- 1Control Systems Lab, School of Mechanical Engineering, National Technical University of Athens, Athens, Greece
- 2Space Exploration, Canadian Space Agency (CSA), Montreal, QC, Canada
- 3Intelligent Robotics and Autonomous Systems Lab, College of Engineering and Applied Science, University of Cincinnati, Cincinnati, OH, United States
- 4Institute of Robotics and Mechatronics, German Aerospace Center (DLR), Oberpfaffenhofen, Germany
Space exploration and exploitation depend on the development of on-orbit robotic capabilities for tasks such as servicing of satellites, removing of orbital debris, or construction and maintenance of orbital assets. Manipulation and capture of objects on-orbit are key enablers for these capabilities. This survey addresses fundamental aspects of manipulation and capture, such as the dynamics of space manipulator systems (SMS), i.e., satellites equipped with manipulators, the contact dynamics between manipulator grippers/payloads and targets, and the methods for identifying properties of SMSs and their targets. Also, it presents recent work of sensing pose and system states, of motion planning for capturing a target, and of feedback control methods for SMS during motion or interaction tasks. Finally, the paper reviews major ground testing testbeds for capture operations, and several notable missions and technologies developed for capture of targets on-orbit.
Introduction
Space exploration and exploitation depend on tasks such as inspecting, refueling, upgrading, repairing, or rescuing satellites, removing of orbital debris, and construction and maintenance of large orbital assets and infrastructures. Until now, all notable servicing tasks have been performed at Low Earth Orbit (LEO) by astronaut Extravehicular Activities (EVAs). However, EVAs are by nature risky operations requiring careful planning and preparation. Unfortunately, this increases mission costs and turn-around time drastically, making servicing missions too costly, of prolonged development, or even unfeasible. For critical space assets located in Geosynchronous Orbits (GEO) or other high-altitude orbits, EVA is not even an option in the foreseeable future.
To execute on-orbit tasks being inaccessible to, or too dangerous for humans, robotic on-orbit servicing (OOS) can be employed, with tasks to be performed by space manipulator systems (SMSs), also called chasers or servicers in the literature. An SMS consists of a satellite base equipped with one or more robotic manipulators (arms) with grappling devices on them and driven by a vision system which allows them to capture a target (client) satellite, or another object. An SMS also can be a large servicing manipulator mounted on a space facility.
Since the 1990s, the paradigm of on-orbit servicing using a SMS has attracted the interest of many researchers, see, for example, (Luo and Sakawa, 1990; Papadopoulos and Moosavian, 1994; Nagamatsu et al., 1996; Hirzinger, et al., 2000; Yoshida et al., 2006; Ma et al., 2007; Rekleitis, et al., 2007; Flores-Abad et al., 2017; Yoshida, 2003; Aghili and Parsa, 2007; Aghili and Parsa, 2009; Aghili, 2012; Aghili, 2020). These research works were motivated by several national and international missions not only for repairing, rescuing, and refueling failed satellites, but also for removal of defunct satellites or space debris (Kawamoto et al., 2003; Aghili and Turin, 2012b). Orbital debris removal using a SMS is also becoming of particular interest as space debris is on the rise, increasing the risk of collisions. Recently, the population growth has reached an unstable point in some congested orbits (Brachet, 2010). All these robotic servicing mission concepts require that a robotic arm captures the target in a safe and secure manner given operational and environmental constraints.
Targets for capture may be cooperative, i.e., a stable and safe target due to its operational Attitude and Orbit Control Subsystem (AOCS), or non-cooperative i.e., an unknown or tumbling target with a varying axis of rotation. They can also be collaborative, i.e., designed for capture or servicing, equipped with visual markers and grapple fixtures, or non-collaborative, as most of today’s satellites. In many cases in the literature, the term cooperative stands for collaborative, too.
As often revealed by ground observations, many on-orbit objects are tumbling in an uncontrolled way (non-cooperative targets), making the robotic capture a very challenging task (Kirchner G., et al., 2017). In fact, although several missions for on-orbit target capture using a SMS have been demonstrated so far, such as JAXA’s ETS-VII (Oda, 1999; Yoshida, 2003), DARPA’s Orbital Express (Whelan et al., 2000), and China’s Aolong-1 (Space Flight, 2016), robotic capture of a tumbling satellite has not been attempted yet.
The SMS for future on-orbit servicing missions will be operated from ground or autonomously, depending on mission constraints, requirements, and the level of technology readiness. Nevertheless, increased autonomy for robotic systems for on-orbit servicing missions is identified as the key technology by space agencies; it represents a critical challenge in space robotics (Center, 2010). This is especially true in the case of servicing non-cooperative targets, where teleoperation cannot be used due to time delays, communication dropouts, operator misperception, limited fields of view, and limited data bandwidth, as all work against a successful capture in a dynamic situation and make it an unsafe practice.
Clearly, only after a manipulator has successfully captured and stabilized a tumbling target, can a service operation be started. Therefore, a common robotic capture task for on-orbit servicing consists of four operational phases (Flores-abad et al., 2014a): a) observation and planning phase, b) final approach phase, c) impact and grasping/capture phase, and d) post-capture stabilization phase. From a different phasing perspective, the operation can be postulated (Aghili, 2013; Lampariello and Hirzinger, 2013) into three primitive operational phases: i) state and parameters estimation phase; ii) pre-grasping phase; and iii) post-grasping phase. Regardless of how to phase the operation, the primary challenges and key requirements for an end-to-end solution are the same.
To achieve safe and reliable OOS tasks, several challenges must be addressed, that render missions difficult and complex (Stieber and Fung, 1991; Flores-abad et al., 2014a). These include identifying a target prior to grasping, planning and control strategies to be employed, SMS performance during capture, and tackling the contact effects of an end-effector coming into physical contact with the target. To obtain a safe and well controlled contact operation, suitable hardware design approaches for manipulators and grippers, effective control methods, and well-planned operation procedures are all required.
Ground-based test and validation of perception and control systems for SMSs performing 3D contact operations is another key challenge in the presence of gravity as most of the large space manipulators cannot even lift themselves in the 1G environment. A number of experimental methods exist, such as suspension testing (Brown and Dolan, 1994), air -bearing supported testing (Schwartz et al., 2003), neutral buoyancy testing (Akin and Howard, 1992), and hardware-in-the-loop simulations (Ma et al., 2004; Ma et al., 2012). Addressing method limitations and increasing their scope is a prerequisite in boosting our confidence in their performance in space.
This paper provides a comprehensive review of research work in manipulation and capture on-orbit. Dynamics of Space Robots in Orbit discusses the dynamics of rigid and flexible elements of SMS in orbit, covering aspects such as the mode they operate in, the initial conditions, and modeling techniques. Contact Dynamics addresses the contact mechanics and motion behavior, both from the physical modeling and simulation viewpoints. System Identification of In-Orbit Robotic Systems is aiming at finding SMS and target properties, both of which are important for planning and control. Sensing of pose and state required for closed-loop control is discussed in Sensing of Pose and State. In Motion Planning, motion planning methods for grasping a target and on-orbit assembly are outlined. Feedback Control reviews feedback control methods and control issues for SMS during motion or interaction tasks. Ground testing testbeds as an essential prerequisite for capture operations are presented in Ground Testbed Facilities. Finally, several relevant missions and key technologies developed for capture of targets on orbit are presented in Missions and Technology.
Dynamics of Space Robots in Orbit
In-orbit space manipulator systems (SMS), see Figure 1, operate in a free-fall environment, where the gravitational effects are present during operations (Abiko and Yoshida, 2001). However, these effects, as well as non-gravitational existing perturbations such as thin air drag, magnetic force, and direct solar radiation pressure can be neglected due to the small-time scale of operations and the magnitude of the forces compared to operational forces (Dubowsky and Papadopoulos, 1993). Regarding spacecraft actuation, a SMS can operate in two main modes:
a) The free-flying mode, in which spacecraft thrusters are active. Then, the system Center of Mass (CoM) can translate. During this mode, magnetorquers or momentum control devices (MCD) such as reaction wheels or momentum gyros, can be active, too. This mode is employed during the final approach of a SMS to its target, so that the target is within the manipulator workspace.
b) The free-floating mode, in which external actions are excluded. As such, all spacecraft thrusters are turned off. Then, the system CoM cannot translate, while the spacecraft translates and rotates in response to manipulator motions. In some cases, the spacecraft attitude must be maintained during manipulator motions to avoid loss of communication with ground stations and solar panel disorientation. In this mode, the spacecraft attitude is controlled actively with momentum control devices (MCD), such as reaction wheels or momentum gyros, while the system CoM does not translate. If MCD are used then the mode is called partial free-floating. The free-floating or the partial free-floating modes are preferred during grasping, since they eliminate sudden motions due to thrusters, and conserve propellant and power.

FIGURE 1. A SMS operating on-orbit (Nanos and Papadopoulos, 2017).
SMS dynamics are important as they contribute to SMS analysis, to their effective simulation prior to deployment, and are needed in the development of advanced controllers. However, they tend to be computationally expensive; hence, methods for increasing the speed of computation are still needed.
Free-Flying Space Manipulator Systems
To increase SMS mobility and perform larger end-effector displacements (Papadopoulos and Dubowsky, 1991b; Lampariello et al., 2003; Lampariello, R., 2013) or/and limit the contact force disturbances during docking operations (Shibli et al., 2005; Flores-abad et al., 2014a), the SMS must operate in the free-flying mode. In this mode, the spacecraft can be transferred and oriented arbitrarily in space. To achieve this, the initial designs were employing thrusters and MCDs controlled by the AOCS for spacecraft position and orientation control, and joint motors, controlled by a separate manipulator control system, for controlling manipulator functions. However, due to dynamic coupling, the motion of the manipulator affects the motion of the spacecraft and vice versa, creating undesired control disturbances (Seweryn and Banaszkiewicz, 2008; Misra and Bai, 2017; Christidi-Loumpasefski et al., 2020). Therefore, although initially each of these control systems would operate independently, the recent trend is to move towards a single and coordinated controller (see Coordinated Control and Handling/Servicing Space Objects).
The kinematics and dynamics of the system can be derived here using the spacecraft CoM as the representative point for the translational motion, following the so-called direct path approach, which in this case results in more compact equations of motion (Moosavian and Papadopoulos, 2004).
The end-effector linear velocity
where
where
The system equations of motion for a free-flying SMS with N joints can be written as
where the spacecraft attitude is defined by the Euler parameters
where
Free-Floating Space Manipulator Systems
For small end-effector motions close to a target, the system may operate in the free-floating mode, during which an uncontrolled motion of the spacecraft arises because of the dynamic coupling between the spacecraft and the manipulator (Papadopoulos and Dubowsky, 1993; Wilde et al., 2018). Free-floating SMS exhibit nonholonomic behavior due to the non-integrability of the angular momentum conservation equation. Two cases are studied in the literature: a) zero initial angular momentum (Papadopoulos and Dubowsky, 1991a; Zong et al., 2020) and b) non-zero initial angular momentum (Nanos and Papadopoulos, 2010; Giordano et al., 2016).
Zero Initial Angular Momentum
In free-floating mode, no external forces act on the system, and therefore the system CoM is fixed in inertial space. Taking the system CoM as a representative point for the translational motion and using barycentric vectors (barycentric vector approach) which reflect both the geometric configuration and mass distribution of the system, decoupling of the total linear and angular motion from the rest of the equations, results (Papadopoulos and Dubowsky, 1991a). This allows the use of controllers for fixed-base manipulators, under some mild conditions (Papadopoulos, 1991).
In case of zero initial angular momentum, the angular momentum conservation yields (Papadopoulos and Dubowsky, 1991a),
where
The end-effector linear velocity
where the Euler parameters
Such systems are subject to path dependent Dynamic Singularities (DS) that complicate their path planning (Papadopoulos and Dubowsky, 1993), and restrict their effective workspace. To allow use of the entire SMS workspace, path planning methodologies allowing the end-effector to follow a desired path and avoiding DS have been proposed (Nanos and Papadopoulos, 2012) (also see Singularity Avoidance).
In the case of a free-floating SMS with N joints, zero angular momentum and negligible disturbances, the reduced equations of motion are (Papadopoulos and Dubowsky, 1991a):
where
Regarding the partial free-floating mode, in which the spacecraft attitude can be controlled with momentum devices only, the SMS equation of motion are (Papadopoulos, 1991)
where
Non-Zero Initial Angular Momentum
Although zero initial system angular momentum is desired before using a SMS in free-floating mode, small collisions with the environment or on-off attitude controller inaccuracies result in small amounts of angular momentum. In principle, momentum can be absorbed using either thrusters or momentum control devices. However, thrusters by their nature use expendable propellants, limiting system life, and due to their on-off nature, they cannot reduce the angular momentum to zero. Momentum control devices require electrical power supplied by solar arrays; however, they tend to saturate and ultimately, also require use of thrusters for de-spinning. Therefore, in practice, a free-floating SMS can have small accumulated angular momentum.
A free-floating SMS with initial angular momentum is an affine system with a drift term (Yamada et al., 1995; Matsuno and Saito, 2001). This term is caused by the angular momentum and complicates the path planning and control of such systems (Nanos and Papadopoulos, 2015a; Nanos and Papadopoulos, 2017; Giordano et al., 2017; Giordano et al., 2018).
In case of non-zero initial angular momentum, the angular momentum conservation is given by (Nanos and Papadopoulos, 2010),
where
The end-effector linear velocity
where the Generalized Jacobian
The reduced equations of motion of a free-floating SMS with non-zero angular momentum take the form (Nanos and Papadopoulos, 2010; Nanos and Papadopoulos, 2017):
where the first two terms of Eq. 11 are the same as those in Eq. 7. The effect of the non-zero angular momentum on the system dynamics is included in term
Recently, the disturbances in the SMS response due to accumulated angular momentum of a rotating reaction wheel have been studied, with the aim of designing a controller compensating for such momentum disturbances (Christidi-Loumpasefski et al., 2020). In Mishra et al. (2020) the inertia-decoupled reduced Euler-Lagrange equations are exploited through the resulting block-diagonal inertia matrix to avoid the need for joint acceleration measurements in regulation tasks, in which a controller stabilizes the configuration of an orbital robot about a setpoint, in the specific setting that its spacecraft velocity is unmeasured. A well-partitioned Coriolis/centrifugal matrix is characterized by useful properties, which aid in the stability analysis.
Flexible Space Manipulator Systems
In space applications, manipulator design differs from that in terrestrial applications. Due to the lack of gravity loading, SMS are designed to be lightweight and long reaching, which introduces link flexibilities. Moreover, lightweight, and flexible structures such as solar arrays, deployable truss antennas are employed (Du and Wang, 2020). Often, their joints are driven by harmonic drives for large gear ratio and compact design, introducing joint flexibility (Ulrich and Sasiadek, 2012). These types of flexibilities may cause vibrations both in the manipulator and the spacecraft during on-orbit servicing especially in tasks where physical contact occurs (Stieber and Fung, 1991; Schneider and Cannon Jr, 1992; Ma et al., 1997; Ma and Wang, 2007).
Considering the gearmotor dynamics and using the barycentric vector approach, the angular momentum conservation for a free-floating SMS, is given by (Nanos and Papadopoulos, 2015b):
where the column vector
Assuming that all system flexibilities are lumped to joint flexibilities, it can be shown that for a free-floating SMS, the link and motor equations are not only dynamically coupled through the joint elastic torques, but also at the acceleration level (Nanos and Papadopoulos, 2015b):
where
A different modelling approach called the singular perturbation method has been proposed for the case the joint stiffness is relatively large, but still finite (Hu and Vucovich, 1997). Then, the system exhibits a two-time scale dynamic behavior in terms of rigid and elastic variables. Using this method, one can apply controllers which consist of a slow control action designed based on a rigid robot model, and a fast control action designed to damp the joint elastic oscillations (Yu and Chen 2014).
The assumption that all system flexibilities are lumped to joint flexibilities is reasonable for SMS with short links. However, in some cases the design of lightweight and long reach manipulators is strongly preferred as it reduces launch mass and increases manipulator reach. A problem of such lightweight space manipulators is the increased structural flexibility of the links, which causes structural vibrations. Flexible links can be modeled as Euler-Bernoulli beams (Green and Sasiadek, 2007; Christidi-Loumpasefski et al., 2020) and a finite-dimensional model of link flexibility can be obtained by the assumed modes technique (Zhang et al., 2020).
Contact Dynamics
All capture and some manipulation operations involve physical contact between the robot and an external object or the environment. Contact operations are among the most difficult operations for a robot, whose contact behavior is governed by contact dynamics. Although contact dynamics of individual rigid or elastic bodies has been extensively studied in the last few decades (Gilardi and Sharf, 2002; Flores and Lankarani, 2016; Natsiavas, 2019), accurate modeling and control of contact behaviors of multibody systems are still challenging for most robotic operations in space, especially when contact interfaces are complex as commonly seen in on-orbit servicing (Flores-abad et al., 2014a), orbital debris removal (Shan et al., 2016) and on-orbit assembly (Piskorz and Jones, 2018). For example, Figure 2 shows a typical battery and its housing structure on the International Space Station (ISS) whose contact geometry is characterized as three cascade peg-in-hole pairs (one rectangular peg/hole and two cylindrical pegs/holes). This is just one of many batteries of different sizes and designs on ISS, which have been maintained by either EVAs or the dual-arm ISS robot Special Purpose Dexterous Manipulator (SPDM). It was found that the insertion or removal of such a battery into or from its housing worksite was one of the most difficult operations of the ISS robot and hence extensive research had to be done to ensure success of these operations (Stieber and Fung, 1991; Ma and Carr, 1998). Therefore, modeling, simulation and verification of contact dynamics and control approaches are always among the most critical parts of space robot development and operations.
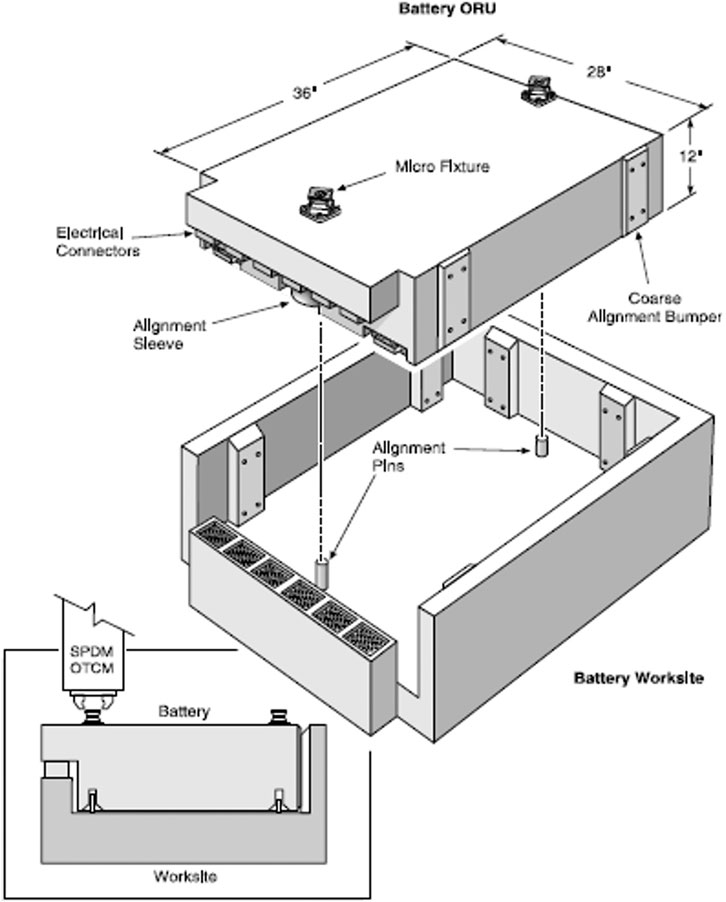
FIGURE 2. An ISS battery and housing with three peg-in-hole contact pairs (Ma and Carr, 1998).
In practice, contact often occurs among mechanical parts with complex geometries of convex and concave mixed topology, which cannot be simply represented by two regular shapes or point-plane contact. The most used modeling method is the surface compliance-based approach (Ma, 1995; Gilardi and Sharf, 2002). With this method, first step is to fully understand how the two contact bodies will contact and engage in the robotic operation. With such an understanding, one can then partition each contact body into many small enough sub-bodies or surfaces, so that all the contacting areas or points, especially these in the concave surfaces, can be accurately represented (Ma, 2000). The next step is to identify all the possible contacts and calculate the geometrically overlapped contact regions between sub-bodies based on the simulated motion states of these contact bodies in the robotic multibody system.
Many CAD or computer graphics algorithms are available for efficient calculation of contact regions (Choi et al., 2010). The final step is to calculate contact forces for all the contact regions. At each contact region, there is a normal force along the surface normal, a material/structural damping force also in the normal direction, and a friction force in the tangential plane of the contacting surfaces (Ma, 1995; Gilardi and Sharf, 2002; Gonthier et al., 2004). Most of the normal contact force models are based on linear spring–dashpot or nonlinear Hertzian spring–dashpot laws with damping terms to accommodate the energy loss (Machado et al., 2012). The traditional one-dimensional Coulomb friction model does not work well for simulating general 3D sticking (jamming) or stick-slip phenomena. This problem was addressed by introducing a 3D bristle friction model in Liang et al. (2012).
Contact dynamics simulations for practical cases with stiff contact materials and complex contact geometries (e.g., manipulator capturing or spacecraft docking) usually are very inefficient because of the required large number of iterative computations and very small numerical integration step size (for numerical stability). Many studies have been devoted to improving efficiency of computational contact models. Mazhar et al. (2015) presented a solution method to simulate the multibody systems with frictional contact. The presented method reduced the required time by one or two orders of magnitude. Navarro and de Souza Braun (2013) determined the normal spring stiffness coefficient of a linear normal contact model through numerical solutions for the overlap between particles in non-linear models.
Boos and McPhee (2013) proposed a volumetric contact dynamics model for the purpose of generating reliable and rapid simulations of contact dynamics, which allows modeling of contact between complex geometries and relatively large contact surfaces, while being less expensive computationally than finite element methods. Ma and Wang (2007) and Liang et al. (2011) presented a method to combine linearized contact force terms with the manipulator’s structural stiffness and damping matrices for model order reduction. The method can improve simulation speed by one or more orders but applies to flexible manipulators with slow motion cases only. Askari (2021) introduced a concept to simulate either soft or conformal contacts and developed mathematically closed-form contact models, which are easy-to-implement while resolving the discontinuity issue with the Kelvin-Voigt model.
A unifying dynamics formulation for nonsmooth multi-body systems subject to changing topology and multiple contacts based on a linear projection operator was presented in Aghili (2019). It follows by development of an energetically consistent model of slipping and sticking frictional impacts for robotic systems in contact with a frictional surface in Aghili (2020). This work reveals that a contact dynamics model can lead to energetic consistency in both slip and stick states upon imposing specific constraints on the coefficient of friction and the coefficient of restitution.
Zhao et al. (2016) developed a multi-point rigid-body contact dynamics model which calculated contact forces using kinematic constraints and Lagrange multipliers. They found that, when the model was applied to an APDS (androgynous peripheral docking system) docking case, the resulting simulation was more efficient than surface-compliance based models. Ma et al. (2020) developed an inverse research strategy towards the establishment of contact force model for complex contacting surfaces by utilizing parameter identification methods. Wang and Liu (2020) revealed the shortcoming of the improved contact stiffness coefficient and developed two different contact force models for the internal and external contact forms associated with the hysteresis damping factor from the Lankarani-Nikravesh contact force model (L-N model). Even with these recent developments regarding model efficiency, real-time contact dynamics simulation for realistic contact operations is still difficult to guarantee due to complex contact geometry and variable numerical integration step size for solving stiff differential equations.
All contact dynamics models for practical capture missions will have many model parameters describing the geometry, stiffness, friction, and material damping properties of the contact interfaces. Accurate identification of these model parameters remains a challenge. Although research efforts have been made for identifying model parameters from hardware tests (Weber et al., 2006; Kim and Ma, 2007; Verscheure et al., 2008), most of the users still have to assume or estimate parameters based on design data. Even if one can identify experimentally these parameters from real contact parts before launch, the parameter values can still change significantly in space due to changing of material properties and the operational environment in space. To address these uncertainties, Liu et al. (2020) proposed a hybrid contact modeling methodology to combine a traditional analytical contact model with a data-driven neuron network model, where the analytical model represents theory-based general contact dynamics, while the neuron-network based data-driven model captures the existing known and unknown unmodelled errors and uncertainties. The data driven model can be trained using machine learning techniques from experimental data collected from repeated testing of real contact hardware, which must be done anyway for all the space systems before they are launched to the space. More research is needed to mature this new hybrid modeling approach. Another area of contact modeling requiring significant further research is the frictional contact problem with large deformation because of the increasing development and applications of soft grasping (e.g., robotic handling of soft/fabric covers of a satellite) or soft robots (Botta et al., 2017; Sun et al., 2021; Sadati et al., 2021).
Again, due to high uncertainties in contact dynamics modeling and simulations, space agencies across the world developed various hardware-in-the-loop (HIL) simulation facilities to test and verify critical contact operations of space robotic systems before they are launched into space. NASA/MSFC first developed an HIL simulation facility to test Space Shuttle docking or berthing to ISS (Tobbe et al., 1991). Canadian Space Agency (CSA) developed SPDM Task Verification Facility (STVF) to test ISS robot SPDM critical contact operations (Piedboeuf et al., 1999; Ma et al., 2004; Aghili, 2019). German Aerospace Center (DLR) developed the European Proximity Operations Simulator (EPOS) to test satellite rendezvous and docking operations for the DEOS and OLEV missions (Boge and Ma, 2011). China Academy of Space Technology (CAST) developed a Manipulator Task Verification Facility to test Chinese space station manipulators on-orbit service operations (Mou et al., 2018). US Naval Research Laboratory (NRL) developed a test facility to test robotic operations for the RSGS mission (Roesler et al., 2017). NASA Goddard Space Flight Center (GSFC) also developed a test facility to test the Space Infrastructure Dexterous Robot (SPIDER) on-orbit servicing operations for the OSAM-1 mission (NASA/GSFC, n.d.). Details of these major facilities are discussed in Section 8.3.
System Identification of In-Orbit Robotic Systems
As system properties may change during operations in space, methods are needed to establish these properties on-orbit for health monitoring, planning and control purposes. Research efforts have focused on the development of methods for rigid satellites, while other efforts have concentrated on the identification of flexible satellites, i.e., satellites with flexible appendages. Both are important elements of satellite (or debris) capture operations, as they reduce the operational risks and allow tuning of the control parameters involved.
Rigid Satellites and Tumbling Objects
To reduce the risk of a defunct rigid satellite capture by a SMS, researchers have proposed methods to identify its parameters in the pre-capture phase while others have developed methods that require the capture phase to be accomplished first, i.e., for the post-capture phase. The methods developed for the identification of rigid satellites in the pre-capture phase can be classified as vision-based and momentum based. Vision-based methods are addressed in detail in Vision-Based State/Inertia Parameter Estimation and Motion Prediction. However, methods relying on vision alone cannot identify all the individual inertia parameters. They estimate the ratios of the moments of inertia, the CoM location, and the orientation of principal axes, only.
To identify the full inertia matrix, momentum-based methods were developed, in which the servicing satellite applies forces and moments to the target. Sheinfeld and Rock (2009) first proposed the preliminary concept; Christidi-Loumpasefski and Papadopoulos (2018) extended it to address the full identification issue, followed by experimental verification. Meng et al. (2019) also proposed the application of an impulse to the satellite by making soft contact using a flexible fish-rod like sticker mounted on the SMS, and the use of data from visual and force sensors to estimate the tumbling motion (pose and linear/angular velocities) and identify all ten inertial parameters (mass, CoM location, and moments and products of inertia) of the satellite. Their simulation study showed that for an object weighing 1,000 kg, only a small force of less than 10 N is sufficient to accomplish the task of identifying all inertial parameters. To avoid physical contact, Meng et al. (2020) showed the feasibility of applying non-contact impulse using eddy current to identify all ten inertial parameters. In the same work they demonstrated experimentally that the method can be used for pre-capture detumbling of a tumbling target, so that the high risk of physical contact with the tumbling object for the capture phase is avoided.
Methods developed for the post-capture phase can be classified into those that use the equations of motion and those based on momentum equations. Murotsu et al. (1994) estimated the inertial parameters of an object captured by a space robot based on the equations of motion derived by the Newton-Euler approach, under the condition that the robot is free-floating. Lampariello and Hirzinger (2005), proposed a method for the identification of the base body and load on the end-effector, using accelerometers. Rackl et al. (2013) addressed problems in the SMS satellite identification, the captured satellite or both, using direct robot joint torque sensing. The methods based on the equations of motion, require acceleration measurements, which are very noisy. However, if torque sensors at the robot joints are available, the use of acceleration measurements can be avoided, to the advantage of the accuracy of the identification process (Rackl et al., 2013). This approach was shown to be more accurate than momentum-based identification methods.
To avoid noise corrupting estimates, several researchers formulated momentum-based identification methods. Murotsu et al. (1994) focused on estimating the inertial parameters of an object captured by a space robot based on the conservation of momentum, under the condition that the robot is free-floating. Ma et al. (2008) made use of a robotic arm to change the inertia distribution of a spacecraft system. Considering measurable velocity changes and computable inertia changes of the robotic arm, the inertia parameters of the spacecraft body were identified. Nguyen-Huynh and Sharf (2013) developed an online momentum-based estimation method for inertial parameter identification of an unknown tumbling target. Chu et al. (2017) estimated the inertial parameters of a captured satellite using contact force information. Xu et al. (2017), proposed a method that uses both equations of motion and momentum equations for identifying all inertial properties of a captured satellite (Murotsu et al., 1994).
Flexible Satellites
Satellites are often equipped with flexible appendages and their identification is well established. Rackl and Lampariello (2014) addressed the effects of flexible appendages to the free-floating dynamics and to the rigid body parameter identification of a SMS satellite/base. A lumped parameter model was used for the flexible appendages and a method to identify its parameters was presented. However, flexible satellites are more often considered as distributed models and are identified based on modal analysis algorithms. Modal analysis of flexible components is studied particularly well for structural applications such as those in civil engineering and extensive literature in this field is available; examples of spacecraft applications exist as well. On-orbit identification experiments of structural modal parameters have been implemented on some spacecraft such as the Hubble Space Telescope (HST) (Anthony and Andersen, 1995), the Galileo spacecraft (Pappa and Juang, 1984), and the Engineering Test Satellite VIII (ETS-VIII) (Kasai et al., 2009). Accelerometer data from the ROSA flight experiment on the ISS were analyzed to identify the ROSA system modal parameters (Chamberlain et al., 2018).
System Identification of Space Manipulator Systems
Space manipulator parameters and kinematics/dynamics models are reasonably understood and measured before launch to space. However, some of the parameters may change in orbit and hence, on-orbit identification or calibration of model parameters is needed. Several researchers have developed methods for rigid SMS, while others have studied the identification of flexible SMS, i.e., SMS with flexible joints and/or flexible links.
Rigid Space Manipulator Systems
The methods developed for the identification of rigid SMS are mainly momentum-based. Yoshida and Abiko (2002) used estimation errors for the reaction wheel momentum to compute the deviations of the parameters of a SMS from the nominal ones. Xu et al. (2017) proposed a method that uses both equations of motion and momentum equations for identifying all inertial properties of each body of a SMS. Christidi-Loumpasefski et al., (2017) proposed a method that allows identification of all system parameters required to reconstruct the free-floating joint-space dynamics of a SMS, based on the angular momentum conservation. This method was enhanced further to identify all system parameters required to reconstruct the free-floating Cartesian-space dynamics of a SMS, based on the angular momentum conservation and kinematics equations (Christidi-Loumpasefski et al., 2020). Naveen et al. (2019) developed a momentum-based method that identifies all parameters required to reconstruct the free-flying dynamics of a SMS, using the linear and angular momentum equations.
Flexible Space Manipulator Systems
Α challenge in the design of space robotic manipulators is to use light materials, suitable for typical on-orbit tasks. Lightweight structures improve the payload-to-arm mass ratio. A drawback of such lightweight manipulators is the increased link structural flexibility. SMS are subject also to joint flexibilities that arise when motion transmission elements such as harmonic drives, transmission belts and long shafts are used. Both types of flexibilities cause vibrations, which are profound when manipulating large payloads; if neglected, poor performance and even control instabilities may result. To tackle flexibilities issues, advanced control strategies are required; however, these need knowledge of system parameters.
Krzyżak et al. (2012) studied the modeling and identification of two-degree-of-freedom (DoF) planar SMS with flexible joints by block-oriented systems. The joint dynamics included non-linear stiffness and friction terms. The manipulator was represented by a Hammerstein model consisting of a memoryless nonlinearity followed by a dynamic linear system. Zhiyu et al. (2019) linearized the dynamic model of a two-DoF planar SMS with flexible links at an arbitrary working point and studied the estimation of the system state-space model during the capture of an unknown object. A recursive tracking approach based on the recursive predictor-based subspace identification algorithm was proposed to identify the manipulator payload mass parameter. Nanos and Papadopoulos (2019) studied the estimation of the full dynamics of a spatial SMS with flexible joints. It was shown that methods based on the angular momentum conservation, which are tolerant to sensor noise, cannot estimate joint flexibility parameters.
A new parameter estimation method, based on the energy balance during the motion of a flexible joint SMS, was developed. The method estimates all system parameters including those that describe the joint flexibilities, requiring measurements of joint angles and rates, spacecraft attitude and angular velocity, and joint torques. Christidi-Loumpasefski et al. (2020) further enhanced the study, applying the energy balance method to the estimation of link flexibility parameters in addition to all SMS inertial and joint flexibility parameters.
Although many identification methods have been developed, difficulties for identifying model parameters of a SMS in operation including flexible and rigid elements, hard nonlinearities, and perhaps sloshing effects, still require further research efforts.
Sensing of Pose and State
Motion State Estimation
Robust relative navigation systems are critical for many current and near-future lunar or space exploration missions to support rendezvous, proximity operations and docking for both crewed and uncrewed vehicles. Reliable relative pose information in full 6-DoF is required during approach and docking of a visiting vehicle with the ISS. It is deemed that the safety of the controlled spacecraft during such proximity maneuvers critically depends on the performance and robustness of the relative navigation systems. Their failure to provide continuous and accurate pose (position and orientation) is considered as a critical hazard or even a catastrophic hazard that can cause failure of the mission all together. This is a challenging issue that must be addressed properly prior to the routine deployment of SMS in orbit.
Several relative navigation sensors exist capable of providing measurements for estimating the pose of objects having relative motion. Application of radar and altimetry for space-borne navigation systems begun more than half a century ago (Kriegsman, 1966), while X-ray pulsars for relative navigation between two spacecraft in deep space was introduced (Emadzadeh and Speyer, 2011; Liu et al. 2015). Other relative navigation methods focus on using Global Position System (GPS) for determining both absolute and relative position between two spacecraft (Wolfe and Speyer, 2004).
Vision systems have been developed capable of estimating the pose of two objects moving with respect to each other. Among them, an active vision system such as a Laser Camera System (LCS) is preferable because of its robustness in the harsh lighting conditions of space (Samson, et al., 2004). Although using radar or GPS for relative navigation systems are with the advantage of long-range distance measurement, they have less resolution and precision compared with vision-based systems. Moreover, the advent of relatively low-cost and commercially available laser range sensors and scanners, which has been greatly exploited for autonomous navigation of robotic vehicles (Lu and Tomizuka, 2006) makes them preferred sensor of choice in relative navigation systems. A rendezvous laser radar was used as the primary navigation to perform unmanned autonomous rendezvous docking experiments in the ETS-VII mission (Mokuno et al., 2004). Vision algorithms for laser scanners have been also developed for motion estimation of free-floating objects to support a variety of on-orbit proximity operations (Masutani et al., 1994; Hillenbrand and Lampariello, 2005; Aghili and Parsa, 2008). In Lingenauber et al. (2017) the potential benefits of plenoptic cameras for robot vision during on-orbit servicing missions were discussed.
The conventional vision-based pose estimation algorithms are essentially 3D registration processes, by which the range data collected from different views are aligned in a common coordinate system. The iterative closest point (ICP) is the cornerstone of 3D vision-based pose estimation algorithm. The iterative procedure minimizes distance between a point cloud in one dataset and the closest points in the other (Besl and McKay, 1992; Greenspan and Yurick, 2003). Typically, one dataset is a set of 3D point-cloud acquired by scanning an object, while the other one is a model set such as a CAD model of the same object. The basic ICP algorithm has proven to be very useful in the processing of range data (Greenspan and Yurick, 2003). Subsequently, several variations on the basic method have been developed to optimize different phases of the algorithm (Greenspan and Yurick, 2003). Convergence of ICP iterations and the accuracy of the fine alignment process depends on quality of the 3-D vision data that can be adversely affected by many factors such as sensor noise, disturbance, outliers, symmetric view of the target, or incomplete scan data.
A review of collaborative and non-collaborative spacecraft pose determination techniques for close-proximity operations can be found in Opromolla et al. (2017). Approaches in visual tracking of a non-collaborative as well as a partially collaborative satellite, to enable close-range rendezvous between a servicer and a target satellite, were presented in Oumer (2016). Experimental results indicate that camera-based methods provide robust and accurate tracking for the approach to malfunctioning satellites in spite of the difficulties associated with specularities and direct sunlight (Oumer, 2016; Lampariello et al., 2021). Taking advantage of the simple dynamics of a free-floating object, which is not acted upon by any external force or moment, researchers have employed different observers to track and predict the motion of free-floating space objects (Hillenbrand and Lampariello, 2005; Aghili and Parsa, 2007). However, relative thrust acceleration was not accounted for, and therefore these methods are not applicable for relative navigation. A robust 6-DoF relative navigation by combining the iterative closet point (ICP) registration algorithm and a noise - adaptive Kalman filter (AKF) in a closed-loop configuration together with using measurements from a laser scanner and an inertial measurement unit (IMU) was presented in Aghili and Su (2016).
Vision-Based State/Inertia Parameter Estimation and Motion Prediction
Visually guided robotic capture of a moving object often requires long-term prediction of the object motion not only for a smooth capture but also because visual feedback may not be continually available, e.g., due to vision obstruction by the robotic arm. The use of laser range data has been proposed for motion estimation of free-floating space objects (Lichter and Dubowsky, 2004; Hillenbrand and Lampariello, 2005; Aghili and Parsa, 2007; Aghili and Parsa, 2009). Lichter and Dubowsky (2004) employed two separate Kalman filters for the rotational and translational dynamics of a free-floating space object to reduce the noise of a range sensor. Since principal inertia of the target are directly included in the state vector to be estimated by a Kalman Filter (KF), a normalization and re-parameterization of the estimated inertia values must be performed at every step of the KF cycle. Hillenbrand and Lampariello (2005) developed a nonlinear least-squares estimation method for long-term motion prediction (<100 s) and for the model identification of a free-tumbling space object. The identification process estimates the six inertia parameters of the target inertia tensor (with respect to an arbitrary constant factor) and the target’s velocity at the initial time of the motion prediction, which is then solved as an Initial Value Problem in the camera frame. Aghili and Parsa (2007, 2009) developed a computationally efficient, noise AKF for the motion estimation and prediction of a free-tumbling target satellite. The filter receives noisy pose measurements from a laser vision system aboard the chaser satellite at a close distance in a neighboring orbit, and estimates the full states, all the inertia parameters of the target satellite, as well as the covariance of the measurement noise. This motion estimation/prediction scheme was further developed for a fault-tolerant pose estimation of space objects (Aghili et al., 2011; Aghili and Su, 2016). The robustness and accuracy of fault-tolerant pose estimation was demonstrated through a hardware-in-the loop simulation setting.
Identification of states and parameters of space objects using minimum set inertial parameters, i.e, in terms of two relative inertia variables, was presented in Aghili (2013). Tweddle et al. (2015), developed a vision-based method that can estimate some of the satellite’s inertial properties. In Setterfield et al. (2018), a procedure for estimating the inertial properties of a passive in-orbit object was presented, in which the principal axes and inertia ratios of the object were estimated using an explicit comparison between the estimated and an analytically predicted body-frame angular velocity. The angular velocity was estimated with finite differences. The method was applied on the Synchronized Position Hold Engage and Reorient Experimental Satellites (SPHERES) and the Visual Estimation for Relative Tracking and Inspection of Generic Objects (VERTIGO) test platform on the ISS with two fast multi-axis tumble trajectories. In Lampariello et al. (2021), the nonlinear least-squares method in Hillenbrand and Lampariello (2005) was extended to perform long-term rotational motion prediction, up to <600 s. The method was compared to a constrained least-squares approach (Benninghoff and Boge, 2015) and to the Extended Kalman Filter (EKF) method in Aghili and Parsa (2009), showing a better performance in critical tumbling states of the target satellite, such as the condition close to a flat spin. Meng et al. (2019) investigated the use of EKF to estimate motion state from noisy vision images as a part of the vision and impulse combined solution for identifying all the inertial parameters. They proposed a scheme of decaying process noise for the covariance matrix, leading to both fast and accurate convergence of the estimate.
The state estimation of the chaser satellite also was recognized in Gallardo et al. (2019) to be of great relevance for the control of a free-floating impedance controller during the capturing phase. In fact, the interfacing of a fast-sampled robot controller with a slow sampled Guidance, Navigation and Control (GNC)-bus on the spacecraft causes performance loss for the robot controller. Additionally, only slow-sampled, and noisy exteroceptive sensors which provide relative pose measurements, may be available for feedback. As such, an EKF was presented which, based on IMU and star/sun trackers sensors, as well as on the slow-sampled poses of the tumbling target derived from visual camera and LIDAR sensors, computes a fast, full state estimation of both servicer and target. A similar task was addressed in Mishra et al. (2019) with a nonlinear observer, which estimates the inertial pose and the velocity of a free-floating non-cooperative target using only relative pose measurements. A novel dynamics model in terms of minimum set inertia parameters was developed in Aghili (2021) that was utilized to design a constrained and adaptive EKF for estimation of not only the states and parameter but also the covariance of the vision sensor noise. This work has demonstrated that incorporation of the minimum set of inertia parameters in the estimator internal model elevates the system degree of observability.
Motion Planning
Spacecraft guidance provides reference trajectories and attitude profiles for the final approach phase of a SMS to reach a berthing point and start capture, docking and servicing operations. Similarly, manipulator motion planning provides joint and end-effector trajectories necessary to grasp a target, mate appropriate interfaces, or perform orbital replacement unit (ORU) exchanges (Dubanchet, et al., 2020). Due to parameter errors and uncertainties, a feedback control, as discussed in Feedback Control, is also needed to complete a capture operation. In the following subsections, the capture of a tumbling target satellite is addressed first, followed by the on-orbit assembly of a large space telescope.
Capture of a Tumbling Target
The task of capturing a free-tumbling target satellite is typically divided into the following steps, as already described in Introduction (see also Figure 3): a state and parameters estimation phase; a pre-grasping phase; a grasping phase, and a post-grasping phase. The pre-grasping phase can be further divided into an approach maneuver of the chaser to a predefined Mating Point near the target; and a pre-grasping maneuver of the robotic arm on the chaser satellite, to move the robot end-effector onto the capture point of the target.
The grasping itself includes soft grasping, during which the chaser and target cannot move away of each other, and hard grasping during which rigidization occurs, see also Arms, Grippers, and End-Effectors. As such, the post-grasping phase first involves a maneuver of the robotic arm on the chaser satellite to stabilize the chaser-target stack (rigidization). The detumbling of the chaser-target stack then follows. The latter is addressed in Post-Grasping Motion Planning and in Capturing/Contacting a Target—Impedance/Compliance Control and Coordinated Control and Handling/Servicing Space Objects as a control problem. The pre-grasping phase requires as input the prediction of the tumbling target’s motion (the prediction task is addressed in Vision-Based State/Inertia Parameter Estimation and Motion Prediction), as postulated in Jacobsen et al. (2002), Aghili (2013) and Lampariello and Hirzinger (2013). The guidance of an SMS to rendezvous and capture a tumbling free-floating object in a safe and secure manner remains a challenging task today.
Chaser Approach Maneuver
The approach maneuver of the chaser to a predefined Mating Point belongs to the AOCS domain, see Free-Flying Space Manipulator Systems. However, free-flying and AOCS tasks tend to overlap, as also described in Coordinated Control and Handling/Servicing Space Objects for feedback control. As such, some pointers are provided here, which may serve as an introduction to the subject.
With a target locally stationary, the approach phase can be achieved by point-to-point planning and depending on the actuation mode, by simple on-off thruster control, and attitude fine-tuning using momentum exchange devices. Capturing a tumbling, non-cooperative target is more challenging, as here velocity matching between the SMS end-effector and the capture point is required. The chaser approach maneuver can be performed with or without synchronization of the chaser motion with that of the target. An example of the former approach can be found in ESA’s e.Deorbit scenario, while of the latter in DLR’s DEOS scenario (see Missions and Mission Studies).
In Jacobsen et al. (2002) a simplex numerical optimization approach is applied to the chaser approach problem, with particular emphasis on safety metrics, such as time to collision. An optimal trajectory was proposed in Ma et al. (2007), in which an iterative algorithm, stemming from an indirect formulation of the optimal control problem for a planar case, was proposed for minimum time and fuel consumption. An extension of this work (Boyarko et al., 2011) considers the full 6-DoF proximity motion dynamics. A guidance method for fuel-optimal trajectories (Breger and How, 2008) employed mixed-integer linear programming (MILP). A simple and widely used algorithm for real-time trajectory planning is the glidescope algorithm (Hablani et al., 2002), which is based on the closed-form solution of the linear Clohessy–Wiltshire equations. A hybrid linear quadratic regulator/artificial potential function (LQR/APF) scheme for the guidance and control of multiple spacecraft proximity maneuvers, was proposed in Bevilacquaa et al. (2011), while methods for guidance and control of a SMS approaching a non-cooperative target were developed in the presence of uncertainty and measurements incompleteness (Somov et al., 2018).
The use of convex programming techniques is another common choice in aerospace guidance and control applications, as described in the survey (Liu, 2014). A convex programming-based guidance scheme (Misra and Bai, 2017) and an optimization technique for the pre-capture trajectory (Aghili, 2009) were proposed, where only the SMS base attitude is controlled (partial free-floating mode), removing the nonholonomic characteristics of the system. In MacPherson et al. (2018), an optimal control strategy to exploit the dynamic robustness of gecko-inspired dry adhesive grippers for the task of grasping a free-floating, spinning object is presented. The spacecraft rendezvous guidance problem was also tackled in the convex programming-based context in Virgili-Llop et al. (2017, 2019), where convexification was applied to the collision avoidance constraints, deriving from the solar appendages of the target. The resulting motion planning method is proven to converge always to a stationary point, independently of the initial guess, in short computation time. The same authors however recognized that the addressed optimization problem still exhibits local minima and propose finding a good minimum with multiple calls of the motion planner online. In Stoneman and Lampariello (2016) emphasis was given to collision avoidance, which was shown to play an important role in the e.Deorbit scenario (see Missions and Mission Studies). The trajectory planning problem is formulated as a state-constrained, nonlinear program (NLP) and solved for many planning queries offline, to provide a set of (close to) globally optimal solutions. This set of solutions can then be used to warm-start the motion planner in an online setting, via regression. A description of a mission pipeline is presented in Albee et al. (2021). This approach, including a target motion prediction functionality, a chaser motion planner, and a chaser tracking controller, will be tested in 2021 on the ISS with the ASTROBEEs.
Pre-Grasping Motion Planning
In deploying a SMS for target capture, a manipulator trajectory is needed to achieve the goal. Several secondary optimization goals, such as obstacle and singularities avoidance, fuel consumption, and base disturbance minimization can be sought, too. In most cases, the SMS is free-floating (full or partial mode), as described in Dynamics of Space Robots in Orbit and Free-Floating Space Manipulator Systems. In the pre-grasping phase, the manipulator arm moves from its home position to intercept a grapple fixture or point on the target at a rendezvous point with zero relative velocity.
Pre-grasping trajectory planning for robotic capturing of a tumbling satellite was presented in Aghili and Parsa (2008) without considering some operational requirements at the time of grasping. An EKF was incorporated in the robot planning to provide estimation of the target’s states and parameters needed for predicted motion trajectories (see Vision-Based State/Inertia Parameter Estimation and Motion Prediction), so that the robot’s end-effector could intercept the target’s grapple-fixture with zero relative velocity (to avoid impact). Capture of a satellite by a two degree-of-freedom manipulator using the Reaction Null Space method was presented in Piersigilli et al. (2010). In Aghili (2012), a predicted motion planning for the pre-grasping phase was presented that allowed minimizing a cost function consisting of a weighted linear sum of the travel time, the distance, the cosine of a line-of-sight angle (feasible alignment for robotic grasping), and a soft constraint on the acceleration limit. The pre-grasping trajectory planning and autonomous grasping of a tumbling using actual vision feedback were successfully demonstrated using a dual-arm robotic system used for simulating the motions of a tumbling satellite and a servicing space robot (Aghili, 2012). In Lampariello and Hirzinger (2013), a direct single shooting method was used to treat the grasping problem with inclusion of robot joint position and velocities constraints (to also account for dynamic singularity avoidance, see also Singularity Avoidance), as well as the chaser free-floating dynamics. Due to the long computation times involved in the motion planning, a look-up table approach was presented in Lampariello and Hirzinger (2013) to provide feasible optimal solutions for a range of spin rates of the target in a useful time, however with computation of the trajectories on a computer on ground. A reactionless approach of a two-arm space robot, in the pre-capture phase, where the motion of the second arm was used as a fuel-free means of attitude disturbance cancellation, was presented in James et al. (2016). In Flores-Abad et al. (2017) an optimal control problem was also formulated with the indirect method in joint space, aiming at minimization of torque applied by the robot on the free-floating chaser, while moving towards the grasping point. The problem was solved numerically, addressing the grasping task under the uncertainty of the initial and final positions of the robot end-effector. Yang et al. (2018) presented a multi-priority coordinated trajectory planning method for a dual-arm SMS to capture a target satellite. The method is based on a projection of the null-space of the generalized relative Jacobian matrix of the robotic system. They showed success of capturing a spinning (at 1°/s) satellite using simulation. In Lampariello et al. (2018) the planning method was extended to handle sensor-driven motion constraints and was validated on DLR’s OOS-SIM hardware-in-the-loop simulator, to allow for sensory-feedback trajectory tracking, with sensory-feedback throughout the complete task execution. In Aghili (2021) an adaptive and fault-tolerant vision-guided robotic system was developed for capturing a space object having drifting and tumbling motions subject to occlusion of the vision system. An optimal path planner brings the robot end-effector to the grasping point of a moving target as quickly as possible, subject to multiple constraints such as acceleration limit, smooth capture, and collision avoidance. Experimental results demonstrated smooth capture of a free-floating satellite mockup in spite of system uncertainties and a complete failure of the vision system due to occlusion. Other ideas resulting in reactionless (in terms of spacecraft attitude) manipulator path-planning, were the Reaction Null Space (Nenchev et al., 1996; Piersigilli et al., 2010) and the Zero Reaction Maneuver (Yoshida et al., 2001).
Post-Grasping Motion Planning
Having grasped the uncontrolled drifting and tumbling target, the space manipulator should gently exert force and torque to the target for stopping its drift and transferring its angular momentum to the servicing SMS. Several studies on optimal path planning for stabilization of a tumbling satellite in the post-grasping phase exist. A path planning method must consider the permissible bounds on the interaction moments between the SMS and its target during detumbling. Otherwise, excessive forces and moments may lead to mechanical damage or actuation saturation of the SMS attitude control system. Other constraints include robot workspace limits and joint velocity limits (especially due to dynamic singularities (Papadopoulos, 1993), see also Singularity Avoidance). The principle of conservation of momentum was first used by Dimitrov and Yoshida (2004) to damp out the chaser-target relative motion. An impedance control scheme for a free-floating space robot in grasping of a tumbling target with model uncertainty was presented by Abiko et al. (2006). These control schemes do not impose motion or force/torque constraints.
The problem of path planning and control of space manipulators to stabilize a tumbling satellite in the post-grasp phase was postulated and addressed in Aghili (2008). The development of fast detumbling maneuvers subject to torque restriction followed (Aghili, 2009). However, the coupling between dynamics of the rotational and translational systems was ignored and thus the planned trajectory was not truly optimal. In Lampariello and Hirzinger (2013) and Lampariello et al. (2018), the post-grasping task (rigidization) was again addressed with the direct single shooting method as an NLP, optimizing the mechanical energy of the robot arm. Particularly, in Lampariello et al. (2018), this phase was re-planned onboard, to account for tracking errors in the previous approach phase (see Pre-Grasping Motion Planning), while favoring the fulfillment of the position-dependent motion constraints (such as collision avoidance and robot manipulator workspace limits). It was in fact found that end-effector forces were well below the operational limits.
Other methods for post-capture control of tethered (the gripper is attached to a space platform through a tether) or articulated space-manipulators have been proposed (Nguyen-Huynh and Sharf, 2013; Wang et al., 2015; Huang et al., 2016; Zhang, et al., 2017; Wang et al., 2018; Huang, et al., 2019). Nguyen-Huynh et al. developed an adaptive reactionless motion and parameter identification in post-capture of a space object grasped by a manipulator (Nguyen-Huynh and Sharf, 2013). Wang et al. (2015) proposed a novel control scheme to realize stabilization of tumbling combinations after target capture by coordination of a tethered space manipulator and thrusters accommodated on the base of the space manipulator. A detumbling strategy and coordination control of kinematically redundant space robots after capturing a tumbling target was proposed by Wang et al. (2018). Chu and Wu (2018) presented a new self-learning soft-grasp control algorithm based on the variable stiffness technology for target capturing by a free-floating space manipulator. Self-collision avoidance and avoiding the collision with target by manipulator links might be another cost function parameters (Huang et al., 2019).
Optimal control strategies for the post-grasping phase, where the optimal controller damps out both translational and rotational motions collaboratively and simultaneously by taking advantage of the coupling between dynamics of translational and rotational systems was proposed in Aghili (2020). The optimal controller minimizes a cost function, which can be time, distance, or energy, while ensuring that the magnitude of the interaction force and torque between the manipulator’s end-effector and the satellite remain below their prescribed safe values. In Virgili-Llop and Romano (2019) the authors extended their work in Virgili-Llop et al. (2019) to solve the guidance task simultaneously for the capture and detumble maneuvers, consolidated by extensive numerical simulations and hardware-in-the-loop experiments. A dual-integral sliding mode planning method based on the reconfiguration of the reaction wheels is proposed in Hana et al. (2020) for the stabilization control problem of a combined spacecraft after multiple impacts during target capture. A non-holonomic path-planning technique based on a particle swarm optimization was proposed and applied to target berthing and target post-capture base re-orientation (Xu, et al., 2009).
Singularity Avoidance
Of relevance to the capture motion planning task is also singularity avoidance, which in the case of free-floating robot dynamics, is particularly challenging, since a given end-effector pose may be singular or not, depending on the path taken to reach it (see Dynamics of Space Robots in Orbit). Efforts have been dedicated to describing the location of the singularities in the robot workspace. The Path Dependent and Path Independent Workspaces were defined (Papadopoulos, 1992; Papadopoulos and Dubowsky, 1993); the latter was used to ensure dynamic singularity-free manipulator motions, while minimizing the SMS base disturbances. To plan manipulator trajectories for free-floating systems, a Lie algebra approach was employed for Cartesian motion planning (Papadopoulos, 1992). To avoid long duration trajectories, a Cartesian point to point path planning methodology using high order polynomials, was employed to specify the desired path directly in joint-space (Tortopidis and Papadopoulos, 2007). The accessibility of final configurations was extended drastically, while free parameters were determined by optimization techniques. Another approach was based on flatness theory extended to three-link spatial space robots (Xu et al., 2008). A similar approach was presented in Agrawal et al. (2009).
By making use of the inverted chain formulation (Abiko et al., 2006) and of free-floating robot dynamics properties presented in Cusumano et al. (2004), an efficient and complete method for generating singularity maps in the joint space of a 6-DoF free-floating robot is presented in Calzolari et al. (2020). Given the location of the singularities, the singularity avoidance can be treated as a collision avoidance problem, to increase the efficiency of the motion planning task in a nonlinear programming setting. Assuming that a Cartesian path is predefined, a method was proposed to yield initial system configurations that ensure that the predefined path avoids dynamic singularities (Nanos and Papadopoulos, 2012).
On-Orbit Assembly
Different works in the literature conceptually discussed the on-orbit assembly of space telescopes. The Rendezvous and Docking assembly principle have different drawbacks, including high risk of collision, high requirement for the GNC system and large fuel consumption (She et al., 2020). To accomplish the task with space robots, the free-floating dynamics is typically omitted, since the parts to be assembled and the robotic arm which assembles them, are both hosted on the same spacecraft.
Examples of robotic assembly planning for this specific task can be found in She et al. (2020) and Martinez-Moritz et al. (2021). The motion planning task was divided in the latter into a global and a local layer. The global layer faces the challenge of first planning the assembly order, as well as of creating the instructions to be followed by the planner of the local layer. Methods to achieve this task solve the so-called robotic assembly planning problem (Martinez-Moritz, et al., 2021). The local layer consists of a constrained path planner that plans manipulation tasks to place single parts into the assembly. Different methodologies may be adopted here, including Rapidly-exploring Random Trees (RRT) - based methods, such as RRT-Connect (Kuffner and LaValle, 2000), Constrained Bi-directional Rapidly Exploring Random Tree (CBiRRT) (Berenson et al., 2009) for sampling-based path planners, CHOMP (Ratliff et al., 2009), STOMP (Kalakrishnan et al., 2011; Martinez-Moritz et al., 2021) and Genetic Algorithms (She et al., 2020) for optimization-based path planners.
Feedback Control
Control Schemes
Many control approaches can be referenced, depending on the task at hand. These include control for approaching a target, for capturing or interacting with a target, and for handling and servicing clients. Special mention must be made to robust control methodologies aiming to reduce the effects of uncertainties.
Control for Target Approach
Several works exist for the spacecraft velocity matching control, usually as a combination of planning and feedback control. An optimal control of a spacecraft approaching a tumbling target was developed in Xin and Pan (2011), minimizing the flexible motion induced by large angular maneuvers, using a nonlinear optimal control technique. In Buckner and Lampariello (2018) a tube-based Model Predictive Control (MPC) controller for tracking was implemented to track motion planning solutions for the chaser approach problem, see also Albee et al. (2021) for a mission pipeline related to these methods.
Capturing/Contacting a Target—Impedance/Compliance Control
The interaction of a SMS with its environment is important in many tasks and many research works focus on this challenge. Although some researchers have paid attention to the importance of contact control and performed various in-orbit contact dynamics analyses since the 90s’ (Ma, 1995), most control studies ignore the control of the contact force itself, as the contact dynamics is highly nonlinear and hard to model and control. Recently, hybrid impedance controllers for the capture and control of a rotating object by a free-floating space manipulator (Wu et al., 2017; Mou et al., 2018a) have been proposed.
In Yoshida et al. (2004), the concept of impedance matching was adapted to model the contact motion between a SMS and a non-cooperative target and studied whether contact with the target is maintained or lost. The virtual mass concept for using impedance control on-orbit has been proposed, aiming to represent the influence of the end-effector impedance on the target (Nakanishi et al., 2010). In Uyama et al. (2012), the impedance controller is considered in coordinates relative to the target, to reduce the dynamics of the contact problem to those of a damped oscillator. In Rodriguez Perez et al. (2018) a novel method for tuning an impedance control scheme was presented, which ensures post-impact velocity matching between the servicer and target satellites. A method for grasping a partially cooperative tumbling satellite with a free-floating robot, by implementing a tracking controller in Cartesian and in joint space, as well as an EKF for providing robustness and a tumbling satellite velocity estimate for feedforward control during grasping, was presented in Lampariello et al. (2018). To capture a target robustly without precise motion tracking and large force interaction, a novel gripper design in conjunction with the application of an impedance control law was proposed in Hirano et al. (2017). To minimize interaction forces between a robot manipulator and a satellite, while maintaining contact, an approach based on direct force control in the presence of a rigid grasp was proposed in Seweryn, et al. (2018), while a solution to minimize the risk of damage to the arm and thereby enhance contact performance was presented in Ma et al. (2015). However, both designs require control mode switching. For the docking of a SMS to a target with an impedance-controlled manipulator (Mitros et al., 2016; Mitros et al., 2017), the relationship of impedance gains to system parameters was established.
To allow for larger workspaces, free-flying SMSs have been considered. An extension of Hogan’s impedance control concept, the Object Impedance Control (OIC) has been developed for multiple robotic arms manipulating a common object (Schneider and Cannon Jr, 1992). To manipulate an object by a free-flying SMS with multiple arms on-orbit, the Multiple Impedance Control (MIC), which exploits the OIC, has been developed (Moosavian and Papadopoulos, 2010; Mitros et al., 2017). An Extended MIC method has been proposed for the dual-arm control of a passive object in space, in the presence of flexible appendages (Zarafshan and Moosavian, 2011). In a disturbance-based impedance controller, an end-effector desired trajectory generator provides the desired impedance behavior, while the desired motion is applied using a simple PD joint torque controller (Flores-Abad et al., 2018). Stolfi et al. (2017) extended the formulation of Impedance Control proposed in Nakanishi and Yoshida (2006) to a two-arm free-flying manipulator system with particular emphasis on the impact and post-impact phase with a target satellite. In Nagaoka et al. (2018) the detumbling and capture of space debris by a dual-arm space robot is accomplished by repeated impact, without precise estimation of the inertial characteristics and surface frictional roughness of a spinning rocket upper stage.
Based on the passivity control method, research, and experimental analysis on flexible joint manipulators with joint torque feedback has been developed in Ott et al. (2004) and Albu-Schaeffer et al. (2004). However, the nonlinear friction that exists at the joints was not explicitly addressed in these works. Thus, in practice these controllers were applied together with additional motor side friction compensation or disturbance observers. An impedance control with adaptive friction compensation for the dexterous robot hand has been proposed in Chen et al. (2011), implementing a friction EKF based observer, for adaptive impedance control of the fingers.
DLR took the lead in implementing the on-orbit impedance control experiment in ROKVISS and conducted an experimental study on joint parameters (Landzettel, et al., 2006). A compliant control mode (including force and impedance control) was tested in orbit with JAXA’s ETS-VII and showed good performance (Oda, 1999). The problem of detecting, isolating, and estimating the contact force for an orbital robot was addressed in Cavenago et al. (2021). A new observer was presented based on the dynamics in terms of the motion of the centroid of the whole robot and the joints, which was compared to the classical base-joint dynamics approach and validated with hardware on ground. The same method was extended in Cavenago et al. (2021) to include reaction wheels to thruster actuation of the base body, as well as a reaction control strategy, which aimed at avoiding the buildup of the contact force and possible instabilities.
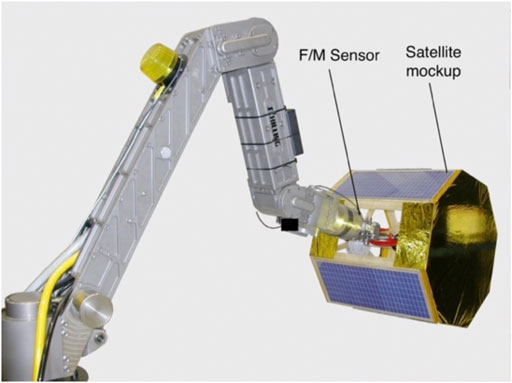
The Special Purpose Dexterous Manipulator (SPDM) has been extensively utilized to handle various ORUs for ISS maintenance operations (Oshinowo et al., 2006). SPDM is a dual arm manipulator where each 7 degree-of-freedom arm is approximately 3.3 m long and is mounted on a single DoF body joint. It can complete human scale delicate servicing tasks with maximum tip velocities 7.5 cm/s-2.5°/s. In the teleoperation mode, SPDM is capable of positioning its end-effector relative to a target within 0.6 cm-2.0°, while in the automatic mode it is capable of adjusting the position and orientation of its end-effector in increments of 0.2 cm or 0.1° in any direction using Force-Moment Accommodation (FMA) control (Fulford, 1999; Aghili et al., 2001; Mukherji et al., 2001; Oshinowo et al., 2006). The capability of a space manipulator to effectively perform tasks involving contact hinges on the availability of an adequately accurate force-moment feedback. For many robots, force feedback is provided by a force-moment sensor (FMS) installed at a robot’s wrist. On-orbit calibration of SPDM force-moment sensors was studied in Aghili (2000).
Coordinated Control and Handling/Servicing Space Objects
When a SMS executes tasks on a serviced vehicle or a passive object (such as orbital assembly part or orbital debris), the control of both the manipulator configuration (to perform the required task) and the spacecraft attitude/position (to avoid collisions and loss of contact with the operations command center), is required. The coordinated control of the spacecraft and its mounted manipulators is an important control mode, which today tends to be addressed by a single controller.
The coordinated control of SMS in which both the spacecraft and its manipulators are controlled was developed employing a Transposed-Jacobian controller with inertial feedback (Papadopoulos and Dubowsky, 1991b). Coordinated control of a spacecraft attitude and its manipulator (partial free-floating mode) for OOS applications was presented in Aghili (2009). Α coordination controller for the combined system of a SMS and its target, considered as a manipulator payload, aimed at controlling the attitude of the target (Huang et al., 2016). A control strategy considering the servicing vehicle base and the manipulator as a single multi-body system subject to coordinated control was presented in Sabatini et al. (2017), with the goal of approaching and grasping a target spacecraft. In De Stefano et al. (2019), a coordinated control was presented for end-effector tracking and base regulation, while focusing on the effects due to the different sampling rates of the manipulator and base controllers, which can generate stability issues. The approach task to a tumbling target with a fully actuated free-flying robot was addressed in Mishra et al. (2020), where a cascade interconnection of a geometric EKF observer and a geometric controller were validated in simulation.
A coordinated control scheme which considers the contribution of reaction wheels to the system angular momentum, has been studied in Jayakody et al. (2016) modifying the Adaptive Variable Structure Control (AVSC) scheme to a SMS. In Antonello et al. (2019), coordinated control of both the servicing vehicle and the manipulator end-effector, in face of disturbances (e.g., point contact with a serviced satellite), was proposed. A method for coordinated control of both the manipulator end-effector and the servicing vehicle attitude, and the translation of the global system CoM, was proposed (Giordano et al., 2019). A control strategy which uses thrusters, reaction wheels, and robotic arm drives in a coordinated way to limit the use of the thrusters in both cases with and without contact is presented in Giordano et al. (2020). A unifying framework for whole-body control of orbital robots can be found in Giordano (2020), in which the advantages of common free-floating and free-flying strategies are merged, resulting in controllers that are more fuel efficient than the classical spacecraft positioning controllers.
To control multi-arm space robots in coordination with the spacecraft base, several schemes have been proposed, such as a model-based control algorithm (Moosavian and Papadopoulos, 1997), and an adaptation of the AVSC (Shi et al., 2017). The use of a second arm as a balancing mechanism, while the primary manipulator performs the desired task, was studied in Xu et al. (2017).
A compliance/impedance controller for the end-effector, integrated as part of a coordinated control scheme can both stabilize the servicing vehicle, and control the manipulator end-effector. A coordinated control method for a single manipulator capturing of a tumbling target, implementing a fast, on-line updating manipulator path planner and end-effector compliance control, was proposed (Gangapersaud et al., 2019). Coordinated detumbling of a non-cooperative captured target, with simultaneous servicing vehicle attitude PD control, was developed in Hirano et al. (2018). However, both abovementioned methods do not consider singularity avoidance or manipulator workspace constraints.
Besides the coordinated control schemes, other controllers have been proposed for the captured target handling task, such as a control method for handling captured passive objects, aiming at reduction of flexibility-induced vibrations (Dubowsky and Boning, 2007), or methods proposed to maintain firm grasp (Hiramatsu and Fitz-Coy, 2007). The handling of a passive object by multiple space robots, was studied in Rekleitis and Papadopoulos (2015), proposing a hybrid control scheme with on-off thruster control of the SMSs, while their manipulators could apply continuous forces on the passive object.
Control in the Presence of Parametric Uncertainties
Two main approaches exist in treating parametric uncertainty: robustness and adaptation. The nonlinear robustness and parameter sensitivity field is rather limited, with most works relying on special features to prove stability under uncertainties. Nonlinear Sliding Mode Control (SMC) (Slotine and Li, 1991) can be used, but it suffers from drawbacks such as excessive control effort (Dastidar, 2010), and state oscillation around the desired values; the later can be mitigated using higher order SMC (Ferrara and Incremona, 2015). Linearization, when applicable, can be employed to allow use of linear robustness tools Rekleitis and Papadopoulos (2014). The problem of tracking control with a guaranteed performance for free-floating SMS with uncertainties and external disturbances, was studied using an adaptive nonlinear
In the adaptation approach, controller parameters are adapted so that the desired response is obtained despite parameter variations (Slotine and Li, 1991). However, they are subject to limitations, especially in free-floating systems, in which classical adaptive control laws are not applicable readily. Thus, while adaptive control has been proposed for free-flying robotic systems (e.g., Ulrich et al., 2016), its use in free-floating ones is restricted. Adaptive control has been proposed for free-floating robotic systems handling a captured passive target, either using the base reaction to dampen vibrations (Abiko and Yoshida, 2010), or generating reactionless manipulator motions not disturbing the spacecraft attitude (Nguyen-Huynh and Sharf, 2013). A task-space adaptive controller has been proposed in Wang et al. (2017), however it requires four adaptation laws simultaneously, and an online solution of a differential equation.
Parameter identification methods can be used to estimate accurately system parameters, and concurrently be used in any stable non-linear controller. Methods for concurrent parameter identification and adaptive control have been proposed for a simplified point-mass system (Espinoza and Roascio, 2017) or for a full space robot that assumes only the last manipulator link (including the captured target) as unknown, while it also requires noisy acceleration measurements (Zong et al., 2019). In Christidi-Loumpasefski et al. (2020) a fast, and reliable parameter identification method previously developed by the authors, was further enhanced, to identify all required parameters for the complete system dynamics reconstruction in Cartesian and joint space and provide on-the-fly accurate parameter estimation for control, resulting in a Self-Tuning Controller (Slotine and Li, 1991).
Visual Servoing
Visual servoing approaches for manipulation of space objects in complex scenarios and automated rendezvous and docking of non-spinning spacecraft have been proposed for various missions (Wertz and Bell, 2003; Ruth and Tracy, 2004; Evans III and Mulder, 2006). Wertz and Bell (2003) gave an overview of hardware and software technologies (sensors and actuators) required for autonomous rendezvous and docking of two spacecraft started at a remote distance. The terminal phase of the Demonstration of Autonomous Rendezvous Technology (DART) mission that includes proximity maneuvers for rendezvous to a cooperative spacecraft under an advanced video guidance sensor is described in Ruth and Tracy (2004).
Adaptive control law for spacecraft rendezvous and docking under measurement uncertainty such as aggregation of sensor calibration parameter, systematic bias, or some stochastic disturbances was proposed in Singla and Junkins (2006) and Aghili and Su (2016). The development and experimental validation of adaptive visual servoing for on-orbit servicing was presented in Aghili (2012); see Figure 3. The vision guidance problem for the shortest time was cast into the optimal control framework pertaining to two sequentially occurring maneuvers in the pre-grasping and post-capturing phases (Aghili, 2013). Adaptive deliberate planning was accomplished by combining a 3D registration algorithm and a constrained estimator allowing real-time estimation of required parameters and states (Aghili and Parsa, 2007). This integrated estimation and control architecture also allows fault detection and recovery of the visual feedback whenever the vision sensor generates erroneous information, i.e., caused by partial or full obstruction vision (Aghili et al., 2011). A visual servoing method for the approach, capture and rigidization of a tumbling target with a free-floating robot was presented in Lampariello et al. (2018). The visual servo was fed a desired command from a combination of a reference trajectory and the output of an EKF. The method was tested on an experimental facility on ground. A fault-tolerant and adaptive visual servoing for capturing free-floaters has been recently presented in Aghili (2021) that allows to choose the most appropriate control action in the face of environmental uncertainties or short-term failure of the vision. Experimental results demonstrated smooth capturing of a free-floating object in the present of partial or complete failure of the vision system.
Telepresence and Teleoperation
Although impressive progress has been made in recent years with respect to the robotic automation level of non-trivial tasks, it is of key importance, especially in the space robotics environment, to be able to react quickly to unforeseen situations or to incorporate the integration of “human” intelligence from the beginning when performing robotic activities in space. To this end, telerobotics is the appropriate paradigm combining robotic (manipulation) and human capabilities (intelligence, strategy, problem solving). In this context, the term telerobotics subsumes the areas of teleoperation up to telepresence. Teleoperation covers the entire range of task execution at a remote location, including the use of intelligent autonomous systems. Telepresence, on the other hand, stands for the possibility of being quasi-immersively present at the remote location as an operator through a robotic avatar. To this end, experiments were carried out in and with the ISS in recent years to cover the entire range of telerobotics. However, it is worth pointing out that these experiments involved interactions with quasi-static environments. The effects of communication time delay and dropouts, of limited bandwidth, as well as of the operator’s misperception and limited field of view, make the execution of tasks on dynamic environments with telerobotic methods, such as the capture of a tumbling target, still challenging today. The ability of an operator’s fast response to a contingency, may be combined with an autonomous capture system in the context of shared control. However, this is a challenge that has not been studied adequately yet.
DLR’s and Roscosmos’s ROKVISS and KONTUR-2 experiments led the way to study the feasibility of employing robots as haptically coupled avatars for the user in both directions between Earth and orbit (Hirzinger et al., 2005; Artigas et al., 2016; KONTUR-2: Force-feedback Teleoperation from the International Space Station, 2016). METERON (Multi-Purpose End-To-End Robotic Operation Network), led/spearheaded by ESA, with partners NASA, Roscosmos, and DLR, conducted a suite of experiments to validate advanced technologies for space robotics operation and telemanipulation. Several robotic assets on Earth, including Rollin’ Justin (DLR), were controlled from on board the ISS using various command modalities. In contrast to KONTUR-2, the METERON SUPVIS Justin experiment placed an intelligent robot co-worker in the scenario of a planetary surface habitat for supervised autonomy teleoperation (Lii et al., 2015; Lii et al., 2018; Schmaus et al., 2018). The experiment aimed to demonstrate how robots, despite significant communication times, can be commanded to solve complex tasks. The local intelligence of the robot was used to implement the commands of an astronaut. However, the technology demonstrated in this scenario can well be applied for the case in which the robot is in orbit and the operator is on ground. NASA’s Robonaut I and II were designed for a wide variety of intra-vehicular activities on the ISS (Ambrose et al., 2000; Diftler et al., 2011). The robot can be teleoperated by coupling its stereo vision and dexterous capability with the user through augmented reality and finger tracking (Bibby and Necessary, 2008; Peters et al., 2003).
NASA, with the support of CSA, has started a Robotic Refueling Mission (RRM) on ISS using CSA’s SPDM (Gefke et al., 2017). RRM is a series of multi-phased ISS payload experiments designed to test and mature the tools and technologies associated with on-orbit robotic fueling services. The hardware is a 1.1 m × 1.1 m × 0.8 m module consisting of four robotic servicing tools, several tool adapters, a fluid (ethanol) transfer system, and multiple task boards, valves, and spacecraft blanketing representative of those found on existing satellites. The tools contained within RRM were actuated and controlled via SPDM, operated at ISS mission control with NASA personnel supporting on-orbit operations remotely from the NASA Goddard Space Flight Center. The primary robotic control method is remote high-level teleoperation with local closed-loop force-moment accommodation (thus reducing contact risk). Phases 1 and 2 of the mission have been successfully completed in 2013 and 2015, respectively. Phase 3 is focusing on technologies needed to transfer and long-term (<3 months) store super-cold cryogenic fluids (NASA, 2021).
Ground Testbed Facilities
Ground testbed facilities have been used for spacecraft control hardware/software verification since various space programs began half a century ago (Schwartz et al., 2003). Due to the high cost of launch and operations associated with on-orbit repair, a spacecraft must operate reliably once it is placed in orbit. Therefore, realistic testing of spacecraft prior to launch, ideally with all hardware/software in place at system level, ought to be undertaken to ensure that the spacecraft functions as intended. One of the challenges of this approach is that testing must take place in a 1-g environment, whereas the actual system will eventually operate in a zero-g environment. This has motivated the building of testbed facilities in various government and university laboratories for the testing and verification of space robotic systems (Wilde et al., 2019).
Zero-G Simulation of Free-Floating Space Objects
Since space manipulators are designed to work in a microgravity environment, they should also be tested in a microgravity environment. There are many technologies available to address the problem of reproducing the microgravity space environment, such as air bearings, cable suspension, neutral buoyancy, free-fall, magnetic suspension, large rotating wheels, and HIL simulation (Flores-abad et al., 2014a). However, of all of these, the air bearings are the most popular in industry for testing spacecraft.
Cable suspension achieves single dimensional weight compensation only. Adding a 3D gimbal at the end of the cable can simulate weightless rotation but it is an unstable emulation because the CoM of the simulated object must always align perfectly with the gimbal center, which is obviously not suitable for robot testing. Neutral buoyancy facilities, i.e., water tanks, have been used extensively for astronaut training. However, a functional spacecraft cannot be submerged in the water; in addition, viscous damping does not allow a space-representative dynamic environment and the water media also significantly affects sensor performance. A free-fall test through flying parabolas in aircraft can achieve zero-g in a 3-D environment but only for less than 30 s of testing time, not long enough for most space robotic operations. Magnetic suspension systems provide only a low force-torque dynamic environment with a small range of motion.
Air-bearing tables (Yoshida, 2003; Papadopoulos et al., 2008; Rybus and Seweryn, 2016) and spherical air-bearings (Schwartz et al., 2003) are commonly used for ground-based testbeds for testing the translation and attitude control systems of a spacecraft. An emulation of zero-g translational motion can be achieved by an air-bearing table on which a spacecraft translates on a flat surface perpendicular to the gravity direction while being floated on a cushion of compressed air with almost no resistance. This technique has been used for testing various space systems such as formation flying (Choset and Kortenkamp, 1999), free-flying space robots (Yoshida, 2003), orbital rendezvous and docking (Matunaga et al., 2000; Aghili and Su, 2016), capturing mechanisms of spacecraft (Kawamoto et al., 2001), and free-flying inspection vehicles (Choset and Kortenkamp, 1999).
Although an air-bearing table system can be utilized to test some physical components of spacecraft control systems, including the sensors and actuators, this system is limited to a two-dimensional planar environment. Spherical air-bearings have been used for spacecraft attitude determination and control hardware/software verification for many years (Schwartz et al., 2003). The earliest development and design of a satellite simulator based on spherical air-bearing with three axes of rotation has evolved into modern testbed facilities (Colebanket al., 1999; Schwartz et al., 2003). A spherical air-bearing yields minimum friction and hence offers a nearly torque-free environment if the CoM is coincident with the bearing’s center of rotation. The main problem with the spherical air bearing is the limited range of motion (within ±45° about horizontal axes) resulting from equipment being affixed to the bearing (Peck et al., 2003). Also, spherical air-bearings are not useful for simulating spacecraft having flexible appendages, because the location of the center-of-mass of such spacecraft is not fixed. Spherical bearings cannot be used to simulate a robot’s weightless rotation either because the mass center of a robot changes when the robot moves.
Although one can envisage combining the two air-bearing technologies in a testbed for reproducing both the rotational and translational motions (Tsiotras, 2014; Saulnier, et al., 2014), having a spacecraft mounted manipulator and complete freedom in all six rigid degrees-of-freedom is still technically difficult to achieve (Schwartz et al., 2003). Air-bearing supported testing of a large space manipulator requires a large and massive test mechanism to support the manipulator and the payload it handles. Since the supporting mechanism must move with its supported manipulator, it will alter the dynamics of the tested manipulator. Yao et al. (2018) recently developed a method to eliminate this unwanted side effect, so that the true dynamics of the tested manipulator can be understood.
Most motion testing systems allow the incorporation of real sensors of a satellite such as gyros and star trackers in HIL simulation loops. However, actuators such as reaction wheels or gas-jet thrusters have been simulated. The main idea in HIL simulation is to combine digital simulation of the robotic arm and physical testing of some of its hardware in the same framework. In other words, under the HIL simulation framework some of the SMS components are simulated by digital models and other components are represented by real physical hardware. Such an approach can take advantage of both digital simulation (for difficult-to-test items such as the long-reach arm in 3D zero-g space) and hardware testing (for difficult-to-model items such as contact dynamics). Rather than testing the control algorithm on a purely mathematical model of the robotic system, one can use real hardware in the simulation loop (Aghili et al., 2006; Aghili and Namvar, 2009). This allows key hardware to be physically tested along with the entire SMS system in operation, which is otherwise impossible in the 1-g environment. It also allows detailed measurement for accurate performance assessment of the system under the test.
The concept of the HIL methodology has also been utilized for design and implementation of various laboratory testbeds to study the dynamic coupling between a space-manipulator and its host spacecraft operating in free space (Dubowsky et al., 1994; Tarao et al., 2000; Yoshida, 2003). A system called the Vehicle Emulation System Model II (VES II) permits the experimental evaluation of planning and control algorithm for mobile terrestrial and space robot systems by using the so-called “admittance control” (Dubowsky et al., 1994). Similar concepts have been also pursued by other space agencies such as, DLR (Krenn and Schaefer, 1999), CSA (Aghili and Piedboeuf, 2000), and NASA (Ananthakrishnan et al., 1996) for different applications. A method to control a manipulator system grasping a rigid-body payload so that the motion of the combined system in consequence of external applied forces to be the same as another free-floating rigid-body (with different inertial properties) was developed in (Aghili and Namvar, 2009). This allows zero-g emulation of a free-floating space object under the test in a 1-g laboratory environment as shown in Figure 4. The controller consisting of motion feedback and force/moment feedback adjusts the motion of the test spacecraft to match that of the flight spacecraft, even if the latter has flexible appendages (such as solar panels) and the former is rigid. Satellite simulator testbed facility based on hardware-in-loop simulation technology to investigate capturing free-floating satellite under 1-g laboratory environment was developed at CSA (Aghili et al., 2008; Aghili and Parsa, 2007; Aghili, 2012). A dual-arm robotic system was utilized at the CSA ground testbed facility for replicating the motion dynamics of a servicer robot and a target satellite; see Figure 3. Ground simulations using hardware in-the-loop simulation to simulate the servicing arm and a parallel motion-based platform to replicate the client satellite has been developed also at NASA’s Goddard Space Flight Center (Carignan et al., 2014). A later and more general overview of the ground test facilities at the same NASA center is given in Roberts (2017). This robotic testbed platform was used to investigate the dynamic interaction between the servicing spacecraft and client satellite (Strube et al., 2012; Brannan and Carignan, 2013; Brannan and Carignan, 2017; Brannan et al., 2018; Brannan et al., 2020).
Space Mechatronics Testbeds
Joint servomechanisms consisting of actuators, sensors, and controllers are among the fundamentals in mechatronics and robotics. Development of any new joint prototype ought to undergo extensive mechanical, electrical, and thermal tests at different stages of the development to make sure that the system works as intended. In robotics applications, these tests can be performed using a robot prototype built on developed joints. However, building a complete prototype of the robotic system is an expensive and inflexible process. Moreover, due to the iterative nature of the design process, the need for multiple robot prototypes makes it even more costly and time consuming. The challenge of testing space manipulators is even greater because they must be tested and validated in a 1-g laboratory environment whereas the actual robotic system will eventually work in an environment with different gravity, temperature, and ambient pressure.
Alternatively, testing of actuators and join prototypes can be carried out by mounting them on a dynamometer. Industrial dynamometers tend to use a flywheel and/or mechanical brake for loading the actuator. However, such a simple load does not represent a real manipulator. Hence, the extent of the test result is limited, and the real performance remains largely unknown until the actual robot becomes operational. Mechatronic testbeds that use dynamometers for testing vehicle dynamics and control have been developed based on the concept of HIL simulation (Brennan and Alleyne, 2000; Tartt and Moskwa, 2001). These test methods are limited to emulating loads with linear dynamics.
Design and development of a testbed facility for testing a range of actuators, used for either space robots were first reported in Aghili (2005, 2006). Unlike industrial dynamometers that apply constant braking torques, or vehicle dynamometers that are capable of emulating linear loads, a dynamometer utilizing active loads that generate loading torques corresponding to a prescribed mode was employed, see Figure 5. High fidelity joint torque emulation is made possible by incorporating the measurement of joint torque as well as joint angles and velocities in a composite feedforward/feedback loop. The role of the feedback control is to modify the simple inertia of the rotors of the load motors to match the nonlinear and coupled dynamics of manipulator links. Such a testbed system allows testing the complete joint prototypes of a manipulator without needing to construct the manipulator. This can reduce significantly the cost associated with the development of space robots, so that the joint prototypes can undergo test under a space-like thermal/vacuum environment.

FIGURE 5. Testing the joints of a space manipulator on a dynamometer using actively controlled loads (CSA).
Space Manipulator Task Verification Facilities
Space robots have become viable means to perform complex extra-vehicular robotic tasks as they have proven to play critical role in construction and maintenance of the ISS. Assembly of the ISS was not possible without the iconic Canadarm2, while the SPDM has been extensively utilized to handle various ORUs for ISS maintenance. Station construction and maintenance operations mostly involve robotic contact tasks and therefore they must be first carefully planned and then properly controlled to avoid wedging, jamming, or overloading during the insertion or removal operation of ORUs. The verification of large space robots on the ground is challenging as these long-reach and lightweight robots are designed to work only in a microgravity environment and thus they cannot do real 3D operations on ground.
Space agencies have built sophisticated testbed facilities for verification and validation of on-orbit contact tasks through implementation of HIL simulation technology using robotic manipulators capable of operating in 1-G laboratory environment. The earliest HIL simulation facility was built to investigate the berthing of a Space Shuttle onto ISS by the Shuttle Remote Manipulator System (Canadarm) (Tobbe et al., 1991). It followed by development of the SPDM Task Verification Facility (STVF) at CSA to verify dexterous tasks to be performed by SPDM on the ISS (Aghili and Piedboeuf, 2000; Ma et al., 2004; Aghili and Piedboeuf, 2006; Aghili, 2019); see Figure 6A. Similar HIL simulator facility to simulate on-orbit servicing robots performing contact tasks have been built at DLR (Krenn and Schaefer, 1999; Ma et al., 2012; Artigas et al., 2015). Bandwidth limitations of HIL simulator involving contact tasks regarding contact stability and fidelity performances have been the subject of several studies (Krenn and Schaefer, 1999; Aghili and Piedboeuf, 2006).

FIGURE 6. (A) SPDM Task Verification Facility (CSA), (B) Capturing task at the OOS-SIM facility (DLR). (C) Manipulator Test and Verification Facility (MTVF) developed by China Academy of Space Technology (Liu, et al., 2018).
More recently, a passivity-based approach for simulating satellite dynamics on a position-controlled robot equipped with a force–torque sensor was presented in De Stefano et al. (2019). Time delay and discrete-time integration effects were analyzed from an energetic perspective and compensated through a passivity-based control strategy to ensure a faithful and stable dynamic simulation with position-controlled robots. The benefits of the proposed strategy were demonstrated on the OOS-SIM, shown in Figure 6B. An exhaustive analysis of energy-based control for simulation of multi-body dynamics using robotic facilities was presented in De Stefano and Marco (2018). The first example of a prolonged contact between the two industrial robots in the OOS-SIM, which results from the loop closure with the torque-controlled Light-Weight Robot (LWR, orange robot Figure 6B) when simulating capture, was presented in Lampariello et al. (2018). A stable prolonged contact was possible thanks to the sufficiently compliant behavior of the LWR, although some periodic disturbances were visible in the equilibrium regulation point, to be attributed to the intrinsic time delay in the simulator.
Since SPDM could not be directly tested for 3D contact operations on ground, after several trade-off studies, a ground-based HIL simulation facility consisting of an SPDM real-time dynamic simulator, a hydraulic manipulator (for mimicking SPDM dynamic behavior), and the real SPDM end-effector and payload mockups was developed at the Canadian Space Agency (CSA) (Aghili and Piedboeuf, 2000; Aghili and Piedboeuf, 2006; Aghili, 2019) for high-fidelity task verification of the SPDM. Since the simulating robot interacts with a physical environment, contact dynamics modeling is not required and hence many technical difficulties associated with contact dynamics modeling are avoided; see Figure 6A. On the other hand, the hydraulic simulating manipulator is not dynamically and even kinematically equivalent to the reference SPDM robot. Therefore, the greatest challenge in a high-fidelity simulating robotic system is to maintain dynamical similarity between the simulating robot and reference robot through proper control architecture. It turns out that this goal can be achieved though closed-loop impedance matching of the two robots so that the ground-based simulating manipulator can generate contact forces and transitional impact which closely match those expected from SPDM during on-orbit operations (Ma et al., 2004; Aghili and Piedboeuf, 2000; Aghili, 2019).
Another challenge for the emulating robot is the uncertainty associated with the environment impedance, which affects the contact stability and fidelity performance of the simulating robot. In essence, these challenges can be addressed by a systematic robust control approach to find the best compromise between fidelity performance and contact stability given varied range of environment impedances and limited bandwidth of the simulating robot. A robust impedance-matching of manipulators is presented in Aghili (2019) to generate high-fidelity contact force profiles in consequence of either operator commands or impulsive force caused by pre-impact velocity to match those of a space robot as closely as possible.
The idea of shaping the dynamics of the emulating manipulator to represent a scenario of interest was also applied in Mishra et al. (2020), where a fixed-based manipulator was used to simulate an orbital robot. The Lagrange-Poincare equations were used to describe the orbital robot’s dynamics, which reveal a block-diagonalized inertia, such that noisy joint acceleration/torque measurements were avoided in the computation of the spacecraft motion due to manipulator interaction, even while considering external forces. The chief advantage of this method is physical consistency of the simulation. The effectiveness of this approach was validated through DLR’s OOS-SIM hardware-in-the-loop simulator of a fully actuated orbital robot, while interacting with the environment. The dynamic shaping idea was also applied in De Stefano et al. (2021), where the OOS-SIM facility was used to simulate the relative motion between a very large tumbling target and a manipulator-equipped spacecraft. By exploiting a Lagrangian matching relative to a nominal motion, the simulated dynamics replicated by the robots enables motions of large satellites to be reproduced. The benefit of the method was demonstrated through experiments on the OOS-SIM facility for the grasping of ENVISAT, a free-tumbling satellite and the largest space debris in Low-Earth-Orbit (see also Other General Software and Hardware Technology Developments).
To support the research and development of the Chinese Space Station Program, an HIL Space Manipulator Test and Verification Facility (MTVF) was developed by the China Academy of Space Technology (Mou et al., 2018; Liu et al., 2018). As shown in Figure 6C, the system consists of two large industrial robots, one physically simulating the 3D motion of the end-effector of a space manipulator or its grasped payload, and the other simulating the payload to be grasped or the worksite the grasped payload will be in contact with Ding et al. (2021). Each of the customer-built industrial robots can handle 300 kg payload. Each industrial robot can translate for a short distance on a rail on the base.
The system used the HIL concept of combining digital simulation of an in-orbit space manipulator and a hardware testbed of real contact hardware. Such an industrial-robot based HIL simulation concept has been widely used in space industry (Flores-abad et al., 2014a). However, the uniqueness of the MTVF is to use custom built industrial robots to achieve better HIL simulation performance with a few special measures: a) it implemented 1,000 Hz commanding cycle in both joint and end-effector control loops for more stable HIL dynamic response; b) it increased gear ratio for smaller maximum speed but higher accelerating capability; c) it had an end-effector force/moment control capability; d) it used a dynamics-model based feedforward loop to reduce nonlinear effects of the industrial robots. These enhanced capabilities are not readily available from commercially-off-the-shelf industrial robots, but they are essential to help achieve stable and accurate HIL simulation of the impact-contact behavior of a space manipulator. Just as all the other existing major HIL simulation facilities, this system also employed the strategy of 6-DoF impedance match in operational space to ensure the fidelity of the HIL contact simulation results.
Missions and Technology
Although proper orbital capture and manipulation missions are still scarce, quite a few studies were carried out in recent years on these topics and many new missions are in plan. The robotic technology related to these missions is also developing at an always increasing pace, as described next.
Missions and Mission Studies
ESA’s and DLR’s OOS Mission Studies
After the pioneering ETS-VII and Orbital Express missions in 1998 and 2007, respectively (Yoshida et al., 2016), in which a cooperative, attitude-controlled target satellite was captured by a free-flying robot, some mission studies focused on the capture of a non-cooperative tumbling target. In DLR’s DEOS study (Reintsema et al., 2010), the mission goal was to capture a small tumbling satellite with a free-floating robot, in both the autonomous and tele-presence operational modes (the latter through an operator on ground). The e.Deorbit study was about an Active Debris Removal mission, promoted by the Clean Space initiative (Clean Space, 2012), given that the ENVISAT was going to be deorbited into the Earth atmosphere (e.deorbit Study Team, 2015). With a length of 26 m and a mass of 8 t, the chaser required to synchronize its motion with the Grasping Point on the target during capture. The two scenarios are shown in Figures 7A,B. In both studies, a torque-controlled kinematically-redundant robotic arm, based on DLR’s robot hardware technology (see Arms, Grippers, and End-Effectors), was used to provide compliant behavior at contact. Details of the e.Deorbit study were provided in Jaekel et al. (2018). Following the latter study, an Airbus DS-led e.Deorbit Consolidation Phase Study was carried out, based on the Airbus Spacetug and an MDA manipulator, in which the capture is preceded by a contactless detumbling maneuver (Estable et al., 2020). In the same spirit, ESA is currently financing the ClearSpace-1 mission (Figure 7C), with a caging capturing concept, consisting of multiple arms wrapping around the target. The latter is intended in this case to be the upper stage of a Vega rocket, with 100 kg of mass.
A different line of development for capturing a satellite for servicing, is the one first developed in the study Orbital Life Extension Vehicle (Smart-OLEV) (Kaiser et al., 2008). Here, the apogee motor of geostationary satellites is used as a docking port for a chaser, equipped with a dedicated docking mechanism. The chaser is then used to provide extra capacity for orbital and attitude control of the target, thus extending the latter’s operational life. The same idea was used ten years later in the two Mission Extension Vehicle (MEV) missions and in the Mission Robot Vehicle (MRV) concept (see Northrop Grumman’s MEV and MRV).
DARPA’s Robotic Servicing of Geosynchronous Satellites (RSGS)
RSGS will be DARPA’s second OOS technology demonstration mission after the Orbital Express mission which was launched in 2007 and successfully demonstrated on-orbit robotic fuel transfer and capture of a cooperative client satellite (launched together with the servicing craft). Unlike Orbital Express and all the other prior OOS missions flown so far, RSGS will directly serve a client satellite in a GEO orbit. The mission (Figure 8) intents to (Parrish, n.d.):
1) demonstrate in or near GEO that a robotic servicing vehicle can perform safe, reliable, useful, and efficient operations, with the flexibility to adapt to a variety of on-orbit missions and conditions;
2) demonstrate satellite servicing mission operations on operational GEO satellites in collaboration with commercial and United States Government spacecraft operators;
3) support the development of a servicer spacecraft with sufficient propellant and payload robustness to enable dozens of missions over several years.
FIGURE 8. Robotic servicing vehicle (RSV) and envisioned missions (Parrish, 2021).
Originally DARPA teamed with Maxar Technologies for developing the RSGS mission. It recently changed the partnership to Northrop Grumman/ATK to integrate the RSGS into a new Northrop Grumman mission called Mission Robotic Vehicle (MRV).
NASA/SSL OSAM-1 (Formerly Restore-L)
According to (NASA/GSFC, n.d.), OSAM-1 mission is planned to perform an autonomous rendezvous with Landsat-7 in low Earth orbit (LEO) followed by refueling and orbit relocation. This endeavor requires two robotic arms and the development of a reliable propellant-transfer system (Figure 9). The Landsat-7 is an unprepared client, not originally designed with on-orbit servicing in mind, and its functional lifespan will be lengthened by this servicing mission. The OSAM-1 spacecraft will also include another payload called Space Infrastructure Dexterous Robot (SPIDER).

FIGURE 9. NASA/SSL OSAM-1 mission (NASA/GSFC, 2021).
SPIDER includes a lightweight 5-m robotic arm, bringing the total number of robotic arms flying on OSAM-1 mission to three. SPIDER will assemble seven elements to form a functional 3-m communications antenna and manufacture a 10-m lightweight composite beam. The robotically assembled antenna will demonstrate Ka-band transmission with a ground station. SPIDER operations will help mature space technologies with many potential cross-cutting applications, including (Shoemaker et al., 2020):
1) enabling new architectures and capabilities for a wide range of government and commercial missions;
2) enabling In-space construction of large communications antennae and telescopes;
3) eliminating volume limits imposed by rockets;
4) replacing some astronaut extravehicular activity tasks with precision robotics; and
5) introducing the potential for longer mission durations enabled by planned or unplanned maintenance.
The mission was originally scheduled to be launched in mid-2020s (Henry, 2020).
Northrop Grumman’s MEV and MRV
Orbital ATK (now part of Northrop Grumman) has developed the Mission Extension Vehicle (MEV) missions in the past few years. They were the first OOS missions developed by a private company purely for commercialization. MEV-1 was launched in October 2019 and completed its historic docking with the Intelsat 901 spacecraft on February 25, 2020. This marked the very first time two commercial satellites docked in orbit. IS-901 resumed communications services on April 2, 2020. MEV-2 was launched and successfully docked with the Intelsat 10-02 (IS-10-02) on April 12, 2021 (Grumman, 2021). MEV-2 is the second Mission Extension Vehicle supplied by Space Logistics LLC, a wholly owned subsidiary of Northrop Grumman. Unlike MEV-1, which docked client IS-901 above the GEO orbit before moving it back into service, MEV-2 docked with the client IS-10-02 directly in its operational GEO orbital location. Both MEV-1 and MEV-2, shown in Figure 10A, are planned to extend their client satellites for a five-year period after which the clients will be placed back into graveyard orbit. Then the servicing vehicles will have an option to service other client satellites on orbit.

FIGURE 10. Northrop Grumman’s (A) MEV (Orbital ATK), and (B) MRV (Grumman, 2021).
Northrop Grumman has recently teamed with DARPA with the RSGS program for the new Mission Robotic Vehicle (MRV), as shown Figure 10B. In the MRV mission, DARPA will provide the robotics payload that will be used to service satellites at a GEO orbit.
The United States Naval Research Laboratory developed the payload for the RSGS program. It consists of two dexterous robotic arms, along with several tools and sensors. Northrop Grumman’ Space Logistics division will provide the bus technologies it developed for the MRV mission (Erwin, 2020).
Other General Software and Hardware Technology Developments
The mission activities go hand in hand with technology developments. In the COMRADE project, ESA has promoted the design, development, and testing of a control system for a free-flying robot for two missions: a) Active Debris Removal (ADR) with a dedicated seven DoF robotic manipulator and LAR gripper end-effector. b) Refueling mission (see also Arms, Grippers, and End-Effectors) Here, a combined controller was tested on the OOS-SIM facility for the capturing of ENVISAT. The controller ran on a LEON4 computer, proving its applicability for space flight. Furthermore, an overview of the design and outcomes of the project were presented in (Colmenarejo et al., 2018), to include a comparison between a robust
Other important software and hardware developments have been undertaken in Europe under the six-year PERASPERA project (PERASPERA, 2014), within the EU Strategic Research Cluster on Space Robotics, aiming, among other things, at the maturation of orbital robotic technologies. The first set of grants (Operational Grants) within this project (2016–2017) was dedicated to the development of common building blocks, to include an operating system or middleware (European Space Robot Control Operating System, ESROCOS), a planning framework (European Robotic Goal-Oriented Autonomous Controller, ERGO), a sensor data fusion framework (InFuse), an integrated sensor suit (I3DS) and a standard interface for robotic manipulation of payloads (SIROM).
Running at the DLR since 2014, the RICADOS project aims at holistic simulation of an on-orbiting servicing mission, from a realistic ground segment (GSOC) to a communication link to a space segment, performing inspection, rendezvous, and capture tasks (Benninghoff et al., 2018). These tasks are partly validated on DLR’s hardware-in-the-loop facilities EPOS and OOS-SIM. Furthermore, the DLR, in cooperation with the MIT, is promoter and developer of an experimental mission with the ASTROBEEs on the ISS, for the approach maneuver of a chaser satellite to a tumbling target. In this mission, the functional sequence consisting of motion prediction, motion planning and robust trajectory tracking, will be tested (Albee et al., 2021). The telepresence technology has also been extensively demonstrated by the DLR in different projects, to include KONTUR-2 (Artigas et al., 2016; Riecke et al., 2016) and METERON (Schmaus et al., 2018).
The initial PERASPERA building blocks were then used in a second set of grants, which developed concepts and technologies for a servicing mission (EROSS), for modular spacecraft assembly and reconfiguration (MOSAR) and for on-orbit assembly of a large space telescope (PULSAR). The goal is to perform an orbital demonstration mission in 2023–24.
In particular, the EROSS project assesses and demonstrates the capability of a manipulator-equipped servicing spacecraft to perform medium and close-range rendezvous, and then to capture and manipulate/service a collaborative client satellite with a highest degree of autonomy, see Figure 11. EROSS reuses and integrates both software (such as ESROCOS, ERGO and INFUSE) and hardware (such as SIROM), developed in previous Operational Grants led in PERASPERA, and previous developments on projects by the European Space Agency, such as the ASSIST project. When required, new designs are produced, such as a new manipulator gripper. To facilitate the varying demands of the different stages of the mission, a versatile GNC architecture is developed, including a Coordinated Control scheme that allows for the simultaneous Model-based PD control of the servicer platform attitude and Compliant Control of the end-effector of the seven Dof manipulator (Dubanchet, et al., 2020).

FIGURE 11. The EROSS Concept includes a free-flying spacecraft equipped with a 7-DoF manipulator (EROSS EU Horizon 2020).
Arms, Grippers, and End-Effectors
The development of hardware for orbital robotics has been very active in the last years. The DLR had tested and validated its robot joint technology in the ROKVISS mission (Yoshida et al., 2016), in which two robot joints were placed on the outer surface of the ISS, between 2005 and 2011. In a recent development, this technology has been improved and used to build a seven-degree of freedom robot manipulator, the Compliant Assistance and Exploration SpAce Robot (CAESAR), shown in Figure 12A (Beyer et al., 2018). Other robotic arms are being developed in the United States, to include DARPA’s FREND arm, as well as the Dragonfly, later developed into the longer SPIDER. A torque-controlled robot is also constructed by TUI with the name of KRAKEN.
FIGURE 12. (A) CAESAR robot arm with SpaceHand (DLR), (B) ASSIST mechanism for refueling satellites (ESA).
ESA focused on developing a cost-effective solution for refueling GEO satellites in space as currently the fuel levels often deplete, for communications satellites, while the payloads are still in good health. A refueling mechanism was developed, called ASSIST, which will allow satellites in the future to be refueled and serviced while on orbit, extending their life, Figure 12B. As is typically the case for most end-effectors, the ASSIST mechanism performs first soft docking (allowing relative motions but not separation) followed by a motorized retraction ending during a hard docking phase (rigidization) using aligning pins (Medina et al., 2017). ASSIST is the reference mission with dedicated 6/7 DoF robotic manipulator and ASSIST end-effector (Visentin, 2020).
In ESA project Predator, the main objective was to design and prototype/demonstrate via functional tests a robotic end-effector gripper breadboard that can be used to capture the Launch Adaptor Ring (LAR) of non-cooperative satellites during a debris removal mission (Visentin, 2020). The Stewart platform-based gripper, which is attached to the tip of the robotic arm, plays an important role in the satellite capture operation as it provides the mechanical and structural interface between the servicer/chaser vehicle and the target satellite during the critical capture and stabilization operations.
Other robot end-effector designs can be found in Jaworski et al. (2017) and Jaekel et al. (2018) for a mechanism which can also clamp to the launch adapter ring of the target satellite and in Trentlage et al. (2016) and Cauligi et al. (2020) for Gecko-inspired grippers. A tool for capturing a non-cooperative target is described in Sun et al. (2020).
Chinese Space Station Manipulators
The China’s Space Station Remote Manipulator System (CSSRMS) consists of two manipulators: a larger manipulator called Chinese Space Station Manipulator (CSSM) and a smaller one called Experimental Module Manipulator (EMM) (Li et al., 2019). The CSSM is a 10.5-m long, 7-joint manipulator designed for transposing and assembling large station modules, handling transportation cargos, assisting the smaller manipulator EMM or an astronaut as a mobile platform (Li et al., 2015). It can manipulate a large payload of 25,000-kg mass at maximum tip linear and angular velocities of 0.02-m/s and 0.15-°/s, respectively, while its unloaded tip velocities can reach up to 0.3-m/s and 3-°/s, respectively, Figure 13A.

FIGURE 13. (A) Chinese Space Station Manipulator (CSSM) (Li et al., 2015), (B) China’s Space Station Remote Manipulator System (CSSRMS) (Liu, 2014).
With its symmetric topology design of two identical ends (Figure 13B), it can relocate itself on the station using its “walking” capability. EMM is a 5-m long, 7-joint manipulator designed for taking care of the station’s exposed experimental platform and optical platform and providing support to EVA activities (Liu, 2014). It can handle a payload of 3,000-kg mass at maximum tip linear and angular speeds of 0.03-m/s and 0.15-°/s, respectively, while its unloaded tip speeds can reach up to 0.2-m/s and 3-°/s. It can operate either from an anchor point on the station or from the tip of CSSM which extends its tip reachability to over 15 m. Both manipulators have force-motion control capability and can be operated either in automated mode or remotely control mode from the space station or a ground station. The two manipulators will be launched to space in 2021–2022 timeframe (Yang, 2021).
Gateway Extravehicular Robotic System
The Lunar Gateway is considered by NASA and the ISS partners for the next flagship human space exploration. The International Space Exploration Coordination Group (ISECG) has also concluded that the Gateway will be critical in expanding human presence to the Moon, Mars and deeper into the Solar System (Merrill et al., 2015; Shireman et al., 2018). The Gateway is a crewed orbiting platform like the ISS, but instead of operating in Low Earth Orbit (LEO), the Gateway will operate in a Moon-centric orbit called near-rectilinear halo orbit (NRHO). Canada contribution to the Gateway program, as a partner of the ISS, is intended to be an extra-vehicular robotics (EVR) system, which is deemed to be the evolution of the iconic robotics element of the ISS known as the Canadarm 2; see Figure 14. The Gateway EVR system as shown in Figure 14 is intended to provide similar services to the Gateway as the Canadarm 2 provides for the ISS, such as maintenance, remove and replacement (R&R) operation of ORUs, inspection, as well as berthing of commercial and international cargo spacecraft to visit Gateway regularly for bringing fresh supply. However, there are new services proposed. One interesting application of the EVR system proposed on the Gateway is the assisted attitude control system (ACS), which can lead to significant fuel saving (Aghili and Rey, 2020).
Traversal of the lunar Gateway along its designated NRHO orbit can impart significant angular momentum to the spacecraft from lunar gravity gradient torques. The stored angular momentum cannot be removed by a magnetic torquer since the magnetic field of the Moon is very weak, while using thrusters may require propellant consumption of 9 kg/year. A cost-effective solution based on a robotically steerable solar sail permitting desaturation of the Gateway’s wheels without using any propellant is proposed in Aghili and Rey (2020). The solar sail is grasped and then optimally positioned and oriented by the designated robotic arm of the Gateway to generate the required torque through solar radiation pressure.
Reconfigurable Robots for On-Orbit Servicing
Robotic manipulators working in space environments often need to change their configuration to meet the demands of a specific task within the constraints of the environment. Particularly in space applications, it is desirable and cost-effective to employ a single versatile robot capable of performing different tasks such as inspection, contact operation, assembly (insertion and removal of objects), and carrying objects (pick and place). Optimal operation of each of these tasks demands a specific manipulator design. For instance, large robots maximizing the structural length index are typically suitable for inspection, robots with maximum manipulability measure are well conditioned for dexterous contact tasks, and configurations maximizing the distance of the robot limbs and extremities from the environment are suitable for payload handling.
Space systems are designed for minimum weight to reduce launch cost. Another design constraint for a space system is that it should be compact enough to be accommodated within its designated space in the launch vehicle. Since the links of a space manipulator are usually long, they must be folded before launch. For example, the Canadarm 2 has two long booms, each of which has a hinge at the middle, which allowed the booms to be folded before launch and then unfolded manually by astronauts in orbit. For on-orbit servicing missions whereby no human operator is present, the robot must be able to deploy itself. The original reconfigurable robot was introduced in Fukuta and Kawauchi (1990) to add versatility to the robotic manipulator. The concept was then developed further in Paredis and Khosla (1995) Cellular robots based on hexagonal modules and the concept of robot molecules was described in Kotay et al. (1998). Another modular reconfigurable manipulator, which had three 6-degree-of-freedom (DoF) arms, was proposed for space applications in Ohkami et al. (1999), Hayashi et al. (2000) and Shibata and Ohkami (2002); the manipulator was designed to be able to brachiate around the Japanese section of the ISS. All these reconfigurable robots are modular, hence needing an effective docking system for connecting and releasing the modules. Reconfigurable robots based on modular joints have been proposed for both terrestrial and space applications (Aghili and Su, 2012). Although modular robots have the great advantage of being able to change their number of links and to create a tree-like structure, they require complex joints for connecting modules, as well as a docking system for exchanging modules. Reconfigurable robots based on lockable telescopic links was first proposed in Aghili and Parsa (2009) to offer a simpler and more effective solution to the problem. Further to the versatility that this design provides, it makes it possible to contain the manipulator in a small volume, which is suitable for launch, see Figure 15.
Conclusion
This survey addressed fundamental aspects of manipulation and capture on orbit, such as the dynamics of SMSs in orbit, the contact dynamics between manipulator grippers and their targets, and the methods for identifying properties of SMSs and of their targets. Also, it presented recent work in the areas of sensing of pose and system states, of motion planning for capturing a target, and of feedback control methods for SMS to perform challenging motion or interaction tasks on orbit. Finally, the paper reviews major ground-based test and verification facilities developed by space agencies across the world for on-orbit robotic capture and service operations, and several recent or near-future missions and technologies developed for technology demonstration and commercialization. Although a lot of research work has been done recently, several important issues remain open and need to be studied, enabling safe and successful proliferation of robotic systems in orbit. The survey discussed these remaining challenges and issues.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abiko, S., Lampariello, R., and Hirzinger, G. (2006). Impedance Control for a Free-Floating Robot in the Grasping of a Tumbling Target with Parameter Uncertainty. In IEEE/RSJ International Conference on Intelligent Robots and Systems, (pp. 1020–1025).
Abiko, S., and Yoshida, K. (2010). Adaptive Reaction Control for Space Robotic Applications with Dynamic Model Uncertainty. Adv. Robotics 24, 1099–1126. doi:10.1163/016918610x501264
Abiko, S., and Yoshida, K. (2001). 6th International Symposium on Artificial Inteligence and Robotics & Robotics in Space (I-SAIRAS). St-Hubert, Quebec, Canada.Post Flight Analysis of ETS-VII Space Robotic Experiments.
Aghili, F. (2006). A Mechatronic Testbed for Revolute-Joint Prototypes of a Manipulator. IEEE Trans. Robotics 22 (5), 1265–1273. doi:10.1109/tro.2006.882962
Aghili, F. (2012). A Prediction and Motion-Planning Scheme for Visually Guided Robotic Capturing of Free-Floating Tumbling Objects with Uncertain Dynamics. IEEE Trans. Robotics 28 (3), 634–649. doi:10.1109/tro.2011.2179581
Aghili, F. (2005).A Robotic Testbed for Zero-G Emulation of Spacecraft. In IEEE/RSJ Int. Conference on Intelligent Robots and Systems. Alberta, Canada, 1033–1040.
Aghili, F. (2012b).Active Orbital Debris Removal Using Space Robotics. In Proc. of International Symposium on Artificial Intelligence, Robotics and Automation in Space i-SAIRAS. Italy: Turin.
Aghili, F. (2009).Coordination Control of a Free-Flying Manipulator and its Base Attitude to Capture and Detumble a Noncooperative Satellite. In IEEE/RSJ International Conference on Intelligent Robots and Systems. St. Louis, USA. doi:10.1109/iros.2009.5353968
Aghili, F., Dupuis, E., Martin, E., and Piedboeuf, J.-C. (2001).Force/Moment Accommodation Control for Tele-Operated Manipulators Performing Contact Tasks in Stiff Environment. In IEEE/RSJ International Conference on Intelligent Robotics and Systems. Maui, Hawaii, 2227–2233.
Aghili, F. (2020). Energetically Consistent Model of Slipping and Sticking Frictional Impacts in Multibody Systems. Multibody Syst. Dyn. 48, 193–209. doi:10.1007/s11044-019-09703-2
Aghili, F. (2021). Fault-Tolerant and Adaptive Visual Serving for Capturing Moving Objects. IEEE/ASME Trans. Mechatron., 1. doi:10.1109/tmech.2021.3087729
Aghili, F., Kuryllo, M., Okouneva, G., and English, C. (2011). Fault-tolerant Position/Attitude Estimation of Free-Floating Space Objects Using a Laser Range Sensor. IEEE Sensors J. 11 (1), 176–185. doi:10.1109/jsen.2010.2056365
Aghili, F. (2019). Modeling and Analysis of Multiple Impacts in Multibody Systems under Unilateral and Bilateral Constrains Based on Linear Projection Operators. Multibody Syst. Dyn. 46, 41–62. doi:10.1007/s11044-018-09658-w
Aghili, F., and Namvar, M. (2009). Scaling Inertia Properties of a Manipulator Payload for 0-g Emulation of Spacecraft. Int. J. Robotics Res. 28 (7), 883–894. doi:10.1177/0278364908099464
Aghili, F., Namvar, M., and Vukovich, G. (2006). IEEE Int. Conference on Robotics & Automation. Orlando, Florida, 3886–3892.Satellite Simulator with a Hydraulic Manipulator.
Aghili, F. (2000).On-orbit Calibration of the SPDM Force-Moment Sensor. In IEEE International Conference on Robotics and Automation. San Francisco, CA.
Aghili, F. (2008). Optimal Control for Robotic Capturing and Passivation of a Tumbling Satellite with Unknown Dynamics AIAA Guidance, Navigation and Control Conference. Honolulu, Hawaii. doi:10.2514/6.2008-7274
Aghili, F. (2009).Optimal Control of a Space Manipulator for Detumbling of a Target Satellite. In IEEE Int. Conference on Robotics & Automation. Kobe, Japan, 3019–3024.
Aghili, F. (2020). Optimal Trajectories and Robot Control for Detumbling a Non-cooperative Satellite. AIAA J. Guidance, Control Dyn. 43 (2), 1952–1959. doi:10.2514/1.g005037
Aghili, F., and Parsa, K. (2009). A Reconfigurable Robot with Lockable Cylindrical Joints. IEEE Trans. Robot. 25 (4), 785–797. doi:10.1109/tro.2009.2017130
Aghili, F., and Parsa, K. (2007). Adaptive Motion Estimation of a Tumbling Satellite Using Laser-Vision Data with Unknown Noise Characteristics. IEEE/RSJ Int. Conf. Intell. Robots Syst., 839–846.
Aghili, F., and Parsa, K. (2008).An Adaptive Vision System for Guidance of a Robotic Manipulator to Capture a Tumbling Satellite with Unknown Dynamics. In IEEE/RSJ Int. Conf. on Intelligent Robots and Systems. Nice, France, 3064–3071.
Aghili, F., Parsa, K., and Martin, E. (2008).Robotic Docking of a Free-Falling Space Object with Occluded Visual Condition. In 9th Int. Symp. on Artificial Intelligence, Robotics & Automation in Space (i-SAIRAS). Los Angeles, CA. doi:10.2514/6.2008-7317
Aghili, F., and Parsa, K. (2009). Motion and Parameter Estimation of Space Objects Using Laser-Vision Data. J. Guidance, Control Dyn. 32 (2), 538–550. doi:10.2514/1.37129
Aghili, F., and Piedboeaeuf, J.-C. (2006). Feb.Emulation of Robots Interacting with Environment. IEEE/ASME Trans. Mechatron. 11 (1), 35–46. doi:10.1109/tmech.2005.863367
Aghili, F., and Piedboeuf, J.-C. (2000).Hardware-in-Loop Simulation of Robots Interacting with Environment via Algebraic Differential Equation. In IEEE/RSJ International Conference on Intelligent Robots and Systems. Takamatsu, Japan, 1590–1596.
Aghili, F. (2013).Pre- and Post-Grasping Robot Motion Planning to Capture and Stabilize a Tumbling/Drifting Free-Floater with Uncertain Dynamics. In IEEE International Conference on Robotics and Automation (ICRA). Karlsruhe, Germany, 5441–5448.
Aghili, F., and Rey, D. (2020). Optimal Trajectories and Robot Control for Detumbling a Non-cooperative Satellite. J. Guidance, Control Dyn. 43 (5), 981–988. doi:10.2514/1.g004758
Aghili, F. (2019). Robust Impedance-Matching of Manipulators Interacting with Uncertain Environments: Application to Task Verification of the Space Station's Dexterous Manipulator. IEEE/ASME Trans. Mechatron. 24 (4), 1565–1576. doi:10.1109/tmech.2019.2928281
Aghili, F., and Su, C.-Y. (2012).Reconfigurable Space Manipulators for In-Orbit Servicing and Space Exploration. In Proc. of International Symposium on Artificial Intelligence, Robotics and Automation in Space i-SAIRAS. Turin, Italy.
Aghili, F., and Su, C.-Y. (2016). Robust Relative Navigation by Integration of ICP and Adaptive Kalman Filter Using Laser Scanner and IMU. Ieee/asme Trans. Mechatron. 21 (4), 2015–2026. doi:10.1109/tmech.2016.2547905
Agrawal, S. K., Pathak, K., Franch, J., Lampariello, R., and Hirzinger, G. (2009). A Differentially Flat Open-Chain Space Robot with Arbitrarily Oriented Joint Axes and Two Momentum Wheels at the Base. IEEE Trans. Automat. Contr. 54 (9), 2185–2191. doi:10.1109/TAC.2009.2026836
Akin, D. L., and Howard, R. D. (1992).Neutral Buoyancy Simulation of Space Telerobotics Operations. In Cooperative Intelligent Robotics in space. SPIE. doi:10.1117/12.56776
Albee, K., Oestreich, C., Specht, C., Espinoza, A., Todd, J., Hokaj, I., et al. (2021). A Robust Observation, Planning, and Control Pipeline for Autonomous Rendezvous with Tumbling Targets. Front. Robotics AI.
Albu-Schaeffer, A., Ott, C., and Hirzinger, G. (2004).A Passivity Based Cartesian Impedance Controller for Flexible Joint Robots Part II: Full State Feedback, Impedance Design and Experiments. In International Conference on Robotics and Automation. USA: New Orleans.
Ambrose, R. O., Aldridge, H., Askew, R. S., Burridge, R. R., Bluethmann, W., Diftler, M., et al. (2000). Robonaut: NASA's Space Humanoid. IEEE Intell. Syst. 15, 57–63. doi:10.1109/5254.867913
Ananthakrishnan, S., Teders, R., and Alder, K. (1996). Role of Estimation in Real-Time Contact Dynamics Enhancement of Space Station Engineering Facility. IEEE Robot. Automat. Mag. 3, 20–28. doi:10.1109/100.540146
Anthony, T., and Andersen, G. (1995). On-orbit Modal Identification of the Hubble Space Telescope. IEEE Am. Control. Conf. 1, 402–406.
Antonello, A., Valverde, A., and Tsiotras, P. (2019). Dynamics and Control of Spacecraft Manipulators with Thrusters and Momentum Exchange Devices. AIAA J. Guidance Control. Dyn. 42 (1). doi:10.2514/1.g003601
Artigas, J., Balachandran, R., Riecke, C., Stelzer, M., Weber, B., Ryu, J.-H., et al. (2016).KONTUR-2: Force-Feedback Teleoperation from the International Space Station. In IEEE International Conference on Robotics and Automation (ICRA). Stockholm, Sweden. doi:10.1109/ICRA.2016.7487246
Artigas, J., De Stefano, M., Rackl, W., Lampariello, R., Brunner, B., Bertleff, W., et al. (2015).The OOS-SIM: An On-Ground Simulation Facility for On-Orbit Servicing Robotic Operations. In IEEE International Conference on Robotics and Automation (ICRA). Seattle, WA, USA: IEEE, 2854–2860. doi:10.1109/ICRA.2015.7139588
Askari, E. (2021). Mathematical Models for Characterizing Non-hertzian Contacts. Appl. Math. Model. 90, 432–447. doi:10.1016/j.apm.2020.08.048
Benninghoff, H., and Boge, T. (2015).Rendezvous Involving a Non-cooperative, Tumbling Target-Estimation of Moments of Inertia and center of Mass of an Unknown Target. In 25th International Symposium on Space Flight Dynamics. Munich, Germany: German Aerospace Center and European Space Agency, 1–16.
Benninghoff, H., Rems, F., Risse, E.-A., Irmisch, P., Ernst, I., and Brunner, B. (2018). RICADOS-rendezvous, Inspection, Capturing and Detumbling by Orbital Servicing. In Proc. of the 7th International Conference on Astrodynamics Tools and Techniques.
Berenson, D., Srinivasa, S. S., Ferguson, D., and Kuffner, J. J. (2009).Manipulation Planning on Constraint Manifolds. In IEEE International Conference on Robotics and Automation ICRA. Kobe, Japan, 625–632. doi:10.1109/ROBOT.2009.5152399
Besl, P. J., and McKay, N. D. (1992). A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 14 (2), 239–256. doi:10.1109/34.121791
Bevilacqua, R., Lehmann, T., and Romano, M. (2011). Development and Experimentation of LQR/APF Guidance and Control for Autonomous Proximity Maneuvers of Multiple Spacecraft. Acta Astronautica 68, 1260–1275. doi:10.1016/j.actaastro.2010.08.012
Beyer, A., Grunwald, G., Heumos, M., Schedl, M., Bayer, R., Bertleff, W., et al. (2018).CAESAR: Space Robotics Technology for Assembly, Maintenance, and Repair. In Proceedings of the International Astronautical Congress. Bremen, Germany: IAC.
Bibby, J., and Necessary, R. (2008). “Robonaut 1 - Telepresence,”. Editor R. Ambrose. & NASA) Retrieved from available at: https://robonaut.jsc.nasa.gov/R1/sub/telepresence.asp.
Boge, T., and Ma, O. (2011). Using Advanced Industrial Robotics for Spacecraft Rendezvous and Docking Simulation. In IEEE international conference on robotics and automation, 1–4.
Boos, M., and McPhee, J. (2013). Volumetric Modeling and Experimental Validation of Normal Contact Dynamic Forces. J. Comput. Nonlinear Dyn. 8 (2). doi:10.1115/1.4006836
Botta, E. M., Sharf, I., and Misra, A. K. (2017). Contact Dynamics Modeling and Simulation of Tether Nets for Space-Debris Capture. JOURNAL GUIDANCE, CONTROL, DYNAMICS 40, 110–123. doi:10.2514/1.g000677
Boyarko, G., Yakimenko, O., and Romano, M. (2011). Optimal Rendezvous Trajectories of a Controlled Spacecraft and a Tumbling Object. J. Guidance, Control Dyn. 34 (4), 1239–1252. doi:10.2514/1.47645
Brachet, G. (2010). Long-term Sustainability of Outer Space activitiesCommittee on the Peaceful Uses of Outer Space. Vienna: UNCOPUOS.
Brannan, J., and Carignan, C. (2013).Modeling Flexible-Body Dynamics in Real-Time Robotic Systems Used in Satellite Servicing Simulations. In AIAA Modeling and Simulation Technologies (MRT) Conference. Boston, Massachusetts. doi:10.2514/6.2013-5157
Brannan, J., Carignan, C., and Roberts, B. (2020).Hybrid Strategy for Evaluating On-Orbit Servicing, Assembly, and Manufacturing Technologies. In The Accelerating Space Commerce, Exploration, and New Discovery (ASCEND). Las Vegas, Nevada: AIAA. doi:10.2514/6.2020-4194
Brannan, J., and Carignan, G. (2017).Interaction of a Robotic Servicing Vehicle with Satellite Flexible Modes during Capture. In AIAA Modeling and Simulation Technologies Conference. Grapevine, Texas, 1–13.
Brannan, J., Scott, N., and Carignan, C. (2018).Robot Servicer Interaction with a Satellite during Capture. In International Symposium on Artificial Intelligence, Robotics and Automation in Space (i-SAIRAS). Madrid, Spain: AIAA.
Breger, L., and How, J. P. (2008). Safe Trajectories for Autonomous Rendezvous of Spacecraft. J. Guidance, Control Dyn. 31 (5), 1478–1489. doi:10.2514/1.29590
Brennan, S., and Alleyne, A. (2000). The Illinois Roadway Simulator: a Mechatronic Testbed for Vehicle Dynamics and Control. Ieee/asme Trans. Mechatron. 5 (4), 349–359. doi:10.1109/3516.891046
Brown, H. B., and Dolan, J. M. (1994). A Novel Gravity Compensation System for Space Robots. In Proceedings of the ASCE Specialty Conference on Robotics for Challenging Environments.
Buckner, C., and Lampariello, R. (2018).Tube-based Model Predictive Control for the Approach Maneuver of a Spacecraft to a Free-Tumbling Target Satellite. In Annual American Control Conference (ACC). Milwaukee, WI, USA: IEEE, 5690–5697. doi:10.23919/ACC.2018.8431558
Calzolari, D., Lampariello, R., and Massimo Giordano, A. (2020). Singularity Maps of Space Robots and Their Application to Gradient-Based Trajectory Planning. In Robotics Science and Systems RSS. Virtual Conference. doi:10.15607/RSS.2020.XVI.015
Carignan, C., Scott, N., and Roderick, S. (2014, June 17-19). Hardware-In-The-Loop Simulation of Satellite Capture on a Ground-Based Robotic Testbed. In Proc. International Symposium on Artificial Intelligence, Robotics and Automation in Space i-SAIRAS.
Cauligi, A., Chen, T. A., Suresh, S., Dille, M., Ruiz, G. R., Vargas, A. M., et al. (2020). Design and Development of a Gecko-Adhesive Gripper for the Astrobee Free-Flying Robot arXiv preprint arXiv:2009.09151.
Cavenago, F., Giordano, A. M., and Massari, M. (2021). Contact Detection, Isolation and Estimation for Orbital Robots through an Observer Based on a Centroid-Joints Dynamics. Acta Astronautica 181, 40–51. doi:10.1016/j.actaastro.2021.01.001
Cavenago, F., Massari, M., Giordano, A. M., and Garofalo, G. (2021). Unexpected Collision Detection, Estimation, and Reaction for a Free-Flying Orbital Robot. J. Guidance, Control Dyn. 44, 967–982. doi:10.2514/1.G005585
Center, G. S. (2010). On-Orbit Satellite Servicing Study. National Aeronautics and Space Administration (NASA).
Chamberlain, M. K., Kiefer, S. H., and Banik, J. (2018). On-Orbit Structural Dynamics Performance of the Roll-Out Solar Array. In AIAA Spacecraft Structures Conference.doi:10.2514/6.2018-1942
Chen, Z., Lii, N. Y., Wimböck, T., Fan, S., and Liu, H. (2011). Experimental Evaluation of Cartesian and Joint Impedance Control with Adaptive Friction Compensation for the Dexterous Robot Hand Dlr-Hit Ii. Int. J. Hum. Robot. 08, 649–671. doi:10.1142/s0219843611002605
Choi, J., Ryu, H. S., Kim, C. W., and Choi, J. H. (2010). An Efficient and Robust Contact Algorithm for a Compliant Contact Force Model between Bodies of Complex Geometry. Multibody Syst. Dyn. 23 (1), 99–120. doi:10.1007/s11044-009-9173-3
Choset, H., and Kortenkamp, D. (1999). Path Planning and Control for Free-Flying Inspection Robot in Space. IEEE 12 (2). doi:10.1061/(asce)0893-1321(1999)12:2(74)
Christidi-Loumpasefski, O.-O., Nanos, K., and Papadopoulos, E. (2020).On Parameter Estimation of Flexible Space Manipulator Systems. In IEEE International Conference on Robotics and Automation. Paris, France. doi:10.1109/iros45743.2020.9340768
Christidi-Loumpasefski, O.-O., Nanos, K., and Papadopoulos, E. (2017).On Parameter Estimation of Space Manipulator Systems Using the Angular Momentum Conservation. In IEEE International Conference on Robotics and Automation. Singapore, Singapore. doi:10.1109/icra.2017.7989641
Christidi-Loumpasefski, O.-O., and Papadopoulos, E. (2018).Parameter Identification of a Space Object in the Pre-capture Phase. In 14th International Symposium on Artificial Intelligence, Robotics and Automation in Space. Madrid, Spain.
Christidi-Loumpasefski, O.-O., Rekleitis, G., and Papadopoulos, E. (2020).Concurrent Parameter Identification and Control for Free-Floating Robotic Systems during On-Orbit Servicing. In IEEE International Conference on Robotics and Automation. Paris, France. doi:10.1109/icra40945.2020.9197187
Chu, M., and Wu, X. (2018). Modeling and Self-Learning Soft-Grasp Control for Free-Floating Space Manipulator during Target Capturing Using Variable Stiffness Method. IEEE Access 6, 7044–7054. doi:10.1109/access.2017.2788400
Chu, Z., Ma, Y., Hou, Y., and Wang, F. (2017). Inertial Parameter Identification Using Contact Force Information for an Unknown Object Captured by a Space Manipulator. Acta Astronautica 131, 69–82. doi:10.1016/j.actaastro.2016.11.019
Clean Space (2012). Retrieved from Safety & Security, ESA. available at: https://www.esa.int/Enabling_Support/Space_Engineering_Technology/Clean_Space.
Colebank, J. E., Jones, R. D., Nagy, G. R., Pllak, R. D., and Mannebach, D. R. (1999). SIMSAT: A Satellite Simulator and Experimental Test Bed for Air Force Research. AIAA Paper, 99–44.
Colmenarejo, P., Branco, J., Santos, N., Serra, P., Telaar, J., Strauch, H., et al. (2018). Methods and Outcomes of the COMRADE Project - Design of Robust Combined Control for Robotic Spacecraft and Manipulator in Servicing Missions: Comparison between between Hinf and Nonlinear Lyapunov-Based Approaches. Bremen, Germany: 69th International Astronautical Congress (IAC).
Cusumano, F., Lampariello, R., and Hirzinger, G. (2004). Development of Tele-Operation Control for a Free-Floating Robot during the Grasping of a Tumbling Target. In International Conference on Intelligent Manipulation and Grasping.
Dastidar, R. G. (2010).On the Advantages and Limitations of Sliding Mode Control for Spacecraft. In AIAA SPACE Conference & Exposition. California: Anaheim. August - 2 September.
De Stefano, M. (2018). Energy-based Control for Simulation of Multi-Body Dynamics Using Robotic Facilities. Italy: Emilia, Italy: PhD Thesis, University of Modena and Reggio-Emilia.
De Stefano, M., Balachandran, R., and Secchi, C. (2020). A Passivity-Based Approach for Simulating Satellite Dynamics with Robots: Discrete-Time Integration and Time-Delay Compensation. IEEE Trans. Robot. 36 (1), 189–203. doi:10.1109/TRO.2019.2945883
De Stefano, M., Mishra, H., Balachandran, R., Lampariello, R., Ott, C., and Secchi, C. (2019). Multi-rate Tracking Control for a Space Robot on a Controlled Satellite: A Passivity-Based Strategy. IEEE Robot. Autom. Lett. 4 (2), 1319–1326. doi:10.1109/LRA.2019.2895420
De Stefano, M., Mishra, H., Giordano, A., Lampariello, R., and Ott, C. (2021). A Relative Dynamics Formulation for Hardwarein-The-Loop Simulation of On-Orbit Robotic Missions. Ieee Robotics Automation Lett.
deorbit Study Team, e. (2015). Statement of Work, Phase B1 of an Active Debris Removal mission (E.DEORBIT Mission. Phase B1). In Reference GSTP-SOW-e.Deorbit. Noordwijk, Holland: European Space Agency.
Diftler, M. A., Permenter, F. A., Hargrave, B. K., Platt, R., Savely, R. T., Ambrose, R. O., et al. (2011). Robonaut 2 - the First Humanoid Robot in Space, in 2011 IEEE International Conference on Robotics and Automation (Shanghai, China: IEEE). doi:10.1109/ICRA.2011.5979830
Dimitrov, D. N., and Yoshida, K. (2004).Momentum Distribution in a Space Manipulator for Facilitating the post-impact Control, in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Sendai, Japan.
Ding, X., Wang, Y., Wang, Y., and Xu, K. (2021). A Review of Structures, Verification, and Calibration Technologies of Space Robotic Systems for On-Orbit Servicing. Sci. China Technol. Sci. 64, 462–480. doi:10.1007/s11431-020-1737-4
Du, Y., and Wang, C. (2020). Dynamic Coupling and Control of Flexible Space Robots. Int. J. Struct. Stab. Dyn. 20 (9). doi:10.1142/s0219455420501035
Dubanchet, V., Bejar Romero, J., Nyborg Gregertsen, K., Austad, H., Gancet, J., Natusiewicz, K., et al. (2020).EROSS Project – European Autonomous Robotic Vehicle for On-Orbit Servicing. In International Symposium on Artificial Intelligence, Robotics and Automation in Space, (i-SAIRAS ’20). USA: Pasadena, California.
Dubowsky, S., and Boning, P. (2007).The Coordinated Control of Space Robot Teams for the On-Orbit Construction of Large Flexible Space Structures. In International Conference on Robotics and Automation, Special Workshop on Space Robotics. Rome, Italy.
Dubowsky, S., Durfee, W., Kulinski, A., Muller, U., Paul, I., and Pennington, J. (1994). The Design and Implementation of a Laboratory Test Bed for Space Robotics: The VES Mod II. In ASME Conf., DE-Vol. 72, Robotics: Kinematics, Dynamics and Control, (pp. 99–108).
Dubowsky, S., and Papadopoulos, E. (1993). The Kinematics, Dynamics, and Control of Free-Flying and Free-Floating Space Robotic Systems. IEEE Trans. Robot. Automat. 9 (5), 531–543. doi:10.1109/70.258046
Emadzadeh, A. A., and Speyer, J. L. (2011). Relative Navigation between Two Spacecraft Using X-ray Pulsars. IEEE Trans. Contr. Syst. Technol. 19 (5), 1021–1035. doi:10.1109/tcst.2010.2068049
Erwin, S. (2020). DARPA Picks Northrop Grumman as its Commercial Partner for Satellite Servicing Program. Retrieved 02 26, 2021, from available at: https://spacenews.com/darpa-picks-northrop-grumman-as-its-commercial-partner-for-satellite-servicing-program/.
Espinoza, A. T., and Roascio, D. (2017).Concurrent Adaptive Control and Parameter Estimation through Composite Adaptation Using Model Reference Adaptive Control/Kalman Filter Methods. In IEEE Conference on Control Technology and Applications (CCTA). USA: Kohala Coast, Hawai'i. August 27-30. doi:10.1109/ccta.2017.8062538
Estable, S., Pruvost, C., Ferreir, E., Telaar, J., Fruhnert, M., Imhof, C., et al. (2020). Capturing and deorbiting Envisat with an Airbus Spacetug. Results from the ESA e.Deorbit consolidation phase study. J. Space Saf. Eng. 7 (1), 52–66. doi:10.1016/j.jsse.2020.01.003
Evans, J. W., Pinon, E., and Mulder, T. A. (2006). Autonomous Rendezvous Guidance and Navigation for Orbital Express and beyond. In 6th AAS/AIAA Space Flight Mechanics Conference,, (pp. 2–-7).
Ferrara, A., and Incremona, G. (2015). Design of an Integral Suboptimal Second-Order Sliding Mode Controller for the Robust Motion Control of Robot Manipulators. IEEE Trans. Control. Syst. Tech. 23, 2316–2325. doi:10.1109/TCST.2015.2420624
Flores, P., and Lankarani, H. M. (2016). Contact Force Models for Multibody Dynamics. Springer. doi:10.1007/978-3-319-30897-5
Flores-Abad, A., Crain, A., Nandayapa, M., Garcia-Teran, M., and Ulrich, S. (2018). Disturbance Observer-Based Impedance Control for a Compliance Capture of an Object in SpaceAIAA Guidance, Navigation, and Control Conference. Florida, USA: Kissimmee. doi:10.2514/6.2018-1329
Flores-abad, A., Ma, O., Pham, K., and Ulrich, S. (2014a). A Review of Space Robotics Technologies for On-Orbit Servicing. Prog. aerospace Sci. 68, 1–26. doi:10.1016/j.paerosci.2014.03.002
Flores-Abad, A., Wei, Z., Ma, O., and Pham, K. (2014b). Optimal Control of Space Robots for Capturing a Tumbling Object with Uncertainties. J. Guidance, Control Dyn., 2014–2017. doi:10.2514/1.G000003
Flores-Abad, A., Zhang, L., Wei, Z., and Ma, O. (2017). Optimal Capture of a Tumbling Object in Orbit Using a Space Manipulator. J. Intell. Robot Syst. 86 (2), 199–211. doi:10.1007/s10846-016-0417-1
Fukuta, T., and Kawauchi, Y. (1990). Cellular Robotic System (CEBOT) as One of the Realization of Self-Organizing Intelligent Universal Manipulator. Proc. IEEE Int. Conf. Robot. Autom., 662–667.
Gallardo, A. P., Mishra, H., Giordano, A. M., and Lampariello, R. (2019).Robust Estimation of Motion States for Free-Floating Tumbling Target Capture. In IEEE Aerospace Conference. Montana, USA: Big SkyIEEE, 1–11. doi:10.1109/AERO.2019.8741802
Gangapersaud, R. A., Liu, G., and de Ruiter, A. (2019). Detumbling a Non-cooperative Space Target with Model Uncertainties Using a Space Manipulator. AIAA J. Guidance Control Dyn. 42 (4). doi:10.2514/1.g003111
Gefke, G. G., Janas, A., and Reed, B. (2017). Advances in Robotic Servicing Technology Development. 2015 AIAA Space Forum. Pasadena: AIAA. doi:10.2514/6.2017-5119
Gilardi, G., and Sharf, I. (2002). Literature Survey of Contact Dynamics Modelling. Mechanism Machine Theor. 37, 1213–1239. doi:10.1016/s0094-114x(02)00045-9
Giordano, A., Garofalo, G., and Albu-Schaffer, A. (2018). Workspace Fixation for Free-Floating Space Robot Operations. Brisbane, QLD, Australia: IEEE International Conference on Robotics and Automation. doi:10.1109/icra.2018.8460478
Giordano, A. M., Dietrich, A., Ott, C., and Albu-Schäffer, A. (2020). Coordination of Thrusters, Reaction Wheels, and Arm in Orbital Robots. Robotics Autonomous Syst. 131, 103564. doi:10.1016/j.robot.2020.103564
Giordano, A. M., Garofalo, G., and Albu-Schaffer, A. (2017). Momentum Dumping for Space RobotsIEEE 56th Annual Conference on Decision and Control. Melbourne, VIC, Australia. doi:10.1109/cdc.2017.8264434
Giordano, A. M., Garofalo, G., De Stefano, M., Ott, C., and Albu-Schaffer, (2016). Dynamics and Control of a Free-Floating Space Robot in Presence of Nonzero Linear and Angular momentaIEEE 55th Conference on Decision and Control. USA: Las Vegas, NV. doi:10.1109/cdc.2016.7799432
Giordano, A. M., Ott, C., and Albu-Schaffer, A. (2019). Coordinated Control of Spacecraft’s Attitude and End-Effector for Space Robots. IEEE Robotics Automation Lett. 4, 2108–2115. doi:10.1109/LRA.2019.2899433
Giordano, A. M. (2020). Whole-body Control of Orbital Robots. Munich, Germany: PhD, Technical University of Munich. doi:10.18235/0002844
Gonthier, Y., McPhee, J., Lange, C., and Piedbœuf, J.-C. (2004). A Regularized Contact Model with Asymmetric Damping and Dwell-Time Dependent Friction. Multibody Syst. Dyn. 11 (3), 209–233. doi:10.1023/b:mubo.0000029392.21648.bc
Green, A., and Sasiadek, J. (2007). Intelligent Tracking Control of a Free-Flying Flexible Space Robot manipulatorAIAA Guidance, Navigation and Control Conference and Exhibit. South Carolina: Hilton Head. doi:10.2514/6.2007-6320
Greenspan, M., and Yurick, M. (2003).Approximate K-D Tree Search for Efficient ICP. In IEEE International Conference on Recent Advances in 3D Digital Imaging and Modeling. Banff, Canada, 442–448.
Grumman, N. (2021). Northrop Grumman and Intelsat Make History with Docking of Second Mission Extension Vehicle to Extend Life of Satellite. available at: https://news.northropgrumman.com/news/releases/northrop-grumman-and-intelsat-make-history-with-docking-of-second-mission-extension-vehicle-to-extend-life-of-satellite.
Hablani, H. B., Tapper, M. L., and Dana-Bashian, D. J. (2002). Guidance and Relative Navigation for Autonomous Rendezvous in a Circular Orbit. J. Guidance, Control Dyn. 25 (3), 553–562. doi:10.2514/2.4916
Han, D., Huang, P., Liu, X., and Yang, Y. (2020). Combined Spacecraft Stabilization Control after Multiple Impacts during the Capture of a Tumbling Target by a Space Robot. Acta Astronautica 176, 24–32. doi:10.1016/j.actaastro.2020.05.035
Hayashi, R., Matunaga, S., and Ohkami, Y. (2000). Capability Evaluation of Reconfigurable Brachiating Space Robot. In 26th Annu. Conf. IEEE Ind. Electron. Soc. Nagoya, Japan, 2461–2466.
Henry, C. (2020). Maxar Wins $142 Million NASA Robotics mission. Retrieved 02 26, 2021, available at: https://spacenews.com/maxar-wins-142-million-nasa-robotics-mission/.
Hillenbrand, U., and Lampariello, R. (2005). Motion and Parameter Estimation of a Free-Floating Space Object from Range Data for Motion Prediction. In 8th International Symposium on Artificial Intelligence and Robotics & Automation in Space.
Hiramatsu, T., and Fitz-Coy, N. (2007).Game Theoretic Approach to Post-Docked Satellite Control. In 20th International Symposium on Space Flight Dynamics. USA: Goddard Space Flight Center.
Hirano, D., Kato, H., and Saito, T. (2018).Online Path Planning and Compliance Control of Space Robot for Capturing Tumbling Large Object. In IEEE/RSJ International Conference on Intelligent Robots and Systems. Madrid, Spain, 1–5. doi:10.1109/iros.2018.8594099
Hirano, D., Kato, H., and Tanishima, N. (2017).Caging-Based Grasp with Flexible Manipulation for Robust Capture of a Free-Floating Target. In IEEE International Conference on Robotics and Automation. Singapore. doi:10.1109/icra.2017.7989645
Hirzinger, G., Brunner, B., Lampariello, R., Landzettel, K., Schott, J., and Steinmetz, B.-M. (2000).Advances in Orbital Robotics. In Advances in orbital robotics. IEEE International Conference on Robotics and Automation. San Francisco, CA, USA: IEEE, 898–907. doi:10.1109/ROBOT.2000.844163
Hirzinger, G., Landzettel, K., Reintsema, D., Preusche, C., Albu-Schaeffer, A., Rebele, B., et al. (2005).ROKVISS – Robotics Component Verification on ISS. In 8th International Symposium on Artifical Intelligence, Robotics and Automation in Space - iSAIRAS. Munich, Germany. Retrieved from available at: https://elib.dlr.de/43891/.
Hu, Y. R., and Vucovich, G. (1997). Modeling and Control of Free-Flying Flexible Joint Coordinated Robots. Monterey, CA, USA: 8th International Conference on Advanced Robotics.
Huang, P., Lu, Y., Wang, M., Meng, Z., Zhang, Y., and Zhang, F. (2019). Postcapture Attitude Takeover Control of a Partially Failed Spacecraft with Parametric Uncertainties. IEEE Trans. Automat. Sci. Eng. 16 (2), 919–930. doi:10.1109/tase.2018.2875139
Huang, P., Wang, D., Zhang, F., Meng, Z., and Liu, Z. (2016). Postcapture Robust Nonlinear Control for Tethered Space Robot with Constraints on Actuator and Velocity of Space Tether. Int. J. Robust. Nonlinear Control. 27 (16), 2824–2841. doi:10.1002/rnc.3712
Huang, P., Wang, M., Meng, Z., Zhang, F., and Liu, Z. (2016). Attitude Coordinated Control for Docked Spacecraft Based on Estimated Coupling Torque. J. Aerospace Eng.
Jacobsen, S., Lee, C., Zhu, C., and Dubowsky, S. (2002). Planning of Safe Kinematic Trajectories for Free Flying Robots Approaching an Uncontrolled Spinning Satellite. Int. Des. Eng. Tech. Conferences Comput. Inf. Eng. Conf. 36533, 1145–1151.
Jaekel, S., Lampariello, R., Rackl, W., De Stefano, M., Oumer, N., Giordano, A. M., et al. (2018). Design and Operational Elements of the Robotic Subsystem for the e.deorbit Debris Removal Mission. Front. Robot. AI 5, 5. doi:10.3389/frobt.2018.00100
James, F., Shah, S., Singh, A., Krishna, K., and Misra, A. (2016). Reactionless Maneuvering of a Space Robot in Precapture Phase. J. Guidance, Control Dyn. 39 (10). doi:10.2514/1.g001828
Jaworski, J., Dudek, L., Wolski, M., Mateja, A., Wittels, P., Labecki, M., et al. (2017). Grippers for Launch Adapter Rings of Non-cooperative Satellites Capture for Active Debris Removal, Space Tug and On-Orbit Satellite Servicing Applications. Holland: ASTRA. ESTEC.
Jayakody, H. S., Shi, L., Katupitiya, J., and Kinkaid, N. (2016). Robust Adaptive Coordination Controller for a Spacecraft Equipped with a Robotic Manipulator. J. Guidance, Control Dyn, 2699–2711.
Kaiser, C., Sjöberg, F., Delcura, J. M., and Eilertsen, B. (2008). SMART-OLEV-An Orbital Life Extension Vehicle for Servicing Commercial Spacecrafts in GEO. Acta Astronautica 63, 400–410. doi:10.1016/j.actaastro.2007.12.053
Kalakrishnan, M., Chitta, S., Theodorou, E., Pastor, P., Schaal, S., and Shanghai, P. R. (2011).STOMP: Stochastic Trajectory Optimization for Motion Planning. In IEEE International Conference on Robotics and Automation ICRA. China, 4569–4574. doi:10.1109/ICRA.2011.5980280
Kasai, T., Yamaguchi, I., Igawa, H., Mitani, S., Ohtani, T., Ikeda, M., et al. (2009). On-Orbit System Identification Experiments of the Engineering Test Satellite-VIII. Trans. JSASS Space Tech. Jpn. 7 (26), Pc_79–Pc_84. doi:10.2322/tstj.7.pc_79
Kawamoto, S., Matsumoto, K., and Wakabayashi, S. (2001).Ground experiment of Mechanical Impulse Method for Uncontrollable Satellite Capturing. In 6th Int. Symposium on Artificial Intelligence and Robotics & Automation in Space: I-SAIRAS. St-Hubert, Canada.
Kawamoto, S., Nishida, S., and Kibe, S. (2003). Research on a Space Debris Removal System. Japan: NAL Res ProgNational Aerospace Lab.
Kim, J.-H., and Ma, O. (2007).Testing of a Contact-Dynamics Parameters Identification Method Using a Robotics-Based Testbed. In IEEE, International Conference on Advanced Robotics. Jeju, Korea, 975–980.
Kirchner, G., et al. (2017).Determination of Attitude and Attitude Motion of Space Debris, Using Laser Ranging and Single-Photon Light Curve Data. In Proceedings of the 7th European Conference on Space Debris. Darmstadt, Germany.
Kotay, K., Rus, D., Vona, M., and McGray, C. (1998). The Self-Reconfiguring Robot Molecule. IEEE Int. Conf. Robot. Autom., 424–431.
Krenn, R., and Schaefer, B. (1999). Limitations of Hardware-In-The Loop Simulations of Space Robotics Dynamics Using Industrial Robots. European space agency,” European Space Agency, Special Publication, ESA SP, 681–686.
Kriegsman, B. A. (1966). Radar-Updated Inertial Navigation of a Continuously-Powered Space Vehicle. IEEE Trans. Aerosp. Electron. Syst. AES-2 (4), 549–565. doi:10.1109/taes.1966.4501887
Krzyżak, A., Sasiadek, J. Z., and Ulrich, S. (2012). Nonparametric Identification of Robot Flexible Joint Space Manipulator. In 17th International Conference on Methods & Models in Automation & Robotics.doi:10.1109/mmar.2012.6347893
Kuffner, J. J., and LaValle, S. M. (2000).RRT-connect: An Efficient Approach to Single-Query Path Planning. In IEEE International Conference on Robotics and Automation ICRA. San Francisco, CA, USA, 995–1001. doi:10.1109/ROBOT.2000.844730
Lampariello, R., Agrawal, S., Hirzinger, G., and May, (2003). Optimal Motion Planning for Free-Flying Robots. Taiwan: International Conference on Robotics and Automation 3, 3029–3035. doi:10.1109/ROBOT.2003.1242056
Lampariello, R., and Hirzinger, G. (2013).Generating Feasible Trajectories for Autonomous On-Orbit Grasping of Spinning Debris in a Useful Time. In IEEE/RSJ International Conference on Intelligent Robots and Systems IROS. Tokyo, Japan, 5652–5659. doi:10.1109/IROS.2013.6697175
Lampariello, R., and Hirzinger, G. (2005).Modeling and Experimental Design for the On-Orbit Inertial Parameter Identification of Free-Flying Space Robots. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Long Beach, California, US: ASME, 881–890. doi:10.1115/DETC2005-85242
Lampariello, R., Mishra, H., Oumer, N., and Peters, J. (2021). Robust Motion Prediction of a Free-Tumbling Satellite with On-Ground Experimental Validation (Accepted). J. Guidance, Control. Dyn.. doi:10.2514/1.G005745
Lampariello, R., Mishra, H., Oumer, N., Schmidt, P., de Stefano, M., and Albu-Schaffer, A. (2018). Tracking Control for the Grasping of a Tumbling Satellite with a Free-Floating Robot. IEEE Robot. Autom. Lett. 3 (4), 3638–3645. doi:10.1109/lra.2018.2855799
Lampariello, R. (2013). On Grasping a Tumbling Debris Object with a Free-Flying Robot. IFAC Proc. Volumes 46 (19), 161–166. doi:10.3182/20130902-5-de-2040.00118
Landzettel, K., Preusche, C., Albu-Schaffer, A., Reintsema, D., Rebele, B., and Hirzinger, G. (2006).Robotic On-Orbit Servicing - DLR's Experience and Perspective. In IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing. doi:10.1109/iros.2006.282164
Li, D., Rao, W., Hu, C., Wang, Y., Tang, Z., and Wang, Y. (2015).Overview of the Chinese Space Station Manipulator. In AIAA SPACE 2015 Conference and Exposition. AIAA. doi:10.2514/6.2015-4540
Li, W.-J., Cheng, D.-Y., Liu, X.-G., Wang, Y.-B., Shi, W.-H., Tang, Z.-X., et al. (2019). On-orbit Service (OOS) of Spacecraft: A Review of Engineering Developments. Prog. Aerospace Sci. 108, 32–120. doi:10.1016/j.paerosci.2019.01.004
Liang, J., Fillmore, S., and Ma, O. (2012). An Extended Bristle Friction Force Model with Experimental Validation. Mechanism Machine Theor. 56, 123–137. doi:10.1016/j.mechmachtheory.2012.06.002
Liang, J., Ma, O., and Liu, C. (2011). Model Reduction of Contact Dynamics Simulation Using a Modified Lyapunov Balancing Method. Frontier Mech. Eng. 6 (4), 123–137. doi:10.1007/s11465-011-0244-9
Lichter, M. D., and Dubowsky, S. (2004).State, Shape, and Parameter Estimation of Space Objects from Range Images. In IEEE International Conference on Robotics and Automation. USA: New Orleans. doi:10.1109/robot.2004.1307513
Lii, N. Y., Leidner, D., Schiele, A., Birkenkampf, P., Bayer, R., Pleintinger, B., et al. (2015).Simulating an Extraterrestrial Environment for Robotic Space Exploration: The METERON SUPVIS-Justin Telerobotic experiment and the Solex Proving Ground. In 13th Symposium on Advanced Space Technologies in Robotics and Automation (ASTRA). Netherlands: Noordwijk. doi:10.1145/2701973.2702022
Lii, N. Y., Riecke, C., Leidner, D., Schätzle, S., Schmaus, P., Weber, B., et al. (2018).The Robot as an Avatar or Co-worker? an Investigation of the Different Teleoperation Modalities through the KONTUR-2 and METERON SUPVIS Justin Space Telerobotic Missions. In Proceedings of the International Astronautical Congress, IAC. 69th International Astronautical Congress (IAC). Bremen, Germany. Retrieved from available at: https://elib.dlr.de/133023/.
Lingenauber, M., Strobl, K. H., Oumer, N. W., and Kriegel, S. (2017).Benefits of Plenoptic Cameras for Robot Vision during Close Range On-Orbit Servicing Maneuvers. In IEEE Aerospace Conference. MT, USA: Big SkyIEEE, 1–18. doi:10.1109/AERO.2017.7943666
Liu, Hong. (2014).Overview of the Chinese Space Station Manipulator. In International Symposium on Artificial Intelligence, Robotics and Automation in Space (i-SAIRAS). Montreal: European Space Agency.
Liu, J., Fang, J. C., Ma, X., Kang, Z. W., and Wu, J. (2015). X-ray Pulsar/starlight Doppler Integrated Navigation for Formation Flight with Ephemerides Errors. IEEE Aerosp. Electron. Syst. Mag. 30 (3), 30–39. doi:10.1109/maes.2014.140074
Liu, Q., Liang, J., and Ma, O. (2020). A Physics-Based and Data-Driven Hybrid Modeling Method for Accurately Simulating Complex Contact Phenomenon. Multibody Syst. Dyn. 50, 97–117. doi:10.1007/s11044-020-09746-w
Liu, Q., Xiao, X., Mou, F., Wu, S., Ma, W., and Hu, C. (2018).Study on a Numerical Simulation of a Manipulator Task Verification Facility System. In 2018 IEEE International Conference on Mechatronics and Automation (ICMA). Changchun: IEEE, 2132–2137.
Lu, G., and Tomizuka, M. (2006). Lidar Sensing for Vehicle Lateral Guidance: Algorithm and Experimental Study. Ieee/asme Trans. Mechatron. 11 (6), 653–660. doi:10.1109/tmech.2006.886192
Luo, Z., and Sakawa, Y. (1990). A Control of a Space Manipulator for Capturing a Tumbling Object. Proc. 29th IEEE Conf. Decis. Control., 103–108.
Ma, G., Jiang, Z., Li, H., Gao, J., Yu, Z., Chen, X., et al. (2015). Hand-eye Servo and Impedance Control for Manipulator Arm to Capture Target Satellite Safely. Robotica 33, 848–864. doi:10.1017/s0263574714000587
Ma, J., Chen, G., Ji, L., Qian, L., and Dong, S. (2020). A General Methodology to Establish the Contact Force Model for Complex Contacting Surfaces. Mech. Syst. Signal Process. 140, 106678. doi:10.1016/j.ymssp.2020.106678
Ma, O., Buhariwala, K., Roger, N., Maclean, J., and Carr, R. (1997). MDSF - A Generic Development and Simulation Facility for Flexible, Complex Robotic Systems. Robotica 15, 49–62. doi:10.1017/s0263574797000076
Ma, O., and Carr, R. (1998). Dynamics Modelling and Simulation of SPDM Operations Part II: SPDM Handling the IEA Battery. IFAC Proc. Volumes 31 (33), 165–170. doi:10.1016/s1474-6670(17)38404-5
Ma, O. (2000).CDT – A General Contact Dynamics Toolkit. In 31st International Symposium on Robotics (ISR 2000). Montreal: IFR, 468–473.
Ma, O. (1995).Contact Dynamics Modelling for the Simulation of the Space Station Manipulators Handling Payloads. In IEEE International Conference on Robotics and Automation. Nagoya, 1252–1258.
Ma, O., Dang, H., and Pham, K. (2008). On-orbit Identification of Inertia Properties of Spacecraft Using a Robotic Arm. J. Guidance, Control Dyn. 31 (No. 6), 1761–1771. doi:10.2514/1.35188
Ma, O., Flores-Abad, A., and Boge, T. (2012). Use of Industrial Robots for Hardware-In-The-Loop Simulation of Satellite Rendezvous and Docking. Acta Astronautica 81, 335–347. doi:10.1016/j.actaastro.2012.08.003
Ma, O., Wang, J., Misra, S., and Liu, M. (2004). On the Validation of SPDM Task Verification Facility. J. Robotic Syst. 21 (5), 219–235. doi:10.1002/rob.20011
Ma, O., and Wang, J. (2007). Model Order Reduction for Impact-Contact Dynamics Simulations of Flexible Manipulators. Robotica 25, 397–407. doi:10.1017/s026357470600316x
Ma, Z., Ma, O., and Shashikanth, B. N. (2007). Optimal Approach to and Alignment with a Rotating Rigid Body for Capture. J. Astronaut Sci. 55 (4), 407–419. doi:10.1007/bf03256532
Machado, M., Moreira, P., Flores, P., and Lankarani, H. M. (2012). Compliant Contact Force Models in Multibody Dynamics: Evolution of the Hertz Contact Theory. Mechanism Machine Theor. 53, 99–121. doi:10.1016/j.mechmachtheory.2012.02.010
MacPherson, R., Hockman, B., Bylard, A., Estrada, M. A., Cutkosky, M. R., and Pavone, M. (2018). “Trajectory Optimization for Dynamic Grasping in Space Using Adhesive Grippers,” in Field and Service Robotics. Editor S. R. Hutter M. (Springer Proceedings in Advanced Robotics), 49–64. doi:10.1007/978-3-319-67361-5_4
Martinez-Moritz, J., Rodrıguez, I., Nottensteiner, K., Lutze, J.-P., Lehner, P., and Roa, A. M. (2021).Hybrid Planning System for In-Space Robotic Assembly of Telescopes Using Segmented Mirror Tiles. In IEEE Aerospace Conference. Montana, USA: Big Sky. doi:10.1109/aero50100.2021.9438399
Masutani, Y., Iwatsu, T., and Miyazaki, F. (1994).Motion Estimation of Unknown Rigid Body under No External Forces and Moments. In IEEE Int. Conf. on Robotics & Automation. San Diego, 1066–1072.
Matsuno, F., and Saito, K. (2001).Attitude Control of a Space Robot with Initial Angular Momentum. In IEEE International Conference on Robotics and Automation. Seoul, South Korea.
Matunaga, S., Yoshihara, K., Takahashi, T., Tsurumi, S., and Ui, K. (2000). Ground experiment Systems for Dual-Manipulator-Based Capture of Damaged Satallites. In IEEE Int. Conference on Intelligent Robots and Sys, (pp. 1847–1852).
Mazhar, H., Heyn, T., Negrut, D., and Tasora, A. (2015). Using Nesterov's Method to Accelerate Multibody Dynamics with Friction and Contact. ACM Trans. Graph. 34 (3), 1–14. doi:10.1145/2735627
Medina, A., Tomassini, A., Suatoni, M., Avilés, M., Solway, N., Coxhill, I., et al. (2017). Towards a Standardized Grasping and Refuelling On-Orbit Servicing for Geo Spacecraft. Acta Astronautica 134, 1–10. doi:10.1016/j.actaastro.2017.01.022
Meng, Q., Liang, J., and Ma, O. (2019). Identification of All the Inertial Parameters of a Non-cooperative Object in Orbit. Aerospace Sci. Tech. 91, 571–582. doi:10.1016/j.ast.2019.05.047
Meng, Q., Zhao, C., Ji, H., and Liang, J. (2020). Identify the Full Inertial Parameters of a Non-cooperative Target with Eddy Current Detumbling. Adv. Space Res. 66, 1792–1802. doi:10.1016/j.asr.2020.05.044
Merrill, R. G., Strange, N., Qu, M., and Hatten, N. (2015). Mars Conjunction Crewed Missions with a Reusable Hybrid Architecture. IEEE Aerospace Conf., 1–14.
Mishra, H., De Stefano, M., Giordano, A. M., Lampariello, R., and Ott, C. (2020). A Geometric Controller for Fully-Actuated Robotic Capture of a Tumbling Target. In 2020 American Control Conference (ACC). Denver, CO, USA: IEEE, 2150–2157. doi:10.23919/ACC45564.2020.9147294
Mishra, H., De Stefano, M., Giordano, A. M., and Ott, C. (2019). A Nonlinear Observer for Free-Floating Target Motion Using Only Pose Measurements. In 2019 American Control Conference (ACC), (pp. 1114–1121). doi:10.23919/ACC.2019.8814815
Mishra, H., De Stefano, M., Giordano, A. M., and Ott, C. (2020).Output Feedback Stabilization of an Orbital Robot. In 2020 59th IEEE Conference on Decision and Control (CDC). IEEE, 1503–1501. doi:10.1109/CDC42340.2020.9304044
Mishra, H., Giordano, A. M., De Stefano, M., Lampariello, R., and Ott, C. (2020).Inertia-Decoupled Equations for Hardware-In-The-Loop Simulation of an Orbital Robot with External Forces. In 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). NV, USA: Las VegasIEEE, 1879–1886. doi:10.1109/IROS45743.2020.9341633
Misra, G., and Bai, X. (2017). November)Optimal Path Planning for Free-Flying Space Manipulators via Sequential Convex Programming. J. Guidance, Control. Dyn. 40 (11). doi:10.2514/1.g002487
Mitros, Z., Paraskevas, I., and Papadopoulos, E. (2016).On Robotic Impact Docking for on Orbit Servicing. In 24th Mediterranean Conference on Control and Automation. Athens, Greece. doi:10.1109/med.2016.7536032
Mitros, Z., Rekleitis, G., Patsiaouras, I., and Papadopoulos, E. (2017).Impedance Control Design for On-Orbit Docking Using an Analytical and Experimental Approach. In 25th Mediterranean Conference on Control and Automation. Malta: Valletta. doi:10.1109/med.2017.7984288
Mokuno, M., Kawano, I., and Suzuki, T. (2004). In-orbit Demonstration of Rendezvous Laser Radar for Unmanned Autonomous Rendezvous Docking. IEEE Trans. Aerosp. Electron. Syst. 40 (2), 617–626. doi:10.1109/taes.2004.1310009
Moosavian, S. A. A., and Papadopoulos, E. (2010). Cooperative Object Manipulation with Contact Impact Using Multiple Impedance Control. Int. J. Control. Autom. Syst. 8 (2), 314–327. doi:10.1007/s12555-010-0218-4
Moosavian, S. A. A., and Papadopoulos, E. (2004). Explicit Dynamics of Space Free-Flyers with Multiple Manipulators via SPACEMAPLE. Adv. Robotics 18, 223–244. doi:10.1163/156855304322758033
Moosavian, S. A., and Papadopoulos, E. (1997). Coordinated Motion Control of Multiple Manipulator Space Free-Flyers. Huntsville, AL, USA: 7th AAS/AIAA Space Flight Mechanics Meeting.
Mou, F., Wu, S., Xiao, X., Zhang, T., and Ma, O. (2018a).Control of a Space Manipulator Capturing a Rotating Object in the Three-Dimensional Space. In 15th International Conference on Ubiquitous Robots (UR). Hawaii, USA: Hawaii Convention Center. doi:10.1109/urai.2018.8441888
Mou, F., Xiao, X., Zhang, T., Liu, Q., Li, D., Hu, C., et al. (2018). A HIL Simulation Facility for Task Verification of the Chinese Space Station Manipulator. In IEEE International Conference on Mechatronics and Automation (ICMA), (pp. 2138–2144).
Mukherji, R., Rey, D., Stieber, M., and Lymer, J. (2001).Special Purpose Dexterous Manipulator (Spdm) Advanced Control Features and Development Test Results. In 6th International Symposium on Artificial Intelligence and Robotics & Automation in Space: i-SAIRAS. St-Hubert, Canada.
Murotsu, Y., Senda, K., Ozaki, M., and Tsujio, S. (1994). Parameter Identification of Unknown Object Handled by Free-Flying Space Robot. J. guidance, Control Dyn. 17 (No. 3), 488–494. doi:10.2514/3.21225
Nagamatsu, H., Kubota, T., and Nakatani, I. (1996). Capture Strategy for Retrieval of a Tumbling Satellite by a Space Robotic Manipulator. IEEE Int. Conf. Robotics Automation, 70–75.
Nagaoka, K., Kameoka, R., and Yoshida, K. (2018). October 16)Repeated Impact-Based Capture of a Spinning Object by a Dual-Arm Space Robot. Front. Robot. AI 5 (15). doi:10.3389/frobt.2018.00115
Nakanishi, H., Uyama, N., and Yoshida, K. (2010).Virtual Mass of Impedance System for Free-Flying Target Capture. In IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, Taiwan. doi:10.1109/iros.2010.5649131
Nakanishi, H., Yoshida, K., and Yoshida, K. (2006). Impedance Control of Free-Flying Space Robot for Orbital Servicing. J. Robot. Mechatron. 18 (5), 608–617. doi:10.20965/jrm.2006.p0608
Nanos, K. (2015). Dynamics, Trajectory Planning, and Control of Space Robotic Systems in the Presence of Angular Momentum and Flexibilities (In Greek). PhD Thesis. Athens, Greece: National Technical University of Athens.
Nanos, K., and Papadopoulos, E. (2015a). Avoiding Dynamic Singularities in Cartesian Motions of Free-Floating Manipulators. IEEE Trans. Aerospace Electron. Syst. 51 (No. 3), 2305–2318. doi:10.1109/taes.2015.140343
Nanos, K., and Papadopoulos, E. G. (2015b). On the Dynamics and Control of Flexible Joint Space Manipulators. Control. Eng. Pract. 45, 230–243. doi:10.1016/j.conengprac.2015.06.009
Nanos, K., and Papadopoulos, E. (2012). On Cartesian Motions with Singularities Avoidance for Free-Floating Space Robots. In IEEE International Conference on Robotics and Automation, (pp. 5398–5403).
Nanos, K., and Papadopoulos, E. (2019).On Parameter Estimation of Space Manipulator Systems with Flexible Joints Using the Energy Balance. In IEEE International Conference on Robotics and Automation. Montreal, Canada. doi:10.1109/icra.2019.8793960
Nanos, K., and Papadopoulos, E. (2017). On the Dynamics and Control of Free-Floating Space Manipulator Systems in the Presence of Angular Momentum. Front. Robot. AI 4, 26. doi:10.3389/frobt.2017.00026
Nanos, K., and Papadopoulos, E. (2010).On the Use of Free-Floating Space Robots in the Presence of Angular Momentum. In IEEE/ASME International Conference on Advanced Intelligent Mechatronics Systems. Montreal, Que. Canada. doi:10.1007/s11370-010-0083-2
NASA (2021). Robotic Refueling Mission 3. NASA: available at: https://nexis.gsfc.nasa.gov/RRM3.html.
NASA/GSFC (2021). OSAM-1: On-Orbit Servicing, Assembly, and Manufacturing-1. Retrieved 02 26, 2021, from available at: https://nexis.gsfc.nasa.gov/osam-1.html.
Natsiavas, S. (2019). Analytical Modeling of Discrete Mechanical Systems Involving Contact, Impact, and Friction. Appl. Mech. Rev. 71 (5). doi:10.1115/1.4044549
Navarro, H. A., and de Souza Braun, M. P. (2013). Determination of the normal spring Stiffness Coefficient in the Linear spring-dashpot Contact Model of Discrete Element Method. Powder Technol. 246, 707–722. doi:10.1016/j.powtec.2013.05.049
Naveen, B., Shah, S. V., and Misra, A. K. (2019). Momentum Model-Based Minimal Parameter Identification of a Space Robot. J. Guidance, Control Dyn. 42 (No. 3), 508–523. doi:10.2514/1.g003541
Nenchev, D., Yoshida, K., and Uchiyama, M. (1996). Reaction Null-Space Based Control of Flexible Structure Mounted Manipulator Systems. In IEEE Decision and Control Conference. Japan: Kobe.
Nguyen-Huynh, T. C., and Sharf, I. (2013). Adaptive Reactionless Motion and Parameter Identification in Postcapture of Space Debris. J. Guidance, Control Dyn. 36 (No. 2), 404–414. doi:10.2514/1.57856
Oda, M. (1999).Space Robot Experiments on NASDA's ETS-VII Satellite-Preliminary Overview of the Experiment Results. In IEEE International Conference on Robotics and Automation. Detroit, USA.
Ohkami, Y., Matunaga, S., Hayashi, R., and Man, Cybern. (1999).Operational Aspects of a Super Redundant Space Robot with Reconfiguration and Brachiating Capability. In Proc. IEEE Int. Conf. Syst. Tokyo, Japan, 178–183.
Opromolla, R., Fasano, G., Rufino, G., and Grassi, M. (2017). A Review of Cooperative and Uncooperative Spacecraft Pose Determination Techniques for Close-Proximity Operations. Prog. Aerospace Sci. 93, 53–72. doi:10.1016/j.paerosci.2017.07.001
Oshinowo, L., Coleshill, E., Rembala, R., Liu, M., and Prasad, S. (2006). Commissioning "Dextre" for On-Orbit Operations. In 57th International Astronasutical Congress. Valencia: IFA. doi:10.2514/6.iac-06-b4.2.02
Ott, C., Albu-Schaeffer, A., Kugi, A., Stamigioli, S., and Hirzinger, G. (2004).A Passivity Based Cartesian Impedance Controller for Flexible Joint Robots Part I: Torque Feedback and Gravity Compensation. In IEEE International Conference on Robotics and Automation. USA: New Orleans. doi:10.1109/robot.2004.1307462
Oumer, N. (2016). Visual Tracking and Motion Estimation for an On-Orbit Servicing of a Satellite. Osnabrueck,Germany: Ph.D. thesis, University of Osnabrueck.
Paielli, R. A., and Bach, R. E. (1993). Attitude Control with Realization of Linear Error Dynamics. AIAA J. Guidance Control. Dyn. 16 (No. 1), 182–189. doi:10.2514/3.11444
Papadopoulos, E., and Dubowsky, S. (1991b).Coordinated Manipulator/Spacecraft Motion Control for Space Robotic Systems. In IEEE International Conference on Robotics and Automation. Sacramento, CA, USA, 1696–1701.
Papadopoulos, E., and Dubowsky, S. (1993). Dynamic Singularities in the Control of Free-Floating Space Manipulators. ASME J. Dynamic Syst. Meas. Control. 115 (No. 1), 44–52. doi:10.1115/1.2897406
Papadopoulos, E., and Dubowsky, S. (1991a). On the Nature of Control Algorithms for Free-Floating Space Manipulators. IEEE Trans. Robot. Automat. 7 (6), 750–758. doi:10.1109/70.105384
Papadopoulos, E. (1993).Large Payload Manipulation by Space Robots. In Proc. of International Conference on Intelligent Robots and Systems (IROS '93). Yokohama, Japan, 2087–2094.
Papadopoulos, E., and Moosavian, S. (1994). Dynamics and Control of Multi-Arm Space Robots during chase and Capture Operations. IEEE/RSJ Int. Conf. Intell. Robots Syst., 1554–1561.
Papadopoulos, E. (1991). On the Dynamics and Control of Space Manipulators. Cambridge, MA, USA: Dept. of Mechanical Engineering, Massachusetts Institute of Technology. doi:10.23919/acc.1991.4791629
Papadopoulos, E., Paraskevas, I., Flessa, T., Nanos, K., Rekleitis, G., and Kontolatis, I. (2008). The NTUA Space Robot Simulator: Design & Results. 10th ESA Workshop on Advanced Space Technologies for Robotics and Automation (ASTRA 2008). Noordwijk, Netherlands: ESA/ESTEC.
Papadopoulos, E. (1992).Path Planning for Space Manipulators Exhibiting Nonholonomic Behavior. In IEEE/RSJ International Conference on Intelligent Robots and Systems. RaleighUSA: North Carolina.
Pappa, R., and Juang, J. N. (1984). Galileo Spacecraft Modal Identification Using an Eigensystem Realization algorithmNASA. AIAA, 1984–1070. doi:10.2514/6.1984-1070
Paredis, C., and Khosla, P. (1995). Design Ofmodular Fault Tolerant Manipulators. Robot: 1st Workshop Algorithmic Found, 371–383.
Parrish, J. (2021). Robotic Servicing of Geosynchronous Satellites (RSGS). Retrieved 02 26, 2021, from available at: https://www.darpa.mil/program/robotic-servicing-of-geosynchronous-satellites.doi:10.5194/acp-2020-1198-ac2
Peck, M. A., Miller, L., Cavender, A. R., Gonzalez, M., and Hintz, T. (2003). An Airbearing-Based Testbed for Mmentum-Control Systems and Spacecraft Line of Sight. American Astronautical Society, 3–127.
PERASPERA (2014). Retrieved from available at: http://www.h2020-peraspera.eu/.
Perez, P. R., De Stefano, M., and Lampariello, R. (2018).Velocity Matching Compliant Control for a Space Robot during Capture of a Free-Floating Target. In IEEE Aerospace Conference Proceedings. MT, USA: Big SkyIEEE. doi:10.1109/AERO.2018.8396733
Peters, R. A., Campbell, C. L., Bluethmann, W. J., and Huber, E. (2003).Robonaut Task Learning through Teleoperation. In 2003 IEEE International Conference on Robotics and Automation. Taipei, Taiwan: IEEE. doi:10.1109/ROBOT.2003.1242017
Piedboeuf, J.-C., De Carufel, J., Aghili, F., and Dupuis, E. (1999). Task Verification Facility for the, Canadian Special Purpose Dextrous Manipulator. Proc. 1999 IEEE Int. Conf. Robotics Automation, 1077–1083.
Piersigilli, P., Sharf, I., and Misra, A. K. (2010). Reactionless Capture of a Satellite by a Two Degree-Of-freedom Manipulator. Acta Astronautica 66 (1), 183–192. doi:10.1016/j.actaastro.2009.05.015
Piskorz, D., and Jones, K. L. (2018). On-orbit Assembly of Space Assets: A Path to Affordable and Adaptable Space Infrastructure. The Aerospace Corporation.
Rackl, W., Lampariello, R., and Albu-Schäffer, A. (2013). Parameter Identification Methods for Free-Floating Space Robots with Direct Torque Sensing. IFAC Proc. Volumes 46 (19), 464–469. doi:10.3182/20130902-5-de-2040.00121
Rackl, W., and Lampariello, R. (2014).Parameter Identification of Free-Floating Robots with Flexible Appendages and Fuel Sloshing. In IEEE International Conference on Modelling, Identification and Control. Austria: Innsbruck. doi:10.1109/icmic.2014.7020740
Ratliff, N., Zucker, M., Bagnell, J. A., and Srinivasa, S. (2009).CHOMP: Gradient Optimization Techniques for Efficient Motion Planning. In IEEE International Conference on Robotics and Automation ICRA. Kobe, Japan, 489–494. doi:10.1109/ROBOT.2009.5152817
Reintsema, D., Thaeter, J., Rathke, A., Naumann, W., Rank, P., and Sommer, J. (2010). DEOS – the German Robotics Approach to Secure and De-orbit Malfunctioned Satellites from Low Earth Orbits. ,i-SAIRAS 2010. Japan: Sapporo.
Rekleitis, G., and Papadopoulos, E. (2014).On Controller Parametric Sensitivity of Passive Object Handling in Space by Robotic Servicers. In International Conference on Intelligent Robots and Systems. Chicago, IL, USA, 14–18.
Rekleitis, G., and Papadopoulos, E. (2015). On-orbit Cooperating Space Robotic Servicers Handling a Passive Object. IEEE Trans. Aerosp. Electron. Syst. 51 (2), 802–814. doi:10.1109/taes.2014.130584
Rekleitis, I., Martin, E., Rouleau, G., L'Archevêque, R., Parsa, K., and Dupuis, E. (2007). Autonomous Capture of a Tumbling Satellite. J. Field Robotics 24 (4), 275–296. doi:10.1002/rob.20194
Riecke, C., Artigas, J., Balachandran, R., Bayer, R., Beyer, A., Brunner, B., et al. (2016). The International Symposium on Artificial Intelligence, Robotics and Automation in Space (I-SAIRAS 2016). Beijing, China.KONTUR-2 MISSION: THE DLR FORCE FEEDBACK JOYSTICK FOR SPACE TELEMANIPULATION FROM THE ISS.
Roberts, B. (2017). Gravity Offload Techniques Utilized at NASA’s Goddard Space Flight Center. In IEEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) workshop. available at: http://hq.wvrtc.com/iros2017/files/roberts-presentation.pdf.
Roesler, G., Jaffe, P., and Henshaw, G. (2017). Orbital Mechanics. IEEE Spectr. 54 (3), 44–50. doi:10.1109/mspec.2017.7864756
Ruth, M., and Tracy, C. (2004). Video-guidance for DART Rendezvous mission. Proc. SPIE 5419, 92–106.
Rybus, T., and Seweryn, K. (2016). Planar Air-Bearing Microgravity Simulators: Review of Applications, Existing Solutions and Design Parameters. Acta Astronautica 120, 239–259. doi:10.1016/j.actaastro.2015.12.018
Rybus, T., Seweryn, K., and Sasiadek, J. Z. (2016).Trajectory Optimization of Space Manipulator with Non-zero Angular Momentum during Orbital Capture Maneuvre. In AIAA Conference on Guidance, Navigation, and Control. San DiegoUSA: California. doi:10.2514/6.2016-0885
Sabatini, M., Gasbarri, P., and Palmerini, G. B. (2017). Coordinated Control of a Space Manipulator Tested by Means of an Air Bearing Free Floating Platform. Acta Astronautica 139, 296–305. doi:10.1016/j.actaastro.2017.07.015
Sadati, S. M. H., Elnaz Naghibi, S., Shiva, A., Michael, B., Renson, L., Howard, M., et al. (2021). TMTDyn: A Matlab Package for Modeling and Control of Hybrid Rigid-Continuum Robots Based on Discretized Lumped System and Reduced Order Models. Int. J. Robotics Res.
Samson, C., English, C., Deslauriers, A., Christie, I., Blais, F., and Ferrie, F. (2004). The Neptec Three-Dimensional Laser Camera System: From Space Mission STS-105 to Terrestrial Applications. Can. Aeronaut. Space J. 50 (2), 115–123. doi:10.5589/q04-009
Saulnier, K., Pérez, D., Huang, R. C., Gallardo, D., Tilton, G., and Bevilacqua, R. (2014). A Six-Degree-Of-freedom Hardware-In-The-Loop Simulator for Small Spacecraft. Acta Astronautica 105 (2), 444–462. doi:10.1016/j.actaastro.2014.10.027
Schmaus, P., Leidner, D., Krüger, T., Schiele, A., Pleintinger, B., Bayer, R., et al. (2018). Preliminary Insights from the METERON SUPVIS Justin Space-Robotics Experiment. IEEE Robot. Autom. Lett. 3 (4), 3836–3843. doi:10.1109/LRA.2018.2856906
Schneider, S. A., and Cannon, R. H. (1992). Object Impedance Control for Cooperative Manipulation: Theory and Experimental Results. IEEE Trans. Robot. Automat. 8 (3), 383–394. doi:10.1109/70.143355
Schwartz, J. L., Peck, M. A., and Hall, C. D. (2003). Historical Review of Air-Bearing Spacecraft Simulators. J. Guidance, Control Dyn. 26 (4), 513–522. doi:10.2514/2.5085
Seddaoui, A., and Saaj, C. M. (2019). Combined Nonlinear H∞ Controller for a Controlled-Floating Space Robot. J. Guidance, Control Dyn. 42 (8), 1878–1885. doi:10.2514/1.g003811
Setterfield, T. P., Miller, D. W., Saenz-Otero, A., Frazzoli, E., and Leonard, J. J. (2018). Inertial Properties Estimation of a Passive On-Orbit Object Using Polhode Analysis. J. Guidance, Control Dyn. 41 (10), 2214–2231. doi:10.2514/1.G003394
Seweryn, K., and Banaszkiewicz, M. (2008).Optimization of the Trajectory of a General Free-Flying Manipulator during the Rendezvous Maneuver. In AIAA Guidance, Navigation and Control Conference and Exhibit. Honolulu, Hawaii. doi:10.2514/6.2008-7273
Seweryn, K., Rybus, T., Colmenarejo, P., Novelli, G., Oles, J., Pietras, M., et al. (2018). Validation of the Robot Rendezvous and Grasping Manoeuvre Using Microgravity Simulators. In IEEE International Conference on Robotic and Automation.doi:10.1109/icra.2018.8460475
Shan, M., Guo, J., and Gill, E. (2016). Review and Comparison of Active Space Debris Capturing and Removal Methods. Prog. Aerospace Sci. 80, 18–32. doi:10.1016/j.paerosci.2015.11.001
She, Y., Li, S., Liu, Y., and Cao, M. (2020). In-orbit Robotic Assembly mission Design and Planning to Construct a Large Space Telescope. J. Astron. Telesc. Instrum. Syst. 6 (1), 1. doi:10.1117/1.JATIS.6.1.017002
Sheinfeld, D., and Rock, S. (2009). Rigid Body Inertia Estimation with Applications to the Capture of a Tumbling Satellite. 19th AAS/AIAA spaceflight Mech. Meet., (pp. Vol. 134, 343–356).
Shi, L., Kayastha, S., and Katupitiya, J. (2017). Robust Coordinated Control of a Dual-Arm Space Robot. Acta Astronautica 138, 475–489. doi:10.1016/j.actaastro.2017.06.009
Shibata, T., and Ohkami, Y. (2002).Development of Brachiating Control System for Reconfigurable Brachiating Space Robot. In 3rd Int. Workshop Robot Motion Control. Poznan, Poland, 255–259.
Shibli, M., Aghili, F., and Su, C. (2005).Modeling of a Free-Flying Space Robot Manipulator in Contact with a Target Satellite. In IEEE Conference on Control Applications. Toronto: Canada, 559–564.
Shireman, K., Montalbano, J., McDonald, M., and Laurini, K. (2018). The ISS Partnership and Human Exploration in Cislunar Space and on the Moon. Bremen, Germany: 69th International Astronautical Congress.
Shoemaker, M. A., Mcintosh, R., Volle, M., and Jacobsohn, J. (2020). OSAM-1 Decommissioning Orbit Design. AAS/AIAA Astrodynamics Specialist Conference.
Singla, P., Subbarao, K., and Junkins, J. L. (2006). Adaptive Output Feedback Control for Spacecraft Rendezvous and Docking under Measurement Uncertainty. J. Guidance, Control Dyn. 29 (4), 892–902. doi:10.2514/1.17498
Somov, Y., Butyrin, Y., Somov, Y., and Somova, T. (2018).Guidance and Control of a Free-Flying Robot at Rendezvous with Noncooperative Space Vehicle. In 5th IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace). Rome, Italy: June, 20–22.
Space Flight (2016). China’s New Orbital Debris Clean-Up Satellite Raises Space Militarization Concerns. Space Flight101: available at: https://spaceflight101.com/long-march-7-maiden-launch/aolong-1-asat-concerns/.
Stieber, M. E., and Fung, P. T. (1991). Control System Challenges Associated with the mobile Servicing System for Space Station Freedom. In Proceedings of the Annual Rocky Mountain Guidance and Control Conference. Keystone: Guidance and control.
Stolfi, A., Gasbarri, P., and Sabatini, M. (2017). A Combined Impedance-PD Approach for Controlling a Dual-Arm Space Manipulator in the Capture of a Non-cooperative Target. Acta Astronautica 139, 243–253. doi:10.1016/j.actaastro.2017.07.014
Stoneman, S., and Lampariello, R. (2016).A Nonlinear Optimization Method to Provide Real-Time Feasible Reference Trajectories to Approach a Tumbling Target Satellite. In International Symposium on Artificial Intelligence, Robotics and Automation in Space i-SAIRAS. Beijing, P.R. China.
Strube, M., Hyslop, A., Carignan, C., and Easley, J. (2012).Ground Simulation of an Autonomous Satellite Rendezvous and Tracking System Using Dual Robotic Systems. In International Symposium on Artificial Intelligence, Robotics and Automation in Space (i-SAIRAS). Italy: Turin.
Sun, D., Liu, C., and Hu, H. (2021). Dynamic Computation of 2D Segment-To-Segment Frictional Contact for a Flexible Multibody System Subject to Large Deformations. Mechanism Machine Theor.
Sun, Y., Liu, Y., Jin, M., Liu, R., and Liu, H. (2020).A Novel Non-cooperative Target Capture Tool for Defunct Satellite. In IEEE International Conference on Mechatronics and Automation. IEEE. doi:10.1109/icma49215.2020.9233784
Tarao, S., Inohira, E., and Uchiyama, M. (2000).Motion Simulation Using a High-Speed Parallel Link Mechanism. In IEEE/RSJ Int. Conf. On Intelligent Robots and Systems. Japan: Takamatsu.
Tartt, C. J., and Moskwa, J. J. (2001).A Hardware-In-The-Loop Transient Diesel Engine Test System for Control and Diagnostic Development. In ASME International Mechanical Engineering Congress and Exposition. New York, NY, 532.
Taveira, T., Siqueira, A., and Terra, M. (2006).Adaptive Nonlinear H-Inf Controllers Applied to a Free-Floating Space Manipulator. In IEEE International Conference on Control Applications. Munich, Germany: IEEE, 1476–1481.
Tobbe, P., Naumann, C., Sutton, W., and Bryan, T. (1991). NASA MSFC Hardware in the Loop Simulations of Automatic Rendezvous and Capture Systems. Washington DC: NASA.
Tortopidis, I., and Papadopoulos, E. (2007). On Point-to-Point Motion Planning for Underactuated Space Manipulator Systems. Robotics Autonomous Syst. 55 (2), 122–131. doi:10.1016/j.robot.2006.07.003
Trentlage, C., Mindermann, P., Ben Larbi, M. K., and Stoll, E. (2016). Development and Test of an Adaptable Docking Mechanism Based on Mushroom-Shaped Adhesive Microstructures. AIAA SPACE. doi:10.2514/6.2016-5486
Tsiotras, P. (2014). ASTROS: A 5DOF Experimental Facility for Research in Space Proximity Operations. Adv. Astronautical Sci. 151, 717–730.
Tweddle, B. E., Saenz‐Otero, A., Leonard, J. J., and Miller, D. W. (2015). Factor Graph Modeling of Rigid‐body Dynamics for Localization, Mapping, and Parameter Estimation of a Spinning Object in Space. J. Field Robotics 32 (No. 6), 897–933. doi:10.1002/rob.21548
Ulrich, S., Saenz-Otero, A., and Barkana, I. (2016). Passivity-Based Adaptive Control of Robotic Spacecraft for Proximity Operations under Uncertainties. J. Guidance, Control Dyn. 39 (6), 1444–1453. doi:10.2514/1.g001491
Ulrich, S., and Sasiadek, J. Z. (2012). Modeling and Direct Adaptive Control of a Flexible-Joint Manipulator. AIAA J. Guidance Control Dyn. 35 (No. 1), 25–39. doi:10.2514/1.54083
Umetani, Y., and Yoshida, K. (1989). Resolved Motion Rate Control of Space Manipulators with Generalized Jacobian Matrix. IEEE Trans. Robotics Automation 5 (No. 3), 303–314. doi:10.1109/70.34766
Uyama, N., Nakanishi, H., Nagaoka, K., and Yoshida, K. (2012).Impedance-based Contact Control of a Free-Flying Space Robot with a Compliant Wrist for Non-cooperative Satellite Capture. In 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Portugal: Vilamoura-AlgarveIEEE. doi:10.1109/IROS.2012.6386082
Verscheure, D., Swevers, J., Bruyninckx, H., and De Schutter, J. (2008).On-line Identification of Contact Dynamics in the Presence of Geometric Uncertainties. In 2008 IEEE International Conference on Robotics and Automation. Pasadena, CA, USA, 851–856.
Virgili-Llop, J., and Romano, M. (2019). Simultaneous Capture and Detumble of a Resident Space Object by a Free-Flying Spacecraft-Manipulator System. Front. Robot. AI 6. doi:10.3389/frobt.2019.00014
Virgili-Llop, J., Zagaris, C., Zappulla, R., Bradstreet, A., and Romano, M. (2019). A Convex-Programming-Based Guidance Algorithm to Capture a Tumbling Object on Orbit Using a Spacecraft Equipped with a Robotic Manipulator. Int. J. Robotics Res. 38 (1), 40–72. doi:10.1177/0278364918804660
Virgili-Llop, J., Zagaris, C., Zappulla, R., Bradstreet, A., and Romano, M. (2017).Laboratory Experiments on the Capture of a Tumbling Object by a Spacecraft–Manipulator System Using a Convex-Programming-Based Guidance. In AAS/AIAA Astrodynamics Specialist Conference. Stevenson, WA, USA, 21–24.
Wang, D., Huang, P., and Meng, Z. (2015). Coordinated Stabilization of Tumbling Targets Using Tethered Space Manipulators. IEEE Trans. Aerosp. Electron. Syst. 51 (3), 2420–2432. doi:10.1109/taes.2015.140530
Wang, G., and Liu, C. (2020). Further Investigation on Improved Viscoelastic Contact Force Model Extended Based on Hertz's Law in Multibody System. Mechanism Machine Theor. 153, 103986. doi:10.1016/j.mechmachtheory.2020.103986
Wang, H., Cheng, L., and Xie, Y. (2017).Task-Space Adaptive Dynamic Modularity Control of Free-Floating Space Manipulators. In IEEE 56th Annual Conference on Decision and Control (CDC). Melbourne, Australia, 12–15. doi:10.1109/cdc.2017.8263859
Wang, M., Luo, J., Yuan, J., and Walter, U. (2018). Detumbling Strategy and Coordination Control of Kinematically Redundant Space Robot after Capturing a Tumbling Target. Nonlinear Dyn. 92 (3), 1023–1043. doi:10.1007/s11071-018-4106-4
Weber, M., Patel, K., Ma, O., and Sharf, I. (2006). Identification of Contact Dynamics Model Parameters from Constrained Robotic Operations. ASME. J. Dyn. Sys., Meas. Control. 128 (2), 307–318. doi:10.1115/1.2192839
Wertz, J. R., and Bell, R. (2003). Autonomous Rendezvous and Docking Technologies — Status and Prospects. Proc. SPIE 5088, 20–30.
Whelan, D., Adler, E., Wilson, S., and Roesler, G. (2000). Darpa Orbital Express Program: Effecting a Revolution in Space-Based Systems,” in Small Payloads in Space.doi:10.1117/12.406656
Wilde, M., Clark, C., and Romano, M. (2019). Historical Survey of Kinematic and Dynamic Spacecraft Simulators for Laboratory Experimentation of On-Orbit Proximity Maneuvers. Prog. Aerospace Sci. 110, 100552. doi:10.1016/j.paerosci.2019.100552
Wilde, M., Kwok Choon, S., Grompone, A., and Romano, M. (2018). Equations of Motion of Free-Floating Spacecraft-Manipulator Systems: An Engineer's Tutorial. Front. Robot. AI 5, 41. doi:10.3389/frobt.2018.00041
Wolfe, J., and Speyer, J. L. (2004).Effective Estimation of Relative Positions in Orbit Using Differential Carrier-phase. In AIAA Guidance, Navigation and Control Conference. Rhode Island. doi:10.2514/6.2004-4777
Wu, S., Mou, F., and Ma, O. (2017).Contact Dynamics and Control of a Space Manipulator Capturing a Rotating Object. In AIAA Guidance, Navigation, and Control Conference. Texas, USA: Grapevine, 9–13.
Xin, M., and Pan, H. (2011). Nonlinear Optimal Control of Spacecraft Approaching a Tumbling Target. Aerospace Sci. Tech. 15 (2), 79–89. doi:10.1016/j.ast.2010.05.009
Xu, W., Hu, Z., Zhang, Y., and Liang, B. (2017). On-orbit Identifying the Inertia Parameters of Space Robotic Systems Using Simple Equivalent Dynamics. Acta Astronautica 132, 131–142. doi:10.1016/j.actaastro.2016.12.031
Xu, W., Li, C., Liang, B., Xu, Y., Liu, Y., and Qiang, W. (2009). Target Berthing and Base Reorientation of Free-Floating Space Robotic System after Capturing. Acta Astronautica 64 (2), 109–126. doi:10.1016/j.actaastro.2008.07.010
Xu, W., Liu, Y., Liang, B., Xu, Y., Li, C., and Qiang, W. (2008). Non-holonomic Path Planning of a Free-Floating Space Robotic System Using Genetic Algorithms. Adv. Robotics 22 (4), 451–476. doi:10.1163/156855308x294680
Xu, W., Meng, D., Liu, H., Wang, X., and Liang, B. (2017). Singularity-free Trajectory Planning of Free-Floating Multiarm Space Robots for Keeping the Base Inertially Stabilized. IEEE Trans. Syst. Man Cybernetics: Syst.
Yamada, K., Yoshikawa, S., and Fujita, Y. (1995). Arm Path Planning of a Space Robot with Angular Momentum. Adv. Robotics 9 (No. 6), 693–709.
Yang, L., Yuan, H., Xu, W., and Hu, Z. (2018). Generalized Relative Jacobian Matrix of Space Robot for Dual-Arm Coordinated Capture. J. Guidance, Control Dyn., 1019–1028.
Yao, H., Ren, W., Ma, O., Chen, T., and Zhao, Z. (2018). Understanding the True Dynamics of Space Manipulators from Air-Bearing Based Ground Testing. J. Guidance, Control. Dyn.
Yoshida, K., and Abiko, S. (2002). Inertia Parameter Identification for a Free-Flying Space robotAIAA Guidance, Navigation, and Control Conference. Monterey, CA, USA. doi:10.2514/6.2002-4568
Yoshida, K., Dimitrov, D., and Nakanishi, H. (2006). On the Capture of Tumbling Satellite by a Space Robot. Beijing, China: IEE/RSJ Int. Conference on Intelligent Robots and Systems. doi:10.1109/iros.2006.281900
Yoshida, K. (2003). Engineering Test Satellite VII Flight Experiments for Space Robot Dynamics and Control: Theories on Laboratory Test Beds Ten Years Ago, Now in Orbit. Int. J. Robotics Res. 22 (5), 321–335. doi:10.1177/0278364903022005003
Yoshida, K., Hashizume, K., and Abiko, S. (2001). Zero Reaction Maneuver: Flight Validation with ETS-VII Space Robot and Extension to Kinematically Redundant Arm. Piscataway, NJ, USA: IEEE International Conferences on Robotics and Automation.
Yoshida, K., Nakanishi, H., Ueno, H., Inaba, N., Nishimaki, T., and Oda, M. (2004). Dynamics, Control and Impedance Matching for Robotic Capture of a Non-cooperative Satellite. Adv. Robotics 18 (2), 175–198. doi:10.1163/156855304322758015
Yoshida, K., Wilcox, B., Hirzinger, G., and Lampariello, R. (2016). “Space Robotics,” in Handbook of Robotics. Editors B. Siciliano, and O. Khatib. 2nd ed. (Cham: Springer), 1423–1462. doi:10.1007/978-3-319-32552-1_55
Yu, X., and Chen, L. (2014).Dynamic Modeling and Control of a Free-Flying Space Robot with Flexible-Link and Flexible-Joints. In IEEE International Conference on Robotics and Automation. Hong Kong, China, 6625–6630.
Zarafshan, P., and Moosavian, S. (2011).Control of a Space Robot with Flexible Members. In IEEE International Conference on Robotics and Automation. Shanghai, China, 9–13. doi:10.1109/icra.2011.5979882
Zhang, B., Liang, B., Wang, Z., Mi, Y., Zhang, Y., and Chen, Z. (2017). Coordinated Stabilization for Space Robot after Capturing a Noncooperative Target with Large Inertia. Acta Astronautica 134, 75–84. doi:10.1016/j.actaastro.2017.01.041
Zhang, Q., Liu, X., and Cai, G. (2020). Dynamics and Control of a Flexible-Link Flexible-Joint Space Robot with Joint Friction. Int. J. Aeronaut. Space Sci.
Zhao, Z., Liu, C., and Chen, T. (2016). Docking Dynamics between Two Spacecrafts with APDSes. Multibody Syst. Dyn. 37 (3), 245–270. doi:10.1007/s11044-015-9477-4
Zhiyu, N. I., Jinguo, L. I., Zhigang, W. U., and Xinhui, S. H. (2019). Identification of the State-Space Model and Payload Mass Parameter of a Flexible Space Manipulator Using a Recursive Subspace Tracking Method. Chin. J. Aeronautics 32 (No. 2), 513–530.
Zong, L., Luo, J., Wang, M., and Yuan, J. (2019). Parameters Concurrent Learning and Reactionless Control in post-capture of Unknown Targets by Space Manipulators. Nonlinear Dyn. 96 (1), 443–457. doi:10.1007/s11071-019-04798-w
Keywords: space robotics, on-orbit servicing, robotic capture on orbit, manipulation in orbit, ground testing of space robots, dynamics and control of space robots, contact dynamics, grippers for space
Citation: Papadopoulos E, Aghili F, Ma O and Lampariello R (2021) Robotic Manipulation and Capture in Space: A Survey. Front. Robot. AI 8:686723. doi: 10.3389/frobt.2021.686723
Received: 27 March 2021; Accepted: 07 July 2021;
Published: 19 July 2021.
Edited by:
Carl Glen Henshaw, United States Naval Research Laboratory, United StatesReviewed by:
Brian Roberts, National Aeronautics and Space Administration, United StatesMarkus Wilde, Florida Institute of Technology, United States
Gordon Roesler, Robots in Space LLC, United States
Tomasz Rybus, Centrum Badań Kosmicznych Polskiej Akademii Nauk (CBK PAN), Poland
Copyright © 2021 Papadopoulos, Aghili, Ma and Lampariello. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Evangelos Papadopoulos, ZWdwYXBhZG9AY2VudHJhbC5udHVhLmdy
 Evangelos Papadopoulos
Evangelos Papadopoulos Farhad Aghili2
Farhad Aghili2 Ou Ma
Ou Ma Roberto Lampariello
Roberto Lampariello