- 1The University of Texas at Arlington Research Institute, Fort Worth, TX, United States
- 2Department of Computer Science and Engineering, University of Texas at Arlington, Arlington, TX, United States
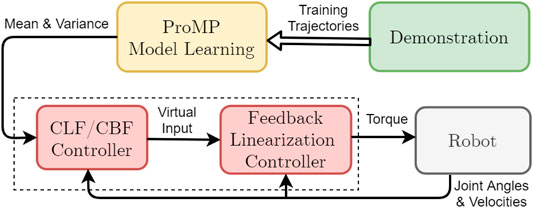
In this paper, we present a novel means of control design for probabilistic movement primitives (ProMPs). Our proposed approach makes use of control barrier functions and control Lyapunov functions defined by a ProMP distribution. Thus, a robot may move along a trajectory within the distribution while guaranteeing that the system state never leaves more than a desired distance from the distribution mean. The control employs feedback linearization to handle nonlinearities in the system dynamics and real-time quadratic programming to ensure a solution exists that satisfies all safety constraints while minimizing control effort. Furthermore, we highlight how the proposed method may allow a designer to emphasize certain safety objectives that are more important than the others. A series of simulations and experiments demonstrate the efficacy of our approach and show it can run in real time.
1 Introduction
The idea of proximity between robots and humans performing useful tasks, in a shared work space, inevitably brings up the issue of safety. In fact, safety is a limiting factor for the development of the autonomous robotic partners (Vicentini, 2021). Furthermore, strict safety requirements pose a major challenge for system integrators and robotics applications designers. When humans and robots share a physical work environment, robots must have control laws that make them verifiably safe around humans. In particular, robot systems need to be capable of detecting task variations, and their motion planning and control algorithms must be flexible enough to allow for variation while guaranteeing safety (Kragic et al., 2018).
Robot motion planning is a rich field of study providing myriad approaches to determine robot trajectories, including in the presence of obstacles (Mohanan and Salgoankar, 2018). Many approaches, such as rapidly exploring random trees (LaValle, 1998; LaValle et al., 2001), probabilistic roadmaps (Hsu et al., 1998; Geraerts and Overmars, 2004), and artificial potential fields (Warren, 1989; Vadakkepat et al., 2000) require predefined static maps for peak performance. In addition, robot motion planning algorithms often require expert design of cost functions, potential functions, and random sampling that are outside the expertise of day-to-day users. The learning from demonstration paradigm can address these shortcomings (Argall et al., 2009; Chernova and Thomaz, 2014) by leveraging the inherent expertise of a human teacher.
Movement primitives (MPs) are a popular approach to encode and generalize human demonstrations for training robots. MPs are modeled through a compact representation of the implicitly continuous and high-dimensional trajectories. For example, dynamic movement primitives (DMPs) use demonstrations to learn a model of the control effort necessary to produce a desired trajectory for a stabilized dynamic system (Ijspeert et al., 2013; Dahlin and Karayiannidis, 2019). Capturing the natural variation in human demonstration of a task can help a robot overcome uncertainty and deviation between the training regime and actual task execution (Gomez-Gonzalez et al., 2020). However, DMPs only encapsulate a single trajectory demonstration and thus lack this flexibility.
Probabilistic movement primitives (ProMPs) are a concept in which a distribution of trajectories is learned from multiple demonstrations. There are several works that have focused on the construction of ProMP controllers. In (Paraschos et al., 2018a), the design of a stochastic ProMP feedback controller was studied by exploiting the property of the covariance derivatives which can be explicitly computed. A model-free ProMP controller that adapts movement to force-torque input was designed in (Paraschos et al., 2018b). In (Calinon and Lee, 2017), the authors designed a model predictive control-based ProMP controller for a linear discrete time system model.
While they have prominent advantages, ProMP methods still present notable shortcomings. For example, prior ProMP approaches require a linearized model of the system in the controller design. This makes the controller less relevant for nonlinear systems such as robotics and autonomous vehicles. Additionally, while ProMPs themselves are fairly simple to generate, their controllers are difficult to implement, vulnerable to noise, sensitive to design parameters, and are variable to initial conditions. These factors limit the ability of non-experts to employ or tune such controllers. Finally, ProMPs by definition are stochastic and distributions of trajectories defined by Gaussian functions have a large support. Thus, the resulting trajectories can deviate far from the mean of the training set.
In recent years, real-time safety-critical control of dynamic systems has received notable consideration (Wieland and Allgöwer, 2007). One important approach is the use of barrier certificates/functions, which leverage off-line iterative optimization algorithms to verify safety for a given dynamical system (Sloth et al., 2012). The notion has been extended to synthesizing safe control laws in real-time using quadratic programming (QP) to find control inputs that satisfy control barrier functions (CBFs) (Ames et al., 2016).
A powerful property of CBFs is that they are easily combined with control Lyapunov functions (CLFs) in the same QP such that the resulting controller guarantees stability while respecting limits and safe regions of the state space (Ames et al., 2019; Cortez et al., 2019; Lopez et al., 2020). Additionally, the QP solved to find a safe, stable control input during run-time can include other optimization terms such as minimizing control effort. Other tasks formulated as cost functions or constraints can be included as well. CBF and CLF based controls have their own downsides, most notably the advanced knowledge necessary to define the barriers and trajectories. Efforts to automate the definition of CBFs and CLFs include mapping temporal logic statements to barriers and trajectories (Srinivasan and Coogan, 2020) and training piece-wise barrier functions for obstacles in the workspace (Saveriano and Lee, 2019).
This work addresses the aforementioned weaknesses of ProMPs and CBFs/CLFs. In our presented approach, the trajectory distribution provided by a ProMP is used to define a CLF and one or more CBFs. Specifically, the ProMP mean is used to define a CLF, and barriers for the CBFs are defined using the standard deviation of the distribution. Thus, the CLF and CBFs are established strictly through human demonstration eschewing the need for advanced control knowledge. The system will roughly track the mean trajectory, with a modicum of freedom to optimize the control effort or other requirements, while guaranteeing that the system never leaves a known neighborhood of the mean.
Since CLF and CBF controllers are intrinsically based on the nonlinear model of the system, our approach overcomes the inherent linearity of ProMP controllers. We demonstrate the effectiveness and computational efficiency of our approach through simulations and experiments with a two-link and a six-link robot. Examples of generated control trajectories by our method for a Universal Robots UR5 are shown in Figure 1. In summary, the salient contributions of this paper are the following.
• We develop a novel means of automating the design of CLFs and CBFs from the distribution delivered by a ProMP.
• We introduce a new control design for ProMPs by combining CLFs and CBFs.
• We demonstrate the practical applicability of the proposed method through experimental validation on a Universal Robots UR5e.
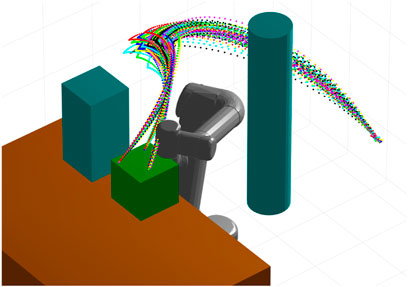
FIGURE 1. A set of robot trajectories generated by our CLF/CBF-based ProMP demonstration and control method. The controller guarantees that the system never leaves a neighborhood defined by the training set and provides a straightforward way to define trajectories that enforce safety constraints in the presence of obstacles. Copyright 2021 IEEE. Reprinted, with permission, from Davoodi et al., 2021.
The remainder of this paper is structured as follows. In Section 2, we review ProMPs, CBFs, CLFs, and robot system dynamics. We detail our approach for a ProMP to define the CLFs and CBFs for optimal control in Section 3. Simulation and experiments are presented in Section 4. Lastly, we conclude with a discussion on future work in Section 5.
2 Background
This section presents necessary background information on ProMPs, CBFs, and CLFs.
Notation: Given a matrix A, we denote its transpose by A⊤. Let the identity and zero matrices, with appropriate dimensions, be denoted by I and 0, respectively. We denote ⋆ as the symmetric entries of a matrix. For a vector field fi(x) and vector of vector fields F(x) = [f1(x), …, fn(x)], let
2.1 Probabilistic Movement Primitives
ProMPs provide a parametric representation of trajectories which can be executed in multiple ways through the use of a probability distribution. A set of basis functions are used to reduce the model parameters and aid learning over the demonstrated trajectories. The trajectory distribution can be defined and generated in any space that accommodates the system (e.g., joint space or task space) (Paraschos et al., 2018a). In this work we consider joint space trajectories and assume the demonstrations to be normally distributed.
Let
where
We marginalize out wi to create the trajectory distribution
Here, the distribution p (ζi, θi) defines a hierarchical Bayesian model over the trajectories ζi (Paraschos et al., 2018a) and
The trajectory can be generated from the ProMP distribution using wi, the basis function Φ(k), and (2). The basis function is chosen based on the type of robot movement which can be either rhythmic or stroke-based. From (Eq. 2), the mean
Multiple demonstrations are needed to learn a distribution over wi. To train a ProMP we use a combination of radial basis and polynomial basis functions. From the demonstrations, the parameters θi can be estimated using maximum likelihood estimation (Lazaric and Ghavamzadeh, 2010). However, when there are insufficient demonstrations this may result in unstable estimates of the ProMP parameters. Therefore, similar to (Gomez-Gonzalez et al., 2020), our method uses a regularization to estimate the ProMP distribution. We maximize θi for the posterior distribution over the ProMP using expectation maximization,
In addition, we make use of Normal-Inverse-Wishart as a prior distribution p (θi) to increase stability when training the ProMP parameters (Gomez-Gonzalez et al., 2020).
2.2 System Modeling
Consider the following control affine nonlinear system
where
The model (4) encompasses the dynamic model of robotic manipulators. We consider the following description of robot motion given by the general form by the Euler-Lagrange equations,
where
2.3 Control Barrier and Control Lyapunov Functions
2.3.1 Control Barrier Functions
Let C be a set for which we wish to verify that x(t) ∈ C, ∀t. Then, C defines a safe set. A smooth function
where Int(C) and ∂C denote the interior and boundary of C, respectively.
Existing approaches to define CBFs include exponential CBFs, reciprocal CBFs, and zeroing CBFs (Ames et al., 2016; Nguyen and Sreenath, 2016). Yet, these methods have trade-offs with respect to ease of definition, boundedness of velocities, speed of convergence, etc. In this work we investigate the use of a reciprocal CBF. This type of CBF has a small value when the states are far from the constraints and it becomes unbounded when the states approach the constraints.
Definition 1(Ames et al., 2014) Given C and h, a function
Remark 1It is worth noting that based on the definition of the safe set (7), if the initial state of the system is inside the safe set (i.e., h(x0) > 0 when the system’s trajectory gets close to the safety boundary) then the CBF condition forces the systems’ trajectories to go back inside the safe set. This is due to the fact that the derivative of h(x(t)) is negative on the boundary which leads the value of B(x) (h(x)) to start decreasing (increasing). Moreover, the constant value γ determines how fast the states of the system can reach the safety boundary.
2.3.2 Control Lyapunov Functions
CLFs can be used to model and design dynamical control system inputs to ensure objectives such as stability, convergence to the origin (or other set point), or convergence to a desired trajectory. In order to have a construction similar to CBFs, we consider exponentially stabilizing CLFs (Ames et al., 2014).
Definition 2In a domain
Having established a CBF to accomplish safety and a CLF to achieve control performance objectives, the two may be unified through a QP. As a result, safe control laws can be computed using the QP to solve the constrained optimization problems at each point in time (Ames et al., 2016).
3 Control Development
Our main goal is to design a controller such that the system output tracks a trajectory within the distribution generated by a ProMP. To this end, we first construct a nonlinear inner-loop control law based on the feedback linearization of (Eq. 5). Then, an outer-loop controller established by a CLF-CBF is designed using the distribution parameters
1. Use the demonstrated trajectories of a robot to train and estimate a ProMP distribution. The ProMP provides the time-varying mean and variance of a trajectory.
2. Develop a feedback linearization controller to obtain a linear and decoupled input-output closed-loop relationship for the error signal.
3. Design a CLF to stabilize the system such that ∀i, qi → μi, where μi is the i-th element of
4. Create a CBF to ensure that the error ei = qi − μi satisfies the safety constraint ∀i, |ei| < σi, where σi is the (1, 1) element of Σi.
The general structure of our proposed system is shown in Figure 2.
3.1 Feedback Linearization Controller
First, we define the trajectory and error vectors as
Next, assume that the decoupling matrix Γ is well-defined and has full rank (Hsu et al., 2015)1. This implies that the system in (Eq. 4) is feedback linearizable and we can prescribe the following control law,
where v is an auxiliary feedback control value. This yields the second order linear system from input v to output e,
By defining
From there, n decoupled systems can be obtained from (Eq. 13),
where
It should be noted that the derivative of the tracking error in (Eq. 14) can be obtained from
To accomplish problem objective 3, it is sufficient to ensure ei → 0. This is accomplished by designing an appropriate CLF. To satisfy problem objective 4, it is adequate to make |ei| < σi. This objective is satisfied by defining suitable CBFs. In the following subsections, the CLFs and CBFs are defined for the system in (Eq. 14). Moreover, the ith controller for each system in (Eq. 14) is designed by combining the corresponding CLFs and CBFs via a QP problem.
3.2 Control Lyapunov Function
Consider the following rapidly exponentially stabilizing-CLF (RES-CLF) (Zhao et al., 2014),
where ϵi is a positive scalar and
In order to exponentially stabilize the system, we want to find vi such that
where c3i is a positive constant value. To guarantee a feasible solution for the QP, the CLF constraint can be relaxed by δi > 0 (Ames et al., 2014) resulting in
This relaxation parameter will be minimized in the QP cost function. It is worth mentioning that by providing a weighting factor on the relaxation parameter δi, the QP can prioritize how close the system should track of a specific trajectory while ensuring that safety is always satisfied.
3.3 Control Barrier Functions
We propose two safety constraints for each system in (Eq. 14). More specifically, each system should satisfy − σi < ei < σi. Consequently, we have the following two safety constraints,
In this work, we assume that the initial conditions satisfy the safety constraints, i.e., the initial tracking errors are in the safe region. From (Eq. 19), it is clear that we have multiple time-varying constraints that should be satisfied simultaneously. Moreover, it is trivial to verify that LGei = 0 and LFLGei ≠ 0, thus the safety constraint has a relative degree of 2. For relative degree-two constraints, the reciprocal CBF is defined as (Hsu et al., 2015),
where j ∈ {1, 2} and aEij, bEij are positive scalars. The following control barrier condition should be satisfied for time varying constraints which leads to time varying CBFs,
Remark 2Note that by choosing small values for aEij and bEij, the system will stop far from the constraint surfaces. On the other hand, by choosing large parameters the system will stop close to the constraints. In some cases, especially in the presence of uncertainties, choosing aEij and bEij to be too large may cause constraint violations (i.e., no solution exists to the QP problem). As a result, based on the given application, a compromise must be considered for choosing these parameters.
3.4 Quadratic Program
As shown in (Eq. 19), two safety constraints need to be satisfied simultaneously for each linearized, decoupled system. Due to this fact, a single controller can be obtained in such a way that guarantees adherence to both constraints (Rauscher et al., 2016). In this subsection, n QPs are proposed to unify RES-CLF and CBFs for each system in (Eq. 14) into a single controller. The n QPs for i ∈ {1, … , n} are defined as
where
Remark 3If feedback linearization is not feasible, or in the case that feedback linearization does not result in independent systems, we should encode the coupling between the joints to train a single ProMP for the multidimensional system. Our proposed approach can be extended to address such cases by defining the safety constraints based on the entire ProMP covariance matrix, not just the diagonal elements. This is an avenue of future exploration.
4 Simulations and Experiments
In this section, we demonstrate different aspects and capabilities of our methodology for the ProMP control of a robotic system via simulations and experiments. The system models and proposed real-time controller were implemented in a MATLAB 2019a environment. All computations were run on a Dell OptiPlex 7050 machine with an Intel Core i7-7700X CPU and 8 GB of memory.
4.1 Case Study 1: Two-Link Robot
We consider a rigid, two-link robot with the dynamic model of (Eq. 5) and the following parameters (Kolhe et al., 2013),
where m1 and m2 are the link masses, l1 and l2 are the lengths of the links, and g is the gravitational acceleration. For the simulations, the values of these variables are selected as m1 = 1, m2 = 1, l1 = 1, l2 = 1, and g = 9.8.
We generated 50 trajectories that achieve a goal position from various starting positions while avoiding three obstacles. Using this dataset, we trained a ProMP with Algorithm 1 from (Gomez-Gonzalez et al., 2020). We used L = 2 basis functions consisting of five radial basis parameters. The results of the ProMP training are presented in Figure 3, where the 50 input trajectories are shown in red. The ProMP mean joint trajectories, μi, are shown in dark green, and in a light-green fill we show μi ± σi. A visualization of the ProMP in the workspace, based on (Sakai et al., 2018), is displayed in Figure 4, where the black circles indicate the location of obstacles. The robot link positions over time are highlighted in red, with different colors representing key end-effector trajectories from the ProMP. The green trajectory is the mean of the ProMP distribution. The other four trajectories result from combinations of μi ± σi, i ∈ {1, 2}.
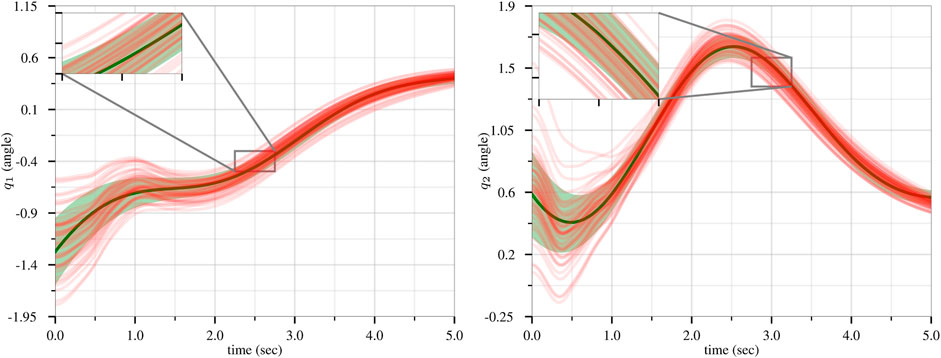
FIGURE 3. Training of the CLF/CBF-based ProMPs for the first joint (left) and second joint (right). The 50 input trajectories are shown in red, and the ProMP mean joint trajectories (μi) are shown in dark green. A light-green fill shows μi ± σi. Copyright 2021 IEEE. Reprinted, with permission, from Davoodi et al., 2021.
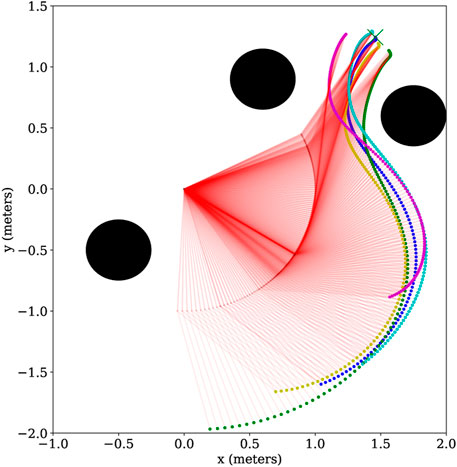
FIGURE 4. A visualization of the two-link CLF/CBF-based ProMP joint trajectories in the robot workspace. The robot link positions over time are shown in red, while the end-effector trajectory following the mean ProMP joint trajectories is shown in green. The four trajectories of the end effector with joint combinations μi ± σi, i ∈{1,2} are illustrated in cyan, blue, yellow and magenta. The black circles correspond to obstacles. Copyright 2021 IEEE. Reprinted, with permission, from Davoodi et al., 2021.
Three sets of simulations were conducted. In each simulation, the CLF parameters were selected as ϵi = 0.1 and c3i = 0.5. In scenario 1, greater priority was given to the CLF than CBF by choosing a high weight, i.e., psc1 = psc2 = 200. Moreover, the CBF design parameters were set to aE11 = aE12 = 20.1, aE21 = aE22 = 20, bE11 = bE12 = 1, bE21 = bE22 = 0.9, γ1 = 10.1, and γ2 = 9. In scenario 2, psci was chosen as psc1 = psc2 = 0.02 which implies that less priority was given to the CLF in comparison with the CBF. Moreover, the CBF parameters in this scenario are the same as the first scenario. To show the effects of changing the CBF parameters aEij, bEij, and γi, we consider another scenario. In scenario 3, aE11 = aE12 = 1.1, aE21 = aE22 = 1.1, bE11 = bE12 = 0.4, bE21 = bE22 = 0.5, γ1 = 1.3, and γ2 = 1.51, with psci = 0.02 as in the second scenario. Consequently, the effects of changing the CBF parameters can be analyzed by comparing the second and third scenarios.
The simulation results are exhibited in Figure 5. In scenario 1, by choosing a large value for psci (more priority given to the CLF than CBF), the system output remains close to the mean trajectory. However, in scenario 2, by considering a small value for psci (more priority given to the CBF than CLF), the system remains safely inside the distribution but does not necessarily stay close to the mean. In scenario 3, it can be seen that by choosing smaller values for aEij, bEij, and γi, the system output will maintain more distance from the constraint surfaces, resulting in remaining closer to the mean trajectory. In short, our proposed method provides a valuable option to the system designer by permitting fine-grained administration of the trajectories while ensuring safety.
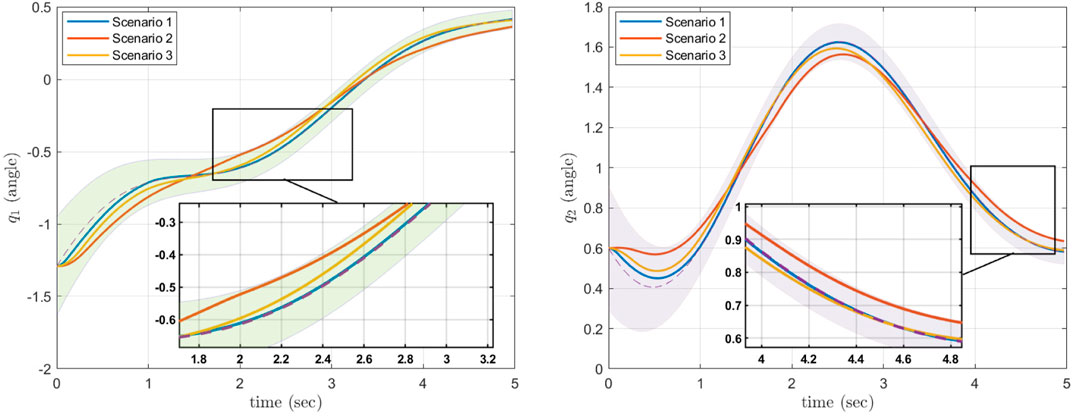
FIGURE 5. The results of the CLF/CBF-based ProMP controller for the first joint (left) and second joint (right). The safe region of μi ± σi, i ∈{1, 2} is shown as a filled “tube.” The control results in different trajectories for distinct values of the weight psci, however all trajectories remain safe. Copyright 2021 IEEE. Reprinted, with permission, from Davoodi et al., 2021.
The primary computational cost of our controller, with respect to time, comes from the fact that it must solve a set of QPs at every time step. In the evaluation simulations, two QP problems are solved in real time (one for each link). The average required time (Tave), maximum time (Tmax), and the standard deviation (std) for solving the QP problems are Tave = {0.0 015s, 0.0 011s}, Tmax = {0.1 148s, 0.0 119s}, std = {0.0 053s, 0.0 006s}. From these results, it is clear that the expected execution time of the QP problems is very small (e.g., in the range of 1 ms). The large maximum times correspond to instances of a single outlier. Hence, the controller is applicable for real-time implementation.
4.2 Comparison With Conventional ProMP Control
One specific aspect of the CLF/CBF-based ProMP controller developed in this work is minimizing the control effort in the optimization problem (Eq. 22) at each time step. This leads to a lower control effort in comparison with a traditional ProMP controller. Another set of simulations were conducted to compare our proposed methodology with the results of (Paraschos et al., 2018a; Mathew, 2018), which is representative as one of the primary works in this field. To provide a fair comparison with our method, the ProMP controller is also applied to the feedback linearizable model of the two-link robot.
We conducted three sets of simulations (designated as the fourth, fifth and sixth scenarios). In scenario 4, we implemented the CLF/CBF-based controller with more priority accorded to the CLF rather than the CBF (similar to scenario 1). In scenario 5, we considered the CLF/CBF-based controller with more priority bestowed to the CBF instead of the CLF (similar to scenario 2). The ProMPs in scenarios 4 and 5 were trained using the library in (Gomez-Gonzalez, 2019). However, we were not able to successfully implement the original controller in (Gomez-Gonzalez, 2019). Therefore, in scenario 6, we trained and implemented the traditional ProMP controller presented in (Paraschos et al., 2018a) using the library presented in (Mathew, 2018). While the ProMPs for our CLF/CBF-based ProMP controller and traditional ProMP controller used the same training set, the resulting ProMP mean and covariance are slightly different. For each scenario, the simulations were run for 100 different initial conditions that were randomly selected within the bound [μ1 ± 0.12, μ2 ± 0.12], where μ1 (0) = − 1.292 5, and μ2 (0) = 0.6.
The simulation results corresponding to these three scenarios are, respectively, shown in Figures 6–8, where the mean of ProMP is highlighted by a dashed orange line, and the mean ± variance bounds are shown with dotted black lines. These results show that all the controllers are robust against uncertainties in the initial conditions. From Figure 6, it can be concluded that by using the CLF/CBF-based controller with high psci, the system quickly converges and tracks the mean trajectory. The system deviates from the mean to take a shorter path in Figure 7, but it is clear that by considering small values for psci the system remains safely inside the distribution. Based on Figure 8, it can be seen that when using a traditional ProMP controller, the system tracks the mean with an error larger than scenario 4. Moreover, the second joint does not remain inside the distribution during certain periods. We posit that the ProMP controller has some lag, akin to a PID controller with proportional gains that are too low. The feedback and feedforward gains of the ProMP controller are determined as functions of the system parameters and ProMP parameters, and they cannot be tuned to reduce tracking error. The ProMP can be “tuned” through the use of via points. To this end, we have added a via point as the last element of the mean trajectory to ensure convergence. These results show that the CLF/CBF-based ProMP controller has better tracking performance when compared to a traditional ProMP controller.
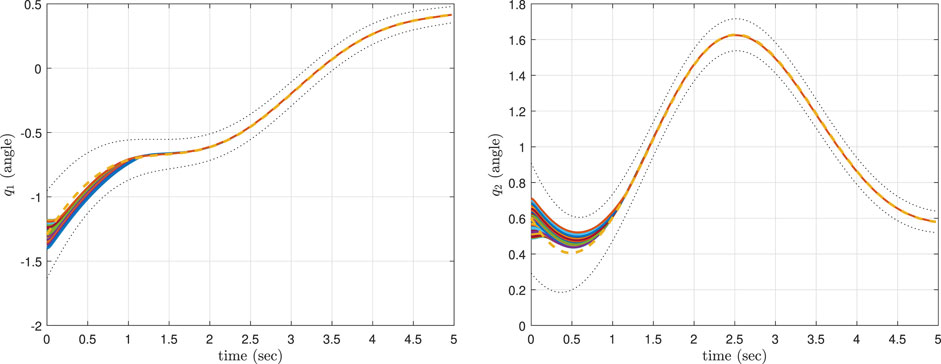
FIGURE 6. The results of the CLF/CBF-based ProMP controller with more priority given to the CLF than the CBF for the first joint (left) and second joint (right).
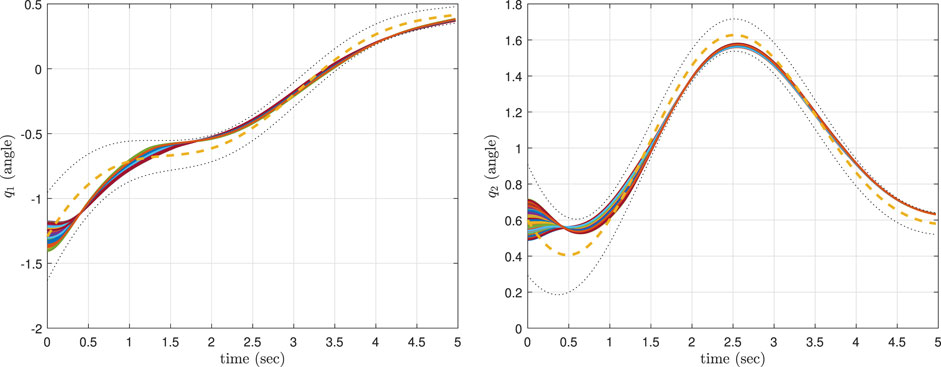
FIGURE 7. The results of the CLF/CBF-based ProMP controller with more priority given to the CBF than the CLF for the first joint (left) and second joint (right).
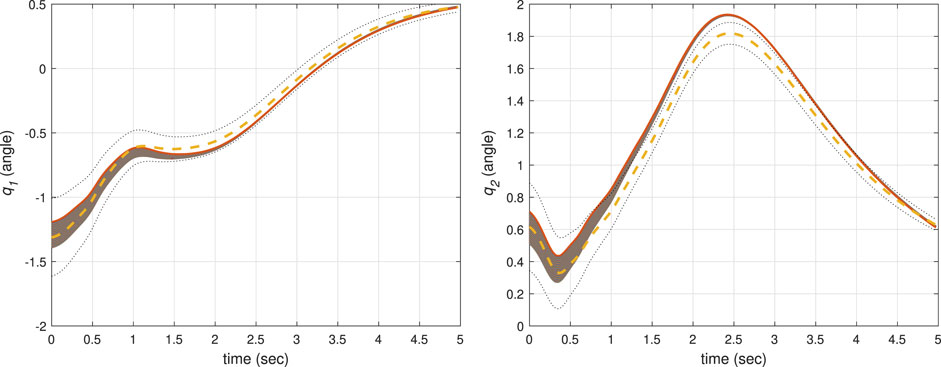
FIGURE 8. The results of a traditional ProMP controller for the first joint (left) and second joint (right).
Figure 9 and Figure 10 summarize the root mean square (RMS) values of the control variables for scenarios 4, 5, and 6 in the form of a boxplot. In these figures, 50% of all the RMS values are placed in the boxes and the median is shown by a red line that divides the box into two parts. The black bars indicate the maximum and minimum values, and the dashed “whiskers” indicate 25% of the values between the box and max/min. Outliers, if any, are indicated by red crosses. From Figure 9, it can be concluded that scenario 4 has larger control values in comparison to scenario 5, i.e., more control effort is needed to be able to effectively track the ProMP mean. This indicates one strength of leveraging trajectory distributions over a single trajectory; the system is given more freedom to reduce the control effort while maintaining safety. Moreover, in contrast with a traditional ProMP controller our methodology has a remarkably lower control effort as shown in Figure 9 and Figure 10.
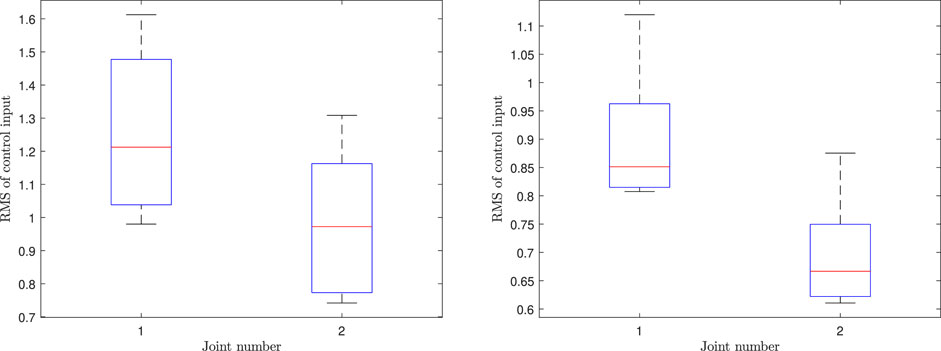
FIGURE 9. The RMS values of control inputs corresponding to the CLF/CBF-based ProMP controller for the fourth scenario (left) and the fifth scenario (right).
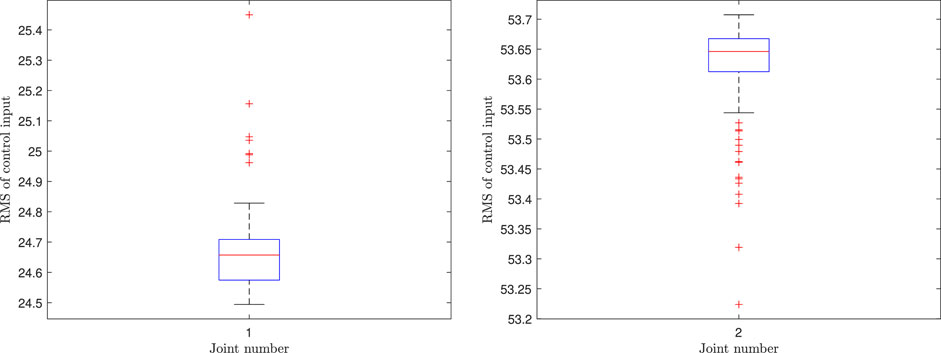
FIGURE 10. The RMS values of control inputs corresponding to a traditional ProMP controller for the first joint (left) and second joint (right).
4.3 Case Study 2: Universal Robots UR5 Six-Link Robot
The equation of motion of the UR5 robot can be written in the form of (Eq. 5), with the following parameters (Spong and Vidyasagar, 2008),
where
where mij are the entries of the inertia matrix. Moreover, the elements of the gravity vector are obtained from
where
We generated 90 joint-space trajectories with defined goals, obstacles, and starting positions. The 90 UR5 trajectories were then used to train a joint-space ProMP using the same parameters as in the two-link robot case study. The following set of CLF and CBF parameters were chosen: ϵ1 = ϵ2 = ϵ3 = ϵ4 = ϵ5 = 0.1, ϵ6 = 0.01, and c3i = 1.1, aEij = 20.1, bEij = 1, and γi = 10.1, i ∈ {1, … , 6}, j ∈ {1, 2}. The simulation environment is depicted in Figure 1 and Figure 11. We consider two different scenarios. In scenario 1, psci = 200, which gives higher importance to the CLF. For scenario 2, psci = 0.001, which implies that the design interest and priority is on the CBF. As is clear from Figure 11, in both scenarios the robot can effectively track the mean of ProMP and simultaneously avoid colliding with environmental obstacles. The running time statistics for solving the QP problems are Tave = [0.001 4, 0.001 1, 0.001 0, 0.001 0, 0.001 1, 0.001 0], Tmax = [0.119 3, 0.012 0, 0.012 8, 0.005 8, 0.031 4, 0.002 8], std = [0.005 3, 0.000 5, 0.000 5, 0.000 3, 0.001 4, 0.000 2]. The large maximum values are again due to a single outlier. Thus, the expected operational time is well within the demands of a robotic system. The cause of the outlier occurrences is an avenue of future research to offer improved performance guarantees.
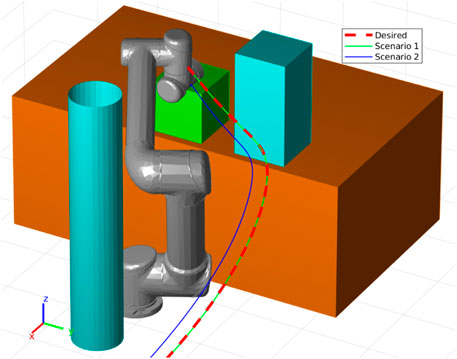
FIGURE 11. The results of the CLF/CBF-based ProMP controller for a UR5 robot. Copyright 2021 IEEE. Reprinted, with permission, from Davoodi et al., 2021.
4.4 Case Study 3: Universal Robots UR5e Six-Link Robot
To conclude this section, we evaluated our CLF/CBF-based ProMP controller using a physical robot with static obstacles. The robot used was a Universal Robots UR5e six-link manipulator with a Robotiq two-finger gripper. In addition to the robot, our environmental setup included the following three static obstacles: a robotic arm, box, and the table that the robot was mounted on.
We tasked a human teacher with demonstrating a pick-and-place procedure to the robot. In our setup, the robot must move from a starting bin to a goal bin located on the other side of a box. We installed a gravity compensation controller on the robot enabling the teacher to directly affect the robot’s joints via kinesthetic teaching. Using this directed learning from demonstration approach allows us to bypass the correspondence problem (Argall et al., 2009). Additionally, kinesthetic teaching retains parity between the demonstration, learning, and execution space of the trajectories. In all, seven demonstrations of the task were conducted. From these demonstrations, we collected the joint angles, velocities, and the associated time steps. It is worth mentioning that care must be taken to collect data that is roughly Gaussian, or at least unimodal. Methods to handle non-Gaussian or multimodal data is an issue to be addressed in future work.
Using this demonstration data, we trained a joint-space ProMP using the same parameters as described in the previous sections. In Figure 12, we see the demonstration data (in green), the respective ProMP mean (red), and one standard deviation of the ProMP (light red). Note that q6, which corresponds to the final wrist joint, was not purposefully actuated by the teacher and is largely static during training. We implemented the CLF/CBF-based ProMP controller with psci = 0.5. The other parameters were selected to be the same as the previous simulations in Section 4.3. Figure 13 depicts the demonstration operation as the human teacher moves the robot arm during the task. The trajectory from the CLF/CBF-based ProMP controller on the UR5e robot is shown in Figure 14.
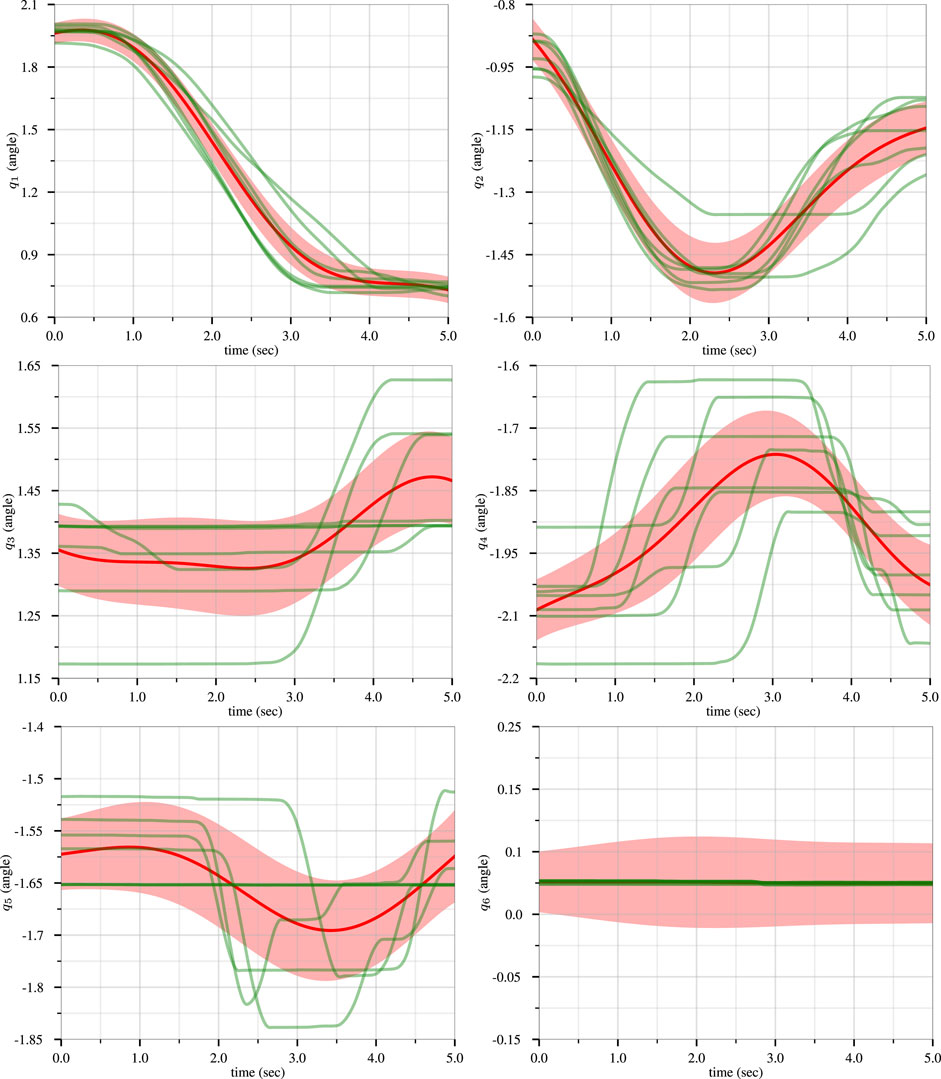
FIGURE 12. The UR5e robot joint trajectories recorded from the human demonstration of the pick-and-place task are shown in green, while the ProMP mean trajectory and one standard deviation of the ProMP are colored red and light red, respectively.
5 Conclusion and Future Work
In this work we solved a ProMP robot guidance problem using a CLF/CBF-based controller. Our approach stabilizes the robot and guarantees that the system output is always inside the distribution generated by a ProMP. The time-varying nature of the ProMP ensures the robot is guided along the distribution at the desired rate. Moreover, our technique allows for prioritizing between strict tracking of ProMP mean and loose but safe tracking of mean trajectory, which is not possible in the native ProMP control design. It was shown, in Section 4.2, that this can reduce control effort at the risk of getting closer to barriers. Simulation and experimental studies on a two-link and six-link robot confirm the viability of our method for designing the controller.
As part of ongoing work, we are investigating the trade-offs of various different CBFs (e.g., zeroing versus reciprocal), other choices of cost functions, and constraints in the QP. Additionally, we are seeking novel methods that automatically define additional barriers to ensure the safe movement of a co-robot around dynamic obstacles (e.g., humans and other robots). This includes the exploration of an active learning framework whereby a co-robot has the capability to select informative trajectories from the ProMP distribution that can then be used for autonomously retraining itself.
Data Availability Statement
The data used in this research includes simulation and experimental results. The authors will provide it upon reasonable request.
Author Contributions
MD lead theoretical development and implementation of CBF/CLF controller. AI lead implementation of ProMP controllers. JC implemented ProMP algorithms and conducted simulations and experiments. WB lead theoretical developments of ProMP and contributed to CLF and CBF design. NG directed the research overall and lead theoretical design of nonlinear control theory. All authors contributed to writing and editing the manuscript and contributed to the theoretical development and analysis of experimental and simulation results.
Funding
This material is based upon work supported by the National Science Foundation (NSF) under Grant No. 1728057 and the University of Texas at Arlington Research Institute. JC was supported by an NSF Graduate Research Fellowship under Grant No. 1746052 and a Tau Beta Pi Fellowship.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1A control designer would confirm that the system has the same number of inputs as outputs and verify that e satisfies a vector relative degree (Kolavennu et al., 2001) condition, typically vector relative degree 2. This implies that the decoupling matrix Γ is well-defined and nonsingular.
References
Ames, A. D., Grizzle, J. W., and Tabuada, P. (2014). “Control Barrier Function Based Quadratic Programs with Application to Adaptive Cruise Control,” in Proceedings of the IEEE Conference on Decision and Control, Los Angeles, CA, USA, December 2014, 6271–6278. doi:10.1109/cdc.2014.7040372
Ames, A. D., Xu, X., Grizzle, J. W., and Tabuada, P. (2016). Control Barrier Function Based Quadratic Programs for Safety Critical Systems. IEEE Trans. Automatic Control. 62, 3861–3876. doi:10.1109/TAC.2016.2638961
Ames, A. D., Coogan, S., Egerstedt, M., Notomista, G., Sreenath, K., and Tabuada, P. (2019). “Control Barrier Functions: Theory and Applications,” in Proceedings of the European Control Conference, Naples, Italy, June 2019, 3420–3431. doi:10.23919/ECC.2019.8796030
Argall, B. D., Chernova, S., Veloso, M., and Browning, B. (2009). A Survey of Robot Learning from Demonstration. Robotics Autonomous Syst. 57, 469–483. doi:10.1016/j.robot.2008.10.024
Calinon, S., and Lee, D. (2017). “Learning Control,” in Humanoid Robotics: A Reference. Editors A. Goswami, and P. Vadakkepat (Berlin/Heidelberg, Germany: Springer), 1261–1312. doi:10.1007/978-94-007-7194-9_68-1
Chernova, S., and Thomaz, A. L. (2014). Robot Learning from Human Teachers. Synth. Lectures Artif. Intelligence Machine Learn. 8, 1–121. doi:10.2200/s00568ed1v01y201402aim028
Cortez, W. S., Oetomo, D., Manzie, C., and Choong, P. (2021). Control Barrier Functions for Mechanical Systems: Theory and Application to Robotic Grasping. IEEE Trans. Contr. Syst. Technol. 29, 530–545. doi:10.1109/TCST.2019.2952317
Dahlin, A., and Karayiannidis, Y. (2019). Adaptive Trajectory Generation under Velocity Constraints Using Dynamical Movement Primitives. IEEE Control. Syst. Lett. 4, 438–443. doi:10.1109/LCSYS.2019.2946761
Davoodi, M., Iqbal, A., Cloud, J. M., Beski, W. J., and Gans, N. R. (2021). “Probabilistic Movement Primitive Control via Control Barrier Functions,” in 2021 IEEE 17th International Conference on Automation Science and Engineering (CASE), Lyon, France, August 23–27, 2021, 697–703. doi:10.1109/CASE49439.2021.9551540
Geraerts, R., and Overmars, M. H. (2004). “A Comparative Study of Probabilistic Roadmap Planners,” in Algorithmic Foundations of Robotics V. Editors J.-D. Boissonnat, J. Burdick, K. Goldberg, and S. Hutchinson (Berlin/Heidelberg, Germany: Springer), 43–57. doi:10.1007/978-3-540-45058-0_4
Gomez-Gonzalez, S., Neumann, G., Scholkopf, B., and Peters, J. (2020). Adaptation and Robust Learning of Probabilistic Movement Primitives. IEEE Trans. Robot. 36, 366–379. doi:10.1109/tro.2019.2937010
Gomez-Gonzalez, S. (2019). Probabilistic Movement Primitive Library. Available at: https://github.com/sebasutp/promp.
Hsu, D., Kavraki, L. E., Latombe, J.-C., Motwani, R., and Sorkin, S. (1998). “On Finding Narrow Passages with Probabilistic Roadmap Planners,” in Proceedings of the Workshop on the Algorithmic Foundations of Robotics, Houston Texas USA, August 1998, 141–154.
Hsu, S.-C., Xu, X., and Ames, A. D. (2015). “Control Barrier Function Based Quadratic Programs with Application to Bipedal Robotic Walking,” in Proceedings of the American Control Conference, Chicago, IL, USA, July, 2015, 4542–4548. doi:10.1109/acc.2015.7172044
Ijspeert, A. J., Nakanishi, J., Hoffmann, H., Pastor, P., and Schaal, S. (2013). Dynamical Movement Primitives: Learning Attractor Models for Motor Behaviors. Neural Comput. 25, 328–373. doi:10.1162/neco_a_00393
Katharina, K. (2014). “Force Estimation in Robotic Manipulators: Modeling, Simulation and Experiments,” (Trondheim, Norway: Norwegian University of Science and Technology). Master’s thesis.
Kolavennu, S., Palanki, S., and Cockburn, J. C. (2001). Nonlinear Control of Nonsquare Multivariable Systems. Chem. Eng. Sci. 56, 2103–2110. doi:10.1016/s0009-2509(00)00470-x
Kolhe, J. P., Shaheed, M., Chandar, T. S., and Talole, S. E. (2013). Robust Control of Robot Manipulators Based on Uncertainty and Disturbance Estimation. Int. J. Robust. Nonlinear Control. 23, 104–122. doi:10.1002/rnc.1823
Kragic, D., Gustafson, J., Karaoguz, H., Jensfelt, P., and Krug, R. (2018). “Interactive, Collaborative Robots: Challenges and Opportunities,” in Proceedings of the International Joint Conference on Artificial Intelligence, Stockholm Sweden, July, 2018, 18–25. doi:10.24963/ijcai.2018/3
LaValle, S. M., Kuffner, J. J., and Donald, B. (2001). Rapidly-exploring Random Trees: Progress and Prospects. Algorithmic Comput. Robotics: New Dir. 5, 293–308. doi:10.1201/9781439864135-43
LaValle, S. M. (1998). Rapidly-exploring Random Trees: A New Tool for Path Planning. Pennsylvania, United States: CiteSeerX.
Lazaric, A., and Ghavamzadeh, M. (2010). “Bayesian Multi-Task Reinforcement Learning,” in Proceedings of the International Conference on Machine Learning, Haifa Israel, June, 2010, 599–606.
Lopez, B. T., Slotine, J.-J. E., and How, J. P. (2020). Robust Adaptive Control Barrier Functions: An Adaptive and Data-Driven Approach to Safety. Control. Syst. Lett. 5, 1031–1036. doi:10.1109/LCSYS.2020.3005923
Mathew, M. (2018). PROMP Library Written in Python. Available at: https://github.com/mjm522/promps_python.
Mohanan, M. G., and Salgoankar, A. (2018). A Survey of Robotic Motion Planning in Dynamic Environments. Robotics Autonomous Syst. 100, 171–185. doi:10.1016/j.robot.2017.10.011
Nguyen, Q., and Sreenath, K. (2016). “Exponential Control Barrier Functions for Enforcing High Relative-Degree Safety-Critical Constraints,” in Proceedings of the American Control Conference, Boston, MA, USA, July 2016, 322–328. doi:10.1109/acc.2016.7524935
Paraschos, A., Daniel, C., Peters, J., and Neumann, G. (2018a). Using Probabilistic Movement Primitives in Robotics. Auton. Robot 42, 529–551. doi:10.1007/s10514-017-9648-7
Paraschos, A., Rueckert, E., Peters, J., and Neumann, G. (2018b). Probabilistic Movement Primitives under Unknown System Dynamics. Adv. Robotics 32, 297–310. doi:10.1080/01691864.2018.1437674
Rauscher, M., Kimmel, M., and Hirche, S. (2016). “Constrained Robot Control Using Control Barrier Functions,” in Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Daejeon, Korea (South), October 2016, 279–285. doi:10.1109/iros.2016.7759067
Sakai, A., Ingram, D., Dinius, J., Chawla, K., Raffin, A., and Paques, A. (2018). Pythonrobotics: a python Code Collection of Robotics Algorithms. arXiv, 1–8. arXiv preprint arXiv:1808.10703.
Saveriano, M., and Lee, D. (2019). Learning Barrier Functions for Constrained Motion Planning with Dynamical Systems. IEEE/RSJ International Conference on Intelligent Robots and Systems, Macau, China, November, 2019, 112–119. doi:10.1109/IROS40897.2019.8967981
Sloth, C., Wisniewski, R., and Pappas, G. J. (2012). “On the Existence of Compositional Barrier Certificates,” in Proceedings of the IEEE Conference on Decision and Control, Maui, HI, USA, December 2012, 4580–4585. doi:10.1109/cdc.2012.6426178
Spong, M. W., and Vidyasagar, M. (2008). Robot Dynamics and Control. Hoboken, New Jersey, United States: John Wiley & Sons.
Srinivasan, M., and Coogan, S. (2021). Control of mobile Robots Using Barrier Functions under Temporal Logic Specifications. IEEE Trans. Robot. 37, 363–374. doi:10.1109/TRO.2020.3031254
Vadakkepat, P., Tan, K. C., and Ming-Liang, W. (2000). “Evolutionary Artificial Potential fields and Their Application in Real Time Robot Path Planning,” in Proceedings of the Congress on Evolutionary Computation (IEEE), La Jolla, CA, USA, July 2000, 256–263.
Vicentini, F. (2021). Collaborative Robotics: A Survey. J. Mech. Des. 143, 040802. doi:10.1115/1.4046238
Warren, C. W. (1989). “Global Path Planning Using Artificial Potential fields,” in Proceedings of the IEEE International Conference on Robotics and Automation, Scottsdale, AZ, USA, May 1989, 316–317.
Wieland, P., and Allgöwer, F. (2007). Constructive Safety Using Control Barrier Functions. IFAC Proc. Volumes 40, 462–467. doi:10.3182/20070822-3-za-2920.00076
Keywords: motion control, movement primitives, learning from demonstration, robot safety, nonlinear control
Citation: Davoodi M, Iqbal A, Cloud JM, Beksi WJ and Gans NR (2022) Safe Robot Trajectory Control Using Probabilistic Movement Primitives and Control Barrier Functions. Front. Robot. AI 9:772228. doi: 10.3389/frobt.2022.772228
Received: 07 September 2021; Accepted: 07 February 2022;
Published: 16 March 2022.
Edited by:
Holger Voos, University of Luxembourg, LuxembourgReviewed by:
Reza Ghabcheloo, Tampere University, FinlandHamed Habibi, University of Luxembourg, Luxembourg
Copyright © 2022 Davoodi, Iqbal, Cloud, Beksi and Gans. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nicholas R. Gans, bmdhbnNAdXRhLmVkdQ==
 Mohammadreza Davoodi
Mohammadreza Davoodi Asif Iqbal
Asif Iqbal Joseph M. Cloud
Joseph M. Cloud William J. Beksi
William J. Beksi Nicholas R. Gans
Nicholas R. Gans