Model-Based Nonlinear Feedback Controllers for Pressure Control of Soft Pneumatic Actuators Using On/Off Valves

1 Introduction

Soft robotics is a rapidly growing field in which the robots are elastically deformable (Rus and Tolley, 2015; Bao et al., 2018; Xu and Wang, 2021). Soft robots can be actuated using dieletric elastomers, shape-memory alloys, magnetic actuation, photo-responsive materials, tendon-driven approaches, or fluid power (El-Atab et al., 2020; Yang et al., 2020). Pneumatic or hydraulic soft robots are used in applications such as minimally invasive surgery (Runciman et al., 2019), rehabilitation (Wehner et al., 2013), elderly assistance (Ansari et al., 2017), safe human–robot interaction (De Greef et al., 2009), and handling of fragile materials (Shintake et al., 2018). Fluid-driven soft robots offer high dexterity and safety, large deformation, good power-to-weight ratio, and low manufacturing cost (El-Atab et al., 2020; Tawk and Alici, 2021). Soft robots are fabricated from soft actuators, including single-, double-, and multi-chambered actuators, fiber-reinforced actuators, and omnidirectional actuators (Gorissen et al., 2017; Xavier et al., 2021a).

Soft pneumatic actuators are usually controlled with proportional or on/off solenoid valves (Skorina et al., 2017; Booth et al., 2018; Wang et al., 2019a; Young et al., 2021). The most popular pneumatic control architecture for soft robotics is the fluidic control board, an open source hardware platform available from the Soft Robotics Toolkit (Soft robotics toolkit, 2019) that was originally employed in the experimental platform of Galloway et al. (2013), Polygerinos et al. (2013), and Polygerinos et al. (2015) and has since then inspired many pneumatic control systems (Onal and Rus, 2013; Luo et al., 2014a; Luo et al., 2014b). The board consists mainly of a diaphragm pump, a set of solenoid valves, and pressure sensors for feedback control. MOSFETs allow the use of Pulse-Width Modulation (PWM) to control the pressure of fluid passing through the valves. Pressure can also be controlled using pressure regulators; however, this allows only one pressure in the whole system. Recently, a number of other open-source pneumatic drivers have also been proposed such as FlowIO (Shtarbanov, 2021), Pneuduino (Ou et al., 2016), and PneuSoRD (Young et al., 2021).

The literature describes various model-based nonlinear control strategies for pneumatic cylinders and hydraulic systems (Rahmat et al., 2011; Weist et al., 2011; Saravanakumar et al., 2017), such as sliding modes (Paul et al., 1994; Richer and Hurmuzlu, 2000; Barth et al., 2002; Nguyen et al., 2007), State-Dependent Riccati Equation (SDRE) (Weickgenannt et al., 2010; Strano and Terzo, 2015; Strano and Terzo, 2016), feedback linearization (Lee et al., 2002; Ke et al., 2007), and adaptive (Tsai and Huang, 2008; Zhihong Rao and Bone, 2008) and fuzzy (Shih and Ma, 1998; Chillari et al., 2001) controllers. In contrast to their rigid counterparts, model-based dynamic controllers for the more recent soft pneumatic actuators are still in their nascent stage (Skorina et al., 2017; Wang et al., 2019a). For pneumatic-driven soft robots, the nonlinearities arising from hyperelastic materials, complex geometries, and the compressibility of air hinder the development of accurate mathematical models. Analytical models for soft actuators have been developed using the piecewise constant curvature approach (Webster and Jones, 2010; Marchese et al., 2014a), the Lagrangian approach (Wang et al., 2019b; Cao et al., 2021a), the Euler–Bernoulli principle (Gorissen et al., 2011; Polygerinos et al., 2015; Xiao et al., 2021), the Castigliano method (Drotman et al., 2017; Drotman et al., 2019), the theory of Cosserat rods (Bartholdt et al., 2021; Berthold et al., 2021), and data-driven approaches (Elgeneidy et al., 2018; Mohamed et al., 2020). Alternatively, a modeling framework for pneumatic systems can be developed using an energy-based approach to derive lumped parameter models for fluid circuit components (Watton, 1989; De Silva, 2004; Karnopp et al., 2012). In particular, pneumatic sources act as current sources, fluidic tubing and channels act as impedances, and fluidic chambers act as capacitances (Onal and Rus, 2013; Marchese et al., 2014a; Xavier et al., 2020). Relying on the electrical circuit equivalence of pneumatic systems, the dynamic behavior of a bending soft actuator can be approximated as a lumped second-order dynamic equation (Onal and Rus, 2013; Skorina et al., 2015).

Using this second-order equation, sliding mode controllers are developed in the works of Skorina et al. (2015), Luo et al. (2017), and Khan and Li (2020) to control the bending angle of soft actuators governed by high-speed on/off solenoid valves. A sliding mode controller with a static mapping function to create a feedforward augmented sliding mode controller is proposed by Skorina et al. (2015), which improved tracking for dynamic trajectories under a payload. A model reference adaptive controller augmented by a feedforward inverse dynamic controller is used by Skorina et al. (2017) to demonstrate the versatility of the proposed control approach. Alternatively, a purely data-driven approach can be used to control the bending angle of soft actuators (Elgeneidy et al., 2018). An observer-based adaptive sliding mode controller using a dynamic model on the basis of the Euler–Lagrange method is proposed by Cao et al. (2021b) to estimate the velocity information and track desired bending angle references.

Experimentally tuned PID and on-off controllers have also been extensively used in fluid-powered soft robots (Khan et al., 2020; Xavier et al., 2021b), such as snake-like (Onal and Rus, 2013), worm-like (Calderón et al., 2016), soft-bodied fish (Marchese et al., 2014b), and manta ray (Suzumori et al., 2007) robots. Automatic tuning of ordinary, piecewise, and fuzzy PI controllers using a heuristic-based coordinate descent algorithm is proposed by Khan et al. (2020), which was shown to generally produce better results than manually tuned parameters. The sliding mode controller in the work of Ibrahim et al. (2019) outperformed the PID controller in the simulation results; however, the PID controller performed best in experimental work, at the expense of higher overshoot and lower robustness to external forces. Conversely, the sliding mode controller with a PID sliding surface in the work of Khan and Li (2020) dampens vibration on deactuation in comparison to an experimentally tuned PID controller.

The articles described above have presented controllers for bending angle or extension motions, i.e., high-level control (George Thuruthel et al., 2018). However, few works have considered the impact of the pneumatic system on the soft actuator performance and developed low-level control (pressure control) strategies. Regardless of the soft actuator design, the pneumatic system critically affects the pressure dynamics of soft actuators (Xavier et al., 2020; Joshi and Paik, 2021). While the actuation mode, force, and displacement are governed by the actuator design and loading conditions, the actuation speed is largely determined by the pressure and flow dynamics of the soft pneumatic actuator (Joshi et al., 2021). Therefore, pressure control plays a major role in the overall performance of soft robots (Skorina et al., 2017; George Thuruthel et al., 2018). In the work of Wang et al. (2019a), a pneumatic model was used to control the bending angle of a pneumatic network actuator using a robust backstepping controller with two-way, two-position on/off valves. Sliding mode controllers are proposed by Ibrahim et al. (2019; 2021) to control the pressure of a soft actuator using proportional valves. In the work of Chen et al. (2020), a pneumatic model is included to control the bending angle of a fiber-reinforced actuator using two three-way, two-position on/off valves with a backstepping-based adaptive robust controller and sliding mode controller. In the work of Falkenhahn et al. (2016), feedback linearization is proposed to control the motion of a bellow-shaped continuum manipulator with proportional valves. Sliding mode controllers are also used by Jouppila et al. (2014) for position control of a pneumatic muscle in a comparative study between three approaches using on/off valves and traditional servo valves. Finally, cascade control structures have also been proposed where the faster inner layer performs pressure control and outer layer is responsible for open-loop angle control (Yi et al., 2018; Zhou et al., 2019).

1.1 Contributions

In this article, analytical and simulations models are developed for the pressure dynamics of soft pneumatic actuators governed by pneumatic systems with three-way, two-position on/off valves and a pressure-regulated receiver, as shown in Figure 1. On the basis of the analytical model, three nonlinear feedback controllers are derived for low-level control of soft actuators: SDRE, sliding mode, and feedback linearization. The tracking performance and robustness of these controllers is enhanced by augmenting the sliding mode and feedback linearization controllers with integral action. The mathematical model is also used to determine a feedforward component that is augmented to a PI controller with anti-windup. The control strategies are evaluated on a simulation model developed in Simscape Fluids and also experimentally on a bending soft pneumatic actuator using an Arduino Due and Simulink. The performance of the controllers is evaluated using metrics for the tracking performance and control effort. The simulation and experimental results demonstrate the effectiveness of the proposed nonlinear controllers for pressure tracking.

FIGURE 1

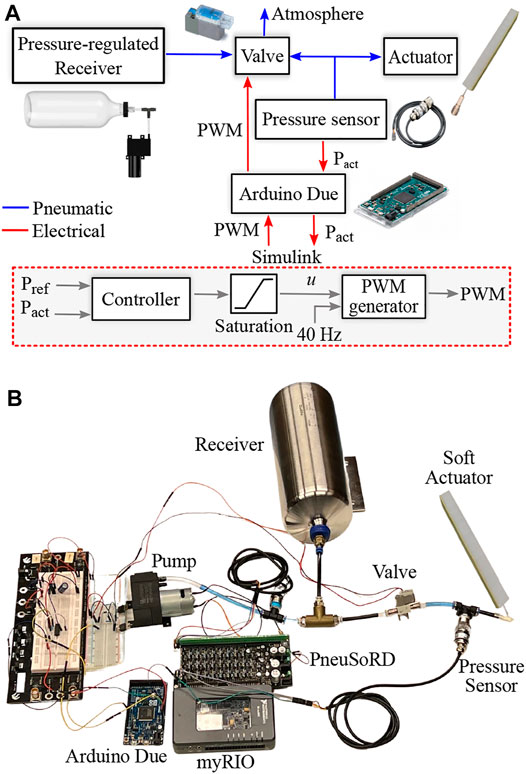
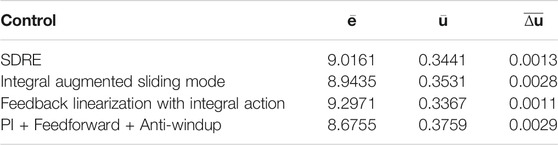
FIGURE 1. Pneumatic system with 3/2 valve and pressure-regulated receiver. The pressure of the soft actuator is regulated by controlling the duty cycle of the valve with a 40-Hz PWM signal. The dotted red box illustrates the implementation of the control strategies in Simulink. (A) High-level description. (B) Physical system.

The remainder of this article is organized as follows. Section 2 describes the air dynamics model for the soft actuator, and Section 3 presents the parameter selection for the pneumatic system. Section 4 describes the model-based nonlinear controllers used in this study. Section 5 presents simulation results for the control strategies based on a model developed within Simscape Fluids. In Section 6, experimental results of the closed-loop tracking performances are evaluated and compared to the simulations. Finally, Section 7 discusses the conclusions of this work.

2 Modeling

The pneumatic system in this work employs a single three-way, two-position on/off valve, a diaphragm pump, and pressure sensors for feedback control, as shown in Figure 1. An air receiver (reservoir) is employed to improve response speed and efficiency while minimizing the peak pump flow rate. The inlet port of the valve is connected to the receiver; the outlet port is connected to the soft actuator. Pressure control in the actuator is performed by controlling the duty cycle of the PWM wave into the valve.

2.1 Fundamental Equations

Two fundamental equations are used to model the air pressure dynamics of the pneumatic system. The polytropic gas law is used to model the actuator pressurization, and the valve model ANSI/(NFPA)T3.21.3 is used to characterize the flow rate during charging and discharging.

1) Polytropic gas law (equation of state)

$P{V}^{\gamma }=constant(1)$

where $P$ is the pressure, $V$ is the volume, and $\gamma$ is the polytropic index. For an isothermal process, $\gamma =1$, whereas, for an isentropic process (adiabatic and reversible), $\gamma =k=c_p/c_v=1.4$. The pressure and volume in the equation above may have various different units. In this work, $P$ has absolute bar units to comply with the valve model and $V$ is in liters. However, note that the pressure is measured and presented in relative kilopascals for the simulation and experimental results; hence, appropriate unit conversions are adopted as required. Differentiating both sides,

$\gamma P{V}^{\gamma -1}\frac{dV}{dt}+V^{\gamma }\frac{dP}{dt}=0\Rightarrow Q=\frac{V}{\gamma P}\frac{dP}{dt}(2)$

where $Q=-\frac{dV}{dt}$ is the volume flow rate into the actuator.

2) Valve model ANSI/(NFPA)T3.21.3

Volumetric flow rate $Q$ (L/s) through a valve is given by

$Q=\frac{114.5u{C}_v\sqrt{P_{low}\mathrm{\Delta }P}}{\sqrt{T_{high}}}(3)$

where $\mathrm{\Delta }P=P_{high}-P_{low}$, $P_{high}$ and $P_{low}$ are the absolute upstream and downstream pressures (bar), $u$ is the duty cycle of the PWM signal applied to the valve, $C_v$ is the flow coefficient, and $T_{high}$ is the upstream temperature (kelvin).

2.2 Pressure Dynamics of Actuator

The net flow into the soft actuator is given by $Q=Q_c-Q_d$, where $Q_c$ and $Q_d$ are the flow rates for the charging and discharging valves. Then, in Eq. 2,

$\frac{d{P}_A}{dt}=\frac{\gamma P_A}{V_A}(Q_c-Q_d)(4)$

where $P_A$ (absolute bar) and $V_A$ (L) are the pressure and volume of the actuator. From Eq. 3,

$Q_c=\frac{114.5u_c{C}_v\sqrt{P_A(P_R-P_A)}}{\sqrt{T_R}}(5)$

$Q_d=\frac{114.5u_d{C}_v\sqrt{P_{atm}(P_A-P_{atm})}}{\sqrt{T_A}}(6)$

where $u_c$ and $u_d$ are the duty cycles for the charging and discharging valves, respectively; $P_R$ is the receiver pressure (absolute bar); and $T_R$ and $T_A$ are receiver and actuator temperatures (kelvin), respectively. Here, $T_R=T_A=T=293.15$K.

Inserting Eqs. 4, 5 into Eq. 4 and defining $\alpha =\frac{114.5\gamma C_v}{V_A\sqrt{T}}$ yields

$\frac{d{P}_A}{dt}=\alpha P_A\left(u_c\sqrt{P_A(P_R-P_A)}-u_d\sqrt{P_{atm}(P_A-P_{atm})}\right)(7)$

For pneumatic systems with a 3/2 valve, a single PWM signal is used; hence, $u_c=u$ and $u_d=(1-u)$. Set $x=P_A$, $c_1=P_R$, and $c_2=P_{atm}$ in Eq. 7; then, the actuator model takes the form

$\dot{x}=f(x)+g(x)u(8)$

$f(x)=-\alpha x\sqrt{c_2(x-c_2)}(9)$

$g(x)=\alpha x\left(\sqrt{x(c_1-x)}+\sqrt{c_2(x-c_2)}\right)(10)$

3 Open-Loop System Design

Prior to evaluating the performance of nonlinear controllers, the open-loop system response is evaluated to determine the physical limitations of the pneumatic system and select the required pneumatic components given soft actuator specifications and desired pressure response characteristics. A parameter selection procedure is proposed by (Xavier et al. (2021b) using the ISO6358 standard for the valves, which can be converted to ANSI/(NFPA) T3.21.3 after valve selection. Following the procedure in the work of Xavier et al. (2021b).

1) Define actuator characteristics and requirements:

$•$ Desired pressure $P_A$ and volume $V_A$ of the actuator: $P_A=$ 60 kPa (161.325 kPa absolute), $V_A=$ 30 ml.

$•$ Desired rise time $T_{rise}$ of the response: $T_{rise}=$ 0.25 s.

$•$ Maximum number of actuation cycles per minute $N$: $N=$ 30 cycles/min.

2) Select receiver parameters:

$•$ $V_R>10\times V_A$: $V_R=$ 2 L.

$•$ $P_R>1.2\times P_A$ and $P_R\in \{\mathrm{100,150,200}\}\text{kPa}$: $P_R=$ 100 kPa.

3) Select valve sonic conductance $C$:

•Use Figure 5 in the work of Xavier et al. (2021b) to determine the normalized conductance $\bar{C}$ for desired $P_A$ and $T_{rise}$: $\bar{C}=$ 1.04.

$•$For the corresponding $\bar{C}$, select $C\ge \bar{C}\times V_A$:

$C\ge$ 0.031 L/(s$\cdot$bar).

4) Select valve configuration:

$•$ three-way, two-position V114 (SMC) with $C=0.037$L/(s$\cdot$bar). Therefore, $C_v=0.008$.

5) Select air pump flow in liters per minute (LPM):

•From Eq. 15, $Q_{Pump}(P_R)\ge Q_{req,3way}$ = 0.6 + 1.3 = 1.9 LPM. Hence, the KYK50BPM pump is selected.

From Equation 4, the volume of air $V_{air}$ (L) consumed during one actuation cycle from atmospheric pressure $P_{atm}$ to the desired pressure $P_A$ is

$V_{air}=\frac{V_A}{\gamma }\ln \left(\frac{P_A}{P_{atm}}\right)(11)$

Consequently, for $N$ actuation cycles per minute, the required flow $Q_{req}$ (LPM) from the air pump to keep the receiver at constant pressure is

$Q_{req}=\frac{N\times V_A}{\gamma }\ln \left(\frac{P_A}{P_{atm}}\right)(12)$

For three-way valves, an additional volume of air is consumed during regulation due to frequent switching and release of air to the atmosphere. The additional flow in liters per second is

$Q_{add}=\frac{114.5u_{ff}{C}_v\sqrt{P_A(P_R-P_A)}}{\sqrt{T}}(13)$

where $u_{ff}$ is the required duty cycle for a desired pressure. This is obtained by setting $\dot{x}=0$ in Eq. 8, which results in

$u_{ff}=\frac{\sqrt{c_2(x_d-c_2)}}{\sqrt{x_d(c_1-x_d)}+\sqrt{c_2(x_d-c_2)}}(14)$

Therefore, the total required flow for three-way valves $Q_{req,3way}$ is

$Q_{req,3way}=Q_{req}+60\times Q_{add}[\text{in\hspace{0.17em}LPM}](15)$

Therefore, the setup investigated here employs the diaphragm pump KYK50BPM, a V114 on/off valve, a 2 L receiver, two pressure sensors (SEN0257, DFRobot) and tubing between each of these elements. The pneumatic soft robotics driver (PneuSoRD) proposed by Young et al. (2021) is used with myRIO to control the pressure of the receiver and minimize sensor noise due to switching of the valve and motor. The inlet port of the valve is connected to the receiver, the outlet port is connected to the soft actuator and the exhaust port is open to atmosphere. The PWM output for the motor is connected to PneuSoRD (Young et al., 2021) and the PWM outputs for the valves are each connected to a BJT transistor (TIP31A) through a 330$\mathrm{\Omega }$ resistor. A flyback diode (1n5817) is added to dissipate energy stored in the solenoid during turn-off.

4 Controller Design

In this section, the three nonlinear controllers are described, in addition to the PI controller with feedforward and anti-windup. SDRE control provides a systematic and effective algorithm for designing nonlinear controllers by allowing nonlinearities in the system states while additionally offering great design flexibility. Sliding mode controllers provide a systematic approach for robust control and have found extensive application in pneumatic systems because switched control laws can provide high performance for systems employing PWM. The feedback linearization approach has a straightforward implementation for single-input, single-output nonlinear systems in normal form (Eq. 8) and allows for the development of various state-space control techniques available for linear systems, such as pole placement and linear quadratic regulator design.

4.1 State-Dependent Riccati Equation Control

The general infinite-horizon nonlinear regulator problem is defined by the minimization of the following performance criterion:

$J={\int }_0^{\infty }{x}^T(t)Q(x)x(t)+u^T(t)R(x)u(t)dt(16)$

with respect to the state $x$ and the control $u$ subject to the nonlinear differential constraint Eq. 8, where $Q(x)\ge 0$ and $R(x)>0$ for all $x$, and $f(x),g(x),R(x),Q(x)\in C^k$, $k\ge 1$. The controller parameters can be tuned by recalling that $Q$ penalizes the tracking error and $R$ penalizes control authority. If the elements of $Q$ are large compared to the elements of $R$, then the states remain small, whereas large values for $R$ guarantee small control inputs.

The SDRE design proceeds as follows (Mracek and Cloutier, 1998; Çimen, 2010; Nekoo, 2019).

1) Use direct parameterization to bring the nonlinear dynamics to the State-Dependent Coefficient form, i.e.,

$\dot{x}=A(x)x+B(x)u(17)$

where

$f(x)=A(x)x\text{\hspace{0.17em},\hspace{0.17em}}B(x)=g(x)(18)$

2) Solve the SDRE

$P(x)A(x)+A^T(x)P(x)-P(x)B(x)R^{-1}(x)B^T(x)P(x)+Q(x)=0(19)$

3) Construct the nonlinear feedback controller

$u=-R^{-1}(x)B^T(x)P(x)x(20)$

For regulation to non-zero set points, the following error variables are defined: $\tilde{x}=x-x_d$ and $\tilde{u}=u-u_d$, where $x_d$ and $u_d$ are the desired (or reference) values. The control objective becomes the minimization of the error, i.e., $\tilde{x}\to 0$ as $t\to \infty$, which implies $x\to x_d$ as $t\to \infty$. The following error system is obtained (refer to Appendix for derivation),

$\dot{\stackrel{̃}{x}}=A(\tilde{x})\tilde{x}+B(\tilde{x})\tilde{u}(21)$

where

$A(\tilde{x})=-\alpha a_1+\alpha a_2{u}_d+\alpha a_1{u}_d+a_3/\tilde{x}$

$B(\tilde{x})=\alpha x_d{a}_2+\alpha \tilde{x}{a}_2+\alpha x_d{a}_1+\alpha \tilde{x}{a}_1$

$a_1=\sqrt{c_2(x_d+\tilde{x}-c_2)}$, $a_2=\sqrt{(x_d+\tilde{x})(c_1-x_d-\tilde{x})}$

$a_3=-\alpha x_d{a}_1+\alpha x_d{a}_2{u}_d+\alpha x_d{a}_1{u}_d+\alpha x_d{a}_{1d}-\alpha x_d{a}_{2d}{u}_d-\alpha x_d{a}_{1d}{u}_d$

$a_{1d}=\sqrt{c_2(x_d-c_2)}$, $a_{2d}=\sqrt{x_d(c_1-x_d)}$

From step (2), the SDRE is

$2P(\tilde{x})A(\tilde{x})-\frac{P^2(\tilde{x})B^2(\tilde{x})}{R(\tilde{x})}+Q(\tilde{x})=0(22)$

whose positive-definite solution is

$P(\tilde{x})=\frac{R(\tilde{x})}{B^2(\tilde{x})}\left(A(\tilde{x})+\sqrt{A^2(\tilde{x})+\frac{B^2(\tilde{x})Q(\tilde{x})}{R(\tilde{x})}}\right)(23)$

From step (3), the control law for the error system is

$\tilde{u}=-\frac{1}{B(\tilde{x})}\left(A(\tilde{x})+\sqrt{A^2(\tilde{x})+\frac{B^2(\tilde{x})Q(\tilde{x})}{R(\tilde{x})}}\right)\tilde{x}(24)$

Therefore, the overall control is $u=u_d+\tilde{u}$, which has a feedback component $\tilde{u}$ and a feedforward component $u_d=u_{ff}$ given by Eq. 14. For this scalar system, the SDRE nonlinear feedback solution and its associated state $\tilde{x}$ and co-state $\lambda =P(\tilde{x})\tilde{x}$ satisfy the conditions for optimality of the nonlinear regulator problem, i.e., $H_u=0$ and $\dot{\lambda }=-H_x$, where $H$ is the Hamiltonian of the system (Mracek and Cloutier, 1998; Naidu, 2002). Because the performance index is convex and the differential constraint is linear in $u$ and because $u$ is a scalar, there exists only one solution which is, therefore, globally asymptotically stable and globally optimal (Çimen, 2012). In addition, because the SDRE can be solved analytically, ${\lim }_{\left|\tilde{x}\right|\to 0}A(\tilde{x})$ does not have to be finite as long as ${\lim }_{\left|\tilde{x}\right|\to 0}A(\tilde{x})\tilde{x}$ is finite. For further details on the proof that these necessary conditions are satisfied and the derivation of the SDRE control law, readers are referred to the works of Cloutier et al. (1996) and Mracek and Cloutier (1998). Note that this exact solution greatly simplifies the implementation of the control law because it does not require the Riccati equation to be solved in each time step. Exact solutions are also proposed by Nekoo and Geranmehr (2013) and Rafee Nekoo (2013), where an online control update formulation is also discussed for more complex systems.

4.2 Integral Augmented Sliding Mode Controller

The conventional sliding surface for sliding mode control (SMC) is given by Slotine and Li (1991)

$s(t)={\left(\frac{\mathrm{d}}{\mathrm{d}t}+\lambda \right)}^{n-1}\tilde{x}(t)(25)$

where $n$ is the order of the system and $\lambda$ is a strictly positive constant. The problem of tracking $x=x_d$ is equivalent to that of remaining on the surface $s(t)$ for all $t>0$; thus, the problem can be reduced to that of keeping the scalar quantity $s$ at zero. The dynamics, while in sliding mode, is given by $\dot{s}=0$, from which the equivalent control $\widehat{u}$ is obtained. To satisfy the sliding condition and ensure that the system trajectories remain on the surface $s(t)=0$ despite uncertainty on the dynamics $f$, a discontinuous control term $u_s$ across $s(t)=0$ is added to $\widehat{u}$: $u=\widehat{u}-k_s\mathrm{sgn}(s)$, where the constant $k_s$ increases with the extent of parametric uncertainty (Slotine and Li, 1991). The two main uncertain parameters are the soft actuator volume, which increases during pressurization, and the receiver pressure, which oscillates due to rapid bursts of flow into the actuator. In general, larger $k_s$ results in faster rise time but increases chattering in the soft actuator response. Therefore, in practice, the $k_s$ values are increased until satisfactory transient performance is achieved while maintaining reasonable control chattering and minimizing control saturation.

The discontinuous control law can be smoothed to achieve a trade-off between chattering and the magnitude of the tracking error. This is achieved by introducing a thin boundary layer around the sliding surface. Hence, SMC law is

$u=\widehat{u}-k_s\text{sat}\left(\frac{s}{\mathrm{\Phi }}\right)=\widehat{u}-k_s\left\{\begin{array}{cc}\frac{s}{\mathrm{\Phi }},\hfill & \left|\frac{s}{\mathrm{\Phi }}\right|\le 1\hfill \\ \mathrm{sgn}\left(\frac{s}{\mathrm{\Phi }}\right),\hfill & \left|\frac{s}{\mathrm{\Phi }}\right|>1\hfill \end{array}\right.(26)$

where $\mathrm{\Phi }$ is the boundary layer thickness.

The tracking accuracy can be improved by introducing integral action into the sliding surface (Eker and Akınal, 2008):

$s(t)={\left(\frac{\mathrm{d}}{\mathrm{d}t}+\lambda \right)}^{n-1}\tilde{x}(t)+k_i{\int }_{t_0}^t\tilde{x}(\tau )\text{d}\tau (27)$

where $k_i$ is the integral gain.

A necessary condition for the output trajectory to remain on the sliding surface is

$\dot{s}=0\Rightarrow \dot{\stackrel{̃}{x}}+k_i\tilde{x}=0(28)$

Choosing $k_i>0$, the characteristic polynomial $s+k_i=0$ is strictly Hurwitz; therefore, $\tilde{x}\to 0$ as $t\to \infty$ and the closed-loop system is globally asymptotically stable. From Eq. 28, the equivalent control is

$\widehat{u}=\frac{1}{g(x)}\left({\dot{x}}_d-f(x)-k_i(x-x_d)\right)(29)$

Therefore, the overall SMC is

$u=\frac{1}{g(x)}\left({\dot{x}}_d-f(x)-k_i(x-x_d)\right)-k_s\text{sat}\left(\frac{s}{\mathrm{\Phi }}\right)(30)$

with $s=\tilde{x}(t)+k_i{\int }_{t_0}^t\tilde{x}(\tau )\text{d}\tau$, $f(x)$ defined in Eq. 9 and $g(x)$ in Eq. 10.

4.3 Feedback Linearization With Integral Action

Here, the pressure of the actuator is defined as the output of the system, i.e., $y=h(x)=x$. Because $\frac{\partial h}{\partial x}\ne 0$, a linear input–output relationship for the system defined in Eq. 8 can be obtained with the control law (Marquez, 2003)

$u=\frac{1}{L_{g}h(x)}\left(-L_{f}h(x)+v\right)(31)$

where $L_{f}h(x)=\frac{\partial h}{\partial x}f(x)$ is the Lie derivative of $h$ with respect to $f$ and $L_{g}h(x)=\frac{\partial h}{\partial x}g(x)$ is the Lie derivative of $h$ with respect to $g$. Because $\frac{\partial h}{\partial x}=1$, the control law becomes

$u=\frac{1}{g(x)}\left(-f(x)+v\right)(32)$

with $f(x)$ defined in Eq. 9 and $g(x)$ in Eq. 10. This control law renders the linear differential equation

$\dot{x}=v(33)$

To compensate for model uncertainties and improve reference tracking, integral action is introduced by augmenting the system with a state that integrates the tracking error $\dot{\sigma }=x-x_d$. Hence, the state-space model is given by

$\left[\begin{array}{c}\hfill \dot{\stackrel{̃}{x}}\hfill \\ \hfill \dot{\sigma }\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill \tilde{x}\hfill \\ \hfill \sigma \hfill \end{array}\right]+\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right]\left(v-{\dot{x}}_d\right)(34)$

Defining $w=v-{\dot{x}}_d$, the gains $k$ and $k_i$ in the control law $w=-k\tilde{x}-k_i\sigma$ can be obtained with standard controller design techniques for linear systems such as pole placement. In practice, the gain $k$ is increased until no significant changes are observed in the rise time of the soft actuator response and $k_i$ is kept at low values because large $k_i$ gains were observed to make the response slower to initial set point changes. Therefore, the linear control component is

$v=-k\tilde{x}(t)-k_i{\int }_{t_0}^t\tilde{x}(\tau )d\tau +{\dot{x}}_d(t)(35)$

Finally, the overall control is obtained by introducing Eq. 35 into Eq. 32.

4.4 PI Controller With Feedforward and Anti-windup

The nonlinear controllers discussed above are compared to a PI controller augmented with feedforward. The inclusion of feedforward improves reference tracking and reduces the control effort from the feedback component, which is responsible to compensate for model uncertainty, i.e., to correct any miscalculation involved in the anticipatory control action inherent in feedforward (Goodwin et al., 2001).

The feedforward component $u_{ff}$ for a desired pressure is obtained from Eq. 14. The overall control law is

$u=-k_p\tilde{x}(t)-k_i{\int }_{t_0}^t\tilde{x}(\tau )d\tau +u_{ff}(36)$

where $k_p$ and $k_i$ are the proportional and integral gains of the PI controller.

Considering the duty cycle of the valve is limited between 0 and 1 and large set point changes are usually desired in soft robotic applications, the integral term becomes unacceptably large leading to poor transient response (e.g., large settling time) without an anti-windup mechanism. Here, anti-windup is implemented using conditional integration (integrator clamping), where the integration is disabled when the duty cycle saturates (Visioli, 2006; Åström and Hägglund, 2006).

5 Simulation Results

5.1 Simscape Model

Using the mathematical model, the duty cycle is directly applied to the valve equations. However, in practical systems, the duty cycle is converted to a PWM wave and then applied to the valve. The system model is developed in Simscape Fluids within MATLAB/Simulink, as shown in Figure 2. The pneumatic components are shown in magenta and include the flow rate source, receiver, pipe, 3/2 solenoid valve, and the soft actuator. The actuator is modeled as a constant volume chamber. This is a reasonable assumption considering fiber-reinforced bending actuators, pneumatic network actuators, 3D/4D-printed actuators, and actuators fabricated with harder silicone rubbers exhibit low levels of volume change due to ballooning (Chen et al., 2020; Xavier et al., 2021b). Pressure sensors are added to the actuator and receiver, and random sensor noise with zero mean and 0.5-kPa variance is added to the pressure measurements.

FIGURE 2

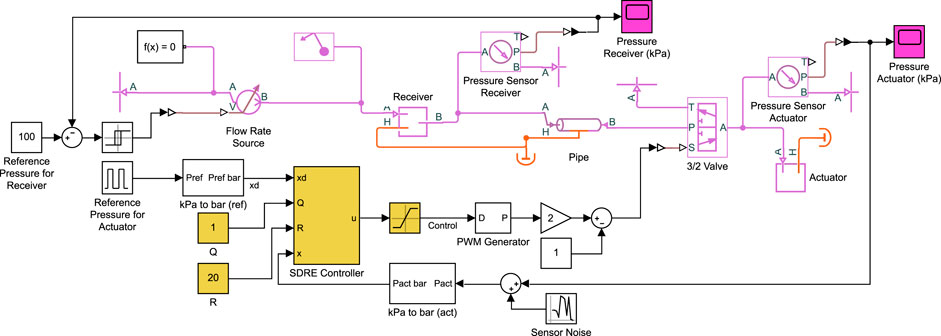
FIGURE 2. Model of pneumatic control system in Simulink. The diaphragm pump is modeled as a volumetric flow rate source, the pneumatic line as a pipe, and the air receiver and actuator as constant volume chambers. Here, the SDRE controller is shown in yellow, where the SDRE controller block contains the implementation of Eqs. 24 and 14. Equivalent blocks are used for the other controllers. Pressure sensors are added to the actuator and receiver and random sensor noise is added to the pressure measurements.

5.2 Performance Evaluation

The control methods proposed in Section 4 are evaluated with simulations using Simscape Fluids. A polytropic index of 1.2 is used in the controller design as this value showed excellent agreement between the mathematical and Simscape models. The tracking performance and control inputs for a reference square wave with a period of 2 s are shown in Figure 3. The controller parameters are tuned empirically via simulation to minimize the settling time and overshoot of the pressure responses following the general guidelines for each controller provided in Section 4.

FIGURE 3

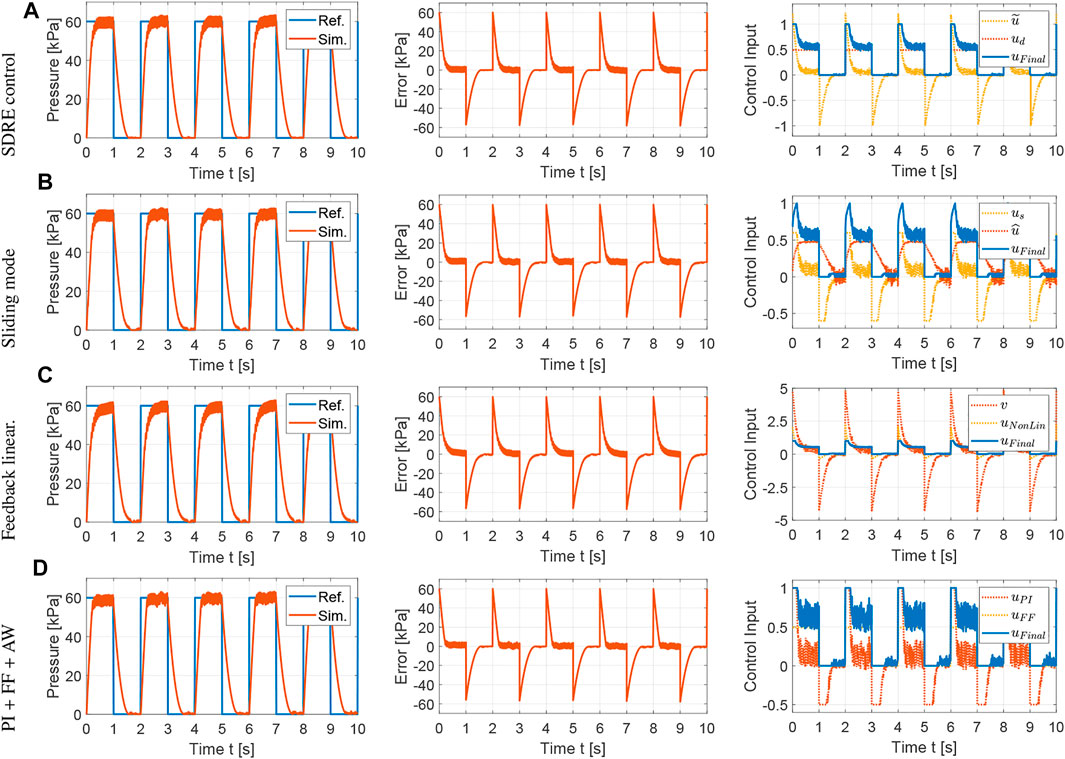
FIGURE 3. Simulation results for the comparison of nonlinear control strategies using the Simscape Fluids model: tracking performance, tracking error and control input for square wave with T = 2 s. (A) SDRE control: $Q=5$ and $R=10$, $\tilde{u}$ is the feedback term, $u_d$ is the feedforward term, and $u_{Final}$ is the control applied to the valve after saturation. (B) Integral augmented sliding mode control: $k_s=0.6$, $k_i=0.01$ and $\mathrm{\Phi }=0.2$, $u_s$ is the discontinuous term, $\widehat{u}$ is the equivalent control, and $u_{Final}$ is the control applied to the valve after saturation. (C) Feedback linearization with integral action: $k=8$ and $k_i=0.01$, $v$ is the linear control term, $u_{NonLin}$ is the total control, and $u_{Final}$ is the control applied to the valve after saturation. (D) PI controller with feedforward and anti-windup: $k_p=5$ and $k_i=0.5$, $u_{PI}$ is the PI control term, $u_{FF}$ is the feedforward term, and $u_{Final}$ is the control applied to the valve after saturation.

The performance of these control strategies is evaluated by three metrics: average tracking error $\bar{e}$, average control input $\bar{u}$, and average control variation $\overline{\mathrm{\Delta }u}$, as given below,

$\bar{e}=\frac{1}{N}\sum _{k=1}^N\left|e(k)\right|,(37)$

$\bar{u}=\frac{1}{N}\sum _{k=1}^N\left|u(k)\right|,(38)$

$\overline{\mathrm{\Delta }u}=\frac{1}{N}\sum _{k=1}^N\left|u(k)-u(k-1)\right|.(39)$

The average tracking error is used to evaluate the tracking performance, the average control input is used to evaluate the amount of control effort, and the average control variation is used to measure the degree of control input chattering. The metrics for the results shown in Figure 3 are summarized in Table 1 using the average over the five actuation cycles. Note that there are small differences between each cycle due to sensor noise, small variations in the receiver pressure, and the viscoelasticity of the silicone rubber. However, these differences are not significant, which supports the robustness of the proposed controllers. The SDRE and sliding mode controllers have similar tracking performance but the SDRE controller displays less chattering and control effort, and slightly faster settling time. Using feedback linearization, high proportional gains were needed to achieve tracking performance comparable to the previous optimal and robust nonlinear control strategies. Although feedback linearization resulted in less chattering, the tracking performance is inferior. Finally, it can be observed that, when the nonlinear model is incorporated into the feedforward component for a PI controller with anti-windup, excellent tracking performance can be achieved. To evaluate the robustness of the control strategies, a range of set points and soft actuator volumes are evaluated in Figures 4, 5, respectively. As shown in Figure 4, all controllers are able to track references at varying pressure ranges, except for the feedback linearization control law, which shows sluggish response for higher pressures. In addition, all controllers are robust to volume changes in the soft actuator, especially the SDRE, sliding mode, and PI with feedforward and anti-windup controllers. Although the actuator has some level of ballooning during actuation, the performance of the controllers is not significantly affected by the constant volume assumption.

TABLE 1

TABLE 1. Performance of control strategies: simulation results for square wave with T = 2 s.

FIGURE 4

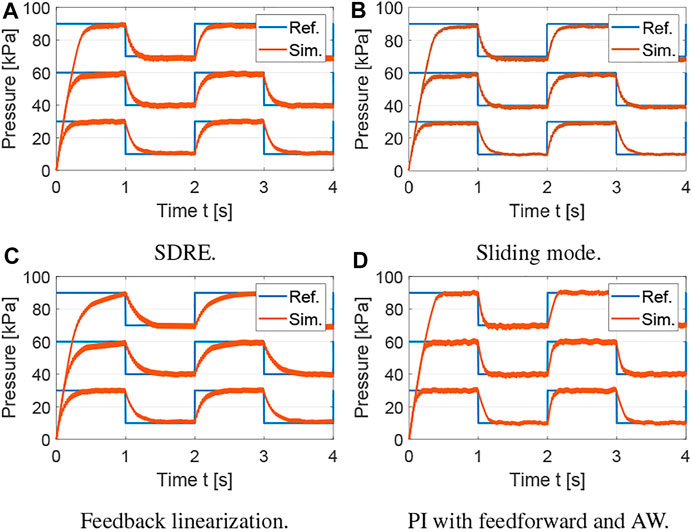
FIGURE 4. Evaluation of robustness of control strategies to variation in pressure references with varying offsets. (A) SDRE. (B) Sliding mode. (C) Feedback linearization. (D) PI with feedforward and AW.

FIGURE 5

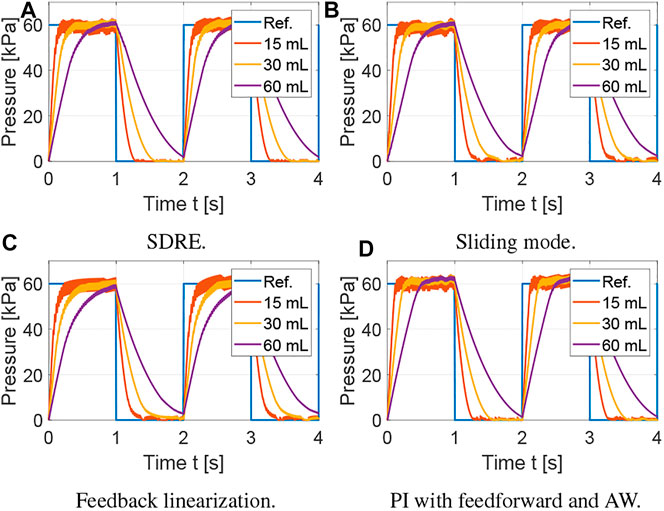
FIGURE 5. Evaluation of robustness of control strategies to variation in actuator volume. For each controller, the results are shown for three actuator volumes: 15, 30, and 60 ml. (A) SDRE. (B) Sliding mode. (C) Feedback linearization. (D) PI with feedforward and AW.

6 Experimental Results

The actuator used in the experimental results is a pneumatic network bending actuator fabricated using standard molding procedures (Marchese et al., 2015; Schmitt et al., 2018), as shown in Figure 1. Molds are designed in Autodesk Inventor and printed using an Original Prusa i3 MK3S (Prusa Research). Silicone rubber (DragonSkin10) forms the main body of the actuator and a strain limiting layer of fiberglass fabric is added to the bottom of the actuator to generate bending. The control strategies are programmed using Simulink; then, the Simulink support package for Arduino hardware and the MinGW64 compiler are used to generate code and interactively communicate in real time with an Arduino Due at a sampling time of 5 ms. To allow for real-time control and data visualization, Simulink is run in external mode over the serial and desired signals are logged for analysis with the Simulation Data Inspector. To reduce the noise level in the pressure sensor, the pressure data is filtered using a moving average filter for the last 10 pressure measurements. An example of the Simulink-Arduino implementation is shown in Figure 6 for the SDRE controller.

FIGURE 6

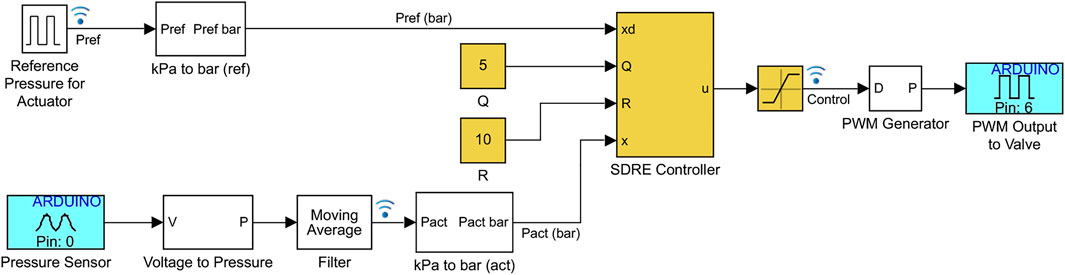
FIGURE 6. Implementation of control strategies with Simulink and Arduino. Here, the SDRE controller is shown in yellow, equivalent blocks are used for the other controllers. The blue blocks indicate the pressure sensor measurements (analog input) and PWM wave applied to the 3/2 valve (digital output).

6.1 Performance Evaluation and Comparison to Simulations

The tracking performance and control inputs for a reference square wave with a period of 2 s are shown in Figure 7. Compared to the simulations, the experimental results show an increased level of chattering due to sensor noise and compliance of the soft actuator. The SDRE and integral augmented sliding mode controllers provided the best tracking performances, with the SDRE controller showing reduced chattering and control effort, as summarized in Table 2. Comparing Tables 1 and 2, it is clear that the PI controller augmented with feedforward and anti-windup performs better in simulation results. However, its performance is still comparable to nonlinear optimal and robust control strategies, i.e., SDRE and SMC, respectively. The rise time for all controller responses are below 0.5 s, which validates the open-loop design procedure for the pneumatic components in Section 3. The response time can be further reduced with larger receiver pressures or valve flow coefficients. It is important to note that the response time is also a function of the internal chamber design of the soft actuator and the length and diameter of the tube connection, which can effectively act as flow restrictions. In this work, a tube with internal diameter of 4 mm and length of 8 cm between the valve and the soft actuator was used to minimize flow resistance and the added volume in the flow path.

FIGURE 7

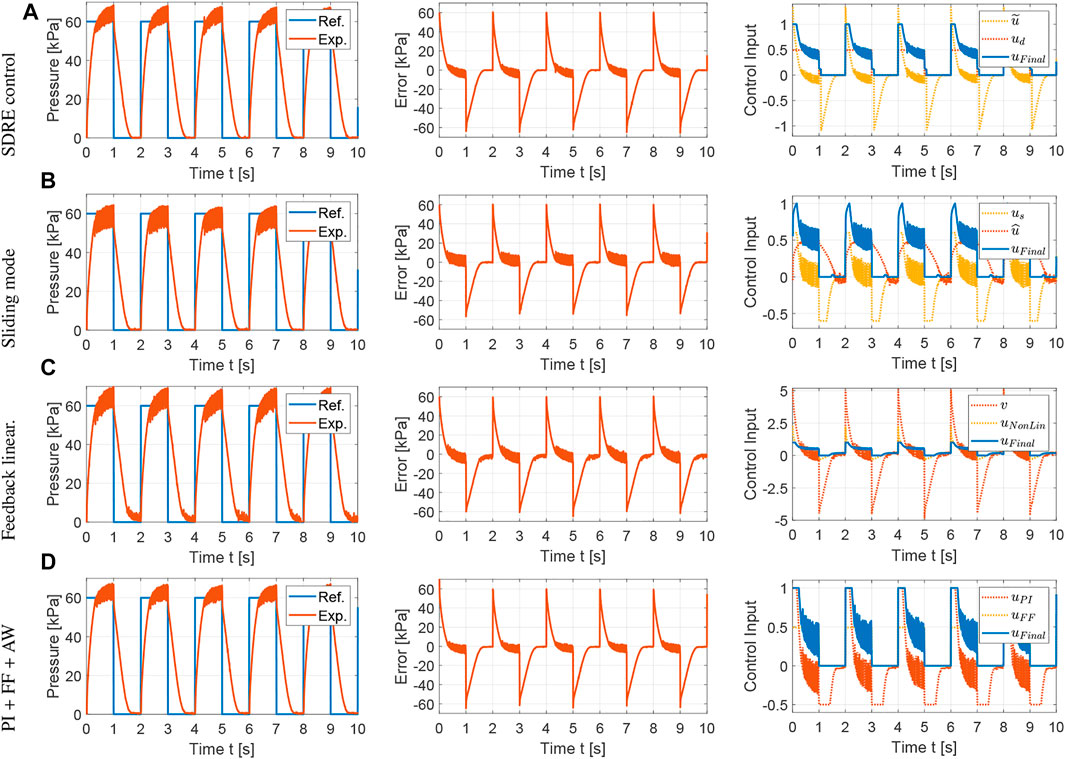
FIGURE 7. Experimental results for the comparison of nonlinear control strategies: tracking performance, tracking error and control input for square wave with T = 2 s. (A) SDRE control: $Q=5$ and $R=10$. (B) Integral augmented sliding mode control: $k_s=0.6$, $k_i=0.01$, and $\mathrm{\Phi }=0.2$. (C) Feedback linearization with integral action: $k=8$ and $k_i=0.01$. (D) PI controller with feedforward and anti-windup: $k_p=5$ and $k_i=0.5$. The description for the control input terms is the same as in Figure 3.

TABLE 2

TABLE 2. Performance of control strategies: experimental results for square wave with T = 2 s.

The tracking performance of the nonlinear controllers is also evaluated for a sine wave with a period of 2 s, as shown in Figure 8. As for the square waves, the SDRE and integral augmented sliding mode controllers provided the best tracking performances with average tracking errors of 2.694 and 2.729, respectively. The feedback linearization controller with integral action and the PI controller augmented with feedforward and anti-windup showed average tracking errors of 3.942 and 3.139.

FIGURE 8

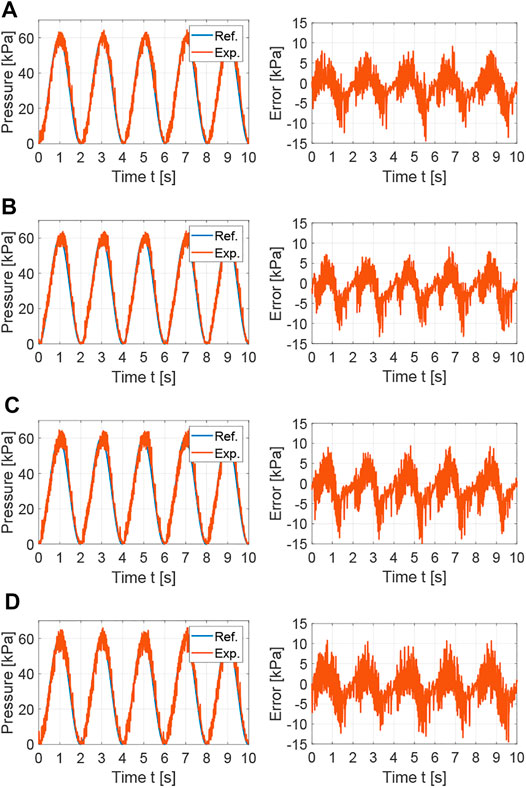
FIGURE 8. Experimental results for the comparison of nonlinear control strategies: tracking performance and error for sine wave with T = 2 s. (A) SDRE control: $Q=50$ and $R=1$. (B) Integral augmented sliding mode control: $k_s=2$, $k_i=0.01$ and $\mathrm{\Phi }=0.2$. (C) Feedback linearization with integral action: $k=40$ and $k_i=0.01$. (D) PI controller with feedforward and anti-windup: $k_p=10$ and $k_i=0.5$.

The chattering observed in the actuator responses in Figures 7, 8 is an inherent characteristic of pneumatic systems with on/off 3/2 valves, where flow is released to atmosphere at the off state of the PWM wave during pressure regulation, which causes the pressure in the actuator to continuously oscillate around its target. This can be reduced using systems with dual on/off 2/2 valves, which allow for an intermediate state where there is no flow in or out of the soft actuator. However, these systems increase control complexity as two inputs are controlled and cost as two valves are required. Alternatively, proportional valves can be used. However, these valves generally are more costly and much larger in size than on/off 3/2 or 2/2 solenoid valves.

7 Conclusion

This article describes the application and comparison of model-based nonlinear feedback controllers for soft pneumatic actuators operated with on/off valves. A model of the pneumatic system is developed, and four control strategies are compared using simulation and experimental results. The SDRE and integral augmented sliding mode controllers exhibited excellent tracking performance in both simulations and experiments. However, the SDRE controller showed less chattering and control effort compared to the sliding mode controller. The PI controller with feedforward and anti-windup performs better in simulations.

Integral action was introduced to the sliding mode and feedback linearization control laws to provide some robustness to model uncertainties. The three most uncertain parameters were as follows: the flow coefficient of the valve, the receiver pressure which decreases slightly during charging, and the actuator volume which increases with pressure. All four controllers showed robustness to varying actuator pressures and volumes. However, the feedback linearization method was noticeably slower at higher pressures and volumes.

On the basis of the experimental results, the authors recommend the SDRE method due to the systematic design process and best combination of fast response and minimum chatter. Whereas some nonlinear control strategies only address stability, the SDRE method directly addresses performance through the specification of a performance index in the nonlinear regulator problem. Furthermore, the state and control weightings can be adjusted with predictable results similar to linear quadratic regulator designs.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author Contributions

MX, YY, and AF conceptualized the study. MX developed the model and control strategies, conducted all the simulations and experiments in this article, and wrote the original draft. YY and AF supervised the project and reviewed and edited the article.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Alejandro Donaire for his assistance with the addition of integral action to the nonlinear controllers.

References

Ansari, Y., Manti, M., Falotico, E., Mollard, Y., Cianchetti, M., and Laschi, C. (2017). Towards the Development of a Soft Manipulator as an Assistive Robot for Personal Care of Elderly People. Int. J. Adv. Robot. Syst. 14 (2), 1729881416687132. doi:10.1177/1729881416687132

CrossRef Full Text | Google Scholar

Åström, K. J., and Hägglund, T. (2006). Advanced PID Control, Vol. 461. Research Triangle, North Carolina, United States: ISA-The Instrumentation, Systems, and Automation Society.

Google Scholar

Bao, G., Fang, H., Chen, L., Wan, Y., Xu, F., Yang, Q., et al. (2018). Soft Robotics: Academic Insights and Perspectives through Bibliometric Analysis. Soft Robotics 5 (3), 229–241. doi:10.1089/soro.2017.0135

PubMed Abstract | CrossRef Full Text | Google Scholar

Barth, E. J., Zhang, J., and Goldfarb, M. (2002). “Sliding Mode Approach to Pwm-Controlled Pneumatic Systems,” in Proceedings of the 2002 American Control Conference (IEEE Cat. No.CH37301), Anchorage, AK, USA, November 2002, 2362–2367. doi:10.1109/acc.2002.1023995

CrossRef Full Text | Google Scholar

Bartholdt, M., Wiese, M., Schappler, M., Spindeldreier, S., and Raatz, A. (2021). “A Parameter Identification Method for Static Cosserat Rod Models: Application to Soft Material Actuators with Exteroceptive Sensors,” in Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, December 2021, 624–631. doi:10.1109/iros51168.2021.9636447

CrossRef Full Text | Google Scholar

Berthold, R., Bartholdt, M. N., Wiese, M., Kahms, S., Spindeldreier, S., and Raatz, A. (2021). “A Preliminary Study of Soft Material Robotic Modelling: Finite Element Method and Cosserat Rod Model,” in Proceedings of the 2021 9th International Conference on Control, Mechatronics and Automation (ICCMA), Belval, Luxembourg, December 2021, 7–13. doi:10.1109/iccma54375.2021.9646194

CrossRef Full Text | Google Scholar

Booth, J. W., Case, J. C., White, E. L., Shah, D. S., and Kramer-Bottiglio, R. (2018). “An Addressable Pneumatic Regulator for Distributed Control of Soft Robots,” in Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, June 2018, 25–30. doi:10.1109/robosoft.2018.8404892

CrossRef Full Text | Google Scholar

Calderón, A. A., Ugalde, J. C., Zagal, J. C., and Pérez-Arancibia, N. O. (2016). “Design, Fabrication and Control of a Multi-Material-Multi-Actuator Soft Robot Inspired by Burrowing Worms,” in Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, March 2016, 31–38.

Google Scholar

Cao, G., Huo, B., Yang, L., Zhang, F., Liu, Y., and Bian, G. (2021). Model-based Robust Tracking Control without Observers for Soft Bending Actuators. IEEE Robot. Autom. Lett. 6 (3), 5175–5182. doi:10.1109/lra.2021.3071952

CrossRef Full Text | Google Scholar

Cao, G., Liu, Y., Jiang, Y., Zhang, F., Bian, G., and Owens, D. H. (2021). Observer-based Continuous Adaptive Sliding Mode Control for Soft Actuators. Nonlinear Dyn. 105, 371–386. doi:10.1007/s11071-021-06606-w

CrossRef Full Text | Google Scholar

Chen, C., Tang, W., Hu, Y., Lin, Y., and Zou, J. (2020). Fiber-reinforced Soft Bending Actuator Control Utilizing On/off Valves. IEEE Robot. Autom. Lett. 5 (4), 6732–6739. doi:10.1109/lra.2020.3015189

CrossRef Full Text | Google Scholar

Chillari, S., Guccione, S., and Muscato, G. (2001). “An Experimental Comparison between Several Pneumatic Position Control Methods,” in Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No.01CH37228), Orlando, FL, USA, August 2002, 1168–1173.

Google Scholar

Çimen, T. (2012). Survey of State-dependent Riccati Equation in Nonlinear Optimal Feedback Control Synthesis. J. Guidance, Control Dyn. 35 (4), 1025–1047. doi:10.2514/1.55821

CrossRef Full Text | Google Scholar

Çimen, T. (2010). Systematic and Effective Design of Nonlinear Feedback Controllers via the State-dependent Riccati Equation (Sdre) Method. Annu. Rev. Control. 34 (1), 32–51. doi:10.1016/j.arcontrol.2010.03.001

CrossRef Full Text | Google Scholar

Cloutier, J. R., D’Souza, C. N., and Mracek, C. P. (1996). “Nonlinear Regulation and Nonlinear H Control via the State-dependent Riccati Equation Technique: Part 1, Theory,” in Proceedings of the International Conference on Nonlinear Problems in Aviation and Aerospace, Daytona Beach, FL USA, May 1996, 117–131.

Google Scholar

De Greef, A., Lambert, P., and Delchambre, A. (2009). Towards Flexible Medical Instruments: Review of Flexible Fluidic Actuators. Precision Eng. 33 (4), 311–321. doi:10.1016/j.precisioneng.2008.10.004

CrossRef Full Text | Google Scholar

De Silva, C. W. (2004). Mechatronics: An Integrated Approach. Boca Raton, Florida, United States: CRC Press.

Google Scholar

Drotman, D., Ishida, M., Jadhav, S., and Tolley, M. T. (2019). Application-driven Design of Soft, 3-d Printed, Pneumatic Actuators with Bellows. Ieee/asme Trans. Mechatron. 24 (1), 78–87. doi:10.1109/tmech.2018.2879299

CrossRef Full Text | Google Scholar

Drotman, D., Jadhav, S., Karimi, M., de Zonia, P., and Tolley, M. T. (2017). “3d Printed Soft Actuators for a Legged Robot Capable of Navigating Unstructured Terrain,” in Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, July 2017, 5532–5538. doi:10.1109/icra.2017.7989652

CrossRef Full Text | Google Scholar

Eker, İ., and Akınal, Ş. A. (2008). Sliding Mode Control with Integral Augmented Sliding Surface: Design and Experimental Application to an Electromechanical System. Electr. Eng. 90 (3), 189–197. doi:10.1007/s00202-007-0073-3

CrossRef Full Text | Google Scholar

El-Atab, N., Mishra, R. B., Al-Modaf, F., Joharji, L., Alsharif, A. A., Alamoudi, H., et al. (2020). Soft Actuators for Soft Robotic Applications: A Review. Adv. Intell. Syst. 2 (10), 2000128. doi:10.1002/aisy.202000128

CrossRef Full Text | Google Scholar

Elgeneidy, K., Lohse, N., and Jackson, M. (2018). Bending Angle Prediction and Control of Soft Pneumatic Actuators with Embedded Flex Sensors - A Data-Driven Approach. Mechatronics 50, 234–247. doi:10.1016/j.mechatronics.2017.10.005

CrossRef Full Text | Google Scholar

Falkenhahn, V., Hildebrandt, A., Neumann, R., and Sawodny, O. (2016). Dynamic Control of the Bionic Handling Assistant. Ieee/asme Trans. Mechatron. 22 (1), 6–17. doi:10.1109/TMECH.2016.2605820

CrossRef Full Text | Google Scholar

Galloway, K., Polygerinos, P., Walsh, C., and Wood, R. (2013). “Mechanically Programmable bend Radius for Fiber-Reinforced Soft Actuators,” in Proceedings of the 2013 16th International Conference on Advanced Robotics (ICAR), Montevideo, Uruguay, March 2013. doi:10.1109/icar.2013.6766586

CrossRef Full Text | Google Scholar

George Thuruthel, T., Ansari, Y., Falotico, E., and Laschi, C. (2018). Control Strategies for Soft Robotic Manipulators: A Survey. Soft Robotics 5 (2), 149–163. doi:10.1089/soro.2017.0007

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodwin, G. C., Graebe, S. F., and Salgado, M. E. (2001). Control System Design, Vol. 240. Hoboken, New Jersey, United States: Prentice-Hall.

Google Scholar

Gorissen, B., De Volder, M., De Greef, A., and Reynaerts, D. (2011). Theoretical and Experimental Analysis of Pneumatic Balloon Microactuators. Sensors Actuators A: Phys. 168 (1), 58–65. doi:10.1016/j.sna.2011.03.057

CrossRef Full Text | Google Scholar

Gorissen, B., Reynaerts, D., Konishi, S., Yoshida, K., Kim, J.-W., and De Volder, M. (2017). Elastic Inflatable Actuators for Soft Robotic Applications. Adv. Mater. 29 (43), 1604977. doi:10.1002/adma.201604977

PubMed Abstract | CrossRef Full Text | Google Scholar

Ibrahim, S., Krause, J. C., Olbrich, A., and Raatz, A. (2021). Modeling and Reconstruction of State Variables for Low-Level Control of Soft Pneumatic Actuators. Front. Robot. AI 8, 32. doi:10.3389/frobt.2021.557830

CrossRef Full Text | Google Scholar

Ibrahim, S., Krause, J. C., and Raatz, A. (2019). “Linear and Nonlinear Low Level Control of a Soft Pneumatic Actuator,” in Proceedings of the 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Korea (South), April 2019, 434–440. doi:10.1109/robosoft.2019.8722737

CrossRef Full Text | Google Scholar

Joshi, S., and Paik, J. (2021). Pneumatic Supply System Parameter Optimization for Soft Actuators. Soft Robotics 8 (2), 152–163. doi:10.1089/soro.2019.0134

PubMed Abstract | CrossRef Full Text | Google Scholar

Joshi, S., Sonar, H., and Paik, J. (2021). Flow Path Optimization for Soft Pneumatic Actuators: Towards Optimal Performance and Portability. IEEE Robot. Autom. Lett. 6 (4), 7949–7956. doi:10.1109/lra.2021.3100626

CrossRef Full Text | Google Scholar

Jouppila, V. T., Gadsden, S. A., Bone, G. M., Ellman, A. U., and Habibi, S. R. (2014). Sliding Mode Control of a Pneumatic Muscle Actuator System with a Pwm Strategy. Int. J. Fluid Power 15 (1), 19–31. doi:10.1080/14399776.2014.893707

CrossRef Full Text | Google Scholar

Karnopp, D. C., Margolis, D. L., and Rosenberg, R. C. (2012). System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems. Hoboken, New Jersey, United States: John Wiley & Sons.

Google Scholar

Ke, J., Kotta, Ü., and Wang, J. (2007). Tracking Control of Nonlinear Pneumatic Actuator Systems Using Static State Feedback Linearization of the Input-Output Map. Proc. Estonian Acad. Sci. Phys. Maths. 56 (1), 47–56. doi:10.3176/phys.math.2007.1.04

CrossRef Full Text | Google Scholar

Khan, A. H., and Li, S. (2020). Sliding Mode Control with Pid Sliding Surface for Active Vibration Damping of Pneumatically Actuated Soft Robots. IEEE Access 8, 88793–88800. doi:10.1109/access.2020.2992997

CrossRef Full Text | Google Scholar

Khan, A. H., Shao, Z., Li, S., Wang, Q., and Guan, N. (2020). Which Is the Best PID Variant for Pneumatic Soft Robots an Experimental Study. Ieee/caa J. Autom. Sinica 7 (2), 451–460. doi:10.1109/jas.2020.1003045

CrossRef Full Text | Google Scholar

Lee, H. K., Choi, G. S., and Choi, G. H. (2002). A Study on Tracking Position Control of Pneumatic Actuators. Mechatronics 12 (6), 813–831. doi:10.1016/s0957-4158(01)00024-1

CrossRef Full Text | Google Scholar

Luo, M., Agheli, M., and Onal, C. D. (2014). Theoretical Modeling and Experimental Analysis of a Pressure-Operated Soft Robotic Snake. Soft Robotics 1 (2), 136–146. doi:10.1089/soro.2013.0011

CrossRef Full Text | Google Scholar

Luo, M., Skorina, E. H., Tao, W., Chen, F., Ozel, S., Sun, Y., et al. (2017). Toward Modular Soft Robotics: Proprioceptive Curvature Sensing and Sliding-Mode Control of Soft Bidirectional Bending Modules. Soft Robotics 4 (2), 117–125. doi:10.1089/soro.2016.0041

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, M., Tao, W., Chen, F., Khuu, T., Ozel, S., and Onal, C. (2014). “Design Improvements and Dynamic Characterization on Fluidic Elastomer Actuators for a Soft Robotic Snake,” in Proceedings of the 2014 IEEE International Conference on Technologies for Practical Robot Applications (TePRA), Woburn, MA, USA, August 2014. doi:10.1109/tepra.2014.6869154

CrossRef Full Text | Google Scholar

Marchese, A. D., Katzschmann, R. K., and Rus, D. (2015). A Recipe for Soft Fluidic Elastomer Robots. Soft Robotics 2 (1), 7–25. doi:10.1089/soro.2014.0022

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchese, A. D., Onal, C. D., and Rus, D. (2014). Autonomous Soft Robotic Fish Capable of Escape Maneuvers Using Fluidic Elastomer Actuators. Soft Robotics 1 (1), 75–87. doi:10.1089/soro.2013.0009

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchese, A., Komorowski, K., Onal, C., and Rus, D. (2014). “Design and Control of a Soft and Continuously Deformable 2d Robotic Manipulation System,” in Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, September 2014, 2189–2196. doi:10.1109/icra.2014.6907161

CrossRef Full Text | Google Scholar

Marquez, H. J. (2003). Nonlinear Control Systems: Analysis and Design. Hoboken, New Jersey, United States: John Wiley.

Google Scholar

Mohamed, M. H., Wagdy, S. H., Atalla, M. A., Rehan Youssef, A., and Maged, S. A. (2020). A Proposed Soft Pneumatic Actuator Control Based on Angle Estimation from Data-Driven Model. Proc. Inst. Mech. Eng. H 234 (6), 612–625. doi:10.1177/0954411920911277

PubMed Abstract | CrossRef Full Text | Google Scholar

Mracek, C. P., and Cloutier, J. R. (1998). Control Designs for the Nonlinear Benchmark Problem via the State-dependent Riccati Equation Method. Int. J. Robust Nonlinear Control. 8 (4-5), 401–433. doi:10.1002/(sici)1099-1239(19980415/30)8:4/5<401:aid-rnc361>3.0.co;2-u

CrossRef Full Text | Google Scholar

Naidu, D. S. (2002). Optimal Control Systems. Boca Raton, Florida, United States: CRC Press.

Google Scholar

Nekoo, S. R., and Geranmehr, B. (2013). Control of Non-affine Systems Using the State-dependent Riccati Equation (Sdre). Majlesi J. Mechatron. Syst. 2 (4).

Google Scholar

Nekoo, S. R. (2019). Tutorial and Review on the State-dependent Riccati Equation. Jand 8 (2), 109–166. doi:10.5890/jand.2019.06.001

CrossRef Full Text | Google Scholar

Nguyen, T., Leavitt, J., Jabbari, F., and Bobrow, J. E. (2007). Accurate Sliding-Mode Control of Pneumatic Systems Using Low-Cost Solenoid Valves. Ieee/asme Trans. Mechatron. 12 (2), 216–219. doi:10.1109/tmech.2007.892821

CrossRef Full Text | Google Scholar

Onal, C. D., and Rus, D. (2013). Autonomous Undulatory Serpentine Locomotion Utilizing Body Dynamics of a Fluidic Soft Robot. Bioinspir. Biomim. 8 (2), 026003. doi:10.1088/1748-3182/8/2/026003

PubMed Abstract | CrossRef Full Text | Google Scholar

Ou, J., Heibeck, F., and Ishii, H. (2016). “Tei 2016 Studio: Inflated Curiosity,” in Proceedings of the TEI '16: Tenth International Conference on Tangible, Embedded, and Embodied Interaction, Eindhoven, Netherlands, February 2016, 766–769.

Google Scholar

Paul, A. K., Mishra, J. E., and Radke, M. G. (1994). Reduced Order Sliding Mode Control for Pneumatic Actuator. IEEE Trans. Contr. Syst. Technol. 2 (3), 271–276. doi:10.1109/87.317984

CrossRef Full Text | Google Scholar

Polygerinos, P., Lyne, S., Wang, Z., Nicolini, L., Mosadegh, B., Whitesides, G., et al. (2013). “Towards a Soft Pneumatic Glove for Hand Rehabilitation,” in Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, January 2013, 1512–1517. doi:10.1109/iros.2013.6696549

CrossRef Full Text | Google Scholar

Polygerinos, P., Wang, Z., Overvelde, J. T. B., Galloway, K. C., Wood, R. J., Bertoldi, K., et al. (2015). Modeling of Soft Fiber-Reinforced Bending Actuators. IEEE Trans. Robot. 31 (3), 778–789. doi:10.1109/tro.2015.2428504

CrossRef Full Text | Google Scholar

Rafee Nekoo, S. (2013). Nonlinear Closed Loop Optimal Control: a Modified State-dependent Riccati Equation. ISA Trans. 52 (2), 285–290. doi:10.1016/j.isatra.2012.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahmat, M., Sunar, N., Salim, S. N. S., Abidin, M. S. Z., Fauzi, A. M., and Ismail, Z. (2011). Review on Modeling and Controller Design in Pneumatic Actuator Control System. Int. J. Smart Sens. Intell. Syst. 4 (4). doi:10.21307/ijssis-2017-460

CrossRef Full Text | Google Scholar

Richer, E., and Hurmuzlu, Y. (2000). A High Performance Pneumatic Force Actuator System: Part II-Nonlinear Controller Design. J. Dyn. Sys. Meas. Control. 122 (3), 426–434. doi:10.1115/1.1286366

CrossRef Full Text | Google Scholar

Runciman, M., Darzi, A., and Mylonas, G. P. (2019). Soft Robotics in Minimally Invasive Surgery. Soft Robotics 6 (4), 423–443. doi:10.1089/soro.2018.0136

PubMed Abstract | CrossRef Full Text | Google Scholar

Rus, D., and Tolley, M. T. (2015). Design, Fabrication and Control of Soft Robots. Nature 521 (7553), 467–475. doi:10.1038/nature14543

PubMed Abstract | CrossRef Full Text | Google Scholar

Saravanakumar, D., Mohan, B., and Muthuramalingam, T. (2017). A Review on Recent Research Trends in Servo Pneumatic Positioning Systems. Precision Eng. 49, 481–492. doi:10.1016/j.precisioneng.2017.01.014

CrossRef Full Text | Google Scholar

Schmitt, F., Piccin, O., Barbé, L., and Bayle, B. (2018). Soft Robots Manufacturing: a Review. Front. Robot. AI 5, 84. doi:10.3389/frobt.2018.00084

PubMed Abstract | CrossRef Full Text | Google Scholar

Shih, M.-C., and Ma, M.-A. (1998). Position Control of a Pneumatic cylinder Using Fuzzy Pwm Control Method. Mechatronics 8 (3), 241–253. doi:10.1016/s0957-4158(98)00005-1

CrossRef Full Text | Google Scholar

Shintake, J., Cacucciolo, V., Floreano, D., and Shea, H. (2018). Soft Robotic Grippers. Adv. Mater. 30 (29), 1707035. doi:10.1002/adma.201707035

PubMed Abstract | CrossRef Full Text | Google Scholar

Shtarbanov, A. (2021). “Flowio Development Platform–The Pneumatic “Raspberry Pi” for Soft Robotics,” in Proceedings of the Extended Abstracts of the 2021 CHI Conference on Human Factors in Computing Systems, Yokohama Japan, May 2021, 1–6.

Google Scholar

Skorina, E. H., Luo, M., Ozel, S., Chen, F., Tao, W., and Onal, C. D. (2015). “Feedforward Augmented Sliding Mode Motion Control of Antagonistic Soft Pneumatic Actuators,” in Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, July 2015, 2544–2549. doi:10.1109/icra.2015.7139540

CrossRef Full Text | Google Scholar

Skorina, E. H., Luo, M., Tao, W., Chen, F., Fu, J., and Onal, C. D. (2017). Adapting to Flexibility: Model Reference Adaptive Control of Soft Bending Actuators. IEEE Robot. Autom. Lett. 2 (2), 964–970. doi:10.1109/lra.2017.2655572

CrossRef Full Text | Google Scholar

Slotine, J.-J. E., and Li, W. (1991). Applied Nonlinear Control. Englewood Cliffs, NJ: Prentice-Hall.

Google Scholar

Soft robotics toolkit (2019). Components. Retrieved on 27/03/2019. [Online]. Available at: https://softroboticstoolkit.com/components.

Google Scholar

Strano, S., and Terzo, M. (2015). A Sdre-Based Tracking Control for a Hydraulic Actuation System. Mech. Syst. Signal Process. 60-61, 715–726. doi:10.1016/j.ymssp.2015.01.027

CrossRef Full Text | Google Scholar

Strano, S., and Terzo, M. (2016). Accurate State Estimation for a Hydraulic Actuator via a SDRE Nonlinear Filter. Mech. Syst. Signal. Process. 75, 576–588. doi:10.1016/j.ymssp.2015.12.002

CrossRef Full Text | Google Scholar

Suzumori, K., Endo, S., Kanda, T., Kato, N., and Suzuki, H. (2007). “A Bending Pneumatic Rubber Actuator Realizing Soft-Bodied Manta Swimming Robot,” in Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, May 2007, 4975–4980. doi:10.1109/robot.2007.364246

CrossRef Full Text | Google Scholar

Tawk, C., and Alici, G. (2021). A Review of 3D‐Printable Soft Pneumatic Actuators and Sensors: Research Challenges and Opportunities. Adv. Intell. Syst. 3, 2000223. doi:10.1002/aisy.202000223

CrossRef Full Text | Google Scholar

Tsai, Y.-C., and Huang, A.-C. (2008). Fat-based Adaptive Control for Pneumatic Servo Systems with Mismatched Uncertainties. Mech. Syst. Signal Process. 22 (6), 1263–1273. doi:10.1016/j.ymssp.2007.10.011

CrossRef Full Text | Google Scholar

Visioli, A. (2006). Practical PID Control. Berlin/Heidelberg, Germany: Springer Science & Business Media.

Google Scholar

Wang, T., Zhang, Y., Chen, Z., and Zhu, S. (2019). Parameter Identification and Model-Based Nonlinear Robust Control of Fluidic Soft Bending Actuators. Ieee/asme Trans. Mechatron. 24 (3), 1346–1355. doi:10.1109/tmech.2019.2909099

CrossRef Full Text | Google Scholar

Wang, T., Zhang, Y., Zhu, Y., and Zhu, S. (2019). A Computationally Efficient Dynamical Model of Fluidic Soft Actuators and its Experimental Verification. Mechatronics 58, 1–8. doi:10.1016/j.mechatronics.2018.11.012

CrossRef Full Text | Google Scholar

Watton, J. (1989). Fluid Power Systems: Modeling, Simulation, Analog and Microcomputer Control. Hoboken, New Jersey, United States: Prentice-Hall.

Google Scholar

Webster, R. J., and Jones, B. A. (2010). Design and Kinematic Modeling of Constant Curvature Continuum Robots: A Review. Int. J. Robotics Res. 29 (13), 1661–1683. doi:10.1177/0278364910368147

CrossRef Full Text | Google Scholar

Wehner, M., Quinlivan, B., Aubin, P. M., Martinez-Villalpando, E., Baumann, M., Stirling, L., et al. (2013). “A Lightweight Soft Exosuit for Gait Assistance,” in 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, May 2013, 3362–3369. doi:10.1109/icra.2013.6631046

CrossRef Full Text | Google Scholar

Weickgenannt, M., Zimmert, N., Klumpp, S., and Sawodny, O. (2010). “Application of Sdre Control to Servopneumatic Drives,” in Proceedings of the 2010 IEEE International Conference on Control Applications, Yokohama, Japan, August 2010, 1725–1730. doi:10.1109/cca.2010.5611228

CrossRef Full Text | Google Scholar

Weist, J., Arteaga, M. A., de la Cruz, L. R., and Hebisch, H. (2011). Model Free Control for Differential Pneumatic Pistons: Experimental Comparison. Int. J. Control 84 (1), 138–164. doi:10.1080/00207179.2010.543154

CrossRef Full Text | Google Scholar

Xavier, M. S., Fleming, A. J., and Yong, Y. K. (2021). Design and Control of Pneumatic Systems for Soft Robotics: a Simulation Approach. IEEE Robot. Autom. Lett. 6 (3), 5800–5807. doi:10.1109/lra.2021.3086425

CrossRef Full Text | Google Scholar

Xavier, M. S., Fleming, A. J., and Yong, Y. K. (2021). Finite Element Modeling of Soft Fluidic Actuators: Overview and Recent Developments. Adv. Intell. Syst. 3 (2), 2000187. doi:10.1002/aisy.202000187

CrossRef Full Text | Google Scholar

Xavier, M. S., Fleming, A. J., and Yong, Y. K. (2020). “Modelling and Simulation of Pneumatic Sources for Soft Robotic Applications,” in Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, August 2020. doi:10.1109/aim43001.2020.9158802

CrossRef Full Text | Google Scholar

Xiao, W., Hu, D., Chen, W., Yang, G., and Han, X. (2021). Modeling and Analysis of Bending Pneumatic Artificial Muscle with Multi-Degree of freedom. Smart Mater. Struct. 30 (9), 095018. doi:10.1088/1361-665x/ac1939

CrossRef Full Text | Google Scholar

Xu, F., and Wang, H. (2021). Soft Robotics: Morphology and Morphology-Inspired Motion Strategy. Ieee/caa J. Autom. Sinica 8 (9), 1500–1522. doi:10.1109/jas.2021.1004105

CrossRef Full Text | Google Scholar

Yang, Y., Wu, Y., Li, C., Yang, X., and Chen, W. (2020). Flexible Actuators for Soft Robotics. Adv. Intell. Syst. 2 (1), 1900077. doi:10.1002/aisy.201900077

CrossRef Full Text | Google Scholar

Yi, J., Chen, X., Song, C., Zhou, J., Liu, Y., Liu, S., et al. (2018). Customizable Three-Dimensional-Printed Origami Soft Robotic Joint with Effective Behavior Shaping for Safe Interactions. IEEE Trans. Robot. 35 (1), 114–123. doi:10.1109/TRO.2018.2871440

CrossRef Full Text | Google Scholar

Young, T. R., Xavier, M. S., Fleming, A. J., and Yong, Y. K. (2021). “A Control and Drive System for Pneumatic Soft Robots: Pneusord,” in Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, December 2021, 2822–2829. doi:10.1109/iros51168.2021.9635874

CrossRef Full Text | Google Scholar

Zhihong Rao, Z., and Bone, G. M. (2008). Nonlinear Modeling and Control of Servo Pneumatic Actuators. IEEE Trans. Contr. Syst. Technol. 16 (3), 562–569. doi:10.1109/tcst.2007.912127

CrossRef Full Text | Google Scholar

Zhou, J., Chen, X., Chang, U., Lu, J.-T., Leung, C. C. Y., Chen, Y., et al. (2019). A Soft-Robotic Approach to Anthropomorphic Robotic Hand Dexterity. IEEE Access 7, 101483–101495. doi:10.1109/access.2019.2929690

CrossRef Full Text | Google Scholar

Appendix-Error System for SDRE Control

Firstly, define the reference system

$\begin{array}{cc}\hfill {\dot{x}}_d=& -\alpha x_d\underset{a_{1d}}{\underbrace{\sqrt{c_2(x_d-c_2)}}}\hfill \\ \hfill & +(\alpha x_d\underset{a_{2d}}{\underbrace{\sqrt{x_d(c_1-x_d)}}}+\alpha x_d\underset{a_{1d}}{\underbrace{\sqrt{c_2(x_d-c_2)}}})u_d\hfill \end{array}(40)$

From the definition of the error variables, $x=x_d+\tilde{x}$ and $u=u_d+\tilde{u}$. Therefore, in Eqs. 8–10,

$\begin{array}{cc}\hfill {\dot{x}}_d+\dot{\stackrel{̃}{x}}=& -\alpha (x_d+\tilde{x})\underset{a_1}{\underbrace{\sqrt{c_2(x_d+\tilde{x}-c_2)}}}\hfill \\ \hfill & +\left\{\alpha (x_d+\tilde{x})\right.\underset{a_2}{\underbrace{\sqrt{\left(x_d+\tilde{x}\right)(c_1-x_d-\tilde{x})}}}\hfill \\ \hfill & +\alpha (x_d+\tilde{x})\underset{a_1}{\underbrace{\sqrt{c_2(x_d+\tilde{x}-c_2)}}}\}(u_d+\tilde{u})\hfill \end{array}(41)$

Using the reference system (Eq. 40) and the definitions of $a_1$, $a_2$, $a_{1d}$, and $a_{2d}$,

$\begin{array}{cc}\hfill \dot{\stackrel{̃}{x}}=& -\alpha \tilde{x}{a}_1+\alpha \tilde{x}{a}_2{u}_d+\alpha \tilde{x}{a}_1{u}_d\hfill \\ \hfill & +(\alpha x_d{a}_2+\alpha \tilde{x}{a}_2+\alpha x_d{a}_1+\alpha \tilde{x}{a}_1)\tilde{u}\hfill \\ \hfill & -\alpha x_d{a}_1+\alpha x_d{a}_2{u}_d+\alpha x_d{a}_1{u}_d\hfill \\ \hfill & +\alpha x_d{a}_{1d}-\alpha x_d{a}_{2d}{u}_d-\alpha x_d{a}_{1d}{u}_d\hfill \end{array}(42)$

The last two lines in the equation above define $a_3$, multiplying $a_3$ by $\tilde{x}/\tilde{x}$ yields

$\begin{array}{cc}\hfill \dot{\stackrel{̃}{x}}=& \underset{A(\tilde{x})}{\underbrace{(-\alpha a_1+\alpha a_2{u}_d+\alpha a_1{u}_d+a_3/\tilde{x})}}\tilde{x}\hfill \\ \hfill & +\underset{B(\tilde{x})}{\underbrace{(\alpha x_d{a}_2+\alpha \tilde{x}{a}_2+\alpha x_d{a}_1+\alpha \tilde{x}{a}_1)}}\tilde{u}\hfill \end{array}(43)$