Phase-dependent transparency in a two-level system with applications to all-optical switching

The phenomenon of transparency, conventionally studied in three and higher level atomic systems, is extended to the case of a two-level system (TLS), where we use a semiclassical framework to describe the transparent propagation of classical fields in a medium of TLS scatterers. We demonstrate a new form of transparency with fast pulses, accounting for the initial state of the TLS, which we call phase-dependent transparency. Using the phenomenon of photon locking, we showed that TLSs initialized in maximum coherence states exhibit transparency to resonant fields when there is phase-matching between the phase of the atomic coherence and that of the probe field. An application to the problem of all-optical switching is also discussed, where on-demand transmission is generated by controlling the relative phase between a $\pi /2$ pump pulse and the transmitted probe pulse.

Introduction

The coherent interaction of matter and light can lead to the emergence of quantum interference between multiple pathways, such as electronic excitation pathways (Fleischhauer et al., 2005), in turn revealing novel quantum phenomena that is of tremendous interest today in the fields of quantum information science and emerging quantum technologies (Lukin et al., 2001; Fleischhauer and Lukin, 2000; Lukin et al., 2000; Körber et al., 2018; Sangouard et al., 2011; Kimble, 2008). An example of one such phenomena is induced transparency, which originated in the study of light-matter interaction in three and higher level atomic systems (Petrosyan et al., 2011; Slusher and Gibbs, 1972). Today, induced transparency has been extended to a large number of systems including optomechanical systems (Weis et al., 2010; Agarwal and Huang, 2010; Xiong and Wu, 2018), plasmonics (Zhang et al., 2008; Kekatpure et al., 2010; Zhu et al., 2014), and coupled microresonators (Naweed et al., 2005; Guo et al., 2021; Huang et al., 2022; Yang et al., 2009). However, we do not see similar results for the simple case of the two-level system (TLS), in the case of observing EIT-like transparency without the inclusion of additional structures for the TLS. For example, the presence of mechanical vibrations in a medium of two level scatterers along with a polychromatic driving field can produce partial and full transparency in the TLS medium (Radeonychev et al., 2006; Radeonychev et al., 2020). More generally, polychromatic driving can lead to the presence of additional scattering channels-effectively expanding the state space of our TLS in the frequency domain and leading to the emergence of EIT-like transparency (Kälin et al., 2004). Additionally, induced transparency in two-level atoms has been realized in the presence of self-induced transparency (SIT) effects, where nearly lossless transmission is observed for pulsed light that has the form of an optical soliton (Chakravarty, 2016). The phenomenon of SIT was first discovered by McCall and Hahn (McCall and Hahn, 1969), where coherent, resonant, fast pulses propagate with anomalously low energy losses in a medium of two-level atoms. We distinguish the form of transparency developed in this paper from SIT, noting that it has more in common with EIT.

Electromagnetically induced transparency (EIT) (Fleischhauer et al., 2005; Marangos, 1998; Harris, 1997; Finkelstein et al., 2023) is one of the most famous examples of transparency, caused by destructive interference of probability amplitudes from multiple pathways between two states in a multilevel system dressed with strong coupling fields. The optical susceptibilities of EIT setups are shown to be sensitive to the phases of driving fields (Sahrai et al., 2007; Yang et al., 2010; Abi-sallouma et al., 2007; Joshi, 2009) with cancellation/amplification of nonlinearities corresponding to dispersive and absorptive effects dependent on the relative phases between different field components. As argued in (Abi-sallouma et al., 2007), the dependence of EIT on quantum interference implies that EIT must then also be dependent on a phase term, owing to the fact that the quantum interference is a result of a coherent interaction. The identification of this phase term would imply the presence of a tunability from transparency to absorption which can even persist in the steady-state regime for more complex systems (Yang et al., 2010; Hu et al., 2005). While EIT, for the case of the 3-level Lambda system, is not sensitive to the relative phase between the pump and probe fields in the steady state limit, this is not the case in the transient regime where there can be a relative phase between the atomic dipole and that of the fields (Abi-sallouma et al., 2007). In this regime, EIT can temporarily become electromagnetically induced absorption (EIA) (Lezama et al., 1999; Akulshin et al., 1998; Korsunsky et al., 1999) due to the destructive interference between the multiple pathways becoming constructive (Abi-sallouma et al., 2007). The ability to engineer such interference effects is a major goal in quantum control theory. Techniques such as pulse shaping and frequency modulation are highly effective in generating dark-state based transfer and interference effects in three and higher level systems, leading to phenomena like adiabatic population transfer (Chathanathil et al., 2023) and EIT respectively. More broadly, quantum control techniques have been instrumental in realizing robust state transfer, especially in the development of one- and two-qubit gates that sustain high fidelity in the presence of stochastic drift and open system effects (Koch et al., 2022). The impact of Markovian and non-Markovian noise on qubit control is examined in (Delben et al., 2023), including scenarios where closed-system quantum control schemes break down, and the use of fast-control strategies for reducing decoherence effects.

A similar concept as phase-dependent transient EIT is used in our work where a relative phase between the atomic coherence and the probe field is used to generate non-steady state transparency. In principle, when the populations in both states of a TLS are equal, the outcome of equal rates of stimulated emission and absorption should result in transparency. We find that this basic principle can be satisfied, but is dependent on the state of the atomic density matrix and the phase of the probe light. Indeed, we show in this work that the phase of the probe field can be chosen to result in no energy transfer if the TLS is in a maximum coherence superposition state and the probe is resonant while being in phase with the atomic coherence. The invariance of the atomic density matrix to a perturbation that satisfies the relative phase condition is called photon locking (Tannor, 2007; Vreeker et al., 1986; Bayer et al., 2009; Bodey et al., 2019) and is implemented to realize transparent propagation of probe pulses in a medium of TLS scatterers. We call the resulting transparency phenomena phase-dependent transparency (PDT). In this work, we also propose a protocol to realize absorptive all-optical switching (Yadav and Bhattacherjee, 2022; Volz et al., 2012) where a relative phase between the probe field and atomic coherence can be used to tune between absorption and transmission. All-optical switching has been realized, based on the principle of perfect photon absorption, in cavity QED schemes with cold atoms interacting with a cavity driven by two fields with some constant relative phase (Agarwal et al., 2016; Guo et al., 2024). One extremely important research area is the realization of optical switching with single-photons (Volz et al., 2012; Shen and Fan, 2005), though this is beyond the scope of this work. Our protocol uses a semi-classical scheme with TLSs interacting with classical pulses, allowing on-demand switching between absorption and transparency in the transient regime.

Materials and methods

We consider the problem of propagation of hundred $\mathrm{p}\mathrm{s}$ pulses in a homogeneous continuous vapor of two-level atoms with density $n$ with no buffer gas and low-moderate optical depth $\alpha <1$, where $L$ is the medium length. Each atom at position $x$ has transition frequency ${\omega }_0$, and is initialized in the maximal coherence state ${\psi }_0$ (with $|⟨1|{\psi }_0⟩⟨{\psi }_0|2⟩|=1/2$) at the retarded time $t-x/c=0$. The optical depth must be restricted to prevent the free polarization field generated by the atomic coherence in the medium from perturbing the maximum coherence state. We use the Maxwell-Bloch equations (Svidzinsky et al., 2015) to model the evolution of the pulse and atomic populations and coherences. A probe pulse, with duration $\tau$ and central time $t_c$, is introduced from the left and reaches the medium at $x=0$. The pulse has waveform $E(x,t)=A(x,t)\cos (kx-{\omega }_{L}t-{\varphi }_0-\varphi (x,t))$, with complex-valued envelope $A(x,t)$, and frequency ${\omega }_L={\omega }_0+{\mathrm{\Delta }}_0$, where ${\mathrm{\Delta }}_0$ is the pulse detuning, and $\varphi (x,t)$ is a general time and position dependent phase. For convenience, we define the time-dependent detuning $\mathrm{\Delta }(x,t)={\mathrm{\Delta }}_0+\dot{\varphi }(x,t)$. We assume that ${\omega }_0\gg |\mathrm{\Delta }(x,t)|,|A(x,t)|$. We obtain the below field interaction Hamiltonian,

$\tilde{H}=-\frac{1}{2}\left(\mathrm{\Delta }\left(t\right){\widehat{\sigma }}_z+\text{Re}\left[\mathrm{\Omega }\left(x_0,t\right)\right]{\widehat{\sigma }}_x-\text{Im}\left[\mathrm{\Omega }\left(x_0,t\right)\right]{\widehat{\sigma }}_y\right)(1)$

where we defined the complex Rabi frequency $\mathrm{\Omega }(x_0,t)=-\mu A(x_0,t)e^{i{\varphi }_0}/\hslash$, where $\mu =⟨1|e\widehat{r}|2⟩$ is the atomic transition dipole moment, after applying the rotating wave approximation to remove fast terms. For comprehensiveness, we account for spontaneous emission processes with decay rate $\mathrm{\Gamma }$. Using the TLS density matrix, $\rho (t)$, for an atom at $x=x_0$, we define the generalized density matrix, $\rho (x,t)$, as a continuous function of position. We make use of the Bloch vector formalism with the goal of obtaining a vectorized equation for the atomic population and coherence terms. We define the Bloch vector $\vec{\sigma }(x,t)$,

$\begin{array}{cc}\hfill & \vec{\sigma }={\left({\sigma }_x,{\sigma }_y,{\sigma }_z\right)}^T\hfill \\ \hfill & {\sigma }_x+i{\sigma }_y=2{\rho }_{21}\hfill \\ \hfill & {\sigma }_z={\rho }_{11}-{\rho }_{22}\hfill \end{array}(2)$

And introduce the driving vector $\vec{v}(x_0,t)={(\text{Re}[\mathrm{\Omega }(x_0,t)],\text{Im}[\mathrm{\Omega }(x_0,t)],-\mathrm{\Delta }(t))}^T$ and obtain a geometric form for the evolution of the Bloch vector using the Hamiltonian (Equation 1),

$\dot{\stackrel{⃗}{\sigma }}=-\vec{v}\times \vec{\sigma }-\mathrm{\Gamma }\left(\vec{\sigma }-{\left(\mathrm{0,0,1}\right)}^T\right)(3)$

where we used the Feynman-Vernon-Hellwarth representation (Tannor, 2007), modified to take into account spontaneous emission. To model the propagation of a probe pulse through a cold vapor of two level atoms we use the semiclassical Maxwell-Bloch equations in the slow-varying-envelope-approximation (SVEA). Assuming that the probe pulse propagates paraxially with a pulse duration much larger than the oscillation frequency $(\tau \gg 2\pi /\omega )$, it follows that the probe pulse can be approximately expanded as a product of a fast oscillation $e^{i(kx-\omega t)}$ and a slow envelope for the probe Rabi frequency $\mathrm{\Omega }(x,t)$ (Svidzinsky et al., 2015).

$\left(\frac{1}{c}\frac{\partial }{\partial t}+\frac{\partial }{\partial z}\right)\mathrm{\Omega }\left(x,t\right)=iP\left(x,t\right)(4)$

We consider the evolution of the probe pulse in response to the macroscopic polarization consisting of the dipole moments of the atomic vapor $P=\frac{n{\mu }^2\omega }{2\hslash {ϵ}_{0}c}{\sigma }^{+}$ where ${\sigma }^{+}=({\sigma }_x+i{\sigma }_y)/2$ (Equation 2). The optical response to the probe pulse, including absorption and dispersion, is obtained by propagating Equations 3, 4. We assume that there is a strong initial polarization $P(x,t_0)$ generated by a forward-directed pump pulse with phase $e^{i(kx-\omega t)}$. In the SVEA, the only coherent field produced is the forward-directed field due to phase-matching enforced by the spatial phase of the coherence. Therefore we do not consider the backwards directed field in our model.

Results

From Equation 3, we obtain an important result. With the assumption that the pulse duration is small enough that there is negligible change to the Bloch vector from spontaneous emission, when $\vec{\sigma }\Vert \vec{v}$, there is no time-dependence to the Bloch vector, in contrast to the general case shown in Figure 1. This is called photon locking (Tannor, 2007; Vreeker et al., 1986). We can understand the phenomenon of photon locking in the TLS by considering the time evolution of the TLS when a pump and probe pulse are sequentially applied. In the case where the pump Rabi phase is zero and the pulse is a resonant $\pi /2$ area pulse, the Bloch vector is rotated to ${\vec{\sigma }}_0={(\mathrm{0,1,0})}^T$. If the probe Rabi phase is also zero (plus a multiple of $2\pi$), then all the population would move to the excited state and we would have ${\vec{\sigma }}_1={(\mathrm{0,0},-1)}^T$ as if a single $\pi$ pulse was applied. We note that in this case, the probe and ${\sigma }^{+}$ are out of phase. However, in the case where the probe Rabi phase is $\pi /2$ (plus a multiple of $\pi$), the probe and ${\sigma }^{+}$ are in-phase, satisfying condition $\vec{\sigma }\Vert \vec{v}$, and this results in no population transfer. Another identification we can make is that ${\vec{\sigma }}_0$ corresponds to an eigenstate of $\tilde{H}$ (Equation 1), which is a time-dependent Hamiltonian that also has time-independent eigenstates-implying that ${\vec{\sigma }}_0$ is also an eigenstate of time evolution.

Figure 1

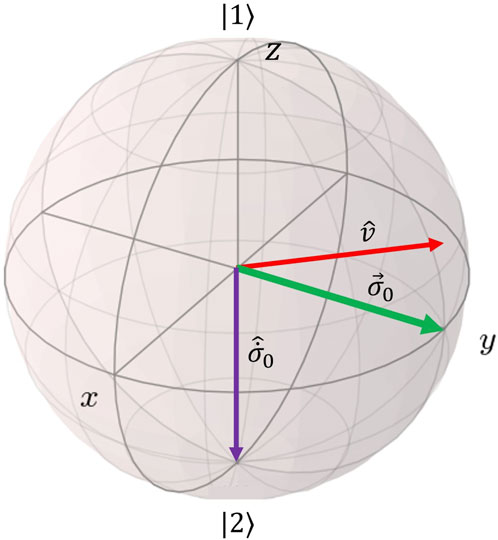
Figure 1. Demonstration of the Bloch vector ${\vec{\sigma }}_0$ (green) evolution by the torque ${\widehat{\dot{\sigma }}}_0$ (purple) induced by the driving vector (red unit vector $\widehat{v}$).

By itself, this condition is insufficient for us to obtain transparency. While the atom undergoes no dynamics from the driving vector when the condition $\vec{\sigma }\Vert \vec{v}$ is satisfied, this does not necessarily imply that the field experiences no change (up to some phase shift). Indeed, an introduction of a chirp or phase to the field will unravel transparency. Unlike the case of EIT, where the absorption pathway is completely suppressed, with photon locking both absorption and stimulated emission processes still occur-such that there can still be a polarization response from a single atom. A nonzero population inversion $({\sigma }_z\ne 0)$ will result in a polarization response to the pulse, that results in the rotation of $\vec{v}$ as the pulse propagates in the medium, hence photon locking by itself is insufficient a criterion for transparency of the TLS medium to the pulse. We find that in the limit where ${\sigma }_z={\mathrm{\Delta }}_0=0$, we obtain the condition that the phase of the atomic coherence must be equal to the Rabi phase ${\varphi }_0$, up to a multiple of $\pi$. The condition for phase-dependent transparency is given explicitly below,

$\begin{array}{c}\hfill {\sigma }_z={\mathrm{\Delta }}_0=0,\arg \left[{\sigma }^{+}\right]=\arg \left[\mathrm{\Omega }\right]\text{mod}\left(\pi \right)\end{array}(5)$

The satisfaction of the above condition (Equation 5) results in phase-dependent transparency, where the scattering processes that result in population shift upwards (absorption) and downwards (stimulated emission) have equal probability amplitudes (in magnitude and phase) and exactly cancel, resulting in no phase shifts to the field. Using the equations of motion for the pulse envelope $\mathrm{\Omega }(x,t)$, we see that this results in no polarization response to the pulse. If the phases of the two scattering amplitudes are not equal up to a multiple of $\pi$, we will observe Rabi flopping (population cycling). On the other hand, if there is some population inversion in the medium (which requires $\mathrm{\Delta }\ne 0$ to satisfy $\vec{v}\times \vec{\sigma }=0$), there will generally be a phase-shift to the pulse after it interacts with the TLS. This altogether justifies the constraint Equation 5. Additionally, we note that all scattering terms preserve the phase of $|{\psi }_0\rangle$, as seen when we calculate the Dyson series, giving us an alternate derivation for the phase matching condition, see Supplementary Material (Ramaswamy and Malinovskaya, 2024).

For the equations of motion of the probe pulse, we utilize the retarded Green’s function to propagate the solution of Equation 3 and Equation 4 using the initial conditions at $t=t_0$ for the probe $\mathrm{\Omega }(x,t)={\mathrm{\Omega }}_0(t-c^{-1}x)$ and Bloch vector $\vec{\sigma }(x,t_0)$. The resulting field is the sum of the free field and the scatterer contributions.

$\begin{array}{cc}\hfill & \mathrm{\Omega }\left(x,t\right)=e^{i/c{\int }_0^{x}d\xi \dot{\varphi }\left(t-c^{-1}\left(x-\xi \right)\right)}\left({\mathrm{\Omega }}_0\left(t-c^{-1}x\right)+i\frac{n{\mu }^2\omega }{2\hslash {ϵ}_{0}c}\right.\hfill \\ \hfill & \left.\times {\int }_0^{x}d\zeta e^{-i/c{\int }_0^{\zeta }d\xi \dot{\varphi }\left(t-c^{-1}\left(x-\xi \right)\right)}{\sigma }^{+}\left(\zeta ,t-c^{-1}\left(x-\zeta \right)\right)\right)\hfill \end{array}(6)$

We also obtain the below integral equation for ${\sigma }^{+}(x,t)$,

$\begin{array}{cc}\hfill & {\sigma }^{+}\left(x,t\right)={\sigma }^{+}\left(x,t_0\right)e^{-\left(\mathrm{\Gamma }/2+i{\mathrm{\Delta }}_0\right)\left(t-t_0\right)}{e}^{-i{\int }_{t_0}^{t}d{t}^{\prime }\dot{\varphi }\left(t^{\prime }\right)}\hfill \\ \hfill & +i{e}^{-i{\int }_{t_0}^{t}d{t}^{\prime }\dot{\varphi }\left(t^{\prime }\right)}{\int }_{t_0}^{t}d{t}^{\prime }\mathrm{\Omega }\left(x,t^{\prime }\right)e^{-\left(\mathrm{\Gamma }/2+i{\mathrm{\Delta }}_0\right)\left(t-t^{\prime }\right)}\hfill \\ \hfill & \times e^{i{\int }_{t_0}^{t^{\prime }}d\zeta \dot{\varphi }\left(\zeta \right)}{\sigma }_z\left(x,t^{\prime }\right)\hfill \end{array}(7)$

which when substituted into Equation 6, separates the free polarization component of the Rabi frequency, ${\mathrm{\Omega }}_f(x,t)=i{\alpha }_0{L}^{-1}{\int }_0^{x}d{x}^{\prime }{\sigma }^{+}(x^{\prime },t_0)\mathrm{\Gamma }{e}^{-(\mathrm{\Gamma }/2+i{\mathrm{\Delta }}_0)(t-t_0-c^{-1}(x-x^{\prime }))}$, from the polarization response to the field, which depends on the population inversion ${\sigma }_z(x,t)$. Here, ${\alpha }_0=\frac{nL{\mu }^2\omega }{2\hslash {ϵ}_{0}c\mathrm{\Gamma }}$ is the optical depth at resonance. When the condition $\tau \ll {\mathrm{\Gamma }}^{-1}$ is satisfied, we can neglect the contribution from spontaneous emission but we retain the term in our simulations for completion. The free polarization field has negligible contribution to the Bloch vector for ${\alpha }_0\tau \ll 1$. As long as ${\sigma }_z=0$ everywhere in the medium, and for all time, there will be no polarization response to the pulse, and the driving vector $\vec{v}(x,t)$ will not rotate. It follows that the field propagates transparently in the atomic medium when the conditions for phase-dependent transparency are satisfied.

To verify the transmission/absorption behavior for different values of the initial phase ${\varphi }_0$, we compute the normalized intensity-time integral:

$Q\left(x\right)={\int }_{-\tau }^{\tau }d{t}^{\prime }|\mathrm{\Omega }\left(x,t^{\prime }\right)/\mathrm{\Omega }\left(0,t^{\prime }\right){|}^2(8)$

In the transparent case $({\varphi }_0=\pi /2)$, the probe and free polarization fields are out of phase by $\pi /2$ and thus do not interfere. Therefore, we subtract the free polarization contribution from the total intensity before calculating $Q(x)$. To analyze the dispersive properties of the medium, we compute the group delay ${\tau }_g(x)$ and the temporal variance ${\sigma }_{\tau }^2(x)$ of the transmitted field,

$\begin{array}{cc}\hfill & {\tau }_g\left(x\right)=\frac{{\int }_{t_0}^{t_1}d{t}^{\prime }{t}^{\prime }|\mathrm{\Omega }\left(x,t^{\prime }\right){|}^2}{{\int }_{t_0}^{t_1}d{t}^{\prime }|\mathrm{\Omega }\left(x,t^{\prime }\right){|}^2}\hfill \\ \hfill & {\sigma }_{\tau }^2\left(x\right)=\frac{{\int }_{t_0}^{t_1}d{t}^{\prime }{\left(t^{\prime }-{\tau }_g\left(x\right)\right)}^2|\mathrm{\Omega }\left(x,t^{\prime }\right){|}^2}{{\int }_{t_0}^{t_1}d{t}^{\prime }|\mathrm{\Omega }\left(x,t^{\prime }\right){|}^2}\hfill \end{array}(9)$

In the absorptive case $({\varphi }_0=0)$, the probe and free polarization fields are both purely imaginary and interfere coherently. As a result, they cannot be individually resolved, and their interaction gives rise to a cross term $2\text{Re}[{\mathrm{\Omega }}_f{\mathrm{\Omega }}_{\text{pr}}^{*}]$ in the intensity. Although the population inversion remains approximately zero $({\sigma }_z\approx 0)$, a strong optical torque is exerted on the Bloch vector due to this coherent interaction, leading to energy transfer that is suppressed in the photon-locking regime. We numerically simulated the propagation of resonant pulses using Equations 3, 6 using the method of lines in space, and integrated the ODE equations in the retarded time coordinate $\tau =t-z/c$. We considered the two cases of ${\varphi }_0=0,\pi /2$, with $\varphi (x,t)=0$, in a medium of Rb-87 atoms initialized in state $\left(|1\rangle +i|2\rangle \right)/\sqrt{2}$, see Figure 2 $({\varphi }_0=0)$ and Figure 3 $({\varphi }_0=\pi /2)$. The decay rate is given by $\mathrm{\Gamma }=(2\pi )6.05\text{\hspace{0.17em}MHz}$. In the absence of photon locking $({\varphi }_0=0)$, we observe the expected absorption of the probe field, as population is transferred to the excited state. This process perturbs the linear evolution of ${\sigma }_z(x,t)$ and ${\sigma }_y(x,t)$ associated with the free polarization field. Coherent interference between the probe and free polarization leads to a pronounced intensity reduction of $-16.9$ dB in $Q(x)$ at $x\approx 0.254$ m, beyond which the intensity increases-see Figure 4.

Figure 2

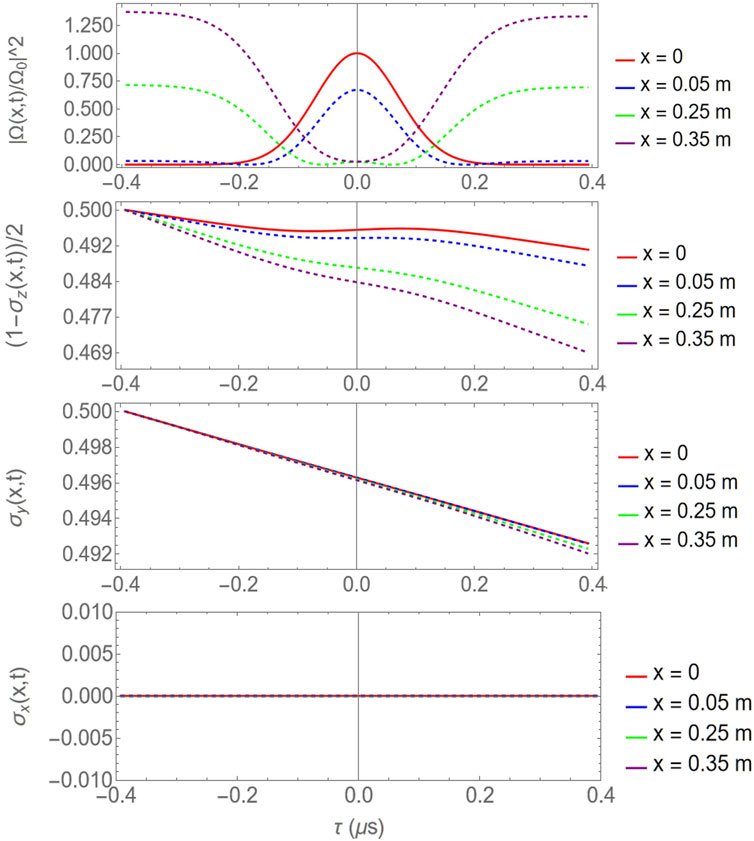
Figure 2. Numerics of the normalized probe intensity (top) and Bloch vector components $({\sigma }_x,{\sigma }_y,(1-{\sigma }_z)/2)$ versus the retarded time $\tau$ at different distances $x$ for the absorptive case $({\varphi }_0=0)$. The incident probe has pulse area $0.004\pi$ and duration $\tau =100\text{\hspace{0.17em}ps}$.

Figure 3

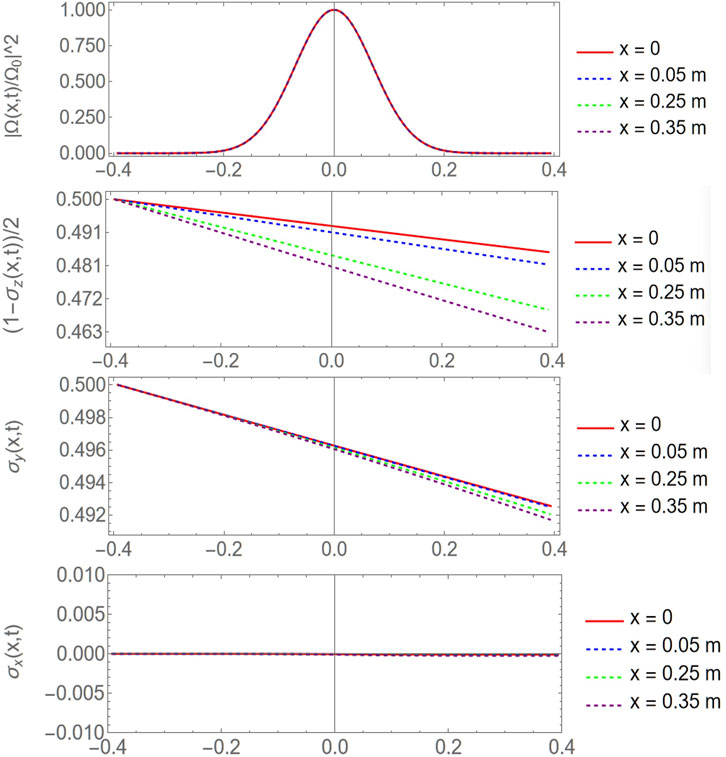
Figure 3. Numerics of the normalized probe intensity (top) and Bloch vector components $({\sigma }_x,{\sigma }_y,(1-{\sigma }_z)/2)$ versus the retarded time $\tau$ at different distances $x$ for the PDT case $({\varphi }_0=\pi /2)$. The incident probe has pulse area $0.004\pi$ and duration $\tau =100\text{\hspace{0.17em}ps}$.

Figure 4

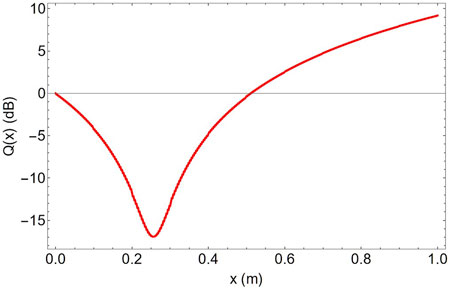
Figure 4. Normalized intensity-time integral $Q(x)$ (in dB units) versus position for the absorptive configuration as in Figure 2.

The dispersive behavior observed in this regime arises from the coherent interference between the probe and the free polarization field. As shown in the plots of the temporal quantities (Equation 9) in Figure 5, for propagation distances $x<0.2$ m, the pulse exhibits significant temporal narrowing, evidenced by a decrease in the temporal variance ${\sigma }_{\tau }^2(x)$, along with a small positive group delay ${\tau }_g(x)>0$. In this region, the probe field amplitude exceeds that of the free polarization, and destructive interference primarily suppresses the resonant spectral components of the probe, effectively preserving its off-resonant spectral components. For $x>0.2$ m, the free polarization becomes dominant, leading to temporal broadening of the total field relative to the input probe. Both the group delay and temporal variance asymptotically approach the characteristic values of the free polarization field alone.

Figure 5

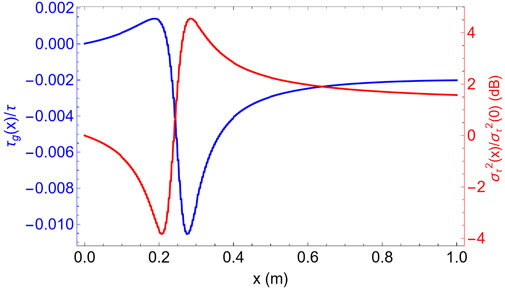
Figure 5. Normalized group delay ${\tau }_g(x)/\tau$ (blue) and normalized temporal variance ${\sigma }_{\tau }^2(x)/{\sigma }_{\tau }^2(0)$ (in dB units) versus position for the absorptive configuration as in Figure 2.

Phase-dependent transparency is obtained for the photon locking case $({\varphi }_0=\pi /2)$ where the probe intensity profile remains unchanged throughout the medium. The change to the atomic Bloch vector $\vec{\sigma }(x,t)$ is purely linear, unlike the absorptive case where absorption of the probe field increased the population inversion ${\sigma }_z$. The persistence of ${\sigma }_z(x,t)\approx 0$, along with the relative phase condition (Equation 5) leads to a vanishing optical response in Equation 7. As shown in Figure 6, the change in the probe intensity-time integral $Q(x)$ remains small—approximately $2\times 10^{-2}$ at $x=1.0\mathrm{m}$. Note that for the total transmitted field, the free polarization field must also be included in the integral for $Q(x)$. Due to the $\pi /2$ phase offset between the probe and free polarization fields, this contribution increases $Q(x)$ without affecting the probe profile. In addition to this negligible absorption, the group delay ${\tau }_g(x)$ and temporal variance ${\sigma }_{\tau }^2(x)$ show minimal variation across the medium (see Figure 7), further supporting our characterization of the observed behavior as PDT. Together, these results confirm that the field propagation satisfies $\mathrm{\Omega }(x,t)\approx {\mathrm{\Omega }}_0(t-x/c)$, in agreement with our numerical simulations.

Figure 6

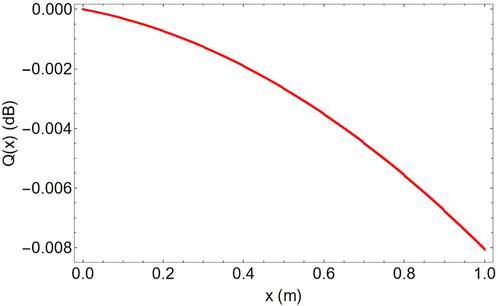
Figure 6. Normalized intensity-time integral $Q(x)$ (in dB units) versus position for the PDT configuration as in Figure 5.

Figure 7

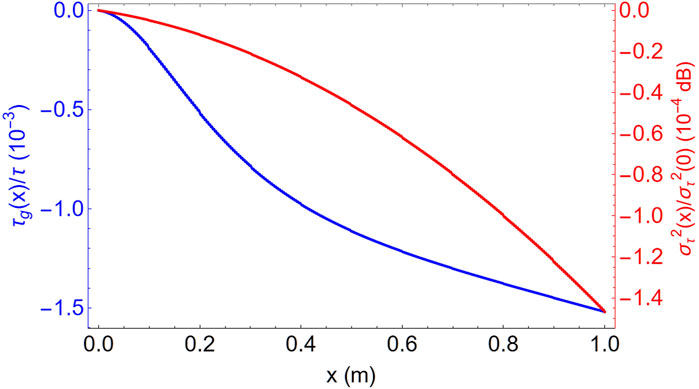
Figure 7. Normalized group delay ${\tau }_g(x)/\tau$ (blue) and normalized temporal variance ${\sigma }_{\tau }^2(x)/{\sigma }_{\tau }^2(0)$ (in dB units) versus position for the PDT configuration as in Figure 5.

Discussion

The transparency phenomenon is robust to the probe detuning to an extent, see Figure 8. For $|\mathrm{\Delta }\tau |\ll |{\mathrm{\Omega }}_0{|}^{-1}$, there is negligible transfer of coherence from ${\sigma }_y$ to ${\sigma }_x$ and hence negligible population transfer. However as the detuning or pulse duration increases, population will either shift to the ground or excited state depending on the sign of $\mathrm{\Delta }$. In the case of initial state $\frac{|1\rangle +i|2\rangle }{\sqrt{2}}$ and ${\varphi }_0=\pi /2$, the Bloch equation (Equation 3) shows that population shifts to the ground state for $\mathrm{\Delta }<0$ and to the excited state for $\mathrm{\Delta }>0$ as we increase $|\mathrm{\Delta }|$. The population transfer cycles between the two states as we increase $|\mathrm{\Delta }|$ further. This occurs because the initially imaginary coherence is transferred to the real coherence at a rate $\mathrm{\Delta }$ and the real coherence is transferred to the population inversion, ${\sigma }_z$, with rate $\text{Im}[\mathrm{\Omega }]$. The signs of $\mathrm{\Delta }$ are reversed for $\varphi =-\pi /2$.

Figure 8

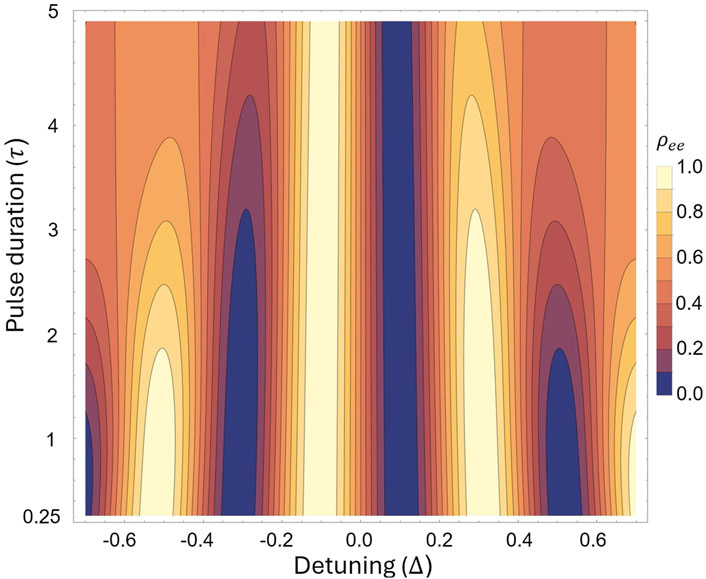
Figure 8. Plot of the excited state population ${\rho }_{ee}$ after interaction with a $\pi /2$ pulse with relative phase zero versus the probe detuning $\mathrm{\Delta }$ and the pulse duration $\tau$, in arbitrary units.

The degradation of phase-dependent transparency (PDT) in the presence of nonzero detuning implies that a thermal velocity distribution in the atomic medium will similarly be detrimental. To examine how a distribution of detunings affects transparency even when the phase-locking condition is satisfied, we introduce a velocity distribution $g(\vec{v})$ and a velocity-dependent detuning $\mathrm{\Delta }(\vec{v})={\mathrm{\Delta }}_0-\vec{k}\cdot \vec{v}$. We assume all atoms, regardless of their velocity class, are initialized in the maximally coherent Bloch state ${(\mathrm{0,1,0})}^T$. We consider the averaged Bloch vector ${\sigma }_{\text{av}}(x,t)=\int dvg(\vec{v})\sigma (x,t;v)$ and expand the general solution to first order in $\mathrm{\Delta }\tau$, assuming that ${\mathrm{\Delta }}_{\text{th}},|{\mathrm{\Omega }}_0|\ll {\tau }^{-1}$ where ${\mathrm{\Delta }}_{\text{th}}$ is the Doppler width. We move to the interaction picture in which the time-dependence of the Rabi frequency is explicitly retained, such that $\vec{v}(x,t)=|\mathrm{\Omega }(x,t)|{(\cos (\mathrm{\Delta }t+\varphi ),\sin (\mathrm{\Delta }t+\varphi ),0)}^T$ and expand to first order. The solution to Equation 3 for $\varphi =\pi /2$ is given by,

$\begin{array}{cc}\hfill & \vec{\sigma }\left(x,t\right)\sim \vec{\sigma }\left(x,t_0\right)-\left(2{\mathrm{\Delta }}_{\text{th}}\tau \right)\left(2{\mathrm{\Omega }}_0\tau \right){\int }_{-2{\mathrm{\Delta }}_{\text{th}}}^{2{\mathrm{\Delta }}_{\text{th}}}dvg\left(\vec{v}\right)\frac{\mathrm{\Delta }\left(\vec{v}\right)}{2{\mathrm{\Delta }}_{\text{th}}}\hfill \\ \hfill & {\left(\frac{\left(2{\mathrm{\Omega }}_0\tau \right)}{2\tau }{\int }_{t_0}^{t}d{t}^{\prime }|\frac{\mathrm{\Omega }\left(x,t^{\prime }\right)}{{\mathrm{\Omega }}_0}{|}^2,0,|\frac{\mathrm{\Omega }\left(x,t\right)}{{\mathrm{\Omega }}_0}|\right)}^T+\mathcal{O}\left({\left({\mathrm{\Delta }}_{\text{th}}\tau \right)}^2\right)\hfill \end{array}(10)$

We can see that all terms in Equation 10 are of the form $c(2{\mathrm{\Delta }}_{\text{th}}\tau ){(2{\mathrm{\Omega }}_0\tau )}^n$, where $|c|\sim 1$. Substituting this term into Equation 6, we similarly see a scaling of the absorption coefficient with ${\mathrm{\Delta }}_{\text{th}}\tau$. It follows that we can suppress the effect of a non-zero detuning and Doppler broadening by enforcing ${\mathrm{\Delta }}_{\text{th}},|{\mathrm{\Omega }}_0|\ll {\tau }^{-1}$.

We have assumed the case of a homogeneous continuous vapor of two-level atoms in our model and assumed no inhomogeneous effects including variations in the spatial profile of the beam, frequency shifts of the atoms and the presence of background scatterer species that produce phase fluctuations in the probe. Due to the coherent nature of photon locking, any effects that disturb the coherent phase relationship between the atoms in the medium and the pulse will degrade PDT. While these effects are beyond the scope of this paper, we detail how our model can be extended to incorporate inhomogeneities for the interested reader. Position-dependent drifts in the transition frequencies of the atoms can be introduced as randomly assigned c-number detunings $\mathrm{\Delta }(x){\sigma }_z(x)$, selected from a Gaussian distribution with $⟨\mathrm{\Delta }(x)⟩=0$, $⟨{(\mathrm{\Delta }(x))}^2⟩={\sigma }_{\mathrm{\Delta }}^2$ to model effects such as inhomogeneous magnetic shifts in a vapor cell or optical trap setup. The effects of these shifts on PDT is similar to the case of Doppler broadening where enforcement of the condition $|2{\sigma }_{\mathrm{\Delta }}\tau |\ll 1$ can be used to suppress drift effects. Inhomogeneities in the probe beam profile can be introduced through phase kicks to the Rabi frequency $\mathrm{\Omega }(x,t)\to \mathrm{\Omega }(x,t)e^{i\varphi (x)}$, similarly selected from a Gaussian distribution with $⟨\varphi (x)⟩=0$, $⟨{(\varphi (x))}^2⟩={\sigma }_{\varphi }^2$. In addition, we can incorporate the effect of decay and phase fluctuations in the field due to scattering from a background species by introducing to the SVEA unidirectional equation (Equation 4) a position dependent decay term $-\kappa (x)\mathrm{\Omega }(x,t)$ and Langevin forces $F(x,t)$ (Scully and Zubairy, 1997). A more rigorous theoretical examination of these effects will be explored in a future work.

As previously mentioned, the transparency effect is sustained when the condition $\tau \ll {\mathrm{\Gamma }}^{-1}$ is satisfied. For larger scatterer densities, spontaneous emission and the free polarization generate a large enough field such that we can no longer neglect the contribution from the first term in Equation 7. We hence do not consider the phenomenon of phase-dependent transparency in the regime where open system dynamics become significant.

The results with PDT yields important conclusions on how we can use the phase of light fields to induce transparency by making the scattering amplitudes for absorption and stimulated emission equal in magnitude and phase. We remark that is different from EIT where the scattering amplitudes for absorption from different pathways sum to zero due to them being $\pi$ out of phase with each other. There is a parallel in that we can tune induced transparency to induced absorption in the non steady-state case by changing the phase of the probe field (Abi-sallouma et al., 2007). Furthermore, in contrast with EIT, our approach would only require optical pumping to a state which is transparent to the probe field, and does not require a coupling field to generate the destructive interference required of EIT.

All-optical switching

The results we developed here have applications in the development of optical switches (Yadav and Bhattacherjee, 2022; Volz et al., 2012). Indeed, phase dependent transparency could provide an easy way to generate on-demand transient absorption and transparency through control of the relative phase between the probe field and atomic coherence. To illustrate this, we introduce a conceptual scheme for all-optical switching in Figure 9. A pump (red) and probe (green) pulse are prepared and joined at the third arm to generate a pulse sequence described by the tuple $(A,{\varphi }_i)$ where $A$ is the pulse area magnitude and ${\varphi }_i$ is the Rabi phase. The distances of the arms $x_i$ are used to set ${\varphi }_i$. The chamber (dark grey) is a medium of two level scatterers that are resonant with the frequencies of the two pulses. The pump pulse drives the system to the maximum coherence state, ${\vec{\sigma }}_0$, and the response to the probe pulse is determined by the relative phase ${\varphi }_2-{\varphi }_1$. Since the $\pi /2$ pump pulse generates an atomic coherence that is $\pi /2$ out of phase with that of the pump pulse, completely transparent transmission of the probe pulse is achieved when ${\varphi }_2-{\varphi }_1\equiv \pi /2\text{mod}(\pi )$. On the other hand, if ${\varphi }_2-{\varphi }_1\equiv 0\text{mod}(2\pi )$, population is transferred to the excited state and we get absorption. We also mention the case for ${\varphi }_2-{\varphi }_1\equiv \pi \text{mod}(2\pi )$ where population is returned to the ground state, resulting in amplification of the probe. After the probe pulse passes, the system is reset, where all the population is returned to the ground state, for application of the next pump-probe pulse sequence. The protocol we developed assumes that the TLSs interact with coherent fields that can be described by a semiclassical Hamiltonian. Therefore the results derived here can be extended to the cavity QED setup of a TLS interacting with a classical control field and cavity driven by a coherent probe field. For the purposes of all-optical switching with fast $(\sim 100\mathrm{p}\mathrm{s})$ pulses, switching contrasts of upwards of $10\mathrm{d}\mathrm{B}$ are required. Using our definition of the intensity-time integral $Q(x)$ (Equation 8), we calculate the switching contrast $S(x)$:

$S\left(x\right)=-10{\log }_{10}\left|\frac{Q_{\text{abs}}\left(x\right)}{Q_{\text{PDT,pr}}\left(x\right)+Q_{\text{PDT,free}}\left(x\right)}\right|(11)$

Figure 9

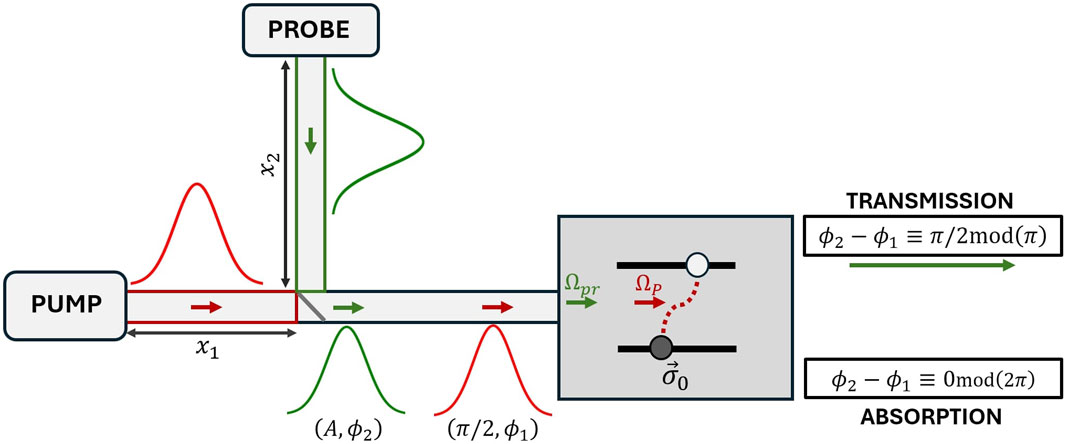
Figure 9. Protocol for all-optical switching using phase-dependent transparency in two-level systems.

The plot of the switching contrast, calculated with Equation 11, in Figure 10 shows that a maximum contrast of $S\sim 19.9\mathrm{d}\mathrm{B}$ is achieved at $x=0.258\text{\hspace{0.17em}m}$, which is well above the $10\mathrm{d}\mathrm{B}$ contrast. In opposition to optical switching schemes based on EIT, the absorptive effect does not scale with the optical depth as the coherent interference between the probe and free polarization leads to an increase in intensity once the free polarization’s intensity is comparable to the probe’s. Nonetheless, the high switching contrast achieved with this simple scheme shows that PDT-based all-optical switchers can be a promising direction for developing classical all-optical switching, especially in the ultrafast regime.

Figure 10

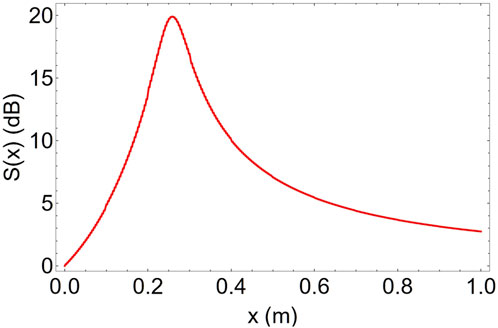
Figure 10. Switching contrast $S(x)$ (11) in dB versus distance $x$ for the PDT optical switcher with density $n=2\times 10^{13}{\mathrm{m}}^{-3}$, pulse area $0.004\pi$, and pulse duration $\tau =100\text{\hspace{0.17em}ps}$.

We have theoretically demonstrated a new form of non-steady state transparency in the two-level system (TLS) with fast hundred ps pulses, which we call phase-dependent transparency (PDT), that is realized when the TLS is in a maximum coherence state and when the relative phase between the probe pulse and atomic coherence is a multiple of $\pi$. We used a semiclassical framework to describe the propagation of classical fields in a medium of TLS scatterers and developed the phase matching condition from a geometric formulation of the Bloch vector equations and the polarization response to the probe field in the SVEA. Our results show that the phase of the probe field can control the absorption response of the medium, enabling transparency in configurations where it is not typically observed—for example, in degenerate hyperfine magnetic manifolds of alkali atoms (Lipsich et al., 2000; Ramaswamy et al., 2023). While our model considers a simplified two-level system and omits effects such as Doppler broadening, spatial inhomogeneity, and dephasing, the core concept of photon locking via a relative pump–probe phase can be generalized to multilevel systems that incorporate these complexities. The findings discussed in this work contribute to the broader understanding of coherence and phase control in non-steady-state transparency. We also proposed a conceptual protocol for implementing all-optical switching using PDT in alkali atom vapor cells with ps optical pulses. Future research may further explore the theoretical limits and experimental feasibility of such switching schemes, including strategies to mitigate decoherence, phase noise, and inhomogeneities.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

AR: Writing – original draft, Writing – review and editing. SM: Conceptualization, Funding acquisition, Investigation, Methodology, Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. We acknowledge funding support from the Office of Naval Research through award N00014-22-1-2374.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frqst.2025.1526469/full#supplementary-material

Data Sheet 1 | Alternate derivation of the phase matching condition using the Dyson series expansion.

References

Abi-sallouma, T., Davis, C. L. J. P., Elliott, E., and Narducci, F. A. (2007). J. Mod. Opt. 54, 2459. doi:10.1080/09500340701742617

CrossRef Full Text | Google Scholar

Agarwal, G. S., Di, K., Wang, L., and Zhu, Y. (2016). Perfect photon absorption in the nonlinear regime of cavity quantum electrodynamics. Phys. Rev. A 93, 063805. doi:10.1103/physreva.93.063805

CrossRef Full Text | Google Scholar

Agarwal, G. S., and Huang, S. (2010). Electromagnetically induced transparency in mechanical effects of light. Phys. Rev. A 81, 041803. doi:10.1103/physreva.81.041803

CrossRef Full Text | Google Scholar

Akulshin, A., Barreiro, S., and Lezama, A. (1998). Electromagnetically induced absorption and transparency due to resonant two-field excitation of quasidegenerate levels in Rb vapor. Phys. Rev. A 57, 2996–3002. doi:10.1103/physreva.57.2996

CrossRef Full Text | Google Scholar

Bayer, T., Wollenhaupt, M., Sarpe-Tudoran, C., and Baumert, T. (2009). Robust photon locking. Phys. Rev. Lett. 102, 023004. doi:10.1103/physrevlett.102.023004

PubMed Abstract | CrossRef Full Text | Google Scholar

Bodey, J. H., Stockill, R., Stockill, R., Denning, E. V., Denning, E. V., Gangloff, D. A., et al. (2019). npj Quantum Inf. 5, 1. doi:10.1038/s41534-019-0206-3

CrossRef Full Text | Google Scholar

Chakravarty, S. (2016). Soliton solutions of coupled maxwell–bloch equations. Phys. Lett. A 380, 1141–1150. doi:10.1016/j.physleta.2015.10.031

CrossRef Full Text | Google Scholar

Chathanathil, J., Ramaswamy, A., Malinovsky, V. S., Budker, D., and Malinovskaya, S. A. (2023). Chirped fractional stimulated raman adiabatic passage. Phys. Rev. A 108, 043710. doi:10.1103/physreva.108.043710

CrossRef Full Text | Google Scholar

Delben, G. J., Beims, M. W., and da Luz, M. G. E. (2023). Control of a qubit under markovian and non-Markovian noise. Phys. Rev. A 108, 012620. doi:10.1103/physreva.108.012620

CrossRef Full Text | Google Scholar

Finkelstein, R., Bali, S., Firstenberg, O., and Novikova, I. (2023). A practical guide to electromagnetically induced transparency in atomic vapor. New J. Phys. 25, 035001. doi:10.1088/1367-2630/acbc40

CrossRef Full Text | Google Scholar

Fleischhauer, M., Imamoglu, A., and Marangos, J. P. (2005). Electromagnetically induced transparency: optics in coherent media. Rev. Mod. Phys. 77, 633–673. doi:10.1103/revmodphys.77.633

CrossRef Full Text | Google Scholar

Fleischhauer, M., and Lukin, M. D. (2000). Dark-state polaritons in electromagnetically induced transparency. Phys. Rev. Lett. 84, 5094–5097. doi:10.1103/physrevlett.84.5094

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, M.-D., Wu, Y.-J., Li, N., Li, H.-F., and Zhou, C.-X. (2024). Optical switch based on tunable perfect photon absorption. Phys. Lett. A 505, 129456. doi:10.1016/j.physleta.2024.129456

CrossRef Full Text | Google Scholar

Guo, S.-T., Zhang, Y.-H., Wu, L.-L., Ye, M.-Y., and Lin, X.-M. (2021). Transition between coupled-resonator-induced transparency and absorption. Phys. Rev. A 103, 033510. doi:10.1103/physreva.103.033510

CrossRef Full Text | Google Scholar

Harris, S. E. (1997). Electromagnetically induced transparency. Phys. Today 50, 36–42. doi:10.1063/1.881806

CrossRef Full Text | Google Scholar

Hu, X.-M., Zou, J.-H., Li, X., Du, D., and Cheng, G.-L. (2005). Amplitude and phase control of trichromatic electromagnetically induced transparency. J. Phys. B Atomic, Mol. Opt. Phys. 38, 683–692. doi:10.1088/0953-4075/38/6/007

CrossRef Full Text | Google Scholar

Huang, X., Wang, T.-J., and Wang, C. (2022). Electromagnetically induced transparency and absorption in directly coupled whispering-gallery mode microcavities. IEEE Photonics J. 14, 1–8. doi:10.1109/jphot.2022.3151506

CrossRef Full Text | Google Scholar

Joshi, A. (2009). Phase-dependent electromagnetically induced transparency and its dispersion properties in a four-level quantum well system. Phys. Rev. B 79, 115315. doi:10.1103/physrevb.79.115315

CrossRef Full Text | Google Scholar

Kälin, M., Gromov, I., and Schweiger, A. (2004). Transparency in two-level spin systems induced by a longitudinal field. Phys. Rev. A 69, 033809. doi:10.1103/physreva.69.033809

CrossRef Full Text | Google Scholar

Kekatpure, R. D., Barnard, E. S., Cai, W., and Brongersma, M. L. (2010). Phase-coupled plasmon-induced transparency. Phys. Rev. Lett. 104, 243902. doi:10.1103/physrevlett.104.243902

PubMed Abstract | CrossRef Full Text | Google Scholar

Kimble, H. J. (2008). The quantum internet. Nature 453, 1023–1030. doi:10.1038/nature07127

PubMed Abstract | CrossRef Full Text | Google Scholar

Koch, C. P., Boscain, U., Calarco, T., Dirr, G., Filipp, S., Glaser, S. J., et al. (2022). Quantum optimal control in quantum technologies. Strategic report on current status, visions and goals for research in Europe. EPJ Quantum Technol. 9, 19. doi:10.1140/epjqt/s40507-022-00138-x

CrossRef Full Text | Google Scholar

Körber, M., Morin, O., Langenfeld, S., Neuzner, A., Ritter, S., and Rempe, G. (2018). Decoherence-protected memory for a single-photon qubit. Nat. Photonics 12, 18–21. doi:10.1038/s41566-017-0050-y

CrossRef Full Text | Google Scholar

Korsunsky, E., Leinfellner, N., Huss, A., Baluschev, S., and Windholz, L. (1999). Phase-dependent electromagnetically induced transparency. Phys. Rev. A 59, 2302–2305. doi:10.1103/physreva.59.2302

CrossRef Full Text | Google Scholar

Lezama, A., Barreiro, S., and Akulshin, A. M. (1999). Electromagnetically induced absorption. Phys. Rev. A 59, 4732–4735. doi:10.1103/physreva.59.4732

CrossRef Full Text | Google Scholar

Lipsich, A., Barreiro, S., Akulshin, A. M., and Lezama, A. (2000). Absorption spectra of driven degenerate two-level atomic systems. Phys. Rev. A 61, 053803. doi:10.1103/physreva.61.053803

CrossRef Full Text | Google Scholar

Lukin, M. D., Fleischhauer, M., Cote, R., Duan, L. M., Jaksch, D., Cirac, J. I., et al. (2001). Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 87, 037901. doi:10.1103/physrevlett.87.037901

PubMed Abstract | CrossRef Full Text | Google Scholar

Lukin, M. D., Yelin, S. F., and Fleischhauer, M. (2000). Entanglement of atomic ensembles by trapping correlated photon states. Phys. Rev. Lett. 84, 4232–4235. doi:10.1103/physrevlett.84.4232

PubMed Abstract | CrossRef Full Text | Google Scholar

Marangos, J. P. (1998). Electromagnetically induced transparency. J. Mod. Opt. 45, 471–503. doi:10.1080/09500349808231909

CrossRef Full Text | Google Scholar

McCall, S. L., and Hahn, E. L. (1969). Self-induced transparency. Phys. Rev. 183, 457–485. doi:10.1103/physrev.183.457

CrossRef Full Text | Google Scholar

Naweed, A., Farca, G., Shopova, S. I., and Rosenberger, A. T. (2005). Induced transparency and absorption in coupled whispering-gallery microresonators. Phys. Rev. A 71, 043804. doi:10.1103/physreva.71.043804

CrossRef Full Text | Google Scholar

Petrosyan, D., Otterbach, J., and Fleischhauer, M. (2011). Electromagnetically induced transparency with rydberg atoms. Phys. Rev. Lett. 107, 213601. doi:10.1103/physrevlett.107.213601

PubMed Abstract | CrossRef Full Text | Google Scholar

Radeonychev, Y. V., Khairulin, I. R., Vagizov, F. G., Scully, M., and Kocharovskaya, O. (2020). Observation of acoustically induced transparency for -Ray photons. Phys. Rev. Lett. 124, 163602. doi:10.1103/PhysRevLett.124.163602

PubMed Abstract | CrossRef Full Text | Google Scholar

Radeonychev, Y. V., Tokman, M. D., Litvak, A. G., and Kocharovskaya, O. (2006). Acoustically induced transparency in optically dense resonance medium. Phys. Rev. Lett. 96, 093602. doi:10.1103/physrevlett.96.093602

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramaswamy, A., Chathanathil, J., Kanta, D., Klinger, E., Papoyan, A., Shmavonyan, S., et al. (2023). Mirrorless lasing: a theoretical perspective. Opt. Mem. Neural Netw. 32, S443–S466. doi:10.3103/s1060992x23070172

CrossRef Full Text | Google Scholar

Ramaswamy, A., and Malinovskaya, A. (2024). Phase-dependent transparency in a two-level system: supplemental material. Hoboken, NJ, USA: Stevens Institute of Technology.

Google Scholar

Sahrai, M., Mahmoudi, M., and Kheradmand, R. (2007). The impact of the relative phase on the transient optical properties of a four-level EIT medium. Phys. Lett. A 367, 408–414. doi:10.1016/j.physleta.2007.03.014

CrossRef Full Text | Google Scholar

Sangouard, N., Simon, C., de Riedmatten, H., and Gisin, N. (2011). Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80. doi:10.1103/revmodphys.83.33

CrossRef Full Text | Google Scholar

Scully, M. O., and Zubairy, M. S. (1997). Quantum optics. Cambridge University Press.

Google Scholar

Shen, J.-T., and Fan, S. (2005). Coherent single photon transport in a one-dimensional waveguide coupled with superconducting quantum bits. Phys. Rev. Lett. 95, 213001. doi:10.1103/physrevlett.95.213001

PubMed Abstract | CrossRef Full Text | Google Scholar

Slusher, R. E., and Gibbs, H. M. (1972). Self-induced transparency in atomic rubidium. Phys. Rev. A 5, 1634–1659. doi:10.1103/physreva.5.1634

CrossRef Full Text | Google Scholar

Svidzinsky, A. A., Zhang, X., and Scully, M. O. (2015). Quantum versus semiclassical description of light interaction with atomic ensembles: revision of the maxwell-bloch equations and single-photon superradiance. Phys. Rev. A 92, 013801. doi:10.1103/physreva.92.013801

CrossRef Full Text | Google Scholar

Tannor, D. (2007). Introduction to quantum mechanics. Sausalito, CA: University Science Books.

Google Scholar

Volz, T., Reinhard, A., Winger, M., Badolato, A., Hennessy, K. J., Hu, E. L., et al. (2012). Ultrafast all-optical switching by single photons. Nat. Photonics 6, 605–609. doi:10.1038/nphoton.2012.181

CrossRef Full Text | Google Scholar

Vreeker, R., Glasbeek, M., Sleva, E., and Zewail, A. (1986). Phase locking of molecular two-level quantum systems: application to ionic solids. Chem. Phys. Lett. 129, 117–119. doi:10.1016/0009-2614(86)80180-4

CrossRef Full Text | Google Scholar

Weis, S., Rivière, R., Deléglise, S., Gavartin, E., Arcizet, O., Schliesser, A., et al. (2010). Optomechanically induced transparency. Science 330, 1520–1523. doi:10.1126/science.1195596

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiong, H., and Wu, Y. (2018). Fundamentals and applications of optomechanically induced transparency. Appl. Phys. Rev. 5, 031305. Available online at: https://pubs.aip.org/aip/apr/article-pdf/doi/10.1063/1.5027122/19740644/031305_1_online.pdf. doi:10.1063/1.5027122

CrossRef Full Text | Google Scholar

Yadav, S., and Bhattacherjee, A. B. (2022). “Quantum optical switches,” in Optical switching: device technology and applications in networks (Wiley), 185–201.

CrossRef Full Text | Google Scholar

Yang, L.-J., Lu, D.-Q., and Zhao, M. (2010). in 2010 symposium on photonics and optoelectronics, 1–4.

Google Scholar

Yang, X., Yu, M., Kwong, D.-L., and Wong, C. W. (2009). All-optical analog to electromagnetically induced transparency in multiple coupled photonic crystal cavities. Phys. Rev. Lett. 102, 173902. doi:10.1103/physrevlett.102.173902

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, S., Genov, D. A., Wang, Y., Liu, M., and Zhang, X. (2008). Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 101, 047401. doi:10.1103/physrevlett.101.047401

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y., Hu, X., Yang, H., and Gong, Q. (2014). On-chip plasmon-induced transparency based on plasmonic coupled nanocavities. Sci. Rep. 4, 3752. doi:10.1038/srep03752

PubMed Abstract | CrossRef Full Text | Google Scholar