Micromotion compensation using dark and bright ion species

Stray electric fields induce excess micromotion in ion traps, limiting experimental performance. We present a new micromotion-compensation technique that utilizes a dark ion in a multi-species bright-dark-bright linear ion crystal. Stray electric fields in the radial plane of the trap deform the crystal axially due to the different masses of dark and bright ions. We exploit the mode softening near the transition to the zig-zag configuration to enhance the crystal deformation and, as a result, increase the method’s sensitivity dramatically. We corroborate our results with a modified ion-displacement compensation method using a single bright ion. Our modification allows us to compensate stray fields on the 2D radial plane from a 1D measurement of the ion position on the camera by controlling the asymmetry of the two radial modes of the trap. Both methods require only a fixed imaging camera and continuous ion-fluorescence detection. As such, they can be readily implemented in most ion-trapping experiments without additional hardware modifications.

Introduction

Excess micromotion (EMM) is the residual motion of an ion in its equilibrium position driven by the radiofrequency (RF) oscillating fields, and it is present in any RF ion trap (Berkeland et al., 1998). While EMM could be used to one’s advantage in some exceptional cases (Navon et al., 2013), typically, compensating EMM below some threshold is a necessary condition for most ion-trapping experiments. A few prominent examples are experiments involving the interaction between ultracold neutral atoms and trapped ions where EMM can limit the energy scale of the interaction (Tomza et al., 2019), optical-atomic clocks where uncompensated EMM could limit the clock’s accuracy (Brewer et al., 2019), and optical trapping of ions where the optical dipole force is overwhelmed by uncompensated stray electric fields in the trap (Huber et al., 2014).

Many techniques for detecting and compensating EMM were developed in the last few decades. The most common (Berkeland et al., 1998) are the resolved-sideband, photon-correlation, and ion-displacement methods. Each technique has its advantages and disadvantages when compared to others (Keller et al., 2015). For example, the resolved-sideband method (Berkeland et al., 1998; Keller et al., 2015) and its recent extension (Arnold et al., 2024) only detect EMM parallel to the laser’s k-vector and require the implementation of coherent-control tools such as narrow linewidth lasers. Here, we focus on a technique for which advanced coherent-control tools are unnecessary.

The minimal requirement for imaging a trapped ion is continuous illumination with a laser to induce ion fluorescence and an imaging system to collect the emitted photons on a camera. With only these tools at hand, EMM compensation can be achieved by observing the position of the ion on the camera for different radio-frequency trapping strengths (Berkeland et al., 1998; Schneider et al., 2012; Gloger et al., 2015; Saito et al., 2021). While 2D information on the ion position is readily extracted from a fluorescence image of an ion, the information regarding the position along the imaging axis is less accessible (Schneider et al., 2012). It requires automated mechanical scanning of the focus (Gloger et al., 2015; Saito et al., 2021) or engineering of the imaging point-spread function (Zhou et al., 2024), which are not standard techniques in ion imaging.

Here, we use a “dark” ion (⁴⁴$\mathrm{C}\mathrm{a}$⁺) embedded in a crystal of “bright” ions (⁴⁰$\mathrm{C}\mathrm{a}$⁺) as a sensitive detector of radial stray electric fields and for EMM compensation. Throughout the paper, we call the central ion “dark” simply because our fluorescence lasers do not address it, whereas they do address the surrounding “bright” ions. Since the radial confinement in linear RF traps depends on the mass of the ion, mixed-species ions, which carry different masses, will acquire a differential shift in their position due to radial stray electric fields (Mokhberi and Willitsch, 2015). This will lead to a deformation of the ion crystal detectable by fluorescence imaging. Minimizing the crystal deformation inevitably indicates the suppression of stray electric fields in the ion trap.

In a linear crystal of bright ions embedded with a dark ion of different mass, a stray radial electric field can be detected by observing the deformation of the crystal along its axis (axial axis), which can be sensitive to a displacement of the dark ion in both radial directions. Thus, by reading the position of the bright ions along the axial axis on the 2D imaging plane, we are sensitive to radial displacements of the dark ion that are both on and out of the imaging plane.

Axial deformation due to radial displacement is quadratic in nature. Hence, we need to enhance the sensitivity of our method further. We do so by working near the transition from a linear to a zig-zag configuration in a bright-dark-bright three-ion crystal (Kaufmann et al., 2012). Near the transition, the frequency of the radial bending mode approaches zero (mode softening) (Fishman et al., 2008), significantly enhancing crystal deformation for a given stray field.

Mixed-species ion crystals are becoming more common in novel ion-trapping quantum technologies such as mixed-species optical atomic clocks (Brewer et al., 2019; Hausser et al., 2025), quantum-logic control of molecular ions (Wolf et al., 2016; Lin et al., 2020; Sinhal et al., 2020; Holzapfel et al., 2024) and highly charged ions (King et al., 2022), and mixed-species quantum computation (Tan et al., 2015; Ballance et al., 2015; Pino et al., 2021; Bruzewicz et al., 2019; Hughes et al., 2020; Negnevitsky et al., 2018), to name a few. Therefore, techniques for compensating EMM in these mixed-species crystals are of high importance (Barrett et al., 2003).

To test the validity of our dark-ion EMM compensation method, we use the technique developed in Refs (Schneider et al., 2012; Gloger et al., 2015; Saito et al., 2021) with a small but useful modification. In these works, EMM compensation was performed by monitoring the position of a single bright ion in the two radial directions while changing the amplitude of the oscillating RF fields. The position of the ion along the imaging axis was retrieved by automated scanning of the imaging focus (Gloger et al., 2015; Saito et al., 2021) or by inferring it from the size of the de-focused point-spread function (Schneider et al., 2012). Here, we show that by changing the ratio between the frequencies of the two radial modes, we can compensate EMM in the two radial directions without the position information along the imaging axis. In our trap, which possesses a large asymmetry ratio at low RF amplitudes, we change the asymmetry by increasing the RF amplitude, which results in a non-linear ion trajectory (Gloger et al., 2015).

In this work, we consider only EMM generated by the ion’s radial displacement from the trap’s RF center. Typically, this is the leading EMM term to compensate, which can acquire the largest value. Other EMM origins exist, such as out-of-phase EMM and axial EMM (Meir et al., 2018), which are typically lower in magnitude. The presented method is insensitive to these EMM sources since they don’t induce a constant shift from the trap’s RF center.

Experiment - dark ion

We use a linear-segmented RF trap similar to the one described in Meir et al. (2018). We load ions to the trap from a heated oven loaded with pure calcium (Ca) grains. We use a 1 + 1′ resonance-enhanced-ionization scheme to load ions to the trap from the flux of neutral atoms emerging from the heated oven. By tuning the first ionization beam to a resonance in neutral Ca, we can selectively ionize different Ca isotopes (Lucas et al., 2004). We load a three-ion crystal made of two ⁴⁰Ca⁺ ions (bright ions) and one ⁴⁴Ca⁺ ion (dark ion) in the center. The cooling and fluorescence lasers are tuned to the resonance of the ⁴⁰Ca⁺ ions, hence the “bright” and ’‘dark” nomenclatures. The RF drive frequency in our experiment is $\mathrm{\Omega }/2\pi =14.5456\text{\hspace{0.17em}MHz}$.

The three-ion crystal transitions from a linear to a zig-zag configuration when the bright-ion radial frequency, ${\omega }_r^b$, is lower than the threshold frequency (see Supplementary Material - dark-ion zig-zag condition),

${\omega }_{r,zz}^b\approx {\omega }_{ax}^b\sqrt{\frac{4}{5}\left(1+\frac{2m_d}{m_b}\right)}.(1)$

here, $m_b$ $(m_d)$ is the bright (dark) ion mass, and ${\omega }_{ax}^b$ is the axial frequency of a single bright ion in the trap. In this experiment, we set this frequency to ${\omega }_{ax}^b/2\pi =260.4\text{\hspace{0.17em}kHz}$. We can relate the radial frequency of a single bright ion in the trap, ${\omega }_r^b$, to the center-of-mass (COM) radial-mode frequency of a bright-dark-bright (bdb) crystal,

${\omega }_{r,\text{COM}}^{\mathit{bdb}}\approx {\omega }_r^b\frac{2}{3}\left(1+\frac{m_b}{2m_d}\right).(2)$

using Equations 1, 2, we get ${\omega }_{r,\text{COM},zz}^{\mathit{bdb}}/2\pi \approx 404\text{\hspace{0.17em}kHz}$ for the transition frequency from linear to zig-zag configuration in terms of the crystal’s COM mode. Note that while the COM radial mode has a finite value near the transition to zig-zag, the bending radial mode, where the two bright ions move out of phase with respect to the dark ion, approaches zero (mode softening):

${\omega }_{r,\text{bend}}^{\mathit{bdb}}\sim \sqrt{{\left({\omega }_r^b\right)}^2-{\left({\omega }_{r,zz}^b\right)}^2}.(3)$

A static electric field $E_r$ in the trap’s center will displace the ion according to (Berkeland et al., 1998)

$d_r\approx \frac{Q{E}_r}{m_i{\left({\omega }_r^i\right)}^2},(4)$

where $Q$ is the electric charge of the ion and the index $i$ indicates a bright $(i=b)$ or a dark $(i=d)$ ion. In a linear ion trap, to a leading order, ${\omega }_{ax}^2\propto m^{-1}$ while ${\omega }_r^2\propto m^{-2}$ such that displacements from the center are different for the dark and bright ions in the radial direction (see Figure 1c). In addition, the displacement scales as $d_r\propto {\omega }^{-2}$. For that, the bending mode, whose frequency approaches zero near the zig-zag transition, governs the ion’s displacement.

Figure 1

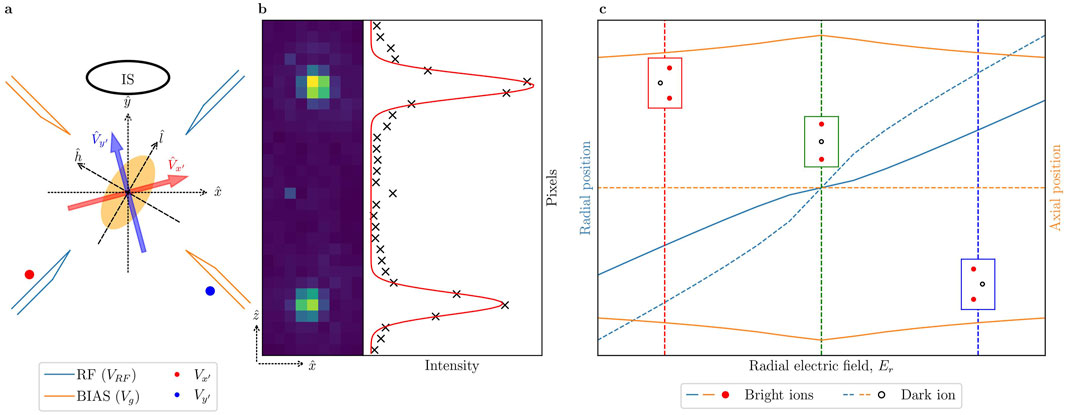
Figure 1. Deformation of a bright-dark-bright Coulomb crystal due to uncompensated EMM. (a) Sketch of a radial cross-section of the ion trap showing the RF (light blue) and BIAS (orange) trap blades, on which we apply RF $(V_{\text{RF}})$ and bias $(V_g)$ trapping voltages. Two compensation rods, $V_{x^{\prime }}$ (red) and $V_{y^{\prime }}$ (blue), create a radial electric field along the ${\widehat{V}}_{x^{\prime }}$ and ${\widehat{V}}_{y^{\prime }}$ directions. The imaging system (IS) captures the position of the ions along one projection of the radial direction $(\widehat{x})$ and the axial direction $(\widehat{z})$, as shown in (b). The displacement of the ions due to external field is dependent on the orientation (dashed axes) and ratio (orange ellipse) of the high $(\widehat{h})$ and low $(\widehat{l})$ radial modes. (b) Sample image of the ions captured by the IS (1 s exposure time, 5 images average). The position of the ions is found by fitting the intensity to a Gaussian in both the vertical and horizontal axes, which are then averaged for multiple frames to reduce their uncertainty. (c) A calculation of the change in the positions of the dark and bright ions as the radial field, $E_r$, is varied. Orange (blue) lines are the axial (radial) position of the bright (solid) and dark (dashed) ions. Green, blue, and red insets show the position of the dark ion (black open circle) compared to the bright ions (red circles) for different values of the radial electric field, marked by dashed, vertical lines.

We control the static electric field amplitude and orientation in the radial plane of the trap by applying voltages ($V_{x^{\prime }}$, $V_{y^{\prime }}$) on two compensation electrodes (see Figure 1a). As we scan the total excess field through its minimum, the dark ion is moved from one side of the crystal to the other as the sign of the external-field flips (see Figure 1c). When the trap is perfectly compensated, the dark ion is found directly between the two bright ions, pushing them to their maximum separation from each other. In the zig-zag configuration, however, the linear arrangement of ions is no longer stable, and as such, the dark ion will jump “over” the trap center. This jump occurs randomly when a fluctuation in the electric fields or a collision with background gasses grants it enough energy to bypass the potential barrier between the two sides of the crystal.

The radial plane of the trap supports two orthogonal modes $({\omega }_{r=h},{\omega }_{r=l})$, which are typically non-degenerate, ${\omega }_h>{\omega }_l$. Specifically, our trap has a large low-to-high radial-frequency ratio of ${\omega }_l/{\omega }_h\approx 0.7$ in the dark-ion experiment. We vary the radial modes’ frequencies and their orientation by changing the amplitude of the RF oscillating fields and the bias voltage, denoted as $V_g$ (see Figure 1a). We measure the trap frequencies via resonant electric-field excitation (“tickle”) (Drewsen et al., 2004). A suitable linear combination of the two compensation voltages allows us to push the ions toward each radial mode.

We record the position of the bright ions on an EM-CCD camera (Figure 1b). The imaging system comprises an objective with a working distance of $\sim$30 mm and a focal length of $\sim$37 mm. The imaging-system magnification is measured to be $\sim$1.13 µm/pixel. The exposure time is 1 s. The image is projected on the trap’s axial axis and on some projection of both the radial modes. In this experiment, we measure the axial distance between the two bright ions (see Figure 1b) from which we can infer the radial displacement of the dark ion from the axial axis.

Results - dark ion

The dependence of the distance between the bright ions on the EMM and the low radial-mode frequency is shown in Figure 2. We vary the compensation voltages, $V_{\perp }=f(V_{x^{\prime }},V_{y^{\prime }})$, to create a field along the direction of the low-frequency mode, ${\omega }_l$, and record the bright-ions positions. Here, $f$ is a linear function of the compensation-electrodes voltage, which we found experimentally (the line orthogonal to the purple line in Figure 3c as we performed the experiment with a bias voltage $V_g=0.6\text{\hspace{0.17em}V}$). We repeat this procedure for different radial-mode trapping frequencies.

Figure 2

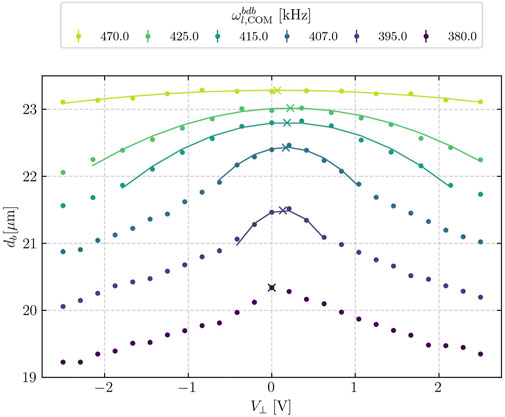
Figure 2. Bright ion separation, $d_b$, as function of an applied radial electric field for different low radial mode frequencies, ${\omega }_{l,\text{COM}}^{\mathit{bdb}}$ (legend). The electric field is applied along the direction of the low radial mode. The trap is compensated (not necessarily at the x-axis origin) when the distance between the bright ions is at its maximum. We extract the compensation value via a local parabola fit to the data (solid lines, cross indicate fit maximum). The measurement peak becomes more pronounced, and the range of quadratic dependence narrows as the radial frequency approaches the transition to zig-zag. Below the transition frequency to zig-zag $(\sim 404\text{\hspace{0.17em}kHz})$, bright ions display a noticeable discontinuity in their positions as the crystal jumps between the zig and zag configurations, with the bright ion distance no longer fitting a parabola when looking far below the transition frequency.

Figure 3

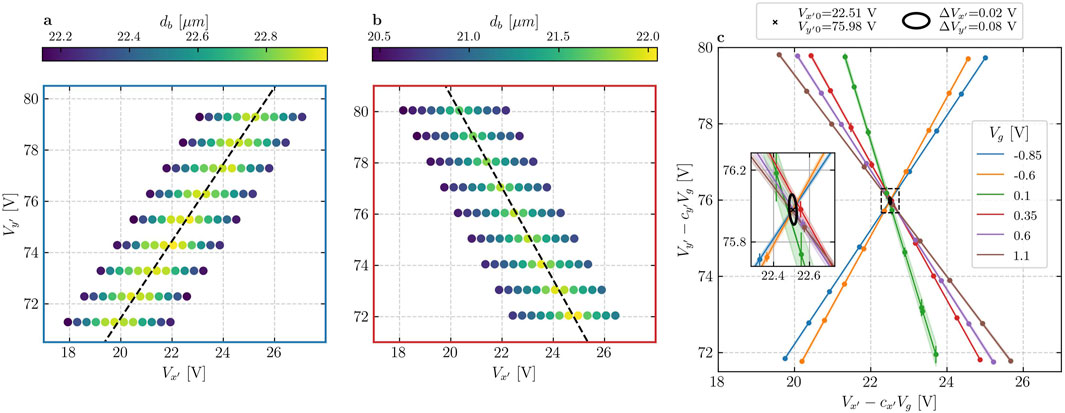
Figure 3. Dark ion EMM compensation. (a,b) Bright ion distance (color scale) as a function of the compensation voltages ($V_{x^{\prime }}$, $V_{y^{\prime }}$) for different bias voltages (a) $V_g=\text{−}0.85\text{\hspace{0.17em}V}$, (b) $V_g=0.35\text{\hspace{0.17em}V}$). Throughout the measurements, we kept the low-radial mode frequency at ${\omega }_{l,\text{COM}}^{\mathit{bdb}}=430\text{\hspace{0.17em}kHz}$ to avoid accidentally crossing the zig-zag transition frequency mid-measurement. The maximal ion distance follows a linear line in ($V_{x^{\prime }}$, $V_{y^{\prime }}$) space (dashed black line), the angle of which is determined by the radial-modes orientation. These lines are identical to those in (c) for bias voltages, $V_g=\text{−}0.85\text{\hspace{0.17em}V}$ (blue) and $V_g=0.35\text{\hspace{0.17em}V}$ (red), as denoted by the color of the frames. (c) Compensation lines for different bias voltages (see legend). Each line is a linear fit as in (a,b), the points being the peaks of the ion distances found for each $V_{y^{\prime }}$ in the 2D scans. The lines are shifted by the dependence of the compensation point on $V_g$ (Equation 6), so they all intersect at a single point ($c_{x^{\prime }}=-0.23\pm 0.07$, $c_{y^{\prime }}=0.57\pm 0.04$)- Equation 7. The ellipse shows the one-sigma error in the estimation of $(V_{x^{\prime }0},V_{y^{\prime }0})$.

As ${\omega }_{l,\text{COM}}^{\mathit{bdb}}$ approaches the zig-zag transition frequency ($\sim 404\text{\hspace{0.17em}kHz}$, see Equation 2), the bending mode confinement approaches zero, making the radial position of the dark ion, and thus the axial size of the crystal, more sensitive to uncompensated EMM. This increase in sensitivity can be seen in the steepness of the peaks in the different curves in Figure 2: Far from the zig-zag transition, the curves look almost entirely flat, making the peak indiscernible. While moving closer to the critical point, the curves grow progressively steeper until the zig-zag transition point, where the measurement is most sensitive.

Below the transition frequency to zig-zag configuration, the dark ion no longer passes through the center of the crystal when $V_{\perp }=0$, as this is not a stable configuration for a zig-zag chain. Instead, the crystal will randomly jump between the zig and zag configurations due to the potential barrier between them, making the estimation of the peak inherently unreliable.

For traps with considerable ratio between the high and low radial frequency modes (Saito and Mukaiyama, 2024) as our own (${\omega }_l/{\omega }_h\approx 0.7$ in the dark-ion experiment), the sufficient sensitivity for dark ion displacement is achieved in only one radial direction: while ${\omega }_l$ approaches the zig-zag transition frequency, ${\omega }_h$ remains far above it, such that the sensitivity of our measurement is diminished (in our trap, ${\omega }_{h,\text{COM}}^{\mathit{bdb}}\approx 590\text{\hspace{0.17em}kHz}$ at the zig-zag transition). As a result, conducting a 2D scan of the bright ion distance vs the compensation voltages results in a “compensation line”, $V_{y^{\prime }}=m{V}_{x^{\prime }}+b$, for which the distance is maximized (see Figures 3a,b). Following this line of minimal sensitivity, the ions are pushed towards the high radial mode, ${\omega }_h$. We cannot determine the location of the compensation point along the line from a single 2D scan (a ratio of ${\omega }_l/{\omega }_h>0.9$ is required for 2D compensation from a single scan - see Figure 2).

To overcome this obstacle, we exploit the ability to tune the orientation of the radial modes in our trap (Saito and Mukaiyama, 2024). By changing the bias voltage $V_g$ from −0.85 V to 1.1 V, we can change the trap’s mode orientation by $\sim 70$° (see Figure 3b). This rotation of ${\omega }_h$ and ${\omega }_l$ allows us to find new compensation lines,

$V_{y^{\prime }}=m_g{V}_{x^{\prime }}+b_g,(5)$

where $m_g$ and $b_g$ are the linear coefficients for a specific bias voltage, $V_g$. The intersection of all these lines should give the value of ($V_{x^{\prime }0}$, $V_{y^{\prime }0}$) for which EMM is compensated.

However, by changing the bias voltage, we also create stray electric fields due to the misalignment of the bias and RF quadrupoles in the trap. This results in a linear dependence of the compensation point on the value of $V_g$:

$\begin{array}{c}\hfill V_{x^{\prime }g}=c_{x^{\prime }}{V}_g+V_{x^{\prime }0},\\ \hfill V_{y^{\prime }g}=c_{y^{\prime }}{V}_g+V_{y^{\prime }0}.\end{array}(6)$

Here, ($V_{x^{\prime }g}$, $V_{y^{\prime }g}$) are the compensation values for some value of $V_g$, ($V_{x^{\prime }0}$, $V_{y^{\prime }0}$) are the compensation values for $V_g=0$, and ($c_{x^{\prime }}$, $c_{y^{\prime }}$) are the linear coefficients, all of which are not known a-priori.

Using Equation 6 to “shift” all compensation lines (Equation 5) due to the effect of $V_g$, we get the following set of linear equations:

$c_{y^{\prime }}{V}_g+V_{y^{\prime }0}=m_g\left(c_{x^{\prime }}{V}_g+V_{x^{\prime }0}\right)+b_g.(7)$

This set of equations has four “free” parameters: $\mathrm{c}\mathrm{x}\prime$, $\mathrm{c}{\mathrm{y}}^{\prime }$, $\mathrm{V}{\mathrm{x}}^{\prime }0$, and $V_{y^{\prime }0}$. Hence, by scanning the 2D compensation voltages for at least four bias voltages, we can extract the compensation points for any value of $\mathrm{V}\mathrm{g}$. The results of this procedure with six different bias voltages are shown in Figure 3c.

Experiment - single ion

To corroborate the EMM compensation results using a dark ion, we measure EMM by monitoring the position of a single bright ion on the camera for different amplitudes of the trapping RF fields (Berkeland et al., 1998; Schneider et al., 2012; Gloger et al., 2015; Saito et al., 2021). Here, we show that for 2D radial EMM compensation, only information on ion displacement along one radial direction is necessary. In our setup, this corresponds to the x-axis, which is perpendicular to the imaging axis. Our technique relies on two necessary conditions: 1) The ability to change the ratio of the trap’s radial modes. 2) The orientation of any of the radial modes should not align with the imaging optical axis. Both of these conditions can be met in a typical ion trap. In our trap, the first is fulfilled by adjusting the RF amplitude (see single-ion section in the Supplementray Material) as our trap possesses large inherent asymmetry between the radial modes (see Figure 5C legend), while the second condition is ensured through a simple adjustment of $V_g$.

As can be seen from Equation 4, the magnitude of the ion’s shift from the trap center due to a stray electric field depends on the radial trapping frequency. Changing the amplitude of the radial trapping fields from maximum to minimum values (denoted as “high” and “low” RF amplitudes) while monitoring the ion’s position shift is an efficient way to detect EMM (Berkeland et al., 1998; Schneider et al., 2012; Gloger et al., 2015; Saito et al., 2021).

In a symmetric trap, where the two radial modes are degenerate $({\omega }_l={\omega }_h)$, the ion is displaced along the direction of the stray electric field (see Figure 4a). In case the field is directed along the imaging-system axis, it will be hard to detect a shift in the position of the ion. In a non-symmetric trap, where the two radial modes are non-degenerate $({\omega }_l<{\omega }_h)$, the ion shifts more towards the low radial mode (Figure 4b). In this case, we can detect a shift in the ion position perpendicular to the imaging axis even though the electric field points along the imaging system axis.

Figure 4

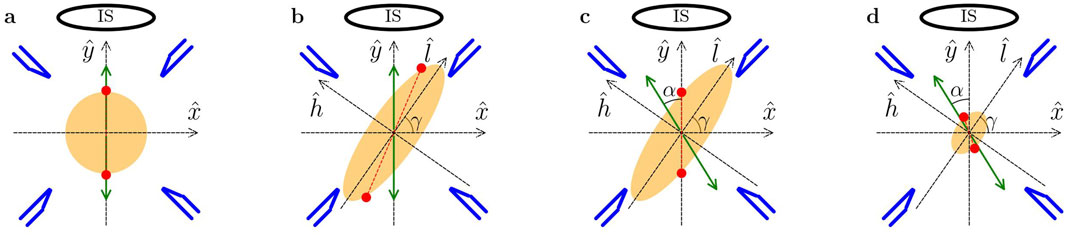
Figure 4. Single-ion radial displacement due to a radial stray electric field. The imaging system (IS) is oriented along the y-axis and can detect only shifts in ion position along the x-axis. The radial mode frequencies (${\omega }_l$, ${\omega }_h$) strength, ratio, and orientation $(\gamma )$ are given by the orange ellipse. (a) ${\omega }_l/{\omega }_h\approx 1$. (b,c) ${\omega }_l/{\omega }_h\approx 0.55$. (d) ${\omega }_l/{\omega }_h\approx 0.77$. (a–d) $\gamma =55$°. The stray electric field (green arrows) orientation is denoted by $\alpha$. (a,b) $\alpha =0$°. (c,d) $\alpha \approx 32$°. The two red dots connected by a dashed red line denotes the position of the ion for varying magnitude of the electric field. Blue blades illustrate the position and orientation of the trap electrodes. Through a change in the ratio of the radial trapping frequencies, undetectable EMM due to unobservable x-displacement, (a,c) can be detected, (b,d) - see text.

However, even for the non-symmetric trap case, an electric field oriented by an angle (see single-ion section in the Supplementary Material),

${\alpha }_0=\gamma -\arctan \left(\tan \left(\gamma \right){\left({\omega }_l/{\omega }_h\right)}^2\right),(8)$

will lead to a non-detectable ion displacement along the imaging axis (Figure 4c). In Equation 8, $\gamma$ is the orientation angle of the radial modes with respect to the lab frame (see Figures 4b–d). Nevertheless, since the angle ${\alpha }_0$ depends on the radial-mode frequency ratio, ${\omega }_l/{\omega }_h$, changing this ratio (see single-ion section in the Supplementray material) allows us to induce detectable ion displacement along the x-axis for any stray-electric-field orientation (Figure 4d).

Results - single ion

The results of EMM compensation with a single bright ion are presented in Figure 5. We scan the compensation-electrodes voltages, $V_{x^{\prime }}$, $V_{y^{\prime }}$, and record the ion’s position for one high and three low RF amplitudes. The high RF amplitude corresponds to ${\omega }_l=1440$ kHz and ${\omega }_h=1500$ kHz for the low and high radial modes, respectively. The three low RF amplitudes correspond to ${\omega }_l=\mathrm{572,449,310}$ kHz for the low radial mode and ${\omega }_h=\mathrm{742,652,565}$ kHz for the high radial mode. We measure the ion displacement along the x-axis, $d_x$, between the high RF amplitude and all low RF amplitudes (data points in Figures 5a–c). For each $V_{y^{\prime }}$ compensation value, there exists a compensation value, $V_{x^{\prime }}$, for which the ion displacement is zero (open circles in Figures 5a–c).

Figure 5

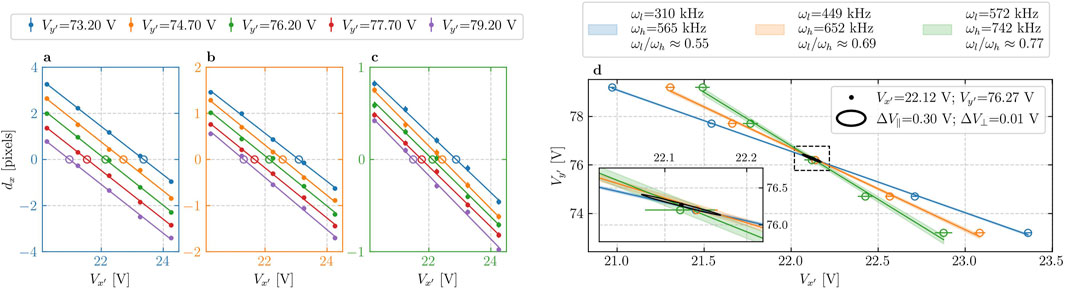
Figure 5. Single-ion EMM compensation. (a–c) Dots are ion relative displacements between high to low RF amplitudes as a function of the $V_{x^{\prime }}$ (x-axis) and $V_{y^{\prime }}$ (color, left-side legend) compensation voltages. High RF amplitude corresponds to $\sim$1.5 MHz radial frequency. The three different low-RF-amplitude radial frequencies and ratios are given in the right-side legend. Errors are not visible at this scale, lines are linear fits, and open circles are estimates from fits for the zero-displacement $V_{x^{\prime }}$ voltages. (d) Zero-displacement trajectories in the $(V_{x^{\prime }},V_{y^{\prime }})$ space. Each color corresponds to a different low-RF amplitude (caption (a–c) box color). Open circles are the fit estimates extracted from (a–c) with the estimation error shown as horizontal lines. Lines are linear fits. All lines cross at the EMM compensation point (black). The ellipse shows the 1$\sigma$ error in the compensation point estimation. The inset zooms into the crossing point. In this experiment, the bias voltage was fixed at a value of $V_g=0.6\text{\hspace{0.17em}V}$.

We plot the zero-displacement compensation values in the ($V_{x^{\prime }}$, $V_{y^{\prime }}$) space (open circles in Figure 5d) and fit them to a linear line. We note that for each low RF amplitude (different radial-mode frequency ratios), the zero-displacement line follows a different angle in the ($V_{x^{\prime }}$, $V_{y^{\prime }}$) space. We find the zero-displacement lines intersection point (black dot in Figure 5d) and uncertainty (black ellipse in Figure 5d). The intersection point corresponds to the EMM compensated point where the radial stray electric field is minimized.

Discussion

To compare our compensation scheme with other works, we relate the change in the compensation-electrodes voltage to the resulting electric field at the trap center. A typical uncertainty of $\mathrm{\Delta }{V}_{x^{\prime }/y^{\prime }}\approx 0.1\text{\hspace{0.17em}V}$ in the compensation voltage (see Figure 3c legend) corresponds to a stray electric-field uncertainty of $\mathrm{\Delta }{E}_r\approx 0.2{\mathrm{V}\mathrm{m}}^{-1}$ (see single-ion section in the Supplementray Material). This level of compensation, which can be reached on a time scale of a few minutes, is consistent with the residual stray-field magnitudes in typical ion-trap experiments (Keller et al., 2015). A more qualitative comparison is difficult to perform due to the different trapping parameters used in various experiments.

On the other hand, a quantitative and direct comparison between the two compensation methods presented in this paper is shown in Figure 6. While the two methods yield similar compensation uncertainties, there is a small discrepancy between them, which cannot be attributed to random error. As the results of the single-ion compensation are consistent before and after the dark-ion measurement, we can rule out drifts as the cause of the discrepancy.

Figure 6

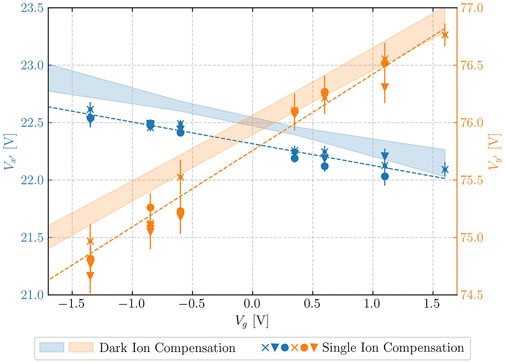
Figure 6. Comparison between the single ion (markers) and dark ion (shaded areas) compensation methods. Error bars of the markers and the width of the shaded area give the $1\sigma$ errors in estimating the compensation values for each method, respectively. The estimated $V_{x^{\prime }}$ (blue, left y-axis) and $V_{y^{\prime }}$ (orange, right y-axis) compensation voltages are shown as a function of the bias voltage $V_g$. Markers correspond to single-ion experiments performed before (cross) and after (first circle and then triangle) the dark-ion experiment. Dashed lines are linear fits for the single-ion data.

One possible systematic effect that differentiates between the two schemes is the presence of the scattering force from the fluorescence laser during the measurements. The scattering force acts as an additional effective stray field in the single-ion scheme (on saturation, the maximal scattering field is $E_{sc,\text{max}}\approx 0.7{\mathrm{V}\mathrm{m}}^{-1}$). To compensate for the effect of the scattering force, we need to apply an equal and antiparallel field, $E_r=-E_{sc}$. In contrast, in the dark-ion scheme, the scattering force acts only on the bright ions, where the dark ion is unaffected by the scattering force, causing additional deformation in the crystal. To compensate for this deformation, we need to apply a compensation field $E_r\approx E_{sc}/(m_d/m_b-1)$ (see scattering-force section in the Supplementray Material). This amounts to $E_r\approx 10E_{sc}$ for our bright and dark ion masses. From the above discussion and the comparison made in Figure 6, we can give an upper bound to the scattering field in our experiment to be $E_{sc}\lesssim 0.1\mathrm{V}\mathrm{m}-1$.

In the single-ion scheme, we perform EMM compensation independently for each bias voltage by exploiting the change in the low-to-high radial frequency ratio when increasing the RF amplitude (see legend in Figure 5d). In contrast, we need to perform several measurements for different bias voltages in the dark-ion scheme, resulting in a linear fit for the EMM compensation as a function of the bias voltage. This is because of the sensitivity scaling in the dark-ion scheme: Since we are detecting axial contraction due to a field that shifts the ions radially, the sensitivity of the dark-ion scheme scales as $s\equiv -\frac{1}{E_r}\frac{d(d_b)}{d{E}_r}\propto {({\omega }_{r,\text{bend}}^{\mathit{bdb}})}^{-4}$ (see Supplementary Material - dark-ion sensitivity). Hence, we need to work close to the zig-zag transition to obtain greater sensitivity as the radial bending mode approaches zero frequency near the transition (Equation 3).

Our trap has a large low-to-high radial-frequency ratio (${\omega }_l/{\omega }_h\approx 0.7$ in the dark-ion experiment). With this large ratio, we cannot obtain sensitivity to the high radial mode while working above the zig-zag transition in the low radial mode. For more symmetric traps $({\omega }_l/{\omega }_h>0.9)$, it should be possible to simultaneously compensate EMM in the two radial directions in a single scan at a specific bias voltage. In contrast, in our trap, the sensitivity of the single-ion method should decrease in more symmetric traps due to a smaller change in the low-to-high radial frequency ratio when changing the RF amplitude. For that, we expect the dark-ion method to be more beneficial in such scenarios. Unfortunately, we cannot meet these symmetric conditions in our experiment.

The dark-ion scheme exploits the phenomena where ions with different masses experience different effective radial trapping potentials when placed within the same trap. As such, we can further enhance the sensitivity of this method by working with dark and bright ions with a greater mass difference. E.g., moving from ⁴⁴$\mathrm{C}\mathrm{a}$⁺ to ¹⁴${\mathrm{N}}_2^{+}$ (mass of 28 atomic-mass units) as the dark ion in this work will increase the sensitivity by a factor of $\sim$18 (see Supplementary material - dark-ion sensitivity). In addition, large mass differences reduce the scattering-force systematic effect, which scales as $m_b/(m_d-m_b)$. Note, however, that the crystal will not be stable in the trap for a mass ratio too large. In case both ions can be imaged by laser fluorescence, it is sensitivity-wise beneficial to put the lighter ion in the center of the crystal (see Supplementary material - dark-ion sensitivity).

Summary

To summarize, we presented two EMM compensation methods that require only a fixed imaging system and continuous fluorescence detection, which makes them compatible and accessible to most ion-trapping experiments as is. Both methods overcome the difficulty of measuring the EMM in the direction parallel to the imaging system. The dark-ion method detects axial deformation of a bright-dark-bright ion crystal due to the bright and dark ions mass difference, while the single-bright-ion method exploits the curved ion trajectory resulting from changes in trap asymmetry. Both methods enable effective EMM compensation, achieving stray electric field amplitudes well below $\sim 1{\mathrm{V}\mathrm{m}}^{-1}$.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

OB: Conceptualization, Formal analysis, Investigation, Methodology, Software, Writing – original draft. DE: Methodology, Software, Writing – review and editing. JD: Methodology, Writing – review and editing. IH: Methodology, Software, Writing – review and editing. ZM: Conceptualization, Formal analysis, Funding acqusition, Supervision, Validation, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. We acknowledge the support of the Diane and Guilford Glazer Foundation Impact Grant for New Scientists, the research grant from the Donald Gordon Foundation and the Ike, Molly and Steven Elias Foundation, the research grant from the Laurie Kayden Foundation, the Center for New Scientists at the Weizmann Institute of Science, the Edith and Nathan Goldenberg Career Development Chair, the Israel Science Foundation (Grant No. 1010/22 and 1364/24), and the Minerva Stiftung with funding from the Federal German Ministry for Education and Research.

Acknowledgments

We thank Roee Ozeri for fruitful discussions and reading of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frqst.2025.1596801/full#supplementary-material

References

Arnold, K., Jayjong, N., Kang, M., Qichen, Q., Zhang, Z., Zhao, Q., et al. (2024). Enhanced micromotion compensation using a phase-modulated light field. Phys. Rev. A 110, 033115. doi:10.1103/physreva.110.033115

CrossRef Full Text | Google Scholar

Ballance, C. J., Schäfer, V. M., Home, J. P., Szwer, D. J., Webster, S. C., Allcock, D. T. C., et al. (2015). Hybrid quantum logic and a test of Bell’s inequality using two different atomic isotopes. Nature 528, 384. doi:10.1038/nature16184

PubMed Abstract | CrossRef Full Text | Google Scholar

Barakhshan, P., Marrs, A., Bhosale, A., Arora, B., Eigenmann, R., and Safronova, M. S. (2022). Portal for high-precision atomic data and computation (version 2.0). Newark, DE, USA: University of Delaware. Available online at: https://www.udel.edu/atom.

Google Scholar

Barrett, M. D., DeMarco, B., Schaetz, T., Meyer, V., Leibfried, D., Britton, J., et al. (2003). Sympathetic cooling of ⁹Be⁺ and ²⁴Mg⁺ for quantum logic. Phys. Rev. A 68, 042302. doi:10.1103/PhysRevA.68.042302

CrossRef Full Text | Google Scholar

Berkeland, D. J., Miller, J. D., Bergquist, J. C., Itano, W. M., and Wineland, D. J. (1998). Minimization of ion micromotion in a Paul trap. J. Appl. Phys. 83, 5025–5033. doi:10.1063/1.367318

CrossRef Full Text | Google Scholar

Brewer, S. M., Chen, J. S., Hankin, A. M., Clements, E. R., Chou, C. W., Wineland, D. J., et al. (2019). ²⁷Al⁺ quantum-logic clock with a systematic uncertainty below 10⁻¹⁸. Phys. Rev. Lett. 123, 033201. doi:10.1103/PhysRevLett.123.033201

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruzewicz, C., McConnell, R., Stuart, J., Sage, J., and Chiaverini, J. (2019). Dual-species, multi-qubit logic primitives for Ca+/Sr+ trapped-ion crystals. Npj Quantum Inf. 5, 102. doi:10.1038/s41534-019-0218-z

CrossRef Full Text | Google Scholar

Drewsen, M., Mortensen, A., Martinussen, R., Staanum, P., and Sørensen, J. L. (2004). Nondestructive identification of cold and extremely localized single molecular ions. Phys. Rev. Lett. 93, 243201. doi:10.1103/physrevlett.93.243201

PubMed Abstract | CrossRef Full Text | Google Scholar

Fishman, S., De Chiara, G., Calarco, T., and Morigi, G. (2008). Structural phase transitions in low-dimensional ion crystals. Phys. Rev. B 77, 064111. doi:10.1103/physrevb.77.064111

CrossRef Full Text | Google Scholar

Gloger, T. F., Kaufmann, P., Kaufmann, D., Baig, M. T., Collath, T., Johanning, M., et al. (2015). Ion-trajectory analysis for micromotion minimization and the measurement of small forces. Phys. Rev. A 92, 043421. doi:10.1103/physreva.92.043421

CrossRef Full Text | Google Scholar

Hausser, H. N., Keller, J., Nordmann, T., Bhatt, N. M., Kiethe, J., Liu, H., et al. (2025). ¹¹⁵In⁺ − ¹⁷²Yb⁺ Coulomb crystal clock with 2.5×10⁻¹⁸ systematic uncertainty. Phys. Rev. Lett. 134, 023201. doi:10.1103/PhysRevLett.134.023201

PubMed Abstract | CrossRef Full Text | Google Scholar

Holzapfel, D., Schmid, F., Schwegler, N., Stadler, O., Stadler, M., Ferk, A., et al. (2024). Quantum control of a single H₂⁺ molecular ion. arXiv:2409.06495 [physics.atom-ph].

Google Scholar

Huber, T., Lambrecht, A., Schmidt, J., Karpa, L., and Schaetz, T. (2014). A far-off-resonance optical trap for a Ba+ ion. Nat. Commun. 5, 5587. doi:10.1038/ncomms6587

PubMed Abstract | CrossRef Full Text | Google Scholar

Hughes, A. C., Schäfer, V. M., Thirumalai, K., Nadlinger, D. P., Woodrow, S. R., Lucas, D. M., et al. (2020). Benchmarking a high-fidelity mixed-species entangling gate. Phys. Rev. Lett. 125, 080504. doi:10.1103/PhysRevLett.125.080504

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaufmann, H., Ulm, S., Jacob, G., Poschinger, U., Landa, H., Retzker, A., et al. (2012). Precise experimental investigation of eigenmodes in a planar ion crystal. Phys. Rev. Lett. 109, 263003. doi:10.1103/physrevlett.109.263003

PubMed Abstract | CrossRef Full Text | Google Scholar

Keller, J., Partner, H. L., Burgermeister, T., and Mehlstäubler, T. E. (2015). Precise determination of micromotion for trapped-ion optical clocks. J. Appl. Phys. 118, 104501. doi:10.1063/1.4930037

CrossRef Full Text | Google Scholar

King, S. A., Spieß, L. J., Micke, P., Wilzewski, A., Leopold, T., Benkler, E., et al. (2022). An optical atomic clock base on a highly charged ion. Nature 611, 43. doi:10.1038/s41586-022-05245-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, Y., Leibrandt, D. R., Leibfried, D., and Chou, C. W. (2020). Quantum entanglement between an atom and a molecule. Nature 581, 273–277. doi:10.1038/s41586-020-2257-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Lucas, D., Ramos, A., Home, J., McDonnell, M., Nakayama, S., Stacey, J.-P., et al. (2004). Isotope-selective photoionization for calcium ion trapping. Phys. Rev. A 69, 012711. doi:10.1103/physreva.69.012711

CrossRef Full Text | Google Scholar

Meir, Z., Sikorsky, T., Ben-shlomi, R., Akerman, N., Pinkas, M., Dallal, Y., et al. (2018). Experimental apparatus for overlapping a ground-state cooled ion with ultracold atoms. J. Mod. Opt. 65, 387. doi:10.1080/09500340.2017.1397217

CrossRef Full Text | Google Scholar

Mokhberi, A., and Willitsch, S. (2015). Structural and energetic properties of molecular Coulomb crystals in a surface-electrode ion trap. New J. Phys. 17, 045008. doi:10.1088/1367-2630/17/4/045008

CrossRef Full Text | Google Scholar

Navon, N., Kotler, S., Akerman, N., Glickman, Y., Almog, I., and Ozeri, R. (2013). Addressing two-level systems variably coupled to an oscillating field. Phys. Rev. Lett. 111, 073001. doi:10.1103/physrevlett.111.073001

PubMed Abstract | CrossRef Full Text | Google Scholar

Negnevitsky, V., Marinelli, M., Mehta, K. K., Lo, H.-Y., Flühmann, C., and Home, J. P. (2018). Repeated multi-qubit readout and feedback with a mixed-species trapped-ion register. Nature 563, 527–531. doi:10.1038/s41586-018-0668-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Pino, J. M., Dreiling, J. M., Figgatt, C., Gaebler, J. P., Moses, S. A., Allman, M., et al. (2021). Demonstration of the trapped-ion quantum CCD computer architecture. Nature 592, 209–213. doi:10.1038/s41586-021-03318-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Saito, R., and Mukaiyama, T. (2024). Determination of principal axes orientation in an ion trap using matter-wave interference. Opt. Express 32, 42616. doi:10.1364/oe.534882

CrossRef Full Text | Google Scholar

Saito, R., Saito, K., and Mukaiyama, T. (2021). Measurement of ion displacement via RF power variation for excess micromotion compensation. J. Appl. Phys. 129. doi:10.1063/5.0046121

CrossRef Full Text | Google Scholar

Schneider, C., Enderlein, M., Huber, T., Dürr, S., and Schaetz, T. (2012). Influence of static electric fields on an optical ion trap. Phys. Rev. A 85, 013422. doi:10.1103/physreva.85.013422

CrossRef Full Text | Google Scholar

Sinhal, M., Meir, Z., Najafian, K., Hegi, G., and Willitsch, S. (2020). Quantum-nondemolition state detection and spectroscopy of single trapped molecules. Science 367, 1213–1218. doi:10.1126/science.aaz9837

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, T. R., Gaebler, J. P., Lin, Y., Wan, Y., Bowler, R., Leibfried, D., et al. (2015). Multi-element logic gates for trapped-ion qubits. Nature 528, 380–383. doi:10.1038/nature16186

PubMed Abstract | CrossRef Full Text | Google Scholar

Tomza, M., Jachymski, K., Gerritsma, R., Negretti, A., Calarco, T., Idziaszek, Z., et al. (2019). Cold hybrid ion-atom systems. Rev. Mod. Phys. 91, 035001. doi:10.1103/revmodphys.91.035001

CrossRef Full Text | Google Scholar

Wolf, F., Wan, Y., Heip, J. C., Gebert, F., Shi, C., and Schmidt, P. O. (2016). Non-destructive state detection for quantum logic spectroscopy of molecular ions. Nature 530, 457–460. doi:10.1038/nature16513

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Y.-z., Zhang, M.-c., Su, W.-b., Wu, C.-w., Xie, Y., Chen, T., et al. (2024). Tracking the extensive three-dimensional motion of single ions by an engineered point-spread function. Nat. Commun. 15, 6483. doi:10.1038/s41467-024-49701-3

PubMed Abstract | CrossRef Full Text | Google Scholar