Establishment of Natural Hazards Mapping Criteria Using Analytic Hierarchy Process (AHP)

Despite the large number of studies on natural hazards mapping and modeling, an increasing number of disasters still occur worldwide. Floods, landslides, and tsunamis, among others, consistently hit vulnerable countries, resulting in increasing death tolls and economic losses in the last decades. The increased reliability of available hazard maps is still insufficient when not fully integrated and incorporated in the respective communities' land use plans. As a pro-active and preventive approach in combatting disasters, land use planning requires the relevant stakeholders' active participation. This study derives the most crucial criteria in the eyes of planners, experts, and decision-makers for natural hazards mapping as part of land use planning and part of disaster risk reduction. These stakeholders and experts establish criteria for flood, landslide, earthquake and storm surge hazard mapping through Multi-criteria Evaluation (MCE). The MCE technique compares the relative merits of different spatially related criteria following the Analytic Hierarchy Process (AHP) through pair-wise comparisons of criteria by experts and the decision-makers. This research process derives a general and consistent list of criteria for hazard mapping initially developed and based in the Philippines, which can be used in subsequent GIS analysis. Results further show the advantages of using AHP in a multi-criteria analysis for decision-making and compliance.

Introduction

Natural hazards, such as earthquakes, hurricanes, volcanic eruptions, and storms, are unavoidable phenomena. Depending upon the geographical location of a place or country, natural hazards could be location-specific, i.e., dependent on the characteristics and specific for one place and not necessarily occurring in other places. Typhoons strike, for example, predominantly in the northern and central parts of the Philippines (Luzon, Visayas) but less frequently in the southern part (Mindanao). This is partly due to the specific nature of the hazard itself and its specific geography. Reversely, multiple hazards may also be present simultaneously in a single area. In highly active volcanic regions, there may be both volcanic eruptions accompanied by earthquakes and tsunamis. Japan is an example of such an area. Hence, natural hazards are present regardless if the country is developed or still developing. It is a global concern that needs to be mitigated and prepared for appropriately.

Numerous strategies have been developed and enacted to manage these hazards worldwide, yet many of these strategies still result in disasters. The management of hazards could be categorized into two types, namely the pro-active and the reactive approaches. A pro-active approach consists of management interventions that emphasize actions and strategies to prevent the conversion of a hazard to a disaster. In this approach, land use planning is an important strategy to manage hazards where places are identified and categorized as highly risky and not suitable for land uses, and whereby the presence of any human activity is assessed based on the degree of necessity. Contrastingly, a reactive approach deals with managing activities after a disaster has happened, such as the (effective) search and rescue operations, the reconstruction activities.

As a pro-active approach, land use planning deals with the proper allocation of lands, not just considering its physical characteristics to function the defined use but also incorporating the probable risks underlying it. This strategy requires a quantitative inventory of hazards and the underlying risks and integrating it into land use planning. Taking into account the existing hazards, they are best visualized and appreciated through mapping and modeling. Although hazard mapping has been practiced for a long time, the uncertainty characteristic of hazards and the changing climate are enough reasons to revisit and recalibrate the existing hazard maps constantly.

There is a tremendous development of different methodologies of producing hazard maps and models in the last decade. Uddin et al. (2013) and Samarasinghea et al. (2010) used remote sensing and GIS technologies in flood risk analysis and management because flood hazard mapping and flood shelter analysis are vital elements in appropriate land use planning for flood-prone areas. With remote sensing, Uddin et al. (2013) used the ArcGIS model builder with mapping using the Object-based Image Analysis (OBIA) implemented in eCognition software, while Samarasinghea et al. (2010) applied the use of HEC-HMS (hydrologic modeling software) that includes several hydrologic methods to simulate the rainfall-runoff process in river basins. Abdalla et al. (2014) used a GIS-supported fuzzy-set approach for flood risk assessment while Nwilo et al. (2012) used GIS and Cellular Framework Approach in flood modeling vulnerability assessment of settlements. In another study, the use of GIS and statistical analysis for land susceptibility mapping was employed by Mancini et al. (2010) and Grozavu et al. (2010). Specifically, they used the Logistic Regression approach to be an adequate tool for assessing landslide susceptibility objectively and quantitatively, providing parameters permitting evaluation of output quality. Maugeri et al. (2009) also used GIS in their study of lifeline seismic hazard developed in a GIS environment, by “Spatial Analysis” and “Field Calculation” techniques, and Alexoudi et al. (2002) used the same technology (GIS) in predicting seismic hazard by developing deterministic and probabilistic scenarios in terms of spectral ordinates.

As mentioned, hazard maps are also area-specific, and the technical aspect as to which these were made and intended to likewise varies from one place to another or from one country to other countries. Depending on the countries' organizational capability to produce such highly accurate maps, oftentimes, the issue of accuracy and precision of the technicalities of hazard mapping is a major concern. The analysis results are greatly affected by data availability and accuracy (Al-Hanbali et al., 2011); therefore, the selection of data sources should be influenced by their accuracy and resolution (Hiscock et al., 1995; Dai et al., 2001). However, even with highly accurate maps, sometimes hazard maps are just made to have maps. It, therefore, defeats the purpose of building a resilient community, especially in support of land use planning and management.

Land use planning is an integral process of the different objectives and goals, including the different preferences for using the land. In most cases, land use planners are always influenced by the organization executives or the decision makers and implementers of the land use plans. Considering these conflicting interests over land use, the use of Multi-criteria Evaluation (MCE) methodology for land use planning is a tool that caters to the different preferences given a set of alternatives to choose from in the decision-making process. Nyeko (2012) objectively used GIS in spatial decision-making, including planning for land use, thereby providing a powerful platform for the organization of map layers (raster logic) and performing logical and mathematical analyses during land suitability analysis. The GIS-based MCE approach extended to focusing on finding optimal sites for hillside development (Chandio and Matori, 2011), land suitability assessment for wind farm development (Latinopoulos and Kechagia, 2015), land suitability assessment for potential rubber expansion (Nguyen et al., 2015), coastal management and planning (Bagheri et al., 2012), and for urban land expansion and development (Yang et al., 2008; Cerreta and De Toro, 2012; Raddad, 2016).

In the context of decision-making, there is already extensive academic literature relating to MCE/MCDA. Different approaches have been introduced in addressing decision-problems for various applications, including site selection, natural hazards mapping, and other spatially-related cases that provide alternative solutions to the problems. The existing MCDA approaches are grouped into four main theoretical trends based on model forms, model development process, and application scope (Pardalos et al., 1995; Siskos and Spyridakos, 1999). These include the (a) Value System Approaches including the AHP/ANP and the Multi-Attribute Value/Utility Theory (MAVT/MAUT), (b) Outranking Relations Approaches including ELECTRE, PROMETHEE as well as TOPSIS and VIKOR, (c) Disaggregation-Aggregation Approach and the (d) Multi-Objective Optimization Approaches (Psomas et al., 2018).

These approaches have been explicitly used in decision-making processes such as the incorporation of Fuzzy AHP and GIS to take care of the vagueness type of uncertainty for urban highway bypass horizontal alignment (Ouma et al., 2014) and the application of GIS-Interval Rough AHP for flood hazard mapping (Gigović et al., 2017). GIS and outranking multi-criteria analysis were also used for land use suitability assessment for housing land with ELECTRE-TRI (Joerin et al., 2001) and the use of BORDA and PROMETHEE for decision making of naval base selection (Ahmadi and Herdiawan, 2021). In another study, a probabilistic or stochastic approach was incorporated into the local MCDA for flood susceptibility assessment using Weighted Linear Combination (WLC) (Tang et al., 2018). The use of Multi-Objective Optimization Approach was explored for evacuation planning (Yuan and Han, 2010), and the Fuzzy Multi-Objective Optimization Approach for treated wastewater allocation (Tayebikhorami et al., 2019) was also used.

In support of land use planning as a tool for disaster risk reduction, GIS-based MCE has gained more popularity in the recent decade, especially in hazard mapping, to actively engage the experts and decision-makers. Although not fully used in the proper land use planning process, numerous works have utilized the GIS-based MCE approach in natural hazards mapping, including for flood hazard mapping (Rahman and Saha, 2007; Wang et al., 2011; Gigović et al., 2017), landslide susceptibility mapping (Baban and Sant, 2005; Feizizadeh and Blaschke, 2011; Mallick et al., 2018), and earthquake susceptibility mapping (Walker et al., 2014; Sabah et al., 2017). Their works positively showed that the capabilities of GIS integrated with MCE technique could be a highly potential approach addressing natural disasters and would entail the active participation of experts and even the decision-makers in land use planning and mapping.

Thus, even in the advances of decision-making approaches, the use of AHP/ANP has been applied more frequently, incorporating spatial analysis using GIS (Psomas et al., 2018), including natural hazards susceptibility mapping.

The advantage of using the MCE technique is that it can combine and compare spatially related criteria. Its goal is to integrate information from multiple criteria to produce an output map of suitability levels (Lai et al., 2013). In this case, those areas that are not risky for natural hazards and are suitable for a specific land use. Evaluation and analysis of these criteria eventually support the goal of developing a resilient community by providing land use plans that are sensitive to natural hazards.

The formulation and selection of criteria is one of the important elements of the multi-criteria evaluations. It is the basis for measuring and evaluating a decision (Eastman et al., 1995). In the evaluation process, MCE establishes preferences between options by reference to an explicit set of objectives that the decision making body has identified, and for which it has established measurable criteria to assess the extent to which the objectives have been achieved (Department for Communities and Local Government-London, 2009). In this context, a criterion is characterized by a score (range of scores) of performance preferred by the decision-maker (Zeleny, 1998). Voogd (1982) defines a “criterion” as a measurable aspect of judgment by which a dimension of various choice possibilities under consideration can be characterized.

Although the set of criteria is the main requirement and condition for the subsequent spatial analysis, the number of criteria should be enough, and the type of criteria should be meaningful to make an effective analysis and arrive at outstanding results. A large number of criteria for one objective tends to confuse decision-makers, while too few criteria may be insufficient to provide all the necessary relevant information (Pourebrahim et al., 2010). As such, the process of choosing and establishing the criteria might at some point be critical and needs sufficient attention and extra care to yield the desired best results.

In MCE, the criteria are the data evidence being considered, and they either support or restrict the alternatives. In this sense, the criteria are generally categorized as “factors” or “constraints.” The factors are the criteria that support the alternatives or that influence (enhance or detract) the viability of the objective under consideration which are represented by the layers referred to as the criterion maps, while the constraints are the criteria that exclude the area from the analysis (López-Marrero et al., 2011; Lai et al., 2013).

The aggregation of the alternatives' local scores with the criteria weights is the final phase in any decision-problem (Kasim and Jemain, 2020). Criteria weights determination is then considered crucial in multi-criteria decision-making models (Zizovic et al., 2020), which can be derived in several ways objectively, subjectively, and in an equal weighting method (Hafezparast et al., 2015). An entropy method is an objective approach, where criteria weights are acquired, disregarding the decision makers' opinion and utilizing the data present in a decision matrix or the intrinsic information contained in the criteria (Kasim and Jemain, 2020). An application of this approach is used in a study for weight determination of glazing properties for Trombe wall systems (Oluah et al., 2019). Another objective approach is the CRiteria Importance Through Intercriteria Correlation (CRITIC) of determining criteria weights (Diakoulaki et al., 1995). In the CRITIC approach, the standard deviations of ranked criteria values and the correlation coefficients of all paired columns determine the criteria contrasts.

Meanwhile, in the subjective approach, the significance of criteria is based on the decision makers' or experts' opinions following their preferences (Zizovic et al., 2020). Examples of the subjective approaches are the rank-based (Sureeyatanapas, 2016) and the AHP method (Saaty, 1980, 2008), which uses pair-wise comparisons based on the experts' preferences.

With the general goal of establishing a decision support system using a GIS-based MCE to support land use planning as a tool for disaster risk reduction, this paper aims at establishing a general set of evaluation criteria that can be referred to spatially. The criteria must be significant in hazard mapping, emphasizing flooding, landslide, earthquake, and storm surge. Although many studies involving hazard mapping have been conducted and produced valuable hazard maps, these are usually for one single or specific hazard only. Therefore, the aim of allocating and regulating land uses in line with managing multiple risks at the same time cannot be fully achieved.

In light of aligning land use planning with disaster mitigation and quandary, this paper aims at deriving a more generic framework of spatially referenced criteria for simultaneous analysis in hazard mapping. Therefore, the key research question objective of this paper is to derive the most appropriate criteria for hazard mapping in the context of specific characteristics of hazards management in the Philippines. To exemplify the participatory approaches of land use planning that fully integrate disaster risk reduction, the study uses the AHP method in weight determination. A time-consuming yet simple and straightforward technique that incorporates decision-makers' or experts' active participation in solving decision-problems such as land use suitability mapping and natural hazards susceptibility mapping. In other words, through the active participation of the people affected, one can create a better and more informed decision-making process (Morales and de Vries, 2021).

This framework must be easier to understand for a non-technical person, easier to perform and execute for government officials and land use planning practitioners, and it must be more country-specific for the Philippines. Although it is said to be country-specific, the said criteria can be replicated, depending upon which area or country the criteria are suitable.

The paper starts with an overview of natural hazards and mapping and their impact on developmental planning on the one hand and the importance of incorporating disaster risk reduction strategies in land use planning using MCE-AHP on the other. The subsequent sections describe how these concepts are linked in current literature, followed by an analysis of how and when MCE-AHP is used as part of natural hazards mapping. We conclude by identifying how the concepts and applications can be improved and the further steps for research.

Methodology

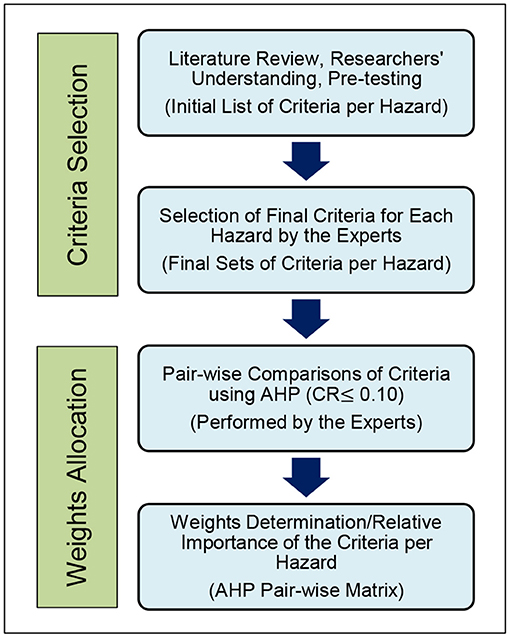
In deriving the criteria for hazard mapping, the formulation and selection of criteria need to have a spatial reference and have a specific significance to the Philippine situation. This is an important step in the execution of MCE. The selection of the evaluation criteria to be used in hazard mapping were initially identified through literature reviews, the researchers' understanding of the objective, and the experts' knowledge (Figure 1). To get into the core of criteria selection, the literature review was conducted to gather relevant information on the already used criteria in similar studies that could be used in a GIS-based MCE. The literatures' primary sources came from known and credible research repositories like research gate, google scholar, science direct, and web of science, using important keywords such as hazard mapping, AHP, MCE/MCDA as the search criteria in the query of relevant papers. A longer list of the probable criteria (Annex 1) per hazard was made due to the literature review. The lists were then subjected to two rounds of pre-testing with Ph.D. students and professionals of related fields.

FIGURE 1

Figure 1. Overall flow of criteria establishment per hazard.

The study is divided into two major parts. The first is selecting the final list of the evaluation criteria per hazard. The second part was the weight determination through pair-wise comparison using the AHP technique (Figure 1). The first part relies on selecting of the criteria performed by 20 experts as decision-makers from the already prepared probable list. Aside from the given list, the experts could likewise add other criteria they consider important in addressing the decision problem. The identified experts are those working within any institution in hazard mapping and land use planning as recommended by colleagues, universities, and related agencies in the Philippines. The final criteria' selection relied on personal face-to-face interviews using a structured questionnaire and using an online platform via google docs. After the experts' majority vote, a shortlist as the final set of criteria per hazard was made considering the recommended guidelines (Malczewski, 1999; Yahaya et al., 2010).

The second part commenced after the finalization of the evaluation criteria. The same set of experts were asked to make the pair-wise comparisons of all the sets of criteria using the AHP approach. The AHP is a method of measurement that derives priority scales through the experts' judgements (Saaty, 2008). It is used in decision-making problems organized hierarchically (Figure 2) at different levels containing a finite number of elements (Mallick et al., 2018). The hierarchical structure of AHP measures and synthesizes various factors of a complex decision-making process and makes it simple to combine the parts in a whole (Russo and Camanho, 2015). In this concept, AHP is considered a decision-making and forecasting method that gives the percentage distribution of decision points in terms of the factors affecting the decision, which can be used if the decision hierarchy can be defined (Sabah et al., 2017).

FIGURE 2

Figure 2. Structured problem with three different hierarchy levels (Chandio and Matori, 2011).

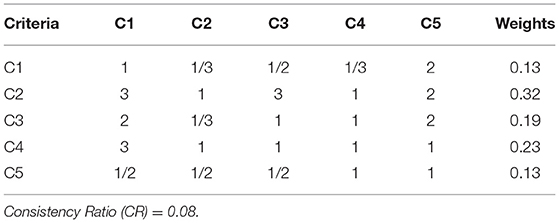
In carrying out the pair-wise comparisons, the decision factors (criteria) are compared with each other using the preference intensity evaluation or the scale of relative importance (Table 1) on a scale of 1–9. The preference scale value of 1 signifies that the two criteria being compared are of equal importance, while 9 signifies that one criterion is extremely preferred as more important than the other criterion being compared. The values 2, 4, 6, and 8 are the median values over the preferred values.

TABLE 1

Table 1. Preference intensity evaluation by binary comparison relatively between criteria in AHP (Ghodsipour, 2003; Rezaei and Tahsili, 2018).

A comparison matrix (Table 2) is then made with the preference intensity evaluation results and correspondingly normalizes the values to solve for the principal Eigen value (λ).

$\begin{array}{ll}\lambda ={\displaystyle \sum _{i=1}^n}C{v}_{ij}& (1)\end{array}$

λ is calculated by averaging the value of the consistency vector, is obtained from the summation of products between each element of Eigen Vector and the normalized relative weight.

TABLE 2

Table 2. An example of pair-wise comparison matrix for assessing the weights of factors.

An observable condition in a decision-making exercise is the presence of inconsistencies dealing with many factors being compared. Although AHP allows for some inconsistency level, it should not exceed a certain threshold (Saaty, 1980, 2008). AHP has the capacity to measure the consistency of the experts' preferences by employing the computation of a suitable Consistency Index (CI) as the deviation or the degree of consistency.

$\begin{array}{ll}CI=\frac{\lambda -n}{n-1}& (2)\end{array}$

The consistency measures will equal the number of comparisons considered (n), so the CI will be equal to zero so as the Consistency Ratio (CR) to make sure that the original preference ratings are consistent. In the computation of CI, the normalized relative weights, the normalized principal Eigen vector, and the principal Eigen value (λ) are first computed. The λ is simply the average of the normalized comparison matrix's Eigen values (Nyeko, 2012). According to Hossain et al. (2007), the essence of AHP is a solution of an Eigen value problem involving the reciprocal matrix comparisons.

$\begin{array}{ll}CR=\frac{CI}{RI}& (3)\end{array}$

Table 3 shows the Random Index (RI) suggested by Saaty for small problems to be used in the CR computation.

TABLE 3

Table 3. Random Index (RI) values for small problems.

On validating the preferences of the experts, a follow-up questions were made to support their choices. Also, they were allowed to have an initial ranking of all the criteria in each set which also agreed to their preferences.

Saaty (1980, 2008) recommended that the acceptable CR be ≤0.10 (or 10%). Higher than the said value means the pair-wise comparisons for the criteria are highly inconsistent in terms of the preferences, hence a need to revise the pair-wise comparisons. The said acceptable consistency ratio is still recognized and used in recent years in several studies such as of Tang et al. (2018) for flood susceptibility assessment, Razandi et al. (2015) in their application of AHP for groundwater potential mapping, Quinta-Nova and Ferreira (2020) on land suitability study for emerging fruit crops and Mansour et al. (2019) where they used AHP for ecotourism land suitability study.

The above processes in criteria establishment using AHP can then be summarized into major steps as follows:

1. Identify the decision problem.

2. Develop a hierarchy construction of the problem at different stages to determine the problem's objectives and outcomes based on the aim, criterion, and alternatives.

3. Perform pair-wise comparisons using the intensity scale and determine the criterion weight correspondingly.

4. Compute for the maximum eigenvalue, consistency ratio, and normalized values for each criterion/alternative.

5. For an unacceptable CR value, i.e., >0.10, the expert is required to repeat his judgment in the pair-wise comparisons till the CR value lies at an acceptable level (Lee and Chan, 2008).

The AHP gained its significance, especially in decision-making, because of its interactive graphical user interfaces, automatic calculation of priorities and variabilities, and sensitivity analysis (Mallick et al., 2018). Perhaps one of its main advantages is it provides the ability to measure the consistency of the decision makers' preferences and manipulate qualitative and quantitative criteria (Gigović et al., 2017). However, the final decision derived using the AHP method is based on subjective evaluations, specifically during pair-wise comparisons (Song et al., 2013; Gigović et al., 2017). The observation is affirmed by Mallick et al. (2018) that the decision-makers in any decision-making problem could be subjective and uncertain about their level of preference mainly because of the incomplete knowledge or information and uncertain within the decision environment. Thus, their preferences are subjective, and their choices are affected by the sufficiency of the information. Additionally, in a decision-making process, Campos et al. (2007) described the term “subjective uncertainty” from scientific ignorance, uncertainty in measurement, the impossibility of confirmation or observation, censorship, or other knowledge deficiency.

Lastly, since many experts are participating in a decision-making process, heterogeneous preferences are often observed. The aim of group decision-making is, therefore, to reach a consensus or an agreement. However, achieving consistent agreement is difficult, especially in AHP methodology with the number of comparison matrices (Ishizaka and Labib, 2011). More especially in convening the experts in a single setting is impossible to organize (distant experts or many experts). Thus, the experts' preferences are convened through geometric mean (Saaty and Vargas, 2005). After ensuring the consistencies of the individual preferences are acceptable, the collective preference was achieved by determining the geometric mean. Adopting the geometric mean instead of the arithmetic mean preserves the matrix's reciprocal property employed in AHP (Aczél and Saaty, 1983).

Results and Discussion

Established Criteria for Hazard Mapping

The Philippines is a country exposed to multiple hazards primarily because of its archipelagic nature and geographical location within the “Pacific Ring of Fire.” This makes the country highly susceptible to earthquakes and volcanic eruptions, tsunami, sea-level rise, storm surges, landslides, floods, and drought (Asian Disaster Reduction Center (ADRC), 2019; UNDRR, 2019). The UNDRR on their knowledge platform for disaster risk reduction shows that from the years 1990 to 2014, the Philippines' top five hazards in terms of frequency include storm, flood, landslide, volcanic eruption, and earthquake. In terms of mortality, the top four hazards include storm, earthquake, flood, and landslide, and in terms of economic losses, the top three hazards are storm, flood, and earthquake (UNDRR Prevention Web, 2017). Although volcanic eruption is included in the top five hazards, the study included only flood, landslide, storm surge, and earthquake, mainly because volcanoes are not throughout the country and the last recorded disastrous volcanic eruption in the Philippines was still in June 1991 (Asian Disaster Reduction Center (ADRC), 2019).

In connection to the four hazards mentioned above, relevant evaluation criteria were identified and used in this study. The final selection of the evaluation criteria is crucial for the analysis and in making decisions about the problem. Primarily, the criteria should be able to answer the decision problem. Although the most common basis in selecting criteria for decision-making is availability and accessibility (Akinci et al., 2013), the important characteristics of criteria should be comprehensive and measurable (Malczewski, 1999; Yahaya et al., 2010). This means that the criteria should clearly indicate the associated object's achievement and their outcomes can be measured for every decision alternative.

Based on the experts' knowledge and preferences, the following are the criteria to be used in GIS-MCE for hazard mapping:

Flood Hazard Mapping. Flood or inundation is an overflowing of a large amount of water beyond its normal confines, especially over what is normally dry. In flood hazard mapping, the experts chose seven relevant criteria: the rainfall/precipitation, distance from the drainage network, slope, land use/land cover, elevation, distance from the rivers, and the size of the river basin/watershed.

Landslide Hazard Mapping. Landslide, in general, is the sliding of a mass of earth or rock from a mountain or cliff. The occurrence of landslides could have different triggering factors, including rain or water, earthquake, and human activities. For landslide hazard mapping, the experts selected five criteria: slope, rainfall/precipitation, elevation, land use/land cover, and soil type.

Earthquake Hazard Mapping. Earthquake is essentially defined as ground shaking due to other events such as plate tectonic movements. Though other researchers and hazard-related agencies regard earthquakes as a triggering factor, the study included earthquakes as a hazard since the effects of ground shaking could be fatal in some instances, like earthquakes with high magnitudes and intensities. For this research, the experts chose five criteria for earthquake hazard mapping: the soil type, liquefaction potential, distance from faults, length of active faults, and history of occurrence.

Storm Surge Mapping. Storm surge is technically defined as the rising of the sea because of atmospheric pressure changes and wind associated with a storm. This hazard generally occurs in countries with shorelines or coastal areas. For storm surge mapping, the experts selected four relevant criteria: the distance from the shoreline, elevation of the area, surge height, and tide.

The above-mentioned sets of criteria were used in the second part of the study which is the derivation of the priority scales. The weights of the criteria were determined by showing their relative importance through pair-wise comparisons based on the experts' knowledge and information in hazard mapping as indicated in their preferences.

Derived Weights of the Criteria Using AHP

The experts' different preferences as the decision-makers who participated in the research were gathered and consequently computed based on the accepted and practiced guidelines of using AHP. Their preferences are correspondingly represented and quantified with the weights of each criterion (Figures 3–6; Annex 2). For the different sets of criteria in each hazard, the corresponding weights were computed per expert (A to T), and the arithmetic means shown in horizontal lines (Figures 3–6) were computed to reflect the overall preference weight but are not used as the final weights to be used in future GIS analysis.

FIGURE 3

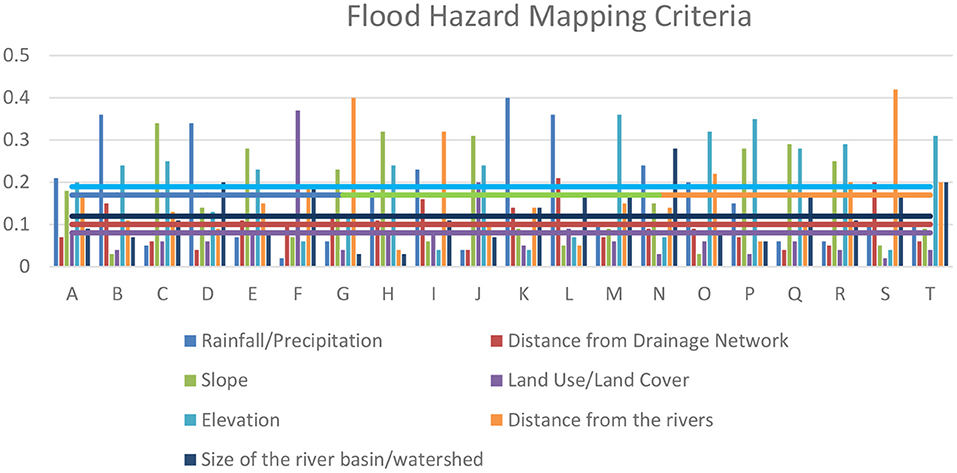
Figure 3. Weights of the criteria for flood hazard mapping using AHP showing the mean values in horizontal lines.

Figure 3 shows the distribution of weights for each of the seven criteria for flood hazard mapping. Although the data reveal small differences in each criterion's average weights (shown in horizontal lines in the graph), the experts gave the biggest weight to the criterion elevation with 0.19. This signifies that higher elevations should be preferred for the allocation of lands for any use in consideration of probable flooding incidence. A notable observation is that among the criteria, the rainfall/precipitation, slope, and the distance from the rivers are on the second rank with equal weights of 0.17, too close to the criterion elevation. This suggests that the experts believe that those criteria are equally important considerations in selecting the best places that are less risky to flooding. The criterion with the least weight of 0.08 is the land use/land cover. Although considered an important criterion, the land use/land cover is the least important in flood hazard mapping.

The same poll of experts expressed their preferences over the criteria for landslide hazard mapping (Figure 4). On average, the highest weight was given to slope with 0.33, which is significantly higher than the rest of the criteria. This is followed by the criterion elevation with a weight of 0.20. This manifests the experts' beliefs that sloping terrain and considerably elevated areas are the most important factors upon which landslides occur. Hence, should be given more attention in landslide hazard mapping. The smallest weight of 0.12 was acquired by the criterion land use/land cover based on the experts' collective preferences.

FIGURE 4

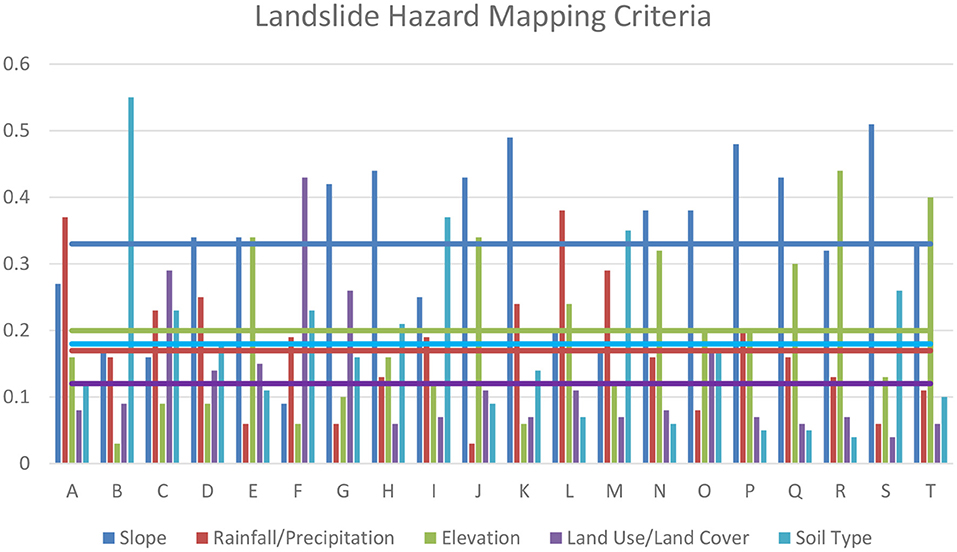
Figure 4. Weights of the criteria for landslide hazard mapping using AHP showing the mean values in horizontal lines.

Figure 5 shows the weights of the criteria for earthquake hazard mapping. On average, the criterion distance from the faults has the highest weight with 0.31 followed by the length of the active faults with 0.24. This signifies that the experts strongly believed that in the occurrence of earthquakes, the places that could be more prone to damages due to ground shaking are those places near to faults, or the distance to faults has a perceived direct relationship to the degree of damage caused by earthquakes. On the other hand, the criterion soil type got the lowest weight of 0.11 based on the experts' preferences. This suggests that the soil type has the least importance in preparing earthquake hazard maps among the criteria in this set.

FIGURE 5

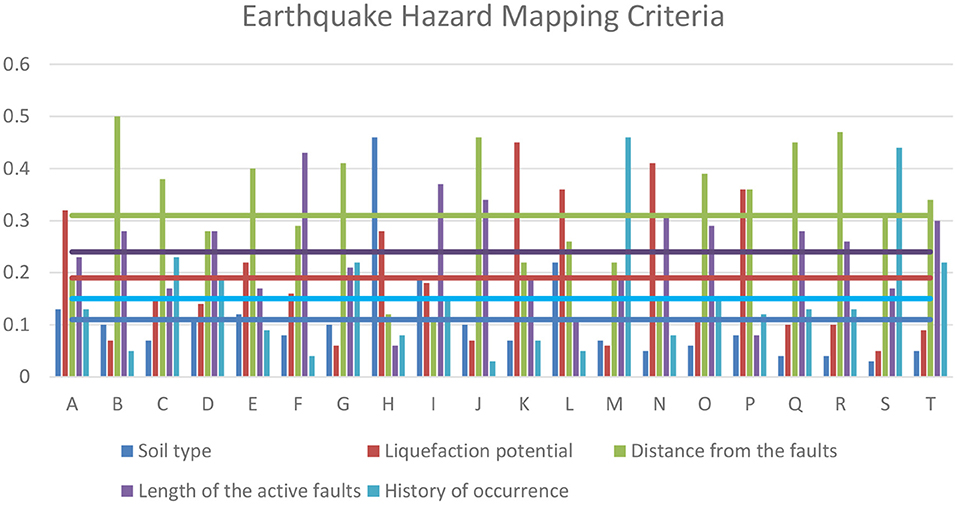
Figure 5. Weights of the criteria for earthquake hazard mapping using AHP showing the mean values in horizontal lines.

On average, the distance from the shoreline has the highest weight of 0.33, followed by the criterion surge height with 0.30 (Figure 6). This implies that the experts' preference in selecting safer places considering probable storm surges is those places farther from the shoreline. The criterion tide acquired the lowest weight with 0.13. This suggests that the tide is the least important among the set of criteria as it is always present, with gradual motion and predictable nature

FIGURE 6

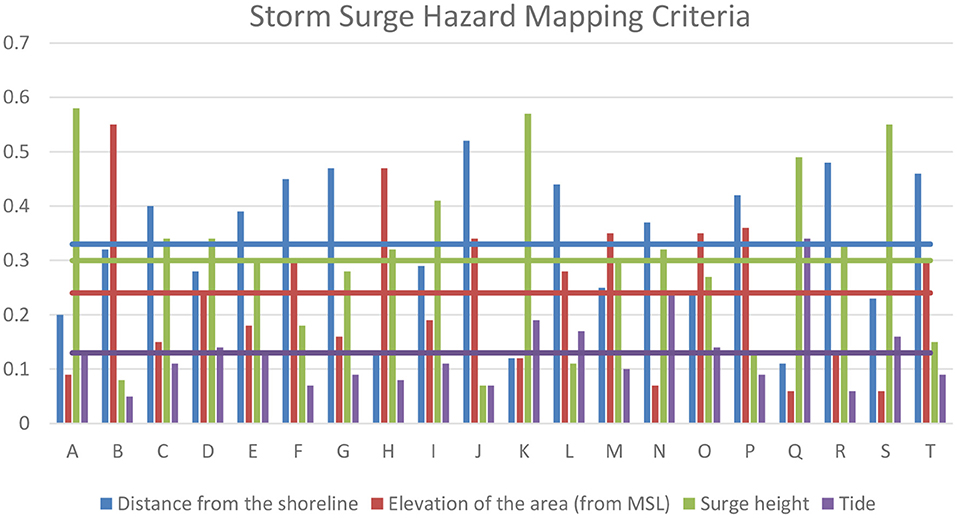
Figure 6. Weights of the criteria for storm surge hazard mapping using AHP showing the mean values in horizontal lines.

It is clear from the corresponding weights (Figures 3–6; Annex 2) that the experts have different preferences on each criterion per hazard mapping. These preferences are directed by the different factors that influence the experts in their choices, such as the level of information they have on each criterion and the type of hazards. Figure 3 shows that the criterion elevation for flood hazard mapping obtained the highest average weight of 0.19. Although more experts preferred the same ranking for elevation with the three highest weights (individual experts) of 0.36, 0.35, and 0.32, it can be noted that three other experts gave a computed weight for the elevation of 0.04, which shows extreme preferences. The same observation applies to Figure 4, which shows that the criterion slope is the most preferred among the five criteria with an average weight of 0.33 in landslide hazard mapping. Contributing to this average weight are the notable three highest individual weights of 0.51, 0.49, and 0.48, however three other extreme preferences can be observed with 0.16, 0.17, and 0.17. It can be deduced that in large-scale decision-making with various decision-makers, heterogeneous preferences would likely arise (Chao et al., 2020). As mentioned in the preceding section, the most important factor that strongly influences the experts' subjective preferences is the level of knowledge and information about the object in the decision-making process (Faro, 2015; Cettolin and Riedli, 2019). The knowledge and information would therefore be dependent on educational backgrounds, training, and experiences, locations, and nature of work as well as decision habits that would determine the way they express their individual preferences (Chen et al., 2015; Chao et al., 2020).

The succeeding tables (Tables 4–7) show the hazard mapping criteria' pair-wise comparison matrices. After ensuring the individual consistencies were achieved (Annex 3), the geometric mean of the individual preferences was computed and subsequently used to fill in the pair-wise comparison matrices representing the collective preferences of the experts who participated in this research. The tables further show the computed weights of the different sets of criteria to be used in subsequent hazard mapping. The overall consistency ratio for the collective preferences and the computed principal Eigen values (λ) are shown in Annex 4.

TABLE 4

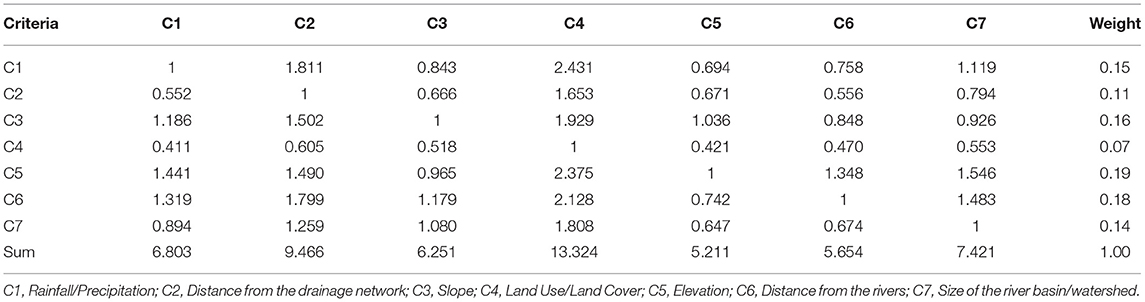
Table 4. Pair-wise comparison matrix of flood hazard mapping criteria using the geometric mean of the preferences.

Table 4 reflects the experts' collective preferences as shown in the matrix of pair-wise comparisons for flood hazard mapping criteria. Seven criteria were compared with each other and the computed weights reveal that the criterion Elevation with a weight of 0.19 is the most preferred, followed by the criterion Distance from the rivers with 0.18. This implies that the experts prefer areas with higher elevations than water bodies like rivers to be safer for development and are more likely to be free from flooding events. On the other hand, the Land use/land cover obtained the lowest weight of 0.07 and the Distance from the drainage network with a computed weight of 0.11, which is 4% greater than the lowest weight.

In the landslide hazard mapping criteria (Table 5), it is pronounced that the experts mostly prefer Slope as the most important criterion in determining areas more likely susceptible to landslides. The slope obtained a computed weight of 0.36 which is 20% higher than the second preferred criterion which is the Elevation having a computed weight of 0.19. The two mentioned criteria suggest that the experts value the physical attributes (topography) of the land (slope and elevation) to be the most important factors in considering areas prone to landslide events. On the other hand, the criterion Land use/land cover is the least preferred criterion in landslide hazard mapping with a computed weight of 0.12.

TABLE 5

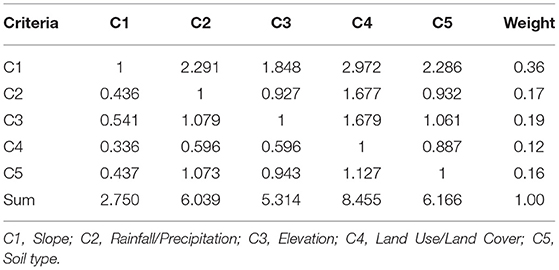
Table 5. Pair-wise comparison matrix of landslide hazard mapping criteria using the geometric mean of the preferences.

Table 6 shows the pair-wise comparison matrix of the earthquake hazard mapping criteria. The collective preferences results show that among the criteria being compared, the criterion Distance from faults got the biggest weight of 0.34, which is 9% higher than the second preferred criterion Length of the active faults having a computed weight of 0.25. This reveals that the experts believed that areas along fault lines are most likely more affected by ground shaking. The table further shows that among the criteria being compared, the least preferred criterion is the Soil type weighting of 0.10.

TABLE 6

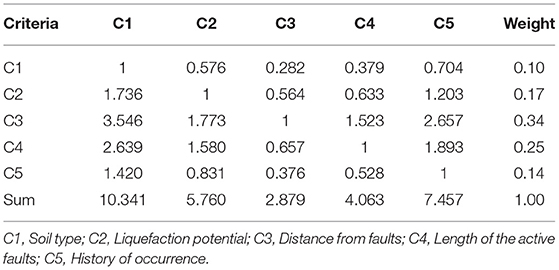
Table 6. Pair-wise comparison matrix of earthquake hazard mapping criteria using the geometric mean of the preferences.

The experts' collective preferences with the criteria for storm surge hazard mapping compared pair-wise (Table 7) reveal that the experts prefer the criterion Distance from the shoreline with a weight of 0.34 as the most important factor in determining areas with high risks for storm surge. Among the criteria compared, the criterion Tide obtained the lowest weight of 0.13, being the least preferred primarily due to the tides' predictive characteristic.

TABLE 7

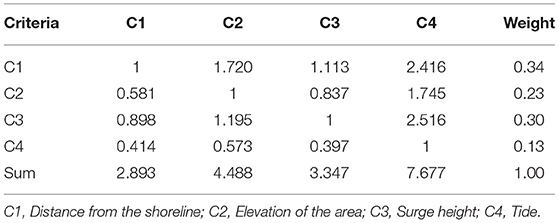
Table 7. Pair-wise comparison matrix of storm surge hazard mapping criteria using the geometric mean of the preferences.

The preceding tables (Tables 4–7) generally show the criteria weights in each set for hazard mapping. The assigned weight to each criterion indicates its relative importance compared to other criteria and can be used in subsequent hazard mapping. The larger the weight, the more important is the criterion in the overall utility (Malczewski, 1999; Drobne and Lisec, 2009), which makes the part on weight determination significant in MCE. Furthermore, the computed weights reflect the experts' overall preferences through geometric mean, which retains the reciprocal property of the matrix in AHP (Aczél and Saaty, 1983). Since the selection of areas for suitability mapping and areas that are hazard-prone is regarded as a decision problem in this research, then the role of the decision-makers is vital in realizing the objective. The existence of heterogeneous preferences was convened in the computation of the geometrical average, which is likewise important in group decision-making in reaching consensus. Additionally, AHP effectively incorporates the different preferences with a certain acceptable threshold of inconsistencies to convene to one decision. In this case, the criteria established with corresponding weights derived through AHP can make potential hazard maps.

Conclusion and Recommendations

Conclusions

The study successfully established the multiple criteria to be used in hazard mapping that could be referenced spatially. The various types of criteria include topographic (slope, elevation), environmental and climatic factors (tide levels, rainfall/precipitation), soil properties (soil type, liquefaction potential), and other hazard-related criteria (length of active faults and surge height). Additionally:

• The criteria derived from this study sought to address the objective of producing hazard maps as a decision function that could be an excellent contribution to land use planning that integrates disaster risk reduction or identifies areas that are not suitable for human habitation due to its unsafe nature.

• The people participation represented by the experts exemplifies the significant role of humans in the decision-making processes even in the presence of highly advanced technologies such as GIS and remote sensing applications and the objective criteria weighting methodologies. In this important contribution, the knowledge and expertise of the people are transformed into priority scales of the criteria and alternatives in a decision-making process.

• The criteria derived herein are generic, i.e., they can be replicated beyond and outside of the Philippines and adapted depending on the locations in which these criteria will be used. The main advantage of the established criteria for multiple hazard mapping is its simplicity and being straightforward, which means the criteria derived are easier to understand and comprehend not just for those experts working in hazard mapping but also for different decision-makers and stakeholders.

• As compared to more complex and technical approaches of hazard mapping and modeling such as those which uses more detailed data (like water runoff, the cross-sectional area of the river, peak ground acceleration), technologies and procedures (e.g., hydrologic modeling), this study established criteria that are common, and universal. The criteria being used in this study can be processed with ease and can be made accessible readily to the public, say via online platforms.

• The AHP used in determining the relative importance of the criteria as in many decision problems successfully derived the corresponding weights of the respective criteria in each hazard mapping. The experts who participated in this study performed the pair-wise comparisons for all the sets of criteria in each hazard type regardless of their specialization, say the type of hazard they are more knowledgeable on and the hazard they have the least information about.

• The extreme preferences of the same criteria being compared pair-wise as performed by the experts indicate their different levels of knowledge and information about the hazards, which determines their subjective preferences. Nevertheless, the study revealed the most important criteria as reflected in the collective preferences to be used in hazard mapping: elevation-flood hazard mapping, slope-landslide hazard mapping, distance from the faults-earthquake hazard mapping, and distance from the shoreline-storm surge hazard mapping.

• A positive note in the case of AHP is that consistency of preferences can be achieved, which is a widely accepted advantage.

Recommendations

• Although the preferences were convened as a collective preference, a rather different result may be achieved if the experts are more homogeneous, like the same specialization and expertise. Therefore, it is recommended that even all these hazard mappings be done simultaneously, each hazard would have different sets of experts performing the pair-wise comparisons with the same background like education, expertise, and line of work to increase the result's reliability.

• Furthermore, since the study is a decision-making exercise, reaching an agreement is the main objective. Although 10–20 is a commonly used number of experts (Yang et al., 2008; Wang et al., 2011; Gigović et al., 2017), the problem lies in the identified experts' originating locations. Hence, for further studies, it is recommended that the experts be assembled in one location to reach a consensus and eventually an agreement. Likewise, there will be an open discussion to support their preferences which would serve as a validation mechanism of their decisions. This would rather entail additional effort, time, and costs.

• Another recommendation would be applying the method at different points in time (that would be affected by the experts' level of information and situation needs) and with a different set of experts from other countries.

• With the classical AHP method used in decision-making, it is recommended to compare and combine the AHP method with other techniques such as the stated choice and Q methodology, which are not commonly used in decision-making. The combination process could open possibilities of leading to sharper results and the potentials of deriving similar views and opinions.

• Lastly, it is further recommended that in minimizing the effects of hazards, not just hazard mapping will be made, but a risk analysis (risk map) still using the criteria established will be made to have in estimation of the highly probable and least probable sectors to be affected, i.e., the number of households and population in danger zones. Also, statistical analysis should be done comparing output maps of these multiple-criteria based on AHP and those produced in other techniques in hazard mapping to validate the final output of this study.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

FM and WV: study conception, design, analysis, and interpretation. FM: data collection and draft manuscript preparation. WV: reviewing and editing of manuscript. All authors contributed to the article and approved the submitted version.

Funding

The APC was funded by the Technical University of Munich (TUM).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors wish to acknowledge the Commission on Higher Education (CHED) and Visayas State University (VSU) of the Philippines, and the Technical University of Munich (TUM) in Germany for all the support and assistance for the whole research work.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsus.2021.667105/full#supplementary-material

References

Abdalla, R., Elawal, Y., Chen, Z., Han, S., and Rui, X. (2014). A GIS-supported fuzzy-set approach for flood risk assessment. Can. Water Resour. J. 39, 3–14. doi: 10.1080/07011784.2014.881058

CrossRef Full Text | Google Scholar

Aczél, J., and Saaty, T. (1983). Procedures for synthesizing ratio judgements. J. Math. Psychol. 27, 93–102. doi: 10.1016/0022-2496(83)90028-7

CrossRef Full Text | Google Scholar

Ahmadi and Herdiawan, D. (2021). The implementation of BORDA and PROMETHEE for decision making of naval base selection. Decis. Sci. Lett. 10, 129–138. doi: 10.5267/j.dsl.2020.11.006

CrossRef Full Text | Google Scholar

Akinci, H., Özalp, A. Y., and Bülent, T. (2013). Agricultural land use suitability using GIS and AHP technique. Comput. Electron. Agric. 97, 71–82. doi: 10.1016/j.compag.2013.07.006

CrossRef Full Text | Google Scholar

Alexoudi, M., Hatzigogos, T. h., and Pitilakis, K. (2002). “Earthquake-hazard assessment in Thessaloniki, Greece,” in Earthquake Loss Estimation and Risk Reduction International Conference (Bucharest).

Al-Hanbali, A., Alsaaideh, B., and Kondoh, A. (2011). Using GIS-based weighted linear combination analysis and remote sensing techniques to select optimum solid waste disposal sites within Mafraq City, Jordan. J. Geogr. Inf. Syst. 3, 267–278. doi: 10.4236/jgis.2011.34023

CrossRef Full Text | Google Scholar

Asian Disaster Reduction Center (ADRC) (2019). Information on Disaster Risk Reduction of the Member Countries: Philippines. Available online at: https://www.adrc.asia/nationinformation.php?NationCode=608andLang=en (accessed on 10 June 2019).

Google Scholar

Baban, S. M. J., and Sant, K. J. (2005). Mapping landslide susceptibility for Caribbean Island of Tobago using GIS, multi-criteria evaluation techniques with a varied weighted approach. Caribb. J. Earth Sci. 38, 11–20.

Google Scholar

Bagheri, M., Sulaiman, W. N. A., and Vaghefi, N. (2012). Land use suitability analysis using multi-crietria decision analysis for coastal management and planning: a case study of Malaysia. J. Environ. Sci. Technol. 5, 364–372. doi: 10.3923/jest.2012.364.372

CrossRef Full Text | Google Scholar

Campos, F., Neves, A., and Campello de Souza, F. M. (2007). “Decision making under subjective uncertainty,” in Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Multi-criteria Decision Making (Honolulu, HI), 85–90. doi: 10.1109/MCDM.2007.369421

PubMed Abstract | CrossRef Full Text | Google Scholar

Cerreta, M., and De Toro, P. (2012). Urbanization suitability maps: a dynamic spatial decision support system for sustainable land use. Earth Syst. Dynam. 3, 157–171. doi: 10.5194/esd-3-157-2012

CrossRef Full Text | Google Scholar

Cettolin, E., and Riedli, A. (2019). Revealed preferences under uncertainty. incomplete preferences for randomization. J. Econ. Theory 181, 574–585. doi: 10.1016/j.jet.2019.03.002

CrossRef Full Text | Google Scholar

Chandio, I. A., and Matori, A. N. B. (2011). GIS-based multi-criteria decision analysis of land suitability for hillside development. Int. J. Environ. Sci. Dev. 2, 469–473. doi: 10.7763/IJESD.2011.V2.171

CrossRef Full Text | Google Scholar

Chao, X., Kou, G. P., Yi, and Viedma, E. H. (2020). Large-Scale Group Decision-Making with Non-cooperative Behaviors and Heterogeneous Preferences: An Application in Financial Inclusion. Eur. J. Oper. Res. 288, 271–293. doi: 10.1016/j.ejor.2020.05.047

CrossRef Full Text | Google Scholar

Chen, X., Zhang, H., and Dong, Y. (2015). The fusion process with heterogeneous preference structure in group decision making: a survey. Inf. Fusion 24, 72–83. doi: 10.1016/j.inffus.2014.11.003

CrossRef Full Text | Google Scholar

Dai, F. C., Lee, C. F., and Zhang, X. H. (2001). GIS-based geo-environmental evaluation for urban land use planning: a case study. Eng. Geol. 61, 257–271. doi: 10.1016/S0013-7952(01)00028-X

CrossRef Full Text | Google Scholar

Department for Communities and Local Government-London (2009). Multi-Criteria Analysis: A Manual. Communities and Local Government, London, United Kingdom.

Google Scholar

Diakoulaki, D., Mavrotas, G., and Papayannakis, L. (1995). Determining objective weights in multiple criteria problems: the CRITIC method. Comput. Oper. Res. 22, 763–770. doi: 10.1016/0305-0548(94)00059-H

CrossRef Full Text | Google Scholar

Drobne, S., and Lisec, A. (2009). Multi-attribute decision analysis in GIS: weighted linear combination and ordered weighted averaging. Informatica 33, 459–474.

Google Scholar

Eastman, J. R., Jin, W., Kyem, P. A. K., and Tolenado, J. (1995). Raster procedures for multi-criteria/multi-objective decisions. Photogramm. Eng. Remote Sens. 61, 539–547.

Faro, J. H. (2015). Variational Bewley preferences. J. Econ. Theory 157, 699–729. doi: 10.1016/j.jet.2015.02.002

CrossRef Full Text | Google Scholar

Feizizadeh, B., and Blaschke, T. (2011). Landslide risk assessment based on gis multi-criteria evaluation: a case study of Bostan-Abad County, Iran. J. Earth Sci. Eng. 1, 66–71.

Google Scholar

Ghodsipour, S. H. (2003). Topics in Multi-Criteria Decision, Vol. 3. Tehran: Amirkabir University of Technology Press.

Gigović, L., Pamučar, D., Bajić, Z., and Drobnjak, S. (2017). Application of GIS-interval rough methodology for flood hazard mapping in Urban areas. Water 9:360. doi: 10.3390/w9060360

CrossRef Full Text | Google Scholar

Grozavu, A., Mărgărint, M. C., and Patriche, C. V. (2010). GIS applications for landslide susceptibility assessment: a case study in Iaşi County (Moldavian Plateau, Romania). Risk Anal. VII, 393–404. doi: 10.2495/RISK100341

CrossRef Full Text | Google Scholar

Hafezparast, M., Araghinejad, S., and Filatova, T. (2015). Comparing the subjective and the objective criteria weighting in agricultural water resources management. Hydrology 3, 38–46. doi: 10.11648/j.hyd.20150304.11

CrossRef Full Text | Google Scholar

Hiscock, K. M., Lovett, A. A., Brainard, J. S., and Parfitt, J. P. (1995). Ground water vulnerability assessment: two case studies using GIS methodology. Q. J. Eng. Geol. Geol. Soc. 28, 179–194. doi: 10.1144/GSL.QJEGH.1995.028.P2.09

CrossRef Full Text | Google Scholar

Hossain, M. S., Chowdhury, S. R., Das, N. G., and Rahaman, M. (2007). Multi-criteria evaluation approach to GIS-based land suitability classification for Tilapia farming in Bangladesh. Aquac. Int. 15, 425–443. doi: 10.1007/s10499-007-9109-y

CrossRef Full Text | Google Scholar

Ishizaka, A., and Labib, A. (2011). Review of the main developments in the analytic hierarchy process. Expert Syst. Appl. 38, 14336–14345. doi: 10.1016/j.eswa.2011.04.143

CrossRef Full Text | Google Scholar

Joerin, F., Thériault, M., and Musy, A. (2001). Using GIS and outranking multi-criteria analysis for land use suitability assessment. Int. J. Geogr. Inf. Sci.15, 153–174. doi: 10.1080/13658810051030487

CrossRef Full Text | Google Scholar

Kasim, M. M., and Jemain, A. A. (2020). Performance of entropy-based criteria weights in solving multi-criteria problems. J. Phys. 1496:012015. doi: 10.1088/1742-6596/1496/1/012015

CrossRef Full Text | Google Scholar

Lai, T., Dragicevic, S., and Schmidt, M. (2013). Integration of multicriteria evaluation and cellular automata methods for landslide simulation modelling. Geomat. Nat. Hazards Risk 4, 355–375. doi: 10.1080/19475705.2012.746243

CrossRef Full Text | Google Scholar

Latinopoulos, D., and Kechagia, K. (2015). A GIS-based multi-criteria evaluation for wind farm site selection. A regional scale application in Greece. Renew. Energy 78, 550–560. doi: 10.1016/j.renene.2015.01.041

CrossRef Full Text | Google Scholar

Lee, G. K. L., and Chan, E. H. W. (2008). The analytic hierarchy process (AHP) approach for assessment of urban renewal proposals. Soc. Indec. Res. 89, 155–168. doi: 10.1007/s11205-007-9228-x

CrossRef Full Text | Google Scholar

López-Marrero, T., González-Toro, A., Heartsill-Scalley, T., and Hermansen-Báez, L. A. (2011). Multi-Criteria Evaluation and Geographic Information Systems for Land-Use Planning and Decision Making [Guide]. Gainesville, FL: USDA Forest Service, Southern Research Station, 8.

Google Scholar

Malczewski, J. (1999). GIS and Multicriteria Decision Analysis. New York, NY: J. Wiley and Sons.

Google Scholar

Mallick, J., Singh, R. K., Alawadh, M. A., Islam, S., Khan, R. A., and Qureshi, M. N. (2018). GIS-based landslide susceptibility evaluation using Fuzzy-AHP multi-criteria decision-making techniques in Abha Watershed, Saudi Arabia. Environ. Earth Sci. 77:276. doi: 10.1007/s12665-018-7451-1

CrossRef Full Text | Google Scholar

Mancini, F., Ceppi, C., and Ritrovato, R. (2010). GIS and statistical analysis for landslide susceptibility mapping in the Daunia Area, Italy. Nat. Hazards Earth Syst. Sci. 10, 1851–1864. doi: 10.5194/nhess-10-1851-2010

CrossRef Full Text | Google Scholar

Mansour, S., Al-Awhadi, T., and Al-Hatrushi, S. (2019). Geospatial-based multi-criteria analysis for ecotourism land suitability using GIS and AHP: a case study of Masirah Island, Oman. J. Ecotourism 19, 148–167. doi: 10.1080/14724049.2019.1663202

CrossRef Full Text | Google Scholar

Maugeri, M., Motta, E., Mussumeci, G., and Raciti, E. (2009). Lifeline seismic hazards: a GIS application. Earthq. Eng. Resist. Struct. VII, 381–392. doi: 10.2495/ERES090351

CrossRef Full Text | Google Scholar

Morales, F. Jr., and de Vries, W. T. (2021). Establishment of land use suitability mapping criteria using analytic hierarchy process (AHP) with practitioners and beneficiaries. Land 10:235. doi: 10.3390/land10030235

CrossRef Full Text | Google Scholar

Nguyen, T. T., Verdoodt, A., Tran, V. Y., and Delbecque, N. (2015). Design of a GIS and multi-criteria based land evaluation procedure for sustainable land use planning at the regional level. Agric. Ecosyst. Environ. 200, 1–11. doi: 10.1016/j.agee.2014.10.015

CrossRef Full Text | Google Scholar

Nwilo, C., Olayinka, D. N., and Adzandeh, A. E. (2012). Flood modelling and vulnerability assessment of settlements in the adamawa state floodplain using GIS and cellular framework approach. Glob. J. Human Sci. 12, 11–20.

Google Scholar

Nyeko, M. (2012). GIS and multi-criteria decision analysis for land use resource planning. J. Geogr. Inf. Syst. 4, 341–348. doi: 10.4236/jgis.2012.44039

CrossRef Full Text | Google Scholar

Oluah, C. K., Akinlabi, E. T., and Njoku, H. O. (2019). Weight determination of glazing properties for trombe wall application in johannesburg: an entropy method implementation. J. Phys. 1378, 1–6. doi: 10.1088/1742-6596/1378/3/032042

CrossRef Full Text | Google Scholar

Ouma, Y. O., Yabann, C., Kirichu, M., and Tateishi, R. (2014). Optimization of urban highway bypass horizontal alignment: a methodological overview of intelligent spatial MCDA approach using fuzzy AHP and GIS. Adv. Civ. Eng. 2014, 1–26. doi: 10.1155/2014/182568

CrossRef Full Text | Google Scholar

Pardalos, P. M., Siskos, Y., and Zopounidis, C. (1995). Editorial: Advances in Multicriteria Analysis. Dordrecht: Kluwer Academic Publishers. doi: 10.1007/978-1-4757-2383-0

CrossRef Full Text | Google Scholar

Pourebrahim, S., Hadipour, M., Mokhtar, M. B., and Mohamed, M. I. H. (2010). Analytic network process for criteria selection in sustainable coastal land use planning. Ocean Coast. Manag. 53, 544–551. doi: 10.1016/j.ocecoaman.2010.06.019

CrossRef Full Text | Google Scholar

Psomas, A., Vryzidis, I., Spyridakos, A., and Mimikou, M. (2018). MCDA approach for agricultural water management in the context of water-energy-land-food nexus. Oper. Res. 21, 689–723. doi: 10.1007/s12351-018-0436-8

CrossRef Full Text | Google Scholar

Quinta-Nova, L., and Ferreira, D. (2020). Land suitability analysis for emerging fruit crops in Central Portugal using GIS. Agric. For. 66, 41–48. doi: 10.17707/AgricultForest.66.1.05

CrossRef Full Text | Google Scholar

Raddad, S. (2016). Integrated a GIS and multi criteria evaluation approach for sustainability analysis of urban expansion in Southeastern Jerusalem Region-Palestine. Am. J. Geogr. Inf. Syst. 5, 24–31. doi: 10.5923/j.ajgis.20160501.03

CrossRef Full Text | Google Scholar

Rahman, M. R., and Saha, S. K. (2007). Flood hazard zonation-a gis aided multi criteria evaluation (MCE) approach with remotely sensed data. Int. J. Geoinform. 3, 25–37.

Google Scholar

Razandi, Y., Pourghasemi, H. R., Neisani, N. S., and Rahmati, O. (2015). Application of analytic hierarchy process, frequency ratio and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 8, 867–883. doi: 10.1007/s12145-015-0220-8

CrossRef Full Text | Google Scholar

Rezaei, A., and Tahsili, S. (2018). Urban vulnerability assessment using AHP. Hindawi Adv. Civ. Eng. 2018:601. doi: 10.1155/2018/2018601

CrossRef Full Text | Google Scholar

Russo, R. D. F. S., and Camanho, R. (2015). Criteria in AHP: a systematic review of literature. Procedia Comput. Sci. 55, 1123–1132. doi: 10.1016/j.procs.2015.07.081

CrossRef Full Text | Google Scholar

Saaty, T. L. (1980). The Analytic Hierarchy Process. New York: McGraw Hill. International, Translated to Russian, Portuguese, and Chinese, Revised editions, Paperback (1996, 2000). Pittsburgh: RWS Publications.

Google Scholar

Saaty, T. L. (2008). Decision making with analytic hierarchy process. Int. J. Serv. Sci. 1, 83–98. doi: 10.1504/IJSSCI.2008.017590

CrossRef Full Text | Google Scholar

Saaty, T. L., and Vargas, L. G. (2005). The possibility of group welfare functions. Int. J. Inf. Technol. Decis. Mak. 4, 167–176. doi: 10.1142/S0219622005001453

CrossRef Full Text | Google Scholar

Sabah, L., Yücedag, I., and Yalcin, C. (2017). Earthquake hazard analysis for districts of Düzce via AHP fuzzy logic methods. J. Cogn. Syst. 2, 43–47.

Google Scholar

Samarasinghea, S. M. J. S., Nandalal, H. K., Weliwitiya, D. P., Fowze, J. S. M., Hazarika, M. K., and Samarakoon, L. (2010). Application of remote sensing and GIS for flood risk analysis: a case study at Kalu-ganga River, Sri Lanka. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 38, 110–115.

Google Scholar

Siskos, Y., and Spyridakos, A. (1999). Intelligent multicriteria decision support: overview and perspectives. Eur J. Oper. Res. 113, 236–246. doi: 10.1016/S0377-2217(98)00213-6

CrossRef Full Text | Google Scholar

Song, W., Ming, X., and Wu, Z. (2013). An integrated rough number-based approach to design concept evaluation under subjective environments. J. Eng. Des. 24, 320–341. doi: 10.1080/09544828.2012.732994

CrossRef Full Text | Google Scholar

Sureeyatanapas, P. (2016). Comparison of ranked-based weighting methods for multi-criteria decision making. KKU Eng. J. 43, 376–379.

Google Scholar

Tang, Z., Yi, S., Wang, C., and Xiao, Y. (2018). Incorporating probabilistic approach into local multi-criteria decision analysis for flood susceptibility assessment. Stoch. Environ. Res. Risk Assess. 32, 701–714. doi: 10.1007/s00477-017-1431-y

CrossRef Full Text | Google Scholar

Tayebikhorami, S., Nikoo, M. R., and Sadegh, M. (2019). A fuzzy multi-objective optimization approach for treated wastewater allocation. Environ. Monit. Assess. 191:468. doi: 10.1007/s10661-019-7557-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Uddin, K., Gurung, D. R., Giriraj, A., and Shrestha, B. (2013). Application of remote sensing and GIS for flood hazard management: a case study from Sindh Province, Pakistan. Am. J. Geogr. Inf. Syst. 2, 1–5. doi: 10.5923/j.ajgis.20130201.01

CrossRef Full Text | Google Scholar

UNDRR (2019). Disaster Risk Reduction in the Philippines: Status Report 2019. United Nations Office for Disaster Risk Reduction (UNDRR), Regional Office for Asia and the Pacific, Bangkok, Thailand.

UNDRR Prevention Web (2017). Philippines: Disaster and Risk Profile. The Knowledge Platform for Disaster Risk Reduction. Available online at: https://www.preventionweb.net/countries/phl/data/ (accessed 15 September, 2017).

Voogd, J. H. (1982). Multi-Criteria Evaluation for Urban and Regional Planning. Delft: Delftsche Uitgevers Maatschappij.

Google Scholar

Walker, B. B., Taylor-Noonan, C., Tabbernor, A., McKinnon, T., Bal, H., Bradley, D., et al. (2014). A multi-criteria evaluation model of earthquake vulnerability in Victoria, British Columbia. Nat. Hazards 74, 1209–1222. doi: 10.1007/s11069-014-1240-2

CrossRef Full Text | Google Scholar

Wang, Y., Li, Z., Tang, Z., and Zeng, G. (2011). A GIS-based spatial multi-criteria approach for flood risk assessment in Dongting Lake Region, Hunan, Central China. Water Resour. Manag. 25, 3465–3484. doi: 10.1007/s11269-011-9866-2

CrossRef Full Text | Google Scholar

Yahaya, S., Ahmad, N., and Abdalla, R. F. (2010). Multicriteria Analysis for flood vulnerable areas in Hadejia-Jama'are River Basin, Nigeria. Eur. J. Sci. Res. 42, 71–83.

Google Scholar

Yang, F., Zeng, G., Du, C., Tang, L., Zhou, J., and Li, Z. (2008). Spatial analyzing system for urban land-use management based on gis and multi-criteria assessment modeling. Prog. Nat. Sci. 18, 1279–1284. doi: 10.1016/j.pnsc.2008.05.007

CrossRef Full Text | Google Scholar

Yuan, F., and Han, L. D. (2010). A multi-objective optimization approach for evacuation planning. Procedia Eng. 3, 217–227. doi: 10.1016/j.proeng.2010.07.020

CrossRef Full Text | Google Scholar

Zeleny, M. (1998). Multiple criteria decision making: eight concepts of optimality. Human Syst. Manag. 17, 97–107.

Google Scholar

Zizovic, M., Marinkovik, D., and Boza, M. (2020). Objective methods for determining criteria weight coefficients: a modification of the CRITIC method. Decis. Making 3, 149–161. doi: 10.31181/dmame2003149z

CrossRef Full Text | Google Scholar