Parental Investments and Educational Outcomes: Trivers–Willard in the U.S.

In the U.S., there is evidence of a Trivers–Willard (T–W) effect in educational attainment, such that the sons of high status fathers attain more education than the daughters, and the daughters of low status fathers attain more education than the sons. This paper seeks to uncover the mechanisms by which this T–W effect occurs. Data are from the High School and Beyond Study by the U.S. National Center for Education Statistics. Results show that the T–W effect is not a result of the fact that fathers are less likely to be present in the homes of children of low status fathers. Other results show that the sons of high status fathers are more likely than daughters to be sent to private high school, whereas the daughters of low status fathers are more likely than sons to be sent to private high school. These parental investments pay off, as the sex gap in academic grade point averages (GPAs) (favoring women) is narrower for the children of high status fathers than the children of low status fathers. In turn, academic GPA in high school helps explain the T–W effect in educational attainment. Parental non-financial investment as measured by student academic expectations as sophomores in high school also helps explain why the sons of high status fathers obtain higher degrees than the daughters. Together, these two factors: student’s academic GPA in high school and his/her expectations of educational attainment, fully explain the T–W effect in educational attainment in the U.S.

Introduction

The Trivers–Willard (henceforth T–W) hypothesis predicts mothers in good condition will invest more in sons, whereas mothers in poorer condition will invest more in daughters (Trivers, 1972; Trivers and Willard, 1973). Investment can be in utero and manifest in sex ratios at birth, or manifest in parental investments after birth. Applied to sex ratios, the T–W hypothesis has garnered empirical support from tests of a number of species, including humans, e.g., see reviews in Cameron (2004), Lazarus (2002), and Cronk (2007), particularly when condition of the mother is measured close to the time of conception.

Trivers and Willard (1973) further note that “the model can be applied to humans differentiated on a socioeconomic scale, as long as the reproductive success of a male at the upper end of the scale exceeds his sister’s, while that of a female at the lower end of the scale exceeds her brother’s.” This suggests that in a stratified society high status mothers will invest more in male offspring, and low status mothers will invest more in female offspring. This is the strategy that will maximize reproductive success, given that in a stratified society, the children of high status mothers are likely to remain high status, whereas the children of low status mothers are likely to remain low status. A high status man can expect to produce more children than a high status woman, whereas a low status woman can expect to produce more offspring than a low status man.

There is evidence that if status is measured as personal income, in contemporary industrialized (and stratified) societies high status men do have more children than high status women, and low status men have fewer children than low status women, on average. For example, in the U.S. and the UK, for men personal income is positively associated with number of offspring for men, whereas it is negatively associated with number of offspring for women (Hopcroft, 2006, 2015; Weeden et al., 2006; Nettle and Pollet, 2008; Huber et al., 2010). In Sweden, both income and education are positively associated with number of offspring for men only and negatively associated with number of offspring for women (Fieder and Huber, 2007; Goodman and Koupil, 2010). In Norway, Lappegård and Rønsen (2013) find that both education and income increase the probability of additional children for men only. In Finland, Nisén et al. (2013) find more highly educated men have more children than highly educated women.

Given the greater reproductive success of high income men compared to high income women, and the greater reproductive success of low income women compared to high income women in the U.S., on average, we would expect the T–W hypothesis to apply. That is, we would expect high status families to invest more in their sons, and low status families to invest more in their daughters. In particular, given the results described above, we may expect that high status families want to ensure that their sons become high income, and low status families want to ensure that their daughters marry a high income man, because this is the strategy that in the U.S. maximizes reproductive success.

Yet parents can rarely ensure high incomes (or any other positive social outcome) for their children. Furthermore, there is no evolutionary or other reason to believe that they are consciously pursuing such outcomes in and of themselves. But we can well imagine that, on average, parents have evolved a psychology that leads them to want to invest in their children to help them succeed socially and economically, and this psychology is likely influenced by their own social position and their perception of environmental factors (Durante et al., 2015). Yet, previous tests of the T–W hypothesis examining investments in children at young ages have given null or mixed results (Freese and Powell, 1999; Keller et al., 2001; Beaulieu and Bugental, 2008; Schnettler, 2011).

In the U.S., the most important way parents help their children succeed socially and economically is by investing in their children’s education. Unlike in other developed countries, in the U.S. responsibility for a child’s education lies primarily with the child’s parents and includes responsibility for choice of school and for paying the costs of tuition; so, investments in their children’s education by parents can be substantial. Most parents are also aware of the importance of education for their children’s success, as education is an important predictor of economic and social outcomes for individuals (Julian and Kominski, 2011; Hout, 2012). Given this, the T–W hypothesis predicts that high status parents will invest more in the education of their sons, whereas low status parents will invest more in the education of their daughters.

Indeed, if educational outcomes are examined, a T–W effect becomes clear. In the U.S., the sons of high status fathers attain more years of education and higher degrees than the daughters, whereas the daughters of low status fathers attain more years of education and higher degrees than the sons. This has been found in a variety of data sets for the U.S. for the period 1972–2000 (Hopcroft, 2005) and the period 2000–2010 (Hopcroft and Martin, 2014). Cox (2003) also found that parents in lower quartiles for parental net worth were more likely to have a daughter who is better educated than a son, whereas parents in the top quartile for parental net worth were more likely to have a son who is better educated than a daughter. These findings occur despite the fact that in the U.S. women now obtain more education then men do, on average. Women in general make up a larger proportion of university populations and earn more than half the higher level degrees granted by U.S. institutions and have done for the last 20 years. For example, in 2010, females earned 60% of all Master’s degrees and 51% of all Doctorates in the U.S. (Aud et al., 2012).

Yet, while this T–W effect in educational attainment is entirely consistent with the differential investment predicted by the T–W hypothesis, it is unclear by what mechanisms these results come about. Most previous research on sex differences in educational outcomes by class of origin has not sought to test the T–W hypothesis and thus does not examine the interaction between parental status and child’s sex on educational attainment. Most recent research has focused on explaining the growing gender gap in high school and college completion, which now favors women [e.g., Buchmann and DiPrete (2006), Legewie and DiPrete (2012), Bertrand and Pan (2013), Autor et al. (2015), and Fortin et al. (2015)] For example, Autor et al. (2015) examine the interaction between family socioeconomic status (measured by an index of mother’s education, father presence, and marital status of parents) and a variety of educational and other outcomes for young boys and girls. Their results are consistent with T–W as they find that disadvantaged environments are more detrimental to boys than girls [see also Buchmann and DiPrete (2006) and Bertrand and Pan (2013)], although their focus on young people precludes an examination of sex differences at the highest levels of educational attainment, where the sons of high status fathers attain higher levels of education than the daughters.

There have been very few explicit tests of the T–W hypothesis as it relates to differential investment in the education of children in the U.S., and these have given mostly null results. Freese and Powell (1999) found no T–W effect in educational investments in children, such as saving money for college, use of private school, having educational objects in the home, talking to children about school, and monitoring of children’s behavior. Hopcroft and Martin (2014) found no T–W effect in whether a child last attended a public or private junior or high school, the amount of tuition paid at the child’s last college, and the amount of total educational loans obtained by the child.

One problem with the Freese and Powell (1999) study is with their measures of family social status. Their measures of family status were family income (measured as the total income earned by the family from all sources) and the highest education of the most highly educated parent. Yet, measures of family income and education do not adequately measure the social ranking of an individual or a family in a stratified society that T–W likely has in mind. In particular, social ranking implies differential social prestige, which measures of family income and measures of the most highly educated parent do not fully capture. It was because of the inadequacy of single measures of social status such as income and education that Blau et al. (1967) initially developed the socioeconomic index (henceforth SEI) of social status, a measure that represents a composite of the average prestige and income for an occupation, along with the average education required for the occupation. We think that because it incorporates the important dimension of social prestige, for purposes of testing the T–W hypothesis the Duncan SEI measure is more appropriate than measures such as income and education, and this is the measure we use here and have used in the past (Hopcroft, 2005; Hopcroft and Martin, 2014).

In this paper, we use the socioeconomic status of the father’s occupation as the best single measure of family social status. This is not to say that mother’s socioeconomic status is unimportant for investment in children. But father’s occupational status is likely the best single measure of family social status, given that fathers are more likely to be employed full time than mothers (and were so at the time our data were collected). Furthermore, if the mother is employed full time, her occupational status is typically similar to the father’s occupational status, given educational homogamy in marriage markets (Kalmijn, 1998). Having two high status money earners in the family does not increase the family’s overall social status beyond that afforded by the earner with the highest status occupation. Because not all fathers are present in the household, and it is likely that the absence of a father has a particularly adverse effect on boys (Buchmann and DiPrete, 2006; Autor et al., 2015), we do measure and include a control for father presence in the home in high school as a predictor of educational attainment.

To measure differential parental investment, we use measures of the financial and non-financial ways that parents invest in their children’s education. Financial investments include whether the child was sent to a private or public high school; whether the child was sent to a public or private college; the selectivity of the child’s first college; the extent of the child’s employment in high school; and how much the child saved from their earnings to pay for college.

Non-financial investment measures include whether the child has a dedicated space in the home to study; and whether the father was present in the home. Father presence is often treated as a measure of family socioeconomic status [e.g., Buchmann and DiPrete (2006) and Autor et al. (2015)]. Yet, the choice of mothers not to marry or to divorce their husbands can also be seen as an investment by mothers in their children, given that if the father is elsewhere his investments in his children are likely diminished. We also use child’s educational expectations as a sophomore in high school (how much education the child expected to attain) as a measure of non-financial investment in children. We assume a child’s expectations in high school largely reflect family expectations, which further reflect family encouragement (or lack of encouragement) for the child’s education.

We also examine the effects of child’s academic ability on educational attainment, and whether this can account for the observed T–W effect in educational attainment. It is possible that the sons of high status men get more education than the daughters because they are more academically capable; and it is also possible that the daughters of low status men get more education than the sons because they are more academically capable. Student ability measures include the child’s PSAT Math (a test administered to high school sophomores in the U.S.) scores as a proxy for IQ; the academic intensity of the child’s high school program; and the child’s high school academic grade point average (GPA).

Data and Measures

The data come from the High School and Beyond (henceforth HS&B) study, which was sponsored by the U.S. Department of Education’s National Center for Education Statistics (NCES). The base-year survey was conducted in the spring term of 1980 using a national probability sample of 1015 secondary schools (including private and religious schools) as the first units of selection. In the second stage, up to 36 seniors and 36 sophomores were selected in each school. A variety of information was collected about students, including details on their high school program of study, test scores, and grades. In addition, data were collected from teachers, principals, and parents to better understand the school and home contexts.

The HS&B sophomore and senior cohorts were surveyed again in 1982, 1984, and 1986; the sophomore cohort was also surveyed in 1992. It is the data on the sophomore cohort in 1992 that is used here. The unweighted response rate at the baseline school level was 70%. Case weights were adjusted for non-response at each level and for each round, and the 1992 case weight is included in the analyses shown here. The data were analyzed with SAS 9.2 using OLS, ordered probit or logistic regression analyses as appropriate.

Ordered probit models were used when the dependent variable consisted of an ordered categorical variable (e.g., highest degree). These models assume an underlying continuum to the ordinal-dependent variable and estimate threshold levels of this continuum, along with parameters for each of the independent variables. The specification used here was

$T_n{}^{*}=\beta \prime z_n+{\epsilon }_n$

where $T_{\text{n}}^{*}$ = latent and continuous measure of highest degree of respondent, z_n = a vector of explanatory variables describing the respondent, β is a vector of parameters to be estimated, and ε_n = a random error term.

The observed and coded highest degree T_n, is determined from the model as follows.

$\begin{array}{l}{T}_n=0\text{\hspace{1em}if}-\infty \le T_n{}^{*}\le {\mu }_1(<\text{HS})\\ T_n=\text{1\hspace{1em}if }{\mu }_1<T_n{}^{*}\le {\mu }_2(HS)\\ T_n=\text{2\hspace{1em}if }{\mu }_2<T_n{}^{*}\le {\mu }_3(\text{Associate Degree})\\ T_n=\text{3\hspace{1em}if }{\mu }_3<T_n{}^{*}\le {\mu }_4(\text{BA})\\ T_n=\text{4\hspace{1em}if }{\mu }_4<T_n{}^{*}\le {\mu }_5(\text{Graduate Degree})\end{array}$

The μ_i in the above equation represents the thresholds ­estimated in the analysis, along with the parameter vector β. The thresholds give cutoffs for predicted values of the dependent variable and allow one to predict dependent variable values for specific values of the independent variables.

Elements of the parameter vector β can be interpreted much as slopes in a multiple regression analysis, with positive signs on the parameters indicating a positive relationship between that variable and the dependent variable. The relationship between the latent, continuous measure of highest degree $T_{\text{n}}^{*}$ and the observed highest degree, T_n may be depicted as follows:

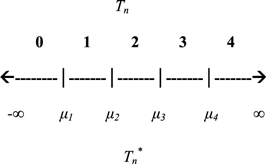
The parameters of the model produced by SAS can be used to predict the Z-score of the probability of the highest ordered outcome. For more information on this model, see Greene (2000).

Logistic regression assumes a binary outcome y (e.g., father present in home), and here it takes the form as follows:

$\begin{array}{c}\text{Log }\left[p_{\text{y}}/\left(1-p_{\text{y}}\right)\right]={\beta }_0+{\beta }_1\text{Sex}+{\beta }_2\text{Father's SEI}+{\beta }_3\text{Age}+{\beta }_4\text{Race}+{\beta }_5\text{Sex}\times \text{Father's SEI}\end{array}$

The slopes (β) can be interpreted much as slopes in a multiple regression analysis, with positive signs on the parameters indicating a positive relationship between that variable and the dependent variable. The parameters of the model produced by SAS can be used to predict the log odds of the outcome in question.

Measures

Educational Attainment

Highest Degree: coded graduate/professional degree = 3, bachelor’s degree = 2, certificate or associates degree = 1, high school or less = 0. This was measured in the 1992 wave of the survey, when the respondents ranged in age from 25 to 32 and had a mean age of 28. Most of the respondents would have completed their education by this age. Although there is very little differentiation of respondents by age in the data set, in the analyses age was controlled.

Family Measures

Father’s occupational status: this is the status of the father’s occupation when the child was in high school in 1980, coded using Duncan SEI scores (Blau et al., 1967). We use this measure as the best available single measure of family social status, for the reasons detailed above. This study uses the transformation from occupation codes to Duncan SEI codes given in Levinsohn et al. (1978), given that these are appropriate for the time period in which the data were collected. The values of this variable range from a low of 7.33 to a high of 70.21 in this dataset.

It would be useful to know the number of siblings a student has. Unfortunately, the 1992 wave of the data set only contains the variable Siblings in Household: coded as yes = 1, no = 0, and thus is less useful as a control for family size. In the following analyses, this variable was not included (including the variable did not change the majority of results reported below).

Race is coded as white = 1, non-white = 0.

Financial Investment Measures

• Private or Public High School: Coded private (includes Catholic) = 1, public = 0.

• Selectivity of first college: Coded highly selective = 3, selective = 2, non-selective = 1, open Door = 0.

• Public or Private college (first college): Coded private 2/4 year college = 1, public 2/4 year college = 0.

• Extent of Employment in High School: Coded 15 + Hours work = 3, <15 h worked = 2, never employed prior to 1981 = 1, never worked = 0.

• Proportion saved for college from high school work: Coded almost all = 2, over half = 1, little to some = 0.

Non-Financial Investment Measures

• Educational Expectations in 1980: coded as graduate/professional degree = 5, bachelor’s degree = 4, associate’s degree = 3, postsecondary vocational degree = 2, high school or less = 1, do not know = 0. The question was phrased as follows: “as things stand now, how far do you expect to get?”

• Have specific place in the home to study: coded have = 1, have not = 0.

This is a measure of family support for student academic achievement.

• Father present in household: Coded 1 = yes. The presence of a biological father in the home may encourage/support the educational aspirations of sons in particular. There is evidence that father absence is particularly harmful for boys (Buchmann and DiPrete, 2006; Autor et al., 2015). This is based on the answer to the question “Which of the following people live in the same household with you? Father?” The next questions specifically asks about a step- or foster-father’s presence so the question on father presence should be regarded as a measure of whether the son has a biological father in the household.

Student Ability Measures

• PSATMath scores = Coded as actual scores.

Quantitative scores on the PSAT (Preliminary Scholastic Aptitude Test) were highly correlated with measured IQ in this time period (Aliotti et al., 1975). So, this measure can be considered a proxy for student IQ.

• Academic Intensity of High School Program: coded with range 0–5 with most intense = 5. A score of the academic intensity of the student’s high school program, as determined by the NCES.

• High School Academic GPA = Coded as actual GPA. This is the student’s overall GPA in academic classes only.

Results

Means and SDs for all variables are given in Table 1.

TABLE 1

Table 1. Descriptive statistics for all variables, high school, and beyond 1992.

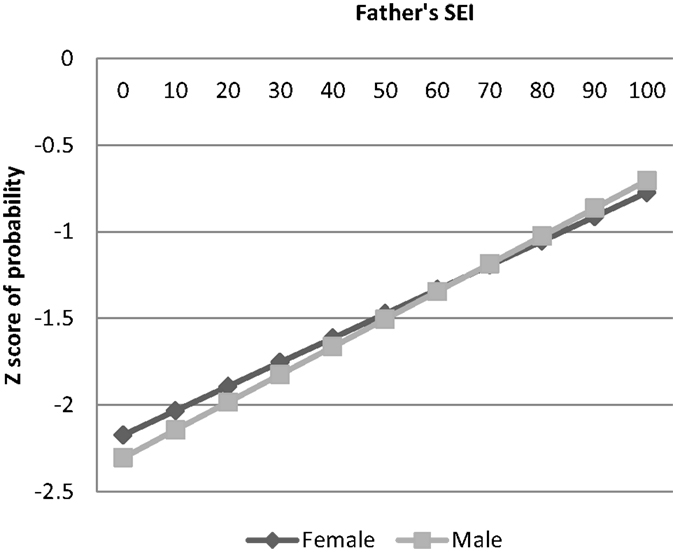
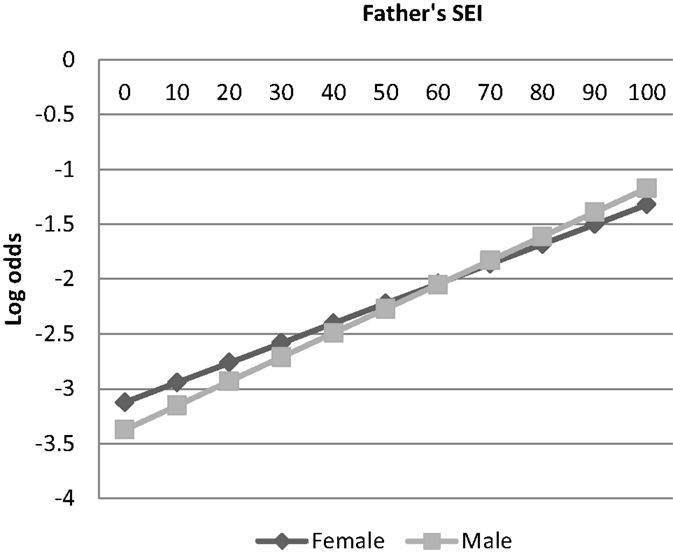
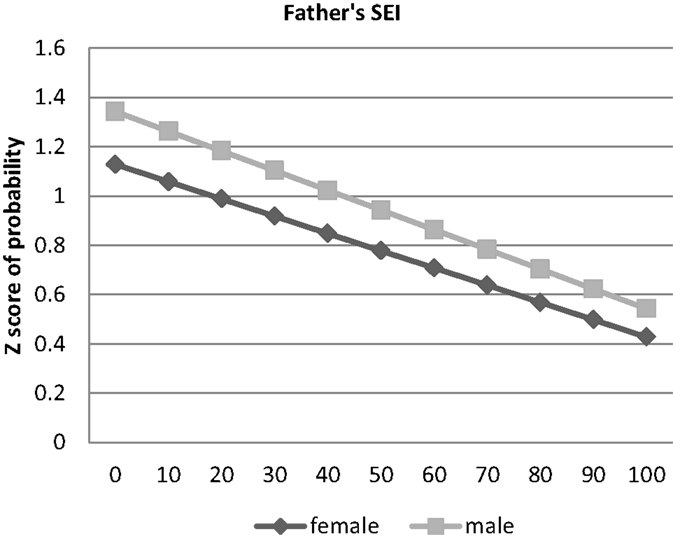
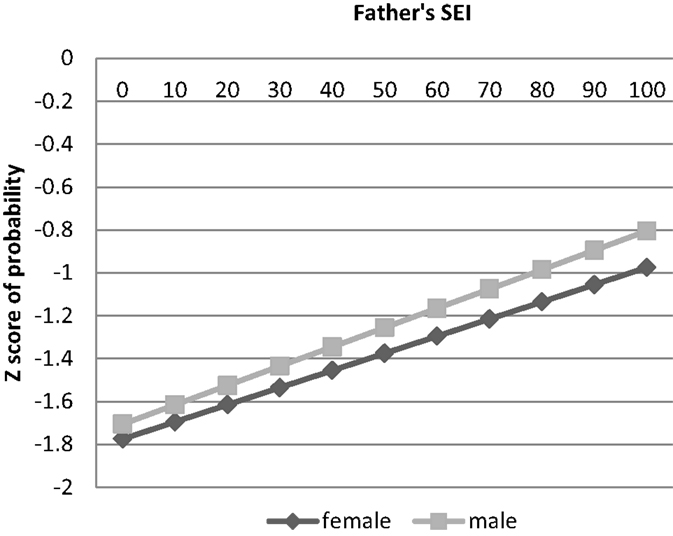
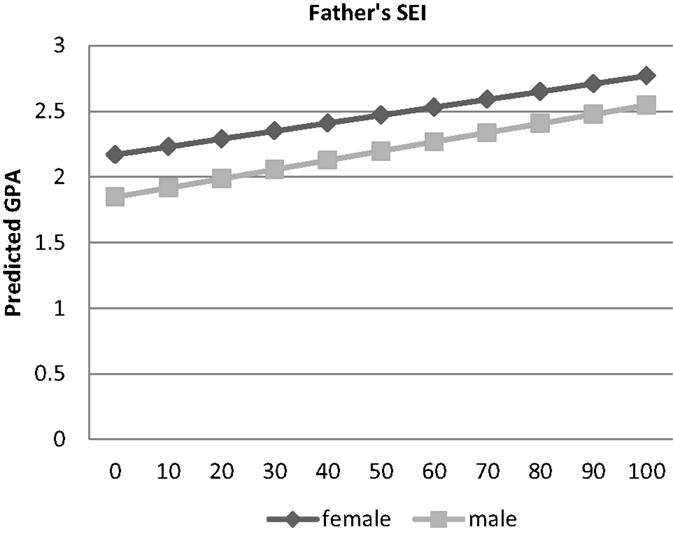
In the first part of the analysis, the original T–W effect in educational attainment is replicated, see the ordered probit analysis in Table 2 Column 1 and Figure 1. In Column 2, the same analysis is performed, this time including a control for father presence. Given the inclusion in all the models of the interaction term between sex and father’s status, the coefficient on the variable sex should be interpreted as the effect of sex for the children of men with zero status. Similarly, the coefficient on the variable father’s status should be interpreted as the effect of father’s status for those whose sex equals 0 (women), whereas the effect of father’s status for males (sex equals 1) is obtained by adding the coefficient on the variable father’s status to the coefficient on the interaction term. In this first model, the effect of sex is negative, showing that the sons of low status men obtain less education than the daughters. The coefficient for the variable SEI is positive, showing that the daughters of high status men obtain more education than the daughters of low status men. The interaction between sex and father’s status is positive and significant, showing that the sons of high status fathers obtain higher degrees than the daughters on average. This replicates findings previously reported for different data sets in Hopcroft (2005) and Hopcroft and Martin (2014).

TABLE 2

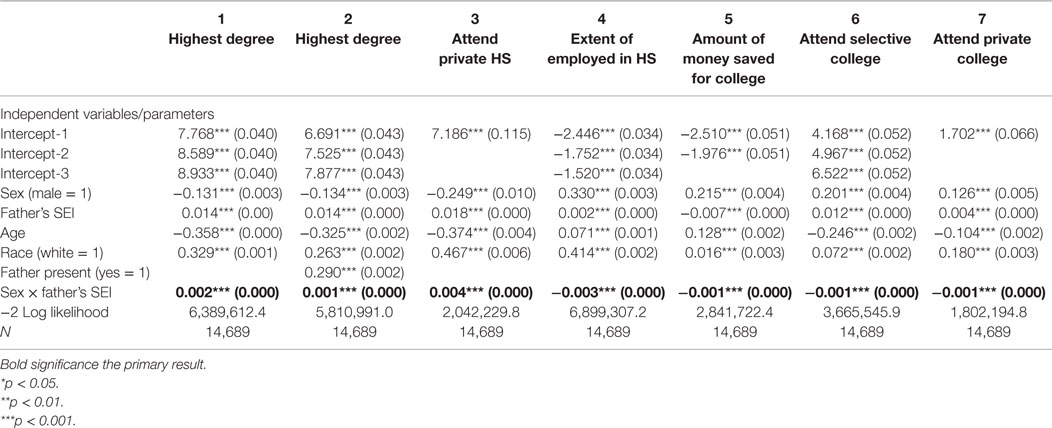
Table 2. Ordered probit and logistic regression parameter estimates, with dependent variables highest degree and measures of parental financial support.

FIGURE 1

Figure 1. Probability of graduate or professional degree, by father’s SEI and sex.

Model 2 includes a control for the variable father presence in high school, and the coefficient for father’s presence shows that a father’s presence has a positive effect on degree attainment. The inclusion of this control reduces the size of the coefficient on the variable for the interaction between sex and SEI, but it remains positive and significant. This shows that the positive effect of father’s status on education remains significantly stronger for sons than for daughters, and this is not due to the greater likelihood of father presence in the households of higher status men.

As the first step to understand the mechanisms involved in producing the T–W effect shown in Model 1, the different measures of financial investment, non-financial investment, and student ability are used as dependent variables, to see if the same T–W effect is seen in these measures. That is, these analyses can answer the questions: do the sons of high status fathers receive more financial investment, more non-financial investment, or have more ability than the daughters? Do the sons of low status fathers receive less financial investment, less non-financial investment, or have less ability than the daughters?

Financial Investments

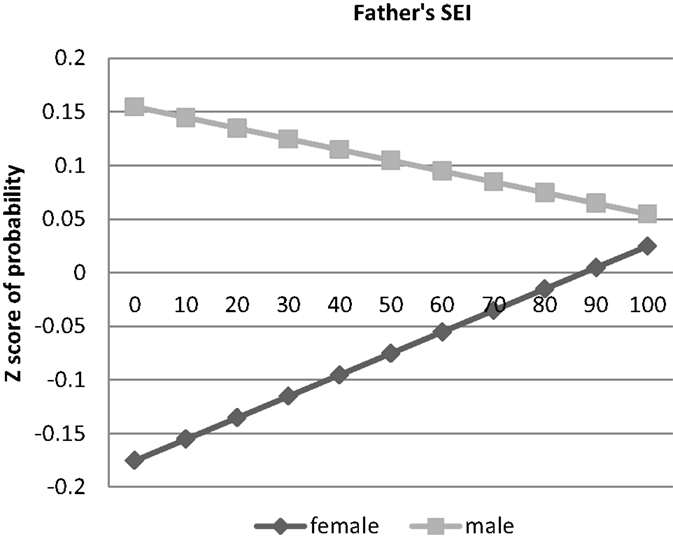
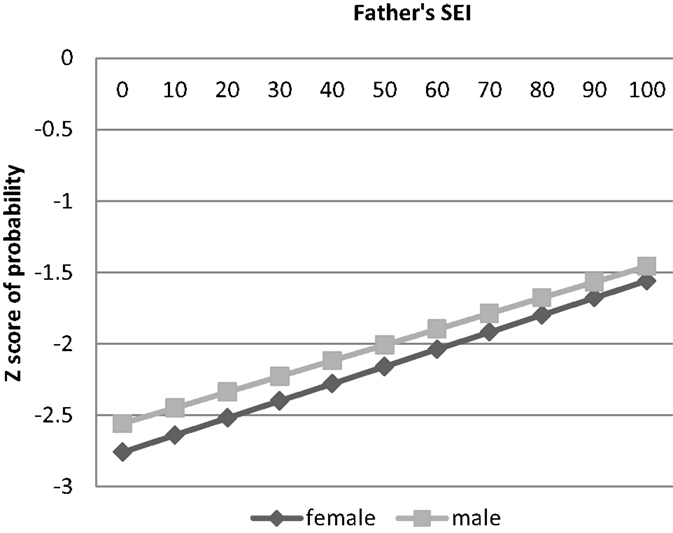
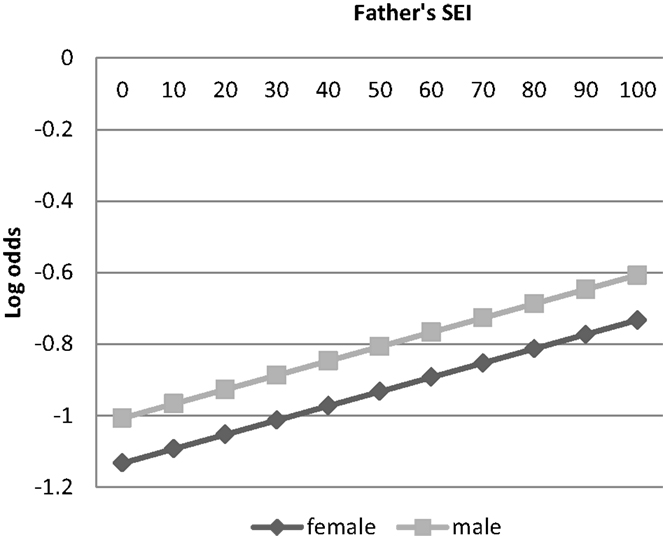
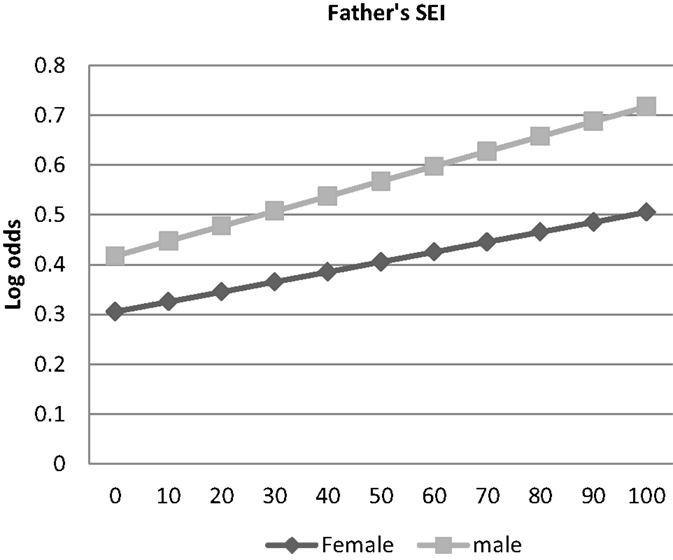
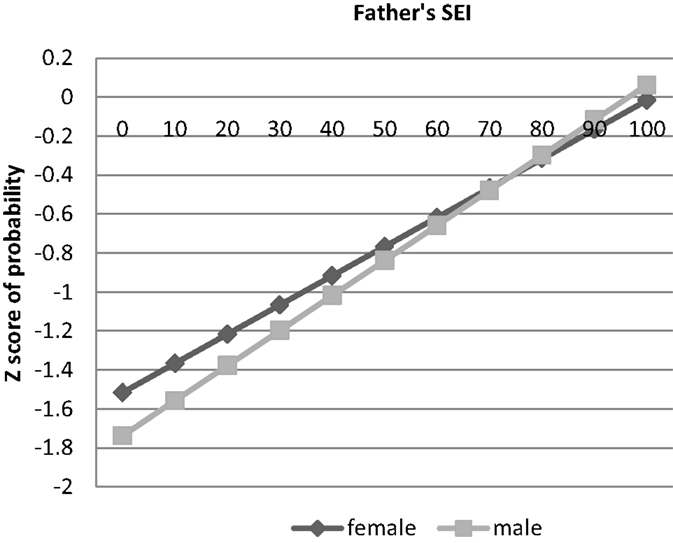
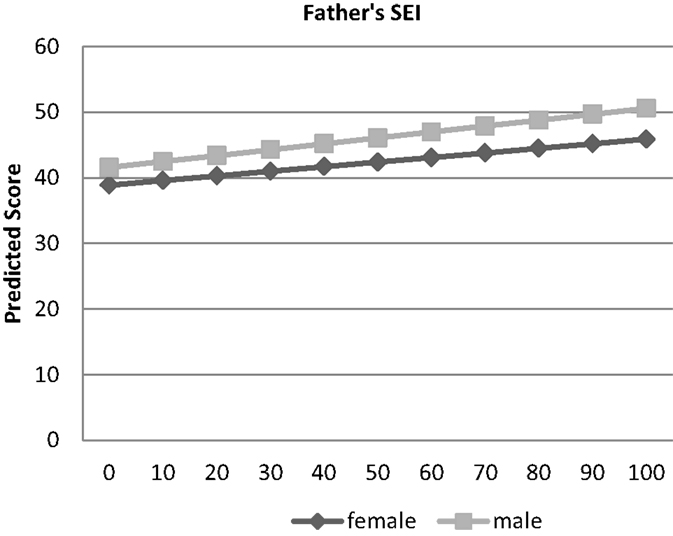
Results for the financial investment measures are given in Models 3–7 of Table 2 and in Figures 2–6. Results of the logistic regression analysis of attendance at private high school given in column 3 of Table 2 show that that consistent with a T–W pattern of investment, the sons of high status fathers are more likely than the daughters to attend private high school, whereas the daughters of low status fathers are more likely than the sons to go to private high school (see Figure 2). Results of the ordered probit analysis of extent of high school employment given in column 4 shows that both the sons of low status men and high status men are more likely than daughters to be extensively employed during high school, although the sex gap is smaller among the children of high status men (see Figure 3). This is also consistent with a T–W pattern of investment, as it suggests that the daughters of low status men and the sons of high status men are discouraged from extensive employment in high school by their parents. Results of the ordered probit analysis of amount of money saved for college given in column 5 shows that sons of both high and low status men save more money for college than the daughters, but the sex gap is smaller among the children of high status men (see Figure 4). This suggests that the sons of high status men are not encouraged to save as much money for college as the sons of low status men, a finding that is also consistent with a T–W effect. These results suggest that these three factors: attending a private high school, amount of employment in high school, and saving money from high school employment – may be part of the mechanism for the T–W effect in educational attainment. To test this, we included each of these factors in three separate analyses with highest degree attained as the dependent variables (analyses not shown). These analyses showed that each of these factors by itself did not substantially change the results described above – the coefficient for the interaction between sex and father’s status remained positive and significant, and the coefficient for the variable sex remained negative. This result suggests that these factors by themselves do not explain the T–W effect in educational attainment in the U.S.

FIGURE 2

Figure 2. Log odds of attending private high school, by father’s SEI and sex.

FIGURE 3

Figure 3. Probability of 15+ hours of employment in high school, by father’s SEI and sex.

FIGURE 4

Figure 4. Probability almost all money saved for college, by father’s SEI and sex.

Other results from ordered probit analysis of attendance at selective college and the logistic regression of attendance at a private college given in Table 2, in columns 6 and 7 and in Figures 5 and 6, do not help explain the T–W effect in educational attainment. Boys are more likely to go to selective colleges over all, and the sex gap is narrower among the children of high status men. Boys are more likely to attend private colleges over all, and the sex gap is narrower among the children of high status men. These results suggest that attending a more selective college or a private college does not fully explain why the sons of high status men get more education than the daughters, and the daughters of low status men get more education than the sons.

FIGURE 5

Figure 5. Probability of attendance at highly selective college, by father’s SEI and sex.

FIGURE 6

Figure 6. Log odds attend private college, by father’s SEI and sex.

Non-Financial Investments

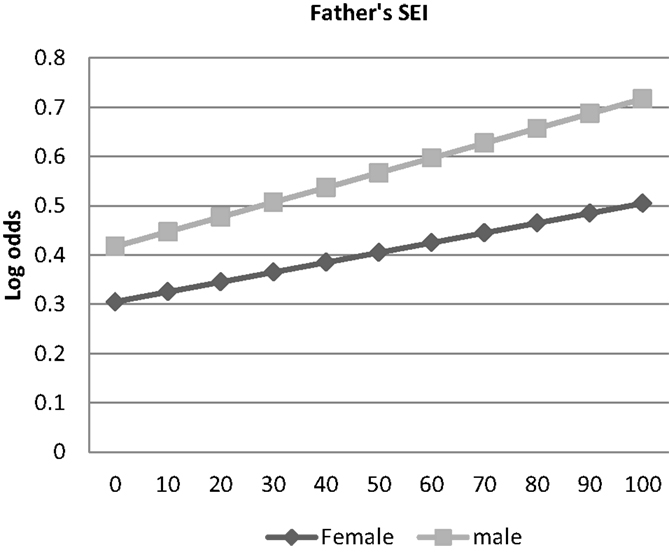
Table 3 gives the results of the analysis using the non-financial investment measures (see also Figures 7–9). As in Table 2, given the inclusion in all the models of the interaction term between sex and father’s status, the coefficient on the variable sex should be interpreted as the effect of sex for the children of men with zero status. Similarly, the coefficient on the variable father’s status should be interpreted as the effect of father’s status for those whose sex equals 0 (women), whereas the effect of father’s status for males (sex equals 1) is obtained by adding the coefficient on the variable father’s status to the coefficient on the interaction term. Results of the logistic regression analysis of having a specific study place in the home in column 1 show that the sons of high status fathers are more likely than daughters to have a specific study place, but that is true also of the sons of low status fathers (Figure 7). Results of the logistic regression in column 2 show that the sons of high status men are more likely than daughters to have their father present in the household, but the same is true of the sons of low status men, so this does not fully explain the T–W effect in educational attainment examined here (see Figure 8). Thus, these two measures do not fully explain why the sons of high status men get more education than the daughters, and the daughters of low status men get more education than the sons.

TABLE 3

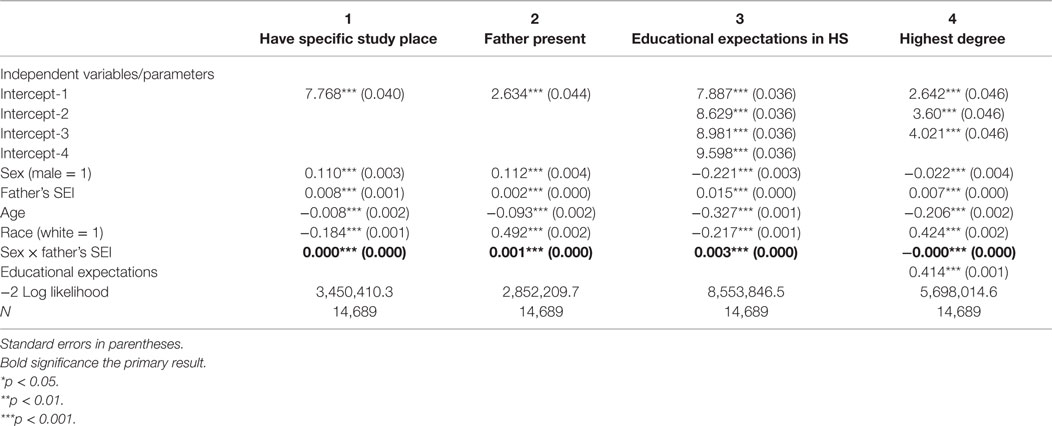
Table 3. Ordered probit and logistic regression parameter estimates, with dependent variables measures of parental non-financial investment and highest degree.

FIGURE 7

Figure 7. Probability of having designated study place, by father’s SEI and sex.

FIGURE 8

Figure 8. Probability of Father present, by father’s SEI and sex.

In the ordered probit analysis with educational expectations of high school sophomores as dependent variable, the T–W effect is seen (see column 3 and Figure 9). The sons of high status fathers have expectations of attaining higher degrees than the daughters, while the daughters of low status fathers have expectations of attaining higher degrees than the sons. This suggests that differential educational expectations in high school may explain the observed T–W effect in educational attainment. Indeed, when education expectations are included in the ordered probit analysis to predict highest degree attained (see column 4), the interaction effect between father’s status and sex remains significant, but reverses in sign. This means that controlling for educational expectations in high school, the daughters of high status fathers attain more education than the sons, although results also show that the sons of low status fathers continue to attain less education than the daughters even with education expectations controlled. This result suggests that the reason that the sons of high status fathers gain more education than the daughters is because they have greater expectations of higher education than the daughters. However, educational expectations do not explain the lower educational attainment of the sons of low status men compared to the daughters, as the coefficient for sex (which can be interpreted as the effect for men when father’s status is 0) continues to be negatively associated with highest degree even with educational expectations controlled.

FIGURE 9

Figure 9. Probability of expectation of graduate or profession degree, by father’s SEI and sex.

Individual Ability

Table 4 gives the results of the analysis of individual ability in columns 1–3 and Figures 10–12. Results in of the OLS regression in column 1 show that the sons of high status men have higher PSATMath scores than the daughters, but so do the sons of low status men (see Figure 10). Results of the ordered probit analysis of the academic intensity of high school program in column 2 show that the sons of high status fathers are more likely to have an academically intense program of study than daughters, but so are the sons of low status men (see Figure 11). Results of the OLS regression in column 3 with academic GPA as dependent variable show that overall males have lower academic GPAs, but the sex gap is smaller among the sons and daughters of high status men (see Figure 12). This suggests that attainment of a high GPA in academic subjects in high school may be part of the mechanism by which the sons of high status men get more education than the daughters. To test this, we put academic GPA in an ordered probit analysis with highest degree attained as the dependent variable. In this analysis, the results changed somewhat. The results (see column 4) show that the sons of high status fathers are more likely to obtain higher degrees than the daughters, but with academic GPA controlled now the sons of low status fathers also obtain higher degrees than the daughters.

TABLE 4

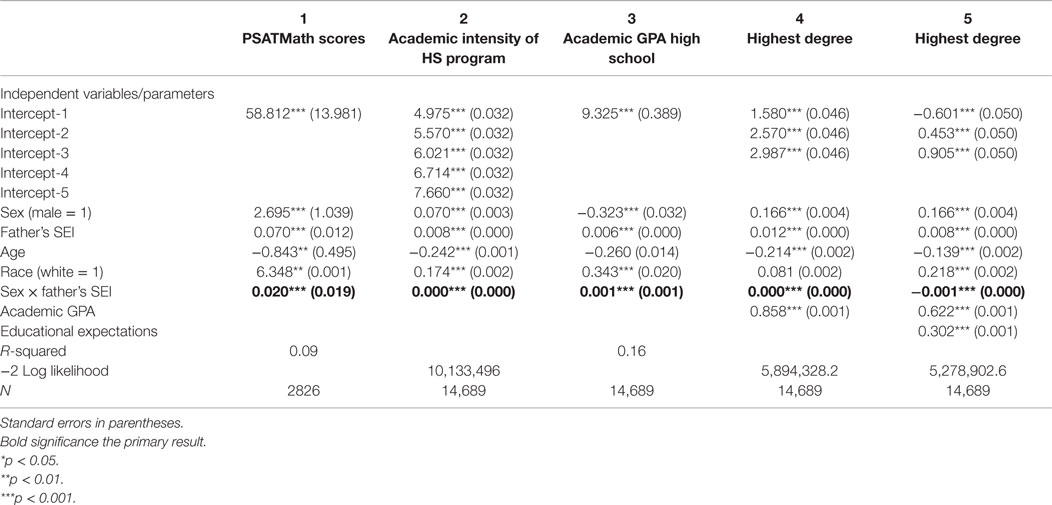
Table 4. Ordered probit and OLS regression parameter estimates, with dependent variables measures of ability and highest degree attained.

FIGURE 10

Figure 10. Predicted PSATMath score, by father’s SEI and sex.

FIGURE 11

Figure 11. Probability of most academically intense high school program, by father’s SEI and sex.

FIGURE 12

Figure 12. Predicted academic GPA, by father’s SEI and sex.

The final ordered probit analysis (column 5) uses educational expectations in high school and academic abilities as measured by academic GPA to predict highest degree attained and includes the interaction between father’s status and student sex. This analysis shows that both academic GPA and education expectations are both positively associated with final educational attainment. This analysis also shows a complete reversal of the original T–W effect – in this analysis controlling for both educational expectations and academic GPA, the sons of high status fathers obtain less education than the daughters, and the sons of low status fathers obtain more education than the daughters. Together, these analyses suggest that the original T–W effect can be entirely explained by these two factors alone: academic GPA and academic expectations in high school. Specifically, the sons of low status fathers obtain less education than the daughters because of low academic GPAs in high school, whereas the sons of high status fathers obtain more education than the daughters because of higher academic attainment expectations in high school.

Discussion and Conclusion

This paper replicates the finding of an interaction between father’s occupational status and children’s educational attainment, such that the sons of high status fathers achieve higher degrees than the daughters, whereas the daughters of low status fathers achieve higher degrees than the sons in the 1992 wave of the 1980 High School and Beyond longitudinal survey. This result has now been found in four different probability samples of the American population at several different points in time [see also Hopcroft (2005) and Hopcroft and Martin (2014); see also Cox (2003)]. This result may be simply characteristic of the U.S. where parents are disproportionately responsible for financing their children’s education. However, similar findings have been found outside of the U.S. For example, Bereczkei and Dunbar (1997) find that the average number of years of education completed by children was higher for Gypsy girls than that completed by Gypsy boys, whereas the number of years of education completed by Hungarian boys was higher than that completed by Hungarian girls. Mulder (1998) found that the sons of both wealthy and poor parents attained more education than the girls, but the sex gap in educational attainment was significantly smaller among the children of poorer parents.

The purpose of this paper was to uncover the mechanisms by which the T–W effect in educational outcomes in the U.S. occurs. A variety of mechanisms were found to contribute. The results show that the sons of high status fathers are more likely than daughters to attend a private high school, are less extensively employed during high school than the sons of low status men, and are less likely to save money from their work than the sons of low status men. The daughters of low status fathers are more likely than the sons to go to private high school and are less likely to be extensively employed during high school than the daughters of high status men.

This suggests that parents are shielding their sons and daughters differentially from work burdens and investing in children’s private high school differentially based on their own status, consistent with the T–W hypothesis. This differential investment pays off in academic GPAs, as although women have higher average academic GPAs than men, the sex gap is narrower among the children of high status men. Academic GPA in high school is in turn an important predictor of a child’s final educational attainment.

The results also show that parents help shape their children’s educational attainment by shaping their expectations about how much education is possible, and they do so in ways consistent with the T–W hypothesis. This analysis showed that the sons of high status fathers expect to attain more education than the daughters; and the sons of low status fathers expect to attain less education than the daughters. Given that educational expectations are an important predictor of highest level of education attained, these differential educational expectations are the second important mechanism for the observed T–W effect.

When both these factors – academic GPA in high school and educational expectations in high school – are controlled, we found that the T–W effect in educational attainment disappears and actually reverses direction. With academic GPA and expectations controlled, the daughters of high status fathers attain more education than the sons, and the sons of low status fathers attain more education than the daughters – the complete reversal of the original finding. This suggests that the original T–W effect in educational attainment is a result of these two factors alone.

Also, instructive is what we did not find in this analysis. Contrary to our expectations, we found that the sons of both low and high status men are more likely to go to highly selective colleges and attend private colleges than daughters, although the sex gap narrows among the children of high status men. Our conclusion is that the T–W effect in educational attainment in the U.S. is not because high status parents are more likely to put their sons in highly selective or private colleges while low status parents are more likely to send their daughters to such places.

We also found that the T–W effect in educational attainment is not because of differential non-financial investments such as having a specific study place in the home, nor does the fact that fathers are less likely to be present in the homes of the sons of low status men account for the T–W effect in educational attainment described here. Although in general low status fathers are less likely to be present in the home than high status fathers, and this is detrimental for boys in particular [see Bertrand and Pan (2013) and Autor et al. (2015)] boys in general are more likely to have a father present in the home than girls. Furthermore, controlling for father presence did not account for the T–W pattern of sex differences in degree attainment documented here. So, while a father’s absence is more detrimental to boys than girls and can help explain the overall sex gap in educational achievement, it cannot explain the T–W pattern of educational attainment documented here.

Similarly, sons of both high and low status men have higher PSATMath scores than daughters, so this measure (a proxy for intelligence) cannot explain the T–W effect in educational attainment presented here. In addition, sons of both low and high status men have more academically intense programs of study in high school than daughters, so this cannot explain the T–W effect in highest degree attained.

We conclude that the results of the analyses presented here suggest that families do differentially invest in their sons’ and daughters’ education depending on their own position in a social hierarchy, as the T–W hypothesis predicts. They do this primarily by shaping their children’s expectations about how much education it is possible for them to attain, and differentially investing in their children financially (in private schooling and shielding children from working in high school) as necessary in order to help them achieve these expectations by earning good grades in high school. Although the interaction effect between sex and father’s occupational status found here and in other studies is small (Hopcroft, 2005; Hopcroft and Martin, 2014), it is unpredicted by any other theory. This further suggests that evolutionary hypotheses, such as the T–W hypothesis, when tested appropriately, can illuminate human social processes in non-obvious ways. Future work should further examine the mechanisms by which parents differentially invest in sons and daughters in ways predicted by the T–W hypothesis by examining additional and more refined measures of both the financial and non-financial investments parents make in children’s education.

Author Contributions

RH is the primary lead author of the article and did most of the writing, the figures, and many of the analyses. DM collaborated on the paper conceptually and did a great deal of the data analysis for this paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Aliotti, N. C., Britt, M. F., and Raskins, G. P. (1975). Relationships among creativity, intelligence, and achievement measures in upward bound students. Psychol. Sch. 12, 423–427. doi: 10.1002/1520-6807(197510)12:4<423::AID-PITS2310120409>3.0.CO;2-Y

CrossRef Full Text | Google Scholar

Aud, S., Hussar, W., Johnson, F., Kena, G., Roth, E., Manning, E., et al. (2012). The Condition of Education 2012 (NCES 2012-045). Washington, DC: U.S. Department of Education, National Center for Education Statistics. Available at: http://nces.ed.gov/pubs2012/2012045.pdf

Google Scholar

Autor, D., Figlio, D., Karbownik, K., Roth, J., and Wasserman, M. (2015). Family Disadvantage and the Gender Gap in Behavioral and Educational Outcomes. Working Paper Series. WP-15-16. Institute for Policy Research Northwestern University. Available at: http://www.k12accountability.org/resources/At-Risk-Students/Boy_Girl_Gap_Autor.pdf

Google Scholar

Beaulieu, D. A., and Bugental, D. (2008). Contingent parental investment: an evolutionary framework for understanding early interaction between mothers and children. Evol. Hum. Behav. 29, 249–255. doi:10.1016/j.evolhumbehav.2008.01.002

CrossRef Full Text | Google Scholar

Bereczkei, T., and Dunbar, R. I. (1997). Female-biased reproductive strategies in a Hungarian Gypsy population. Proc. R. Soc. London Ser. B 264, 17–22. doi:10.1098/rspb.1997.0003

CrossRef Full Text | Google Scholar

Bertrand, M., and Pan, J. (2013). The trouble with boys: social influences and the gender gap in disruptive behavior. Am. Econ. J. Appl. Econ. 5, 32–64. doi:10.1257/app.5.1.32

CrossRef Full Text | Google Scholar

Blau, P. M., Duncan, O. D., In Collaboration with Andrea Tyree. (1967). The American Occupational Structure. New York: Wiley.

Google Scholar

Buchmann, C., and DiPrete, T. A. (2006). The growing female advantage in college completion: the role of family background and academic achievement. Am. Sociol. Rev. 71, 515–541. doi:10.1177/000312240607100401

CrossRef Full Text | Google Scholar

Cameron, E. Z. (2004). Facultative adjustment of mammalian sex ratios in support of the Trivers-Willard hypothesis: evidence for a mechanism. Proc. R. Soc. London Ser. B 271, 1723–1728. doi:10.1098/rspb.2004.2773

CrossRef Full Text | Google Scholar

Cox, D. (2003). “Private transfers within the family: mothers, fathers, sons, and daughters,” in Death and Dollars: The Role of Gifts and Bequests in America, eds A. Munnell and A. Sundén (Washington, DC: Brookings Institution Press), 168–217.

Google Scholar

Cronk, L. (2007). Boy or girl: gender preferences from a Darwinian point of view. Reprod. Biomed. Online 15, 23–32. doi:10.1016/S1472-6483(10)60546-9

CrossRef Full Text | Google Scholar

Durante, K., Griskevicius, V., Redden, J. P., and White, A. E. (2015). Spending on daughters versus sons in economic recessions. J. Consum. Res. 42, 435–456. doi:10.1093/jcr/ucv023

CrossRef Full Text | Google Scholar

Fieder, M., and Huber, S. (2007). The effects of sex and childlessness on the association between status and reproductive output in modern society. Evol. Hum. Behav. 28, 392–398. doi:10.1016/j.evolhumbehav.2007.05.004

CrossRef Full Text | Google Scholar

Fortin, N. M., Oreopoulos, P., and Phipps, S. (2015). Leaving boys behind: Gender disparities in high academic achievement. J. Hum. Resour. 50, 549–579. doi:10.3368/jhr.50.3.549

CrossRef Full Text | Google Scholar

Freese, J., and Powell, B. (1999). Sociobiology, status and parental investment in sons and daughters: testing the T/W hypothesis. Am. J. Sociol. 104, 1704–1743. doi:10.1086/210221

CrossRef Full Text | Google Scholar

Goodman, A., and Koupil, I. (2010). The effect of school performance upon marriage and long-term reproductive success in 10,000 Swedish males and females born 1915-1929. Evol. Hum. Behav. 31, 425–435. doi:10.1016/j.evolhumbehav.2010.06.002

CrossRef Full Text | Google Scholar

Greene, W. H. (2000). Econometric analysis (4th ed.). Englewood Cliffs: Prentice Hall.

Google Scholar

Hopcroft, R. L. (2005). Parental status and differential investment in sons and daughters: T-W revisited. Soc. Forces 83, 1111–1136. doi:10.1353/sof.2005.0035

CrossRef Full Text | Google Scholar

Hopcroft, R. L. (2006). Sex, status and reproductive success in the contemporary U.S. Evol. Hum. Behav. 27, 104–120. doi:10.1016/j.evolhumbehav.2005.07.004

CrossRef Full Text | Google Scholar

Hopcroft, R. L. (2015). Sex differences in the relationship between status and number of offspring in the contemporary U.S. Evol. Hum. Behav. 36, 146–151. doi:10.1016/j.evolhumbehav.2014.10.003

CrossRef Full Text | Google Scholar

Hopcroft, R. L., and Martin, D. O. (2014). The primary parental investment in children in the contemporary U.S. is education: testing the Trivers-Willard hypothesis of parental investment. Hum. Nat. 25, 235–250. doi:10.1007/s12110-014-9197-0

CrossRef Full Text | Google Scholar

Hout, M. (2012). Social and economic returns to college education in the United States. Annu. Rev. Sociol. 38, 379–400. doi:10.1146/annurev.soc.012809.102503

CrossRef Full Text | Google Scholar

Huber, S., Bookstein, F., and Fieder, M. (2010). Socio-economic status and reproduction in modern women – an evolutionary-ecological perspective. Am. J. Hum. Biol. 22, 578–587. doi:10.1002/ajhb.21048

CrossRef Full Text | Google Scholar

Julian, T. A., and Kominski, R. A. (2011). Education and Synthetic Work-Life Earnings Estimates. American Community Survey Reports, ACS-14. Washington, DC: U.S. Census Bureau.

Google Scholar

Kalmijn, M. (1998). Homogamy: causes, patterns, trends. Annu. Rev. Sociol. 24, 395. doi:10.1146/annurev.soc.24.1.395

CrossRef Full Text | Google Scholar

Keller, M. C., Nesse, R. M., and Hofferth, S. (2001). The T/W hypothesis of parental investment. No effect in the contemporary United States. Evol. Hum. Behav. 22, 343–360. doi:10.1016/S1090-5138(01)00075-7

CrossRef Full Text | Google Scholar

Lappegård, T., and Rønsen, M. (2013). Socioeconomic differences in multipartner fertility among Norwegian men. Demography 50, 1135–1153. doi:10.1007/s13524-012-0165-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Lazarus, J. (2002). “Human sex ratios: adaptations and mechanisms, problems and prospects,” in Sex Ratios: Concepts and Research Methods, ed. I. C. W. Hardy (Cambridge: Cambridge University Press), 287–311.

Google Scholar

Legewie, J., and DiPrete, T. A. (2012). School context and the gender gap in educational achievement. Am. Sociol. Rev. 77, 463–485. doi:10.1177/0003122412440802

CrossRef Full Text | Google Scholar

Levinsohn, J., Henderson, L. B., Riccobono, J. A., and Moore, R. P. (1978). National Longitudinal Study Base Year, First, Second and Third Follow-Up. Data File Users Manual. Volume 1. Research Triangle Park, NC: Center for Educational Research and Evaluation, Research Triangle Institute.

Google Scholar

Mulder, M. B. (1998). Brothers and sisters: how sibling interactions affect optimal parental allocations. Hum. Nat. 9, 119–161. doi:10.1007/s12110-998-1001-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Nettle, D., and Pollet, T. V. (2008). Natural selection on male wealth in humans. Am. Nat. 172, 658–666. doi:10.1086/591690

PubMed Abstract | CrossRef Full Text | Google Scholar

Nisén, J., Martikainen, P., Kaprio, J., and Silventoinen, K. (2013). Educational differences in completed fertility: a behavioral genetic study of Finnish male and female twins. Demography 50, 1399–1420. doi:10.1007/s13524-012-0186-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Schnettler, S. (2011). Nature Plus Nurture Equals love? A Test of the T/W Hypothesis of Differential Parental Investment on the Basis of Sociological and Biological Explanations [Dissertation].

Google Scholar

Trivers, R. L. (1972). “Parental investment and sexual selection,” in Sexual Selection and the Descent of Man, 1871–1971, ed. B. Campbell (Chicago: Aldine), 136–179.

Google Scholar

Trivers, R. L., and Willard, D. E. (1973). Natural selection of parental ability to vary the sex ratio of offspring. Science 179, 90–92. doi:10.1126/science.179.4068.90

PubMed Abstract | CrossRef Full Text | Google Scholar

Weeden, J., Abrams, M. J., Green, M. C., and Sabini, J. (2006). Do high-status people really have fewer children? Hum. Nat. 17, 377–392. doi:10.1007/s12110-006-1001-3

CrossRef Full Text | Google Scholar