- 1Department of Physics, University of Alberta, Edmonton, AB, Canada
- 2Applied Mathematics and Plasma Physics, Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM, United States
Energetic electron beams have been proposed for tracing magnetic field lines from the magnetosphere down to the ionosphere, in active experiments aimed at diagnosing mechanisms at play in the coupling between magnetosphere and ionosphere. It is recognized however that in the absence of an efficient mitigation technique, this approach would lead to unacceptably large spacecraft charging and positive potential buildup, which would result in environmental hazard for the spacecraft. This problem would be particularly acute in low density regions of the magnetosphere of interest in the study of magnetic field reconnection and substorm dynamics. A solution to this predicament could consist of creating a plasma contactor whereby a gas puff would be ionized, leading to the evacuation of positive charges and collection of cold electrons, thus compensating for the charges lost in the electron beam. A possible alternative is presented here, which consists of attaching a large passive conducting surface to the spacecraft, a “tethered capacitor”, from which negative charges would be drawn to compensate for those lost from the beam. This capacitor would then charge to a large positive potential, leaving the spacecraft and electron gun at a lower, acceptable positive potential. The tethered capacitor could have a relatively small mass; consisting only of a thin conducting surface that would be “inflated” as a result of repulsive electrostatic forces. This charge mitigation concept, as applied to active electron beam experiments, is explored using three dimensional particle-in-cell (PIC) simulations from which scaling laws can be inferred for the spacecraft and tethered capacitor potentials under proposed electron beam operations.
1. Introduction
Electron guns have been used on several satellites to perform a variety of active experiments, including controlling the floating potential (Whipple and Olsen, 1980; Koons and Cohen, 1982; Pedersen et al., 1984), and diagnosing distant parts of the magnetosphere along magnetic field lines (Hendrickson et al., 1975; Wilhelm et al., 1980; Winckler, 1980, 1992; Nemzek et al., 1992; Grandal and North, 2012). An interesting proposal to elucidate the long-standing problem of magnetosphere-ionosphere coupling and, more generally, of what creates auroral forms, involves the injection of energetic electrons along field lines (i.e., in the loss cone), from satellites in near geostationary orbits. By monitoring light emitted by atoms excited by these electrons entering the upper atmosphere, this approach would map unambiguously the ionospheric footpoint of the magnetospheric spacecraft. Combined with suitable measurements of the magnetospheric and ionospheric state, it would determine what magnetospheric conditions are related to the wide variety of auroral forms. The approach considered here consists of emitting 1 MeV electron pulses along magnetic field lines from a satellite in elliptic near geostationary orbit, sampling the magnetosphere at altitudes between 30,000 and 50,000 km. The orbit inclination and argument of the perigee would be such as to maximize the time spent over the TREx array in Canada (Donovan, 2015a,b). Electrons would be injected in a succession of 0.5 s pulses, each comprising 100, 10 mA minipulses of duration 0.5 ms followed by a 4.5 ms rest period. Following each 0.5 s pulse, there would be a half second of rest to allow for batteries to recharge, and the process would be repeated. The average electron current emitted over the 0.5 s period would then be 1 mA. This pulsed operation of the electron beam would enable the detection of the beam spot in the atmosphere through blinking against a bright auroral background. One technical difficulty is that owing to the low plasma density in the region of interest (ne ~ 106 m−3), neutralization from collecting background electrons alone would not be sufficient to prevent the spacecraft from reaching unacceptably large positive potentials. Indeed, with space parameters of interest here, assuming balance between background electron collection and the 1 mA average current emitted during the first 0.5 s of each pulse, a simple orbital-motion-limited (OML) (Mott-Smith and Langmuir, 1926; Sudit and Woods, 1994; Allen et al., 2000) estimate of the floating potential leads to a value of the order 45 kV. Not only these values are unacceptably large for spacecraft safety but they would also cause energetic electrons to strike spacecraft components, requiring careful consideration from the perspective of internal charging. A promising solution proposed to avoid the buildup of such large potentials consists of using a “plasma contactor” whereby a relatively dense plasma cloud would be created near the spacecraft. As the spacecraft potential increases, electrons from the plasma would be attracted to the satellite while ions would be repelled (Delzanno et al., 2015; Lucco Castello et al., 2018), thus maintaining the floating potential at a lower value through emission of significant ion currents by the contactor cloud. Plasma contactors or hollow cathodes have proven their effectiveness in laboratory (Stenzel and Urrutia, 1990; Williams and Wilbur, 1990) and space (Olsen, 1985; Patterson et al., 1993; Katz et al., 1994; Comfort et al., 1998; Safránková et al., 2002) for controlling satellite floating potentials. In addition, ion beam emission (Schmidt et al., 1995; Torkar et al., 2001) and the release of neutral gas (Gilchrist et al., 1990) have also been used to mitigate satellite charging in space. The alternative considered here consists of attaching a large tethered passive surface capacitor, from which electrons would be drawn as needed by the active spacecraft in order to maintain its floating potential to an acceptable level. This capacitor could consist of an electrostatically “inflatable” conducting foil held by a boom at a fixed distance from the satellite. During the emission of electron pulses, as negative current would be drawn from the capacitor, its potential would increase to large positive values until on average, the capacitor and the spacecraft collect sufficient background electrons to balance lost electron beam charges. The feasibility of this concept is assessed quantitatively in the following sections.
In section 2, we first present a simple estimate of the conditions required for current balance for the spacecraft-capacitor system when collected currents and voltages are assumed to be constant. These results are then used to derive an empirical scaling law for the current collected by the capacitor under various operational scenarios. The following section considers the time dependence of the voltages and collected currents when the electron beam is in operation. This is then followed by section 4 in which a simple analytic model is presented to estimate the peak potential and collected currents at the end of 0.5 ms of beam emission. A summary and conclusions are presented in section 5
2. Steady State Current Balance
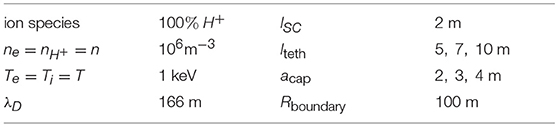
Our goal is to find a satellite-tethered-capacitor configuration that satisfies current balance during the 0.5 s when the electron accelerator is operated, such that the satellite and capacitor potentials remain at an acceptable level. To start with, we consider steady state conditions, in which the spacecraft and capacitor are at fixed potentials, and calculate the currents collected under different conditions. For the purpose of the estimate, a simple geometry is assumed for the assembly. It consists of a cubic satellite bus with side length lSC = 2 m, a thin tether of length lteth to which a spherical conducting sphere of radius acap is attached, as illustrated in Figure 1. The spacecraft surface is assumed to be equipotential at voltage VSC = 1 kV, while the tether and capacitor are assumed to be at the same voltage Vcap. For simplicity, a pure fully ionized non-drifting electron-proton plasma background is assumed, and the magnetic field is assumed to be zero. Our calculations are based on fully kinetic Particle In Cell (PIC) simulations made with PTetra (Marchand, 2012; Marchand and Resendiz Lira, 2017), an explicit electrostatic code which uses unstructured tetrahedral meshes to discretize the simulation domain. In the simulations we consider tether lengths lteth varying from 5 to 10 m, and capacitor voltages Vcap from 10 to 25 kV. In all cases, including the time dependent solution considered in section 3, the emitted electron beam is not included in the simulations. The charge lost in the beam is accounted for indirectly by subtracting the emitted charges from the capacitor at each simulation time step. That is, the electron gun mounted on the spacecraft is assumed to draw all its current from the capacitor. The simulation domain is discretized with a mesh consisting of approximately 3.5 million tetrahedra and 600, 000 vertices. Approximately 200 million macro-particles are used to represent electrons and ions in the PIC simulations. In all cases the simulation domain is delimited by a spherical boundary of radius Rboundary = 100 m where the potential is assumed to be zero. The radius of the outer boundary must be sufficiently large for the incoming electron flux at the boundary to be significantly larger than the average 1 mA that must be collected by the spacecraft-capacitor assembly. If the outer boundary is not far enough and the incoming flux is <1 mA, the entire simulation becomes nearly depleted of electrons, the spacecraft potential increases without bounds, and no steady state solution can be found. Assuming a background Maxwellian distribution, in order for the electron flux at the outer boundary to match the required current, the following condition must be satisfied (Laframboise, 1966):
where k is the Boltzmann constant, and me is the electron mass.
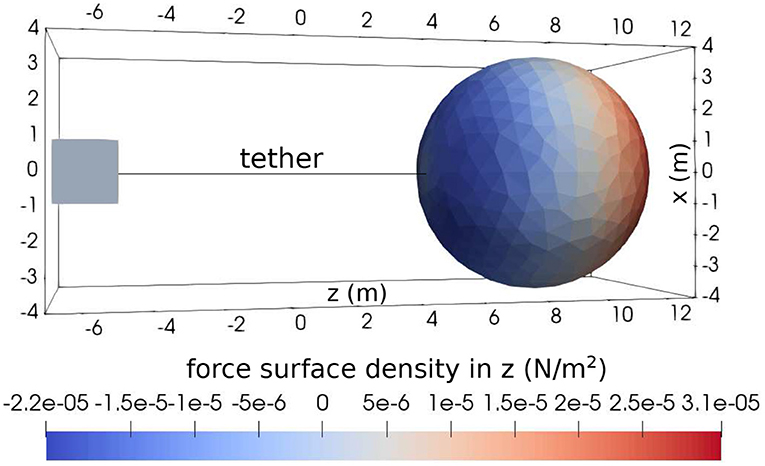
Figure 1. Illustration of the spacecraft, tether, and spherical capacitor geometry assumed in the simulations. The colors on the sphere show the component of the electric force surface density along z, computed at t = 5.5 ms in the time dependent simulation.
With the space-plasma parameters considered here this gives a radius of approximately 10 m. Different radii have been considered including 50, 75, and 100 m. Only the latter has been used throughout as being sufficiently far from the spacecraft-capacitor assembly. A summary of the plasma and simulation parameters is given in Table 1
Collected currents were computed with different values of tether lengths lteth, capacitor radius acap and capacitor potentials Vcap. Table 2 lists the currents collected by the spacecraft bus, the capacitor, and the total collected current computed with the different configurations considered. The range of parameters was selected so as to yield a total collected current close to the Itotal = 1 mA objective, and from which a simple analytic fit can be constructed. The table shows that in all cases considered, most of the collected current is from the spherical capacitor. Thus guided by the OML expression for the electron current collected by a positive conducting sphere, we fitted the total collected current with
where e is the unit charge and TeV is the temperature in eV. In Equation 2 fitting parameters α, β, and γ are set to best approximate simulation results. For an isolated sphere, idealized OML theory would predict 1, 0, and 1 for α, β, and γ, respectively. Deviations from these values are allowed to account for the presence of the nearby spacecraft, the length, and bias voltage of the tether. This expression is fitted to the data in Table 2 so as to minimize the maximum relative error. The result, α = 0.983, β = 0.050, and γ = 1.000, fits all data points with a maximum relative error of 6.6%. This analytic fit can also be used to find conditions under which a given current will be collected at steady state, for satellite and tethered capacitor parameters in the range of those considered in Table 2. For example, a 7 m tether with a 3 m radius capacitor biased to 10 kV should be adequate to balance the average 1 mA current lost while emitting electron pulses on the “Magnetosphere-Ionosphere Observatory (MIO)” (Borovsky, 2002; Delzanno et al., 2016). From the fit and Table 2, it is also clear that different electron currents could be collected from background plasma, with modified configuration parameters.
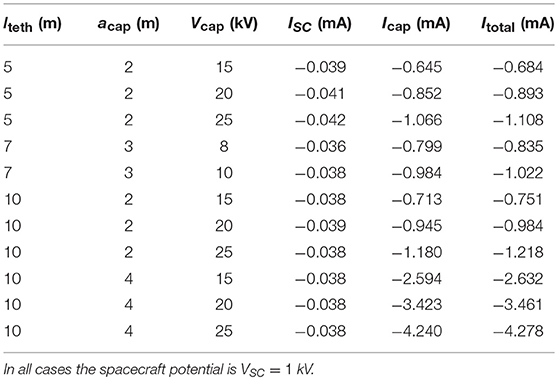
Table 2. Steady state currents collected by the spacecraft and the tethered capacitor for the different configurations considered.
3. Time-Dependent Solution
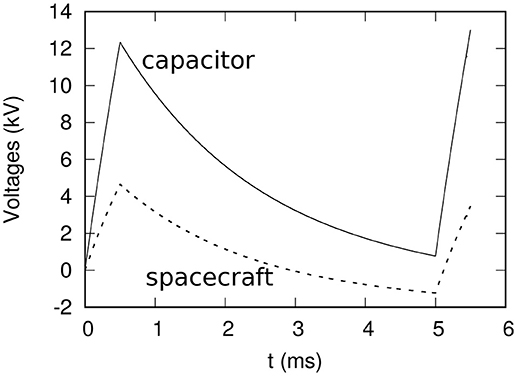
The results presented so far have focused on currents collected assuming constant spacecraft and capacitor voltages. From Table 2 and the analytic fit 2 it appears that under these conditions it should be possible for the spacecraft-capacitor assembly to collect the 1 mA current required to balance the average current lost during the 5 ms period of a minipulse (i.e., 0.5 ms of electron gun operation at 10 mA followed by 4.5 ms without emission). The steady state currents for given voltages would be applicable to the actual experiment provided that the spacecraft and capacitor voltages remain approximately constant during a full 5.0 ms of a minipulse. This in turn would be valid if the relaxation time of the system were larger than 5.0 ms; that is, if the voltages didn't change significantly during the 4.5 ms beam rest period. However, simulations indicate otherwise. The relaxation times for the voltage and collected currents are found to be of order 2 ms, which implies that while the estimates obtained assuming steady state potentials are indicative of how collected currents relate to voltages under the assumed geometries, they cannot be seen as quantitatively accurate. This is apparent in Figures 2, 3 for the time evolution of the voltages and collected currents, assuming a 10 m tether and a 4 m spherical capacitor. These results were obtained assuming a uniform plasma and zero potential on all components at time t = 0. In the simulation, the full current of the electron beam is assumed to come from the sphere. Any charging of the spacecraft is from the impact of surrounding plasma particles. During the first 0.5 ms when electrons are being fired, the capacitor and spacecraft voltages increase almost linearly to 12.3 and 4.66 kV, respectively. This is accompanied by a nearly linear drop in the collected current reaching −2.23 and −0.12 mA for the sphere and spacecraft, respectively. In the following 4.5 ms rest period both voltages and currents relax quasi-exponentially toward an equilibrium. The first 0.5 ms of the following minipulse was also simulated to ascertain whether differences in the initial condition would result in significant changes in the time evolution of the system. At time 5.5 ms, the spacecraft voltage is 3.47 kV and that of the capacitor, 13.0 kV, while the collected currents are −0.10 and −2.3 mA, respectively. These values being relatively close to the ones found at t = 0.5 ms, we conclude that the time evolution of the potentials and collected currents calculated in the first 5.0 ms provide a good representation of what would be found within subsequent minipulses. It follows from the rapid decay, occurring on a time scale of order 2 ms, that both satellite and capacitor would equilibrate with space environment within 20–50 ms. This is longer than the 4.5 ms separating successive minipulses, but sufficiently short for an equilibrium to be reached during the 0.5 s rest period separating different pulses.
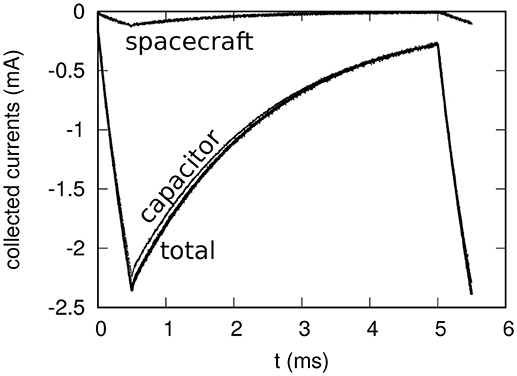
Figure 3. Collected current by the spacecraft, the capacitor and the sum of the two, over a 5.5 ms time period.
It is noteworthy that toward the end of the 5 ms cycle, the spacecraft potential becomes negative. This is due in part to the decrease in the capacitor potential, and to the collection of a fraction of the electrons attracted to the capacitor. Finally, the force between the spacecraft bus and capacitor has been calculated by integrating the force surface density; that is, the force per unit surface area, over both surfaces, as
where the integration is carried out over the entire surface of a given object, ϵ0 is the free space permittivity, E is the magnitude of the electric field at the surface, and is the unit vector perpendicular to the surface pointing outward. The z component of the force surface density exerted on the spherical capacitor computed at time 5.5 ms is illustrated in Figure 1. The figure shows an approximate cos(θ) profile, where θ is the angle between the direction along the tether and the radial position on the sphere, with an offset of approximately 4.5 × 10−6 Nm−2. The computed net force along the z direction is N, corresponding to a repulsive force with respect to the satellite. The force between the spacecraft and the sphere, while small, would likely become attractive during part of a 5.0 ms period; in particular when the spacecraft becomes negative while the sphere remains positive. If the average force were to be attractive, a possible solution would be to use a tether with sufficient rigidity to keep spacecraft and capacitor apart.
4. Analytic Approximation
The time dependent results just considered suggest a simple analytic model to capture the essential of the system response to the emission of electron beam pulses. Assuming that the potential at the spacecraft is due mainly to the influence of the nearby capacitor, the spacecraft potential should be
Considering the large Debye length in this environment, the capacitor voltage is approximated as for a sphere in vacuum:
where, assuming zero initial charge,
is the negative of the charge emitted in the beam in time t, plus the charge collected from incident background electrons. In this expression, use is made of the fact that, during the 0.5 ms period when the electron beam is fired, Iplasma(t) increases approximately linearly with time. Omitting the explicit time dependence in Iplasma for brevity and assuming V > 0, we then approximate Iplasma with the OML theory, which yields
Substituting 7 in 6, and evaluating the numerical values of physical constants, equation 5 becomes
where V, acap, Ibeam, and t are in SI units, and TkeV is the temperature in keV. With the parameters considered in the time dependent simulation, a = 4 m, Ibeam = −0.01 A, and T = 1 keV, the predicted capacitor potential from 8 at time t = 5 × 10−4 s is V ~ 10 kV. Using this estimate for V in the top part of Eq. 7, we find Iplasma ~ 1.9 mA. Finally, the spacecraft potential estimated with 8 at t = 0.5 ms is VSC ~ 2.67 kV. Compared with computed values, these estimates are of course approximate, with relative errors ranging from ~20% for the predicted capacitor voltage and collected current from background plasma, to ~50% for the spacecraft potential. While approximate, this simple model should be useful in exploring parameter space and finding optimal conditions for the proposed approach to be applied.
5. Summary and Conclusion
An alternative to plasma contactors has been presented as a possible means of mitigation for spacecraft charging occurring when electron beams are emitted in a tenuous plasma. The solution consists of attaching a capacitor with a large conducting surface area to a spacecraft from which current can be drawn to compensate for the current injected by the electron beam. As a result, the capacitor becomes strongly positively charged, thus reducing positive increases in the spacecraft potential, and mitigating possibly adverse effects. For the parameters considered here, with a collecting surface area larger than that of the spacecraft, the conducting capacitor can collect sufficient electron current from background plasma to balance an average electron beam current of order 1 mA, while maintaining a potential of order 10 kV. Assuming constant voltages for the spacecraft and capacitor, scaling laws were derived for the collected current which suggest that it might be practical to apply this approach to mitigate spacecraft charging in active electron beam emission experiments. A simulation has also been made to explore the time evolution of the voltages and collected currents. Three time periods have been considered, including the 0.5 ms of beam emission, followed by a 4.5 ms when the electron beam is turned off, and a subsequent 0.5 ms of beam emission. Voltages and collected currents exhibit significant variations in time, with extrema at the end of 0.5 ms period of beam emission, with an approximate exponential decay during the following 4.5 ms rest period. The average values found for the collected currents, however, are consistent with results obtained in the steady state approximation. A simple analytic model was constructed that can capture the dependence of the tethered capacitor voltage and collected current as a function of time and other physical parameters. Predictions made with this model can only be viewed as approximate, but they should prove useful, in conjunction with kinetic simulations, to explore and optimize system parameters.
In this paper, we have focused on the conditions where the spacecraft charges to values of order of 1 kV. This is acceptable from the perspective of the emission of the electron beam (since the beam energy is much larger than 1 kV) and for spacecraft safety (provided that the spacecraft platform is designed to avoid differential charging and the risk of electrostatic discharges). However, kV potentials can perturb local plasma measurements, meaning that one would then have reliable measurements only in-between (0.5 s) pulses. One could increase the tether length and/or the capacitor size to decrease the spacecraft potential. Furthermore, in a real mission the main spacecraft carrying the electron gun could be accompanied by daughter spacecraft sufficiently far not to be affected by perturbations resulting from the beam emission, and from which plasma environment parameters and their gradients would be measured (Borovsky, 2002; Dors et al., this issue).
Clearly, for this approach to be practical, it would be necessary for on-board electronics to draw negative current from the capacitor when it is at voltages well above that of the spacecraft. Assuming a 10 kV potential difference, the energy needed to extract a charge of −10 mA × 0.5 ms from the spheres should be of order 0.05 J, which is much less than the 10 mA × 0.5 ms × 1 MV = 5 J energy in each electron pulse. We recall that several simplifying assumptions have been made in this work. The spacecraft, tether, and capacitor have been somewhat idealized, and several physical effects such as photo-electron emission and secondary electron emission have been neglected. Considering the typically large positive voltages of the assembly and the low energy of photo or secondary electrons (a few eV) however, any emitted electron would almost certainly be accelerated back to the emitting surface. One point to consider is the possibility that a fraction of the background incident energetic electrons, with thermal energy 1 keV plus the energy of ~10 kV gained when reaching the capacitor, would go through it if the material that the capacitor is made of does not have sufficient stopping power. In this study, a simple sphere was considered, with the suggestion that it could consist of an electrostatically “inflatable” foil. In order to ensure that incident energetic electrons be captured by the capacitor, however, other geometries with adequate material properties should be considered in future studies.
Data Availability Statement
The datasets analyzed in this study are contained in the manuscript itself.
Author Contributions
RM was mainly responsible for carrying out the simulations. RM and GD contributed though discussions and in the interpretation of the results.
Funding
This work was supported in part by the Natural Sciences and Engineering Council of Canada, and by the Laboratory Directed Research and Development program (LDRD), under the auspices of the National Nuclear Security Administration of the U.S. Department of Energy by Los Alamos National Laboratory, operated by Los Alamos National Security LLC under contract DE-AC52-06NA25396. RM made use of the Compute Canada computing facility to carry out numerical simulations.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Dr. Joe Borovsky for insightful discussions and input.
References
Allen, J., Annaratone, B., and De Angelis, U. (2000). On the orbital motion limited theory for a small body at floating potential in a maxwellian plasma. J. Plasma Phys. 63, 299–309. doi: 10.1017/S0022377800008345
Borovsky, J. (2002). The Magnetosphere-Ionosphere Observatory (MIO). Los Alamos Natl. Lab., Los Alamos, NM. Available online at: http://www.lanl.gov/csse/MIOwriteup.pdf
Comfort, R., Moore, T., Craven, P., Pollock, C., Mozer, F., and Williamson, W. (1998). Spacecraft potential control by the plasma source instrument on the POLAR satellite. J. Spacecraft Rockets 35, 845–849. doi: 10.2514/2.7586
Delzanno, G., Borovsky, J., Thomsen, M., Moulton, J., and MacDonald, E. (2015). Future beam experiments in the magnetosphere with plasma contactors: how do we get the charge off the spacecraft? J. Geophys. Res. Space Phys. 120, 3647–3664. doi: 10.1002/2014JA020608
Delzanno, G. L., Borovsky, J. E., Thomsen, M. F., Gilchrist, B. E., and Sanchez, E. (2016). Can an electron gun solve the outstanding problem of magnetosphere-ionosphere connectivity? J. Geophys. Res. Space Phys. 121, 6769–6773.
Donovan, E. (2015a). The transition region explorer: observing the multi-scale dynamics of geospace. AGU Fall Meeting Abstracts, (San Francisco, CA).
Donovan, E. (2015b). The Transition Region Explorer (TREx). Available online at: http://aurora.phys.ucalgary.ca/public/trex/TREx_factsheet.png
Gilchrist, B. E., Banks, P. M., Neubert, T., Williamson, P. R., Myers, N. B., Raitt, W. J., and Sasaki, S. (1990). Electron collection enhancement arising from neutral gas jets on a charged vehicle in the ionosphere. J. Geophys. Res. Space Phys. 95, 2469–2475. doi: 10.1029/JA095iA03p02469
Grandal, B., and North, A. (2012). Artificial Particle Beams in Space Plasma Studies, Vol. 79. Springer Science & Business Media.
Hendrickson, R. A., McEntire, R. W., and Winckler, J. (1975). Echo i: an experimental analysis of local effects and conjugate return echoes from an electron beam injected into the magnetosphere by a sounding rocket. Planet. Space Sci. 23, 1431–1444. doi: 10.1016/0032-0633(75)90039-2
Katz, I., Barfield, J., Burch, J., Marshall, J., Gibson, W., Neubert, T., et al. (1994). Interactions between the space experiments with particle plasma contactor and the ionosphere. J. Spacecraft Rockets 31, 1079–1084. doi: 10.2514/3.26562
Koons, H., and Cohen, H. (1982). “Plasma waves and electrical discharges stimulated by beam operations on a high altitude satellite,” in in Artificial Particle Beams in Space Plasma Studies, ed B. Grandal (Boston, MA: Springer), 111–120.
Laframboise, J. G. (1966). Theory of Spherical and Cylindrical Langmuir Probes in a Collisionless, Maxwellian Plasma at Rest. Ph.D. thesis, University of Toronto.
Lucco Castello, F. L., Delzanno, G. L., Borovsky, J. E., Miars, G., Leon, O., and Gilchrist, B. E. (2018). Spacecraft-charging mitigation of a high-power electron beam emitted by a magnetospheric spacecraft: simple theoretical model for the transient of the spacecraft potential. J. Geophys. Res. Space Phys. 123, 6424–6442. doi: 10.1029/2017JA024926
Marchand, R. (2012). PTetra, a tool to simulate low orbit satellite-plasma interaction. IEEE Trans. Plasma Sci. 40, 217–229. doi: 10.1109/TPS.2011.2172638
Marchand, R., and Resendiz Lira, P. A. (2017). Kinetic simulation of spacecraft–environment interaction. IEEE Trans. Plasma Sci. 45, 535–554. doi: 10.1109/TPS.2017.2682229
Mott-Smith, H. M., and Langmuir, I. (1926). The theory of collectors in gaseous discharges. Phys. Rev. 28:727. doi: 10.1103/PhysRev.28.727
Nemzek, R., Malcolm, P., and Winckler, J. (1992). Comparison of echo 7 field line length measurements to magnetospheric model predictions. J. Geophys. Res. Space Phys. 97, 1279–1287. doi: 10.1029/91JA02658
Olsen, R. (1985). Experiments in charge control at geosynchronous orbit-ats-5 and ats-6. J. Spacecraft Rockets 22, 254–264. doi: 10.2514/3.25742
Patterson, M. J., Hamley, J. A., Sarver-Verhey, T., Soulas, G. C., Parkes, J., Ohlinger, W. L., et al. (1993). Plasma contactor technology for space station freedom. AIAA Paper (Irvine, CA), 93–2228.
Pedersen, A., Cattell, C., Fälthammar, C.-G., Formisano, V., Lindqvist, P.-A., Mozer, F., et al. (1984). Quasistatic electric field measurements with spherical double probes on the GEOS and ISEE satellites. Space Sci. Rev. 37, 269–312.
Safránková, J., and Omar, A. (2002). “Actively produced high-energy electron bursts within the magnetosphere: the APEX project,” in Annales Geophysicae, Vol. 20, 1529–1538. doi: 10.5194/angeo-20-1529-2002
Schmidt, R., Arends, H., Pedersen, A., Rüdenauer, F., Fehringer, M., Narheim, B., et al. (1995). Results from active spacecraft potential control on the geotail spacecraft. J. Geophys. Res. Space Phys. 100, 17253–17259. doi: 10.1029/95JA01552
Stenzel, R., and Urrutia, J. (1990). Currents between tethered electrodes in a magnetized laboratory plasma. J. Geophys. Res. Space Phys. 95, 6209–6226. doi: 10.1029/JA095iA05p06209
Sudit, I. D., and Woods, R. C. (1994). A study of the accuracy of various langmuir probe theories. J. Appl. Phys. 76, 4488–4498. doi: 10.1063/1.357280
Torkar, K., Riedler, W., Escoubet, C., Fehringer, M., Schmidt, R., Grard, R., et al. (2001). Active spacecraft potential for Cluster–implementation and first results. Ann. Geophys. (2001) 19, 1289–1302. doi: 10.5194/angeo-19-1289-2001
Whipple, E., and Olsen, R. (1980). “Importance of differential charging for controlling both natural and induced vehicle potentials on ats-5 and ats-6,” in NASA Conference Publication 2182, AFGL-TR-81-0270, 887.
Wilhelm, K., Bernstein, W., and Whalen, B. (1980). Study of electric fields parallel to the magnetic lines of force using artificially injected energetic electrons. Geophys. Res. Lett. 7, 117–120. doi: 10.1029/GL007i002p00117
Williams, J. D., and Wilbur, P. J. (1990). Experimental study of plasma contactor phenomena. J. Spacecraft Rockets 27, 634–641. doi: 10.2514/3.26192
Winckler, J. R. (1980). The application of artificial electron beams to magnetospheric research. Rev. Geophys. 18, 659–682. doi: 10.1029/RG018i003p00659
Keywords: charge mitigation, charge collection enhancement, teneous magnetospheric plasma, magnetosphere-ionosphere coupling, spacecraft charging, electron beam, tethered capacitor
Citation: Marchand R and Delzanno GL (2018) Tethered Capacitor Charge Mitigation in Electron Beam Experiments. Front. Astron. Space Sci. 5:42. doi: 10.3389/fspas.2018.00042
Received: 29 September 2018; Accepted: 28 November 2018;
Published: 13 December 2018.
Edited by:
Hermann Lühr, Helmholtz Center Potsdam German Geophysical Research Center (GFZ), Helmholtz Association of German Research Centers (HZ), GermanyReviewed by:
Yasuhito Narita, Austrian Academy of Sciences (OAW), AustriaOctav Marghitu, National Institute for Laser Plasma and Radiation Physics, Romania
Copyright © 2018 Marchand and Delzanno. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Richard Marchand, cmljaGFyZC5tYXJjaGFuZEB1YWxiZXJ0YS5jYQ==
 Richard Marchand
Richard Marchand Gian Luca Delzanno
Gian Luca Delzanno