An Asymptotically Safe Guide to Quantum Gravity and Matter

1. Invitation to Asymptotic Safety

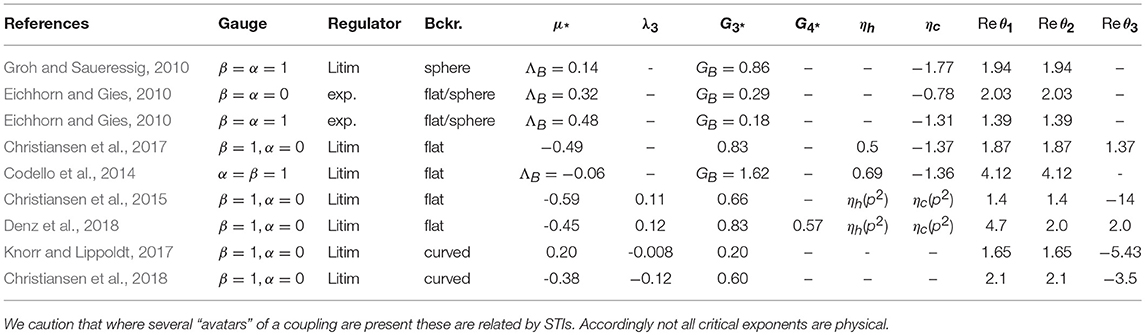
Asymptotic safety (Weinberg, 1980) is a quantum-field theoretic paradigm providing an ultraviolet (UV) extension or completion for effective field theories. The high-momentum regime of an asymptotically safe theory is scale invariant, cf. Figure 1. It is governed by a fixed point of the Renormalization Group (RG) flow of couplings. As such, asymptotic safety is an example of a fruitful transfer of ideas from statistical physics to high-energy physics: In the former, interacting RG fixed points provide universality classes for continuous phase transitions (Wilson and Fisher, 1972; Zinn-Justin, 2002), in the latter these generalize asymptotic freedom to a scale-invariant UV completion with residual interactions. This paradigm is being explored for physics beyond the Standard Model in several promising ways. Following the discovery of perturbative asymptotic safety in weakly-coupled gauge-Yukawa models in four dimensions (Litim and Sannino, 2014), the search for asymptotically safe extensions of the Standard Model with new degrees of freedom close to the electroweak scale is ongoing. Mechanisms for asymptotic safety also exist in nonrenormalizable settings, making it a candidate paradigm for quantum gravity (Weinberg, 1980; Reuter, 1998). After the discovery of the Higgs boson (Aad, 2012; Chatrchyan, 2012), we know that the Standard Model can consistently be extended up to the Planck scale (Bezrukov et al., 2012; Buttazzo et al., 2013; Bezrukov and Shaposhnikov, 2015). Hence, the interplay of the Standard Model with quantum fluctuations of gravity within a quantum field theoretic setting is under active exploration.

FIGURE 1

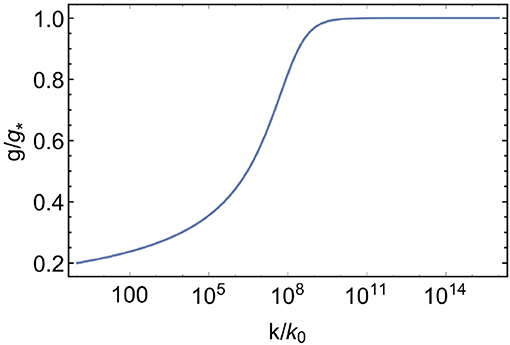
Figure 1. Schematic RG flow for an asymptotically safe coupling. Beyond the transition scale at $k/k_0\approx 10^9$, (approximate) scale-invariance is realized; full scale-invariance is realized asymptotically at k/k₀ → ∞.

This review aims at providing an introduction to asymptotic safety for non-experts, highlighting mechanisms that generate asymptotically safe physics, explaining how these could play a role in settings relevant for high-energy physics and discussing open questions of (potentially) asymptotically safe models. An extensive bibliography is intended to serve as a guide to further reading, providing more comprehensive and in-depth answers to many points only touched upon briefly here.

2. Asymptotic Safety - the Key Idea

Quantum fluctuations induce a momentum-scale dependence in the couplings of a model, breaking scale invariance even in classically scale-invariant models. Scale invariance is restored at RG fixed points. These can be non-interacting, in which case the theory is asymptotically free, or interacting in at least one of the couplings, in which case the theory is asymptotically safe. Both fixed points underlie theories that are fundamental in a Wilsonian sense: For a theory that is discretized, e.g., on a lattice, an RG fixed point guarantees that a continuum limit exists. Scale-invariance protects the running couplings in a model from Landau poles which can signal a breakdown of a description of an interacting system by this model because of triviality¹. Hence, the introduction of new physics is one viable theoretical option instead of a necessity.

Scale-invariance requires a fixed point in the dimensionless couplings g_i, obtained from their dimensionful counterparts $\overline{g}$_i with canonical dimension d_{$\overline{g}$i} by multiplication with an appropriate power of the RG scale k

$\begin{array}{ll}{g}_i(k)={\overline{g}}_i(k)k^{-d_{{\overline{g}}_i}}.& (1)\end{array}$

A scale-invariant point is a zero of all beta functions,

$\begin{array}{ll}{\beta }_{g_i}=k{\partial }_k{g}_i(k)=0\text{\hspace{1em}at\hspace{1em}}{g}_i=g_{i*}.& (2)\end{array}$

Then, dimensionful couplings² scale with their canonical dimensionality, i.e., ${\overline{g}}_i(k)~k^{d_{{\overline{g}}_i}}$, since g_i(k) = g_i* = const in a scale-invariant regime. This must hold for all couplings in the infinite-dimensional theory space, spanned by all interactions allowed by symmetries, including higher-order, i.e., canonically irrelevant interactions. Quantum fluctuations generically generate all interactions, as familiar from effective field theories. Moreover, there is no a priori physical argument to exclude higher-order terms from the dynamics. The restriction to perturbatively renormalizable terms that is commonly assumed is actually an automatic consequence of the universality class of the Gaussian, i.e., free fixed point which renders higher-order terms irrelevant for perturbative low-energy physics.

2.1. Predictivity in the Infinite-Dimensional Space of Couplings

The main consequence of an RG fixed point is not that it provides a fundamental theory—after all, experiments are limited to finite scales—but that it generates universal predictions for low-energy physics. It imposes relations between the couplings encoding the location of the UV-critical surface of the fixed point. This hypersurface is spanned by all couplings along which RG trajectories emanate from the fixed point as one lowers k toward the infrared (IR). The corresponding relevant directions parameterize the deviation from scale invariance, i.e., the flow toward the IR can only deviate from the fixed point along the relevant directions. They constitute free parameters, as a range of values of relevant couplings can be reached along different trajectories emanating from the fixed point, cf. Figure 2. It can be more intuitive to understand that a free parameter is associated to such a direction, as IR-repulsiveness equals UV-attractivity. Irrespective of its IR value, a UV-attractive coupling reaches the fixed point at high scales as one reverses the flow toward the UV. (Nevertheless, recall that although we measure physics at low energies and try to extrapolate toward viable UV physics, nature works the other way: IR physics emerges as a consequence of UV physics).

FIGURE 2

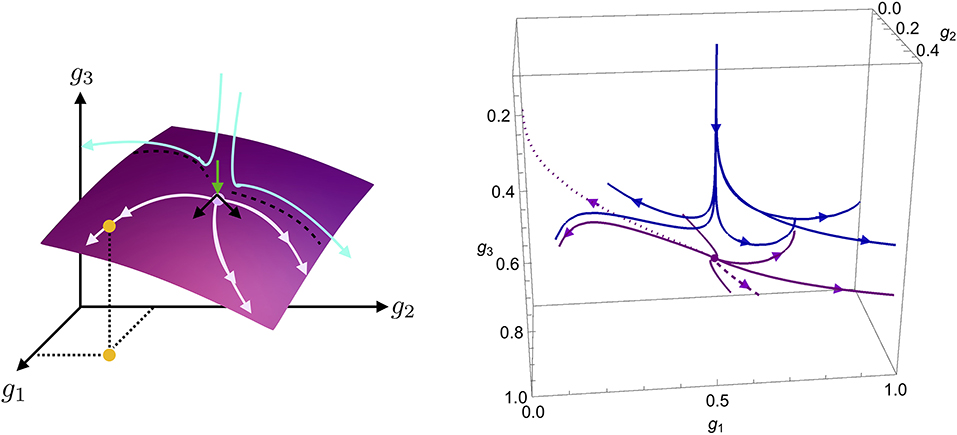
Figure 2. Left panel: Illustration of a fixed point (light purple dot) with its UV critical hypersurface (purple). RG trajectories starting off the critical hypersurface (teal) are pulled toward the fixed point along the irrelevant direction (roughly aligned with g₃), before the IR repulsive directions g₁ and g₂ kick in and drive the flow away from the fixed point. The linearized flow is indicated by the black (relevant directions) and green (irrelevant direction) arrows. Right panel: A fixed point with two relevant directions in the space of three couplings g_1,2,3, where g₃ corresponds to the IR attractive direction. The purple trajectories emanate from the fixed point, and g_{2, 3} fully determine the deviation from scale invariance. The arrows indicate the RG flow toward the IR. The corresponding beta functions of one canonically marginal, relevant and irrelevant interaction are given by ${\beta }_{g_1}=2g_1-3g_1^2-3g_1^2{g}_2$, β_g2 = −2g₂ + 2g₁ − 3g₁g₂ and ${\beta }_{g_3}=-g_1{g}_3+g_3^3$.

Toward the IR, the irrelevant, i.e., IR-attractive directions are automatically pulled toward the fixed point, cf. Figure 2. Accordingly, no free parameter is associated to them – this is the universality-generating property of an RG fixed point: Initializing the RG flow at some scale k₀, the flow maps a UV interval of values for an irrelevant coupling at k₀ to a much smaller IR interval. The latter shrinks to zero as one takes k₀ → ∞. As a one-coupling example with an IR attractive fixed point, consider

$\begin{array}{ll}{\beta }_g=g(g-g_{*}),& (3)\end{array}$

with the solution

$\begin{array}{ll}g(k)=\frac{g_{*}}{1+{\left(\frac{k}{k_0}\right)}^{g_{*}}\left(\frac{g_{*}}{g_0}-1\right)},& (4)\end{array}$

where g(k₀) = g₀. As the initial scale k₀ → ∞, g(k) → g_*. For a finite k₀, the difference g(k) − g_* goes to zero as k/k₀ → 0. For a trajectory that emanates from the fixed point, there is no freedom of choice for the value for an irrelevant direction: the fixed-point requirement restricts the flow to lie within the critical hypersurface, resulting in completely determined values for the irrelevant directions. For instance, at the free fixed point, higher-order couplings do not play a role in the IR: the RG flow drives them toward zero for all perturbative initial conditions in the UV. This generates universality and independence of the IR physics from the UV physics in all but the (marginally) relevant couplings.

To determine the set of IR-repulsive (= UV attractive) directions, it suffices to examine the linearized flow about the fixed point³ at $\overrightarrow{g}={\overrightarrow{g}}_{*}$,

$\begin{array}{ll}{\beta }_{g_i}={\displaystyle \sum _j}\frac{\partial {\beta }_{g_i}}{\partial g_j}{|}_{\overrightarrow{g}={\overrightarrow{g}}_{*}}(g_j-g_{j*})+{O}{(g_j-g_{j*})}^2.& (5)\end{array}$

In terms of the critical exponents⁴

$\begin{array}{ll}{\theta }_I=-\text{eig}{{M}}_{ij}=-\text{eig}\frac{\partial {\beta }_{g_i}}{\partial g_j}{|}_{\overrightarrow{g}={\overrightarrow{g}}_{*}},& (6)\end{array}$

and corresponding (right) eigenvectors V^I, the solution to Equation (5) is

$\begin{array}{ll}{g}_i(k)=g_{i*}+{\displaystyle \sum _I}{c}_I{V}_i^I{\left(\frac{k}{k_0}\right)}^{-{\theta }_I}.& (7)\end{array}$

k₀ is an arbitrary reference scale and c_I are constants of integration. Typically, the set of couplings $\overrightarrow{g}$ does not diagonalize the stability matrix ${{M}}_{ij}$ at $\overrightarrow{g}={\overrightarrow{g}}_{*}$ and the eigenvectors V^I are superpositions. As the stability matrix need not be symmetric, the eigenvalues need not be real. Their imaginary part results in a spiraling behavior of the flow in the vicinity of the fixed point, where the real part determines whether the spiraling is inwards or outwards. To determine the set of free parameters, it therefore suffices to consider the real parts. For the following discussion we will thus assume that the eigenvalues are real. For θ_I > 0, the corresponding eigenvector V^I constitutes an IR repulsive direction: Toward the IR, the distance to the fixed-point regime grows, and the IR values of couplings appearing in V^I depend on c_I. Fixing this free parameter requires experimental input. Accordingly, predictivity requires a finite number of directions with θ_I > 0.

In contrast, for θ_I < 0, the IR values of couplings are independent of the corresponding c_I, cf. Equation (7): For θ_I < 0, any deviation from the fixed-point value in V^I is washed out by the RG flow to the IR. Once a choice of coordinates in theory space is made, the critical hypersurface typically exhibits curvature. If the critical hypersurface had no curvature, the values of irrelevant couplings would be constant. Curvature of the critical hypersurface generates a scale dependence which is completely fixed once the values of all relevant couplings are specified, cf. Figure 2. The values of the corresponding irrelevant couplings depend on the scale, but not independently of the relevant couplings, cf. green trajectory in Figure 3.

FIGURE 3

Figure 3. Left panel: The beta functions ${\beta }_g=2g-2g^2$ and ${\beta }_y=-gy+2y^3$ feature a fixed point at $g=1,y=1/\sqrt{2}$ that has one UV attractive and one IR attractive direction. The UV critical surface is indicated in green, the IR critical surface in red. The RG flow toward the IR is attracted toward the UV critical surface, such that the relation between g and y that parameterizes the UV critical surface is approximately realized also for trajectories (in purple) that start off the UV critical surface. Right panel: The flow described by ${\beta }_g=2g-2g^2$ and ${\beta }_{g_2}=-2g_2+2g_2^2$ features a fixed point at g = g₂ = 1, which is IR attractive in g₂ and where the UV critical surface has no curvature. Therefore, g₂(k) = 1 for the trajectories emanating from this fixed point.

For asymptotic safety, the finite contribution to the θ_I due to residual interactions at ${\overrightarrow{g}}_{*}$ shifts the critical exponents away from the canonical dimensions of couplings, e.g.,

$\begin{array}{ll}{\theta }_i=-\frac{\partial {\beta }_i}{\partial g_i}{|}_{g_i=g_{i*}}=-\frac{\partial }{\partial g_i}({\partial }_t{\overline{g}}_i{k}^{-d_{{\overline{g}}_i}}){|}_{g_i=g_{i*}}=d_{{\overline{g}}_i}{g}_{i*}+\eta (g_{i*}^2),& (8)\end{array}$

for a coupling g_i that is an eigendirection of ${{M}}_{ij}$. This can enhance the predictive power of interacting over free fixed points.

The interpretation of asymptotic safety as a way of imposing predictivity on a model specified by its field content and symmetries is crucial in the context of quantum gravity. The simplest interpretation of the Planck scale suggests that it acts as a minimal length, inducing discreteness for quantum-gravity models at the kinematical level. This might suggest that one need not search for a continuum limit in quantum gravity. Yet, by requiring a continuum limit one restricts the dynamics to a trajectory within the critical surface, leaving just a finite number of free parameters to determine the dynamics at all scales. In the presence of an explicit cutoff scale, the microscopic dynamics might be defined anywhere in the theory space, requiring specification of an infinite number of couplings for the UV dynamics (see also Eichhorn, 2018b). Similarly, predictivity at high scales breaks down in effective field theories. Moreover, physical discreteness can arise in quantum gravity even in a continuum theory, through the dynamical emergence of a scale (see e.g., Reuter and Schwindt, 2006; Percacci and Vacca, 2010), or through discreteness in the spectra of operators (Rovelli and Smolin, 1995; Ashtekar and Lewandowski, 1997).

2.2. Asymptotic Safety in a Nutshell

The development of the Standard Model was based on the principle of renormalizability. This is one way of implementing predictivity, i.e., constructing a low-energy theory with a finite number of free parameters.Yet, as, e.g., ϕ⁴ theory in 4 dimensions highlights, a perturbatively renormalizable theory is not guaranteed to exist as a fundamental theory in the Wilsonian sense, due to the triviality problem. Analogously, the Standard Model is actually expected to be an effective low-energy theory. Asymptotic safety is a paradigm that combines the requirement of predictivity with the possibility of obtaining a fundamental theory through an RG fixed point at high momenta with a finite number of relevant directions. The fixed point ensures nonperturbative renormalizability, while the finite dimensionality of the critical hypersurface guarantees predictivity of the model.

2.3. Non-fundamental Asymptotic Safety

Instead of providing a “fundamental” UV completion, asymptotic safety might serve as one step forward in our understanding of microscopic physics, with more fundamental physics to be discovered beyond. While providing a UV completion for some RG trajectories, a fixed point can simultaneously act as an IR attractor for a more fundamental description. This follows, as a fixed point's UV repulsive directions correspond to its IR attractive directions. Hence, it is a misconception that a fixed point is either UV or IR - whether trajectories emanate from it in the UV, or approach it in the IR depends on the initial conditions for the RG flow. Given two fixed points connected by an RG trajectory, the distinction into a UV and an IR fixed point (which is also expected to satisfy the a-theorem Cardy, 1988) follows from the trajectory.

For specificity, assume that a cutoff scale k_UV exists, such that for k > k_UV a (quasilocal) quantum field theoretic description is impossible or requires additional fields and/or symmetries. At k ≤ k_UV, the dynamics can be described in the asymptotically safe theory space. Initial conditions for the RG flow are determined by the underlying fundamental model at k = k_UV. It they lie close to or on the IR-critical surface of a fixed point, the flow is attracted toward the fixed point along its IR-attractive directions. The flow is actually driven toward the UV-critical surface, cf. purple trajectories in Figure 3. Trajectories can even spend a large amount of RG “time” close to the fixed point. At k_trans < k_UV the effect of the IR-repulsive directions kicks in and the flow is driven away from the fixed point along its IR-repulsive directions. This trajectory will result in IR-values of couplings close to those of a “true” fixed-point trajectory (cf. Figure 3 see Percacci and Vacca, 2010). The above is nothing but a detailed account of how a fixed point generates IR universality. Thus, asymptotically safe fixed points could generate universal IR predictions, even in the presence of k_UV.

2.4. Mechanisms for and Selected Examples of Asymptotic Safety

A special case of an RG fixed point is that of an asymptotically free one. To generate it, antiscreening contributions have to dominate in the beta function of the respective coupling. In contrast, asymptotic safety is generated by several different mechanisms and can be realized both in the perturbative and the nonperturbative regime, i.e., with near-Gaussian or far-from-Gaussian critical exponents. As a second key difference, an interacting fixed point allows to combine finite, predictable IR values of couplings with UV completeness. For the free fixed point, finite IR values typically require the corresponding coupling to be an IR repulsive direction, i.e., relevant. This negates the possibility to predict the value of the coupling which remains a free parameter based on the free fixed point alone. (Of course, an interacting fixed point can dominate the flow in the IR, at which the coupling in question could be IR attractive. In this case it is again the universality class of the interacting fixed point which provides a prediction for a finite value of a coupling).

2.4.1. Canonical Scaling vs. Quantum Effects

This mechanism is available for couplings which are asymptotically free in their critical dimension d_crit, where they are dimensionless, i.e., their one-loop beta function is given by

$\begin{array}{ll}{\beta }_{g_i}{|}_{d=d_{\text{crit}}}={\beta }_1{g}_i^{\#},& (9)\end{array}$

with β₁ < 0 and # = 2, 3. In d = d_crit + ϵ, the coupling is dimensionful, $g_i={\overline{g}}_i{k}^{cϵ}$, where c > 0 depends on the coupling under consideration. For ϵ ≪ 1, the one-loop beta function reads

$\begin{array}{ll}{\beta }_{g_i}{|}_{d=d_{\text{crit}}+ϵ}=cϵg_i+{\beta }_1{g}_i^{\#}.& (10)\end{array}$

An interacting fixed point lies at

$\begin{array}{ll}{g}_i^{*}={\left(-\frac{cϵ}{{\beta }_1}\right)}^{1/(\#-1)}.& (11)\end{array}$

This mechanism is realized in Yang-Mills theory in d = 4 + ϵ (Peskin, 1980), nonlinear sigma models in d = 2 + ϵ (Polyakov, 1975; Bardeen et al., 1976; Friedan, 1980; Higashijima and Itou, 2003; Codello and Percacci, 2009; Fabbrichesi et al., 2011) and the Gross-Neveu model in d = 2 + ϵ (Gawedzki and Kupiainen, 1985; Kikukawa and Yamawaki, 1990; de Calan et al., 1991; He et al., 1992; Hands et al., 1993; Braun et al., 2011).

For Yang-Mills theory, the ϵ-expansion has been extended up to fourth order, indicating a fixed point in d = 5 (Morris, 2005), cf. Figure 4, corroborating functional RG results (Gies, 2003), in contrast to lattice results (Knechtli and Rinaldi, 2016). For instance, consider SU(3) Yang-Mills, cf. Figure 4. The ϵ expansion in Morris (2005) yields for $\tilde{\alpha }=\frac{6}{{(4\pi )}^2}{g}^2$

$\begin{array}{ll}{\beta }_{\tilde{\alpha }}=ϵ\tilde{\alpha }-b_1{\tilde{\alpha }}^2-b_2{\tilde{\alpha }}^3-b_3{\tilde{\alpha }}^4-b_4{\tilde{\alpha }}^5,& (12)\end{array}$

$\begin{array}{ll}{b}_1=3.67,b_2=5.67,b_3=13.23,b_4=39.43+\frac{51.22}{9},& (13)\end{array}$

resulting in

$\begin{array}{ll}{\tilde{\alpha }}_{*}=0.272ϵ-0.115{ϵ}^2+0.024{ϵ}^3-0.016{ϵ}^4.& (14)\end{array}$

Couplings which are marginally irrelevant in their critical dimension d_c can achieve interacting fixed points for d < d_c, where they correspond to irrelevant directions. In contrast to the case in d_c, where the free fixed point results in a vanishing coupling at all scales in order to be a UV fixed point (triviality problem), in d = d_c − ϵ, the interacting fixed point requires a unique finite value of the coupling in the IR, corresponding to the fixed-point value, unless the UV critical hypersurface is curved. Thus, the interacting theory is UV complete for one unique value of the coupling. Conversely, asymptotically free trajectories reach the interacting fixed point in the IR.

FIGURE 4

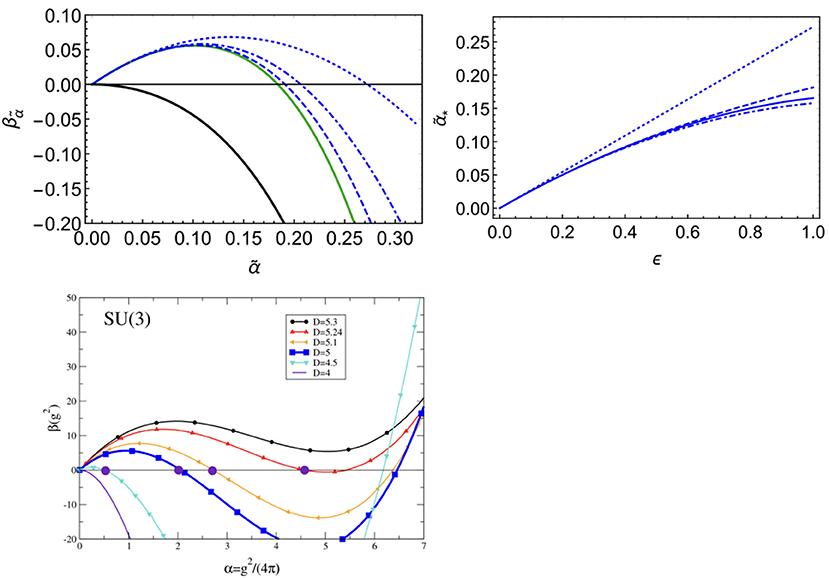
Figure 4. Left upper panel: Based on results in Morris (2005), the beta function for SU(3) Yang-Mills theory in the epsilon expansion for $\tilde{\alpha }=\frac{6}{{(4\pi )}^2}{g}^2$ for ϵ = 0 (black line), ϵ = 1 at one loop (dotted), two loops (dot-dashed), three loops (dashed) and four loops (green). Right upper panel: Fixed-point value for α as a function of ϵ up to ϵ (dotted), ϵ² (dot-dashed), ϵ³ (dashed), and ϵ⁴ (continuous) emerge from the free fixed point at d → d_crit, i.e., ϵ → 0. Lower panel: Results from the FRG calculation taken from Gies (2003) for $\alpha =\frac{g^2}{4\pi }$.

For instance, for scalar theories, the marginally irrelevant nature of the quartic coupling in d = 4 implies the existence of a fixed point in d = 4 − ϵ. The well-known Wilson-Fisher fixed point is IR attractive in the quartic coupling (Wilson and Fisher, 1972) and serves as the IR endpoint of an asymptotically free trajectory. It has been characterized with various methods (Guida and Zinn-Justin, 1998; Campostrini et al., 1999; Pelissetto and Vicari, 2002; Canet et al., 2003; Litim and Zappala, 2011; El-Showk et al., 2012, 2014; Gliozzi and Rago, 2014) and serves as a benchmark example for many techniques. For d > 4, a possible fixed point (Fei et al., 2014) lies at negative quartic coupling, appearing to be at odds with a stable microscopic potential (Percacci and Vacca, 2014; Eichhorn et al., 2016).

Fixed points generated by such a mechanism are weakly coupled at small ϵ, where the critical exponent is equal to minus the canonical dimension.

A key example is gravity: Slightly above its critical dimension d = 2, where the Einstein action is purely topological, the beta function for the dimensionless Newton coupling $G=G_N{k}^{d-2}$ at one loop reads (Weinberg, 1980; Gastmans et al., 1978; Christensen and Duff, 1978),

$\begin{array}{ll}{\beta }_G=ϵG-{\beta }_1{G}^2,\mathrm{\text{such that }}{G}_{*}=\frac{ϵ}{{\beta }_1},\theta =-ϵ,& (15)\end{array}$

where β₁ depends on the parameterization of metric fluctuations h_μν around a background $\overline{g}$_μν. Note that in these calculations the Jacobian that arises in the path-integral measure from relating the different parameterizations is not taken into account. Specifically the functional RG in the limit d → 2 yields (Percacci and Vacca, 2015)

$\begin{array}{ll}{\beta }_1=-\frac{2(19-38\beta +13{\beta }^2)}{3(1-{\beta }^2)},& (16)\end{array}$

for the linear parameterization g_μν = $\overline{g}$_μν + h_μν,

$\begin{array}{ll}{\beta }_1=-\frac{2(25-38\beta +19{\beta }^2)}{3{(1-\beta )}^2},& (17)\end{array}$

for the exponential parameterization g_μν = ${\overline{g}}_{\mu \kappa }{\text{exp}\left[\text{h}..\right]}_{\nu }^{\kappa },$

where β is a gauge parameter, such that for β → 0 the result β₁ = −38/3 is found (Tsao, 1977; Brown, 1977; Kawai and Ninomiya, 1990; Jack and Jones, 1991) for the linear parameterization and β₁ = −50/3 for the exponential parameterization (David, 1988; Distler and Kawai, 1989; Kawai et al., 1993a,b, 1996; Aida et al., 1994; Nishimura et al., 1994; Aida and Kitazawa, 1997; Codello and D'Odorico, 2015). A continuous extension to d = 4 might be possible (Falls, 2015, 2017).

2.4.2. One-Loop vs. Higher-Loop

In perturbation theory, the signs of the one-loop and two-loop coefficients can differ, leading to a cancellation at a finite fixed-point value, schematically

$\begin{array}{ll}{\beta }_{g_i}={\beta }_1{g}_i^{{\#}_1}+{\beta }_2{g}_i^{{\#}_2}+\dots & (18)\end{array}$

with

$\begin{array}{ll}{\beta }_{g_i}{|}_{g_i=g_{i*}}=0,g_{i*}={\left(\frac{-{\beta }_1}{{\beta }_2}\right)}^{\frac{1}{{\#}_2-{\#}_1}}.& (19)\end{array}$

The fixed point is real for sign(β₂) = −sign(β₁). For it to lie at small values, where higher-loop terms are small, we require |β₁| < |β₂|. Actually, the two-loop coefficient is a proxy for the higher-loop terms: the fixed point is generated by the competing signs of the one-loop vs. the “effective” two-loop term. As one extends the asymptotic perturbative series to higher loops, the fixed-point value shifts to compensate for the change, but as long as the sign of the “effective” two-loop term is unchanged, a fixed point exists, cf. Figure 5.

FIGURE 5

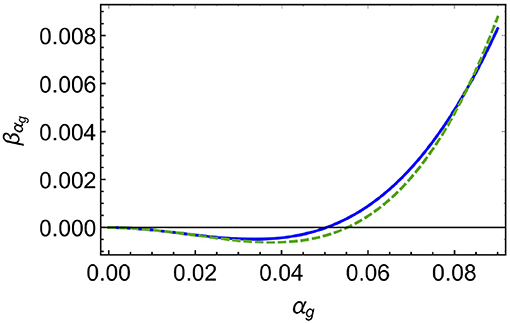
Figure 5. Beta function of the gauge coupling α_g for the model in Litim and Sannino (2014) at next-to-leading order (two loop, blue continuous line) and next-to-next-to-leading order (three loop, green dashed line), cf. Equation (34) for the two-loop beta function. The fixed-point value for α_y at the corresponding order has been inserted and ϵ = 0.1 has been chosen.

The interacting fixed point is IR attractive (repulsive) for β₁ < 0(> 0). Additionally, a UV (IR) attractive fixed point lies at g_i* = 0. Therefore, a complete trajectory exists between the free (interacting) fixed point in the UV and the interacting (free) fixed point in the IR for β₁ < 0(> 0). The former case is known as the Banks-Zaks fixed point in the case of non-Abelian gauge theories (Caswell, 1974; Banks and Zaks, 1982). The latter underlies new developments in gauge-Yukawa models (Litim and Sannino, 2014), see section 3.

2.4.3. Competing Degrees of Freedom

In models with several degrees of freedom, a scale-invariant fixed-point regime can be achieved if the effect of different degrees of freedom can balance out - either within a perturbative expansion or at the nonperturbative level and for dimensionless as well as dimensionful couplings. Schematically,

$\begin{array}{ll}{\beta }_g={\beta }_g^{(\text{d}.\text{o}.\text{f}.1)}-{\beta }_g^{(\text{d}.\text{o}.\text{f}.2)},& (20)\end{array}$

where, e.g., d.o.f1 might be a bosonic and d.o.f.2 a fermionic contribution. (N = 4) super Yang Mills could be seen as a special example (Sohnius, 1985).

A competition of fermionic and bosonic degrees of freedom also occurs in the beta function of a quartic scalar coupling which couples to fermions through a Yukawa coupling. This competition actually underlies Higgs mass bounds in the SM (Altarelli and Isidori, 1994; Hambye and Riesselmann, 1997). Perturbatively, the Yukawa coupling in simple Yukawa models is UV unsafe. Hints for a nonperturbative fixed point have been found (Gies and Scherer, 2010; Gies et al., 2010), but been called into question in Vacca and Zambelli (2015) in extended truncations of the RG flow.

3. Gauge-Yukawa Models: Asymptotic Safety at Weak Coupling

In d = 4 dimensions, gauge-Yukawa models can exhibit perturbative asymptotic safety, discovered in Litim and Sannino (2014), achieved through a balance of one- vs. two-loop effects. We follow Litim and Sannino (2014) and consider a simple gauge theory with gauge coupling g with

$\begin{array}{ll}{\alpha }_g=\frac{g^2}{{(4\pi )}^2},& (21)\end{array}$

with 2-loop beta function

$\begin{array}{ll}{\beta }_{{\alpha }_g}=(-B+C{\alpha }_g){\alpha }_g^2.& (22)\end{array}$

An interacting fixed point lies at

$\begin{array}{ll}{\alpha }_{g*}=\frac{B}{C}.& (23)\end{array}$

For the case B > 0, C > 0, this is the Banks-Zaks fixed point (Banks and Zaks, 1982), which is IR attractive in the gauge coupling. Accordingly, a complete RG trajectory can be constructed, emanating from the free fixed point in the UV and ending in a conformal regime in the IR. This can be achieved within the conformal window, e.g., $11/2N_c<N_f<34N_c^3/(13N_c^2-3)$ for N_f fermions in the fundamental representation of SU(N_c), Ryttov and Shrock (2011); Pica and Sannino (2011), and Ryttov and Shrock (2016).

Asymptotic safety in the form of an IR-repulsive interacting fixed point occurs where asymptotic freedom is lost, i.e., the antiscreening effect of non-Abelian gauge bosons is overcompensated by the screening effect of charged matter. This requires B < 0 (see Caswell, 1974; Tarasov and Vladimirov, 1977; Jones, 1982; Machacek and Vaughn, 1983), and accordingly C < 0 for the coupling g to be real. As shown in Caswell (1974), see also Bond and Litim (2017), this is not possible to achieve with fermions only. Adding scalars to the model provides a Yukawa coupling

$\begin{array}{ll}{\alpha }_y=\frac{y^2}{(4{\pi }^2)},& (24)\end{array}$

that results in

$\begin{array}{ll}C\to C-D{\alpha }_y.& (25)\end{array}$

This facilitates asymptotic safety. The one-loop Yukawa beta function reads

$\begin{array}{ll}{\beta }_{{\alpha }_y}={\partial }_t{\alpha }_y=(E{\alpha }_y-F{\alpha }_g){\alpha }_y,& (26)\end{array}$

see Fischler and Oliensis (1982) and Machacek and Vaughn (1984) for two-loop results. The above system of beta functions admits three solutions

$\begin{array}{ll}{\alpha }_{g*}=0,{\alpha }_{y*}=0,& (27)\end{array}$

$\begin{array}{ll}{\alpha }_{g*}=\frac{B}{C},{\alpha }_{y*}=0,& (28)\end{array}$

$\begin{array}{ll}{\alpha }_{g*}=\frac{B}{C-D\frac{F}{E}},{\alpha }_{y*}=\frac{B}{C-D\frac{F}{E}}\frac{F}{E},& (29)\end{array}$

where appropriate conditions on the coefficients of the beta function ensure that fixed-point values are real. The second fixed point is a generalization of the Banks-Zaks fixed point. The fully interacting fixed point has one IR attractive and one IR-repulsive direction. The corresponding critical exponents are

$\begin{array}{l}{\theta }_{1,2}=\frac{-BE}{2{(CE-DF)}^2}(-BCE-CEF+D{F}^2\pm \\ \sqrt{B^2{C}^2{E}^2-2BF(CE-2DF)(CE-DF)+F^2{(CE-DF)}^2}).& (30)\end{array}$

Perturbative asymptotic safety in four-dimensional gauge theories requires the presence of fermions and scalars (Litim and Sannino, 2014), providing a possible justification for the existence of fundamental scalars in nature. Moreover, (gravity-free) theories in four dimensions cannot exhibit weakly-coupled fixed points, i.e., arising from a balance of one-loop vs. two-loop effects, unless gauge interactions are present (Bond and Litim, 2017, 2018a). This explains why tentative proposals for interacting fixed points in four-dimensional fermion-scalar theories lie in a nonperturbative regime (Gies and Scherer, 2010; Eichhorn et al., 2018a).

As couplings can be rescaled arbitrarily (without an impact on the critical exponents), the fixed-point values of couplings do not automatically convey information on whether the fixed point is perturbative. To achieve strict perturbative control over the fixed point, the critical exponents should be arbitrarily close to the canonical ones. This can be achieved in the Veneziano limit which allows to continuously emerge the fixed point from the free one. Hence we now focus on an SU(N_c) gauge theory with N_f flavors of Dirac fermions in the fundamental representation to take the Veneziano-limit, Veneziano (1979),

$\begin{array}{ll}{N}_f\to \infty ,N_c\to \infty ,\mathrm{\text{with }}ϵ=\frac{N_f}{N_c}-\frac{11}{2}\mathrm{\text{finite}}.& (31)\end{array}$

C = 25 (Caswell, 1974) holds in this limit without Yukawa interactions. The simplest way to add a N_f × N_f matrix H of complex scalars is to have them uncharged under the gauge group,

$\begin{array}{ll}{ℒ}_{H-\text{pot}}=-u\text{Tr}{\left(H^{†}H\right)}^2-v{\left(\text{Tr}{H}^{†}H\right)}^2& (32)\end{array}$

Then the two quartic couplings decouple from the beta functions for the gauge and Yukawa coupling at the above order in perturbation theory and in the Veneziano limit (Litim and Sannino, 2014, see Jack and Osborn, 1984; Machacek and Vaughn, 1985; Ford et al., 1992) for the two-loop beta functions.

In the limit (31), fixed-point values are controlled by ϵ and remain perturbative for ϵ < < 1 (Litim and Sannino, 2014). For a study of gauge groups and representations for which such a fixed point exists (see Bond et al., 2018). Asymptotic safety is achieved in appropriately rescaled couplings that guarantee well-behaved large-N-beta functions,

$\begin{array}{ll}{\tilde{\alpha }}_y=\frac{y^2{N}_c}{16{\pi }^2},{\tilde{\alpha }}_g=\frac{g^2{N}_c}{16{\pi }^2}.& (33)\end{array}$

The beta functions read

$\begin{array}{ll}{\beta }_{{\tilde{\alpha }}_g}={\tilde{\alpha }}_g^2\left(\frac{4}{3}ϵ+\left(25+\frac{26}{3}ϵ\right){\tilde{\alpha }}_g-2{\left(\frac{11}{2}+ϵ\right)}^2{\tilde{\alpha }}_y\right),& (34)\end{array}$

$\begin{array}{ll}{\beta }_{{\tilde{\alpha }}_y}={\tilde{\alpha }}_y\left((13+2ϵ){\tilde{\alpha }}_y-6{\tilde{\alpha }}_g\right).& (35)\end{array}$

While the one-and two-loop contribution of the gauge coupling to ${\beta }_{{\tilde{\alpha }}_g}$ are positive, the contribution of the Yukawa coupling is negative. Accordingly a finite fixed-point value of the Yukawa coupling induces a physically acceptable fixed point, i.e., ${\tilde{\alpha }}_{g*}>0$. In turn, the positive contribution $~{\tilde{\alpha }}_y$ in ${\beta }_{{\tilde{\alpha }}_y}$ can balance against the negative one $~{\tilde{\alpha }}_g$ to generate a physically acceptable fixed point at ${\tilde{\alpha }}_y>0$. This results in an interacting fixed point emerging from the Gaussian one, since ϵ can become arbitrarily small for large enough numbers of fields,

$\begin{array}{l}{\tilde{\alpha }}_{g*}=\frac{26ϵ+4{ϵ}^2}{57-46ϵ-8{ϵ}^2},\\ {\tilde{\alpha }}_{y*}=\frac{12ϵ}{57-46ϵ-8{ϵ}^2}.& (36)\end{array}$

To leading order in ϵ, the critical exponents are given by

$\begin{array}{ll}{\theta }_1=\frac{104}{171}{ϵ}^2,{\theta }_2=-\frac{52}{19}ϵ,& (37)\end{array}$

which go back to the canonical, vanishing values for ϵ → 0. There is one IR repulsive and one IR attractive direction, fixing the Yukawa coupling at all scales in terms of the gauge coupling (or vice-versa). In other words, the value of one of the couplings in terms of the other is a prediction of the setting.

In a setting with “non-fundamental” asymptotic safety (with new physics kicking in at some k_UV), it is important that the velocity of the flow in the IR-attractive direction is of order ϵ, whereas it is of order ϵ² in the IR-repulsive direction. At the transition scale to the more fundamental description, initial conditions for the values of couplings are typically not the fixed-point values. Toward the IR, the flow is pulled toward the fixed point along the IR-attractive direction with a velocity ${O}(ϵ)$ and repelled from the fixed point along the IR-repulsive direction with a velocity ${O}({ϵ}^2)$. Accordingly, near-fixed-point scaling could determine the behavior of a larger class of trajectories, cf. Figure 6.

FIGURE 6

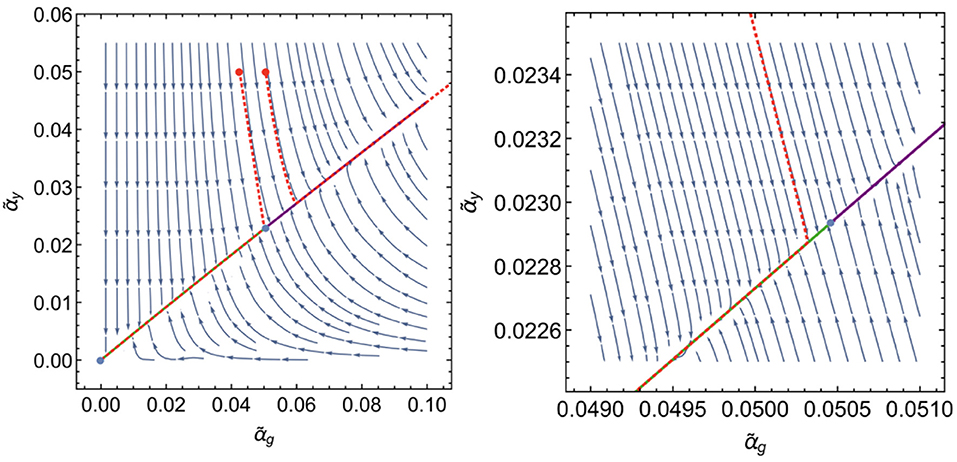
Figure 6. The flow toward the IR from the fixed point in Equation (36) for ϵ = 1/10 features one strongly IR attractive and one weakly IR repulsive direction. The green and purple, thick, continuous lines are the two only “true” fixed-point trajectories. Initial conditions in the UV away from the fixed point (red dots) result in trajectories that are indistinguishably close to the fixed-point trajectories in the IR. The right panel shows a zoom into the vicinity of the fixed point, where the “non-fundamental” trajectory narrowly misses the fixed point, but approaches the critical hypersurface arbitrarily closely, resulting in universal predictions in the IR.

At the next order in the approximation, quartic scalar self-interactions have to be included. For the corresponding large N couplings

$\begin{array}{ll}{\alpha }_h=\frac{u{N}_f}{16{\pi }^2},{\alpha }_v=\frac{v{N}_f}{16{\pi }^2},& (38)\end{array}$

the one-loop beta functions are given by Jack and Osborn (1984); Machacek and Vaughn (1985), and Ford et al. (1992)

$\begin{array}{ll}{\beta }_{{\alpha }_h}=-(11+2ϵ){\tilde{\alpha }}_y^2+4{\alpha }_h({\tilde{\alpha }}_y+2{\alpha }_h),& (39)\end{array}$

$\begin{array}{ll}{\beta }_{{\alpha }_v}=12{\alpha }_h^2+4{\alpha }_v({\alpha }_v+4{\alpha }_h+{\tilde{\alpha }}_y).& (40)\end{array}$

Due to the Yukawa coupling, fermionic fluctuations generate a scalar potential (cf. first term in Equation 39) and cannot be set to zero consistently if ${\tilde{\alpha }}_{y*}\ne 0$; therefore a nontrivial fixed point of the system ${\tilde{\alpha }}_y,{\tilde{\alpha }}_g,{\alpha }_v,{\alpha }_h$ has to be found. To satisfy Weyl consistency conditions (see below), the beta function of the gauge coupling is extended to three-loop order and that of the Yukawa coupling to two-loop order, where there is also a contribution ~α_h. The double-trace coupling α_v decouples from the remainder of the system. The system admits a joint, asymptotically safe fixed point at α_h* > 0, and α_v* < 0 with α_h* + α_v* > 0, indicating a fixed-point potential that is bounded from below Litim and Sannino (2014). A study of the effective potential that includes quantum fluctuations at all scales on a trajectory emanating from the fixed point also indicates its stability (Litim et al., 2016). At the fixed point, the scalar couplings are irrelevant, therefore the full model only features one free parameter.

The inclusion of two-loop effects in the gauge coupling and one-loop effects in the Yukawa coupling (or three-loop in the gauge, two-loop in the Yukawa, and one loop in the scalar couplings) is suggested by Weyl consistency conditions (Jack and Osborn, 1990, 2014), which relate derivatives of beta functions. They arise by considering the model on a curved (but fixed) background and performing Weyl rescalings of the metric. As two subsequent Weyl rescalings commute, it follows that $\frac{\partial {\beta }^i}{\partial g_j}=\frac{\partial {\beta }^j}{\partial g_i}$. Herein ${\beta }^i={\chi }^{ij}{\beta }_j$, where χ^ij is a metric in the space of couplings which depends on the couplings. An expression for χ^ij for gauge-Yukawa models has been derived in Antipin et al. (2013).

These conditions should hold for the full RG flow and can be imposed on the perturbative expansion. For a discussion of the corresponding ordering scheme for beta functions as well as other systematic choices of perturbative orders in the context of gauge-Yukawa theories (see also Bond et al., 2018).

Residual interactions in canonically marginal couplings at an interacting fixed point provide finite contributions to beta functions of higher-order, canonically irrelevant couplings. Higher-order couplings in the scalar potential develop near-Gaussian fixed-point values of their own (Buyukbese and Litim, 2017). Accordingly, their scaling exponents follow the expectation that these couplings should remain irrelevant at a perturbative asymptotically safe fixed point.

The interacting fixed point in gauge-Yukawa systems constitutes a four-dimensional example of asymptotic safety, established within perturbation theory. It provides a new universality class which calls for an in-depth study of its possible extensions and generalizations.

The extension to a supersymmetric setting has been discussed in Intriligator and Sannino (2015); Bajc and Sannino (2016); Bond and Litim (2017); and Bajc and Dondi (2018). While perturbative asymptotic safety cannot be realized in the supersymmetric setting with a simple gauge-group (Intriligator and Sannino, 2015), it can exist in settings with semi-simple gauge groups (Bond and Litim, 2017; Bajc and Dondi, 2018). This highlights how an added symmetry can allow to derive strong no-go-theorems for asymptotic safety.

The fixed-point structure in gauge-Yukawa models is more intricate in a setting away from four dimensions (Codello et al., 2016) (or under the inclusion of potential quantum-gravity effects Christiansen et al., 2017), where the degeneracy of the free fixed point is lifted, and fixed-point collisions can occur.

Given that asymptotic safety appears in a range of gauge theories where asymptotic freedom is lost, the phase diagram of gauge theories could be richer than previously thought. In fact, indications for an interacting fixed point at leading order in 1/N_f go back to Palanques-Mestre and Pascual (1984) and Gracey (1996), see Holdom (2011) for a recap and a discussion of higher orders in 1/N_f. With a view toward the potential phenomenological importance of such fixed points (Antipin and Sannino, 2017; Antipin et al., 2018a), employ a resummation of the fermionic bubble diagrams that contribute at leading order in 1/N_f to all orders in perturbation theory to the beta function for the non-Abelian gauge coupling. This provides indications for an interacting fixed point: In a 1/N_f expansion, the first nontrivial order vanishes in the large N_f limit, unless there is a value of the coupling where it features a pole. In that case, depending on the sign of that contribution, a zero of the beta function can be generated. Indeed a corresponding pole can be found, providing an indication for a fixed point at a non-perturbatively large value of the gauge coupling. A similar resummation for the gauge contribution to the leading nontrivial order of the beta function of the Yukawa coupling has been performed in Kowalska and Sessolo (2018), see also Alanne and Blasi (2018) and Alanne and Blasi (2018).

The a-theorem (Cardy, 1988) has been explored in this setting (Antipin et al., 2018b; Dondi et al., 2018), showing that, as expected, the Jack and Osborn a function (Jack and Osborn, 2014) takes a larger value at the UV fixed point than at the IR fixed point.

These developments pave the way for asymptotically safe model building beyond the Standard Model (e.g., Abel and Sannino, 2017a,b; Bond et al., 2017; Mann et al., 2017; Molinaro et al., 2018).

3.1. Asymptotically Safe Phenomenology

The idea that scale-invariance is realized in physics beyond the Standard Model has received a lot of attention (see e.g., Meissner and Nicolai, 2007; Shaposhnikov and Zenhausern, 2009a,b; Holthausen et al., 2013; Khoze, 2013; Lindner et al., 2014; Gies and Zambelli, 2017; Lewandowski et al., 2018), mostly focusing on settings with classical scale invariance. It is therefore highly intriguing to explore whether extensions of the Standard Model are asymptotically safe along the lines in Litim and Sannino (2014), realizing quantum scale invariance. Measurements showing a decreasing SU(3) coupling as a function of energy only cover a finite energy range and hence do not exclude asymptotic safety.

Steps toward an asymptotically safe Standard Model include the observation that asymptotic safety can be achieved in semi-simple gauge groups (Esbensen et al., 2016; Bond and Litim, 2018b) and with chiral fermions (Mølgaard and Sannino, 2017). To render the non-Abelian Standard Model gauge couplings asymptotically safe, new fermionic states transforming in nontrivial representation of SU(2) and/or SU(3), have to be added. Asymptotic safety might be achieved for one of the non-Abelian gauge couplings, with the others becoming asymptotically free, depending on the representation the new (vectorlike) fermions transform in Kowalska et al. (2017). The matching scale, essentially corresponding to the mass scale of the new fermions, which separates the regime of power-law running below the fixed point from the regime of logarithmic running in the Standard Model, adds new free parameters to these models.

Yet, the non-Abelian gauge groups of the Standard Model are SU(2) and SU(3), not SU(N_c) with N_c → ∞, as required for the Veneziano limit. Accordingly, the addition of fermions to the Standard Model such that the non-Abelian gauge couplings, together with the BSM Yukawa coupling become asymptotically safe (Bond et al., 2017; Mann et al., 2017), is difficult to reconcile with a perturbative nature of the extension (Barducci et al., 2018), at least if one also insists on solving the U(1) triviality problem. This is evident, e.g., in the large values of the critical exponents that lead to a fast flow away from the fixed point toward the IR (see e.g., Bond et al., 2017; Mann et al., 2017). Hence, large N_f fixed points (Palanques-Mestre and Pascual, 1984; Gracey, 1996; Holdom, 2011; Antipin and Sannino, 2017; Antipin et al., 2018a; Kowalska and Sessolo, 2018) play a key role in these developments. Accommodating the Higgs at the correct mass is a challenge (Pelaggi et al., 2018). This could change in a grand unified setting (Molinaro et al., 2018), which could also become asymptotically safe (Abel and Sannino, 2017b).

Asymptotic safety beyond the Standard Model could have intriguing phenomenological consequences in astrophysics and cosmology (Nielsen et al., 2015). For instance, asymptotically safe dark matter could accommodate a significant running of the portal coupling to visible matter between the dark-matter-mass scale—relevant for thermal production of dark matter in the early universe—and the scale of direct detection experiments (Sannino and Shoemaker, 2015). In the WIMP-paradigm, the dark matter relic density is linked to the probability of direct detection, since the cross-section for dark-matter-annihilation into Standard Model particles is related to the cross-section for dark matter scattering off Standard Model particles. Hence, the lack of direct detection has put severe constraints on the paradigm (Tan et al., 2016; Akerib et al., 2017; Aprile et al., 2018). These might be circumvented by introducing additional fields, providing a new parameter that decreases the tension between direct experimental bounds on the cross-section and the relic-density constraints. Asymptotic safety could provide an alternative explanation (Sannino and Shoemaker, 2015): the value of the coupling at the higher scale is larger as it approaches an interacting fixed point. This might accommodate thermal production of the full dark matter relic density while being consistent with bounds from direct searches.

4. Asymptotically Safe Quantum Gravity

4.1. Status of Asymptotic Safety in Gravity

Einstein gravity, quantized perturbatively, loses predictivity at (trans)planckian scales due to its perturbative nonrenormalizability. Infinitely many free parameters are associated with counterterms required to absorb new divergences appearing at every loop order⁵ (Deser and Nieuwenhuizen, 1974a,b; 't Hooft and Veltman, 1974; Goroff and Sagnotti, 1986; van de Ven, 1992). At momenta p below the Planck scale, only a finite number of the counterterms contribute (Donoghue, 1994a,b) if one assumes that the corresponding dimensionless couplings are all of order one. Then, higher-order terms are suppressed by ${(p/M_{\text{Planck}})}^{\#}$, # > 2. Thus, gravity and quantum physics are actually compatible, but a perturbative quantization only holds up to the Planck scale (Donoghue, 2012). The key challenge is to find an ultraviolet completion. The minimalistic and conservative nature of asymptotic safety as compared to many other approaches to quantum gravity make it a useful starting point for this endeavor: If this ansatz for quantum gravity fails, more radical notions on the quantum nature of spacetime are required.

As the free fixed point is IR attractive in the Newton coupling,⁶ the first mechanism for asymptotic safety cf. Sec. 2.4.1, which is realized in d = 2 + ϵ dimensions (Brown, 1977; Tsao, 1977; Christensen and Duff, 1978; Gastmans et al., 1978; Weinberg, 1980; David, 1988; Distler and Kawai, 1989; Kawai and Ninomiya, 1990; Jack and Jones, 1991; Kawai et al., 1993a,b, 1996; Aida et al., 1994; Nishimura et al., 1994; Aida and Kitazawa, 1997; Codello and D'Odorico, 2015), might also determine the fate of gravity in d = 4 dimensions. The physical mechanism behind asymptotic safety in gravity (Nink and Reuter, 2013) is the antiscreening nature of metric fluctuations that shield the Newton coupling, similar to the effect of self-interacting gluons in the Yang-Mills vacuum.

An extension of the ϵ expansion to higher order, combined with an appropriate resummation, could provide indications for or against a fixed point in four dimensions. This is also a goal of discrete approaches to the gravitational path-integral where spacetime configurations are constructed from scratch from microscopic building blocks: Causal (Ambjorn et al., 2000, 2001) (and possibly also Euclidean Laiho and Coumbe, 2011; Laiho et al., 2017) Dynamical Triangulations) (CDT) feature a higher-order phase transition (Ambjorn et al., 2011, 2012, 2017) facilitating a continuum limit. This could provide a universality class for quantum gravity. Complementary to Monte Carlo simulations of dynamical triangulations, an analytical approach to search for a suitable continuum limit is based on tensor models (Ambjorn et al., 1991; Godfrey and Gross, 1991; Gross, 1992; Benedetti and Gurau, 2012; Gurau, 2016), see Sec. 4.2.4. Lattice studies based on Euclidean Regge calculus have also been put forward as indications for asymptotic safety (Hamber, 2009, 2015).

Intriguingly, perturbative techniques in d = 4 yield indications for an asymptotically safe fixed point (Codello and Percacci, 2006; Niedermaier, 2009, 2010), providing a hint at a near-perturbative nature of asymptotically safe gravity.

Most of the compelling evidence for asymptotic safety in gravity comes from Euclidean functional RG (FRG) studies based on the Wetterich equation⁷. This framework provides beta functions for the dependence of couplings on the momentum scale k. The scale is introduced into the generating functional through an infrared cutoff function $R_k(p^2)$, called the regulator,

$\begin{array}{ll}{Z}_k\left[J\right]=\int {D}\phi e^{-S\left[\phi \right]-\frac{1}{2}\text{Tr}\phi R_k(p^2)\phi +\text{Tr}J\phi },& (41)\end{array}$

$\begin{array}{ll}{\Gamma }_k\left[\varphi \right]={\displaystyle \underset{J}{\text{sup}}}(\text{Tr}J\varphi -\text{ln}{Z}_k\left[J\right])-\frac{1}{2}\text{Tr}\varphi R_k(p^2)\varphi ,{\langle \phi \rangle }_k=\varphi ,& (42)\end{array}$

reducing to the standard definitions at k = 0. $R_k(p^2)$ and its derivative $k{\partial }_k{R}_k(p^2)$ are sketched in Figure 7. This setup provides a flow equation, the Wetterich equation (Wetterich, 1993), also Ellwanger (1994) and Morris (1994), pioneered for gauge theories in Reuter and Wetterich (1994) and gravity in Reuter (1998). The regulator acts as a simultaneous IR- and UV cutoff, such that the change of a coupling at scale k is mainly driven by quantum fluctuations at that scale:

$\begin{array}{ll}{\partial }_t{\Gamma }_k=k{\partial }_k{\Gamma }_k=\frac{1}{2}\text{Tr}\left[{\left(\frac{{\delta }^2{\Gamma }_k\left[\varphi \right]}{\delta {\varphi }^2}+R_k\right)}^{-1}{\partial }_t{R}_k\right].& (43)\end{array}$

For gravity, the covariant Laplacian $\bar{\Delta }$ with respect to an auxiliary background metric $\overline{g}$_μν takes the role of the momentum p², Reuter (1998); Dou and Percacci (1998); Souma (1999), and Lauscher and Reuter (2002). For general introductions and reviews (see Berges et al., 2002; Polonyi, 2003; Pawlowski, 2007; Rosten, 2010; Braun, 2012; Delamotte, 2012; Gies, 2012, for gravity, see Reuter and Saueressig, 2012; Nink et al., 2013; Ashtekar et al., 2014; Percacci, 2017; Eichhorn, 2018a). The method is well-suited to models with dimensionful couplings, and therefore widely-used in condensed-matter physics and statistical physics (Kopietz et al., 2010; Metzner et al., 2012; Platt et al., 2013). Its relation to perturbation theory, which is straightforward at one loop, has been explored at higher loops in Papenbrock and Wetterich (1995) and Codello et al. (2014).

FIGURE 7

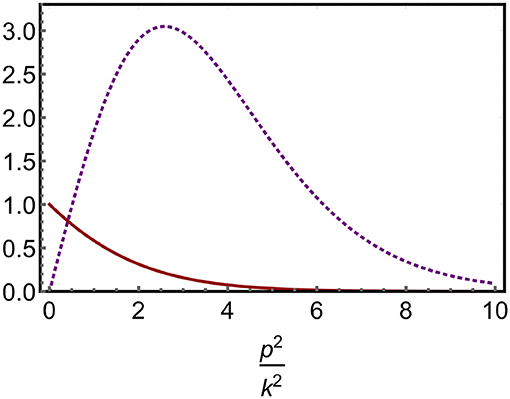
Figure 7. The regulator $R_k(p^2)$ (continuous red line) acts as a suppression term for IR modes. In the flow equation Equation (43) its derivative with respect to k (dotted purple line) acts as a suppression for UV modes, as well, such that the main contribution to the scale dependence of the dynamics at k comes from modes at that momentum scale.

The FRG tracks the scale dependence of all couplings that are compatible with the symmetries, not just the perturbatively renormalizable interactions. For practical calculations, theory space is truncated to a (typically finite-dimensional) subspace, introducing a systematic error. To highlight that quantitative results can already be achieved in relatively small truncations, we provide the leading scaling exponents for the Ising model in Table 1.

TABLE 1

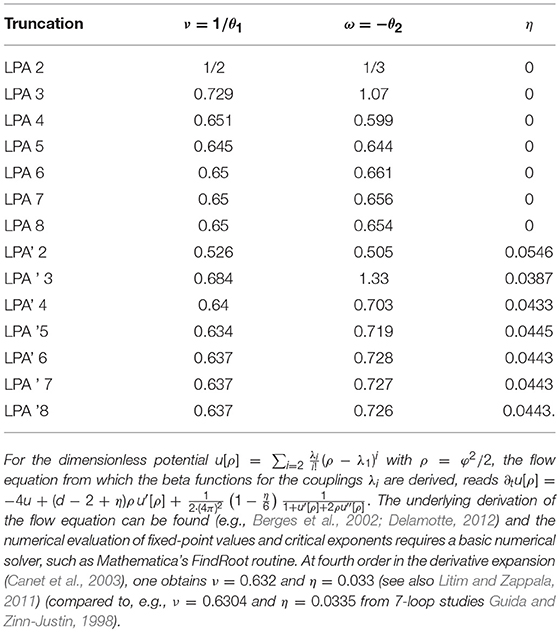
Table 1. Relevant and leading irrelevant critical exponent as well as the anomalous dimension for the Ising model obtained with the FRG in a derivative expansion to leading order (local potential approximation, LPA, to order 2n in the field) and next-to-order (LPA') with field-independent anomalous dimension.

For fixed points that arise via the mechanism in section 2.4.1, the scaling is near-canonical near the critical dimension, providing a systematic way to devise truncations that include all relevant couplings. There are indications that in quantum gravity four dimensions is close to two in the sense that the canonical dimension is a good predictor of relevance at the fixed point (Falls et al., 2013, 2016), enabling the setup of robust truncations by canonical power-counting. These indications require further confirmation, e.g., by including operators of the form R□ⁿR (De Alwis, 2018).

Considerable evidence for the existence of the interacting Reuter fixed point has accumulated, starting from the seminal work (Dou and Percacci, 1998; Reuter, 1998; Souma, 1999; Lauscher and Reuter, 2002; Reuter and Saueressig, 2002), employing truncations of the form

$\begin{array}{l}{\Gamma }_k=-\frac{1}{16\pi G_N}\int d^{4}x\sqrt{g}(R-2\Lambda )+{\Gamma }_{k\text{higher}-\text{order}}+\frac{1}{32\pi G_N\alpha }\\ \int d^{4}x\sqrt{\overline{g}}{\overline{g}}^{\mu \nu }\left({\bar{D}}^{\kappa }{h}_{\mu \kappa }-\frac{1+\beta }{4}{\bar{D}}_{\mu }h\right)\left({\bar{D}}^{\lambda }{h}_{\nu \lambda }-\frac{1+\beta }{4}{\bar{D}}_{\nu }h\right)\\ -\sqrt{2}\int d^{4}x\sqrt{\overline{g}}{\bar{c}}_{\mu }\left(({\overline{g}}^{\mu \rho }{\bar{D}}^{\kappa }{g}_{\rho \nu }{D}_{\kappa }+{\bar{D}}^{\kappa }{g}_{\kappa \nu }{D}_{\rho })-\frac{1+\beta }{2}{\bar{D}}^{\mu }{D}_{\nu }\right)c^{\nu }.& (44)\end{array}$

The third term is a gauge fixing term with two parameters α, β (see, e.g., Falkenberg and Odintsov, 1998; Gies et al., 2015; de Brito et al., 2018 for studies of the off-shell gauge dependence and Benedetti, 2012 for gauge-independent on-shell results) and the third line is the corresponding Faddeev-Popov operator⁸. Barred quantities refer to a background metric $\overline{g}$_μν with respect to which the metric g_μν can be gauge fixed, and a local coarse-graining scheme is set up. The fluctuation field is

$\begin{array}{ll}{h}_{\mu \nu }=g_{\mu \nu }-{\overline{g}}_{\mu \nu }.& (45)\end{array}$

A discussion of background-independence is given in section 4.2.3. All results below are in the background-approximation, where g_μν = $\overline{g}$_μν is used in the RG flow. Results from selected key truncations are summarized in Table 2.

TABLE 2

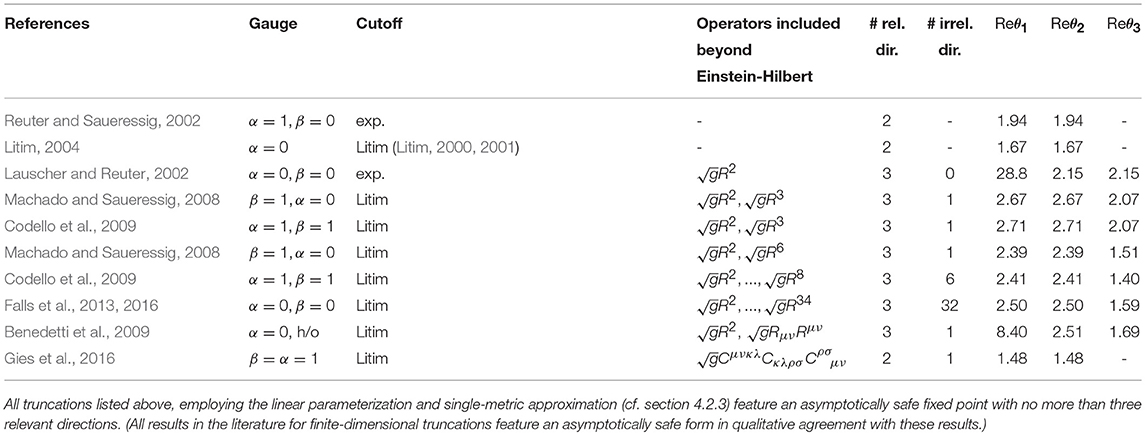
Table 2. The operators beyond Einstein-Hilbert, the number of relevant/irrelevant directions, and the values of the positive critical exponents are indicated.

For purposes of illustration, we also quote beta functions in the Einstein-Hilbert truncation with $G=G_N{k}^2$ and λ = Λ/k² from Codello et al. (2009), with anomalous dimensions η_h(c) for the metric (ghost) (e.g., in Donà et al., 2014), and for the functional $f(\tilde{R})$, from Benedetti and Caravelli (2012) as found in Dietz and Morris (2013a).

$\begin{array}{l}{\beta }_G=2G-\frac{G^2}{12·4\pi }\left(\frac{52(4-{\eta }_h)}{1-2\lambda }+40(4-{\eta }_c)\right),\\ {\beta }_{\lambda }=-2\lambda +\frac{G}{12·4\pi }\left(\frac{20(6-{\eta }_h)}{1-2\lambda }-16(6-{\eta }_c)\right)-\frac{G\lambda }{12·4\pi }\left(\frac{52(4-{\eta }_h)}{1-2\lambda }+40(4-{\eta }_c)\right),& (46)\end{array}$

$\begin{array}{l}{\partial }_{t}f=4f-2\tilde{R}{f}^{\prime }+\frac{1}{384{\pi }^2}[-20\frac{{\partial }_t{f}^{\prime }-2\tilde{R}{f}^{″}+8f^{\prime }}{(\tilde{R}-2)f^{\prime }-2f}-36-12-5{\tilde{R}}^2\\ +\frac{({\tilde{R}}^4-54{\tilde{R}}^2-54)({\partial }_t{f}^{″}-2\tilde{R}{f}^{‴})-({\tilde{R}}^3+18{\tilde{R}}^2+12)({\partial }_t{f}^{\prime }-2\tilde{R}{f}^{″}+2f^{\prime })-36({\tilde{R}}^2+2)(f^{\prime }+6f^{″})}{2\left(-9f^{″}+(\tilde{R}-3)f^{\prime }-2f\right)}].& (47)\end{array}$

Here, $\tilde{R}=R/k^2$ is the dimensionless curvature and primes denote derivatives with respect to $\tilde{R}$. Equation (47) provides the beta functions for couplings of Rⁿ upon a Taylor expansion in the curvature.

The Newton coupling and cosmological constant are relevant, cf. Figure 8. Accordingly, the IR value of the cosmological constant is unrestricted. The choice of different fixed-point trajectories in Figure 8 results in different values of the dimensionful cosmological constant in the IR Λ_IR. To realize ${\Lambda }_{\text{IR}}/M_{\text{Pl}}^2<<1$, a specific trajectory has to be chosen. The question, why this particular trajectory is realized, is the finetuning “problem.” Yet, any relevant coupling is actually linked to a similar question. For instance, the value of the QCD coupling at the electroweak scale would be different on other, also asymptotically free trajectories. The question how a more fundamental principle selects one out of many viable trajectories for the relevant couplings exists irrespective of whether the coupling is logarithmically or power-law sensitive to the momentum scale. (The need for successive tuning at each order in perturbation theory for the power-law case is a consequence of that particular approximation scheme, not a signature of a consistency problem of the theory).

FIGURE 8

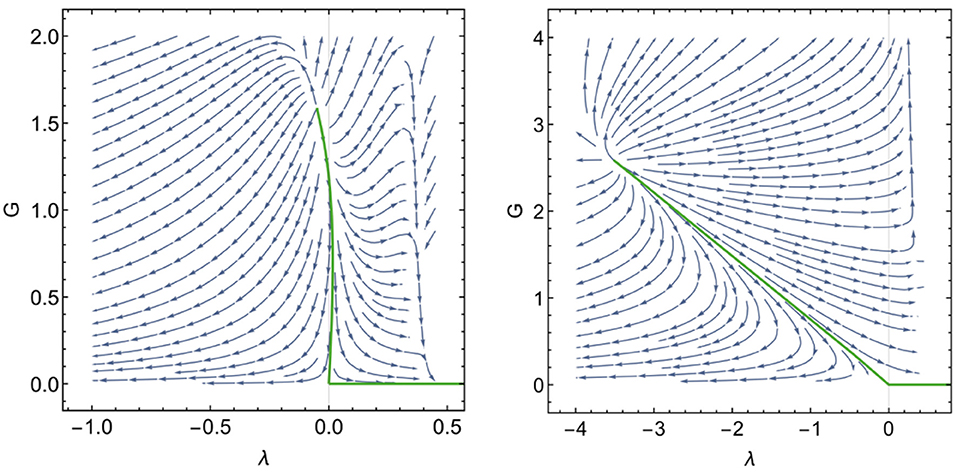
Figure 8. The RG flow to the IR in the Einstein-Hilbert truncation in the setup discussed in Donà et al. (2014) for a type Ia cutoff features a trajectory—passing very close to the free fixed point—on which the dimensionful Newton coupling and cosmological constant reach constant values in the IR in agreement with measurements. Left panel: pure gravity case; right panel: including minimally coupled matter as in the Standard Model (4 scalars, 12 vectors, 45 Weyl fermions). The two eigendirections of the fixed point are superposition of G and λ.

At the interacting Reuter fixed point, canonical ordering appears to hold⁹, cf. Table 2. This provides a scheme to set up consistent truncations: Assume for simplicity that the operators in Table 2 diagonalize the stability matrix, resulting in critical exponents

$\begin{array}{ll}{\theta }_i=d_{{\overline{g}}_i}+{\eta }_i.& (48)\end{array}$

Unless the anomalous scaling contribution η_i would grow with the canonical dimension, the canonical dimension dominates for canonically highly irrelevant couplings, rendering them irrelevant at an interacting fixed point. In fact, already at the level of canonically marginal couplings of R² and $R_{\mu \nu }{R}^{\mu \nu }$, there appears to be only one relevant direction¹⁰. All canonically irrelevant operators that have been examined are irrelevant at the fixed point. In Falls et al. (2013) and Falls et al. (2016), the normalized difference of canonical and quantum scaling dimension decreases with decreasing canonical dimension for Rⁿ, cf. Figure 9. The near-Gaussian scaling spectrum (at higher orders in the curvature expansion) is also in line with the possibility to find indications of asymptotic safety from perturbation theory (Codello and Percacci, 2006; Niedermaier, 2009, 2010).

FIGURE 9

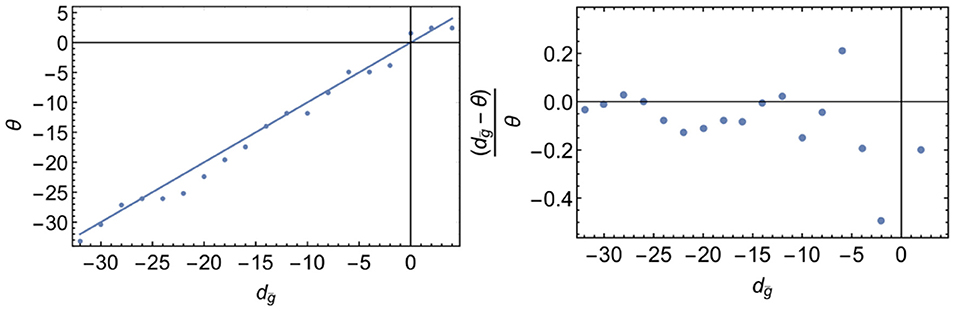
Figure 9. Data from Falls et al. (2016) on the critical exponents in a truncation $\sum _n\sqrt{g}{R}^n$, compared to the canonical dimension.

Systematic truncation errors can be estimated given that in approximations schemes for QFTS, dependencies on unphysical parameters arise even at the level of observables. The better the approximation, the weaker such a dependence. Tests include gauge-parameter dependence (Gies et al., 2015), regulator dependence (Reuter and Saueressig, 2002) and dependence on the parameterization for metric fluctuations (Gies et al., 2015; Ohta et al., 2016; de Brito et al., 2018).

Going beyond finite-dimensional truncations, the closed fixed-point equation for $f(\tilde{R})$, e.g., Equation (47) has been investigated. Depending on the choice of regulator, it contains a varying number of fixed singularities, as the regulator introduces additional field-dependence in the background approximation. Thus, specific choices of the regulator allow for global solutions (Benedetti and Caravelli, 2012; Demmel et al., 2012; Dietz and Morris, 2013a,b; Demmel et al., 2015; Ohta et al., 2015) while others do not (Codello et al., 2009). One might conclude that extensions of the truncation are required, going beyond the background- approximation for $f(\tilde{R})$ (see Christiansen et al., 2018, see section 4.2).

Many gravitational theories are classically dynamically equivalent to GR. Thus different theory spaces could allow for asymptotic safety (Krasnov and Percacci, 2018). For instance, the vielbein and the connection can be treated as independent variables (Daum and Reuter, 2012, 2013; Harst and Reuter, 2015, 2016), or torsion can be included (Pagani and Percacci, 2015; Reuter and Schollmeyer, 2016). The dimension of theory space and the number of relevant couplings decrease by one (Eichhorn, 2015) in unimodular gravity (Unruh, 1989; Finkelstein et al., 2001; Ellis et al., 2011), where the determinant of the metric is a fixed density, removing the cosmological constant from the action. Further, fluctuations in topology, dimensionality, signature etc. might be included in the gravitational path integral. The corresponding additional configurations either prevent the existence of a continuum limit/ RG fixed point, lead to an asymptotically safe fixed point in the same universality class as Table 2, or provide another gravitational universality class which differs in its physical implications and can therefore (in principle) be probed experimentally.

In two dimensions, the conformal field theory underlying asymptotic safety has been studied (Nink and Reuter, 2016). In d = 4, scale-invariance need not imply conformal invariance (in fact, sufficient conditions for this are not known). If it were possible to extend the conformal bootstrap program (Simmons-Duffin, 2016) to a gravitational setting, a search for the corresponding universality class with relevant directions according to Table 2 might answer whether there is a conformal theory behind asymptotically safe gravity.

4.2. Open Questions & Future Perspectives

4.2.1. Lorentzian Signature

There is no simple Wick-rotation in quantum gravity, thus the above results do not directly imply Lorentzian asymptotic safety. In an ADM decomposition of the metric, the change of signature can be implemented by changing one parameter. This has been used in Manrique et al. (2011a) to find hints for asymptotic safety in a Lorentzian setting for the Einstein-Hilbert truncation. Further, RG flows in the ADM decomposition have been explored in Rechenberger and Saueressig (2013), Biemans et al. (2017), and Biemans et al. (2017). The FRG can be formulated in a Lorentzian setting (Floerchinger, 2012), underlying the study of real-time correlators, e.g., in QCD (Pawlowski and Strodthoff, 2015).

Alternatively, a proposal (Eichhorn, 2018b) to search for Lorentzian asymptotic safety employs causal set quantum gravity. This is an intrinsically Lorentzian, discrete approach to quantum gravity, based on the path integral over all causal sets (Bombelli et al., 1987). Under the restriction to manifoldlike causal sets (implemented as a path integral over sprinklings Henson, 2006; Dowker, 2013) the space of couplings might feature a second-order phase transition (Surya, 2012; Glaser, 2018).

4.2.2. Propagating Degrees of Freedom

Higher-order derivatives in QFTs on a flat background generically imply an instability in the kinetic term (Ostrogradsky, 1985; Woodard, 2015), translating into a violation of reflection positivity for the Euclidean propagator (Arici et al., 2017). In a quantum setting, the unboundedness of the Hamiltonian can be traded for unitarity violation through negative-norm states in the Hilbert space (Woodard, 2015).

In quantum gravity, an analysis of unitarity is presumably rather more subtle for several reasons.

Firstly, positivity violation in gauge-variant propagators occurs in unitary theories such as QCD (Cucchieri et al., 2005; Bowman et al., 2007). [A direct analogy with QCD has been proposed for (asymptotically free higher-derivative) gravity in Holdom and Ren, 2016a,b.] The physical “graviton” as the transverse traceless part of the metric propagator is defined perturbatively; but non-perturbatively no local separation of gauge and physical degrees of freedom is possible.

Secondly, an instability in the flat-space propagator is not in conflict with observations, given that the cosmological background appears to be FRW-like.

Thirdly, Ostrogradski instabilities occur under a crucial assumption, namely that of finitely many higher-order terms. Yet the case with infinitely higher order terms can feature a well-defined propagator, translating into a well-posed initial value problem at the level of the equations of motion (Barnaby and Kamran, 2008). Examples include string-field theory, see Barnaby and Kamran (2008) and references therein. Accordingly, truncated dynamics in asymptotically safe gravity might contain spurious instabilities (just as an analysis of a truncated effective action for string theory would).

Fourth, even at the level of curvature-squared actions, the mass of the “ghost” (analyzed around flat space) runs as a function of momentum. Hence, such ghosts might not appear as physical states (see Floreanini and Percacci, 1995; Benedetti et al., 2009; Becker et al., 2017).

Finally, if asymptotic safety is “non-fundamental” (cf. section 2.3), the mass-scale of the ghosts (if these exist on physically relevant backgrounds) sets an upper bound on k_UV.

CDT satisfies reflection positivity (Ambjorn et al., 2000, 2001). Thus, its continuum limit, which might correspond to asymptotically safe gravity, inherits this property. As many other examples, this reinforces that the quest to understand quantum spacetime can be accelerated by searching for links between quantum-gravity approaches.

In addition to ghost-like states, higher-order gravity can (but again, need not) contain additional propagating degrees of freedom. These might be of phenomenological interest, e.g., driving inflation or leading to modifications of GR detectable in black holes and/or gravitational waves.

Determining the spectrum of propagating gravitational degrees of freedom in asymptotically safe gravity is an important outstanding question. A comprehensive answer in the FRG approach requires studying the full propagator (at k = 0, where all quantum fluctuations contribute) around a solution to the quantum equations of motion.

4.2.3. Background Independence

Background independence is a key property of quantum gravity, meaning that all configurations in the path integral should be treated on an equal footing. This appears to be at odds with the introduction of a local coarse graining scheme, as this relies on a metric. Specifically, the regulator in the flow equation depends on a background metric $\overline{g}$_μν. Additionally, a local formulation of gauge theories requires gauge fixing to derive the propagator. The flow equation is based on a background gauge-fixing. Nevertheless, background independence can be achieved, if all backgrounds are treated on the same footing (Becker and Reuter, 2014), i.e., if g_μν and $\overline{g}$_μν are both kept as distinct arguments of the flowing action. In the limit k → 0, where the regulator vanishes, setting g_μν = $\overline{g}$_μν yields an effective action that inherits diffeomorphism invariance and therefore background independence from the auxiliary background-diffeomorphism invariance that is kept intact for an appropriate choice of gauge fixing and regulator function. Therefore, ultimately we are interested in Γ_k→0[$\overline{g}$_μν, g_μν = $\overline{g}$_μν], or Γ_k→0[$\overline{g}$_μν, h_μν = 0], respectively. Crucially, the flow is driven by the fluctuation propagator, ${\left({\Gamma }_k^{(0,2)}\left[{\overline{g}}_{\mu \nu },g_{\mu \nu }\right]\right)}^{-1}={\left(\frac{{\delta }^2}{\delta g_{\kappa \lambda }\delta g_{\rho \sigma }}{\Gamma }_k\left[{\overline{g}}_{\mu \nu },g_{\mu \nu }\right]\right)}^{-1}$, or, equivalently, ${\left({\Gamma }_k^{(0,2)}\left[{\overline{g}}_{\mu \nu },h_{\mu \nu }\right]\right)}^{-1}$. As the regulator and gauge fixing break the symmetry between g_μν and $\overline{g}$_μν, this is not the same as ${\left({\Gamma }_k^{(2,0)}\left[{\overline{g}}_{\mu \nu },g_{\mu \nu }\right]\right)}^{-1}$. Schematically,

$\begin{array}{l}{\partial }_t{\Gamma }_k[{\Phi }_{\text{bck}},{\Phi }_{\text{phys}}]=\frac{1}{2}\text{Tr}[{\left(\frac{{\delta }^2{\Gamma }_k[{\Phi }_{\text{bck}},{\Phi }_{\text{phys}}]}{\delta {\Phi }_{\text{phys}}^2}+R_k[{\Phi }_{\text{bck}}]\right)}^{-1}\\ {\partial }_t{R}_k[{\Phi }_{\text{bck}}]].& (49)\end{array}$

In the background approximation, one equates Φ_phys = Φ_bck after the derivation of $\frac{{\delta }^2{\Gamma }_k\left[{\Phi }_{\text{bck}},{\Phi }_{\text{phys}},\right]}{\delta {\Phi }_{\text{phys}}^2}$. Accordingly, projections on field monomials pick up the auxiliary background-field dependence of the regulator in this approximation.

As an intermediate step to obtaining an effective action that respects background independence, one has to derive the flow of the fluctuation field propagator (Christiansen et al., 2017, 2016, 2015; Denz et al., 2018) in a setting that makes explicit use of a background. Alternatively, one can map this to a “bimetric” truncation, in which the propagator of the full metric is distinguished from the background metric, and drives the RG flow (Manrique and Reuter, 2010; Manrique et al., 2011b,c; Becker and Reuter, 2014), see Table 3.

TABLE 3

Table 3. Fixed-point results from Becker and Reuter (2014) for the “dynamical” couplings in the Einstein-Hilbert truncation and their background counterparts.

The fluctuation-field dynamics are not protected by an auxiliary diffeomorphism invariance (as the background dynamics is). Accordingly, the theory space is that of a spin-2-field, with (modified) Slavnov-Taylor identities relating different couplings as a consequence of the symmetry. In a vertex expansion, this results in distinct “avatars” of couplings. For instance, expanding the Einstein-Hilbert action to nth order in the fluctuation field results in n “avatars” of the Newton coupling and cosmological constant, λ_n and G_n. Table 4 lists fixed-point results for these “avatars”. We use the notation μ = −2λ₂ and also provide the fluctuation field anomalous dimension η_h and ghost anomalous dimension η_c. Where their full momentum dependence has been evaluated, as in Christiansen et al. (2017); Christiansen et al. (2015); and Denz et al. (2018), the numbers provided refer to anomalous dimensions at vanishing momentum. “Hybrid” calculations, which evaluate the anomalous dimensions of the fluctuation fields, but equate the background and fluctuation Newton couplings, G_B and cosmological constants, Λ_B are included.

TABLE 4

Table 4. Fixed-point results for fluctuation couplings.

The example of a background-deformed regularization for scalar field theory shows how the background dependence of the regulator can spoil the study of fixed-point results for the Wilson-Fisher fixed point (Bridle et al., 2014). A symmetry identity, namely the shift Ward-identity, follows from background independence. It is structurally similar to the flow equation and relates the background-field-dependence on $\bar{\varphi }$ and the fluctuation-field-dependence on φ of the flowing action (Reuter and Wetterich, 1997; Litim and Pawlowski, 2002; Bridle et al., 2014; Safari, 2016),

$\begin{array}{ll}\frac{\delta {\Gamma }_k}{\delta \bar{\varphi }}-\frac{\delta {\Gamma }_k}{\delta \phi }=\frac{1}{2}\text{Tr}\left[{\left(\frac{{\delta }^2{\Gamma }_k}{\delta {\phi }^2}+R_k\left[\bar{\varphi }\right]\right)}^{-1}\frac{\delta R_k\left[\bar{\varphi }\right]}{\delta \bar{\varphi }}\right].& (50)\end{array}$

Imposing the shift Ward-identity allows to recover background-independent results (Bridle et al., 2014). In a similar spirit, studies imposing the shift Ward identity in background- approximations for gravity (where the analog of Equation (50) is supplemented by contributions from the gauge fixing sector) have been performed in Morris (2016); Percacci and Vacca (2017); Labus et al. (2016); Ohta (2017); and Nieto et al. (2017).

Dynamical triangulations are background-independent as there is no preferred configuration and even the foliation structure in CDTs appears to be dispensable (Jordan and Loll, 2013). Therefore, establishing whether a universal continuum limit exists in the same universality class (i.e., with matching physical critical exponents) as FRG studies indicate, tests background independence of asymptotically safe gravity. One can either approach this by the well-tested method of computer simulations, based on a Monte-Carlo approach, or explore tensor models (see Sec. 4.2.4).

4.2.4. The RG Perspective on (Discrete) Quantum Gravity

The use of RG ideas in quantum gravity has been gaining traction in various forms over the last few years. Interacting fixed points play a role in several different approaches (see, e.g., Eichhorn and Koslowski, 2013, 2018; Ambjorn et al., 2014; Benedetti et al., 2015; Bahr and Steinhaus, 2016, 2017; Dittrich et al., 2016a,b; Dittrich, 2017; Ben Geloun et al., 2018) and references therein. In particular, in models that introduce a discretization, RG tools enable searches for a universal continuum limit encoded in RG fixed points. As one example, consider tensor models. These are spacetime-free models which encode the gluing of fundamental building blocks of a triangulation in their combinatorics. They generate the sum over all simplicial pseudomanifolds (triangulations) through their Feynman-diagram expansion, thereby generalizing the success-story of matrix models (Di Francesco et al., 1995) to higher dimensions (Ambjorn et al., 1991; Godfrey and Gross, 1991; Gross, 1992). A universal continuum limit might exist if the couplings are tuned to critical values while the tensor size N is taken to infinity (Gurau, 2011). This limit corresponds to a fixed point of an abstract, non-local RG flow set up in the tensor size N, Brezin and Zinn-Justin (1992) and Eichhorn and Koslowski (2013). This coarse-graining flow goes from many degrees of freedom (large N), to fewer degrees of freedom (small N). It is background independent by making no reference to locality or spacetime. Therefore, if a viable fixed point, leading to a physically acceptable phase of spacetime (where the “emergent” spacetime is four dimensional at large scales) can be identified, this provides an indication for a universal continuum limit - i.e., asymptotic safety - in a background independent setting. In Eichhorn and Koslowski (2013) an FRG approach was proposed for matrix models and generalized for tensor models in Eichhorn and Koslowski (2018), also triggering activity in related group field theories (e.g., Benedetti et al., 2015; Ben Geloun et al., 2018).

4.2.5. Toward Asymptotically Safe Phenomenology in Astrophysics and Cosmology

As a candidate for a model of quantum spacetime, asymptotic safety should explain the structure of spacetime in the very early universe (see Bonanno and Saueressig, 2017) for a review and in those regions of black-hole spacetimes that contain classical curvature singularities. Within the FRG language, the UV physics is encoded in the limit of the full effective action Γ_k→0 in which physical scales, e.g., curvature scales, are taken to (trans)planckian values. External physical scales can act as an IR cutoff for quantum fluctuations, as is most easily seen for the external momenta in scattering processes. This motivates the use of “RG improvement” techniques that provide quantum-gravity “inspired” models. The RG-improvement is performed by upgrading all couplings to running couplings and subsequently identifying k with a physical scale of the system in question, either at the level of the action, the equations of motion or the classical solutions. In settings with a high degree of symmetry and correspondingly a single physical scale, the identification is unique and dictated by dimensional arguments (e.g., k² ~ R is the unique choice for a deSitter-type setting).“RG improved” results indicate dimensional reduction of the spectral dimension (Lauscher and Reuter, 2005; Reuter and Saueressig, 2011; Calcagni et al., 2013), singularity resolution in black holes (Bonanno and Reuter, 1999, 2000, 2006; Falls et al., 2012; Becker and Reuter, 2012; Falls and Litim, 2014; Koch and Saueressig, 2014a,b; Kofinas and Zarikas, 2015; Pawlowski and Stock, 2018; Adeifeoba et al., 2018), finite entanglement entropy (Pagani and Reuter, 2018) as well as an inflationary regime generated through quantum gravity effects (Bonanno and Reuter, 2008; Bonanno et al., 2011a,b; Reuter and Saueressig, 2013; Kofinas and Zarikas, 2016).

5. Asymptotically Safe Quantum Gravity and Matter

Our universe contains gravitational and matter degrees of freedom which are coupled to each other. Thus, to understand the quantum structure of spacetime in our universe it is neither necessary nor sufficient to show consistency of quantum- gravity models disregarding matter. This does not imply that quantum gravity must be a unified theory of all interactions, or that it needs to contain matter as fundamental degrees of freedom. It simply means that at observationally accessible scales accessible, all degrees of freedom, gravitational and matter, must be accounted for and their predicted dynamics compatible with observations. As the Standard Model contains N_S = 4 scalars, N_V = 12 and N_D = 24 fermions (including right-handed neutrinos) but there is only one metric, the microscopic gravitational dynamics might even be well-approximated by the dynamics obtained from an appropriate large N_i approximation.

The measured Higgs mass of M_h ≈ 125GeV (Aad, 2012; Chatrchyan, 2012) lies within a narrow band where no new physics is required for the consistency of the Standard Model below the Planck scale. A Higgs mass higher than about 180 GeV (Hambye and Riesselmann, 1997) leads to Landau-pole type behavior in the quartic coupling below the Planck scale. In the absence of higher-order terms in the Higgs potential (see e.g.,Branchina and Messina, 2013; Gies et al., 2014; Eichhorn et al., 2015) the lower bound on the Higgs mass from absolute vacuum stability lies at M_h = 129GeV in a three-loop study for Λ_NP = M_Pl, (Bezrukov et al., 2012), rendering the electroweak vacuum metastable. As its lifetime exceeds the age of the universe (Elias-Miro et al., 2012), see Markkanen et al. (2018) for a review, the next scale of new physics for the Standard Model could be the Planck scale. Such a “desert” provides an exciting opportunity for quantum gravity: The initial conditions for the RG flow of matter interactions are set by quantum gravity at the Planck scale. In the absence of the “desert,” new physics at intermediate scales could shield the quantum gravity scale from view. Conversely, in a “desert”-like setting, there is a direct link between Planck-scale physics and electroweak-scale physics.

5.1. Impact of Quantum Gravity on Matter

There are two effects of asymptotically safe gravity on matter in truncated FRG studies. Firstly, it generates nonzero fixed-point values for particular higher-order matter couplings, see section 5.1.1. Secondly, it impacts the scale dependence of the canonically marginal Standard Model couplings, see section 5.1.2. Both effects result in observational consistency constraints on the microscopic gravitational parameter space.

5.1.1. Matter Interacts in the Presence of Asymptotically Safe Quantum Gravity

The interacting nature of the asymptotically safe gravitational dynamics percolates into the matter sector. There cannot be UV fixed point with all matter interactions set to zero, Eichhorn and Gies (2011)^{11 12}. Interactions respecting the global symmetries of the kinetic terms for matter fields cannot be set to zero consistently (Eichhorn and Held, 2017). Finite contributions to their beta functions are generated by gravitational fluctuations. These prevent a free fixed point, as they are independent of the matter coupling and instead scale with the Newton coupling G (Eichhorn and Gies, 2011; Eichhorn, 2012; Eichhorn et al., 2016; Christiansen and Eichhorn, 2017; Eichhorn and Held, 2017; Eichhorn et al., 2018e). Thus, the free fixed point that exists in the limit of vanishing Newton coupling, G → 0, is shifted to a finite value, the shifted Gaussian fixed point (sGFP). Matter couplings $\bar{\chi }$ invariant under the global symmetries of the kinetic terms¹³ feature canonical dimensions $d_{\bar{\chi }}<0$ in d = 4. Schematically, the FRG beta function reads

$\begin{array}{ll}{\beta }_{\chi }=-d_{\bar{\chi }}\chi +{\#}_1{G}_{\text{eff}}\chi +{\#}_2{G}_{\text{eff}}^2+{\#}_3{\chi }^{\#}.& (51)\end{array}$

We focus on # = 2 (see Eichhorn and Gies, 2011; Eichhorn, 2012; Eichhorn et al., 2016; Christiansen and Eichhorn, 2017; Eichhorn and Held, 2017). $G_{\text{eff}}=\frac{G}{1+\mu }-\frac{G}{(1+{\mu }^2)}$ parameterizes the effective strength of gravity fluctuations in the Einstein-Hilbert truncation (see Eichhorn and Held, 2017) for higher-order terms. The fixed points are

$\begin{array}{ll}{\chi }_{1/2*}=\frac{d-{\#}_1{G}_{\text{eff}}\pm \sqrt{-4{\#}_2{\#}_3{G}_{\text{eff}}^2+{({\#}_1{G}_{\text{eff}}-d_{\bar{\chi }})}^2}}{2{\#}_3},& (52)\end{array}$

such that χ_1* is the sGFP. For sign#₃ = sign#₂, these two fixed points collide at

$\begin{array}{ll}{G}_{\text{eff},\text{crit}}=\frac{d_{\bar{\chi }}}{{\#}_1-2\sqrt{{\#}_2{\#}_3}}.& (53)\end{array}$

Beyond, the sGFP is complex, thus G > G_eff,crit is inconsistent. As G_eff measures the effective strength of gravity fluctuations, G_eff,crit marks the (truncation dependent) weak-gravity bound. Once gravitational fluctuations exceed this bound, cf. Figure 10, they trigger novel divergences in matter couplings, restricting the viable microscopic parameter space to the remaining region. As the induced matter couplings are canonically irrelevant, they are power-law suppressed below the Planck scale and presumably irrelevant for particle physics at lower scales.

FIGURE 10

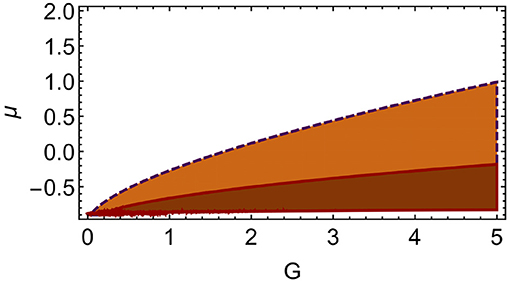
Figure 10. The weak gravity bound in the (G, μ = −2Λ) plane for the Yang-Mills system (from Christiansen and Eichhorn, 2017) in orange, bounded by the dark dashed line, and the weak gravity bound in scalar-fermion systems (from Eichhorn et al., 2016; Eichhorn and Held, 2017) in dark red, bounded by the red continuous line, lie close to each other.

5.1.2. A Link That Could Matter: From the Planck Scale to the Electroweak Scale

Asymptotically safe gravity could uniquely fix the values of marginally irrelevant Standard Model (SM)-couplings (Abelian gauge couplings, Yukawas, Higgs quartic) at the Planck scale. This might allow to confront asymptotic safety with observations, since those couplings run logarithmically below the Planck scale, retaining a “memory” of their Planck-scale values.

For the marginal SM couplings g_SM, the quantum-gravity contribution to β_gSM is linear in g_SM, as the gravitational RG flow cannot generate the SM interactions once they are set to zero due to their distinct symmetry structure (Eichhorn and Held, 2017). Technically, this is encoded in the diagrams underlying the FRG flow (see, e.g., Eichhorn et al., 2016; Christiansen and Eichhorn, 2017; Eichhorn and Held, 2017; Eichhorn, 2018; Eichhorn and Versteegen, 2018). Hence, the quantum-gravity contribution is

$\begin{array}{ll}{\beta }_{g_{\text{SM}}}{|}_{\text{grav}}=-f_{g_{\text{SM}}}{g}_{\text{SM}},& (54)\end{array}$

where f_gSM ~ G is the contribution of metric fluctuations to the corresponding interaction vertex and additionally contains the gravity contribution to the anomalous dimensions of the matter fields. This contribution acts like a scaling dimension, i.e., like an effective change in spacetime dimensionality. For canonically irrelevant couplings, a UV completion requires f_gSM > 0, resembling an effective dimensional reduction. It is unclear whether and how this fits with other indications for dimensional reduction in quantum gravity (Carlip, 2017).

Asymptotic freedom in non-Abelian gauge theories is a key cornerstone in the construction of the SM. This property could persist, as

$\begin{array}{ll}{\beta }_g=-f_{g}g-{\#}_g{g}^3,\dots & (55)\end{array}$

for gauge couplings g, where f_g ≥ 0 holds in all FRG studies to date (Daum et al., 2010; Folkerts et al., 2012; Harst and Reuter, 2011; Christiansen and Eichhorn, 2017; Eichhorn and Versteegen, 2018; Christiansen et al., 2017). #_g depends on the gauge group and matter content while the gravity contribution is blind to the internal index structure and accordingly gauge-group independent. Additional gravity contributions are indirect ones, arising through quantum-gravity-induced higher-order interactions which couple into the flow of the gauge coupling (Christiansen and Eichhorn, 2017) (note that the sign of the w-term in η is incorrect; accordingly this indirect contribution strengthens asymptotic freedom.)

The non-universality of beta functions, setting in at three loops for dimensionless couplings, starts at leading order for dimensionful couplings. Hence, the gravity contributions to beta functions in approximations differ in different schemes (see Robinson and Wilczek, 2006; Pietrykowski, 2007, 2013; Toms, 2007, 2008, 2009, 2010, 2011; Ebert et al., 2008, 2009; Mackay and Toms, 2010; Rodigast and Schuster, 2010; Anber et al., 2011; Felipe et al., 2011; Anber and Donoghue, 2012; Ellis et al., 2012; Narain and anishetty, 2013; Gonzalez-Martin and Martin, 2017) for perturbative studies. At the level of observables, such dependences must cancel. The same physics is encoded in different ways in distinct schemes. As the FRG is applicable to settings with dimensionful couplings (including a multitude of extensively probed universality classes in statistical physics), one could argue that it is well-suited to explore quantum gravity in simpler approximations. The non-universality of the gravity-contribution is reflected in the regulator-dependence of f_g in truncations: Within a background-field study, $f_g=\frac{6}{\pi }G{\Phi }_1^1(0)$ (Daum et al., 2010), where ${\Phi }_1^1(0)>0$ always holds, but the value depends on the choice of regulator, e.g., ${\Phi }_1^1(0)=1$ for the Litim-cutoff and ${\Phi }_1^1(0)={\pi }^2/6$ for the exponential cutoff. This dependence is expected to cancel against regulator-dependence of gravitational fixed-point values (at least at the level of physical observables).

For the Abelian gauge coupling the free fixed point is IR attractive in the absence of gravity, such that the observation of a nonvanishing Abelian gauge coupling in the IR presumably prevents an asymptotically free UV completion of the SM (Gell-Mann and Low, 1954). The quantum gravity contribution is the same as in the non-Abelian case (cf. Equation 55), thus

$\begin{array}{ll}{\beta }_{g_Y}=-f_g{g}_Y+\frac{41}{6}\frac{g_Y^3}{16{\pi }^2}+\dots & (56)\end{array}$

Fixed points of Equation (56) lie at

$\begin{array}{ll}{g}_{Y,*1}=0,g_{Y,*2}=\sqrt{\frac{f_{g}6·16{\pi }^2}{41}}.& (57)\end{array}$

The first is IR repulsive, the second IR attractive. If it lies at small enough values, then higher-order terms remain negligible and Equation (56) suffices to analyze the consequences. According to Equation (56), the IR repulsive fixed point at g_{Y * 1} = 0 can be connected to a range of values for g_Y at the Planck scale¹⁴. However, no values above an upper bound, g_Y = g_{Y * 2}, can be reached, as g_{Y * 2} is IR attractive, cf. Figure 11. Only one unique trajectory emanates from g_{Y * 2}. Along this trajectory, g_Y(k) = const until quantum-gravity contributions switch off below the Planck scale, where f_g quickly drops to tiny values and SM fields drive the flow. Unlike in the SM without the gravity-extension, the initial condition for the RG flow of g_Y is fixed at the Planck scale. Testing whether this results in an observationally viable value at the electroweak scale constitutes a strong observational test of the model. It also highlights that confronting quantum gravity with observations might be possible without reaching Planckian energies.

FIGURE 11

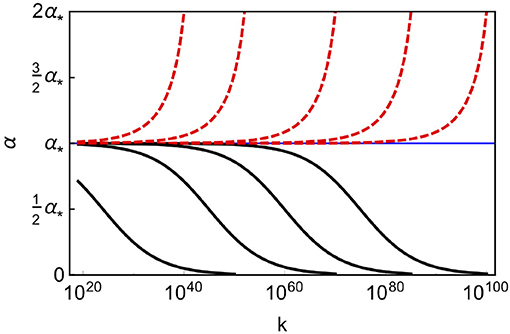
Figure 11. The transplanckian RG flow for $\alpha =g_Y^2/(4\pi )$ described by Equation (56) features trajectories emanating from the free fixed point (black, continuous line), which approach the interacting fixed point at α_*. One unique trajectories (blue, thin line) is the fixed-point trajectory for the interacting fixed point. UV unsafe trajectories are pulled toward the IR fixed point as well (red, dashed lines). Adapted from Eichhorn et al. (2018d).

The fixed-point structure underlying such “retrodictions” was found for the Abelian gauge coupling in Harst and Reuter (2011), further explored in Eichhorn and Versteegen (2018), cf. right panel in Figure 12 and extended to a GUT setting in Eichhorn et al. (2018d).

FIGURE 12

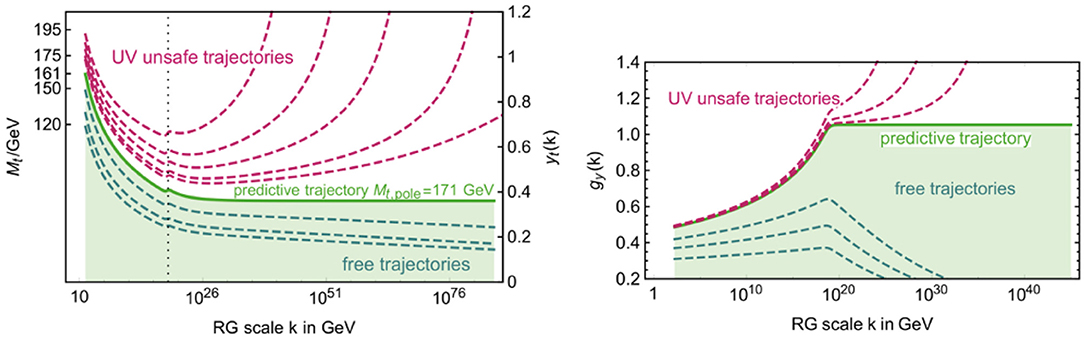
Figure 12. From Eichhorn and Held (2018) and Eichhorn and Versteegen (2018). Based on the beta functions (Equations 56, 58) with f_g > 0 and f_y > 0, respectively, an IR attractive fixed point results in a unique trajectory and serves as an upper bound.

FIGURE 13

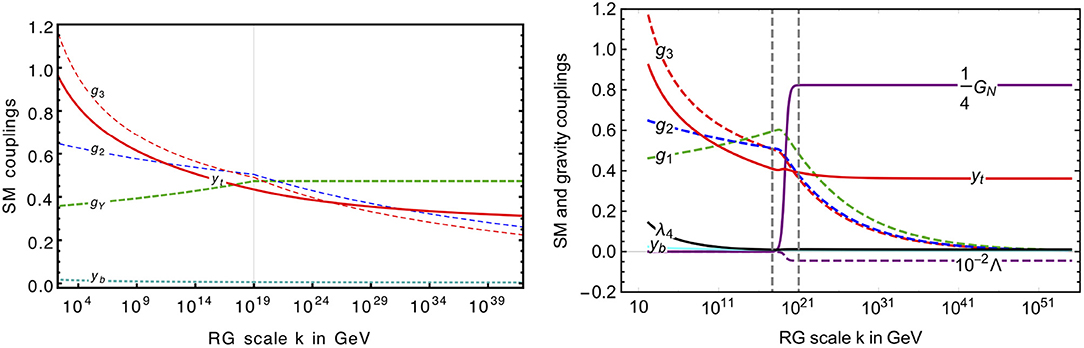
Figure 13. Both panels: RG flows in an approximation as in Equation (56), see Eichhorn and Held (2018) and Eichhorn and Held (2018) for details. Left panel: Flow of gauge couplings and top and bottom Yukawa with quantum-gravity parameterized by $f_g=9.8·10^{-3}$ and $f_y=1.13·10^{-4}$ above the Planck scale and f_g = 0 = f_y below the Planck scale as in Eichhorn and Held (2018). Right panel: Standard-Model RG flow including running gravitational couplings as in Donà et al. (2014) and is taken from Eichhorn and Held (2018).

In Zanusso et al. (2010); Vacca and Zanusso (2010); Oda and Yamada (2016); Eichhorn et al. (2016); Eichhorn and Held (2017); and Hamada and Yamada (2017), the gravity-contribution f_y to the Yukawa sector was calculated. Using beta functions of the form

$\begin{array}{l}{\beta }_{y_{t(b)}}=\frac{y_{t(b)}}{16{\pi }^2}\left(\frac{3y_{b(t)}^2}{2}+\frac{9y_{t(b)}^2}{2}-\frac{9}{4}{g}_2^2-8g_3^2\right)-f_y{y}_{t(b)}\\ -\frac{3y_{t(b)}}{16{\pi }^2}\left(\frac{1}{36}+Y_{t(b)}^2\right)g_Y^2,& (58)\end{array}$

for the quarks of the third generation, with Y_t = 2/3, Y_b = −1/3, supplemented by the assumption that the gauge sector of the SM is asymptotically free, and gravitational fixed-point values from a background-approximation results in a uniquely fixed top mass of about 170 GeV (Eichhorn and Held, 2018), cf. left panel of Figure 12.

Intriguingly, the SM beta functions with gravity in the approximation defined by Equations (57, 58) also admit an interacting fixed point such that the top Yukawa, bottom Yukawa and Abelian gauge coupling are fixed uniquely. They reach IR values in the vicinity of the observed ones, if the two gravity contributions f_g and f_y take appropriate values (Eichhorn and Held, 2018). In this scenario, the difference between top mass and bottom mass is generated through an interacting fixed point induced by gravity due to their different charges.

The fixed-point structure could be simpler in the scalar sector. Asymptotically safe quantum gravity flattens the Higgs potential: If all other SM couplings are asymptotically free, a fixed point at vanishing Higgs potential exists in line with intact shift-symmetry (Eichhorn and Held, 2017). It is IR attractive (Narain and Percacci, 2010; Percacci and Vacca, 2015; Labus et al., 2016; Oda and Yamada, 2016; Hamada and Yamada, 2017; Eichhorn, 2018). This extends to the Higgs portal coupling to scalar dark matter (Eichhorn, 2018). Taking the corresponding fixed-point values λ_h* = 0 (for the Higgs quartic) and λ_hχ* = 0 (for the Higgs portal coupling) as initial conditions for the RG flow at the Planck scale, and setting all SM couplings to their observationally preferred Planck-scale values, one reaches a Higgs mass in the vicinity of the observed value, while the Higgs portal coupling remains zero at all scales. The first is a prediction (Shaposhnikov and Wetterich, 2010) put forward before the discovery of the Higgs at the LHC (Aad, 2012; Chatrchyan, 2012), see also Bezrukov et al. (2012). The second appears to be consistent with the non-detection of a scalar Higgs portal through direct searches (Athron et al., 2017; Aprile et al., 2018).

“Retrodictions” of SM couplings could be a much more generic consequence of quantum gravity than just of asymptotic safety as discussed in section 2.3.

5.2. Impact of Matter on Quantum Gravity – Backreaction Matters?

The impact of quantum fluctuations of matter on the gravitational fixed point has been studied in simple truncations. The corresponding theory space also contains non-minimal matter-curvature couplings (Narain and Percacci, 2010; Percacci and Vacca, 2015; Eichhorn and Lippoldt, 2017; Eichhorn et al., 2018e).

Matter fields deform the gravitational fixed point in truncations. Adding a small number of matter fields leads to the continued existence of a viable interacting fixed point. At larger number of matter fields, there are indications that further extensions of the truncation could be required (Meibohm et al., 2016; Eichhorn et al., 2018b).

Assuming that asymptotic safety in gravity is driven by antiscreening metric fluctuations inducing a fixed point in the Newton coupling, the matter contribution to β_G is critical. Specifically,

$\begin{array}{ll}{\beta }_G{|}_{\text{matter}}=N_S{G}^2{a}_S+N_D{G}^2{a}_D+N_V{G}^2{a}_V,& (59)\end{array}$

where a_S > 0 (Donà et al., 2014; Percacci and Vacca, 2015; Meibohm et al., 2016; Labus et al., 2016; Don‘a et al., 2016; Biemans et al., 2017; Alkofer and Saueressig, 2018; Eichhorn et al., 2018b), agreeing with perturbative studies for d = 2 + ϵ dimensions (Christensen and Duff, 1978) and studies of the one-loop effective action using heat-kernel techniques (Kabat, 1995; Larsen and Wilczek, 1996). Similarly, fermions screen the Newton coupling¹⁵ a_D > 0 (Donà et al., 2014; Meibohm et al., 2016; Eichhorn et al., 2018c), in agreement with perturbative studies (Kabat, 1995; Larsen and Wilczek, 1996). For vectors, a_V < 0 (Donà et al., 2014; Christiansen et al., 2017; Biemans et al., 2017; Alkofer and Saueressig, 2018; Eichhorn et al., 2018c), also found with perturbative techniques (Kabat, 1995; Larsen and Wilczek, 1996). Background and fluctuation results are in agreement on this result (for fluctuation results, it is crucial to include the anomalous dimensions Don‘a et al., 2016; Eichhorn et al., 2018b).

A strong indication for (near-perturbative) asymptotic safety in matter-gravity systems comes from a comparison (Eichhorn et al., 2018b,c) of distinct “avatars” of the Newton coupling (Don‘a et al., 2016). It can be read off from the three-graviton vertex as well as gravity-matter vertices, just like the gauge coupling in gauge theories. For a dimensionless gauge coupling in the perturbative regime, two-loop universality equates the different avatars. Beyond perturbation theory, the Slavnov-Taylor-identities relating the avatars become nontrivial. Simply put, the stronger quantum effects are, the less trivial are the relation of classically equal couplings. Eichhorn et al. (2018b,c) observe an effective universality of distinct avatars of the Newton coupling, which agree within an estimate of the systematic truncation error. This signals a near-perturbative nature of asymptotically safe gravity. Further, the delicate cancellations required between different contributions to the beta functions in order to achieve effective universality strongly point toward a physical fixed point instead of a truncation artifact.

6. Outlook

Asymptotically safe models are of inherent theoretical interest when it comes to a comprehensive understanding of fundamental quantum field theories. Exciting progress in the last few years even hints at a possibility of asymptotically safe extensions of the Standard Model – with or without gravity. In quantum gravity, the idea of asymptotic safety resonates with a wider effort to analyze quantum spacetime from a Renormalization Group point of view. Hence, the many intriguing open questions that remain to be answered in this area appear worth tackling, and the new (asymptotically safe) perspective on high-energy physics is exciting and potentially useful to explore.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I would like to thank all participants and speakers of the workshop Asymptotic safety in a dark universe at Perimeter Institute in June 2018, the conference Quantum spacetime and the Renormalization Group in Bad Honnef in June 2018 and the workshop on Quantum fields – from fundamental question to phenomenological applications at MITP in September 2018 for stimulating discussions, and in particular acknowledge helpful discussions with L. Freidel, D. Litim, J. Pawlowski, M. Reuter, F. Sannino and C. Wetterich that have informed this review. It is a particular pleasure to thank all current and past members of my research group for successful collaborations, inspiring discussions and for joining in the (only asymptotically safe) quest for quantum gravity. I acknowledge support by the DFG under grant no. Ei/1037-1.

Footnotes

1. ^ Models affected by the triviality problem can only hold up to arbitrarily high momentum scales if the coupling vanishes at all scales, rendering the models noninteracting, or trivial. Establishing triviality requires going beyond perturbation theory. Nonetheless, an intuitive understanding of the problem can be gained from perturbation theory, e.g., in scalar λϕ⁴ theory in four dimensions. The one-loop beta function for the quartic self-interaction λ is ${\beta }_{\lambda }=\#{\lambda }^2$, where # > 0 holds. Integrating the beta function leads to a logarithmic divergence. Pushing the scale Λ of the divergence (the Landau pole) to infinity requires λ₀ = λ(k₀) = 0, since $\Lambda /k_0=e^{\frac{1}{\#{\lambda }_0}}$.

2. ^ Weinberg (1980) motivates the focus on dimensionless couplings g_i instead of their dimensionful counterparts $\overline{g}$_i by requiring finiteness of observables. Measurable quantities at some energy scale E, e.g., a scattering cross-section σ, can be written as $\sigma =E^{\#}f(g_i)$, where # is the canonical dimension of σ, multiplied by a function of the dimensionless couplings g_i that enter. Herein the RG scale is equated to a physical energy scale. If the dimensionless couplings diverge at a finite energy scale, this typically entails divergences in physical quantities.

3. ^ To determine the basin of attraction of the fixed point, one numerically integrates the RG flow to generate full trajectories.

4. ^ The opposite sign convention is sometimes used in the literature.

5. ^ The enhanced symmetry in supergravity rules out many of these counterterms, shifting the expected order of divergence in the maximally supersymmetric theory to higher orders (Bern et al., 2017, 2018).

6. ^ In the higher-derivative theory with the additional invariants R² and $R_{\mu \nu }{R}^{\mu \nu }$ the marginal couplings are asymptotically free (Stelle, 1977; Fradkin and Tseytlin, 1982; Avramidi and Barvinsky, 1985). Around flat space, this theory features a kinetic instability (see Salvio, 2018) for a review. Breaking Lorentz symmetry allows to use higher-order spatial derivatives while keeping the action at second order in time derivatives (Horava, 2009), resulting in perturbatively renormalizability. Yet, the projectable version propagates an additional scalar that becomes nonperturbative in the IR. As the non-projectable version features a larger number of couplings, asymptotic freedom has only been established in 2+1 (Barvinsky et al., 2017) dimensions and not 3+1, as well as in the large N limit for N scalars coupled to Horava gravity (D'Odorico et al., 2014). Constraints from pulsars (Yagi et al., 2014) and gravitational waves from a neutron-star merger (Emir Gümrükçüoğlu et al., 2018) constrain these models.

7. ^ A variant of the Polchinski equation also provides support for the asymptotic-safety conjecture (de Alwis, 2018).

8. ^ A nontrivial wave-function renormalization (Eichhorn and Gies, 2010; Groh and Saueressig, 2010) and ghost terms beyond the Faddeev-Popov are generated by the flow and have nonvanishing fixed-point values (Eichhorn, 2013).

9. ^ A combined truncation of Gies et al. (2016) with the operators in Benedetti et al. (2009) remains to be explored.

10. ^ Results in the exponential parameterization even yield one relevant direction less (Ohta et al., 2016; de Brito et al., 2018).

11. ^ That four-fermion interactions are generated by quantum gravity fluctuations but remain finite implies that chiral symmetry, protecting the light fermions of the Standard Model, remains intact (see also Meibohm and Pawlowski, 2016; Eichhorn and Held, 2017). The effective background curvature in the UV can nevertheless break chiral symmetry (Gies and Martini, 2018).

12. ^ In d ≠ 4, where specific matter models feature interacting fixed points, it is an intriguing question whether a new, combined universality class for matter and asymptotically safe gravity exists (see e.g., Elizalde et al., 1996; Percacci and Vacca, 2015; Labus et al., 2016).

13. ^ Notwithstanding arguments that suggest that quantum gravity should break global symmetries (Kallosh et al., 1995), studies of the FRG flow in truncations indicate the opposite result. This might be tied to the potential existence of black-hole remnants in asymptotic safety (Bonanno and Reuter, 2000; Falls et al., 2012). This implies that, e.g., Standard-Model couplings do not feature a contribution ~#₂, only a term ~#₁.

14. ^ Couplings that are asymptotically free, not asymptotically safe, already run at transplanckian scales.

15. ^ For the background Newton coupling, this is more subtle: Choosing to impose the regulator on the spectrum of ∇², or on /∇² = ∇² − R/4 results in a different sign of the fermionic contribution to the running of G (Dona and Percacci, 2013 see also Alkofer, 2018; Alkofer and Saueressig, 2018). This highlights that the (unphysical) background-field dependence of the regulator can alter results in the background approximation in simple truncations, suggesting the need for a fluctuation calculation. The first choice agrees with the result from fluctuations calculations.

References

Aad, G. (2012). Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012:716. doi: 10.1016/j.physletb.2012.08.020

CrossRef Full Text | Google Scholar

Abel, S., and Sannino, F. (2017a). Radiative symmetry breaking from interacting UV fixed points. Phys. Rev. D 96:056028. doi: 10.1103/PhysRevD.96.056028

CrossRef Full Text | Google Scholar

Abel, S., and Sannino, F. (2017b). Framework for an asymptotically safe standard model via dynamical breaking. Phys. Rev. D 96:055021. doi: 10.1103/PhysRevD.96.055021

CrossRef Full Text | Google Scholar

Adeifeoba, A., Eichhorn, A., and Platania, A. (2018). Towards conditions for black-hole singularity-resolution in asymptotically safe quantum gravity. arXiv:1808.03472 [gr-qc].

Google Scholar

Aida, T., and Kitazawa, Y. (1997). Two loop prediction for scaling exponents in (2+epsilon)-dimensional quantum gravity. Nucl. Phys. B 491:427. doi: 10.1016/S0550-3213(97)00091-6

CrossRef Full Text | Google Scholar

Aida, T., Kitazawa, Y., Kawai, H., and Ninomiya, M. (1994). Conformal invariance and renormalization group in quantum gravity near two-dimensions. Nucl. Phys. B 427:158. doi: 10.1016/0550-3213(94)90273-9

CrossRef Full Text | Google Scholar

Akerib, D. S., Alsum, S., Araújo, H. M., Bai, X., Bailey, A. J., Balajthy, J., et al. (2017). Results from a search for dark matter in the complete LUX exposure. Phys. Rev. Lett. 118:021303. doi: 10.1103/PhysRevLett.118.021303

PubMed Abstract | CrossRef Full Text | Google Scholar

Alanne, T., and Blasi, S. (2018). The abelian gauge-Yukawa β-functions at large N_f. arXiv:1808.03252 [hep-ph].

Alanne, T., and Blasi, S. (2018). The β-function for Yukawa theory at large N_f. JHEP 1808:081.

Alkofer, N. (2018). Asymptotically safe f(R)-gravity coupled to matter II: global solutions. arXiv:1809.06162 [hep-th].

Alkofer, N., and Saueressig, F. (2018). Asymptotically safe f(R)-gravity coupled to matter I: the polynomial case arXiv:1802.00498 [hep-th]

Altarelli, G., and Isidori, G. (1994). Lower limit on the Higgs mass in the standard model: an Update. Phys. Lett. B 337:141. doi: 10.1016/0370-2693(94)91458-3

CrossRef Full Text | Google Scholar

Ambjorn, J., Coumbe, D., Gizbert-Studnicki, J., Gorlich, A., and Jurkiewicz, J. (2017). New higher-order transition in causal dynamical triangulations. Phys. Rev. D 95:124029. doi: 10.1103/PhysRevD.95.124029

CrossRef Full Text | Google Scholar

Ambjorn, J., Durhuus, B., and Jonsson, T. (1991). Three-dimensional simplicial quantum gravity and generalized matrix models. Mod. Phys. Lett. A 6:1133. doi: 10.1142/S0217732391001184

CrossRef Full Text | Google Scholar

Ambjorn, J., Görlich, A., Jurkiewicz, J., Kreienbuehl, A., and Loll, R. (2014). Renormalization group flow in CDT. Class. Quant. Grav. 31:165003. doi: 10.1088/0264-9381/31/16/165003

CrossRef Full Text | Google Scholar

Ambjorn, J., Jordan, S., Jurkiewicz, J., and Loll, R. (2011). A second-order phase transition in CDT. Phys. Rev. Lett. 107:211303. doi: 10.1103/PhysRevLett.107.211303

CrossRef Full Text | Google Scholar

Ambjorn, J., Jordan, v, Jurkiewicz, J., and Loll, R. (2012). Second- and first-order phase transitions in CDT. Phys. Rev. D 85:124044. doi: 10.1103/PhysRevD.85.124044

CrossRef Full Text | Google Scholar

Ambjorn, J., Jurkiewicz, J., and Loll, R. (2000). A nonperturbative lorentzian path integral for gravity. Phys. Rev. Lett. 85:924. doi: 10.1103/PhysRevLett.85.924

PubMed Abstract | CrossRef Full Text | Google Scholar

Ambjorn, J., Jurkiewicz, J., and Loll, R. (2001). Dynamically triangulating lorentzian quantum gravity. Nucl. Phys. B 610:347. doi: 10.1016/S0550-3213(01)00297-8

CrossRef Full Text | Google Scholar

Anber, M. M., and Donoghue, J. F. (2012) On the running of the gravitational constant. Phys. Rev. D 85:104016. doi: 10.1103/PhysRevD.85.104016

CrossRef Full Text | Google Scholar

Anber, M. M., Donoghue, J. F., and El-Houssieny, M. (2011) Running couplings operator mixing in the gravitational corrections to coupling constants. Phys. Rev. D 83:124003. doi: 10.1103/PhysRevD.83.124003

CrossRef Full Text | Google Scholar

Antipin, O., Dondi, N. A., Sannino, F., Thomsen, A. E., and Wang, Z. W. (2018a). Gauge-Yukawa theories: beta functions at large N_f. arXiv:1803.09770 [hep-ph].

Antipin, O., Dondi, N. A., Sannino, F., and Thomsen, A. E. (2018b). The a-theorem at large N_f. arXiv:1808.00482 [hep-th].

Google Scholar

Antipin, O., Gillioz, M., Mølgaard, E., and Sannino, F. (2013). The a theorem for gauge-Yukawa theories beyond Banks-Zaks fixed point. Phys. Rev. D 87:125017. doi: 10.1103/PhysRevD.87.125017

CrossRef Full Text | Google Scholar

Antipin, O., and Sannino, F. (2017). Conformal window 2.0: the large N_f safe story. arXiv:1709.02354 [hep-ph].

Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Althueser, L., Amaro, F. D., et al. (2018). Dark matter search results from a one ton-year exposure of XENON1T. Phys. Rev. Lett. 121:111302. doi: 10.1103/PhysRevLett.121.111302

PubMed Abstract | CrossRef Full Text | Google Scholar

Arici, F., Becker, D., Ripken, C., Saueressig, F., and van Suijlekom, W. D. (2017). Reflection positivity in higher derivative scalar theories. arXiv:1712.04308 [hep-th].

Google Scholar

Ashtekar, A., and Lewandowski, J. (1997). Quantum theory of geometry. 1: Area operators. Class. Q. Grav. 14:A55. doi: 10.1088/0264-9381/14/1A/006

CrossRef Full Text

Ashtekar, A., Reuter, M., and Rovelli, C. (2014). From general relativity to quantum gravity. arXiv:1408.4336 [gr-qc].

Google Scholar

Athron, P., Balázs, C., Bringmann, T., Buckley, A., Chrzaszcz, M., Conrad, J., et al. (2017). Status of the scalar singlet dark matter model. Eur. Phys. J. C. 77:568. doi: 10.1140/epjc/s10052-017-5113-1

CrossRef Full Text | Google Scholar

Avramidi, I. G., and Barvinsky, A. O. (1985). Asymptotic freedom in higher derivative quantum gravity. Phys. Lett. 159B:269. doi: 10.1016/0370-2693(85)90248-5

CrossRef Full Text | Google Scholar

Bahr, B., and Steinhaus, S. (2016). Numerical evidence for a phase transition in 4d spin foam quantum gravity. Phys. Rev. Lett. 117: 141302. doi: 10.1103/PhysRevLett.117.141302

PubMed Abstract | CrossRef Full Text | Google Scholar

Bahr, B., and Steinhaus, S. (2017). Hypercuboidal renormalization in spin foam quantum gravity. Phys. Rev. D. 95:126006. doi: 10.1103/PhysRevD.95.126006

CrossRef Full Text | Google Scholar

Bajc, B., Dondi, N. A., and Sannino, F. (2018). Safe sUSY. JHEP 1803:005. doi: 10.1007/JHEP03(2018)005

CrossRef Full Text | Google Scholar

Bajc, B., and Sannino, F. (2016). Asymptotically safe grand unification. JHEP 1612:141. doi: 10.1007/JHEP12(2016)141

CrossRef Full Text | Google Scholar

Banks, T., and Zaks, A. (1982). On the phase structure of vector-like gauge theories with massless fermions. Nucl. Phys. B 196:189. doi: 10.1016/0550-3213(82)90035-9

CrossRef Full Text | Google Scholar

Bardeen, W. A., Lee, B. W., and Shrock, R. E. (1976). Phase transition in the nonlinear σ Model in 2 + ϵ dimensional continuum. Phys. Rev. D 14:985. doi: 10.1103/PhysRevD.14.985

CrossRef Full Text | Google Scholar

Barducci, D., Fabbrichesi, M., Nieto, C. M., Percacci, R., and Skrinjar, V. (2018). In search of a UV completion of the standard model-78.000 models that don't work. arXiv:1807.05584 [hep-ph]. doi: 10.1007/JHEP11(2018)057

CrossRef Full Text | Google Scholar

Barnaby, N., and Kamran, N. (2008). Dynamics with infinitely many derivatives: the initial value problem. JHEP 0802:008. doi: 10.1088/1126-6708/2008/02/008

CrossRef Full Text | Google Scholar

Barvinsky, A. O., Blas, D., Herrero-Valea, M., Sibiryakov, S. M., and Steinwachs, C. F. (2017). Hořava gravity is asymptotically free (in 2+1 dimensions). Phys. Rev. Lett. 119:211301. doi: 10.1103/PhysRevLett.119.211301

PubMed Abstract | CrossRef Full Text | Google Scholar

Becker, D., and Reuter, M. (2012). Running boundary actions, asymptotic safety, and black hole thermodynamics. JHEP 1207:172. doi: 10.1007/JHEP07(2012)172

CrossRef Full Text | Google Scholar

Becker, D., and Reuter, M. (2014). En route to background independence: broken split-symmetry, and how to restore it with bi-metric average actions. Annals Phys. 350:225. doi: 10.1016/j.aop.2014.07.023

CrossRef Full Text | Google Scholar

Becker, D., Ripken, C., and Saueressig, F. (2017). On avoiding Ostrogradski instabilities within Asymptotic Safety. JHEP 1712:121. doi: 10.1007/JHEP12(2017)121

CrossRef Full Text | Google Scholar

Ben Geloun, J., Koslowski, T. A., Oriti, D., and Pereira, A. D. (2018). Functional renormalization group analysis of rank 3 tensorial group field theory: the full quartic invariant truncation. Phys. Rev. D 97:126018. doi: 10.1103/PhysRevD.97.126018

CrossRef Full Text | Google Scholar

Benedetti, D. (2012). Asymptotic safety goes on shell. New J. Phys. 14:015005. doi: 10.1088/1367-2630/14/1/015005

CrossRef Full Text | Google Scholar

Benedetti, D., Ben Geloun, J., and Oriti, D. (2015). Functional renormalisation group approach for tensorial group field theory: a rank-3 model. JHEP 1503:084. doi: 10.1007/JHEP03(2015)084

CrossRef Full Text | Google Scholar

Benedetti, D., and Caravelli, F. (2012). The local potential approximation in quantum gravity. JHEP 1206:017. doi: 10.1007/JHEP06(2012)017

CrossRef Full Text | Google Scholar

Benedetti, D., and Gurau, R. (2012). Phase transition in dually weighted colored tensor models. Nucl. Phys. B 855:420. doi: 10.1016/j.nuclphysb.2011.10.015

CrossRef Full Text | Google Scholar

Benedetti, D., Machado, P. F., and Saueressig, F. (2009). Asymptotic safety in higher-derivative gravity. Mod. Phys. Lett. A 24:2233. doi: 10.1142/S0217732309031521

CrossRef Full Text | Google Scholar

Berges, J., Tetradis, N., and Wetterich, C. (2002). Nonperturbative renormalization flow in quantum field theory and statistical physics. Phys. Rept. 363, 223–386. doi: 10.1016/S0370-1573(01)00098-9

CrossRef Full Text | Google Scholar

Bern, Z., Carrasco, J. J., Chen, W. M., Edison, A., Johansson, H., Parra-Martinez, J., et al. (2018). Ultraviolet properties of ${N}=8$ supergravity at five Loops. arXiv:1804.09311 [hep-th].

Google Scholar

Bern, Z., Carrasco, J. J. M., Chen, W. M., Johansson, H., Roiban, R., and Zeng, M. (2017). Five-loop four-point integrand of N = 8 supergravity as a generalized double copy. Phys. Rev. D 96:126012. doi: 10.1103/PhysRevD.96.126012

CrossRef Full Text

Bezrukov, F., Kalmykov, M. Y., Kniehl, B. A., and Shaposhnikov, M. (2012). Higgs boson mass and new physics. JHEP 1210:140. doi: 10.1007/JHEP10(2012)140

CrossRef Full Text | Google Scholar

Bezrukov, F., and Shaposhnikov, M. (2015). Why should we care about the top quark Yukawa coupling? J. Exp. Theor. Phys. 120:335.

Biemans, J., Platania, A., and Saueressig, F. (2017). Renormalization group fixed points of foliated gravity-matter systems. JHEP 1705:093. doi: 10.1007/JHEP05(2017)093

CrossRef Full Text | Google Scholar

Biemans, J., Platania, A., and Saueressig, F. (2017). Quantum gravity on foliated spacetimes: asymptotically safe and sound. Phys. Rev. D 95:086013. doi: 10.1103/PhysRevD.95.086013

CrossRef Full Text | Google Scholar

Bombelli, L., Lee, J., Meyer, D., and Sorkin, R. (1987). Space-time as a causal set. Phys. Rev. Lett. 59:521. doi: 10.1103/PhysRevLett.59.521

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonanno, A., Contillo, A., and Percacci, R. (2011a). Inflationary solutions in asymptotically safe f(R) theories. Class. Quant. Grav. 28:145026. doi: 10.1088/0264-9381/28/14/145026

CrossRef Full Text

Bonanno, A., and Reuter, M. (1999). Quantum gravity effects near the null black hole singularity. Phys. Rev. D. 60:084011. doi: 10.1103/PhysRevD.60.084011

CrossRef Full Text | Google Scholar

Bonanno, A., and Reuter, M. (2000). Renormalization group improved black hole space-times. Phys. Rev. D. 62:043008. doi: 10.1103/PhysRevD.62.043008

CrossRef Full Text | Google Scholar

Bonanno, A., and Reuter, M. (2006). Spacetime structure of an evaporating black hole in quantum gravity. Phys. Rev. D. 73:083005. doi: 10.1103/PhysRevD.73.083005

CrossRef Full Text | Google Scholar

Bonanno, A., and Reuter, M. (2008). Primordial entropy production and lambda-driven inflation from quantum Einstein gravity. J. Phys. Conf. Ser. 140:012008. doi: 10.1088/1742-6596/140/1/012008

CrossRef Full Text | Google Scholar

Bonanno, A., and Reuter, M. (2011b). Entropy production during asymptotically safe inflation. Entropy 13:274. doi: 10.3390/e13010274

CrossRef Full Text | Google Scholar

Bonanno, A., and Saueressig, F. (2017). Asymptotically safe cosmology–a status report. Comptes Rendus Physique 18:254. doi: 10.1016/j.crhy.2017.02.002

CrossRef Full Text | Google Scholar

Bond, A. D., Hiller, G., Kowalska, K., and Litim, D. F. (2017). Directions for model building from asymptotic safety. JHEP 1708:004. doi: 10.1007/JHEP08(2017)004

CrossRef Full Text | Google Scholar

Bond, A. D., and Litim, D. F. (2017). Theorems for asymptotic safety of Gauge theories. Eur. Phys. J. C 77:429. doi: 10.1140/epjc/s10052-017-4976-5

CrossRef Full Text | Google Scholar

Bond, A. D., and Litim, D. F. (2017). Asymptotic safety guaranteed in supersymmetry. Phys. Rev. Lett. 119:211601. doi: 10.1103/PhysRevLett.119.211601

PubMed Abstract | CrossRef Full Text | Google Scholar

Bond, A. D., and Litim, D. F. (2018a). Price of asymptotic safety. arXiv:1801.08527 [hep-th].

Google Scholar

Bond, A. D., and Litim, D. F. (2018b). More asymptotic safety guaranteed. Phys. Rev. D 97:085008. doi: 10.1103/PhysRevD.97.085008

CrossRef Full Text | Google Scholar

Bond, A. D., Litim, D. F., Medina Vazquez, G., and Steudtner, T. (2018). UV conformal window for asymptotic safety. Phys. Rev. D 97:036019. doi: 10.1103/PhysRevD.97.036019

CrossRef Full Text | Google Scholar

Bowman, P. O., Heller, U. M., Leinweber, D. B. Parappilly, M. B., Sternbeck, A., von Smekal, L., et al. (2007). Scaling behavior and positivity violation of the gluon propagator in full QCD. Phys. Rev. D 76:094505. doi: 10.1103/PhysRevD.76.094505

CrossRef Full Text | Google Scholar

Branchina, V., and Messina, E. (2013). Stability, higgs boson mass and new physics. Phys. Rev. Lett. 111:241801. doi: 10.1103/PhysRevLett.111.241801

PubMed Abstract | CrossRef Full Text | Google Scholar

Braun, J. (2012). Fermion interactions and universal behavior in strongly interacting theories. J. Phys. G 39:033001. doi: 10.1088/0954-3899/39/3/033001

CrossRef Full Text | Google Scholar

Braun, J., Gies, H., and Scherer, D. D. (2011). Asymptotic safety: a simple example. Phys. Rev. D 83:085012. doi: 10.1103/PhysRevD.83.085012

CrossRef Full Text | Google Scholar

Brezin, E., and Zinn-Justin, J. (1992). Renormalization group approach to matrix models. Phys. Lett. B. 288:54. doi: 10.1016/0370-2693(92)91953-7

CrossRef Full Text | Google Scholar

Bridle, I. H., Dietz, J. A., and Morris, T. R. (2017). The local potential approximation in the background field formalism. JHEP 1403:093. doi: 10.1007/JHEP03(2014)093

CrossRef Full Text | Google Scholar

Brown, L. S. (1977). Stress tensor trace anomaly in a gravitational metric: scalar fields. Phys. Rev. D 15:1469. doi: 10.1103/PhysRevD.15.1469

CrossRef Full Text | Google Scholar

Buttazzo, D., Degrassi, G., Giardino, P. P., Giudice, G. F., Sala, F., Salvio, A., et al. (2013). Investigating the near-criticality of the Higgs boson. JHEP 1312:089. doi: 10.1007/JHEP12(2013)089

CrossRef Full Text | Google Scholar

Buyukbese, T., and Litim, D. F. (2017). Asymptotic safety of gauge theories beyond marginal interactions. PoS LATTICE 2016:233. doi: 10.22323/1.256.0233

CrossRef Full Text | Google Scholar

Calcagni, G., Eichhorn, A., and Saueressig, F. (2013). Probing the quantum nature of spacetime by diffusion. Phys. Rev. D 87:124028. doi: 10.1103/PhysRevD.87.124028

CrossRef Full Text | Google Scholar

Campostrini, M., Pelissetto, A., Rossi, P., and Vicari, E. (1999). Improved high temperature expansion and critical equation of state of three-dimensional Ising-like systems. Phys. Rev. E 60:3526. doi: 10.1103/PhysRevE.60.3526

PubMed Abstract | CrossRef Full Text | Google Scholar

Canet, L., Delamotte, B., Mouhanna, D., and Vidal, J. (2003). Nonperturbative renormalization group approach to the Ising model: a Derivative expansion at order partial**4. Phys. Rev.B 68:064421. doi: 10.1103/PhysRevB.68.064421

CrossRef Full Text | Google Scholar

Cardy, J. L. (1988). Is there a c theorem in four-dimensions? Phys. Lett. B 215:749. doi: 10.1016/0370-2693(88)90054-8

CrossRef Full Text

Carlip, S. (2017). Dimension and dimensional reduction in quantum gravity. Class. Quant. Grav. 34:193001. doi: 10.1088/1361-6382/aa8535

CrossRef Full Text | Google Scholar

Caswell, W. E. (1974). Asymptotic behavior of nonabelian gauge theories to two loop order. Phys. Rev. Lett. 33:244. doi: 10.1103/PhysRevLett.33.244

CrossRef Full Text | Google Scholar

Chatrchyan, S. (2012). Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716:30. doi: 10.1016/j.physletb.2012.08.021

CrossRef Full Text | Google Scholar

Christensen, S. M., and Duff, M. J. (1978). Quantum gravity in two + ϵ dimensions. Phys. Lett. 79B:213. doi: 10.1016/0370-2693(78)90225-3

CrossRef Full Text | Google Scholar

Christiansen, N., and Eichhorn, A. (2017). An asymptotically safe solution to the U(1) triviality problem. Phys. Lett. B. 770:154. doi: 10.1016/j.physletb.2017.04.047

CrossRef Full Text | Google Scholar

Christiansen, N., Eichhorn, A., and Held, A. (2017). Is scale-invariance in gauge-Yukawa systems compatible with the graviton? Phys. Rev. D 96:084021. doi: 10.1103/PhysRevD.96.084021

CrossRef Full Text

Christiansen, N., Falls, K., Pawlowski, J. M., and Reichert, M. (2018). Curvature dependence of quantum gravity. Phys. Rev. D 97:046007. doi: 10.1103/PhysRevD.97.046007

CrossRef Full Text | Google Scholar

Christiansen, N., Knorr, B., Meibohm, J., Pawlowski, J. M., and Reichert, M. (2015). Local Quantum Gravity. Phys. Rev. D 92:121501. doi: 10.1103/PhysRevD.92.121501

CrossRef Full Text | Google Scholar

Christiansen, N., Knorr, B., Pawlowski, J. M., and Rodigast, A. (2016). Global flows in quantum gravity. Phys. Rev. D 93:044036. doi: 10.1103/PhysRevD.93.044036

CrossRef Full Text | Google Scholar

Christiansen, N., Litim, D. F., Pawlowski, J. M., and Reichert, M. (2017). One force to rule them all: asymptotic safety of gravity with matter. arXiv:1710.04669 [hep-th].

Google Scholar

Christiansen, N., Litim, D. F., Pawlowski, J. M., and Rodigast, A. (2017). Fixed points and infrared completion of quantum gravity. Phys. Lett. B 728:114. doi: 10.1016/j.physletb.2013.11.025

CrossRef Full Text | Google Scholar

Codello, A., Demmel, M., and Zanusso, O. (2014). Scheme dependence and universality in the functional renormalization group. Phys. Rev. D 90:027701. doi: 10.1103/PhysRevD.90.027701

CrossRef Full Text | Google Scholar

Codello, A., and D'Odorico, G. (2015). Scaling and renormalization in two dimensional quantum gravity. Phys. Rev. D 92:024026. doi: 10.1103/PhysRevD.92.024026

CrossRef Full Text | Google Scholar

Codello, A., D'Odorico, G., and Pagani, C. (2014). Consistent closure of renormalization group flow equations in quantum gravity. Phys. Rev. D. 89:081701. doi: 10.1103/PhysRevD.89.081701

CrossRef Full Text | Google Scholar

Codello, A., Langæble, K., Litim, D. F., and Sannino, F. (2016). Conformal Gauge-Yukawa theories away from four dimensions. JHEP 1607:118. doi: 10.1007/JHEP07(2016)118

CrossRef Full Text | Google Scholar

Codello, A., and Percacci, R. (2006). Fixed points of higher derivative gravity. Phys. Rev. Lett. 97:221301. doi: 10.1103/PhysRevLett.97.221301

PubMed Abstract | CrossRef Full Text | Google Scholar

Codello, A., and Percacci, R. (2009). Fixed points of nonlinear sigma models in d>2. Phys. Lett. B 672:280. doi: 10.1016/j.physletb.2009.01.032

CrossRef Full Text | Google Scholar

Codello, A., Percacci, R., and Rahmede, C. (2009). Investigating the ultraviolet properties of gravity with a wilsonian renormalization group equation. Annals Phys. 324:414. doi: 10.1016/j.aop.2008.08.008

CrossRef Full Text | Google Scholar

Cucchieri, A., Mendes, T., and Taurines, A. R. (2005). Positivity violation for the lattice Landau gluon propagator. Phys. Rev. D 71:051902. doi: 10.1103/PhysRevD.71.051902

CrossRef Full Text | Google Scholar

Daum, J.-E., and Reuter, M. (2012). Renormalization group flow of the holst action. Phys. Lett. B 710:215. doi: 10.1016/j.physletb.2012.01.046

CrossRef Full Text | Google Scholar

Daum, J. E., Harst, U., and Reuter, M. (2010). Running gauge coupling in asymptotically safe quantum gravity. JHEP 1001:084. doi: 10.1007/JHEP01(2010)084

CrossRef Full Text | Google Scholar

Daum, J. E., and Reuter, M. (2013). Einstein-cartan gravity, asymptotic safety, and the running immirzi parameter. Annals Phys. 334:351. doi: 10.1016/j.aop.2013.04.002

CrossRef Full Text | Google Scholar

David, F. (1988). Conformal field theories coupled to 2D gravity in the conformal gauge. Mod. Phys. Lett. A 3:1651. doi: 10.1142/S0217732388001975

CrossRef Full Text | Google Scholar

de Alwis, S. P. (2018). Exact RG flow equations and quantum gravity. JHEP 1803:118. doi: 10.1007/JHEP03(2018)118

CrossRef Full Text | Google Scholar

De Alwis, S. P. (2018). Higher derivative corrections to lower order RG flow equations. arXiv:1809.04671 [hep-th].

Google Scholar

de Brito, G. P., Ohta, N., Pereira, A. D., Tomaz, A. A., and Yamada, M. (2018). Asymptotic safety and field parametrization dependence in the f(R) truncation. arXiv:1805.09656 [hep-th].

Google Scholar

de Calan, C., Faria da Veiga, P. A., Magnen, J., and Seneor, R. (1991). Constructing the three-dimensional gross-neveu model with a large number of flavor components. Phys. Rev. Lett. 66:3233. doi: 10.1103/PhysRevLett.66.3233

PubMed Abstract | CrossRef Full Text | Google Scholar

Delamotte, B. (2012). An introduction to the nonperturbative renormalization group. Lect. Notes Phys. 852:49. doi: 10.1007/978-3-642-27320-9_2

CrossRef Full Text | Google Scholar

Demmel, M., Saueressig, F., and Zanusso, O. (2012). Fixed-functionals of three-dimensional quantum Einstein Gravity. JHEP 1211:131. doi: 10.1007/JHEP11(2012)131

CrossRef Full Text | Google Scholar

Demmel, M., Saueressig, F., and Zanusso, O. (2015). A proper fixed functional for four-dimensional Quantum Einstein Gravity. JHEP 1508:113. doi: 10.1007/JHEP08(2015)113

CrossRef Full Text | Google Scholar

Denz, T., Pawlowski, J. M., and Reichert, M. (2018). Towards apparent convergence in asymptotically safe quantum gravity. Eur. Phys. J. C 78:336. doi: 10.1140/epjc/s10052-018-5806-0

CrossRef Full Text | Google Scholar

Deser, S., and Nieuwenhuizen, P. V. (1974a). Nonrenormalizability of quantized fermion gravitation interactions. Lett. Nuovo Cim. 2:218.

Google Scholar

Deser, S., and Nieuwenhuizen, P. V. (1974b). Nonrenormalizability of the quantized einstein-maxwell system. Phys. Rev. Lett. 32:245.

Google Scholar

Di Francesco, P., Ginsparg, P., H., and Zinn-Justin, J. (1995). 2-D Gravity and random matrices. Phys. Rept. 254:1. doi: 10.1016/0370-1573(94)00084-G

CrossRef Full Text | Google Scholar

Dietz, J. A., and Morris, T. R. (2013a). Asymptotic safety in the f(R) approximation. JHEP1301:108. doi: 10.1007/JHEP01(2013)108

CrossRef Full Text | Google Scholar

Dietz, J. A., and Morris, T. R. (2013b). Redundant operators in the exact renormalisation group and in the f(R) approximation to asymptotic safety. JHEP 1307:064. doi: 10.1007/JHEP07(2013)064

CrossRef Full Text | Google Scholar

Distler, J., and Kawai, H. (1989). Conformal field theory and 2D quantum gravity. Nucl. Phys. B 321:509. doi: 10.1016/0550-3213(89)90354-4

CrossRef Full Text | Google Scholar

Dittrich, B. (2017). “The continuum limit of loop quantum gravity-a framework for solving the theory,” in 100 Years of General Relativity Loop Quantum Gravity, eds A. Ashtekar and J. Pullin (Singapore: World Scientific Publishing), 153–179. doi: 10.1142/9789813220003_0006

CrossRef Full Text | Google Scholar

Dittrich, B., Mizera, S, and Steinhaus, S. (2016a). Decorated tensor network renormalization for lattice gauge theories and spin foam models. New J. Phys. 18:053009. doi: 10.1088/1367-2630/18/5/053009

CrossRef Full Text | Google Scholar

Dittrich, B., Schnetter, E., Seth, C. J., and Steinhaus, S. (2016b). Coarse graining flow of spin foam intertwiners. Phys. Rev. D. 94: 124050. doi: 10.1103/PhysRevD.94.124050

CrossRef Full Text | Google Scholar

D'Odorico, G., Saueressig, F., and Schutten, M. (2014). Asymptotic freedom in Horava-lifshitz gravity. Phys. Rev. Lett. 113:171101. doi: 10.1103/PhysRevLett.113.171101

PubMed Abstract | CrossRef Full Text | Google Scholar

Don‘a, P., Eichhorn, A., Labus, P., and Percacci, R. (2016). Asymptotic safety in an interacting system of gravity and scalar matter. Phys. Rev. D. 93:044049. doi: 10.1103/PhysRevD.93.044049

CrossRef Full Text | Google Scholar

Donà, P., Eichhorn, A., and Percacci, R. (2014). Matter matters in asymptotically safe quantum gravity. Phys. Rev. D 89:084035. doi: 10.1103/PhysRevD.89.084035

CrossRef Full Text | Google Scholar

Dona, P., and Percacci, R. (2013). Functional renormalization with fermions and tetrads. Phys. Rev. D. 87:045002. doi: 10.1103/PhysRevD.87.045002

CrossRef Full Text | Google Scholar

Dondi, N. A., Prochazka, V., and Sannino, V (2018). Conformal Data of fundamental Gauge-Yukawa Theories. Phys. Rev. D 98:045002. doi: 10.1103/PhysRevD.98.045002

CrossRef Full Text | Google Scholar

Donoghue, J. F. (1994a). Leading quantum correction to the Newtonian potential. Phys. Rev. Lett. 72:2996. doi: 10.1103/PhysRevLett.72.2996

PubMed Abstract | CrossRef Full Text | Google Scholar

Donoghue, J. F. (1994b). General relativity as an effective field theory: the leading quantum corrections. Phys. Rev. D 50:3874. doi: 10.1103/PhysRevD.50.3874

PubMed Abstract | CrossRef Full Text | Google Scholar

Donoghue, J. F. (2012). The effective field theory treatment of quantum gravity. AIP Conf. Proc. 1483:73. doi: 10.1063/1.4756964

CrossRef Full Text | Google Scholar

Dou, D., and Percacci, R. (1998). The running gravitational couplings. Class. Q. Grav. 15:3449. doi: 10.1088/0264-9381/15/11/011

CrossRef Full Text | Google Scholar

Dowker, F. (2013). Introduction to causal sets and their phenomenology. Gen. Rel. Grav. 45:1651. doi: 10.1007/s10714-013-1569-y

CrossRef Full Text | Google Scholar

Ebert, D., Plefka, J., and Rodigast, A. (2008). Absence of gravitational contributions to the running Yang-Mills coupling Phys. Lett. B. 660:579. doi: 10.1016/j.physletb.2008.01.037

CrossRef Full Text

Ebert, D., Plefka, J., and Rodigast, A. (2009). Gravitational contributions to the running yang-mills coupling in large extra-dimensional brane worlds. JHEP 0902:028. doi: 10.1088/1126-6708/2009/02/028

CrossRef Full Text | Google Scholar

Eichhorn, A. (2012). Quantum-gravity-induced matter self-interactions in the asymptotic-safety scenario. Phys. Rev. D. 86:105021. doi: 10.1103/PhysRevD.86.105021

CrossRef Full Text | Google Scholar

Eichhorn, A. (2013). Faddeev-popov ghosts in quantum gravity beyond perturbation theory. Phys. Rev. D 87:124016. doi: 10.1103/PhysRevD.87.124016

CrossRef Full Text | Google Scholar

Eichhorn, A. (2015). The renormalization group flow of unimodular f(R) gravity. JHEP 1504:096. doi: 10.1007/JHEP04(2015)096

CrossRef Full Text | Google Scholar

Eichhorn, A. (2018a). Status of the asymptotic safety paradigm for quantum gravity and matter. Found. Phys. 48:1407. doi: 10.1007/s10701-018-0196-6

CrossRef Full Text | Google Scholar

Eichhorn, A. (2018b). Towards coarse graining of discrete Lorentzian quantum gravity. Class. Quant. Grav. 35:044001. doi: 10.1088/1361-6382/aaa0a3

CrossRef Full Text | Google Scholar

Eichhorn, A., and Gies, H. (2010). Ghost anomalous dimension in asymptotically safe quantum gravity. Phys. Rev. D 81:104010. doi: 10.1103/PhysRevD.81.104010

CrossRef Full Text | Google Scholar

Eichhorn, A., and Gies, H. (2011). Light fermions in quantum gravity. New J. Phys. 13:125012. doi: 10.1088/1367-2630/13/12/125012

CrossRef Full Text | Google Scholar

Eichhorn, A., Gies, H., Jaeckel, J., Plehn, T., Scherer, M. M., and Sondenheimer, R. (2015). The higgs mass and the scale of new physics. JHEP 1504:022. doi: 10.1007/JHEP04(2015)022

CrossRef Full Text | Google Scholar

Eichhorn, A., Hamada, Y., Lumma, J., and Yamada, M. (2018). Quantum gravity fluctuations flatten the Planck-scale higgs potential. Phys. Rev. D. 97:086004. doi: 10.1103/PhysRevD.97.086004

CrossRef Full Text | Google Scholar

Eichhorn, A., and Held, A. (2017). Viability of quantum-gravity induced ultraviolet completions for matter. Phys. Rev. D. 96:086025. doi: 10.1103/PhysRevD.96.086025

CrossRef Full Text | Google Scholar

Eichhorn, A., and Held, A. (2018). Mass difference for charged quarks from quantum gravity. Phys. Rev. Lett. 121:151302. doi: 10.1103/PhysRevLett.121.151302

PubMed Abstract | CrossRef Full Text | Google Scholar

Eichhorn, A., and Held, A. (2018). Top mass from asymptotic safety. Phys. Lett. B 777:217. doi: 10.1016/j.physletb.2017.12.040

CrossRef Full Text | Google Scholar

Eichhorn, A., Held, A., and Griend, P. V. (2018a). Asymptotic safety in the dark. arXiv:1802.08589 [hep-ph].

Google Scholar

Eichhorn, A., Held, A., and Pawlowski, J. M. (2016). Quantum-gravity effects on a Higgs-Yukawa model. Phys. Rev. D. 94:104027. doi: 10.1103/PhysRevD.94.104027

CrossRef Full Text | Google Scholar

Eichhorn, A., Held, A., and Wetterich, C. (2018d). Quantum-gravity predictions for the fine-structure constant. Phys. Lett. B 782:198. doi: 10.1016/j.physletb.2018.05.016

CrossRef Full Text | Google Scholar

Eichhorn, A., Janssen, L., and Scherer, M. M. (2016). Critical O(N) models above four dimensions: small-N solutions and stability. Phys. Rev. D 93:125021. doi: 10.1103/PhysRevD.93.125021

CrossRef Full Text | Google Scholar

Eichhorn, A., and Koslowski, T. (2013). Continuum limit in matrix models for quantum gravity from the functional renormalization Group. Phys. Rev. D. 88:084016. doi: 10.1103/PhysRevD.88.084016

CrossRef Full Text

Eichhorn, A., and Koslowski, T. (2018). Flowing to the continuum in discrete tensor models for quantum gravity. Ann. Inst. H. Poincare Comb. Phys. Interact. 5:173. doi :10.4171/AIHPD/52

CrossRef Full Text | Google Scholar

Eichhorn, A., Labus, P., Pawlowski, J. M., and Reichert, M. (2018b). Effective universality in quantum gravity. arXiv:1804.00012 [hep-th].

Google Scholar

Eichhorn, A., and Lippoldt, S. (2017). Quantum gravity and standard-model-like fermions. Phys. Lett. B. 767:142. doi: 10.1016/j.physletb.2017.01.064

CrossRef Full Text | Google Scholar

Eichhorn, A., Lippoldt, S., Pawlowski, J. M., Reichert, M., and Schiffer, M. (2018c). How perturbative is quantum gravity? arXiv:1810.02828 [hep-th].

Eichhorn, A., Lippoldt, S., and Skrinjar, V. (2018e). Nonminimal hints for asymptotic safety. Phys. Rev. D. 97:026002. doi: 10.1103/PhysRevD.97.026002

CrossRef Full Text | Google Scholar

Eichhorn, A., and Versteegen, F. (2018). Upper bound on the abelian gauge coupling from asymptotic safety. JHEP 1801:030. doi: 10.1007/JHEP01(2018)030

CrossRef Full Text | Google Scholar

Elias-Miro, J., Espinosa, J. R., Giudice, G. F., Isidori, G., Riotto, A., and Strumia, A. (2012). Higgs mass implications on the stability of the electroweak vacuum. Phys. Lett. B 709:222. doi: 10.1016/j.physletb.2012.02.013

CrossRef Full Text | Google Scholar

Elizalde, E., Odintsov, S. D., and Romeo, A. (1996). Renormalization group properties of higher derivative quantum gravity with matter in (4-epsilon)-dimensions Nucl. Phys. B. 462:315. doi: 10.1016/0550-3213(95)00674-5

CrossRef Full Text

Ellis, G. F. R., van Elst, H., Murugan, J., and Uzan, J. P. (2011). On the trace-free Einstein equations as a viable alternative to general relativity. Class. Quant. Grav. 28:225007. doi: 10.1088/0264-9381/28/22/225007

CrossRef Full Text | Google Scholar

Ellis, J., and Mavromatos, N. E. (2012). On the interpretation of gravitational corrections to gauge couplings Phys. Lett. B. 711:139. doi: 10.1016/j.physletb.2012.04.005

CrossRef Full Text

Ellwanger, U. (1994). FLow equations for N point functions and bound states. Z. Phys. C 62:503. doi: 10.1007/BF01555911

CrossRef Full Text | Google Scholar

El-Showk, S., Paulos, M. F., Poland, D., Rychkov, S., Simmons-Duffin, D., and Vichi, A. (2012). Solving the 3D ising model with the conformal bootstrap. Phys. Rev. D 86:025022. doi: 10.1103/PhysRevD.86.025022

CrossRef Full Text | Google Scholar

El-Showk, S., Paulos, M. F., Poland, D., Rychkov, S., Simmons-Duffin, D., and Vichi, A. (2014). Solving the 3d ising model with the conformal bootstrap II. c-Minimization and precise critical exponents. J. Stat. Phys. 157:869. doi: 10.1007/s10955-014-1042-7

CrossRef Full Text | Google Scholar

Emir Gümrükçüoğlu, A., Saravani, M., and Sotiriou, T. P. (2018). Horava gravity after GW170817. Phys. Rev. D 97:024032. doi: 10.1103/PhysRevD.97.024032

CrossRef Full Text | Google Scholar

Esbensen, J. K., Ryttov, T. A., and Sannino, F. (2016). Quantum critical behavior of semisimple gauge theories. Phys. Rev. D 93:045009. doi: 10.1103/PhysRevD.93.045009

CrossRef Full Text | Google Scholar

Fabbrichesi, M., Percacci, R., Tonero, A., and Zanusso, O. (2011). Asymptotic safety and the gauged SU(N) nonlinear σ-model. Phys. Rev. D 83:025016. doi: 10.1103/PhysRevD.83.025016

CrossRef Full Text | Google Scholar

Falkenberg, S., and Odintsov, S. D. (1998). Gauge dependence of the effective average action in Einstein gravity. Int. J. Mod. Phys. A 13:607. doi: 10.1142/S0217751X98000263

CrossRef Full Text | Google Scholar

Falls, K. (2015). Renormalization of newton's constant. Phys. Rev. D 92:124057. doi: 10.1103/PhysRevD.92.124057

CrossRef Full Text | Google Scholar

Falls, K. (2017). Physical renormalization schemes and asymptotic safety in quantum gravity. Phys. Rev. D 96:126016. doi: 10.1103/PhysRevD.96.126016

CrossRef Full Text | Google Scholar

Falls, K., and Litim, D. F. (2014). Black hole thermodynamics under the microscope. Phys. Rev. D 89:084002. doi: 10.1103/PhysRevD.89.084002

CrossRef Full Text | Google Scholar

Falls, K., Litim, D. F., Nikolakopoulos, K., and Rahmede, C. (2013). A bootstrap towards asymptotic safety. arXiv:1301.4191 [hep-th].

Google Scholar

Falls, K., Litim, D. F., Nikolakopoulos, K., and Rahmede, C. (2016). Further evidence for asymptotic safety of quantum gravity. Phys. Rev. D 93:104022. doi: 10.1103/PhysRevD.93.104022

CrossRef Full Text | Google Scholar

Falls, K., Litim, D. F., and Raghuraman, A. (2012). Black holes and asymptotically safe gravity. Int. J. Mod. Phys. A. 27:1250019. doi: 10.1142/S0217751X12500194

CrossRef Full Text | Google Scholar

Fei, L., Giombi, S., and Klebanov, I. R. (2014). Critical O(N) models in 6−ϵ dimensions. Phys. Rev. D 90:025018. doi: 10.1103/PhysRevD.90.025018

CrossRef Full Text

Felipe, J. C. C., Brito, L. C. T., Sampaio, M., and Nemes, M. C. (2011). Quantum gravitational contributions to the beta function of quantum electrodynamics. Phys. Lett. B 700:86. doi: 10.1016/j.physletb.2011.04.061

CrossRef Full Text | Google Scholar

Finkelstein, D. R., Galiautdinov, A. A., and Baugh, J. E. (2001). Unimodular relativity and cosmological constant. J. Math. Phys. 42:340. doi: 10.1063/1.1328077

CrossRef Full Text | Google Scholar

Fischler, M., and Oliensis, J. (1982). Two loop corrections to the evolution of the higgs-yukawa coupling constant. Phys. Lett. 119B:385. doi: 10.1016/0370-2693(82)90695-5

CrossRef Full Text | Google Scholar

Floerchinger, S. (2012). Analytic continuation of functional renormalization group equations. JHEP 1205:021. doi: 10.1007/JHEP05(2012)021

CrossRef Full Text | Google Scholar

Floreanini, R., and Percacci, R. (1995). The renormalization group flow of the Dilaton potential. Phys. Rev. D 52:896. doi: 10.1103/PhysRevD.52.896

PubMed Abstract | CrossRef Full Text | Google Scholar

Folkerts, S., Litim, D. F., and Pawlowski, J. M. (2012). Asymptotic freedom of Yang-Mills theory with gravity. Phys. Lett. B. 709:234. doi: 10.1016/j.physletb.2012.02.002

CrossRef Full Text | Google Scholar

Ford, C., Jack, I., and Jones, D. R. T. (1992). The standard model effective potential at two loops. Nucl. Phys. B 387:373. doi: 10.1016/0550-3213(92)90165-8

CrossRef Full Text | Google Scholar

Fradkin, E. S., and Tseytlin, A. A. (1982). Renormalizable asymptotically free quantum theory of gravity. Nucl. Phys. B 201:469. doi: 10.1016/0550-3213(82)90444-8

CrossRef Full Text | Google Scholar

Friedan, D. (1980). Nonlinear models in two epsilon dimensions. Phys. Rev. Lett. 45: 1057. doi: 10.1103/PhysRevLett.45.1057

CrossRef Full Text | Google Scholar

Gastmans, R., Kallosh, R., and Truffin, C. (1978). Quantum gravity near two-dimensions. Nucl. Phys. B 133:417. doi: 10.1016/0550-3213(78)90234-1

CrossRef Full Text | Google Scholar

Gawedzki, K., and Kupiainen, A. (1985). Renormalizing the nonrenormalizable. Phys. Rev. Lett. 55:363. doi: 10.1103/PhysRevLett.55.363

CrossRef Full Text | Google Scholar

Gell-Mann, M., and Low, F. E. (1954). Quantum electrodynamics at small distances. Phys. Rev. 95:1300. doi: 10.1103/PhysRev.95.1300

CrossRef Full Text | Google Scholar

Gies, H. (2003). Renormalizability of gauge theories in extra dimensions. Phys. Rev. D 68:085015. doi: 10.1103/PhysRevD.68.085015

CrossRef Full Text | Google Scholar

Gies, H. (2012). Introduction to the functional RG and applications to gauge theories. Lect. Notes Phys. 852:287. doi: 10.1007/978-3-642-27320-9_6

CrossRef Full Text | Google Scholar

Gies, H., Gneiting, C., and Sondenheimer, R. (2014). Higgs mass bounds from renormalization flow for a simple yukawa model. Phys. Rev. D 89:045012. doi: 10.1103/PhysRevD.89.045012

CrossRef Full Text | Google Scholar

Gies, H., Knorr, B., and Lippoldt, S. (2015). Generalized parametrization dependence in quantum gravity. Phys. Rev. D 92:084020. doi: 10.1103/PhysRevD.92.084020

CrossRef Full Text | Google Scholar

Gies, H., Knorr, B., Lippoldt, S., and Saueressig, F. (2016). Gravitational two-loop counterterm is asymptotically safe. Phys. Rev. Lett. 116:211302. doi: 10.1103/PhysRevLett.116.211302

PubMed Abstract | CrossRef Full Text | Google Scholar

Gies, H., and Martini, R. (2018). Curvature bound from gravitational catalysis. Phys. Rev. D. 97:085017. doi: 10.1103/PhysRevD.97.085017

CrossRef Full Text | Google Scholar

Gies, H., Rechenberger, S., and Scherer, M. M. (2010). Towards an asymptotic-safety scenario for chiral Yukawa systems. Eur. Phys. J. C 66:403. doi: 10.1140/epjc/s10052-010-1257-y

CrossRef Full Text | Google Scholar

Gies, H., and Scherer, M. M. (2010). Asymptotic safety of simple Yukawa systems. Eur. Phys. J. C 66:387. doi: 10.1140/epjc/s10052-010-1256-z

CrossRef Full Text | Google Scholar

Gies, H., and Zambelli, L. (2017). Non-abelian higgs models: paving the way for asymptotic freedom. Phys. Rev. D 96:025003. doi: 10.1103/PhysRevD.96.025003

CrossRef Full Text | Google Scholar

Glaser, L. (2018). The ising model coupled to 2d orders. Class. Quant. Grav. 35:084001. doi: 10.1088/1361-6382/aab139

CrossRef Full Text | Google Scholar

Gliozzi, F., and Rago, A. (2014). Critical exponents of the 3d Ising and related models from Conformal Bootstrap. JHEP 1410:042. doi: 10.1007/JHEP10(2014)042

CrossRef Full Text | Google Scholar

Godfrey, N., and Gross, M. (1991). Simplicial quantum gravity in more than two-dimensions. Phys. Rev. D 43:1749. doi: 10.1103/PhysRevD.43.R1749

PubMed Abstract | CrossRef Full Text | Google Scholar

Gonzalez-Martin, S., and Martin, C. P. (2017). Do the gravitational corrections to the beta functions of the quartic and Yukawa couplings have an intrinsic physical meaning? Phys. Lett. B 773:585. doi: 10.1016/j.physletb.2017.09.011

CrossRef Full Text

Goroff, M. H., and Sagnotti, A. (1986). The ultraviolet behavior Of einstein gravity. Nucl. Phys. B 266:709.

Google Scholar

Gracey, J. A. (1996). The QCD beta function at O[1/N(f)]. Phys. Lett. B 373:178. doi: 10.1016/0370-2693(96)00105-0

CrossRef Full Text | Google Scholar

Groh, K., and Saueressig, F. (2010). Ghost wave-function renormalization in asymptotically safe quantum gravity. J. Phys. A 43:365403. doi: 10.1088/1751-8113/43/36/365403

CrossRef Full Text | Google Scholar

Gross, M. (1992). Tensor models and simplicial quantum gravity in >2-D. Nucl. Phys. Proc. Suppl. 25A:144. doi: 10.1016/S0920-5632(05)80015-5

CrossRef Full Text | Google Scholar

Guida, R., and Zinn-Justin, J. (1998). Critical exponents of the N vector model. J. Phys. A 31:8103. doi: 10.1088/0305-4470/31

CrossRef Full Text | Google Scholar

Gurau, R. (2011). The 1/N expansion of colored tensor models. Annales Henri Poincare 12:829. doi: 10.1007/s00023-011-0101-8

CrossRef Full Text | Google Scholar

Gurau, R. (2016). Invitation to random tensors. SIGMA 12:094. doi: 10.3842/SIGMA.2016.094

CrossRef Full Text | Google Scholar

Hamada, Y., and Yamada, M. (2017). Asymptotic safety of higher derivative quantum gravity non-minimally coupled with a matter system. JHEP 1708:070. doi: 10.1007/JHEP08(2017)070

CrossRef Full Text | Google Scholar

Hamber, H. W. (2009). Quantum gravity on the lattice. Gen. Relat. Grav. 41:817. doi: 10.1007/s10714-009-0769-y

CrossRef Full Text | Google Scholar

Hamber, H. W. (2015). Scaling exponents for lattice quantum gravity in four dimensions. Phys. Rev. D 92:064017. doi: 10.1103/PhysRevD.92.064017

CrossRef Full Text | Google Scholar

Hambye, T., and Riesselmann, K. (1997). Matching conditions and Higgs mass upper bounds revisited. Phys. Rev. D 55:7255. doi: 10.1103/PhysRevD.55.7255 [hep-ph/9610272].

CrossRef Full Text | Google Scholar

Hands, S., Kocic, A., and Kogut, J. B. (1993). Four fermi theories in fewer than four-dimensions. Annals Phys. 224:29. doi: 10.1006/aphy.1993.1039

CrossRef Full Text | Google Scholar

Harst, U., and Reuter, M. (2011). QED coupled to QEG. JHEP 1105, 119. doi: 10.1007/JHEP05(2011)119

CrossRef Full Text | Google Scholar

Harst, U., and Reuter, M. (2015). A new functional flow equation for Einstein–cartan quantum gravity. Annals Phys. 354:637. doi: 10.1016/j.aop.2015.01.006

CrossRef Full Text | Google Scholar

Harst, U., and Reuter, M. (2016). On selfdual spin-connections and asymptotic safety. Phys. Lett. B 753:395. doi: 10.1016/j.physletb.2015.12.016

CrossRef Full Text | Google Scholar

He, H. J., Kuang, Y. P., Wang, Q., and Yi, Y. P. (1992). Effective potential, renormalization, and nontrivial ultraviolet fixed point in D-dimensional four fermion theories (2 < D < 4) to order 1N in 1N expansion. Phys. Rev. D 45:4610. doi: 10.1103/PhysRevD.45.4610

CrossRef Full Text | Google Scholar

Henson, J. (2006). “The causal set approach to quantum gravity,” in Approaches to Quantum Gravity, ed D. Oriti (Cambridge), 393–413.

Google Scholar

Higashijima, K., and Itou, E. (2003). Three-dimensional nonlinear sigma models in the Wilsonian renormalization method. Prog. Theor. Phys. 110:563. doi: 10.1143/PTP.110.563

CrossRef Full Text | Google Scholar

Holdom, B. (2011). Large N flavor beta-functions: a recap. Phys. Lett. B 694:74. doi: 10.1016/j.physletb.2010.09.037

CrossRef Full Text | Google Scholar

Holdom, B., and Ren, J. (2016a). QCD analogy for quantum gravity. Phys. Rev. D 93:124030. doi: 10.1103/PhysRevD.93.124030

CrossRef Full Text | Google Scholar

Holdom, B., and Ren, J. (2016b). Quadratic gravity: from weak to strong. Int. J. Mod. Phys. D 25:1643004. doi: 10.1142/S0218271816430045

CrossRef Full Text | Google Scholar

Holthausen, M., Kubo, J., Lim, K. S., and Lindner, M. (2013). Electroweak and conformal symmetry breaking by a strongly coupled hidden sector. JHEP 1312:076. doi: 10.1007/JHEP12(2013)076

CrossRef Full Text | Google Scholar

Horava, P. (2009). Quantum gravity at a lifshitz point. Phys. Rev. D 79:084008. doi: 10.1103/PhysRevD.79.084008

CrossRef Full Text | Google Scholar

Intriligator, K., and Sannino, F. (2015). Supersymmetric asymptotic safety is not guaranteed. JHEP 1511:023. doi: 10.1007/JHEP11(2015)023

CrossRef Full Text | Google Scholar

Jack, I., and Jones, D. R. T. (1991). The epsilon expansion of two-dimensional quantum gravity. Nucl. Phys. B 358:695. doi: 10.1016/0550-3213(91)90430-6

CrossRef Full Text | Google Scholar

Jack, I., and Osborn, H. (1984). Background field calculations in curved space-time. 1. General formalism and application to scalar fields. Nucl. Phys. B 234:331. doi: 10.1016/0550-3213(84)90067-1

CrossRef Full Text | Google Scholar

Jack, I., and Osborn, H. (1990). Analogs for the c Theorem for Four-dimensional renormalizable field theories. Nucl. Phys. B 343:647. doi: 10.1016/0550-3213(90)90584-Z

CrossRef Full Text

Jack, I., and Osborn, H. (2014). Constraints on RG flow for four dimensional quantum field theories. Nucl. Phys. B 883:425. doi: 10.1016/j.nuclphysb.2014.03.018

CrossRef Full Text | Google Scholar

Jones, D. R. T. (1982). The two loop beta function for a G(1) x G(2) Gauge Theory. Phys. Rev. D 25:581. doi: 10.1103/PhysRevD.25.581

CrossRef Full Text | Google Scholar

Jordan, S., and Loll, R. (2013). Causal dynamical triangulations without preferred foliation. Phys. Lett. B. 724:155. doi: 10.1016/j.physletb.2013.06.007

CrossRef Full Text | Google Scholar

Kabat, D. N. (1995). Black hole entropy and entropy of entanglement. Nucl. Phys. B. 453:281. doi: 10.1016/0550-3213(95)00443-V

CrossRef Full Text | Google Scholar

Kallosh, R., Linde, A. D., Linde, D. A., and Susskind, L. (1995). Gravity and global symmetries. Phys. Rev. D. 52:912. doi: 10.1103/PhysRevD.52.912

PubMed Abstract | CrossRef Full Text | Google Scholar

Kawai, H., Kitazawa, Y., and Ninomiya, M. (1993a). Scaling exponents in quantum gravity near two-dimensions. Nucl. Phys. B 393:280. doi: 10.1016/0550-3213(93)90246-L

CrossRef Full Text | Google Scholar

Kawai, H., Kitazawa, Y., and Ninomiya, M. (1993b). Ultraviolet stable fixed point and scaling relations in (2+epsilon)-dimensional quantum gravity. Nucl. Phys. B 404:684. doi: 10.1016/0550-3213(93)90594-F

CrossRef Full Text | Google Scholar

Kawai, H., Kitazawa, Y., and Ninomiya, M. (1996). Renormalizability of quantum gravity near two-dimensions. Nucl. Phys. B 467:313. doi: 10.1016/0550-3213(96)00119-8

CrossRef Full Text | Google Scholar

Kawai, H., and Ninomiya, M. (1990). Renormalization group and quantum gravity. Nucl. Phys. B 336:115. doi: 10.1016/0550-3213(90)90345-E

CrossRef Full Text | Google Scholar

Khoze, V. V. (2013). Inflation and dark matter in the higgs portal of classically scale invariant standard model. JHEP 1311:215. doi: 10.1007/JHEP11(2013)215

CrossRef Full Text | Google Scholar

Kikukawa, Y., and Yamawaki, K. (1990). Ultraviolet fixed point structure of renormalizable four fermion theory in less than four-dimensions. Phys. Lett. B 234:497. doi: 10.1016/0370-2693(90)92046-L

CrossRef Full Text | Google Scholar

Knechtli, F., and Rinaldi, E. (2016). Extra-dimensional models on the lattice. Int. J. Mod. Phys. A 31:1643002. doi: 10.1142/S0217751X16430028

CrossRef Full Text | Google Scholar

Knorr, B., and Lippoldt, S. (2017). Correlation functions on a curved background. Phys. Rev. D. 96:065020. doi: 10.1103/PhysRevD.96.065020

CrossRef Full Text | Google Scholar

Koch, B., and Saueressig, F. (2014a). Structural aspects of asymptotically safe black holes. Class. Quant. Grav. 31:015006. doi: 10.1088/0264-9381/31/1/015006

CrossRef Full Text | Google Scholar

Koch, B., and Saueressig, F. (2014b). Black holes within asymptotic safety. Int. J. Mod. Phys. A 29:1430011. doi: 10.1142/S0217751X14300117

CrossRef Full Text | Google Scholar

Kofinas, G., and Zarikas, V. (2015). Avoidance of singularities in asymptotically safe quantum Einstein gravity. JCAP 1510:069. doi: 10.1088/1475-7516/2015/10/069

CrossRef Full Text | Google Scholar

Kofinas, G., and Zarikas, V. (2016). Asymptotically safe gravity and non-singular inflationary big bang with vacuum birth. Phys. Rev. D. 94:103514. doi: 10.1103/PhysRevD.94.103514

CrossRef Full Text | Google Scholar

Kopietz, P., Bartosch, L., and Schütz, F. (2010). Introduction to the functional renormalization group. Lect. Notes Phys. 798:1. doi: 10.1007/978-3-642-05094-7

CrossRef Full Text | Google Scholar

Kowalska, K., Bond, A., Hiller, G., and Litim, D. (2017). Towards an asymptotically safe completion of the standard model. PoS EPS HEP2017:542. doi: 10.22323/1.314.0542

CrossRef Full Text | Google Scholar

Kowalska, K., and Sessolo, E. M. (2018). Gauge contribution to the 1/N_F expansion of the Yukawa coupling beta function. JHEP 1804, 027. doi: 10.1007/JHEP04(2018)027

CrossRef Full Text

Krasnov, K., and Percacci, R. (2018). Gravity and unification: a review. Class. Quant. Grav. 35:143001. doi: 10.1088/1361-6382/aac58d

CrossRef Full Text | Google Scholar

Labus, P., Morris, T. R., and Slade, Z. H. (2016). Background independence in a background dependent renormalization group. Phys. Rev. D 94:024007. doi: 10.1103/PhysRevD.94.024007

CrossRef Full Text | Google Scholar

Labus, P., Percacci, R., and Vacca, G. P. (2016). Asymptotic safety in O(N) scalar models coupled to gravity. Phys. Lett. B. 753:274. doi: 10.1016/j.physletb.2015.12.022

CrossRef Full Text

Laiho, J., Bassler, S., Coumbe, D., Du, D., and Neelakanta, J. T. (2017). Lattice quantum gravity and asymptotic safety. Phys. Rev. D 96:064015. doi: 10.1103/PhysRevD.96.064015

CrossRef Full Text | Google Scholar

Laiho, J., and Coumbe, D. (2011). Evidence for asymptotic safety from lattice quantum gravity. Phys. Rev. Lett. 107:161301. doi: 10.1103/PhysRevLett.107.161301

PubMed Abstract | CrossRef Full Text | Google Scholar

Larsen, F., and Wilczek, F. (1996). Renormalization of black hole entropy and of the gravitational coupling constant. Nucl. Phys. B. 458:249. doi: 10.1016/0550-3213(95)00548-X

CrossRef Full Text | Google Scholar

Lauscher, O., and Reuter, M. (2002). Ultraviolet fixed point and generalized flow equation of quantum gravity. Phys. Rev. D 65:025013. doi: 10.1103/PhysRevD.65.025013

CrossRef Full Text | Google Scholar

Lauscher, O., and Reuter, M. (2002). Flow equation of quantum Einstein gravity in a higher derivative truncation. Phys. Rev. D 66:025026. doi: 10.1103/PhysRevD.66.025026

CrossRef Full Text | Google Scholar

Lauscher, O., and Reuter, M. (2005). Fractal spacetime structure in asymptotically safe gravity. JHEP 0510:050. doi: 10.1088/1126-6708/2005/10/050

CrossRef Full Text | Google Scholar

Lewandowski, A., Meissner, K. A., and Nicolai, H. (2018). Conformal standard model, leptogenesis and dark matter. Phys. Rev. D 97:035024. doi: 10.1103/PhysRevD.97.035024

CrossRef Full Text | Google Scholar

Lindner, M., Schmidt, S., and Smirnov, J. (2014). Neutrino masses and conformal electro-weak symmetry breaking. JHEP 1410:177. doi: 10.1007/JHEP10(2014)177

CrossRef Full Text | Google Scholar

Litim, D. F. (2000). Optimization of the exact renormalization group. Phys. Lett. B 486:92. doi: 10.1016/S0370-2693(00)00748-6

CrossRef Full Text | Google Scholar

Litim, D. F. (2001). Optimized renormalization group flows. Phys. Rev. D 64:105007. doi: 10.1103/PhysRevD.64.105007

CrossRef Full Text | Google Scholar

Litim, D. F. (2004). Fixed points of quantum gravity. Phys. Rev. Lett. 92:201301. doi: 10.1103/PhysRevLett.92.201301

PubMed Abstract | CrossRef Full Text | Google Scholar

Litim, D. F., Mojaza, M., and Sannino, F. (2016). Vacuum stability of asymptotically safe gauge-Yukawa theories. JHEP 1601:081. doi: 10.1007/JHEP01(2016)081

CrossRef Full Text | Google Scholar

Litim, D. F., and Pawlowski, J. M. (2002). Wilsonian flows and background fields. Phys. Lett. B 546:279. doi: 10.1016/S0370-2693(02)02693-X

CrossRef Full Text | Google Scholar

Litim, D. F., and Sannino, F. (2014). Asymptotic safety guaranteed. JHEP 1412:178. doi: 10.1007/JHEP12(2014)178

CrossRef Full Text | Google Scholar

Litim, D. F., and Zappala, D. (2011). Ising exponents from the functional renormalisation group. Phys. Rev. D 83:085009. doi: 10.1103/PhysRevD.83.085009

CrossRef Full Text | Google Scholar

Machacek, M. E., and Vaughn, M. T. (1983). Two loop renormalization group equations in a general quantum field theory. 1. Wave function renormalization. Nucl. Phys. B 222:83. doi: 10.1016/0550-3213(83)90610-7

CrossRef Full Text | Google Scholar

Machacek, M. E., and Vaughn, M. T. (1984). Two loop renormalization group equations in a general quantum field theory. 2. Yukawa Couplings. Nucl. Phys. B 236:221. doi: 10.1016/0550-3213(84)90533-9

CrossRef Full Text | Google Scholar

Machacek, M. E., and Vaughn, M. T. (1985). Two loop renormalization group equations in a general quantum field Theory. 3. Scalar quartic couplings. Nucl. Phys. B 249:70. doi: 10.1016/0550-3213(85)90040-9

CrossRef Full Text | Google Scholar

Machado, P. F., and Saueressig, F. (2008). On the renormalization group flow of f(R)-gravity. Phys. Rev. D 77:124045. doi: 10.1103/PhysRevD.77.124045

CrossRef Full Text | Google Scholar

Mackay, P. T., and Toms, D. J. (2010) Quantum gravity scalar fields. Phys. Lett. B. 684:251. doi: 10.1016/j.physletb.2009.12.032

CrossRef Full Text | Google Scholar

Mann, R., Meffe, J., Sannino, F., Steele, T., Wang, Z. W., and Zhang, C. (2017). Asymptotically safe standard model via vectorlike fermions. Phys. Rev. Lett. 119:261802. doi: 10.1103/PhysRevLett.119.261802

PubMed Abstract | CrossRef Full Text | Google Scholar

Manrique, E., Rechenberger, S., and Saueressig, F. (2011a). Asymptotically safe lorentzian gravity. Phys. Rev. Lett. 106:251302. doi: 10.1103/PhysRevLett.106.251302

PubMed Abstract | CrossRef Full Text | Google Scholar

Manrique, E., and Reuter, M. (2010). Bimetric truncations for quantum Einstein gravity and asymptotic safety. Annals Phys. 325:785. doi: 10.1016/j.aop.2009.11.009

CrossRef Full Text | Google Scholar

Manrique, E., Reuter, M., and Saueressig, F. (2011b). Matter induced bimetric actions for gravity. Annals Phys. 326:440. doi: 10.1016/j.aop.2010.11.003

CrossRef Full Text | Google Scholar

Manrique, E., Reuter, M., and Saueressig, F. (2011c). Bimetric renormalization group flows in quantum Einstein gravity. Annals Phys. 326: 463. doi: 10.1016/j.aop.2010.11.006

CrossRef Full Text | Google Scholar

Markkanen, T., Rajantie, A., and Stopyra, S. (2018). Cosmological aspects of higgs vacuum metastability arXiv:1809.06923 [astro-ph.CO].

Meibohm, J., and Pawlowski, J. M. (2016). Chiral fermions in asymptotically safe quantum gravity. Eur. Phys. J. C. 76, no. 5, 285. doi: 10.1140/epjc/s10052-016-4132-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Meibohm, J., Pawlowski, J. M., and Reichert, M. (2016) Asymptotic safety of gravity-matter systems. Phys. Rev. D. 93:084035. doi: 10.1103/PhysRevD.93.084035

CrossRef Full Text | Google Scholar

Meissner, K. A., and Nicolai, H. (2007). Conformal symmetry and the standard model. Phys. Lett. B 648:312. doi: 10.1016/j.physletb.2007.03.023

CrossRef Full Text | Google Scholar

Metzner, W., Salmhofer, M., Honerkamp, C., Meden, V., and Schönhammer, K. (2012). Functional renormalization group approach to correlated fermion systems. Rev. Mod. Phys. 84:299. doi: 10.1103/RevModPhys.84.299

CrossRef Full Text | Google Scholar

Mølgaard, E., and Sannino, F. (2017). Asymptotically safe and free chiral theories with and without scalars. Phys. Rev. D 96:056004. doi: 10.1103/PhysRevD.96.056004

CrossRef Full Text | Google Scholar

Molinaro, E., Sannino, F., and Wang, Z. W. (2018). Safe pati-salam. arXiv:1807.03669 [hep-ph].

Google Scholar

Morris, T. R. (1994). The exact renormalization group and approximate solutions. Int. J. Mod. Phys. A 9:2411.

Google Scholar

Morris, T. R. (2005). Renormalizable extra-dimensional models. JHEP 0501:2. doi: 10.1088/1126-6708/2005/01/002

CrossRef Full Text | Google Scholar

Morris, T. R. (2016). Large curvature and background scale independence in single-metric approximations to asymptotic safety. JHEP 1611:160. doi: 10.1007/JHEP11(2016)160

CrossRef Full Text | Google Scholar

Narain, G., and Percacci, R. (2010). Renormalization group flow in scalar-tensor theories. I. Class. Quant. Grav. 27:075001. doi: 10.1088/0264-9381/27/7/075001

CrossRef Full Text | Google Scholar

Narain, R., and Anishetty, R. (2013). Running couplings in quantum theory of gravity coupled with gauge fields. JHEP 1310:203. doi: 10.1007/JHEP10(2013)203

CrossRef Full Text | Google Scholar

Niedermaier, M. (2010). Gravitational fixed points and asymptotic safety from perturbation theory. Nucl. Phys. B 833:226. doi: 10.1016/j.nuclphysb.2010.01.016

CrossRef Full Text | Google Scholar

Niedermaier, M. R. (2009). Gravitational fixed points from perturbation theory. Phys. Rev. Lett. 103:101303. doi: 10.1103/PhysRevLett.103.101303

PubMed Abstract | CrossRef Full Text | Google Scholar

Nielsen, N. G., Sannino, F., and Svendsen, O. (2015). Inflation from asymptotically safe theories. Phys. Rev. D 91:103521. doi: 10.1103/PhysRevD.91.103521

CrossRef Full Text | Google Scholar

Nieto, C. M., Percacci, R., and Skrinjar, V. (2017). Split weyl transformations in quantum gravity. Phys. Rev. D 96:106019. doi: 10.1103/PhysRevD.96.106019 [arXiv:1708.09760 (gr-qc)].

CrossRef Full Text | Google Scholar

Nink, A., and Reuter, M. (2013). On the physical mechanism underlying Asymptotic Safety. JHEP 1301:062. doi: 10.1007/JHEP01(2013)062

CrossRef Full Text | Google Scholar

Nink, A., and Reuter, M. (2016). The unitary conformal field theory behind 2D Asymptotic Safety. JHEP 1602:167. doi: 10.1007/JHEP02(2016)167

CrossRef Full Text | Google Scholar

Nink, A., Reuter, M., and Saueressig, F. (2013). Asymptotic safety in quantum gravity. Scholarpedia 8:31015. doi: 10.4249/scholarpedia.31015

CrossRef Full Text | Google Scholar

Nishimura, J., Tamura, S., and Tsuchiya, A. (1994). R**2 gravity in (2+epsilon)-dimensional quantum gravity. Mod. Phys. Lett. A 9:3565. doi: 10.1142/S0217732394003403

CrossRef Full Text

Oda, K. y., and Yamada, M. (2016). Non-minimal coupling in higgs–yukawa model with asymptotically safe gravity. Class. Quant. Grav. 33:125011. doi: 10.1088/0264-9381/33/12/125011

CrossRef Full Text | Google Scholar

Ohta, N. (2017). Background scale independence in quantum gravity. PTEP 2017:033E02. doi: 10.1093/ptep/ptx020

CrossRef Full Text | Google Scholar

Ohta, N., Percacci, R., and Pereira, A. D. (2016). Gauges and functional measures in quantum gravity I: Einstein theory. JHEP 1606:115. doi: 10.1007/JHEP06(2016)115

CrossRef Full Text | Google Scholar

Ohta, N., Percacci, R., and Vacca, G. P. (2015). Flow equation for f(R) gravity and some of its exact solutions. Phys. Rev. D 92:061501. doi: 10.1103/PhysRevD.92.061501

CrossRef Full Text

Ohta, N., Percacci, R., and Vacca, G. P. (2016). Renormalization group equation and scaling solutions for f(R) gravity in exponential parametrization. Eur. Phys. J. C 76:46. doi: 10.1140/epjc/s10052-016-3895-1

CrossRef Full Text | Google Scholar

Ostrogradsky, M. (1985). Mémoires sur les équations différentielles, relatives au problème des isopérimétres. Mem. Acad. St. Petersbourg 6:385.

Google Scholar

Pagani, C., and Percacci, R. (2015). Quantum gravity with torsion and non-metricity. Class. Quant. Grav. 32:195019. doi: 10.1088/0264-9381/32/19/195019

CrossRef Full Text | Google Scholar

Pagani, C., and Reuter, M. (2018). Finite entanglement entropy in asymptotically safe quantum gravity. JHEP 1807:039. doi: 10.1007/JHEP07(2018)039

CrossRef Full Text | Google Scholar

Palanques-Mestre, A., and Pascual, P (1984). The 1/N⁻f expansion of the γ and beta functions in QED. Commun. Math. Phys. 95:277. doi: 10.1007/BF01212398

CrossRef Full Text | Google Scholar

Papenbrock, T., and Wetterich, C. (1995). Two loop results from one loop computations and nonperturbative solutions of exact evolution equations. Z. Phys. C 65:519. doi: 10.1007/BF01556140

CrossRef Full Text | Google Scholar

Pawlowski, J. M. (2007). Aspects of the functional renormalisation group. Annals Phys. 322:2831. doi: 10.1016/j.aop.2007.01.007

CrossRef Full Text | Google Scholar

Pawlowski, J. M., and Stock, D. (2018). Quantum improved schwarzschild-(A)dS and Kerr-(A)dS space-times. [arXiv:1807.10512 hep-th].

Google Scholar

Pawlowski, J. M., and Strodthoff, N. (2015). Real time correlation functions and the functional renormalization group. Phys. Rev. D 92:094009. doi: 10.1103/PhysRevD.92.094009

CrossRef Full Text | Google Scholar

Pelaggi, G. M., Plascencia, A. D., Salvio, A., Sannino, F., Smirnov, J., and Strumia, A. (2018). Asymptotically safe standard model extensions? Phys. Rev. D 97:095013. doi: 10.1103/PhysRevD.97.095013

CrossRef Full Text

Pelissetto, A., and Vicari, E. (2002). Critical phenomena and renormalization group theory. Phys. Rept. 368:549. doi: 10.1016/S0370-1573(02)00219-3

CrossRef Full Text | Google Scholar

Percacci, R. (2017). “An introduction to covariant quantum gravity and asymptotic safety,” in 100 years of General Relativity (Book 3), ed A. Ashtekar (Singapore: World Scientific Publishing).

Google Scholar

Percacci, R., and Vacca, G. P. (2014). Are there scaling solutions in the O(N)-models for large N in d > 4 ? Phys. Rev. D 90:107702. doi: 10.1103/PhysRevD.90.107702

CrossRef Full Text

Percacci, R., and Vacca, G. P. (2015). Search of scaling solutions in scalar-tensor gravity. Eur. Phys. J. C 75:188. doi: 10.1140/epjc/s10052-015-3410-0

CrossRef Full Text | Google Scholar

Percacci, R., and Vacca, G. P. (2017). The background scale ward identity in quantum gravity. Eur. Phys. J. C 77, 52. doi: 10.1140/epjc/s10052-017-4619-x

CrossRef Full Text | Google Scholar

Percacci, R., and Vacca, P. G. (2010). Asymptotic safety, emergence and minimal length. Class. Q. Grav. 27:245026 doi: 10.1088/0264-9381/27/24/245026

CrossRef Full Text | Google Scholar

Peskin, M. E. (1980). Critical point behavior Of the Wilson Loop. Phys. Lett. 94B:161. doi: 10.1016/0370-2693(80)90848-5

CrossRef Full Text | Google Scholar

Pica, C., and Sannino, F. (2011). UV and IR zeros of Gauge theories at the four loop order and beyond. Phys. Rev. D 83:035013. doi: 10.1103/PhysRevD.83.035013

CrossRef Full Text | Google Scholar

Pietrykowski, A. R. (2007). Gauge dependence of gravitational correction to running of gauge couplings. Phys. Rev. Lett. 98:061801. doi: 10.1103/PhysRevLett.98.061801

PubMed Abstract | CrossRef Full Text | Google Scholar

Pietrykowski, A. R. (2013). Interacting scalar fields in the context of effective quantum gravity. Phys. Rev. D. 87:024026. doi: 10.1103/PhysRevD.87.024026

CrossRef Full Text | Google Scholar

Platt, C., Hanke, W., and Thomale, R. (2013). Functional renormalization group for multi-orbital Fermi surface instabilities. Adv. Phys. 62, 453–562. doi: 10.1080/00018732.2013.862020

CrossRef Full Text | Google Scholar

Polonyi, J. (2003). Lectures on the functional renormalization group method. Central Eur. J. Phys. 1:1. doi: 10.2478/BF02475552

CrossRef Full Text | Google Scholar

Polyakov, A. M. (1975). Interaction of goldstone particles in two-dimensions. Applications to ferromagnets and massive yang-mills fields. Phys. Lett. 59B:79. doi: 10.1016/0370-2693(75)90161-6

CrossRef Full Text | Google Scholar

Rechenberger, S., and Saueressig, F. (2013). A functional renormalization group equation for foliated spacetimes. JHEP 1303:010. doi: 10.1007/JHEP03(2013)010

CrossRef Full Text | Google Scholar

Reuter, M. (1998) non-perturbative evolution equation for quantum gravity. Phys. Rev. D 57:971.

Google Scholar

Reuter, M., and Saueressig, F. (2002). Renormalization group flow of quantum gravity in the Einstein-Hilbert truncation. Phys. Rev. D 65:065016. doi: 10.1103/PhysRevD.65.065016

CrossRef Full Text | Google Scholar

Reuter, M., and Saueressig, F. (2011). Fractal space-times under the microscope: a renormalization group view on monte carlo data. JHEP 1112:012. doi: 10.1007/JHEP12(2011)012

CrossRef Full Text | Google Scholar

Reuter, M., and Saueressig, F. (2012). Quantum einstein gravity. New J. Phys. 14:055022. doi: 10.1088/1367-2630/14/5/055022

CrossRef Full Text | Google Scholar

Reuter, M., and Saueressig, F. (2013). Asymptotic safety, fractals, and cosmology. Lect. Notes Phys. 863:185. doi: 10.1007/978-3-642-33036-0_8

CrossRef Full Text | Google Scholar

Reuter, M., and Schollmeyer, G. M. (2016). The metric on field space, functional renormalization, and metric–torsion quantum gravity. Annals Phys. 367:125. doi: 10.1016/j.aop.2015.12.004

CrossRef Full Text | Google Scholar

Reuter, M., and Schwindt, J. M. (2006) A Minimal length from the cutoff modes in asymptotically safe quantum gravity. JHEP 601:070. doi: 10.1088/1126-6708/2006/01/070

CrossRef Full Text | Google Scholar

Reuter, M., and Wetterich, C. (1994). Effective average action for gauge theories and exact evolution equations. Nucl. Phys. B 417, 181. doi: 10.1016/0550-3213(94)90543-6

CrossRef Full Text | Google Scholar

Reuter, M., and Wetterich, C. (1997). Gluon condensation in nonperturbative flow equations. Phys. Rev. D 56:7893. doi: 10.1103/PhysRevD.56.7893

CrossRef Full Text | Google Scholar

Robinson, S. P., and Wilczek, F. (2006). Gravitational correction to running of gauge couplings. Phys. Rev. Lett. 96:231601. doi: 10.1103/PhysRevLett.96.231601

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodigast, A., and Schuster, T. (2010). Gravitational corrections to Yukawa and phi**4 interactions. Phys. Rev. Lett. 104:081301. doi: 10.1103/PhysRevLett.104.081301

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosten, O. J. (2010). Fundamentals of the exact renormalization group. arXiv:1003.1366 [hep-th].

Google Scholar

Rovelli, C., and Smolin, L. (1995). Discreteness of area and volume in quantum gravity. Nucl. Phys. B 442:593.

Google Scholar

Ryttov, T. A., and Shrock, R. (2011). Higher-Loop corrections to the infrared evolution of a Gauge Theory with fermions. Phys. Rev. D 83:056011. doi: 10.1103/PhysRevD.83.056011

CrossRef Full Text | Google Scholar

Ryttov, T. A., and Shrock, R. (2016). Infrared zero of β and value of γ_m for an SU(3) Gauge Theory at the five-loop level. Phys. Rev. D 94:105015. doi: 10.1103/PhysRevD.94.105015

CrossRef Full Text

Safari, M. (2016). Splitting ward identity. Eur. Phys. J. C 76:201. doi: 10.1140/epjc/s10052-016-4036-6

CrossRef Full Text | Google Scholar

Salvio, A. (2018). Quadratic gravity. arXiv:1804.09944 [hep-th].

Google Scholar

Sannino, F., and Shoemaker, I. M. (2015). Asymptotically safe dark matter. Phys. Rev. D 92:043518. doi: 10.1103/PhysRevD.92.043518

CrossRef Full Text | Google Scholar

Shaposhnikov, M., and Wetterich, C. (2010). Asymptotic safety of gravity and the higgs boson mass Phys. Lett. B. 683:196. doi: 10.1016/j.physletb.2009.12.022

CrossRef Full Text

Shaposhnikov, M., and Zenhausern, D. (2009a). Scale invariance, unimodular gravity and dark energy. Phys. Lett. B 671:187. doi: 10.1016/j.physletb.2008.11.054

CrossRef Full Text | Google Scholar

Shaposhnikov, M., and Zenhausern, D. (2009b). Quantum scale invariance, cosmological constant and hierarchy problem. Phys. Lett. B 671:162. doi: 10.1016/j.physletb.2008.11.041

CrossRef Full Text | Google Scholar

Simmons-Duffin, D. (2016). The conformal bootstrap. doi: 10.1142/9789813149441_0001

CrossRef Full Text

Sohnius, M. F. (1985). Introducing supersymmetry. Phys. Rept. 128:39. doi: 10.1016/0370-1573(85)90023-7

CrossRef Full Text | Google Scholar

Souma, W. (1999). Nontrivial ultraviolet fixed point in quantum gravity. Prog. Theor. Phys. 102:181. doi: 10.1143/PTP.102.181

CrossRef Full Text | Google Scholar

Stelle, K. S. (1977). Renormalization of higher derivative quantum gravity. Phys. Rev. D 16:953. doi: 10.1103/PhysRevD.16.953

CrossRef Full Text | Google Scholar

Surya, S. (2012). Evidence for a phase transition in 2D causal set quantum gravity. Class. Quant. Grav. 29:132001. doi: 10.1088/0264-9381/29/13/132001

CrossRef Full Text | Google Scholar

't Hooft, G., and Veltman, M. J. G. (1974). One loop divergencies in the theory of gravitation. Annales poincare. Phys. Theor. A 20:69.

Google Scholar

Tan, A., Xiao, M., Cui, X., Chen, X., Chen, Y., Fang, D., et al. (2016). Dark matter results from first 98.7 days of data from the PandaX-II experiment. Phys. Rev. Lett. 117:121303. doi: 10.1103/PhysRevLett.117.121303

PubMed Abstract | CrossRef Full Text | Google Scholar

Tarasov, O. V., and Vladimirov, A. A. (1977). Two loop renormalization of the Yang-Mills Theory in an Arbitrary Gauge. Sov. J. Nucl. Phys. 25:585.

Google Scholar

Toms, D. J. (2007). Quantum gravity and charge renormalization. Phys. Rev. D. 76:045015. doi: 10.1103/PhysRevD.76.045015

CrossRef Full Text | Google Scholar

Toms, D. J. (2008). Cosmological constant and quantum gravitational corrections to the running fine structure constant. Phys. Rev. Lett. 101:131301. doi: 10.1103/PhysRevLett.101.131301

PubMed Abstract | CrossRef Full Text | Google Scholar

Toms, D. J. (2009). Quantum gravity, gauge coupling constants, and the cosmological constant. Phys. Rev. D. 80:064040. doi: 10.1103/PhysRevD.80.064040

CrossRef Full Text | Google Scholar

Toms, D. J. (2010). Quantum gravitational contributions to quantum electrodynamics Nature 468:56. doi: 10.1038/nature09506

CrossRef Full Text

Toms, D. J. (2011). Quadratic divergences and quantum gravitational contributions to gauge coupling constants. Phys. Rev. D. 84:084016. doi: 10.1103/PhysRevD.84.084016

CrossRef Full Text | Google Scholar

Tsao, H. S. (1977). Conformal anomalies in a general background metric. Phys. Lett. 68B:79. doi: 10.1016/0370-2693(77)90039-9

CrossRef Full Text | Google Scholar

Unruh, W. G. (1989). A unimodular theory Of canonical quantum gravity. Phys. Rev. D 40:1048.

PubMed Abstract | Google Scholar

Vacca, G. P., and Zambelli, L. (2015). Multimeson Yukawa interactions at criticality. Phys. Rev. D 91:125003. doi: 10.1103/PhysRevD.91.125003

CrossRef Full Text | Google Scholar

Vacca, G. P., and Zanusso, O. (2010). Asymptotic safety in Einstein gravity and scalar-fermion matter. Phys. Rev. Lett. 105:231601. doi: 10.1103/PhysRevLett.105.231601

PubMed Abstract | CrossRef Full Text | Google Scholar

van de Ven, A. E. M. (1992). Two loop quantum gravity. Nucl. Phys. B 378, 309.

Google Scholar

Veneziano, G. (1979). U(1) without instantons. Nucl. Phys. B 159:213. doi: 10.1016/0550-3213(79)90332-8

CrossRef Full Text | Google Scholar

Weinberg, S. (1980). “UV divergences in quantum theories of gravitation,” in SPIRES Entry, eds S. W., and Hawking, W. Israel (Cambridge: Cambridge University Press), 790–831. Available online at: http://www.slac.stanford.edu/spires/find/hep/www?irn=784877

Google Scholar

Wetterich, C. (1993). Exact evolution equation for the effective potential. Phys. Lett. B 301:90.

Google Scholar

Wilson, K. G., and Fisher, M. E. (1972). Critical exponents in 3.99 dimensions. Phys. Rev. Lett. 28:240. doi: 10.1103/PhysRevLett.28.240

CrossRef Full Text | Google Scholar

Woodard, R. P. (2015). Ostrogradsky's theorem on Hamiltonian instability. Scholarpedia 10:32243. doi: 10.4249/scholarpedia.32243

CrossRef Full Text | Google Scholar

Yagi, K., Blas, D., Barausse, E., and Yunes, N. (2014). Constraints on einstein-Æther theory and Horava gravity from binary pulsar observations. Phys. Rev. D 89:084067.

Google Scholar

Zanusso, O., Zambelli, L., Vacca, G. P., and Percacci, R. (2010). Gravitational corrections to Yukawa systems. Phys. Lett. B 689:90. doi: 10.1016/j.physletb.2010.04.043

CrossRef Full Text | Google Scholar

Zinn-Justin, J. (2002). Quantum field theory and critical phenomena. Int. Ser. Monogr. Phys. 113:1. doi: 10.1093/acprof:oso/9780198509233.001.0001

CrossRef Full Text | Google Scholar