- 1Plasma Theory and Applications Group, Los Alamos National Laboratory, Los Alamos, NM, United States
- 2Syntek Technolgies Inc., Arlington, VA, United States
- 3Department of Physics and Astronomy, University of California, Los Angeles, Los Angeles, CA, United States
In the decade from the mid 80's to the mid 90's there was considerable interest in the generation of diamagnetic cavities produced by the sub-Alfvenic expansion of heavy ions across a background magnetic field. Examples included the AMPTE and CRRES barium releases in the magnetotail and magnetosphere as well as laser experiments at various laboratories in the United States and the Soviet Union. In all of these experiments field-aligned striations and other small-scale structures were produced as the cavities formed. Local and non-local linear theory as well as full particle (PIC), hybrid, and Hall-MHD simulations (mostly 2-D) were developed and used to understand at least qualitatively the features of these experiments. Much of this review is a summary of this work, with the addition of some new 3-D PIC and Hall-MHD simulations that clarify old issues associated with the origin and evolution of cavities and their surface features. In the last part of this review we discuss recent extensions of the earlier efforts: new space observations of cavity-like structures as well as new laboratory experiments and calculations with greatly improved diagnostics of cavities formed by expansions of laser-produced ions at super-Alfvenic speeds both across and along the background magnetic field.
Introduction
Many active experiments in space involve the release of canisters of neutral barium atoms. Barium has the very interesting property that it has a very long photo-ionization time, ~30 s. This allows the formation of large clouds of barium ions expanding across the ambient magnetic field. Such ion expansions exclude the magnetic field, creating a magnetic cavity. The Active Magnetospheric Particle Tracer Experiment (AMPTE) mission launched in 1984 (Valenzuela et al., 1986) and a second mission, the Combined Release and Radiation Effects Satellite (CRRES) launched in 1991, which released smaller amounts of chemicals, were carried out to provide information of how newborn ions in the magnetotail or upstream of the bow shock traveled throughout the magnetosphere. For example, AMPTE produced artificial comets with the release of barium as well as lithium upstream and just behind the bow shock. Similarly, there were releases in the magnetotail; the barium ions produced large clouds (radius ~200 km) that were visible from the Earth. The top panel in Figure 1 shows the magnetic field magnitude as a function of time as measured by the magnetometer on the release module (Lühr et al., 1988) during the first magnetotail experiment on March 21, 1985 (Figure 12, Bernhardt et al., 1987). The diamagnetic cavity, with |B| ≈ 0, appears shortly after the release time, 9:20:38, and extends out to 9:26:20, as the cavity collapses and the cloud moves relative to the spacecraft. Optical measurements from the ground confirm the density and velocity profiles of the barium as a function of time. Cavity Formation and Properties of this review provides a simple derivation of the dynamics of the cavity formation that has been shown to be consistent with the AMPTE data. Results from experiments of cavity formation performed in the laboratory using a source of expanding energetic ions from a target irradiated by a laser will also be discussed that suggest the commonality of the diamagnetic cavity formation process.
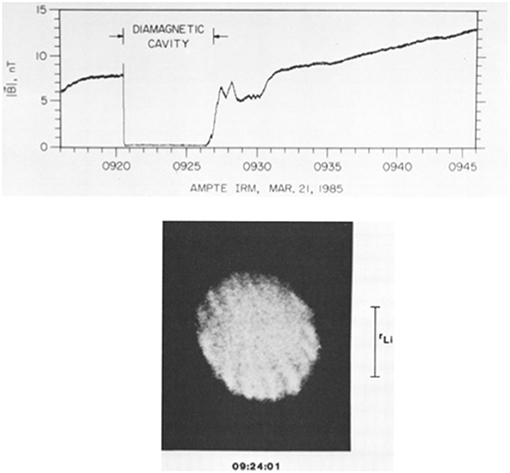
Figure 1. Results from the 21 March 1985 AMPTE magnetotail release. [top] Magnetic field magnitude measured by the IRM satellite showing the magnetic cavity. The diamagnetic cavity, with |B| ~ 0, appears right at the release time, 9:20:38, and extends out to 9:26:20, as the cavity collapses and the cloud moves relative to the spacecraft. [bottom] CCD image of the cloud at time of maximum expansion, t = 9:24:01, when the cloud radius is 210 km ~ the barium ion gyroradius, rLi. The bright areas correspond to higher plasma density. The top panel is from Figure 12, the bottom panel from Figure 18 in Bernhardt et al. (1987). The figures are reproduced with permission from The American Geophysical Union.
The lower panel of Figure 1 is a photograph of the same AMPTE barium cloud obtained from a CCD camera on the ground in White Sands, NM (Figure 18, Bernhardt et al., 1987). This photo was taken at about the time that the cloud has reached maximum expansion across the magnetic field and shows field-aligned striations on the surface of the cloud. Striations are commonly observed on barium clouds, but most often seen at later time at longer wavelengths when the cloud collapses radially and elongates along the ambient magnetic field. Short wavelength striations are also frequently observed in laboratory experiments. The origin and properties of these structures are the subject of Striation Growth and Evolution.
It is interesting to note that historically the chemical release experiments in space (AMPTE to CRRES) occurred in about the same time frame as the laboratory experiments were being fielded in both the U.S. and the Soviet Union. The experiments will be described in Cavity Formation and Properties and Striation Growth and Evolution, and have been discussed in reviews by Akimoto et al. (1988), Zakharov (2003), and Zakharov et al. (2006). These two groups of activities were not programmatically related, and much theory and simulation work was directed toward one or the other type of experiment. As we show later, the theory and simulation program at the Naval Research Laboratory (NRL) was active in both the AMPTE and CRRES missions, and was also the home of a significant laser experimental effort, so they were well-situated to connect these two seemingly different efforts.
In contrast to this experience track is one recently proposed by Howes (2018). In his review he argues that laboratory experiments can now replace space experiments, because laboratory experiments are cheaper, are easier to field, have more controllable boundary and initial conditions, and are more readily reproducible/repeatable. He gives examples of laboratory experiments that are addressing issues of direct importance to space plasmas physics. These include: plasma turbulence, magnetic reconnection, particle acceleration, collisionless shocks, kinetic, and fluid instabilities, as well as other processes. He does recognize, however, that space experiments do have larger spatial and longer temporal domains, use smaller size probes relative to plasma scales and provide 3-D velocity diagnostics that are important for some types of experiments. In this review, we discuss the formation and evolution of diamagnetic cavities—a very active area of research three decades ago in which there were significant and complementary efforts in space and laboratory experiments. Interest does continue at present, albeit in somewhat different physical regimes in the laboratory, but without corresponding active space experiments. While the Howes review (2018) discusses how laboratory experiments can now be used to understand space plasma physics issues, the present paper stresses the important role of the interplay of space and laboratory activities that led to basic understanding of diamagnetic cavities in the previous generation. As we emphasize in this review, a broad-based array of both laboratory and space experiments addressed by a wider range of theoretical and simulation techniques that can span both spatial and temporal scales of laboratory and space conditions could be beneficial to the needs of different funding sponsors.
The fundamental question we address in this review is what we did, or did not, know concerning the nature of diamagnetic cavities by 1993, and how recent work has improved this understanding. The basic goals of this review related to this overarching question are as follows. First, we recall the basic physics of cavity formation and look back at the original experiments that validated this model (Cavity Formation and Properties). Second, we review a variety of previous experiments conducted in both space and in the laboratory to investigate the main dynamical features of cavities—namely the formation of field-aligned surface striations. We discuss related theory and simulations that describe at least qualitatively the mechanisms for the growth of these surface waves. And we address recent experiments and 3-D simulations that have improved this overall understanding (Striation Growth and Evolution). Third, we discuss present-day interest in cavities—new phenomena in space and laboratory experiments and simulations to investigate magnetic cavities in different regimes (Extensions). Finally, in Conclusions we provide a short summary and suggest where research in diamagnetic cavity phenomena may be headed in the future.
Cavity Formation and Properties
The formation of a diamagnetic cavity, such as the AMPTE magnetotail magnetic cavity shown in Figure 1, can be understood from a simple pressure balance argument based on conservation of energy (e.g., Gisler and Lemons, 1989; Ripin et al., 1993). We consider the 3-D radial expansion of an ideal, perfectly conducting dense plasma of radius R, velocity V and total mass M in a uniform magnetic field Bo. The properties of the expansion are determined by the work the plasma does in pushing the magnetic field out of the volume that it occupies. The final size of the cavity results from the equilibration between the (thermal) pressure of the expanded plasma and the external magnetic field pressure. The stopping radius (RB) and the duration of the expansion (to) are found using the conservation of energy Eo:
where initially V(t = 0) = Vd, R(0) = 0 and thus Eo = MV/2. The expansion continues until t = to, when V(to) = 0, R(to) = RB, with Eo = (B/2μo)(4πR/3). From equating these two expressions for Eo, we find RB = (3μoMV/4πB)1/3; RB is referred to as the magnetic confinement radius. In this simple picture, we neglect any additional thermal energy or internal Ohmic heating. In the next section we will go beyond this model to look in detail at the current on the edge of the expanding plasma and how it leads to cavity formation and plasma heating.
Later, we will also need to know the rate of deceleration of the plasma cloud. By taking the time derivative of Equation (1), with dEo/dt = 0, we obtain
(with g > 0), which evidently increases as R2 and reaches its maximum at R = RB,
One can also integrate to get R(t) and V(t) and find to ≈ 1.3 RB/Vd.
In similar fashion in the case where the expansion is cylindrical in two dimensions (with cylinder of length L), so that the excluded magnetic energy is B r2Lπ/2μo, we can show, with RB = (μo MV/B Lπ)1/2, that
so that gmax = V/RB at R = RB and Vdto/RB = π/2. The difference in the rate of deceleration of the plasma near the end of the expansion between 2-D (~ R) and 3-D (~ R2), and the maximum deceleration gmax/(V/RB) = 1 in 2-D and 1.5 in 3-D, will appear in the development of the surface striations is shown in the next section. It should also be noted that in 2-D a slightly different result occurs if free expansion is allowed in the axial direction (Gisler and Lemons, 1989). Also at least in simulation, it is possible to have a one-dimensional expansion as well, with the excluded magnetic energy, BL2R/2μo. In this case the velocity decreases linearly in time, Vdto/RB = 0.5 and g = 0.5V/RB is a constant.
In the AMPTE case, ground based observations indicated that the maximum cavity radius was about 210 km. Estimating the initial plasma mass is a bit difficult because only a fraction of the barium atoms that are released become ionized. Ground-based measurements could also confirm that the expanding barium plasma compressed into a thin shell, leading to a narrow current layer. This current loop provides the magnetic field that cancels out the background field inside the loop, forming the diamagnetic cavity. Like the Lühr et al. (1988) observations of the AMPTE diamagnetic cavity measured by the release spacecraft (IRM) shown in Figure 1, direct spacecraft measurements of the diamagnetic cavity formation from smaller barium releases in the CRRES program were also carried out (e.g., Bernhardt, 1992).
Diamagnetic cavities were also produced in laboratory experiments in about the same time frame as the AMPTE barium releases. For example, at the Naval Research Laboratory the 30 J Pharos III glass laser was used to illuminate an aluminum target in a low density plasma embedded in a strong magnetic field (B ~ 0.1–1 kG) (Ripin et al., 1987, 1990, 1993). Magnetic probes were used to measure the magnetic field excluded by the expanding target plasma, although the initial measurements were not very accurate. Another experiment (Dimonte and Wiley, 1991) employed the two-beam 200 J Janus laser and various target materials at Lawrence Livermore National Laboratory and included a magneto-optic imaging probe (MIP) that was developed and used to obtain accurate measurements of the magnetic field. This technique uses Faraday rotation to measure the magnetic field profile continuously in space and time, as shown in the top panels of Figure 2 (Figure 3 in Dimonte and Wiley, 1991). The top left panels present streak camera images across a transverse cut vs. time, showing the cavity expanding to a maximum radius (~3 cm) and then collapsing. The line-outs at various times in the right side of the top panel show that the field is indeed totally excluded in the cavity and the magnetic field gradient at the cavity boundary is relatively steep. Other experiments were carried out in Novosibirsk, USSR, using a 1 kJ CO2 laser and observed similar behavior (Zakharov et al., 1999; Zakharov, 2002).
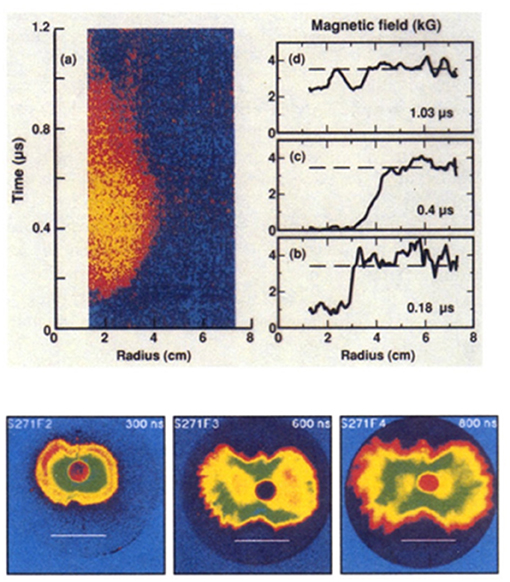
Figure 2. Results of laser experiment by Dimonte and Wiley (1991) showing: [top] radius vs. time of the magnetic cavity from MIP measurements (left; blue region corresponds to the ambient magnetic field ~4 kG, orange to zero magnetic field) and (right) corresponding line-outs at various times showing well-developed cavity at t = 0.4 μs. [bottom] False color images of expanding plasma cloud at various times (300, 600, 800 ns)–the two laser beams hit the target from the left and right sides of the picture and plasma expands outward producing short-wavelength modes on the surface. Here the magnetic field (out of the plane) is 3.5 kG. The top panels are from Figure 3, bottom panels from Figure 2 in Dimonte and Wiley (1991). The figures are reproduced with permission from The American Physical Society.
Striation Growth and Evolution
While the formation of a magnetic cavity is consistent with conservation of energy and magnetic field exclusion in both space and laboratory experiments was expected, the development of field-aligned flute modes on the surface of the expanding plasma cloud was a more surprising feature. One example is the CCD image of the AMPTE magnetotail release that was already shown in Figure 1. With in situ measurements from a single spacecraft it would have been difficult to infer the character of these structures. In this section we discuss the experiments, theory and simulations, which led to a good understanding of how such surface features develop, in the years during and immediately after the space chemical releases and the laboratory laser experiments were carried out. We conclude with a discussion of more recent high-resolution experiments and simulations that have further enhanced our knowledge of the underlying processes.
Experiments
In some laser experiments small-scale short-wavelength striations appeared at the edge of the cavity, reminiscent of the AMPTE release shown earlier in Figure 1. Examples include the early small-scale experiments by Okada et al. (1981, Figure 3) the Ripin et al. experiments (Figure 6, 1993), Zakharov et al., experiments (Figure 3, 1996), and also the Dimonte and Wiley (1991, Figure 2) experiments. An example of this type of behavior from the Dimonte and Wiley experiment is shown in the bottom panel of Figure 2 displaying false color images of expanding plasma cloud at various times (300, 600, 800 ns). In this experiment the two laser beams hit the target from the left and right sides of the picture and plasma expands outward producing short-wavelength modes on the surface. However, in other experiments, larger flutes were observed (e.g., Ripin et al., 1990 Figure 2; Ripin et al., 1993, Figure 3), which showed unusual, finger-like projections. Similarly, in some experiments where large flutes were observed, the overall cavity size was smaller (i.e., r < RB) and the flutes extended some distance beyond r = RB. This suggested that another experimental parameter also plays an important role. As originally shown by Zakharov et al. (Dimonte and Wiley (1986), this parameter is the ratio of the gyroradius of the expanding target ions (of charge Zde and mass md), ρd = Vd/ωcd (where the ion gyrofrequency is ωcd = ZdeBo/md) to RB. For small ρd/RB, small-scale flute modes are generated and cavity sizes are R ~ RB; larger flutes and smaller cavities result when ρd/RB ~ 1. Dimonte and Wiley (1991) changed the magnetic field, the laser energy and the target material in their experiment to vary ρd/RB and modify the size of the resulting cavities to verify these predictions. The ratio ρd/RB determines how magnetized are the target ions during the expansion, which can be expressed in terms of the size of the Hall-term in a Hall-MHD description of the cavity dynamics, as discussed later. In cases of very energetic target ions, where ρd/RB >> 1, the expanding plasma generates a jet-like penetration across the magnetic field and creates only a small magnetic cavity, as shown in experiments by Mostovych et al. (1989) and Plechaty et al. (2013). Short-wavelength surface modes that are observed in this regime are likely due to a lower hybrid velocity shear (i.e., Kelvin-Helmholtz-like) instability (Peyser et al., 1992).
Further analysis of the flutes observed in the NRL experiments suggest that they could appear before the cavity reached its final size, and there could be a turn-on condition that in some experiments seemed to be independent of the magnetic field (Ripin et al., 1993). There were also suggestions that as the flutes grew, their wavelengths increased, although it was not clear whether this occurs by mode coupling, mode coalescence, or some other non-linear process. Dimonte and Wiley (1991) were able to obtain wavenumber spectra that showed such a shift to longer wavelengths. Other observations showed that flutes seem to bend in the direction of electro gyro-motion and the tips of the flutes were observed at times to bifurcate (Ripin et al., 1993). Again, we emphasize that the reproducibility of these laboratory experiments and the ability to vary parameters independently were important to document the behavior of the surface striations as they grew and developed, perhaps non-linearly.
Theory
In the pressure-balance model presented in Cavity Formation and Properties, the expanding plasma slows down as it does work in excluding the background magnetic field to form a diamagnetic cavity. The deceleration of the spherically expanding plasma (–g, g > 0) is given by Equation (2). The plasma is also heated, and equilibrium is achieved when the thermalized sphere of plasma is in pressure balance with the external magnetic field. Here we go beyond the simple dynamical model and look in more detail at the physics of the expanding plasma to understand the generation of the plasma current that leads to the expulsion of the magnetic field, the formation of flute modes and the resulting thermalization of the plasma.
At the leading edge of the expanding plasma cloud there is a density gradient εn given by
defined so that εn > 0 at this interface. One then expects that the interface between the expanding but decelerating plasma and the magnetic field would be unstable to a Rayleigh-Taylor instability, the growth rate of which according to MHD is
However, in the case of expanding cavities produced in active experiments, the cavity is usually small compared to the wavelength of the Rayleigh-Taylor instability and the observed waves on the surface of the cavity are evidently smaller than the cavity diameter. In this case one needs to include the Hall term in the wave analysis. With the addition of this term, Hassam and Huba (1987) and Huba et al. (1987) have shown that a shorter wavelength, faster growing instability occurs with growth rate
In contrast to the usual Rayleigh-Taylor instability, in this “Large-Larmor Radius” (LLR) Rayleigh-Taylor instability the character of the unstable modes is different: the fluid motion of the plasma is current-free, rather than divergence-free, producing finger-like projections of the plasma into the magnetic field region, rather than the usual spike-and-bubble configuration characteristic of a Rayleigh-Taylor instability. Figure 3 shows the growth rates of both the Rayleigh-Taylor and the LLR instability as a function of the inverse density scale length εn. These solutions are derived from solving a set of single fluid MHD equations (blue curve) as well as equations containing the Hall term (red curve) (Hassam and Huba, 1987).
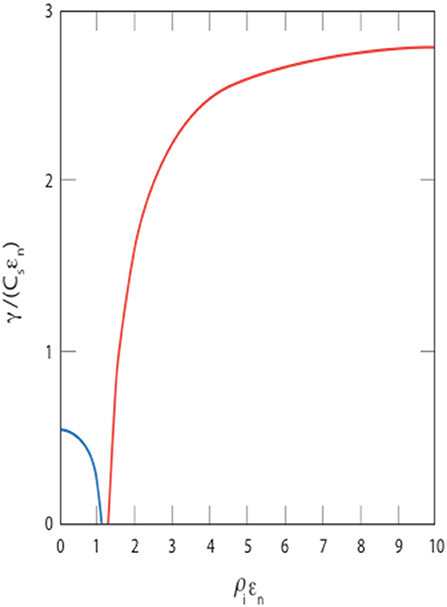
Figure 3. Calculated growth rate of the usual Rayleigh-Taylor instability (blue curve) and the Large Larmor Radius Rayleigh Taylor instability (red curve) as a function of ρiεn. Solutions come from solving set of single fluid MHD Equations (blue curve) with the addition of the Hall term (red curve). The figure is redrawn from the original Figure 1 in Hassam and Huba (1987), with permission from The American Geophysical Union.
An alternative way to understand this new type of Rayleigh-Taylor-like instability is from a kinetic point of view (Winske, 1988, 1989). The expanding plasma compresses into a thin shell as the ions exclude the magnetic field and a radial electric field Er (< 0) drags the electrons and magnetic field along to keep the plasma quasi-neutral, as shown in the left panels Figure 4 (Figure 1 in Winske, 1989). In terms of the radial ion momentum equation (for unmagnetized ions)
with the ion pressure given in terms of the ion temperature, Pi = ni(r)Ti with Ti = miv/2 assumed simply as a constant, the radial electric field can be written as
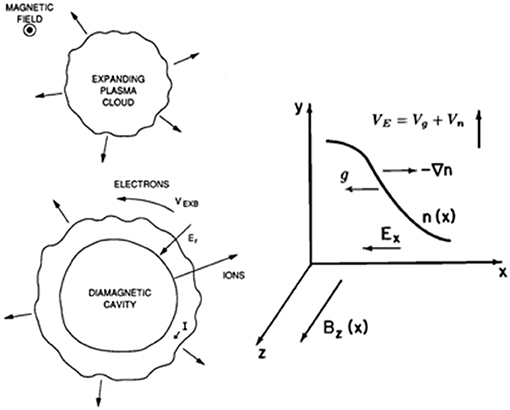
Figure 4. Left panels show schematic of expanding plasma cloud compressing into a thin shell, showing the radial electric field and electron and ion azimuthal drifts, from Figure 1 in Winske (1989), reproduced with permission from the American Institute of Physics. Right panel shows corresponding density profile, direction of the density gradient, the deceleration, the radial electric field, the cross-field drift and the magnetic field in slab geometry used in the linear analysis, from Figure 1 in Winske (1988), reproduced with permission from The American Geophysical Union.
In the rest frame of the ions, the electrons (E × B) drift in the azimuthal direction
due to a combination of the “gravitational drift” Vg and the ion diamagnetic drift Vn. This azimuthal, relative electron-ion drift provides the current that produces a magnetic field which opposes the background magnetic field leading to the formation of the cavity. The electron-ion drift also gives rise to a fast-growing electrostatic instability. This instability was originally discussed by Davidson and Gladd (1975) and Gladd (1976), who studied decelerating plasma sheaths (g > 0) in imploding theta-pinch plasmas, and Okada et al. (1979), who suggested that the instability could occur in expanding magnetized laser plasmas. The geometry for the linear analysis is shown in the right side of Figure 4 (Figure 1 in Winske, 1988). With Vg = 0, the resulting instability is the well-known lower hybrid drift instability (Krall and Liewer, 1971); the real frequency ωr, the maximum growth rate γm and corresponding wavenumber km at maximum growth are given by
where ωLH = ωpi/(1/)1/2≈ ωci(mi/me)1/2. When Vg >> Vn, the instability reduces to the LLR solution of Hassam and Huba (1987).
Figure 5 compares solutions a simplified linear dispersion relation (electrostatic, cold electrons, cold ions) showing the real and imaginary part of the frequency vs. wavenumber for two cases: blue curves (Vn/vA = 1, Vg = 0) and red curves (Vn/vA = 1, Vg = 3) (Figures 2, 3 in Winske, 1989). Here the ion beta is assumed to be βi = 0.2 = v/v, with vi the ion thermal speed and vA the Alfven speed. With Vg = 0 the wave properties are those expected of the lower hybrid drift instability, i.e., high frequency, fast growing, short wavelength unstable modes. Whereas, with the inclusion of Vg = 3 vA, the instability grows even faster, with maximum growth occurring at longer wavelength. It should be noted that from Cavity Formation and Properties, the deceleration of the expanding plasma increases as the plasma expands and reaches its maximum as the plasma stops. In addition, the density gradient at the leading edge can also change in time. Thus, when doing linear theory for specific experimental conditions, such as the AMPTE releases, one typically uses average values for the plasma parameters, rather than trying to determine more realistic local values during the plasma expansion. In addition to appearing as the observed flute modes, the unstable waves also heat both electrons and ions, thus leading to the thermalized state of the expanded plasma when it comes to rest as the magnetic cavity reaches its maximum size.
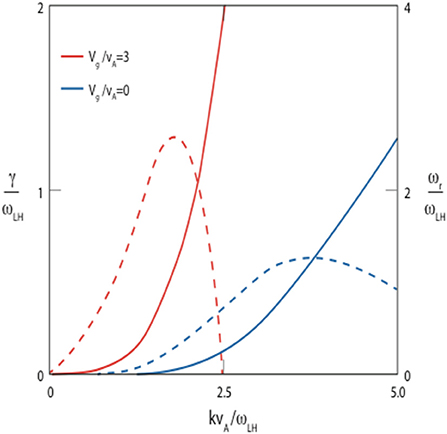
Figure 5. Results of linear theory showing real frequency (ωr, solid curves) and growth rates (γ, dashed curves) as a function of wavenumber for Vg = 0 (blue curves) and Vg = 3 vA (red curves). Frequencies are normalized by the lower hybrid frequency ωLH, velocity by the Alfven speed vA and wavenumbers by ωLH/vA. Adding the gravitational drift increases the growth rate, corresponding real frequency and reduces the wavenumber at maximum growth (Winske, 1988). The figure is redrawn from Figures 2, 3 in Winske (1989), with permission from The American Institute of Physics.
Huba et al. (1990) generalized the kinetic local linear theory to include additional effects, namely ion-neutral collisions and related Pedersen drifts, generalized magnetization effects of the ions through the use of Gordeyev integrals, and electromagnetic effects on the electrons. They also employed proper electron and ion distribution functions in setting up the equilibrium. Numerical solutions, in which the role of the gravitational drift were emphasized, were presented as well as analytic solutions of the dispersion equation in various limits. Parameters for the AMPTE and CRRES barium releases in space as well as for the NRL laser experiment were carefully compiled and used in the linear theory calculations that were then compared with measurements. Good qualitative agreement was found in all cases, but generally, the linear theory gives wavelengths of the fastest growing modes that are too short (often by an order of magnitude) compared with observations.
The linear theory of these fast-growing instabilities augmented by the gravitational drift was also extended to include non-local effects to provide a more realistic picture of the interface between the expanding plasma cloud and the magnetic field. Huba et al. (1989) modified the Hall-MHD model and Gladd and Brecht (1991) extended the kinetic model. In both cases eigenfunctions were obtained that characterize the radial structure of the electric field at the interface. Peak growth rates obtained from the non-local analysis were also consistent with those obtained from local theory, again emphasizing that linear theory tends to overestimate the growth rates of the most unstable waves.
Simulations
A number of 2-D simulations of the development of striations on expanding plasma clouds were also carried out, using a variety of plasma models to both show the validity of the linear theory calculations and also to examine the non-linear behavior. (We defer showing examples of the instability development in the simulations to later in the section when recent 3-D simulations will be discussed and compared with the earlier 2-D calculations). Huba et al. (1987) conducted MHD and Hall-MHD simulations in a slab geometry (denser fluid supposed by lighter fluid and stronger magnetic field) with an imposed “gravity.” In the MHD simulations, the usual “spike and bubble” structure appears. In the Hall-MHD simulations, the character of the modes is much different, i.e., shorter wavelength, faster-growing, more finger-like structures appear (also see Winske, 1996). Similar MHD and Hall-MHD simulations (Huba et al., 1992, 1993) were also done later for the G-4 and G-10 barium releases associated with the CRRES mission. No striations appeared in the simulations using the MHD equations, whereas flute modes rapidly formed when the Hall-MHD term was added to the calculations Also in these simulations the flutes evolved to longer wavelengths in time while the tips of the flutes seemed to continue to propagate outwards even when most of the barium ions had stopped.
Similarly, full-particle 2-D simulations of expanding plasma clouds were carried out by Winske (1988, 1989). Consistent with linear theory, very short wavelength modes appeared and grew on lower-hybrid time scales (e.g., Figure 11 in Winske, 1988). Analysis of the wave amplitudes indicated that growth during the linear stage was consistent with linear theory and wave generation occurs at very short wavelength. However, it should be pointed out that such waves could have been seeded on the expanding cloud at early times by the computational grid. In addition, the saturation of the waves was much larger than expected from usual arguments for the lower hybrid drift instability (Liewer and Davidson, 1977). In this case the continuing expansion of the plasma cloud keeps the radial electric field, which gives rise to the azimuthal current, large so that the system continues to be driven to much higher wave levels that persist until the plasma stops expanding. Some coalescence to longer wavelengths appeared after the plasma stopped and the instability saturated. In various simulations, as ρd/RB was increased, the size of the flutes became larger and the final cavity size was smaller (Winske, 1989). These results were consistent with the experimental results of Dimonte and Wiley (1991) and Zakharov et al. (2006). A number of other full particle simulations were also carried out by various groups, using different initial conditions and plasma parameters (see review by Akimoto et al., 1988). Such calculations demonstrate the robustness of the instability generation mechanism.
Hybrid simulations, in which the electrons are treated as a massless fluid, the ions are treated kinetically using particle-in-cell techniques and electromagnetic fields are considered in the low-frequency approximation (e.g., Winske and Gary, 2007), were also been carried out for expanding plasma clouds in both 2-D and 3-D geometries (Brecht and Thomas, 1988; Brecht and Gladd, 1992). Because of the lack of electron inertia, linear theory in this case indicates that the linear growth rate of surface flute modes increases with wavenumber out to the resolution of the calculation. In this case it is necessary to initialize the simulations with a prescribed short wavelength perturbation. As the plasma expands, this mode grows at a rate consistent with linear theory and continues to dominate to saturation. Later, there may be coalescence to longer wavelengths. Such simulations provide an interesting compromise between Hall-MHD and full particle simulations. Hybrid simulations with a finite electron mass have also been carried out in a 2-D slab geometry (in which case the deceleration is slower, being constant in time and space) that show mode coalescence at late times that increases in simulations where the ion to electron mass ratio is increased (Sgro et al., 1989).
Summary
By the early 90's, the experimental programs were essentially finished and most of the modeling had also been completed. The consensus among those who had worked on this problem could be summarized in a schematic figure, Figure 6 (from Figure 17 in Huba et al., 1990). The figure shows the (random) development of short wavelength modes as the plasma cloud compresses into a thin, expanding shell. By the time of saturation, the instability had evolved to longer wavelength modes. At even later time, these evolved modes continue to grow and expand outward, even as the inner edge of the cavity begins to collapse. This picture was consistent with experiments and simulations at that time, but evidently did not provide a detailed explanation. Zakharov et al. (1986) proposed a mechanism to explain why the cavity seemed smaller and the flutes larger when ρd/RB was larger, based on the competition between expansion and diffusion. Qualitatively this model is consistent with experiments and simulations, which indicate that the instability, and the resulting diffusion, are larger when ρd/RB is large (Winske, 1989).
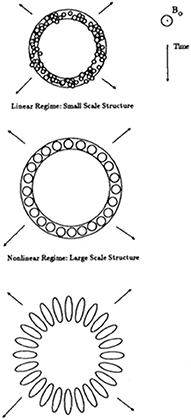
Figure 6. Pictorial representation of the understanding of striation formation and development from Figure 17 in Huba et al. (1990), showing progression from small random waves generated in the expanding shell at early times, coalescence to larger wavelengths and then expansion of the longer wavelengths modes beyond the surface of the shell at later times. The figure is reproduced with permission from The American Institute of Physics.
New Work
In the last few years new experiments and simulations have shed further light on the processes of flute mode generation and non-linear development. For example, experiments at the University of California Los Angeles (UCLA) by Collette and Gekelman (2011) used a much smaller laser, ~1.2 J, but one which could be fired in sync with the background plasma that is produced at 1 Hz in the Large Plasma Device (LAPD) (Gekelman et al., 1991). In addition, small computer-controlled probes that measure the components of the magnetic field could be moved automatically every few shots so that the dynamics of the cavity formation could be carefully mapped out from the B field components and the current J (computed from ∇ × B) in space and time. For example, the current structure that produces the diamagnetic cavity inferred from such measurements is shown in the right panel of Figure 7 (Figure 6 in Collette and Gekelman, 2011). Even though the cavity sizes in these experiments were small (~few cm), the movable probe measurements can be converted into movies and fast photographs can be used to measure the growth and development of flutes, as shown in the left stack of panels in Figure 7 (Collette and Gekelman, 2011, Figure 2). These experiments demonstrate that while they are in a somewhat different physical regime, in terms of dimensionless parameters they are consistent with earlier space and laboratory experiments. The very high-resolution results show the development and evolution of very short wavelength modes that coalesce into larger structures. The presence of collisional effects in these experiments could also be quantified and indicate that the collapse of the cavity occurs much faster than expected from collisional diffusion.

Figure 7. Results of the laser experiment by Collette and Gekelman (2011) showing: [left] series of high resolution photos at various times showing development of small-scale flute models on the expanding plasma shell; [right] composite of magnetic field probe measurements to show the magnetic field lines (blue) and azimuthal current structure (red) around the expanding shell (the brown cylinder to the right represents the target). The left panels are from Figure 2, the right panel from Figure 6 in Collette and Gekelman (2011), reproduced with permission from The American Institute of Physics.
In addition to new experiments, new simulations of diamagnetic cavities have also been recently carried out. For example, Huba has performed new 3D ideal and Hall MHD simulations of an expanding ion cloud. For these simulations the ions are deposited using
where n0 = 5 × 104 cm−3 is the initial neutral density, σi = 0.14 s−1 is the ionization rate, V0 = 1 km/s is the expansion velocity, and Δr0 = 0.5 km. The simulation is initialized at t = 2 s with an initial spherical shell of expanding ions at a radius r = 2 km. Additionally, there is a 1D background magnetic field Bz = 10−4 G. These parameters are chosen for numerical expediency and do not represent a specific magnetospheric barium release. The grid used is 100 × 100 × 100 and is non-uniform; the extent of the grid perpendicular to B is ± 55 λi and along B is ± 140 λi, where λi is the ion inertial length.
The results are shown in Figures 8, 9. We show an isodensity contour ni = 700 cm−3 at times t = 15 s and 32 s for the ideal MHD case (left panels) and Hall MHD case (right panels). The z-axis is aligned with the background magnetic field. In Figure 8 the view of the contours is along the z-axis, i.e., along the magnetic field. At t = 15 s both the ideal and Hall MHD cases are essentially identical. However, at t = 32 s the ideal MHD case is basically unstructured, while the Hall MHD case has become unstable and large-scale density irregularities have developed. In Figure 9 the view of the contours is perpendicular to the background magnetic field. Again, at t = 15 s both the ideal and Hall MHD cases are essentially identical, but the contours are more extended along the magnetic field because the ions can freely expand along this axis. At t = 32 s the ideal MHD case is not structured and the extension along the magnetic field is more pronounced. The Hall MHD case shows the development of density irregularities that are filamented along the magnetic field, as expected.
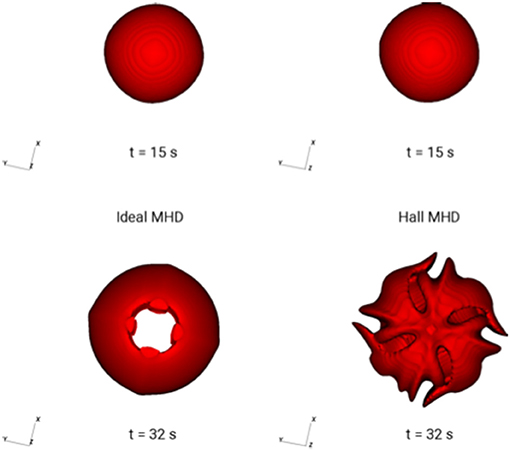
Figure 8. Isodensity contours of the expanding ion cloud viewed along the magnetic field at times t = 15 and 32 s for the ideal and Hall MHD cases.
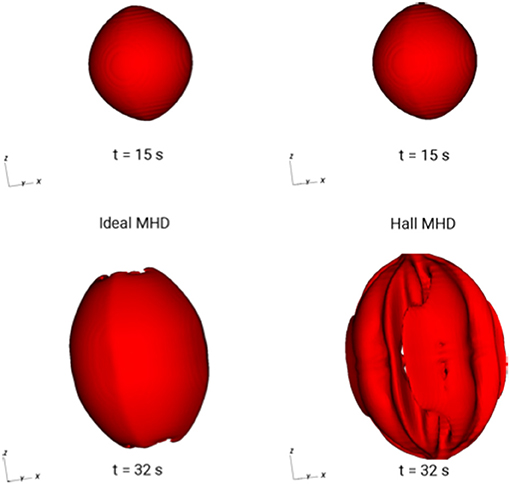
Figure 9. Isodensity contours of the expanding ion cloud viewed perpendicular to the magnetic field at times t = 15 and 32 s for the ideal and Hall MHD cases.
The earlier full particle simulations (Winske, 1988, 1989) of short wavelength flute modes developing on the surface of an expanding debris plasma cloud were carried out in two spatial dimensions perpendicular to the background magnetic field. The observed wavelengths were in qualitative agreement with the linear theory of the generalized lower hybrid drift instability. The initial wavelengths were very short, perhaps limited by the grid resolution, but they developed into somewhat longer wavelength structures in time. While it was expected that there would be some changes if the simulations were run in 3-D rather than 2-D, i.e., the deceleration of the cloud is stronger in 3-D and develops later in the expansion as shown in Figure 5, it was not possible to carry out 3-D simulations of even modest size three decades ago. With the development of modern 3-D particle codes, e.g., VPIC (Bowers et al., 2008), and the readily available computing resources, 3-D simulations have now been done and compared with 2-D, as shown in Figure 10. The parameters of the simulation are very similar to those in Winske (1988); the debris ions have md/me = 100, initial cloud density nd/no = 25, initial radius = 2 c/ωpe, expansion velocity vd = vA, ωpe/ωce = 5. The system size is 25 × 25 c/ωpe in 2-D, using 5 million simulation particles to represent the debris ions and electrons and 25 million particles each to present the background ions and electrons. Similarly, the system size is 25 × 25 × 25 c/ωpe in 3-D, using ~1 billion simulation particles to represent the debris ions and electrons and 8.3 billion particles each to present the background ions and electrons. Figure 10 shows a summary of the two simulations. The left side of the figure shows color contours of the debris electron density in 2-D (left panels) and 3-D (right panels) at various times. At the early time (ωcet = 25, corresponding to ωLHt ≈ 2.5), the instability in 2-D has begun to grow. By ωcet = 50, the instability is well-developed in 2-D and just starting to grow in 3-D. By ωcet = 75 the instability is fully developed in 2-D with well-defined, but low-density flute modes extending beyond the radius of the cavity. In 3-D the instability is not yet as well-developed, but flute modes growing at slightly longer wavelength are apparent. The panel on the right of Figure 10 shows the 3-D image of the debris electron density at ωcet = 75 that more clearly reveals the field-aligned striations on the surface and how they would appear to an external viewer. The black “fuzz” represents a low-density halo of electrons that have been able to propagate away from the outer edge of the cavity. Overall, these comparative calculations are consistent with expectations: linear theory would suggest that the instability should develop somewhat slower in 3-D at slightly longer wavelengths due to the difference of the deceleration, g(t). And from the 3-D perspective the striations on the surface are reminiscent of the AMPTE image (Figure 1). Evidently, more quantitative comparisons from these simulations need to be carried out to examine what are the levels of the fluctuating electric fields and how the linear modes coalesce in time.
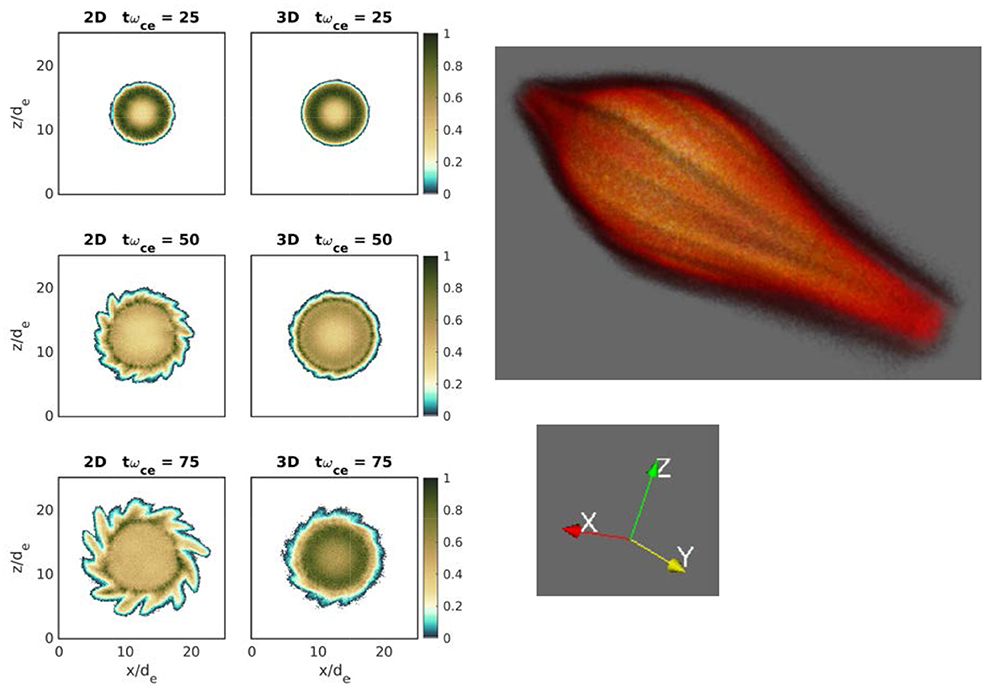
Figure 10. Results of 2-D and 3-D VPIC particle simulations: left panels show 2-D debris electron density in the plane perpendicular to the magnetic field from (left) 2-D run and (right) 3-D run at three times (top row – ωcet = 25, when the instability just begins to develop in the 2-D run; middle row – ωcet = 50, when instability is fully developed in 2-D but just starting in 3-D; lower row – ωcet = 75, when instability is fully developed). The right panel shows a 3-D picture of the debris electron cloud surface at this later time, ωcet = 75, showing the cloud expansion along the magnetic field (y-direction) and how the surface perturbations would appear to an external viewer.
Extensions
Finally, we consider more recent work related to magnetic cavity formation. In this case we consider expansion of a dense target plasma across a magnetized background plasma, but with the expansion speed greater than the Alfven speed. As we show, the physics becomes different as the interaction is dominated by the dynamics of the background plasma as the cavity forms and this interaction determine the cavity size.
Recall that in the initial discussion of the cavity size, the energy equation, Equation (1), was used, assuming that the background density was so low that it could be ignored. Here the opposite limit is considered, where the background density is large and its contribution dominates that of the magnetic field. Instead of Equation (1), conservation of momentum is used to determine the distance over which the expanding target mass M overruns an equivalent mass of background plasma (ion mass mi, ion density no), the so-call equal mass radius Rm:
Comparing the equal mass radius with the magnetic confinement radius, RB, determined from Equation (1), we find
where vA is the Alfven speed based on the background plasma density and the magnetic field. It is evident from Equation (14) that the expanding plasma will stop (and hence determine the size of the magnetic cavity) at R = RB if the background plasma density is low so that the expansion speed is less than the Alfven speed. Similarly, if the background density is larger and thus the Alfven speed is smaller, the expanding plasma stops, and the cavity radius is determined, by the equal mass radius, Rm. As we discuss later, in this case the expanding debris ions transfer their momentum to the background ions through a process known as Larmor coupling. Another important aspect of cavities produced by super-Alfven Mach number expansions (Vd > vA) is that there are no flute modes generated on the cavity surface, as we discuss later.
The AMPTE mission conducted heavy ion releases in solar wind in front of and just behind the bow shock. In this case the solar wind flow is significantly larger than the Alfven speed so that in the solar wind frame the photoionized barium and lithium ions are super-Alfvenic. Observations of these events (Lühr et al., 1986; Valenzuela et al., 1986) do show cavity formation, but with very small cavities resulting from the lithium releases. But more significant observations involved the subsequent motion of the plasma cloud in the solar wind after the cavity collapses, for example, the barium release of Dec. 27, 1984. There was some dispute about the initial motion of the cloud transverse to the solar wind flow, which Papadopoulos et al. (1987) explained in terms of the motional electric field in the solar wind. There was also considerable interest about the subsequent behavior of the lithium ions that were picked up by the solar wind and formed an artificial comet (Valenzuela et al., 1986).
In recent years laboratory experiments have also been done using high-power lasers to generate high-energy target ions that expand at super-Alfvenic speeds across a background magnetic field, both at UCLA on LAPD using the > 100 J Raptor laser (Niemann et al., 2012) and at the Laser Institute in Novosibirsk. Experiments and simulations (Clark et al., 2013, 2014; Niemann et al., 2013, 2014; Schaeffer et al., 2014, 2015; Shaikhislamov et al., 2015) exhibited cavity formation and development. More importantly, they showed that a collisionless shock wave is generated that separates from the edge of the cavity and propagates outward. In the super-Alfvenic case, the pickup of the background ions allows the momentum of the outward streaming target ions to be transferred to the background ions. Equation (13) indicates that the expanding target ions transfer their momentum and energy to the background ions to conserve momentum, but does not indicate how this occurs. Because these are collisionless plasmas, the transfer cannot occur through collisional interactions, but instead involves the electromagnetic fields. In particular, the coupling occurs through the transverse electric field (Eφ), which is the same mechanism that allows newborn ions in the solar wind to be “picked up,” i.e., accelerated up to the solar wind speed to form an artificial comet (Papadopoulos et al., 1987). Because of the presence of the electric field, the background ions are initially accelerated in the azimuthal direction, and then by gyromotion in the magnetic field acquire a large positive radial velocity, as the radially expanding debris ions also start to bend in the magnetic field and decrease their radial velocity (eventually with their radial velocity going to zero). This mechanism, known as Larmor coupling, has been investigated by Bashurin et al. (1983), Hewett et al. (2011) and more recently by Bondarenko et al. (2017b). It has also been recently demonstrated in the laboratory using ion spectroscopy (Bondarenko et al., 2017a) as well as with ion current probes (Prokopov et al., 2016). It is to be noted that because the background ions continue to carry momentum and energy outward, at the cavity boundary the magnetic disturbance does not stop but continues propagating outward as a collisionless shock wave.
The formation of the magnetic cavity in the UCLA experiments is measured using magnetic field probes. Five probes at different radial positions are mounted on a rod, which is moved each time the laser is fired (once every 45 min) in order to map out in space and time the magnetic field intensity. The top panel in Figure 11 shows one such compiled figure (Figure 5, Clark et al., 2014). Values of the magnetic field B/Bo at various probe positions are plotted as a function of time (with positions and time given both in actual and normalized units). (Near the target there are no measurements). Two features stand out. The dark blue region, corresponding to B ~ 0, is the developing magnetic cavity, which eventually expands out to r ~ 35 cm, corresponding to ~7 c/ωpi. The red region is the compressed magnetic field that forms early in time and propagates away from the cavity at Alfven Mach number MA ~ 2.
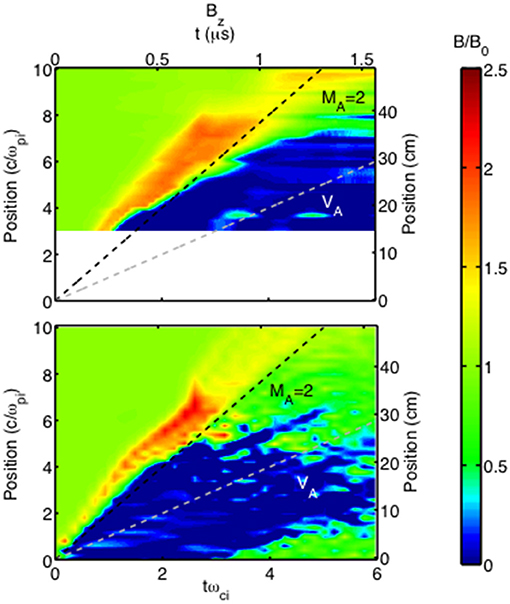
Figure 11. Comparison between experimental data from the UCLA laser experiment (top) and a 2-D hybrid simulation (bottom). The plots show the magnetic field magnitude, B/Bo, as a function of time and space. The formation and evolution of the magnetic cavity (blue region) and the development of a collisionless shock at the edge of the cavity (red) are clearly visible in each plot and show good agreement between simulation and experiment. The plot is from Figure 5 of Clark et al. (2014) and is reproduced with permission from The American Physical Society.
Simulation is an important tool in these experiments, since at present there are no diagnostics to measure the plasma properties of either the debris ions or the background ions. Two-dimensional hybrid simulations (Clark et al., 2013, 2014; Niemann et al., 2013, 2014; Schaeffer et al., 2014, 2015) have been carried out for the conditions in the experiments and generally are in good agreement. The bottom panel of Figure 11 shows the comparison of the simulations (Figure 5, Clark et al., 2014) for the experimental conditions in the top panel, plotting the magnetic field magnitude vs. space and time in the same format on the same scales. The simulation reproduces the size of the cavity and the speed of the outgoing magnetic wave. The measured magnetic field change across the wave front can be shown to be consistent with the jump conditions that are satisfied for a collisionless shock wave. The 2-D simulations of the experiment also show that as the cavity develops, flute modes do not appear on the surface and some of the target ions have diffused beyond the cavity boundary (Clark et al., 2013, 2014). A number of experiments of this type have been carried out with different initial conditions that help define the criteria for which a collisionless shock can be generated (Schaeffer et al., 2017a).
It is also possible to redirect the laser beam so that it enters the plasma chamber at a small angle with respect to the axial magnetic field. By repositioning the target closer to one end of the plasma column, one can then study the dynamics of energetic debris ions streaming along the magnetic field. As before, the expansion of the energetic debris ions from the target produces a magnetic cavity, which can be measured by magnetic probes, as shown in Figure 12 (Heuer et al., 2018, private communication). In this case a small (~20 J) laser that fires at the same rate that the background plasma is generated is used to make the cavity, allowing very detailed probe measurements in 3-D. The cavity has a small transverse scale (radius ~3 cm) but is greatly expanded along the field (~12 cm). The interaction of the debris ions with this cavity tends to scatter a majority of the ions outward toward the walls of the chamber where they are lost. But a fraction of the debris ions do continue to propagate along the magnetic field at several times the Alfven speed and generate electromagnetic waves (Heuer et al., 2018). Magnetic probes at various positions downstream from the target measure the magnetic wave components along and transverse to the ambient field. Hybrid simulations and theory are then used to compare the computed wave properties with the measurements (Weidl et al., 2016); good agreement is obtained.
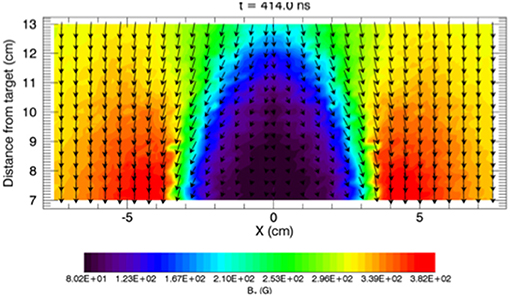
Figure 12. Magnetic probe measurements of the magnetic field direction and magnitude (arrows) produced by a low Mach number (MA ~ 1) expansion of target ions with laser beam oriented along the background magnetic field. The magnetic cavity (purple region) forms just in front of the target (Heuer et al., 2018, private communication).
Lastly, it should be pointed out that other types of magnetic cavities occur in space near the bow shock. These structures were originally called hot diamagnetic cavities (Thomsen et al., 1988) or hot flow anomalies (Schwartz et al., 1988) and were thought to be relatively small-scale entities just upstream of the shock. These structures result from interactions of discontinuities or steepened waves in the solar wind with the bow shock. The disruption of the shock allows downstream ions to flow into the solar wind, somewhat similar to a chemical ion release upstream of the bow shock, creating a cavity-like structure. These are not genuine “diamagnetic cavities” in the sense that the expanding, hotter plasma density from the magnetosheath is not much greater than the background (solar wind) density and thus the magnetic field is not totally excluded inside the cavity. The size of these cavities can vary widely. More recent observations (with simultaneous multi-spacecraft measurements) and 2-D hybrid simulations indicate they can extend over significant portion of the bow shock (Omidi et al., 2013).
Conclusions
The formation and properties of diamagnetic cavities were very active areas of space and laboratory plasma research several decades ago with both ion release experiments in space and laser-produced ion expansion experiments in the laboratory. Both types of experiments demonstrated magnetic field exclusion by the expanding release/target generated plasma and subsequent cavity formation. They also showed formation of field-aligned striations on the cavity surface, with wavelengths of the flute modes less than the ion gyroradius and much smaller than the cavity size. Linear theory indicated that a generalized lower-hybrid instability driven by both the density gradient at the edge of the cavity and more importantly, an additional drift due to the deceleration of the cavity surface could be the source of such unstable flute modes. Hall-MHD and particle simulations verified the instability mechanism, although there were issues concerning the observed wavelengths being much longer than the most unstable modes predicted by linear theory. By the early 90's, when the experimental campaigns were winding down, this was the state of our understanding (i.e., Figure 6).
Since then, there have been some additional laboratory experiments of sub-Alfvenic plasma expansions with improved diagnostics. But most importantly, very recent 3-D Hall-MHD and full particle simulations more clearly reveal that the initial development of the instability does occur at very short wavelength—perhaps even determined by grid resolution in the calculations—but the instability rapidly evolves to somewhat longer wavelengths, more consistent with the experimental measurements. Even though the effect of the deceleration of the plasma is a stronger effect in 3-D compared to 2-D, and the (linear) instability behavior is consistent with this difference, overall there are not new effects that arise in three dimensions. This was not totally unexpected since for the phenomena that we are interested in, namely cavities and surface striations, we have already demonstrated in this review that the space experiments, which are three-dimensional, are similar in many ways to the laser experiments that are essentially two-dimensional.
Most recent experimental and computational research has been devoted to debris ion expansions at greater than the Alfven speed as well as expansions along, rather than across the magnetic field. In these cases, cavities are still produced, but instead of flute modes at the surface, collisionless shock waves propagate outward from the cavity when the expansion is primarily perpendicular to the ambient magnetic field and various types of ion beam-driven electromagnetic waves are produced in parallel expansions. While space observations reveal many properties of shocks and related particle acceleration that can be studied in the laboratory. Howes (2018), the laboratory experiments are unique for clarifying the time-dependent processes of how cavities form and shocks are generated. In the future it may be possible to conduct such experiments in larger facilities with imposed inhomogeneous background plasmas and magnetic fields. For example, experiments at the Omega EP laser facility have already demonstrated that high-Alfven-Mach number shocks can be generated (Schaeffer et al., 2017b). Interesting new results from such experiments concerning cavity sizes and shapes, as well as wave generation and non-linear development, verified by appropriate 2-D and 3-D Hall-MHD, full particle and hybrid simulations, could eventually lead to new interest for active experiments in space. One promising candidate is a proposed small barium release via a rocket launch to generate lower hybrid turbulence and whistler waves (Ganguli et al., 2015).
Author Contributions
DW wrote much of the text and put the manuscript together. He was responsible for putting together 7 of the figures and related text. JH provided results of new calculations, resulting in 2 figures plus related text. CN provided 2 figures and related text. AL provided results of new calculations, resulting in 1 figure plus related text.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Work at Los Alamos and UCLA was supported in part by the Defense Threat Reduction Agency. A portion of this research was done while JH was at the Naval Research Laboratory.
References
Akimoto, K., Galvez, M., Gary, S. P., Sgro, A. G., and Winske, D. (1988). Prompt structuring of a plasma expanding in an external magnetic field. J. Geomag. Geoelectr. 40, 1161–1191. doi: 10.5636/jgg.40.1161
Bashurin, V., Golubev, A. I., and Terekhin, V. A. (1983). The collisionless deceleration of an ionized cloud dispersing in a uniform plasma in a magnetic field. J. Appl. Mech. Tech. Phys. 24, 614–622. doi: 10.1007/BF00905870
Bernhardt, P. A. (1992). Probing the magnetosphere using chemical releases from the combined release and radiation effects satellite. Phys. Fluids B 4, 2249–2256. doi: 10.1063/1.860193
Bernhardt, P. A., Roussel-Dupre, R. A., Pongratz, M. B., Haerendel, G., Valenzuela, A., Gurnett, D. A., et al. (1987). Observations and theory of the AMPTE magnetotail barium releases. J. Geophys. Res. 92, 5777–5794. doi: 10.1029/JA092iA06p05777
Bondarenko, A. S., Schaeffer, D. B., Everson, E. T., Clark, S. E., Lee, B. R., Constantin, C. G., et al. (2017a). Collisionless momentum transfer in space and astrophysical explosions. Nature Phys. 13, 573–577. doi: 10.1038/nphys4041
Bondarenko, A. S., Schaeffer, D. B., Everson, E. T., Clark, S. E., Lee, B. R., Constantin, C. G., et al. (2017b). Laboratory study of collisionless coupling between explosive debris plasma and magnetized ambient plasma. Phys. Plasmas 24:082110. doi: 10.1063/1.4995480
Bowers, K. S., Albright, B. J., Yin, L., Bergen, B., and Kwan, T. J. T. (2008). Ultrahigh, performance three-dimensional electromagnetic relativistic kinetic plasma simulation. Phys. Plasmas 15:055703. doi: 10.1063/1.2840133
Brecht, S. H., and Gladd, N. T. (1992). Structuring of a plasma shell expanding into a magnetized plasma at sub-Alfvenic speed. IEEE Trans. Plasma Sci. 20, 678–690. doi: 10.1109/27.199514
Brecht, S. H., and Thomas, V. A. (1988). Multidimensional simulations using hybrid particle codes. Computer Phys. Comm. 48, 135–143. doi: 10.1016/0010-4655(88)90031-8
Clark, S. E., Everson, E. T., Schaeffer, D. B., Bondarenko, A. S., Constantin, C. G., Niemann, C., et al. (2014). Enhanced collisionless shock formation in a magnetized plasma containing a density gradient. Phys. Rev. E. 90:041101 (R). doi: 10.1103/PhysRevE.90.041101
Clark, S. E., Winske, D., Schaeffer, D. B., Everson, E. T., Bondarenko, A. S., Constantin, C. G., et al. (2013). Hybrid simulation of shock formation for super-Alfvenic expansion of laser ablated debris through an ambient, magnetized plasma. Phys. Plasmas 20:082129. doi: 10.1063/1.4819251
Collette, A., and Gekelman, W. (2011). Structure of an exploding laser-produced plasma. Phys. Plasmas 18:055705. doi: 10.1063/1.3567525
Davidson, R. C., and Gladd, N. T. (1975). Anomalous transport properties associated with the lower-hybrid-drift instability. Phys. Fluids 18, 1327–1335. doi: 10.1063/1.861021
Dimonte, G., and Wiley, L. G. (1991). Dynamics of exploding plasmas in a magnetic field. Phys. Rev. Lett. 67, 1755–1758. doi: 10.1103/PhysRevLett.67.1755
Ganguli, G., Crabtree, C., Mithaiwala, M., Rudakov, L., and Scales, W. (2015). Evolution of lower hybrid turbulence in the ionosphere. Phys. Plasmas 22:112904. doi: 10.1063/1.4936281
Gekelman, W., Pfister, H., Lucky, Z., Bamber, J., Leneman, D., and Maggs, J. (1991). Design, construction, and properties of the large plasma research device – The LAPD at UCLA. Rev. Sci. Instrum. 62, 2875–2883. doi: 10.1063/1.1142175
Gisler, G., and Lemons, D. S. (1989). Dynamics of a plasma expanding into a uniform magnetic field. J. Geophys. Res. 94, 10145–10149. doi: 10.1029/JA094iA08p10145
Gladd, N. T. (1976). The lower hybrid drift instability and the modified two stream instability in high density theta pinch environments. Plasma Phys. 18, 27–40. doi: 10.1088/0032-1028/18/1/002
Gladd, N. T., and Brecht, S. H. (1991). Nonlocal theory of lower-hybrid-drift instability for a plasma shell expanding into a magnetic field. Phys. Fluids B 3, 3232–3247. doi: 10.1063/1.859754
Hassam, A. B., and Huba, J. D. (1987). Structuring of the AMPTE magnetotail barium releases. Geophys. Lett. 14, 60–63. doi: 10.1029/GL014i001p00060
Heuer, P. V., Weidl, M. S., Dorst, R. S., Schaeffer, D. B., Bondarenko, A. S., Tripathi, S.K. P., et al. (2018). Observations of a field-aligned ion/ion-beam instability in a magnetized laboratory plasma. Phys. Plasmas 25:032104. doi: 10.1063/1.5017637
Hewett, D. W., Brecht, S. H., and Larson, D. L. (2011). The physics of ion decoupling in magnetized plasma expansions. J. Geophys. Res. 116:A11310. doi: 10.1029/2011JA016904
Howes, G. G. (2018). Laboratory space physics: investigating the physics of space plasmas in the laboratory. Phys. Plasmas 25:055501. doi: 10.1063/1.5025421
Huba, J. D., Bernhardt, P. A., Fedder, J. A., Lyon, J. G., and Mitchell, H. G. (1993). Modelling the plasma dynamics of the CRRES G-9 and G-10 barium releases. Adv. Space Res. 13, 45–54. doi: 10.1016/0273-1177(93)90049-H
Huba, J. D., Bernhardt, P. A., and Lyon, J. G. (1992). Preliminary study of the CRRES magnetospheric barium releases. J. Geophys. Res. 97, 11–24. doi: 10.1029/91JA02144
Huba, J. D., Hassam, A. B., and Satyanarayana, P. (1989). Nonlocal theory of the Rayleigh-Taylor instability in the limit of unmagnetized ions. Phys. Fluids B 1, 931–941. doi: 10.1063/1.859017
Huba, J. D., Hassam, A. B., and Winske, D. (1990). Stability of sub-Alfvenic expansions. Phys. Fluids B 2, 1676–1697. doi: 10.1063/1.859441
Huba, J. D., Lyon, J. G., and Hassam, A. B. (1987). Theory and simulations of the Rayleigh-Taylor instability in the limit of large Larmor radius. Phys. Rev. Lett. 59, 2971–2974. doi: 10.1103/PhysRevLett.59.2971
Krall, N. A., and Liewer, P. C. (1971). Low-frequency instabilities in magnetic pulses. Phys. Rev. A 4, 2094–2103. doi: 10.1103/PhysRevA.4.2094
Liewer, P. C., and Davidson, R. C. (1977). Sheath broadening by the lower-hybrid-drift instability in post-implosion theta pinches. Nucl. Fusion 17, 85–100. doi: 10.1088/0029-5515/17/1/008
Lühr, H., Klöcker, N., and Acuña, M. H. (1988). The diamagnetic effect during AMPTE's tail releases: initial results. Adv. Space Phys. 8, 1–14.
Lühr, H., Southwood, D. J., Klöcker, N., Dunlop, M. W., Mier-Jedrzejowicz, W. A. C., Rijnbeek, R. P., et al. (1986). In situ magnetic field observations of the AMPTE artificial comet. Nature 320, 708–711. doi: 10.1038/320708a0
Mostovych, A. N., Ripin, B. H., and Stamper, J. A. (1989). Laser-produced plasma jets: collimation and instability in strong transverse magnetic fields. Phys. Rev. Lett. 62, 2837–2840. doi: 10.1103/PhysRevLett.62.2837
Niemann, C., Constantin, C. G., Schaeffer, D. B., Tauschwitz, A., Weiland, T., Lucky, Z., et al. (2012). Raptor: a high-energy Nd:glass laser facility for collisionless laboratory astrophysics. J. Instrum. 7:P03010. doi: 10.1088/1748-0221/7/03/P03010
Niemann, C., Gekelman, W., Constantin, C. G., Everson, E. T., Schaeffer, D. B., Bondarenko, A. S., et al. (2014). Observation of collisionless shocks in a large current-free laboratory plasma. Geophys. Res. Lett. 41, 7413–7418. doi: 10.1002/2014GL061820
Niemann, C., Gekelman, W., Constantin, C. G., Everson, E. T., Schaeffer, D. B., Clark, S. E., et al. (2013). Dynamics of exploding plasmas in a large magnetized plasma. Phys. Plasmas 20:012108. doi: 10.1063/1.4773911
Okada, S., Sato, K., and Sekiguchi, T. (1979). Possibility of lower-hybrid-drift instability in laser produced plasmas in a uniform magnetic field. J. Phys. Soc. JPN 46, 355–356. doi: 10.1143/JPSJ.46.355
Okada, S., Sato, K., and Sekiguchi, T. (1981). Behavior of laser produced plasma in a uniform magnetic field – plasma instabilities. Jpn. J. Appl. Phys. 20, 157–165. doi: 10.1143/JJAP.20.157
Omidi, N., Zhang, H., Sibeck, D., and Turner, D. (2013). Spontaneous hot flow anomalies at quasi-parallel shocks: 2. Hybrid Simul. J. Geophys. Res. 118, 173–180. doi: 10.1029/2012JA018099
Papadopoulos, K., Lui, A. T. Y., and Huba, J. D. (1987). Collisionless coupling in the AMPTE artificial comet. J. Geophys. Res. 92, 47–54. doi: 10.1029/JA092iA01p00047
Peyser, T. A., Manka, C. K., Ripin, B. H., and Ganguli, G. (1992). Electron-ion hybrid instability in laser-produced plasma expansions across magnetic fields. Phys. Fluids B 4, 2448–2458. doi: 10.1063/1.860213
Plechaty, C., Presura, R., and Esaulov, A. A. (2013). Focusing of an explosive plasma expansion in a transverse magnetic field. Phys. Rev. Lett. 111:185002. doi: 10.1103/PhysRevLett.111.185002
Prokopov, P. A., Zakharov, Y. P., Tishchenko, V. N., Shaikhislamov, I. F., Boyarintsev, E. L., Melekhov, A. V., et al. (2016). Laser plasma simulations of the generation processes of Alfven and collisionless shock waves in space plasma. J. Phys. Conf. Ser. 769:012086. doi: 10.1088/1742-6596/769/1/012086
Ripin, B. H., Huba, J. D., McLean, E. A., Manka, C. K., Peyser, T., Burris, H. R., et al. (1993). Sub-Alfvenic plasma expansion. Phys. Fluids B 5, 3491–3506. doi: 10.1063/1.860825
Ripin, B. H., Manka, C. K., Peyser, T. A., McLean, E. A., Stamper, J. A., Mostovych, A. N., et al. (1990). Laboratory laser-produced astrophysical-like plasmas. Laser Particle Beams 8, 183–190. doi: 10.1017/S026303460000793X
Ripin, B. H., McLean, E. A., Manka, C. K., Pawley, C., Stamper, J. A., Peyser, T. A., et al. (1987). Large-Larmor-radius interchange instability. Phys. Rev. Lett. 59, 2299–2302. doi: 10.1103/PhysRevLett.59.2299
Schaeffer, D. B., Everson, E. T., Bondarenko, A. S., Clark, S. E., Constantin, C. G., Vincena, S., et al. (2014). Laser-driven magnetized quasi-perpendicular collisionless shocks on the Large Plasma Device. Phys. Plasmas 21:056312. doi: 10.1063/1.4876608
Schaeffer, D. B., Everson, E. T., Bondarenko, A. S., Clark, S. E., Constantin, C. G., Winske, D., et al. (2015). Experimental study of subcritical laboratory magnetized collisionless shocks using a laser-driven magnetic piston. Phys. Plasmas 22:113101. doi: 10.1063/1.4934983
Schaeffer, D. B., Fox, W., Haberberger, D., Fiksel, G., Bhattacharjee, A., Barnak, D. H., et al. (2017b). Generation and evolution of high-Mach-number laser-driven magnetized collisionless shocks in the laboratory. Phys. Rev. Lett. 119:025001. doi: 10.1103/PhysRevLett.119.025001
Schaeffer, D. B., Winske, D., Larson, D. J., Cowee, M. M., Constantin, C. G., Bondarenko, A. S., et al. (2017a). On the generation of magnetized collisionless shocks in the large plasma device. Phys. Plasmas 24:041405. doi: 10.1063/1.4978882
Schwartz, S. J., Kessel, R. L., Brown, C. C., Woolliscroft, L. C., Dunlop, M. W., Farrugia, C. J., et al. (1988). Active current sheets near the Earth's bow shock. J. Geophys. Res. 93, 11295–11310.
Sgro, A. G., Gary, S. P., and Lemons, D. S. (1989). Expanding plasma structure and its evolution toward long wavelengths. Phys. Fluids B 1, 1890–1899. doi: 10.1063/1.859196
Shaikhislamov, I. F., Zakharov, Y. P., Posukh, V. G., Melekhov, A. V., Boyarintsev, E. L., Ponomarenko, A. G., et al. (2015). Experimental study of collisionless super-Alfvenic interaction of interpenetrating plasma flows. Plasma Phys. Rpt. 41, 399–407. doi: 10.1134/S1063780X15050050
Thomsen, M. F., Gosling, J. T., Bame, S. J., Quest, K. B., Russell, C. T., and Fuselier, S. A. (1988). On the origin of hot diamagnetic cavities near the Earth's bow shock. J. Geophys. Res. 93, 11311–11325.
Valenzuela, A., Haerendel, G., Föppl, H., Melzner, F., Neuss, H., Rieger, E., et al. (1986). The AMPTE artificial comet experiments. Nature 320, 700–703. doi: 10.1038/320700a0
Weidl, M. S., Winske, D., Jenko, F., and Niemann, C. (2016). Hybrid simulations of a parallel collisionless shock in the Large Plasma Device. Phys. Plasmas 23:122102. doi: 10.1063/1.4971231
Winske, D. (1988). Short wavelength modes on expanding plasma clouds. J. Geophys. Res. 93, 2539–2552. doi: 10.1029/JA093iA04p02539
Winske, D. (1989). Development of flute modes on expanding plasma clouds. Phys. Fluids B 1, 1900–1910. doi: 10.1063/1.858922
Winske, D. (1996). Regimes of the magnetized Rayleigh-Taylor instability. Phys. Plasmas 3, 3966–3974. doi: 10.1063/1.871569
Winske, D., and Gary, S. P. (2007). Hybrid simulations of debris-ambient ion interactions in astrophysical explosions. J. Geophys. Res. 112:A10303. doi: 10.1029/2007JA012276
Zakharov, Y.u P., Melekhov, A. V., Orishich, A. M., Ponomarenko, A. G., Posukh, V. G., and Shaikhislamov, I. F. (1999). Diamagnetic cavity of plasma clouds expanding into magnetized media. J. Plasma Fus. Res. Ser. 2, 398–401.
Zakharov, Y.u P., Orishich, A. M., Ponomarenko, A. G., and Posukh, V. G. (1986). Effectiveness of the slowing of expanding clouds of diamagnetic plasma by a magnetic field (experimental). Sov. J. Plasma Phys. 12, 674–678.
Zakharov, Y. P. (2002). Laboratory simulation of artificial plasma releases in space. Adv. Space Res. 9, 1335–1344. doi: 10.1016/S0273-1177(02)00184-9
Zakharov, Y. P. (2003). Collisionless laboratory astrophysics with lasers. IEEE Trans. Plasma Sci. 31, 1243–1251. doi: 10.1109/TPS.2003.820957
Zakharov, Y. P., Antonov, V. M., Boyarintsev, E. L., Melekhov, A. V., Posukh, V. G., Shaikhislamov, I. F., et al. (2006). Role of the Hall flute instability in the interaction of laser and space plasmas with a magnetic field. Plasma Phys. Repts. 32, 183–204. doi: 10.1134/S1063780X06030020
Keywords: magnetic cavities, plasma instabiities, active experiments in space, kinetic plasma simulations, Hall-MHD simulations
Citation: Winske D, Huba JD, Niemann C and Le A (2019) Recalling and Updating Research on Diamagnetic Cavities: Experiments, Theory, Simulations. Front. Astron. Space Sci. 5:51. doi: 10.3389/fspas.2018.00051
Received: 28 November 2018; Accepted: 21 December 2018;
Published: 28 January 2019.
Edited by:
Joseph Eric Borovsky, Space Science Institute, United StatesReviewed by:
Hermann Lühr, Helmholtz Center Potsdam German Geophysical Research Center (GFZ), Helmholtz Association of German Research Centers (HZ), GermanyYasuhito Narita, Austrian Academy of Sciences (OAW), Austria
Copyright © 2019 Winske, Huba, Niemann and Le. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dan Winske, d2luc2tlQGxhbmwuZ292
 Dan Winske
Dan Winske Joseph D. Huba2
Joseph D. Huba2