Artificial Aurora Experiments and Application to Natural Aurora

A review is given of the effects observed during injections of powerful electron beams from sounding rockets into the upper atmosphere. Data come from in situ particle and wave measurements near a beam-emitting rocket and ground-based optical, wideband radiowave, and radar observations. The overall data cannot be explained solely by collisional degradation of energetic electrons but require collisionless beam-plasma interactions (BPI) be taken into account. The beam-plasma discharge theory describes the features of the region near a beam-emitting rocket, where the beam-excited plasma waves energize plasma electrons, which then ignite the discharge. The observations far beneath the rocket reveal a double-peak structure of artificial auroral rays, which can be understood in terms of the beam-excited strong Langmuir turbulence being affected by collisions of ionospheric electrons. This leads to the enhanced energization of ionospheric electrons in a narrow layer termed the plasma turbulence layer (PTL), which explains the upper peak. Similar double-peak structures or a sharp upper boundary in rayed auroral arcs have been observed in the auroral ionosphere by optical, radar, and rocket observations, and called Enhanced Aurora. A striking resemblance between Enhanced and Artificial Aurora altitude profiles indicates that they are created by the above BPI process which results in the PTL.

1. Introduction

Aurora, also known as polar or northern lights (aurora borealis) or southern lights (aurora australis), is a natural airglow in the Earth's sky, such as shown in Figure 1. As auroras were formerly thought to be the first light of dawn, the name “Aurora” came from the Latin word for “dawn, morning light,” while “Borealis” was coined by Galileo in 1619 from the Roman goddess of the dawn and the Greek name for the north wind (Siscoe, 1986). Aurora is seen mainly at high latitudes in the auroral zone, the position of which is controlled by the geomagnetic activity (e.g., Meng et al., 1991). It is produced when fluxes of energetic electrons precipitate along the magnetic field into the upper atmosphere at altitudes below ~130 km.

FIGURE 1

Figure 1. Examples of auroral displays: (a) Corona and (b) rayed arcs (https://en.wikipedia.org/wiki/Aurora).

It is thus straightforward to employ electron beams injected from a space vehicle with controlled parameters to explore Artificial Aurora (AA) generated in the upper atmosphere. Such (active) AA experiments have been conducted from sounding rockets and the Spacelab (e.g., Davis et al., 1971, 1980; Hess et al., 1971; Cambou et al., 1975, 1978, 1980; O'Neil et al., 1978a,b; Maehlum et al., 1980a; Jacobsen, 1982; Obayashi et al., 1984; Neubert et al., 1986; Kawashima, 1988; Goerke et al., 1992; Burch et al., 1993). Besides exploring Artificial Aurora, active electron beam experiments, beginning with the Echo 1 experiment (Hendrickson et al., 1971), used injected beams as probes for studying the remote natural processes along the magnetic field. Comprehensive reviews of the “Electron Echo” series and similar experiments have been given by Winckler (1980, 1992) and Kellogg (1992).

The present survey mainly focuses on the AA experiments with primarily downward electron injections. The early experiments were focused on the optical features of Artificial Aurora, then investigation of electron beam-plasma interactions became the main driving force. Because of the limited scope of this review, the setup of different experiments, as well as the electron and ion injectors and diagnostic suites onboard and on the ground, are described only schematically. The presentation is also limited to sounding rocket experiments at altitudes at and below ~200 km to avoid the effects of return currents caused by a positive potential of beam-emitting vehicles (e.g., Linson, 1982; Obayashi et al., 1984; Managadze et al., 1988; Frank et al., 1989). The main conclusion of these experiments is that the overall dataset cannot be explained solely by collisional degradation of the beam electrons and requires collisionless beam-plasma interactions (BPI) be taken into account. This stimulated numerous laboratory experiments and theoretical studies discussed during international symposiums on active experiments in space (e.g., Reme, 1980; Grandal, 1982a; Burke, 1983).

This chapter is organized as follows. The salient features of the “classical aurora” limited to collisional impact processes are summarized in section 2. Section 3 gives a review of the effects observed during injections of powerful electron beams from sounding rockets in the ionosphere. Data come from in situ measurements of the luminescence, thermal and suprathermal populations, and beam electrons near a beam-emitting space vehicle, as well as from ground-based optical, radar, and radioemission observations. A brief survey of the BPI theory, which was developed to address the observed unexpected effects, is presented in section 4.

The processes in the near-rocket region are explained by the beam-plasma discharge (BPD) theory (Galeev et al., 1976; Mishin and Ruzhin, 1980a, 1981; Rowland et al., 1981a; Papadopoulos, 1982, 1986; Mishin et al., 1989; Sotnikov et al., 1992) outlined in section 5. The AA rays far from the rocket reveal a special regime of strong Langmuir turbulence in which the wave spectrum in the beam-plasma system, and thus acceleration of suprathermal electrons, is controlled by collisional damping (Izhovkina and Mishin, 1979; Volokitin and Mishin, 1979; Mishin et al., 1981, 1989). The developed theory explained several puzzling features of natural aurora, which is dubbed Enhanced Aurora by Hallinan et al. (1985). Enhanced Aurora (EA) is discussed in the final section. As a rule, only the basic concepts on a semi-qualitative level are given, just sufficient for understanding experimental results. Details and rigorous derivations can be found in the referenced original papers, reviews, and textbooks. Plots and images have been adjusted and sometimes additionally annotated with respect to the originals.

Before presenting the principal experimental results, it is instructive to discuss briefly the “classical” auroral features that follow from collisional interaction of energetic electrons with the neutral atmosphere.

2. Beam-Atmosphere Interaction: “Classical Aurora”

The collisional or single-particle approach (SPA) considers processes of ionization, dissociation, and excitation of atmospheric constituents (N₂, O, and O₂) by electron impact (e.g., Rees, 1989). In each ionization event precipitating (primary) electrons with energies ε_b ~ 1–10 keV lose energy, Δε_ion = ε_ion + ε_s, where ε_ion is the ionization energy and ε_s is the energy of the new-born (secondary) electron. Degradation of primary and secondary electrons along the path is usually calculated using Monte Carlo technique. The energy dissipation rate can be estimated from Bethe's formula

$\begin{array}{ll}\frac{d\epsilon }{dh}\approx -\frac{\epsilon }{l_{\epsilon }(h)}\propto N(h)& (1)\end{array}$

Here l_ε ≈ (υ/ν_ion)ε/ 〈Δε_ion〉 and ν_ion is the mean free path and ionization frequency of electrons with the initial energy $\epsilon =\frac{1}{2}{m}_e{v}^2$, respectively; 〈Δε_ion〉 ≈ 32 eV is the average energy loss in air; v is the electron speed; and N(h) is the neutral gas density at a given altitude, h. Equation (1) is valid as long as Δε_ion ≪ ε.

The altitude profile of optical emissions at a wavelength λ is determined by the volume emission rate (VER). For the prompt emissions, for which quenching is negligible, the VER reduces to the excitation rate

$\begin{array}{ll}{Q}_{\lambda }=4\pi {{\displaystyle \int }}_{{\epsilon }_{\lambda }}^{\infty }{\sigma }_{\lambda }(\epsilon )\Phi (\epsilon )d\epsilon ·\left[X\right]& (2)\end{array}$

Here ε_λ and σ_λ are the excitation energy and cross-section, respectively, [X] is the density of the neutral species, $\Phi (\epsilon )=\frac{2\epsilon }{m_e^2}F(\epsilon )$ is the differential omnidirectional number flux, m_e is the electron mass, and F(ε) is the distribution function.

The aurora's color is determined by the wavelengths, λ, of electromagnetic radiation emitted by atoms and molecules in the upper atmosphere, mainly atomic oxygen (O) and molecular nitrogen (N₂), impacted by energetic electrons. The excitation energy is a good indicator of the electron energy distribution. For example, ε_λ for the green- (λ = 557.7 nm), blue- (427.8), and violet-line (391.4) emissions are about 4.2, 18.9, and 20 eV, respectively. As the excitation cross-sections are small at ε > 500 eV, the auroral glow is mainly determined by suprathermal, T_e ≪ ε < 500 eV, electrons with the distribution function F_s(ε). Here T_e is the electron temperature, which usually does not exceed ~0.3 eV.

The suprathermal population is created due to degradation of secondary electrons. In the local approximation, the suprathermal (omnidirectional) flux, ${\Phi }_s(\epsilon )=(2\epsilon /m_e^2)F_s(\epsilon )$, can be approximated by a power law function

$\begin{array}{ll}{\Phi }_s(\epsilon )\approx \frac{3}{2\pi m_e{v}_c}{n}_s{\left(\frac{{\epsilon }_c}{\epsilon }\right)}^{p_s}\text{at }\epsilon >{\epsilon }_c& (3)\end{array}$

with the spectral index p_s ≈ 3.5, the density of the secondary electrons n_s ~ 10 · n_b (the density of the primary electron flux), and ${\epsilon }_c=m_e{v}_c^2/2\approx 6$ eV. At ε < ε_c ≈ 6 eV, the distribution is very sensitive to the neutral composition because of considerable differences between cross-sections for various components. The local approximation is valid until the atmosphere scale height, H_N, greatly exceeds v/ν_il, where ν_il(ε) is the frequency of inelastic collisions. Note that the spectral index for the (directional) magnetic field-aligned flux is p_s − 1 ≈ 2.5.

Figure 2 shows a typical altitude profile of auroral luminosity calculated for the initial energy ε_b = 7.2 keV using Monte Carlo method (Izhovkina and Mishin, 1979). Apparently, above the peak, at h > h_m ≈ 110 km, the brightness is proportional to the neutral density N, which is consistent with Equation (1). The peak altitude, h_m, and thickness, Δh_m, can be estimated from the conditions $l_b^{(m)}=l_{{\epsilon }_b}(h_m)\approx H_N$ and Δh_m ~ H_N(h_m), respectively. Both h_m and Δh_m decrease with increasing ε_b, since the primary electrons penetrate the denser and cooler atmosphere. These features, together with the spectrum Φ_s(ε) (3) and the associative VER (2), constitute the “classical aurora” paradigm that is widely used for calculating the auroral E-region conductivity and power released by precipitating electrons.

FIGURE 2

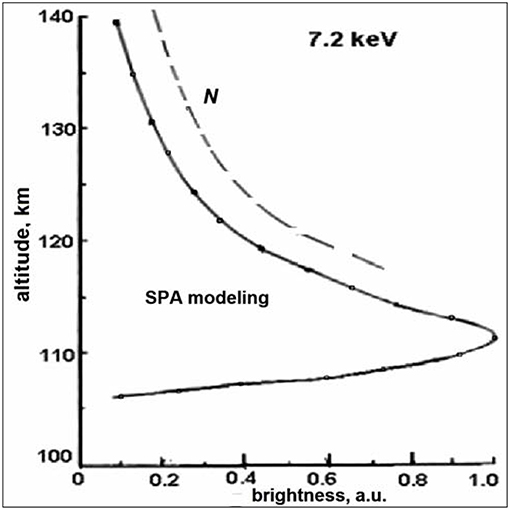
Figure 2. Auroral altitude profile for ε_b = 7.2 keV primary electrons. The dashed line shows the relative neutral density from the MSIS model. Adapted from Izhovkina and Mishin (1979). Reprinted by permission from Geomagnetism and Aeronomy.

The next section presents the “anomalous” features of Artificial Aurora that were unforeseen by the collisional approach.

3. Artificial Aurora Experiments

We start with the observations during the Zarnitza-2 experiment carried out in September 1975 (Cambou et al., 1975; Dokukin et al., 1981; Ivchenko et al., 1981). It is worth noting that Zarnitza 1 and 2 together with the ARAKS (Artificial Radiation and Aurora between Kerguelen and Soviet Union) “North” and “East” experiments constituted the French-Soviet program led by F. Cambou and R. Sagdeev. The electron beam and cesium plasma injectors were put by a rotation-stabilized meteorological rocket into a ballistic trajectory with a 155 km apogee (Figure 3). Ground-based diagnostic instruments, including a low-light TV camera, a dual frequency (22.5 and 33.8 MHz) radar, and a broadband (27–51 MHz) VHF radio receiver, provided enough information to describe the effects of injected electrons.

FIGURE 3

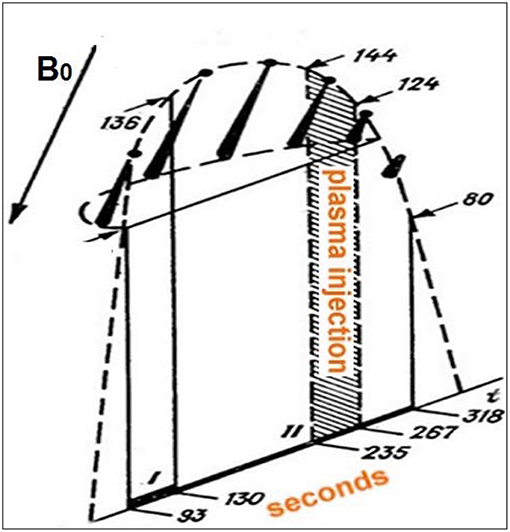
Figure 3. Cartoon depicting the Zarnitza-2 rocket trajectory with electron and plasma injections. The numbers 136, …80 indicate the altitude in kilometers. After Dokukin et al. (1981). Reprinted by permission from COSPAR.

Electron injections were started at h ≈ 109 km, with the beam energy and current of 9.3 keV and 0.27 A, respectively, and switched to 7 keV and 0.45 A at h ≈ 136 km. The injection duty cycle comprised of 0.67 and 0.04 s pulses with 100% modulation at 2 kHz and 0.75 s gaps between the pulses. The beam was primarily directed downwards with the initial cone angle of 1°. Because of the rocket's spin with T_spin ≈ 3.4 s, the injection angle, θ₀, to the magnetic field B₀ varied between the extrema, i.e., θ_min ≤ θ₀ ≤ θ_max, with θ_min (θ_max) changing periodically between 40° and 28° (70° and 92°) in 58 s due to the rocket's axis precession.

3.1. Artificial Aurora

In the course of the experiment, a remote low-light TV camera recorded 350–700 nm emissions at 5 frames/s and exposition time of 0.17 s (Ivchenko et al., 1981). All typical auroral lines have been identified in the emission spectrum. Left frame in Figure 4 is made up of two of about eighty nearly-identical AA images during injections near apogee (Mishin et al., 1981). The luminosity profiles were obtained using microphotometric analysis of the optical emissions along the AA rays and taking the aspect angle condition into account. Each profile features a bright glow near the beam-emitting rocket and two luminosity peaks far from the rocket. The agreement between the observed and calculated AA lower boundary indicates that the beam energy is close to the nominal (cf. Davis et al., 1971; Rees et al., 1976). That is, the rocket potential is small, which agrees with the measurements onboard (Dokukin et al., 1981).

FIGURE 4

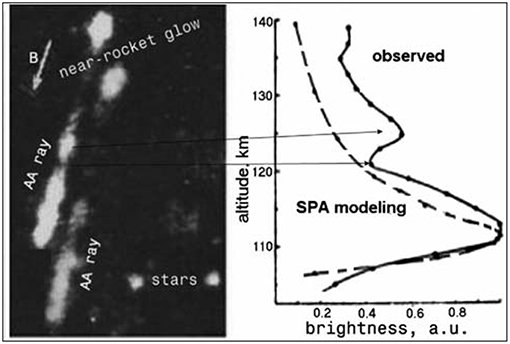
Figure 4. (Left) An example of the near-rocket glow and Artificial Auroral rays in Zarnitza 2 (see text). (Right) The altitude-profile of the leftmost AA ray with a Monte Carlo profile superimposed. After Mishin et al. (1981). Reprinted by permission from COSPAR.

The AA brightness agrees with Monte Carlo calculations below 120 km (cf. Figure 2), but above the observed luminosity substantially exceeds the collisional level. Besides, the lower peak is slightly wider than the SPA profile, indicating some additional (~10%) scatter of the beam energy. A slight increase of the energy of some part of the beam electrons indicated by the lowest portion of the profile can possibly be explained by Kainer et al.'s (1972) mechanism.

Now we turn to describe the characteristics of the near-rocket glow (NRG), suprathermal electrons, VHF radioemission, and fast scattering of the beam electrons dubbed “prompt echoes.”

3.2. Near-Rocket Glow and Suprathermal Electrons

Figure 5 shows the AA radiation from the near-rocket glow (NRG) in the course of the Zarnitza 2 and Polar 5 (Maehlum et al., 1980b,c; Grandal, 1982b) experiments, respectively. The variation of the relative radiation flux, F_R/F₀, from the near-rocket glow (NRG) with altitude and injection angle (Figures 5A–C) does not follow the SPA predictions (Ivchenko et al., 1981). Here F₀ ≈ 2.5·10¹⁸ photon/s is the radiation flux from a point source at altitude 100 km, which produces the same flux density, 2·10³ photon/cm²s, on the ground as the faintest detectable star of the 9th stellar magnitude. On average, the NRG radiation barely changes near apogee. The scatter of the values between 190 and 220 s is due to unstable electric power supply that resulted in the data loss during 220–250 s. Note that fluxes at altitudes ~150 and 115–120 km are of the same order, F_R/F₀ ~ 10–15, while the neutral density changes by more than a factor of ten.

FIGURE 5

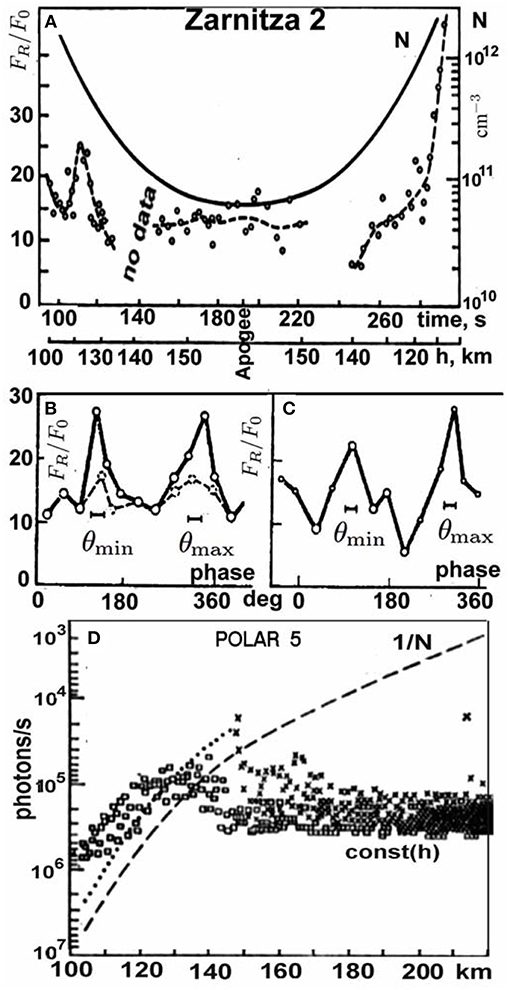
Figure 5. (A) The radiation flux in the units of F₀ from the NRG in Zarnitza 2 averaged over 3–4 neighboring frames (circles). The dashed (solid) line shows the trend of F_R (the neutral density, N, in cm⁻³). (mid) Variation of the flux with the rocket spin phase for the intervals 150–290 s (the solid line) and 150–220 s (dashed) averaged over (B) 7 or 14 frames taken at ≤0.6 s from the start of long pulses and (C) 3 or 8 frames taken within 0.2 s. The phases for θ_min and θ_max are indicated. After Ivchenko et al. (1981). (D) The beam-induced luminescence in photon/s at λ = 391.4 nm during Polar 5. The dashed line shows 1/N scaled. After Maehlum et al. (1980b) and Grandal (1982b). Reprinted by permission from Geomagnetism and Aeronomy and Plenum Press.

The presence of two almost equal maxima of F_R during one rocket rotation at the extrema of the injection angle, ${\theta }_{min}\approx 30^{\bullet }$ and ${\theta }_{max}\approx 80^{\bullet }$, also contradicts to the SPA predictions. Taking the average photon energy of 2–3 eV (mainly 391.4-nm photons) gives the radiated power of ~30–45 W. That is, the NRG radiates about one percent of the beam power. These values are of the same order as in the Zarnitza 1 experiment (Cambou et al., 1975) and much larger than the collisional limit. The latter is true for the flux during the whole flight.

Quite similar results have been obtained in the Polar 5 “mother-daughter” rocket experiment (Maehlum et al., 1980b,c; Grandal, 1982b) conducted in February 1976. An electron accelerator on the “daughter” payload produced a ~10 keV electron beam with the maximum current of 0.13 A, which was pulsed at a repetition period 0.4 s. Each pulse comprised five 2-ms sub-pulses separated by 2 ms gaps. The “mother” payload carried a 391.4 nm phometer with the sampling rate of 2.5 kHz and diagnostic instruments for monitoring scattered and secondary electrons, as well as wave effects. The payloads separated slowly, so their distance across B₀ reached about 80 m in the end of flight.

Figure 5D shows the luminescence at 391.4 nm detected by the photometer during beam injections. The observed light level follows the neutral density below 130 km but is fairly constant in the altitude range from 150 km to apogee at 220 km and much larger than that produced by the beam electrons. The latter agrees well with the observations of the electron population in the NRG (Figure 6) with many more suprathermal electrons, the source of airglow, than produced by direct impact.

FIGURE 6

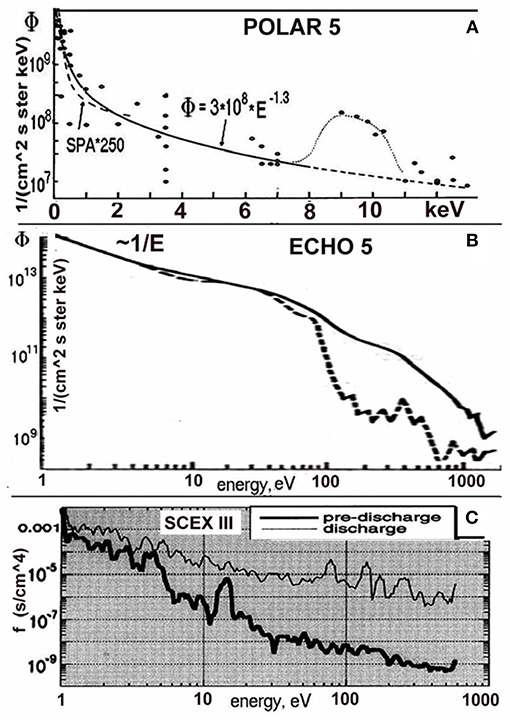
Figure 6. (A) Suprathermal and beam electron spectra in Polar 5. The dashed line shows the SPA spectrum multiplied by 250. After Maehlum et al. (1980b) and Grandal (1982b). Suprathermal electron spectra in (B) Echo 5 with/without (the dashed/solid line) neutral gas injections, and (C) SCEX III. After Arnoldy et al. (1985) and Bale et al. (1995). Reprinted by permission from Elsevier, Plenum Press, and the American Geophysical Union.

Indeed, the suprathermal flux at energies less than 1 keV in Figure 6A greatly exceeds the SPA spectrum and has a power law spectrum, Φ(ε) ∝ ε^−1.3, i.e., with the spectral index ~ p_s/3 (Equation 3). The same is true for suprathermal electron spectra observed during the Echo 5 (Arnoldy et al., 1985; Winckler, 1992) and the Several Compatible Experiments (SCEX) III (Goerke et al., 1992; Bale et al., 1995) experiments in November 1979 and February 1990, respectively. During Echo 5, three electron guns injected a 25 keV and 0.6 A electron beam. Each 4-ms injection comprised 0.5 ms turn-on and turn-off pulses and three 1-ms pulses repeated every 20 ms in a 90 pulse “fast” series. Particles were measured every 200 ms aboard the same payload. Due to the electrode voltage sweep failure of the particle detectors at 132 s flight time, only 0.5 and 8 keV particles were measured at 80° and 0° pitch angles, respectively. The suprathermal electron fluxes (Figure 6B) observed earlier in the flight without (the solid line) and with (dashed) cold nitrogen gas injections have the power law spectrum, Φ(ε) ∝ ε⁻¹, until the flux drops at about 100 eV as the neutral density increased near the rocket. Note beforehand that the latter is in good agreement with the BPI theory prediction (section 4.5).

The SCEX III rocket with a 375 km apogee carried two payloads with a variety of scientific sensors (e.g., Goerke et al., 1992; Bale et al., 1995). An electron gun was located on the aft payload injecting electrons at various energies up to 6 keV and currents from 1 to 60 mA. The neutral density measured on the aft and forward payload showed a significant enhancement over atmospheric models probably caused by severe outgassing. The plots in Figure 6C show suprathermal populations obtained during two 0.16 s sweeps of the retarding potential analyzer (RPA) aboard the aft payload near apogee at 315 s flight time. The “pre-discharge” and “discharge” curve corresponds to the beam current below and above 10 mA, respectively. Above 10-20 mA, the measured (quasi-directional) electron flux averaged over electron energy and 391.4 nm luminosity averaged over 200 s of photometer data (Bale et al., 1995, Figures 2, 4) grow nonlinearly with the beam current. The flux's spectral index is ≈2.3 (close to the SPA's) during the pre-discharge regime and decreases to ≈1.2 at greater currents.

The concurrent optical and radar observations in Zarnitza 2 established that the near-rocket glow near apogee had a cylindrical shape with the dimensions of ~10 m across and ~300 m along B₀ (Dokukin et al., 1981). Similarly, the Polar 5 (Grandal, 1982b), Electron 2 (Jacobsen, 1982), and the U.S./Canadian electron accelerator experiment (Duprat et al., 1983) with mother-daughter payload configurations measured the dimensions of the hot electron/plasma cloud to be ~100 m along B₀ and several beam Larmor radii transverse to B₀.

As 391.4 nm emission indicates ionization of nitrogen, the airglow data, consistent with suprathermal electrons at ε > ε_ion, unequivocally point to enhanced ionization taking place in the near-rocket region. This conclusion is supported by concurrent observations of the radar backscatter and intense very high frequency (VHF) radioemission from the near-rocket region at frequencies greatly exceeding the plasma frequency of the ambient plasma (Mishin and Ruzhin, 1980b; Dokukin et al., 1981; Goerke et al., 1992) presented next.

3.3. VHF Radioemission From the Near-Rocket Region in Zarnitza 2 and ARAKS

Figure 7 illustrates the evolution of the VHF spectrum with the injection height and pitch angle during 0.67 s pulses in Zarnitza 2 and the temporal development during 20 ms pulses in ARAKS. In Zarnitza 2, a broadband continuous spectrum of beam-induced VHF electromagnetic waves was detected by a ground-based radio spectrograph with a 27–51 MHz bandwidth (Dokukin et al., 1981). It is seen in Figures 7A,B that the radioemission appears during each 0.67 s injection pulse and is modulated by the rocket's spin. This modulation is due to the variation of the injection pitch angle (cf. Figures 5B,C) and also clearly depends on the spin phase. The radio burst near 50 MHz of a 5–10 MHz width at the beginning of the injection pulse is a rapid drift from lower to higher frequencies within the spectrograph sweeping time of 20 ms.

FIGURE 7

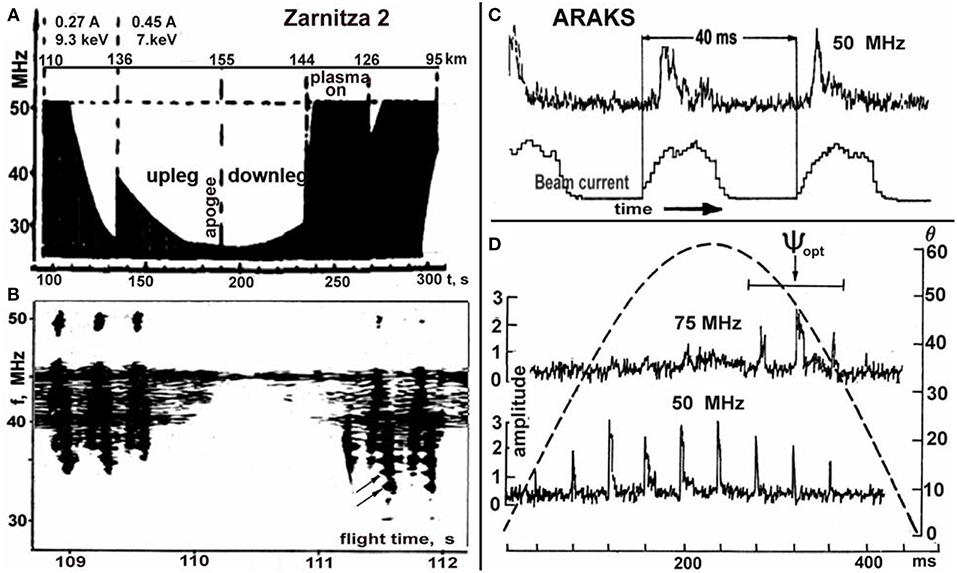
Figure 7. VHF radioemission in Zarnitza 2 and ARAKS: Variation of the broadband spectrum in Zarnitza 2 with (A) altitude and (B) the rocket's spin (one long pulse per 2 revolutions). Arrows indicate the specral maxima at (s + 1/2)f_ce. Adapted from Dokukin et al. (1981). (C) Delay of radioemission at 50 MHz relative to the start of 20 ms pulses in ARAKS and (D) dependence of radioemission at 75 MHz on the phase of the rocket's rotation. The dashed curve shows the beam pitch angle θ₀. After Mishin and Ruzhin (1980b). Reprinted by permission from COSPAR.

During the first injection regime, the maximum frequency averaged over several long pulses between 120 and ≈130 km decreased with altitude as N^1/4. After transition to the second regime and until the plasma generator was turned on, f_max is approximated as follows

$\begin{array}{ll}{f}_{max}=\text{const}{\left(\frac{I_b}{v_b}\frac{N}{V_{R\perp }}\right)}^{1/2}& (4)\end{array}$

Here V_R⊥ is the rocket's speed across the magnetic field, which differs significantly between the upleg and downleg parts of the trajectory. The dependence of the NRG plasma growth on V_R⊥ was predicted theoretically by Galeev et al. (1976).

Assuming that f_max (4) is the increased plasma (Langmuir) frequency, $f_{pe}\approx 9\sqrt{n_e}$ kHz, gives the plasma density in the NRG, n_e ∝ I_bN/v_bV_R⊥. The spectral density of the electromagnetic flux was at least 10⁻²⁰ W/m²Hz, which exceeds more than ten times the detection threshold. Assuming a point source at about 300 km distance gives ~100 W of the total radiated power for a 10 MHz band emission, i.e., ~3 percent of the beam power, which is of the same order as the radiated optical power. As shown in Figure 7B, the spectrum has maxima (buldges) centered at half-integral harmonics of the electron gyrofrequency, f_ce, i.e., f_s ≈ (s + 1/2)f_ce, with integers s ≥ 20 to ≈ 30 (Dokukin et al., 1981, Figure 10). This “gyro structure” is clearly seen only in a certain height range from 110 to 128 km and 105–115 km in the first and second injection regime, respectively. Near apogee, the radioemission at ≥27 MHz appears only twice during one rocket's rotation as a brief pulse. At the same time, the VHF radar data show radioemission at the radar frequency of 22.5 MHz during the whole injection pulse, i.e., two rotations of the rocket.

The temporal development of radioemission and its dependence on the phase of the rocket' spin was studied in details during the ARAKS “East” experiment using five narrowband receivers located at the launching site (Mishin and Ruzhin, 1980b). A 0.5 A and 27 or 13 keV electron beam was injected at various angles, φ, with respect to the axis of the rocket. As in Zarnitza 2, the spectral density of the VHF electromagnetic flux was at least 10⁻²⁰ W/m²Hz. Figures 7C,D illustrates the features of 50 and 75 MHz emissions generated by 20 ms injections of 13 keV electrons at φ = 30° (pitch angles θ ≈ 0°–60°) in the altitude range of 111.2–103.7 km.

One can see the time delay of a few milliseconds with respect to the start of 20 ms pulses. The time delay for 75 MHz emissions is greater than that for 50 MHz by a few ms (Mishin and Ruzhin, 1980b, Figure 6). The generation of the higher-frequency emission depends on the phase of the rocket's rotation, ψ, which is counted off from the axis aligned with V_R⊥. This dependence results from rotation of the beam guiding center with the spinning rocket, ΔV_⊥ ~ 2πr_cb/T_spin, where r_cb = v_b sin θ/ω_ce is the beam Larmor radius (Mishin and Ruzhin, 1980a). The total speed of the guiding center across B₀ amounts to V_⊥ = V_R⊥ + ΔV_⊥(ψ). It is minimized at the “optimum” phase, ψ → ψ_opt, when the guiding center moves against V_R⊥. In the ARAKS experiment, ΔV_⊥(ψ)/V_R⊥ reached up to 30%.

3.4. Prompt Electron Echoes

Besides the enhanced number of suprathermal electrons in the NRG, strong scattering of beam electrons occurs in the vicinity of a beam-emitting payload (Hendrickson et al., 1971; Winckler et al., 1975; Gringauz et al., 1980; Lyakhov and Managadze, 1980; Maehlum et al., 1980c; Winckler, 1980, 1992; Arnoldy et al., 1985; Wilhelm et al., 1985). This effect is dubbed prompt electron echoes (PEE) as the backscattered electrons are detected within ≤100 ms even during upward beam injections. Figure 8 shows the results from the Echo 5 and ARAKS experiments (Gringauz et al., 1980; Arnoldy et al., 1985). Clearly, above 140 km the scattered flux is almost independent of the neutral density, while the SPA predicts the decrease by a factor of 30. By the same token, the Polar 5 data reveal (Maehlum et al., 1980c) that an initially-collimated beam significantly broadens over pitch angles in less than one gyroperiod, i.e., ~10⁻⁶ s. Furthermore, in addition to the beam core, a noticeable part of beam electrons is scattered over large pitch angles up to ~180°. At altitudes 150 to 180 km, the flux of these “halo” electrons varies with the distance, d_⊥ (in meters), between the mother and daughter payloads as

$\begin{array}{ll}{\Phi }_{obs}=3·10^{7}exp(-0.07·d_{\perp }),& (5)\end{array}$

which is about 10² times greater than collisional scattering can produce.

FIGURE 8

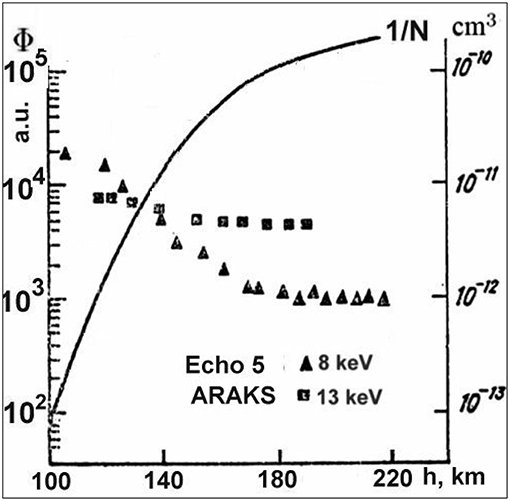
Figure 8. Variation of the scattered beam electrons in the ARAKS (squares) and Echo 5 (triangles) experiments. The solid line shows the model value of N⁻¹ in cm³. After Grandal (1982a) and Arnoldy et al. (1985). Reprinted by permission from COSPAR and American Geophysical Union.

In summary, the observed near-rocket glow, suprathermal electrons, VHF radioemission, and prompt electron echoes, as well as the fine altitudinal structure of AA rays, point to much stronger interaction of injected electrons with the upper atmosphere than provided by electron collisions. Next, a brief survey is presented of the theory of collisionless beam-plasma interaction (BPI) resulting in the beam-plasma discharge (BPD) near beam-emitting payloads and the double-peak structure of artificial and natural aurora rays.

4. Beam- Ionospheric Plasma Interaction

The upper atmosphere is, in fact, a weakly-ionized plasma, the ionosphere, with the plasma density n_e ≪ N. Conventionally (e.g., Ichimaru, 1973), ionized gases can be regarded as plasma if their behavior is dominated by the collective response of charged particles due to the long-range Coulomb force. Charged particles in motion generate electromagnetic fields that affect motion of other particles, thereby making a fast remote response to local perturbations. The distance over which charges in plasma are shielded is the electron Debye radius, r_D = v_Te/ω_pe, where ω_pe = 2πf_pe (the Langmuir frequency) and v_Te is the electron thermal velocity. The number of particles in the Debye sphere in plasmas is large, $N_D=4\pi n_e{r}_D^3\gg 1$. In collisional plasmas, the plasma frequency is supposed to significantly exceed the collision frequency of plasma electrons, ν_e.

Henceforth, the density, mass, electric (magnetic, B₀) fields, and frequency, f = ω/2π, are taken in cm⁻³, grams, V/m (Gauss), and Hz, respectively. Temperature, T_e,i, is taken in units of energy, electronvolts (1 eV = 11,605 K). We consider only one singly-charged ion species with the ion-to-electron mass ratio $m_i/m_e={\mu }^{-1}=3·10^4$ and 6 · 10⁴ in the F- and E-region ionosphere at altitudes around ~200 km and ~ 100–130 km, respectively.

4.1. Plasma Waves

A symbiotic relationship between plasma particles and fields results in a wide variety of collective motions, i.e., plasma waves. Of those, the most important for the BPI are high-frequency (HF) plasma modes. In a weakly-magnetized (ω_ce ≪ ω_pe) plasma, their frequencies away from the electron gyroharmonics, sω_ce, are

$\begin{array}{ll}{\omega }_{\text{k}}={\omega }_{pe}\left(1+\frac{3}{2}{k}^2{r}_D^2+\frac{{\omega }_{ce}^2}{{\omega }_{pe}^2}{sin}^2\alpha \right)& (6)\end{array}$

with the wavenumber k, the propagation angle α = arccos(k·B₀/kB₀), and $k^2{r}_D^2\ll 1$. It reduces to the Langmuir (L) branch, ${\omega }_l\approx {\omega }_{pe}(1+\frac{3}{2}{k}^2{r}_D^2)$ at α = 0 (k = k_∥) and to the upper hybrid (UH) branch, ${\omega }_{uh}\approx \sqrt{{\omega }_{pe}^2+{\omega }_{ce}^2}$ at α = π/2 (k = k_⊥). The spectral energy density of a broad Langmuir spectrum, $\delta \text{E}(\text{r},t)=\sum _{\text{K}}{\text{E}}_{\text{k}}{e}^{i\text{kr}-i{\omega }_{\text{k}}t}$ is $W_l\approx \sum |{\text{E}}_{\text{k}}{|}^2/4\pi$.

The other important branch of electrostatic (E = −∇ϕ) HF waves is the electron Bernstein (EB) mode with frequencies approaching sω_ce at both $k_{\perp }^{-1}\gg r_{ce}$ and ≪r_ce (the electron Larmor radius). Near k_⊥r_ce ~ 1, they have a wide maximum around half-integral gyroharmonics, ω_s ≈ (s + 1/2)ω_ce, where the group velocity tends to zero (e.g., Mikhailovskii, 1974). It is worth noting that in the magnetospheric community such waves, routinely observed in the plasma sheet region associated with diffuse aurora (e.g., Ashour-Abdalla and Kennel, 1978; Khazanov, 2011), are called electron cyclotron harmonics (ECH).

It is instructive to recall the well-known wave-particle quantum-mechanical analogy (e.g., Ichimaru, 1973), which helps to understand the wave properties in an inhomogeneous plasma. Since ω_k(r, k) is constant in stationary media, we have $d{\omega }_{\text{k}}=d\text{r}\frac{\partial {\omega }_{\text{k}}}{\partial \text{r}}{\displaystyle {|}_{\text{k}}+d\text{k}\frac{\partial {\omega }_{\text{k}}}{\partial \text{k}}{|}_{\text{r}}}=0$ or

$\begin{array}{ll}\frac{d}{dt}\text{r}={\text{v}}_g=\frac{\partial }{\partial \text{k}}{\omega }_{\text{k}};\frac{d}{dt}\text{k}=-\frac{\partial }{\partial \text{r}}{\omega }_{\text{k}}& (7)\end{array}$

That is, the wave vector changes in such a way that the frequency is preserved. Equations (7) are the Hamilton equations for unit-mass particles (plasmons) with the “energy” ω_k and “momentum” k, moving with the (group) velocity v_g. It is also convenient to introduce the number of plasmons as N_k = W_k/ω_k.

Let us consider Langmuir plasmons moving in a one-dimensional density depletion (cavity), n(x) = n₀(1 − |δn(x)|) centered at x = x_c, with the width $L_n\gg k_c^{-1}$ (k_c = k(x_c)). Expanding ω_pe(n) gives ${\omega }_l/{\omega }_{p0}-1\approx \frac{1}{2}\delta n(x)+\frac{3}{2}{k}^2(x)r_D^2$, so the Hamiltonian can be represented as the sum of the kinetic energy, ${\epsilon }_k={\text{k}}^2/2$, and potential, $U(x)=2\delta n(x)/3r_D^2$. As it follows from (7), $\frac{d}{dt}{\text{k}=\text{v}}_g\frac{\partial }{\partial \text{r}}\text{k}>0$ (“acceleration”) and $\frac{d}{dt}\text{k}<0$ (“deceleration”) for plasmons moving toward and from the cavity's center, respectively. Evidently, the cavity plays a role of the potential hole for plasmons that are trapped inside if the Hamiltonian is negative, i.e., −U(x_c) > ε_k(x_c) or

$\begin{array}{ll}\left|\delta n(x_c)\right|>3k_c^2{r}_D^2,& (8)\end{array}$

and move freely otherwise.

4.2. Resonance Wave-Particle Interaction

Let us consider plane Langmuir waves, $\text{E}(\text{r},t)={\text{E}}_{\text{k}}{e}^{i\text{kr}-i{\omega }_{\text{k}}t}$, moving along the magnetic field (∥z) much faster than the bulk of electrons, i.e., v_Te ≪ ω_k/k_z = v_ph (the phase velocity). Thus, only a small group of fast particles can be in resonance with the waves, i.e., v_∥ = v_res = (ω_k − sω_ce)/k_∥, with s = 0, ±1, ±2, etc. It is called the Cherenkov resonance at s = 0 and the cyclotron resonance otherwise. It is instructive to give an example of the resonance wave-particle interaction in isotropic plasmas. The equation of motion of an electron with the unperturbed velocity v₀ = const reads

$\begin{array}{ll}\frac{d}{dt}{\text{r}=\text{v}}_0+{\text{v}}_E;\frac{d}{dt}{\text{v}}_E=\frac{-e}{m_e}{\text{E}}_{\text{k}}exp(i\text{kr}-i{\omega }_{\text{k}}t)& (9)\end{array}$

(e is the elementary charge). Linearizing in the wave field yields the quiver velocity

$\begin{array}{ll}{\text{v}}_E\approx -\frac{ie}{m{\omega }_{\text{k}}^{\prime }}{\text{E}}_{\text{k}}{e}^{-i{\omega }_{\text{k}}^{\prime }t}& (10)\end{array}$

where ${\omega }_{\text{k}}^{\prime }={\omega }_{\text{k}}-{\text{kv}}_0$ is the Doppler-shifted wave frequency. The work of the electric field, $\propto \overline{\text{Re}(\delta \text{v})·\text{Re}(E)}$, upon non-resonance particles, ${\omega }_{\text{k}}^{\prime }\ne 0$, vanishes as the positive and negative contributions on average cancel each other. For resonance particles, ${\omega }_{\text{k}}^{\prime }\to 0$, the linearization procedure is invalid, and Equation (9) must be solved explicitly. Taking k along the z axis, in the reference system of the wave, $z^{\prime }=z-v_{ph}t$, yields the equation of motion in a periodic wave potential

$\begin{array}{ll}\frac{d^2}{d{t}^2}\xi +{\omega }_{tr}^{2}sin\xi =0& (11)\end{array}$

Here ξ = kz′ is the relative phase, ϕ_{k, ω} is the amplitude of the potential, and ${\omega }_{tr}=\sqrt{\frac{e}{m_e}{k}^2|{\varphi }_{\text{k}}|}$. Nearly at the resonance, ξ ≪ 1, Equation (11) reduces to a classic (mechanical) oscillator with ξ ≈ ξ₀ cos(ω_trt). That is, particles in the resonance zone, $v_z^{(-)}<v_z<v_z^{(+)}$, where

$\begin{array}{ll}{v}_z^{(\pm )}=v_{ph}\pm v_{tr}\text{ and }{v}_{tr}=\sqrt{\frac{e}{m_e}|{\varphi }_{\text{k}}|}\ll v_{Te},& (12)\end{array}$

are trapped and oscillate around the minimum potential energy, maintaining the constant phase relative to the wave for many wave periods (e.g., Galeev and Sagdeev, 1979). The particles exchange energy with the wave

$\begin{array}{ll}\Delta \epsilon =2m_e{v}_{ph}(v_{ph}-v_z)& (13)\end{array}$

after reflection from a moving potential barrier. That is, slow ($v_z^{(-)}$) particles are “kicked” along by the wave and gain energy, while fast ($v_z^{(+)}$) particles push on the wave and lose energy. The net energy exchange is defined by the difference, $F_0(v_z^{(+)})-F_0(v_z^{(-)})\approx 2v_{tr}{\displaystyle \frac{\partial F_0}{\partial v_z}{|}_{v_{ph}}}$, between the population of the two groups with the distribution function F₀(v). It is negative in a Maxwellian plasma, so the waves are damped. This resonance, collisionless damping is named the Landau damping. In a magnetoactive plasma, oblique waves are subjected to the cyclotron damping as well. Therefore, in thermal equilibrium waves exist at the thermal noise level, W ~ n_eT_e/N_D.

In non-equilibrium plasma, the population of fast particles can dominate in a certain velocity domain so that waves in resonance with these particles will gain energy and grow. This process (inverse Landau or cyclotron damping) is called plasma instability.

4.3. Beam (Bump–in-Tail) Instability

Let a collimated, u = v_∥ ≫ v_⊥, “warm” and tenuous, $1>\Delta u_b/u_b>>{(n_b/n_e)}^{1/3}$, electron beam with the beam density, n_b ≪ n_e, and the mean energy, ε_b ≫ T_e, precipitates into the ionosphere along the magnetic field. Such distribution function is known as a “bump-in-tail,” meaning the tail of the whole electron distribution with the bulk, secondary, and beam electrons. As ∂F_b/∂u > 0 at u_b − Δu_b < u < u_b, Langmuir waves with phase velocities within this range will grow at a rate (e.g., Mikhailovskii, 1974)

$\begin{array}{ll}{\Gamma }_r=\frac{d{W}_r}{W_{r}dt}={\gamma }_b-{\nu }_e\approx {\omega }_{pe}\frac{\pi n_b}{n_e}{\left(\frac{u_b}{\Delta u_b}\right)}^2-{\nu }_e-{\gamma }_{nl}& (14)\end{array}$

Here W_r is the spectral energy density of the beam-resonant waves, k_∥ = k_r, γ_nl is the rate of spectral transfer due to nonlinear mode coupling (see below), and ${\nu }_e\approx 10^{-7}{T}_e^{5/6}N$ at T_e < 0.4 eV and $\approx 10^{-7}{T}_e^{1/2}N$ at 0.4 < T_e ≤ 100 eV below ~ 200 km. Calling for Γ_r > 0 at γ_nl = 0 gives the limiting neutral density

$\begin{array}{ll}N<N_{max}\approx 1.5·10^{12}\frac{{\gamma }_b}{{\omega }_{pe}}{T}_e^{-5/6}{n}_e^{1/2}\text{ c}{\text{m}}^{-3}& (15)\end{array}$

Taking $n_e~10^5$ cm⁻³, T_e ~ 0.1 eV, n_b ~ 1 cm⁻³, and Δv_b/v_b ~ 0.1 yields for the standard neutral atmosphere that the instability develops at altitudes above h_min = h(N_max) ~ 105 km.

The wave excitation goes at the expense of the beam energy leading to widening of the beam distribution and thus decrease of γ_b. In a steady state, the dissipation rate is determined by the energy flux balance

$\begin{array}{ll}{n}_b\frac{\partial }{\partial z}{\langle u_b\epsilon \rangle }_b=-\frac{\partial }{\partial z}{v}_g{W}_r\approx -{\Gamma }_r{W}_r& (16)\end{array}$

where < … > _b means averaging over the beam distribution. The beam speed greatly exceeds the wave group velocity, v_g ≈ 3T_e/m_eu_b, so in the absence of nonlinear interactions W_r is greater than n_bε_b by a factor of v_b/v_g ~ ε_b/T_e.

The relaxation length, l_rel, is a distance from the beam entry into the plasma over which the instability stabilizes at some Δu_b(l_rel) = Δu_∞. It can be estimated from Equation (16) as follows

$\begin{array}{ll}{l}_{rel}~\Lambda \frac{\Delta u_{\infty }}{{\gamma }_b^{\infty }}\frac{n_b{\epsilon }_b}{W_r}& (17)\end{array}$

Here Λ ~ ln (N_D) ~ 10 is a numerical coefficient accounting for the growth of the waves from the thermal level. In order to determine the level of the beam-excited waves, W_r, one should allow for nonlinear wave interactions resulting in the energy transfer from the resonance region at a rate γ_nl. The efficiency of this nonlinear damping is governed by the parameter of nonlinearity, w = W/n₀T_e ≪ 1.

4.4. Nonlinear Effects

Disregarding wave-wave interactions and using the statistical description of waves with random phases, results in the quasilinear approximation (Vedenov et al., 1962). It is valid only for very tenuous beams irrelevant to our problem. The next step in w is taking account of the induced scattering, in which electrons interact with beats of different randomly-phased modes (e.g., Galeev and Sagdeev, 1979). This weak turbulence (WT) approximation is valid until the beam density exceeds

$\begin{array}{ll}{n}_b^{(th)}\approx 0.1\mu \frac{T_i}{T_e}{n}_e~(1-3)·10^{-6}{n}_e& (18)\end{array}$

(Galeev, 1975; Papadopoulos, 1975; Galeev et al., 1977). Then, the beam relaxation is described in terms of strong Langmuir turbulence (SLT).

The SLT regime is inherently tied to the tendency of Langmuir plasmons to accumulate inside density depletions or cavities, δn_s = n_e/n₀ − 1 < 0. Namely, the waves of wavelengths ~ k⁻¹ are trapped if $\left|\delta n_s\right|>3k^2{r}_D^2$ (Equation 8). The resulting excess of the wave pressure, $\delta W_l\approx W_l\left|\delta n_s\right|/3k^2{r}_D^2$, exceeds the thermal pressure imbalance, δp_e = n₀T_eδn_s, if $w_l>w_{th}=3k^2{r}_D^2$. In this case, the ponderomotive force, −∇δW_l, pushes plasma out of the cavity, which further deepens and traps yet more plasmons in a positive-feedback loop. As a result, initial modulations grow with time. At W_l/n₀T_e ≫ W_th, the growth rate of this modulational instability (MI) is

$\begin{array}{ll}{\gamma }_{mi}(W_l)\approx {\omega }_{pe}\sqrt{\frac{\mu w_l}{3}}& (19)\end{array}$

As trapping inside a cavity leads to strong correlation of the wave phases, such that the WT condition of random phases (e.g., Galeev and Sagdeev, 1979) is violated, this regime has been termed strong Langmuir turbulence (SLT).

Cavities with trapped strongly-correlated Langmuir oscillations are termed cavitons and subjected to collapse (Zakharov, 1972). Their evolution depends on the dimension, d, and can be understood from simple arguments (e.g., Sagdeev, 1979). The conservation of the plasmons' number in a cavity of the size, l, yields |E²(t)| ∝ l^−d(t). The wavelengths of the trapped plasmons are also of the order of l, i.e., k ~ 1/l. The trapping condition yields $l^{-1}~k\propto |\delta n_s{|}^{1/2}$, indicating that a deepening cavity narrows, collapses, as time progresses. Since $\left|\delta p_e\right|\propto T_e\left|\delta n_s\right|\propto l^{-2}$ and |E²| ∝ l^−d, the thermal pressure will ultimately balance the HF pressure for d = 1, thus forming one-dimensional cavitons. In two (three) dimensions, the speed of collapse persists (accelerates) with time.

In a weakly-magnetized plasma, ω_ce ≪ ω_pe, the cavitons at $\left|\delta n_s\right|\ll {\omega }_{ce}^2/{\omega }_{pe}^2$ are pancake-like, with the dimensions

$\begin{array}{ll}{l}_{\parallel }~k_{\parallel }^{-1}~r_D|\delta n_s{|}^{-1/2}~l_{\perp }\frac{{\omega }_{pe}}{{\omega }_{ce}}|\delta n_s{|}^{1/2}& (20)\end{array}$

(e.g., Rowland et al., 1981b; Shapiro and Shevchenko, 1984; Robinson, 1997). The basic signatures of the SLT development in various beam-plasma systems have been observed in laboratory experiments (e.g., Cheung et al., 1982; Karfidov and Lukina, 1997; Robinson, 1997; Vyacheslavov et al., 2002).

The phase velocity of plasmons in collapsing cavitons, ~ ω_pe/k(t), decreases with time, so eventually plasmons are absorbed by plasma electrons due to Landau and transit-time damping. As a result, a small group of suprathermal electrons gains energy, while the HF pressure in the caviton drops and collapse is arrested due to the wave energy “burnout.” Ultimately, a dynamic equilibrium is reached between the pumping energy into cavitons in the long-scale source region, $k_L\le r_D^{-1}\sqrt{w_L/3}$, and short-scale transfer by collapsing cavitons (W_cav) into the absorption interval, k ≥ k_a (e.g., Galeev et al., 1977). The energy density in the source region, $W_L>W_{cav}>W_a={\int }_{{}_{k\ge k_a}}{W}_{k}dk$, comprises the MI-excited (non-trapped) long-scale waves.

In collisionless isothermal plasmas one gets at γ_b ≫ μω_pe (Galeev et al., 1977)

$\begin{array}{ll}{w}_r\approx 3{\left(\frac{\mu {\gamma }_b}{{\omega }_{pe}}\right)}^{1/2}\ll w_L\approx 3\frac{{\gamma }_b}{{\omega }_{pe}}& (21)\end{array}$

In collisional plasmas, Equations (18) and (21) hold for ν_e/ω_pe < 3T_e/2ε_b. In the opposite case, the MI threshold is $w_{th}^{(c)}\approx 2{\nu }_e/{\omega }_{pe}$ and the threshold beam density becomes (Volokitin and Mishin, 1979)

$\begin{array}{ll}{n}_b^{(c)}\approx 0.1n_e\mu \frac{T_i}{T_e}\frac{{\nu }_e}{{\omega }_{pe}}\frac{{\epsilon }_b}{T_e}& (22)\end{array}$

If $W_L>>W_r>W_{th}^{(c)}$, the MI growth rate is of the same order as γ_mi (19). However, as follows from eq. (21), γ_mi(W_L) < ν_e at

$\begin{array}{ll}{\nu }_e>{\nu }_{*}\approx {\left(\mu {\gamma }_b{\omega }_{pe}\right)}^{1/2}& (23)\end{array}$

collisional damping is faster than collapse. Since the nonlinear transfer rate due to collapse reduces, the level of plasma waves in this “collisional SLT” regime increases over that in Equation (21) and becomes (Volokitin and Mishin, 1979; Mishin and Telegin, 1989)

$\begin{array}{ll}{w}_r^{(*)}\approx \frac{3{\nu }_e}{{\omega }_{pe}}\ll w_L^{(*)}\approx \frac{3}{\mu }{\left(\frac{{\nu }_e}{{\omega }_{pe}}\right)}^2& (24)\end{array}$

Now the relaxation length can be estimated using Equations (17), (21), and (24)

$\begin{array}{ll}{l}_b~v_b\frac{{\epsilon }_b}{T_e}{\left(\frac{\Delta u_{\infty }}{v_b}\right)}^3\{\begin{array}{c}{\nu }_{\ast }^{-1}\text{\hspace{0.17em}at\hspace{0.17em}}{\nu }_e<{\nu }_{\ast }\\ {\nu }_e^{-1}\text{\hspace{0.17em}at\hspace{0.17em}}{\nu }_e>{\nu }_{\ast }\end{array}& (25)\end{array}$

In addition, in the presence of short-scale, q ≫ k_L, density irregularities, $\delta n_s(\text{r})=\sum _q\text{Re}(\delta n_{q}exp(iqz))$, long-scale plasmons are transferred into the short scales via conversion, $L_{k_L}+\delta n_s\to L_q^{\prime }$ (Galeev et al., 1977). For a wideband random-phase oscillations, $\left|\delta n_q\right|<3q^2{r}_D^2$, the conversion rate is

$\begin{array}{ll}{\gamma }_{conv}\approx {{\displaystyle \sum }}_{\text{q}}{\nu }_l(\text{q})\frac{{\langle |\delta n{|}^2\rangle }_{\text{q}}}{36q^4{r}_D^4}\ll {\nu }_l(\text{q})<3{\omega }_{pe}{q}^2{r}_D^2& (26)\end{array}$

Here ν_l(k) is the total (collisional + Landau) damping rate and ${\langle |\delta n{|}^2\rangle }_{\text{q}}$ is the phase-averaged spectral energy. The conversion process dominates at γ_conv > γ_mi(w_L). Applying a similar procedure to the electromagnetic version of the Zakharov equation (e.g., Shapiro and Shevchenko, 1984), one can describe resonant scatter of radio waves on ion density oscillations (e.g., Mishin et al., 1992).

The value of T_e in Equation (25) is the average energy of the bulk electrons, T_e = T_h, heated by the beam-excited turbulence at a rate

$\begin{array}{ll}{\tau }_{heat}^{-1}\approx \frac{2}{3}{\nu }_e(T_e)W_l/n_e& (27)\end{array}$

At altitudes below ~130 km the growth of T_e is limited mainly by inelastic losses, ν_il(T_e) = δ_il(T_e)ν_e(T_e). The coefficient of inelastic losses at h = 150-180 km, calculated using the Majeed and Strickland (1997) tabulations, is ${\delta }_{il}(T_e)\approx (0.1\to 1.5)·10^{-2}\to 0.1\to 0.3\to 0.1$ at T_e ≈ (0.2 → 0.45) → 0.6 → 5 → 10 eV. Assuming the ambient temperature T₀ = 0.2 eV and $W_l/n_e{T}_0~10^{-3}$-10⁻² in a steady state, one gets the temperature of heated electrons T_h ≈ T₀(1 + 2w_l/3δ_e(T_h)) ≈ 0.3–0.5 eV.

4.5. Acceleration of Suprathermal Electrons

The SLT acceleration of suprathermal (tail) electrons is, probably, the most important consequence of the BPI for artificial and natural aurora. In brief, the short-scale, k > k_a, plasmons in collapsing cavities are absorbed by a small group of plasma electrons. Their distribution function along the magnetic field can be found from the kinetic equation

$\begin{array}{ll}\frac{d}{dt}{F}_t=\frac{{\omega }_{pe}^2}{m_e{n}_0}\frac{\partial }{\partial u}\frac{W_{{\omega }_k/u}}{u}\frac{\partial F_t}{\partial u}\equiv \frac{\partial }{\partial u}D(u)\frac{\partial F_t}{\partial u}& (28)\end{array}$

As a result, a suprathermal tail, ε ≫ T_e, is formed, with a power-law distribution

$\begin{array}{ll}{F}_t(\epsilon )=\frac{n_t}{8\pi v_{min}^3}{\left(\frac{\epsilon }{{\epsilon }_{min}}\right)}^{-p_t}\text{ at }{\epsilon }_{max}\ge \epsilon \ge {\epsilon }_{min}& (29)\end{array}$

In a Maxwellian isotropic plasma (F₀ = F_M), theoretical estimates give the spectral index p_t ≈ 7/4 − 9/4 and the minimum energy, ${\epsilon }_{min}^{(M)}~10T_e$; while the matching condition, F_t(ε_min) = F₀(ε_min), yields $n_t^{(M)}~10^{-4}{n}_e$ (Galeev et al., 1977; Pelleiter, 1982). One-dimensional numerical simulations yield p_t ≈ 3/2 (Galeev et al., 1983; Wang et al., 1997). Figure 9 illustrates the wave spectrum and electron distribution in the developed strong Langmuir turbulence.

FIGURE 9

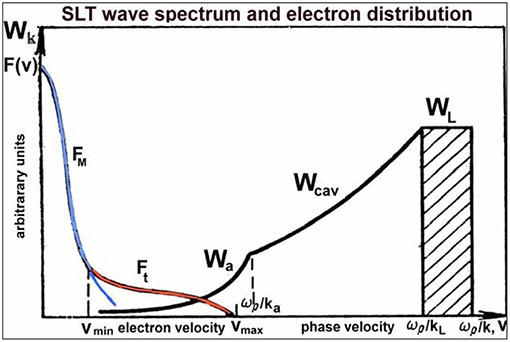
Figure 9. Cartoon depicting the wave spectrum and electron distribution in the developed strong Langmuir turbulence. The wave energy in the long-scale source (W_L at ω_l/k ≥ ω_pe/k_L), transfer (W_cav at ω_pe/k_a < ω_l/k ≤ ω_pe/k_L), and absorption (W_a at ω_l/k ≤ ω_pe/k_a) intervals are indicated by the striped rectangle and solid black curves, respectively. The blue and red solid lines indicate the bulk and accelerated tail populations, respectively. After Shapiro and Shevchenko (1984). Reprinted by permission from Plenum Press.

Substituting the accelerated flux Φ_t(ε) into Equation (2) with σ_λ = σ_ion gives the ionization rate, which can be approximated as (Mishin and Telegin, 1989)

$\begin{array}{ll}{q}_{ion}^{(t)}\approx n_b{\nu }_e(T_e)\frac{3T_e}{{\epsilon }_{ion}}{\left(\frac{u_b}{\Delta u_b}\right)}^4& (30)\end{array}$

A remark is in order. In the presence of the ambient (“seed”) suprathermal population, such as secondary electrons with the distribution F_s(ε) ≫ F_M(ε) at $\epsilon \ge {\epsilon }_{min}^{(M)}$, the absorption rate increases and collapse is arrested at greater scales than in a Maxwellian plasma. That is, ${\epsilon }_{min}^{(s)}\gg {\epsilon }_{min}^{(M)}$ and thus many more energetic electrons are accelerated (Mishin and Telegin, 1986). Another effect of electron-neutral collisions is that ε_max depends on inelastic losses of the accelerated electrons, ~ ν_ion(ε), that maximize at ε_m ~ 100 eV. Evidently, as soon as the rate of inelastic losses, ν_il(ε_L) at ${\epsilon }_L\approx 10^4{W}_L/n_e<{\epsilon }_m$, exceeds the acceleration rate, m_eD(u_L)/8πε_L, the expansion of the tail, $F_t(\epsilon )\propto {\epsilon }^{-p_t}$, stops (cf. Figure 6B). In the SLT regime (24), it occurs at $N>N_m\approx 10^8\sqrt{n_e}$ cm⁻³ (Volokitin and Mishin, 1979; Mishin, 2010).

4.6. SLT Acceleration in High-Power Radio Wave Experiments

It seems relevant to briefly discuss the SLT acceleration of suprathermal electrons producing artificial aurora and ionization in active space experiments with high-power radio waves (Mishin and Pedersen, 2011; Eliasson et al., 2012, 2015; Mishin et al., 2016). Here Langmuir waves are parametrically driven by ordinary (O) pump waves near the reflection altitude, h₀, where the pump frequency, f_o, matches the local plasma frequency, f_pe(h₀) (the interested reader is referred to Streltsov et al., 2018 review). Figure 10 exemplifies the results of the Eliasson et al. (2012, 2015) full-wave one-dimensional simulations with various input pump amplitudes, E_in, for radio beam pointings at and between the geographic zenith (vertical, V) and the geomagnetic field direction (magnetic zenith, MZ) at the High-frequency Active Auroral Research Program (HAARP) facility at Gakona, Alaska, USA. The simulation details are given in Eliasson et al. (2012, 2015). Note only that the nonlinearity parameter, $w\propto E_{in}^2/8\pi n_e{T}_e$, exceeds the thershold for the SLT regime to develop.

FIGURE 10

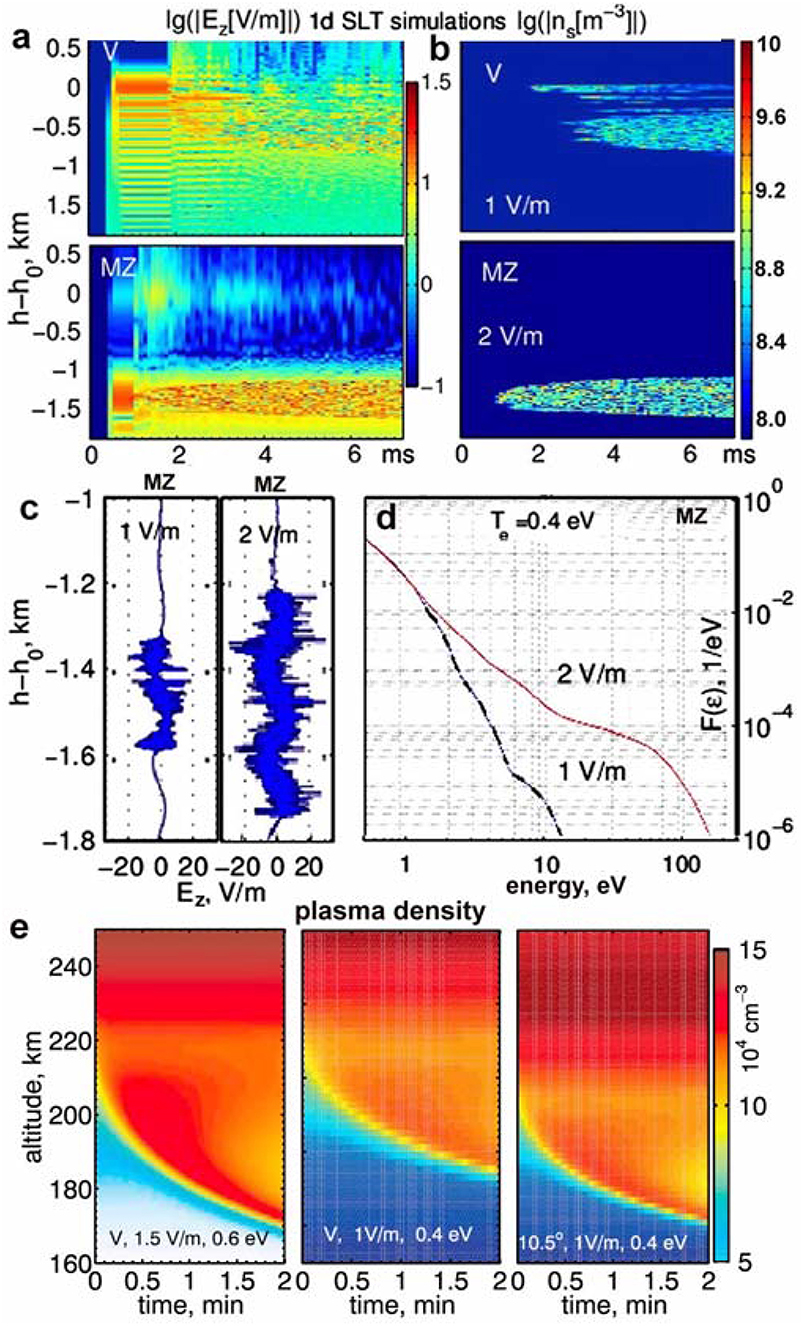
Figure 10. Time-vs.-altitude color-coded plots of (a) log₁₀(|E_z[V/m]|) and (b) log₁₀(|δn_s[m⁻³]|) for E_in = 1 and 2 V/m at V and MZ, as indicated in plots; (c) turbulent electric fields, E_z, (d) the distribution function, F_t(ε) = F_t(u)du/dε; and (e) time-vs.-altitude plots of the plasma density at V and 10.5° S calculated for various E_in and T_e indicated in frames. Adapted from Eliasson et al. (2012, 2015). Reprinted by permission from the American Geophysical Union.

Figures 10a,b illustrates the development of the longitudinal (Langmuir) electric field, E_z, and cavitons, δn_s, for vertical and MZ injections with E_in = 1 and 2 V/m. Omitting the features of their spatial distribution related to the radio wave propagation, we point out that in 1–2 ms the initial (Airy) structure starts breaking into small-scale turbulence. In saturation, solitary wave packets in the SLT region are trapped in density cavitons. It is seen that the SLT region of the altitudinal extent, l_LT, is sandwiched between the WT regions with turbulent electric fields but without cavitons. The appearance of the electromagnetic waves near h₀ at MZ is due to $O+\delta n_k\to O^{{}^{\prime }}$ conversion on short-scale ion density oscillations (Equation 26) in the SLT region. Figures 10c,d show the turbulent electric fields, δE_sat, and the electron energy distribution, F_t(ε) = F_t(u)du/dε, at the end of the simulation runs.

At each injection angle, the simulated spectral width, Δk, as well as δE_sat and l_LT, increase with E_in. These factors and the input value of T_e lead to considerable differences in F_t(ε). Overall, the main part of F_t(ε) at ε_max ≥ ε ≥ ε_min can be fitted by a power law, $F_t(\epsilon )\propto {\epsilon }^{-p_t}$, with the relative tail density, $10^4{n}_t/n_e$, between 2 and 6 and p_t between ≈1.5 and 2. The maximum energy, ε_max, at altitudes h ≥ 170 km depends mainly on the transit time, τ_∥ ~ l_LT/u_max, while inelastic losses dominate below 170 km. In particular, F_t(ε) at 10.5° S is more enhanced than at vertical due to greater l_LT. At MZ for E_in = 2 V/m, F_t(ε) is close to that at vertical for E_in = 1.5 V/m (Eliasson et al., 2012, Figure 8). This explains the differences in the patches (layers) of artificial plasma descending from the initial interaction altitude at various input parameters shown in Figure 10e.

The downward propagation of the artificial plasma produced by the accelerated electron tail is due to the fact that the electrons propagating along the geomagnetic field create the new plasma resonance condition for the incident radio wave below the initial resonance. This way, an ionizing wavefront created by the SLT-accelerated electrons is formed (Mishin and Pedersen, 2011; Eliasson et al., 2012). Furthermore, the presence of the ambient suprathermal population (photoelectrons) facilitates the SLT acceleration (Mishin et al., 2004, 2016; Eliasson et al., 2018), quite similar to the effect of secondary electrons in auroral plasmas (Mishin and Telegin, 1986). The consequences of the photoelectrons in the sunlit ionosphere are the decreased threshold, the greater downward speeds, and the decay of the persistent artificial ionization at the terminal altitude after sunlit-to-dark transition.

Next we explore the effect of transition from the “collisionless” to “collisional” SLT regime at ν_e > ν_* (23).

4.7. Plasma-Turbulence Layer

At ν > ν_* (23), the plasma turbulence level increases as $W_L^{(*)}~{\nu }_e^2$ (24). Thus, the condition ν_e(h_*) = ν_* defines the upper boundary, h_*, of the layer of enhanced plasma turbulence termed the Plasma Turbulence Layer or the PTL (Mishin and Telegin, 1989; Mishin et al., 1989). Balancing the heating rate (27) by inelastic losses gives

$\begin{array}{ll}{\delta }_{il}(T_e)\approx 3\frac{{\gamma }_b}{{\omega }_{pe}}\{\begin{array}{l}1\text{\hspace{1em}at\hspace{1em}}{\nu }_e<{\nu }_{\ast }\hfill \\ {\left({\nu }_e/{\nu }_{\ast }\right)}^2\text{\hspace{0.17em}at\hspace{1em}}{\nu }_e>{\nu }_{\ast }\hfill \end{array}& (31)\end{array}$

As follows from (31), for ${\gamma }_b/{\omega }_{pe}~(0.3-1)10^{-3}$ the temperature T_e reaches ≈0.3-0.45 eV in the PTL and does not exceed ≈0.25 eV above h_*. Since $q_{ion}^{(t)}$ (30) increases with T_e, the auroral luminosity is peaked inside the PTL and greatly enhanced over the collisional (SPA) limit, q_b ~ n_bν_b. This regime continues until ν_e(h) increases to ${\nu }_e(h_{*}^{*})={\nu }_{*}^{*}\approx 0.3{\mu }^{1/2}{\omega }_{pe}$. Below $h_{*}^{*}$, deep cavities are not created and $w_{r*}^{*}~w_{L*}^{*}~{\mu }^{-1}{\left(\frac{{\gamma }_b}{{\omega }_{pe}}\right)}^2$, so collapse and concomitant suprathermal electron acceleration are inhibited. For typical auroral beam-plasma parameters, $n_b/n_e~10^{-5}$ and Δu/u_b ~ 0.2, the value of ${\nu }_{*}^{*}$ is of the order of 3ν_*. This means that for the standard neutral atmosphere scale height, H_N ~ 5 km, the overall PTL thickness is of the order of 5 km.

Figure 11 illustrates a scenario (Mishin et al., 1981; Mishin and Telegin, 1989; Mishin, 2010) of the formation of a double-peaked ionization/luminosity profile of auroral rays due to the PTL (cf. Figure 4). The lower peak ($q_{ion}^{(c)}$) is caused by the collisional ionization of neutral gas by the primary (beam) electrons, while the upper layer, i.e., the PTL, is due to accelerated suprathermal electrons. For a few keV beams, both peaks will overlap, so that the observer would see only one thick layer with a sharp upper boundary.

FIGURE 11

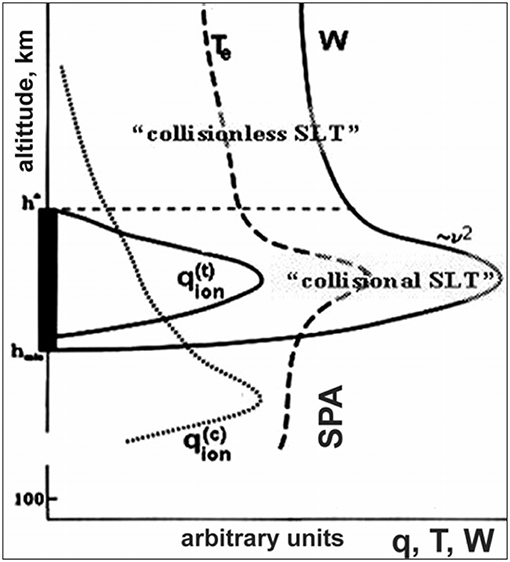
Figure 11. Schematic representation of the Plasma Turbulence Layer (PTL) indicated by the black rectangle and a double-peaked ionization profile. The dotted curve presents the collisional (SPA) ionization profile, $q_{ion}^{(c)}.$ The dashed curve shows the electron temperature profile of the heated plasma. The solid curves show the altitudinal profiles of the wave energy density, W, and ionization rate of the accelerated electrons, $q_{ion}^{(t)}$. The dashed horizaontal line indicates the PTL upper boundary. After Mishin (2010). Reprinted by permission from the American Institute of Physics.

This scenario agrees well with the altitude profile of artificial auroral rays far from the beam-emitting rocket (Figure 4) and natural auroral rays (section 6). Note that artificial beams expand across B₀ due to collisional diffusion, so that the beam density far beneath the rocket in Zarnitza 2 was ~ 1 cm⁻³ (Izhovkina, 1978), i.e., close to that of natural beams. Also, one should bear in mind that beams lose only ≤20% of their energy in the BPD region, acquiring the velocity scatter Δu/u_b ~ 0.1–0.2 (Mishin and Ruzhin, 1980a, 1981).

A remark is in order. So far our consideration was limited to collisionless interaction of a warm, tenuous (bump-in-tail) beam pertinent to natural and artificial auroral rays. With regards to the near-rocket plasma, this approximation becomes applicable after the plasma density significantly increases over the background in the beam-plasma discharge, which is described below. In addition to the beam instability, highly oblique EB/ECH waves can also be excited for electron injections at large pitch angles due to the non-equilibrium beam distribution over transverse velocities (e.g., Mikhailovskii, 1974). In the following, both the Langmuir- and EB/ECH-related processes are outlined.

5. Beam-Plasma Discharge

It has long been known that injection of powerful electron beams in neutral gas may result in the avalanche-like ionization accompanied by strong plasma oscillations (e.g., Getty and Smullin, 1963; Vlasenko et al., 1976a; Bernstein et al., 1978, 1979; Szuszczewicz et al., 1979). This phenomenon is termed the Beam-Plasma Discharge (BPD) to emphasize the chief role of the beam-excited waves. As any discharge, BPD develops under certain breakdown conditions that can be readily obtained in a simplified form.

5.1. Qualitative Considerations

At first glance, BPD can be treated similar to the classical high-frequency (HF, ω₀ ≫ ν_e) discharge (e.g., MacDonald, 1966), in which the pump waves are excited by the injected beam. In the HF discharge theory, the key parameter is the pump threshold amplitude, E_hf, as a function of the applied frequency (ω₀), gas density (N), and size (L) of the discharge gap. The Townsend criterion requires that an electron must acquire enough energy to produce at least one ionizating impact before disappearing from the gap due to recombination and diffusion. Replacing W_l in Equation (27) by $W_{hf}={({\omega }_{pe}/{\omega }_0)}^2|E_{hf}{|}^2/4\pi$ gives the time of the electron heating up to the energy ε_h ≥ ε_ion. In HF discharges ${\tau }_{hf}\propto {\epsilon }_h{\nu }_e^{-1}({\epsilon }_h)|E_{hf}{|}^{-2}$ is much greater than τ_ion, so the breakdown criterion reduces to

$\begin{array}{ll}{\tau }_{hf}<{\tau }_{loss}& (32)\end{array}$

In the BPD, the pump waves are generated via the beam instability. Therefore, the first step is to find the critical beam density, $n_b^{(cr)}$, necessary for the instability to develop. Let n_cr be the minimum plasma density for which the instability can develop at given N and γ_b, similar to the reverse condition (15). As the pre-discharge ionization is created solely by the beam electrons at a rate q_b ~ ν_bn_b (ν_b = ν_ion(ε_b)), the instability criterion follows from the ionization balance (Lebedev et al., 1976)

$\begin{array}{ll}{n}_b>n_b^{(cr)}~n_{cr}{({\nu }_b{\tau }_{loss})}^{-1}& (33)\end{array}$

Conditionally, the BPD problem may be divided into the “beam” and “discharge” parts. The former considers the beam ralaxation to find the input parameters, i.e., the excited wave spectrum and the size of the discharge “gap,” for the latter. Then, the energization (heating and acceleration) of plasma electrons with subsequent ionization is calculated. The solution of the first part critically depends on the plasma density and temperature that vary during the breakdown. Nonetheless, the two parts can be considered independently because the BPI timescale is much shorter than τ_ion. That is, the beam relaxation in the course of the breakdown comes about as in a stationary plasma with the density n_e = n_e(t) and temperature T_h(t).

The avalanche starts at some point, t_*, when the ionization by plasma electrons, q_ion = ν_ion(T_h)n_e(t_*), becomes greater than ν_bn_b. Therefore, the BPD threshold is the Townsend condition (32) with the left-hand side replaced by t_*. If suprathermal electrons are disregarded, t_* is of the order of the heating time of the bulk electrons, τ_heat. The latter can be estimated from Equation (27) substituting W_l in a generic form W_l = a_bn_bε_b, where a_b is a coefficient defined by the beam relaxation regime. This yields the criterion for a self-sustained discharge

$\begin{array}{lll}{\tau }_{heat}& ~& 3{\nu }_{ion}^{-1}(T_h)\frac{n_{cr}{\epsilon }_{ion}}{a_b{n}_b{\epsilon }_b}<{\tau }_{loss}\\ \mathrm{or }{n}_b& >& n_b^{(d)}~({\epsilon }_{ion}/a_b{\epsilon }_b)n_b^{(cr)}& (34)\end{array}$

Here we accounted for the fact that ${\nu }_b~3·10^{-8}$ N s⁻¹ for 3–10 keV electrons is of the order of $\frac{1}{3}{\nu }_{ion}(T_h)$ at T_h ≥ 1 eV (e.g., Majeed and Strickland, 1997). The condition (34) is satisfied automatically at $n_b>n_b^{(cr)}$ if $a_b>{\epsilon }_{ion}/{\epsilon }_b~10^{-3}$, which is valid already for rather tenuous (“weak”) beams, $1\gg n_b/n_{cr}>10^{-6}$.

For injections at h > 100 km, the requirement (33) becomes obsolete as the beam instability develops already in the ambient ionospheric plasma of the density n₀. A finite cross-section of injected beams reduces the growth rate but not quenches the instability (e.g., Alekhin et al., 1972). Furthermore, the values of τ_heat and τ_loss at the beginning of the BPD significantly differ from that for weak beams. The main difference stems from the beam energy density, n_bε_b, being much greater than the gas kinetic pressure of the ambient plasma, n₀T₀. This makes the BPI/BPD regime at the start of the breakdown drastically differ from the presented above (Volokitin and Mishin, 1978; Mishin and Ruzhin, 1980a, 1981).

5.2. Initial Stage of the BPD

5.2.1. Beam Instability

Following Alekhin et al. (1972) and Gendrin (1974), let us consider a cylindrical (“pencil”) beam injected with the beam current, I_b ≪ I_cr, divergence angle, $\Delta {\theta }_0<{\theta }_{*}=({\omega }_{ce}/{\omega }_{p0}){(I_b/I_{lim})}^{1/2}\ll 1,$ and initial radius, r₀. Here the limiting current, $I_{lim}={\epsilon }_b{v}_b/e\approx 30·{\tilde{\epsilon }}_b^{3/2}$ [A], with ${\tilde{\epsilon }}_b=0.1{\epsilon }_b\left[\text{keV}\right]$, defines the injection current at which the beam is locked by the space charge. The initial beam density, $n_b^{(0)}=I_b/e{u}_b\pi r_0^2$, greatly exceeds $n_0~10^5$ cm⁻³ for currents I_b > 0.1 A and ε_b < 10 keV (${\tilde{\epsilon }}_b<1$). Therefore, the beam expands radially due to electrostatic repulsion. For ω_pe(n₀) = ω_p0 > ω_ce and injections at small pitch angles θ₀ < θ_*, the beam quickly (in $~{\omega }_{p0}^{-1}$) expands to

$\begin{array}{ll}{r}_{b*}\approx (v_b/{\omega }_{p0}){(I_b/I_{lim})}^{1/2}\approx 50{\tilde{\epsilon }}_b^{-1/4}\sqrt{I_b/{\tilde{n}}_0}\text{cm},& (35)\end{array}$

so its density reduces to $n_{b*}\approx n_0=10^5·{\tilde{n}}_0$ cm⁻³ and the velocity/pitch-angle scatter increases to $\Delta v_b^{*}/v_b~\Delta {\theta }_{*}~{(I_b/I_{lim})}^{1/2}$. For ω_p0 < ω_ce, the beam expands to r_b*(ω_p0/ω_ce) and its density becomes $n_0{({\omega }_{ce}/{\omega }_{p0})}^2$ (Gendrin, 1974).

At injection angles θ₀ > θ_*, the beam executes a Larmor spiral with a hollow radial cross-section bounded by the beam gyroradius, r_cb = v_b sin θ_o/ω_ce (cf. Winckler, 1992, Figure 2). As for small angles, electrostatic repulsion makes the radial beam thickness of $\delta r_{*}\approx r_{b*}^2/(2r_{cb}cos{\theta }_0)$, so its density nears to n₀. A helical structure rapidly transforms into a pencil-like (cf. Winckler, 1992, Figure 2) as the excited EB/ECH oscillations scatter beam electrons, thus broadening their pitch-angle distribution and enhancing radial diffusion (see shortly).

A generic form of the distribution function of a cylindrical beam injected at θ₀ > θ_* can be represented as

$\begin{array}{ll}{F}_b(\text{v},r)=n_b(r)F_{\parallel }(\frac{u-u_b}{\Delta u_0})F_{\perp }(\frac{v_{\perp }-v_{b\perp }}{\Delta v_{\perp 0}})& (36)\end{array}$

with the beam density, $n_b=I_b/(\pi e{r}_{\perp }^2{u}_b)$, and the radial thickness, r_⊥. Here u_b = v_bcos θ₀, v_b⊥ = v_b sin θ₀, Δu₀ ≪ u_b, Δv_⊥0 ≪ v_b⊥, $\int F_{\parallel }{F}_{\perp }{d}^{3}v=1$, and F_{∥, ⊥}(x) has a maximum (“bump”) at x → 0 and tends to 0 at |x| → ∞. Taking r_⊥ ~ r_cb = v_b sin θ₀/ω_ce, gives $n_b\approx 10^3{I}_b{\tilde{\epsilon }}_b^{-3/2}/{sin}^2{\theta }_{0}cos{\theta }_0$ cm⁻³. Using a hollow-cylinder beam does not change the basic results concerning the instability development.

In a uniform beam-plasma system, a “cold,” $\Delta u/u_b<{(n_b/n_e)}^{1/3}<1$, beam excites Langmuir oscillations, ω_k0 ≈ ω_p0 ≈ k₀u_b, at the growth rate ${\gamma }_c\approx {\omega }_{p0}{(n_b/n_0)}^{1/3}$ (e.g., Mikhailovskii, 1974). For a bounded beam of a radial extent r_⊥, the growth rate depends on whether the inhomogeneity parameter, ξ₀ = k₀r_⊥, is smaller or greater than the root of the first kind, first order Bessel function, ξ₁ ≈ 3.75. That is, short-scale waves, ξ₀ ≫ 1, develop as for an unbounded beam, in accordance with general considerations. For θ₀ < θ_*, the radius r_⊥ is ≈ r_b* (35) and ${\xi }_0\approx {(I_b/I_{lim})}^{1/2}\ll 1$. For a “tenuous” beam, $n_b<n_0{\omega }_{ce}^2/({\omega }_{p0}^2-{\omega }_{ce}^2)$, the growth rate becomes (Alekhin et al., 1972)

$\begin{array}{ll}{\gamma }_c^{(<)}\approx {\omega }_{p0}{\left(I_b/2I_{lim}{\xi }_1^2\right)}^{1/3}& (37)\end{array}$

For a “dense” beam, $n_b>n_0{\omega }_{ce}^2/({\omega }_{p0}^2-{\omega }_{ce}^2)$, waves at ${\omega }_k\approx \sqrt{{\omega }_{p0}^2-{\omega }_{ce}^2}\approx k{u}_b$ grow at a rate

$\begin{array}{ll}{\gamma }_c^{\left(>\right)}\approx {\omega }_k{\left(\frac{{\omega }_{ce}}{{\omega }_{p0}}\right)}^{1/2}{\left(\frac{I_b}{I_{lim}}\right)}^{1/4}& (38)\end{array}$

The radial extent of the wave excitation region, and thus of the discharge,

$\begin{array}{ll}{R}_d~\frac{v_b}{{\omega }_{ce}}\{\begin{array}{l}\left|\sin {\theta }_0\right|{\left({\xi }_1/{\xi }_0\right)}^{1/3}\text{\hspace{1em}at\hspace{1em}}{\theta }_0>{\theta }_{\ast }\hfill \\ {\left(I_{\lim }/I_b\right)}^{1/4}\text{\hspace{0.17em}at\hspace{1em}}{\theta }_0\le {\theta }_{\ast }\hfill \end{array}& (39)\end{array}$

significantly excees the beam gyroradius, particularly, at small injection pitch angles. In fact, the radial size is even greater because the wave amplitudes outside R_d (39) decrease as $~{(R_d/r)}^{1/2}exp(-r/R_d)$ (Alekhin et al., 1972). This agrees with the laboratory (e.g., Fainberg, 1962; Kharchenko et al., 1962; Bernstein et al., 1978; Jost et al., 1982) and mother-daughter (Maehlum et al., 1980b,c; Grandal, 1982b; Jacobsen, 1982; Duprat et al., 1983) measurements.

As already noted, the instability due to the bump in transverse velocities is important at θ₀ ≫ θ_*. At Δv_⊥0 → 0, the distribution function, $F_{\perp }\left(\frac{v_{\perp }-v_{b\perp }}{\Delta v_{\perp 0}}\right)$ tends to the Dirac delta function, δ(v_⊥ − v_b⊥), known and as a “ring” or “oscillator” distribution (e.g., Mikhailovskii, 1974). In a uniform beam-plasma system, EB/ECH oscillations can develop with almost any possible ratio of ξ_⊥ = k_⊥v_b⊥/ω_ce. Similar to the bump-in-tail instability, the beam radial inhomogeneity is less significant for short-scale, ξ_⊥ ≫ 1, oscillations. For those, the maximum growth rate is reached at ω_k ≈ ω_uh ≈ k_zu_b + sω_ce

$\begin{array}{ll}{\gamma }_o\approx {\omega }_{uh}{\left(\frac{n_b}{\pi n_0}\right)}^{1/3}{\left(\frac{k_z}{k}\right)}^{2/3}{\xi }_0^{-1/3}& (40)\end{array}$

If k_z → 0, the maximum growth rate at ω_k ≈ ω_uh ~ sω_ce (s ≥ 2) reduces to ${\gamma }_s\approx 0.1\left({\omega }_{p0}^2/{\omega }_{ce}\right){(n_b/n_0)}^{1/2}$ and at s ≫ 1 tends to ${\gamma }_s\approx {\omega }_{p0}{(n_b/n_0)}^{a_s}$, where a_s = 1/2 at $n_b/n_0<{\omega }_{ce}^2/{\omega }_{p0}^2$ and 2/5 otherwise (e.g., Mikhailovskii, 1974).

5.2.2. Relaxation of Cold Beams

As the excited spectrum is narrow, Δk ≪ γ_c/u_b, and width of the resonance region, |u − v_ph| ~ γ_c/k₀, is greater than Δu₀, it is safe considering interaction with a quasi-monochromatic Langmuir oscillation. Henceforth, γ_c stands for ${\gamma }_c^{(<)}$ or ${\gamma }_c^{(>)}$, whichever applicable. The wave growth slows down when the beam electrons become trapped by the wave potential and change the relative phase bouncing back and forth in the potential hole. The beam velocity scatter, Δu_tr/u_b, increases over the saturation time ~10/γ_c to ~ γ_c/ω_p0 at the wave amplitude (e.g., Onishchenko et al., 1970; van Wakeren and Hopman, 1972; Abe et al., 1979)

$\begin{array}{ll}{\displaystyle \left|E_0^{(tr)}\right|}\approx {(8\pi n_b{\epsilon }_b{\gamma }_c/{\omega }_{p0})}^{1/2}|cos{\theta }_0|& (41)\end{array}$

That is, the instability is saturated along the relaxation length, $l_{rel}^{(tr)}~10u_b/{\gamma }_c~100$–300 m.

The saturation of the ring/oscillator instability also occurs due to trapping of the beam electrons at the wave amplitude ${\displaystyle |E_{\theta }^{(tr)}{\displaystyle |}\approx |E_{\parallel }^{(tr)}|}$ (41) with γ_c and cosθ₀ replaced by γ_osc or γ_s and sin θ₀, respectively (e.g., Kitsenko et al., 1974; Aburjania et al., 1978). In the saturated state, the scatter of perpendicular velocities is of the order of γ_{o, s}/ω_uh ~ 0.2–0.3. Since the wave frequency exceeds the cyclotron frequency, the trapped beam electrons are unmagnetized and pulled by the wave across the magnetic field, ultimately filling the void in the center and expanding over the beam gyroradius. This is consistent with the data concerning the beam structure (Bernstein et al., 1979), as well as the distortion of single particle trajectories for beam currents above the threshold (Maehlum et al., 1980c).

5.2.3. Electron Heating and Ionization

If the beam is relatively weak and $W_{tr}={\displaystyle |E_0^{(tr)}{|}^2}/4\pi <n_0{T}_0$, the electron heating rate is given by equation (27) with the coefficient of inelastic losses, δ_il(T_h), adjusted to higher values of T_h > 1 eV. However, W_tr > n₀T₀ for I_b ≥ 0.1 A and ε_b ≤ 10 keV, so the quiver velocity, v_E (10), for the wave (41) is greater than the thermal electron velocity and r_E = v_E/ω_p0 > r_D(T₀). This results in excitation of secondary Langmuir waves, E_p, and low-frequency, $\Omega \le {\mu }^{1/2}{\omega }_{p0}$, density oscillations, δn_p, via an aperiodic parametric instability, $E_0^{(tr)}\to E_p+\delta n_p$, with the maximum growth rate, ${\gamma }_p~{\mu }^{1/3}{\omega }_{p0}$, at ${\text{k}=\text{k}}_p\approx 1.8{\text{r}}_E/r_E^2$ (Kruer and Dawson, 1971; De Groot and Katz, 1973). Trapping of thermal electrons by the secondary waves makes the electron orbits intersect at ${\tau }_p\approx 10{\gamma }_p^{-1}~20$ μs. This leads to the fast, less than $f_{p0}^{-1}$, heating of the bulk electrons up to $T_h\approx T_E\approx \frac{1}{2}{m}_e{v}_E^2$ (De Groot and Katz, 1973). Substituting ${\displaystyle \left|E_0^{(tr)}\right|}$ (41) into v_E (10), yields

$\begin{array}{ll}{T}_h={\epsilon }_{ion}·{\tilde{T}}_h\approx {\epsilon }_b\frac{n_b}{n_0}\frac{{\gamma }_c}{{\omega }_{p0}}{cos}^2{\theta }_0& (42)\end{array}$

That is, the collisionless heating time, ${\tau }_{heat}^{(c)}~10(1+{\gamma }_c/{\gamma }_p)/{\gamma }_c$, is much faster than the collisonal time. For the ring/oscillator beam, the value of T_h follows from ${\displaystyle \left|E_{\theta }^{(tr)}\right|}$. It is worth noting that the fast heating was observed in the Bauer et al. (1992) laboratory experiment. High electron temperatures in the near zone were reported by Gringauz et al. (1981, up to ~100 eV), Jacobsen (1982), and Arnoldy et al. (1985).

At $n_0~10^5$ cm⁻³ and $1.5<{\tilde{T}}_h<10$, the ionization rate, ${\nu }_{ion}(T_h)~10^{-8}{\tilde{T}}_h^{1/2}N$, exceeds ${\tau }_p^{-1}$ at

$\begin{array}{ll}N>N_{hf}\approx 10^{10}\sqrt{n_0/{\tilde{T}}_h}~3·10^{12}/{\tilde{T}}_h^{1/2}\text{ c}{\text{m}}^{-3}& (43)\end{array}$

or h < h_hf ≈ 110 - 120 km. Here the BPD criterion is alike the HF discharge (32), while at higher altitudes it becomes ${\nu }_{ion}^{-1}(T_h)<{\tau }_{loss}$. The lifetime of the heated electrons is determined mainly by transverse diffusion, ${\tau }_{d\perp }~R_d^2/{\nu }_e(T_h)r_{ce}^2$. However, the time of injection into the same magnetic tube is limited due to the transverse speed of the beam guiding center, τ_R ~ r_cb/V_⊥, with V_⊥ = V_R⊥ + ΔV_⊥(ψ) (see section 3.3). It is worth noting that Vlasenko et al. (1976a) have observed that the BPD is inhibited at some critical speed of the gas flow across the electron beam.

At high altitudes, the BPD condition reduces to ${\tau }_R>{\nu }_{ion}^{-1}(T_h)$, which yields (Mishin and Ruzhin, 1980a)

$\begin{array}{ll}N>N_{\min }\approx {10}^{10}{V}_{R\perp }\{\begin{array}{l}3{\tilde{\epsilon }}_b^{1/4}{I}_b^{-1/2}\text{\hspace{0.17em}at\hspace{0.17em}}{\theta }_0\le {\theta }_{\ast }\hfill \\ \frac{{\omega }_{p0}}{2{\omega }_{ce}}{I}_b^{-2/3}\text{\hspace{0.17em}at\hspace{0.17em}}{\theta }_0>{\theta }_{\ast }\hfill \end{array}{\text{cm}}^{-3}& (44)\end{array}$

For injection currents ~0.5 A, ${\tilde{\epsilon }}_b~1$, and V_R⊥ ~ 0.3 km/s, the BPD condition (44) yields h(N_min) = h_max ~ 160–170 km.

A few remarks are in order. Interaction of beam electrons with short-scale, k ≫ ω_pe/v_b, oscillations results in fast pitch-angle scattering with the effective “collision” frequency (Mishin et al., 1989; Mishin et al., 1994; Khazanov et al., 1993)

$\begin{array}{ll}{\nu }_{eff}\approx {\omega }_{pe}{\displaystyle \sum _k}\frac{W_k}{k{r}_D{n}_e{T}_h}{\left(\frac{T_h}{{\epsilon }_b}\right)}^{3/2}& (45)\end{array}$

which greatly exceeds the collisional frequency, ~ ν_b, at altitudes above ~120 km. Numerical simulations (Khazanov et al., 1993; Mishin et al., 1994) have shown that this process suffices to explain the basic features of the prompt electron echo (section 3.4).

Thus far, only perpendicular diffusion was considered. However, at injection angles close to π/2 the field-aligned extent of the discharge gap, $~l_{rel}^{(tr)}·{\theta }_{*}$, is so small that the parallel diffusion becomes dominant and limits the discharge ignition. Therefore, besides parallel injections, the optimal BPD conditions are achieved at injection angles ≤ 80° (cf. Figure 5).

Next, the conversion rate (26) increases to ${\gamma }_{conv}\approx {\omega }_{pe}\langle |\delta n_k{|}^2\rangle$ for $k~r_D^{-1}$ (Volokitin and Mishin, 1978). In the heated plasma, the low-frequency density oscillations, $k~k_p~r_D^{-1}(T_h)$, are saturated at $\langle |\delta n_p{|}^2\rangle ~2{\mu }^{1/3}$ (De Groot and Katz, 1973), thus yielding ${\gamma }_{conv}^{(p)}\approx 2{\mu }^{1/3}{\omega }_{pe}$. If ${\gamma }_{conv}^{(p)}>{\gamma }_c$ (${\gamma }_{conv}^{(p)}>{\gamma }_{osc}$ or γ_s), the beam (ring) instability is suppressed. That is, the heated plasma is “cleared” for the beam propagation and the BPI starts in the adjacent region. This way, the heated region will move away from the rocket at a speed $u_T^{(p)}~l_{rel}^{(tr)}/{\tau }_p$ (Mishin and Ruzhin, 1980a, 1981).

The short-scale density oscillations in the “cleared” region decay due to various dissipative processes including diffusion and induced scattering on ions within the decay time ${\tau }_{osc}~10{\tau }_{heat}^{(c)}$. As soon as ${\gamma }_{conv}^{(p)}$ drops below γ_c (γ_o or γ_s), the BPI resumes in the initial region and is suppressed again after the heating time, ${\tau }_{heat}^{(c)}$. The obvious corollary is that the BPI in each individual gap, $~l_{rel}^{(tr)}$, proceeds in a quasi-periodic series of short, $~{\tau }_{heat}^{(c)}$, pulses of enhanced wave activity and particle energization repeated at ~ τ_osc. Such behavior is typical of laboratory experiments with intense cold beams (e.g., Kharchenko et al., 1962; Cabral, 1976; Vlasenko et al., 1976b) and has also been observed in active experiments (e.g., Gringauz et al., 1981; Kawashima, 1988). Evidently, at altitudes above h_max this “oscillatory” regime persists over the duration of injection pulses.

During the oscillation period, τ_osc, the newly-born plasma cools off due to thermal conduction and inelastic losses down to T_e ~ 1 eV and the ionization rate decreases. However, as the diffusion time is greater than τ_osc, the plasma density, n_e, in the heated region increases with the average rate ${\overline{\tau }}_{ion}^{-1}$. As long as $n_b^{(0)}$ remains greater than n_e, the “initial stage” regime holds. When n_e rises to $n_b^{(0)}$ at the time ${\tau }_0~{\overline{\tau }}_{ion}ln(n_b^{(0)}/n_0)~10N_{min}/N$ ms, electrostatic repulsion ends and the beam preserves its initial snape. However, the instability development proceeds as before and even faster because of the increase of ω_pe. After a few τ₀, the plasma density, n_e, significantly exceeds $n_b^{(0)}$ so that the “warm”-beam approximation (section 4) becomes applicable. Actually, that can happen even earlier due to radial diffusion of beam electrons scattered off persisting short-scale oscillations at the rate (45), which is indicated by the prompt electron echo (section 3.4).

5.3. Stationary BPD

There are the principal differences between the stationary and initial BPD regimes. First, a cold beam excites convective modes with the group velocity v_g ~ u_b, while a warm beam excites Langmuir waves (6) with v_g ≪ u_b. As result, the energy density of the excited waves remains very high even for n_b ≪ n_e, as well as the electron temperature. Next, in addition to ionization by the heated thermal plasma electrons, accelerated suprathermal electrons can contribute significantly to the BPD ignition when strong Langmuir turbulence determines the beam relaxation (Mishin and Ruzhin, 1980a, 1981; Rowland et al., 1981a; Papadopoulos, 1982, 1986; Sharp, 1982; Omelchenko et al., 1992; Sotnikov et al., 1992). If the SLT development is inhibited, the bulk electron heating is the only source for the BPD. Here the BPD development is similar to that of the HF discharge, as discussed in section 5.1.

As the neutral density in the NRG region varies during the flight, the beam relaxation regime changes accordingly. Let us first consider the region where $n_b>n_b^{(c)}$ (22). At ν_e < ν_* (23), as follows from the heat balance (31) with ${\gamma }_b/{\omega }_{pe}~10^{-2}-10^{-1}$, the electron temperature is T_h ~ 1–5 eV. The ionization by the thermal bulk electrons is determined by a Maxwellian tail, i.e., $q_M~10^{-8}{n}_{e}Nexp(-{\tilde{T}}_h^{-1})$. However, the main contribution comes from suprathermal electrons (29). Comparng the ionization rate $q_{ion}^{(t)}$ (30) with τ_R yields the maximum plasma density in a stationary discharge of the order of

$\begin{array}{ll}{n}_{max}^{(t)}~n_b{\nu }_e(T_h)\frac{10T_h}{{\epsilon }_{ion}}{\left(\frac{u_b}{\Delta u_b}\right)}^4\frac{r_{\perp }}{V_{R\perp }}\propto \frac{I_b}{u_b}\frac{N}{V_{R\perp }}& (46)\end{array}$

This dependence is similar to the observed $f_{max}\propto \sqrt{n_{max}}$ (4).

As soon as ${\nu }_e>{\nu }_{*}^{*}$ or N > N_md, the electron temperature increases but the acceleration of suprathermal electrons is inhibited. Here the palsma density is determined by the balance between ionization by thermal electrons and radial diffusion to give $n_{max}^{(t)}\propto N^{2/5}$ and then ∝ N^3/2, as collisional damping reduces the beam spreading and hence the excited wave energy. The lower BPD boundary is determined by the neutral density, N_max, at which collisional damping inhibits the development of the cold-beam instability (Mishin and Ruzhin, 1980a; Dokukin et al., 1981).

These results pertain to the beam instability. As far as the ring/ocillatory instability is concerned, its development at ω_pe/ω_ce ~ s ≫ 1 proceeds even faster than at the initial stage. As a result the beam distribution over transverse velocities widens such that the wave energy grows to ~ (0.1 − 0.3)n_bε_b. Here, the strong electron heating is the main contributor to the BPD development. Since the group velocity at ω_k/ω_ce ≈ s + 1/2 tends to zero, these waves are most enhanced (cf. Ashour-Abdalla and Kennel, 1978; Ashour-Abdalla et al., 1980), which explains the gyrofeatures in Figure 7B. As the ring instability growth rates are smaller than γ_c, it is suppressed at higher altitudes. Figure 12 illustrates the BPD regimes vs. altitude and the range of altitudes (neutral gas densities) where the various BPD features were observed.

FIGURE 12

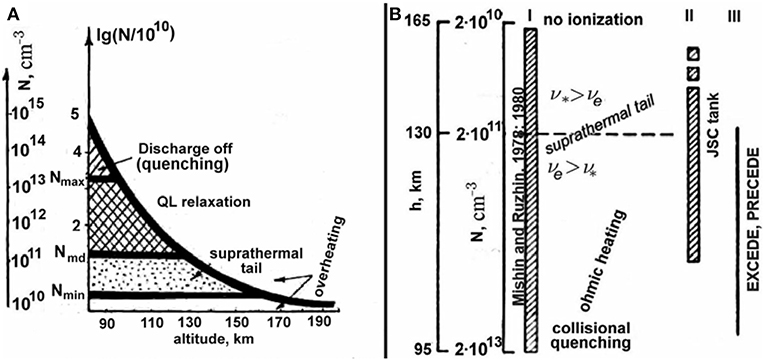
Figure 12. (A) The different stationary BPD regimes vs. altitude defined by the beam relaxation regimes. Adapted from Mishin and Ruzhin (1980a). (B) Altitude and neutral density range over which BPD is expected. The first stripped column indicates the range expected from Mishin and Ruzhin's analysis. The second stripped column indicates the parameter range over which BPD has been observed in the large tank at the Jonson Space Center. The vertical line on the right indicates the altitude range over which the EXCEDE and PRECEDE experiments with currents far beyond the BPD thereshold were conducted. Adapted from Linson (1982). Reprinted by permission from Plenum Press.

Finally, using the heated bulk and accelerated tail electrons it is easy to show that the total power of optical emissions radiated from the NRG is of the order of a few per cent of the beam power (Ivchenko et al., 1981; Mishin and Ruzhin, 1981). The power of VHF radioemission estimated assuming conversion of Langmuir waves on density oscillations inherent in unstable beam-plasma systems also reaches a few percent of the beam power (Galeev et al., 1976; Mishin and Ruzhin, 1981).

6. Enhanced Aurora

The distribution of precipitating electrons, F_b(v), varies significantly in time and space creating various auroral forms with latitudinal scale lengths from tens of kilometers down to hundred meters (e.g., Meng et al., 1991). Some of the measured distributions of auroral electrons do exhibit the bump-in-the-tail feature. Its origin is beyond the scope of this survey.

6.1. Auroral Electrons

Figure 13 exemplifies auroral beam and suprathermal electron spectra observed over auroral arcs (e.g., Reasoner and Chappell, 1973; Arnoldy et al., 1974; Feldman and Doering, 1975; Bryant et al., 1978). In Figure 13B, the primary flux is approximated by a Gaussian distribution of the density n_b = 0.6 cm⁻³, energy scatter Δε_b ≈ 2.9 keV, and ε_b ≈ 10.2 keV (the dashed line). These beam parameters easily suffice the BPI conditions described in sections 4.3 and 4.4. Therefore, the beam relaxation can be described by the BPI theory outlined there. In particular, the relaxation length, l_b (25) at ν_e < ν_* (23) exceeds the distance between the acceleration region of auroral beams (e.g., Meng et al., 1991) and the E-region ionosphere. This explains why the bump-in-tail distributions, such as in Figures 13A,B, are preserved along the path (Galeev, 1975; Papadopoulos, 1975).

FIGURE 13

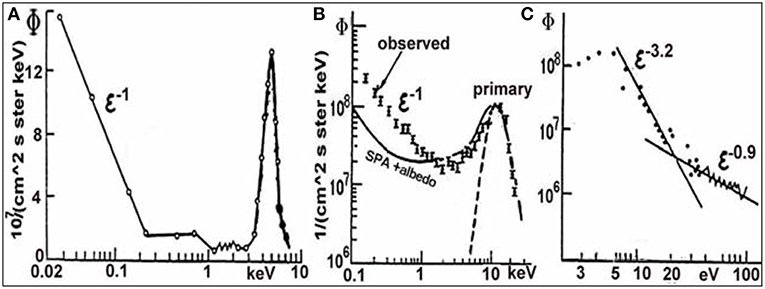
Figure 13. Differential number fluxes over auroral arcs with the ‘bump-in-the tail' distribution of primary electrons and flat power-law spectra of secondary electrons. Dots and circles show the observed fluxes, while dashed and solid lines show (B) a Gaussian approximation and (C) power-law trends. Adapted from (A) Arnoldy et al. (1974). (B) Bryant et al. (1978), and (C) Feldman and Doering (1975). Reprinted by permission from the American Geophysical Union.

As in Figures 6A,B, the suprathermal spectrum in the range ≥6–1,000 eV is well approximated by a power law Φ(ε) ~ ε⁻¹. It is considerably flatter than the SPA spectrum (3) shown by the solid line in Figure 6B. In frame c, a SPA-like spectrum over the class II arc changes to a flatter one at ε ≥ ε_min ≈ 20 eV, i.e., ${\epsilon }_{min}\gg {\epsilon }_{min}^{(M)}$. The overall observations show that the spectrum of suprathermal electrons over arcs is not formed solely on account of the collisional interaction but can be explained in terms of the SLT acceleration (Papadopoulos and Coffey, 1974; Galeev, 1975; Matthews et al., 1976; Mishin and Telegin, 1986). It is worth to note that recent incoherent scatter radar observations (Isham et al., 2012; Akbari et al., 2013) do reveal the signatures of strong Langmuir turbulence in auroral plasma, quite similar to that in high-power radio wave experiments.

6.2. Luminosity and Ionization Profiles

A typical representation of the altitude-profile of auroral luminosity/ionization is illustrated by Figure 2. However, Donahue et al. (1968) reported on rocket measurements of auroral emissions at 557.7 and 391.4 nm, both having narrow local maxima at 115 and 130 km. Similarly, ground-based optical imagers detected either double-peaked auroral rays of about the same thickness, displaced in altitude by about 5–15 km, or one thick layer with the sharp upper boundary below about 130 km, with the characteristic scale length of only a fraction of H_N (Oguti, 1975; Stenbaek-Nielsen and Hallinan, 1979; Dzyubenko et al., 1980; Hallinan et al., 1985). This phenomenon was called “Enhanced Aurora.” Similar layers of auroral ionization were also detected from sounding rockets (Swider and Narcisi, 1977; Morioka et al., 1988), the EISCAT UHF incoherent scatter radar (Wahlund et al., 1989; Schlesier et al., 1997), and a dual-altitude 90-MHz radar system (Timofeev and Miroshnikov, 1982). There were efforts to explain such double-peak profiles by the collisional interaction invoking two precipitating electron populations, i.e., a monoenergetic field-aligned beam and an isotropic beam of a higher energy. However, these efforts failed to fit the upper peak and sharp upper boundary.

Figures 14A,B shows double-peaked auroral rays observed near Tixie Bay by a side-looking low-light TV camera, the same as used in Zarnitza 2, and their luminosity profiles (Dzyubenko et al., 1980). The upper peaks are by a factor of two narrower than the minimum possible from the SPA, while the lower peak matches the SPA predictions (cf. Figure 4). Shown below (Figure 14C) is an example of a rayed arc with the sharp upper boundary (Hallinan et al., 1985).

FIGURE 14

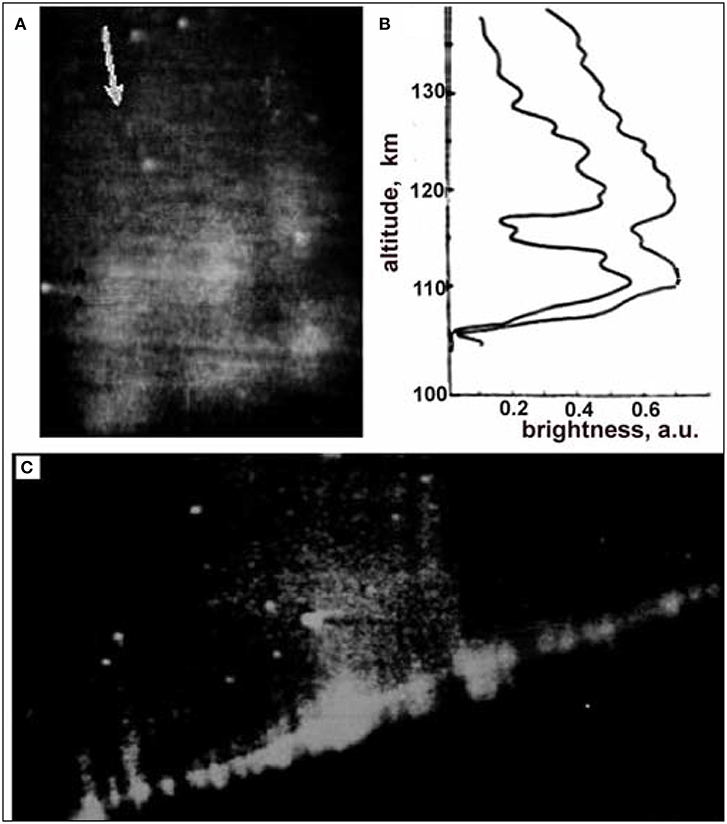
Figure 14. (A) Auroral rays along the magnetic field indicated by the arrow and (B) their luminosity profiles. Adapted from Dzyubenko et al. (1980). (C) A rayed arc with the sharp upper boundary. After Hallinan et al. (1985). Reprinted by permission from the American Institute of Physics and American Geophysical Union.

More than fifty narrow layers of the enhanced electron temperature co-located with the plasma density peaks in the altitude range ≥ 115–150 km have been found in the EISCAT UHF radar database (Schlesier et al., 1997). One sample is shown in Figures 15A,B, where the thin layers in T_e and n_e are emphasized by thick lines. Note that the ion temperature is significantly smaller than the peak value of T_e ≈ 3, 000 K and that the overall density profile has two peaks. A similar double-peaked ionization profile (Figure 15C) was observed in pulsating aurora (Wahlund et al., 1989). Dashed lines show the SPA profiles calculated for ε_b = 3.8 and 10 keV. As for auroral rays, the difference with the SPA profile for the upper peak is evident.

FIGURE 15

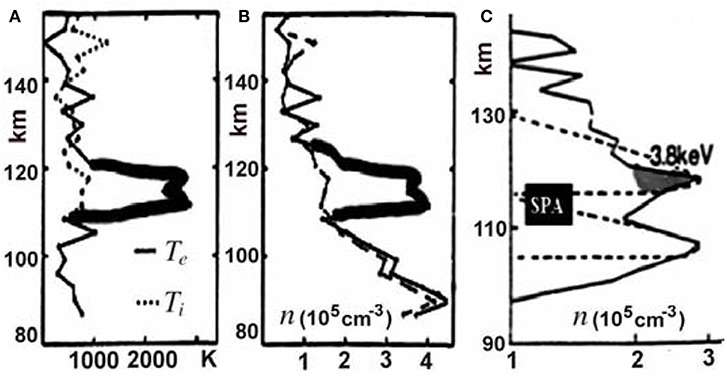
Figure 15. Thin layers of the (A) elevated electron temperature and (B) electron density indicated by thick lines (after Schlesier et al., 1997); and (C) a double-peaked ionization profile in pulsating aurora. Dashed lines show the SPA profiles calculated for ε_b ≈ 3.8 and 10 keV. After Wahlund et al. (1989). Reprinted by permission from the American Geophysical Union.

A striking resemblance between the Enhanced and Artificial Aurora (Figure 4) profiles is evident. Given that the parameters of electron beams far beneath the rocket are close to that of natural beams, it is safe to conclude that their generation mechanisms have much in common. It is obvious that the sought-for mechanism is the one that creates the plasma turbulence layer.

7. Conclusion

The effects of powerful electron beams injected from sounding rockets into the upper atmosphere to create artificial aurora are outlined. Data come from in situ measurements of the luminescence, thermal and suprathermal populations, and beam electrons near a beam-emitting space vehicle, as well as from ground-based optical, radar, and radioemission observations. The overall dataset cannot be explained solely by collisional degradation of energetic electrons but demands collisionless beam-plasma interactions (BPI) be taken into account. A brief survey of the BPI theory in a weakly-ionized plasma is presented. The basic processes of the near-rocket region are described in terms of the beam-plasma discharge (BPD) ignited by plasma electrons energized by the beam-excited plasma turbulence. Depending on the ambient plasma and atmospheric densities, there are several regimes of the BPD development. The observations of artificial auroral rays far beneath the rocket indicate that turbulence regime and thus the relaxation of radially expanded beams are strongly affected by collisions of plasma electrons. As a result, the energy density of plasma waves and concomitant energization of plasma electrons are enhanced in a narrow layer termed the plasma turbulence layer (PTL). The PTL formation results in an upper peak in a double-peak structure of artificial auroral rays. Some examples of optical and incoherent scatter radar observations of the luminosity and ionization profiles of rayed auroral arcs exhibiting two peaks or a sharp upper boundary are presented. Such auroral forms have been called Enhanced Aurora. An evident resemblance between Enhanced and Artificial Aurora points to their common generation mechanism, which is the one that creates the plasma turbulence layer.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was supported by the Air Force Office of Scientific Research LRIR 16RV COR277 and 19RV COR038.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abe, H., Fukumasa, O., and Itatani, R. (1979). Computer simulation of nonlinear interaction between a cold beam an a weakly collisional plasma. Phys. Fluids 22, 310–320. doi: 10.1063/1.862582

CrossRef Full Text | Google Scholar

Aburjania, G., Pankratov, I., and Kitsenko, A. (1978). Nonlienar stage of charged particle jet interaction with plasma in magnetic field. Sov. J. Plasma Phys. 4, 227–234.

Akbari, H., Semeter, J., Nicolls, M., Broughton, M., and LaBelle, J. (2013). Localization of auroral Langmuir turbulence in thin layers. J. Geophys. Res. Space Phys. 118, 3576–3583. doi: 10.1002/jgra.50314

CrossRef Full Text | Google Scholar

Alekhin, Y., Karpman, V., Ryutov, D., and Sagdeev, R. (1972). Stability of an electron beam injected along the magnetic field lines. Cosmic Electrodyn. 2, 280–291.

Arnoldy, R., Lewis, P., and Isaacson, P. (1974). Field-aligned auroral electron fluxes. J. Geophys. Res. 79, 4208–4221. doi: 10.1029/JA079i028p04208

CrossRef Full Text | Google Scholar

Arnoldy, R., Pollock, C., and Winckler, J. (1985). The energization of electrons and ions by electron beams injected in the ionosphere. J. Geophys. Res. 90:5197. doi: 10.1029/JA090iA06p05197

CrossRef Full Text | Google Scholar

Ashour-Abdalla, M., and Kennel, C. (1978). Nonconvective and convective electron cyclotron harmonic instabilities. J. Geophys. Res. 83, 1531–1543. doi: 10.1029/JA083iA04p01531

CrossRef Full Text | Google Scholar

Ashour-Abdalla, M., Leboeuf, J., Dawson, J., and Kennel, C. (1980). A simulation study of cold electron heating by loss cone instabilities. Geophys. Res. Lett. 7, 889–892. doi: 10.1029/GL007i011p00889

CrossRef Full Text | Google Scholar

Bale, S., Kellogg, P., Monson, S., Anderson, H., and Potter, D. (1995). Suprathermal electrons associated with a plasma discharge on an active sounding rocket experiment. J. Geophys. Res. 100, 23749–23754. doi: 10.1029/95JA01630

CrossRef Full Text | Google Scholar

Bauer, B., Wong, A., Decyk, V., and Rosental, G. (1992). Experimental observation of super strong electron plasma waves and wave breaking. Phys. Rev. Lett. 68, 3706–3709. doi: 10.1103/PhysRevLett.68.3706

CrossRef Full Text | Google Scholar

Bernstein, W., Leinbach, H., Kellogg, P., Monson, S., Hallinan, T, Garriott, O. K., et al. (1978). Electron beam injection experiments: the beam-plasma discharge at low pressures and magnetic field strengths. Geophys. Res. Lett. 5, 127–130. doi: 10.1029/GL005i002p00127

CrossRef Full Text | Google Scholar

Bernstein, W., Leinbagh, H., Kellogg, P., Monson, S., and Hallinan, T. (1979). Further laboratory measurements of the beam-plasma discharge. J. Geophys. Res. 84:7271. doi: 10.1029/JA084iA12p07271

CrossRef Full Text | Google Scholar

Bryant, D., Hall, D., and Lepine, D. (1978). Electron acceleration in an array of auroral arcs. Planet Space Sci. 26, 81–90.

Google Scholar

Burch, J., Mende, S. B., Kawashima, N., Roberts, W. T., Taylor, W. W. L., Neubert, T., et al. (1993). Artificial auroras in the upper atmosphere: 1. Electron beam injections. Geophys. Res. Lett. 20, 491–494. doi: 10.1029/93GL00595

CrossRef Full Text | Google Scholar

Burke, W. (ed.). (1983). “Active experiments in space,” in Alpbach, Austria, May 24-28, 1983, ESA, Vol. SP-195 (Paris: European Space Agency), 375.

Google Scholar

Cabral, J. (1976). Nonlinear space-time evolution of the electron cyclotron instability in a beam plasma experiment. Plasma Phys. 18, 719–735. doi: 10.1088/0032-1028/18/9/007

CrossRef Full Text | Google Scholar

Cambou, F., Dokoukine, V., Lavergnat, J., Pellat, R., Reme, H., Saint-Marc, A., et al. (1980). General description of the ARAKS experiments. Ann. Geophys. 36, 271–283.

Google Scholar

Cambou, F., Dokukin, V., Ivchenko, V., Managadze, G., Migulin, V., Nazarenko, O., et al. (1975). The Zarnitza rocket experiment of electron injection. Space Res. 15, 491–500.

Google Scholar

Cambou, F., Lavergnat, J., Migulin, V., Morozov, V., Paton, B., Pellat, R., et al. (1978). ARAKS - controlled or puzzling experiment? Nature 271, 723–726. doi: 10.1038/271723a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheung, P., Wong, A., Darrow, C., and Qian, S. (1982). Simultaneous observations of caviton formation, spiky turbulence, and electromagnetic radiation. Phys. Rev. Lett. 48, 1348–1351. doi: 10.1103/PhysRevLett.48.1348

CrossRef Full Text | Google Scholar

Davis, T., Hallinan, T., Mead, G., Mead, J., Trichel, M., and Hess, W. (1971). Artificial aurora experiment: ground-based optical observations. J. Geophys. Res. 76, 6082–6092. doi: 10.1029/JA076i025p06082

CrossRef Full Text | Google Scholar

Davis, T., Wescott, E., Hallinan, T., Stenbaek-Nielsen, H., Hess, W., Trichel, M., et al. (1980). Artificial aurora conjugate to a rocket-borne electron accelerator. J. Geophys. Res. 85, 1722–1728. doi: 10.1029/JA085iA04p01722

CrossRef Full Text | Google Scholar

De Groot, J., and Katz, J. (1973). Anomalous plasma heating by a very strong high-frequency electric field. Phys. Fluids 16, 401–407. doi: 10.1063/1.1694355

CrossRef Full Text | Google Scholar

Dokukin, V., Ivchenko, V., Markeev, A., Milinevsky, G., Mishin, E., Ruzhin, Y., et al. (1981). Results of ZARNITSA-2, A rocket experiment on artificial electron beam injection in the ionosphere. Adv. Space Res. 1, 5–15.

Google Scholar

Donahue, T., Parkinson, T., Zipf, E., Doering, J., Fastie, W., and Miller, R. (1968). Excitation of the auroral green line by dissociative recombination of the oxygen molecular ion: analysis of two rocket experiments. Planet. Space Sci. 16, 737–748. doi: 10.1016/0032-0633(68)90078-0

CrossRef Full Text | Google Scholar

Duprat, G., Whalen, B., McNamara, A., and Bernstein, W. (1983). Measurements of the stability of energetic electron beams in the ionosphere. J. Geophys. Res. 88:3095. doi: 10.1029/JA088iA04p03095

CrossRef Full Text | Google Scholar

Dzyubenko, N., Ivchenko, V., Milinevsky, G., and Mishin, E. (1980). Influence of plasma collective effects on aurora borealis streamers. Sov. Phys. JETP Lett. 31, 607–610.

Eliasson, B., Milikh, G., Liu, T., Shao, X., and Papadopoulos, K. (2018). Simulations of the generation of energetic electrons and the formation of descending artificial plasma layers during HF-heating at Arecibo. J. Geophys. Res. Space Phys. 123, 10301–10309. doi: 10.1029/2018JA026073

CrossRef Full Text | Google Scholar

Eliasson, B., Milikh, G., Shao, X., Mishin, E., and Papadopoulos, K. (2015). Incidence angle dependence of Langmuir turbulence and artificial ionospheric layers driven by high-power HF-heating. J. Plasma Phys. 81:415810201. doi: 10.1017/S0022377814000968

CrossRef Full Text | Google Scholar

Eliasson, B., Shao, X., Milikh, G., Mishin, E., and Papadopoulos, K. (2012). Numerical modeling of artificial ionospheric layers driven by high-power HF-heating. J. Geophys. Res. 117:A10321. doi: 10.1029/2012JA018105

CrossRef Full Text | Google Scholar

Fainberg, Y. (1962). The interaction of charged particle beams with plasma. J. Nucl. Energy Part C Plasma Phys. 4, 203–220. doi: 10.1088/0368-3281/4/3/309

CrossRef Full Text | Google Scholar

Feldman, P., and Doering, J. (1975). Auroral electrons and the optical emissions of nitrogen. J. Geophys. Res. 80, 2808–2812. doi: 10.1029/JA080i019p02808

CrossRef Full Text | Google Scholar

Frank, L., Paterson, W., Ashour-Abdalla, M., Schriver, D., Kurth, W., Gurnett, D., et al. (1989). Electron velocity distributions and plasma waves associated with the injection of an electron beam into the ionosphere. J. Geophys. Res. 94, 6995–7001.

Google Scholar

Galeev, A. (1975). “Plasma turbulence in the magnetosphere with special regards to plasma heating,” in Physics of the Hot Plasma in the Magnetosphere, eds B. Hultqvist and L. Stenflo (New York, NY: Plenum Press), 251–270.

Google Scholar

Galeev, A., Mishin, E., Sagdeev, R., Shapiro, V., and Shevchenko, V. (1976). Discharge in the region around a rocket following an electron beam injection in the ionosphere. Sov. Phys. Doklady, 21, 641–644.

Galeev, A., and Sagdeev, R. (1979). “Nonlinear plasma theory,” in Reviews of Plasma Physics, Vol. 7, ed M. Leontovich (New York, NY: Consultants Bureau), 1–180.

Google Scholar

Galeev, A., Sagdeev, R., Shapiro, V., and Shevchenko, V. (1977). Relaxation of high-current electron beams and the modulational instability. Sov. Phys. JETP 45, 266–271.

Galeev, A., Sagdeev, R., Shapiro, V., and Shevehenko, V. (1983). “Beam plasma discharge and suprathermal electron tails,” in Active Experiments in Space (Alpbach, Austria, May 24-28, 1983), ESA, ed W. Burke, Vol. SP-195 (Paris: European Space Agency), 151–155.

Google Scholar

Gendrin, R. (1974). Initial expansion phase of an artificially injected electron beam. Planet. Space Sci. 22, 613–615. doi: 10.1016/0032-0633(74)90097-X

CrossRef Full Text | Google Scholar

Getty, W., and Smullin, L. (1963). Beam-plasma discharge: buildup of oscillations. J. Appl. Phys. 34, 3421–3429. doi: 10.1063/1.1729220

CrossRef Full Text | Google Scholar

Goerke, R., Kellogg, P., Monson, S., Franz, R., Nemzek, R., Anderson, H., et al. (1992). Observations of VHF emissions from 50-mA electron beam injections in the ionosphere that are associated with beam-induced discharges. J. Geophys. Res. 97, 1319–1335. doi: 10.1029/91JA02431

CrossRef Full Text | Google Scholar

Grandal, B. (ed.). (1982a). Artificial Particle Beams in Space Plasma Studies, NATO Advanced Study Institutes Series B, Vol. 79. New York, NY: Plenum Press.

Grandal, B. (1982b). “Highlights of the observations in the polar 5 electron accelerator rocket experiment,” in Artificial Particle Beams in Space Plasma Studies. NATO Advanced Study Institutes Series B, Vol. 79, ed B. Grandal (New York, NY: Plenum Press), 159-174.

Google Scholar

Gringauz, K., Mishin, E., Shutte, N., and Volokitin, A. (1981). Rocket potential measurements during electron beam injection into the ionosphere. Adv. Space Res. 1, 69–76. doi: 10.1016/0273-1177(81)90273-8

CrossRef Full Text | Google Scholar

Gringauz, K., Shutte, N. Smirnova, L., Reme, H., Saint-Marc, A., and Vigo, J. (1980). Natural precipitation of electrons and effects observed during the operation of the electron gun during the ARAKS experiment. Ann. Geophys. 36, 363–370.

Google Scholar

Hallinan, T., Stenbaek-Nielsen, H., and Deehr, C. (1985). Enhanced aurora. J. Geophys. Res. 90, 8461–8475. doi: 10.1029/JA090iA09p08461

CrossRef Full Text | Google Scholar

Hendrickson, R., McEntire, R., and Winckler, J. (1971). Electron echo experiment: a new magnetospheric probe. Nature 230, 564–566. doi: 10.1038/230564a0

CrossRef Full Text | Google Scholar

Hess, W., Trichel, M., Davis, T., Beggs, W., Kraft, G., Stassinopoulos, E., et al. (1971). Artificial Aurora experiment: experiment and principal results. J. Geophys. Res. 76, 6067–6081. doi: 10.1029/JA076i025p06067

CrossRef Full Text | Google Scholar

Ichimaru, S. (1973). Basic Principles in Plasma Physics: A Statistical Approach. San Francisco, CA: Benjamin-Cummings.

Google Scholar

Isham, B., Rietveld, M., Guio, P., Forme, F., Grydeland, T., and Mjlhus, E. (2012). Cavitating Langmuir turbulence in the terrestrial aurora. Phys. Rev. Lett. 108:105003. doi: 10.1103/PhysRevLett.108.105003

PubMed Abstract | CrossRef Full Text | Google Scholar

Ivchenko, V., Milinevsky, G., Mishin, E., and Ruzhin, Y. (1981). Optical observations of near-rocket glow in the “Zarnitsa-2” Experiment. Geomagn. Aeron., Engl. Edition 19, 398–399.

Izhovkina, N. (1978). Spreading of the distribution function of an electron beam in the ionosphere as a function of the distance to the iniection point. Geomagn. Aeron. Engl. Edition 18, 352–253.

Google Scholar

Izhovkina, N., and Mishin, E. (1979). Possibility of triggering beam-plasma discharge during injections of auroral electrons into the ionosphere. Geomagn. Aeron. Engl. Edition 19, 398–399.

Google Scholar

Jacobsen, T. (1982). “Observations of plasma heating effects in the ionosphere by a rocket borne electron accelerator,” in Artificial Particle Beams in Space Plasma Studies. NATO Advanced Study Institutes Series B, Vol. 79, ed B. Grandal (New York, NY: Plenum Press), 175–198.

Google Scholar

Jost, R., Anderson, H., Bernstein, W., and Kellogg, P. (1982). “Radial dependensce of HF wave field strength in the BPD column,” in Artificial Particle Beams in Space Plasma Studies, NATO Advanced Study Institute, Vol. 79, ed B. Grandal (New York, NY: Plenum Press), 431–438.

Google Scholar

Kainer, S., Dawson, J., and Coffey, T. (1972). Alternating current instability produced by the two-stream instability. Phys. Fluids 15, 2419–2422. doi: 10.1063/1.1693886

CrossRef Full Text | Google Scholar

Karfidov, D., and Lukina, N. (1997). Electrical fields in a plasma with strong Langmuir turbulence. Phys. Lett. A 232, 443–446. doi: 10.1016/S0375-9601(97)00379-4

CrossRef Full Text | Google Scholar

Kawashima, N. (1988). Electron beam experiment in space. J. Geomag. Geoelectr. 40, 1269–1281. doi: 10.5636/jgg.40.1269

CrossRef Full Text | Google Scholar

Kellogg, P. (1992). Electron beams and their interactions with the ionosphere-a review of the E||B series. Adv. Space Res. 12, 15–28. doi: 10.1016/0273-1177(92)90345-X

CrossRef Full Text | Google Scholar

Kharchenko, I., Fainberg, Y., Nikolayev, R., Kornilov, E., Lutsenko, E., and Pedenko, N. (1962). Interaction of an electron beam with a plasma in a magnetic field. Nuclear Fusion Suppl. 3, 1101–1106.

Google Scholar

Khazanov, G. (2011). Kinetic Theory of Inner Magnetospheric Plasma. New York, NY: Springer.

Google Scholar

Khazanov, G., Neubert, T., Gefan, G., Trukhan, A., and Mishin, E. (1993). A kinetic description of electron beam injection from Spacecraft. Geophys. Res. Lett. 20, 1999–2002. doi: 10.1029/93GL01981

CrossRef Full Text | Google Scholar

Kitsenko, A., Pankratov, I., and Stepanov, K. (1974). The nonlinear phase of monochromatic-oscillation excitation by a charged-particle beam in a plasma located in a magnetic field. Sov. Phys. JETP 39, 77–81.

Google Scholar

Kruer, W., and Dawson, J. (1971). Anomalous heating of plasma electrons driven by a large transverse field at ω = ω_pe. Phys. Fluids 14, 1003–1005. doi: 10.1063/1.1693529

CrossRef Full Text | Google Scholar

Lebedev, P., Onishchenko, I., Tkach, I., Fainberg, I., and Shevchenko, V. (1976). Theory of the beam-plasma discharge. Soviet Journ. Plasma Phys. 2, 222–225.

Google Scholar

Linson, L. (1982). “Charge neutralization as studied experimentally and theoretically,” in Artificial Particle Beams in Space Plasma Studies, NATO Advanced Study Institute, Vol. 79, ed B. Grandal (New York, NY: Plenum Press), 573–596.

Google Scholar

Lyakhov, S., and Managadze, G. (1980). Observations of fluxes of electrons scattered by the atmosphere in the second ARAKS experiment of January 26, 1975. Ann. Geophys. 36, 375–380.

Google Scholar

MacDonald, A. (1966). Microwave Breakdown in Gases. New York, NY: Wiley.

Maehlum, B., Grandal, B, Jacobsen, T., and Troim, J. (1980c). Polar 5 - An electron accelerator experiment within an aurora. 2. Scattering of an artificially produced electron beam in the atmosphere. Planet. Space Sci. 28, 279–289. doi: 10.1016/0032-0633(80)90018-5

CrossRef Full Text | Google Scholar

Maehlum, B., Maseide, K., Aarsnes, K., Egeland, A., Grandal, B., Holtet, J., et al. (1980a). Polar 5 - an electron accelerator experiment within an aurora. 1. Instrumentation and geophysical conditions. Planet. Space Sci. 28, 259–278. doi: 10.1016/0032-0633(80)90017-3

CrossRef Full Text | Google Scholar

Maehlum, B., Thrane, E., and Troim, J. (1980b). Polar 5 - An electron accelerator experiment within an aurora.4. Measurements of the 391.4 nm light produced by an artificial electron beam in the upper atmosphere. Planet. Space Sci. 28, 309–319. doi: 10.1016/0032-0633(80)90020-3

CrossRef Full Text | Google Scholar

Majeed, T., and Strickland, D. (1997). New survey of electron impact cross sections for photoelectron and auroral electron energy loss calculations. J. Phys. Chem. Ref. Data 26, 335–349. doi: 10.1063/1.556008

CrossRef Full Text | Google Scholar

Managadze, G., Balebanov, V., Burchudladze, A., Gaugua, T., Leonov, N., Lyakhov, S., et al. (1988). Potential observation of an electron emitting rocket payload and other related plasma measurements. Planet. Space Sci. 36:399. doi: 10.1016/0032-0633(88)90128-6

CrossRef Full Text | Google Scholar

Matthews, D., Pongrats, M., and Papadopoulos, K. (1976). Nonlinear production of suprathermal tails in auroral electrons. J. Geophys. Res. 81, 123–129. doi: 10.1029/JA081i001p00123

CrossRef Full Text | Google Scholar

Meng, C.-I., Rycroft, M., and Frank, L. (eds.). (1991). Auroral Physics. Cambridge: Cambridge University Press.

Google Scholar

Mikhailovskii, A (1974), Theory of Plasma Instabilities. Vol. 1: Instabilities of a Homogeneous Plasma. New York, NY: Consultants Bureau.

Mishin, E. (2010). “Nonlinear plasma effects in natural and artificial aurora,” in AIP Proceedings Modern Challenges in Nonlinear Plasma Physics, Vol. CP 1320, eds D. Vassiliadis, S. Fung, X. Shao, I. Daglis, and J. Huba (Washington, DC), 177–184.

Google Scholar

Mishin, E., Burke, W., and Pedersen, T. (2004). On the onset of HF-induced airglow at HAARP. J. Geophys. Res. 109:A02305. doi: 10.1029/2003JA010205

CrossRef Full Text | Google Scholar

Mishin, E., Ivchenko, V., and Milinevsky, G. (1981). Fine structure of artificial auroral rays. Adv. Space Res. 1, 163–165. doi: 10.1016/0273-1177(81)90286-6

CrossRef Full Text | Google Scholar

Mishin, E., Lukjanova, L., Makarenko, S., and Atamaniuk, B. (1992). Radio wave dissipation in turbulent auroral plasma during the precipitation of energetic electrons. Radio Sci. 27, 283–287. doi: 10.1029/91RS02631

CrossRef Full Text | Google Scholar

Mishin, E., and Pedersen, T. (2011). Ionizing wave via high-power HF acceleration. Geophys. Res. Lett. 38:L01105. doi: 10.1029/2010GL046045

CrossRef Full Text | Google Scholar

Mishin, E., and Ruzhin, Y. (1980a). The model of beam-plasma discharge in the rocket environment during an electron beam injection in the ionosphere. Ann. Geophys. 36, 423–432.

Google Scholar

Mishin, E., and Ruzhin, Y. (1980b). The dynamics of HF radio emission in the ARAKS experiment. Ann. Geophys. 36, 357–362.

Google Scholar

Mishin, E., and Ruzhin, Y. (1981). Beam-plasma discharge in near rocket region. Adv. Space Res. 1, 47–59. doi: 10.1016/0273-1177(81)90271-4

CrossRef Full Text | Google Scholar

Mishin, E., Ruzhin, Yu., and Telegin, V. (1989). The Interaction of Electron Beams with Ionospheric Plasma (in Russian). Leningrad: Gidrometeoizdat.

Mishin, E., and Telegin, V (1986), Spectrum of suprathermal electrons in the auroral plasma. Sov. J. Plasma Phys. 12, 509–510.

Google Scholar

Mishin, E., and Telegin, V. (1989). Effects of plasma turbulence in Aurorae. Geomagn. Aeron. Engl. Edition 29, 1–13.

Google Scholar

Mishin, E., Trukhan, A., Gefan, G., and Drozdov, A. (1994). Numerical simulation of “Fast Electro Echo” accompanying artificial injection of electron beams in ionosphere. Geomagn. Aeron. Engl. Edition 33, 558–561.

Mishin, E., Watkins, B., Lehtinen, N., Eliasson, B., Pedersen, T., and Grach, S. (2016). Artificial ionospheric layers driven by high-frequency radiowaves: an assessment. J. Geophys. Res. Space Physics, 121, 3497–3524. doi: 10.1002/2015JA021823

CrossRef Full Text | Google Scholar

Morioka, A., Oya, H., Miyoka, H., Ono, T., Obara, T., Yamagishi, H., et al. (1988). Wave-particle interaction in the auroral ionosphere in LF and HF ranges: results from Antarctic rocket observations. J. Geomag. Geoelectr. 40, 923–937. doi: 10.5636/jgg.40.923

CrossRef Full Text | Google Scholar

Neubert, T., Taylor, W. W. L., Storey, L. R. O., Kawashima, N., Roberts, W. T., Reasoner, D. L., et al. (1986). Waves generated during electron beam emissions from the space shuttle. J. Geophys. Res. 91, 11321–11329. doi: 10.1029/JA091iA10p11321

CrossRef Full Text | Google Scholar

Obayashi, T, Kawashima, N, Kuriki, K, Nagatomo, M, Ninomiya, K, Sasaki, S, et al. (1984). Space experiments with particle accelerators. Science 225, 195–196. doi: 10.1126/science.225.4658.195

PubMed Abstract | CrossRef Full Text | Google Scholar

Oguti, T. (1975). Two-tiered auroral band. J. Atmos. Terr. Phys. 37, 1501–1504. doi: 10.1016/0021-9169(75)90082-3

CrossRef Full Text | Google Scholar

Omelchenko, Yu., Sotnikov, V., Shapiro, V., and Shevchenko, V. (1992). Strong Langmuir turbulence and beam-plasma discharge in the ionospheric plasma. Planet. Space Sci. 40, 535–540. doi: 10.1016/0032-0633(92)90172-K

CrossRef Full Text | Google Scholar

O'Neil, R., Bien, F., Burt, D., Sandock, J., and Stair, A. Jr. (1978a). Summarized results of the artificial aurora experiment, PRECEDE. J. Geophys. Res. 83, 3273–3280. doi: 10.1029/JA083iA07p03273

CrossRef Full Text | Google Scholar

O'Neil, R., Lee, E., Stair, A. Jr, and Ulwick, J. (1978b). EXCEDE II Test, an artificial aurora experiment: ground-based optical observations. J. Geophys. Res. 83, 3281–3288. doi: 10.1029/JA083iA07p03281

CrossRef Full Text | Google Scholar

Onishchenko, I., Linetskii, A., Matsiborko, N., Shapiro, V., and Shevchenko, V. (1970). On nonlinear theory of monochromatic plasma wave excitation by an electron beam. Sov. Phys. JETP Lett. 12, 281–285.

Papadopoulos, K. (1975). Nonlinear stabilization of beam plasma interaction by parametric effects. Phys. Fluids 18, 1769–1777. doi: 10.1063/1.861096

CrossRef Full Text | Google Scholar

Papadopoulos, K. (1982). “Theory of beam plasma discharge,” in Artificial Particle Beams in Space Plasma Studies, NATO Advanced Study Institute, Vol. 79, ed B. Grandal (New York, NY: Plenum Press), 505–524.

Google Scholar

Papadopoulos, K. (1986). Scaling of the beam plasma discharge for low magnetic fields. J. Geophys. Res. 91, 1627–1631. doi: 10.1029/JA091iA02p01627

CrossRef Full Text | Google Scholar

Papadopoulos, K., and Coffey, T (1974), Nonthermal features of the auroral plasma due to precipitating electrons. J. Geophys. Res. 79, 674–676. doi: 10.1029/JA079i004p00674

CrossRef Full Text | Google Scholar

Pelleiter, G. (1982). Generation of a high energy electron tail by strong Langmuir turbulence in a plasma. Phys. Rev. Lett. 49, 782–785. doi: 10.1103/PhysRevLett.49.782

CrossRef Full Text | Google Scholar

Reasoner, D., and Chappell, C. (1973). Twin-payload observation of incident and backscattered auroral electrons. J. Geophys. Res. 78, 2176–2186. doi: 10.1029/JA078i013p02176

CrossRef Full Text | Google Scholar

Rees, M. (1989). Physics and Chemistry of the Upper Atmosphere. New York, NY: Cambridge University Press.

Google Scholar

Rees, M., Romick, G., Anderson, H., and Casserly, R. Jr. (1976). Calculation of auroral emissions from measured auroral precipitation: comparison with observation. J. Geophys. Res. 81, 5091–5096. doi: 10.1029/JA081i028p05091

CrossRef Full Text | Google Scholar

Reme, H. (ed.). (1980). Special issue on the results of the active French-Soviet ARAKS experiments. Ann. Geophys. 36:3.

Robinson, P. (1997). Nonlinear wave collapse and strong turbulence. Rev. Mod. Phys. 69, 507–573. doi: 10.1103/RevModPhys.69.507

CrossRef Full Text | Google Scholar

Rowland, H., Chang, C., and Papadopoulos, K. (1981a). Scaling of the beam-plasma discharge. Phys. Rev. Lett. 86, 9215–9218.

Google Scholar

Rowland, H., Lyon, J., and Papadopoulos, K. (1981b). Strong Langmuir turbulence in one and two dimensions. J. Geophys. Res. 46, 346–348.

Google Scholar

Sagdeev, R. (1979). The 1976 oppenheimer lectures: critical problems in plasma astrophysics. Rev. of Mod. Phys. 51, 1–20.

Google Scholar

Schlesier, A., Mishin, E., and Schlegel, K. (1997). “Non-collisional” ionization and temperature layers in the auroral E/F₁ layer: EISCAT observations. Geophys. Res. Lett. 24, 1407–1410. doi: 10.1029/97GL01178

CrossRef Full Text | Google Scholar

Shapiro, V., and Shevchenko, V. (1984). “Strong turbulence of plasma oscillations,” in Handbook of Plasma Physics. Basic Plasma Physics, Vol. 2, eds A. Galeev and R. Sudan (New York, NY: Elsevier), 123–182.

Google Scholar

Sharp, W. (1982). Suprathermal electrons produced by beam-plasma discharge. Geophys. Res. Lett. 9, 869–872. doi: 10.1029/GL009i008p00869

CrossRef Full Text | Google Scholar

Siscoe, G. (1986). An historical footnote on the origin of ‘aurora borealis’. Hist. Geophys. 2:11. doi: 10.1029/HG002p0011

CrossRef Full Text | Google Scholar

Sotnikov, V., Omelchenko, Yu., Shapiro, V., Shevchenko, V., Ashour-Abdalla, M., and Schriver, D. (1992). A model of beam-plasma discharge in a nonuniform plasma. Phys Fluids B 4, 3562–3568. doi: 10.1063/1.860363

CrossRef Full Text | Google Scholar

Stenbaek-Nielsen, H., and Hallinan, T. (1979). Pulsating aurora: evidence for non-collisional thermalisation of precipitating electrons. J. Geophys. Res. 84, 3257–3272. doi: 10.1029/JA084iA07p03257

CrossRef Full Text | Google Scholar

Streltsov, A., Berthelier, J.-J., Chernyshov, A., Frolov, V., Honary, F., Kosch, M., et al. (2018). Past, present and future of active radio frequency experiments in space. Space Sci. Rev. 214, 118–240. doi: 10.1007/s11214-018-0549-7

CrossRef Full Text | Google Scholar

Swider, W., and Narcisi, R. (1977). Auroral E-region: ion composition and nitric oxide. Planet. Space Sci. 25, 103–106. doi: 10.1016/0032-0633(77)90014-9

CrossRef Full Text | Google Scholar

Szuszczewicz, E., Walker, O., Holmes, O, and Leinbach, H (1979). Plasma diffusion in a space-simulation beam-plasma discharge. Geophys. Res. Lett 6, 201–204. doi: 10.1029/GL006i003p00201

CrossRef Full Text | Google Scholar

Timofeev, E., and Miroshnikov, Y. (1982). Altitude characteristics of radar aurora as seen by 90 MHz double-altitude radar system operated at Karmaselga. J. Geophys. Res. 87, 44–54.

Google Scholar

van Wakeren, J., and Hopman, H. (1972). Trapping of electrons in large-amplitude electrostatic fFields resulting from beam-plasma interaction. Phys. Rev. Lett. 28, 295–298. doi: 10.1103/PhysRevLett.28.295

CrossRef Full Text | Google Scholar

Vedenov, A., Velikhov, E., and Sagdeev, R. (1962). Quasilinear theory of plasma oscillations, Nucl. Fusion Suppl. 2, 465–475.

Google Scholar

Vlasenko, S., Popovich, V., and Kharchenko, I. (1976a). Formation of beam-plasma discharge as an electron beam is injected into a gas flow. Sov. J. Plasma Phys. 2, 149–152.

Google Scholar

Vlasenko, S., Popovich, V., and Kharchenko, I. (1976b). Radiation and density fluctuations of a beam-plasma discharge without a magnetic field. Sov. J. Plasma Phys. 2, 152–156.

Google Scholar

Volokitin, A., and Mishin, E. (1978). Initial stage of the neutralization of a rocket during electron beam injection into ionosphere. Sov. J. Plasma Phys. 4, 531–532.

Google Scholar

Volokitin, A., and Mishin, E. (1979). On electron beam relaxation in the plasma with rare collisions. Sov. J. Plasma Phys. 5, 654–656.

Vyacheslavov, L., Burmasov, V., Kandaurov, I., Kruglyakov, E., Meshkov, O., Popov, S., et al. (2002). Strong Langmuir turbulence with and without collapse: experimental study. Plasma Phys. Control. Fusion, 44, B279–B291. doi: 10.1088/0741-3335/44/12B/320

CrossRef Full Text | Google Scholar

Wahlund, J., Opgenoorth, H., and Rothwell, P. (1989). Observation of thin aurnral ionization layers by EISCAT in connection with pulsating aurora. J. Gcophys. Res. 94, 17223–17233. doi: 10.1029/JA094iA12p17223

CrossRef Full Text | Google Scholar

Wang, J., Newman, D., and Goldman, M. (1997). Vlasov simulations of electron heating by Langmuir turbulence near the critical altitude in the radiation-modified ionosphere. J. Atmos. Sol. Terr. Phys. 59, 2461–2474. doi: 10.1016/S1364-6826(96)00140-X

CrossRef Full Text | Google Scholar

Wilhelm, K., Bernstein, W., Kellogg, P., and Whalen, B. (1985). Fast magnetospheric ehoes of energetic electron beams. J. Geophys. Res. 90, 491–504. doi: 10.1029/JA090iA01p00491

CrossRef Full Text | Google Scholar

Winckler, J., Arnoldy, R., and Hendrickson, R. (1975). Echo 2: a study of electron beams injected into the high-latitude ionosphere from a large sounding rocket. J. Geophys. Res. 80, 2083–2088. doi: 10.1029/JA080i016p02083

CrossRef Full Text | Google Scholar

Winckler, J. R. (1980). The application of artifical electron beams to magnetospheric research. Rev. Geophys. Space Phys. 18, 659–682. doi: 10.1029/RG018i003p00659

CrossRef Full Text | Google Scholar

Winckler, J. R. (1992). Controlled experiments in the Earth's magnetosphere with artifical electron beams. Rev. Mod. Phys. 64, 859–871. doi: 10.1103/RevModPhys.64.859

CrossRef Full Text | Google Scholar

Zakharov, V. (1972). Collapse of Langmuir waves. Soviet Phys. JETP 35, 908–914.

Google Scholar

Notation

B₀ - the ambient magnetic field

L - Langmuir waves

EB - electron Bernstein waves

F_M - the Maxwellian distribution

F_s - the distribution function of secondary electrons

F_t - the accelerated tail distribution function

MI - modulational instability

Primary waves -the waves excited by the beam

SLT- strong Langmuir turbulence

SST - superstrong (Langmuir) turbulence

T_spin - the rocket's rotation period

WT - weak turbulence

W_k - the wave spectral energy density

$l_n=dln{n}_e/dh{|}^{-1}$- the plasma density scale height

$n_t^{ion}$ - the density of the ionizing (ε > ε_ion) electrons

r_D - the Debye radius

r_cb − the Larmor radius of the beam electrons

w = W/n₀T_e - the dimensionless parameter of nonlinearity

w_th - the modulational instability threshold

γ_mi - the modulational instability growth rate

${\alpha }_t^{ion}=n_t^{ion}/n_c$ - the relative density of ionizing (ε > ε_ion) electrons

ε_ion - the ionization energy

ε_min (ε_max) - the minimum (maximum) energy of the accelerated electrons

θ - pitch angle

λ_T - the mean free path of thermal electrons

μ = m_e/m_i - the electron-to-ion mass ratio

ν_il - the frequency of inelastic collisions

ν_ion - the ionization frequency