Stability of a Rotating Asteroid Housing a Space Station

Today there are numerous studies on asteroid mining. They elaborate on selecting the right objects, prospecting missions, potential asteroid redirection, and the mining process itself. For economic reasons, most studies focus on mining candidates in the 100–500 m size-range. Also, suggestions regarding the design and implementation of space stations or even colonies inside the caverns of mined asteroids exist. Caverns provide the advantages of confined material in near-zero gravity during mining and later the hull will shield the inside from radiation. Existing studies focus on creating the necessary artificial gravity by rotating structures that are built inside the asteroid. Here, we assume the entire mined asteroid to rotate at a sufficient rate for artificial gravity and investigate its use for housing a habitat inside. In this study we present how to estimate the necessary spin rate assuming a cylindrical space station inside a mined asteroid and discuss the implications arising from substantial material stress given the required rotation rate. We estimate the required material strength using two relatively simple analytical models and discuss applicability to rocky near-Earth asteroids.

1. Introduction

Sustaining human life on a station built inside a mined asteroid is a task which will require expertise in many fields. There needs to be air to breathe, water to drink, and the appropriate recycling systems, as well as food and light. Nevertheless, one of the most important prerequisites for a human body to stay healthy is gravity.

Taking plants to space and zero gravity is not as big a problem as taking a human body into this hostile environment. Plants do adapt to zero gravity relatively easily which is shown by many experiments performed both on the ISS (International Space Station) as well as on the ground with artificial microgravity (for example, see Kitaya et al., 2000, 2001; Kiss et al., 2009).

The human body however, reacts sensitive to zero gravity. The lack of an up and down direction in space affects endothelial cells (Versari et al., 2013), blood distribution to endocrine and reflex mechanisms controlling body water homeostasis and blood pressure (e.g., Taibbi et al., 2013), and it results in muscle wasting (Gopalakrishnan et al., 2010), severe bone loss (Keyak et al., 2009), immune depression (e.g., Cogoli, 1993; Battista et al., 2012; Gasperi et al., 2014), and ophthalmic problems (Nelson et al., 2014).

A study on how much gravity is needed to keep the human body upright was performed by Harris et al. (2014). They found that the threshold level of gravity needed to influence a persons orientation judgment is about 15 % of the gravity on Earth's surface, which is approximately the gravity acting on the Lunar surface. Martian gravity, 38 % of Earth's gravity, should be enough for astronauts to orient themselves and maintain balance.

As a consequence of a lack of experiments on the influence of reduced gravity on the human body we adopt the value of 38 % of Earth's gravity (g_E) as starting point for our theoretical approach. We assume that a rotation of the asteroid has to cause an artificial gravity of minimum 0.38 g_E in order to sustain long term healthy conditions for humans on the station.

Present suggestions to tackle this challenge of providing sufficient gravity rely on habitats in rotating wheels or tori that create gravity: Grandl and Bazso (2013) suggest self-sustained colonies up to 2000 people. Other studies somewhat vaguely mention augmenting the natural rotation with additional artificial rotation (Taylor et al., 2008). We elaborate on the latter and explore the feasibility and viability of creating artificial gravity for a habitat by putting the entire asteroid to rotation at a rate sufficient to generate the desired gravity.

An important aspect which directly affects applicability of this approach is sufficient material strength to sustain the required rotation rates. Although little is known about the exact composition of asteroids in the relevant size domain (≲ 0.5 km), observational data on fast rotators indicate individual objects with notable material strength. 2000 DO₈, the fastest rotator in the IAU Minor Planet Center's list¹ has a rotation period of 1.3 min. Assuming a long axis of about 80 m for this object, (Pravec et al., 2002) find a minimum tensile strength of approx. 2 × 10⁴ Pa, three orders of magnitude less than the typical tensile strength of solid rock. Other studies focusing on still smaller bodies (13–420 cm) such as meteoroids conclude bulk strengths upon atmospheric entry in the range 0.1–3.6 MPa (Popova et al., 2011); investigating larger objects, Borovička (2016) concludes that most meteoroids in the 1–20 m size range are fractured rocks with strengths of 0.1–10 MPa. When the latter observation-based findings are combined with the strength decreasing as the negative 1/2 power of diameter (Holsapple, 2007) a 500 m asteroid will have material strengths between 4 kPa and 2 MPa, which effectively limits the rotation rate they will be able to sustain. Theoretical estimates of the maximum spin rate of solid, rocky asteroids in the strength regime (asteroids smaller than about 10 km) based on Holsapple (2007)'s Equation (5.11) range from 1.3 rpm for a friction angle of zero to 1.9 rpm for a friction angle of 45°, respectively².

We start with initial considerations regarding the required spin rate of a space station with sufficient artificial gravity (section 2). Section 3 elaborates on the stress acting on the asteroidal hull and formulates two analytical models for the tensile and shear stresses as a function of the asteroid size, the dimensions of the space station, the required artificial gravity level, and the bulk density of the asteroid material. Section 4 applies our formulation to a near-Earth asteroid maximizing the usable area of the space station while observing maximum stress constraints. Finally, conclusions and an outlook on further related research is given in section 5.

2. Initial Considerations

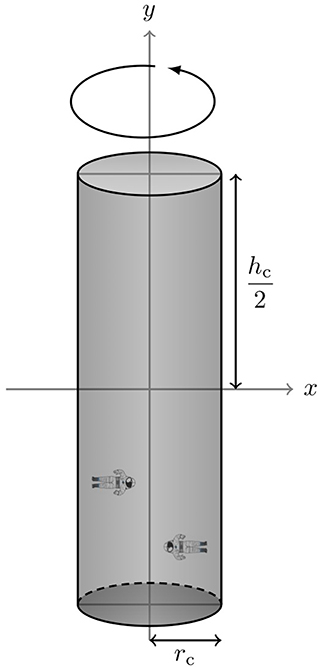
Let's assume a cylindrical space station with height h_c and radius r_c as depicted in Figure 1. Letting the cylinder rotate about its symmetry axis y with angular velocity ω will create an acceleration of

$\begin{array}{ll}{g}_{\text{c}}={\omega }^2{r}_{\text{c}}& (1)\end{array}$

acting on objects on the lateral surface. For a certain artificial gravity level the required rotation rate ω and rotation period T are then given by

$\begin{array}{ll}\omega =\sqrt{\frac{g_{\text{c}}}{r_{\text{c}}}},T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{r_{\text{c}}}{g_{\text{c}}}}.& (2)\end{array}$

Considering a size range of r_c = 50…250 m for example, the rotation rates would need to be between 1.17 and 2.6 rpm (rotations per minute) to create artificial gravity necessary for sustaining extended stays on the station (assuming 0.38 g_E as discussed above). Figure 2 gives an overview of rotation rates for a range of radii and gravity levels. The area usable for a space station subject to artificial gravity is the lateral surface of the cylinder S,

$\begin{array}{ll}S=2\pi r_{\text{c}}{h}_{\text{c}}.& (3)\end{array}$

FIGURE 1

Figure 1. Sketch of a cylindrical space station of height h_c and radius r_c.

FIGURE 2

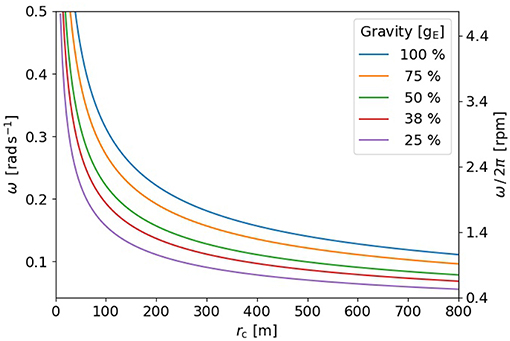
Figure 2. Rotation rates ω in rad s⁻¹ and rpm necessary to achieve an artificial gravity of g_c on the lateral surface of a cylinder with radius r_c.

3. Estimating Tensile and Shear Stress

The station is to be built inside a mined asteroid. Imposing a spin rate sufficient for providing artificial gravity on the lateral surface of the cylinder will create a substantial load on the asteroid material due to centrifugal forces. While little is known on material properties of small asteroids subject to our study, we rely on assumed material strength. Here, we assume that the asteroid is made of homogeneous, solid material such as basaltic silicate rock, for instance. We estimate the load on the asteroid material in simplified models: the tensile stress acting on the asteroid cross section is related to assumed tensile strength of solid silicate rock.

Figure 3 shows our geometrical model of a spheroidal asteroid with semi-axes a and b, respectively. The cavern is centered and cylindrical with respective radius r_c and height h_c. Due to the elliptical cross-section, the lateral distance d between the cavern and the asteroid's surface is given by

$\begin{array}{ll}d=\frac{b}{a}\sqrt{a^2-\frac{{h_{\text{c}}}^2}{4}}-r_{\text{c}}.& (4)\end{array}$

For a feasible solution, the cavern needs to be inside the asteroid in its entirety, which translates to the condition d > 0 or

$\begin{array}{ll}{r}_{\text{c}}<\frac{b}{a}\sqrt{a^2-\frac{{h_{\text{c}}}^2}{4}}.& (5)\end{array}$

The whole body will rotate about its symmetry axis y at a rate ω providing sufficient artificial gravity on the lateral surface of the space station with radius r_c. We assume rigid body rotation.

FIGURE 3

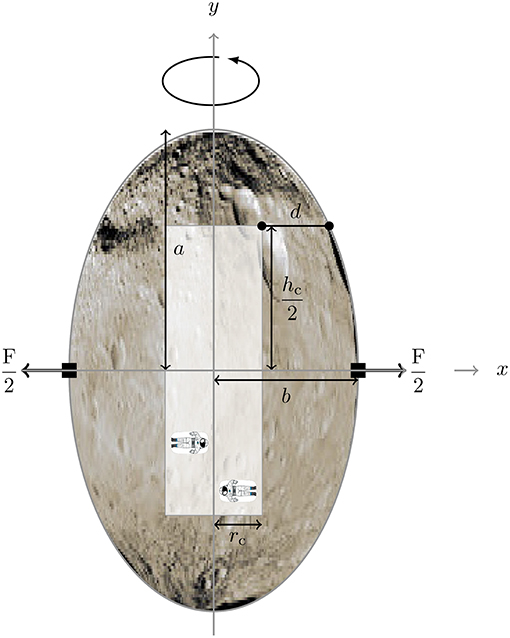
Figure 3. Sketch of asteroid with cylindrical cavern used to house a space station. Picture: Asteroid Vesta. Credit: NASA/JPL-Caltech/UCAL/MPS/DLR/IDA.

3.1. Model 1

In this model centrifugal forces that are acting on the asteroid material exert a load on an arbitrary symmetry plane. We determine the tensile stress that results from this load. The total centrifugal force F₁ pulling two halves of the asteroid apart is given by

$\begin{array}{ll}{F}_1=2{\displaystyle \underset{\genfrac{}{}{0ex}{}{\text{asteroid}}{\text{half}}}{\int }}\text{d}F=2{\displaystyle \underset{\genfrac{}{}{0ex}{}{\text{asteroid}}{\text{half}}}{\int }}\text{d}(m{\omega }^{2}r)=2{\omega }^2\rho {\displaystyle \underset{\genfrac{}{}{0ex}{}{\text{asteroid}}{\text{half}}}{\int }}r\text{d}V.& (6)\end{array}$

Here, we use the mass m of a volume element, the uniform asteroid density ρ, and the distance r of a volume element from the rotation axis. Transforming into cylindrical coordinates symmetrical w.r.t. the y-axis (dV = r dr dy dφ) and considering that there will be no contribution from the void of height h_c and radius r_c (see Figure 3) gives

$\begin{array}{ll}{F}_1=2{\omega }^2\rho \left[{\displaystyle \underset{0}{\overset{\pi }{\int }}}\text{d}\phi {\displaystyle \underset{-a}{\overset{a}{\int }}}\text{d}y{\displaystyle \underset{0}{\overset{\frac{b}{a}\sqrt{a^2-y^2}}{\int }}}{r}^2\text{d}r-{\displaystyle \underset{0}{\overset{\pi }{\int }}}\text{d}\phi {\displaystyle \underset{-h_{\text{c}}/2}{\overset{h_{\text{c}}/2}{\int }}}\text{d}y{\displaystyle \underset{0}{\overset{r_{\text{c}}}{\int }}}{r}^2\text{d}r\right].& (7)\end{array}$

Note that $r(y)=\frac{b}{a}\sqrt{a^2-y^2}$ holds for the elliptical cross section. Integrating (details given in Appendix A) yields

$\begin{array}{ll}{F}_1=\pi {\omega }^2\rho \left(\frac{\pi }{4}a{b}^3-\frac{2}{3}{r_{\text{c}}}^3{h}_{\text{c}}\right).& (8)\end{array}$

This load acts on the asteroid's cross section A = π a b − 2r_c h_c (cf. Figure 3) resulting in tensile stress σ₁ = F₁/A of

$\begin{array}{ll}{\sigma }_1=\frac{F_1}{A}=\frac{\pi {\omega }^2\rho }{12}\left(\frac{3\pi a{b}^3-8{r_{\text{c}}}^3{h}_{\text{c}}}{\pi ab-2r_{\text{c}}{h}_{\text{c}}}\right).& (9)\end{array}$

As we are interested in the stress resulting from a desired artificial gravity g_c we substitute ω² from (2) and get

$\begin{array}{ll}{\sigma }_1=\frac{\pi \rho g_{\text{c}}}{12r_{\text{c}}}\left(\frac{3\pi a{b}^3-8{r_{\text{c}}}^3{h}_{\text{c}}}{\pi ab-2r_{\text{c}}{h}_{\text{c}}}\right).& (10)\end{array}$

By introducing the dimensionless quantities

$\begin{array}{ll}{h_{\text{c}}}^{\prime }=\frac{h_{\text{c}}}{a},{r_{\text{c}}}^{\prime }=\frac{r_{\text{c}}}{b}& (11)\end{array}$

we can separate the parameters specific to individual asteroids and show that σ scales linearly with each of material density ρ, desired artificial gravity g_c, and asteroid semi-minor axis b. Inserting ${h_{\text{c}}}^{\prime }$ and ${r_{\text{c}}}^{\prime }$ into (10) yields

$\begin{array}{ll}{\sigma }_1=\frac{\pi \rho g_{\text{c}}b}{12{r_{\text{c}}}^{\prime }}\left(\frac{3\pi -8{r_{\text{c}}{ }^{\prime }}^3{h_{\text{c}}}^{\prime }}{\pi -2{r_{\text{c}}}^{\prime }{h_{\text{c}}}^{\prime }}\right)=\rho g_{\text{c}}b·f({r_{\text{c}}}^{\prime },{h_{\text{c}}}^{\prime }).& (12)\end{array}$

Hence, it is sufficient to study $f({r_{\text{c}}}^{\prime },{h_{\text{c}}}^{\prime })$ to get estimates for the stresses in asteroids of arbitrary density and semi-minor axis rotating at a rate providing the desired artificial gravity. Figure 4 shows σ₁ contours assuming parameters ρ = 1 g cm⁻³, g_c = 1 g_E, and b = 1 m. For different parameter values the numbers scale linearly with ρ, g_c, and b. The white area in Figure 4 corresponds to illegal combinations of r_c and h_c that violate condition (5) demanding the space station has to be inside the asteroid in its entirety.

FIGURE 4

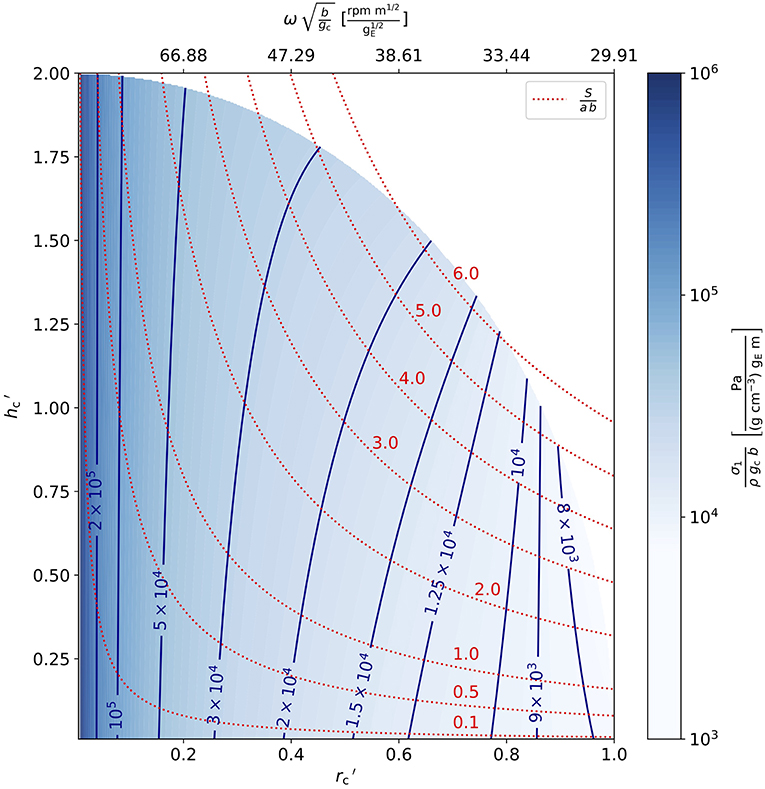
Figure 4. Model 1 material stress for different dimensions of the space station (dimensionless radius r_c and height h_c). The blue contour lines give the ratio $\frac{{\sigma }_1}{\rho g_{\text{c}}b}$ for ρ given in g cm⁻³, g_c measured in units of g_E, and b measured in meters, respectively. The dotted red lines give contours of the ratio $\frac{S}{ab}$ obtained via (14), the upper x-axis gives the scaled rotation rate.

The required rotation rate as a function of space station radius r_c and desired artificial gravity g_c is given in (2), scales according to

$\begin{array}{ll}\omega =\sqrt{\frac{g_{\text{c}}}{r_{\text{c}}}}=\sqrt{\frac{{\text{g}}_{\text{E}}}{b}}\sqrt{\frac{g_{\text{c}}\left[{\text{g}}_{\text{E}}\right]}{{r_{\text{c}}}^{\prime }}},& (13)\end{array}$

and is indicated on the upper x-axis. As we will be interested in the usable surface area of the station S, we indicate its dimensionless variant

$\begin{array}{ll}\frac{S}{ab}=2\pi {r_{\text{c}}}^{\prime }{h_{\text{c}}}^{\prime }& (14)\end{array}$

as red, dotted contour lines in Figure 4. For any assumed maximum material strength, the solution for maximum S suggests a radius of the cylinder r_c that extends all the way to the surface (d = 0, cf. Figure 3). This is however, the edge case of our model 1 that estimates material load by assuming two halves of the asteroid driven apart by centrifugal forces. As soon as d gets very small the “two halves” assumption fails. Therefore, we estimate material load by another model which will be more accurate at the edge case, i.e., very small values of the distance to the surface d.

3.2. Model 2

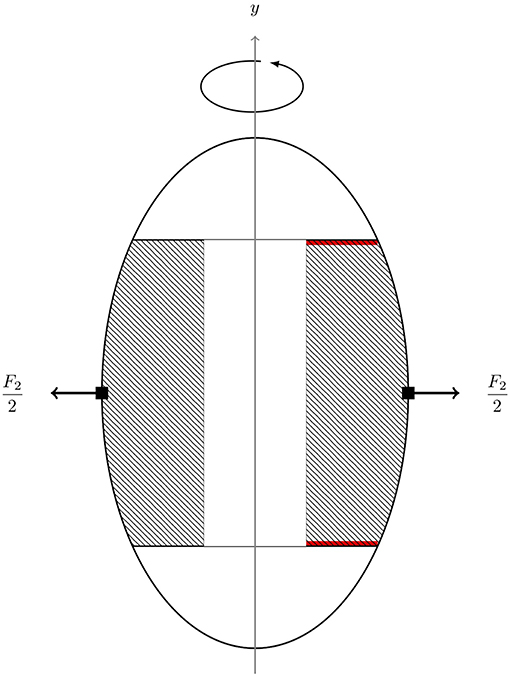
Rather than focusing on two entire halves of the hollowed-out asteroid, this model studies the “mantle” outside the space station. This is the solid torus created by sweeping the right part of the hashed surface between the red lines at y = ±h_c/2 in Figure 5 around the y-axis. As the radius of the space station approaches the asteroid's hull, the centrifugal forces attempting to shear away this torus may get significant. This shearing load acts on the two annuli resulting from rotating the red lines in Figure 5 about the y-axis. In addition to overcoming the shear strength of the asteroid material however, the tensile strength of the cross section (the hashed area in Figure 5) has to be exceeded by the load exerted by the centrifugal force.

FIGURE 5

Figure 5. Simplified sketch of cavity for clarification. Force acting on material.

Similar to calculating F₁ in section 3.1, the centrifugal force F₂ can be derived by transforming to cylindrical coordinates as follows:

$\begin{array}{lll}{F}_2& ={\omega }^2\rho {\displaystyle \underset{\genfrac{}{}{0ex}{}{\text{shaded volume}}{\genfrac{}{}{0ex}{}{\text{in }\text{Figure}5,}{\text{i}.\text{e}.,\left|y\right|\le h_{\text{c}}/2}}}{\int }}r\text{d}V={\omega }^2\rho {\displaystyle \underset{\left|y\right|\le \frac{1}{2}{h}_{\text{c}}}{\int }}{r}^2\text{ d}r\text{ d}y\text{ d}\phi & (15)\end{array}$

$\begin{array}{ll}={\omega }^2\rho {\displaystyle \underset{0}{\overset{2\pi }{\int }}}\text{d}\phi {\displaystyle \underset{-\frac{1}{2}{h}_{\text{c}}}{\overset{\frac{1}{2}{h}_{\text{c}}}{\int }}}\text{d}y{\displaystyle \underset{r_{\text{c}}}{\overset{\frac{b}{a}\sqrt{a^2-y^2}}{\int }}}\text{d}r{r}^2.& (16)\end{array}$

Integrating (Appendix B gives the detailed steps) yields a rather lengthy expression for the centrifugal force:

$\begin{array}{l}{F}_2=\frac{2\pi {\omega }^2\rho }{3}\{\frac{1}{8}{\left(\frac{b}{a}\right)}^3[h_{\text{c}}\left(5a^2-\frac{h_{\text{c}}^2}{2}\right)\sqrt{a^2-\frac{h_{\text{c}}^2}{4}}\\ +6a^4\arcsin \frac{h_{\text{c}}}{2a}]-h_{\text{c}}{r}_{\text{c}}^3\}.& (17)\end{array}$

This force exerts a tensile load on the asteroid's cross section A^t between y = −h_c/2 and y = h_c/2 and a shear load on the two annuli of area A^s given by rotating the red lines in Figure 5 about the y-axis. The surface area A^t is given by (cf. Figure 5)

$\begin{array}{l}{A}^t=2\left[{\displaystyle \underset{-h_{\text{c}}/2}{\overset{h_{\text{c}}/2}{\int }}}x(y)\text{d}y-h_{\text{c}}{r}_{\text{c}}\right]=4{\displaystyle \underset{0}{\overset{h_{\text{c}}/2}{\int }}}\frac{b}{a}\sqrt{a^2-\frac{y^2}{4}}\text{d}y-2h_{\text{c}}{r}_{\text{c}}\\ =\frac{4b}{a}{\left[\frac{y}{4}\sqrt{4a^2-y^2}+a^{2}arctan\frac{y}{\sqrt{4a^2-y^2}}\right]}_0^{\frac{h}{2}}-2h_{\text{c}}{r}_{\text{c}}\end{array}$

and using the identity $\arcsin x=\arctan (x/\sqrt{1-x^2)}$ we get

$\begin{array}{ll}{A}^t=\frac{b{h}_{\text{c}}}{2a}\sqrt{4a^2-\frac{{h_{\text{c}}}^2}{4}}+4abarcsin\frac{h_{\text{c}}}{4a}-2h_{\text{c}}{r}_{\text{c}}.& (18)\end{array}$

Each of the annuli has a surface of A^s,

$\begin{array}{lll}{A}^s& =\pi \left[{(r_{\text{c}}+d)}^2-{r_{\text{c}}}^2\right]=\pi \left[\frac{b^2}{a^2}\left(a^2-\frac{{h_{\text{c}}}^2}{4}\right)-{r_{\text{c}}}^2\right]& (19)\end{array}$

$\begin{array}{ll}=\pi \left[b^2\left(1-\frac{{h_{\text{c}}}^2}{4a^2}\right)-{r_{\text{c}}}^2\right].& (20)\end{array}$

Combining Equations (17), (18), and (20), we obtain the average stress σ₂ in this model,

$\begin{array}{ll}{\sigma }_2=\frac{F_2}{A^t+2A^s},& (21)\end{array}$

for the complete—rather unwieldy—formulation of the stress please refer to Appendix C. Unlike it is the case in model 1, we cannot formulate σ₂ in a scaling way using the dimensionless quantities r_c and h_c. For the asteroids in scope of this study though, σ₂ is usually smaller than σ₁, but increases if the space station radius gets closer to the asteroid's surface. In the following section 4 we will demonstrate this by comparing the two models for a fictitious, yet realistic asteroid.

4. Application to a Realistic Asteroid

We will apply the analytic models 1 and 2 to a rocky asteroid with dimensions 500 × 390 m. There is a number of similar-sized rocky near-Earth asteroids, e.g., 3757 Anagolay, 99942 Apophis, 3361 Orpheus, 308635 (2005 YU55), 419624 (SO16), etc. (cf. JPL, 2018). As little is known about the composition and material properties of these objects, we assume they are composed of basaltic rock with a bulk density of ρ = 2.7 g cm⁻³. Tensile strength values for basalt are in the range of approx. 12…14 MPa (Stowe, 1969), shear strengths are approx. 8…36 MPa (Karaman et al., 2015), which provides an order-of-magnitude framework of the expected material strength data that is also compatible with the ≈10 MPa for Georgia Keystone granite measured by Housen and Holsapple (1999). Following Holsapple (2007), strength is decreasing with the body's average radius to the power of −1/2 (strength ~ (ab²)^−1/6), which suggests an upper limit of the order of 0.7 MPa, likely less as indicated by observations. Finally, we will assume a desired artificial gravity level of g_c = 0.38 g_E as discussed in section 1.

Figures 6, 7 show the resulting stresses along with the usable space station surface and required rotation rates predicted by models 1 and 2, respectively. While the maximum stresses are comparable between the two models, the patterns and minimum stresses differ significantly. In model 1, apart from the above mentioned edge case problem, we note material stresses that exceed the assumed strength by a factor of two up to an order of magnitude. While stresses for “thinner” tori (i.e., larger r_c) are of the same order of magnitude in both models, model 2 (Figure 7) predicts systematically lower stresses of down to ≲ 0.1 MPa for space stations deeper inside the asteroid in their entirety. In order to estimate the size of a feasible space station, we implemented a small nonlinear optimization model in GAMS (GAMS Development Corporation, 2019) that finds r_c and h_c which maximize the usable surface area S while maintaining a gravity level of g_c = 0.38 g_E and several assumed strength limits (0.05–0.7 MPa), all smaller than the suggested upper limit. Table 1 lists the resulting space station dimensions. Note that the required rotation rates are in the 1.3–1.4 rpm range.

FIGURE 6

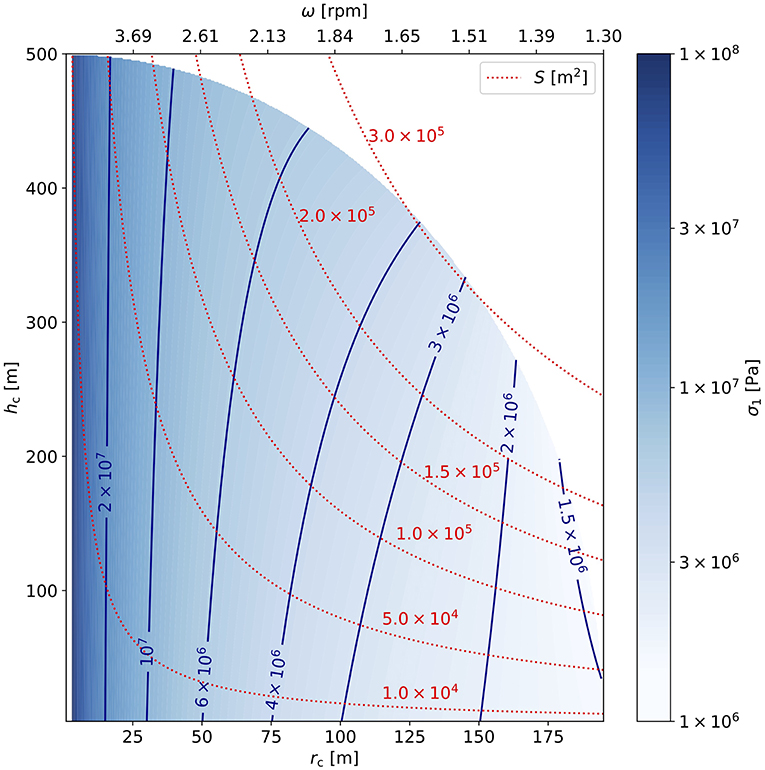
Figure 6. Model 1 results for artificial gravity of 0.38 g_E in a space station of radius r_c and height h_c, the color code and the blue contour lines give the tensile stress σ₁ resulting from the required rotation rate obtained via (9). The red dotted lines give the usable surface area S of the space station, the upper x-axis denotes the required rotation rate.

FIGURE 7

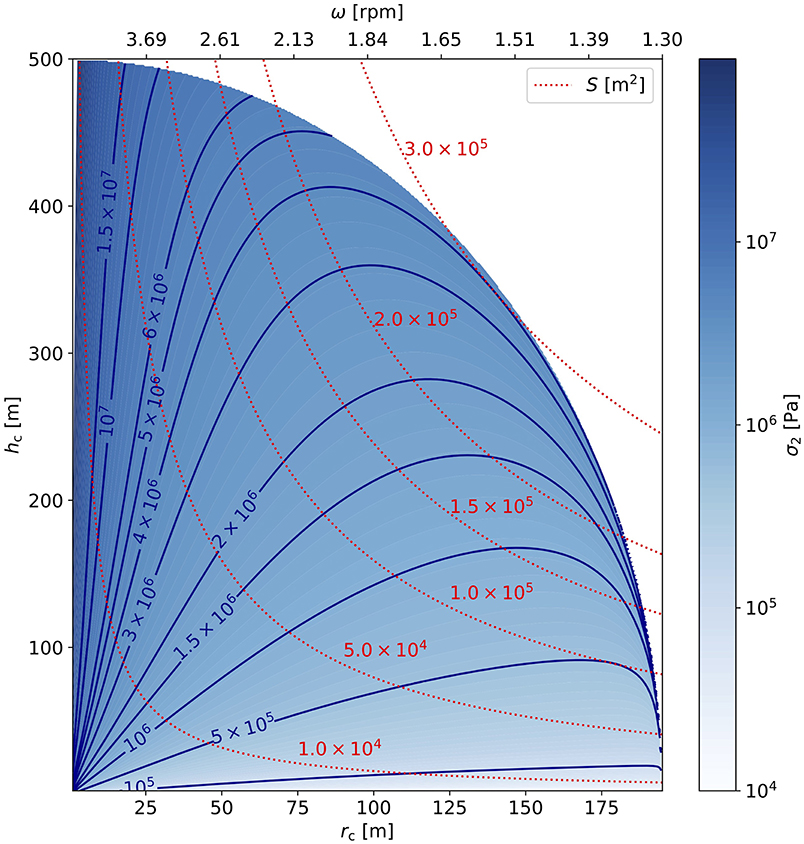
Figure 7. Model 2 results for artificial gravity of 0.38 g_E in a space station of radius r_c and height h_c, the color code and the blue contour lines give the combined tensile and shear stress resulting from the required rotation rate obtained via (9). The red dotted lines give the usable surface area S of the space station, the upper x-axis denotes the required rotation rate.

TABLE 1

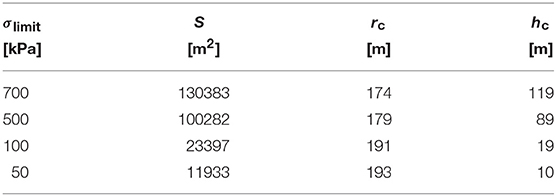
Table 1. Space station dimensions r_c, h_c, and usable area S for model 2 stress estimates and material strength σ_limit. See text for details.

5. Conclusions and Further Research

We established two simple analytical models for estimating whether a candidate for asteroid mining may be suitable for hosting a space station with artificial gravity. The novelty in our approach is to investigate whether the asteroidal hull—once set to rotation as a whole—can sustain the material loads resulting from a sufficiently high rotation rate. Model 2 predicts material loads resulting from centrifugal forces of the order of the material strength of solid, rocky bodies in the considered size range ≲ 500 m. It is still unclear however, whether the required rotation rates of more than 1 rpm can be sustained by an asteroid. Strength estimates derived from meteoroid studies and theoretical models indicate that the required spin rates are at the border of being realistic (cf. sections 1 and 4). On the other hand, the fastest-spinning asteroid observed so far has a period of 1.3 min (Pravec et al., 2002), but the inventory of sub-km asteroids is far from being complete. Hence, we cannot completely rule out that a space station with some level of artificial gravity in the cavern of a mined asteroid is infeasible if its dimensions are chosen right and if the material composition and material strength of the asteroid are known to a satisfactory level of accuracy. Practical applications will crucially depend on knowing not only the composition but also the internal structure of candidate bodies. As missions to these asteroids seem inevitable for such studies, decisions on inhabiting such asteroids may only be possible after mining operations have started. Also, the methods of actually initiating the rotation at the required rate is subject to further investigations. Hypothetically, starts and landings of spacecraft during the mining process might contribute to building up angular momentum of the asteroid.

Currently, we are working on a more realistic analytic approach for determining the detailed shape of the cavern housing the space station taking into account the internal density profile and a better analytical model eliminating the discrepancy of our models 1 and 2.

In the past, we successfully conducted smooth particle hydrodynamics (SPH) simulations of asteroids (e.g., Maindl et al., 2013; in review; Haghighipour et al., 2018). As our analytical study is approximative in nature we plan to conduct a series of SPH simulations with different material models and varying porosity. First results deploying the p − α porosity model (Jutzi et al., 2008) confirm the analytical model results (order of magnitude) for competent rock but suggest a disproportionately strong decline in material stress with increasingly porous asteroid material (Maindl et al., 2019). They need to be refined with carefully designed damage models, though.This will allow to numerically verify the predictions of the simplified analytical models presented here as well as future models and to further investigate the behavior of rotating bodies with substantial internal caverns. With that we will be able to investigate the applicability of our approach to possibly smaller asteroids and/or lower artificial gravity levels more thoroughly.

Author Contributions

TIM developed the analytical models and performed most of the calculations. He wrote about 70 % of the paper and created most of the figures. RM provided various aspects of the analytical approximations, helped in the calculations, and contributed to the representation of the individual equations. He wrote about 15 % of the paper. BL contributed to the quality of the analytical models, researched the details of required artificial gravity levels, and created the pictorials of the asteroid with the cylindrical cavern. She wrote about 15 % of the paper.

Funding

This project received seed funding from the Dubai Future Foundation through Guaana.com open research platform. The authors also acknowledge support by the FWF Austrian Science Fund project S11603-N16.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors are indebted to Dr. C. M. Schäfer for carefully checking the formulae and wish to thank Drs. Á. Bazsó and C. Lhotka for many fruitful discussions and constructive feedback. The authors also wish to thank the reviewers for their constructive feedback which significantly improved the quality of this paper.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2019.00037/full#supplementary-material

Footnotes

1. ^https://www.minorplanetcenter.net/iau/lists/LightcurveDat.html

2. ^Assumed spheroidal asteroid: semi-axes a = 250 m, b = c = 195 m, density ρ = 2.7 g cm⁻³, $\text{strength}=10^7{\bar{r}}^{-1/2}$, $\bar{r}={(abc)}^{1/3}$. Note that these high spin rates have not been observed so far.

References

Battista, N., Meloni, M. A., Bari, M., Mastrangelo, N., Galleri, G., Rapino, C., et al. (2012). 5-Lipoxygenase-dependent apoptosis of human lymphocytes in the International Space Station: data from the ROALD experiment. FASEB J. 26, 1791–1798. doi: 10.1096/fj.11-199406

PubMed Abstract | CrossRef Full Text | Google Scholar

Borovička, J. (2016). “Are some meteoroids rubble piles?,” in Asteroids: New Observations, New Models, volume 318 of IAU Symposium, eds S. R. Chesley, A. Morbidelli, R. Jedicke, and D. Farnocchia (Cambridge, UK: Cambridge University Press), 80–85. doi: 10.1017/S174392131500873X

CrossRef Full Text

Cogoli, A. (1993). The effect of space flight on human cellular immunity. Environ. Med. 37, 107–116.

PubMed Abstract | Google Scholar

GAMS Development Corporation (2019). General Algebraic Modeling System (GAMS) Release 26.1.0. Fairfax, VA: GAMS Development Corporation.

Gasperi, V., Rapino, C., Battista, N., Bari, M., Mastrangelo, N., Angeletti, S., et al. (2014). A functional interplay between 5-lipoxygenase and μ-calpain affects survival and cytokine profile of human Jurkat T lymphocyte exposed to simulated microgravity. Biomed. Res. Int. 2014:782390. doi: 10.1155/2014/782390

PubMed Abstract | CrossRef Full Text | Google Scholar

Gopalakrishnan, R., Genc, K. O., Rice, A. J., Lee, S. M., Evans, H. J., Maender, C. C., Ilaslan, H., et al. (2010). Muscle volume, strength, endurance, and exercise loads during 6-month missions in space. Aviat. Space Environ. Med. 81, 91–102. doi: 10.3357/ASEM.2583.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Grandl, W., and Bazso, A. (2013). “Near earth asteroids – prospection, orbit modification, mining and habitation,” in Asteroids: Prospective Energy and Material Resources, ed V. Badescu (Berlin; Heidelberg: Springer), 415–438.

Google Scholar

Haghighipour, N., Maindl, T. I., Schäfer, C. M., and Wandel, O. J. (2018). Triggering the activation of main belt comets: the effect of porosity. Aphys J 855:60. doi: 10.3847/1538-4357/aaa7f3

CrossRef Full Text | Google Scholar

Harris, L. R., Herpers, R., Hofhammer, T., and Jenkin, M. (2014). How much gravity is needed to establish the perceptual upright? PLoS ONE 9:e106207. doi: 10.1371/journal.pone.0106207

PubMed Abstract | CrossRef Full Text | Google Scholar

Holsapple, K. A. (2007). Spin limits of Solar System bodies: from the small fast-rotators to 2003 EL61. Icarus 187, 500–509. doi: 10.1016/j.icarus.2006.08.012

CrossRef Full Text | Google Scholar

Housen, K. R., and Holsapple, K. A. (1999). Scale Effects in Strength-Dominated Collisions of Rocky Asteroids. Icarus 142, 21–33. doi: 10.1006/icar.1999.6206

CrossRef Full Text | Google Scholar

JPL (2018). JPL Small Body Database (2018-11-10). Pasadena, CA.

Jutzi, M., Benz, W., and Michel, P. (2008). Numerical simulations of impacts involving porous bodies. I. Implementing sub-resolution porosity in a 3D SPH hydrocode. Icarus 198, 242–255. doi: 10.1016/j.icarus.2008.06.013

CrossRef Full Text | Google Scholar

Karaman, K., Cihangir, F., Ercikdi, B., Kesimal, A., and Demirel, S. (2015). Utilization of the Brazilian test for estimating the uniaxial compressive strength and shear strength parameters. J. Southern Afr. Inst. Min. Metal. 115, 185–192. doi: 10.17159/2411-9717/2015/v115n3a3

CrossRef Full Text | Google Scholar

Keyak, J. H., Koyama, A. K., LeBlanc, A., Lu, Y., and Lang, T. F. (2009). Reduction in proximal femoral strength due to long-duration spaceflight. Bone 44, 449–453. doi: 10.1016/j.bone.2008.11.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiss, J. Z., Kumar, P., Millar, K. D. L., Edelmann, R. E., and Correll, M. J. (2009). Operations of a spaceflight experiment to investigate plant tropisms. Adv. Space Res. 44, 879–886. doi: 10.1016/j.asr.2009.06.007

CrossRef Full Text | Google Scholar

Kitaya, Y., Kawai, M., Tsuruyama, J., Takahashi, H., Tani, A., Goto, E., et al. (2001). The effect of gravity on surface temperature and net photosynthetic rate of plant leaves. Adv. Space Res. 28, 659–664. doi: 10.1016/S0273-1177(01)00375-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Kitaya, Y., Tani, A., Goto, E., Saito, T., and Takahashi, H. (2000). Development of a plant growth unit for growing plants over a long-term life cycle under microgravity conditions. Adv. Space Res. 26, 281–288. doi: 10.1016/S0273-1177(99)00572-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Maindl, T. I., Schäfer, C., Speith, R., Süli, Á., Forgács-Dajka, E., and Dvorak, R. (2013). SPH-based simulation of multi-material asteroid collisions. Astron. Nachrichten 334, 996–999. doi: 10.1002/asna.201311979

CrossRef Full Text | Google Scholar

Maindl, T. I., Schäfer, C. M., Loibnegger, B., and Miksch, R. (2019). “Tensile loads in porous rotating asteroids with artificial caverns,” in Lunar and Planetary Science Conference, volume 50 of Lunar and Planetary Science Conference (The Woodlands, TX), 1094.

Nelson, E. S., Mulugeta, L., and Myers, J. G. (2014). Microgravity-induced fluid shift and ophthalmic changes. Life 4, 621–665. doi: 10.3390/life4040621

PubMed Abstract | CrossRef Full Text | Google Scholar

Popova, O., Borovička, J., Hartmann, W. K., Spurný, P., Gnos, E., Nemtchinov, I., et al. (2011). Very low strengths of interplanetary meteoroids and small asteroids. Meteor. Planet. Sci. 46, 1525–1550. doi: 10.1111/j.1945-5100.2011.01247.x

CrossRef Full Text | Google Scholar

Pravec, P., Harris, A. W., and Michalowski, T. (2002). “Asteroid rotations,” in Asteroids III, eds W. F. Bottke Jr., A. Cellino, P. Paolicchi, and R. P. Binzel (Tucson, AZ: University of Arizona Press), 113–122.

Stowe, R. L. (1969). Strength and Deformation Properties of Granite, Basalt, Limestone, and Tuff at Various Loading Rates. Misc. paper C-69-1, Army Engineer Waterways Experiment Station (Vicksburg, MS).

Google Scholar

Taibbi, G., Kaplovitz, K., Cromwell, R. L., Godley, B. F., Zanello, S. B., and Vizzeri, G. (2013). Effects of 30-day head-down bed rest on ocular structures and visual function in a healthy subject. Aviat. Space Environ. Med. 84, 148–154. doi: 10.3357/ASEM.3520.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Taylor, T. C., Grandl, W., Pinni, M., and Benaroya, H. (2008). “Space colony from a commercial asteroid mining company town,” in Space Technology and Applications International Forum-STAIF 2008 volume 969 of American Institute of Physics Conference Series, ed M. S. El-Genk (Melville, NY), 934–941.

Google Scholar

Versari, S., Longinotti, G., Barenghi, L., Maier, J. A., and Bradamante, S. (2013). The challenging environment on board the International Space Station affects endothelial cell function by triggering oxidative stress through thioredoxin interacting protein overexpression: the ESA-SPHINX experiment. FASEB J. 27, 4466–4475. doi: 10.1096/fj.13-229195

PubMed Abstract | CrossRef Full Text | Google Scholar