Effect of Field-Line Curvature on the Ionospheric Accessibility of Relativistic Electron Beam Experiments

1. Introduction

Plasma sheet transport is primarily driven by coupling of the magnetosphere and solar wind and has distinctly different behavior based on the orientation of the interplanetary magnetic field (IMF) with respect to the earth's dipole field (Wing et al., 2014, and references therin). Under northward IMF conditions, plasma convection weakens and transport may be dominated by turbulent flows (Borovsky and Funsten, 2003; Wang et al., 2010; Merkin et al., 2013). Under southward conditions, convection is stronger and may involve localized transient flows moving earthward (Angelopoulos et al., 1992; Sergeev, 2005; Birn et al., 2011; Wiltberger et al., 2015). Although transport of flux from the dayside to the nightside can be steady under southward IMF conditions, return of the flux to the dayside can be inhibited leading to the storage of flux in the plasma sheet and eventual release through substorms (Akasofu, 1964).

Observations in the ionosphere can provide insight into convection processes in the magnetotail (Sergeev, 2005; Bristow, 2008; Nishimura et al., 2010). The electric field responsible for magnetotail convection maps into the ionosphere (Ridley et al., 1998; Ruohoniemi and Baker, 1998) and auroral displays result in regions where flows twist magnetic fields, leading to field-aligned currents and electron precipitation. Diffuse particle precipitation detected by low altitude satellites can also provide a global picture of the plasma populations in the magnetotail (Wing and Newell, 1998; Wing et al., 2005; Wing and Johnson, 2009). However, connecting these ionospheric observations with magnetotail processes is complicated because the magnetic field mapping is not known precisely (Willis et al., 1997a,b). In order to understand the causal relationship between ionospheric observations and events/populations in the magnetosphere, it is necessary to map field-lines in the magnetosphere to their ionospheric footpoints. The use of empirical or MHD modeling techniques has made it possible to infer the mechanisms behind ionospheric observations; however, these results still involve significant uncertainty.

Having satellites configured with an electron beam generator is a promising method to map regions in the magnetosphere to the ionosphere by firing electrons into the loss cone and observing the precipitation from the ground (see Sanchez et al. in review). Experiments involving the artificial injection of electrons along magnetic field-lines in the magnetosphere has already shown feasibility of detecting electron beams (Winckler, 1980). However, it has been theorized (Neubert and Banks, 1992) that relativistic electron beams would be more stable than the beams used in these experiments (which had energies up to 40 keV) due to the higher relativistic mass and lower beam density. It is also suggested by simple linear analysis that relativistic beams traveling through the magnetosphere are stable to two-stream instabilities (Galvez and Borovsky, 1988), and relativistic beams entering the ionosphere are stable to resistive hose, ion hose, and filamentation instabilities (Gilchrist et al., 2001). Nevertheless, relativistic beams do come with their own issues, as discussed by Porazik et al. (2014), due to the fact that the first adiabatic invariant will not necessarily be conserved to zeroth order. Using a second order asymptotic expansion derived by Gardner (1966), it was shown that the dependence on field-line curvature in the higher order terms of μ has a substantial effect on the loss cone. There are two important consequences of this fact that we discuss in this paper.

First, the fact that the loss cone is reduced by increasing field-line curvature is highly relevant in the case of satellites positioned near the equatorial plane at midnight local time. The magnetotail stretches during times of increased activity, which may cause the field-line curvature at the position of the satellite to increase significantly. However, the activity in these regions is relevant to understanding the magnetosphere-ionosphere connection. Therefore, it is useful to systematically examine how field-line curvature affects ionospheric accessibility in the regions under consideration in order to determine magnetotail configurations that would permit the technique to be used successfully without a significant reduction of beam precipitation due to curvature effects.

A second important consequence of this study is the possibility to infer field-line curvature by varying the energy of the beam. The curvature is an important variable that describes magnetotail stretching and current sheet thickness. As such, it would be particularly useful for considerations of stability of the magnetotail to ballooning instability and/or reconnection. For example, if the magnetic field curvature is known, it would provide a significant constraint of magnetotail equilibria and therefore could potentially be used to constrain equilibrium models used for stability analysis (Cheng, 1995; Cheng and Zaharia, 2004).

A relatively simple threshold condition relating beam energy and curvature can be obtained when the accelerator is aimed in the direction of the magnetic field. For field-aligned electrons, Gardner's formula takes the simple form:

$\begin{array}{ll}\mu =\bar{\mu }{\rho }^2{\kappa }^2& (1)\end{array}$

where ρ = γmv/qB, $\bar{\mu }=\gamma m{v}^2/2B$, and κ is the magnitude of the field-line curvature, given by $\overrightarrow{\kappa }=(\widehat{b}·\nabla )\widehat{b}$ where $\widehat{b}=\overrightarrow{B}/B$. Field-aligned electron beams are therefore expected to precipitate if

$\begin{array}{ll}{\rho }^2{\kappa }^2<B/B_i& (2)\end{array}$

where B_i is the magnitude of the field at the ionospheric footpoint. These beams can therefore be used to obtain information about the field-line curvature at the launch position. If precipitation of the beam is observed, then it must be true that

$\begin{array}{ll}{R}_c>\rho \sqrt{\frac{B_i}{B}}& (3)\end{array}$

where R_c = 1/κ. Although obtaining a lower bound on the radius of curvature may be useful, this relationship seems to reveal an opportunity for directly measuring the curvature if the accelerator is capable of varying the energy of the beam. If all of the particles are fired exactly in the direction of the field, then one would only need to increase the energy until precipitation is no longer observed, indicating that the above inequality is no longer satisfied and $R_c=\rho \sqrt{B_i/B}$. However, no accelerator will be capable of firing every electron exactly in the direction of the field. It must be shown that, for an electron beam aimed in the direction of $\overrightarrow{B}$ and having some pitch angle spread Δ, the fraction of particles simultaneously fired that are in the loss cone will significantly decrease at the critical energy where $\rho =R_c\sqrt{B/B_i}$ in order to fully validate this concept.

2. Methodology

At a given energy and initial launch position, we will express the initial velocity of electrons by the angles (ϕ, α), which are defined by:

$\begin{array}{ll}\begin{array}{c}tan(\varphi )=\frac{\overrightarrow{v}·\widehat{N}}{\overrightarrow{v}·\widehat{N_b}}\\ cos(\alpha )=\frac{\overrightarrow{v}·\overrightarrow{B}}{vB}\end{array}& (4)\end{array}$

where $\widehat{N}$ and $\widehat{N_b}$ are the normal and bi-normal vectors of the field line at the launch point, respectively. Note that ϕ and α are merely the azimuthal and lateral angles in conventional spherical coordinates where the z-axis is aligned with $\overrightarrow{B}$. Given an initial launch position $\overrightarrow{x}$, a beam energy E, and initial velocity defined by the pair of angles (ϕ, α), we denote the value of the magnetic moment for electrons given by Gardner's formula by $\mu (\overrightarrow{x},E,\varphi ,\alpha )$. We then define the loss cone as the set:

$\begin{array}{ll}LC(\overrightarrow{x},E)=\{(\varphi ,\alpha )|\mu (\overrightarrow{x},E,\varphi ,\alpha )\le \gamma m{v}^2/2B_i\}& (5)\end{array}$

If μ is conserved to second order, ionospheric accessibility at a given energy and launch position can be expressed through the surface area of the loss cone in velocity space, given by

$\begin{array}{ll}A(\overrightarrow{x},E)={\displaystyle {\int }_{LC(\overrightarrow{x},E)}\sin }(\alpha )d\alpha d\varphi & (6)\end{array}$

see the Appendix for a detailed explanation of how A may be computed most efficiently. If μ is not conserved to second order, then A can not be expected to represent ionospheric accessibility. This fact is especially important in the case where A is not monotonic along field-lines. In many of these cases, A will change sharply along the field-line, which conflicts with the assumption that μ is conserved to second order. For this reason, we will consider an alternative accessibility metric to A:

$\begin{array}{ll}{A}^{\star }(\overrightarrow{x},E)=\min \{A(\overrightarrow{y},E)|\overrightarrow{y}\in X\}& (7)\end{array}$

where X is the set of points containing the point $\overrightarrow{x}$ that all lie on the same field-line and lie between the point $\overrightarrow{x}$ and the ionospheric footpoint.

In order to validate the idea of using variable energy accelerators to measure field-line curvature, we must investigate the accessibility of field-aligned beams near the critical energy, defined by:

$\begin{array}{ll}{E}_c=m{c}^2(\sqrt{1+\frac{{\Omega }^2{R}_c^2}{c^2}\frac{B}{B_i}}-1)& (8)\end{array}$

where Ω = qB/m. Note that Ω is the non-relativistic gyrofrequency and the actual gyrofrequency is Ω/γ. E_c is the energy where $\rho =R_c\sqrt{B/B_i}$, and is therefore the threshold energy above which electrons having initial velocity exactly aligned with $\overrightarrow{B}$ will not precipitate in the ionosphere. For the sake of simplicity, we will suppose that the instantaneous density of the beam is normally distributed in α with standard deviation σ:

$\begin{array}{ll}n(\alpha )=\frac{exp\frac{-{\alpha }^2}{2{\sigma }^2}}{\sqrt{2{\pi }^3}\sigma erf(\frac{\Delta }{\sigma \sqrt{2}})}& (9)\end{array}$

where Δ is the pitch angle spread of the beam. One can check that this distribution satisfies the normalization condition:

$\begin{array}{ll}{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^{\Delta }n}}(\alpha )d\alpha d\varphi =1& (10)\end{array}$

Given a beam energy and initial launch position, the fraction of particles instantaneously fired from the beam that are in the loss cone can be determined simply by drawing a sufficiently large number of pairs (ϕ, α) from this distribution and computing the fraction of those pairs that are in the set LC.

3. Results

In order to systematically investigate the consequences of tail stretching for beam accessibility, we calculate A on the midnight meridional plane using the Tsyganenko 1989 model (Tsyganenko, 1989) with K_p ranging between 1 and 7, where we assume a 1 MeV beam (see Figure 1). Field-lines are also shown so that the changes in the field-line curvature can be seen visually. As K_p increases, it is visibly apparent that the field-line curvature increases on the equatorial plane and decreases away from the equatorial plane. The dark regions indicate regions of relatively small A, which implies low beam accessibility. For K_p = 1 and K_p = 2, A is smallest in regions where field-line curvature is greatest. However, for K_p > 2, this trend is broken for X < −7R_E. In these cases, A is seen to be large on the equatorial plane, and essentially vanishes in regions immediately above and below the equatorial plane. This reduction in accessibility is due to terms in Gardner's formula that depend on ∂κ/∂n or ∂κ/∂s, where $\partial /\partial n=\widehat{N}·\nabla$ and $\partial /\partial s=\widehat{b}·\nabla$. If the higher order derivatives of the curves are large, then these terms increase μ so that A is significantly reduced. However, for |Z| > 1R_E, A consistently increases as K_p increases due to the reduction of field-line curvature in these regions.

FIGURE 1

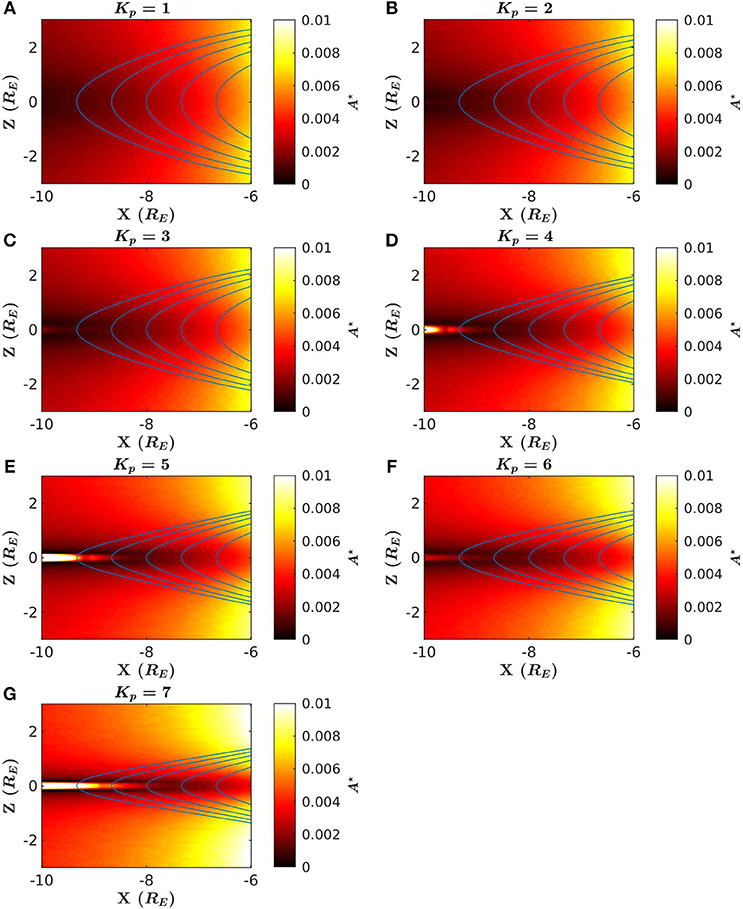
Figure 1. A plotted over midnight local time for various K_p assuming a beam energy of 1 MeV: (A) K_p = 1, (B) K_p = 2, (C) K_p = 3, (D) K_p = 4, (E) K_p = 5, (F) K_p = 6, (G) K_p = 7. Blue curves represent field-lines that intersect chosen values of X on the equatorial plane. Darker and lighter regions indicate regions with smaller and greater values of A, respectively. Note that A is not expected to reflect accessibility at the equatorial plane for high K_p.

It should be noted that although the equatorial μ in these cases can be consistent with ionospheric precipitation, it is unlikely in this case that μ is actually conserved through the dark regions just above the equatorial regions where A vanishes. As mentioned previously, A is only a reflection of beam accessibility if μ is conserved to second order. However, high gradients in A conflict with the assumption that μ is conserved, implying that electron beams are not generally accessible to the ionosphere when launched from any region equatorward of the region of low accessibility. In other words, if a particle were to move along the field line from the equatorial plane into a dark region, there would be no path of accessibility from that dark region to the ionosphere that conserves magnetic moment. For this reason, A^⋆ is a better reflection of beam accessibility (see Figure 2). From this figure, it is more clearly seen that accessibility at the equatorial plane decreases as K_p increases. It should be noted that there may be paths of accessibility for particles for which the magnetic moment is not conserved, but such precipitation cannot be predicted reliably due to the chaotic nature of orbits in the plasma sheet (Chen et al., 1990).

FIGURE 2

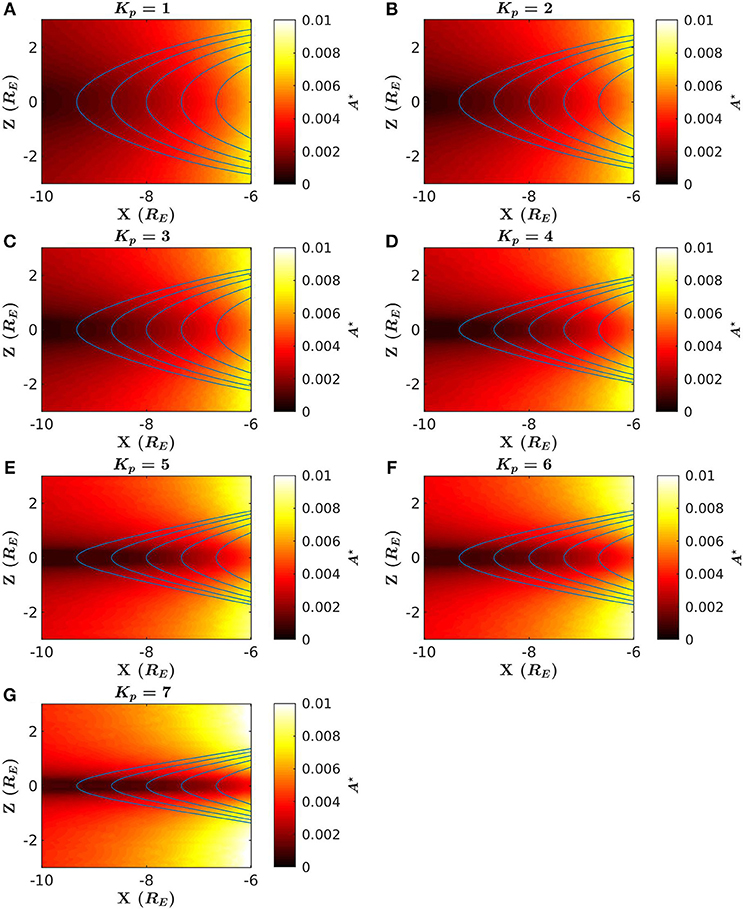
Figure 2. A^⋆ plotted over midnight local time for various K_p assuming a beam energy of 1 MeV: (A) K_p = 1, (B) K_p = 2, (C) K_p = 3, (D) K_p = 4, (E) K_p = 5, (F) K_p = 6, (G) K_p = 7. Blue curves represent field-lines that intersect chosen values of X on the equatorial plane. Darker and lighter regions indicate regions with smaller and greater values of A^⋆, respectively.

If μ is conserved to second order, then a beam fired with pitch angle α that precipitates in the northern hemisphere is also expected to precipitate in the southern hemisphere if the pitch angle were instead chosen to be π−α. However, in the same way that μ is not expected to be conserved for electrons fired from the equatorial plane, μ is likewise not expected to be conserved for electrons passing through the equatorial plane. Therefore, although electron beams away from the equatorial plane are reliably accessible to at least one of the two hemispheres, the beams cannot be simultaneously accessible to both the northern and southern hemispheres when the tail is stretched. This consequence must be taken into consideration if ground observers are not stationed at locations both in the northern and southern hemispheres. It should also be noted that this limitation is not seen for non-relativistic beam experiments (Winckler, 1980) or for experiments involving satellites in geosynchronous orbit.

Figure 3 shows the fraction of particles fired into the loss cone in the case of a field-aligned beam with realistic beam spread Δ = 0.005 (see Sanchez et al. in review), with σ = Δ/3, and for energies above and below the E_c. All other parameters are chosen to correspond with a satellite positioned on local time midnight, at the equatorial plane, and at a radial distance of 8 R_E with K_p = 1. It is seen that the fraction of particles in the loss cone decreases significantly at E_c. If μ is conserved to second order, then it follows that the fraction of particles that precipitate in the ionosphere should be expected to decrease significantly at this threshold.

FIGURE 3

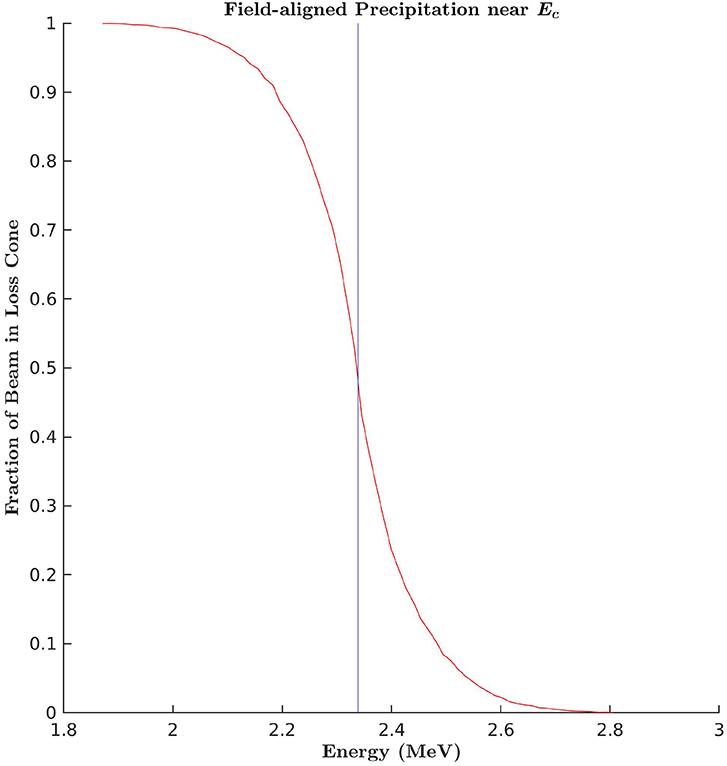
Figure 3. The fraction of particles fired into the loss cone plotted against beam energy in the case of a field-aligned beam with Δ = 0.005, σ = Δ/3. E_c is represented by the blue line.

4. Conclusions

The results above suggest that as the magnetotail is stretched and magnetic curvature increases there will be a reduction of accessibility in the equatorial plane |Z| < 1R_E and an increase of accessibility in regions where |Z| > 1R_E where μ is expected to be conserved. In these regions, increasing K_p corresponds with increasing A^⋆ in all cases, indicating that ionospheric accessibility is increased when the tail is stretched and field-line curvature is reduced. These results show that tail stretching may create difficulty in performing electron beam experiments if the satellite is positioned on the equatorial plane. However, because this issue is not seen for launch positions where |Z| > 1R_E, it may still be possible to use relativistic beams to map field-lines from the ionosphere to locations near the plasma sheet. This result validates one aspect of the idea that electron beams may be used to study the relationship between plasma sheet dynamics and observations in the ionosphere. Alternatively, our results generally suggest that relativistic electron beams could be used to map field lines within geosynchronous orbit for a wide range of geomagnetic conditions.

For field-aligned beams, we have shown that the fraction of particles that precipitate in the ionosphere decreases sharply around E_c. If the accelerator were capable of varying the beam energy from below E_c, ground observers would be able to detect the change in precipitation at E_c and would therefore be able to infer the field-line curvature (see Powis et al., in review, for details surrounding ground observations of electron beam experiments in general). The ability to directly measure aspects of the field-line geometry would be a substantial aid in constraining models of the magnetic field of Earth's inner magnetosphere. In addition to measuring curvature, the arc length of field-lines between the launch and precipitation points may be directly measured using low energy keV field-aligned beams. In this case, μ is well approximated by the zeroth order term, so v_∥≈v. The total distance that the electrons travel is therefore equal to the arc-length of the field-line. The ability to measure both the arc length and curvature of field-lines in the magnetosphere using a single satellite is a very attractive opportunity, and our results demonstrate that the issue of using this kind of information to properly constrain models is a topic worthy of extensive study (see Willard et al. in review).

These results do not provide insight into situations involving magnetic fields that are not well described by the Tsyganenko 1989 model, which could occur in a turbulent or reconnecting plasma sheet where small-scale curvature could be found. However, we expect that such configurations offer less accessibility than that described by the Tsyganenko model. These results also do not provide insight into how the accessibility may be affected by waves found in the magnetosphere or created by the beam itself, which may have the effect of scattering electrons out of the loss cone even if they are initially fired into it. However, calculations carried out by Glauert and Horne (2005) seem to show that pitch angle scattering based on typically observed wave amplitudes is not significant for relativistic electrons with small initial pitch angle that interact with whistler mode, EMIC, and Z mode waves. In these cases, no bounce-averaged diffusion coefficient was determined for electrons with small initial pitch angle since these electrons were not immediately scattered out of the loss cone, which indicates that wave particle interaction would not be a significant effect for electron beams fired with small pitch angle. Nevertheless, Glauert and Horne's calculations do not show that this is generally the case for beams fired into the loss cone, and further investigation of beam stability and wave saturation is required in order to completely rule out the significance of this effect on the overall accessibility.

Author Contributions

JW wrote the manuscript and made the calculations with help from JJ, in consultation with ES, JS, AP, and IK. JJ devised the project. All authors discussed the results prior to and during the preparation of the manuscript.

Funding

Work at Andrews University is performed under NASA Grants NNX17AI47G, NNX16AR10G, NNH15AB17I, NNX16AQ87G, NNX17AI50G, NNX15AJ01G, and 80NSSC18K0835 and NSF Grant AGS1832207.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the National Science Foundation and the National Aeronautics and Space Administration for supporting this research.

References

Akasofu, S.-I. (1964). The development of the auroral substorm. Planet. Space Sci. 12, 273–282. doi: 10.1016/0032-0633(64)90151-5

CrossRef Full Text | Google Scholar

Angelopoulos, V., Baumjohann, W., Kennel, C. F., Coronti, F. V., Kivelson, M. G., Pellat, R., et al. (1992). Bursty bulk flows in the inner central plasma sheet. J. Geophys. Res. 97, 4027–4039. doi: 10.1029/91JA02701

CrossRef Full Text | Google Scholar

Birn, J., Nakamura, R., Panov, E. V., and Hesse, M. (2011). Bursty bulk flows and dipolarization in mhd simulations of magnetotail reconnection. J. Geophys. Res. 116:A01210. doi: 10.1029/2010JA016083

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Funsten, H. O. (2003). Mhd turbulence in the earth's plasma sheet: dynamics, dissipation, and driving. J. Geophys. Res. 108:1284. doi: 10.1029/2002JA009625

CrossRef Full Text | Google Scholar

Bristow, W. (2008). Statistics of velocity fluctuations observed by superdarn under steady interplanetary magnetic field conditions. J. Geophys. Res. 113:A11202. doi: 10.1029/2008JA013203

CrossRef Full Text | Google Scholar

Chen, J., Burkhart, G. R., and Huang, C. Y. (1990). Observational signatures of nonlinear magnetotail particle dynamics. Geophys. Res. Lett. 17, 2237–2240. doi: 10.1029/GL017i012p02237

CrossRef Full Text | Google Scholar

Cheng, C. Z. (1995). Three-dimensional magnetospheric equilibrium with isotropic pressure. Geophys. Res. Lett. 22, 2401–2404. doi: 10.1029/95GL02308

CrossRef Full Text | Google Scholar

Cheng, C. Z., and Zaharia, S. (2004). Mhd ballooning instability in the plasma sheet. Geophys. Res. Lett. 31:L06809. doi: 10.1029/2003GL018823

CrossRef Full Text | Google Scholar

Galvez, M., and Borovsky, J. E. (1988). The electrostatic two-stream instability driven by slab-shaped and cylindrical beams injected into plasmas. Phys. Fluids 31:857. doi: 10.1063/1.866767

CrossRef Full Text | Google Scholar

Gardner, C. S. (1966). Magnetic moment to second order for axisymmetric static field. Phys. Fluids 9:1997. doi: 10.1063/1.1761557

CrossRef Full Text | Google Scholar

Gilchrist, B. E., Khazanov, G., Krause, L. H., and Neubert, T. (2001). Study of Relativistic Electron Beam Propagation in the Atmosphere-Ionosphere-Magnetosphere. Technical report, University of Michigan, Ann Arbor, MI.

Google Scholar

Glauert, S. A., and Horne, R. B. (2005). Calculation of pitch angle and energy diffusion coefficients with the PADIE code. J. Geophys. Res. 110:A04206. doi: 10.1029/2004JA010851

CrossRef Full Text | Google Scholar

Merkin, V. G., Lyon, J. G., and Claudepierre, S. G. (2013). Kelvin-helmholtz instability of the magnetospheric boundary in a three-dimensional global mhd simulation during northward imf conditions. J. Geophys. Res. 118, 5478–5496. doi: 10.1002/jgra.50520

CrossRef Full Text | Google Scholar

Neubert, T., and Banks, P. M. (1992). Recent results from studies of electron beam phenomena in space plasmas. Planet. Space Sci. 40, 153–183. doi: 10.1016/0032-0633(92)90055-S

CrossRef Full Text | Google Scholar

Nishimura, Y., Lyons, L., Zou, S., Angelopoulos, V., and Mende, S. (2010). Substorm triggering by new plasma intrusion: themis all-sky imager observations. J. Geophys. Res. 115:A07222. doi: 10.1029/2009JA015166

CrossRef Full Text | Google Scholar

Porazik, P., Johnson, J. R., Kaganovich, I., and Sanchez, E. (2014). Modification of the loss cone for energetic particles. Geophys. Res. Lett. 41, 8107–8113. doi: 10.1002/2014GL061869

CrossRef Full Text | Google Scholar

Ridley, A. J., Lu, G., Clauer, C. R., and Papitashvili, V. O. (1998). A statistical study of the ionospheric convection response to changing interplanetary magnetic field conditions using the assimilative mapping of ionospheric electrodynamics technique. J. Geophys. Res. 103, 4023–4040. doi: 10.1029/97JA03328

CrossRef Full Text | Google Scholar

Ruohoniemi, J. M., and Baker, K. B. (1998). Large-scale imaging of high-latitude convection with super dual auroral radar network hf radar observations. J. Geophys. Res. 103, 20797–20811. doi: 10.1029/98JA01288

CrossRef Full Text | Google Scholar

Sergeev, V. A. (2005). “Bursty bulk flows and their ionospheric footprints,” in Multiscale Processes in the Earth's Magnetosphere: From Interball to Cluster, NATO Science Series II: Mathematics, Physics and Chemistry, Vol. 178, eds J. A. Sauvaud and Z. Němeček (Dordrecht: Springer). Available online at: https://link.springer.com/chapter/10.1007/1-4020-2768-0_16#aboutcontent

Google Scholar

Tsyganenko, N. (1989). A magnetospheric magnetic field model with a warped tail current sheet. Planet. Space Sci. 37, 5–20. doi: 10.1016/0032-0633(89)90066-4

CrossRef Full Text | Google Scholar

Wang, C.-P., Lyons, L. R., Nagai, T., Weygand, J. M., and Lui, A. T. Y. (2010). Evolution of plasma sheet particle content under different interplanetary magnetic field conditions. J. Geophys. Res. 115:A06210. doi: 10.1029/2009JA015028

CrossRef Full Text | Google Scholar

Willis, D. M., Singh, J. R., and Comer, J. (1997a). Uncertainties in field-line tracing in the magnetosphere. Part I: the axisymmetric part of the internal geomagnetic field. Ann. Geophys. 15, 165–180. doi: 10.1007/s00585-997-0165-4

CrossRef Full Text | Google Scholar

Willis, D. M., Singh, J. R., and Freeman, K. S. C. (1997b). Uncertainties in field-line tracing in the magnetosphere. Part II: the complete internal geomagnetic field. Ann. Geophys. 15, 181–196. doi: 10.1007/s00585-997-0181-4

CrossRef Full Text | Google Scholar

Wiltberger, M., Merkin, V., Lyon, J. G., and Ohtani, S. (2015). High-resolution global magnetohydrodynamic simulation of bursty bulk flows. J. Geophys. Res. 120, 4555–4566. doi: 10.1002/2015JA021080

CrossRef Full Text | Google Scholar

Winckler, J. R. (1980). The application of artificial electron beams to magnetospheric research. Rev. Geophys. 18:659. doi: 10.1029/RG018i003p00659

CrossRef Full Text | Google Scholar

Wing, S., and Johnson, J. R. (2009). Substorm entropies. J. Geophys. Res. 114:A00D07. doi: 10.1029/2008JA013989

CrossRef Full Text | Google Scholar

Wing, S., Johnson, J. R., Chaston, C. C., Echim, M., Escoubet, C. P., Lavraud, B., et al. (2014). Review of solar wind entry into and transport within the plasma sheet. Space Sci. Rev. 184, 33–86. doi: 10.1007/s11214-014-0108-9

CrossRef Full Text | Google Scholar

Wing, S., Johnson, J. R., Newell, P. T., and Meng, C.-I. (2005). Dawn-dusk asymmetries, ion spectra, and sources in the northward interplanetary magnetic field plasma sheet. J. Geophys. Res. 110:A08205. doi: 10.1029/2005JA011086

CrossRef Full Text | Google Scholar

Wing, S., and Newell, P. T. (1998). Central plasma sheet ion properties as inferred from ionospheric observations. J. Geophys. Res. 103, 6785–6800. doi: 10.1029/97JA02994

CrossRef Full Text | Google Scholar

A. Appendix

The angular coordinates used to formalize the concept of loss cone surface area, although useful for the purpose of describing the concept, are not the preferred coordinates to use when calculating A. For this purpose, it is convenient to apply a coordinate transformation (λ, β) = T(ϕ, α), where the initial velocity corresponding to the angles (λ, β) satisfy the relations:

$\begin{array}{ll}\begin{array}{c}\text{tan}(\lambda )=\frac{\overrightarrow{v}·{\hat{e}}_1}{\overrightarrow{v}·{\hat{e}}_2}\\ \text{cos}(\beta )=\frac{\overrightarrow{v}·{\overrightarrow{v}}_0}{v^2}\end{array}& (\mathrm{A1})\end{array}$

where ${\overrightarrow{v}}_0=v{ê}_1\times {ê}_2$ is the initial velocity of the trajectory having μ = 0. Note that, like the previous coordinate system, this is nothing more than a conventional spherical coordinate system where the z-axis is aligned with a particular direction. In this case, λ and β are azimuthal and lateral angles for a spherical coordinate system with the z-axis aligned with ${\overrightarrow{v}}_0$. As described by Porazik et al. (2014), ${\overrightarrow{v}}_0$ is not exactly aligned with the magnetic field and will always have a perpendicular component that is aligned with the drift. The transformation T is therefore simply a rotation of the system about the normal axis $\widehat{N}$ by an angle α₀ such that $cos({\alpha }_0)={\overrightarrow{v}}_0·\overrightarrow{B}/vB$. Setting ${\widehat{v}}_0·\widehat{N}=0$ in Gardner's formula, α₀ can be easily computed by solving

$\begin{array}{l}(K_1^2-K_3+K_4)w^4+(K_2-2K_1)w^3+(1+K_3-2K_1^2)w^2\\ +2K_{1}w+K_1^2=0& (\mathrm{A2})\end{array}$

where w = sin(α₀) and

$\begin{array}{l}{K}_1=\rho \kappa \\ K_2=\frac{\rho }{B}\frac{\partial B}{\partial n}\\ K_3={\rho }^2(\frac{1}{2r^2}\frac{B_r^2}{B^2}+\frac{B_r}{2r{B}^2}\frac{\partial B}{\partial s}-\frac{\kappa B_z}{4rB}+\frac{1}{8}{(\frac{1}{B}\frac{\partial B}{\partial s})}^2-\frac{11}{4}{\kappa }^2\\ +\frac{9\kappa }{2B}\frac{\partial B}{\partial n}-\frac{7}{4}\frac{\partial \kappa }{\partial n})\\ K_4={\rho }^2(\frac{B_r^2}{8r^2{B}^2}-\frac{B_r}{8r{B}^2}\frac{\partial B}{\partial s}-\frac{B_z}{8r{B}^2}\frac{\partial B}{\partial n}-\frac{5}{32}{(\frac{1}{B}\frac{\partial B}{\partial s})}^2\\ +\frac{15}{8}{(\frac{1}{B}\frac{\partial B}{\partial n})}^2-\frac{5}{8}\frac{1}{B}\frac{{\partial }^{2}B}{\partial n^2})& (\mathrm{A3})\end{array}$

The precise choice of unit vectors ê₁ and ê₂ is not important so long as ê₁·ê₂ = 0. This degree of ambiguity merely corresponds to a phase offset in the angle λ. For this analysis, we make the choice that λ = 0 should correspond to velocities where $\overrightarrow{v}·\widehat{N}=0$ and $\overrightarrow{v}·\overrightarrow{B}\times \nabla B>0$.

In the original coordinate system, it was found by Porazik et al. that a given angle ϕ may correspond with two different points on the loss cone boundary. Conveniently, this is not a feature of these new coordinates, and one can check that every point on the loss cone boundary has a unique value of λ. This fact makes the integral A far more straight forward to calculate. In these new coordinates, the integral takes the form

$\begin{array}{ll}A={\displaystyle {\int }_0^{2\pi }[}1-\cos ({\beta }_b(\lambda ))]d\lambda & (\mathrm{A4})\end{array}$

where $\mu =\gamma m{v}^2/2B_i$ when (λ, β) = (λ, β_b(λ)). The above expression can be very easily approximated with high precision using the trapezoidal rule.