Nuclear Reactions of Astrophysical Interest

1. Introduction

Nuclear reactions are responsible for the nucleosynthesis, i.e., for the formation of the elements in the Universe (Bethe, 1939; Burbidge et al., 1957). Big-Bang nucleosynthesis mainly produces ²H, ³He, and α particles. This primordial nucleosynthesis is followed by the formation of early stars where elements up to Fe are produced. Heavier elements are then synthesized by various processes, such as neutron capture (Reifarth et al., 2018), neutrino-induced reactions (Alvarez-Ruso et al., 2018), explosive events in supernovae (Wiescher et al., 2012), and the rapid-neutron process in neutron-star mergers (Thielemann et al., 2017). Astrophysical scenarios and stellar models are discussed in many textbooks (see e.g., Clayton, 1983; Rolfs and Rodney, 1988; Iliadis, 2007; Thompson and Nunes, 2009) and review articles (see e.g., Aprahamian et al., 2005; José and Iliadis, 2011; Wiescher et al., 2012).

The role of nuclear physics in astrophysics is fundamental, and this discipline is referred to as nuclear astrophysics. It essentially started with the pioneering work of Bethe (1939). Later, the various cycles of stellar evolution were described in the seminal review by Burbidge et al., known as B²FH (Burbidge et al., 1957). Many observational properties find their origin in nuclear physics. (i) A typical example is the $0_2^{+}$ level of ¹²C, known as the Hoyle state (Hoyle, 1954), which was predicted from the observed ¹²C abundance in the Universe, and found experimentally later. The formation of ¹²C is currently well-understood from the triple α process. (ii) From the observed abundances of the elements, a gap between masses 5 and 8 is explained by the particle instability of ⁵He and ⁵Li. (iii) In the high-mass region of the abundance distribution, peaks are clearly observed, and are explained by the existence of magic numbers in nuclear physics. Magic nuclei are strongly bound, and therefore difficult to destroy by photodissociation. (iv) The abundance distribution also presents an “even-odd” effect, even nuclei being more abundant; again the origin of this effect stems from nuclear binding energies since odd-mass nuclei are less bound and therefore more fragile than even-mass nuclei. Recent reviews on nuclear astrophysics can be found in Bertulani and Kajino (2016) and Liccardo et al. (2018).

Stellar models require many nuclear inputs. A huge number (up to several thousands) of reaction rates, involving charged particles (protons and alphas) and neutrons, are needed in nucleosynthesis networks (Wiescher et al., 2012). Reactions involving charged particles are transfer and capture processes. The former stem from the nuclear force, and the latter from the electromagnetic interaction. When both channels are open, the transfer cross section is always much larger than the capture cross section. A challenge for nuclear physicists is to determine the cross sections at stellar energies, which are in general much lower than the Coulomb barrier. Except in a few cases, direct measurements in this low-energy range (referred to as the “Gamow peak”) are not possible, since the cross sections are too low to be measured in the laboratory. Although experimental techniques have been strongly developed over the last decades (Broggini et al., 2010), a theoretical support is often necessary to complement the data, and in particular to extrapolate them down to stellar energies.

Owing to the experimental difficulties associated with direct measurements, several indirect techniques have been developed: the Trojan Horse method (Baur, 1986; Tumino et al., 2013; Spitaleri et al., 2019), the Coulomb breakup method (Baur et al., 1986), or the Asymptotic Normalization Coefficient method (ANC, see Mukhamedzhanov et al., 2001). The main advantage of these indirect approaches is to circumvent the smallness of the cross sections. However, they require a precise theoretical modeling to determine the relevant cross sections from the data.

The calculation of the cross sections is of course based on the scattering theory. Various models are being used in the literature. Owing to the low energies relevant in nuclear astrophysics, and to the low level densities, the optical model (also referred to as “potential model”) can be used for capture reactions (Tombrello and Parker, 1963; Bertulani, 2003). Heavy-ion fusion reactions are also described by this model, even if different variants exist (Canto et al., 2006). Impressive developments have been performed in the framework of microscopic models, which present an important predictive power since they rely on a nucleon-nucleon interaction only. Solving a many-body Schrödinger equation for scattering states is however a difficult task, and the cluster approximation (Horiuchi et al., 2012) is used in most calculations. However, recent works succeeded to address, in a microscopic theory, the ²H(d,γ)⁴He (Arai et al., 2011), ³He(d,p)⁴He (Navrátil and Quaglioni, 2012), and ³He(α, γ)⁷Be (Neff, 2011; Dohet-Eraly et al., 2016) reactions without the cluster approximation. Recent progress has been made in Effective Field Theories (Zhang et al., 2018). These calculations are highly computer demanding, and are currently limited to low-mass systems.

The models discussed above are, in principle, independent of experimental data. In practice, however, available data are used to assess their reliability, and/or to tune some important parameter(s). In contrast, the phenomenological R-matrix theory (see for example Barker and Kajino, 1991; Descouvemont and Baye, 2010) explicitly relies on the existence of data, but is an efficient tool to analyse reactions of astrophysical interest. The cross sections can be parameterized by a small number of real, energy-independent, parameters. This fitting procedure requires the availability of experimental data, but in general allows a reliable extrapolation down to stellar energies. The R-matrix theory deals with capture, transfer and elastic scattering on an equal footing. In practice, however, the R-matrix theory is limited to reactions where the level density is limited (typically up to a few levels per MeV).

When the mass increases, the level density is in general too large for cluster models or for an R-matrix approach. In that situation, the cross section essentially depends on properties of the compound nucleus. Here the shell model (Richter et al., 2011) provides information on resonance properties, such as energies, spins, widths, etc. An extension to the continuum has been developed (Chatterjee et al., 2006). The Hauser-Feshbach formalism (Rauscher et al., 1997) is also widely used in high-mass systems, with a high level density.

A specificity of nuclear astrophysics is to require a large number of reaction rates. These reaction rates are obtained from various sources, experimental as well as theoretical. A link between nuclear physics and astrophysics can be established by compilations, where the authors provide an evaluation of the available data, and recommend reaction rates. The first compilations were performed by the Caltech group (Caughlan and Fowler, 1988), and then improved in various ways: evaluation of uncertainties, improved numerical treatment, update of experimental data, etc. Some compilations address specific reactions, such as Big-Bang nucleosynthesis (Descouvemont et al., 2004; Coc et al., 2012) or solar fusion reactions (Adelberger et al., 2011), but other works cover a wider range (Angulo et al., 1999; Longland et al., 2010).

In this review, we discuss the current status of reaction models in nuclear astrophysics. We focus on charged-particle induced reactions, which represent one of the main inputs in stellar evolution. In section 2, we present an overview of the different cross sections involved in the nucleosynthesis. In section 3 we briefly describe some theoretical models used for nuclear reactions. Applications are presented in section 4. The conclusion and outlook are presented in section 5.

2. Cross Sections for Nuclear Astrophysics

2.1. Scattering Wave Functions

In this section, we present an outline of the reaction theory needed for nuclear astrophysics. In particular, we are dealing with low energies, around and below the Coulomb barrier. The goal is to model different processes, such as transfer or capture reactions. We start from a general formalism of scattering theory, and then apply it to different models. This outline is of course very brief, and we refer to textbooks (e.g., Satchler, 1983; Canto and Hussein, 2013) for a more detailed presentation.

The main goal of scattering models is to solve the Schrödinger equation

$\begin{array}{ll}H\Psi =E\Psi & (1)\end{array}$

for positive energies E (this energy is defined from the reaction threshold). In this equation, H is the Hamiltonian, and Ψ is the nucleus-nucleus wave function. For the sake of simplicity we assume here that the internal structure of the colliding nuclei is neglected and that the spin of the target is zero. Consequently, the Hamiltonian only depends on the relative coordinate r. For a system with charges (Z₁e, Z₂e) and nucleon numbers (A₁, A₂), it is written as

$\begin{array}{ll}H=-\frac{{\hslash }^2}{2\mu m_N}{\Delta }_r+V_N(r)+V_C(r),& (2)\end{array}$

where, m_N is the nucleon mass and μ = A₁A₂/(A₁ + A₂) is the dimensionless reduced mass of the system. In Equation (2), V_N(r) and V_C(r) are the nuclear and Coulomb potentials, respectively. In general V_N(r) depends on the angular momentum and on the spin. A partial wave with total spin J and angular momentum L is given by

$\begin{array}{ll}{\Psi }_L^{JM}(r)=\frac{1}{r}{g}_L^J(r){\left[Y_L({\Omega }_r)\otimes {\chi }_s\right]}^{JM},& (3)\end{array}$

where the spinor χ_s is associated with the spin. In most cases, s = 0 or s = 1/2 (the latter case covers the frequent situation of nucleon scattering). The relative function $g_L^J(r)$ is given by the one-dimension Schrödinger equation

$\begin{array}{ll}-\frac{{\hslash }^2}{2\mu m_N}\left(\frac{d^2}{d{r}^2}-\frac{L(L+1)}{r^2}+V_N(r)+V_C(r)\right)g_L^J(r)=E{g}_L^J(r),& (4)\end{array}$

and must be solved for scattering states (E > 0) or for bound states (E < 0) with the corresponding boundary conditions. Efficient techniques are based on the Numerov algorithm (Raynal, 1972) or on the R-matrix method (Descouvemont and Baye, 2010).

At large distances, the nuclear potential V_N in (2) is negligible. For a scattering state, the radial wave function tends to

$\begin{array}{ll}{g}_L^J(r){\displaystyle \underset{r\to \infty }{\to }}{I}_L(kr)-U_L^J{O}_L(kr),& (5)\end{array}$

where I_L(x) and O_L(x) are the incoming and outgoing Coulomb functions (see section 2.2), and $U_L^J$ is the scattering matrix (in single-channel calculations, it is a 1 × 1 matrix). The scattering matrix depends on the nuclear potential, and provides the elastic cross sections. For real potentials, usually used in astrophysics, we have the property

$\begin{array}{ll}\left|U_L^J\right|=1.& (6)\end{array}$

The phase shift ${\delta }_L^J$ is defined from

$\begin{array}{ll}{U}_L^J=\text{exp}(2i{\delta }_L^J),& (7)\end{array}$

and is real. At energies above the Coulomb barrier, complex potentials are often used. The imaginary part simulates absorption, and the model is referred to as the “optical model” (Satchler, 1983). In that case, we have

$\begin{array}{ll}\left|U_L^J\right|\le 1,& (8)\end{array}$

and the phase shift contains an imaginary part.

Generalizations can be performed in various directions. A first possibility is to extend the wave function (3) to multichannel calculations as

$\begin{array}{ll}{\Psi }_L^{JM}(r)=\frac{1}{r}{\displaystyle \sum _{cLI}}{g}_{cLI}^J(r){\left[Y_L({\Omega }_r)\otimes {\left[{\varphi }_c^{I_1}\otimes {\varphi }_c^{I_2}\right]}^I\right]}^{JM},& (9)\end{array}$

where ${\varphi }_c^{I_1}$ and ${\varphi }_c^{I_2}$ are the internal wave functions with spins I₁ and I₂, and where I is the channel spin. Equation (4) is replaced by a system of coupled equations.

In Equations (3) and (9), antisymmetrization effects between the target and the projectile are neglected. However, they can be partly simulated by an appropriate choice of the nucleus-nucleus potential (Friedrich, 1981; Baye, 1987). A second generalization aims to explicitly include antisymmetrization effects. In microscopic cluster models (Descouvemont and Dufour, 2012), the wave function is defined as

$\begin{array}{ll}{\Psi }_L^{JM}={A}\frac{1}{r}{\displaystyle \sum _{cLI}}{g}_{cLI}^J(r){\left[Y_L({\Omega }_r)\otimes {\left[{\varphi }_c^{I_1}({\xi }_1)\otimes {\varphi }_c^{I_2}({\xi }_2)\right]}^I\right]}^{JM},& (10)\end{array}$

where ${A}$ is the A-nucleon antisymmetrization operator. The internal wave functions are defined in the shell model and depend on a set of internal coordinates (ξ_i). We will briefly describe microscopic models in section 3.

2.2. General Properties of Low-Energy Reactions

Before discussing applications specific to nuclear astrophysics, we address here some general properties of the cross sections at low energies, typical of stellar conditions. In this energy regime, the scattering between charged particles is essentially governed by the Coulomb interaction. In other words, we can neglect the structure of the nuclei, and reduce the Schrödinger equation to a two-body problem. For a given angular momentum L, the wave function depends on the relative coordinate r. The radial Schrödinger equation only involves the Coulomb potential and reads, at c.m. energy E,

$\begin{array}{ll}-\frac{{\hslash }^2}{2\mu m_N}\left(\frac{d^2}{d{r}^2}-\frac{L(L+1)}{r^2}\right)g_L(r)+\frac{Z_1{Z}_2{e}^2}{r}{g}_L(r)=E{g}_L(r),& (11)\end{array}$

where we have dropped index J. The solutions of Equation (11) are the regular and irregular Coulomb functions F_L(η, kr) and G_L(η, kr) (Thompson, 2010). They depend on the wave number k, and on the Sommerfeld parameter η

$\begin{array}{l}k=\sqrt{\frac{2\mu m_{N}E}{{\hslash }^2}},\\ \eta =\frac{Z_1{Z}_2{e}^2}{\hslash v}\approx 0.158Z_1{Z}_2\sqrt{\frac{\mu }{E}}(E\text{ in MeV}),& (12)\end{array}$

where v = ℏk/μm_N is the relative velocity.

From the Coulomb functions, one defines the incoming and outgoing functions as

$\begin{array}{l}{I}_L(\eta ,x)=G_L(\eta ,x)-i{F}_L(\eta ,x),\\ O_L(\eta ,x)=G_L(\eta ,x)+i{F}_L(\eta ,x).& (13)\end{array}$

The penetration factor P_L and the shift factor S_L are obtained, at a radius a, from

$\begin{array}{l}{P}_L(E,a)=ka/\left[F_L^2(\eta ,ka)+G_L^2(\eta ,ka)\right]\\ S_L(E,a)=\left[F_L(\eta ,ka)F_L^{\prime }(\eta ,ka)+G_L(\eta ,ka)G_L^{\prime }(\eta ,ka)\right]P_L(E,a),& (14)\end{array}$

where the prime denotes the derivative with respect to ka. The penetration factor can be approximately interpreted as the probability to cross the Coulomb barrier, and therefore strongly depends on energy (strictly speaking, however, P_L is not a probability since it may be larger than unity). Below the Coulomb barrier, it essentially depends on energy as

$\begin{array}{ll}{P}_L(E,a)~\text{exp}(-2\pi \eta ).& (15)\end{array}$

This term represents the main contribution to the energy dependence for L = 0. Higher-order corrections can be found in Clayton (1983) and Afanasjev et al. (2012). The penetration factor is illustrated in Figure 1 for a light system p+¹²C, and for an heavier system α+¹²C. The Coulomb barriers are around 1.6 and 3.2 MeV, respectively. As expected, the centrifugal barrier reduces the penetration factor. This effect is stronger for light systems, where the reduced mass is small. Some dependence upon the radius a shows up, but is weak at very low energies.

FIGURE 1

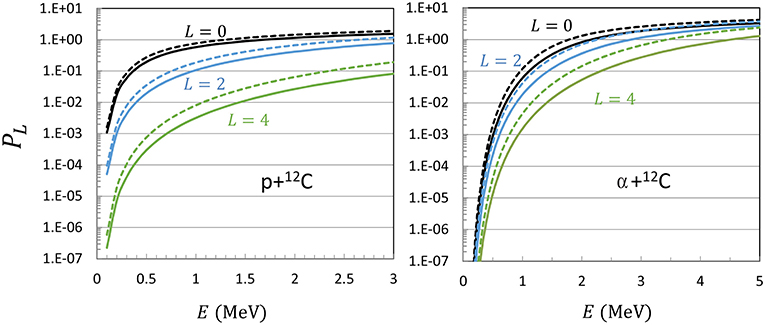
Figure 1. Penetration factor (14) for the p+¹²C (left) and α+¹²C (right) systems. Solid and dashed lines correspond to a = 5 fm and a = 6 fm, respectively.

The fast energy dependence (15) is common to all low-energy cross sections. For this reason, nuclear astrophysicists use the S factor

$\begin{array}{ll}S(E)=\sigma (E)E\text{ exp}(2\pi \eta ),& (16)\end{array}$

which presents a smooth energy dependence for non-resonant reactions. It contains the nuclear information on the reaction.

Resonances play an important role in many reactions. Near a resonance energy E_R in a partial wave J_R, a cross section σ(E) can be written at the Breit-Wigner approximation as

$\begin{array}{ll}\sigma (E)\approx \frac{\pi }{k^2}\frac{2J_R+1}{(2I_1+1)(2I_2+1)}\frac{{\Gamma }_i(E){\Gamma }_f(E)}{{(E-E_R)}^2+\Gamma {(E)}^2/4},& (17)\end{array}$

where Γ_i and Γ_f are the partial widths in the initial and final channels, Γ is the total width, and (I₁, I₂) are the spins of the colliding nuclei. This definition is valid for transfer as well as for capture reactions. In both cases, the entrance width Γ_i(E) is a particle width, often a proton or an alpha width. Its energy dependence is given by

$\begin{array}{ll}{\Gamma }_i(E)={\Gamma }_i\frac{P_L(E,a)}{P_L(E_R,a)}=2{\gamma }_i^2{P}_L(E,a),& (18)\end{array}$

where Γ_i is the width at energy E_R, and ${\gamma }_i^2$ is called the reduced width (Descouvemont and Baye, 2010). Notice that the energy variation slightly depends on the radius a. The Breit-Wigner approximation is a particular case of the more general R-matrix theory (Lane and Thomas, 1958; Descouvemont and Baye, 2010), where several resonances may overlap.

According to Equation (15), the width of a resonance gets very narrow when the energy decreases. The reduced width ${\gamma }_i^2$ reflects the cluster structure of the resonance (Descouvemont and Baye, 2010) and is defined even for bound states (in that case the total width is Γ_i = 0 since the penetration factor vanishes). It does not depend on energy. Consequently, even a state presenting a strong cluster structure may be characterized by a small total width if it is located at low energies. As the entrance width depends on the penetration factor, the fast Coulomb dependence is also removed in the resonant S factor [Equation (16) with the cross section (17)].

In transfer reactions, Γ_f(E) is also a particle width, and the previous discussion is still valid. Notice that, in general, the L values are different (see a discussion and examples in Descouvemont, 2003). However, the Q value must be taken into account as

$\begin{array}{ll}{\Gamma }_f(E)=2{\gamma }_f^2{P}_L(E+Q,a)& (19)\end{array}$

where ${\gamma }_f^2$ is the reduced width of the resonance in the exit channel. If the threshold energy Q is large (typically a few MeV), the corresponding penetration factor presents a slow energy dependence, and the final width is approximated by a constant. This is not true in a few specific reactions, where the Q value is small (or even negative), and where the energy dependence of (19) is not negligible (an example is ¹⁷O(α,n)²⁰Ne where Q = 0.586 MeV).

In capture reactions, the width of the exit channel Γ_f is the γ width. The energy dependence is given by the theory of electromagnetic transitions and reads

$\begin{array}{ll}{\Gamma }_{\gamma }(E)={\Gamma }_{\gamma }{\left(\frac{E-E_f}{E_R-E_f}\right)}^{2\lambda +1},& (20)\end{array}$

where Γ_γ is the γ width at the resonance energy, λ is the order of the electromagnetic transition, and E_f the energy of the final nuclear state (E_f < 0). In general this energy dependence is rather weak, and can be neglected. Owing to the lower amplitude of the electromagnetic interaction compared to the nuclear force, γ widths are in general much lower than particle widths (in light nuclei Γ_γ ≲ 1 eV).

The total width Γ(E) in (17) is in general defined as the sum of the partial widths,

$\begin{array}{ll}\Gamma (E)={\Gamma }_i(E)+{\Gamma }_f(E).& (21)\end{array}$

If more than two channels are open, the total width should include all partial widths of the resonance.

2.3. Radiative-Capture Reactions

Radiative-capture reactions play an important role in the nucleosynthesis (Iliadis, 2007). They can be seen as a transition from an initial scattering state to a final bound state of the system. This process arises from the electromagnetic interaction, and can therefore be treated in the perturbation theory (Rose and Brink, 1967). If H_e is the photon-emission Hamiltonian for the nuclear system, the capture cross section to a final state with spin J_f and parity π_f is given by

$\begin{array}{l}\frac{d{\sigma }_c}{d{\Omega }_{\gamma }}(E,J_f{\pi }_f)=\frac{k_{\gamma }}{2\pi \hslash }\frac{1}{(2I_1+1)(2I_2+1)}\\ \times {\displaystyle \sum _{q{\nu }_1{\nu }_2{M}_f}}|\langle {\Psi }^{J_f{M}_f{\pi }_f}|H_e(q,{\Omega }_{\gamma })|{\Psi }^{{\nu }_1{\nu }_2}\rangle {|}^2,& (22)\end{array}$

where Ω_γ is the photon angle, q = ±1 is the photon polarization, and ${\Psi }^{J_f{M}_f{\pi }_f}$ the final-state wave function. Here ν₁ and ν₂ are the spin projections of the colliding nuclei.

To compute the cross section, the initial wave function ${\Psi }^{{\nu }_1{\nu }_2}$ is expanded in partial waves, and the electromagnetic operator is expanded in multipoles ${{M}}_{\lambda \mu }^{\sigma }$ (Rose and Brink, 1967). At the long wavelength approximation, the electric (σ = E) and magnetic (σ = M) multipole operators are given by

$\begin{array}{l}{{M}}_{\lambda \mu }^E=e{\displaystyle \sum _i^A}{g}_{\ell }(i)r_i^{\lambda }{Y}_{\lambda }^{\mu }({\Omega }_{r_i}),\\ {{M}}_{\lambda \mu }^M={\mu }_N{\displaystyle \sum _i^A}\left[\frac{2}{\lambda +1}{g}_{\ell }(i){\ell }_i+g_s(i)s_i\right]·\nabla r_i^{\lambda }{Y}_{\lambda }^{\mu }({\Omega }_{r_i}),& (23)\end{array}$

with

$\begin{array}{l}{g}_{\ell }(i)=1/2-t_{iz},\\ g_s(i)=g_p(1/2-t_{iz})+g_n(1/2+t_{iz}),& (24)\end{array}$

where t_iz is the isospin projection of nucleon i, and g_p, g_n are the gyromagnetic factors of the proton (g_p = 5.586) and of the neutron (g_n = −3.826) (μ_N = eℏ/m_Nc is the nuclear magneton). Equations (23) are written in the framework of a microscopic approach. Simplified expressions, valid for two-particle systems can be found (e.g., in Bertulani, 2003; Descouvemont, 2003). After integration over the photon angle Ω_γ, the total cross section is given by

$\begin{array}{l}{\sigma }_c(E,J_f{\pi }_f)=\frac{2J_f+1}{(2I_1+1)(2I_2+1)}\frac{8\pi }{\hslash }\\ \times {\displaystyle \sum _{\sigma \lambda J_i{I}_{\omega }{L}_{\omega }}}\frac{k_{\gamma }^{2\lambda +1}}{2L_{\omega }+1}\frac{(\lambda +1)}{\lambda (2\lambda +1)!{!}^2}\\ |\langle {\Psi }^{J_f{\pi }_f}\left|\right|{{M}}_{\lambda }^{\sigma }\left|\right|{\Psi }_{L_{\omega }{I}_{\omega }}^{J_i{\pi }_i}(E)\rangle {|}^2,& (25)\end{array}$

where J_i and π_i are the spin and parity in the entrance channel, and where L_ω and I_ω are the channel spin and the orbital momentum. The summations in (25) are limited by the usual selection rules

$\begin{array}{l}|J_i-J_f|\le \lambda \le J_i+J_f,\\ {\pi }_i{\pi }_f={(-)}^{\lambda }(\text{for }\sigma =E),\\ {\pi }_i{\pi }_f={(-)}^{\lambda +1}(\text{for }\sigma =M).& (26)\end{array}$

In addition, the long-wavelength approximation (k_γR ≪ 1, where R is a typical dimension of the system) strongly reduces the summation over λ. In many cases, a single multipole is important.

As in the previous subsection we only give the integrated cross section, where no interference between multipoles and partial waves shows up. In contrast, the differential cross section (22) involves interference terms (see more detail in Descouvemont, 2003).

2.4. Transfer Reactions

In a transfer reaction (also denoted as “rearrangement reaction”), some nucleons are exchanged between the target and the projectile. A typical example in astrophysics is the ¹³C(α,n)¹⁶O reaction, where two protons and one neutron are stripped from the α particle to ¹³C, to produce ¹⁶O. Transfer processes arise from the nuclear interaction and the corresponding cross sections are usually much larger than the capture cross sections, arising from the electromagnetic interaction. For example, the ¹³C(α,n)¹⁶O cross section is larger by several order of magnitude than the ¹³C(α, γ)¹⁷O cross section.

If Ω = (θ, ϕ) is the relative direction of the nuclei in the final channel, the transfer cross section (Descouvemont and Baye, 2010) is given by

$\begin{array}{ll}\frac{d{\sigma }_t}{d\Omega }(E,i\to f)=\frac{\pi }{k^2}\frac{1}{(2I_1+1)(2I_2+1)}{\displaystyle \sum _j}{A}_j(E)P_j(\text{cos }\theta ),& (27)\end{array}$

where the anisotropy coefficients A_j(E) are defined as

$\begin{array}{l}{A}_j(E)=\frac{1}{4\pi }{\displaystyle \sum _{J\pi \ell LI}}{\displaystyle \sum _{J^{\prime }{\pi }^{\prime }{\ell }^{\prime }{L}^{\prime }{I}^{\prime }}}{(-)}^{I-I^{\prime }}Z(j,J,J^{\prime },\ell ,L,I)Z(j,J,J^{\prime },{\ell }^{\prime },L^{\prime },I^{\prime })\\ U_{i\ell I,f{\ell }^{\prime }{I}^{\prime }}^{J\pi }(E)U_{iLI,f{L}^{\prime }{I}^{\prime }}^{J^{\prime }{\pi }^{\prime }*}(E).& (28)\end{array}$

and U^Jπ represents the collision matrix generalized to multichannel systems. Coefficients Z are defined as

$\begin{array}{l}Z(j,J,J^{\prime },\ell ,L,I)={\left[(2J+1)(2J^{\prime }+1)(2\ell +1)(2L+1)\right]}^{1/2}\\ <\ell 0L0|j0>\left\{\begin{array}{ccc}\ell & L& j\\ J^{\prime }& J& I\end{array}\right\}.& (29)\end{array}$

Again, definition (27) is model independent. The choice of the model only affects the collision matrix. As for radiative capture, the important quantity in astrophysics is the integrated cross section

$\begin{array}{ll}{\sigma }_t(E,i\to f)=\frac{\pi }{k^2}{\displaystyle \sum _{J\pi }}\frac{2J+1}{(2I_1+1)(2I_2+1)}{\displaystyle \sum _{L{L}^{\prime }I{I}^{\prime }}}|U_{iLI,f{L}^{\prime }{I}^{\prime }}^{J\pi }(E){|}^2.& (30)\end{array}$

The discussion of subsection 2.3 remains valid: in general a few terms are important in (30), since only low L values contribute at energies below the Coulomb barrier.

2.5. Fusion Reactions

A number of nuclear reactions that occur in stars are fusion reactions, involving light to medium-mass nuclei. Important examples are the carbon and oxygen burning processes in massive stars. The angular momentum and energy-dependent transmission coefficient T_f(L, E) is then used in the cross section formula to obtain the fusion cross section σ_f

$\begin{array}{ll}{\sigma }_f(E)=\frac{\pi }{k^2}(1+{\delta }_{12}){\displaystyle \sum _L}(2L+1)T_f(L,E),& (31)\end{array}$

where δ₁₂ = 1 for symmetric systems and 0 otherwise. For symmetric systems the sum runs over even L values only.

Within an optical model approach to fusion (in that case, $\left|U_L^J\right|<1$), the transmission coefficient is given by

$\begin{array}{ll}{T}_f(L,E)=1-|U_L^J{|}^2.& (32)\end{array}$

However, at very low energies, $U_L^J\approx 1$, and this technique is not accurate. From the continuity equation, the transmission coefficient (32) is strictly equivalent to

$\begin{array}{ll}{T}_f(L,E)=-\frac{2}{\hslash v}{\displaystyle \int }|g_L(r){|}^{2}W(r)dr,& (33)\end{array}$

where W(r) is the imaginary part of the optical potential that represents absorption due to fusion, and g_L(r) is the exact (single-channel) wave function (Hussein, 1984; Canto et al., 2006).

2.6. Weak-Capture Cross Sections

For low-mass stars, the nucleosynthesis is initiated by the p(p,e⁺ν)d reaction, which occurs through the weak interaction. Since the corresponding Hamiltonian is much smaller than the nuclear and electromagnetic Hamiltonians, the cross section is very small. Estimates in optimal experimental conditions (Rolfs and Rodney, 1988) predict one event per 10⁶ years! Fortunately, theoretical models are quite accurate (Kamionkowski and Bahcall, 1994; Marcucci et al., 2013). The cross section is shown to be proportional to

$\begin{array}{ll}{\sigma }_{pp}(E)~|<{\Psi }_d^{1^{+}}||{{M}}_F+{\lambda }^2{{M}}_{GT}||{\Psi }_{pp}(E)>{|}^2,& (34)\end{array}$

where ${\Psi }_d^{1^{+}}$ is the deuteron wave function, Ψ_pp(E) is the p − p scattering wave function and ${{M}}_F$ and ${{M}}_{GT}$ are the Fermi and Gamow-Teller operators, respectively. In (34), λ² is the ratio of axial-vector to vector coupling constants. A recent calculation (Gaspard et al., 2019) provides S(0) ≈ 3.95 × 10⁻²⁵ MeV-b, which is considerably lower than values obtained for capture or transfer reactions.

3. Reaction Models in Nuclear Astrophysics

3.1. Microscopic Models

Microscopic models are based on fundamental principles of quantum mechanics, such as the treatment of all nucleons, with exact antisymmetrization of the wave functions. Neglecting three-body forces, the Hamiltonian of a A-nucleon system is written as

$\begin{array}{ll}H={\displaystyle \sum _{i=1}^A}{T}_i+{\displaystyle \sum _{i<j=1}^A}{V}_{ij},& (35)\end{array}$

where T_i is the kinetic energy and V_ij a nucleon-nucleon interaction (Wildermuth and Tang, 1977).

The Schrödinger equation associated with this Hamiltonian cannot be solved exactly when A > 3. For very light systems (A ~ 4 − 5) efficient methods (Kievsky et al., 2008) exist, even for continuum states (Navrátil et al., 2010). However, most reactions relevant in nuclear astrophysics involve heavier nuclei, essentially with nucleon or α projectiles. Recent developments of ab initio models (see e.g., Caurier and Navrátil, 2006; Navrátil and Quaglioni, 2011) are quite successful for spectroscopic properties of low-lying states. These models make use of realistic interactions, including three-body forces, and fitted on many properties of the nucleon-nucleon system. Recent works succeeded in applying ab initio calculations to nuclear astrophysics (see e.g., Arai et al., 2011; Neff, 2011; Dohet-Eraly et al., 2016; Marcucci, 2018). However, a consistent description of bound and scattering states of an A-body problem remains a challenging task (Navrátil et al., 2010), in particular for transfer reactions.

In the cluster approximation, it is assumed that the nucleons are grouped in clusters (Wildermuth and Tang, 1977; Descouvemont and Dufour, 2012). The internal wave functions of the clusters are denoted as ${\varphi }_i^{I_i{\pi }_i{\nu }_i}({\xi }_i)$, where I_i and π_i are the spin and parity of cluster i, and ξ_i represents a set of their internal coordinates. In a two-cluster system, a channel function is defined as

$\begin{array}{ll}{\phi }_{LI}^{JM\pi }({\Omega }_r,{\xi }_1,{\xi }_2)={\left[Y_L({\Omega }_r)\otimes {\left[{\varphi }_1^{I_1{\pi }_1}({\xi }_1)\otimes {\varphi }_2^{I_2{\pi }_2}({\xi }_2)\right]}^I\right]}^{JM},& (36)\end{array}$

where different quantum numbers show up: the channel spin I, the relative angular momentum L, the total spin J and the total parity $\pi ={\pi }_1{\pi }_2{(-)}^L$.

As discussed in section 2.1, the total wave function of the A-nucleon system is written, in a microscopic cluster model, as

$\begin{array}{ll}{\Psi }^{JM\pi }={\displaystyle \sum _{cLI}}{\Psi }_{cLI}^{JM\pi }={\displaystyle \sum _{cLI}}{A}{g}_{cLI}^{J\pi }(r){\phi }_{cLI}^{JM\pi }({\Omega }_r,{\xi }_1,{\xi }_2),& (37)\end{array}$

which corresponds to the Resonating Group (RGM) definition (Horiuchi, 1977; Descouvemont and Dufour, 2012). Index c refers to different two-cluster arrangements, and ${A}$ is the antisymmetrization operator. In most applications, the internal cluster wave functions ${\varphi }_i^{I_i{\pi }_i{\nu }_i}$ are defined in the shell model. Accordingly, the nucleon-nucleon interaction must be adapted to this choice, which leads to effective forces, such as the Volkov (Volkov, 1965) or the Minnesota (Thompson et al., 1977) interactions. The relative wave functions $g_{cLI}^{J\pi }(r)$ are to be determined from the Schrödinger equation, which is transformed into a integro-differential equation involving a non-local potential (Horiuchi, 1977). In practice, this relative function is expanded over Gaussian functions (Wildermuth and Tang, 1977; Dufour and Descouvemont, 2011), which corresponds to the Generator Coordinate Method (GCM). The numerical calculations can be made systematic with the GCM, which is not the case for the RGM.

The main advantage of cluster models with respect to other microscopic theories is their ability to deal with reactions, as well as with nuclear spectroscopy. The first applications were done for reactions involving light nuclei, such as d, ³He or α particles (Liu et al., 1981; Hofmann and Hale, 1997). More recently, much work has been devoted to the improvement of the internal wave functions: multicluster descriptions (Descouvemont and Baye, 1994), large-basis shell model extensions (Descouvemont, 1996), or monopolar distortion (Baye and Kruglanski, 1992).

3.2. The Potential Model

Solving the Schrödinger equation associated with a many-body system is a difficult problem, which does not have an exact solution when the nucleon number is larger than three. The potential model is fairly simple to use, and has been applied to several reactions in low-energy nuclear physics (Tombrello, 1965; Bertulani, 2003). The basic assumptions of the potential model are: (i) the nucleon-nucleon interaction is replaced by a nucleus-nucleus force V(r), which depends on the relative coordinate r only; (ii) the wave functions of the unified nucleus can be described by a cluster structure with A₁ + A₂ nucleons; (iii) the internal structure of the nuclei does not play any role. Since we are dealing with low energies, the potential is in general real. The extension to higher energies, which requires complex potentials to simulate absorption channels, is known as the optical model. A generalization to coupled-channel problems is also possible, but seldom used in nuclear astrophysics.

The radial function $g_L^{J\pi }(r)$ for bound and scattering states is deduced from Equation (4). According to the application, the choice of the nuclear contribution is guided by experimental constraints. In radiative-capture calculations it is crucial to reproduce the final-state energy. If phase shifts are available, they can be used to determine the initial potential.

Besides experimental constraints, the nucleus-nucleus potential must follow requirements arising from microscopic arguments (Kukulin et al., 1983; Baye and Descouvemont, 1985). In the microscopic wave function (37), it can be shown that, under some assumptions, there are non-vanishing radial functions $g_{cLI}^{J\pi }(r)$ which yield ${\Psi }_{cLI}^{JM\pi }=0$ after application of the antisymmetrization operator ${A}$. These radial functions are called “forbidden states,” and their number depends on the system and on the angular momentum. To illustrate the problem, let us consider the α+p system where the α particle is described in the shell model. Since the s-shell is filled by the α orbitals, the external proton cannot occupy this s-shell state, which corresponds to a forbidden state. We refer the reader to Buck et al. (1977), Kukulin et al. (1983), and Baye and Descouvemont (1985) for more information. The occurrence of forbidden states can be simulated by an adequate choice of the potential. According to Buck et al. (1977), the potential must contain a number of bound states n_r, equal to the number of forbidden states. This prescription leads to deep potentials, since they involve additional (unphysical) bound states. The calculation of n_r is in general not obvious, except for nucleus-nucleon systems.

In this simple model, the capture cross sections are deduced from integrals involving scattering functions $g_{L_{i}I}^{J_i{\pi }_i}(r)$ at energy E, and bound-state wave functions $g_{L_{f}I}^{J_f{\pi }_f}(r)$

$\begin{array}{ll}{I}_{if}^{\lambda }(E)={\displaystyle \int }{g}_{L_i}^{J_i{\pi }_i}(E,r)r^{\lambda }{g}_{L_f}^{J_f{\pi }_f}(r)dr.& (38)\end{array}$

We refer to Bertulani (2003) for more detail.

The main advantage of the potential model is its simplicity. However, it assumes from the very beginning that the final bound state presents the two-body structure of the entrance channel. This is also true for resonances, which must be described by the adopted nucleus-nucleus structure. This hypothesis is not always valid. In the ¹⁶O(α, γ)²⁰Ne reaction for example, the $0_1^{+}$ ground state and the $0_4^{+}$ broad resonance are well described by an α+¹⁶O structure, but the $0_2^{+}$ and $0_3^{+}$ resonances would require other configurations, such as α+¹⁶O^* or p+¹⁹F. This problem is more and more frequent as the level density increases. Another well-known example is the ¹⁵O(α, γ)¹⁹Ne reaction where most of the ¹⁹Ne low-lying states can be accurately reproduced by an α+¹⁵O structure, but where the resonance important for astrophysics (3/2⁺ at E_c.m. = 0.50 MeV) most likely presents another structure (Dufour and Descouvemont, 2000).

3.3. The Phenomenological R-Matrix Method

The R-matrix method is well-known in atomic and nuclear physics (Descouvemont and Baye, 2010). The basic idea is to divide the space in two regions: the internal region (with radius a), where the nuclear force is important, and the external region, where the interaction between the nuclei is governed by the Coulomb force only. Although the R-matrix parameters do depend on the channel radius a, the sensitivity of the cross section with respect to its choice is quite weak. In the R-matrix method, the energy dependence of the cross sections is obtained from Coulomb functions, as expected from the Schrödinger equation.

In the phenomenological variant of the R-matrix method, the physics of the internal region is determined by a number N of poles, which are characterized by their energies E_λ and reduced widths γ_λi. In a multichannel problem, the R-matrix at energy E is defined as

$\begin{array}{ll}{R}_{if}(E)={\displaystyle \sum _{\lambda =1}^N}\frac{{\gamma }_{\lambda i}{\gamma }_{\lambda f}}{E_{\lambda }-E},& (39)\end{array}$

which must be determined for each partial wave Jπ (not written for the sake of clarity). Indices i and f refer to the initial and final channels. The pole properties are associated with the physical energy and width of resonances, but not strictly equal. This is known as the difference between “formal” and “observed” parameters, deduced from experiment.

The scattering matrices, and therefore the cross sections, are directly determined from the R matrices in the different partial waves (see Lane and Thomas, 1958; Descouvemont and Baye, 2010 for detail). When a single-channel is involved (i = f = 1), the scattering matrix is written as

$\begin{array}{ll}U=\frac{I(ka)}{O(ka)}\frac{1-(S-iP)R}{1-(S+iP)R},& (40)\end{array}$

where P(E) and S(E) are the penetration and shift factors, respectively. In that case, the R-matrix has a dimension 1 × 1. This definition can be easily extended to multichannel calculations (Descouvemont and Baye, 2010). The phase shift is defined by

$\begin{array}{ll}U=\text{exp}(2i\delta )=\text{exp}(2i({\delta }_{\text{HS}}+{\delta }_{\text{R}})),& (41)\end{array}$

where δ_HS is the hard-sphere phase shift which is obtained with R = 0, and therefore with γ_λi = 0. The hard-sphere and R-matrix phase shifts are obtained from

$\begin{array}{l}{\delta }_{\text{HS}}=-arctan\frac{F(ka)}{G(ka)},\\ {\delta }_{\text{R}}=arctan\frac{PR}{1-SR}.& (42)\end{array}$

Let us discuss the calculation of resonance properties. The pole energies E_λ and reduced widths γ_λ (see Equation 39) are associated with the poles of the R-matrix, and therefore depend on the conditions of the calculation, such as the radius a. In a single-channel problem, the resonance energies $E_i^r$, also referred to as the “observed” energies, are defined as the energies where the R-matrix phase shift is δ_R = π/2. According to (42), $E_i^{\text{r}}$ are therefore solutions of the equation

$\begin{array}{ll}S(E_i^{\text{r}})R(E_i^{\text{r}})=1.& (43)\end{array}$

On the other hand, the “observed” width enters the Breit-Wigner parameterization near the resonance energy

$\begin{array}{ll}{\delta }_{\text{R}}(E)\approx arctan\frac{{\Gamma }_i(E)}{2(E_i^{\text{r}}-E)},& (44)\end{array}$

which gives, by using (42)

$\begin{array}{ll}{\Gamma }_i(E)=2P(E)\frac{R(E_i^{\text{r}})}{{\left[S(E)R(E)\right]}_{E=E_i^{\text{r}}}^{\prime }}=2P(E){\tilde{\gamma }}_i^2,& (45)\end{array}$

and defines ${\tilde{\gamma }}_i^2$ as the “observed” reduced width of the resonance. We also have

$\begin{array}{ll}{\Gamma }_i(E)={\Gamma }_i\frac{P(E)}{P(E_i^{\text{r}})},& (46)\end{array}$

where Γ_i is the width calculated at the resonance energy.

If the pole number N is larger than unity, or in multichannel calculations, the definition of $E_i^{\text{r}}$ and of ${\tilde{\gamma }}_i^2$ is not analytical and requires numerical calculations (Angulo and Descouvemont, 2000; Brune, 2002). We illustrate here a simple but frequent situation of a single-channel calculation with N = 1. The phase shift (42) is

$\begin{array}{ll}{\delta }_{\text{R}}(E)=arctan\frac{{\Gamma }_1(E)}{2(E_1-E-{\gamma }_1^{2}S(E))},& (47)\end{array}$

which is equivalent to (44) if we set

$\begin{array}{l}{E}_1^{\text{r}}=E_1-{\tilde{\gamma }}_1^{2}S(E_1^{\text{r}})\\ {\tilde{\gamma }}_1^2={\gamma }_1^2/(1+{\gamma }_1^2{S}^{\prime }(E_1^{\text{r}})),& (48)\end{array}$

where S′(E) = dS/dE. These formulas provide a simple link between calculated and observed values. To derive (48) we have used the Thomas approximation where the shift factor is linearized near $E_1^{\text{r}}$ as

$\begin{array}{ll}S(E)\approx S(E_1^{\text{r}})+(E-E_1^{\text{r}})S^{\prime }(E_1^{\text{r}}).& (49)\end{array}$

This approximation is in general quite accurate. The term ${\tilde{\gamma }}_1^2{S}^{\prime }(E_1^{\text{r}})$ is called the shift factor; it is proportional to the reduced width and is therefore large for strongly deformed states. With Equation (48), the fitting procedure can be used from the observed parameters. It presents important simplifications when some of the parameters (such as bound-state or resonance energies) are known from experiment, and therefore should be constant during the fit.

The phenomenological R-matrix method can be applied to transfer as well as to capture reactions. It is usually used to investigate resonant reactions but is also suited to describe non-resonant processes. In the latter case, the non-resonant behavior is simulated by a high-energy pole, referred to as the background contribution, which makes the R-matrix nearly energy independent. In nuclear astrophysics, a famous application is the ¹²C(α, γ)¹⁶O reaction. Experimental cross sections are available down to E ≈ 1 MeV, whereas the relevant stellar energy is close to 0.3 MeV. The R-matrix parameters are fitted to the available data, and then used to extrapolate the cross section to stellar energies (see a review in deBoer et al., 2017).

3.4. Indirect Methods

The main problem of nuclear astrophysics is the smallness of the cross sections at stellar energies. Further, in some reactions the availability of the required beam at the right energy may be difficult to obtain. These issues spurred interest in devising indirect methods (Tribble et al., 2014; Mukhamedzhanov and Rogachev, 2017), whereby the induced desired reaction is extracted from another reaction. We give below a brief overview of some indirect methods.

3.4.1. The Trojan Horse Method

The basic idea behind the Trojan Horse Method (Baur, 1986; Typel and Baur, 2003; Tumino et al., 2013; Spitaleri et al., 2019) is to use the three-body reaction,

$\begin{array}{ll}a+A\to b+(x+A)\to b+(c+C),& (50)\end{array}$

to extract the cross section of the desired x+A → c+C two-body reaction. In the entrance channel, nucleus a presents a cluster structure a = b + x, and cluster x is transferred to the target A. In this process, cluster b acts as a spectator.

Using the Plane Wave Impulse Approximation and the spectator model (Typel and Baur, 2003), the cross section of process (50) is factorized as

$\begin{array}{ll}\frac{d^3\sigma }{d{E}_{c}d{\Omega }_{c}d{\Omega }_C}=K{\left(\frac{d\sigma }{d\Omega }\right)}_{\text{off}}|\Phi (k_{xb}){|}^2,& (51)\end{array}$

where K is a kinematic factor. In this equation, ${\left(\frac{d\sigma }{d\Omega }\right)}_{\text{off}}$ is the half-off-energy-shell differential cross section for the two-body reaction, x + A → c + C, and Φ(k_xb) is the Fourier transform of the ground state wave function of nucleus a(= b + x).

The main advantage of the Trojan Horse Method is that the cross section (51) is not affected by Coulomb effects, and is therefore more accessible than cross sections of astrophysical interest. Dividing it by a calculated $K|\Phi (k_{xb}){|}^2$ provides the desired cross section ${\left(\frac{d\sigma }{d\Omega }\right)}_{\text{off}}$. We refer the reader to Tribble et al. (2014) and Spitaleri et al. (2019) for recent reviews. The Trojan Horse Method has been applied to many reactions (see a review in Tumino et al., 2013). A recent example is the measurement of the ²H(d,p)³H and ²H(d,n)³He cross sections from 2 keV to 1.5 MeV (Tumino et al., 2011). An ³He beam was used to measure the three-body ²H(³He,p³H)¹H and ²H(³He,n³He)¹H cross sections. Here nucleus a is ³He=d+p, and the deuteron cluster (x in our notations) is transferred to the target. This approach provides ²H(d,p)³H and ²H(d,n)³He cross sections free of electron screening effects.

3.4.2. Coulomb Dissociation

The Coulomb breakup method (Baur et al., 1986, 2001) has been suggested in experiments using radioactive beams to address the problem of small cross sections. The photodissociation reaction

$\begin{array}{ll}c+\gamma \to a+b& (52)\end{array}$

represents the reverse process of the capture reaction

$\begin{array}{ll}a+b\to c+\gamma ,& (53)\end{array}$

and their cross sections σ_d and σ_c are related by the balance theorem

$\begin{array}{ll}{\sigma }_d(E)=\frac{(2I_a+1)(2I_b+1)}{2(2I_c+1)}\frac{k^2}{k_{\gamma }^2}{\sigma }_c(E),& (54)\end{array}$

where I_i represents the spin of nucleus i In most applications, the photon wavelength k_γ is much larger than the particle wavelength k, which means that

$\begin{array}{ll}\frac{k^2}{k_{\gamma }^2}\gg 1,& (55)\end{array}$

and σ_d is significantly larger than σ_c. This method is therefore a good way to compensate the smallness of capture cross sections at low energies. It is, however, limited to capture reactions toward the ground state of nucleus c.

The ⁶Li→α+d breakup reaction was used to assess the method (Kiener et al., 1991), and reinvestigated recently (Hammache et al., 2010). Coulomb breakup has also been used with radioactive beams, to investigate reactions, such as ¹⁴O→¹³N+p (Motobayashi et al., 1991; Kiener et al., 1993) or ⁸B→⁷Be+p (Motobayashi et al., 1994; Kikuchi et al., 1998; Schümann et al., 2006). The importance of the nuclear interaction on the Coulomb dissociation has been discussed, for example, in Kumar and Bonaccorso (2012).

3.4.3. The Asymptotic Normalization Coefficient (ANC) Method

At large distances, the radial wave function for bound states tends to a Whittaker function (Abramowitz and Stegun, 1972); we have

$\begin{array}{ll}{g}_L^{J\pi }(r){\displaystyle \underset{r\to \infty }{\to }}{C}_L^{J\pi }{W}_{-\eta ,L+1/2}(2k_{B}r),& (56)\end{array}$

where $C_L^{J\pi }$ is the so-called “asymptotic normalization coefficient” (ANC). For weakly bound states, the exponential decrease is slow, and the main contribution to the electromagnetic matrix elements arises from large distances. The capture cross section is then essentially determined by the ANC. A typical example is the ⁷Be(p,γ)⁸B reaction, where the ⁸B ground state is bound by 137 keV only. Of course, this is true at very low energies only (typically ≤ 100 keV); for higher energies, the inner part of the wave function and, consequently, the nuclear interaction play a role.

When the external-capture approximation is valid, the capture cross section to a final state f can be written as

$\begin{array}{ll}{\sigma }_c(E,J_f{\pi }_f)\approx |C_{L_f}^{J_f{\pi }_f}{|}^2{\tilde{\sigma }}_c(E,J_f{\pi }_f),& (57)\end{array}$

where ${\tilde{\sigma }}_f(E,J_f{\pi }_f)$ is independent of the model; its energy dependence is given by the properties of the Coulomb functions (Baye and Brainis, 2000). The measurement of the ANC is based on transfer reactions where a nucleon of the projectile is transferred to the target. Energies must be large enough to ensure a peripheral process which is sensitive to the external part of the wave functions only. An example is the ⁷Be(³He,d)⁸B reaction which has been used to determine the ANC of ⁸B (Mukhamedzhanov et al., 1995).

4. Applications

4.1. Applications of Microscopic Models

The knowledge of the ²H(d,γ)⁴He, ²H(d,p)³H, and ²H(d,n)³He cross sections at astrophysical energies is of great interest. Aside from the astrophysical interest, the ²H(d,γ)⁴He capture reaction is extremely important from the nuclear physics viewpoint because its cross section at low energies (below 0.3 MeV) is expected to be dominated by D-wave components in the α particle. Hence it should be very sensitive to the tensor force in the NN interaction (Sabourov et al., 2004).

An ab initio model has been used to study the phase shifts of the p+³He (Arai et al., 2010) and d+d, p+³H, n+³He (Arai et al., 2011) systems. For the two-body NN interaction V_ij, two different realistic potentials are used: AV8′ (Pudliner et al., 1997) and G3RS (Tamagaki, 1968), that consist of central, tensor, and spin-orbit components. Because the main aim is to clarify the role of the tensor force, it is useful to compare results obtained with the realistic interactions with that of an effective NN interaction that contains no tensor force. The MN central potential (Thompson et al., 1977) is adopted with the standard value for the admixture parameter u = 1.

The ²H(d,p)³H and ²H(d,n)³He reactions play an important role in Big-Bang nucleosynthesis. As the observed D/H ratio is currently known with 1.5% accuracy, a high precision is required for the reaction rates. The cross sections have been measured by several groups (Leonard et al., 2006; Tumino et al., 2014), but the extrapolations down to low energies are still uncertain. A compilation of the latest data has been undertaken to reduce the extrapolation uncertainties (Coc et al., 2015). The ²H(d,p)³H and ²H(d,n)³He S factors are presented in Figure 2. They mainly occur from the transitions of the d + d ⁵S₂ channel to the D-wave continuum of p+³H or n+³He, which is due to the tensor force. Without the tensor force, these cross sections cannot be reproduced.

FIGURE 2

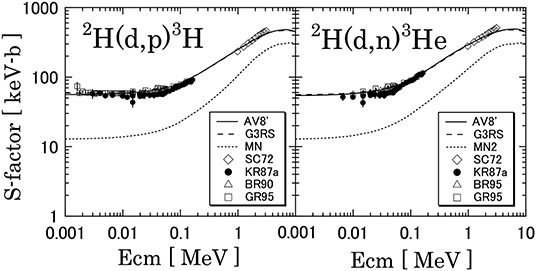
Figure 2. ²H(d,p)³H and ²H(d,n)³He astrophysical S-factors calculated with the realistic AV8′+ G3RS potential (solid lines) and with the effective MN potential (dotted lines). See Angulo et al. (1999) for the experimental data. Reprinted figure with permission from Arai et al. (2011). Copyright (2011) by the American Physical Society.

More recently, the ³He(α, γ)⁷Be and ³H(α, γ)⁷Li cross sections were computed in the no-core shell model (NCSM) (Dohet-Eraly et al., 2016). The authors used a renormalized chiral nucleon-nucleon interaction. In addition to NCSM states, which are optimized for bound states of the seven-nucleon systems, a specific treatment of the α+³He and α+³H configuration is introduced, yielding the NCSM with continuum. With this correction, bound-state properties and elastic phase shifts are well-reproduced. Figure 3 shows the corresponding S-factors, which are compared with previous ab initio models (Nollett, 2001; Neff, 2011). Significant differences exist, due to convergence problems and to the use of different nucleon-nucleon interactions.

FIGURE 3

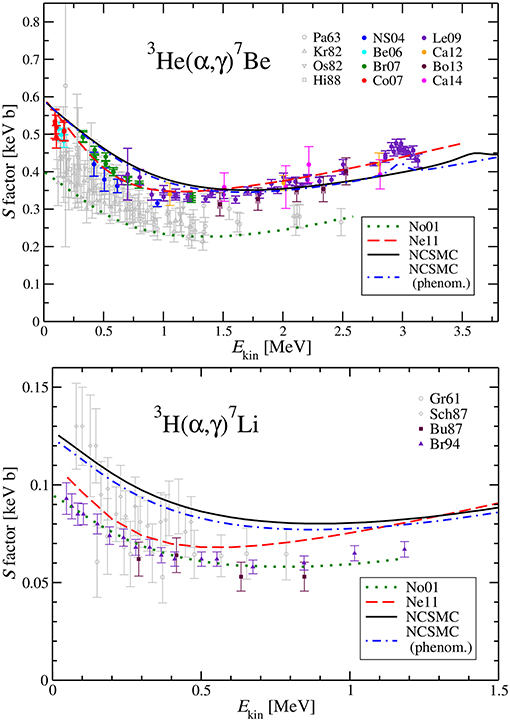
Figure 3. ³He(α, γ)⁷Be and ³H(α, γ)⁷Li S-factors computed with the No Core Shell model (solid lines). The other lines represent alternative calculations (see Dohet-Eraly et al., 2016 for details and for the references to the data). Reprinted from Dohet-Eraly et al. (2016) with permission from Elsevier.

4.2. Applications of the Potential Model

The first applications of the potential model were devoted to the ³He(α, γ)⁷Be (Tombrello and Parker, 1963; Buck et al., 1985) and the ⁷Be(p,γ)⁸B (Robertson, 1973; Typel et al., 1997) reactions. Both reactions are essentially non-resonant at low energies, and the final bound states can be fairly well-described by a two-cluster structure. Most applications in the literature are performed with local potentials. More recently, the influence of the non-locality was investigated by Tian et al. (2018). Applications to fusion reactions can be found, for example, in Chien et al. (2018) (single-channel model) and Assunção and Descouvemont (2013) (multichannel model).

We present in Figure 4 the ³He(α, γ)⁷Be S-factor computed with the potential of Buck et al. (1985), and compare with some experimental data sets. The goal is not to provide a fit of the data, but rather to illustrate the use of the potential model in a simple example. The α+³He potential contains a spin-orbit term; it reproduces several spectroscopic properties of ⁷Be and of ⁷Li. We show separately the contributions of the s wave ($L_i=0,J_i=1/2^{+}$) and of the d wave ($L_i=2,J_i=3/2^{+},5/2^{+}$). Around E = 0 the main contribution comes from L_i = 0, but L_i = 2 cannot be neglected at energies where data are available.

FIGURE 4

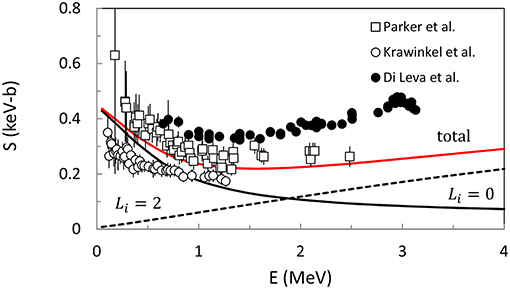
Figure 4. ³He(α, γ)⁷Be S-factor computed in the potential model. The L_i = 0 and L_i = 2 components are shown separately. The data are taken from Parker and Kavanagh (1963), Kräwinkel et al. (1982), and Di Leva et al. (2009).

As discussed in section 3, the capture cross sections are determined from integrals involving the initial and final wave functions. Let us define

$\begin{array}{ll}I(r)=g^{J_f}(r)r^{\lambda }{g}^{J_i}(r),& (58)\end{array}$

whose integral provides the electric component of the cross section. In Figure 5, we present this integrand for typical energies. For the ³He(α, γ)⁷Be reaction, the maximum of I(r) is located near r_max = 10 fm. At low energy the initial function $g^{J_i}(r)$ decreases rapidly in the nuclear region; conversely, the final function $g^{J_f}(r)$ is maximal in this region, and exponentially decreases as

$\begin{array}{ll}{g}^{J_f}(r)=C_f{W}_{-\eta ,{\ell }_f+1/2}(2k_{B}r)~C_f\text{ exp}(-k_{B}r)/{\rho }^{\eta },& (59)\end{array}$

where k_B is the wave number of the bound state. The decrease is therefore faster for large k_B values, and hence for large binding energies. For very low binding energies, such as in ⁸B (−137 keV), we have r_max ≈ 40 fm and integrand (58) is non-negligible up to 150 fm. Accordingly, integrals (38) must be performed up to large r values to ensure the convergence.

FIGURE 5

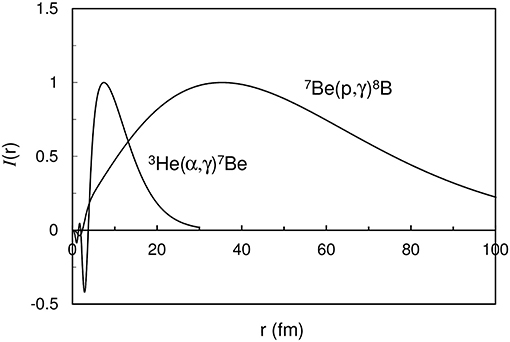
Figure 5. Integrand (58) at 0.02 MeV for ⁷Be(p,γ)⁸B, and at 0.1 MeV for ³He(α, γ)⁷Be (λ = 1). The normalization is arbitrary.

4.3. Applications of the R-Matrix Method

Besides the typical application of the R-matrix to the ¹²C(α, γ)¹⁶O reaction (deBoer et al., 2017), various reactions have been analyzed recently in the R-matrix approach. Some examples are ¹⁴N(p,γ)¹⁵O (Li et al., 2016) or ¹³C(p, γ)¹⁴N (Chakraborty et al., 2015). Here we discuss in more detail a recent R-matrix analysis of the ¹⁸O(p,α)¹⁵N cross section which has been measured in the underground laboratory of the Gran Sasso (LUNA) (Bruno et al., 2019). This reaction influences the abundances of ¹⁵N, ¹⁸O and ¹⁹F isotopes, critical to constrain a wide variety of stellar models.

At stellar temperatures, the rate is mainly determined by the properties of three 1/2⁺ (ℓ = 0) resonances at center of mass energies 0.143, 0.610, and 0.800 MeV. For the latter two resonances, results on their energy and partial widths are inconsistent (La Cognata et al., 2008), and important differences have also been reported between the cross sections of different datasets at low energies. The main goal of Bruno et al. (2019) was to measure the non-resonant component of the cross section of the ¹⁸O(p,α)¹⁵N reaction at proton beam energies from E_p = 360 to 60 keV, extending the range of direct measurements to stellar energies. From the cross section measurements, the strength of resonances of astrophysical interest could be determined.

An important advantage of the R-matrix theory is that some parameters are common to different reactions. In the present case, resonance energies, and proton widths are common to the ¹⁸O(p,p)¹⁸O and ¹⁸O(p,α)¹⁵N cross sections. Only the α widths are specific to ¹⁸O(p,α)¹⁵N. This property therefore provides several constraints on the parameter sets. Ideally, the cross sections should be measured at several angles, which permits to add further constraints.

The LUNA data and the fits of the ¹⁸O(p,p)¹⁸O and ¹⁸O(p,α)¹⁵N cross sections are shown in Figures 6, 7, respectively. Several resonances are included in the fit (see Bruno et al., 2019 for detail). Both fits are excellent, with common parameters (energies and proton widths of resonances). The new data set (Bruno et al., 2019) suggest a new resonance at E_cm = 110 keV.

FIGURE 6

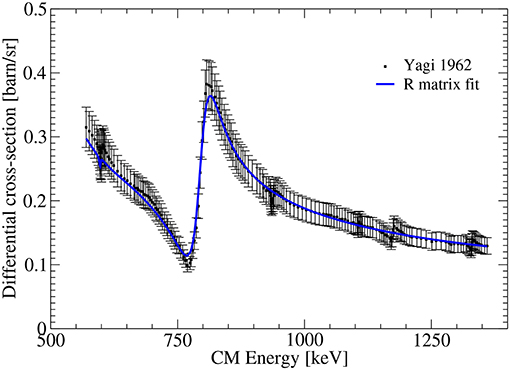
Figure 6. ¹⁸O(p,p)¹⁸O differential cross section at θ = 140° with the R-matrix fit. The data are taken from Yagi (1962). Reprinted from Bruno et al. (2019) with permission from Elsevier.

FIGURE 7

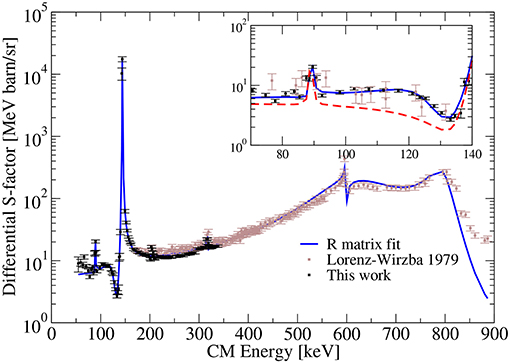
Figure 7. ¹⁸O(p,α)¹⁵N differential S-factor at θ = 135° with the R-matrix fit. The red dashed lined in the inset shows the effect of removing the new state at E = 106 keV. Reprinted from Bruno et al. (2019) with permission from Elsevier.

5. Conclusion

Nuclear astrophysics is a broad field, where many nuclear inputs are necessary. In particular, charged-particle cross sections are quite important, and difficult to measure, owing to the low energies and cross sections. Another characteristic of nuclear astrophysics is that there is almost no systematics. In the low-mass region, each reaction presents its own peculiarities and difficulties, in the theoretical as well as in the experimental viewpoints. Nevertheless some hierarchy can be established among reactions of astrophysical interest. Transfer reactions, arising from the nuclear interaction, present cross sections larger than capture cross sections which have an electromagnetic origin. In addition, the resonant or non-resonant nature of a reaction also affects the amplitude of the cross section.

We have discussed different theoretical models often used in nuclear astrophysics. The potential model and the R-matrix method are widely applied in this field; they are fairly simple and well-adapted to low-energy reactions. On the other hand, microscopic cluster models have a stronger predictive power, since they only rely on a nucleon-nucleon interaction, and on the assumption of a cluster structure for the nucleus. Finally, indirect methods are more and more developed since they overcome the major difficulty of nuclear astrophysics, i.e., the smallness of the cross sections.

A very impressive amount of work has been devoted to nuclear astrophysics in the last decades. Although most reactions involving light nuclei are sufficiently known, some reactions, such as ¹²C(α, γ)¹⁶O or ¹²C+¹²C, still require much effort to reach the accuracy needed for stellar models. In the nucleosynthesis of heavy elements (s process, p process), further problems arise from the level densities and the cross sections should be determined from statistical models. A better knowledge of these cross sections represents a challenge for the future.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was supported by the Fonds de la Recherche Scientifique-FNRS under Grant Numbers 4.45.10.08 and J.0049.19. Computational resources have been provided by the Consortium des Équipements de Calcul Intensif (CÉCI), funded by the Fonds de la Recherche Scientifique de Belgique (F.R.S.-FNRS) under Grant No. 2.5020.11 and by the Walloon Region. PD was Directeur de Recherches of F.R.S.-FNRS, Belgium.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abramowitz, M., and Stegun, I. A. (1972). Handbook of Mathematical Functions. London: Dover.

Google Scholar

Adelberger, E. G., Balantekin, A. B., Bemmerer, D., Bertulani, C. A., Chen, J. W., Costantini, H., et al. (2011). Solar fusion cross sections II: the pp chain and CNO cycles. Rev. Mod. Phys. 83:195. doi: 10.1103/RevModPhys.83.195

CrossRef Full Text | Google Scholar

Afanasjev, A. V., Beard, M., Chugunov, A. I., Wiescher, M., and Yakovlev, D. G. (2012). Large collection of astrophysical S factors and their compact representation. Phys. Rev. C 85:054615. doi: 10.1103/PhysRevC.85.054615

CrossRef Full Text | Google Scholar

Alvarez-Ruso, L., Sajjad Athar, M., Barbaro, M. B., Cherdack, D., Christy, M. E., Coloma, P., et al. (2018). NuSTEC¹ White Paper: Status and challenges of neutrino–nucleus scattering Prog. Part. Nucl. Phys. 100, 1–68. doi: 10.1016/j.ppnp.2018.01.006

CrossRef Full Text | Google Scholar

Angulo, C., Arnould, M., Rayet, M., Descouvemont, P., Baye, D., Leclercq-Willain, C., et al. (1999). A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 656, 3–183. doi: 10.1016/S0375-9474(99)00030-5

CrossRef Full Text | Google Scholar

Angulo, C., and Descouvemont, P. (2000). R-matrix analysis of interference effects in ¹²c(α,α)¹²c and ¹²c(α,γ)¹⁶o. Phys. Rev. C 61:064611. doi: 10.1103/PhysRevC.61.064611

CrossRef Full Text | Google Scholar

Aprahamian, A., Langanke, K., and Wiescher, M. (2005). Nuclear structure aspects in nuclear astrophysics. Prog. Part. Nucl. Phys. 54, 535–613. doi: 10.1016/j.ppnp.2004.09.002

CrossRef Full Text | Google Scholar

Arai, K., Aoyama, S., and Suzuki, Y. (2010). Microscopic cluster model study of ³He + p scattering. Phys. Rev. C 81:037301. doi: 10.1103/PhysRevC.81.037301

CrossRef Full Text | Google Scholar

Arai, K., Aoyama, S., Suzuki, Y., Descouvemont, P., and Baye, D. (2011). Tensor force manifestations in Ab Initio study of the ²H(d,γ)⁴He, ²H(d,p)³H, and ²H(d,n)³He reactions. Phys. Rev. Lett. 107:132502. doi: 10.1103/PhysRevLett.107.132502

PubMed Abstract | CrossRef Full Text | Google Scholar

Assunção, M., and Descouvemont, P. (2013). Role of the hoyle state in ¹²C + ¹²C fusion. Phys. Lett. B 723, 355–359. doi: 10.1016/j.physletb.2013.05.030

CrossRef Full Text | Google Scholar

Barker, F. C., and Kajino, T. (1991). The 12C(α, γ)16o cross section at low energies. Aust. J. Phys. 44, 369–396. doi: 10.1071/PH910369

CrossRef Full Text | Google Scholar

Baur, G. (1986). Breakup reactions as an indirect method to investigate low-energy charged-particle reactions relevant for nuclear astrophysics. Phys. Lett. B 178, 135–138. doi: 10.1016/0370-2693(86)91483-8

CrossRef Full Text | Google Scholar

Baur, G., Bertulani, C. A., and Rebel, H. (1986). Coulomb dissociation as a source of information on radiative capture processes of astrophysical interest. Nucl. Phys. A 458, 188–204. doi: 10.1016/0375-9474(86)90290-3

CrossRef Full Text | Google Scholar

Baur, G., Hencken, K., Trautmann, D., Typel, S., and Wolter, H. H. (2001). Electromagnetic dissociation as a tool for nuclear structure and astrophysics. Prog. Part. Nucl. Phys. 46, 99–108. doi: 10.1016/S0146-6410(01)00113-2

CrossRef Full Text | Google Scholar

Baye, D. (1987). Supersymmetry between deep and shallow nucleus-nucleus potentials. Phys. Rev. Lett. 58, 2738–2741. doi: 10.1103/PhysRevLett.58.2738

PubMed Abstract | CrossRef Full Text | Google Scholar

Baye, D., and Brainis, E. (2000). Zero-energy determination of the astrophysical s factor and effective-range expansions. Phys. Rev. C 61:025801. doi: 10.1103/PhysRevC.61.025801

CrossRef Full Text | Google Scholar

Baye, D., and Descouvemont, P. (1985). Antisymmetrization effects in radiative capture reactions. Ann. Phys. 165, 115–147. doi: 10.1016/S0003-4916(85)80007-5

CrossRef Full Text | Google Scholar

Baye, D., and Kruglanski, M. (1992). α + α scattering in a microscopic model with monopolar distortion. Phys. Rev. C 45, 1321–1332. doi: 10.1103/PhysRevC.45.1321

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertulani, C. A. (2003). RADCAP: A potential model tool for direct capture reactions. Comput. Phys. Commun. 156, 123–141. doi: 10.1016/S0010-4655(03)00441-7

CrossRef Full Text | Google Scholar

Bertulani, C. A., and Kajino, T. (2016). Frontiers in nuclear astrophysics. Prog. Part. Nucl. Phys. 89, 56–100. doi: 10.1016/j.ppnp.2016.04.001

CrossRef Full Text | Google Scholar

Bethe, H. A. (1939). Energy production in stars. Phys. Rev. 55, 103. doi: 10.1007/BF01325636

CrossRef Full Text | Google Scholar

Broggini, C., Bemmerer, D., Guglielmetti, A., and Menegazzo, R. (2010). LUNA: Nuclear astrophysics deep underground. Ann. Rev. Nucl. Part. Sci. 60, 53–73. doi: 10.1146/annurev.nucl.012809.104526

CrossRef Full Text | Google Scholar

Brune, C. R. (2002). Alternative parametrization of R-matrix theory. Phys. Rev. C 66:044611. doi: 10.1103/PhysRevC.66.044611

CrossRef Full Text | Google Scholar

Bruno, C. G., Aliotta, M., Descouvemont, P., Best, A., Davinson, T., Bemmerer, D., et al. (2019). Improved astrophysical rate for the ¹⁸O(p,α)¹⁵N reaction by underground measurements. Phys. Lett. B 790, 237–242. doi: 10.1016/j.physletb.2019.01.017

CrossRef Full Text | Google Scholar

Buck, B., Baldock, R. A., and Rubio, J. A. (1985). Cluster model of A = 7 nuclei and the astrophysical s factor for ³He(α,γ)⁷Be at zero energy. J. Phys. G 11, L11–L16. doi: 10.1088/0305-4616/11/1/003

CrossRef Full Text | Google Scholar

Buck, B., Friedrich, H., and Wheatley, C. (1977). Local potential models for the scattering of complex nuclei. Nucl. Phys. A 275, 246–268. doi: 10.1109/TNS.1977.4329048

CrossRef Full Text | Google Scholar

Burbidge, E. M., Burbidge, G. R., Fowler, W. A., and Hoyle, F. (1957). Synthesis of the elements in stars. Rev. Mod. Phys. 29, 547–650. doi: 10.1103/RevModPhys.29.547

CrossRef Full Text | Google Scholar

Canto, L. F., Gomes, P. R. S., Donangelo, R., and Hussein, M. S. (2006). Fusion and breakup of weakly bound nuclei. Phys. Rep. 424, 1–111. doi: 10.1016/j.physrep.2005.10.006

CrossRef Full Text | Google Scholar

Canto, L. F., and Hussein, M. S. (2013). Scattering Theory of Molecules, Atoms and Nuclei. Singapore: World Scientific Publishing.

Google Scholar

Caughlan, G. R., and Fowler, W. A. (1988). Thermonuclear reaction rates v. At. Data. Nucl. Data Tables 40, 283–334. doi: 10.1016/0092-640X(88)90009-5

CrossRef Full Text | Google Scholar

Caurier, E., and Navrátil, P. (2006). Proton radii of ^{4, 6, 8}He isotopes from high-precision nucleon-nucleon interactions. Phys. Rev. C 73:021302. doi: 10.1103/PhysRevC.73.021302

CrossRef Full Text | Google Scholar

Chakraborty, S., deBoer, R., Mukherjee, A., and Roy, S. (2015). Systematic R-matrix analysis of the ¹³C(p, γ)¹⁴N capture reaction. Phys. Rev. C 91:045801. doi: 10.1103/PhysRevC.91.049905

CrossRef Full Text | Google Scholar

Chatterjee, R., Okolowicz, J., and Ploszajczak, M. (2006). Description of the ¹⁷F(p,γ)¹⁸Ne radiative capture reaction in the continuum shell model. Nucl. Phys. A 764, 528–550. doi: 10.1016/j.nuclphysa.2005.10.002

CrossRef Full Text | Google Scholar

Chien, L. H., Khoa, D. T., Cuong, D. C., and Phuc, N. H. (2018). Consistent mean-field description of the ¹²C + ¹²C optical potential at low energies and the astrophysical s factor. Phys. Rev. C 98:064604. doi: 10.3952/physics.v57i4.3597

CrossRef Full Text | Google Scholar

Clayton, D. D. (1983). Principles of Stellar Evolution and Nucleosynthesis. Chicago, IL: The University of Chicago Press.

Google Scholar

Coc, A., Goriely, S., Xu, Y., Saimpert, M., and Vangioni, E. (2012). Standard big bang nucleosynthesis up to cno with an improved extended nuclear network. Astrophys. J. 744:158. doi: 10.1088/0004-637X/744/2/158

CrossRef Full Text | Google Scholar

Coc, A., Petitjean, P., Uzan, J. P., Vangioni, E., Descouvemont, P., Iliadis, C., et al. (2015). New reaction rates for improved primordial D/H calculation and the cosmic evolution of deuterium. Phys. Rev. D 92:123526. doi: 10.1103/PhysRevD.92.123526

CrossRef Full Text | Google Scholar

deBoer, R. J., Görres, J., Wiescher, M., Azuma, R. E., Best, A., Brune, C. R., et al. (2017). The ¹²C(α, γ)¹⁶O reaction and its implications for stellar helium burning. Rev. Mod. Phys. 89:035007. doi: 10.1103/RevModPhys.89.035007

CrossRef Full Text | Google Scholar

Descouvemont, P. (1996). Application of an extended cluster model to the ⁸Li(α,n)¹¹B reaction. Nucl. Phys. A 596, 285–298. doi: 10.1016/0375-9474(95)00409-2

CrossRef Full Text | Google Scholar

Descouvemont, P. (2003). Theoretical Models for Nuclear Astrophysics. New York, NY: Nova Science.

Google Scholar

Descouvemont, P., Adahchour, A., Angulo, C., Coc, A., and Vangioni-Flam, E. (2004). Compilation and R-matrix analysis of big bang nuclear reaction rates. At. Data Nucl. Data Tables 88, 203–236. doi: 10.1016/j.adt.2004.08.001

CrossRef Full Text | Google Scholar

Descouvemont, P., and Baye, D. (1994). ⁷Li+ p and ⁷Be+ n reactions in a microscopic three-cluster model. Nucl. Phys. A 573, 28–46. doi: 10.1016/0375-9474(94)90013-2

CrossRef Full Text | Google Scholar

Descouvemont, P., and Baye, D. (2010). The R-matrix theory. Rep. Prog. Phys. 73:036301. doi: 10.1088/0034-4885/73/3/036301

CrossRef Full Text | Google Scholar

Descouvemont, P., and Dufour, M. (2012). Clusters in Nuclei, Vol. 2, Lecture Notes in Physics, Vol. 848. Berlin; Heidelberg: Springer.

Google Scholar

Di Leva, A., Gialanella, L., Kunz, R., Rogalla, D., Schürmann, D., Strieder, F., et al. (2009). Stellar and primordial nucleosynthesis of ⁷be: Measurement of ³he(α, γ)⁷be. Phys. Rev. Lett. 102:232502. doi: 10.1103/PhysRevLett.102.232502

PubMed Abstract | CrossRef Full Text | Google Scholar

Dohet-Eraly, J., Navrátil, P., Quaglioni, S., Horiuchi, W., Hupin, G., and Raimondi, F. (2016). ³He(α,γ)⁷Be and ³H(α,γ)⁷Li astrophysical S factors from the no-core shell model with continuum. Phys. Lett. B 757, 430–436. doi: 10.1016/j.physletb.2016.04.021

CrossRef Full Text | Google Scholar

Dufour, M., and Descouvemont, P. (2000). The ¹⁵N(α,γ)¹⁹F and ¹⁵O(α,γ)¹⁹Ne reactions in a microscopic multicluster model. Nucl. Phys. A 672, 153–164. doi: 10.1016/S0375-9474(00)00054-3

CrossRef Full Text | Google Scholar

Dufour, M., and Descouvemont, P. (2011). Low-lying resonances in the 16b nucleus. Phys. Lett. B 696, 237–240. doi: 10.1016/j.physletb.2010.12.032

CrossRef Full Text | Google Scholar

Friedrich, H. (1981). Microscopic nucleus-nucleus potentials. Phys. Rep. 74C, 209–275. doi: 10.1016/0370-1573(81)90131-9

CrossRef Full Text | Google Scholar

Gaspard, D., Sparenberg, J. M., Wenda, Q., and Baye, D. (2019). Complex-energy analysis of proton-proton fusion. Phys. Rev. C 100:035805. doi: 10.1103/PhysRevC.100.035805

CrossRef Full Text | Google Scholar

Hammache, F., Heil, M., Typel, S., Galaviz, D., Sümmerer, K., Coc, A., et al. (2010). High-energy breakup of ⁶Li as a tool to study the big bang nucleosynthesis reaction ²H(α, γ)⁶Li. Phys. Rev. C 82:065803. doi: 10.1103/PhysRevC.82.065803

CrossRef Full Text | Google Scholar

Hofmann, H. M., and Hale, G. M. (1997). Microscopic calculation of the 4he system. Nucl. Phys. A 613, 69–106. doi: 10.1016/S0375-9474(96)00418-6

CrossRef Full Text | Google Scholar

Horiuchi, H. (1977). Kernels of gcm, rgm and ocm and their calculation methods. Prog. Theor. Phys. Suppl. 62, 90–190. doi: 10.1143/PTPS.62.90

CrossRef Full Text | Google Scholar

Horiuchi, H., Ikeda, K., and Katō, K. (2012). Recent developments in nuclear cluster physics. Prog. Theor. Phys. Suppl. 192:1. doi: 10.1143/PTPS.192.1

CrossRef Full Text | Google Scholar

Hoyle, F. (1954). On nuclear reactions occuring in very hot stars.i. the synthesis of elements from carbon to nickel. Astrophys. J. Suppl. 1:121. doi: 10.1086/190005

CrossRef Full Text | Google Scholar

Hussein, M. S. (1984). Theory of the heavy-ion fusion cross section. Phys. Rev. C 30:1962. doi: 10.1103/PhysRevC.30.1962

CrossRef Full Text | Google Scholar

Iliadis, C. (2007). Nuclear Physics of Stars. Weinheim: Wiley-VCH Verlag GmbH.

Google Scholar

José, J., and Iliadis, C. (2011). Nuclear astrophysics: the unfinished quest for the origin of the elements. Rep. Prog. Phys. 74:096901. doi: 10.1088/0034-4885/74/9/096901

CrossRef Full Text | Google Scholar

Kamionkowski, M., and Bahcall, J. N. (1994). The rate of the proton-proton reaction. Astrophys. J. 420:884. doi: 10.1086/173612

CrossRef Full Text | Google Scholar

Kiener, J., Gils, H. J., Rebel, H., Zagromski, S., Gsottschneider, G., Heide, N., et al. (1991). Measurements of the coulomb dissociation cross section of 156 mev ⁶Li projectiles at extremely low relative fragment energies of astrophysical interest. Phys. Rev. C 44, 2195–2208. doi: 10.1103/PhysRevC.44.2195

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiener, J., Lefebvre, A., Aguer, P., Bacri, C. O., Bimbot, R. B., Borderie, G. B., et al. (1993). Determination of the ¹³N(p, γ)¹⁴O reaction rate through the coulomb break-up of a ¹⁴O radioactive beam. Nucl. Phys. A 552, 66–81. doi: 10.1016/0375-9474(93)90331-Q

CrossRef Full Text | Google Scholar

Kievsky, A., Rosati, S., Viviani, M., Marcucci, L. E., and Girlanda, L. (2008). A high-precision variational approach to three- and four-nucleon bound and zero-energy scattering states. J. Phys. G 35:063101. doi: 10.1088/0954-3899/35/6/063101

CrossRef Full Text | Google Scholar

Kikuchi, T., Motobayashi, T., Iwasa, N., Ando, Y., Kurokawa, M., Moriya, S., et al. (1998). Further measurement of the ⁷Be(p,γ)⁸B cross section at low energies with the coulomb dissociation of ⁸B. Eur. Phys. J. A 3, 213–215.

Google Scholar

Kräwinkel, H., Becker, H. W., Buchmann, L., Görres, J., Kettner, K. U., Kieser, W. E., et al. (1982). The ³He(α,γ)⁷Be reaction and the solar neutrino problem. Zeit. Phys. A 304, 307–332. doi: 10.1007/BF01421513

CrossRef Full Text | Google Scholar

Kukulin, V. I., Neudatchin, V. G., Obukhovski, I. T., and Smirnov, Y. F. (1983). Clusters as Subsystems in Light Nuclei. Braunschweig: Vieweg.

Google Scholar

Kumar, R., and Bonaccorso, A. (2012). Interplay of nuclear and coulomb effects in proton breakup from exotic nuclei. Phys. Rev. C 86:061601. doi: 10.1103/PhysRevC.86.061601

CrossRef Full Text | Google Scholar

La Cognata, M., Spitaleri, C., Mukhamedzhanov, A. M., Irgaziev, B., Tribble, R. E., Banu, A., et al. (2008). Measurement of the 20 and 90 kev resonances in the ¹⁸O(p,α)¹⁵N reaction via the trojan horse method. Phys. Rev. Lett. 101:152501. doi: 10.1103/PhysRevLett.101.152501

PubMed Abstract | CrossRef Full Text | Google Scholar

Lane, A. M., and Thomas, R. G. (1958). R-matrix theory of nuclear reactions. Rev. Mod. Phys. 30, 257–353. doi: 10.1103/RevModPhys.30.257

CrossRef Full Text | Google Scholar

Leonard, D. S., Karwowski, H. J., Brune, C. R., Fisher, B. M., and Ludwig, E. J. (2006). Precision measurements of ²H(d,p)³H and ²H(d,n)³He total cross sections at big bang nucleosynthesis energies. Phys. Rev. C 73:045801. doi: 10.1103/PhysRevC.73.045801

CrossRef Full Text | Google Scholar

Li, Q., Görres, J., deBoer, R. J., Imbriani, G., Best, A., Kontos, A., et al. (2016). Cross section measurement of ¹⁴N(p, γ)¹⁵O in the cno cycle. Phys. Rev. C 93:055806. doi: 10.1103/PhysRevC.93.055806

CrossRef Full Text | Google Scholar

Liccardo, V., Malheiro, M., Hussein, M., Carlson, B., and Frederico, T. (2018). Nuclear processes in astrophysics: Recent progress. Eur. Phys. J. A 54:221. doi: 10.1140/epja/i2018-12648-5

CrossRef Full Text | Google Scholar

Liu, Q. K. K., Kanada, H., and Tang, Y. C. (1981). Microscopic study of ³He(α, γ)⁷Be electric-dipole capture reaction. Phys. Rev. C 23, 645–656. doi: 10.1103/PhysRevC.23.645

CrossRef Full Text | Google Scholar

Longland, R., Iliadis, C., Champagne, A., Newton, J., Ugalde, C., Coc, A., et al. (2010). Charged-particle thermonuclear reaction rates: I. monte carlo method and statistical distributions. Nucl. Phys. A 841, 1–30. doi: 10.1016/j.nuclphysa.2010.04.008

CrossRef Full Text | Google Scholar

Marcucci, L. E. (2018). Recent progress in ab-initio studies of nuclear reactions of astrophysical interest with a ≤ 3. J. Phys. Conf. Series 981:012019. doi: 10.1088/1742-6596/981/1/012019

CrossRef Full Text | Google Scholar

Marcucci, L. E., Schiavilla, R., and Viviani, M. (2013). Proton-proton weak capture in chiral effective field theory. Phys. Rev. Lett. 110:192503. doi: 10.1103/PhysRevLett.110.192503

PubMed Abstract | CrossRef Full Text | Google Scholar

Motobayashi, T., Iwasa, N., Ando, Y., Kurokawa, M., Murakami, H., Gen, J. R., et al. (1994). Coulomb dissociation of ⁸B and the ⁷Be(p,γ)⁸B reaction at low energies. Phys. Rev. Lett. 73, 2680–2683. doi: 10.1103/PhysRevLett.73.2680

CrossRef Full Text | Google Scholar

Motobayashi, T., Takei, T., Kox, S., Perrin, C., Merchez, F. K., Ieki, D. R., et al. (1991). Determination of the astrophysical ¹³N(p,γ)¹⁴O cross section through the coulomb dissociation method. Phys. Lett. B 264, 259–263. doi: 10.1016/0370-2693(91)90345-Q

CrossRef Full Text | Google Scholar

Mukhamedzhanov, A. M., Gagliardi, C. A., and Tribble, R. E. (2001). Asymptotic normalization coefficients, spectroscopic factors, and direct radiative capture rates. Phys. Rev. C 63:024612. doi: 10.1103/PhysRevC.63.024612

CrossRef Full Text | Google Scholar

Mukhamedzhanov, A. M., and Rogachev, G. V. (2017). Radiative capture reactions via indirect methods. Phys. Rev. C 96:045811. doi: 10.1103/PhysRevC.96.045811

CrossRef Full Text | Google Scholar

Mukhamedzhanov, A. M., Tribble, R. E., and Timofeyuk, N. K. (1995). Possibility to determine the astrophysical s factor for the ⁷Be(p,γ)⁸B radiative capture from analysis of the ⁷Be(³He,d)⁸B reaction. Phys. Rev. C 51, 3472–3478. doi: 10.1103/PhysRevC.51.3472

PubMed Abstract | CrossRef Full Text | Google Scholar

Navrátil, P., and Quaglioni, S. (2011). Ab initio many-body calculations of deuteron-⁴He scattering and ⁶Li states. Phys. Rev. C 83:044609. doi: 10.1103/PhysRevC.83.044609

CrossRef Full Text | Google Scholar

Navrátil, P., and Quaglioni, S. (2012). Ab Initio many-body calculations of the ³H(d,n)⁴He and ³He(d,p)⁴He fusion reactions. Phys. Rev. Lett. 108:042503. doi: 10.1103/PhysRevLett.108.042503

PubMed Abstract | CrossRef Full Text | Google Scholar

Navrátil, P., Roth, R., and Quaglioni, S. (2010). Ab initio many-body calculations of nucleon scattering on ⁴He, ⁷Li, ⁷Be, ¹²C, and ¹⁶O. Phys. Rev. C 82:034609. doi: 10.1103/PhysRevC.82.034609

CrossRef Full Text | Google Scholar

Neff, T. (2011). Microscopic calculation of the ³He(α, γ)⁷Be and ³H(α, γ)⁷Li capture cross sections using realistic interactions. Phys. Rev. Lett. 106:042502. doi: 10.1103/PhysRevLett.106.042502

PubMed Abstract | CrossRef Full Text | Google Scholar

Nollett, K. M. (2001). Radiative α-capture cross sections from realistic nucleon-nucleon interactions and variational monte carlo wave functions. Phys. Rev. C 63:054002. doi: 10.1103/PhysRevC.63.054002

CrossRef Full Text | Google Scholar

Parker, P. D., and Kavanagh, R. W. (1963). He³(α, γ)Be⁷ reaction. Phys. Rev. 131, 2578–2582. doi: 10.1103/PhysRev.131.2578

CrossRef Full Text | Google Scholar

Pudliner, B. S., Pandharipande, V. R., Carlson, J., Pieper, S. C., and Wiringa, R. B. (1997). Quantum monte carlo calculations of nuclei with a < 7. Phys. Rev. C 56:1720. doi: 10.1103/PhysRevC.56.1720

CrossRef Full Text | Google Scholar

Rauscher, T., Thielemann, F. K., and Kratz, K. L. (1997). Nuclear level density and the determination of thermonuclear rates for astrophysics. Phys. Rev. C 56, 1613–1625. doi: 10.1103/PhysRevC.56.1613

CrossRef Full Text | Google Scholar

Raynal, J. (1972). Computing as a Language of Physics, Trieste 1971. Vienna: IAEA. 281.

Reifarth, R., Erbacher, P., Fiebiger, S., Göbel, K., Heftrich, T., Heil, M., et al. (2018). Neutron-induced cross sections. Eur. Phys. J. Plus 133:424. doi: 10.1140/epjp/i2018-12295-3

CrossRef Full Text | Google Scholar

Richter, W., Brown, B. A., Signoracci, A., and Wiescher, M. (2011). Shell-model studies of the rp reaction ²⁵Al(p,γ)²⁶Si. Prog. Part. Nucl. Phys. 66, 283–286. doi: 10.1016/j.ppnp.2011.01.021

CrossRef Full Text | Google Scholar

Robertson, R. G. H. (1973). Proton capture by ⁷Be and the solar neutrino problem. Phys. Rev. C 7, 543–547. doi: 10.1103/PhysRevC.7.543

CrossRef Full Text | Google Scholar

Rolfs, C., and Rodney, W. S. (1988). Cauldrons in the Cosmos. Chicago, IL: The University of Chicago Press.

Google Scholar

Rose, H. J., and Brink, D. M. (1967). Angular distributions of gamma rays in terms of phase-defined reduced matrix elements. Rev. Mod. Phys. 39, 306–347. doi: 10.1103/RevModPhys.39.306

CrossRef Full Text | Google Scholar

Sabourov, K., Ahmed, M. W., Canon, S. R., Crowley, B., Joshi, K., Kelley, J. H., et al. (2004). Experimental and theoretical study of the ²H($\overrightarrow{d}$,γ)⁴ He reaction below E_c.m. = 60keV. Phys. Rev. C 70:064601. doi: 10.1103/PhysRevC.70.064601

CrossRef Full Text | Google Scholar

Satchler, G. R. (1983). Direct Nuclear Reactions. Oxford: Oxford University Press.

Google Scholar

Schümann, F., Typel, S., Hammache, F., Sümmerer, K., Uhlig, F., Böttcher, I., et al. (2006). Low-energy cross section of the ⁷Be(p,γ)⁸B solar fusion reaction from the coulomb dissociation of ⁸B. Phys. Rev. C 73:015806. doi: 10.1103/PhysRevLett.73.015806

CrossRef Full Text | Google Scholar

Spitaleri, C., La Cognata, M., Lamia, L., Pizzone, R. G., and Tumino, A. (2019). Astrophysics studies with the trojan horse method. Eur. Phys. J. A 55:161. doi: 10.1140/epja/i2019-12833-0

CrossRef Full Text | Google Scholar

Tamagaki, R. (1968). Repulsive core of effective alpha-alpha potential and the pauli principle. Suppl. Prog. Theor. Phys. E68, 242–258. doi: 10.1143/PTPS.E68.242

CrossRef Full Text | Google Scholar

Thielemann, F., Eichler, M., Panov, I., and Wehmeyer, B. (2017). Neutron star mergers and nucleosynthesis of heavy elements. Ann. Rev. Nucl. Part. Sci. 67, 253–274. doi: 10.1146/annurev-nucl-101916-123246

CrossRef Full Text | Google Scholar

Thompson, D. R., LeMere, M., and Tang, Y. C. (1977). Systematic investigation of scattering problems with the resonating-group method. Nucl. Phys. A 286, 53–66. doi: 10.1016/0375-9474(77)90007-0

CrossRef Full Text | Google Scholar

Thompson, I., and Nunes, F. (2009). Nuclear Reactions for Astrophysics: Principles, Calculation and Applications of Low-Energy Reactions. Cambridge: Cambridge University Press.

Google Scholar

Thompson, I. J. (2010). NIST Handbook of Mathematical Functions. Cambridge: Cambridge University Press.

Google Scholar

Tian, Y., Pang, D. Y., and Ma, Z. Y. (2018). Effects of nonlocality of nuclear potentials on direct capture reactions. Phys. Rev. C 97:064615. doi: 10.1103/PhysRevC.97.064615

CrossRef Full Text | Google Scholar

Tombrello, T. A. (1965). The capture of protons by 7Be. Nucl. Phys. 71, 459–464. doi: 10.1016/0029-5582(65)90733-9

CrossRef Full Text | Google Scholar

Tombrello, T. A., and Parker, P. D. (1963). Direct-capture model for the He³(α, γ)Be⁷ and T(α, γ)Li⁷ reactions. Phys. Rev. 131, 2582–2589. doi: 10.1103/PhysRev.131.2582

CrossRef Full Text | Google Scholar

Tribble, R. E., Bertulani, C. A., Cognata, M. L., Mukhamedzhanov, A. M., and Spitaleri, C. (2014). Indirect techniques in nuclear astrophysics: a review. Rep. Prog. Phys. 77:106901. doi: 10.1088/0034-4885/77/10/106901

PubMed Abstract | CrossRef Full Text | Google Scholar

Tumino, A., Spartá, R., Spitaleri, C., Mukhamedzhanov, A. M., Typel, S., Pizzone, R. G., et al. (2014). New determination of the ²H(d,p)³H and ²H(d,n)³He reaction rates at astrophysical energies. Astrophys. J. 785:96. doi: 10.1088/0004-637X/785/2/96

CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., Cherubini, S., Gulino, M., La Cognata, M., Lamia, L., et al. (2013). New advances in the trojan horse method as an indirect approach to nuclear astrophysics. Few Body Syst. 54, 745–753. doi: 10.1007/s00601-013-0690-5

CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., Mukhamedzhanov, A. M., Typel, S., Aliotta, M., Burjan, V., et al. (2011). Low-energy fusion reactions via the trojan horse method. Phys. Lett. B 700, 111–115. doi: 10.1016/j.physletb.2011.05.001

CrossRef Full Text | Google Scholar

Typel, S., and Baur, G. (2003). Theory of the trojan-horse method. Ann. Phys. 305, 228–265. doi: 10.1016/S0003-4916(03)00060-5

CrossRef Full Text | Google Scholar

Typel, S., Wolter, H. H., and Baur, G. (1997). Higher-order effects in the coulomb dissociation of 8b into ⁷Be+P. Nucl. Phys. A 613, 147–164. doi: 10.1016/S0375-9474(96)00415-0

CrossRef Full Text | Google Scholar

Volkov, A. B. (1965). Equilibrium deformation calculations of the ground state energies of 1p shell nuclei. Nucl. Phys. 74, 33–58. doi: 10.1016/0029-5582(65)90244-0

CrossRef Full Text | Google Scholar

Wiescher, M., Käppeler, F., and Langanke, K. (2012). Critical reactions in contemporary nuclear astrophysics. Ann. Rev. Astron. Astrophys. 50, 165–210. doi: 10.1146/annurev-astro-081811-125543

CrossRef Full Text | Google Scholar

Wildermuth, K., and Tang, Y. C. (1977). A Unified Theory of the Nucleus. Braunschweig: Vieweg.

Google Scholar

Yagi, K. (1962). Analysis of elastic scattering of protons by o18 and the energy levels of f19. J. Phys. Soc. Japan 17:604. doi: 10.1143/JPSJ.17.604

CrossRef Full Text | Google Scholar

Zhang, X., Nollett, K. M., and Phillips, D. R. (2018). Models, measurements, and effective field theory: Proton capture on ⁷Be at next-to-leading order. Phys. Rev. C 98:034616. doi: 10.3952/physics.v58i1.3647

CrossRef Full Text | Google Scholar