- 1Los Alamos National Laboratory, Los Alamos, NM, United States
- 2NASA, Goddard Spaceflight Center, Greenbelt, MD, United States
- 3SRI International, Menlo Park, CA, United States
- 4Department of Physics and Astronomy, The University of Calgary, Calgary, AB, Canada
- 5Space Science Institute, Boulder, CO, United States
The 1970s and 1980s were heydays for using active electron beam experiments to probe some of the fundamental physical processes that occur throughout the heliosphere and in astrophysical contexts. Electron beam experiments were used to study spacecraft charging and spacecraft-plasma coupling; beam-plasma interaction physics; magnetic bounce and drift physics; auroral physics; wave generation; and military applications. While these experiments were enormously successful, they were also limited by the technologies that were available at that time. New advances in space instrumentation, data collection, and accelerator technologies enable a revolutionary new generation of active experiments using electron beams in space. In this paper we discuss such an experiment, the Beam Plasma Interactions Experiment (Beam PIE), a sounding rocket experiment designed to (a) advance high-electron mobility transistor-based radio frequency (RF) linear accelerator electron technology for space applications and (b) study the production of whistler and X-mode waves by modulated electron beams.
Introduction
Active space experiments using electron beams started in the 1970s primarily to study spacecraft charging effects (e.g., Mullen et al., 1986; Sasaki et al., 1986, 1988; Banks et al., 1990). In those experiments electron beams could produce controlled amounts of “artificial” charging in order to better understand the physical processes involved in spacecraft charging and neutralization and to investigate the effects of severe charging on spacecraft systems. Later electron beams were used to conduct a variety of innovative and successful active physics experiments involving beam-plasma interactions (e.g., Gendrin, 1974; Cambou et al., 1978, 1980), magnetic bounce and drift physics (e.g., Hendrickson et al., 1975, 1976; Winckler et al., 1975), and the generation of VLF wave emissions (e.g., Monson et al., 1976; Dechambre et al., 1980; Obayashi et al., 1982; Farrell et al., 1988; Neubert et al., 1988; Reeves et al., 1988, 1990a,b). Los Alamos National Laboratory also tested a neutralized H− particle beam in the BEAR (Beam Experiment Aboard a Rocket) program as part of the US Strategic Defense Initiative.
Studies of wave-generation and wave-particle interactions using electron beams were of particular interest in the early days of active experiments. The experiments of the 1980's were able to demonstrate the ability to produce propagating electromagnetic waves; to identify that the strongest emissions were whistler-mode and; to establish a general agreement with analytic theory (Harker and Banks, 1985, 1987; Reeves et al., 1990b).
Theoretical work on beam-plasma-wave generation began in the 1960s and was further developed specifically for the active experiments program (e.g., Harker and Banks, 1983, 1985; Farrell et al., 1989). As with a physical antenna each beam pulse acts as a current source. The plasma through which the beam propagates responds according to the resonance condition:
where ω is the frequency of the mode, k|| is the wave vector along the background magnetic field (i.e., in the parallel direction), v|| is the parallel beam velocity, γ is the beam relativistic factor, ωce is the electron cyclotron frequency and s is an integer number with s=0 corresponding to the Landau resonance and s≠ 0 describing cyclotron resonance. The waves are emitted as Cherenkov radiation as described by e.g., Farrell et al. (1989). Harker and Banks (1985) calculated the whistler-mode wave power expected from a pulsed electron beam and Reeves et al. (1990b) found that the Spacelab 2 observations generally showed the predicted dependence on modulation frequency, duty cycle, and pitch angle. However, both the accelerator and receiver technologies available for the early electron beam experiments were quite limited. For example, the Spacelab 2 experiment could only operate at a single beam energy (1 keV) and current (100 mA). Only the modulation frequency and duty cycle could be varied. The wave receiver was a 1D analog audio recorder with a 10 kHz passband. No information on Poynting flux, wave normal angle, or polarization could be obtained.
Recently, Los Alamos National Laboratory and NASA's Goddard Spaceflight Center have been awarded a grant to conduct active experiments on beam-wave generation using state-of-the-art linear electron accelerators, wave receivers, and plasma instrumentation. The project is funded through NASA's Low Cost Access to Space (LCAS) sounding rocket program. The experiment is called the Beam Plasma Interactions Experiment, or Beam PIE, and is scheduled to launch in spring of 2021 nominally from Poker Flat, AK. In the remainder of this paper we discuss the experimental setup, objectives, and expected results based on theory, modeling, and simulation.
Experimental Objectives
Waves and wave-particle interactions play a critical role in some of the most important dynamics in space and astrophysical plasmas by mediating the exchange of energy between fields and particles. The Earth's radiation belts are a good example of such a system. In addition to the ULF wave-particle interactions that drive radial diffusion (and betatron/Fermi acceleration), plasmas injected from the magnetotail into the inner magnetosphere form distributions that are energetically unstable. Depending on the nature of the plasma distributions and the ambient field and plasma conditions, those unstable distributions produce whistler-mode chorus, electromagnetic ion cyclotron (EMIC), magnetosonic, electron cyclotron harmonic, and other waves. Those waves, in turn, strongly affect the dynamics of the radiation belts. Whistler-mode chorus waves, for example, can strongly accelerate 100s keV “seed” electrons to MeV energies. These wave-particle interactions are considered to be the dominant radiation belt electron acceleration mechanism for at least a subset of events (Reeves et al., 2013; Thorne et al., 2013; Baker et al., 2014). EMIC waves can strongly pitch angle scatter radiation belt electrons and are candidates for rapid radiation belt losses (for at least some events and some energies) (e.g., Jordanova et al., 2008; Ukhorskiy and Sitnov, 2012; Usanova et al., 2014). Countless other examples can be found throughout the heliosphere: in the corona, solar wind, planetary magnetospheres, ionospheres, heliopause, and essentially every plasma system where we have wave and particle observations. Besides the scientific interest associated with the natural environment, wave-particle interaction physics can have very important practical applications such as radiation belt remediation (Carlsten et al., 2019).
There are many sources of free energy for wave generation and much study has been devoted to linear, quasi-linear, and non-linear instabilities that occur, naturally, in space [see e.g., Gary (1993)]. An alternative approach is a more active experimental technique, namely using an artificial electron beam to generate the waves. Accelerator-produced electron beams are “artificial” only in the sense that we can precisely control the characteristics of the beam to produce waves with equally precise and testable characteristics.
The objective of the Beam Plasma Interactions Experiment is to discover and characterize fundamental wave-particle interactions by generating waves using a modulated energetic electron beam, characterizing the wave properties to test theoretical and model predictions. As a secondary objective we will determine if the beam-generated wave fields are strong enough to produce measurable scattering of ambient ionospheric electron populations. The main specific objectives of Beam PIE are to:
• Demonstrate, for the first time, advanced RF linear electron accelerator instrumentation for space experiments.
• Quantitatively test theories of how energetic electron beams couple to plasmas to stimulate whistler-mode radiation.
• Discover and characterize how energetic electron beams couple to plasmas to stimulate propagating R-X-mode radiation.
Beam Pie—The Beam Plasma Interactions Experiment
Experimental Concept of Operations
Beam PIE will utilize a “mother-daughter” rocket configuration in which one rocket segment, the “accelerator” will house the electron beam and power systems and the other section, the “receiver” will house the fields, waves, and particle detectors. The payload layout in launch configuration and placement of the instruments on the two payloads are shown schematically in Figure 1.
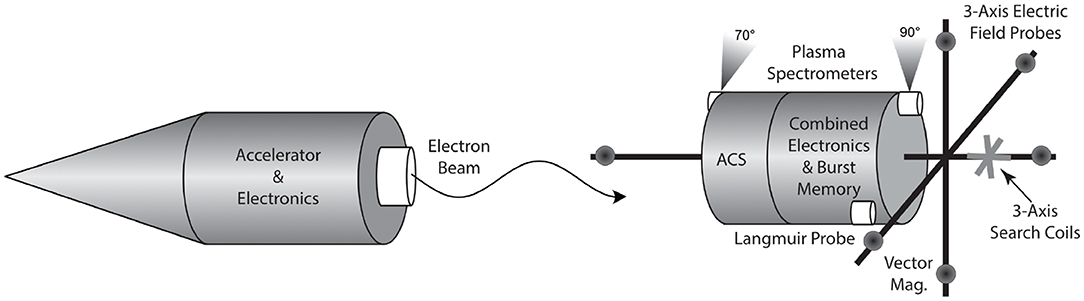
Figure 1. Schematic of the Beam PIE payload and instrument locations. The Accelerator Payload contains only the accelerator and associated electronics. After payload separation it will be aligned roughly along the magnetic field and boosted to a higher altitude. The Receiver Payload consists of 3-axis electric and magnetic field probes, a wave digitizer/receiver, a plasma spectrometer, a Langmuir probe, a vector magnetometer and associated electronics [see sections DC and Wave Electric Field Detectors–Energetic Electron Spectrometer (APES)]. An attitude control system (ACS) will be used to achieve a spin rate for the receiver payload of ~1 Hz. The same ACS will orient the payloads such that they will be aligned ±2° to the magnetic field at apogee which achieves ±5° for all altitudes above 300 km.
After achieving operational altitude and immediately after engine cutoff an attitude control system (ACS) will be used to orient the payloads such that they will be aligned ±2° to the magnetic field at apogee which achieves ±5° for all altitudes above 300 km. The orientation of the magnetic field is known much more precisely from models and previous rocket missions but some margin of error is built into the mission success criteria. At all times through flight, magnetometers on both the accelerator and receiver payloads will provide more precise knowledge of the orientation with respect to B and therefore beam pitch angle and receiver “spin tone.”
The accelerator and receiver segments will be spring-separated to place the accelerator segment on a higher altitude trajectory (apogee ~500 km) and the receiver segment on a lower-altitude trajectory with ~1 km peak separation as achievable by the spring system (Figure 2). With the rocket body oriented along B the separation creates a V primarily in the B direction. Thus, separation of the accelerator and receiver payloads is roughly field-aligned with minimal separation in the perpendicular to B direction. GPS receivers on both payloads will provide knowledge of the payload separations both along and perpendicular to B.
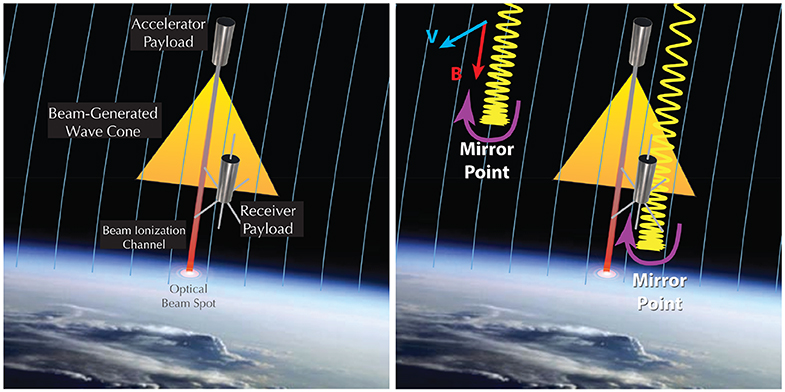
Figure 2. Schematic of the Beam PIE concept of operations. The Accelerator Payload directs the electron beam down the magnetic field line. The beam-generated waves spread out in a cone of wave power. The waves are detected and characterized by the Receiver Payload flying at a somewhat lower altitude. In the region where waves are present, they resonantly pitch angle scatter ambient ionospheric electrons which lowers their magnetic mirror points and increases the flux of upward going electrons detected at the Receiver Payload.
The electron beam on the accelerator segment will be aligned with the rocket body and therefore also directed downward along the magnetic field line. The beam will be operated in a sequence of beam “firings.” The Beam PIE linear accelerator is capable of producing beams with energies ranging from ~10–50 keV. The accelerator electronics are capable of modulating the beam at frequencies from a few Hz up to 1 MHz. Modulation frequencies of ~2–25 kHz optimize the generation of whistler-mode waves. Coherence effects maximize power at the beam modulation frequency and harmonics thereof (Harker and Banks, 1985). In the R-X mode, waves are generated at frequencies between the plasma and upper hybrid frequency regardless of the beam modulation frequency but coherence effects favor very short beam pulses (see Figures 10, 11). Using frequencies of 1 MHz and duty cycles <10% produces pulses of <100 ns which should concentrate nearly all the wave power in the R-X mode. Theory and modeling predict that both the division of power between the whistler and R-X-mode waves, and the characteristics (power, frequency, wave vector, polarization, etc.) of each wave mode, should be a strong function of the beam parameters and thus a sensitive test of our understanding of beam-plasma-wave interactions (Expected dependencies are discussed further in section Expected Results from Theory, Modeling, and Simulation).
The receiver payload includes a 3-axis electric field measurement, 3-axis search coil, fluxgate magnetometer, and a full waveform capture digital receiver that will exquisitely characterize the waves generated by the beam from the accelerator payload. The receiver payload will also measure the parameters needed to calculate the wave dispersion relation: the background magnetic field, electron temperature, and absolute electron density.
It is not our objective to measure the electron beam itself on the receiver payload. Although the plasma instrument is capable of that measurement, the beam is guided by the magnetic field and the gyroradius of the beam is extremely small relative to the size of the receiver payload. Therefore, only very precise (and fortuitous) magnetic conjunction would allow direct detection of the beam. Rather, the experiment is designed to measure beam-generated waves and scattering of ambient electrons—neither of which requires precise magnetic conjugacy.
The phase velocities of both whistler and R-X-mode waves that are generated by the electron beam are equal to the beam velocity. The group velocity of the whistler waves is in the same direction as the beam itself (i.e., downward). Those waves are fast and propagate mostly field aligned. On the other hand, the R-X-mode waves have a much smaller group velocity, oriented opposite to the beam over a wide range of angles that strongly depends on frequency. Thus, in order for the instruments in the receiver payload to detect the R-X mode waves generated by the beam injected from the accelerator payload, the receiver must be in or above the wave generation region. As is discussed above, the two payloads are spring-separated so that their distance increases with time, reaching a peak separation of about 1 km during the ~400 s duration of the experiment. The minimum separation during operation is on the order of ~100 m, since the beam firing sequence starts tens of seconds after the two payloads start to separate. The power of the waves emitted by the beam is maximized when the characteristic size of the beam pulse along the field is less or comparable to the wavelength of the mode to be excited. The expansion of the beam pulses imposes a constraint on the size of the emission region (see Section Expected Results from Theory, Modeling, and Simulation), which is stronger for R-X modes due to their smaller wavelength. Preliminary calculations indicate that the beam may continue to efficiently excite R-X modes waves over distance of several hundred meters (Delzanno and Roytershteyn, 2019), implying that the receiver payload will travel through the R-X wave generation region (which is created almost instantaneously since the beam pulses travel at a fraction of the speed of light) as its distance relative to the main payload increases. Furthermore, R-X mode waves created below the receiver payload will move upward and at least some of them will be captured by the receiver, possibly in the far-field depending on the actual cross-field separation between the two payloads. Since whistlers have significantly larger wavelength, the size of the whistler-wave-generation region is significantly larger and the receiver will be comfortably inside it. Further, the receiver could also capture whistler waves generated above the receiver payload and moving downward. We note that, in general, the area of the beam itself is only a few gyro-radii but the area over which waves can be detected is much larger. For waves propagating ±20° with respect to B, a 1 km accelerator-receiver separation produces cone of wave power ~700 m in diameter. Larger propagation angles, of course, produce a larger area of radiated power. Therefore, while the accelerator and receiver should be roughly field-aligned, considerable cross-field separations are not at all problematic and can in fact allow measurements in the far-field.
It is well-known that whistler mode waves pitch angle scatter electrons through Langmuir and gyro-resonant wave-particle interactions but the electron scattering by R-X-mode waves has not been tested in space. If the R-X-mode waves are sufficiently strong they would be expected to very efficiently pitch angle scatter ambient (background) ionospheric electrons and we will also check for this effect. Because of their polarization R-X-mode waves pitch angle scatter electrons that are traveling in the same direction as the wave phase velocity– in this case that means electrons moving down the field lines. The accelerator and receiver payloads will both operate at ~300–500 km, well above the nominal atmospheric absorption altitude of ~100 km for 10 s keV electrons. Therefore, the pitch angle distribution will have a large atmospheric loss cone and very strong anisotropies when comparing the upward and downward directed hemispheres. When the beam-generated waves are off, few particles will mirror below the receiver payload and therefore few particles should be measured moving up the field. When the beam is on, we will look for pitch angle scattering of ambient ionospheric electrons by looking at a change in the flux of upward-going electrons. A change in upward-going electrons could indicate that the waves are scattering electrons to lower mirror altitudes or that these electrons could have been precipitated (Figure 2B). To make this measurement we include two plasma spectrometers capable of measuring 0–30 keV electrons [see section Energetic Electron Spectrometer (APES)]. The receiver payload will be spinning and oriented with the spin axis aligned to the Earth's magnetic field so one plasma spectrometer will be oriented at 90° to measure locally mirroring electrons and one will be mounted facing “downward” to measure upward going electrons that have mirrored below the receiver payload. The “downward-looking” spectrometer will be oriented 70° to the spin axis which will measure electrons mirroring at ~100 km altitude (Whistler mode waves resonate with electrons propagating in the opposite direction as the waves and also resonate with much higher energy electrons so whistler mode scattering is not readily measured with this experimental set up).
Beam PIE Instrumentation
As discussed above, Beam PIE is a standard “mother-daughter” rocket configuration consisting of a main payload and a subpayload. The main “receiver” payload will house the fields, waves, and particle detectors and will be equipped with an ACS (attitude control system). The “daughter,” or “accelerator” subpayload, located forward of the main payload, will house the electron beam accelerator and power system (Figure 1).
Linear Electron Accelerator
The electron accelerator is shown schematically in Figure 3. The electron beam is generated in a DC ~10-keV “electron gun” and injected into a single 5-GHz RF cavity which can accelerate the beam an additional 40 keV for a total nominal energy range of ~10–50 keV.
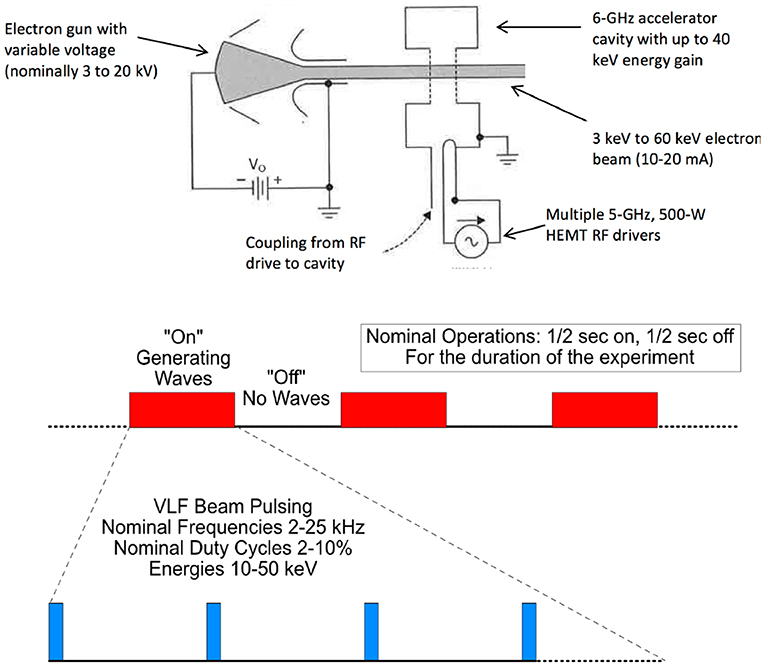
Figure 3. (Top) Schematic of the electron beam accelerator. The beam is initially created with a 10 kV COTS electron “gun.” For higher energies the beam is further accelerated a linear RF cavity driven by four high electron mobility transistors (HEMTs). (bottom) A schematic of the beam operations and VLF pulsing sequence.
When operating at 10 keV, the electron gun will produce 20 mA of current. A bare accelerator system produces a beam with ~100% E/E which is too large for efficient wave generation. Therefore, we will use a chicane magnet at the beam aperture to reduce the beam E/E to ~10%. This also reduces the emitted beam current to ~ <2 mA which is sufficiently small that no significant spacecraft charging is produced.
The 10 keV electron gun is commercial off the shelf (COTS). The accelerator cavity uses a novel LANL design that adapts common laboratory RF linear accelerator (linac) components to be suitable to space applications. One novel feature of the design is the use of high-electron mobility transistors (HEMTs) to energize the RF cavity (Figure 4). HEMTs greatly reduce power consumption and associated waste heat.

Figure 4. Left: Measured power at 5 GHz from a HEMT as a function of time. Middle: Power amplifier board (HEMT is the white square) which is used to drive the 5 GHz cavity. Right: 5 GHz RF cavity halves (in front) and assembled in a vacuum enclosure for testing with beam (background).
A notional electron beam pulse format is also shown in Figure 3. Nominal operations consist of a sequence of ½ second beam pulses separated by ½ second when the beam is off and no waves are being generated. Each ½ s of beam on time can utilize a different combination of beam energy, RF frequency, and beam duty cycle. Additionally, the range of rocket altitudes provides a range of background plasma and magnetic field conditions allowing a wide range of beam-plasma-wave interaction conditions to be investigated. The ½ s intervals when the beam (and waves) are off allows unambiguous separation of beam-generated waves from naturally occurring wave conditions.
DC and Wave Electric Field Detectors
The Beam PIE wave receiver will gather measurements of both ambient waves and plasma structures as well as plasma waves excited by the electron beams. The DC and AC vector electric field will be measured using the standard double probe technique (e.g., Pfaff, 1996). In this manner, spherical sensors with embedded pre-amps will be extended on three independent, tri-axial double probes. This configuration provides a full, three dimensional electric field measurement that will completely parameterize the vector electric field (DC to 5 MHz) including DC and wave electric fields parallel to the magnetic field direction (Figure 5).
The double probes include inner spheres (situated 0.5 m inboard of the outer spheres) to serve as multiple baseline electric field detectors or spaced receivers (Pfaff and Marionni, 1998). These “double-double” probes are similar to ones flown successfully in the auroral E-region Rocket/Radar Instability Study (ERRRIS) (rockets 21.097 and 21.100) and Cusp Transient Features Campaign (rockets 36.152, 36.153). Measurable phase shifts from these separated receivers not only establish the electrostatic nature of any ELF/VLF wave modes associated with the electron beams, but also provide a measure of their wavelength and phase velocity.
The wave receiver also includes an HF channel to observe the presence of any waves near the electron plasma frequency, such as HF Langmuir waves. The electronics will return continuous FFT power spectra of the ambient plasma environment. Furthermore, a burst memory will gather vector AC fields (three components) sampled at 10 Msample/sec each synchronized with the electron beams with ample time prior and after the actual beam discharge. Importantly, the bust waveform capture capability and dedicated telemetry system allow the opportunity for discovery of phenomena outside of the primary experimental objectives including instabilities and potential non-linear effects.
Langmuir Probe
A fixed-biased Langmuir probe will be flown in order to observe the electron plasma number density and its fluctuations. The Langmuir probe will be oriented perpendicular to the spin axis and magnetic field direction to minimize spin effects. In addition to pre-launch calibration curves and theory, the Langmuir probe will be normalized using simultaneous ground-based Poker Flat Rocket Range ionosonde data, as well as plasma wave data where applicable.
Vector Magnetometer
The Goddard Space Flight Center will furnish a vector fluxgate magnetometer similar to that flown on numerous sounding rocket experiments to measure the currents associated with the aurora, the Sq current system, and the equatorial electrojet. This magnetometer is a commercially procured Bartington type (or equivalent) for which 18-bit A/D converters will be built at the Goddard Space Flight Center. The electronics are part of the electric field electronics. These instruments provide tri-axial measurements to a resolution better than ± 1 nT. This performance is sufficient to detect VLF whistler mode waves as well as the potential effects of field-aligned currents. The magnetic field component of MHz R-X mode waves will not be measured in this experiment.
Search Coil
The Search Coil unit is an AC magnetic field sensor capable of detecting the B-field vector of an electromagnetic plasma or radio wave. Each coil has many thousands of turns to convert a wave's dB/dt into an output sensor voltage between 10 Hz and 100 kHz. The analog output V(t) from each sensor can then drive an ADC for inclusion in the data stream for return and subsequent spectral analysis. Figure 6 shows a set of flight units built by Goddard Space Flight Center for the Air Force's DSX mission (Scherbarth et al., 2009).
Combined Electronics and Burst Memory
The electronics for the combined DC/Wave electric field instrument and the fluxgate and search coil magnetic field instruments, as well as the Langmuir probe, will be integrated into a combined electronics assembly built by Goddard. Similar unites have been flown on numerous previous experiments. The Goddard group will also provide a burst memory for the payload that will be synchronized with the electron beams, as was successfully carried out as part of the fields experiment for the APEX high density beam releases (see Pfaff et al., 2004). The burst memory will gather precursor data prior to the beam activation, to ensure that the fastest particles and wave modes associated with the release itself will be captured. The burst memory will record HF and MF vector data gathered by the electric field detectors.
Energetic Electron Spectrometer (APES)
The preceding instruments, as described, are all required for the primary Beam PIE science objectives—generation of whistler and R-X-mode waves with a novel linear electron accelerator. We also note that the previously-discussed receiver payload instruments can operate in any orientation with respect to the magnetic field and can operate equally well on a non-spinning platform.
The secondary objective of Beam PIE, however, is to study the effect of the waves on ambient electrons. Specifically we investigate pitch angle scattering by R-X mode waves.
The Beam PIE energetic electron spectrometer (known as the Acute Precipitating Electron Spectrometer, APES) uses magnetic deflection to measure the locally-mirroring and upward-going electrons with high cadence over a 150 eV to >30 keV energy range. The APES field of view is 10° × 10°. One APES spectrometer is oriented at ~90° to the ambient magnetic field to measure locally-mirroring electron. The other is oriented at 70° to the spin axis in order to measure upward-going electrons that mirror below the rocket at ~100 km altitude. An increase in the ratio of upward going electrons to locally-mirroring electrons indicates pitch angle scattering by the R-X mode waves.
APES [described in detail in Michell et al. (2016)] uses a micro-channel plate (MCP) detection system with 50 discrete anodes (energies). Ray tracing analysis of the magnetic deflection system to be used is presented in Figure 7 next to a photograph of the APES instrument that flew on the GREECE mission.

Figure 7. A ray tracing of the magnetic deflection system for APES, showing the paths of electrons of different energies (left), a photograph of the APES that flew on the GREECE mission (middle), and field-aligned electron measurements from the GREECE mission (right).
Ground-Based Diagnostics
To the extent feasible, radar and optical ground-based instrumentation will be used to measure the properties of the ambient plasma before and during the beam injection and to remotely measure the ionospheric effects of the primary beam energy deposition and enhanced precipitation from wave-particle interactions. The effects that we will be looking for is the electron density (Ne) perturbation over background, measured with incoherent scatter radar and optical emissions using ground-based imagers.
The Poker Flat Incoherent Scatter Radar (PFISR) is operated by SRI International on behalf of the National Science Foundation and it will be operated during the rocket flight. PFISR is a modular, UHF phased-array capable of beam steering on a pulse-to-pulse basis (Nicolls et al., 2007). PFISR operations will start at least 2 h before and continue at least 2 h after the rocket's launch window.
The radar's mode of operation for the Beam PIE rocket flight will consist of multiple beams with orientations selected to measure the ambient Ne and convection along the foot-point of the rocket's trajectory and its vicinity, as well as the perturbation Ne caused by the energy deposition of the electron beam. Measurements of the electron density perturbations as a function of beam energy and current will provide diagnostics of beam propagation from the accelerator payload and energy deposition into the atmosphere. Detection of optical emissions from the interaction of the beam with the atmosphere provide opportunities for additional beam diagnostics. The optical emissions are similar to naturally-occurring aurora but, with this active experiment we have precise knowledge of beam energies, currents, and frequencies [e.g., Marshall et al. (2014)].
Expected Results From Theory, Modeling, and Simulation
Expected Results—Wave Generation
The primary objectives of the Beam Plasma Interactions Experiment are to test our understanding of wave generation through beam-plasma interactions. We will independently test the generation of whistler-mode and R-X-mode waves as well as the partitioning of energy between the modes. Wave diagnostics include wave spectral power density, polarization, ellipticity, and Poynting flux. While the space physics community has come to understand the power of such measurements, what makes Beam PIE unique is the ability to do active, controlled experiments with unprecedented flexibility in pulsed electron beam parameters. We have the ability to independently vary beam energy, pulse frequency, and duty cycle. In addition, the trajectory of the rocket naturally samples different background plasma conditions (density, temperature and magnetic field strength) that determine the plasma wave dispersion relation.
For wave generation, the starting point is the theory of Harker and Banks (Harker and Banks, 1983 labeled “HB” in the following; 1985; 1987) which solves the cold plasma dispersion relation to obtain the wave amplitudes for a sequence of beam pulses with finite length (labeled “lp”) along the direction of motion, while the pulses are infinitesimal in the perpendicular direction. These pulses are assumed to move with a constant velocity and pitch angle α relative to the background magnetic field and the response of the plasma to the beam pulses is calculated in the framework of cold-plasma linear theory. The HB theory was developed in the 1980's, stemming from earlier work that calculated the radiated power from a point charge (McKenzie, 1963; Mansfield, 1967) and was used for the interpretation of ionospheric electron-beam experiments such as Spacelab 1 and 2 (Gurnett et al., 1986; Bush et al., 1987; Farrell et al., 1988, 1989; Reeves et al., 1988, 1990a,b; Farrell and Goertz, 1990). It is used here as a reference and, later in this section, we discuss its limitations and the physical effects that will need to be incorporated for more accurate predictions of waves generated by Beam PIE.
In order to obtain realistic parameters for Beam PIE, we have used the International Reference Ionosphere (IRI) model for the month of March 2009 at 0 Local Time and for altitudes between 300 and 500 km. The corresponding average density is n = 3.8·104 cm−3. The average magnetic field for the same altitudes at the Poker Flat (Alaska) launch site is B0 = 4.7·10−5 T. These parameters give the ratio of the electron plasma frequency (ωpe) to the cyclotron frequency (ωce) equal to ωpe/ωce = 1.33. In what follows, we assume hydrogen ions.
Generation of Whistler Waves
Figure 8 shows the power spectral density obtained from HB in the whistler regime (ω ≤ ωce), for three beam energies equal to 14, 34, and 54 keV. The former value corresponds to the maximum energy obtained from the DC electron gun, while the latter value is the maximum energy achievable after the RF accelerator cavity. The calculation is performed for a single beam pulse of length corresponding to the pulse period tp = 100 ns and the power spectral density is in units of [] (where qp is the pulse charge, ϵ0 is the permittivity of vacuum and c is the speed of light). We have also used a beam pitch angle α = 1° to account for inaccuracies in beam pointing relative to our target of injection aligned to the background magnetic field and only computed contributions due to the Landau resonance (as appropriate for a field-aligned beam). Note also that a finite pitch angle is necessary to obtain a finite total radiated power (McKenzie, 1963). Figure 8 (left) shows that the whistler signal breaks into two distinct frequency bands for E = 34 keV and shrinks considerably in frequency for E = 54 keV. Consistently, the whistler radiated power drops by two orders of magnitude for energies above E ~ 35 keV.
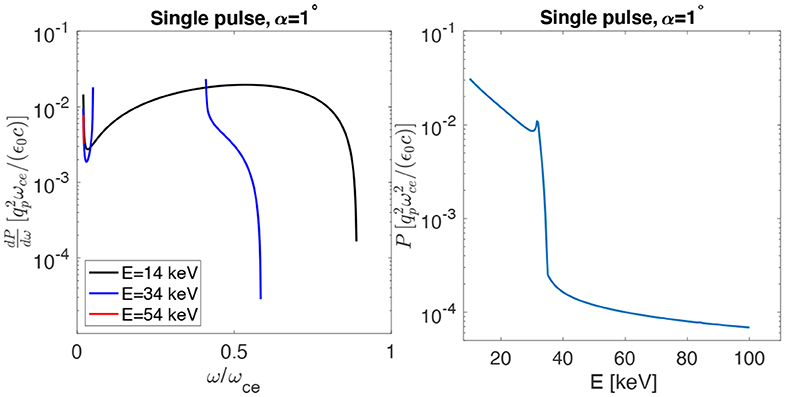
Figure 8. Power spectral density and integrated power for beam-generated whistler waves for different beam energies.
Generation of R-X-Mode Waves
The whistler branch is not the only regime where the beam can couple with a magnetized plasma. Figure 9 (left) shows the power spectral density vs. frequency with the same format of Figure 8, extending the frequency range from ω = ωpe to the upper hybrid frequency ωuh = 1.64ωce. Comparing against Figure 8 shows that the R-X-mode wave signal is quite similar for the beam energies considered and, most important, it can be orders of magnitude stronger than the whistler mode signal. The total radiated power in Figure 9 (right) shows a decreasing trend with beam energy but is several orders of magnitudes higher that the power radiated in the whistler range for all cases considered. These results indicate that highest radiation and, hence, highest beam-plasma coupling may be achieved through the R-X-mode.
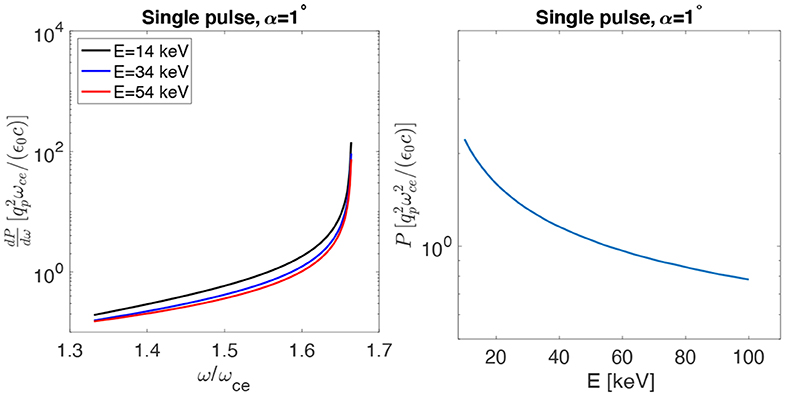
Figure 9. Power spectral density and integrated power for beam-generated R-X-mode radiation for different beam energies.
Beam Operations for Wave Generation
While we have demonstrated that both whistler and R-X-modes can be excited by an electron beam, a primary objective of Beam PIE is to use controlled experiments to quantitatively test our understanding of beam-plasma-wave interactions. The beam parameters that can be user-selected are beam energy (i.e., velocity), modulation frequency, and pulse duty cycle. We have designed nominal beam operation modes to test each of these parameters.
An example of the predicted energy partitioning between whistler and R-X-mode waves is shown in Figures 10, 11, together with more detailed examples of wave dependence on beam parameters. Figure 10 is obtained for beam energy E = 14 keV, pitch angle α = 1°, 100 pulses of length corresponding to 100 ns and varying the duty-cycle between 5 and 20%. This corresponds to a beam modulation between 500 kHz and 2 MHz, which targets the R-X mode. Indeed, despite the fact that both whistler and R-X modes are generated, the total radiated power is overwhelmingly in the R-X modes. Figure 11 is obtained for the same parameters of Figure 10, except that the duty-cycle is fixed at 5% and the pulse length is varied between 1 μs and 4 μs. Since the duty-cycle is constant, varying the pulse length implies a modulation between 12.5 kHz and 50 kHz, i.e., in the whistler regime. Unlike the case in Figure 10, in this case the radiated power in whistler and R-X mode waves is comparable. Note that the total normalized radiated power in Figure 11 is lower than that in Figure 10 because it is plotted in units of []. For the same beam current, a 1 μs beam pulse has 10 times larger pulse charge than a 100 ns beam pulse, implying that in reality the total radiated power in dimensional units is comparable in the two cases. In each of these cases both whistler and R-X-mode waves are generated. We note, however, that the partitioning of wave energy, the spectral shape in each mode, and the harmonic structures are all strongly frequency dependent providing a very sensitive test of the theory of beam-plasma-wave interactions.
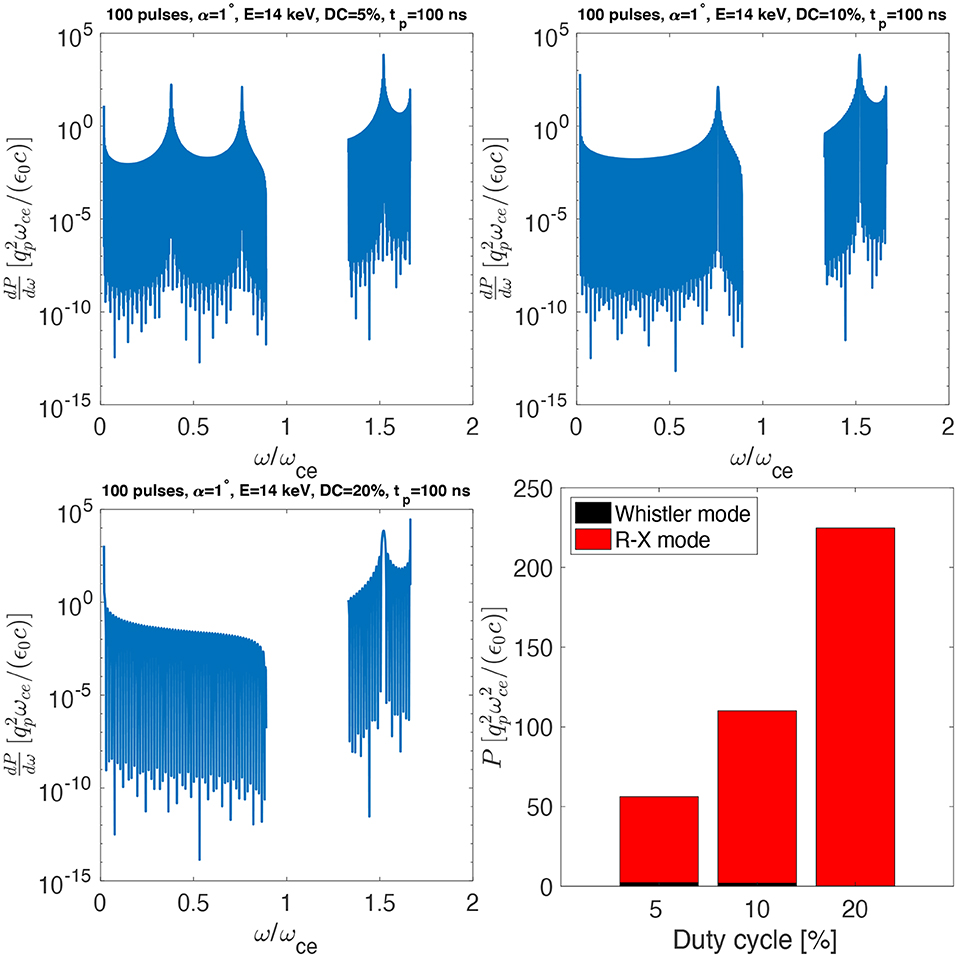
Figure 10. Predicted Whistler (ω/ωce < 1) and R-X-mode (ω/ωce > 1.3) wave power spectra for a 14 keV beam with varying pulsing duty cycles (top and bottom-left panels). Note the discrete harmonic structure. The bottom-right panel shows the partition of the total integrated power between whistler and R-X modes.
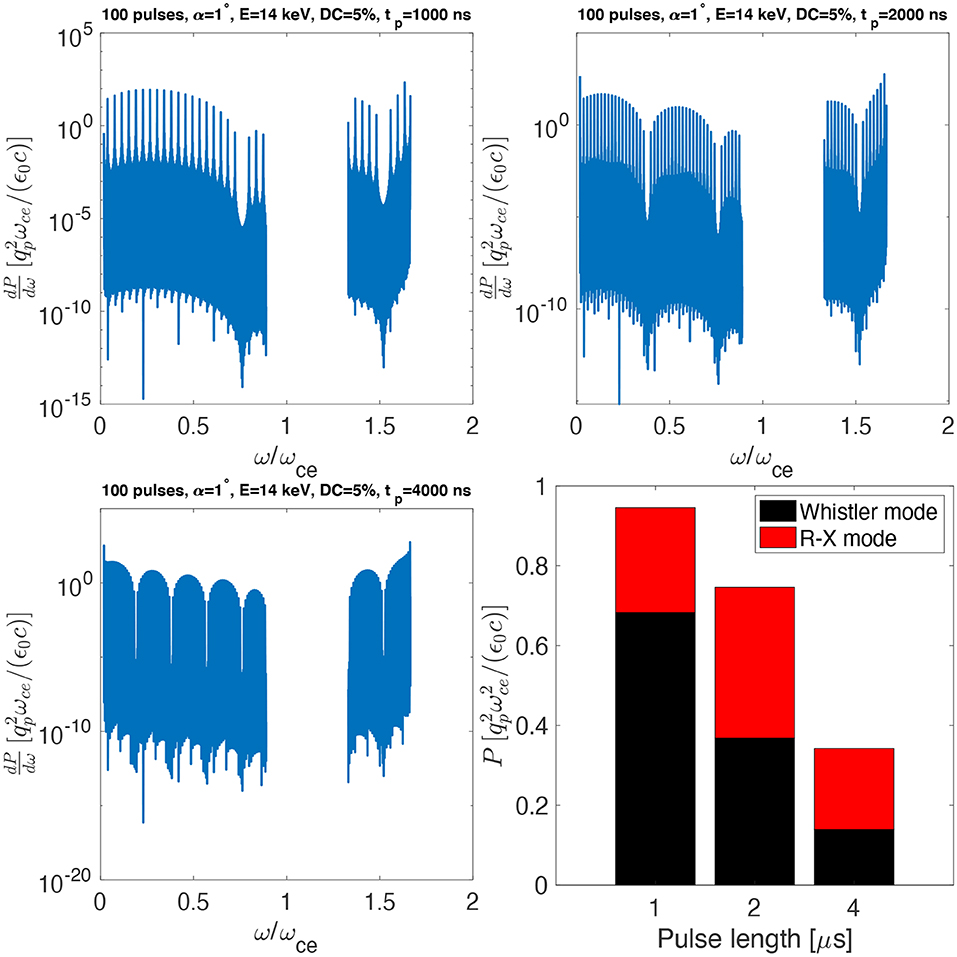
Figure 11. Predicted Whistler (ω/ωce < 1) and R-X-mode (ω/ωce > 1.3) wave power spectra for a 14 keV beam with 5% pulsing duty cycle. The top and bottom-left panels differ only in beam pulse length. The bottom-right panel shows the partition of the total integrated power between whistler and R-X modes.
Simulation Support for Beam PIE
The HB theory provides a good starting point to estimate the response of a magnetized plasma to a pulsed electron beam. However, it has a number of limitations that need to be addressed to improve the accuracy of the Beam PIE predictions. In particular, the theory assumes an infinitesimal transverse direction of the beam and is based on cold-plasma theory. These approximations imply that there are resonances at the lower- and upper-hybrid frequencies where the power spectral density diverges, even though the total radiated power remains finite (for non-zero pitch angles). The behavior of the power spectral density near resonances affects the total radiated power and the partition between whistler and R-X modes—particularly the power in the R-X modes since the power spectral density is monotonically increasing toward the upper-hybrid frequency, c.f. Figure 9. There are several effects that can regularize the power spectral density (finite transverse beam size, thermal effects, non-linear effects and collisions) around resonances and that need to be properly considered. Furthermore, the HB theory does not take into account beam dynamics nor the potential feedback between the plasma and the beam. The beam dynamics are important because the beam pulses can radiate efficiently (i.e., coherently) in certain wavelengths only if the longitudinal extension of the beam pulse is smaller/comparable to the excited wavelengths and this affects the longitudinal extension of the radiated wave field. The beam dynamics are in itself fairly complex since the beam can expand longitudinally due to its space-charge, while oscillating transversely due to the combined effects of space charge and the Lorentz force. How much the beam pulse charge is neutralized by the background plasma also affects the beam dynamics. Last, the feedback between beam and plasma is a possible source of instability, whose effect on the radiation pattern needs to be evaluated. Generally speaking, earlier work showed that the small, finite-size beam radius decreases the growth rate of the electrostatic two-stream instability (Galvez and Borovsky, 1988) and early active experiments showed that beams could propagate long-distances in space (Winckler, 1982). A Spacelab experiment, on the other hand, showed radiation levels consistent with coherent Cherenkov emission and attributed it to beam bunching due to the two-stream instability (Farrell et al., 1989). Note that the criteria for beam instability is expected to be k∥Vb ~ ωpe, where Vb is the beam velocity (Gary, 1993). Since this is approximately the same criterion for R-X mode emission, it gives a pulse length for instability comparable to that where coherent effects will quench radiation into R-X modes. Thus, using short (100 ns) pulses maximizes radiation into R-X modes but also prevents the development of the instability. Longer pulses (either directly from the accelerator or elongated by pulse expansion via space-charge effects) could potentially become unstable and create bunches and this regime will also be tested by Beam PIE.
As a first step to address the limitations just discussed, we have modified the HB theory to account for pulses of finite transverse size, assuming pulses with a Gaussian shape characterized by a width along and perpendicular to the magnetic field, l|| and l⊥, respectively. While a cylindrical shape is characteristic of pulses when they leave the RF accelerator (B. Carlsten, personal communication), a Gaussian shape might be more appropriate on longer time-scales of beam dynamics. We have applied the finite-transverse-size HB theory to the same case presented in Figure 10, for a beam with l⊥ = 0.1 m and l|| = 3.4 m. The results for the partition of the radiated power between whistler and R-X modes vs. duty cycle are shown in Figure 12 (left), where one can see that the radiated power is still dominated by R-X modes but it is lower by ~ 20–30% than what shown in Figure 10. Figure 12 (right) shows the applications of the finite-transverse-size HB theory to the same case presented in Figure 11, for a beam with l⊥ = 0.1 m and l|| = 34 m (pulse length = 1 μs), l|| = 69 m (2 μs) and l|| = 138 m (4 μs), for a 5% duty cycle. While there is small reduction in the whistler radiated power, one can see that radiation in R-X modes is completely quenched (c.f. Figure 11) since the pulse lengths are now larger than the characteristic wavelength of the modes. These results emphasize the importance of treating beam dynamics and the pulse evolution in the determination of the beam-generated wave field.
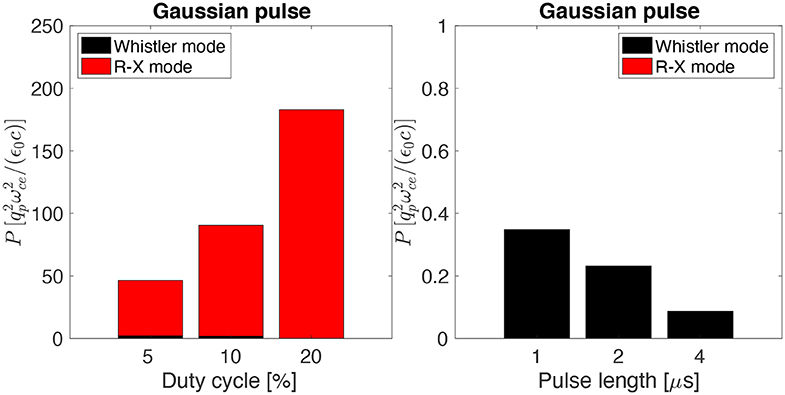
Figure 12. Predicted Whistler (ω/ωce < 1) and R-X-mode (ω/ωce > 1.3) partition of radiated wave power for a 14 keV beam made of 100 pulses with a Gaussian shape: (left) pulse length 100 ns for different duty cycles; (right) 5% duty cycle for different pulse lengths.
Furthermore, in order to address the issue of beam dynamics and stability, we have adopted a two-pronged approach. First, we are performing simulations of wave emission by a pulsed beam of a given shape with a highly accurate three-dimensional Vlasov code called the Spectral Plasma Solver (SPS) (Delzanno, 2015; Vencels et al., 2016; Roytershteyn and Delzanno, 2018). Second, we are performing simulations of beam pulse dynamics using the Particle-In-Cell (PIC) simulation code VPIC (Bowers et al., 2008). The properties of the spectral and PIC methods complement each other, so that such an approach allows for the most efficient exploration of the processes of interest.
SPS uses a spectral decomposition of the plasma distribution function in terms of Hermite polynomials in velocity space, a Fourier decomposition in physical space (appropriate for problems with periodic boundary conditions) and an implicit time discretization. The velocity-space spectral decomposition is such that one can describe the plasma as a macroscopic fluid with the low-order moments of the expansion, while the kinetic physics is retained by adding more moments (Vencels et al., 2015). The beam simulations are performed using NH = 4 Hermite polynomials in each velocity direction (corresponding to a fluid approximation) and the number of spatial modes along x, y, z directions equal correspondingly to 150, 150, and 248. The beam, implemented as an external current in the simulation, moves along z axis aligned with the external magnetic field B0.
Figure 13a shows the By component of the magnetic field (normalized to B0) at the end of a simulation (ωpet = 120) with E = 14 keV for a single beam pulse. The pulse is introduced into SPS as an external current produced by a cylindrical pulse with a total charge of 2 nC uniformly distributed inside the cylinder (shown as a black rectangle at z/de ~ 32). The initial length of the pulse corresponds to a 100 ns beam pulse, while its radius is equal to 0.1 de. In this SPS simulation, we follow the longitudinal dynamics of the pulse due to its own space charge but do not model the transverse dynamics of the pulse (see section First-principle simulations of Beam Dynamics). Also, we do not account for any potential neutralization of the beam pulse charge due to the background plasma. Two modes of radiation are clearly visible: the whistler mode (with longer wavelengths) and the R-X-mode (with shorter wavelengths). As the pulse propagates, its length increases and at z/de ~ 25 the length of the pulse becomes comparable to the wavelength of the R-X-mode plasma wave. Above this point the radiation is dominated by the whistler mode waves as radiation in the R-X-mode decreases significantly due to coherence effects as expected from radiation theory (c.f. Figure 12). The wave spectrum of the radiation field from the single pulse simulation is shown in panel (b) where the presence of the two modes can be further differentiated. Panel (c) in Figure 13 shows radiation from a 10-pulse finite-length beam with the same parameters as in Figure 13a but modulated by a frequency equal to (ωpe + ωuh)/2 corresponding to a frequency of R-X-mode plasma waves. As expected from HB theory (Figure 10), the radiation is dominated by the R-X-mode. This is also confirmed by a spectrum of the radiation shown in panel (d). At z/de ~ 27 the pulses (shown by black rectangles) merge and the radiation field is dramatically reduced by coherence effects. Figure 13c suggests that, for the parameters considered, radiation in the R-X mode would be maximized over ~20 de (i.e., ~600 m). Future work will revisit this type of simulations including the transverse beam dynamics, beam energy spread and beam-pulse neutralization to make more accurate predictions of the extension of the R-X-mode wave field and optimize the separation between accelerator and receiver payloads accordingly.
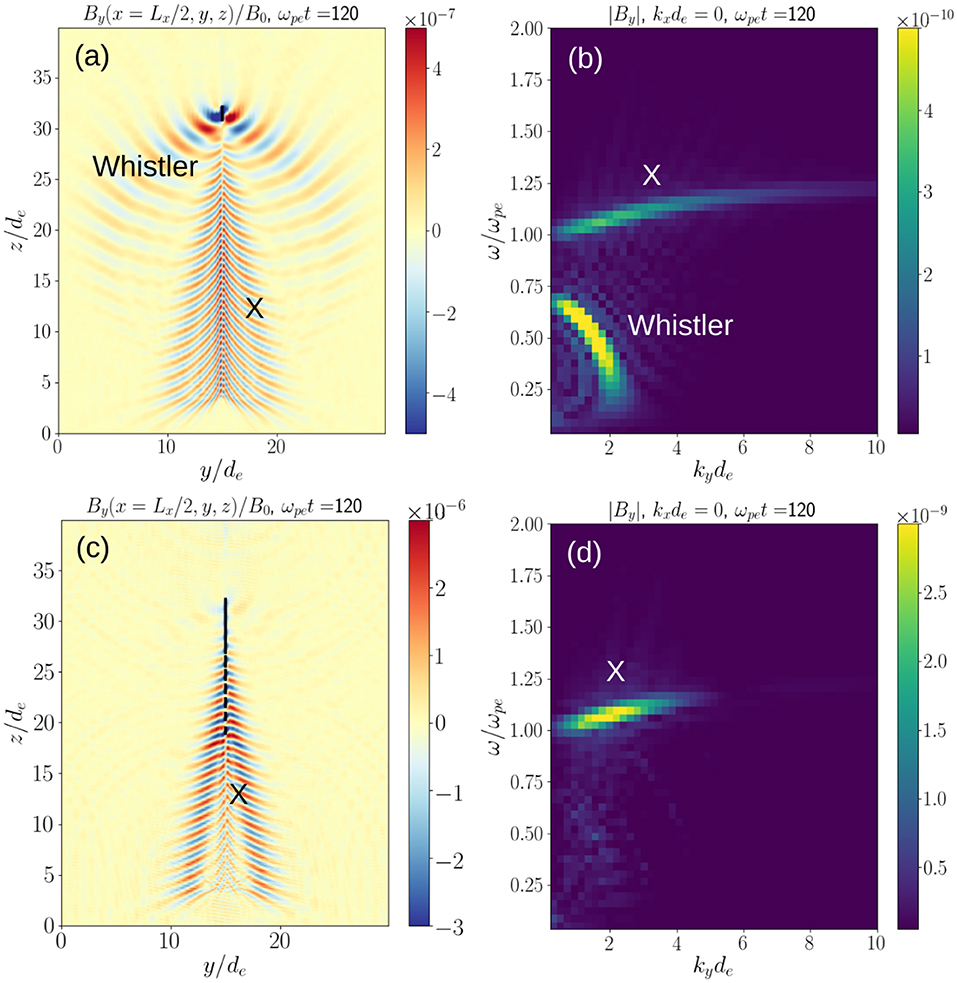
Figure 13. The By radiation field at ωpet = 120 generated by (a) single beam pulse and (c) 10-pulse beam modulated by a high frequency characteristic of R-X-mode waves. The energy of each pulse is 14 keV and charge per pulse is 2 nC. The corresponding spectra are shown in panels (b,d).
A detailed comparison of wave generation and SPS simulations for a Gaussian pulse can be found in Delzanno and Roytershteyn (2019).
The type of simulations presented in Figure 13 already remove some of the limitations of the HB theory. By accounting for finite-size beam pulses, thermal and non-linear effects, we can compute a finite radiated power in the whistler and R-X modes and compute the corresponding wave amplitudes for Beam PIE. In addition, a model for beam dynamics, which includes also the transverse dynamics, is being implemented in SPS, thus allowing calculations of the effect of the beam dynamics on the wave field and, in particular, of its extent before coherence effects reduce the waves amplitude.
First-Principle Simulations of Beam Dynamics
The spectral plasma solver (SPS) simulations described in the previous section allow us to assess properties of the (relatively weak) radiated field. However, their computational cost would increase dramatically if the beam dynamics and feedback between the beam pulses and the magnetized plasma were fully resolved. Particle in Cell (PIC) methodology offers a convenient alternative to study such processes. The trade-off is that the radiated field is not accurately described, mostly due to statistical noise associated with the finite number of computational particles.
Here we discuss some of the results from a preliminary VPIC simulation intended to study dynamics of beam pulses. The VPIC code solves a system of relativistic Maxwell-Vlasov equations for each plasma species in a 3D domain of spatial extent Lx = Ly ≈ 0.065de and Lz ≈ 5.5de with uniform magnetic field in the z direction. Boundary conditions corresponding to a perfect electric conductor are used on x and y boundaries and a perfect magnetic conductor on z boundaries. The number of cells is 200 × 200 × 16384. The simulation is initialized with a uniform, two-component plasma with the following parameters: , ωpe/ωce = 1.3, mi/me = 1, 836. As the simulation progresses, beam pulses with energy Eb = 14KeV are injected at z ≈ 0 with a δ-function distribution in energy. The beam electrons are treated as a separate plasma species. The initial beam radius is and the initial beam density is approximately 38 times higher than the background. The length of a single pulse is approximately tp1ωpe ≈ 1 and the time interval between pulses is tp2ωpe ≈ 2π. The beam is injected with zero pitch angle. The beam particles are absorbed at the other end of the domain at z ≈ Lz. In the simulation discussed here, no additional positive charge is injected in the system to compensate for the injected beam charge.
As the beam pulse is injected, the electrostatic repulsion drives its rapid expansion transversely and, to a lesser degree, longitudinally, along the beam propagation direction (also aligned with the background magnetic field). This is illustrated in Figure 14, which shows density-weighted mean-square radius of the pulses as a function of z, the coordinate along the magnetic field. The transverse expansion is counterbalanced by the Lorentz force, such that mean beam radius oscillates in z. We note that in this simulation the pulses are injected with zero pitch angle spread and, hence, the dynamic value of the beam pulse radius is quite smaller than that used in the studies of Figure 13, rb = 0.1de. The transverse structure of a single pulse is shown in Figure 15. Here, the top panel shows an isosurface of constant beam density (beam density equal to 0.1 of the reference background density for the case shown). The middle panel shows profiles of background ion and electron densities, as well as the profile of the beam density along the cut indicated in the top panel. Profiles of the electric field Ex and the beam rotation velocity Uby along the same cut are shown in the bottom panel. Several important observations could be immediately made: i) individual beam pulses are shaped by a combined action of electrostatic repulsion, Lorentz forces, and instabilities; ii) the resulting microscopic structure is quite complex, but overall the beam pulse maintains coherence on spatial scales relevant to wave emission; iii) the beam pulse is partially charge-neutralized by the electrons of the background plasma, which reduces the severity of the electrostatic repulsion.
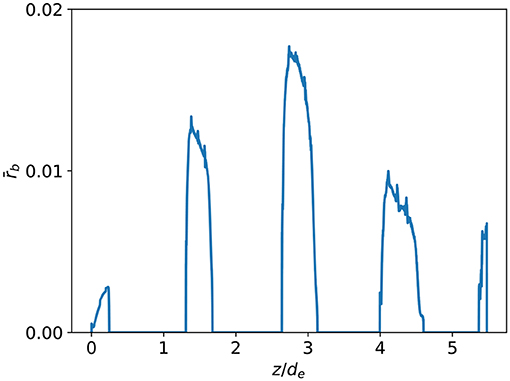
Figure 14. Density-weighted radius (normalized to de) of beam pulses in a PIC simulation of beam dynamics as a function of the distance along the background magnetic field. The velocity is normalized to the E × B drift value corresponding to the peak electric field, while E× is normalized to its peak value.
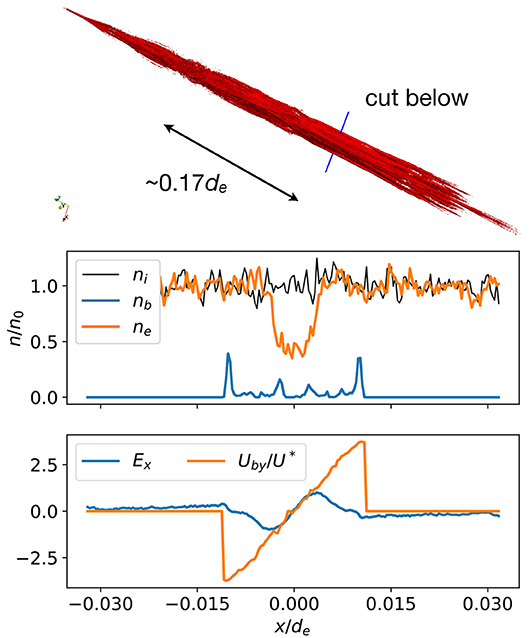
Figure 15. Top panel: isosurface of constant beam density for a beam pulse in PIC simulation of beam dynamics. The region shown corresponds to the pulse between 4de ≤ z ≤ 4.5de (see Figure 14). Middle panel: profiles of the beam density and those of the background ion and electron densities along the cut at ≈ 4.2de, indicated in the top panel. Bottom panel: profiles of radial electric field and transverse (rotational) beam velocity. The velocity is normalized to the E x B drift value corresponding to the peak electric field.
Discussion
This paper describes the Beam-Plasma Interactions Experiment. Beam PIE is an active experiment that uses a novel linear accelerator based electron beam and advanced wave and plasma diagnostics instruments to test beam wave-generation physics in greater detail than previously possible. The experiment uses a mother-daughter payload with the higher-altitude payload carrying the linear accelerator and the lower-altitude payload carrying a suite of wave and particle detectors. The first objective of the experiment is to conduct the first tests of modern linear accelerator technology in space which, if successful, could enable a new generation of active experiments. The second objective is to test the generation of whistler waves by the electron beam over a range of parameters (energy, modulation frequency, and duty cycle) not previously investigated in space. The third objective is to test the generation of R-X-mode radiation by the electron beam—an experiment that has not previously been done. The partitioning of energy and the detailed characteristics of the whistler vs. R-X-mode waves should be a sensitive test of our understanding of beam-plasma-wave interactions.
One example of a future active experiment is the Magnetosphere-Ionosphere Connections Explorer (CONNEX). The objective of this mission concept is to understand the magnetospheric processes that produce different types of auroral forms. It would use a multi-cell RF linear accelerator to accelerate electrons to energies up to 1 MeV. The beam is strong enough to produce a visible spot in the auroral ionosphere to test the magnetic connectivity between the auroral ionosphere and the dipole-to-tail transition region in the equatorial magnetosphere. We note, however, that the design of the CONNEX beam would also allow pulsed-beam operations and therefore the opportunity to test the generation of waves by pulsed electron beams under magnetospheric (rather than ionospheric) conditions. Both CONNEX and the USAF DSX experiment (which uses a physical antenna to generate waves) could provide technology demonstrations for future active modification of the space environment including remediation of artificial radiation belts from High Altitude Nuclear Explosions (Reeves, 2018; Carlsten et al., 2019).
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
GR is PI of the Beam PIE mission and PF is deputy PI and payload manager. GD, KY, and VR are responsible for the simulation and modeling work shown. BC, JL, MH, and DN make up the electron accelerator team. RP is Goddard lead and responsible for the DC and AC electric field experiments as well as the fluxgate magnetometer. WF is responsible for the search coil. DR is responsible for the Langmuir probe. MS is responsible for the electron plasma spectrometer. ERS, ES, and ED are responsible for ground observations.
Funding
Funding for the Beam PIE investigation is provided by the National Aeronautics and Space Administration, NASA, under grant number 80HQTR18T0078. GD was supported by the US Department of Energy through the Los Alamos National Laboratory, Laboratory Directed Research and Development (LDRD) program. KY acknowledges support from the Center for Space and Earth Science (CSES) of the Los Alamos National Laboratory. The Los Alamos National Laboratory LDRD and CSES program offices were not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy. The simulation work used resources provided by the Los Alamos National Laboratory Institutional Computing Program. Contributions of VR were supported by NSF award 1707275 and NASA award 80NSSC18K1232. PIC simulations were conducting using resources provided by the NASA High-End Computing Program through the NASA Advanced Supercomputing Division at Ames Research Center as well as resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.
Conflict of Interest
ERS was employed by company SRI International.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to the Magnetosphere-Ionosphere Connections (CONNEX) satellite team for close collaborations and many fruitful discussions.
References
Baker, D. N., Jaynes, A. N., Li, X., Henderson, M. G., Kanekal, S. G., Reeves, G. D., et al. (2014). Gradual diffusion and punctuated phase space density enhancements of highly relativistic electrons: Van Allen Probes observations. Geophys. Res. Lett, 41, 1351–1358. doi: 10.1002/2013GL058942
Banks, P. M., Gilchrist, B. E., Neubert, T., Myers, N., Raitt, W. J., Williamson, P. R., et al. (1990). Charge-2 rocket observations of vehicle charging and charge neutralization. Adv. Space Res, 10, 133–136. doi: 10.1016/0273-1177(90)90286-9
Bowers, K. J., Albright, B. J., Yin, L., Bergen, B., and Kwan, T. J. T. (2008). Ultrahigh performance three-dimensional electromagnetic relativistic kinetic plasma simulation. Phys. Plasmas 15:055703. doi: 10.1063/1.2840133
Bush, R. I., Reeves, G. D., Banks, P. M., Neubert, T., Williamson, P. R., Raitt, W. J., et al. (1987). Electromagnetic fields from pulsed electron beam experiments in space: Spacelab-2 results. Geophys. Res. Lett. 14, 1015–1018. doi: 10.1029/GL014i010p01015
Cambou, F., Dokoukine, V. S., Lavergnat, J., Pellat, R., Reme, H., Saint-Marc, A., et al. (1980). General description of the ARAKS experiments. Ann. Geophys. 36, 271–284.
Cambou, F., Lavergnat, J., Migulin, V. V., Morozov, A. I., Paton, B. E., Pellat, R., et al. (1978). ARAKS—Controlled or puzzling experiment? Nature 271, 723–726. doi: 10.1038/271723a0
Carlsten, B. E., Patrick Colestock, L., Gregory Cunningham, S., Gian Luca, D., Eric Dors, E., Michael Holloway, A., et al. (2019). Radiation-belt remediation using space-based antennas and electron beams. IEEE Trans. Plasma Sci. 47, 2045–2063. doi: 10.1109/TPS.2019.2910829
Dechambre, M., Kushnerevsky Yu, V., Lavergnat, J., Pellat, R., Pulinets, S. A., and Selegei, V. V. (1980). Waves observed by the ARAKS experiments: the whistler mode. Ann. Geophys. 36, 341–349.
Delzanno, G. L. (2015). Multi-dimensional, fully-implicit, spectral method for the Vlasov–Maxwell equations with exact conservation laws in discrete form. J. Comput. Phys. 301, 338–356. doi: 10.1016/j.jcp.2015.07.028
Delzanno, G. L., and Roytershteyn, V. (2019). High-frequency plasma waves and pitch angle scattering induced by pulsed electron beams. J. Geophys. Res. 124, 7543–7552. doi: 10.1029/2019JA027046
Farrell, W. M. A. D., Gurnett Banks, P. M., Bush, R. I., and Raitt, W. J. (1988). An analysis of whistler-mode radiation from the Spacelab-2 electron beam. J. Geophys Res. 93, 153–161. doi: 10.1029/JA093iA01p00153
Farrell, W. M., and Goertz, C. K. (1990). The coherent Cerenkov radiated power from a group of field-aligned test particles in a magnetoplasma. Planet. Space Sci. 38, 373–381. doi: 10.1016/0032-0633(90)90103-W
Farrell, W. M., Gurnett, D. A., and Goertz, C. K. (1989). Coherent Cerenkov radiation from the Spacelab 2 electron beam. J. Geophys. Res. 94, 443–452. doi: 10.1029/JA094iA01p00443
Galvez, M., and Borovsky, J. E. (1988). The electrostatic two-stream instability driven by slab-shaped and cylindrical beams injected into plasmas. Phys. Fluids 31, 857–862. doi: 10.1063/1.866767
Gary, S. P. (1993). Theory of Space Microinstabilities. New York, NY: Cambridge University Press. doi: 10.1017/CBO9780511551512
Gendrin, R. (1974). The French-Soviet ‘ARAKS’ experiment. Space Sci. Rev. 15, 905–931. doi: 10.1007/BF00241068
Gurnett, D. A., Kurth, W. S., Steinberg, J. T., Banks, P. M., Bush, R. I., and Raitt, W. J. (1986). Whistler-mode radiation from the Spacelab 2 electron beam. Geophys. Res. Lett. 13, 225–228. doi: 10.1029/GL013i003p00225
Harker, K. J., and Banks, P. M. (1983). Radiation from pulsed electron beams in space plasmas. Planet. Space Sci. 19, 454–470. doi: 10.1029/RS019i002p00454
Harker, K. J., and Banks, P. M. (1985). Radiation from long pulse train electron beams in space plasmas. Planet. Space Sci. 33, 953–963. doi: 10.1016/0032-0633(85)90109-6
Harker, K. J., and Banks, P. M. (1987). Near fields in the vicinity of pulsed electron beams in space. Planet. Space Sci. 35, 11–19. doi: 10.1016/0032-0633(87)90139-5
Hendrickson, R. A., McEntire, R. W., and Winckler, J. R. (1975). Echo 1: an experimental analysis of local effects and conjugate return echoes from an electron beam injected into the magnetosphere by a sounding rocket. Planet. Space Sci. 23:1431. doi: 10.1016/0032-0633(75)90039-2
Hendrickson, R. A., Winckler, J. R., and Arnoldy, R. L. (1976). Echo III: the study of electric and magnetic fields with conjugate echoes from artificial electron beams injected into the auroral zone ionosphere. Geophys. Res. Lett. 3, 409–412. doi: 10.1029/GL003i007p00409
Jordanova, V. K., Albert, J., and Miyoshi, Y. (2008). Relativistic electron precipitation by EMIC waves from self-consistent global simulations. J. Geophys. Res. 113, 1–11. doi: 10.1029/2008JA013239
Mansfield, V. N. (1967). Radiation from a charged particle spiraling in a cold magnetoplasma. Astrophys. J. 147, 672–680. doi: 10.1086/149043
Marshall, R. A., Nicolls, M., Sanchez, E., Lehtinen, N. G., and Neilson, J. (2014). Diagnostics of an artificial relativistic electron beam interacting with the atmosphere. J. Geophys. Res. 119, 8560–8577. doi: 10.1002/2014JA020427
McKenzie, J. F. (1963). Cerenkov radiation in a magneto-ionic medium (with application to the generation of low-frequency electromagnetic radiation in the exosphere by the passage of charged corpuscular streams). Philosoph. Trans. R Soc. 255, 585–606. doi: 10.1098/rsta.1963.0012
Michell, R. G., Samara, M., Grubbs, G., Ogasawara, K., Miller, G., Trevino, J. A., et al. (2016). APES: acute precipitating electron spectrometer-a high time resolution monodirectional magnetic deflection electron spectrometer. J. Geophys. Res. 121, 5959–5965. doi: 10.1002/2016JA022637
Monson, S. J., Kellogg, P. J., and Cartwright, D. G. (1976). Whistler mode plasma waves observed on electron Echo 2. J. Geophys. Res. 81, 2193–2199. doi: 10.1029/JA081i013p02193
Mullen, E. G., Gussenhoven, M. S., Hardy, D. A., Aggson, T. A., Ledley, B. G., and Whipple, E. (1986). SCATHA survey of high-level spacecraft charging in sunlight. J. Geophys. Res. 91, 1474–1490. doi: 10.1029/JA091iA02p01474
Neubert, T., Hawkins, J. G., Reeves, G. D., Banks, P. M., Bush, R. I., Williamson, P. R., et al. (1988). Pulsed electron-beam emission in space. J. Geomagn. Geoelectr. 40, 1221–1233. doi: 10.5636/jgg.40.1221
Nicolls, M. J., Heinselman, C. J., Hope, E. A., Ranjan, S., Kelley, M. C., and Kelly, J. D. (2007). Imaging of polar mesosphere summer echoes with the 450 MHz poker flat advanced modular incoherent scatter radar. Geophys. Res. Lett. 34, 1–6. doi: 10.1029/2007GL031476
Obayashi, T., Kawashima, N., Kuriki, K., Nagatomo, N., Ninomiya, K., Sasaki, S., et al. (1982). “Space experiments with particle accelerators (SEPAC),” in Artificial Particle Beams in Space Plasma Studies, ed Grandal, B. (Springer: Plenum, NY), 659–672. doi: 10.1007/978-1-4684-4223-6_44
Pfaff, R. (1996). “In-situ measurement techniques for ionospheric research,” in Modern Ionospheric Science, eds H. Kohl, et al. (Munich: European Geophysical Society), 459–551.
Pfaff, R., Freudenreich, H., Bounds, S., Erlandson, R., Delamere, P., Meng, C. I., et al. (2004). Electric field, magnetic field, and density measurements on the active plasma experiment. Spacecraft J. Rockets 42, 521–532. doi: 10.2514/1.11945
Pfaff, R., and Marionni, P. A. (1998). “Multiple-baseline spaced receivers,” in Measurement Techniques in Space Plasmas: Fields, ed Pfaff, R., et al. (American Geophysical Union), 161–167. doi: 10.1029/GM103p0161
Reeves, G. D. (2018). “Electron beams for radiation belt remediation,” in Proceedings of the ANS RPSD 2018 - 20th Topical Meeting of the Radiation Protection & Shielding Division of ANS, American Nuclear Society (LaGrange Park, IL, Santa Fe, NM), 26–31.
Reeves, G. D., Banks, P. M., Neubert, T., Bush, R. I., Williamson, P. R., Fraser-Smith, A. C., et al. (1988). VLF wave emissions by pulsed and DC electron beams in space. 1, Spacelab 2 observations. J. Geophys. Res. 93, 14699–14756. doi: 10.1029/JA093iA12p14699
Reeves, G. D., Banks, P. M., Neubert, T., and Harker, K. J. (1990a). VLF Wave emissions by pulsed and DC electron-beams in space. 2. Analysis of spacelab-2 results. J. Geophys. Res. Space 95, 6505–6517. doi: 10.1029/JA095iA05p06505
Reeves, G. D., Banks, P. M., Neubert, T., Harker, K. J., Gurnett, D. A., and Raitt, W. J. (1990b). Spacelab 2 electron beam wave stimulation: studies of important parameters, J Geophys Res-Space 95, 10655–10670. doi: 10.1029/JA095iA07p10655
Reeves, G. D., Spence, H. E., Henderson, M. G., Morley, S. K., Friedel, R. H., Funsten, H. O., et al. (2013). Electron acceleration in the heart of the Van Allen radiation belts. Science 341, 991–994. doi: 10.1126/science.1237743
Roytershteyn, V., and Delzanno, G. L. (2018). Spectral approach to plasma kinetic simulations based on hermite decomposition in the velocity space. Front. Astronomy Space Sci. 5, 1–11. doi: 10.3389/fspas.2018.00027
Sasaki, S., Kawashima, N., Kuriki, K., Yanagisawa, M., and Obayashi, T. (1986). Vehicle charging observed in SEPAC Spacelab-1 experiment. J. Spacecraft Rockets 23, 194–199. doi: 10.2514/3.25801
Sasaki, S., Oyama, K. I., Kawashima, N., Obayashi, T., Hirao, K., Raitt, W. J., et al. (1988). Tethered rocket experiment (CHARGE-2) initial results on electrodynamics. Radio Sci. 23, 975–988. doi: 10.1029/RS023i006p00975
Scherbarth, M., Smith, D., Adler, A., Stuart, J., and Ginet, G. (2009). AFRL's demonstration and science experiments (DSX) mission. Proc. SPIE 7438, 1–10. doi: 10.1117/12.824898
Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013). Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504, 411–414. doi: 10.1038/nature12889
Ukhorskiy, Y., and Sitnov, M. I. (2012). Dynamics of radiation belt particles. Space Sci. Rev. 179, 545–578. doi: 10.1007/978-1-4899-7433-4_17
Usanova, M. E., Drozdov, A., Orlova, K., Mann, I. R., Shprits, Y., Robertson, M. T., et al. (2014). Effect of EMIC waves on relativistic and ultrarelativistic electron populations: Ground- based and Van Allen Probes observations. Geophys. Res. Lett. 41, 1375–1381. doi: 10.1002/2013GL059024
Vencels, J., Delzanno, G. L., Johnson, A., Peng, I. B., Laure, E., and Markidis, S. (2015). Spectral solver for multi-scale plasma physics simulations with dynamically adaptive number of moments. Proced. Comput. Sci. 51, 1148–1157. doi: 10.1016/j.procs.2015.05.284
Vencels, J., Delzanno, G. L., Manzini, G., Markidis, S., Peng, I. B., and Roytershteyn, V. (2016). SpectralPlasmaSolver: a spectral code for multiscale simulations of collisionless. magnetized plasmas. J. Phys. 719, 012022–012033. doi: 10.1088/1742-6596/719/1/012022
Winckler, J. R. (1982). “The use of artificial electron beams as probes of the distant magnetosphere,” in Artificial Particle Beams in Space Plasma Studies, ed Grandal, B. (Springer), 1–34. doi: 10.2514/6.1982-142
Keywords: active experiments, electron beam, wave-particle interactions, energetic particles, radiation belts, remediation, space physics
Citation: Reeves GD, Delzanno GL, Fernandes PA, Yakymenko K, Carlsten BE, Lewellen JW, Holloway MA, Nguyen DC, Pfaff RF, Farrell WM, Rowland DE, Samara M, Sanchez ER, Spanswick E, Donovan EF and Roytershteyn V (2020) The Beam Plasma Interactions Experiment: An Active Experiment Using Pulsed Electron Beams. Front. Astron. Space Sci. 7:23. doi: 10.3389/fspas.2020.00023
Received: 19 February 2020; Accepted: 30 April 2020;
Published: 17 June 2020.
Edited by:
Marian Lazar, Ruhr-Universität Bochum, GermanyReviewed by:
David Malaspina, University of Colorado Boulder, United StatesPeter Haesung Yoon, University of Maryland, United States
Copyright © 2020 Reeves, Delzanno, Fernandes, Yakymenko, Carlsten, Lewellen, Holloway, Nguyen, Pfaff, Farrell, Rowland, Samara, Sanchez, Spanswick, Donovan and Roytershteyn. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Geoffrey D. Reeves, cmVldmVzQGxhbmwuZ292
 Geoffrey D. Reeves
Geoffrey D. Reeves Gian Luca Delzanno
Gian Luca Delzanno Philip A. Fernandes1
Philip A. Fernandes1 John W. Lewellen
John W. Lewellen Michael A. Holloway
Michael A. Holloway Dinh C. Nguyen
Dinh C. Nguyen Ennio R. Sanchez
Ennio R. Sanchez Eric F. Donovan
Eric F. Donovan
