A Brief Overview of Black Hole-Neutron Star Mergers

1. Introduction

The first observation by the LIGO-Virgo collaboration (LVC) of gravitational waves (GWs) coming from merging black holes (Abbott et al., 2016, GW150914) and neutron stars (Abbott et al., 2017c, GW170817) made GW astrophysics a reality. Since then, the LVC has confirmed an additional 9 binary black holes (BBH) (Abbott et al., 2019), with dozens of other systems announced in public alerts¹. BBH mergers were also discovered by an independent search pipeline used on publicly available LVC data (Venumadhav et al., 2019). Most recently, an event that may have been a second binary neutron star (BNS) merger was reported by the LVC (Abbott et al., 2020, GW190425)².

BNS and black hole-neutron star (BHNS) systems play an especially interesting role in this new field of astrophysics. By observing neutron star mergers, we gather information about the equation of state of neutron stars (Flanagan and Hinderer, 2008; Abbott et al., 2018), about the origin of heavy elements produced through r-process nucleosynthesis (Freiburghaus et al., 1999; Drout et al., 2017; Pian et al., 2017), and about the expansion rate of the Universe (Abbott et al., 2017b; Hotokezaka et al., 2019). Neutron star mergers also power at least a subset of short gamma-ray bursts (SGRBs) (Abbott et al., 2017a), as well as UV/optical/infrared kilonovae (Li and Paczynski, 1998; Roberts et al., 2011; Chornock et al., 2017; Coulter et al., 2017; Cowperthwaite et al., 2017; Evans et al., 2017; Nicholl et al., 2017; Soares-Santos et al., 2017; Villar et al., 2017), and radio emission from ultra-relativistic jets and mildly relativistic outflows (Nakar and Piran, 2011; Hotokezaka et al., 2016; Mooley et al., 2018). The event rates of BNS and BHNS mergers remain however very uncertain (Abadie et al., 2010; Belczynski et al., 2016; Abbott et al., 2020). Only two potential BNS mergers have been officially confirmed so far, and no BHNS mergers, even though a number of candidates can be found within the LVC's public alerts.

The evolution of BHNS binaries can be divided into three main phases: a millions-of-years long inspiral during which the two objects slowly lose energy and angular momentum to GW emission; a merger phase lasting about 1 ms and resulting in either the tidal disruption of the neutron star (see Figure 1) or its plunge into the black hole; and, for disrupting systems only, a seconds-long post-merger phase during which more matter is ejected or accreted onto the black hole. These three phases happen on widely different timescales, and involve different physical processes and observable signals. In this manuscript, we will review each stage of a BHNS's evolution in turn, and discuss important properties of the associated GW and electromagnetic (EM) signals.

FIGURE 1

Figure 1. Time evolution of a disrupting BHNS binary, including: onset of mass accretion (top left), unstable mass transfer (top right), evolution into a long tidal tail (bottom left), and circularization into an accretion disk (bottom right).

BHNS systems cover a high-dimensional and largely unconstrained parameter space. Our priors for the properties of black holes and neutron stars in BHNS binaries come from their observation in other types of binary systems or from theoretical considerations, and are accordingly quite uncertain. While most neutron stars observed in BNS systems have masses in the [1.2 − 1.6]M_⊙ range (Özel et al., 2012), more massive neutron stars exist, up to at least ~ 2M_⊙ (Demorest et al., 2010; Antoniadis et al., 2013). Most galactic black holes have masses of [5 − 15]M_⊙ (Özel et al., 2010), but black holes observed through GWs are often more massive (Abbott et al., 2019). Whether black holes can be formed within the “mass gap” between the most massive neutron stars and ~5M_⊙ also remains an important open question. The magnitude and orientation of black hole spins are unknown, and while most BHNS binaries are expected to have negligible eccentricities (Peters and Mathews, 1963), eccentric BHNS binaries cannot entirely be ruled out and have evolutions very distinct from circular binaries (Stephens et al., 2011). Obtaining reliable models for the observable signals powered by BHNS binaries across this vast parameter space can be difficult, yet the dependence of these signals in the properties of BHNS binaries is what allows us to extract valuable information from observations. In this review, we mostly consider circular binaries, leaving as free parameters the masses M_{NS, BH} of the compact objects, their dimensionless spins ${\overrightarrow{\chi }}_{\text{NS},\text{BH}}$, and the equation of state of dense nuclear matter, which sets the radius R_NS of a given neutron star.

2. Binary Inspiral

From an observational point of view, the millions of years of GW driven inspiral that eventually result in the merger of a BHNS binary constitute an extended dark age between the supernova explosion that created the neutron star and the bright GW and EM emissions that accompany the merger. Ground-based GW detectors, such as LIGO and Virgo only become sensitive to BHNS binaries seconds to minutes before merger. Most of our efforts thus focus on understanding the very end of the inspiral. To first order, the GW-driven inspiral of BHNS binaries proceeds as for black holes of the same masses and spins. GW detectors are mostly sensitive to the chirp mass

$\begin{array}{ll}{M}_c=\frac{{\left(M_{\text{NS}}{M}_{\text{BH}}\right)}^{3/5}}{{\left(M_{\text{BH}}+M_{\text{NS}}\right)}^{1/5}}& (1)\end{array}$

of a system, while individual mass measurements suffer from large statistical errors for all but the brightest events. As for BNS systems, the main observable effect of the finite size of neutron stars before merger is the acceleration of the GW-driven inspiral due to tides (Flanagan and Hinderer, 2008): large neutron stars merge earlier than more compact stars. GW detectors are primarily sensitive to the resulting change in the phase of the GW signal. To first order, that change is linear in the dimensionless tidal deformability parameter (Hinderer et al., 2010), defined for BHNS systems as

$\begin{array}{ll}\tilde{\Lambda }=\frac{32}{39}\frac{M_{\text{NS}}^4\left(M_{\text{NS}}+12M_{\text{BH}}\right)}{{\left(M_{\text{NS}}+M_{\text{BH}}\right)}^5}\frac{k_2}{C_{\text{NS}}^5}& (2)\end{array}$

with $C_{\text{NS}}=M_{\text{NS}}G/(R_{\text{NS}}{c}^2)$ the compaction of the neutron star, and k₂ its dimensionless l = 2 Love number. Both k₂ and R_NS depend on the equation of state of nuclear matter inside the neutron star. Unfortunately, $\tilde{\Lambda }$ becomes very small when M_BH ≫ M_NS. As a result, finite size effects in BHNS mergers are expected to be detectable only for close-by events involving low-mass black holes (Lackey et al., 2014). The usefulness of BHNS binaries for the determination of the neutron star equation of state largely depends on the event rate of BHNS mergers that involve low-mass black holes. The existence of black holes within the supposed “mass gap” would be particularly convenient in that respect. For reference, recent results from the LVC (Abbott et al., 2018), NICER (Miller et al., 2019; Riley et al., 2019), and joint analysis of both datasets (Landry et al., 2020; Raaijmakers et al., 2020) find R_NS ~ (10.5 − 14.5) km, with variations due to the chosen astrophysical data, equation of state model and maximum NS mass.

Additionally, it can be difficult to unequivocally determine that a given GW signal is powered by a BHNS merger. In the absence of an EM signal, our main method to determine the nature of merging compact objects is to use their inferred masses, and to assume that any object below a fixed threshold mass is a neutron star. This clearly introduces an untested astrophysical prior in the interpretation of the data. It can also be difficult to determine whether a system is a high mass ratio BHNS system or a more symmetric BBH system with the same chirp mass (Hannam et al., 2013)³. Furthermore, if black holes are commonly formed with large spins misaligned with the orbital angular momentum of the binary, BHNS binaries may experience significant orbital precession. As the GW templates currently used by detection pipelines do not take orbital precession into account, this could lead to the loss of a significant fraction (~30%) of BHNS systems (Harry et al., 2014), with an observational bias toward the detection of non-processing systems. Analysis of the observed population of BHNS binaries thus require careful consideration of observational biases and of the probabilistic nature of the characterization of a signal as a BHNS system.

Finally, we note that the availability of reliable GW templates is crucial to the analysis of merger events. In that respect, significant progress have been made in recent years on precessing waveform models (Schmidt et al., 2012; Hannam et al., 2014; Pan et al., 2014; Smith et al., 2016; Khan et al., 2019; Varma et al., 2019), which may be of particular importance for BHNS systems, and on the inclusion of tidal effects in waveform models (Lackey et al., 2014; Bernuzzi et al., 2015; Hinderer et al., 2016; Dietrich et al., 2017; Nagar et al., 2018). Recent high-accuracy numerical simulations of BHNS inspirals (Foucart et al., 2019) show reasonable agreement between tidal models and simulations, except for rapidly spinning neutron stars. It should however be noted that state-of-the art simulations still have numerical errors at the level of ~10–20% of the phase difference between BBH and BHNS waveforms, which puts a limit on how far waveform models can be tested in practice.

3. Merger Dynamics

The merger of a BHNS binary follows one out of two potential pathways: either the neutron star is disrupted by the tidal field of the black hole, leading to mass ejection and the formation of an accretion torus around the black hole; or the neutron star plunges into the black hole whole. Qualitatively, the physical processes leading to these two potential outcomes are well-understood (Lattimer and Schramm, 1976). As the binary spirals in, the neutron star first reaches either the radius of the innermost stable circular orbit (ISCO) of the black hole R_ISCO, or the disruption radius R_dis. Roughly speaking, disruption happens if R_dis ≳ R_ISCO, i.e., if the neutron star is tidally disrupted outside of the ISCO. This division between disrupting and non-disrupting systems creates two classes of events with very distinct observational properties.

Qualitatively, if the neutron star is treated as a test mass and the black hole spin is aligned with the orbital angular momentum of the binary, the ISCO radius scales as $R_{\text{ISCO}}=f({\chi }_{\text{BH}})G{M}_{\text{BH}}/c^2$, with f a function ranging from 1 to 9 and decreasing for increasing (prograde) spins (Bardeen et al., 1972). For large mass ratios and in Newtonian physics, the disruption radius scales as $R_{\text{dis}}~k{(M_{\text{BH}}/M_{\text{NS}})}^{1/3}{R}_{\text{NS}}$, with k a numerical constant with a mild dependence on the equation of state and the black hole spin (Fishbone, 1973; Wiggins and Lai, 2000). From these simple scalings, we deduce that disruption will be favored for (a) low-mass black holes; (b) prograde black hole spins; and (c) large neutron star radii.

A more quantitative understanding requires general relativistic simulations (Duez et al., 2008; Etienne et al., 2009; Chawla et al., 2010; Kyutoku et al., 2010; Foucart et al., 2012; Kawaguchi et al., 2015). Simulations tell us that for quasi-circular binaries, mass transfer is always unstable. We can also predict which systems disrupt (see Figure 2), and for disrupting systems how much mass remains outside of the black hole after disruption (Pannarale et al., 2011; Foucart, 2012; Foucart et al., 2018)—typically a few tenths of a solar mass. While these predictions were first made for systems with aligned black hole spins, simulations also show that for misaligned black hole spins, simply using in fitting formulae the aligned component of the black hole spin or replacing the ISCO radius by the radius of the innermost stable spherical orbit (ISSO) provides reasonably accurate predictions (Foucart et al., 2013b; Stone et al., 2013; Kawaguchi et al., 2015). Overall, the outcome of a BHNS merger can be predicted with reasonable accuracy as a function of just three dimensionless parameters: the symmetric mass ratio $\eta =M_{\text{NS}}{M}_{\text{BH}}/{(M_{\text{NS}}+M_{\text{BH}})}^2$, the aligned component of the dimensionless black hole spin χ_∥, and the neutron star compaction C_NS (Foucart et al., 2018). However, these models do not apply to systems with large eccentricities: partial disruption of the neutron star is then possible (Stephens et al., 2011), and we do not have reliable predictions for the outcome of the merger in the larger-dimensional parameter space of eccentric BHNS systems. There have also been too few simulations to robustly characterize binaries with rapidly rotating neutron stars.

FIGURE 2

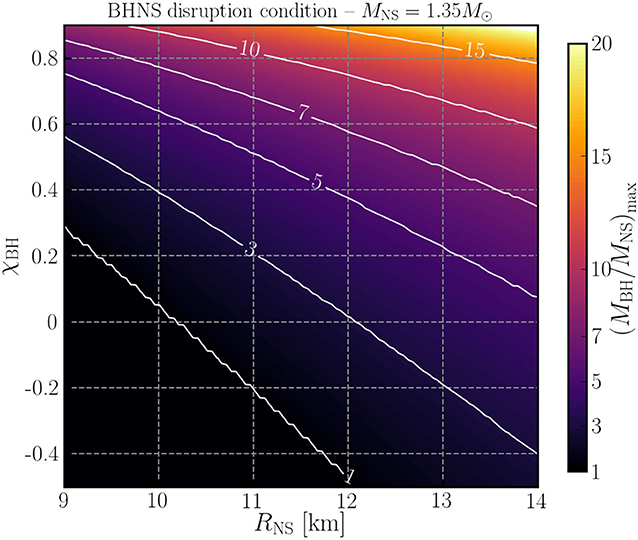
Figure 2. Maximum value of the mass ratio M_BH/M_NS for which a BHNS system will disrupt as a function of the neutron star radius R_NS and aligned component of the dimensionless black hole spin χ_BH, assuming M_NS = 1.35M_⊙ (Foucart et al., 2018). Results for other M_NS can be obtained by looking at the disruption condition at constant $C_{\text{NS}}=G{M}_{\text{NS}}/(R_{\text{NS}}{c}^2)$.

For non-disrupting BHNS systems, the merger ends the interesting part of the evolution. The GW signal is practically identical to a BBH system with the same component masses and spins (Foucart et al., 2013a; Lackey et al., 2014), there is neither mass ejection nor accretion disk, and we do not expect detectable post-merger EM signals. In the rest of this review, we will thus focus on the more interesting disrupting BHNS systems. However, disrupting systems may very well be a small minority of the observed BHNS binaries. Even a relatively low mass black hole (M_BH ~ 7M_⊙) requires a moderate-to-high black hole spin χ_∥ ≳ (0.2−0.7) to disrupt neutron stars with equations of state compatible with GW170817. The BBH systems detected so far have black holes of high mass and/or low spin (Abbott et al., 2019; Venumadhav et al., 2019) that would be highly unlikely to disrupt neutron stars—though the rapidly spinning BH candidate reported in Zackay et al. (2019) provides some hope for the existence of disrupting BHNS binaries. While we should be ready for a population of disrupting BHNS mergers, we should acknowledge that the idea that most BHNS mergers undergo tidal disruption is currently disfavored.

Disrupting BHNS systems provide us with a wealth of additional information. First, the GW signal is cut off when disruption occurs, at a frequency f_cut ~ (1−1.5) kHz that depends on the equation of state of the neutron star. The inclusion of that cut-off frequency in waveform models (Lackey et al., 2014; Pannarale et al., 2015) can help constrain the equation of state of neutron stars, complementing the information provided by the tidal dephasing (Lackey et al., 2012; Lackey et al., 2014). Second, a disrupting BHNS binary typically ejects a few percents of a solar mass of material. The ejection of neutron-rich matter at mildly relativistic speeds is extremely important to the study of BHNS and BNS mergers: as the ejecta expands into the surrounding interstellar medium, it undergoes r-process nucleosynthesis, forming many of the heavy elements observed today on Earth. The outcome of the r-process is not, however, unique: more neutron-rich ejecta (approximately, with <~25% protons) forms heavier r-process elements than more neutron-poor ejecta (Wanajo et al., 2014; Lippuner and Roberts, 2015). This matters if we wish to understand nucleosynthesis in the Universe, but also to understand the properties of the observable optical/infrared kilonovae powered by radioactive decays in the ejecta. If heavier r-process elements are produced, the opacity of the ejecta increases, causing the kilonova to be dimmer, of longer duration, and shifted from the optical to the infrared (Kasen et al., 2013). Kilonova signals also contain information about the mass, velocity, composition, and geometry of the ejecta (Barnes and Kasen, 2013; Kawaguchi et al., 2016). Thus, if we can connect the ejecta properties to the parameters of the binary, we can use kilonovae observations to complement and cross-check GW observations of BHNS systems. In BHNS system, the merger ejecta, or dynamical ejecta, has fairly well-constrained properties. It is cold, very neutron-rich (~5% protons), and moves at an average velocity v ~ (0.1−0.3)c. It is also quite different from the dynamical ejecta of BNS mergers: there is more mass ejection in disrupting BHNS binaries, the ejecta is very asymmetric, and there is no neutron poor component to the ejecta that may power an optical kilonova. Fits to the result of numerical simulations have provided us with relatively robust predictions for its mass (Kawaguchi et al., 2016) and asymptotic velocity (Kawaguchi et al., 2016; Foucart et al., 2017) that can be used to develop kilonovae models. While higher accuracy predictions for the properties of the dynamical ejecta would certainly be useful in the long term, this phase of the evolution is quite well-understood when compared to the formation and evolution of post-merger remnants.

4. Post-Merger Remnants

In our description of the evolution of BHNS binaries, we have so far only considered the effects of general relativity (GWs, ISCO, …), of ideal hydrodynamics (tides and tidal disruption), and of the nuclear equation of state of cold dense matter in neutrinoless beta-equilibrium. During inspiral and merger, this is generally sufficient to capture the most important observable features of BHNS binaries. This changes dramatically after merger: as bound matter from the disrupted neutron star begins to circularize, mostly through hydrodynamical shocks and interactions between the tidal tail and the forming accretion disk, magnetic fields and neutrinos start to play an important role. Magnetic fields and turbulent eddies will grow due to the Kelvin-Helmholtz instability at the disk-tail boundary, heating the disk and driving outflows (Kiuchi et al., 2015), while neutrinos cool the denser regions of the disk and heat its corona (Lee et al., 2009; Deaton et al., 2013; Janiuk et al., 2013; Foucart et al., 2015). Neutrino absorption in the corona can drive a disk wind (Dessart et al., 2009) and, more importantly, preferential absorption of electron neutrinos over electron antineutrinos leads to an increase in the ratio of protons to neutrons in the outflows (Foucart et al., 2015). At later times the growth of the magnetorotational instability leads to an increase in the strength of the magnetic field, angular momentum transport and heating in the disk, accretion of matter onto the black hole, and the production of mildly relativistic outflows for multiple seconds after the merger (Fernández and Metzger, 2013; Siegel and Metzger, 2017; Fernández et al., 2019). Finally, depending on the large-scale structure of the magnetic field after merger, continuous or more intermittent relativistic jets may be produced ~0.1–1 s after merger (Paschalidis et al., 2015; Siegel and Metzger, 2017; Ruiz et al., 2018; Christie et al., 2019), potentially leading to the production of a SGRB.

Numerical simulations and theoretical models have made important strides in the study of post-merger remnants over the last decade, yet this remains by far the most uncertain part of the evolution. A first problem is that only one magnetohydrodynamics simulation has used sufficient resolution to capture the growth of the Kelvin-Helmholtz instability at the disk-tail boundary (Kiuchi et al., 2015), and it did not include any treatment of the neutrinos. In the absence of cooling, it predicted massive outflows from the forming disk (50% of the disk mass, an amount comparable to the dynamical ejecta). Lower-resolution simulations including neutrino cooling did not observe significant outflows at this stage (Deaton et al., 2013; Foucart et al., 2015), but lacked the heating provided by the Kelvin-Helmholtz instability. The physical answer lies somewhere in between these two extremes, leaving a large uncertainty regarding the mass of hot, mildly relativistic matter that may be ejected during the circularization of the accretion disk. This is particularly problematic because these early post-merger outflows could be the main source of optical kilonovae in BHNS systems.

A second important source of uncertainty is the large scale structure of the magnetic field after merger. Merger simulations have produced jets when a strong dipolar magnetic field was initialized outside of the neutron star before merger (Paschalidis et al., 2015; Ruiz et al., 2018), but no simulation has resolved the growth of a large-scale magnetic field from realistic initial field strengths. On the other hand, simulations of post-merger remnants show that the large scale structure of the magnetic field has a significant impact on the jet power and the ejected mass (Christie et al., 2019). This leaves us with important open questions regarding the connection between SGRB properties and the pre-merger characteristics of a BHNS binary, as well as regarding the mechanism for the production of relativistic jets, e.g., whether a strong magnetic field outside of the neutron star leads to the production of a jet ~100 ms after merger (Paschalidis et al., 2015; Ruiz et al., 2018), or a dynamo mechanism within the disk creates a jet later on Christie et al. (2019).

One reliable constant in post-merger studies of BHNS systems is that a large fraction ~(15–50)% of the bound matter remaining around the black hole after the disruption of a neutron star is ejected in mildly relativistic outflows. There is, however, a wide range of outflow mechanisms. We observe early outflows (≲1 s post-merger) due to turbulent heating at the disk-tail interface (Kiuchi et al., 2015) and in the inner regions of the disk (Siegel and Metzger, 2017; Fernández et al., 2019), as well as delayed outflows due to viscous heating and recombination of alpha-particles in the disk (Fernández and Metzger, 2013; Christie et al., 2019; Fernández et al., 2019). The former have highly uncertain masses, velocities and compositions, in part due to uncertain initial conditions in the post-merger remnant, and in part due to missing physics in the simulations (particularly neutrino radiation transport). The latter are better understood: they are relatively slow (v ≲ 0.05c), and formed of ~20–30% protons.

As post-merger outflows in BHNS mergers have a total mass roughly similar to that of the dynamical ejecta, they have a large impact on the properties of BHNS-powered kilonovae. Uncertainties in their mass (by a factor of 2–3), velocity, and composition (neutron rich/neutron poor) are the main source of error in the construction of theoretical models of BHNS outflows today. A better understanding of the post-merger winds, along with better nuclear models and improved understanding of the heating rate of merger outflows (Barnes et al., 2016), are critical to the production of reliable kilonova models for BHNS binaries. Currently, models either ignore the post-merger ejecta (Kawaguchi et al., 2016), take only some of the post-merger outflows into account (Barbieri et al., 2020), or suffer from large uncertainties due to our lack of understanding of the post-merger ejecta (Andreoni et al., 2019; Coughlin et al., 2019).

Finally, let us comment briefly on our understanding of BHNS binaries as engines for SGRBs. Relativistic jets have now been produced in simulations of BHNS merger (Paschalidis et al., 2015; Ruiz et al., 2018)⁴ and/or of their post-merger remnant disks (Siegel and Metzger, 2017; Christie et al., 2019). We also know that the properties of the jet depend on the large scale structure of the post-merger magnetic field. However, connecting that large scale structure to the pre-merger properties of the system remains an important unsolved problem. It is unclear whether observations or simulations will first constrain the magnetic field structure of the remnant of a BHNS merger. At the moment, the most reliable information that comes from the joint observation of a SGRB and GW signal from a BHNS binary is that the neutron star was disrupted.

5. Discussion

With the advent of GW astronomy, the study of BHNS mergers is undergoing a rapid transformation. More efforts are now being directed toward the modeling and interpretation of multi-messenger observations of binary mergers. It has also become clear that the study of BHNS systems suffers from significant complications when compared with BNS systems: statistical uncertainties in the individual masses of the merging compact objects make it difficult to unequivocally characterize a GW event as a BHNS binary, and many BHNS binaries likely involve high-mass and/or low-spin black holes for which the neutron star plunges whole into the black hole, preventing the emission of detectable post-merger EM signals.

To make optimal use of the available observational data, reliable models of the GW and EM signals powered by BHNS binaries are required. On the GW side, a number of models including finite-size effects for BHNS and/or BNS systems have been developed (Lackey et al., 2014; Bernuzzi et al., 2015; Hinderer et al., 2016; Dietrich et al., 2017; Nagar et al., 2018). Before merger, these models agree with numerical simulations of BHNS binaries within current numerical errors, except in the most extreme cases tested so far (Foucart et al., 2019). Models for the impact on the GW signal of the disruption of the neutron star have more room to improve: they remain only order-of-magnitude accurate, and typically limited in their coverage of the BHNS parameter space (Lackey et al., 2014; Pannarale et al., 2015).

On the EM side, a first model combining information from SGRBs and kilonovae was recently developed by Barbieri et al. (2020), adding to a previously developed model for the kilonova signals powered by the dynamical ejecta of BHNS mergers (Kawaguchi et al., 2016). Existing models remain however limited by our lack of understanding of post-merger outflows, as well as by nuclear physics and radiation transport uncertainties (Barnes et al., 2016). In particular, the large scale structure of magnetic fields within and outside of the post-merger accretion disk is not, at this point, well-constrained by merger simulations, despite its large impact on post-merger outflows and on the properties of SGRBs (Christie et al., 2019). To make optimal use of upcoming multi-messenger observations (or even non-detections), it is thus important to develop improved kilonova and SGRB models, and properly characterize model uncertainties.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

FF gratefully acknowledges support from the NSF through grant PHY-1806278, from NASA through grant 80NSSC18K0565, and from the DOE through grant DE-SC0020435.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^Public alerts from the LVC are available online at https://gracedb.ligo.org/.

2. ^GW190425 has observed masses that could also plausibly be explained as a very low mass BHNS merger, if ~ (2−3)M_⊙ black holes exist.

3. ^If we allow for primordial black holes within the same mass range as neutron stars, low-mass BHNS mergers can also mimic BNS systems, even if we observe an EM counterpart (Hinderer et al., 2019).

4. ^“Jets” here are outflow regions with large Poynting flux, that cannot reach Lorentz factor of more than a few due to the limits of existing merger simulations.

References

Abadie, J., Abbott, B. P., Abbott, R., Abernathy, M., Accadia, T., Acernese, F., et al. (2010). Predictions for the rates of compact binary coalescences observable by ground-based gravitational-wave detectors. Class. Quantum Grav. 27:173001. doi: 10.1088/0264-9381/27/11/114007

CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016). GW150914: first results from the search for binary black hole coalescence with advanced LIGO. Phys. Rev. D 93:122003. doi: 10.1103/PhysRevD.93.122003

CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2019). GWTC-1: a gravitational-wave transient catalog of compact binary mergers observed by LIGO and virgo during the first and second observing runs. Phys. Rev. X 9:031040. doi: 10.1103/PhysRevX.9.031040

CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2020). GW190425: observation of a compact binary coalescence with total mass ~ 3.4M_⊙. Astrophys. J. Lett. (2020) 892:L3. doi: 10.3847/2041-8213/ab75f5

CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2017a). Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 848:L13. doi: 10.3847/2041-8213/aa920c

CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2017b). A gravitational-wave standard siren measurement of the Hubble constant. Nature 551, 85–88. doi: 10.1038/nature24471

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2017c). GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119:161101. doi: 10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2018). GW170817: measurements of neutron star radii and equation of state. Phys. Rev. Lett. 121:161101. doi: 10.1103/PhysRevLett.121.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Andreoni, I., Goldstein, D. A., Kasliwal, M. M., Nugent, P. E., Zhou, R., Newman, J. A., et al. (2019). GROWTH on S190814bv: deep synoptic limits on the optical/near-infrared counterpart to a neutron star-black hole merger. Astrophys. J. 890:131. doi: 10.3847/1538-4357/ab6a1b

CrossRef Full Text | Google Scholar

Antoniadis, J., Freire, P. C. C., Wex, N., Tauris, T. M., Lynch, R. S., van Kerkwijk, M. H., et al. (2013). A massive pulsar in a compact relativistic binary. Science 340:6131. doi: 10.1126/science.1233232

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbieri, C., Salafia, O. S., Perego, A., Colpi, M., and Ghirlanda, G. (2020). Electromagnetic counterparts of black hole-neutron star mergers: dependence on the neutron star properties. Eur. Phys. J. A 56:8. doi: 10.1140/epja/s10050-019-00013-x

CrossRef Full Text | Google Scholar

Bardeen, J. M., Press, W. H., and Teukolsky, S. A. (1972). Rotating black holes: locally nonrotating frames, energy extraction, and scalar synchrotron radiation. Astrophys. J. 178:347. doi: 10.1086/151796

CrossRef Full Text | Google Scholar

Barnes, J., and Kasen, D. (2013). Effect of a high opacity on the light curves of radioactively powered transients from compact object mergers. Astrophys. J. 775:18. doi: 10.1088/0004-637X/775/1/18

CrossRef Full Text | Google Scholar

Barnes, J., Kasen, D., Wu, M.-R., and Mart'inez-Pinedo, G. (2016). Radioactivity and thermalization in the ejecta of compact object mergers and their impact on kilonova light curves. Astrophys. J. 829:110. doi: 10.3847/0004-637X/829/2/110

CrossRef Full Text | Google Scholar

Belczynski, K., Repetto, S., Holz, D. E., O'Shaughnessy, R., Bulik, T., Berti, E., et al. (2016). Compact binary merger rates: comparison with LIGO/Virgo upper limits. Astrophys. J. 819:108. doi: 10.3847/0004-637X/819/2/108

CrossRef Full Text | Google Scholar

Bernuzzi, S., Nagar, A., Dietrich, T., and Damour, T. (2015). Modeling the dynamics of tidally interacting binary neutron stars up to the merger. Phys. Rev. Lett. 114:161103. doi: 10.1103/PhysRevLett.114.161103

PubMed Abstract | CrossRef Full Text | Google Scholar

Chawla, S., Anderson, M., Besselman, M., Lehner, L., Liebling, S. L., Motl, P. M., et al. (2010). Mergers of magnetized neutron stars with spinning black holes: disruption, accretion and fallback. Phys. Rev. Lett. 105:111101. doi: 10.1103/PhysRevLett.105.111101

PubMed Abstract | CrossRef Full Text | Google Scholar

Chornock, R., Berger, E., Kasen, D., Cowperthwaite, P. S., Nicholl, M., Villar, V. A., et al. (2017). The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. IV. Detection of near-infrared signatures of R-process nucleosynthesis with Gemini-South. Astrophys. J. Lett. 848:L19. doi: 10.3847/2041-8213/aa905c

CrossRef Full Text | Google Scholar

Christie, I. M., Lalakos, A., Tchekhovskoy, A., Fernández, R., Foucart, F., Quataert, E., et al. (2019). The role of magnetic field geometry in the evolution of neutron star merger accretion discs. Mon. Not. R. Astron. Soc. 490, 4811–4825. doi: 10.1093/mnras/stz2552

CrossRef Full Text | Google Scholar

Coughlin, M. W., Dietrich, T., Antier, S., Bulla, M., Foucart, F., Hotokezaka, K., et al. (2019). Implications of the search for optical counterparts during the first six months of the advanced LIGO's and Advanced Virgo's third observing run: possible limits on the ejecta mass and binary properties. Mon. Not. R. Astron. Soc. 492, 863–876. doi: 10.1093/mnras/stz3457

CrossRef Full Text | Google Scholar

Coulter, D. A., Foley, R. J., Kilpatrick, C. D., Drout, M. R., Piro, A. L., Shappee, B. J., et al. (2017). Swope Supernova Survey 2017a (SSS17a), the optical counterpart to a gravitational wave source. Science 358, 1556–1558. doi: 10.1126/science.aap9811

PubMed Abstract | CrossRef Full Text | Google Scholar

Cowperthwaite, P. S., Berger, E., Villar, V. A., Metzger, B. D., Nicholl, M., Chornock, R., et al. (2017). The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. II. UV, optical, and near-infrared light curves and comparison to kilonova models. Astrophys. J. 848:L17. doi: 10.3847/2041-8213/aa8fc7

CrossRef Full Text | Google Scholar

Deaton, M. B., Duez, M. D., Foucart, F., O'Connor, E., Ott, C. D., Kidder, L. E., et al. (2013). Black hole-neutron star mergers with a hot nuclear equation of state: outflow and neutrino-cooled disk for a low-mass, high-spin case. Astrophys. J. 776:47. doi: 10.1088/0004-637X/776/1/47

CrossRef Full Text | Google Scholar

Demorest, P., Pennucci, T., Ransom, S., Roberts, M., and Hessels, J. (2010). Shapiro delay measurement of a two solar mass neutron star. Nature 467, 1081–1083. doi: 10.1038/nature09466

PubMed Abstract | CrossRef Full Text | Google Scholar

Dessart, L., Ott, C. D., Burrows, A., Rosswog, S., and Livne, E. (2009). Neutrino signatures and the neutrino-driven wind in binary neutron star mergers. Astrophys. J. 690, 1681–1705. doi: 10.1088/0004-637X/690/2/1681

CrossRef Full Text | Google Scholar

Dietrich, T., Bernuzzi, S., and Tichy, W. (2017). Closed-form tidal approximants for binary neutron star gravitational waveforms constructed from high-resolution numerical relativity simulations. Phys. Rev. D 96:121501. doi: 10.1103/PhysRevD.96.121501

CrossRef Full Text | Google Scholar

Drout, M. R., Piro, A. L., Shappee, B. J., Kilpatrick, C. D., Simon, J. D., Contreras, C., et al. (2017). Light curves of the neutron star merger GW170817/SSS17a: implications for R-process nucleosynthesis. Science 358, 1570–1574. doi: 10.1126/science.aaq0049

PubMed Abstract | CrossRef Full Text | Google Scholar

Duez, M. D., Foucart, F., Kidder, L. E., Pfeiffer, H. P., Scheel, M. A., and Teukolsky, S. A. (2008). Evolving black hole-neutron star binaries in general relativity using pseudospectral and finite difference methods. Phys. Rev. D 78:104015. doi: 10.1103/PhysRevD.78.104015

CrossRef Full Text | Google Scholar

Etienne, Z. B., Liu, Y. T., Shapiro, S. L., and Baumgarte, T. W. (2009). Relativistic simulations of black hole-neutron star mergers: effects of black-hole spin. Phys. Rev. D 79:044024. doi: 10.1103/PhysRevD.79.044024

CrossRef Full Text | Google Scholar

Evans, P. A., Cenko, S. B., Kennea, J. A., Emery, S. W. K., Kuin, N. P. M., Korobkin, O., et al. (2017). Swift and NuSTAR observations of GW170817: detection of a blue kilonova. Science 358, 1565–1570. doi: 10.1126/science.aap9580

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernández, R., and Metzger, B. D. (2013). Delayed outflows from black hole accretion tori following neutron star binary coalescence. Mon. Not. R. Astron. Soc. 435, 502–517. doi: 10.1093/mnras/stt1312

CrossRef Full Text | Google Scholar

Fernández, R., Tchekhovskoy, A., Quataert, E., Foucart, F., and Kasen, D. (2019). Long-term GRMHD simulations of neutron star merger accretion discs: implications for electromagnetic counterparts. Mon. Not. R. Astron. Soc. 482, 3373–3393. doi: 10.1093/mnras/sty2932

CrossRef Full Text | Google Scholar

Fishbone, L. G. (1973). The relativistic Roche problem. I. Equilibrium theory for a body in equatorial, circular orbit around a Kerr black hole. Astrophys. J. 185, 43–68. doi: 10.1086/152395

CrossRef Full Text | Google Scholar

Flanagan, É. É., and Hinderer, T. (2008). Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 77:021502. doi: 10.1103/PhysRevD.77.021502

CrossRef Full Text | Google Scholar

Foucart, F. (2012). Black-hole-neutron-star mergers: disk mass predictions. Phys. Rev. D 86:124007. doi: 10.1103/PhysRevD.86.124007

CrossRef Full Text | Google Scholar

Foucart, F., Buchman, L., Duez, M. D., Grudich, M., Kidder, L. E., MacDonald, I., et al. (2013a). First direct comparison of nondisrupting neutron star-black hole and binary black hole merger simulations. Phys. Rev. D 88:064017. doi: 10.1103/PhysRevD.88.064017

CrossRef Full Text | Google Scholar

Foucart, F., Deaton, M. B., Duez, M. D., Kidder, L. E., MacDonald, I., Ott, C. D., et al. (2013b). Black hole-neutron star mergers at realistic mass ratios: equation of state and spin orientation effects. Phys. Rev. D 87:084006. doi: 10.1103/PhysRevD.87.084006

CrossRef Full Text | Google Scholar

Foucart, F., Desai, D., Brege, W., Duez, M. D., Kasen, D., Hemberger, D. A., et al. (2017). Dynamical ejecta from precessing neutron star-black hole mergers with a hot, nuclear-theory based equation of state. Class. Quant. Grav. 34:044002. doi: 10.1088/1361-6382/aa573b

CrossRef Full Text | Google Scholar

Foucart, F., Duez, M. D., Hinderer, T., Caro, J., Williamson, A. R., Boyle, M., et al. (2019). Gravitational waveforms from spectral Einstein code simulations: neutron star-neutron star and low-mass black hole-neutron star binaries. Phys. Rev. D 99:044008. doi: 10.1103/PhysRevD.99.044008

CrossRef Full Text | Google Scholar

Foucart, F., Duez, M. D., Kidder, L. E., Scheel, M. A., Szilágyi, B., and Teukolsky, S. A. (2012). Black hole-neutron star mergers for 10M_⊙ black holes. Phys. Rev. D 85:044015. doi: 10.1103/PhysRevD.85.044015

CrossRef Full Text | Google Scholar

Foucart, F., Hinderer, T., and Nissanke, S. (2018). Remnant baryon mass in neutron star-black hole mergers: predictions for binary neutron star mimickers and rapidly spinning black holes. Phys. Rev. D 98:081501. doi: 10.1103/PhysRevD.98.081501

CrossRef Full Text | Google Scholar

Foucart, F., O'Connor, E., Roberts, L., Duez, M. D., Haas, R., Kidder, L. E., et al. (2015). Post-merger evolution of a neutron star-black hole binary with neutrino transport. Phys. Rev. D 91:124021. doi: 10.1103/PhysRevD.91.124021

CrossRef Full Text | Google Scholar

Freiburghaus, C., Rosswog, S., and Thielemann, F.-K. (1999). R-process in neutron star mergers. Astrophys. J. Lett. 525, L121–L124. doi: 10.1086/312343

PubMed Abstract | CrossRef Full Text | Google Scholar

Hannam, M., Brown, D. A., Fairhurst, S., Fryer, C. L., and Harry, I. W. (2013). When can gravitational-wave observations distinguish between black holes and neutron stars? Astrophys. J. Lett. 766:L14. doi: 10.1088/2041-8205/766/1/L14

CrossRef Full Text | Google Scholar

Hannam, M., Schmidt, P., Bohé, A., Haegel, L., Husa, S., Ohme, F., et al. (2014). A simple model of complete precessing black-hole-binary gravitational waveforms. Phys. Rev. Lett. 113:151101. doi: 10.1103/PhysRevLett.113.151101

PubMed Abstract | CrossRef Full Text | Google Scholar

Harry, I. W., Nitz, A. H., Brown, D. A., Lundgren, A. P., Ochsner, E., and Keppel, D. (2014). Investigating the effect of precession on searches for neutron-star-black-hole binaries with advanced LIGO. Phys. Rev. D 89:024010. doi: 10.1103/PhysRevD.89.024010

CrossRef Full Text | Google Scholar

Hinderer, T., Lackey, B. D., Lang, R. N., and Read, J. S. (2010). Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 81:123016. doi: 10.1103/PhysRevD.81.123016

CrossRef Full Text | Google Scholar

Hinderer, T., Nissanke, S., Foucart, F., Hotokezaka, K., Vincent, T., Kasliwal, M., et al. (2019). Distinguishing the nature of comparable-mass neutron star binary systems with multimessenger observations: GW170817 case study. Phys. Rev. D 100:06321. doi: 10.1103/PhysRevD.100.063021

CrossRef Full Text | Google Scholar

Hinderer, T., Taracchini, A., Foucart, F., Buonanno, A., Steinhoff, J., Duez, M., et al. (2016). Effects of neutron-star dynamic tides on gravitational waveforms within the effective-one-body approach. Phys. Rev. Lett. 116:181101. doi: 10.1103/PhysRevLett.116.181101

PubMed Abstract | CrossRef Full Text | Google Scholar

Hotokezaka, K., Nakar, E., Gottlieb, O., Nissanke, S., Masuda, K., Hallinan, G., et al. (2019). A Hubble constant measurement from superluminal motion of the jet in GW170817. Nat. Astron. 3, 940–944. doi: 10.1038/s41550-019-0820-1

CrossRef Full Text | Google Scholar

Hotokezaka, K., Nissanke, S., Hallinan, G., Lazio, T. J. W., Nakar, E., and Piran, T. (2016). Radio counterparts of compact binary mergers detectable in gravitational waves: a simulation for an optimized survey. Astrophys. J. 831:190. doi: 10.3847/0004-637X/831/2/190

CrossRef Full Text | Google Scholar

Janiuk, A., Mioduszewski, P., and Moscibrodzka, M. (2013). Accretion and outflow from a magnetized, neutrino cooled torus around the gamma ray burst central engine. Astrophys. J. 776:105. doi: 10.1088/0004-637X/776/2/105

CrossRef Full Text | Google Scholar

Kasen, D., Badnell, N. R., and Barnes, J. (2013). Opacities and spectra of the R-process ejecta from neutron star mergers. Astrophys. J. 774:25. doi: 10.1088/0004-637X/774/1/25

CrossRef Full Text | Google Scholar

Kawaguchi, K., Kyutoku, K., Nakano, H., Okawa, H., Shibata, M., and Taniguchi, K. (2015). Black hole-neutron star binary merger: dependence on black hole spin orientation and equation of state. Phys. Rev. D 92:024014. doi: 10.1103/PhysRevD.92.024014

CrossRef Full Text | Google Scholar

Kawaguchi, K., Kyutoku, K., Shibata, M., and Tanaka, M. (2016). Models of kilonova/macronova emission from black hole–neutron star mergers. Astrophys. J. 825:52. doi: 10.3847/0004-637X/825/1/52

CrossRef Full Text | Google Scholar

Khan, S., Chatziioannou, K., Hannam, M., and Ohme, F. (2019). Phenomenological model for the gravitational-wave signal from precessing binary black holes with two-spin effects. Phys. Rev. D 100:024059. doi: 10.1103/PhysRevD.100.024059

CrossRef Full Text | Google Scholar

Kiuchi, K., Sekiguchi, Y., Kyutoku, K., Shibata, M., Taniguchi, K., and Wada, T. (2015). High resolution magnetohydrodynamic simulation of black hole-neutron star merger: Mass ejection and short gamma ray bursts. Phys. Rev. D 92:064034. doi: 10.1103/PhysRevD.92.064034

CrossRef Full Text | Google Scholar

Kyutoku, K., Shibata, M., and Taniguchi, K. (2010). Gravitational waves from nonspinning black hole-neutron star binaries: dependence on equations of state. Phys. Rev. D 82:044049. doi: 10.1103/PhysRevD.82.044049

CrossRef Full Text | Google Scholar

Lackey, B. D., Kyutoku, K., Shibata, M., Brady, P. R., and Friedman, J. L. (2012). Extracting equation of state parameters from black hole-neutron star mergers: Nonspinning black holes. Phys. Rev. D 85:044061. doi: 10.1103/PhysRevD.85.044061

CrossRef Full Text | Google Scholar

Lackey, B. D., Kyutoku, K., Shibata, M., Brady, P. R., and Friedman, J. L. (2014). Extracting equation of state parameters from black hole-neutron star mergers: aligned-spin black holes and a preliminary waveform model. Phys. Rev. D 89:043009. doi: 10.1103/PhysRevD.89.043009

CrossRef Full Text | Google Scholar

Landry, P., Essick, R., and Chatziioannou, K. (2020). Nonparametric constraints on neutron star matter with existing and upcoming gravitational wave and pulsar observations. Phys. Rev. D 101:123007. doi: 10.1103/PhysRevD.101.123007

CrossRef Full Text | Google Scholar

Lattimer, J. M., and Schramm, D. N. (1976). The tidal disruption of neutron stars by black holes in close binaries. Astrophys. J. 210, 549–567. doi: 10.1086/154860

CrossRef Full Text | Google Scholar

Lee, W. H., Ramirez-Ruiz, E., and Diego-Lopez-Camara (2009). Phase transitions and He-synthesis driven winds in neutrino cooled accretion disks: prospects for late flares in short gamma-ray bursts. Astrophys. J. 699, L93–L96. doi: 10.1088/0004-637X/699/2/L93

CrossRef Full Text | Google Scholar

Li, L.-X., and Paczynski, B. (1998). Transient events from neutron star mergers. Astrophys. J. 507:L59. doi: 10.1086/311680

CrossRef Full Text | Google Scholar

Lippuner, J., and Roberts, L. F. (2015). R-process lanthanide production and heating rates in kilonovae. Astrophys. J. 815:82. doi: 10.1088/0004-637X/815/2/82

CrossRef Full Text | Google Scholar

Miller, M., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2019). PSR J0030+0451 mass and radius from NICER data and implications for the properties of neutron star matter. Astrophys. J. Lett. 887:L24. doi: 10.3847/2041-8213/ab50c5

CrossRef Full Text | Google Scholar

Mooley, K. P., Deller, A. T., Gottlieb, O., Nakar, E., Hallinan, G., Bourke, S., et al. (2018). Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 561, 355–359. doi: 10.1038/s41586-018-0486-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagar, A., Bernuzzi, S., Del Pozzo, W., Riemenschneider, G., Akcay, S., Carullo, G., et al. (2018). Time-domain effective-one-body gravitational waveforms for coalescing compact binaries with nonprecessing spins, tides and self-spin effects. Phys. Rev. D 98:104052. doi: 10.1103/PhysRevD.98.104052

CrossRef Full Text | Google Scholar

Nakar, E., and Piran, T. (2011). Radio remnants of compact binary mergers–the electromagnetic signal that will follow the gravitational waves. Nature 478, 82–84. doi: 10.1038/nature10365

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicholl, M., Berger, E., Kasen, D., Metzger, B. D., Elias, J., Briceño, C., et al. (2017). The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. III. Optical and UV spectra of a blue kilonova from fast polar ejecta. Astrophys. J. Lett. 848:L18. doi: 10.3847/2041-8213/aa9029

CrossRef Full Text | Google Scholar

Özel, F., Psaltis, D., Narayan, R., and McClintock, J. E. (2010). The black hole mass distribution in the galaxy. Astrophys. J. 725:1918. doi: 10.1088/0004-637X/725/2/1918

CrossRef Full Text | Google Scholar

Özel, F., Psaltis, D., Narayan, R., and Santos Villarreal, A. (2012). On the mass distribution and birth masses of neutron stars. Astrophys. J. 757:55. doi: 10.1088/0004-637X/757/1/55

CrossRef Full Text | Google Scholar

Pan, Y., Buonanno, A., Taracchini, A., Kidder, L. E., Mroué, A. H., Pfeiffer, H. P., et al. (2014). Inspiral-merger-ringdown waveforms of spinning, precessing black-hole binaries in the effective-one-body formalism. Phys. Rev. D 89:084006. doi: 10.1103/PhysRevD.89.084006

CrossRef Full Text | Google Scholar

Pannarale, F., Berti, E., Kyutoku, K., Lackey, B. D., and Shibata, M. (2015). Aligned spin neutron star-black hole mergers: a gravitational waveform amplitude model. Phys. Rev. D 92:084050. doi: 10.1103/PhysRevD.92.084050

CrossRef Full Text | Google Scholar

Pannarale, F., Tonita, A., and Rezzolla, L. (2011). Black hole-neutron star mergers and short GRBs: a relativistic toy model to estimate the mass of the torus. Astrophys. J. 727:95. doi: 10.1088/0004-637X/727/2/95

CrossRef Full Text | Google Scholar

Paschalidis, V., Ruiz, M., and Shapiro, S. L. (2015). Relativistic simulations of black hole-neutron star coalescence: the jet emerges. Astrophys. J. 806:L14. doi: 10.1088/2041-8205/806/1/L14

CrossRef Full Text | Google Scholar

Peters, P. C., and Mathews, J. (1963). Gravitational radiation from point masses in a Keplerian orbit. Phys. Rev. 131:435. doi: 10.1103/PhysRev.131.435

CrossRef Full Text | Google Scholar

Pian, E., D'Avanzo, P., Benetti, S., Branchesi, M., Brocato, E., Campana, S., et al. (2017). Spectroscopic identification of r-process nucleosynthesis in a double neutron-star merger. Nature 551, 67–70. doi: 10.1038/nature24298

PubMed Abstract | CrossRef Full Text | Google Scholar

Raaijmakers, G., Greif, S. K., Riley, T. E., Hinderer, T., Hebeler, K., Schwenk, A., et al. (2020). Constraining the dense matter equation of state with joint analysis of NICER and LIGO/Virgo measurements. Astrophys. J. Lett. 893:L21. doi: 10.3847/2041-8213/ab822f

CrossRef Full Text | Google Scholar

Riley, T. E., Watts, A. L., Bogdanov, S., Ray, P. S., Ludlam, R. M., Guillot, S., et al. (2019). A NICER view of PSR J0030+0451: millisecond pulsar parameter estimation. Astrophys. J. Lett. 887:L21. doi: 10.3847/2041-8213/ab481c

CrossRef Full Text | Google Scholar

Roberts, L. F., Kasen, D., Lee, W. H., and Ramirez-Ruiz, E. (2011). Electromagnetic transients powered by nuclear decay in the tidal tails of coalescing compact binaries. Astrophys. J. Lett. 736:L21. doi: 10.1088/2041-8205/736/1/L21

CrossRef Full Text | Google Scholar

Ruiz, M., Shapiro, S. L., and Tsokaros, A. (2018). Jet launching from binary black hole-neutron star mergers: dependence on black hole spin, binary mass ratio and magnetic field orientation. Phys. Rev. D 98:123017. doi: 10.1103/PhysRevD.98.123017

CrossRef Full Text | Google Scholar

Schmidt, P., Hannam, M., and Husa, S. (2012). Towards models of gravitational waveforms from generic binaries: a simple approximate mapping between precessing and non-precessing inspiral signals. Phys. Rev. D 86:104063. doi: 10.1103/PhysRevD.86.104063

CrossRef Full Text | Google Scholar

Siegel, D. M., and Metzger, B. D. (2017). Three-dimensional general-relativistic magnetohydrodynamic simulations of remnant accretion disks from neutron star mergers: outflows and r-process nucleosynthesis. Phys. Rev. Lett. 119:231102. doi: 10.1103/PhysRevLett.119.231102

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, R., Field, S. E., Blackburn, K., Haster, C.-J., Pürrer, M., Raymond, V., et al. (2016). Fast and accurate inference on gravitational waves from precessing compact binaries. Phys. Rev. D 94:044031. doi: 10.1103/PhysRevD.94.044031

CrossRef Full Text | Google Scholar

Soares-Santos, M., Holz, D. E., Annis, J., Chornock, R., Herner, K., Berger, E., et al. (2017). The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. I. Discovery of the optical counterpart using the dark energy camera. Astrophys. J. Lett. 848:L16. doi: 10.3847/2041-8213/aa9055

CrossRef Full Text | Google Scholar

Stephens, B. C., East, W. E., and Pretorius, F. (2011). Eccentric black hole-neutron star mergers. Astrophys. J. 737:L5. doi: 10.1088/2041-8205/737/1/L5

CrossRef Full Text | Google Scholar

Stone, N., Loeb, A., and Berger, E. (2013). Pulsations in short gamma ray bursts from black hole-neutron star mergers. Phys. Rev. D 87, 084053. doi: 10.1103/PhysRevD.87.084053

CrossRef Full Text | Google Scholar

Varma, V., Field, S. E., Scheel, M. A., Blackman, J., Gerosa, D., Stein, L. C., et al. (2019). Surrogate models for precessing binary black hole simulations with unequal masses. Phys. Rev. Res. 1:033015. doi: 10.1103/PhysRevResearch.1.033015

CrossRef Full Text | Google Scholar

Venumadhav, T., Zackay, B., Roulet, J., Dai, L., and Zaldarriaga, M. (2019). New binary black hole mergers in the second observing run of advanced LIGO and advanced Virgo. Phys. Rev. D 101:083030. doi: 10.1103/PhysRevD.101.083030

CrossRef Full Text | Google Scholar

Villar, V. A., Guillochon, J., Berger, E., Metzger, B. D., Cowperthwaite, P. S., Nicholl, M., et al. (2017). The combined ultraviolet, optical, and near-infrared light curves of the kilonova associated with the binary neutron star merger GW170817: unified data set, analytic models, and physical implications. Astrophys. J. 851:L21. doi: 10.3847/2041-8213/aa9c84

CrossRef Full Text | Google Scholar

Wanajo, S., Sekiguchi, Y., Nishimura, N., Kiuchi, K., Kyutoku, K., and Shibata, M. (2014). Production of all the R-process nuclides in the dynamical ejecta of neutron star mergers. Astrophys. J. Lett. 789:L39. doi: 10.1088/2041-8205/789/2/L39

CrossRef Full Text | Google Scholar

Wiggins, P., and Lai, D. (2000). Tidal interaction between a fluid star and a Kerr black hole: relativistic Roche-Riemann model. Astrophys. J. 532:530. doi: 10.1086/308565

CrossRef Full Text | Google Scholar

Zackay, B., Venumadhav, T., Dai, L., Roulet, J., and Zaldarriaga, M. (2019). Highly spinning and aligned binary black hole merger in the advanced LIGO first observing run. Phys. Rev. D 100:023007. doi: 10.1103/PhysRevD.100.023007

CrossRef Full Text | Google Scholar