Theoretical Predictions of Surface Light Element Abundances in Protostellar and Pre-Main Sequence Phase

Theoretical prediction of surface stellar abundances of light elements–lithium, beryllium, and boron–represents one of the most interesting open problems in astrophysics. As well known, several measurements of ⁷Li abundances in stellar atmospheres point out a disagreement between predictions and observations in different stellar evolutionary phases, rising doubts about the capability of present stellar models to precisely reproduce stellar envelope characteristics. The problem takes different aspects in the various evolutionary phases; the present analysis is restricted to protostellar and pre-Main Sequence phases. Light elements are burned at relatively low temperatures (T from $\approx 2$ to $\approx 5$ million degrees) and thus in the early evolutionary stages of a star they are gradually destroyed at different depths of stellar interior mainly by (p, α) burning reactions, in dependence on the stellar mass. Their surface abundances are strongly influenced by the nuclear cross sections, as well as by the extension toward the stellar interior of the convective envelope and by the temperature at its bottom, which depend on the characteristics of the star (mass and chemical composition) as well as on the energy transport in the convective stellar envelope. In recent years, a great effort has been made to improve the precision of light element burning cross sections. However, theoretical predictions surface light element abundance are challenging because they are also influenced by the uncertainties in the input physics adopted in the calculations as well as the efficiency of several standard and non-standard physical processes active in young stars (i.e. diffusion, radiative levitation, magnetic fields, rotation). Moreover, it is still not completely clear how much the previous protostellar evolution affects the pre-Main Sequence characteristics and thus the light element depletion. This paper presents the state-of-the-art of theoretical predictions for protostars and pre-Main Sequence stars and their light element surface abundances, discussing the role of (p, α) nuclear reaction rates and other input physics on the stellar evolution and on the temporal evolution of the predicted surface abundances.

1 Introduction

Light elements – lithium, beryllium and boron (hereafter Li, Be and B) – are burned at relatively low temperatures (T from $\approx 2$ to $\approx 5$ million degrees) easy to reach in stellar interiors at the bottom of the convective envelope, even during the early pre-Main Sequence (pre-MS) evolution. Therefore, surface light elements are depleted if the mixing processes become efficient enough to bring them down to the destruction region. This property makes such elements very good tracers of the mixing efficiency in stellar envelopes whose theoretical treatment is still a difficult task in stellar physics. Due to the different burning temperatures, the comparison between theory and observation for Li, Be and B, if possible, would be very useful to constrain theoretical models and in particular the extension of the convective envelope. The most of the observations concern the abundance of ⁷Li because, in most stars, surface ⁶Li is completely destroyed during the pre-MS phase and Be and B isotopic measurements are very problematic (e.g., Cunha, 2010; Kaufer, 2010; Delgado Mena et al., 2012).

A huge amount of data for surface ⁷Li abundances are available both for disk, thick disk and halo field stars and for open clusters; however, the well known discrepancy between predictions and observations of this quantity in clusters or in the Sun (the so-called “lithium-problem”) is still an open question (see e.g., Charbonnel et al., 2000; Jeffries, 2000; Piau and Turck-Chièze, 2002; Xiong and Deng, 2002; Sestito et al., 2003; Jeffries, 2006; Talon, 2008).

The theoretical prediction of surface light element abundances is complex because they are sensitive to both the input physics (i.e., equation of state, reaction rates, opacity, etc…) and chemical element abundances (i.e., initial abundance of deuterium, helium, metals, etc…) adopted in stellar models, together with the assumed efficiency of microscopic diffusion and radiative acceleration (see e.g., Piau and Turck-Chièze, 2002; Richard et al., 2002; Burke et al., 2004; Richard et al., 2005; Tognelli et al., 2012; Tognelli et al., 2015). The situation is even more complicated because surface light element abundances seem to be affected by additional “non standard” physical processes, not routinely included in stellar evolutionary codes, as the possible presence of relevant magnetic fields and mass accretion processes in some young pre-MS stars (see e.g., Baraffe and Chabrier, 2010; MacDonald and Mullan, 2012; Feiden and Chaboyer, 2013; Somers and Pinsonneault, 2014; Somers and Pinsonneault, 2015). Moreover, rotation-induced mixing, turbulent mixing, gravity waves and mass loss processes could play a role, though mainly for Main Sequence and more evolved stars (see e.g., Montalbán and Schatzman, 2000; Talon and Charbonnel, 2010; Pace et al., 2012; Charbonnel et al., 2013 and references therein).

The pre-MS is the first stellar phase where the star evolves as a fully formed object. To reach this evolutionary stage, the future star has to accrete mass, until its final value, in the previous “protostellar phase.” The details of this phase, when matter of the protostellar cloud is still falling on the surface of the protostar, are complex and uncertain. The full understanding of how the protostellar accreting phase affects the predictions for pre-MS characteristics (and thus light element abundances) is still an open problem. The inclusion of the protostellar accretion phase in evolutionary codes produces stars in the early pre-MS phase different from what expected in standard non accreting models, in which stars essentially contract along the Hayashi track. This eventually results in differences between standard and accreting models still visible during the whole pre-MS or the MS phase, with effects on both the structure and chemical composition of the stellar models (Baraffe et al., 2009; Baraffe and Chabrier, 2010; Tognelli et al., 2013; Kunitomo et al., 2018; Tognelli et al., 2020).

Light element burning cross sections are fundamental ingredients in the predictions of the time behavior of light element stellar surface abundances. In recent years new values for (p,α) reaction rates have been proposed, mainly estimated using the Trojan Horse Method, greatly improving the precision of these quantities.

The present review summarizes the state-of-the-art of theoretical predictions for protostars and pre-MS stars and their light element surface abundances, in the light of recent improvements in the adopted input physics, updated reaction rates and description of the formation and evolution of pre-MS stars.

The paper is structured as it follows. In Section 2 we qualitatively show the location of observed young pre-MS stars in the HR diagram and we compared it to the predictions of standard non accreting models. In Section 3 we give a brief overview of the main characteristics and evolutionary stages of a pre-MS model without protostellar accretion. In Section 4 we introduce the protostellar accretion phase, discussing the differences between spherical and disc accretion, along with the main parameters the determine the structure of an accreting protostar. In Section 5 we analyze the burning of light elements (Li, Be and B) in pre-MS stars and the predicted surface abundances during the pre-MS for stellar models of different masses without or with protostellar accretion phase. In Section 6 we review the impact of updated cross sections for the burning of light elements and their impact in the predictions of surface abundances in pre-MS stellar models. In Section 7 we summarize the main aspects highlighted in the review.

2 Observational Data of Pre-Main Sequence Stars as Test of Theoretical Models

This review is focused on theoretical predictions for protostellar/pre-MS models, which can be validated only through comparison with observational data. Given the difficulty in directly observing the stellar formation and the protostellar phase, only an investigation of the characteristics of very young pre-MS stars, close to the end of the protostellar phase, can indirectly give information on the previous accretion period. The availability of observations for very young pre-MS stars is thus fundamental. A great number of data is available for young pre-MS stars (ages $\sim 1$ Myr) with solar or slightly sub-solar metallicity; among these objects, some of them show a still detectable accretion disc, or protoplanetary disc, and very low accretion rates (see e.g. Hartmann and Kenyon, 1996; Muzerolle et al., 2000; Calvet et al., 2005; Muzerolle et al., 2005a; Muzerolle et al., 2005b; Bae et al., 2013; Ingleby et al., 2014). Such residual accretion discs show clear footprints of a previous accretion phase.

As an example, Figure 1 shows a sample of young pre-MS stars compared to standard isochrones from 0.1 to 10 Myr and evolutionary tracks for masses in the range [0.01, 1.0] ${\mathrm{M}}_{\odot }$ (Tognelli et al., 2011). Such observed stars are fully formed, in the sense that the measured accretion rates are extremely small, thus, they have already reached their final mass. Thus they can be considered stars evolving as constant mass structures. This figure is intended to qualitatively show the position of observed young stars in a HR diagram; they are located in a region which theoretically corresponds to pre-MS models undergoing to a gravitational contraction (we will discuss this evolutionary stage in more details in Section 3). Standard stellar models generally agree with data for young stars in the colour-magnitude (CM) or in the HR diagram (see e.g., Tognelli, 2013; Randich et al., 2018), as qualitatively shown in figure. We remark that stellar models should be able to populate such region of the HR diagram where young stars are observed. Thus, the simple comparison with observations of young associations/clusters (especially in the GAIA era) in the HR/CM diagram can put strong constraints on stellar evolution theoretical predictions (see e.g., Babusiaux et al., 2018; Randich et al., 2018; Bossini et al., 2019). This is a fundamental point especially when accretion phases are taken into account (see Section 4), helping in constraining free parameters adopted in model computations.

FIGURE 1

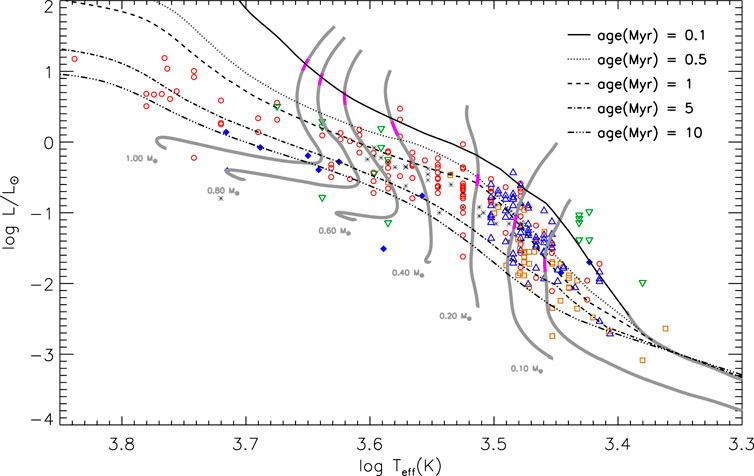
FIGURE 1. HR diagram for young pre-MS stars extracted from the literature, compared with a set of standard evolutionary models and isochrones from the PISA database (Tognelli et al., 2011; Tognelli et al., 2018).

Other constraints are provided from pre-MS stars in double-lined eclipsing binary (EB) systems, whose masses and radii can be determined with high precision. In recent years, an increasing number of EB systems have been studied in detail, giving the possibility to check pre-MS model predictions against data (see e.g., Mathieu et al., 2007; Gennaro et al., 2012).

Further constraints come from the measurements in low-mass stars of the surface abundance of lithium-7, which, being an element whose destruction rate is extremely sensitive to the temperature, can be used to test the temporal evolution of the pre-MS stellar structures (Charbonnel et al., 2000; Piau and Turck-Chièze, 2002; Randich, 2010; Tognelli et al., 2012). These issues will be discussed in the present rewiew.

3 General Characteristics of Standard Pre-Main Sequence Evolution

The pre-MS evolution starts at the end of the accretion phase and ends with the Zero Age Main Sequence, or simply ZAMS, position¹. The star is totally formed, and the mass can be considered constant at least for the whole pre-MS and Main Sequence (MS) evolution. The first consistent description of the pre-MS evolution was given by Hayashi (1961) and Hayashi and Nakano (1963); the basic idea is that a pre-MS star starts from a cold, expanse and luminous model. Due to the low temperatures, the opacity of the stellar matter is large and thus the radiative temperature gradient in the whole structure is larger than the adiabatic one. This leads to convective motions extended within the entire stellar structure; thus the star is fully mixed and chemically homogeneous. Figure 2 shows an example of the evolution of pre-MS solar metallicity low mass stars in the mass range [0.1, 1.0] ${\mathrm{M}}_{\odot }$ computed using the PISA stellar evolutionary code (Degl’Innocenti et al., 2008; Dell’Omodarme et al., 2012), with the adopted input physics/parameters described in Tognelli et al. (2018) and Tognelli et al. (2020); the same figure also shows a qualitative representation of some of the main evolutionary stages characteristics of such mass range.

FIGURE 2

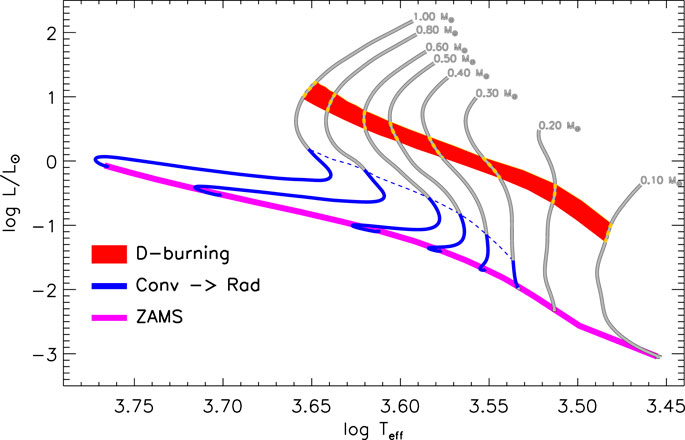
FIGURE 2. HR diagram for low-mass stars with indicated the main evolutionary stages during the pre-MS evolution: Hayashi track (fully convective star, gray line), partially convective star (blue line), locus of the Zero Age Main Sequence (ZAMS, magenta line). The locus corresponding to the deuterium burning is indicated by the red stripe.

Due to their low temperatures, during these first stages of the standard pre-MS evolution, stars cannot produce the nuclear energy required to balance the surface energy losses by radiation and their evolution essentially consists in a gravitational contraction. The evolution time scale is thus given by the thermal (Kelvin-Helmholtz) time scale, which is the time of energy transport throughout the star. It is common to define the Kelvin-Helmholtz time scale as the ratio between the total gravitational energy of the star and its luminosity L:

${\tau }_{KH}=\frac{\beta }{2}\frac{G{M}^2}{RL}.(1)$

The factor β takes into account the density profile inside the star. For an (unrealistic) model of homogeneous and spherical star with a constant density, $\beta =5/3$. The gravitational contraction leads to an internal temperature increase. We recall that for non-degenerate structures² the central temperature, $T_c$, depends on the stellar mass M, the radius R and the chemical composition (mean molecular weight μ) in the following way:

$T_c\propto \frac{\mu M}{R}.(2)$

From the relation above a contraction naturally leads to a rise in $T_c$. Using this result, the Stephan-Boltzmann law $\left(L\propto R^2{T}_{\mathrm{eff}}^{\mathrm{4}}\right)$ and the virial theorem, it can be shown that the luminosity of the star decreases following a simple power law, $L\propto t^{-2/3}$.

The gravitational contraction is the only energy source until the central temperature reaches about 10⁶ K, when the deuterium burning reaction D(p,γ)³He (D-burning) becomes efficient. Such a reaction generates the energy required to maintain the star stable on nuclear time scales, longer than the thermal one. This is guaranteed also by the steep dependence on the temperature of the energy generation rate, ${\mathit{\in }}_{pD}$, $\left({\mathit{\in }}_{pD}\propto T_c^{12}\right)$; such a dependence limits the $T_c$ increase, halting the gravitational contraction (because of the $T_c\propto 1/R$ relation).

The ignition of the D-burning, due to the produced energy flux, maintains the star fully convective and deuterium is burnt in the whole star. The D-burning phase is shown in Figure 2 as a the red stripe, which indicates the part of the Hayashi track where D-burning provides more than 10% of the total stellar luminosity, for stars with different masses.

The nuclear time scale of D-burning depends on the characteristics of the star, mainly on the mass. The luminosity of a star at the beginning D-burning phase increases with the stellar mass; this means that increasing the stellar mass the D-burning increases its efficiency to balance the higher energy losses at the stellar surface. Thus the rate of deuterium destruction increases with mass. The typical nuclear D-burning time scale for masses in the range $0.1-1{\mathrm{M}}_{\odot }$ varies between about 0.1–2 Myr, depending on the mass; as an example the D-burning phase lasts about 1–2 × 10⁶ yr for $0.1{\mathrm{M}}_{\odot }$ and about 10⁵ yr for a $1{\mathrm{M}}_{\odot }$ (see e.g., Chabrier and Baraffe, 1997; D’Antona and Mazzitelli, 1997; Tognelli et al., 2011).

The duration of the D-burning phase in pre-MS depends not only on the stellar mass but it is also proportional to the original stellar deuterium mass fraction abundance. Observations suggest that for disc stars a value of $X_D\approx 2\times {10}^{-5}$ should be adopted (see e.g., the review by Sembach, 2010); such a value is smaller than that predicted by the BBN ($X_D\approx 4\times {10}^{-5}$, see e.g., Steigman et al., 2007; Pettini et al., 2008; Pitrou et al., 2018; Mossa et al., 2020), as expected – e.g., by galactic evolution models – because deuterium is destroyed in stars.

Once deuterium has been completely exhausted in the whole star a pure gravitational contraction phase starts again. As for the previous evolution the stellar luminosity is well approximated by the power law $L\propto t^{-2/3}$. This second gravitational contraction increases the temperature and density in the inner region of the star. Depending on the total mass, such a temperature increase could lead to a drop in the radiative opacity ${\kappa }_R$. For stars with $M\mathrm{\gtrsim }0.3{\mathrm{M}}_{\odot }$ , the internal opacity drop reduces the radiative gradient leading to the formation of a central radiative stable zone. As a consequence of this fact, the star leaves the Hayashi track in the HR diagram, shifting toward larger temperatures as the radiative core grows in mass, until the star efficiently ignites the central hydrogen burning (reaching the ZAMS). This part of the stellar evolution is traditionally called the Henyey track and corresponds to the blue part of the evolutionary track in Figure 2. For $M\mathrm{<}0.3{\mathrm{M}}_{\odot }$, the temperature increase is not enough to produce such an opacity drop and the star continues its contraction along the Hayashi line. In this mass range, if the total mass is larger than approximately $0.08{\mathrm{M}}_{\odot }$, the contraction continues until the central temperature is large enough to ignite central hydrogen burning, which becomes the main energy source of the star (see e.g., Iben, 2013). On the other hand, if $M\mathrm{<}0.08{\mathrm{M}}_{\odot }$, during the contraction the star become so dense that the pressure is dominated by the degenerate electron contribution; in such a configuration the pressure is only very slightly dependent on the temperature. Then the contraction slows down and the star (called brown dwarf) evolves along a cooling sequence which, in the HR diagram, follows a precise mass-radius relation.

This general picture describes the evolution of a pre-MS star in the standard case; theoretical calculations are started when the star is a fully formed object, chemically homogeneous at high luminosity (large radius) on the Hayashi line. However, it is well known that stars undergo a formation phase, the protostellar phase, during which the mass is accreted from the protostellar cloud and/or from a disk to reach the final stellar mass. The inclusion of such a phase could, at least in principle, modify the standard theoretical picture.

4 Protostellar Accretion Phase

The stellar formation process starts with the collapse and the fragmentation of a molecular cloud that contracts forming denser cores which eventually become protostars and then stars. During this process, the protostellar mass progressively increases as the matter in the cloud falls onto the central dense object. The cloud collapse is a complex hydrodynamic problem, in which one has also to take into account cooling processes by molecules and dust. At a given time during the collapse a stable hydrostatic core forms, on which mass continues to fall, so that the accretion treatment does not require anymore hydrodinamical models (e.g., Stahler et al., 1980a; Stahler et al., 1980b; Stahler et al., 1981; Hartmann et al., 1997; Baraffe et al., 2012).

Protostellar accretion has been analyzed in the literature starting from the pioneering works by Stahler et al. (1980a), Stahler (1988), Palla and Stahler (1991), Palla and Stahler (1992), Palla and Stahler (1993), Hartmann et al. (1997), and Siess and Livio (1997), to more recent works by Baraffe et al. (2009), Hosokawa and Omukai (2009a), Baraffe and Chabrier (2010), Tognelli (2013), Kunitomo et al. (2017) and Tognelli et al. (2020). Depending on the characteristics of the accretion assumed in the computations (chemical composition, magnetic fields, rotation, geometry…) the collapse of the cloud and the stellar formation can produce different evolution whose footprints are still visible in pre-MS stars.

4.1 Cloud Collapse and Protostellar Accretion

The main phases of the protostellar evolution are briefly described below (for more details see Larson, 1969; Larson, 1972; Larson, 2003).

• Isothermal collapse: The protostellar cloud, during its first collapse (until the central density is lower than about 10⁻¹³ g·cm⁻³) does not warm, because its density is too low to trap the energy produced by the contraction. When the density further increases above this limit the radiation can be partially trapped.

• Formation of the first Larson core: the energy trapped inside the denser regions of the cloud prevent a further collapse of this region. A first temporarily hydrostatic core forms (with a mass of about $0.01{\mathrm{M}}_{\odot }$ and a radius of several AU) out of which the matter is still falling on the core. A transition region (shock front) develops close to the core surface where the matter settles and passes from supersonic to subsonic.

• Second collapse: the hydrostatic core contracts as long as it radiates energy from its surface. So, although its mass is increasing due to mass accretion, its radius shrinks. The contraction of the core leads to a temperature rise, until the temperature of molecular hydrogen dissociation $\left(T\sim 2000\mathrm{K}\right)$ is reached. Then contraction energy does not warm anymore the core but it’s used to dissociate $H_2$, forcing the core to break the condition of hydrostatic equilibrium. At this stage, the core density and pressure increase.

• Formation of the second Larson core: when $H_2$ is fully dissociated a further increase of density and pressure, due to contraction, while mass is still falling radially on the core, leads to a second, hydrostatic equilibrium for the central core with a mass of the order of $\sim 0.001{\mathrm{M}}_{\odot }$ (=1 M_J, Jupiter mass) and a radius of about $1{\mathrm{R}}_{\odot }$. From this moment on the central objects maintains its hydrostatic configuration while its mass increases.

The protostellar evolutionary phases listed above are quite general (for solar metallicity stars) and almost independent of the computation details. Larson (1969) remarked that at some stages of the cloud evolution a hydrostatic central object (second Larson core) forms that can be considered the first protostellar core. The characteristics of this core (i.e., mass, radius, density and central temperature) appear to be barely sensitive to the adopted cloud initial conditions or to the adopted input physics (see e.g., Masunaga and Inutsuka, 2000; Machida et al., 2008; Tomida et al., 2013; Vaytet et al., 2013). Reasonable intervals for the mass, radius and temperature of the stable hydrostatic core are: mass range of 1–20 M_J, radius values of $0.5-10{\mathrm{R}}_{\odot }$ and central temperature of 2–6 × 10⁴ K.

In the HR diagram of Figure 3 the sequence that identifies the end of the protostellar accretion (when the star becomes visible) is compared to standard isochrones. Interestingly, the end of the protostellar evolution is very close to the position of the 1 Myr standard isochrone. Larson (1969) and Larson (1972) adopting selected accretion parameters, followed the subsequent evolution until the Hayashi track, finding that low mass stars $\left(M<1{\mathrm{M}}_{\odot }\right)$ attain, after the protostellar accretion, characteristics similar to that of standard evolution along the Hayashi track. In contrast, as the mass increases $\left(M\mathrm{>2}{\mathrm{M}}_{\odot }\right)$, models skip the Hayashi line, ending the protostellar phase closer and closer to the MS position, where they join the “standard” track.

FIGURE 3

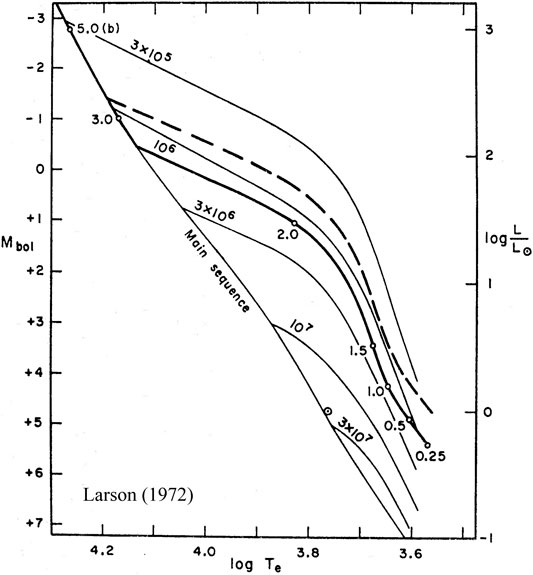
FIGURE 3. Comparison between standard isochrones (thin solid lines) and the loci of the end of protostellar accreting sequence for two different initial temperatures of the cloud (10 K thick solid and 20 K thick dashed line). Circles mark the position of 0.25, 0.5, 1, 1.5, 2, 3, and $5{\mathrm{M}}_{\odot }$ models. Figure adapted from Larson (1972).

It is worth to remark that theoretical models for the protostellar evolution cannot be easily checked with observations, as these accreting phases occur when the star is still embedded inside the cloud and thus the central core is largely masked by the matter around it.

4.2 Protostellar Accretion in Hydrostatic Stellar Evolution Codes

As already discussed, hydrodynamic evolution of accreting stars is still a challenging task from the computational point of view. However, concerning the central protostar, it’s not needed to employ a hydrodynamic code, as the protostar itself is in hydrostatic equilibrium after the formation of the second Larson core. In this approximation, the central object can be described using a mono dimensional hydrostatic stellar evolutionary code (see e.g. Stahler et al., 1980a; Stahler et al., 1980b; Siess and Livio, 1997).

On the other hand, hydrodynamic models are needed to predict the structure of the envelope surrounding the protostar, which does not satisfy the hydrostatic conditions but it’s essential to determine the characteristics of the accretion flow. More precisely, the envelope gives information about the accretion rate, the percentage of the energy of the falling matter transferred to the star and the accretion geometry. Information about these quantities are needed inputs for hydrostatic protostellar models. Due to the still present uncertainty on hydrodynamic calculations, all the previous accretion parameters are affected by not negligible theoretical indeterminacy, as briefly summarized below.

• Accretion rate. The accretion rate $\left(\dot{m}\right)$ defines the rate at which the star changes its mass; $\dot{m}$ can vary by orders of magnitude during the accretion phase, passing from $\dot{m}<{10}^{-6}-{10}^{-7}{\mathrm{M}}_{\odot }/\mathrm{yr}$ (quiescent accretion) to rapid and intense episodes of mass accretion (bursts) with $\dot{m}\sim {10}^{-4}-{10}^{-3}{\mathrm{M}}_{\odot }/\mathrm{yr}$, e.g., as observed in FU Ori stars (Hartmann and Kenyon, 1996; Audard et al., 2014; Hartmann et al., 2016).

• Energy transferred by the accreted matter. The matter falling to the star before reaching the stellar surface has a kinetic energy that can be estimated approximating the matter velocity to the free fall one. However, when it settles on the stellar surface, the kinetic energy has become equal to zero, so the kinetic energy has been converted into another energy form. It can be thermal energy carried inside the star (the accreted matter is hot), or the energy can be partially or totally radiated (photons) before the matter reaches the stellar surface (at the shock front). The fraction of the kinetic energy transferred to the protostar depends on the characteristics of the accretion flow (i.e., density, accretion geometry, accretion rate, see e.g., Baraffe et al., 2012).

The difficulty in treating simultaneously the protostar and the envelope evolution requires some simplifications, which mainly concern the geometry of the accreting protostar-envelope system:

• Spherical accretion (see e.g., Stahler et al., 1980a; Stahler, 1988; Palla and Stahler, 1991; Palla and Stahler, 1992; Palla and Stahler, 1993; Hosokawa and Omukai, 2009a). The star is supposed to be deeply embedded into the parental cloud and the matter falls on it almost radially. The whole stellar surface is subjected to the accretion and the energy radiated by the star can be reabsorbed by the envelope. The whole protostellar accretion occurs as a radial infall from a cloud that has mass enough to generate the star, at a fixed value of the accretion rate.

• Disc accretion (Hartmann et al., 1997; Siess and Livio, 1997; Baraffe et al., 2009; Baraffe and Chabrier, 2010; Tognelli, 2013; Kunitomo et al., 2017). The matter falls from a boundary layer of a circumstellar disc and reaches the star via accretion streams. Most of the stellar surface is not subjected by the accretion and the star is free to radiate its energy, most of which is lost in space. The disc is assumed to be totally decoupled from the central star and it is not treated in the stellar evolution codes. The parameters that define the accretion (accretion rate, disk lifetime, accretion energy) are considered as external free parameters which can be obtained from detailed accretion disc evolution calculations (e.g., Vorobyov and Basu, 2010; Baraffe et al., 2012).

The spherical accretion scenario is likely to describe the first stages of the formation of the protostar when it is still embedded within the cloud that retains an approximate spherical geometry. However, observations suggest that at some stage of protostellar evolution, the cloud collapses to a disc – because of angular momentum conservation – and that it is during the disc accretion that the star gains most of its final mass (see e.g., Natta et al., 2000; Meyer et al., 2007; Watson et al., 2007; Machida et al., 2010 and references therein). So, both scenarios are interesting and describe a part of the protostellar accretion.

The most important difference between spherical and disc accretion, which deeply affects the protostellar evolution, is the amount of energy retained by the accreted matter. Indeed, while in the spherical accretion it’s possible to estimate the amount of energy retained by the accreted matter, in disc accretion this quantity is defined by a free parameter $\left({\alpha }_{\mathrm{acc}}\right)$. The impact of ${\alpha }_{\mathrm{acc}}$ on the evolution is discussed in the next sections.

4.3 Spherical and Disc Protostellar Accretion

The spherical accretion scenario applies to a star that is deeply embedded in a gas cloud. In this case, the evolution of the star and of the envelope have to be treated simultaneously. This allows (at least in principle) to have a consistent evaluation of the accretion rate and the amount of thermal energy that the accretion flows bring inside the star. Qualitatively, the energy emitted from the stellar surface is not free to escape into space since it has to interact with the matter around the star. Thus such an energy is partially reabsorbed by the matter in the envelope, and it eventually reaches the star. The effect of this process is that the star has a kind of external energy source that warms up the stellar surface. The injection of thermal energy from the accreted mass forces the star to expand or at least to compensate for the radius decrease caused by injection of mass.

The impact of spherical accretion on the formation of pre-MS stars has been largely analyzed in the pioneering works by Larson (Larson, 1969; Larson, 1972; Stahler et al., 1980a; Stahler, 1988; Palla and Stahler, 1991; Palla and Stahler, 1992; Palla and Stahler, 1993), and more recently also by Hosokawa and collaborators (Hosokawa and Omukai, 2009a; Hosokawa and Omukai, 2009b; Hosokawa et al., 2010; Hosokawa et al., 2011). One of the main results of such a spherical accretion scenario is that stars during the accretion phase remain bright and with large radii. Using a mild and constant accretion rate of ${10}^{-5}{\mathrm{M}}_{\odot }/\mathrm{yr}$, it is possible to obtain fully accreted stars in a region of the HR diagram that corresponds to the upper envelope of the locus where young pre-MS stars are observed (see Figure 4). This sequence was called “birthline,” that is the locus of stars with different masses where the accretion ends and the stars become optically visible (Palla and Stahler, 1993).

FIGURE 4

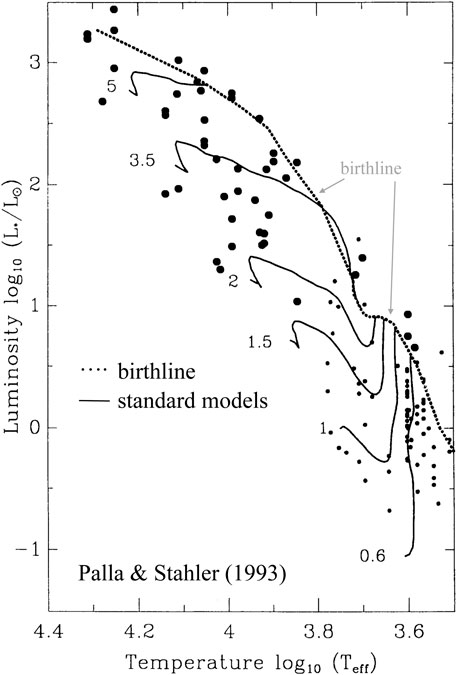
FIGURE 4. Comparison between standard tracks (solid lines) and the birthline (dotted line). Dots represent T Tauri and Herbig Ae/Be stars. Figure adapted from Palla and Stahler (1993).

More recent sets of birthlines can be found in Hosokawa and Omukai (2009a): such accretion models was computed for different values of the accretion rate (from ${10}^{-6}$ to ${10}^{-3}{\mathrm{M}}_{\odot }/\mathrm{yr}$), adopting a spherical protostellar accretion code (similar to that used by Stahler and Palla). They showed that increasing $\dot{m}$, the birthline moves toward larger luminosities and radii, thus still in full agreement with the observations. Moreover, since spherical accretion models produce low-mass stars (on the birthline) in a region that corresponds to the top of the Hayashi track of standard stellar models (see Figure 4), the differences between standard and spherical accreting models in pre-MS low-mass stars are negligible. This validates the results of standard evolutionary tracks/isochrones (at least for ages higher than 1 Myr).

However, it’s commonly accepted that stars do not accrete mass spherically during their entire protostellar phase; on the contrary they gain most of their mass from an accretion disc. This motivates the detailed study of protostellar accretion from a disk geometry. Differently from the spherical accretion, in the disc geometry the accretion streams cover only a very limited part of the stellar surface (few percent, see e.g., Hartmann et al., 1997) and almost the whole star is free to radiate its energy into space. Another difference is that all the accretion parameters (i.e., accretion rate, fraction of energy inside the accreted matter, etc..) are treated as external parameters in disc accretion models.

In the disc accretion geometry, it’s possible to follow also an analytic approach to analyze the main characteristics of the accreting star. Following the formalism presented in Hartmann et al. (1997), it’s possible to write a simple equation for the temporal evolution of the accreting star radius:

$\frac{\dot{R}}{R}=\frac{7}{3}\frac{R}{G{M}^2}\left[{\beta }_D-L_{\mathrm{ph}}+\left({\alpha }_{\mathrm{acc}}-\frac{1}{7}\right)\frac{G{M}^2}{R}\frac{\dot{m}}{M}\right](3)$

where M and R are the stellar mass and radius, ${\beta }_D$ expresses the luminosity due to the deuterium burning (D-burning), $L_{\mathrm{ph}}$ is the luminosity of the stellar surface, $\dot{m}$ is the mass accretion rate and ${\alpha }_{\mathrm{acc}}$ represents the fraction of the accretion energy deposed into the star (thermal energy of the accreted matter).

Equation 3 contains three terms: the first and second are the normal terms that define the evolution of the star with a surface radiative loss $\left(L_{\mathrm{ph}}\right)$ with the inclusion of D-burning energy production ${\beta }_D$, while the last term represents the accretion effect, which is proportional to $\dot{m}$. This term accounts for the fraction of the thermal energy of the accreted matter retained by the star, ${\alpha }_{\mathrm{acc}}$. Such a parameter has to be specified as an external free parameter, ranging from 0 (no energy acquired by the star) to about 1 (or 1/2 in case of thin disc, see e.g., Siess and Livio, 1997). From the same equation, it’s also evident that ${\alpha }_{\mathrm{acc}}=1/7\equiv {\alpha }_{\mathrm{acc},\mathrm{cr}}$ defines a critical value; for ${\alpha }_{\mathrm{acc}}\mathrm{<}{\alpha }_{\mathrm{acc},\mathrm{cr}}$ the third term is negative, and it contributes to the contraction of the star. For ${\alpha }_{\mathrm{acc}}\mathrm{>}{\alpha }_{\mathrm{acc},\mathrm{cr}}$ the same term produces a radius expansion. It is common to refer to the case ${\alpha }_{\mathrm{acc}}\sim 0$ (or ${\alpha }_{\mathrm{acc}}\ll {\alpha }_{\mathrm{acc},\mathrm{cr}}$) as cold disc accretion and ${\alpha }_{\mathrm{acc}}\mathrm{>}{\alpha }_{\mathrm{acc},\mathrm{cr}}$ as hot disc accretion.

Looking at Eq. 3 it is clear that a radius expansion requires a positive value of the right side of the equation, which can be obtained or via an efficient deuterium burning (large ${\beta }_D$) or via an efficient accretion energy transport into the protostar $\left({\alpha }_{\mathrm{acc}}\mathrm{>}{\alpha }_{\mathrm{acc},\mathrm{cr}}\right)$. These two cases are discussed separately in the next two sections.

4.4 D-Burning During Protostellar Accretion

To check if the D-burning alone can produce a protostar with a large radius, in agreement with observations, we assume ${\alpha }_{\mathrm{acc}}=0$. From eq. 3, to produce a radius increase, D-burning has to supply the star with enough energy to counterbalance the radiative losses at the stellar surface plus the gravitational energy decrease caused by the mass ingestion. If this condition is not satisfied, the protostar contracts and the resulting model at the end of the protostellar phase has a radius much smaller than that observed in young disk stars and expected in spherical accretion cases. The dependency of the radius on original deuterium abundance $X_{\mathrm{D}}$ has been investigated in Tognelli (2013) and more recently in Kunitomo et al. (2017). In Kunitomo et al. (2017) the authors assumed for the second Larson core mass the value $M_{\mathrm{seed}}=0.01{\mathrm{M}}_{\odot }$ (=10 M_J). Figure 5 shows a comparison between birthlines obtained assuming different values of $X_{\mathrm{D}}$, for a cold accretion scenario with M_seed = 10 M_J. When no deuterium is taken into account in the stellar matter, the star inevitably contracts: in this model, the star ignites the hydrogen burning close to the end of the protostellar accretion, thus totally skipping the pre-MS evolution. The situation changes increasing the deuterium mass fraction abundance in the star. To partially reproduce the standard pre-MS evolution, a deuterium content of $X_D\approx 4\times {10}^{-5}$ (i.e., 40 ppm) is required. If a more reliable deuterium content is adopted, $X_D\approx 2\times {10}^{-5}$, the models with protostellar accretion converges to standard models only in the Henyey track; in this case, the evolution along the Hayashi track is missed contrarily to what observed in young clusters. We want to comment about the fact that the uncertainty on galactic deuterium mass fraction abundance is not larger than 10 ppm (see e.g., Figure 2 and Table 1 in Sembach, 2010), thus an initial deuterium content of $X_D\approx 40\mathrm{ppm}$ is an over estimation for disk stars. This fact seems to indicate that deuterium alone is not capable of maintaining the star bright enough to reconcile protostellar cold accretion models and the results obtained in a standard non accreting scenario.

FIGURE 5

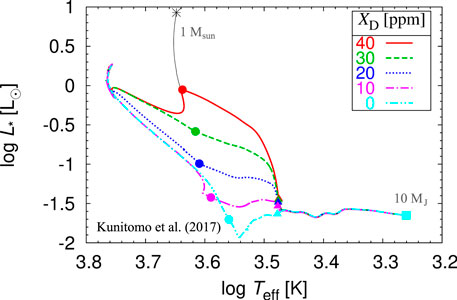
FIGURE 5. Effect of different deuterium original abundances (see labels), $X_{\mathrm{D}}$, on the protostellar evolution of $1{\mathrm{M}}_{\odot }$ model. The protostellar accretion starts with a seed mass of 10 M_J, with a constant accretion rate of ${10}^{-5}{\mathrm{M}}_{\odot }$·yr⁻¹. Filled circles indicate the end of the protostellar accretion phase and triangles the beginning of D-burning. Figure adapted from Kunitomo et al. (2017).

4.5 Accretion Energy

There is another natural way to obtain a radius expansion in protostars, which is assuming that the ingested matter retains part of its internal energy; this means to assume a value of ${\alpha }_{\mathrm{acc}}>{\alpha }_{\mathrm{acc},\mathrm{cr}}$. In Hartmann et al. (1997) it was shown that non-cold accretion models $\left({\alpha }_{\mathrm{acc}}>{\alpha }_{\mathrm{acc},\mathrm{cr}}\right)$ can attain a radius expansion large enough to reproduce observed stars; in this case the disc accretion mimics spherical-accretion birthline obtained by Stahler (1988). More recently, Kunitomo et al. (2017) analyzed in more details the impact of ${\alpha }_{\mathrm{acc}}$ on the formation of a $1{\mathrm{M}}_{\odot }$ model, finding that the inclusion of a certain fraction of the total accretion energy [i.e., ${\alpha }_{\mathrm{acc}}\in \left(\mathrm{0,1}\right)$] in the star is capable of maintaining the structure at large radii. Figure 6 shows the birthline computed in Tognelli (2013) – by means of the PISA stellar evolutionary code – for solar metallicity stars using three values of ${\alpha }_{\mathrm{acc}}=0$ (cold case), 0.5 and 1 (hot case), for a seed mass value of 5 M_J. From Figure 6, it is evident that adopting a value of ${\alpha }_{\mathrm{acc}}\ge 0.5$ models on the birthline are bright and intersect the standard evolutionary tracks in the standard Hayashi track, for all the selected mass range [0.1, 2.0] ${\mathrm{M}}_{\odot }$. Recently, Tognelli et al. (2020) have obtained similar results for metal poor models: they showed that even in the low metallicity case, the inclusion of accretion energy produces expanse objects that intersect the Hayashi track of standard non accreting models at the end of the protostellar accretion stage.

FIGURE 6

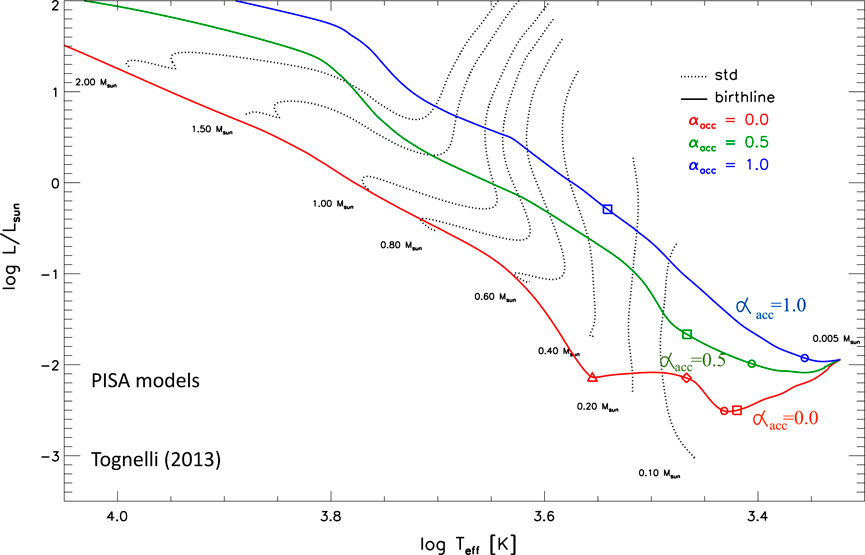
FIGURE 6. Effect of ${\alpha }_{\mathrm{acc}}$ on the protostellar evolution for three values of, 0 (cold accretion), 0.5 and 1 (hot accretion). Dotted lines are standard pre-MS tracks. Figure adapted from Tognelli (2013).

4.6 Connecting the Standard pre-MS and the Protostellar Accretion Phase

From the previous discussion, it emerges that, depending on the characteristics of the protostellar accretion, the protostar could end its first evolution with a structure similar or in some cases profoundly different from that obtained in a normal gravitational contraction along the Hayashi track. The largest discrepancy with standard pre-MS evolution occurs in the case of cold accretion starting from a seed of the order of few Jupiter masses, as in that case the classical Hayashi track is almost completely skipped (see e.g., Baraffe et al., 2009; Tognelli et al., 2020).

Figure 7 shows the evolution in the HR diagram of cold accretion models starting from different $M_{\mathrm{seed}}$ and ending with different final masses, as discussed in details in Baraffe et al. (2009). It is difficult to reproduce the Hayashi track of pre-MS stars starting from $M_{\mathrm{seed}}$ of few Jupiter masses (i.e., cases A, B, D). Moreover, the position of the 1 Myr model (filled square) in accretion models is relatively far from the standard 1 Myr isochrone; in most of the cases, the position of pre-MS models with the inclusion of cold protostellar accretion at 1 Myr is very close to the standard non accreting 10 Myr isochrone, witnessing the strong impact of cold accretion on pre-MS evolution.

FIGURE 7

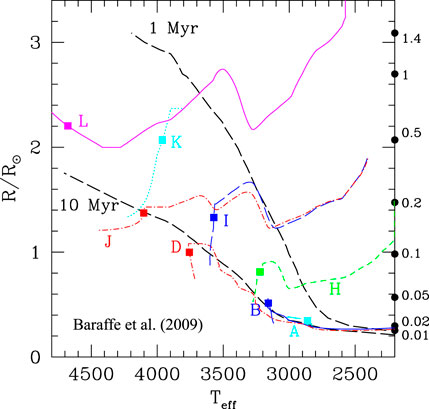
FIGURE 7. Evolution in the HR diagram of protostellar models with different values of $M_{\mathrm{seed}}$, compared with the standard 1 and 10 Myr isochrones (black long dashed lines). The different letters indicate models with different seeds and final masses $\left(M_{fin}\right)$, in particular (A) M_seed = 1 M_J, M_fin = $0.05{\mathrm{M}}_{\odot }$ (B) M_seed = 1 M_J, M_fin = $0.1{\mathrm{M}}_{\odot }$ (D) M_seed= 1 M_J, M_fin = $0.5{\mathrm{M}}_{\odot }$ (H) M_seed = 10 M_J, M_fin = $0.21{\mathrm{M}}_{\odot }$ (I) M_seed = 50 M_J, M_fin = $0.55{\mathrm{M}}_{\odot }$ (J) M_fin = $1.05{\mathrm{M}}_{\odot }$ (K) M_seed = 100 M_J, M_fin = $1.1{\mathrm{M}}_{\odot }$ (L) M_seed = 100 M_J, M_fin = $1.85{\mathrm{M}}_{\odot }$. Filled squares represent the position of the 1 Myr model. Figure adapted from Baraffe et al. (2009).

As discussed, it is likely that stars first accrete in a spherical hot scenario and then, at a given stage, switch to a disk-like accretion. In this case the transition from hot to cold accretion occurs for some value of the protostellar mass (possibly dependent on the amount of mass available in the cloud/disk). This mixed scenario has been investigated by Hosokawa et al. (2011) to show that the protostar remains bright enough to end the protostellar phase close to a Hayashi track. Top panel of Figure 8 shows the models by Hosokawa et al. (2011). The purely hot accretion scenario (purple solid line), which corresponds to a hot birthline obtained assuming a spherical accretion, attains large luminosities and radii well above the standard 1 Myr isochrone. Figure shows also the results of models where the accretion switches from hot to cold at a given value of the stellar mass, namely $0.03{\mathrm{M}}_{\odot }$ (magenta dashed line), $0.1{\mathrm{M}}_{\odot }$ (magenta solid line) and at $0.3{\mathrm{M}}_{\odot }$ (magenta dotted line). It is interesting to notice that in all cases, the birthline is still quite luminous, being very close to the 1 Myr isochrone. Similar results have been obtained for metal poor models by Tognelli et al. (2020) (bottom panel of Figure 8).

FIGURE 8

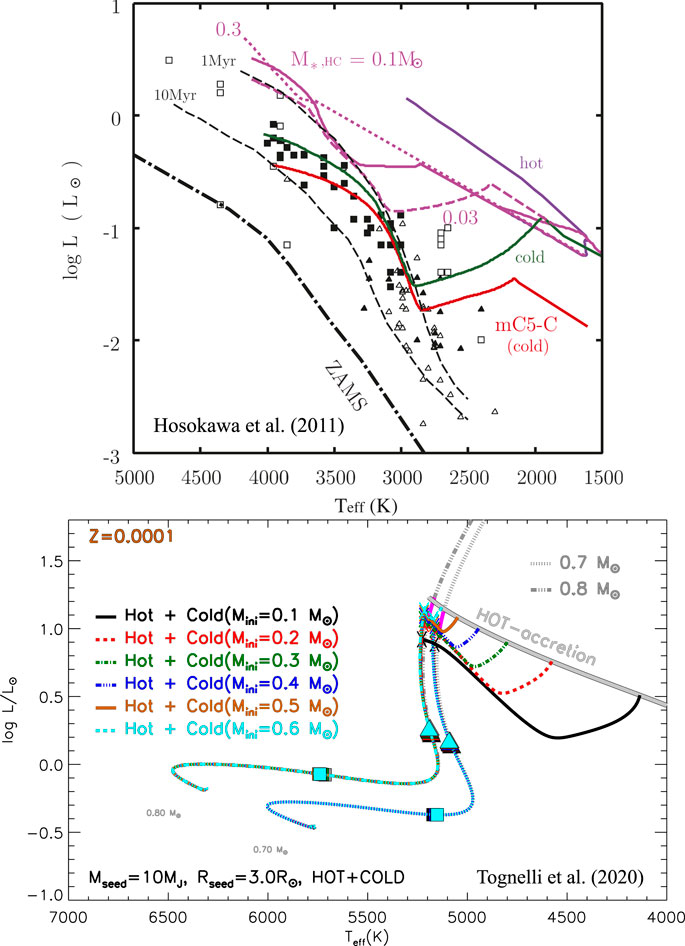
FIGURE 8. Evolution in the HR diagram of purely and partially hot models computed with an accretion rate $\dot{m}={10}^{-5}{\mathrm{M}}_{\odot }/\mathrm{yr}$. Top panel: comparison between purely hot (solid purple line), purely cold (green and red solid lines) and hot + cold birthlines (magenta lines). The two purely cold cases differ for the seed radius, $3.7{\mathrm{R}}_{\odot }$ (green line) and $1.5{\mathrm{R}}_{\odot }$ (red line, mC5-C). The accretion switches from hot to cold at a given value of the mass, which is $0.03{\mathrm{M}}_{\odot }$ (magenta dashed line), $0.1{\mathrm{M}}_{\odot }$ (magenta solid line), and $0.3{\mathrm{M}}_{\odot }$ (magenta dotted line). Black lines are isochrones of 1 and 10 Myr (dashed lines) and the ZAMS (dot-dashed line) for standard non accreting models. Squares, triangles and circles represent observations of some young pre-MS stars. Figure adapted from Hosokawa et al. (2011). Bottom panel: models at low metallicity (Z = 0.0001) for a total final mass of 0.7 and $0.8{\mathrm{M}}_{\odot }$. The accretion switches from hot to cold at a mass value 0.1, 0.2, 0.3, 0.4, 0.5, and $0.6{\mathrm{M}}_{\odot }$ as indicated in the labels. The thick gray line represents the hot birhtline $\left({\alpha }_{\mathrm{acc}}=1\right)$. Figure adapted from Tognelli et al. (2020).

Baraffe et al. (2009) and Baraffe et al. (2012) investigated also the possibility to produce bright objects using an episodic accretion. The basic idea behind the models is that during intense bursts mass accretion phases the protostar can accrete matter in the hot-accretion configuration [${\alpha }_{\mathrm{acc}}>{\alpha }_{\mathrm{acc},\mathrm{cr}}$, see the Appendix in Baraffe et al. (2012)], to switch back to cold accretion at the end of each burst. The authors showed that in this case it’s still possible to produce models that end their protostellar accretion close to the standard position of the Hayashi track, to reproduce data (see also Tognelli et al., 2020 for metal poor protostars).

What emerges from the previous analysis is that, if one assumes masses and radii typical of the second Larson core, cold models cannot produce the observed bright stars in young clusters, but it is required the presence of hot accretion phases. Thus, the results seem quite comfortable: in most hot disk or spherical geometry, the protostellar accretion leads to pre-MS models with characteristics similar to those predicted in standard pre-MS evolution. More importantly, the position in the HR diagram of such models is in agreement with observational data. On the contrary, for the accretion parameters leading to a final mass model different to that of the standard one, as in the cold accretion scenario, the position in the HR diagram is in disagreement with disk star observations, rising doubts about the validity of such models.

5 Light Elements Surface Abundances and Nuclear Burning During the pre-MS Phase

Lithium, together with beryllium and boron, belong to the class of light elements burnt in pre-MS, because of their relatively low nuclear destruction temperature (between 2–5 million degree). The threshold values for the burning temperature depend mainly on the considered element, on the stellar mass (density and evolutionary stage) and slightly on the chemical composition of the star (in particular on helium and metals abundances). For pre-MS solar metallicity stars in the mass interval [0.08, 1.0] ${\mathrm{M}}_{\odot }$, the ranges of burning temperatures for the different elements approximately are: 2.4–3.5 × 10⁶ K [T(^6,7Li)], 3.5–4.0 × 10⁶ K [T(⁹Be)] and 4.2–5.0 × 10⁶ K [T(^10,11B)]. In the literature the temperatures given for the burning are sometimes slightly different form the values reported here; the reason is that usually authors do not take into account that stars with different masses ignites these elements at slightly different temperatures because the nuclear burning rates also depends (even if at a lower level) on the density in the region where the burning occurs. Moreover, such temperatures can be different for MS or pre-MS stars with the same mass because of the different time scales in which light elements are destroyed. In MS stars the evolutionary time scale is much longer than that in pre-MS (for the same mass and chemical composition) consequently a smaller burning rate due to a smaller threshold temperature at the bottom of the convective envelope, is compensated by the longer time during which that element is destroyed. As a result the burning of light elements in MS can efficiently occur even at thresholds temperature smaller than those required in pre-MS. Due to the differences in their burning temperatures in pre-MS, Li, Be and B are gradually destroyed at different depths inside the stellar interior and at different ages, in dependence on the stellar mass. As an example, Figure 9 shows the portion along the evolutionary track where surface Li, Be and B are burnt at the bottom of the convective envelope in a set of solar chemical composition stars in the mass range [0.08, 1.0] ${\mathrm{M}}_{\odot }$. It is interesting to notice that while Li is burnt (at the bottom of the convective envelope) in the whole selected mass range, surface ⁹Be burning occurs only for masses between about 0.08 and $0.5{\mathrm{M}}_{\odot }$, while B is burnt in an even smaller mass range (about 0.1–$0.3{\mathrm{M}}_{\odot }$).

FIGURE 9

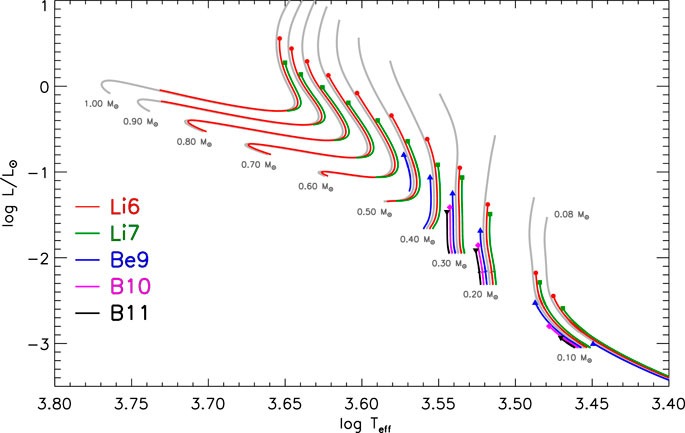
FIGURE 9. Evolutionary tracks for solar metallicity in the HR diagram with indicated the regions where surface light element abundances decrease due to burning (where the temperature at the bottom of the convective envelope is higher than the burning temperature of Li, Be and B). The stellar models have been computed using the PISA evolutionary code with the same input parameters described in Lamia et al. (2015).

The abundance of light elements at the stellar surface are strongly influenced by the nuclear burning as well as by the inwards extension of the convective envelope and by the temperature at its bottom. Consequently, the comparison between theory and observation for Li, Be and B surface abundances are useful to constrain theoretical models and in particular the convective envelope depth.

From the observational point of view, most of the data for light elements concern the abundance of ⁷Li whose line (at 670.779 nm) can be safely resolved even in cold stars, as witnessed by the huge amount of data for stars in clusters or isolated stars at different metallicities (see e.g., Sestito and Randich, 2005; Delgado Mena et al., 2014; Delgado Mena et al., 2015; Aguilera-Gómez et al., 2018 and references therein).

⁶Li burns at a lower temperature with respect to ⁷Li, consequently it’s almost completely destroyed when ⁷Li burning becomes efficient. Thus a potential detection of observable amounts of ⁶Li in stellar atmospheres would constrain the destruction of the less fragile ⁷Li (Copi et al., 1997). Since the depth of the convective zone increases with metallicity, ⁶Li is almost completely depleted in high metallicity disk stars, as in the Sun (see e.g., Asplund et al., 2009) and it is below the detection level also for most thick disk and halo stars (see e.g., Spite and Spite, 2010). The possible abundance of ⁶Li below the limit of detection also for halo stars could be explained by the fact that the amount of ⁶Li formed by the standard Big Bang and by the cosmic rays is supposed to be very low. Moreover, a very small ⁶Li abundance in these stars would be very difficult to detect, in particular because the lines (doublets) of ⁶Li and ⁷Li are overlapping (see also discussion in Sec. 5.5).

Beryllium and boron measurements are more problematic than ⁷Li observations. ⁹Be abundance is measured using near-UV lines, only in stars with $T_{\mathrm{eff}}\mathrm{\gtrsim }5000\mathrm{K}$, which corresponds in pre-MS to a mass range where Be is expected to be preserved and not destroyed (see e.g., Garcia Lopez et al., 1995; Santos et al., 2004; Randich et al., 2007; Smiljanic et al., 2010; Delgado Mena et al., 2012; Lamia et al., 2015).

The abundance of the boron isotopes is even more difficult to measure than Be because the boron lines fall mainly in the UV part of the spectra where the Earth atmosphere is not transparent. In addition, for disk metallicity stars, B lines suffer strong blending problems (see, e.g., Cunha, 2010). Similarly to Be, B abundance are available in a mass range where B is expected to be not burnt in standard models. Despite the observational difficulties Be and B surface abundances data are available for some stars even at low metallicities (see e.g., Boesgaard and Novicki, 2005; Lodders et al., 2009; Tan et al., 2009; Primas, 2010; Boesgaard et al., 2011). In the observed stars, the ratio ¹¹B/¹⁰B seems to be of the order of four, in agreement with solar values and meteorite results, even if it is very difficult to spectroscopically discriminate among the boron isotopes (see, e.g., Proffitt and Quigley, 1999; Prantzos, 2012). Be and B surface abundances have been also measured in the Sun where, as expected, they are not burned (see e.g., Asplund et al., 2005; Asplund et al., 2009; Lodders et al., 2009; Lodders, 2010).

The temperatures for light elements burning can be reached in stellar interiors during the pre-MS evolution of stars with masses larger than about 0.05–$0.1{\mathrm{M}}_{\odot }$ (depending on the requested burning threshold temperature). We recall that at the beginning of the pre-MS evolutions stars are, independently of their mass, fully convective. Thus, if a nuclear burning occurs at this evolutionary stage, the burning affects the chemical abundance in the whole star, from the center to the surface. However, as the star contracts and warms up, the opacity decreases at the stellar center and stars with $M\mathrm{\gtrsim }0.3{\mathrm{M}}_{\odot }$ develop a radiative core. From this moment on the chemical evolution of the surface is (during the pre-MS) decoupled from that of the center if the bottom of the convective envelope does not reach a region deep and hot enough to process –via nuclear burning– the surface matter. Thus, for partially convective pre-MS stars, a condition to have a partial surface depletion of a specific element is that the bottom of the convective envelope reaches a temperature high enough to make nuclear burning efficient and then recedes toward the external parts of the star at lower temperatures.

Figure 10 shows the temporal evolution of the temperature at the bottom of the convective envelope, $T_{\mathrm{bce}}$, for stars with different masses between 0.08 and $1.0{\mathrm{M}}_{\odot }$ at solar metallicity, with indicated the approximate values for the Li, Be and B burning temperatures. In fully convective stars $T_{\mathrm{bce}}$ coincides with the central temperature, T_c. When stars are fully convective $T_{\mathrm{bce}}$ progressively increases until the star reaches the ZAMS, while in stars that develop a radiative core $T_{\mathrm{bce}}$ stops increasing when the radiative core forms and $T_{\mathrm{bce}}$ slowly decreases as the radiative core grows in mass. This has a direct impact on the interval of time during which the surface light elements depletion occurs. Considering e.g., ⁷Li abundance in fully convective stars (i.e. $\mathrm{M\le }0.3{\mathrm{M}}_{\odot }$), $T_{\mathrm{bce}}$ overcomes T(⁷Li) at young ages (i.e., about 50 Myr for $0.1{\mathrm{M}}_{\odot }$ and 5 Myr for $0.3{\mathrm{M}}_{\odot }$); then surface Li burning continues during the whole pre-MS and MS phase. Since $T_{\mathrm{bce}}$ continuously increases, the burning efficiency increases too. On the other hand, in partially convective stars $T_{\mathrm{bce}}$ reaches a maximum and then decreases as the star evolves toward the ZAMS. For $M\mathrm{\gtrsim }0.5{\mathrm{M}}_{\odot }$, $T_{\mathrm{bce}}$ decreases below T(⁷Li) at some point during the pre-MS, thus halting the lithium burning at the bottom of the convective envelope. From this moment on, surface lithium abundance remains constant during the pre-MS phase. Figure 10 also shows that increasing the mass of the star the time interval during which surface lithium is destroyed is shorter and the maximum value of $T_{\mathrm{bce}}$ reduces too; this is due to the fact that increasing the mass the convective envelope becomes thinner. This indicates that, increasing the mass, surface lithium is destroyed progressively less efficiently.

FIGURE 10

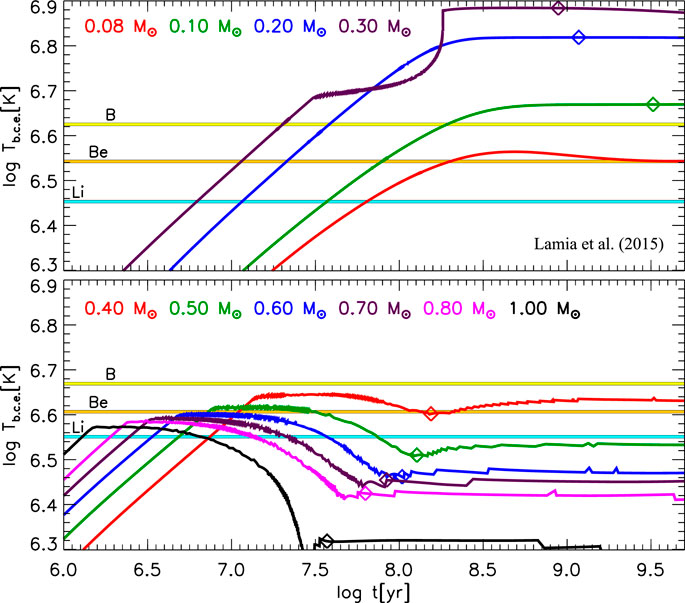
FIGURE 10. Temporal evolution of the temperature at the bottom of the convective envelope for masses in the range [0.08,1.0] ${\mathrm{M}}_{\odot }$. The threshold temperature required to ignite Li, Be and B burning are indicated as colored horizontal lines. The ZAMS position is marked by a diamond. The not regular behavior of the $0.3{\mathrm{M}}_{\odot }$ model at $\log t\left(yr\right)\sim 7.5-8.3$ is caused by the formation of a transient convective core before the ZAMS [figure adapted from Lamia et al. (2015)].

The situation is similar for the other light elements; clearly one has to take into account the different burning temperatures, so that the mass range in which Be and B are destroyed at the base of the convective envelope is different from that in which lithium is burned. As an example, for solar composition models, Be can be burnt at the bottom of the convective envelope in the mass interval $0.08\mathrm{\lesssim }M/{\mathrm{M}}_{\odot }\mathrm{\lesssim }0.5$. On the other hand B in destroyed only in the mass range $0.1\mathrm{\lesssim }M/{\mathrm{M}}_{\odot }\mathrm{\lesssim }0.3$.

Figure 11 gives an example of the ⁷Li surface abundance time behavior predicted for stars in the mass range [0.08, 1.0] ${\mathrm{M}}_{\odot }$; it’s important to notice that ligh element surface abundances depend not only on the capability of $T_{\mathrm{bce}}$ to overcome the threshold temperature for the considered element, but also on the duration of the burning and on the difference between the threshold and $T_{\mathrm{bce}}$. In particular, this last quantity is very important because the burning rate of light elements is proportional to $T^a$ with $a\approx 20$ for lithium, $a\approx 23$ for beryllium and $a\approx 25$ for boron.

FIGURE 11

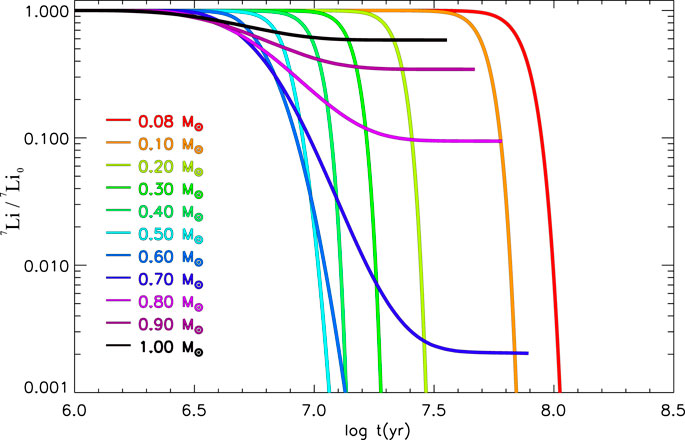
FIGURE 11. Temporal evolution of surface lithium abundance (normalized to the initial one) during the pre-MS for stars in the mass range [0.08, 1.0] ${\mathrm{M}}_{\odot }$ and solar chemical composition. Stellar models have been computed using the same input parameters described in Lamia et al. (2015).

Referring to Figure 11, in fully convective stars, i.e., $M\mathrm{\lesssim }0.3{\mathrm{M}}_{\odot }$, at a fixed age, the surface lithium depletion progressively increases increasing the stellar mass. For partially convective models, this behavior breaks up and, at a fixed age, the lithium depletion decreases as the mass increases. This is clearly visible in the figure comparing e.g., the predicted lithium abundance at about $\log t\left(yr\right)=7.5$ for 0.7, 0.8, 0.9, and $1.0{\mathrm{M}}_{\odot }$ models. The amount of residual surface lithium increases with the mass, as the consequence of the decrease of $T_{\mathrm{bce}}$ (in time) when the radiative core forms and grows.

Figures 10, 11 refer to a standard evolution, where the star is fully formed at the top of the Hayashi track. The situation can be different if protostellar accretion is taken into account, in particular in those cases where the star at the end of the protostellar phase is compact and faint, which corresponds essentially to the case of cold accretion models. This could affect light element burning in two different ways: 1) in principle for some possible values of the accretion parameters it could be possible the burning of light elements (most likely lithium) during the protostellar phase 2) accretion can change the pre-MS stellar characteristics with respect to those already predicted by the standard scenario so that the light element burning efficiency is changed too. We will discuss the effect of the protostellar accretion on the surface chemical composition in Section 5.2.

5.1 Surface Lithium Abundance in Open Clusters

Many questions are still open about the large discrepancies between the predicted and observed surface lithium abundance in young clusters, where standard models tend to underestimate the surface abundance at a given age (see e.g., D’Antona et al., 2000; D’Antona and Montalbán, 2003; Jeffries, 2006; Tognelli et al., 2012 and references therein). Moreover the presence of a large scatter in the observed Li abundance among stars with similar $T_{\mathrm{eff}}$ in young clusters poses questions about the possible mechanisms producing different amounts of lithium depletion in stars with the same mass, age and chemical composition (Jeffries, 2000; King et al., 2000; Clarke et al., 2004; Xiong and Deng, 2006; King et al., 2010).

It is worth noticing that, qualitatively, standard models (without accretion) are capable to produce a pattern of lithium vs. mass (or $T_{\mathrm{eff}}$) similar to that observed in young clusters. This pattern can be divided into three regions, and, referring to Figure 12, it can be summarized as it follows:

FIGURE 12

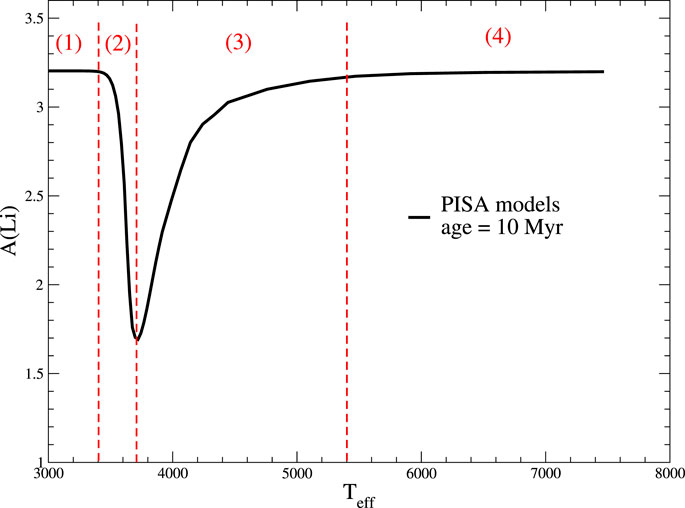
FIGURE 12. Theoretical surface lithium abundance predicted for solar metallicity stars at 10 Myr, as obtained in standard evolutionary models using the PISA evolutionary code.

• Starting from a certain value of the effective temperature (that depends on the cluster age) the surface lithium content, at a given cluster age, increases with the $T_{\mathrm{eff}}$ (or the stellar mass), until it reaches a plateau corresponding to stars that do not deplete Li (hot stars). Regions (3)–(4) in Figure 12 correspond to partially convective models of increasing mass. As previously discussed, the more massive is the star, the thinner is the convective envelope and, in turn, the less efficient is the surface Li depletion. The plateau corresponds to stars with a convective envelope so thin that T_bce < T(⁷Li).

• For lower masses (and thus $T_{\mathrm{eff}}$), e.g., in regions (1)–(2), stars are fully convective and lithium is burned in the whole star. At a fixed age the lithium burning efficiency increases with the stellar mass and lithium surface abundance rapidly changes varying the stellar mass.

• In region (1), reducing the mass (or $T_{\mathrm{eff}}$), one approaches the minimum mass that reaches the Li burning temperature in fully convective stars. Below this minimum mass the surface lithium abundance is constant and equal to the original value.

5.2 Lithium Abundance Evolution During Protostellar Accretion

As discussed in the previous section, the inclusion of the protostellar accretion phase could (in dependence of the adopted accretion parameters) drastically alter the evolution of a pre-MS star. In this section we briefly review the main effects of the protostellar accretion phase on the surface lithium abundance during the protostellar and pre-MS evolution as a function of the different possible accretion parameters.

This problem was first analyzed by Baraffe and Chabrier (2010), who showed that the inclusion of protostellar accretion in solar metallicity stars with different input parameters can lead to a variety of cases for which the resulting lithium abundance (in pre-MS or in MS) is different from what expected in standard pre-MS evolution (see also Baraffe et al., 2012; Tognelli, 2013; Kunitomo et al., 2018). We recall that accretion models depend on many parameters, but the main quantities that strongly affect the pre-MS evolution are the seed mass and the accretion energy deposed into the star. The general picture that emerges is that in cold accretion models lithium is efficiently destroyed during the protostellar accretion or at the very beginning of the pre-MS phase. Thus these stars should show a very low surface lithium content.

A detailed analysis of the effect of the protostellar accretion on surface lithium abundance for different subsolar metallicities ($Z=0.005$, $Z=0.001$, and $Z=0.0001$) was discussed in Tognelli et al. (2020). We also performed some tests to verify that what obtained for sub-solar metallicity is still valid at solar metallicities.

The results by Tognelli et al. (2020), similarly to what already obtained by Baraffe and Chabrier (2010), show that two scenarios can be found:

• Pure cold accretion case. The accretion leads to stellar structures at the end of the protostellar phase different with respect to standard non accreting models, affecting also the lithium burning efficiency. If the seed mass is of the order of few Jupiter masses, the models result to be so compact and hot that start to efficiently deplete lithium before the end of the accretion phase. The level of depletion is mainly determined by the seed mass and it’s only slightly affected by the other accretion parameters (accretion rates, initial radius). After the protostellar phase, for masses larger than about 0.1–$0.2{\mathrm{M}}_{\odot }$, lithium is completely destroyed in an extremely hot and fully convective pre-MS structure. This prediction is in complete disagreement with observations available for young clusters, where $M\approx 0.8$–$1{\mathrm{M}}_{\odot }$ stars show no relevant lithium depletion (see Section 5.4 for more details). Moreover, such accreting models are in disagreement with the observed position of very young disk pre-MS stars in the HR diagram. The disagreement between data and accretion models is partially mitigated if a larger seed mass is adopted (of the order of 10 M_J). In this case it is possible to reduce the level of lithium depletion in very low mass stars (i.e., $M\mathrm{\lesssim }0.3{\mathrm{M}}_{\odot }$), but not for stars close to $1{\mathrm{M}}_{\odot }$ where lithium is totally depleted in pre-MS.

• Hot accretion case. In Section 4.6 we showed that if stars accrete part of their mass during an hot accretion phase (during which the protostar is maintained at large radius by the accretion energy), the star at the end of the accretion phase is more similar to a standard evolutionary models. In this case, protostars are relatively cold and they do not deplete an appreciable amount of Li. Then, when the star enters the pre-MS the residual lithium is essentially equal to the original one, as predicted by models without accretion and from this moment on the lithium evolution proceeds as in standard stellar evolutionary models.

These two scenarios embrace many other possible solutions, obtained by modify/tuning the accretion parameters and the accretion history to produce, at least in principle, intermediate scenarios. However, a fine tuning of the accretion parameters that depends also on the stellar mass is unlikely and could produce artificial results (Tognelli et al., 2020). The two extreme scenarios highlight an important point. The expected Li abundance is strictly connected to the protostellar evolution. Stars that due to the inclusion of the protostellar accretion skip the Hayashi track (i.e., pure cold accretion) undergo to an efficient lithium burning during the protostellar phase, in disagreement with standard predictions. This kind of models are excluded, at least for disk metallicities, by observational data.

The possible effects of accretion on stellar characteristics and Li temporal evolution could also be linked to the question of the luminosity spread observed in star forming regions. The problem consists in the fact that stars with the same $T_{\mathrm{eff}}$ and the same chemical composition show different luminosities (see e.g., Hillenbrand, 2009; Jeffries, 2009; Da Rio et al., 2010a; Da Rio et al., 2010b). A possible dependence on the protostellar accretion of such a luminosity spread was analyzed by Baraffe et al. (2009); the adoption of a different accretion history during the protostellar phase can strongly affect the luminosity and $T_{\mathrm{eff}}$ of a star at the end of the protostellar phase, as already discussed in previous sections. If this is the case, faint stars, which experienced cold accretion, should show a clear lower lithium content than bright ones. In other words, such a luminosity spread should directly reflect in a surface lithium content spread. This point deserves to be further investigated to clearly confirm or exclude the presence of a correlation between lithium content and luminosity in star forming regions.

5.3 Lithium in Old Metal Poor Stars

An interesting aspect to be discussed about lithium evolution is the cosmological lithium problem. Halo stars show a lithium plateau for $T_{\mathrm{eff}}>5900\mathrm{K}$ and [Fe/H] < −1.5, the so called Spite plateau (Spite and Spite, 1982a; Spite & Spite, 1982b), with a constant logarithmic lithium abundance³A(Li)-2.4 (Charbonnel and Primas, 2005; Asplund et al., 2006; Meléndez et al., 2010; Sbordone et al., 2010), and references therein. From the theoretical point of view, stars with such temperatures and metallicities are expected to preserve their initial lithium content, moreover galactic enrichment due to cosmic rays and spallation processes should be totally negligible at such low metallicities. Thus the Spite plateau is expected to represent the primordial lithium content produced during the big bang nucleosynthesis (BBN).

However, BBN predicts a primordial lithium content of A(Li)-2.75, (see e.g., Cyburt et al., 2016; Pitrou et al., 2018). This estimate depends on the density of baryons, which is related to the fluctuations of the cosmic microwave background measured with WMAP and Planck satellites. The BBN predictions for the primordial lithium abundance are thus 0.3–0.6 dex larger than the Spite plateau value. This discrepancy constitutes the so called “cosmological lithium problem.” Several attempts to introduce new physics (exotic particles) or to review the reaction rates during the BBN have been performed, but without any firm conclusion (see e.g., Fields, 2011; Pizzone et al., 2014; Goudelis et al., 2016; Coc and Vangioni, 2017; Damone et al., 2018; Lamia et al., 2019).

Similarly, on the stellar evolution side, the problem has been analyzed to find a possible mechanism to deplete the same lithium amount for the stars with different masses and metallicities which populate the Spite plateau. Diffusion has been investigated as a possible solution, as it slowly brings surface lithium below the convective region (Richard et al., 2005). This process acts on timescales typical of the MS evolution, but its efficiency depends on the stellar mass and thus in the mass range corresponding to the Spite Plateau the effect of diffusion increases with $T_{\mathrm{eff}}$. Thus no Spite plateau would be possible without tuning the diffusion efficiency. Also turbulent mixing could produce an effect similar to that of pure diffusion, on similar time scales, but also in this case an ad hoc tuning is required (see e.g., Richard et al., 2005; Spite et al., 2012 and references therein). Also mass loss coupled to diffusion and turbulent mixing can be tuned to produce a constant lithium depletion along the Spite plateau (Swenson, 1995; Vauclair and Charbonnel, 1995), but, again, there is the need for a fine tuning of the parameters.

Another possibility is that lithium depletion occurs during the pre-MS. In this case, Fu et al. (2015) suggested that a certain level of undershooting⁴ at the bottom of the convective envelope of pre-MS stars could increase the depletion of surface lithium. In addition, a residual matter accretion, regulated by the stellar luminosity, could provide gas with pristine chemical composition (and thus lithium to the star), obtaining in pre-MS the depletion level required to produce the Spite plateau. However, in such models, MS diffusion must be inhibited to avoid a $T_{\mathrm{eff}}$ (or mass) dependent depletion on MS time scales.

Recently Tognelli et al. (2020) analyzed the possibility to produce a constant lithium depletion in pre-MS taking into account in the models the protostellar evolution with different accretion parameters. As discussed in Sec. s 4.6 and 5.2, depending on the scenario adopted during the protostellar evolution, stars at the beginning of the pre-MS can be profoundly different from the ones evolved starting from the Hayashi track. The reason is that the protostellar phase can deeply affect the thermal structure of a star. As a result, it’s possible to induce a lithium depletion in pre-MS or even during the protostellar phase, but it requires the adoption of a fine tuning of the parameters that govern the stellar mass acretion (see e.g., Fu et al., 2015; Tognelli et al., 2020). Moreover, as already discussed, the models that show a significant Li depletion, follow a pre-MS evolution in the HR diagram that is different to that observed for high metallicity pre-MS stars. The lack of Galactic very young and metal poor stellar systems, in which one could observe pre-MS stars with Spite plateau metallicities, avoid the possibility to restrict the range of valid accretion parameters and reach firm conclusions.

To conclude, the proposed mechanisms could in principle alleviate the cosmological lithium problem, but the weakness of all these suggested solutions is that a fine tuning of the parameters is still required to produce a constant lithium depletion reproducing the Spite plateau.

5.4 Uncertainties on Predicted Surface Lithium Abundance

The predicted depletion of surface lithium abundance (and, in general, of the light element surface abundances) is affected by the uncertainties on the input physics adopted in stellar models and on the assumed chemical composition, that influence the extension of convective envelope and temperature structure of the star. In particular, also the uncertainty on the nuclear burning cross sections plays a role in the light element abundance predictions. In the literature there are several attempts to estimate the impact of the uncertainties on the parameters/input physics adopted in stellar models on the predictions of lithium abundance in low and very-low mass stars (see e.g., Piau and Turck-Chièze, 2002; Burke et al., 2004; Tognelli et al., 2012; Tognelli et al., 2015). The quantities that mainly affects lithium, as analyzed in the quoted papers, are the following (see e.g., Chapter 3 in Tognelli, 2013):

• Radiative opacity and equation of state. The extension of the convective envelope is determined by the Schwarzschild criterion which simply states that a region is convective if the radiative temperature gradient $\left[{\nabla }_{rad}\equiv {\left(d\log T/d\log P\right)}_{rad}\right]$ is larger than the adiabatic one. The radiative gradient is proportional to the Rosseland mean radiative opacity ${\kappa }_R$, thus change in ${\kappa }_R$ directly affects the position of the convective unstable boundary. Generally an uncertainty on ${\kappa }_R$ of about $\pm 5\%$ is assumed in the computations (Badnell et al., 2005; Blancard et al., 2012; Mondet et al., 2015). Similarly an uncertainty on the adiabatic gradient, ${\nabla }_{ad}$, thus in the equation of state, modifies the position of the bottom of the convective envelope. An increase in ${\kappa }_R$ or a decrease of ${\nabla }_{ad}$ lead to an extension of the convective envelope that can reach deeper and hotter layers, increasing the efficiency of surface lithium burning (see e.g., Tognelli, 2013). The variation of surface lithium abundance, due to the change in the equation of state or radiative opacity, strongly depends on the selected mass range and age. However, in those models that efficiently deplete lithium (e.g., for 0.7 and $0.8{\mathrm{M}}_{\odot }$) a variation in lithium abundance of approximately 0.1–0.2 dex (due to equation of state uncertainty) and 0.4–0.5 dex (due to opacity error) can be obtained. In the worst cases (i.e., $M\sim 0.6{\mathrm{M}}_{\odot }$) a variation of $5\%$ of the radiative opacity can lead to a difference of ∼0.8 dex in the predicted lithium content. The effect on surface lithium of the equation of state or radiative opacity reduces as the mass increases.

• Outer boundary conditions. The outer boundary conditions are the pressure $P_{atm}$ and temperature $T_{atm}$ at the bottom of the atmosphere. These quantity deeply affect the temperature profile in the convective envelope thus modifying also its depth. The uncertainty on $\left(P_{atm},T_{atm}\right)$ it is not provided by stellar atmospheric calculations, but one can test the effect on the stellar characteristics of the adoption of different atmospheric models available in the literature (see e.g., Tognelli et al., 2011). As said above, the effect on lithium depends on the mass/age of the models; a typical variation of 0.3–0.5 dex is expected, which reduces as the mass increases..

• Mixing length parameter. The convection efficiency in super-adiabatic regimes in 1D stellar evolution codes commonly relies on mixing-length theory (MLT) (Böhm-Vitense, 1958). In this formalism, the scale on which the heat is efficiently transported by convection is defined as $\ell ={\alpha }_{\mathrm{ML}}\times H_p$, where $H_p$ is the local pressure scale height and ${\alpha }_{\mathrm{ML}}$ is the mixing length parameter, a free parameter to be calibrated. The extension of the convective envelope and thus the temperature at its bottom and the surface lithium abundance are strongly affected by the adopted ${\alpha }_{\mathrm{ML}}$. The adoption of different values of this quantity within plausible ranges can produce a variation of surface lithium abundance as large as one order of magnitude in those stars where the external envelope is largely super adiabatic and where lithium is efficiently destroyed at the bottom of the convective envelope (i.e., for masses in the range [0.5, 1.0] ${\mathrm{M}}_{\odot }$ (see e.g., Piau and Turck-Chièze, 2002; Tognelli et al., 2012).

• Nuclear cross section. The error on the cross section for the ⁷Li(p, $\alpha$)⁴He reaction directly affects the rate at which lithium is destroyed and thus its temporal evolution. Since the energy released by such reactions is inconsequential for the stellar structure, the only effect is on the surface lithium content at a fixed age. In Section 6 we will discuss this point in more detail.

• Chemical composition. The initial abundance of helium (Y) and metals (Z) in the star is not known, but it can be estimated from the observed [Fe/H], assuming for metal rich stars the same relative abundance of metals of the Sun, while for metal poor galactic stars a suitable alpha-enhancement must be introduced⁵. The conversion of [Fe/H] into Y and Z depends on the assumed values of: 1) the primordial helium mass fraction produced in the BBN $\left(Y_p\right)$, 2) the metal-to-helium enrichment ratio $\left(\Delta Y/\Delta Z\right)$, 3) the metal-to-hydrogen ratio in the Sun $\left[{\left(Z/X\right)}_{\odot }\right]$, 4) and the [α/Fe] (alpha-enhancement) for metal poor stars (Gennaro et al., 2012; Tognelli et al., 2012; Tognelli et al., 2015). The observational error on [Fe/H] has thus to be combined with the uncertainties of such quantities, to estimate the final global uncertainty on the initial helium and metal mass fraction to be used in the computation of stellar models (see e.g., Gennaro et al., 2012; Tognelli et al., 2012; Tognelli et al., 2015); for solar chemical composition, the uncertainty on Y and Z are estimated to be of the order of 4–5% for Y and about 20% for Z (Tognelli et al., 2015). The variations of Y and Z have a strong impact on the lithium burning because they change both the extension of the convective envelope and the temperature inside a star (see e.g., Piau and Turck-Chièze, 2002; Tognelli, 2013; Tognelli et al., 2015); the uncertainty on the chemical composition can produce a variation of the surface lithium abundance up to one order of magnitude, especially in stars with $M\mathrm{\lesssim }0.7{\mathrm{M}}_{\odot }$. The effect reduces at larger masses.

Tognelli (2013) quantitatively evaluated the impact on the predicted surface lithium abundance of the uncertainties in the input physics and in the initial chemical composition discussed above, calculating upper and lower limits of surface ⁷Li in stellar models. Figure 13 shows the estimated upper/lower limits (plotted as error bars) of surface lithium abundance and effective temperature, due to the contribution of the input physics uncertainties (top panel) and chemical composition indeterminacy (bottom panel). Stars with different masses at different ages typical of young clusters are shown (for more details on the procedure adopted to obtain these limits see Tognelli et al., 2012; Tognelli, 2013). The errors on the present input physics and the typical uncertainties on the adopted chemical composition have a drastic impact on the predicted surface lithium abundance, which can vary by more than one order of magnitude, especially for stars with $T_{\mathrm{eff}}\mathrm{\lesssim }4700\mathrm{K}$.

FIGURE 13

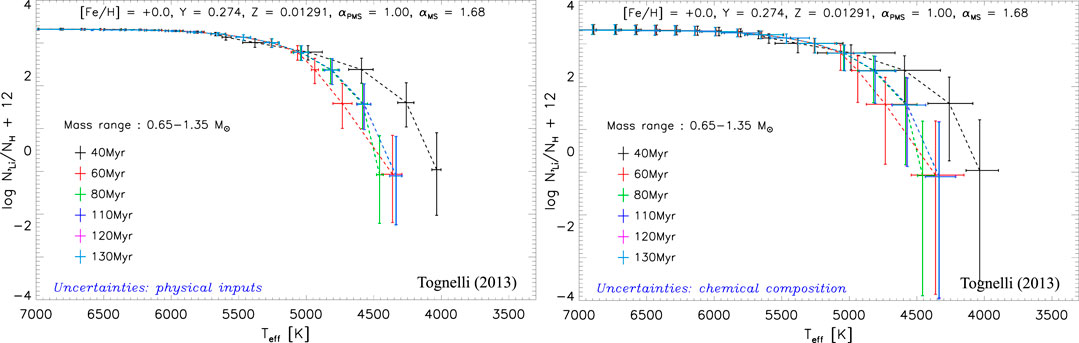
FIGURE 13. Uncertainties on surface lithium abundance and effective temperature due to the errors on adopted input physics (left panel) and chemical composition (right panel). Figure adapted from Tognelli (2013).

In standard models, the only possibility to deplete surface lithium in pre-MS is via convective mixing. If the bottom of the convective envelope reaches a region hot enough to burn lithium, then the surface lithium decreases in time. The level of depletion depends on a key parameter in convective stars, which is the efficiency of convective energy transport. A more efficient convective transport produces hotter stars that consequently experience a more efficient lithium burning. The opposite occurs if the convection efficiency reduces.

A precise physical treatment of external convection would require three-dimensional hydrodynamic models which have been improved in recent years, but only for limited regions of the star corresponding mainly to the atmospheric regions (see e.g., Nordlund et al., 2009; Collet et al., 2011; Freytag et al., 2012; Magic et al., 2013; Trampedach et al., 2013; Trampedach et al., 2014; Trampedach et al., 2015; Pratt et al., 2016, and references therein). These codes are state-of-the-art (magneto) hydrodynamic code that solves the time-dependent hydrodynamic equations for mass, momentum, and energy conservation, coupled with the 3D radiative transfer equation, in order to correctly account for the interaction between the radiation field and the plasma. However, hydrodynamic calculations still cannot cover the wide range of physics quantities needed to model the Galactic stellar populations. Moreover, their results cannot be easily adopted in stellar evolutionary codes, although attempts to implement approximations directly based on 3D simulations in 1D stellar models exist in the literature (e.g., Lydon et al., 1992; Ludwig et al., 1999; Arnett et al., 2015; Arnett et al., 2018). The commonly adopted procedure to treat the convection efficiency in super-adiabatic regimes in 1D stellar evolution codes relies on mixing-length theory (MLT) (Böhm-Vitense, 1958), where convection efficiency depends on the free parameter ${\alpha }_{\mathrm{ML}}$. A variation of such a parameter can produce a large effect on the surface lithium abundance at a given age in stars with a super-adiabatic envelope. This effect is particularly important in stars with masses larger than about 0.5–$0.6{\mathrm{M}}_{\odot }$. It has been shown in the literature that models with a reduced convection efficiency (${\alpha }_{\mathrm{ML}}<$${{\displaystyle {\alpha }_{\mathrm{ML}}}}_{\odot }$, solar calibrated value) attains a better agreement with data for both young clusters and binary stars (Piau and Turck-Chièze, 2002; D’Antona and Montalbán, 2003; Tognelli et al., 2012).

Figure 14 shows the results obtained by Tognelli et al. (2012) where the observed surface lithium abundance in five young open clusters (IC2602, α Per, Blanco1, Pleiades and NGC2516) has been compared to theoretical predictions obtained adopting two different values for the mixing length parameter during the Pre-MS phase: one calibrated on MS stars to reproduce their colors and the other corresponding to a much less efficient convective energy transport. The best value to be used in pre-MS has been estimated in order to reproduce the A(Li) vs. $T_{\mathrm{eff}}$ pattern. The availability of young clusters to perform such an analysis (ages below 100–150 Myr) is mandatory to avoid possible effects due to MS non-standard mixing processes which act on timescales of the order of ∼ Gyr. Referring to Figure 14, it is evident that in all cases, the adoption of a constant value of ${\alpha }_{\mathrm{ML}}$ (calibrated on MS stars) produces a lithium depletion much larger than observed. On the other hand it is possible to tune ${\alpha }_{\mathrm{ML}}$ during the pre-MS to reproduce the observed lithium pattern and the most important result is that the derived ${\alpha }_{\mathrm{ML}}$ in pre-MS is independent of the cluster age and on the stellar mass. The authors derived a value of ${\alpha }_{\mathrm{ML},\mathrm{PMS}}=1$. We mention that the reduction of the efficiency of superadiabatic convection in stellar envelope has been put forward as a plausible mechanism to explain the discrepancies in the radius observed and predicted in pre-MS binary systems. A value of ${\alpha }_{\mathrm{ML}}\sim 1$ has been suggested to explain the radius in young binary systems (see e.g., Gennaro et al., 2012).

FIGURE 14

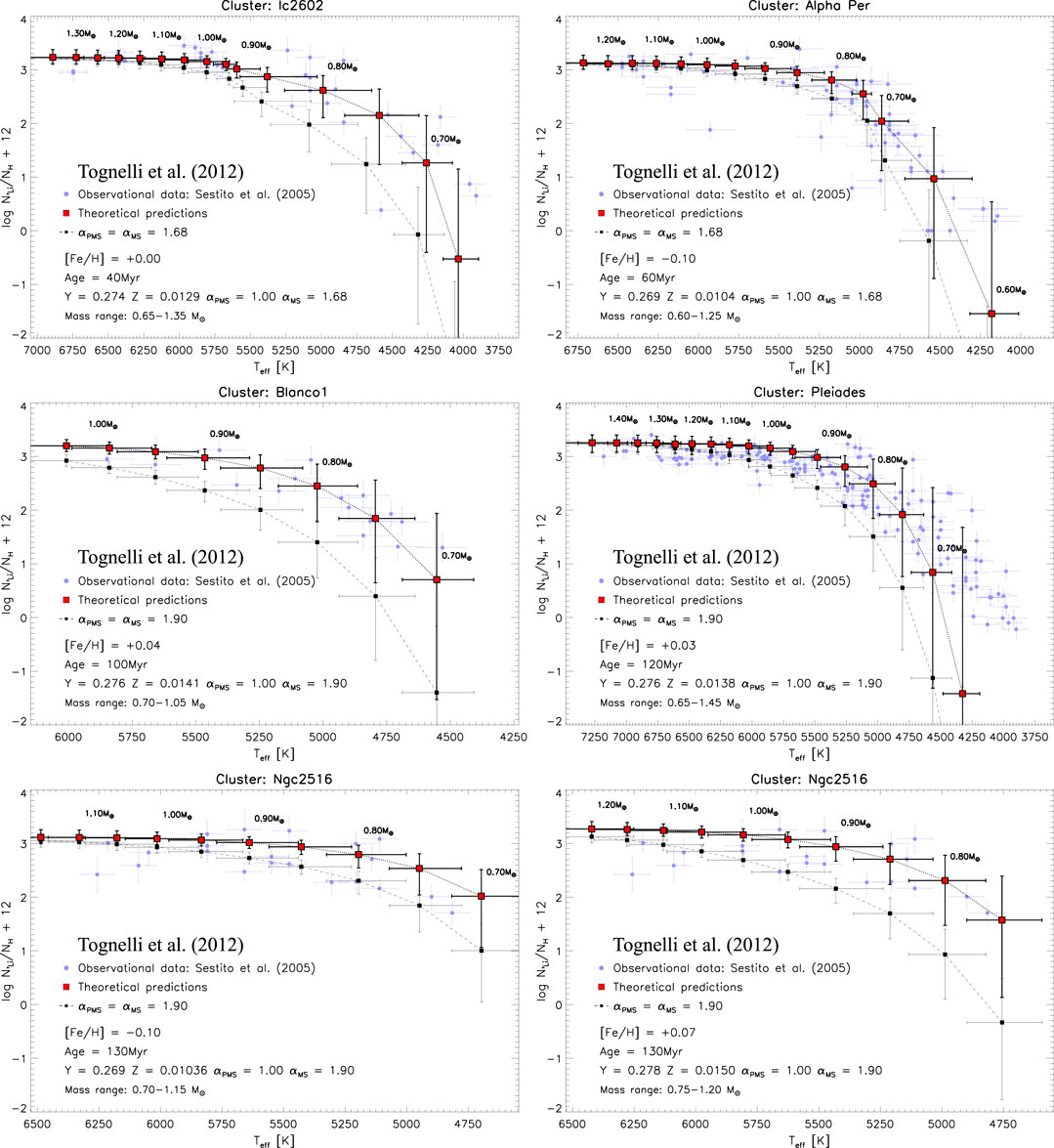
FIGURE 14. Comparison between data and theoretical model predictions for surface lithium in young clusters. Models with the same mixing length parameter in pre-MS and MS phases, calibrated with MS stars, are shown as dashed lines while models with calibrated convection efficiency in MS and artificially reduced mixing length parameter $\left({\alpha }_{\mathrm{ML}}=1\right)$ in pre-MS are shown as continuous lines. In the case of NGC2516, the models were computed using two different values of [Fe/H], [Fe/H] = -0.10 (bottom left panel) and [Fe/H] = +0.07 (bottom right panel), as reported in the literature. Figure adapted from Tognelli et al. (2012).

As said, ${\alpha }_{\mathrm{ML}}$ is a free parameter which reflects the present not precise knowledge of external convection efficiency, thus one should find a physical reason for its variation during the evolution of a given star. A reduced convection efficiency could be motivated by the attempt in 1D evolutionary codes to mimic the main effects of some non-standard mechanisms active in young stars, such as the presence of a not negligible magnetic field (especially in the convective region, see e.g., Ventura et al., 1998). To this regard (Feiden and Chaboyer, 2013) found that the inclusion of a magnetic field in partially convective stars produces a radius expansion caused by the inhibition of convection efficiency in the convective envelope (see also Feiden and Chaboyer, 2012). Figure 15 shows the results of their work on evolutionary models computed with and without the inclusion of a magnetic field. The models are compared to the characteristics of YY Gem binary system (both stars have masses of about $0.6{\mathrm{M}}_{\odot }$Torres and Ribas, 2002). Such a system exhibit evidences of a relatively strong magnetic field (surface spots, X-ray, gyrosynchrotron radio emissions, flaring events). Standard models underestimate the radius of the components by about 8%, a difference that can be erased if a magnetic field of 4–5 KG is included in the computations. The stronger is the magnetic field the larger the radius of the star at the same age (left panel). In the radius vs. $T_{\mathrm{eff}}$ plane, the inclusion of a magnetic field produces a cooler and brighter star (see right panel of Figure 15). Feiden and Chaboyer (2013) also showed that it is possible to reproduce the main effects of a magnetic field in 1D non-magnetic stellar models by using a properly tuned value of the mixing length parameter. To do this an ${\alpha }_{\mathrm{ML}}$ value lower than the solar calibrated one (i.e., close to unity) should be adopted.

FIGURE 15

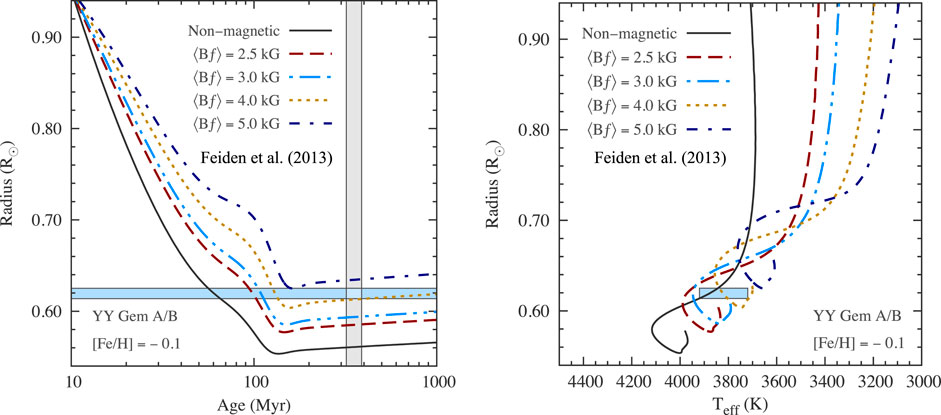
FIGURE 15. Effect of magnetic fields (for the labeled surface magnetic field strength <B f>) on the radius evolution of a partially convective pre-MS star $\left(M=\mathrm{0}\mathrm{.599}{\mathrm{M}}_{\odot }\right)$. The radius is compared to that of the observed YY Gem binary system (horizontal and vertical stripes). Left panel: radius vs. age. Right panel: stellar radius vs. $T_{\mathrm{eff}}$ for magnetic and non magnetic models. Figure adapted from Feiden and Chaboyer (2013).

The presence of a magnetic field makes the star cooler and modifies the temperature stratification inside the star: this has a direct impact on surface lithium burning efficiency (Feiden, 2016). Supplementary Figure S1 shows the comparison between the expected surface lithium abundance as a function of $T_{\mathrm{eff}}$ in standard non magnetic models of 5 and 10 Myr compared to a model of 10 Myr in which a magnetic field is included [the magnetic field strength B_eq shown in figure varies with the mass but in the mass range 0.1–$1{\mathrm{M}}_{\odot }$ it is of the order of 2–2.6 KG]. The inclusion of the magnetic field has a strong impact on the resulting lithium abundance, drastically reducing the level of depletion and thus pointing in the direction to improve the agreement between data and model predictions for pre-MS stars.

Another aspect related to the presence of magnetic field in the star is the possibility to include in stellar models a surface spots coverage fraction (see e.g., Jackson and Jeffries, 2014; Somers and Pinsonneault, 2015). The effect of the spots is to reduce the outgoing flux at the stellar surface producing a radius inflation and a decrease of the stellar effective temperature. Such an effect goes in the same direction of an artificially decreased convection efficiency and, as expected, leads to a cooler envelope and to a less efficient lithium burning. Supplementary Figure S2 shows an application of stellar models with surface spots to the surface lithium abundance observed in the Pleiades cluster (see Somers and Pinsonneault, 2015). Standard models predict a level of pre-MS lithium depletion larger than that observed. The agreement can be restored assuming that a certain fraction of the stellar surface is covered by spots; increasing the coverage fraction, the models are cooler and thus the surface lithium depletion is reduced. It’s important to notice that the presence of magnetic fields of different strength or a different spot coverage fraction in stars with similar mass can introduce a star-to-star scatter in the surface lithium abundance. This could partially answer another important open question about young clusters, i.e., which is the cause of a spread in the lithium abundance, measured in stars with similar effective temperature. The extent of such spread is much larger than the quoted uncertainties, so it represents a real spread (see e.g., Xiong and Deng, 2006). The inclusion of a different surface spots coverage or different magnetic fields strength could produce stars with similar effective temperatures (but different total masses) thus leading to an apparent dispersion in the lithium abundance.

Additional mechanisms that can alter the level of lithium burning in stars have been analyzed in the literature. An induced extra mixing due to the presence of rotation, gravity waves, diffusion, or mass loss has been put forward to reproduce the surface lithium abundance pattern typical of older stars (ages $\mathrm{\gtrsim }500$ Myr). However, such mechanisms are not relevant for the evolution of young pre-MS stars and thus we will not discuss them in this context (see e.g., Landin et al., 2006; Eggenberger et al., 2012; Charbonnel et al., 2013).

5.5 Uncertainties on Atmospheric Models for Surface Lithium Abundance Determination

The determination of surface element abundances involves the interpretation of the observed absorption lines through atmospheric models as accurate as possible. However modeling stellar atmospheres is a difficult task and the uncertainties on the measurements of surface element abundance clearly affects the comparison between theory and observations. Here we limit to briefly discuss the main difficulties in modeling realistic stellar atmospheres, the interested reader can find more details in other reviews (see e.g., Jofré et al., 2019).

The photosphere of low mass stars is covered with a complex and stochastic pattern – associated with convective heat transport – of downflowing cooler plasma and bright areas where hot plasma rises, the so called granulation (Nordlund et al., 2009). As already discussed, convection is a difficult process to understand, because it is non-local and three-dimensional, involving non-linear interactions over many disparate length scales. In recent years it has become possible to use numerical three-dimensional (3D) radiative hydrodynamical (RHD) codes to study stellar convection in atmosphere such as Stagger Code (Nordlund et al., 2009; Collet et al., 2011) and CO5BOLD (Freytag et al., 2012). Nowadays, the use of large grids of simulations covering a substantial range of values of effective temperature and surface gravity for stars in different regions of the HR diagram (Ludwig et al., 2009; Magic et al., 2013; Trampedach et al., 2013) have proven that the convection-related surface structures have different size, depth, and temporal variations, depending on the stellar type (Beeck et al., 2013; Tremblay et al., 2013; Magic and Asplund, 2014). Moreover, the related activity (in addition to other phenomena such as magnetic spots, rotation, dust, etc.) has an impact in stellar parameter determination (Bigot et al., 2011; Chiavassa et al., 2012; Creevey et al., 2012), radial velocity (Allende Prieto et al., 2013; Chiavassa et al., 2018), chemical abundances estimates (Asplund et al., 2009; Caffau et al., 2011), and photometric colors (Bonifacio et al., 2018; Chiavassa et al., 2018).

Chemical abundance ratios inferred from spectra of cool stars is based on the understanding of limitations and uncertainties of spectroscopic analyses. In this context, radiation transfer in the atmospheres of late-type stars generally takes place under non-local thermodynamic equilibrium (NLTE) conditions, rather than the idealized LTE (Asplund, 2005). The full 3D NLTE treatment would require to compute NLTE radiative transfer inside radiative hydrodynamical simulations and coupling it to the equations of gas movements. In these simulations the computational cost is dominated by the radiative transfer calculations which can be greatly reduced by adopting an approximated solution based on the opacity binning or multi-group method (Nordlund, 1982). However, introducing NLTE calculations at this stage would largely increase the computation time making very complicated to obtain a relaxed simulation. This is why 3D NLTE radiative transfer calculations are only affordable in a post-processing manner, i.e., each 3D RHD simulation is computed in LTE and then the so called <3D> models are computed averaging multiple snapshots of 3D RHD simulations over regions of equal optical depth and over the time series (e.g., Asplund et al., 2004; Caffau et al., 2009; Magic et al., 2013; Lind et al., 2017; Nordlander et al., 2017; Amarsi et al., 2018). This approach offers a middle-ground between full 3D NLTE and 1D NLTE, by accounting for NLTE in model atoms of arbitrary size, and through the use of time-independent 1D structures derived from the full 3D hydrodynamic simulations (Bergemann et al., 2017). Using this method, Wang et al. (2021) derived a new 3D NLTE solar abundance of A(Li) = 0.96 ± 0.05, which is 0.09 dex lower than the commonly used value and provided a grids of synthetic spectra and abundance corrections publicly available. Eventually, it has also become possible to undertake large samples of observations from disk and halo stars with this 3D NLTE analysis (Amarsi et al., 2019; Bergemann et al., 2019). Unluckily at present 3D atmospheric calculations are not still available for Pre-Main Sequence atmospheres.

The measurement of surface lithium abundances constitutes an important example of efforts undertaken in this field. In Sec. 5 we mentioned that the stellar surface abundance of ⁶Li is expected to be negligible, moreover its identification is very difficult. The presence of ⁶Li in metal-poor halo stars can only be derived from the asymmetry in the red wing of the ⁷Li doublet line at 670.8 nm. Several authors attempted to detect ⁶Li using 1D hydrostatic models and assuming LTE for a number of metal-poor stars with [Fe/H], lower than −2 dex (Cayrel et al., 1999; Asplund et al., 2006). Cayrel et al. (2007) pointed out that the intrinsic line asymmetry – due to the stellar surface convection – in the ⁷Li doublet would be almost indistinguishable from the asymmetry produced by a weak ⁶Li blend on a (presumed) symmetric ⁷Li profile.

The total line strength of the Li resonance line determines the ⁷Li-abundance and the shape of the line profile determines the isotopic ratio due to the shift between ⁶Li and ⁷Li isotopic components. Thus it’s critical to resolve the strongly differential NLTE effects on the granules and inter-granular regions (Supplementary Figure S3), because they have a preferential influence over the blue- and red-shifted part of the line profile, respectively (Lind et al., 2013). To investigate this aspect, Steffen et al. (2012) and Lind et al. (2013) used a 3D NLTE treatment with 3D RHD simulation snapshots carried out with CO5BOLD and Stagger Code, respectively. They re-analyzed the Li feature in some metal-poor stars and were not able to confirm the previous claimed detection of ⁶Li. However, they pointed out that a full understanding of 3D NLTE line formation is necessary to make correct measurements of ⁶Li, even though from their studies they could give only upper limits for the isotopic ratio ⁶Li/⁷Li. In particular, the 3D NLTE approach is important to characterize the calibration lines, to decrease the observational error. Eventually, a very recent publication by González Hernández et al. (2019), confirms the non detection of ⁶Li for a very metal poor binary star [(Fe/H) ∼−3.7 dex], finding an upper limit for the isotopic ratio of ⁶Li/⁷Li$< 10\text{\%}$.

6 Effects of Light Element Burning Cross Sections on Pre-Main Sequence Characteristics and on Light Element Surface Abundances

The predicted temporal evolution of light elements is affected by the stellar evolutionary stage and by the model structure, which depends on the input physics adopted in the computations. One of the key ingredients is the adopted light element burning cross section, as derived from measurements of indirect/direct processes. Thus it’s worth discussing how the recent determination of such cross sections at energies relevant for stellar evolution have changed the prediction of surface light element abundances in low mass stars.

For stellar calculation the reaction rate of a two body process can be written in the following way (see e.g., Rolfs and Rodney, 1988),

$N_A{\langle \sigma v\rangle }_b=\sqrt{\frac{8}{\pi \mu }}\frac{N_A}{{\left(K_{B}T\right)}^{\frac{3}{2}}}{\displaystyle \underset{0}{\overset{+\infty }{\int }}\sigma {\left(E\right)}_{b}E{e}^{-\frac{E}{K_{B}T}}dE}\left(\mathrm{c}{\mathrm{m}}^3\mathrm{mo}{\mathrm{l}}^{-1}{\mathrm{s}}^{-1}\right)(4)$

where $\sigma \left(E\right)$ is the cross section of the process, the subscript b means that the reaction rate is for two bare nuclei (i.e., without any electron screening effect), T is the temperature in Kelvin (K). In stellar evolution calculations, the energy at which the process occurs are generally so small that it is convenient to write the cross section in terms of another quantity called the astrophysical factor $S\left(E\right)$ defined as it follows,

$S{\left(E\right)}_b=E\sigma {\left(E\right)}_b{e}^{2\pi \eta \left(E\right)}(5)$

with $\eta \left(E\right)$ the Sommerfeld parameter related to the tunnel effect of two interacting charged particles, that can be written as:

$2\pi \eta \left(E\right)=\frac{Z_1{Z}_2{e}^2}{2{\epsilon }_0\hslash }\sqrt{\frac{\mu }{2E_{\mathrm{cm}}}}=31.3998Z_1{Z}_2\sqrt{\frac{A_{\mu }}{E_{\mathrm{cm}}\left(\mathrm{KeV}\right)}}(6)$

where $\mu =m_1{m}_2/\left(m_1+m_2\right)$ is the reduced mass and $A_{\mu }$ is the same quantity but expressed in atomic mass units (amu), $E_{\mathrm{cm}}\left(\mathrm{KeV}\right)$ is the energy in the center of mass expressed in KeV. Using this quantity, Eq. 4 assumes the following form,

$N_A{\langle \sigma v\rangle }_b=\sqrt{\frac{8}{\pi \mu }}\frac{N_A}{K_B{T}^{\frac{3}{2}}}{\displaystyle \underset{0}{\overset{+\infty }{\int }}S{\left(E\right)}_b{e}^{-2\pi \eta \left(E\right)-\frac{E}{K_{B}T}}dE}\left(\mathrm{c}{\mathrm{m}}^3\mathrm{mo}{\mathrm{l}}^{-1}{\mathrm{s}}^{-1}\right)(7)$

For many application in stellar astrophysics, it is possible to expand the astrophysical factor around a specific value of the energy, thus obtaining,

$S\left(E\right)\approx S\left(E_0\right)\left[1+\frac{S\text{'}\left(E_0\right)}{S\left(E_0\right)}\left(E-E_0\right)+\frac{1}{2}\frac{S\text{'}\text{'}\left(E_0\right)}{S\left(E_0\right)}{\left(E-E_0\right)}^2+\dots \right](8)$

The quantity $E_0$ is also known as the Gamow peak energy, and it corresponds to the energy where the exponential quantity inside the integral in Eq. 7 has its maximum value. $E_0$ is defined in the following way (Rolfs and Rodney, 1988),

$E_0=1.22{\left(A_{\mu }{Z}_1^2{Z}_2^2{T}_6^2\right)}^{\frac{1}{3}}\left(\mathrm{KeV}\right)(9)$

with $T_6$ the temperature expressed in million kelvin.

The expansion of $S\left(E\right)$ given above depends on the temperature at which the considered reaction occurs (thorough $E_0$), which in turn depends on the stellar mass. However, at low energy typical of reactions in stars, $S\left(E\right)$ varies slowly with the energy, thus it is convenient to expand $S\left(E\right)$ around $E\approx 0$: in this case the reaction rate can be evaluated knowing $S\left(0\right)$ and its derivatives [usually it is enough to have $S\text{'}\left(0\right)$ and $S\text{'}\text{'}\left(0\right)$].

Light element (p,α) reaction rates have been recently revised through the indirect Trojan Horse Method (THM, see e.g., Baur, 1986; Spitaleri et al., 2003; Spitaleri et al., 2016; Spitaleri et al., 2019 and references therein), which is particularly useful to measure cross sections at astrophysical energies by-passing extrapolation procedure, often affected by systematic uncertainties due, for instance, to electron screening effects. THM allows to measure the astrophysically relevant cross sections in correspondence, or very close, to the Gamow peak without experiencing the lowering of the signal-to-noize ratio due to the presence of the Coulomb barrier between the interacting charged particles. Moreover in the last years THM was successfully applied to reactions induced by unstable beams Pizzone et al. (2016) and Lamia et al. (2019) as well as neutron induced reactions which may play a role also in the context of light element nucleosynthesis and BBN. In particular the ³He(n,p)³H was studied at the astrophysically relevant energies (see Pizzone et al., 2020 and references therein). THM was also applied to reactions between heavier systems, which are relevant in the late stellar evolutionary stages (Tumino et al., 2018). We will discuss the effects of these improvements and of the present errors on nuclear cross sections on the light elements surface abundance calculations in pre-Main Sequence stars.

6.1 Effects of Deuterium Burning Cross Sections on pre-MS Evolution

As discussed in Sec. s 3, 4.3 and 4.4, deuterium burning plays a crucial role in the first stages of pre-MS or protostellar evolution. The value of the cross section of the p(D,γ)³He process in stellar conditions has been reported by several authors (see Adelberger et al., 2011 for a review) both from measurements and theoretical calculations along with its uncertainty. Adelberger et al. (2011) redetermined the best value for the astrophysical factor $S\left(E\right)$ for such a reaction at zero energy $\left[S\left(0\right)\right]$ and the uncertainty on it, concluding that the current uncertainty on $S\left(0\right)$ for such burning reaction is $\approx 7\%$. Recently, Mossa et al. (2020) redetermined the D+p cross sections at energies typical of the BBN (between 32–263 KeV) – thus larger than those used in stellar calculations – estimating an uncertainty of about $3\%$.

We tested the impact on pre-MS evolution of the D+p cross section variation, using the uncertainty given by Adelberger et al. (2011) at stellar energies, which is $\pm 7\%$. Such a variation of the deuterium burning reaction rate produces a negligible effect on the stellar structure evolution. The negligible effect is related to the large dependency on the temperature of the p(D,γ)³He burning channel (about $T^{12}$); if $S\left(0\right)$ is artificially varied (e.g., reduced) by 7% (independently of the temperature), to obtain the same energy production rate, which sustains the star, an increase of the burning temperature is required. However, given the high temperature dependency of the rate, a very small temperature variation is enough to restore the energy production. Thus the models are essentially unaffected by the current uncertainty on the p(D,γ)³He reaction rate. From this analysis we can conclude that the main uncertainty source on the D-burning phase in stellar models is the error on the initial deuterium abundance which can be as large as 50% as discussed in Section 4.4.

Recently Tumino et al. (2014) (see also Tumino et al., 2011) measured the reaction rate for two additional channels involving the D-burning, namely the D(D,p)³H and the D(D,n)³He processes, using the THM; such burning channels could potentially contribute to the D-burning in stars. Supplementary Figure S4 shows, for the quoted reactions, the THM rates compared to the ones of still widely used NACRE compilation (Angulo et al., 1999), of the JINA REACLIB (Cyburt, 2004) and to the (Descouvemont et al., 2004) rates. The estimated uncertainty on the analyzed burning channels (of about 5%) are also shown. At temperatures typical of stellar deuterium burning (∼10⁶ K) the D(D,p)³H is about 5% larger than the NACRE, while it is much larger (about 15%) than the value reported in Cyburt (2004). The differences sensitively reduce at larger temperatures, more important for cosmological calculations. If the Descouvemont et al. (2004) rate is considered, the difference with THM is very small at stellar temperatures (below 1%), while it increases at larger temperatures, reaching about 5% at $T\sim {10}^9\mathrm{K}$.

The new THM rate for the D(D,n)³He reaction is ∼10% larger than the others (NACRE, JINA and (Descouvemont et al., 2004)) for temperatures smaller than about $5\times {10}^7\mathrm{K}$. At larger temperatures the differences reduce and for $T\mathrm{\gtrsim }2\times {10}^8\mathrm{K}$ the THM rate is smaller than the others by about 5–10%. Tumino et al. (2014) evaluated the effect of the new rates in stellar models, showing that the change in the cross sections does not produce any effect on the stellar structure. The result was expected because such burning channels are quite negligible in stellar models, where D is mainly destroyed via the p(D,γ)³He channel. On the contrary, these reactions could be more important for BBN (Cyburt, 2004; Coc and Vangioni, 2010). Tumino et al. (2014) estimated that the new reaction rates could result in a variation of the primordial deuterium abundance inferred from the BBN by about $2\%$, while an impact on the ⁷Li abundance up to about 10% is expected.

6.2 Stellar Surface Abundance of Light Elements and Updated (p,α) Reaction Rates

The energy produced in the Li, Be and B nuclear reactions is negligible and such reactions do not affect stellar structures evolution. However, the surface abundances of light elements strongly depend on the nuclear burning (Tognelli et al., 2019). The different fragility of Li, Be and B against (p,α) destruction reactions potentially allows to investigate the characteristics of different depths of the stellar interior.

In Supplementary Figures S5, S10 the reaction rates for the most relevant light element burning (p,α) reactions calculated with the THM are shown and compared with the JINA REACLIB and the less recent, but still widely used, NACRE rates. The results are discussed below.

6.2.1 ⁶Li and ⁷Li Surface Abundance and (p,α) Reaction Rates Efficiency

The first attempts to apply THM (p,α) reaction rates to pre-MS lithium surface abundance calculations were performed by Pizzone et al. (2003) and Pizzone et al. (2005) (hereafter pt05) and successively updated, after re-normalization to recently released direct data, in Lamia et al. (2012) and Lamia et al. (2013). The left panel of Supplementary Figure S5 shows the ⁶Li(p,α)³He reaction rate obtained using the THM compared to the pt05 rate available on the JINA REACLIB page. The THM estimated rate deviates from the pt05 by about 15% at a temperature of $\mathrm{T}\approx {10}^{6}K$, typical of ⁶Li burning in the pre-MS phase, a value that is larger than the current estimated uncertainty (about 10%) on the rate itself.

Lamia et al. (2013) evaluated the effect on the surface ⁶Li abundance of the update of the ⁶Li+p reaction rate for a range of stellar masses at three different metallicities [(Fe/H) = −0.5, −1.0, and −2.0]. Supplementary Figure S6 shows the time evolution of the surface ⁶Li abundance – normalized to the original value– obtained adopting the three different ⁶Li(p,α)³He reaction rates – THM, JINA (pt05), and NACRE. From Supplementary Figure S6 it is evident that ⁶Li depletion, at fixed burning reaction rate, varies significantly for different masses and metallicities. This can be understood recalling that the higher the metallicity (or the lower the stellar mass) the deeper and hotter the base of the convective envelope. Note that among the most massive models (i.e., $M=1.2{\mathrm{M}}_{\odot }$), which have the thinnest external convective envelopes, only that with the highest metallicity [i.e., (Fe/H) = −0.5] efficiently depletes surface ⁶Li. In the selected [Fe/H] range, the difference in the ⁶Li depletion between the THM and NACRE models ranges from about 13% (for $M=1.2{\mathrm{M}}_{\odot }$) to about 60% (for $M=1.0{\mathrm{M}}_{\odot }$). The difference reduces if JINA rate is adopted, as expected due to the smaller differences between the two rates.

Right panel of Supplementary Figure S5 shows the comparison between the THM and NACRE ⁷Li + p reaction rate; the difference is of about 13% at a temperature of $\mathrm{T}\approx {10}^6\mathrm{K}$, not much larger than the current uncertainty on the rate (about 10%). Supplementary Figure S7 shows the time evolution of the surface ⁷Li abundance for different masses when THM and NACRE ⁷Li + p reaction rates are adopted. The differences between the two calculations range from about 7% (for $M=1.0{\mathrm{M}}_{\odot }$) to about 25% (for $M=0.6{\mathrm{M}}_{\odot }$).

In general, the effect of adopting different ⁶Li and ⁷Li burning reaction rates, although not negligible, is less important than the effects due to errors in other quantities used in the computation of a stellar model, such as the original chemical composition, external convection efficiency, or the uncertainties in some other physical inputs adopted in the calculations (e.g., opacity and equation of state, see Sec. 5.4 and the discussions in Pizzone et al., 2010 and Tognelli et al., 2012). Thus, at the moment an uncertainty on the burning reaction rate of the order of 10% is not the main error source in the determination of the surface lithium abundance in stellar models (Lamia et al., 2012; Lamia et al., 2013).

6.2.2 Lithium Depletion Boundary

In the mass range $M\approx 0.06-0.4{\mathrm{M}}_{\odot }$ (the exact values depending on the chemical composition), ⁷Li is completely destroyed in pre-MS in fully convective structures. The larger is the mass the higher is the temperature inside the star, and consequently the earlier is the onset of lithium burning. The larger temperature in more massive stars produces also a more efficient lithium burning, and consequently the age at which lithium is fully depleted in such convective stars strongly depends on the stellar mass. In a coeval population of stars with ages between about 15 and 350 Myr, one would expect to observe a sharp transition in very low-mass regime between stars with and without surface lithium at a given mass (corresponding to the higher stellar mass that, at the cluster age, fully destroy lithium). Such a transition, usually called the Lithium Depletion Boundary (LDB), is a powerful age indicator (see e.g., D’Antona and Mazzitelli, 1994) thanks to the connection between luminosity, mass and age. Supplementary Figure S8 shows an example of the age vs. luminosity relation for stars located at the LDB in the mass range [0.06 ÷ 0.4] ${\mathrm{M}}_{\odot }$.

The method of LDB has been successfully adopted to assign ages to young clusters as a competitive method to the use of isochrone fitting (e.g., Barrado y Navascués et al., 1999; Oliveira et al., 2003; Jeffries and Oliveira, 2005; Manzi et al., 2008; Dobbie et al., 2010; Jeffries et al., 2013; Binks and Jeffries, 2014; Juarez et al., 2014; Dahm, 2015; Dupuy et al., 2016; Martín et al., 2018; Martín et al., 2020 and references therein). The uncertainties on age determination through the LDB technique have been analyzed in Burke et al. (2004) and, more recently, in Tognelli et al. (2015); the main uncertainties that potentially affect the LDB age determination are those already discussed in Section 5.4. Supplementary Figure S9 shows the relative age uncertainty on LDB age determination obtained by Tognelli et al. (2015) taking into account the errors on the adopted input physics and chemical composition. The shaded area has been obtained by a cumulative variation of all the considered input physics and chemical abundances within their uncertainties (going into more detail would require a too long discussion out of the purposes of this review, see the quoted paper for additional information). The uncertainty of the method depends on the stellar luminosity (or mass) at the LDB, which, in turn, translates in an age, but it is in any case lower than about 10%. As a general comment, faint stars that correspond to LDB ages of the order of 50–60 Myr $\left(0.06\mathrm{\lesssim }M/{\mathrm{M}}_{\odot }\mathrm{\lesssim }0.1\right)$ have errors of the order of about 5%, an uncertainty that increases increasing the stellar luminosity at the LDB and thus the derived age. Tognelli et al. (2015) showed that a large part of the uncertainty on the LDB $\left(\sim 40\%\right)$ comes from the chemical composition indetermination while the lithium burning rate causes a variation of the LDB age of about 1%.

6.2.3 ⁹Be and ¹⁰B Surface Abundance and (p,α) Reaction Rates Efficiency

Supplementary Figure S10 shows the comparison between the recent THM reaction rates and other reaction rates used in the literature. The THM ⁹Be(p,α)⁶Li rate (at temperatures of few million degrees) is about 25% larger than NACRE and the uncertainty on the THM ⁹Be burning rate is about 25% (blue dashed area in the figure). The THM reaction rate is quite similar to that in the recent NACRE II (Xu et al., 2013), even if the THM uncertainty region is sensibly smaller than that of the NACRE II rate, see (Lamia et al., 2015). Left panel of Supplementary Figure S11 shows the comparison between the predicted surface Be abundances computed using the THM reaction rate and the NACRE reaction rate, for solar metallicity stars. The higher THM rate leads to a faster ⁹Be destruction consequently, at the same age, models with the THM rate show a lower ⁹Be surface abundance with respect to models with the NACRE rate. The differences in the predicted surface abundances are significant in those models where ⁹Be is efficiently destroyed (i.e., for $M\mathrm{\lesssim }0.5{\mathrm{M}}_{\odot }$).

We recall that in stars, ⁹Be is destroyed through two channels: ⁹Be(p,α)⁶Li (R₁, the rate analyzed by Lamia et al., 2015) and ⁹Be(p, 2α)²H (R₂). The ratio R₁/${\mathrm{R}}_2\approx 1.2$, for stellar conditions at the temperature of interest; thus the R₂ contribution to beryllium destruction is not negligible. Changing only R₁, as done in Lamia et al. (2015) affects the final beryllium abundance by a factor that is given by the R₁ reaction rate change (about 25%) multiplied by the probability that the ⁹Be burning occurs in that channel, i.e., 25% × R₁/(R₁ + R₂ ) $\approx 14\%$, thus leading to a change in the predicted Beryllium abundance lower than what expected if only R₁ channel was active in stars. The effect of the THM uncertainty on the ⁹Be(p,α)⁶Li rate – approximately 25% which is equal to the difference with respect to NACRE rate – is expected to produce a variation of the predicted ⁹Be surface abundance of the same order of magnitude discussed above.

Right panel of Supplementary Figure S10 shows the comparison between the THM and the NACRE rate for the ¹⁰B(p,α)⁷Be reaction: at temperatures of a few millions of kelvin, the THM rate is ∼30% lower than the NACRE one. The error of the THM rate at the temperatures of interest is about 20%. However if the THM rate is compared with the one of the updated NACRE II Compilation (Xu et al., 2013), the differences are significantly reduced, see (Lamia et al., 2015).

The effect of the different ¹⁰B(p,α)⁷Be reaction rates on surface B abundance in low mass stars (at solar metallicity) is shown in the right panel of Supplementary Figure S11. The lower THM ¹⁰B(p,α)⁷Be cross section leads to a smaller ¹⁰B destruction and thus to a larger surface ¹⁰B abundance at a fixed age. Due to the higher ¹⁰B burning temperature with respect to ⁹Be, the effect of reaction rate change is significant only for masses $M\mathrm{\lesssim }0.4{\mathrm{M}}_{\odot }$. Also notice that the typical timescale at a fixed mass where ¹⁰B is destroyed is longer than that of ⁹Be.

For completeness in Supplementary Figure S11 we point out for ages typical of MS evolution [e.g., $\log t\mathrm{\gtrsim }8.5$ for $M=0.5{\mathrm{M}}_{\odot }$ for the ⁹Be abundance behavior and for $M=0.4{\mathrm{M}}_{\odot }$ for ¹⁰B] the effect of microscopic diffusion, which leads to the settling of light elements toward the stellar interior.

Supplementary Figure S12 shows the surface logarithmic abundances of ⁹Be and ¹⁰B as a function of the effective temperature, $T_{\mathrm{eff}}$. Although observational ⁹Be and ¹⁰B abundances are still not available for the low temperature/mass regimes typical of efficient ⁹Be and/or ¹⁰B burning, it is worth to estimate the role of the improvements in nuclear physics in surface abundance predictions. The models are computed using the THM and NACRE reaction rates discussed above; we remind that $T_{\mathrm{eff}}$ is not affected by the change of the (p,α) rates. Each curve represents the abundance isochrone, i.e., the locus of models with the same age but different masses. For those models where ⁹Be (¹⁰B) burns the differences between the adoption of the NACRE and THM reaction rates can be as large as about 0.2–0.3 dex for ⁹Be and almost 1 dex for ¹⁰B.

To our knowledge, an analysis of the dependence of surface ⁹Be or ¹⁰B abundances on the errors in input physics and chemical composition adopted in the calculations is not available in the literature. However, it’s a good approximation assuming a Be and B burning sensitivity to the input physics similar to that obtained for ⁷Li, as the burning temperatures are not much different. Under this assumption, the effects of the uncertainty on (p,α) Be and B burning reaction rates is not the dominant error source for the surface abundance predictions of such elements.

7 Summary and Conclusion

Surface light elements abundances prediction in stellar models is a difficult task because it’s affected by several errors in the adopted input physics and uncertainties in the efficiency of some physical mechanisms as e.g., convection in the stellar envelope. Moreover, pre-MS characteristics and surface light element abundances depend on the previous protostellar phase, which is the phase when the star forms. Analysis of the effects of different choices of accretion parameters (accretion rate, radius and mass of the first stable hydrostatic protostar, accretion history, accretion geometry, the amount of energy transferred from the accreted matter to the accreting star, etc..) on the subsequent pre-MS evolution have been performed in the literature. The results show that if the accretion process leads to bright and extended structures at the end of the protostellar phase the stellar characteristics (including the surface light element abundances) are very similar to those of standard (non-accreting) pre-MS models with the same final mass. The structure of a pre-MS star at the end of the accretion phase is affected by the inclusion of the protostellar accretion only for a restricted range of accretion parameters, mainly in the so called “cold accretion scenario.” In these cases a significant reduction of the surface light element abundances during the protostellar phase (in contrast to standard models) has been obtained; however the position of the stars in the HR diagram is in disagreement with observations for disk stars, rising doubts about the validity of the adopted accretion parameters.

Protostellar accretion in low mass halo stars was suggested in the literature as one of the possible solutions for the cosmological lithium problem. However, theoretical calculations show that the reproduction of the Spite Plateau would require a fine tuning of the parameters that govern the protostellar phase and, more important, the models with the required Li depletion follow a pre-MS evolution in the HR diagram which is quite different to the one observed for high metallicity pre-MS stars. Comparison between theoretical predictions and observations for surface lithium abundance in young open clusters still show discrepancies. During the pre-MS phase surface Li abundance is strongly influenced by the nuclear burning as well as by the extension toward the interior of the convective envelope and by the temperature at its bottom. These last two quantities depend on the input physics adopted in the calculations (radiative opacity, atmospheric models etc..), on the assumed stellar chemical composition and on the convection efficiency in superadiabatic regions, whose precise physical treatment is not still fully available.

Comparison between predictions and observations for pre-MS stars in open clusters suggest a less efficient convection during the pre-MS phase with respect to the Main Sequence. This is true even if one takes into account the uncertainties on the results due to the errors in the adopted input physics and assumed chemical composition. A possible explanation of this result could be the fact that in 1D evolutionary codes a reduced convection efficiency could mimic the main effects of some non-standard mechanisms active in young stars, such as the presence of a not negligible magnetic field and/or surface spot coverage.

The energy produced by the Li, Be, B burning reactions is negligible, thus their effects on stellar structures are irrelevant. However, the surface abundances of light elements strongly depends on the nuclear burning and thus on the adopted reaction rates. The only nuclear burning that during the pre-MS or protostellar accretion phase affects stellar evolution is the deuterium burning. The impact on pre-MS evolution of a variation of the p(D,γ)³He reaction rate by its present uncertainty (±7%) has been analyzed in the literature, finding a negligible effect on stellar models. Two other D-burning channels have been considered, namely the D(D,p)³H and the D(D,n)³He. However, as expected, the inclusion of such channels does not produce relevant effects on pre-MS evolution as the largest part of deuterium is destroyed via p(D,γ)³He.

The effects on the other light elements surface abundance predictions of the still present (even if greatly reduced) uncertainty on (p,α) cross sections have been evaluated in detail and compared to the influence on the results of the errors in the other physics ingredients and in the stellar chemical composition. Light element (p,α) reaction rates have been recently revised through the indirect Trojan Horse method (THM), sensibly reducing their estimated uncertainty and finding differences with previous estimates at the energies of astrophysical interest. In general, differences in the predicted surface Li, Be, B abundances if the THM or the less recent but still widely used NACRE reaction rates are adopted are significant for stars in which light elements are efficiently burned.

The current uncertainty on the ⁶Li and ⁷Li proton capture reaction rates is of the order of 10%. Numerical calculations show that the effects on the ⁶Li and ⁷Li surface abundances due to this uncertainty, although not negligible, are less important than the influence of errors in other quantities used in the computation of a stellar model. The present errors on the ⁹Be(p,α)⁶Li and ¹⁰B(p,α)⁷Be rates, at the temperatures of interest, are, respectively, of about 25 and 20%. Due to the higher ⁹Be and ¹⁰B burning temperature, with respect to the Li burning, the effects of the reaction rate change/uncertainty are significant only for masses lower than $M\mathrm{\lesssim }0.5{\mathrm{M}}_{\odot }$ and $M\mathrm{\lesssim }0.4{\mathrm{M}}_{\odot }$, respectively.

In conclusion, recent cross section measurements for light element (p,α) burning reactions sensibly reduced their uncertainty, even if it is still not negligible. Pre-Main Sequence theoretical calculations and consequently prediction for light element surface abundances are affected by several uncertainty sources: the not precise knowledge of the protostellar evolution and the efficiency of superadiabatic convection, the still present errors on the input physics adopted in the calculations and in the assumed stellar chemical composition. On the other hand, the errors on light element nuclear cross sections do not constitute the main uncertainty source for the prediction of light elements surface abundances.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work has been partially supported by INFN (Iniziativa specifica TAsP) and the Pisa University project PRA 2018/2019 “Le stelle come laboratori cosmici di fisica fondamentale.”

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer OS declared a past co-authorship with one of the authors RP to the handling editor.

Acknowledgments

AC acknowledges the support of the “visiting fellow” program (BVF 2019) of the Pisa University. ET acknowledges INAF-OAAb for the fellowship “Analisi dell’influenza dell’evoluzione protostellare sull’abbondanza superficiale di elementi leggeri in stelle di piccola massa in fase di pre-sequenza principale.” LL acknowledges the program “Starting Grant 2020” by University of Catania.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.604872/full#supplementary-material

Footnotes

¹The ZAMS corresponds to the phase when central hydrogen begins to be burned into helium with secondary burning elements at equilibrium and nuclear energy production fully supporting the star.

²When talking about degeneration we refer to electron quantum degeneracy.

³$A\left(Li\right)$ indicates an observational notation for abundances, where A(Li) = log N_Li/N_H + 12, with N being the number of particles of a given specie.

⁴The term “undershooting” indicates a sink of the external convection toward the stellar interior larger than the one predicted in classical models i.e., by the Schwarzschild criterion.

⁵With alpha enhancement one indicates an enhancement of the relative abundance of α elements (C, O, Ne, Mg, Si, S, Ar and Ca) with respect to the solar composition. It is generally expressed as: [α/Fe] = $\log {\left({\mathrm{N}}_{\alpha }/{\mathrm{N}}_{Fe}\right)}_{\mathrm{star}}-\log {\left({\mathrm{N}}_{\alpha }/{\mathrm{N}}_{Fe}\right)}_{\odot }$.

References

Adelberger, E. G., García, A., Robertson, R. G. H., Snover, K. A., Balantekin, A. B., Heeger, K., et al. (2011). Solar fusion cross sections. II. The pp chain and CNO cycles. Rev. Mod. Phys. 83, 195–246. doi:10.1103/RevModPhys.83.195

CrossRef Full Text | Google Scholar

Aguilera-Gómez, C., Ramírez, I., and Chanamé, J. (2018). Lithium abundance patterns of late-F stars: an in-depth analysis of the lithium desert. A&A 614, A55. doi:10.1051/0004-6361/201732209

CrossRef Full Text | Google Scholar

Allende Prieto, C., Koesterke, L., Ludwig, H.-G., Freytag, B., and Caffau, E. (2013). Convective line shifts for the Gaia RVS from the CIFIST 3D model atmosphere grid. A&A 550, A103. doi:10.1051/0004-6361/201220064

CrossRef Full Text | Google Scholar

Amarsi, A. M., Barklem, P. S., Asplund, M., Collet, R., and Zatsarinny, O. (2018). Inelastic O+H collisions and the O I 777 nm solar centre-to-limb variation. A&A 616, A89. doi:10.1051/0004-6361/201832770

CrossRef Full Text | Google Scholar

Amarsi, A. M., Nissen, P. E., and Skúladóttir, Á. (2019). Carbon, oxygen, and iron abundances in disk and halo stars. Implications of 3D non-LTE spectral line formation. A&A 630, A104. doi:10.1051/0004-6361/201936265

CrossRef Full Text | Google Scholar

Angulo, C., Arnould, M., Rayet, M., Descouvemont, P., Baye, D., Leclercq-Willain, C., et al. (1999). A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A. 656, 3–183.

CrossRef Full Text | Google Scholar

Arnett, W. D., Meakin, C., Hirschi, R., Cristini, A., Georgy, C., Campbell, S., et al. (2018). 3D simulations and MLT: II. RA-ILES results. arXiv e-prints. arXiv:1810.04659

Google Scholar

Arnett, W. D., Meakin, C., Viallet, M., Campbell, S. W., Lattanzio, J. C., and Mocák, M. (2015). Beyond mixing-length theory: a step toward 321D. ApJ 809, 30. doi:10.1088/0004-637X/809/1/30

CrossRef Full Text | Google Scholar

Asplund, M. (2005). New light on stellar abundance analyses: departures from LTE and homogeneity. ARA&A 43, 481–530. doi:10.1146/annurev.astro.42.053102.134001

CrossRef Full Text | Google Scholar

Asplund, M., Grevesse, N., Sauval, A. J., Allende Prieto, C., and Kiselman, D. (2004). Line formation in solar granulation. IV. [O I], O I and OH lines and the photospheric O abundance. A&A 417, 751–768. doi:10.1051/0004-6361:20034328

CrossRef Full Text | Google Scholar

Asplund, M., Grevesse, N., Sauval, A. J., and Scott, P. (2009). The chemical composition of the Sun. ARA&A 47, 481–522. doi:10.1146/annurev.astro.46.060407.145222

CrossRef Full Text | Google Scholar

Asplund, M., Grevesse, N., and Sauval, A. J. (2005). “The solar chemical composition,”. Cosmic abundances as records of stellar evolution and nucleosynthesis. Editors T. G. BarnesIII, and F. N. Bash (San Francisco: Astronomical Society of the Pacific Conference Series), Vol. 336, 25.

Google Scholar

Asplund, M., Lambert, D. L., Nissen, P. E., Primas, F., and Smith, V. V. (2006). Lithium isotopic abundances in metal-poor halo stars. ApJ 644, 229–259. doi:10.1086/503538

CrossRef Full Text | Google Scholar

Audard, M., Ábrahám, P., Dunham, M. M., Green, J. D., Grosso, N., Hamaguchi, K., et al. (2014). “Episodic accretion in young stars,”. Protostars and planets VI. Editors H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning, 387. doi:10.2458/azu˙uapress˙9780816531240-ch017

CrossRef Full Text | Google Scholar

Gaia Collaboration Babusiaux, C., van Leeuwen, F., Barstow, M. A., Jordi, C., Vallenari, A., et al. (2018). Gaia data release 2. Observational hertzsprung-russell diagrams. A&A 616, A10. doi:10.1051/0004-6361/201832843

CrossRef Full Text | Google Scholar

Badnell, N. R., Bautista, M. A., Butler, K., Delahaye, F., Mendoza, C., Palmeri, P., et al. (2005). Updated opacities from the opacity project. MNRAS 360, 458–464. doi:10.1111/j.1365-2966.2005.08991.x

CrossRef Full Text | Google Scholar

Bae, J., Hartmann, L., Zhu, Z., and Gammie, C. (2013). Variable accretion outbursts in protostellar evolution. ApJ 764, 141. doi:10.1088/0004-637X/764/2/141

CrossRef Full Text | Google Scholar

Baraffe, I., and Chabrier, G. (2010). Effect of episodic accretion on the structure and the lithium depletion of low-mass stars and planet-hosting stars. A&A 521, A44. doi:10.1051/0004-6361/201014979

CrossRef Full Text | Google Scholar

Baraffe, I., Chabrier, G., and Gallardo, J. (2009). Episodic accretion at early stages of evolution of low-mass stars and Brown dwarfs: a solution for the observed luminosity spread in H-R diagrams? ApJl 702, L27–L31. doi:10.1088/0004-637X/702/1/L27

CrossRef Full Text | Google Scholar

Baraffe, I., Vorobyov, E., and Chabrier, G. (2012). Observed luminosity spread in young clusters and FU Ori stars: a unified picture. ApJ 756, 118. doi:10.1088/0004-637X/756/2/118

CrossRef Full Text | Google Scholar

Barrado y Navascués, D., Stauffer, J. R., and Patten, B. M. (1999). The lithium-depletion boundary and the age of the young open cluster IC 2391. ApJl 522, L53–L56. doi:10.1086/312212

CrossRef Full Text | Google Scholar

Baur, G. (1986). Breakup reactions as an indirect method to investigate low-energy charged-particle reactions relevant for nuclear astrophysics. Phys. Lett. B 178, 135–138.

CrossRef Full Text | Google Scholar

Beeck, B., Cameron, R. H., Reiners, A., and Schüssler, M. (2013). Three-dimensional simulations of near-surface convection in main-sequence stars. II. Properties of granulation and spectral lines. A&A 558, A49. doi:10.1051/0004-6361/201321345

CrossRef Full Text | Google Scholar

Bergemann, M., Collet, R., Amarsi, A. M., Kovalev, M., Ruchti, G., and Magic, Z. (2017). Non-local thermodynamic equilibrium stellar spectroscopy with 1D and <3D> models. I. Methods and application to magnesium abundances in standard stars. ApJ 847, 15. doi:10.3847/1538-4357/aa88cb

CrossRef Full Text | Google Scholar

Bergemann, M., Gallagher, A. J., Eitner, P., Bautista, M., Collet, R., Yakovleva, S. A., et al. (2019). Observational constraints on the origin of the elements. I. 3D NLTE formation of Mn lines in late-type stars. A&A 631, A80. doi:10.1051/0004-6361/201935811

CrossRef Full Text | Google Scholar

Bigot, L., Mourard, D., Berio, P., Thévenin, F., Ligi, R., Tallon-Bosc, I., et al. (2011). The diameter of the CoRoT target HD 49933. Combining the 3D limb darkening, asteroseismology, and interferometry. A&A 534, L3. doi:10.1051/0004-6361/201117349

CrossRef Full Text | Google Scholar

Binks, A. S., and Jeffries, R. D. (2014). A lithium depletion boundary age of 21 Myr for the Beta Pictoris moving group. MNRAS 438, L11–L15. doi:10.1093/mnrasl/slt141

CrossRef Full Text | Google Scholar

Blancard, C., Cossé, P., and Faussurier, G. (2012). Solar mixture opacity calculations using detailed configuration and level accounting treatments. ApJ 745, 10. doi:10.1088/0004-637X/745/1/10

CrossRef Full Text | Google Scholar

Boesgaard, A. M., and Novicki, M. C. (2005). Beryllium in the ultra-lithium-deficient, metal-poor halo dwarf g186-26. ApJl 633, L125–L128. doi:10.1086/498021

CrossRef Full Text | Google Scholar

Boesgaard, A. M., Rich, J. A., Levesque, E. M., and Bowler, B. P. (2011). Beryllium and alpha-element abundances in a large sample of metal-poor stars. ApJ 743, 140. doi:10.1088/0004-637X/743/2/140

CrossRef Full Text | Google Scholar

Böhm-Vitense, E. (1958). Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen. Z. Astrophysik 46, 108.

Google Scholar

Bonifacio, P., Caffau, E., Ludwig, H. G., Steffen, M., Castelli, F., Gallagher, A. J., et al. (2018). Using the CIFIST grid of COBOLD 3D model atmospheres to study the effects of stellar granulation on photometric colours. I. Grids of 3D corrections in the UBVRI, 2MASS, HIPPARCOS, Gaia, and SDSS systems. A&A 611, A68. doi:10.1051/0004-6361/201732232

CrossRef Full Text | Google Scholar

Bossini, D., Vallenari, A., Bragaglia, A., Cantat-Gaudin, T., Sordo, R., Balaguer-Núñez, L., et al. (2019). Age determination for 269 Gaia DR2 open clusters. A&A 623, A108. doi:10.1051/0004-6361/201834693

CrossRef Full Text | Google Scholar

Burke, C. J., Pinsonneault, M. H., and Sills, A. (2004). Theoretical examination of the lithium depletion boundary. ApJ 604, 272–283. doi:10.1086/381242

CrossRef Full Text | Google Scholar

Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., and Bonifacio, P. (2011). Solar chemical abundances determined with a CO5BOLD 3D model atmosphere. Sol. Phys. 268, 255–269. doi:10.1007/s11207-010-9541-4

CrossRef Full Text | Google Scholar

Caffau, E., Maiorca, E., Bonifacio, P., Faraggiana, R., Steffen, M., Ludwig, H.-G., et al. (2009). The solar photospheric nitrogen abundance. Analysis of atomic transitions with 3D and 1D model atmospheres. A&A 498, 877–884. doi:10.1051/0004-6361/200810859

CrossRef Full Text | Google Scholar

Calvet, N., Briceño, C., Hernández, J., Hoyer, S., Hartmann, L., Sicilia-Aguilar, A., et al. (2005). Disk evolution in the orion OB1 association. AJ 129, 935–946. doi:10.1086/426910

CrossRef Full Text | Google Scholar

Cayrel, R., Spite, M., Spite, F., Vangioni-Flam, E., Cassé, M., and Audouze, J. (1999). New high S/N observations of the (6Li)/(7) Li blend in HD 84937 and two other metal-poor stars. A&A 343, 923–932.

Google Scholar

Cayrel, R., Steffen, M., Chand, H., Bonifacio, P., Spite, M., Spite, F., et al. (2007). Line shift, line asymmetry, and the 6̂Li/7̂Li isotopic ratio determination. A&A 473, L37–L40. doi:10.1051/0004-6361:20078342

CrossRef Full Text | Google Scholar

Chabrier, G., and Baraffe, I. (1997). Structure and evolution of low-mass stars. A&A 327, 1039–1053.

Google Scholar

Charbonnel, C., Decressin, T., Amard, L., Palacios, A., and Talon, S. (2013). Impact of internal gravity waves on the rotation profile inside pre-main sequence low-mass stars. A&A 554, A40. doi:10.1051/0004-6361/201321277

CrossRef Full Text | Google Scholar

Charbonnel, C., Deliyannis, C. P., and Pinsonneault, M. (2000). “Sinks of light elements in stars - Part III (invited paper),”. The light elements and their evolution. Editors L. da Silva, R. de Medeiros, and M. Spite, Vol. 198, 87.

CrossRef Full Text | Google Scholar

Charbonnel, C., and Primas, F. (2005). The lithium content of the Galactic Halo stars. A&A 442, 961–992. doi:10.1051/0004-6361:20042491

CrossRef Full Text | Google Scholar

Chiavassa, A., Bigot, L., Kervella, P., Matter, A., Lopez, B., Collet, R., et al. (2012). Three-dimensional interferometric, spectrometric, and planetary views of Procyon. A&A 540, A5. doi:10.1051/0004-6361/201118652

CrossRef Full Text | Google Scholar

Chiavassa, A., Casagrande, L., Collet, R., Magic, Z., Bigot, L., Thévenin, F., et al. (2018). The STAGGER-grid: a grid of 3D stellar atmosphere models. V. Synthetic stellar spectra and broad-band photometry. A&A 611, A11. doi:10.1051/0004-6361/201732147

CrossRef Full Text | Google Scholar

Clarke, D., MacDonald, E. C., and Owens, S. (2004). Li abundance/surface activity connections in solar-type Pleiades. A&A 415, 677–684. doi:10.1051/0004-6361:20034620

CrossRef Full Text | Google Scholar

Coc, A., and Vangioni, E. (2010). Big-Bang nucleosynthesis with updated nuclear data, J. Phys. Conf. Ser. Journal of physics conference series, 202. 012001. doi:10.1088/1742-6596/202/1/012001

CrossRef Full Text | Google Scholar

Coc, A., and Vangioni, E. (2017). Primordial nucleosynthesis. Int. J. Mod. Phys. E 26, 1741002. doi:10.1142/S0218301317410026

CrossRef Full Text | Google Scholar

Collet, R., Hayek, W., Asplund, M., Nordlund, Å., Trampedach, R., and Gudiksen, B. (2011). Three-dimensional surface convection simulations of metal-poor stars. The effect of scattering on the photospheric temperature stratification. A&A 528, A32. doi:10.1051/0004-6361/201016151

CrossRef Full Text | Google Scholar

Copi, C. J., Schramm, D. N., and Turner, M. S. (1997). Big-bang nucleosynthesis limit to the number of neutrino species. Phys. Rev. 55, 3389–3393. doi:10.1103/PhysRevD.55.3389

CrossRef Full Text | Google Scholar

Creevey, O. L., Thévenin, F., Boyajian, T. S., Kervella, P., Chiavassa, A., Bigot, L., et al. (2012). Fundamental properties of the Population II fiducial stars ¡ASTROBJ¿HD 122563¡/ASTROBJ¿ and ¡ASTROBJ¿Gmb 1830¡/ASTROBJ¿ from CHARA interferometric observations. A&A 545, A17. doi:10.1051/0004-6361/201219651

CrossRef Full Text | Google Scholar

Cunha, K. (2010). “Boron abundances in the Galactic disk,”. Light elements in the universe. Editors C. Charbonnel, M. Tosi, F. Primas, and C. Chiappini (IAU Symposium), Vol. 268, 243–248. doi:10.1017/S1743921310004199

CrossRef Full Text | Google Scholar

Cyburt, R. H., Fields, B. D., Olive, K. A., and Yeh, T.-H. (2016). Big bang nucleosynthesis: present status. Rev. Mod. Phys. 88, 015004. doi:10.1103/RevModPhys.88.015004

CrossRef Full Text | Google Scholar

Cyburt, R. H. (2004). Primordial nucleosynthesis for the new cosmology: determining uncertainties and examining concordance. Phys. Rev. 70, 023505. doi:10.1103/PhysRevD.70.023505

CrossRef Full Text | Google Scholar

Da Rio, N., Gouliermis, D. A., and Gennaro, M. (2010a). A new method for the assessment of age and age spread of pre-main-sequence stars in young stellar associations of the magellanic clouds. ApJ 723, 166–183. doi:10.1088/0004-637X/723/1/166

CrossRef Full Text | Google Scholar

Da Rio, N., Robberto, M., Soderblom, D. R., Panagia, N., Hillenbrand, L. A., Palla, F., et al. (2010b). A multi-color optical survey of the orion nebula cluster. II. The H-R diagram. ApJ 722, 1092–1114. doi:10.1088/0004-637X/722/2/1092

CrossRef Full Text | Google Scholar

Dahm, S. E. (2015). Reexamining the lithium depletion boundary in the Pleiades and the inferred age of the cluster. ApJ 813, 108. doi:10.1088/0004-637X/813/2/108

CrossRef Full Text | Google Scholar

Damone, L., Barbagallo, M., Mastromarco, M., Mengoni, A., Cosentino, L., Maugeri, E., et al. (2018). Be (n ,p ) Li reaction and the cosmological lithium problem: measurement of the cross section in a wide energy range at n_TOF at CERN. Phys. Rev. Lett. 121, 042701. doi:10.1103/PhysRevLett.121.042701

PubMed Abstract | CrossRef Full Text | Google Scholar

Degl’Innocenti, S., Prada Moroni, P. G., Marconi, M., and Ruoppo, A. (2008). The FRANEC stellar evolutionary code. Ap&SS 316, 25–30. doi:10.1007/s10509-007-9560-2

CrossRef Full Text | Google Scholar

Delgado Mena, E., Bertrán de Lis, S., Adibekyan, V. Z., Sousa, S. G., Figueira, P., Mortier, A., et al. (2015). Li abundances in F stars: planets, rotation, and Galactic evolution. A&A 576, A69. doi:10.1051/0004-6361/201425433

CrossRef Full Text | Google Scholar

Delgado Mena, E., Israelian, G., González Hernández, J. I., Santos, N. C., and Rebolo, R. (2012). Be abundances in cool main-sequence stars with exoplanets. ApJ 746, 47. doi:10.1088/0004-637X/746/1/47

CrossRef Full Text | Google Scholar

Delgado Mena, E., Israelian, G., González Hernández, J. I., Sousa, S. G., Mortier, A., Santos, N. C., et al. (2014). Li depletion in solar analogues with exoplanets. Extending the sample. A&A 562, A92. doi:10.1051/0004-6361/201321493

CrossRef Full Text | Google Scholar

Dell’Omodarme, M., Valle, G., Degl’Innocenti, S., and Prada Moroni, P. G. (2012). The Pisa stellar evolution data base for low-mass stars. A&A 540, A26. doi:10.1051/0004-6361/201118632

CrossRef Full Text | Google Scholar

Descouvemont, P., Adahchour, A., Angulo, C., Coc, A., and Vangioni-Flam, E. (2004). Compilation and R-matrix analysis of Big Bang nuclear reaction rates. At. Data Nucl. Data Tables 88, 203–236. doi:10.1016/j.adt.2004.08.001

CrossRef Full Text | Google Scholar

Dobbie, P. D., Lodieu, N., and Sharp, R. G. (2010). IC 2602: a lithium depletion boundary age and new candidate low-mass stellar members. MNRAS 409, 1002–1012. doi:10.1111/j.1365-2966.2010.17355.x

CrossRef Full Text | Google Scholar

Dupuy, T. J., Forbrich, J., Rizzuto, A., Mann, A. W., Aller, K., Liu, M. C., et al. (2016). High-precision radio and infrared astrometry of LSPM J1314+1320AB. II. Testing pre-main-sequence models at the lithium depletion boundary with dynamical masses. ApJ 827, 23. doi:10.3847/0004-637X/827/1/23

CrossRef Full Text | Google Scholar

D’Antona, F., and Mazzitelli, I. (1997). Evolution of low mass stars. Mem. Soc. Astron. Italiana 68, 807.

Google Scholar

D’Antona, F., and Mazzitelli, I. (1994). New pre-main-sequence tracks for M less than or equal to 2.5 solar mass as tests of opacities and convection model. ApJS 90, 467–500. doi:10.1086/191867

CrossRef Full Text | Google Scholar

D’Antona, F., and Montalbán, J. (2003). Efficiency of convection and Pre-Main Sequence lithium depletion. A&A 412, 213–218. doi:10.1051/0004-6361:20031410

CrossRef Full Text | Google Scholar

D’Antona, F., Ventura, P., and Mazzitelli, I. (2000). First results on pre-main-sequence evolution, including a magnetic field. ApJ 543, L77–L80. doi:10.1086/318172

CrossRef Full Text | Google Scholar

Eggenberger, P., Haemmerlé, L., Meynet, G., and Maeder, A. (2012). Impact of rotation and disc lifetime on pre-main sequence lithium depletion of solar-type stars. A&A 539, A70. doi:10.1051/0004-6361/201118432

CrossRef Full Text | Google Scholar

Feiden, G. A., and Chaboyer, B. (2013). Magnetic inhibition of convection and the fundamental properties of low-mass stars. I. Stars with a radiative core. ApJ 779, 183. doi:10.1088/0004-637X/779/2/183

CrossRef Full Text | Google Scholar

Feiden, G. A., and Chaboyer, B. (2012). Reevaluating the mass-radius relation for low-mass, main-sequence stars. ApJ 757, 42. doi:10.1088/0004-637X/757/1/42

CrossRef Full Text | Google Scholar

Feiden, G. A. (2016). Magnetic inhibition of convection and the fundamental properties of low-mass stars. III. A consistent 10 Myr age for the Upper Scorpius OB association. A&A 593, A99. doi:10.1051/0004-6361/201527613

CrossRef Full Text | Google Scholar

Fields, B. D. (2011). The primordial lithium problem. Annu. Rev. Nucl. Part. Sci. 61, 47–68. doi:10.1146/annurev-nucl-102010-130445

CrossRef Full Text | Google Scholar

Freytag, B., Steffen, M., Ludwig, H. G., Wedemeyer-Böhm, S., Schaffenberger, W., and Steiner, O. (2012). Simulations of stellar convection with CO5BOLD. J. Comput. Phys. 231, 919–959. doi:10.1016/j.jcp.2011.09.026

CrossRef Full Text | Google Scholar

Fu, X., Bressan, A., Molaro, P., and Marigo, P. (2015). Lithium evolution in metal-poor stars: from pre-main sequence to the Spite plateau. MNRAS 452, 3256–3265. doi:10.1093/mnras/stv1384

CrossRef Full Text | Google Scholar

Garcia Lopez, R. J., Rebolo, R., and Perez de Taoro, M. R. (1995). Beryllium abundances in late-type Hyades dwarf stars. A&A 302, 184.

Google Scholar

Gennaro, M., Prada Moroni, P. G., and Tognelli, E. (2012). Testing pre-main-sequence models: the power of a Bayesian approach. MNRAS 420, 986–1018. doi:10.1111/j.1365-2966.2011.19945.x

CrossRef Full Text | Google Scholar

González Hernández, J. I., Bonifacio, P., Caffau, E., Ludwig, H. G., Steffen, M., Monaco, L., et al. (2019). The Li/Li isotopic ratio in the metal-poor binary CS22876-032. A&A 628, A111. doi:10.1051/0004-6361/201936011

CrossRef Full Text | Google Scholar

Goudelis, A., Pospelov, M., and Pradler, J. (2016). Light particle solution to the cosmic lithium problem. Phys. Rev. Lett. 116, 211303. doi:10.1103/PhysRevLett.116.211303

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartmann, L., Cassen, P., and Kenyon, S. J. (1997). Disk accretion and the stellar birthline. ApJ 475, 770. doi:10.1086/303547

CrossRef Full Text | Google Scholar

Hartmann, L., Herczeg, G., and Calvet, N. (2016). Accretion onto pre-main-sequence stars. ARA&A 54, 135–180. doi:10.1146/annurev-astro-081915-023347

CrossRef Full Text | Google Scholar

Hartmann, L., and Kenyon, S. J. (1996). The FU orionis phenomenon. ARA&A 34, 207–240. doi:10.1146/annurev.astro.34.1.207

CrossRef Full Text | Google Scholar

Hayashi, C., and Nakano, T. (1963). Evolution of stars of small masses in the pre-main-sequence stages. Prog. Theor. Phys. 30, 460–474. doi:10.1143/PTP.30.460

CrossRef Full Text | Google Scholar

Hayashi, C. (1961). Stellar evolution in early phases of gravitational contraction. PASJ 13, 450–452.

Google Scholar

Hillenbrand, L. A. (2009). “Age-related observations of low mass pre-main and young main sequence stars,”. The ages of stars. Editors E. E. Mamajek, D. R. Soderblom, and R. F. G. Wyse (IAU Symposium), Vol. 258, 81–94. doi:10.1017/S1743921309031731

CrossRef Full Text | Google Scholar

Hosokawa, T., Offner, S. S. R., and Krumholz, M. R. (2011). On the reliability of stellar ages and age spreads inferred from pre-main-sequence evolutionary models. ApJ 738, 140. doi:10.1088/0004-637X/738/2/140

CrossRef Full Text | Google Scholar

Hosokawa, T., and Omukai, K. (2009a). Evolution of massive protostars with high accretion rates. ApJ 691, 823–846. doi:10.1088/0004-637X/691/1/823

CrossRef Full Text | Google Scholar

Hosokawa, T., and Omukai, K. (2009b). Low-metallicity protostars and the maximum stellar mass resulting from radiative feedback: spherically symmetric calculations. ApJ 703, 1810–1818. doi:10.1088/0004-637X/703/2/1810

CrossRef Full Text | Google Scholar

Hosokawa, T., Yorke, H. W., and Omukai, K. (2010). Evolution of massive protostars via disk accretion. ApJ 721, 478–492. doi:10.1088/0004-637X/721/1/478

CrossRef Full Text | Google Scholar

Iben, I. (2013). Stellar evolution physics. in Physical Processes in stellar interiors, Vol. 1.

Ingleby, L., Calvet, N., Hernández, J., Hartmann, L., Briceno, C., Miller, J., et al. (2014). The evolution of accretion in young stellar objects: strong accretors at 3-10 myr. ApJ 790, 47. doi:10.1088/0004-637X/790/1/47

CrossRef Full Text | Google Scholar

Jackson, R. J., and Jeffries, R. D. (2014). The effect of star-spots on the ages of low-mass stars determined from the lithium depletion boundary. MNRAS 445, 4306–4315. doi:10.1093/mnras/stu2076

CrossRef Full Text | Google Scholar

Jeffries, R. D. (2006). Pre-main-sequence lithium depletion (chemical abundances and mixing in stars in the milky way and its satellites, 163. ESO ASTROPHYSICS SYMPOSIASpringer-Verlag, 163. 978-3-540-34135-2.

Jeffries, R. D. (2009). “Age spreads in star forming regions?,” in The ages of stars. Of IAU symposium. Editors E. E. Mamajek, D. R. Soderblom, and R. F. G. Wyse, Vol. 258, 95–102. doi:10.1017/S1743921309031743

CrossRef Full Text | Google Scholar

Jeffries, R. D. (2000). “Lithium depletion in open clusters,”. Stellar clusters and associations: convection, rotation, and dynamos. Editors R. Pallavicini, G. Micela, and S. Sciortino (Astronomical Society of the Pacific Conference Series), Vol. 198, 245.

Google Scholar

Jeffries, R. D., Naylor, T., Mayne, N. J., Bell, C. P. M., and Littlefair, S. P. (2013). A lithium depletion boundary age of 22 Myr for NGC 1960. MNRAS 434, 2438–2450. doi:10.1093/mnras/stt1180

CrossRef Full Text | Google Scholar

Jeffries, R. D., and Oliveira, J. M. (2005). The lithium depletion boundary in NGC 2547 as a test of pre-main-sequence evolutionary models. MNRAS 358, 13–29. doi:10.1111/j.1365-2966.2005.08820.x

CrossRef Full Text | Google Scholar

Jofré, P., Heiter, U., and Soubiran, C. (2019). Accuracy and precision of industrial stellar abundances. ARA&A 57, 571–616. doi:10.1146/annurev-astro-091918-104509

CrossRef Full Text | Google Scholar

Juarez, A. J., Cargile, P. A., James, D. J., and Stassun, K. G. (2014). An improved determination of the lithium depletion boundary age of Blanco 1 and a first look on the effects of magnetic activity. ApJ 795, 143. doi:10.1088/0004-637X/795/2/143

CrossRef Full Text | Google Scholar

Kaufer, A. (2010). “Observations of light elements in massive stars,”. Light elements in the universe. Editors C. Charbonnel, M. Tosi, F. Primas, and C. Chiappini (IAU Symposium), Vol. 268, 317–324. doi:10.1017/S1743921310004291

CrossRef Full Text | Google Scholar

King, J. R., Krishnamurthi, A., and Pinsonneault, M. H. (2000). The lithium-rotation correlation in the Pleiades revisited. AJ 119, 859–872. doi:10.1086/301205

CrossRef Full Text | Google Scholar

King, J. R., Schuler, S. C., Hobbs, L. M., and Pinsonneault, M. H. (2010). Li I and K I scatter in cool Pleiades dwarfs. ApJ 710, 1610–1618. doi:10.1088/0004-637X/710/2/1610

CrossRef Full Text | Google Scholar

Kunitomo, M., Guillot, T., Ida, S., and Takeuchi, T. (2018). Revisiting the pre-main-sequence evolution of stars. II. Consequences of planet formation on stellar surface composition. A&A 618, A132. doi:10.1051/0004-6361/201833127

CrossRef Full Text | Google Scholar

Kunitomo, M., Guillot, T., Takeuchi, T., and Ida, S. (2017). Revisiting the pre-main-sequence evolution of stars. I. Importance of accretion efficiency and deuterium abundance. A&A 599, A49. doi:10.1051/0004-6361/201628260

CrossRef Full Text | Google Scholar

Lamia, L., Mazzocco, M., Pizzone, R. G., Hayakawa, S., La Cognata, M., Spitaleri, C., et al. (2019). Cross-section measurement of the cosmologically relevant Be(n,α)He reaction over a broad energy range in a single experiment. Astrophysical J. 879, 23. doi:10.3847/1538-4357/ab2234

CrossRef Full Text | Google Scholar

Lamia, L., Spitaleri, C., La Cognata, M., Palmerini, S., and Pizzone, R. G. (2012). Recent evaluation of the Li(p, α)He reaction rate at astrophysical energies via the Trojan Horse method. A&A 541, A158. doi:10.1051/0004-6361/201219014

CrossRef Full Text | Google Scholar

Lamia, L., Spitaleri, C., Pizzone, R. G., Tognelli, E., Tumino, A., Degl’Innocenti, S., et al. (2013). An updated Li(p, α)He reaction rate at astrophysical energies with the trojan horse method. ApJ 768, 65. doi:10.1088/0004-637X/768/1/65

CrossRef Full Text | Google Scholar

Lamia, L., Spitaleri, C., Tognelli, E., Degl’Innocenti, S., Pizzone, R. G., and Prada Moroni, P. G. (2015). Astrophysical impact of the updated Be(p,α)Li and B(p,α)Be reaction rates as deduced by THM. ApJ 811, 99. doi:10.1088/0004-637X/811/2/99

CrossRef Full Text | Google Scholar

Landin, N. R., Ventura, P., D’Antona, F., Mendes, L. T. S., and Vaz, L. P. R. (2006). Non-gray rotating stellar models and the evolutionary history of the Orion Nebular Cluster. A&A 456, 269–282. doi:10.1051/0004-6361:20054011

CrossRef Full Text | Google Scholar

Larson, R. B. (1969). Numerical calculations of the dynamics of collapsing proto-star. MNRAS 145, 271.

CrossRef Full Text | Google Scholar

Larson, R. B. (1972). The evolution of spherical protostars with masses 0.25 M_solar to 10 M_solar. MNRAS 157, 121. doi:10.1093/mnras/157.2.121

CrossRef Full Text | Google Scholar

Larson, R. B. (2003). The physics of star formation. Rep. Prog. Phys. 66, 1651–1697. doi:10.1088/0034-4885/66/10/R03

CrossRef Full Text | Google Scholar

Lind, K., Amarsi, A. M., Asplund, M., Barklem, P. S., Bautista, M., Bergemann, M., et al. (2017). Non-LTE line formation of Fe in late-type stars - IV. Modelling of the solar centre-to-limb variation in 3D. MNRAS 468, 4311–4322. doi:10.1093/mnras/stx673

CrossRef Full Text | Google Scholar

Lind, K., Melendez, J., Asplund, M., Collet, R., and Magic, Z. (2013). The lithium isotopic ratio in very metal-poor stars. A&A 554, A96. doi:10.1051/0004-6361/201321406

CrossRef Full Text | Google Scholar

Lodders, K., Plame, H., and Gail, H. (2009). Abundances of the elements in the solar system. In Landolt-börnstein - group VI Astronomy and astrophysics numerical data and functional relationships in science and technology volume 4B: solar system. Edited by J.E. Trümper, 4. 44. doi:10.1007/978-3-540-88055-4˙34

CrossRef Full Text | Google Scholar

Lodders, K. (2010). Solar system Abundances of the elements. Astrophysics Space Sci. Proc. 16, 379. doi:10.1007/978-3-642-10352-0˙8

CrossRef Full Text | Google Scholar

Ludwig, H.-G., Freytag, B., and Steffen, M. (1999). A calibration of the mixing-length for solar-type stars based on hydrodynamical simulations. I. Methodical aspects and results for solar metallicity. A&A 346, 111–124.

Google Scholar

Ludwig, H., Caffau, E., Steffen, M., Freytag, B., Bonifacio, P., and Kučinskas, A. (2009). The CIFIST 3D model atmosphere grid. Mem. Soc. Astron. Italiana 80, 711.

Google Scholar

Lydon, T. J., Fox, P. A., and Sofia, S. (1992). A formulation of convection for stellar structure and evolution calculations without the mixing-length theory approximations. I. Application to the Sun. ApJ 397, 701. doi:10.1086/171826

CrossRef Full Text | Google Scholar

Mathieu, R. D., BaraffeSimon, I. M., Stassun, K. G., and White, R. (2007). Dynamical mass measurements of pre-main-sequence stars: fundamental tests of the physics of young stars. Protostars and Planets V, 411–425.

Google Scholar

MacDonald, J., and Mullan, D. J. (2012). Precision modelling of M dwarf stars: the magnetic components of CM Draconis. MNRAS 421, 3084–3101. doi:10.1111/j.1365-2966.2012.20531.x

CrossRef Full Text | Google Scholar

Machida, M. N., Inutsuka, S.-i., and Matsumoto, T. (2010). formation process of the circumstellar disk: long-term simulations in the main accretion phase of star formation. ApJ 724, 1006–1020. doi:10.1088/0004-637X/724/2/1006

CrossRef Full Text | Google Scholar

Machida, M. N., Inutsuka, S.-i., and Matsumoto, T. (2008). High- and low-velocity magnetized outflows in the star formation process in a gravitationally collapsing cloud. ApJ 676, 1088–1108. doi:10.1086/528364

CrossRef Full Text | Google Scholar

Magic, Z., and Asplund, M. (2014). Surface appearance of stellar granulation.The Stagger-grid: a grid of 3D stellar atmosphere models - VI. arXiv e-prints. arXiv:1405.7628.

Google Scholar

Magic, Z., Collet, R., Asplund, M., Trampedach, R., Hayek, W., Chiavassa, A., et al. (2013). The Stagger-grid: a grid of 3D stellar atmosphere models. I. Methods and general properties. A&A 557, A26. doi:10.1051/0004-6361/201321274

CrossRef Full Text | Google Scholar

Manzi, S., Randich, S., de Wit, W. J., and Palla, F. (2008). Detection of the lithium depletion boundary in the young open cluster IC 4665. A&A 479, 141–148. doi:10.1051/0004-6361:20078226

CrossRef Full Text | Google Scholar

Martín, E. L., Lodieu, N., and Béjar, V. J. S. (2020). Search for the sub-stellar lithium depletion boundary in the open star cluster Coma Berenices. A&A 640, A9. doi:10.1051/0004-6361/202037907

CrossRef Full Text | Google Scholar

Martín, E. L., Lodieu, N., Pavlenko, Y., and Béjar, V. J. S. (2018). The lithium depletion boundary and the age of the hyades cluster. ApJ 856, 40. doi:10.3847/1538-4357/aaaeb8

CrossRef Full Text | Google Scholar

Masunaga, H., and Inutsuka, S.-i. (2000). A radiation hydrodynamic model for protostellar collapse. II. The second collapse and the birth of a protostar. ApJ 531, 350–365. doi:10.1086/308439

CrossRef Full Text | Google Scholar

Meléndez, J., Ramírez, I., Casagrande, L., Asplund, M., Gustafsson, B., Yong, D., et al. (2010). The solar, exoplanet and cosmological lithium problems. Ap&SS 328, 193–200. doi:10.1007/s10509-009-0187-3

CrossRef Full Text | Google Scholar

Meyer, M. R., Backman, D. E., Weinberger, A. J., and Wyatt, M. C. (2007). “Evolution of circumstellar disks around normal stars: placing our solar system in context,” in Protostars and planets V. Editors B. Reipurth, D. Jewitt, and K. Keil, 573.

Google Scholar

Mondet, G., Blancard, C., Cossé, P., and Faussurier, G. (2015). Opacity calculations for solar mixtures. ApJS 220, 2. doi:10.1088/0067-0049/220/1/2

CrossRef Full Text | Google Scholar

Montalbán, J., and Schatzman, E. (2000). Mixing by internal waves. III. Li and Be abundance dependence on spectral type, age and rotation. A&A 354, 943–959.

Google Scholar

Mossa, V., Stöckel, K., Cavanna, F., Ferraro, F., Aliotta, M., Barile, F., et al. (2020). The baryon density of the Universe from an improved rate of deuterium burning. Nature 587, 210–213. doi:10.1038/s41586-020-2878-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Muzerolle, J., Calvet, N., Briceño, C., Hartmann, L., and Hillenbrand, L. (2000). Disk accretion in the 10 MYR old T Tauri stars TW hydrae and hen 3-600a. ApJ 535, L47–L50. doi:10.1086/312691

PubMed Abstract | CrossRef Full Text | Google Scholar

Muzerolle, J., Luhman, K. L., Briceño, C., Hartmann, L., and Calvet, N. (2005a). Measuring accretion in young substellar objects: approaching the planetary mass regime. ApJ 625, 906–912. doi:10.1086/429483

CrossRef Full Text | Google Scholar

Muzerolle, J., Megeath, S. T., Flaherty, K. M., Gordon, K. D., Rieke, G. H., Young, E. T., et al. (2005b). The outburst of V1647 orionis revealed by spitzer. ApJ 620, L107–L110. doi:10.1086/428832

CrossRef Full Text | Google Scholar

Natta, A., Grinin, V., and Mannings, V. (2000). “Properties and evolution of disks around pre-main-sequence stars of intermediate mass,” in Protostars and planets IV. Editors V. Mannings, A. P. Boss, and S. S. Russell, 559–588.

Google Scholar

Nordlander, T., Amarsi, A. M., Lind, K., Asplund, M., Barklem, P. S., Casey, A. R., et al. (2017). 3D NLTE analysis of the most iron-deficient star, SMSS0313-6708. A&A 597, A6. doi:10.1051/0004-6361/201629202

CrossRef Full Text | Google Scholar

Nordlund, A. (1982). Numerical simulations of the solar granulation. I - basic equations and methods. A&A 107, 1–10.

Google Scholar

Nordlund, Å., Stein, R. F., and Asplund, M. (2009). Solar surface convection. Living Rev. Solar Phys. 6, 2.

PubMed Abstract | CrossRef Full Text | Google Scholar

Oliveira, J. M., Jeffries, R. D., Devey, C. R., Barrado y Navascués, D., Naylor, T., Stauffer, J. R., et al. (2003). The lithium depletion boundary and the age of NGC 2547. MNRAS 342, 651–663. doi:10.1046/j.1365-8711.2003.06592.x

CrossRef Full Text | Google Scholar

Pace, G., Castro, M., Meléndez, J., Théado, S., and do Nascimento, J.-D. (2012). Lithium in M 67: from the main sequence to the red giant branch. A&A 541, A150. doi:10.1051/0004-6361/201117704

CrossRef Full Text | Google Scholar

Palla, F., and Stahler, S. W. (1991). The evolution of intermediate-mass protostars. I - basic results. ApJ 375, 288–299. doi:10.1086/170188

CrossRef Full Text | Google Scholar

Palla, F., and Stahler, S. W. (1992). The evolution of intermediate-mass protostars. II. Influence of the accretion flow. ApJ 392, 667. doi:10.1086/171468

CrossRef Full Text | Google Scholar

Palla, F., and Stahler, S. W. (1993). The pre-main-sequence evolution of intermediate-mass stars. ApJ 418, 414. doi:10.1086/173402

CrossRef Full Text | Google Scholar

Pettini, M., Zych, B. J., Murphy, M. T., Lewis, A., and Steidel, C. C. (2008). Deuterium abundance in the most metal-poor damped Lyman alpha system: converging on h. MNRAS 391, 1499–1510. doi:10.1111/j.1365-2966.2008.13921.x

CrossRef Full Text | Google Scholar

Piau, L., and Turck-Chièze, S. (2002). Lithium depletion in pre-main-sequence solar-like stars. ApJ 566, 419–434. doi:10.1086/324277

CrossRef Full Text | Google Scholar

Pitrou, C., Coc, A., Uzan, J.-P., and Vangioni, E. (2018). Precision big bang nucleosynthesis with improved Helium-4 predictions. Phys. Rep. 754, 1–66. doi:10.1016/j.physrep.2018.04.005

CrossRef Full Text | Google Scholar

Pizzone, R. G., Roeder, B. T., McCleskey, M., Trache, L., Tribble, R. E., Spitaleri, C., et al. (2016). Trojan Horse measurement of the F(p,α)O astrophysical S(E)-factor. Eur. Phys. J. A 52, 24. doi:10.1140/epja/i2016-16024-3

CrossRef Full Text | Google Scholar

Pizzone, R. G., Spampinato, C., Spartá, R., Couder, M., Tan, W., Burjan, V., et al. (2020). Indirect measurement of the He (n,p)H reaction cross section at Big Bang energies. Eur. Phys. J. A 56, 199. doi:10.1140/epja/s10050-020-00212-x

CrossRef Full Text | Google Scholar

Pizzone, R. G., Spartá, R., Bertulani, C. A., Spitaleri, C., La Cognata, M., Lalmansingh, J., et al. (2014). Big bang nucleosynthesis revisited via trojan horse method measurements. Astrophysical J. 786, 112.

CrossRef Full Text | Google Scholar

Pizzone, R. G., Spitaleri, C., Cherubini, S., La Cognata, M., Lamia, L., Romano, S., et al. (2010). Trojan Horse Method: a tool to explore electron screening effect. J. Phys. Conf. Ser. 202, 012018. doi:10.1088/1742-6596/202/1/012018

CrossRef Full Text | Google Scholar

Pizzone, R. G., Spitaleri, C., Lattuada, M., Cherubini, S., Musumarra, A., Pellegriti, M. G., et al. (2003). Proton-induced lithium destruction cross-section and its astrophysical implications. Astron. Astrophysics 398, 423–427.

CrossRef Full Text | Google Scholar

Pizzone, R. G., Tumino, A., Degl’Innocenti, S., Spitaleri, C., Cherubini, S., Musumarra, A., et al. (2005). Trojan horse estimate of bare nucleus astrophysical s (e)-factor for the li (p, α) he reaction and its astrophysical implications. Astron. Astrophysics 438, 779–784.

CrossRef Full Text | Google Scholar

Prantzos, N. (2012). Production and evolution of Li, Be, and B isotopes in the Galaxy. A&A 542, A67. doi:10.1051/0004-6361/201219043

CrossRef Full Text | Google Scholar

Pratt, J., Baraffe, I., Goffrey, T., Geroux, C., Viallet, M., Folini, D., et al. (2016). Spherical-shell boundaries for two-dimensional compressible convection in a star. A&A 593, A121. doi:10.1051/0004-6361/201628296

CrossRef Full Text | Google Scholar

Primas, F. (2010). “Beryllium and boron in metal-poor stars,”. Light elements in the universe. Editors C. Charbonnel, M. Tosi, F. Primas, and C. Chiappini (IAU Symposium), Vol. 268, 221–230. doi:10.1017/S1743921310004163

CrossRef Full Text | Google Scholar

Proffitt, C. R., and Quigley, M. F. (1999). Boron abundances in early-B stars: the B 3 2065.8 angstroms line in IUE data. American astronomical society meeting abstracts, Vol. 195. American Astronomical Society Meeting Abstracts

Google Scholar

Randich, S. (2010). “Lithium and beryllium in Population I dwarf stars,”. Light elements in the universe. Editors C. Charbonnel, M. Tosi, F. Primas, and C. Chiappini (IAU Symposium), Vol. 268, 275–283. doi:10.1017/S1743921310004242

CrossRef Full Text | Google Scholar

Randich, S., Primas, F., Pasquini, L., Sestito, P., and Pallavicini, R. (2007). Tracing mixing in stars: new beryllium observations of the open clusters NGC 2516, Hyades, and M 67. A&A 469, 163–172. doi:10.1051/0004-6361:20066218

CrossRef Full Text | Google Scholar

Randich, S., Tognelli, E., Jackson, R., Jeffries, R. D., Degl’Innocenti, S., Pancino, E., et al. (2018). The Gaia-ESO Survey: open clusters in Gaia-DR1 . A way forward to stellar age calibration. A&A 612, A99. doi:10.1051/0004-6361/201731738

CrossRef Full Text | Google Scholar

Richard, O., Michaud, G., and Richer, J. (2005). Implications of WMAP observations on Li abundance and stellar evolution models. ApJ 619, 538–548. doi:10.1086/426470

CrossRef Full Text | Google Scholar

Richard, O., Michaud, G., Richer, J., Turcotte, S., Turck-Chièze, S., and VandenBerg, D. A. (2002). Models of metal-poor stars with gravitational settling and radiative accelerations. I. Evolution and abundance anomalies. ApJ 568, 979–997. doi:10.1086/338952

CrossRef Full Text | Google Scholar

Rolfs, C. E., and Rodney, W. S. (1988). Cauldrons in the cosmos: nuclear astrophysics. Chicago, IL: Univ. Chicago Press.

Santos, N. C., Israelian, G., Randich, S., García López, R. J., and Rebolo, R. (2004). Beryllium anomalies in solar-type field stars. A&A 425, 1013–1027. doi:10.1051/0004-6361:20040510

CrossRef Full Text | Google Scholar

Sbordone, L., Bonifacio, P., Caffau, E., Ludwig, H.-G., Behara, N. T., González Hernández, J. I., et al. (2010). The metal-poor end of the Spite plateau. I. Stellar parameters, metallicities, and lithium abundances. A&A 522, A26. doi:10.1051/0004-6361/200913282

CrossRef Full Text | Google Scholar

Sembach, K. (2010). “Measurements of deuterium in the milky way,”. IAU symposium. Editors C. Charbonnel, M. Tosi, F. Primas, and C. Chiappini (IAU Symposium), Vol. 268, 43–52. doi:10.1017/S1743921310003856

CrossRef Full Text | Google Scholar

Sestito, P., Randich, S., Mermilliod, J. C., and Pallavicini, R. (2003). The evolution of lithium depletion in young open clusters: NGC 6475. A&A 407, 289–301. doi:10.1051/0004-6361:20030723

CrossRef Full Text | Google Scholar

Sestito, P., and Randich, S. (2005). Time scales of Li evolution: a homogeneous analysis of open clusters from ZAMS to late-MS. A&A 442, 615–627. doi:10.1051/0004-6361:20053482

CrossRef Full Text | Google Scholar

Siess, L., and Livio, M. (1997). On the rotational evolution of young low-mass stars. ApJ 490, 785. doi:10.1086/304905

CrossRef Full Text | Google Scholar

Smiljanic, R., Pasquini, L., Charbonnel, C., and Lagarde, N. (2010). Beryllium abundances along the evolutionary sequence of the open cluster IC 4651 - a new test for hydrodynamical stellar models. A&A 510, A50. doi:10.1051/0004-6361/200912957

CrossRef Full Text | Google Scholar

Somers, G., and Pinsonneault, M. H. (2014). A tale of two anomalies: depletion, dispersion, and the connection between the stellar lithium spread and inflated radii on the pre-main sequence. ApJ 790, 72. doi:10.1088/0004-637X/790/1/72

CrossRef Full Text | Google Scholar

Somers, G., and Pinsonneault, M. H. (2015). Older and colder: the impact of starspots on pre-main-sequence stellar evolution. ApJ 807, 174. doi:10.1088/0004-637X/807/2/174

CrossRef Full Text | Google Scholar

Spitaleri, C., Cherubini, S., del Zoppo, A., Di Pietro, A., Figuera, P., Gulino, M., et al. (2003). The trojan horse method in nuclear astrophysics. Nucl. Phys. A. 719, C99–C106. doi:10.1016/S0375-9474(03)00975-8

CrossRef Full Text | Google Scholar

Spitaleri, C., La Cognata, M., Lamia, L., Mukhamedzhanov, A. M., and Pizzone, R. G. (2016). Nuclear astrophysics and the trojan horse method. Eur. Phys. J. A 52, 77.

CrossRef Full Text | Google Scholar

Spitaleri, C., La Cognata, M., Lamia, L., Pizzone, R. G., and Tumino, A. (2019). Astrophysics studies with the trojan horse method. Eur. Phys. J. A 55, 161.

CrossRef Full Text | Google Scholar

Spite, F., and Spite, M. (1982a). Abundance of lithium in unevolved halo stars and old disk stars - interpretation and consequences. A&A 115, 357–366.

Google Scholar

Spite, M., Spite, F., and Bonifacio, P. (2012). The cosmic lithium problem . an observer’s perspective. Memorie della Societa Astronomica Italiana Supplementi 22, 9.

Google Scholar

Spite, M., and Spite, F. (2010). “Li isotopes in metal-poor halo dwarfs: a more and more complicated story,”. Light elements in the universe. Editors C. Charbonnel, M. Tosi, F. Primas, and C. Chiappini (IAU Symposium), Vol. 268, 201–210. doi:10.1017/S1743921310004138

CrossRef Full Text | Google Scholar

Spite, M., and Spite, F. (1982b). Lithium abundance at the formation of the Galaxy. Nature 297, 483–485. doi:10.1038/297483a0

CrossRef Full Text | Google Scholar

Stahler, S. W. (1988). Deuterium and the stellar birthline. ApJ 332, 804. doi:10.1086/166694

CrossRef Full Text | Google Scholar

Stahler, S. W., Shu, F. H., and Taam, R. E. (1980a). The evolution of protostars. I - global formulation and results. ApJ 241, 637–654. doi:10.1086/158377

CrossRef Full Text | Google Scholar

Stahler, S. W., Shu, F. H., and Taam, R. E. (1980b). The evolution of protostars. II - the hydrostatic core. ApJ 242, 226–241. doi:10.1086/158459

CrossRef Full Text | Google Scholar

Stahler, S. W., Shu, F. H., and Taam, R. E. (1981). The evolution of protostars. III - the accretion envelope. ApJ 248, 727–737. doi:10.1086/159197

CrossRef Full Text | Google Scholar

Steffen, M., Cayrel, R., Caffau, E., Bonifacio, P., Ludwig, H. G., and Spite, M. (2012). Li detection in metal-poor stars: can 3D model atmospheres solve the second lithium problem?. Memorie della Societa Astronomica Italiana Supplementi 22, 152.

Google Scholar

Steigman, G., Romano, D., and Tosi, M. (2007). Connecting the primordial and Galactic deuterium abundances. MNRAS 378, 576–580. doi:10.1111/j.1365-2966.2007.11780.x

CrossRef Full Text | Google Scholar

Swenson, F. J. (1995). Lithium in halo dwarfs: the undoing of diffusion by mass loss. ApJ 438, L87–L90. doi:10.1086/187722

CrossRef Full Text | Google Scholar

Talon, S., and Charbonnel, C. (2010). “Light elements as diagnostics on the structure and evolution of low-mass stars,”. IAU symposium. Editors C. Charbonnel, M. Tosi, and F. Primas (& C. ChiappiniIAU Symposium), Vol. 268, 365–374. doi:10.1017/S1743921310004485

CrossRef Full Text | Google Scholar

Talon, S. (2008). Mixing processes in rotating stars. Mem. Soc. Astron. Italiana 79, 569.

Google Scholar

Tan, K. F., Shi, J. R., and Zhao, G. (2009). Beryllium abundances in metal-poor stars. MNRAS 392, 205–215. doi:10.1111/j.1365-2966.2008.14027.x

CrossRef Full Text | Google Scholar

Tognelli, E., Degl’Innocenti, S., and Prada Moroni, P. G. (2012). Li surface abundance in pre-main sequence stars. Testing theory against clusters and binary systems. A&A 548, A41. doi:10.1051/0004-6361/201219111

CrossRef Full Text | Google Scholar

Tognelli, E., Lamia, L., Pizzone, R. G., Degl’Innocenti, S., Prada Moroni, P. G., Romano, S., et al. (2019). Stellar surface abundance of light elements and updated (p,α) reaction rates. Nuclei in the cosmos XV, 219, 449–452. doi:10.1007/978-3-030-13876-9˙87

CrossRef Full Text | Google Scholar

Tognelli, E., Prada Moroni, P. G., and Degl’Innocenti, S. (2015). Cumulative theoretical uncertainties in lithium depletion boundary age. MNRAS 449, 3741–3754. doi:10.1093/mnras/stv577

CrossRef Full Text | Google Scholar

Tgnelli, E., Prada Moroni, P. G., Degl’Innocenti, S., Salaris, M., and Cassisi, S. (2020). Protostellar accretion in low mass metal poor stars and the cosmological lithium problem. A&A 638, A81. doi:10.1051/0004-6361/201936723

CrossRef Full Text | Google Scholar

Tognelli, E., Prada Moroni, P. G., and Degl’Innocenti, S. (2013). The PISA Pre-Main Sequence accreting models. Protostars and planets VI posters.

Google Scholar

Tognelli, E., Prada Moroni, P. G., and Degl’Innocenti, S. (2011). The Pisa pre-main sequence tracks and isochrones. A database covering a wide range of Z, Y, mass, and age values. A&A 533, A109. doi:10.1051/0004-6361/200913913

CrossRef Full Text | Google Scholar

Tognelli, E., Prada Moroni, P. G., and Degl’Innocenti, S. (2018). Theoretical uncertainties on the radius of low- and very-low-mass stars. MNRAS 476, 27–42. doi:10.1093/mnras/sty195

CrossRef Full Text | Google Scholar

Tognelli, E. (2013). The Pisa pre-main sequence stellar evolutionary models: results for non-accreting and accreting models. Pisa, Italy: PhD dissertation, University of Pisa Available at:https://etd.adm.unipi.it/t/etd-05312013-140950/.

Tomida, K., Tomisaka, K., Matsumoto, T., Hori, Y., Okuzumi, S., Machida, M. N., et al. (2013). Radiation magnetohydrodynamic simulations of protostellar collapse: protostellar core formation. ApJ 763, 6. doi:10.1088/0004-637X/763/1/6

CrossRef Full Text | Google Scholar

Torres, G., and Ribas, I. (2002). Absolute dimensions of the M-type eclipsing binary YY geminorum (Castor C): a challenge to evolutionary models in the lower main sequence. ApJ 567, 1140–1165. doi:10.1086/338587

CrossRef Full Text | Google Scholar

Trampedach, R., Asplund, M., Collet, R., Nordlund, Å., and Stein, R. F. (2013). A grid of three-dimensional stellar atmosphere models of solar metallicity. I. General properties, granulation, and atmospheric expansion. ApJ 769, 18. doi:10.1088/0004-637X/769/1/18

CrossRef Full Text | Google Scholar

Trampedach, R., Christensen-Dalsgaard, J., Asplund, M., Stein, R. F., and Nordlund, Å. (2015). The surface of stellar models - now with more 3D simulations!. European physical journal web of conferences, 101. European Physical Journal Web of Conferences, 06064. doi:10.1051/epjconf/201510106064

CrossRef Full Text | Google Scholar

Trampedach, R., Stein, R. F., Christensen-Dalsgaard, J., Nordlund, Å., and Asplund, M. (2014). Improvements to stellar structure models, based on a grid of 3D convection simulations - I. T(τ) relations. MNRAS 442, 805–820. doi:10.1093/mnras/stu889

CrossRef Full Text | Google Scholar

Tremblay, P. E., Ludwig, H. G., Freytag, B., Steffen, M., and Caffau, E. (2013). Granulation properties of giants, dwarfs, and white dwarfs from the CIFIST 3D model atmosphere grid. A&A 557, A7. doi:10.1051/0004-6361/201321878

CrossRef Full Text | Google Scholar

Tumino, A., Spartà, R., Spitaleri, C., Mukhamedzhanov, A. M., Typel, S., Pizzone, R. G., et al. (2014). New determination of the H(d,p)H and H(d, n)He reaction rates at astrophysical energies. ApJ 785, 96. doi:10.1088/0004-637X/785/2/96

CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., La Cognata, M., Cherubini, S., Guardo, G. L., Gulino, M., et al. (2018). An increase in the C + C fusion rate from resonances at astrophysical energies. Nature 557, 687–690. doi:10.1038/s41586-018-0149-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., Mukhamedzhanov, A. M., Typel, S., Aliotta, M., Burjan, V., et al. (2011). Low-energy d+d fusion reactions via the Trojan Horse Method. Phys. Lett. B 700, 111–115. doi:10.1016/j.physletb.2011.05.001

CrossRef Full Text | Google Scholar

Vauclair, S., and Charbonnel, C. (1995). Influence of a stellar wind on the lithium depletion in halo stars: a new step towards the lithium primordial abundance. A&A 295, 715.

Google Scholar

Vaytet, N., Chabrier, G., Audit, E., Commerçon, B., Masson, J., Ferguson, J., et al. (2013). Simulations of protostellar collapse using multigroup radiation hydrodynamics. II. The second collapse. A&A 557, A90. doi:10.1051/0004-6361/201321423

CrossRef Full Text | Google Scholar

Ventura, P., Zeppieri, A., Mazzitelli, I., and D’Antona, F. (1998). Pre-main sequence Lithium burning: the quest for a new structural parameter. A&A 331, 1011–1021.

Google Scholar

Vorobyov, E. I., and Basu, S. (2010). The burst mode of accretion and disk fragmentation in the early embedded stages of star formation. ApJ 719, 1896–1911. doi:10.1088/0004-637X/719/2/1896

CrossRef Full Text | Google Scholar

Wang, E. X., Nordlander, T., Asplund, M., Amarsi, A. M., Lind, K., and Zhou, Y. (2021). 3D NLTE spectral line formation of lithium in late-type stars. MNRAS 500, 2159–2176. doi:10.1093/mnras/staa3381

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, A. M., Stapelfeldt, K. R., Wood, K., and Ménard, F. (2007). “Multiwavelength imaging of young stellar object disks: toward an understanding of disk structure and dust evolution,” in Protostars and planets VI. Editors B. Reipurth, D. Jewitt, and K. Keil, 523.

Google Scholar

Xiong, D.-R., and Deng, L.-C. (2006). A re-examination of the dispersion of lithium abundance of Pleiades member stars. ChA&A 30, 24–40. doi:10.1016/j.chinastron.2006.01.003

CrossRef Full Text | Google Scholar

Xiong, D. R., and Deng, L. (2002). The extent of the solar overshooting zone deduced from Li abundance. MNRAS 336, 511–519. doi:10.1046/j.1365-8711.2002.05767.x

CrossRef Full Text | Google Scholar

Xu, Y., Takahashi, K., Goriely, S., Arnould, M., Ohta, M., and Utsunomiya, H. (2013). Nacre II: an update of the NACRE compilation of charged-particle-induced thermonuclear reaction rates for nuclei with mass number A<16. Nucl. Phys. A 918, 61–169. doi:10.1016/j.nuclphysa.2013.09.007

CrossRef Full Text | Google Scholar