Formation of Interstellar Silicate Dust via Nanocluster Aggregation: Insights From Quantum Chemistry Simulations

The issue of formation of dust grains in the interstellar medium is still a matter of debate. One of the most developed proposals suggests that atomic and heteromolecular seeds bind together to initiate a nucleation process leading to the formation of nanostructures resembling very small grain components. In the case of silicates, nucleated systems can result in molecular nanoclusters with diameters ≤ 2 nm. A reasonable path to further increase the size of these proto-silicate nanoclusters is by mutual aggregation. The present work deals with modeling this proto-silicate nanocluster aggregation process by means of quantum chemical density functional theory calculations. We simulate nanocluster aggregation by progressively reducing the size of a periodic array of initially well-separated nanoclusters. The resulting aggregation leads to a set of silicate bulk structures with gradually increasing density which we analyze with respect to structure, energetics and spectroscopic properties. Our results indicate that aggregation is a highly energetically favorable process, in which the infrared spectra of the finally formed amorphous silicates match well with astronomical observations.

Introduction

Interstellar matter consists of gaseous molecules and submicron solid state particles commonly referred to as dust grains. Ninety nine percentage of the interstellar mass belongs to the former group while a meager 1% to the latter one. This matter is not evenly distributed and often accumulates in condensed regions between stars, forming interstellar clouds (Tielens, 2013; van Dishoeck, 2014). Despite making up only a tiny fraction of the interstellar mass, dust grains are pivotal constituents which assist in the build-up the molecular diversity and complexity of the interstellar medium (ISM) (Williams and Herbst, 2002; Hama and Watanabe, 2013). Indeed, the formation of different simple molecules [some of them of fundamental relevance such as H₂, (Kerkeni and Bromley, 2013; Vidali, 2013; Navarro-Ruiz et al., 2014a, 2015, 2016) H₂O (van Dishoeck et al., 2013; Molpeceres et al., 2019) and CH₃OH (Watanabe et al., 2003; Rimola et al., 2014)] as well as complex organic molecules (Öberg, 2016; Herbst, 2017; Zamirri et al., 2019b) (e.g., CH₃CHO or NH₂CHO) (Enrique-Romero et al., 2016, 2019; Rimola et al., 2018) has been postulated to exclusively occur on the surface of grains. Co-adsorption at catalytic surface sites accelerate these formation reactions, which would not otherwise occur in the gas phase.

In the ISM, dust particles can be found as bare grains of refractory materials or covered in ices, depending on the conditions of the interstellar clouds where they are found. In diffuse clouds the temperature is typically between 50–100 K with gas densities in the range 10–10² cm⁻³. Here, bare grains predominate because UV photons can penetrate the cloud, destroying any molecular complex species. Grains consist of either carbonaceous materials (Ehrenfreund and Charnley, 2000; Tielens, 2008) or silicates (Henning, 2010) (i.e., refractory materials), depending on the C/O ratio where they nucleate, grow and form. In dense molecular clouds (with temperatures as low as 5–10 K and a gas density of ~10⁴ cm⁻³), the low permeability of UV photons into the cloud allows the formation/accretion of simple volatile species, which convert into ice mantles covering the refractory grains. The most predominant component of the interstellar ices is H₂O, but other species are also relatively abundant, such as NH₃, CO, CO₂, and CH₃OH (Boogert et al., 2015).

Most bare interstellar grains are made of silicates, which are a class of naturally occurring inorganic materials with a large diversity in chemical composition and structural properties. All silicates are based on the [SiO₄]⁴⁻ building block with divalent cations compensating the negative charge. In interstellar grains the most common cation is Mg²⁺, followed to a lesser extent by Fe²⁺, as dictated by the relative interstellar abundances. Two main classes of interstellar silicates have been identified: olivines and pyroxenes, with general chemical compositions Mg_2xFe_(2−2x)SiO₄ and Mg_xFe_(1−x)SiO₃ (x = 0–1), respectively. These interstellar grain silicates are usually structurally amorphous, although crystalline silicates have also been detected (Molster and Kemper, 2005). Evidence of amorphicity is provided by astronomical infrared (IR) observations, where mid-IR measurements show two broad bands centered at 9.7 μm (~1,100 cm⁻¹) and 18 μm (~550 cm⁻¹) (Henning, 2010), attributed to the ν(SiO) stretching and δ(OSiO) bending modes. These bands are usually found to be heavily broadened, which is indicative of the wide distribution of bond lengths and angles characteristic of amorphous systems. We note that this assignment of broadened bands to amorphous silicate grains should be used with care in the case of very small grains (Zamirri et al., 2019a).

The elementary steps leading to silicate grain formation is not yet fully understood. The commonly held current view is that silicate dust nucleates in outflows of dying stars, in which atomic and molecular seeds bind together to initiate the nucleation process (Weinberger, 2005; Ercolano et al., 2007; Jones, 2007; Matsuura et al., 2011). Some thermodynamically viable pathways for the initial stages of silicate nucleation in circumstellar environments have been studied by computational chemistry techniques, indicating that heteromolecular aggregation of Mg, SiO and H₂O could be a plausible mechanism, rather than direct nucleation of atomic O, Mg and Si (Goumans and Bromley, 2012, 2013). The silicate dust grains formed in such processes are thought to be of the order 0.1 μm in diameter (dust grain monomers) when they leave the star and enter the ISM. There, these grains are subject to supernovae shockwaves and dust grain collisions which shatter these grains into small nanosized fragments (Jones et al., 1996; Hirashita and Kobayashi, 2013). There is also laboratory evidence that small silicate dust grains may (re)form in the ISM (Rouillé et al., 2014). It is thus estimated that the ISM could contain a significant population of nano-sized proto-silicates (Li and Draine, 2001b), which will eventually form part of the diffuse and dense clouds.

Interestingly, proto-silicate nanoclusters have properties that match relatively well with the physico-chemical features of very small grain (VSG) components (of size ≤ 20 nm) (Li and Draine, 2001a; Rouillé et al., 2014), the optical properties of which cannot be described by bulk material measurements. VSGs may be responsible for the UV bump in the IS extinction curve and a significant fraction of the mid-IR emission (Rapacioli et al., 2005; Pilleri et al., 2012, 2015). Although carbonaceous materials (e.g., polycyclic aromatic hydrocarbons, hydrogenated amorphous carbon) have been advocated to be the main constituent of VSGs, there could also be a significant component formed from proto-silicate nanoclusters/nanoparticles. VSG proto-silicates can be understood as intermediate species from which larger silicates (i.e., grain monomers) are formed from the nucleation seed. A reasonable process would involve the production of different proto-silicate nanoclusters driven by harsh external phenomena (e.g., cosmic ray hits or shock waves) and subsequent aggregation by intermolecular attractive forces between nanoclusters. Interestingly, since nanoclusters are inherently not crystalline-like (Escatllar et al., 2019; Zamirri et al., 2019a), direct aggregates are expected to exhibit an amorphous structural state.

Quantum chemical computations have been used to investigate on the physico-chemical properties of interstellar silicates (Goumans and Bromley, 2011; Kerkeni and Bromley, 2013; Navarro-Ruiz et al., 2014a,b; Navarro-Ruiz et al., 2015, 2016; Oueslati et al., 2015; Kerkeni et al., 2017, 2019; Molpeceres et al., 2019), demonstrating the extreme usefulness of this approach by providing unique results at an atomic scale related to their structure, reactivity and vibrational features. In the present work, the aggregation between proto-silicate nanoclusters to form silicate bulk aggregates is investigated by means of quantum chemical simulations. To this end, a modeling strategy based on the gradual reduction in size of a periodic unit cell centered on a proto-silicate nanocluster, thus decreasing the distance between repeated nanoclusters, is employed. The resulting increasingly condensed systems during this procedure have been analyzed from a structural, energetic and spectroscopic points of view giving new insights into the plausibility of the proto-silicate aggregation processes.

Methods

Theoretical calculations were carried out with the CRYSTAL14 code (Dovesi et al., 2014); a program dedicated to simulating all-electron periodic and molecular systems. Simulations were performed with density functional theory (DFT) calculations using the hybrid B3LYP functional (Lee et al., 1988; Becke, 1993) in combination with the following Gaussian basis sets: (8s)-(511sp)-(1d) for Mg, (8s)-(6311sp)-(1d) for Si, and (8s)-(411sp)-(1d) for O. A reliable performance of this methodology for simulating the structure and spectroscopic properties of silicates is evidenced by different theoretical works, where results of DFT calculations using the B3LYP functional are found to compare very well with experimental measurements related to IR, Raman and reflectance spectroscopy (Noel et al., 2006; De La Pierre et al., 2011, 2013; Navarro-Ruiz et al., 2014b; Martínez-González et al., 2018).

The shrinking factor of the reciprocal space net was set to 3, defining a total of 14 k points in the irreducible Brillouin zone (IBZ) (Monkhorst and Pack, 1976). The overlap integrals controlling the Coulomb and exchange series were set to 10⁻⁶ and 10⁻¹⁶. The SCF criterion was set to 10⁻⁷ Hartrees. Geometry optimizations were performed using the quasi-Newton algorithm, combining the quadratic step (BFGS scheme) with a linear one (Civalleri et al., 2001; Doll, 2001).

Simulated IR spectra were obtained by computing the vibrational frequencies of the studied systems at the Γ point (point k = 0 in IBZ) within the harmonic approximation. The Hessian matrix was obtained numerically (i.e., via the central difference formula), in which second-energy derivatives are calculated by displacing each of the 3N optimized nuclear positions by a small amount (u = 0.003 Å) (Pascale et al., 2004). The SCF criterion convergence to numerically construct the Hessian matrix was set to 10⁻¹¹ Hartrees in order to ensure sufficiently accurate numerical derivatives for calculating frequencies. IR intensity values of the normal modes were calculated through the variation of the dipole moment along the corresponding modes using a set of localized Wannier functions (Zicovich-Wilson et al., 2001, 2002). We note that anharmonicity is very unlikely to be significant in our systems as they do not contain light atoms (e.g., H) and the aggregation process is interpreted to occur at the very low temperatures of the ISM, and thus only low energy vibrational states are populated. Accordingly, we consider the harmonic approximation to be sufficiently accurate for the description of the vibrational spectra.

Visualization and manipulation of the structures, including visual inspection of the calculated frequencies for band assignment, have been carried out with the MOLDRAW program (Ugliengo et al., 1993). Figures were rendered with the POVRAY program.

Results and Discussion

The underlying idea is to assess if aggregation of proto-silicate nanoclusters can result in the formation of silicate grains present in the ISM. To this end, construction of bulk silicate structures from gradually bringing together molecular silicate nanoclusters was firstly performed. Then, a structural and energetic analysis of the obtained structures was carried out to assess the stability of these aggregates with respect to the respective bulk crystalline silicate system. Finally, simulated IR spectra were compared with observational data for actual IR silicates in the ISM. Cartesian/fractional coordinates of the studied systems are available in the Supplementary Material.

Construction of Aggregated Silicates

The initial structure from which the aggregated silicate systems are generated is the Mg₆Si₃O₁₂ nanocluster (Sil-0 in Figures 1, 2), which has the forsterite stoichiometry (i.e., Mg₂SiO₄) and contains three formula units. Sil-0 was found as one of the most energetically stable nanocluster isomers of this size in global optimization searches using Monte Carlo basin hopping approach (Escatllar et al., 2019). In Escatllar et al. (2019) DFT based calculations were carried out using the PBE0 hybrid functional, while our work employed the B3LYP hybrid functional. Despite this methodological difference, structural parameters for Sil-0 provided by both methods compare extremely well.

FIGURE 1

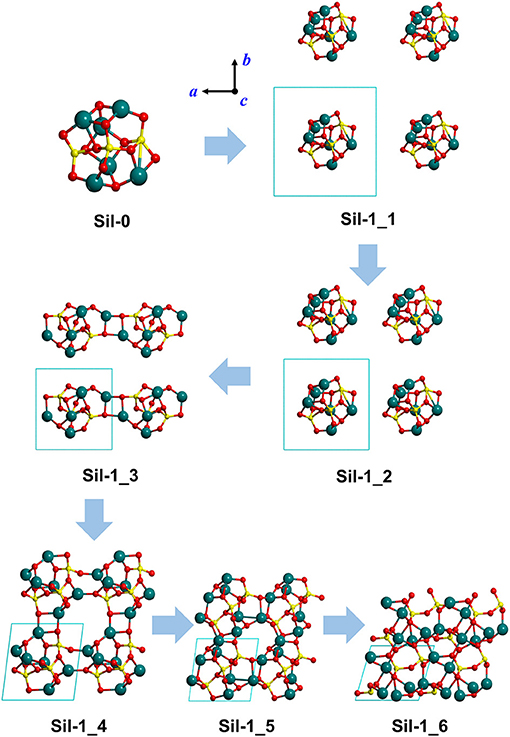
Figure 1. Optimized silicate structures derived from the progressive reduction of the periodic unit cell size as a strategy to mimic proto-silicate aggregation. For Sil-1_1, Sil-1_2, and Sil-1_3, unit cell parameters were fixed to the initial values, while for Sil-1_4, Sil-1_5, and Sil-1_6 they were included in the optimization process. Atom color key: Si—yellow, Mg—blue, O—red.

FIGURE 2

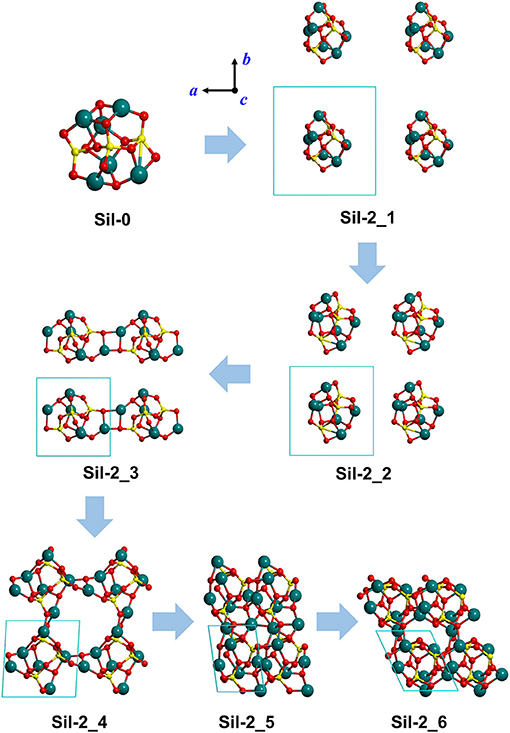
Figure 2. Optimized silicate structures derived from the progressive reduction of the periodic unit cell size as a strategy to mimic proto-silicate aggregation. For Sil-2_1, Sil-2_2, and Sil-2_3, unit cell parameters were fixed to the initial values, while for Sil-2_4, Sil-2_5, and Sil-2_6 they were included in the optimization process. These structures result from the aggregation of the same nanocluster as shown in Figure 1, but with a different initial rotational orientation within the periodic unit cell. Atom color key: Si—yellow, Mg—blue, O—red.

Our “virtual” aggregation process (represented in Figures 1, 2) is explained as follows. The first step was to apply periodic boundary conditions to Sil-0. That is, the nanocluster was introduced inside a cubic box (i.e., the unit cell) that was repeated periodically in the three spatial dimensions. The initial lattice parameters of the unit cell were set to a = b = c = 12 Å and α = β = γ = 90°. Once the periodic system was generated, the atomic positions of the nanocluster were optimized, keeping the lattice parameters fixed to avoid interactions between replicated nanoclusters. Due to the relatively large values of a, b and c, the first system is simply a relatively isolated Sil-0 nanocluster inside the unit cell, which keeps its molecular structure (see Sil-1_1 in Figure 1), meaning that there are no significant interactions between periodically replicated nanoclusters.

From this starting point, the values of a, b and c were progressively decreased (shown in Figure 1), hence reducing the size of the unit cell, in which the internal atomic positions of the system were relaxed with fixed lattice parameters. With each reduction in cell size, the replicated nanoclusters were closer to each other (see Sil-1_1 and Sil-1_2 structures of Figure 1), up to a point in which interaction between nanoclusters took place. Indeed, structure Sil-1_3 of Figure 1 shows the formation of Mg-O bonds between two adjacent nanoclusters. At this point, we can consider that aggregation is starting to occur.

Once this situation was reached (i.e., interaction between replicated nanoclusters), during this aggregation phase both internal atomic positions and lattice cell parameters were optimised in order to better allow the interacting nanoclusters to reach a stable relaxed energy minimum. This final aggregation process led to the formation of several extended amorphous silicates with different structures and densities (see Sil-1_4, Sil-1_5, and Sil-1_6 and Table 1).

TABLE 1

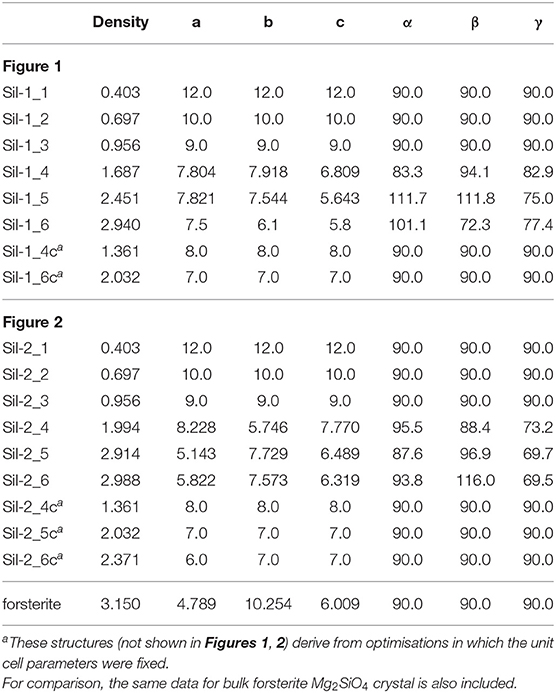
Table 1. Densities (in g cm⁻³) and lattice cell parameters (distances in Å and angles in degrees) of the periodic silicate structures shown in Figures 1, 2.

Finally, we note that the structures of the resulting amorphous silicates derived from our aggregation procedure depend on the initial orientation of the nanocluster inside the periodic box. This effect is shown in the aggregated structures in Figures 1 and 2, respectively, where in the latter case, the nanocluster was rotated 45° with respect to the c axis as compared to the former. This change in initial conditions was found to significantly influence the detailed atomic structures during aggregation, especially those generated in the final aggregation steps, in which the unit cell parameters were optimized (e.g., compare Sil-1_4, Sil-1_5 and Sil-1_6 with Sil-2_4, Sil-2_5, and Sil-2_6, respectively).

Structural and Energetic Analysis

Figures 1, 2 show the optimized silicate systems adopting the abovementioned nanocluster aggregation procedure. The first generated structures (Sil-1_1/Sil-2_1 and Sil-1_2/Sil-2_2 in Figures 1, 2) are periodic arrays of isolated silicate nanoclusters. Since these structures do not significantly interact with respective images (the closest inter-cluster distances are ≈6.1 Å and ≈4.0 Å, respectively), they do not suffer structural variation with respect to the original nanocluster.

The first replica-interacting systems (structures Sil-1_3 and Sil-2_3 in Figures 1, 2) show the formation of Mg-O bonds between images forming a square (MgO)₂ ring. These interactions take place when the unit cell parameters are a = b = c = 9 Å. This suggests that inter-cluster Mg-O interactions could trigger the silicate aggregation between nanoclusters. This is reasonable since interaction between these two atom types is essentially electrostatic (i.e., formally between Mg²⁺ and O²⁻ ions). From these initially interacting structures, slight reduction of the unit cell size, followed by full geometry optimization, quickly leads to the formation of extended porous silicates, namely, silicates with cavities inside the structures (see Sil-1_4 and Sil-2_4 structures in Figures 1, 2). Indeed, in both systems, the nanocluster replicas interact along the three periodic directions in such a way that a cavity between them is created. These pores have diameters of ≈7–8 Å, which is a suitable size to encapsulate small gaseous molecules. Thus, if the proto-silicate nanoclusters were capable to possess adsorbed molecules on their surfaces, they could potentially be retained during the aggregation process and finally become confined inside the formed porous.

Further reduction of the unit cell size leads to the formation of dense silicates (see e.g., Sil-1_6) with no pores. Interestingly, these compressed systems appear to be totally amorphous materials since the atomic positions do not seem to follow any regularity in space. This amorphous nature will be further explored by their simulated IR spectra (see below).

The relative energy of these “generated + optimized” systems with respect to that of the forsterite bulk Mg₂SiO₄ crystal (considered here as our reference system) as a function of system density is reported in Figure 3. The values of these energies are also reported in Table 2. Values are normalized with respect to the four Mg₂SiO₄ units present in the crystalline unit cell. The energy plots can also be understood as the energy variation of the systems with respect to the distance between proto-silicate units, where a high density implies a smaller inter-silicate distance and vice versa.

FIGURE 3

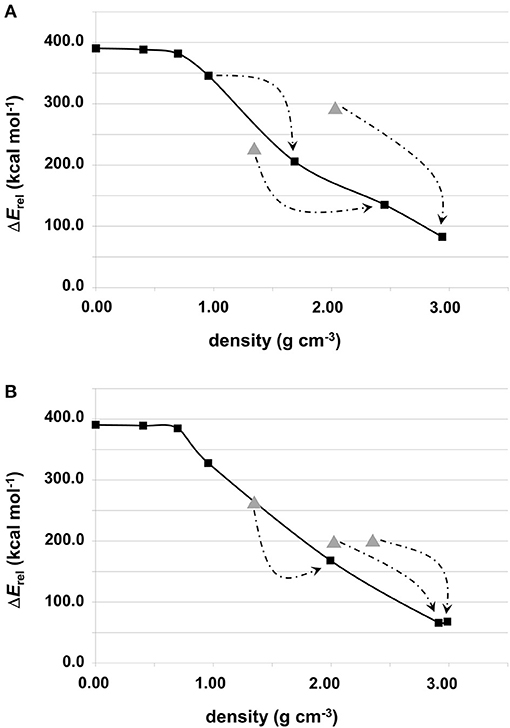
Figure 3. Relative energies (in kcal mol⁻¹) of the Mg₆Si₃O₁₂-based aggregates with respect to the bulk forsterite Mg₂SiO₄ crystal as a function of their density. Values are normalized with respect to the four Mg₂SiO₄ units present in the crystalline unit cell: (A) for systems shown in Figure 1; (B) for systems shown in Figure 2. Values labeled by triangles refer to compressed structures without optimizing their unit cells (see text for more details). Arrows indicate the system formed upon full geometry (i.e., atomic positions + cell parameters) optimization. The molecular nanocluster system is considered to have density 0 g cm⁻³, as the lattice parameters are effectively infinite.

TABLE 2

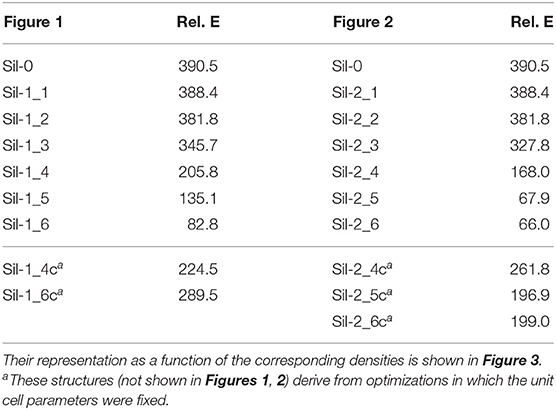
Table 2. Relative energies (in kcal mol⁻¹) of the periodic silicate structures shown in Figures 1, 2 with respect to the bulk forsterite Mg₂SiO₄ crystal (per unit formula).

Among the different silicates studied here, crystalline forsterite is the most stable one, while the molecular nanocluster is the least stable. This is not surprising as: (i) for extended systems crystalline structures tend to be more stable than amorphous ones, and (ii) nanoclusters have a high percentage of undercoordinated surface atoms resulting in highly reconstructed and strained non-crystalline structures (Escatllar et al., 2019), leading to large instabilities. In our case, the isolated Mg₆Si₃O₁₂ nanocluster is approximately 390 kcal mol⁻¹ higher in energy than crystalline bulk Mg₂SiO₄.

For periodic structures without interactions between replicas, their energetic stability is, as expected, the same as the Mg₆Si₃O₁₂ nanocluster. Once interaction between clusters begins, the relative energies of the system with respect to forsterite decreases. For the first interacting systems, relative energies are still relatively high (330–345 kcal mol⁻¹), as the interaction is limited to a strained (MgO)₂ ring. However, for the subsequent increasingly interacting systems, relative energies significantly drop: the porous silicates lie 170–200 kcal mol⁻¹ above the energy of forsterite and the corresponding relative energies our densest silicates are <100 kcal mol⁻¹.

In the plots in Figure 3, the relative energies of compressed systems without optimized unit cell parameters are also represented (gray triangle points). The arrows indicate the resulting structures when full optimization (i.e., atomic positions + cell parameters) was performed from those without optimizing the unit cell. These later structures are more energetically unstable than their optimized unit cell analogues as the constrained cell parameters lead to artificially overly compressed structures which exhibit high geometrical strains. Therefore, we do not consider these systems as representative.

Analysis of Simulated IR Spectra

Figure 4 shows the simulated IR spectra associated with the silicate structures reported in Figures 1 (black spectra) and 2 (red spectra), while Table 3 reports the calculated intensities and the vibrational mode assignment of the IR bands presented in Figure 4. For the sake of comparison, IR data related to the crystalline Mg₂SiO₄ forsterite is also included. In Figure 4, gray shading indicates the positions of the IR bands for general interstellar silicates obtained from astronomical observations, which are centered at ca. 1,000 cm⁻¹ and ca. 550 cm⁻¹. The IR spectra of the molecular nanocluster and the crystalline bulk are also available in the literature (Navarro-Ruiz et al., 2014b; Martínez-González et al., 2018; Escatllar et al., 2019).

FIGURE 4

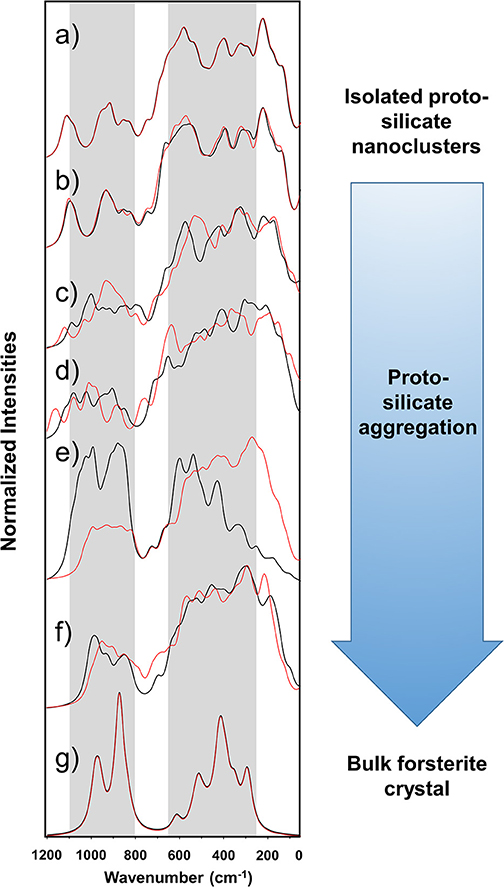
Figure 4. Calculated IR spectra of the silicate aggregates. The calculated IR spectra of the Mg₆Si₃O₁₂ nanocluster and the crystalline forsterite bulk are also included. Gray shading indicates the bands from observational measurements, centered at ca. 1,000 and 550 cm⁻¹, the width of which being the corresponding full width at half maximum (FWHM) ranges [from Henning (2010)]. Black spectra are those for the systems shown in Figure 1 (Sil-1_1 is omitted because it is equal to Sil-0). Red spectra are those for the systems shown in Figure 2 (Sil-2_1 is omitted because it is equal to Sil-0). The spectra are superimposed to show that irrespective of the aggregation process route the final dense structures are very similar observationally. (a) Sil-0, (b) Sil-1_2 and Sil-2_2, (c) Sil-1_3 and Sil-2_3, (d) Sil-1_4 and Sil-2_4, (e) Sil-1_5 and Sil-2_5, (f) Sil-1_6 and Sil-2_6, and (g) forsterite crystalline Mg₂SiO₄ bulk. Intensities are normalized to 100 with respect to the most intense band and accordingly they are in arbitrary units.

TABLE 3

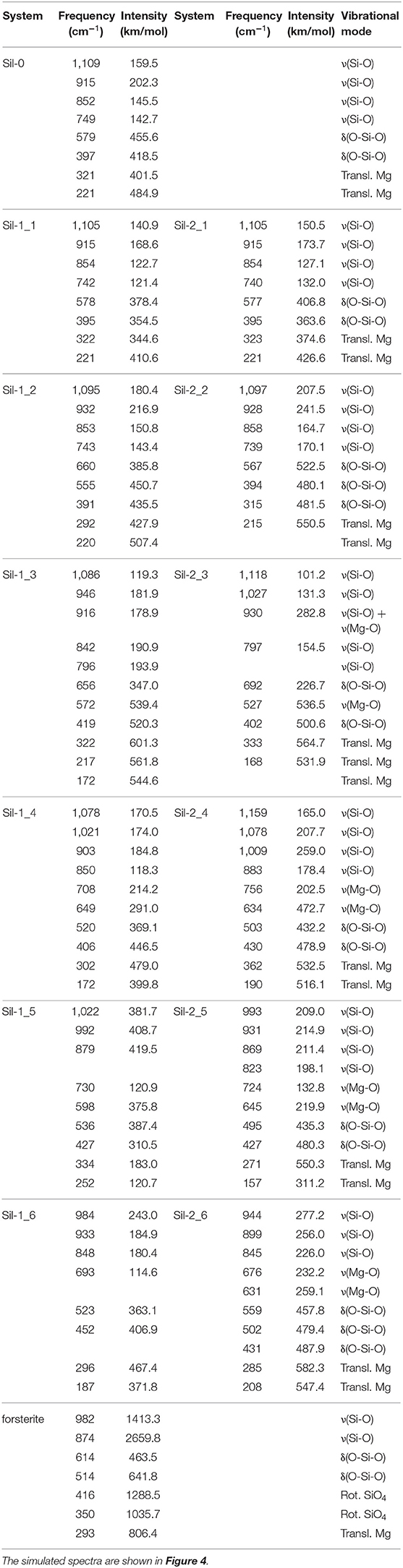
Table 3. Calculated frequencies and intensities, and assignment of the corresponding vibrational modes of the IR bands for the studied systems.

The forsterite spectrum shows a set of well-defined, relatively sharp IR bands (Figure 4g). Bands peaked between 1,000 and 800 cm⁻¹ are assigned to the ν(Si-O) stretching modes, those between 600 and 500 cm⁻¹ to δ(O-Si-O) bending modes, those around 400 cm⁻¹ to rotational motions of the SiO₄ tetrahedra, and those around 350 cm⁻¹ to translational motions of the metal cations. In contrast, the IR spectrum of the Mg₆Si₃O₁₂ nanocluster (Figure 4a) displays a wider variety of bands. This is due to the nanocluster's lack of internal symmetry, which splits the IR bands into several signals because of the non-equivalent vibrations of the moieties. Despite this, IR assignments can also be grouped in a similar way as the crystalline ones.

In relation to the progressively reduced silicates, the IR spectra of the periodic non-interacting replicas systems (Sil-1_2 and Sil-2_2 of Figures 1, 2, respectively) are, expectedly, almost identical than that of the molecular nanocluster (compare spectra of Figure 4a with b). Changes start when the replicas of adjacent cells start to interact (Sil-1_3 and Sil-1_4 of Figure 1, and Sil-2_3 and Sil-2_4 of Figure 2). Because of the presence of the newly formed Mg-O bonds, some new bands assigned to the ν(Mg-O) appear; in particular, the bands around 1,000 cm⁻¹ (see spectra of Figures 4c,d), which were lacking in the non-interacting-replicas systems. The presence of these new bands converts the IR profiles into a more continuous band through the 1,200–800 cm⁻¹ range. Due to this, the regions between the stretching vibrations and the rest of vibrations are more clearly differentiated in two broad bands. Such a differentiation is even more defined in the periodic fully interacting-replicas systems (i.e., Sil-1_5 and Sil-1_6 of Figure 1 and Sil-2_5 and Sil-2_6 of Figure 2). For these systems, the IR spectra match well those of the bulk amorphous Mg₂SiO₄ silicates, namely, two very broad bands between 1,100 and 800 cm⁻¹ and between 600 and 200 cm⁻¹ (see spectra of Figures 4e,g). These IR features are in good agreement with those of large amorphous silicate models (Martínez-González et al., 2018) and observational measurements (Henning, 2010). In view of these results, the first interacting-replicas systems (Sil-1_3, Sil-1_4, Sil-2_3, and Sil-2_4) can be considered as transient states involved in the aggregation processes from proto-silicate nanoclusters to amorphous silicates.

It is finally worth mentioning that the superimposition of the two sets of spectra shown in Figure 4, from the Sil-1 and Sil-2 aggregation, although having different initial conditions, tend to produce bulk amorphous silicates with very similar IR profiles. This is an important fact because is suggests that, irrespective of the detailed route of the aggregation process, the resulting structures arising from each aggregation process are very similar observationally.

Conclusions

In this work we investigate theoretically the aggregation of proto-silicate nanoclusters (i.e., small silicate clusters) as a way to form interstellar silicate grains. The study is performed by means of periodic quantum mechanical simulations using DFT based calculations employing the hybrid B3LYP functional; a method known to be reliable for modeling silicate systems.

Using a stable Mg₆Si₃O₁₂ nanocluster as initial guess structure to form silicate aggregates, the adopted strategy to simulate the aggregation process is based on the progressive reduction in size of a 3D periodic unit cell centered on the nanocluster. Upon decreasing the lattice parameters, the nanocluster replicas in adjacent unit cells start to interact to form extended Mg₂SiO₄ silicate materials with progressively increasing density.

Our results indicate that the first interaction between nanocluster replicas takes place between Mg and O atoms, forming (MgO)₂ rings. These tenuously linked intermediate-aggregated systems exhibit internal cavities rendering them as nanoporous materials. Further reduction in size of the periodic box gives rise to systems in which the porosity disappears, leading to dense amorphous materials.

Energetic analysis of the resulting structures shows that all of them lie higher in energy than the forsterite Mg₂SiO₄ crystal bulk. The most unstable system is the isolated Mg₆Si₃O₁₂ proto-silicate nanocluster (ca. 400 kcal mol⁻¹ with respect to forsterite per formula unit). Once proto-silicate replicas start to interact, corresponding relative energies significantly decrease. The porous systems lie ca. 170–200 kcal mol⁻¹ above the forsterite, while the densest non-porous materials are <100 kcal mol⁻¹ the crystalline bulk. This increasingly stabilization of the systems formed during the compression is indicative that the aggregation process does not present energetic hindrances, at least thermodynamically and at very low temperatures.

The IR spectra of non-interacting replica systems are practically identical to the isolated Mg₆Si₃O₁₂ nanocluster, whereas for the interacting cases additional bands arise. For the porous systems, particular bands at ca. 900 cm⁻¹ appear due to the new ν(Mg-O) vibrations, while for the densest ones two very broad bands at 1,100–800 cm⁻¹ and 600–200 cm⁻¹ are exhibited. These bands are representatives of the amorphous nature of the structures and match fairly well with the astronomical IR observational. Interestingly, irrespective of the detailed proto-silicate aggregation processes, the resulting dense silicate structures show similar IR features, indicating that they are observationally very similar.

In summary, our results provide evidence that formation of interstellar silicate grains through proto-silicate aggregation is a feasible process, since the aggregation steps are energetically favorable and the final amorphous systems exhibit IR properties in fair agreement with those obtained observationally.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

All authors participated in the initial conception of the research idea and in the discussion of the results. AR did the quantum chemical simulations and participated in the writing and editing of the manuscript. SB participated in the writing and editing of the manuscript.

Funding

This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme grant agreement no. 865657 for the project Quantum Chemistry on Interstellar Grains (QUANTUMGRAIN). We acknowledge financial support from the Spanish Ministerio de Ciencia, Innnovación y Universidades (projects CTQ2017-89132-P, RTI2018-095460-B-100, and MDM-2017-0767 via the Spanish Structures of Excellence María de Maeztu program) and the Generalitat de Catalunya (projects 2017SGR1323 and 2017SGR13).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

AR is indebted to the Ramón y Cajal program. The Red Española de Supercomputación (RES) and Consorci de Serveis Universitaris de Catalunya (CSUC) are also acknowledged for the provision of supercomputing time.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.659494/full#supplementary-material

References

Becke, A. D. (1993). Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652. doi: 10.1063/1.464913

CrossRef Full Text

Boogert, A. C. A., Gerakines, P. A., and Whittet, D. C. B. (2015). Observations of the icy Universe. Annu. Rev. Astron. Astrophys. 53, 541–581. doi: 10.1146/annurev-astro-082214-122348

CrossRef Full Text | Google Scholar

Civalleri, B., D'arco, P., Orlando, R., Saunders, V. R., and Dovesi, R. (2001). Hartree-Fock geometry optimisation of periodic systems with the CRYSTAL code. Chem. Phys. Lett. 348, 131–138. doi: 10.1016/S0009-2614(01)01081-8

CrossRef Full Text | Google Scholar

De La Pierre, M., Carteret, C., Orlando, R., and Dovesi, R. (2013). Use of Ab initio methods for the interpretation of the experimental IR reflectance spectra of crystalline compounds. J. Comput. Chem. 34, 1476–1485. doi: 10.1002/jcc.23283

PubMed Abstract | CrossRef Full Text | Google Scholar

De La Pierre, M., Orlando, R., Maschio, L., Doll, K., Ugliengo, P., and Dovesi, R. (2011). Performance of six functionals (LDA, PBE, PBESOL, B3LYP, PBE0, and WC1LYP) in the simulation of vibrational and dielectric properties of crystalline compounds. The case of forsterite Mg₂SiO₄. J. Comput. Chem. 32, 1775–1784. doi: 10.1002/jcc.21750

PubMed Abstract | CrossRef Full Text | Google Scholar

Doll, K. (2001). Implementation of analytical Hartree-Fock gradient for periodic systems. Comput. Phys. Comm. 137, 74–78. doi: 10.1016/S0010-4655(01)00172-2

CrossRef Full Text | Google Scholar

Dovesi, R., Orlando, R., Erba, A., Zicovich-Wilson, C. M., Civalleri, B., Casassa, S., et al. (2014). CRYSTAL14: a program for the ab initio investigation of crystalline solids. Int. J. Quantum Chem. 114, 1287–1317. doi: 10.1002/qua.24658

CrossRef Full Text | Google Scholar

Ehrenfreund, P., and Charnley, S. B. (2000). Organic molecules in the interstellar medium, comets, and meteorites: a voyage from dark clouds to the early Earth. Annu. Rev. Astron. Astrophys. 38, 427–483. doi: 10.1146/annurev.astro.38.1.427

CrossRef Full Text | Google Scholar

Enrique-Romero, J., Rimola, A., Ceccarelli, C., and Balucani, N. (2016). The (impossible?) formation of acetaldehyde on the grain surfaces: insights from quantum chemical calculations. Mon. Not. R. Astron. Soc. 459, L6–L10. doi: 10.1093/mnrasl/slw031

CrossRef Full Text | Google Scholar

Enrique-Romero, J., Rimola, A., Ceccarelli, C., Ugliengo, P., Balucani, N., and Skouteris, D. (2019). Reactivity of HCO with CH₃ and NH₂ on water ice surfaces. A comprehensive accurate quantum chemistry study. ACS Earth Space Chem. 3, 2158–2170. doi: 10.1021/acsearthspacechem.9b00156

CrossRef Full Text | Google Scholar

Ercolano, B., Barlow, M. J., and Sugerman, B. E. K. (2007). Dust yields in clumpy supernova shells: SN 1987A revisited. Mon. Not. R. Astron. Soc. 375, 753–763. doi: 10.1111/j.1365-2966.2006.11336.x

CrossRef Full Text | Google Scholar

Escatllar, A. M., Lazaukas, T., Woodley, S. M., and Bromley, S. T. (2019). Structure and properties of nanosilicates with olivine (Mg₂SiO₄)_N and pyroxene (MgSiO₃)_N compositions. ACS Earth Space Chem. 3, 2390–2403. doi: 10.1021/acsearthspacechem.9b00139

PubMed Abstract | CrossRef Full Text | Google Scholar

Goumans, T. P. M., and Bromley, S. T. (2011). Hydrogen and oxygen adsorption on a nanosilicate – a quantum chemical study. Mon. Not. R. Astron. Soc. 414, 1285–1291. doi: 10.1111/j.1365-2966.2011.18463.x

CrossRef Full Text | Google Scholar

Goumans, T. P. M., and Bromley, S. T. (2012). Efficient nucleation of stardust silicates via heteromolecular homogeneous condensation. Mon. Not. R. Astron. Soc. 420, 3344–3349. doi: 10.1111/j.1365-2966.2011.20255.x

CrossRef Full Text | Google Scholar

Goumans, T. P. M., and Bromley, S. T. (2013). Stardust silicate nucleation kick-started by SiO+TiO₂. Philos. Trans. R. Soc. A 371:20110580. doi: 10.1098/rsta.2011.0580

CrossRef Full Text | Google Scholar

Hama, T., and Watanabe, N. (2013). Surface processes on interstellar amorphous solid water: Adsorption, diffusion, tunneling reactions, and nuclear-spin conversion. Chem. Rev. 113, 8783–8839. doi: 10.1021/cr4000978

PubMed Abstract | CrossRef Full Text | Google Scholar

Henning, T. (2010). Cosmic silicates. Annu. Rev. Astron. Astrophys. 48, 21–46. doi: 10.1146/annurev-astro-081309-130815

CrossRef Full Text | Google Scholar

Herbst, E. (2017). The synthesis of large interstellar molecules. Int. Rev. Phys. Chem. 36, 287–331. doi: 10.1080/0144235X.2017.1293974

CrossRef Full Text | Google Scholar

Hirashita, H., and Kobayashi, H. (2013). Evolution of dust grain size distribution by shattering in the interstellar medium: Robustness and uncertainty. Earth Planets Space 65:2. doi: 10.5047/eps.2013.03.008

CrossRef Full Text | Google Scholar

Jones, A. P. (2007). The mineralogy of cosmic dust: astromineralogy. Eur. J. Mineral. 19, 771–782. doi: 10.1127/0935-1221/2007/0019-1766

CrossRef Full Text | Google Scholar

Jones, A. P., Tielens, A. G. G. M., and Hollenbach, D. J. (1996). Grain Shattering in Shocks: The 321 Interstellar Grain Size Distribution. Astrophys J. 469:740. doi: 10.1086/177823

CrossRef Full Text | Google Scholar

Kerkeni, B., Bacchus-Montabonel, M.-C., Shan, X., and Bromley, S. T. (2019). Understanding H2 formation on hydroxylated pyroxene nanoclusters: Ab initio study of the reaction energetics and kinetics. J. Phys. Chem. A 123, 9282–9291 doi: 10.1021/acs.jpca.9b06713

PubMed Abstract | CrossRef Full Text | Google Scholar

Kerkeni, B., Bacchus-Montabonel, M. C., and Bromley, S. T. (2017). How hydroxylation affects hydrogen adsorption and formation on nanosilicates. Mol. Astrophys., 7, 1–8. doi: 10.1016/j.molap.2017.04.001

CrossRef Full Text | Google Scholar

Kerkeni, B., and Bromley, S. T. (2013). Competing mechanisms of catalytic H₂ formation and dissociation on ultrasmall silicate nanocluster dust grains. Mon. Not. R. Astron. Soc. 435, 1486–1492. doi: 10.1093/mnras/stt1389

CrossRef Full Text | Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electr8on density. Phys. Rev. B 37, 785–789. doi: 10.1103/PhysRevB.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, A., and Draine, B. T. (2001a). Infrared emission from interstellar dust. II. The diffuse interstellar medium. Astrophys. J. 554, 778–802. doi: 10.1086/323147

CrossRef Full Text | Google Scholar

Li, A., and Draine, B. T. (2001b). On ultrasmall silicate grains in the diffuse interstellar medium. Astrophys. J. Lett. 550, L213–L217. doi: 10.1086/319640

CrossRef Full Text | Google Scholar

Martínez-González, J. Á., Navarro-Ruiz, J., and Rimola, A. (2018). Multiscale computational simulation of amorphous silicates' structural, dielectric, and vibrational spectroscopic properties. Minerals 8:353. doi: 10.3390/min8080353

CrossRef Full Text | Google Scholar

Matsuura, M., Dwek, E., Meixner, M., Otsuka, M., Babler, B., Barlow, M. J., et al. (2011). Herschel detects a massive dust reservoir in supernova 1987A. Science 333:1258. doi: 10.1126/science.1205983

PubMed Abstract | CrossRef Full Text | Google Scholar

Molpeceres, G., Rimola, A., Ceccarelli, C., Kästner, J., Ugliengo, P., and Mat,é, B. (2019). Silicate-mediated interstellar water formation: a theoretical study. Mon. Not. R. Astron. Soc. 482, 5389–5400. doi: 10.1093/mnras/sty3024

PubMed Abstract | CrossRef Full Text | Google Scholar

Molster, F., and Kemper, C. (2005). Crystalline Silicates. Space Sci. Rev. 119, 3–28. doi: 10.1007/s11214-005-8066-x

CrossRef Full Text | Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special points for brillouin-zone integrations. Phys. Rev. B 13, 5188–5192. doi: 10.1103/PhysRevB.13.5188

CrossRef Full Text | Google Scholar

Navarro-Ruiz, J., Martínez-González, J. Á., Sodupe, M., Ugliengo, P., and Rimola, A. (2015). Relevance of silicate surface morphology in interstellar H₂ formation. Insights from quantum chemical calculations. Mon. Not. R. Astron. Soc. 453, 914–924. doi: 10.1093/mnras/stv1628

CrossRef Full Text | Google Scholar

Navarro-Ruiz, J., Sodupe, M., Ugliengo, P., and Rimola, A. (2014a). Interstellar H adsorption and H₂ formation on the crystalline (010) forsterite surface: A B3LYP-D2^* periodic study. Phys. Chem. Chem. Phys. 16, 17447–17457. doi: 10.1039/C4CP00819G

PubMed Abstract | CrossRef Full Text | Google Scholar

Navarro-Ruiz, J., Ugliengo, P., Rimola, A., and Sodupe, M. (2014b). B3LYP Periodic Study of the Physicochemical Properties of the Nonpolar (010) Mg-Pure and Fe-Containing Olivine Surfaces. J. Phys. Chem. A 118, 5866–5875. doi: 10.1021/jp4118198

PubMed Abstract | CrossRef Full Text | Google Scholar

Navarro-Ruiz, J., Ugliengo, P., Sodupe, M., and Rimola, A. (2016). Does Fe²⁺ in olivine-based interstellar grains play any role in the formation of H₂? Atomistic insights from DFT periodic simulations. Chem. Commun. 52, 6873–6876. doi: 10.1039/C6CC02313D

CrossRef Full Text | Google Scholar

Noel, Y., Catti, M., D'Arco, P., and Dovesi, R. (2006). The vibrational frequencies of forsterite Mg₂SiO₄: an all-electron ab initio study with the CRYSTAL code. Phys. Chem. Miner. 33, 383–393. doi: 10.1007/s00269-006-0085-y

CrossRef Full Text | Google Scholar

Öberg, K. I. (2016). Photochemistry and astrochemistry: photochemical pathways to interstellar complex organic molecules. Chem. Rev. 116, 9631–9663. doi: 10.1021/acs.chemrev.5b00694

PubMed Abstract | CrossRef Full Text | Google Scholar

Oueslati, I., Kerkeni, B., and Bromley, S. T. (2015). Trends in the adsorption and reactivity of hydrogen on magnesium silicate nanoclusters. Phys. Chem. Chem. Phys. 17, 8951–8963. doi: 10.1039/C4CP05128A

PubMed Abstract | CrossRef Full Text | Google Scholar

Pascale, F., Zicovich-Wilson, C. M., Gejo, F. L., Civalleri, B., Orlando, R., and Dovesi, R. (2004). The calculation of the vibrational frequencies of crystalline compounds and its implementation in the CRYSTAL code. J. Comput. Chem. 25, 888–897. doi: 10.1002/jcc.20019

PubMed Abstract | CrossRef Full Text | Google Scholar

Pilleri, P., Joblin, C., Boulanger, F., and Onaka, T. (2015). Mixed aliphatic and aromatic composition of evaporating very small grains in NGC 7023 revealed by the 3.4/3.3 μm ratio. Astron. Astrophys. 577:A16. doi: 10.1051/0004-6361/201425590

PubMed Abstract | CrossRef Full Text | Google Scholar

Pilleri, P., Montillaud, J., Berné, O., and Joblin, C. (2012). Evaporating very small grains as tracers of the UV radiation field in photo-dissociation regions. Astron. Astrophys. 542:A69. doi: 10.1051/0004-6361/201015915

CrossRef Full Text | Google Scholar

Rapacioli, M., Joblin, C., and Boissel, P. (2005). Spectroscopy of polycyclic aromatic hydrocarbons and very small grains in photodissociation regions. Astron. Astrophys. 429, 193–204. doi: 10.1051/0004-6361:20041247

CrossRef Full Text | Google Scholar

Rimola, A., Skouteris, D., Balucani, N., Ceccarelli, C., Enrique-Romero, J., Taquet, V., et al. (2018). Can formamide be formed on interstellar ice? An atomistic perspective. ACS Earth Space Chem. 2, 720–734. doi: 10.1021/acsearthspacechem.7b00156

CrossRef Full Text | Google Scholar

Rimola, A., Taquet, V., Ugliengo, P., Balucani, N., and Ceccarelli, C. (2014). Combined quantum chemical and modeling study of CO hydrogenation on water ice. Astron. Astrophys. 572:A70. doi: 10.1051/0004-6361/201424046

CrossRef Full Text | Google Scholar

Rouillé, G., Jäger, C., Krasnokutski, S. A., Krebsz, M., and Henning, T. (2014). Cold condensation of dust in the ISM. Faraday Discuss. 168, 449–460. doi: 10.1039/C4FD00010B

PubMed Abstract | CrossRef Full Text | Google Scholar

Tielens, A. G. G. M. (2008). Interstellar Polycyclic Aromatic Hydrocarbon Molecules. Annu. Rev. Astron. Astrophys. 46, 289–337. doi: 10.1146/annurev.astro.46.060407.145211

PubMed Abstract | CrossRef Full Text | Google Scholar

Tielens, A. G. G. M. (2013). The molecular universe. Rev. Modern Phys. 85, 1021–1081. doi: 10.1103/RevModPhys.85.1021

CrossRef Full Text | Google Scholar

Ugliengo, P., Viterbo, D., and Chiari, G. (1993). MOLDRAW: molecular graphics on a personal computrer. Z. Kristallogr. 1993, 207–209. doi: 10.1524/zkri.1993.207.Part-1.9

CrossRef Full Text | Google Scholar

van Dishoeck, E. F. (2014). Astrochemistry of dust, ice and gas: introduction and overview. Faraday Discuss. 168, 9–47. doi: 10.1039/C4FD00140K

PubMed Abstract | CrossRef Full Text | Google Scholar

van Dishoeck, E. F., Herbst, E., and Neufeld, D. A. (2013). Interstellar water chemistry: from laboratory to observations. Chem. Rev. 113, 9043–9085. doi: 10.1021/cr4003177

PubMed Abstract | CrossRef Full Text | Google Scholar

Vidali, G. (2013). H2 Formation on interstellar grains. Chem. Rev. 113:8762–8782. doi: 10.1021/cr400156b

PubMed Abstract | CrossRef Full Text | Google Scholar

Watanabe, N., Shiraki, T., and Kouchi, A. (2003). The dependence of H₂CO and CH₃OH formation on the temperature and thickness of H₂O-CO ice during the successive hydrogenation of CO. Astrophys. J. 588, L121–L124. doi: 10.1086/375634

CrossRef Full Text | Google Scholar

Weinberger, A. J. (2005). Construction-site inspection. Nature 433, 114–115. doi: 10.1038/433114a

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, D. A., and Herbst, E. (2002). It's a dusty Universe: surface science in space. Surf. Sci. 500, 823–837. doi: 10.1016/S0039-6028(01)01538-2

CrossRef Full Text | Google Scholar

Zamirri, L., Macià Escatllar, A., Mariñoso Guiu, J., Ugliengo, P., and Bromley, S. T. (2019a). What can infrared spectra tell us about the crystallinity of nanosized interstellar silicate dust grains? ACS Earth Space Chem. 3, 2323–2338. doi: 10.1021/acsearthspacechem.9b00157

CrossRef Full Text | Google Scholar

Zamirri, L., Ugliengo, P., Ceccarelli, C., and Rimola, A. (2019b). Quantum mechanical investigations on the formation of complex organic molecules on interstellar ice mantles. review and perspectives. ACS Earth Space Chem. 3, 1499–1523. doi: 10.1021/acsearthspacechem.9b00082

CrossRef Full Text | Google Scholar

Zicovich-Wilson, C. M., Bert, A., Roetti, C., Dovesi, R., and Saunders, V. R. (2002). Characterization of the electronic structure of crystalline compounds through their localized wannier functions. J. Chem. Phys. 116, 1120–1127. doi: 10.1063/1.1425406

CrossRef Full Text | Google Scholar

Zicovich-Wilson, C. M., Dovesi, R., and Saunders, V. R. (2001). A general method to obtain well localized wannier functions for composite energy bands in linear combination of atomic orbital periodic calculations. J. Chem. Phys. 115, 9708–9719. doi: 10.1063/1.1415745

CrossRef Full Text | Google Scholar