Effect of Binding Energies on the Encounter Desorption

The abundance of interstellar ice constituents is usually expressed with respect to the water ice because, in denser regions, a significant portion of the interstellar grain surface would be covered by water ice. The binding energy (BE) or adsorption energy of the interstellar species regulates the chemical complexity of the interstellar grain mantle. Due to the high abundance of water ice, the BE of surface species with the water is usually provided and widely used in astrochemical modeling. However, the hydrogen molecules would cover some part of the grain mantle in the denser and colder part of the interstellar medium. Even at around ∼10 K, few atoms and simple molecules with lower adsorption energies can migrate through the surface. The BE of the surface species with H₂ substrate would be very different from that of a water substrate. However, adequate information regarding these differences is lacking. Here, we employ the quantum chemical calculation to provide the BE of 95 interstellar species with H₂ substrate. These are representative of the BEs of species to a H₂ overlayer on a grain surface. On average, we notice that the BE with the H₂ monomer substrate is almost ten times lower than the BE of these species reported earlier with the H₂O c-tetramer configuration. The encounter desorption of H and H₂ was introduced [with ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_2\right)=45\text{K}$ and ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)=23\text{K}$] to have a realistic estimation of the abundances of the surface species in the colder and denser region. Our quantum chemical calculations yield higher adsorption energy of H₂ than that of H [$\text{E}\text{D}\left(\text{H},{\text{H}}_2\right)$ = 23–25 K and $\text{E}\text{D}\left({\text{H}}_2,{\text{H}}_2\right)$ = 67–79 K]. We further implement an astrochemical model to study the effect of encounter desorption with the present realistic estimation. The encounter desorption of the N atom [calculations yield ${\text{E}}_{\text{D}}\left(\text{N},{\text{H}}_2\right)=83\text{K}$] is introduced to study the differences with its inclusion.

1 Introduction

Interstellar grains mainly consist of amorphous silicate and some form of carbonaceous materials (Li, 2004). It is now well established that these grains can significantly constrain the chemical composition of molecular clouds or star-forming regions. In the cloud’s denser regions, where the temperature is reasonably low (∼10 K), the grain surface would be covered by icy layers. A sizable portion of these icy layers may contain water molecules. Thus, providing the binding energies (BEs) with the water as a substrate is proper. In reality, the surface species would face a bare grain in the diffuse region. Some ice layers would grow on the top of this grain surface in the denser medium and host the incoming species. The composition of this ice layer depends on the initial elemental abundance of the species in that region. It would not necessarily always be H₂O-dominated. There are ample examples of the presence of a notable portion of CO, CO₂, CH₄, NH₃, CH₃OH, etc., on the ice (Gibb et al., 2004; Das et al., 2010; Das and Chakrabarti, 2011; Das et al., 2016; Gorai et al., 2020a).

Hydrogen molecules are ubiquitous in denser regions of the interstellar medium (ISM). Thus, its accretion rate on the grain is much higher in comparison to the others. However, because of the low adsorption energy, it can be easily desorbed from the grain. Despite this, a significant portion of the grain mantle would be covered by molecular hydrogen, especially around the cold and dense interstellar condition. This inhomogeneous surface coverage could influence the mobility of the other surface species. Initially, the encounter desorption mechanism was introduced by Hincelin et al. (2015) to eliminate the overestimation of the abundance of molecular hydrogen on the grain. This desorption process occurs during surface diffusion and is induced by the presence of repulsive inter-H₂ forces, effectively reducing the BE of H₂. They considered ${\text{gH}}_2+{\text{gH}}_2\to {\text{H}}_2+{\text{gH}}_2$, where “g” designates the grain surface species. They obtained an excellent match within the microscopic Monte Carlo method and the rate equation approach when they implemented this unique approach. The Monte Carlo approach is best suited for monitoring the chemical composition of the grain mantle. However, it is time-consuming (Chakrabarti et al., 2006a; Chakrabarti et al., 2006b; Cuppen and Herbst, 2007; Das et al., 2008a; Das et al., 2010; Das and Chakrabarti, 2011; Das et al., 2016). Recently, Chang et al. (2021) considered a similar process and included H’s desorption by a similar mechanism. They considered $\text{gH}+{\text{gH}}_2\to \text{H}+{\text{gH}}_2$, which means whenever the surface H meets one surface H₂, surface H desorb with a certain probability. They reported a significant difference between the formation of some key surface species with the inclusion of this treatment.

A substantial amount of BE values are available from the temperature-programmed desorption (TPD) studies on various model substrates like graphite, diamond-like carbon, amorphous or crystalline silica, silicates, water, and other ice surfaces (Collings et al., 2004; Noble et al., 2012; Ward et al., 2012; Dulieu et al., 2013). But, the BE of the species with H₂ substrate is yet to be known. Cuppen and Herbst (2007) had estimated the BE of H atom on H₂ substrate ∼45 K by following Vidali et al. (1991). They also estimated the BEs of O, OH, ${\text{H}}_2,{\text{O}}_2,{\text{H}}_2\text{O},{\text{O}}_3,{\text{O}}_2\text{H},\text{and}{\text{H}}_2{\text{O}}_2$ with the H₂ substrate by scaling its obtained BE with H₂O substrate with the ratio of BE between the BE of H with water substrate and with H₂ substrate.

A vital impediment in examining the encounter desorption with other species is the shortage of information about the adsorption energy of these species with H₂ molecule. Here, we employ quantum chemical calculations to determine the adsorption energy of these species with H₂ molecule. Obtained BE assessments are executed in our Chemical Model of Molecular Cloud (hereafter CMMC) (Das et al., 2015a; Das et al., 2015b; Gorai et al., 2017a; Gorai et al., 2017b; Sil et al., 2018; Gorai et al., 2020b). The encounter desorption effect is vital during the prestellar core phase. Studying the formation of stars is one of the essential intricacies of astrophysics. A complete understanding of the star formation process is yet to be established. However, in brief, stars are formed by a long condensation process (Pagani et al., 2013). In the beginning, warm diffuse material (∼8000 K) converts into a cold neutral atomic gas (∼100 K and ∼10–100 cm⁻³). After further evolution, it transforms into a more dense region (10²–10⁴ cm⁻³ and ∼10–20 K). If no other heating source is present, then a dense core (>10⁴ cm⁻³) appears in some places of these turbulent materials. Some of these cores further evolve into prestellar cores (>10⁵ cm⁻³) (Bergin and Tafalla, 2007; Keto and Caselli, 2008). Prestellar cores further continue their evolution for the formation of the protostar. Due to the accretion of atoms and molecules, gas-phase abundance is depleting, whereas the molecular ice mantles form. The chemical composition of the grain mantle is mainly governed by the addition of atomic hydrogen with the atoms or simple molecules. The chemical composition of the bulk ices further varies with the star formation process associated with it. Depending on this, it is expected that the ice composition would be very different in various places. However, from the infrared observations, it was observed that the significant repositories of interstellar hydrogen, oxygen, carbon, and nitrogen are H₂O, CH₃OH, H₂CO, CO, CO₂, CH₄, and NH₃ (Gibb et al., 2000; Whittet et al., 2007; Öberg et al., 2008; Boogert et al., 2015).

This article is compiled as follows. In Section 2, we confer computational methodology. Discussion and results are presented in Section 3, and finally, in Section 4, we conclude.

2 Computational Details

2.1 Quantum Chemical Calculations

Here, we have utilized the Gaussian 09 suite of programs (Frisch et al., 2013) for quantum chemical calculations. In a periodic treatment of surface adsorption phenomena, the BE is related to the interaction energy, (ΔE), as follows:

$BE=-\text{Δ}E.(1)$

For a bounded adsorbate, the BE is a positive quantity and is defined as follows:

$BE=\left(E_{surface}+E_{species}\right)-E_{ss},(2)$

where ${\text{E}}_{\text{ss}}$ is the optimized energy for the complex system where a species is placed at a suitable distance from the grain surface. ${\text{E}}_{\text{surface}}$ and ${\text{E}}_{\text{species}}$ are the optimized energies of the grain surface and species, respectively.

To find the optimized energy of all structures, we have used a second-order Møller–Plesset (MP2) method with an aug-cc-pVDZ basis set (Dunning and Thom, 1989). We have considered 95 interstellar species for the computation of their BEs with the H₂ substrate. To make the calculation more straightforward, we have considered a monomer configuration of the H₂ molecule as an adsorbent. The adsorbates noted in Table 1 are placed at a suitable distance from the adsorbent with a weak bond so that a van der Waals interaction occurs during the optimization. All the optimized geometries are provided in the supplementary information. We must confess that the interstellar species considered in this study are often larger than the H₂. Since the estimated BEs are different in different locations, this may lead to a fallacious estimation. It is recommended to take the average whenever different binding sites are found. Despite these flaws, it can provide us with a general picture and startup initiative to compare the BE of a species with the water and H₂ substrate. Following the BE calculations carried out by Das et al. (2018) (see Tables 2 and 3), here we have not considered the ZPE and BSSE corrections for our BE calculations. All the obtained BE values are noted in Table 1. It is interesting to note that except for phosphorous, the calculated adsorption energy of most of the abundant atoms (H, C, N, O, and S) with the H₂ substrate is found to be <100 K.

TABLE 1

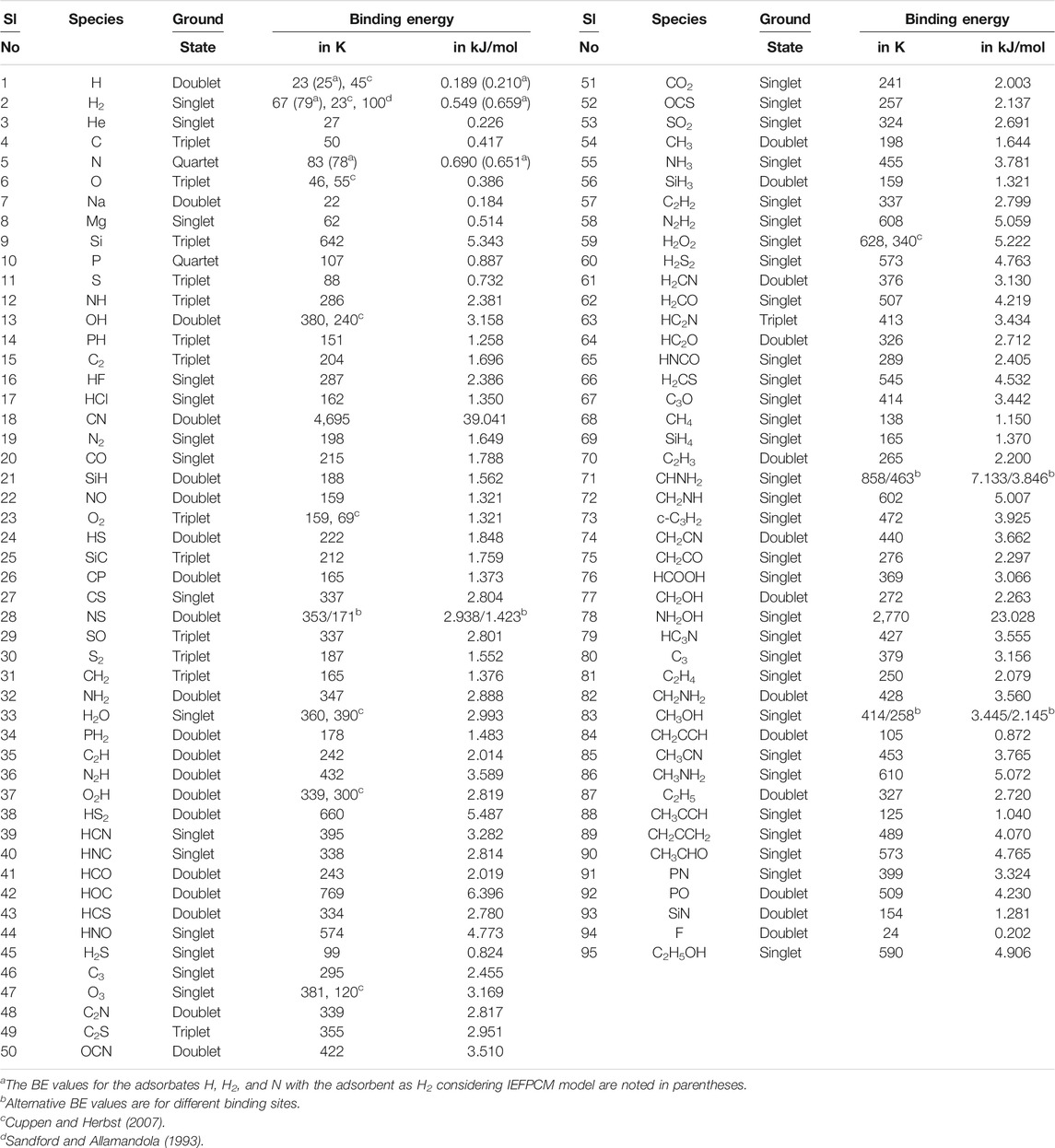
TABLE 1. Calculated binding energy (with MP2/aug-cc-pVDZ) of various species with H₂ monomer surface.

TABLE 2

TABLE 2. Initial elemental abundances considered in this study.

TABLE 3

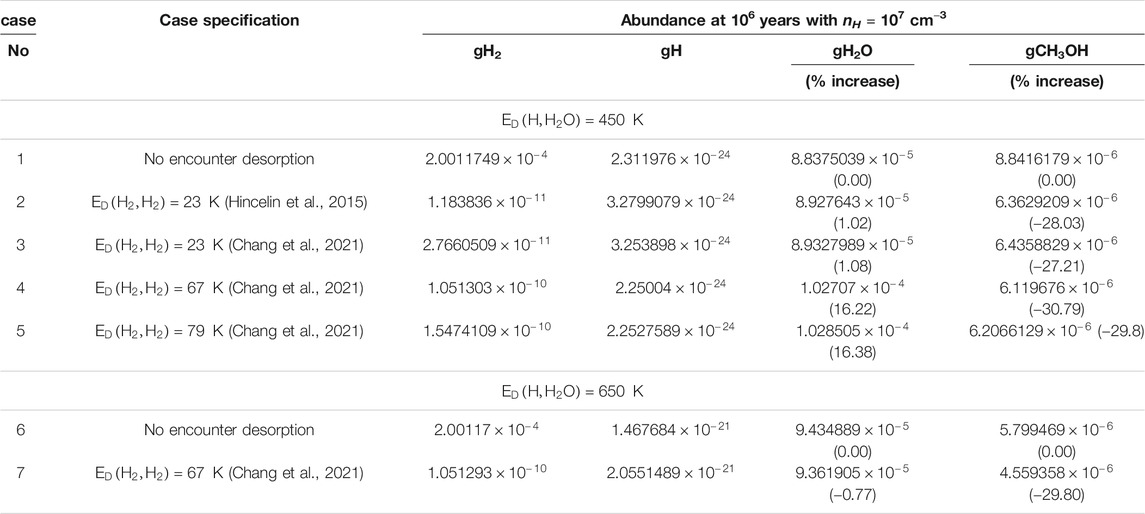
TABLE 3. The obtained abundance of gH₂, gH, gH₂O, and gCH₃OH for the effect of encounter desorption of H₂ under various situations with $R=0.35$, $n_H={10}^7{\text{cm}}^{-3}$, and $T=10\text{K}$.

In Table 1, we have reported the BE values obtained by considering a free-standing H₂ interacting with a species. But in reality, this H₂ would be pre-adsorbed and can feel the surface. It would yield a different BE than the previous case. To check the effect of condensed H₂O in the ice phase, we also have calculated the interaction energy by considering the molecule embedded in a continuum solvation field. For this purpose, we have examined the local effects and the integral equation formalism (IEF) variant of the polarizable continuum model (PCM) (Cancès et al., 1997; Tomasi et al., 2005) with water as a solvent (Gorai et al., 2020a). The obtained values for H, H₂, and N with the IEFPCM model are noted in Table 1 (in parentheses). The two calculations significantly differ. For example, with the free-standing H₂, we have the BE of H, H₂, and N ∼23 K, 67 K, and 83 K, respectively, whereas with the IEFPCM model, we have obtained ∼25 K, 79 K, and 78 K, respectively. So, the free-standing H₂ underestimated the BE of H and H₂ by 2 and 12 K, whereas it overestimated N’s case by 5 K. We also provided in Table 1 the literature BE values (Sandford and Allamandola, 1993; Cuppen and Herbst, 2007) (if available) for the comparison.

Das et al. (2018) provided BEs of the ∼100 interstellar species considering the c-tetramer configuration of water molecules. Table 1 shows the BE of the roughly same interstellar species with the H₂ monomer. We have noticed that the obtained BEs with H₂ are much smaller than those of the water tetramer configuration. On average, we have received almost 10 times lower BEs with the H₂ surface. Table 1 shows the ground state of the species used to calculate the BE. The values of BE are very much sensitive on the chosen ground state spin multiplicity. To evaluate the ground state spin multiplicity of each species, we have taken the help of Gaussian 09 suite of program. The way to check for the ground state spin multiplicity is to run separate calculations (job type “opt + freq”), each with different spin multiplicities, and then compare the results between them. The lowest energy electronic state solution of the chosen spin multiplicity is the ground state noted for the species in Table 1.

2.2 Astrochemical Model

We have included the encounter desorption phenomenon in our CMMC code (Das et al., 2015a; Das et al., 2015b; Das et al., 2016; Gorai et al., 2017a; Gorai et al., 2017b; Sil et al., 2018; Gorai et al., 2020b) to study its effect. The surface chemistry network of our model is mostly adopted from Ruaud et al. (2015), Das et al. (2015b), and Gorai et al. (2020b). The gas-phase network of the CMMC model is mainly adopted from the UMIST database (McElroy et al., 2013). Additionally, we have also included the deuterated gas-phase chemical network from the UMIST. A cosmic ray rate of 1.3 × 10⁻¹⁷ s⁻¹ is considered in all our models. Cosmic ray–induced desorption and nonthermal desorption rates with a fiducial parameter of 0.01 is considered. For all the grain surface species, we have adopted a photodesorption rate of 1 × 10⁴ per incident UV photon (Ruaud et al., 2015). A sticking coefficient of 1.0 is considered for the neutral species except for the H and H₂. The sticking coefficients of H and H₂ are considered by following the relation proposed by Chaabouni et al. (2012). Following Garrod and Pauly (2011), here we have implemented the competition between diffusion, desorption, and reaction. For the diffusion energy (E_b), we have considered R × adsorption energy (E_D). Here, R is a scaling factor that can vary between 0.35 and 0.8 (Garrod et al., 2007). The BE of the species is mostly considered from Wakelam et al. (2017), and a few from Das et al. (2018). Table 2 refers to the adopted initial abundances concerning the total hydrogen nuclei in all forms. Except for HD’s value in Table 2, elemental abundances are taken from Semenov et al. (2010). We considered the initial abundances of HD from Roberts and Millar (2000).

The encounter desorption effect was first introduced by Hincelin et al. (2015). The rate of encounter desorption of H₂ on the surface of H₂ is defined as follows:

$E{n}_{H_2}=\frac{1}{2}{k}_{H_2,H_2}g{H}_{2}g{H}_{2}P\left(H_2,H_2\right),(3)$

where gH₂ is the surface concentration of H₂ molecules in cm⁻³, $\text{P}\left({\text{H}}_2,{\text{H}}_2\right)$ defines the probability of desorption over the diffusion, and ${\text{k}}_{{\text{H}}_2,{\text{H}}_2}$ is the diffusion rate coefficient over the H₂O substrate. ${\text{k}}_{{\text{H}}_2,{\text{H}}_2}$ is defined as follows (Hasegawa et al., 1992):

$k_{H_2,H_2}=\kappa \left(R_{diff{H}_2}+R_{diff{H}_2}\right)/n_d{\text{cm}}^3{\text{s}}^{-1}.(4)$

In the above equation, $n_d$ is the dust-grain number density, κ is the probability for the reaction to happen (unity for the exothermic reaction without activation energy), and $R_{diff}$ is the diffusion of the species. $\text{P}\left({\text{H}}_2,{\text{H}}_2\right)$ in Eq. 3 is defined as follows:

$\text{P}\left({\text{H}}_2,{\text{H}}_2\right)=\frac{\text{Desorption}\text{rate}\text{of}{\text{H}}_2\text{on}{\text{H}}_2\text{substrate}}{\text{Desorption}\text{rate}\text{of}{\text{H}}_2\text{on}{\text{H}}_2\text{substrate}+\text{Diffusion}\text{of}{\text{H}}_2\text{on}{\text{H}}_2\text{substrate}}.(5)$

There would be various desorption factors (by thermal, reactive, cosmic ray, etc.). The thermal desorption is defined as $\nu \text{exp}\left(-{\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)/\text{T}\right){\text{s}}^{\mathrm{–}1}$, where T is the dust temperature. Similarly, there would be various diffusion mechanisms, but thermal diffusion would be dominating. It is defined as $\nu \text{exp}\left(-{\text{E}}_{\text{b}}\left({\text{H}}_2,{\text{H}}_2\right)/\text{T}\right)/\text{S}\left({\text{s}}^{-1}\right)=\text{thermal}\text{hopping}\text{rate}/\text{number}\text{of}\text{sites}\left({\text{s}}^{-1}\right)$. Here, we have used $\text{Diffusion}\text{energy}\left({\text{E}}_{\text{b}}\right)=\text{R}\times \text{Adsorption}\text{energy}\left({\text{E}}_{\text{D}}\right)$. Recently, Chang et al. (2021) has extended this work by considering the encounter desorption of the H atom. In their definition of the encounter desorption of H₂, in Eq. 5, they used the hopping rate of H₂ on H₂ substrate instead of the diffusion rate of H₂ on H₂ substrate. Following the prescription defined by Chang et al. (2021), the encounter desorption of species X is defined as follows:

${\text{En}}_{\text{X},{\text{H}}_2}=\frac{{\text{h}}_{\text{X},{\text{H}}_2}}{\text{S}}\text{gX}{\text{gH}}_2\text{P}\left(\text{X},{\text{H}}_2\right){\text{P}}_{\text{X}},(6)$

where ${\text{h}}_{\text{X},{\text{H}}_2}$ is the hopping rate over H₂O surface $\left[\nu exp\left(-{\text{E}}_{\text{b}}\left(\text{X},{\text{H}}_2\right)/\text{T}\right)\right]$, P (X,H₂) is the desorption probability of gX while encountering with gH₂, and P_X denotes the probability of gX to migrate at the location of gH₂ over the H₂O substrate. P (X,H₂) and P_X are defined as follows:

$\text{P}\left(\text{X},{\text{H}}_2\right)=\frac{\text{Desorption}\text{rate}\text{of}\text{X}\text{on}{\text{H}}_2\text{substrate}}{\text{Desorption}\text{rate}\text{of}\text{X}\text{on}{\text{H}}_2\text{substrate}+\text{Hopping}\text{rate}\text{of}\text{X}\text{on}{\text{H}}_2\text{substrate}},(7)$

$P_X=\frac{\text{Hopping}\text{rate}\text{of}\text{X}\text{on}{\text{H}}_2\text{O}\text{substrate}}{\text{Hopping}\text{rate}\text{of}\text{X}\text{on}{\text{H}}_2\text{O}\text{substrate}+\text{Hopping}\text{rate}\text{of}{\text{H}}_2\text{on}{\text{H}}_2\text{O}\text{substrate}}.(8)$

3 Results and Discussion

3.1 Encounter Desorption of H₂

First of all, we have benchmarked our model with Hincelin et al. (2015). In Figure 1, we have compared our results with those obtained in Hincelin et al. (2015). For this comparison, following Hincelin et al. (2015), we have used T = 10 K, ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\text{O}\right)=440\text{K}$, ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_2\text{O}\right)=450\text{K}$, ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)=23\text{K}$, and R = 0.5. Solid curves in Figure 1 represent the cases obtained here, and the rest are extracted from Hincelin et al. (2015) by using the online tool of Rohatgi (2020). Our results with and without encounter desorption show an excellent match with Hincelin et al. (2015). Presently in the KIDA database (kida.astrophy.u-bordeaux.fr), more updated BE values were listed. It suggests that ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_2\text{O}\right)=650\text{K}$. The results obtained from our quantum chemical calculations shown in Table 1 represent the estimated BE values with the H₂ substrate. In the following section, we have used these updated energy values, and the effects of their changes are discussed.

FIGURE 1

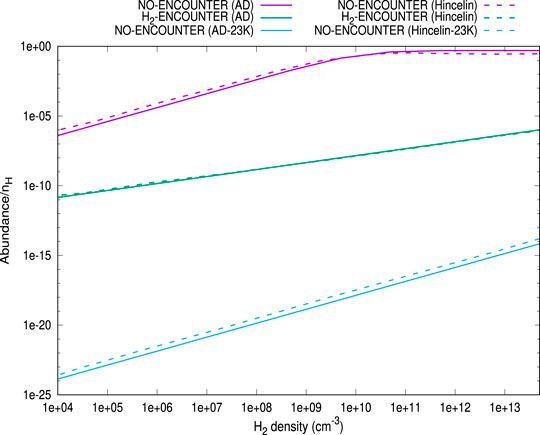
FIGURE 1. The comparison between Figure 2 of Hincelin et al. (2015) and the cases obtained here. We have extracted Figure 2 of Hincelin et al. (2015) by using the online tool of Rohatgi (2020). Three cases are shown: (A) no encounter desorption is considered with ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\text{O}\right)=440\text{K}$, (B) no encounter desorption is considered with ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)=23\text{K}$, (C) encounter desorption of H₂ was considered with ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\text{O}\right)=440\text{K,}$ and ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)=23\text{K}$. We have noticed an excellent match between our calculated (solid curves) steady-state abundance of H₂ on grain surface and that obtained in Hincelin et al. (2015) (dashed curves).

3.1.1 gH₂

Figure 2 shows the time evolution of gH₂ by considering $n_H={10}^7{\text{cm}}^{-3}$, $T=10\text{K,}$ and $R=0.35-0.80$. Interestingly, the abundance of gH₂ seems to be invariant with R’s changes, whereas it strongly depends on R in encounter desorption. R’s lower value means a quicker hopping rate, whereas a higher value represents a delayed hopping rate. With the increase in R, gH₂ abundance raises for the encounter desorption case. It means that as we rise R’s value, the encounter desorption effect depreciates. The left panel of Figure 5 exposes that with the increase in R’s value, a steady decrease in the ratio between the gH₂ abundance with no encounter desorption case (NE) and with encounter desorption case (EN) is obtained. The probability of the encounter desorption is inversely proportional to the rate of diffusion (Eq. 5) or hopping (Eq. 7). Since the increase in the value of R induces faster diffusion and hopping, it is lowering the encounter desorption probability of H₂ as expected. Figure 3 shows the time evolution of gH₂ with NE and EN when we have used $R=0.35$, $T=10\text{K,}$ and $n_H={10}^4\mathrm{–}{10}^7{\text{cm}}^{-3}$. In both cases, abundances of gH₂ increase with the density. The middle panel of Figure 5 shows the gH₂ abundance ratio between NE and EN with density. It depicts that the effect of encounter desorption is more pronounced for higher density. Figure 4 shows the gH₂ abundances when we have used $n_H={10}^7$, $R=0.35$, and T = 5–20 K. In the right panel of Figure 5, we have shown the gH₂ abundance ratio obtained between NE and EN with the temperature changes. From the figures, it is seen that the effect of encounter desorption is maximum toward the lower temperature (∼10 K), and it ceases around 20 K. The curve is similar to the H₂ formation efficiency discussed in Chakrabarti et al. (2006a), Chakrabarti et al. (2006b) for olivine grain. With the decrease in temperature, H atoms’ mobility decreases. Thus, the formation rate decreases. With the increase in temperature, the hopping rate increases, which can increase the formation efficiency, but at the same time, the residence time of H atoms decreases which affects the H₂ formation efficiency. As a result, the H₂ formation efficiency is maximum at around ∼10 K, and the encounter desorption effect is pronounced at the peak hydrogen formation efficiency.

FIGURE 2

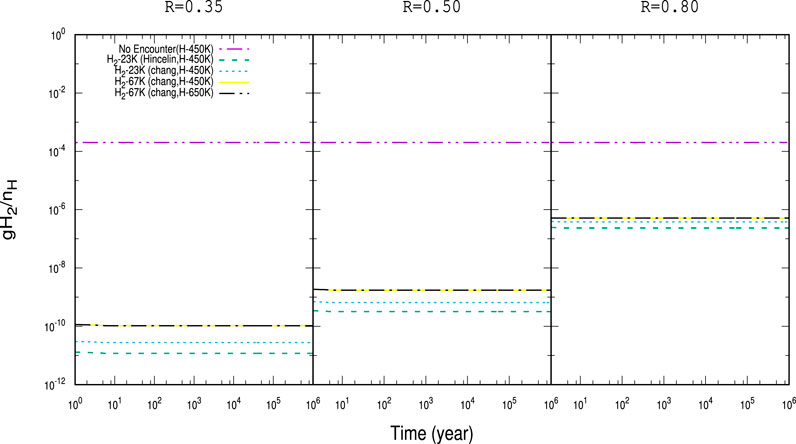
FIGURE 2. Time evolution of the abundances of gH₂ with $n_H={10}^7{\text{cm}}^{-3}$ and $T=10\text{K}$ are shown for $R=0.35$, 0.5, and 0.8. The dash-dotted purple curve represents the time evolution of gH₂ abundance with the no encounter desorption [with ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_2\text{O}\right)=450\text{K}$]. It depicts that the gH₂ abundance remains roughly invariant with the changes in R. However, when encounter desorption is introduced, gH₂ abundance increases with the R. The time evolution of the gH₂ abundance with ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)=23\text{K}$ and ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_{2}0\right)=450\text{K}$ is shown with the green dashed line when the method of Hincelin et al. (2015) is used and blue dotted line when the method of Chang et al. (2012) is used. gH₂ abundances obtained with our estimated BE value [i.e., ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)=67\text{K}$] are shown with a solid yellow line. For this case, we have used ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_2\text{O}\right)=450\text{K}$ and the method used in Chang et al. (2021). With the black dash-dotted line, the time evolution of gH₂ abundance is shown with ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_2\text{O}\right)=650\text{K}$ and method of Chang et al. (2021). We have seen significant differences when we have used different energy barriers and different methods (Hincelin et al., 2015; Chang et al., 2021). Obtained values of gH₂ are further noted in Table 3 for better understanding.

FIGURE 3

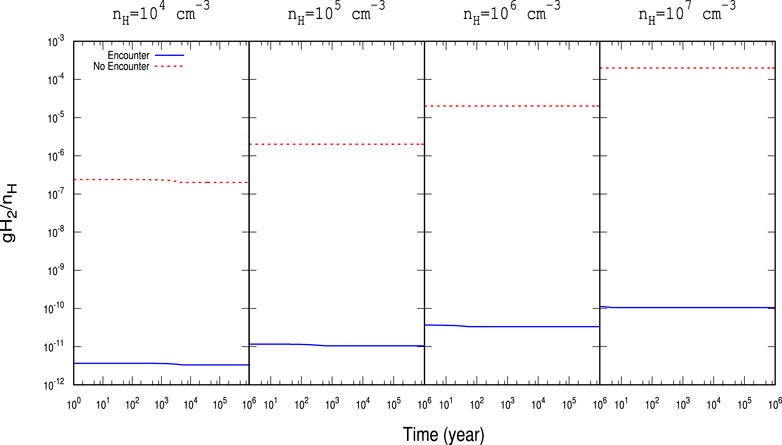
FIGURE 3. Time evolution of gH₂ with $R=0.35$ and various ${\text{n}}_{\text{H}}$ (${10}^4,{10}^5,{10}^6$, and ${10}^7{\text{cm}}^{-3}$) are shown. It depicts that the effect of encounter desorption increases with the increase in density.

FIGURE 4

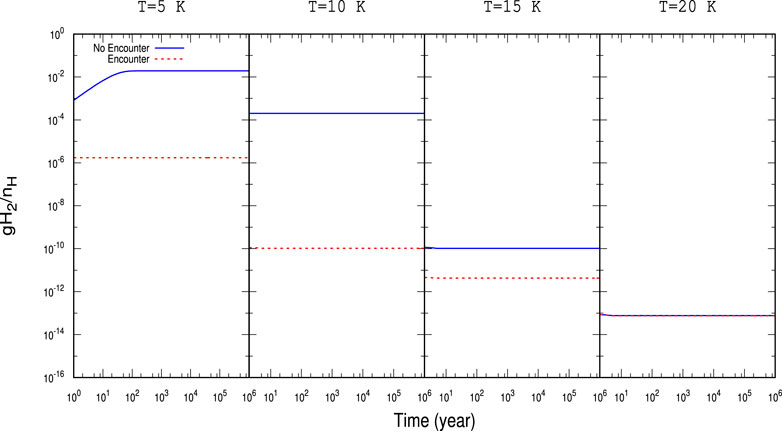
FIGURE 4. Time evolution of gH₂ with $R=0.35$, $n_H={10}^7{\text{cm}}^{-3},$ and various temperatures (5, 10, 15, and 20 K) are shown. It depicts that the effect of encounter desorption decreases with the increase in temperature.

FIGURE 5

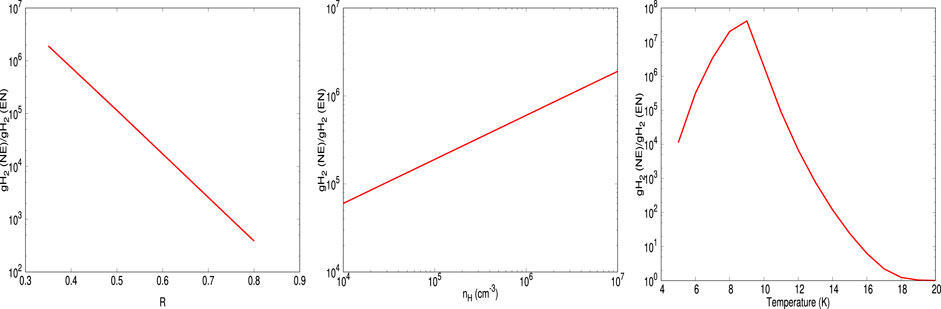
FIGURE 5. The ratio between the final abundances of gH₂ obtained with the no encounter (NE) desorption and encounter desorption (EN) is shown. From left to right, it shows the variation of this ratio with R, ${\text{n}}_{\text{H}}$, and temperature, respectively.

For a better illustration, the obtained abundances with $R=0.35$, T = 10 K, and $n_H={10}^7{\text{cm}}^{-3}$ are noted in Table 3 at the end of the total simulation time (∼10⁶ years). Chang et al. (2021) considered the competition between hopping rate and desorption rate of H₂ (Eq. 7), whereas (Hincelin et al., 2015) considered the battle between the diffusion and desorption rate of H₂ (Eq. 5). This difference in consideration resulting ∼ two times higher abundance of gH₂ with the consideration of Chang et al. (2021) compared to Hincelin et al. (2015) (see case 2 and 3 of Table 3 and Figure 2). Our quantum chemical calculation yields $E_D\left(H_2,H_2\right)=67\text{K}$, which is higher than it was used in the earlier literature value of 23 K (Cuppen and Herbst, 2007; Hincelin et al., 2015; Chang et al., 2021). The computed adsorption energy is further increased to 79 K when we have considered the IEFPCM model. Table 3 shows that increase in the BE [$E_D\left(H_2,H_2\right)=67\text{K}$, and 79 K, case 4 and 5 of Table 3] results in sequentially higher surface coverage of gH₂ than it was with $E_D\left(H_2,H_2\right)=23\text{K}$ (case 3 of Table 3). In case 5 of Table 3, we have noted the abundance of gH₂ when no encounter desorption effect is considered, but a higher adsorption energy of H atom is used [$E_D\left(H,H_{2}O\right)=650\text{K}$]. Case 6 of Table 3 also considered this adsorption energy of H atom along with $E_D\left(H_2,H_2\right)=67\text{K}$, and the method of Chang et al. (2021) is used. A comparison between the abundance of gH₂ of case 4 and case 6 (the difference between these two cases are in consideration of the adsorption energy of gH) yields a marginal decrease in the abundance of gH₂ when higher adsorption energy of gH is used.

3.1.2 gH

The obtained abundance of gH is noted in Table 3. The gH abundance is marginally decreased in Chang et al. (2021) compared to Hincelin et al. (2015). The use of higher ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)$ (∼67 K and 79 K) decreases the value of gH compared to case 2. However, the use of the H atom’s higher adsorption energy (650 K) can increase the gH abundance by a couple of orders of magnitude (see case 7 of Table 3).

3.1.3 gH₂O and gCH₃OH

The effect of the encounter desorption on the other major surface species (gH₂O and gCH₃OH) is also shown in Table 3. In the bracketed term, we have noted the percentage increase in their abundances from the case where no encounter desorption was considered [for $E_D\left(H,H_{2}O\right)=450\text{K}$ and 650 K, respectively]. Table 3 depicts that the consideration of encounter desorption of H₂ can significantly change (decrease by ∼27–30%) the methanol abundance (case 3 and case 7) from that was obtained with the no encounter desorption (case 1 and case 6). However, the changes in the surface abundance of water are minimal (∼±1%) for the addition of the encounter desorption of H₂. These changes (increase or decrease) are highly dependent on the adsorption energy of H, temperature, density, and the value of R (∼0.35 noted in Table 3). The changes in $E_D\left(H_2,H_2\right)$ from 23 to 67 K can influence the surface abundance of methanol and water. For example, in between case 3 and case 4 of Table 3, we can see that there is a significant increase (∼15%) in the abundance of gH₂O when higher adsorption energy [$E_D\left(H_2,H_2\right)=67\text{K}$] is used. However, this higher adsorption energy can marginally under-produce the methanol on the grain. In brief, from Table 3, it is clear that the encounter desorption can significantly change the abundances of surface species. Still, these changes are highly dependent on the adopted adsorption energy with the water and H₂ ice and adopted physical parameters ($n_H$, R, T).

3.2 Encounter Desorption of Other Species

The idea of encounter desorption Hincelin et al. (2015) primarily arose to eliminate the enhanced surface coverage of H₂ in the relatively denser and colder medium. Since H₂ has lower adsorption energy with the water surface (∼440 K), it could move on the surface very fast and occupy a position on the top of another H₂ molecule. Comparatively, in the denser and colder region, the chances of this occurrence enhance. Since the H₂ molecule on H₂ has negligible BE [23 K used in Cuppen and Herbst (2007), Hincelin et al. (2015)], it could easily desorb back to the gas phase. Other surface species can, of course, meet with H₂, but the idea of this encounter desorption arises when the species can occupy a position on the top of the H₂ molecule. For example, a carbon atom is having a BE of 10,000 K (Wakelam et al., 2017). H₂ could quickly meet one C atom on the grain surface, but due to the lower mobility of atomic carbon at a low temperature, every time H₂ will be on the top of the carbon atom. Since the whole C-H₂ system is attached to the water substrate, this will not satisfy the encounter desorption probability. Among the various key elements considered in this study, gH, gN, and gF have the BE of 650 K (Wakelam et al., 2017), 720 K (Wakelam et al., 2017), and 800 K (listed in the original OSU gas-grain code from Eric Herbst group in 2006), respectively, with the water ice. It yields a reasonable time scale for hopping even at a low grain temperature (∼10 K). Since the initial elemental abundance of F is negligible, we can neglect its contribution. The hopping time scale is heavily dependent on the assumed value of R. For example, by considering $R=0.35$, at 10 K, the hopping time scale for gH and gN is $1.12\times {10}^4$ years [with ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_2\text{O}\right)=650\text{K}$] and $4.61\times {10}^{-3}$ years [with ${\text{E}}_{\text{D}}\left(\text{N},{\text{H}}_2\text{O}\right)=720\text{K}$], respectively. It changes to 1.9 and 226 years for H and N atoms, respectively, for $R=0.5$. Since the typical lifetime of a dark cloud is ∼10⁶ years, the criterion related to the encounter desorption is often satisfied. Among the di-atomic species, H₂ is only having a faster swapping rate (having BE 440 K, which corresponds to a hopping time scale of $\sim 1.24\times {10}^{-7}$ years and $9\times {10}^{-5}$ years, respectively, with R = 0.35 and R = 0.5). Looking at the faster hopping rate and their abundances on the grain surface, we have extended the consideration of the encounter desorption of these species. We have considered $\text{gX}+{\text{gH}}_2\to \text{X}+{\text{gH}}_2$, where X refers to H₂, H, and N.

In Figure 6, we have shown the time evolution of the abundances of gH, gH₂, gN, gD, and gHD with $n_H={10}^7{\text{cm}}^{-3}$, $T=10\text{K}$, and $R=0.35$. The encounter desorption of H₂ and without the encounter desorption effect are shown to show the differences. Figure 6 depicts that the abundances of gN, gH, and gH₂ have a reasonably high surface coverage. Since these species have a reasonable hopping rate at the low temperature, encounter desorption of these species need to be considered in the chemical model. Here, we have included the encounter desorption of these species sequentially to check their effect on the final abundances of some of the key surface species (gH₂O, gCH₃OH, and gNH₃). To check the effect of encounter desorption of the other species, we have sequentially included the encounter desorption of H₂, H, and N. Figure 7 shows the time evolution of the encounter desorption of gH₂O, gCH₃OH, and gNH₃. We have already discussed the encounter desorption of gH₂ in Section 3.1. Figure 7 shows that when we have included the encounter desorption of the H atom and N atom, the time evolution of the abundances shows significant changes in abundance. It depicts that considering the effect of encounter desorption of N atom can substantially increase the abundances of gH₂O, gCH₃OH, and gNH₃ for the physical condition considered here ($n_H={10}^7{\text{cm}}^{-3}$, $T=10\text{K}$, and $R=0.35$). We further have included the encounter desorption of D and HD by considering the same BE as it was obtained for H and H₂ with the H₂ substrate. The cumulative effect (by considering the encounter desorption of H, H₂, N, D, and HD together) on the abundances is shown with the dotted curve. We have noticed that the abundance profile considering the cumulative effect shows a notable difference from that obtained with the no encounter desorption case. But the cumulative effect marginally differs from the encounter desorption effect of H₂. In Figure 8, we have shown the temperature variation of the final abundances of water, methanol, and ammonia with respect to total hydrogen nuclei in all forms. It shows that the ice phase abundances of methanol, water, and ammonia can strongly deviate from the no encounter desorption case. As in Figure 7, we have also seen that the cumulative effect of the encounter desorption marginally deviates from the encounter desorption of H₂. Around 20 K, we have noticed a great match between the cumulative encounter desorption case (dash-dotted cyan line), H₂ encounter desorption case (solid red line), and no encounter desorption case (solid black line). The right panel of Figure 5 shows that as we have increased the temperature beyond 10 K, the effect of the encounter desorption of H₂ starts to decrease. Around 20 K, it roughly diminishes. Since the cumulative effect follows the nature of H₂ encounter desorption, it also matches with the no encounter desorption case at ∼20 K.

FIGURE 6

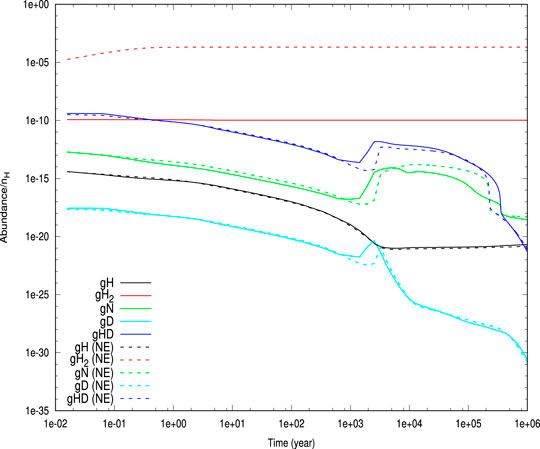
FIGURE 6. Time evolution of the abundances of H, H₂, D, HD, and N obtained from our simulation is shown. Solid curves represent the cases by considering the encounter desorption [with ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)=67\text{K}$] of H₂ and no encounter desorption (dashed curves) with ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_2\text{O}\right)=650\text{K}$, $n_H={10}^7{\text{cm}}^{-3}$, $T=10\text{K}$, and $R=0.35$.

FIGURE 7

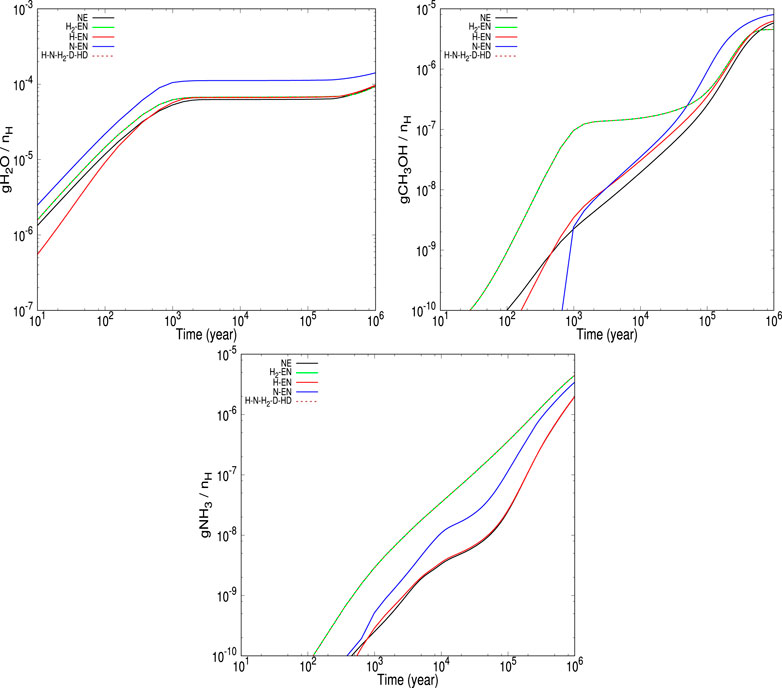
FIGURE 7. The time evolution of the abundances of ice phase water (first panel), methanol (second panel), and ammonia (third panel) is shown for $n_H={10}^7{\text{cm}}^{-3}$, $T=10\text{K}$, and $R=0.35$. It shows a significant difference between the consideration of encounter desorption (solid green line for H₂, solid red line for H, and solid blue line for N) and without encounter desorption (black line). The encounter desorption of H, N, H₂, D, and HD are collectively considered (brown dotted line) and show that it marginally deviates from the encounter desorption of H₂.

FIGURE 8

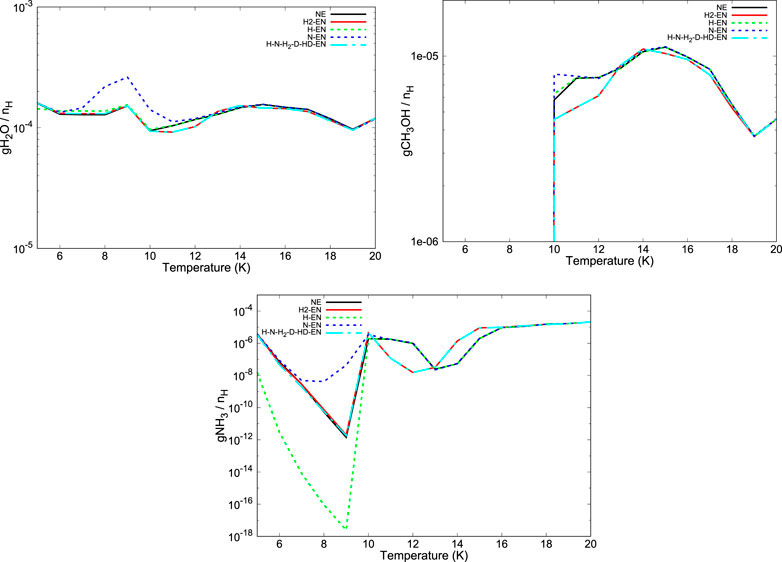
FIGURE 8. Temperature variation of the abundances of ice phase water (first panel), methanol (second panel), and ammonia (third panel) is shown for $n_H={10}^7{\text{cm}}^{-3}$ and $R=0.35$. It shows a significant difference between the consideration of encounter desorption and without encounter desorption (black line). The encounter desorption of H, N, H₂, D, and HD are collectively considered, and as like Figure 7, it marginally varies from the encounter desorption of H₂.

4 Conclusion

Here, we have provided realistic BEs of the interstellar species with the H₂ substrate. Supported with these BE values, we further have implemented our CMMC model to check the encounter desorption effect of H₂, H, and N on the interstellar ices. Following are the major highlights of this study.

• Our quantum chemical calculation finds a lower BE value (∼10 times) of all the species than it was obtained with the water (Das et al., 2018) substrate.

• Earlier in the literature, ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)=23\text{K}$ (Cuppen and Herbst, 2007; Hincelin et al., 2015; Chang et al., 2021) and ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_2\right)=45\text{K}$ (Cuppen and Herbst, 2007; Chang et al., 2021) are used. Our quantum chemical calculations find an opposite trend with ${\text{E}}_{\text{D}}\left({\text{H}}_2,{\text{H}}_2\right)=67\text{K}$ and ${\text{E}}_{\text{D}}\left(\text{H},{\text{H}}_2\right)=23\text{K}$. Sil et al. (2017) also explored that BE of the H₂ molecule always remains higher than that of the H atom considering different adsorbents like benzene, silica, and water cluster. The consideration of these updated adsorption energies show a significant deviation in the abundances of the surface species.

• Our modeling results suggest that the inclusion of the encounter desorption of the H, H₂, and N can affect the abundances of the major surface constituents like water, methanol, and ammonia. The cumulative effect roughly resembles a similar abundance with that obtained with the H₂’s encounter desorption only. For a bit higher temperature (∼20 K), when the encounter desorption effect of H₂ ceases, the encounter desorption of the cumulative cases exactly matches with the no encounter desorption case.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

MS acknowledges DST, the Government of India, for providing financial assistance through the DST-INSPIRE Fellowship [IF160109] scheme. SA and SS acknowledge Indian Center for Space Physics for allowing them to continue their M. Sc. project work. This research was possible in part due to a Grant-In-Aid from the Higher Education Department of the Government of West Bengal.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.671622/full#supplementary-material

References

Bergin, E. A., and Tafalla, M. (2007). Cold Dark Clouds: The Initial Conditions for Star Formation. Annu. Rev. Astron. Astrophysics 45, 339–396. doi:10.1146/annurev.astro.45.071206.100404

CrossRef Full Text | Google Scholar

Boogert, A. C. A., Gerakines, P. A., and Whittet, D. C. B. (2015). Observations of the Icy Universe. Annu. Rev. Astron. Astrophysics 53, 541–581. doi:10.1146/annurev-astro-082214-122348

CrossRef Full Text | Google Scholar

Cancès, E., Mennucci, B., and Tomasi, J. (1997). A New Integral Equation Formalism for the Polarizable Continuum Model: Theoretical Background and Applications to Isotropic and Anisotropic Dielectrics. J. Chem. Phys. 107, 3032–3041. doi:10.1063/1.474659

CrossRef Full Text | Google Scholar

Chaabouni, H., Bergeron, H., Baouche, S., Dulieu, F., Matar, E., Congiu, E., et al. (2012). Sticking Coefficient of Hydrogen and Deuterium on Silicates under Interstellar Conditions. Astron. Astrophysics 538, A128. doi:10.1051/0004-6361/201117409

CrossRef Full Text | Google Scholar

Chakrabarti, S. K., Das, A., Acharyya, K., and Chakrabarti, S. (2006a). Effective Grain Surface Area in the Formation of Molecular Hydrogen in Interstellar Clouds. Astron. Astrophysics 457, 167–170. doi:10.1051/0004-6361:20065335

CrossRef Full Text | Google Scholar

Chakrabarti, S. K., Das, A., Acharyya, K., and Chakrabarti, S. (2006b). Recombination Efficiency of Molecular Hydrogen on Interstellar Grains-II. A Numerical Study. Bull. Astronom. Soc. India 34, 299. https://ui.adsabs.harvard.edu/abs/2006BASI...34..299C/abstract

Google Scholar

Chang, Q., Zheng, X. L., Zhang, X., Quan, D. H., Lu, Y., Meng, Q. K., et al. (2021). On the Encounter Desorption of Hydrogen Atoms on an Ice Mantle. Res. Astron. Astrophys. 21, 039. doi:10.1088/1674-4527/21/2/39

CrossRef Full Text | Google Scholar

Collings, M. P., Anderson, M. A., Chen, R., Dever, J. W., Viti, S., Williams, D. A., et al. (2004). A Laboratory Survey of the Thermal Desorption of Astrophysically Relevant Molecules. Monthly Notices R. Astronom. Soc. 354, 1133–1140. doi:10.1111/j.1365-2966.2004.08272.x

CrossRef Full Text | Google Scholar

Cuppen, H. M., and Herbst, E. (2007). Simulation of the Formation and Morphology of Ice Mantles on Interstellar Grains. Astrophysical J. 668, 294–309. doi:10.1086/521014

CrossRef Full Text | Google Scholar

Das, A., Acharyya, K., Chakrabarti, S., and Chakrabarti, S. K. (2008a). Formation of Water and Methanol in Star Forming Molecular Clouds. Astron. Astrophysics 486, 209–220. doi:10.1051/0004-6361:20078422

CrossRef Full Text | Google Scholar

Das, A., Acharyya, K., and Chakrabarti, S. K. (2010). Effects of Initial Condition and Cloud Density on the Composition of the Grain Mantle. Monthly Notices R. Astronomical Soc. 409, 789–800. doi:10.1111/j.1365-2966.2010.17343.x

CrossRef Full Text | Google Scholar

Das, A., and Chakrabarti, S. K. (2011). Composition and Evolution of Interstellar Grain Mantle under the Effects of Photodissociation. Monthly Notices R. Astronomical Soc. 418, 545–555. doi:10.1111/j.1365-2966.2011.19503.x

CrossRef Full Text | Google Scholar

Das, A., Majumdar, L., Chakrabarti, S. K., and Sahu, D. (2015b). Deuterium Enrichment of the Interstellar Medium. New Astron. 35, 53–70. doi:10.1016/j.newast.2014.07.006

CrossRef Full Text | Google Scholar

Das, A., Majumdar, L., Sahu, D., Gorai, P., Sivaraman, B., and Chakrabarti, S. K. (2015a). Methyl Acetate and its Singly Deuterated Isotopomers in the Interstellar Medium. Astrophys. J. 808, 21. doi:10.1088/0004-637X/808/1/21

CrossRef Full Text | Google Scholar

Das, A., Sahu, D., Majumdar, L., and Chakrabarti, S. K. (2016). Deuterium Enrichment of the Interstellar Grain Mantle. Monthly Notices R. Astronomical Soc. 455, 540–551. doi:10.1093/mnras/stv2264

CrossRef Full Text | Google Scholar

Das, A., Sil, M., Gorai, P., Chakrabarti, Si. K., and Loison, J. C. (2018). An Approach to Estimate the Binding Energy of Interstellar Species. Astrophys. J. Suppl. Ser. 237, 9. doi:10.3847/1538-4365/aac886

CrossRef Full Text | Google Scholar

Dulieu, F., Congiu, E., Noble, J., Baouche, S., Chaabouni, H., Moudens, A., et al. (2013). How Micron-Sized Dust Particles Determine the Chemistry of Our Universe. Sci. Rep. 3, 1338. doi:10.1038/srep01338

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunning J Thom, H. (1989). Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2013). Gaussian 09 Revision D.01. Wallingford CT: Gaussian Inc.

Garrod, R. T., and Pauly, T. (2011). On the Formation of CO² and Other Interstellar Ices. Astrophysical J. 735, 15. doi:10.1088/0004-637X/735/1/15

CrossRef Full Text | Google Scholar

Garrod, R. T., Wakelam, V., and Herbst, E. (2007). Non-thermal Desorption from Interstellar Dust Grains via Exothermic Surface Reactions. Astron. Astrophys. 467, 1103–1115. doi:10.1051/0004-6361:20066704

CrossRef Full Text | Google Scholar

Gibb, E. L., Whittet, D. C. B., Boogert, A. C. A., and Tielens, A. G. G. M. (2004). Interstellar Ice: The Infrared Space Observatory Legacy. Astrophys. J. Suppl. Ser. 151, 35–73. doi:10.1086/381182

CrossRef Full Text | Google Scholar

Gibb, E. L., Whittet, D. C. B., Schutte, W. A., Boogert, A. C. A., Chiar, J. E., Ehrenfreund, P., et al. (2000). An Inventory of Interstellar Ices toward the Embedded Protostar W33a. Astrophysical J. 536, 347–356. doi:10.1086/308940

CrossRef Full Text | Google Scholar

Gorai, P., Bhat, B., Sil, M., Mondal, S. K., Ghosh, R., Chakrabarti, S. K., et al. (2020b). Identification of Prebiotic Molecules Containing Peptide-like Bonds in a Hot Molecular Core, G10.47+0.03. Astrophys. J. 895, 86. doi:10.3847/1538-4357/ab8871

CrossRef Full Text | Google Scholar

Gorai, P., Das, A., Das, A., Sivaraman, B., Etim, E. E., and Chakrabarti, Si. K. (2017a). A Search for Interstellar Monohydric Thiols. Astrophys. J. 836, 70. doi:10.3847/1538-4357/836/1/70

CrossRef Full Text | Google Scholar

Gorai, P., Das, A., Majumdar, L., Chakrabarti, S. K., Sivaraman, B., and Herbst, E. (2017b). The Possibility of Forming Propargyl Alcohol in the Interstellar Medium. Mol. Astrophys. 6, 36–46. doi:10.1016/j.molap.2017.01.004

CrossRef Full Text | Google Scholar

Gorai, P., Sil, M., Das, A., Sivaraman, B., Chakrabarti, S. K., Ioppolo, S., et al. (2020a). Systematic Study on the Absorption Features of Interstellar Ices in the Presence of Impurities. ACS Earth Space Chem. 4, 920–946. doi:10.1021/acsearthspacechem.0c00098

CrossRef Full Text | Google Scholar

Hasegawa, T. I., Herbst, E., and Leung, C. M. (1992). Models of Gas-Grain Chemistry in Dense Interstellar Clouds with Complex Organic Molecules. Astrophys. J. Suppl. Ser. 82, 167. doi:10.1086/191713

CrossRef Full Text | Google Scholar

Hincelin, U., Chang, Q., and Herbst, E. (2015). A New and Simple Approach to Determine the Abundance of Hydrogen Molecules on Interstellar Ice Mantles. Astron. Astrophys. 574, A24. doi:10.1051/0004-6361/201424807

CrossRef Full Text | Google Scholar

Keto, E., and Caselli, P. (2008). The Different Structures of the Two Classes of Starless Cores. Astrophysical J. 683, 238–247. doi:10.1086/589147

CrossRef Full Text | Google Scholar

Li, A. (2004). Interaction of Nanoparticles with Radiation. in Astrophysics of Dust. Editors A. N. Witt, G. C. Clayton, and B. T. Draine (Astronomical Society of the Pacific Conference Series), Estes Park, CO, 309, 417.

Google Scholar

McElroy, D., Walsh, C., Markwick, A. J., Cordiner, M. A., Smith, K., and Millar, T. J. (2013). The UMIST Database for Astrochemistry 2012. Astron. Astrophysics 550, A36. doi:10.1051/0004-6361/201220465

CrossRef Full Text | Google Scholar

Noble, J. A., Congiu, E., Dulieu, F., and Fraser, H. J. (2012). Thermal Desorption Characteristics of CO, O² and CO² on Non-porous Water, Crystalline Water and Silicate Surfaces at Submonolayer and Multilayer Coverages. Monthly Notices R. Astronomical Soc. 421, 768–779. doi:10.1111/j.1365-2966.2011.20351.x

CrossRef Full Text | Google Scholar

Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., Blake, G. A., Evans, N. J., Lahuis, F., et al. (2008). The C2dspitzerspectroscopic Survey of Ices Around Low-Mass Young Stellar Objects. III. CH4. Astrophys. J. 678, 1032–1041. doi:10.1086/533432

CrossRef Full Text | Google Scholar

Pagani, L., Lesaffre, P., Roueff, E., Jorfi, M., Honvault, P., González-Lezana, T., et al. (2013). Philosophical Trans. R. Soc. A: Math. Phys. Eng. Sci. 370, 5201–5212. doi:10.11.1098/rsta.2012.0027

CrossRef Full Text

Roberts, H., and Millar, T. J. (2000). Modelling of Deuterium Chemistry and its Application to Molecular Clouds. Astron. Astrophysics 361, 388–398. https://ui.adsabs.harvard.edu/abs/2000A%26A...361..388R/abstract

Google Scholar

Rohatgi, A. (2020). Webplotdigitizer. Version 4.4.

Ruaud, M., Loison, J. C., Hickson, K. M., Gratier, P., Hersant, F., and Wakelam, V. (2015). Modelling Complex Organic Molecules in Dense Regions: Eley-Rideal and Complex Induced Reaction. Monthly Notices R. Astronomical Soc. 447, 4004–4017. doi:10.1093/mnras/stu2709

CrossRef Full Text | Google Scholar

Sandford, S. A., and Allamandola, L. J. (1993). H2 in Interstellar and Extragalactic Ices: Infrared Characteristics, Ultraviolet Production, and Implications. Astrophys. J. Lett. 409, L65. doi:10.1086/186861

CrossRef Full Text | Google Scholar

Semenov, D., Hersant, F., Wakelam, V., Dutrey, A., Chapillon, E., Guilloteau, S., et al. (2010). Chemistry in Disks. IV. Benchmarking Gas-Grain Chemical Models with Surface Reactions. Astron. Astrophys. 522, A42. doi:10.1051/0004-6361/201015149

CrossRef Full Text | Google Scholar

Sil, M., Gorai, P., Das, A., Bhat, B., Etim, E. E., and Chakrabarti, S. K. (2018). Chemical Modeling for Predicting the Abundances of Certain Aldimines and Amines in Hot Cores. Astrophys. J. 853, 139. doi:10.3847/1538-4357/aa984d

CrossRef Full Text | Google Scholar

Sil, M., Gorai, P., Das, A., Sahu, D., and Chakrabarti, S. K. (2017). Adsorption Energies of H and H: a Quantum-Chemical Study. Eur. Phys. J. D 71, 45. doi:10.1140/epjd/e2017-70610-4

CrossRef Full Text | Google Scholar

Tomasi, J., Mennucci, B., and Cammi, R. (2005). Quantum Mechanical Continuum Solvation Models. Chem. Rev. 105, 2999–3094. doi:10.1021/cr9904009PMID: 16092826

PubMed Abstract | CrossRef Full Text | Google Scholar

Vidali, G., Ihm, G., Kim, H. Y., and Cole, M. W. (1991). Potentials of Physical Adsorption. Surf. Sci. Rep. 12, 135–181. doi:10.1016/0167-5729(91)90012-M

CrossRef Full Text | Google Scholar

Wakelam, V., Loison, J. C., Mereau, R., and Ruaud, M. (2017). Binding Energies: New Values and Impact on the Efficiency of Chemical Desorption. Mol. Astrophys. 6, 22–35. doi:10.1016/j.molap.2017.01.002

CrossRef Full Text | Google Scholar

Ward, M. D., Hogg, I. A., and Price, S. D. (2012). Thermal Reactions of Oxygen Atoms with CS at Low Temperatures on Interstellar Dust. Monthly Notices R. Astronom. Soc. 425, 1264–1269. doi:10.1111/j.1365-2966.2012.21520.x

CrossRef Full Text | Google Scholar

Whittet, D. C. B., Shenoy, S. S., Bergin, E. A., Chiar, J. E., Gerakines, P. A., Gibb, E. L., et al. (2007). The Abundance of Carbon Dioxide Ice in the Quiescent Intracloud Medium. Astrophys. J. 655, 332–341. doi:10.1086/509772

CrossRef Full Text | Google Scholar