A Brief Review on Primordial Black Holes as Dark Matter

1 Introduction

The hypothesis of the formation of black holes (BHs) in the early Universe was first suggested in 1967 by Zeldovich and Novikov (Zel’dovich and Novikov, 1967), and independently by Hawking in 1971 (Hawking, 1971). Soon after, the possibility that primordial black holes (PBHs) could account for at least part of the DM became obvious (Chapline, 1975; Meszaros, 1975). At that time, the DM question started to be outlined as one of the fundamental problems in cosmology [see, e.g., the reviews in Sanders (2010); Bertone and Hooper (2018)]. DM (partly) composed by PBHs constitutes an exciting possibility, presenting an enormous number of observable signatures which can constrain its parameter space, as shall be detailed in Sec. 6. The variety of phenomenological effects produced by PBHs allows placing stringent bounds on the abundance of PBHs, usually indicated by the energy fraction of DM as PBHs, $f_{\text{PBH}}={\text{Ω}}_{\text{PBH}}/{\text{Ω}}_{\text{DM}}$, with ${\text{Ω}}_{\text{PBH}}$ and ${\text{Ω}}_{\text{DM}}$ the ratios of energy densities and critical density. Moreover, since PBHs are usually expected to be formed before nucleosynthesis, BBN constraints on the baryon abundance do not apply to them, as they do not intervene in the nucleosynthesis of elements, and thus, can be regarded as non-baryonic DM (Carr and Kühnel, 2020). Several recent reviews are devoted to discuss PBHs in great detail (see, e.g., Sasaki et al., 2018; Carr and Kühnel, 2020; Carr et al., 2020; Green and Kavanagh, 2021).

Shortly after the first detection of gravitational waves from a merger of $\sim 30M_{\odot }$ BHs by LIGO (Abbott et al., 2016), the question whether these could be of primordial nature was raised (Bird et al., 2016). Analysis of posterior data from the gravitational wave detectors LIGO and Virgo showed that the detected mergers are compatible with the hypothesis of their components being of primordial nature, although there is no strong preference over stellar BHs (Sasaki et al., 2016; Ali-Haïmoud et al., 2017; Clesse and García-Bellido, 2017; Clesse and García-Bellido, 2018; Garcia-Bellido et al., 2020; De Luca et al., 2020b; De Luca et al., 2021; Wong et al., 2021). PBHs with a lognormal mass function have been claimed to better fit data than BHs from astrophysical origin (Dolgov et al., 2020), although this is in contrast to the results ofHall et al. (2020), and a mixed population seems compatible or even favored (Hütsi et al., 2021).

Unlike stellar BHs, formed from the collapse of a massive star, which can present masses only above $\sim 3M_{\odot }$ [the Tolman–Oppenheimer–Volkoff limit (Oppenheimer and Volkoff, 1939; Tolman, 1939)], PBHs could be produced with any mass. Thus, a positive measurement of a BH with a mass lower than $\sim 3M_{\odot }$ would be a confirmation of the existence of primordial, non-stellar BHs (Clesse and García-Bellido, 2018). PBHs could also conform intermediate mass BHs, with masses between $\sim {10}^2{M}_{\odot }$ and ${10}^5{M}_{\odot }$, too massive to be originated from a single star. It is the case of the merger event of BHs with masses $\sim 60M_{\odot }$ and $\sim 80M_{\odot }$, producing a remnant BH of $\sim 150M_{\odot }$, in a so far mostly unobserved range of masses (Abbott et al., 2020). Furthermore, PBHs could constitute the seeds for super massive black holes (SMBHs), present in the nuclei of most galaxies, with masses ranging from ${10}^5{M}_{\odot }$ to ${10}^{10}{M}_{\odot }$, and already existing at redshifts $z>6$ (Carr and Silk, 2018). Such massive objects can hardly be produced from accreting stellar remnant BHs (Volonteri, 2010). However, the existence of massive enough PBHs may act as seeds for the SMBHs, from which they could have grown by accretion.

PBH formation is already present in standard cosmologies, although extremely unlikely. However, their production usually requires some exotic inflationary scenarios or physics beyond the Standard Model (BSM) in order to obtain a large enough abundance. The typically considered formation mechanism of PBHs arises from the direct collapse of primordial fluctuations, whose power is enhanced at small scales as a consequence of some inflationary potential, as we shall further comment on below. There are, however, other scenarios which naturally predict a population of PBHs as a result of phase transitions in the early Universe and by the collapse of topological defects (Hawking et al., 1982; Hawking, 1989; Polnarev and Zembowicz, 1991; Garriga et al., 2016; Deng et al., 2017; Deng and Vilenkin, 2017). Hence, the existence of PBHs would provide valuable hints about the still unknown physics of the very early Universe (see, e.g., Polnarev and Khlopov, 1985; Khlopov, 2010; Belotsky et al., 2014), and may allow to probe high-energy scales and supersymmetric theories (Ketov and Khlopov, 2019).

In this review, the most relevant aspects of PBHs as DM are briefly discussed, such as the mechanism of formation in Section 2, the initial abundance and mass distribution in Section 3, the process of accretion in Section 4 and other PBH features, which could leave imprints on different observables, in Section 5. Current observational constraints on their population are summarized in Section 6, and we conclude in Section 7.

2 Formation and Conditions of Collapse

The mass of a BH which collapsed in the early Universe depends on its formation time. A BH can be characterized by an extremely dense amount of matter in a very compact region, i.e., within the well-known Schwarzschild radius, $R_S=2G{M}_{\text{PBH}}/c^2\sim 3M_{\text{PBH}}/M_{\odot }\mathrm{km}$. Thus, the mean density inside that region can be estimated as ${\rho }_S=M_{\text{PBH}}/\left(4\pi R_S^3/3\right)\sim {10}^{18}{\left(M/M_{\odot }\right)}^{-2}\mathrm{g}\mathrm{c}{\mathrm{m}}^{-3}$. On the other hand, the mean density of the universe in the radiation era scales with time as ${\rho }_c\sim {10}^6{\left(t/\text{s}\right)}^{-2}\mathrm{g}\mathrm{c}{\mathrm{m}}^{-3}$. In order to have PBH formation, densities at least of the order of the mean inside the BH horizon, ${\rho }_c\sim {\rho }_S$, are needed. Therefore, the mass of the resulting PBHs should be of the order of the horizon mass at that time, i.e., the mass within a region of the size of the Hubble horizon, $M_{\text{PBH}}\sim M_{\text{H}}$ (Carr, 1975), which is defined as

$M_{\text{H}}=\frac{4}{3}\overline{\rho }{\left(\frac{c}{H}\right)}^3=\frac{c^3}{2GH}\sim {10}^{15}\text{\hspace{0.17em}g\hspace{0.17em}}\left(\frac{t}{{10}^{-23}\text{s}}\right) .(1)$

PBHs with masses of $\sim M_{\odot }\simeq 2\times {10}^{33}\mathrm{g}$ would have been formed at around the QCD phase transition, at $t\sim {10}^{-6}\mathrm{s}$. Since the PBH mass is roughly given by the mass within the horizon, it means that fluctuations entering the horizon can collapse into PBHs. A detailed calculation shows that $M_{\text{PBH}}=\gamma M_{\text{H}}$, where the proportionality factor γ depends on the details of gravitational collapse, and gets values lower than 1. Early estimates showed that it can be approximated as $\gamma \simeq c_s^{3/2}\simeq 0.2$, with $c_s=1/3$ the sound speed at the radiation epoch (Carr, 1975) More refined results show that the PBH mass is given by a scaling relation with the overdensityδ, $M_{\text{PBH}}=\kappa {\left(\delta -{\delta }_c\right)}^{\alpha }$ (Niemeyer and Jedamzik, 1998; Niemeyer and Jedamzik, 1999), where κ and α are order unity constants, which depend on the background cosmology and on the shape of the perturbation (Niemeyer and Jedamzik, 1998; Niemeyer and Jedamzik, 1999; Musco et al., 2005), and${\delta }_c\simeq c_s^2$ is the collapse threshold [see, e.g., Escrivà et al., 2021; Musco et al., 2021 for recent accurate computations]. Figure 1 depicts a sketch of the process of PBH formation.

FIGURE 1

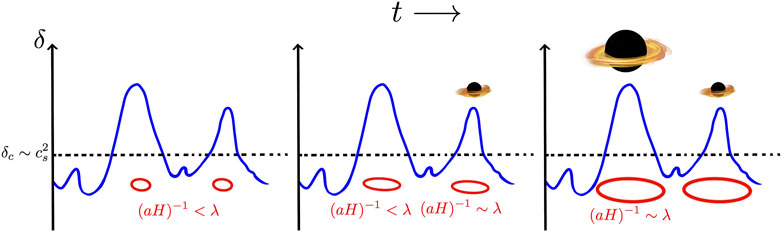
FIGURE 1. Sketch of the formation of PBHs from overdensities for three different successive moments. When fluctuations larger than a critical threshold ${\delta }_c\sim c_s^2$ enter the horizon, i.e., their wavelength $\lambda =2\pi /k$ (which characterizes the size of the perturbation) is of the order of the Hubble horizon ${\left(aH\right)}^{-1}$, the overdense region collapses and a PBH is produced. As can be seen in Eqs 1, 2, longer modes (large λ, low k) enter the horizon later and lead to more massive PBHs.

Since PBHs are formed when fluctuations cross the horizon by the time of formation, $t_f$, their mass can be related to the wavelength of perturbations. When the mode of wavenumber k crosses the horizon, the condition $a\left(t_f\right)H\left(t_f\right)=k$ holds. Since the mass of PBHs is proportional to the horizon mass at the moment of formation, $M_{\text{PBH}}\propto \gamma H^{-1}$, at the radiation dominated era (Sasaki et al., 2018),

$M_{\text{PBH}}\simeq 30M_{\odot }\left(\frac{\gamma }{0.2}\right){\left(\frac{2.9\times {10}^5\text{Mpc}}{k}\right)}^2 .(2)$

Hence, probing a given scale k could constrain a PBH population of its corresponding mass. Furthermore, an enhancement in the power spectrum around that scale would result in a large number of PBHs of such masses. In this review, we shall only consider PBHs formed during the radiation era. Those produced before inflation ends would have been diluted due to their negligible density during the inflationary accelerated expansion. PBHs formed during the matter-dominated era, or in an early matter domination era previous to the radiation era, have also been considered in the literature, and may have different imprints, since the conditions of collapse are less restrictive, and could start from smaller inhomogeneities (see, e.g., Green and Kavanagh, 2021).

3 Abundance and Mass Function OF PBHS

It is possible to estimate the initial abundance of PBHs at the moment of formation, taking into account all overdensities above the threshold for collapse, ${\delta }_c\simeq 1/3$. Assuming a Gaussian probability distribution, $P\left(\delta \right)$, for the overdensities with variance ${\sigma }^2\left(M\right)$ at a mass scale M, the initial abundance, defined as $\beta \left(M_{\text{H}}\right)={\rho }_{\text{PBH}}\left(t_f\right)/{\rho }_{\text{tot}}\left(t_f\right)$, is given by (Sasaki et al., 2018; Green and Kavanagh, 2021)

$\beta \left(M_{\text{PBH}}\right)\simeq \gamma {\displaystyle \underset{{\delta }_c}{\overset{\infty }{\int }}P\left(\delta \right)d\delta }\simeq \gamma \sqrt{\frac{2}{\pi }}\frac{\sigma \left(M_{\text{PBH}}\right)}{{\delta }_c}\text{exp}\left[-\frac{{\delta }_c^2}{2{\sigma }^2\left(M_{\text{PBH}}\right)}\right] ,(3)$

where in the last equality, $\sigma \left(M_{\text{H}}\right)\ll {\delta }_c$ has been assumed. For the standard cosmological scenario with an initial scale invariant power spectrum, at CMB scales, the amplitude of the fluctuations is around $\sigma \left(M_{\text{PBH}}\right)\sim {10}^{-5}$, leading to $\beta \sim {10}^{-5}\text{exp}\left(-{10}^{10}\right)$, which is completely negligible (Green, 2014). Therefore, in order to have a relevant population of PBHs, larger values of the initial power spectrum are needed. On the other hand, the assumption of a Gaussian distribution may not be consistent with enhanced fluctuations and the presence of PBHs, so deviations are unavoidable (Franciolini et al., 2018; De Luca et al., 2019b) [except for specific inflation models presenting an inflection point Atal and Germani (2019)]. Non-gaussianities could have a great impact on the initial fraction and lead to a larger population, as well as leaving detectable signatures in gravitational waves (Cai et al., 2019). Finally, note that the above formula follows the simple Press-Schechter approach, whereas to account for the non-universal nature of the threshold, the use of peak theory provides more accurate results (Green et al., 2004; Germani and Musco, 2019). Its validity, however, is limited to relatively narrow power spectra, while broader spectra require the use of non-linear statistics (Germani and Sheth, 2020).

Nonetheless, although the initial fraction β is a very small quantity, since matter and radiation densities scale differently with redshift [$\propto {\left(1+z\right)}^3$ and $\propto {\left(1+z\right)}^4$ respectively], the PBH contribution can become relevant at current times. The fraction $\beta \left(M\right)$ can be related to the current density parameters of PBH and radiation, ${\text{Ω}}_{\text{PBH}}$ and ${\text{Ω}}_{\gamma }$, as (Carr et al., 2010),

${\text{Ω}}_{\text{PBH}}\left(M\right)=\beta \left(M\right)\left(1+z_f\right){\text{Ω}}_{\gamma }\simeq {\gamma }^{1/2}\left[\frac{\beta \left(M\right)}{1.15\times {10}^{-8}}\right]{\left(\frac{M}{M_{\odot }}\right)}^{-1/2} .(4)$

For initial fractions as low as $\beta \sim {10}^{-8}$ of solar mass BHs, the fraction of energy in PBHs could be, thus, of order unity.

Depending on the specific mechanism of formation, a population of PBHs with different masses could be generated. The specific shape of the enhancement of fluctuations determines the mass distribution function. Sharp peaks in the power spectrum imply approximately monochromatic distributions. For instance, chaotic new inflation may give rise to relatively narrow peaks (Yokoyama, 1998; Saito et al., 2008). However, inflation models with an inflection point in a plateau of the potential (García-Bellido, 2017; García-Bellido and Ruiz Morales, 2017), or hybrid inflation (Clesse and García-Bellido, 2015), predict, instead, extended mass functions, which can span over a large range of PBHs masses. In this review, we focus on monochromatic distributions for simplicity, although it is possible to translate constraints to extended mass functions, which can be very stringent despite the fact of having more parameters to fit (Carr et al., 2017; Bellomo et al., 2018). Nonetheless, even if there are bounds that exclude $f_{\text{PBH}}\sim 1$ in the monochromatic case, there are choices for the mass function which allow PBHs to constitute most or all of the DM abundance (Lehmann et al., 2018; Ashoorioon et al., 2020; Sureda et al., 2020).

4 Accretion Onto PBHS

One of the consequences of the existence of PBHs with greater impact on different observables is the process of accretion. Infalling matter onto PBHs would release radiation, injecting energy into the surrounding medium, and strongly impacting its thermal state, leaving significant observable signatures. The physics of accretion is highly complex, but one can attempt a simplified approach considering the spherical non-relativistic limit, following the seminal work by Bondi (1952). In this framework, the BH is treated as a point mass surrounded by matter, embedded in a medium which tends to constant density far enough from the BH. The relevant scale is the so-called Bondi radius, defined by

$r_{\text{B}}=\frac{G{M}_{\text{PBH}}}{c_{s,\infty }^2} ,(5)$

where $c_{s,\infty }$ is the speed of sound far enough from the PBH. At distances around $\sim r_{\text{B}}$, the accretion process starts to become relevant, and the velocity of the accreted matter reaches $v\sim c_{s,\infty }$, when the density is still close to the boundary value, ${\rho }_{\infty }$. Taking into account the velocity of the BH relative to the medium, $v_{\text{rel}}$, one can write the accretion rate as (Bondi, 1952)

${\dot{M}}_{\text{PBH}}=4\pi \lambda {\rho }_{\infty }\frac{{\left(G{M}_{\text{PBH}}\right)}^2}{{\left(c_{s,\infty }^2+v_{\text{rel}}^2\right)}^{3/2}} ,(6)$

where the parameter λ is the dimensionless accretion rate and depends on the equation of state, but it is order $\sim 1$ for the cases of interest (Ali-Haïmoud and Kamionkowski, 2017). In the early Universe, $v_{\text{rel}}$ can be estimated as the baryon-DM relative velocity, computed in linear theory. Its root-mean-square value is approximately constant before recombination, dropping linearly with $1+z$ at later times (Ali-Haïmoud and Kamionkowski, 2017).

On the other hand, real BHs spin and form an accreting disk. Thus, the spherical symmetric case may not be applicable. Even though PBH spins are expected to be small, an accretion disk would form if the angular momentum is large enough to keep matter orbiting at Keplerian orbits at distances much larger than the innermost stable orbits, which are roughy given by the Schwarzschild radius (Agol and Kamionkowski, 2002). Applying this criterion, the formation of accretion disks around PBHs has been suggested to occur if the condition $f_{\text{PBH}}{M}_{\text{PBH}}/M_{\odot }\ll {\left[\left(1+z\right)/730\right]}^3$ is fulfilled (Poulin et al., 2017b). This is satisified for $M_{\text{PBH}}\mathrm{\gtrsim }{M}_{\odot }$ and large enough abundances at the epoch of CMB decoupling or at later times. Some of the results outlined above are still valid if the dimensionless accretion rate λ is suppresed by roughly two orders of magnitude, after accounting for viscosity effects and matter outflows through jets (Poulin et al., 2017b).

The matter falling onto BHs is greatly accelerated, which gives rise to radiative emission of high-energy photons by processes such as bremsstrahlung. The luminosity of accreting BHs is proportional to its accretion rate, and can be written as (Xie and Yuan, 2012)

$L_{\text{acc}}=\mathrm{ϵ}\left({\dot{M}}_{\text{PBH}}\right){\dot{M}}_{\text{PBH}} ,(7)$

where $\mathrm{ϵ}\left({\dot{M}}_{\text{PBH}}\right)$ denotes the radiative efficiency, which is in general a complicated function of the accretion rate ${\dot{M}}_{\text{PBH}}$, and depends upon the geometry, viscosity and other hydrodynamical considerations.

If the accretion disk is optically thin, most of the energy released through viscous dissipation is radiated away, and the luminosities obtained can be close to the Eddington luminosity, $L_{\text{Edd}}$, explaining the extreme brightness of many far Active Galactic Nuclei (AGN) (Shakura and Sunyaev, 1973). However, PBHs, like nearby astrophysical BHs, may radiate in a much less efficient way, through the Advective-Dominated-Accretion-Flow (ADAF) (Ichimaru, 1977; Rees et al., 1982; Narayan and Yi, 1994; Narayan and Yi, 1995) (see, e.g., Yuan and Narayan, 2014 for a review). In this scenario, the dynamics is ruled by advective currents, forming a hot thick disk. Most of the emitted energy is deposited in the same accretion disk, heating it up. Thus, only a small portion of energy is released to the surrounding medium, the radiative process being inefficient. In the ADAF scenario, the efficiency function can be fitted by a broken power-law formula, with the slopes and amplitudes dependent on the mass range and the specific modeling of viscosity effects (Xie and Yuan, 2012).

Finally, the energy emitted in the accretion processes is deposited through different channels into the medium. The energy deposition rate for each channel reads (Ali-Haïmoud and Kamionkowski, 2017; Poulin et al., 2017b)

${\left(\frac{d{E}_c}{dVdt}\right)}_{\text{dep}}=f_c\left(z\right)L_{\text{acc}}{n}_{\text{PBH}}=f_c\left(z\right)L_{\text{acc}}\frac{f_{\text{PBH}}{\rho }_{\text{DM}}}{M_{\text{PBH}}} ,(8)$

where the subscript c denotes the channel in which energy is deposited, namely: ionization, heating, or atomic excitations (where the $\text{Ly}\alpha$ transitions are the most relevant ones). The energy deposition factors $f_c\left(z\right)$ quantify the fraction of energy which goes to the different channels, and has been computed numerically (Slatyer, 2016). This energy injection would affect different types of observables, as we briefly outline below.

5 Other Generic Features

A noteworthy phenomenon of BHs is that of evaporation. Due to quantum effects in curved spacetimes, BHs may emit particles at their event horizon, as was noticed in Hawking (1974). The emitted radiation would have a nearly thermal black body spectrum, with a temperature given by (Carr et al., 2010)

$T_{\text{BH}}=\frac{\hslash c^3}{8\pi k_{B}GM}\sim {10}^{-7}\text{\hspace{0.17em}K\hspace{0.17em}}\frac{M_{\odot }}{M} ,(9)$

which is known as Hawking temperature. Due to this emission, BHs would slowly lose mass until completely evaporate. The lifetime of a PBH of initial mass M is (Lopresto, 2003)

$\tau \left(M\right)\sim {10}^{64}\text{\hspace{0.17em}yr\hspace{0.17em}}{\left(\frac{M}{M_{\odot }}\right)}^3 .(10)$

Thus, the lower the PBH mass, the earlier it evaporates. Those with masses of 10¹⁵ g or below would have already evaporated by now, having lifetimes shorter than the age of the Universe (Page, 1976), so they cannot contribute to the current DM abundance. These evaporation products or the effects they produce in different observables can be search for in a variety of experiments, probing different mass ranges. Detailed computations of the emitted spectra can be performed by codes such as BlackHawk Arbey and Auffinger (2019).

Another important feature is that of clustering. If fluctuations are originally Gaussian distributed and around a relatively narrow peak, PBHs are not expected to be originated in clusters, being initially randomly distributed on small scales (Ali-Haïmoud, 2018; Desjacques and Riotto, 2018). However, either primordial non-gaussianities or a broad peak in the power spectrum could lead to a significant initial clustering (Ballesteros et al., 2018; Suyama and Yokoyama, 2019) [although broad spectra have also been argued not to produce appreciable clustering (Moradinezhad Dizgah et al., 2019)]. Anyway, PBHs could become bounded as the Universe evolves. A proper determination of their clustering properties at later times is of great importance, for instance, in order to estimate their merger rates (Desjacques and Riotto, 2018; De Luca et al., 2020a). Indeed, the formation of clusters could alleviate some constraints on the PBH abundance (Belotsky et al., 2019).

On another hand, since PBHs would be formed from the collapse of high density peaks relatively spherically symmetric, their torques and angular momentum are expected to be small (Chiba and Yokoyama, 2017; Mirbabayi et al., 2020). It is usually quantified with the dimensionless spin parameter, $\mathcal{S}=S/\left(G{M}_{\text{PBH}}^2\right)$, where S is the spin. Estimations of for PBHs show that it is a small quantity, equal or lower than 0.01 (De Luca et al., 2019a). In contrast, astrophysical BHs are expected to have substantially larger spins, since angular momentum must be conserved during the collapse of their stars of origin, which are often rotating. Hence, the spin can serve as a good proxy to distinguish the nature of a population of BHs. The measurement of low spin parameters could represent a hint for the detection of PBHs. The latest Bayesian analyses of LIGO/Virgo mergers suggest that low values of the spin parameter are strongly preferred by data, regardless of the assumed priors (Garcia-Bellido et al., 2020). Note, however, that the PBH mass and spin depend on the accretion mechanism and their time evolution is correlated (De Luca et al., 2020c).

Furthermore, due to the discrete nature of PBHs, a Poisson shot noise contribution to the matter power spectrum, constant in wavenumber, $P_{\text{sn}}\left(k\right)\propto f_{\text{PBH}}^2{\overline{n}}_{\text{PBH}}^{-1}\propto f_{\text{PBH}}{M}_{\text{PBH}}$, would be expected (Afshordi et al., 2003; Gong and Kitajima, 2017). PBHs fluctuations give rise to isocurvature modes (Afshordi et al., 2003; Chisholm, 2006; Inman and Ali-Haïmoud, 2019), and thus, affect only at scales smaller than the horizon at the epoch of matter-radiation equality (Peacock, 1999). Therefore, this leads to an enhancement in the matter power spectrum, increasing the population of low-mass halos, which can be constrained by large scale structure and Lyα forest analyses. This effect is different from the one induced by other non-CDM candidates, such as warm DM or fuzzy DM, which suppress small scale fluctuations, washing out small structures. This contribution becomes relevant for low-mass halos not large enough to cool and collapse to form stars, which are commonly known as minihalos. It has been argued that this enhancement may produce a non-negligible 21 cm signal from the neutral hydrogen in minihalos (Gong and Kitajima, 2017, Gong and Kitajima, 2018). However, consistently accounting for the heating of the IGM due to PBH accretion increases the Jeans mass and suppresses the minihalo 21 cm signal, making it almost negligible (Mena et al., 2019).

6 Observational Constraints on PBHS as DM

PBHs can impact cosmology and astrophysics in a wide range of ways, leaving different observational effects which allow to constrain their properties. In this section, we review the most important bounds on the current fraction of PBHs as DM, $f_{\text{PBH}}={\text{Ω}}_{\text{PBH}}/{\text{Ω}}_{\text{DM}}$, for a wide range of masses $M_{\text{PBH}}$, for monochromatic mass functions. A collection of limits from the different probes is depicted in Figure 2. For a more comprehensive list of constraints, see Green and Kavanagh (2021); Carr and Kühnel (2020).

FIGURE 2

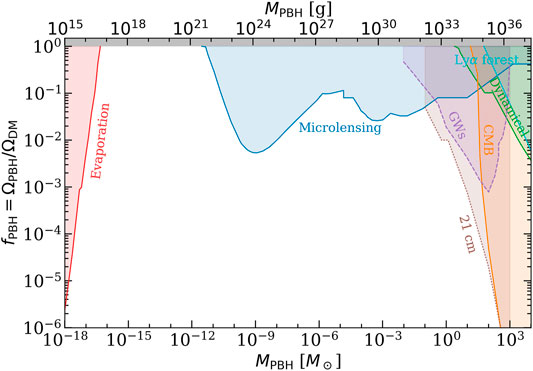
FIGURE 2. Compilation of constraints on the PBH fraction (with respect to DM) as a function of the PBH mass, assuming a monochromatic mass function. The different probes considered are: impact of PBH evaporation (red) on the extragalactic γ-ray background (Carr et al., 2010) and on the CMB spectrum (Clark et al., 2017); non-observation of microlensing events (blue) from the MACHO (Alcock et al., 2001), EROS (Tisserand et al., 2007), Kepler (Griest et al., 2014), Icarus (Oguri et al., 2018), OGLE (Niikura et al., 2019b) and Subaru-HSC (Croon et al., 2020) collaborations; PBH accretion signatures on the CMB (orange), assuming spherical accretion of PBHs within halos (Serpico et al., 2020); dynamical constraints, such as disruption of stellar systems by the presence of PBHs (green), on wide binaries (Monroy-Rodríguez and Allen, 2014) and on ultra-faint dwarf galaxies (Brandt, 2016); power spectrum from the Lyα forest (cyan) (Murgia et al., 2019); merger rates from gravitational waves (purple), either from individual mergers (Kavanagh et al., 2018; Abbott et al., 2019) or from searches of stochastic gravitational wave background (Chen and Huang, 2020). Gravitational waves limits are denoted by dashed lines, since they could be invalidated (Boehm et al., 2021). Dotted brown line corresponds to forecasts from the 21 cm power spectrum with SKA sensitivities (Mena et al., 2019) and from 21 cm forest prospects (Villanueva-Domingo and Ichiki, 2021). Figure created with the publicly available Python code PBHbounds (Kavanagh, 2019).

Evaporation

Since BHs emit energy due to Hawking radiation, those with a lifetime shorter than the age of the Universe must have disintegrated nowadays, a fact which excludes PBHs with $M_{\text{PBH}}<M_{\text{*}}\simeq 4\times {10}^{14}\mathrm{g}$ to form part of the current DM (Page, 1976). Moreover, PBHs with masses small enough, although still present, should emit a strong γ ray and cosmic ray background which could be observed. Absence of its detection strongly constrains the range of masses $M_{\text{PBH}}\mathrm{\lesssim }{10}^{17}\mathrm{g}$. In particular, the maximum fraction allowed is $f_{\text{PBH}}\mathrm{\lesssim }2\times {10}^{-8}{\left(M_{\text{PBH}}/M_{\text{*}}\right)}^{3+\mathrm{ϵ}}$, with $\mathrm{ϵ}\sim 0.1-0.4$ (Carr et al., 2016). Comparable limits have been found from INTEGRAL and COMPTEL observations of the Galactic Center (DeRocco and Graham, 2019; Laha, 2019; Coogan et al., 2020; Laha et al., 2020). Furthermore, bounds from the isotropic X-ray and soft gamma-ray background have also been recently updated (Ballesteros et al., 2020; Iguaz et al., 2021). Additionally, data on the diffuse supernova neutrino background at Super-Kamiokande are also able to set constraints (Dasgupta et al., 2020).

Microlensing

If a compact object crosses the line of sight of a star, it may produce a so-called microlensing effect, which implies a transient and achromatic amplification of its flux. The range of masses of the objects which can produce it span from $5\times {10}^{-10}$ to $\sim 100M_{\odot }$ (Paczynski, 1986; Green and Kavanagh, 2021). The non-detection of these events leads to bounds on the maximum abundance of PBHs about $f_{\text{PBH}}\mathrm{\lesssim }0.01-0.1$ by the MACHO (Alcock et al., 2001) and EROS (Tisserand et al., 2007) surveys in the Large and Small Magellanic Clouds, the Subaru Hyper Suprime Cam (HSC) in M31 (Andromeda) (Niikura et al., 2019a) and the Optical Gravitational Lensing Experiment (OGLE) in the Galactic bulge (Niikura et al., 2019b). Nonetheless, the existence of Earth-mass PBHs $\left(M_{\text{PBH}}\sim {10}^{-5}{M}_{\odot }\right)$ with a fraction $f_{\text{PBH}}\sim 0.03$ could explain the observed excess of six microlensing events found in the OGLE data (Mróz et al., 2017), which is consistent with other constraints in this range of PBHs masses (Niikura et al., 2019b). Although this may constitute a hint of their existence, it cannot be regarded as a detection of PBHs, since these microlensing observations could also be explained by free-floating planets. There are some caveats regarding the results of the MACHO collaboration (Hawkins, 2015), since the limits reported are model dependent and could be biased by the assumption of an over-massive halo. Moreover, the results of the MACHO and EROS projects have been found to be statistically incompatible. Therefore, these bounds are not completely reliable, and PBHs could not be definitely ruled out within this range of masses. Variations of the lensing effect in type Ia Supernovae (Zumalacárregui and Seljak, 2018) and gamma-ray bursts (Barnacka et al., 2012) have also been proposed to constrain the PBH parameter space, although these limits have been later invalidated (Garcia-Bellido et al., 2017; Katz et al., 2018).

Gravitational Waves

The observation of BH mergers by LIGO and Virgo collaborations can be employed to constrain the allowed number of PBHs. Demanding that the predicted merger rates of PBH binaries cannot exceed the ones measured by gravitational waves, tight upper bounds of $f_{\text{PBH}}\mathrm{\lesssim }0.01$ have been found for PBHs masses between 1 and 300 $M_{\odot }$ (Ali-Haïmoud et al., 2017; Kavanagh et al., 2018). The non-observation of a stochastic gravitational wave background of mergers expected from a population of PBHs has also been used to constrain their abundace (Chen and Huang, 2020). However, to derive these limits, BHs have been treated as Schwarzschild BHs, while it would be more appropiate to use cosmological BH solutions embedded in a FLRW metric, such as the Thakurta metric (Thakurta, 1981). This implies a time-dependent mass, and that PBH binaries created before galaxy formation would have merged at much earlier times, allowing to obtain merger rates consistent with the LIGO observations, and completely avoiding these constraints (Boehm et al., 2021).

Dynamical Constraints

Due to two-body interactions, kinetic energies of systems of different masses usually become balanced and match. If a stellar system also has an additional MACHO population, its stars would gain kinetic energy and, due to the virial theorem, the system would expand. Therefore, the presence of PBHs would dynamically heat star clusters, making them larger and with higher velocity dispersions, leading to an eventual dissolution into its host galaxy. Populations with high mass to luminosity ratios are more sensitive to this effect, as happens with ultra faint dwarf galaxies (UFDW), which would be disrupted by the presence of PBHs. Making use of these effects, tight bounds have been obtained at $f_{\text{PBH}}\sim {10}^{-3}$ for $M_{\text{PBH}}\sim {10}^4{M}_{\odot }$, weakening at lower masses down to $f_{\text{PBH}}\mathrm{\lesssim }1$ for $M_{\text{PBH}}\sim 10M_{\odot }$ (Brandt, 2016). In a similar way, wide binary stellar systems may be perturbed by compact objects, potentially being disrupted after multiple encounters. The separation distribution of wide binaries restricts the PBH fraction from $f_{\text{PBH}}\mathrm{\lesssim }1$ for $M_{\text{PBH}}\simeq 3M_{\odot }$ down to $f_{\text{PBH}}\mathrm{\lesssim }0.1$ at $M_{\text{PBH}}\mathrm{\gtrsim }70M_{\odot }$ (Monroy-Rodríguez and Allen, 2014).

CMB

Radiation emitted either by accretion or from Hawking evaporation may affect the CMB spectrum in two ways: producing spectral distortions and modifying temperature anisotropies. The energetic radiation can enhance the ionization rate, delay recombination and shift the peaks of the CMB anisotropy spectrum, as well as induce more diffusion damping. The polarization spectrum could also be modified, since the increase of the free electron fraction would increase the Thomson optical depth and enhance the reionization bump at large angular scales. Although early CMB analyses (Ricotti et al., 2008) found very stringent bounds on the allowed abundance of accreting PBHs, later works revisited these computations and found much milder constraints (Horowitz, 2016; Ali-Haïmoud and Kamionkowski, 2017). On another hand, while the former constraints rely on the assumption of spherical accretion, accreting disks have been argued to be more realistic for PBHs, resulting in tighter limits (Poulin et al., 2017b). Taking into account that PBHs could be immersed in DM halos with higher densities than the background, their accretion rates would be increased, also leading to more stringent constraints (Serpico et al., 2020). CMB limits from accretion are currently the most stringent ones for masses $\mathrm{\gtrsim }10M_{\odot }$. The main caveat is their dependence on some details of the accretion mechanisms, such as the effective velocity and the accretion rate, which may not be very well understood yet.

On the other hand, the energy injection from PBHs evaporation would produce anisotropies and spectral distortions in the CMB spectrum, which would also limit the maximum abundance, leading to similar costraints to those obtained from the extra-galactic γ-ray background commented above (Clark et al., 2017; Poulin et al., 2017a; Acharya and Khatri, 2020). Besides energy injection from accretion of BH evaporation, spectral distortions can also be produced by other means, such as the diffusion of photons due to Silk damping at small scales. This allows the translation of constraints on spectral distortions from FIRAS to stringent upper bounds on the PBH abundance, for masses $M_{\text{PBH}}>{10}^5{M}_{\odot }$ (Nakama et al., 2018).

Lyα Forest

The discrete nature of PBHs would lead to a shot-noize contribution to the matter power spectrum, enchancing small scale fluctuations. Observations of the Lyα forest, which traces matter distribution at small scales, have been employed to extract limits on the maximum allowed fraction of PBHs (Afshordi et al., 2003). The shot-noize contribution to the power spectrum depends on the joint product $f_{\text{PBH}}{M}_{\text{PBH}}$, for which the upper bound $f_{\text{PBH}}{M}_{\text{PBH}}\le 60M_{\odot }$ has been obtained (Murgia et al., 2019). The drawback of this method is on the priors of the reionization modeling and, as any Lyα forest analysis, is model dependent.

21 cm Cosmology

The 21 cm line signal from the hyperfine structure of the hydrogen is highly sensitive to the thermal state of the IGM, and thus, energy injection from PBH accretion or evaporation may leave strong observable signatures. The first claimed measurement of a global absorption dip by the EDGES collaboration (Bowman et al., 2018) may lead to competitive bounds on the PBH abundance, either from accretion processes (Hektor et al., 2018) or from energy injection by evaporation (Clark et al., 2018; Halder and Banerjee, 2021; Halder and Pandey, 2021). It must be noted, however, that the EDGES signal has not been confirmed yet by other experiments, and it has been argued that it could be explained by alternative mechanisms (Hills et al., 2018; Bradley et al., 2019; Sims and Pober, 2020). On the other hand, although the cosmological 21 cm power spectrum has not been detected yet, forecasts with future experiments such as HERA and SKA have shown that 21 cm power spectrum data from these two radiotelescopes could potentially improve the bounds up to $f_{\text{PBH}}<{10}^{-2}-{10}^{-6}$ for masses above $M_{\odot }$ (Mena et al., 2019). The 21 cm forest observed as absorption troughs in the spectra of radio sources at $z\sim 10-15$ could also provide similar limits on the PBH abundance, due to the Poisson shot noise and to the accretion heating effect (Villanueva-Domingo and Ichiki, 2021).

7 Conclusion

The extremely rich physics involved in the formation, evolution and distribution of PBHs implies a large number of observable effects which allow probing them. A myriad of constraints are present for a large range of PBHs masses. In recent years some of these limits, as those from microlensing, femtolensing, CMB accretion or BH mergers, have been revisited. Some of these bounds have been significantly weakened or have even disappeared, opening windows in the parameter space where PBHs could still form a substantial part of the DM, if not all. On the other hand, future experiments with better sensitivities may be able to reach yet unexplored regions in the parameter space and tighten up current limits. New probes, such as the 21 cm line pursued in radio interferometers like SKA, will present a promising and powerful way to proof or refute the existence of PBHs formed in the early universe and their potential contribution to the DM in the Universe.

Author Contributions

PV-D is the main author of the text and the figures. OM and SP-R have substantially collaborated in the editing process.

Funding

PV and OM are supported by the Spanish grants FPA2017-85985-P and PROMETEO/2019/083. SP is supported by the Spanish FEDER/MCIU-AEI grant FPA2017-84543-P, and partially, by the Portuguese FCT (UID/FIS/00777/2019 and CERN/FIS-PAR/0004/2019). All authors acknowledge support from the European ITN project HIDDeN (H2020-MSCA-ITN-2019//860881-HIDDeN).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abbott, B. P., Abbott, R., Abbott, T., Abbott, D., Abernathy, M. R., Acernese, K., et al. (2016). Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 116, 061102. doi:10.1103/PhysRevLett.116.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Abbott, S., Abraham, F., Acernese, K., et al. (2019). Search for Subsolar Mass Ultracompact Binaries in Advanced LIGO’s Second Observing Run. Phys. Rev. Lett. 123, 161102. doi:10.1103/PhysRevLett.123.161102

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, R., Abbott, S., Abraham, F., Acernese, K., Ackley, C., Adams, R. X., et al. (2020). GW190521: a Binary Black Hole Merger with a Total Mass of 150 M⊙. Phys. Rev. Lett. 125, 101102. doi:10.1103/PhysRevLett.125.101102

PubMed Abstract | CrossRef Full Text | Google Scholar

Acharya, S. K., and Khatri, R. (2020). CMB Spectral Distortions Constraints on Primordial Black Holes, Cosmic Strings and Long Lived Unstable Particles Revisited. JCAP 02, 010. doi:10.1088/1475-7516/2020/02/010

CrossRef Full Text | Google Scholar

Afshordi, N., McDonald, P., and Spergel, D. N. (2003). Primordial Black Holes as Dark Matter: the Power Spectrum and Evaporation of Early Structures. ApJ 594, L71–L74. doi:10.1086/378763

CrossRef Full Text | Google Scholar

Agol, E., and Kamionkowski, M. (2002). X-rays from Isolated Black Holes in the Milky Way. Mon. Not. Roy. Astron. Soc. 334, 553. doi:10.1046/j.1365-8711.2002.05523.x

CrossRef Full Text | Google Scholar

Alcock, C., Allsman, R. A., Alves, D. R., Axelrod, T. S., Becker, A. C., Bennett, D. P., et al. (2001). MACHO Project Limits on Black Hole Dark Matter in the 1-30 M Range. Astrophys. J. Lett. 550, L169. doi:10.1086/319636

CrossRef Full Text | Google Scholar

Ali-Haïmoud, Y. (2018). Correlation Function of High-Threshold Regions and Application to the Initial Small-Scale Clustering of Primordial Black Holes. Phys. Rev. Lett. 121, 081304. doi:10.1103/PhysRevLett.121.081304

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali-Haïmoud, Y., and Kamionkowski, M. (2017). Cosmic Microwave Background Limits on Accreting Primordial Black Holes. Phys. Rev. D95, 043534. doi:10.1103/PhysRevD.95.043534

CrossRef Full Text | Google Scholar

Ali-Haïmoud, Y., Kovetz, E. D., and Kamionkowski, M. (2017). Merger Rate of Primordial Black-Hole Binaries. Phys. Rev. D 96, 123523. doi:10.1103/PhysRevD.96.123523

CrossRef Full Text | Google Scholar

Arbey, A., and Auffinger, J. (2019). BlackHawk: a Public Code for Calculating the Hawking Evaporation Spectra of Any Black Hole Distribution. Eur. Phys. J. C 79, 693. doi:10.1140/epjc/s10052-019-7161-1

CrossRef Full Text | Google Scholar

Ashoorioon, A., Rostami, A., and Firouzjaee, J. T. (2020). “Charting the Landscape in Our Neighborhood from the PBHs Mass Distribution and GWs,”.

Google Scholar

Atal, V., and Germani, C. (2019). The Role of Non-gaussianities in Primordial Black Hole Formation. Phys. Dark Univ. 24, 100275. doi:10.1016/j.dark.2019.100275

CrossRef Full Text | Google Scholar

Ballesteros, G., Coronado-Blázquez, J., and Gaggero, D. (2020). X-ray and Gamma-ray Limits on the Primordial Black Hole Abundance from Hawking Radiation. Phys. Lett. B 808, 135624. doi:10.1016/j.physletb.2020.135624

CrossRef Full Text | Google Scholar

Ballesteros, G., Serpico, P. D., and Taoso, M. (2018). On the Merger Rate of Primordial Black Holes: Effects of Nearest Neighbours Distribution and Clustering. J. Cosmology Astropart. Phys. 2018, 043. doi:10.1088/1475-7516/2018/10/043

CrossRef Full Text | Google Scholar

Barnacka, A., Glicenstein, J. F., and Moderski, R. (2012). New Constraints on Primordial Black Holes Abundance from Femtolensing of Gamma-ray Bursts. Phys. Rev. D 86, 043001. doi:10.1103/PhysRevD.86.043001

CrossRef Full Text | Google Scholar

Bellomo, N., Bernal, J. L., Raccanelli, A., and Verde, L. (2018). Primordial Black Holes as Dark Matter: Converting Constraints from Monochromatic to Extended Mass Distributions. J. Cosmology Astropart. Phys. 2018, 004. doi:10.1088/1475-7516/2018/01/004

CrossRef Full Text | Google Scholar

Belotsky, K. M., Dokuchaev, V. I., Eroshenko, Y. N., Esipova, E. A., Khlopov, M. Y., Khromykh, L. A., et al. (2019). Clusters of Primordial Black Holes. Eur. Phys. J. C 79, 246. doi:10.1140/epjc/s10052-019-6741-4

CrossRef Full Text | Google Scholar

Belotsky, K. M., Dmitriev, A. D., Esipova, E. A., Gani, V. A., Grobov, A. V., et al. (2014). Signatures of Primordial Black Hole Dark Matter. Mod. Phys. Lett. A. 29, 1440005. doi:10.1142/S0217732314400057

CrossRef Full Text | Google Scholar

Bertone, G., and Hooper, D. (2018). History of Dark Matter. Rev. Mod. Phys. 90, 045002. doi:10.1103/RevModPhys.90.045002

CrossRef Full Text | Google Scholar

Bird, S., Cholis, I., Muñoz, J. B., Ali-Haïmoud, Y., Kamionkowski, M., et al. (2016). Did LIGO Detect Dark Matter? Phys. Rev. Lett. 116, 201301. doi:10.1103/PhysRevLett.116.201301

PubMed Abstract | CrossRef Full Text | Google Scholar

Boehm, C., Kobakhidze, A., O’hare, C. A. J., Picker, Z. S. C., and Sakellariadou, M. (2021). Eliminating the LIGO Bounds on Primordial Black Hole Dark Matter. JCAP 03, 078. doi:10.1088/1475-7516/2021/03/078

CrossRef Full Text | Google Scholar

Bondi, H. (1952). On Spherically Symmetrical Accretion. MNRAS 112, 195. doi:10.1093/mnras/112.2.195

CrossRef Full Text | Google Scholar

Bowman, J. D., Rogers, A. E. E., Monsalve, R. A., Mozdzen, T. J., and Mahesh, N. (2018). An Absorption Profile Centred at 78 Megahertz in the Sky-Averaged Spectrum. Nature 555, 67–70. doi:10.1038/nature25792

PubMed Abstract | CrossRef Full Text | Google Scholar

Bradley, R. F., Tauscher, K., Rapetti, D., and Burns, J. O. (2019). A Ground Plane Artifact that Induces an Absorption Profile in Averaged Spectra from Global 21 Cm Measurements, with Possible Application to EDGES. ApJ 874, 153. doi:10.3847/1538-4357/ab0d8b

CrossRef Full Text | Google Scholar

Brandt, T. D. (2016). Constraints on MACHO Dark Matter from Compact Stellar Systems in Ultra-faint dwarf Galaxies. ApJ 824, L31. doi:10.3847/2041-8205/824/2/L31

CrossRef Full Text | Google Scholar

Cai, R.-g., Pi, S., and Sasaki, M. (2019). Gravitational Waves Induced by Non-gaussian Scalar Perturbations. Phys. Rev. Lett. 122, 201101. doi:10.1103/PhysRevLett.122.201101

PubMed Abstract | CrossRef Full Text | Google Scholar

Carr, B. J. (1975). The Primordial Black Hole Mass Spectrum. ApJ 201, 1–19. doi:10.1086/153853

CrossRef Full Text | Google Scholar

Carr, B. J., Kohri, K., Sendouda, Y., and Yokoyama, J. (2010). New Cosmological Constraints on Primordial Black Holes. Phys. Rev. D 81, 104019. doi:10.1103/PhysRevD.81.104019

CrossRef Full Text | Google Scholar

Carr, B., Kohri, K., Sendouda, Y., and Yokoyama, J. (2020). “Constraints on Primordial Black Holes,”.

Google Scholar

Carr, B., and Kühnel, F. (2020). Primordial Black Holes as Dark Matter: Recent Developments. Annu. Rev. Nucl. Part. Sci. 70, 355–394. doi:10.1146/annurev-nucl-050520-125911

CrossRef Full Text | Google Scholar

Carr, B., Kühnel, F., and Sandstad, M. (2016). Primordial Black Holes as Dark Matter. Phys. Rev. D 94, 083504. doi:10.1103/PhysRevD.94.083504

CrossRef Full Text | Google Scholar

Carr, B., Raidal, M., Tenkanen, T., Vaskonen, V., and Veermäe, H. (2017). Primordial Black Hole Constraints for Extended Mass Functions. Phys. Rev. D 96, 023514. doi:10.1103/PhysRevD.96.023514

CrossRef Full Text | Google Scholar

Carr, B., and Silk, J. (2018). Primordial Black Holes as Generators of Cosmic Structures. MNRAS 478, 3756–3775. doi:10.1093/mnras/sty1204

CrossRef Full Text | Google Scholar

Chapline, G. F. (1975). Cosmological Effects of Primordial Black Holes. Nat. J. C 253, 251–252. doi:10.1038/253251a0

CrossRef Full Text | Google Scholar

Chen, Z.-C., and Huang, Q.-G. (2020). Distinguishing Primordial Black Holes from Astrophysical Black Holes by Einstein Telescope and Cosmic Explorer. J. Cosmology Astropart. Phys. 2020, 039. doi:10.1088/1475-7516/2020/08/039

CrossRef Full Text | Google Scholar

Chiba, T., and Yokoyama, S. (2017). Spin Distribution of Primordial Black Holes. PTEP 2017, 083E01. doi:10.1093/ptep/ptx087

CrossRef Full Text | Google Scholar

Chisholm, J. R. (2006). Clustering of Primordial Black Holes: Basic Results. Phys. Rev. D 73, 083504. doi:10.1103/PhysRevD.73.083504

CrossRef Full Text | Google Scholar

Clark, S., Dutta, B., Gao, Y., Ma, Y.-Z., and Strigari, L. E. (2018). 21 Cm Limits on Decaying Dark Matter and Primordial Black Holes. Phys. Rev. D 98, 043006. doi:10.1103/PhysRevD.98.043006

CrossRef Full Text | Google Scholar

Clark, S., Dutta, B., Gao, Y., Strigari, L. E., and Watson, S. (2017). Planck Constraint on Relic Primordial Black Holes. Phys. Rev. D 95, 083006. doi:10.1103/PhysRevD.95.083006

CrossRef Full Text | Google Scholar

Clesse, S., and García-Bellido, J. (2015). Massive Primordial Black Holes from Hybrid Inflation as Dark Matter and the Seeds of Galaxies. Phys. Rev. D 92, 023524. doi:10.1103/PhysRevD.92.023524

CrossRef Full Text | Google Scholar

Clesse, S., and García-Bellido, J. (2018). Seven Hints for Primordial Black Hole Dark Matter. Phys. Dark Universe 22, 137–146. doi:10.1016/j.dark.2018.08.004

CrossRef Full Text | Google Scholar

Clesse, S., and García-Bellido, J. (2017). The Clustering of Massive Primordial Black Holes as Dark Matter: Measuring Their Mass Distribution with Advanced LIGO. Phys. Dark Univ. 15, 142–147. doi:10.1016/j.dark.2016.10.002

CrossRef Full Text | Google Scholar

Coogan, A., Morrison, L., and Profumo, S. (2020). Direct Detection of Hawking Radiation from Asteroid-Mass Primordial Black Holes. Phys. Rev. Lett. 126, 171101. doi:10.1103/PhysRevLett.126.171101

CrossRef Full Text | Google Scholar

Croon, D., McKeen, D., Raj, N., and Wang, Z. (2020). Subaru-HSC through a Different Lens: Microlensing by Extended Dark Matter Structures. Phys. Rev. D 102, 083021. doi:10.1103/PhysRevD.102.083021

CrossRef Full Text | Google Scholar

Dasgupta, B., Laha, R., and Ray, A. (2020). Neutrino and Positron Constraints on Spinning Primordial Black Hole Dark Matter. Phys. Rev. Lett. 125, 101101. doi:10.1103/PhysRevLett.125.101101

PubMed Abstract | CrossRef Full Text | Google Scholar

De Luca, V., Desjacques, V., Franciolini, G., Malhotra, A., and Riotto, A. (2019a). The Initial Spin Probability Distribution of Primordial Black Holes. J. Cosmology Astropart. Phys. 2019, 018. doi:10.1088/1475-7516/2019/05/018

CrossRef Full Text | Google Scholar

De Luca, V., Desjacques, V., Franciolini, G., and Riotto, A. (2020a). The Clustering Evolution of Primordial Black Holes. JCAP 11, 028. doi:10.1088/1475-7516/2020/11/028

CrossRef Full Text | Google Scholar

De Luca, V., Franciolini, G., Kehagias, A., Peloso, M., Riotto, A., and Ünal, C. (2019b). The Ineludible Non-gaussianity of the Primordial Black Hole Abundance. J. Cosmology Astropart. Phys. 2019, 048. doi:10.1088/1475-7516/2019/07/048

CrossRef Full Text | Google Scholar

De Luca, V., Franciolini, G., Pani, P., and Riotto, A. (2021). Bayesian Evidence for Both Astrophysical and Primordial Black Holes: Mapping the GWTC-2 Catalog to Third-Generation Detectors, J. Cosmology Astroparticle Phys., 2021, 003. doi:10.1088/1475-7516/2021/05/003

CrossRef Full Text | Google Scholar

De Luca, V., Franciolini, G., Pani, P., and Riotto, A. (2020b). Primordial Black Holes Confront LIGO/Virgo Data: Current Situation. JCAP 06, 044. doi:10.1088/1475-7516/2020/06/044

CrossRef Full Text | Google Scholar

De Luca, V., Franciolini, G., Pani, P., and Riotto, A. (2020c). The Evolution of Primordial Black Holes and Their Final Observable Spins. JCAP 04, 052. doi:10.1088/1475-7516/2020/04/052

CrossRef Full Text | Google Scholar

Deng, H., Garriga, J., and Vilenkin, A. (2017). Primordial Black Hole and Wormhole Formation by Domain walls. J. Cosmology Astropart. Phys. 2017, 050. doi:10.1088/1475-7516/2017/04/050

CrossRef Full Text | Google Scholar

Deng, H., and Vilenkin, A. (2017). Primordial Black Hole Formation by Vacuum Bubbles. J. Cosmology Astropart. Phys. 2017, 044. doi:10.1088/1475-7516/2017/12/044

CrossRef Full Text | Google Scholar

DeRocco, W., and Graham, P. W. (2019). Constraining Primordial Black Hole Abundance with the Galactic 511 keV Line. Phys. Rev. Lett. 123, 251102. doi:10.1103/PhysRevLett.123.251102

PubMed Abstract | CrossRef Full Text | Google Scholar

Desjacques, V., and Riotto, A. (2018). Spatial Clustering of Primordial Black Holes. Phys. Rev. D 98, 123533. doi:10.1103/PhysRevD.98.123533

CrossRef Full Text | Google Scholar

Dolgov, A. D., Kuranov, A. G., Mitichkin, N. A., Porey, S., Postnov, K. A., Sazhina, O. S., et al. (2020). On Mass Distribution of Coalescing Black Holes. JCAP 12, 017. doi:10.1088/1475-7516/2020/12/017

CrossRef Full Text | Google Scholar

Escrivà, A., Germani, C., and Sheth, R. K. (2021). Analytical Thresholds for Black Hole Formation in General Cosmological Backgrounds. JCAP 01, 030. doi:10.1088/1475-7516/2021/01/030

CrossRef Full Text | Google Scholar

Franciolini, G., Kehagias, A., Matarrese, S., and Riotto, A. (2018). Primordial Black Holes from Inflation and Non-gaussianity. J. Cosmology Astropart. Phys. 2018. 016 doi:10.1088/1475-7516/2018/03/016

CrossRef Full Text | Google Scholar

García-Bellido, J. (2017). Massive Primordial Black Holes as Dark Matter and Their Detection with Gravitational Waves. J. Phys. Conf. Ser. 840, 012032. doi:10.1088/1742-6596/840/1/012032

CrossRef Full Text | Google Scholar

Garcia-Bellido, J., Clesse, S., and Fleury, P. (2017). LIGO Lo(g)Normal MACHO: Primordial Black Holes Survive SN Lensing Constraints. Phys. Dark Univ. 20, 95–100. doi:10.1016/j.dark.2018.04.005

CrossRef Full Text | Google Scholar

Garcia-Bellido, J., Nuño Siles, J. F., and Ruiz Morales, E. (2020). Bayesian Analysis of the Spin Distribution of LIGO/Virgo Black Holes. Phys. Dark Universe 31, 100791. doi:10.1016/j.dark.2021.100791

CrossRef Full Text | Google Scholar

García-Bellido, J., and Ruiz Morales, E. (2017). Primordial Black Holes from Single Field Models of Inflation. Phys. Dark Universe 18, 47–54. doi:10.1016/j.dark.2017.09.007

CrossRef Full Text | Google Scholar

Garriga, J., Vilenkin, A., and Zhang, J. (2016). Black Holes and the Multiverse. J. Cosmology Astropart. Phys. 2016, 064. doi:10.1088/1475-7516/2016/02/064

CrossRef Full Text | Google Scholar

Germani, C., and Musco, I. (2019). Abundance of Primordial Black Holes Depends on the Shape of the Inflationary Power Spectrum. Phys. Rev. Lett. 122, 141302. doi:10.1103/PhysRevLett.122.141302

PubMed Abstract | CrossRef Full Text | Google Scholar

Germani, C., and Sheth, R. K. (2020). Nonlinear Statistics of Primordial Black Holes from Gaussian Curvature Perturbations. Phys. Rev. D 101, 063520. doi:10.1103/PhysRevD.101.063520

CrossRef Full Text | Google Scholar

Gong, J.-O., and Kitajima, N. (2018). Distribution of Primordial Black Holes and 21cm Signature. JCAP 1811, 041. doi:10.1088/1475-7516/2018/11/041

CrossRef Full Text | Google Scholar

Gong, J.-O., and Kitajima, N. (2017). Small-scale Structure and 21cm Fluctuations by Primordial Black Holes. JCAP 1708, 017. doi:10.1088/1475-7516/2017/08/017

CrossRef Full Text | Google Scholar

Green, A. M., and Kavanagh, B. J. (2021). Primordial Black Holes as a Dark Matter Candidate. J. Phys. G 48, 4. doi:10.1088/1361-6471/abc534

CrossRef Full Text | Google Scholar

Green, A. M., Liddle, A. R., Malik, K. A., and Sasaki, M. (2004). A New Calculation of the Mass Fraction of Primordial Black Holes. Phys. Rev. D 70, 041502. doi:10.1103/PhysRevD.70.041502

CrossRef Full Text | Google Scholar

Green, A. M. (2014). Primordial Black Holes: Sirens of the Early Universe. Quan. Aspects Black Holes 178, 129–149. doi:10.1007/978-3-319-10852-0_5

CrossRef Full Text | Google Scholar

Griest, K., Cieplak, A. M., and Lehner, M. J. (2014). Experimental Limits on Primordial Black Hole Dark Matter from the First 2 Yr of Kepler Data. Astrophys. J. 786, 158. doi:10.1088/0004-637X/786/2/158

CrossRef Full Text | Google Scholar

Halder, A., and Banerjee, S. (2021). Bounds on Abundance of Primordial Black Hole and Dark Matter from EDGES 21-cm Signal. Phys. Rev. D 103, 063044. doi:10.1103/PhysRevD.103.063044

CrossRef Full Text | Google Scholar

Halder, A., and Pandey, M. (2021). Investigating the Effect of PBH, Dark Matter – Baryon and Dark Matter – Dark Energy Interaction on EDGES in 21cm Signal

Google Scholar

Hall, A., Gow, A. D., and Byrnes, C. T. (2020). Bayesian Analysis of LIGO-Virgo Mergers: Primordial vs. Astrophysical Black Hole Populations. Phys. Rev. D 102, 123524. doi:10.1103/PhysRevD.102.123524

CrossRef Full Text | Google Scholar

Hawking, S. (1989). Black Holes from Cosmic Strings. Phys. Lett. B 231, 237–239. doi:10.1016/0370-2693(89)90206-2

CrossRef Full Text | Google Scholar

Hawking, S. (1971). Gravitationally Collapsed Objects of Very Low Mass. MNRAS 152, 75. doi:10.1093/mnras/152.1.75

CrossRef Full Text | Google Scholar

Hawking, S. W. (1974). Black Hole Explosions? Nat. J. C 248, 30–31. doi:10.1038/248030a0

CrossRef Full Text | Google Scholar

Hawking, S. W., Moss, I. G., and Stewart, J. M. (1982). Bubble Collisions in the Very Early Universe. Phys. Rev. D 26, 2681–2693. doi:10.1103/PhysRevD.26.2681

CrossRef Full Text | Google Scholar

Hawkins, M. R. S. (2015). A New Look at Microlensing Limits on Dark Matter in the Galactic Halo. A&A 575, A107. doi:10.1051/0004-6361/201425400

CrossRef Full Text | Google Scholar

Hektor, A., Hütsi, G., Marzola, L., Raidal, M., Vaskonen, V., and Veermäe, H. (2018). Constraining Primordial Black Holes with the EDGES 21-cm Absorption Signal. Phys. Rev. D 98, 023503. doi:10.1103/PhysRevD.98.023503

CrossRef Full Text | Google Scholar

Hills, R., Kulkarni, G., Meerburg, P. D., and Puchwein, E. (2018). Concerns about Modelling of the EDGES Data. Nat. J. C 564, E32–E34. doi:10.1038/s41586-018-0796-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Horowitz, B. (2016). Revisiting Primordial Black Holes Constraints from Ionization History

Google Scholar

Hütsi, G., Raidal, M., Vaskonen, V., and Veermäe, H. (2021). Two Populations of LIGO-Virgo Black Holes. JCAP 03, 068. doi:10.1088/1475-7516/2021/03/068

CrossRef Full Text | Google Scholar

Ichimaru, S. (1977). Bimodal Behavior of Accretion Disks - Theory and Application to Cygnus X-1 Transitions. Astrophys. J. 214, 840–855. doi:10.1086/155314

CrossRef Full Text | Google Scholar

Iguaz, J., Serpico, P. D., and Siegert, T. (2021). Isotropic X-ray Bound on Primordial Black Hole Dark Matter

Google Scholar

Inman, D., and Ali-Haïmoud, Y. (2019). Early Structure Formation in Primordial Black Hole Cosmologies. Phys. Rev. D 100, 083528. doi:10.1103/PhysRevD.100.083528

CrossRef Full Text | Google Scholar

Katz, A., Kopp, J., Sibiryakov, S., and Xue, W. (2018). Femtolensing by Dark Matter Revisited. J. Cosmology Astropart. Phys. 2018, 005. doi:10.1088/1475-7516/2018/12/005

CrossRef Full Text | Google Scholar

Kavanagh, B. J. [Dataset](2019). Bradkav/Pbhbounds: Release version. doi:10.5281/zenodo.3538999

CrossRef Full Text | Google Scholar

Kavanagh, B. J., Gaggero, D., and Bertone, G. (2018). Merger Rate of a Subdominant Population of Primordial Black Holes. Phys. Rev. D 98, 023536. doi:10.1103/PhysRevD.98.023536

CrossRef Full Text | Google Scholar

Ketov, S. V., and Khlopov, M. Y. (2019). Cosmological Probes of Supersymmetric Field Theory Models at Superhigh Energy Scales. Symmetry 11, 511. doi:10.3390/sym11040511

CrossRef Full Text | Google Scholar

Khlopov, M. Y. (2010). Primordial Black Holes. Res. Astron. Astrophys. 10, 495–528. doi:10.1088/1674-4527/10/6/001

CrossRef Full Text | Google Scholar

Laha, R., Muñoz, J. B., and Slatyer, T. R. (2020). INTEGRAL Constraints on Primordial Black Holes and Particle Dark Matter. Phys. Rev. D 101, 123514. doi:10.1103/PhysRevD.101.123514

CrossRef Full Text | Google Scholar

Laha, R. (2019). Primordial Black Holes as a Dark Matter Candidate Are Severely Constrained by the Galactic center 511 keV γ -ray Line. Phys. Rev. Lett. 123, 251101. doi:10.1103/PhysRevLett.123.251101

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmann, B. V., Profumo, S., and Yant, J. (2018). The Maximal-Density Mass Function for Primordial Black Hole Dark Matter. JCAP 04, 007. doi:10.1088/1475-7516/2018/04/007

CrossRef Full Text | Google Scholar

Lopresto, M. C. (2003). Some Simple Black Hole Thermodynamics. Phys. Teach. 41, 299–301. doi:10.1119/1.1571268

CrossRef Full Text | Google Scholar

Mena, O., Palomares-Ruiz, S., Villanueva-Domingo, P., and Witte, S. J. (2019). Constraining the Primordial Black Hole Abundance with 21-cm Cosmology. Phys. Rev. D100, 043540. doi:10.1103/PhysRevD.100.043540

CrossRef Full Text | Google Scholar

Meszaros, P. (1975). Primeval Black Holes and Galaxy Formation. A&A 38, 5–13.

Google Scholar

Mirbabayi, M., Gruzinov, A., and Noreña, J. (2020). Spin of Primordial Black Holes. JCAP 03, 017. doi:10.1088/1475-7516/2020/03/017

CrossRef Full Text | Google Scholar

Monroy-Rodríguez, M. A., and Allen, C. (2014). The End of the MACHO Era Revisited: New Limits on MACHO Masses from Halo Wide Binaries. ApJ 790, 159. doi:10.1088/0004-637X/790/2/159

CrossRef Full Text | Google Scholar

Moradinezhad Dizgah, A., Franciolini, G., and Riotto, A. (2019). Primordial Black Holes from Broad Spectra: Abundance and Clustering. J. Cosmology Astropart. Phys. 2019, 001. doi:10.1088/1475-7516/2019/11/001

CrossRef Full Text | Google Scholar

Mróz, P., Udalski, A., Skowron, J., Poleski, R., Kozlowski, S., Szymanski, M. K., et al. (2017). No Large Population of Unbound or Wide-Orbit Jupiter-mass Planets. Nat. J. C 548, 183–186. doi:10.1038/nature23276

CrossRef Full Text | Google Scholar

Murgia, R., Scelfo, G., Viel, M., and Raccanelli, A. (2019). Lyman-α forest Constraints on Primordial Black Holes as Dark Matter. Phys. Rev. Lett. 123, 071102. doi:10.1103/PhysRevLett.123.071102

PubMed Abstract | CrossRef Full Text | Google Scholar

Musco, I., De Luca, V., Franciolini, G., and Riotto, A. (2021). Threshold for Primordial Black Holes. II. A Simple Analytic Prescription. Phys. Rev. D 103, 063538. doi:10.1103/PhysRevD.103.063538

CrossRef Full Text | Google Scholar

Musco, I., Miller, J. C., and Rezzolla, L. (2005). Computations of Primordial Black Hole Formation. Class. Quant. Grav. 22, 1405–1424. doi:10.1088/0264-9381/22/7/013

CrossRef Full Text | Google Scholar

Nakama, T., Carr, B., and Silk, J. (2018). Limits on Primordial Black Holes from μ Distortions in Cosmic Microwave Background. Phys. Rev. D 97, 043525. doi:10.1103/PhysRevD.97.043525

CrossRef Full Text | Google Scholar

Narayan, R., and Yi, I. (1995). Advection Dominated Accretion: Underfed Black Holes and Neutron Stars. Astrophys. J. 452, 710. doi:10.1086/176343

CrossRef Full Text | Google Scholar

Narayan, R., and Yi, I. (1994). Advection-dominated Accretion: a Self-Similar Solution. ApJ 428, L13. doi:10.1086/187381

CrossRef Full Text | Google Scholar

Niemeyer, J. C., and Jedamzik, K. (1999). Dynamics of Primordial Black Hole Formation. Phys. Rev. D 59, 124013. doi:10.1103/PhysRevD.59.124013

CrossRef Full Text | Google Scholar

Niemeyer, J. C., and Jedamzik, K. (1998). Near-critical Gravitational Collapse and the Initial Mass Function of Primordial Black Holes. Phys. Rev. Lett. 80, 5481–5484. doi:10.1103/PhysRevLett.80.5481

CrossRef Full Text | Google Scholar

Niikura, H., Takada, M., Yasuda, N., Lupton, R. H., Sumi, T., More, S., et al. (2019a). Microlensing Constraints on Primordial Black Holes with Subaru/HSC Andromeda Observations. Nat. Astron. 3, 524–534. doi:10.1038/s41550-019-0723-1

CrossRef Full Text | Google Scholar

Niikura, H., Takada, M., Yokoyama, S., Sumi, T., and Masaki, S. (2019b). Constraints on Earth-Mass Primordial Black Holes from OGLE 5-year Microlensing Events. Phys. Rev. D 99, 083503. doi:10.1103/PhysRevD.99.083503

CrossRef Full Text | Google Scholar

Oguri, M., Diego, J. M., Kaiser, N., Kelly, P. L., and Broadhurst, T. (2018). Understanding Caustic Crossings in Giant Arcs: Characteristic Scales, Event Rates, and Constraints on Compact Dark Matter. Phys. Rev. D 97, 023518. doi:10.1103/PhysRevD.97.023518

CrossRef Full Text | Google Scholar

Oppenheimer, J. R., and Volkoff, G. M. (1939). On Massive Neutron Cores. Phys. Rev. 55, 374–381. doi:10.1103/PhysRev.55.374

CrossRef Full Text | Google Scholar

Paczynski, B. (1986). Gravitational Microlensing by the Galactic Halo. ApJ 304, 1. doi:10.1086/164140

CrossRef Full Text | Google Scholar

Page, D. N. (1976). Particle Emission Rates from a Black Hole. II. Massless Particles from a Rotating Hole. Phys. Rev. D 14, 3260–3273. doi:10.1103/PhysRevD.14.3260

CrossRef Full Text | Google Scholar

Peacock, J. A. (1999). Cosmological Physics. Cambridge University Press. doi:10.1017/CBO9780511804533

CrossRef Full Text

Polnarev, A. G., and Khlopov, M. Y. (1985). Cosmology, Primordial Black Holes, and Supermassive Particles. Sov. Phys. Usp. 28, 213–232. doi:10.1070/PU1985v028n03ABEH003858

CrossRef Full Text | Google Scholar

Polnarev, A., and Zembowicz, R. (1991). Formation of Primordial Black Holes by Cosmic Strings. Phys. Rev. D 43, 1106–1109. doi:10.1103/PhysRevD.43.1106

CrossRef Full Text | Google Scholar

Poulin, V., Lesgourgues, J., and Serpico, P. D. (2017a). Cosmological Constraints on Exotic Injection of Electromagnetic Energy. JCAP 03, 043. doi:10.1088/1475-7516/2017/03/043

CrossRef Full Text | Google Scholar

Poulin, V., Serpico, P. D., Calore, F., Clesse, S., and Kohri, K. (2017b). CMB Bounds on Disk-Accreting Massive Primordial Black Holes. Phys. Rev. D96, 083524. doi:10.1103/PhysRevD.96.083524

CrossRef Full Text | Google Scholar

Rees, M. J., Phinney, E. S., Begelman, M. C., and Blandford, R. D. (1982). Ion Supported Tori and the Origin of Radio Jets. Nature 295, 17–21. doi:10.1038/295017a0

CrossRef Full Text | Google Scholar

Ricotti, M., Ostriker, J. P., and Mack, K. J. (2008). Effect of Primordial Black Holes on the Cosmic Microwave Background and Cosmological Parameter Estimates. ApJ 680, 829–845. doi:10.1086/587831

CrossRef Full Text | Google Scholar

Saito, R., Yokoyama, J., and Nagata, R. (2008). Single-field Inflation, Anomalous Enhancement of Superhorizon Fluctuations and Non-gaussianity in Primordial Black Hole Formation. J. Cosmology Astropart. Phys. 2008, 024. doi:10.1088/1475-7516/2008/06/024

CrossRef Full Text | Google Scholar

Sanders, R. H. (2010). The Dark Matter Problem: A Historical Perspective. Cambridge University Press.

CrossRef Full Text

Sasaki, M., Suyama, T., Tanaka, T., and Yokoyama, S. (2016). Primordial Black Hole Scenario for the Gravitational-Wave Wvent GW150914. Phys. Rev. Lett. 117, 061101. doi:10.1103/PhysRevLett.117.061101

PubMed Abstract | CrossRef Full Text | Google Scholar

Sasaki, M., Suyama, T., Tanaka, T., and Yokoyama, S. (2018). Primordial Black Holes—Perspectives in Gravitational Wave Astronomy. Class. Quant. Grav. 35, 063001. doi:10.1088/1361-6382/aaa7b4

CrossRef Full Text | Google Scholar

Serpico, P. D., Poulin, V., Inman, D., and Kohri, K. (2020). Cosmic Microwave Background Bounds on Primordial Black Holes Including Dark Matter Halo Accretion. Phys. Rev. Res. 2, 023204. doi:10.1103/PhysRevResearch.2.023204

CrossRef Full Text | Google Scholar

Shakura, N. I., and Sunyaev, R. A. (1973). Black Holes in Binary Systems. Observational Appearance. Astron. Astrophys. 24, 337–355.

Google Scholar

Sims, P. H., and Pober, J. C. (2020). Testing for Calibration Systematics in the EDGES Low-Band Data Using Bayesian Model Selection. MNRAS 492, 22–38. doi:10.1093/mnras/stz3388

CrossRef Full Text | Google Scholar

Slatyer, T. R. (2016). Indirect Dark Matter Signatures in the Cosmic Dark Ages II. Ionization, Heating and Photon Production from Arbitrary Energy Injections. Phys. Rev. D93, 023521. doi:10.1103/PhysRevD.93.023521

CrossRef Full Text | Google Scholar

Sureda, J., Magaña, J., Araya, I. J., and Padilla, N. D. (2020). Press-Schechter Primordial Black Hole Mass Functions and Their Observational Constraints

Google Scholar

Suyama, T., and Yokoyama, S. (2019). Clustering of Primordial Black Holes with Non-gaussian Initial Fluctuations. Prog. Theor. Exp. Phys. 2019, 103E02. doi:10.1093/ptep/ptz105

CrossRef Full Text | Google Scholar

Thakurta, S. N. G. (1981). Kerr Metric in an Expanding Universe. Indian J. Phys. 55B, 304–310.

Google Scholar

Tisserand, P., Le Guillou, L., Afonso, C., Albert, J. N., Andersen, J., Ansari, E., et al. (2007). Limits on the MACHO Content of the Galactic Halo from the EROS-2 Survey of the Magellanic Clouds. Astron. Astrophys. 469, 387–404. doi:10.1051/0004-6361:20066017

CrossRef Full Text | Google Scholar

Tolman, R. C. (1939). Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 55, 364–373. doi:10.1103/PhysRev.55.364

CrossRef Full Text | Google Scholar

Villanueva-Domingo, P., and Ichiki, K. (2021). 21 Cm forest Constraints on Primordial Black Holes (Preprint) Arxiv

Google Scholar

Volonteri, M. (2010). Formation of Supermassive Black Holes. Astron. Astrophysics Rev. 18, 279–315. doi:10.1007/s00159-010-0029-x

CrossRef Full Text | Google Scholar

Wong, K. W. K., Franciolini, G., De Luca, V., Baibhav, V., Berti, E., Pani, P., et al. (2021). Constraining the Primordial Black Hole Scenario with Bayesian Inference and Machine Learning: the GWTC-2 Gravitational Wave Catalog. Phys. Rev. D 103, 023026. doi:10.1103/PhysRevD.103.023026

CrossRef Full Text | Google Scholar

Xie, F.-G., and Yuan, F. (2012). The Radiative Efficiency of Hot Accretion Flows. Mon. Not. Roy. Astron. Soc. 427, 1580. doi:10.1111/j.1365-2966.2012.22030.x

CrossRef Full Text | Google Scholar

Yokoyama, J. (1998). Chaotic New Inflation and Formation of Primordial Black Holes. Phys. Rev. D 58, 083510. doi:10.1103/PhysRevD.58.083510

CrossRef Full Text | Google Scholar

Yuan, F., and Narayan, R. (2014). Hot Accretion Flows Around Black Holes. Ann. Rev. Astron. Astrophys. 52, 529–588. doi:10.1146/annurev-astro-082812-141003

CrossRef Full Text | Google Scholar

Zel’dovich, Y. B., and Novikov, I. D. (1967). The Hypothesis of Cores Retarded during Expansion and the Hot Cosmological Model. Soviet Ast 10, 602.

Google Scholar

Zumalacárregui, M., and Seljak, U. (2018). Limits on Stellar-Mass Compact Objects as Dark Matter from Gravitational Lensing of Type Ia Supernovae. Phys. Rev. Lett. 121, 141101. doi:10.1103/PhysRevLett.121.141101

PubMed Abstract | CrossRef Full Text | Google Scholar