- Department of Mathematics and Mechanics, St. Petersburg State University, St. Petersburg, Russia
Model kinetic equations are proposed for the description of ionized monoatomic gas mixture flows. The mixtures are assumed enough rarefied to be treated as ideal gases after multiple ionization steps. The model equations contain the equilibrium distribution functions for the components of the gas mixtures under consideration like it was done in BGK equations and their well-known generalizations. However, in this paper the new forms of the equilibrium distribution functions are used which correspond to the entropy maximum under the constraints of momentum, total energy, nuclei and electrons (both bound and free) conservation. It is shown that the derived model equations allow us to study the local equilibrium flows of the ionized gases and the transport processes of energy, nuclei and electrons in the non-equilibrium conditions.
1 Introduction
When studying gas flows near bodies moving in the upper atmosphere, it is necessary to take into account the dissociation and ionization processes. Therefore, many theoretical studies are devoted to consideration of the transport processes in gas flows with electronic degrees of freedom, ionization and recombination [see, for example, (Zhdanov, 2009; Capitelli et al., 2012; Bruno et al., 2007; Bruno et al., 2008; Istomin and Kustova, 2014; Zhdanov and Stepanenko, 2016a; Zhdanov and Stepanenko, 2016b; Istomin and Kustova, 2017; Istomin and Kustova, 2017)]. At present, a special attention is concentrated on the kinetic description problems of the ionized gas flows with multiple ion species [see, for example, the generalization (Simakov and Molvig, 2016) of the Braginskij ion fluid description of unmagnetized plasma (Braginskii, 1958) and Ref. (Arslanbekov and Kolobov, 2018)].
The present study is devoted to the kinetic description of monoatomic gas mixtures with multiple ion species. The mixtures are assumed enough rarefied to be treated as ideal gases and to be described in terms of single-particle distribution functions even after multiple ionization steps. Under these conditions one can use the generalized Boltzmann equations like it was done for the description of gas mixtures with excitation of molecular internal degrees of freedom and chemical reactions [see, for example, (Loureiro and Amorim, 2016; Ferziger and Kaper, 1972; Vallander et al., 1977; Giovangigli, 1999; Rydalevskaya, 2003; Nagnibeda and Kustova, 2009; Loureiro and Amorim, 2016)].
In derivation of any kinetic equations, the principal difficulties are connected with the complex structure of their integral collisions operators. Therefore, full collision operators were replaced with model collision operators, first in the kinetic equations derived by Bhatnagar, Gross and Krook (BGK) for simple monoatomic gases (Bhatnagar et al., 1954). Further, the BGK model was generalized for the gas mixtures with the internal degrees of freedom of molecules and with chemical reactions [see, for example, (Morse, 1964; Hanson and Morse, 1967; Groppi and Spiga, 2004)].
In the present paper, the generalization of the BGK model is proposed for the kinetic description of the multiply ionized monoatomic gases mixtures. In the model kinetic equations the new form of the local equilibrium distribution functions for the atoms, ions and free electrons is used. These model equations allow us to derive the reduced systems of the macroscopic conservation equations.
2 Generalization of BGK Model
Consider the flow of an ionized gas mixture which consists of the neutral atoms
If the translational energy of particles is described classically or quasi-classically and their internal energy is assumed quantum, then for the determination of the ionized gas mixtures states one can use the distribution functions
where
It should be noted that the normalization conditions for the functions
In Ref. (Rydalevskaya, 2017), the equilibrium distribution functions
In the present study, to find local equilibrium functions
where k is the Boltzmann constant; W,
One can consider that
where
If one neglects the exchange effects and assumes
then the expression Eq. 4 can be rewritten in the form [see (Rydalevskaya, 2003; Rydalevskaya, 2017)]
Using the Stirling formula, we obtain
To determine the local equilibrium values
Here
The constraints which correspond to the momentum conservation can be presented in the form:
In ionized monoatomic gas flow, in addition to the energy and momentum there are
Using the method of Lagrange multipliers, for the determination of entropy density Eq. 6 maximum under constraints Eq. 7, we obtain equilibrium values
where
If the translational energy of particles is described quasi-classically and their internal energy is assumed quantum, then it is possible to turn from the numbers
where h is Planck’s constant,
To determine unknown parameters
The conservation of momentum can be written in the form
where
Introducing the particles peculiar velocities
where
For the determination of coefficients
Here
3 System of the Macroscopic Conservation Equations
The equations for the macroscopic parameters
The equation of momentum conservation is obtained as a sum of two relations. One of them follows from the kinetic Eq. 15, after multiplying them by
where
is the stress tensor.
The equation of total energy conservation is derived similarly, combining two parts. One of them follows from Eq. 15, after multiplying them by
where
is the transport energy flux.
The equations for the conservation of the nuclei
where
are the transport fluxes of the nuclei
Derivation of the conservation equation for the total number of electrons
where
is the transport flux of the electrons.
One may note that the continuity equation for density ϱ in the ionized gas mixtures is the consequence of Eqs 28, 30. Indeed, the equation
is obtained after the addition of the multiplied by the nuclei masses
and
The macroscopic Eqs 23, 26, 28 and 30 do not differ from the corresponding conservation equations which can be obtained from the kinetic equations of the Boltzmann’s type. To close the system of Eqs 23, 26, 28 and 30, it is necessary to specify the stress tensor
4 Equilibrium and Non-equilibrium Solutions of the Model Kinetic Equations
The distribution functions Eq. 17 and Eq. 18 are the equilibrium solutions of Eqs 15, 16.
If parameters
For the calculation of the equilibrium composition the gas mixture under consideration it is necessary to determine the partition functions
The temperature dependencies of the equilibrium relative concentrations of the atoms, ions and free electrons in the monoatomic ionized nitrogen at atmospheric pressure are shown in (Rydalevskaya, 2017). In the present paper the such temperature dependencies one can show for the ionized mixture monoatomic oxygen (see Figure 1).
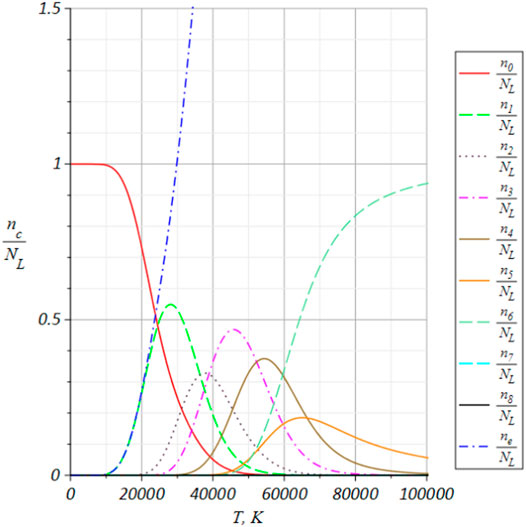
FIGURE 1. The temperature dependencies of the equilibrium relative concentrations of the atoms, ions and free electrons in the monoatomic ionized oxygen (
In non-equilibrium conditions one can turn in model equations to the dimensionless form.
In the case when a mean time θ, characterizing the rate of the macroscopic parameters variation, is known, one can introduce the dimensionless parameter
If
Under these conditions, for the solution of the model Eq. 15 and Eq. 16 one can use the Chapman–Enskog method (CEM), see, for example, (Chapman and Cowling, 1970; Ferziger and Kaper, 1972; Vallander et al., 1977; Giovangigli, 1999; Rydalevskaya, 2003; Nagnibeda and Kustova, 2009).
Substituting the expansions Eq. 26 and Eq. 27 in dimensionless model equations Eq. 7 and Eq. 8, equating the terms under the ε identical degrees and reverting to dimensionless variables, we can write
The operators
The solutions of Eqs 15, 16 in the zero-order approximation of CEM coincide with the equilibrium distribution functions
where
As a result, for the description of the local equilibrium flows of ionized gas mixtures we have the set of conservation equations:
In the present situation, one can consider that Eqs 39–42 provide the closed description of the local equilibrium flows of multiply ionized monoatomic gases mixtures. One can note that the systems of these equations allow us to deduce the series of integral relations and to obtain the analytical formulae for the study of the ionization processes influence on adiabatic coefficient and a sound velocity (Romanova and Rydalevskaya, 2017; Romanova and Rydalevskaya, 2018).
After the transition to the following approximation of CEM, we can obtain the solution of the model kinetic Eq. 15 and Eq. 16 in first-order approximation. Under these conditions relations Eq. 36 and Eq. 37 have the form:
Relations Eq. 17 and Eq. 43 allow us to find the distribution functions for the atoms
5 Conclusions
In the paper the model kinetic equations for the study of the weakly non-equilibrium flows of multi-component plasma are proposed.
These equations are the generalization of BGK model where the equilibrium distribution functions of the atoms and ions depend on the number N of corresponding chemical element in the periodic system and electric charge of the particle [see (Rydalevskaya, 2017)].
It is shown that such model equations allow one to derive the systems of the conservation equations for the energy, momentum, the numbers of the nuclei of different species and the electrons (both bound and free).
It is shown that these systems provide the closed description for local equilibrium flows of the plasma with multiple ions species.
For the solution of the model kinetic equations under consideration the Chapman–Enskog method is proposed.
It should be noted that an application of the model kinetic Eq. 15, Eq. 16 with local equilibrium functions Eq. 17 and Eq. 18 can be very important when the ionization degree of gas medium and the probabilities of the electronic energy excitation, ionization and neutralization of microscopic particles are unknown.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
MR proposed a generalization of the BGK model. YV obtained the solution of the model kinetic equations. All authors contributed to manuscript revision, read, and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank E. Kustova for useful advices.
Footnotes
References
Arslanbekov, R., and Kolobov, V. (2018). Adaptive Kinetic-Fluid Models for Expanding Plasmas. J. Phys.: Conf. Ser. 1031, 012018. doi:10.1088/1742-6596/1031/1/012018
Bhatnagar, P. L., Gross, E. P., and Krook, M. (1954). A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 94, 511–525. doi:10.1103/PhysRev.94.511
Braginskii, S. I. (1958). Transport Phenomena in a Completely Ionized Two-Temperature Plasma. Journal of Experimental and Theoretical Physics 6, 358.
Bruno, D., Capitelli, M., Catalfamo, C., and Laricchiuta, A. (2008). Cutoff Criteria of Electronic Partition Functions and Transport Properties of Atomic Hydrogen Thermal Plasmas. Physics of Plasmas 15, 112306. doi:10.1063/1.3012566
Bruno, D., Capitelli, M., Catalfamo, C., and Laricchiuta, A. (2007). Transport of Internal Electronic Energy in Atomic Hydrogen Thermal Plasmas. Physics of Plasmas 14, 072308. doi:10.1063/1.2752518
Capitelli, M., Colonna, G., and D’Angola, A. (2012). Fundamental Aspects of Plasma Chemical Physics. New York: Springer.
Chapman, S., and Cowling, T. (1970). The Mathematical Theory of Non-Uniform Gases. Cambridge: Cambridge Univ. Press.
D'Angola, A., Colonna, G., Gorse, C., and Capitelli, M. (2008). Thermodynamic and transport properties in equilibrium air plasmas in a wide pressure and temperature range. Eur. Phys. J. D. 46, 129–150. doi:10.1140/epjd/e2007-00305-4
Ferziger, J. H., and Kaper, H. G. (1972). Mathematical Theory of Transport Processes in Gases. Amsterdam: North Holland Publ. Co.
Giordano, D., Capitelli, M., and Colonna, G. (1994). Tables of Internal Partition Functions and Thermodynamics Properties of High-Temperature Air Species from 50 K to 100000 K. Paris: European Space Agency (ESA).
Groppi, M., and Spiga, G. (2004). A Bhatnagar-Gross-Krook-type approach for chemically reacting gas mixtures. Physics of Fluids 16, 4273–4284. doi:10.1063/1.1808651
Hanson, F. B., and Morse, T. F. (1967). Kinetic Models for a Gas with Internal Structure. Phys. Fluids 10, 345–353. doi:10.1063/1.1762114
Istomin, V. A., and Kustova, E. V. (2014). Effect of Electronic Excitation on High-Temperature Flows behind Strong Shock Waves. AIP Conference Proceedings 1628, 1221–1228. doi:10.1063/1.4902731
Istomin, V. A., and Kustova, E. V. (2017). State-Specific Transport Properties of Partially Ionized Flows of Electronically Excited Atomic Gases. Chemical Physics 485-486, 125–139. doi:10.1016/j.chemphys.2017.01.012
Istomin, V. A., and Kustova, E. V. (2017). Transport coefficients and heat fluxes in non-equilibrium high-temperature flows with electronic excitation. Physics of Plasmas 24, 022109. doi:10.1063/1.4975315
Loureiro, J., and Amorim, J. (2016). Kinetics and Spectroscopy of Low Temperature Plasmas. Switzerland: Springer. doi:10.1007/978-3-319-09253-9
Morse, T. F. (1964). Kinetic Model for Gases with Internal Degrees of Freedom. Phys. Fluids 7, 159–169. doi:10.1063/1.1711128
Nagnibeda, E. A., and Kustova, E. V. (2009). Non-Equilibrium Reacting Gas Flows. Berlin-Heidelberg: Springer-Verlag.
Romanova, M. S., and Rydalevskaya, M. A. (2017). Determination of equilibrium composition of thermally ionized monoatomic gas under different physical conditions. Tech. Phys. 62, 677–683. doi:10.1134/S1063784217050243
Romanova, M. S., and Rydalevskaya, M. A. (2018). Motion integrals and sound velocity in local equilibrium flows of ionized monatomic gases. Mathematics. Mechanics. Astronomy 5, 310–320.
Rydalevskaya, M. A. (2017). Simplified method for calculation of equilibrium plasma composition. Physica A: Statistical Mechanics and its Applications 476, 49–57. doi:10.1016/j.physa.2017.02.025
Rydalevskaya, M. A. (2003). Statistical and Kinetic Models in Physical-Chemical Gas Dynamics. St. Petersburg: St. Petersburg Univ. Press.
Simakov, A. N., and Molvig, K. (2016). Hydrodynamic Description of an Unmagnetized Plasma with Multiple Ion Species. I. General Formulation. Phys. Plasmas 23, 032115. doi:10.1063/1.4943894
Vallander, S. V., Nagnibeda, E. A., and Kustova, E. V. (1977). Some Quations of the Kinetic Theory of the Chemical Reacting Gas Mixtures. Leningrad: Leningrad Univ. Press.
Zhdanov, V. M., and Stepanenko, A. A. (2016a). Kinetic Theory of Transport Processes in Partially Ionized Reactive Plasma, I: General Transport Equations. Physica A: Statistical Mechanics and its Applications 446, 35–53. doi:10.1016/j.physa.2015.11.012
Keywords: model kinetic equations, ionized gas mixtures, equilibrium distribution functions, macroscopic conservation equation, BGK model
Citation: Rydalevskaya MA and Voroshilova YN (2021) Model Kinetic Equations for Multiply Ionized Gas Mixtures. Front. Astron. Space Sci. 8:696328. doi: 10.3389/fspas.2021.696328
Received: 16 April 2021; Accepted: 07 June 2021;
Published: 21 June 2021.
Edited by:
Gianpiero Colonna, National Research Council (CNR), ItalyReviewed by:
Dmitry Levko, Esgee Technologies, United StatesJayr Amorim, Instituto de Tecnologia da Aeronáutica (ITA), Brazil
Copyright © 2021 Rydalevskaya and Voroshilova. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Maria A. Rydalevskaya, cnlkYWxldnNrYUByYW1ibGVyLnJ1
 Maria A. Rydalevskaya
Maria A. Rydalevskaya Yulia N. Voroshilova
Yulia N. Voroshilova