Weak Turbulence and Quasilinear Diffusion for Relativistic Wave-Particle Interactions Via a Markov Approach

We derive weak turbulence and quasilinear models for relativistic charged particle dynamics in pitch-angle and energy space, due to interactions with electromagnetic waves propagating (anti-)parallel to a uniform background magnetic field. We use a Markovian approach that starts from the consideration of single particle motion in a prescribed electromagnetic field. This Markovian approach has a number of benefits, including: 1) the evident self-consistent relationship between a more general weak turbulence theory and the standard resonant diffusion quasilinear theory (as is commonly used in e.g. radiation belt and solar wind modeling); 2) the general nature of the Fokker-Planck equation that can be derived without any prior assumptions regarding its form; 3) the clear dependence of the form of the Fokker-Planck equation and the transport coefficients on given specific timescales. The quasilinear diffusion coefficients that we derive are not new in and of themselves, but this concise derivation and discussion of the weak turbulence and quasilinear theories using the Markovian framework is physically very instructive. The results presented herein form fundamental groundwork for future studies that consider phenomena for which some of the assumptions made in this manuscript may be relaxed.

1 Introduction

Quasilinear diffusion theory forms the basis of much of the modeling and interpretation of particle transport and energization due to interactions with electromagnetic waves; at terrestrial (Horne et al., 2005; Summers, 2005; Thorne, 2010) and planetary (Woodfield et al., 2014; Kollmann et al., 2018) radiation belts; in the solar atmosphere and solar wind (Steinacker and Miller, 1992; Vocks et al., 2005; Vocks, 2012; Verscharen and Chandran, 2013; Jeong et al., 2020); and for the dynamics of cosmic rays (Schlickeiser, 1989; Mertsch, 2020).

The classic derivations of quasilinear theory (Drummond and Pines, 1962; Vedenov et al., 1962; Kennel and Engelmann, 1966; Lerche, 1968; Lyons, 1974; Summers, 2005) not only provide the form of the Fokker-Planck equation to describe the particle dynamics, but also the diffusion coefficients that encode the effect of the resonant wave-particle interactions as a function of the background magnetic field strength, plasma refractive index, and electromagnetic wave spectral properties. It is also possible to derive the diffusion coefficients due to resonant wave-particle interactions via a different technique, i.e., a Hamiltonian analysis of single particle interactions with given wave modes (e.g., see Albert (2001); Albert (2010)). Furthermore, Lemons (2012) has demonstrated a quite general method to derive both the form of the Fokker-Planck equation itself, as well as the transport coefficients that apply in a particular circumstance.

The method presented by Lemons (2012) (building on work presented in Lemons et al. (2009)) is in principle quite general and could be applied to a wide range of phenomena, but was applied to a particular restricted case in that paper, namely particle pitch-angle dynamics due to interactions with a stationary transverse magnetic field only. Using a Markovian analysis [e.g., see Wang and Uhlenbeck (1945); Reif (2009); Zheng et al. (2019); Allanson et al. (2020)] Lemons (2012) derives a theory to describe both the weak turbulence and quasilinear regimes. Despite the fact that the electromagnetic perturbation considered is a stationary magnetic field only, the equations derived by Lemons (2012) do in fact reproduce the standard form for pitch-angle diffusion by field-aligned propagating electromagnetic waves using the quasilinear theory - for the particular case of pitch-angle diffusion only. This corresponds to the subset of plasma environments in which the plasma frequency is significantly larger than the gyrofrequency (f_pe ≫ f_ce, e.g., see Eq. 8 in Summers and Thorne (2003)).

In this paper, we study relativistic particle dynamics due to interactions with travelling electromagnetic waves, and therefore build upon the work by Lemons (2012) who considered time-invariant magnetic fields. This addition allows us to study both energy and pitch-angle dynamics, and is therefore applicable in regions with any value of f_pe/f_ce. Some of the most important expressions in this paper may not be new in and of themselves (e.g. the quasilinear theory for field-aligned waves). However, this concise self-consistent derivation and discussion of both the weak turbulence and quasilinear theories by using the Markovian framework is physically very instructive. We emphasize that the methods presented herein do allow in principle for the derivation of not only the transport (drift and diffusion) coefficients, but also the very form of the transport (Fokker-Planck) equation itself, based upon prescribed electromagnetic waves and some sensible physical assumptions.

In Section 2 we present the derivation of the general Fokker-Planck equation in energy and pitch-angle space, using the Chapman-Kolmogorov equation as a starting point, and we indicate its relationship to the most basic form (i.e., the non-bounce-averaged and two-dimensional form in e.g., Glauert and Horne (2005); Summers (2005)) of the energy and pitch-angle diffusion equation as is employed in radiation belt studies (although typically after a bounce-averaging procedure (Glauert et al., 2014)). In Section 3 we calculate the exact relativistic equations of motion for particle position, gyrophase, pitch-angle and kinetic energy, due to interactions with field-aligned electromagnetic waves. In Section 4 we present the main calculations and results of this paper, namely the derivation of the weak turbulence and quasilinear diffusion coefficients. We conclude and discuss future possible directions in Section 5, which may include the relaxing of some assumptions as presented in this manuscript.

2 Fokker-Planck Equation Derived Using Markov Theory

Consider a spatially uniform (or equivalently, a spatially averaged) collisionless particle distribution function, g_s = g_s(p, t), for particle species s, normalized according to

$\int g_s\left(\mathbf{p},t\right)d^{3}p=n_s,$

where ∫d³p is taken to be the integral over all relativistic momentum space ( − ∞ < p_x, p_y, p_z < ∞), and n_s is the number density (such that Vn_s = N_s, with N_s the total number of particles in a spatial volume V). The relativistic momentum is defined as p = γm_0sv, with v the velocity, $\gamma ={(1-v^2/c^2)}^{-1/2}$, m_0s the rest mass, and c the speed of light in a vacuum. Under the assumption of a gyrotropic distribution function (g_s(p, t) = g_s(p_∥, p_⊥, t)), we can reduce the triple integration to a double integration according to,

$2\pi {\int }_{p_{\parallel }=-\infty }^{p_{\parallel }=\infty }{\int }_{p_{\perp }=0}^{p_{\perp }=\infty }{g}_s\left(p_{\parallel },p_{\perp },t\right)p_{\perp }d{p}_{\perp }d{p}_{\parallel }=n_s,$

where p_∥ = p ⋅B₀/|B₀| and p_⊥ = |p ×B₀|/|B₀|, for B₀ the local background magnetic field, and we assume that B₀ = |B₀| > 0 without loss of generality. The relativistic momentum and kinetic energy, E, are related by p²c² = E(E + 2E_Rs) (Glauert and Horne, 2005), for E_Rs = m_0sc² the rest-mass energy. To clarify, E is the relativistic kinetic energy only, and not the total relativistic energy. Furthermore, the particle pitch angle, 0 < α < π, is defined by p_∥ = |p| cos α and p_⊥ = |p| sin α. Using these definitions and the Jacobian relation, dp_⊥dp_∥ = c⁻²(E + E_Rs)dEdα, we can rewrite the integrals so that

$\frac{2\pi }{c^3}{\int }_{\alpha =0}^{\alpha =\pi }{\int }_{E=0}^{E=\infty }{f}_s\left(E,\alpha ,t\right)\left(E+E_{\text{Rs}}\right)\sqrt{E\left(E+2E_{\text{Rs}}\right)}\mathrm{s}\mathrm{i}\mathrm{n}\alpha dEd\alpha =n_s,$

where we have made the association g_s(p_∥, p_⊥, t) = f_s(E, α, t). From hereon in we will dispense with the s subscript for brevity. We will now derive the general form of the equation that evolves f in time, as is consistent with Markovian stochastic particle dynamics in energy and pitch-angle space.

2.1 Fokker-Planck Equation in a General Form

Markovian dynamics are a special example of a stochastic/random process, and are essentially characterized by the requirement that the conditional probability of a given future state (at an immediately successive time t = t₀ + Δt) only depends on the current state (at t = t₀) (Wang and Uhlenbeck, 1945; Zheng et al., 2019). The Markovian stochastic formalism is appropriate to use in this paper since we are seeking a solution of particle motion in a statistical sense (i.e., the evolution of a particle distribution function), and not a deterministic sense (i.e., the exact dynamics of a very large number of particles).

The Chapman-Kolmogorov equation is the basic equation for Markov theory, and is also sometimes known as the Einstein-Smoluchowski equation, (e.g., see Wang and Uhlenbeck (1945); Einstein (1956); Reif (2009); Zheng et al. (2019)). The Chapman-Kolmogorov equation for f, adapted to be written in energy and pitch-angle space, is

$\begin{array}{ccc}\hfill & \hfill & f\left(E,\alpha ,t+\mathrm{\Delta }t\right)\left(E+E_{\text{R}}\right)\sqrt{E\left(E+2E_{\text{R}}\right)}\sin \alpha \hfill \\ \hfill & \hfill & ={\int }_{E^{\prime }=0}^{\infty }{\int }_{{\alpha }^{\prime }=0}^{\pi }\mathrm{\Psi }\left(E,\alpha ;E^{\prime },{\alpha }^{\prime },\mathrm{\Delta }t\right)f\left(E^{\prime },{\alpha }^{\prime },t\right)\left(E^{\prime }+E_{\text{R}}\right)\sqrt{E^{\prime }\left(E^{\prime }+2E_{\text{R}}\right)}\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }^{\prime }d{E}^{\prime }d{\alpha }^{\prime }.\hfill \end{array}$

Here, Ψ(E, α; E′, α′, Δt) is the transition probability density that a particle located at (E′, α′) at time t will reach (E, α) at time t + Δt. Using a standardized procedure based on so-called “Kramers-Moyal” theory (essentially using Taylor series, and as described in e.g. Wang and Uhlenbeck (1945); Einstein (1956); Walt (1994); Reif (2009); Roederer and Zhang (2013); Lemons (2012); Zheng et al. (2019)), we derive the following Fokker-Planck equation

$\begin{array}{ccc}\hfill \frac{\partial f}{\partial t}& =\hfill & -\frac{1}{G_1}\frac{\partial }{\partial E}\left(G_1{\mathcal{C}}_{E}f\right)-\frac{1}{G_2}\frac{\partial }{\partial \alpha }\left(G_2{\mathcal{C}}_{\alpha }f\right)\hfill \\ \hfill & \hfill & +\frac{1}{G_1}\frac{{\partial }^2}{\partial E^2}\left(G_1{\mathcal{D}}_{EE}f\right)+\frac{1}{G_2}\frac{{\partial }^2}{\partial {\alpha }^2}\left(G_2{\mathcal{D}}_{\alpha \alpha }f\right)+\frac{2}{G_1{G}_2}\frac{{\partial }^2}{\partial \alpha \partial E}\left(G_1{G}_2{\mathcal{D}}_{E\alpha }f\right),\hfill \end{array}(1)$

for $G_1(E)=(E+E_{\text{R}})\sqrt{E(E+2E_{\text{R}})}$ and G₂(α) =  sin α, and the drift and diffusion coefficients defined as

$\begin{array}{ccc}\hfill \left\{{\mathcal{C}}_{\alpha },{\mathcal{C}}_E\right\}& =\hfill & \left\{\frac{⟨\mathrm{\Delta }\alpha ⟩}{\mathrm{\Delta }t},\frac{⟨\mathrm{\Delta }E⟩}{\mathrm{\Delta }t}\right\},\hfill \\ \hfill \left\{{\mathcal{D}}_{\alpha \alpha },{\mathcal{D}}_{E\alpha },{\mathcal{D}}_{EE}\right\}& =\hfill & \left\{\frac{⟨{\left(\mathrm{\Delta }\alpha \right)}^2⟩}{2\mathrm{\Delta }t},\frac{⟨\mathrm{\Delta }E\mathrm{\Delta }\alpha ⟩}{2\mathrm{\Delta }t},\frac{⟨{\left(\mathrm{\Delta }E\right)}^2⟩}{2\mathrm{\Delta }t}\right\},\hfill \end{array}$

where ⟨…⟩ denotes a suitable statistical or ensemble average, and the set notation {…} is used only to write the definitions in a compact manner. The denominator in the transport coefficients, Δt = t − t₀, is a ‘suitable’ timescale over which to consider the drift/diffusion, and helps to define the increments Δα = α(t₀ + Δt) − α(t₀), ΔE = E(t₀ + Δt) − E(t₀) (e.g., see Liu et al. (2010); Liu et al. (2012)); Lemons (2012); Allanson et al. (2019); Allanson et al. (2020) for discussions regarding ensemble averages and timescales). Note that here we are using the same formal definitions of transport coefficients as in e.g., Lemons (2012); Glauert et al. (2014), such that ${\mathcal{C}}_{\alpha }$, ${\mathcal{C}}_E$, ${\mathcal{D}}_{\alpha \alpha }$, ${\mathcal{D}}_{\alpha E}$, and ${\mathcal{D}}_{EE}$, have units of s⁻¹, Js⁻¹, s⁻¹, Js⁻¹ and J²s⁻¹, respectively.

Equation 1 is the Fokker-Planck equation that describes particle transport (diffusion and drift) in relativistic kinetic energy and pitch-angle space, under the assumption of Markovian stochastic dynamics and a uniform background magnetic field. It is currently written in a very general form, and an investigation of the particle dynamics in a given system (i.e., a given set of background and perturbative forces and considered timescales) may reveal the exact form of the diffusion and drift coefficients, their relationship, and thus the exact form of Eq. 1 itself.

2.2 Fokker-Planck Equation Reduced to a More Familiar Form

Equation 1 can be re-written as

$\begin{array}{ccc}\hfill \frac{\partial f}{\partial t}& =\hfill & -\frac{1}{G_1}\frac{\partial }{\partial E}\left[f\left(G_1{\mathcal{C}}_E-\frac{\partial }{\partial E}\left(G_1{\mathcal{D}}_{EE}\right)-\frac{G_1}{G_2}\frac{\partial }{\partial \alpha }\left(G_2{\mathcal{D}}_{\alpha E}\right)\right)\right]\hfill \\ \hfill & \hfill & -\frac{1}{G_2}\frac{\partial }{\partial \alpha }\left[f\left(G_2{\mathcal{C}}_{\alpha }-\frac{\partial }{\partial \alpha }\left(G_2{\mathcal{D}}_{\alpha \alpha }\right)-\frac{G_2}{G_1}\frac{\partial }{\partial E}\left(G_1{\mathcal{D}}_{\alpha E}\right)\right)\right]\hfill \\ \hfill & \hfill & +\frac{1}{G_1}\frac{\partial }{\partial E}\left[G_1\left({\mathcal{D}}_{EE}\frac{\partial f}{\partial E}+{\mathcal{D}}_{\alpha E}\frac{\partial f}{\partial \alpha }\right)\right]\hfill \\ \hfill & \hfill & +\frac{1}{G_2}\frac{\partial }{\partial \alpha }\left[G_2\left({\mathcal{D}}_{\alpha \alpha }\frac{\partial f}{\partial \alpha }+{\mathcal{D}}_{\alpha E}\frac{\partial f}{\partial E}\right)\right].\hfill \end{array}$

Examination of the particle dynamics in a given system can reveal the relationship between the drift and diffusion coefficients, sometimes known as the “drift-diffusion relation” (e.g. see Lemons (2012)). As one specific example, consider that the following drift-diffusion relations could be satisfied,

$\begin{array}{ccc}\hfill {\mathcal{C}}_E& =\hfill & \frac{1}{G_1}\frac{\partial }{\partial E}\left(G_1{\mathcal{D}}_{EE}\right)+\frac{1}{G_2}\frac{\partial }{\partial \alpha }\left(G_2{\mathcal{D}}_{\alpha E}\right),\hfill \end{array}(2)$

$\begin{array}{ccc}\hfill {\mathcal{C}}_{\alpha }& =\hfill & \frac{1}{G_2}\frac{\partial }{\partial \alpha }\left(G_2{\mathcal{D}}_{\alpha \alpha }\right)+\frac{1}{G_1}\frac{\partial }{\partial E}\left(G_1{\mathcal{D}}_{\alpha E}\right),\hfill \end{array}(3)$

then Eq. 1 reduces to the following transport equation for energy and pitch angle diffusion

$\begin{array}{ccc}\hfill \frac{\partial f}{\partial t}& =\hfill & \frac{1}{\sin \alpha }\frac{\partial }{\partial \alpha }\left[\sin \alpha \left({\mathcal{D}}_{\alpha \alpha }\frac{\partial f}{\partial \alpha }+{\mathcal{D}}_{\alpha E}\frac{\partial f}{\partial E}\right)\right]\hfill \\ \hfill & +\hfill & \frac{1}{\left(E+E_{\text{R}}\right)\sqrt{E\left(E+2E_{\text{R}}\right)}}\frac{\partial }{\partial E}\left[\left(E+E_{\text{R}}\right)\sqrt{E\left(E+2E_{\text{R}}\right)}\left({\mathcal{D}}_{EE}\frac{\partial f}{\partial E}+{\mathcal{D}}_{\alpha E}\frac{\partial f}{\partial \alpha }\right)\right].\hfill \end{array}(4)$

Equation 4 is exactly consistent with the standard relativistic quasilinear equation as derived via a different approach (see discussion of derivations and regions of applicability in Sections 1 and 5), used to describe energy and pitch-angle dynamics due to wave-particle interactions in the resonant diffusion quasilinear theory (Glauert and Horne, 2005; Summers, 2005) prior to ‘bounce-averaging’.

Equation 4 (or some variant thereof that may also include dynamics in real/radial space, and/or a so-called ‘bounce-/drift-averaging’ procedure) is often known as ‘the diffusion equation’ in the terrestrial and planetary magnetospheric communities. This reflects the fact that one can only see diffusion coefficents “$\mathcal{D}$” playing a role in the dynamics. The exact form of “the diffusion equation” (e.g., see Kennel and Engelmann (1966); Schulz and Lanzerotti (1974)) is a result of the most typical derivation method employed—essentially a perturbative analysis of the Vlasov-Maxwell system (see a discussion in Section 5 of this paper).

However it is important to note that some form of drift processes are in principle playing a role, despite the fact they do not appear in Eq. 4. The drift-diffusion relations in Eqs 2, 3 demonstrate this fact. Equations 2, 3 do not state that the drift coefficients “$\mathcal{C}$” = 0, but rather that “$\mathcal{C}$” takes a restricted set of values such that the only drift to occur is determined by gradients in the diffusion coefficients themselves (e.g., see discussions in Lemons (2012) and Zheng et al. (2019) for the slightly simpler cases of dynamics in pitch-angle space only and a single “action-integral” space only, respectively). These insights are one benefit of using this Markovian approach—and one can conclude that Eq. 4 describes a particular subset of a more rich set of possible particle dynamics, that are described by Eq. 1.

It is therefore of great interest to try and derive Fokker-Planck equations for a given system using the Markovian approach (as opposed to the historically more standard Vlasov-Maxwell approach), to see if we can gain more insights regarding energetic particle dynamics. One important question is to discover when a more standard “diffusion equation” such as Eq. 4 is appropriate, and when a more rich formalism such as Eq. 1 is necessary.

3 Exact Equations of Motion

We consider a right-handed xyz co-ordinate system, with a uniform background magnetic field B₀ = (B₀, 0, 0) defining x as the “parallel’” direction, with “perpendicular” quantities in the yz plane. Particle velocities are defined according to

$\mathbf{v}=\left(v_x,v_y,v_z\right)=|\mathbf{v}|\left(\cos \alpha ,\sin \alpha \cos \varphi ,\sin \alpha \sin \varphi \right).$

The magnetic components of a field-aligned electromagnetic spectrum can be expressed as a sum over all considered wave-modes k. We define $\mathbf{k}=\bar{k}|{\mathrm{\Omega }}_0|c^{-1}\widehat{\mathbf{x}}$, with Ω₀ = qB₀/(m₀γ) the signed relativistic gyrofrequency in the background field B₀, and $\bar{k}$ a dimensionless variable such that $-\infty <\bar{k}<\infty$. We can define the magnetic wave fields using Fourier transforms over the dimensionless variable $\bar{k}$

$\begin{array}{ccc}\hfill B_y\left(x,t\right)& =\hfill & \frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\tilde{B}}_y\left(\bar{k},x,t\right)d\bar{k}=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\tilde{B}\left(\bar{k}\right)\cos \psi \left(\bar{k},x,t\right)d\bar{k},\hfill \end{array}(5)$

$\begin{array}{ccc}\hfill B_z\left(x,t\right)& =\hfill & \frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\tilde{B}}_z\left(\bar{k},x,t\right)d\bar{k}=\mp \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\tilde{B}\left(\bar{k}\right)\sin \psi \left(\bar{k},x,t\right)d\bar{k}.\hfill \end{array}(6)$

The ∓ sign corresponds to right-/left-handed waves (e.g., field-aligned whistler-mode and electromagnetic ion-cyclotron waves respectively). Note that by using a dimensionless $\bar{k}$, this implies that $\tilde{B}(\bar{k})$ has the same dimensions as B₀, i.e. that of a magnetic field. The phase is defined by $\psi (\bar{k},x,t)=\mathbf{k}\cdot \mathbf{x}-\omega (\bar{k})\mathrm{\Delta }t=\bar{k}|{\mathrm{\Omega }}_0|c^{-1}x-\omega (\bar{k})\mathrm{\Delta }t$, with $\omega =\omega (\bar{k})$ the dispersion relation of mode $\bar{k}$. For completeness, the Fourier amplitudes of the magnetic and electric perturbations, $\tilde{\mathbf{B}}(\bar{k},x,t)$ and $\tilde{\mathcal{E}}(\bar{k},x,t)$ respectively, associated with a given single wave mode characterized by the wave-vector k, are defined by

$\begin{array}{ccc}\hfill \tilde{\mathbf{B}}\left(\bar{k},x,t\right)& =\hfill & \left(0,{\tilde{B}}_y\left(\bar{k},x,t\right),{\tilde{B}}_z\left(\bar{k},x,t\right)\right)=\tilde{B}\left(\bar{k}\right)\left(0,\cos \psi \left(\bar{k},x,t\right),\mp \sin \psi \left(\bar{k},x,t\right)\right)\left.\right),\hfill \end{array}(7)$

$\begin{array}{ccc}\hfill \tilde{\mathcal{E}}\left(\bar{k},x,t\right)& =\hfill & \left(0,{\tilde{\mathcal{E}}}_y\left(\bar{k},x,t\right),{\tilde{\mathcal{E}}}_z\left(\bar{k},x,t\right)\right)=v_{\text{ph}}\left(\bar{k}\right)\left(0,{\tilde{B}}_z\left(\bar{k},x,t\right),-{\tilde{B}}_y\left(\bar{k},x,t\right)\right),\hfill \end{array}(8)$

where we have used the assumption that the electromagnetic fields $\propto e^{i(\mathbf{k}\cdot \mathbf{x}-\omega (\bar{k})(t-t_0))}$, such that $\nabla \times \tilde{\mathcal{E}}=i\mathbf{k}\times \tilde{\mathcal{E}}$, $\partial \tilde{\mathbf{B}}/\partial t=-i\omega (\bar{k})\tilde{\mathbf{B}}$, and $v_{\text{ph}}(\bar{k})=\omega (\bar{k})/|\mathbf{k}|$. The electric components of the wave can then be constructed from Eqs 5, 6 by using Eq. 8.

Starting from the Lorentz force law $(\mathbf{F}=q(\mathcal{E}+\mathbf{v}\times \mathbf{B}))$, we derive the exact relativistic equations of motion for particle position x, gyrophase ϕ, pitch-angle α, and kinetic energy E, due to interactions with a field-aligned right-/left-handed electromagnetic spectrum as defined by Eqs 5, 6. The details of this process are in Supplementary Appendix A, and the results are given by Eqs 9–12 below.

$\begin{array}{ccc}\hfill \frac{dx}{dt}& =\hfill & |\mathbf{v}|\cos \alpha =v_{\parallel }=c\frac{\sqrt{E\left(E+2E_{\text{R}}\right)}}{E+E_{\text{R}}}\cos \alpha ,\hfill \end{array}(9)$

$\begin{array}{ccc}\hfill \frac{dE}{dt}& =\hfill & \mp \frac{{\mathrm{\Omega }}_0}{2\pi }\sqrt{E\left(E+2E_{\text{R}}\right)}\sin \alpha {\int }_{-\infty }^{\infty }\frac{1}{\eta \left(\bar{k}\right)}ϵ\left(\bar{k}\right)\sin \zeta \left(\bar{k},x,t\right)d\bar{k},\hfill \end{array}(10)$

$\begin{array}{ccc}\hfill \frac{d\alpha }{dt}& =\hfill & \pm \frac{{\mathrm{\Omega }}_0}{2\pi }{\int }_{-\infty }^{\infty }\left(1-\frac{1}{\eta \left(\bar{k}\right)}\frac{E+E_{\text{R}}}{\sqrt{E\left(E+2E_{\text{R}}\right)}}\cos \alpha \right)ϵ\left(\bar{k}\right)\sin \zeta \left(\bar{k},x,t\right)d\bar{k},\hfill \end{array}(11)$

$\begin{array}{ccc}\hfill \frac{d\varphi }{dt}& =\hfill & {\mathrm{\Omega }}_0\left[-1+\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\left(\cot \alpha -\frac{1}{\eta \left(\bar{k}\right)\sin \alpha }\frac{E+E_{\text{R}}}{\sqrt{E\left(E+2E_{\text{R}}\right)}}\right)ϵ\left(\bar{k}\right)\cos \zeta \left(\bar{k},x,t\right)d\bar{k}\right],\hfill \end{array}(12)$

with $\zeta (\bar{k},x,t)=\psi (\bar{k},x,t)\pm \varphi (x,t)$ a combination of wave phase and particle gyrophase; $ϵ(\bar{k})=\tilde{B}(\bar{k})/B_0$ a dimensionless/normalised magnitude of magnetic wave field mode $\bar{k}$; and $\eta (\bar{k})=|\mathbf{k}|c/\omega (\bar{k})$ the refractive index of mode $\bar{k}$. In Table 1 we list many (but not all) of the important algebraic symbols used in this manuscript.

TABLE 1

TABLE 1. Many of the important algebraic symbols that are used in this article.

4 Derivation of the Weak Turbulence Transport Coefficients

4.1 Expansions of the Equations of Motion

The equations of motion Eqs 9–12 are nonlinear, coupled ordinary differential equations in the variables (x, E, α, ϕ). Therefore we seek solutions via expansion in a small dimensionless parameter, and the form of the equations suggests that $ϵ(\bar{k})$ is a sensible small parameter to choose. This is an example of a solution in a regime of “weak turbulence” (e.g., see Sagdeev and Galeev (1969)), which in our context will mean to solve the equations of motion up to and including the second order in $ϵ(\bar{k})$.

In the same way as was done in Lemons (2012), we look for solutions up to and including second order, i.e., of the form

$\begin{array}{ccc}\hfill x\left(t\right)& \approx \hfill & x^{\left(0\right)}\left(t\right)+x^{\left(1\right)}\left(t\right)+x^{\left(2\right)}\left(t\right),\hfill \end{array}(13)$

$\begin{array}{ccc}\hfill E\left(t\right)& \approx \hfill & E^{\left(0\right)}\left(t\right)+E^{\left(1\right)}\left(t\right)+E^{\left(2\right)}\left(t\right),\hfill \end{array}(14)$

$\begin{array}{ccc}\hfill \alpha \left(t\right)& \approx \hfill & {\alpha }^{\left(0\right)}\left(t\right)+{\alpha }^{\left(1\right)}\left(t\right)+{\alpha }^{\left(2\right)}\left(t\right),\hfill \end{array}(15)$

$\begin{array}{ccc}\hfill \varphi \left(t\right)& \approx \hfill & {\varphi }^{\left(0\right)}\left(t\right)+{\varphi }^{\left(1\right)}\left(t\right)+{\varphi }^{\left(2\right)}\left(t\right),\hfill \end{array}(16)$

such that terms with a “(n)” superscript are proportional to ϵⁿ. Without loss of generality, we state the following initial conditions: x(t₀) = x⁽⁰⁾(t₀) = x₀; E(t₀) = E⁽⁰⁾(t₀) = E₀; α(t₀) = α⁽⁰⁾(t₀) = α₀; and ϕ(t₀) = ϕ⁽⁰⁾(t₀) = ϕ₀. Therefore

$x^{\left(1\right)}\left(t_0\right)=x^{\left(2\right)}\left(t_0\right)=E^{\left(1\right)}\left(t_0\right)=E^{\left(2\right)}\left(t_0\right)={\alpha }^{\left(1\right)}\left(t_0\right)={\alpha }^{\left(2\right)}\left(t_0\right)={\varphi }^{\left(1\right)}\left(t_0\right)={\varphi }^{\left(2\right)}\left(t_0\right)=0.(17)$

Inserting Eqs 13–16 into the equations of motion Eqs 9–12 leads to zeroth-, first- and second-order equations of motion for x⁽⁰⁾, x⁽¹⁾, x⁽²⁾, E⁽⁰⁾, E⁽¹⁾, E⁽²⁾, α⁽⁰⁾, α⁽¹⁾, α⁽²⁾, ϕ⁽⁰⁾, ϕ⁽¹⁾ and ϕ⁽²⁾. Full details of this expansion process and solution methods are given in Supplementary Appendix B.

4.2 Diffusion Coefficients for Weak Turbulence

In this paper we have considered integral sums of Fourier modes (Fourier transforms) for the electromagnetic perturbations. This corresponds to an infinite spatial domain (whereas a finite spatial domain would correspond to a finite sum of discrete Fourier modes). Therefore we conduct a spatial average over − L/2 < x < L/2 but formally send L → ∞. The further averaging procedure that we will consider will be over gyrophase, ϕ. In particular we will assume that (to zeroth order) particles are uniformly distributed over position x and phase ϕ, i.e. x⁽⁰⁾(t) and ϕ⁽⁰⁾(t) remain uniformly distributed over [ − L/2, L/2] and [0, 2π] respectively. This “random-phase” approximation (Lemons et al., 2009; Lemons, 2012) is standard in the derivations of quasilinear theory (e.g., assumptions regarding spatial and azimuthal/gyrotropic symmetries of the distribution function in Kennel and Engelmann (1966)). We therefore define the ensemble averaging ⟨…⟩ for a generic function A as

$⟨A⟩=\underset{L\to \infty }{\lim }\frac{1}{L}{\int }_{-L/2}^{L/2}\left(\frac{1}{2\pi }{\int }_0^{2\pi }\mathit{A}\mathit{d}{\varphi }_0\right)d{x}_0.(18)$

We use this definition of ensemble averaging to complete the derivation of the weak turbulence diffusion coefficients in Supplementary Appendices B, C. Note that the integrals are performed “over the initial conditions” for particle position and gyrophase, x₀ and ϕ₀ respectively. The zeroth-order solutions for x⁽⁰⁾(t) and ϕ⁽⁰⁾(t) in Supplementary Appendix B demonstrate that particles initially uniformly distributed in x₀ and ϕ₀ will stay uniformly distributed at all later times t, to zeroth-order. Therefore the assumption of random-phase is justified and consistent to zeroth-order. This corresponds philosophically to the “integration over unperturbed (i.e., zeroth-order) orbits, as is commonplace in the aforementioned Vlasov-Maxwell treatments of quasilinear theory (e.g., see Kennel and Engelmann (1966); Verscharen and Chandran (2013).

We note that the expansions defined by Eqs 14, 15, the initial conditions of Eq. 17, and the zeroth-order solutions of the equation of motion in Supplementary Appendix B lead to the following definitions (up to second-order)

$\begin{array}{ccc}\hfill \mathrm{\Delta }\alpha =\alpha \left(t_0+\mathrm{\Delta }t\right)-\alpha \left(t_0\right)& \approx \hfill & {\alpha }^{\left(1\right)}\left(t_0+\mathrm{\Delta }t\right)+{\alpha }^{\left(2\right)}\left(t_0+\mathrm{\Delta }t\right),\hfill \\ \hfill \mathrm{\Delta }E=E\left(t_0+\mathrm{\Delta }t\right)-E\left(t_0\right)& \approx \hfill & E^{\left(1\right)}\left(t_0+\mathrm{\Delta }t\right)+E^{\left(2\right)}\left(t_0+\mathrm{\Delta }t\right).\hfill \end{array}$

Therefore, considering contributions to the diffusion coefficients in energy and pitch-angle up space up to and including second order in $ϵ(\bar{k})$ leads to

$\left\{{\mathcal{D}}_{\alpha \alpha },{\mathcal{D}}_{\alpha E},{\mathcal{D}}_{EE}\right\}\approx \left\{\frac{⟨{{\alpha }^{\left(1\right)}}^2⟩}{2\mathrm{\Delta }t},\frac{⟨{\alpha }^{\left(1\right)}{E}^{\left(1\right)}⟩}{2\mathrm{\Delta }t},\frac{⟨{E^{\left(1\right)}}^2⟩}{2\mathrm{\Delta }t}\right\}.(19)$

The calculations in Supplementary Appendices B, C then provide the following weak turbulence expressions

$\begin{array}{ccc}\hfill {\mathcal{D}}_{\alpha \alpha }& =\hfill & \frac{|{\mathrm{\Omega }}_0|}{4\pi }\frac{c}{|{\mathrm{\Omega }}_0|}{\int }_{-\infty }^{\infty }\left[\underset{L\to \infty }{\lim }\left(\frac{1}{L}{ϵ}^2\left(\bar{k}\right)\right)\right]{\left(1-\frac{\omega \left(\bar{k}\right)}{\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}}{\cos }^2{\alpha }_0\right)}^2\hfill \\ \hfill & \hfill & \times \frac{\left\{1-\cos \left[\left(\left(\omega \left(\bar{k}\right)-\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}\right)/{\mathrm{\Omega }}_0\pm 1\right)\mathrm{\Delta }t{\mathrm{\Omega }}_0\right]\right\}}{\mathrm{\Delta }t|{\mathrm{\Omega }}_0|{\left(\left(\omega \left(\bar{k}\right)-\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}\right)/{\mathrm{\Omega }}_0\pm 1\right)}^2}d\bar{k}\hfill \end{array}(20)$

$\begin{array}{ccc}\hfill {\mathcal{D}}_{\alpha E}& =\hfill & -\frac{|{\mathrm{\Omega }}_0|}{4\pi }\frac{c}{|{\mathrm{\Omega }}_0|}\sqrt{E_0\left(E_0+2E_R\right)}\sin {\alpha }_0{\int }_{-\infty }^{\infty }\left[\underset{L\to \infty }{\lim }\left(\frac{1}{L}{ϵ}^2\left(\bar{k}\right)\right)\right]\frac{1}{\eta \left(\bar{k}\right)}\left(1-\frac{\omega \left(\bar{k}\right)}{\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}}{\cos }^2{\alpha }_0\right)\hfill \\ \hfill & \hfill & \times \frac{\left\{1-\cos \left[\left(\left(\omega \left(\bar{k}\right)-\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}\right)/{\mathrm{\Omega }}_0\pm 1\right)\mathrm{\Delta }t{\mathrm{\Omega }}_0\right]\right\}}{\mathrm{\Delta }t|{\mathrm{\Omega }}_0|{\left(\left(\omega \left(\bar{k}\right)-\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}\right)/{\mathrm{\Omega }}_0\pm 1\right)}^2}d\bar{k}\hfill \end{array}(21)$

$\begin{array}{ccc}\hfill {\mathcal{D}}_{EE}& =\hfill & \frac{|{\mathrm{\Omega }}_0|}{4\pi }\frac{c}{|{\mathrm{\Omega }}_0|}\left(E_0\left(E_0+2E_R\right)\right){\sin }^2{\alpha }_0{\int }_{-\infty }^{\infty }\left[\underset{L\to \infty }{\lim }\left(\frac{1}{L}{ϵ}^2\left(\bar{k}\right)\right)\right]\frac{1}{\eta {\left(\bar{k}\right)}^2}\hfill \\ \hfill & \hfill & \times \frac{\left\{1-\cos \left[\left(\left(\omega \left(\bar{k}\right)-\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}\right)/{\mathrm{\Omega }}_0\pm 1\right)\mathrm{\Delta }t{\mathrm{\Omega }}_0\right]\right\}}{\mathrm{\Delta }t|{\mathrm{\Omega }}_0|{\left(\left(\omega \left(\bar{k}\right)-\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}\right)/{\mathrm{\Omega }}_0\pm 1\right)}^2}d\bar{k}\hfill \end{array}(22)$

with

${\mathbf{v}}_{\parallel }^{\left(0\right)}=c\frac{\sqrt{E_0\left(E_0+2E_R\right)}}{E_0+E_R}\cos {\alpha }_0\widehat{\mathbf{x}},(23)$

the zeroth order approximation solution for the parallel velocity (i.e. the unperturbed solution).

Equations 20–22 show that the weak turbulence diffusion coefficients all involve integrating over a time-dependent factor that we define as A

$A=\frac{\left[1-\cos \left(R\mathrm{\Delta }t{\mathrm{\Omega }}_0\right)\right]}{R^2\mathrm{\Delta }t|{\mathrm{\Omega }}_0|},(24)$

with

$R=\left(\omega \left(\bar{k}\right)-\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}\right)/{\mathrm{\Omega }}_0\pm 1.(25)$

The term designated by R determines how close to resonance a given particle is with a given right-/left-handed electromagnetic wave mode (described by $\omega =\omega (\bar{k})$). R = 0 indicates an exact cyclotron resonance (e.g., see Tsurutani and Lakhina (1997)), and larger values of |R| indicate that a wave and particle are further away from resonance. In Figure 1 we plot some important features of A.

FIGURE 1

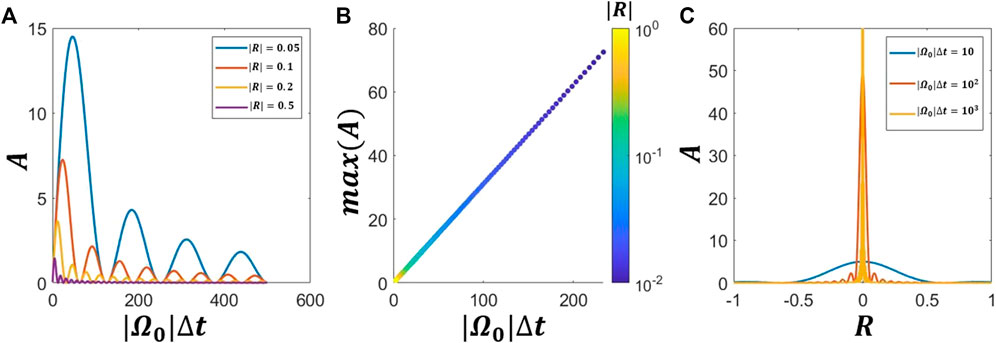
FIGURE 1. In (A) we show A as a function of |Ω₀|Δt, for given fixed values of R = 0.05, 0.1, 0.2, 0.5. In (B) we show the maximum value of A that is obtained, as a function of the value of |Ω₀|Δt, and for given fixed values of R from R = 10⁻² to R = 1 (see colour bar). In (C) we show A as a function of R, for given fixed values of |Ω₀|Δt = 10, 10², 10³.

In Figure 1A we show A as a function of |Ω₀|Δt, for given fixed values of |R| = 0.05, 0.1, 0.2, 0.5. There are two important features to note: 1) A and therefore the weak turbulence diffusion coefficients demonstrate a periodic dependence on the elapsed timescale Δt (albeit with the contributions becoming less significant as |Ω₀|Δt → ∞); 2) for smaller values of |R| (i.e., closer to cyclotron resonance), the contribution to the weak turbulence coefficients from this factor A is more significant, at all times.

In Figure 1B we show the maximum value of A that is obtained, as a function of the value of |Ω₀|Δt, and for given fixed values of |R| from R = 10⁻² to R = 1 (see colour bar). When |R| indicates that waves and particles are closer to resonance (i.e. |R| is closer to 0), then A maximizes at later times (this can also be seen from Figure 1A). One important implication to note is that particles further away from resonance (larger values of |R|) contribute most to A at earlier times.

In Figure 1C we show A as a function of R, for given fixed values of |Ω₀|Δt = 10, 10², 10³. This shows that as |Ω₀|Δt → ∞, the weak turbulence diffusion coefficients are essentially determined only via particles that are close to or exactly in resonance |R| ≈ 0. Equivalently, for smaller elapsed times |Ω₀|Δt, we can state that the contribution to diffusion from non-resonant particles is non-negligible and worthy of consideration.

4.3 Diffusion Coefficients in Resonant Diffusion Quasilinear Theory

The expressions for the diffusion coefficients, “$\mathcal{D}$”, defined by Eqs 20–22 are in principle valid for any Δt that satisfies Δt_C ≤ Δt ≪ 1/|D|, for Δt_C a particle de-correlation time (e.g., see Liu et al. (2010); Lemons (2012); Osmane and Lejosne (2021) for discussions of the de-correlation time). The standard interpretation of the quasilinear theory in this context is to understand that Δt_C ≫|Ω₀|⁻¹, i.e., that particles decorrelate over many gyroperiods. As we let Δt|Ω₀| → ∞ in our formalism, we see that A tends to zero everywhere away from R = 0. At R = 0, the limit as Δt|Ω₀| → ∞ is at first not clear, and so we can use l’Hopital’s rule to show that

$\underset{\mathrm{\Delta }t|{\mathrm{\Omega }}_0|\to \infty }{\lim }\frac{1-\cos \left(R\mathrm{\Delta }t{\mathrm{\Omega }}_0\right)}{\mathrm{\Delta }t|{\mathrm{\Omega }}_0|R^2}=\underset{\mathrm{\Delta }t|{\mathrm{\Omega }}_0|\to \infty }{\lim }\left|\frac{\sin \left(R\mathrm{\Delta }t{\mathrm{\Omega }}_0\right)}{R}\right|=\pi \delta \left(R\right),$

via one definition of the Dirac delta function. This gives

${\mathcal{D}}_{\alpha \alpha ,QL}=\frac{{\mathrm{\Omega }}_0^2}{W_0}\frac{\pi }{2}{\int }_{-\infty }^{\infty }\tilde{W}\left(\bar{k}\right){\left(1-\frac{\omega \left(\bar{k}\right)}{\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}}{\cos }^2{\alpha }_0\right)}^2\delta \left(\omega \left(\bar{k}\right)-\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}\pm {\mathrm{\Omega }}_0\right)d\bar{k},(26)$

making use of: (i) δ(X/Ω₀) = |Ω₀|δ(X); (ii) defining $W_0=B_0^2/(2{\mu }_0)$ as the background magnetic field energy density; (iii) and defining

$\tilde{W}\left(\bar{k}\right)=\frac{1}{2\pi }\frac{c}{|{\mathrm{\Omega }}_0|}\underset{L\to \infty }{\lim }\frac{1}{L}\frac{{\tilde{B}}^2\left(\bar{k}\right)}{2{\mu }_0},$

the magnetic wave energy density associated with mode $\mathbf{k}=|{\mathrm{\Omega }}_0|c^{-1}\bar{k}\widehat{\mathbf{x}}$. $\tilde{W}(\bar{k})$ is defined such that the spatially averaged magnetic wave energy density associated with the magnetic wave turbulent spectrum, W_wave, is defined as

$W_{\text{wave}}=\frac{B_{\text{wave}}^2}{2{\mu }_0}={\int }_{-\infty }^{\infty }\tilde{W}\left(\bar{k}\right)d\bar{k}.$

Note that the “lim_L→∞1/L” does not send all results to zero. This spatial average (over an infinite domain) is common in studies of quasilinear theory (e.g., see Kennel and Engelmann (1966); Summers (2005)). In fact, the “1/L” factor in the denominator competes with an “L” factor in the numerator due to the fact that the integral over all space (i.e., L) of $B_y^2+B_z^2=(B_y+i{B}_z)(B_y-i{B}_z)$ yields

$L{B}_{\text{wave}}^2=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\tilde{B}}^2\left(k\right)dk=\frac{1}{2\pi }\frac{c}{|{\mathrm{\Omega }}_0|}{\int }_{-\infty }^{\infty }{\tilde{B}}^2\left(\bar{k}\right)d\bar{k}.(27)$

A discussion of this feature is given in Lyons (1974), for example.

Similarly, we obtain

$\begin{array}{ccc}\hfill {\mathcal{D}}_{\alpha E,QL}& =\hfill & -\frac{{\mathrm{\Omega }}_0^2}{W_0}\frac{\pi }{2}\sin {\alpha }_0\sqrt{E_0\left(E_0+2E_R\right)}\hfill \\ \hfill & \hfill & \times {\int }_{-\infty }^{\infty }\tilde{W}\left(\bar{k}\right)\frac{1}{\eta \left(\bar{k}\right)}\left(1-\frac{\omega \left(\bar{k}\right)}{\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}}{\cos }^2{\alpha }_0\right)\delta \left(\omega \left(\bar{k}\right)-\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}\pm {\mathrm{\Omega }}_0\right)d\bar{k},\hfill \end{array}(28)$

$\begin{array}{ccc}\hfill {\mathcal{D}}_{EE,QL}& =\hfill & \frac{{\mathrm{\Omega }}_0^2}{W_0}\frac{\pi }{2}{\sin }^2{\alpha }_0\left(E_0\left(E_0+2E_R\right)\right){\int }_{-\infty }^{\infty }\tilde{W}\left(\bar{k}\right)\frac{1}{{\eta }^2\left(\bar{k}\right)}\delta \left(\omega \left(\bar{k}\right)-\mathbf{k}\cdot {\mathbf{v}}_{\parallel }^{\left(0\right)}\pm {\mathrm{\Omega }}_0\right)d\bar{k}.\hfill \end{array}(29)$

The definitions of “$\mathcal{D}$” in equations Eqs 26, 28, 29 are consistent with those in the standard relativistic and non-bounce-averaged quasilinear theory, e.g., see Glauert and Horne (2005); Summers (2005).

Therefore, taking |Ω₀|Δt → ∞ has allowed us to obtain the time-independent quasilinear diffusion coefficients in energy and pitch-angle space, from the corresponding time-dependent weak turbulence coefficients. This calculation and process mirrors the same result as presented in Lemons (2012), for the more restricted pitch-angle case.

5 Discussion

5.1 Weak Turbulence Diffusion Coefficients

The first main result of this paper is the derivation of the diffusion coefficients, ${\mathcal{D}}_{\alpha \alpha }$, ${\mathcal{D}}_{\alpha E}$ and ${\mathcal{D}}_{EE}$, under the assumption of “weak turbulence” only–namely that the amplitude of the “k^th” mode is much smaller than that of the background uniform field, $ϵ(\bar{k})=\tilde{B}(\bar{k})/B_0\ll 1$. Under this assumption, we spatially average and impose one further condition of “random phase” (i.e., particles uniformly distributed over gyrophase, and also known as gyrotropy), to obtain the weak turbulence diffusion coefficients in Eqs 20–22.

The result is a diffusion coefficient, “$\mathcal{D}$”, that is not only a function of the plasma refractive index, background magnetic field strength and electromagnetic wave perturbation spectrum, but also a function of elapsed timescale, Δt. The expressions in Eqs 20–22 are in principle valid for any Δt that satisfies Δt_C ≤ Δt ≪ 1/|D|, for Δt_C a particle de-correlation time. The details and properties of these weak turbulence diffusion coefficients require further investigation (in particular their dependency on time). However, we note that it is now well established that the considered elapsed timescale can play a crucial role on the nature of particle diffusion in energy and pitch-angle space (e.g., see Watt et al. (2021)). A careful consideration of the elapsed timescale has been shown to be important in the interpretation of the diffusion coefficient and general nature of the charged particle dynamics: for situations with zero wave-growth rate (e.g., see Liu et al. (2010); Liu et al. (2012); Lemons (2012); Allanson et al. (2020)); but also in the context of growing and saturating wave modes (e.g., see Camporeale and Zimbardo (2015); Allanson et al. (2021))

One particularly interesting observation to make is that when considered over finite timescales, the weak turbulence diffusion coefficients demonstrate the contribution towards particle diffusion of wave modes that are not in exact resonance (R ≠ 0). Specifically, the terms in the integrand of Eqs 20–22 admit contributions towards particle diffusion (i.e. for a specific value of energy and pitch angle) from a range of wave modes (i.e., different values of $\bar{k}$), i.e. not only those wave modes that satisfy the cyclotron resonance condition (R = 0). This phenomenon is known as resonance broadening—the importance of which has been noted by numerous authors (e.g., see Dupree (1966); Karimabadi and Menyuk (1991); Karimabadi et al. (1992); Cai et al. (2020)).

Furthermore, we note that Lemons (2012) discussed some possible restrictions to the validity of the general methodology that they, and we, present. Namely, that for very small pitch angles the assumption of a very small magnetic field perturbation (as compared to the background magnetic field strength) may not be sufficient to derive meaningful weak turbulence and quasilinear theories. This is essentially due to the appearance of a cot α factor appearing in the equation for dϕ/dt (Eq. 3b in Lemons (2012), and note that they use θ in place of α). Lemons (2012) develop a “small-correlation time” theory to specifically investigate the small pitch angle regime, but explain that it will be difficult to demonstrate the validity of their theory. Equation 12 in this manuscript demonstrates that there may be a similar regime of interest for the system that we consider. However, these considerations are subtle and are beyond the scope of this study.

It will be interesting to further investigate the properties of the weak turbulence diffusion coefficients: 1) the nature of their dependency on elapsed timescale Δt; 2) and the role of the resonance-broadening effect (and in particular its correspondence to the pre-existing literature). These considerations are left for future work and are beyond the scope of this study.

5.2 Quasilinear Diffusion as a Limit of Weak Turbulence

The second main result of this paper is a new derivation via the Markov method of the pitch-angle and energy diffusion coefficients (${\mathcal{D}}_{\alpha \alpha ,QL}$, ${\mathcal{D}}_{\alpha E,QL}$ and ${\mathcal{D}}_{EE,QL}$), that are equivalent to those used in the standard relativistic quasilinear theory, in the resonant diffusion limit (e.g., see Glauert and Horne (2005); Summers (2005)). These results are given in Eqs 26–29, and are derived from the weak turbulence diffusion coefficients in Eqs 20–22 under the assumptions of elapsed times much greater than the gyroperiod, Δt ≫ 1/|Ω₀|. These results build on the pitch-angle diffusion results similarly derived by Lemons (2012). We have derived these equations in the context of field-aligned waves only. Because the waves are field-aligned, an integral over wave normal angle is avoided, as is the sum over different resonance numbers, which would be required in a treatment of obliquely propagating wave modes (e.g., see Lyons (1974); Glauert and Horne (2005); Albert (2005). It will be interesting in future works to consider non-zero wave normal angles.

5.3 Novel Derivation of the Weak Turbulence and Quasilinear Diffusion Theories

The standard derivations of the quasilinear theory (Drummond and Pines, 1962; Vedenov et al., 1962; Kennel and Engelmann, 1966; Lerche, 1968; Lyons, 1974; Summers, 2005) are founded upon a perturbative analysis of the Vlasov-Maxwell equations (e.g., see Schindler (2007)), and describe the evolution of a gyrophase-averaged (gyrotropic) particle distribution function in an infinite and homogeneous collisionless plasma with a uniform and static background magnetic field, although we do note a comparatively recent example of a derivation by Brizard and Chan (2004) that does include spatial inhomogeneities from the very outset. The standard derivations rely on a number of assumptions: 1) sufficiently small electromagnetic wave power and a correspondingly sufficiently large spectral width (e.g., see Karpman (1974); Tong et al. (2019)); 2) sufficiently small wave growth rates and slowly varying wave spectra, and a correspondingly slowly varying spatially averaged distribution function (e.g., see Kennel and Engelmann (1966); Davidson et al. (1972)); 3) a wave spectrum that satisfies the so-called “Chirikov resonance overlap condition” (e.g., see Zaslavskiĭ and Chirikov (1972); Artemyev et al. (2015)). Quasilinear theory in the limit of resonant diffusion further restricts that wave growth rates actually tend to zero (Kennel and Engelmann, 1966), and this is the version of the quaslinear theory that is commonly used in numerical radiation belt diffusion models (e.g., see Beutier and Boscher (1995); Albert et al. (2009); Su et al. (2010); Subbotin et al. (2010); Glauert et al. (2014)).

The approach presented in this paper to derive the weak turbulence and quasilinear diffusion coefficients has some important benefits. Firstly, our derivations rely on fewer technical assumptions than those mentioned above for the case of the quasilinear theory in the resonant diffusion limit (zero wave growth rate). Ultimately, the main two assumptions are the small wave amplitudes ϵ_k, and the “random-phase” criteria. Secondly, we believe that the theory has a very intuitive and “user-friendly” entry point, namely an expansion of particle trajectories that obey the Lorentz force law, $\mathbf{F}=q(\mathcal{E}+\mathbf{v}\times \mathbf{B})$, under the influence of prescribed electromagnetic waves expressed as Fourier transforms. There may be considerable algebra that follows, but the route through the calculation is quite straightforward to understand and is based on commonly used techniques. Furthermore, the emergent dependence of the transport coefficients on timescale is one example of the insight that can be derived using this approach. We anticipate that this approach can be used to derive transport equations and associated transport coefficients for a wider variety of systems and circumstances, and we leave this for future work, e.g., electromagnetic fields with non-zero wave normal angles.

5.4 Nonlinear Wave-Particle Interactions

Numerous observations have shown the prevalence of high-amplitude electromagnetic whistler-mode and ion-cyclotron waves in the Earth’s inner magnetosphere (Cattell et al., 2008; Cully et al., 2008; Breneman et al., 2011; Kellogg et al., 2011; Wilson et al., 2011; Hendry et al., 2019; Tyler et al., 2019; Zhang et al., 2019; Zhang et al., 2021), such as are responsible for local changes in the energy and pitch-angle of radiation belt electrons. These high “nonlinear” wave amplitudes cast some doubt on the applicability of the quasilinear theory in such cases. Furthermore, a number of co-ordinated wave and particle measurements have directly demonstrated the existence of nonlinear wave-particle interactions in the Earth’s inner magnetosphere (Agapitov et al., 2015; Foster et al., 2016; Kurita et al., 2018; Mozer et al., 2018; Shumko et al., 2018). Therefore, an improved theoretical understanding and modelling capability of radiation belt dynamics that incorporates the most appropriate elements of the quasilinear and nonlinear theories of wave-particle interactions is an important and outstanding question (e.g., see Omura et al. (2008); Albert et al. (2013); Tao et al. (2012a,b); Omura et al. (2015); Camporeale (2015); Camporeale and Zimbardo (2015); Artemyev et al. (2018); Mourenas et al. (2018); Vainchtein et al. (2018); Zheng et al. (2019); Gan et al. (2020); Allanson et al. (2020); Allanson et al. (2021)).

Theoretical and modeling studies (Albert and Bortnik, 2009; Liu et al., 2012; Zheng et al., 2012; Lee et al., 2018; Artemyev et al., 2018; Vainchtein et al., 2018; Mourenas et al., 2018; Zheng et al., 2019; Gan et al., 2020; Allanson et al. (2020); Allanson et al. (2021)) indicate that an effective incorporation of nonlinear wave-particle interactions into existing modeling paradigms may require the addition of extra, or modified, transport coefficients (or some other addition) to the version of the Fokker-Planck equation that is currently used (e.g., see Schulz and Lanzerotti (1974); Glauert et al. (2014)). There are a number of candidate methods to achieve this (or a similar) goal, and a number of these are summarized in Artemyev et al. (2021). A fully nonlinear model of wave-particle interactions in the radiation belts would necessarily need to include inhomogeneous background magnetic fields and number density, to incorporate: 1) phase decorrelation specifically due the inhomogeneity itself (e.g., see Albert (2010)): 2) nonlinear effects known as phase bunching and phase trapping (e.g., see Omura et al. (2008)). We do not include such spatial inhomogeneities and therefore cannot describe these associated effects. However, we emphasize that the methods in this paper do present a consistent mechanism that allows for the derivation of not only the transport (drift and diffusion) coefficients, but also the very form of the transport (Fokker-Planck) equation itself, based upon prescribed electromagnetic waves and some sensible physical assumptions. In future works, we could derive drift-diffusion relations such as Eqs 2, 3 from first principles for other situations, as opposed to a-priori assuming them to hold. This advance is one of the main benefits of using the approach demonstrated in this paper, and it remains to be seen if these methods can be applied to include the inhomogeneous cases.

6 Summary

In this paper we have presented new derivations of relativistic weak turbulence and quasilinear diffusion models. These models describe charged particle dynamics due to interactions with right-/left-handed electromagnetic waves, and specifically for the case of waves that are travelling parallel (and/or anti-parallel) to the direction of the background magnetic field. The approach differs from the most standard methods of derivation, that are based upon the Vlasov-Maxwell set of equations (e.g., see Kennel and Engelmann (1966)). Instead, our approach uses the principles of Markovian dynamics, and is fundamentally based on solutions to the single-particle Lorentz force equation, $\mathbf{F}=q(\mathcal{E}+\mathbf{v}\times \mathbf{B})$. In particular, we expand the relevant equations of motion up to second order in a small parameter, $ϵ(\bar{k})=\tilde{B}(\bar{k})/|{\mathbf{B}}_0|$, (the relative magnitude of magnetic perturbations to the background magnetic field), and then ensemble average the solutions to obtain the diffusion coefficients. The approach used in this paper builds upon the work by Lemons (2012), in which pitch-angle dynamics were considered due to interactions with a static magnetic field profile. The main conclusions and results of this paper are as follows:

• A derivation and discussion of the general Fokker-Planck equation to describe stochastic charged particle dynamics in energy and pitch-angle space, using Markov theory (Eq. 1; Section 2). This equation includes all possible advective and diffusive dynamics, in principle. The form of the drift and diffusion coefficients are then to be determined on a system-by-system basis. In this paper we solve for the diffusive dynamics only, and leave investigations of the drift coefficients and drift-diffusion relations for future works;

• In sections 3 and 4 we solve the Lorentz force law using expansions in the small parameter $ϵ(\bar{k})$, and then ensemble average the results to derive the diffusion coefficients for a weak turbulence approximations. The obtained diffusion coefficients ${\mathcal{D}}_{\alpha \alpha },{\mathcal{D}}_{\alpha E}$ and ${\mathcal{D}}_{EE}$ Eqs 20–22 are in principle valid for any elapsed time Δt provided Δt_C ≤ Δt ≪ 1/|D|, for Δt_C the particle de-correlation time. These weak turbulence diffusion coefficients: 1) display an interesting dependency on Δt; 2) and also explicitly incorporate the effects of non-resonant particles, as well as the standard effects of cycolotron-resonant particles;

• The weak turbulence diffusion coefficients recover the standard form as used in the resonant-diffusion limit of relativistic quasilinear theory (e.g., see Glauert and Horne (2005); Summers (2005)), when we consider elapsed timescales much greater than a gyroperiod (i.e., we allow Δt ≫ 1/|Ω₀|, and formally |Ω₀|Δt → ∞);

• Whilst the form of the quasilinear diffusion coefficients is not new in and of itself, our new derivation has a number of benefits, including: 1) the evident self-consistent relationship between a more general weak turbulence theory and the standard resonant diffusion quasilinear theory (as is commonly used in e.g. radiation belt and solar wind modeling); 2) the general nature of the Fokker-Planck equation that can be derived without any prior assumptions regarding its form; 3) the clear dependence of the form of the Fokker-Planck equation and the transport coefficients on given specific timescales.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

OA derived the equations and wrote the article. TE reproduced the equations and consulted on the article. CW 1) consulted on the article; 2) discussed key themes with OA on many occasions; 3) and provided Figure 1. TN 1) consulted on the article; 2) provided key early input with regards to the ensemble averaging method.

Funding

OA acknowledges financial support from the University of Exeter and from the United Kingdom Natural Environment Research Council (NERC) Independent Research Fellowship NE/V013963/1. OA and CW acknowledge financial support from the NERC Highlight Topic Grant NE/P017274/1 (Rad-Sat), and from United Kingdom Science and Technology Facilities Council (STFC) via Consolidated Grant ST/W000369/1. TE acknowledges financial support from an Early Career Fellowship, split jointly by the Leverhulme Trust (ECF-2019-155) and the University of Leicester in the first instance (2019-21), but presently the University of Glasgow (2021-). TN acknowledges financial support from the STFC via Consolidated Grant ST/S000402/1. The University of Exeter cover the Open Access Publication Fee via a UKRI block grant.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.805699/full#supplementary-material

References

Agapitov, O. V., Artemyev, A. V., Mourenas, D., Mozer, F. S., and Krasnoselskikh, V. (2015). Nonlinear Local Parallel Acceleration of Electrons through Landau Trapping by Oblique Whistler Mode Waves in the Outer Radiation belt. Geophys. Res. Lett. 42, 10,140–10,149. doi:10.1002/2015GL066887

CrossRef Full Text | Google Scholar

Albert, J. M., and Bortnik, J. (2009). Nonlinear Interaction of Radiation belt Electrons with Electromagnetic Ion Cyclotron Waves. Geophys. Res. Lett. 36, L12110. doi:10.1029/2009GL038904

CrossRef Full Text | Google Scholar

Albert, J. M. (2001). Comparison of Pitch Angle Diffusion by Turbulent and Monochromatic Whistler Waves. J. Geophys. Res. 106, 8477–8482. doi:10.1029/2000JA000304

CrossRef Full Text | Google Scholar

Albert, J. M. (2010). Diffusion by One Wave and by many Waves. J. Geophys. Res. 115, A00F05. doi:10.1029/2009JA014732

CrossRef Full Text | Google Scholar

Albert, J. M. (2005). Evaluation of Quasi-Linear Diffusion Coefficients for Whistler Mode Waves in a Plasma with Arbitrary Density Ratio. J. Geophys. Res. 110, A03218. doi:10.1029/2004JA010844

CrossRef Full Text | Google Scholar

Albert, J. M., Meredith, N. P., and Horne, R. B. (2009). Three-dimensional Diffusion Simulation of Outer Radiation belt Electrons during the 9 October 1990 Magnetic Storm. J. Geophys. Res. Space Phys. 114, A09214. doi:10.1029/2009ja014336

CrossRef Full Text | Google Scholar

Albert, J. M., Tao, X., and Bortnik, J. (2013). Aspects of Nonlinear Wave-Particle Interactions. Editors D Summers, I. R. Mann, D. N. Baker, and M Schulz, 199, 255–264. Washington, DC: American Geophysical Union. doi:10.1029/2012GM001324 https://agupubs.onlinelibrary.wiley.com/doi/book/10.1029/GM199.

CrossRef Full Text | Google Scholar

Allanson, O., Watt, C. E. J., Allison, H. J., and Ratcliffe, H. (2021). Electron Diffusion and Advection during Nonlinear Interactions with Whistler-Mode Waves. J. Geophys. Res. Space Phys. 126, e2020JA028793. doi:10.1029/2020ja028793

CrossRef Full Text | Google Scholar

Allanson, O., Watt, C. E. J., Ratcliffe, H., Allison, H. J., Meredith, N. P., Bentley, S. N., et al. (2020). Particle-in-cell Experiments Examine Electron Diffusion by Whistler-Mode Waves: 2. Quasi-Linear and Nonlinear Dynamics. J. Geophys. Res. Space Phys. 125, e2020JA027949. doi:10.1029/2020JA027949

CrossRef Full Text | Google Scholar

Allanson, O., Watt, C. E. J., Ratcliffe, H., Meredith, N. P., Allison, H. J., Bentley, S. N., et al. (2019). Particle‐in‐cell Experiments Examine Electron Diffusion by Whistler‐mode Waves: 1. Benchmarking with a Cold Plasma. J. Geophys. Res. Space Phys. 124, 8893–8912. doi:10.1029/2019JA027088

CrossRef Full Text | Google Scholar

Artemyev, A. V., Mourenas, D., Agapitov, O. V., and Krasnoselskikh, V. V. (2015). Relativistic Electron Scattering by Magnetosonic Waves: Effects of Discrete Wave Emission and High Wave Amplitudes. Phys. Plasmas 22, 062901. doi:10.1063/1.4922061

CrossRef Full Text | Google Scholar

Artemyev, A. V., Neishtadt, A. I., Vasiliev, A. A., and Mourenas, D. (2018). Long-term Evolution of Electron Distribution Function Due to Nonlinear Resonant Interaction with Whistler Mode Waves. J. Plasma Phys. 84, 905840206. doi:10.1017/S0022377818000260

CrossRef Full Text | Google Scholar

Artemyev, A. V., Neishtadt, A. I., Vasiliev, A. A., Zhang, X.-J., Mourenas, D., and Vainchtein, D. (2021). Long-term Dynamics Driven by Resonant Wave-Particle Interactions: from Hamiltonian Resonance Theory to Phase Space Mapping. J. Plasma Phys. 87, 835870201. doi:10.1017/S0022377821000246

CrossRef Full Text | Google Scholar

Beutier, T., and Boscher, D. (1995). A Three-Dimensional Analysis of the Electron Radiation belt by the Salammbô Code. J. Geophys. Res. 100, 14853–14861. doi:10.1029/94JA03066

CrossRef Full Text | Google Scholar

Breneman, A., Cattell, C., Wygant, J., Kersten, K., Wilson, L. B., Schreiner, S., et al. (2011). Large-amplitude Transmitter-Associated and Lightning-Associated Whistler Waves in the Earth's Inner Plasmasphere at L < 2. J. Geophys. Res. 116, A06310. doi:10.1029/2010JA016288

CrossRef Full Text | Google Scholar

Brizard, A. J., and Chan, A. A. (2004). Relativistic Quasilinear Diffusion in Axisymmetric Magnetic Geometry for Arbitrary-Frequency Electromagnetic Fluctuations. Phys. Plasmas 11, 4220–4229. doi:10.1063/1.1773554

CrossRef Full Text | Google Scholar

Cai, B., Wu, Y., and Tao, X. (2020). Effects of Nonlinear Resonance Broadening on Interactions between Electrons and Whistler Mode Waves. Geophys. Res. Lett. 47, e2020GL087991. doi:10.1029/2020GL087991

CrossRef Full Text | Google Scholar

Camporeale, E. (2015). Resonant and Nonresonant Whistlers-Particle Interaction in the Radiation Belts. Geophys. Res. Lett. 42, 3114–3121. doi:10.1002/2015GL063874

CrossRef Full Text | Google Scholar

Camporeale, E., and Zimbardo, G. (2015). Wave-particle Interactions with Parallel Whistler Waves: Nonlinear and Time-dependent Effects Revealed by Particle-In-Cell Simulations. Phys. Plasmas 22, 092104. doi:10.1063/1.4929853

CrossRef Full Text | Google Scholar

Cattell, C., Wygant, J. R., Goetz, K., Kersten, K., Kellogg, P. J., von Rosenvinge, T., et al. (2008). Discovery of Very Large Amplitude Whistler-Mode Waves in Earth's Radiation Belts. Geophys. Res. Lett. 35, L01105. doi:10.1029/2007GL032009

CrossRef Full Text | Google Scholar

Cully, C. M., Bonnell, J. W., and Ergun, R. E. (2008). Themis Observations of Long-Lived Regions of Large-Amplitude Whistler Waves in the Inner Magnetosphere. Geophys. Res. Lett. 35, L17S16. doi:10.1029/2008GL033643

CrossRef Full Text | Google Scholar

Davidson, R. C., Hammer, D. A., Haber, I., and Wagner, C. E. (1972). Nonlinear Development of Electromagnetic Instabilities in Anisotropic Plasmas. Phys. Fluids 15, 317–333. doi:10.1063/1.1693910

CrossRef Full Text | Google Scholar

Drummond, W. E., and Pines, D. (1962). Nonlinear Stability of Plasma Oscillations. Nucl. Fusion Suppl. 3, 1049–1058.

Google Scholar

Dupree, T. H. (1966). A Perturbation Theory for strong Plasma Turbulence. Phys. Fluids 9, 1773–1782. doi:10.1063/1.1761932

CrossRef Full Text | Google Scholar

Einstein, A. (1956). Investigations on the Theory of the Brownian Movement. Dover Books on Physics Series. New York, NY: Dover Publications.

Google Scholar

Foster, J. C., Erickson, P. J., Baker, D. N., Jaynes, A. N., Mishin, E. V., Fennel, J. F., et al. (2016). Observations of the Impenetrable Barrier, the Plasmapause, and the VLF Bubble during the 17 March 2015 Storm. J. Geophys. Res. Space Phys. 121, 5537–5548. doi:10.1002/2016JA022509

CrossRef Full Text | Google Scholar

Gan, L., Li, W., Ma, Q., Albert, J., Artemyev, A., and Bortnik, J. (2020). Nonlinear Interactions between Radiation belt Electrons and Chorus Waves: Dependence on Wave Amplitude Modulation. Geophys. Res. Lett. 47, e2019GL085987. doi:10.1029/2019GL085987

CrossRef Full Text | Google Scholar

Glauert, S. A., and Horne, R. B. (2005). Calculation of Pitch Angle and Energy Diffusion Coefficients with the PADIE Code. J. Geophys. Res. 110, A04206. doi:10.1029/2004JA010851

CrossRef Full Text | Google Scholar

Glauert, S. A., Horne, R. B., and Meredith, N. P. (2014). Three‐dimensional Electron Radiation belt Simulations Using the BAS Radiation Belt Model with New Diffusion Models for Chorus, Plasmaspheric Hiss, and Lightning‐generated Whistlers. J. Geophys. Res. Space Phys. 119, 268–289. doi:10.1002/2013JA019281

CrossRef Full Text | Google Scholar

Hendry, A. T., Santolik, O., Kletzing, C. A., Rodger, C. J., Shiokawa, K., and Baishev, D. (2019). Multi‐instrument Observation of Nonlinear EMIC‐Driven Electron Precipitation at Sub-MeV Energies. Geophys. Res. Lett. 46, 7248–7257. doi:10.1029/2019GL082401

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Shprits, Y. Y., Meredith, N. P., Glauert, S. A., Smith, A. J., et al. (2005). Wave Acceleration of Electrons in the Van Allen Radiation Belts. Nature 437, 227–230. doi:10.1038/nature03939

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeong, S.-Y., Verscharen, D., Wicks, R. T., and Fazakerley, A. N. (2020). A Quasi-Linear Diffusion Model for Resonant Wave-Particle Instability in Homogeneous Plasma. ApJ 902, 128. doi:10.3847/1538-4357/abb099

CrossRef Full Text | Google Scholar

Karimabadi, H., Krauss-Varban, D., and Terasawa, T. (1992). Physics of Pitch Angle Scattering and Velocity Diffusion, 1. Theory. J. Geophys. Res. 97, 13853–13864. doi:10.1029/92JA00997

CrossRef Full Text | Google Scholar

Karimabadi, H., and Menyuk, C. R. (1991). A Fast and Accurate Method of Calculating Particle Diffusion: Application to the Ionosphere. J. Geophys. Res. 96, 9669–9687. doi:10.1029/91JA00315

CrossRef Full Text | Google Scholar

Karpman, V. I. (1974). Nonlinear Effects in the ELF Waves Propagating along the Magnetic Field in the Magnetosphere. Space Sci. Rev. 16, 361–388. doi:10.1007/BF00171564

CrossRef Full Text | Google Scholar

Kellogg, P. J., Cattell, C. A., Goetz, K., Monson, S. J., and Wilson, L. B. (2011). Large Amplitude Whistlers in the Magnetosphere Observed with Wind-Waves. J. Geophys. Res. 116, A09224. doi:10.1029/2010JA015919

CrossRef Full Text | Google Scholar

Kennel, C. F., and Engelmann, F. (1966). Velocity Space Diffusion from Weak Plasma Turbulence in a Magnetic Field. Phys. Fluids 9, 2377–2388. doi:10.1063/1.1761629

CrossRef Full Text | Google Scholar

Kollmann, P., Roussos, E., Paranicas, C., Woodfield, E. E., Mauk, B. H., Clark, G., et al. (2018). Electron Acceleration to Mev Energies at jupiter and Saturn. J. Geophys. Res. Space Phys. 123, 9110–9129. doi:10.1029/2018ja025665

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurita, S., Miyoshi, Y., Kasahara, S., Yokota, S., Kasahara, Y., Matsuda, S., et al. (2018). Deformation of Electron Pitch Angle Distributions Caused by Upper Band Chorus Observed by the Arase Satellite. Geophys. Res. Lett. 45, 7996–8004. doi:10.1029/2018GL079104

CrossRef Full Text | Google Scholar

Lee, S.-Y., Lee, E., Seough, J., Lee, J.-g., Hwang, J., Lee, J.-J., et al. (2018). Simulation and Quasi-Linear Theory of Whistler Anisotropy Instability. J. Geophys. Res. Space Phys. 123, 3277–3290. doi:10.1029/2017ja024960

CrossRef Full Text | Google Scholar

Lemons, D. S., Liu, K., Winske, D., and Gary, S. P. (2009). Stochastic Analysis of Pitch Angle Scattering of Charged Particles by Transverse Magnetic Waves. Phys. Plasmas 16, 112306. doi:10.1063/1.3264738

CrossRef Full Text | Google Scholar

Lemons, D. S. (2012). Pitch Angle Scattering of Relativistic Electrons from Stationary Magnetic Waves: Continuous Markov Process and Quasilinear Theory. Phys. Plasmas 19, 012306. doi:10.1063/1.3676156

CrossRef Full Text | Google Scholar

Lerche, I. (1968). Quasilinear Theory of Resonant Diffusion in a Magneto-Active, Relativistic Plasma. Phys. Fluids 11, 1720–1727. doi:10.1063/1.1692186

CrossRef Full Text | Google Scholar

Liu, K., Lemons, D. S., Winske, D., and Gary, S. P. (2010). Relativistic Electron Scattering by Electromagnetic Ion Cyclotron Fluctuations: Test Particle Simulations. J. Geophys. Res. 115, A04204. doi:10.1029/2009JA014807

CrossRef Full Text | Google Scholar

Liu, K., Winske, D., Gary, S. P., and Reeves, G. D. (2012). Relativistic Electron Scattering by Large Amplitude Electromagnetic Ion Cyclotron Waves: The Role of Phase Bunching and Trapping. J. Geophys. Res. 117, A06218. doi:10.1029/2011JA017476

CrossRef Full Text | Google Scholar

Lyons, L. R. (1974). General Relations for Resonant Particle Diffusion in Pitch Angle and Energy. J. Plasma Phys. 12, 45–49. doi:10.1017/S0022377800024910

CrossRef Full Text | Google Scholar

Mertsch, P. (2020). Test Particle Simulations of Cosmic Rays. Astrophys Space Sci. 365, 135. doi:10.1007/s10509-020-03832-3

CrossRef Full Text | Google Scholar

Mourenas, D., Zhang, X.-J., Artemyev, A. V., Angelopoulos, V., Thorne, R. M., Bortnik, J., et al. (2018). Electron Nonlinear Resonant Interaction with Short and Intense Parallel Chorus Wave Packets. J. Geophys. Res. Space Phys. 123, 4979–4999. doi:10.1029/2018JA025417

CrossRef Full Text | Google Scholar

Mozer, F. S., Agapitov, O. V., Blake, J. B., and Vasko, I. Y. (2018). Simultaneous Observations of Lower Band Chorus Emissions at the Equator and Microburst Precipitating Electrons in the Ionosphere. Geophys. Res. Lett. 45, 511–516. doi:10.1002/2017GL076120

CrossRef Full Text | Google Scholar

Omura, Y., Katoh, Y., and Summers, D. (2008). Theory and Simulation of the Generation of Whistler-Mode Chorus. J. Geophys. Res. 113, A04223. doi:10.1029/2007JA012622

CrossRef Full Text | Google Scholar

Omura, Y., Miyashita, Y., Yoshikawa, M., Summers, D., Hikishima, M., Ebihara, Y., et al. (2015). Formation Process of Relativistic Electron Flux through Interaction with Chorus Emissions in the Earth's Inner Magnetosphere. J. Geophys. Res. Space Phys. 120, 9545–9562. doi:10.1002/2015JA021563

CrossRef Full Text | Google Scholar

Osmane, A., and Lejosne, S. (2021). Radial Diffusion of Planetary Radiation Belts' Particles by Fluctuations with Finite Correlation Time. ApJ 912, 142. doi:10.3847/1538-4357/abf04b

CrossRef Full Text | Google Scholar

Reif, F. (2009). Fundamentals of Statistical and Thermal Physics. Long Grove, Illinois: Waveland Press.

Google Scholar

Roederer, J., and Zhang, H. (2013). Dynamics of Magnetically Trapped Particles: Foundations of the Physics of Radiation Belts and Space Plasmas. Astrophysics and Space Science Library. Springer Berlin Heidelberg.

Google Scholar

Sagdeev, R. Z., and Galeev, A. A. (1969). Nonlinear Plasma Theory (New York: W.A. Benjamin, Inc.).

Google Scholar

Schindler, K. (2007). Physics of Space Plasma Activity. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Schlickeiser, R. (1989). Cosmic-ray Transport and Acceleration. I - Derivation of the Kinetic Equation and Application to Cosmic Rays in Static Cold media. II - Cosmic Rays in Moving Cold media with Application to Diffusive Shock Wave Acceleration. ApJ 336, 243. doi:10.1086/167009

CrossRef Full Text | Google Scholar

Schulz, M., and Lanzerotti, L. (1974). Particle Diffusion in the Radiation Belts. Physics and chemistry in space. Berlin-Heidelberg: Springer-Verlag. doi:10.1007/978-3-642-65675-0

CrossRef Full Text | Google Scholar

Shumko, M., Turner, D. L., O'Brien, T. P., Claudepierre, S. G., Sample, J., Hartley, D. P., et al. (2018). Evidence of Microbursts Observed Near the Equatorial Plane in the Outer Van allen Radiation belt. Geophys. Res. Lett. 45, 8044–8053. doi:10.1029/2018GL078451

CrossRef Full Text | Google Scholar

Steinacker, J., and Miller, J. A. (1992). Stochastic Gyroresonant Electron Acceleration in a Low-Beta Plasma. I - Interaction with Parallel Transverse Cold Plasma Waves. ApJ 393, 764. doi:10.1086/171544

CrossRef Full Text | Google Scholar

Su, Z., Xiao, F., Zheng, H., and Wang, S. (2010). STEERB: A Three-Dimensional Code for Storm-Time Evolution of Electron Radiation belt. J. Geophys. Res. 115, A09208. doi:10.1029/2009JA015210

CrossRef Full Text | Google Scholar

Subbotin, D., Shprits, Y., and Ni, B. (2010). Three-dimensional Verb Radiation belt Simulations Including Mixed Diffusion. J. Geophys. Res. 115, A03205. doi:10.1029/2009JA015070

CrossRef Full Text | Google Scholar

Summers, D. (2005). Quasi-linear Diffusion Coefficients for Field-Aligned Electromagnetic Waves with Applications to the Magnetosphere. J. Geophys. Res. 110. doi:10.1029/2005JA011159

CrossRef Full Text | Google Scholar

Summers, D., and Thorne, R. M. (2003). Relativistic Electron Pitch-Angle Scattering by Electromagnetic Ion Cyclotron Waves during Geomagnetic Storms. J. Geophys. Res. 108 (A4), 1143. doi:10.1029/2002JA009489

CrossRef Full Text | Google Scholar

Tao, X., Bortnik, J., Albert, J. M., and Thorne, R. M. (2012a). Comparison of Bounce-Averaged Quasi-Linear Diffusion Coefficients for Parallel Propagating Whistler Mode Waves with Test Particle Simulations. J. Geophys. Res. 117, A10205. doi:10.1029/2012JA017931

CrossRef Full Text | Google Scholar

Tao, X., Bortnik, J., Thorne, R. M., Albert, J. M., and Li, W. (2012b). Effects of Amplitude Modulation on Nonlinear Interactions between Electrons and Chorus Waves. Geophys. Res. Lett., L0610239. doi:10.1029/2012GL051202

CrossRef Full Text | Google Scholar

Thorne, R. M. (2010). Radiation belt Dynamics: The Importance of Wave-Particle Interactions. Geophys. Res. Lett. 37, L22107. doi:10.1029/2010GL044990

CrossRef Full Text | Google Scholar

Tong, Y., Vasko, I. Y., Artemyev, A. V., Bale, S. D., and Mozer, F. S. (2019). Statistical study of whistler waves in the solar wind at 1 au. ApJ 878, 41. doi:10.3847/1538-4357/ab1f05

CrossRef Full Text | Google Scholar

Tsurutani, B. T., and Lakhina, G. S. (1997). Some Basic Concepts of Wave-Particle Interactions in Collisionless Plasmas. Rev. Geophys. 35, 491–501. doi:10.1029/97RG02200

CrossRef Full Text | Google Scholar

Tyler, E., Breneman, A., Cattell, C., Wygant, J., Thaller, S., and Malaspina, D. (2019). Statistical Occurrence and Distribution of High‐Amplitude Whistler Mode Waves in the Outer Radiation Belt. Geophys. Res. Lett. 46, 2328–2336. doi:10.1029/2019GL082292

CrossRef Full Text | Google Scholar

Vainchtein, D., Zhang, X. J., Artemyev, A. V., Mourenas, D., Angelopoulos, V., and Thorne, R. M. (2018). Evolution of Electron Distribution Driven by Nonlinear Resonances with Intense Field‐Aligned Chorus Waves. J. Geophys. Res. Space Phys. 123, 8149–8169. doi:10.1029/2018JA025654

CrossRef Full Text | Google Scholar

Vedenov, A. A., Velikhov, E., and Sagdeev, R. (1962). Quasilinear Theory of Plasma Oscillations. Nucl. Fusion Suppl. 2, 465–475.

Google Scholar

Verscharen, D., and Chandran, B. D. G. (2013). The Dispersion Relations and Instability Thresholds of Oblique Plasma Modes in the Presence of an Ion Beam. ApJ 764, 88. doi:10.1088/0004-637x/764/1/88

CrossRef Full Text | Google Scholar

Vocks, C. (2012). Kinetic Models for Whistler Wave Scattering of Electrons in the Solar Corona and Wind. Space Sci. Rev. 172, 303–314. doi:10.1007/s11214-011-9749-0

CrossRef Full Text | Google Scholar

Vocks, C., Salem, C., Lin, R. P., and Mann, G. (2005). Electron Halo and Strahl Formation in the Solar Wind by Resonant Interaction with Whistler Waves. ApJ 627, 540–549. doi:10.1086/430119

CrossRef Full Text | Google Scholar

Walt, M. (1994). Introduction to Geomagnetically Trapped Radiation. Cambridge Atmospheric and Space Science Series. Cambridge, United Kingdom: Cambridge University Press. doi:10.1017/CBO9780511524981

CrossRef Full Text | Google Scholar

Wang, M. C., and Uhlenbeck, G. E. (1945). On the Theory of the Brownian Motion II. Rev. Mod. Phys. 17, 323–342. doi:10.1103/RevModPhys.17.323

CrossRef Full Text | Google Scholar

Watt, C. E. J., Allison, H. J., Thompson, R. L., Bentley, S. N., Meredith, N. P., Glauert, S. A., et al. (2021). The Implications of Temporal Variability in Wave-Particle Interactions in Earth’s Radiation Belts. Geophys. Res. Lett. 48. doi:10.1029/2020GL089962

CrossRef Full Text | Google Scholar

Wilson, L. B., Cattell, C. A., Kellogg, P. J., Wygant, J. R., Goetz, K., Breneman, A., et al. (2011). The Properties of Large Amplitude Whistler Mode Waves in the Magnetosphere: Propagation and Relationship with Geomagnetic Activity. Geophys. Res. Lett. 38. doi:10.1029/2011GL048671

CrossRef Full Text | Google Scholar

Woodfield, E. E., Horne, R. B., Glauert, S. A., Menietti, J. D., and Shprits, Y. Y. (2014). The Origin of Jupiter's Outer Radiation belt. J. Geophys. Res. Space Phys. 119, 3490–3502. doi:10.1002/2014JA019891

CrossRef Full Text | Google Scholar

Zaslavskiĭ, G. M., and Chirikov, B. V. (1972). Stochastic Instability of Non-linear Oscillations. Sov. Phys. Usp. 14, 549–568. doi:10.1070/pu1972v014n05abeh004669

CrossRef Full Text | Google Scholar

Zhang, X.-J., Mourenas, D., Shen, X.-C., Qin, M., Artemyev, A. V., Ma, Q., et al. (2021). Dependence of Relativistic Electron Precipitation in the Ionosphere on Emic Wave Minimum Resonant Energy at the Conjugate Equator. J. Geophys. Res. Space Phys. 126. doi:10.1029/2021JA029193

CrossRef Full Text | Google Scholar

Zhang, X. J., Mourenas, D., Artemyev, A. V., Angelopoulos, V., Bortnik, J., Thorne, R. M., et al. (2019). Nonlinear Electron Interaction with Intense Chorus Waves: Statistics of Occurrence Rates. Geophys. Res. Lett. 46, 7182–7190. doi:10.1029/2019GL083833

CrossRef Full Text | Google Scholar

Zheng, L., Chen, L., and Zhu, H. (2019). Modeling Energetic Electron Nonlinear Wave‐Particle Interactions with Electromagnetic Ion Cyclotron Waves. J. Geophys. Res. Space Phys. 124, 3436–3453. doi:10.1029/2018JA026156

CrossRef Full Text | Google Scholar

Zheng, Q., Zheng, Y., Fok, M.-C., and Lui, A. T. Y. (2012). Electron Energy Diffusion and Advection Due to Non-linear Electron-Chorus Wave Interactions. J. Atmos. Solar-Terrestrial Phys. 80, 152–160. doi:10.1016/j.jastp.2012.01.011

CrossRef Full Text | Google Scholar