Cascading parametric decay coupling between whistler and ion acoustic waves: Darwin particle-in-cell simulations

1 Introduction

Finite-amplitude electromagnetic fluctuations known as whistler waves are frequently observed in the Earth’s magnetosphere (Burtis and Helliwell, 1969; Maksimovic et al., 2001; Cattell et al., 2008) and solar wind (Lacombe et al., 2014; Tong et al., 2019; Agapitov et al., 2020; Cattell et al., 2021). They are known to play a significant role in regulating the electron populations in the radiation belt region (Thorne, 2010), especially during active periods of geomagnetic activity (Meredith et al., 2001; Reeves et al., 2013; Mourenas et al., 2014). In addition to the nonlinear interactions between the whistler waves and resonant electrons in this space plasma environment (Agapitov et al., 2015a), these waves contribute to heating and acceleration processes in the solar wind (Vocks et al., 2005) and magnetosheath regions (Huang et al., 2018). The nonlinear resonant wave-particle interaction manifests itself as the frequency chirping phenomena in the whistler mode chorus waves (Omura et al., 2008; Gao et al., 2014). Multiband chorus waves have been detected by the THEMIS satellites and nonlinear wave-wave coupling mechanisms have been proposed as a potential generation mechanism for this observation (Gao et al., 2016), and more recently, the origin of the chorus emission period has been linked to the drift velocity of energetic electrons (Gao et al., 2022). Furthermore, an analysis of waveforms from the Van Allen Probes has revealed possible parametric coupling between whistler waves and electron acoustic modes (Agapitov et al., 2015b).

Under certain conditions, large amplitude monochromatic plasma waves are nonlinearly unstable and can decay into other types of fluctuations. One such nonlinear process is the parametric decay instability in which a forward propagating parent wave decays into two daughter waves (Forslund et al., 1972). The decay instability has been investigated in whistler mode waves Umeda et al. (2014), circularly polarized Alfvén waves (Terasawa et al., 1986), Langmuir waves (Umeda and Ito, 2008), and light waves (Usui et al., 2002). In the parametric decay instability of parallel propagating whistler waves, a backward propagating daughter whistler wave and forward or backward ion acoustic or electron acoustic wave mode are involved. The instability threshold is determined by the product of the damping rates of the daughter waves, which can be large due to the increased Landau damping rate of the ion acoustic waves, particularly when the electron and ion temperatures are comparable in the plasma. When the ion and electron temperatures are comparable there is a possibility of parametric decay via an ion quasimode, however, this involves non-parallel propagation (Shukla, 1977).

Previous studies of the whistler wave parametric decay instability have been made using one and two-dimensional fully electromagnetic particle-in-cell (PIC) simulation models (Umeda et al., 2014, 2018; Ke et al., 2018). For a large amplitude pump whistler wave (δB_w/B_o ∼ 0.3) and frequency near the electron cyclotron frequency, the energy of the electron bulk velocity supporting the parent wave is converted into thermal energy perpendicular to the background magnetic field. This increase of perpendicular thermal energy relative to parallel thermal energy triggered an electron temperature anisotropy instability which in turn, caused heating and acceleration of the electrons. For smaller amplitudes (δB_w/B_o ∼ 0.03–0.07) and only parallel propagation, it was found that proton heating and field-aligned acceleration occurred through the Landau resonance due to the enhanced ion acoustic wave. Above δB_w/B_o ∼ 0.05 it has been reported that a secondary parametric decay of the daughter whistler wave can occur (Karbashewski, 2017; Ke et al., 2017). Two-dimensional simulations indicate that the 2D decay instability is quite different compared to purely parallel propagation, with different time scales and wave-particle interaction dynamics (Umeda et al., 2017; Ke et al., 2018).

The purpose of this paper is to investigate the growth and subsequent nonlinear evolution of the parametrically unstable, parallel propagating electron whistler modes. Since the ion dynamics are essential, we use a magneto-inductive PIC simulation (Darwin model) (Busnardo-Neto et al., 1977) which allows for larger time steps due to the exclusion of the light wave branch. The threshold, growth rate, and saturation dynamics of the parametric decay instability are investigated and one of the main results is the establishment of the threshold condition for initiation of multiple decays of the daughter modes generated from the initial single wave decay process.

The organization of this paper is as follows: in Section 2 we detail the relevant theory for the coupling and parametric decay instability between whistler waves and ion acoustic waves and outline the setup of the UPIC simulation software; in Section 3 we present the simulation results and analysis of the parametric decay pathways; and in Section 4 we make a comparison of the simulation results with models, discuss relevant regimes for the observation of the instability, and summarize the main results.

2 Theory and modeling

2.1 Whistler-ion acoustic parametric decay

In this section, we present a model for the ponderomotive coupling and parametric decay of a whistler wave into daughter whistler and ion acoustic waves. We consider a uniform plasma with a background magnetic field oriented along the x-component of a Cartesian coordinate system, $\mathbf{B}=B_0\widehat{\mathbf{x}}$. Electromagnetic and electrostatic waves are considered to propagate with wave vectors parallel to the background magnetic field and thus the transverse electromagnetic wave fields will be strictly in the yz-components, and the longitudinal electrostatic field is strictly in the x-component. The whistler wave dispersion relation for parallel propagation with respect to the background magnetic field is derived from the cold plasma dispersion relation for magnetized plasmas, or Lassen-Appleton-Hartree equation, as, (Lassen, 1926; Appleton, 1927; Hartree, 1931; Gurnett and Bhattacharjee, 2005),

$\frac{k^2{c}^2}{{\omega }_{pe}^2}\simeq 1-\frac{{\omega }_{pe}}{\omega \left(\omega -{\omega }_{ce}\right)}(1)$

where ω_pe is the electron plasma frequency and ω_ce is the electron cyclotron frequency; in formulating the dispersion ion motion has been neglected. Figure 1 is a plot of ω/ω_pe as a function of kc/ω_pe with Eq. 1 shown by the black dotted curve; ω_ce/ω_pe = 1/3 is used to construct the curve and is the same as the ratio used in the simulations presented herein. The parallel propagating whistler wave is a right-hand, circularly polarized, transverse electromagnetic wave that approaches a resonance at ω_ce as k increases. Near the resonance, the wavelength is on the order of the electron cyclotron radius and the phase velocity and group velocity of the whistler wave both approach zero. The wave-particle interactions are strong near resonance and the wave will experience cyclotron damping as energy is transferred to the electrons; as a result, the whistler branch is more strongly damped as k increases.

FIGURE 1

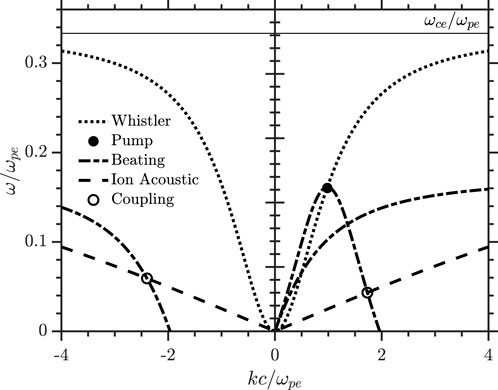
FIGURE 1. Ponderomotive coupling between whistler waves and ion acoustic waves. A pump whistler wave (black filled circle) creates ponderomotive beat patterns (black dash-dotted curve) with the whistler wave branch (black dotted curve). The ion acoustic branch (black dashed curve) is coupled to the pump whistler wave and whistler branch where it intersects with the pondermotive beating (black hollow circles). The solid black line indicates ω_ce/ω_pe =1/3.

Ion acoustic waves (IAWs) are low-frequency electrostatic, longitudinal waves manifesting as oscillations of the plasma ions and electrons that are analogous to collisional sound waves in a gas. The dispersion relation for ion acoustic waves of singly ionized ions is dependent on both the temperature of the electrons, T_e, and ions, T_i, as well as the mass of the ions, M, and defines the ion acoustic velocity c_s,

$c_s={\left(\frac{{\gamma }_e{k}_B{T}_e}{M}\frac{1}{1+k^2{\lambda }_{De}^2}+\frac{{\gamma }_i{k}_B{T}_i}{M}\right)}^{1/2}(2)$

where k_B is the Boltzmann constant, λ_De is the electron Debye length, and γ_s is the heat capacity ratio with γ_i = 3 for ions in one-dimension and γ_e = 1 for isothermal electrons (Chen, 1984). Ion acoustic waves experience heavy Landau damping by ions moving at velocities near the ion acoustic phase velocity, thus the waves become significant only when T_e ≫ T_i and the contribution of the ion temperature term becomes negligible. Under this assumption, an inspection of Eq. 2 reveals that the ion acoustic wave has a nearly linear relationship between ω and k until $k^2{\lambda }_{De}^2\gg 1$, at which point the ion acoustic wave approaches a resonance at the ion plasma frequency ω_pi; this condition is only for large k and for the relevant parameter space of the present study the ion acoustic wave is dispersionless $(c_s^2\approx k_B{T}_e/M)$. The dashed black curve in Figure 1 shows Eq. 2 for the parameters used in the simulation, which will be detailed in Section 2.2.

The coupling of whistler waves, which are transverse electromagnetic waves, and ion acoustic waves, which are longitudinal electrostatic waves, is achieved through the ponderomotive force, or Miller force (Miller, 1958). The ponderomotive force is a nonlinear effect that has been used to describe many plasma phenomena, such as the self-focusing of lasers in a plasma (Max, 1976), electromagnetic-electrostatic mode conversion in non-uniform plasmas (Morales and Lee, 1974), and density structures in the auroral ionosphere (Bellan and Stasiewicz, 1998). The force arises due to spatial variations in the amplitude of an oscillating electric field δE = E_s(r) cos (ωt); the force per m³ on the electrons in a plasma is (Chen, 1984),

${\mathbf{F}}_{\mathbf{p}}=-\frac{{ϵ}_0}{2}\frac{{\omega }_{pe}^2}{{\omega }^2}\nabla ⟨E_s^2⟩(3)$

where ⟨…⟩ indicates a time average over the period of the wave, 2π/ω. The force is the same for both electrostatic and electromagnetic perturbations though the mechanism behind the force is different. In the electrostatic case, particles are forced into regions of lower field amplitude by the larger electric force in high field regions. In the case of an electromagnetic wave, the force arises from a second order Lorentz v × B force along the wave vector that varies with the spatial variation of the electric field. In both cases, the Miller force due to the spatial variations of the electric field results in a build-up of particle density in lower field regions. Equation 3 is for electrons, but one can see that the ponderomotive force is proportional to the spatial gradient of the electric field as well as the density of the region and will therefore be felt by all charged particles. However, because of the mass dependence, the effect is smaller for ions relative to the force on electrons by a factor of m_e/M. Thus, the ponderomotive force on the ions can often be neglected; however, at low frequencies, the ions will respond to the charged regions created by the ponderomotive force on electrons.

A subset of nonlinear wave-wave interactions are known as parametric decay instabilities and involve a three-wave coupling between a pump wave and two daughter modes. The three coupled waves involved must satisfy a set of matching conditions Neubert (1982).

${\omega }_w={\omega }_T\pm {\omega }_L(4)$

${\mathbf{k}}_w={\mathbf{k}}_T\pm {\mathbf{k}}_L(5)$

Where the subscript w refers to the pump wave, the subscript T refers to the transverse daughter wave, and the subscript L is the longitudinal daughter wave. In Section 3 we present 1-D PIC simulations designed to observe parametric coupling of an imposed, monochromatic, pump whistler wave with daughter whistler and IAW waves that exist in the plasma as thermal modes. The pump whistler forms spatial beats in the transverse electric fields with each of the thermal whistler modes and this sets up a ponderomotive force in the parallel direction equal to,

${\mathbf{F}}_{\mathbf{P}}=-\frac{{ϵ}_0}{2}\frac{{\omega }_{pe}^2}{{\omega }^2}\nabla \langle {\left({\mathbf{E}}_w+{\mathbf{E}}_T\right)}^2\rangle \simeq -{ϵ}_0\frac{{\omega }_{pe}^2}{{\omega }_B^2}\nabla \langle {\mathbf{E}}_w\cdot {\mathbf{E}}_T\rangle (6)$

where we assume a uniform pump wave with $⟨E_w^2⟩=0$, the gradient of the $⟨E_T^2⟩$ term is small and may be discarded, and only the cross term ⟨E_w ⋅E_T⟩ will contribute to the ponderomotive force. Here, we denote all of the whistler modes apart from the pump as E_T. The ponderomotive beating will force low amplitude electrostatic perturbations parallel to B₀ with frequency ω_B = ω_w − ω_T and wavenumber k_B = k_w − k_T when ω_w > ω_T, and frequency ω_B = ω_T − ω_w and wavenumber k_B = k_T − k_w when ω_T > ω_w. In Figure 1 the pump whistler is indicated by a filled black circle and the ponderomotive beating patterns are indicated by the dash-dotted curves. In Section 3 we will demonstrate that this ponderomotive beating of the whistler branch with a monochromatic pump does form low amplitude electrostatic wave perturbations with the pattern predicted in Figure 1.

The ponderomotive beating branch facilitates coupling to an ion acoustic mode at (k_L, ω_L), so long as k_B ≈ k_L and ω_B ≈ ω_L, and forms a set of three coupled waves between the pump, daughter whistler, and daughter IAW. The ponderomotive force will drive the growth of the resonant IAW which will in return drive the growth of the resonant daughter whistler. The location of the electrostatic coupling in ωk-space between the electromagnetic whistler modes and electrostatic IAW occurs at the intersections of the pondermotive beating and IAW branch; this is indicated in Figure 1 by the hollow circles. For the present electrostatic mode, only beating with counter-propagating whistler waves will lead to a parametric decay channel.

In the regime where ω_ce < ω_pe the whistler wave pump generates parametric instabilities above a certain threshold amplitude. The parametric instability that is dominant over a wide range of parameters is the ion decay instability. Near the threshold amplitude, with the matching conditions satisfied, the threshold is given by (Nishikawa, 1968; Forslund et al., 1972),

${\left(\frac{B_w}{B_o}\right)}^2>8\left(1+{\left(\frac{c{k}_w}{{\omega }_{pe}}\right)}^2\right){\beta }_e\left(\frac{{\gamma }_T}{{\omega }_T}\right)\left(\frac{{\gamma }_L}{{\omega }_L}\right)(7)$

where k_w is the pump wavenumber, electron plasma beta is defined as ${\beta }_e=8\pi n{T}_e/B_o^2$, and γ_T and γ_L are the damping rates of the transverse and longitudinal daughter modes, respectively. The frequency and wavenumber matching conditions require ω_L ≃ 2k_wc_s and ω_T ≃ ω_w at − k_w. Therefore, the product of the linear damping rates of the transverse and longitudinal daughter modes essentially determines the threshold amplitude needed to excite the parametric decay instability. These damping rates can be computed from linear kinetic theory to give an estimate of threshold pump wave amplitude.

Above threshold, the real frequency and maximum growth rate of the parametrically unstable ion wave are given by ω ≈ ω_L + iΓ, where ω_L ≃ 2k_wc_s and,

$\frac{\mathrm{\Gamma }}{{\omega }_T}\simeq \sqrt{\frac{{\omega }_{ci}}{{\omega }_L}}\frac{B_w}{B_o}(8)$

This result implies that the growth rate scales linearly with pump wave amplitude and is inversely proportional to the square root of the ion mass. These analytical results will be used to compare with the simulations. We mention here that the equation for the ion wave growth rate is obtained from the dispersion relation for the three-wave mode coupling presented in (Forslund et al., 1972).

2.2 Simulation setup

To investigate the nonlinear growth and saturation of the parametric decay instability for parallel propagating monochromatic whistler waves the Darwin particle-in-cell (PIC) simulation model is used and based on the spectral code developed as part of the UCLA particle-in-cell (UPIC) framework (Decyk, 2007). The simulation has previously been used to model the whistler wave instabilities driven by the temperature anisotropy in the solar wind and Earth’s magnetosphere (Hughes et al., 2016).

The Darwin PIC model removes the transverse component of the displacement current in Ampere’s law, therefore, the high-frequency light waves are excluded while leaving the other waves, such as the whistler wave, unaffected (Busnardo-Neto et al., 1977). In comparison to the conventional explicit electromagnetic PIC model, the Darwin PIC method is more computationally efficient since the Courant condition for the time step is not restricted to following the light waves. The grid spacing, Δ_x, is required to resolve the Debye length to avoid numerical heating of the plasma. Since we focus on the parametric decay of the parallel propagating whistler wave, a 1-D PIC simulation model with periodic boundary conditions is utilized. Fully 3-D electromagnetic fields and velocities are included but only spatial variation in the x-direction is present. A uniform background magnetic field is imposed along the x-axis.

The UPIC code uses dimensionless parameters where time is normalized to the plasma frequency, t → ω_pet, space is normalized to the grid spacing, x → x/Δ_x, where the grid spacing is determined by the dimensionless thermal velocity of the electrons v_te → v_te/Δ_xω_pe and is an input to the code, the charge of each species s is normalized to the elementary charge, q_s → q_s/e, the mass of each species is normalized to the mass of an electron, m_s → m_s/m_e, and these provide the necessary normalizations for all other quantities (Decyk, 2007). The simulation input parameters used, unless otherwise stated, are the time step Δ_t = 0.2ω_pet, electron thermal velocity v_te = 1.00, number of time steps N_t = 5001, number of grid cells N_x = 512, number of particles per species N_p = 184320, and cyclotron frequency ω_ce/ω_pe = 1/3, c/ω_peΔ_x = 10, electron-ion temperature ratio T_e/T_i = 100, and electron-ion mass ratio M/m_e = 16.

The choice of the low mass ratio is justified and made for several reasons: (i) computational efficiency, higher mass ratios require significantly more time steps to resolve the long time scales associated with ion dynamics and require a larger spatial grid to achieve sufficient k-space resolution; (ii) increasing the IAW frequency to the order of the whistler waves, this makes the illustration of the dynamics in both simulations and theoretical descriptions more clear; and (iii) part of the motivation for this work is a similar process that could occur for the EAW, the low mass ratio IAW decay is a precursor for studies of the EAW with a similar dispersion.

The UPIC code was modified to enable the external driving of transverse electric fields. The whistler wave driving is accomplished by adding sinusoidal wave fields each iteration to the self-consistent electric fields; the amplitude is slowly increased as the system responds to the external fields and when done correctly the wave continues to propagate once the driver is turned off. To launch a whistler wave the external driver needs to be right-hand circularly polarized and the external electric fields added to the self-consistent fields are.

$E_{wz}=E_w\left(t\right)\cos \left(k_{w}x-{\omega }_{w}t\right)(9)$

$E_{wy}=E_w\left(t\right)\sin \left(k_{w}x-{\omega }_{w}t\right)(10)$

In all simulations, the amplitude E_w(t) increases linearly to some maximum at ω_pet = 100 and the driver fields are eliminated. The driven wave mode is chosen to have ω_w ≈ 0.161ω_pe and k_wc/ω_pe ≈ 0.98 corresponding to mode number m_w = 8 where k = 2πm/N_x. The amplitude of the self-consistently propagating electromagnetic wave is determined from the magnetic field at ω_pet = 150. It is not necessary to perturb the transverse magnetic fields and velocities as the system will respond each iteration to the pumped electric fields and set up the necessary conditions for the wave to continue propagating if the pump is matched to a real mode of the plasma. Additionally, since a parallel whistler mode has no longitudinal component the particles are loaded uniformly at time ω_pet = 0.

3 Results

We begin this section by demonstrating with the PIC simulation the ponderomotive beating model outlined in Section 2.1. Throughout this section a quantity A in xt-space may be shown in kt-space and mω-space (i.e. kω-space); the spatially Fourier transformed quantity will be denoted as $\bar{A}$ and the spatio-temporally Fourier transformed quantity will be denoted as $\tilde{A}$. Figure 2A shows the transverse electric field fluctuations $\delta {\tilde{E}}_y$ and illustrates the thermal whistler branch in a simulation where the ions remain fixed, the wave driver is kept off, and the electrons are relatively cold at v_te = 0.10 to reduce the cyclotron damping at frequencies close to ω_ce. The theoretical curve for the whistler branch from Figure 1 is shown by the white dashed line and is in excellent agreement with the simulation. It is these low amplitude whistler waves that will form spatial beats in the transverse electric fields with the pump wave to produce the ponderomotive force along x.

FIGURE 2

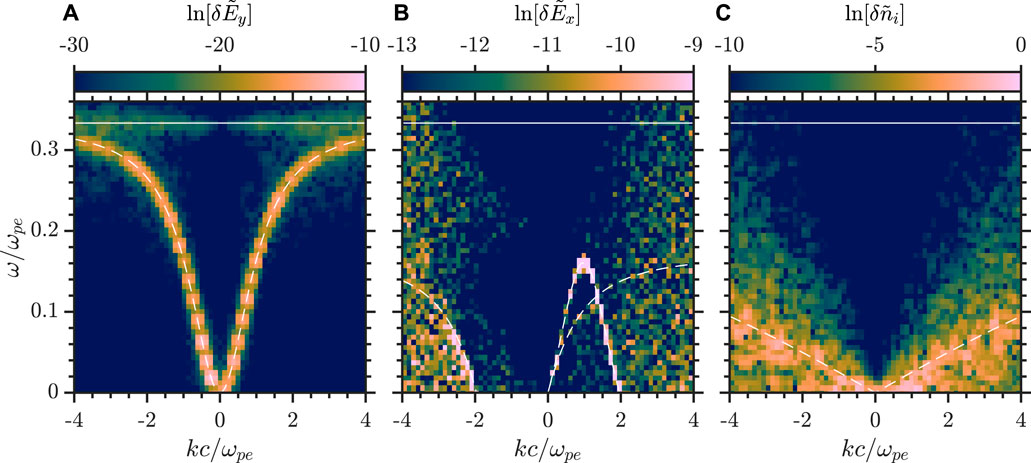
FIGURE 2. (A) Whistler branch visible in $\delta {\tilde{E}}_y$ in a cold electron, fixed ion simulation. (B) Ponderomotive coupling pattern in $\delta {\tilde{E}}_x$ for a low amplitude pump whistler (δB_w/B₀=0.1) in a cold electron, fixed ion simulation. (C) Ion acoustic branch seen in $\delta {\tilde{n}}_i$ in a hot electron, cold ion simulation (T_e/T_i =100). The solid line in each is ω_ce/ω_pe and the dashed curves represent the respective branch shown in each panel.

Figure 2B shows the longitudinal field fluctuations $\delta {\tilde{E}}_x$ for the same simulation parameters but with the driven wave launched with an amplitude of δB_w/B₀ ∼ 0.1. With no electrostatic wave to couple to due to the fixed ions, the low amplitude ponderomotive beating patterns are observed and show remarkable agreement with the theoretical curves. The beating with whistler waves higher than the pump is suppressed relative to the low-frequency waves, as is the beating with co-propagating waves when compared to the counter-propagating waves; thus it may be expected that the dominant decay path will involve the lower frequency counter-propagating whistler and co-propagating IAW highlighted in Figure 1. Next, the electron thermal velocity is returned to the nominal value of v_te = 1.00, the moving ions are introduced and the driven wave is removed; the resulting thermal ion acoustic fluctuations in $\delta {\tilde{n}}_i$ are shown in Figure 2C and again are in good agreement with the predicted dispersion.

The ingredients for observing the parametric decay of the whistler wave are all contained in Figure 2 and demonstrate the ponderomotive model. The inclusion of the pump wave with the nominal simulation parameters creates the situation where the parametric decay may be observed for a large enough amplitude pump. The first observed decay activity occurs at δB_w/B₀ = 0.028. Figure 3 shows the simulation result for a pump wave with amplitude δB_w/B₀ = 0.032. In Figure 3A the xt-space evolution of δE_y shows the linear growth of the pump whistler and its subsequent self-consistent propagation after ω_pet = 100. In Figure 3B the same is seen at mode number m = 8 in kt-space. At ω_pet ≈ 350 we observe the rapid growth of a monochromatic electromagnetic wave counter-propagating to the pump wave. This is confirmed as a whistler wave in Figure 3C where the pump mode and a daughter whistler mode are observed at m_w = 8 and m_T1 = −6 along the whistler branch.

FIGURE 3

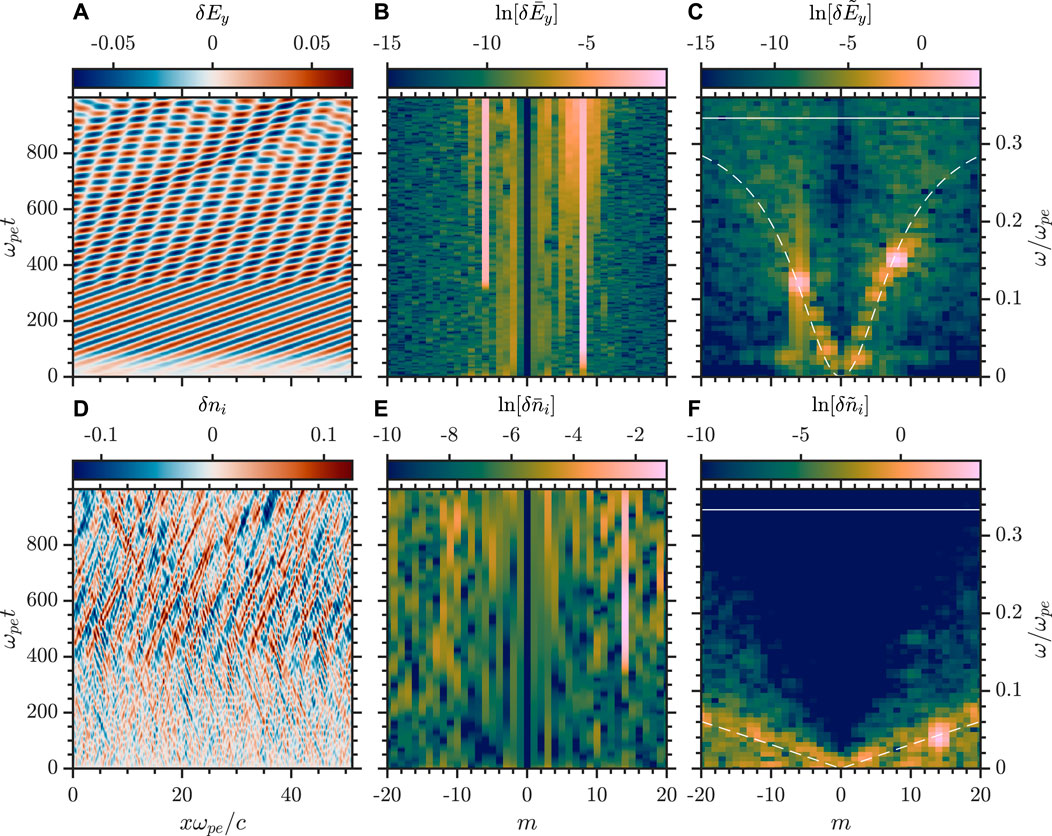
FIGURE 3. Single parametric decay of whistler wave with δB_w/B₀=0.032 (A),(B), and (C) xt-space, mt-space, and mω-space of δE_y, respectively (D),(E), and (F) xt-space, mt-space, and mω-space of δn_i, respectively. Dashed curves indicate the whistler and IAW branches in (C) and (F), respectively, and the solid line is ω_ce/ω_pe. The mode number m is related to the wave number by the relation k =2πm/N_x.

In Figure 3D, E we observe the growth of an electrostatic structure in δn_i and $\delta {\bar{n}}_i$, respectively, coinciding with the growth of the whistler wave at ω_pet ≈ 350. The kω-space of $\delta {\tilde{n}}_i$ in Figure 3F shows this is an ion acoustic daughter wave at m_L1 = 14. The parametric decay conditions in Eqs 4, 5 for the wave frequency and mode number yield: ω_T1 + ω_L1 = (0.119 + 0.038)ω_pe = 0.157ω_pe and m_T1 + m_L1 = −6 + 14 = 8; this is approximately equal to ω_w and matches m_w. Figure 4A shows the expected parametric decay path for a counter-propagating daughter whistler wave with ω_T < ω_w; a comparison of the theoretical and observed decay shows a small difference due to the non-integer mode numbers that are unavailable to the spectral code.

FIGURE 4

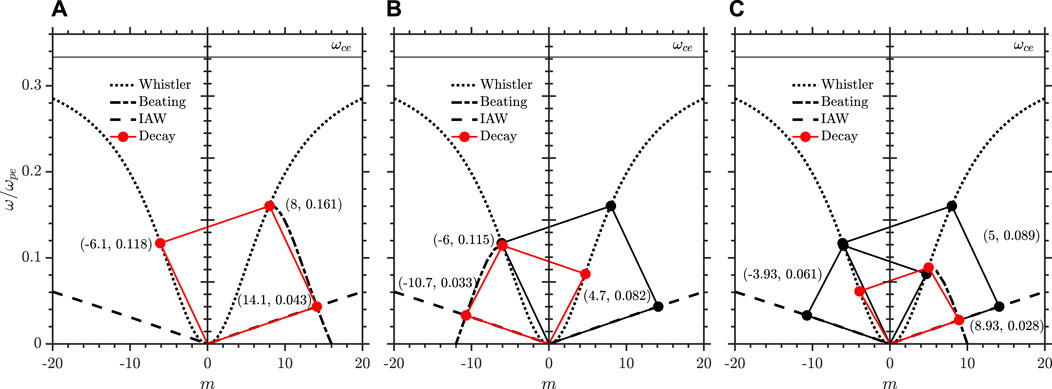
FIGURE 4. Cascading parametric decay paths. The dotted curve is the whistler branch, the dash-dotted black curve is the ponderomotive beating with the counter-propagating low-frequency whistlers, and the dashed black line is the ion acoustic wave. The parametric 3-wave coupling is indicated by the solid red curve where the (x, y) pairs in each panel are the locations of the red circles (A) Primary decay of pump whistler wave. (B) Secondary decay of the daughter whistler wave. (C) Tertiary decay of the secondary daughter whistler wave.

In Figure 1 we highlighted that there were two possible locations for coupling to the ion acoustic wave in kω-space by a given pump wave; for both couplings, the daughter whistler wave is counter-propagating with the pump wave, however, one corresponds to ω_T < ω_w and the other to ω_T > ω_w. While the latter is certainly a possible decay channel, the former dominates and this is likely due to the increased cyclotron damping of the higher whistler modes. This is supported by the amplitude of the pondermotive beat modes in Figure 2B that show beats with ω_T < ω_w whistler modes are the strongest and the beating becomes nearly non-existent as ω_T approaches ω_ce. Though not investigated here, the coupling to the counter-propagating IAW and counter-propagating whistler with ω_T > ω_w could conceivably occur under the right conditions.

Figure 5 presents the simulation result for a pump wave with amplitude δB_w/B₀ = 0.052 in the same format as Figure 3. The growth of the T1 wave begins earlier at ω_pet ≈ 200 but the rate of the growth is considerably reduced as seen in the panel of $\delta {\bar{E}}_y$. The T1 mode is accompanied by the simultaneous and more rapid growth of another electromagnetic mode; this is confirmed to be a counter-propagating (with respect to T1) whistler wave, T2, at m_T2 = 5 and ω_T2 = 0.107ω_pe. In the ion fluctuations, there is first the growth of the L1 mode and this is followed by the growth of a co-propagating (with respect to T1) ion acoustic structure, L2, at m_L2 = −11 and ω_L2 = 0.019ω_pe.

FIGURE 5

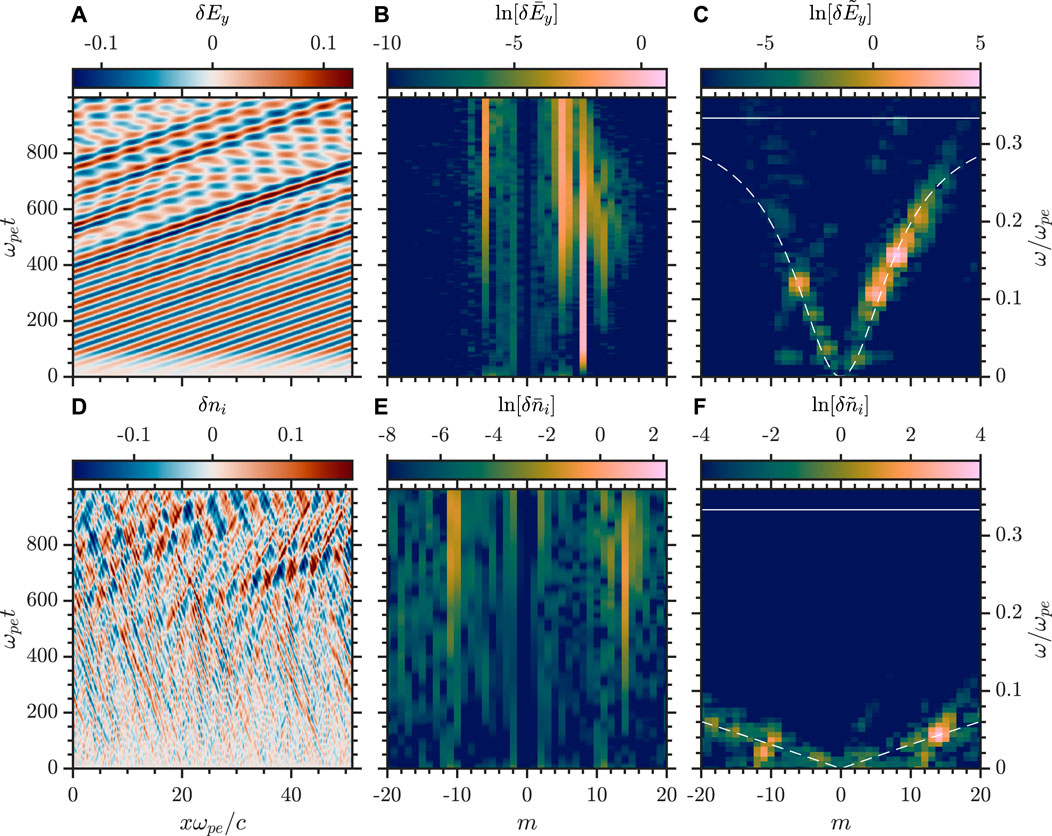
FIGURE 5. Double parametric decay of whistler wave with δB_w/B₀=0.052 (A),(B), and (C) xt-space, mt-space, and mω-space of δE_y, respectively (D),(E), and (F) xt-space, mt-space, and mω-space of δn_i, respectively. Dashed lines indicate the whistler and IAW branches in (C) and (F), respectively, and the solid line is ω_ce/ω_pe.

The observed decay path is still the primary decay seen at lower pump amplitudes, however, this is accompanied by a secondary decay. The growth of the primary decay is significantly reduced due to the cascade of energy to the secondary decay as the pump wave drives the growth of all four daughter waves. The expected matching conditions of the secondary decay channel are shown in Figure 4B, where m_T1 = −6 is explicitly used as the intermediate pump wave, and agree favourably with the simulation results. Notably, the mode numbers again are non-integers and this explains the small discrepancies between the simulation and prediction. The threshold for the secondary decay occurs at δB_w/B₀ ≈ 0.036 and can be identified by a rapid reduction in the growth rate of the primary daughter modes as will be discussed in Section 4.

Increasing the pump wave further to δB_w/B₀ ≳ 0.063 results in a tertiary decay channel of another counter-propagating whistler wave and IAW to L1. This is shown in Figure 6 for δB_w/B₀ = 0.103 in the same format as Figures 3, 5. In the δE_y and $\delta {\bar{E}}_y$ plots we observe a larger growth rate for the primary decay, followed by the secondary, and finally the tertiary, T3 mode. However, in the δn_i and $\delta {\bar{n}}_i$ panels the L1 structure is observed to grow to a very large amplitude at ω_pet ≈ 300 and become highly nonlinear; this is evidenced by the development of a mirror mode at m*L1 = −14 and the zero frequency content at m_L1 and $m_{L1}^{*}$ in the $\delta {\tilde{n}}_i$ plot. The structure initially propagates with the ion acoustic velocity but slows and becomes nearly stationary as the wave steepens; the structure is short-lived and decays rapidly as energy cascades to the other daughter modes. Given the continuous cascade of parametric decays, it is interesting this over-driven primary IAW regime does not lead to a quaternary decay or even higher decay channels that provide a sink for the excess pump energy.

FIGURE 6

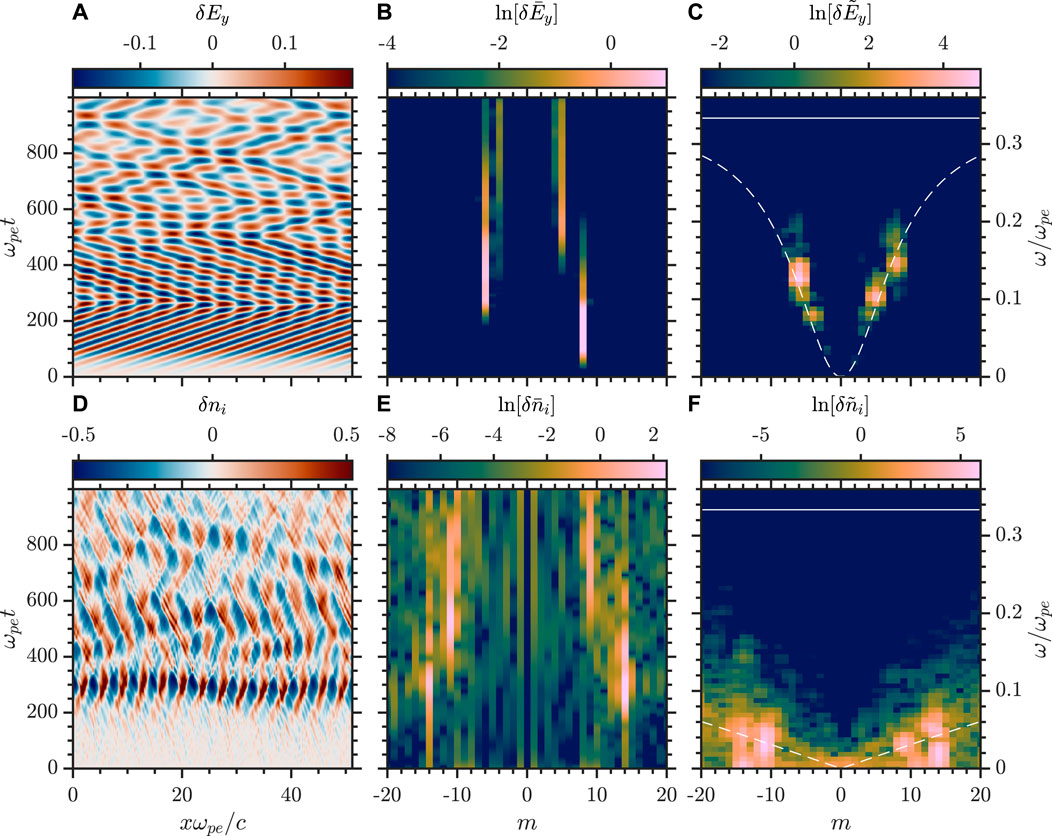
FIGURE 6. Triple parametric decay of whistler wave with δB_w/B₀=0.103 (A),(B), and (C) xt-space, mt-space, and mω-space of δE_y, respectively (D),(E), and (F) xt-space, mt-space, and mω-space of δn_i, respectively. Dashed lines indicate the whistler and IAW branches in (C) and (F), respectively, and the solid line is ω_ce/ω_pe.

The electromagnetic modes remain linear and follow a clearly defined decay path with all four whistler modes highlighted in the $\delta {\tilde{E}}_y$ plot; similarly, apart from the zero frequency modes, the three daughter IAWs are observed in $\delta {\tilde{n}}_i$. The tertiary whistler mode T3 has m_T3 = −4 and ω_T3 = 0.075ω_pe, and the tertiary IAW L3 has m_L3 = 9 and ω_L3 = 0.031ω_pe. These modes meet the matching conditions with T2 and are close to the expected decay channel in Figure 4C.

Lastly, we investigate a case with cascading parametric decays for a higher mass ratio of M/m_e = 400 to demonstrate the universality of the effect. The grid size has been expanded to N_x = 2048, while the number of particles per cell has been kept constant by increasing the total number of particles per species to N_p = 737280. We choose here to pump mode number m_w = 20 (ω_w ≈ 0.09) — and not m_w = 32 for a direct comparison to the smaller grid—to keep the dynamics in xt-space more easily visible; this is expected to somewhat reduce the threshold for instability, and indeed the primary decay threshold is observed to be δB_w/B₀ ≈ 0.02, however, to observe a cascade still requires the amplitude to be well above the threshold. The small IAW frequency at the relevant mode numbers for decay to occur means that the whistler modes involved have very little spread in frequency and mode number compared with the previous cases; the primary decay has m_T1 = −19 and ω_T1 ≈ 0.08 for the daughter whistler, and M_L1 = 39 and ω_T1 ≈ 0.01 for the daughter IAW. Thus, any cascade will be observed as a sequential decrease in mode number for the subsequent daughter modes. Figure 7 presents the cascade at the higher mass ratio in the same format as the previous cases. It is clear from the evolution of the dominant mode numbers in the mt-space diagrams that a parametric decay cascade is occurring. We again observe nonlinear and nearly stationary structures in the ion density as there is considerable power in the zero-frequency modes.

FIGURE 7

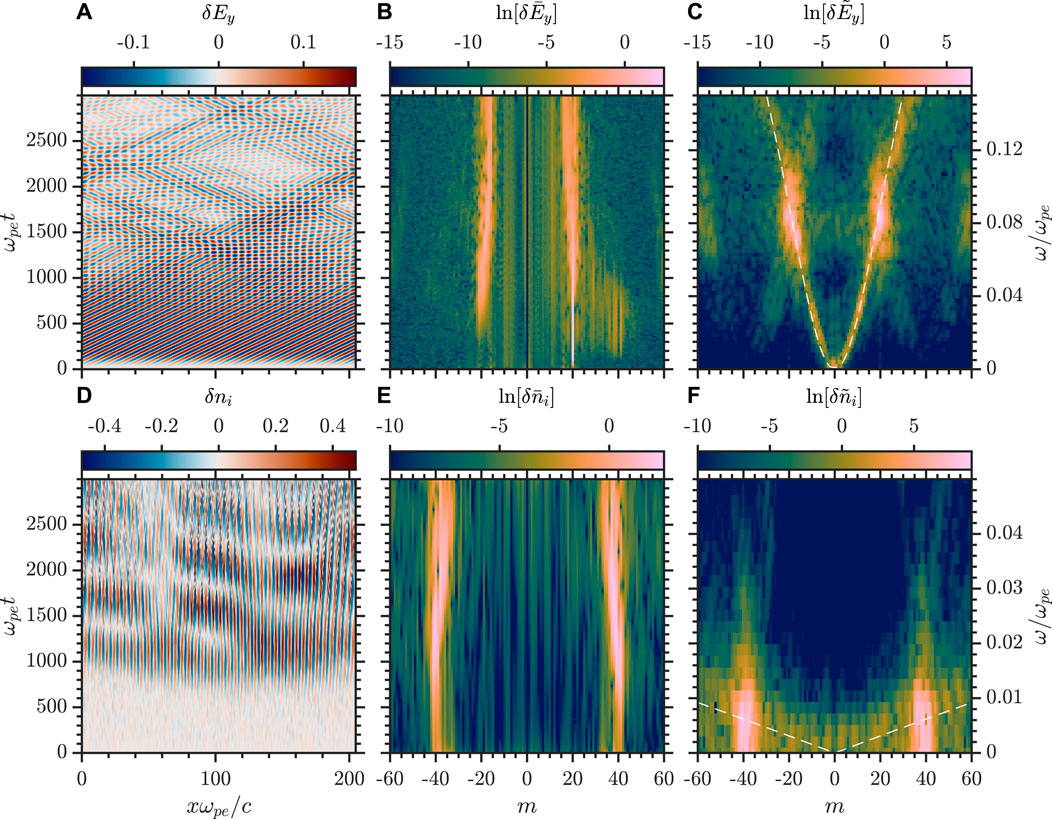
FIGURE 7. Triple parametric decay of whistler wave with δB_w/B₀=0.095 with a mass ratio of M/m_e =400 (A),(B), and (C) xt-space, mt-space, and mω-space of δE_y, respectively (D),(E), and (F) xt-space, mt-space, and mω-space of δn_i, respectively. Dashed lines indicate the whistler and IAW branches in (C) and (F), respectively, and the solid line is ω_ce/ω_pe.

4 Discussion

In this section, we discuss the dynamics of the daughter wave growth, parametric instability thresholds, relevance to the radiation belts and solar wind, and finish with a summary of the main results. Figure 8 displays the evolution of the field and particle energies and the mode growth for the triple parametric decay case in Figure 6. Figure 8A displays the fractional transverse and longitudinal electric field energy, relative to the total electric field energy; Figure 8B displays the fractional energy of the electromagnetic fields and kinetic energies of the electrons and ions; and Figures 8C, D show the m vs t growth of the whistler and IAW daughter modes, respectively. The initial ramp of the driven whistler wave puts the majority of the field energy into the transverse component. The first decay of the pump and subsequent growth of the nonlinear ion acoustic structure occurs at ω_pet = 300 and rapid transfer of energy from the transverse to the longitudinal electrostatic field occurs simultaneously. This is accompanied by a small growth in the electron and ion kinetic energies (B), though only minimal heating is observed throughout the decay process. The growth of the primary decay is rapid and the whistler wave T1 experiences only slight damping (C) in comparison to the IAW damping (D); this results in the growth of the transverse fraction compared to the longitudinal. Each subsequent decay is observed in the fractional electric field energy (D) as an increase in the longitudinal fraction and subsequent decay.

FIGURE 8

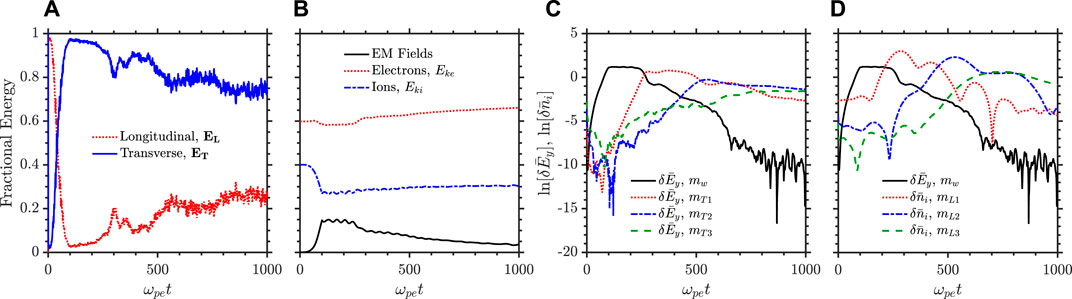
FIGURE 8. Analysis of energy transfer and wave growth during the triple decay for δB_w/B₀=0.103 (A) Fractional electric field energy that is contained in the longitudinal electric field (red dotted curve) and transverse electric field (blue solid curve) (B) Fractional energy of the electromagnetic fields (black solid curve), electron kinetic energy (red dotted curve), and ion kinetic energy (blue dash-dotted curve) (C) and (D) growth of the parametric decay modes for the daughter whistler and ion acoustic waves, respectively. The solid black curve is the pump whistler, the red dotted curve is the primary decay, the blue dash-dotted curve is the secondary decay, and the green dashed curve is the tertiary decay.

The growth rates, γ/ω_pe, of the daughter modes can be extracted from the mt-space for each pump wave amplitude. Figure 9 shows these growth rates from δB_w/B₀ ∼ 0.016–0.103. The scaling of the growth rate for the ion acoustic mode with pump mode amplitude is shown in Figure 9B and this agrees with the trend obtained in Eq. 8. Quantitatively, the theoretical growth rates are lower than the simulation values indicating that modifications to the theory are needed in this parameter regime.

FIGURE 9

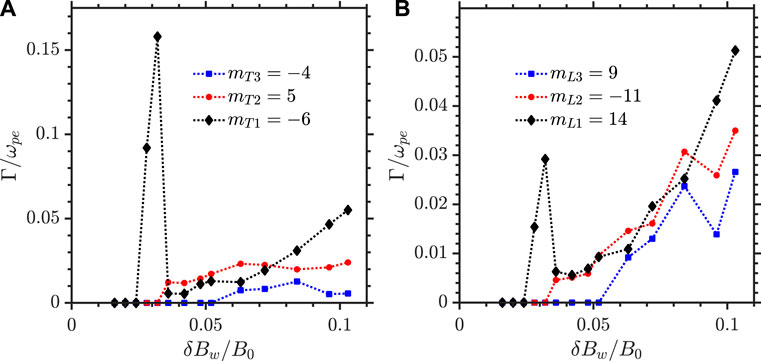
FIGURE 9. Growth rates of whistler and IAW modes as the pump amplitude, δB_P/B₀, increases show clear transitions between single, double and triple decay (A) Whistler modes. (B) IAW modes.

The threshold value of the single parametric decay instability from the simulations is δB_w/B₀ ∼ 0.028 and the theoretical value obtained from Eq. 7 is found to be δB_w/B₀ ∼ 0.042, using the linear kinetic theory results for the daughter mode damping rates. This discrepancy is possibly due to the linear orbit approximations used to compute the damping rates. Damping rates used from the simulation, Figure 8D, gives a threshold value of δB_w/B₀ ∼ 0.030 which is in closer agreement with the measured simulation value.

At δB_w/B₀ ∼ 0.036 the secondary decay threshold is reached and the growth rates of the primary whistler and IAW modes rapidly drop. At the threshold, the growth rate of the secondary whistler mode exceeds that of the primary whistler, while the ion acoustic wave growth rates are comparable to each other. The tertiary threshold is reached at δB_w/B₀ ∼ 0.063, as the pump amplitude is increased the secondary and tertiary whistler growth rates appear to saturate while the primary whistler growth rate increases linearly with the pump amplitude. The IAW rates all continue to increase with the primary IAW exceeding the growth rate prior to any of the cascades.

While this study is focused on the parametric interaction of whistlers with ion acoustic waves, there is the possibility of a similar parametric interaction with the electron acoustic wave (EAW) that has been proposed by Agapitov et al. (2015b) as a generation mechanism of nonlinear electrostatic structures observed in the Earth’s radiation belts. The electron acoustic wave is heavily damped and can largely be ignored in a plasma with a single electron component, i.e. an electron population associated with a single temperature. However, under certain conditions, in plasmas with both hot (subscript h) and cold (subscript c) electron populations the electron acoustic wave becomes only weakly damped; the conditions for this were first mapped by Gary and Tokar (1985) and are approximately T_h/T_c > 10 and 0 < n_c < 0.8n_e where n_c + n_h = n_e. In Figure 10A we show a possible setup for observation of the whistler-EAW parametric instability, and in Figure 10B we demonstrate the existence of the lightly damped EAW in the UPIC simulation. The parameters for the EAW are T_h/T_c = 100, n_c/n_e = 0.1, vth = 3.16, and ω_ce = 3ω_pe/4. As outlined in Figure 10A the pump wave should decay to a co-propagating EAW and counter-propagating whistler, in a similar fashion to the IAW coupling. However, from preliminary studies we observe that the dominant coupling of the whistler wave is to the electron plasma (Langmuir) wave branch (upper branch in Figure 10) that is more unstable than the EAW. It is possible to drive the EAW instability with a relative drift between the hot and cold populations (Gary, 1987) and this condition was present in the observations by Agapitov et al. (2015b); this relative drift configuration may be required to observe the whistler-EAW parametric instability.

FIGURE 10

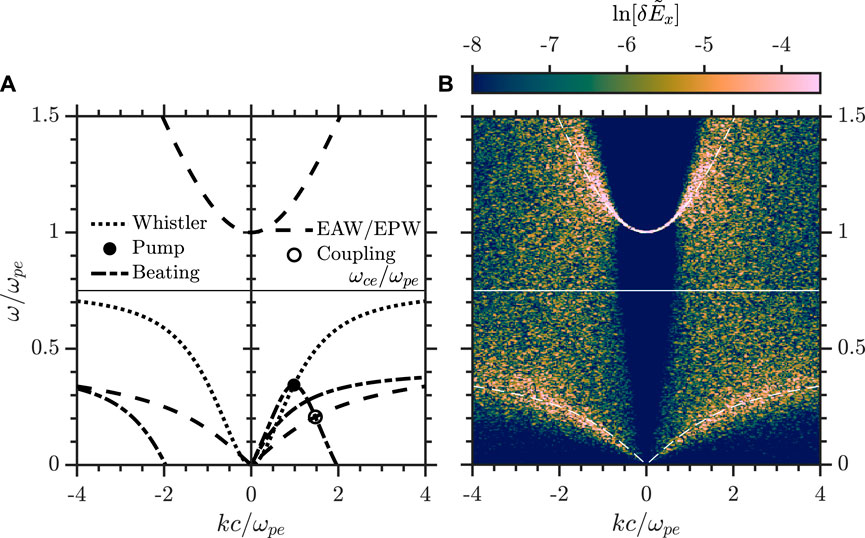
FIGURE 10. Ponderomotive coupling between whistler waves and electron acoustic waves (EAW). (A) In the same format as Figure 1, the pondermotive beating of the pump whistler wave and whistler branch can couple to the electron acoustic wave of a two-electron-species plasma (B) Demonstration of the electron acoustic mode in the UPIC simulation using T_h/T_c =100, vth =3.16 (v_tc =0.316), n_h =0.9n_e (n_c =0.1n_e), and ω_ce/ω_pe =3/4.

Recently, Parker Solar Probe has revealed that wave-wave interactions may be as common in the solar wind as they are in the Earth’s magnetosphere (Ma et al., 2021). Whistler waves are assumed to control the generation of the superthermal electrons in the solar corona and their dynamics during propagation in the solar wind (Vocks and Mann, 2003; Vocks et al., 2005). The recent observations by Solar Orbiter showed only anti-sunward propagation of whistler waves at around 100 R_⊙ (solar radii) (Kretzschmar et al., 2021). However, observations of the Parker Solar Probe at heliocentric distances from 20 to 50 R_⊙ revealed whistler waves propagating sunward (Agapitov et al., 2020; Dudok de Wit et al., 2022), anti-sunward (Dudok de Wit et al., 2022), and counter-streaming whistlers (Karbashews et al., 2022). The sunward propagating whistler waves can significantly contribute to scattering the strahl electrons into the halo population (Vocks et al., 2005; Roberg-Clark et al., 2019). The higher amplitude of these waves (5–10 times greater compared to whistlers observed by Solar Orbiter) can suggest the local generation of these waves (supported by the localized region of whistlers observation: above 22–25 R_⊙ (Cattell et al., 2022)) by electron instabilities (probably together with anti-sunward waves) or from a turbulent cascade of anti-sunward whistler waves generated locally by beam instabilities. Observations of ion acoustic waves in this region (reported in (Mozer et al., 2020) and earlier from Helios observations (Gurnett and Frank, 1978)) make the parametric cascading through the ion acoustic mode to be a potentially feasible generation mechanism of the observed sunward propagating whistler population.

The main results of this paper can be summarized as follows. A Darwin particle-in-cell (PIC) simulation model has been used to study the parametric decay instability of parallel propagating whistler waves in the presence of an undamped ion acoustic wave (IAW). A field-aligned monochromatic whistler wave is launched and couples to a counter-propagating whistler mode and co-propagating ion acoustic mode. The coupling of the electromagnetic fields to the electrostatic field via the ponderomotive force forms spatio-temporal beat patterns in the longitudinal electric field generated by the counter-propagating whistlers and pump whistler wave. The threshold amplitude for the instability is determined and agrees with a prediction using the ion decay instability. As the amplitude of the pump whistler wave is increased, secondary and tertiary decay thresholds are reached and are observed to cascade from the daughter whistler modes. At the largest amplitude (δB_w/B₀ ∼ 0.1) the primary IAW evolves into a short-lived and highly nonlinear structure. The growth rate scaling with amplitude for the primary decay channel compares favourably with analytical expressions. We presented preliminary results on the parametric coupling of whistler waves with the electron acoustic wave (EAW).

Concerning future studies, the present simulation model will be used to explore the conditions under which parametric instability involving the EAW can be present as has been observed in space plasmas. Plasma conditions that support an undamped electron acoustic wave are likely to also have a weakly damped ion acoustic wave; future simulations could be performed with both modes present to determine the dominant electrostatic coupling and under what conditions this holds. Last, the present study focused on 1-D processes, similar 2-D and/or 3-D studies could provide insight into parametric interactions of oblique whistler waves that are commonly found in both the magnetosphere and solar wind.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SK ran the simulations, formulated the whistler-ion acoustic ponderomotive coupling and parametric decay model, produced the figures, and wrote parts of the theory and discussion sections and the majority of the results section. RS advised on the simulations, compared the simulation results with the for instability thresholds and growth rates, and wrote parts of the theory and discussion sections and the majority of the introduction. OA reviewed the results, advised on manuscript content, and contributed to the introduction and discussion sections.

Funding

SK acknowledges support from NSERC, NASA grants 80NNSC19K0264, 80NNSC19K0848, and NSF grant 1914670, RS acknowledges support from NSERC, and OA. acknowledges support from 80NNSC19K0848, 80NSSC22K0522, 80NSSC20K0218, 80NSSC22K0433, 80NSSC21K1770, and NSF grant number 191467.

Acknowledgments

We would like to acknowledge the assistance of Viktor Decyk with using the UPIC simulation software, and acknowledge the use of the perceptually uniform and colour-vision-deficiency friendly colour maps developed by Crameri et al. (2020) for public use.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agapitov, O. V., Artemyev, A. V., Mourenas, D., Mozer, F. S., and Krasnoselskikh, V. (2015a). Nonlinear local parallel acceleration of electrons through landau trapping by oblique whistler mode waves in the outer radiation belt. Geophys. Res. Lett. 42, 2015GL066887. doi:10.1002/2015GL066887

CrossRef Full Text | Google Scholar

Agapitov, O. V., Krasnoselskikh, V., Mozer, F. S., Artemyev, A. V., and Volokitin, A. S. (2015b). Generation of nonlinear electric field bursts in the outer radiation belt through the parametric decay of whistler waves. Geophys. Res. Lett. 42, 3715–3722. doi:10.1002/2015GL064145

CrossRef Full Text | Google Scholar

Agapitov, O. V., Wit, T. Dd, Mozer, F. S., Bonnell, J. W., Drake, J. F., Malaspina, D., et al. (2020). Sunward-propagating whistler waves collocated with localized magnetic field holes in the solar wind: Parker solar probe observations at 35.7 R_⊙ radii. Astrophys. J. 891, L20. doi:10.3847/2041-8213/ab799c

CrossRef Full Text | Google Scholar

Appleton, E. V. (1927). URSI proceedings. Brussels: Washington General Assembly.

Google Scholar

Bellan, P. M., and Stasiewicz, K. (1998). Fine-scale cavitation of ionospheric plasma caused by inertial alfvén wave ponderomotive force. Phys. Rev. Lett. 80, 3523–3526. doi:10.1103/physrevlett.80.3523

CrossRef Full Text | Google Scholar

Burtis, W. J., and Helliwell, R. A. (1969). Banded chorus—A new type of vlf radiation observed in the magnetosphere by ogo 1 and ogo 3. J. Geophys. Res. 74, 3002–3010. doi:10.1029/JA074i011p03002

CrossRef Full Text | Google Scholar

Busnardo-Neto, J., Pritchett, P., Lin, A., and Dawson, J. (1977). A self-consistent magnetostatic particle code for numerical simulation of plasmas. J. Comput. Phys. 23, 300–312. doi:10.1016/0021-9991(77)90096-1

CrossRef Full Text | Google Scholar

Cattell, C., Breneman, A., Dombeck, J., Hanson, E., Johnson, M., Halekas, J., et al. (2022). Parker solar probe evidence for the absence of whistlers close to the sun to scatter strahl and to regulate heat flux. Astrophys. J. Lett. 924, L33. doi:10.3847/2041-8213/ac4015

CrossRef Full Text | Google Scholar

Cattell, C., Breneman, A., Dombeck, J., Short, B., Wygant, J., Halekas, J., et al. (2021). Parker solar probe evidence for scattering of electrons in the young solar wind by narrowband whistler-mode waves. Astrophys. J. Lett. 911, L29. doi:10.3847/2041-8213/abefdd

CrossRef Full Text | Google Scholar

Cattell, C., Wygant, J. R., Goetz, K., Kersten, K., Kellogg, P. J., von Rosenvinge, T., et al. (2008). Discovery of very large amplitude whistler-mode waves in earth’s radiation belts. Geophys. Res. Lett. 35, L01105. doi:10.1029/2007GL032009

CrossRef Full Text | Google Scholar

Chen, F. F. (1984). Introduction to plasma physics and controlled fusion. 2nd edn. New York: Plenum Press.

Google Scholar

Crameri, F., Shephard, G. E., and Heron, P. J. (2020). The misuse of colour in science communication. Nat. Commun. 11, 5444. doi:10.1038/s41467-020-19160-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Decyk, V. K. (2007). Upic: A framework for massively parallel particle-in-cell codes. Comput. Phys. Commun. 177, 95–97. doi:10.1016/j.cpc.2007.02.092

CrossRef Full Text | Google Scholar

Dudok de Wit, T., Krasnoselskikh, V. V., Agapitov, O., Froment, C., Larosa, A., Bale, S. D., et al. (2022). First results from the SCM search-coil magnetometer on parker solar probe. JGR. Space Phys. 127, e2021JA030018. doi:10.1029/2021JA030018

CrossRef Full Text | Google Scholar

Forslund, D. W., Kindel, J. M., and Lindman, E. L. (1972). Parametric excitation of electromagnetic waves. Phys. Rev. Lett. 29, 249–252. doi:10.1103/PhysRevLett.29.249

CrossRef Full Text | Google Scholar

Gao, X., Chen, R., Lu, Q., Chen, L., Chen, H., and Wang, X. (2022). Observational evidence for the origin of repetitive chorus emissions. Geophys. Res. Lett. 49, e2022GL099000. doi:10.1029/2022GL099000

CrossRef Full Text | Google Scholar

Gao, X., Li, W., Thorne, R. M., Bortnik, J., Angelopoulos, V., Lu, Q., et al. (2014). New evidence for generation mechanisms of discrete and hiss-like whistler mode waves. Geophys. Res. Lett. 41, 4805–4811. doi:10.1002/2014GL060707

CrossRef Full Text | Google Scholar

Gao, X., Lu, Q., Bortnik, J., Li, W., Chen, L., and Wang, S. (2016). Generation of multiband chorus by lower band cascade in the earth’s magnetosphere. Geophys. Res. Lett. 43, 2343–2350. doi:10.1002/2016GL068313

CrossRef Full Text | Google Scholar

Gary, S. P. (1987). The electron/electron acoustic instability. Phys. Fluids (1994). 30, 2745–2749. doi:10.1063/1.866040

CrossRef Full Text | Google Scholar

Gary, S. P., and Tokar, R. L. (1985). The electron-acoustic mode. Phys. Fluids (1994). 28, 2439–2441. doi:10.1063/1.865250

CrossRef Full Text | Google Scholar

Gurnett, D. A., and Bhattacharjee, A. (2005). Introduction to plasma physics: With space and laboratory applications. Cambridge University Press, 84–90.

Google Scholar

Gurnett, D. A., and Frank, L. A. (1978). Ion acoustic waves in the solar wind. J. Geophys. Res. 83, 58–74. doi:10.1029/JA083iA01p00058

CrossRef Full Text | Google Scholar

Hartree, D. R. (1931). The propagation of electromagnetic waves in a refracting medium in a magnetic field. Math. Proc. Camb. Phil. Soc. 27, 143–162. doi:10.1017/S0305004100009440

CrossRef Full Text | Google Scholar

Huang, S. Y., Sahraoui, F., Yuan, Z. G., Contel, O. L., Breuillard, H., He, J. S., et al. (2018). Observations of whistler waves correlated with electron-scale coherent structures in the magnetosheath turbulent plasma. Astrophys. J. 861, 29. doi:10.3847/1538-4357/aac831

CrossRef Full Text | Google Scholar

Hughes, R. S., Wang, J., Decyk, V. K., and Gary, S. P. (2016). Effects of variations in electron thermal velocity on the whistler anisotropy instability: Particle-in-cell simulations. Phys. Plasmas 23, 042106. doi:10.1063/1.4945748

CrossRef Full Text | Google Scholar

Karbashews, S., Agapitov, O. V., and Kim, H. Y. (2022). Counter-streaming whistlers collocated with magnetic field inhomogeneities in the solar wind: Parker solar probe observations during encounter 1 at 42.6r⊙. The Astrophysical Journal in Preparation.

Google Scholar

Karbashewski, S. (2017). Large amplitude whistler waves: Nonlinear dynamics and interactions. Master’s thesis. Edmonton, AB: University of Alberta. doi:10.7939/R33776B4R

CrossRef Full Text | Google Scholar

Ke, Y., Gao, X., Lu, Q., Hao, Y., and Wang, S. (2018). Parametric decay of oblique whistler waves in the earth’s magnetosphere: 2-d pic simulations. Phys. Plasmas 25, 072901. doi:10.1063/1.5037763

CrossRef Full Text | Google Scholar

Ke, Y., Gao, X., Lu, Q., and Wang, S. (2017). Parametric decay of a parallel propagating monochromatic whistler wave: Particle-in-cell simulations. Phys. Plasmas 24, 012108. doi:10.1063/1.4974160

CrossRef Full Text | Google Scholar

Kretzschmar, M., Chust, T., Krasnoselskikh, V., Graham, D., Colomban, L., Maksimovic, M., et al. (2021). Whistler waves observed by solar orbiter/RPW between 0.5 AU and 1 AU. Astron. Astrophys. 656, A24. doi:10.1051/0004-6361/202140945

CrossRef Full Text | Google Scholar

Lacombe, C., Alexandrova, O., Matteini, L., SantolÃk, O., Cornilleau-Wehrlin, N., Mangeney, A., et al. (2014). Whistler mode waves and the electron heat flux in the solar wind:clusterobservations. Astrophys. J. 796, 5. doi:10.1088/0004-637X/796/1/5

CrossRef Full Text | Google Scholar

Lassen, H. I. (1926). Über die ionisation der atmosphäre und ihren einfluß auf die ausbreitung der kurzen elektrischen wellen der drahtlosen telegraphie. Z. für Hochfrequenztech. 28, 109.

Google Scholar

Ma, J., Gao, X., Yang, Z., Tsurutani, B. T., Liu, M., Lu, Q., et al. (2021). Nonlinear wave–wave coupling related to whistler-mode and electron bernstein waves observed by the parker solar probe. Astrophys. J. 918, 26. doi:10.3847/1538-4357/ac0ef4

CrossRef Full Text | Google Scholar

Maksimovic, M., Harvey, C. C., Santolík, O., Lacombe, C., de Conchy, Y., Hubert, D., et al. (2001). Polarisation and propagation of lion roars in the dusk side magnetosheath. Ann. Geophys. 19, 1429–1438. doi:10.5194/angeo-19-1429-2001

CrossRef Full Text | Google Scholar

Max, C. E. (1976). Strong self-focusing due to the ponderomotive force in plasmas. Phys. Fluids (1994). 19, 74–77. doi:10.1063/1.861305

CrossRef Full Text | Google Scholar

Meredith, N. P., Horne, R. B., and Anderson, R. R. (2001). Substorm dependence of chorus amplitudes: Implications for the acceleration of electrons to relativistic energies. J. Geophys. Res. 106, 13165–13178. doi:10.1029/2000JA900156

CrossRef Full Text | Google Scholar

Miller, M. A. (1958). Motion of charged particles in the high-frequency electromagnetic fields. Radiophysics 1, 110–123.

Google Scholar

Morales, G. J., and Lee, Y. C. (1974). Ponderomotive-force effects in a nonuniform plasma. Phys. Rev. Lett. 33, 1016–1019. doi:10.1103/physrevlett.33.1016

CrossRef Full Text | Google Scholar

Mourenas, D., Artemyev, A. V., Agapitov, O. V., Krasnoselskikh, V., and Li, W. (2014). Approximate analytical solutions for the trapped electron distribution due to quasi-linear diffusion by whistler mode waves. JGR. Space Phys. 119, 9962–9977. doi:10.1002/2014JA020443

CrossRef Full Text | Google Scholar

Mozer, F. S., Bonnell, J. W., Bowen, T. A., Schumm, G., and Vasko, I. Y. (2020). Large-amplitude, wideband, Doppler-shifted, ion acoustic waves observed on the parker solar probe. Astrophys. J. 901, 107. doi:10.3847/1538-4357/abafb4

CrossRef Full Text | Google Scholar

Neubert, T. (1982). Stimulated scattering of whistler waves by ion acoustic waves in the magnetosphere. Phys. Scr. 26, 239–247. doi:10.1088/0031-8949/26/3/016

CrossRef Full Text | Google Scholar

Nishikawa, K. (1968). Parametric excitation of coupled waves i. general formulation. J. Phys. Soc. Jpn. 24, 916–922. doi:10.1143/JPSJ.24.916

CrossRef Full Text | Google Scholar

Omura, Y., Katoh, Y., and Summers, D. (2008). Theory and simulation of the generation of whistler-mode chorus. J. Geophys. Res. 113. doi:10.1029/2007JA012622

CrossRef Full Text | Google Scholar

Reeves, G. D., Spence, H. E., Henderson, M. G., Morley, S. K., Friedel, R. H. W., Funsten, H. O., et al. (2013). Electron acceleration in the heart of the van allen radiation belts. Science 341, 991–994. doi:10.1126/science.1237743

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberg-Clark, G. T., Agapitov, O., Drake, J. F., and Swisdak, M. (2019). Scattering of energetic electrons by heat-flux-driven whistlers in flares. Astrophys. J. 887, 190. doi:10.3847/1538-4357/ab5114

CrossRef Full Text | Google Scholar

Shukla, P. K. (1977). Parametric coupling of a large-amplitude whistler wave with ion quasimodes in plasmas. Phys. Rev. A 16, 1294–1296. doi:10.1103/PhysRevA.16.1294

CrossRef Full Text | Google Scholar

Terasawa, T., Hoshino, M., Sakai, J. I., and Hada, T. (1986). Decay instability of finite-amplitude circularly polarized alfven waves: A numerical simulation of stimulated brillouin scattering. J. Geophys. Res. 91, 4171–4187. doi:10.1029/JA091iA04p04171

CrossRef Full Text | Google Scholar

Thorne, R. M. (2010). Radiation belt dynamics: The importance of wave-particle interactions. Geophys. Res. Lett. 37. doi:10.1029/2010GL044990

CrossRef Full Text | Google Scholar

Tong, Y., Vasko, I. Y., Artemyev, A. V., Bale, S. D., and Mozer, F. S. (2019). Statistical study of whistler waves in the solar wind at 1 au. Astrophys. J. 878, 41. doi:10.3847/1538-4357/ab1f05

CrossRef Full Text | Google Scholar

Umeda, T., and Ito, T. (2008). Vlasov simulation of Langmuir decay instability. Phys. Plasmas 15, 084503. doi:10.1063/1.2965494

CrossRef Full Text | Google Scholar

Umeda, T., Saito, S., and Nariyuki, Y. (2018). Decay of nonlinear whistler mode waves: 1D versus 2D. Phys. Plasmas 25, 072118. doi:10.1063/1.5031483

CrossRef Full Text | Google Scholar

Umeda, T., Saito, S., and Nariyuki, Y. (2014). Electron acceleration during the decay of nonlinear whistler waves in low-beta electron-ion plasma. Astrophys. J. 794, 63. doi:10.1088/0004-637X/794/1/63

CrossRef Full Text | Google Scholar

Umeda, T., Saito, S., and Nariyuki, Y. (2017). Rapid decay of nonlinear whistler waves in two dimensions: Full particle simulation. Phys. Plasmas 24, 054503. doi:10.1063/1.4982609

CrossRef Full Text | Google Scholar

Usui, H., Matsumoto, H., and Gendrin, R. (2002). Numerical simulations of a three-wave coupling occurring in the ionospheric plasma. Nonlinear process. geophys. 9, 1–10. doi:10.5194/npg-9-1-2002

CrossRef Full Text | Google Scholar

Vocks, C., and Mann, G. (2003). Generation of suprathermal electrons by resonant wave-particle interaction in the solar corona and wind. Astrophys. J. 593, 1134–1145. doi:10.1086/376682

CrossRef Full Text | Google Scholar

Vocks, C., Salem, C., Lin, R. P., and Mann, G. (2005). Electron halo and strahl formation in the solar wind by resonant interaction with whistler waves. Astrophys. J. 627, 540–549. doi:10.1086/430119

CrossRef Full Text | Google Scholar