Electromagnetic solitons and their stability in relativistic degenerate dense plasmas with two electron species

The evolution of electromagnetic (EM) solitons due to nonlinear coupling of circularly polarized intense laser pulses with low-frequency electron-acoustic perturbations is studied in relativistic degenerate dense astrophysical plasmas with two groups of electrons: a sparse population of classical relativistic electrons and a dense population of relativistic degenerate electron gas. Different forms of localized stationary solutions are obtained and their properties are analyzed. Using the Vakhitov-Kolokolov stability criterion, the conditions for the existence and stability of a moving EM soliton are also studied. It is noted that the stable and unstable regions shift around the plane of soliton eigenfrequency and the soliton velocity due to the effects of relativistic degeneracy, the fraction of classical to degenerate electrons and the EM wave frequency. Furthermore, while the standing solitons exhibit stable profiles for a longer time, the moving solitons, however, can be stable or unstable depending on the degree of electron degeneracy, the soliton eigenfrequency and the soliton velocity. The latter with an enhanced value can eventually lead to a soliton collapse. The results should be useful for understanding the formation of solitons in the coupling of highly intense laser pulses with slow response of degenerate dense plasmas in the next generation laser-plasma interaction experiments as well as the novel features of x-ray and γ-ray pulses that originate from compact astrophysical objects.

1 Introduction

The nonlinear propagation of intense electromagnetic (EM) waves in plasmas is typically associated with a wide variety of interesting nonlinear phenomena, such as the generation of wakefields (Roy et al., 2019), parametric instabilities (Quesnel et al., 1997; Barr et al., 1999; Gleixner and Kumar, 2020), harmonic generation (Mori et al., 1993; Shen et al., 1995), self-focusing of wave envelopes (Esarey et al., 1997), generation of intense electric and magnetic fields (Borghesi et al., 2002b; Wagner et al., 2004), and localization of EM waves as solitons (Farina and Bulanov, 2001; Sundar et al., 2011; Roy et al., 2019). One particular class of waves that caught attention in the context of laser-plasma interactions in relativistic regimes is the EM solitons. Many years back, in 1956, Akhiezer and Polovin proposed a set of relativistic electron fluid equations coupled to the Maxwell equations to model the interactions of intense EM waves with plasmas and found exact nonlinear wave solutions (solitons) in relativistic plasmas. Such EM solitons are high-frequency laser pulses that are typically modulated by low-frequency plasma density perturbations and that propagate without any diffraction or spreading out of waves. They appear in the context of various plasma environments and have potential applications, e.g., in laser fusion and plasma-based particle accelerators (Sen and Kaw, 1994; Esirkepov et al., 2002; Farina and Bulanov, 2005). Relativistic EM solitons have been observed in two-dimensional (2D) and three-dimensional (3D) particle-in-cell (PIC) simulations (Bulanov et al., 1999; Sentoku et al., 1999; Esirkepov et al., 2002) and also detected in experiments using proton imaging techniques (Borghesi et al., 2002b,a). It has also been shown (Bulanov et al., 1999; Esirkepov et al., 2002) that nearly twenty five to forty percent of the laser pulse energy goes into the generation of EM solitons or soliton-like structures which may persist as appreciable signatures in the forms of modulated pulses in the radiation spectra (ranging from radio to γ-rays) that emanate from compact astrophysical objects.

The interaction of highly intense laser pulse or EM waves with ponderomotive force driven slow response of plasma density perturbations has been known to be one of the most powerful mechanisms for the generation of wakefields or the formation of EM solitons and hence for particle acceleration at relativistic speed in high intensity electromagnetic fields. Although in high density regimes the Fermi pressure seems to be the dominant effect, the main dominating force in such nonlinear interactions is typically the EM wave ponderomotive force. It has been seen that the degeneracy Fermi pressure mainly contributes to the wave dispersion and hence plays key roles for the transition from wakefield generation to the soliton formation [See, e.g., (Roy et al., 2019) and references therein]. There are some other effects such as spin-orbit interaction (Asenjo et al., 2012, 2011; Morandi et al., 2014), the Darwin term (Asenjo et al., 2012, 2011), and pair-production (Hebenstreit et al., 2011) which may, however, become important in some other contexts than the present theory. It is to be noted that the mechanism of soliton formation considered here may not be directly related to the quantum electrodynamics in which the Schwinger limit is applicable. The electrons achieve relativistic speed by the ponderomotive force of the highly intense EM fields, and high density degenerate plasmas can thus be generated simultaneously, e.g., with the production of X-rays and γ-rays in the environments of compact astrophysical objects like white dwarfs.

The formation of envelope solitons in the interactions of circularly polarized EM waves with cold plasmas have been studied by Kozlov et al. (1979). They employed the quasineutral approximations to establish the existence of small-amplitude localized solutions in the form of drifting solitons. A subsequent numerical investigation has been focused on EM solitons of relativistic amplitude (Kozlov et al., 1979). Mima et al. (Mima et al., 1986) studied the propagation characteristics of solitary waves and predicted as possible charged particle acceleration mechanism. Furthermore, Kaw et al. (Kaw et al., 1992) solved a set of coupled nonlinear equations for modulated light pulses and electron plasma waves, and discussed the nonlinear relationship among the group velocity, amplitude, and the frequency of envelope solitons. Farina and Bulanov (Farina and Bulanov, 2001) investigated the influence of ion motion on relativistic solitonic structures and they showed that the amplitude of moving solitons can be limited by this influence. In an another investigation and in a weakly relativistic regime, the nonlinear propagation of one-dimensional weakly nonlinear solitary waves in cold plasmas was studied using the reductive perturbation technique by Kuehl and Zhang, 1993. The nonlinear theory of weakly relativistic circularly polarized EM pulses in warm plasmas in the forms of bright and dark solitons was considered by Poornakala et al. (2002) in different parameter regimes. The one-dimensional (1D) dynamics of EM solitons in relativistic electron–ion plasmas has also been studied (Lontano et al., 2003, 2002). Furthermore, the existence of single- and multiple-peak solitary structures and their stability, mutual interaction and propagation in inhomogeneous cold plasmas were examined by Saxena et al. (2006). Recently, using the Vakhitov-Kolokolov criterion, the stability and dynamical evolution of linearly polarized EM solitons were studied in the framework of a generalized nonlinear Schrödinger (GNLS) equation in relativistic degenerate dense plasmas (Roy and Misra, 2020). However, the present work considers the interactions of circularly polarized EM waves with two groups of electrons (one classical relativistic hot electron species with a small concentration and the bulk relativistic degenerate electron gas). While the two-electron species in plasmas support low-frequency electron-acoustic waves Misra et al. (2021), the single species electrons with stationary background of ions as in (Roy and Misra, 2020) are rather relevant for high-frequency Langmuir waves. So, the evolution equations and the results, to be obtained in the present study, will be significantly different from those of the work of (Roy and Misra, 2020). In an another work, the nonlinear coupling of EM waves and low-frequency electron-acoustic density fluctuations was considered by Shatashvili et al. (2020) in relativistic astrophysical plasmas with two-temperature electrons. They reported that the modulated EM waves can propagate in the subsonic or supersonic regimes. However, the existence criterion, the dynamical evolution and stability of EM solitons were not studied in this investigation.

The aim of this work is to advance the previous theory (Shatashvili et al., 2020) of EM waves in relativistic degenerate dense plasmas and to report the detailed analysis for the existence of different kinds of localized soliton solutions, their stability analysis using the Vakhitov-Kolokolov criterion, as well as their dynamical evolution by a simulation approach. It is found that the parameter domains for the stable and unstable regions predicted in the linear analysis well agree with the simulation results. The motivation for studying a two-temperature electron plasma is due to fact that although there is no direct observational evidence for the existence of two groups of electrons in relativistic degenerate regimes, based on the information available from the theories and some relevant observations, it is expected that such highly relativistic degenerate astrophysical plasmas coexisting with classical relativistic hot electron flow can exist, e.g., during the formation of relativistic jets due to accretion-induced collapsing of white dwarfs into black holes (Begelman et al., 1984; Kryvdyk, 1999; Kryvdyk and Agapitov, 2007). The relativistic dense plasmas where the background distribution of electrons deviates from the thermodynamic equilibrium can also appear in the context of laser produced plasmas or ion beam driven plasmas (Gibbon, 2005; Hau-Riege, 2011). In such cases, the system energy mostly flows into the electrons, thereby generating fully degenerate electrons with long tails or partially degenerate electrons with high temperature tails, and allowing the division of background electrons with two different temperatures. The excitation of low-frequency electron-acoustic waves in these systems are believed to play key roles in the nonlinear wave coupling and the formation of coherent structures like solitons.

2 Basic equations

The nonlinear coupling of high-frequency circularly polarized intense EM waves and slow plasma response of low-frequency electron-acoustic perturbations in unmagnetized plasmas composed of a dense relativistic degenerate electron gas (with number density n_d ≡ n_d0 + δn_d), a sparse population of nondegenerate classical electrons (with number density n_cl ≡ n_cl0 + δn_cl), and immobile ions is governed by the following Zakharov-like equations (Shatashvili et al., 2020).

$2i\left(\frac{\partial }{\partial t}+v_g\frac{\partial }{\partial z}\right)A+b_0\frac{{\partial }^{2}A}{\partial z^2}+b_{1}NA+b_2|A{|}^{2}A=0,(1)$

$\left(\frac{{\partial }^2}{\partial t^2}-\frac{{\partial }^2}{\partial z^2}\right)N=-3b_3\frac{{\partial }^2|A{|}^2}{\partial z^2},(2)$

where N ≡ δn_d/n_d0 is the dimensionless degenerate electron density perturbation and A ≡ eA/mc² is the dimensionless EM wave vector potential with e denoting the elementary charge, m the electron mass, and c the speed of light in vacuum. In Eqs. 1, 2, the time and space coordinates are normalized according to t → tω₀ and z → zω₀/c_s, where ω₀ (k₀) is the EM wave frequency (wave number) given by the high-frequency dispersion relation: ${\omega }_0^2=c^2{k}_0^2+{\mathrm{\Omega }}_d^2+\alpha {\omega }_{ed}^2$ and c_s is the electron-acoustic speed, defined by, $c_s^2=(1/3)\alpha c^2{R}_0^2/\sqrt{1+R_0^2}$. Here, ${\omega }_{ed}\equiv \sqrt{4\pi n_{d0}{e}^2/m}$ is the plasma oscillation frequency of degenerate electrons, ${\mathrm{\Omega }}_d^2={\omega }_{ed}^2/\sqrt{1+R_0^2}$, α = n_cl0/n_d0 (≪ 1) is the ratio between the equilibrium number densities of classical and degenerate electrons, and $R_0=\hslash {(3{\pi }^2{n}_{d0})}^{1/3}/mc$ measures the degree of electron degeneracy, i.e., R₀ ≪ 1 (≫ 1) corresponds to weakly relativistic (ultra-relativistic) degenerate plasmas. Also, v_g is the EM wave group velocity normalized by c_s, $b_0=\left(d{v}_g/d{k}_0\right){\omega }_0/c_s^2$ represents the group velocity dispersion, $b_1={\left({\omega }_{ed}/{\omega }_0\right)}^2\left(1-{\kappa }^2/\sqrt{1+R_0^2}\right)$ is associated with the nonlocal nonlinearity, $b_2={\left({\omega }_{ed}/{\omega }_0\right)}^2\left(\alpha +{\kappa }^2/{(1+R_0^2)}^{3/2}\right)$ is the coefficient of the cubic nonlinear term, and $b_3=\left(\sqrt{1+R_0^2}-{\kappa }^2\right)/R_0^2$ with $2/3<{\kappa }^2\equiv 1-R_0^2/3(1+R_0^2)<1$ corresponds to the ponderomotive nonlinearity.

The model Eqs. 1, 2 have been derived using a set of relativistic fluid equations coupled to the Maxwell equations on several assumptions, namely, the thermodynamic temperature of classical electrons is much lower than the Fermi temperature, the characteristic wave frequency is much higher than the de Broglie frequency, and the EM pump wave is weakly relativistic. Furthermore, it has been assumed that the two electron species have different effective masses (m_d > m_cl) in which the effective mass of classical electrons (m_cl) is determined by their thermodynamic temperature while that of degenerate electrons (m_d) is determined by their number density Shatashvili et al. (2020). The model was essentially derived to explore novel nonlinear coupling of high-frequency EM waves with low-frequency electron-acoustic waves and the modulational instability induced by the new physics originating due to the flow of classical relativistic electrons in relativistic degenerate plasmas Shatashvili et al. (2020). Such plasmas, coexisting with a classical hot accumulating astrophysical flow, are interesting and important plasma ingredients in the environments of white dwarf stars, e.g., during the relativistic jet formation from collapsing white dwarfs to black holes (Begelman et al., 1984; Kryvdyk, 1999; Kryvdyk and Agapitov, 2007). The model can similarly be used to explore the new particle-acceleration mechanism via the formation of wakefield generation and EM solitons in which the degeneracy pressure can play a decisive role for the transition from wakefield generation to soliton formation (Roy et al., 2019).

It is to be noted that although there are similar works in the literature along the lines of the present study, no previous results in the literature can be recovered in some particular limits, namely nonrelativistic plasma flow or weakly relativistic degeneracy (classical) of the present model Eqs. 1, 2. However, there are some studies on electromagnetic envelope solitons in relativistic magnetized plasmas based on the NLS formalism. For example, starting from a set of relativistic fluid equations coupled to the circularly polarized EM wave equation, Borhanian et al. (Borhanian et al., 2009) studied the modulational instability and the evolution of circularly polarized EM wave envelopes in magnetized plasmas. Their formalism was based on a multiple scale perturbation approach to derive the NLS equation (without any nonlocal nonlinearity) which is distinctive from the present approach. Furthermore, the existence and the properties of standing high-frequency EM solitons were studied by Mikaberidze and Berezhiani, 2015 in a fully degenerate overdense electron plasma by considering a set of relativistic fluid and Maxwell equations. Their evolution equations for traveling EM solitons are similar to Eqs. 3, 4 obtained in Section 3. Since the formalism considered in these studies is different from the present one, one cannot recover the previous results even in some particular cases as mentioned before.

3 Localized stationary soliton

Before we investigate the conditions for the existence of EM solitons and their stability, we first look for some simple localized stationary soliton solutions that relativistic two-temperature plasmas can support and that are correlated with the plasma density depletion. So, looking for a localized stationary soliton solution of Eqs. 1, 2, we introduce the coordinate transformations ξ = z − v_gt, τ = t, and assume the vector potential A to be of the form A = a(ξ) exp(iωτ) and N ≡ N(ξ), where ω is the EM soliton eigenfrequency. Under these transformations Eqs. 1, 2 reduce to

$b_0\frac{d^{2}a}{d{\xi }^2}-2\omega a+b_{1}Na+b_2{a}^3=0,(3)$

$\left(v_g^2-1\right)\frac{d^{2}N}{d{\xi }^2}=-3b_3\frac{d^2{a}^2}{d{\xi }^2}.(4)$

Solving Eq. 4 yields the following expression for the density perturbation.

$N=\frac{3b_3}{1-v_g^2}{a}^2.(5)$

Here, we note that since 2/3 < κ² < 1, b₃ is always positive. Also, from the high-frequency dispersion relation and the expression for the electron-acoustic speed c_s stated in Section 2, it can be noted that v_g > 1 holds (for which we have a density depression) in the moderate or weakly relativistic degenerate regime. However, v_g < 1 holds (for which we have a density hump) for R₀ ≫ 1, i.e., in the ultra-relativistic regime. Thus, it follows that the stationary localized EM solitons may exist in a wide range of values of the degeneracy parameter R₀. Since the density perturbation cannot vanish in the region of EM field localization, there is no possibility of the formation of cavitation at some point in the region.

Next, eliminating N from Eqs. 3, 5, we obtain the following nonlinear differential equation for the wave amplitude a.

$\frac{d^{2}a}{d{\xi }^2}-\mu a+f\left(a^2\right)a=0,(6)$

where μ = 2ω/b₀ is the nonlinear frequency shift measuring the inverse of the square of the characteristic width of the soliton and f is the nonlinear function of the wave amplitude, given by,

$f\left(a^2\right)=\frac{1}{b_0}\left(b_2+\frac{3b_1{b}_3}{1-v_g^2}\right)a^2.(7)$

Clearly, |f| is an increasing function of a. However, considering f as a function of k₀ (or ω₀) we note that while its absolute value increases in a small interval 0 ≲ k₀ ≲ 0.1, the same decreases in the other small sub-interval 0.1 < k₀ ≲ 0.3 and tends to vanish for k₀ ≳ 0.3. In the latter, the localized soliton solution may not exist. Furthermore, |f| becomes higher (> 1) with higher values of the degeneracy parameter R₀ ≳ 30 and with a small increment of α and ω. Thus, there must be some parameter restrictions for which the nonlinearity is not too high, i.e., |f|≲ 1 or a bit more for the existence of EM solitons with amplitude a ∼ O(1).

In what follows, we integrate Eq. 6 and use the boundary conditions, namely a → 0, da/dξ → 0, and d²a/dξ² → 0 as ξ → ±∞ to obtain the following energy balance equation for the motion of a pseudoparticle of unit mass in which a plays the role of a pseudo-coordinate and ξ that of the pseudo-time.

$\frac{1}{2}{\left(\frac{da}{d\xi }\right)}^2+V\left(a\right)=0,(8)$

where the pseudopotential V(a) is given by

$V\left(a\right)=\frac{1}{4b_0}\left(b_2+\frac{3b_1{b}_3}{1-v_g^2}\right)a^4-\frac{1}{2}\mu a^2.(9)$

For the existence of finite-amplitude EM solitons, the pseudopotential V must satisfy the following conditions:

1) V(0) = V′(0) = 0.

2) V′′(a) < 0 at a = 0, so that the fixed point at the origin becomes unstable.

3) V(a_m ≠ 0) = 0 and V′(a_m) ≷ 0 according to when the solitary waves are compressive (with positive potential, i.e., a > 0) or rarefactive (with negative potential, i.e., a < 0). Here, $a_m=\sqrt{4\omega /[b_2+3b_1{b}_3/(1-v_g^2)]}$ represents the soliton amplitude.

When the above conditions are satisfied one can then integrate Eq. 8 and use the boundary conditions stated before to find the following soliton solution.

$a\left(\xi \right)=a_m\text{sech}\left(\xi /\mathrm{\Delta }\right),(10)$

where $\mathrm{\Delta }=\sqrt{b_0/2\omega }$ is the width of the EM soliton. Since the amplitude a_m is to be real, we must have either v_g < 1 or $v_g>\sqrt{1+3b_1{b}_3/b_2}$. We note that v_g < 1 is satisfied either in the regime of k₀ ≪ 1 for a moderate value of R₀ or in the regime 0 ≤ k₀ ≲ 1 with R₀ ≫ 1. Thus, EM solitons in relativistic degenerate plasmas can travel as subsonic and supersonic waves (Shatashvili et al., 2020).

We numerically verify the aforementioned conditions for the existence of EM solitons in different parameter regimes and plot the Sagdeev potential V(a) against a and the corresponding soliton profiles as shown in Figure 1. We note that the conditions for V(a) are satisfied in a wide range of values of R₀ including R₀ ≪ 1 and R₀ ≫ 1 implying that EM solitons can exist both in the weakly relativistic and ultra-relativistic regimes. However, as noted before in highly degenerate regimes (R₀ ≳ 30), the nonlinear function f tends to become much higher in magnitude. So, such highly degenerate regimes may not be admissible for the existence of soliton solution in the particular form. From the subplot (a) of Figure 1 it is evident that for certain parameter values, V(a) crosses the a-axis at a = a_m and V < 0 for 0 < a < a_m. Such a_m is the amplitude of the soliton as is evident from the profiles in subplot (b). The width of the soliton can also be obtained either using the relation W = |a_m/V_min| from the profiles of V(a) [subplot (a)] or from the profiles of a(ξ) [subplot (b)]. Here, V_min represents the absolute minimum value of V. When a value of either the degeneracy parameter R₀ or the soliton frequency ω (or the wave number k₀) is increased, a significant increment (reduction) of the soliton amplitude (width) is noticed. However, the amplitude remains the same and the width gets reduced when a fraction of classical to degenerate electrons are slightly enhanced.

FIGURE 1

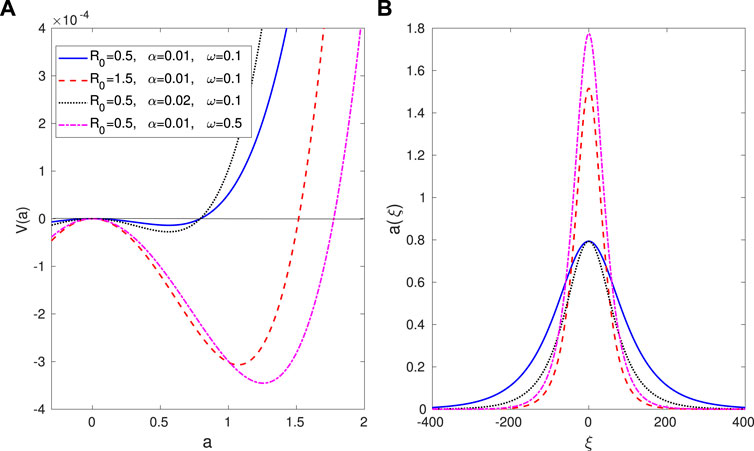
FIGURE 1. The Sagdeev potential V(a) [subplot (A)] and the corresponding soliton solutions a(ξ) [subplot (B)] are shown for different values of the parameters as in the legends with a fixed value of k₀ = 0.3.

4 Stability of electromagnetic solitons

In this section, we focus on the evolution of slowly varying weakly nonlinear small amplitude circularly polarized EM wave envelopes and their stability in relativistic degenerate dense plasmas. So, we introduce a slowly varying complex envelope in the form:

$A=\frac{1}{2}\left(a{e}^{-it}+a^{}{e}^{it}\right),N=\frac{1}{2}\left(N_2{e}^{-i2t}+N_2^{}{e}^{i2t}\right),(11)$

where we have considered the odd harmonics (first order) for the vector potential A and even harmonics (second order) for the density perturbation N. Since we are looking for an evolution equation for the wave potential A of the NLS type, the contributions of other harmonics may not be so important. In Eq. 11, the asterisk denotes the complex conjugate of the physical quantity. Substituting the expansions of Eq. 11 into Eq. 2 and collecting the second harmonic terms ∼ exp(−i2t), we obtain the following expression for N₂.

$N_2=\frac{3}{8}{b}_3\frac{{\partial }^2{a}^2}{\partial z^2}.(12)$

Next, substituting the expansions of Eq. 12 into Eq. 1 and collecting the first harmonic terms ∼ exp(−it), we obtain the following equation for the EM wave amplitude a.

$i\left(\frac{\partial }{\partial t}+v_g\frac{\partial }{\partial z}\right)a+P\frac{{\partial }^{2}a}{\partial z^2}+Q_1|a{|}^{2}a+Q_2\frac{{\partial }^2{a}^2}{\partial z^2}{a}^{}=0.(13)$

Eq. 13 can further be reduced to the following form by applying the transformations ξ = z − v_gt and τ = t, i.e.,

$i\frac{\partial a}{\partial \tau }+P\frac{{\partial }^{2}a}{\partial {\xi }^2}+Q_1|a{|}^{2}a+Q_2\frac{{\partial }^2{a}^2}{\partial {\xi }^2}{a}^{}=0,(14)$

where the coefficients of the dispersion (p) and the local (Q₁) and nonlocal (Q₂) nonlinear coefficients are

$P=\frac{1}{2}{b}_0,Q_1=\frac{3}{8}{b}_2,Q_2=\frac{3}{32}{b}_1{b}_3.(15)$

Eq. 14 is in the form of a generalized nonlinear Schrödinger (GNLS) equation in which the cubic (local) and derivative (nonlocal) nonlinearities are significantly modified by the effects of the relativistic degeneracy of dense electrons, percentage of nondegenerate electrons as well as the EM pump wave frequency. Here, by the local nonlinearity we mean the effect that occurs due to the interactions of different kinds of carrier harmonic modes (including self-interactions) at nonlinear regimes. On the other hand, the nonlocal nonlinearity appears due to the ponderomotive force of EM wave fields on the slow response of plasma density fluctuations. In the limit of R₀ ≪ 1, the nonlocal effect tends to become less significant and the local cubic nonlinearity prevails. However, as one gradually enters from the weakly to ultra-relativistic regimes with R₀ ≫ 1, the nonlocal term dominates over the local nonlinearity in the domain of higher values of k₀. Thus, it becomes significant to study the evolution of localized wave envelopes and their stability especially in the relativistic degeneracy regime. So, we look for a localized stationary solution of Eq. 14 in the form of a moving soliton (distinctive from that in Section 3) as $a=\rho (\eta )\exp \left[i\theta (\eta )+i{\lambda }^2\tau \right]$ where η = ξ − v₀τ with v₀ denoting the soliton velocity (which, in general, is different from v_g) in the moving frame of reference. Next, substituting this solution into Eq. 14, we obtain the following coupled equations for the soliton phase and the amplitude.

$\beta {\theta }_{\eta \eta }\rho +\left(4\beta -2b_0\right){\rho }_{\eta }{\theta }_{\eta }-2v_0{\rho }_{\eta }=0,(16)$

$\begin{array}{ll}\hfill {\rho }_{\eta \eta }+\frac{3}{8\beta }{b}_1{b}_3\rho {\rho }_{\eta }^2& =\frac{3}{4\beta }{\rho }^3\left(b_1{b}_3{\theta }_{\eta }^2-b_2\right)\hfill \\ \hfill & +\frac{\rho }{\beta }\left(2{\lambda }^2-2{\theta }_{\eta }{v}_0+b_0{\theta }_{\eta }^2\right),\hfill \end{array}(17)$

where β = b₀ + (3/8)b₁b₃ρ². Integrating Eq. 16 and using the boundary conditions, namely ρ, ρ_η, ρ_ηη → 0 as η → ±∞, we obtain dθ/dη ≈ v₀/b₀, whereas Eq. 17 gives on integration

${\rho }_{\eta }^2=\frac{{\rho }^2}{b_0\beta }\left[2{\lambda }^2{b}_0-v_0^2-\frac{3}{8}{b}_0\left(b_2-b_1{b}_3\frac{v_0^2}{b_o^2}\right){\rho }^2\right].(18)$

Further integration of Eq.18 gives a soliton solution in the following implicit form.

$\begin{array}{ll}\hfill \pm \eta & =\sqrt{\frac{3b_1{b}_3{\rho }_0^2{b}_0}{8\left(2{\lambda }^2{b}_0-v_0^2\right)}}{\tan }^{-1}\left(\sqrt{\frac{8\beta /3b_1{b}_3}{{\rho }_0^2\left(1-{\rho }^2/{\rho }_0^2\right)}}\right)\hfill \\ \hfill & +\frac{\left(b_0/2\right)}{\sqrt{2{\lambda }^2{b}_0-v_0^2}}\ln \left|\frac{\sqrt{\beta }-\sqrt{b_o\left(1-{\rho }^2/{\rho }_0^2\right)}}{\sqrt{\beta }+\sqrt{b_o\left(1-{\rho }^2/{\rho }_0^2\right)}}\right|,\hfill \end{array}(19)$

where ρ₀ is the maximum amplitude of the soliton, given by,

${\rho }_0^2=\frac{8}{3}\frac{\left(2{\lambda }^2{b}_0-v_0^2\right)b_0}{b_2{b}_0^2-b_1{b}_3{v}_0^2}.(20)$

From Eqs. 19, 20 it follows that the conditions for the existence of real solutions require

$2{\lambda }^2{b}_0-v_0^2>0,b_2{b}_0^2-b_1{b}_3{v}_0^2>0.(21)$

We will consider these conditions and discuss about the existence domains in more details shortly. In fact, Eq. 19 describes two branches of soliton solutions which are symmetric about the origin and which, when combined together, form a complete soliton profile. The characteristics of these solitons are displayed in Figure 2 for different values of the parameters, namely the degeneracy parameter R₀, the soliton velocity v₀ and the eigenfrequency λ. It is noted that in contrast to the effects of the soliton velocity, i.e., by increasing values of which the soliton amplitude decreases but the width broadens, the effects of the electron degeneracy and the eigenfrequency are to enhance the soliton amplitude but to reduce the width significantly as similar to those observed in Figure 1. The percentage of classical electrons α has also the similar effects on the soliton profiles as in Figure 1. Physically, for the present model, the wave dispersion is provided by the degeneracy pressure of electrons as well as by the separation of charged particles (Poisson equation). However, as the values of the degeneracy parameter R₀ increase, the coefficients of the group velocity dispersion p and the nonlocal nonlinearity (associated with the ponderomotive force) Q₂ tend to decrease but those of the cubic nonlinearity Q₁ increase and remain smaller than Q₂ in the regime 0 < R₀ ≲ 20. As a result, the increased wave energy from amplification is accommodated by an increase in soliton amplitude and a reduction in its width. If the density ratio α is slightly increased or if one considers the high- or ultra-relativistic degeneracy regimes, the ponderomotive nonlinearity tends to dominate over the cubic nonlinearity which results into a depletion of both the amplitude and width. However, some other nonlinear phenomena including the soliton collapse can also take place which we will examine in the end of this section.

FIGURE 2

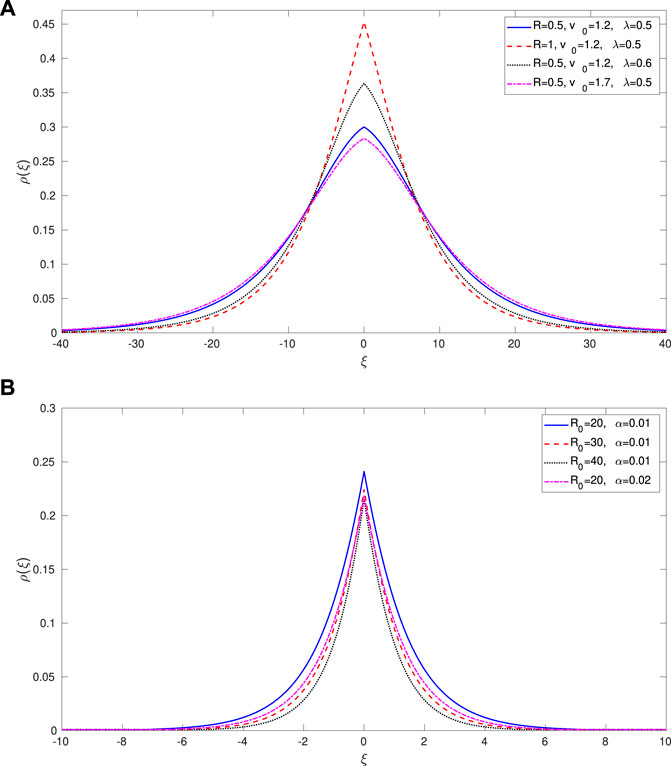
FIGURE 2. Two branches of soliton solutions [Eq. 19], symmetric about the origin, are plotted against ξ with a fixed α = 0.01 and different values of the parameters as in the legends. While subplot (A) is shown for a moderate value of R₀, subplot (B) is for relatively a higher value of R₀. The soliton characteristics are significantly modified due to different degrees of relativistic degeneracy.

It is to be mentioned that the profiles in Figure 2 are not exactly the cusp solitons. The spiky shape appears due to numerical plots of the two functions with plus and minus signs in Eq. 19 separately, which seem to mismatch at the top of the curves. The latter may be a sort of numerical error. However, cusp solitons may appear in the context of NLS equations with saturating nonlinearities [See, e.g., (Wadati et al., 1980)].

It is now imperative to study the stability of the moving solitons given by Eq. 19. To this end, we use the Vakhitov-Kolokolov stability criterion (Vakhitov and Kolokolov, 1973) according to which the solitons are said to be stable against a longitudial perturbation if

$\frac{d{P}_0}{d{\lambda }^2}>0,(22)$

where P₀ is the soliton photon number, defined by,

$P_0=\int |a{|}^{2}d\xi .(23)$

The expression for P₀(λ) can be obtained by integrating Eq. 18 with respect to η with the limits for ρ as 0 and ρ₀, and using Eq. 23 as

$\begin{array}{ll}\hfill P_0\left(\lambda \right)& =\frac{\sqrt{8}{b}_0}{\sqrt{3\left(b_2{b}_0^2-b_1{b}_3{v}_0^2\right)}}\hfill \\ \hfill & \times \left[\frac{\sqrt{2}{\beta }_0}{\sqrt{3b_1{b}_3}}{\cot }^{-1}\left(\sqrt{\frac{8b_0}{3b_1{b}_3{\rho }_0^2}}\right)-{\rho }_0\sqrt{\frac{b_0}{4}}\right],\hfill \end{array}(24)$

where ${\beta }_0=b_0+(3/8)b_1{b}_3{\rho }_0^2$ (the value of β at ρ = ρ₀). Thus, according to the stability condition [Eq. 22], the moving EM soliton (19) is said to be stable in the region λ < λ_s and unstable in the region λ > λ_s, where λ_s is some critical value of λ at which P₀ achieves a local maximum and beyond which dP₀/dλ² < 0. Since finding an analytic form of λ_s is extremely difficult, we try to obtain its values by a numerical approach for different sets of values of the parameters. The profiles of P₀(λ) and the corresponding values of λ_s are exhibited in Figure 3 with the variations of the degeneracy parameter R₀, the soliton velocity v₀ and the classical to degenerate electron number density ratio α. The stable and unstable regions can be predicted, respectively, with the conditions λ < λ_s, dP₀/dλ² > 0 and λ > λ_s, dP₀/dλ² < 0. It is found that, an increase of each of R₀, v₀ and k shifts the instability threshold λ_s towards its higher values, implying that the stability domains (λ < λ_s) are significantly enhanced. This means that, in contrast to linearly polarized EM waves (Roy and Misra, 2020), the circularly polarized EM solitons cab be stable in high density degenerate plasmas with two-temperature electrons.

FIGURE 3

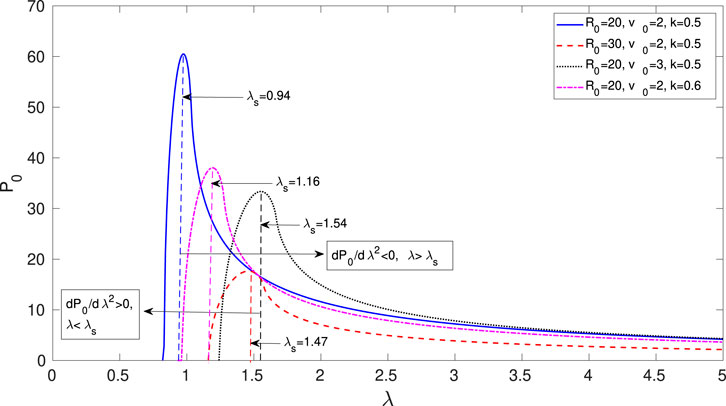
FIGURE 3. The soliton photon number P₀(λ) is plotted against the eigenfrequency λ with a fixed α = 0.01 and for different values of the other parameters as in the legends. The solitons are stable (unstable) in the regions λ < λ_s, dP₀/dλ² > 0 (λ > λ_s, dP₀/dλ² < 0).

Next, apart from the Vakhitov-Kolokolov stability criterion, we also examine if there be any constraints on the parameters λ and v₀ in order to have a real soliton solution Eq. 19. These constraints together with the stability criterion stated before can provide the existence as well as the stable and unstable regions of EM solitons. In this context, we find the limits for the parameters λ and/or v₀ from Eq. 21 as

$v_0<v_s\equiv b_0\min \left\{\sqrt{2}\lambda ,\sqrt{b_2/b_1{b}_3}\right\}.(25)$

Thus, considering Eqs. 21, 22, 25, we obtain the regions for the existence of EM solitons and their stability/instability in the (v₀, λ)-plane as shown in Figure 4. Different critical values of λ and v₀ are indicated by the text arrows and so are v₀ > v_s where no soliton solution exists. Thus, the existence regions together with the stable and unstable regions are those satisfy the conditions: λ < λ_s, v₀ < v_s, dP₀/dλ² > 0 (Stable) and λ < λ_s, v₀ < v_s, dP₀/dλ² < 0 (Unstable) as indicated in the subplots. We find that as the value of the degeneracy parameter R₀ increases, the stable/unstable regions shift towards unstable/stable ones with a significant reduction of v_s but a significant increase of λ_s. The wave number k₀ has also similar effects on the stable and unstable regions, however, a change in λ_s is not so effective. Although in the region of v₀ > v_s, no real analytic soliton solution [cf. Eq. 19] exists, there may be some other numerical solution of Eq. 14. Such a discrepancy may occur due to an initial small phase difference between the approximate analytical and numerical solutions in the particular region. It is to be noted that the Vakhitov-Kolokolov criterion is suitable only for the linear stability of EM solitons that involve exponential growth or decay of wave modes. It cannot predict the nonlinear evolution of unstable envelope solitons or the stability of localized solutions that have arbitrary profiles. However, due to the presence of both the cubic and nonlocal nonlinearities, the GNLS equation can admit, apart from the envelope solitons, the soliton collapse or some other nonlinear features which are out of scope of the present study.

FIGURE 4

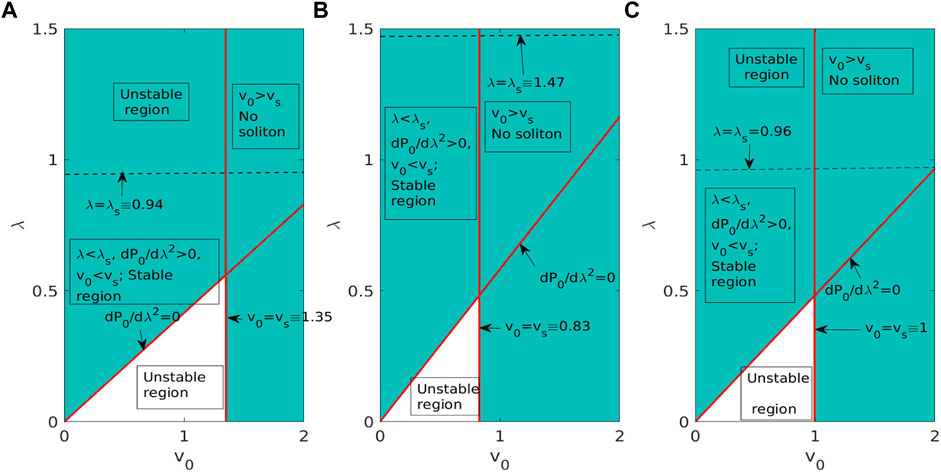
FIGURE 4. The stable and unstable regions as well as the existence domains of EM solitons are shown in the (v₀, λ)-plane for diferent values of the parameters: (A) R₀ = 20, α = 0.01, k₀ = 0.5, (B) R₀ = 30, α = 0.01, k₀ = 0.5, and (C) R₀ = 20, α = 0.01, k₀ = 0.6.

Relying on the existence as well as the stable and unstable regions of EM solitons obtained so far in the (v₀, λ)-plane, we now study the dynamical evolution of EM solitons by a numerical simulation approach. The aim is also to verify whether these regions indeed support the numerical soliton solutions. So, we solve Eq. 14 by using the Runge-Kutta scheme with a time step size Δτ = 0.001 and the initial condition (at τ = 0): a(ξ) ∼ a₀sech²(ξ/8) exp(−iv₀ξ). Figure 5 shows the evolution of EM solitons after time τ = 150 with the spatial interval − 200 ≤ ξ ≤ 200 and 1,000 grid points for different values of the parameters that fall in the existence and stable/unstable regions. As an illustration, we consider two unstable regions with 1) R₀ = 20, λ = 1.5, v₀ = 0.6, α = 0.01, k₀ = 0.5 [subplot (a)] and 2) R₀ = 30, λ = 0.2, v₀ = 5, α = 0.01, k₀ = 0.5 [subplot (c)] and a stable region with R₀ = 30, λ = 0.2, v₀ = 0.6, α = 0.01, k₀ = 0.5 [subplot (b)]. It is seen that as time goes on, the initial profile tends to radiate and as the nonlinear and dispersion effects intervene the dynamics, the soliton evolves into either a stable pulse or an unstable one. Furthermore, the standing soliton with v₀ = 0, R₀ = 20, amplitude a₀ ∼ 0.7, λ = 0.2, and photon number P₀ = 1.64 in the stable region oscillates around ξ = 0 with a frequency close to the EM wave frequency and it remains stable for a longer time interval. However, as the velocity is increased, the moving soliton with v₀ = 0.6, R₀ = 30, amplitude a₀ ∼ 0.7, λ = 0.2, and photon number P₀ = 17.6 in the stable region propagates towards the upstream region and it displays an increase of the wave amplitude [subplot (b)]. Physically, an increase of the soliton velocity results into a reduction of the relative eigenfrequency $\mathrm{\Lambda }\equiv \sqrt{{\lambda }^2-v_0^2/b_0}$ but an enhancement of the photon number which, in turn, increases the soliton amplitude. However, as time progresses the moving soliton mitigates to a stable structure. On the other hand, by increasing the eigenfrequency λ = 1.5 but retaining the soliton speed at v₀ = 0.6 with a different value of R₀ = 20 [subplot (a)], we find that the photon number is reduced to P₀ = 1.05. As a result the soliton in the unstable region exhibits a decay of its amplitude and as time elapses, it reaches towards a steady state stable soliton. Next, further considering an increased value of the soliton velocity (v₀ = 5), however, retaining R₀ = 30 and λ = 0.2 that fall in the unstable region we find that the soliton photon number increases and the soliton can no longer travel undistorted, i.e., its amplitude aperiodically grows and eventually leads to a collapse [subplot (c)].

FIGURE 5

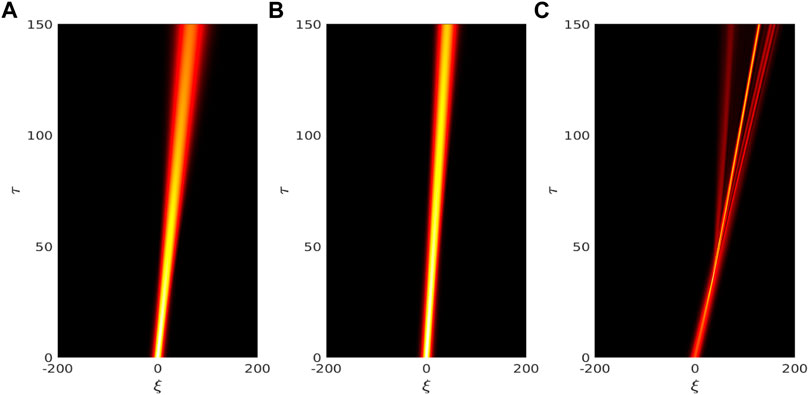
FIGURE 5. Dynamical evolution of EM solitons [Numerical solution of Eq. 14] for different parameter values that correspond to stable [subplot (B)] and unstable [subplots (A) and (C)] regions [cf. Figure 4]. The parameter values for the subplots (A) to (C), respectively, are R₀ = 20, λ = 1.5, v₀ = 0.6, α = 0.01, k₀ = 0.5; R₀ = 30, λ = 0.2, v₀ = 0.6, α = 0.01, k₀ = 0.5; and R₀ = 30, λ = 0.2, v₀ = 2, α = 0.01, k₀ = 0.5.

5 Summary and conclusion

We have studied the generation of EM solitons in the nonlinear interactions between a circularly polarized intense EM pulse and low-frequency electron-acoustic density fluctuations that are driven by the EM wave ponderomotive force in relativistic degenerate dense plasmas with two groups of electrons. The evolution of such solitons is described by a coupled set of nonlinear equations for the EM vector potential and the density fluctuations associated with the slow plasma response (Shatashvili et al., 2020). Stationary localized soliton solutions of the coupled equations are obtained and their characteristics are analyzed with the parameters that correspond to the relativistic degeneracy of electrons (R₀), the fraction of classical to degenerate electrons (α) and the EM wave frequency (ω₀).

Using the Vakhitov-Kolokolov stability criterion, we have also studied the existence conditions and performed a linear stability analysis of a moving soliton whose evolution is governed by a GNLS equation with both the cubic (local) and derivative (nonlocal) nonlinearities. Different stable and unstable regions are obtained which shift around the (v₀, λ)-plane due to variations of the parameters R₀, α, and ω₀ that correspond to different physical regimes in astrophysical settings. Here, v₀ is the soliton velocity and λ is the eigenfrequency. A direct numerical simulation of the generalized GNLS equation reveals that the parameter domains for the stability and instability of EM solitons well agree with those predicted using the Vakhitov-Kolokolov stability criterion. It is also found that an initially launched moving soliton with an increased velocity in the instability domain eventually collapses after a finite interval of time due to higher nonlocal nonlinear effects than the cubic nonlinearity.

To conclude, it has been observed that relativistic high density degenerate plasmas deviating from thermodynamic equilibrium can appear not only in the context of laser produced plasmas or beam driven plasmas but also in compact astrophysical objects like white dwarf stars, neutron stars (Gibbon, 2005; Hau-Riege, 2011). In these environments, since the system energy flows mostly into the electrons, they may appear either as a group of partially degenerate electrons with high temperature tails or a group of relativistic classical and fully degenerate electrons. Such plasmas are known to support low-frequency electron-acoustic waves (Misra et al., 2021) which play key roles in the nonlinear wave dynamics. Furthermore, these compact astrophysical objects emanate different EM radiation spectra ranging from radio to γ-rays. So, interactions of these intense pulses with high-density plasmas may give rise the formation of solitons and other coherent structures as localized bursts of x-rays and γ-rays. In this respect, the present theoretical results could be useful for understanding the characteristics of x-ray and γ-ray pulses as well as for the next generation intense laser-solid density plasma interaction experiments.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

AM acknowledges support from Science and Engineering Research Board (SERB, Government of India) through a research project with sanction order no. CRG/2018/004475 and Fee Support (Ref: DSC-07033608101PRD).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Asenjo, F. A., Muñoz, V., Valdivia, J. A., and Mahajan, S. M. (2011). A hydrodynamical model for relativistic spin quantum plasmas. Phys. Plasmas 18, 012107. doi:10.1063/1.3533448

CrossRef Full Text | Google Scholar

Asenjo, F. A., Zamanian, J., Marklund, M., Brodin, G., and Johansson, P. (2012). Semi-relativistic effects in spin-1/2 quantum plasmas. New J. Phys. 14, 073042. doi:10.1088/1367-2630/14/7/073042

CrossRef Full Text | Google Scholar

Barr, H. C., Mason, P., and Parr, D. M. (1999). Electron parametric instabilities driven by relativistically intense laser light in plasma. Phys. Rev. Lett. 83, 1606–1609. doi:10.1103/PhysRevLett.83.1606

CrossRef Full Text | Google Scholar

Begelman, M. C., Blandford, R. D., and Rees, M. J. (1984). Theory of extragalactic radio sources. Rev. Mod. Phys. 56, 255–351. doi:10.1103/RevModPhys.56.255

CrossRef Full Text | Google Scholar

Borghesi, M., Bulanov, S., Campbell, D. H., Clarke, R. J., Esirkepov, T. Z., Galimberti, M., et al. (2002a). Macroscopic evidence of soliton formation in multiterawatt laser-plasma interaction. Phys. Rev. Lett. 88, 135002. doi:10.1103/PhysRevLett.88.135002

PubMed Abstract | CrossRef Full Text | Google Scholar

Borghesi, M., Campbell, D. H., Schiavi, A., Haines, M. G., Willi, O., MacKinnon, A. J., et al. (2002b). Electric field detection in laser-plasma interaction experiments via the proton imaging technique. Phys. Plasmas 9, 2214–2220. doi:10.1063/1.1459457

CrossRef Full Text | Google Scholar

Borhanian, J., Kourakis, I., and Sobhanian, S. (2009). Electromagnetic envelope solitons in magnetized plasma. Phys. Lett. A 373, 3667–3677. doi:10.1016/j.physleta.2009.08.010

CrossRef Full Text | Google Scholar

Bulanov, S. V., Esirkepov, T. Z., Naumova, N. M., Pegoraro, F., and Vshivkov, V. A. (1999). Solitonlike electromagnetic waves behind a superintense laser pulse in a plasma. Phys. Rev. Lett. 82, 3440–3443. doi:10.1103/PhysRevLett.82.3440

CrossRef Full Text | Google Scholar

Esarey, E., Sprangle, P., Krall, J., and Ting, A. (1997). Self-focusing and guiding of short laser pulses in ionizing gases and plasmas. IEEE J. Quantum Electron. 33, 1879–1914. doi:10.1109/3.641305

CrossRef Full Text | Google Scholar

Esirkepov, T., Nishihara, K., Bulanov, S. V., and Pegoraro, F. (2002). Three-dimensional relativistic electromagnetic subcycle solitons. Phys. Rev. Lett. 89, 275002. doi:10.1103/PhysRevLett.89.275002

PubMed Abstract | CrossRef Full Text | Google Scholar

Farina, D., and Bulanov, S. V. (2005). Dynamics of relativistic solitons. Plasma Phys. control. Fusion 47, A73–A80. doi:10.1088/0741-3335/47/5a/007

CrossRef Full Text | Google Scholar

Farina, D., and Bulanov, S. V. (2001). Relativistic electromagnetic solitons in the electron-ion plasma. Phys. Rev. Lett. 86, 5289–5292. doi:10.1103/PhysRevLett.86.5289

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibbon, P. (2005). Short pulse laser interactions with matter. PUBLISHED BY IMPERIAL COLLEGE PRESS AND DISTRIBUTED BY WORLD SCIENTIFIC PUBLISHING CO. doi:10.1142/p116

CrossRef Full Text | Google Scholar

Gleixner, F., and Kumar, N. (2020). Electronic parametric instabilities of an ultrarelativistic laser pulse in a plasma. Phys. Rev. E 101, 033201. doi:10.1103/physreve.101.033201

PubMed Abstract | CrossRef Full Text | Google Scholar

Hau-Riege, S. (2011). Examples of X-ray–matter interaction. chap 10, 239–261. doi:10.1002/9783527636365.ch10

CrossRef Full Text | Google Scholar

Hebenstreit, F., Ilderton, A., and Marklund, M. (2011). Pair production: The view from the lightfront. Phys. Rev. D. 84, 125022. doi:10.1103/PhysRevD.84.125022

CrossRef Full Text | Google Scholar

Kaw, P. K., Sen, A., and Katsouleas, T. (1992). Nonlinear 1d laser pulse solitons in a plasma. Phys. Rev. Lett. 68, 3172–3175. doi:10.1103/PhysRevLett.68.3172

PubMed Abstract | CrossRef Full Text | Google Scholar

Kozlov, V. A., Litvak, A. G., and Suvorov, E. V. (1979). Envelope solitons of relativistic strong electromagnetic waves. Sov. Phys. - JETP Engl. Transl.); (United States) 49, 1.

Google Scholar

Kryvdyk, V., and Agapitov, A. (2007). Relativistic jets from accretion-induced collapsing white dwarfs. In 15th European Workshop on White Dwarfs Astronomical Society of the Pacific Conference Series, September 2007, eds. R. Napiwotzki, and M. R. Burleigh., 411

Google Scholar

Kryvdyk, V. (1999). Electromagnetic radiation from collapsing stars — I. The power-series distribution of particles in magnetospheres. Mon. Notices R. Astronomical Soc. 309, 593–598. doi:10.1046/j.1365-8711.1999.02869.x

CrossRef Full Text | Google Scholar

Kuehl, H. H., and Zhang, C. Y. (1993). One-dimensional, weakly nonlinear electromagnetic solitary waves in a plasma. Phys. Rev. E 48, 1316–1323. doi:10.1103/PhysRevE.48.1316

PubMed Abstract | CrossRef Full Text | Google Scholar

Lontano, M., Bulanov, S. V., Koga, J., Passoni, M., and Tajima, T. (2002). A kinetic model for the one-dimensional electromagnetic solitons in an isothermal plasma. Phys. Plasmas 9, 2562–2568. doi:10.1063/1.1476307

CrossRef Full Text | Google Scholar

Lontano, M., Passoni, M., and Bulanov, S. V. (2003). Relativistic electromagnetic solitons in a warm quasineutral electron–ion plasma. Phys. Plasmas 10, 639–649. doi:10.1063/1.1544666

CrossRef Full Text | Google Scholar

Mikaberidze, G., and Berezhiani, V. (2015). Standing electromagnetic solitons in degenerate relativistic plasmas. Phys. Lett. A 379, 2730–2734. doi:10.1016/j.physleta.2015.08.009

CrossRef Full Text | Google Scholar

Mima, K., Ohsuga, T., Takabe, H., Nishihara, K., Taijma, T., Zaidman, E., et al. (1986). Wakeless triple-soliton accelerator. Phys. Rev. Lett. 57, 1421–1424. doi:10.1103/PhysRevLett.57.1421

PubMed Abstract | CrossRef Full Text | Google Scholar

Misra, A. P., Chatterjee, D., and Brodin, G. (2021). Landau damping of electron-acoustic waves due to multi-plasmon resonances. Phys. Plasmas 28, 112102. doi:10.1063/5.0061716

CrossRef Full Text | Google Scholar

Morandi, O., Zamanian, J., Manfredi, G., and Hervieux, P.-A. (2014). Quantum-relativistic hydrodynamic model for a spin-polarized electron gas interacting with light. Phys. Rev. E 90, 013103. doi:10.1103/PhysRevE.90.013103

PubMed Abstract | CrossRef Full Text | Google Scholar

Mori, W., Decker, C., and Leemans, W. (1993). Relativistic harmonic content of nonlinear electromagnetic waves in underdense plasmas. IEEE Trans. Plasma Sci. IEEE Nucl. Plasma Sci. Soc. 21, 110–119. doi:10.1109/27.221109

CrossRef Full Text | Google Scholar

Poornakala, S., Das, A., Kaw, P. K., Sen, A., Sheng, Z. M., Sentoku, Y., et al. (2002). Weakly relativistic one-dimensional laser pulse envelope solitons in a warm plasma. Phys. Plasmas 9, 3802–3810. doi:10.1063/1.1496085

CrossRef Full Text | Google Scholar

Quesnel, B., Mora, P., Adam, J. C., Héron, A., and Laval, G. (1997). Electron parametric instabilities of ultraintense laser pulses propagating in plasmas of arbitrary density. Phys. Plasmas 4, 3358–3368. doi:10.1063/1.872494

CrossRef Full Text | Google Scholar

Roy, S., Chatterjee, D., and Misra, A. P. (2019). Generation of wakefields and electromagnetic solitons in relativistic degenerate plasmas. Phys. Scr. 95, 015603. doi:10.1088/1402-4896/ab447d

CrossRef Full Text | Google Scholar

Roy, S., and Misra, A. P. (2020). Stability and evolution of electromagnetic solitons in relativistic degenerate laser plasmas. J. Plasma Phys. 86, 905860611. doi:10.1017/S0022377820001452

CrossRef Full Text | Google Scholar

Saxena, V., Das, A., Sen, A., and Kaw, P. (2006). Fluid simulation studies of the dynamical behavior of one-dimensional relativistic electromagnetic solitons. Phys. Plasmas 13, 032309. doi:10.1063/1.2187447

CrossRef Full Text | Google Scholar

Sen, A., and Kaw, P. K. (1994). Nonlinear 1d laser pulse solitons for particle acceleration. Phys. Scr. 1994, 47–50. doi:10.1088/0031-8949/1994/t50/007

CrossRef Full Text | Google Scholar

Sentoku, Y., Esirkepov, T. Z., Mima, K., Nishihara, K., Califano, F., Pegoraro, F., et al. (1999). Bursts of superreflected laser light from inhomogeneous plasmas due to the generation of relativistic solitary waves. Phys. Rev. Lett. 83, 3434–3437. doi:10.1103/physrevlett.83.3434

CrossRef Full Text | Google Scholar

Shatashvili, N. L., Mahajan, S. M., and Berezhiani, V. I. (2020). Nonlinear coupling of electromagnetic and electron acoustic waves in multi-species degenerate astrophysical plasma. Phys. Plasmas 27, 012903. doi:10.1063/1.5135959

CrossRef Full Text | Google Scholar

Shen, B., Yu, W., Zeng, G., and Xu, Z. (1995). Relativistic harmonic generation by intense laser in plasmas. Phys. Plasmas 2, 4631–4634. doi:10.1063/1.870953

CrossRef Full Text | Google Scholar

Sundar, S., Das, A., Saxena, V., Kaw, P., and Sen, A. (2011). Relativistic electromagnetic flat top solitons and their stability. Phys. Plasmas 18, 112112. doi:10.1063/1.3662441

CrossRef Full Text | Google Scholar

Vakhitov, N. G., and Kolokolov, A. A. (1973). Stationary solutions of the wave equation in a medium with nonlinearity saturation. Radiophys. Quantum Electron. 16, 783–789. doi:10.1007/BF01031343

CrossRef Full Text | Google Scholar

Wadati, M., Ichikawa, Y. H., and Shimizu, T. (1980). Cusp soliton of a new integrable nonlinear evolution equation. Prog. Theor. Phys. 64, 1959–1967. doi:10.1143/PTP.64.1959

CrossRef Full Text | Google Scholar

Wagner, U., Tatarakis, M., Gopal, A., Beg, F. N., Clark, E. L., Dangor, A. E., et al. (2004). Laboratory measurements of 0.7 GG magnetic fields generated during high-intensity laser interactions with dense plasmas. Phys. Rev. E 70, 026401. doi:10.1103/PhysRevE.70.026401

PubMed Abstract | CrossRef Full Text | Google Scholar