Abstract
The recent astronomical detection of c-C3HC2H and l-C5H2 has led to increased interest in C5H2 isomers and their relative stability. The present work provides the first complete list of anharmonic vibrational spectral data with infrared intensities for three such isomers as well as including the first set of rotational data for the bipyramidal C5H2 isomer allowing for these molecules to serve as potential tracers of interstellar carbon. All three isomers have fundamental vibrational frequencies with at least one notably intense fundamental frequency. The l-C5H2 isomer has, by far, the highest intensities out of the three isomers at 2076.3 cm−1 (738 km mol−1) and 1887.5 cm−1 (182 km mol −1). The c-C3HC2H isomer has one intense peak at 3460.6 cm−1 (84 km mol−1), and the bipyramidal C5H2 isomer has one intense peak at 489.3 cm−1 (78 km mol−1). The relative intensities highlight that while l-C5H2 is not the lowest energy isomer, its notable intensities should make it more detectable in the infrared than the lower energy c-C3HC2H form. The bipyramidal isomer is firmly established here to lie 44.98 kcal mol−1 above the cyclic form. The explicitly correlated coupled cluster rovibrational spectral data presented herein should assist with future laboratory studies of these C5H2 isomers and aid in detection in astronomical environments especially through the newly operational James Webb Space Telescope.
1 Introduction
The unidentified infrared bands (UIRs) are unattributed spectral features observed in virtually all types of astronomical objects whose provenance is not firmly established (Peeters et al., 2002). The UIRs were first recognized in 1973 in the 8–13 μm region and have since been detected in nebulae and in the diffuse interstellar medium (ISM) among other astronomical environments (Peeters et al., 2002). The UIRs were first believed to originate from mostly grain mantle molecules (Allamandola et al., 1979). However, since 1984 most of the UIR spectral features have been hypothesized to be caused by polycyclic aromatic hydrocarbons (PAHs) (Leger and Puget, 1984; Sellgren, 1984; Molster et al., 2001). One difficulty with supporting this so-called PAH hypothesis is that most PAHs are not rotationally active at worst or weakly dipolar at best. This leads many PAHs to be poor candidates for rotational astronomical detection, which has been the primary vehicle for most astrochemical molecular observation including the recent detection of PAH-like molecules (Cabezas et al., 2021; Cernicharo et al., 2021). However, some small PAH-like molecules, like isomers of C5H2, have a lower symmetry which can allow for a nonzero dipole moment and possible rotational activity. Recently, two isomers of C5H2, l-C5H2 and ethynyl cyclopropenylidene (c-C3HC2H), have been independently detected in Taurus Molecular Cloud-1 and pathways of formation have been determined experimentally and supported theoretically (He et al., 2020; Cabezas et al., 2021; Cernicharo et al., 2021; Karton and Thimmakondu, 2022). The detection of C5H2 isomers could allude to other rotationally dark PAHs lurking in the interstellar medium. Insight into the presence, and identity, of PAHs in various astronomical environments can shed light on the chemical and physical aspects of these environments and how they contribute to the UIRs (Tielens, 2008). Additionally the recently launched James Webb Space Telescope (JWST) will allow for more detections through vibrational/infrared spectroscopy which can be used for the detection of PAHs that previously could not be detected through rotational spectroscopy.
In addition to the astronomical interest, previous theoretical works have disagreed about the relative energy of C5H2 isomers. These have been quantum chemically computed using coupled cluster theory at the CCSD/DZP, CCSD/TZ2P, and CCSD(T)/cc-pVTZ levels, but there are still discrepancies in the relative energies (Balaji and Michl, 1988; Seburg et al., 1997; Veis et al., 2008). Specifically, the bipyramidyl C5H2 isomer, shown in Figure 1, has an inconsistent magnitude of relative energy when compared to other C5H2 isomers depending on the level of theory utilized (Balaji and Michl, 1988; Seburg et al., 1997; Veis et al., 2008). A previous study at the HF/6-31G* level (Pople et al., 1993) places bipyramidal C5H2 100 kcal mol−1 higher than other C5H2 isomers while another study utilizing MBPT(2)/6-31G* puts the bipyramidal C5H2 isomer only 30 kcal mol−1 higher (Balaji and Michl, 1988; Pople et al., 1993; Seburg et al., 1997). Furthermore, previous density functional and coupled cluster theory computations also place the bipyramidyl C5H2 isomer 47–70 kcal mol−1 higher than other isomers (Seburg et al., 1997; Karton and Thimmakondu, 2022). Despite the different levels of theory agreeing that the bipyramidyl C5H2 isomer is not the lowest energy isomer, there is a clear disagreement on the magnitude of energy difference for the isomer (Balaji and Michl, 1988; Pople et al., 1993; Seburg et al., 1997; Karton and Thimmakondu, 2022). Determining more accurate relative energies is necessary because the ambient energy in the ISM allows for the formation of non-global-minimum structures. However, the energy can not be too much higher; a higher energy difference closer to 100 kcal mol −1 is much more unreasonable for formation in the ISM (Seburg et al., 1997). Newer, higher-level computations could help to settle the disagreements as to the relative energy of the bipyramidal C5H2 structure compared to the other isomers of C5H2. A further look into the l-C5H2 isomer, shown in Figure 2, and the c-C3HC2H isomer, shown in Figure 3, can provide a common reference to determine the relative energy of the bipyramidal C5H2 isomer. Additionally the c-C3HC2H isomer and the l-C5H2 isomer have been detected in the laboratory by Fourier transform spectrometry which provides a benchmark to the theoretical methods utilized herein (McCarthy et al., 1997; Travers et al., 1997).
FIGURE 1

Bipyramidal C5H2.
FIGURE 2
l-C5H2.
FIGURE 3

c-C3HC2H.
The present work utilizes high level quantum chemical computations to compute molecular structures, energies, and spectroscopic data for the bipyramidal C5H2 isomer shown in Figure 1, the l-C5H2 isomer shown in Figure 2, and the c-C3HC2H isomer shown in Figure 3. The spectroscopic data is computed using quartic force fields (QFFs) which are fourth-order Taylor series expansions of the internuclear potential energy portion of the Watson Hamiltonian (Fortenberry and Lee, 2019). QFFs based on coupled cluster theory at the singles, doubles, and perturbative triples level within the explicitly correlated F12b construction [CCSD(T)-F12b] (Adler et al., 2007; Knizia et al., 2009) and a triple-ζ basis set can frequently achieve agreement to within 5–7 cm−1 of gas-phase experimental vibrational frequencies (Gardner et al., 2021). However a shortcoming of this method is that the rotational constants are only accurate to about 60 MHz (Agbaglo et al., 2019; Agbaglo and Fortenberry, 2019a,b; Watrous et al., 2021). An improvement would be to utilize a composite method combining core-correlated CCSD(T)-F12b with the cc-pCVTZ-F12 basis set and a correction for scalar relativity (Watrous et al., 2021). This method is referred to as F12-TZ-cCR and offers closer agreement, compared to previous methods, to experimental rotational constants on the order of 7.5 MHz which is necessary for accurate detection (Westbrook et al., 2021b; Watrous et al., 2021). Thus the fundamental vibrational frequencies and rotational constants at this level of theory provided here will lend theoretical support to experiments that will help NASA missions such as the Stratospheric Observatory for Infrared Astronomy (SOFIA) and JWST to facilitate the detection of these isomers in space.
2 Computational details
All four levels of theory in the present work utilize CCSD(T)-F12b (Raghavachari et al., 1989; Adler et al., 2007; Knizia et al., 2009; Shavitt and Bartlett, 2009). The first two QFFs use the cc-pVXZ-F12 basis sets (Peterson et al., 2008; Yousaf and Peterson, 2008; Knizia et al., 2009) where X is D or T. This combination is abbreviated as F12-XZ in the following. F12-DZ and F12-TZ QFFs are utilized for all three isomers. The other two levels of theory are based on core-correlated CCSD(T)-F12b with the cc-pCVXZ-F12 basis sets, (Watrous et al., 2021), where X is again D or T. Additionally this method includes a correction for scalar relativity computed with canonical CCSD(T) with a cc-pVTZ-DK basis set (Douglas and Kroll, 1974; Jansen and Hess, 1989). This combination is hereafter referred to as F12-XZ-cCR. F12-DZ-cCR and F12-TZ-cCR QFFs are only utilized for the c-C3HC2H isomer due to the substantial increase in computational cost. The QFF for the c-C3HC2H isomer is composed of 20,641 displacements from the equilibrium geometry along the symmetry-internal coordinates (SICs) shown below with atom labels corresponding to Figure 3.
The QFFs for the l-C5H2 and bipyramidal C5H2 isomers are run directly in Cartesian coordinates composed of 46,064 points and 38,968 points respectively. This increase in the number of points for Cartesians instead of SICs exacerbates the increase in computational cost that would be needed for the F12-DZ-cCR and F12-TZ-cCR methods. For the SIC-based QFFs, the geometry is first optimized at each of the four levels of theory, then each geometry is displaced by 0.005 Å or 0.005 radians along the SICs to form the QFF. For the c-C3HC2H isomer, in addition to the previous displacements, the out-of-plane bends (OPB) are instead displaced by 0.010 Å or 0.010 radians to help combat the well-known OPB problem (Westbrook et al., 2020; Lee and Fortenberry, 2021). At each of the displaced geometries, single-point energies are calculated. The resulting energies are then fit by a least-squares procedure to yield the optimized geometry. A refit to the function minimum zeroes the gradients and yields the new equilibrium geometry as well as the corresponding force constants. The force constants are then converted from SICs to Cartesian coordinates by using the INTDER program (Allen and coworkers, 2005). For the Cartesian QFFs, each geometry is first optimized at the F12-DZ and F12-TZ levels of theory. Then, each geometry is displaced by 0.005 Å along the Cartesian x, y, and z axes. For l-C5H2 at the F12-DZ level of theory, each geometry was displaced by 0.010 Å in the out-of-plane coordinates. The force constants are computed numerically by central finite differences (Westbrook et al., 2021b).
For all of the QFFs, the rovibrational spectral data is computed using the SPECTRO software package (Gaw et al., 1991) which uses the Cartesian force constants in vibrational perturbation theory at second order (Watson, 1977; Papousek and Aliev, 1982; Franke et al., 2021) and second-order rotational perturbation theory (Mills, 1972). Type-1 and -2 Fermi resonances, Fermi polyads (Martin and Taylor, 1997) and Coriolis resonances are taken into account to further increase the accuracy of the rovibrational data (Martin et al., 1995; Martin and Taylor, 1997). These are shown in Supplementary Tables S1–S3 of the Supplemental Information (SI) along with the optimized geometrical parameters and T1 diagnostics shown in Supplementary Tables S4–S6. The anharmonic zero point vibrational energy (ZPVE) from the refit geometry, refit energy (only for the SIC QFF), and energy from the optimized minima are added together to calculate the relative energy.
The geometry optimizations, harmonic frequencies, single point energies, and dipole moments are computed using the Molpro 2020.1 software package (Werner et al., 2020). The dipole moments are computed at the F12-TZ level of theory. Double-harmonic and anharmonic infrared intensities are computed using Gaussian16 (Frisch et al., 2016) with the MP2/aug-cc-pVTZ (Møller and Plesset, 1934; Kendall et al., 1992), B3LYP/aug-cc-pVTZ (Yang et al., 1986; Lee et al., 1988; Becke, 1993), and B3LYP/N07D (Barone et al., 2008) levels of theory. Previous work has shown semi-quantitative accuracy for harmonic infrared intensities for the MP2 level of theory for a substantial decrease in cost relative to higher-level computations (Yu et al., 2015; Finney et al., 2016; Westbrook et al.,2021a).
3 Results and discussion
The relative energies of l-C5H2, c-C3HC2H, and bipyramidal C5H2 are compared at the F12-DZ and the F12-TZ levels of theory as shown in Table 1. The relative energies of the c-C3HC2H and l-C5H2 isomers are similar to previous (Seburg et al., 1997) relative energy computations with the l-C5H2 isomer being 13.79 kcal mol−1 higher in energy than the c-C3HC2H isomer. However, the bipyramidal C5H2 isomer is lower in relative energy than some previous computations (Balaji and Michl, 1988; Pople et al., 1993; Seburg et al., 1997). The relative energy of the bipyramidal C5H2 isomer at the F12-TZ level of theory is 44.98 kcal mol−1 compared to the c-C3HC2H isomer. This relative energy is much closer to the previous MBPT(2)/6-31G* calculations, at about 30 kcal mol−1, as opposed to previous calculations at the HF/6-31G* level of theory where the relative energy was roughly 100 kcal mol−1 higher than other C5H2 isomers (Balaji and Michl, 1988; Pople et al., 1993; Seburg et al., 1997). While this highly-symmetric isomer gives indication of possessing multi-reference effects due to its large T1 diagnostic (0.059), the extent to which this will affect the relative energies is left for future work.
TABLE 1
| Isomer | F12-DZ | F12-TZ | CCSD(T)/cc-pVTZa | CCSDT(Q)/CBSb |
|---|---|---|---|---|
| c-C3HC2H | 0.00 | 0.00 | 2.01 | 0.66 |
| l-C5H2 | 13.86 | 13.79 | 13.82 | 13.53 |
| bipyramidyl C5H2 | 45.90 | 44.98 | 47.51 |
Relative energy of C5H2 Isomers in kcal mol−1 compared to previous experiment.
From Ref. (Seburg et al., 1997) where energies are relative to a lower energy isomer.
From Ref. (Karton and Thimmakondu, 2022) where energies are relative to a lower energy isomer.
3.1 Rotational constants
Out of the three isomers, the l-C5H2 isomer has the largest dipole moment of 5.94 D and its equilibrium (e) and vibrationally-averaged (0) rotational constants, shown in Table 2, demonstrate near prolate character (κ = − 0.99987 for the F12-TZ level of theory, where κ is defined as (2B0 − A0 − C0)/(A0 − C0)). This large dipole moment has helped with detection of the molecule through rotational spectroscopy. The F12-DZ and F12-TZ rotational constants agree well with a maximum relative difference of 0.57% in the B0 rotational constant. Compared to experimental Fourier transform microwave spectroscopy (McCarthy et al., 1997), the F12-TZ B0 and C0 rotational constants differ from experiment by only 3.0 MHz (0.13%) and 1.1 MHz (0.05%) respectively. This benchmarking constrains the expected accuracy for other, unknown spectral observables provided in this work. The A0 rotational constant differs from experiment by 10,200 MHz (3.67%), but the error for the A0 rotational constant is known to have a higher error for near prolate molecules (Gardner et al., 2021). The complete set of the vibrationally excited rotational constants are reported in Supplementary Table S7 of the SI. The quartic and sextic distortion constants in the S-reduced Hamiltonian are reported in Table 2. The DJ constant is about 13 Hz lower than experiment while the DJK constant differs from experiment by around 24 kHz at the F12-DZ level of theory, but has a much higher difference at the F12-TZ level of theory at around 2,596 kHz. While DJK often exhibits minor effects on the rotational spectrum of near-prolate molecules (Stein et al., 2015), this erroneous l-C5H2DJK value for F12-TZ (and, in fact, all of its sextic distortion constants, as well) presently stems from a compounding error brought about by the step size and the resulting QFF improperly representing these data. The F12-DZ data are consistent within step size and experimental comparison implying that these data are reliable as are the F12-TZ data behaving in similar ways.
TABLE 2
| F12-DZ | F12-TZ | ||||
|---|---|---|---|---|---|
| Constant | Units | 0.005 | 0.010 | 0.005 | Exp.a |
| A e | MHz | 290162.5 | 290162.5 | 290123.6 | |
| B e | MHz | 2290.1 | 2290.1 | 2296.4 | |
| C e | MHz | 2272.1 | 2272.1 | 2278.4 | |
| A 0 | MHz | 286248.3 | 286245.9 | 287832.8 | 277600 |
| B 0 | MHz | 2294.6 | 2294.5 | 2307.8 | 2304.7844 |
| C 0 | MHz | 2275.7 | 2275.7 | 2286.9 | 2285.8053 |
| D J | Hz | 92.822 | 92.831 | 91.191 | 104 |
| D JK | kHz | 70.773 | 71.920 | 2,642.5 | 46.4 |
| D K | MHz | 22.182 | 22.180 | 19.676 | |
| d 1 | mHz | −771.6 | −771.6 | −775.9 | |
| d 2 | mHz | −285.6 | −282.0 | 1,081.6 | |
| H J | nHz | −558.98 | −516.46 | −216,800 | |
| H JK | mHz | 238.14 | 232.78 | 11,321 | |
| H KJ | kHz | −1.8080 | −1.4656 | −478.98 | |
| H K | kHz | 6.9698 | 6.6280 | 484.19 | |
| h 1 | nHz | −50.873 | −105.28 | −36970 | |
| h 2 | mHz | 1.1503 | 1.0644 | −0.015785 | |
| h 3 | nHz | 121.91 | 115.04 | −2042.6 | |
| μ | D | 5.94 | |||
| κ | −0.99987 | −0.99987 | −0.99985 | ||
Rotational constants of l-C5H2 compared to previous experimenta.
From McCarthy et al., 1997.
The c-C3HC2H isomer has a smaller dipole moment than the l-C5H2 isomer at 3.59 D. The c-C3HC2H isomer also shows near prolate character (κ = − 0.98026 at the F12-TZ-cCR level of theory) as exhibited by the rotational constants B0 and C0 being almost the same as shown in Table 3. The F12-TZ-cCR data agrees extremely well with previous Fourier transform spectrometry results (Travers et al., 1997), differing by only 1.1 MHz (0.03%) for the B0 rotational constant, 0.96 MHz (0.03%) for the C0 rotational constant, and even 15 MHz (0.04%) for the A0 rotational constant. Both the F12-DZ-cCR and F12-TZ-cCR methods produce rotational constants closer to experiment than F12-DZ and F12-TZ which in line with previous work (Watrous et al., 2021). Doubling the step size for the OBPs has little-to-no effect in the rotational constants as expected. The S-reduced Hamiltonian quartic and sextic distortion constants are reported in Table 3, and the DK constant compares well with experiment, only differing by 0.2 kHz at the F12-TZ-cCR level of theory. The experimental DJ rotational constant is 288 Hz while the computed DJ rotational constant is 246.14 Hz. However, the computed A-reduced Hamiltonian ΔJ, determined in this work, has a value of 285.28 Hz which aligns closely with the reported experimental value, suggesting a potential misattribution in the experimental work.
TABLE 3
| F12-DZ | F12-DZ-cCR | F12-TZ | F12-TZ-cCR | |||||
|---|---|---|---|---|---|---|---|---|
| Constant | Units | 0.005 | 0.010 | 0.005 | 0.010 | 0.010 | 0.010 | Exp.a |
| A e | MHz | 34593.7 | 34593.7 | 34768.1 | 34768.1 | 34629.3 | 34835.3 | |
| B e | MHz | 3410.1 | 3410.1 | 3424.5 | 3424.5 | 3413.1 | 3429.6 | |
| C e | MHz | 3104.1 | 3104.1 | 3117.5 | 3,117.5 | 3106.7 | 3122.3 | |
| A 0 | MHz | 34386.9 | 34398.1 | 34578.6 | 34578.7 | 34449.4 | 34654.1 | 34638.701 |
| B 0 | MHz | 3406.0 | 3406.2 | 3420.9 | 3420.7 | 3409.9 | 3426.0 | 3424.8768 |
| C 0 | MHz | 3095.8 | 3096.1 | 3,109.8 | 3109.6 | 3099.6 | 3114.6 | 3113.6386 |
| D J | Hz | 245.00 | 245.00 | 246.72 | 246.71 | 244.68 | 246.14 | 288 |
| D K | kHz | 29.813 | 29.801 | 29.780 | 29.788 | 29.659 | 29.795 | 29.5 |
| D JK | kHz | 105.97 | 105.80 | 107.72 | 106.72 | 105.79 | 106.57 | |
| d 1 | Hz | −28.524 | −28.523 | −28.662 | −28.663 | −28.472 | −28.589 | |
| d 2 | Hz | −19.625 | −19.617 | −19.581 | −19.586 | −19.524 | −19.570 | |
| H J | μHz | −173.88 | −173.55 | −172.98 | −172.73 | −170.73 | −171.01 | |
| H JK | mHz | 106.73 | 106.531 | 106.24 | 105.97 | 104.63 | 105.22 | |
| H KJ | Hz | −4.0028 | −3.9978 | −3.9473 | −3.9491 | −3.8877 | −39.167 | |
| H K | Hz | 4.0870 | 4.0827 | 4.0363 | 4.0384 | 3.9812 | 40.157 | |
| h 1 | μHz | −13.184 | −13.165 | −13.022 | −13.040 | −12.987 | −12.952 | |
| h 2 | μHz | 90.284 | 90.145 | 89.750 | 89.589 | 88.667 | 88.905 | |
| h 3 | μHz | 18.237 | 18.222 | 18.092 | 18.098 | 17.999 | 18.007 | |
| μ | D | 3.59 | ||||||
| κ | −0.98018 | −0.98019 | −0.98023 | −0.98023 | −0.9802 | −0.98025 | ||
Rotational constants of c-C3HC2H compared to previous experimenta.
From Travers et al., 1997.
Unlike the other two isomers, the bipyramidal C5H2 isomer does not have a dipole due to its D3h symmetry. Even so, the rotational constants for the bipyramidal C5H2 isomer are given in Table 4 for completeness. Additionally, the molecule is oblate and has only B0 and C0 rotational constants. The bipyramidal C5H2 molecule has not been detected in astrophysical observations or even observed experimentally. The F12-DZ and the F12-TZ methods have good agreement differing by only 9.2 MHz for the C0 rotational constant. Hence, the results presented here provide the most accurate predictions of its rotational constants which may be helpful for the accurate kinetic rate determination or the thermochemical analysis that requires the full rotational partition function.
TABLE 4
| Constant | Units | F12-DZ | F12-TZ |
|---|---|---|---|
| B e | MHz | 12733.1 | 12742.1 |
| C e | MHz | 9145.2 | 9153.0 |
| B 0 | MHz | 12647.4 | 12656.6 |
| C 0 | MHz | 9055.4 | 9063.7 |
| D J | KHz | 2.979 | 2.979 |
| D JK | kHz | 6.770 | 6.718 |
| D K | kHz | 1.676 | 1.751 |
| d 1 | mHz | 48.6 | 2.06 |
| d 2 | mHz | 8.42 | 1.21 |
| H J | mHz | 1.736 | 1.746 |
| H JK | mHz | −10.886 | −11.033 |
| H KJ | mHz | 9.011 | 9.935 |
| H K | mHz | 21.254 | 20.669 |
| h 1 | μHz | 0.702 | −1.215 |
| h 2 | μHz | 1.282 | −2.913 |
| h 3 | μHz | 263.914 | 257.523 |
Rotational constants of bipyramidal C5H2.
3.2 Vibrational frequencies
The l-C5H2 isomer has the largest anharmonic intensities out of the three C5H2 isomers, as shown in Table 5. The two most intense modes are ν3 with an intensity of 738 km mol−1 at 2076.3 cm−1 (4.81 μm) and ν4 with an intensity of 182 km mol−1 at 1887.5 cm−1 (5.30 μm). These intensities represent the movements in the linear carbon chain and are up to ten times larger than the anti-symmetric stretch in water, which has an intensity of about 70 km mol−1 at the same level of theory. The large intensities of these two frequencies imply that l-C5H2 should be observable right at the edge of the NIRspec instrument onboard JWST in a region often bereft of known transitions for organic molecules. Out of the three levels of theory in this work used to compute intensities, only the B3LYP/N07D results are reported for the l-C5H2 isomer as it is the only method with all real frequencies in line with the present high-level computations. The previous theory used to compute the intensities agrees qualitatively with the order of intensities computed with B3LYP/N07D. Additionally, the N07D basis set is designed to handle hydrocarbon systems like this and has been used to produce anharmonic frequencies in reasonable agreement with experiment (Barone et al., 2008; Barone et al., 2013). However in this case, the anharmonic frequencies produced by B3LYP/N07D fall short in comparison with the fundamental frequencies produced by the F12-TZ level of theory. In contrast, the F12-DZ and F12-TZ anharmonic frequencies have relatively close agreement. The exceptions to this are the modes involving an in-plane bend (IPB) or OPB of the carbon chain, ν10-ν15. The portions of the QFF involving these modes have problems with the cubic and quartic force constants. Those modes are reported as the harmonic values, and most anharmonic corrections are within the margin of error for the levels of theory. A larger step size is also used at the F12-DZ level of theory to combat the OPB problem (Fortenberry et al., 2018; Westbrook et al., 2020; Lee and Fortenberry, 2021; Lee and Fortenberry, 2021). However there is no significant improvement of the issue. As a result, the larger step size is not repeated for the F12-TZ level of theory. This will not affect possible detection via JWST because the NIRSpec and MIRI instruments on the JWST only capture spectra to about 333 cm−1, but the resolution drops for the lower frequencies below 2000 cm−1 since the larger range MIRI instrument does not have the same capabilities as NIRspec. The harmonic frequencies for both the F12-DZ and F12-TZ levels of theory agree well with previous theoretical harmonic frequencies for most modes (Karton and Thimmakondu, 2022), but vary more for the OPB and IPB which is likely due to the aforementioned OPB problem (Westbrook et al., 2020; Lee and Fortenberry, 2021).
TABLE 5
| F12-DZ | F12-TZ | B3LYP/N07D | Previous theoryb | |||||
|---|---|---|---|---|---|---|---|---|
| Description | 0.005 | 0.010 | 0.005 | Freq | f | Freq | f | |
| ω 1 (b2) | C-H Anti-Sym Stretch | 3,219.4 | 3219.4 | 3215.5 | 3,199.1 | 1 | 3,215.1 | 0.0 |
| ω 2 (a1) | C-H Sym Stretch | 3127.7 | 3127.7 | 3125.1 | 3117.5 | 1 | 3127.3 | 0.6 |
| ω 3 (a1) | (C1-C2) - (C2-C3) + (C3-C4) - (C4-C5) | 2145.3 | 2,145.3 | 2,153.5 | 2212.7 | 806 | 2,151.6 | 677.1 |
| ω 4 (a1) | (C1-C2) - (C2-C3) - (C3-C4) + (C4-C5) | 1924.4 | 1924.4 | 1935.2 | 1974.6 | 206 | 1921.8 | 176.6 |
| ω 5 (a1) | H-C-C Sym Bend | 1503.9 | 1503.9 | 1506.9 | 1513.8 | 9 | 1,503.5 | 7.7 |
| ω 6 (a1) | (C1-C2) + (C2-C3) - (C3-C4) - (C4-C5) | 1349.5 | 1349.5 | 1355.8 | 1369.9 | 7 | 1346.9 | 18.0 |
| ω 7 (b2) | H-C-C Anti-Sym Bend | 1033.7 | 1,033.7 | 1030.7 | 1031.0 | 1 | 1030.3 | 0.4 |
| ω 8 (b1) | C5 OPB | 936.0 | 936.3 | 941.4 | 968.6 | 34 | 943.4 | 31.6 |
| ω 9 (a1) | (C1-C2) + (C2-C3) + (C3-C4) + (C4-C5) | 749.0 | 749.0 | 752.2 | 769.8 | 1 | 745.5 | 0.4 |
| ω 10 (b1) | C3-C4 OPB | 534.0 | 534.3 | 536.1 | 656.4 | 7 | 576.2 | 2.8 |
| ω 11 (b2) | C2-C3 IPB | 398.4 | 398.4 | 411.7 | 527.6 | 4 | 445.4 | 0.9 |
| ω 12 (b1) | C2-C4 OPB | 244.8 | 244.7 | 239.9 | 314.8 | 7 | 270.9 | 8.5 |
| ω 13 (b2) | C2-C4 IPB | 231.1 | 231.1 | 230.9 | 286.2 | 7 | 254.9 | 5.7 |
| ω 14 (b2) | C1-C5 IPB | 133.3 | 133.3 | 123.2 | 148.3 | 1 | 139.3 | 0.0 |
| ω 15 (b1) | C1 OPB | 110.8 | 110.7 | 104.3 | 143.7 | 2 | 122.3 | 3.1 |
| ZPVE | 8758.4 | 8812.5 | 8948.0 | |||||
| ν 1 (b2) | C-H Anti-Sym Stretch | 3073.7 | 3066.1 | 3078.2 | 3047.4 | 1 | ||
| ν 2 (a1) | C-H Sym Stretch | 3019.2 | 3011.6 | 2,955.4 | 3013.1 | 2 | ||
| ν 3 (a1) | (C1-C2) - (C2-C3) + (C3-C4) - (C4-C5) | 2098.9 | 2090.6 | 2076.3 | 2170.4 | 738 | ||
| ν 4 (a1) | (C1-C2) - (C2-C3) - (C3-C4) + (C4-C5) | 1898.0 | 1894.9 | 1887.5 | 1944.1 | 182 | ||
| ν 5 (a1) | H-C-C Sym Bend | 1472.0 | 1467.4 | 1,43.8 | 1483.5 | 6 | ||
| ν 6 (a1) | (C1-C2) + (C2-C3) - (C3-C4) - (C4-C5) | 1340.7 | 1334.1 | 1318.9 | 1350.5 | 6 | ||
| ν 7 (b2) | H-C-C Anti-Sym Bend | 1022.5 | 1018.7 | 1155.4 | 1011.6 | 1 | ||
| ν 8 (b1) | C5 OPB | 924.6 | 923.8 | 769.0 | 944.8 | 35 | ||
| ν 9 (a1) | (C1-C2) + (C2-C3) + (C3-C4) + (C4-C5) | 741.0 | 730.1 | 756.4 | 772.4 | 1 | ||
| ν 10 (b1) | C3-C4 OPB | 534.0a | 534.3a | 536.1a | 365.8 | 7 | ||
| ν 11 (b2) | C2-C3 IPB | 398.4a | 398.4a | 411.7a | 285.8 | 2 | ||
| ν 12 (b1) | C2-C4 OPB | 224.8a | 244.7a | 239.9a | 244.3 | 4 | ||
| ν 13 (b2) | C2-C4 IPB | 231.1a | 231.1a | 230.9a | 247.5 | 9 | ||
| ν 14 (b2) | C1-C5 IPB | 133.3a | 133.3a | 123.2a | 151.6 | 1 | ||
| ν 15 (b1) | C1 OPB | 110.8a | 110.7a | 104.3a | 133.7 | 2 | ||
F12-DZ and F12-TZ harmonic and fundamental vibrational frequencies and B3LYP/N07D intensities (in km mol−1) of l-C5H2 compared to previous theory computed at the fc-CCSD(T)/cc-pVTZ level of theoryb.
Harmonic values reported.
Previous theory from Karton and Thimmakondu, 2022.
For the c-C3HC2H isomer, the vibrational frequencies are in Table 6, and the double-harmonic intensities are in Table 7. The c-C3HC2H isomer has two intense peaks with the most intense peak being the acetylene C-H stretch, ν1, at 3,347.8 cm−1 (2.99 μm) with an anharmonic intensity of 84 km mol−1 at the B3LYP/N07D level of theory. The second most intense peak is the C5-C6-H7 in-plane bend (IPB), ν11, at 577.9 cm −1 (17.3 μm) with an intensity of 52 km mol−1. The intensity changes depending on which level of theory is used to calculate the double-harmonic intensities, but all three methods computed for the intensities agree on the qualitative order of intensities for the modes, as does the previous theory (Karton and Thimmakondu, 2022). The intensities for c-C3HC2H are not as strong as the intensities for l-C5H2, but are still strong enough for detection.
TABLE 6
| F12-DZ | F12-DZ-cCR | F12-TZ | F12-TZ-cCR | Previous Theoryb | ||||
|---|---|---|---|---|---|---|---|---|
| Description | 0.005 | 0.010 | 0.005 | 0.010 | 0.010 | 0.010 | ||
| ω 1 (a′) | Acetylene C-H Stretch | 3454.7 | 3454.7 | 3459.8 | 3459.8 | 3,454.2 | 3460.6 | 3457.0 |
| ω 2 (a′) | Ring CH Stretch | 3261.1 | 3261.1 | 3266.4 | 3266.4 | 3,259.9 | 3266.7 | 3261.4 |
| ω 3 (a′) | C5 In-Plane Motion | 2166.4 | 2166.4 | 2172.6 | 2172.6 | 2,167.9 | 2176.2 | 2163.8 |
| ω 4 (a′) | C4-C5 Out-of-Plane Motion | 1713.4 | 1713.4 | 1719.3 | 1719.3 | 1715.1 | 1722.9 | 1708.0 |
| ω 5 (a′) | (C2-C3) + (C3-C4) Stretch | 1278.5 | 1,278.6 | 1,283.9 | 1283.9 | 1279.7 | 1286.5 | 1269.8 |
| ω 6 (a′) | (C2-C3) - (C3-C4) Stretch | 1117.4 | 1117.4 | 1122.5 | 1122.5 | 1119.8 | 1126.1 | 1107.9 |
| ω 7 (a′) | C3-C2-H1 IPB | 949.9 | 949.9 | 953.8 | 953.8 | 948.5 | 952.3 | 945.8 |
| ω 8 (a″) | C3-C2-H1 OPB | 892.9 | 893.2 | 895.9 | 895.9 | 893.7 | 898.2 | 891.2 |
| ω 9 (a″) | C5-C6-H7 OPB | 710.0 | 710.0 | 714.8 | 714.8 | 713.9 | 717.8 | 705.4 |
| ω 10 (a′) | C4-C5 Stretch | 696.0 | 696.0 | 698.6 | 698.6 | 697.5 | 700.9 | 692.1 |
| ω 11 (a′) | C5-C6-H7 IPB | 604.4 | 604.4 | 608.7 | 608.7 | 611.3 | 615.6 | 601.8 |
| ω 12 (a″) | C4-C5 Out-Of Plane Motion | 510.4 | 510.4 | 511.6 | 511.6 | 517.7 | 521.7 | 520.4 |
| ω 13 (a′) | C4-C5 In Plane Motion | 498.8 | 498.8 | 502.4 | 502.4 | 504.3 | 508.9 | 500.1 |
| ω 14 (a″) | C5-C6 Out-Of-Plane Motion | 201.8 | 201.8 | 202.8 | 202.7 | 202.6 | 203.6 | 212.9 |
| ω 15 (a′) | C5-C6 In-Plane Motion | 189.2 | 189.2 | 190.7 | 190.7 | 190.8 | 192.0 | 193.0 |
| ZPVE | 7869.7 | 8908.0 | 9383.5 | 9115.5 | 9234.5 | 9069.4 | ||
| ν 1 (a′) | Acetylene C-H Stretch | 3412.6 | 3341.7 | 3311.3 | 3328.8 | 3346.4 | 3347.8 | |
| ν 2 (a′) | Ring CH Stretch | 3034.4 | 3,102.4 | 3137.1 | 3139.1 | 3145.4 | 3,127.1 | |
| ν 3 (a′) | C5 In-Plane Motion | 2168.0 | 2131.8 | 2,123.4 | 2,128.7 | 2,124.3 | 2135.5 | |
| ν 4 (a′) | C4-C5 Out-of-Plane Motion | 1673.6 | 1675.5 | 1675.2 | 1681.4 | 1685.3 | 1706.8 | |
| ν 5 (a′) | (C2-C3) + (C3-C4) Stretch | 1138.0 | 1,199.5 | 1,262.1 | 1,265.1 | 1,285.6 | 1256.3 | |
| ν 6 (a′) | (C2-C3) - (C3-C4) Stretch | 1194.6 | 1,113.6 | 1073.5 | 1090.0 | 1073.9 | 1061.0 | |
| ν 7 (a′) | C3-C2-H1 IPB | 949.9a | 891.7 | 944.2 | 958.9 | 948.5a | 916.2 | |
| ν 8 (a″) | C3-C2-H1 OPB | 892.9a | 848.5 | 895.9a | 865.1 | 893.7a | 898.2a | |
| ν 9 (a″) | C5-C6-H7 OPB | 710.0a | 684.7 | 711.6 | 689.8 | 705.2 | 646.6 | |
| ν 10 (a′) | C4-C5 Stretch | 696.0a | 698.2 | 675.1 | 690.3 | 674.7 | 700.9a | |
| ν 11 (a′) | C5-C6-H7 IPB | 555.1 | 574.6 | 574.4 | 585.6 | 595.0 | 577.9 | |
| ν 12 (a″) | C4-C5 Out-Of Plane Motion | 510.4a | 510.4a | 511.6a | 511.6a | 517.7a | 521.7a | |
| ν 13 (a′) | C4-C5 In Plane Motion | 498.8a | 476.6 | 502.1 | 506.6 | 504.3a | 500.7 | |
| ν 14 (a″) | C5-C6 Out-Of-Plane Motion | 201.8a | 201.8a | 202.8a | 202.7a | 202.6a | 203.6a | |
| ν 15 (a′) | C5-C6 In-Plane Motion | 189.2a | 189.2a | 190.7a | 190.7a | 190.8a | 169.5 | |
Harmonic and fundamental vibrational frequencies of c-C3HC2H compared to previous theory computed at the fc-CCSD(T)/cc-pVTZ level of theoryb.
Harmonic values reported.
Previous theory from Karton and Thimmakondu, 2022.
TABLE 7
| MP2/TZ | B3LYP/TZ | B3LYP/N07D | Previous theorya | |||||
|---|---|---|---|---|---|---|---|---|
| Description | Freq | f | Freq | f | Freq | f | f | |
| ω 1 (a′) | Acetylene C-H Stretch | 3474.6 | 85 | 3461.2 | 90 | 3478.7 | 100 | 71.1 |
| ω 2 (a′) | Ring CH Stretch | 3283.4 | 2 | 3234.4 | 1 | 3250.2 | 1 | 1.1 |
| ω 3 (a′) | C5 In-Plane Motion | 2145.1 | 6 | 2192.6 | 3 | 2193.7 | 3 | 10.6 |
| ω 4 (a′) | C4-C5 Out-of-Plane Motion | 1703.2 | 4 | 1719.7 | 5 | 1724.9 | 6 | 5.0 |
| ω 5 (a′) | (C2-C3) + (C3-C4) Stretch | 1286.9 | 32 | 1280.3 | 38 | 1275.1 | 39 | 41.2 |
| ω 6 (a′) | (C2-C3) - (C3-C4) Stretch | 1128.9 | 3 | 1,108.7 | 8 | 1103.3 | 7 | 6.5 |
| ω 7 (a′) | C3-C2-H1 IPB | 944.6 | 3 | 951.9 | 2 | 943.8 | 3 | 2.3 |
| ω 8 (a″) | C3-C2-H1 OPB | 902.0 | 13 | 899.9 | 15 | 880.8 | 17 | 17.1 |
| ω 9 (a″) | C5-C6-H7 OPB | 687.5 | 31 | 756.5 | 27 | 744.4 | 36 | 28.7 |
| ω 10 (a′) | C4-C5 Stretch | 704.2 | 2 | 708.8 | 1 | 706.5 | 1 | 1.7 |
| ω 11 (a′) | C5-C6-H7 IPB | 614.5 | 45 | 610.1 | 54 | 595.4 | 65 | 49.2 |
| ω 12 (a″) | C4-C5 Out-Of Plane Motion | 531.9 | 2 | 549.5 | 5 | 562.2 | 2 | 1.9 |
| ω 13 (a′) | C4-C5 In Plane Motion | 503.0 | 3 | 530.7 | 4 | 538.2 | 2 | 2.4 |
| ω 14 (a″) | C5-C6 Out-Of-Plane Motion | 206.5 | 1 | 218.6 | 1 | 238.4 | 1 | 0.9 |
| ω 15 (a′) | C5-C6 In-Plane Motion | 188.0 | 7 | 202.3 | 7 | 211.9 | 6 | 5.7 |
| ν 1 (a′) | Acetylene C-H Stretch | 3,351.6 | 78 | 3,335.6 | 81 | 3353.6 | 84 | |
| ν 2 (a′) | Ring CH Stretch | 3,156.9 | 1 | 3106.0 | 1 | 3117.9 | 1 | |
| ν 3 (a′) | C5 In-Plane Motion | 2113.8 | 3 | 2152.0 | 2 | 2152.1 | 2 | |
| ν 4 (a′) | C4-C5 Out-of-Plane Motion | 1667.0 | 3 | 1,677.7 | 4 | 1681.0 | 4 | |
| ν 5 (a′) | (C2-C3) + (C3-C4) Stretch | 1253.1 | 29 | 1,249.3 | 36 | 1245.1 | 34 | |
| ν 6 (a′) | (C2-C3) - (C3-C4) Stretch | 1107.2 | 1 | 1078.6 | 3 | 1075.4 | 3 | |
| ν 7 (a′) | C3-C2-H1 IPB | 921.5 | 4 | 930.7 | 3 | 922.3 | 4 | |
| ν 8 (a″) | C3-C2-H1 OPB | 886.1 | 13 | 885.1 | 15 | 871.0 | 20 | |
| ν 9 (a″) | C5-C6-H7 OPB | 673.0 | 31 | 742.5 | 28 | 691.3 | 30 | |
| ν 10 (a′) | C4-C5 Stretch | 703.3 | 1 | 696.9 | 1 | 696.1 | 1 | |
| ν 11 (a′) | C5-C6-H7 IPB | 613.0 | 43 | 592.7 | 55 | 555.0 | 52 | |
| ν 12 (a″) | C4-C5 Out-Of Plane Motion | 532.8 | 3 | 545.0 | 4 | 508.1 | 1 | |
| ν 13 (a′) | C4-C5 In Plane Motion | 497.4 | 4 | 526.4 | 4 | 491.7 | 9 | |
| ν 14 (a″) | C5-C6 Out-Of-Plane Motion | 210.5 | 1 | 220.2 | 1 | 212.0 | 1 | |
| ν 15 (a′) | C5-C6 In-Plane Motion | 192.2 | 7 | 201.7 | 7 | 195.7 | 5 | |
Intensities in km mol−1 of c-C3HC2H compared to previous theory computed at the fc-CCSD(T)/cc-pVTZ level of theorya.
Previous theory from Karton and Thimmakondu, 2022.
For the c-C3HC2H, there are differences in the anharmonic frequencies between the levels of theory and step sizes as shown in Table 6. Fundamental frequencies ν12, ν14, and ν15 produce questionable positive anharmonicities, although they are below or on the lower edge of the range to be detected through the aforementioned instruments on JWST. Additionally, these three modes have a maximum intensity of 5 km mol−1. Both considerations make these frequencies unlikely to be detected. Increasing the level of theory to F12-DZ-cCR improves the anharmonic correction for the ν9, ν10, and ν13 fundamentals. The doubled step size in the OPB coordinates further improves the anharmonic correction for F12-DZ and F12-DZ-cCR. As a result only the doubled step size is calculated at the higher levels of theory due to the increased computational cost. Similarly, this doubled step size helps the anharmonic correction for ν7 and ν8 with F12-DZ and F12-DZ-cCR. There is much less variation in the harmonic frequencies between the levels of theory. Additionally, the harmonic frequencies compare well to previous theory (Karton and Thimmakondu, 2022). Figure 4 shows a simulated spectrum of the F12-TZ-cCR anharmonic frequencies and the B3LYP/N07D intensities with all bands incorporated; only those with notable intensities are present.
FIGURE 4
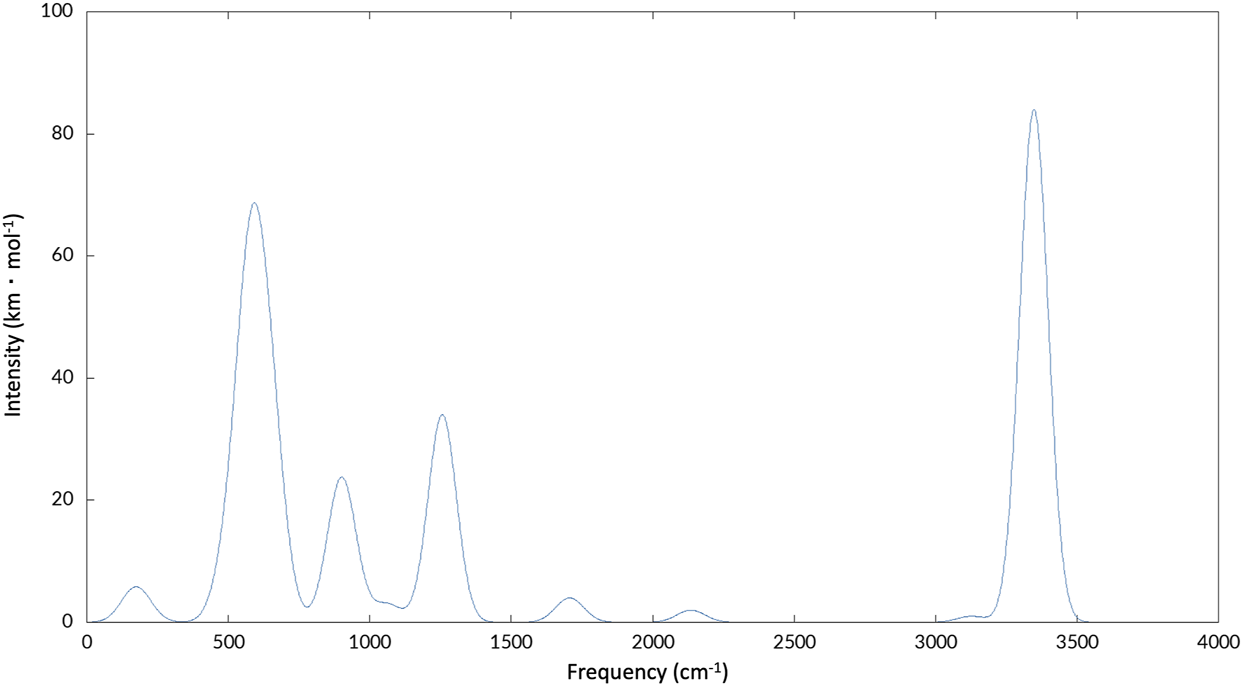
Simulated spectrum of c-C3HC2H.
For the bipyramidal C5H2 isomer, the vibrational frequencies for the F12-DZ and F12-TZ QFFs, shown in Table 8, have close agreement for most of the frequencies. The bipyramidal C5H2 isomer has one intense frequency in which is ν10, the symmetric C2-C3 + C2-C4 stretch, with an intensity of 78 km mol−1 at 426.1 cm −1 (23.5 μm) which is slightly smaller than the c-C3H2H isomer and much smaller than the most intense peaks for the l-C5H2 isomer. Unlike the other isomers, the bipyramidal C5H2 isomer only has three other fundamentals that have intensities over 10 km mol−1 at the B3LYP/N07D level of theory. These are ν4 at 1,273.6 cm−1 (7.85 μm), ν5 at 1,108.7 cm−1 (9.02 μm), and ν8 at 829.5 cm−1 (12.0 μm). While the different methods differ in the quantitative value of the intensities, they again agree qualitatively with each other and with previous theory on what will be the most and least intense peaks (Karton and Thimmakondu, 2022). However only having one fundamental with a large intensity could increase the difficulty for the detection of the bipyramidal C5H2 isomer compared to the other two isomers. The F12-DZ and the F12-TZ QFFs show good agreement for the harmonic and anharmonic fundamental frequencies and the harmonic frequencies further show good agreement to previous theory (Karton and Thimmakondu, 2022). The largest discrepancy arises in ν10, with a difference of 26.5 cm−1, but a majority of the frequencies agree to within 3 cm−1. However, given the greater computational rigor of F12-TZ, its data should be considered the more reliable of the two.
TABLE 8
| F12-DZ | F12-TZ | MP2/TZ | B3LYP/TZ | B3LYP/N07D | Previous theorya | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Description | Freq | f | Freq | f | Freq | f | Freq | f | |||
| C-H Sym Stretch | 3331.6 | 3329.5 | 3376.0 | – | 3311.0 | – | 3319.9 | – | 3331.6 | 0.0 | |
| C-H Anti-Sym Stretch | 3330.0 | 3327.8 | 3,374.7 | 30 | 3309.4 | 11 | 3318.5 | 9 | 3330.0 | 12.3 | |
| C1-C5 Stretch | 1307.1 | 1308.7 | 1,302.2 | – | 1314.5 | – | 1329.5 | – | 1299.7 | 0.0 | |
| C1-C Ring - C5-C Ring Stretch | 1288.3 | 1290.4 | 1,298.0 | 29 | 1,289.5 | 28 | 1302.8 | 24 | 1276.2 | 19.6 | |
| ω 5 (e′) | H-CC Sym Bend | 1128.2 | 1126.8 | 1079.6 | 5 | 1129.2 | 10 | 1136.8 | 10 | 1129.0 | 8.3 |
| ω 6 (e″) | H-CC Anti-Sym Bend | 1010.9 | 1008.3 | 978.1 | – | 1017.8 | – | 1,024.1 | – | 1011.5 | 0.0 |
| C1-C2,C3,C4-C5 Stretch | 852.2 | 851.5 | 913.1 | – | 837.5 | – | 834.4 | – | 846.8 | 0.0 | |
| ω 8 (e′) | C2-C3 - C2-C4 Stretch | 842.5 | 844.1 | 813.4 | 30 | 850.4 | 15 | 857.5 | 16 | 839.4 | 20.4 |
| ω 9 (e″) | C1-C2 - C2-C5 Stretch | 783.8 | 786.2 | 807.0 | – | 734.2 | – | 771.1 | – | 777.1 | 0.0 |
| ω 10 (e′) | C2-C3 + C2-C4 Stretch | 488.7 | 489.3 | 382.4 | 82 | 525.9 | 48 | 530.7 | 46 | 490.7 | 49.9 |
| ZPVE | 9228.0 | 9187.4 | |||||||||
| C-H Sym Stretch | 3190.5 | 3190.4 | 3,240.7 | 1 | 3187.4 | 1 | 3189.1 | 1 | |||
| C-H Anti-Sym Stretch | 3146.4 | 3139.3 | 3239.6 | 30 | 3187.0 | 10 | 3188.8 | 7 | |||
| C1-C5 Stretch | 1250.9 | 1253.0 | 1271.2 | 1 | 1262.9 | 1 | 1283.3 | 1 | |||
| C1-C Ring - C5-C Ring Stretch | 1273.4 | 1273.6 | 1269.6 | 27 | 1318.5 | 27 | 1334.3 | 23 | |||
| ν 5 (e′) | H-CC Sym Bend | 1126.4 | 1108.7 | 1048.7 | 5 | 1103.8 | 9 | 1108.7 | 11 | ||
| ν 6 (e″) | H-CC Anti-Sym Bend | 1009.1 | 995.2 | 953.7 | – | 1001.5 | – | 1001.2 | - | ||
| C1-C2,C3,C4-C5 Stretch | 834.4 | 832.4 | 914.3 | 1 | 850.4 | 3 | 847.0 | 1 | |||
| ν 8 (e′) | C2-C3 - C2-C4 Stretch | 830.1 | 829.5 | 800.2 | 30 | 836.9 | 12 | 842.3 | 14 | ||
| ν 9 (e″) | C1-C2 - C2-C5 | 756.3 | 759.2 | 770.8 | – | 719.7 | – | 752.9 | – | ||
| ν 10 (e′) | C2-C3 + C2-C4 | 452.6 | 426.1 | 344.9 | 78 | 524.2 | 50 | 526.6 | 47 | ||
F12-DZ and F12-TZ harmonic and fundamental frequencies of bipyramidal C5H2 with intensities in km mol−1 compared to previous theory computed at the fc-CCSD(T)/cc-pVTZ level of theorya.
Previous theory from Karton and Thimmakondu, 2022.
4 Conclusion
The large intensities for some of the fundamental frequencies in all of the isomers may facilitate the detection of these C5H2 structures via JWST. Such spectral data could lead to the identification for some UIRs as well as unknown transitions of known interstellar molecules such as l-C5H2 and c-C3HC2H. The bipyramidal C5H2 isomer has some of the lowest intensities of the three isomers but still has one peak at 426.1 cm−1 (23.5 μm) with an intensity of 78 km mol−1. The c-C3HC2H isomer has one intense fundamental frequency at 3,347.8 cm−1 with an intensity of 84 km mol−1. The l-C5H2 isomer has the two highest intensities out of the three isomers for its ν4 at 1887.5 cm−1 with a large intensity of 182 km mol−1 and ν3 at 2076.3 cm−1 with a very large intensity of 738 km mol−1 making this fundamental the most likely of the group especially since, again, l-C5H2 has been previously detected via radioastronomy. The F12-TZ methodology produces rotational constants for l-C5H2 within 3 MHz (0.13%) for the B0 and C0 rotational constants. Improving upon this high level of accuracy, the F12-TZ-cCR methodology for c-C3HC2H produces B0 and C0 rotational constants within 1.1 MHz (0.03%) of experiment. This close agreement to experiment lends supports to the accuracy of the other theoretical values, notably the fundamental vibrational frequencies, reported herein. Out of the three C5H2 isomers presented in this work, the c-C3HC2H isomer has the lowest relative energy, with l-C5H2 13.79 kcal mol−1 higher in line with previous work (Seburg et al., 1997). The bipyramidal C5H2 isomer is 44.98 kcal mol−1 higher in energy compared previous computations which places this D3h isomer 100 kcal mol−1 or more higher than other C5H2 isomers (Seburg et al., 1997). The dipole moments for the c-C3HC2H and l-C5H2 isomers are large at 3.59 D and 5.94 D, respectively, which has facilitated the previous detections of the isomers in space through rotational spectroscopy. Overall, the anharmonic vibrational frequencies and rotational constants presented herein may help to facilitate the laboratory or astronomical detection of unknown transitions of known molecules. In particular, the high-intensity fundamental frequencies of each molecule that fall within the high-resolution range of JWST may also help to disentangle some of the heretofore unidentified features in the UIRs.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
AW, BW, and RF contributed to conception and design of the study. AW performed the computations. AW and BW analyzed the data. AW wrote the first draft of the manuscript, and BW and RF edited the manuscript. RF secured funding for the research and provided administration for the project. All authors contributed to manuscript revision, read, and approved the submitted version.
Acknowledgments
The authors wish to acknowledge funding from NASA grant NNX17AH15G, NSF grant CHE-1757888, NSF grant OIA-1757220, and the University of Mississippi’s College of Liberal Arts as well as computational resources from the Mississippi Center for Supercomputing Research (MCSR).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.1051535/full#supplementary-material
References
1
Adler T. B. Knizia G. Werner H.-J. (2007). A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys.127, 221106. 10.1063/1.2817618
2
Agbaglo D. Fortenberry R. C. (2019b). The performance of explicitly correlated wavefunctions [CCSD(T)-F12b] in the computation of anharmonic vibrational frequencies. Chem. Phys. Lett.734, 136720. 10.1016/j.cplett.2019.136720
3
Agbaglo D. Fortenberry R. C. (2019a). The performance of explicitly correlated methods for the computation of anharmonic vibrational frequencies. Int. J. Quantum Chem.119, e25899. 10.1002/qua.25899
4
Agbaglo D. Lee T. J. Thackston R. Fortenberry R. C. (2019). A small molecule with PAH vibrational properties and a detectable rotational spectrum: c-(C)C3H2, cyclopropenylidenyl carbene. Astrophys. J.871, 236. 10.3847/1538-4357/aaf85a
5
Allamandola L. J. Greenberg J. M. Norman C. A. (1979). On the middle infra-red fluorescence and absorption of molecules in grain mantles. Astron. Astrophys.77, 66–74.
6
Allen W. D. coworkers (2005). INTDER 2005 is a general program written by W. D. Allen and coworkers, which performs vibrational analysis and higher-order non-linear transformations, Athens, GA: University of Georgia.
7
Balaji V. Michl J. (1988). New strained organic molecules: Theory guides experiment. Pure Appl. Chem.60, 189–194. 10.1351/pac198860020189
8
Barone V. Biczysko M. Bloino J. Egidi F. Puzzarini C. (2013). Accurate structure, thermodynamics, and spectroscopy of medium-sized radicals by hybrid coupled cluster/density functional theory approaches: The case of phenyl radical. J. Chem. Phys.138 (23), 234303.
9
Barone V. Cimino P. Stendardo E. (2008). Development and validation of the B3LYP/N07D computational model for structural parameter and magnetic tensors of large free radicals. J. Chem. Theory Comput.4, 751–764. 10.1021/ct800034c
10
Becke A. D. (1993). Density-functional thermochemistry. III. the role of exact exchange. J. Chem. Phys.98, 5648–5652. 10.1063/1.464913
11
Cabezas C. Tercero B. Agúndez M. Marcelino N. Pardo J. R. de Vicente P. et al (2021). Cumulene carbenes in TMC-1: Astronomical discovery of l-H2C5. Astron. Astrophys.650, L9. 10.1051/0004-6361/202141274
12
Cernicharo J. Agúndez M. Cabezas C. Tercero B. Marcelino N. Pardo J. R. et al (2021). Pure hydrocarbon cycles in TMC-1: Discovery of ethynyl cyclopropenylidene, cyclopentadiene, and indene. Astron. Astrophys.649, L15. 10.1051/0004-6361/202141156
13
Douglas M. Kroll N. (1974). Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. (N. Y).82, 89–155. 10.1016/0003-4916(74)90333-9
14
Finney B. Fortenberry R. C. Francisco J. S. Peterson K. A. (2016). A spectroscopic case for SPSi detection: The third-row in a single molecule. J. Chem. Phys.145, 124311. 10.1063/1.4963337
15
Fortenberry R. C. Lee T. J. (2019). Computational vibrational spectroscopy for the detection of molecules in space. Ann. Rep. Comput. Chem.15, 173–202. 10.1016/bs.arcc.2019.08.006
16
Fortenberry R. C. Novak C. M. Lee T. J. (2018). Rovibrational analysis of c-SiC2H2: Further evidence for out-of-plane bending issues in correlated methods. J. Chem. Phys.149, 024303. 10.1063/1.5043166
17
Franke P. R. Stanton J. F. Douberly G. E. (2021). How to VPT2: Accurate and intuitive simulations of CH stretching infrared spectra using VPT2+K with large effective Hamiltonian resonance treatments. J. Phys. Chem. A125, 1301–1324. 10.1021/acs.jpca.0c09526
18
Frisch M. J. Trucks G. W. Schlegel H. B. Scuseria G. E. Robb M. A. Cheeseman J. R. et al (2016). Gaussian 16 revision C.01. Wallingford CT: Gaussian Inc.
19
Gardner M. B. Westbrook B. R. Fortenberry R. C. Lee T. J. (2021). Highly-accurate quartic force fields for the prediction of anharmonic rotational constants and fundamental vibrational frequencies. Spectrochimica Acta Part A Mol. Biomol. Spectrosc.248, 119184. 10.1016/j.saa.2020.119184
20
Gaw J. F. Willets A. Green W. H. Handy N. C. (1991). SPECTRO: A program for the derivation of spectrscopic constants from provided quartic force fields and cubic dipole fields. Advances in Molecular Vibrations and Collision Dynamics. Editor Joel M.BowmanMark A.Ratner (Greenwich, Connecticut: JAI Press, Inc.), 170–185.
21
He C. Galimova G. R. Luo Y. Kaiser R. I. Eckhardt A. K. Sun R. et al (2020). A chemical dynamics study on the gas-phase formation of triplet and singlet C5H2 carbenes. Proc. Natl. Acad. Sci. U. S. A.117, 30142–30150. 10.1073/pnas.2019257117
22
Jansen G. Hess B. A. (1989). Revision of the douglas-kroll transformation. Phys. Rev. A39, 6016–6017. 10.1103/physreva.39.6016
23
Karton A. Thimmakondu V. S. (2022). From molecules with a planar tetracoordinate carbon to an astronomically known C5H2 carbene. J. Phys. Chem. A126, 2561–2568. 10.1021/acs.jpca.2c01261
24
Kendall R. A. Dunning T. H. Harrison R. J. (1992). Electron affinities of the first-row atoms revisited. systematic basis sets and wave functions. J. Chem. Phys.96, 6796–6806. 10.1063/1.462569
25
Knizia G. Adler T. B. Werner H.-J. (2009). Simplified CCSD(T)-F12 methods: Theory and benchmarks. J. Chem. Phys.130, 054104. 10.1063/1.3054300
26
Lee C. Yang W. T. Parr R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B37, 785–789. 10.1103/physrevb.37.785
27
Lee T. J. Fortenberry R. C. (2021). The unsolved issue with out-of-plane bending frequencies for C C multiply bonded systems. Spectrochimica Acta Part A Mol. Biomol. Spectrosc.248, 119148. 10.1016/j.saa.2020.119148
28
Leger A. Puget J. L. (1984). Identification of the “unidentified IR emission features” of interstellar dust?Astron. Astrophys.137, L5–L8.
29
Martin J. M. L. Lee T. J. Taylor P. R. François J.-P. (1995). The anharmonic force field of ethylene, C2H4, by means of accurate ab initio calculations. J. Chem. Phys.103, 2589–2602. 10.1063/1.469681
30
Martin J. M. L. Taylor P. R. (1997). Accurate ab initio quartic force field for trans-HNNH and treatment of resonance polyads. Spectrochimica Acta Part A Mol. Biomol. Spectrosc.53, 1039–1050. 10.1016/s1386-1425(96)01869-0
31
McCarthy M. C. Travers M. J. Kovács A. Gottlieb C. A. Thaddeus P. (1997). Eight new carbon chain molecules. Astrophys. J. Suppl. Ser.113, 105–120. 10.1086/313050
32
Mills I. M. (1972). “Vibration-rotation structure in asymmetric- and symmetric-top molecules,” in Molecular spectroscopy - modern research. Editors RaoK. N.MathewsC. W. (New York: Academic Press), 115–140.
33
Møller C. Plesset M. S. (1934). Note on an approximation treatment for many-electron systems. Phys. Rev.46, 618–622. 10.1103/physrev.46.618
34
Molster F. J. Lim T. L. Sylvester R. J. Waters L. B. F. M. Barlow M. J. Beintema D. A. et al (2001). The complete ISO spectrum of NGC 6302. Astron. Astrophys.372, 165–172. 10.1051/0004-6361:20010465
35
Papousek D. Aliev M. R. (1982). Molecular vibration-rotation spectra. Amsterdam: Elsevier.
36
Peeters E. Hony S. Van Kerckhoven C. Tielens A. G. G. M. Allamandola L. J. Hudgins D. M. et al (2002). The rich 6 to 9 μm spectrum of interstellar PAHs. Astron. Astrophys.390, 1089–1113. 10.1051/0004-6361:20020773
37
Peterson K. A. Adler T. B. Werner H.-J. (2008). Systematically convergent basis sets for explicitly correlated wavefunctions: The atoms H, He, B-Ne, and Al-Ar. J. Chem. Phys.128, 084102. 10.1063/1.2831537
38
Pople J. A. Scott A. P. Wong M. W. Radom L. (1993). Scaling factors for obtaining fundamental vibrational frequencies and zero-point energies from HF/6-31G* and MP2/6-31G* harmonic frequencies. Isr. J. Chem.33, 345–350. 10.1002/ijch.199300041
39
Raghavachari K. Trucks G. W. Pople J. A. Head-Gordon M. (1989). A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett.157, 479–483. 10.1016/s0009-2614(89)87395-6
40
Seburg R. A. McMahon R. J. Stanton J. F. Gauss J. (1997). Structures and stabilities of C5H2 isomers: Quantum chemical studies. J. Am. Chem. Soc.119, 10838–10845. 10.1021/ja971412j
41
Sellgren K. (1984). The near-infrared continuum emission of visual reflection nebulae. Astrophys. J.277, 623–633. 10.1086/161733
42
Shavitt I. Bartlett R. J. (2009). Many-body methods in Chemistry and physics: MBPT and coupled-cluster theory. Cambridge: Cambridge University Press.
43
Stein C. Weser O. Schroder B. Botschwina P. (2015). High-level theoretical spectroscopic parameters for three ions of astrochemical interest. Mol. Phys.113, 2169–2178. 10.1080/00268976.2015.1017019
44
Tielens A. G. G. M. (2008). Interstellar polycyclic aromatic hydrocarbon molecules. Annu. Rev. Astron. Astrophys.46, 289–337. 10.1146/annurev.astro.46.060407.145211
45
Travers M. J. McCarthy M. C. Gottlieb C. A. Thaddeus P. (1997). Laboratory detection of the ring-chain molecule C5H2. Astrophys. J.483, L135–L138. 10.1086/310744
46
Veis L. Čàrsky P. Pittner J. Michl J. (2008). Coupled cluster study of polycyclopentanes: Structure and properties of C5H2n, n = 0-4. Collect. Czechoslov. Chem. Commun.73, 1525–1551. 10.1135/cccc20081525
47
Watrous A. G. Westbrook B. R. Fortenberry R. C. (2021). F12-TZ-cCR: A methodology for faster and still highly-accurate quartic force fields. J. Phys. Chem. A125, 10532–10540. 10.1021/acs.jpca.1c08355
48
Watson J. K. G. (1977). “Aspects of quartic and sextic centrifugal effects on rotational energy levels,” in Vibrational spectra and structure. Editor DuringJ. R. (Amsterdam: Elsevier), 1–89.
49
Werner H.-J. Knowles P. J. Manby F. R. Black J. A. Doll K. Heßelmann A. et al (2020). Molpro, version 2020.1, a package of ab initio programs. WIREs Comput. Mol. Sci.2, 242–253. See http://www.molpro.net. 10.1002/wcms.82
50
Westbrook B. R. Del Rio W. A. Lee T. J. Fortenberry R. C. (2020). Overcoming the out-of-plane bending issue in an aromatic hydrocarbon: The anharmonic vibrational frequencies of c-(CH)C3H2+. Phys. Chem. Chem. Phys.22, 12951–12958. 10.1039/d0cp01889a
51
Westbrook B. R. Patel D. J. Dallas J. D. Swartzfager G. C. Lee T. J. Fortenberry R. C. (2021a). Fundamental vibrational frequencies and spectroscopic constants of substituted cyclopropenylidene (c-C3HX, x=F, Cl, CN). J. Phys. Chem. A125, 8860–8868. 10.1021/acs.jpca.1c06576
52
Westbrook B. R. Valencia E. M. Rushing S. C. Tschumper G. S. Fortenberry R. C. (2021b). Anharmonic vibrational frequencies of ammonia borane (BH3NH3). J. Chem. Phys.154, 041104. 10.1063/5.0040050
53
Yang W. T. Parr R. G. Lee C. T. (1986). Various functionals for the kinetic energy density of an atom or molecule. Phys. Rev. A34, 4586–4590. 10.1103/physreva.34.4586
54
Yousaf K. E. Peterson K. A. (2008). Optimized auxiliary basis sets for explicitly correlated methods. J. Chem. Phys.129, 184108. 10.1063/1.3009271
55
Yu Q. Bowman J. M. Fortenberry R. C. Mancini J. S. Lee T. J. Crawford T. D. et al (2015). The structure, anharmonic vibrational frequencies, and intensities of NNHNN+. J. Phys. Chem. A119, 11623–11631. 10.1021/acs.jpca.5b09682
Summary
Keywords
rotational spectroscopy, vibrational spectroscopy, infrared observations, coupled cluster theory, astrochemistry, carbon chemistry
Citation
Watrous AG, Westbrook BR and Fortenberry RC (2022) Theoretical spectra and energetics for c-C3HC2H, l-C5H2, and bipyramidal D3h C5H2. Front. Astron. Space Sci. 9:1051535. doi: 10.3389/fspas.2022.1051535
Received
22 September 2022
Accepted
25 October 2022
Published
14 November 2022
Volume
9 - 2022
Edited by
Mattia Melosso, Scuola Superiore Meridionale, Italy
Reviewed by
Silvia Alessandrini, Scuola Normale Superiore, Italy
Qian Gou, Chongqing University, China
Updates
Copyright
© 2022 Watrous, Westbrook and Fortenberry.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ryan C. Fortenberry, r410@olemiss.edu
This article was submitted to Astrochemistry, a section of the journal Frontiers in Astronomy and Space Sciences
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.