- 1The Johns Hopkins University Applied Physics Laboratory, Laurel, MD, United States
- 2Physics Department, University of New Hampshire, Durham, NH, United States
- 3Southwest Research Institute, San Antonio, TX, United States
Motivated by MMS mission observations near magnetic reconnection sites, we have developed a new empirical reconstruction (ER) model of the three-dimensional (3D) magnetic field and the associated plasma currents. Our approach combines both the measurements from a constellation of satellites and a set of physics-based equations as physical constraints to build spatially smooth distributions. This ER model directly minimizes the loss function that characterizes the model-measurement differences and the model departures from linear or nonlinear physical constraints using an efficient stochastic optimization method by which the effects of random measurement errors can be effectively included. Depending on the availability of the measured parameters and the adopted physical constraints on the reconstructed fields, the ER model could be either slightly over-determined or under-determined, yielding nearly identical reconstructed fields when solved by the stochastic optimization method. As a result, the ER model remains valid and operational even if the input measurements are incomplete. Two sets of new indices associated respectively with the model-measurement differences and the model departures are introduced to objectively measure the accuracy and quality of the reconstructed fields. While applying the reconstruction model to observations of an electron diffusion region (EDR) observed by NASA’s Magnetospheric Multiscale (MMS) mission, we examine the relative contributions of the errors in the plasma current density arising from random measurement errors and linear approximations made in application of the curlometer technique. It was found that the errors in the plasma current density calculated directly from the measured magnetic fields using a linear approximation were mostly contributed from the nonlinear configuration of the 3D magnetic fields.
Introduction
Visualization of Earth’s magnetosphere is an effective way to understand the magnetospheric environment and its associated physical processes. However, historically our exploration and understanding have been limited to either remote sensing (energetic neutral atom imaging, e.g., IMAGE, TWINS) or in-situ point-wise measurements made from satellites in space, from either single- (e.g., Geotail, Polar) or multi-satellite (e.g., THEMIS, Cluster, MMS) missions. One technique to translate discrete point-wise satellite measurements into a 3D visualization is to develop a reconstruction model that captures the fundamental magnetic field (B) and plasma field as characterized by the plasma current density (J)—measured independently from the magnetic field—in the neighborhood of the measurement domain. Introduction of magnetohydrodynamic (MHD) equations could also lead to the reconstruction of additional field variables such as plasma velocity (U) and electric field (E). It is understood that MHD is not appropriate just at the localized site of the electron diffusion region (EDR) where the X-point becomes a singularity in an ideal MHD model and the diffusion is parameterized by a bulk parameter of resistivity in a resistive MHD model (Priest, 2016). Our goal is to visualize the broader regions surrounding the EDR site. Depending on specific science problems, the magnetic and plasma fields can be reconstructed either from a set of global measurements to yield a climatological configuration covering the entire magnetosphere (e.g., Tsyganenko and Sitnov, 2007) or from a set of in-situ measurements along satellite paths to yield a localized configuration in both space and time (e.g., Dunlop et al., 1988; Dunlop et al., 2002). This paper focuses on the localized reconstruction.
Previously, there have been two categories of models for reconstructing localized fields (e.g., B and J) in Earth’s magnetosphere. The first uses the Grad-Shafranov reconstruction (GSR) technique to produce reconstruction field maps of (B, J) and U by solving a set of MHD equations where the measurements are used as boundary conditions to constrain the reconstructed field (e.g., Sonnerup and Guo, 1996; Hasegawa et al., 2004; Hasegawa et al., 2005; Sonnerup and Teh, 2008; Zhu and Lui, 2012; Sonnerup et al., 2016). The GSR technique was developed for a force-free magnetic-field configuration (e.g., Sturrock, 1994) and was mainly used to derive two-dimensional stationary and coherent MHD structure in the magnetosphere (e.g., Sonnerup and Guo, 1996). In this category of approaches, the spatial configuration of the reconstructed fields is determined by solving a full set of self-consistent MHD partial differential equations that extensively describe various physical processes relating different parameters. This reconstruction approach can effectively yield and solve a full set of physics-based model for (B, J) and U using measurements obtained by a single satellite along its trajectory as the boundary conditions.
The second category of reconstruction approaches reconstructs the field maps of (B, J) by empirically fitting a prescribed spatial configuration of the field maps to the point-wise in-situ satellite measurements forming a finite volume with multiple lines and faces in space (e.g., Dunlop et al., 1988; Dunlop et al., 2002; Torbert et al., 2020). We may call this category of techniques an “empirical reconstruction” (ER). This ER approach is especially effective and useful for reconstructing (B, J) fields from multi-satellite measurements. Unlike the GSR techniques where the spatial configuration of the fields (B, J) and U is solved from the measurements based on a full set of MHD equations, the ER models prescribe the spatial configurations of (B, J) guided by in-situ measurements and use only limited number of physical equations as constraints, such as
to determine the model parameters. In Eq. 1a,
Assuming a linear approximation for the spatial variation of the modeled B, Dunlop et al. (1988) introduced a curlometer technique to reconstruct the J field solely from the measured B based on one MHD equation (Eq. 1a). The authors also proposed an objective index called the “quality indicator” to measure the accuracy or quality of the reconstructed J field. In Torbert et al. (2020), an ER model for both B and J fields produced by assuming a nonlinear function for B was developed based on point-wise measurements of (B, J) from MMS and physical constraints from Eqs. 1a, b. For a reconstruction model with a nonlinear variation in B, we expect the reconstructed B and J fields to be more accurate and of higher quality than those derived from the curlometer technique, which is founded upon a linear approximation for the B field. Such an improvement is especially important near EDRs where the magnetic field lines are expected to be highly curved and the plasma field plays an important role in the localized reconnection process. Note that the ER model by Torbert et al. (2020) was developed as an evenly determined problem, i.e., the numbers of unknown parameters and constraints are equal, from the perspective of the more general data analysis technique for which an extra constraint is needed to add to the model that will affect the quality of the reconstructed fields. In addition, the quality and the factors affecting the reconstruction quality are difficult to quantify.
In this paper, we develop a new 3D ER model by using a stochastic optimization method to construct the smooth fields. This new ER model is a generalization of the previous ER models for which additional measurements and MHD equations can be flexibly introduced in the same model framework. In addition, the model effectively considers and quantifies the effects of random errors arising from uncertainties in the in-situ measurements. Furthermore, this stochastic optimization approach introduces additional flexibility into the model by allowing it to work regardless of whether the parameters considered are over- or under-defined. The central idea of the previous ER models is the utilization of the MHD Eq. 1a that derives J field from a prescribed analytic B field to fit the point-wise measurements and to perform the reconstructions. Note that Eq. 1a is derived by neglecting the displacement current in Ampere’s Law and is one of several important equations in an MHD system. The validity of Eq. 1a is based on the MHD fundamental assumption that the fields vary on the same time and length scales as the plasma parameters (Boyd and Sanderson, 2003). Two other important MHD equations similar to Eq. 1a are Ohm’s Law
which derives the electric field E from the plasma velocity U for a given B field, and Faraday’s Law of Induction, which relates the plasma resistivity (η) to the rest of the fields (Boyd and Sanderson, 2003)
Here, Eq. 2 plays a role similar to Eq. 1a in that an analytic E field can be derived from a prescribed analytic U field for given (B, η). Note that the plasma resistivity η can be considered a parametric measure of the particle acceleration and energy conversion near EDRs. Alternatively, it can also be considered as a phenomenological parameter to be used as a proxy to locate the EDRs of reconnection (e.g., Scudder, 2016; Yamada et al., 2016). In particular, the ultimate inclusion of this aspect of particle acceleration—and thus connection to recent MMS energetic particle observations near EDRs (e.g., Cohen et al., 2021; Turner et al., 2021)—motivated development of this new reconstruction approach.
For an ER model that only adopts one or two MHD linear equations, the problem can be solved by a traditional least-squares method that solves a set of linear algebraic equations (e.g., Dunlop et al., 1988; Dunlop et al., 2002; Denton et al., 2020; Torbert et al., 2020). When additional and, more importantly, nonlinear MHD equations such as Eqs. 2, 3 are included, a more practical approach is to solve the model parameters by directly minimizing a “loss function” that characterizes the model-measurement differences and the model departures from the above MHD equations (Eqs. 1–3). The new ER model introduced here solves for the reconstruction parameters by directly minimizing this loss function, which will be discussed in detail in Section 2. Note that the term “model departure” here means violation of a physical constraint—e.g., a violation of Eq. 1b in the reconstructed model. Such a violation arises either from the measurement errors on which the ER model is built or from the nature of the ER with a prescribed configuration—e.g., a linear or quadratic functional form in B field.
The new 3D ER model presented here has been built on the basis of directly minimizing the loss function L (or y) using a stochastic optimization method. For a linear system such as one using only Eqs. 1a, b, the model parameters could also be solved by the traditional least-squares method if the reconstruction is formulated in an even-determined or an over-determined problem. Comparing to the traditional least-squares method that solves a set of linear algebraic equations, this alternative method has several merits. First, the system could be nonlinear or the loss function L is not necessarily in a quadratic form with respect to the model parameters. The nonlinearity becomes unavoidable when the plasma resistivity is included in an ER model that uses MHD Eqs. 1–3. The loss function L, to be discussed in detail in Section 2 for the present ideal MHD ER model, has a quadratic form for which the model parameters could also be derived by solving a set of linear algebraic equations when an additional constraint is used to formulate the problem into an even-determined one (e.g., Denton et al., 2020; Torbert et al., 2020). However, our detailed discussions on how to specify and select different components of L clearly also show the flexibility of the new model that allows other constraints corresponding to the point-wise measurements of (U, E) fields and Eqs. 2, 3 to be added to the reconstruction without much change in the algorithmic structure. Second, the effect of the measurement errors is explicitly included in the reconstruction model (see Section 3.1). While by nature all parameters of stochastic algorithms are random variables, there are two sources of uncertainties in practice for a physical problem: 1) the measurements carry random errors and 2) physical relations used in the loss function constraints are not perfect. Both uncertainty sources are included in the stochastic optimization method, which gives a solution with its accuracy limited by the error term
In Section 2, we describe how to build an ER model that includes two critical steps: 1) design of a loss function and 2) use of an efficient optimization technique to solve for the model parameters. Section 3 defines several indices that measure the accuracy and quality of the reconstruction model and presents the model results for a test case near a previously-studied EDR event (Torbert et al., 2018; Torbert et al., 2020) observed in the magnetotail by the Magnetospheric Multiscale (MMS) mission (Burch et al., 2016). Section 4 provides a few concluding remarks.
Model Description
The first step to build an ER model is to design a “loss function” based on the available measurements and a set of adopted MHD equations such as those shown in Eqs. 1–3. In general, an analytic and smooth specification of the field variables (B, U, η) will automatically lead to analytic and smooth functions for (J, E) fields by use of Eqs. 1a, 2. This procedure allows analytic evaluations of all modeled fields at any space-time grids to be compared with the available measurements. The loss function is defined as a collection of various constraints corresponding to the model-measurement differences and the model departures from the adopted MHD equations, such as Eqs. 1–3. In practice, other complementary physical equations may serve as additional constrains. For example, just as to Eq. 1b that imposes a strong constraint on the reconstructed B field, the plasma velocity U may satisfy an approximate continuity equation
The second step to build an ER model is to solve for the model parameters by minimizing the defined loss function. When the MHD equations are linear, such as those shown in Eqs. 1a, b, the model parameters can be derived by a traditional least-squares method that solves a set of linear algebraic equations. Alternatively, the model parameters can also be solved by directly minimizing the loss function. This approach is especially useful when the adopted MHD equations contain nonlinear components, which generally cannot be converted to a set of linear algebraic equations. In this paper, we use a stochastic optimization method called the “simultaneous perturbation stochastic approximation” (SPSA) method to directly minimize the loss function regardless of whether or not the system contains nonlinear terms (e.g., Spall, 1998a; Zhu and Spall, 2002; Spall, 2003). In addition, random errors are treated directly in the loss function and the SPSA solution procedure so that the effects of measurement uncertainties can be examined. Once the model parameters are obtained, the last step to build an ER model is to diagnose the accuracy and the quality of the reconstructed fields. Such a post-diagnostic procedure is necessary because the ER models are built on both measurements that contain random measurement errors and adopted MHD equations that do not form a closed system.
Design of the Loss Function for the Reconstruction Model for an Ideal Magnetohydrodynamic System
To demonstrate how the aforementioned three steps are implemented, we first apply this new 3D ER model to an MHD system that only contains point-wise measurements of (B, J) fields together with MHD Eqs 1a, b as has been extensively investigated by the traditional least-squares method (e.g., Denton et al., 2020; Torbert et al., 2020). This reconstruction model can be considered an ER model for an ideal MHD system because the effect of resistivity (η) is not included. Extension to a more comprehensive nonlinear ER model that uses Eqs. 1–3 with point-wise measurements of (B, J) and (U, E) fields and incorporates the effects of plasma resistivity contained in Eqs. 2, 3 near the EDRs will be presented in our future investigations.
Here, we follow Torbert et al. (2020) and prescribe the form of the reconstructed field by expressing the time-independent magnetic field B as a quadratic function of the spatial coordinate r by a second-order Taylor expansion of a vector field
where
where
Given MMS measurements at the vertices
The generalized loss function (L) has the following form
where the individual components of the loss function
with
We first note the similarities and differences between
Application of a Stochastic Optimization Algorithm to Solve for Model Parameters and Selection of Loss Function Components
In this new 3D ER model, the model parameters in Eq. 5 are solved by directly minimizing the loss function L defined in Eq. 6 using a stochastic optimization algorithm called the SPSA method (Spall, 1998a; Spall, 1998b; Spall, 2003) through an iterative procedure that also naturally incorporates the errors for the measured fields
In practice, the SPSA method solves for the model parameters that minimize the following dimensionless loss function (y) with a random perturbation that characterizes the measurement errors (Supplementary Eqs. A4a, b in Supplementary Appendix A)
where L is given by Eq. 6,
When all the loss function components in Eq. 6
To explain why using
Results
To test our new model and to also demonstrate the third step of diagnosing the accuracy and the quality of the reconstructed fields while building an ER model, we use MMS measurements from the magnetotail EDR event of 11 July 2017. During this event, the MMS constellation traversed a reconnection region in the earthward and northward directions while remaining near the neutral plane (Torbert et al., 2018). Figure 1 shows 7 s of magnetic field
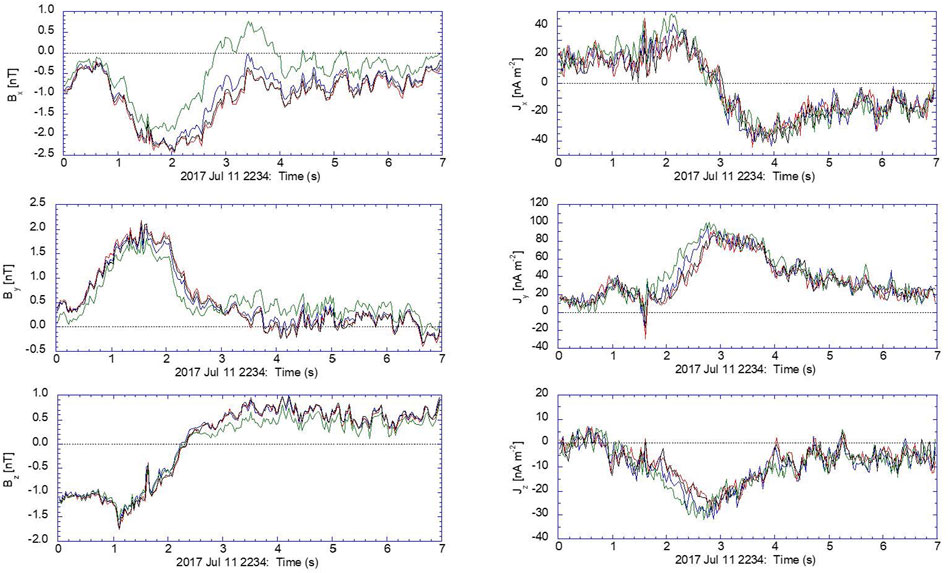
FIGURE 1. Measurements from the four MMS spacecraft (MMS1, MMS2, MMS3, MMS4) on 11 July 2017 showing (left) the measured magnetic field
Error Consideration and Quality Indicators
Note that the measurement errors here include uncertainties in both the instrumentation and subsequent processing of the data. However, the random errors in Eq. 8 are associated with the unbiased instrument noise. Here, we estimate the errors by directly calculating the parameter variability included in the data series. In Figure 2, we show both the means
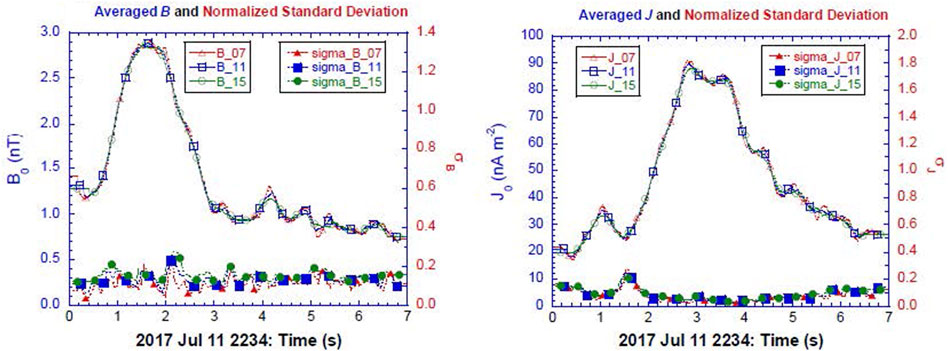
FIGURE 2. Mean and normalized standard deviation fields derived from the MMS measurements. The means and standard deviations are calculated on a moving window with a width of 7 (red), 11 (blue), and 15 (green) time steps, respectively. Panels (A) and (B) correspond to the B field and J field, respectively.
Given model parameters
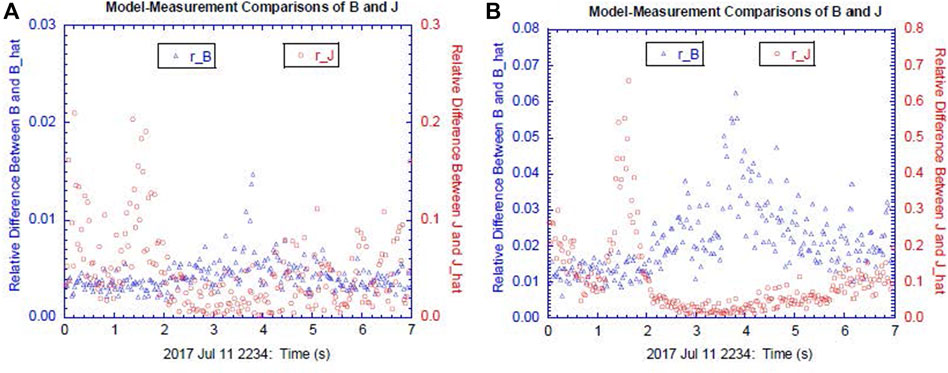
FIGURE 3. Relative differences
The results from a pair of reconstructions with
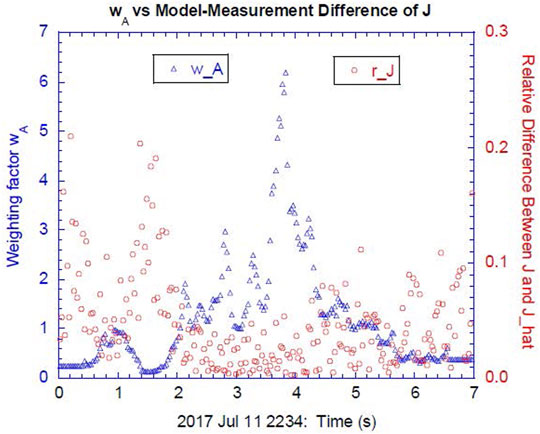
FIGURE 4. Weighting factor
Unlike reconstruction models based on the GSR technique, where the reconstructed fields are mainly derived by various physical relations, the new ER model presented here is mainly data-driven, directly fitting the modeled fields to the measured fields. Since the design of the general loss function highlighted in Eqs. 6, 7 also contains a component of the model departures characterizing a few physical constraints, the validity of those constraints can be used as a measure of the quality of the ER model in addition to the two indices
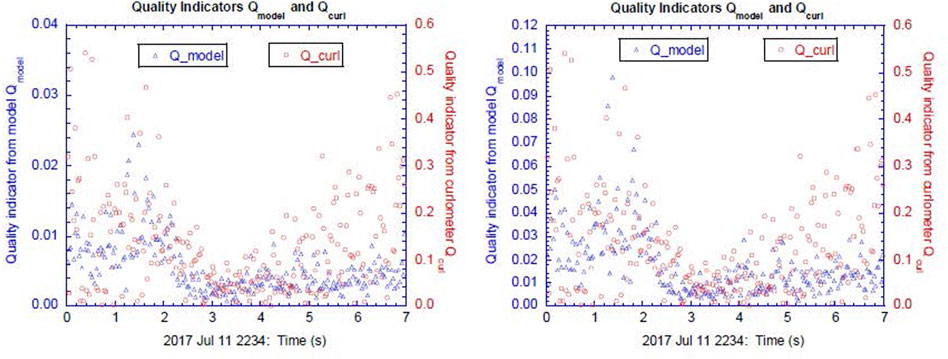
FIGURE 5. Quality indicators
In the above,
We now turn to the loss function component
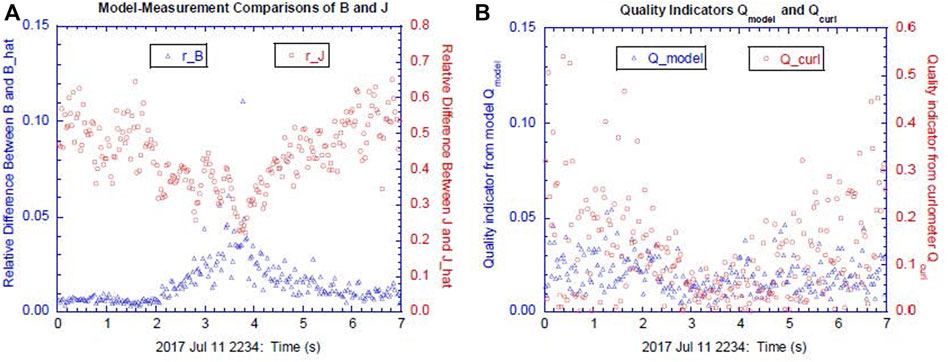
FIGURE 6. (A) Relative differences
At this stage, it is also interesting to examine a largely under-determined setting of excluding both
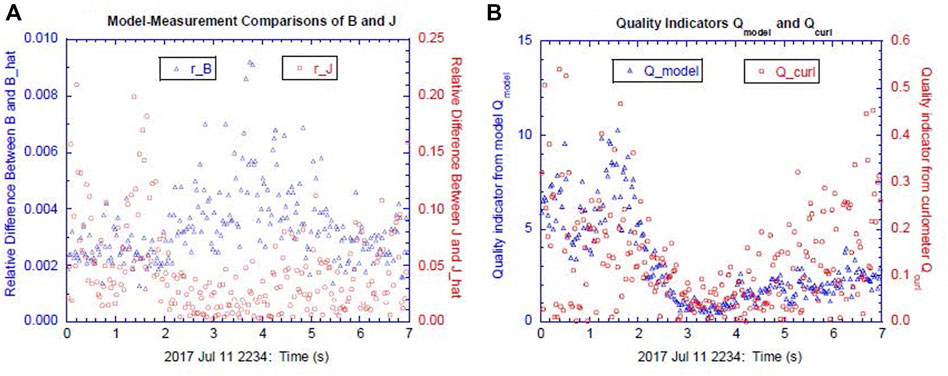
FIGURE 7. (A) Relative differences
The other more important implication of this test run for a largely under-determined setting with only 24 constraints for a 30-parameter reconstruction model is that the current ER model can be directly applied to reconstructing fields with a set of incomplete measurements. The stochastic optimization algorithms can solve for model parameters under the same algorithmic framework regardless whether the problem is over- or under-determined. For example, for a default setting of the current ER model with 33 constraints, the algorithm can be directly applied to an incomplete set of MMS measurements if the
The Reconstructed Fields
We now present the reconstructed fields based on the MMS measurements shown in Figure 1. A reconstruction model can be developed in either an L-M-N coordinate system derived from the minimum variance analysis or in a fixed system, such as GSE that is used in the present reconstruction model. One purpose of adopting the L-M-N coordinate system to develop a reconstruction model is to take advantage of the ability to neglect changes in the minimum variance direction to convert a slightly under-determined problem into an even-determined one (Denton et al., 2020; Torbert et al., 2020). When the reconstructed field varies rapidly with time, the constructed L-M-N coordinate may also change accordingly. Under such a circumstance, the reconstructed fields at different time instances cannot be directly compared with each other. Our reconstruction model based on the SPSA stochastic optimization method can automatically accommodate an over-determined or under-determined setting of the model as discussed above. As a result, the fields reconstructed at different temporal instances but on the common, fixed GSE coordinate system can be directly compared.
We present the reconstructed fields in a local GSE coordinate X-Y-Z such that
where
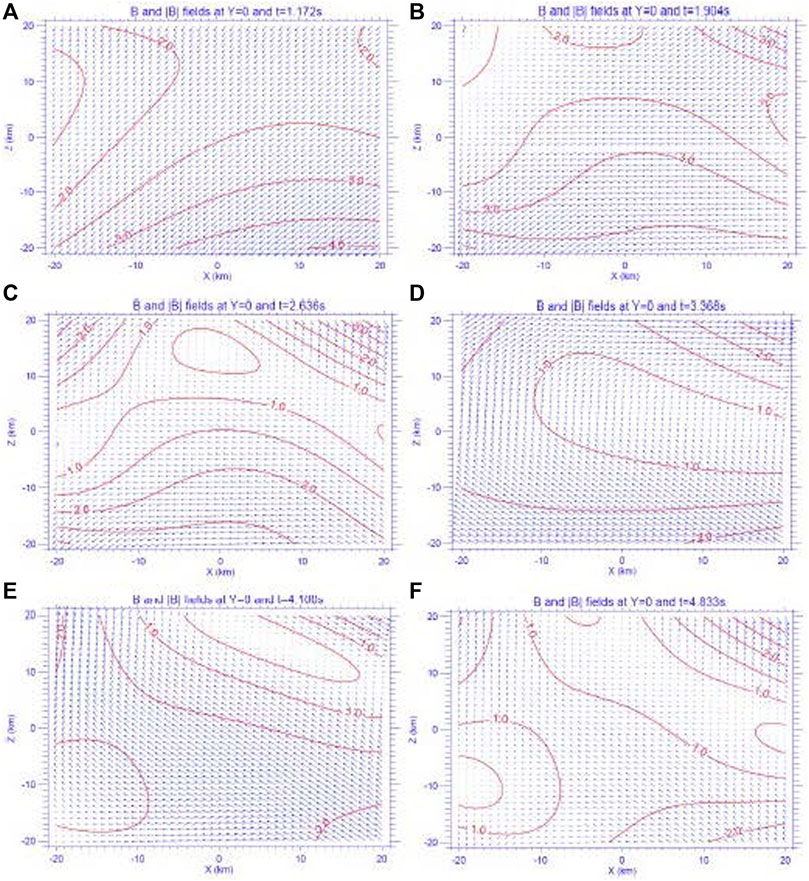
FIGURE 8. Modeled B fields projected into and its magnitude |B| (in nT) evaluated on the X-Z plane of Y = 0 at six time instances of (A)
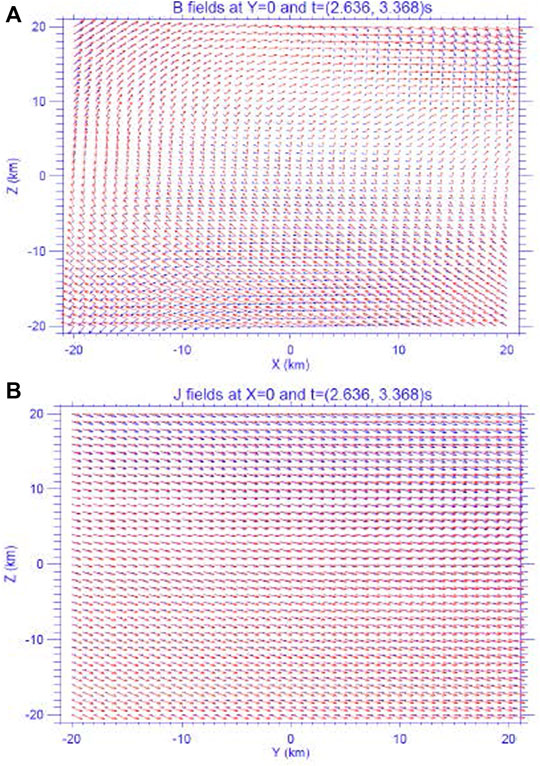
FIGURE 9. (A) Modeled B fields projected into the X-Z plane of Y = 0 at two times of
Conclusion
A new ER model for the 3D magnetic field and plasma current field has been developed by use of a stochastic optimization method called SPSA. This reconstruction model adopts an empirical approach by fitting the prescribed analytic functions for the magnetic and plasma fields to the point-wise measurements from a constellation of satellites with a set of physical constraints determined by the MHD equations. The fitness is defined by a general loss function that consists of the model-measurement differences and the model departures from linear or nonlinear physical constraints. The new ER model directly minimizes the loss function using a stochastic optimization method called SPSA algorithm for which the effect of the random measurement errors is also included. We presented the concrete steps of how to implement this ER model to a special case of having the MMS-measured fields
We have introduced the indices
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
XZ: Proposed the original idea, developed the model, and wrote the paper. IC: Provided the data, refined the idea, and revised the paper. BM: Refined the idea and revised the paper. RN: Refined the idea and revised the paper. DT: Refined the idea through various discussions. RT: Refined the idea.
Funding
This research was supported by the Magnetospheric Multiscale (MMS) mission of NASA’s Science Directorate Heliophysics Division via subcontract to the Southwest Research Institute (NNG04EB99C) and NASA Grant NNX10AB84G.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
Constructive comments on SPSA applications from James C. Spall and Richard Denton are greatly appreciated. We also thank Daniel J. Gershman and others on MMS team for the FPI current density and magnetic field measurements used in this paper. Constructive comments from two reviewers are also appreciated.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.878403/full#supplementary-material
References
Bhatnagar, S., Prasad, H. L., and Prashanth, L. A. (2013). Stochastic Recursive Algorithms for Optimization - Simultaneous Perturbation Method. New York: Springer, 302.
Boyd, T. J., and Sanderson, J. J. (2003). The Physics of Plasmas. Cambridge: Cambridge University Press, 532.
Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric Multiscale Overview and Science Objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9
Chanteur, G. (1998). “Spatial Interpolation for Four Spacecraft: Theory,” in Analysis Methods for Multi-Spacecraft Data. Editors G. Paschmann, and P. W. Daly (Bern, Switzerl, and Paris, France: The International Space Science InstituteEuropean Space Agency), 395–418. Chap. 12.
Chin, D. C. (1999). Simultaneous Perturbation Method for Processing Magnetospheric Images. Opt. Eng. 38, 606–611. doi:10.1117/1.602104
Chong, E. K. P., and Zak, S. H. (2001). An Introduction to Optimization. Second Edition. New York: John Wiley & Sons, 476.
Cohen, I. J., Turner, D. L., Mauk, B. H., Bingham, S. T., Blake, J. B., Fennell, J. F., et al. (2021). Characteristics of Energetic Electrons Near Active Magnetotail Reconnection Sites: Statistical Evidence for Local Energization. Geophys. Res. Lett. 48, e2020GL090087. doi:10.1029/2020GL090087
Denton, R. E., Torbert, R. B., Hasegawa, H., Dors, I., Genestreti, K. J., Argall, M. R., et al. (2020). Polynomial Reconstruction of the Reconnection Magnetic Field Observed by Multiple Spacecraft. J. Geophys. Res. Space Phys. 125, e2019JA027481. doi:10.1029/2019JA027481
Dunlop, M. W., Balogh, A., Glassmeier, K.-H., and Robert, P. (2002). Four-point Cluster Application of Magnetic Field Analysis Tools: The Curlometer. J. Geophys. Res. 107 (A11), 1384. doi:10.1029/2001JA005088
Dunlop, M. W., Southwood, D. J., Glassmeier, K.-H., and Neubauer, F. M. (1988). Analysis of Multipoint Magnetometer Data. Adv. Space Res. 8, 273–277. doi:10.1016/0273-1177(88)90141-x
Gurnett, D. A., and Bhattacharjee, A. (2005). Introduction to Plasma Physics – with Space and Laboratory Applications. Cambridge: Cambridge University Press, 452.
Harvey, C. C. (1998). “Spatial Gradients and the Volumetric Tensor,” in Analysis Methods for Multi-Spacecraft Data. Editors G. Paschmann, and P. W. Daly (Bern, Switzerl, and Paris, France: The International Space Science InstituteEuropean Space Agency), 307–322. Chap. 12.
Hasegawa, H., Sonnerup, B. U. Ö., Dunlop, M. W., Balogh, A., Haaland, S. E., Klecker, B., et al. (2004). Reconstruction of Two-Dimensional Magnetopause Structures from Cluster Observations: Verification of Method. Ann. Geophys. 22, 1251–1266. doi:10.5194/angeo-22-1251-2004
Hasegawa, H., Sonnerup, B. U. Ö., Klecker, B., Paschmann, G., Dunlop, M. W., and Rème, H. (2005). Optimal Reconstruction of Magnetopause Structures from Cluster Data. Ann. Geophys. 23, 973–982. doi:10.5194/angeo-23-973-2005
Holton, J. R. (2004). An Introduction to Dynamic Meteorology. Fourth Edition. New York: Elsevier Academic Press, 535.
Menke, W. (1989). Geophysical Data Analysis: Discrete Inverse Theory. Revised Edition. New York: Academic Press, 289.
Middleton, H., and Masson, A. (2016). The Curlometer Technique: A Beginner’s Guide. CSA Technical Note. ESDC-CSA-TN-0001. Madrid, Spain: European Space Astronomy Centre, 19.
Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., et al. (2016). Fast Plasma Investigation for Magnetospheric Multiscale. Space Sci. Rev. 199, 331–406. doi:10.1007/s11214-016-0245-4
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (1992). Numerical Recipes in Fortran. The Arts of Scientific Computing. Second Edition. Cambridge: Cambridge University Press, 963.
Priest, E. (2016). “MHD Structures in Three-Dimensional Reconnection,” in Magnetic Reconnection – Concepts and Applications. Editors W. Gonzalez, and E. Parker (Switzerland: Springer), 101–142. doi:10.1007/978-3-319-26432-5_3
Robert, P., Roux, A., Harvey, C. C., Dunlop, M. W., Daly, P. W., and Glassmeier, K. H. (1998). “Tetrahedron Geometric Factors,” in Analysis Methods for Multi-Spacecraft Data. Editors G. Paschmann, and P. W. Daly (Bern, Switzerl, and Paris, France: The International Space Science InstituteEuropean Space Agency), 323–348. Chap. 13.
Roelof, E. C., Mauk, B. H., and Meier, R. R. (1993). Simulations of EUV and ENA Magnetospheric Images Based on the Rice Convection Model. Proc. Spie, Instrumentation Magnetospheric Imagery 2008, 202–213.
Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., et al. (2016). The Magnetospheric Multiscale Magnetometers. Space Sci. Rev. 199, 189–256. doi:10.1007/s11214-014-0057-3
Scudder, J. D. (2016). “Collisionless Reconnection and Electron Demagnetization,” in Magnetic Reconnection – Concepts and Applications. Editors W. Gonzalez, and E. Parker (Switzerland: Springer), 33–100. doi:10.1007/978-3-319-26432-5_2
Sonnerup, B. U. Ö., and Guo, M. (1996). Magnetopause Transects. Geophys. Res. Lett. 23, 3679–3682. doi:10.1029/96gl03573
Sonnerup, B. U. Ö., Hasegawa, H., Denton, R. E., and Nakamura, T. K. M. (2016). Reconstruction of the Electron Diffusion Region. J. Geophys. Res. Space Physics 121, 4279–4290. doi:10.1002/2016JA022430
Sonnerup, B. U. Ö., and Teh, W.-L. (2008). Reconstruction of Two-Dimensional Coherent MHD Structures in a Space Plasma: The Theory. J. Geophys. Res. 113. doi:10.1029/2007JA012718
Spall, J. C. (2000). Adaptive Stochastic Approximation by the Simultaneous Perturbation Method. IEEE Trans. Automat. Contr. 45, 1839–1853. doi:10.1109/tac.2000.880982
Spall, J. C. (1998a). An Overview of the Simultaneous Perturbation Method for Efficient Optimization. Johns Hopkins APL Tech. Dig. 19, 482–492.
Spall, J. C. (1998b). Implementation of the Simultaneous Perturbation Algorithm for Stochastic Optimization. IEEE Trans. Aerosp. Electron. Syst. 34 (3), 817–823. doi:10.1109/7.705889
Spall, J. C. (2003). Introduction to Stochastic Search and Optimization: Estimation, Simulation, and Control. New York: John Wiley & Sons, 595.
Spall, J. C. (1992). Multivariate Stochastic Approximation Using a Simultaneous Perturbation Gradient Approximation. IEEE Trans. Automat. Contr. 37, 332–341. doi:10.1109/9.119632
Sturrock, P. A. (1994). Plasma Physics: An Introduction to the Theory of Astrophysical, Geophysical and Laboratory Plasmas. Cambridge: Cambridge University Press, 335.
Torbert, R. B., Burch, J. L., Phan, T. D., Hesse, M., Argall, M. R., Shuster, J., et al. (2018). Electron-scale Dynamics of the Diffusion Region during Symmetric Magnetic Reconnection in Space. Science 362 (6421), 1391–1395. doi:10.1126/science.aat2998
Torbert, R. B., Dors, I., Argall, M. R., Genestreti, K. J., Burch, J. L., Farrugia, C. J., et al. (2020). A New Method of 3‐D Magnetic Field Reconstruction. Geophys. Res. Lett. 47, e2019GL085542. doi:10.1029/2019gl085542
Tsyganenko, N. A., and Sitnov, M. I. (2007). Magnetospheric Configurations from a High-Resolution Data-Based Magnetic Field Model. J. Geophys. Res. 112. doi:10.1029/2007JA012260
Turner, D. L., Cohen, I. J., Bingham, S. T., Stephens, G. K., Sitnov, M. I., Mauk, B. H., et al. (2021). Characteristics of Energetic Electrons Near Active Magnetotail Reconnection Sites: Tracers of a Complex Magnetic Topology and Evidence of Localized Acceleration. Geophys. Res. Lett. 48, e2020GL090089. doi:10.1029/2020GL090089
Yamada, M., Yoo, J., and Zenitani, S. (2016). “Energy Conversion and Inventory of a Prototypical Magnetic Reconnection Layer,” in Magnetic Reconnection – Concepts and Applications. Editors W. Gonzalez, and E. Parker (Switzerland: Springer), 143–179. doi:10.1007/978-3-319-26432-5_4
Zhu, X., and Lui, A. T. Y. (2012). Reconstruction of Neighboring Plasma Environment along a Satellite Path by a Barotropic Plasma Model. J. Atmos. Solar-Terrestrial Phys. 77, 46–56. doi:10.1016/j.jastp.2011.11.005
Keywords: stochastic optimization, empirical reconstruction model, magnetospheric reconnection, simultaneous perturbation stochastic approximation, loss function
Citation: Zhu X, Cohen IJ, Mauk BH, Nikoukar R, Turner DL and Torbert RB (2022) A New Three-Dimensional Empirical Reconstruction Model Using a Stochastic Optimization Method. Front. Astron. Space Sci. 9:878403. doi: 10.3389/fspas.2022.878403
Received: 18 February 2022; Accepted: 07 April 2022;
Published: 09 May 2022.
Edited by:
Olga Verkhoglyadova, NASA Jet Propulsion Laboratory (JPL), United StatesReviewed by:
Bogdan Hnat, University of Warwick, United KingdomYasuhito Narita, Austrian Academy of Sciences (OeAW), Austria
Copyright © 2022 Zhu, Cohen, Mauk, Nikoukar, Turner and Torbert. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xun Zhu, eHVuLnpodUBqaHVhcGwuZWR1
 Xun Zhu
Xun Zhu Ian J. Cohen1
Ian J. Cohen1 Barry H. Mauk
Barry H. Mauk