Using mutual information to investigate non-linear correlation between AE index, ULF Pc5 wave activity and electron precipitation

In this study, we use mutual information from information theory to investigate non-linear correlation between geomagnetic activity indicated by auroral electrojet (AE) index with both the global ultra low frequency (ULF) Pc5 wave power and medium energy (≥30 keV) electron precipitation at the central outer radiation belt. To investigate the energy and magnetic local time (MLT) dependence of the non-linearity, we calculate the mutual information and Pearson correlation coefficient separately for three different energy ranges (30–100 keV, 100–300 keV and ≥300 keV) and four different MLT sectors (0–6, 6–12, 12–18, 18–24). We compare results from 2 years 2004 and 2007 representing geomagnetically more active and less active years, respectively. The correlation analysis between the AE index and electron precipitation shows a clear MLT and energy dependence in both active and quiet conditions. In the two lowest energy ranges of the medium energy electrons (30–100 keV and 100–300 keV) both non-linear correlation and Pearson correlation indicate strong dependence with the AE index in the dawn sector. The linear dependence indicated by the Pearson correlation coefficient decreases from dawn to dusk while the change in the non-linear correlation is smaller indicating an increase in the non-linearity from dawn to dusk. The non-linearity between the AE index and electron precipitation is larger at all MLT sectors except MLTs 6–12 during geomagnetically more active year when larger amount of the activity is driven by interplanetary coronal mass ejections (ICMEs) compared to lower activity year with high speed stream (HSS) and stream interaction region (SIR) driven activity. These results indicate that the processes leading to electron precipitation become more non-linear in the dusk and during geomagnetically more active times when the activity is driven by ICMEs. The non-linearity between the AE index and global ULF Pc5 activity is relatively low and seems not to be affected by the difference in the geomagnetic activity during the 2 years studied.

1 Introduction

Earth’s radiation belts (e.g., Van Allen, 1981; Li and Hudson, 2019) are occupied by energetic electrons and ions that are trapped in the geomagnetic field. The outer radiation belt above L ≳ 3 consists mostly of energetic electrons from a few hundred keVs up to ultra-relativistic energies. The behavior of energetic electrons is affected by multiple different waves modes that are present in the inner magnetosphere (e.g., Baker et al., 2019). The main source of the medium energy electrons (tens to hundreds of keVs) are injections from the Earth’s magnetotail during substorms (e.g., Jaynes et al., 2015a). The substorm activity in the magnetotail is captured well by the auroral electrojet (AE) index (e.g., Newell and Gjerloev, 2011). AE index measures the total electrojet activity at the auroral latitudes. It is calculated from magnetometer stations located under the auroral oval as a difference between the AU and AL indices (AE = AU-AL), which are measures of the maximum magnetic field perturbation caused by the strongest eastward and westward currents of the auroral oval, respectively (Davis and Sugiura, 1966). AE index below 300 nT indicates quiet time conditions, during medium activity AE index is 300–1500 nT and AE index increases over 1500 nT during intense AE activity. In a recent statistical study, Nesse Tyssøy et al. (2021) demonstrated that AE index is a good proxy for the precipitation of the medium energy electrons ($\ge 30$ keV).

Whistler-mode chorus waves have been found to act as both loss and acceleration mechanism of the radiation belt electrons (e.g., Kennel and Petschek, 1966; Reeves et al., 2003; Thorne et al., 2013; Artemyev et al., 2014; Li et al., 2014). Chorus waves are driven by the anisotropic distribution function of the electrons injected from the plasma sheet during a substorm process and they are mainly observed on dawn side from midnight to noon (e.g., Meredith et al., 2020). They are right-hand polarized waves that are observed usually in two frequency bands: lower-band chorus waves with frequencies 0.1–0.5 f_ce and upper-band chorus waves with frequencies 0.5–0.8 f_ce, where f_ce is the equatorial electron cyclotron frequency. The cyclotron resonant interactions between the radiation belt electrons and the chorus waves may progressively accelerate lower energy electrons to high energies up to MeVs (e.g., Jaynes et al., 2015b). The chorus wave generation, growth and subsequent wave-particle interactions can also scatter electrons of keVs to hundreds of keVs into the loss cone causing them to precipitate to the upper atmosphere causing both the diffuse (e.g. Thorne et al., 2010; Ni et al., 2016) and pulsating (Nishimura et al., 2010; Kasahara et al., 2018) aurora. Lam et al. (2010) conducted a correlation analysis between the precipitating $>30$ keV electron fluxes and bounce averaged pitch angle diffusion coefficients for lower-band chorus during strong geomagnetic activity (AE $>300$ nT). They found high linear Pearson correlation coefficients $(>0.8)$ at morning hours and at larger L-shells (L > 5.1). The upper-band chorus waves have been found to cause the resonant scattering of $<5$ keV electrons whereas for higher energy electrons (30–100 keV) the lower-band chorus waves are the dominant scattering process especially near the edge of the loss cone (e.g., Ni et al., 2008).

The electron population in the outer radiation belt is also affected by ultra low frequency (ULF) waves in the Pc4 (6.7–22 mHz corresponding to period of 45–150 s) and Pc5 (1.7–6.7 mHz corresponding to period of 150–600 s) range (e.g., Elkington et al., 2003; Shprits et al., 2008; Mann et al., 2013, 2016; Zong et al., 2017). These waves can be generated externally by the solar wind-magnetosphere interactions (e.g., Kepko and Spence, 2003; Rae et al., 2005; Claudepierre et al., 2008, 2010; Zhang et al., 2010; Hwang and Sibeck, 2016; Wang et al., 2017) or internally by the drift-bounce resonance, which can be driven by ions injected from the magnetotail during substorms (e.g. Chen and Hasegawa, 1991; Zolotukhina et al., 2008; James et al., 2016; Yamakawa et al., 2019). Pc5 ULF waves can be divided to toroidal and poloidal modes (or combinations of both modes), based on the direction of magnetic field fluctuations. Magnetic field fluctuations of the toroidal mode oscillate in the azimuthal direction and poloidal mode is observed in the radial magnetic field component (Hudson et al., 2004). The toroidal ULF mode can reach the ground magnetometers but the poloidal mode can only be observed from the spacecraft observations (Shi et al., 2018). ULF waves can accelerate radiation belt electrons via drift resonance causing radial diffusion (e.g., Elkington et al., 1999; Elkington et al., 2003) and can increase the energetic electron flux up to an order of magnitude (Su et al., 2015).

Previous studies have demonstrated that the statistical dependence between the solar wind and the radiation belts and their electrons in the inner magnetosphere can be non-linear in nature (e.g., Reeves et al., 2011; Kellerman and Shprits, 2012; Wing et al., 2016, 2021; Simms et al., 2021). For example, the combined simultaneous or subsequent interaction of different wave modes with the radiation belt electrons can be non-linear (Simms et al., 2018, 2021). However, commonly used Pearson correlation coefficient only measures the linear dependencies and does not unveil the possible non-linear correlations. Information theory techniques such as mutual information can be used to reveal non-linear dependencies (e.g. Johnson and Wing, 2005; Wing et al., 2016; Cameron et al., 2019; Wing et al., 2021; Osmane et al., 2022). These techniques have been previously used in space plasma physics to study e.g., geoeffectiveness of solar wind shocks with different front orientations (Cameron et al., 2019), solar wind drivers of radiation belt electron fluxes (Wing et al., 2016, 2021) and how geostationary seed and relativistic electron fluxes correlate with the ULF waves (Osmane et al., 2022).

In this paper, we utilize mutual information from information theory to quantify the non-linear correlation coefficient and compare it with the linear Pearson correlation coefficient between substorm activity indicated by the AE index and global Pc5 ULF wave power and AE index and precipitating medium energy electrons at L-shells from 5 to 7. We compare results from years 2004 and 2007, representing geomagnetically more active and less active years, respectively. The correlation analysis between the AE index and geosynchronous and groundbased Pc5 ULF wave indices indicate low non-linearity. We investigate the correlation between the AE index and electron precipitation separately for three different energy ranges of the medium energy electrons (30–100 keV, 100–300 keV and $>$300 keV) and from four MLT sectors (0–6, 6–12, 12–18, 18–24). This paper is organized as follows. The data and the methods used in this study are described in Section 2, the results are presented in Section 3, and discussed in Section 4.

2 Data and methods

2.1 Solar wind and geomagnetic activity

The solar wind plasma parameters, the interplanetary magnetic field (IMF), and the auroral electrojet index (AE) are obtained from the NASA OMNIWeb (https://omniweb.gsfc.nasa.gov). Solar wind OMNI data (plotted in Figure 1) is propagated to the Earth’s bow shock. We use OMNI data with 1 min resolution and calculate the hourly maximum for the AE index, AE_max, which is used in the mutual information and correlation calculations, because we are interested in the impact of the peak geomagnetic activity. The correlation coefficient and mutual information with different time offsets behaves very similarly for both the hourly maximum and hourly mean of the AE index but the latter yields slightly lower values.

FIGURE 1

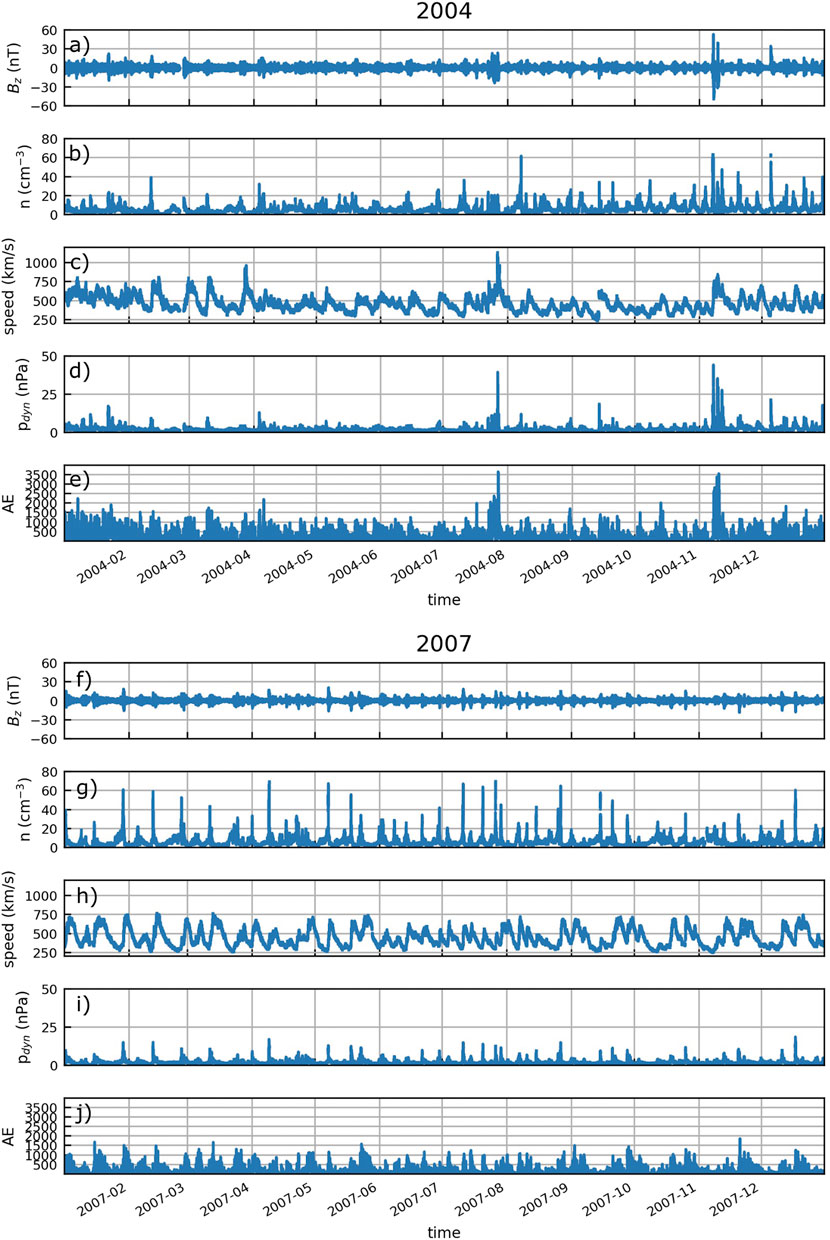
FIGURE 1. Overview of the solar wind parameters, IMF north-south component B_z, number density n, solar wind speed, dynamic pressure p_dyn and AE index from 2004 (A–E) and 2007 (F–J).

2.2 Wave activity

ULF wave indices, T_geo and T_gr, are 1 h resolution measurements of the total spectral power of the magnetic field fluctuations from geosynchronous and ground based observations, respectively, in the 2–7 mHz frequency band obtained from the data archive: http://ulf.gcras.ru/archive.html (Kozyreva et al., 2007). The ground based ULF wave index T_gr is obtained from ground-based magnetometers at 60°–70° latitude from the Northern hemisphere. The geosynchronous T_geo is calculated using the data from GOES spacecraft that are located on the geosynchronous orbit at 6.6 R_E on the equatorial plane. The ULF wave indices used in this study are defined as logarithm in base 10 of the total spectral power.

2.3 Precipitating electrons

Electron precipitation data is obtained from polar-orbiting low-altitude Polar Operational Environmental Satellite (POES). The Medium Energy Proton and Electron Detector (MEPED) instrument of the Space Environment Monitor (SEM-2) Suite on board POES spacecraft (NOAA-15, NOAA-16, NOAA-17, NOAA-18 and MetOp-02) measures electrons with 0° and 90° telescopes. At higher latitudes, where the magnetic field lines are almost radial, the 0° telescope measures primarily the electrons in the loss cone while 90° measures the trapped electron population, but it can flip to opposite at the lower latitudes (Asikainen and Mursula, 2013). The angle of view of both telescopes is 30° and they measure electrons in the energy channels $>30\mathrm{k}\mathrm{e}\mathrm{V}$, $>100\mathrm{k}\mathrm{e}\mathrm{V}$, $>300\mathrm{k}\mathrm{e}\mathrm{V}$. The proton contamination and other instrumental problems affecting the POES measurements (see e.g. Rodger et al., 2013) have been corrected from the POES data used in this study (Asikainen and Mursula, 2013; Asikainen, 2017). We want to focus on the region of the outer radiation belt outside the plasmapause, therefore, we use electron precipitation observations at the L shells from 5 to 7 and all MLTs divided into four sectors (0–6, 6–12, 12–18, 18–24 MLT).

At high latitudes local bounce loss cone is usually larger than the field of view of the POES telescopes, and thus the 0° telescope underestimates the precipitating electrons, while at the higher latitudes the 90° telescope observes part of the precipitating flux (e.g., Hargreaves et al., 2010; Rodger et al., 2013). Therefore we estimate the precipitating flux, J_precip, as geometric mean between the parallel and perpendicular fluxes, J₀ and J₉₀, respectively, following the approach used by Hargreaves et al. (2010), Rodger et al. (2013), George et al. (2020), and Nesse Tyssøy et al. (2022):

$J_{\mathit{precip}}=\sqrt{J_0\cdot J_{90}}.(1)$

We note that some amount of trapped population seen by 90° telescope of POES spacecraft is always included in the estimated J_precip, which could cause underestimation of the total precipitated flux during time periods when the trapped electron flux is low and precipitated flux is high as well as overestimation of the total flux during times of high trapped flux. Nevertheless, this approach will provide much better estimation for the qualitative analysis of the electron precipitation in this study compared to using only the 0° telescope measurements. To calculate the estimated precipitation separately for each energy range 30–100 keV, 100–300 keV, and $>300$ keV, we first subtract the higher energy range channel from the lower ones (i.e. to get the 30–100 keV electrons the channel $>100$ keV is subtracted from channel $>30$ keV) before calculating J_precip.

2.4 Mutual information

Pearson correlation coefficient only measures linear correlation between two quantities and does not detect the relationships that are non-linear in nature. A useful measure that also considers non-linear relationships is Mutual Information (MI) from information theory (e.g. Li, 1990; Cover and Thomas, 2006). It quantifies the amount of information that random variables X and Y share. The method is described more in detail by Osmane et al. (2022) but it is presented briefly below. Entropy, H, is commonly used as a measure of the uncertainty, which for each variable can be defined as

$H\left(X\right)=-\sum _{x\in X}p\left(x\right)\log p\left(x\right);H\left(Y\right)=-\sum _{y\in Y}p\left(y\right)\log p\left(y\right)(2)$

where p(x) and p(y) refer to probability mass functions of variables X and Y, respectively. The joint entropy of the two variables is

$H\left(X,Y\right)=-\sum _{x,y}p\left(x,y\right)\log \left(p\left(x,y\right)\right)(3)$

The mutual information MI between two variables X and Y is defined as:

$\begin{array}{lll}\hfill MI\left(X,Y\right)=H\left(X\right)+H\left(Y\right)-H\left(X,Y\right)& =\sum _{y\in Y}\sum _{x\in X}p\left(x,y\right){\log }_2\hfill & \left(\frac{p\left(x,y\right)}{p\left(x\right)p\left(y\right)}\right),\hfill \end{array}(4)$

where p (x, y) is the joint probability mass function of X and Y. Mutual information is invariant with respect to reparametrization of the variables, i.e., MI(X, Y) = MI(X′, Y′) for homeomorphisms X′ = F(X) and Y′ = G(Y) (Kraskov et al., 2004). This means, for example, that the value of mutual information is same for MI(X, Y) and MI(log  X, log  Y).

Mutual information contains both linear and non-linear information from the relation between two variables. In a case where the two variables have normal distributions and the joint distribution is a bivariate normal, MI can be compared to the linear correlation coefficient, ρ, through:

$\mathrm{M}\mathrm{I}=-\frac{1}{2}\log \left(1-{\rho }^2\right),(5)$

giving an estimation for the information adjusted correlation for the certain value of MI:

${\rho }_{\mathit{adj}}=\sqrt{1-2^{-2\mathrm{M}\mathrm{I}}},(6)$

which can be applied for any joint distribution of two variables. Information adjusted correlation coefficient, ρ_adj, can be compared with the Pearson correlation coefficient to give an estimation if the Pearson correlation has underestimated the dependence of the two variables due to existing non-linearities. In this study, we quantify the non-linearity as:

$1-\frac{|{\rho }_{\mathit{P}}|}{{\rho }_{\mathit{adj}}}.(7)$

If the information adjusted correlation is larger than the linear Pearson correlation coefficient, the investigated variables have some statistically significant non-linear dependencies and the non-linearity term becomes larger. In the case of the information adjusted correlation being comparable to the Pearson correlation, the non-linear dependencies are not significant or they are not present and the non-linearity is close to zero.

We follow the same procedure to calculate the MI for two variables as Osmane et al. (2022) by binning the data sets used using Freedman-Diaconis rule (Freedman and Diaconis, 1981). This method discretizes the variables, which leads to biases in the in the estimation of the MI that depend on the total number of the measurement points (N) and the statistical dependence between the two variables studied. To estimate an error for the mutual information caused by the discretization of the variables, we calculate so called zero baseline level similarly as described by Osmane et al. (2022). This is done by calculating the mutual information for 200 shuffles of the data sets for each time lag and calculating its standard deviation σ_MI. In Figure 2 and 4 the baseline is shown as the orange line and the shaded area is 3σ_MI. We estimate the error of the ρ_adj by calculating error propagation using Equation 6, where we use ΔMI = 3σ_MI. For the Pearson correlation coefficient we estimate the error by calculating the correlation coefficient for 200 shuffles of the two data sets, and the error is three times the standard deviation of the result (Δρ_P = 3σ_P).

FIGURE 2

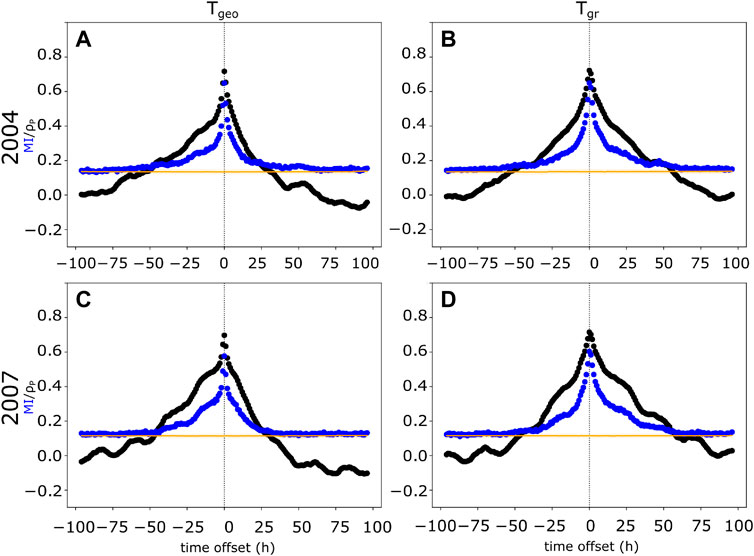
FIGURE 2. Calculation of the MI and Pearson correlation coefficient for [log₁₀AE_max(t), T_geo (t + τ)] and [log₁₀AE_max(t), T_gr (t + τ)], where τ varies between ± 96 h. T_geo and T_gr are the global ULF indices for geosynchronous and ground-based observations, respectively. Panels (A) and (B) show results from year 2004 and panels (C) and (D) show results from 2007. The blue dots show the calculated MI and black dots indicate the linear Pearson correlation coefficient. The positive time offset indicates that AE index would precede the ULF wave indices and the negative time offset indicates the opposite. The orange line indicates the zero baseline.

Mutual information is an integrated measure over how connected two variables are. In order to investigate how the certain values of the two variables are connected, a pointwise mutual information can be used. Definition of pointwise mutual information (PMI) is

$\mathrm{P}\mathrm{M}\mathrm{I}\left(x,y\right)={\log }_2\left(\frac{p\left(x,y\right)}{p\left(x\right)p\left(y\right)}\right).(8)$

PMI can be used to investigate if a pair of x and y values occur together more often than would be expected from two independent distributions. The parameter would be zero for all x and y if X and Y were independent. PMI for some pair of x and y tells that they occur together 2^PMI times more/less often than they would for independent distributions (e.g., Cameron et al., 2019). For example, PMI$>1$ tells that the pair of observed x and y occurs more than twice as often $(>2^1)$ as would be expected from independent variables. Similarly PMI$<-1$ means that the observed pair of x and y occurred less than half as frequently $(<2^{-1})$ than they would have occurred for independent variables.

3 Results

We compare data from two different years: year 2004 that coincides with early declining phase of Solar Cycle 23 and year 2007 that coincides with the late declining phase of the cycle 23. Figure 1 shows the solar wind conditions and geomagnetic activity from both years from the OMNI data base with 1 min resolution. Year 2004 features a few periods of particularly intense AE activity (AE $>$ 1500 nT) associated to strong Earth-impacting interplanetary coronal mass ejections (ICMEs; e.g., Kilpua et al., 2017), but overall both years have frequent medium and intense level AE activity (AE $\sim 500-1500$ nT). During the year 2004, however, AE activity seems more continuous while in 2007 it increases and wanes periodically. This likely reflects that in 2007 the clear majority of geomagnetically active periods were related to stream interaction regions (SIRs) and high speed solar wind streams (HSS), while ICMEs had a significant contribution in 2004 (Asikainen and Ruopsa, 2016). The Richardson and Cane ICME list (http://www.srl.caltech.edu/ACE/ASC/DATA/level3/icmetable2.htm) reports 20 ICMEs in the near-Earth solar wind in 2004, while in 2007 only 2 ICMEs were identified. It is also interesting to note that in 2007 there were frequent high dynamics pressure intervals, presumably related to compression at SIRs.

3.1 Geomagnetic activity vs. ULF wave activity

As an indicator of the geomagnetic activity we use the hourly maximum of the AE index (AE_max). Because it can vary multiple orders of magnitude, we use logarithm of the AE index (log₁₀AE_max) in the mutual information and correlation coefficient calculations. Figure 2 shows the results of the correlation analysis calculated with different time offsets (τ) ranging from −96 to +96 h for both years. We calculate the MI (blue dots) and ρ_P (black dots) between the AE index and ULF wave activity, [log₁₀AE_max(t), T_geo∕gr (t + τ)]. Positive time offset indicates that the changes in AE index precede the ULF wave power, whereas negative time offset would imply the opposite (i.e., corresponding changes observed in AE index at time t would be observed in ULF wave index at time t + τ for positive time offset and t − |τ| for negative τ).

Figure 2 shows that the mutual information and Pearson correlation peak with zero time offset (τ_max = 0) for [log₁₀AE_max(t), T_geo∕gr (t + τ)] in case of both the geosynchronous and ground based ULF wave indices. The time offset of the maximum value of the mutual information τ_max, maximum mutual information MI, the information adjusted correlation ρ_adj (calculated from the mutual information using Equation 6), and the corresponding Pearson correlation coefficient ρ_P are listed in Table 1. The information adjusted correlation is slightly higher than the Pearson correlation for all investigated cases suggesting some non-linear dependencies between AE and ULF wave activity. For 2004 the Pearson correlation and information adjusted correlation are the same for both geosynchronous and ground based ULF wave indices. For 2007 the Pearson correlation is also within the error limits for both ULF indices and the difference in the information adjusted correlation is not significant. We calculate the non-linearity defined by Equation 7. There are no significant differences in the non-linearity between the geomagnetically more (2004) and less (2007) active years and the geosyncrhonous and ground based ULF wave indices.

TABLE 1

TABLE 1. Maximum value of the Mutual Information at time offset τ_max, the corresponding information adjusted correlation, ρ_adj, and Pearson correlation coefficient, ρ_P, with the time offset τ_max for [log₁₀AE_max(t), T_geo (t + τ)] and [log₁₀AE_max(t), T_gr (t + τ)].

Figure 3 shows the map of the pointwise mutual information (PMI) calculated for the zero time offset, i.e., when the mutual information and Pearson correlation peak (Figure 2). The color scale of the PMI map is saturated at values ≤ −1 and $\ge 1$, to highlight the areas where the log₁₀AE_max and the ULF indices occur 2 times less/more frequently (2^PMI) than would be expected from independent variables. Overall, the maps look similar for both geosynchronous and groundbased ULF indices (left and right column, respectively) and years (top row 2004 and bottom row 2007). A few stronger geomagnetic storms occurred in 2004 and, therefore, AE index and also the ULF wave indices reach higher values in 2004 than in 2007. The lowest ULF wave activity ($<-0.5$ for T_geo and $<1.0$ for T_gr) always occurs with the log₁₀AE_max < 2 (AE_max < 100 nT). The PMI map also shows the general positive correlation between AE index and the ULF wave indices. High ULF wave activity rarely occurs with low AE index, and the ULF wave power is always elevated during intense AE activity. The largest ULF wave index values can occur over broad range of AE activity, also during the times of relatively weak AE activity (log₁₀AE_max ∼ 2.7 i.e. AE_max ∼ 500 nT). These are likely caused by periods of increased dynamic pressure or high solar wind speed during northward IMF that can generate ULF wave activity as mentioned in the Introduction.

FIGURE 3

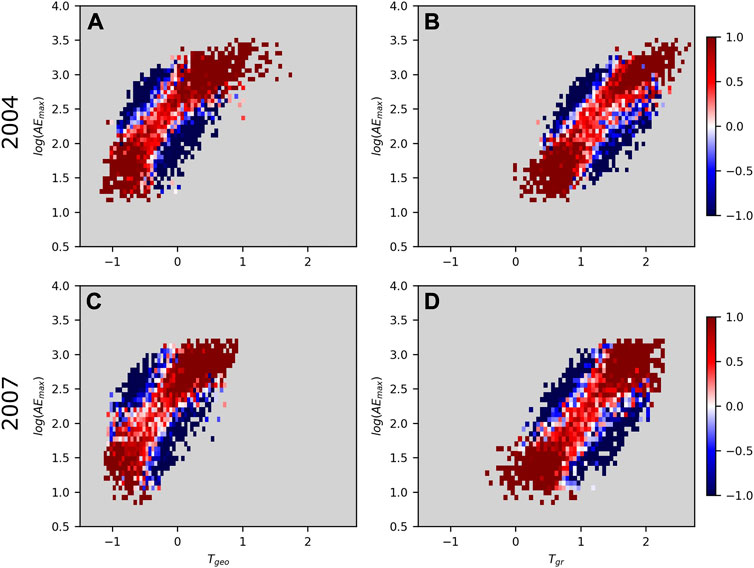
FIGURE 3. PMI map of the log₁₀AE_max and the geosynchronous ULF wave index T_geo and ground based T_gr, in panels (A) and (B) from year 2004 and panels (C) and (D) from year 2007. The color scale is saturated at values $>1$ and $<-1$, to highlight the areas where the log₁₀AE_max and T_geo∕gr occur more than twice or less than half as frequently (2^PMI) as would be expected if the variables were independent.

3.2 Geomagnetic activity vs. electron precipitation

Next, we investigate the relationship between the AE index and electron precipitation. We calculate MI and Pearson correlation coefficient for the logarithm of hourly maximum value of AE ([log₁₀  AE_max(t), log₁₀ (J_precip) (t + τ)], separately for three different energy ranges (30–100 keV, 100–300 keV and $>$300 keV) and for four different MLT sections (0–6, 6–12, 12–18, 18–24 MLT). We use the logarithm of the J_precip because it can vary over five orders of magnitude during the observed time period. Figure 4 shows the mutual information (blue dots) and Pearson correlation coefficient (black) with different time offsets ranging from ±96 h from year 2004 (as in Figure 2). Columns show the different MLT regions and rows corresponds to the different energy ranges. Positive time offset again indicates that the changes in AE precede the precipitation and negative would imply the opposite. Figure 4 shows that electron precipitation in the 30–100 keV range has a clear peak in both mutual information and Pearson correlations at all MLT sectors. In the dawn sector the peak is quite narrow, but the peak spreads and has lower correlation values in the dusk sector. The tails at positive time lags are more pronounced showing that variations in AE precede variation in electron precipitation, as expected. Results from 2007 overall show similar behaviour (see Supplementary Figure S1).

FIGURE 4

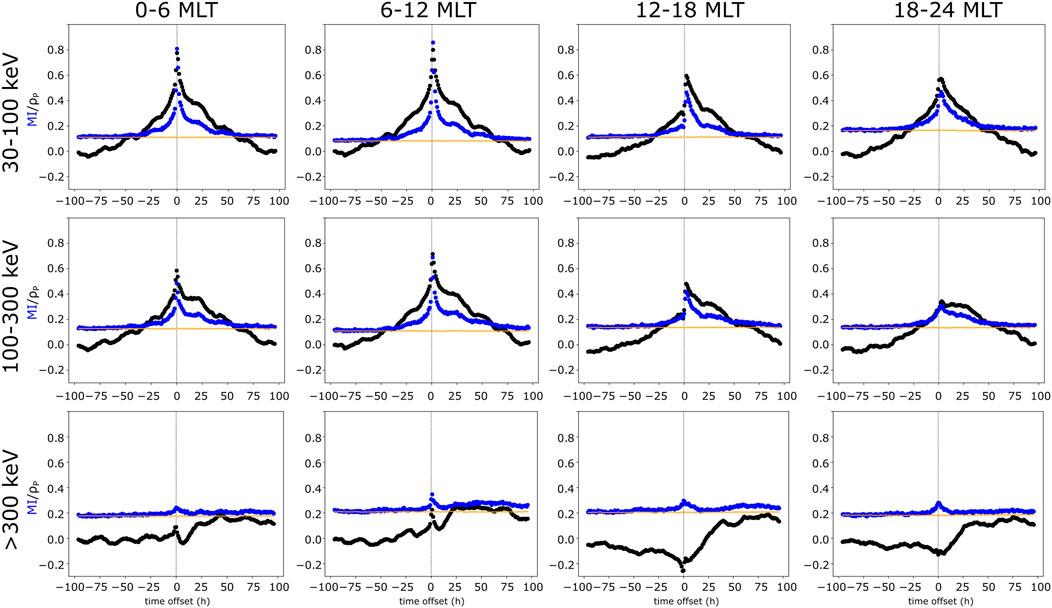
FIGURE 4. Calculation of the MI (blue) and Pearson correlation coefficient (black) between log₁₀AE_max and log₁₀ (J₃₀₋₁₀₀) (top row), log₁₀ (J_100−300) (middle row), and log₁₀ (J_>300) (bottom row) from 2004 with different time offsets [log₁₀AE_max(t), log₁₀(J) (t + τ)]. Columns show the results from different MLT regions. The orange line is the zero baseline.

For both years investigated, τ_max, maximum MI, the information adjusted correlation ρ_adj (calculated using Eq. 6) and corresponding ρ_P are listed in Table 2 and illustrated in Figure 5 as a function of MLT sector. The y-axis of the panels on the top row show the correlation coefficient and the bottom panel shows the non-linearity (Equation 7). For both 2004 and 2007, ρ_adj and ρ_P are considerably higher in the dawn side (0–6 and 6–12 MLT regions) than during the dusk hours (12–18 MLT and 18–24 MLT). The Pearson correlation coefficient decreases more when moving from early morning to evening MLTs than the information corrected correlation and, therefore, the non-linearity (Equation 7) is larger at dusk hours than at dawn hours as can be seen in the bottom panel of Figure 5. This indicates that the relationship between the AE index and precipitation of 30–100 keV electrons is more non-linear in the dusk side of the magnetosphere than at dawn. It is also interesting to note that the time lag of the maximum adjusted correlation increases with MLT. The lag is 0 at 0–6 MLT section, 1 h at 6–12 MLT and finally 2 h in the dusk corresponding to the eastward drift period of ∼30 keV equatorial electrons. The information adjusted correlation has similar values for both 2004 and 2007, while the Pearson correlation is higher and therefore, non-linearity is smaller for the geomagnetically less active year 2007.

TABLE 2

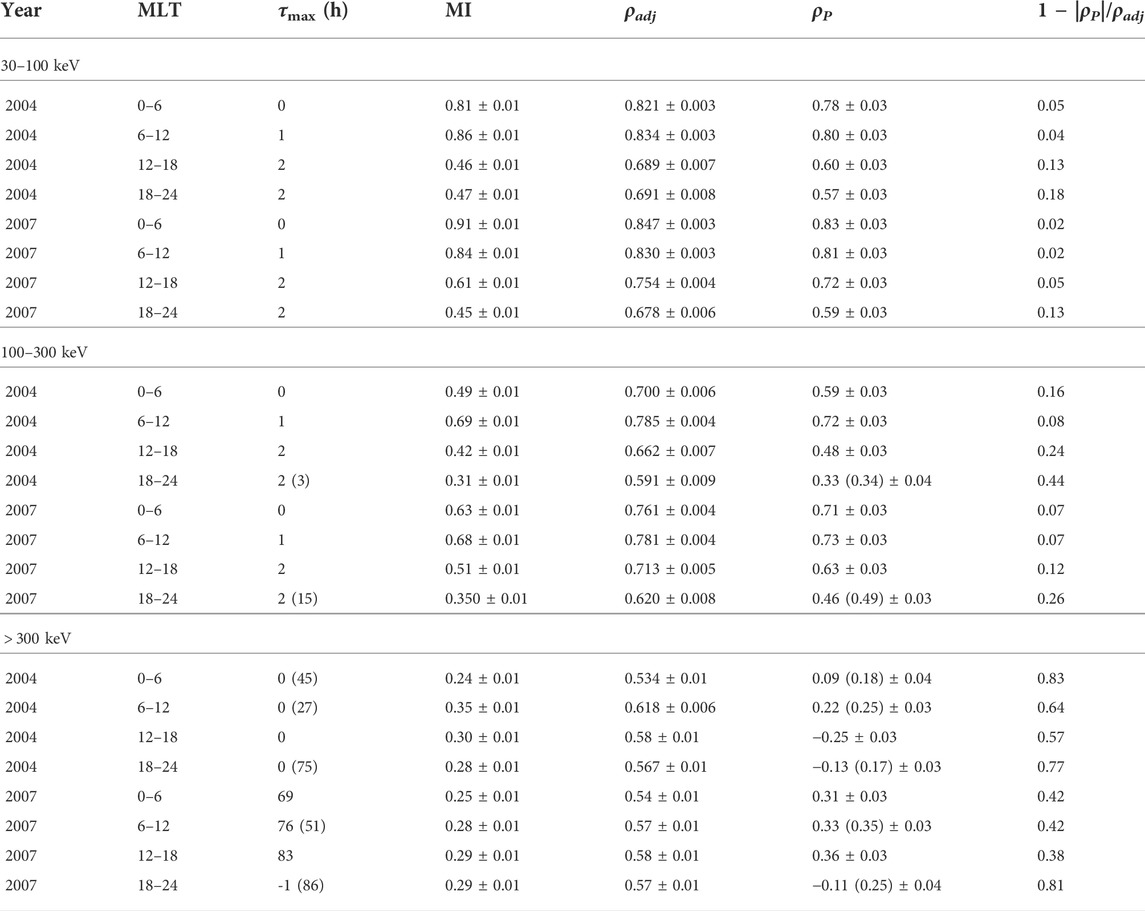
TABLE 2. Maximum value of the Mutual Information at time offset τ_max, the information adjusted correlation, ρ_adj, and Pearson correlation coefficient ρ_P, for AE index and electron precipitation in three different energy ranges [log₁₀AE_max(t), log₁₀ (J_precip) (t + τ)]. The value in the parenthesis in τ_max column indicate if the maximum of the ρ_P occur at different τ than maximum of the MI at τ_max, the corresponding ρ_P is given in the parenthesis in the sixth column.

FIGURE 5

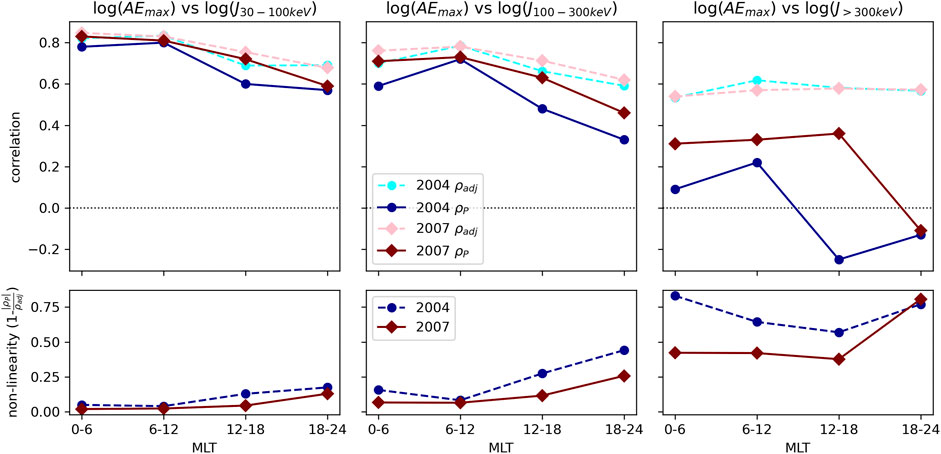
FIGURE 5. Top row shows information adjusted correlation and Pearson correlation coefficient between AE index and 30–100 keV precipitation (left column), 100–300 keV precipitation (middle column), and $>300$ keV precipitation (right). The bottom row shows the non-linearity (1 − |ρ_P|/ρ_adj) for each evaluated energy range. The darker colored data points indicate ρ_P and lighter color ρ_adj. Circles indicate results from 2004 and diamonds from 2007.

The correlation analysis of the precipitation of 100–300 keV electrons (see Table 2 and Figures 4, 5) shows similar behavior as the results for the 30–100 keV electrons discussed above. Both non-linear and Pearson correlation peak at 6–12 MLT region, and the Pearson correlation is smaller on the dusk side of the magnetosphere than in the dawn. The ρ_adj values are overall slightly lower for the 100–300 keV electrons than for the 30–100 keV electrons. The non-linearity behaves also quite similarly for the 100–300 keV electrons as for the 30–100 keV electrons, except in the dusk the drop in the Pearson correlation is more significant and therefore the increase in the non-linearity from dawn to dusk is larger.

Finally, the results clearly show that for the highest energy electrons ($>$300 keV), the correlation of the AE index and electron precipitation behave differently from the precipitation of the lower energy electrons. The information adjusted correlation remains between 0.60 and 0.67 for all MLTs. The absolute value of the Pearson correlation is low $(<0.3)$ and it changes sign with different time offsets as can be seen on the bottom row of Figure 4 and from Table 2. In some cases the Pearson correlation coefficient and MI peak with different time offsets (τ_max indicates the maximum MI), however, the Pearson correlation coefficient indicates low correlation at all time offsets between the AE index and the higher energy electrons (Figure 4).

The PMI maps for AE index and electron precipitation at different energy ranges and MLT regions from year 2004 are shown in Figure 6 (from 2007 see Supplementary Figure S2). The maps are constructed using the time offset of maximum MI (τ_max in Table 2) for the [log₁₀AE_max(t), log  J_30−100keV (t + τ_max)]. Again, the dark red (blue) regions show where the PMI $\ge 1$ $(\le -1)$, meaning that the pair of values occurs more than twice (less than half) as often together as would be expected from independent variables. These PMI maps show the change in the correlation between the AE index and the precipitating electron flux from dawn hours (0–12 MLT) to the dusk hours (12–24 MLT) and with increasing energy. For both 30–100 keV and 100–300 keV electrons the logarithm of the precipitating electron flux log (J_precip) remains below 4 during the quiet geomagnetic activity (i.e., AE_max < 300 nT) showing that there is no strong precipitation at geomagnetically quiet times. Strong precipitation (log (J_precip) > 5) can occur with wide range of AE values during medium and high activity (AE_max > 300 nT). The PMI map for $>300$ keV electrons show no linear correlation. During quiet times (AE_max < 300 nT) the PMI is positive around log (J_precip) ≈ 3 but at those flux values the PMI becomes negative with increasing AE index. The lower (log (J_precip) < 2.5) and higher (log (J_precip) > 3.5) fluxes occur more likely during increased geomagnetic activity instead. This might suggest that during increased geomagnetic activity the flux of higher energy electrons can get either increased or depleted. This could happen also in a few cases for the 100–300 keV electrons in the dusk (12–18 and 18–24 MLT sections), where PMI gets positive values also for low precipitating electron fluxes (log (J_precip) ≈ 2) during medium geomagnetic activity.

FIGURE 6

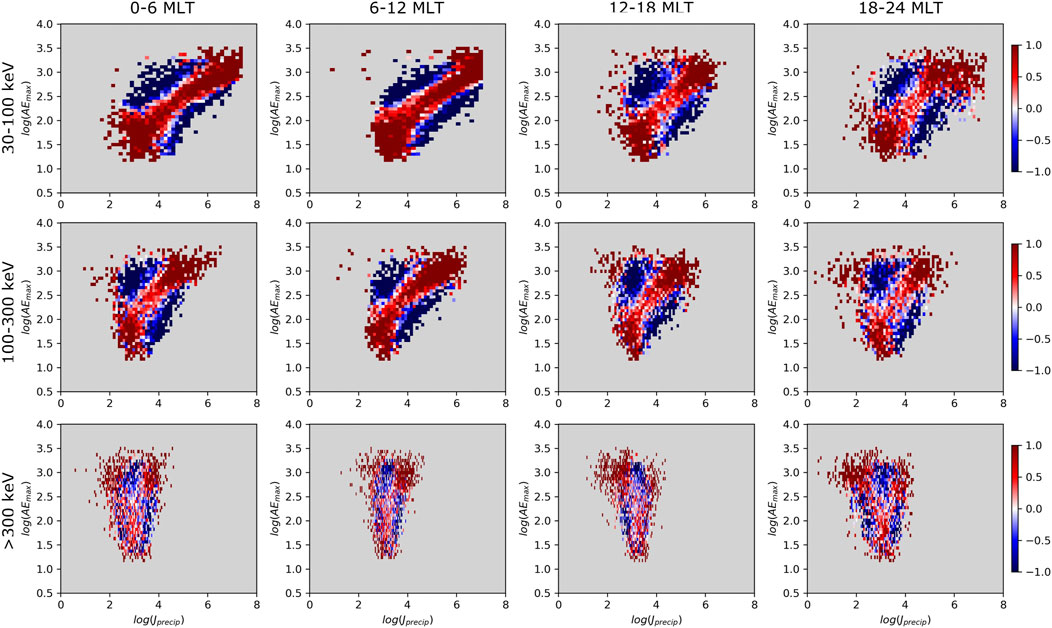
FIGURE 6. PMI map of log₁₀AE_max and log₁₀ (J₃₀₋₁₀₀) (top row), log₁₀ (J_100−300) (middle row), and log₁₀ (J_>300) (bottom row) from 2004. The columns show results from different MLT regions. Each panel is plotted with the time offset τ_max indicated in Table 2. The color scale is saturated at values $>1$ and $<-1$, to highlight the areas where the log₁₀AE_max and log₁₀ (J_precip) occur more than twice or less than half as frequently (2^PMI) as would be expected if the variables were independent.

4 Discussion and conclusions

In this paper, we used mutual information from information theory to study the linear and non-linear dependencies between the AE index as the indicator of the level of geomagnetic activity, Pc5 ULF wave activity given by the global ULF wave index and electron precipitation. We evaluate the correlations for the AE index and electron precipitation separately for three different medium energy ranges (30–100 keV, 100–300 keV, and $>$300 keV) and for four MLT regions (0–6, 6–12, 12–18, 18–24). We compared the results from two full years 2004 and 2007 representing geomagnetically more active and more quiet years, respectively. We used the logarithm of the hourly maximum of the AE index for the mutual information and the Pearson correlation coefficient calculation. We note that the calculated electron precipitation is just estimation of the total precipitated flux that could be overestimated during periods of high trapped flux and underestimated during time periods of low trapped flux but high precipitated flux.

Radiation belt electrons at medium energies from tens to a few hundreds of keVs that are injected from the magnetotail during substorms are typically called source electrons as they act as the source of the whistler mode chorus waves. Previous studies have shown that both the precipitating and trapped electrons within this energy range in the outer radiation belts are well correlated with the AE index (e.g. Katsavrias et al., 2021; Nesse Tyssøy et al., 2021). Our results are consistent with the previous studies and show that both the mutual information and Pearson correlation coefficient between AE index and electron precipitation in the energy ranges 30–100 keV and 100–300 keV indicate strong linear correlation (ρ_P > 0.78) on the dawn side of the magnetosphere. A recent statistical analysis over a full solar cycle of daily averaged data by Nesse Tyssøy et al. (2021) showed that the AE index is a good proxy for the precipitation of $\ge 30$keV energy electrons. The authors used electron precipitation from NOAA/POES at three energy ranges ($>43$ keV, $>114$ keV and $>292$ keV), and found that the electrons from the lowest of these energy ranges respond to the AE fastest and the correlation is largest, while the correlation decreases and the time lag increases with increasing energy of the precipitating electrons being 2 days for the $>292$ keV electrons. This is consistent especially with year 2007 (see Table 2; Supplementary), where the non-linear and linear correlation increases with larger time offsets especially at MLT sectors 6–12 and 12–18.

The drift period of equatorial electrons within the 30–100 keV energy range at L shells 5 to 7 varies between 1 and 5 h. These times correspond well with the increasing time lag of the maximum information adjusted correlation between the AE index and the electron precipitation. At MLTs 0–6 the correlation peaks within the first hour (0 time lag). As the electrons drift eastward the MI peaks with one hour time lag at the MLT 6–12 and in the dusk side of the magnetosphere the time lag is two hours. As the electrons drift they excite chorus waves. This generation process itself causes precipitation of source energy electrons and the chorus waves also start interacting and causing precipitation of seed energy ($\sim 300-700$ keV) electrons. The time lags for the peak mutual information between AE and higher energy electrons ($>300$ keV) occur at zero time offset for 2004 and multiple days for 2007 (Table 2). The linear correlation coefficients peak with couple of days delay also for 2004, although the Pearson correlation values indicate no significant ($\le 0.3$ for 2004) or low correlation ($\le 0.36$ for 2007). These results could reflect the dominance of precipitating of seed energy electrons that start immediately as the chorus waves are generated. The effect progresses gradually to higher energies (e.g., Jaynes et al., 2015b).

We find that the linear Pearson correlation between the AE index and electron precipitation in the energy range from 30–300 keV decrease from dawn to dusk, while the decrease in the mutual information (and the information adjusted correlation) is relatively smaller with MLT compared to the Pearson correlation. Our results, therefore, indicate that the linear statistical dependence between the AE index and precipitating electrons is stronger at MLTs$<$12, while relationship appears to be more non-linear from noon to evening sector (MLT$>$12). Previous studies have shown that the chorus wave activity driven by the source electrons injected from the magnetotail during the substorm activity have been found to correlate well with the precipitation of the 30–100 keV electrons outside the plasmapause (e.g., Lam et al., 2010; Chen et al., 2014). Chorus waves are mainly exited between 0–12 MLT (e.g., Meredith et al., 2020), therefore, it is likely that they are the main cause of the high linear correlation observed between AE index and 30–300 keV electron precipitation at dawn. The cause of the persisting non-linear relationship between AE index and the precipitating electrons at dusk may be related to excitation of multiple different wave modes and their combined effect of scattering the electrons to the loss cone. In the dusk, the EMIC waves are the dominating cause of the precipitation of the MeV electrons, but they have been found to be responsible also of precipitation of sub-MeV electrons down to $\sim 100$ keV (e.g., Blum et al., 2019; Hendry et al., 2019). Other possible wave modes that are known to precipitate electrons from a few tens to a few hundred keV range at dusk are magnetosonic mode (e.g., Ma et al., 2016) and hiss (inside the plasmasphere) (e.g., Ma et al., 2021). Another factor causing larger non-linearity in the dusk may be the related to the changes and asymmetries of the electron convection and drift trajectories. Some electrons that drift around the Earth might get lost from the radiation belts before they reach the dusk side or they may end up outside the L shell range investigated in this study.

The Pearson correlation coefficient between the AE index and the electron precipitation at energies 30–100 keV and 100–300 keV is lower for geomagnetically more active year 2004 than for a quieter year 2007 within all other MLT sectors except 6–12, where the high correlation between AE index and electron precipitation is maintained for different solar cycle phases even when typical drivers of geomagnetic activity are different. The difference in the information adjusted correlation between the 2 years is smaller than difference in the linear correlations. In 2004 significant part of the observed geomagnetic activity is driven by ICMEs while in 2007 the activity is mainly caused by SIRs and HSSs (e.g. Asikainen and Ruopsa, 2016; Kilpua et al., 2017). Previous studies have shown that the geomagnetic activity driven by ICMEs is different from HSS driven activity (e.g., Holappa et al., 2014; Asikainen and Ruopsa, 2016). ICMEs are responsible for driving intense geomagnetic storm and the magnetospheric response can vary depending on the properties of the ICMEs (e.g., Borovsky and Denton, 2006), while the substorm process is mainly driven by HHSs (e.g., Tanskanen et al., 2005). Therefore, our results indicate that during geomagnetic activity driven by SIRs and HSSs, the dependency between the AE index and electron precipitation remains more linear while the ICME driven activity cause the response of the inner magnetospheric processes leading to particle precipitation on the dusk side to become more non-linear because ICMEs cause strong and rapid changes in the inner magnetosphere that could vary significantly depending on the properties of the ICMEs.

The non-linearity of the correlation between the AE index and the global ULF wave indices is small for both geosynchronous and groundbased indices. The Pearson correlation coefficient is a little bit smaller than the information adjusted correlation suggesting that some non-linearities could be present but they are not very significant. The correlation coefficients between the AE index and the global ULF wave indices do not show significant difference between the 2 years studied. The information adjusted correlation is slightly smaller for 2007 than 2004, but the difference does not impact the non-linearity significantly. Therefore, the correlation analysis of the AE index and global Pc5 ULF wave indices suggest that the level of the non-linearity does not depend on the level of the geomagnetic activity or its driver (ICMEs in 2004 and SIRs ans HSSs in 2007 as discussed above).

In summary, this study shows that non-linearity of the correlation between the geomagnetic activity indicated by the AE index and the precipitation of the medium energy electrons is dependent on the energy of the electrons and MLT. The non-linear correlation between the AE index and electrons in the energy ranges 30–100 keV and 100–300 keV persist at all MLTs while the significant linear dependence is only present on the pre-noon hours. The linear correlation between the AE index and the electron precipitation is also lower during the geomagnetically more active year when larger portion of the geomagnetic activity is driven by ICMEs. This suggests that during the geomagnetic activity driven by ICMEs the magnetosphere becomes more non-linear or there is a larger variability between each ICME driven storm compared to SIR and HSS driven activity. The correlation analysis between the AE index and ULF Pc5 indices, on the other hand, shows that the non-linearity between the geomagnetic activity and ULF Pc5 wave activity is not very high and it is not affected by the different drivers and intensity of the geomagnetic activity of the 2 years studied.

Author contributions

SH performed the data analysis and wrote the paper. All coauthors assisted with the interpretation of the results and provided comments on the paper. TA provided the POES data that included the corrections from the proton contamination and other instrumental problems. MS wrote the analysis scripts used in this study to analyse the data.

Funding

This research has been supported by the Finnish Centre of Excellence in Research of Sustainable Space, Project 1312390. EKJK acknowledges the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme Project SolMAG 724391, and Academy of Finland project 1310445. AO and MS acknowledge funding from the Academy of Finland by the profiling action on Matter and Materials (grant no. 318913). HG acknowledges the Consolidator grant 682068-PRESTISSIMO. TA was supported by the Academy of Finland via PRediction of SPace climate and its Effects in ClimaTe, PROSPECT, (Project 321440) research project.

Acknowledgments

We gratefully acknowledge the Finnish Center of Excellence in Research of Sustainable Space and the Academy of Finland for their funding.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.987913/full#supplementary-material

References

Artemyev, A. V., Vasiliev, A. A., Mourenas, D., Agapitov, O. V., Krasnoselskikh, V., Boscher, D., et al. (2014). Fast transport of resonant electrons in phase space due to nonlinear trapping by whistler waves. Geophys. Res. Lett. 41, 5727–5733. doi:10.1002/2014GL061380

CrossRef Full Text | Google Scholar

Asikainen, T. (2017). “Calibrated and corrected POES/MEPED energetic particle observations,” in The ESPAS e-infrastructure: Access to data in near-Earth space. Editors A. Belehaki, M. Hapgood, and J. Watermann (Les Ulis, France: EDP Science), 57–69. doi:10.1051/978-2-7598-1949-2

CrossRef Full Text | Google Scholar

Asikainen, T., and Mursula, K. (2013). Correcting the noaa/meped energetic electron fluxes for detector efficiency and proton contamination. J. Geophys. Res. Space Phys. 118, 6500–6510. doi:10.1002/jgra.50584

CrossRef Full Text | Google Scholar

Asikainen, T., and Ruopsa, M. (2016). Solar wind drivers of energetic electron precipitation. J. Geophys. Res. Space Phys. 121, 2209–2225. doi:10.1002/2015JA022215

CrossRef Full Text | Google Scholar

Baker, D. N., Hoxie, V., Zhao, H., Jaynes, A. N., Kanekal, S., Li, X., et al. (2019). Multiyear measurements of radiation belt electrons: Acceleration, transport, and loss. JGR. Space Phys. 124, 2588–2602. doi:10.1029/2018JA026259

PubMed Abstract | CrossRef Full Text | Google Scholar

Blum, L., Artemyev, A., Agapitov, O., Mourenas, D., Boardsen, S., and Schiller, Q. (2019). Emic wave-driven bounce resonance scattering of energetic electrons in the inner magnetosphere. JGR. Space Phys. 124, 2484–2496. doi:10.1029/2018JA026427

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Denton, M. H. (2006). Differences between cme-driven storms and cir-driven storms. J. Geophys. Res. 111, A07S08. doi:10.1029/2005JA011447

CrossRef Full Text | Google Scholar

Cameron, T. G., Jackel, B., and Oliveira, D. M. (2019). Using mutual information to determine geoeffectiveness of solar wind phase fronts with different front orientations. JGR. Space Phys. 124, 1582–1592. doi:10.1029/2018JA026080

CrossRef Full Text | Google Scholar

Chen, L., and Hasegawa, A. (1991). Kinetic theory of geomagnetic pulsations 1. Internal excitations by energetic particles. J. Geophys. Res. 96, 1503–1512. doi:10.1029/90JA02346

CrossRef Full Text | Google Scholar

Chen, Y., Reeves, G. D., Friedel, R. H. W., and Cunningham, G. S. (2014). Global time-dependent chorus maps from low-earth-orbit electron precipitation and van allen probes data. Geophys. Res. Lett. 41, 755–761. doi:10.1002/2013GL059181

CrossRef Full Text | Google Scholar

Claudepierre, S. G., Elkington, S. R., and Wiltberger, M. (2008). Solar wind driving of magnetospheric ULF waves: Pulsations driven by velocity shear at the magnetopause. J. Geophys. Res. 113, A05218. doi:10.1029/2007JA012890

CrossRef Full Text | Google Scholar

Claudepierre, S. G., Hudson, M. K., Lotko, W., Lyon, J. G., and Denton, R. E. (2010). Solar wind driving of magnetospheric ULF waves: Field line resonances driven by dynamic pressure fluctuations. J. Geophys. Res. 115, A11202. doi:10.1029/2010JA015399

CrossRef Full Text | Google Scholar

Cover, T. M., and Thomas, J. A. (2006). Elements of information theory. Second Edition. Hoboken, New Jersey: John Wiley & Sons.

Google Scholar

Davis, T. N., and Sugiura, M. (1966). Auroral electrojet activity index ae and its universal time variations. J. Geophys. Res. 71, 785–801. doi:10.1029/JZ071i003p00785

CrossRef Full Text | Google Scholar

Elkington, S. R., Hudson, M. K., and Chan, A. A. (1999). Acceleration of relativistic electrons via drift-resonant interaction with toroidal-mode pc-5 ulf oscillations. Geophys. Res. Lett. 26, 3273–3276. doi:10.1029/1999GL003659

CrossRef Full Text | Google Scholar

Elkington, S. R., Hudson, M. K., and Chan, A. A. (2003). Resonant acceleration and diffusion of outer zone electrons in an asymmetric geomagnetic field. J. Geophys. Res. 108, 1116. doi:10.1029/2001JA009202

CrossRef Full Text | Google Scholar

Freedman, D., and Diaconis, P. (1981). On the histogram as a density estimator:l2 theory. Z. Wahrscheinlichkeitstheorie Verw. Geb. 57, 453–476. doi:10.1007/bf01025868

CrossRef Full Text | Google Scholar

George, H., Kilpua, E., Osmane, A., Asikainen, T., Kalliokoski, M. M. H., Rodger, C. J., et al. (2020). Outer Van Allen belt trapped and precipitating electron flux responses to two interplanetary magnetic clouds of opposite polarity. Ann. Geophys. 38, 931–951. doi:10.5194/angeo-38-931-2020

CrossRef Full Text | Google Scholar

Hargreaves, J. K., Birch, M. J., and Evans, D. S. (2010). On the fine structure of medium energy electron fluxes in the auroral zone and related effects in the ionospheric D-region. Ann. Geophys. 28, 1107–1120. doi:10.5194/angeo-28-1107-2010

CrossRef Full Text | Google Scholar

Hendry, A. T., Santolik, O., Kletzing, C. A., Rodger, C. J., Shiokawa, K., and Baishev, D. (2019). Multi-instrument observation of nonlinear emic-driven electron precipitation at sub–mev energies. Geophys. Res. Lett. 46, 7248–7257. doi:10.1029/2019GL082401

CrossRef Full Text | Google Scholar

Holappa, L., Mursula, K., and Asikainen, T. (2014). A new method to estimate annual solar wind parameters and contributions of different solar wind structures to geomagnetic activity. J. Geophys. Res. Space Phys. 119, 9407–9418. doi:10.1002/2014JA020599

CrossRef Full Text | Google Scholar

Hudson, M. K., Denton, R. E., Lessard, M. R., Miftakhova, E. G., and Anderson, R. R. (2004). A study of pc-5 ulf oscillations. Ann. Geophys. 22, 289–302. doi:10.5194/angeo-22-289-2004

CrossRef Full Text | Google Scholar

Hwang, K. J., and Sibeck, D. G. (2016). Role of low-frequency boundary waves in the dynamics of the dayside magnetopause and the inner magnetosphere. Wash. D.C. Am. Geophys. Union Geophys. Monogr. Ser. 216, 213–239. doi:10.1002/9781119055006.ch13

CrossRef Full Text | Google Scholar

James, M. K., Yeoman, T. K., Mager, P. N., and Klimushkin, D. Y. (2016). Multiradar observations of substorm-driven ulf waves. J. Geophys. Res. Space Phys. 121, 5213–5232. doi:10.1002/2015JA022102

CrossRef Full Text | Google Scholar

Jaynes, A. N., Baker, D. N., Singer, H. J., Rodriguez, J. V., Loto’aniu, T. M., Ali, A. F., et al. (2015a). Source and seed populations for relativistic electrons: Their roles in radiation belt changes. JGR. Space Phys. 120, 7240–7254. doi:10.1002/2015JA021234

CrossRef Full Text | Google Scholar

Jaynes, A. N., Lessard, M. R., Takahashi, K., Ali, A. F., Malaspina, D. M., Michell, R. G., et al. (2015b). Correlated pc4–5 ulf waves, whistler-mode chorus, and pulsating aurora observed by the van allen probes and ground-based systems. JGR. Space Phys. 120, 8749–8761. doi:10.1002/2015JA021380

CrossRef Full Text | Google Scholar

Johnson, J. R., and Wing, S. (2005). A solar cycle dependence of nonlinearity in magnetospheric activity. J. Geophys. Res. 110. doi:10.1029/2004JA010638

CrossRef Full Text | Google Scholar

Kasahara, S., Miyoshi, Y., Yokota, S., Mitani, T., Kasahara, Y., Matsuda, S., et al. (2018). Pulsating aurora from electron scattering by chorus waves. Nature 554, 337–340. doi:10.1038/nature25505

PubMed Abstract | CrossRef Full Text | Google Scholar

Katsavrias, C., Aminalragia–Giamini, S., Papadimitriou, C., Sandberg, I., Jiggens, P., Daglis, I., et al. (2021). On the interplanetary parameter schemes which drive the variability of the source/seed electron population at geo. JGR. Space Phys. 126, e2020JA028939. doi:10.1029/2020JA028939

CrossRef Full Text | Google Scholar

Kellerman, A. C., and Shprits, Y. Y. (2012). On the influence of solar wind conditions on the outer-electron radiation belt. J. Geophys. Res. 117. doi:10.1029/2011JA017253

CrossRef Full Text | Google Scholar

Kennel, C. F., and Petschek, H. E. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. 71, 1–28. doi:10.1029/JZ071i001p00001

CrossRef Full Text | Google Scholar

Kepko, L., and Spence, H. E. (2003). Observations of discrete, global magnetospheric oscillations directly driven by solar wind density variations. J. Geophys. Res. 108, 1257. doi:10.1029/2002JA009676

CrossRef Full Text | Google Scholar

Kilpua, E., Koskinen, H. E. J., and Pulkkinen, T. I. (2017). Coronal mass ejections and their sheath regions in interplanetary space. Living Rev. Sol. Phys. 14, 5. doi:10.1007/s41116-017-0009-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Kozyreva, O., Pilipenko, V., Engebretson, M., Yumoto, K., Watermann, J., and Romanova, N. (2007). In search of a new ulf wave index: Comparison of pc5 power with dynamics of geostationary relativistic electrons. Planet. Space Sci.Ultra-Low Freq. Waves Magnetos. 55, 755–769. doi:10.1016/j.pss.2006.03.013

CrossRef Full Text | Google Scholar

Kraskov, A., Stögbauer, H., and Grassberger, P. (2004). Estimating mutual information. Phys. Rev. E 69, 066138. doi:10.1103/PhysRevE.69.066138

CrossRef Full Text | Google Scholar

Lam, M. M., Horne, R. B., Meredith, N. P., Glauert, S. A., Moffat-Griffin, T., and Green, J. C. (2010). Origin of energetic electron precipitation >30 kev into the atmosphere. J. Geophys. Res. 115. doi:10.1029/2009JA014619

CrossRef Full Text | Google Scholar

Li, W., and Hudson, M. K. (2019). Earth’s van allen radiation belts: From discovery to the van allen probes era. JGR. Space Phys. 124, 8319–8351. doi:10.1029/2018JA025940

CrossRef Full Text | Google Scholar

Li, W. (1990). Mutual information functions versus correlation functions. J. Stat. Phys. 60, 823–837. doi:10.1007/BF01025996

CrossRef Full Text | Google Scholar

Li, W., Thorne, R. M., Ma, Q., Ni, B., Bortnik, J., Baker, D. N., et al. (2014). Radiation belt electron acceleration by chorus waves during the 17 March 2013 storm. JGR. Space Phys. 119, 4681–4693. doi:10.1002/2014JA019945

CrossRef Full Text | Google Scholar

Ma, Q., Li, W., Thorne, R. M., Bortnik, J., Kletzing, C. A., Kurth, W. S., et al. (2016). Electron scattering by magnetosonic waves in the inner magnetosphere. JGR. Space Phys. 121, 274–285. doi:10.1002/2015JA021992

CrossRef Full Text | Google Scholar

Ma, Q., Li, W., Zhang, X. J., Bortnik, J., Shen, X. C., Connor, H. K., et al. (2021). Global survey of electron precipitation due to hiss waves in the earth’s plasmasphere and plumes. JGR. Space Phys. 126, e2021JA029644. doi:10.1029/2021JA029644

CrossRef Full Text | Google Scholar

Mann, I. R., Lee, E. A., Claudepierre, S. G., Fennell, J. F., Degeling, A., Rae, I. J., et al. (2013). Discovery of the action of a geophysical synchrotron in the Earth’s Van Allen radiation belts. Nat. Commun. 4, 2795. doi:10.1038/ncomms3795

CrossRef Full Text | Google Scholar

Mann, I. R., Ozeke, L. G., Murphy, K. R., Claudepierre, S. G., Turner, D. L., Baker, D. N., et al. (2016). Explaining the dynamics of the ultra-relativistic third Van Allen radiation belt. Nat. Phys. 12, 978–983. doi:10.1038/nphys3799

CrossRef Full Text | Google Scholar

Meredith, N. P., Horne, R. B., Shen, X.-C., Li, W., and Bortnik, J. (2020). Global model of whistler mode chorus in the near-equatorial region (—λ_m— 18). Geophys. Res. Lett. 47, e87311. doi:10.1029/2020GL087311

CrossRef Full Text | Google Scholar

Nesse Tyssøy, H., Partamies, N., Babu, E. M., Smith-Johnsen, C., and Salice, J. A. (2021). The predictive capabilities of the auroral electrojet index for medium energy electron precipitation. Front. Astron. Space Sci. 8, 167. doi:10.3389/fspas.2021.714146

CrossRef Full Text | Google Scholar

Nesse Tyssøy, H., Sinnhuber, M., Asikainen, T., Bender, S., Clilverd, M. A., Funke, B., et al. (2022). Heppa iii intercomparison experiment on electron precipitation impacts: 1. Estimated ionization rates during a geomagnetic active period in april 2010. JGR. Space Phys. 127, e2021JA029128. doi:10.1029/2021JA029128

CrossRef Full Text | Google Scholar

Newell, P. T., and Gjerloev, J. W. (2011). Evaluation of supermag auroral electrojet indices as indicators of substorms and auroral power. J. Geophys. Res. 116. doi:10.1029/2011JA016779

CrossRef Full Text | Google Scholar

Ni, B., Thorne, R. M., Shprits, Y. Y., and Bortnik, J. (2008). Resonant scattering of plasma sheet electrons by whistler-mode chorus: Contribution to diffuse auroral precipitation. Geophys. Res. Lett. 35, L11106. doi:10.1029/2008GL034032

CrossRef Full Text | Google Scholar

Ni, B., Thorne, R. M., Zhang, X., Bortnik, J., Pu, Z., Xie, L., et al. (2016). Origins of the earth’s diffuse auroral precipitation. Space Sci. Rev. 200, 205–259. doi:10.1007/s11214-016-0234-7

CrossRef Full Text | Google Scholar

Nishimura, Y., Bortnik, J., Li, W., Thorne, R. M., Lyons, L. R., Angelopoulos, V., et al. (2010). Identifying the driver of pulsating aurora. Science 330, 81–84. doi:10.1126/science.1193186

PubMed Abstract | CrossRef Full Text | Google Scholar

Osmane, A., Savola, M., Kilpua, E., Koskinen, H., Borovsky, J. E., and Kalliokoski, M. (2022). Quantifying the non-linear dependence of energetic electron fluxes in the earth’s radiation belts with radial diffusion drivers. Ann. Geophys. 40, 37–53. doi:10.5194/angeo-40-37-2022

CrossRef Full Text | Google Scholar

Rae, I. J., Donovan, E. F., Mann, I. R., Fenrich, F. R., Watt, C. E. J., Milling, D. K., et al. (2005). Evolution and characteristics of global Pc5 ULF waves during a high solar wind speed interval. J. Geophys. Res. 110, A12211. doi:10.1029/2005JA011007

CrossRef Full Text | Google Scholar

Reeves, G. D., McAdams, K. L., Friedel, R. H. W., and O’Brien, T. P. (2003). Acceleration and loss of relativistic electrons during geomagnetic storms. Geophys. Res. Lett. 30, 1529. doi:10.1029/2002GL016513

CrossRef Full Text | Google Scholar

Reeves, G. D., Morley, S. K., Friedel, R. H. W., Henderson, M. G., Cayton, T. E., Cunningham, G., et al. (2011). On the relationship between relativistic electron flux and solar wind velocity: Paulikas and blake revisited. J. Geophys. Res. 116. doi:10.1029/2010JA015735

CrossRef Full Text | Google Scholar

Rodger, C. J., Kavanagh, A. J., Clilverd, M. A., and Marple, S. R. (2013). Comparison between poes energetic electron precipitation observations and riometer absorptions: Implications for determining true precipitation fluxes. J. Geophys. Res. Space Phys. 118, 7810–7821. doi:10.1002/2013JA019439

CrossRef Full Text | Google Scholar

Shi, X., Baker, J. B. H., Ruohoniemi, J. M., Hartinger, M. D., Murphy, K. R., Rodriguez, J. V., et al. (2018). Long-lasting poloidal ULF waves observed by multiple satellites and high-latitude SuperDARN radars. JGR. Space Phys. 123, 8422–8438. doi:10.1029/2018JA026003

PubMed Abstract | CrossRef Full Text | Google Scholar

Shprits, Y. Y., Elkington, S. R., Meredith, N. P., and Subbotin, D. A. (2008). Review of modeling of losses and sources of relativistic electrons in the outer radiation belt I: Radial transport. J. Atmos. Solar-Terrestrial Phys. 70, 1679–1693. doi:10.1016/j.jastp.2008.06.008

CrossRef Full Text | Google Scholar

Simms, L. E., Engebretson, M. J., Clilverd, M. A., Rodger, C. J., and Reeves, G. D. (2018). Nonlinear and synergistic effects of ulf pc5, vlf chorus, and emic waves on relativistic electron flux at geosynchronous orbit. J. Geophys. Res. Space Phys. 123, 4755–4766. doi:10.1029/2017JA025003

CrossRef Full Text | Google Scholar

Simms, L. E., Engebretson, M. J., Rodger, C. J., Dimitrakoudis, S., Mann, I. R., and Chi, P. J. (2021). The combined influence of lower band chorus and ulf waves on radiation belt electron fluxes at individual l-shells. JGR. Space Phys. 126, e2020JA028755. doi:10.1029/2020JA028755

CrossRef Full Text | Google Scholar

Su, Z., Zhu, H., Xiao, F., Zong, Q. G., Zhou, X. Z., Zheng, H., et al. (2015). Ultra-low-frequency wave-driven diffusion of radiation belt relativistic electrons. Nat. Commun. 6, 10096. doi:10.1038/ncomms10096

PubMed Abstract | CrossRef Full Text | Google Scholar

Tanskanen, E. I., Slavin, J. A., Tanskanen, A. J., Viljanen, A., Pulkkinen, T. I., Koskinen, H. E. J., et al. (2005). Magnetospheric substorms are strongly modulated by interplanetary high-speed streams. Geophys. Res. Lett. 32, L16104. doi:10.1029/2005GL023318

CrossRef Full Text | Google Scholar

Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013). Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504, 411–414. doi:10.1038/nature12889

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, R. M., Ni, B., Tao, X., Horne, R. B., and Meredith, N. P. (2010). Scattering by chorus waves as the dominant cause of diffuse auroral precipitation. Nature 467, 943–946. doi:10.1038/nature09467

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Allen, J. A. (1981). “Observations of high intensity radiation by satellites 1958 Alpha and 1958 Gamma,” in Space science comes of age: Perspectives in the history of the space Sciences. Editors P. A. Hanle, V. D. Chamberlain, and S. G. Brush, 58–73.

Google Scholar

Wang, C.-P., Thorne, R., Liu, T. Z., Hartinger, M. D., Nagai, T., Angelopoulos, V., et al. (2017). A multispacecraft event study of Pc5 ultralow-frequency waves in the magnetosphere and their external drivers. JGR. Space Phys. 122, 5132–5147. doi:10.1002/2016JA023610

CrossRef Full Text | Google Scholar

Wing, S., Johnson, J. R., Camporeale, E., and Reeves, G. D. (2016). Information theoretical approach to discovering solar wind drivers of the outer radiation belt. JGR. Space Phys. 121, 9378–9399. doi:10.1002/2016JA022711

CrossRef Full Text | Google Scholar

Wing, S., Johnson, J. R., Turner, D. L., Ukhorskiy, A., and Boyd, A. J. (2021). Untangling the solar wind and magnetospheric drivers of the radiation belt electrons. Earth Space Sci. Open Archive 66. doi:10.1002/essoar.10508584.1

CrossRef Full Text | Google Scholar

Yamakawa, T., Seki, K., Amano, T., Takahashi, N., and Miyoshi, Y. (2019). Excitation of storm time pc5 ulf waves by ring current ions based on the drift-kinetic simulation. Geophys. Res. Lett. 46, 1911–1918. doi:10.1029/2018GL081573

CrossRef Full Text | Google Scholar

Zhang, X. Y., Zong, Q.-G., Wang, Y. F., Zhang, H., Xie, L., Fu, S. Y., et al. (2010). Ulf waves excited by negative/positive solar wind dynamic pressure impulses at geosynchronous orbit. J. Geophys. Res. 115. doi:10.1029/2009JA015016

CrossRef Full Text | Google Scholar

Zolotukhina, N. A., Mager, P. N., and Klimushkin, D. Y. (2008). Pc5 waves generated by substorm injection: A case study. Ann. Geophys. 26, 2053–2059. doi:10.5194/angeo-26-2053-2008

CrossRef Full Text | Google Scholar

Zong, Q., Rankin, R., and Zhou, X. (2017). The interaction of ultra-low-frequency pc3-5 waves with charged particles in Earth’s magnetosphere. Rev. Mod. Plasma Phys. 1, 10. doi:10.1007/s41614-017-0011-4

CrossRef Full Text | Google Scholar