- 1Fesenkov Astrophysical Institute, Almaty, Kazakhstan
- 2Department of Physics and Technology, Al-Farabi Kazakh National University, Almaty, Kazakhstan
Within the modified potential cluster model (MPCM) with forbidden states, the total cross sections are calculated for capture in the ground and first excited states of the 9Li nucleus in the n8Li channel in the energy range from 10−5 eV to 5 MeV based on Е1 and M1 transitions. The experimentally proved resonance at Ec.m. = 0.232 MeV in the 4P5/2 wave and ab initio-predicted 4P3/2 resonance at 1.32 MeV [Phys. Rev. C 103, 035801 (2021)] are considered. The strong impact of the asymptotic constant and channel spectroscopic factors on the total capture cross sections are responsible for the variation in the absolute values within factor two. As a consequence, the thermal cross sections are
1 Introduction
The implication of an 8Li(n,γ)9Li reaction is under discussion since it was included in the following primordial nucleosynthesis chain suggested by Mao and Champagne (1991) and Kajino (1995):
The experimental study of the 8Li(n,γ)9Li reaction performed using the Coulomb dissociation method reported by Zecher et al. (1998) is still the only study since 1998 and provides only two cross-section points. The promising prospect for new experimental measurements is reported in the recent proposal of the study of the breakup of 9Li on a 208Pb target at a different energy regime (Gupta et al., 2022). This process is included in one of the chains of primordial nucleosynthesis.
Since this reaction plays a bridge role from the synthesis of light-seed nuclei A ≤ 7 to the heavy elements, theoretical model calculations are in high demand. The early theoretical calculations of cross sections and reaction rates presented by Malaney et al. (1988), Mao and Champagne (1991), Thielemann et al. (1991), Descouvemont (1993), Rauscher et al. (1994), Bertulani (1999), Kobayashi et al. (2003), Li et al. (2005), Guimarães et al. (2007), Banerjee et al. (2008), and Ma et al. (2012) differ significantly from each other (see Table 6 in Section 7 for details). A modern investigation of the 8Li(n,γ)9Li reaction is provided by microscopic models by McCracken et al. (2021) and Dong et al. (2022).
It is important to note that along with the sequence (1), other branching options involving 8Li are possible: for example, the chain 7Li(n,γ)8Li(α,n)11B(n,γ)12B(β+)12C was suggested as a possible explanation for the production of A ≥ 12 nuclides, observed in very metal-poor stars (Paradellis et al., 1990). Paradellis et al. (1990) raised a series of studies of the 8Li(α,n)11B reaction, covering the test of an inhomogeneous Big Bang model (Cherubini et al., 2004), as well as C-N-O Big Bang nucleosynthesis (BBN) (Su-Qing et al., 2010) at temperatures T9 = 0.5–1.2. The key role of the 8Li(α,n)11B reaction is recognized in the production of seed nuclei at T9 = 2.5–5, later burnt to heavier elements via r-capture reactions, during type II supernova explosions (La Cognata and Del Zoppo, 2011). It is worth noting that the reaction 8Li(α,n)11B has been more extensively studied than the radiative neutron capture on 8Li, but their rates differ from each other within an order of magnitude (Das et al., 2017; Mondal et al., 2022). Hence, the continuation of the 7Li(n,γ)8Li chain remains an open area of investigation, and further studies are needed. Specifically, there is no definitive conclusion regarding the comparability of the reaction rates for 8Li(n,γ)9Li and 8Li(α,n)11B during the crucial temperature range of a standard BBN from 0.1 to 1 T9.
Present consideration of the 8Li(n,γ)9Li reaction is performed in the framework of the modified potential cluster model (MPCM) (Dubovichenko, 2015; Dubovichenko, 2019). This model is based on classifying discrete and continuum orbital states by Young diagrams {f}, which effectively includes the Pauli principle while constructing the corresponding wave functions. Our results (Dubovichenko and Dzhazairov-Kakhramanov, 2016) need to be considered due to our recent research on the 7Li(n,γ)8Li reaction (Burkovа et al., 2021). It was suggested that for the 8Li nucleus, it is necessary to use the Young diagram {431} instead of {44}, assumed previously in Dubovichenko and Dzhazairov-Kakhramanov (2016). Such a diagram changed the entire structure of forbidden and allowed states for the interaction potentials in the n + 8Li channel. Therefore, we examined this effect while calculating the total cross sections and reaction rates. The low-lying resonance at Jπ = 5/2− at the energy Ex = 4.296(15) MeV is considered in comparison with our previous study (Dubovichenko and Dzhazairov-Kakhramanov, 2016).
Recently, the properties of 9Li-bound states and low-lying resonances were studied within the no-core shell model with continuum (NCSMC) (McCracken et al., 2021). The authors note that the ab initio-calculated 7Li(n,γ)8Li total cross section at the energies 20 keV to 1.6 MeV in the center-of-mass reference frame is nearly a factor two higher than that of our previous result (Dubovichenko and Dzhazairov-Kakhramanov, 2016). In the present work, we explain the origin of this discrepancy and come to an acceptable agreement with McCracken et al. (2021). The results of the low-temperature reaction rates at T9 < 1 still remain in question.
Radiative neutron capture reaction rates on 6,7,8Li nuclei are compared to estimate the “neutron poisoning” lithium isotope destruction.
This work is organized as follows: Section 2 presents the main aspects of the MPCM. Section 3 covers calculation methods. Classification of orbital states and interaction potentials are given in Section 4 and Section 5, respectively. Section 6 presents the total cross sections. Reaction rates are provided in Section 7. The conclusion is given in Section 8.
2 A brief review of the MPCM
The MPCM has been used to calculate the astrophysical S-factor and total cross section of a number of reactions (Dubovichenko, 2015; Dubovichenko, 2019), also employing the classification of orbital states according to the Young diagrams (Nemets et al., 1988; Neudatchin et al., 1992). The main feature of the MPCM is the concept of states forbidden by the Pauli principle, which are orthogonal to the allowed states. The interaction potentials are constructed to fit this orthogonality condition (Dubovichenko and Uzikov, 2011). The evident success of the MPCM in describing the total cross sections of 40 radiative capture reactions is proved, under the assumption of two-body clustering both in initial and final channels, in monographs (Dubovichenko, 2015; Dubovichenko, 2019) and reviews (Dubovichenko and Dzhazairov-Kakhramanov, 2017).
The MPCM was introduced in one of our papers about 10 years ago [see (Dubovichenko et al., 2013)], but in terms of meaning and calculation methods, we have operated with this model since the 1980s (Dubovichenko and Zhusupov, 1984a; Dubovichenko and Zhusupov, 1984b; Dubovichenko and Dzhazairov-Kakhramanov, 1990; Dubovichenko et al., 1990). It is important to note that the first classification of cluster states, according to Young diagrams, was introduced in the works of V. G. Neudatchin et al. in the early 1970s (Neudatchin et al., 1971; Neudatchin et al., 1972). We extended this theory to other light nuclei with A ≤ 8 (Itzykson and Nauenberg, 1966; Dubovichenko, 1997).
The basic principles of the MPCM are formulated in an extended version in recent papers (Dubovichenko et al., 2022a; Dubovichenko et al., 2023a). In summary, the MPCM is a two-particle model that accounts for the internal characteristics of clusters, such as their sizes, charges, and masses. The Pauli principle is implemented via the exclusion of the forbidden states, manifesting in proper node behavior of the radial wave function. Potentials of the bound states are constructed based on asymptotic constants and binding energies. Potentials of the scattering processes are built based on the spectra of the final nucleus or the scattering phase shifts of the particles of the input channel. Parameters of the potentials are fixed or variable within the asymptotic constant error intervals and vary within the energy or width errors of resonant or excited states. The radial wave functions of both continuous and discrete states are constructed to match the appropriate asymptotic behaviors.
3 Calculation methods
We use well-known formulas for the total cross sections and matrix elements for the operators of electromagnetic NJ transitions (Dubovichenko, 2015; Dubovichenko, 2019). These expressions are given in reviews (Angulo et al., 1999; Dubovichenko, 1997):
The matrix elements of convection electric EJ transitions have the following form:
The spin part of the magnetic dipole process M1(S) at J = 1 is defined as
The notations in Eqs 2–8, i.e., Si, Sf, Lf, Li, Ji, and Jf, are the spins, orbital, and total angular momentums in the initial (i) and final (f) channels; m1, m2, Z1, and Z2 are the masses and charges of the particles of the initial channel; IJ is the integral over the radial wave functions of initial χi and final χf states, and the radial part of the multiple operators; m = m1+m2; and μ1 and μ2 are the magnetic moments of the clusters.
The neutron mass m1 = mn = 1.00866491597 amu (NIST, 2019), and the 8Li mass is
The radial scattering and bound state functions χi and χf in the overlap integrals
The asymptotic normalization coefficient (ANC) ANC is related to the experimental asymptotic constant C by the following expression (Mukhamedzhanov and Tribble, 1999):
where Sf is the spectroscopic factor and C is the dimensional asymptotic constant (AC), which is also represented in terms of the asymptotic wave functions:
For a continuous spectrum,
The calculating methods of other quantities within the framework of the MPCM, i.e., root-mean mass and charge radii or binding energy, are given, for example, in our works (Dubovichenko, 2015; Dubovichenko, 2019; Dubovichenko and Dzhazairov-Kakhramanov, 2015). The energies of bound states are searched for by the finite difference method outlined by Dubovichenko (2012), Dubovichenko (2015), and Dubovichenko (2019). One can use the variational method to control the correctness of these energies, and such a procedure has been used, for example, by La Cognata and Del Zoppo (2011), Das et al. (2017), and in Supplementary Appendix SA of the study by Dubovichenko and Dzhazairov-Kakhramanov (2015). It should be noted that the accuracy of searching for the binding energy by these methods in some cluster systems can reach up to 10 meV or 0.01 eV (Dubovichenko et al., 2017). The calculation details for a number of cluster systems are presented in books (La Cognata and Del Zoppo, 2011; Das et al., 2017) and reviews (Neudatchin et al., 1992; Tilley et al., 2002; Dubovichenko, 2012; Dubovichenko and Dzhazairov-Kakhramanov, 2015; Sukhoruchkin and Soroko, 2016; Dubovichenko et al., 2017; Burkovа et al., 2021).
4 Classification and structure of 9Li states
For the 8Li nucleus, as shown by Burkovа et al. (2021), we consider the Young orbital diagram (431), so for the n8Li system, we consider {431} × {1} = {531} + {441} + {432}. The diagram {531} corresponds to L = 1, 2, and 3 and is forbidden since the s-shell cannot contain five nucleons (Neudatchin et al., 1992). Allowed diagrams {441} and {432} may be put in compliance with the GS of the 9Li nucleus in the n8Li channel alone with the orbital angular momentum L = 1. Following Neudatchin et al. (1992), the scattering states turn out to be mixed by {441} + {432} diagrams, while the bound states refer only to the {441} diagram. It should be noted that forbidden states appear as bound only in both discrete and continuous spectra.
To reconstruct the GS total angular momentum, parity, and isospin Jπ, Т = 3/2−, 3/2 of 9Li, we used the 8Li data Jπ, Т = 2+, 1 obtained by Tilley et al. (2002). The spin channel n + 8Li is defined by the vector addition of 8Li and n total spins, i.e., S = 2 + 1/2, and allows two states S = 3/2 and S = 5/2. Therefore, a spin-mixed 4+6P3/2 state is possible for the GS (in the spectral notation 2S+1LJ), but we consider it a pure 4P3/2 state. There is only one excited state at an energy of 2.691(5) MeV relative to the GS and binding energy Eb = −1.3729(5) MeV. The first excited state (1st ES) with Jπ = 1/2− is assumed a 4P1/2 state.
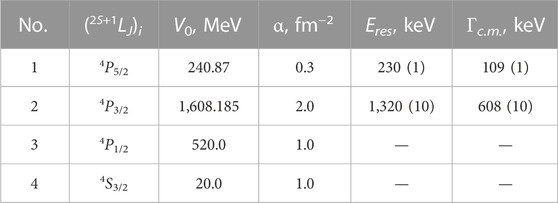
Figure 1 illustrates the spectrum of the 9Li nucleus in the n8Li channel. The reliable, experimentally confirmed complete data on the total angular momentum, parity, excitation energy Ex, and width Γc.m. are known for the first resonant state only (Tilley et al., 2002; Sukhoruchkin and Soroko, 2016).

FIGURE 1. Energy spectrum of 9Li in MeV (Tilley et al., 2002; Sukhoruchkin and Soroko, 2016). Data (*) comprise the ab initio prediction of McCracken et al. (2021).
This state with Jπ = 5/2− is located at an excitation energy Ex = 4.296(15) MeV relative to GS or 0.232(15) MeV relative to the threshold energy Eth of the n8Li channel. Such a state is considered as a quartet 4P5/2 wave. Dubovichenko (2012) and Dubovichenko et al. (2017)reported the width Γc.m. = 100(30) keV. Based on these data, it is possible to construct a completely unambiguous 4P5/2 elastic scattering potential with a bound forbidden state. The variations in potential parameters may come only within the accuracy of the resonance width.
The second excited state at Ex = 5.38(6) MeV [1.32(6) MeV above Eth] with the width Γc.m. = 600(100) keV is identified as a 3/2− state in recent works (McCracken et al., 2021). For the third excited state, experimental data provide a value of Ex at 6.430(15) MeV and Γc.m. = 40(20) keV, but the total angular momentum and parity 7/2− were only predicted by McCracken et al. (2021). We consider the strong E1 and M1 transitions as the estimation of E2 transition shows its minor role (Dubovichenko and Dzhazairov-Kakhramanov, 2016).
Table 1 presents all treated transitions to the ground and first excited states of 9Li in the n8Li channel and
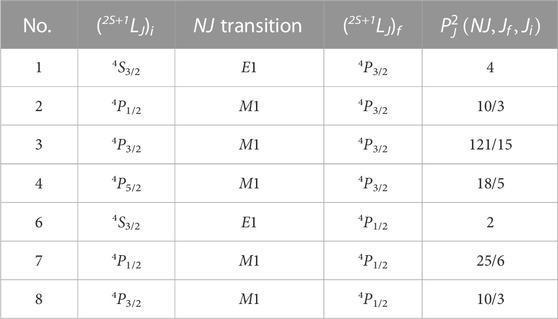
TABLE 1. Multipole transitions to GS and first ES of the 9Li nucleus in the n8Li channel and coefficients
5 Interaction potentials
To construct the interaction potentials for the scattering states, we used the resonant-state parameters Ex, Γc.m., and Jπ. Non-resonant waves are provided by the potentials leading to the phase shifts close to zero (if there are no forbidden states), or to 180o if such a state appears in the classification of orbital states according to the Young diagrams.
The parameters of bound state potentials are conditioned by reproducing the data on the binding energy, matter, and charge radii, and the asymptotic constant (Dubovichenko, 2015; Dubovichenko, 2019; Dubovichenko and Dzhazairov-Kakhramanov, 2015).
The nuclear two-body interaction potential is represented as a Gaussoid (Dubovichenko, 2015; Dubovichenko, 2019):
5.1 Continuous spectrum
The potential parameters of Eq. 12 are listed in Table 2. These reproduce well the data on the 4P5/2 and 4P3/2 resonant states (Tilley et al., 2002; Sukhoruchkin and Soroko, 2016). As for the non-resonant-state 4P1/2, the corresponding potential is deep enough to include the forbidden state. The S-wave does not appear in the 9Li spectrum neither as the bound state nor as the resonant state. Therefore, the corresponding potential in Table 2 might lead to zero or near-zero phase shifts.
The corresponding calculated phase shifts are shown in Figure 2. The
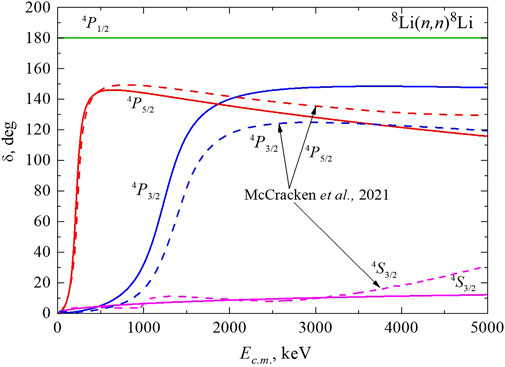
FIGURE 2. Phase shifts of elastic n8Li scattering: solid curves are the results of MPCM calculations with the potential parameters given in Table 2; dashed curves are ab initio results obtained by McCracken et al. (2021) (digitalized).
The comparison between phase shifts obtained in the MPCM and ab initio NCSMC calculations [digitalized data obtained by McCracken et al. (2021)] is shown in Figure 2. Phase shifts
5.2 Discrete spectrum
The following data on the ANC are considered to build the GS potential. The experimental values are deduced from the data on the neutron transfer reaction 8Li(d,p)9Lig.s. obtained by Guimarães et al. (2006). ANC = 0.96(8) fm−1/2, and in the study by Tilley et al. (2002), ANC = 1.15(14) fm−1/2. Their average value ANC = 1.06(10) fm−1/2 agrees with the results obtained by Timofeyuk (2013), who reported a calculated value of 1.08 fm−1/2 for ANC GS. Timofeyuk (2013) also provided theoretical values of the spectroscopic factors 0.6 and 1.1 obtained by two methods, which correspond to an average value of Sf = 0.85(25). Other data on the spectroscopic factors are given in Table 3.
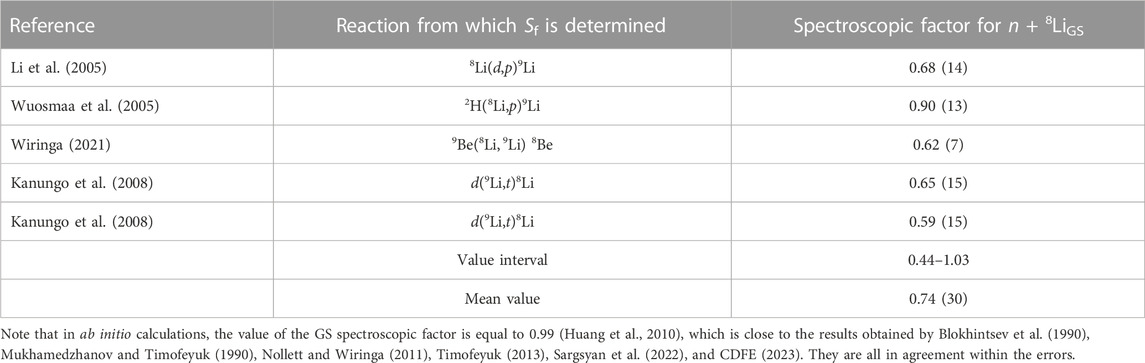
TABLE 3. Spectroscopic factors for the GS of 9Li in the n + 8Li channel from the studies by Li et al. (2005), Wuosmaa et al. (2005), Kanungo et al. (2008), and Wiringa (2021).
Estimation within the aforementioned limits for ANC = 0.88–1.29 fm−1/2, and the range for the spectroscopic factor Sf = 0.44–1.03 (Table 3) results in Cw = 0.95–2.03. In recent ab initio extended network calculations, ANC = 1.23(6) fm−1/2 was reported, along with spectroscopic factors Sf = 0.83–1.06 (Mukhamedzhanov and Timofeyuk, 1990). At the edges of these intervals, we obtain Cw = 1.30–1.42.
Huang et al. (2010) and Sargsyan et al. (2022)obtained, for the first ES of the 9Li nucleus, ANC = 0.4 fm−1/2 (unfortunately, no uncertainties are available) at Sf = 0.55, which leads to C = 0.54 fm−1/2 or the dimensionless constant Cw = 0.77 at Sf = 0.698.
In CDFE (2023) for GS, the calculations yield ANC = 1.140(13) fm−1/2, and for the first ES, ANC = 0.308(7) fm−1/2, which leads to Сw = 0.60(1) at Sf = 0.55. Timofeyuk (2013) reported, for the first ES, ANC = 0.33 fm−1/2 at
The potential parameters for the bound ground and excited states of the 9Li in n8Li channel are summarized in Table 4. In the present calculations, we use an 8Li radius equal to 2.327 ± 0.0298 fm (Sánchez et al., 2007). The radius of 9Li is 2.2462 ± 0.0315 fm (Sánchez et al., 2007). Nörtershäuser et al. (2005)used radii values 2.299(32) fm for 8Li and 2.217(35) fm for 9Li. Dubovichenko et al. (2022b) obtained, for these radii, 2.30(4) fm and 2.24(4) fm. The neutron charge radius is assumed to be zero, and the mass radius of 0.8414 fm coincides with the known proton radius (NIST, 2019).

TABLE 4. Parameters of the bound ground and excited state potentials of the 9Li in n8Li channel and calculated asymptotic constant Cw, Rch, and Rm radii, and binding energy Eb.
The upper and lower sets refer to the GS and first ES interaction potentials, respectively, defined in Table 4, and differ by the Cw values but lead to the same binding channel energy.
6 Total cross sections of radiative n8Li capture
The results of the present calculation of the integral total and partial cross sections are shown in Figure 3A. Strong sensitivity on the Cw values is observed for the upper and lower sets. The input of the first ES into the total cross sections is negligible if compared with that of the GS in both cases. The dipole electric E1 transition from the 4S3/2 wave to 4P3/2, 1/2 bound states provides low-energy cross sections and serves as a base for the resonant magnetic M1 transitions. Both resonances 4P5/2 and 4P3/2 are present at the energies ∼230 keV and 1.32 MeV.
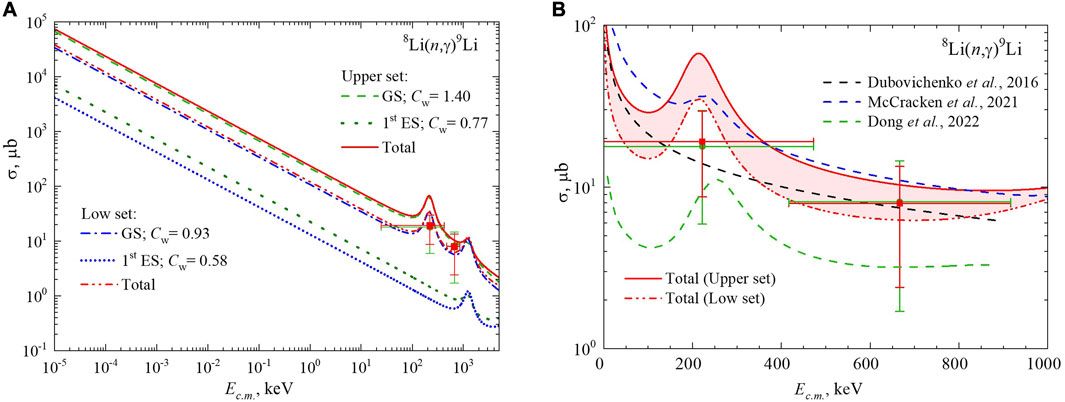
FIGURE 3. Total cross sections of radiative 8Li(n,γ)9Li capture in the GS and first ES of the 9Li nucleus. Experimental data on 9Li Coulomb dissociation obtained by Zecher et al. (1998): green dots on the Pb target and red squares on the U target. (A) MPCM calculations are explained in the legend. (B) Comparison of the MPCM and microscopic calculations: present MPCM total cross sections are the same as in panel (A), the blue dashed curve shows the ab initio results obtained by McCracken et al. (2021), and the green dashed curve shows the results obtained by Dong et al. (2022) (digitalized). The black dashed curve shows our previous results obtained by Dubovichenko and Dzhazairov-Kakhramanov (2016).
The comparison of the cross sections calculated in the MPCM and within the microscopic models (McCracken et al., 2021; Dong et al., 2022), along with the experimental data (Zecher et al., 1998), is shown in Figure 3B. The red band is obtained by varying Cw between 0.93 and 1.4. The results on σ(E) obtained by Dong et al. (2022) differ essentially in the whole energy range and reach the lower error bar limits only. Therefore, it is more reasonable to compare the MPCM and ab initio results obtained by McCracken et al. (2021). The difference is observed at the energies close to the first resonance 4P5/2: the lower set (red dash-double-dotted curve) and ab initio cross sections (blue dashed curve) are comparable, contrary to the upper set application (red solid curve). Out of the resonance range Ec.m. > 300 keV and up to 1 MeV, the upper set and ab initio cross sections practically coincide and fit the second experimental point fairly well. The low-energy cross-section part is discussed in the following sections.
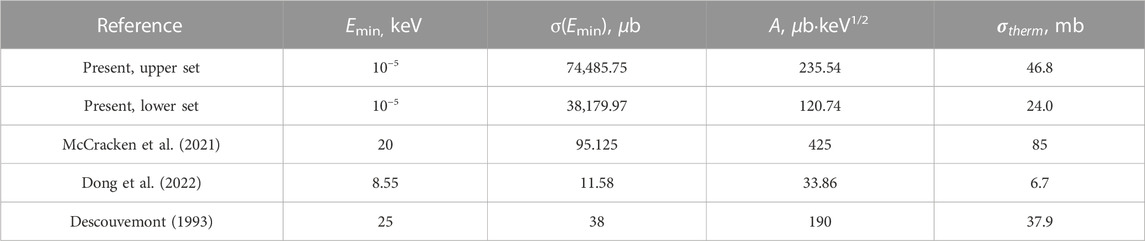
The total capture cross section of thermal and cold neutrons shows the following energy dependence (Dubovichenko, 2015; Dubovichenko, 2019):
Based on one available point, the σ(Emin) constant A(μb·keV1/2) is determined, and calculation of the thermal cross section at 25.3 meV may be implemented according to Eq. 13. The results on
A comparison between various
7 Reaction rate of radiative n8Li capture
The well-known expression for the radiative neutron capture reaction rate in terms of the Maxwellian averaged cross sections is
where E is expressed in MeV, the total cross section σ(E) is represented in μb, μ is the reduced mass in amu, and T9 is the temperature in 109 K (Norman and Schramm, 1979). Based on the total cross sections shown in Figure 3A, the corresponding reaction rates are presented in Figure 4A. The band refers to the upper and lower sets of GS and first ES interaction potentials, as shown in Table 4, applied to calculate total cross sections. The temperature dependence of
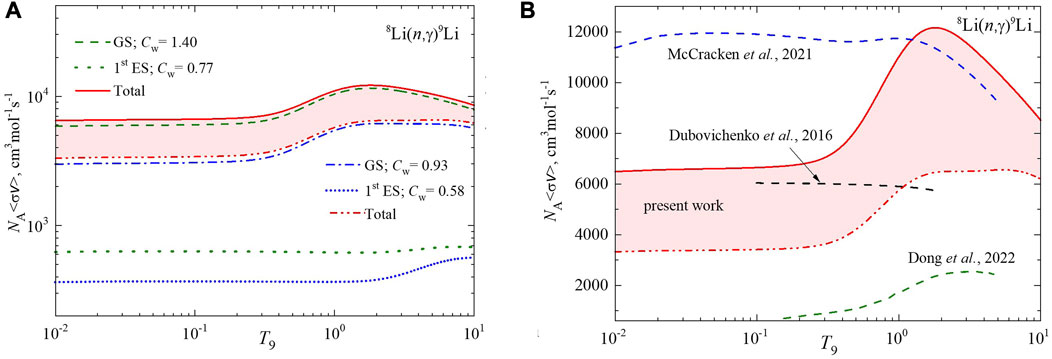
FIGURE 4. Reaction rate of radiative 8Li(n,γ)9Li capture to the GS and first ES of 9Li. (A) MPCM calculations are explained in the legend. (B) Comparison of MPCM and microscopic calculations: present MPCM reaction rates are the same as in panel (A), the blue dashed curve shows the ab initio results obtained by McCracken et al. (2021), and the green dashed curve shows the results obtained by Dong et al. (2022) (digitalized). The black dashed curve shows our previous results from Dubovichenko and Dzhazairov-Kakhramanov (2016).
A comparison of MPCM new results and calculations obtained by McCracken et al. (2021) and Dong et al. (2022), as well as our early data obtained by Dubovichenko and Dzhazairov-Kakhramanov (2016), is presented in Figure 4B. The ab initio reaction rate (McCracken et al., 2021) (blue dashed curve) exceeds our results at low temperatures and approximately coincides in the resonance region. A noticeable decrease in
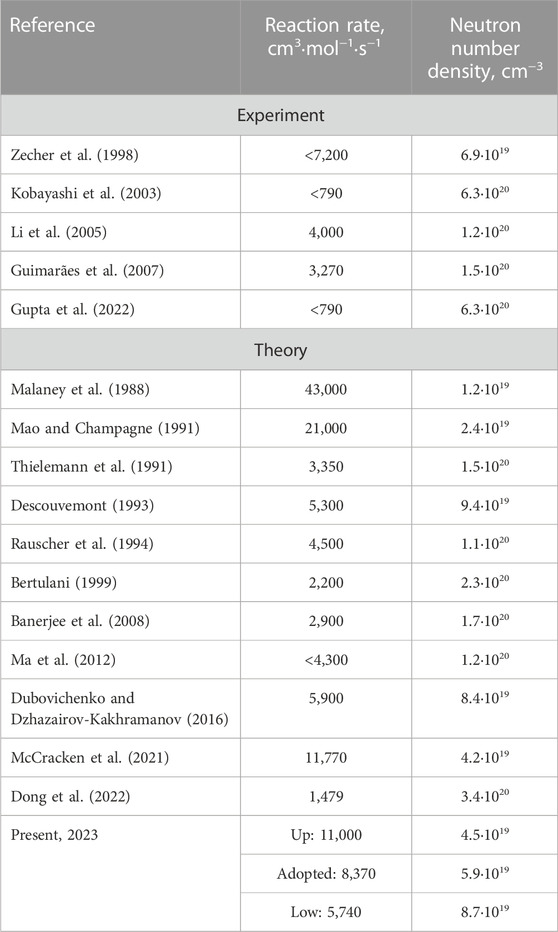
Since 1988 (Malaney et al., 1988), significant efforts have been made to find the consensus on the reaction rate value at T9 = 1, useful in the context of BBN. Table 6 shows the comparison of different results for the reaction rates, which are partially taken from the studies by Kobayashi et al. (2003), Banerjee et al. (2008), Dubovichenko and Dzhazairov-Kakhramanov (2016), and Dong et al. (2022).
We complemented the data on the reaction rates with the neutron number densities nn, which may be referred to as the r-process ignition threshold density since it is calculated under the condition of equality of the 8Li mean lifetime and neutron capture time τβ ≈ τ(n,γ) following the general definitions of the Nuclear Data Evaluation Project (2021):
The isotope 8Li is unstable with a half-life time t1/2 = 838.79 ± 0.36 ms (Kajino et al., 2019) or τβ = 1.186 s. The estimated neutron number densities nn given in Table 6 condition the start of the r-process on 8Li at T9 = 1 and lay in the interval 1.2·1019–6.3·1020 cm−3, which brings forth a difference of up to the factor 50 with respect to the listed datasets. Following the study by Dubovichenko et al. (2019), the typical conditions for the r-process nn∼3·1023 cm−3 and T9∼1 require both an explosive environment and high-density neutron-rich matter. In this context, the difference in the reaction rate data given in Table 6 seems not so crucial.
We still see a challenge in finding any cross-points that allow us to resolve the problem of variable 8Li(n,γ)9Li reaction rates. One point we assume is related to the thermal cross sections for the 6,7,8Li isotopes discussed in Section 6 (Table 5). Another one is based on our experience of studying the radiative capture reaction rates on the group of the neighboring isotopes. For example, it was found that low-temperature reaction rates for 10-13B(n,γ)11-14B conditioned by the S-wave capture outside of the resonance energy region show some regularity—the higher the channel threshold, the higher the reaction rate (Dubovichenko et al., 2020; Dubovichenko et al., 2021; Dubovichenko et al., 2023a; Dubovichenko et al., 2023b). The same effect is observed for the proton capture on the nitrogen isotopes 12,13,15N(p,γ)13,14,16O (Kubono et al., 2016), and an exception is given by the reaction 14N(p,γ)15O as S-wave capture occurs via a weak E2 transition contrary to more advanced E1 or M1.
Figure 5 shows the reactions rates on lithium isotopes 6,7,8Li calculated in the MPCM. We observe that the order of magnitude of
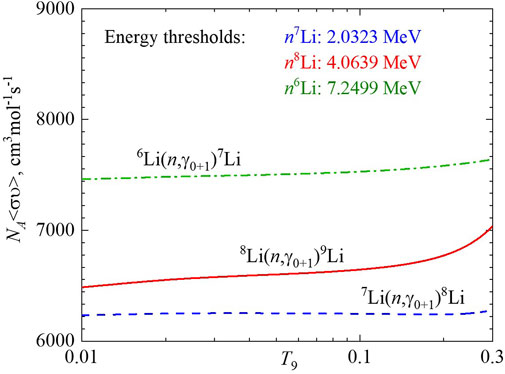
FIGURE 5. The reaction rates of radiative neutron capture for 6Li(n,γ0+1)7Li (Firestone and Revay, 2016), 7Li(n,γ0+1)8Li (Burkovа et al., 2021), and 8Li(n,γ0+1)9Li present results for the upper set in Figure 4. Threshold energies Eth are given in square brackets.
8 Conclusion
Following our new results on the 7Li(n,γ0+1)8Li reaction (Burkovа et al., 2021), we reconsider the reaction 8Li(n,γ0+1)9Li. The total cross sections and reaction rates are calculated for the reaction 8Li(n,γ0+1)9Li, including the corrections inserted for the interaction potentials comparing the early work (Dubovichenko and Dzhazairov-Kakhramanov, 2016).
The experimentally proved resonance at Ec.m. = 0.232 MeV in the 4P5/2 wave and ab initio-predicted 4P3/2 resonance at 1.32 MeV (McCracken et al., 2021) are considered. The intensity of 4P5/2 resonance depends strongly on the range of asymptotic constants Cw, as well as the cross sections as a whole, which is observed in the temperature T9 dependence of the reaction rates.
The minor role of the (n,γ1) process is proved; therefore, the GS transitions are dominant. The variation in the GS asymptotic constant Cw = 0.93–1.40 leads to the values of the reaction rate 5,740–11,000 cm3·mol−1·s−1 at temperature T9 = 1 relevant for the r-formation of 9Li. The upper value nearly coincides with the ab initio reaction rate 11,770 cm3·mol−1·s−1 at T9 = 1 (McCracken et al., 2021), but we acknowledge this agreement as occasional.
We suggest two criteria to narrow down the range of reaction rates in our study. The first one concerns the values of thermal cross sections. Analysis of
The second criterion is related to the reaction rates of radiative neutron capture on lithium isotopes 6,7,8Li. The examined correlation between the energy thresholds and order of reaction rates at low temperatures beyond the possible resonances T9 < 0.2 leads to the conclusion that upper-set calculations are more reasonable (see Figure 5).
The recent results on the reaction rates obtained by McCracken et al. (2021) and Dong et al. (2022) show substantial differences, both qualitative and quantitative. The present calculations do not eliminate this discrepancy. The new measurements proposed by Gupta et al. (2022) may clarify the situation.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
The work was supported by the grant of the Ministry of Education and Science of the Republic of Kazakhstan, No. AP09259021.
Acknowledgments
The authors sincerely thank P. Navratil for providing the numerical results on the cross section and reaction rate obtained by McCracken et al. (2021), and discussing some issues.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1251743/full#supplementary-material
References
Angulo, C., Arnould, M., Rayet, M., Descouvemont, P., Baye, D., Leclercq-Willain, C., et al. (1999). A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 656, 3–183. doi:10.1016/S0375-9474(99)00030-5
Banerjee, P., Chatterjee, R., and Shyam, R. (2008). Coulomb dissociation of 9Li and the rate of the 8Li(n,γ)9Li reaction. Phys. Rev. C 78, 035804. doi:10.1103/PhysRevC.78.035804
Bertulani, C. A. (1999). The astrophysical reaction 8Li(n,γ)9Li from measurements by reverse kinematics. J. Phys. G Nucl. Part. Phys. 25, 1959–1963. doi:10.1088/0954-3899/25/9/313
Blokhintsev, L. D., Mukhamedzhanov, A. M., and Timofeyuk, N. K. (1990). The vertex constant of virtual decay t→d+n and a nucleon-nucleon potential. Ukranian J. Phys. 35, 341–345.
Burkovа, N. A., Dubovichenkо, S. B., Dzhazairov-Kakhramanov А, V., and Nurakhmetova, S. Z. (2021). Comparative role of the 7Li(n,γ)8Li reaction in Big Bang nucleosynthesis. J. Phys. G Nucl. Part. Phys. 48, 045201. doi:10.1088/1361-6471/abe2b5
Caughlan, G. R., and Fowler, W. A. (1988). Thermonuclear reaction rates V. A. T. Data Nucl. Data Tables 40, 283–334. doi:10.1016/0092-640X(88)90009-5
CDFE (2023). Chart of nucleus shape and size parameters. Available at: http://cdfe.sinp.msu.ru/cgi-bin/muh/radcard.cgi?z=3& a=9& td=123456 (Accessed June 1, 2023).
Cherubini, S., Figuera, P., Musumarra, A., Agodi, C., Alba, R., Calabretta, L., et al. (2004). 8Li(α,n)11B at big bang temperatures: neutron counting with a low intensity 8Li radioactive beamn. AIP Conf. Proc. 701, 68–72. doi:10.1063/1.1691688
Coc, A. (2016). Primordial nucleosynthesis. J. Phys. Conf. Ser. 665, 012001. doi:10.1088/1742-6596/665/1/012001
Das, S. K., Fukuda, T., Mizoi, Y., Ishiyama, H., Miyatake, H., Watanabe, Y. X., et al. (2017). New measurement of the 8Li(α,n)11B reaction in a lower-energy region below the Coulomb barrier. Phys. Rev. C 95, 055805. doi:10.1103/PhysRevC.95.055805
Descouvemont, P. (1993). The 8Li(n,γ)9Li and 8B(p,γ)9C mirror reactions in a microscopic cluster model. Astrophys. J. 405, 518. doi:10.1086/172383
Dong, G. X., Wang, X. B., Michel, N., and Płoszajczak, M. (2022). Gamow shell model description of the radiative capture reaction 8Li(n,γ)9Li. Phys. Rev. C 105, 064608. doi:10.1103/PhysRevC.105.064608
Dubovichenko, S., Dzhazairov-Kakhramanov, A., and Afanasyeva, N. (2013). Radiative neutron capture on 9Be, 14C, 14N, 15N and 16O at thermal and astrophysical energies. Int. J. Mod. Phys. E 22, 1350075. doi:10.1142/S0218301313500754
Dubovichenko, S., and Dzhazairov-Kakhramanov, A. (2017). Study of the nucleon radiative captures 8Li(n,γ)9Li, 9Be(p,γ)10B, 10Be(n,γ)11Be, 10B(p,γ)11C, and 16O(p,γ)17F at thermal and astrophysical energies. Int. J. Mod. Phys. E 26, 1630009. doi:10.1142/S0218301316300095
Dubovichenko, S. B., Burkova, N. A., and Dzhazairov-Kakhramanov, A. V. (2019). Influence of low-lying resonances on reaction rates for 10B(n,γ)11B capture. Nucl. Phys. A 992, 121625. doi:10.1016/j.nuclphysa.2019.121625
Dubovichenko, S. B., Burkova, N. A., Dzhazairov-Kakhramanov, A. V., and Tkachenko, A. S. (2020). Influence of resonances on the 11B(n,γ)12B capture reaction rate. Capture to the ground state of 12B. Astropart. Phys. 123, 102481. doi:10.1016/j.astropartphys.2020.102481
Dubovichenko, S. B., Burkova, N. A., Dzhazairov-Kakhramanov, A. V., and Yertaiuly, A. (2021). 12B(n,γ)13B reaction as an alternative path to astrophysical synthesis of 13C isotope. Nucl. Phys. A 1011, 122197. doi:10.1016/j.nuclphysa.2021.122197
Dubovichenko, S. B., Burkova, N. A., Kezerashvili, R. Y., Tkachenko, A. S., and Yeleusheva, B. M. (2023b). The astrophysical S−factor and reaction rate for 15N(p,γ)16O within the modified potential cluster model. arXiv:2303.14680v2 [nucl-th].
Dubovichenko, S. B., Burkova, N. A., Tkachenko, A. S., and Dzhazairov-Kakhramanov, A. V. (2023a). Influence of resonances on the 11B(n,γ)12B reaction rate. Capture to the excited states of 12B. Int. J. Mod. Phys. E 32. doi:10.1142/S0218301323500088
Dubovichenko, S. B., Burkova, N. A., and Tkachenko, A. S. (2022b). Reaction rate of radiative n6Li capture in the temperature range from 0.01 to 10 T9. Nucl. Phys. A 1027, 122520. doi:10.1016/j.nuclphysa.2022.122520
Dubovichenko, S. B., and Dzhazairov-Kakhramanov, A. V. (2016). The Reaction8Li(n,γ)9Li at Astrophysical Energies And Its Role In Primordial Nucleosynthesis. Astrophys. J. 819, 78. doi:10.3847/0004-637X/819/1/78
Dubovichenko, S. B., Dzhazairov-Kakhramanov, A. V., and Afanasyeva, N. V. (2017). New results for reaction rate of the proton radiative capture on 3H. Nucl. Phys. A 963, 52–67. doi:10.1016/j.nuclphysa.2017.04.006
Dubovichenko, S. B., and Dzhazairov-Kakhramanov, A. V. (1990). Potential description of elastic nd, dd, n4He, and d3He scattering. Soviet J. Nucl. Phys. USSR 51, 971–977.
Dubovichenko, S. B., and Dzhazairov-Kakhramanov, A. V. (2015). Thermonuclear processes for three body system in the potential cluster model. Nucl. Phys. A 941, 335–363. doi:10.1016/j.nuclphysa.2015.07.009
Dubovichenko, S. B. (1997). Electromagnetic effects in light nuclei and the cluster potential model. Phys. Part. Nucl. 28, 615. doi:10.1134/1.953057
Dubovichenko, S. B. (2012). Methods for calculating nuclear characteristics. Nuclear and thermonuclear processes. Second edition. Saarbrucken, Germany: Lambert Acad. Publ., 425.
Dubovichenko, S. B., Neudachin, V. G., Sakharuk, A. A., and Smirnov, YuF. (1990). Generalized potential description of interaction of the hightest pt and ph nuclei. Izv. Akad. Nauk. SSSR 54, 911–916.
Dubovichenko, S. B. (2019). Radiative neutron capture and primordial nucleosynthesis of the Universe. First English edition. Berlin: De Gruyter, 310.
Dubovichenko, S. B. (2015). Thermonuclear processes in stars and Universe. Second Edition. Saarbrucken: Scholar’s Press, 332.
Dubovichenko, S. B., Tkachenko, A. S., Kezerashvili, R. Y., Burkova, N. A., and Dzhazairov-Kakhramanov, A. V. (2022a). 6Li(p,γ)7Be reaction rate in the light of the new data of the Laboratory for Underground Nuclear Astrophysics. Phys. Rev. C 105, 065806. doi:10.1103/PhysRevC.105.065806
Dubovichenko, S. B., and Uzikov, Y. N. (2011). Astrophysical S factors of reactions with light nuclei. Phys. Part. Nucl. 42, 251–301. doi:10.1134/S1063779611020031
Dubovichenko, S. B., and Zhusupov, M. A. (1984a). Some characteristics of 7Li in αt model for potentials with forbidden states. Sov. Jour Nucl. Phys. USSR 39, 1378–1381.
Dubovichenko, S. B., and Zhusupov, M. A. (1984b). The structure of light nuclei with A=6,7,8 in cluster models for potential with forbidden states. Izv. Akad. Nauk. SSSR 48, 935–937.
Firestone, R. B., and Revay, Z. (2016). Thermal neutron radiative cross sections for 6,7Li, 9Be, 10,11B, 12,13C, and 14,15N. Phys. Rev. C 93, 054306. doi:10.1103/PhysRevC.93.054306
Guimarães, V., Camargo, O., Lichtenthaler, R., Barioni, A., Kolata, J. J., Amro, H., et al. (2006). “Investigation of nucleosynthesis capture reactions by using 8Li radioactive beam transfer reactions,” in Proceedings of International Symposium on Nuclear Astrophysics - Nuclei in the Cosmos - IX — PoS(NIC-IX), CERN, Geneva, 25-30 June 2006 (Trieste, Italy: Sissa Medialab). doi:10.22323/1.028.0108
Guimarães, V., Lichtenthäler, R., Camargo, O., Barioni, A., Assunção, M., Kolata, J. J., et al. (2007). Neutron transfer reactions induced by 8Li on 9Li. Phys. Rev. C 75, 054602. doi:10.1103/PhysRevC.75.054602
Guo, B., Li, Z. H., Liu, W. P., Bai, X. X., Lian, G., Yan, S. Q., et al. (2005). The 8Li(d,p)9Li reaction and astrophysical 8B(p,γ)9C reaction rate. Nucl. Phys. A 761, 162–172. doi:10.1016/j.nuclphysa.2005.07.013
Gupta, D., Kundalia, K., Ali, Sk M., and Mitra, R. (2022). Break up of 9Li to study the 8Li(n,γ) reaction. European organization for nuclear research Proposal to the ISOLDE and Neutron Time-of-Flight Committee.
Huang, J. T., Bertulani, C. A., and Guimarães, V. (2010). Radiative capture of nucleons at astrophysical energies with single-particle states. A. T. Data Nucl. Data Tables 96, 824–847. doi:10.1016/j.adt.2010.06.004
Iliadis, C. (2015). Nuclear physics of stars. Second. Weinheim, Germany: Wiley-VCH Verlag GmbH & Co. KGaA, 672.
Itzykson, C., and Nauenberg, M. (1966). Unitary groups: representations and decompositions. Rev. Mod. Phys. 38, 95–120. doi:10.1103/RevModPhys.38.95
Kajino, T., Aoki, W., Balantekin, A. B., Diehl, R., Famiano, M. A., and Mathews, G. J. (2019). Current status of r-process nucleosynthesis. Prog. Part Nucl. Phys. 107, 109–166. doi:10.1016/j.ppnp.2019.02.008
Kajino, T. (1995). Inhomogeneous big-bang model, revived, and evolution of the light elements in cosmic rays. Nucl. Phys. A 588, c339–c343. doi:10.1016/0375-9474(95)00159-X
Kanungo, R., Andreyev, A. N., Buchmann, L., Davids, B., Hackman, G., Howell, D., et al. (2008). Spectroscopic factors for the 9Li ground state and N=6 shell closure. Phys. Lett. B 660, 26–31. doi:10.1016/j.physletb.2007.12.024
Kobayashi, H., Ieki, K., Horváth, Á., Galonsky, A., Carlin, N., Deák, F., et al. (2003). Astrophysical reaction rate for the 8Li(n,γ)9Li reaction. Phys. Rev. C 67, 015806. doi:10.1103/PhysRevC.67.015806
Kubono, S., Yamaguchi, H., Hayakawa, S., Hou, S. Q., and He, J. J. (2016). Explosive nuclear burning in the pp-chain region and the breakout processes. EPJ Web Conf. 109, 01001. doi:10.1051/epjconf/201610901001
La Cognata, M., and Del Zoppo, A. (2011). The 8Li(α,n)11B reaction rate at astrophysical temperatures. Astrophys. J. 736, 148. doi:10.1088/0004-637X/736/2/148
Li, Z. H., Liu, W. P., Bai, X. X., Guo, B., Lian, G., Yan, S. Q., et al. (2005). The 8Li(d,p)9Li reaction and the astrophysical 8Li(n,γ)9Li reaction rate. Phys. Rev. C 71, 052801. doi:10.1103/PhysRevC.71.052801
Ma, H-L., Dong, B-G., Yan, Y-L., and Zhang, X-Z. (2012). Shell model study on the astrophysical neutron capture of 8Li. Eur. Phys. J. A 48, 125. doi:10.1140/epja/i2012-12125-3
R. A. Malaney, W. F. Fowler, and G. J. Matthews (Editors) (1988). Origin and distribution of the elements (Singapore: World Scientific).
Mao, Z. Q., and Champagne, A. E. (1991). The 8Li(n,γ)9Li reaction and primordial nucleosynthesis. Nucl. Phys. A 522, 568–577. doi:10.1016/0375-9474(91)90081-G
McCracken, C., Navrátil, P., McCoy, A., Quaglioni, S., and Hupin, G. (2021). Microscopic investigation of the 8Li(n,γ)9Li reaction. Phys. Rev. C 103, 035801. doi:10.1103/PhysRevC.103.035801
Mondal, S., Das, P., Senapati, E., Pandit, D., Dey, B., De, A., et al. (2022). Analysis of cross-section, S-factor and thermonuclear reaction rate of 8Li(α,n)11B and 14N(p,γ)15O using TALYS and EMPIRE nuclear reaction codes. Int. J. Mod. Phys. E 31. doi:10.1142/S0218301322500641
Mukhamedzhanov, A. M., and Timofeyuk, N. K. (1990). Microscopic calculation of nucleon separation vertex constant for 1p shell nuclei. J. Soviet Nucl. Phys. 51, 431–441.
Mukhamedzhanov, A. M., and Tribble, R. E. (1999). Connection between asymptotic normalization coefficients, subthreshold bound states, and resonances. Phys. Rev. C 59, 3418–3424. doi:10.1103/PhysRevC.59.3418
Nemets, O. F., Neudatchin, V. G., Rudchik, A. T., and Smirnov, Y. F.Tchuvil'sky YuM (1988). Nucleon association in atomic nuclei and the nuclear reactions of the many nucleons transfers. Kiev: Naukova dumka, 488.
Neudatchin, V. G., Kukulin, V. I., Boyarkina, A. N., and Korennoy, V. P. (1972). A microscopically substantiated optical potential for the α-t system, including nucleon exchange. Lett. al Nuovo Cimento 5, 834–838. doi:10.1007/BF02812319
Neudatchin, V. G., Kukulin, V. I., Korotkikh, V. L., and Korennoy, V. P. (1971). A microscopically substantiated local optical potential for α-α- scattering. Phys. Lett. B 34, 581–583. doi:10.1016/0370-2693(71)90142-0
Neudatchin, V. G., Kukulin, V. I., Pomerantsev, V. N., and Sakharuk, A. A. (1992). Generalized potential-model description of mutual scattering of the lightest p+d, d+3He nuclei and the corresponding photonuclear reactions. Phys. Rev. C 45, 1512–1527. doi:10.1103/PhysRevC.45.1512
Neugart, R., Balabanski, D. L., Blaum, K., Borremans, D., Himpe, P., Kowalska, M., et al. (2008). Precision measurement of 11Li moments: influence of halo neutrons on the 9Li core. Phys. Rev. Lett. 101, 132502. doi:10.1103/PhysRevLett.101.132502
NIST (2019). Fundamental physical constants. Available at: https://physics.nist.gov/cuu/Constants/index.html (Accessed June 1, 2023).
Nollett, K. M., and Wiringa, R. B. (2011). Asymptotic normalization coefficients from ab initio calculations. Phys. Rev. C 83, 041001. doi:10.1103/PhysRevC.83.041001
Norman, E. B., and Schramm, D. N. (1979). On the conditions required for the r-process. Astrophysical J. 228, 881–892. doi:10.1086/156914
Nörtershäuser, W., Bushaw, B. A., Dax, A., Drake, G. W. F., Ewald, G., Götte, S., et al. (2005). Measurement of the nuclear charge radii of 8,9Li. Eur. Phys. J. A 25, 199–200. doi:10.1140/epjad/i2005-06-053-9
Nuclear Data Evaluation Project (2021). Triangle universities nuclear laboratory. 8Li β-decay evaluated data. Available at: https://nucldata.tunl.duke.edu/nucldata/GroundStatedecays/08Li.shtml#halflife (Accessed April 25, 2023).
Paradellis, T., Kossionides, S., Doukellis, G., Aslanoglou, X., Assimakopoulos, P., Pakou, A., et al. (1990). Astrophysical S(E) factor of 8Li (α,n0)11B and inhomogeneous Big Bang nucleosynthesis. Z. fur Phys. A At. Nucl. 337, 211–220. doi:10.1007/BF01294294
Plattner, G. R., and Viollier, R. D. (1981). Coupling constants of commonly used nuclear probes. Nucl. Phys. A 365, 8–12. doi:10.1016/0375-9474(81)90384-5
Rauscher, T., Applegate, J. H., Cowan, J. J., Thielemann, F-K., and Wiescher, M. (1994). Production of heavy elements in inhomogeneous cosmologies. Astrophys. J. 429, 499. doi:10.1086/174339
Sánchez, R., Nörtershäuser, W., Dax, A., Ewald, G., Götte, S., Kirchner, R., et al. (2007). “Nuclear charge radius of 11Li,” in Laser 2006 (Berlin, Heidelberg: Springer Berlin Heidelberg), 181–188. doi:10.1007/978-3-540-71113-1_17
Sargsyan, G. H., Launey, K. D., Shaffer, R. M., Marley, S. T., Dudeck, N., Mercenne, A., et al. (2022). Ab initio single-neutron spectroscopic overlaps in lithium isotopes. arXiv:2210.08843 [nucl-th].
Su-Qing, H., Kai-Su, W., Yong-Shou, C., Neng-Chuan, S., and Zhi-Hong, L. (2010). The main path to C, N, O elements in big bang nucleosynthesis. Chin. Phys. Lett. 27, 082601. doi:10.1088/0256-307X/27/8/082601
Sukhoruchkin, S. I., and Soroko, Z. N. (2016). Excited nuclear states. Berlin Heidelberg: Springer. doi:10.1007/978-3-662-48875-1
Thielemann, F. K., Applegate, J. H., Cowan, J. H., and Wiescher, M. (1991). “Production of heavy elements in inhomogeneous cosmologies,” in Nuclei in the cosmos. Editor H. Oberhummer (Baden/Vienna: Springer-Verlag, Heildelberg), 248.
Tilley, D. R., Cheves, C. M., Godwin, J. L., Hale, G. M., Hofmann, H. M., Kelley, J. H., et al. (2002). Energy levels of light nuclei A=5,6,7. Nucl. Phys. A 708, 3–163. doi:10.1016/S0375-9474(02)00597-3
Timofeyuk, N. K. (2013). Spectroscopic factors and asymptotic normalization coefficients for 0p-shell nuclei: recent updates. Phys. Rev. C 88, 044315. doi:10.1103/PhysRevC.88.044315
Varlamov, V., Ishkhanov, B., and Komarov, S. Y. (2015). Nuclear wallet cards database. Available at: http://cdfe.sinp.msu.ru/services/ground/NuclChart_release.html (Accessed June 1, 2023).
Wiringa, R. B. (2021). Spectroscopic overlaps. Available at: http://www.phy.anl.gov/theory/research/overlap (Accessed May 30, 2023).
Wuosmaa, A. H., Rehm, K. E., Greene, J. P., Henderson, D. J., Janssens, R. V. F., Jiang, C. L., et al. (2005). Neutron spectroscopic factors in 9Li from 2H(8Li,p)9Li. Phys. Rev. Lett. 94, 082502. doi:10.1103/PhysRevLett.94.082502
Keywords: nuclear astrophysics, thermal and astrophysical energies, n8Li system, total cross sections, reaction rate, cluster model
Citation: Dubovichenko SB, Yeleusheva BM, Burkova NA and Tkachenko AS (2023) The reaction rate of radiative n8Li capture in the range from 0.01 to 10 T9. Front. Astron. Space Sci. 10:1251743. doi: 10.3389/fspas.2023.1251743
Received: 02 July 2023; Accepted: 10 August 2023;
Published: 01 September 2023.
Edited by:
Denise Piatti, University of Padua, ItalyReviewed by:
Andres Arazi, National Atomic Energy Commission, ArgentinaGiuseppe Ferdinando D'Agata, University of Catania, Italy
Copyright © 2023 Dubovichenko, Yeleusheva, Burkova and Tkachenko. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: S. B. Dubovichenko, ZHVib3ZpY2hlbmtvQGdtYWlsLmNvbQ==
 S. B. Dubovichenko
S. B. Dubovichenko B. M. Yeleusheva
B. M. Yeleusheva N. A. Burkova1,2
N. A. Burkova1,2 A. S. Tkachenko
A. S. Tkachenko