- 1Space Environment and Radio Engineering, Electronic, Electrical and Systems Engineering, School of Engineering, University of Birmingham, Birmingham, United Kingdom
- 2Environmental Mathematics, Department of Earth and Environmental Sciences, University of Exeter, Penryn, United Kingdom
- 3Department of Mathematics, University of Exeter, Exeter, United Kingdom
- 4Department of Atmospheric and Oceanic Sciences, University of California at Los Angeles, Los Angeles, CA, United States
- 5Department of Physics, University of Helsinki, Helsinki, Finland
- 6United States Air Force Research Laboratory, Albuquerque, NM, United States
- 7Department of Mathematics, Physics and Electrical Engineering, Northumbria University, Newcastle upon Tyne, United Kingdom
- 8Centre for Fusion, Space and Astrophysics, University of Warwick, Coventry, United Kingdom
- 9Department of Mathematics and Statistics, University of Tromso, Tromsø, Norway
- 10International Space Science Institute, Bern, Switzerland
- 11British Antarctic Survey, Cambridge, United Kingdom
- 12School of Mathematics and Statistics, University of St Andrews, St Andrews, United Kingdom
- 13Department of Physics and Astronomy, University of Iowa, Iowa City, IA, United States
- 14Grantham Research Institute on Climate Change and the Environment, London School of Economics and Political Science, London, United Kingdom
Quasilinear theories have been shown to well describe a range of transport phenomena in magnetospheric, space, astrophysical and laboratory plasma “weak turbulence” scenarios. It is well known that the resonant diffusion quasilinear theory for the case of a uniform background field may formally describe particle dynamics when the electromagnetic wave amplitude and growth rates are sufficiently “small”, and the bandwidth is sufficiently “large”. However, it is important to note that for a given wave spectrum that would be expected to give rise to quasilinear transport, the quasilinear theory may indeed apply for given range of resonant pitch-angles and energies, but may not apply for some smaller, or larger, values of resonant pitch-angle and energy. That is to say that the applicability of the quasilinear theory can be pitch-angle dependent, even in the case of a uniform background magnetic field. If indeed the quasilinear theory does apply, the motion of particles with different pitch-angles are still characterised by different timescales. Using a high-performance test-particle code, we present a detailed analysis of the applicability of quasilinear theory to a range of different wave spectra that would otherwise “appear quasilinear” if presented by e.g., satellite survey-mode data. We present these analyses as a function of wave amplitude, wave coherence and resonant particle velocities (energies and pitch-angles), and contextualise the results using theory of resonant overlap and small amplitude criteria. In doing so, we identify and classify five different transport regimes that are a function of particle pitch-angle. The results in our paper demonstrate that there can be a significant variety of particle responses (as a function of pitch-angle) for very similar looking survey-mode electromagnetic wave products, even if they appear to satisfy all appropriate quasilinear criteria. In recent years there have been a sequence of very interesting and important results in this domain, and we argue in favour of continuing efforts on: (i) the development of new transport theories to understand the importance of these, and other, diverse electron responses; (ii) which are informed by statistical analyses of the relationship between burst- and survey-mode spacecraft data.
1 Introduction
A grand challenge problem in radiation belt science is the understanding and parameterisation of the relative contributions of quasilinear and nonlinear wave-particle interactions respectively (e.g., see Bortnik et al. (2008a); Omura et al. (2008); Albert et al. (2012); Tao et al. (2012b); Allanson et al. (2021); Artemyev et al. (2021b); Gan et al. (2022); Allanson et al. (2023)). Informed by spacecraft observations (e.g., Agapitov et al., 2015; Foster et al., 2017; Kurita et al., 2018; Mozer et al., 2018; Shumko et al., 2018; Zhang et al., 2019; Tsai et al., 2022; Zhang et al., 2022), many theoretical/analytical and numerical advances have been made in recent years (see discussions and context in e.g., Vainchtein et al. (2018); Mourenas et al. (2018); Lukin et al. (2021); Allanson et al. (2022); Albert et al. (2022b); Bortnik et al. (2022); Frantsuzov et al. (2023); Artemyev et al. (2022) in the context of local wave-particle interactions; Lejosne (2019); Desai et al. (2021); Osmane and Lejosne (2021); Camporeale et al. (2022); Lejosne et al. (2022); Osmane et al. (2023); Lejosne and Albert (2023) considering radial transport; as well as Brizard and Chan (2022) for a combined and self-consistent formalism). Recent works have also pioneered the importance of including inherent ‘sub-grid’ variability of particle dynamics in radiation belt modelling (Watt et al., 2017; Watt et al., 2019; Ross et al., 2020; Ross et al., 2021; Watt et al., 2021; Watt et al., 2022), and machine learning techniques to parameterise wave particle interactions (Kluth et al., 2022).
The dominant features, dynamics, acceleration and decay of the outer radiation belt can often be well reproduced using numerical codes that utilise the quasilinear theory: over sufficiently ‘long’ timescales (usually significant numbers of drift periods) and ‘large’ (bounce- and/or drift-averaged) lengthscales (e.g., see Thorne et al. (2013); Tu et al. (2014); Li et al. (2014); Su et al. (2016); Drozdov et al. (2017); Glauert et al. (2018); Ma et al. (2018); Allison and Shprits (2020); Ross et al. (2021); Summers and Stone (2022). While we must acknowledge the many successes of current models, the sustained interest in the field is clearly based upon the fact that we do not yet always capture all details of acceleration, loss and decay for all values/ranges of energy and pitch-angle simultaneously (e.g., see discussion in Green et al. (2004); Kersten et al. (2014); Ma et al. (2015); Ni et al. (2015); Drozdov et al. (2015); Mourenas et al. (2016); Kessel (2016); Li and Hudson (2019); Ripoll et al. (2020); Lejosne et al. (2022); Osmane et al. (2023)). To give a subset of examples that pertain to velocity-space transport, it is clear that there are still many outstanding questions regarding: (a) the cumulative/‘long term’ effects of nonlinear wave-particle interactions that either may or may not be explained via a quasilinear-esque approach applied over a given timescale (Artemyev et al., 2022; Frantsuzov et al., 2023; Vargas et al., 2023; Lukin et al., 2024); (b) the short timescale and small lengthscale effects that likely cannot be explained by quasilinear theory on any timescale, and that may have a macroscopic/non-neglible contribution - for example, but not limited to: microbursts driven via nonlinear interactions (Osmane et al., 2016; 2017; Mozer et al., 2018; Shumko et al., 2018); and resonance broadening corrections to chorus and EMIC diffusion rates for equatorial particles (Cai et al., 2020; Tonoian et al., 2022).
Radiation belt models solve particular examples of Fokker-Planck diffusion equations Schulz and Lanzerotti (1974); Roederer and Zhang (2013) and are implemented most typically in 3D (E, αeq, L⋆) (e.g., see Varotsou et al. (2005); Subbotin and Shprits (2009); Tu et al. (2013); Glauert et al. (2014); Ma et al. (2018); Wang et al. (2020)), but sometimes in 4D to additionally incorporate magnetic local time or latitudinal variations (e.g., see Fok et al. (2011); Shprits et al. (2015)). The version of the quasilinear theory used in radiation belt models is ‘parasitic’, in the sense that there is no feedback of the particle densities and currents on the waves (known as the resonant diffusion limit of the quasilinear theory (Kennel and Engelmann, 1966)). Most models currently parameterise ‘local’ diffusion via bounce- and drift-averaged versions of the quasilinear diffusion coefficients, themselves derived for an infinite uniform plasma in a gyrotropic (independent of gyrophase) velocity space (e.g., relativistic kinetic energy E, and pitch-angle α) Glauert and Horne (2005). The bounce-averaging procedure (as introduced by Roberts (1969); Lyons et al. (1972) produces an averaged diffusion coefficient that is calculated as a time-weighted mean of the local expression (the local expression is calculated by (Kennel and Engelmann, 1966; Lerche, 1968)). The time-weighting is calculated via consideration of the adiabatic motion that the particle would have followed, had it not been disturbed by a wave. The drift-averaging procedure then further averages these bounce-averaged diffusion coefficients over all magnetic local time. We also note other recently developed approaches to radiation belt modelling that involve the incorporation of test particles into different varieties of global-scale simulation (Desai et al., 2021; Chan et al., 2023; Lukin et al., 2024).
Therefore, it is the diffusion coefficients calculated in the infinite and uniform domain that currently underpin the local (velocity-space) transport in operational radiation belt models, and so that is the formalism that we examine in this work. We note that a number of works have analysed the validity of the bounce-averaged diffusion coefficients for specific examples of narrowband/coherent wave-modes and dipolar background field structures (e.g., see (Bortnik et al., 2008a; Albert, 2010; Tao and Bortnik, 2010; Artemyev et al., 2023), which have been generalised to broadband wave modes in e.g., Gan et al. (2022); Artemyev et al. (2022); Frantsuzov et al. (2023). Importantly, and depending on the value of relevant parameters, the inhomogeneity of the background magnetic field in these cases can mean that bounce-averaged quasilinear theories are valid, in circumstances when otherwise one would not have expected this to be the case.
Fundamentally, by using the Fokker-Planck diffusion equations, we need a description of the diffusion coefficients, which capture the sub-grid physics of the wave-particle interaction itself, summarising its efficacy as a function of energy and pitch-angle. Diffusion coefficients arise due to many different wave modes from the “zoo” of naturally-occurring electromagnetic waves in the magnetosphere. We do not yet have fully self-consistent kinetic plasma physics methods of modelling all electron interactions over global magnetospheric scales. There are self-consistent numerical experiments of magnetospheric wave activity (e.g., Devine et al., 1995; Hikishima et al., 2009; Hikishima et al., 2010; Hikishima and Omura, 2012; Nunn and Omura, 2012; Ke et al., 2017; Ratcliffe and Watt, 2017; Allanson et al., 2019; Fan et al., 2019; Li et al., 2019; Allanson et al., 2020; Hikishima et al., 2020; Allanson et al., 2021; Zhang X.-J. et al., 2021; Chen et al., 2022; Nogi and Omura, 2023), but it is necessary to constrain these experiments in order that they are computationally tractable.
The temporal and spatial variability of the waves is not fully understood (e.g., Zhang et al., 2021a; Zhang et al., 2021b), and so models of diffusion coefficients are constructed from statistical descriptions of wave activity obtained from many years of spacecraft and ground-based observation (Pahud et al., 2009; Li et al., 2011; Rae et al., 2012; Agapitov et al., 2013; Spasojevic et al., 2015; Malaspina et al., 2017; Hartley et al., 2018; Bentley et al., 2019; Meredith et al., 2019; Meredith et al., 2020; Sarris et al., 2022). Spacecraft can provide information regarding wave amplitude, frequency and wave-normal angle; in addition to indirect measures of local number density (via wave spectra or spacecraft potential); and observations of the strength of the local magnetic field. All of these observations provide a snapshot of information at discrete times along the spacecraft track. Wave information is obtained as a discrete Fourier transform (i.e., a Fourier Series), derived from a discrete time series over short intervals. These data are combined together to form models of the diffusion coefficients (Horne et al., 2013; Orlova et al., 2014; Sandhu et al., 2021; Wong et al., 2022; Murphy et al., 2023). What is important is to consider how we use those observations in terms of the theory of quasilinear and nonlinear wave interactions.
The aim of this work is to present a thorough exploration of the variety of particle transport regimes during interactions with different varieties of field-aligned waveforms in a uniform background magnetic field, and to assess the applicability/validity of quasilinear theory for these cases. One key point is that all results presented relate to waveforms that (when Fourier transformed according to standard techniques as used on operational scientific spacecraft, and as discussed in e.g., Kletzing et al. (2013); Kletzing et al. (2023)) ‘look quasilinear’ in all aspects. In Figure 1 we present analytical wave forms and subsequently derived wave spectra to illustrate this point. Figures 1A–C show time-series of the By component of whistler-mode wave spectra constructed exactly as done for this article, and to be discussed further in Section 2. In Figures 1D–F we present the respective power spectra for these wave forms that were calculated using a standard numerical Fast Fourier Transform (FFT) routine. In Figures 1G–I we further plot power spectra for the same wave-forms but calculated exactly as per the FFT engine on the Van Allen Probes EMFISIS Wave Frequency Receiver (WFR) instruments. Therefore Figures 1G–I represent protypical wave spectra that one might expect to download as a EMFISIS WFR survey mode data product (Kletzing et al., 2013; Kletzing et al., 2023). Figures 1A–F demonstrate three possible examples to demonstrate the (infinite) variety of waveforms and wave spectral forms that could in principle be underlying these survey mode spectral prototypes. The waveforms that we choose are somewhat idealised, but this is in order to allow us to probe different physical phenomena in a precise manner, as is very common practice (Tao et al., 2011; Tao et al., 2014). The results in this paper seek to understand the variety of particle responses for essentially identical looking survey-mode products 1 (g)-(i), which appear to satisfy all appropriate quasilinear criteria. In particular, we highlight the variety of responses that are possible as a function of pitch-angle, since we believe that this feature is often overlooked, and does relate directly to more complicated scenarios such as those in e.g., Bortnik et al. (2008b); Albert and Bortnik (2009); Albert (2010); Tao et al. (2012a); Gan et al. (2020), Gan et al. (2022); Artemyev et al. (2023).
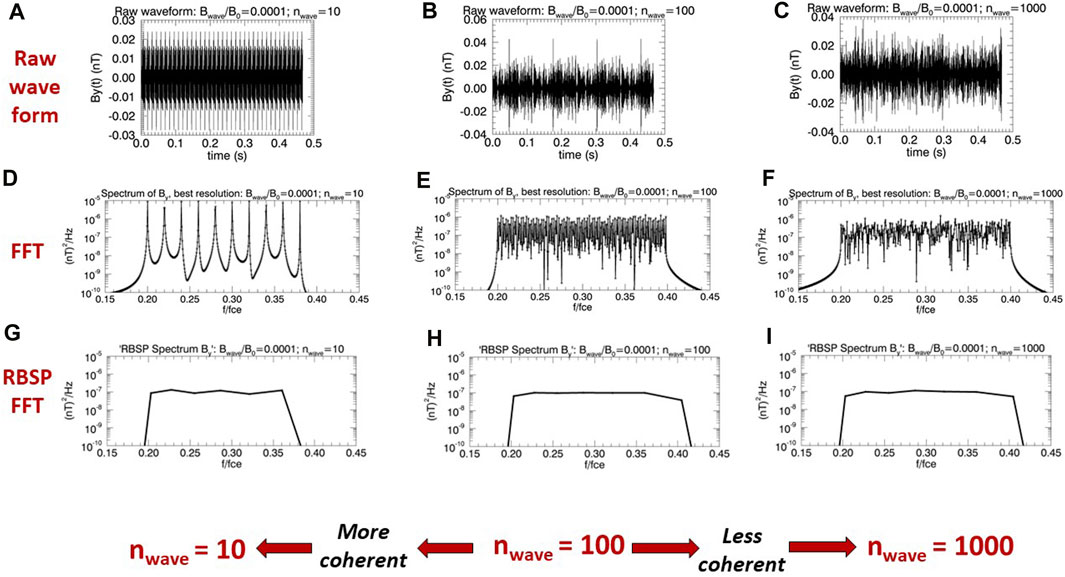
FIGURE 1. (A–C) show a 0.468s time-series of the By component of whistler-mode wave spectra constructed exactly as done for this article, with nwave =10,100,1000 respectively and a fixed value of Bwave/B0=10–4. (D–F) show the respective spectra for these wave forms that were calculated using a standard numerical FFT routine. (G–I) plot Fourier spectra for the same wave-forms but calculated exactly as per the FFT engine on the Van Allen Probes EMFISIS WFR (Kletzing et al., 2013; Kletzing et al., 2023).
In Section 2 we demonstrate that the applicability of the quasilinear theory to a wave power-spectral-density that one might obtain from survey-mode on a spacecraft depends on the pitch-angle of interest, and also on information that cannot be obtained from the survey-mode data itself. We show this via numerical experiment and plasma physics theory. In addition, we show that even for a survey-mode wave spectrum that essentially satisfies all possible quasilinear requirements, there are noteworthy time-dependent phenomena that occur at small and large-pitch angles, to be defined. In Section 3 we present a thorough discussion and relate these results to others recently obtained in the literature, and also to ‘more realistic’ physical scenarios. Section 4 includes a summary of the results obtained and presented, an indication of worthwhile future work, implications, and questions raised.
2 The regime of particle transport in response to a given wave spectrum is dependent on the pitch-angle
2.1 The small amplitude criterion underpinning quasilinear theory
Under the assumption of a quasi-static (vanishing growth/damping rate) electromagnetic wave power spectral density in a uniform plasma with uniform magnetic field, there is an important condition that should be satisfied in order for quasilinear theory to be valid. This condition is essentially that of small wave amplitudes as described in e.g., Kennel and Engelmann (1966), but made more precise and in relation to the wave bandwidth, as described/used in Karpman (1974); Le Queau and Roux (1987); Tong et al. (2019); Kuzichev et al. (2023). The condition requires that the wave amplitudes are sufficiently small, or equivalently that the wave spectra is sufficiently broad, and can be written as follows (see equation 2.18 in Karpman (1974) or just above Eq. 8 in Tong et al. (2019))
with v the particle velocity; B0 > 0 the magnitude of the background magnetic field; ωce = qB0/(m0γ) the signed and relativistic gyrofrequency (for relativistic gamma
Note the appearance of the
1. A function of particle pitch-angle, for a given fixed wave spectrum,
2. More readily satisfied for small pitch-angles (closer to 0°), and more difficult to satisfy for large pitch-angles (closer to 90°).
2.2 The chirikov resonance overlap criterion underpinning quasilinear theory
2.2.1 On fourier series representations
Conversely, there is also a condition on wave amplitudes being sufficiently large. In order to explain this, we will first need to clarify some fundamentals regarding the electromagnetic waves. Theoretical diffusion coefficients are usually derived with respect to Fourier transform representations of the electromagnetic waves (e.g., see Kennel and Engelmann (1966)). These are formally valid over infinite spatial domain and temporal domains, only. In particular, the electromagnetic field wave power is defined as the average over (infinite) space, and is calculated by integrating over all continuous frequency space (Lyons, 1974; Allanson et al., 2022). All continuous frequencies can be considered, because (and only because) the temporal domain is infinite.
In contrast, the spatial domain of a real space plasma phenomenon is finite in extent. Likewise, the timeframe considered for some phenomenon is finite. As such (and due to elementary mathematical/physical considerations), one can only obtain a discrete Fourier series representation of an electromagnetic wave field for a finite spatio-temporal domain observed ‘in nature’. The lowest non-zero frequency that can be observed will be unambiguosuly determined by the total elapsed (finite) time, and likewise the largest wavelength that can be observed will be unambiguously determined by the total spatial extent. This is not a technical/theoretical artifice, but a fundamental aspect of the nature of the problem considered. There will be (a countably) infinite number of frequencies/wavelengths that can be used in the Fourier series representation, but they will fundamentally be discrete.
In further contrast, when one considers the input/output of a numerical experiment, or the measurements in a laboratory experiment, or indeed the observations made by a spacecraft instrument, we have the further restriction of measurements made at discrete time and space. This further limits the range of frequencies and wavelengths that can be considered, and sets an upper limit to frequency (lower limit to wavelength), as determined by the Nyquist criterion. This will give a finite number of (necessarily discrete) frequencies and wavelengths.
All of this is to say (in preparation for what follows), that the notion of a Fourier series is not a theoretical artifice or a mathematical hiccup, but in actual fact a fundamental consequence of the fact that we require a representation over finite spatio-temporal domains. There is then the added clarification that this representation is countably infinite in number (but discrete) for continuous time (i.e., what a real Newtonian particle ‘observes’); but finite and discrete in an experiment/observation.
2.2.2 The overlap criterion
The overlap criterion dictates that the Fourier wave amplitudes Bw,k for mode k are sufficiently large so as to enable stochasticity (i.e., diffusion) via resonant island overlap (Chirikov, 1960; Zaslavskiĭ and Chirikov, 1972; Chirikov, 1979; Lichtenberg and Lieberman, 1992; Matsoukis et al., 1998; Wykes et al., 2001; Artemyev et al., 2015). If the islands do not overlap in the given region of velocity space that corresponds to given mode k, then the particles resonant with mode k will evolve deterministically (i.e., not diffusion) in accordance with their interaction with that one resonant mode. This criterion states that ‘adjacent’ (in ω, k space) wave amplitudes must be sufficiently large so as to appear incoherent to the resonating particles, and is expressed approximately as
for vwidth = 2ωtr,k/k the trapping width in velocity space for mode k (for
with vr1 and vr2 the values of two resonant velocites adjacent to each other in k space, as determined by solutions to the cyclotron resonance condition for our scenario with k = k‖ (ω − k‖v‖ = |ωce|/γ),
for vph,k = ω/k the phase velocity. Note the appearance of the particle pitch-angle in Eq. 3. Once again, there are two fundamental points to note here. The Chirikov resonance-overlap criterion enabling the application of the quasilinear theory is
1. A function of particle pitch-angle, for a given fixed wave spectrum,
2. More difficult to satisfy for small pitch-angles (closer to 0°), and more readily satified for large pitch-angles (closer to 90°).
2.2.3 Island overlap enables phase randomisation which enables transition to stochasticity
There are many derivations of electrostatic and/or electromagnetic quasilinear theory in the literature (e.g., Vedenov et al. (1962); Drummond and Pines (1962); Andronov and Trakhtengerts (1964); Rowlands et al. (1966); Kennel and Engelmann (1966); Hall and Sturrock (1967); Lerche (1968); Sagdeev and Galeev (1969); Kulsrud and Pearce (1969); Lyons et al. (1972); Melrose (1980); Schlickeiser (1989); Steinacker and Miller (1992); Stix (1992); Walker (1993); Albert (2001); Swanson (2003); Brizard and Chan (2004); Albert (2010); Lemons (2012); Brizard and Chan (2022); Allanson et al. (2022); Cunningham (2023). The majority of those derivations utilise a perturbative Vlasov-Poisson/Maxwell approach in a uniform geometry, but there are the following exceptions: (i) Lyons et al. (1972) and Stix (1992) further apply bounce-averaging procedures; (ii) Albert (2001), Albert (2010) use an approach that is based upon a Hamiltonian analysis of single particle motions, and also include an inhomogeneous background field; (iii) Lemons (2012); Allanson et al. (2022) use a Markov approach; (iv) Brizard and Chan (2004), Brizard and Chan (2022) use a Hamiltonian/Vlasov-Maxwell approach in an axisymmetric field.
Underlying all of these derivations is the key observation that the diffusion equation evolves a distribution function on a ‘slow’ timescale, as determined by the action of sufficiently many wave-particle interactions that themselves occur on a separate ‘fast’ timescale (Brizard and Chan, 2001). The separation between slow and fast is essentially determined by a transition from deterministic to stochastic trajectories (achieved via decorrelation of particle dynamics), and will usually occur after ‘many’ wave-/gyro-periods, leading to validity of the so-called random-phase approximation (Karpman, 1974; Lemons, 2012), as discussed in Section 2.1. As described and/or demonstrated in Chirikov (1960); Smith and Kaufman (1978); Smith et al. (1980); Matsoukis et al. (1998); Lichtenberg and Lieberman (1992); Karimabadi et al. (1992); Sigov and Levchenko (1996); Neishtadt (1999); Wykes et al. (2001); Kaufman (2009); Ukhorskiy and Sitnov (2013); Artemyev et al. (2015); Escande (2018); Kaufman and Cohen (2019), the notion of the Chirikov resonance overlap is fundamental to this entire philosophy, despite the fact that it is rarely mentioned in respective derivations of the quasilinear theory.
2.3 The quasilinear prediction
The relativistic resonant limit quasilinear theory for field-aligned waves as presented in e.g., Lerche (1968); Albert (2005); Glauert and Horne (2005); Summers (2005); Allanson et al. (2022) gives energy, pitch-angle and mixed diffusion coefficients as follows
for W(k) here defined with respect to the energy density of the spatially and temporally averaged (root-mean-square) magnetic wave amplitude
with the sum over roots (of multiplicity one), xj, of a generic function R(x) Summers (2005). These diffusion coefficient formulae are implemented in the following specific ‘diffusive’ example of a (in principle more general, e.g., see Zheng et al. (2019); Allanson et al. (2022)) Fokker-Planck equation
for
2.4 Different particle transport regimes for different pitch-angles
In this work we are interested in the wave effects on particles and not vice versa, thus allowing the use of a test-particle code. In order to examine the fundamental particle reponse to different wave spectra as a function of particle pitch angle, we use high-performance test-particle numerical experiments (open access and open source at https://github.com/donglai96/taiparticle-uniform) that solve the full relativistic equations of motion for charged particles interacting with electromagnetic fields and waves
for p = m0γv the relativistic momentum, and uniform background magnetic field
With ϕj = kjz − ωjt + ϕ0j for randomised ϕ0j; ωj = ωmin + jΔω; and kj determined via the cold plasma dispersion relation (Stix, 1992). We choose (ωmin, ωmax) = (0.2|ωce|, 0.4|ωce|), for ωce the signed, non-relativistic gyrofrequency, and this frequency range therefore determines the value of Δω via Δω = (ωmax − ωmin)/(nwave − 1). The choice of a parallel-propagating wave spectrum fixes Bxj = Byj = Bj for each independent value of j (likewise Exj = Eyj = Ej). We further assume that the spectrum has uniform Fourier amplitude, and therefore that all Bj are the same as each other. It can be shown that in the case of a uniform spectrum their values are determined as
We choose system parameters B0 = 140nT, n = 1cm−3, and therefore fpe/fce ≈ 7.2, for fpe the electron plasma frequency, and fce = |ωce|/(2π) ≈ 3919 Hz the non-relativistic and unsigned ordinary electron gyrofrequency. These are the same parameters as were chosen in Tao et al. (2011); Allanson et al. (2019), Allanson et al. (2020); Cai et al. (2020). Separate experiments are run for individual particle populations. In each experiment, electron ensembles consisting of 120 members are initialised with identical values of kinetic energy and pitch-angle, such that they are resonant with a mode in the center of the spectrum at f = 0.3fce, according to Eq. 4. We note that the code is implemented to ensure that there is a well-defined mode with f = 0.3|fce|. These particles are initialised with randomly distributed gyrophase between 0 and 2π.
The run-time of the experiments is 4,000 relativistic gyroperiods, i.e. 4000γ/|fce| (which is 1.02s for γ = 1, and 1.02γs otherwise), significantly extending the range of previous similar experiments that have validated and constrained the quasilinear theory in a uniform homogeneous setting (Liu et al., 2010; Tao et al., 2011; Allanson et al., 2019; Allanson et al., 2020; Cai et al., 2020). The equations of motion are solved via a Boris algorithm (see Birdsall and Langdon (2004), and as described in section 2.2 of Arber et al. (2015)), with timestep Δt set at 1/500 of the relativistic gyroperiod, Δt = γ/(500fce). We track the pitch-angle, relativistic kinetic energy, and gyrophase of each particle, and output the value of these parameters every 100Δt, i.e. 5 times every relativistic gyroperiod. We specifically note whether the small amplitude criteria (Eq. 1) and/or the Chirikov resonance-overlap criteria (Eq. 3) are being satisified in each case.
We run 126 (=3*3*14) individual experiments. For each of the three values of nwave = 10, 100, 1000, and three values of Brms/|B0| = 10–5, 10–4, 10–3, we run 14 experiments for initial pitch-angle values given as
We will not present the outcome of all 126 experiments in the main text, but all plots are given in the Supporting Information S1. In the manuscript, we will highlight the main conclusions that can be drawn.
3 Dependence of particle dynamics on pitch-angle and wave coherence
In Figures 2–5 we plot nine sub-figures, each with four plots. These show the pitch-angle and gyrophase response of 120 electrons with (initially) uniformly distributed gyrophase that are resonant with f = 0.3|fce|, and for different values of pitch angle and energy. We present these results for different values of Bwave/B0 and nwave, as indicated on the figure. Each horizontal row of three sub-figures presents results for a fixed value of Bwave/B0 (and varying nwave = 10, 100, 1000), and each vertical column of three sub-figures presents results for a fixed value of nwave (and varying Bwave/B0 = 10–5, 10–4, 10–3). Each sub-figure presents four plots as a function of time (4,000 relativistic gyroperiods), namely; (i) a pitch-angle scatter plot of all 120 particles; (ii) ⟨(Δα)2⟩; (iii) ⟨Δα⟩; (iv) a gyrophase scatter plot of all 120 particles.
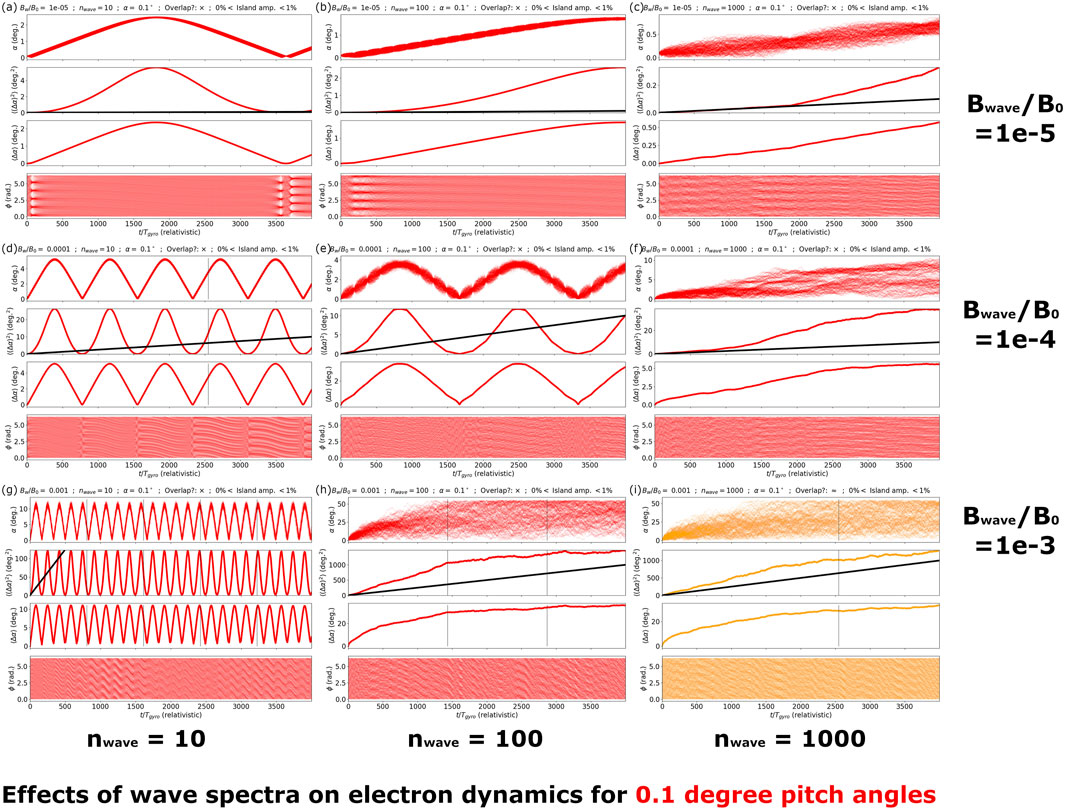
FIGURE 2. Demonstrating the effect of wave coherence and wave amplitude on particle trajectories for α =0.1°, E =5.463 keV. All details pertaining to sub-figures (A–I) are described in Section 3.
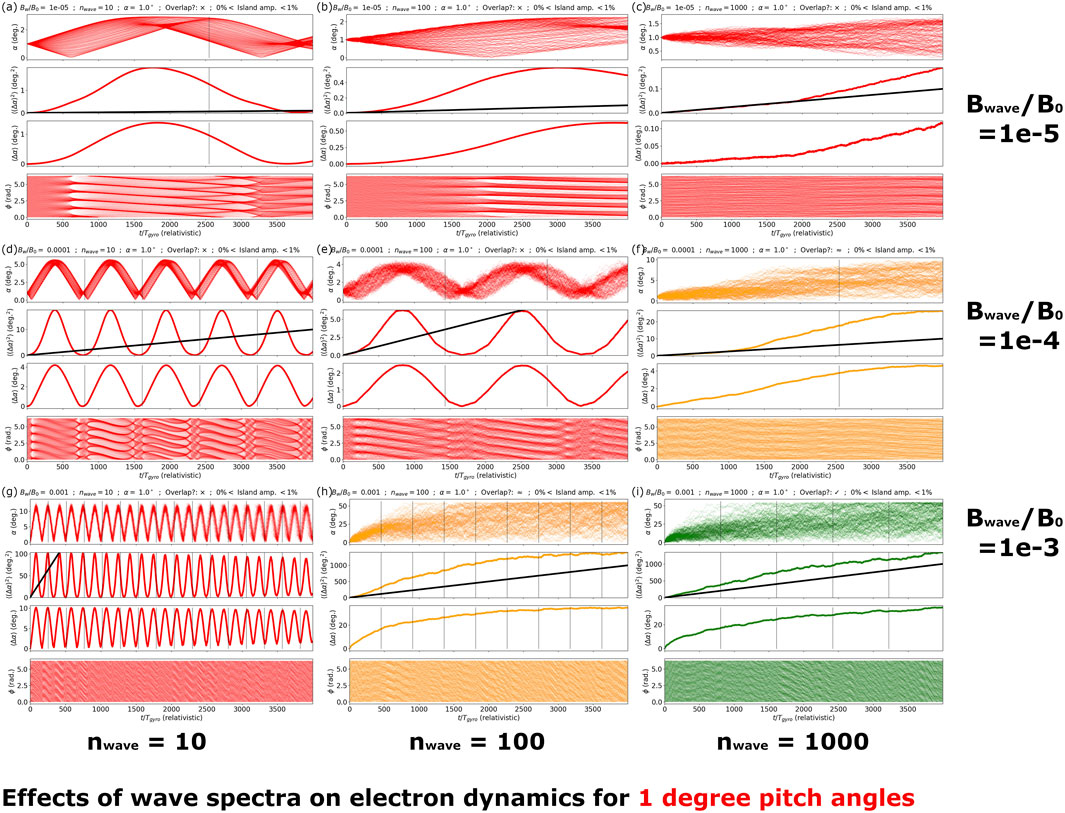
FIGURE 3. Demonstrating the effect of wave coherence and wave amplitude on particle trajectories for α =1°, E =5.465 keV. All details pertaining to sub-figures (A–I) are described in Section 3.
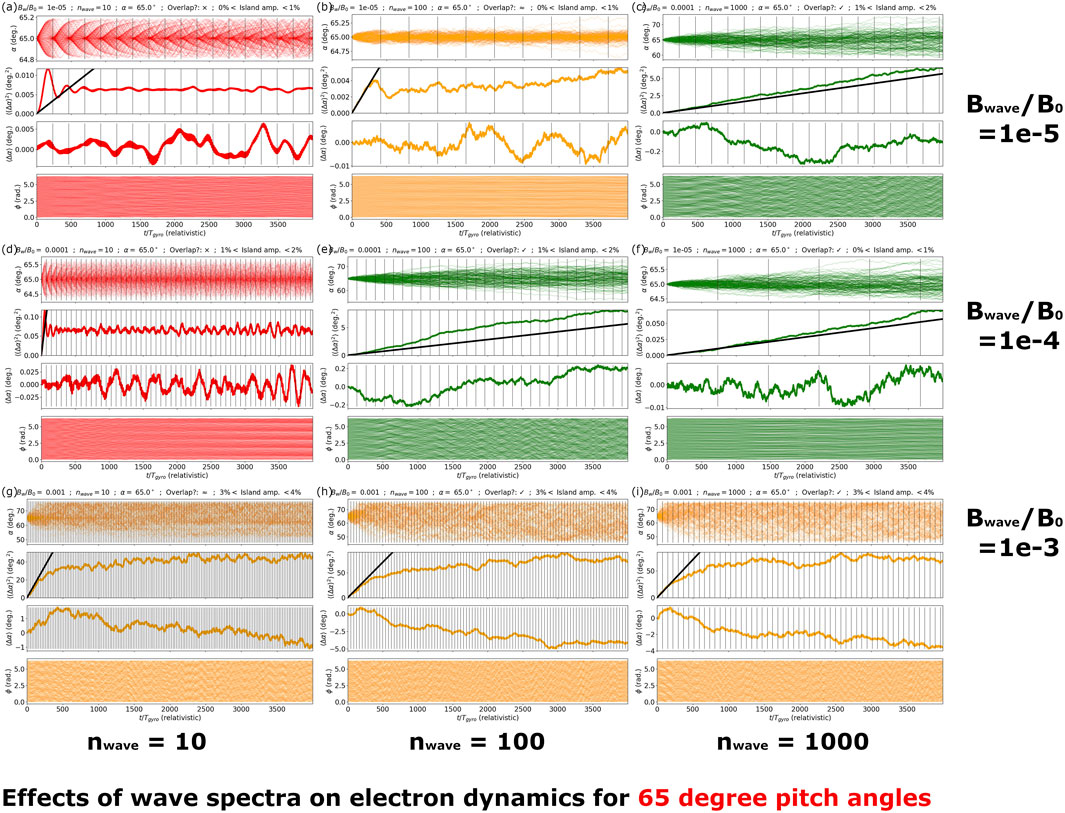
FIGURE 4. Demonstrating the effect of wave coherence and wave amplitude on particle trajectories for α =65°, E =28.751 keV. All details pertaining to sub-figures (A–I) are described in Section 3.
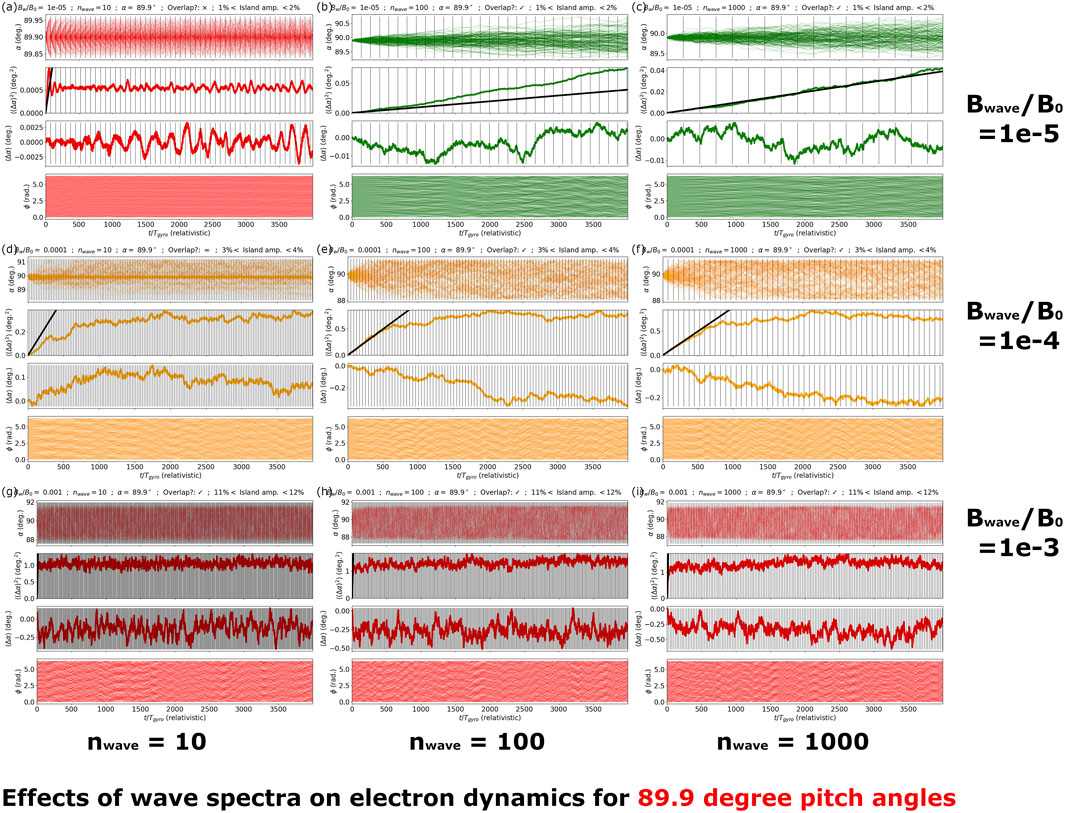
FIGURE 5. Demonstrating the effect of wave coherence and wave amplitude on particle trajectories for α =89.9°, E =1150.233 keV
In the title of each sub-figure, we further indicate whether or not the two important ‘quasilinear criteria’ as described in Sections II A,B are satisfied for this experiment. We define “overlap?” to be satisfied (“✓”) if Equation 3 is satisfied by a margin greater than 50% (i.e., vwidth ≥ (3/2)Δv/2); borderline (“ ≈ ”) if the margin is within the range 2/3–3/2; and not satisfied (“X”) for the cases with vwidth < (2/3)Δv/2. Furthermore we define “island amplitude” to be the ratio (converted to a percentage) of the resonant island centred on f = 0.3|fce|, when compared to the wave spectrum bandwidth, (see Eq. 1), which should be very small for validity of the quasilinear theory.
We combine the outcome of these tests to colour code the plots as follows, to indicate whether or not the quasilinear theory criteria are satisfied, according to the following:
• Green: Overlap criteria is satisfied, and island amplitude criteria is
• Orange: Overlap criteria is borderline, and/or amplitude criteria is
• Red: Overlap criteria is not satisfied, and/or island amplitude criteria is
Note that the exact values for the boundaries that we choose for overlap and amplitude criteria are (within reason) somewhat arbitrary, but are nonetheless sensible and chosen to be indicative of different regimes.
For all plots of ⟨(Δα)2⟩, we overplot in black the linear response predicted by resonant limit quasilinear theory according to Eq. 7. Furthermore, we also plot (as vertical grey lines) integer multiples of (1/2) (2π/ωtr,k), namely, multiples of “half-trapping-periods” for the mode k that corresponds to f = 0.3|fce|, with a trapping period defined as 2π/ωtr,k. A half-trapping-period represents the (theoretical) return of particles to the exact resonant parallel velocity, if they are exhibiting deterministic trajectories, e.g., see phase space plots in Dysthe (1971); Wykes et al. (2001).
In the Supporting Information S1 we further present similar figures for all 126 experiments as previously discussed. These figures further include analagous quantities for transport in energy space, omitted in the main text for brevity, and also since energy transport is exactly correlated to pitch-angle transport for the special case of parallel-propagting waves (Brice, 1964; Allanson et al., 2019).
3.1 The small and very small pitch-angle regimes
In Figures 2A–I we present the pitch-angle and gyrophase response for particles initially resonant with f = 0.3|fce| for α = 0.1°, E = 5.463 keV. It is clear that the resonant overlap criteria can be difficult to satisfy for such a small pitch angle, with only case 2(i) demonstrating a satisfaction of the overlap criteria. There is also a good and sustained agreement with the quasilinear theory prediction for that case, and an apparently sustained randomised gyrophase distribution. Having said that, the ‘drift’ ⟨Δα⟩ observed for case 2(i) is substantial. We remind that ‘drift’ and ‘true advection’ are not the same thing (Lemons, 2012; Zheng et al., 2019; Allanson et al., 2022), and so it may be the case that this drift can be attributed to that expected within the domain of quasilinear theory itself, pending further investigation beyond the scope of this work. For all other sub-figures, we can see that the overlap criteria is not satisfied, but the small wave-amplitude criteria is satisfied. There are a diverse range of particle responses, that can be characterised as follows:
• Deterministic periodic trapping. Cases 2(a) (b), 2(d) (e) and 2(g) resolve periodic deterministic trapped electron trajectories in pitch-angle space, with the gyrophase response also obeying a corresponding periodic behaviour. It is clear that the quasilinear prediction does not describe these cases (although it is of course not expected to do so in this case);
• An initial ‘convex response’ (∝ tn, n > 1) followed by a ‘saturation’. Cases 2(c) and 2(f) demonstrate an initial response for early times which appears to be reasonably well fitted by the quasilinear theory very early on, followed by enhanced transport. There is no obvious discernible correlation between structure in the gyrophase response and the pitch-angle response;
• ‘Concave response’ (∝ tn, n < 1). Cases 2(h) and 2(i) appear phenomenologically similar, although case 2(i) satisfies the overlap criteria as previously discussed (and appears well described by the quasilinear prediction), whereas case 2(h) does not.
To summarise, we see that it is challenging but not impossible to satisfy the quasilinear conditions at such a small pitch-angle. There are a range of particle responses, described by a range of behaviours varying from deterministic trapping to quasilinear diffusion. The corresponding measured drift in all cases is non-negligible. For those particle responses that are deterministic, we do see a corresponding periodic structure in the gyrophase response, which makes sense when one considers the technicalities of trapping by resonant islands. Having said that, the periodicity of these trapped populations does not match well with the predictions using the trapping period as overplotted. However, we suggest that this is due to the fact that trapping islands are necessarily distorted at small pitch-angles (Artemyev et al., 2021a; Albert et al., 2021).
In Figures 3A–I we present the pitch-angle and gyrophase response for particles initially resonant with f = 0.3|fce| for α = 1°, E = 5.465 keV. The results for this value are broady similar to those presented in Figure 2, with a few exceptions. The main differences are as follows:
• We observe a closer matching of the deterministic periodic motion to that predicted by the integer multiples of the half-trapping-periods, and in particular for Figures 3D, E;
• We observe that one additional case satisfies the Chirikov overlap criterion (Figure 3F). Interestingly, the quasilinear theory matches very well for this case, but only for a portion of the run-time, with the electron response then rising and saturating, as in other presented cases;
• a number of the sub-figures (in particular Figures 3A, B, D, E) demonstrate a significant and periodic ordering of particles in gyrophase space, with particular gyrophases being favoured during a trapping half-period, and then subsequently re-mixed.
This figure therefore demonstrates that there is a notable difference between particle dynamics at very small (i.e., close to 0°), and small (i.e., at the boundary of resonant overlap, and perhaps close to the loss cone) pitch-angles. This fact is well-known based on a number of recent studies that consider the context of an inhomogeneous background magnetic field (e.g., see Albert et al. (2021); Artemyev et al. (2021a)), and here we demonstrate a related phenomenon for the case of a uniform background magnetic field.
3.2 The quasilinear regimes
The two core requirements for validity of the quasilinear theory (low-amplitude perturbations and resonant island overlap) have been defined in Section 2 A,B. We here emphasise that all experiments that are expected to satisfy the quasilinear theory (i.e., when these two conditions are satisfied, and with the ‘low-amplitude/island amplitude’ criterion being at or below a few percent) show either good or very good agreement with the quasilinear diffusion coefficient for a certain amount of time. Further, there are some cases when the conditions are not satisfied, and yet we still observe a partial agreement with the quasilinear theory, which is very interesting to note, and certainly motivates future work.
In Figures 4A–I we present the pitch-angle and gyrophase response for particles initially resonant with f = 0.3|fce| for α = 65°, E = 28.751 keV. The main features that we observe here are the following:
• Fewer examples (if any) display (quasi-)deterministic trajectories. Collective periodic motions are observable via the scatter plots in Figures 4A, D. Howevever this is of a fundamentally different nature to the deterministic oscillations demonstrated in some examples in Figures 2, 3. In Figures 4A, D there is a dispersion and subsequent coalescence of particles on trapping timescales, as indicated by the vertical lines. Chirikov resonant overlap is not demonstrated in these examples, and so we suggest that this behaviour can be attributed to particles ‘hopping’ in ‘gyroangle-wave-phase’ space from one island to another (‘horizontally’ if one considers the standard island diagrams, e.g., see Dysthe (1971)), without significantly changing velocity.
• Correspondingly, we observe that the quasilinear theory is frequently valid (overlap and small amplitude criteria satisfied), and this is reflected by the particle behaviour in sub-Figures 4C, E–I). However, we make the important note that the linear response has an inherent time-limitation ∝ 1/D that decreases as island amplitude increases.
• Interestingly, cases 4(b) and 4(d) demonstrate an apparent satisfaction of the quasilinear prediction for a brief initial phase, despite not satisfying the overlap criterion. This timescale is of the order of a half-trapping period. It is interesting to consider this within the context of the theories presented by e.g., Albert (2010), in which it is shown that one resonant island can give rise to diffusive trajectories in an inhomogenous magnetic field, due to the fact that the resonant island is moving in phase space. In that case, a resonant interaction can give rise to diffusion provided the particles interact with the wave-particle potential (i.e., the resonant island) transiently, and therefore avoid trapping or bunching.
• Negligible drift is observed in all cases except for 4(g)-(i), of the order of a few degrees. Once again, it is not the purpose of this paper to ascertain whether or not this motion is ‘diffusion-induced’ or true advection (see discussion in Section III A and e.g., Lemons (2012); Zheng et al. (2019); Allanson et al. (2022) and references therein). But it will be important to consider in future studies, after further theoretical developments.
3.3 The large pitch-angle regime
In Figures 5A–I we present the pitch-angle and gyrophase response for particles initially resonant with f = 0.3|fce| for α = 89.9°, E = 1150.233 keV
3.4 A summary of the different regimes
In Figure 6 we collect together the main conclusions that we draw from experiments performed in this paper, and in particular the different ‘species’ in the ‘zoo’ of particle responses. We classify five different varieties of particle response, according to
1. Very small pitch-angle with no overlap. In these cases the resonant overlap criteria is not satisfied, particles evolve deterministically due to trapping in resonant islands with e.g., Δα ∝ sin (Ct), for C < ωtr,k some constant. However, the trapping period does not fit the standard trapping period formulae (Omura, 2021), but this is not surprising given that trapping islands are deformed at very small pitch-angles (Le Queau and Roux, 1987; Artemyev et al., 2021a; Albert et al., 2021);
2. Small pitch angle with no overlap. Again, the resonant overlap criteria is not satisfied, and particles evolve deterministically due to trapping in resonant islands with e.g., Δα ∝ sin (ωtr,kt);
3. Small pitch-angle with overlap. The quasilinear theory is technically valid but dynamics may not reproduce the standard linear response for a long time, if at all. We observe Δα ∝ t and there is evidence to suggest that the governing equation in such cases may not be the standard ‘diffusion equation’ since additional advective terms may be required Lemons (2012). In any case, it is important to note that the diffusive component of the dynamics are likely still well described by the diffusion equation, despite the fact that we do not observe the linear response (Vanden Eijnden, 1997). This is clearly a complicated issue and requires further investigation;
4. The standard quasilinear regime. Resonance overlap and small amplitude criteria are satisfied, and Δα ∝ t1/2. We see the standard linear response, however this will saturate after some departure timescale ∝ 1/D (Liu et al., 2010; Lemons, 2012);
5. The large pitch-angle regime. Quasilinear theory may or may not technically be valid since the overlap criteria will be satisfied but the small wave-amplitude criteria may be broken. This regime is characterised by an initial response that very rapidly saturates. It often seems to be the case that the linear response is well matched by the quasilinear theory, even if only for a very short time.
These different regimes are demarcated in Figure 6. As nwave → ∞ for a fixed Bwave then this picture will tend to a function of pitch angle according to Eq. 1 in this paper (equation 2.18 of Karpman (1974)), independent of the resonant overlap criteria, leaving only three distinct regimes. As nwave increases for a fixed Bwave, then islands overlap more readily, because island width (ωtr,k/k) decreases
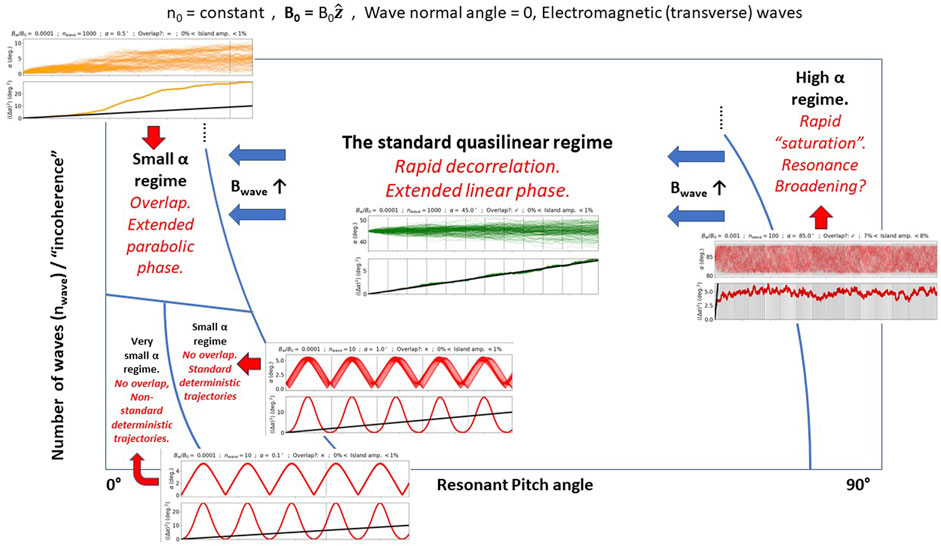
FIGURE 6. A schematic to describe different regimes of particle transport as a function of initial pitch-angle and the incoherence of the wave spectrum.
4 Discussion
4.1 A zoo of possibilities for the particle response for a given sample of survey-mode spacecraft data
We return now to the modelling of diffusion coefficients that drive radiation belt models. It is important to note that electromagnetic observations from spacecraft that are used to build empirical wave maps for use in constructing diffusion coefficients are usually ‘survey-mode’ spectra. As one example, the Van Allen Probes spacraft produce survey mode spectra of electromagnetic waveforms via the EMFISIS WFR instrument (Kletzing et al., 2013; Kletzing et al., 2023) with a cadence of 6s, and a discrete Fourier Transform that is performed over a 0.468s sub-section of the “continuous waveform burst-mode” data (sampled at 35 kHz over a 5.968s interval (Kletzing et al., 2023)). This survey mode spectra is therefore ‘averaged’ in the sense that it is composed using all burst-mode waveforms collected over a given 0.468s period, and it is implicitly assumed to represent the 6s period. Furthermore the frequency bins used are quasi-logarithmically spaced and therefore the powers in each bin represent averages over that logarithmically sized bin. Therefore, the spectra are siginifcantly averaged both temporally and in frequency space (Tyler et al., 2019a; Tyler et al., 2019b).
In Figure 1 we present analytical wave forms and subsequently derived wave spectra to illustrate this point. Figures 1A–C show a 0.468s time-series of the By component of whistler-mode wave spectra constructed exactly as done for this article, with nwave = 10, 100, 1000 respectively and a fixed value of Bwave/B0 = 10–4. In Figures 1D–F we present the respective spectra for these wave forms that were calculated using a standard numerical FFT routine. In Figures 1G–I we further plot Fourier spectra for the same wave-forms but calculated exactly as per the FFT engine on the Van Allen Probes EMFISIS WFR instruments, as described above using quasi-logarithmic bins. Therefore Figures 1G–I represent prototypical wave spectra that one might expect to download as a EMFISIS WFR survey mode data product. Figures 1A–F demonstrate the variety of waveforms and wave spectral forms that could in principle be underlying these survey mode spectral prototypes. The results in our paper therefore demonstrate how one can obtain a significant variety of particle responses (as a function of pitch-angle) for essentially identical looking survey-mode products, even if they appear to satisfy all appropriate quasilinear criteria.
As discussed and implied by many authors (e.g., see Cully et al. (2008); Wilson et al., 2011; Breneman et al. (2011); Kellogg et al. (2011); Li et al. (2011); Santolík et al. (2014); Tyler et al. (2019b); Watt et al. (2017); Watt et al. (2019); Zhang et al. (2019); Zhang et al. (2020b); Zhang et al. (2020a)), these features imply that there could be a wide variability of waveform amplitudes and structures in time-frequency space for ‘similar-looking’ survey-mode spectra, and this has significant implications for the resultant particle transport (Zhang et al., 2020a; Zhang et al., 2020b; Allanson et al., 2021; Frantsuzov et al., 2023). Significant recent progress has been made in statistical analyses of the effects of the underlying “burst mode wave structure” of nonlinear whistler-mode waves on electron dynamics (e.g., see Artemyev et al. (2022) and references therein), ultimately aiming to charaterise diverse electron responses via effective diffusion coefficients that may scale with wave amplitude to powers other than two, depenmding on wave amplitude and wave packet duration.
It will be interesting in future work to assess the relative occurences of the different particle regimes indicated in Figure 6. It is true to say that the different wave fields used in the numerical experiments in this paper are somewhat idealised (e.g., Figures 1D, E), but they are chosen as such in order to isolate different regimes in which fundamentally different kinds of phenomena occur. Future work should focus on constraining the relative occurences of the different particle transport regimes by comparing with spacecraft data. Nonetheless, this idealisation does not detract from the main conclusions/contributions of this work, namely,: (i) to our knowledge, the most extensive numerical examination of electron scattering regimes for field-aligned and static R or L mode spectra in a cold and uniform plasma with uniform background magnetic field (expanding upon Liu et al. (2010); Tao et al. (2011); Allanson et al. (2019); Allanson et al. (2020); (ii) the key observation that extensively averaged spectra such as are provided via survey mode products can obscure significant structure in the wave spectrum, and that this can therefore imply a mulipliicity of electron responses; (iii) this multiplicity of electron responses is demonstrated, and is a strong function of resonant particle pitch-angle (and therefore energy), wave amplitude and wave coherence.
Further, and to give a specific example, whilst the spectra in e.g., Figures 1D, E, could be argued to have unphysical attributes (namely, the periodicity of the ‘spikes’ in frequency space), this exact feature is inconsequential for the electrons of interest, which are chosen to be resonant with the ‘spike’ at f = 0.3fce. The dynamics of those electrons will be determined by wave power that is either at or very much local to f = 0.3fce, and the non-zero ‘noise’ that is surrounding it. It is certainly not uncommon to observe ‘spikes’ in whistler-mode wave spectra (e.g., but not limited to chorus and transmitter mode waves), especially when one considers higher resolution data (e.g., see Cully et al. (2008); Wilson et al., 2011; Breneman et al. (2011); Kellogg et al. (2011); Li et al. (2011); Santolík et al. (2014); Tyler et al. (2019b); Watt et al. (2017); Watt et al. (2019); Zhang et al. (2019); Zhang et al. (2020b); Zhang et al. (2020a)). Therefore we believe that the electron dynamics associated with the waves in Figures 1D, E are certainly relevant, and in fact demonstrate the trapping of electrons in the island associated with the frequency for which the peak of the ‘spike’ occurs.
4.2 Relationship with work done in the context of an inhomogeneous background magnetic field
Most frequently, treatments on ‘non-quasilinear’ interactions have historically considered the effect of resonant interactions between coherent/monochrommatic electromagnetic waves on electrons in an inhomogeneous background field (e.g., see Tao et al. (2020); Omura (2021); Albert et al. (2022a); Artemyev et al. (2023) and references therein), although we note works that consider the effects of incoherent/broadband waves in inhomogeneous fields (Tao et al., 2012a; Artemyev et al., 2022; Gan et al., 2022; Frantsuzov et al., 2023). Furthermore, one could consider the additional effects of one or more of amplitude modulation (Tao et al., 2012b; Tao et al., 2013; Gan et al., 2020), rapid frequency variations and phase decoherence (Zhang et al., 2020b; Zhang X.-J. et al., 2021), and sequential resonant interactions (Tao et al., 2014), for a fully realistic treatment such as in An et al. (2022).
In short, the one foundational idea that unites many of these works in the inhomogeneous regime is the notion of the inhomogeneity parameter, a dimensionless ratio of the influence of the wave field to the background field inhomogeneity (Omura et al., 2008; Albert et al., 2012; Artemyev et al., 2023). For the case of a monochromatic coherent wave, then analysis based on the inhomogeneity parameter shows that dynamics can be described using bounce-averaged quasilinear diffusion coefficients for sufficiently small wave amplitudes and sufficiently large values of |∇B0|. Then, more complicated and perhaps more realistic wave form spectral varieties make this dichotomy more nuanced, e.g., see Artemyev et al. (2022).
Furthermore, there has recently been significant work that specifically aims to understand deviations from quasilinear diffusion theory (either whistler-mode or electromagnetic ion-cyclotron waves) for small pitch-angles in the context of an inhomogeneous background magnetic field (Grach and Demekhov, 2018; Kitahara and Katoh, 2019; Artemyev et al., 2021a; Albert et al., 2021; Albert et al., 2022a; Bortnik et al., 2022; Hanzelka et al., 2023), or large pitch angles within the context of a homogeneous background magnetic field (Camporeale, 2015; Camporeale and Zimbardo, 2015; Cai et al., 2020), and also a dipolar field (Tonoian et al., 2022).
The results of all of these studies can certainly be framed within the resonant island paradigm, as in our study. Furthermore, there are clear links between our results and those presented by Cai et al. (2020) within the context of resonance broadening (Dupree, 1966; Salat, 1988; Karimabadi and Menyuk, 1991; Karimabadi et al., 1992), meriting further investigation. We reiterate that the reasons for considering all of these important features (background magnetic field inhomogeneity, wave amplitude modulation, phase decoherence) are clear and beyond reproach, namely, to best represent and describe physical reality. However, in this study we make the choice to directly probe weak turbulence/quasilinear theories (Kennel and Engelmann, 1966; Lerche, 1968; Lyons et al., 1972; Summers, 2005; Allanson et al., 2022) that currently form the foundations of radiation belt models (Subbotin and Shprits, 2009; Tu et al., 2013; Glauert et al., 2014; Ma et al., 2018; Wang et al., 2020), prior to bounce- and drift-averaging Roberts (1969); Lyons et al. (1972).
This manuscript contributes to this wider body of work by specifically considering wave modes that at first appearances may appear relatively benign, namely, low amplitude-broadband and in the case of a uniform background field. We demonstrate that there is a range of particle responses permissible to wave spectra that ‘look quasilinear’, and that these behaviours are a function of pitch-angle and wave coherence. This motivates further future observational and theoretical studies, including those that may derive new transport theories for such phenomena.
4.3 On the extraction of diffusion coefficients from numerical experiments
It has been noted in a number of recent works that (even in the quasilinear regime), and for a given ‘short’ initial decorrelation time, the particle response (e.g., for pitch-angle ⟨(Δα)2⟩) may not evolve ∝ t1 (Allanson et al., 2019; Allanson et al., 2020), and likely will evolve ∝ t2 (Liu et al., 2010; Lemons, 2012; Escande, 2018). Therefore, when extracting a ‘diffusion coefficient’ from experimental data, one may obtain a Dexperiment ∝ t1 over that short time. This at first would appear to be a violation of the quasilinear predictions Dquasilinear ∝ t0. However, this ‘convex/parabolic’ particle response (⟨(Δα)2⟩∝ t2) may not in fact violate the assumptions of quasilinear theory, and is likely a natural initial transient phase of a quasilinear system that can (conditions permitting) later develop into the ‘linear’ particle response (⟨(Δα)2⟩∝ t1) that is standard for quasilinear theory (Vanden Eijnden, 1997; Liu et al., 2010; Escande, 2018).
Very interestingly, Lemons (2012) indicated that, nonetheless, a new form of the Fokker-Planck equation may be required in such a regime during early decorrelation times (in the case of pitch-angle dynamics only), despite the fact that the quasilinear conditions of the electromagnetic perturbations are satisfied (in their case it was magnetic perturbations only). We leave investigations of this nature for our system to future work, noting that related (analogous) phenomena have been recently described in Lejosne and Albert (2023) for the case of radial transport.
5 Summary
We present a detailed analyis of the resonant electron response to whistler mode waves in a uniform background magnetic field using a test-particle code. The waves are uniformly distributed between 0.2 and 0.4 of the electron gyrofrequency, and parallel-propagating. We vary the coherence of the wave spectrum and we further vary the value of wave amplitude to create a two-dimensional parameter space. We analyse the electron response as a function of initial pitch-angle, and compare to the evolution predicted by the relativistic resonant limit quasilinear theory.
One of the immediate practical implications is to consider the multiplicity of electron responses that could in truth be occurring in nature when electrons respond to waveforms that are consistent with a given survey-mode wave spectra downloaded from spacecraft. This motivates future studies that consider the diversity of waveforms that exist in burst-mode datasets for ‘apparently quasilinear’ survey-mode spectra (as depicted in Figure 1 and discussed in Section 4.1), and the corresponding implications of these diverse responses in statistical models of electron dynamics.
We interpret the results obtained within the context of the two relevant conditions for the validity of the quasilinear theory (in this system), namely, the Chirikov resonant overlap criteria and the small amplitude criteria. Both of these criteria are a function of pitch-angle, even in the regime of a uniform background magnetic field. We find five distinct regimes/‘species’ in the ‘zoo’ of particle responses (summarised in Figure 6), and our main conclusions are as follows:
1. ‘Intermediate pitch-angles/the standard quasilinear regime’: reassuringly, we observe that the quasilinear theory well matches the evolution of the electrons in almost all cases when it is predicted to do so. However, the pitch-angle range that this relates to is very much a function of wave coherence and wave amplitude. Furthermore, the duration of the ‘linear particle response’ that is predicted by quasilinear theory is variable (∝ 1/D).
2. ‘Small pitch-angle quasilinear regime’: interestingly, there are occasions at small pitch-angles where the quasilinear theory is technically valid, but we observe an extended ‘convex/parabolic’ phase. As discussed, this is not entirely unexpected and not a refutation of the diffusive Fokker-Planck equation in order to describe the diffusive component of the dynamics (Vanden Eijnden, 1997), however there is good reason to expect that there may be an additional and ‘true’ advective component to the dynamics for this transient phase (Lemons, 2012), but this remains a hypothesis at the current stage until further analysis is performed (beyond the scope of this manuscript).
3. ‘Small pitch-angle deterministic regime’: for sufficiently small pitch-angles stochasticity is prevented and the particles demonstrate a periodic and deterministic trajectory over the timescale considered, with periodicity determined by the trapping period (in the framework of resonant islands). This is a manifestation of the fact that the Chirikov resonant overlap criterion has not been satisfied.
4. ‘Very small pitch-angle deterministic regime’: here, particles respond in almost exactly the same way as in case 3., except for the fact that they do not oscillate with the period as predicted by standard trapping theory. We attribute this to the now well-known fact that resonant islands are necessarily deformed at very small pitch-angles.
5. ‘Large pitch-angle regime’: if the pitch-angle is sufficiently large, then ‘extreme overlap’ and/or the wave-amplitude result in electron trajectories that briefly transport in a manner that is often well matched by quasilinear theory but very rapidly saturate. It will be important in the future to consider this phenomenon within the context of resonance broadening theory (Dupree, 1966; Karimabadi and Menyuk, 1991; Cai et al., 2020), and the related so-called ‘90° problem’ for quasilinear theory (Camporeale, 2015; Camporeale and Zimbardo, 2015).
6. One feature that is common to regimes two to five, is that often (but not always) it appears that the linear response predicted by quasilinear theory well matches the transport for an initial short time. We will not overly speculate here what we believe may be causing this, but it certainly merits future work, and we believe (based on the conclusions presented in e.g., Lemons (2012)) that the Markovian formalism developed in Allanson et al. (2022) may be particularly well suited to analysing these phenomena. In particular the regimes of one or more of small pitch-angle, small times, large pitch-angles, all as a function of the underlying wave spectra.
7. A continuum of responses: all of the above mentioned conclusions are a function of the value of nwave and Bwave. The relationship is quite complex, but is discussed thoroughly within this work. The results presented in this paper certainly motivate further works that seek to find a unified description that can access all different five regimes for different parameter values.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
OA: Writing–original draft, Writing–review and editing. DM: Writing–original draft, Writing–review and editing. AO: Writing–original draft, Writing–review and editing. JA: Writing–original draft, Writing–review and editing. JB: Writing–original draft, Writing–review and editing. CW: Writing–original draft, Writing–review and editing. SC: Writing–original draft, Writing–review and editing. JS: Writing–original draft, Writing–review and editing. DR: Writing–original draft, Writing–review and editing. NM: Writing–original draft, Writing–review and editing. TE: Writing–original draft, Writing–review and editing. TN: Writing–original draft, Writing–review and editing. DH: Writing–original draft, Writing–review and editing. RB: Writing–original draft, Writing–review and editing. NW: Writing–original draft, Writing–review and editing. SE: Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. OA would like to acknowledge financial support from the University of Birmingham, the University of Exeter, and also from the United Kingdom Research and Innovation (UKRI) Natural Environment Research Council (NERC) Independent Research Fellowship NE/V013963/1 and NE/V013963/2, and the UKRI NERC GW4+ DTP2 studentship project (4253) 2697077. OA and CEJW acknowledge financial support from the NERC Highlight Topic Grant NE/P017274/1 (Rad-Sat), and from United Kingdom Science and Technology Facilities Council (STFC) via Consolidated Grant ST/W000369/1. DM and JB would like to gratefully acknowledge support from NASA award 80NSSC20K1270 and NASA/CCMC award 80NSSC23K0324. JB would like to acknowledge NSF/GEM award 2025706 and DM further acknowledges the UCLA Dissertation Year Fellowship. Support for AO was provided by the Academy of Finland profiling action Matter and Materials (grant # 318913). JA acknowledges support from AFOSR grant 2022RVCOR002. NPM would like to acknowledge funding from the Natural Environment Research Council grants NE/V00249X/1 (Sat-Risk), NE/R016038/1 and NE/X000389/1. RB would like to acknowledge the UKRI NERC GW4+ DTP2 studentship project (4253) 2697077. DR is grateful to the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme Dispersive Hydrodynamics where work on this paper was undertaken. DR was also supported by Engineering and Physical Sciences Research Council (EPSRC) grant no EP/R014604/1. SC acknowledges support from ISSI via the J. Geiss fellowship. SC and NW acknowledge support from the AFOSR grant FA8655-22-1-7056. TE and TN acknowledge support from UKRI Science and Technology Facilities Council (STFC) consolidated grant number ST/W001195/1. Support for DPH was provided by NASA grants 80NSSC21K0519 and 80NSSC20K1324. SE aknowledges support from the United Kingdom Space Weather Instrumentation, Measurement, Modelling and Risk (SWIMMR) Programme, Natural Environment Research Council (NERC) Grant NE/V002708/1.
Acknowledgments
The authors would like to acknowledge helpful discussions with Anton Artemyev (UCLA), Alain Brizard (St Michael’s College), Anthony Chan (Rice University), Solène Lejosne (UC Berkeley), Ivan Vasko (UC Berkeley), Lynn Wilson III (NASA GSFC), and Xiaojia Zhang (UT Dallas).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1332931/full#supplementary-material
References
Agapitov, O., Artemyev, A., Krasnoselskikh, V., Khotyaintsev, Y. V., Mourenas, D., Breuillard, H., et al. (2013). Statistics of whistler mode waves in the outer radiation belt: cluster staff-sa measurements. J. Geophys. Res. Space Phys. 118, 3407–3420. doi:10.1002/jgra.50312
Agapitov, O. V., Artemyev, A. V., Mourenas, D., Mozer, F. S., and Krasnoselskikh, V. (2015). Nonlinear local parallel acceleration of electrons through landau trapping by oblique whistler mode waves in the outer radiation belt. Geophys. Res. Lett. 42, 10140–10149. doi:10.1002/2015GL066887
Albert, J. M. (2001). Comparison of pitch angle diffusion by turbulent and monochromatic whistler waves. J. Geophys. Res. Space Phys. 106, 8477–8482. doi:10.1029/2000JA000304
Albert, J. M. (2005). Evaluation of quasi-linear diffusion coefficients for whistler mode waves in a plasma with arbitrary density ratio. J. Geophys. Res. Space Phys. 110, 2004JA010844. doi:10.1029/2004JA010844
Albert, J. M. (2009). The coupling of quasi-linear pitch angle and energy diffusion. J. Atmos. Solar-Terrestrial Phys. 71, 1664–1668. doi:10.1016/j.jastp.2008.11.014
Albert, J. M. (2010). Diffusion by one wave and by many waves. J. Geophys. Res. Space Phys. 115, 2009JA014732. doi:10.1029/2009JA014732
Albert, J. M. (2013). Comment on “on the numerical simulation of particle dynamics in the radiation belt. part i: implicit and semi-implicit schemes” and “on the numerical simulation of particle dynamics in the radiation belt. part ii: procedure based on the diagonalization of the diffusion tensor” by e. camporeale et al. J. Geophys. Res. Space Phys. 118, 7762–7764. doi:10.1002/2013JA019126
Albert, J. M., Artemyev, A., Li, W., Gan, L., and Ma, Q. (2022a). Analytical results for phase bunching in the pendulum model of wave-particle interactions. Front. Astronomy Space Sci. 9, 971358. doi:10.3389/fspas.2022.971358
Albert, J. M., Artemyev, A., Li, W., Gan, L., and Ma, Q. (2022b). Equations of motion near cyclotron resonance. Front. Astronomy Space Sci. 9, 910224. doi:10.3389/fspas.2022.910224
Albert, J. M., Artemyev, A. V., Li, W., Gan, L., and Ma, Q. (2021). Models of resonant wave-particle interactions. J. Geophys. Res. Space Phys. 126, e2021JA029216. doi:10.1029/2021JA029216
Albert, J. M., and Bortnik, J. (2009). Nonlinear interaction of radiation belt electrons with electromagnetic ion cyclotron waves. Geophys. Res. Lett. 36, 2009GL038904. doi:10.1029/2009GL038904
Albert, J. M., Tao, X., and Bortnik, J. (2012). Aspects of nonlinear wave-particle interactions. United States: American Geophysical Union, 255–264. doi:10.1029/2012GM001324
Allanson, O., Elsden, T., Watt, C., and Neukirch, T. (2022). Weak turbulence and quasilinear diffusion for relativistic wave-particle interactions via a markov approach. Front. Astronomy Space Sci. 8, 805699. doi:10.3389/fspas.2021.805699
Allanson, O., Watt, C. E. J., Allison, H. J., and Ratcliffe, H. (2021). Electron diffusion and advection during nonlinear interactions with whistler-mode waves. J. Geophys. Res. Space Phys. 126, e2020JA028793. doi:10.1029/2020JA028793
Allanson, O., Watt, C. E. J., Ratcliffe, H., Allison, H. J., Meredith, N. P., Bentley, S. N., et al. (2020). Particle-in-cell experiments examine electron diffusion by whistler-mode waves: 2. quasi-linear and nonlinear dynamics. J. Geophys. Res. Space Phys. 125, e2020JA027949. doi:10.1029/2020JA027949
Allanson, O., Watt, C. E. J., Ratcliffe, H., Meredith, N. P., Allison, H. J., Bentley, S. N., et al. (2019). Particle-in-cell experiments examine electron diffusion by whistler-mode waves: 1. benchmarking with a cold plasma. J. Geophys. Res. Space Phys. 124, 8893–8912. doi:10.1029/2019JA027088
Allanson, O., Zhang, X.-J., and Omura, Y. (2023). Quasilinear and nonlinear wave-particle interactions in magnetospheric plasmas. Lausanne: Frontiers Media SA. doi:10.3389/978-2-8325-3710-7
Allison, H. J., and Shprits, Y. Y. (2020). Local heating of radiation belt electrons to ultra-relativistic energies. Nat. Commun. 11, 4533. doi:10.1038/s41467-020-18053-z
An, Z., Wu, Y., and Tao, X. (2022). Electron dynamics in a chorus wave field generated from particle-in-cell simulations. Geophys. Res. Lett. 49, e2022GL097778. doi:10.1029/2022GL097778
Andronov, A. A., and Trakhtengerts, V. V. (1964). Kinetic instability of the earth’s outer radiation belt. Geomagnetism Aeronomy 4, 233–242.
Arber, T. D., Bennett, K., Brady, C. S., Lawrence-Douglas, A., Ramsay, M. G., Sircombe, N. J., et al. (2015). Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys. Control. Fusion 57, 113001–113026. doi:10.1088/0741-3335/57/11/113001
Artemyev, A. V., Albert, J. M., Neishtadt, A. I., and Mourenas, D. (2023). The effect of wave frequency drift on the electron nonlinear resonant interaction with whistler-mode waves. Phys. Plasmas 30, 012901. doi:10.1063/5.0131297
Artemyev, A. V., Mourenas, D., Agapitov, O. V., and Krasnoselskikh, V. V. (2015). Relativistic electron scattering by magnetosonic waves: effects of discrete wave emission and high wave amplitudes. Phys. Plasmas 22, 062901. doi:10.1063/1.4922061
Artemyev, A. V., Mourenas, D., Zhang, X.-J., and Vainchtein, D. (2022). On the incorporation of nonlinear resonant wave-particle interactions into radiation belt models. J. Geophys. Res. Space Phys. 127, e2022JA030853. doi:10.1029/2022JA030853
Artemyev, A. V., Neishtadt, A. I., Albert, J. M., Gan, L., Li, W., and Ma, Q. (2021a). Theoretical model of the nonlinear resonant interaction of whistler-mode waves and field-aligned electrons. Phys. Plasmas 28, 052902. doi:10.1063/5.0046635
Artemyev, A. V., Neishtadt, A. I., Vasiliev, A. A., Zhang, X.-J., Mourenas, D., and Vainchtein, D. (2021b). Long-term dynamics driven by resonant wave–particle interactions: from Hamiltonian resonance theory to phase space mapping. J. Plasma Phys. 87, 835870201. doi:10.1017/S0022377821000246
Bentley, S. N., Watt, C. E. J., Rae, I. J., Owens, M. J., Murphy, K., Lockwood, M., et al. (2019). Capturing uncertainty in magnetospheric ultralow frequency wave models. Space Weather 17, 599–618. doi:10.1029/2018SW002102
Birdsall, C., and Langdon, A. (2004). “Plasma physics via computer simulation,” in Series in plasma physics and fluid dynamics (United Kingdom: Taylor and Francis).
Bortnik, J., Albert, J. M., Artemyev, A., Li, W., Jun, C.-W., Grach, V. S., et al. (2022). Amplitude dependence of nonlinear precipitation blocking of relativistic electrons by large amplitude emic waves. Geophys. Res. Lett. 49, e2022GL098365. doi:10.1029/2022GL098365
Bortnik, J., Thorne, R. M., and Inan, U. S. (2008a). Nonlinear interaction of energetic electrons with large amplitude chorus. Geophys. Res. Lett. 35, 2008GL035500. doi:10.1029/2008GL035500
Bortnik, J., Thorne, R. M., and Meredith, N. P. (2008b). The unexpected origin of plasmaspheric hiss from discrete chorus emissions. Nature 452, 62–66. doi:10.1038/nature06741
Breneman, A., Cattell, C., Wygant, J., Kersten, K., Wilson, L. B., Schreiner, S., et al. (2011). Large-amplitude transmitter-associated and lightning-associated whistler waves in the earth’s inner plasmasphere at l < 2. J. Geophys. Res. Space Phys. 116. doi:10.1029/2010JA016288
Brice, N. (1964). Fundamentals of very low frequency emission generation mechanisms. J. Geophys. Res. 69, 4515–4522. doi:10.1029/JZ069i021p04515
Brizard, A. J., and Chan, A. A. (2001). Relativistic bounce-averaged quasilinear diffusion equation for low-frequency electromagnetic fluctuations. Phys. Plasmas 8, 4762–4771. doi:10.1063/1.1408623
Brizard, A. J., and Chan, A. A. (2004). Relativistic quasilinear diffusion in axisymmetric magnetic geometry for arbitrary-frequency electromagnetic fluctuations. Phys. Plasmas 11, 4220–4229. doi:10.1063/1.1773554
Brizard, A. J., and Chan, A. A. (2022). Hamiltonian formulations of quasilinear theory for magnetized plasmas. Front. Astronomy Space Sci. 9, 1010133. doi:10.3389/fspas.2022.1010133
Cai, B., Wu, Y., and Tao, X. (2020). Effects of nonlinear resonance broadening on interactions between electrons and whistler mode waves. Geophys. Res. Lett. 47, e2020GL087991. doi:10.1029/2020GL087991
Camporeale, E. (2015). Resonant and nonresonant whistlers-particle interaction in the radiation belts. Geophys. Res. Lett. 42, 3114–3121. doi:10.1002/2015GL063874
Camporeale, E., Delzanno, G. L., Zaharia, S., and Koller, J. (2013). On the numerical simulation of particle dynamics in the radiation belt: 2. procedure based on the diagonalization of the diffusion tensor. J. Geophys. Res. Space Phys. 118, 3476–3484. doi:10.1002/jgra.50278
Camporeale, E., Wilkie, G. J., Drozdov, A. Y., and Bortnik, J. (2022). Data-driven discovery of fokker-planck equation for the earth’s radiation belts electrons using physics-informed neural networks. J. Geophys. Res. Space Phys. 127, e2022JA030377. doi:10.1029/2022JA030377
Camporeale, E., and Zimbardo, G. (2015). Wave-particle interactions with parallel whistler waves: nonlinear and time-dependent effects revealed by particle-in-cell simulations. Phys. Plasmas 22, 092104. doi:10.1063/1.4929853
Chan, A. A., Elkington, S. R., Longley, W. J., Aldhurais, S. A., Alam, S. S., Albert, J. M., et al. (2023). Simulation of radiation belt wave-particle interactions in an mhd-particle framework. Front. Astronomy Space Sci. 10, 1239160. doi:10.3389/fspas.2023.1239160
Chen, H., Gao, X., Lu, Q., Fan, K., Ke, Y., Wang, X., et al. (2022). Gap formation around 0.5ωe in the whistler-mode waves due to the plateau-like shape in the parallel electron distribution: 2d pic simulations. J. Geophys. Res. Space Phys. 127, e2021JA030119. doi:10.1029/2021JA030119
Chirikov, B. V. (1960). Resonance processes in magnetic traps. J. Nucl. Energy. Part C, Plasma Phys. Accel. Thermonucl. Res. 1, 253–260. doi:10.1088/0368-3281/1/4/311
Chirikov, B. V. (1979). A universal instability of many-dimensional oscillator systems. Phys. Rep. 52, 263–379. doi:10.1016/0370-1573(79)90023-1
Cully, C. M., Bonnell, J. W., and Ergun, R. E. (2008). Themis observations of long-lived regions of large-amplitude whistler waves in the inner magnetosphere. Geophys. Res. Lett. 35, 2008GL033643. doi:10.1029/2008GL033643
Cunningham, G. S. (2023). Resolution of a few problems in the application of quasilinear theory to calculating diffusion coefficients in heliophysics. J. Geophys. Res. Space Phys. 128, e2023JA031703. doi:10.1029/2023JA031703
Desai, R. T., Eastwood, J. P., Horne, R. B., Allison, H. J., Allanson, O., Watt, C. E. J., et al. (2021). Drift orbit bifurcations and cross-field transport in the outer radiation belt: global mhd and integrated test-particle simulations. J. Geophys. Res. Space Phys. 126, e2021JA029802. doi:10.1029/2021JA029802
Devine, P. E., Chapman, S. C., and Eastwood, J. W. (1995). One- and two-dimensional simulations of whistler mode waves in an anisotropic plasma. J. Geophys. Res. Space Phys. 100, 17189–17203. doi:10.1029/95ja00842
Drozdov, A. Y., Shprits, Y. Y., Orlova, K. G., Kellerman, A. C., Subbotin, D. A., Baker, D. N., et al. (2015). Energetic, relativistic, and ultrarelativistic electrons: comparison of long-term verb code simulations with van allen probes measurements. J. Geophys. Res. Space Phys. 120, 3574–3587. doi:10.1002/2014JA020637
Drozdov, A. Y., Shprits, Y. Y., Usanova, M. E., Aseev, N. A., Kellerman, A. C., and Zhu, H. (2017). Emic wave parameterization in the long-term verb code simulation. J. Geophys. Res. Space Phys. 122, 8488–8501. doi:10.1002/2017JA024389
Drummond, W. E., and Pines, D. (1962). Nonlinear stability of plasma oscillations. Nucl. Fusion Suppl. 3, 1049–1058.
Dupree, T. H. (1966). A perturbation theory for strong plasma turbulence. Phys. Fluids 9, 1773–1782. doi:10.1063/1.1761932
Dysthe, K. B. (1971). Some studies of triggered whistler emissions. J. Geophys. Res. 76, 6915–6931. doi:10.1029/JA076i028p06915
Escande, D. F. (2018). From thermonuclear fusion to Hamiltonian chaos. Eur. Phys. J. H 43, 397–420. doi:10.1140/epjh/e2016-70063-5
Fan, K., Gao, X., Lu, Q., Guo, J., and Wang, S. (2019). The effects of thermal electrons on whistler mode waves excited by anisotropic hot electrons: linear theory and 2-d pic simulations. J. Geophys. Res. Space Phys. 124, 5234–5245. doi:10.1029/2019JA026463
Fok, M.-C., Glocer, A., Zheng, Q., Horne, R., Meredith, N., Albert, J., et al. (2011). Recent developments in the radiation belt environment model. J. Atmos. Solar-Terrestrial Phys. 73, 1435–1443. doi:10.1016/j.jastp.2010.09.033
Foster, J. C., Erickson, P. J., Omura, Y., Baker, D. N., Kletzing, C. A., and Claudepierre, S. G. (2017). Van allen probes observations of prompt mev radiation belt electron acceleration in nonlinear interactions with vlf chorus. J. Geophys. Res. Space Phys. 122, 324–339. doi:10.1002/2016JA023429
Frantsuzov, V. A., Artemyev, A. V., Zhang, X.-J., Allanson, O., Shustov, P. I., and Petrukovich, A. A. (2023). Diffusive scattering of energetic electrons by intense whistler-mode waves in an inhomogeneous plasma. J. Plasma Phys. 89, 905890101. doi:10.1017/S0022377822001271
Gan, L., Li, W., Ma, Q., Albert, J., Artemyev, A., and Bortnik, J. (2020). Nonlinear interactions between radiation belt electrons and chorus waves: dependence on wave amplitude modulation. Geophys. Res. Lett. 47, e2019GL085987. doi:10.1029/2019GL085987
Gan, L., Li, W., Ma, Q., Artemyev, A. V., and Albert, J. M. (2022). Dependence of nonlinear effects on whistler-mode wave bandwidth and amplitude: a perspective from diffusion coefficients. J. Geophys. Res. Space Phys. 127, e2021JA030063. doi:10.1029/2021JA030063
Glauert, S. A., and Horne, R. B. (2005). Calculation of pitch angle and energy diffusion coefficients with the PADIE code. J. Geophys. Res. 110, A04206. doi:10.1029/2004JA010851
Glauert, S. A., Horne, R. B., and Meredith, N. P. (2014). Three-dimensional electron radiation belt simulations using the bas radiation belt model with new diffusion models for chorus, plasmaspheric hiss, and lightning-generated whistlers. J. Geophys. Res. Space Phys. 119, 268–289. doi:10.1002/2013JA019281
Glauert, S. A., Horne, R. B., and Meredith, N. P. (2018). A 30-year simulation of the outer electron radiation belt. Space Weather 16, 1498–1522. doi:10.1029/2018SW001981
Grach, V. S., and Demekhov, A. G. (2018). Resonance interaction of relativistic electrons with ion-cyclotron waves. I. Specific features of the nonlinear interaction regimes. Radiophys. Quantum Electron. 60, 942–959. doi:10.1007/s11141-018-9860-0
Green, J. C., Onsager, T. G., O’Brien, T. P., and Baker, D. N. (2004). Testing loss mechanisms capable of rapidly depleting relativistic electron flux in the earth’s outer radiation belt. J. Geophys. Res. Space Phys. 109, 2004JA010579. doi:10.1029/2004JA010579
Hall, D. E., and Sturrock, P. A. (1967). Diffusion, scattering, and acceleration of particles by stochastic electromagnetic fields. Phys. Fluids 10, 2620–2628. doi:10.1063/1.1762084
Hanzelka, M., Li, W., and Ma, Q. (2023). Parametric analysis of pitch angle scattering and losses of relativistic electrons by oblique EMIC waves. Front. Astronomy Space Sci. 10, 1163515. doi:10.3389/fspas.2023.1163515
Hartley, D. P., Kletzing, C. A., Santolík, O., Chen, L., and Horne, R. B. (2018). Statistical properties of plasmaspheric hiss from van allen probes observations. J. Geophys. Res. Space Phys. 123, 2605–2619. doi:10.1002/2017JA024593
Hikishima, M., and Omura, Y. (2012). Particle simulations of whistler-mode rising-tone emissions triggered by waves with different amplitudes. J. Geophys. Res. Space Phys. 117, 2011JA017428. doi:10.1029/2011JA017428
Hikishima, M., Omura, Y., and Summers, D. (2010). Self-consistent particle simulation of whistler mode triggered emissions. J. Geophys. Res. Space Phys. 115, 2010JA015860. doi:10.1029/2010JA015860
Hikishima, M., Omura, Y., and Summers, D. (2020). Particle simulation of the generation of plasmaspheric hiss. J. Geophys. Res. Space Phys. 125, e2020JA027973. doi:10.1029/2020JA027973
Hikishima, M., Yagitani, S., Omura, Y., and Nagano, I. (2009). Full particle simulation of whistler-mode rising chorus emissions in the magnetosphere. JGR Space Phys. 114, 2008ja013625. doi:10.1029/2008ja013625
Horne, R. B., Kersten, T., Glauert, S. A., Meredith, N. P., Boscher, D., Sicard-Piet, A., et al. (2013). A new diffusion matrix for whistler mode chorus waves. J. Geophys. Res. Space Phys. 118, 6302–6318. doi:10.1002/jgra.50594
Karimabadi, H., Krauss-Varban, D., and Terasawa, T. (1992). Physics of pitch angle scattering and velocity diffusion, 1. theory. J. Geophys. Res. Space Phys. 97, 13853–13864. doi:10.1029/92JA00997
Karimabadi, H., and Menyuk, C. R. (1991). A fast and accurate method of calculating particle diffusion: application to the ionosphere. J. Geophys. Res. Space Phys. 96, 9669–9687. doi:10.1029/91JA00315
Karpman, V. (1974). Nonlinear effects in the ELF waves propagating along the magnetic field in the magnetosphere. Space Sci. Rev. 16, 361–388. doi:10.1007/BF00171564
Kaufman, A. N. (2009). A half-century in plasma physics. J. Phys. Conf. Ser. 169, 012002. doi:10.1088/1742-6596/169/1/012002
Kaufman, A. N., and Cohen, B. I. (2019). Theoretical plasma physics. J. Plasma Phys. 85, 205850601. doi:10.1017/S0022377819000667
Ke, Y., Gao, X., Lu, Q., Wang, X., and Wang, S. (2017). Generation of rising-tone chorus in a two-dimensional mirror field by using the general curvilinear pic code. J. Geophys. Res. Space Phys. 122, 8154–8165. doi:10.1002/2017JA024178
Kellogg, P. J., Cattell, C. A., Goetz, K., Monson, S. J., and Wilson, L. B. (2011). Large amplitude whistlers in the magnetosphere observed with wind-waves. J. Geophys. Res. Space Phys. 116, 2010JA015919. doi:10.1029/2010JA015919
Kennel, C. F., and Engelmann, F. (1966). Velocity space diffusion from weak plasma turbulence in a magnetic field. Phys. Fluids 9, 2377–2388. doi:10.1063/1.1761629
Kersten, T., Horne, R. B., Glauert, S. A., Meredith, N. P., Fraser, B. J., and Grew, R. S. (2014). Electron losses from the radiation belts caused by emic waves. J. Geophys. Res. Space Phys. 119, 8820–8837. doi:10.1002/2014JA020366
Kessel, M. (2016). Things we do not yet understand about solar driving of the radiation belts. J. Geophys. Res. Space Phys. 121, 5549–5552. doi:10.1002/2016JA022472
Kitahara, M., and Katoh, Y. (2019). Anomalous trapping of low pitch angle electrons by coherent whistler mode waves. J. Geophys. Res. Space Phys. 124, 5568–5583. doi:10.1029/2019JA026493
Kletzing, C. A., Bortnik, J., Hospodarsky, G., Kurth, W. S., Santolik, O., Smitth, C. W., et al. (2023). The electric and magnetic fields instrument suite and integrated science (EMFISIS): science, data, and usage best practices. Space Sci. Rev. 219, 28. doi:10.1007/s11214-023-00973-z
Kletzing, C. A., Kurth, W. S., Acuna, M., MacDowall, R. J., Torbert, R. B., Averkamp, T., et al. (2013). The electric and magnetic field instrument suite and integrated science (EMFISIS) on RBSP. Space Sci. Rev. 179, 127–181. doi:10.1007/s11214-013-9993-6
Kluth, G., Ripoll, J. F., Has, S., Fischer, A., Mougeot, M., and Camporeale, E. (2022). Machine learning methods applied to the global modeling of event-driven pitch angle diffusion coefficients during high speed streams. Front. Phys. 10, 786639. doi:10.3389/fphy.2022.786639
Kulsrud, R., and Pearce, W. P. (1969). The effect of wave-particle interactions on the propagation of cosmic rays. Astrophysical J. 156, 445. doi:10.1086/149981
Kurita, S., Miyoshi, Y., Kasahara, S., Yokota, S., Kasahara, Y., Matsuda, S., et al. (2018). Deformation of electron pitch angle distributions caused by upper band chorus observed by the arase satellite. Geophys. Res. Lett. 45, 7996–8004. doi:10.1029/2018GL079104
Kuzichev, I. V., Vasko, I. Y., Artemyev, A. V., Bale, S. D., and Mozer, F. S. (2023). Particle-in-cell simulations of sunward and anti-sunward whistler waves in the solar wind. Astrophysical J. 959, 65. doi:10.3847/1538-4357/acfd28
Lejosne, S. (2019). Analytic expressions for radial diffusion. J. Geophys. Res. Space Phys. 124, 4278–4294. doi:10.1029/2019JA026786
Lejosne, S., and Albert, J. M. (2023). Drift phase resolved diffusive radiation belt model: 1. theoretical framework. Front. Astronomy Space Sci. 10, 1200485. doi:10.3389/fspas.2023.1200485
Lejosne, S., Allison, H. J., Blum, L. W., Drozdov, A. Y., Hartinger, M. D., Hudson, M. K., et al. (2022). Differentiating between the leading processes for electron radiation belt acceleration. Front. Astronomy Space Sci. 9, 896245. doi:10.3389/fspas.2022.896245
Lemons, D. S. (2012). Pitch angle scattering of relativistic electrons from stationary magnetic waves: continuous markov process and quasilinear theory. Phys. Plasmas 19, 012306. doi:10.1063/1.3676156
Le Queau, D., and Roux, A. (1987). Quasi-monochromatic wave particle interactions in magnetospheric plasmas. Sol. Phys. 111, 59–80. doi:10.1007/BF00145441
Lerche, I. (1968). Quasilinear theory of resonant diffusion in a magnetoactive, relativistic plasma. Phys. Fluids 11, 1720–1727. doi:10.1063/1.1692186
Li, J., Bortnik, J., An, X., Li, W., Angelopoulos, V., Thorne, R. M., et al. (2019). Origin of two-band chorus in the radiation belt of Earth. Nat. Commun. 10, 4672. doi:10.1038/s41467-019-12561-3
Li, W., Bortnik, J., Thorne, R. M., and Angelopoulos, V. (2011). Global distribution of wave amplitudes and wave normal angles of chorus waves using themis wave observations. J. Geophys. Res. Space Phys. 116, 2011JA017035. doi:10.1029/2011JA017035
Li, W., and Hudson, M. (2019). Earth’s van allen radiation belts: from discovery to the van allen probes era. J. Geophys. Res. Space Phys. 124, 8319–8351. doi:10.1029/2018JA025940
Li, W., Thorne, R. M., Ma, Q., Ni, B., Bortnik, J., Baker, D. N., et al. (2014). Radiation belt electron acceleration by chorus waves during the 17 march 2013 storm. J. Geophys. Res. Space Phys. 119, 4681–4693. doi:10.1002/2014JA019945
Liu, K., Lemons, D. S., Winske, D., and Gary, S. P. (2010). Relativistic electron scattering by electromagnetic ion cyclotron fluctuations: test particle simulations. J. Geophys. Res. Space Phys. 115, 2009JA014807. doi:10.1029/2009JA014807
Lukin, A. S., Artemyev, A. V., and Petrukovich, A. A. (2021). On application of stochastic differential equations for simulation of nonlinear wave–particle resonant interactions. Phys. Plasmas 28, 092904. doi:10.1063/5.0058054
Lukin, A. S., Artemyev, A. V., Zhang, X.-J., Allanson, O., and Tao, X. (2024). On the two approaches to incorporate wave-particle resonant effects into global test particle simulations. J. Geophys. Res. Space Phys. 129, e2023JA032163. doi:10.1029/2023JA032163
Lyons, L. R. (1974). General relations for resonant particle diffusion in pitch angle and energy. J. Plasma Phys. 12, 45–49. doi:10.1017/S0022377800024910
Lyons, L. R., Thorne, R. M., and Kennel, C. F. (1972). Pitch-angle diffusion of radiation belt electrons within the plasmasphere. J. Geophys. Res. 77, 3455–3474. doi:10.1029/JA077i019p03455
Ma, Q., Li, W., Bortnik, J., Thorne, R. M., Chu, X., Ozeke, L. G., et al. (2018). Quantitative evaluation of radial diffusion and local acceleration processes during gem challenge events. J. Geophys. Res. Space Phys. 123, 1938–1952. doi:10.1002/2017JA025114
Ma, Q., Li, W., Thorne, R. M., Ni, B., Kletzing, C. A., Kurth, W. S., et al. (2015). Modeling inward diffusion and slow decay of energetic electrons in the earth’s outer radiation belt. Geophys. Res. Lett. 42, 987–995. doi:10.1002/2014gl062977
Malaspina, D. M., Jaynes, A. N., Hospodarsky, G., Bortnik, J., Ergun, R. E., and Wygant, J. (2017). Statistical properties of low-frequency plasmaspheric hiss. J. Geophys. Res. Space Phys. 122, 8340–8352. doi:10.1002/2017JA024328
Matsoukis, S. K., Chapman, S., and Rowlands, G. (1998). Whistler mode wave coupling effects on electron dynamics in the near earth magnetosphere. Geophys. Res. Lett. 25, 265–268. doi:10.1029/97GL03716
Melrose, D. (1980). Plasma astrophysics: nonthermal processes in diffuse magnetized plasmas. Astrophysical applications. V. 2. New York: Gordon and Breach Science Publishers.
Meredith, N. P., Horne, R. B., Clilverd, M. A., and Ross, J. P. J. (2019). An investigation of vlf transmitter wave power in the inner radiation belt and slot region. J. Geophys. Res. Space Phys. 124, 5246–5259. doi:10.1029/2019JA026715
Meredith, N. P., Horne, R. B., Shen, X.-C., Li, W., and Bortnik, J. (2020). Global model of whistler mode chorus in the near-equatorial region (— λm| < 18°). Geophys. Res. Lett. 47, e2020GL087311. doi:10.1029/2020GL087311
Mourenas, D., Artemyev, A. V., Ma, Q., Agapitov, O. V., and Li, W. (2016). Fast dropouts of multi-mev electrons due to combined effects of emic and whistler mode waves. Geophys. Res. Lett. 43, 4155–4163. doi:10.1002/2016gl068921
Mourenas, D., Zhang, X.-J., Artemyev, A. V., Angelopoulos, V., Thorne, R. M., Bortnik, J., et al. (2018). Electron nonlinear resonant interaction with short and intense parallel chorus wave packets. J. Geophys. Res. Space Phys. 123, 4979–4999. doi:10.1029/2018JA025417
Mozer, F. S., Agapitov, O. V., Blake, J. B., and Vasko, I. Y. (2018). Simultaneous observations of lower band chorus emissions at the equator and microburst precipitating electrons in the ionosphere. Geophys. Res. Lett. 45, 511–516. doi:10.1002/2017GL076120
Murphy, K. R., Sandhu, J., Rae, I. J., Daggitt, T., Glauert, S., Horne, R. B., et al. (2023). A new four-component l*-dependent model for radial diffusion based on solar wind and magnetospheric drivers of ulf waves. Space Weather 21, e2023SW003440. doi:10.1029/2023SW003440
Neishtadt, A. (1999). On adiabatic invariance in two-frequency systems. Dordrecht: Springer Netherlands, 193–212. doi:10.1007/978-94-011-4673-9_17
Ni, B., Cao, X., Zou, Z., Zhou, C., Gu, X., Bortnik, J., et al. (2015). Resonant scattering of outer zone relativistic electrons by multiband emic waves and resultant electron loss time scales. J. Geophys. Res. Space Phys. 120, 7357–7373. doi:10.1002/2015JA021466
Nogi, T., and Omura, Y. (2023). Upstream shift of generation region of whistler-mode rising-tone emissions in the magnetosphere. J. Geophys. Res. Space Phys. 128, e2022JA031024. doi:10.1029/2022JA031024
Nunn, D., and Omura, Y. (2012). A computational and theoretical analysis of falling frequency vlf emissions. J. Geophys. Res. Space Phys. 117, 2012ja017557. doi:10.1029/2012ja017557
Omura, Y. (2021). Nonlinear wave growth theory of whistler-mode chorus and hiss emissions in the magnetosphere. Earth, Planets Space 73, 95. doi:10.1186/s40623-021-01380-w
Omura, Y., Katoh, Y., and Summers, D. (2008). Theory and simulation of the generation of whistler-mode chorus. J. Geophys. Res. Space Phys. 113, 2007JA012622. doi:10.1029/2007JA012622
Orlova, K., Spasojevic, M., and Shprits, Y. (2014). Activity-dependent global model of electron loss inside the plasmasphere. Geophys. Res. Lett. 41, 3744–3751. doi:10.1002/2014GL060100
Osmane, A., Kilpua, E., George, H., Allanson, O., and Kalliokoski, M. (2023). Linear, quasi-linear and nonlinear radial transport in the earth’s radiation belts. Astrophysical J. Letter. doi:10.3847/1538-4365/acff6a
Osmane, A., and Lejosne, S. (2021). Radial diffusion of planetary radiation belts’ particles by fluctuations with finite correlation time. Astrophysical J. 912, 142. doi:10.3847/1538-4357/abf04b
Osmane, A., Turner, D. L., Wilson, L. B., Dimmock, A. P., and Pulkkinen, T. I. (2017). Subcritical growth of electron phase-space holes in planetary radiation belts. Astrophysical J. 846, 83. doi:10.3847/1538-4357/aa8367
Osmane, A., Wilson, L. B., Blum, L., and Pulkkinen, T. I. (2016). On the connection between microbursts and nonlinear electronic structures in planetary radiation belts. Astrophysical J. 816, 51. doi:10.3847/0004-637x/816/2/51
Pahud, D., Rae, I., Mann, I., Murphy, K., and Amalraj, V. (2009). Ground-based pc5 ulf wave power: solar wind speed and mlt dependence. J. Atmos. Solar-Terrestrial Phys. 71, 1082–1092. doi:10.1016/j.jastp.2008.12.004
Rae, I. J., Mann, I. R., Murphy, K. R., Ozeke, L. G., Milling, D. K., Chan, A. A., et al. (2012). Ground-based magnetometer determination of in situ pc4–5 ulf electric field wave spectra as a function of solar wind speed. J. Geophys. Res. Space Phys. 117, 2011ja017335. doi:10.1029/2011ja017335
Ratcliffe, H., and Watt, C. E. J. (2017). Self-consistent formation of a 0.5 cyclotron frequency gap in magnetospheric whistler mode waves. J. Geophys. Res. Space Phys. 122, 8166–8180. doi:10.1002/2017JA024399
Ripoll, J.-F., Claudepierre, S. G., Ukhorskiy, A. Y., Colpitts, C., Li, X., Fennell, J. F., et al. (2020). Particle dynamics in the earth’s radiation belts: review of current research and open questions. J. Geophys. Res. Space Phys. 125, e2019JA026735. doi:10.1029/2019JA026735
Roberts, C. S. (1969). Pitch-angle diffusion of electrons in the magnetosphere. Rev. Geophys. 7, 305–337. doi:10.1029/rg007i001p00305
Roederer, J., and Zhang, H. (2013). “Dynamics of magnetically trapped particles: foundations of the physics of radiation belts and space plasmas,” in Astrophysics and space science library (Berlin, Germany: Springer Berlin Heidelberg).
Ross, J. P. J., Glauert, S. A., Horne, R. B., Watt, C. E., Meredith, N. P., and Woodfield, E. E. (2020). A new approach to constructing models of electron diffusion by emic waves in the radiation belts. Geophys. Res. Lett. 47, e2020GL088976. doi:10.1029/2020GL088976
Ross, J. P. J., Glauert, S. A., Horne, R. B., Watt, C. E. J., and Meredith, N. P. (2021). On the variability of emic waves and the consequences for the relativistic electron radiation belt population. J. Geophys. Res. Space Phys. 126, e2021JA029754. doi:10.1029/2021JA029754
Rowlands, J., Shapiro, V. D., and Shevchenko, V. I. (1966). Quasilinear theory of plasma cyclotron instability. Soviet J. Exp. Theor. Phys. 23, 651.
Salat, A. (1988). Exact resonance broadening theory of diffusion in random electric fields. Phys. Fluids 31, 1499–1504. doi:10.1063/1.866689
Sandhu, J. K., Rae, I. J., Wygant, J. R., Breneman, A. W., Tian, S., Watt, C. E. J., et al. (2021). Ulf wave driven radial diffusion during geomagnetic storms: a statistical analysis of van allen probes observations. J. Geophys. Res. Space Phys. 126, e2020JA029024. doi:10.1029/2020JA029024
Santolík, O., Kletzing, C. A., Kurth, W. S., Hospodarsky, G. B., and Bounds, S. R. (2014). Fine structure of large-amplitude chorus wave packets. Geophys. Res. Lett. 41, 293–299. doi:10.1002/2013GL058889
Sarris, T. E., Li, X., Zhao, H., Papadakis, K., Liu, W., Tu, W., et al. (2022). Distribution of ulf wave power in magnetic latitude and local time using themis and arase measurements. J. Geophys. Res. Space Phys. 127, e2022JA030469. doi:10.1029/2022JA030469
Schlickeiser, R. (1989). Cosmic-ray transport and acceleration. I - derivation of the kinetic equation and application to cosmic rays in static cold media. II - cosmic rays in moving cold media with application to diffusive shock wave acceleration. Astrophysical J. 336, 243. doi:10.1086/167009
Schulz, M., and Lanzerotti, L. (1974). “Particle diffusion in the radiation belts,” in Physics and chemistry in space (New York: Springer-Verlag).
Shprits, Y. Y., Kellerman, A. C., Drozdov, A. Y., Spence, H. E., Reeves, G. D., and Baker, D. N. (2015). Combined convective and diffusive simulations: verb-4d comparison with 17 march 2013 van allen probes observations. Geophys. Res. Lett. 42, 9600–9608. doi:10.1002/2015gl065230
Shumko, M., Turner, D. L., O’Brien, T. P., Claudepierre, S. G., Sample, J., Hartley, D. P., et al. (2018). Evidence of microbursts observed near the equatorial plane in the outer van allen radiation belt. Geophys. Res. Lett. 45, 8044–8053. doi:10.1029/2018GL078451
Sigov, Y. S., and Levchenko, V. D. (1996). Beam - plasma interaction and correlation phenomena in open vlasov systems. Plasma Phys. Control. Fusion 38, A49–A65. doi:10.1088/0741-3335/38/12A/005
Smith, G. R., Byers, J. A., and LoDestro, L. L. (1980). Superadiabatic and stochastic ion motion in the presence of a wave in a mirror-machine plasma. Phys. Fluids 23, 278–286. doi:10.1063/1.862960
Smith, G. R., and Kaufman, A. N. (1978). Stochastic acceleration by an obliquely propagating wave-an example of overlapping resonances. Phys. Fluids 21, 2230–2241. doi:10.1063/1.862161
Spasojevic, M., Shprits, Y. Y., and Orlova, K. (2015). Global empirical models of plasmaspheric hiss using van allen probes. J. Geophys. Res. Space Phys. 120, 10370–10383. doi:10.1002/2015JA021803
Steinacker, J., and Miller, J. A. (1992). Stochastic gyroresonant electron acceleration in a low-beta plasma. I. Interaction with parallel transverse cold plasma waves. Astrophysical J. 393, 764. doi:10.1086/171544
Su, Z., Gao, Z., Zhu, H., Li, W., Zheng, H., Wang, Y., et al. (2016). Nonstorm time dropout of radiation belt electron fluxes on 24 september 2013. J. Geophys. Res. Space Phys. 121, 6400–6416. doi:10.1002/2016JA022546
Subbotin, D. A., and Shprits, Y. Y. (2009). Three-dimensional modeling of the radiation belts using the versatile electron radiation belt (verb) code. Space Weather 7, 2008SW000452. doi:10.1029/2008SW000452
Summers, D. (2005). Quasi-linear diffusion coefficients for field-aligned electromagnetic waves with applications to the magnetosphere. J. Geophys. Res. Space Phys. 110, 2005JA011159. doi:10.1029/2005JA011159
Summers, D., and Stone, S. (2022). Analysis of radiation belt “killer” electron energy spectra. J. Geophys. Res. Space Phys. 127, e2022JA030698. doi:10.1029/2022JA030698
Swanson, D. (2003). “Plasma waves,” in Series in plasma physics. 2nd Edition (United Kingdom: Taylor and Francis).
Tao, X., and Bortnik, J. (2010). Nonlinear interactions between relativistic radiation belt electrons and oblique whistler mode waves. Nonlinear Process. Geophys. 17, 599–604. doi:10.5194/npg-17-599-2010
Tao, X., Bortnik, J., Albert, J., Thorne, R., and Li, W. (2013). The importance of amplitude modulation in nonlinear interactions between electrons and large amplitude whistler waves. J. Atmos. Solar-Terrestrial Phys. 99, 67–72. doi:10.1016/j.jastp.2012.05.012
Tao, X., Bortnik, J., Albert, J. M., Liu, K., and Thorne, R. M. (2011). Comparison of quasilinear diffusion coefficients for parallel propagating whistler mode waves with test particle simulations. Geophys. Res. Lett. 38, 2011GL046787. doi:10.1029/2011GL046787
Tao, X., Bortnik, J., Albert, J. M., and Thorne, R. M. (2012a). Comparison of bounce-averaged quasi-linear diffusion coefficients for parallel propagating whistler mode waves with test particle simulations. J. Geophys. Res. Space Phys. 117, 2012JA017931. doi:10.1029/2012JA017931
Tao, X., Bortnik, J., Albert, J. M., Thorne, R. M., and Li, W. (2014). Effects of discreteness of chorus waves on quasilinear diffusion-based modeling of energetic electron dynamics. J. Geophys. Res. Space Phys. 119, 8848–8857. doi:10.1002/2014JA020022
Tao, X., Bortnik, J., Thorne, R. M., Albert, J. M., and Li, W. (2012b). Effects of amplitude modulation on nonlinear interactions between electrons and chorus waves. Geophys. Res. Lett. 39, 2012GL051202. doi:10.1029/2012GL051202
Tao, X., Zonca, F., Chen, L., and Wu, Y. (2020). Theoretical and numerical studies of chorus waves: a review. Sci. China Earth Sci. 63, 78–92. doi:10.1007/s11430-019-9384-6
Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013). Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504, 411–414. doi:10.1038/nature12889
Tong, Y., Vasko, I. Y., Artemyev, A. V., Bale, S. D., and Mozer, F. S. (2019). Statistical study of whistler waves in the solar wind at 1 au. Astrophysical J. 878, 41. doi:10.3847/1538-4357/ab1f05
Tonoian, D. S., Artemyev, A. V., Zhang, X.-J., Shevelev, M. M., and Vainchtein, D. L. (2022). Resonance broadening effect for relativistic electron interaction with electromagnetic ion cyclotron waves. Phys. Plasmas 29, 082903. doi:10.1063/5.0101792
Tsai, E., Artemyev, A., Zhang, X.-J., and Angelopoulos, V. (2022). Relativistic electron precipitation driven by nonlinear resonance with whistler-mode waves. J. Geophys. Res. Space Phys. 127, e2022JA030338. doi:10.1029/2022JA030338
Tu, W., Cunningham, G. S., Chen, Y., Henderson, M. G., Camporeale, E., and Reeves, G. D. (2013). Modeling radiation belt electron dynamics during gem challenge intervals with the dream3d diffusion model. J. Geophys. Res. Space Phys. 118, 6197–6211. doi:10.1002/jgra.50560
Tu, W., Cunningham, G. S., Chen, Y., Morley, S. K., Reeves, G. D., Blake, J. B., et al. (2014). Event-specific chorus wave and electron seed population models in dream3d using the van allen probes. Geophys. Res. Lett. 41, 1359–1366. doi:10.1002/2013GL058819
Tyler, E., Breneman, A., Cattell, C., Wygant, J., Thaller, S., and Malaspina, D. (2019a). Statistical distribution of whistler mode waves in the radiation belts with large magnetic field amplitudes and comparison to large electric field amplitudes. J. Geophys. Res. Space Phys. 124, 6541–6552. doi:10.1029/2019JA026913
Tyler, E., Breneman, A., Cattell, C., Wygant, J., Thaller, S., and Malaspina, D. (2019b). Statistical occurrence and distribution of high-amplitude whistler mode waves in the outer radiation belt. Geophys. Res. Lett. 46, 2328–2336. doi:10.1029/2019GL082292
Ukhorskiy, A. Y., and Sitnov, M. I. (2013). Dynamics of radiation belt particles. Space Sci. Rev. 179, 545–578. doi:10.1007/s11214-012-9938-5
Vainchtein, D., Zhang, X.-J., Artemyev, A. V., Mourenas, D., Angelopoulos, V., and Thorne, R. M. (2018). Evolution of electron distribution driven by nonlinear resonances with intense field-aligned chorus waves. J. Geophys. Res. Space Phys. 123, 8149–8169. doi:10.1029/2018JA025654
Vanden Eijnden, E. (1997). Some remarks on the quasilinear treatment of the stochastic acceleration problem. Phys. Plasmas 4, 1486–1488. doi:10.1063/1.872548
Vargas, A. D., Artemyev, A. V., Zhang, X.-J., and Albert, J. (2023). Role of “positive phase bunching” effect for long-term electron flux dynamics due to resonances with whistler-mode waves. Phys. Plasmas 30, 112905. doi:10.1063/5.0169278
Varotsou, A., Boscher, D., Bourdarie, S., Horne, R. B., Glauert, S. A., and Meredith, N. P. (2005). Simulation of the outer radiation belt electrons near geosynchronous orbit including both radial diffusion and resonant interaction with whistler-mode chorus waves. Geophys. Res. Lett. 32, 2005GL023282. doi:10.1029/2005GL023282
Vedenov, A. A., Velikhov, E., and Sagdeev, R. (1962). Quasilinear theory of plasma oscillations. Nucl. Fusion Suppl. 2, 465–475.
Walker, A. (1993). “Plasma waves in the magnetosphere,” in Physics and chemistry in space (Berlin, Heidelberg: Springer).
Wang, D., Shprits, Y. Y., Zhelavskaya, I. S., Effenberger, F., Castillo, A. M., Drozdov, A. Y., et al. (2020). The effect of plasma boundaries on the dynamic evolution of relativistic radiation belt electrons. J. Geophys. Res. Space Phys. 125, e2019JA027422. doi:10.1029/2019JA027422
Watt, C. E. J., Allison, H. J., Bentley, S. N., Thompson, R. L., Rae, I. J., Allanson, O., et al. (2022). Temporal variability of quasi-linear pitch-angle diffusion. Front. Astronomy Space Sci. 9, 1004634. doi:10.3389/fspas.2022.1004634
Watt, C. E. J., Allison, H. J., Meredith, N. P., Thompson, R. L., Bentley, S. N., Rae, I. J., et al. (2019). Variability of quasilinear diffusion coefficients for plasmaspheric hiss. J. Geophys. Res. Space Phys. 124, 8488–8506. doi:10.1029/2018JA026401
Watt, C. E. J., Allison, H. J., Thompson, R. L., Bentley, S. N., Meredith, N. P., Glauert, S. A., et al. (2021). The implications of temporal variability in wave-particle interactions in earth’s radiation belts. Geophys. Res. Lett. 48, e2020GL089962. doi:10.1029/2020GL089962
Watt, C. E. J., Rae, I. J., Murphy, K. R., Anekallu, C., Bentley, S. N., and Forsyth, C. (2017). The parameterization of wave-particle interactions in the Outer Radiation Belt. J. Geophys. Res. Space Phys. 122, 9545–9551. doi:10.1002/2017JA024339
Wilson, L. B., Cattell, C. A., Kellogg, P. J., Wygant, J. R., Goetz, K., Breneman, A., et al. (2011). The properties of large amplitude whistler mode waves in the magnetosphere: propagation and relationship with geomagnetic activity. Geophys. Res. Lett. 38, 2011GL048671. doi:10.1029/2011GL048671
Wong, J.-M., Meredith, N. P., Horne, R. B., Glauert, S. A., and Ross, J. P. J. (2022). Electron diffusion by magnetosonic waves in the earth’s radiation belts. J. Geophys. Res. Space Phys. 127, e2021JA030196. doi:10.1029/2021JA030196
Wykes, W. J., Chapman, S. C., and Rowlands, G. (2001). Stochastic pitch angle diffusion due to electron-whistler wave–particle interactions. Phys. Plasmas 8, 2953–2962. doi:10.1063/1.1371953
Zaslavskiĭ, G. M., and Chirikov, B. V. (1972). Stochastic instability of non-linear oscillations. Sov. Phys. Uspekhi 14, 549–568. doi:10.1070/pu1972v014n05abeh004669
Zhang, S., Rae, I. J., Watt, C. E. J., Degeling, A. W., Tian, A., Shi, Q., et al. (2021a). Determining the global scale size of chorus waves in the magnetosphere. J. Geophys. Res. Space Phys. 126, e2021JA029569. doi:10.1029/2021JA029569
Zhang, S., Rae, I. J., Watt, C. E. J., Degeling, A. W., Tian, A., Shi, Q., et al. (2021b). Determining the temporal and spatial coherence of plasmaspheric hiss waves in the magnetosphere. J. Geophys. Res. Space Phys. 126, e2020JA028635. doi:10.1029/2020JA028635
Zhang, X.-J., Agapitov, O., Artemyev, A. V., Mourenas, D., Angelopoulos, V., Kurth, W. S., et al. (2020a). Phase decoherence within intense chorus wave packets constrains the efficiency of nonlinear resonant electron acceleration. Geophys. Res. Lett. 47, e2020GL089807. doi:10.1029/2020GL089807
Zhang, X.-J., Artemyev, A., Angelopoulos, V., Tsai, E., Wilkins, C., Kasahara, S., et al. (2022). Superfast precipitation of energetic electrons in the radiation belts of the Earth. Nat. Commun. 13, 1611. doi:10.1038/s41467-022-29291-8
Zhang, X.-J., Demekhov, A. G., Katoh, Y., Nunn, D., Tao, X., Mourenas, D., et al. (2021c). Fine structure of chorus wave packets: comparison between observations and wave generation models. J. Geophys. Res. Space Phys. 126, e2021JA029330. doi:10.1029/2021JA029330
Zhang, X.-J., Mourenas, D., Artemyev, A. V., Angelopoulos, V., Bortnik, J., Thorne, R. M., et al. (2019). Nonlinear electron interaction with intense chorus waves: statistics of occurrence rates. Geophys. Res. Lett. 46, 7182–7190. doi:10.1029/2019GL083833
Zhang, X.-J., Mourenas, D., Artemyev, A. V., Angelopoulos, V., Kurth, W. S., Kletzing, C. A., et al. (2020b). Rapid frequency variations within intense chorus wave packets. Geophys. Res. Lett. 47, e2020GL088853. doi:10.1029/2020GL088853
Keywords: space plasma, plasma waves, wave-particle interactions, quasilinear theory, radiation belts, pitch-angle, diffusion, test-particle
Citation: Allanson O, Ma D, Osmane A, Albert JM, Bortnik J, Watt CEJ, Chapman SC, Spencer J, Ratliff DJ, Meredith NP, Elsden T, Neukirch T, Hartley DP, Black R, Watkins NW and Elvidge S (2024) The challenge to understand the zoo of particle transport regimes during resonant wave-particle interactions for given survey-mode wave spectra. Front. Astron. Space Sci. 11:1332931. doi: 10.3389/fspas.2024.1332931
Received: 03 November 2023; Accepted: 27 February 2024;
Published: 13 March 2024.
Edited by:
Joseph E. Borovsky, Space Science Institute (SSI), United StatesReviewed by:
Danny Summers, Memorial University of Newfoundland, CanadaIvan Vasko, University of California, Berkeley, United States
Copyright © 2024 Allanson, Ma, Osmane, Albert, Bortnik, Watt, Chapman, Spencer, Ratliff, Meredith, Elsden, Neukirch, Hartley, Black, Watkins and Elvidge. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Oliver Allanson, by5kLmFsbGFuc29uQGJoYW0uYWMudWs=
 Oliver Allanson
Oliver Allanson Donglai Ma
Donglai Ma Adnane Osmane
Adnane Osmane Jay M. Albert
Jay M. Albert Jacob Bortnik
Jacob Bortnik Clare E. J. Watt
Clare E. J. Watt Sandra C. Chapman
Sandra C. Chapman Joseph Spencer
Joseph Spencer Daniel J. Ratliff7
Daniel J. Ratliff7 Nigel P. Meredith
Nigel P. Meredith Thomas Neukirch
Thomas Neukirch David P. Hartley
David P. Hartley