Long-term investigation of an open cluster Berkeley 65

We present a decade-long investigation of a poorly studied cluster, Berkeley 65 (Be 65), using deep optical data from the telescopes of ARIES, Nainital Observatory. We estimate its radius ($R_{\mathit{cluster}}$ = 1.6′, aspect ratio of $\sim$1.1), distance (2.0 $\pm$ 0.1 kpc) and age ($\sim$160 Myrs). A clear turn-off point at $\sim$1.7 ${\text{M}}_{\odot }$ in the mass function suggests the escape of low-mass stars, and the lower photometric mass compared to the dynamical mass indicates ongoing disruption due to external forces. Our long-baseline optical photometric data also identifies 64 periodic and 16 non-periodic stars in this region. We have presented the light curves and the classification of those variables. The periodic stars have periods ranging from $\sim$0.05 days to $\sim$3.00 days and amplitude ranges from $\sim$8 mmag to $\sim$700 mmag. The nonperiodic stars show variation from $\sim$30 mmag to $\sim$500 mmag. The periodic stars include main-sequence pulsating variables such as Slow Pulsating B-type, $\delta$ Scuti, RR Lyrae, and $\gamma$ Doradus. We report a detached binary system and rotating variables similar to BY Draconis-type stars exhibiting variable brightness caused by starspots, chromospheric activity, and magnetic field-related phenomena.

1 Introduction

Most stars are believed to form in clusters within molecular clouds (Lada and Lada, 2003) and are ideal sites to study star formation and stellar/galaxy evolution. The mass function distribution in a cluster (having a broad mass range) is an ideal statistical tool to investigate the star formation process. The dynamics of stars in the clusters, as well as the structure of clusters measured as a function of cluster age, hold important clues on the processes of galaxy evolution. The long-term monitoring of stars in the cluster also gives important clues on the internal physical processes related to their evolution, through their photometric variability behavior (Lada and Lada, 2003; Allen et al., 2007; Grasha et al., 2017; Grasha et al., 2018).

The star clusters, which are primarily formed in the Galactic disc, are subjected to disturbance, such as disc shock, spiral arm passage, molecular cloud encounters, etc., (Spitzer and Harm, 1958; Kruijssen, 2012). As star clusters evolve, the removal of gas due to stellar feedback, along with gravitational interactions among stars and binary systems, gradually weakens the cluster’s gravitational potential. This process results in the expansion of the cluster and can ultimately lead to its partial or complete dissolution into the surrounding galactic field (e.g., Spitzer and Harm, 1958; Dib et al., 2011; Parker and Meyer, 2012; Dib et al., 2013; Parker and Dale, 2013; Pfalzner and Kaczmarek, 2013; Brinkmann et al., 2017; Dib et al., 2018). In the Galactic disc, open clusters typically have a lifespan of approximately 200 Myr before they begin to break apart (Bonatto et al., 2006; Yang et al., 2013). Clusters that survive beyond this period often develop distorted shapes and become less tightly bound, increasing their likelihood of breaking apart. After breaking apart, these former clusters give rise to moving groups and add stars to the field population (see also, Sharma et al., 2020). Thus, open clusters are the sites to study the galaxy’s evolution and dynamics (Tang et al., 2019).

Open clusters also harbor various types of variable stars, including pulsating, rotating, eclipsing binaries, and non-periodic variables, in a broad mass spectrum. Pulsating variables, such as $\beta$ Cep, $\delta$ Scuti stars, $\gamma$ Doradus ($\gamma$ Dor) stars, and Slowly Pulsating B-type (SPB) stars, exhibit variable amplitudes ranging from a few millimagnitude (mmag) to hundreds of mmag over periods of hours to days. These stars are particularly valuable for investigating the internal structure and evolution as their variability arises from radial and non-radial pulsations (Gautschy and Saio, 1993; Kim et al., 2001; Kang et al., 2007; Chehlaeh et al., 2018). On the other hand, rotating variables show periodic variability due to the modulation of stellar spots caused by stellar rotation. The variability amplitudes for these variables typically range from a few mmag to tens of mmag over days. The study of variability in these stars provides direct information about angular momentum evolution and magnetic activity (Messina, et al., 2008). Overall, studying long-term photometric variability in stars gives us an essential insight into how different mechanisms evolve during the life span of stars.

Thus, considering the above points, an intermediate-age open cluster (a few 100 Myr age, having most of the stars in the main sequence) located in the Galactic plane is ideally suited to study the dynamics and stellar evolution simultaneously. Similar studies on star clusters have been carried out in the past decade. However, most of these studies are not always based on deep and long-term photometric data and usually lack membership determination based on high-quality proper motion (PM) data. This paper presents a photometric study of a poorly studied open cluster, Berkeley 65 (hereafter, Be 65; Figure 1). Be 65 is a Trumpler Class I 2p open cluster (Ruprecht, 1966) in Cassiopeia constellation, located at ${\alpha }_{2000}=02^{h}39^{m}00^s$, ${\delta }_{2000}=+60°25^{\prime }00^{″}$ ($l=135.8480°$, b = $+0.2588°$). The primary aim of the current study is to understand the dynamical state of this cluster precisely and to identify various types of variables in this region by using our decade-long photometric monitoring of this cluster along with high-quality data in archives, such as PM information from Gaia’s third data release (Gaia Collaboration et al., 2023).

Figure 1

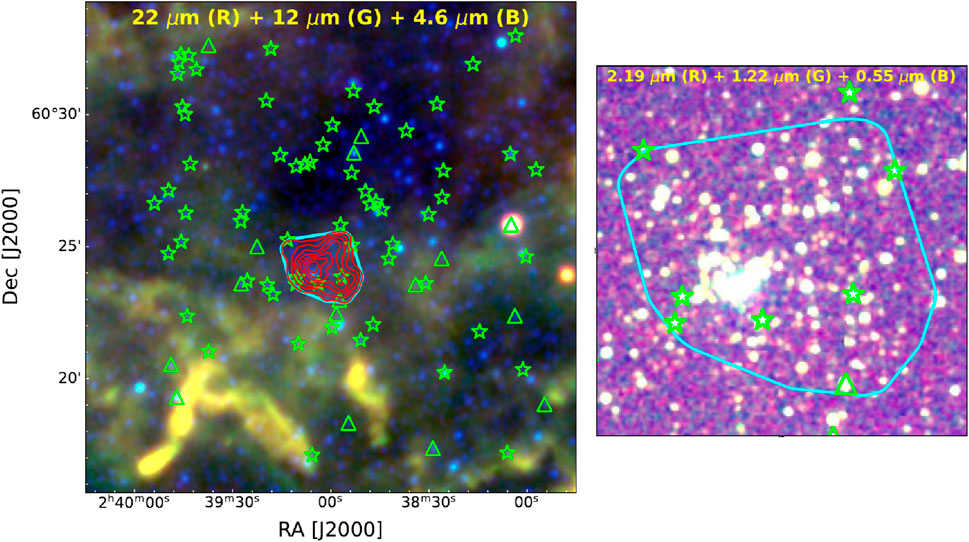
Figure 1. Left panel: Color composite image of the Be 65 cluster region covering $\sim 20^{\prime }\times$ ${20}^{\prime }$ FoV, using the W2 (4.6 $\mu$m), W3 (12 $\mu$m), and W4 (22 $\mu$m) WISE images, shown as blue, green, and red colors, respectively. The red contours are the stellar iso-density contours generated using the nearest neighbor method from the 2MASS data (see Section 4.1). The cyan color convex hull indicates the extent of the Be 65 cluster. The green open stars and triangles denote the identified periodic and non-periodic variables. Right panel: Zoomed-in image of the cluster region. This color-composite image comprises 2MASS $K$, $J$ band, and observed $V$ band images shown as red, green, and blue, respectively.

This paper is organized as follows: Section 2 presents the observations and data reduction. Section 3 outlines the methods used to derive the cluster parameters and identify variable stars. In Section 4, we discuss the physical and dynamical properties of the cluster Be 65, as well as the characteristics and classification of the identified variables. Finally, Section 5 provides a summary of our findings and conclusions.

2 Observations and data reduction

2.1 Optical photometric data

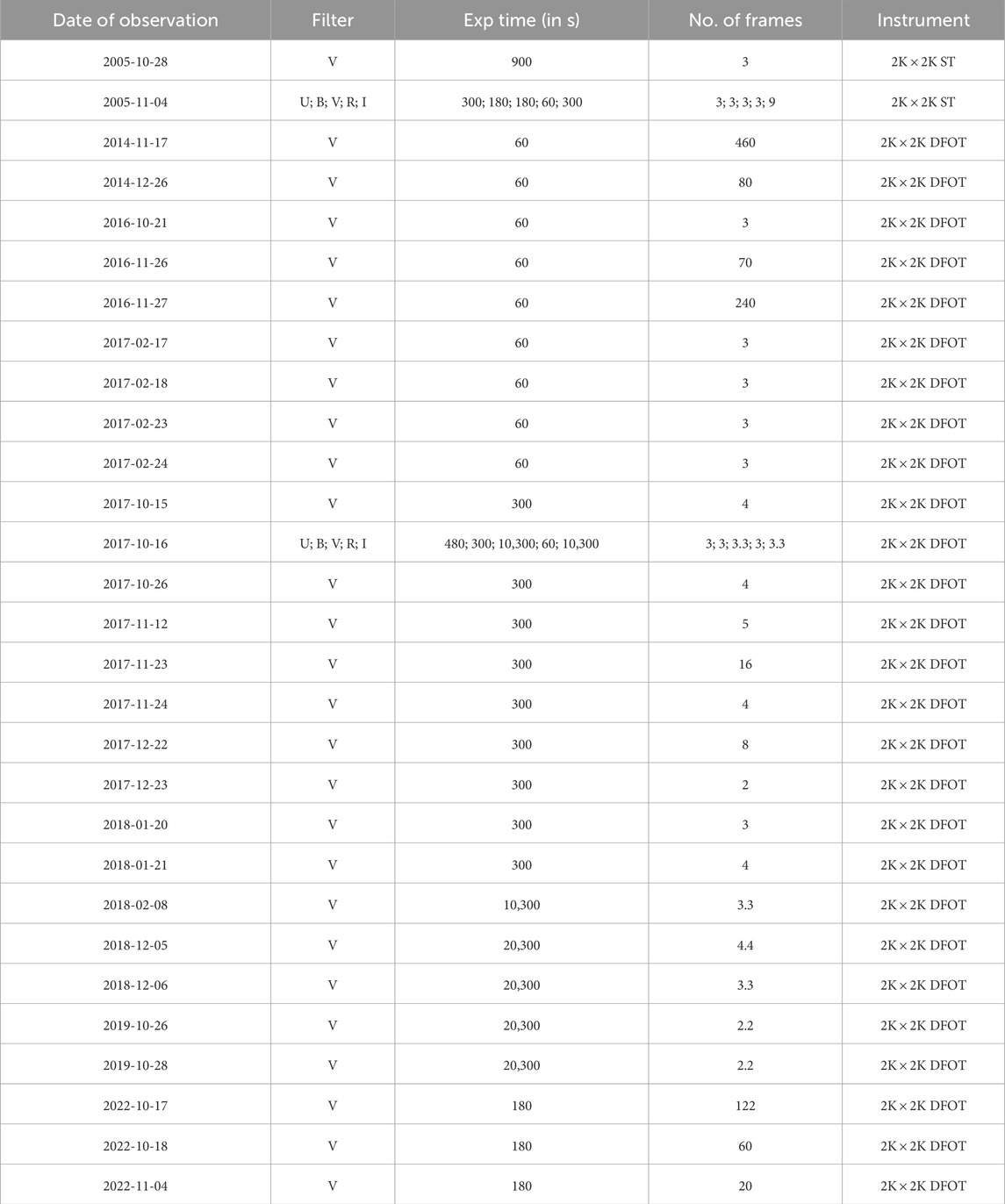
The long-term photometric monitoring of Be 65 was done using the 1.3 m f/4 Devasthal Fast Optical Telescope (DFOT) at the Aryabhatta Research Institute of Observational Sciences (ARIES), located at Devasthal, India. The telescope has a 2K$\times$2K CCD camera with a field of view (FoV) of $\sim 18^{\prime }.4\times 18{.}^{\prime }4$. The CCD has a $\sim$ 0.54 arcsec/pixel plate scale with a pixel size of $\sim$ 13.5 $\mu$m. The gain and read-out noise of the CCD are $\sim$2.0 electrons/ADU and $\sim$ 7.0 electrons, respectively (Sagar et al., 2012). About 1200 frames were taken in the Johnson $V$ filter over twenty-nine nights, from 2005 October 28 to 2022 November 04, including rigorous observation on two full nights and a few observations in the Johnson $U$, $B$, and Cousins $R,I$ bands. We have also observed the Be 65 cluster by 1.04 m ARIES Sampurnanand Telescope (ST), Nainital, in broadband $U$, $B$, $V$, $R_C$ and $I_C$ filters using the 2K $\times$ 2K CCD camera having a FoV of $13^{\prime }.5\times 13^{\prime }.5$ (Sagar et al., 2012; Kaur et al., 2020). The observing nights had good weather conditions, with a typical full width at half maxima (FWHM) for stellar images of around $1.5^{″}-2^{″}$. The detailed log of observations is given in Table 1.

Table 1

Table 1. Log of observations.

The basic data reduction, including image cleaning, photometry, and astrometry, was done using the standard procedure explained in Sharma et al. (2020) and Kaur et al. (2020). The Be 65 field was observed on the same night (04 November 2005) as was NGC 6910 cluster (Kaur et al., 2020) along with a standard field (SA98, Landolt, 1992). The typical seeing value on that night was $\sim$ 7 pixels $(\sim 3^{″})$, and observations were conducted under good atmospheric conditions. Thus, we have used the same calibration equations, as generated by Kaur et al. (2020), to transform instrumental magnitudes of several bright stars in the Be 65 field into standard Vega systems. For subsequent observations of Be 65 using the 1.3 m telescope, it was not necessary to observe additional standard stars because the field already contained several bright stars with established standard magnitudes. Thus, to calibrate the 1.3 m observations, a set of new transformation coefficients were directly derived from the standard and instrumental magnitudes of the local standard stars. While there is a possibility that some of these stars may be variable, the statistical impact is minimized due to the large number of stars used. This approach also helps reduce errors associated with differences in airmass between standard stars and target stars, and it mitigates instrumental effects in the calibration equations. The current observations can detect stars faint up to V$\sim$22 mag with photometric errors less than 0.1 mag. For the present analysis, we have used only those stars whose error in magnitude in different bands is less than 0.1 mag. We transformed the pixel coordinates into celestial coordinates (RA and Dec) using the Graphical Astronomy and Image Analysis (GAIA¹) tool with a root-mean-square (RMS) less than 0.5″.

2.2 Archival photometric data

We have also used the photometric point source catalog from the following archives:

1. We obtained near-infrared (NIR) JHKs photometric data from the 2MASS All-Sky Point Source Catalog (Cutri et al., 2003; Skrutskie et al., 2006) for a stellar distribution study (see Section 3.1). This catalog provides complete and reliable NIR photometry down to the 15.8, 15.1, and 14.3 magnitude limits in J (1.24 $\mu$m), H (1.66 $\mu$m), and $K_s$ (2.16 $\mu$m). We analyzed only sources with good photometric precision (photometric uncertainties less than 0.1 mag).

2. We have used data from Gaia’s third data release, Gaia DR3 (Gaia Collaboration et al., 2023). Gaia DR3 provides astrometric positions, parallaxes, radial velocities, and proper motions for over 1.8 billion sources brighter than 21 mag in the G (0.33-1.05$\mu$m) photometric band. Precise magnitudes in three photometric bands G, $G_{BP}$(0.33-0.68$\mu$m), and $G_{RP}$(0.63-1.05 $\mu$m) are provided for up to 1.4 billion sources, along with astrophysical parameters and variability information for millions of objects. We have downloaded the Gaia DR3 data from the data archive². We have used this data to discriminate between members and non-members of the clusters (see Supplementary Appendix S1.1).

3 Methodology

3.1 Structure of the cluster

As stars are less attenuated by dust and gas in NIR bands in comparison to optical bands, we have used the 2MASS All-Sky Point Source Catalog to investigate the distribution of stellar density in the Be 65 region, covering $\sim 20^{\prime }\times$ ${20}^{\prime }$ FoV. A surface density map is produced using the nearest neighbor method as described in Gutermuth et al. (2005), Gutermuth et al. (2009) and Sharma et al. (2016). Briefly, the local surface density was computed using a grid with a resolution of 5 pixels ($\sim$ 2.5 arcsec). At each grid point, the distance to the 20th nearest star was determined. Then the local surface density $(\sigma )$ at each grid point [i,j] was estimated using the following equation:

$\sigma \left(i,j\right)=\frac{N}{\pi \times {\left(r_N\right)}^2}(1)$

where $r_N$ is the calculated distance of the nearest 20th stars from the grid point, and $N$ is the number of stars (i.e., 20) within a local area of radius $r_N$. Then the calculated surface density map was smoothed to a $3\times 3$ ${\text{pixels}}^2$ grid.

The resulting density contours, shown as red curves in the left panel of Figure 1, have the lowest contour level set at 1$\sigma$ above the mean stellar density $(8+2stars/arcmi{n}^2)$ with contour intervals of 1$\sigma$ (2 stars/$arcmi{n}^2$). The contours reveal a clear enhancement in stellar density in the central region.

3.2 Extinction, distance, and age of the cluster

We have used an optical $(U-B)$ versus $(B-V)$ two-color diagram (TCD) (see left panel in Figure 2) to estimate the reddening toward the Be 65 cluster (Verma et al., 2023; Sharma et al., 2024). We have plotted the probable member stars (see Supplementary Appendix S1.1) that are within the convex hull as black dots along with zero-age main sequence (ZAMS; dashed line in blue color in Figure 2) taken from Pecaut and Mamajek (2013). We have shifted the ZAMS along the reddening vector (with a slope of $E(U-B)/E(B-V)=0.72$, corresponding to $R_V$ = 3.1) to match the distribution of stars with minimum reddening in the cluster direction (blue solid curve in the left panel of Figure 2). Only stars of spectral type A or earlier have been selected for the reddening analysis to obtain a more reliable result. This choice is motivated by the desire to minimize several effects of factors like metallicity, unresolved binaries, rotating stars, low mass pre-main sequence (PMS), and photometric errors, which can introduce uncertainties for later type stars (see Phelps and Janes, 1994 and ref therein). In this way, the minimum reddening value $(E{(B-V)}_{\mathit{min}})$ is estimated as 0.92 mag ($A_V$ = 2.85 mag). The approximate error in this estimate is 0.05 mag, as outlined in Phelps and Janes (1994).

Figure 2

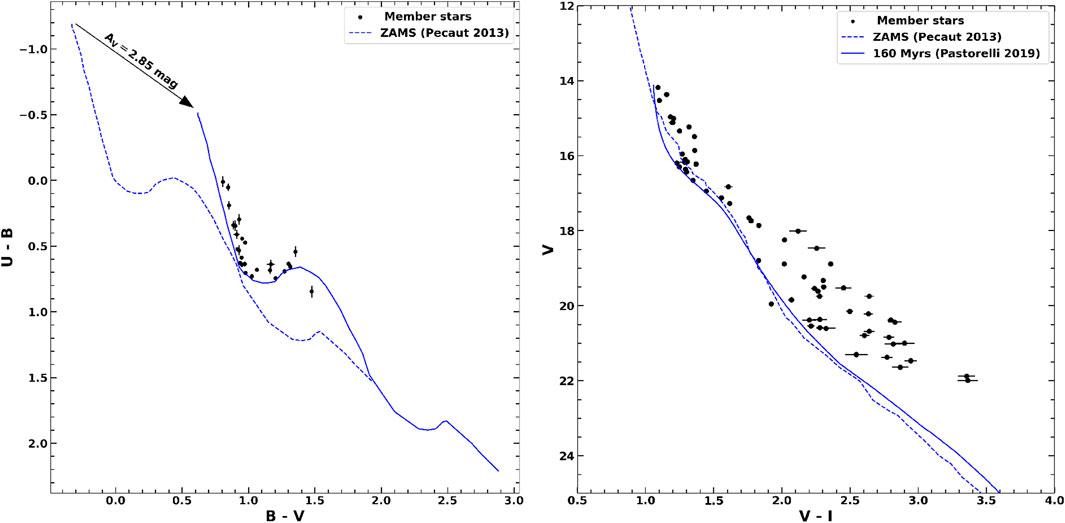
Figure 2. Left panel: $U-B$ V/s $B-V$ TCD for Be 65. The cluster member stars inside the convex hull are represented as black dots. The dashed blue line is the theoretical ZAMS curve taken from Pecaut and Mamajek (2013). The solid blue line is the reddened ZAMS curve along the reddening vector (black arrow) with $E(B-V)=0.92$ mag. Right panel: $V$ vs. $(V-I)$ CMD for Be 65. The solid blue curve represents the theoretical isochrone taken from Pastorelli et al. (2019) for age 160 Myrs and solar metallicity (i.e., Z = 0.02), and the dashed blue curve is the theoretical ZAMS taken from Pecaut and Mamajek (2013). Both curves are corrected for distance and extinction value for Be 65 (i.e., 2.0 kpc and $A_V=2.85$ mag).

To calculate the distance of the Be 65 cluster, we have selected 11 relatively brighter (V $<$16 mag) member stars (see Supplementary Appendix S1.1) which are inside the cluster extent, i.e., convex hull (see Section 4.1). These selected member stars have a parallax error of less than 0.1 mas. The distances of these selected member stars were obtained from Bailer-Jones et al. (2021), and the mean of the distances of these stars has been considered as the distance of the cluster, i.e., 2.0 $\pm$ 0.1 kpc. To further verify the estimated distance and extinction of the cluster, we applied the isochrone fitting method to its color-magnitude diagram (CMD), a technique that has been successfully utilized in numerous previous studies (Phelps and Janes, 1994; Schmeja and Klessen, 2006; Sharma et al., 2016; Pandey et al., 2020). Specifically, we used the $V$ vs. $(V-I)$ CMD, as shown in the right panel of Figure 2. We have shown the distribution of member stars (see Supplementary Appendix S1.1) within the convex hull as black dots. The blue dashed curve is the ZAMS curve taken from Pecaut and Mamajek (2013) corrected for distance and minimum extinction. A good match of ZAMS with the distribution of member stars provides additional confirmation of the cluster’s distance and extinction estimates.

The ages of young clusters are typically estimated using dereddened CMDs, either by comparing the most massive stars with post-main-sequence evolutionary tracks, if significant stellar evolution is evident, or by fitting PMS isochrones to the lower-mass, still-contracting population (Phelps and Janes, 1994; Lata et al., 2014a; Sharma et al., 2020; Rangwal et al., 2023; Verma et al., 2023). The brighter blue stars typically serve as key constraints in isochrone fitting (Phelps and Janes, 1994). To determine the age of Be 65 cluster, we utilized the optical CMD (V versus V–I), presented in the right panel of Figure 2 (Lata et al., 2014b; Sharma et al., 2020; Rangwal et al., 2023). The ZAMS (Pecaut and Mamajek, 2013), corrected for the cluster’s distance and reddening, is overlaid as a dashed blue curve. The brightest star on the main sequence has an estimated mass of approximately 3.5 ${\text{M}}_{\odot }$. By visually fitting isochrones from Pastorelli et al. (2019), we find that an isochrone corresponding to an age 160 Myr (solid blue curve) aligns well with the observed member stars in the CMD. The uncertainty in the estimated age is influenced by factors such as differential reddening within the cluster and an extended period of star formation, both of which contribute to scatter in CMD (Phelps and Janes, 1994). Given that we have corrected the isochrone using the minimum observed reddening value, and considering the variability in extinction across the cluster, we adopt a minimum age uncertainty of approximately 40 Myr.

3.3 Mass function

The distribution of stellar masses during a star formation event is known as the initial mass function (IMF). The study of the IMF is crucial for understanding the star formation process and star clusters’ subsequent chemical and dynamical evolution (Kroupa, 2002). However, directly determining the IMF for a cluster is not possible due to the dynamic evolution of the stellar system. Therefore, we have estimated the present-day mass function (MF) of the Be 65 cluster. The MF is commonly represented by a power law equation, $\mathrm{\Phi }\propto m^{\mathrm{\Gamma }}$, and the slope of the MF is denoted as:

$\mathrm{\Gamma }=\frac{dlog\left(\mathrm{\Phi }\right)}{dlog\left(m\right)};\mathrm{\Phi }=N\left(log\left(m\right)\right)(2)$

Where $\mathrm{\Phi }$ is the number of stars, corrected for completeness factor (CF), per unit logarithmic mass interval.

To estimate the CF, we used the ADDSTAR routine from DAOPHOT II (Stetson, 1987; Stetson, 1992). The detailed methodology is described in Sagar and Richtler (1991). In summary, artificial stars with known magnitudes and positions were randomly added to the original image. These modified frames were then re-reduced using the same reduction procedures as the original data. The CF as a function of magnitude was determined by calculating the ratio of recovered artificial stars to the total number of added stars within each magnitude bin. To better sample the fainter end of the luminosity function, a more number of artificial stars were added in the lower magnitude ranges. The number of added stars was limited to approximately 15$\%$ of the total star count in order to preserve the original crowding conditions. The right panel of Figure 3 shows the CF versus magnitude plot in $V$ and $I$ bands for the cluster region. As expected, the CF decreases when we go towards the fainter end.

Figure 3

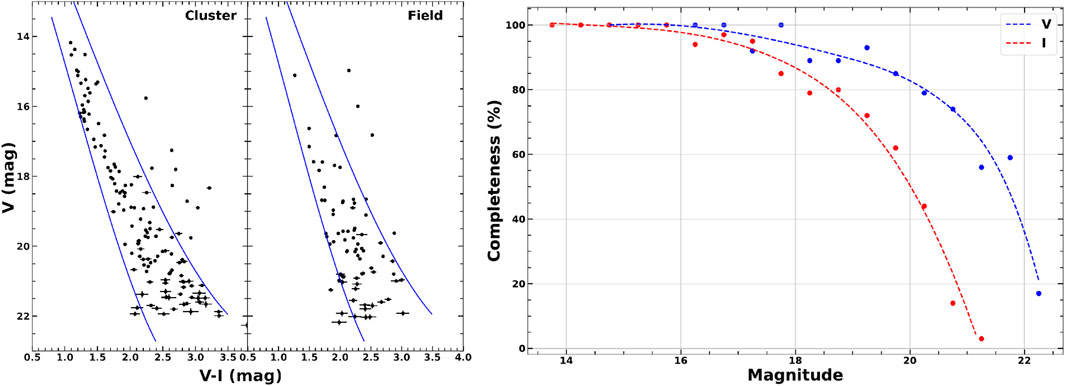
Figure 3. Left panel: $V$ vs. $(V-I)$ CMD for the stars in cluster and field regions. The blue line envelopes are created to select well-defined MS stars for LF and MF calculation for Be 65. Right panel: Completeness factor for the cluster region of Be 65 as a function of magnitude. The red and blue dots are completeness factors derived using photometric $I$ and $V$ band data, respectively. The dashed lines are respective smoothed splines.

The left panel of Figure 3 presents the CMDs for stars in both the cluster and field regions. We defined an envelope to select well-defined MS stars in each region (cf. Sharma et al. 2008), to reduce field star contamination in the cluster region. To construct the cluster’s luminosity function (LF), we subtracted the CF-corrected star counts in the field region from those in the cluster region, in different mag bins within the envelopes in the CMDs. Finally, the magnitude bins in the LF were converted into mass bins using a 160 Myr isochrone from Pecaut and Mamajek (2013), and the resulting MF distribution is shown in Figure 4.

Figure 4

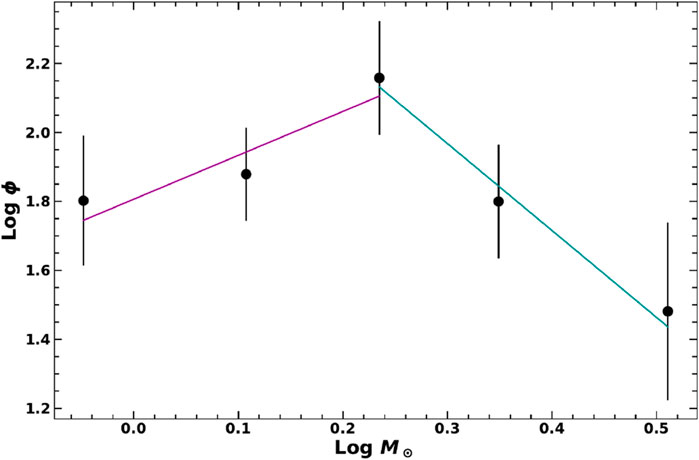
Figure 4. Mass function distribution for the Be 65 cluster. The error bars represented with MF data points (filled black dots) are $\pm \sqrt{N}$ errors. The solid cyan and magenta lines are the least-squares fits to the MF data points.

3.4 Identification of variables

Our long-term photometric monitoring of Be 65 is ideal for identifying this region’s long-period and short-term variables. We have used differential photometric techniques to identify variable stars in the field. This technique is particularly useful for removing the star’s brightness variation due to atmospheric conditions on the night of observation and instrumental signatures. It is important to note that the error in calculated magnitude increases as the stars become fainter. Therefore, a brighter star cannot be used as a comparison star for the faint stars, as larger magnitude errors can obscure the star’s variation. To overcome this, we divided all the stars into different magnitude bins with a bin size of 1 mag. We computed the magnitude differences for each magnitude bin for every possible pair of stars in a frame. We selected the comparison stars for which the standard deviation in the magnitude difference was the minimum. After selecting the comparison star, we determined the magnitude difference between the comparison star and target stars in each magnitude bin. Subsequently, we generated light curves (LCs) by plotting the resulting $△$V (magnitude difference) against the Modified Julian Date (MJD). We visually inspected all the LCs in the initial step to identify any signs of variability. If a star displayed a consistent visual variation greater than the scatter observed in the comparison star, it was classified as a variable star. The Lomb-Scargle periodogram (Lomb, 1976; Scargle, 1982) is then used to determine the period of all periodic variable stars. As data is highly unevenly sampled, false periods can also show up in the periodogram. Therefore, we have confirmed the period of the periodic variable by plotting their phase-folded LCs. The phase values in these phase-folded LCs are binned so that each bin, with a bin size of 0.01, contains a single data point. In this way, we have identified 64 periodic stars toward the Be 65 cluster. For those variables for which no periods were estimated (16) successfully, we call them non-periodic variables. In Figure 5, we show the sample LCs of periodic (V42) and non-periodic (V15) stars. In Figure 6, the power spectrum and phase-folded LC (in the upper and middle panel, respectively) of a periodic star V42 is shown, while in the lower panel, the phase-folded LC of a detected eclipsing binary (for detail, see Section 4.4) is shown. The LCs of all variable stars are provided in Supplementary Material, and their derived parameters (e.g., coordinates, V magnitudes, periods, amplitudes, etc.) are given in Table 2. Variables with distances (taken from Bailer-Jones et al., 2021) falling within the one-sigma range of the estimated cluster distance (as discussed in Section 3.2) are classified as member stars (35) in Table 2, while the remaining are considered field stars (45). Although many of the member variables lie outside the apparent cluster extent (see Figure 1), this may be due to their dispersal from the cluster as a result of an ongoing disruption process. Figure 7 illustrates the RMS dispersion of magnitudes for all the observed stars as a function of their V magnitude. As expected, there is an increase in dispersion towards the fainter end of the magnitude range. The identified variables are represented by open blue stars (periodic) and open blue triangles (non-periodic). In this figure, some stars with a very high RMS are not classified as variables. This could be due to unusually high photometric errors (e.g., bad pixels within the star, the presence of a nearby brighter star, cosmic correction residuals).

Figure 5

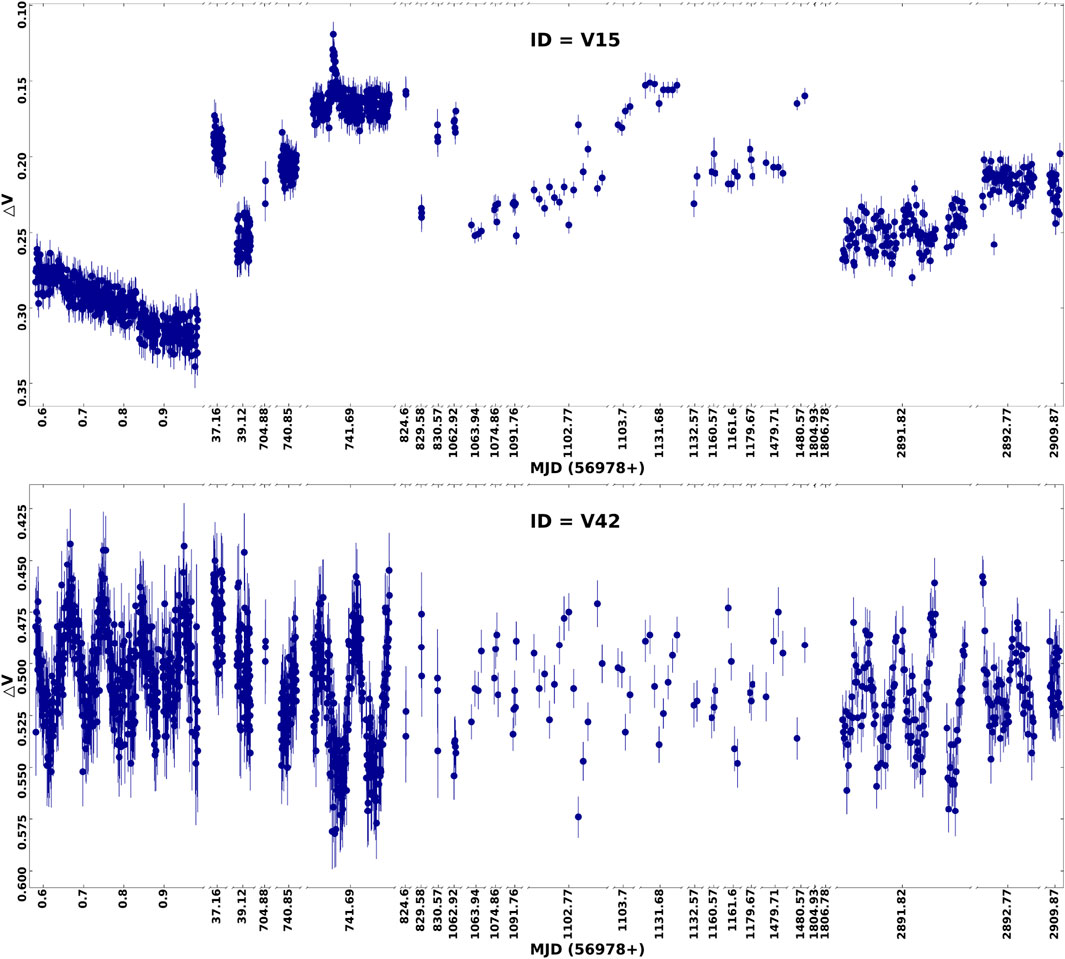
Figure 5. Samples of the light curves: in the upper panel, the light curve of a non-periodic variable (V15) is shown. The light curve of a periodic variable (V42) is shown in the lower panel.

Figure 6

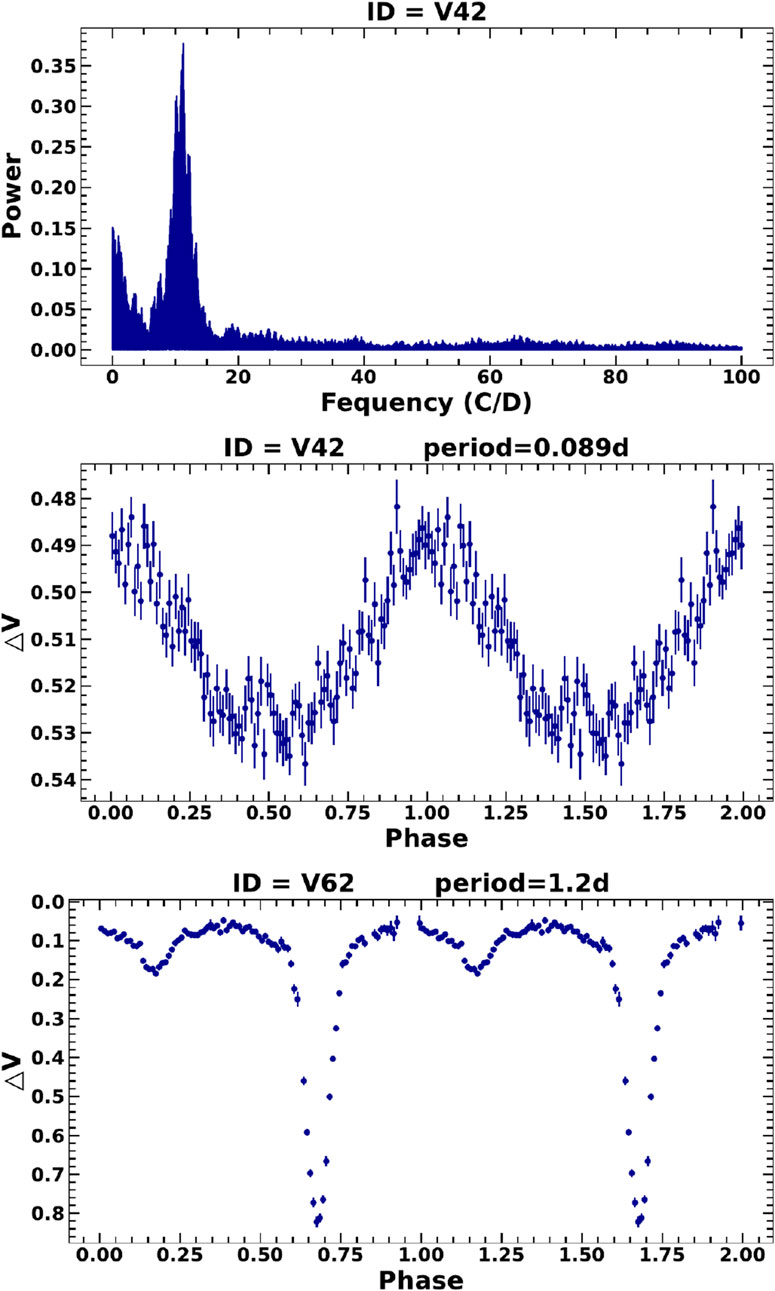
Figure 6. Upper panel: The power spectrum of a periodic star (V42) derived using Lomb-Scargle periodogram (Lomb, 1976; Scargle, 1982). Middle panel: the phase-folded light curve of the same periodic star (V42) using the period as 0.089 days. Lower panel: The phase-folded light curve of a detected eclipsing binary (V62); approx. 1.2 days is used as a period to fold the light curve.

Table 2

Table 2. Catalog of the variable stars.

Figure 7

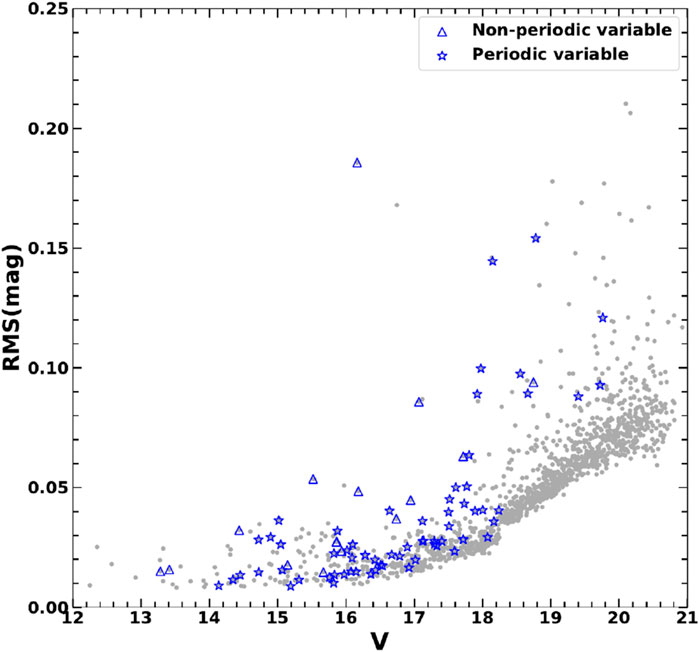
Figure 7. RMS dispersion of magnitudes for all the target stars as a function of their V magnitude. The grey dots represent the stars in FoV towards the Be 65 cluster, while the blue open triangles and stars represent non-periodic and periodic variables towards the Be 65 cluster.

4 Results

4.1 Physical properties of the Be 65 cluster

Using the surface density estimates derived from Equation 1, the peak density is found to be located at ${\alpha }_{2000}=02^{h}39^{m}05^s$, ${\delta }_{2000}=+60°24^{\prime }30^{″}$. As the cluster does not have perfectly spherical symmetric morphology, we define its area using a convex hull³, represented by the cyan-colored curve in the right panel of Figure 1 (see Schmeja and Klessen, 2006, for details). The Qhull⁴ program is used to compute the convex hull for the stars located within the lowest density contour. We estimated the area of cluster $A_{\mathit{cluster}}$, as the area under the convex hull normalized by a geometrical factor that considers the ratio of objects contained within the convex hull versus those situated on its boundary (cf. Sharma et al., 2020, and references therein). Then, the cluster radius, $R_{\mathit{cluster}}$, is determined as the radius of a circle with the same area as $A_{\mathit{cluster}}$. Additionally, we have computed the circular radial size, $R_{\mathit{circle}}$, which is defined as half of the maximum distance between any two members within the cluster. It represents the radius of the smallest possible circle that contains the entire grouping. In this way, we have estimated the $A_{\mathit{cluster}}$, $R_{\mathit{cluster}}$ and aspect ratio $R_{\mathit{circle}}^2/R_{\mathit{cluster}}^2$ (Gutermuth et al., 2009) for the Be 65 cluster as 8.3 $arcmi{n}^2$, 1.6′ and 1.1, respectively.

The minimum reddening value $(E{(B-V)}_{\mathit{min}})$ towards Be 65 cluster is estimated as $0.92\pm 0.05$ mag ($A_V$ = 2.85 mag). The seemingly less scattered distribution of stars in the TCD hints toward the negligible differential reddening or gas/dust in this cluster. This hints towards the evolved phase of this cluster. Our PM and CMD fitting analysis confirms the distance of this cluster as 2.0 $\pm$ 0.1 kpc. The cluster’s age, estimated from the turn-off point of the brightest member star for the cluster, is estimated as $\sim 160$ Myrs.

Although there is a scatter in the MF distribution, a distinct change in slope can be observed at log$(M_{\odot })\approx 0.23$ (or $M\approx 1.7M_{\odot })$. This break in the MF slope has also been observed in previous studies of other clusters (e.g., Sharma et al., 2007; Jose et al., 2008). We calculated distinct $\mathrm{\Gamma }$ using Equation 2 on either side of the observed break using a least-squares fitting method. The MF slope in the relatively higher-mass $(1.7M_{\odot }\le M\le 3.5M_{\odot })$ regime is found to be −2.52 $\pm$0.15, whereas the MF slope in the low-mass regime $(0.9M_{\odot }\le M\le 1.7M_{\odot })$ is estimated as 1.27 $\pm$0.33.

4.2 Dynamical state of the cluster

In our study, we used the minimum spanning tree (MST⁵) method (Allison et al., 2009; Olczak et al., 2011; Dib et al., 2018), to investigate mass segregation within the Be 65 cluster region. We used the mass segregation ratio (MSR, ${\mathrm{\Gamma }}_{\mathit{MSR}}$) to quantify mass segregation. The ${\mathrm{\Gamma }}_{\mathit{MSR}}$ was calculated by constructing MSTs for two groups: the massive member stars (with magnitudes G$<$17) and an equal number of randomly selected stars from all cluster members within the cluster region. For each group, the total edge length of the MST was computed over 100 iterations, and the mean edge lengths were determined. The ${\mathrm{\Gamma }}_{\mathit{MSR}}$ was then obtained by taking the ratio of the mean edge length of the random sample to that of the massive stars. The uncertainty in the ${\mathrm{\Gamma }}_{\mathit{MSR}}$ was estimated as the standard deviation of the MST edge lengths of random samples (for details, see Sharma et al., 2020). The calculated value of ${\mathrm{\Gamma }}_{\mathit{MSR}}$ for the Be 65 cluster is $1.1\pm 1.2$. This indicates the presence of mass segregation, suggesting a concentration of massive stars towards the central region of the cluster (for further details, see Sharma et al., 2020; 2023; Kaur et al., 2023). To explore whether the observed mass segregation in Be 65 originates from the dynamical relaxation or is inherent in its formation, we calculated the dynamical relaxation time, $T_E$, as $\sim$4.4 Myr based on the sample of member stars in the Be 65 cluster (for more information, refer to Sharma et al., 2020). The probable age of the cluster is calculated as 160 Myr (see Section 3.2), which is much higher than the $T_E$. Thus, the cluster can be considered dynamically relaxed. Even considering a loss of 50$\%$ of stars due to data incompleteness, the dynamical relaxation time will be $T_E\sim 7.5$ Myr. However, this remains considerably smaller than the age of the Be 65 cluster (i.e., $\sim$ 160 Myr). This suggests that the observed mass segregation in this cluster could result from the dynamical evolution of stars.

One of the consequences of the mass segregation process is the increased vulnerability of the lowest-mass members to be ejected from the system (e.g., see Mathieu, 1984). Thus, we estimated the tidal radius ‘$r_t$’ of Be 65, following the methodology outlined by Sharma et al. (2020). To calculate the tidal radius, we first derived the cluster stars’ MF distribution using the member stars’ LF (as described in Section 3.3). The total mass of the Be 65 cluster is estimated to be 82 $M_{\odot }$ up to the completeness limit of the observed photometric V band data, corresponding to 0.9 $M_{\odot }$. Based on these calculations, the tidal radius is approximately 6.3 pc. If we missed 50$\%$ of the cluster mass in the lower mass bins due to data incompleteness, the resulting tidal radius ‘$r_t$’ would be approximately 8 pc. We then compared the photometric mass with the dynamical mass (${\text{M}}_{\mathit{dyn,tid}}$) for stars within the tidal radius to quantify this cluster’s dynamical status further. The dynamical mass is calculated by,

$M_{\mathit{dyn,tid}}\sim \frac{r_t{\sigma }_{3D}^2}{G}(3)$

Where $r_t$ is the 3D tidal radius, and ${\sigma }_{3D}$ is the 3D velocity dispersion (Fleck et al., 2006; Tang et al., 2019). Assuming an isotropic velocity distribution within the tidal radius, ${\sigma }_{3D}^2$ is 3 times the 1D velocity dispersion ${\sigma }^2$ of cluster members. Using the typical radial velocity dispersion of 1 km ${\text{s}}^{-1}$ for open clusters (Girard et al., 1989), the $M_{\mathit{dyn,tid}}$ from Equation 3, for Be 65 cluster comes out to be $\sim$5581 ${\text{M}}_{\odot }$. This is much higher than the estimated photometric mass of Be 65 within the tidal radius, i.e., $\sim$164 ${\text{M}}_{\odot }$, suggesting that this cluster has lost stellar mass and, thus, is under the process of disruption.

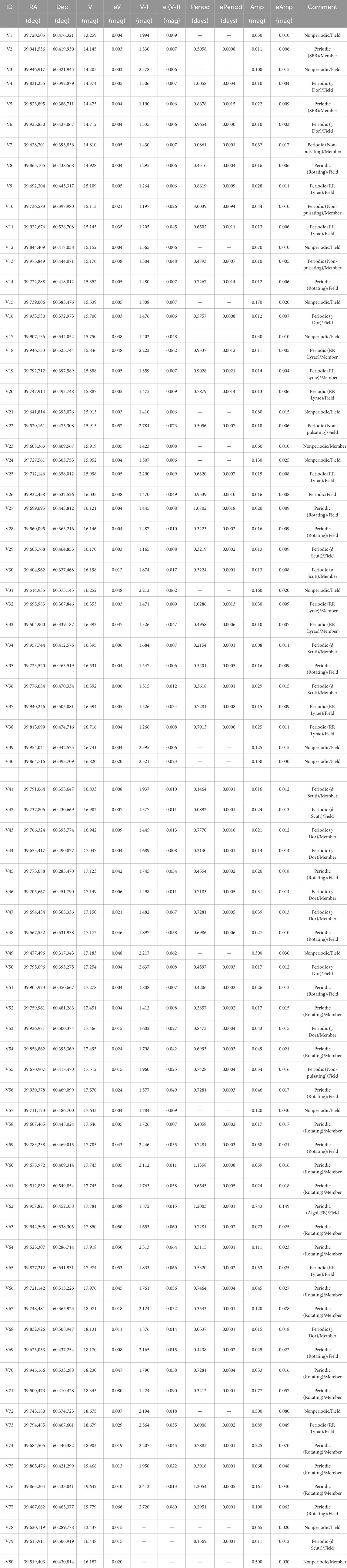
4.3 Physical properties of the variables

Figure 8 shows the distribution of amplitude and period of the variables identified in the present study. The amplitude and period of the periodic stars range from $\sim$8 mmag to $\sim$700 mmag and $\sim$0.05 days to $\sim$3.00 days, respectively. At the same time, the amplitude of non-periodic stars ranges from $\sim$30 mmag to $\sim$500 mmag. The period distribution peaks around 0.7 days for all the periodic variables. The amplitudes for non-periodic stars show a more or less flat distribution, whereas the periodic variables favor smaller amplitudes in their variability.

Figure 8

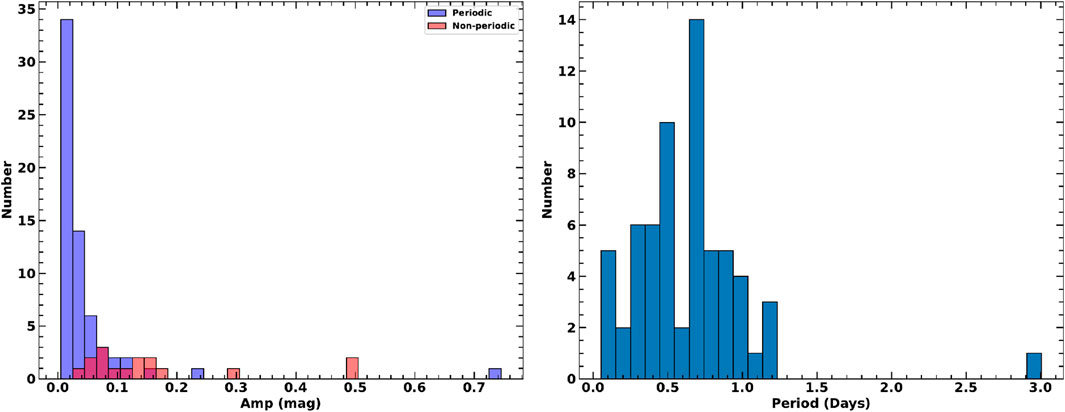
Figure 8. In the left panel, the histogram shows the amplitude distribution of variable stars. The right panel shows the period distribution of periodic stars.

The physical parameters, such as the age and mass of the cluster member variables, can be easily derived from their position in the CMD. However, it can’t be done for other field variables as we don’t know their exact extinction and distance. Thus, we utilized the Green et al. (2019) map to determine the extinction values for these field variables. Subsequently, employing these extinction values along with the distances obtained from Bailer-Jones et al. (2021), we derived the absolute magnitude in the V band $(M_V)$ for the field variables. By comparing the estimated $M_V$ values with the standard $M_V$ values in Pecaut and Mamajek (2013), we got the values of luminosity (log$(L/L_{\odot })$) and temperature (log$(T_{\mathit{eff}})$) for all the variables. In Figure 9, the Hertzsprung-Russell (HR) diagram (log$(L/L_{\odot })$ vs. log$(T_{\mathit{eff}})$) is plotted for all the periodic variables in the FoV. In this HR diagram, the dotted blue line is the MS curve taken from Pecaut and Mamajek (2013). The location of $\beta$ Cep, SPB, and $\delta$ Scuti stars in the HR diagram are represented by the dotted magenta line and solid black and blue lines, respectively (Miglio et al., 2007; Balona et al., 2011). The magenta dashed lines show the location of the $\gamma$ Dor stars (Warner et al., 2003). The green dots represent the field periodic variables, whereas the red open circles represent the member periodic variables. The distribution of the current sample of periodic variables in the HR diagram suggests that they have a large mass range (0.5-3.0 ${\text{M}}_{\odot }$); however, most are between $\sim$ 1-2 ${\text{M}}_{\odot }$.

Figure 9

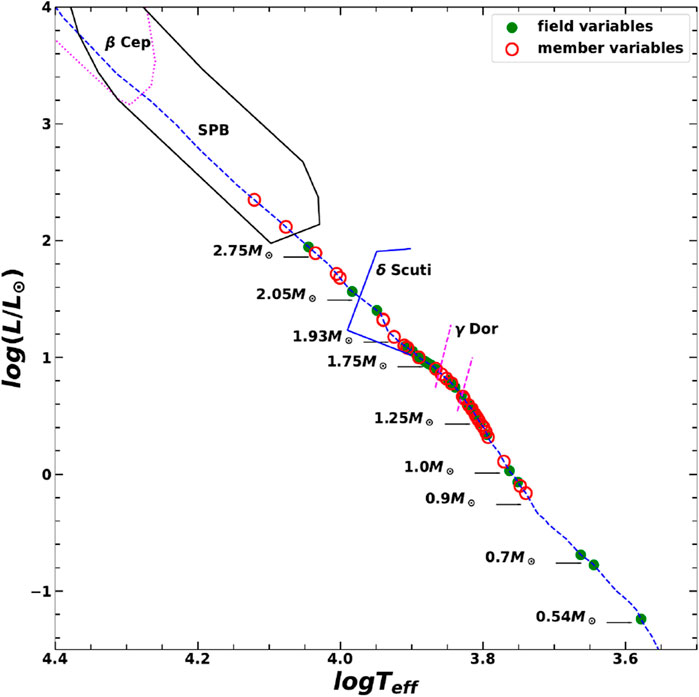
Figure 9. Hertzsprung-Russell (log$(L/L_{\odot })$ vs. log$(T_{\mathit{eff}})$) diagram for periodic variables within the FoV. The dotted blue line is the MS curve from Pecaut and Mamajek (2013). The green dots and red open circles represent the field and member periodic variables, respectively. The dotted magenta line shows the location of $\beta$ Cep-type MS variables, whereas the solid black line shows the location of SPB variables. The solid blue line shows the instability strip of $\delta$ Scuti stars, and the magenta dashed line shows the location of $\gamma$ Dor variables (Warner et al., 2003; Miglio et al., 2007; Balona et al., 2011).

4.4 Classification of variables

We have not detected any PMS signatures in the identified variables, as outlined in the study by Gutermuth et al. (2009); Koenig and Leisawitz (2014); Sharma et al. (2016). Thus, considering the identified variable as MS variables, we tried to classify these variables into various known type classes. Our approach involved classifying these stars based on their period, variability amplitude, position in the HR diagram, and the shape of their LCs.

4.4.1 Pulsating variables

$\beta$ Cep stars, which are pulsating MS variables, occupy a position above the upper MS on the HR diagram (dotted magenta line in Figure 9) and have early B spectral types (Handler and Meingast, 2011). They exhibit periods ranging from 0.1 to 0.6 days and amplitudes ranging from $\sim$10 mmag to $\sim$300 mmag. On the other hand, SPB stars are located just below the instability strip of $\beta$ Cep variables (Waelkens, 1991). These stars display complex oscillations with multiple periods, attributed to non-radial g-mode pulsations driven by the $\kappa$ mechanism (Gautschy and Saio, 1993; Fedurco et al., 2020). Typically, these variables have periods ranging from half a day to a few days in some instances (Stankov and Handler, 2005). $\delta$ Scuti stars are pulsating MS stars with spectral types A and F. They undergo radial and non-radial pulsations, with periods typically ranging from $\sim$ 0.008 days–0.42 days (Sánchez Arias et al., 2017; Martinez-Vazquez et al., 2023). The amplitude of brightness variations is generally small, on the order of a few mmag to a few hundred mmag (Pietrukowicz et al., 2020; Soszyński et al., 2021). Another group of pulsation variables is known as $\gamma$ Dor, with periods ranging from several hours to a few days and amplitudes ranging from a few tens of mmag to hundreds of mmag. These stars are located below the instability strip of $\delta$ Scuti stars, and their instability strip overlaps with that of $\delta$ Scuti stars (Warner et al., 2003; Ibanoglu et al., 2018).

In our study, we identified two stars with periodic variations (V2 and V5) positioned within the SPB region on the HR diagram (refer to Figure 9). These stars have periods of 0.5058 $\pm$ 0.0008 days and 0.8678 $\pm$ 0.0015 days, respectively. Consequently, we classify these stars as SPB-type variable stars. The 19 periodic variables fall within the $\delta$ Scuti instability strip on the HR diagram. These stars exhibit periods that span from $\sim$0.09 days to $\sim$1.03 days, and their amplitudes range from $\sim$8 mmag to $\sim$90 mmag. Among them, 7 stars have periods that fall within the typical range of $\delta$ Scuti variables. Furthermore, the LCs of these stars are well in agreement with the LCs of $\delta$ Scuti stars available in the literature (see, Pietrukowicz et al., 2020). Thus, these stars are marked as $\delta$ Scuti in Table 2. The remaining 12 stars are marked as “RR Lyrae” stars as RR Lyrae stars have the same spectral type as $\delta$ Scuti but larger periods Mullen et al., 2023; Gao et al., 2025. The 9 identified periodic variables, with periods ranging from $\sim$0.21 days to $\sim$1.01 days and amplitudes ranging from $\sim$10 mmag to $\sim$43 mmag, are located within the $\gamma$ Dor instability strip in the HR diagram. These stars are classified as $\gamma$ Dor in Table 2. One periodic variable, V68, located just below the $\gamma$ Dor instability strip, has a period (0.0537 $\pm$ 0.0001 days; very short for rotating variable), amplitude ($\sim$15 mmag), and shape of the light curve, similar to that of a pulsating star. Considering the potential errors in the calculated luminosity and temperature values, we have marked this variable as “$\gamma$ Dor” in Table 2.

4.4.2 Non-pulsating variables

A group of five stars, V7, V10, V13, V22, and V55, are located within the gap between the SPB and $\delta$ Scuti instability regions. Mowlavi et al. (2013) found these types of stars in the open cluster NGC 3766, where they observed a significant population of newly identified variable stars occupying the region between SPB and $\delta$ Scuti stars, where standard stellar models do not predict any pulsation (Balona et al., 2011; Mowlavi et al., 2013; Szewczuk and Daszyńska-Daszkiewicz, 2017). However, it has been observed that stars do exist in this gap and are classified as non-pulsating variables despite actually pulsating. This pulsation may be attributed to rapid rotation, which alters the internal conditions of the stars (Balona et al., 2011). The findings of Mowlavi et al. (2013) were further supported by Lata et al. (2014a), Lata et al. (2019) in their study of the young clusters NGC 1893 and Stock 8. Mowlavi et al. (2013) reported that the periods of these variable stars range from 0.1 to 0.7 days, with amplitudes between 1 and 4 mmag. On the other hand, Lata et al. (2014b) identified a new class of variables in NGC 1893, with periods ranging from 0.17 to 0.58 days and amplitude variations between 7 and 19 mmag. In the case of Stock 8, Lata et al. (2019) identified similar variables, with amplitudes of up to 40 mmag and periods of up to 0.364 days. In this study, the newly identified class of variables have periods ranging from 0.09 to 0.74 days, with amplitudes ranging from 10 to 44 mmag. However, one newly identified class variable (V10) has a period of $\sim$ 3 days and an amplitude of 44 mmag. These variables are marked as “Non-pulsating” in Table 2.

4.4.3 Eclipsing binary

The shape of the LC of one identified periodic variable, V62, suggests that this variable is the probable candidate for an eclipsing binary (EB). Based on the distinct primary and secondary minima observed in the LC of V62, it can be concluded that this star is a detached binary system. The period of the complete cycle for this EB is calculated as 1.2 days. The brightness variation during primary and secondary minima is calculated as approximately 800 mmag and 150 mmag, respectively. The phase-folded LC is given in the lower panel of Figure 6. This star is listed in VizieR Online Data Catalog: KISOGP (Ren et al., 2021) as an Algol-type eclipsing binary with a period 1.2003209$\pm$0.0000029 days and with an eclipsing ratio 0.245. This star is also identified by Gaia DR3 (Gaia Collaboration, 2022) as EB with similar period and brightness variation in the G band.

4.4.4 Rotating variables

This section discusses those variable stars that are located below the $\gamma$ Dor instability strip in the HR diagram. The mass and period range (i.e., solar to subsolar and few hours to few days, respectively) of these variables are well in agreement with the BY Draconis (BY Dra) type variables. BY Dra stars are main-sequence stars belonging to the FGKM spectral types. They exhibit variable brightness caused by starspots, chromospheric activity, and other phenomena related to their magnetic fields (Chahal et al., 2022). These stars are quasi-periodic and change the shape of their LC over a month. The typical amplitude for the BY Dor variable is a few hundred mmag. The 26 identified periodic variables are classified as probable BY Dor in the present work. The period and amplitude of these 28 variables range from approximately 0.30 days–1.20 days and 12 mmag to 225 mmag, respectively. Three of these variables, V48, V52, and V77, are identified by Gaia DR3 (Gaia Collaboration, 2022) as solar-like, RS Canum Venaticorum type and short-time variables, respectively.

4.4.5 Non-periodic variables

The sixteen identified variables are marked as non-periodic in the present study. Two are classified as cluster members, and fourteen are field populations (see Section 3.4). The non-member variables show amplitudes ranging from $\sim$ 30 mmag to 500 mmag, and the member variables have amplitudes $\sim$ 60 mmag and 500 mmag. One of the member variables (V80) is classified as a long-period (with period $\sim$ 691.4704 days) variable by the Gaia variability pipeline (Lebzelter et al., 2023). However, our analysis categorized this variable as non-periodic due to insufficient data to determine its periodicity in the LC. The variables, V15, V31, and V57 are classified as solar-like variable in Gaia DR3 (Gaia Collaboration, 2022). The periods for V31 and V57 are mentioned as 1.67 days and 4.1 days, respectively.

One periodic variable star, V26, could not be classified due to the lack of distance information in Bailer-Jones et al., 2021. Therefore, we have labeled it as “Periodic/Field” in Table 2.

5 Summary and conclusion

We have used deep optical photometric data from the ARIES telescopes to study the physical properties of a poorly studied cluster, Be 65. The shape of this cluster is more or less circular, with an aspect ratio of 1.1. The center of the cluster is found to be at ${\alpha }_{2000}=02^{h}39^{m}05^s$, ${\delta }_{2000}=+60°24^{\prime }30^{″}$ and the size and area of the cluster are estimated as $R_{\mathit{cluster}}$ = 1.6′ (=0.95 pc at a distance of 2 kpc) and $A_{\mathit{cluster}}$ = 8.3 $arcmi{n}^2$, respectively. Using the PM data from Gaia DR3, we have identified members of this cluster. We have estimated this cluster’s distance to 2.0 $\pm$ 0.1 kpc based on the parallax of member stars and isochrone fitting on optical CMD. The brightest member stars of the cluster are estimated to be 3.5 ${\text{M}}_{\odot }$ massive, and based on the turn-off point, the age of this cluster is estimated as $\sim$ 160 Myrs. We have found evidence of mass segregation in this cluster, and the comparison of the age of this cluster (160 Myr) with its dynamical age (7.5 Myr) suggests that the observed mass segregation can be due to the internal dynamical evolution of the cluster. The MF slope in this cluster’s relatively higher-mass $(1.7M_{\odot }\le M\le 3.5M_{\odot })$ regime is estimated as −2.52, steeper than the Salpeter value of −1.35, and the MF shows a turn-off in its distribution at bit higher mass (at $\sim$1.7 ${\text{M}}_{\odot }$). The MF slope of +1.27 at the lowest mass bin $(0.8M_{\odot }\le M\le 1.7M_{\odot })$ suggests fewer low-mass stars in this cluster. Thus, the overall MF distribution hints towards losing low-mass stars probably due to the dynamical evolution in the Be 65 cluster. The low value of the estimated photometric mass, i.e., $\sim$164 ${\text{M}}_{\odot }$, in comparison to its dynamical mass ($\sim$5581 ${\text{M}}_{\odot }$), confirms that this cluster has lost stellar mass and, thus, is under the process of disruption. A cluster can disrupt under the influence of both the internal and external dynamical evolution (see also, Tang et al., 2019). The stellar system can lose a substantial fraction of its stars in a time scale of ${\tau }_{\text{evap}}\sim 100\times T_E$ due to internal dynamical evolution (Shu, 1982; Binney and Tremaine, 1987). External disturbances, such as tidal forces from nearby giant molecular clouds or star clusters, passages through Galactic spiral arms or discs, or shear forces caused by Galactic differential rotation, can further speed up the cluster’s disintegration. The Be 65 cluster, located within the Galactic disc in an environment of gas and dust (see Figure 1), with an age of approximately 160 Myr, seems to have lost stars much earlier than its ${\tau }_{\text{evap}}$ ($\sim$0.75 Gyr) time scale, suggesting dominant roles of the external forces in its dynamical evolution.

Using a homogeneous decade-long baseline optical data, we also searched for the variables in the direction of the Be 65 cluster region. We have identified 64 periodic and 16 non-periodic stars, with periods ranging from 0.05 days to 3 days and amplitudes ranging from approximately 8 mmag to 742 mmag. Out of them, 35 are found to be members of the cluster Be 65, and the remaining ones are the field population. Using the position in the HR diagram and the shape of the LCs, we have characterized the variability properties of the periodic stars. Of them, 31 are categorized as main-sequence pulsating variables of different types, such as SPB (2), $\delta$ Scuti (7), RR Lyrae (12), and $\gamma$ Dor (10). We have found 5 variables that do not follow the standard pulsation models and fall between SPB and $\delta$ Scuti instability regions. Their pulsation may be attributed to rapid rotation, which alters the internal conditions of the stars (Balona et al., 2011). We also found a detached binary system (V62) based on its distinct primary and secondary minima observed in the LC. We have identified 26 rotating variables with mass and period ranges (i.e., solar to subsolar and a few hours to a few days, respectively) similar to BY Dra-type variables. They exhibit variable brightness caused by starspots, chromospheric activity, and other phenomena related to their magnetic fields. The 16 identified variables are categorized as non-periodic, as we cannot phase-fold their light LCs. These variables show 30 mmag to 500 mmag amplitude range. A few of them (V15, V31, and V57) are classified as solar-like variables in Gaia DR3.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

TC: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Writing – original draft. SS: Conceptualization, Data curation, Investigation, Methodology, Supervision, Writing – review and editing. KS: Writing – review and editing. JP: Formal Analysis, Investigation, Writing – review and editing. AV: Data curation, Validation, Writing – review and editing. HK: Data curation, Formal Analysis, Investigation, Methodology, Software, Writing – review and editing. Mamta: Data curation, Writing – review and editing. MC: Data curation, Writing – review and editing. DO: Conceptualization, Writing – review and editing. AS: Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. DO acknowledges the support of the Department of Atomic Energy, Government of India, under project identification no. RTI 4002. AV acknowledges the financial support of DST-INSPIRE (No.: DST/INSPIRE Fellowship/2019/IF190550).

Acknowledgments

The observations reported in this paper were obtained by using the 1.3 m Devasthal Fast Optical Telescope (DFOT) and 1.04 m Sampurnand Telescope (ST), Nainital, India. This work made use of data from the Two Micron All Sky Survey (a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation), and archival data obtained with the Spitzer Space Telescope and Wide Infrared Survey Explorer (operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the NASA. This publication also made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). We thank both the referees for their constructive suggestions, which significantly improved the clarity of the paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2025.1608196/full#supplementary-material

Footnotes

¹https://astro.dur.ac.uk/∼pdraper/gaia/gaia.html

²https://www.cosmos.esa.int/web/gaia/data-release-3

³Convex hull is an irregular polygon enclosing all points in a grouping with internal angles between two contiguous sides of less than 180 $\mathrm{deg}$.

⁴Barber, C. B., D.P. Dobkin, and H.T. Huhdanpaa,” The Quickhull Algorithm for Convex Hulls,” ACM Transactions on Mathematical Software, 22(4):469-483 December 1996, www.qhull.org.

⁵The MST is a network of branches that connects a set of points while minimizing the total branch length and avoiding any loops (Battinelli, 1991). This algorithm has lately become a popular tool to search for clusters of stars since it is independent from the star’s density number (Gutermuth et al., 2009; Chavarría et al., 2014; Sharma et al., 2016).

References

Allen, L., Megeath, S. T., Gutermuth, R., Myers, P. C., Wolk, S., Adams, F. C., et al. (2007). “The structure and evolution of young stellar clusters,” in Protostars and planets V. Editors B. Reipurth, D. Jewitt, and K. Keil, 361. doi:10.48550/arXiv.astro-ph/0603096

CrossRef Full Text | Google Scholar

Allison, R. J., Goodwin, S. P., Parker, R. J., Portegies Zwart, S. F., de Grijs, R., and Kouwenhoven, M. B. N. (2009). Using the minimum spanning tree to trace mass segregation. MNRAS 395, 1449–1454. doi:10.1111/j.1365-2966.2009.14508.x

CrossRef Full Text | Google Scholar

Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., and Andrae, R. (2021). Estimating distances from parallaxes. V. Geometric and photogeometric distances to 1.47 billion stars in Gaia early data release 3. AJ 161. Astron. J. 161, 147. doi:10.3847/1538-3881/abd806

CrossRef Full Text | Google Scholar

Balona, L. A., Pigulski, A., De Cat, P., Handler, G., Gutiérrez-Soto, J., Engelbrecht, C. A., et al. (2011). Kepler observations of the variability in B-type stars. MNRAS 413, 2403–2420. doi:10.1111/j.1365-2966.2011.18311.x

CrossRef Full Text | Google Scholar

Battinelli, P. (1991). A new identification technique for OB associations: OB associations in the Small Magellanic Cloud. A&A 244, 69.

Google Scholar

Binney, J., and Tremaine, S. (1987). Galactic dynamics. Princeton, NJ, United States: Princeton University Press.

CrossRef Full Text | Google Scholar

Bonatto, C., Kerber, L. O., Bica, E., and Santiago, B. X. (2006). Probing disk properties with open clusters. A&A 446, 121–135. doi:10.1051/0004-6361:20053573

CrossRef Full Text | Google Scholar

Brinkmann, N., Banerjee, S., Motwani, B., and Kroupa, P. (2017). The bound fraction of young star clusters. A&A 600, A49. doi:10.1051/0004-6361/201629312

CrossRef Full Text | Google Scholar

Chahal, D., de Grijs, R., Kamath, D., and Chen, X. (2022). Statistics of BY Draconis chromospheric variable stars. MNRAS 514, 4932–4943. doi:10.1093/mnras/stac1660

CrossRef Full Text | Google Scholar

Chavarría, L., Allen, L., Brunt, C., Hora, J. L., Muench, A., and Fazio, G. (2014). A multiwavelength study of embedded clusters in W5-east, NGC 7538, S235, S252 and S254-S258. MNRAS 439, 3719–3754. doi:10.1093/mnras/stu224

CrossRef Full Text | Google Scholar

Chehlaeh, N., Mkrtichian, D., Lampens, P., Komonjinda, S., Kim, S.-L., Van Cauteren, P., et al. (2018). Photometric study and search for variable stars in the intermediate-age open cluster NGC 2126. Mon. Notices R. Astronomical Soc. 480, 1850–1863. doi:10.1093/mnras/sty1906

CrossRef Full Text | Google Scholar

Cutri, R. M., Skrutskie, M. F., van Dyk, S., Beichman, C. A., Carpenter, J. M., Chester, T., et al. (2003). VizieR online data catalog: 2MASS all-sky catalog of point sources (Cutri+ 2003). VizieR Online Data Cat, II/246.

Google Scholar

Dib, S., Gutkin, J., Brandner, W., and Basu, S. (2013). Feedback-regulated star formation - II. Dual constraints on the SFE and the age spread of stars in massive clusters. MNRAS 436, 3727–3740. doi:10.1093/mnras/stt1857

CrossRef Full Text | Google Scholar

Dib, S., Piau, L., Mohanty, S., and Braine, J. (2011). Star formation efficiency as a function of metallicity: from star clusters to galaxies. MNRAS 415, 3439–3454. doi:10.1111/j.1365-2966.2011.18966.x

CrossRef Full Text | Google Scholar

Dib, S., Schmeja, S., and Parker, R. J. (2018). Structure and mass segregation in Galactic stellar clusters. MNRAS 473, 849–859. doi:10.1093/mnras/stx2413

CrossRef Full Text | Google Scholar

Fedurco, M., Paunzen, E., Hümmerich, S., Bernhard, K., and Parimucha, Š. (2020). Pulsational properties of ten new slowly pulsating B stars. A&A 633, A122. doi:10.1051/0004-6361/201935478

CrossRef Full Text | Google Scholar

Fleck, J. J., Boily, C. M., Lançon, A., and Deiters, S. (2006). On the mass of dense star clusters in starburst galaxies from spectrophotometry. MNRAS 369, 1392–1406. doi:10.1111/j.1365-2966.2006.10390.x

CrossRef Full Text | Google Scholar

Gaia Collaboration (2022). VizieR online data catalog: Gaia DR3 Part 4. Var. (Gaia Collab. 2022). VizieR Online Data Catalog, I/358.

Google Scholar

Gaia Collaboration Vallenari, A., Brown, A. G. A., Prusti, T., de Bruijne, J. H. J., Arenou, F., et al. (2023). Gaia data release 3 - summary of the content and survey properties. A&A 674, A1. doi:10.1051/0004-6361/202243940

CrossRef Full Text | Google Scholar

Gao, X., Chen, X., Wang, S., and Liu, J. (2025). Classification of periodic variable stars from TESS. ApJS 276, 57. doi:10.3847/1538-4365/ad9dd6

CrossRef Full Text | Google Scholar

Gautschy, A., and Saio, H. (1993). On non-radial oscillations of B-type stars. MNRAS 262, 213–219. doi:10.1093/mnras/262.1.213

CrossRef Full Text | Google Scholar

Girard, T. M., Grundy, W. M., Lopez, C. E., and van Altena, W. F. (1989). Relative proper motions and the stellar velocity dispersion of the open cluster M67. AJ 98, 227. doi:10.1086/115139

CrossRef Full Text | Google Scholar

Grasha, K., Calzetti, D., Bittle, L., Johnson, K. E., Donovan Meyer, J., Kennicutt, R. C., et al. (2018). Connecting young star clusters to CO molecular gas in NGC 7793 with ALMA-LEGUS. MNRAS 481, 1016–1027. doi:10.1093/mnras/sty2154

CrossRef Full Text | Google Scholar

Grasha, K., Elmegreen, B. G., Calzetti, D., Adamo, A., Aloisi, A., Bright, S. N., et al. (2017). Hierarchical star formation in turbulent media: evidence from young star clusters. ApJ 842, 25. doi:10.3847/1538-4357/aa740b

CrossRef Full Text | Google Scholar

Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., and Finkbeiner, D. (2019). A 3D dust map based on Gaia, pan-STARRS 1, and 2MASS. ApJ 887, 93. doi:10.3847/1538-4357/ab5362

CrossRef Full Text | Google Scholar

Gutermuth, R. A., Megeath, S. T., Myers, P. C., Allen, L. E., Pipher, J. L., and Fazio, G. G. (2009). A spitzer survey of young stellar clusters within one kiloparsec of the sun: cluster core extraction and basic structural analysis. ApJS 184, 18–83. doi:10.1088/0067-0049/184/1/18

CrossRef Full Text | Google Scholar

Gutermuth, R. A., Megeath, S. T., Pipher, J. L., Williams, J. P., Allen, L. E., Myers, P. C., et al. (2005). The initial configuration of young stellar clusters: a K-band number counts analysis of the surface density of stars. ApJ 632, 397–420. doi:10.1086/432460

CrossRef Full Text | Google Scholar

Handler and Meingast Meingast, S. (2011). New β cephei stars in the young open cluster ngc 637. A&A 533, A70. doi:10.1051/0004-6361/201116874

CrossRef Full Text | Google Scholar

Ibanoglu, C., Çakırlı, Ö., and Sipahi, E. (2018). The first comprehensive catalog of γ Dor pulsators and their characteristics. New A 62, 70–84. doi:10.1016/j.newast.2018.01.004

CrossRef Full Text | Google Scholar

Jose, J., Pandey, A. K., Ojha, D. K., Ogura, K., Chen, W. P., Bhatt, B. C., et al. (2008). Stellar contents and star formation in the young open cluster Stock 8. Mon. Notices R. Astronomical Soc. 384, 1675–1700. doi:10.1111/j.1365-2966.2007.12825.x

CrossRef Full Text | Google Scholar

Kang, Y. B., Kim, S. L., Rey, S. C., Lee, C. U., Kim, Y. H., Koo, J. R., et al. (2007). Variable stars in the open cluster NGC 2099 (M37). PASP 119, 239–250. doi:10.1086/513883

CrossRef Full Text | Google Scholar

Kaur, H., Sharma, S., Dewangan, L. K., Ojha, D. K., Durgapal, A., and Panwar, N. (2020). Unveiling the physical conditions in NGC 6910. ApJ 896, 29. doi:10.3847/1538-4357/ab9122

CrossRef Full Text | Google Scholar

Kaur, H., Sharma, S., Durgapal, A., Dewangan, L. K., Verma, A., Panwar, N., et al. (2023). Structural analysis of open cluster Bochum 2. J. Astrophysics Astronomy 44, 66. doi:10.1007/s12036-023-09953-9

CrossRef Full Text | Google Scholar

Kim, S. L., Chun, M. Y., Park, B. G., Lee, S. H., Sung, H., Ann, H. B., et al. (2001). Search for short-period variable stars in the open cluster NGC 2301. A&A 371, 571–578. doi:10.1051/0004-6361:20010403

CrossRef Full Text | Google Scholar

Koenig, X. P., and Leisawitz, D. T. (2014). A classification scheme for young stellar objects using the wide-field infrared survey explorer AllWISE catalog: revealing low-density star formation in the outer galaxy. ApJ 791, 131. doi:10.1088/0004-637X/791/2/131

CrossRef Full Text | Google Scholar

Kroupa, P. (2002). The initial mass function of stars: evidence for uniformity in variable systems. Science 295, 82–91. doi:10.1126/science.1067524

PubMed Abstract | CrossRef Full Text | Google Scholar

Kruijssen, J. M. D. (2012). On the fraction of star formation occurring in bound stellar clusters. MNRAS 426, 3008–3040. doi:10.1111/j.1365-2966.2012.21923.x

CrossRef Full Text | Google Scholar

Lada, C. J., and Lada, E. A. (2003). Embedded clusters in molecular clouds. Annu. Rev. Astronomy Astrophysics 41, 57–115. doi:10.1146/annurev.astro.41.011802.094844

CrossRef Full Text | Google Scholar

Landolt, A. U. (1992). UBVRI photometric standard stars in the magnitude range 11.5-16.0 around the celestial equator. AJ 104, 340. doi:10.1086/116242

CrossRef Full Text | Google Scholar

Lata, S., Pandey, A., Sharma, S., Bonatto, C., and Yadav, R. K. (2014a). Photometric study of five open star clusters. New Astron. 26, 77–85. doi:10.1016/j.newast.2013.06.003

CrossRef Full Text | Google Scholar

Lata, S., Pandey, A. K., Kesh Yadav, R., Richichi, A., Irawati, P., Panwar, N., et al. (2019). Short-period variable stars in young open cluster Stock 8. AJ 158, 68. doi:10.3847/1538-3881/ab298c

CrossRef Full Text | Google Scholar

Lata, S., Yadav, R. K., Pandey, A. K., Richichi, A., Eswaraiah, C., Kumar, B., et al. (2014b). Main-sequence variable stars in young open cluster NGC 1893. MNRAS 442, 273–284. doi:10.1093/mnras/stu726

CrossRef Full Text | Google Scholar

Lebzelter, T., Mowlavi, N., Lecoeur-Taibi, I., Trabucchi, M., Audard, M., García-Lario, P., et al. (2023). Gaia Data Release 3. The second Gaia catalogue of long-period variable candidates. A&A 674, A15. doi:10.1051/0004-6361/202244241

CrossRef Full Text | Google Scholar

Lomb, N. R. (1976). Least-squares frequency analysis of unequally spaced data. Ap&SS 39, 447–462. doi:10.1007/BF00648343

CrossRef Full Text | Google Scholar

Martinez-Vazquez, C. E., Salinas, R., Vivas, A. K., and Catelan, M. (2023). “Breaking the laws”: a segmented period-luminosity relation in delta Scuti stars. Am. Astronomical Soc. Meet. Abstr. 241, 10.

Google Scholar

Mathieu, R. D. (1984). The structure and dynamics of the open cluster M 11. ApJ 284, 643–662. doi:10.1086/162447

CrossRef Full Text | Google Scholar

Messina, S., Distefano, E., Parihar, P., Kang, Y. B., Kim, S.-L., Rey, S.-C., et al. (2008). RACE-OC project: rotation and variability in the open cluster NGC 2099 (M 37). A&A 483, 253–262. doi:10.1051/0004-6361:20079216

CrossRef Full Text | Google Scholar

Miglio, A., Montalbán, J., and Dupret, M. A. (2007). Revised instability domains of SPB and β Cephei stars. Commun. Asteroseismol. 151, 48–56. doi:10.1553/cia151s48

CrossRef Full Text | Google Scholar

Mowlavi, N., Barblan, F., Saesen, S., and Eyer, L. (2013). Stellar variability in open clusters. I. A new class of variable stars in NGC 3766. A&A 554, A108. doi:10.1051/0004-6361/201321065

CrossRef Full Text | Google Scholar

Mullen, J. P., Marengo, M., Martínez-Vázquez, C. E., Chaboyer, B., Bono, G., Braga, V. F., et al. (2023). RR Lyrae mid-infrared period-luminosity-metallicity and period-Wesenheit-Metallicity relations based on Gaia DR3 parallaxes. ApJ 945, 83. doi:10.3847/1538-4357/acb20a

CrossRef Full Text | Google Scholar

Olczak, C., Spurzem, R., and Henning, T. (2011). A highly efficient measure of mass segregation in star clusters. A&A 532, A119. doi:10.1051/0004-6361/201116902

CrossRef Full Text | Google Scholar

Pandey, R., Sharma, S., Panwar, N., Dewangan, L. K., Ojha, D. K., Bisen, D. P., et al. (2020). Stellar cores in the sh 2-305 H II region. ApJ 891, 81. doi:10.3847/1538-4357/ab6dc7

CrossRef Full Text | Google Scholar

Parker, R. J., and Dale, J. E. (2013). Imprints of feedback in young gasless clusters? MNRAS 432, 986–997. doi:10.1093/mnras/stt517

CrossRef Full Text | Google Scholar

Parker, R. J., and Meyer, M. R. (2012). Characterizing the dynamical state of star clusters from snapshots of their spatial distributions. MNRAS 427, 637–650. doi:10.1111/j.1365-2966.2012.21851.x

CrossRef Full Text | Google Scholar

Pastorelli, G., Marigo, P., Girardi, L., Chen, Y., Rubele, S., Trabucchi, M., et al. (2019). Constraining the thermally pulsing asymptotic giant branch phase with resolved stellar populations in the Small Magellanic Cloud. MNRAS 485, 5666–5692. doi:10.1093/mnras/stz725

CrossRef Full Text | Google Scholar

Pecaut, M. J., and Mamajek, E. E. (2013). Intrinsic colors, temperatures, and bolometric corrections of pre-main-sequence stars. ApJS 208, 9. doi:10.1088/0067-0049/208/1/9

CrossRef Full Text | Google Scholar

Pfalzner, S., and Kaczmarek, T. (2013). The expansion of massive young star clusters - observation meets theory. A&A 559, A38. doi:10.1051/0004-6361/201322134

CrossRef Full Text | Google Scholar

Phelps, R. L., and Janes, K. A. (1994). Young open clusters as probes of the star formation process. 1: an atlas of open cluster photometry. ApJS 90, 31. doi:10.1086/191857

CrossRef Full Text | Google Scholar

Pietrukowicz, P., Soszyński, I., Netzel, H., Wrona, M., Udalski, A., Szymański, M. K., et al. (2020). Over 10000 δ Scuti stars toward the galactic bulge from OGLE-IV. Acta Astron 70, 241–263. doi:10.32023/0001-5237/70.4.1

CrossRef Full Text | Google Scholar

Rangwal, G., Yadav, R. K. S., Bisht, D., Durgapal, A., and Sariya, D. P. (2023). Investigating kinematics and dynamics of three open clusters towards Galactic anticentre. Mon. Notices R. Astronomical Soc. 523, 1867–1884. doi:10.1093/mnras/stad1517

CrossRef Full Text | Google Scholar

Ren, F., de Grijs, R., Zhang, H., Deng, L., Chen, X., Matsunaga, N., et al. (2021). VizieR online data catalog: KISOGP: 7055 eclipsing binaries with KWFC (Ren+, 2021). Strasbourg, France: VizieR Online Data Catalog. doi:10.26093/cds/vizier.51610176

CrossRef Full Text | Google Scholar

Ruprecht, J. (1966). Classification of open star clusters. Bull. Astronomical Institutes Czechoslov. 17, 33.

Google Scholar

Sagar, R., Kumar, B., Omar, A., and Joshi, Y. C. (2012). New optical telescopes at Devasthal observatory: 1.3-m installed and 3.6-m upcoming. Astronomical Soc. India Conf. Ser. 4, 173. doi:10.1117/12.925634

CrossRef Full Text | Google Scholar

Sagar, R., and Richtler, T. (1991). Mass functions of five Large Magellanic Cloud star clusters. A&A 250, 324.

Google Scholar

Sánchez Arias, J. P., Córsico, A. H., and Althaus, L. G. (2017). Asteroseismology of hybrid δ Scuti-γ Doradus pulsating stars. A&A 597, A29. doi:10.1051/0004-6361/201629126

CrossRef Full Text | Google Scholar

Scargle, J. D. (1982). Studies in astronomical time series analysis. II. Statistical aspects of spectral analysis of unevenly spaced data. ApJ 263, 835–853. doi:10.1086/160554

CrossRef Full Text | Google Scholar

Schmeja, S., and Klessen, R. S. (2006). Evolving structures of star-forming clusters. A&A 449, 151–159. doi:10.1051/0004-6361:20054464

CrossRef Full Text | Google Scholar

Sharma, S., Dewangan, L., Panwar, N., Kaur, H., Ojha, D. K., Yadav, R., et al. (2023). Teutsch 76: a deep near-infrared study. J. Astrophysics Astronomy 44, 46. doi:10.1007/s12036-023-09936-w

CrossRef Full Text | Google Scholar

Sharma, S., Ghosh, A., Ojha, D. K., Pandey, R., Sinha, T., Pandey, A. K., et al. (2020). The disintegrating old open cluster Czernik 3. MNRAS 498, 2309–2322. doi:10.1093/mnras/staa2412

CrossRef Full Text | Google Scholar

Sharma, S., Pandey, A. K., Borissova, J., Ojha, D. K., Ivanov, V. D., Ogura, K., et al. (2016). Structural studies of eight bright rimmed clouds in the southern hemisphere. Astronomical J. 151, 126. doi:10.3847/0004-6256/151/5/126

CrossRef Full Text | Google Scholar

Sharma, S., Pandey, A. K., Ogura, K., Aoki, T., Pandey, K., Sandhu, T. S., et al. (2008). Mass functions and photometric binaries in nine open clusters. Astronomical J. 135, 1934–1945. doi:10.1088/0004-6256/135/5/1934

CrossRef Full Text | Google Scholar

Sharma, S., Pandey, A. K., Ojha, D. K., Chen, W. P., Ghosh, S. K., Bhatt, B. C., et al. (2007). Star formation in young star cluster NGC 1893. Mon. Notices R. Astronomical Soc. 380, 1141–1160. doi:10.1111/j.1365-2966.2007.12156.x

CrossRef Full Text | Google Scholar

Sharma, S., Verma, A., Mallick, K., Dewangan, L. K., Kaur, H., Yadav, R. K., et al. (2024). Cluster Formation in a filamentary cloud: the case of the stellar cluster NGC 2316. AJ 167, 106. doi:10.3847/1538-3881/ad19cd

CrossRef Full Text | Google Scholar

Shu, F. H. (1982). The Physical Universe. New York: McGraw Hill.

Google Scholar

Skrutskie, M. F., Cutri, R. M., Stiening, R., Weinberg, M. D., Schneider, S., Carpenter, J. M., et al. (2006). The two Micron all Sky survey (2MASS). AJ 131, 1163–1183. doi:10.1086/498708

CrossRef Full Text | Google Scholar

Soszyński, I., Pietrukowicz, P., Skowron, J., Udalski, A., Szymański, M. K., Skowron, D. M., et al. (2021). Over 24 000 δ Scuti stars in the galactic bulge and disk from the OGLE survey. Acta Astron 71, 189–204. doi:10.32023/0001-5237/71.3.1

CrossRef Full Text | Google Scholar

Spitzer, L., and Harm, R. (1958). Evaporation of stars from isolated clusters. ApJ 127, 544. doi:10.1086/146486

CrossRef Full Text | Google Scholar

Stankov, A., and Handler, G. (2005). Catalog of galactic β cephei stars. ApJS 158, 193–216. doi:10.1086/429408

CrossRef Full Text | Google Scholar

Stetson, P. B. (1987). DAOPHOT: a computer program for crowded-field stellar photometry. PASP 99, 191. doi:10.1086/131977

CrossRef Full Text | Google Scholar

Stetson, P. B. (1992). “More experiments with DAOPHOT II and WF/PC images,” in Astronomical data analysis software and systems I. Editors D. M. Worrall, C. Biemesderfer, and J. Barnes (San Francisco, CA: Astronomical Society of the Pacific Conference Series), 25, 297.

Google Scholar

Szewczuk, W., and Daszyńska-Daszkiewicz, J. (2017). Domains of pulsational instability of low-frequency modes in rotating upper main sequence stars. MNRAS 469, 13–46. doi:10.1093/mnras/stx738

CrossRef Full Text | Google Scholar

Tang, S.-Y., Pang, X., Yuan, Z., Chen, W. P., Hong, J., Goldman, B., et al. (2019). Discovery of tidal tails in disrupting open clusters: coma berenices and a neighbor stellar group. ApJ 877, 12. doi:10.3847/1538-4357/ab13b0

CrossRef Full Text | Google Scholar

Verma, A., Sharma, S., Dewangan, L., Pandey, R., Baug, T., Ojha, D. K., et al. (2023). Kronberger 55: a candidate for end-dominated collapse scenario. J. Astrophysics Astronomy 44, 52. doi:10.1007/s12036-023-09932-0

CrossRef Full Text | Google Scholar

Waelkens, C. (1991). Slowly pulsating B stars. A&A 246, 453.

Google Scholar

Warner, P. B., Kaye, A. B., and Guzik, J. A. (2003). A theoretical γ Doradus instability strip. ApJ 593, 1049–1055. doi:10.1086/376727

CrossRef Full Text | Google Scholar

Yang, S.-C., Sarajedini, A., Deliyannis, C. P., Sarrazine, A. R., Kim, S. C., and Kyeong, J. (2013). WIYN open cluster study LII: wide-field CCD photometry of the old open cluster NGC 6819. ApJ 762, 3. doi:10.1088/0004-637X/762/1/3

CrossRef Full Text | Google Scholar