- 1School of GeoSciences, University of Edinburgh, Edinburgh, United Kingdom
- 2School of Mathematics, University of Edinburgh, Edinburgh, United Kingdom
The epidemic type aftershock sequence (ETAS) model is widely used to model seismic sequences and underpins operational earthquake forecasting (OEF). However, it remains challenging to assess the reliability of inverted ETAS parameters for numerous reasons. For example, the most common algorithms just return point estimates with little quantification of uncertainty. At the same time, Bayesian Markov chain Monte Carlo implementations remain slow to run and do not scale well, and few have been extended to include spatial structure. This makes it difficult to explore the effects of stochastic uncertainty. Here, we present a new approach to ETAS modeling using an alternative Bayesian method, the integrated nested Laplace approximation (INLA). We have implemented this model in a new R-Package called ETAS.inlabru, which is built on the R packages R-INLA and inlabru. Our study has included extending these packages, which provided tools for modeling log-Gaussian Cox processes, to include the self-exciting Hawkes process that ETAS is a special case of. While we just present the temporal component here, the model scales to a spatio-temporal model and may include a variety of spatial covariates. This is a fast method that returns joint posteriors on the ETAS background and triggering parameters. Using a series of synthetic case studies, we explore the robustness of ETAS inversions using this method of inversion. We also included runnable notebooks to reproduce the figures in this article as part of the package's GitHub repository. We demonstrate that reliable estimates of the model parameters require that the catalog data contain periods of relative quiescence, as well as triggered sequences. We explore the robustness of the method under stochastic uncertainty in the training data and show that the method is robust to a wide range of starting conditions. We show how the inclusion of historic earthquakes prior to the modeled time window affects the quality of the inversion. Finally, we show that rate-dependent incompleteness of earthquake catalogs after large earthquakes have a significant and detrimental effect on the ETAS posteriors. We believe that the speed of the inlabru inversion, which includes a rigorous estimation of uncertainty, will enable a deeper exploration of how to use ETAS robustly for seismicity modeling and operational earthquake forecasting.
1. Introduction
The epidemic type aftershock sequence (ETAS) model [1–3] is one of the cornerstones of seismicity modeling. It models evolving seismic sequences in terms of background seismicity and seismicity triggered by previous events. As such, it is a self-exciting point process model, which is commonly termed a Hawkes process [4] in the statistical literature. ETAS achieves this by combining several empirical relationships for seismicity. The ETAS model enables us to generate synthetic earthquake sequences and to invert earthquake space-time-magnitude data for the underlying ETAS parameters that characterize both the background and triggering rates. However, the likelihood space for some parameters is notoriously flat, and many factors can affect the robustness of the results.
There are many different implementations of the ETAS model. The most common approach for determining ETAS parameters is the maximum-likelihood method which returns a point estimate on the ETAS parameters using an optimization algorithm (e.g., [5]). In some cases, uncertainty is quoted using the Hessian matrix. Bayesian alternatives are available; for example, the “bayesianETAS” R-package [6] uses the Markov chain Monte Carlo (MCMC) method to return full posteriors. However, MCMC methods are notoriously slow as building the Markov chain is an inherently linear algorithm requiring many successive runs of a forward model based on the previous results. A major benefit of Bayesian methods is that they better describe uncertainty. We have developed a new Bayesian ETAS package using the integrated nested Laplace approximation (INLA) instead of MCMC; this is implemented in the R-Package ETAS.inlabru and will be made available through the Comprehensive R Archive Network (CRAN). The results presented, in this article, are reproducible using this package and a series of Rmd notebooks. Unlike the MCMC implementations, our method does not rely on a latent variable to classify whether events are background or triggered.
The integrated nested Laplace approximation (INLA [7]) and inlabru [8] offer a fast approach for Bayesian modeling of spatial, temporal, and spatio-temporal point process data and have had over 10 years of development. The INLA method is a well-known alternative to MCMC methods to perform Bayesian inference. It has been successfully applied in a variety of fields, such as seismic hazard [9, 10], air pollution [11], disease mapping [12–15], genetics [16], public health [17], and ecology [18, 19], as well as more examples can be found in Bakka et al. [20], Blangiardo et al. [21], and Gómez-Rubio [22].
To date, the main limitation of the application of inlabru to seismicity was that it only addressed log-Gaussian Cox Processes [23], which do not include self-exciting clustering. Serafini et al. [24] addressed this specific limitation by showing how the methodology used for log-Gaussian Cox processes could be extended to model self-exciting Hawkes processes [4, 25], using R-INLA and inlabru, when the function form of the triggering function can be integrated. The novelty of our approach resides in the likelihood approximation. We decompose the log-likelihood into the sum of many small components, where each is linearly approximated with respect to the posterior mode using a truncated Taylor expansion. This means that the log-likelihood is exact at the posterior mode and the accuracy of the approximation decreases as we move away from that point. Furthermore, the linear approximation and the optimization routine to determine the posterior mode are internally performed by the inlabru package. In this study, the specific application to the ETAS model was presented. The temporal model provides posteriors on the background rate and all ETAS parameters.
ETAS.inlabru provides the functions to be approximated while the user provides the data and specifies the priors. The advantages of our approach are both in terms of computational time and its scalability to include relevant covariates [9] such as maps of faults, strain rates, in addition to earthquake catalog data to introduce alternative structures to the parameters (e.g., considering one of them as temporally, or spatially, varying).
Here, we present a broad analysis of how the inlabru inversion performs on synthetic earthquake catalogs where we know all of the controlling parameters. We explore the performance of the inversion as a function of the training catalog length, the impact of large events that happen to occur in the sequence, the consequence of short-term incompleteness after large events as well as various inlabru model choices. These results are generic and not specific to our implementation of the ETAS model—rather our fast Bayesian model allows us to make a more rapid assessment of potential biases derived from the likelihood function itself. We want the reader to come away with an understanding of when the ETAS model is likely to describe a sequence well, be able to identify sources of potential bias, understand how synthetic modeling allows us to explore potential data quality issues, and decide whether fitting an ETAS model is an appropriate way to proceed.
2. Method
In this section, we introduce our inlabru implementation of the temporal ETAS model and refer the reader to Serafini et al. [24] for a complete description of the mathematical formulation.
2.1. The temporal ETAS model
The temporal ETAS model is a marked Hawkes process model, where the marking variable is the magnitude of the events. The ETAS model is composed of three parts: a background rate term, a triggered events rate representing the rate of events induced by past seismicity, and a magnitude distribution independent from space and time. Given the independence between the magnitude distribution and the time distribution of the events, the ETAS conditional intensity is usually the product between a Hawkes process model describing only the location and a magnitude distribution π(m).
More formally, the ETAS conditional intensity function evaluated at a generic time point t ∈ (T1, T2), T1, T2 ≥ 0, T1 < T2 having observed the events , where M0 is the minimum magnitude in the catalog which needs to be completely sampled, and N(t) is the counting process associated with the Hawkes process representing the number of events recorded up to time t (included), is given by the following:
where λHawkes is the conditional intensity of a temporal Hawkes process describing the occurrence times only. In our ETAS implementation, this is given by the following:
The parameters of the model are μ, K, α, c ≥ 0 and p > 1. Different parametrizations of the ETAS model exist; we focus on this one because it has proven to be the most suitable parametrization for our method.
In seismology, the magnitude distribution, π(m) is commonly assumed to be independent of space and time for simplicity of analysis. In this study, we take this to be the Gutenberg–Richter distribution with a b-value of 1. In this section, we focus on the Hawkes part of the model, assuming the parameters of the magnitude distribution are determined independently. From now on, for ease of notation, where not specified differently, we refer to λHawkes as simply λ.
2.2. Hawkes process log-likelihood approximation for inlabru
The Hawkes process is implemented in inlabru by decomposing its log-likelihood function (Equation 3) into multiple parts, the sum of which returns the exact log-likelihood at the point we expand it about. We linearly approximate the single components with respect to the posterior mode and apply the integrated nested Laplace approximation (INLA) method to perform inference on the parameters of the model. Both the linearization and the optimization, to find the posterior mode, are performed internally by inlabru. Our package, ETAS.inlabru, provides inlabru with the ETAS-specific functions representing the log-likelihood component to be approximated. We outline the decomposition below.
Having observed a catalog of events , the Hawkes process log-likelihood is given by the following:
where θ is a vector of the model parameters, is the history of events up to time ti, and
The above integral can be considered the sum of two parts, the number of background events Λ0(T1, T2) and the remaining summation, which is referred to as the sum of the number of triggered events by each event ti, namely Λi(T1, T2). We approximate the integral by linearizing the functions Λ0(T1, T2) and Λi(T1, T2). This means that the resulting approximate integral is the sum of linear functions of the parameters.
However, we concluded that this approximation alone is not sufficiently accurate. To increase the accuracy of the approximation, for each integral Λi(T1, T2), we further consider a partition of the integration interval [max(T1, ti), T2] in Bi bins, such that , and if j < k. By doing this, the integral becomes:
In this way, the integral is decomposed in terms providing a more accurate approximation. We discuss the options for temporal binning in Section 2.3.
Substituting Equations (5) into (3), the Hawkes process log-likelihood can be written as follows:
In our approximation, we linearise the logarithm of each element within summations with respect to the posterior mode θ*. Other choices led to a non-convergent model [24]. In this case, the approximate log-likelihood becomes:
where for a generic function f(θ) with argument θ ∈ Θ ⊂ ℝm, the linearized version with respect to a point θ* is given by a truncated Taylor expansion:
The other key component is the functions for each of the three incremental components in Equation (6) that needs to be linearized in this way. These are provided in ETAS.inlabru and will be discussed in Section 2.4.
2.3. Temporal binning
For each event, time binning is used in Equation (5) to improve the accuracy of the integration of the term describing the sum of the number of triggered events. The binning strategy is fundamental because the number of bins determines, up to a certain limit, the accuracy of this component of the approximation. Considering more bins enhances the accuracy of the approximation but increases the computational time because it increases the number of quantities to be approximated. Also, we cannot reduce the approximation error to zero, and the numerical value of the integral in each bin goes to zero increasing the number of bins, which can be problematic in terms of numerical stability. We found that the ETAS model considered here, having approximately 10 bins for each observed point is usually enough, and that is best considering higher resolution bins close to the triggering event. In fact, the function
varies the most for the value of t close to ti and becomes almost constant moving away from ti. This means that we need shorter bins close to ti, to capture the variation, and wider bins far from ti where the rate changes more slowly.
We choose a binning strategy defined by three parameters Δ, δ > 0, and . The bins relative to the observed point ti are given by the following:
where, ni ≤ nmax is the maximum n ∈ {0, 1, 2, 3, …} such that . The parameter Δ regulates the length of the first bin, δ regulates the length ratio between consecutive bins, and the value nmax regulates the maximum number of bins.
This strategy presents two advantages. The first is that we have shorter bins close to the point ti and wider bins as we move away from that point. The second is that the first (or second, or third, or any) bin has the same length for all points. This is useful because the integral in a bin is a function of the bin length and not of the absolute position of the bin. This means that we need to calculate the value of the integral in the first (second, third, or any) bin once time and reuse the same result for all events. This significantly reduces the computational burden.
2.4. Functions to be linearized
This section and the next one illustrate what we need to provide to inlabru to approximate Hawkes process model. This one focuses on the functions to be provided, while the next one on how they are combined to obtain the desired approximation. Regarding the functions to be provided, we remark that those are already present in the ETAS.inlabru package, thus, the user does not have to provide anything apart from the data, the area of interest, and the prior parameters. However, these sections are useful to understand what happens under the curtains and if one wants to extend this approach to more complicated ETAS implementations.
To build an ETAS model, we need to provide functions for each of the components of the likelihood function (Equation 6). The linearization and the finding of the mode θ* are managed automatically by the inlabru package. We only have to provide the functions to be linearized. Specifically, we need to provide the logarithm of the functions needed to approximate the integral and the logarithm of the conditional intensity. More formally, for our approximation of the ETAS model (i.e., for each term in Equation 6), ETAS.inlabru provides the functions:
and
For full details, refer to Serafini et al. [24].
2.5. Implementation details: The poisson count model trick
This subsection is helpful for those wanting to understand the source code; it describes a computational trick that might appear unusual at first. It can be skipped without a loss of understanding of mathematics.
Our implementation in inlabru works by combining three INLA Poisson models on different datasets. The use of the INLA Poisson model, here, is related to computational efficiency purposes; it does not have any specific statistical meaning. Specifically, we leverage the internal log-likelihood used for Poisson models in R-INLA (and inlabru) to obtain the approximate Hawkes process log-likelihood as part of a computational trick.
More formally, INLA has the special feature of allowing the user to work with Poisson counts models with exposures equal to zero (which should be improper). A generic Poisson model for counts ci, i = 1, …, n observed at locations ti, i = 1, …, n with exposure E1, …, En with log-intensity log λP(t) = f(t, θ), in inlabru has log-likelihood given by the following:
Each Hawkes process log-likelihood component (Equation 6) is approximated using one surrogate Poisson model with log-likelihood given by Equation (13) and an appropriate choice of counts and exposures data. Table 1 reports the approximation for each log-likelihood component with details on the surrogate Poisson model used to represent it. For example, the first part (integrated background rate) is represented by a Poisson model with log-intensity , this will be automatically linearized by inlabru. Given that, the integrated background rate is just a scalar and not a summation, and therefore we only need one observation to represent it, assuming counts equal 0 and exposures equal 1. Table 1 shows that to represent a Hawkes process model having observed n events, we need events with Bh number of bins in the approximation of the expected number of induced events by observation h.
Furthermore, Table 1 lists the components needed to approximate the ETAS log-likelihood, which will be internally considered surrogate Poisson log-intensities by inlabru. More specifically, we only need to create the datasets with counts ci, exposures ei, and the information on the events xi representing the different log-likelihood components; and, to provide the functions and log λ(t). The linearization is automatically performed by inlabru, as well as the retrieving of the parameters' posterior distribution.
More detail on how to build the functions in the ETAS.inlabru package can be found at https://github.com/Serra314/Hawkes_process_tutorials/tree/main/how_to_build_Hawkes.
2.6. Prior specification
We have to set the priors for the parameters. The INLA method is designed for latent Gaussian models, which means that all the unobservable parameters have to be Gaussian. This seems in contrast with the positivity constraint of the ETAS parameters μ, K, α, c, p, but we have a solution.
Our idea is to use an internal scale where the parameters have a Gaussian distribution and to transform them before using them in log-likelihood components calculations. We refer to the internal scale as INLA scale and to the parameters in the INLA scale as θ. In practice, all parameters have a standard Gaussian prior in the INLA scale, and they are transformed to be distributed according to a target distribution in the ETAS scale. Specifically, assuming that θ has a standard Gaussian distribution with cumulative distribution function (CDF) Φ(θ), and calling the inverse of the CDF of the target distribution for the parameter, we can switch between the Gaussian and the target distributions using the following:
where η(θ) has a distribution with CDF FY(·).
The ETAS.inlabru R-package uses the following default priors in the ETAS scale,
however, they can be changed to different distributions that better describe the available prior information.
The package inlabru provides a function to easily implement such transformation. The function is called bru_forward_transformation and takes in input the quantile function of the target distribution and its parameters. Below, we report three examples of transformations such that the parameters in the ETAS scale have a Gamma, Uniform, or Log-Gaussian distribution. We show the empirical density obtained by transforming the same sample of values from a standard Gaussian distribution.
The prior for μ is the one that will most commonly need to be modified as it changes with the size of the domain being modeled. We choose Gamma(shape = aμ, rate = bμ) prior for μ. The mean of the distribution is given by aμ/bμ = 1 event/day; the variance is , and the skewness . One strategy for setting these parameters is to estimate an upper limit on the rate by dividing the duration of the catalog total number of events; this is likely an overestimate as it combines the triggered and background events. One might choose to pick a mean rate that is half of this, which defines the ratio of aμ and bμ. There is then some trade-off in the variance and skewness parameters.
Samples drawn from the priors used in this article are shown in Figures 1A–E, including lines showing the initial and true values that will be used through the majority of the results. The sensitivity to the choice of initial values is the first part of the results section. Please note how broad these priors, are as this is helpful to see how much more informative the posteriors we generate are from these initial distributions.
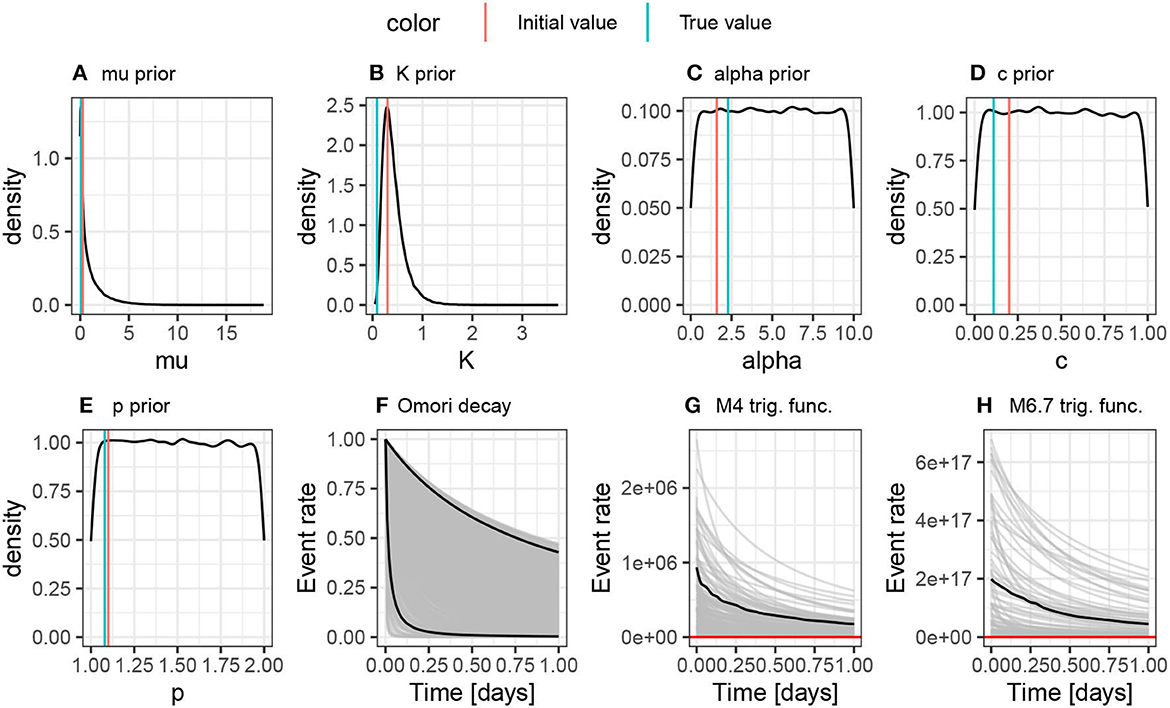
Figure 1. (A–E) Show samples from the priors on the ETAS scale that we use throughout this article. They are intentionally broad. The red line shows the initial value used for the majority of the analyses in this article, and the green line shows the true value. (F–H) Show samples of the triggering functions derived from these priors. The permit a very wide range of triggering behaviors, including unrealistically large numbers of events; these should be used for comparison with the triggering functions derived from the fitted posterior distributions later in the article.
The ETAS parameters themselves are not easy to interpret given that it is their combination in the Omori decay and triggering functions that we are most interested in. We draw 1000 samples from the prior to generate samples of the Omori decay, the triggering function for an M4 event and the triggering function of an M6.7 event (Figures 1F–H). We see that these priors produce a wide range of behavior, including unrealistically large productivity compared to real earthquake process. This information is useful for comparison with the triggering functions derived from sampling posteriors later in the article.
2.7. Fitting the model
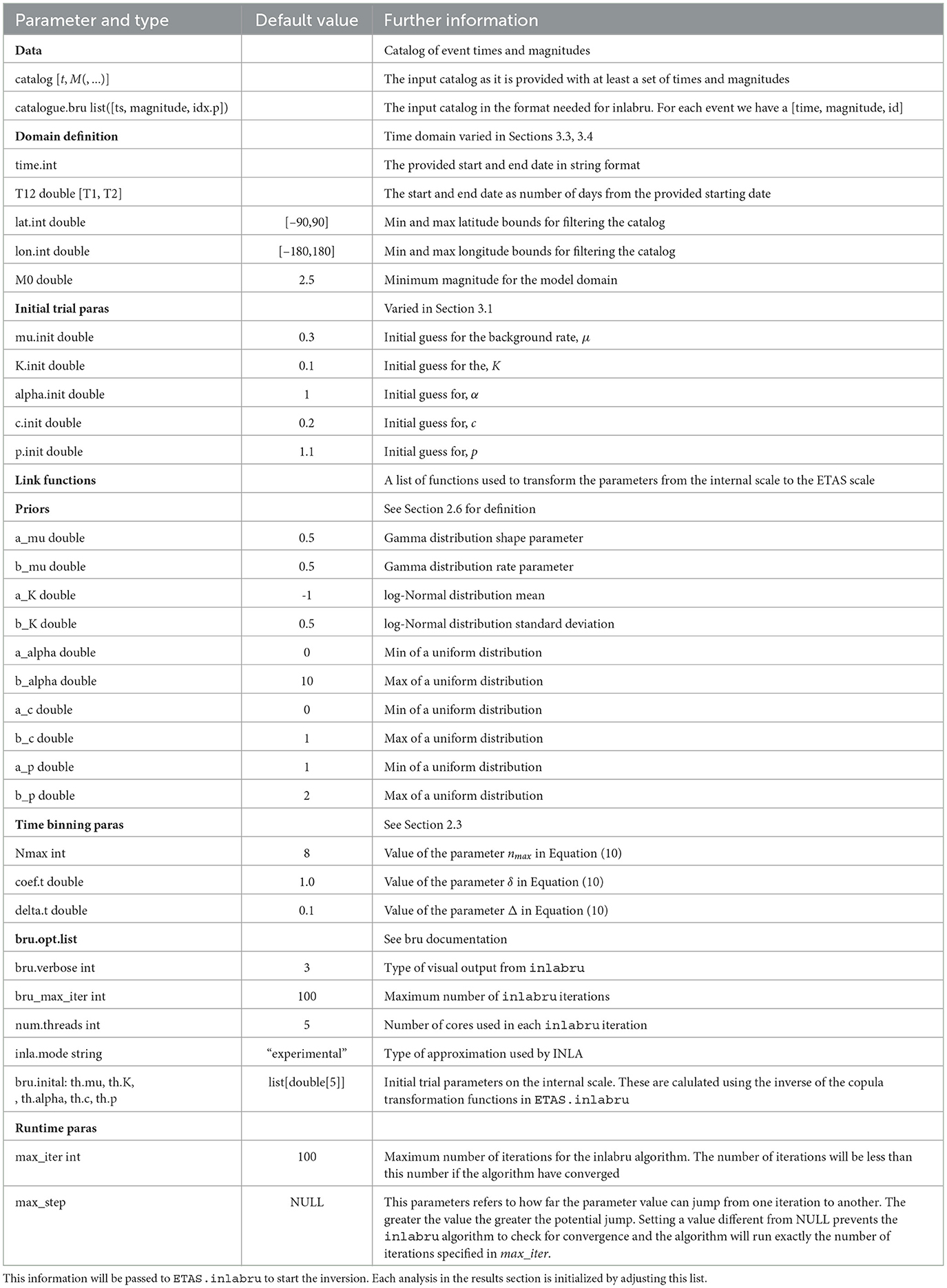
The function Temporal.ETAS.fit(list.input) performs the ETAS inversion. The list.input object is a structured list containing the raw catalog, the catalog formatted for inlabru, definition of the model domain, an initial set of trail parameters on the ETAS scale, the link functions used to transform from the internal scale to the ETAS scale, parameters to set each of the priors, parameters to generate the time binning, and a series of runtime parameters that control the behavior of inlabru. There is a complete description of the parameters in Table 2, which cross-references to the section of the article that describes their role.
In the Section 3, we vary the catalog, start times, and the initial set of trial parameters. To achieve this, we create a default list.input object and then modify these inputs by hand—the notebooks provided demonstrate how to do this.
Once we call Temporal.ETAS.fit(list.input), the iterative fitting of the model parameters is handled automatically by inlabru until they converge or max_iter iterations have occurred. For a comprehensive discussion of the underlying mathematical framework, we refer the reader to Serafini et al. [24].
The iterative process is illustrated in Figure 2 and outlines each of the steps below.
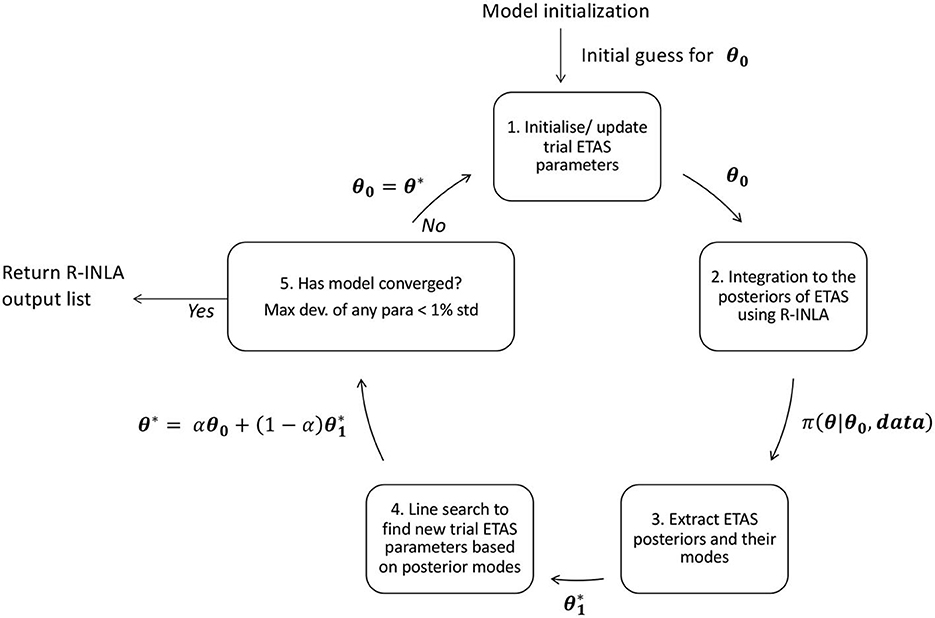
Figure 2. Schematic diagram showing the inlabru workflow which iteratively updates a set of trial ETAS parameters.
2.7.1. Step 1: Initialize/update trial ETAS parameter set
We start with a set of trial ETAS parameters θ0 = (μ0, K0, α0, p0, c0) which will be used as the linearization point for the linear approximation. These initial values should lie within their respective priors. They could be sampled from the priors, but it is possible that a very unrealistic parameter combination might be chosen. These parameters will be updated in each loop of the inlabru algorithm. In general, extreme parametrizations (e.g., parameters smaller than 10−5 or > 20) should be avoided. Usually, setting all the parameters to 1 (expect p which could be set to 1.1) is a safe choice. Another approach could be to use the maximum-likelihood estimate.
2.7.2. Step 2. Integrated nested laplace approximation
ETAS.inlabru contains the ETAS functions that will be internally linearized (refer to Section 2.4) about an arbitrary point and then integrated. The nested integration is performed by R-INLA, but this is managed by inlabru, so we never need to call it directly. The R-INLA output returns a comprehensive output, including the joint posteriors (for an overview of R-INLA output, refer to Krainski et al. [26]).
2.7.3. Step 3. Extract the ETAS posteriors and their modes
From the R-INLA output, we extract the modes of the approximated posteriors . In early iterations, this point is usually far away from the true mode posterior; this depends on the point θ0 used as starting point. The approximate posterior mode tends to true one as the iterations run.
2.7.4. Step 4. Line search to update modal parameters
At this point, we have the initial set of trial ETAS parameters θ0 that were used as the linearization point, and the posterior modes derived from R-INLA . The value of the linearization point is updated to , where the scaling α is determined by the line search method.1
2.7.5. Step 5. Evaluation of convergence
Convergence is evaluated by comparing θ* and θ0. By default, convergence is established when there is a difference between each parameter pair is less than a 1% of the parameter standard deviation. The value 1% can be modified by the user. If convergence has not been achieved and the maximum number of iterations has not occurred, we set and return to step 1 using the new linearization point as the set of trial parameters.
2.8. Generation of synthetic catalogs
The final component of this article is the production of synthetic catalogs to be analzsed. The synthetics are constructed leveraging the branching structure of the ETAS model. Specifically, for temporal models, background events are selected randomly in the provided time window with a rate equal to μ. Then, the offsprings of each background event are sampled from an inhomogeneous Poisson process with intensity given by the triggering function. This process is repeated until no offsprings are generated in the time frame chosen for the simulation.
Using ETAS.inlabru, we generate catalogs with a duration of 1,000 days with a background rate of μ = 0.1 events per day and ETAS triggering parameters of c = 0.11, p = 1.08, α = 2.29, and K = 0.089. We take a b-value of 1 for the Gutenberg–Richter magnitude distribution. The lower magnitude threshold M0 = 2.5, which is motivated by catalogs such as those in the Apennines of Italy or for Ridgecrest in California.
We also use two different scenarios, a seeded version of these catalogs where we impose an extra M6.7 event on day 500, and an unseeded catalog where the events are purely generated by the ETAS model. This leads to catalogs which are relatively active in the former case and relatively quiet in the latter case. Using these scenarios, we can generate different stochastic samples of events to produce a range of catalogs consistent with these parameterizations.
The associated R Markdown notebook in the GitHub repository2 allows the reader to see how we have implemented these catalogs for the range of models investigated in the results.
3. Results
We present the performance of the ETAS.inlabru inversion across a range of synthetic case studies motivated by various challenges of analyzing real earthquake catalogs. We are interested in the accuracy and precision of the inversion compared with the original ETAS parameterization, understanding sources of systematic bias derived from differences in the catalogs being modeled, and the computational efficiency of the method.
All of the analyses start with one or more catalogs of 1,000 days in length, generated using a constant background rate of μ = 0.1 events/day above a constant magnitude threshold of M0 = 2.5, and true ETAS parameters are listed on the top row of Table 3. We choose to use this minimum magnitude motivated by common real values in regions, such as California and the Apennines, Italy.
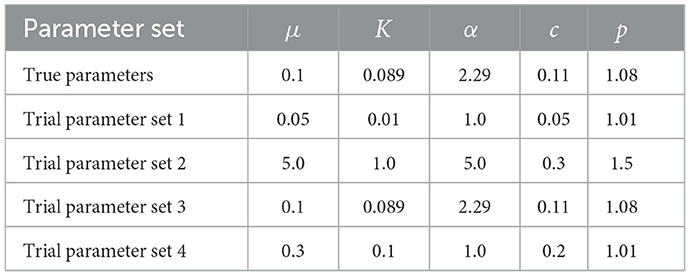
Table 3. The true ETAS parameters and the four sets of different initial conditions used in analyzing the catalogs in Figure 3 to produce the ETAS posteriors in Figure 4.
A consequence of choosing the 1,000-day window is that there will not be a fixed number of events when comparing different samples as some samples contain large events while others are relatively quiet. We make this choice because we believe that it represents the closest analogy to the data challenge faced by practitioners. However, we will be explicit in exploring the implications of this choice.
Within the sequences, there are three different timescales or frequencies that inter-relate. The duration of the synthetic catalogs, the background rate and the rate at which aftershocks decay (e.g., Touati et al. [27]). A short catalog would be one which only samples several background events or perhaps a single mainshock-aftershock sequence, or less. A long catalog would contain periods dominated by small background events and also separate periods containing relatively isolated mainshock aftershock sequences. Clearly, there is scope for a whole range of behavior in between. Given that the accuracy of the ETAS inversion is conditional on the catalog, we should therefore expect factors such as the catalog duration, rate of background events and the presence of large events to influence the ability of the algorithms to find accurate solutions.
3.1. Impact of varying the initial trial ETAS parameter set, θ0
Where algorithms require an initial set of trial starting parameters, it is important to test whether the results are robust irrespective of the choice of starting conditions. We explore the influence of the initial conditions by generating two catalog (refer to Figure 3) using the ETAS model with the true parameters given on the top row of Table 3. They are both 1,000-days long, and the second catalog has an M6.7 event seeded on day 500 to produce a more active sequence (Figure 3B). We then invert each catalog using the different sets of trial ETAS parameters also given in Table 3; the third set of initial parameters includes the true solution.

Figure 3. Two catalogs we use when varying the starting point for the ETAS parameters. (A) Unseeded catalog, nEvents = 217. (B) Catalog seeded with M6.7 event on day 500, nEvents = 2,530.
The first catalog is relatively quiet and has only 217 events (Figure 3A). All four sets initial trial parameters find the same posteriors (Figure 4A). inlabru provides a good estimate of the background rate μ for this catalog. The other posteriors are the parameters that govern the rate of self-exciting triggering. These posteriors are all skew, and some of the posteriors are strongly influenced by their priors, for example, the posterior for p spans the entire range of its prior (compare Figure 1 for the priors and Figure 4A for the posteriors). The posteriors for the triggering parameters are relatively broad because the data are not sufficient to produce a narrow likelihood function.
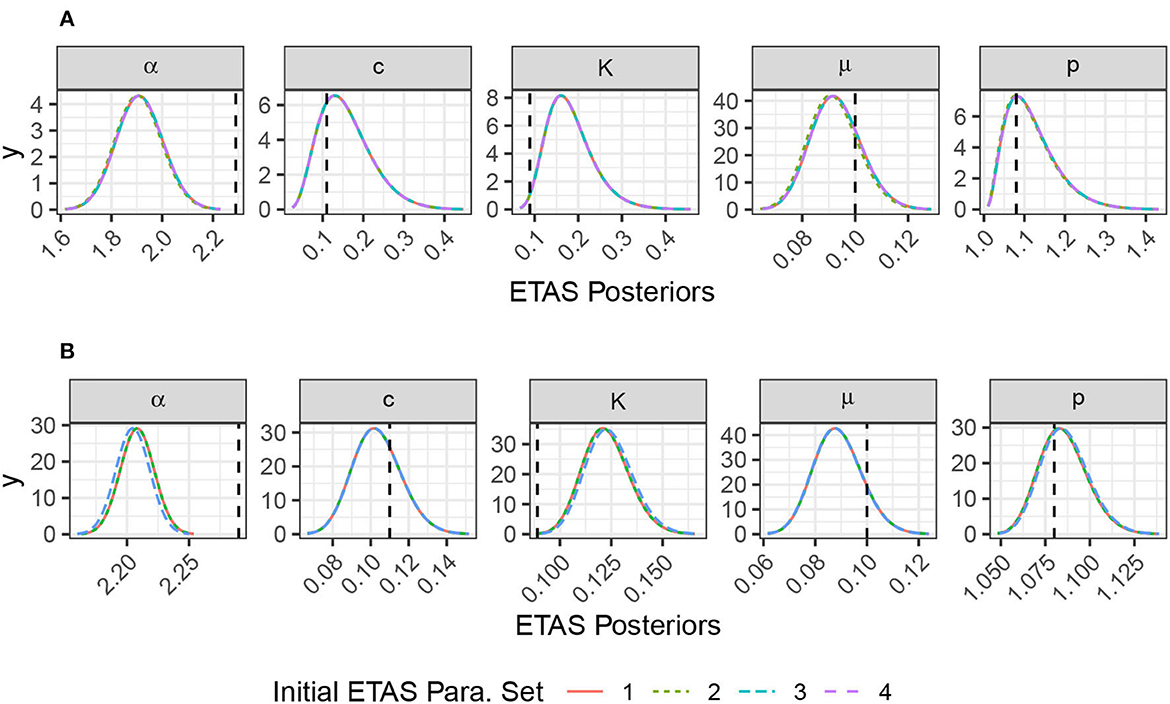
Figure 4. Posteriors for the inversion of the catalogs in Figure 3 are given four different starting points. The vertical black line shows the true values used when generating the synthetic catalogs. Note the very different scales on the x-axis. (A) Inversion of a 1,000-day catalog with no large events, nEvents = 217. (B) Inversion of a 1,000-day catalog with a M6.7 on day 500, nEvents = 2,530.
In the second catalog, we have seeded an M6.7 event on day 500 (Figure 3B). This catalog has a well defined aftershock sequence and, therefore, contains significantly more events, 2530 events in total. Again, all four sets of initial trial parameters find the same posteriors (Figure 4B). The posterior for the background rate, μ, remains well resolved, and there is no reduction in its standard deviation; this indicates that both catalogs have sufficient information to resolve the background rate, even though they are dominated by aftershocks. All of the posteriors for the triggering parameters are significantly narrower than for the first unseeded catalog. This is down to two factors; first there are many more events in the seeded catalog, and second the well-resolved aftershock sequence makes it much easier to constrain the triggering parameters.
All of these models find similar posteriors irrespective of the initial trial ETAS parameters set. It is important that the priors are set broad enough to allow the potential for the posteriors to resolve the true value. This is particularly evident for the quieter model where the posteriors on the triggering parameter's rely on more information from the priors.
In real catalogs, the prior the background rate needs to be set with care because, when considering a purely temporal model, it will vary depending upon the spatial extent being considered; i.e., the background rate of a temporal model when considering a global dataset would be significantly higher than just California. Furthermore, changing the lower magnitude limit significantly changes the total number of background events.
It is difficult to interpret the ETAS posteriors directly, thus, we explore the triggering function by sampling the parameter posteriors 100 times, calculating the triggering functions for these posterior samples, and plotting the ensemble of triggering functions (Figure 5). The first column shows the Omori function, which is the temporal decay of the triggering function, but without the magnitude dependent term, and is, therefore, also independent of the ETAS α parameter. The larger uncertainty in the posteriors for the unseeded quieter catalog (Figure 3A) propagate through to much larger variability in the Omori decay (Figure 5A) than when the sequence is seeded with the large event in the sequence (Figure 5B). It is reassuring to see that the Omori decay from the sequence seeded with the M6.7 event lies within the confidence intervals of that derived from the quieter unseeded sequence. This implies that the prior is sufficiently broad to capture these extremes in catalog type.
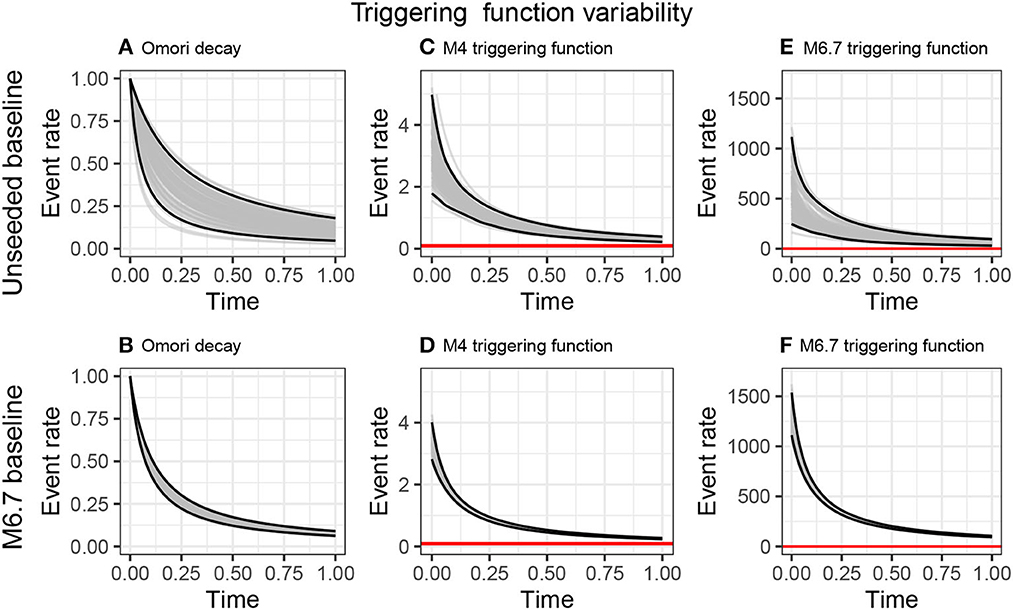
Figure 5. Propagation of ETAS parameter uncertainty on the triggering functions. We take 100 samples of the ETAS posteriors for the 1,000-day quiescent baseline (A, C, E) and the 1,000-day catalog with an M6.7 on day 500 (B, D, F) and use these samples to explore variability in the Omori decay (A, B), the time-triggering function following an M4 event, and the time-triggering function following an M6.7 event.
When incorporating the magnitude dependence, any bias or uncertainty in α becomes important. The figures show the triggering functions for magnitude 4.0 and 6.7 events over 24 hours. While the triggering functions for the M4 events are nested similarly to the Omori sequences; the triggering functions for the M6.7 event are systematically different. The posteriors from the training catalog were seeded with an M6.7 event result an initial event rate 50% higher, and the two distributions barely overlap.
We conclude that the choice of training data could have a significant effect on the forecasts of seismicity rate after large events. In the next section, we explore the robustness of these results to stochastic uncertainty in the training catalogs.
3.2. Impact of stochastic variability
We extend the analysis of the previous section to explore the impact of stochastic variability. We produce 10 synthetic catalogs for both the unseeded and M6.7 seeded catalogs and compare the parameters posterior distribution.
In the family of catalogs where we did not seed large event (Figure 6), we see posteriors of the background rate, μ, that are distributed about the true background rate (Figure 8A) and captured well. By contrast, we mostly see very large uncertainty in the posteriors for the triggering parameters. However, the true values generally still lie within these posteriors. The very broad posteriors correspond to catalogs that had very few triggered sequences in them. Such broad posteriors illustrate how the Bayesian approach enables us to see where the data did not have sufficient power to narrow the priors significantly; this is useful in evaluating the robustness of a fit. Moreover, the large posterior uncertainty on the parameters would propagate through to large uncertainty in the triggering function if used within a forecast with a rigorous quantification of uncertainty. Synthetic catalogs 3 and 6 (Figure 6) contain the largest number of events (1,842 and 930 events, respectively) as a result of the events triggered by a largely random event; these cases have correspondingly tighter and more accurate posteriors for the triggering parameters (Figure 8A). Similarly, catalogs 1 and 9 have the next highest number of events (265 and 245 events, respectively), and these also have the next most informative posteriors. catalogs 2 and 5 have the fewest events (117 and 128, respectively) and produce posteriors that are significantly informed by the priors, as can be seen the range of values being explored.
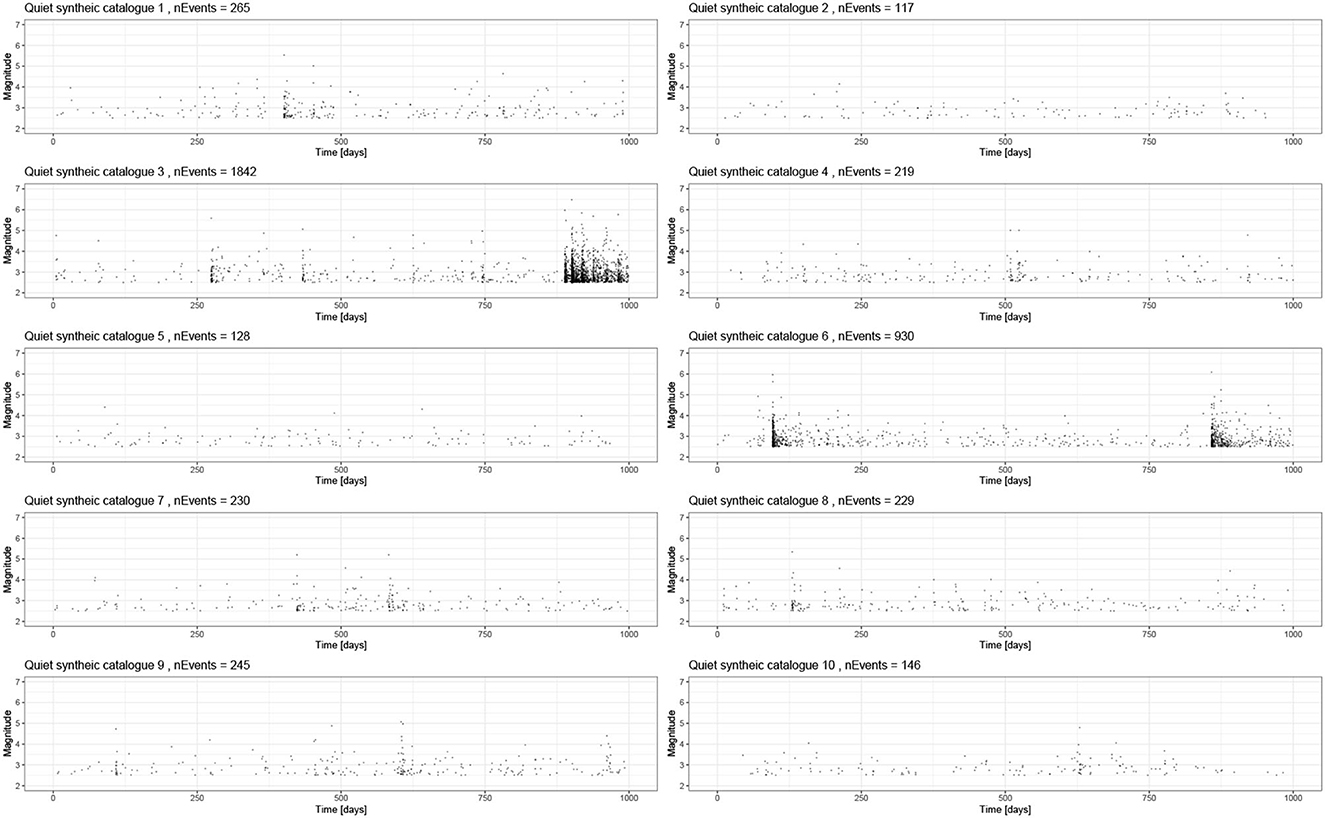
Figure 6. A total of 10 synthetic catalogs based on the baseline model of 1,000-days with background events but no large seeded event. All parameters are the same between the runs, and these just capture the stochastic uncertainty. These are all inverted using inlabru, and the family of posteriors is presented in Figure 10.
Considering the 10 seeded catalogs (Figure 7), we see a complementary story in the posteriors (Figure 8B). Again, the posteriors for the background rate are distributed about the true value and show a similar spread to the unseeded case. All of the triggering parameters have much tighter posteriors. Even though some of the triggering parameter posteriors do not contain the true value, and the percentage error remains small. This is due to the stochastic variability of these catalogs, and this bias should decrease for longer catalogs.
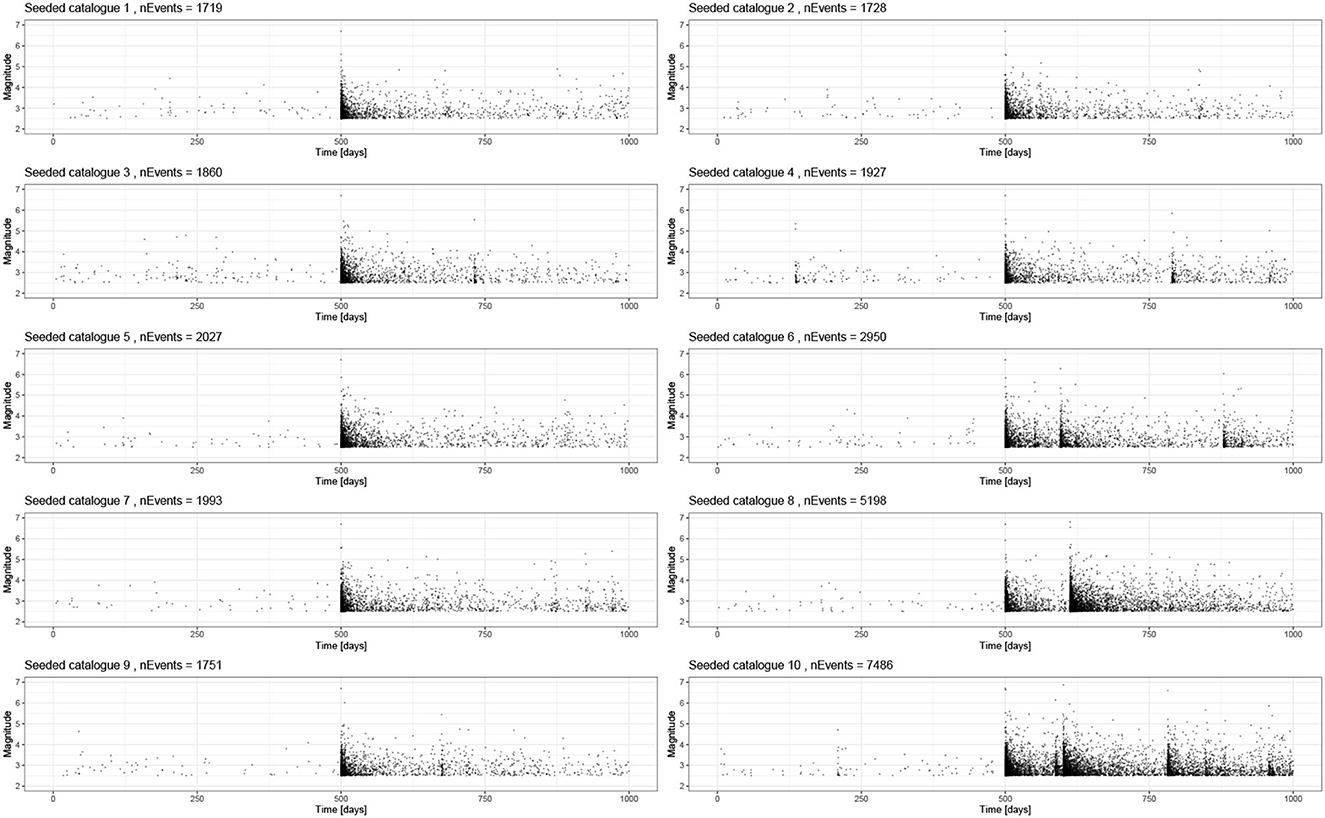
Figure 7. A total of 10 synthetic catalogs based on the baseline model of 1,000-days with background events and an M6.7 event on day 500. All parameters are the same between the runs, and these just capture the stochastic uncertainty. These are all inverted using inlabru, and the family of posteriors is presented in Figure 10.
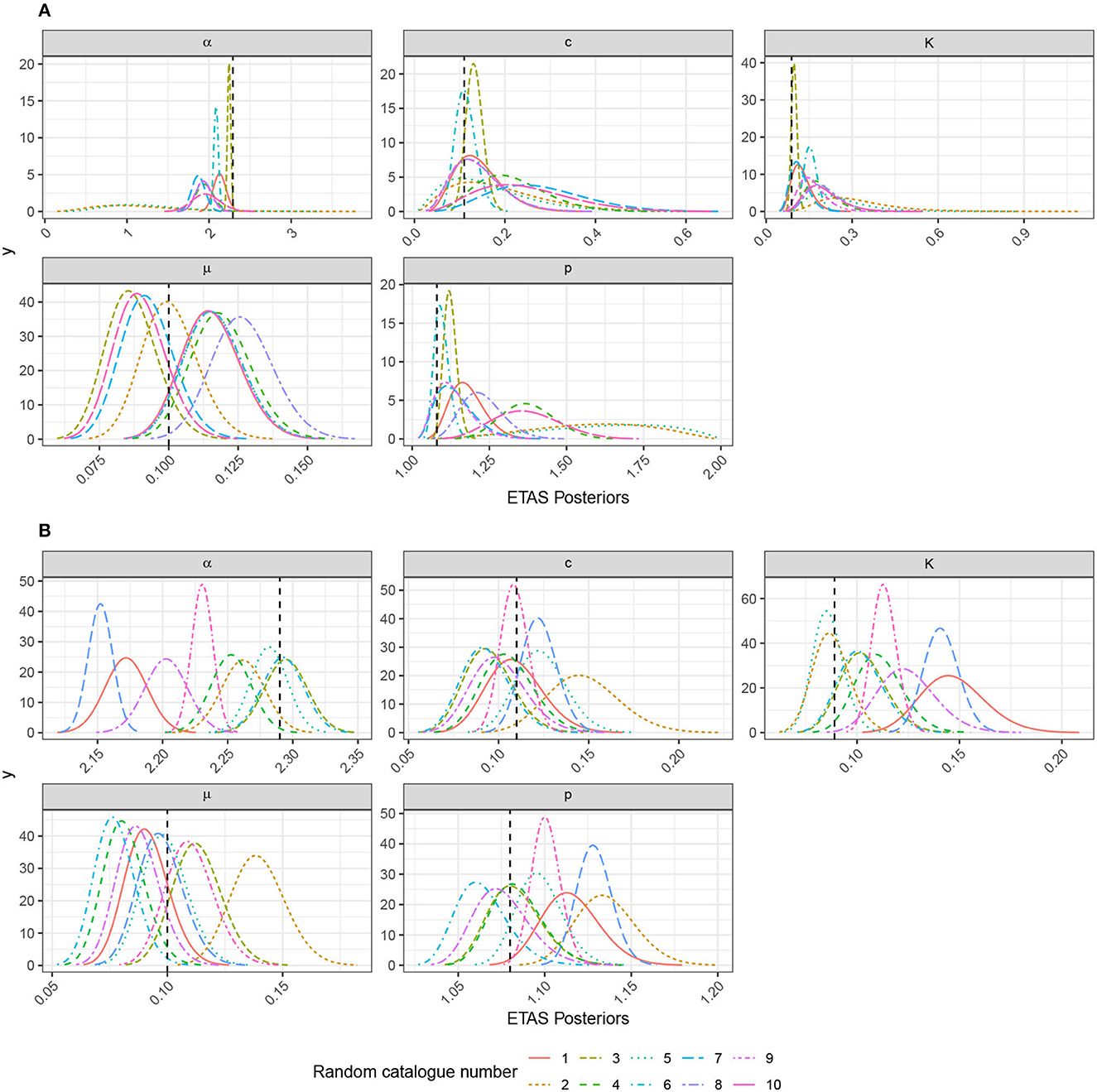
Figure 8. Posteriors that explore the impact of stochastic variability on the inverted ETAS parameters using inlabru. These are based on the relatively quiet catalogs in Figure 6 and those with a large event seeded on day 500 in Figure 7. The catalog numbers can be cross-referenced between the figures. (A) Impact of stochastic variability for 1,000-day catalog with no large events seeded. (B) Impact of stochastic variability for 1,000-day catalog with an M6.7 event seeded on day 500.
There is always trade-off between α and K, which is difficult to resolve. K describes the magnitude independent productivity seen in the Omori law and α describes how the full triggering function productivity varies with magnitude; consequently, one requires many sequences from parents of different magnitudes to resolve K and α well.
Studies which are seeking to assign a physical cause to spatial and/or temporal variability of the background and triggering parameters should ensure that the variability cannot be explained by the stochastic nature of finite earthquake catalogs. The methods presented here provide one possible tool for doing this.
The runtime for a model with 2,000 events is 6 min on a laptop. We find that not only is our inlabru method 10 times faster than “bayesianETAS” for catalogs of more than 2,500 events but also that it scales relatively linearly with the number of events. We inverted a catalog with 15,000 events in 70 min, and it is likely this can be speeded up further using the high performance sparse matrix solver pardiso package.
The inversions of synthetic data presented here show that the stochastic variability in the training catalogs produces understandable variability in the posteriors. More data and sequences containing both triggered sequences and background allow us to resolve all parameters well. Better resolution of α and K would require aftershock sequences from parents of different sizes. We see that only having lower magnitude events leads to broad posteriors on the triggering parameters. The following section explores the impact of reducing the amount of background data on the resolution of μ for the seeded sequences.
3.3. Importance of a representative sample
The motivation for applying the ETAS model is sometimes the presence of an “interesting” feature, such as an evolving or complex aftershock sequence following a notable event. In this section, we explore whether it is important to have both quiet periods, as well as the aftershock sequence itself for accurately recovering the true parameterization. This motivates defining what a representative sample looks like; evaluating this in practice is non-trivial, but we can outline what is insufficient.
We start with the 1,000-day catalog including an M6.7 event seeded on day 500. We then generate catalog subsets by eliminating the first 250, 400, 500, and 501 days of the catalog (start dates of subcatalogs shown as vertical-dashed lines in Figure 9A) and rerun the inlabru ETAS inversion on these subsets. Since the initial period is relatively quiet, we do not remove a large proportion of the events—however, we are removing events from the period where the background events are relatively uncontaminated by triggered events. In doing this, we explore what the necessary data requirements are for us to expect that inlabru can reliably estimate both the background and triggering parameters. When we remove 501 days, we are also removing the seeded mainshock from the subcatalog.
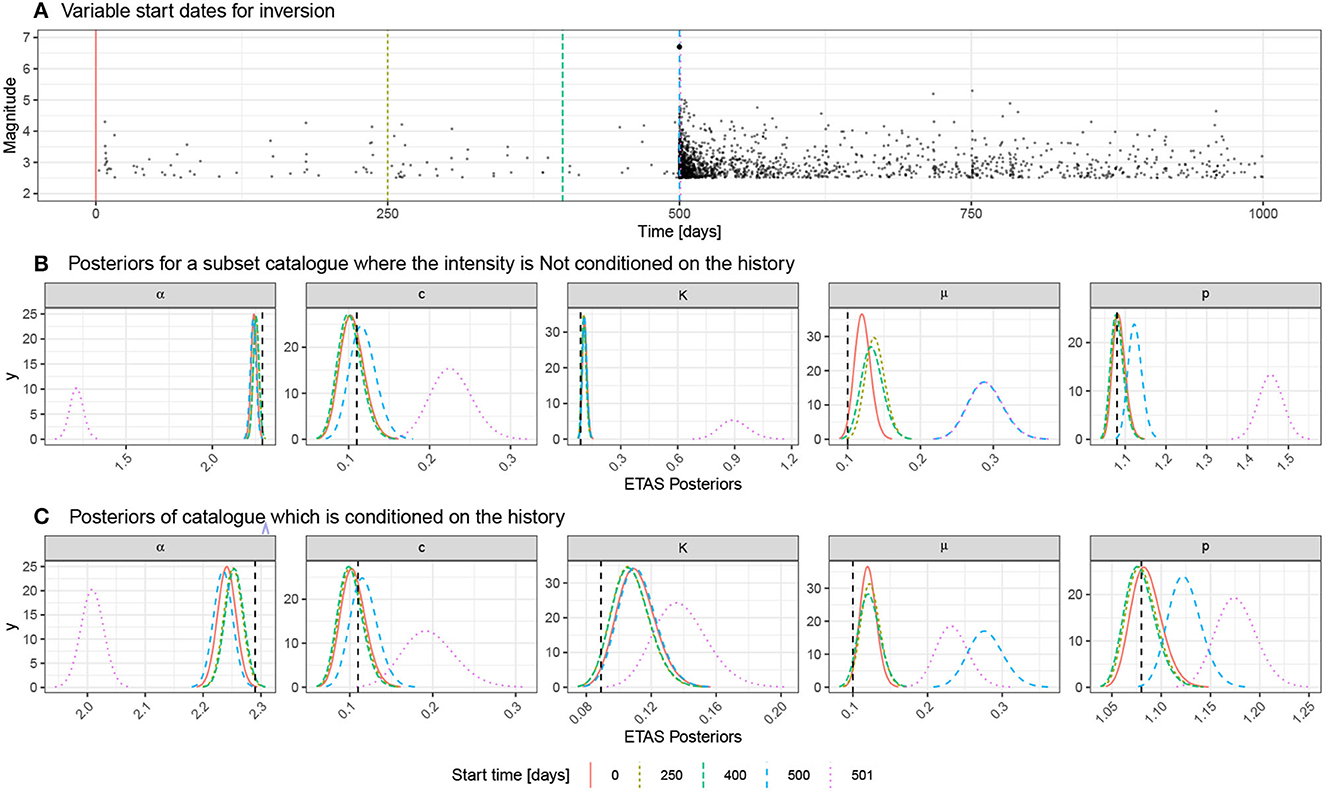
Figure 9. (A) Catalog used to explore the concept of a representative sample and history conditioning. The baseline case on the top row has 500 days of background and an M6.7 event on day 500 with the sequence being recorded until day 1000. We vary the start date for the analysis to remove the first 250 days, 400 days, 500 days, and 501 days. In the last two cases, there is no background period remaining, and the large event is also prior to the catalog subset for the final case. (B) Posteriors of the ETAS parameters for each of the catalog subsets when we crop the subcatalog and do not use the preceding data to condition the model. (C) Rather than cropping out subcatalogs, we now retain the events preceding the start of the model domain and use these when estimating the triggering function. This produces a notably improved performance for the start date on day 501 when the large event is no longer within the model domain.
First, we consider what happens to the posterior of the background rate, μ, as the length of the subcatalogs is shortened. With 500 days of background before the seeded event, we resolve μ accurately. As the quiet background is progressively removed, the model estimate of μ systematically rises. When there is between 250 and 100 days of background data, the mode overestimates the data-generating parameter by approximately 30%, but it still lies within the posterior distributions (turquoise and brown curves for μ in Figure 9B). When there is no background period, the overestimation of μ (blue curve for μ in Figure 9B) is on the order of a factor of 2.5. The estimate corresponds to the level of seismicity at the end of the model domain which has not decayed back to the background rate. From an operational perspective, it is much easier to extend the start date of training data back before the sequence of interest started than to wait until the background rate has been recovered. We should, therefore, expect an analysis looking for time-varying background rate during the sequences carries a risk of bias by this effect.
All of the models, apart from the one starting on day 501, contain the M6.7 event and 500 days of its aftershocks (Figure 9A). In these cases, the triggering parameters are well described by the posteriors (Figure 9B). However, where the model domain starts on day 501, we lose the M6.7 event and its aftershocks on the first day. This results in significant bias in all the triggering parameters, as well as the background rate (Pink curve in Figure 9B). Modeling of specific sequences needs particular care to be taken in the choice of model domain and exclusion of the mainshock from the analysis can pose a major problem in conditioning the ETAS parameters.
The results already presented in Figure 8 showed that the inversion scheme struggles to recover the triggering parameters, when there is no significant sequence in the dataset. Combined with the results of having no background period in this section, we argue that a representative sample should include periods of activity and inactivity if both the background rate and triggering parameters are to be estimated reliably. We also suggest mainshocks of different magnitudes would help for resolving α. By running synthetics such as the ones presented here, one can gain insight into the data requirements in specific case studies.
The model, where the mainshock was not part of the sub-catalog, was particularly biased (pink curve in Figure 9B). In the next section, we explore whether we can correct for this by including the triggering effects of events that occurred prior to the temporal domain being evaluated.
3.4. Impact of historic run-in period
In the previous section, we explicitly cropped out subcatalogs and ran the analysis on that subset of the data, effectively throwing the rest away. We demonstrated the consequences removing the M6.7 mainshock from the sub-catalog being analyzed; the posteriors on the triggering parameters and background became significantly biased (Figure 9B). This example talks to the wider need for the intensity function to be conditioned on historic events prior to the start of the model domain. This is a common issue in modeling regions that have experienced the largest earthquakes.
In ETAS.inlabru, we have another option when analyzing catalog subsets. Rather than cropping out the data, we can provide an extended catalog and specify a model domain that is smaller than the whole dataset. For the time component, this means that events prior to the temporal domain will have their triggering contributions to the model domain taken into account. This approach crops off events beyond the temporal model domain because they do not have a causal impact on the results. The model domain is defined using “T1” and “T2” in the input list for the start and end time, respectively. inlabru assumes any events in the catalog prior to “T1” should be used to historic preconditioning.
In practice, this complicates the implementation of the time binning because events occurring prior to the start of the model domain only need to be evaluated from “T1” onward. The breaking of similarity of the time bins has a penalty in the speed of the implementation.
The results of conditioning the inversion using the historic events can be seen in Figure 9C and should be compared to the equivalent results for the cases where the subcatalogs did not have this preconditioning (Figure 9B). As the start date increases, the inclusion of small background events in the history has little effect on the results because their triggering effect is small. However, a significant improvement in the estimated posteriors is seen, when the M6.7 mainshock is removed from the model domain (c.f. pink lines for each parameter in Figures 9B, C). The historic preconditioning improves the estimation of all the triggering parameters, when the mainshock is missing.
In the analysis of real catalogs, this effect will be particularly relevant when there have been very large past earthquakes, which are still influencing today's rates.
3.5. Impact of short-term incompleteness
Finally, we explore the effect of short-term incompleteness after large mainshocks on the inverted parameters. This rate-dependent incompleteness occurs because is hard to resolve the waveforms of small earthquakes when overprinted by many larger events, yet the effect is short-lived.
We take a 1,000-day catalog with an M6.7 event seeded on day 500 and then introduce a temporary increase in the completeness threshold after the M6.7 event using the functional form suggested by Helmstetter et al. [28],
where, Mi and ti are the magnitude and occurrence time of the event, we are modeling the incompleteness for, t is the time we wish to evaluate the new completeness threshold for, and G and H are parameters of the model. We do not address here how these parameters should be determined in a real dataset and, informed by van der Elst [29], we set them to 3.8 and 1.0, respectively, for our synthetic study. Furthermore, in this exploratory analysis we do not include incompleteness effects for other events in the sequence—so it should be considered a relatively conservative analysis.
We perform the inversion on the original catalog and the one where short-term incompleteness has removed a number of events (Figure 10) and compare the posteriors (Figure 11).
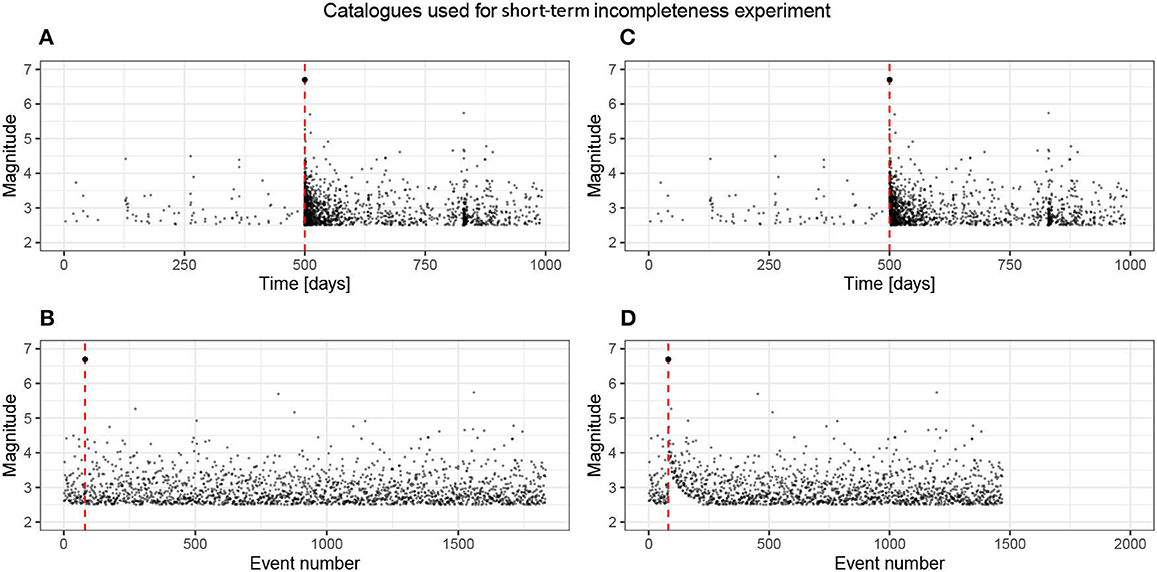
Figure 10. Plots of the complete baseline catalog and the catalog with incompleteness artificially introduced using the functional form suggested by Helmstetter et al. [28]. The complete catalog contains 1,832 events, and the incomplete has 1,469 events. The time-magnitude plot does not present this incompleteness well because it occurs in the very short term after the M6.7 event. The plot of magnitude as a function of event number clearly highlights the temporally varying incompleteness just after the large event. (A) Complete catalog, nEvents = 1,832, (B) Complete, (C) Incomplete catalog, nEvents = 1,469, and (D) Incomplete.
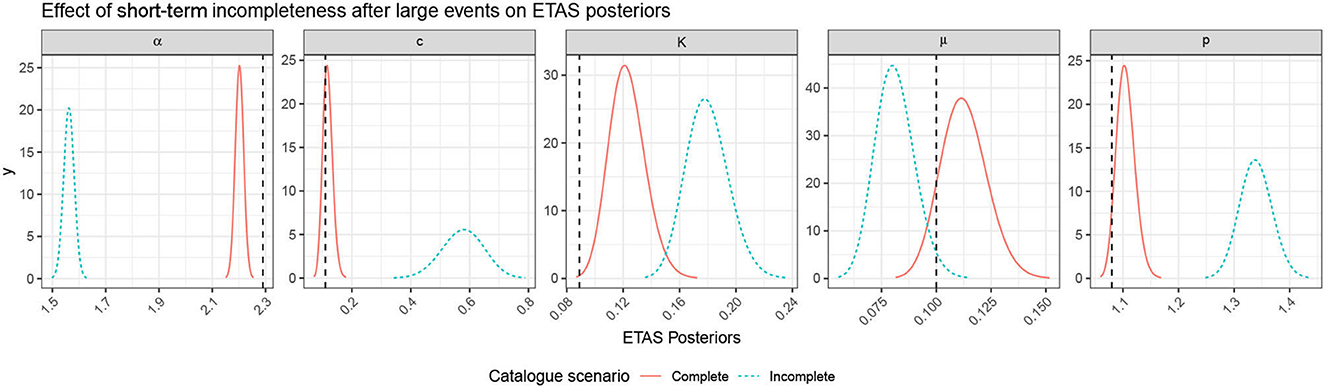
Figure 11. Plot comparing the posteriors of the complete and incomplete catalogs presented in Figure 10. The true parameters are shown with the black-dashed lines.
The complete catalog contained 1832 events, and the incomplete catalog contains 1469 events (Figure 10). This is difficult to see on the event time plot as most of these events are very close in time to the mainshock, so we have also plotted the magnitudes as a function of the event number; here, we see that after the mainshock (red-dashed line), there is a transient in the completeness threshold.
All of the parameter estimates in the incomplete catalog are now notably more biased, and their standard deviation has not increased to compensate for this, so the true values lie significantly outwith the posteriors (Figure 11) and are therefore biased. The incomplete catalog underestimates the background rate as there are fewer events in the same time period. Propagating the triggering parameter posteriors to compare the triggering functions, we see extremely different triggering behavior (Figure 12). The Omori decay for the incomplete catalog is longer lasting but the productivity, driven by α and K, is systematically lower.

Figure 12. Propagation of ETAS parameter uncertainty on the triggering functions. We take 100 samples of the ETAS posteriors for the complete 1,000-day catalog with an M6.7 on day 500 (A, C, E) and for the temporally incomplete version of this catalog, as described in the text. We then use these samples to explore variability in the Omori decay (A, B), the time-triggering function following an M4 event (C, D), and the time-triggering function following an M7.6 event (E, F).
The bias in the predicted triggering functions arising from short-term incompleteness is significant and cannot be ignored within an OEF context. Solving this problem within inlabru is beyond the scope of this article.
4. Discussion
Having analyzed a range of synthetic datasets, we now emphasize the lessons learned we should carry forward for the analysis of real sequences.
Reliable inversions can only result from data that are representative of the processes the model is trying to capture. This means that datasets need to contain both productive sequences and periods that resolve the background without being overprinted by triggered events. The main difference between α and K is that the former describes how the productivity varies with the magnitude of the triggering event while the latter is a magnitude insensitive productivity. If we are to resolve these uniquely, the training data would need relatively isolated sequences that are triggered by mainshocks of different; this will be challenging in many use cases.
Interpreting the results of an ETAS inversion is non-trivial. We advocate the routine analysis of synthetic to understand what it is possible to resolve in principle.
Preconditioning models using large historic events can be significant. By considering samples of the triggering functions once can pre-determine the magnitude of events that need to be included as a function of time.
The use of synthetic modeling should be, particularly, important if time-varying background rates are being inferred from the inversion of catalog subsets in moving windows using the ETAS model.
The impact of short-term incompleteness following large events is very significant and needs to be addressed either by raising the magnitude of completeness or formal modeling of the incompleteness. Resolving this for ETAS.inlabru is beyond the scope of this article.
These are some of the considerations we explored here, but different use cases will present other modeling challenges that can be effectively explored through similar suits of synthetic modeling.
5. Conclusion
ETAS.inlabru is a fast and reliable tool for approximate Bayesian inference of the temporal ETAS model. The advantage of INLA over MCMC-based methods is that it is much faster. For large models, INLA finds a solution where MCMC methods would take far too long. For smaller problems, the speed of computation allows us to take a more exploratory and interactive approach to model construction and testing [30].
The exploratory approach illustrated here can be used to identify and understand sources of uncertainty and bias in the ETAS parameter posteriors that are derived from the structural and stochastic nature of the training data. We identify the need for a representative sample to contain periods of relative quiescence, as well as sequences with clear triggering behavior, if all parameters are to be well resolved.
Where studies focus solely on active sequences, the background rate can be erroneously estimated to be several times larger than the real background rate, and the triggering parameters erroneously imply more rapidly decaying sequences than the true underlying parameterization would. This implies that caution is needed in studies that allow the parameters to vary in time using windowing methods. While one cannot conclusively rule out that background rates and triggering behaviors may vary, we advocate that a stationary model with constant parameters should be adopted unless there is compelling evidence independent of the ETAS inversion, Colfiorito being a case in point (e.g., [31]).
Rate-dependent incompleteness severely degrades the accuracy of the ETAS inversion and needs to be addressed directly.
The use of synthetic modeling, as presented here, provides a basis for discriminating when variations in the posteriors of ETAS parameters can be explained by deficiencies in the training data, and when there is likely a robust and potentially useful signal. Such exploration requires a fast method for performing the inversion. The interpretation is easier when full posteriors can be compared, as opposed to just having point estimates. inlabru is, particularly, well suited to this task.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/edinburgh-seismicity-hub/ETAS.inlabru.
Author contributions
The writing of this article and the analyzes presented in this article were led by MN. The ETAS model was implemented within inlabru by FS. FL provided advice on the implementation of the ETAS model using inlabru. IM reviewed the article and led the corresponding RISE workpackage. All authors contributed to the article and approved the submitted version.
Funding
This study was funded by the Real-Time Earthquake Risk Reduction for a Resilient Europe RISE project, which has received funding from the European Union's Horizon 2020 Research and Innovation Program under grant Agreement 821115. MN and IM were additionally funded by the NSFGEO-NERC grant NE/R000794/1.
Acknowledgments
All the code to produce the present results is written in the R programming language. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) license to any author accepted manuscript version arising from this submission.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2023.1126759/full#supplementary-material
Footnotes
1. ^https://inlabru-org.github.io/inlabru/articles/method.html
2. ^https://github.com/edinburgh-seismicity-hub/ETAS.inlabru/settings
References
1. Ogata Y. Statistical models for earthquake occurrences and residual analysis for point processes. J Am Stat Assoc. (1988) 83:9–27. doi: 10.1080/01621459.1988.10478560
2. Ogata Y, Zhuang J. Space-time ETAS models and an improved extension. Tectonophysics. (2006) 413:13–23. doi: 10.1016/j.tecto.2005.10.016
3. Ogata Y. Significant improvements of the space-time ETAS model for forecasting of accurate baseline seismicity. Earth Planets Space. (2011) 63:217–29. doi: 10.5047/eps.2010.09.001
4. Hawkes AG. Spectra of some self-exciting and mutually exciting point processes. Biometrika. (1971) 58:83–90. doi: 10.1093/biomet/58.1.83
5. Jalilian A. ETAS: an R package for fitting the space-time ETAS model to earthquake data. J Stat Software Code Snippets. (2019) 88:1–39. doi: 10.18637/jss.v088.c01
6. Ross GJ. Bayesian estimation of the ETAS model for earthquake occurrences. Bull Seismol Soc Am. (2021) 111:1473–80. doi: 10.1785/0120200198
7. Rue H, Riebler A, Sørbye SH, Illian JB, Simpson DP, Lindgren FK. Bayesian computing with INLA: a review. Ann Rev Stat Appl. (2017) 4:395–421. doi: 10.1146/annurev-statistics-060116-054045
8. Bachl FE, Lindgren F, Borchers DL, Illian JB. inlabru: an R package for Bayesian spatial modelling from ecological survey data. Methods Ecol Evol. (2019) 10:760–6. doi: 10.1111/2041-210X.13168
9. Bayliss K, Naylor M, Illian J, Main IG. Data-Driven optimization of seismicity models using diverse data sets: generation, evaluation, and ranking using Inlabru. J Geophys Res Solid Earth. (2020) 125:e2020JB020226. doi: 10.1029/2020JB020226
10. Bayliss K, Naylor M, Kamranzad F, Main I. Pseudo-prospective testing of 5-year earthquake forecasts for California using inlabru. Natural Hazards Earth Syst Sci. (2022) 22:3231–46. doi: 10.5194/nhess-22-3231-2022
11. Forlani C, Bhatt S, Cameletti M, Krainski E, Blangiardo M. A joint Bayesian space-time model to integrate spatially misaligned air pollution data in R-INLA. Environmetrics. (2020) 31:e2644. doi: 10.1002/env.2644
12. Riebler A, Sørbye SH, Simpson D, Rue H. An intuitive Bayesian spatial model for disease mapping that accounts for scaling. Stat Methods Med Res. (2016) 25:1145–65. doi: 10.1177/0962280216660421
13. Santermans E, Robesyn E, Ganyani T, Sudre B, Faes C, Quinten C, et al. Spatiotemporal evolution of Ebola virus disease at sub-national level during the 2014 West Africa epidemic: model scrutiny and data meagreness. PLoS ONE. (2016) 11:e0147172. doi: 10.1371/journal.pone.0147172
14. Schrödle B, Held L. A primer on disease mapping and ecological regression using INLA. Comput Stat. (2011) 26:241–58. doi: 10.1007/s00180-010-0208-2
15. Schrödle B, Held L. Spatio-temporal disease mapping using INLA. Environmetrics. (2011) 22:725–34. doi: 10.1002/env.1065
16. Opitz N, Marcon C, Paschold A, Malik WA, Lithio A, Brandt R, et al. Extensive tissue-specific transcriptomic plasticity in maize primary roots upon water deficit. J Exp Bot. (2016) 67:1095–107. doi: 10.1093/jxb/erv453
17. Halonen JI, Hansell AL, Gulliver J, Morley D, Blangiardo M, Fecht D, et al. Road traffic noise is associated with increased cardiovascular morbidity and mortality and all-cause mortality in London. Eur Heart J. (2015) 36:2653–61. doi: 10.1093/eurheartj/ehv216
18. Roos NC, Carvalho AR, Lopes PF, Pennino MG. Modeling sensitive parrotfish (Labridae: Scarini) habitats along the Brazilian coast. Mar Environ Res. (2015) 110:92–100. doi: 10.1016/j.marenvres.2015.08.005
19. Teng J, Ding S, Zhang H, Wang K, Hu X. Bayesian spatiotemporal modelling analysis of hemorrhagic fever with renal syndrome outbreaks in China using R-INLA. Zoonoses Public Health. (2022) 2022:12999. doi: 10.1111/zph.12999
20. Bakka H, Rue H, Fuglstad GA, Riebler A, Bolin D, Illian J, et al. Spatial modeling with R-INLA: a review. Wiley Interdisc Rev Comput Stat. (2018) 10:e1443. doi: 10.1002/wics.1443
21. Blangiardo M, Cameletti M, Baio G, Rue H. Spatial and spatio-temporal models with R-INLA. Spat Spatio Temporal Epidemiol. (2013) 4:33–49. doi: 10.1016/j.sste.2012.12.001
23. Taylor BM, Diggle PJ. INLA or MCMC? A tutorial and comparative evaluation for spatial prediction in log-Gaussian Cox processes. J Stat Comput Simulat. (2014) 84:2266–84. doi: 10.1080/00949655.2013.788653
24. Serafini F, Lindgren F, Naylor M. Approximation of bayesian Hawkes process models with Inlabru. arXiv preprint arXiv:220613360. (2022). doi: 10.48550/arXiv.2206.13360
25. Hawkes AG. Point spectra of some mutually exciting point processes. J R Stat Soc B. (1971) 33:438–43. doi: 10.1111/j.2517-6161.1971.tb01530.x
26. Krainski E, Gomez-Rubio V, Bakka H, Lenzi A, Castro-Camilo D, Simpson D, et al. EnglishAdvanced Spatial Modeling with Stochastic Partial Differential Equations Using R and INLA. 1st ed. Australia: CRC Press (2019).
27. Touati S, Naylor M, Main IG. Origin and nonuniversality of the earthquake interevent time distribution. Phys Rev Lett. (2009) 102:168501. doi: 10.1103/PhysRevLett.102.168501
28. Helmstetter A, Kagan YY, Jackson DD. Comparison of short-term and time-independent earthquake forecast models for Southern California. Bull Seismol Soc Am. (2006) 96:90–106. doi: 10.1785/0120050067
29. van der Elst NJ. B-Positive: a robust estimator of aftershock magnitude distribution in transiently incomplete catalogs. J Geophy ResSolid Earth. (2021) 126:e2020JB021027. doi: 10.1029/2020JB021027
30. Wang, Yue Y, Faraway. Bayesian Regression Modeling with INLA. UK United Kingdom: Chapman & Hall (2018). doi: 10.1201/9781351165761
Keywords: Hawkes process, INLA, seismicity, ETAS, earthquake forecasting
Citation: Naylor M, Serafini F, Lindgren F and Main IG (2023) Bayesian modeling of the temporal evolution of seismicity using the ETAS.inlabru package. Front. Appl. Math. Stat. 9:1126759. doi: 10.3389/fams.2023.1126759
Received: 18 December 2022; Accepted: 23 January 2023;
Published: 23 March 2023.
Edited by:
Jiancang Zhuang, Institute of Statistical Mathematics, JapanReviewed by:
Andrea Llenos, United States Geological Survey (USGS), United StatesRobert Shcherbakov, Western University, Canada
Copyright © 2023 Naylor, Serafini, Lindgren and Main. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mark Naylor, bWFyay5uYXlsb3JAZWQuYWMudWs=
 Mark Naylor
Mark Naylor Francesco Serafini1,2
Francesco Serafini1,2 Finn Lindgren
Finn Lindgren Ian G. Main
Ian G. Main