- 1Faculty of Mechanical Engineering, Babol Noshirvani University of Technology, Babol, Iran
- 2Faculty of Engineering and Applied Science, Industrial Systems Engineering, University of Regina Canada, Regina, SK, Canada
- 3Department of Management, University of Tabriz, Tabriz, Iran
- 4Department of Management, University of Hormozgan, Bandar Abbas, Iran
- 5Binaloud Institute of Higher Education, Mashhad, Iran
- 6Department of Mechanical Engineering, Darmstadt University of Technology, Darmstadt, Germany
- 7Department of Management, University of Tehran, Tehran, Iran
- 8Department of Management, Islamic Azad University of Bojnourd, Bojnord, Iran
The Circular Economy of the Automotive Industry’s Sustainable Supply Chain in the Case of Lithium-Ion Batteries is pioneering in environmental protection and ecological resource utilization. In addition to solving environmental problems, this method provides economic benefits by reducing the need for raw materials and lowering manufacturing costs. However, introducing a circular economy approach in the lithium-ion battery supply chain has numerous risks and challenges. This study addresses these challenges by crafting a framework that encapsulates the risks involved. It identifies the risks that evolving circular economy strategies might bring to the lithium-ion battery supply chain through an integrated Gray Delphi–DEMATEL–ANP method. Furthermore, this work introduces the Gray Degree of Possibility to unveil worst-case scenarios in risk analysis and extends it into zero-sum Game Theory. The study then formulates an improved zero-sum game model to determine optimal strategies for mitigating these risks. The numerical analysis reveals that, according to the proposed methodology, Environmental Pollution Risk emerges as the most critical, with a definite weight of 0.1525. This is followed by the Support Program Deficiency Risk at 0.1452 and the Improper Waste Management Risk at 0.1372.
1 Introduction
The sustainable supply chain in the lithium-ion battery circular economy within the automotive industry has numerous environmental and economic benefits (1, 2). By encouraging re-use, repackaging, and re-cycling of batteries, it reduces continuous extraction of raw materials like lithium, cobalt, and nickel used in the manufacture of these batteries, which not only are finite but are also associated with environmental degradation (3). Such a decrease in dependence on raw materials will, in turn, reduce the carbon footprint of battery production, besides reducing the environmental impact from mining and processing activities according to other scholars. Apart from the above, the circular economy promotes the extended life and resource efficiency of batteries, thus supporting the broad sustainability goals of the automotive industry. The circular economy will help in sustaining a competitive supply chain, not only reducing the impact on the environment. It will help companies in handling pertinent risks with the disruption in supply and surge in pricing volatility in international markets through lowering the dependency on new raw materials. Such critical materials can be made more stable and predictable in the supply by engaging in the recycling and reusing of batteries, which is plainly crucial in the ever-increasing demand of electric vehicles. It further enhances innovation in the design of batteries and recycling technologies to spur more innovation in the sector. Supply chain sustainability in a circular economy is not only good for the environment, its benefits also tie into business strategic purposes and resources management in an efficient and cost-effective manner. There has been important research in the context of the lithium-ion battery circular economy in the automotive industry on the sustainable supply chain over the past years. It is worth noting that the importance of circular strategies in preventing the environmental and social risks related to the supply chain of lithium-ion batteries has been further underlined in these studies (4–6). For example, in comparing circular economy strategies for the U.S. and Australia, Collis et al. (7). They established that there was a need for recycling infrastructures to be strong enough to handle end-of-life lithium-ion batteries from various electric vehicles and emphasized the strong role of policy interventions in establishing circular economy practices (7). In another report, Madrid noted that companies operating in automotive manufacturing chains that have adopted circular economy practices released reports of impressive rates of carbon emissions and waste production reductions, proving perfect applicability of the automotive industry circular economy (8). These studies point out that, for ensuring supply chain sustainability in lithium-ion batteries for the automotive industry, the underpinning has to be provided by the strategies of a circular economy. Similarly, Baars et al. (9) point out that while new technologies will likely reduce just how much cobalt is needed within EV batteries, it may very well shift that resource burden away from cobalt and on to another, such as nickel; thus, mixes of technological improvement and recycling systems should be developed. Islam and Iyer-Raniga (10) describe various ways that spent LIBs can be recycled and elaborate on the need for circular business models and stakeholder engagement in order to create a sustainable supply chain. Kurz et al. (11) applied life cycle assessment methodology to demonstrate that substantial LIB recycling-driven environmental benefits are very technology- and process route-specific, such that bad legislation on the design of circular strategies but could be counterproductive. Cordisco et al. (12) propose a model of a sustainable circular economy by embedding the reuse of LIBs into the concept of a circular economy with social inclusion, therefore promoting both environmental sustainability and social equity. Albertsen et al. (13) investigate the adoption of circular business models by European vehicle manufacturers and call for extended cooperation and initiation of policies on repair, refurbishment, and repurposing of LIBs. Alessia et al. (14) provide an overview of the lithium supply chain and show that a decentralized recycling strategy may more appropriately fit the circular economy principles, thereby making them more sustainable and efficient by extension. Meanwhile, Lahane and Kant (15, 16) set out to identify risks in the implementation of circular supply chains and propose a hybrid framework to help decision-makers develop sustainable strategies. Heath et al. (17) through a critical review, found that in many practices concerning the Circular Economy for LIBs, there are important lacunae in present research, and the necessity for an expanded focus on more than recycling technology, to include the economic, environmental, and policy considerations at play. If there is a huge benefit to the sustainable supply chain of the lithium-ion battery circular economy that prevails in the automotive industry, various risks include the potential disruption of the supply chain due to scarcity in some critical raw materials and the complexity of recycling processes, challenges resulting from ensuring effective traceability across the supply chain. Risk assessment of sustainable supply chains for the lithium-ion battery circular economy is important, given the increasing dependence developing on vehicles from the automotive industry. Mitigating such risks is very important to the sustainability and reliability of the supply chain so as to assure attaining the environmental goals of the automotive industry and maintaining market competitiveness. Baars et al. (9) underline the fact that, while a circular economy strategy could reduce cobalt dependency for LIBs used in EVs, it would further increase the demand for other materials like nickel and an integrated recycling system. Sopha et al. (18) identify major barriers: poor effectiveness of policies, lack of safety standards, and high recycling costs, proposing a framework for optimizing the EV battery circular supply chain. Doose et al. (19) underline how new generations of batteries will require advanced recycling processes and closed material cycles to both manage spent batteries and secure raw material supplies. Azadnia et al. (20) provide insight into the European context through the identification of market, social, and regulatory barriers to the implementation of effective reverse logistics for end-of-life LIBs. Bag et al. (21) discuss issues in adopting digital manufacturing for automotive parts in the context of a circular economy, with particular attention to data security risks. Kayikci et al. (22) identify, by means of the fuzzy DEMATEL method, barriers to the implementation of SSCE comprising a lack of governmental support, integration problems, and complex product design. Albertsen et al. (13) contribute circular business models for LIBs in relation to challenges in policy development and operationalization within the automotive industry. Hua et al. (61) propose a 5R principle: reduce, redesign, remanufacture, repurpose, and recycle to cope with challenges related to managing retired LIB sustainable value chains, pointing out the need for advanced technologies and regulations.
Several advances were made pertaining to the field of multi-criteria decision making, including fuzzy logic and its extensions (15, 16, 23–26), and gray numbers (27). While the publications provide a good amount of insight into the risks and challenges associated with circular economy strategies in the lithium-ion battery supply chain, at this point, no comprehensive model that considers risk assessment and countermeasure evaluation exists. In this regard, G-MCDM has been used to evaluate and rank the identified risks within a structured approach for understanding their relative severity and impact on the supply chain. A zero-sum game theory approach was followed to further explore the worst-case scenario and develop effective strategies to mitigate these risks. In this research, the risks were modeled as a player and the strategies against those risks also as a player. This provided an orderly review of interactions between the risks and mitigation strategies to ensure the picked countermeasures are robust and effective in attending to the most critical vulnerabilities within a supply chain. The contribution of the paper is as follows:
1. Development of the theory of zero-sum games based on the Gray Degree of Possibility to identify the worst case of risk occurrence.
2. Identifying the optimal strategy for dealing with risks and challenges associated with implementing circular economy strategies in the lithium-ion battery supply chain using improved zero-sum games based on the Gray Degree of Possibility.
3. Classification of risks associated with implementing circular economy strategies in the lithium-ion battery supply chain in a sustainable supply chain using integrated Gray Delphi-DEMATEL-ANP.
2 Literature review
2.1 MCDM in risk assessment
Recent studies have employed advanced decision-making frameworks such as Game Theory and Decision-Making to some real problem (28–31). Lahane and Kant (15, 16) have suggested a hybrid model based on Pythagorean fuzzy AHP (PF-AHP) integrated with Pythagorean fuzzy VIKOR (PF-VIKOR) to rank the solutions for mitigating risks in circular supply chains. It identifies and ranks the risks involved in the implementation of circular economy strategies, hence providing the decision-maker with a structured way to focus efforts on effective solutions. According to Lahane and Kant (15, 16), the approach identifies and ranks the risk involved in the implementation of the circular economy strategy, hence providing the structured way to the decision-maker to concentrate efforts on effective solutions. (22), discuss the barriers of adopting smart and sustainable circular economy in the automotive industry. This study applied the fuzzy DEMATEL method to analyze the barriers related to technology, producers, consumers, and policy. It identifies the key barriers to SSCE implementation as a lack of governmental support, integration issues amongst supply chain partners, and complex product designs. Chhimwal et al. (32) use a Bayesian Network methodology for risk propagation analysis in a circular supply chain network. The approach detects and measures the risks affecting supply chain performance and provides valuable insights into the relationships of interdependent factors in the network. Chhimwal et al. (32) apply the DEMATEL method to evaluate the relationship between SSCF-targeted and CE-targeted performance. It identifies the major measures of SSCF related to the enhancement of the CE-targeted outcomes, where it points out the flexibility issue in the sustainable supply chains. Kazemian et al. (33) introduce a hybrid DEMATEL-ANP approach to evaluating network-level supply chain resilience. This tool is capable of quantifying the interdependencies between the factors and strategies for resilience in a very robust framework towards improving supply chain resilience against risks. Kazemian et al. (33) developed a framework using Game Theory models for risk management in supply chain networks. Applications over the validated framework prove its effective in analyzing strategic interactions among entities in the supply chain in identifying optimal strategies for risk mitigation (34). The sustainability associated with waste management is when evaluated based on circular economy strategies through this fuzzy three-stage group multi-criteria decision-making approach that integrates fuzzy DEMATEL, fuzzy ANP, and fuzzy MULTIMOORA (35). This makes provisions for the determination of sustainability indices and the optimal selection of circular economy strategies in a comprehensive manner by Fetanat et al. (35). The authors of this paper proposed another novel extension of the DEMATEL approach, that is, the Pythagorean fuzzy DEMATEL, for the probabilistic safety analysis of processes. This new method is capable of effective prioritization of critical events and corrective actions under consideration of various influencing factors, making it highly effective in the prioritization of complex systems (36). The application of the game theoretical models underpinning a dual-channel green supply chain has been brought out by Alizadeh-Basban and Taleizadeh (37). Here, the incorporation of pricing strategies with remanufacturing process arrangements and marketing efforts turns out to be an area where game theory can find huge effectiveness in maximizing the attainment of circular economy outcomes. Optimum in practical issues (38–40) show improved sustainability and efficiency of the supply chain achieved through minimizing the environmental risk and maximizing the resources used (41).
2.2 Circular economy in lithium-ion batteries
The circular economy, in the context of lithium-ion batteries, forms part of the sustainable supply chain for the automotive industry through an end-of-life recovery strategy of reducing environmental impacts and enhancing resource efficiency. In particular, increasing recycling, material reuse, and material recovery aim at waste minimization and promotion of closed-loop systems to extend product life cycles. This approach contributes to the prevention of environmental problems and has economic advantages by reducing raw material usage and decreasing the production cost (15, 16, 42, 43). Notwithstanding, setting up circular economy strategies for the lithium-ion battery supply chain is accompanied by significant risks resulting from process complexity, regulatory barriers, market, and technological uncertainties. According to Baars et al. (9), circular economy strategies could help reduce EV batteries’ dependence on primary raw materials, such as cobalt. This study has inferred that new technologies, though efficient in reducing cobalt demand, merely transfer the pressure to other metals like nickel. Hence, supply chain risks can only be reduced by proper integration between technological improvement and effective recycling systems. The focus of the research by Islam and Iyer-Raniga (10) is on the spent LIB recycling process, with an emphasis on how the circular business model and stakeholder engagement need to go hand in hand toward creating a sustainable supply chain. Indications by the authors are that greater efforts are needed in policy development, material tracking, and in recycling techniques, notably the relatively new DPR process that seems very promising but requires further investigation.
Kurz et al. (11) applied LCA to establish the environmental impact of LIB recycling. Their result points out that the ecological benefit arising from the recycling process strongly depends on the kind of cell technology and the chosen recycling process. According to Kurz et al. (11), poorly designed and applied circular strategies can turn out to be very negative in terms of environmental impact, so careful implementation is needed. Cordisco et al. (12) provide a new direction that links reusability with social inclusion for disadvantaged people. Their research proposed a model of a circular economy in which not only the environmental but also the associated social equity issues would be attended to by giving an opportunity to involve disadvantaged groups in the recovery and reuse of the generated waste LIBs. Albertsen et al. (13) examine the trends in the adoption of circular business models by vehicle manufacturers in Europe, with an emphasis on repair, refurbishment, and repurposing LIBs. This paper calls for collaboration among stakeholders and policy development processes in support of circular economy strategies within the automotive industry. Alessia et al. (14) delivered an in-depth review of the lithium supply chain, outlining the difficulties of integrating primary and secondary production to contribute to reducing environmental impacts. The research showed that a more sustainable and efficient way to recycle might be by decentralized recycling, closer to the markets and aligned with the principles of the circular economy. Lahane and Kant (15, 16) comment on the risk factors associated with the implementation of circular supply chains. They propose a hybrid framework to rank solutions, which mitigates the risk and could be of help to a decision maker in developing efficient strategies for sustainable supply chain management.
Heath et al. (17) have done some critical review to garner key research gaps and future opportunities in relation to the LIBs circular economy. The recommendations have been that the focus, instead, shifts away from just recycling technology to other broader aspects: economic, environmental, and policy—these will give a comprehensive approach toward implementing the concept of a circular economy. Literature indicates that, even when quite promising, circular economy strategies for both the reduction of environmental and resource-related risk of LIBs do call for a holistic approach: technological innovation, effective recycling processes, social inclusion, and robust policy frameworks. The lithium-ion battery supply chain is long, and its critical raw materials are lithium, cobalt, and nickel, generally regarded as key metals associated with environmental and social risks. The circular economy can help reduce these risks through value-chain actions targeted at reusing, recycling, and re-purposing batteries to reduce significantly dependency on virgin materials. The challenges for deploying circular strategies lie in the area of effective material traceability, next to developing robust recycling infrastructure, and addressing possible supply chain disruptions in view of evolving regulatory frameworks and market demand. Influence on the sustainability of the lithium-ion battery supply chain is also exerted by the geographic distribution of raw material sources, often from high social and environmental risk regions related to child labor and occupational hazards. All these factors put together can help make a comprehensive risk assessment while integrating the dimensions of social, environmental, and economic concerns into a resilient supply chain. A transition to a circular economy would not only reduce environmental footprints but also improve security of supply chains due to reduced dependence on critical materials associated with efficient processes for recycling and recovery.
With increased popularity of electric vehicles, dependence on LIBs has also increased. Transition to EVs presents many challenges and risks, especially within practices of circular economy and sustainable supply chains. This literature review identifies key risks, challenges, and barriers outlined in recent research looking into the circular economy and the management of the LIB supply chain within the automotive industry. Baars et al. (9) present the risks associated with growing demand for raw materials necessary in LIBs of EVs, such as cobalt. The paper shows how, even though circular economy strategies decrease dependency on primary raw materials, they might create new challenges connected with enhanced demand for other metals like nickel. The authors argue that a holistic recycling system is key to combating such risks. Sopha et al. (18) discuss in detail the barriers to strategy implementation for EVBs within the context of the circular economy. In this study, the top three barriers are inefficient government policy, a lack of safety standards, and high recycling costs. These barriers are not independent and therefore call for concurrent strategies. The authors have developed a conceptual framework for addressing these challenges and optimizing the circular supply chain system.
According to Doose et al. (19), high recovery rates for metals during LIB recycling are within reach now that the next generations of batteries are soon to hit the market. As this paper will reveal, the degree of advanced recycling processes and the related dangers in dismantling of batteries result in a call for closed material cycles concerning the availability of raw materials and to make the production of batteries sustainable. Azadnia et al. (20), in their quest to identify hurdles facing the effective implementation of reverse logistics for EV LIBs, find out that the “market and social” and “policy and regulations” are the leading identified barriers. “These identified barriers were found to seriously influence EoL LIB effective management; therefore, working on such barriers is crucial to attain circular economy goals,” states Azadnia et al. (20). Bag et al. (21) examine the barriers in the adoption of digital manufacturing under a circular economy for automotive parts. According to this study, technological challenges, more specifically risks pertaining to data security, are critical to consider. The study thus implies that challenges like these have to be tackled if sustainability in the automotive supply chain is to be actualized. Albertsen et al. (13) study how circular business models for LIBs could be applied to the automotive industry and major applications by European car manufacturers. Among the findings were several identified challenges linked to policy development and the operationalization towards circular strategies that improved policy for increased uptake of circular economy practices. Hua et al. (61) provide a detailed discussion of the issues associated with the sustainable value chain management of the end-of-life LIBs. It proposes that 5R, viz. reduce, redesign, remanufacture, repurpose, and recycle can be the key tenets for addressing the same. The paper also points towards the need for higher technology and better regulation as preconditions if the value chain of LIB has to be sustainable. Advanced game theory and gray set methods are used to find the best strategies for reducing potential obstacles and challenges during the implementation of circular economy principles in this critical field. In general, the main and secondary obstacles for the implementation of the circular economy in the sustainable supply chain in lithium batteries are shown in Table 1.
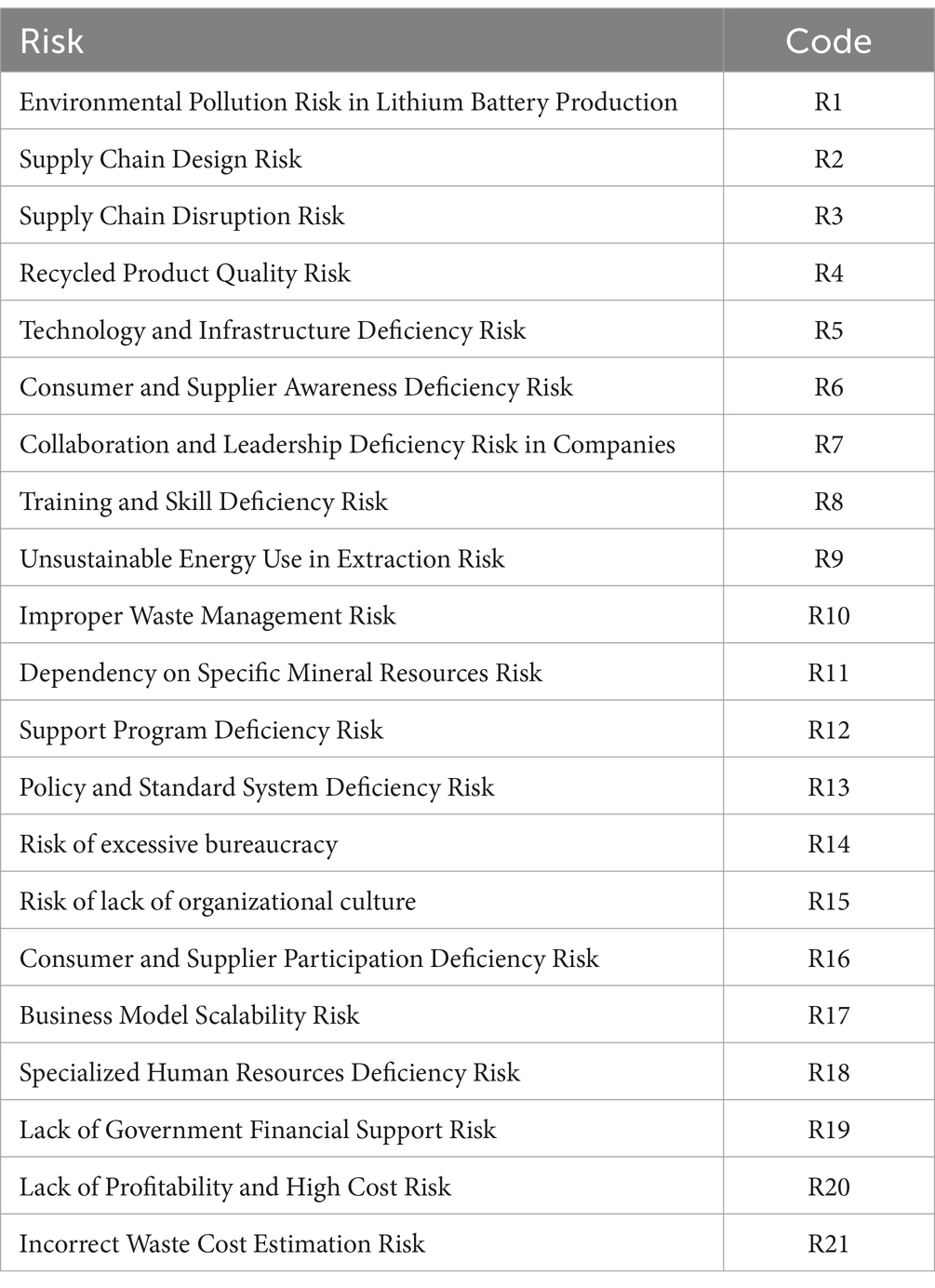
Table 1. Barriers to implementing circular economy in sustainable supply chain in lithium battery (48–51, 55).
3 Research methodology
Gray System Theory was first proposed by Deng in the context of Gray. It gives a framework for handling system complexity with incomplete information. Completely white information represents clarity, while black represents unknown information. On the other hand, a lot of information in most systems is not completely known or completely unknown but is partially in the state of knowledge referred to as gray information. Gray systems are therefore characterized by completely known and completely unknown information. Their main characteristic is that they hold incomplete information. One of the central ideas in this theory is that of a “gray number,” which is an uncertain quantity whose values lie between a certain range, bounded by some known lower and upper limit. Such an interval-based representation of uncertainty is applicable in situations where it is not possible to describe the system fully using the traditional probability density or membership functions. Gray Relational Analysis is a component of Gray System Theory, which has the objective of tackling uncertainty through the focus on vague or imprecise problems needing processing, particularly discrete data and incomplete information. In its work, GRA utilizes traditional deterministic numbers to handle uncertain problems; hence, it provides a means of enhancing the expression of system uncertainties where the availability of complete information is not guaranteed (62).
The subject has been investigated to assess and prioritize the alternatives. The evaluation of options involves the use of gray-scale numbers ranging from 1 to 10 for each criterion (62).
The Likert scale (Table 2) along with the descriptive terms provided by the experts have been used for evaluation. Gray numbers are used in this context for the evaluation process.
3.1 Sum of gray numbers
The sum of two gray numbers G1 = [G1,min,G1,max] and G2 = [G2,min,G2,max] is defined as another gray number. The sum is computed by adding the corresponding lower and upper bounds of the gray numbers in Equation 1.
3.2 Difference of gray numbers
The difference between two gray numbers G1 = [G1,min,G1,max] and G2 = [G2,min,G2,max] is defined by subtracting the corresponding bounds in Equation 2.
3.3 Multiplication of gray numbers
The multiplication of two gray numbers G1 = [G1,min,G1,max] and G2 = [G2,min,G2,max] is defined by considering the product of all combinations of the bounds, with the resulting gray number being the interval from the minimum to the maximum of these products in Equation 3.
3.4 Division of gray numbers
The division of two gray numbers G1 = [G1,min,G1,max] and G2 = [G2,min,G2,max] (assuming G2 does not include zero) is computed by dividing all combinations of the bounds, with the resulting gray number being the interval from the minimum to the maximum of these quotients as Equation 4.
3.5 Scalar multiplication of gray numbers
The multiplication of a gray number G = [Gmin,Gmax] by a scalar k is straightforward and involves multiplying both bounds by k in Equation 5.
3.6 Inverse of a gray number
The inverse of a gray number G = [Gmin,Gmax] (assuming 0 ∉ G) is defined as another gray number that is the interval formed by the inverses of the bounds in Equation 6.
These operations provide a mathematical foundation for performing calculations with gray numbers, making them a powerful tool for handling uncertainty in mathematical models.
3.7 Gray degree of possibility
The Gray Degree of Possibility is a concept within gray system theory used to quantify the degree to which a certain event or value is possible within the framework of gray numbers. It is a measure that compares the overlap between a given interval (gray number) and a specific target interval or value, expressing the likelihood that the true value lies within the target interval.
Given two gray numbers G1 = [G1,min,G1,max] and G2 = [G2,min,G2,max], the Gray Degree of Possibility γ(G1,G2) is calculated as in Equation 7:
Where:
Length of the overlap between G1 and G2 is defined as Overlap(G1,G2) = max(0,min(G1,max,G2,max) − max(G1,min,G2,min)) and Length of G2 is defined as Length(G2) = G2,max − G2,min. Thus, the full formula for the Gray Degree of Possibility becomes in Equation 8:
3.8 Interpretation
The Gray Degree of Possibility γ(G1,G2) yields a value between 0 and 1:
• A value of 1 indicates that G1 is fully contained within G2.
• A value of 0 indicates that there is no overlap between G1 and G2.
• Intermediate values indicate partial overlap, reflecting the degree to which the values of G1 are possible within the interval G2.
This concept is particularly useful in decision-making and analysis under uncertainty, as it allows for the quantification of how likely one uncertain range is to fall within another.
3.9 DEMATEL method under gray numbers
The DEMATEL method is a popular MCDM approach used to model and analyze complex causal relationships among factors in a system (58). When combined with gray numbers, DEMATEL can handle the uncertainty and imprecision inherent in real-world data more effectively. Below is a step-by-step explanation of the Gray DEMATEL method, including the relevant formulas (15, 16, 30, 44).
Step 1: Define the problem and identify criteria.
Define the decision-making problem and identify the set of criteria (factors) C1,C2,…,Cn that will be analyzed.
Step 2: Construct the direct-influence matrix using gray numbers.
Collect expert opinions to evaluate the direct influence of one criterion on another using gray numbers.
Gray Direct-Influence Matrix G: Each element Gij in the matrix G represents the influence of criterion Ci on criterion Cj and is expressed as a gray number as Equation 9:
Step 3: Normalize the direct-influence matrix.
Normalize the gray direct-influence matrix to ensure that the sums of the rows and columns are within the interval [0, 1] in Equation 10.
where , and N is the normalized gray direct-influence matrix.
Step 4: Compute the total-influence matrix.
Compute the total influence (direct and indirect) that each criterion has on others.
Total-Influence Matrix T is in Equation 11.
Here, I is the identity matrix, and (I − N)−1 is the inverse matrix of (I − N).
Step 5: Extract the gray total-influence matrix.
Extract the total-influence matrix while maintaining the gray number format.
Gray Total-Influence Matrix T is in Equation 12.
where each element Tij = [Tijmin,Tijmax] represents the total influence of criterion Ci on Cj.
Step 6: Calculate the sum of rows and columns.
Calculate the sum of rows (denoted as Di) and columns (denoted as Rj) in the total-influence matrix is in Equation 13.
Here, Di represents the total influence given by criterion Ci, and Rj represents the total influence received by criterion Cj.
Step 7: Determine the impact-relation map.
Visualize the causal relationships between the criteria.
Prominence Pi: The prominence of each criterion is calculated as Pi = Di + Ri.
Relation Ni: The net effect (relation) of each criterion is calculated as Ni = Di − Ri.
Interpretation: Positive Ni values indicate that the criterion is a net cause, while negative values indicate it is a net effect.
Step 8: Analyze the results and make decisions.
Analyze the impact-relation map to understand the causal relationships and make informed decisions.
The criteria with high prominence and positive relation are typically key drivers in the system and should be prioritized in decision making. The DEMATEL method under gray numbers extends the traditional DEMATEL approach by incorporating gray numbers to handle uncertainty and imprecision in the data. This enables more robust and reliable analysis of complex systems where information may be incomplete or ambiguous.
3.10 Gray ANP
The (ANP) is a generalization of the (AHP) and is used to solve complex decision-making problems that involve interdependencies among criteria and alternatives. When combined with gray numbers, ANP can effectively handle uncertainty and imprecision in the data. Below is a step-by-step explanation of the ANP method under gray numbers, including the relevant formulas.
Step 1: Define the problem and construct the network model.
Objective: Define the decision-making problem and construct a network model that includes clusters, criteria, and alternatives. Unlike AHP, which uses a hierarchical structure, ANP allows for the interrelationship among elements within and between clusters.
Step 2: Construct pairwise comparison matrices using gray numbers.
Objective: Use expert opinions to evaluate the relative importance of elements within each cluster, as well as the influence of elements across different clusters.
Gray Pairwise Comparison Matrix G: Each element Gij in the matrix G represents the relative importance or influence of element i over element j and is expressed as a gray number as Equation 14:
where Gij = [Gminij,Gmaxij].
Step 3: Normalize the pairwise comparison matrices.
Objective: Normalize the gray pairwise comparison matrices to ensure the sums of the columns are equal to 1, which is required for the calculation of the supermatrix.
For each element Gij in the matrix in Equation 15:
After normalization, each column in the matrix should sum to 1.
Step 4: Construct the initial supermatrix.
Objective: Formulate the initial supermatrix by organizing the normalized gray pairwise comparison matrices into a single matrix that represents the entire network’s structure.
Supermatrix W: The supermatrix is a block matrix where each block represents the influence of a set of elements in one cluster on another set of elements in a different (or the same) cluster in Equation 16.
Each block Wkl is a submatrix corresponding to the relationships between elements in cluster k and cluster l.
Step 5: Construct the weighted supermatrix.
Adjust the initial supermatrix to reflect the relative importance of each cluster within the network. This is done by multiplying each block in the supermatrix by the corresponding cluster’s priority. Weighted Supermatrix W ′ is as where wk is the weight (priority) of cluster k, and Wkl is the block from the initial supermatrix corresponding to the relationship between cluster k and cluster l.
Step 6: Calculate the limit supermatrix.
Compute the limit supermatrix by raising the weighted supermatrix to sufficiently high powers until it converges to a stable matrix where all columns are identical. This limit matrix reflects the long-term influence of each element on others. Limit Supermatrix W″ is as . This operation is typically done by matrix multiplication until the super matrix stabilizes (converges).
Step 7: Extract the priorities.
Extract the priorities (weights) of the decision alternatives from the limit supermatrix. The final priorities of the alternatives can be found in the corresponding rows of the limit supermatrix. The priority of each alternative is given by the corresponding entry in the limit supermatrix. For decision-making, these priorities can be used to rank the alternatives.
Step 8: Sensitivity analysis.
Perform a sensitivity analysis to assess the stability of the results under different scenarios or variations in the input data. Change the input data (e.g., the gray numbers in the pairwise comparisons) slightly and observe how the final priorities change. This helps to ensure that the decision-making process is robust under uncertainty.
3.11 Zero-sum game theory expanded based on gray degree of possibility
In a zero-sum game under gray numbers, we account for uncertainty and imprecision in the payoffs using gray numbers. We also include nonlinear programming constraints to further refine the decision-making process. Below is the step-by-step method, including the formulation of constraints.
Step 1: Calculate the gray degree of possibility.
Gray Degree of Possibility between the gray payoffs of different strategies to quantify the likelihood of one strategy outperforming another under uncertainty. Given two gray numbers G1 = [G1,min,G1,max] and G2 = [G2,min,G2,max], the Gray Degree of Possibility γ(G1,G2) is defined as Equation 17:
Step 2: Construct the gray decision matrix.
Formulate the gray decision matrix that represents the gray payoffs for each strategy pair between two players.
Gray Decision Matrix M: The decision matrix is defined by the gray payoffs, where each element Mij is a gray number representing the payoff to Player 1 when Player 1 chooses strategy i and Player 2 chooses strategy j in Equation 18.
where each element Mij = [Mijmin,Mijmax] is a gray number.
Step 3: Formulate the objective function based on gray degree of possibility.
Define the objective function for Player 1 based on maximizing the Gray Degree of Possibility.
Objective Function for Player 1: Player 1 aims to maximize the minimum Gray Degree of Possibility between the payoff of their chosen strategy and the payoffs of the other strategies.
For each strategy i of Player 1, the objective function can be expressed as:
where γ(Mij,Mkj) is the Gray Degree of Possibility that the payoff Mij is at least as large as Mkj for each strategy k of Player 1, given the strategy j chosen by Player 2.
Step 4: Formulate the nonlinear programming constraints.
In the context of a zero-sum game, the inclusion of nonlinear programming constraints adds a layer of complexity that may be necessary to model real world decision-making scenarios. These constraints can take various forms, including but not limited to:
1. Budget Constraints: Limits on the total resources available to each player is where ci is the cost associated with strategy i and B is the total budget available.
2. Probability Constraints: Ensures that the probabilities assigned to strategies sum to 1 and where pi represents the probability of choosing strategy i.
3. Risk Constraints: Limits the maximum allowable risk or uncertainty is as , where ri is the risk associated with strategy i and R is the maximum allowable risk.
4. Equality/Non-Equality Constraints: Enforces specific requirements or relationships among variables in Equation 19.
where f(x1,x2,…,xm) is a nonlinear function representing the relationship between the strategies.
Step 5: Identify the optimal strategy for Player 1.
Determine the strategy i∗ that maximizes Player 1’s minimum Gray Degree of Possibility while satisfying all nonlinear constraints.
Optimal Strategy: The optimal strategy i∗ for Player 1 is the one that maximizes the minimum Gray Degree of Possibility across all possible strategies of Player 2, subject to the nonlinear constraints as i∗ = argmaxi minj γ(Mij,Mkj) for all k ≠ i subject to constraints.
Step 6: Formulate the problem for Player 2 (dual problem).
Similarly, Player 2’s objective is to minimize the maximum Gray Degree of Possibility that Player 1’s strategy outperforms their strategy, subject to the nonlinear constraints.
For each strategy j of Player 2, the objective function can be expressed as Minimize maxi γ(Mij,Mik), for all k ≠ j subject to constraints.
Step 7: Identify the optimal strategy for Player 2.
Determine the strategy j∗ that minimizes Player 2’s maximum Gray Degree of Possibility while satisfying all nonlinear constraints.
Optimal Strategy: The optimal strategy j∗ for Player 2 is the one that minimizes the maximum Gray Degree of Possibility across all possible strategies of Player 1, subject to the nonlinear constraints in Equation 20.
Step 8: Calculate the game value.
Compute the value of the game, which represents the expected outcome when both players adopt their optimal strategies.
Game Value: The value of the game is the gray number corresponding to the payoff at the optimal strategies i∗ and j∗ the Game Value = Mi∗ j ∗.
The zero-sum game theory model under gray numbers, with an objective function based on the Gray Degree of Possibility and additional nonlinear programming constraints, offers a comprehensive framework for decision making in uncertain and complex environments. By incorporating gray numbers and nonlinear constraints, this model allows for more realistic and flexible solutions that can better accommodate real-world limitations and uncertainties.
4 Finding
4.1 Demographic information
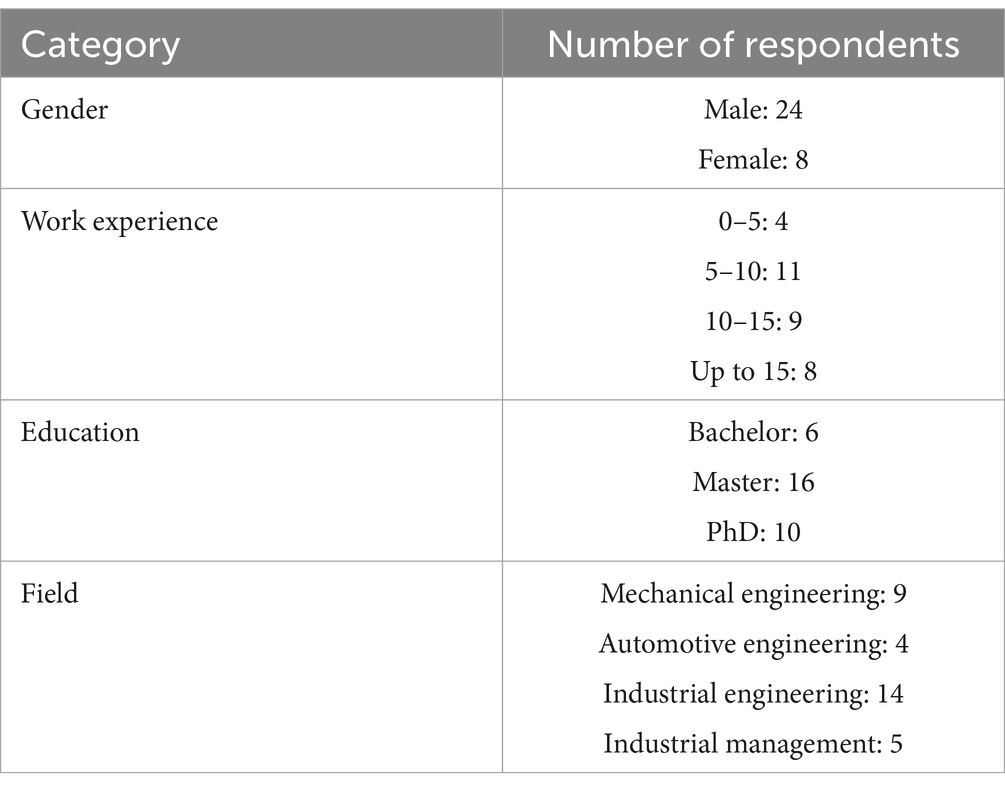
The experts have been selected by the researchers to answer with purposeful judgmental sampling Demographic information is in Table 3.
4.2 Finding of MCDM
In this section, the results of the collected data analysis are presented. First, the obstacles in the circular economy of lithium-ion battery in the sustainable supply chain in the automotive industry have been identified using the Gray Delphi method. The Gray ANP method has been used to rank the circular economy implementation sub-criteria. Gray DEMATEL technique Gray DEMATEL has been used to determine the relationships between the main obstacles. Excel software and python were used to analyze the obtained data.
In the primary stage, risks were determined and chosen from the circular economy of lithium-ion batteries in the sustainable supply chain in the automotive industry. For validation and reliability, gray Delphi Technique was employed. To perform this gray Delphi Technique, a questionnaire with desired criteria is sent separately on individual basis to all group members and done secretly. The gray Delphi method was carried out in three stages, and Kendall’s coefficient of agreement for the first, second and third rounds of the gray Delphi sub-criterion was 0.711, 0.752 and 0.768, respectively, which shows the convergence of the respondents’ opinions and the congruence of their opinions, and therefore gray Delphi confirmed and it stopped. Considering that all the critical values are greater than 0.5, all the risks were accepted.
Stage 1: Initial identification of risk.
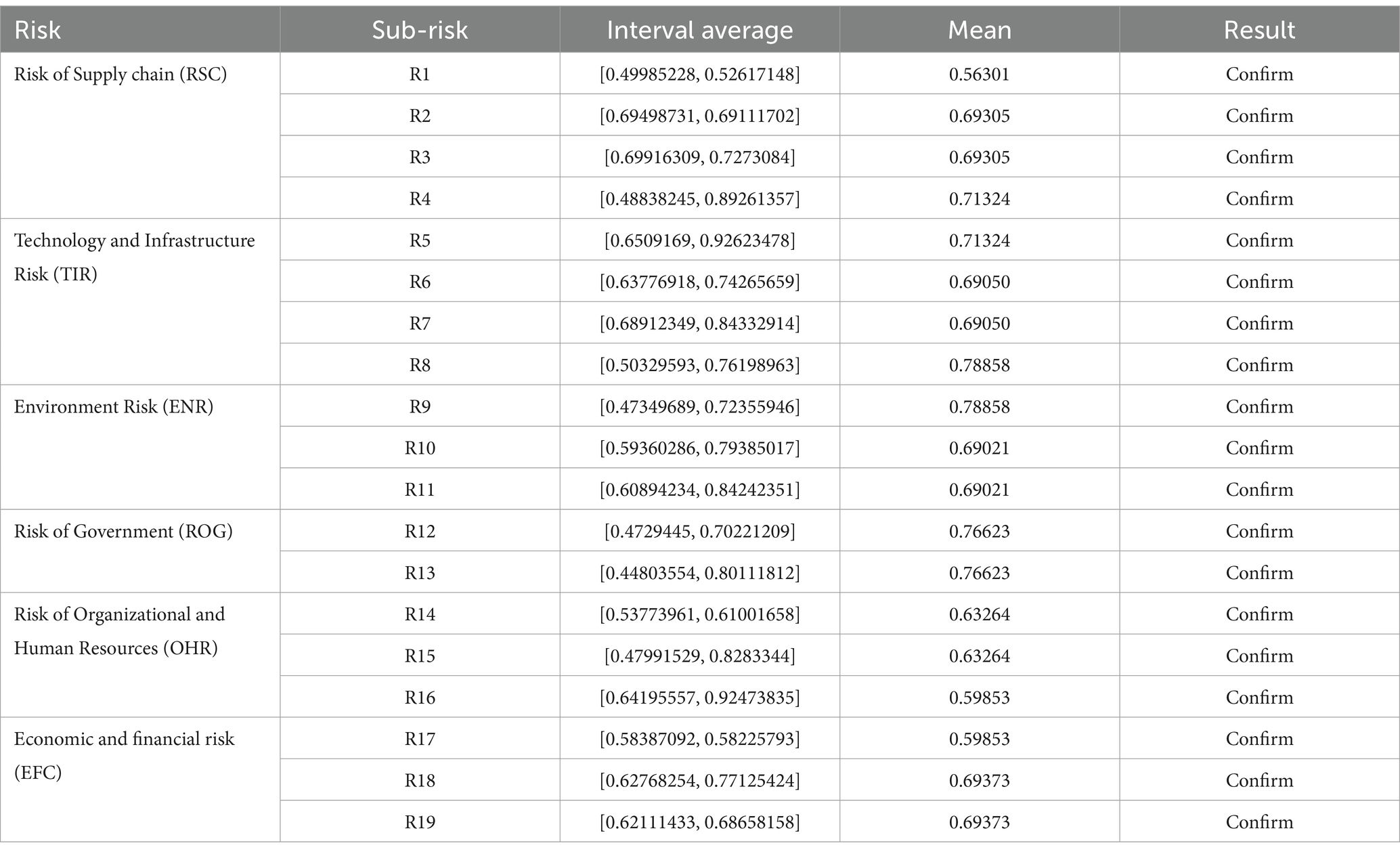
Identification of Criteria: Initially, 21 criteria were identified as potential sub-risks related to the Environmental Pollution Risk in Lithium Battery Production. These criteria spanned various domains including supply chain design, recycled product quality, technology and infrastructure, consumer awareness, and organizational culture, among others. First Round of Expert Evaluation: In the first round, experts were asked to assess these 21 criteria. They provided their assessments, and two criteria were deemed less significant and thus eliminated from further consideration. The remaining 19 criteria were retained for further evaluation. Refinement of Criteria: Based on the feedback and evaluation from experts, the list of criteria was refined, resulting in a shorter list of 19 criteria. The two eliminated criteria were “Excessive Bureaucracy Risk” and “Organizational Culture Deficiency Risk.”
Stage 2: Interval-based evaluation.
The remaining 19 criteria were then subjected to a more detailed assessment. In this round, experts were asked to provide interval-based evaluations, which considered both the mean value and the interval average for each criterion. The data from this round was analyzed to determine the confirmatory status of each criterion. This involved calculating both the mean and the interval averages, allowing for a more nuanced understanding of the risks associated with each criterion. All 19 criteria were confirmed based on their interval-based evaluations. These criteria were found to be relevant and were thus included in the final stage of the Delphi process.
Stage 3: Final confirmation and reporting.
Final Expert Consensus: In the final stage showed in Table 4, experts reviewed the results of the interval-based evaluations. The consensus was reached that all 19 criteria should be retained as they were found to be significant in the context of Environmental Pollution Risk in Lithium Battery Production.
Kendall’s coefficient of agreement for the first, second and third rounds of Delphi sub-criteria was 0.711, 0.752 and 0.768, respectively, which shows the convergence of the respondents’ opinions and the agreement of their opinions, and therefore Delphi was approved and stopped.
4.2.1 Gray ANP
The researchers have adopted the (GANP) to the procedure of giving importance to the inputs into the model. The figure below informs the GANP model to settle the model pattern for the criterion and a set of sub-criteria. This research applied the Gray ANP show in Figure 1 to determine the relative importance of the indicators and criteria model.
4.2.1.1 Determining the priority of the main criteria based on the goal
To make the initial network analysis, the major criteria have been compared in pairs systematically, as per the objective. Pair-wise comparison is simply a process of comparing every element within a cluster with each of its other members. Thus, the number of comparisons made in a cluster containing ‘n’ components is: (n(n−1))/2. Since there are 19 risks involved, the number of comparisons made is 171. Therefore, 171 comparisons have been made by a panel of experts. Gray scale is used by experts for quantifying their point of view. The third chapter defines the gray scale used in the gray network analysis procedure. Gray spectrum was initially used in collecting the experts’ opinions. The Gray ANP technique has utilized the geometric mean approach for integration of opinions by experts. After the construction of the matrix of pairwise comparisons, the eigenvector has been calculated. First, the geometric mean of each line is calculated as Equation 21.
The cumulative total of the items in the preferences column is computed as Equation 22.
Next, step is to sum up all the preferences column items. The sum of all preferences column items is divided by that criteria’s values sum, to normalize those preferences for that criterion. Since values are gray scale; we can simply multiply the sum of all the grayscale lines with their reciprocal. Finding the inverse of total is an essential step. Results of data normalization procedure will be presented in Table 5.
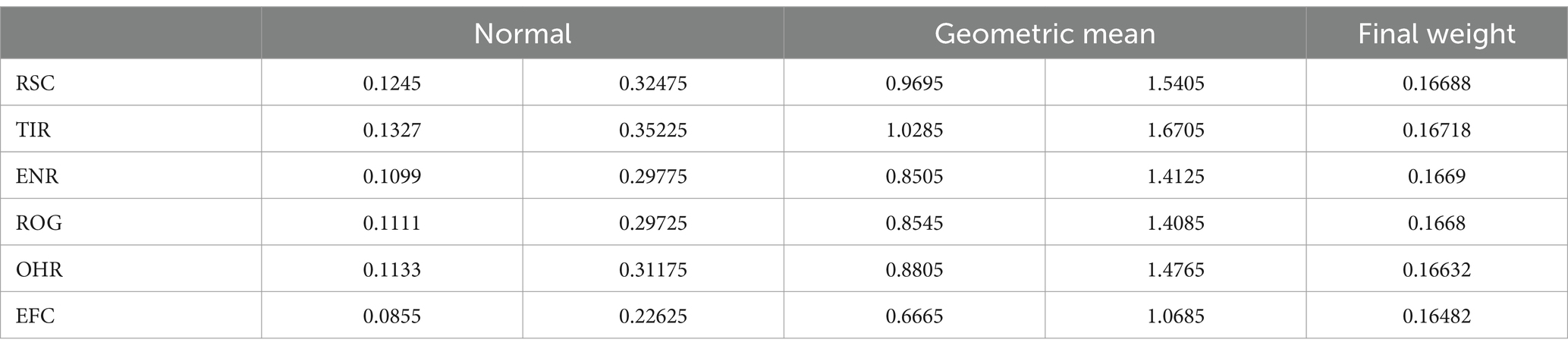
The results of calculating the weights of the main research criteria are presented in Table 6.
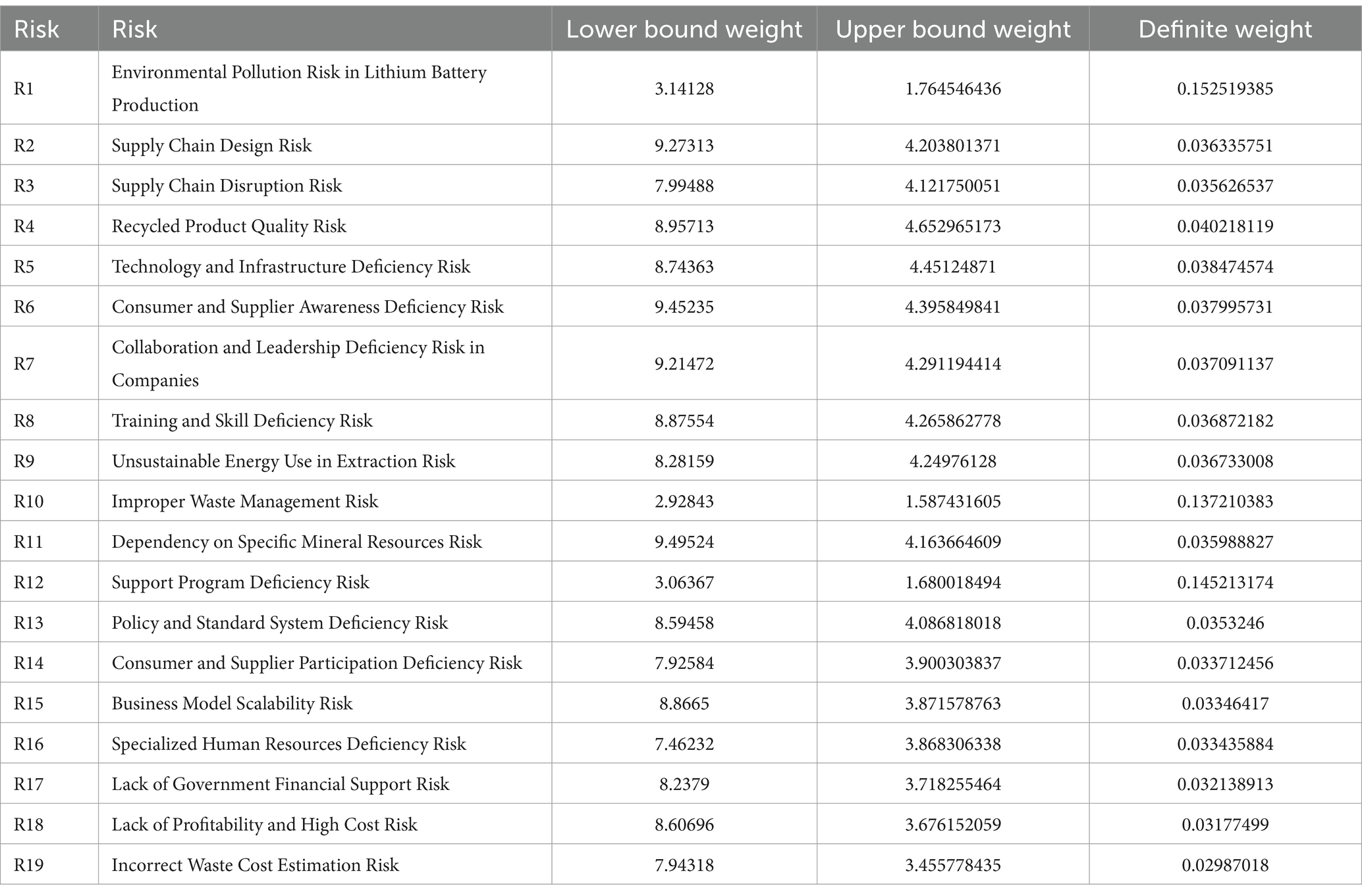
Each obtained gray weight and normalized values are related to the main criteria. At last, grey numbers have been whitened (definite) calculating the average value of the limits. Based on the special vector obtained Criterion TIR with a weight of 0.16718 is the most important and Criterion EFC with a weight of 0.16482 is the last priority. The comparison rate discrepancy was established at 0.036, less than 0.1; hence the comparisons made are reliable.
4.2.1.2 Final priority of indicators with gray DANP technique
4.2.1.2.1 Calculation of unbalanced supermatrix, balanced supermatrix and limit supermatrix
The final weight is obtained by displaying the outcome of the comparison of the main criteria, based on the objective and internal correlations between the criteria, in a super matrix. In this case, the super matrix will be known as the major or imbalanced super matrix. To obtain the overall priority of the indicators with interdependencies, the internally prioritized vectors, that is, computed w are entered in the respective columns of a matrix. Using the identified inter linkages in the present research, the above super matrix-I of this study will be of the following nature in Equation 23:
The super matrix embeds the vector W21, which expresses the relative importance of each of the main criteria with respect to the goal. In this study, the vector W22 measures the pairwise evaluation of the interrelationships between the main criteria derived from the output produced by applying the Gray DEMATEL method. The W32 vector presents the importance of each sub-criterion within its respective cluster. A coefficient value of zero would indicate that the components have no influence on each other where the rows and columns intersect. In the second round of the Gray ANP method, pairwise comparison of the sub-criteria under each criterion has been presented in Table 7 and Figure 2.
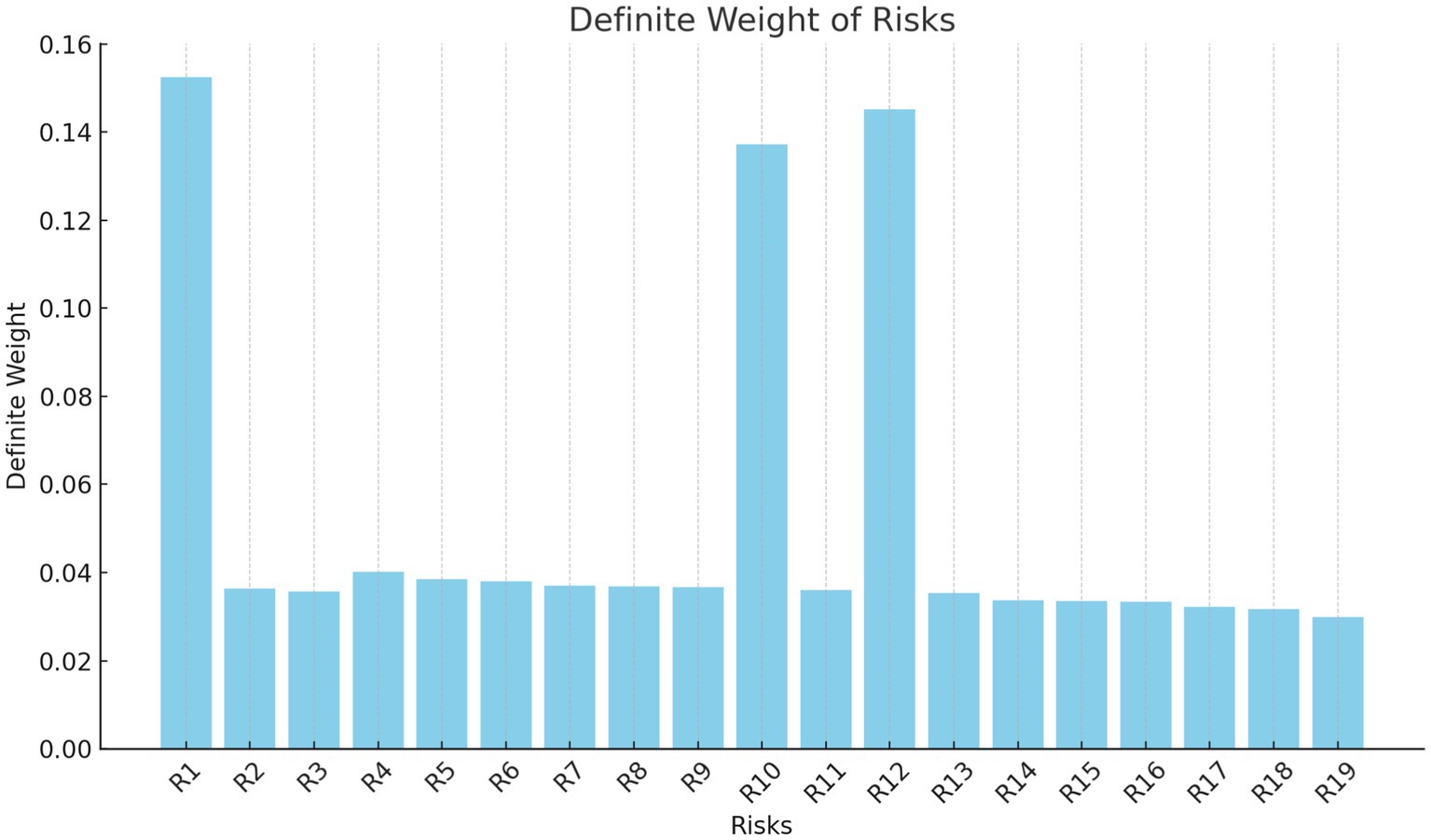
The three most critical risks in lithium battery production, based on their weights, are Environmental Pollution Risk (0.1525), Improper Waste Management Risk (0.1372), and Support Program Deficiency Risk (0.1452). These risks underscore the significant environmental challenges in the industry, highlighting the urgent need for sustainable practices to manage pollution and waste effectively. The high weight of the Support Program Deficiency Risk also indicates the necessity for robust support systems, including training and regulatory compliance, to address these challenges and ensure the industry’s long-term viability. Prioritizing these areas is essential for minimizing environmental impact and maintaining sustainable production processes.
4.2.2 Gray DEMATEL
Step 1: Define the risks and evaluation criteria.
The criteria are based on grey linguistic terms, which have been mapped to grey intervals:
Step 2: Construct the grey direct influence matrix.
The direct influence matrix A is populated using grey intervals. Each element aij is represented as an interval [aLij,aUij], where aLij is the lower bound and aUij is the upper bound of the grey interval.
Step 3: Normalize the grey direct influence matrix.
The grey direct influence matrix A is normalized by ensuring that each interval is divided by the maximum sum of the intervals in any row as Equation 24.
Step 4: Compute the grey total influence matrix T.
The grey total influence matrix T is calculated using the following in Equation 25:
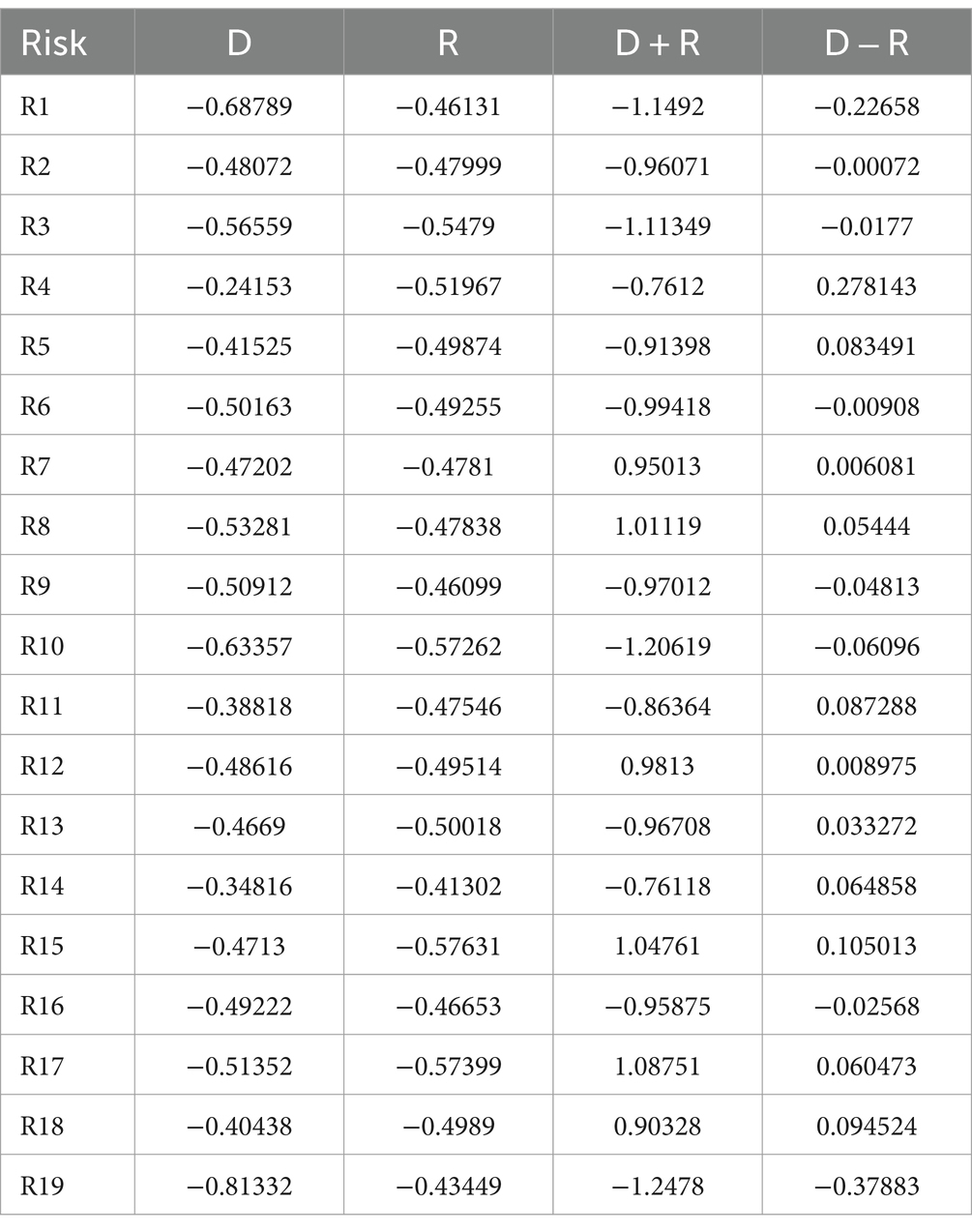
Step 5: Calculate grey D and R values show in Table 8.
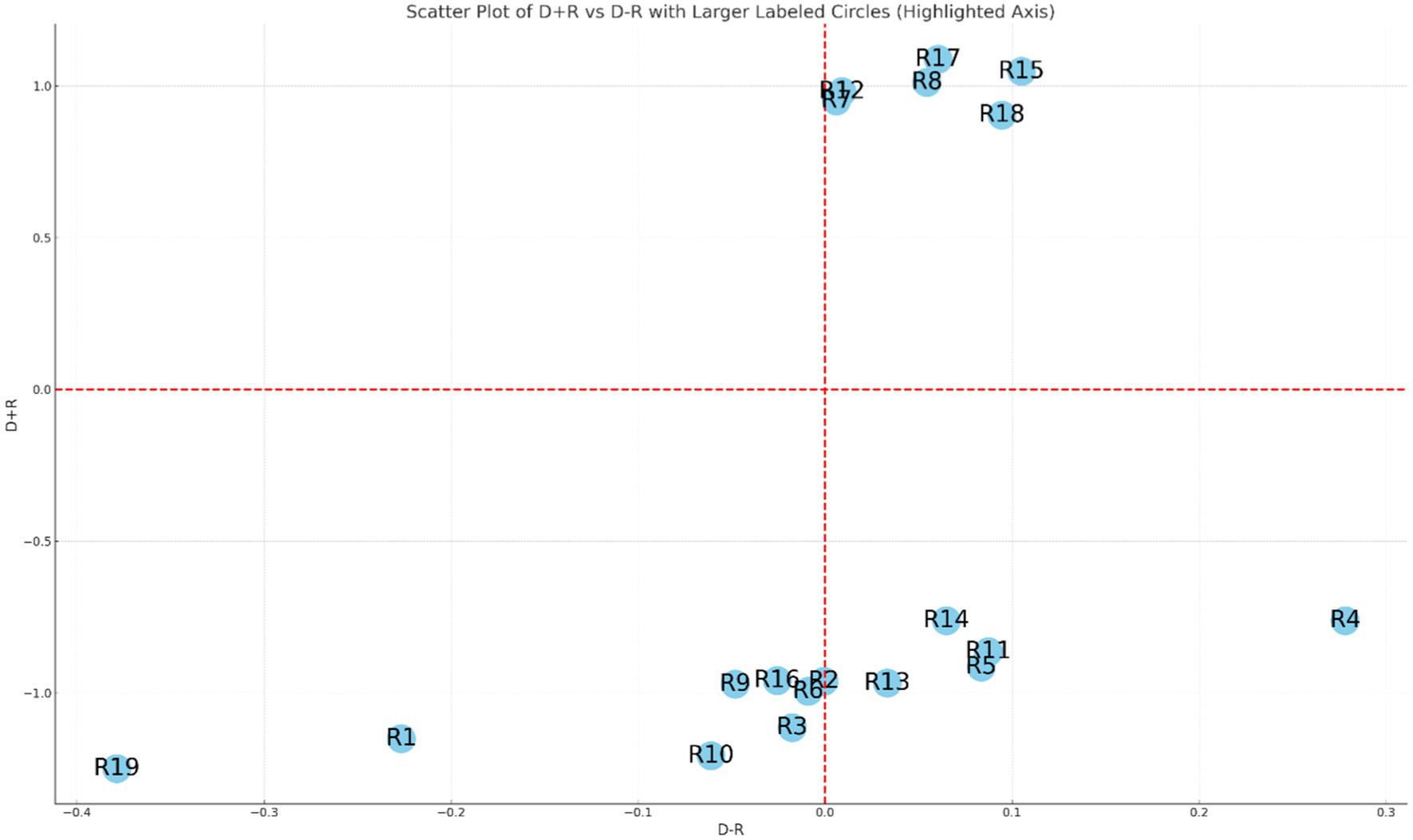
In the Gray DEMATEL method analysis (see Figure 3), the results are categorized based on the values of D + R and D − R. For the risks where both D + R and D − R values are positive, they are positioned in the upper right quadrant of the positive section of the diagram. The chart is divided into four quadrants by the red dashed lines at D + R = 0 and D − R = 0. Each quadrant represents a different characteristic of the risks:
1. Top-Right Quadrant (Positive D + R, Positive D − R):
Risks in this quadrant, such as R7, R8, R12, R15, R17, and R18, are both influential and have a strong impact on other factors in the system. These risks not only influence others but are also relatively independent of being influenced by other risks. They are the driving factors in the system and play a crucial role in shaping the overall risk environment.
1. Top-Left Quadrant (Positive D + R, Negative D − R):
No risks are located in this quadrant in the current plot. If there were any, they would represent risks that are strongly influenced by other factors but also have a moderate impact on other risks. These are somewhat balanced in terms of influence and being influenced.
1. Bottom-Right Quadrant (Negative D + R, Positive D − R):
Risks in this quadrant, such as R4, are influential but also highly dependent on the influence of other risks. These risks have a significant impact on the system but are also susceptible to changes and influences from other factors. They play a dual role in the system, both as influencers and influenced elements.
1. Bottom-Left Quadrant (Negative D + R, Negative D − R):
Risks located here, such as R1, R2, R3, R9, R10, R16, and R19, are not only influenced by other factors but also have a lower impact on the system. These risks are more passive, being predominantly on the receiving end of influences within the system. They are considered less critical in terms of their ability to drive or alter the overall risk profile.
These risks exert an influence on other risks, meaning they are influential factors. For example, R7, R8, R12, R15, R17, and R18 fall into this category, indicating they have a significant impact on the system under consideration. On the other hand, risks where both D + R and D − R values are negative are located in the lower left quadrant of the negative section. These risks are considered to be influenced by other factors rather than being influential themselves. This includes R1, R2, R3, R9, R10, R16, and R19, indicating that these risks are more dependent on other factors within the system.
4.3 Game theory finding
Step 1: Define the players and strategies.
• Player 1: The risks (19 risks, R1,R2,…, R19)
• Player 2: The strategies to counter these risks (6 strategies, S1,S2,…,S6)
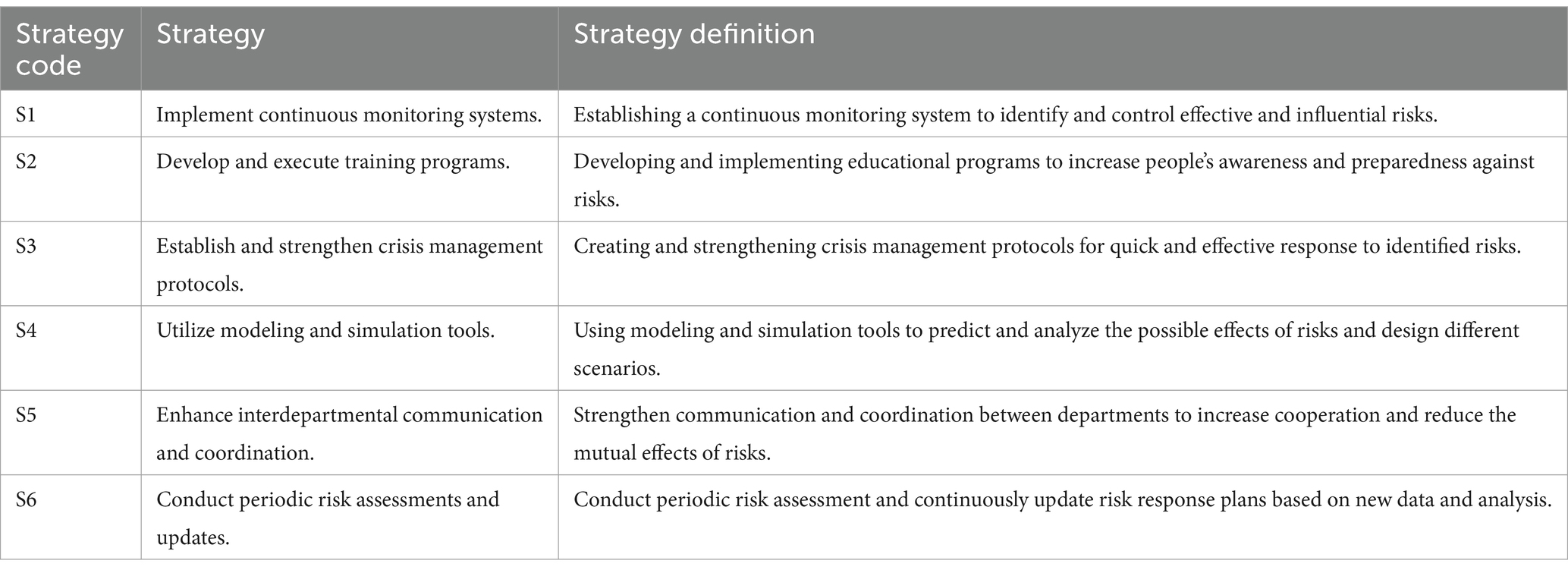
To deal with these risks, the following solutions can be used (see Table 9).
Step 2: Construct the gray decision matrix.
We will create a decision matrix where the elements represent the payoffs (impact or loss) of Player 1 (risks) against Player 2’s strategies. Each element is a gray interval.
Step 3: Calculate the gray degree of possibility.
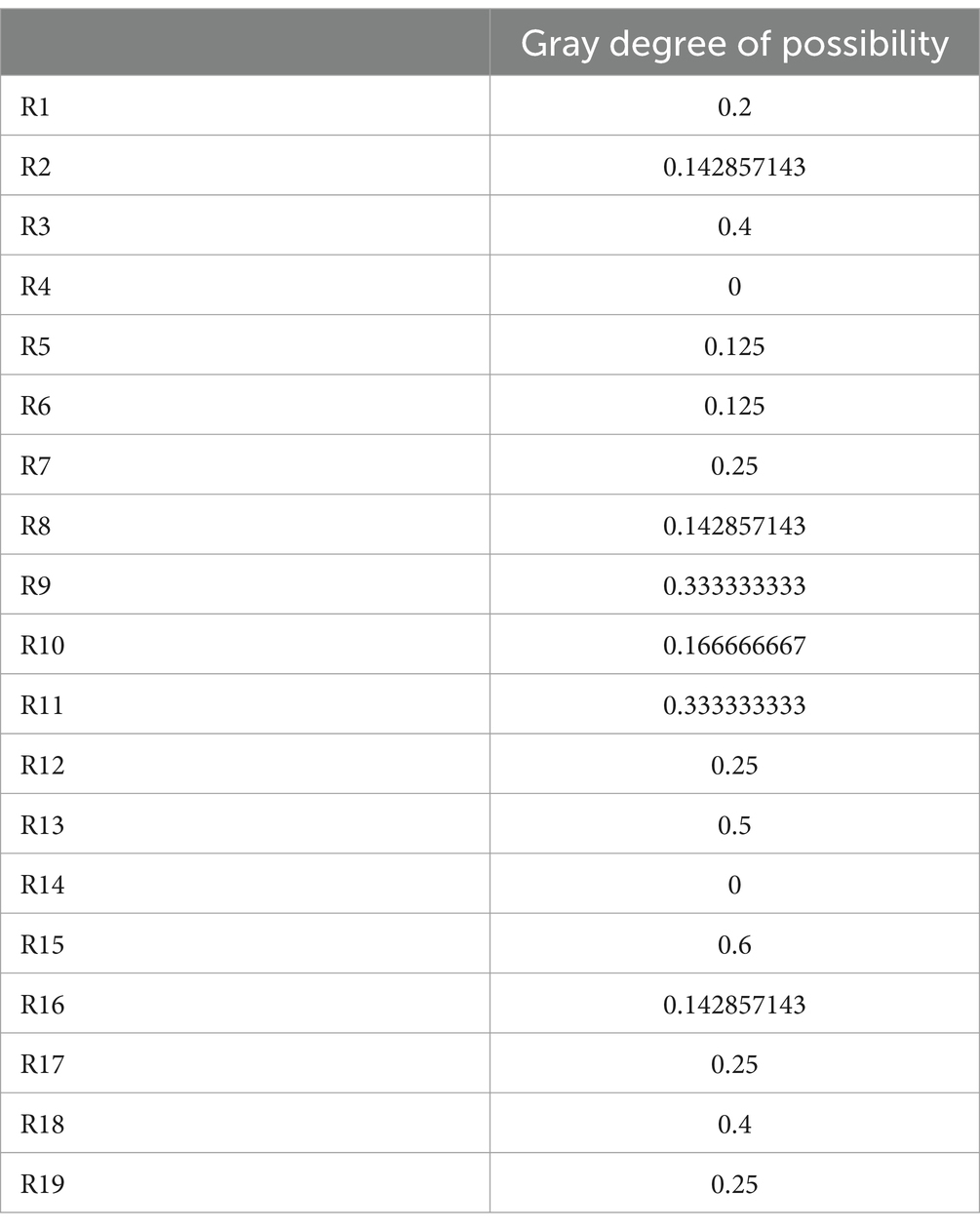
For each element in the decision matrix, we’ll calculate the Gray Degree of Possibility that the payoff from one strategy is at least as large as the payoff from another strategy showed in Tables 10, 11.
Step 4: Formulate the objective function.
The objective function for Player 1 is to minimize the impact (loss), while for Player 2, it’s to maximize the impact (or minimize the efficiency of Player 1’s chosen risk strategy). The players will use the Gray Degree of Possibility as part of their strategy formulation.
Step 5: Apply nonlinear programming constraints.
These constraints include budget limits, probability constraints, risk limits, and any other relevant non-linear relationships.
To mathematically analyze the probability of the worst-case scenario occurring, we consider the intervals provided for each risk as representing possible values the risks could take. For each risk Ri, the interval [Li,Ui] where Li is the lower bound and Ui is the upper bound, can be interpreted as a uniform distribution of potential risk values within this range. The uniform distribution assumption implies that any value within the interval is equally likely, leading to a constant probability density function for the interval.
The probability of the worst-case scenario, denoted Pworst, is then the probability that the actual risk value is close to the lower bound Li. Since the PDF for a uniform distribution is across the interval, the narrowness of the interval (Ui − Li) plays a crucial role. A narrower interval indicates less variability in the possible outcomes, which implies a higher concentration of probability near the lower bound. Specifically, if we define a small ϵ such that Li ≤ x ≤ Li + ϵ, the probability that the risk Ri falls within this small range near the lower bound is given by Equation 26:
This shows that the probability Pworst increases as the interval (Ui − Li) decreases, making the worst-case scenario more probable for risks with smaller ranges. Conversely, larger intervals suggest greater uncertainty and a lower probability that the actual risk is close to Li.
Moreover, considering the cumulative distribution function (CDF) of the uniform distribution, the CDF at the lower bound Li is 0, and it gradually increases to 1 as we approach the upper bound Ui. Therefore, the CDF’s steepness, which is inversely proportional to the interval’s length, further supports that narrower intervals lead to a higher likelihood that the risk remains near the lower bound.
In conclusion, mathematically, the probability of the worst-case scenario is inversely related to the width of the risk intervals. The narrower the interval, the more concentrated the probability near the lower bound, and thus, the higher the likelihood of encountering the worst-case scenario. This insight provides a quantitative foundation for prioritizing risks with smaller intervals in risk management strategies, as they are statistically more likely to realize their worst-case outcomes.
Step 6: Solve for optimal strategies.
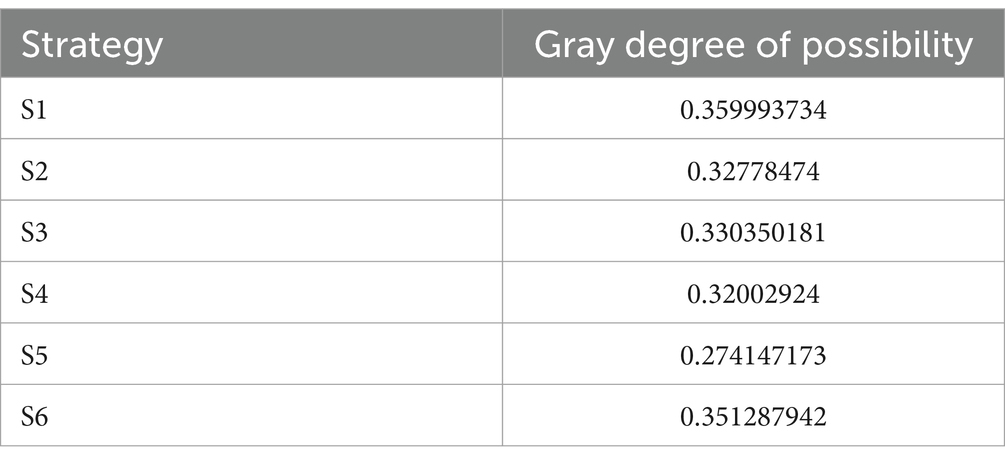
We will determine the optimal solution for strategies for both players using the Gray Degree of Possibility and constraints show in Tables 12, 13.
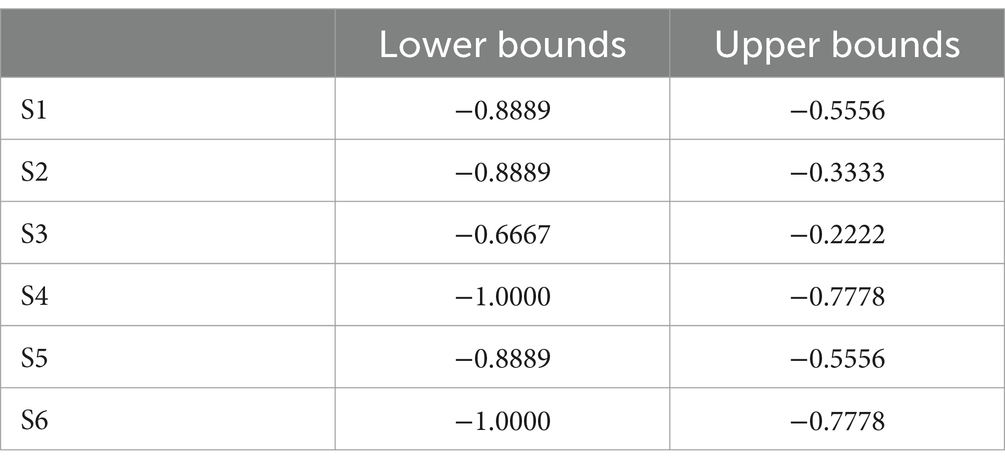
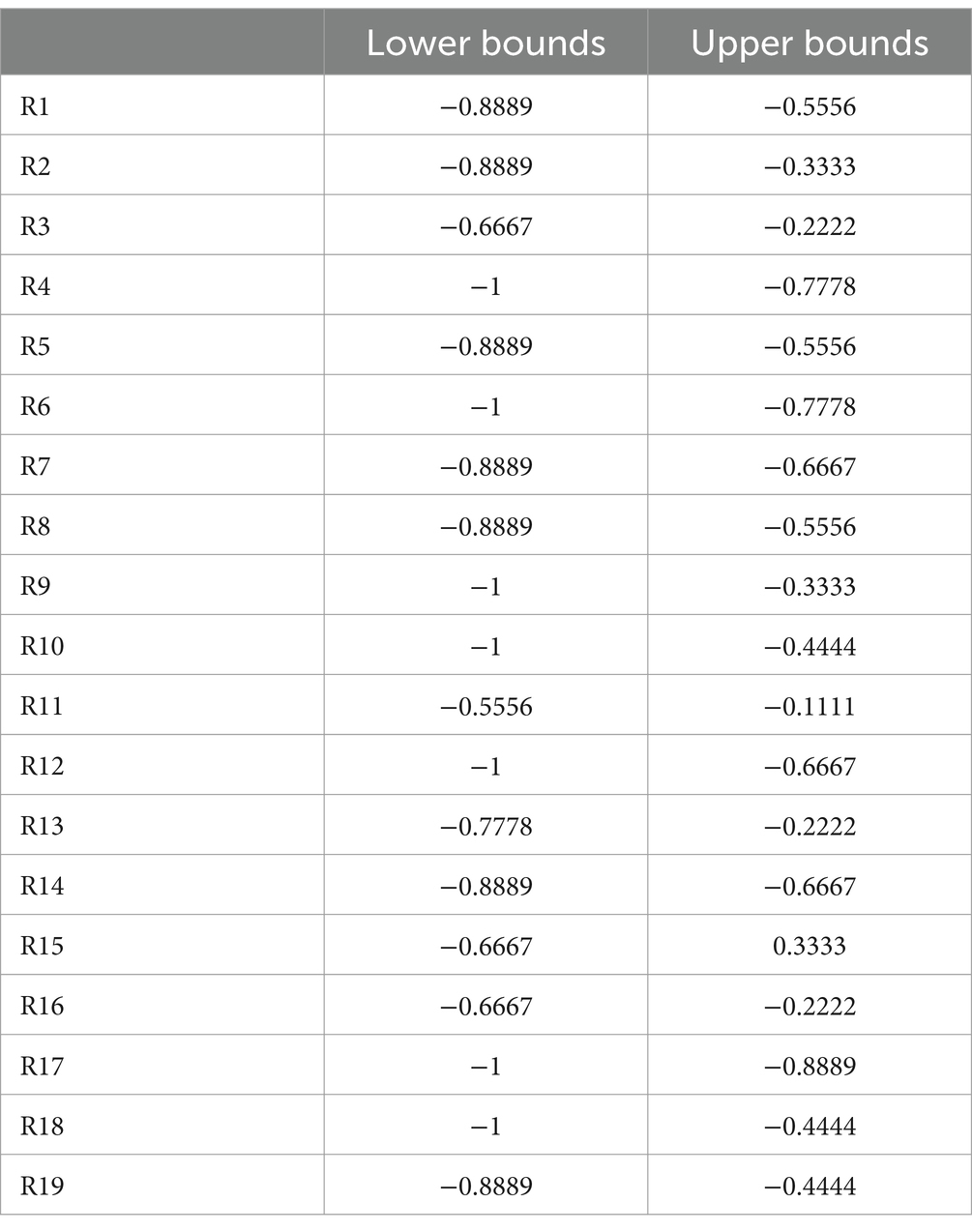
In the analysis of zero-sum game theory, optimal solutions are typically selected based on the criteria of lower bounds and upper bounds. These criteria represent the worst and best possible outcomes when facing risks, respectively. Specifically, the lower bound indicates the minimum value that a strategy can yield, while the upper bound represents the maximum possible value for that strategy.
The optimal strategy in this context is one that minimizes potential losses in the worst-case scenario (i.e., has a higher lower bound) while also maximizing potential gains in the best-case scenario (i.e., has a higher upper bound). Based on this, Strategy S3, with a lower bound of −0.6667 and an upper bound of −0.2222, appears to be the most optimal choice. This strategy offers the least loss in the worst case and the highest gain in the best case compared to the others. On the other hand, Strategies S4 and S6, with lower bounds of −1.0000, pose a higher risk in the worst scenarios, and thus, should generally be avoided if possible. Selecting Strategy S3 seems prudent due to its relative balance between the lower and upper bounds, making it a more robust choice. This strategy demonstrates stability in the worst-case scenarios and has the potential to achieve better outcomes, making it a suitable solution for managing risks, particularly when optimizing results across a range of possible scenarios is essential.
Based on the given output data for the risk intervals, we can perform a detailed analysis to identify which risks are more likely to exhibit their worst-case scenarios and which risks have a broader range of possible outcomes, indicating greater uncertainty.
R7 and R14 have identical intervals, [−0.8889, −0.6667], suggesting a high probability that the actual risk value will be close to the lower bound of −0.8889. Similarly, R11, with an interval of [−0.5556, −0.1111], also indicates a higher likelihood that the actual risk will be nearer to −0.5556. These risks have relatively narrow intervals, meaning there is less variability in the possible outcomes.
R9 has a wide interval of [−1, −0.3333], which means the actual risk could range significantly, making it less likely that the worst-case scenario (−1) will occur. R15, with an interval extending into positive values [−0.6667, 0.3333], shows even greater variability, further reducing the probability that the risk will hit its worst-case value. Such risks, while potentially less likely to reach their worst outcomes, require strategies that account for their wider range of possible impacts.
R4, R6, R17, R12 risks include the extreme lower bound of −1, which could represent the most severe potential outcomes. While R4 and R6 share the same interval [−1, −0.7778], indicating some probability concentration near the lower bound, R17, with the narrower interval of [−1, −0.8889], suggests an even higher likelihood that the risk will indeed be close to −1. R12, although broader, still has the potential to reach −1, highlighting the importance of considering these extreme cases in risk assessments. These risks should be carefully monitored because their worst-case outcomes are more probable. These risks have broader intervals, indicating a higher degree of uncertainty regarding the actual risk value.
The analysis of the output data reveals that risks with narrower intervals, such as R7, R14, and R11, have a higher probability of realizing their worst-case outcomes, and therefore, these should be prioritized in risk mitigation strategies. On the other hand, risks with broader intervals, like R9 and R15, suggest higher uncertainty, which may require different management approaches to address the wider range of potential impacts. Finally, risks with intervals including the extreme value of −1 demand special attention due to their potential severity, despite the varying probabilities of these outcomes.
Step 7: Determine the optimal game value.
The value of the game represents the expected outcome when both players play optimally.
Amount is 0.7778.
4.4 Sensitive analysis
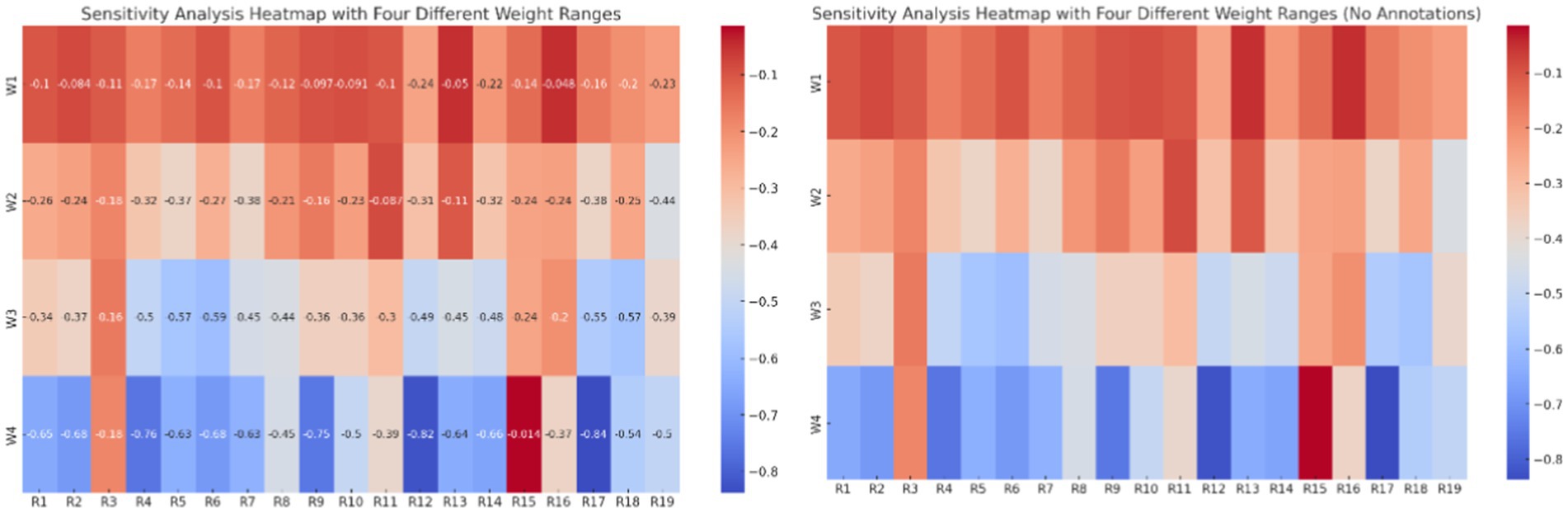
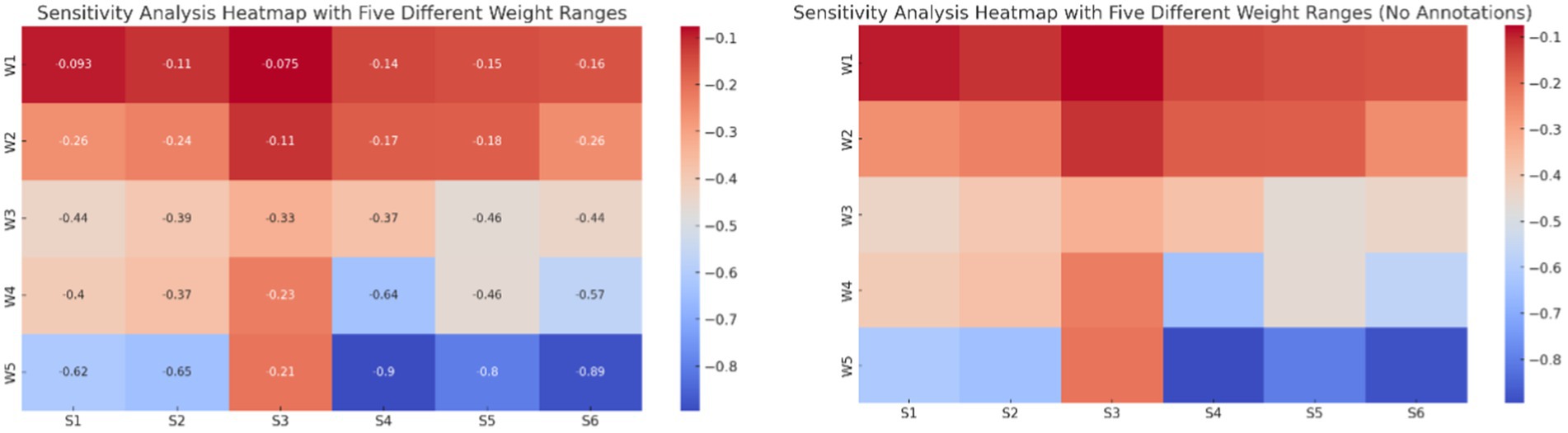
The sensitivity analysis heatmap (Figure 1) illustrates the impact of different weight ranges on 19 identified risks (R1 to R19). Each weight range corresponds to a scenario where one weight is given more emphasis, and the others are adjusted accordingly. This allows us to observe how sensitive each risk is to changes in the weight distribution. The color gradient, from red (higher values) to blue (lower values), visually represents the impact of each weighting scenario on the risks.
From the heatmap, it is evident that certain risks exhibit significant sensitivity under specific weight scenarios. For example, risks like R4, R5, R6, and R16 show noticeable variations in their values across the different weight ranges, indicating that these risks are highly sensitive to changes in weight distribution. These risks might require more attention in scenarios where certain risk factors are prioritized, as their outcomes could vary greatly depending on the specific conditions. On the other hand, risks like R1, R2, and R3 appear less sensitive, with their values remaining relatively stable across the different weight ranges. This stability suggests that these risks are more robust to changes in weight distribution. Overall, this analysis helps identify which risks are more likely to be influenced by prioritization changes and which remain stable regardless of the weighting. Decision-makers can use this information to allocate resources more effectively, focusing on the risks that are most sensitive to the prioritized factors. This approach allows for a more targeted risk management strategy, ensuring that the most volatile risks are closely monitored and mitigated under different scenarios.
The sensitivity analysis heatmap (Figure 4) presented shows the impact of different weight scenarios on six risk mitigation strategies (S1 to S6). Each weight scenario corresponds to a situation where one of the weights is given an 80% emphasis, while the remaining 20% is equally distributed among the other weight factors. This approach simulates the influence of prioritizing one risk mitigation strategy over the others, allowing us to observe how each strategy responds when it is more heavily weighted. From the heatmap, we can see varying degrees of sensitivity across the different strategies. Strategies that show higher values under certain weight scenarios are more influenced when that particular weight is prioritized. For example, if S1 displays a higher value under the W1 scenario, it suggests that this strategy is most effective when W1 is emphasized. Conversely, strategies with lower values under specific weight scenarios indicate less sensitivity to those conditions, implying that these strategies are more robust or less dependent on that particular emphasis. This analysis helps in identifying which risk mitigation strategies are most effective under different prioritization conditions and can guide decision-makers in selecting the appropriate strategy based on the relative importance of different risk factors.
5 Discussion
The three highest-risk factors identified in the Gray ANP method for lithium battery production are the Environmental Pollution Risk, Support Program Deficiency Risk, and Improper Waste Management Risk. The Environmental Pollution Risk carries the highest definite weight of 0.152519385, indicating its critical importance. This risk is paramount due to the significant potential for environmental degradation during lithium battery production, involving hazardous materials that can cause long-term ecological harm if not properly managed. The substantial difference in weight between this risk and others underscores its dominance and the pressing need for effective mitigation strategies to safeguard environmental health. The environmental pollution risks associated with lithium battery production present significant challenges to the sustainable supply chain within the lithium-ion battery circular economy, particularly in the automotive industry. The critical concern lies in the environmental and social impacts resulting from the extraction, processing, and disposal of materials used in lithium-ion batteries, including lithium, cobalt, and nickel. These impacts threaten the long-term sustainability of supply chains as the demand for electric vehicles continues to surge. For instance, studies have highlighted the substantial environmental burdens of large-scale lithium-ion battery production, emphasizing that scaling up production could exacerbate these issues unless supply chains are optimized for sustainability. Moreover, the integration of circular economy principles, such as recycling and reuse, is vital to mitigating these environmental risks. These principles not only aim to reduce the environmental footprint but also to secure material supply by recovering valuable metals from spent batteries (59, 63). Furthermore, research emphasizes the importance of robust regulatory frameworks and circular business models to ensure the sustainable recycling of lithium-ion batteries. The European Union’s Battery Regulation, for example, aims to ensure the sustainability of batteries through stringent recycling targets, which could globally influence supply chains if successfully implemented (54, 57). In addition, the circularity of lithium-ion battery materials has the potential to alleviate some of the critical environmental impacts, with recycling processes recovering significant percentages of metals like cobalt, nickel, and lithium. These processes, however, must be optimized to avoid shifting the environmental burden to other stages of the supply chain (57, 59). The ongoing development of closed-loop recycling methods, which focus on the direct regeneration of battery cathodes, offers promising advancements in reducing both environmental impact and supply chain vulnerabilities (45).
The Support Program Deficiency Risk, with a definite weight of 0.145213174, is the second most significant. This risk highlights the essential role of adequate support programs in the successful implementation of sustainable practices within the supply chain. The high weight assigned to this risk reflects its potential to exacerbate other risks, particularly those related to resource management and regulatory compliance, if appropriate support systems are not in place. The deficiency in support programs presents a significant risk to the sustainable supply chain in the lithium-ion battery circular economy within the automotive industry. The integration of circular economy principles is heavily reliant on robust governmental and institutional support, including policies, economic incentives, and regulatory frameworks. Studies indicate that inadequate support programs can lead to insufficient recycling rates, higher costs, and logistical challenges, thereby undermining the sustainability of the supply chain. For instance, a study highlighted that inefficient government policies and lack of safety standards are among the most significant barriers to the successful implementation of circular economy strategies in the electric vehicle battery sector (18). Similarly, inadequate policy frameworks were identified as a major obstacle in achieving the economic feasibility of lithium-ion battery recycling, which is critical for the circular economy model (10). Moreover, the lack of comprehensive support programs hampers the ability to establish resilient closed-loop supply chains, which are essential for reducing environmental impacts and securing material supplies. Research emphasizes the need for robust support mechanisms, such as economic incentives and regulations, to drive the circular economy in the automotive sector, ensuring that recycling and reuse processes are both economically viable and environmentally sustainable (46). Additionally, the success of circular business models is contingent upon the alignment of supply chain stakeholders and the presence of adequate support programs to facilitate collaboration and innovation (8). Thus, addressing the support program deficiency is critical to advancing sustainable supply chains in the lithium-ion battery circular economy, particularly within the automotive industry.
Lastly, the Improper Waste Management Risk, with a definite weight of 0.137210383, is the third most critical. This risk emphasizes the importance of handling waste responsibly in lithium battery production. Improper waste management can lead to severe environmental contamination and can result in financial and reputational damage for companies. Although slightly lower in weight compared to the top two risks, its close proximity in value underscores its significance. The interconnected nature of these risks highlights the complex challenges in maintaining both environmental and operational sustainability in lithium battery production. Improper waste management poses a significant risk to the sustainable supply chain in the lithium-ion battery circular economy within the automotive industry. As electric vehicles (EVs) become more prevalent, the improper disposal of spent lithium-ion batteries threatens both environmental safety and the efficiency of recycling processes critical to the circular economy. Studies have shown that without proper waste management, significant amounts of valuable materials like lithium, cobalt, and nickel are lost, reducing the efficiency of recycling and increasing the demand for raw material extraction. This inefficiency disrupts the sustainability of supply chains, leading to higher costs and environmental degradation. For example, research highlights that improper waste management leads to increased emissions and resource inefficiencies, which could be mitigated through improved recycling technologies and stricter regulatory frameworks (10). Moreover, the sustainability of the lithium-ion battery supply chain is heavily dependent on the adoption of circular economy practices, which require effective waste management to close the loop on material usage. Inefficiencies in current waste management practices, such as the lack of robust recycling infrastructure and inadequate policy enforcement, exacerbate the environmental risks associated with the end-of-life phase of lithium-ion batteries. Studies have called for the integration of advanced recycling techniques and the development of comprehensive waste management strategies to ensure the sustainability of the supply chain. These strategies are essential for reducing the environmental footprint of lithium-ion batteries and enhancing the resilience of the supply chain (45, 47). Effective waste management is therefore crucial not only for environmental protection but also for maintaining a sustainable and efficient lithium-ion battery supply chain in the automotive industry.
In the context of zero-sum game theory, the selection of optimal strategies often hinges on the careful consideration of lower and upper bounds, which represent the range of possible outcomes under risk. These bounds are crucial for decision-makers who must account for both the worst-case and best-case scenarios. Specifically, the lower bound indicates the minimum value that a strategy can yield, reflecting the worst possible outcome, while the upper bound represents the maximum value, highlighting the best possible outcome under optimal conditions. The strategy that best balances these bounds is typically considered the most robust, as it minimizes potential losses while maximizing potential gains. Comparative analysis of different strategies under this framework reveals that Strategy S3, with a lower bound of −0.6667 and an upper bound of −0.2222, emerges as the most optimal choice. This strategy outperforms others, particularly Strategies S4 and S6, which have lower bounds of −1.0000. The significantly lower bound of these strategies suggests a higher risk in worst-case scenarios, making them fewer desirable choices when the objective is to mitigate risk. The advantage of Strategy S3 lies in its ability to offer the least loss in the worst case while also having the potential to achieve relatively higher gains in the best case. This dual benefit underscores the importance of balance in strategic decision-making, particularly in uncertain environments where the outcomes can vary widely. In conclusion, Strategy S3’s balance between minimizing potential losses and maximizing potential gains makes it a robust and optimal choice in the context of zero-sum game theory. The academic consensus reinforces the importance of selecting strategies that offer stability in the face of risk, supporting the prudence of choosing Strategy S3 over less balanced alternatives.
6 Implications of the study
In order to effectively manage the risks identified in the sustainable supply chain of the circular economy of lithium-ion batteries in the automotive industry, some practical and managerial suggestions are presented. First, strengthening support programs and government policies through strict regulation and providing economic incentives for battery recycling and reuse can help reduce the risk of insufficient program support. Second, improving waste management through the development of advanced recycling infrastructure and the implementation of strict standards for the safe collection, transport, and disposal of batteries can reduce the risks associated with improper waste management. Also, creating extensive collaborations between different parts of the supply chain and encouraging the use of new recycling technologies can help reduce environmental impacts and increase the sustainability of the supply chain. Applying a comprehensive approach to managing these risks can lead to improving resource efficiency, reducing costs, and reducing environmental pollution.
7 Conclusion
The importance of this research lies in its focus on optimizing decision-making in highly uncertain environments, such as those governed by zero-sum game theory, and its practical application to the sustainable supply chain of lithium-ion batteries in the automotive industry. As the demand for electric vehicles continues to rise, the efficient management of risks associated with battery production, recycling, and waste management becomes increasingly critical. This study not only advances theoretical understanding by identifying optimal strategies that balance potential losses and gains but also offers actionable insights that can help industry stakeholders navigate the complex challenges of sustainability. By addressing these issues, the research contributes to the development of more resilient and environmentally responsible supply chains, which are essential for the long-term success of the automotive industry and the broader transition to a sustainable, circular economy. The findings of this study highlight the importance of strategic decision-making in the context of zero-sum game theory, where the optimal strategy is determined by a careful balance between lower and upper bounds. Strategy S3, with its relatively higher lower bound of −0.6667 and upper bound of −0.2222, emerges as the most robust choice. This strategy not only minimizes potential losses in the worst-case scenario but also maximizes potential gains in the best-case scenario. The comparative analysis demonstrates that strategies with lower bounds, such as S4 and S6, pose a higher risk in worst-case scenarios, making them less desirable for risk-averse decision-makers. The advantage of Strategy S3 lies in its ability to provide stability and potential gains, offering a balanced approach that is essential in uncertain environments. This study reinforces the significance of selecting strategies that balance risk and reward, particularly in scenarios where outcomes can vary widely.
The practical implications of this research are profound, especially in the sustainable supply chain management of lithium-ion batteries within the automotive industry. To mitigate the risks identified, it is essential to strengthen support programs and government policies, particularly through stringent regulations and economic incentives that promote battery recycling and reuse. Additionally, improving waste management practices by developing advanced recycling infrastructure and implementing strict standards for safe battery handling can significantly reduce environmental risks. Encouraging collaboration across the supply chain and adopting new recycling technologies are also crucial for enhancing sustainability. These managerial suggestions, grounded in the study’s findings, provide a comprehensive approach to managing risks, ultimately leading to more efficient resource use, cost reductions, and a reduction in environmental pollution. One of the significant limitations of this research is the scarcity of resources and expertise available in the context of developing countries, particularly regarding the sustainable supply chain management of lithium-ion batteries. In these regions, the lack of robust data and limited access to advanced recycling technologies pose challenges to the practical implementation of the study’s recommendations. Additionally, the shortage of skilled professionals and experts in sustainable practices further hinders the development and optimization of effective strategies. For future research, the application of hesitant fuzzy sets and interval-valued hesitant fuzzy sets is proposed within the game theory matrix to address the complexities of decision-making under uncertainty. These advanced fuzzy set approaches like Probabilistic Hesitant Fuzzy allow for a more nuanced representation of uncertainty and hesitation, which are inherent in real-world scenarios, particularly in contexts where precise data is scarce or decision-makers face conflicting information.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
Ethical approval was not required for the studies involving humans because there is no factor for personal information and the information was asked by the questionnaire with the consent of the respondents and the confidentiality of their personal information. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
MA: Writing – original draft, Writing – review & editing. MG: Methodology, Validation, Writing – review & editing. BH: Writing – review & editing. SJ: Writing – original draft. SR: Methodology, Supervision, Writing – original draft, Writing – review & editing. MK: Software, Writing – original draft. ST: Funding acquisition, Writing – original draft, Writing – review & editing. NS: Writing – review & editing. EB: Formal analysis, Project administration, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Chen, Z, Yildizbasi, A, Wang, Y, and Sarkis, J. Safety in lithium-ion battery circularity activities: a framework and evaluation methodology. Resour Conserv Recycl. (2023) 193:106962. doi: 10.1016/j.resconrec.2023.106962
2. Wang, D, Sun, J, and Wei, C. Influencing factor analysis and enterprise evaluation of lithium-ion battery recycling based on improved DEMATEL method. J Intell Fuzzy Syst. (2024) 46:6149–69. doi: 10.3233/JIFS-224124
3. Bridge, G, and Faigen, E. Towards the lithium-ion battery production network: thinking beyond mineral supply chains. Energy Res Soc Sci. (2022) 89:102659. doi: 10.1016/j.erss.2022.102659
4. Parthasarathy, TN, Narayanamoorthy, S, Devi, NSK, Pamucar, D, Simic, V, and Kang, D. An idiosyncratic interval valued picture q-rung Orthopair fuzzy decision-making model for electric vehicle battery charging technology selection. International Journal of Fuzzy Systems. (2024) 26:1–16. doi: 10.1007/s40815-024-01683-6
5. Virmani, N, Agarwal, V, Karuppiah, K, Agarwal, S, Raut, RD, and Paul, SK. Mitigating barriers to adopting electric vehicles in an emerging economy context. J Clean Prod. (2023) 414:137557. doi: 10.1016/j.jclepro.2023.137557
6. Zkik, K, Belhadi, A, Rehman Khan, SA, Kamble, SS, Oudani, M, and Touriki, FE. Exploration of barriers and enablers of blockchain adoption for sustainable performance: implications for e-enabled agriculture supply chains. Int J Log Res Appl. (2023) 26:1498–535. doi: 10.1080/13675567.2022.2088707
7. Collis, GE, Dai, Q, Loh, JS, Lipson, A, Gaines, L, Zhao, Y, et al. Closing the loop on LIB waste: a comparison of the current challenges and opportunities for the US and Australia towards a sustainable energy future. Recycling. (2023) 8:78. doi: 10.3390/recycling8050078
8. Madrid, JA . Circular economy in automotive manufacturing: recycling and sustainability. Int J Adv Res Sci Commun Technol. (2023) 3:814–5. doi: 10.48175/IJARSCT-11964
9. Baars, J, Domenech, T, Bleischwitz, R, Melin, HE, and Heidrich, O. Circular economy strategies for electric vehicle batteries reduce reliance on raw materials. Nat Sustain. (2021) 4:71–9. doi: 10.1038/s41893-020-00607-0
10. Islam, MT, and Iyer-Raniga, U. Lithium-ion battery recycling in the circular economy: a review. Recycling. (2022) 2022:33. doi: 10.3390/recycling7030033
11. Kurz, L, Forster, S, Wörner, R, and Reichert, F. Environmental impacts of specific Recyclates in European battery regulatory-compliant Lithium-ion cell manufacturing. Sustain For. (2022) 15:103. doi: 10.3390/su15010103
12. Cordisco, A, Melloni, R, and Botti, L. Sustainable circular economy for the integration of disadvantaged people: a preliminary study on the reuse of Lithium-ion batteries. Sustain For. (2022) 14:8158. doi: 10.3390/su14138158
13. Albertsen, L, Richter, JL, Peck, P, Dalhammar, C, and Plepys, A. Circular business models for electric vehicle lithium-ion batteries: an analysis of current practices of vehicle manufacturers and policies in the EU. Resour Conserv Recycl. (2021) 172:105658. doi: 10.1016/j.resconrec.2021.105658
14. Alessia, A, Alessandro, B, Maria, VG, Carlos, VA, and Francesca, B. Challenges for sustainable lithium supply: a critical review. J Clean Prod. (2021) 300:126954. doi: 10.1016/j.jclepro.2021.126954
15. Lahane, S, and Kant, R. Evaluating the circular supply chain implementation barriers using Pythagorean fuzzy AHP-DEMATEL approach. Clean Logist Supply Chain. (2021) 2:100014. doi: 10.1016/j.clscn.2021.100014
16. Lahane, S, and Kant, R. Evaluation and ranking of solutions to mitigate circular supply chain risks. Sustain Prod Consum. (2021) 27:753–73. doi: 10.1016/j.spc.2021.01.034
17. Heath, GA, Ravikumar, D, Hansen, B, and Kupets, E. A critical review of the circular economy for lithium-ion batteries and photovoltaic modules–status, challenges, and opportunities. J Air Waste Manage Assoc. (2022) 72:478–539. doi: 10.1080/10962247.2022.2068878
18. Sopha, BM, Purnamasari, DM, and Ma’mun, S. Barriers and enablers of circular economy implementation for electric-vehicle batteries: from systematic literature review to conceptual framework. Sustain For. (2022) 14:6359. doi: 10.3390/su14106359
19. Doose, S, Mayer, JK, Michalowski, P, and Kwade, A. Challenges in ecofriendly battery recycling and closed material cycles: a perspective on future lithium battery generations. Metals. (2021) 11:291. doi: 10.3390/met11020291
20. Azadnia, AH, Onofrei, G, and Ghadimi, P. Electric vehicles lithium-ion batteries reverse logistics implementation barriers analysis: a TISM-MICMAC approach. Resour Conserv Recycl. (2021) 174:105751. doi: 10.1016/j.resconrec.2021.105751
21. Bag, S, Sahu, AK, Kilbourn, P, Pisa, N, Dhamija, P, and Sahu, AK. Modeling barriers of digital manufacturing in a circular economy for enhancing sustainability. Int J Product Perform Manag. (2022) 71:833–69. doi: 10.1108/IJPPM-12-2020-0637
22. Kayikci, Y, Kazancoglu, Y, Lafci, C, and Gozacan, N. Exploring barriers to smart and sustainable circular economy: the case of an automotive eco-cluster. J Clean Prod. (2021) 314:127920. doi: 10.1016/j.jclepro.2021.127920
23. Devi, NSK, Narayanamoorthy, S, Parthasarathy, TN, Thilagasree, CS, Pamucar, D, Simic, V, et al. An integrated bipolar picture fuzzy decision driven system to scrutinize foodwaste treatment technology through assorted factor analysis. Comput Model Eng Sci. (2024) 140:2665–87. doi: 10.32604/cmes.2024.050954
24. Karkehabadi, A, Homayoun, H, and Sasan, A (2024). SMOOT: saliency guided mask optimized online training. In 2024 IEEE 17th Dallas circuits and systems conference (DCAS) (pp. 1–6). IEEE.
25. Parthasarathy, TN, Narayanamoorthy, S, Thilagasree, CS, Marimuthu, PR, Salahshour, S, Ferrara, M, et al. An enhanced fuzzy IDOCRIW-COCOSO multi-attribute decision making algorithm for decisive electric vehicle battery recycling method. Results Eng. (2024) 22:102272. doi: 10.1016/j.rineng.2024.102272
26. Sabetahd, R, Mousavi Ghasemi, SA, Vafaei Poursorkhabi, R, Mohammadzadeh, A, and Zandi, Y. Response attenuation of a structure equipped with ATMD under seismic excitations using methods of online simple adaptive controller and online adaptive Type-2 neural-fuzzy controller. Comput Intell Neurosci. (2022) 2022:5832043. doi: 10.1155/2022/5832043
27. Parthasarathy, TN, Narayanamoorthy, S, Sulaiman, R, Elamir, AM, Ahmadian, A, and Kang, D. An end-to-end categorizing strategy for green energy sources: picture q-rung orthopair fuzzy exprom-ii: Mada approach. Sustain Energy Technol Assess. (2024) 63:103658. doi: 10.1016/j.seta.2024.103658
28. Karkehabadi, A, Homayoun, H, and Sasan, A (2024). FFCL: forward-forward net with cortical loops, training and inference on edge without Backpropogation. In proceedings of the Great Lakes symposium on VLSI 2024 (pp. 626-632).
29. Karuppiah, K, and Sankaranarayanan, B. An integrated multi-criteria decision-making approach for evaluating e-waste mitigation strategies. Appl Soft Comput. (2023) 144:110420. doi: 10.1016/j.asoc.2023.110420
30. Li, Y, Zhao, G, Wu, P, and Qiu, J. An integrated gray DEMATEL and ANP method for evaluating the green mining performance of underground gold mines. Sustain For. (2022) 14:6812. doi: 10.3390/su14116812
31. Narayanamoorthy, S, Parthasarathy, TN, Pragathi, S, Shanmugam, P, Baleanu, D, Ahmadian, A, et al. The novel augmented Fermatean MCDM perspectives for identifying the optimal renewable energy power plant location. Sustain Energy Technol Assess. (2022) 53:102488. doi: 10.1016/j.seta.2022.102488
32. Chhimwal, M, Agrawal, S, and Kumar, G. Measuring circular supply chain risk: a Bayesian network methodology. Sustain For. (2021) 13:8448. doi: 10.3390/su13158448
33. Kazemian, I, Torabi, SA, Zobel, CW, Li, Y, and Baghersad, M. A multi-attribute supply chain network resilience assessment framework based on SNA-inspired indicators. Oper Res. (2022) 22:1853–83. doi: 10.1007/s12351-021-00644-3
34. Chaudhary, K, Chaudhary, G, and Khari, M. Applying game theory models for risk Management in Supply Chain Networks. Full Length Article. (2023) 10:42. doi: 10.54216/AJBOR.100104
35. Fetanat, A, Tayebi, M, and Shafipour, G. Management of waste electrical and electronic equipment based on circular economy strategies: navigating a sustainability transition toward waste management sector. Clean Techn Environ Policy. (2021) 23:343–69. doi: 10.1007/s10098-020-02006-7
36. Yazdi, M, Nedjati, A, Zarei, E, and Abbassi, R. A novel extension of DEMATEL approach for probabilistic safety analysis in process systems. Saf Sci. (2020) 121:119–36. doi: 10.1016/j.ssci.2019.09.006
37. Alizadeh-Basban, N, and Taleizadeh, AA. A hybrid circular economy-game theoretical approach in a dual-channel green supply chain considering sale’s effort, delivery time, and hybrid remanufacturing. J Clean Prod. (2020) 250:119521. doi: 10.1016/j.jclepro.2019.119521
38. Bakhshi, M, Karkehabadi, A, and Razavian, SB (2024). Revolutionizing medical diagnosis with novel teaching-learning-based optimization. In 2024 international conference on emerging smart computing and informatics (ESCI) (pp. 1–6). IEEE.
39. Karkehabadi, A, Bakhshi, M, and Razavian, SB (2024). Optimizing underwater IoT routing with multi-criteria decision making and uncertainty weights. arXiv preprint arXiv:2405.11513.
40. Mohammadzadeh, M, Anisi, A, and Sheikholeslami, M. Multi-objective optimization and thermodynamic assessment of a solar unit with a novel tube shape equipped with a helical tape. Appl Therm Eng. (2024) 254:123851. doi: 10.1016/j.applthermaleng.2024.123851
41. Singh, S, Kumar, S, and Kumar, A. Identifying disruptions by COVID-19 and devising strategies to build robust supply chain–a case study illustration of India's energy storage sector. Benchmarking Int J. (2023). doi: 10.1108/BIJ-06-2023-0405
42. Guan, Y, Liu, Z, Du, Y, and Xu, D. Evaluating batteries for renewable energy storage: a hybrid MCDM framework based on combined objective weights and uncertainty-preserved COPRAS. J Renew Sustain Energy. (2023) 15. doi: 10.1063/5.0153007
43. Kumar, NM, and Chopra, SS. Leveraging blockchain and smart contract technologies to overcome circular economy implementation challenges. Sustain For. (2022) 14:9492. doi: 10.3390/su14159492
44. Alimohammadlou, M, and Alinejad, S. Challenges of blockchain implementation in SMEs’ supply chains: an integrated IT2F-BWM and IT2F-DEMATEL method. Electron Commer Res. (2023):1–43. doi: 10.1007/s10660-023-09696-3
45. Yang, T, Luo, D, Yu, A, and Chen, Z. Enabling future closed-loop recycling of spent lithium-ion batteries: direct cathode regeneration. Adv Mater. (2023) 35:2203218. doi: 10.1002/adma.202203218
46. Lotfi, R, Nazarpour, H, Gharehbaghi, A, Sarkhosh, SMH, and Khanbaba, A. Viable closed-loop supply chain network by considering robustness and risk as a circular economy. Environ Sci Pollut Res. (2022) 29:70285–304. doi: 10.1007/s11356-022-20713-0
47. Meegoda, JN, Malladi, S, and Zayas, IC. End-of-life management of electric vehicle lithium-ion batteries in the United States. Clean Technol. (2022) 4:1162–74. doi: 10.3390/cleantechnol4040071
48. Hu, X, Wang, C, Lim, MK, Chen, W-Q, Teng, L, Wang, P, et al. Critical systemic risk sources in global lithium-ion battery supply networks: static and dynamic network perspectives. Renew Sust Energ Rev. (2023) 173:113083. doi: 10.1016/j.rser.2022.113083
49. Karuppiah, K, Sankaranarayanan, B, Venkatesh, VG, Ali, SM, and Shi, Y. A causal sustainable evaluation of barriers to remanufacturing: An emerging economy perspective. Environ Dev Sustain. (2023):1–38. doi: 10.1007/s10668-023-03779-9
50. Miao, Y, Liu, L, Xu, K, and Li, J. High concentration from resources to market heightens risk for power lithium-ion battery supply chains globally. Environ Sci Pollut Res. (2023) 30:65558–71. doi: 10.1007/s11356-023-27035-9
51. Öztürk, C, Chen, Z, and Yildizbasi, A. The Lithium-ion battery supply chain In: J Sarkis , editor. The Palgrave handbook of supply chain management. Cham: Palgrave Macmillan (2024)
52. Anisi, A, Kremer, GO, and Olafsson, S. Insights from dynamic pricing scenarios for multiple-generation product lines with an agent-based model using text mining and sentiment analysis. Int J Adv Prod Res. (2024) 1:24–45. doi: 10.62743/uad.7352
53. da Silva Lima, L, Cocquyt, L, Mancini, L, Cadena, E, and Dewulf, J. The role of raw materials to achieve the sustainable development goals: tracing the risks and positive contributions of cobalt along the lithium ion battery supply chain. J Ind Ecol. (2023) 27:777–94. doi: 10.1111/jiec.13336
54. Bai, C, Sarkis, J, Yin, F, and Dou, Y. Sustainable supply chain flexibility and its relationship to circular economy-target performance. Int J Prod Res. (2020) 58:5893–910. doi: 10.1080/00207543.2019.1661532
55. Bhalaji, RKA, Bathrinath, S, and Koppiahraj, K (2023). A best worst method to evaluate the risks in the fireworks industry: implications for risk mitigation. In AIP conference proceedings (Vol. 2904, No. 1). AIP Publishing.
56. Hua, Y, Zhou, S, Huang, Y, Liu, X, Ling, H, Zhou, X, et al. Sustainable value chain of retired lithium-ion batteries for electric vehicles. J Power Sources. (2020) 478:228753. doi: 10.1016/j.jpowsour.2020.228753
57. Omair, M, Alkahtani, M, Ayaz, K, Hussain, G, and Buhl, J. Supply chain modelling of the automobile multi-stage production considering circular economy by waste management using recycling and reworking operations. Sustain For. (2022) 14:15428. doi: 10.3390/su142215428
58. Ponnambalam, SG, Sankaranarayanan, B, Karuppiah, K, Thinakaran, S, Chandravelu, P, and Lam, HL. Analysing the barriers involved in recycling the textile waste in India using fuzzy DEMATEL. Sustain For. (2023) 15:8864. doi: 10.3390/su15118864
59. Sadeghi, M, Mahmoudi, A, Deng, X, and Luo, X. Prioritizing requirements for implementing blockchain technology in construction supply chain based on circular economy: fuzzy ordinal priority approach. Int J Environ Sci Technol. (2023) 20:4991–5012. doi: 10.1007/s13762-022-04298-2
60. Sheth, RP, Ranawat, NS, Chakraborty, A, Mishra, RP, and Khandelwal, M. The lithium-ion battery recycling process from a circular economy perspective—a review and future directions. Energies. (2023) 16:3228. doi: 10.3390/en16073228
61. Hua, Y, Zhou, S, Huang, Y, Liu, X, Ling, H, Zhou, X, et al. Sustainable value chain of retired lithium-ion batteries for electric vehicles. J Power Sources (2020) 478:228753.
62. Cui, H, Songwei, D, Jiayi, H, Mengqi, C, Bodong, H, Jingshun, Z, et al. “A hybrid MCDM model with Monte Carlo simulation to improve decision-making stability and reliability.” Information Sciences (2023) 647:119439.
Keywords: risk management, lithium-ion battery, MCDM, circular economy, sustainable supply chain, optimization, zero-sum game theory
Citation: Afroozi MA, Gramifar M, Hazratifar B, Jowkar S, Razavian SB, Keshvari MM, Tabatabaei SA, Sazegar N and Bojnourdi EZ (2024) Risk assessment in lithium-ion battery circular economy in sustainable supply chain in automotive industry using gray degree of possibility in game theory and MCDM. Front. Appl. Math. Stat. 10:1362200. doi: 10.3389/fams.2024.1362200
Edited by:
Indranil SenGupta, Hunter College (CUNY), United StatesReviewed by:
Karuppiah Koppiahraj, Saveetha University, IndiaSamayan Narayanamoorthy, Bharathiar University, India
Copyright © 2024 Afroozi, Gramifar, Hazratifar, Jowkar, Razavian, Keshvari, Tabatabaei, Sazegar and Bojnourdi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sayed Alireza Tabatabaei, c2F5ZWRhbGlyZXphLnRhYmF0YWJhZWlAc3R1ZC50dS1kYXJtc3RhZHQuZGU=
 Mohsen Alizadeh Afroozi1
Mohsen Alizadeh Afroozi1 Seyed Behnam Razavian
Seyed Behnam Razavian Sayed Alireza Tabatabaei
Sayed Alireza Tabatabaei