Analysis of new mathematical model for rabies through wavelet method

Rabies is a fatal zoonotic disease caused by a virus, primarily spread through bites or saliva. Dogs are the main source of human infections worldwide. This article introduces a new mathematical model using fractional differential equations to analyze rabies transmission dynamics. The model consists of four compartments: susceptible and infected populations of both humans and animals, forming a system of fractional differential equations (SOFDEs). The modified Hermite wavelet collocation method (HWCM) is used to solve these equations by converting them into a non-linear algebraic system. Newton-Raphson's approach determines the unknown Hermite coefficients, and the results are compared with ND Solver and RK4 methods. Visual and numerical analysis confirms the proposed method's superior accuracy and effectiveness.

1 Introduction

Dogs are the primary carrier of most human cases of rabies worldwide. Rabies is an acute and deadly zoonotic virus illness that primarily affects all species of mammals and other animals [1]. Animal saliva is the primary reservoir for the rabies virus, although it can also be detected in tears, semen, urine, and other bodily fluids [2]. Once clinical symptoms appear, there is no doubt about the virus's death rate since it affects the central nervous system and causes cerebral dysfunction in the brain [3]. Furthermore, with a case fatality rate that is almost 100%, rabies has the highest of all traditional infectious diseases. Humans contract rabies mostly from dogs, and the disease is primarily spread by dog bites or scratches, particularly from infected dogs [4]. Direct contact with a wound or mucosal surface (such as the nose, mouth, or eye) infected with a rabid dog's saliva can also spread rabies. Rabies can be transmitted by aerosols or tissue and organ transplantation in humans and other species. Early rabies symptoms include fever with discomfort, tingling, sore throat, hypersalivation, cough, vomiting, nausea, and burning sensation or prickling (paraesthesia) at the site of an animal bite. These symptoms are similar to the flu [5]. Subsequently, when the virus spreads throughout the central nervous system, a deadly and progressive inflammation of the brain and spinal cord occurs, leading to paralysis and hyperactivity. Most rabies cases in humans and dogs occur during incubation, the interval between exposure to the virus and the onset of symptoms. However, this interval can vary, ranging from 1 week to a year, contingent on variables such as the site of virus entry and viral load [6]. The incubation period may extend to 7 years in severe circumstances [7, 8].

Except in Antarctica and the Arctic, rabies is still a very deadly disease that affects practically every country in the world to varied degrees. The natural seclusion of islands such as the Seychelles, Australia, New Zealand, and Mauritius is beneficial. A teenage kid in Wisconsin managed to survive rabies in 2004, although the reasons for this positive outcome are still unknown. Every year, rabies causes between 50,000 and 60,000 deaths, as well as 1.74 million DALYs (disability-adjusted life years) to be lost [9, 10]. Over 99% of these fatalities take place in underdeveloped nations where the disease is widespread in the population of domestic dogs. The World Health Organization (WHO) classifies rabies as a “100% vaccine-preventable disease” [11]. Caroll et al. recognized the three most popular rabies control methods as population control, dog mass vaccination, and epidemiological surveillance [12]. Immediate wound cleaning with soap and water following contact with a suspected rabid animal is one of the additional preventive strategies against rabies [13]. There are vaccinations for treating rabies that can be given either before or after exposure and are developed from different types of tissue culture or chicken embryos. Cultural, societal, and economic aspects make it difficult to control the disease, even with annual treatment and control costs exceeding 500 million [14]. Due to the extensive international mobility of animals and people, it seems inevitable that rabies will continue to be brought into nations that have never before experienced the disease [15].

Studying the mathematical model of rabies is crucial for several reasons:

Understanding disease dynamics: Mathematical models help researchers understand how rabies spreads through populations, including factors such as transmission rates, infection cycles, and the impact of various interventions. This understanding is essential for predicting outbreaks and planning effective responses. Optimizing control strategies: Models can simulate different control strategies, such as vaccination campaigns, quarantine measures, or changes in wildlife management. By analyzing these simulations, public health officials can determine the most cost-effective and efficient approaches to control and eventually eliminate rabies. Resource Allocation: Mathematical models can help allocate resources effectively. For instance, they can predict the number of vaccines needed in different regions and times, ensuring that limited resources are used where they are most needed to prevent outbreaks. Predicting outbreaks: Models can forecast the likelihood of future rabies outbreaks based on current data and trends. This predictive capability is critical for preparing and implementing preventive measures before an outbreak occurs. Evaluating intervention impact: By using models to simulate the impact of various interventions, researchers can assess their effectiveness in reducing the incidence of rabies. This helps fine-tune strategies and make data-driven decisions to improve public health outcomes. Informing policy decisions: Policymakers can use insights from mathematical models to make informed decisions about rabies control policies, such as vaccination requirements for pets or wildlife management practices. Educational and training tools: Mathematical models can serve as educational tools for training public health professionals, veterinarians, and researchers, helping them to understand the complexities of disease transmission and control. Addressing emerging challenges: As new challenges arise, such as changes in animal populations or human behavior, mathematical models can be adapted to address these issues and provide updated recommendations for rabies control.

Mathematical models are invaluable for enhancing our understanding of rabies and improving our ability to control and prevent this potentially fatal disease.

Fractional calculus is a branch of mathematical analysis that extends the concept of integer-order differentiation and integration to non-integer (fractional or real) orders. Unlike classical calculus, which deals with derivatives and integrals of integer orders, fractional calculus provides a more generalized and flexible framework to describe complex dynamical systems with memory effects, hereditary properties, and anomalous diffusion. The origins of fractional calculus date back to the 17th century when Leibniz and L'Hospital first discussed the possibility of taking derivatives of non-integer orders. However, significant developments occurred only in the 19th and 20th centuries with the formalization of fractional derivatives and integrals through various definitions, including the Riemann-Liouville, Caputo, and Grunwald-Letnikov approaches. Fractional calculus has gained widespread applications in diverse scientific and engineering disciplines due to its ability to describe real-world phenomena more accurately than classical integer-order models. Some key reasons for its importance include the following: Memory and non-local effects: Many natural and engineering systems exhibit memory-dependent behaviors, where past states influence the current dynamics. Fractional derivatives inherently account for such memory effects. Generalization of classical models: Fractional differential equations are a natural extension of traditional differential equations, offering greater flexibility in modeling complex systems. Anomalous diffusion and power-law behavior: Many physical and biological processes, such as viscoelasticity, fluid mechanics, and epidemiology, exhibit anomalous diffusion, which is best captured using fractional-order models.

Joseph Fourier's findings in the early 1800s state that sines and cosines could be used to create a variety of functions revolutionized mathematical analysis. As a result of this finding, techniques for approximating extra functions by superimposing distinct functions were developed. Sines and cosines might be a better choice for estimating noisy signals, even if necessary to create Fourier analysis. For this reason, mathematicians have been looking for more efficient methods of approximating these signals. Note that these functions have limitless extensions because they are non-local. As a result, they are unable to represent sharp spikes accurately. Wavelet theory is one intriguing and recent advancement in mathematics. Wavelet numerical methods have become increasingly popular in various fields due to their versatility and effectiveness in handling complex problems. Here is an overview of the scope and applications of wavelet numerical methods: Wavelets decompose signals into different frequency components, which can be useful for noise reduction and signal reconstruction. Techniques such as JPEG2000 use wavelets for image compression, offering better quality and compression ratios than traditional methods. Wavelets help in removing noise from images while preserving important features and edges. Wavelet methods can solve PDEs by providing efficient and adaptive representations of solutions. This is particularly useful in problems involving irregular domains and helps create adaptive meshes that refine only where necessary, improving computational efficiency and accuracy. They are used to construct mathematical models requiring multi-resolution analysis, providing a powerful tool for studying complex phenomena across scales. Wavelets are used in financial modeling to analyze price movements and volatility, helping assess and predict risk. With this, wavelet numerical methods are notable for their ability to handle data with varying degrees of smoothness and discontinuities, making them highly effective across various applications. Their versatility and ability to provide both time and frequency domain information make them a valuable tool in modern computational techniques.

Wavelet numerical methods leverage wavelet transforms to solve various numerical problems, particularly differential equations, signal processing, and data analysis. Wavelet numerical methods are used to solve partial differential equations (PDEs) and other complex differential equations more efficiently. They provide a flexible approach to handling problems with variable coefficients and irregular domains. For instance: Wavelet Galerkin methods: These methods use wavelet bases to approximate solutions to differential equations. They offer advantages in terms of accuracy and convergence rates. Wavelet collocation methods: These methods approximate solutions by collocating the equations at specific points using wavelets, which can effectively handle irregular domains and boundary conditions. Wavelet methods can improve the stability and accuracy of numerical algorithms, especially for problems with sharp gradients or discontinuities. They offer a way to handle irregularities and singularities more effectively than traditional methods. Wavelet numerical methods are versatile and can be adapted to various problems and applications. Their flexibility in handling different data types and domains makes them a valuable tool in theoretical and applied contexts. In addition, these methods enhance the efficiency, accuracy, and flexibility of numerical computations. Their ability to handle multiscale data, adapt to different problem characteristics, and improve computational performance makes them essential in modern numerical analysis and scientific computing. Numerous fields have seen its application, including biology, time-frequency analysis, signal analysis for waveform segmentation and representation, and straightforward, quick implementation methods. The introduction of wavelet theory in the mid-1980s significantly impacted applied and pure mathematics. In the past 30 years, wavelet techniques for the numerical approximation of differential equations (DE) have attracted much attention due to their orthogonality, compact support, etc. Numerous wavelet techniques can be used to solve DE numerically. For instance, Lepik et al. [16, 17] investigated the numerical solution of DE by the Haar wavelet technique. Yeshwanth et al. investigated the Chlamydia transmission using the HWM [18], and Darweesh et al. solved Fredholm integro DE using the Haar wavelet method [19]. Manohara et al. employed Bernoulli wavelets on [20] biological models; Shiralashetti et al. employed Laguerre wavelets [21] to resolve a differential equation system; Preetham et al. addressed Bernoulli wavelet method for the flow of a viscous fluid [22]. While Mulimani developed the solutions of brain tumor model [23], Mishra et al. employed the Taylor wavelet [24] to non-linear singular value concerns. Yeshwanth et al. examined the smoking model [25] using the Haar wavelet collocation approach. Kumbinarasaiah et al. used the HWM to discuss the impact of global warming [26]. Marriage divorce model through modified Hermite wavelet [27]. Since rabies is a fatal viral disease, studying it with the help of Mathematical models gives a clear understanding of the spread of the disease. Traditional integer-order models often fail to capture long-term memory effects and delayed responses in epidemiological systems. Rabies exhibit a prolonged incubation period, requiring a more flexible modeling approach that accounts for historical dependence. Fractional-order models provide a better fit to real-world epidemiological data, improving prediction accuracy and intervention planning. Understanding the impact of fractional derivatives on stability, equilibrium points, and control measures is crucial for effective rabies management strategies. The obtained results are contrasted with the RK4 solution, the ND Solver, and the Haar wavelet method (HWM). The recommended plan provides the most straightforward and effective approach to fixing FDEs. Since no one has used HWCM to examine these models in the literature study, we are motivated to investigate this model utilizing the available approaches. This article is organized as follows: The model's formulation and definition of Fractional derivative and Hermite wavelet are covered in Section 2. Hermite wavelet OMI and convergence analysis, uniqueness, and existence of solution are performed in Section 3. The method for solving this problem is presented in Section 4, and the application of the proposed scheme is explained in Section 5. The article is concluded in Section 6.

2 Model formulation, preliminaries of Hermite wavelets, and Fractional derivative

The mathematical model of Rabies has two populations: human and animal populations. The human and animal populations are further divided into two sub-populations at time t: susceptible human population $\mathcal{S}(t)$, infected human population $\mathcal{I}(t)$, susceptible animal population $\mathcal{U}(t)$, and infected animal population $\mathcal{V}(t)$. The following system of differential equations represents the model,

$\begin{array}{ll}\begin{array}{l}\begin{array}{l}{D}_{\tau }^{\beta }\mathcal{S}(\tau )=\lambda -b\mathcal{S}ℐ-c\mathcal{S}\mathcal{V}-d\mathcal{S},\hfill \\ D_{\tau }^{\beta }ℐ(\tau )=b\mathcal{S}ℐ-(d+e)ℐ,\hfill \\ D_{\tau }^{\beta }\mathcal{U}(\tau )=\Lambda -g\mathcal{U}\mathcal{V}-h\mathcal{U},\hfill \\ D_{\tau }^{\beta }\mathcal{V}(\tau )=g\mathcal{U}\mathcal{V}-i\mathcal{V},\hfill \end{array}\}\hfill \end{array}& (1)\end{array}$

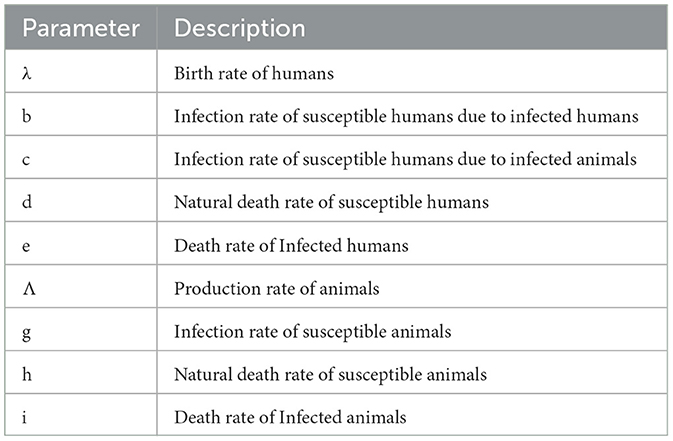
with initial data, $\mathcal{S}\left[0\right]\ge 0$, $\mathcal{I}\left[0\right]\ge 0$, $\mathcal{U}\left[0\right]\ge 0$, $\mathcal{V}\left[0\right]\ge 0$. Figure 1 shows the flow of dependent variables of the rabies model (Equation 2.1). Table 1 explains the model's parameter values. The susceptible human population $\mathcal{S}(t)$ is increasing at a rate birth rate (λ) and decreasing at an infection rate of susceptible humans due to infected humans and animals (b & c) and natural death rate (d). The infected human population $\mathcal{I}(t)$ is increasing at an infection rate of susceptible humans due to infected humans (b) and decreasing due to natural death rate and death rate due to infected humans (d & e). Similarly, the susceptible animal population $\mathcal{U}(t)$ is increasing at a production rate (Λ) and decreasing due to the infection rate of susceptible animals and the natural death rate of susceptible animals (g & h). The infected animal population $\mathcal{V}(t)$ is increasing at an infection rate of susceptible animals (g) and decreasing due to the death rate of infected animals (i).

Figure 1

Figure 1. Rabies model flowchart.

Table 1

Table 1. Overview of the rabies model's parameters.

Definition 1. The Riemann-Liouville's fractional integral of g∈C_μ of the order δ≥0 defined as,

$Q_s^{\beta }=\{\begin{array}{l}g(s)if\delta =0\hfill \\ \frac{1}{\Gamma (\beta )}{\displaystyle {\int }_0^s{(s-t)}^{\beta -1}}g(t)dtif\delta >0.\hfill \end{array}$

The gamma function is indicated here by the symbol Γ where C_μ is continuous linear space.

Definition 2. The Caputo fractional derivative of g(s)∈C_μ is defined as [28]:

$\frac{{\partial }^{\beta }g(s)}{\partial s^{\beta }}=\frac{1}{\Gamma (q-\beta )}{\displaystyle {\int }_0^s{(s-t)}^{q-\beta -1}}{g}^{(q)}(t)dt$

for q−1 < β ≤ q, q is any positive integer, s>0, $g(s)\in C_{\mu }^q,\mu \ge -1$. $C_{\mu }^q$ is continuous linear space containing g^q(s).

A single translated and dilated function known as the mother wavelet is the basis of a family of functions known as wavelets. When the dilation parameter a and translation parameter b fluctuate continuously, we have the following family of continuous wavelets:

${\phi }_{a,b}(y)=|a{|}^{-\frac{1}{2}}\phi (\frac{y-b}{a}),\forall a,b\in R,a\ne 0.$

Parameters a and b can have only discrete values if they are restricted to $a=a_0^{-k}$, $b=n{b}_0{a}_0^{-k}$, a₀>1, and b₀>0. This is the family of discrete wavelets we have,

$\begin{array}{l}{\phi }_{k,n}(x)=|a{|}^{-\frac{1}{2}}\phi (a_0^{k}x-n{b}_0),\forall a,b\in R,a\ne 0,\end{array}$

The wavelet basis for L²(ℝ) is formed by φ_{k, n}. Specifically, φ_{k, n}(y) forms an orthonormal basis when a₀ = 2 and b₀ = 1.

Definition 3. Hermite wavelets are defined as [29],

$\begin{array}{ll}{\phi }_{n,m}(y)=\{\begin{array}{l}\frac{2^{\frac{k+1}{2}}}{\sqrt{\pi }}{\mathscr{H}}_m(2^{k}y-2n+1),\frac{n-1}{2^{k-1}}\le y<\frac{n}{2^{k-1}}\hfill \\ 0,otherwise\hfill \end{array}& (2)\end{array}$

where m ranges from 0 to M−1. In this instance, the Hermite polynomials ${\mathcal{H}}_m(y)$ satisfy the recurrence formula and have degree m for the weight function $\mathcal{W}(y)=\sqrt{1-y^2}$ on the real line ℝ. ${\mathcal{H}}_0(y)=1$, ${\mathcal{H}}_1(y)=2y$, ${\mathcal{H}}_{m+2}(y)=-2(m+1){\mathcal{H}}_{m+1}(y)$.

3 Operational matrix of integration (OMI)

The Hermite wavelets OMI for k = 1 and M = 6 is shown in this section. The following lists the six basis functions on [0, 1):

$\begin{array}{ll}\begin{array}{l}{\phi }_{1,0}(t)=\frac{2}{\sqrt{\pi }},\\ {\phi }_{1,1}(t)=\frac{2}{\sqrt{\pi }}(4t-2),\\ {\phi }_{1,2}(t)=\frac{2}{\sqrt{\pi }}(16t^2-16t+2),\\ {\phi }_{1,3}(t)=\frac{2}{\sqrt{\pi }}(64t^3-96t^2+36t-2),\\ {\phi }_{1,4}(t)=\frac{2}{\sqrt{\pi }}(256t^4+512t^2+320t^2-64t+2),\\ {\phi }_{1,5}(t)=\frac{2}{\sqrt{\pi }}(1024t^5-2560t^4+2240t^3-800t^3+100t-2).\end{array}\}& (3)\end{array}$

by using the collocation points $t_i=\frac{2i-1}{2^{k}M}$, where i = 1, 2, …, 2^k−1M. The corresponding $\mathcal{H}$ can be represented as follows by collocating the base functions with the collocation above points:

$\mathscr{H}=\left[\begin{array}{cccccc}\frac{2}{\sqrt{\pi }}& \frac{2}{\sqrt{\pi }}& \frac{2}{\sqrt{\pi }}& \frac{2}{\sqrt{\pi }}& \frac{2}{\sqrt{\pi }}& \frac{2}{\sqrt{\pi }}\\ -\frac{10}{3\sqrt{\pi }}& -\frac{2}{\sqrt{\pi }}& -\frac{2}{3\sqrt{\pi }}& \frac{2}{3\sqrt{\pi }}& \frac{2}{\sqrt{\pi }}& \frac{10}{3\sqrt{\pi }}\\ \frac{14}{9\sqrt{\pi }}& -\frac{2}{\sqrt{\pi }}& -\frac{34}{9\sqrt{\pi }}& -\frac{34}{9\pi }& -\frac{2}{\sqrt{\pi }}& \frac{14}{9\sqrt{\pi }}\\ \frac{290}{27\sqrt{\pi }}& \frac{10}{\sqrt{\pi }}& \frac{106}{27\sqrt{\pi }}& -\frac{106}{27\sqrt{\pi }}& -\frac{10}{\sqrt{\pi }}& -\frac{290}{27\sqrt{\pi }}\\ -\frac{2206}{81\sqrt{\pi }}& \frac{2}{\sqrt{\pi }}& \frac{1730}{81\sqrt{\pi }}& \frac{1730}{81\sqrt{\pi }}& \frac{2}{\sqrt{\pi }}& -\frac{2206}{81\sqrt{\pi }}\\ -\frac{9850}{243\sqrt{\pi }}& -\frac{82}{\sqrt{\pi }}& -\frac{9362}{243\sqrt{\pi }}& \frac{9362}{243\sqrt{\pi }}& \frac{82}{\sqrt{\pi }}& \frac{9850}{243\sqrt{\pi }}\end{array}\right]$

Integrate Eqn. 3 with respect to t between 0 and t. We obtain

$\begin{array}{ll}\begin{array}{l}{\displaystyle {\int }_0^t{\phi }_{1,0}}(t)=\frac{2}{\sqrt{\pi }}t,\\ {\displaystyle {\int }_0^t{\phi }_{1,1}}(t)=\frac{2}{\sqrt{\pi }}(2t^2-2t),\\ {\displaystyle {\int }_0^t{\phi }_{1,2}}(t)=\frac{2}{\sqrt{\pi }}(16t^3-8t^2+2t),\\ {\displaystyle {\int }_0^t{\phi }_{1,3}}(t)=\frac{2}{\sqrt{\pi }}(16t^4-32t^3-18t^2-2t),\\ {\displaystyle {\int }_0^t{\phi }_{1,4}}(t)=\frac{2}{\sqrt{\pi }}(\frac{256}{5}{t}^5-128t^4+\frac{320}{3}{t}^3-32t^2+2t),\\ {\displaystyle {\int }_0^t{\phi }_{1,5}}(t)=\frac{2}{\sqrt{\pi }}(\frac{512}{3}{t}^6-512t^5+560t^4-\frac{800}{3}{t}^3+50t^2-2t).\end{array}\}& (4)\end{array}$

To obtain the first OMI ${\mathscr{H}}^{\prime }$, collocate Equation 4.

${\mathscr{H}}^{\prime }=\left[\begin{array}{cccccc}\frac{1}{6\sqrt{\pi }}& \frac{1}{2\sqrt{\pi }}& \frac{5}{6\sqrt{\pi }}& \frac{7}{6\sqrt{\pi }}& \frac{3}{2\sqrt{\pi }}& \frac{11}{6\sqrt{\pi }}\\ -\frac{11}{6\sqrt{\pi }}& -\frac{3}{4\sqrt{\pi }}& -\frac{35}{36\sqrt{\pi }}& -\frac{35}{36\sqrt{\pi }}& -\frac{3}{4\sqrt{\pi }}& -\frac{11}{36\sqrt{\pi }}\\ \frac{37}{162\sqrt{\pi }}& \frac{1}{6\sqrt{\pi }}& -\frac{55}{162\sqrt{\pi }}& -\frac{161}{162\sqrt{\pi }}& -\frac{3}{2\sqrt{\pi }}& \frac{253}{162\sqrt{\pi }}\\ \frac{517}{648\sqrt{\pi }}& \frac{21}{8\sqrt{\pi }}& \frac{2485}{648\sqrt{\pi }}& \frac{2485}{648\sqrt{\pi }}& \frac{21}{8\sqrt{\pi }}& \frac{517}{648\sqrt{\pi }}\\ -\frac{6869}{2430\sqrt{\pi }}& -\frac{49}{10\sqrt{\pi }}& -\frac{1325}{486\sqrt{\pi }}& \frac{2737}{2430\sqrt{\pi }}& \frac{33}{10\sqrt{\pi }}& \frac{2981}{2430\sqrt{\pi }}\\ -\frac{10241}{8748\sqrt{\pi }}& -\frac{51}{4\sqrt{\pi }}& -\frac{207305}{8748\sqrt{\pi }}& -\frac{207305}{8748\sqrt{\pi }}& -\frac{51}{4\sqrt{\pi }}& -\frac{10241}{8748\sqrt{\pi }}\end{array}\right]$

Similarly, OMI is as follows for M = 2 and k = 2,

$\begin{array}{ll}\begin{array}{l}{\phi }_{1,0}(t)=\frac{2}{\sqrt{\pi }},\\ {\phi }_{1,1}(t)=4\sqrt{\frac{2}{\pi }}(-1+4t),\\ {\phi }_{2,0}(t)=\frac{2}{\sqrt{\pi }},\\ {\phi }_{2,1}(t)=4\sqrt{\frac{2}{\pi }}(-3+4t).\end{array}\}& (5)\end{array}$

by using the collocation points $x_i=\frac{2i-1}{2^{k}M}$, where i = 1, 2, …, 2^k−1M. Collocating the basis functions with the collocation points as follows will yield an expression for $\mathcal{H}$ as follows:

$\mathscr{H}=\left[\begin{array}{cccc}2\sqrt{\frac{2}{\pi }}& 2\sqrt{\frac{2}{\pi }}& 0& 0\\ -2\sqrt{\frac{2}{\pi }}& 2\sqrt{\frac{2}{\pi }}& 0& 0\\ 0& 0& 2\sqrt{\frac{2}{\pi }}& 2\sqrt{\frac{2}{\pi }}\\ 0& 0& -2\sqrt{\frac{2}{\pi }}& 2\sqrt{\frac{2}{\pi }}\end{array}\right]$

Integrate Eqn. 5 with respect to t between 0 to t. We get

$\begin{array}{ll}\begin{array}{l}{\displaystyle {\int }_0^t{\phi }_{1,0}}(t)=2\sqrt{\frac{2}{\pi }}t,\\ {\displaystyle {\int }_0^t{\phi }_{1,1}}(t)=-4\sqrt{\frac{2}{\pi }}t+8\sqrt{\frac{2}{\pi }}{t}^2,\\ {\displaystyle {\int }_0^t{\phi }_{2,0}}(t)=2\sqrt{\frac{2}{\pi }}t,\\ {\displaystyle {\int }_0^t{\phi }_{2,1}}(t)=-12\sqrt{\frac{2}{\pi }}t+8\sqrt{\frac{2}{\pi }}{t}^2.\end{array}\}& (6)\end{array}$

To obtain the first OMI ${\mathscr{H}}^{\prime }$, collocate Equation 6.

${\mathscr{H}}^{\prime }=\left[\begin{array}{cccc}\frac{1}{2\sqrt{2\pi }}& \frac{3}{2\sqrt{2\pi }}& 0& 0\\ -\frac{3}{4\sqrt{2\pi }}& -\frac{3}{2\sqrt{4\pi }}& 0& 0\\ 0& 0& \frac{5}{2\sqrt{2\pi }}& \frac{7}{2\sqrt{2\pi }}\\ 0& 0& -\frac{35}{4\sqrt{2\pi }}& -\frac{35}{4\sqrt{2\pi }}\end{array}\right]$

Similarly, we can design the OMI with a different sequence.

3.1 Convergence analysis, uniqueness, and existence of solution

Theorem 1. Let y(x) be a continuous bounded function in the Hilbert space H²[0, 1), then the Hermite wavelets expansion of y(x) converges to it [30].

Theorem 2. Let ℝⁿ be polynomial space of degree n+1 over field ℝ and y:[a, b] → ℝⁿ be the solution of arbitrary linear second order differential equation, then the solution for such differential equation by the present method is exact [30].

Theorem 3. Suppose y∈C^p[0, 1) is an p times continuously differentiable function such that $y=\sum _{n=1}^{2^{k-1}}{y}_n(x)$ and {ϕ_{n, m}} be a sequence of Hermite wavelets, where n = 1, …, 2^k−1 and m = 0, …, M−1, k is any positive integer. Let Y_n = L({ϕ_{n, m}}) be the linear space spanned by {ϕ_{n, m}}. If $C_n^T{H}_n(x)$ is best approximation to y_n from Y_n, then C^TH(x) approximates y with following error bound [31]:

$\begin{array}{l}||y-C^{T}H(x)|{|}_2\le \frac{K}{\sqrt{(2p+1)}{2}^{(k+1)(p+\frac{1}{2})}}\end{array}$

where,

$K=max{y}^p(\zeta )\forall \zeta \in [\frac{n-1}{2^{k-1}},\frac{n}{2^{k-1}})$

Theorem 4. Let z(y) ∈ L²(ℝ) be a continuous bounded function defined on [0, 1), then the Hermite wavelet expansion of z(y) is uniformly converges to it.

Proof. Consider z(y) be a continuous function defined on [0, 1) and |z(y)| ≤ μ, where μ is a positive real number. Then, we define z(y) in the form

$\begin{array}{l}z(y)={\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \sum _{j=0}^{\infty }}{c}_{i,j}{W}_{i,j}(y),\end{array}$

where c_{i, j} = $\langle z(y),{\mathcal{W}}_{i,j}(y)\rangle$, and 〈, 〉 denotes inner product. Then, the Hermite wavelet coefficients of continuous functions z(y) are defined as

$\begin{array}{l}{c}_{i,j}={\displaystyle {\int }_{I}z}(y)W_{i,j}(y)dy,\\ c_{i,j}={\displaystyle {\int }_{I}z}(y)\frac{2^{\frac{k+1}{2}}}{\sqrt{\pi }}{\mathscr{H}}_m(2^{k}y-2n+1)dy.\end{array}$

where $I=\mathrm{[}\frac{n-1}{2^{k-1}},\frac{n}{2^{k-1}}\mathrm{)}$. Put 2^kτ−2n+1 = p, then

$\begin{array}{l}{c}_{i,j}=\frac{2^{\frac{k+1}{2}}}{\sqrt{\pi }}{\displaystyle {\int }_{I}z}(\frac{p-1+2n}{2^{k-1}}){\mathscr{H}}_m(p)\frac{dp}{2^k},\\ c_{i,j}=\frac{2^{-\frac{k+1}{2}}}{\sqrt{\pi }}[{\displaystyle {\int }_{I}z}(\frac{p-1+2n}{2^k}){\mathscr{H}}_m(p)dp],\end{array}$

By generalized mean value theorem for integrals

$c_{i,j}=\frac{2^{-\frac{k+1}{2}}}{\sqrt{\pi }}z\left(\frac{\xi -1+2n}{2^k}\right)[{\displaystyle {\int }_0^1{\mathscr{H}}_m}(p)dp],$

where ξ∈(−1, 1). Since ${\mathcal{H}}_m(p)$ is a bounded continuous function. Put ${\displaystyle {\int }_0^1{\mathscr{H}}_m}(p)dp=h$

$\left|c_{i,j}\right|=\left|\frac{2^{-\frac{k+1}{2}}}{\sqrt{\pi }}\right||z(\frac{\xi -1+2n}{2^k})|h.$

Since z is bounded by μ. Hence $|C_{i,j}|=\left|\frac{2^{-\frac{k+1}{2}}}{\sqrt{\pi }}\mu h\right|.$. Where $\mu =z(\frac{\xi -1+2n}{2^k})$. Therefore, ${\displaystyle \sum _{i,j=0}^{\infty }{c}_{i,j}}$ is absolutely convergent. Hence, the Hermite wavelet expansion z(y) converges uniformly to it.                              ⃣

Theorem 5. The solution of the considered model (1) exists and is unique in the region A×[0, T], where

$\begin{array}{l}A=(\mathcal{S},ℐ,\mathcal{U},\mathcal{V})\in {ℝ}^4:||S||<k_1,||ℐ||<k_2,||\mathcal{U}||<k_3,||\mathcal{V}||\\ <k_4,T<\infty .\end{array}$

Proof. Let $W(\tau )=(\mathcal{S}(\tau ),\mathcal{I}(\tau ),\mathcal{U}(\tau ),\mathcal{V}(\tau ))$ and $\overline{W}(\tau )=(\overline{\mathcal{S}}(\tau ),\overline{\mathcal{I}}(\tau ),\overline{\mathcal{U}}(\tau ),\overline{\mathcal{V}}(\tau ))$. Consider a function Z(U, τ) on A×[0, T] and its decomposed form is

$Z(U,\tau )=(Z_1(W,\tau ),Z_2(W,\tau ),Z_3(W,\tau ),Z_4(W,\tau )),$

with Z₁, Z₂, Z₃, and Z₄ are

$\begin{array}{ll}{Z}_1(U,\tau )& =\lambda -b\mathcal{S}\mathcal{I}-c\mathcal{S}\mathcal{V}-d\mathcal{S},\\ Z_2(U,\tau )& =b\mathcal{S}\mathcal{I}-(d+e)\mathcal{I},\\ Z_3(U,\tau )& =\Lambda -g\mathcal{U}\mathcal{V}-h\mathcal{U},\\ Z_4(U,\tau )& =g\mathcal{U}\mathcal{V}-i\mathcal{V},\end{array}$

Norm is taken as

$||W(\tau )||={\displaystyle \underset{\tau \in \left[0,T\right]}{sup}}|W(\tau )\&m={\displaystyle \underset{A}{sup}}||Z(W,\tau )||$

Consider

$\begin{array}{l}||Z(W,\tau )-Z(\overline{W},\tau )||\\ =||\lambda -b\mathcal{S}ℐ-c\mathcal{S}\mathcal{V}-d\mathcal{S}-\lambda +b\overline{\mathcal{S}}\overline{ℐ}+c\overline{\mathcal{S}}\overline{\mathcal{V}}+d\overline{\mathcal{S}}+\\ b\mathcal{S}ℐ-(d+e)ℐ-b\overline{\mathcal{S}}\overline{ℐ}+(d+e)\overline{ℐ}+\Lambda -g\mathcal{U}\mathcal{V}-h\mathcal{U}-\\ \Lambda +g\overline{\mathcal{U}}\overline{\mathcal{V}}+h\overline{\mathcal{U}}+g\mathcal{U}\mathcal{V}-i\mathcal{V}-g\overline{\mathcal{U}}\overline{\mathcal{V}}+i\overline{\mathcal{V}}||\\ \\ =(\lambda -b{k}_2-c{k}_4-d)||\mathcal{S}-\overline{\mathcal{S}}||\\ +(b{k}_1-(d+e))||ℐ-\overline{ℐ}||\\ +(\Lambda -g{k}_4-h)||\mathcal{U}-\overline{\mathcal{U}}||\\ +(g{k}_3-i)||\mathcal{V}-\overline{\mathcal{V}}||.\end{array}$

This implies

$\begin{array}{l}||Z(W,\tau )-Z(\overline{W},\tau )||\le {\psi }_1||\mathcal{S}-\overline{\mathcal{S}}||+{\psi }_2||ℐ-\overline{ℐ}||\\ +{\psi }_3||\mathcal{U}-\overline{\mathcal{U}}||+{\psi }_4||\mathcal{V}-\overline{\mathcal{V}}||,& (7)\end{array}$

where,

$\begin{array}{ll}{\psi }_1& =\lambda -b{k}_2-c{k}_4-d,\\ {\psi }_2& =b{k}_1-(d+e),\\ {\psi }_3& =\Lambda -g{k}_4-h,\\ {\psi }_4& =g{k}_3-i,\end{array}$

put ψ = max{ψ₁, ψ₂, ψ₃, ψ₄} then we obtain

$\begin{array}{ll}||Z(W,\tau )-Z(\overline{W},\tau )||\le \psi ||W(\tau )-\overline{W}(\tau )||& (8)\end{array}$

This equation represents Lipschitz continuity of Z(W, τ). We obtain the following equation on constructing a picard's operator Δ, using the function Z and fractional integral

$\begin{array}{ll}\Delta W=W(0)+I^{\alpha }Z(W,\tau )& (9)\end{array}$

Now, we need to show that Δ is a contraction operator.That is, Δ contracts the distance between points in metric space. Consider

$\begin{array}{ll}||W^{\tau }-W(0)||\le \beta & (10)\end{array}$

from (9)

$\begin{array}{ll}||W(\tau )-W(0)||\le I^{\alpha }(1)||Z(W,\tau )||\le \frac{T^{\alpha }}{\Gamma (\alpha +1)}m<\beta & (11)\end{array}$

Again

$\begin{array}{l}||\Delta W-\Delta \overline{W}||=||I^{\alpha }[Z(W,\tau )-Z(\tau ,\overline{W})]||\\ \le I^{\alpha }(1)||Z(W,\tau )-Z(\overline{W},\tau )||\\ \le \frac{T^{\alpha }}{\Gamma (\alpha +1)}\psi ||W-\overline{W}||\end{array}$

put $\frac{T^{\alpha }}{\Gamma (\alpha +1)}\psi =\varphi$ then $||\Delta W-\Delta \overline{W}||\le \varphi ||W-\overline{W}||$ this shows that Δ is a contraction mapping. Therefore, Δ possesses a unique fixed point. Hence, by Banach's fixed point theorem, the fractional differential equation represented by Equation 7 possesses a unique solution.                              ⃣

4 Hermite wavelet collocation method

Collocation methods in numerical analysis offer several distinct advantages, especially when solving differential equations and other related problems. Here are some key benefits: Simplicity of implementation: collocation methods are relatively straightforward to implement. They involve choosing a set of collocation points and ensuring that the solution satisfies the differential equation at those points. This simplicity makes them easier to apply than more complex numerical methods. Flexibility in choice of basis functions: collocation methods can use various basis functions, such as polynomials, splines, or other functions, depending on the problem. This flexibility allows for tailoring the method to the specific differential equation or problem domain characteristics. Local accuracy: by focusing on ensuring that the solution satisfies the differential equation at specific collocation points, these methods can achieve high local accuracy. This is particularly useful for problems where high precision is needed in certain domain regions. Handling complex geometries: collocation methods can be applied to problems with complex geometries or boundary conditions. They can effectively handle irregular domains and varying boundary conditions by choosing appropriate collocation points and basis functions. Convergence properties: collocation methods can exhibit good convergence properties, especially when appropriate basis functions and collocation points are chosen. For example, when the degree of the polynomial increases, utilizing polynomial basis functions can result in fast convergence to the exact solution. Compatibility with adaptive methods: collocation methods can be combined with adaptive strategies to improve efficiency and accuracy. For example, adaptive refinement of collocation points can be used to focus computational resources on regions where the solution exhibits rapid changes or high gradients. Efficient computation: in many cases, collocation methods can lead to relatively easy linear equation systems, especially when using well-chosen basis functions. This can make the numerical solution process more efficient than methods requiring iterative solvers or complex discretization. Application to time-dependent problems: collocation methods can be effectively applied to time-dependent partial differential equations by discretizing the time variable and applying collocation to the spatial part of the problem. This allows for the analysis of dynamic systems with varying temporal behavior. Error analysis: error analysis for collocation methods is often more straightforward than for other numerical methods. The choice of basis functions and collocation points can be analyzed to estimate and control the error in the numerical solution. Modularity: Collocation methods can be modular and adaptable. For example, you can use different collocation points or basis functions in other domain regions, allowing for a customized approach that fits the specific problem requirements.

Collocation methods provide a powerful and flexible tool for solving various numerical problems, particularly differential equations, by leveraging their simplicity, accuracy, and adaptability. Here, we considered the Hermite wavelet collocation method. There are two approaches to improve the correctness of the solution using this method. First, the domain should be made smaller and the terms (more basic elements) larger. We implemented both simultaneously in the current study to achieve the required accuracy in the solution. We can select more basis elements by breaking the supplied domain into smaller parts. In the end, the solutions are combined linearly. Consider the following partition of $\mathrm{[}\frac{n-1}{2^{k-1}},\frac{n}{2^{k-1}}\mathrm{)}$ in the form $B_k={\cup }_{n=1}^{2^{k-1}}\mathrm{[}\frac{n-1}{2^{k-1}},\frac{n}{2^{k-1}}\mathrm{)}$, where n = 1, 2, …, 2^k−1, and k = 1, 2, ….

Consider the approximation as

$\begin{array}{ll}{z}_{i,k}^{\prime }(\tau )={\displaystyle \sum _{n=1}^{2^{k-1}}}{\displaystyle \sum _{m=0}^{M-1}}{p}_{n,m}^i{\psi }_{n,m}(\tau ),& (12)\end{array}$

where k denotes the solution's domain and i denotes the independent variables. $P_{n,m}^i$ are unknown coefficients of Hermite wavelets, and wavelet basis elements are ψ_{n, m}(τ).

$\begin{array}{ll}{z}_{i,k}^{\prime }=P_{n,m}^i{\text{Ψ}}_{n,m}(\tau ),& (13)\end{array}$

where, $P_{n,m}^i=[p_{1,0}^i,p_{1,1}^i,\dots p_{1,M-1}^i,p_{2,0}^i,\dots p_{2,M-1}^i,\dots p_{2^{k-1},0}^i,\dots p_{2^{k-1},M-1}^i]{\Psi }_{n,m}(\tau )={[{\psi }_{1,0}(\tau ),\dots {\psi }_{1,M-1}(\tau ),{\psi }_{2,0}(\tau ),\dots {\psi }_{2,M-1}(\tau ),\dots {\psi }_{2^{k-1},0}(\tau ),\dots {\psi }_{2^{k-1},M-1}(\tau )]}^T$ Define characteristic function $\Lambda {(\tau )}_{\begin{array}{c}\mathrm{\text{particular one}}\\ \mathrm{\text{connected components of}}{B}_k\end{array}}$ = $\{\begin{array}{l}1,if\tau \in particularoneconnectedcomponentof{B}_k,\hfill \\ 0,if\tau \notin particularoneconnectedcomponentof{B}_k.\hfill \end{array}$ Now, the general approximation is considered as,

$\begin{array}{l}{Z}_i^{\prime }(\tau )={\displaystyle \sum _{\begin{array}{c}\text{vary on each}\\ \text{components of}{B}_k\end{array}}}{\Lambda }_k(\tau )z_{i,k}^{\prime }(\tau ),\forall \tau \in B_k,k\in N\end{array}$

Now, let us select the collocation points as ${\tau }_j=\frac{2i_j-1}{2^k(2^{k-1})M}$, where $i_{j=1,\dots ,k}=1,2,\dots ,2^{k-1}M$.

$\begin{array}{ll}{Z}_i^{\prime }({\tau }_j)={\displaystyle \sum _{\begin{array}{c}\text{vary on each}\\ \text{components of}{B}_k\end{array}}}\Lambda ({\tau }_j)z_{i,k}^{\prime }({\tau }_j)& (14)\end{array}$

The matrix representation of (Eqn. 14) is

$\begin{array}{ll}{Z}_i^{\prime }({\tau }_j)=\sum {\Lambda }_k({\tau }_j)P_{n,m}^i{H}_{B_k},& (15)\end{array}$

where section 2 defines H_Bk. integrate (15) from 0 to x. We obtain

$\begin{array}{ll}{Z}_i({\tau }_j)=Z_i(0)+\sum \Lambda ({\tau }_j)P_{n,m}^i{H}_{Dk}^{\prime }& (16)\end{array}$

Fractionally differentiating (Eqn 16) of order β. We obtain

$\begin{array}{ll}{Z}_i^{\beta }({\tau }_j)=Z_i^{\beta }(0)+\sum \Lambda ({\tau }_j)P_{n,m}^i{H}_{Dk}^{\beta }& (17)\end{array}$

In the provided fractional model (2.1), replace (14), (16), and (17). We obtain the following system of equations,

$\begin{array}{l}{Z}_i(P_{1,0}^1,\dots ,P_{1,M-1}^1,P_{2,0}^1,\dots ,P_{2,M-1}^1,\dots ,P_{2^{k-1},0}^1,\dots ,P_{2^{k-1},M-1}^1,\\ P_{1,0}^2,\dots ,P_{1,M-1}^2,\dots ,\\ P_{2^{k-1},0}^2,\dots ,P_{2^{k-1},M-1}^2,\dots ,P_{1,0}^9,\dots ,P_{1,M-1}^9,\dots ,P_{2^{k-1},0}^9,\dots ,P_{2^{k-1},M-1}^9)=0,\end{array}$

where, i = 1, 2, …, 42^k−1M. The Newton-Raphson approach is used in the following ways to obtain the Hermite wavelet coefficients $P_{n,m}^1$, $P_{n,m}^2$,…, $P_{n,m}^4$: Regarding K = 1, 2, 3, 4. The slope intercept is $P_{(n,m)i+1}^K$, which may be written using Taylor series expansion. The $P_{n,m}^K$ represents the initial guess of the root,

$\begin{array}{l}{Z}_{1,i+1}=Z_{1,i}+(P_{(1,0),i+1}^K-P_{(1,0),i}^K)\frac{\partial Z_{1,i}}{\partial P_{(1,0)}^K}+(P_{(2,0),i+1}^K-P_{(2,0),i}^K)\\ \frac{\partial Z_{1,i}}{\partial P_{(2,0)}^K}+,\dots ,+\\ (P_{(2^{k-1},M-1),i+1}^K-P_{(2^{k-1},M-1),i}^K)\frac{\partial Z_{1,i}}{\partial P_{(2^{k-1},M-1)}^K},\end{array}$

Applying the same method of Taylor series expansion for $Z_2,\dots ,Z_{42^{k-1}M}$ and expanding it to 42^k−1M equations, we obtain

$\begin{array}{l}\frac{\partial Z_{k,i}}{\partial P_{(1,0)}^K}{P}_{1,i+1}^K+\frac{\partial Z_{k,i}}{\partial P_{(2,0)}^K}{P}_{2,i+1}^K+,\dots ,+\frac{\partial Z_{k,i}}{\partial P_{(2^{k-1},M-1)}^K}{P}_{m,i+1}^K\\ =-Z_{k,i}+P_{1,i}^K\frac{\partial Z_{k,i}}{\partial P_{(1,0)}^K}\\ +P_{2,i}^K\frac{\partial Z_{k,i}}{\partial P_{(2,0)}^K}+,\dots ,+P_{m,i}^K\frac{\partial Z_{k,i}}{\partial P_{(2^{k-1},M-1)}^K},& (18)\end{array}$

The equations are shown by the first subscript k, and the function at the present value (i) or at the next value (i+1) is shown by the second subscript. For Equation (18), the matrix notation is as follows:

$\begin{array}{ll}\left[Q\right]\left[P_{i+1}^K\right]=-\left[Z\right]+\left[Q\right]\left[P_i^K\right].& (19)\end{array}$

When the Jacobian matrix made up of partial derivatives is used to express the partial derivatives assessed at i:

$[Q]=\left[\begin{array}{l}\frac{\partial Z_{1,i}}{\partial P_{(1,0)}^K}\frac{\partial Z_{1,i}}{\partial P_{(2,0)}^K}\cdots \frac{\partial Z_{1,i}}{\partial P_{(2^{k-1},M-1)}^K}\\ \frac{\partial Z_{2,i}}{\partial P_{(1,0)}^K}\frac{\partial Z_{2,i}}{\partial P_{(2,0)}^K}\cdots \frac{\partial Z_{2,i}}{\partial P_{(2^{k-1},M-1)}^K}\\ ⋮\cdots ⋮\\ \frac{\partial Z_{42^{k-1}M,i}}{\partial P_{(1,0)}^K}\frac{\partial Z_{42^{k-1}M,i}}{\partial P_{(2,0)}^K}\cdots \frac{\partial Z_{42^{k-1}M,i}}{\partial P_{(2^{k-1},M-1)}^K}\end{array}\right]$

The vector form expression for the start and final values is as follows:${\left[P_i^K\right]}^T$ = $\left[\begin{array}{cccc}{P}_{(1,0),i}^K& P_{(2,0),i}^K& \cdots & P_{(2^{k-1},M-1),i}^K\\ \end{array}\right]$, ${\left[P_{i+1}^K\right]}^T$ = $\left[\begin{array}{cccc}{P}_{(1,0),i+1}^K& P_{(2,0),i+1}^K& \cdots & P_{(2^{k-1},M-1),i+1}^K\end{array}\right]$, and [Z]^T=$\left[\begin{array}{cccc}{Z}_{1,i}& Z_{2,i}& \cdots & Z_{42^{k-1}M,i}\end{array}\right]$Multiplying the inverse of the Jacobian to Equation 19

$\begin{array}{ll}\left[P_{i+1}^K\right]=\left[P_i^K\right]-{\left[Q\right]}^{-1}\left[Z\right].& (20)\end{array}$

Using (20), we derive the Hermite wavelet coefficients $P_{n,m}^K$. By replacing $P_{n,m}^K$, we obtain the desired solution of Equation 16 of order β.

5 Numerical results

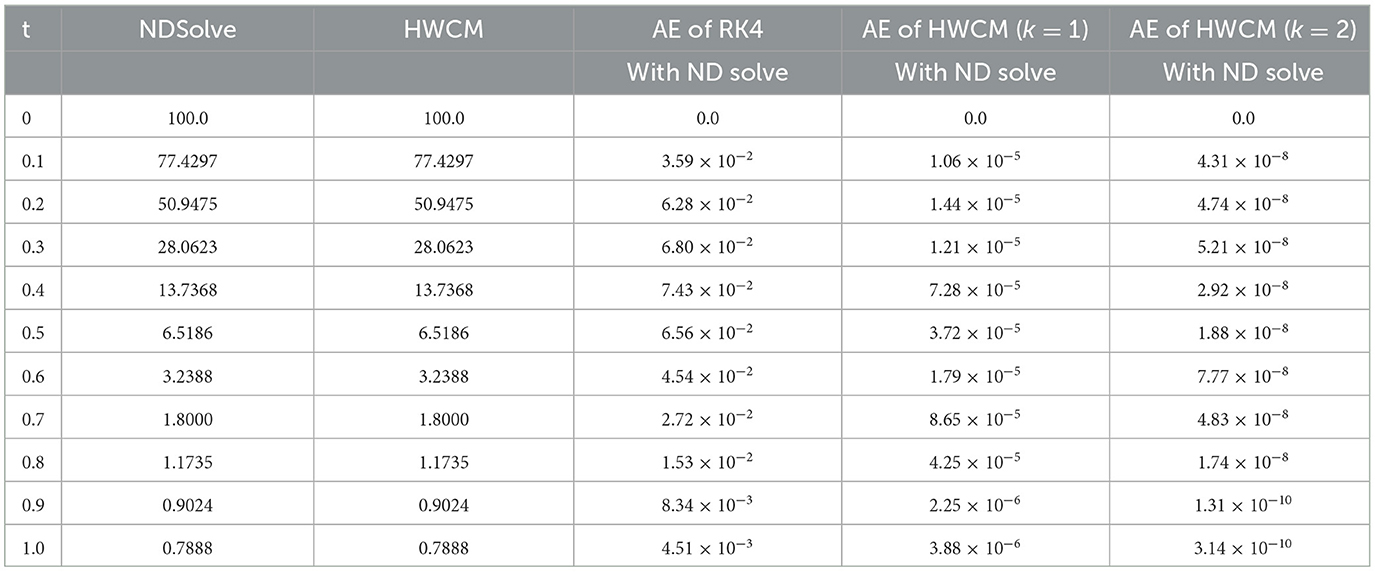
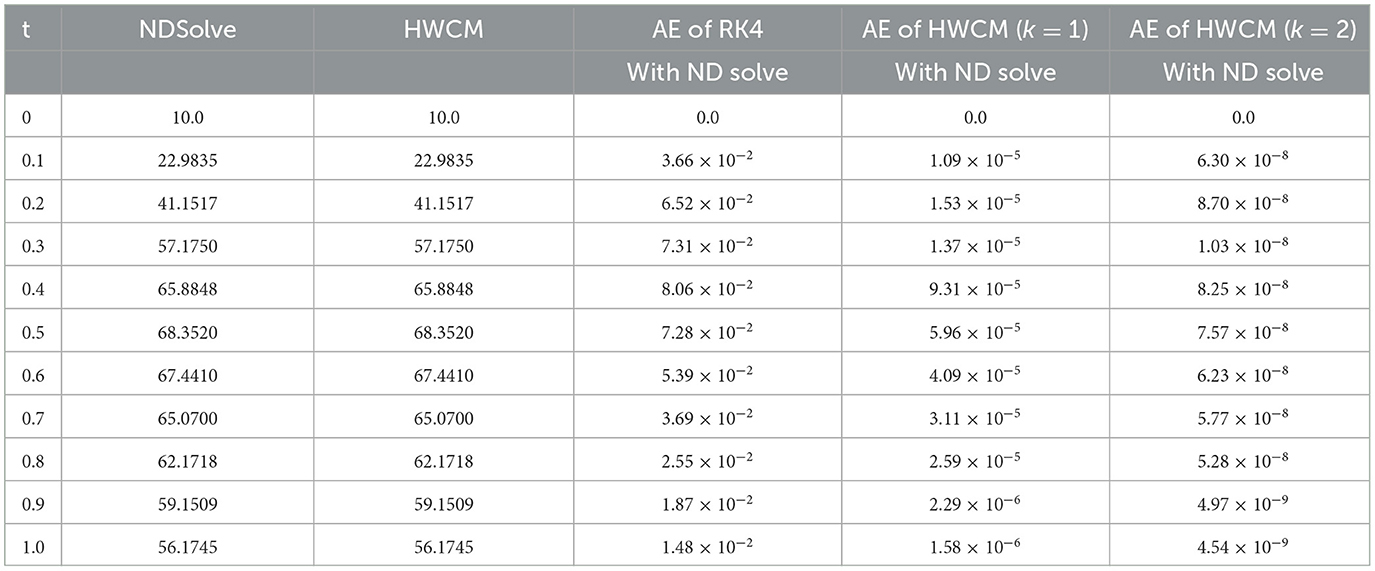
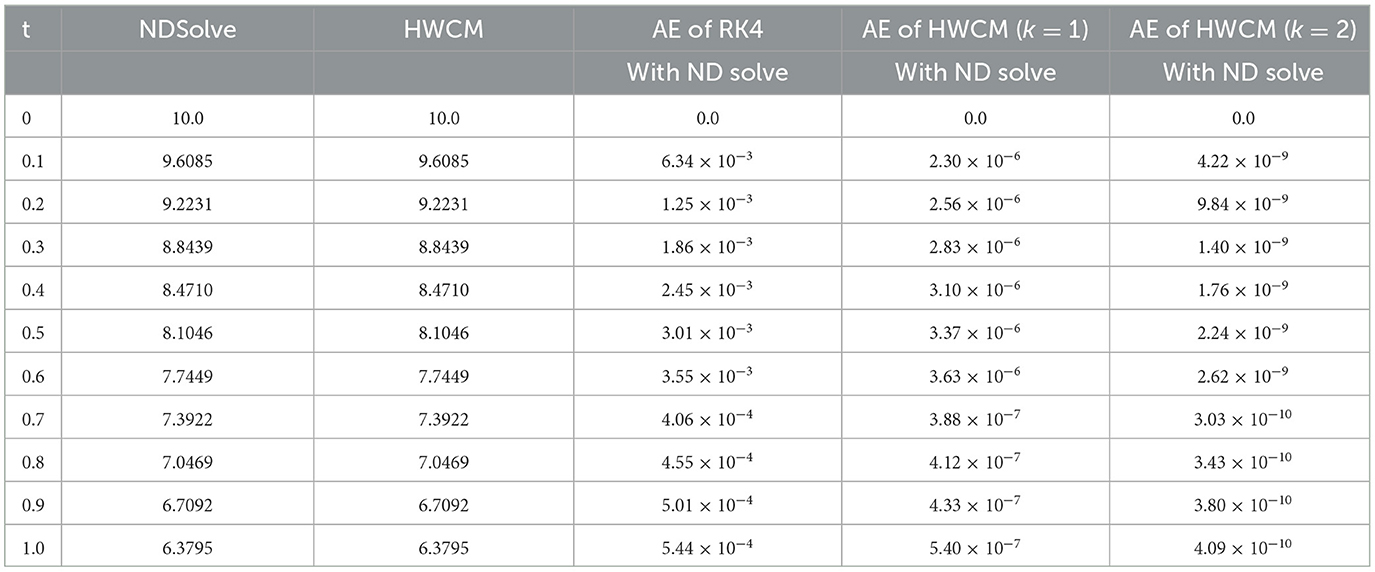
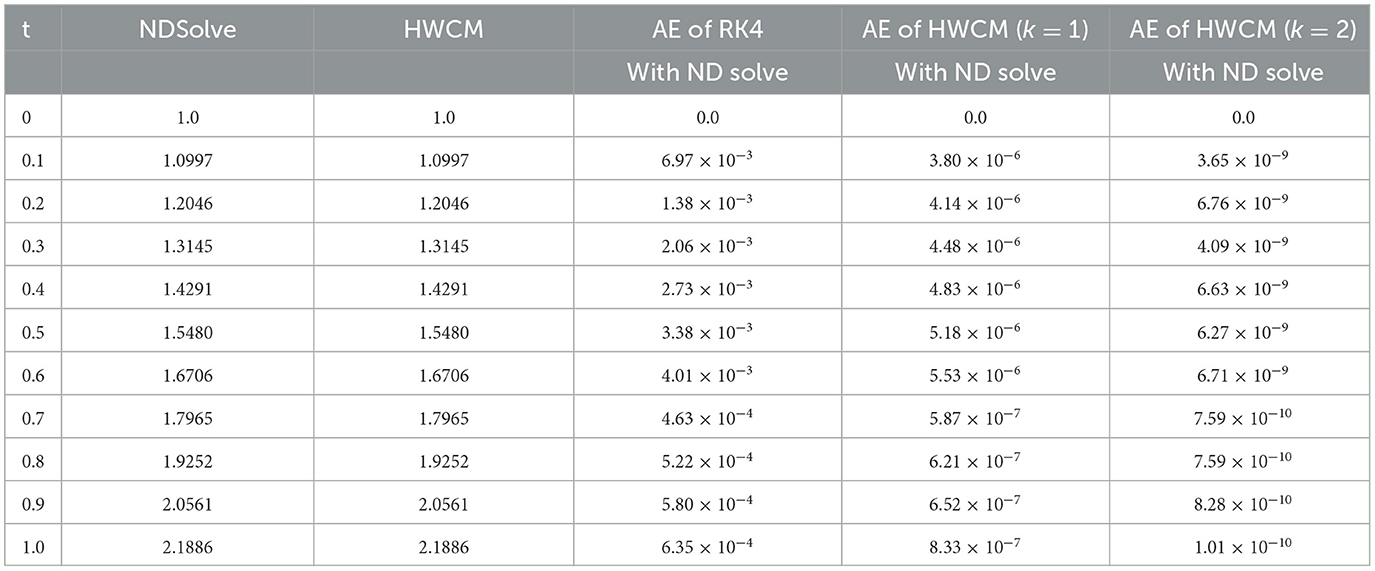
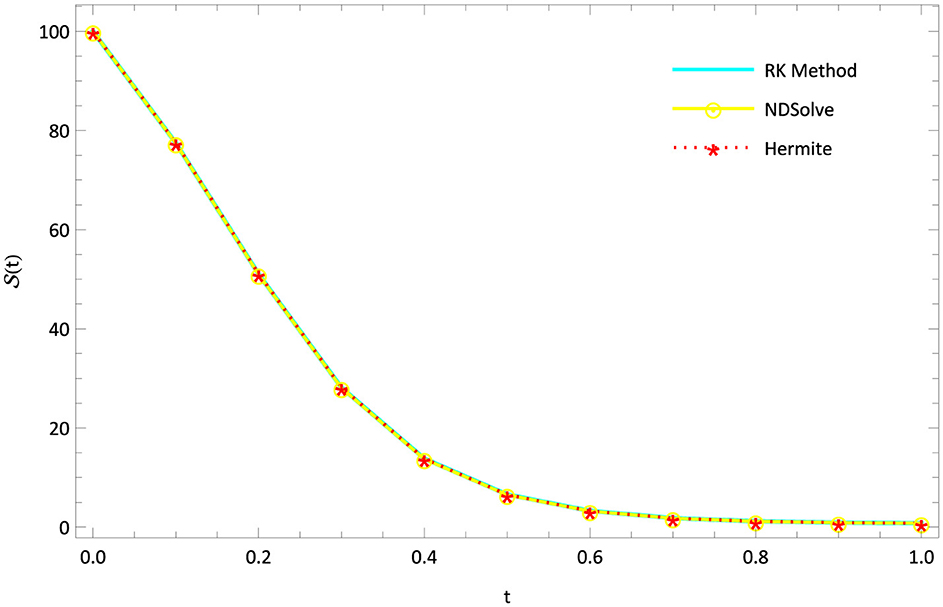
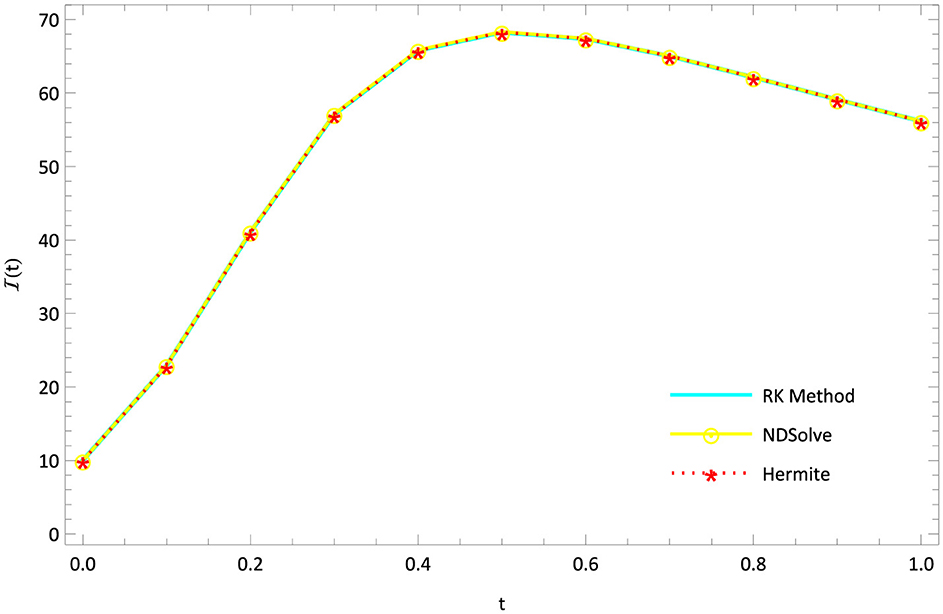
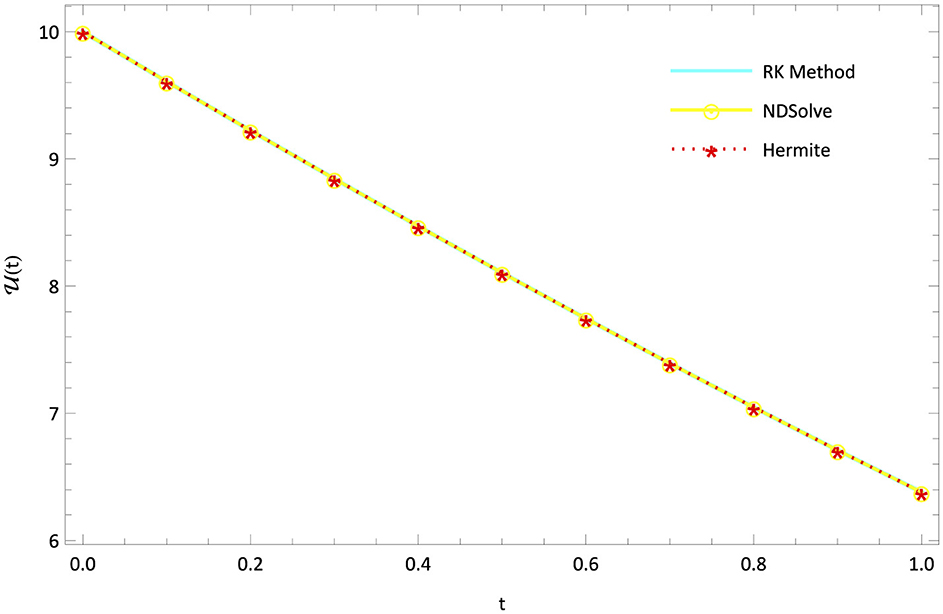
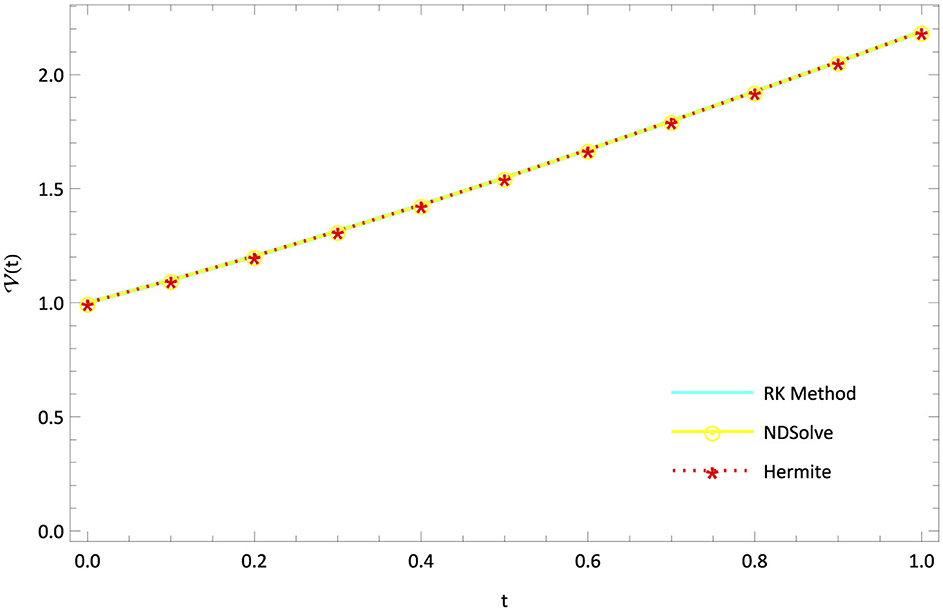
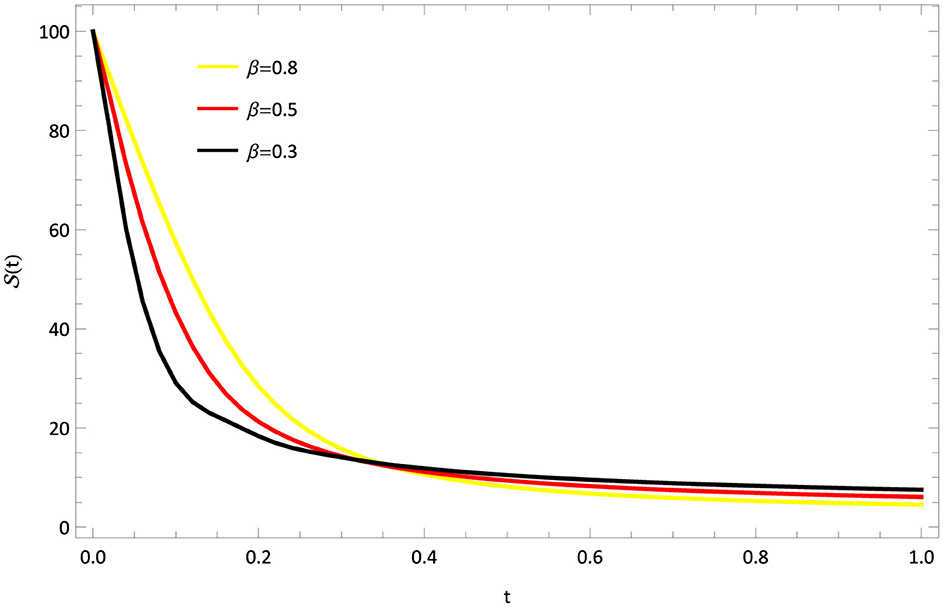
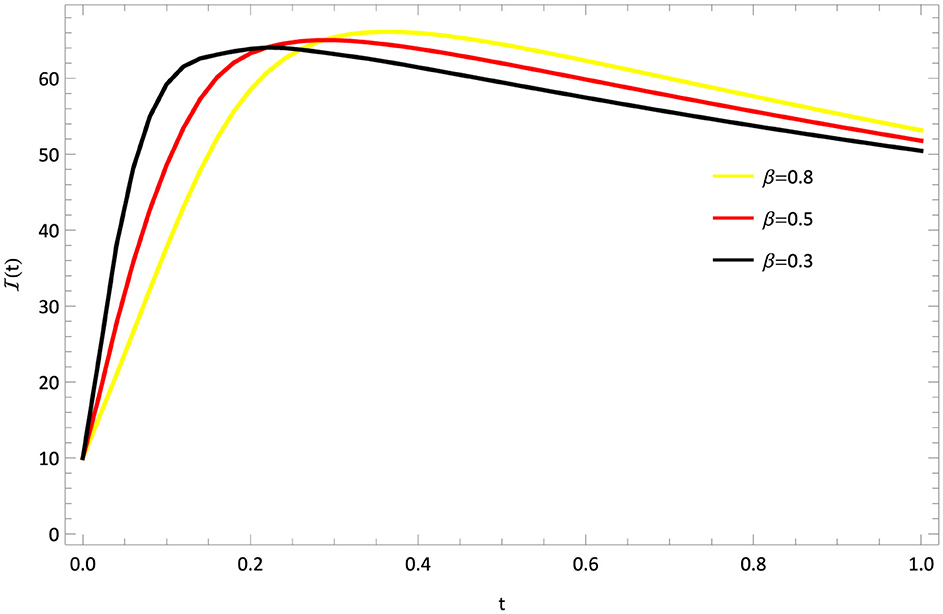
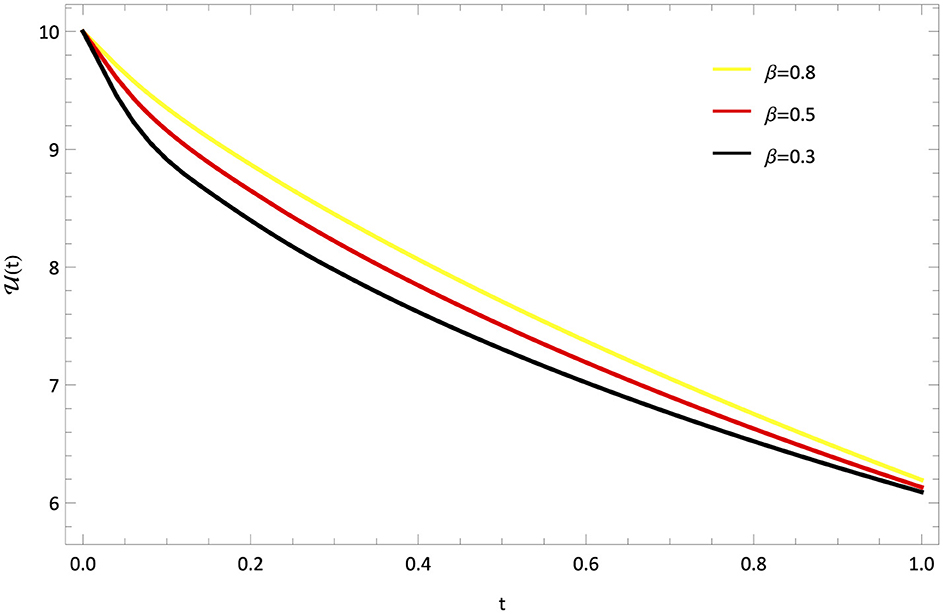
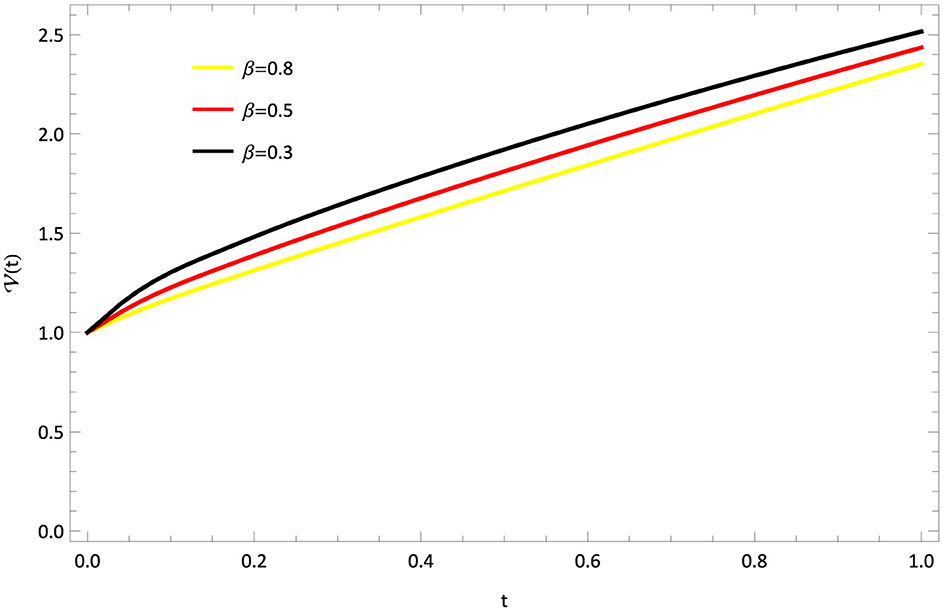
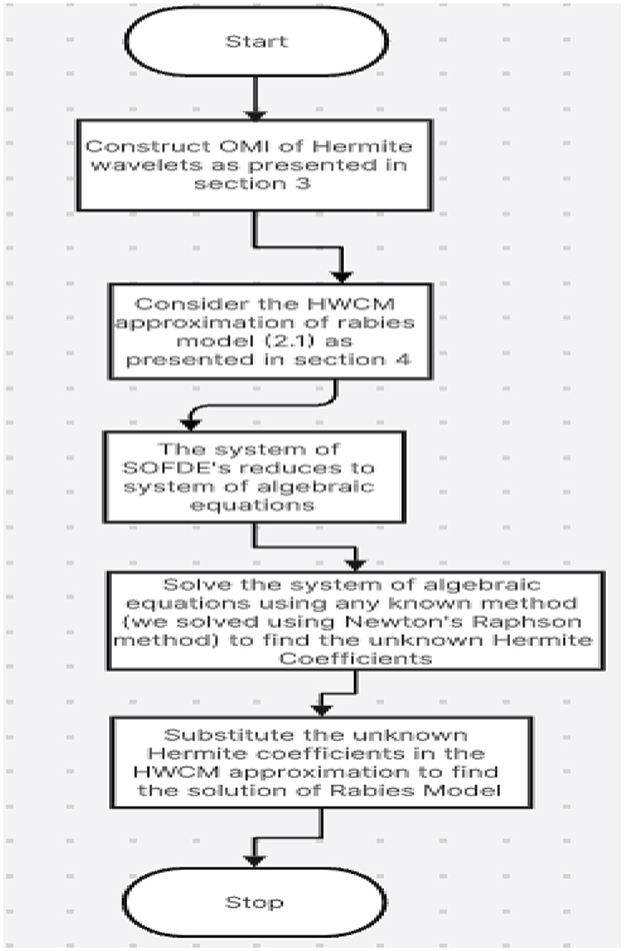
The mathematical model of Rabies presented in section 2 is studied with the presented HWCM under the following model constraints: $\mathcal{S}(0)=100$, $\mathcal{I}(0)=10$, $\mathcal{U}(0)=10$, $\mathcal{V}(0)=1$ and λ = 5, b = 0.1, c = 0.5, d = 0.5, e = 0.1, Λ = 0.055, g = 0.1, h = 0.3, i = 0.03. The numerical depictions and pictorial comparisons of $\mathcal{S}(\tau )$, $\mathcal{I}(\tau )$, $\mathcal{U}(\tau )$, $\mathcal{V}(\tau )$ are done with ND Solver, RK4, and the present approach. The numerical depictions are shown in Tables 2–5 with various methods. The pictorial representation of RK4, ND Solve, and Hermite are represented in Figures 2–5. Figures 6–9 show the pictorial depiction for fractional values of β. We also conclude that, compared to the corresponding integer-order model, the suggested model under Caputo–the fractional order derivative produces more flexible and fruitful results. The results for integer and fractional orders show how quickly and easily the problems can be solved using the newly adjusted Hermite wavelet matrix.

Table 2

Table 2. Numerical depiction of $\mathcal{S}$ with various methods.

Table 3

Table 3. Numerical depiction of $\mathcal{I}$ with various methods.

Table 4

Table 4. Numerical depiction of $\mathcal{U}$ with various methods.

Table 5

Table 5. Numerical depiction of $\mathcal{V}$ with various methods.

Figure 2

Figure 2. Pictorial representation of $\mathcal{S}$ with various methods.

Figure 3

Figure 3. Pictorial representation of $\mathcal{I}$ with various methods.

Figure 4

Figure 4. Pictorial representation of $\mathcal{U}$ with various methods.

Figure 5

Figure 5. Pictorial representation of $\mathcal{V}$ with various methods.

Figure 6

Figure 6. Pictorial representation of $\mathcal{S}$ for various values of β.

Figure 7

Figure 7. Pictorial representation of $\mathcal{I}$ for various values of β.

Figure 8

Figure 8. Pictorial representation of $\mathcal{U}$ for various values of β.

Figure 9

Figure 9. Graphical representation of $\mathcal{V}$ for various values of β.

Variation of the birth rate of humans (λ): the graphic representation of the variation of $\mathcal{S}(t)$, $\mathcal{I}(t)$ that affects the susceptible, infected human population is shown in Figure 10. As the birth rate of humans λ rises, so the susceptible human population $\mathcal{S}(t)$, the infected human population $\mathcal{I}(t)$, increases.

Figure 10

Figure 10. Pictorial depiction of variation of λ.

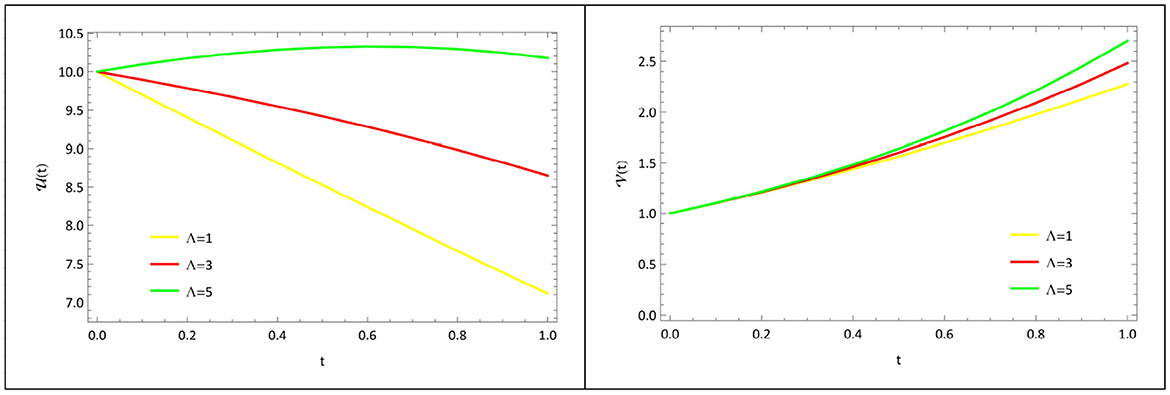
Variation of the production rate of animals (Λ): the graphic representation of the variation of $\mathcal{U}(t)$, $\mathcal{V}(t)$ that affects the susceptible, infected animal population is shown in Figure 11. As the Production rate of animals Λ rises, so the susceptible animal population $\mathcal{U}(t)$, the infected animal population $\mathcal{V}(t)$, increases.

Figure 11

Figure 11. Pictorial depiction of variation of Λ.

Variation of the natural death rate of susceptible humans (d): the graphic representation of the variation of $\mathcal{S}(t)$, $\mathcal{I}(t)$ that affects the susceptible, infected human population is shown in Figure 12. As the natural death rate of susceptible humans d rises, so the susceptible human population $\mathcal{S}(t)$, the infected human population $\mathcal{I}(t)$, decreases.

Figure 12

Figure 12. Pictorial depiction of variation of d.

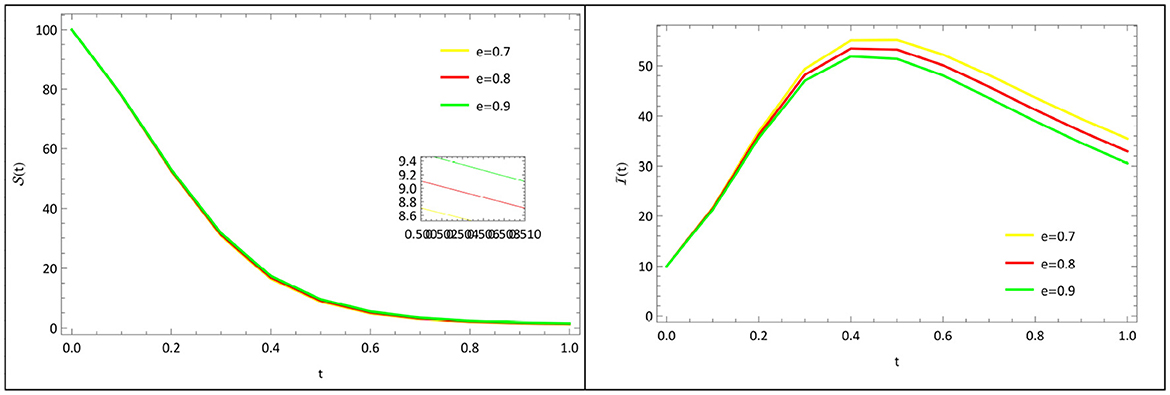
Variation of the death rate of infected humans (e): The graphic representation of the variation of $\mathcal{S}(t)$, $\mathcal{I}(t)$ that affects the susceptible, infected human population is shown in Figure 13. As the death rate of infected humans e rises, the susceptible human population $\mathcal{S}(t)$ increases, whereas the infected human population $\mathcal{I}(t)$ decreases.

Figure 13

Figure 13. Pictorial depiction of variation of e.

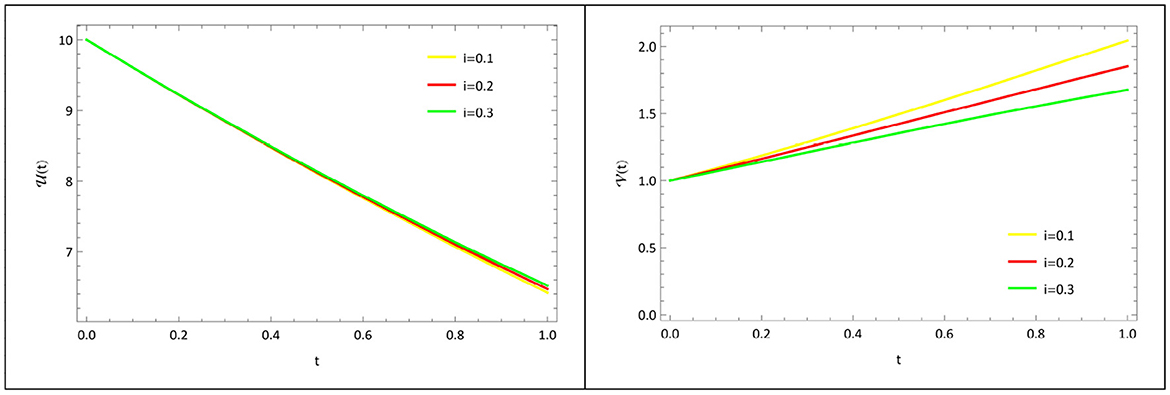
Variation of the death rate of infected animals (i): The graphic representation of the variation of $\mathcal{U}(t)$, $\mathcal{V}(t)$ that affects the susceptible, infected animal population is shown in Figure 14. As the death rate of infected animals i rises, the susceptible animal population $\mathcal{U}(t)$ increases, whereas the infected animal population $\mathcal{V}(t)$ decreases.

Figure 14

Figure 14. Pictorial depiction of variation of i.

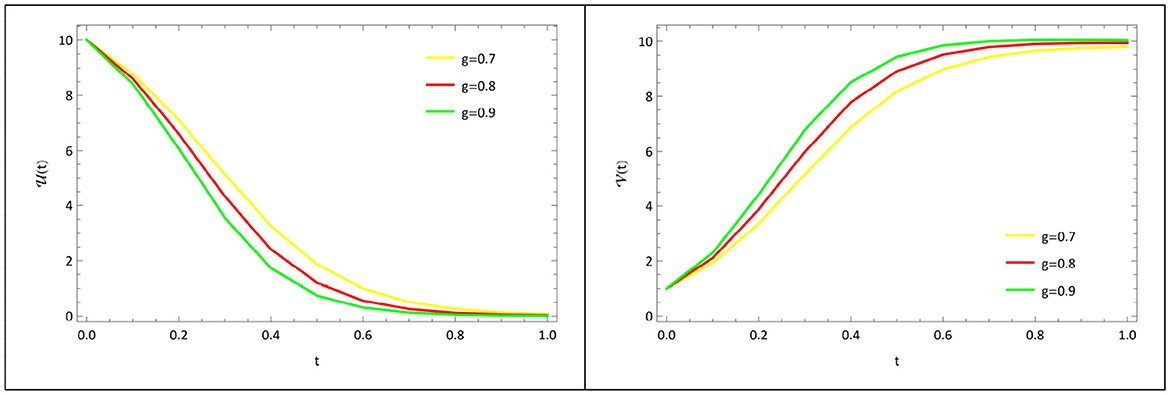
Variation of the infection rate of susceptible animals (g): the graphic representation of the variation of $\mathcal{U}(t)$, $\mathcal{V}(t)$ that affects the susceptible, infected animal population is shown in Figure 15. As the infection rate of susceptible animals g rises, the susceptible animal population $\mathcal{U}(t)$ decreases, whereas the infected animal population $\mathcal{V}(t)$ increases.

Figure 15

Figure 15. Pictorial depiction of variation of g.

6 Conclusion

A rabies model uses mathematical and computational techniques to analyze disease transmission and develop effective control strategies. This study presents an efficient and accurate solution for the non-linear rabies model with fractional-order equations using the Hermite wavelet collocation method (HWCM) (Figure 16). The method constructs an operational matrix for numerical solutions using Hermite wavelets, demonstrating consistency with Mathematica's NDSolver. The Results, supported by tables and figures, confirm that HWCM outperforms traditional numerical models in accuracy. The study also shows that a moderate number of Hermite wavelets is sufficient for precise results, making this approach computationally efficient and easy to implement. Preventive strategies such as mass dog vaccination, public awareness campaigns, pre- and post-exposure prophylaxis, and stray animal management are crucial to controlling rabies. Avoiding contact with stray animals and improving surveillance further help in reducing transmission. The study reinforces that rabies can be effectively managed and controlled with proper vaccination and awareness.

Figure 16

Figure 16. Flowchart of HWCM.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RY: Conceptualization, Formal analysis, Software, Validation, Visualization, Writing – original draft. SK: Conceptualization, Methodology, Supervision, Writing – review & editing. SD: Funding acquisition, Investigation, Supervision, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The authors express their affection for the DST-SERB, Govt. of India, New Delhi, for the financial support under Empowerment and Equity Opportunities for Excellence in Science for 2023–2026. F.No.EEQ/2022/620 Dated:07/02/2023.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chapwanya M, Lubuma JMS, Terefe YA. Analysis and dynamically consistent nonstandard discretization for a rabies model in humans and dogs. Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales Serie A Matematicas. (2016) 110:783–98. doi: 10.1007/s13398-015-0266-y

Crossref Full Text | Google Scholar

2. Clinic M. Rabies-Symptoms, and Causes. Available online at: https://www.mayoclinic.org/diseases-conditions/rabies/symptoms-causes/syc-20351821 (2016). (accessed June 2019).

Google Scholar

3. Haupt W. Rabies risk of exposure and current trends in prevention of human cases. Vaccine. (1999) 17:1742–9. doi: 10.1016/S0264-410X(98)00447-2

Crossref Full Text | Google Scholar

4. Zhang J, Jin Z, Sun GQ, Zhou T, Ruan S. Analysis of rabies in China: transmission dynamics and control. PLoS ONE. (2011) 6:e20891. doi: 10.1371/journal.pone.0020891

PubMed Abstract | Crossref Full Text | Google Scholar

5. Chen J, Zou L, Jin Z, Ruan S. Modeling the geographic spread of rabies in China. PLoS Negl Trop Dis. (2015) 9:e0003772. doi: 10.1371/journal.pntd.0003772

PubMed Abstract | Crossref Full Text | Google Scholar

6. Carroll MJ, Singer A, Smith GC, Cowan DP, Massei G. The use of immunocontraception to improve rabies eradication in urban dog populations. Wildlife Research. (2010) 37:676–87. doi: 10.1071/WR10027

Crossref Full Text | Google Scholar

7. Abdulmajid S, Hassan AS. Analysis of time delayed Rabies model in human and dog populations with controls. Afrika Matematika. (2021) 32:1067–85. doi: 10.1007/s13370-021-00882-w

Crossref Full Text | Google Scholar

8. Layan M, Dellicour S, Baele G, Cauchemez S, Bourhy H. Mathematical modelling and phylodynamics for the study of dog rabies dynamics and control: a scoping review. PLoS Negl Trop Dis. (2021) 15:e0009449. doi: 10.1371/journal.pntd.0009449

PubMed Abstract | Crossref Full Text | Google Scholar

9. Beyene TJ, Mourits MC, Hogeveen H. Dog rabies data reported to multinational organizations from Southern and Eastern African countries. BMC Res Notes. (2017) 10:1–5. doi: 10.1186/s13104-017-2527-7

PubMed Abstract | Crossref Full Text | Google Scholar

10. Wang X, Lou JIE. Two dynamic models about rabies between dogs and human. J Biol Syst. (2008) 16:519–29. doi: 10.1142/S0218339008002666

Crossref Full Text | Google Scholar

11. WHO. Rabies Fact Sheet. Geneva: WHO (2019).

Google Scholar

12. Jemberu WT, Molla W, Almaw G, Alemu S. Incidence of rabies in humans and domestic animals and people's awareness in North Gondar Zone, Ethiopia. PLoS Negl Trop Dis. (2013) 7:e2216. doi: 10.1371/journal.pntd.0002216

PubMed Abstract | Crossref Full Text | Google Scholar

13. Yibrah M, Damtie D. Incidence of human rabies exposure and associated factors at the Gondar Health Center, Ethiopia: a three-year retrospective study. Infect Dis Poverty. (2015) 4:1–6. doi: 10.1186/2049-9957-4-3

PubMed Abstract | Crossref Full Text | Google Scholar

14. Beyer HL, Hampson K, Lembo T, Cleaveland S, Kaare M, Haydon DT. Metapopulation dynamics of rabies and the efficacy of vaccination. Proc R Soc B Biol Sci. (2011) 278:2182–90. doi: 10.1098/rspb.2010.2312

PubMed Abstract | Crossref Full Text | Google Scholar

15. Aydogan SM, Baleanu D, Mohammadi H, Rezapour S. On the mathematical model of Rabies by using the fractional Caputo–Fabrizio derivative. Adv Differ Equ. (2020) 2020:382. doi: 10.1186/s13662-020-02798-4

Crossref Full Text | Google Scholar

16. Lepik U. Numerical solution of differential equations using Haar wavelets. Math Comput Simul. (2005) 68:127–43. doi: 10.1016/j.matcom.2004.10.005

Crossref Full Text | Google Scholar

17. Guf JS, Jiang WS. The Haar wavelets operational matrix of integration. Int J Syst Sci. (1996) 27:623–8. doi: 10.1080/00207729608929258

Crossref Full Text | Google Scholar

18. Kumbinarasaiah S, Yeshwanth R. A study on Chlamydia transmission in United States through the Haar wavelet technique. Results in Cont Optimizat. (2024) 14:100396. doi: 10.1016/j.rico.2024.100396

Crossref Full Text | Google Scholar

19. Darweesh A, Al-Khaled K, Al-Yaqeen OA. Haar wavelets method for solving class of coupled systems of linear fractional fredholm integro-differential equations. Heliyon. 9:e19717. doi: 10.1016/j.heliyon.2023.e19717

PubMed Abstract | Crossref Full Text | Google Scholar

20. Li F, Baskonus HM, Kumbinarasaiah S, Manohara G, Gao W, Ilhan E. An efficient numerical scheme for biological models in the frame of Bernoulli wavelets. Comput Model Eng Sci. (2023) 137:028069. doi: 10.32604/cmes.2023.028069

Crossref Full Text | Google Scholar

21. Shiralashetti SC, Kumbinarasaiah S. Laguerre wavelets exact parseval frame-based numerical method for the solution of system of differential equations. Int J Appl Comput Math. (2020) 6:1–16. doi: 10.1007/s40819-020-00848-9

Crossref Full Text | Google Scholar

22. Kumbinarasaiah S, Preetham MP. Applications of the Bernoulli wavelet collocation method in the analysis of MHD boundary layer flow of a viscous fluid. J Umm Al-Qura Univer Appl Sci. (2023) 9:1–14. doi: 10.1007/s43994-022-00013-6

Crossref Full Text | Google Scholar

23. Mulimani M, Kumbinarasaiah S. Numerical solution for a fractional operator-based mathematical model of a brain tumour. J Analy. (2024) 1–31. doi: 10.1007/s41478-024-00769-6

Crossref Full Text | Google Scholar

24. Vivek KM, Mishra SN. Solution of linear and nonlinear singular value problems using operational matrix of integration of Taylor wavelets. J Taibah Univer Sci. (2023) 17:2241716. doi: 10.1080/16583655.2023.2241716

Crossref Full Text | Google Scholar

25. Kumbinarasaiah S, Yeshwanth R. A numerical study of the evolution of smoking habit model through Haar wavelet technique. Int J Dynam Cont. (2024) 12:3179–97. doi: 10.1007/s40435-024-01422-7

Crossref Full Text | Google Scholar

26. Kumbinarasaiah S, Yeshwanth R. Investigation of the wavelet method impact on the mathematical model of global warming effects on marine ecosystems. J Appl Mathem Comp. (2024) 70:4601–27. doi: 10.1007/s12190-024-02147-8

Crossref Full Text | Google Scholar

27. Yeshwanth R, Kumbinarasaiah S. Numerical Analysis of Marriage-Divorce Model Using New Modified Hermite Wavelet Collocation Technique. Operations Research Forum.

Google Scholar

28. Yan L, Kumbinarasaiah S, Manohara G, Baskonus HM, Cattani C. Numerical solution of fractional PDEs through wavelet approach. Zeitschrift fur angewandte Mathematik und Physik. (2024) 75:61. doi: 10.1007/s00033-024-02195-x

Crossref Full Text | Google Scholar

29. Shiralashetti SC, Kumbinarasaiah S. Hermite wavelets operational matrix of integration for the numerical solution of nonlinear singular initial value problems. Alexandria Eng J. (2018) 54:2591–600. doi: 10.1016/j.aej.2017.07.014

Crossref Full Text | Google Scholar

30. Kumbinarasaiah S. Hermite wavelets approach for the multi-term fractional differential equations. J Interdiscipl Mathem. (2021) 24:1241–62. doi: 10.1080/09720502.2020.1820705

Crossref Full Text | Google Scholar

31. Shiralashetti SC, Kumbinarasaiah S. New generalized operational matrix of integration to solve nonlinear singular boundary value problems using Hermite wavelets. Arab J Basic Appl Sci. (2019) 26:385–96. doi: 10.1080/25765299.2019.1646090

Crossref Full Text | Google Scholar