- 1Courant Institute of Mathematical Sciences, New York University, New York, NY, United States
- 2Aryabhatta Research Institute of Observational Sciences (ARIES), Nainital, India
- 3Georgia Institute of Technology, Atlanta, GA, United States
Owing to the current and upcoming extensive surveys studying the stellar variability, accurate and quicker methods are required for the astronomers to automate the classification of variable stars. The traditional approach of classification requires the calculation of the period of the observed light curve and assigning different variability patterns of phase folded light curves to different classes. However, applying these methods becomes difficult if the light curves are sparse or contain temporal gaps. Also, period finding algorithms start slowing down and become redundant in such scenarios. In this work, we present a new automated method, 1D CNN-LSTM, for classifying variable stars using a hybrid neural network of one-dimensional CNN and LSTM network which employs the raw time-series data from the variable stars. We apply the network to classify the time-series data obtained from the OGLE and the CRTS survey. We report the best average accuracy of 85% and F1 score of 0.71 for classifying five classes from the OGLE survey. We simultaneously apply other existing classification methods to our dataset and compare the results.
1 Introduction
Variable stars have served a pivotal role in expanding our knowledge about various aspects of the universe. These systems have been extensively used for a vast range of studies with their implications on stellar and galactic astrophysics, cosmology, and planetary formation research. A few notable studies are estimating distances to galaxies within and beyond the Local Group and measuring the Hubble constant (Feast, 1999; Freedman et al., 2001; Clementini et al., 2003; Vilardell et al., 2007; Harris et al., 2010; Bhardwaj et al., 2016; Riess et al., 2016; Ripepi et al., 2017), studying chemical composition of different galactic regions (Smith, 1995; Luck et al., 2006; Pedicelli et al., 2009; Genovali et al., 2014), probing stellar structure and evolution (Catelan and Smith, 2015; Christensen-Dalsgaard, 2016; Das et al., 2020, and references therein), studying planetary formation through pre-main-sequence stars (Bell et al., 2013; Ribas et al., 2015), etc.
Recent advancements in astronomical instrumentation has resulted in an avalanche of time-series data from dedicated time-domain surveys such as Optical Gravitational Lensing Experiment (OGLE; Udalski et al., 1993; Soszyński., 2015, Soszyński., 2016, Soszyński., 2018), All-Sky Automated Survey (ASAS; Pojmanski, 2002), Catalina Real-Time Transient Survey (CRTS; Drake et al., 2009; Djorgovski et al., 2011), Zwicky Transient Facility (ZTF; Bellm et al., 2019), and upcoming Vera C. Rubin Observatory (previously Large Synoptic Survey Telescope; LSST Science Collaboration et al., 2009), etc. These databases consist of multiple photometric observations with corresponding time-stamps (light curves) for different variable sources. Classifying these sources based on their light curves helps us in understanding the responsible mechanisms behind the variability and provides insight into their interior structure and formation. The abundance of data from the modern surveys and relevance of variable stars to various domains of astrophysics has heightened the need for automated methods for quick and accurate classification of variable star light curves.
Development of automated methods for classifying variable star’s light curves has seen an upward trend in recent years and has formed the core of many latest studies. A common approach for the automated classification is to extract the periodic and non-periodic features from the light curves and feed them to the machine-learning (ML) classifiers. Periodic features primarily consist of period and Fourier decomposition parameters whereas non-periodic features are mostly statistical parameters (Ferreira Lopes and Cross, 2017). An automated method developed by Debosscher et al. (2007) uses a set of 28 features which are derived from the Fourier analysis of the time-series. These features are mainly the amplitudes, phases, and frequencies obtained from the Fourier fit which are supplied to Gaussian Mixture and ML classifiers for the supervised training. Dubath et al. (2011) present an automatic classification process using statistical parameters such as mean, skewness, standard deviation, and kurtosis as classification attributes. They used Random Forest (RF) for the classification and also estimate the importance of each attribute. Richards et al. (2011) combine the periodic features with the non-periodic features proposed by Butler and Bloom (2011). They demonstrate the application of various ML based classifiers to automatically classify large number of variability classes. They also attempt hierarchical classification using hierarchical single-label classification (HSC) and hierarchical multi-label classification (HMC) using RFs. Nun et al. (2015) offer a Python library called FATS (Feature Analysis for Time Series) intended to standardize the feature extraction process from a given time-series. Kim and Bailer-Jones (2016) develop a package, called UPSILoN, which uses 16 extracted features from the light curves and classifies light curves using Random Forest (RF) technique. Pashchenko et al. (2018) attempt the problem of variability detection using machine learning methods: Support Vector Machines (SVM), Neural Nets (NN), Random Forests (RF), etc. These methods are applied to 18 features which represent the scatter and/or correlation between points in a given light curve.
Feature based classification methods have shown to produce results with good accuracy but these methods make an inherent assumption about the availability of reasonable number of time-stamps for a given light curve. For example, UPSILoN recommends having more than 80 data points in a light curve for obtaining satisfactory precision and recall values. It is known that many light curves from these surveys are noisy and contain temporal gaps due to various reasons related to observational constraints and survey design. Also, the difference in cadence choices among different surveys can potentially make the feature-extraction (and classification) process heterogeneous and survey-dependent. For this reason the recent works have emphasized the need for classification models based on 1) the raw light curve data, or 2) the features not requiring any pre-processing such as light curve folding, Fourier decomposition, etc. The feature extraction can be achieved either in a supervised or unsupervised fashion. These necessities are primarily driven by the fact that the time-series data might be sparse (and therefore not good enough to estimate the period) and can contain gaps in the observations.
Rather than providing the hand-crafted features for classification, recent studies focus on employing the raw time-series data and take advantages from the improved deep-learning (DL) frameworks. Mahabal et al. (2017) process the raw-light curves to generate dm-dt maps. These mappings reflect the difference between the magnitudes (dm) and the corresponding time-stamps (dt) for each pair in the light curve. These differences are binned in fixed dm and dt ranges to obtain the attributes having a uniform dimension for each light curve. These attributes are mapped in 2-dimensions as an image and corresponding class labels are provided to the Convolutional Neural Network (CNN) for training the model. Naul et al. (2018) demonstrate the use of recurrent neural network (RNN) based autoencoder for unsupervised and effective feature extraction. They use the latent space features at the end of encoding layers as representative of the light curves but with reduced dimensionality. This step addresses the issue of light curves with varying length which is a limitation with most ML/DL classifiers. However, they show that encoding-decoding process is more accurate with the period-folded light curves and therefore they use the latent space features obtained from the folded light curves for further classification using Random Forest. Aguirre et al. (2019) consider taking the difference between consecutive time and magnitude values in a light curve to generate two vectors, one each for time and magnitude. These difference vectors form a matrix with two rows and as many columns as the number of difference values. This matrix is passed to a 1D convolutional neural network for training the classification model where time and magnitude difference vectors are treated as two separate channels (similar to different color channels in an image). Carrasco-Davis et al. (2019) show the application of recurrent convolutional neural network (RCNN) to the sequence of images and obtain a recall value of 94% on the data from the High cadence Transient Survey (HiTS). Becker et al. (2020) also make use of RNN and achieve the classification accuracy of 95% in the main variability classes. To address the problem of static classification models, which require re-training as the new data arrives, Zorich et al. (2020) present a probabilistic classification model for the light curves with a continuous stream of data. They demonstrate the application of this approach on the data from CoRot, OGLE and MACHO catalogs.
In the present work, we use a deep-learning framework called Long Short-Term Memory (LSTM; Hochreiter and Schmidhuber, 1997) networks which are specifically designed for handling time-series data and propagate learning from the data to the deeper layers. These models are capable of learning long as well as short-term temporal features and can accommodate the input light curves of varying length. We propose a hybrid network of 1D CNN and LSTM model to classify light curves into different variability classes. Our approach is similar to the image captioning neural model introduced in Vinyals et al. (2014) which combined 2D CNN on images with the LSTM model. In the hybrid model, CNN layers learn to generate the features efficiently and the LSTM part carries out the task of finding the correlations among different observations at varying timescales of an input light curve. These are fed to a fully connected classification layer to predict the variability class. For training the classification model, we use the raw light curve data as an input to the network without any feature-extraction process. This aspect gives this implementation an edge over the previous works. We also implement the 2D CNN method (Mahabal et al., 2017) on our dataset where we consider a modified strategy for generating the dm-dt images. We finally compare the results from the two approaches: 1D CNN-LSTM and 2D CNN.
This paper is organized as follows. In Section 2, we describe the data used in this work for training/testing the classification models and the pre-processing steps required for 2D CNN and 1D CNN-LSTM implementations. Following this, in Section 3 and Section 4, we briefly overview of the two deep learning techniques used for the classification. Section 5 presents the results obtained using the two approaches. Discussion on the results and conclusions are presented in Section 6 with an outline of the road-map for the future work.
2 Data and Pre-Processing
We obtain the archival time-series data from two surveys, OGLE and CRTS, for variability classification. Both datasets contain a large number of light curves and the respective variability classes (labels). We select only a few of these classes which have enough number of distinct light curves (∼ 500 or more) for a stable training of the classification model. We include five variable star classes from OGLE in our dataset, namely classical Cepheids, δ Scuti, Eclipsing Binaries, Long Period Variables, and RR Lyrae. We consider only those light curves that have at least 100 data points to ensure that the network gets a sufficient number of data points to discover the correlations between them and extract useful features for classifying the type of variability. The OGLE database contains 165,105 light curves for Eclipsing Binaries but we select only 50,000 of them to avoid their dominance in the training and keep the computation feasible (though their number is still larger than the other four classes). The total number of OGLE light curves belonging to all the classes are 104,006 in our dataset. From the CRTS survey, we consider the light curves for seven variable star classes. These include Contact Binaries (EW), Detached Binaries (EA), three types of RR Lyrae (RRab, RRc, RRd), Rotating Variables (RSCVn) and Long Period Variables (LPV). The total number of CRTS light curves in our sample are 68,867. The summary of light curves selected in each variability class from the OGLE and CRTS surveys is provided in Table 1.
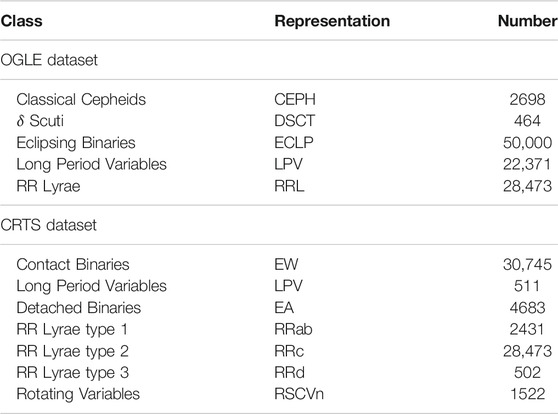
TABLE 1. Summary of light curves belonging to different variability classes obtained from the OGLE and CRTS surveys. The number of samples belonging to different classes in the last column have been adopted from the respective surveys.
We notice that some variability classes are over represented in terms of the number of light curves in both datasets. However, we find that decreasing or increasing their number in the training sample just affects the training time and does not influence the classification accuracy in any significant manner. We use the two datasets separately for training and testing the 2D CNN and 1D CNN-LSTM models.
2.1 Bi-Dimensional Histograms
2D CNN model proposed in Mahabal et al. (2017) was applied to the light curves from the CRTS-North survey (CRTS-N; Mahabal et al., 2012). We apply the same method to a different dataset from the CRTS and OGLE surveys. As the name suggests, the 2D CNN model works on the two-dimensional datasets, like images, whereas light curves are uni-dimensional in nature depicting the variation in brightness as a function of time (left panel in Figure 2). Therefore we pre-process the light curves to generate bi-dimensional histograms (also called dm-dt mappings) and make them suitable for applying a 2D CNN model. To generate bi-dimensional histograms, we follow the same recipe as proposed in the source paper with a few modifications in the binning criteria as discussed below.
We compute the difference in magnitude and time for each pair of data points in the light curve. To find an appropriate number of bins, rather than using fixed bin ranges, we used Freedman-Diaconis rule (Freedman and Diaconis, 1981). Freedman Diaconis estimator computes bin width using the number of data points in a sequence and interquartile range. The estimator was applied to both variations, magnitude and time, individually. We adopt the Freedman-Diaconis rule as opposed to the original binning ranges as it takes into consideration that each light curve might have observations at different times. It automatically adjusts the bin range for a given density of points. We plot these bin sizes as histograms for checking the variations in magnitude and time. We finally consider the median of the histogram range as the number of bins for both time and magnitude variations. This provides the most frequent number of bins for a given survey. This way, we find that the number of bins for the CRTS survey for time and magnitude variations turns out to be 53 and 90 respectively which results in an image of pixel size 90 × 53 with three color channels (R, G, and B). We use the same number of time and magnitude bins for the OGLE survey. A few examples of bi-dimensional histograms generated from the OGLE light curves are shown in Figure 1.
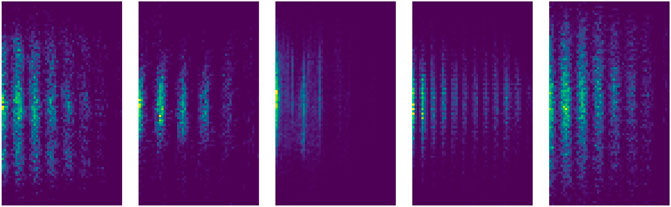
FIGURE 1. Representative bi-dimensional histograms generated from the OGLE light curves for five variability classes (from left to right): Cepheids, δ-Scuti variables, Eclipsing Binaries, Long-period Variables, and RR Lyrae. The x- and y-axis in each of the five panels are the number of pixels (53 along x-axis and 90 along y-axis). The blue and yellow color represent the pixels with the least and the most number of points respectively.
2.2 Padded Time-Series Light Curves
The primary motivation to consider a 1D CNN model (with LSTM) comes from the fact that the raw light curves are one-dimensional sequences. Any rearrangement of these sequences can potentially cause information loss. However, if the variability is periodic in nature and the accurate period is known, the phase-folded light curve can be more informative than the raw light curve. Figure 2 shows one example of a classical Cepheid light curve from OGLE. It is clear that the raw light curve shown in the left panel has no discernible pattern whereas the lower panel clearly shows a smooth sinusoidal-like variation with periodicity. Traditional methods of light curve classification use phase-folded light curves and other criteria based on Fourier parameters, period-luminosity relations, period-color relations, etc. which require the value of period to be known. But the process of period determination becomes challenging as well as computationally expensive in various circumstances such as lack of points in the light curves, insufficient coverage over different phases, etc. Therefore a classification model should be able to use the raw light curves without phase-folding or rearranging them.
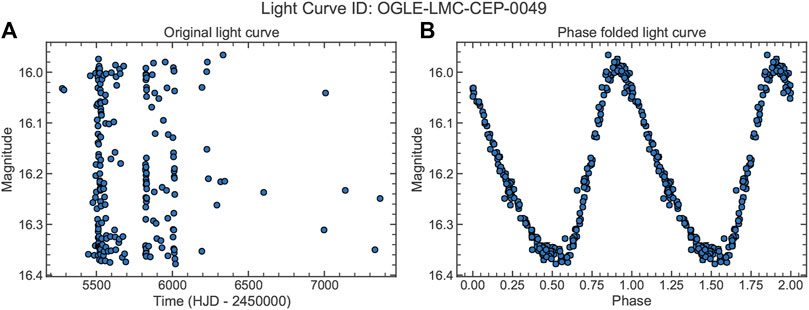
FIGURE 2. Light curve for a classical Cepheid from the OGLE survey. (A) shows the original light curve whereas (B) shows the phase-folded light curve with an estimated period of 3.8497 days. The light curve id is mentioned as the title of the plot.
We propose a 1D CNN model that accepts the light curves without any pre-processing. The light curve data contains variable-length sequences but the computation of the classification model requires all input sequences of the same length. To make all light curves of the same length, we use zero padding at the end of the light curves. This step ensures that the shape of all input light curves remains consistent.
3 Convolutional Neural Networks
Convolutional Neural Networks (CNN or ConvNets; Hinton, 2006; Bengio, 2009; Lecun et al., 2015) have been widely accepted as an excellent tool to identify patterns in astronomical data from diverse sub-domains (Dieleman et al., 2015; Fabbro et al., 2018; Metcalf et al., 2019). These have been utilized in astronomy for numerous classification and regression problems. Many studies have shown that a so-called deep-learning framework like CNN performs better than conventional machine learning algorithms (Kim and Brunner, 2017; Sharma et al., 2020).
A CNN is a kind of deep neural network commonly used for identifying features and patterns in imagery data. It consists of an input layer, an output layer, and multiple hidden layers. The hidden layers include convolutional layers, activation layers, pooling layers, fully connected layers, and normalization layers. Convolutional layers convolve the input image array with the filters and pass the outputs to the succeeding layer. Each convolution layer outputs a new set of activations. Pooling layers are used to decrease the size of the parameters by downsampling the features. Maxpooling is a type of pooling where the maximum value of a section of input is used in the next layer. This helps in generalizing the features and the reduction in features help CNN train quicker. Average pooling is another pooling technique where the average of the pooling window is used in the succeeding layer. Fully connected layers learn the features created from previous layers. Neurons in fully connected layers are connected to all activations of the previous layers. Normalization layers normalize the activations of the previous layers which helps in reducing overfitting. In this work, we use the same CNN architecture as prescribed in Mahabal et al. (2017). The schematic diagram of the architecture is shown in Figure 3.

FIGURE 3. Schematic diagram showing the architecture of Convolutional Neural Network for the OGLE dataset. Different layers in the network are shown as different block and the layer names are indicated at the top of each block. The input images are of shape 90 × 53 × 3. First conv layer uses a kernel size of 3 × 3 but the subsequent layers uses a bigger kernel size of 5 × 5 to find bigger patterns. The same architecture is used for the CRTS dataset except the final classification layer which instead contains seven nodes corresponding to seven variablity classes present in the CRTS. To update the network parameters while training, we use Adam optimizer (Kingma and Ba, 2014) function with the learning rate fixed to 0.0002.
4 1D CNN - LSTM
Inspired from the visual cortex system of animals (Hubel and Wiesel, 1968; Fukushima, 1980), CNNs are mainly used for learning local spatial features and the correlations among the neighbouring points in 2D signals like images. However, in recent years, the applications of CNNs have also been extended to other domains using one-dimensional data, e.g., spectral and time-series analysis, natural language processing, protein sequences, etc. Kiranyaz et al. (2019) provide a careful and detailed overview of 1D CNNs and discuss their applications to several problems. 1D CNNs have shown excellent capabilities to learn patterns and generating features from fixed length 1D data like time-series. We combine 1D CNN with the LSTM networks for classifying light curves.
Long Short Term Memory networks are a type of RNNs having the ability to remember sequences for a long period of time. LSTM networks are used for learning from the sequential data like time-series, speech, and video (Graves and Schmidhuber, 2005; Wang and Jiang, 2015; Karim et al., 2018; Brunel et al., 2019). LSTM networks possess the property of selectively remembering past sections of the data. LSTM networks use three types of gates, namely update gate, forget gate, and output gate. The update gate is used in the current state. The forget gate is used to filter past outputs and the output gate is used to compute the final output. LSTM networks overcome the vanishing gradient problem by using the forget gate which helps in using previous outputs. This property helps LSTM networks to have an edge over conventional feed-forward neural network and RNNs. One example of LSTM networks applied to an astronomical problem is provided in Zhang and Zou (2018). The authors implement the LSTM models for time-series prediction from the light curves. Evaluation of the results based on the mean squared error showed promising prediction for the future points in the time-series. A similar model has been shown to preform well in Czech et al. (2018) for classifying transient radio frequency interference.
In this work, a hybrid network of 1D CNN and LSTM is used to classify the variable star light curves. LSTMs with 1D CNNs help the classification model to learn long and short term patterns, correlations, and dependencies in the input light curve. The convolutional layers in the network create features from the input sequences. They learn to create these features in a way to reduce the error in the prediction. These features are then used by the LSTM to produce its output activations. The output of the final LSTM layer is flattened. The flattened sequence of features is passed to fully connected layers that learn these features. The final softmax layer predicts the variable star classes with respective probabilities. The proposed networks consists of total 10 layers with 4 convolutional layers, 2 Maxpooling layers, 2 LSTM layers, and 2 fully connected layers. We use a kernel size of 3 × 1 for first 2 convolutional layers and 5 × 1 for last 2 convolutional layers. The filter size of convolutional and LSTM layers are in increasing fashion. It is followed by two fully connected layers containing 1024 and 512 neurons respectively. The final “softmax” classification layer has five units for each of the five variability classes from OGLE. Full architecture of the model is presented in Figure 4.
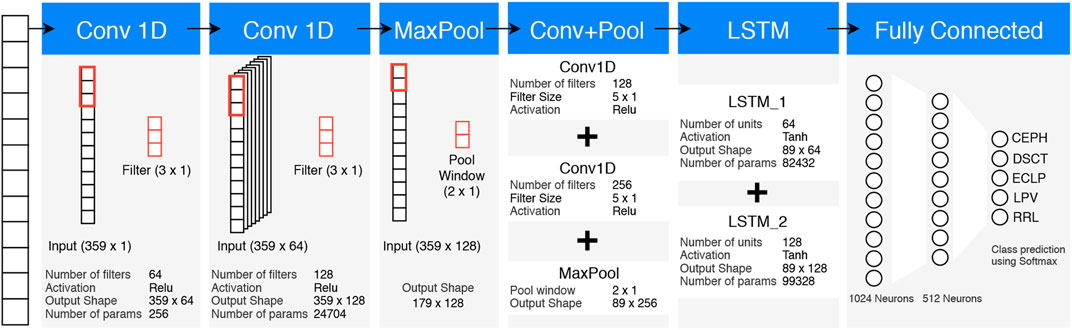
FIGURE 4. Schematic diagram showing the architecture of 1D CNN-LSTM model for the OGLE dataset. The input sequences are padded with zeroes to maintain the constant length of 359 in the OGLE survey and 546 in the CRTS survey for all light curves. Each block represent different type of layers as indicated by the header. The same architecture is used for the CRTS dataset except the final classification layer which instead contains seven nodes corresponding to seven variability classes present in the CRTS.
5 Results
For training the classification models described in Section 3 and Section 4, we use a single NVIDIA GeForce GTX 1060 6GB graphics processing unit. We use CUDA enabled Tensorflow (Abadi et al., 2015) environment for training the models in Python. Since the number of light curves in different classes are highly imbalanced, therefore we give extra weights to the less presented class while training. The weights are assigned in accordance with the numbers of the light curves. To check the overall performance of the classification models, we use the standard metrics: precision, recall, accuracy, and F1 Score.
As described in Section 2, we need to generate the bi-dimensional histograms for providing as inputs to 2D CNNs. We use histogram2d function from Python library NumPy to prepapre the bi-dimensional histograms. We use 60, 20, and 20% of the ligthcurves for training, validation, and testing the classification models respectively. While dividing the dataset into training, testing, and validation samples, we ensure that the ratio of the variable classes remains the same across all the three data portions.
Application of 1D CNN-LSTM model does not require any pre-processing except the padding of the light curves. 1D CNN-LSTM has the advantage of using a smaller number of free parameters to perform classification. This could be a favourable approach in situations where the data is big and computing resources are limited. We use the same splitting criteria of 60%–20%–20% for the two datasets.
5.1 2D CNN on OGLE and CRTS
We train and validate the 2D CNN model on 80% data from the OGLE and CRTS for multi-class classification problem where the number of classes are five and seven, respectively. The model is trained for 100 epochs and each training epoch takes about 165 s. Testing the CNN model on the remaining 20% data from OGLE gives an overall accuracy of 97.5%. For the CRTS dataset, we obtain an accuracy of 74.5%. As the number of light curves belonging to δ Scuti are on a lower side, we experiment with the classification using only the other four classes and get an overall accuracy of 99%. We note the similar increase in the accuracy for the CRTS dataset after removing classes with lesser number of light curves: LPV and RRd. The classification metrics using CNN for OGLE and CRTS are shown in Table 2. The normalized confusion matrix for OGLE is presented in Figure 5).

TABLE 2. Results of classification using 2D CNN on bi-dimensional histograms prepared from the OGLE and the CRTS survey light curves.
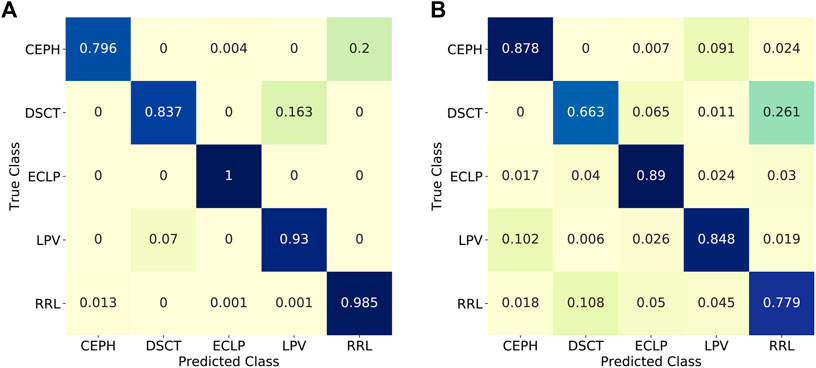
FIGURE 5. Classification results on the test set from OGLE using the 2D CNN (A) and 1D CNN-LSTM (B) models in the form of a normalized confusion matrix. Numbers in each cell represent the fraction of light curves belonging to a true and predicted class. Cells are color-coded according to the numbers in the cell.
5.2 1D CNN-LSTM on OGLE and CRTS
For applying 1D CNN-LSTM model, we examine the distribution of the number of observations in light curves in our dataset. We find that the distribution peaks at 359 for the OGLE and 546 for the CRTS. This means that most light curves in OGLE have 359 data points. To make all the light curves of equal length, the ones with lesser number of observation are padded with zeros at the end of the sequence. The light curves having more number of observations are clipped at 359th observation assuming that these observations will have sufficient information to classify the type of variability. We adopt the same strategy for the CRTS dataset.
We use the CuDNNLSTM layer, which is a faster LSTM implementation and runs only on GPU. The batch size of 32 was used for training 1D CNN-LSTM. The average time for one training epoch is around 75 s. Each classes is given weights according to the number of members in that class. We obtain average accuracy of 85 and 67% for the OGLE and the CRTS lightcurves, respectively. The results of 1D CNN-LSTM on both the datasets are presented in Table 3. The confusion matrix for the OGLE dataset is presented in Figure 5.
6 Conclusions and Discussion
We present two approaches for classifying variable stars using Deep Learning techniques. While the 2D CNN model requires generating dm-dt mappings or bi-dimensional histograms, 1D CNN-LSTM does not require any pre-processing (except padding the light curves to maintain the uniform length for all the light curves) and is a step forward towards classifying light curves without providing engineered features or pre-processing. To classify bi-dimensional histogram images, we use the standard and well-established classification tool, the ConvNets, which perform very well on the OGLE dataset. We find that the classification performance on the CRTS dataset is suboptimal. In the second approach, we use a combined network of 1D CNN and LSTM to classify light curves. This approach does not require any pre-processing which saves a lot of time to generate bi-dimensional histograms. Also, the total training time using 1D CNN-LSTM is reduced by a factor of half as compared to the 2D CNN model. Despite gaining on the overall computation time front, we realize that the performance of 1D CNN-LSTM model is not at par with the 2D CNN approach. Lower accuracy hints that there could be potential shortcomings in the 1D CNN model which bars its performance as the feature extractor. It is also possible that the LSTM layers are unable to correlate the observations at varying time lengths. This aspect of disentangling the problem with the two types of layers needs further investigation.
The degraded performance on the CRTS dataset as compared to the OGLE dataset is a common difficulty faced by both the models. We note that ∼86% of the light curves in the CRTS dataset come only from the two classes: the contact binaries (EWs) and RR Lyrae Type 2 (RRc). Since these two classes have very similar sinusoidal light curves with similar periodicity, most classification algorithms fail to distinguish between these two classes. It should also be noted that the CRTS dataset contains three RR Lyrae sub-classes: RRab, RRc, and RRd. RRab and RRc stars pulsate in the fundamental and first-overtone mode, respectively, whereas RRd stars pulsate in mixed mode between the fundamental and first overtone. The light curves for these classes also look very similar which makes the classification among these classes more difficult.
Despite giving a lesser accuracy, we are able to show that the proposed 1D CNN-LSTM model has the potential to perform the task of classifying variable star light curves without any pre-processing (e.g., converting original time-series to different forms). Moreover, we see that 1D CNN-LSTM gives better results than the 2D CNN approach for certain classes in the CRTS dataset. For example, 1D CNN-LSTM performs better in separating out the light curves from EWs and RRc classes. For these two groups, 2D CNN is able to classify 42% RRc light curves correctly and labels wrongly 50% of the RRc light curves as contact binaries. On the other hand, 1D CNN-LSTM model shows marginally better accuracy of 45% for the RRc light curves and classifies incorrectly 41% light curves as contact binaries. About ∼8% of the RRc light curves are classified as RRab. We make the same observation for the light curves from the RRab and EW classes. Only 29% of the RRab light curves are correctly classified by 2D CNN and 51% light curves are wrongly classified to EW class, whereas 1D CNN-LSTM classifies 55% of the light curves correctly and assigns wrongly only 22% of the light curves as EW. Similarly, while only 69% of the LPVs are correctly classified by the 2D CNN model, the 1D CNN-LSTM model achieves an accuracy of 80% in classifying them. These results, summarized in Table 4, highlight the superiority of the 1D LSTM-CNN model over 2D CNN in distinguishing very similar looking light curves.
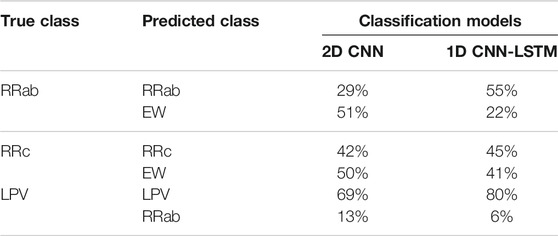
TABLE 4. Comparison of classification results for three variability classes from the CRTS dataset using 2D CNN and 1D CNN-LSTM models. The two rows for each true class represent the correct classification (to the actual class) and mis-classification (to the other class indicated in the second row) percentages, respectively.
As a future scope of this work, we will investigate the other binning strategies along with the ones proposed in Mahabal et al. (2017) and perform detailed comparisons with the bi-dimensional histogram, 1D LSTM-CNN approaches and other prevailing classification techniques. With the demonstrated success of the 1D LSTM-CNN model, we would experiment more with the architecture by optimizing the model hyperparameters, which requires more computational resources. We would also like to explore the capability of the hyperparameter optimized model in classifying light curves from different surveys and examining their performance in case of the sparse light curves. These tests would confirm the robustness of the model against various differences among surveys, e.g., cadence, instrumentation, etc. A more sophisticated approach to classify light curves could use a combination of two parallel CNNs, a 1D CNN for the light curves and another 2D CNN for the science (or difference) images. The features generated using these two networks can be merged and transferred to the final classification layer. The 2D CNN in this alternative approach could provide the required assistance to the 1D CNN-LSTM model to surpass the achieved accuracy by a stand-alone 1D CNN-LSTM model.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://crts.caltech.edu/, http://ogle.astrouw.edu.pl/.
Author Contributions
SB and KS conceived the project. SB performed all computational analysis. KS and AG contributed for intellectual suggestions for the project and helped in the optimization of machine learning algorithm. The manuscript was written by SB and KS. All authors read and approved the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We would like to thank Ajit Kembhavi, Kaustubh Vaghamre, and Ashish Mahabal for their valuable suggestions and key inputs. We are also thankful to the referees for their helpful comments that improved the quality of the manuscript.
References
Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2015). TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. Software available from tensorflow.org.
Aguirre, C., Pichara, K., and Becker, I. (2019). Deep Multi-Survey Classification of Variable Stars. MNRAS 482, 5078–5092. doi:10.1093/mnras/sty2836
Becker, I., Pichara, K., Catelan, M., Protopapas, P., Aguirre, C., and Nikzat, F. (2020). Scalable End-To-End Recurrent Neural Network for Variable star Classification. MNRAS 493, 2981–2995. doi:10.1093/mnras/staa350
Bell, C. P. M., Naylor, T., Mayne, N. J., Jeffries, R. D., and Littlefair, S. P. (2013). Pre-main-sequence Isochrones - II. Revising star and Planet Formation Time-Scales. MNRAS 434, 806–831. doi:10.1093/mnras/stt1075
Bellm, E. C., Kulkarni, S. R., Graham, M. J., Dekany, R., Smith, R. M., Riddle, R., et al. (2019). The Zwicky Transient Facility: System Overview, Performance, and First Results PASP 131, 018002.
Bengio, Y. (2009). Learning Deep Architectures for AI. FNT Machine Learn. 2, 1–127. doi:10.1561/2200000006
Bhardwaj, A., Kanbur, S. M., Macri, L. M., Singh, H. P., Ngeow, C.-C., Wagner-Kaiser, R., et al. (2016). Large Magellanic Cloud Near-Infrared Synoptic Survey. Ii. The Wesenheit Relations and Their Application to the Distance Scale. Astronomical J. 151, 88. doi:10.3847/0004-6256/151/4/88
Brunel, A., Pasquet, J., Pasquet, J., Rodriguez, N., Comby, F., Fouchez, D., et al. (2019). A CNN Adapted to Time Series for the Classification of Supernovae. Electron. Imaging 2019, 90–91. doi:10.2352/issn.2470-1173.2019.14.color-090
Butler, N. R., and Bloom, J. S. (2011). Optimal Time-Series Selection of Quasars. The Astronomical JournalAJ 141, 93. doi:10.1088/0004-6256/141/3/93
Carrasco-Davis, R., Cabrera-Vives, G., Förster, F., Estévez, P. A., Huijse, P., Protopapas, P., et al. (2019). Deep Learning for Image Sequence Classification of Astronomical Events. PASP 131, 108006. doi:10.1088/1538-3873/aaef12
Clementini, G., Gratton, R., Bragaglia, A., Carretta, E., Di Fabrizio, L., and Maio, M. (2003). Distance to the Large Magellanic Cloud: The RR Lyrae Stars. AJ 125, 1309–1329. doi:10.1086/367773
Czech, D., Mishra, A., and Inggs, M. (2018). A CNN and LSTM-Based Approach to Classifying Transient Radio Frequency Interference. Astron. Comput. 25, 52–57. doi:10.1016/j.ascom.2018.07.002
Das, S., Kanbur, S. M., Bellinger, E. P., Bhardwaj, A., Singh, H. P., Meerdink, B., et al. (2020). The Stellar Photosphere-Hydrogen Ionization Front Interaction in Classical Pulsators: A Theoretical Explanation for Observed Period-Colour Relations. MNRAS 493, 29–37. doi:10.14361/9783839453506-004
Debosscher, J., Sarro, L. M., Aerts, C., Cuypers, J., Vandenbussche, B., Garrido, R., et al. (2007). Automated Supervised Classification of Variable Stars. A&A 475, 1159–1183. doi:10.1051/0004-6361:20077638
Dieleman, S., Willett, K. W., and Dambre, J. (2015). Rotation-invariant Convolutional Neural Networks for Galaxy Morphology Prediction. Monthly Notices R. Astronomical Soc. 450, 1441–1459. doi:10.1093/mnras/stv632
Djorgovski, S. G., Donalek, C., Mahabal, A., Moghaddam, B., Turmon, M., Graham, M., et al. (2011). Towards an Automated Classification of Transient Events in Synoptic Sky Surveys. arXiv E-Prints. arXiv:1110.4655.
Drake, A. J., Djorgovski, S. G., Mahabal, A., Beshore, E., Larson, S., Graham, M. J., et al. (2009). First Results from the Catalina Real-Time Transient Survey. ApJ 696, 870–884. doi:10.1088/0004-637x/696/1/870
Dubath, P., Rimoldini, L., Süveges, M., Blomme, J., López, M., Sarro, L. M., et al. (2011). Random forest Automated Supervised Classification of Hipparcos Periodic Variable Stars. MNRAS 414, 2602–2617. doi:10.1111/j.1365-2966.2011.18575.x
Fabbro, S., Venn, K. A., O'Briain, T., Bialek, S., Kielty, C. L., Jahandar, F., et al. (2018). An Application of Deep Learning in the Analysis of Stellar Spectra. MNRAS 475, 2978–2993. doi:10.1093/mnras/stx3298
Feast, M. (1999). Cepheids as Distance Indicators. Publ. Astron. Soc. Pac. 111, 775–793. doi:10.1086/316386
Ferreira Lopes, C. E., and Cross, N. J. G. (2017). New Insights into Time Series Analysis. A&A 604, A121. doi:10.1051/0004-6361/201630109
Freedman, D., and Diaconis, P. (1981). On the Histogram as a Density Estimator:L 2 Theory. Z. Wahrscheinlichkeitstheorie Verw Gebiete 57, 453–476. doi:10.1007/bf01025868
Freedman, W. L., Madore, B. F., Gibson, B. K., Ferrarese, L., Kelson, D. D., Sakai, S., et al. (2001). Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant. ApJ 553, 47.
Fukushima, K. (1980). Neocognitron: A Self-Organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position. Biol. Cybernetics 36, 193–202. doi:10.1007/bf00344251
Genovali, K., Lemasle, B., Bono, G., Romaniello, M., Fabrizio, M., Ferraro, I., et al. (2014). On the fine Structure of the Cepheid Metallicity Gradient in the Galactic Thin Disk. A&A 566, A37. doi:10.1051/0004-6361/201323198
Graves, A., and Schmidhuber, J. (2005). Framewise Phoneme Classification with Bidirectional LSTM and Other Neural Network Architectures. Neural Networks 18, 602–610. iJCNN 2005. doi:10.1016/j.neunet.2005.06.042
Harris, G. L. H., Rejkuba, M., and Harris, W. E. (2010). The Distance to NGC 5128 (Centaurus A). Publ. – Astron. Soc. Aust. 27, 457–462. doi:10.1071/as09061
Hinton, G. E. (2006). Reducing the Dimensionality of Data with Neural Networks. Science 313, 504–507. doi:10.1126/science.1127647
Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735
Hubel, D. H., and Wiesel, T. N. (1968). Receptive fields and Functional Architecture of Monkey Striate Cortex. J. Physiol. (London) 195, 215–243. doi:10.1113/jphysiol.1968.sp008455
Karim, F., Majumdar, S., Darabi, H., and Chen, S. (2018). LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 6, 1662–1669. doi:10.1109/access.2017.2779939
Kim, D.-W., and Bailer-Jones, C. A. L. (2016). A Package for the Automated Classification of Periodic Variable Stars. A&A 587, A18. doi:10.1051/0004-6361/201527188
Kim, E. J., and Brunner, R. J. (2017). Star-galaxy Classification Using Deep Convolutional Neural Networks. Mon. Not. R. Astron. Soc. 464, 4463–4475. doi:10.1093/mnras/stw2672
Kiranyaz, S., Ince, T., Abdeljaber, O., Avci, O., and Gabbouj, M. (2019). “ICASSP 2019,” in 2019 IEEE International Conference on Acoustics, Speech and Signal Processing. New York: ICASSP, 8360–8364.
Lecun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature 521, 436–444. doi:10.1038/nature14539
Luck, R. E., Kovtyukh, V. V., and Andrievsky, S. M. (2006). The Distribution of the Elements in the Galactic Disk. Astron. J. 132, 902–918. doi:10.1086/505687
Mahabal, A. A., Donalek, C., Djorgovski, S. G., Drake, A. J., Graham, M. J., Williams, R., Chen, Y., Moghaddam, B., and Turmon, M. (2012). Real-Time Classification of Transient Events in Synoptic Sky Surveys, 7, in IAU Symposium, Vol. 285, New Horizons in Time Domain Astronomy, Griffin E., Hanisch R., and Seaman R., eds., pp. 355–357. doi:10.1017/s1743921312001056
Mahabal, A., Sheth, K., Gieseke, F., Pai, A., Djorgovski, S. G., Drake, A., et al. (2017). CSS/CRTS/PTF Collaboration. Honolulu, HI: 2017 IEEE Symposium Series on Computational Intelligence (SSCI). arXiv:1709.06257.
Metcalf, R. B., Meneghetti, M., Avestruz, C., Bellagamba, F., Bom, C. R., Bertin, E., et al. (2019). The Strong Gravitational Lens Finding Challenge. A&A 625, A119.
Naul, B., Bloom, J. S., Pérez, F., and van der Walt, S. (2018). A Recurrent Neural Network for Classification of Unevenly Sampled Variable Stars. Nat. Astron. 2, 151–155. doi:10.1038/s41550-017-0321-z
Nun, I., Protopapas, P., Sim, B., Zhu, M., Dave, R., Castro, N., et al. 2015, arXiv e-prints, arXiv:1506.00010
Pashchenko, I. N., Sokolovsky, K. V., and Gavras, P. (2018). Machine Learning Search for Variable Stars. MNRAS 475, 2326–2343. doi:10.1093/mnras/stx3222
Pedicelli, S., Bono, G., Lemasle, B., François, P., Groenewegen, M., Lub, J., et al. (2009). On the Metallicity Gradient of the Galactic Disk. A&A 504, 81–86. doi:10.1051/0004-6361/200912504
Ribas, Á., Bouy, H., and Merín, B. (2015). Protoplanetary Disk Lifetimes vs. Stellar Mass and Possible Implications for Giant Planet Populations. A&A 576, A52. doi:10.1051/0004-6361/201424846
Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., et al. (2011). On Machine-Learned Classification of Variable Stars with Sparse and Noisy Time-Series Data. ApJ 733, 10. doi:10.1088/0004-637x/733/1/10
Riess, A. G., Macri, L. M., Hoffmann, S. L., Scolnic, D., Casertano, S., Filippenko, A. V., et al. (2016). A 2.4% Determination of the Local Value of the Hubble Constant. ApJ 826, 56. doi:10.3847/0004-637x/826/1/56
Ripepi, V., Cioni, M.-R. L., Moretti, M. I., Marconi, M., Bekki, K., Clementini, G., et al. (2017). The VMC Survey - XXV. The 3D Structure of the Small Magellanic Cloud from Classical Cepheids. MNRAS 472, 808–827. doi:10.1093/mnras/stx2096
Sharma, K., Kembhavi, A., Kembhavi, A., Sivarani, T., Abraham, S., and Vaghmare, K. (2020). Application of Convolutional Neural Networks for Stellar Spectral Classification. MNRAS 491, 2280–2300. doi:10.1093/mnras/stz3100
Udalski, A., Szymanski, M., Kaluzny, J., Kubiak, M., Krzeminski, W., Mateo, M., et al. (1993). Acta Astron, 43, 289.
Vilardell, F., Jordi, C., and Ribas, I. (2007). A Comprehensive Study of Cepheid Variables in the Andromeda Galaxy. A&A 473, 847–855. doi:10.1051/0004-6361:20077960
Zhang, R., and Zou, Q. (2018). Time Series Prediction and Anomaly Detection of Light Curve Using LSTM Neural Network. J. Phys. Conf. Ser. 1061, 012012. doi:10.1088/1742-6596/1061/1/012012
Keywords: deep learning, convolutional neural networks, long short term memory, variable star classification, big data and analytics
Citation: Bassi S, Sharma K and Gomekar A (2021) Classification of Variable Stars Light Curves Using Long Short Term Memory Network. Front. Astron. Space Sci. 8:718139. doi: 10.3389/fspas.2021.718139
Received: 31 May 2021; Accepted: 15 September 2021;
Published: 08 November 2021.
Edited by:
Xiangru Li, South China Normal University, ChinaReviewed by:
Jean Baptiste Marquette, UMR5804 Laboratoire d’astrophysique de Bordeaux (LAB), FranceAngel Berihuete, Universidad de Cádiz, Spain
Copyright © 2021 Bassi, Sharma and Gomekar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Saksham Bassi, c2I3Nzg3QG55dS5lZHU=
 Saksham Bassi
Saksham Bassi Kaushal Sharma
Kaushal Sharma Atharva Gomekar3
Atharva Gomekar3