- 1Department of Physics and Astronomy, Rice University, Houston, TX, United States
- 2Department of Physics and Astronomy, University of Iowa, Iowa City, IA, United States
- 3Laboratory for Atmospheric and Space Physics, University of Colorado Boulder, Boulder, CO, United States
- 4Goddard Space Flight Center, NASA, Greenbelt, MD, United States
- 5British Antarctic Survey, Natural Environment Research Council, Cambridge, United Kingdom
Efforts to model and predict energetic electron fluxes in the radiation belts are highly sensitive to local wave-particle interactions. In this study, we use multi-point measurements of precipitating and trapped electron fluxes to investigate the dynamic variation of chorus wave-particle interactions during the 17 March 2013 storm. Quasilinear theory characterizes the chorus wave-particle interaction as a diffusive process, with the diffusion coefficients depending on the particle energy and pitch angle, as well as the background plasma parameters such as the wave intensity and plasma density. These plasma parameters in the radiation belts are spatially localized and time-varying, so we construct event-specific diffusion coefficients using MEPED (onboard POES/MetOp) measurements of electron fluxes at low Earth orbit. This new method provides realistic diffusion coefficients for chorus waves that account for changes in the wave intensity, the plasma density, and the magnetic field strength in the outer radiation belt. We show that the inferred chorus intensity is significantly lower than previous estimates that use MEPED observations since the same amount of increased precipitation by 30–300 keV electrons can be explained by a change in the plasma density. This technique therefore allows for us to create time varying, global maps of the plasma-gyrofrequency ratio (fpe/fce), and therefore plasma density, in the outer radiation belts using the MEPED measurements. The global density estimates compare reasonably well to in situ density measurements from RBSP-B.
1 Introduction
The Earth’s radiation belts are composed of highly energetic electrons and ions that interact with the colder, denser background plasma. This collocation of the dense background plasma and the radiation belts creates a natural laboratory for studying wave-particle interactions in a plasma. The cold plasma generates several types of waves, including whistler-mode chorus waves driven by an electron temperature anisotropy. The higher energy radiation belt particles play no role in the generation of chorus waves, but they strongly interact with the waves through collisionless Landau and cyclotron damping. This wave-particle interaction can pitch angle scatter electrons near the resonant energy, causing them to precipitate into the ionosphere where they can drive the aurora (e.g., Abel and Thorne, 1998).
In this study, we are interested in calculating event-specific chorus diffusion coefficients for later use in the K2 modeling framework. K2 models the time evolution of electron phase-space density using test particles in MHD fields (Elkington et al. 2002, 2004). This MHD-test particle method allows for accurate modeling of both global effects such as radial transport and magnetopause shadowing (Elkington et al., 1999, 2003; Fei et al., 2006), as well as local wave-particle interactions such as quasilinear diffusion due to chorus waves modeled by a 2D Stochastic Differential Equation (Tao et al., 2008; Zheng et al., 2014). The wave-particle interaction is strongly determined by the wave properties in the radiation belts, and in this paper we develop a novel method for estimating these wave properties on a dynamic, global scale.
In the radiation belts, the colder background plasma is typically anisotropic with a higher temperature in the direction perpendicular to Earth’s magnetic field. Electron populations with this temperature anisotropy drive an instability that produces whistler-mode chorus waves, while anisotropic ion populations produce electromagnetic ion-cylotron (EMIC) waves (Kennel and Petschek, 1966; Omura et al., 2009). The whistler-mode chorus waves interact strongly with relativistic electrons and are the focus of this current study due to the ability to measure their precipitation into the ionosphere using the MEPED instrument on the POES and MetOp spacecrafts. EMIC waves are also important for the diffusion and loss of highly energetic electrons (>4 MeV) (Ross et al., 2020, 2021) and will be the subject of future studies.
Since the energetic electrons have no role in generating chorus waves, the wave-particle interaction is best described through the diffusion equation obtained by quasilinear theory. Quasilinear theory is a modification to typical linear solutions of the Boltzmann equation, where a slow time dependence is included for the zeroth order terms. In effect, this allows the Boltzmann equation to be solved for the case where the initial electron distribution is changing in time due to the wave losing energy to the electrons through Landau and cyclotron damping. This solution results in a standard diffusion equation, with the diffusion coefficients depending on the wave properties (Lyons and Williams, 1984).
To model the diffusion process accurately and efficiently, we need to specify a priori the properties of the chorus waves in the radiation belts. This is traditionally done through assembling statistical maps of the wave intensity
The remainder of this paper is organized as follows. In Section 2 the calculation of quasilinear diffusion coefficients is reviewed. The MEPED data used is provided in Section 3. In Section 4 we detail the new method for using the MEPED data to calculate event-specific chorus diffusion coefficients. Section 5 then shows the chorus intensities and plasma densities estimated from scaling the diffusion coefficients, followed by a discussion of further applications in Section 6.
2 Quasilinear diffusion coefficients
2.1 Theory overview
The Boltzmann equation plus Maxwell’s equations provide a closed set of equations to describe the kinetic behavior of a plasma. Typical solutions to this set of equations involve a perturbation approach where the velocity distribution is in the form of
The quasilinear solution to the Boltzmann equation for electromagnetic waves and relativistic particle energies is derived in Kennel and Engelmann (1966) and Lyons and Williams (1984). The solution is of the form of a diffusion equation:
Where the diffusion coefficients are all in units of 1/s, and form the symmetric matrix
The calculation of diffusion coefficients is detailed in Glauert and Horne (2005). In this paper we use all 4 components of the diffusion tensor in Eq. 2, however we will only show the equations for
where
There is an implicit summation over all of the wave modes
The parameters
The diffusion coefficient for a particle with a given pitch angle and momentum is calculated by first solving the dispersion relation in Appendix A simultaneously with Eq. 7 to obtain the resonant wave frequency and wavenumber. The unspecified parameters in Eq. 4 are then: the wave amplitude at the resonant frequency,
The basic motion of radiation belt particles is to bounce between mirror points in each hemisphere. Along this trajectory the wave properties and background plasma will change, so the diffusion coefficients are bounce-averaged. For the pitch angle diffusion coefficient, the bounce averaging is done as (Glauert and Horne, 2005)
where
2.2 Statistical chorus diffusion coefficients
The baseline set of diffusion coefficients used in this paper are calculated using the PADIE (Pitch Angle and Energy Diffusion of Ions and Electrons) model (Glauert and Horne, 2005; Horne et al., 2013) with the procedure given in Reidy et al. (2021) and the wave dataset from Meredith et al. (2020). This set of diffusion coefficients is based on statistical aggregation of wave parameters from the DE 1, Double Star TC1, and THEMIS (A, D, E) satellites, and plasma density measurements from the CRRES satellite. The wave and plasma data used in the diffusion coefficients are binned at half integer values of L-shell, 1-hour increments of MLT, and for Kp index values of 0, 1, 2, 3, and 4+. Figure 1 shows the pitch angle, momentum, and mixed diffusion coefficients at different Kp bins for the same MLT and L-shell.
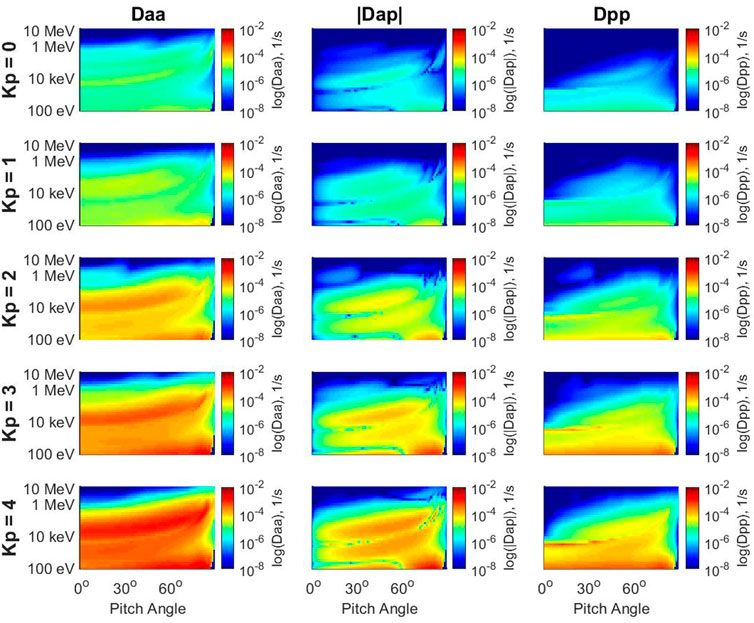
FIGURE 1. Diffusion coefficients binned by Kp index for L = 5, and MLT from 6:00 to 07:00. Note the color scale and axes are the same in each plot. The energies range from 100 eV up to 10 MeV, and the equatorial pitch angle ranges from 0.5° to 89°.
The diffusion coefficients from PADIE will be scaled with MEPED data for wave intensity, Bw, and the plasma-gyrofrequency ratio,
This proportionality also holds for
3 Medium Energy Proton and Electron Detector (MEPED) observations
Energetic electron fluxes are measured at ∼800 km altitudes using the NOAA Polar Orbiting Environmental Satellites (POES) and the European Space Agency Meteorological Observational (MetOp) satellites. The Medium Energy Proton and Electron Detector (MEPED) instrument onboard the POES and MetOp satellites measures incident electron fluxes in 4 energy channels (>30 keV, >100 keV, >300 keV, and >700 keV) with two detectors having different pointing angles. The nominal 0° detector is pointed to the spacecraft zenith, and measures electrons within the loss cone that are precipitating into the ionosphere (when at high latitudes). The nominal 90° detector is pointed behind the spacecraft’s trajectory, and measures electrons that are trapped in the radiation belts and have mirror points just below the spacecraft’s altitude. The angular width of each detector is approximately 30°, however the MEPED detectors admit fluxes through the full 180° face due to the energetic particles penetrating the shielding. This issue is discussed thoroughly in Selesnick et al. (2020), which used Monte Carlo simulations to compute accurate angular response functions for each detector. All analysis of MEPED data in this paper utilizes the angular response functions from Selesnick et al. (2020).
The construction of the MEPED instrument minimized the cross-contamination between the proton and electron channels. However, low energy protons at the right incidence angle are able to enter the electron detector where they produce a false count (Pettit et al., 2021). To account for proton contamination, we use the MEPED dataset from Pettit et al. (2019, 2021) which corrects for proton contamination by fitting the proton detector counts to obtain differential fluxes that are subtracted from the electron channels.
The POES and MetOp satellites are in polar orbit planes, providing a wide range of local time coverage. However, this coverage leaves significant gaps in the data when binning by L shell, MLT, and time. We fill these gaps in data by taking a 2-D linear interpolation in time (UT) and MLT, using the fillmissing function in MATLAB with linear interpolation. This makes the assumption that precipitation is highly localized in L shell, and therefore adjacent bins in L shell are not strongly correlated. In Figure 2 is a plot of the precipitating (0° detector) to trapped (90° detector) flux ratio on March 17-18, 2013, measured by the NOAA POES 15, 16, 17, 18, and 19 satellites, along with MetOp 1 and 2. Figure 2 shows the data filled in to create maps of precipitating/trapped flux in 1-hour local time bins, 0.5 L-shell bins. The data is later binned in 3-hour MLT increments for analysis in Section 4, however Figure 2 shows 6-hour MLT bins for space constraints.
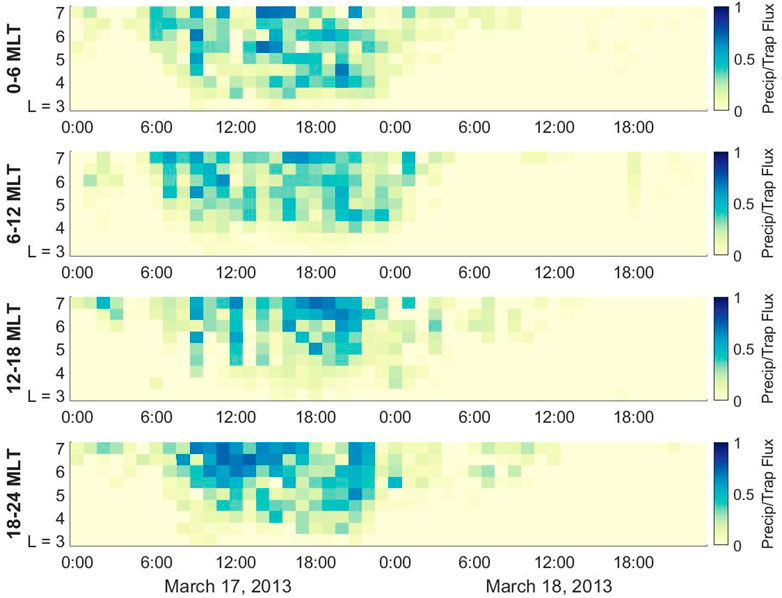
FIGURE 2. MEPED measurements of precipitating to trapped flux ratio as a function of MLT, L-shell, and universal time on March 17-18, 2013. The data are binned in 1 h time (UT) intervals and 0.5 L-shell intervals. The data are obtained from the NOAA POES 15, 16, 17, 18, and 19 satellites, along with MetOp 1 and 2.
4 Event-specific diffusion coefficients
4.1 Inferring chorus wave intensity
The method of using MEPED observations of electron fluxes in order to estimate chorus wave intensity was first developed in Li et al. (2013) and Ni et al. (2014). This method compares the observed precipitating/trapped electron flux ratio from MEPED to the ratio obtained by solving a 1-D diffusion equation in Kennel and Petschek (1966). The predicted flux inside the loss cone, corresponding to the 0-degree MEPED telescope, is (Kennel and Petschek, 1966)
where I0 and I1 are modified Bessel functions. The corresponding flux outside the loss cone, corresponding to the 90-degree MEPED telescope, is (Kennel and Petschek, 1966)
In both equations,
where
The integrations in Eqs 10, 11 are over a finite energy range,
The remaining integration variables
The tilt angle
Eq. 14 can be used to write the local pitch angle
where we denote
The Li et al. (2013) and Ni et al. (2014) method for scaling diffusion coefficients for chorus intensity is as follows:
1) Specify the statistical diffusion coefficient to scale,
2) Calculate the predicted ratio of precipitating to trapped flux,
3) Choose a scaling factor s and recalculate
4) Repeat step 3 for a wide range of scaling factors to calculate the function
5) Obtain the measured precipitating to trapped flux ratio from MEPED data,
6) Solve for
7) The scaled diffusion coefficients are then
This method can be applied without ever knowing the chorus wave intensity used in PADIE to calculate
where
Figure 3 shows an example of this scaling process, with Eq. 16 used to plot
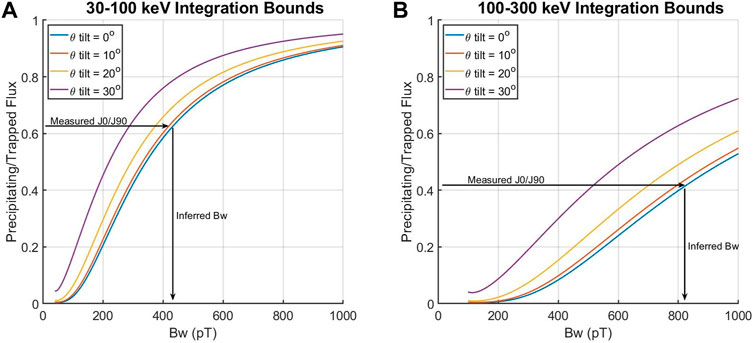
FIGURE 3. Sample calculations of the predicted ratio of precipitating to trapped flux using Eqs 10, 11, 12, 13, 14, 15, with different detector tilt angles. The inferred chorus intensity is obtained by finding where the curve for
4.2 Inferring plasma density
The method for scaling chorus intensity using MEPED data produces different estimates of the chorus intensity in the 30–100 keV and 100–300 keV energy ranges (Figure 3). This discrepancy was noticed in Ni et al. (2014), where they attributed the difference to 1) lower uncertainties in the measured 30–100 keV fluxes due to higher count rates, and 2) the increased importance of momentum diffusion at higher energies. We offer an alternative explanation: the diffusion coefficients assume an inaccurate plasma-gyrofrequency ratio,
Eqs 3, 4, 5 show how the pitch angle diffusion coefficient is calculated. The plasma-gyrofrequency ratio does not explicitly enter into those equations, but it does change the dispersion relation for chorus waves. From Appendix A, the chorus dispersion relation for parallel propagating waves (
which is solved simultaneously with the Landau/cyclotron resonance condition in Eq. 5. For parallel propagating waves the resonance condition yields
Substituting Eq. 18 into Eq. 17, and utilizing
This is a cubic equation in
For parallel propagating waves only the
Eq. 20 shows that two sets of parameters (subscripts 0 and 1) lead to the same solution of
This can be solved for
Using
with the quadratic solution
Notice that in the nonrelativistic limit, and for
Eq. 25 provides an approximate relation between two different particles with different energies and plasma frequencies that yields the same solution of the dispersion relation for the chorus frequency. These two sets of particle energy and plasma-gyrofrequency parameters will therefore yield approximately the same diffusion coefficients, providing a fast and simple way of scaling
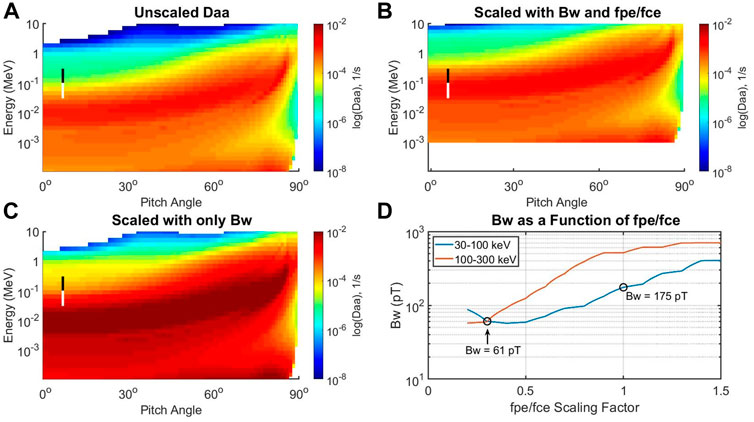
FIGURE 4. Scaling diffusion coefficients for
Eq. 25 gives a quick and approximate way to shift the diffusion coefficients up and down in energy when
1) Specify the statistical diffusion coefficient to scale,
2) Use the method in Section 4.1 to calculate the chorus intensity in the 30–100 keV band,
3) Select a range of scaling factors r for the plasma-gyrofrequency ratio.
4) Use Eq. 25 to shift the diffusion coefficient in energy, substituting
5) Repeat the method in Section 4.1 to construct the curves for chorus intensity
6) Find the intersection of the curves
5 Results
The previous section outlines two methods for scaling diffusion coefficients using observed flux ratios at low Earth orbit. The method in Section 4.1, originally developed by Li et al. (2013) and Ni et al. (2014) only uses a single energy range of 30–100 keV to infer chorus intensity,
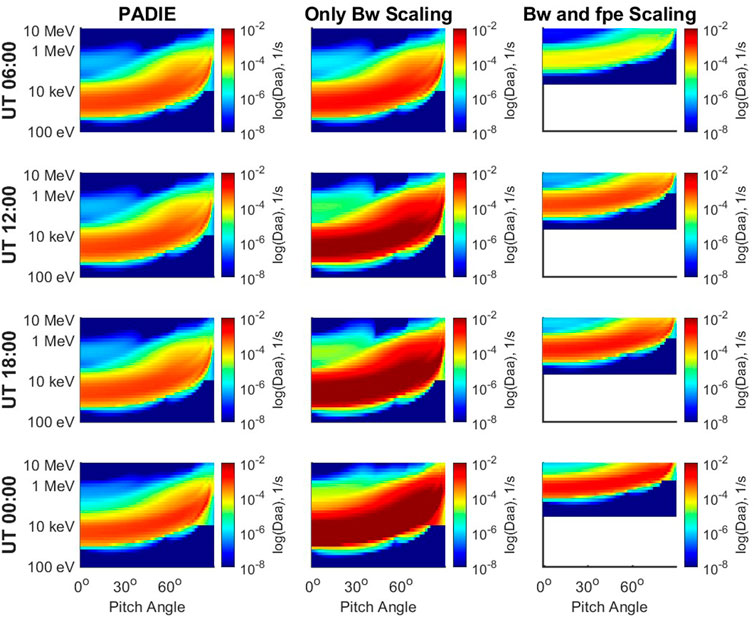
FIGURE 5. Pitch angle diffusion coefficients
Figure 6 shows a snapshot of the results of scaling
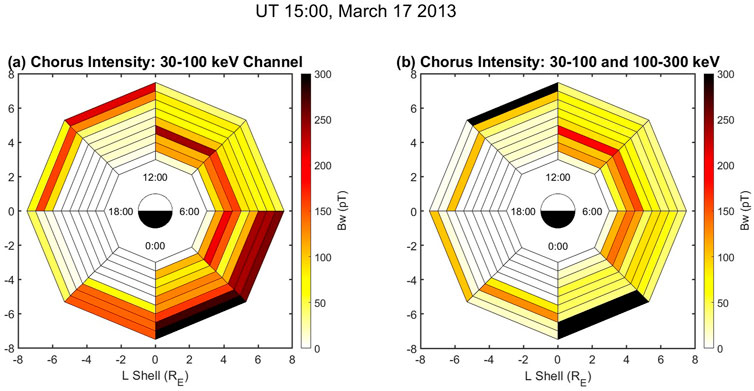
FIGURE 6. Inferred values of chorus wave intensity, Bw. In plot (A) the diffusion coefficients are scaled using only the 30–100 keV range from MEPED. In plot (B) the diffusion coefficients are scaled using the new method that accounts for changes in plasma density by matching the 30–100 keV and 100–300 keV results. The inferred chorus intensity using only the 30–100 keV range (plot a) is consistently larger than the inferred chorus intensity using both energy ranges to account for changes in
The new method for scaling diffusion coefficients enables us to infer what
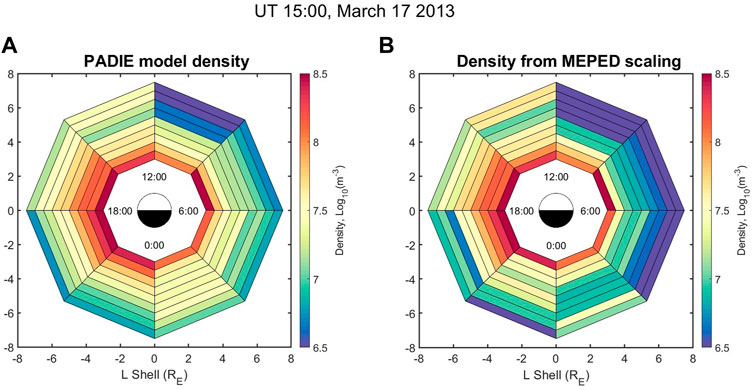
FIGURE 7. Snapshot of equatorial density. Plot (A) shows the statistical density model used to calculate diffusion coefficients with PADIE (Meredith et al., 2020). In plot (B) the inferred density is shown from the new scaling method that utilizes both the 30–100 keV and 100–300 keV energy ranges from MEPED. A movie showing the inferred density at every time step is included in the supplemental materials.
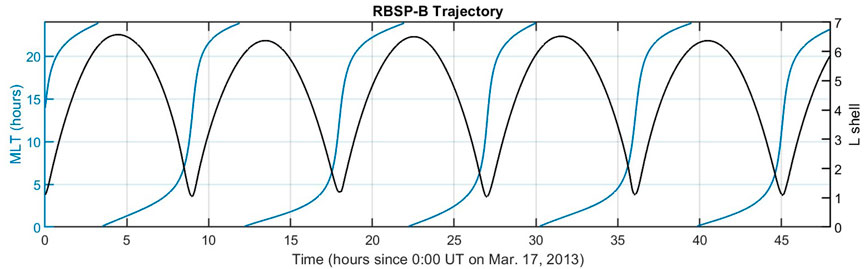
The estimated densities are compared to Van Allen Probes measurements (Kurth et al., 2015) in Figure 8. The densities are obtained from the EMFISIS instrument onboard the RBSP-B spacecraft. During the 17 March 2013 event the satellite apogee was on the nightside, and therefore sampled MLT ranges of approximately 21:00 to 04:00 when in the radiation belt (defined as L ≥ 3). Figure 9 shows the same date-model comparison but plotting the plasma-gyrofrequency ratio
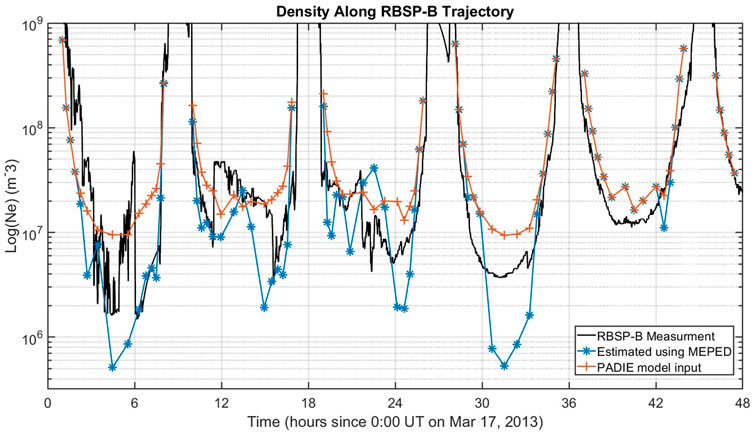
FIGURE 8. Comparison of estimated densities to Van Allen Probes measurements. The densities measured by the RBSP-B spacecraft are shown in (black), for time periods where the spacecraft was in the radiation belts (L ≥ 3). The densities estimated using the MEPED scaling method in Section 4.2 are shown in the (blue) curve, with reasonable agreement to RBSP-B. However, much of this agreement with observations is due to the high quality of the statistical density model used in the PADIE code (orange).
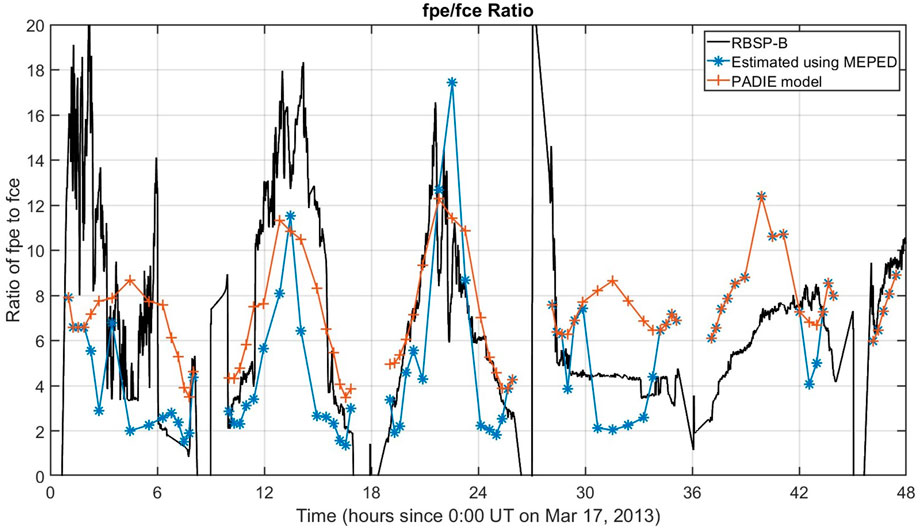
FIGURE 9. Same as Figure 8, except showing the plasma-gyrofrequency ratio
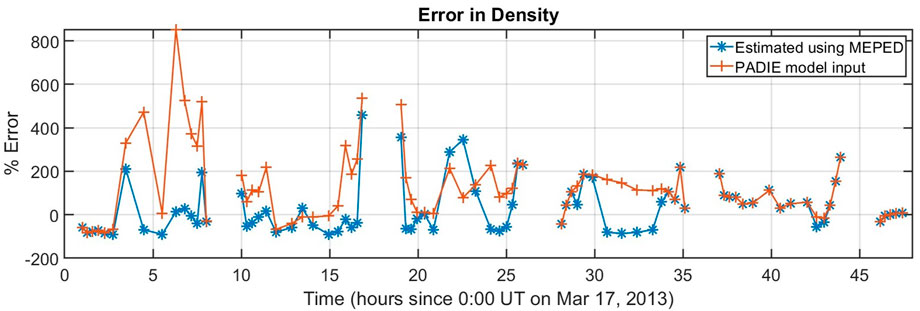
FIGURE 10. Error analysis of the density models. The percent error is computed as error = 100*(model-RBSP)/RBSP, where RBSP is the density measured by RBSP-B, and the model densities are from the MEPED scaling estimates (blue), and the PADIE statistical model (orange). By this metric, the MEPED estimated densities are typically closer to the RBSP-B measurements than the PADIE model is.
6 Conclusion
Modeling wave-particle interaction in the radiation belts requires event-specific diffusion coefficients for each of the relevant waves. Whistler-mode chorus waves strongly interact with electrons in the 10 keV to 1 MeV range and will pitch angle scatter those electrons into the loss cone where they precipitate into the upper atmosphere. The MEPED instrument on the POES/MetOp spacecrafts measures the precipitating and trapped flux of electrons in this energy range, allowing the estimation of the wave parameters in the radiation belts. In this paper, we expanded the method from Li et al. (2013) and Ni et al. (2014) to estimate chorus intensity and the plasma-gyrofrequency ratio,
Estimating the plasma-gyrofrequency ratio provides global, dynamic maps of the plasma density as discussed in Section 4.2. The global maps were compared to Van Allen Probes measurements of the density, showing moderately better percent errors than the statistical PADIE density model. This density estimation is not an exact process, and is limited by the following issues and approximations:
1) The scaling in Eq. 25 assumes parallel propagating chorus waves near the equator are the dominant driver of precipitating electrons measured by MEPED. The scaling equation breaks down in the relativistic limit, so care must be used to avoid scaling MeV energies down into the 30–300 keV integration range. In this paper, the diffusion coefficients needed to be scaled up in energy, so we did not encounter this issue.
2) The POES and MetOp satellites do not provide global coverage. An interpolation scheme was used to fill in spatial and temporal gaps in the data.
3) The scaling method is for the plasma-gyrofrequency ratio
4) This method only applies to time periods with enhanced chorus activity, since there needs to be enhanced electron precipitation in the 30–300 keV range. Furthermore, all precipitation in the 30–300 keV range is attributed to chorus waves and ignores all other wave modes in the radiation belts.
Furthermore, this method could be improved by skipping the energy scaling in Eq. 25 and instead using a large database of precomputed diffusion coefficients at various values of
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: The data, diffusion coefficients, and code used in this paper are available on Zenodo at doi: 10.5281/zenodo.7154151. The POES MEPED data is available at the National Centers for Environmental Information (NCEI) at https://www.ngdc.noaa.gov/stp/satellite/poes/dataaccess.html. The Van Allen Probes densities were obtained from the EMFISIS instrument and are available at https://emfisis.physics.uiowa.edu.
Author contributions
WL developed the methodology and analysis in this study and wrote the first draft of the manuscript. AC, AJ, and SE contributed to the conception and development of the study. JP processed the MEPED dataset. JR, SG, and RH provided the PADIE diffusion coefficients and model inputs. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
WL was supported by the NASA Living With a Star Jack Eddy Postdoctoral Fellowship Program, administered by UCAR’s Cooperative Programs for the Advancement of Earth System Science (CPAESS) under award #NNX16AK22G. WL, AC, AJ, and SE were supported by NASA H-SR grant #NNX17AI51G and NASA LWS grant #80NSSC21K1323. JP acknowledges funding from the NSF Coupling, Energetics and Dynamics of Atmospheric Regions, grant AGS 1651428 and the NASA Living With a Star program, grant NNX14AH54G. RH, SG, and JR were supported by NERC grant NE/V00249X/1 (Sat-Risk). RH and SG were supported by NERC National Capability grant NE/R016038/1 and NERC National Public Good activity grant NE/R016445/1.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.1063329/full#supplementary-material
References
Abel, B., and Thorne, R. M. (1998). Electron scattering loss in earth's inner magnetosphere: 1. Dominant physical processes. J. Geophys. Res. 103 (A2), 2385–2396. doi:10.1029/97JA02919styled
Albert, J. M., Meredith, N. P., and Horne, R. B. (2009). Three-dimensional diffusion simulation of outer radiation belt electrons during the 9 October 1990 magnetic storm. J. Geophys. Res. 114, A09214. doi:10.1029/2009JA014336styled
Bellan, P. M. (2006). Fundamentals of plasma physics. Cambridge, UK: Cambridge University Press. doi:10.1017/CBO9780511807183styled
Elkington, S. R., Hudson, M. K., and Chan, A. A. (1999). Acceleration of relativistic electrons via drift-resonant interaction with toroidal mode Pc-5 ULF oscillations. Geophys. Res. Lett. 26 (21), 3273–3276. doi:10.1029/1999GL003659styled
Elkington, S. R., Hudson, M. K., and Chan, A. A. (2003). Resonant acceleration and diffusion of outer zone electrons in an asymmetric geomagnetic field. J. Geophys. Res. 108, 1116. doi:10.1029/2001ja009202styled
Elkington, S. R., Hudson, M. K., Wiltberger, M. J., and Lyon, J. G. (2002). MHD/Particle simulations of radiation belt dynamics. J. Atmos. Sol. Terr. Phys. 64 (5-6), 607–615. doi:10.1016/S1364-6826(02)00018-4styled
Elkington, S. R., Wiltberger, M., Chan, A. A., and Baker, D. N. (2004). Physical models of the geospace radiation environment. J. Atmos. Sol. Terr. Phys. 66, 1371–1387. doi:10.1016/j.jastp.2004.03.023styled
Fei, Y., Chan, A. A., Elkington, S. R., and Wiltberger, M. J. (2006). Radial diffusion and MHD particle simulations of relativistic electron transport by ULF waves in the September 1998 storm. J. Geophys. Res. 111, A12209. doi:10.1029/2005JA011211styled
Glauert, S. A., and Horne, R. B. (2005). Calculation of pitch angle and energy diffusion coefficients with the PADIE code. J. Geophys. Res. 110, A04206. doi:10.1029/2004JA010851styled
Horne, R. B., Kersten, T., Glauert, S. A., Meredith, N. P., Boscher, D., Sicard-Piet, A., et al. (2013). A new diffusion matrix for whistler mode chorus waves. J. Geophys. Res. Space Phys. 118, 6302–6318. doi:10.1002/jgra.50594styled
Kennel, C. F., and Engelmann, F. (1966). Velocity space diffusion from weak plasma turbulence in a magnetic field. Phys. Fluids (1994). 9, 2377–2388. doi:10.1063/1.1761629styled
Kennel, C. F., and Petschek, H. E. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. 71 (1), 1–28. doi:10.1029/JZ071i001p00001styled
Kurth, W. S., De Pascuale, S., Faden, J. B., Kletzing, C. A., Hospodarsky, G. B., Thaller, S., et al. (2015). Electron densities inferred from plasma wave spectra obtained by the Waves instrument on Van Allen Probes. JGR. Space Phys. 120, 904–914. doi:10.1002/2014JA020857styled
Li, W., Ni, B., Thorne, R. M., Bortnik, J., Green, J. C., Kletzing, C. A., et al. (2013). Constructing the global distribution of chorus wave intensity using measurements of electrons by the POES satellites and waves by the Van Allen Probes. Geophys. Res. Lett. 40, 4526–4532. doi:10.1002/grl.50920styled
Lyons, L. R., and Williams, D. J. (1984). Quantitative aspects of magnetospheric physics. New York: Springer.styled
Ma, Q., Li, W., Bortnik, J., Thorne, R. M., Chu, X., Ozeke, L. G., et al. (2018). Quantitative evaluation of radial diffusion and local acceleration processes during GEM challenge events. JGR. Space Phys. 123, 1938–1952. doi:10.1002/2017JA025114styled
Malaspina, D. M., Jaynes, A. N., Elkington, S., Chan, A., Hospodarsky, G., and Wygant, J. (2021). Testing the organization of lower-band whistler-mode chorus wave properties by plasmapause location. JGR. Space Phys. 126, e2020JA028458. doi:10.1029/2020JA028458styled
Meredith, N. P., Horne, R. B., Shen, X.-C., Li, W., and Bortnik, J. (2020). Global model of whistler mode chorus in the near-equatorial region (|λm|< 18°). Geophys. Res. Lett. 47, e2020GL087311. doi:10.1029/2020GL087311styled
Ni, B., Li, W., Thorne, R. M., Bortnik, J., Green, J. C., Kletzing, C. A., et al. (2014). A novel technique to construct the global distribution of whistler mode chorus wave intensity using low-altitude POES electron data. J. Geophys. Res. Space Phys. 119, 5685–5699. doi:10.1002/2014JA019935styled
Omura, Y., Hikishima, M., Katoh, Y., Summers, D., and Yagitani, S. (2009). Nonlinear mechanisms of lower-band and upper-band VLF chorus emissions in the magnetosphere. J. Geophys. Res. 114, A07217. doi:10.1029/2009JA014206styled
Pettit, J. M., Randall, C. E., Peck, E. D., and Harvey, V. L. (2021). A new MEPED-based precipitating electron data set. J. Geophys. Res. Space Phys. 126, e2021JA029667. doi:10.1029/2021JA029667styled
Pettit, J. M., Randall, C. E., Peck, E. D., Marsh, D. R., van de Kamp, M., Fang, X., et al. (2019). Atmospheric effects of >30-keV energetic electron precipitation in the southern hemisphere winter during 2003. JGR. Space Phys. 124, 8138–8153. doi:10.1029/2019JA026868styled
Reidy, J. A., Horne, R. B., Glauert, S. A., Clilverd, M. A., Meredith, N. P., Woodfield, E. E., et al. (2021). Comparing electron precipitation fluxes calculated from pitch angle diffusion coefficients to LEO satellite observations. JGR. Space Phys. 126, e2020JA028410. doi:10.1029/2020JA028410styled
Ross, J. P. J., Glauert, S. A., Horne, R. B., Watt, C. E. J., and Meredith, N. P. (2021). On the variability of EMIC waves and the consequences for the relativistic electron radiation belt population. JGR. Space Phys. 126, e2021JA029754. doi:10.1029/2021JA029754styled
Ross, J. P. J., Glauert, S. A., Horne, R. B., Watt, C. E., Meredith, N. P., and Woodfield, E. E. (2020). A new approach to constructing models of electron diffusion by EMIC waves in the radiation belts. Geophys. Res. Lett. 47, e2020GL088976. doi:10.1029/2020GL088976styled
Selesnick, R. S., Tu, W., Yando, K. B., Millan, R. M., and Redmon, R. J. (2020). POES/MEPED angular response functions and the precipitating radiation belt electron flux. JGR. Space Phys. 125, e2020JA028240. doi:10.1029/2020JA028240styled
Tao, X., Chan, A. A., Albert, J. M., and Miller, J. A. (2008). Stochastic modeling of multidimensional diffusion in the radiation belts. J. Geophys. Res. 113, A07212. doi:10.1029/2007JA012985styled
Zhang, X.-J., Mourenas, D., Artemyev, A. V., Angelopoulos, V., Bortnik, J., Thorne, R. M., et al. (2019). Nonlinear electron interaction with intense chorus waves: Statistics of occurrence rates. Geophys. Res. Lett. 46, 7182–7190. doi:10.1029/2019GL083833styled
Appendix A: Whistler dispersion relation
The cold plasma dispersion relation is (Bellan, 2006):
Where
The Whistler mode is obtained by solving
From Eq. A4,
The Whistler mode corresponds to the R-mode solution, and Electromagnetic ion-cyclotron (EMIC) waves come from the L-mode solution, so we have
From the definitions of S and D, and ignoring ion terms,
We are interested in solutions where
This shows that R is strictly positive in the Whistler regime
With Eqs A10, A12, we obtain the dispersion relation for parallel propagating Whistler waves:
In Section 4.2 we use this dispersion relation along with the Landau/cyclotron resonance condition to solve for the Whistler mode frequency that is resonant with electrons at a specified energy and pitch angle.
Keywords: radiation belts, wave-particle interaction, quasilinear diffusion, SDE modeling, chorus waves, density measurements, POES/MetOp, van allen probes
Citation: Longley WJ, Chan AA, Jaynes AN, Elkington SR, Pettit JM, Ross JPJ, Glauert SA and Horne RB (2022) Using MEPED observations to infer plasma density and chorus intensity in the radiation belts. Front. Astron. Space Sci. 9:1063329. doi: 10.3389/fspas.2022.1063329
Received: 06 October 2022; Accepted: 04 November 2022;
Published: 21 November 2022.
Edited by:
Stanislav Boldyrev, University of Wisconsin-Madison, United StatesReviewed by:
Binbin Ni, Wuhan University, ChinaIvan Vasko, University of California, Berkeley, United States
Copyright © 2022 Longley, Chan, Jaynes, Elkington, Pettit, Ross, Glauert and Horne. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: William J. Longley, d2xvbmdsZXlAcmljZS5lZHU=
 William J. Longley
William J. Longley Anthony A. Chan
Anthony A. Chan Allison N. Jaynes
Allison N. Jaynes Scot R. Elkington
Scot R. Elkington Joshua M. Pettit
Joshua M. Pettit Johnathan P. J. Ross
Johnathan P. J. Ross Sarah A. Glauert
Sarah A. Glauert Richard B. Horne
Richard B. Horne