Recent progresses in strange quark stars

According to the hypothesis that strange quark matter may be the true ground state of matter at extremely high densities, strange quark stars should be stable and could exist in the Universe. It is possible that pulsars may actually be strange stars, but not neutron stars. Here we present a short review on recent progresses in the field of strange quark stars. First, three popular phenomenological models widely used to describe strange quark matter are introduced, with special attention being paid on the corresponding equation of state in each model. Combining the equation of state with the Tolman-Oppenheimer-Volkov equations, the inner structure and mass-radius relation can be obtained for the whole sequence of strange stars. Tidal deformability and oscillations (both radial and non-radial oscillations), which are sensitive to the composition and the equations of state, are then described. Hybrid stars as a special kind of quark stars are discussed. Several other interesting aspects of strange stars are also included. For example, strong gravitational wave emissions may be generated by strange stars through various mechanisms, which may help identify strange stars via observations. Especially, close-in strange quark planets with respect to their hosts may provide a unique test for the existence of strange quark objects. Fierce electromagnetic bursts could also be generated by strange stars. The energy may come from the phase transition of neutron stars to strange stars, or from the merger of binary strange stars. The collapse of the strange star crust can also release a huge amount of energy. It is shown that strange quark stars may be involved in short gamma-ray bursts and fast radio bursts.

1 Introduction

Strange quark matter, which is a mixture consisting of almost equal numbers of deconfined up, down, and strange quarks, may be true ground state of dense matter (Witten, 1984; Farhi and Jaffe, 1984). If such a strange quark matter hypothesis is correct, then the observed pulsars may actually be strange quark stars (also shortened as strange stars). Strange quark stars (SQS), which involve extraordinarily high densities, intense gravitational fields and strong electromagnetic fields (Alcock et al., 1986; Colpi and Miller, 1992), provide ideal natural laboratories for exploring physics under extreme astrophysical conditions. However, the nature of the strongly interacting matter under such extreme densities is still quite unclear, leading to large uncertainties in the internal structure of strange stars. A lot of efforts have been devoted to the theoretical and observational aspects of strange stars, but many issues still remain unsolved in the field.

Strange quark matter is inherently self-bound by the strong interactions of quarks. As a result, compact stars composed of strange quark matter could be bare strange stars whose density reduces to zero abruptly at the surface. However, a strange star can also have a thin crust composed of normal nuclear matter (Glendenning and Weber, 1992). Because the maximum density of the crust is five times lower than the neutron drip density (Huang and Lu, 1997), the light crust has an almost negligible effect on the internal structure of strange stars (Zdunik, 2002). However, it could significantly change the characteristics of electromagnetic emissions from such compact stars. Also, collapse of the crust could lead to some kinds of electromagnetic bursts or even emission of gravitational waves.

Interestingly, according to the strange quark matter hypothesis, strange quark dwarfs and even strange quark planets could also exist. They may be produced due to the contamination of white dwarfs/planets by strange nuggets in the Universe. While the stability of these low-mass strange objects is still highly debated (Glendenning et al., 1995; Fraga et al., 2001; Vartanyan et al., 2012; Vartanyan et al., 2014; Alford et al., 2017; Di Clemente et al., 2023; Gonçalves et al., 2023), they could provide valuable opportunities for identifying strange stars due to their significant difference from normal matter white dwarfs and planets (Huang and Yu, 2017; Kuerban et al., 2020; Wang et al., 2021; Kurban et al., 2022b).

The study of strange stars is an active and rapidly developing field. In the past few decades, various observational aspects of strange stars have been studied. In this review, we are going to present a brief description on some recent progresses concerning strange stars. Hybrid stars, in which quark matter and hadronic matter may coexist, are also discussed. The structure of our paper is organized as follows. The properties and internal structure of strange stars are introduced in Section 2. Especially, several popular phenomenological models describing the strong interaction among quarks are presented. Tidal deformability and oscillations, which are closely related to the internal structure, are also introduced. As a special kind of quark stars, hybrid stars are discussed in Section 3, paying special attention on the transition between different phases. In Section 4, gravitational wave (GW) emissions from various strange quark objects are discussed. Possible connection between some violent electromagnetic bursts (e.g., gamma-ray bursts and fast radio bursts) and strange stars are introduced in Section 5. Finally, Section 6 presents the conclusions and some further discussion.

2 Internal structure of strange stars

While thousands of pulsars have been observed, the internal composition and structure of them are still controversial. This enigma is closely connected with the interaction and properties of matter under extreme densities and temperatures, thus is an important issue involving fundamental physics. Theoretically, pulsars could be neutron stars or quark stars. In the quark star case, they could either be three-flavor (u, d, s) strange stars, or could even be two-flavor (u, d) quark stars. The existence of the so called hybrid stars is also suggested, which usually include a quark matter core encompassed by normal nuclear matter (Ivanenko and Kurdgelaidze, 1965; Annala et al., 2020; Menezes, 2021).

Equation of state (EOS), which gives the relation between pressure and energy density, is an important factor that determines the structure and overall properties of compact stars. EOS is generally dependent on the composition and temperature of the dense matter. In principle, EOS could be derived by considering the strong interaction of microscopic particles that constitute the dense matter. However, due to the complexity of strong interaction and our poor understanding on it, an accurate derivation of the EOS is still impossible. Various models have been proposed to describe the strong interaction of quarks. In this section, we will introduce several widely used quark interaction models. The internal structure of compact stars based on these models will also be addressed. Note that some further complicated ingredients such as the magnetic field and the spin of the star should also be included when they play a non-negligible role in some extreme cases.

2.1 MIT bag model

The MIT bag model, initially proposed in the 1970s by Chodos et al. (1974a, 1974b), is a phenomenological theoretical description aiming at explaining the structure of hadrons. In this framework, the finite space containing hadrons is regarded as a “bag.” Hadrons in the bag are composed of free quarks, including up, down, and strange quarks in case of strange stars. Such a confinement is not a dynamical outcome of any underlying theory but rather a feature imposed by hand, achieved through the imposition of particular boundary conditions (Buballa, 2005).

The general form of the EOS of this model is (Shafeeque et al., 2023; Lohakare et al., 2023)

$P=k\left(ϵc^2-4B\right),(1)$

where $P$ denotes the pressure within the bag, $ϵ$ represents the energy density, and $c$ is the velocity of light. The parameter $k$ is a constant that depends upon the mass of strange quarks $(m_s)$ and the quantum chromodynamics (QCD) coupling constant. Specifically, for $m_s=0$, $k=1/3$. $B$ signifies the pressure of the bag, corresponding to the energy density when the bag is in a vacuum state. It is a free parameter that could be determined by considering the hadron spectra or other experimental data.

The bag constant is also equivalent to the critical pressure of deconfinement, resulting in a pressure differential across the surface of the bag. The characteristics of quark confinement can be described qualitatively by the bag constant. However, it is too simple to describe asymptotic freedom at increasing energy scales, a crucial property associated with QCD. Anyway, the model has only one free parameter $(B)$, making it the simplest theory to compute the EOS of strange quark matter.

2.2 NJL model

The Nambu-Jona-Lasinio (NJL) model is initially proposed by Nambu and Jona-Lasinio (1961a, 1961b) to describe the interaction between nucleons. It was extended by Eguchi and Sugawara (1974) to include up and down quarks. Kikkawa (1976) further developed the theory to encompass three flavors of quarks, including up, down, and strange quarks. In this review, we utilize the three-flavor NJL model to describe quark matter inside strange stars. The model exhibits spontaneous breaking of chiral symmetry, which is essential for understanding the large nucleon mass and the dynamic generation of fermion masses. Additionally, the model is noteworthy for its solvability, allowing for simple analytical results obtained in certain limiting cases.

The Lagrangian of three-flavor NJL model is generally expressed as

$\mathcal{L}=\bar{\psi }\left(i{\gamma }^{\mu }{\partial }_{\mu }-m\right)\psi +{\mathcal{L}}^{\left(4\right)}+{\mathcal{L}}^{\left(6\right)},$

where $\psi ={({\psi }_u,{\psi }_d,{\psi }_s)}^{\text{T}}$ represents the quark field, ${\gamma }^{\mu }$ denotes the Dirac matrix, $m=diag(m_u,m_d,m_s)$ is the fluid quark mass matrix, and ${\partial }_{\mu }$ is the partial differential operator in four-dimensional spacetime. ${\mathcal{L}}^{(4)}$ and ${\mathcal{L}}^{(6)}$ correspond to four-fermion interaction and six-fermion interaction terms, respectively, representing two-body and three-body interactions. The isospin symmetry indicates that $m_u=m_d$, but $m_s$ differs from both $m_u$ and $m_d$, thereby manifesting the $SU(3)$ symmetry breaking in the three-flavor NJL model.

Since quark confinement is not directly reflected in the NJL model, it is often used in conjunction with the bag constant $(B)$ to derive the EOS. Comparing with the MIT bag model, the confinement is a dynamical outcome in the NJL model rather than being imposed by hand. However, similar to the MIT bag model, the NJL model also fails to explain the characteristics of asymptotic freedom. Additionally, in this model, the interaction between quarks is regarded as point-to-point interaction without the inclusion of gluons. Consequently, it is not a renormalizable field theory, and a regularization scheme must be specified to address the improper integrals that arise (Klevansky, 1992). For more details, readers can refer to the review articles by Klevansky (1992) and Buballa (2005).

2.3 Quasi-particle model

The quasi-particle model is another phenomenological approach for strange quark matter. Peshier et al. (1994) and Gorenstein and Yang (1995) initially employed this model to describe the quark-gluon plasma with strong interactions. Here we present a short introduction to the model. First, the pressure at zero temperature and finite chemical potential can be expressed as a model-independent formula (He et al., 2007; Zong and Sun, 2008b; Zong and Sun, 2008a),

$P\left(\mu \right)=P\left(\mu \right){|}_{\mu =0}+{\int }_0^{\mu }\mathrm{d}{\mu }^{\prime }\rho \left({\mu }^{\prime }\right),$

where $\mu$ denotes the chemical potential, $P(\mu ){|}_{\mu =0}$ signifies the pressure at zero chemical potential, and $\rho (\mu )$ is the number density of quarks.

To calculate the pressure, the primary challenge lies in computing the number density of quarks, which relies on the quark propagator. However, calculating the quark propagator directly from the first principles of QCD is impractical. Therefore, we have to employ approximations and then use the quasi-particle model. In this model, particles are treated as an ideal gas composed of non-interaction quasi-particles, with their masses depending on the temperature and density. This model simplifies the calculation of particle interactions, making computations more tractable. In this way, the EOS is derived in the framework of the quasi-particle model as (Zhao et al., 2010)

$P\left(\mu \right)=P\left(\mu \right){|}_{\mu =0}+\frac{3}{{\pi }^2}{\int }_0^{\mu }\mathrm{d}{\mu }^{\prime }\theta \left({\mu }^{\prime }-m\left({\mu }^{\prime }\right)\right){\left({\left({\mu }^{\prime }\right)}^2-m{\left({\mu }^{\prime }\right)}^2\right)}^{3/2},$

where $m(\mu )$ is the effective mass and $\theta$ is the Heaviside step function. Here, three colors and three flavors have been considered for quarks.

In view of quark confinement, the energy density in the vacuum is lower than that of free quarks. Consequently, the vacuum pressure at zero chemical potential ($P(\mu ){|}_{\mu =0}$) is negative. Using the MIT bag model for reference, we can set $P(\mu ){|}_{\mu =0}=-B$. In this framework, quarks are treated as Fermi gas at high chemical potentials, which to some extent reflects the asymptotic freedom property of QCD. It also matches well with the results of Lattice QCD (Peshier et al., 2000; Peshier et al., 2002; Rebhan and Romatschke, 2003).

2.4 Tolman-Oppenheimer-Volkoff equation

Due to the extremely high density of strange stars accompanied by strong gravity, the effects of spacetime curvature cannot be ignored. Consequently, the structure of strange stars has to be studied in the context of General Relativity. The Tolman-Oppenheimer-Volkoff (TOV) equation (Oppenheimer and Volkoff, 1939; Tolman, 1939), should be employed to infer the structure of such compact objects, which assumes that the interior of the star is composed of spherically symmetric ideal fluid. Using spherical coordinates of $(x^0,x^1,x^2,x^3)=(t,r,\theta ,\varphi )$, the generalized Schwarzschild metric is (Oppenheimer and Volkoff, 1939)

$d{s}^2=-e^{\sigma \left(r\right)}d{t}^2+e^{\eta \left(r\right)}d{r}^2+r^{2}d{\theta }^2+r^{2}si{n}^2\theta d{\varphi }^2,(2)$

where $\sigma (r)$ and $\eta (r)$ are functions of radial coordinates. Comparing it with the spacetime interval, $d{s}^2=g_{ab}d{x}^{a}d{x}^b$, the nonzero covariant components of the metric tensor $g_{ab}$ can be obtained as

$g_{tt}=-e^{\sigma \left(r\right)},g_{rr}=e^{\eta \left(r\right)},\hspace{0.5em}{g}_{\theta \theta }=r^2,\hspace{0.5em}{g}_{\varphi \varphi }=r^{2}sin{\theta }^2.(3)$

The energy-momentum tensor of such a ideal fluid is given by

$T^{ab}=\left(p+ϵ\right)u^a{u}^b+p{g}^{ab},(4)$

where $p$ is the pressure and $ϵ$ is the energy density. For a static spherically symmetric star, the pressure and energy density are functions of the r-coordinate, i.e., $p(r)$ and $ϵ(r)$. $u^a$ and $u^b$ are four-dimension velocities. Equation 4 can be rewritten as

$T_b^a=\left(p+ϵ\right)u^a{u}_b+p{\delta }_b^a.$

Since the star is static, there are no spatial components for the four velocities, i.e., $u^i=0(i=\mathrm{1,2,3}),u^0=u^t=1/\sqrt{-g_{tt}}$. Considering the normalization condition of $u^a{u}_b=-1$, we have (Tolman, 1934)

$T_0^0=-ϵ,$

$T_a^a=p\left(a=\mathrm{1,2,3}\right).$

The Einstein’s field equation is

$R_{ab}-\frac{1}{2}R{g}_{ab}+\mathrm{\Lambda }{g}_{ab}=\frac{8\pi G}{c^4}{T}_{ab},(5)$

where $R_{ab}$ is the Ricci curvature tensor, $R$ is the scalar curvature, $\mathrm{\Lambda }$ is the cosmological constant, $G$ is Newton’s gravitational constant and $c$ is the speed of light. For simplicity, we take $c=1$ hereinafter. The cosmological constant $\mathrm{\Lambda }$ is negligible for compact stars.

The Ricci tensor is expressed as (Glendenning, 1996)

$R_{ab}={\mathrm{\Gamma }}_{a\alpha ,b}^{\alpha }-{\mathrm{\Gamma }}_{ab,\alpha }^{\alpha }+{\mathrm{\Gamma }}_{a\beta }^{\alpha }{\mathrm{\Gamma }}_{b\alpha }^{\beta }-{\mathrm{\Gamma }}_{ab}^{\alpha }{\mathrm{\Gamma }}_{\alpha \beta }^{\beta },(6)$

where the Christoffel symbol is defined as

${\mathrm{\Gamma }}_{ab}^{\lambda }=\frac{1}{2}{g}^{\lambda \kappa }\left(g_{\kappa a,b}+g_{\kappa b,a}-g_{ab,\kappa }\right).$

Using the metric tensor of Equation 3, we can obtain the non-zero Christoffel symbols as (Glendenning, 1996)

$4{\mathrm{\Gamma }}_{00}^1=\frac{1}{2}{\sigma }^{\prime }{e}^{\sigma -\lambda },{\mathrm{\Gamma }}_{10}^0=\frac{1}{2}{\sigma }^{\prime },$

${\mathrm{\Gamma }}_{11}^1=\frac{1}{2}{\eta }^{\prime },{\mathrm{\Gamma }}_{12}^2={\mathrm{\Gamma }}_{13}^3=\frac{1}{r},$

${\mathrm{\Gamma }}_{22}^1=-r{e}^{-\eta },{\mathrm{\Gamma }}_{23}^3=cot\theta ,$

${\mathrm{\Gamma }}_{33}^1=-rsi{n}^2\theta e^{-\eta },{\mathrm{\Gamma }}_{33}^2=-sin\theta cos\theta .$

Here the primes denote differentiation with respect to the r-coordinate. Then the nonzero components of the Ricci tensor in Equation 6 is derived as (Glendenning, 1996)

$R_{00}=e^{\sigma -\eta }\left(-\frac{{\sigma }^{″}}{2}-\frac{{\sigma }^{\prime }}{r}+\frac{{\sigma }^{\prime }}{4}\left({\eta }^{\prime }-{\sigma }^{\prime }\right)\right),$

$R_{11}=\frac{{\sigma }^{″}}{2}-\frac{{\eta }^{\prime }}{r}+\frac{{\sigma }^{\prime }}{4}\left({\sigma }^{\prime }-{\eta }^{\prime }\right),$

$R_{22}=e^{-\eta }\left(1+\frac{r}{2}\left({\sigma }^{\prime }-{\eta }^{\prime }\right)\right)-1,$

$R_{33}=R_{22}si{n}^2\theta .$

Furthermore, we have

$R_b^a=g^{aa}{R}_{ab}.$

The scalar curvature is obtained from the trace of the Ricci tensor,

$R=g^{ab}{R}_{ab}=R_a^a.$

The Einstein’s field Equation 5 can be rewritten as,

$R_b^a-\frac{1}{2}R{\delta }_b^a=8\pi G{T}_b^a.$

Substituting $R_b^a$, $R$ and $T_b^a$ into the equation, we have

$R_0^0-\frac{1}{2}R{\delta }_0^0=e^{-\eta }\left(\frac{1}{r^2}-\frac{{\eta }^{\prime }}{r}\right)-\frac{1}{r^2}=-8\pi Gϵ,$

$R_1^1-\frac{1}{2}R{\delta }_1^1=e^{-\eta }\left(\frac{1}{r^2}+\frac{{\sigma }^{\prime }}{r}\right)-\frac{1}{r^2}=8\pi Gp,$

$R_2^2-\frac{1}{2}R{\delta }_2^2=e^{-\eta }\left(\frac{{\sigma }^{″}}{2}-\frac{{\sigma }^{\prime }{\eta }^{\prime }}{4}+\frac{{\sigma }^{\prime 2}}{4}+\frac{{\sigma }^{\prime }}{2r}-\frac{{\eta }^{\prime }}{2r}\right)=8\pi Gp,$

$R_3^3-\frac{1}{2}R{\delta }_3^3=e^{-\eta }\left(\frac{{\sigma }^{″}}{2}-\frac{{\sigma }^{\prime }{\eta }^{\prime }}{4}+\frac{{\sigma }^{\prime 2}}{4}+\frac{{\sigma }^{\prime }}{2r}-\frac{{\eta }^{\prime }}{2r}\right)=8\pi Gp.$

Note that the last two equations are identical, hence there are only three independent equations.

The boundary conditions can be taken as the Schwarzschild metric vacuum solution, which gives (Tolman, 1939)

$-e^{\sigma \left(r\right)}=1-\frac{2GM}{r},e^{\eta \left(r\right)}=-{\left(1-\frac{2GM}{r}\right)}^{-1},$

where $M$ is the mass of the whole star. The TOV equation can then be derived as (Oppenheimer and Volkoff, 1939)

$\frac{\mathrm{d}p\left(r\right)}{\mathrm{d}r}=-\frac{G\left(ϵ+p\right)\left(m+4\pi r^{3}p\right)}{r\left(r-2Gm\right)}.(7)$

Here the mass included inside a sphere of radius $r$ is

$m\left(r\right)=4\pi {\int }_0^rϵ\left(x\right)x^{2}dx,$

which can be equivalently expressed in the differential form of

$\frac{\mathrm{d}m\left(r\right)}{\mathrm{d}r}=4\pi r^2ϵ.(8)$

Given the pressure and energy density at the center of the star, i.e., $p(0)$ or $ϵ(0)$, we can calculate the mass and radius of a compact star by solving Equations 30, 32.

Typical mass-radius curves of bare strange stars derived by using the MIT bag model are shown in the left panel of Figure 1 (Deb et al., 2017). On the other hand, the mass-radius curves of crusted strange stars are shown in the right panel of Figure 1 (Huang and Lu, 1997). This mass-radius relationship help us understand the maximum and minimum limits of mass, the upper limit of radius, the density distribution and even the stability condition of strange stars. We can also compare the theoretically predicted parameters with observational data to test the model and gain insights into the nature of matter under extreme conditions.

Figure 1

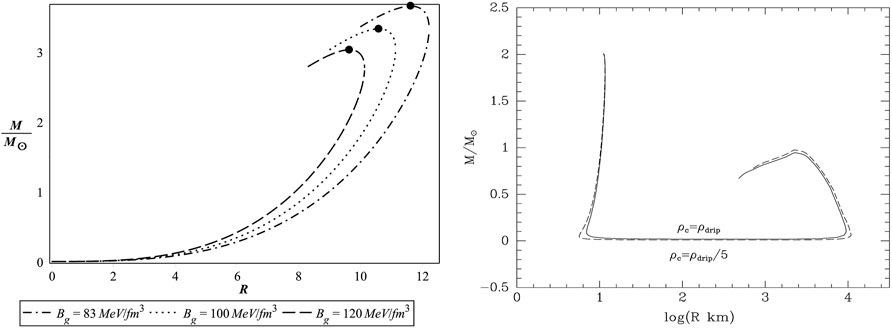
Figure 1. Mass (normalized in solar masses) versus radius (km) for strange stars. Left panel: bare strange stars. Three different values are taken for the bag constant, i.e., 83, 100 and 120 MeV/fm³. The filled circle on each curve represents the maximum-mass star (Deb et al., 2017). Right panel: crusted strange stars. The solid and dashed lines represent the bottom density of neutron drip density $({\rho }_{\text{drip}})$ and ${\rho }_{\text{drip}}/5$, respectively (Huang and Lu, 1997).

2.5 Tidal deformability and love numbers

In the framework of General Relativity, an external tidal field perturbs the spacetime geometry around a star, leading to changes in the metric coefficients. These changes can be analytically expressed in the asymptotic region far from the star. For a spherically symmetric static star with a mass of $m$, the metric coefficient $g_{tt}$ in the local rest frame (which is asymptotically Cartesian and mass-centered coordinates) at a distance of $r$ can be given by solving the Einstein’s field equation, which is (Thorne, 1998)

$\begin{array}{ll}\hfill -\frac{1+g_{tt}}{2}& =-\frac{m}{r}-\frac{\left(3n^i{n}^j-{\delta }^{ij}\right)Q_{ij}}{2r^3}+\mathcal{O}\left(r^{-4}\right)\hfill \\ \hfill & +\frac{E_{ij}}{2}{r}^2{n}^i{n}^j++\mathcal{O}\left(r^3\right),\hfill \end{array}(9)$

where $n^i=x^i/r$. This expression is in units of $G=c=1$. The first term on the right hand is a general relativistic correction for the classical Newtonian gravitational potential. The symmetric and traceless tensors $Q_{ij}$ and $E_{ij}$ represent the quadrupole moment and the external quadrupolar tidal field, respectively.

The distortion of an object caused by external gravitational forces can be described by a linear function between the quadrupole moment $Q_{ij}$ and the external quadrupolar tidal field $E_{ij}$ (Flanagan and Hinderer, 2008; Hinderer, 2008),

$Q_{ij}=-\lambda E_{ij},$

where the coefficient $\lambda$ is the so called tidal deformability. It represents the extent to which the star deforms under the influence of a specific tidal force. A commonly used dimensionless tidal deformation parameter is then defined as,

$\mathrm{\Lambda }=\frac{\lambda }{m^5}.$

Another useful dimensionless tidal Love number $(k_2)$ connected with the coefficient $\lambda$ as

$k_2=\frac{3}{2}\lambda R^{-5},$

where $R$ is the radius of the star. $k_2$ is called the Love number, which represents the second spherical harmonic function (for the angular quantum number $l=2$) used in calculating the metric in Equation 9. It can be calculated as Hinderer (2008)

$\begin{array}{ll}\hfill k_2& =\frac{8C^5}{5}{\left(1-2C\right)}^2\left[2+2C\left(y-1\right)-y\right]\hfill \\ \hfill & \times \left\{2C\left[6-3y+3C\left(5y-8\right)\right]\right.\hfill \\ \hfill & +4C^3\left[13-11y+C\left(3y-2\right)+2C^2\left(1+y\right)\right]\hfill \\ \hfill & {\left.+3{\left(1-2C\right)}^2\left[2-y+2C\left(y-1\right)\right]\ln \left(1-2C\right)\right\}}^{-1},\hfill \end{array}$

where $C=m/R$ is the compactness of the star. The function $y=y(r)$ satisfies the differential equation of (Postnikov et al., 2010; Takátsy and Kovács, 2020)

$\begin{array}{ll}\hfill y\left(r\right)\frac{dy\left(r\right)}{dr}& +y{\left(r\right)}^2+Q\left(r\right)r^2\hfill \\ \hfill & +y\left(r\right)e^{\eta \left(r\right)}\left[1+4\pi r^2\left(p\left(r\right)-ϵ\left(r\right)\right)\right]=0,\hfill \end{array}$

where $p(r)$ and $ϵ(r)$ are the pressure and energy density, respectively. $Q(r)$ is expressed as

$\begin{array}{ll}\hfill Q\left(r\right)& =4\pi e^{\eta \left(r\right)}\left(5ϵ\left(r\right)+9p\left(r\right)+\frac{p\left(r\right)+ϵ\left(r\right)}{c_s^2\left(r\right)}\right)\hfill \\ \hfill & -6\frac{e^{\eta \left(r\right)}}{r^2}-{\left({\sigma }^{\prime }\left(r\right)\right)}^2,\hfill \end{array}$

where $c_s(r)=\sqrt{dp/dϵ}$ is the sound speed. $\sigma (r)$ and $\eta (r)$ are metric functions defined in Equation 2. Taking the boundary condition as $y(0)=2$ (Damour and Nagar, 2009), the tidal Love number $k_2$ can be conveniently calculated by solving the TOV equation.

The tidal Love number $k_2$ is strongly dependent on the EOS of a star. Different EOSs of neutron stars and strange quark stars result in different $k_2$. Thus the tidal deformability could be a useful probe that could help distinguish between neutron stars and strange stars (Postnikov et al., 2010).

2.6 Oscillations and quasi-normal modes

Oscillations are closely relevant to the stability of stars and are sensitive to the equation of state and the composition. In this aspect, quasi-normal modes are usually discussed instead of normal modes, because the stars are practically in a system with energy losses due to gravitational radiation and other dissipative effects. The frequency of a quasi-normal mode is usually expressed as a complex number, in which the real part represents the actual oscillation frequency and the imaginary part indicates the decay rate.

Quasi-normal modes include two parts, the radial oscillation and non-radial oscillation. Radial oscillation refers to the oscillation of the compact star in the radial direction. Non-radial oscillation refers to the oscillation in a non-radial direction, which is usually described by spherical harmonics. Quasi-normal modes of non-radial oscillation are more complex and involve different mode types, such as f-mode, p-mode, and g-mode. Studying these quasi-normal modes can reveal oscillatory behaviors of compact stars under gravitational wave emissions and other dissipative effects, and help probe their internal structure.

2.6.1 Radial oscillations

Radial oscillations of compact stars are investigated firstly by Chandrasekhar (1964a, 1964b). Usually adiabatic oscillations are considered: the whole star oscillates like a retractable spring to expand and shrink periodically. Assuming a spherical symmetry and considering small-amplitude radial oscillations, we can introduce a time-dependent radial displacement $\delta r(r,t)$ of a fluid element at $r$, which is expressed as

$\delta r\left(r,t\right)=X\left(r\right)e^{i\omega t},$

where $X(r)$ represents the oscillation amplitude and $\omega$ is the oscillation frequency.

Under small perturbations, the contributions from nonlinear terms can be ignored. The differential equation of the radial displacement $(X(r))$ was derived by Chandrasekhar (1964b) as

$\begin{array}{ll}\hfill Y\frac{d^{2}X}{d^{2}r}& +\left(\frac{dY}{dr}-Z+4\pi r\gamma p{e}^{\eta }-\frac{1}{2}\frac{d\sigma }{dr}\right)\frac{dX}{dr}\hfill \\ \hfill & +\left[\frac{1}{2}{\left(\frac{d\sigma }{dr}\right)}^2+\frac{2m}{r^3}{e}^{\eta }-\frac{dZ}{dr}-4\pi \left(ϵ+p\right)Zr{e}^{\eta }+{\omega }^2{e}^{\eta -\sigma }\right]X=0,\hfill \end{array}$

where

$Y\left(r\right)=\gamma p/\left(ϵ+p\right),$

$Z\left(r\right)=Y\left(-\frac{2}{r}+\frac{1}{2}\frac{d\sigma }{dr}\right).$

Here $\sigma (r)$ and $\eta (r)$ are again the functions defined in Equation 2. $\gamma$ is the adiabatic index determined by the equation of state,

$\gamma =\frac{ϵ+p}{p}\frac{dp}{dϵ}.$

Using the adiabatic index, $Y$ can be expressed as

$\begin{array}{ll}\hfill Y\left(r\right)& =\frac{dp}{dϵ}\hfill \\ \hfill & \equiv c_s^2,\hfill \end{array}$

where $c_s$ is the sound speed.

To calculate $X(r)$, two boundary conditions must be specified. First, the fluid at the center of the star is assumed to remain at rest, i.e.,

$X\left(0\right)=0.$

Second, the pressure perturbation vanishes at the stellar surface, which means the Lagrangian variation of the pressure should also vanish, i.e.,

$\mathrm{\Delta }p=-e^{\sigma /2}{r}^{-2}\gamma p\frac{d}{dr}\left(r^2{e}^{-\sigma /2}X\right)=0.$

Under these conditions, the eigenvalue of ${\omega }^2$ and the corresponding radial eigenfunction of $X(r)$ can be solved. The radial oscillation frequencies are directly linked to the mean density and elastic properties, providing information about the internal pressure and density distribution inside the star (Benvenuto and Horvath, 1991; Vaeth and Chanmugam, 1992; Jiménez and Fraga, 2019; Bora and Dev Goswami, 2021; Rather et al., 2023).

In most cases, the stellar stability against radial oscillations is investigated by applying the Bardeen-Thorne-Meltzer (BTM) criterion (Bardeen et al., 1966). The BTM criterion is usually expressed as follows: when moving toward the direction of increasing central pressure along the mass-radius curve, at each extremum, one previously stable radial mode becomes unstable if the curve bends counterclockwise, while one previously unstable radial mode becomes stable if the curve bends clockwise. For bare strange quark objects which include the whole bare strange planet-bare strange star series, the conclusion on the stability is quite clear. All configurations before the mass-radius curve reaches its maximum are stable, with stars of higher central pressure unstable. It means that all the bare strange planets and bare strange dwarfs are stable.

However, in the cases of crusted strange quark objects, things become more complicated. At first glance, strange dwarfs seem to be unstable according to the BTM criterion (see the right panel of Figure 1). By contrast, Glendenning et al. (1995) solved the Sturm-Liouville problem governing stellar stability and claimed that strange dwarfs are in fact stable. They found that all the eigenvalues of the radial oscillation mode are positive. It is argued that the strange quark core stabilizes the strange dwarf. Nevertheless, the detailed mechanism on how the strange quark core stabilizes the strange dwarf is not addressed. Later, Alford et al. (2017) revisited the problem and solved the Sturm–Liouville problem again. They found that the lowest eigenvalue of the radial oscillation mode is negative, which means strange dwarfs are unstable. They argued that the lowest eigenvalue was essentially omitted by Glendenning et al. (1995). Recently, Di Clemente et al. (2023) and Gonçalves et al. (2023) further examined the issue and found that the difference between Glendenning et al. (1995) and Alford et al. (2017) is due to the different matching condition used at the interface between strange quark core and nuclear crust. Alford et al. (2017) have used the so-called rapid conversion condition, while the calculations of Glendenning et al. (1995) correspond to the slow conversion condition. As a result, Di Clemente et al. (2023) and Gonçalves et al. (2023) concluded that strange dwarfs are “slow-stable” — being stable only when the phase transition process between strange quark matter and nuclear matter is slower than the radial perturbation.

In fact, the term “slow-stable” is generally used to describe hybrid stars, where the central quark matter is encompassed by nuclear matter and the two kinds of matter can transfer to each other through phase transition. However, in the context of crusted strange dwarfs and planets, the crust and strange core are separated by a strong electric field. There is a “gap” (of several hundreds fermis) between strange quark matter and nuclear matter so that the two “phases” do not contact with each other. As a result, inside strange dwarfs and strange planets, phase transition essentially cannot proceed between the quark matter and the hadronic matter at the bottom of the crust. In other words, these light strange quark objects generally satisfy the slow conversion condition and they are in the “slow-stable” state. To conclude, the electric field between strange core and the crust guarantees the stability of strange dwarfs and strange planets against usual radial perturbations. However, note that a too large perturbation may still be able to cause the crust of a strange dwarf to collapse.

2.6.2 Non-radial oscillations

Non-radial oscillations of neutron stars was initially studied by Thorne and Campolattaro (1967), which are especially important for gravitational wave emissions (Price and Thorne, 1969). For simplicity, we adopt the Cowling approximation (Cowling, 1941; McDermott et al., 1988) and ignore the gravitational perturbations in spacetime. Denoting the deviation of the fluid element from its equilibrium position as ${\xi }^i$, we have (Sotani et al., 2011),

${\xi }^i=\left(e^{-\eta /2}W,-V{\partial }_{\theta },-Vsi{n}^{-2}\theta {\partial }_{\varphi }\right)r^{-2}{Y}_{lm},$

where $i=r,\theta ,\varphi$ in this subsection, $W$ and $V$ are perturbation functions of $t$ and $r$, and $Y_{lm}$ is the spherical harmonics. The perturbation of the four-velocity $\delta u^a$ can then be written as

$\delta u^a=\left(0,e^{-\eta /2}{\partial }_{t}W,-{\partial }_{t}V{\partial }_{\theta },-{\partial }_{t}Vsi{n}^{-2}\theta {\partial }_{\varphi }\right)r^{-2}{e}^{-\varphi }{Y}_{lm}.$

Note that the energy momentum tensor satisfies (Sotani et al., 2011; Curi et al., 2022)

$\delta \left({\nabla }_b{T}^{ab}\right)={\nabla }_b\delta T^{ab}=0.$

Assuming that the perturbations are harmonic functions of time, i.e., $W(r,t)=W(r)e^{i\omega t}$ and $V(r,t)=V(r)e^{i\omega t}$, the oscillation equations in the Cowling approximation can be simplified as

$\begin{array}{ll}\hfill W^{\prime }& =\frac{dϵ}{dp}\left[{\omega }^2{r}^2{e}^{\eta /2-\sigma }V+\frac{1}{2}{\sigma }^{\prime }W\right]-l\left(l+1\right)e^{\eta /2}V,\hfill \\ \hfill V^{\prime }& ={\sigma }^{\prime }V-e^{\eta /2}\frac{W}{r^2}.\hfill \end{array}$

To solve these equations, we again need to specify two boundary conditions. First, the Lagrangian perturbation of pressure should vanish at the stellar surface, i.e.,

$\mathrm{\Delta }p={\omega }^2{r}^2{e}^{\eta /2-\sigma }V+\frac{1}{2}{\sigma }^{\prime }W=0.$

Second, the perturbation functions of $W(r,t)$ and $V(r,t)$ satisfy

$\begin{array}{ll}\hfill W\left(r\right)& =C{r}^{l+1}+\mathcal{O}\left(r^{l+3}\right),\hfill \\ \hfill V\left(r\right)& =C{r}^l/l+\mathcal{O}\left(r^{l+2}\right),\hfill \end{array}$

at the star center $(r=0)$, where $C$ is a constant.

Solving this eigenvalue problem, we can determine the characteristic frequency $\omega$ and the corresponding characteristic function ${\xi }^i$ associated with the non-radial oscillations. The solutions are classified into distinct oscillation modes according to the nature of the characteristic frequencies and eigenfunctions, which mainly include:

f-modes (fundamental modes): This is the lowest order mode of non-radial oscillations. Their frequencies are typically high. They are primarily driven by the global deformation of fluid dynamics, reflecting the overall deformation of the star.

p-modes (pressure modes): For these modes, the frequency is typically high and it increases with the increasing mode order. They are primarily driven by pressure waves (sound waves) in the fluid, reflecting the pressure distribution and the speed of sound inside the star.

g-modes (gravity modes): The frequency is usually low. They are primarily driven by buoyancy forces, reflecting the density gradients and thermal gradients inside the star.

Note that under the Cowling approximation, the non-radial oscillation equations cannot effectively describe the $\omega$-modes (gravitational wave modes) due to the ignoring of the metric perturbations. $\omega$-modes are driven solely by gravitational waves, reflecting the spacetime undulations instead of material movements. To investigate the gravitational emissions accurately, metric perturbations in the framework of General Relativity should be considered and the coupling between the fluid dynamics equations and the Einstein’s field equations should be solved (Kokkotas and Schutz, 1992; Andersson and Kokkotas, 1996; Andersson and Kokkotas, 1998).

3 Hybrid stars

A compact star is conceptually divided into five parts, the atmosphere, the outer crust, the inner crust, the outer core, and the inner core (Weber, 2005). The atmosphere is a thin layer of plasma, typically several centimeters in thickness. The outer crust is composed of atomic nuclei and free electrons, with the density being lower than $10^{11}$ g/cm³. In the inner crust, the density becomes higher but is still less than $10^{14}$ g/cm³. Atomic nucleus are disintegrated and neutrons overflow from the nucleus. In the outer core, the density increases to exceed the nuclear saturation density so that the matter is composed of neutrons, protons, electrons, and muons. In this region, all plasmas are strongly degenerate, with electrons and muons behaving like ideal Fermi gases, while protons and neutrons, among other fermionic fluids, may exist in a state of superfluidity or superconductivity. Many-body nucleon interaction models are necessary to solve for the equation of state of matter in this section under the conditions of beta equilibrium and electric neutrality. When the compact star is massive enough, it will have a special region at the center, the inner core. In this case, the density and pressure will be high enough to transform hadronic matter into quark matter (either with or without strange quarks). The transition may occur at several times of the nuclear saturation density and quark matter could coexist with hadronic matter at around the transition region. We call these stars hybrid stars. Whether a strange star or a hybrid star is more stable can be judged by comparing the energy per baryon, which is defined as the ratio of energy density $ϵ$ to baryon number density $n_B$

$E/A=\frac{ϵ}{n_B}.$

Currently, there is no ideal theory that can satisfactory describe the hadronic phase and the quark phase jointly. So, different models are employed to describe hadronic phase and quark phase separately. The two phases are then connected at the transition region, trying to match with each other through a particular construction, i.e., either the Maxwell construction or the Gibbs construction. Several popular models widely used to describe quark matter have been introduced in Section 2. Similarly, we have many models for hadronic matter, including the relativistic mean field (RMF) models (Walecka, 1975; Alaverdyan, 2009; Dutra et al., 2014) and the Brueckner-Hartree-Fock (BHF) approaches (Li et al., 2010; Li and Schulze, 2012; Tong et al., 2022). For example, NL3, TM1, DD-ME2, and FSU Gold models are popular RMF models, while the Akmal-Pandharipande-Ravenhall (APR) model (Akmal et al., 1998; Gusakov et al., 2005; Schneider et al., 2019), is a typical BHF approach.

Here we will focus on the transition from the hadronic phase to the quark phase. Due to unknown physics, the transition could be a smooth crossover, a sharp first-order transition involving a latent heat, or even a critical point signaling a second-order phase transition. Two methods have been engaged to math the two phases at the transition region, i.e., the Maxwell construction or the Gibbs construction.

3.1 Maxwell construction

The Maxwell construction describes a fist-order transition from hadronic matter to quark matter. In this case, the baryon number is conserved and the two phases are in equilibrium. There could be a sharp interface between the two phases so that the transition is a definite phase transitio, as shown in the left panel of Figure 2. When the pressure $(P)$ is higher than the critical point $(P_0)$, the matter is in the quark configuration, while when $P$ is lower than $P_0$, the matter is in the hadronic phase. To avoid the instabilities caused by the long-range nature of electromagnetic forces, each of the two phases have to maintain electric neutrality independently, i.e.,

$q^{\mathit{quark}}=q^{\mathit{hadron}}=0.$

Figure 2

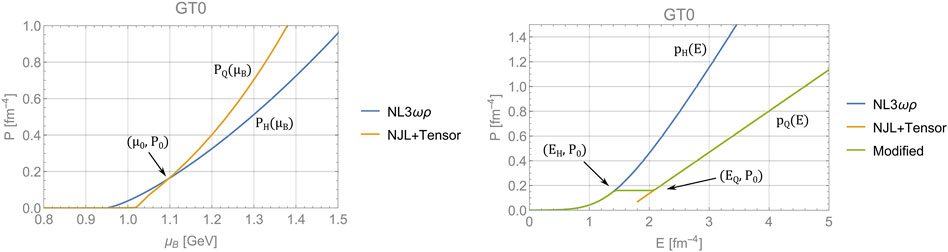
Figure 2. The Maxwell construction between hadronic matter and quark matter (Matsuoka et al., 2018). The hadronic phase (NL3$\omega \rho$ model) and quark phase (NJL model) are represented by blue lines and orange lines, respectively. The green line illustrates the overall EOS. GT0 in the figure means the tensor interaction is zero.

Under this fist-order transition, three equilibrium conditions should also be satisfied, i.e., the chemical potential equilibrium

${\mu }_B^{\mathit{quark}}={\mu }_B^{\mathit{hadron}}=\mu ={\mu }_n,$

the mechanical equilibrium

$P^{\mathit{quark}}\left(\mu ,T\right)=P^{\mathit{hadron}}\left(\mu ,T\right),$

and the thermal equilibrium

$T^{\mathit{quark}}=T^{\mathit{hadron}}=T,$

where ${\mu }_B$ is the chemical potential of baryons, $\mu$ is the chemical potential of the whole system, ${\mu }_n$ is the chemical potential of neutron, and $T$ is temperature. The chemical potential equilibrium and mechanical equilibrium conditions are also reflected in Figure 2.

The overall EOS of a hybrid star is shown in the right panel of Figure 2. There is a “plateau” in the EOS curve, which corresponds to the transition between the hadronic phase and the quark phase. Note that the pressure is a continuous function inside the star, but there is a discontinuity in the energy density at the transition point. Such a jump in the energy density is also known as “latent heat,” which is a hallmark characteristic of a first-order phase transition.

3.2 Gibbs construction

The Gibbs construction is widely employed to describe the complex mixed matter inside compact stars (Glendenning, 1992). For the “complex” mixed phase possibly existed inside hybrid stars, keeping local electric neutrality independently is unreasonable, because the particles can interact with each other in a complicated way. Therefore, charge is conserved and electric neutrality is maintained only for the whole system, but not for each phase. This is a much weaker constraint comparing to that in the Maxwell construction.

According to the Gibbs construction, the chemical potential of each component is still equal between different phases, i.e.,

${\mu }_B^{\mathit{quark}}={\mu }_B^{\mathit{hadron}}=\mu ={\mu }_n,$

${\mu }_Q^{\mathit{quark}}={\mu }_Q^{\mathit{hadron}}={\mu }_e,$

where the subscript $B$ and $Q$ represent the baryon phase and quark phase, respectively. ${\mu }_e$ is the chemical potential of electrons, which appears only in the quark phase. For the pressure and temperature, we also have

$P^{\mathit{quark}}\left(\mu ,T\right)=P^{\mathit{hadron}}\left(\mu ,T\right),$

$T^{\mathit{quark}}=T^{\mathit{hadron}}=T.$

For simplicity, we could take the temperature as zero, i.e., $T=0$. In this way, hadrons and quarks can not only coexist but also mix together in hybrid stars. So, the Gibbs construction is more flexible than the Maxwell construction.

The global electronic neutral condition is expressed as

$\chi q^{\mathit{quark}}+\left(1-\chi \right)q^{\mathit{hadron}}=0,$

where $\chi$ is the volume fraction of quarks that satisfies $0\le \chi \le 1$. In the mixed region, we have

$\chi =\frac{V^{\mathit{quark}}}{V^{\mathit{quark}}+V^{\mathit{hadron}}}.$

Then the energy density of the mixed region is

${ϵ}^{\mathit{mixed}}=\chi {ϵ}^{\mathit{quark}}+\left(1-\chi \right){ϵ}^{\mathit{hadron}},$

and the baryon number density is

${\rho }^{\mathit{mixed}}=\chi {\rho }^{\mathit{quark}}+\left(1-\chi \right){\rho }^{\mathit{hadron}}.$

Comparing with the fixed parameters in the Maxwell construction, the parameters in the Gibbs construction are decided by the percentage of hadrons and quarks. In this case, the energy density is a continuous function and the conversion is smooth rather than a sharp phase boundary existed in the Maxwell construction. It is possible that there is no critical point of any phase transition, but only a crossover from hadronic matter to quark matter in the transition region. Figure 3 illustrates a typical Gibbs construction between hadronic matter and quark matter. The hadronic EOS used in the figure is from Ghosh et al. (1995) and the quark EOS is the effective mass bag model (Schertler et al., 1997; Schertler et al., 1998). The pressure is plot as the function of two independent chemical potentials (${\mu }_n$, ${\mu }_e$). The intersection curve of the two pressure surfaces shows the solution of the Gibbs condition, where the mixed phase presents. In this transition region, all physical parameters change continuously and the free energy of the mixed phase is at a minimum.

Figure 3

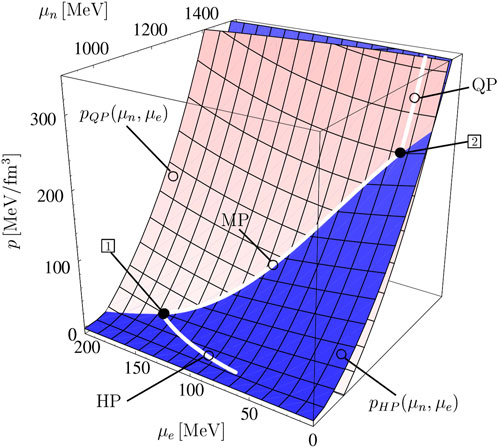
Figure 3. The Gibbs construction between hadronic matter and quark matter (Schertler et al., 2000). The pressure of the hadronic phase $(p_{HP})$ and the quark phase $(p_{QP})$ is plot as a function of the two independent chemical potentials of ${\mu }_n$ and ${\mu }_e$. The intersection curve of the two pressure planes corresponds to the Gibbs condition, where the mixed phase exist. The white lines of $HP$ and $QP$ on the pressure surfaces show the pressure of the hadronic phase and the quark phase under the condition of charge neutrality, respectively.

The Gibbs construction is originally utilized to delineate the multi-phase equilibrium. The chemical potentials of each species are equal in the two phases when they coexist, which satisfies the fundamental requirement for thermodynamic equilibrium. It is not only pertinent to describe first-order phase transitions, but also can be employed to depict higher-order phase transitions and crossover phenomena under suitable circumstances.

4 GW emission from strange stars

GW emission was first proposed by Einstein as a prediction of the General Theory of Relativity (Einstein, 1916; Einstein, 1918). Any changes in the distribution of matter may lead to the variation of the curvature of space-time, causing energy to be carried away in the form of gravitational waves. The detection of GW signals in 2015 by the LIGO collaboration (Abbott et al., 2016) marks the beginning of a new multi-messenger era in astronomy. Many efforts have been made to explore various possible mechanisms that could generate GWs efficiently. Compact stars, due to their extreme density and dynamic motion, serve as crucial sources of GWs. In this aspect, GW emission associated with strange stars may have some special features since their internal composition and structure are different from normal neutron stars. We thus could potentially use GW observations to help identify strange stars.

4.1 GWs from binary strange star systems

Coalescence of binary systems is the most significant stellar GW sources. BH-BH, BH-NS, and NS-NS binary systems are common GW sources. Here we focus on binaries containing strange quark stars, such as BH-SQS and SQS-SQS systems. The detection of the controversial GW190814 event, which involves a possible mass-gap compact object (2.5 – $2.67M_{\odot }$), has drawn a wide attention in the community. Although most researchers believe it could be a neutron star, the possibility that it is a strange star has also been discussed in numerous studies (Bombaci et al., 2021; Miao et al., 2021; Roupas et al., 2021; Lopes and Menezes, 2022; Oikonomou and Moustakidis, 2023). Interestingly, two frequently mentioned GW events, GW170817 and GW190425, are suggested to originate from SQS-SQS systems by Miao et al. (2021), Kumar et al. (2022), and Sagun et al. (2023). Furthermore, theoretical calculations of GW radiation from SQS-SQS binary systems have been preformed by Limousin et al. (2005), Gondek-Rosinska and Limousin (2008), and Bauswein et al. (2010). Moraes and Miranda (2014) even studied the possible existence of NS-SQS binaries and investigated their GW emission.

It should be noted that binary systems containing low-mass strange quark objects can also be strong GW sources. For instance, Lü et al. (2009) investigated GW emission from a white dwarf (WD)–strange dwarf system. Moreover, Perot et al. (2023) argued that GW signal could serve as a better probe to distinguish between strange dwarfs from white dwarfs in binaries. More interestingly, strange quark planets could also stably exist. It is proposed that the merger of a strange quark planet with a SQS can also lead to strong GW emission (Geng et al., 2015; Zhang et al., 2024). Generally, GW emission from merging SQS-strange quark planet will be too weak to be detected if it happens at cosmological distances. However, such events occurring in our Galaxy or in nearby local galaxies is detectable for the Advanced LIGO (Harry and LIGO Scientific Collaboration, 2010) and Einstein Telescope (Hild et al., 2008). Figure 4 shows that the strain spectral amplitude of GWs from coalescing SQS–strange quark planet systems is well above the detection limit when they happen in our Galaxy or in local galaxies. At the same time, we could also try to identify strange quark objects by searching for close-in planets around pulsars. The period of normal matter planet around a pulsar cannot be less than 6,100s, since it would be tidally disrupted in such a close orbit. On the contrary, the period of strange quark planet could be much less than 6,100s due to its extreme high density. Using this method, several extrasolar planetary systems that contain a close-in planet have been argued to be possible candidates of strange planetary systems (Kuerban et al., 2020). Since these extrasolar planetary systems are all relatively close to us, Figure 5 shows that if they merge, the GW emission will be well above the detection limit of current and future GW experiments (Kuerban et al., 2020).

Figure 4

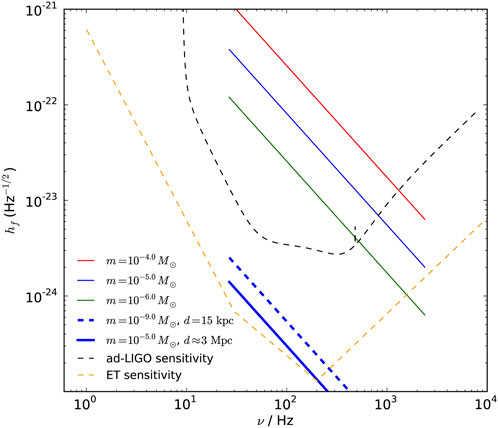
Figure 4. Strain spectral amplitude of GWs against frequency for coalescing SQS-strange quark planet systems (Geng et al., 2015). Various masses are assumed for the strange quark planet, and different distances are taken for the system. The sensitivity curves of advance-LIGO and ET are also shown for comparison.

Figure 5

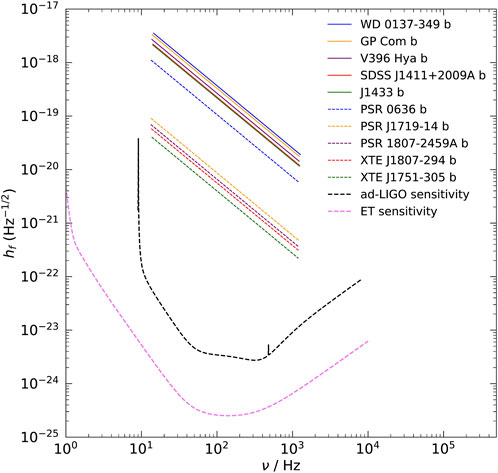
Figure 5. Strain spectral amplitude of GWs against frequency for coalescing strange quark matter planetary systems (Kuerban et al., 2020). The names of the candidate strange quark planets are marked in the plot. This figure shows the strain spectral amplitude of the GW emission when they finally merge with their host in the future.

Recently, Zou and Huang (2022) studied the GW emission produced when a primordial black hole inspirals inside a strange star. The black hole will grow when it swallows the matter from the strange star. It will finally fall toward the center of the strange star and convert the whole star into a stellar mass black hole. During the process, strong GWs will be emitted, whose frequence falls in the range of various ground-based GW detectors, such as the Advanced Virgo, Advanced LIGO, LIGO A+ upgrade, Einstein Telescope (ET), and Cosmic Explorer (CE). More importantly, the GW signals will be different from that produced when a primordial black hole inspirals inside a neutron star, as illustrated in Figure 6. Observation of such GW events thus could provide a useful discrimination between strange stars and neutron stars.

Figure 6

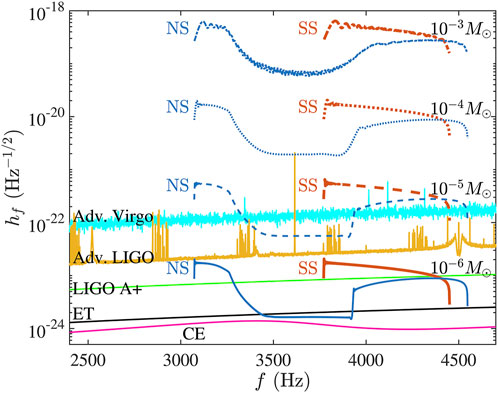
Figure 6. Strain spectral amplitude of GWs against frequency for a primordial black hole inspiraling inside a strange star or a neutron star (Zou and Huang, 2022). The system is assumed to be at 1 kpc from us. The sensitivity curves of several GW experiments are shown for comparison.

4.2 GWs from other mechanisms concerning strange stars

Aside from merger events, the collapse of a neutron star induced by a phase transition to a strange star can also lead to strong GW emission. An increase in the central density of a neutron star can trigger a phase transition from hadronic matter to deconfined quark matter within the core. This transition may lead to the collapse of the whole neutron star into a more compact strange star, accompanied by the emission of GWs. Lin et al. (2006) and Abdikamalov et al. (2009) utilized hydrodynamic simulations to investigate the phase transition process and computed the GW emissions. Recently, Yip et al. (2023) incorporated magnetic fields into their numerical studies to explore the formation of a magnetized strange star and computed the GW signals through general relativistic magnetohydrodynamics simulations. These studies reveal that the emitted GW spectrum is primarily dominated by two fundamental modes: the quasi-radial F mode $(l=0)$ and the quadrupolar ²$f$ mode $(l=2)$. Additionally, Yip et al. (2023) demonstrated that observations of these fundamental modes can help measure the magnetic field strength of the interior toroidal field and the baryonic mass fraction of matter in the mixed phase.

In addition to transient GWs produced from catastrophic events, continuous GW emission can also arise from global oscillations of strange stars. Specifically, r-mode oscillations occurring in rotating SQSs (Andersson et al., 2002; Rupak and Jaikumar, 2013; Wang et al., 2019) are potential mechanisms to produce continuous GWs. The r-mode instability leads to a gradual loss of angular momentum from the compact star, causing it to spin down and emit continuous GWs. Additionally, Gondek-Rosińska et al. (2003) proposed that a triaxial, “bar shaped” strange star could be an efficient source of continuous GW radiation, which is called the bar-mode GW emission. Continuous GW emissions are generally much weaker as compared with that of the catastrophic GW events (Zou et al., 2022). However, with the improvement in the sensitivity of future detectors, GWs from r-mode and bar-mode instabilities may be detectable, which will provide a novel tool for probing the dense matter in compact stars.

The number of detected GW events is increasing rapidly in recent years. Although most of the observed GW events are produced by mergering binary black holes and are not directly related to neutron stars/strange stars, it is possible that more and more GW events involving neutron stars/strange stars will be detected in the near future. GW observations will be a powerful tool to reveal the internal composition and structure of pulsars.

5 Electromagnetic bursts from strange stars

With a strong gravity and magnetic field, a strange star can accrete matter from the surrounding medium or from a companion star. This will lead to some kinds of electromagnetic bursts, such as gamma-ray bursts (GRBs) and fast radio bursts (FRBs).

5.1 GRBs from strange stars

GRBs are one of the most violent stellar explosions. The isotropic equivalent $\gamma$-ray energy released in a typical GRB is in a range of $10^{50}$ – $10^{53}$ ergs. GRBs can be classified into two categories according to their duration, i.e., long GRBs that last for longer than $\sim$ 2 s and short GRBs shorter than $\sim$ 2 s. After more than 50 years of study, it is now generally believed that long GRBs are produced by the collapse of massive stars, while short GRBs are produced by the merger of binary compact stars. However, the possibility that some GRBs are produced by other mechanisms still cannot be expelled (Levan et al., 2016; Zou et al., 2021). For example, strange stars could be involved in some of these fierce bursts.

The conversion of neutron stars to strange stars through a phase transition process will lead to the release of a huge amount of energy, which would be large enough to produce short GRBs (Cheng and Dai, 1996; Bombaci and Datta, 2000; Wang et al., 2000; Shu et al., 2017; Prasad and Mallick, 2018). Many factors can trigger the phase transition process. First, when a neutron star accretes matter from the ambient environment, its mass increases and will finally exceed a maximum value, beyond which the whole star will collapse and be transferred to a strange star. For example, Berezhiani et al. (2003) argued that the central object produced in supernova explosion may be metastable. It could accrete the fall-back matter and collapse to form a strange star. Second, nuclear reactions inside neutron stars can change their internal structure. When the pressure, density and temperature are high enough, neutron matter can transfer to form quark matter. Drago et al. (2004) considered color superconductivity in strange stars and found that diquark condensate could occur, which further increases the energy release during the conversion process. Thirdly, sudden fluctuations of density inside neutron stars can create a “seed” of strange quark matter, which triggers the phase transition and propagates outward to the stellar surface. Mallick and Sahu (2014) found that during the spin down process, the central density of a massive neutron star may increase significantly, triggering a phase transition. The effect of magnetic field in the process is also considered. When a neutron star is converted into a strange star, the energy released during the process is of the magnitude of $\sim 10^{53}$ ergs, sufficient enough to power cosmological short GRBs.

A strange star can be covered by a normal matter crust. The collapse of the crust can also release a large amount of energy and produce an electromagnetic burst. According to Equation 1, the density is a finite value for strange quark matter when the pressure is zero, indicating that it is self-bound. As a result, the mass of strange stars can have a very wide range, i.e., from planetary mass strange objects to nearly two-solar-mass strange stars. On the surface of strange quark matter, quarks are confined by short-range strong interactions, while electrons are confined by long-range electromagnetic interactions. It leads to the formation of an electric field on a lengthscale of hundreds of fermis. The intensity of the electric field can be up to $10^{17}$ V ${\mathrm{c}\mathrm{m}}^{-1}$. Due to the presence of this strong electric field, normal nuclear matter are expelled and accumulates over the surface to form a crust (Alcock et al., 1986; Huang and Lu, 1997). Numerical simulations by Jia and Huang (2004) shows that when a strange star accretes matter, the crust will collapse to trigger a short burst. If the accretion continues, the crust will be re-built and re-collapse again and again, resulting in periodic explosive activities. This mechanism may account for some kinds of soft gamma-ray repeaters.

5.2 FRBs from strange stars

FRBs are fast radio bursts that happen randomly from the sky, typically lasting for a timescale of milliseconds (Lorimer et al., 2007; Thornton et al., 2013). Despite their short durations, the energy released during the burst is immense. About seven hundred FRB sources have been discovered to date, with nearly 30 of them confirmed to exhibit repeating explosive activities. However, the possibility that other FRB sources may also be repeating still cannot be expelled yet. Comprehensive statistical analyses on the properties of repeating FRBs have been extensively carried out based on current astronomical observations, imposing various constraints on their nature (Li et al., 2017; Li et al., 2021; Hu and Huang, 2023), but the origin of FRBs still remains an open problem in need of further investigations.

Various models have been proposed to explain the observational characteristics of FRBs. For non-repeating FRBs, Geng and Huang (2015) and Geng et al. (2020) suggested that they could result from the collision between a compact star and an asteroid. Subsequently, for repeating bursts, researchers went further to argue that they may arise from multiple collisions as magnetized NSs travel through asteroid belts (Dai et al., 2016). On the other hand, Kurban et al. (2022a) and Nurmamat et al. (2024) proposed that repeating bursts may originate from the tidal interactions in a highly elliptical planetary system, in which either a neutron star or a strange star could be involved. In their framework, a planet moves in a highly elliptical orbit around the compact star. The planet will be partially disrupted every time it passes through the periastron since it is very close to the compact host star, generating smaller clumps that finally collide with the host to produce periodically repeating FRBs. These models can satisfactorily explain many of the observed features of repeating FRB sources.

In the previous subsection, we have mentioned that GRBs could originate from the collapse of the crust of a strange star. Similarly, it is also plausible that FRBs may be triggered by such processes, especially when the strange star is a strongly magnetized object. Enormous energy is released during the collapse, giving birth to a large amount of electron/positron pairs. The calculations by Zhang et al. (2018) show that these electron/positron pairs would be accelerated to relativistic velocities far above the polar cap region of the strange star, streaming out along the magnetic field lines and ultimately resulting in a short burst in radio waves. More interestingly, Geng et al. (2021) found that the collapse of the crust of a strange star could happen repeatedly, thus can also serve as a potential mechanism for periodic repeating FRBs. In their framework, the strange star accretes matter from its companion. The accretion flow streams along the magnetic field lines and accumulate in the polar cap region. When the matter at the cap becomes too heavy, the local crust will collapse, triggering an FRB. The crust can be re-built when the accretion process continues and may collapse again once it is overloaded. Periodically repeating FRBs are generated in this way. It should be noted that the active window and quiescent stage in one period could be governed by thermal-viscous instabilities (see Figure 7).

Figure 7

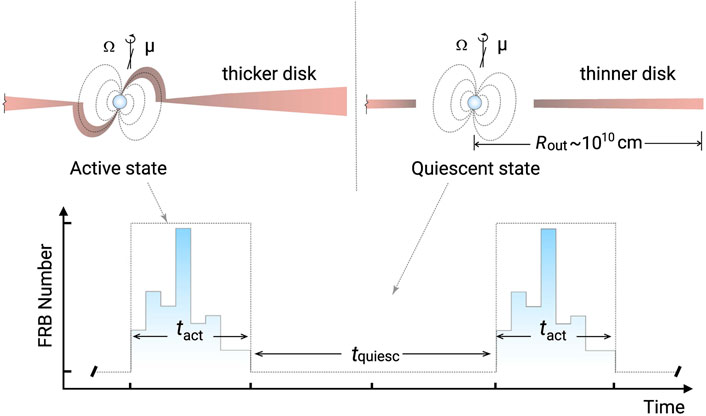
Figure 7. Schematic illustration of periodic repeating fast radio bursts produced in the strange star crust collapse scenario (Geng et al., 2021). In the active state, the accretion rate is high, leading to frequent burst activities. In the quiescent state, the accretion rate is low, and no burst will be generated.

6 Concluding remarks

Strange quark matter could be the true ground state of matter at extreme densities. Such a hypothesis need to be tested through astronomical investigations. Essentially, we should try to discriminate between neutron stars and strange stars through observations. In this article, we present a brief review on some recent progresses in this field. Various models describing quark confinement are introduced. The corresponding EOS derived from these models are presented and compared. By combining these EOSs with the TOV equations, we can calculate the inner structure of strange stars, deriving the mass-radius relation for the whole sequence of strange quark objects. The tidal deformability and the Love number measured through gravitational wave observations may help diagnose the EOS. Radial and non-radial oscillations with different modes can also be used to probe the internal structure of strange stars. The properties of hybrid stars, in which quarks and hadrons may coexist, are also discussed. Some special kinds of electromagnetic bursts could also be connected with strange stars and can be used as a probe of these exotic objects.

GW observation is a hopeful tool to test the existence of strange stars. The coalescence of binary compact systems which includes at lease one strange object could lead to strong GW emission. Previously, people mainly concentrate on relatively high mass binaries, such as BH-SQS and SQS-SQS systems. In the past decade, it is found that when a low mass strange quark planet merge with its host strange star, strong GW emission will also be generated and could be detectable to us if the merger event happens in our Galaxy or in local galaxies (Geng et al., 2015). Furthermore, strange quark planets revolving around their host strange star in a close-in orbit could even be persistent GW sources (Kuerban et al., 2020; Zhang et al., 2024), which could be potential goals of space-based GW experiments in the future. Apart from binary interactions, collapses induced by phase transitions (e.g., from hadronic matter to deconfined quark matter) and global oscillations are also likely to generate GW emission, which could also be tested by the next-generation GW detectors.

GRBs and FRBs are fierce events possibly connected to strange stars. The merger of double strange stars can produce a short GRB, which is very similar to that of binary neutron star coalescence. Additionally, the conversion of neutron stars to strange stars may also act as the energy sources for short GRBs. The total energy released during this phase transition process is estimated to be $\sim 10^{53}$ ergs, which is large enough to power short GRBs occurring at cosmological distances. Furthermore, the collapse of the crust of strange stars could also act as a special mechanism to release a large amount of energy, which could explain FRBs (either one-off or repeating) or some weaker GRBs. The collapse may be triggered by accretion process that makes the crust overloaded. Finally, the collision of an asteroid with a strange star will also lead to some interesting phenomena, which still need to be investigated in detail in the future.

Author contributions

X-LZ: Conceptualization, Investigation, Writing–original draft, Validation. Y-FH: Conceptualization, Funding acquisition, Validation, Writing–review and editing. Z-CZ: Conceptualization, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was supported by the National Natural Science Foundation of China (Grant Nos. 12233002), by National SKA Program of China No. 2020SKA0120300, by the National Key R&D Program of China (2021YFA0718500).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016). Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102. doi:10.1103/PhysRevLett.116.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

Abdikamalov, E. B., Dimmelmeier, H., Rezzolla, L., and Miller, J. C. (2009). Relativistic simulations of the phase-transition-induced collapse of neutron stars. Mon. Not. R. Astron. Soc. 392, 52–76. doi:10.1111/j.1365-2966.2008.14056.x

CrossRef Full Text | Google Scholar

Akmal, A., Pandharipande, V. R., and Ravenhall, D. G. (1998). Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 58, 1804–1828. doi:10.1103/PhysRevC.58.1804

CrossRef Full Text | Google Scholar

Alaverdyan, G. B. (2009). Relativistic mean-field theory equation of state of neutron star matter and a Maxwellian phase transition to strange quark matter. Astrophysics 52, 132–150. doi:10.1007/s10511-009-9043-y

CrossRef Full Text | Google Scholar

Alcock, C., Farhi, E., and Olinto, A. (1986). Strange stars. Astrophys. J. 310, 261. doi:10.1086/164679

CrossRef Full Text | Google Scholar

Alford, M. G., Harris, S. P., and Sachdeva, P. S. (2017). On the stability of strange dwarf hybrid stars. Astrophys. J. 847, 109. doi:10.3847/1538-4357/aa8509

CrossRef Full Text | Google Scholar

Andersson, N., Jones, D. I., and Kokkotas, K. D. (2002). Strange stars as persistent sources of gravitational waves. Mon. Not. R. Astron. Soc. 337, 1224–1232. doi:10.1046/j.1365-8711.2002.05837.x

CrossRef Full Text | Google Scholar

Andersson, N., and Kokkotas, K. D. (1996). Gravitational waves and pulsating stars: what can we learn from future observations? Phys. Rev. Lett. 77, 4134–4137. doi:10.1103/PhysRevLett.77.4134

PubMed Abstract | CrossRef Full Text | Google Scholar

Andersson, N., and Kokkotas, K. D. (1998). Towards gravitational wave asteroseismology. Mon. Notices R. Astronomical Soc. 299, 1059–1068. doi:10.1046/j.1365-8711.1998.01840.x

CrossRef Full Text | Google Scholar

Annala, E., Gorda, T., Kurkela, A., Nättilä, J., and Vuorinen, A. (2020). Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 16, 907–910. doi:10.1038/s41567-020-0914-9

CrossRef Full Text | Google Scholar

Bardeen, J. M., Thorne, K. S., and Meltzer, D. W. (1966). A catalogue of methods for studying the normal modes of radial pulsation of general-relativistic stellar models. ApJ 145, 505. doi:10.1086/148791

CrossRef Full Text | Google Scholar

Bauswein, A., Oechslin, R., and Janka, H. T. (2010). Discriminating strange star mergers from neutron star mergers by gravitational-wave measurements. Phys. Rev. D. 81, 024012. doi:10.1103/PhysRevD.81.024012

CrossRef Full Text | Google Scholar

Benvenuto, O. G., and Horvath, J. E. (1991). Radial pulsations of strange stars and the internal composition of pulsars. Mon. Not. Roy. Astron. Soc. 250, 679–682. doi:10.1093/mnras/250.4.679

CrossRef Full Text | Google Scholar

Berezhiani, Z., Bombaci, I., Drago, A., Frontera, F., and Lavagno, A. (2003). Gamma-ray bursts from delayed collapse of neutron stars to quark matter stars. Astrophys. J. 586, 1250–1253. doi:10.1086/367756

CrossRef Full Text | Google Scholar

Bombaci, I., and Datta, B. (2000). Conversion of neutron stars to strange stars as the central engine of gamma-ray bursts. Astrophys. J. Lett. 530, L69–L72. doi:10.1086/312497

CrossRef Full Text | Google Scholar

Bombaci, I., Drago, A., Logoteta, D., Pagliara, G., and Vidaña, I. (2021). Was gw190814 a black hole–strange quark star system? Phys. Rev. Lett. 126, 162702. doi:10.1103/PhysRevLett.126.162702

PubMed Abstract | CrossRef Full Text | Google Scholar

Bora, J., and Dev Goswami, U. (2021). Radial oscillations and gravitational wave echoes of strange stars for various equations of state. Mon. Not. Roy. Astron. Soc. 502, 1557–1568. doi:10.1093/mnras/stab050

CrossRef Full Text | Google Scholar

Buballa, M. (2005). NJL-model analysis of dense quark matter. Phys. Rep. 407, 205–376. doi:10.1016/j.physrep.2004.11.004

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1964a). Dynamical instability of gaseous masses approaching the Schwarzschild limit in general relativity. Phys. Rev. Lett. 12, 114–116. doi:10.1103/PhysRevLett.12.114

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1964b). The dynamical instability of gaseous masses approaching the Schwarzschild limit in general relativity. Astrophys. J. 140, 417. doi:10.1086/147938

CrossRef Full Text | Google Scholar

Cheng, K. S., and Dai, Z. G. (1996). Conversion of neutron stars to strange stars as a possible origin of γ-ray bursts. Phys. Rev. Lett. 77, 1210–1213. doi:10.1103/PhysRevLett.77.1210

PubMed Abstract | CrossRef Full Text | Google Scholar

Chodos, A., Jaffe, R. L., Johnson, K., and Thorn, C. B. (1974a). Baryon structure in the bag theory. Phys. Rev. D. 10, 2599–2604. doi:10.1103/PhysRevD.10.2599

CrossRef Full Text | Google Scholar

Chodos, A., Jaffe, R. L., Johnson, K., Thorn, C. B., and Weisskopf, V. F. (1974b). New extended model of hadrons. Phys. Rev. D. 9, 3471–3495. doi:10.1103/PhysRevD.9.3471

CrossRef Full Text | Google Scholar

Colpi, M., and Miller, J. C. (1992). Rotational properties of strange stars. Astrophys. J. 388, 513. doi:10.1086/171170

CrossRef Full Text | Google Scholar

Cowling, T. G. (1941). The non-radial oscillations of polytropic stars. Mon. Notices R. Astronomical Soc. 101, 367–375. doi:10.1093/mnras/101.8.367

CrossRef Full Text | Google Scholar

Curi, E. J. A., Castro, L. B., Flores, C. V., and Lenzi, C. H. (2022). Non-radial oscillations and global stellar properties of anisotropic compact stars using realistic equations of state. Eur. Phys. J. C 82, 527. doi:10.1140/epjc/s10052-022-10498-4

CrossRef Full Text | Google Scholar

Dai, Z. G., Wang, J. S., Wu, X. F., and Huang, Y. F. (2016). Repeating fast radio bursts from highly magnetized pulsars traveling through asteroid belts. Astrophys. J. 829, 27. doi:10.3847/0004-637X/829/1/27

CrossRef Full Text | Google Scholar

Damour, T., and Nagar, A. (2009). Relativistic tidal properties of neutron stars. Phys. Rev. D. 80, 084035. doi:10.1103/PhysRevD.80.084035

CrossRef Full Text | Google Scholar

Deb, D., Chowdhury, S. R., Ray, S., Rahaman, F., and Guha, B. K. (2017). Relativistic model for anisotropic strange stars. Ann. Phys. 387, 239–252. doi:10.1016/j.aop.2017.10.010

CrossRef Full Text | Google Scholar

Di Clemente, F., Drago, A., Char, P., and Pagliara, G. (2023). Stability and instability of strange dwarfs. Astron. Astrophys. 678, L1. doi:10.1051/0004-6361/202347607

CrossRef Full Text | Google Scholar

Drago, A., Lavagno, A., and Pagliara, G. (2004). The Supernova-GRB connection. Eur. Phys. J. A 19, 197–201. doi:10.1140/epjad/s2004-03-033-9

CrossRef Full Text | Google Scholar

Dutra, M., Lourenço, O., Avancini, S. S., Carlson, B. V., Delfino, A., Menezes, D. P., et al. (2014). Relativistic mean-field hadronic models under nuclear matter constraints. Phys. Rev. C 90, 055203. doi:10.1103/PhysRevC.90.055203

CrossRef Full Text | Google Scholar

Eguchi, T., and Sugawara, H. (1974). Extended model of elementary particles based on an analogy with superconductivity. Phys. Rev. D. 10, 4257–4262. doi:10.1103/PhysRevD.10.4257

CrossRef Full Text | Google Scholar

Einstein, A. (1916). Näherungsweise Integration der Feldgleichungen der Gravitation. Sitzungsber. Königl. Preuss. Akad. Wiss., 688–696.

Google Scholar

Einstein, A. (1918). Über gravitationswellen. Sitzungsber. Königl. Preuss. Akad. Wiss, 154–167.

Google Scholar

Farhi, E., and Jaffe, R. L. (1984). Strange matter. Phys. Rev. D. 30, 2379–2390. doi:10.1103/PhysRevD.30.2379

CrossRef Full Text | Google Scholar

Flanagan, É. É., and Hinderer, T. (2008). Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D. 77, 021502. doi:10.1103/PhysRevD.77.021502

CrossRef Full Text | Google Scholar

Fraga, E. S., Pisarski, R. D., and Schaffner-Bielich, J. (2001). Small, dense quark stars from perturbative QCD. Phys. Rev. D. 63, 121702. doi:10.1103/PhysRevD.63.121702

CrossRef Full Text | Google Scholar

Geng, J., Li, B., and Huang, Y. (2021). Repeating fast radio bursts from collapses of the crust of a strange star. Innov 2, 100152. doi:10.1016/j.xinn.2021.100152

CrossRef Full Text | Google Scholar

Geng, J. J., and Huang, Y. F. (2015). Fast radio bursts: collisions between neutron stars and asteroids/comets. Astrophys. J. 809, 24. doi:10.1088/0004-637X/809/1/24

CrossRef Full Text | Google Scholar

Geng, J. J., Huang, Y. F., and Lu, T. (2015). Coalescence of strange-quark planets with strange stars: a new kind of source for gravitational wave bursts. Astrophys. J. 804, 21. doi:10.1088/0004-637X/804/1/21

CrossRef Full Text | Google Scholar

Geng, J.-J., Li, B., Li, L.-B., Xiong, S.-L., Kuiper, R., and Huang, Y.-F. (2020). FRB 200428: an impact between an asteroid and a magnetar. Astrophys. J. Lett. 898, L55. doi:10.3847/2041-8213/aba83c

CrossRef Full Text | Google Scholar

Ghosh, S. K., Phatak, S. C., and Sahu, P. K. (1995). Hybrid stars and quark hadron phase transition in chiral colour dielectric model. Zeitschrift fur Physik A Hadrons Nucl. 352, 457–466. doi:10.1007/BF01299764

CrossRef Full Text | Google Scholar

Glendenning, N. (1996). Compact stars: nuclear physics, particle physics and general relativity. 2nd Edn. New York, NY: Springer.

Google Scholar

Glendenning, N. K. (1992). First-order phase transitions with more than one conserved charge: consequences for neutron stars. Phys. Rev. D. 46, 1274–1287. doi:10.1103/PhysRevD.46.1274

PubMed Abstract | CrossRef Full Text | Google Scholar

Glendenning, N. K., Kettner, C., and Weber, F. (1995). From strange stars to strange dwarfs. Astrophys. J. 450, 253. doi:10.1086/176136

CrossRef Full Text | Google Scholar

Glendenning, N. K., and Weber, F. (1992). Nuclear solid crust on rotating strange quark stars. Astrophys. J. 400, 647. doi:10.1086/172026

CrossRef Full Text | Google Scholar

Gonçalves, V. P., Jiménez, J. C., and Lazzari, L. (2023). Revisiting the stability of strange-dwarf stars and strange planets. Eur. Phys. J. A 59, 251. doi:10.1140/epja/s10050-023-01175-5

CrossRef Full Text | Google Scholar

Gondek-Rosińska, D., Gourgoulhon, E., and Haensel, P. (2003). Are rotating strange quark stars good sources of gravitational waves? Astron. Astrophys. 412, 777–790. doi:10.1051/0004-6361:20031431

CrossRef Full Text | Google Scholar

Gondek-Rosinska, D., and Limousin, F. (2008). The final phase of inspiral of strange quark star binaries. Available at: https://hal.archives-ouvertes.fr/hal-00227502 (Accessed March 15, 2018).

Google Scholar

Gorenstein, M. I., and Yang, S. N. (1995). Gluon plasma with a medium-dependent dispersion relation. Phys. Rev. D. 52, 5206–5212. doi:10.1103/PhysRevD.52.5206

PubMed Abstract | CrossRef Full Text | Google Scholar

Gusakov, M. E., Kaminker, A. D., Yakovlev, D. G., and Gnedin, O. Y. (2005). The cooling of Akmal--Pandharipande--Ravenhall neutron star models. Mon. Not. Roy. Astron. Soc. 363, 555–562. doi:10.1111/j.1365-2966.2005.09459.x

CrossRef Full Text | Google Scholar

Harry, G. M.LIGO Scientific Collaboration (2010). Advanced LIGO: the next generation of gravitational wave detectors. Cl. Quantum Gravity 27, 084006. doi:10.1088/0264-9381/27/8/084006

CrossRef Full Text | Google Scholar

He, M., Sun, W.-m., Feng, H.-t., and Zong, H.-s. (2007). A model study of QCD phase transition. J. Phys. G. Nucl. Part. Phys. 34, 2655–2663. doi:10.1088/0954-3899/34/12/010

CrossRef Full Text | Google Scholar

Hild, S., Chelkowski, S., and Freise, A. (2008). Pushing towards the ET sensitivity using ‘conventional’ technology. doi:10.48550/arXiv.0810.0604

CrossRef Full Text | Google Scholar

Hinderer, T. (2008). Tidal Love numbers of neutron stars. Astrophys. J. 677, 1216–1220. [Erratum: Astrophys.J. 697, 964 (2009)]. doi:10.1086/533487

CrossRef Full Text | Google Scholar

Hu, C.-R., and Huang, Y.-F. (2023). A comprehensive analysis of repeating fast radio bursts. Astrophys. J. Suppl. Ser. 269, 17. doi:10.3847/1538-4365/acf566

CrossRef Full Text | Google Scholar

Huang, Y. F., and Lu, T. (1997). Strange stars: how dense can their crust be? A&A 325, 189–194.

Google Scholar

Huang, Y. F., and Yu, Y. B. (2017). Searching for strange quark matter objects in exoplanets. Astrophys. J. 848, 115. doi:10.3847/1538-4357/aa8b63

CrossRef Full Text | Google Scholar

Ivanenko, D. D., and Kurdgelaidze, D. F. (1965). Hypothesis concerning quark stars. Astrophysics 1, 251–252. doi:10.1007/BF01042830

CrossRef Full Text | Google Scholar

Jia, J.-j., and Huang, Y.-f. (2004). A numerical study of the collapse of the crust of strange stars. Chin. Astron. Astrophys. 28, 144–153. doi:10.1016/S0275-1062(04)90017-3

CrossRef Full Text | Google Scholar

Jiménez, J. C., and Fraga, E. S. (2019). Radial oscillations of quark stars from perturbative QCD. Phys. Rev. D. 100, 114041. doi:10.1103/PhysRevD.100.114041

CrossRef Full Text | Google Scholar

Kikkawa, K. (1976). Quantum corrections in superconductor models. Prog. Theor. Phys. 56, 947–955. doi:10.1143/PTP.56.947

CrossRef Full Text | Google Scholar

Klevansky, S. P. (1992). The Nambu-Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 64, 649–708. doi:10.1103/RevModPhys.64.649

CrossRef Full Text | Google Scholar

Kokkotas, K. D., and Schutz, B. F. (1992). W-modes - a new family of normal modes of pulsating relativistic stars. Mon. Notices R. Astronomical Soc. 255, 119–128. doi:10.1093/mnras/255.1.119

CrossRef Full Text | Google Scholar

Kuerban, A., Geng, J.-J., Huang, Y.-F., Zong, H.-S., and Gong, H. (2020). Close-in exoplanets as candidates for strange quark matter objects. Astrophys. J. 890, 41. doi:10.3847/1538-4357/ab698b

CrossRef Full Text | Google Scholar

Kumar, A., Thapa, V. B., and Sinha, M. (2022). Compact star merger events with stars composed of interacting strange quark matter. Mon. Not. R. Astron. Soc. 513, 3788–3797. doi:10.1093/mnras/stac1150

CrossRef Full Text | Google Scholar

Kurban, A., Huang, Y.-F., Geng, J.-J., Li, B., Xu, F., Wang, X., et al. (2022a). Periodic repeating fast radio bursts: interaction between a magnetized neutron star and its planet in an eccentric orbit. Astrophys. J. 928, 94. doi:10.3847/1538-4357/ac558f

CrossRef Full Text | Google Scholar

Kurban, A., Huang, Y.-F., Geng, J.-J., and Zong, H.-S. (2022b). Searching for strange quark matter objects among white dwarfs. Phys. Lett. B 832, 137204. doi:10.1016/j.physletb.2022.137204

CrossRef Full Text | Google Scholar

Levan, A., Crowther, P., de Grijs, R., Langer, N., Xu, D., and Yoon, S.-C. (2016). Gamma-ray burst progenitors. Space Sci. Rev. 202, 33–78. doi:10.1007/s11214-016-0312-x

CrossRef Full Text | Google Scholar

Li, A., Zhou, X. R., Burgio, G. F., and Schulze, H. J. (2010). Protoneutron stars in the Brueckner-Hartree-Fock approach and finite-temperature kaon condensation. Phys. Rev. C 81, 025806. doi:10.1103/PhysRevC.81.025806

CrossRef Full Text | Google Scholar

Li, L.-B., Huang, Y.-F., Zhang, Z.-B., Li, D., and Li, B. (2017). Intensity distribution function and statistical properties of fast radio bursts. Res. Astron. Astrophys. 17, 6. doi:10.1088/1674-4527/17/1/6

CrossRef Full Text | Google Scholar

Li, X. J., Dong, X. F., Zhang, Z. B., and Li, D. (2021). Long and short fast radio bursts are different from repeating and nonrepeating transients. Astrophys. J. 923, 230. doi:10.3847/1538-4357/ac3085

CrossRef Full Text | Google Scholar

Li, Z. H., and Schulze, H. J. (2012). Nuclear matter with chiral forces in Brueckner-Hartree-Fock approximation. Phys. Rev. C 85, 064002. doi:10.1103/PhysRevC.85.064002

CrossRef Full Text | Google Scholar

Limousin, F., Gondek-Rosińska, D., and Gourgoulhon, E. (2005). Last orbits of binary strange quark stars. Phys. Rev. D. 71, 064012. doi:10.1103/PhysRevD.71.064012

CrossRef Full Text | Google Scholar

Lin, L. M., Cheng, K. S., Chu, M. C., and Suen, W. M. (2006). Gravitational waves from phase-transition-induced collapse of neutron stars. Astrophys. J. 639, 382–396. doi:10.1086/499202

CrossRef Full Text | Google Scholar

Lohakare, S. V., Maurya, S. K., Singh, K. N., Mishra, B., and Errehymy, A. (2023). Influence of three parameters on maximum mass and stability of strange star under linear f(Q) - action. Mon. Not. R. Astron. Soc. 526, 3796–3814. doi:10.1093/mnras/stad2861

CrossRef Full Text | Google Scholar

Lopes, L. L., and Menezes, D. P. (2022). On the nature of the mass-gap object in the GW190814 event. Astrophys. J. 936, 41. doi:10.3847/1538-4357/ac81c4

CrossRef Full Text | Google Scholar

Lorimer, D. R., Bailes, M., McLaughlin, M. A., Narkevic, D. J., and Crawford, F. (2007). A bright millisecond radio burst of extragalactic origin. Sci. 318, 777–780. doi:10.1126/science.1147532

PubMed Abstract | CrossRef Full Text | Google Scholar

Lü, Z.-K., Wu, S.-W., and Zeng, Z.-C. (2009). Gravitational wave radiation from a double white dwarf system inside our galaxy: a potential method for seeking strange dwarfs. Res. Astron. Astrophys. 9, 745–750. doi:10.1088/1674-4527/9/7/002

CrossRef Full Text | Google Scholar

Mallick, R., and Sahu, P. K. (2014). Phase transitions in neutron star and magnetars and their connection with high energetic bursts in astrophysics. Nucl. Phys. A 921, 96–113. doi:10.1016/j.nuclphysa.2013.11.009

CrossRef Full Text | Google Scholar

Matsuoka, H., Tsue, Y., Da Providência, J. a., Providência, C., and Yamamura, M. (2018). Hybrid stars from the NJL model with a tensor-interaction. Phys. Rev. D. 98, 074027. doi:10.1103/PhysRevD.98.074027

CrossRef Full Text | Google Scholar

McDermott, P. N., van Horn, H. M., and Hansen, C. J. (1988). Nonradial oscillations of neutron stars. Astrophys. J. 325, 725. doi:10.1086/166044

CrossRef Full Text | Google Scholar

Menezes, D. P. (2021). A neutron star is born. Universe 7, 267. doi:10.3390/universe7080267

CrossRef Full Text | Google Scholar

Miao, Z., Jiang, J.-L., Li, A., and Chen, L.-W. (2021). Bayesian inference of strange star equation of state using the GW170817 and GW190425 data. Astrophys. J. Lett. 917, L22. doi:10.3847/2041-8213/ac194d

CrossRef Full Text | Google Scholar

Moraes, P. H. R. S., and Miranda, O. D. (2014). Probing strange stars with advanced gravitational wave detectors. Mon. Not. R. Astron. Soc. 445, L11–L15. doi:10.1093/mnrasl/slu124

CrossRef Full Text | Google Scholar

Nambu, Y., and Jona-Lasinio, G. (1961a). Dynamical model of elementary particles based on an analogy with superconductivity. I. Phys. Rev. 122, 345–358. doi:10.1103/PhysRev.122.345

CrossRef Full Text | Google Scholar

Nambu, Y., and Jona-Lasinio, G. (1961b). Dynamical model of elementary particles based on an analogy with superconductivity. II. Phys. Rev. 124, 246–254. doi:10.1103/PhysRev.124.246

CrossRef Full Text | Google Scholar

Nurmamat, N., Huang, Y.-F., Geng, J.-J., Kurban, A., and Li, B. (2024). Repeating fast radio bursts produced by a strange star interacting with its planet in an eccentric orbit. Eur. Phys. J. C 84, 210. doi:10.1140/epjc/s10052-024-12572-5

CrossRef Full Text | Google Scholar

Oikonomou, P. T., and Moustakidis, C. C. (2023). Color-flavor locked quark stars in light of the compact object in the hess j1731-347 and the gw190814 event. Phys. Rev. D. 108, 063010. doi:10.1103/PhysRevD.108.063010

CrossRef Full Text | Google Scholar

Oppenheimer, J. R., and Volkoff, G. M. (1939). On massive neutron cores. Phys. Rev. 55, 374–381. doi:10.1103/PhysRev.55.374

CrossRef Full Text | Google Scholar

Perot, L., Chamel, N., and Vallet, P. (2023). Unmasking strange dwarfs with gravitational-wave observations. Phys. Rev. D. 107, 103004. doi:10.1103/PhysRevD.107.103004

CrossRef Full Text | Google Scholar

Peshier, A., Kämpfer, B., Pavlenko, O. P., and Soff, G. (1994). An effective model of the quark-gluon plasma with thermal parton masses. Phys. Lett. B 337, 235–239. doi:10.1016/0370-2693(94)90969-5

CrossRef Full Text | Google Scholar

Peshier, A., Kampfer, B., and Soff, G. (2000). Equation of state of deconfined matter at finite chemical potential in a quasiparticle description. Phys. Rev. C 61, 045203. doi:10.1103/PhysRevC.61.045203

CrossRef Full Text | Google Scholar

Peshier, A., Kämpfer, B., and Soff, G. (2002). From QCD lattice calculations to the equation of state of quark matter. Phys. Rev. D. 66, 094003. doi:10.1103/PhysRevD.66.094003

CrossRef Full Text | Google Scholar

Postnikov, S., Prakash, M., and Lattimer, J. M. (2010). Tidal love numbers of neutron and self-bound quark stars. Phys. Rev. D. 82, 024016. doi:10.1103/PhysRevD.82.024016

CrossRef Full Text | Google Scholar

Prasad, R., and Mallick, R. (2018). Dynamical phase transition in neutron stars. Astrophys. J. 859, 57. doi:10.3847/1538-4357/aabf3b

CrossRef Full Text | Google Scholar

Price, R., and Thorne, K. S. (1969). Non-radial pulsation of general-relativistic stellar models. II. Properties of the gravitational waves. Astrophys. J. 155, 163. doi:10.1086/149857

CrossRef Full Text | Google Scholar

Rather, I. A., Panotopoulos, G., and Lopes, I. (2023). Quark models and radial oscillations: decoding the HESS J1731-347 compact object’s equation of state. Eur. Phys. J. C 83, 1065. doi:10.1140/epjc/s10052-023-12223-1

CrossRef Full Text | Google Scholar

Rebhan, A., and Romatschke, P. (2003). Hard-thermal-loop quasiparticle models of deconfined QCD at finite chemical potential. Phys. Rev. D. 68, 025022. doi:10.1103/PhysRevD.68.025022

CrossRef Full Text | Google Scholar

Roupas, Z., Panotopoulos, G., and Lopes, I. (2021). Qcd color superconductivity in compact stars: color-flavor locked quark star candidate for the gravitational-wave signal gw190814. Phys. Rev. D. 103, 083015. doi:10.1103/PhysRevD.103.083015

CrossRef Full Text | Google Scholar

Rupak, G., and Jaikumar, P. (2013). r-mode instability in quark stars with a crystalline crust. Phys. Rev. C 88, 065801. doi:10.1103/PhysRevC.88.065801

CrossRef Full Text | Google Scholar

Sagun, V., Giangrandi, E., Dietrich, T., Ivanytskyi, O., Negreiros, R., and Providência, C. (2023). What is the nature of the hess j1731-347 compact object? Astrophys. J. 958, 49. doi:10.3847/1538-4357/acfc9e

CrossRef Full Text | Google Scholar

Schertler, K., Greiner, C., Sahu, P. K., and Thoma, M. H. (1998). The influence of medium effects on the gross structure of hybrid stars. Nucl. Phys. A 637, 451–465. doi:10.1016/S0375-9474(98)00330-3

CrossRef Full Text | Google Scholar

Schertler, K., Greiner, C., Schaffner-Bielich, J., and Thoma, M. H. (2000). Quark phases in neutron stars and a third family of compact stars as signature for phase transitions¹. Nuc. Phys. A 677, 463–490. doi:10.1016/S0375-9474(00)00305-5

CrossRef Full Text | Google Scholar

Schertler, K., Greiner, C., and Thoma, M. H. (1997). Medium effects in strange quark matter and strange stars. Nucl. Phys. A 616, 659–679. doi:10.1016/S0375-9474(97)00014-6

CrossRef Full Text | Google Scholar

Schneider, A. S., Constantinou, C., Muccioli, B., and Prakash, M. (2019). Akmal-Pandharipande-Ravenhall equation of state for simulations of supernovae, neutron stars, and binary mergers. Phys. Rev. C 100, 025803. doi:10.1103/PhysRevC.100.025803

CrossRef Full Text | Google Scholar

Shafeeque, M., Mathew, A., and Nandy, M. K. (2023). Maximal mass of the neutron star with a deconfined quark core. J. Astrophys. Astron. 44, 63. doi:10.1007/s12036-023-09957-5

CrossRef Full Text | Google Scholar

Shu, X.-Y., Huang, Y.-F., and Zong, H.-S. (2017). Gamma-ray bursts generated from phase transition of neutron stars to quark stars. Mod. Phys. Lett. A 32, 1750027. doi:10.1142/S0217732317500274

CrossRef Full Text | Google Scholar

Sotani, H., Yasutake, N., Maruyama, T., and Tatsumi, T. (2011). Signatures of hadron-quark mixed phase in gravitational waves. Phys. Rev. D. 83, 024014. doi:10.1103/PhysRevD.83.024014

CrossRef Full Text | Google Scholar

Takátsy, J., and Kovács, P. (2020). Comment on “tidal love numbers of neutron and self-bound quark stars”. Phys. Rev. D. 102, 028501. doi:10.1103/PhysRevD.102.028501

CrossRef Full Text | Google Scholar

Thorne, K. S. (1998). Tidal stabilization of rigidly rotating, fully relativistic neutron stars. Phys. Rev. D. 58, 124031. doi:10.1103/PhysRevD.58.124031

CrossRef Full Text | Google Scholar

Thorne, K. S., and Campolattaro, A. (1967). Non-radial pulsation of general-relativistic stellar models. I. Analytic analysis for L ≥ 2. Astrophys. J. 149, 591. doi:10.1086/149288

CrossRef Full Text | Google Scholar

Thornton, D., Stappers, B., Bailes, M., Barsdell, B., Bates, S., Bhat, N. D. R., et al. (2013). A population of fast radio bursts at cosmological distances. Sci 341, 53–56. doi:10.1126/science.1236789

PubMed Abstract | CrossRef Full Text | Google Scholar

Tolman, R. C. (1934) “Relativity, thermodynamics, and cosmology,”. Oxford: Clarendon Press, 501.

Google Scholar

Tolman, R. C. (1939). Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 55, 364–373. doi:10.1103/PhysRev.55.364

CrossRef Full Text | Google Scholar

Tong, H., Wang, C., and Wang, S. (2022). Nuclear matter and neutron stars from relativistic brueckner–Hartree–Fock theory. Astrophys. J. 930, 137. doi:10.3847/1538-4357/ac65fc

CrossRef Full Text | Google Scholar

Vaeth, H. M., and Chanmugam, G. (1992). Radial oscillations of neutron stars and strange stars. Astronomy Astrophysics 260, 250–254.

Google Scholar

Vartanyan, Y. L., Hajyan, G. S., Grigoryan, A. K., and Sarkisyan, T. R. (2012). Stability valley for strange dwarfs. Astrophys. 55, 98–109. doi:10.1007/s10511-012-9216-y

CrossRef Full Text | Google Scholar

Vartanyan, Y. L., Hajyan, G. S., Grigoryan, A. K., and Sarkisyan, T. R. (2014). Stability of strange dwarfs: a comparison with observations. J. Phys. Conf. Ser. 496, 012009. doi:10.1088/1742-6596/496/1/012009

CrossRef Full Text | Google Scholar

Walecka, J. D. (1975). Equation of state for neutron matter at finite T in a relativistic mean-field theory. Phys. Lett. B 59, 109–112. doi:10.1016/0370-2693(75)90678-4

CrossRef Full Text | Google Scholar

Wang, X., Kuerban, A., Geng, J.-J., Xu, F., Zhang, X.-L., Zuo, B.-J., et al. (2021). Tidal deformability of strange quark planets and strange dwarfs. Phys. Rev. D. 104, 123028. doi:10.1103/PhysRevD.104.123028

CrossRef Full Text | Google Scholar

Wang, X. Y., Dai, Z. G., Lu, T., Wei, D. M., and Huang, Y. F. (2000). A possible model for the supernova/gamma-ray burst connection. Astron. Astrophys. 357, 543–547. doi:10.48550/arXiv.astro-ph/9910029

CrossRef Full Text | Google Scholar

Wang, Y.-B., Zhou, X., Wang, N., and Liu, X.-W. (2019). The r-mode instability windows of strange stars. Res. Astron. Astrophys. 19, 030. doi:10.1088/1674-4527/19/2/30

CrossRef Full Text | Google Scholar

Weber, F. (2005). Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 54, 193–288. doi:10.1016/j.ppnp.2004.07.001

CrossRef Full Text | Google Scholar

Witten, E. (1984). Cosmic separation of phases. Phys. Rev. D. 30, 272–285. doi:10.1103/PhysRevD.30.272

CrossRef Full Text | Google Scholar

Yip, A. K. L., Chi-Kit Cheong, P., and Li, T. G. F. (2023). Gravitational wave signatures from the phase-transition-induced collapse of a magnetized neutron star. doi:10.48550/arXiv.2305.15181

CrossRef Full Text | Google Scholar

Zdunik, J. L. (2002). On the minimum radius of strange stars with crust. Astron. Astrophys. 394, 641–645. doi:10.1051/0004-6361:20021177

CrossRef Full Text | Google Scholar

Zhang, X.-L., Zou, Z.-C., Huang, Y.-F., Gao, H.-X., Wang, P., Cui, L., et al. (2024). Gravitational wave emission from close-in strange quark planets around strange stars with magnetic interactions. Mon. Not. R. Astron. Soc. 531, 3905–3911. doi:10.1093/mnras/stae1400

CrossRef Full Text | Google Scholar

Zhang, Y., Geng, J.-J., and Huang, Y.-F. (2018). Fast radio bursts from the collapse of strange star crusts. Astrophys. J. 858, 88. doi:10.3847/1538-4357/aabaee

CrossRef Full Text | Google Scholar

Zhao, A. M., Cao, J., Luo, L.-J., Sun, W.-M., and Zong, H.-S. (2010). The equation of state of quasi-particle model of quark-gluon plasma at finite chemical potential. Mod. Phys. Lett. A 25, 47–54. doi:10.1142/S0217732310031361

CrossRef Full Text | Google Scholar

Zong, H.-S., and Sun, W.-M. (2008a). A model study of the equation of state of QCD. Int. J. Mod. Phys. A 23, 3591–3612. doi:10.1142/S0217751X08040457

CrossRef Full Text | Google Scholar

Zong, H.-S., and Sun, W.-M. (2008b). Calculation of the equation of state of QCD at finite chemical and zero temperature. Phys. Rev. D. 78, 054001. doi:10.1103/PhysRevD.78.054001

CrossRef Full Text | Google Scholar

Zou, Z.-C., and Huang, Y.-F. (2022). Gravitational-wave emission from a primordial black hole inspiraling inside a compact star: a novel probe for dense matter equation of state. Astrophys. J. Lett. 928, L13. doi:10.3847/2041-8213/ac5ea6

CrossRef Full Text | Google Scholar

Zou, Z.-C., Huang, Y.-F., and Zhang, X.-L. (2022). Gravitational waves from strange star core–crust oscillation. Universe 8, 442. doi:10.3390/universe8090442

CrossRef Full Text | Google Scholar

Zou, Z.-C., Zhang, B.-B., Huang, Y.-F., and Zhao, X.-H. (2021). Gamma-ray burst in a binary system. Astrophys. J. 921, 2. doi:10.3847/1538-4357/ac1b2d

CrossRef Full Text | Google Scholar