Collisional thermalization of minor ions in the solar wind

Introduction: As the solar wind transits through the heliosphere, Coulomb collisions among constituent particles drives it toward local thermodynamic equilibrium. Prior studies of ion collisions in the solar wind have focused on the two most abundant solar wind ions: protons (ionized hydrogen) and α-particles (fully ionized helium).

Methods: Some of the studies have used the technique of collisional analysis to incorporate the effects of collisions and expansion, to extrapolate the evolution of solar-wind ion temperature ratios. This study is the first to apply collisional analysis to the minor ions in the solar wind: carbon, oxygen and iron. Observations of ion temperature ratios in the near-Earth solar wind (r = 1.0 au) are used to predict their values closer to the Sun (r = 0.1 au).

Results: Ion measurements from the Advanced Composition Explorer (ACE) mission were used as individual boundary conditions for the equations of collisional analysis, which were solved numerically to make predictions of the temperature ratios. By using a large dataset spanning twelve years, the distributions of ion temperature ratios measured at r = 1.0 au can be compared to those predicted at r = 0.1 au.

Discussion: The predicted distributions suggest that the ratio of minor-ion temperatures to that of protons is significantly higher closer to the Sun, which is consistent with expectations for a zone of preferential minor-ion heating in/near the solar corona.

1 Introduction

While the solar wind is primarily composed of protons, $\alpha$-particles and electrons (Verscharen et al., 2019), trace amounts of minor ions are also present (Isenberg and Hollweg, 1983; Schmelz et al., 2012). Energy and momentum are exchanged among solar wind particles through collisions, which move the system toward thermodynamic equilibrium (Griem, 1963). These collisions are Coulomb collisions, which are “soft”, small-angle, electrostatic deflections (Marsch, 2006). The rate of these Coulomb collisions in the solar wind is low due to the plasma’s high temperature and low density (Verscharen et al., 2019). As a result, departures from local thermodynamic equilibrium (LTE; Griem, 1963) are often persist well into the solar wind’s expansion through the heliosphere.

A commonly studied non-LTE features of the solar wind is unequal ion temperatures, which can be quantified by the ratio

${\theta }_{ji}=\frac{T_j}{T_i},(1)$

where $T_j$ and $T_i$ are the scalar temperatures of two ion species, $j$ and $i$, respectively. The temperature ratio of the solar wind’s most abundant ions, protons $(i=\mathrm{p})$ and $\alpha$-particles $(j=\alpha )$ have received the most attention in the literature (Feldman et al., 1974; Marsch et al., 1982; Neugebauer, 1976; Kasper et al., 2008; Maruca et al., 2013; Kasper et al., 2017). This study, though, focuses on the temperature ratios of minor ions with protons and in particular considers carbon (${\mathrm{C}}^{5+}$; $j=\mathrm{C}$), oxygen (${\mathrm{O}}^{6+}$; $j=\mathrm{O}$), and iron (${\mathrm{F}\mathrm{e}}^{10+}$; $j=\mathrm{F}\mathrm{e}$). The effects of collisions on the temperature ratios of these and other minor ions have been considered in some previous studies (Hefti et al., 1998; Tracy et al., 2015; Tracy et al., 2016), though this work has primarily focused on using Coulomb number (see, e.g., Verscharen et al., 2019, Section 3.2.6) to quantify the thermalization process. However, as detailed in the following, this study for the first time applies collisional analysis, a more sophisticated tool, to analyze the thermalization of minor ions in the solar wind.

Section 2 provides an overview of collisional analysis applied to ion temperature ratios. The data used in this study are described in Section 3. Section 4 describes the results of applying collisional analysis to these data, and Section 5 summarizes the study’s key findings.

2 Methodology

Collisional analysis, which was first introduced by Maruca et al. (2013), is an analytical method for quantifying the effects of collisions on the non-LTE features of an individual parcel of solar-wind plasma. The work of Maruca et al. (2013) and Johnson et al. (2023) focused on the unequal temperature of $\alpha$-particles relative to protons, as quantified by the ratio ${\theta }_{\alpha \mathrm{p}}$ (Equation 1), while the work of Johnson et al. (2024) elected to focus on differential flow. This study broadens those earlier works to consider the temperatures of additional minor ion species relative to protons: ${\theta }_{j\mathrm{p}}$. The ion temperatures, densities, and velocities of a given parcel of plasma are measured in-situ by a spacecraft located at a given distance, $r$, from the Sun. Collisional analysis uses the appropriate collisional operator to determine the radial evolution of a particular non-LTE feature. Maruca et al. (2013) showed that the radial gradient in ${\theta }_{j\mathrm{p}}$ due to Coulomb collisions is

$\frac{d{\theta }_{j\mathrm{p}}}{dr}=\left(2.6\times 10^7\frac{{\mathrm{c}\mathrm{m}}^3{\mathrm{K}}^{3/2}\mathrm{k}\mathrm{m}}{\mathrm{s}\mathrm{a}\mathrm{u}}\right)\left(\frac{n_{\text{p}}\left(r\right)}{v_{\text{p},\mathrm{r}}\left(r\right)T_{\text{p}}^{3/2}\left(r\right)}\right)\times \left(\frac{{\mu }_j^{1/2}{Z}_j^2\left(1-{\theta }_{j\mathrm{p}}\right)\left(1+{\eta }_{j\mathrm{p}}{\theta }_{j\mathrm{p}}\right)}{{\left({\mu }_j+{\theta }_{j\mathrm{p}}\right)}^{3/2}}\right)\ln {\lambda }_{j\mathrm{p}},(2)$

where $n_j$ and $n_{\text{p}}$ are respectively the number densities of $j$-particles and protons, $v_{\text{p},\mathrm{r}}$ is the radial component of the proton bulk velocity, and ${\mu }_j$ and $Z_j$ are respectively the mass and charge of a $j$-particle relative to those of a proton. Additionally,

$\ln {\lambda }_{j\mathrm{p}}=9+\ln \left[\left(\frac{1}{{\mathrm{c}\mathrm{m}}^{3/2}{\mathrm{K}}^{3/2}}\right)\frac{T_j+{\mu }_j{T}_{\text{p}}}{Z_j\left({\mu }_j+1\right)}{\left(\frac{n_{\text{p}}}{T_{\text{p}}}+\frac{n_j{Z}_j^2}{T_j}\right)}^{-1/2}\right],(3)$

is the Coulomb logarithm and

${\eta }_{j\mathrm{p}}=\frac{n_j}{n_{\text{p}}}.(4)$

Equation 2, after substituting Equation 3 can be numerically integrated using a set of in-situ measurements as a boundary condition to find the radial evolution of the temperature ratio: ${\theta }_{j\mathrm{p}}(r)$. A notable advantage of collisional analysis (versus, e.g., Coulomb number) is that solar wind’s expansion can be directly accounted for by allowing proton density, radial speed, and temperature to scale radially. This study used the average scales reported by Hellinger et al. (2011):

$n_{\text{p}}\left(r\right)\propto r^{-1.8},v_{\text{p,\hspace{0.17em}}r}\left(r\right)\propto r^{-0.2},\mathrm{a}\mathrm{n}\mathrm{d}{T}_{\text{p}}\left(r\right)\propto r^{-0.74}.(5)$

The scaling relationships from Hellinger et al. (2011) and shown in Equation 5, were selected to ensure consistency with previous applications of collisional analysis (e.g., Maruca et al., 2013; Johnson et al., 2023; Johnson et al., 2024). However, more recent studies, such as (i.e., Maruca et al., 2023), have suggested that the radial solar wind speed between $0.1-1.0\mathrm{a}\mathrm{u}$ may increase or remain approximately constant. Preliminary tests using alternative scalings (e.g., $v_{\text{p,\hspace{0.17em}}r}(r)\propto r^0$) produced qualitatively similar results for ${\theta }_{j\mathrm{p}}(r)$, indicating that the key trends are not highly sensitive to the exact velocity profile. These other scaling relationships have been found to give comparable results, although a detailed sensitivity study is planned for future work.

3 Data

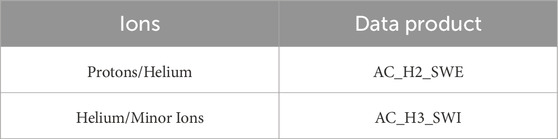
This study used data from the Advanced Composition Explorer (ACE; Stone et al., 1998), which is maintained at the first Lagrange (L1) point of the Sun-Earth system. In-situ measurements of plasma parameters were derived from the Solar Wind Electron, Proton and Alpha Monitor (SWEPAM; McComas et al., 1998) and the Solar Wind Ion Composition Spectrometer (SWICS). Observations are taken from 1998 August 19 through 2011 August 20. This end data was chosen to avoid the complications of a SWICS hardware anomaly (Shearer et al., 2014).

The minor ion data (Gloeckler, 2023) had a 2-h cadence and consisted of 59,179 data points while the proton data (McComas, 2022) had a 1-h cadence and consisted of 104,939 data points. The original data products used in this research are listed in Table 1. The proton data, originally recorded at a 1-h cadence, were resampled to match the 2-h timestamps of the SWICS data. This was done by averaging all available SWEPAM measurements within $\pm 1$ hour of each SWICS time bin. This method was verified by repeating the averaging using 64-s cadence Level-2 SWEPAM data and found negligible differences in the resulting ${\theta }_{j\mathrm{p}}$ distributions, confirming the temporal matching was robust despite occasional data gaps. After the resampling was performed the data set contained 52,469 data points. Filtering was then performed to remove data with low quality or large uncertainties. Specifically, for SWICS ion data, the only retained points had a quality flag of “0,” indicating good data. Records containing fill values, defined as placeholder entries used when no valid measurement was available (typically $-1$ or large invalid values), were also removed. In addition, measurements with large uncertainties in $\alpha$-particle density—specifically, where the reported uncertainty exceeded $50\%$ of the measurement—were excluded from the dataset. After averaging and filtering the data set contained 37,645 data points. To ensure that this analysis reflects quiescent solar wind conditions, time intervals associated with interplanetary coronal mass ejections (ICMEs) were excluded. Specifically, all measurements labeled as “ICME” in the SWICS Level-2 SW-type parameter were removed. This approach was used to minimize contamination from transient plasma populations known to exhibit non-representative ion temperatures and composition profiles.

Table 1

Table 1. Data products used for proton, helium and minor ion measurements.

From the provided thermal speeds the scalar temperatures were computed according to

$v_{th}=\sqrt{\frac{2k_{\text{B}}{T}_j}{m_j}},(6)$

where for $j$- particle species $T_j$ is the scalar temperature and $m_j$ is the mass, $k_{\text{B}}$ is the Boltzmann constant. It should be noted that SWICS thermal speeds are derived from the one-dimensional projection of the ion velocity distribution along the bulk flow direction. This contrasts with datasets such as Wind, where full three-dimensional distribution functions are used to compute scalar temperatures. While collisional analysis as applied here uses scalar temperatures as input, the use of $1\mathrm{D}$ thermal speeds may introduce modest biases in comparison with $3\mathrm{D}$-resolved values. These biases are expected to be consistent across the dataset and do not qualitatively affect the trends examined in this study.

Element abundance ratios were used to compute the respective density ratios, the number densities of minor ions (${\mathrm{C}}^{5+}$, ${\mathrm{O}}^{6+}$, ${\mathrm{F}\mathrm{e}}^{10+}$) were estimated using the ${\mathrm{H}\mathrm{e}}^{2+}$ number density from SWICS, in combination with the elemental abundance ratios reported in the Level-2 dataset (e.g., $\mathrm{H}\mathrm{e}/\mathrm{O}$, $\mathrm{C}/\mathrm{O}$ and $\mathrm{F}\mathrm{e}/\mathrm{O}$). Specifically, the SWICS-derived ${\mathrm{H}\mathrm{e}}^{2+}$ density was used first as a reference, then applied the reported elemental abundance ratios to infer the densities of carbon, oxygen, and iron. It should be noted that the SWICS Level-2 release notes include a caution regarding the use of absolute ${\mathrm{H}\mathrm{e}}^{2+}$ density values and $\mathrm{H}\mathrm{e}/\mathrm{O}$ ratios, particularly with respect to their dependence on solar wind speed (SWICS Team, 2018). In this study, the ${\mathrm{H}\mathrm{e}}^{2+}$ density was used only as a reference to scale relative elemental abundances and compute ${\eta }_{j\mathrm{p}}$ ratios, and not to draw conclusions about absolute helium abundance. As such, the results are not expected to be sensitive to potential systematic offsets in the ${\mathrm{H}\mathrm{e}}^{2+}$ values. Nevertheless, the limitations of the dataset are acknowledged and will be taken into consideration in future work.

It was assumed that the dominant charge states for each species were ${\mathrm{C}}^{5+}$, ${\mathrm{O}}^{6+}$ and ${\mathrm{F}\mathrm{e}}^{10+}$, respectively, based on typical solar wind conditions, and treated these ions as representative of the elemental population for the purposes of the collisional analysis. This approach provides consistent relative densities for use in Equation 4, although assumes that the dominant charge state (${\mathrm{C}}^{5+}$, ${\mathrm{O}}^{6+}$ and ${\mathrm{F}\mathrm{e}}^{10+}$) adequately represents the elemental abundance. It is acknowledged that charge-state distributions can vary significantly depending on solar wind type and conditions, for instance, the ionic fraction of ${\mathrm{C}}^{5+}$ relative to the sum of ${\mathrm{C}}^{4+}-{\mathrm{C}}^{6+}$ may range from 0.2 to $0.8$, and the ionic fraction of ${\mathrm{F}\mathrm{e}}^{10+}$ relative to the sum of ${\mathrm{F}\mathrm{e}}^{6+}-{\mathrm{F}\mathrm{e}}^{20+}$ may range from 0.2 to $0.3$. These variations could introduce systematic uncertainty in the estimated $n_{j\mathrm{p}}$ values, potentially by a factor of $2--5$. A future version of this analysis will incorporate ionic fractions from the ACE Level-2 AC H5 SWI data product to compute charge-state-specific density ratios.

4 Results

Each of Figures 1–4 shows this study’s results for a different ion species: $\alpha$-particles $({\mathrm{H}\mathrm{e}}^{2+})$, carbon $({\mathrm{C}}^{5+})$, oxygen $({\mathrm{O}}^{6+})$, and iron $({\mathrm{F}\mathrm{e}}^{10+})$, respectively. Each figure shows two plots. The left plot shows the probability distribution of ${\theta }_{j\mathrm{p}}$-values as measured at $r=1.0\mathrm{a}\mathrm{u}$ by ACE (Section 3). The right plot shows the probability distribution of ${\theta }_{j\mathrm{p}}$-values predicted for $r=0.1\mathrm{a}\mathrm{u}$ by collisional analysis (Section 2) applied to the individual ACE measurements. Key percentiles of the distributions in Figures 1–4 are listed in Tables 2–5. Within each figure, the range of ${\theta }_{j\mathrm{p}}$-values shown is the same for both plots, but different ranges are used for different figures. In general, the distribution of ${\theta }_{j\mathrm{p}}$-values increases as the mass ratio $m_j/m_{\text{p}}$ increases due to the effects of (super-)mass-proportional heating processes (Marsch, 2006; Kasper et al., 2017; Tracy et al., 2016). Each plot shows its ${\theta }_{j\mathrm{p}}$-range divided into 30 equally sized bins. The probability density was approximated by dividing the number of data in each bin by the total number of data and by the ${\theta }_{j\mathrm{p}}$-width of the bin (per Maruca et al., 2011). It is worth noting that the predicted ${\theta }_{j\mathrm{p}}$ distributions for heavier ions (Figures 1–4, Right) are broadly distributed and do not exhibit clear modal peaks. While this trend aligns with the expected increase in temperature ratio with mass due to preferential heating, the lack of distinct features may reflect limitations imposed by the time-averaged nature of the ACE dataset. As such, caution is warranted when drawing direct comparisons between these predicted distributions and past observational studies from MESSENGER or PSP, which benefit from higher-cadence measurements.

Figure 1

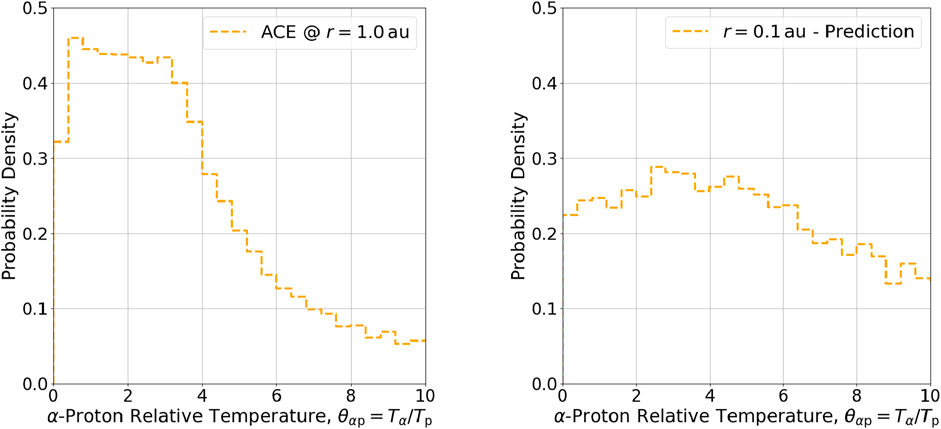
Figure 1. Histogram of observed values of ${\theta }_{\alpha \mathrm{p}}\equiv T_{\alpha }/T_{\text{p}}$ at $r=1.0\mathrm{a}\mathrm{u}$ (Left) and of the predicted ${\theta }_{\alpha \mathrm{p}}$-values (Right). The prediction is based on collisional analysis and extends the measured values to the heliocentric distance $r=0.1\mathrm{a}\mathrm{u}$. Bin counts have been normalized to approximate probability density (Maruca et al., 2011).

Figure 2

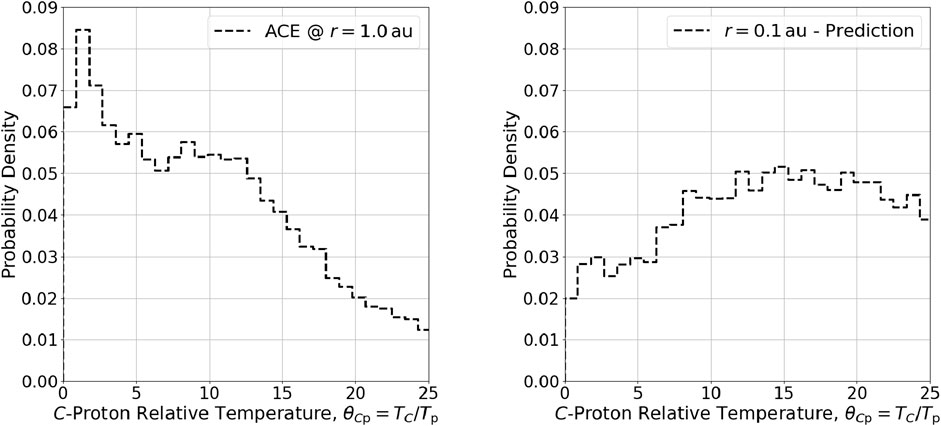
Figure 2. Histogram of observed values of ${\theta }_{\text{C\hspace{0.17em}p}}\equiv T_{\text{C}}/T_{\text{p}}$ at $r=1.0\mathrm{a}\mathrm{u}$ (Left) and of the predicted ${\theta }_{\text{C\hspace{0.17em}p}}$-values (Right). The prediction is based on collisional analysis and extends the measured values to the heliocentric distance $r=0.1\mathrm{a}\mathrm{u}$. Bin counts have been normalized to approximate probability density (Maruca et al., 2011).

Figure 3

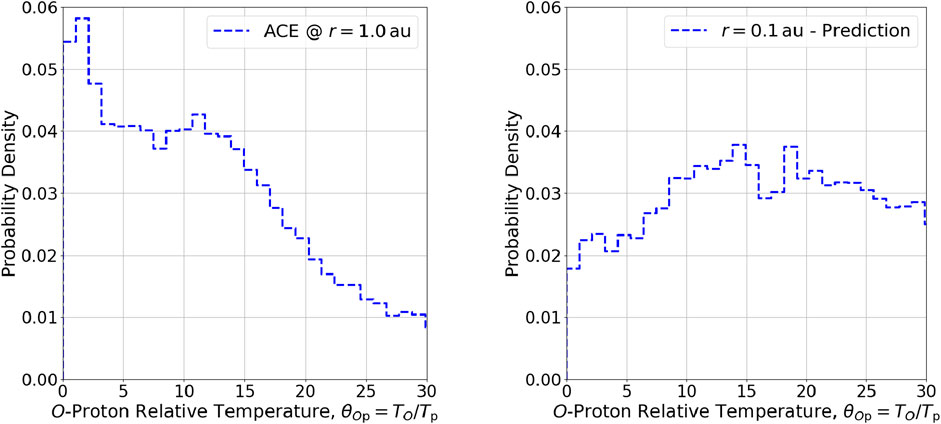
Figure 3. Histogram of observed values of ${\theta }_{\text{O\hspace{0.17em}p}}\equiv T_{\text{O}}/T_{\text{p}}$ at $r=1.0\mathrm{a}\mathrm{u}$ (Left) and of the predicted ${\theta }_{\text{O\hspace{0.17em}p}}$-values (Right). The prediction is based on collisional analysis and extends the measured values to the heliocentric distance $r=0.1\mathrm{a}\mathrm{u}$. Bin counts have been normalized to approximate probability density (Maruca et al., 2011).

Figure 4

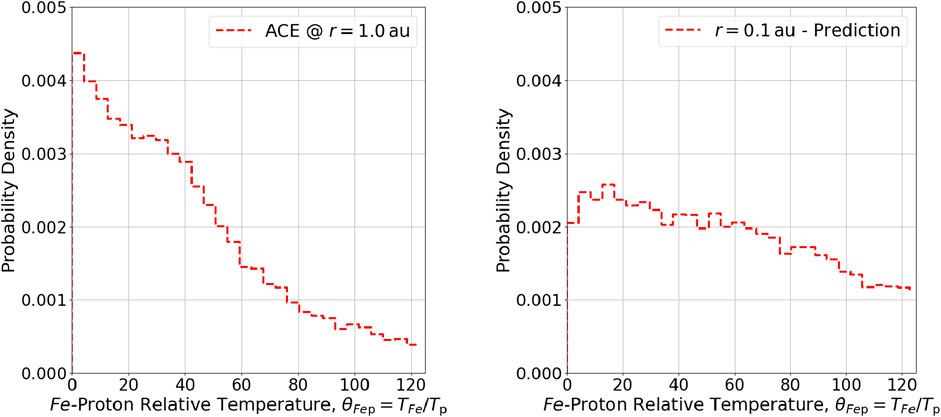
Figure 4. Histogram of observed values of ${\theta }_{\text{Fe\hspace{0.17em}p}}\equiv T_{\text{Fe}}/T_{\text{p}}$ at $r=1.0\mathrm{a}\mathrm{u}$ (Left) and of the predicted ${\theta }_{\text{Fe\hspace{0.17em}p}}$-values (Right). The prediction is based on collisional analysis and extends the measured values to the heliocentric distance $r=0.1\mathrm{a}\mathrm{u}$. Bin counts have been normalized to approximate probability density (Maruca et al., 2011).

Table 2

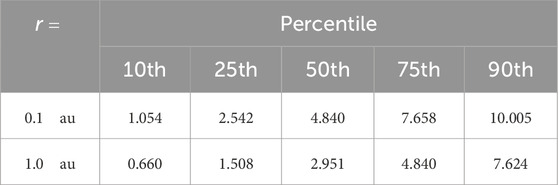
Table 2. Percentiles for the $\alpha$-proton relative temperature distribution from Figure 1.

Table 3

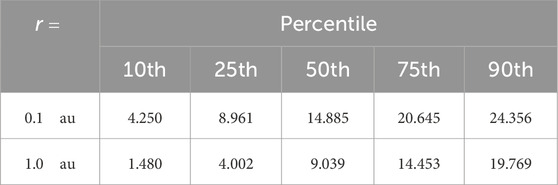
Table 3. Percentiles for the carbon-proton relative temperature distribution from Figure 2.

Table 4

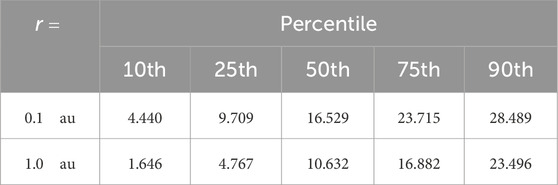
Table 4. Percentiles for the oxygen-proton relative temperature distribution from Figure 3.

Table 5

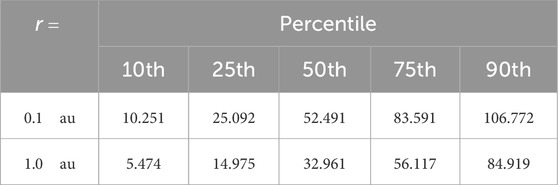
Table 5. Percentiles for the iron-proton relative temperature distribution from Figure 4.

5 Discussion

The right-hand plots in Figures 1–4 show testable predictions for the distribution of relative temperatures in the inner heliosphere $(r=0.1\mathrm{a}\mathrm{u})$. Each plot shows a single peak, mono-modal distribution. The median ($50^{\text{th}}$-percentile), predicted ${\theta }_{j\mathrm{p}}$-value for each species (Tables 2–5) roughly corresponds to the mass ratio of $j$-particles to protons $(m_j/m_{\text{p}})$, which suggests the actions of mass-proportional and/or super-mass-proportional heating of minor ions in the solar corona. This would be consistent with the “zone” of preferential heating presented by Kasper et al. (2017) and Holmes et al. (2024).

At present, the only comparison with observations that can be made is for the $\alpha$-particles as observed by PSP (Fox et al., 2016; Kasper et al., 2016). The predicted ${\theta }_{\alpha \mathrm{p}}$-distribution from this study has a median value of ${\theta }_{\mathrm{\alpha }\mathrm{p}}\approx 4.8$, which corresponds to the center of the broad central plateau in Figure 1 (right plot). While observations with PSP by Johnson et al. (2023), specifically Figure 1 have shown a broad peak at ${\theta }_{\mathrm{\alpha }\mathrm{p}}\approx 5.6$, predictions for $r=0.1\mathrm{a}\mathrm{u}$ made by Maruca et al. (2013) using Wind data expected a peak at ${\theta }_{\alpha \mathrm{p}}\approx 5.4$. This level of agreement, while not exact, is consistent with general expectations from collisional evolution, considering the uncertainties in both in-situ measurements and boundary conditions used in the model. Note that the PSP and Wind data differ in instrument sensitivity, cadence, and sampling intervals, and that the ACE dataset used here reflects longer integration times that may smooth transient high-temperature features. To date, no observations of minor ion relative temperatures have been made close to the Sun, but Gershman et al. (2012), Figure 10 used MESSENGER data from $r\approx 0.3\mathrm{a}\mathrm{u}$ to find a broad distribution of ${\theta }_{\text{Cp}}$- and/or ${\theta }_{\text{Op}}$-values ranging very roughly from 10 to 60.

The left-hand plots in Figures 1–4 show observations for the distribution of relative temperatures in the near-Earth $(r=1.0\mathrm{a}\mathrm{u})$ solar wind. These plots generally show a bimodal distribution with two distinct peaks: one at ${\theta }_{j\mathrm{p}}\approx 1$ corresponding to local thermodynamic equilibrium and a second at a higher ${\theta }_{j\mathrm{p}}$-value. These observational distributions differ from those reported using PSP and Wind, which show more distinct bimodal structures, especially for ${\theta }_{\mathrm{\alpha }\mathrm{p}}$. The ACE data in this study were collected at a 2 h cadence, which can smooth out transient temperature structures and wash out kinetic features such as distinct modal peaks. This limitation is particularly important when interpreting kinetic effects like preferential ion heating or multi-population dynamics, which evolve on much shorter timescales. Therefore, the ACE dataset may underestimate the presence of such features, especially when compared to the higher-cadence data.

Previous studies using proton and $\alpha$-particle data from the Wind spacecraft (e.g., Kasper et al., 2008; Maruca et al., 2013; Johnson et al., 2023) also found a bimodal distribution in ${\theta }_{\alpha \mathrm{p}}$-values, though there were several key differences between their ${\theta }_{\alpha \mathrm{p}}$-distributions and that shown in the left plot of Figure 1. First, the Wind studies found the two peaks in their ${\theta }_{\alpha \mathrm{p}}$-distributions to more distinct, while the distribution in this study shows the peaks barely separated (forming a plateau). Second, the Wind studies found the second peak to be located at ${\theta }_{\alpha \mathrm{p}}\approx 4.5$ versus closer to ${\theta }_{\alpha \mathrm{p}}\approx 3.5$ in this study of ACE data. Mostly like, these differences arise from the vastly different measurement cadences for Wind and ACE datasets: approximately 90 s and 2 h, respectively. The measurement cadence on ACE is so long to allow sufficient integration time to measure the heavy ion species (including carbon, oxygen, and iron, which Wind does not typically measure), but this does mean that its instruments are averaging over short-time-scale fluctuations in ion temperature. Future studies with higher time-resolution datasets, such as those from PSP or upcoming missions, will be critical to resolving whether the predicted trends persist at finer temporal scales and to further test the assumptions underlying collisional analysis.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

EJ: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. BM: Conceptualization, Funding acquisition, Methodology, Resources, Supervision, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors were partially supported by the NSF Award No. 1931435. This research used PlasmaPy, an open source Python package developed by the community for plasma science PlasmaPy (2021).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Feldman, W. C., Asbridge, J. R., and Bame, S. J. (1974). The solar wind He2+ to H+ temperature ratio. J. Geophys. Res. (1896-1977) 79, 2319–2323. doi:10.1029/JA079i016p02319

CrossRef Full Text | Google Scholar

Fox, N. J., Velli, M. C., Bale, S. D., Decker, R., Driesman, A., Howard, R. A., et al. (2016). The solar probe plus mission: humanity’s first visit to our star. Space Sci. Rev. 204, 7–48. doi:10.1007/s11214-015-0211-6

CrossRef Full Text | Google Scholar

Gershman, D. J., Zurbuchen, T. H., Fisk, L. A., Gilbert, J. A., Raines, J. M., Anderson, B. J., et al. (2012). Solar wind alpha particles and heavy ions in the inner heliosphere observed with MESSENGER. J. Geophys. Res. Space Phys. 117. doi:10.1029/2012JA017829

CrossRef Full Text | Google Scholar

Gloeckler, G. (2023). ACE solar wind ion composition spectrometer (SWICS) solar wind plasma elemental and isotopic density, speed, thermal speed, charge state, and ratio parameters. MA, United States: NASA Space Physics Data Facility. doi:10.48322/mvcn-0276

CrossRef Full Text | Google Scholar

Griem, H. R. (1963). Validity of local thermal equilibrium in plasma spectroscopy. Phys. Rev. 131, 1170–1176. doi:10.1103/PhysRev.131.1170

CrossRef Full Text | Google Scholar

Hefti, S., Grünwaldt, H., Ipavich, F. M., Bochsler, P., Hovestadt, D., Aellig, M. R., et al. (1998). Kinetic properties of solar wind minor ions and protons measured with SOHO/CELIAS. J. Geophys. Res. Space Phys. 103, 29697–29704. doi:10.1029/1998JA900022

CrossRef Full Text | Google Scholar

Hellinger, P., Matteini, L., Štverák, v., Trávníček, P. M., and Marsch, E. (2011). Heating and cooling of protons in the fast solar wind between 0.3 and 1 AU: helios revisited. J. Geophys. Res. Space Phys. 116. doi:10.1029/2011JA016674

CrossRef Full Text | Google Scholar

Holmes, J., Kasper, J., Klein, K. G., Lepri, S. T., and Raines, J. M. (2024). Zone of preferential heating for minor ions in the solar wind. Astrophysical J. 964, 19. doi:10.3847/1538-4357/ad23ea

CrossRef Full Text | Google Scholar

Isenberg, P. A., and Hollweg, J. V. (1983). On the preferential acceleration and heating of solar wind heavy ions. J. Geophys. Res. 88, 3923–3935. doi:10.1029/JA088iA05p03923

CrossRef Full Text | Google Scholar

Johnson, E., Maruca, B. A., McManus, M., Klein, K. G., Lichko, E. R., Verniero, J., et al. (2023). Anterograde collisional analysis of solar wind ions. Astrophysical J. 950, 51. doi:10.3847/1538-4357/accc32

CrossRef Full Text | Google Scholar

Johnson, E., Maruca, B. A., McManus, M., Stevens, M., Klein, K. G., and Mostafavi, P. (2024). Application of collisional analysis to the differential velocity of solar wind ions. Front. Astronomy Space Sci. 10. doi:10.3389/fspas.2023.1284913

CrossRef Full Text | Google Scholar

Kasper, J. C., Abiad, R., Austin, G., Balat-Pichelin, M., Bale, S. D., Belcher, J. W., et al. (2016). Solar wind electrons alphas and protons (SWEAP) investigation: design of the solar wind and coronal plasma instrument suite for solar probe plus. Space Sci. Rev. 204, 131–186. doi:10.1007/s11214-015-0206-3

CrossRef Full Text | Google Scholar

Kasper, J. C., Klein, K. G., Weber, T., Maksimovic, M., Zaslavsky, A., Bale, S. D., et al. (2017). A zone of preferential ion heating extends tens of solar radii from the Sun. Astrophysical J. 849, 126. doi:10.3847/1538-4357/aa84b1

CrossRef Full Text | Google Scholar

Kasper, J. C., Lazarus, A. J., and Gary, S. P. (2008). Hot solar-wind helium: direct evidence for local heating by Alfvén-Cyclotron dissipation. Phys. Rev. Lett. 101, 261103. doi:10.1103/PhysRevLett.101.261103

PubMed Abstract | CrossRef Full Text | Google Scholar

Marsch, E. (2006). Kinetic physics of the solar corona and solar wind. Living Rev. Sol. Phys. 3. doi:10.12942/lrsp-2006-1

CrossRef Full Text | Google Scholar

Marsch, E., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn, R., and Neubauer, F. M. (1982). Solar wind helium ions: observations of the Helios solar probes between 0.3 and 1 AU. J. Geophys. Res. Space Phys. 87, 35–51. doi:10.1029/JA087iA01p00035

CrossRef Full Text | Google Scholar

Maruca, B. A., Bale, S. D., Sorriso-Valvo, L., Kasper, J. C., and Stevens, M. L. (2013). Collisional thermalization of hydrogen and helium in solar-wind plasma. Phys. Rev. Lett. 111, 241101. doi:10.1103/physrevlett.111.241101

PubMed Abstract | CrossRef Full Text | Google Scholar

Maruca, B. A., Kasper, J. C., and Bale, S. D. (2011). What are the relative roles of heating and cooling in generating solar wind temperature anisotropies? Phys. Rev. Lett. 107, 201101. doi:10.1103/PhysRevLett.107.201101

PubMed Abstract | CrossRef Full Text | Google Scholar

Maruca, B. A., Qudsi, R. A., Alterman, B. L., Walsh, B. M., Korreck, K. E., Verscharen, D., et al. (2023). The trans-heliospheric survey. Astron. Astrophys. 675, A196. doi:10.1051/0004-6361/202345951

CrossRef Full Text | Google Scholar

McComas, D. (2022). ACE solar wind electron, proton, and alpha monitor. MA, United States: NASA Space Physics Data Facility. doi:10.48322/9w01-2555

CrossRef Full Text | Google Scholar

McComas, D. J., Bame, S. J., Barker, P., Feldman, W. C., Phillips, J. L., Riley, P., et al. (1998). Solar wind electron proton alpha monitor (SWEPAM) for the advanced composition explorer. Space Sci. Rev. 86, 563–612. doi:10.1023/A:1005040232597

CrossRef Full Text | Google Scholar

Neugebauer, M. (1976). The role of Coulomb collisions in limiting differential flow and temperature differences in the solar wind. J. Geophys. Res. (1896-1977) 81, 78–82. doi:10.1029/JA081i001p00078

CrossRef Full Text | Google Scholar

Schmelz, J. T., Reames, D. V., von Steiger, R., and Basu, S. (2012). Composition of the solar corona, solar wind and solar energetic particles. Astrophysical J. 755, 33. doi:10.1088/0004-637x/755/1/33

CrossRef Full Text | Google Scholar

Shearer, P., von Steiger, R., Raines, J. M., Lepri, S. T., Thomas, J. W., Gilbert, J. A., et al. (2014). The solar wind neon abundance observed with ACE/SWICS and ULYSSES/SWICS. Astrophysical J. 789, 60. doi:10.1088/0004-637X/789/1/60

CrossRef Full Text | Google Scholar

Stone, E. C., Frandsen, A. M., Mewaldt, R. A., Christian, E. R., Margolies, D., Ormes, J. F., et al. (1998). The advanced composition explorer. Space Sci. Rev. 86, 1–22. doi:10.1023/A:1005082526237

CrossRef Full Text | Google Scholar

SWICS Team (2018). ACE SWICS level-2 data release notes. NASA Space Physics Data Facility. Available online at: https://izw1.caltech.edu/ACE/ASC/DATA/level2/ssv4/swics_lv2_v4_release_notes.txt.

Google Scholar

Tracy, P. J., Kasper, J. C., Raines, J. M., Shearer, P., Gilbert, J. A., and Zurbuchen, T. H. (2016). Constraining solar wind heating processes by kinetic properties of heavy ions. Phys. Rev. Lett. 116, 255101. doi:10.1103/PhysRevLett.116.255101

PubMed Abstract | CrossRef Full Text | Google Scholar

Tracy, P. J., Kasper, J. C., Zurbuchen, T. H., Raines, J. M., Shearer, P., and Gilbert, J. (2015). Thermalization of heavy ions in the solar wind. Astrophysical J. 812, 170. doi:10.1088/0004-637x/812/2/170

CrossRef Full Text | Google Scholar

Verscharen, D., Klein, K. G., and Maruca, B. A. (2019). The multi-scale nature of the Solar Wind. Living Rev. Sol. Phys. 16, 5. doi:10.1007/s41116-019-0021-0

PubMed Abstract | CrossRef Full Text | Google Scholar