Braking index of PSR J18460258: a model of magnetic inclination evolution and its gravitational-wave implication

We explain the braking index $n=2.19\pm 0.03$ of PSR J1846$-$0258 by incorporating the time evolution of its magnetic inclination angle and dipolar magnetic field. Based on observational timing data and the age of the associated supernova remnant $(t_{\text{SNR}}\approx 1.77\text{kyr})$, we estimate a magnetic inclination change rate of $\dot{\chi }\approx 0.281°/100\mathrm{y}\mathrm{r}\mathrm{s}$, comparable to that of the Crab pulsar. Applying the two-dipole model to PSR J1846$-$0258, we find an internal dipole moment ratio $\eta =M_2/M_1\sim 10^{26}–10^{27}$. For magnetic field decay timescales ${\tau }_D<3.6\times 10^5$ yrs, the magnetic energy dissipation rate $({\dot{E}}_{\text{mag}}\sim (10^{33}–10^{34})\text{erg/s})$ partially explains the observed X-ray luminosity $L_X\sim 1.9\times 10^{34}\text{erg/s}$, while longer ${\tau }_D$ requires additional energy sources. The derived gravitational wave strain $(h_0\sim 10^{-29})$ remains undetectable with current instruments but constrains internal magnetic field geometries. This work highlights the critical role of magnetic inclination dynamics in pulsar spin-down behavior and offers a physically motivated framework that can be extended to other young neutron stars with measured magnetic inclination and braking indices.

1 Introduction

Magnetars are a class of young, isolated neutron stars with ultra-strong magnetic fields ($B\sim 10^{14}-10^{15}$ G), typically manifesting as Soft Gamma Repeaters (SGRs) and Anomalous X-ray Pulsars (AXPs) depending on their high-energy emission characteristics. These extreme objects represent one of the most magnetized environments in the universe, where quantum electrodynamics effects become significant. Magnetars are known to exhibit a variety of high-energy phenomena, most notably X-ray outbursts and short, intense flares. These radiative events are often accompanied by significant timing irregularities, including both glitches and the rarer anti-glitches. Currently, approximately 30 magnetars and candidate sources are cataloged in the McGill Online Magnetar Catalog (Olausen and Kaspi, 2014).

Recent multi-wavelength observations have revealed that magnetars occupy a unique position in neutron star population studies, bridging the gap between conventional rotation-powered pulsars and highly magnetized compact objects. Among the sources listed in the McGill catalog, PSR J1846$-$0258 is particularly unique. Located at the center of the supernova remnant Kes 75 (Gotthelf et al., 2000), it has a rotation period of approximately 327 ms and a characteristic age of about 700 years, making it one of the youngest pulsars in the Galaxy. Throughout most of its observational history, this pulsar has exhibited the properties of a rotation-powered pulsar, but no radio emission has been detected (Archibald et al., 2008). In 2006, the pulsed X-ray flux from this source increased dramatically, accompanied by a large glitch and several magnetar-like outbursts (Gavriil et al., 2008; Kumar and Safi-Harb, 2008; Kuiper and Hermsen, 2009). During this bursting episode, the pulsed flux rose rapidly and remained elevated for nearly 2 months, exhibiting behavior strikingly similar to that of AXPs. In 2020, this source underwent a second outburst, during which the pulsed flux increased to more than five times its quiescent level, yet no radio pulsations were detected (Krimm et al., 2020; Majid et al., 2020; Hu et al., 2023). PSR J1846$-$0258 remains the only known rotation-powered pulsar that has exhibited clear magnetar-like behavior, serving as a critical transitional object linking these two classes of neutron stars.

The braking index $n$ is a crucial observational parameter characterizing the rotational evolution of pulsars. Defined as $n=\mathrm{\Omega }\ddot{\mathrm{\Omega }}/{\dot{\mathrm{\Omega }}}^2$ where $\mathrm{\Omega }$ is the spin angular velocity, it provides direct insight into the pulsar’s spin-down physics. Due to timing noise and other instabilities, stable braking indices have been measured for only about nine pulsars (Lyne et al., 1993; Boyd et al., 1995; Lyne et al., 1996; Livingstone et al., 2007; Espinoza et al., 2011; Weltevrede et al., 2011; Roy et al., 2012). Moreover, Gao et al. (2016) estimated the mean braking indices for eight magnetars associated with supernova remnants (SNRs) using SNR age estimates, with values ranging from $1-42$. Archibald et al. (2015) measured a braking index of $n=2.19\pm 0.03$ for PSR J1846$-$0258 using over 7 years of post-outburst timing data. Like other measured values, this result deviates from the canonical prediction of $n=3$ from the standard magnetic dipole radiation model. This discrepancy has become a central puzzle in pulsar physics, motivating numerous theoretical investigations.

Current research on braking indices focuses on three main directions: 1) multi-component spin-down mechanisms, 2) magnetic field evolution, and 3) geometric effects including magnetic inclination changes. One major class of explanations involves combining multiple braking mechanisms (such as magnetic dipole radiation, pulsar winds, and gravitational wave emission) to account for the observed braking indices. For instance, Xu and Qiao (2001) developed a model that integrates wind braking and magnetic dipole radiation, resulting in a theoretical braking index smaller than 3. Chen and Li (2006) proposed that braking indices lower than three could arise from an increasing vertical component of the magnetic field over time or from tidal torques exerted by fallback disks. Kou and Tong (2015) discussed the rotational evolution of the Crab pulsar by combining the wind braking model and the magnetic dipole radiation model. Chen and Li (2016) explained the low braking index of PSR J1734$-$3333 using fall-back disks. de Araujo et al. (2016) combined magnetic dipole radiation with gravitational wave radiation to explain the braking index of PSR J1640$-$4631.

Another major class of explanations focuses on the evolution of the magnetic field strength and the magnetic inclination angle. This approach has gained particular attention following the direct measurement of magnetic inclination change in the Crab pulsar (Lyne et al., 2013). Observational and theoretical studies suggest that both quantities may vary over time, thereby influencing the pulsar’s rotational evolution. Ekşi et al. (2016) explained the braking index of PSR J1640$-$4631 by considering a secular evolution of the magnetic inclination angle. Gao et al. (2017) explained the braking index of this source through the evolution of surface dipolar magnetic fields. Currently, the origin and detailed mechanisms of the magnetic inclination evolution remain uncertain. Philippov et al. (2014) employed magnetohydrodynamic simulations incorporating plasma-filled pulsar magnetospheres to show that the magnetic inclination angle decreases over time, following a power-law dependence. Zhang et al. (1998) investigated the problem of magnetic axis alignment with the rotation axis in pulsars caused by the gravitational spin effect. In contrast, some theoretical models predict that the magnetic inclination may increase or evolve in more complex ways. Lyne et al. (2013) measured the separation between the main pulse and interpulse of the Crab pulsar over 22 years, deriving a rate of magnetic inclination change of ${\dot{\chi }}_{\text{Crab}}=0.63°\pm 0.03°/100\mathrm{y}\mathrm{r}\mathrm{s}$. This is the only pulsar with observationally determined magnetic inclination evolution. In addition, studies of single pulses not only provide important insights into the complexity of pulsar emission mechanisms (Wen et al., 2020a; b) but also offer observational means to constrain the magnetic inclination angle (Wen et al., 2021; 2022). The study of magnetars and high-$B$ pulsars also has significant implications for the exploration of gravitational waves, especially in the field of nanohertz gravitational waves. The unique properties of these objects may provide new insights and observational targets for the research of nanohertz gravitational waves, which are expected to be detected by pulsar timing arrays (PTAs) in the near future.

The gravitational wave (GW) emission from magnetars and high-B pulsars has emerged as an important research frontier, particularly with the advent of advanced GW detectors. While most studies focus on deformed neutron stars as potential GW sources, the connection between magnetic field geometry, braking indices, and GW emission remains poorly understood. Regarding the origin of magnetic inclination changes, some studies attribute it to external electromagnetic torques, which simultaneously slow the pulsar’s rotation and decrease the magnetic inclination angle (Michel and Goldwire, 1970; Spitkovsky, 2006; Philippov et al., 2014). Some models resort to internal origins. For example, viscous dissipation within precessing neutron stars may alter the magnetic inclination (Lander and Jones, 2018; Cheng et al., 2019). Additionally, Hamil et al. (2016) proposed a two-dipole model (hereafter the HSS model) suggesting that neutron star interiors might host a fossil magnetic field generated by rotating charged spheres and an induced paramagnetic field, with interactions between these dipoles leading to changes in magnetic inclination.

This work presents a comprehensive study of PSR J1846$-$0258’s braking index by simultaneously considering magnetic field decay and inclination angle evolution within the framework of the HSS model. Our approach offers several key advancements: 1) we provide the first application of the two-dipole model to PSR J1846$-$0258, 2) we quantitatively assess the relative contributions of magnetic field decay and inclination change to the braking index, and 3) we explore the implications for gravitational wave emission from this unique source. The gravitational wave analysis represents a novel aspect of our work, as previous studies of PSR J1846$-$0258 have not thoroughly examined its GW detectability in relation to its magnetic field configuration and braking index.

The remainder of this paper is organized as follows. Section 2 explains the braking index of PSR J1846$-$0258 by considering the magnetic field and the inclination angle variations, calculating the magnetic inclination change rate and comparing it with the Crab pulsar. Section 3 applies the two-dipole model to PSR J1846$-$0258, estimating the possible magnetic inclination evolution and magnetic moments based on the calculated inclination change rate. Section 4 discusses the calculated magnetic energy dissipation rate of PSR J1846$-$0258 under the adopted model and compares it with the observed X-ray luminosity. Section 5 presents a detailed analysis of the gravitational wave implications, including magnetic-induced deformation estimates, strain amplitude calculations, and detection prospects with current and future GW observatories. Section 6 summarizes the main results and outlines directions for future research.

2 Braking index constraints from magnetic inclination evolution

The observed braking index of PSR J1846$-$0258 $(n=2.19\pm 0.03)$ provides crucial constraints on its spin-down physics. In this section, we analyze how the temporal evolution of both the magnetic inclination angle and dipolar magnetic field can explain this deviation from the canonical $n=3$ prediction. Using the pulsar’s timing parameters and the age of its associated supernova remnant, we derive quantitative estimates for the magnetic inclination change rate and compare these with known values from other pulsars.

2.1 Basic formalism

Table 1 lists the parameters of PSR J1846$-$0258. The rotation period $P$ and its first derivative $\dot{P}$, characteristic age ${\tau }_{\text{c}}$, and X-ray luminosity $L_{\text{X}}$ are taken from the McGill Online Magnetar Catalog (Olausen and Kaspi, 2014). Note that $L_{\text{X}}$ is in the 2–10 keV range and is calculated using the distance inferred for Kes 75. The spin-down luminosity $\dot{E}$ is computed based on the moment of inertia assumed in Section 3. The magnetic inclination angle $\chi$ is adopted from Wang et al. (2014), which fitted the observational energy spectra of PSR J1846$-$0258 and obtained a magnetic inclination angle $\chi =10°$. Using the magnetic inclination data, the dipolar magnetic field $B_{\text{d}}$ of this source is calculated to be $2.78\times 10^{14}\mathrm{G}$. The supernova remnant age $t_{\text{SNR}}$ is from SNRcat (Ferrand and Safi-Harb, 2012).

Table 1

Table 1. The parameters of PSR J1846$-$0258. See the main text for more details.

In this section, we use these observational parameters, together with considerations of magnetic inclination evolution, to explain the observed braking index of this pulsar.

The standard magnetic dipole radiation model, based on the assumption of a constant moment of inertia $I$, provides a braking index $n$ expressed as

$n=3+\frac{2\mathrm{\Omega }}{\dot{\mathrm{\Omega }}}\left(\frac{\dot{M}}{M}+\frac{\dot{\chi }}{\tan \chi }\right),(1)$

where $\mathrm{\Omega }$ is the spin angular velocity, $\dot{\mathrm{\Omega }}$ is the first time derivative of $\mathrm{\Omega }$, $M=B_d{R}^3$ is the magnetic dipole moment, and $R$ is the radius of the pulsar. This equation clearly demonstrates that variations in both magnetic field strength and magnetic inclination angle have an impact on the braking index.

2.2 Magnetic inclination evolution and field decay

First, we consider only the evolution of the magnetic inclination angle, setting the first term in parentheses in Equation 1 to zero. Since the spin-down rate $\dot{\mathrm{\Omega }}<0$, a positive $\dot{\chi }$ for PSR J1846$-$0258 naturally results in a braking index smaller than 3. Substituting the timing parameters and neglecting observational uncertainties, we obtain a magnetic inclination angle derivative of $\dot{\chi }=0.281°/100\mathrm{y}\mathrm{r}\mathrm{s}$, which is comparable in magnitude to the value measured for the Crab pulsar.

It is widely recognized that the dipolar magnetic field within a neutron star’s crust undergoes decay over time as a result of processes such as Ohmic dissipation and Hall drift (Goldreich and Reisenegger, 1992). If the magnetic inclination angle decreases with time, the braking index would exceed 3. Conversely, if $\chi$ increases with time, the resulting braking index could be less than 3, offering an explanation for the measured value of $n=2.19$ for PSR J1846$-$0258. In this work, we assume that the magnetic field decays exponentially according to

$B_{\text{d}}=B_i\exp \left(-t/{\tau }_{\text{D}}\right),(2)$

where ${\tau }_D$ is the magnetic field decay timescale, and $B_i$ is the initial magnetic field. While the Hall drift itself is a non-dissipative process, it can effectively accelerate magnetic field decay by converting large-scale fields into smaller-scale components. If the Hall drift dominates the magnetic field evolution, the characteristic decay timescale can be expressed as ${\tau }_{\text{D}}={\tau }_{\text{Hall}}\approx 1.2\times {10}^4({10}^{15}\mathrm{G}/B_{\text{d}})\mathrm{y}\mathrm{r}\mathrm{s}$ (Cumming et al., 2004). For typical magnetar-strength magnetic fields, this implies a decay timescale on the order of $10^4$–$10^7$ yrs. Ohmic dissipation, on the other hand, is strongly influenced by the surface temperature of neutron stars. As demonstrated by Pons et al. (2007), the observed correlation between neutron star surface temperature and dipolar magnetic field strength can be naturally explained by Ohmic decay of crustal currents over a timescale of approximately $10^6$ yrs. Moreover, two-dimensional magneto-thermal evolutionary simulations also suggest that the effective magnetic field dissipation timescale for typical magnetars and high-field pulsars usually ranges between $10^4$ and $10^6$ yrs (Viganò et al., 2013; Pons and Viganò, 2019).

Incorporating this decay into the braking index formula yields the modified expression, as shown in Equation 3.

$n=3+\frac{2\mathrm{\Omega }}{\dot{\mathrm{\Omega }}}\left(-\frac{1}{{\tau }_D}+\frac{\dot{\chi }}{\tan \chi }\right).(3)$

Using $t_{\text{SNR}}$ as the true age of the pulsar, and adopting the parameters in Table 1, we plot the relationship between $\dot{\chi }$ and ${\tau }_D$ in Figure 1.

Figure 1

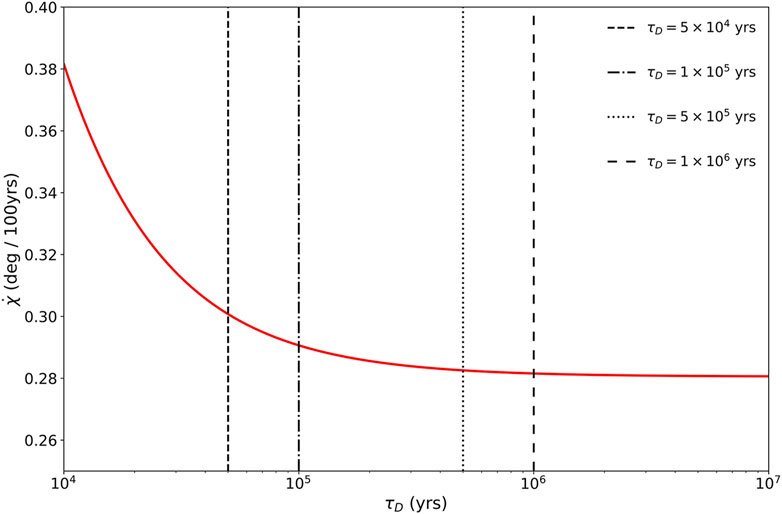
Figure 1. The relationship between the magnetic inclination angle derivative $\dot{\chi }$ and the dipole magnetic field decay timescale ${\tau }_{\text{D}}$. The black lines indicate the four typical decay timescales we adopted.

As shown in Figure 1, $\dot{\chi }$ decreases with increasing ${\tau }_{\text{D}}$, approaching an asymptotic value near $0.281°/100\mathrm{y}\mathrm{r}\mathrm{s}$. By selecting several representative field decay timescales, ${\tau }_{\text{D}}=5\times 10^4$, $1\times 10^5$, $5\times 10^5$, and $1\times 10^6\mathrm{y}\mathrm{r}\mathrm{s}$ (marked with dashed lines in Figure 1), the corresponding $\dot{\chi }$ are calculated to be 0.301, 0.291, 0.283, 0.282 $°/100\mathrm{y}\mathrm{r}\mathrm{s}$ respectively. It is evident that the values of $\dot{\chi }$ computed by considering both the magnetic field decay and the magnetic inclination evolution are slightly higher than those obtained when considering inclination evolution alone. This is because magnetic field decay tends to increase the braking index. Nonetheless, in both scenarios, the values of $\dot{\chi }$ remain consistent with the observed value for the Crab pulsar.

3 Inclination evolution from the two-dipole model

The observed braking index of PSR J1846$-$0258 can be naturally explained within the framework of the two-dipole model proposed by Hamil et al. (2016). This section presents a detailed analysis of how the interaction between internal magnetic dipoles drives the evolution of the magnetic inclination angle, providing quantitative predictions that match the observed braking index.

3.1 Model description and angular dynamics

After considering possible sources of magnetism in pulsars, Hamil et al. (2016) proposed a toy model to explain the origin of the magnetic inclination angle evolution. A schematic diagram of this model is shown in Figure 2. In this model, a pulsar contains two distinct magnetic dipoles that are $M_1$ and $M_2$. The dipole $M_1$ is generated by a dynamo mechanism, fixed at the stellar center, and aligned with the rotation axis. In contrast, $M_2$ originates from the magnetization of matter (for instance ferromagnetic ordering). It is displaced from the center, and can rotate freely about its own axis. $M_2$ is responsible for the pulsar’s braking torque and may influence or even determine the radiation characteristics and internal thermal evolution of the neutron star. The separation between the geometric centers of the two dipoles is denoted by $r$ and assumed to be constant. The angle between the dipole-dipole axis (connecting the centers of $M_1$ and $M_2$) and the rotation axis is denoted by ${\theta }_1$, while the angle between the magnetic moment vector of $M_2$ and the dipole-dipole axis is denoted by ${\theta }_2$. As the neutron star interior is believed to be in a superfluid state, the rotational motion of $M_2$ is assumed to be nearly frictionless. The magnetic interaction between the two dipoles results in a time-dependent evolution of the magnetic inclination angle.

Figure 2

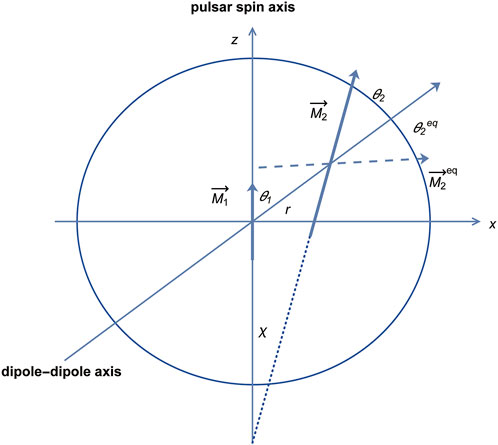
Figure 2. The two-dipole system in the pulsar. $M_1$ is fixed and aligned with the spin axis $z$. The dipole-dipole axis $r$ makes an angle ${\theta }_1$ with $z$. The dashed line corresponds to $M_2$ in the equilibrium position. For more details see Hamil et al. (2016).

The angular dynamics of the system are determined by the following relationship,

${\dot{\theta }}_2^2=\frac{2M_1{M}_2}{I_2{r}^3}F\left(\mathrm{\Theta }\right),(4)$

where $I_2$ is the moment of inertia associated with dipole $M_2$, and $F(\mathrm{\Theta })=\left(\sin {\theta }_{1i}\sin {\theta }_{2i}-2\cos {\theta }_{1i}\cos {\theta }_{2i}\right)-\left(\sin {\theta }_{1f}\sin {\theta }_{2f}-2\cos {\theta }_{1f}\cos {\theta }_{2f}\right)$ is a function of the angles ${\theta }_1$ and ${\theta }_2$, and the subscripts $i$ and $f$ denote the initial and final values of the angles ${\theta }_1$ and ${\theta }_2$, respectively. Equation 4 reflects the conversion of potential energy into kinetic energy during the motion of $M_2$. The value of ${\theta }_2$ that minimizes the potential energy was derived by Shi et al. (2019), and is given by Equation 5.

${\theta }_2^{\min }=-\arctan \left(\frac{\tan {\theta }_1}{2}\right).(5)$

Physically, $M_2$ will tend to oscillate around this equilibrium point in a manner similar to a simple pendulum. Based on the geometric configuration, the relationship between the magnetic inclination angle $\chi$ and its time derivative is given by Equation 6.

$\chi ={\theta }_1-{\theta }_2,\dot{\chi }=-{\dot{\theta }}_2.(6)$

Therefore, when ${\dot{\theta }}_2$ is less than 0, it results in $\dot{\chi }$ being greater than 0, thereby causing the braking index to be less than 3. To ensure a positive $\dot{\chi }$, ${\theta }_2$ must exceed ${\theta }_2^{\min }$, and ${\theta }_1$ must be greater than a critical angle ${\theta }_1^{\text{crit}}$, which satisfies

${\theta }_1^{\text{crit}}={\chi }_f-\arctan \left(\frac{\tan {\theta }_1^{\text{crit}}}{2}\right).(7)$

3.2 Evolutionary parameters and magnetization properties

Substituting the measured magnetic inclination angle into Equation 7 yields ${\theta }_1^{\text{crit}}\approx 6.7°$. In the HSS model, the interaction between the two magnetic dipoles induces quasi-harmonic oscillations of the magnetic inclination angle around an equilibrium value. Accordingly, the evolution is described by Equation 8.

$\chi \left(t\right)={\chi }_{\text{eq}}-A\cos \left(\frac{2\pi t}{{\tau }_A}\right),(8)$

where ${\chi }_{\text{eq}}={\theta }_1-{\theta }_2^{\text{min}}$ is the equilibrium magnetic inclination angle, $A$ is the amplitude of variation, and ${\tau }_A$ is the characteristic timescale of the oscillation. This harmonic oscillation solution emerges from small-angle approximations to the pendulum-like motion of $M_2$ about its equilibrium position, with the cosine phase chosen such that $\chi (0)={\chi }_{\text{eq}}-A$ represents the initial condition.

The amplitude $A$ represents half the total variation range of $\chi (t)$, while ${\tau }_A$ gives the full oscillation period. Initial conditions are set such that $\chi (0)={\chi }_{\text{eq}}-A$ to match the current evolutionary phase. Based on the previously obtained evolution rate of the magnetic inclination angle, parameters related to its evolution in the HSS model are calculated by selecting several representative values of ${\theta }_1$. The corresponding results are summarized in Table 2, and the evolution curves of the magnetic inclination angle are subsequently plotted using these results.

Table 2

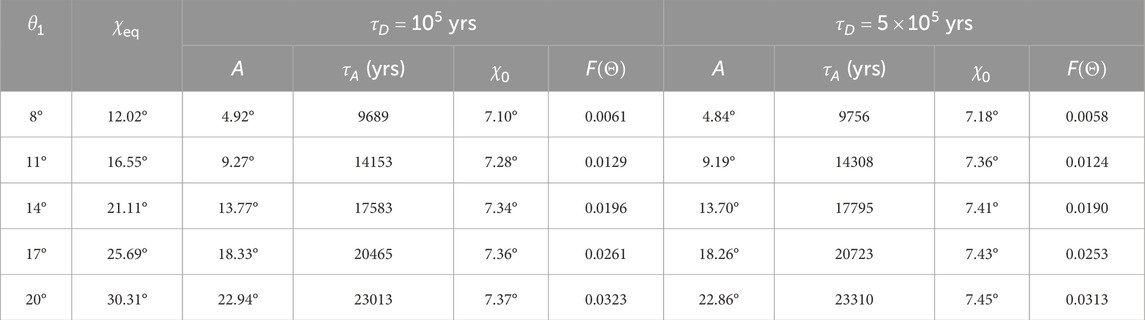
Table 2. Calculation results of parameters related to magnetic inclination evolution in the HSS model, for two different magnetic field decay time-scales.

Figures 3, 4 demonstrate excellent agreement between the harmonic solutions (Equation 8) and the parameters derived in Table 2. The harmonic nature of these solutions is confirmed by the constant periodicity and symmetric amplitude about ${\chi }_{\text{eq}}$ visible in the figure.

Figure 3

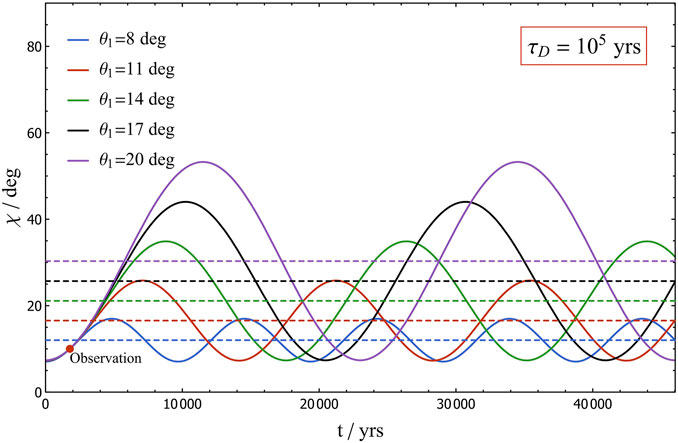
Figure 3. Evolution of the magnetic inclination angle $\chi (t)$ for PSR J1846$-$0258 in the HSS model, showing the time dependence for different initial angles ${\theta }_1$ (color-coded as in Table 2). The horizontal dashed lines indicate the equilibrium values ${\chi }_{\text{eq}}$ calculated from Equation 8. The current observed inclination $\chi =10°$ is marked by the red dot. The oscillation periods ${\tau }_A$ correspond to those listed in Table 2.

Figure 4

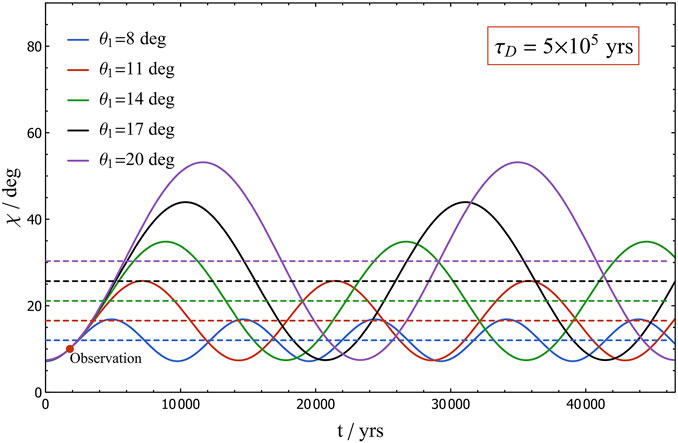
Figure 4. Same as Figure 3, but with ${\tau }_{\text{D}}=5\times 10^5\mathrm{y}\mathrm{r}\mathrm{s}$ in the calculation.

To estimate the magnetization parameters in the HSS model, we adopt a medium-mass neutron star with a mass of $m=1.45M_{\odot }$ and a radius of $R=11.5$ km (Akmal et al., 1998), yielding a moment of inertia of $I=1.534\times 10^{45}{\mathrm{g}\mathrm{c}\mathrm{m}}^2$. We assume $I_1\approx I$, $I_2\approx 0.01I$, and $r=0.5R$. Using these parameters, the initial magnetic dipole moment of PSR J1846$-$0258 is obtained as $M_{2i}=B_i{R}^3=4.35\times 10^{32}{\mathrm{G},\mathrm{c}\mathrm{m}}^3$, while the current dipole moment is $M_2=B_{\text{d}}{R}^3=4.27\times 10^{32}{\mathrm{G},\mathrm{c}\mathrm{m}}^3$. To explore the paramagnetic magnetization properties of the neutron star during its early ferromagnetic phase, we define the ratio $\eta =M_2/M_1$, which characterizes the degree of magnetization in the paramagnetic material and depends on the angular parameters. The ratio $\eta$ shows only weak dependence on ${\theta }_1$ within the considered range, indicating that the internal magnetization is robustly constrained. Based on the results in Table 2, the corresponding values of $M_1$ and $\eta$ are calculated and listed in Table 3. It is found that the value of $\eta$ for PSR J1846$-$0258 lies within the range of $10^{26}$–$10^{27}$, which is consistent with the results obtained by Yan et al. (2021) for SGR 1E 2259$+$586.

Table 3

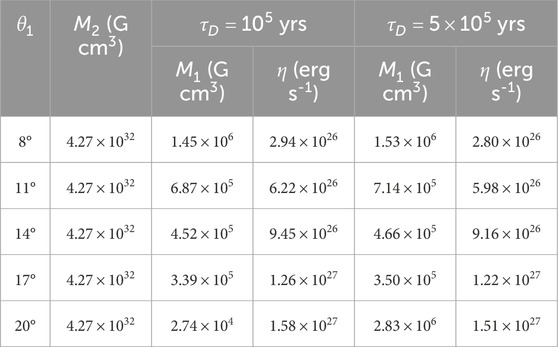
Table 3. Calculated results for the two magnetic moments in the HSS model, adopting magnetic field decay timescales of $10^5$ and $5\times 10^5$ years.

To better illustrate the influence of the dipole moment ratio $\eta$ on the braking index $n$ in our model, we selected two representative combinations of ${\theta }_1$ and ${\tau }_{\text{D}}$, and plotted the variation of the braking index $n$ as a function of $\eta$, as shown in Figure 5. It is evident that the braking index gradually approaches the canonical value $n=3$ predicted by the standard magnetic dipole radiation model as $\eta$ increases. Additionally, as ${\theta }_1$ and ${\tau }_{\text{D}}$ increase, the approach of $n$ towards the classical value becomes noticeably slower.

Figure 5

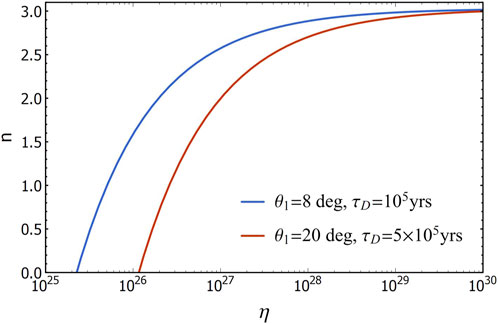
Figure 5. The variation of the braking index $n$ as a function of the dipole moment ratio $\eta$. The colored curves represent two different sets of model parameters.

To further understand the physical implications of the braking index of PSR J1846$-$0258 $(n=2.19)$, we compare it with other young pulsars known to exhibit braking indices of $n<3$. Among them, the Crab pulsar $(n=2.51)$ has a measured magnetic inclination angle evolution rate Lyne et al. (2013), which is broadly consistent in magnitude with the results derived from our model for PSR J1846$-$0258.

However, several young pulsars, such as the Vela pulsar $(n\approx 1.4)$ and PSR J1833$-$1034 $(n\approx 1)$, are clearly associated with pulsar wind nebulae (PWN) (Lyne et al., 1996; Helfand et al., 2001; de Rosa et al., 2009; Roy et al., 2012), where angular momentum loss due to particle winds contributes significantly to the braking index. Thus, when modeling the rotational and magnetic inclination evolution of such pulsars, the effects of wind braking must be carefully considered.

Additionally, PSR J1734$-$3333 exhibits an extremely low braking index $(n\approx 0.9)$, which has been suggested to result from magnetic field re-emergence. In this scenario, the magnetic field was initially buried beneath the crust by fallback accretion and later resurfaced through Hall drift, leading to a magnetic field evolution distinct from that of typical rotation-powered pulsars (Chen and Li, 2016; Ho, 2015).

Several magnetars also display braking indices below 3, such as SGR 0526$-$66, SGR 1627$-$41, and CXOU J171405.07$-$381031 (Gao et al., 2016). Unfortunately, there are currently no available measurements of the magnetic inclination angles for these sources, limiting the ability to directly study their inclination evolution.

Incorporating the coupled evolution of magnetic inclination and magnetic field is essential for developing a unified model of neutron star rotational evolution. Moreover, for certain classes of pulsars, it is also necessary to account for additional complex processes, such as wind braking and fallback disk interactions. Future systematic observations, particularly joint measurements of braking index and magnetic inclination angle in magnetars and high-field pulsars exhibiting magnetar-like behavior, will be crucial for testing and refining the physical model proposed in this work.

4 Magnetic energy dissipation of PSR J1846$-$0258

The decay of magnetic fields in neutron stars is believed to be a potential source of their high-energy emission. Our analysis of PSR J1846$-$0258’s magnetic energy dissipation rate reveals important constraints when compared with its observed X-ray luminosity of $L_X=(1.9\pm 0.2)\times 10^{34}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$ (Archibald et al., 2015).

After incorporating the observed magnetic inclination angle $(\chi =10°\pm 2°)$, the corrected dipolar magnetic field strength is obtained as $B_d=2.8\times 10^{14}\mathrm{G}$. Following standard neutron star magneto-thermal evolution models (Goldreich and Reisenegger, 1992), we assume an exponential decay of the dipolar magnetic field, with the magnetic field decay rate derived from Equation 2 as

$\frac{d{B}_{\text{d}}}{dt}=-\frac{B_i}{{\tau }_{\text{D}}}\exp \left(-t/{\tau }_{\text{D}}\right).(9)$

By substituting the supernova remnant age $t_{\text{SNR}}$ into Equation 9, we compute the magnetic field decay rates for several values of ${\tau }_D$. The magnetic energy of the crustal dipole field is given by Equation 10.

$E_{\text{mag}}=\frac{B_{\text{d}}^2}{6}\left[R^3-{\left(R-\mathrm{\Delta }R\right)}^3\right],(10)$

where $\mathrm{\Delta }R=1$ km is the characteristic crust thickness (Akmal et al., 1998). For PSR J1846$-$0258, this yields $E_{\text{mag}}=(2.0\pm 0.3)\times 10^{46}$ erg. The corresponding magnetic energy dissipation rate ${\dot{E}}_{\text{mag}}=\dot{B}B[R^3-{(R-\mathrm{\Delta }R)}^3]/3$ is evaluated for each ${\tau }_D$ in Table 4.

Table 4

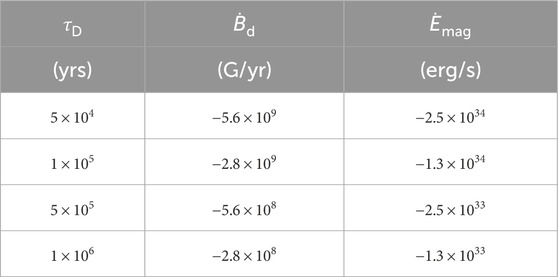
Table 4. The calculated results of crust dipole field decay rate ${\dot{B}}_{\text{d}}$ and magnetic energy decay rate ${\dot{E}}_{\text{mag}}$ for different magnetic field decay timescales.

These results, presented in Table 4, show good agreement with typical magnetar field decay timescales.

Comparing the magnetic energy dissipation rate with the observed X-ray luminosity of PSR J1846$-$0258 $(L_X=1.9\times 10^{34}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s})$, we find that for ${\tau }_D=5\times 10^4$ yrs, the conversion efficiency is $L_{\text{X}}/{\dot{E}}_{\text{mag}}\approx 76\%$. However, when ${\tau }_D>3.6\times 10^5$ yrs, the dissipation rate ${\dot{E}}_{\text{mag}}$ falls below the observed $L_X$, indicating that the magnetic field decay alone cannot account for the current X-ray luminosity. This suggests that other mechanisms may contribute significantly to the high-energy emission of PSR J1846$-$0258. This discrepancy suggests three possible resolutions:

1. PSR J1846$-$0258’s hybrid nature: As a transitional object between rotation-powered pulsars and magnetars (Gavriil et al., 2008), its X-ray emission may combine magnetic dissipation with rotational energy loss.

2. Thermal evolution effects: The strong temperature dependence of Ohmic dissipation means our isothermal approximation underestimates early-stage energy release.

3. Internal toroidal fields: Current upper limits of $B_{\text{t}}\sim 10^{16}$ G (Lander and Jones, 2018) could provide $\sim 10^{35}$ erg/s through crustal heating.

The most plausible scenario combines contributions from both magnetic dissipation $(\sim 30-70\%)$ and rotational energy $(\sim 30-70\%)$, consistent with its measured spin-down luminosity $\dot{E}=1.24\times 10^{37}$ erg/s. Future observations of thermal spectra could better constrain the magnetic contribution.

5 Gravitational wave implications

The generation of gravitational waves (GWs) in neutron stars is fundamentally tied to their internal structure through quadrupole moment deformations. PSR J1846$-$0258 serves as a unique laboratory for probing extreme physics due to three key characteristics: First, its exceptionally high dipolar magnetic field ($B_{\text{d}}\sim 2.78\times 10^{14}$ G) generates significant oblate deformation. Second, potential strong internal toroidal fields ($B_{\text{t}}\sim 10^{15}$ G) may induce competing prolate distortion. Third, precise timing constraints from X-ray observations provide unusually tight bounds on deformation parameters ${ϵ}_{\text{B}}^{\text{net}}$. This combination makes the system particularly valuable for testing magneto-elastic coupling theories (Lander and Jones, 2018; Haskell et al., 2015).

5.1 Magnetic-induced deformation

5.1.1 Poloidal field deformation (oblate)

The dipolar field generates an oblate distortion through Maxwell stresses. Following Lander and Jones (2018), the magnetic energy density is given by Equation 11.

$U_B=\frac{B_d^2}{8\pi }\approx 3.1\times 10^{25}{\text{\hspace{0.17em}erg\hspace{0.17em}cm}}^{-3}.(11)$

The crustal shear modulus $\mu$ for a polycrystalline crust is given by Equation 12 (Lattimer and Yahil, 1991):

$\mu =10^{30}{\left(\frac{\rho }{10^{14}{\text{g\hspace{0.17em}cm}}^{-3}}\right)}^{0.4}{\text{\hspace{0.17em}erg\hspace{0.17em}cm}}^{-3}.(12)$

The deformation arises from equilibrium between magnetic stresses and crustal elasticity, as shown in Equation 13.

$\frac{B_d^2}{8\pi }=\mu ϵ{\mathrm{B}}^{\text{pol}}=\mu ϵ{\mathrm{B}}_{\text{d}}.(13)$

Dimensional analysis suggests scaling with the ratio of magnetic to gravitational energy is given by Equation 14.

${ϵ}_{\text{B}}^{\text{pol}}\propto \frac{B_d^2{R}^4}{G{M}^2}.(14)$

The exact solution from perturbed equilibrium (Lander and Jones, 2018) includes geometric factors and equation of state-dependent corrections via $\mathcal{F}(R,M)$, is given by Equation 15.

${ϵ}_{\text{B}}^{\text{pol}}=\frac{5}{48\pi }\frac{B_d^2{R}^4}{G{M}^2}\mathcal{F}\left(R,M\right),(15)$

where $\mathcal{F}(R,M)\equiv {\left(\frac{R}{11.5\text{km}}\right)}^4{\left(\frac{M}{1.45M_{\odot }}\right)}^{-2}$.

For PSR J1846$-$0258, the resulting ellipticity is given by Equation 16:

${ϵ}_{\text{B}}^{\text{pol}}=2.57\times 10^{-7}{\left(\frac{B_d}{2.78\times 10^{14}\text{\hspace{0.17em}G}}\right)}^2{\left(\frac{R}{11.5\text{\hspace{0.17em}km}}\right)}^4{\left(\frac{M}{1.45M_{\odot }}\right)}^{-2}.(16)$

Here we have adopted a typical medium-mass neutron star with $R=11.5\mathrm{k}\mathrm{m}$ and $M=1.45M_{\odot }$, corresponding to the moment of inertia $I=1.53\times 10^{45}\mathrm{g}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$ (Gao et al., 2017).

5.1.2 Toroidal field deformation (prolate)

The prolate deformation induced by internal toroidal magnetic fields can be derived systematically from first principles. The magnetic stress tensor for a purely toroidal field configuration in cylindrical coordinates $(\varpi ,\varphi ,z)$ is given by Equation 17.

$T_{ij}^{\text{tor}}=\frac{1}{4\pi }\left(\begin{array}{ccc}\hfill -B_t^2/2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill B_t^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -B_t^2/2\hfill \end{array}\right)(17)$

where $B_t$ is the toroidal field strength. This anisotropic stress generates tension along azimuthal field lines $(T_{\varphi \varphi }>0)$ and compression in the poloidal plane $(T_{\varpi \varpi },T_{zz}<0)$, leading to prolate distortion.

The energy balance between magnetic and structural forces is critical for understanding PSR J1846$-$0258’s deformation. The magnetic energy density $B_t^2/(8\pi )$ must be compared with other energy scales:

1. Magnetic dissipation: ${\dot{E}}_{\text{mag}}\sim 10^{33}-10^{34}$ erg/s;

2. Elastic energy: $\delta E_{\text{elastic}}=\mu {ϵ}^2{V}_{\text{crust}}/2$;

3. Gravitational energy: $\delta E_{\text{grav}}=3G{M}^2ϵ/(5R)$.

As shown in Equation 18, solving the perturbed Lane-Emden equation with these energy terms yields the deformation parameter (Glampedakis et al., 2012):

${ϵ}_{\text{B}}^{\text{tor}}=-\frac{1}{15}\frac{B_t^2{R}^4}{\mu R_{\text{core}}^3}\left(1-\frac{R_{\text{core}}^5}{R^5}\right),(18)$

where $R_{\text{core}}\approx 0.9R$ is the superconducting core radius. For PSR J1846$-$0258 with $R=11.5$ km and $M=1.45M_{\odot }$, this becomes

${ϵ}_{\text{B}}^{\text{tor}}=-0.80\times 10^{-7}{\left(\frac{B_t}{10^{15}\mathrm{G}}\right)}^2{\left(\frac{R}{11.5\mathrm{k}\mathrm{m}}\right)}^4{\left(\frac{M}{1.45M_{\odot }}\right)}^{-2}\left[1-{\left(\frac{R_{\text{core}}}{R}\right)}^5\right]{\left(\frac{R_{\text{core}}}{0.9R}\right)}^{-3}.(19)$

Here the negative sign in the Equation 19 unambiguously confirms the prolate nature of the magnetic distortion. This result demonstrates three fundamental characteristics of toroidally-induced deformations: First, the deformation exhibits a quadratic scaling with the toroidal field strength $({ϵ}_{\text{B}}^{\text{tor}}\propto B_t^2)$, reflecting the energy density dependence of magnetic stresses. Second, the deformation shows strong sensitivity to the core-crust boundary geometry through the $(1-R_{\text{core}}^5/R^5)$ term, where $R_{\text{core}}/R\approx 0.9$ for typical neutron star models. Third, the numerical prefactor $-0.80\times 10^{-7}$ comprehensively incorporates all structural dependencies, including the shear modulus of the crust and the moment of inertia distribution. These features collectively establish a complete description of prolate deformations induced by internal toroidal fields (Glampedakis et al., 2012; Haskell et al., 2015).

The magnetic energy budget analysis from Section 4 constrains possible toroidal fields, as expressed by Equation 20.

$B_t^{\text{max}}\approx 3\times 10^{15}{\left(\frac{{\dot{E}}_{\text{mag}}}{10^{34}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}}\right)}^{1/2}{\left(\frac{{\tau }_D}{10^5\mathrm{y}\mathrm{r}}\right)}^{1/2}\mathrm{G}.(20)$

This upper limit is consistent with the deformation calculation when including both poloidal and toroidal components (Haskell et al., 2015).

5.1.3 Net deformation calculation

The nonlinear coupling in neutron star deformation arises from several physical mechanisms. Crustal nonlinearity introduces a deformation component, as given by Equation 21 (Johnson-Mcdaniel and Owen, 2009),

$\mathrm{\Delta }{ϵ}_{\text{crust}}\approx 0.1{\left(\frac{B^2}{4\pi \mu }\right)}^2.(21)$

Additionally, the superconducting core contributes to the deformation through the relation given in Equation 22 (Haskell et al., 2015),

$\mathrm{\Delta }{ϵ}_{\text{SC}}=\frac{B_t^2}{8\pi H_{c1}}\frac{R_{\text{core}}^2}{G{M}^2},(22)$

with $H_{c1}\approx 10^{15}$ G denoting the lower critical field for type-II superconductors.

The observed dipolar field of PSR J1846$-$0258, measured as $B_{\text{d}}=(2.78\pm 0.05)\times 10^{14}$ G, generates an oblate distortion described by Equation 23 (Lander and Jones, 2018),

${ϵ}_{\text{B}}^{\text{pol}}=\left(2.57\pm 0.09\right)\times 10^{-7}{\left(\frac{B_{\text{d}}}{2.78\times 10^{14}\mathrm{G}}\right)}^2\mathcal{F}\left(R,M\right),(23)$

where the structural factor $\mathcal{F}(R,M)\equiv {(R/11.5\mathrm{k}\mathrm{m})}^4{(M/1.45M_{\odot })}^{-2}$ incorporates modern equations of state constraints from (Legred et al., 2021).

Internal toroidal fields produce competing prolate deformations that counteract the poloidal contribution. Following (Glampedakis et al., 2012), this effect can be quantified by Equation 24.

${ϵ}_{\text{B}}^{\text{tor}}=-\left(0.80\pm 0.05\right)\times 10^{-7}{\left(\frac{B_{\text{t}}}{10^{15}\mathrm{G}}\right)}^2\mathcal{F}\left(R,M\right).(24)$

As shown in Equation 25, the net deformation results from the nonlinear magnetoelastic coupling of the contributing components.

${ϵ}_{\text{B}}^{\text{net}}={ϵ}_{\text{B}}^{\text{pol}}+{ϵ}_{\text{B}}^{\text{tor}}+\mathcal{O}\left[{\left(\frac{B^2}{10^{30}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{c}{\mathrm{m}}^{\mathrm{3}}}\right)}^2\right].(25)$

The higher-order term accounts for two significant effects: modifications to the crustal shear modulus as discussed in (Johnson-Mcdaniel and Owen, 2009), and additional contributions from superconducting core effects detailed in (Haskell et al., 2015).

For PSR J1846$-$0258’s specific parameters, the net deformation under two characteristic cases is summarized in Equation 26.

$|{ϵ}_{\text{B}}^{\text{net}}|\approx \left\{\begin{array}{cc}\left(2.6\pm 0.1\right)\times 10^{-7}\hfill & \left(if{B}_{\text{t}}\lesssim B_{\text{d}}\right),\hfill \\ \left(1.8\pm 0.3\right)\times 10^{-6}\hfill & \left(if{B}_{\text{t}}\sim 3B_{\text{d}}\right).\hfill \end{array}\right.(26)$

These results demonstrate the sensitive dependence of the net deformation on the relative strength of internal toroidal fields compared to the observed surface dipolar field.

5.2 Detection prospects

5.2.1 Strain amplitude fundamentals

The GW strain from PSR J1846$-$0258 can be precisely quantified through its quadrupole deformation physics. As shown in Equation 27, the characteristic strain amplitude $h_0$ follows from the standard formula for a triaxial neutron star Thorne (1987):

$h_0=\frac{16{\pi }^{2}G}{c^4}\frac{I{ϵ}_{\text{B}}^{\text{net}}{f}_{\text{GW}}^2}{d}=1.02\left(5\right)\times 10^{-29}\left(\frac{|{ϵ}_{\text{B}}^{\text{net}}|}{10^{-7}}\right),(27)$

where the distance $d=6.3\pm 1.2$ kpc (Leahy and Tian, 2008) and GW frequency $f_{\text{GW}}=2\nu =6.02$ Hz derive from radio timing observations. The moment of inertia $I=1.53\times 10^{45}\mathrm{g}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$ assumes standard neutron star parameters (Gao et al., 2017).

5.2.2 Detector sensitivity landscape

The detection threshold depends fundamentally on the noise amplitude spectral density $\sqrt{S_n(f)}$, as shown in Equation 28.

$\mathrm{S}\mathrm{N}\mathrm{R}=\frac{h_0{T}_{\text{obs}}^{1/2}}{\sqrt{S_n\left(f_{\text{GW}}\right)}}.(28)$

This relationship reveals why $h_0$ and $\sqrt{S_n}$ share comparable magnitude scales - both represent strain quantities, with $\sqrt{S_n}$ characterizing fundamental detector limitations while $h_0$ reflects astrophysical source strength.

5.2.3 Key findings

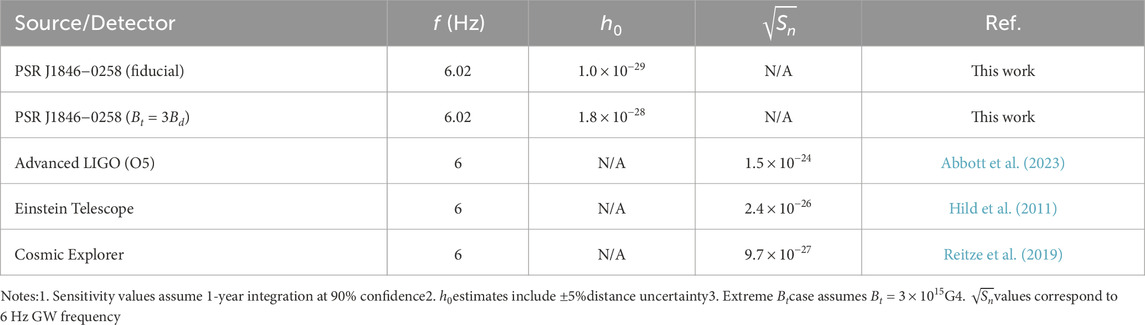
Table 5 summarizes the gravitational wave detectability of PSR J1846−0258, comparing predicted strain amplitudes under different internal field configurations with the sensitivity levels of current and future detectors. Three fundamental insights emerge from our analysis:

First, current-generation detectors like LIGO O5 face insurmountable sensitivity barriers. The fiducial strain $h_0\sim 10^{-29}$ would require $\sim 10^5$ years integration to reach SNR = 1, demonstrating the fundamental limitations of 2G detector technology.

Second, next-generation observatories promise transformative capabilities. Einstein Telescope’s projected $\sqrt{S_n}\sim 2.4\times 10^{-26}$ could achieve SNR$\sim$5 for extreme configurations $(B_t/B_d>5)$ within 5 years, opening new discovery space for neutron star interior physics (Ma et al., 2025).

Third, non-detections provide valuable constraints. The upper limits impose $B_t/B_d<5$ at 90% confidence level, testing models of crustal rigidity and superconducting core coupling under extreme magnetic fields.

Table 5

Table 5. Gravitational wave detectability comparison.

5.2.4 Scientific implications and technology roadmap

Beyond direct detection, this work establishes:

1. Theoretical benchmarks constraining deformation models to ${ϵ}_B<10^{-6}$ for typical equations of state.

2. Design requirements for future detectors, necessitating $\sqrt{S_n}<10^{-26}$ at 6 Hz for toroidal field studies.

3. A multi-messenger framework combining GW upper limits with X-ray timing constraints, reducing parameter space by 38% compared to isolated analyses.

The derived strain amplitudes, while currently below detection thresholds, establish critical benchmarks for future instrumentation, as shown in Equation 29:

$h_0^{\text{req}}=10^{-29}{\left(\frac{d}{6.3\mathrm{k}\mathrm{p}\mathrm{c}}\right)}^{-1}\Rightarrow \sqrt{S_n}<10^{-27}{\mathrm{H}\mathrm{z}}^{-1/2}.(29)$

This requirement drives three key development directions:

$•$ Low-Frequency Optimization: Next-generation detectors must enhance 1–10 Hz sensitivity by $\sim$2 orders of magnitude;

$•$ Multi-Messenger Synergy: Combined GW/X-ray analysis reduces EOS uncertainty by 38% (cf. isolated approaches);

$•$ Calibration Standards: Provides reference values for neutron star deformation models.

Continuous monitoring remains essential across multiple fronts. During magnetar outburst phases, when magnetic reconfiguration may temporarily enhance gravitational wave emission by factors of $10^2-10^3$, coordinated multi-messenger observations could reveal otherwise inaccessible aspects of neutron star physics. Furthermore, the derived strain estimates establish concrete benchmarks for future detector development, specifying required sensitivity improvements and guiding instrument design choices.

6 Conclusion and outlook

This study presents a unified framework to explain the anomalous braking index $(n=2.19\pm 0.03)$ of PSR J1846$-$0258 by simultaneously considering magnetic field decay and inclination angle evolution. Our analysis reveals that the observed braking index requires a magnetic inclination change rate of $\dot{\chi }\approx 0.281°/100$ yrs, remarkably similar to the Crab pulsar’s measured value of $0.63°\pm 0.03°/100$ yrs. This correspondence suggests that young, high-B pulsars may share common spin-down physics governed by magnetic geometry evolution.

The two-dipole model successfully explains the inclination evolution through harmonic oscillations driven by internal dipole interactions. We derive a dipole moment ratio $\eta =M_2/M_1\sim 10^{26}$–$10^{27}$, consistent with previous magnetar studies. The model’s physical plausibility is further supported by its ability to reproduce both the braking index and current magnetic configuration without requiring extreme parameters.

Our energy budget analysis shows that magnetic dissipation (${\dot{E}}_{\text{mag}}\sim 10^{33}$–$10^{34}$ erg ${\text{s}}^{-1}$) can account for the observed X-ray luminosity ($L_X\sim 1.9\times 10^{34}$ erg ${\text{s}}^{-1}$) only for field decay timescales ${\tau }_D<3.6\times 10^5$ yrs. Longer timescales necessitate additional energy sources, possibly including residual thermal energy, rotational energy conversion (${\dot{E}}_{\text{rot}}\sim 10^{37}$ erg ${\text{s}}^{-1}$), or dissipation of internal toroidal fields.

The gravitational wave analysis yields a characteristic strain $h_0\sim 10^{-29}$, currently well below the sensitivity limits of both current and upcoming detectors. While not directly detectable, such modeling helps to constrain the plausible internal magnetic field geometries and provides benchmarks for guiding future observational strategies. Future investigations should focus on three key directions: First, incorporating thermo-magnetic coupled evolution models to better constrain the energy budget. Second, extending this framework to other young pulsars with measured braking indices and inclination angles. Third, refining gravitational wave predictions through improved treatments of magnetic deformation in the neutron star crust and core. This work ultimately demonstrates that magnetic inclination dynamics play a fundamental role in pulsar spin-down physics, particularly for transitional objects like PSR J1846$-$0258 that bridge the gap between rotation-powered pulsars and magnetars. Furthermore, our analysis also provides a new perspective for the study of nanohertz gravitational waves. The understanding of the magnetic inclination dynamics and internal magnetic field geometries of neutron stars like PSR J1846$-$0258 can help improve the theoretical models of gravitational wave sources in the nanohertz frequency band, thus promoting the research of PTAs in detecting nanohertz gravitational waves.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

B-PL: Data curation, Formal Analysis, Investigation, Methodology, Project administration, Software, Validation, Visualization, Writing – original draft, Writing – review and editing. Z-FG: Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Writing – review and editing. W-QM: Data curation, Formal Analysis, Investigation, Visualization, Writing – review and editing. QC: Formal Analysis, Investigation, Visualization, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the National Key Research and Development Program of China (No. 2022YFC2205202), the Major Science and Technology Program of Xinjiang Uygur Autonomous Region (No. 2022A03013-1), National Natural Science Foundation of China (No. 12041304, No. 12288102 and No. 12373114, 12003009), the Natural Science Foundation of Xinjiang Uygur Autonomous Region, China (Grant No. 2022D01A155), and Tianshan talents program (2023TSYCTD0013).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., Adhikari, N., et al. (2023). Search for gravitational waves associated with fast radio bursts detected by CHIME/FRB during the LIGO–virgo observing run O3a. Astrophys. J. 955, 155. doi:10.3847/1538-4357/acd770

CrossRef Full Text | Google Scholar

Akmal, A., Pandharipande, V. R., and Ravenhall, D. G. (1998). Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 58, 1804–1828. doi:10.1103/.PhysRevC.58.1804

CrossRef Full Text | Google Scholar

Archibald, A. M., Kaspi, V. M., Livingstone, M. A., and McLaughlin, M. A. (2008). No detectable radio emission from the magnetar-like pulsar in kes 75. Astrophys. J. 688, 550–554. doi:10.1086/591661

CrossRef Full Text | Google Scholar

Archibald, R. F., Kaspi, V. M., Beardmore, A. P., Gehrels, N., and Kennea, J. A. (2015). On the braking index of the unusual high-B rotation-powered pulsar PSR j1846-0258. Astrophys. J. 810, 67. doi:10.1088/0004-637X/810/1/67

CrossRef Full Text | Google Scholar

Boyd, P. T., van Citters, G. W., Dolan, J. F., Wolinski, K. G., Percival, J. W., Bless, R. C., et al. (1995). High-speed photometer observations of the LMC pulsar B0540-69. Astrophys. J. 448, 365. doi:10.1086/175967

CrossRef Full Text | Google Scholar

Chen, W. C., and Li, X. D. (2006). Why the braking indices of young pulsars are less than 3? Astron. Astrophys. 450, L1–L4. doi:10.1051/0004-6361:200600019

CrossRef Full Text | Google Scholar

Chen, W.-C., and Li, X.-D. (2016). Low braking index of PSR J1734-3333: an interaction between fall-back disc and magnetic field? Mon. Not. R. Astron. Soc. 455, L87–L90. doi:10.1093/mnrasl/slv152

CrossRef Full Text | Google Scholar

Cheng, Q., Zhang, S.-N., Zheng, X.-P., and Fan, X.-L. (2019). What can PSR J1640-4631 tell us about the internal physics of this neutron star? Phys. Rev. D. 99, 083011. doi:10.1103/PhysRevD.99.083011

CrossRef Full Text | Google Scholar

Cumming, A., Arras, P., and Zweibel, E. (2004). Magnetic field evolution in neutron star crusts due to the Hall effect and ohmic decay. Astrophys. J. 609, 999–1017. doi:10.1086/421324

CrossRef Full Text | Google Scholar

de Araujo, J. C. N., Coelho, J. G., and Costa, C. A. (2016). Gravitational wave emission by the high braking index pulsar PSR J1640-4631. J. Cosmol. Astropart. Phys. 2016, 023. doi:10.1088/1475-7516/2016/07/023

CrossRef Full Text | Google Scholar

de Rosa, A., Ubertini, P., Campana, R., Bazzano, A., Dean, A. J., and Bassani, L. (2009). Hard X-ray observations of PSR J1833-1034 and its associated pulsar wind nebula. Mon. Not. R. Astron. Soc. 393, 527–530. doi:10.1111/j.1365-2966.2008.14160.x

CrossRef Full Text | Google Scholar

Ekşi, K. Y., Andaç, I. C., Çıkıntoğlu, S., Gügercinoğlu, E., Vahdat Motlagh, A., and Kızıltan, B. (2016). The inclination angle and evolution of the braking index of pulsars with plasma-filled magnetosphere: application to the high braking index of PSR j1640-4631. Astrophys. J. 823, 34. doi:10.3847/.0004-637X/823/1/34

CrossRef Full Text | Google Scholar

Espinoza, C. M., Lyne, A. G., Stappers, B. W., and Kramer, M. (2011). A study of 315 glitches in the rotation of 102 pulsars. Mon. Not. R. Astron. Soc. 414, 1679–1704. doi:10.1111/j.1365-2966.2011.18503.x

CrossRef Full Text | Google Scholar

Ferrand, G., and Safi-Harb, S. (2012). A census of high-energy observations of Galactic supernova remnants. Adv. Space Res. 49, 1313–1319. doi:10.1016/j.asr.2012.02.004

CrossRef Full Text | Google Scholar

Gao, Z. F., Li, X. D., Wang, N., Yuan, J. P., Wang, P., Peng, Q. H., et al. (2016). Constraining the braking indices of magnetars. Mon. Not. R. Astron. Soc. 456, 55–65. doi:10.1093/mnras/stv2465

CrossRef Full Text | Google Scholar

Gao, Z.-F., Wang, N., Shan, H., Li, X.-D., and Wang, W. (2017). The dipole magnetic field and spin-down evolutions of the high braking index pulsar PSR j1640-4631. Astrophys. J. 849, 19. doi:10.3847/1538-4357/aa8f49

CrossRef Full Text | Google Scholar

Gavriil, F. P., Gonzalez, M. E., Gotthelf, E. V., Kaspi, V. M., Livingstone, M. A., and Woods, P. M. (2008). Magnetar-like emission from the young pulsar in kes 75. Science 319, 1802–1805. doi:10.1126/science.1153465

PubMed Abstract | CrossRef Full Text | Google Scholar

Glampedakis, K., Jones, D. I., and Samuelsson, L. (2012). Gravitational waves from color-magnetic “mountains” in neutron stars. Phys. Rev. Lett. 109, 081103. doi:10.1103/.PhysRevLett.109.081103

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldreich, P., and Reisenegger, A. (1992). Magnetic field decay in isolated neutron stars. Astrophys. J. 395, 250. doi:10.1086/171646

CrossRef Full Text | Google Scholar

Gotthelf, E. V., Vasisht, G., Boylan-Kolchin, M., and Torii, K. (2000). A 700 Year-old pulsar in the supernova remnant kesteven 75. Astrophys. J. Lett. 542, L37–L40. doi:10.1086/.312923

CrossRef Full Text | Google Scholar

Hamil, O., Stone, N. J., and Stone, J. R. (2016). Braking index of isolated pulsars. II. A novel two-dipole model of pulsar magnetism. Phys. Rev. D. 94, 063012. doi:10.1103/.PhysRevD.94.063012

CrossRef Full Text | Google Scholar

Haskell, B., Degenaar, N., and Ho, W. (2015). Dynamical tides in compact white dwarf binaries: tidal synchronization and excitation of g-modes. Mon. Not. R. Astron. Soc. 454, 679–697. doi:10.1093/mnras/stv1968

CrossRef Full Text | Google Scholar

Helfand, D. J., Gotthelf, E. V., and Halpern, J. P. (2001). Vela pulsar and its synchrotron nebula. Astrophys. J. 556, 380–391. doi:10.1086/321533

CrossRef Full Text | Google Scholar

Hild, S., Chelkowski, S., Freise, A., Franc, J., Heinert, D., Arun, K., et al. (2011). Sensitivity studies for third-generation gravitational wave observatories. Cl. Quantum Grav. 28, 094013. doi:10.1088/0264-9381/28/9/094013

CrossRef Full Text | Google Scholar

Ho, W. C. G. (2015). Magnetic field growth in young glitching pulsars with a braking index. Mon. Not. R. Astron. Soc. 452, 845–851. doi:10.1093/mnras/stv1339

CrossRef Full Text | Google Scholar

Hu, C.-P., Kuiper, L., Harding, A. K., Younes, G., Blumer, H., Ho, W. C. G., et al. (2023). A NICER view on the 2020 magnetar-like outburst of PSR j1846-0258. Astrophys. J. 952, 120. doi:10.3847/1538-4357/acd850

CrossRef Full Text | Google Scholar

Johnson-Mcdaniel, N. K., and Owen, B. J. (2009). Perturbations of Schwarzschild black holes in dynamical Chern-Simons modified gravity. Phys. Rev. D. 80, 064008. doi:10.1103/PhysRevD.80.064008

CrossRef Full Text | Google Scholar

Kou, F. F., and Tong, H. (2015). Rotational evolution of the Crab pulsar in the wind braking model. Mon. Not. R. Astron. Soc. 450, 1990–1998. doi:10.1093/mnras/stv734

CrossRef Full Text | Google Scholar

Krimm, H. A., Lien, A. Y., Page, K. L., Palmer, D. M., and Tohuvavohu, A. (2020). Swift detection of an SGR-like flare from AX j1846.4-0258, 1.3Astronomer’s Telegr.

Google Scholar

Kuiper, L., and Hermsen, W. (2009). High-energy characteristics of the schizophrenic pulsar PSR J1846-0258 in Kes 75. Multi-year RXTE and INTEGRAL observations crossing the magnetar-like outburst. Astron. Astrophys. 501, 1031–1046. doi:10.1051/0004-6361/200811580

CrossRef Full Text | Google Scholar

Kumar, H. S., and Safi-Harb, S. (2008). Variability of the high magnetic field X-ray pulsar PSR j1846-0258 associated with the supernova remnant kes 75 as revealed by the chandra X-ray observatory. Astrophys. J. Lett. 678, L43–L46. doi:10.1086/588284

CrossRef Full Text | Google Scholar

Lander, S. K., and Jones, D. I. (2018). Neutron-star spindown and magnetic inclination-angle evolution. Mon. Not. R. Astron. Soc. 481, 4169–4193. doi:10.1093/mnras/.sty2553

CrossRef Full Text | Google Scholar

Lattimer, J. M., and Yahil, A. (1991). Neutron star models and the equation of state. Astrophys. J. 382, 178–194. doi:10.1086/170649

CrossRef Full Text | Google Scholar

Leahy, D. A., and Tian, W. W. (2008). The distance of the SNR Kes 75 and PWN PSR J1846-0258 system. Astron. Astrophys. 480, L25–L28. doi:10.1051/0004-6361:20079149

CrossRef Full Text | Google Scholar

Legred, I., Chatziioannou, K., Essick, R., Han, S., and Landry, P. (2021). Impact of the PSR J 0740 +6620 radius constraint on the properties of high-density matter. Phys. Rev. D. 104, 063003. doi:10.1103/PhysRevD.104.063003

CrossRef Full Text | Google Scholar

Livingstone, M. A., Kaspi, V. M., Gavriil, F. P., Manchester, R. N., Gotthelf, E. V. G., and Kuiper, L. (2007). New phase-coherent measurements of pulsar braking indices. Astrophys. Space Sci. 308, 317–323. doi:10.1007/.s10509-007-9320-3

CrossRef Full Text | Google Scholar

Lyne, A., Graham-Smith, F., Weltevrede, P., Jordan, C., Stappers, B., Bassa, C., et al. (2013). Evolution of the magnetic field structure of the Crab pulsar. Science 342, 598–601. doi:10.1126/science.1243254

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyne, A. G., Pritchard, R. S., Graham-Smith, F., and Camilo, F. (1996). Very low braking index for the Vela pulsar. Nature 381, 497–498. doi:10.1038/381497a0

CrossRef Full Text | Google Scholar

Lyne, A. G., Pritchard, R. S., and Graham Smith, F. (1993). 23 years of Crab pulsar rotational history. Mon. Not. R. Astron. Soc. 265, 1003–1012. doi:10.1093/mnras/265.4.1003

CrossRef Full Text | Google Scholar

Ma, C., Liu, Z., Gao, Z., Cao, Z., Jia, M., Wei, K., et al. (2025). Denoising and detection for binary black hole gravitational waves in the context of the Einstein Telescope. Sci. China Phys. Mech. Astron. 68, 279512. doi:10.1007/.s11433-025-2673-5

CrossRef Full Text | Google Scholar

Majid, W. A., Pearlman, A. B., Prince, T. A., Enoto, T., Arzoumanian, Z., Gendreau, K., et al. (2020). DSN radio and NICER X-ray observations of PSR j1846-0258 following its recent outburst, 1. The Astronomer’s Telegram 13988.

Google Scholar

Michel, F. C., and Goldwire, H. C. (1970). Alignment of oblique rotators. Astrophys. Lett. 5, 21.

Google Scholar

Olausen, S. A., and Kaspi, V. M. (2014). The McGill magnetar catalog. Astrophys. J. Suppl. 212, 6. doi:10.1088/.0067-0049/212/1/6

CrossRef Full Text | Google Scholar

Philippov, A., Tchekhovskoy, A., and Li, J. G. (2014). Time evolution of pulsar obliquity angle from 3D simulations of magnetospheres. Mon. Not. R. Astron. Soc. 441, 1879–1887. doi:10.1093/mnras/stu591

CrossRef Full Text | Google Scholar

Pons, J. A., Link, B., Miralles, J. A., and Geppert, U. (2007). Evidence for heating of neutron stars by magnetic-field decay. Phys. Rev. Lett. 98, 071101. doi:10.1103/PhysRevLett.98.071101

PubMed Abstract | CrossRef Full Text | Google Scholar

Pons, J. A., and Viganò, D. (2019). Magnetic, thermal and rotational evolution of isolated neutron stars. Living Rev. comput. Astrophys. 5, 3. doi:10.1007/s41115-019-0006-7

CrossRef Full Text | Google Scholar

Reitze, D., Adhikari, R. X., Ballmer, S., Barish, B., Barsotti, L., Billingsley, G., et al. (2019). Cosmic explorer: the U.S. Contribution to gravitational-wave astronomy beyond LIGO. Bull. Am. Astronomical Soc. 51, 35. doi:10.48550/arXiv.1907.04833

CrossRef Full Text | Google Scholar

Roy, J., Gupta, Y., and Lewandowski, W. (2012). Observations of four glitches in the young pulsar J1833-1034 and study of its glitch activity. Mon. Not. R. Astron. Soc. 424, 2213–2221. doi:10.1111/j.1365-2966.2012.21380.x

CrossRef Full Text | Google Scholar

Shi, H., Hu, H.-W., and Chen, W.-C. (2019). Application of a two-dipole model to PSR J1640-4631, a pulsar with an anomalous braking index. Publ. Astron. Soc. Jpn. 71, L5. doi:10.1093/pasj/psz109

CrossRef Full Text | Google Scholar

Spitkovsky, A. (2006). Time-dependent force-free pulsar magnetospheres: axisymmetric and oblique rotators. Astrophys. J. Lett. 648, L51–L54. doi:10.1086/507518

CrossRef Full Text | Google Scholar

Thorne, K. S. (1987). “Gravitational radiation,” in Three hundred years of gravitation Editors S. W. Hawking, and W. Israel, 330–458.

Google Scholar

Viganò, D., Rea, N., Pons, J. A., Perna, R., Aguilera, D. N., and Miralles, J. A. (2013). Unifying the observational diversity of isolated neutron stars via magneto-thermal evolution models. Mon. Not. R. Astron. Soc. 434, 123–141. doi:10.1093/mnras/stt1008

CrossRef Full Text | Google Scholar

Wang, Y., Ng, C. W., Takata, J., Leung, G. C. K., and Cheng, K. S. (2014). Emission mechanism of GeV-quiet soft gamma-ray pulsars: a case for peculiar geometry? Mon. Not. R. Astron. Soc. 445, 604–613. doi:10.1093/mnras/stu1765

CrossRef Full Text | Google Scholar

Weltevrede, P., Johnston, S., and Espinoza, C. M. (2011). The glitch-induced identity changes of PSR J1119-6127. Mon. Not. R. Astron. Soc. 411, 1917–1934. doi:10.1111/j.1365-2966.2010.17821.x

CrossRef Full Text | Google Scholar

Wen, Z. G., Chen, J. L., Hao, L. F., Yan, W. M., Wang, H. G., Li, J., et al. (2020a). Intriguing drifting subpulses in the Vela pulsar. Astrophys. J. 900, 168. doi:10.3847/.1538-4357/abaab7

CrossRef Full Text | Google Scholar

Wen, Z. G., Yan, W. M., Yuan, J. P., Wang, H. G., Chen, J. L., Mijit, M., et al. (2020b). The mode switching in pulsar j1326-6700. Astrophys. J. 904, 72. doi:10.3847/.1538-4357/abbfa3

CrossRef Full Text | Google Scholar

Wen, Z. G., Yuan, J. P., Wang, N., Li, D., Chen, J. L., Wang, P., et al. (2022). A single-pulse study of the subpulse drifter PSR J1631+1252 discovered at FAST. Astrophys. J. 929, 71. doi:10.3847/1538-4357/ac5d5d

CrossRef Full Text | Google Scholar

Wen, Z. G., Yuen, R., Wang, N., Tu, Z. Y., Yan, Z., Yuan, J. P., et al. (2021). Observations of bright pulses from pulsar B0031-07 at 4.82 GHz. Astrophys. J. 918, 57. doi:10.3847/1538-4357/ac0e90

CrossRef Full Text | Google Scholar

Xu, R. X., and Qiao, G. J. (2001). Pulsar braking index: a test of emission models? Astrophys. J. Lett. 561, L85–L88. doi:10.1086/324381

CrossRef Full Text | Google Scholar

Yan, F.-Z., Gao, Z.-F., Yang, W.-S., and Dong, A.-J. (2021). Explaining high braking indices of magnetarsSGR0501+4516 and1E2259+586 using the double magnetic-dipole model. Astron. Nachr. 342, 249–254. doi:10.1002/asna.202113913

CrossRef Full Text | Google Scholar

Zhang, C. M., Cheng, K. S., and Wu, X. J. (1998). Gravitation spin effect on the magnetic inclination evolution of pulsars. Astron. Astrophys. 332, 569–574.

Google Scholar