Analyzing cryptographic algorithm efficiency with in graph-based encryption models

This research paper investigates the efficiency of cryptographic algorithms within graph-based encryption models such as star graph, focusing on their computational performance and security robustness. In this study, we analyze the performance of RSA and ElGamal cryptographic algorithms by evaluating time and space complexity across various file types, including text, image, audio, and data of different sizes. The encryption process is modeled using graph structures such as the Star graph, along with other well-known algorithms like A^*, Dijkstra, Bellman-Ford, and Floyd-Warshall for comparative analysis and performance benchmarking. Consequently, this research conducts a comparative analysis of RSA and ElGamal cryptographic algorithms by applying them to mixed data, including binary, text, and image files. The CPU's internal clock was employed to record the execution time of encryption and decryption operations, facilitating the assessment of time complexity for both algorithms. The CPU's internal memory was employed to monitor and record memory usage during the encryption and decryption operations performed on mixed datasets. Accordingly, the evaluation of the encryption algorithms was conducted using criteria such as encryption time, decryption time, and throughput to determine their relative performance. In evaluating cryptographic approaches, factors such as response time, confidentiality, bandwidth, and integrity are considered. Experimental results indicate that RSA demonstrates superior time efficiency and resource utilization, whereas the ElGamal algorithm exhibits greater memory efficiency and resourcefulness. This study evaluates RSA and ElGamal encryption on text, image, audio, and data files of varying sizes using graph-based models. The Star graph algorithm is adopted for its simplicity and low computational cost, and its performance is compared against A^*, Dijkstra, and Bellman-Ford algorithms. Results show that the Star model offers near-optimal paths with significantly reduced processing time, demonstrating high confidence in efficiency for lightweight encryption tasks. We have added computational performance, logical confidence, and optimality conditions of the proposed Star-based encryption model. The Star algorithm, integrated with RSA/ElGamal encryption, is benchmarked against classical pathfinding algorithms like A^*, Dijkstra, and Bellman-Ford, commonly used for routing and shortest-path computations. Computational performance of (i) the worst-case time complexity of star algorithm (proposed) is O(b^d) where b is the branching factor and d is the depth and space complexity is O(E + V) where E is the number of edges and V is the number of nodes, high (central node access) traversal efficiency, excellent (centralized graph encoding) suitability for graph-based encryption, very high structural simplicity, (ii) the worst case time complexity of A^* Algorithm is O(b^d) where b is the branching factor and d is the depth and space complexity is O(E + V) where E is the number of edges and V is the number of nodes, high (with good heuristic) traversal efficiency, good (needs proper graph abstraction) suitability for graph-based encryption, moderate structural simplicity, (iii) the average case time complexity and best case time complexity of Dijkstra's Algorithm is O((V + E) log V) and the worst case time complexity is O((V²) logV) and space complexity is O(V) where V is the number of vertices, moderate to high traversal efficiency, fair (efficient in weighted graphs) suitability for graph-based encryption, moderate structural simplicity, and (iv) Bellman-Ford Algorithm is O(V^*E) time complexity and O(V) space complexity where V is the number of vertices and E is the number of edges, low traversal efficiency, limited (computationally expensive) suitability for graph-based encryption, moderate structural simplicity.

1 Introduction

Data security involves implementing strategies to safeguard digital information against unauthorized disclosure and modification across computing and communication infrastructures. Given the exponential growth in data communication and transfer volumes, coupled with the escalating frequency and sophistication of cyber threats, ensuring robust data security has become more critical than ever. This urgency is underscored by the increasing number of data breaches and cyberattacks targeting sensitive information across various sectors (Li et al., 2022). Consequently, research in data security has rapidly advanced, leading to significant developments in related fields such as cryptography. These advancements have resulted in the creation of sophisticated encryption techniques, including quantum-resistant algorithms and homomorphic encryption, which enhance the protection of sensitive information across various applications. Cryptography is the practice of securing information by converting readable data (plaintext) into an unreadable format (ciphertext) through encryption, and then reverting it back to its original form via decryption. This process ensures that only authorized parties can access the original information (Adeniyi et al., 2022). Cryptography is the discipline dedicated to safeguarding information by transforming it into an unreadable format for unauthorized individuals during storage and transmission. This process, known as encryption, converts plaintext into ciphertext, ensuring that only authorized parties can revert it back to its original form through decryption. By employing mathematical techniques, cryptography ensures data confidentiality, integrity, and authenticity, making it a fundamental component of modern information security systems (Panda and Nag, 2015). Plaintext, also known as clear text, refers to data in its original, readable form that has not been encrypted. It serves as the fundamental input for encryption processes, where it is transformed into ciphertext to protect its confidentiality. Understanding and managing plaintext is crucial in information security, as it pertains to ensuring data confidentiality, integrity, and authentication (Singh et al., 2022).

Our focus is on evaluating the performance of algorithm through the utilization of graph theory and algebraic concepts (West, 2001). In graph theory, a star graph is a type of tree graph characterized by a central node connected directly to all other nodes, which are known as leaves. This structure is a specific case of a complete bipartite graph, denoted as K_{1, n} where “1” represents the central node and “n” denotes the number of leaf nodes. The star graph S_n+1 on n+1 vertices can be represented as the corona product $K_1\odot \overline{K_n}$ where K₁ is a complete graph on one vertex, and K_n is a complete graph on n vertices. Similarly, the corona graph of a cycle C_n with K₁, denoted as C_n⊙K₁ is a graph on 2n vertices obtained by attaching n pendant edges to the cycle C_n. Each vertex of the cycle is connected to a new pendant vertex, enhancing the cycle's connectivity.

Several recent studies have focused on evaluating the performance of RSA and ElGamal cryptographic algorithms, particularly concerning their time and space complexities when applied to mixed data. This section provides a comprehensive summary of these studies, analyzing the methodologies employed and their relevance to the current research. The authors conducted a comparative analysis of RSA and ElGamal cryptographic algorithms, focusing on their energy efficiency and impact on network longevity.

The remainder of this paper is organized as follows. Section 2 presents an overview of the background of the proposed work including a survey of already published techniques regarding their security concerns. Section 3 elaborates the proposed framework of algorithm. We then discuss the implementation of the proposed work with result in Section 4. Discussion presented in Section 5 and finally, Section 6 concludes the paper along with future scope.

2 Related work

Kayalvizhi et al. (2010), utilizing a cluster-based wireless sensor network topology within the NS2 simulation environment, they assessed how each algorithm influences power consumption and overall network lifespan. The study revealed that RSA tends to consume 14.5% less power compared to ElGamal, thereby potentially extending the operational duration was limited to 10 sensor nodes of the wireless sensor networks. Researchers have implemented various cryptographic algorithms in Java to enhance cloud data security, focusing on both symmetric techniques (AES, DES, and Blowfish) and asymmetric methods (RSA). Performance evaluations revealed that Blowfish demonstrated the fastest processing time, followed by AES and DES, with RSA being the slowest. In terms of memory usage, Blowfish, AES, and 3DES consumed similar amounts, whereas RSA utilized approximately twice as much memory as the symmetric algorithms. These findings suggest that Blowfish offers superior speed and efficient memory usage, making it suitable for applications where performance is critical. AES provides a balance between speed and security, while RSA, despite its higher resource consumption, remains valuable for scenarios requiring robust asymmetric encryption (Arora et al., 2013). In Boni et al. (2015), the authors proposed an innovative approach to enhance the Diffie-Hellman key exchange algorithm by introducing the Multiplicative Key Exchange (MKE) technique. This method simplifies the key generation process, reducing computational complexity. Their findings indicate that MKE outperforms the traditional Diffie-Hellman algorithm in terms of execution time, requiring fewer computations. This approach is particularly beneficial in scenarios where rapid key generation is essential, such as in less complex systems with minimal setup requirements. In their study, the authors analyzed the performance of RSA and ElGamal algorithms concerning computing speeds for securing, ensuring confidentiality, and authenticating text data. They employed the computer's internal clock to measure and compare the execution times of both algorithms across various text data inputs, aiming to determine which method is more computationally effective. The implementation was tested using text files of different sizes. The results indicated that RSA is more computationally efficient than ElGamal, leading to better performance. However, a limitation of this research is the use of text data with limited character sizes (Okeyinka, 2015). In another study, the authors evaluated the performance of LUC, ElGamal, and RSA algorithms in text encryption. Each algorithm was implemented across various text samples to measure encryption and decryption times. The findings indicated that RSA exhibited superior performance in encryption speed, while LUC demonstrated enhanced efficiency during decryption. The scope of the study was confined to encrypting secret messages in textual format (Sari et al., 2020). Ni et al. (2021) collaboratively developed novel encryption algorithms utilizing specific graph structures, notably corona graphs and bipartite graphs, to enhance secure message transmission. In Desai et al. (2022) and Behera and Gountia (2024), the authors conducted a comprehensive analysis of several asymmetric public key cryptosystems, focusing on performance-based criteria and metrics. Their research entailed an in-depth comparative examination of RSA, ElGamal, and ECC-ElGamal algorithms. The study aimed to derive clear conclusions regarding the performance requirements of these algorithms. Notably, the research highlighted that Elliptic Curve Cryptography (ECC) offers significant advantages in terms of smaller key sizes and higher computational efficiency, making it well-suited for modern devices with limited processing capabilities, such as smart cards and IoT devices. In Parenreng and Wahid (2022), the study proposed a hybrid cryptographic approach that utilizes the ElGamal encryption model for secure symmetric key distribution, coupled with the Advanced Encryption Standard (AES) algorithm for encrypting message content. This combination leverages the strengths of both asymmetric and symmetric encryption techniques to enhance email security. The implementation was integrated into an email system, effectively encrypting messages and data transmitted via email. The primary objective was to address prevalent email security challenges, particularly the risk of data leakage during email transmission. In this research article (Ali et al., 2024), the authors collectively developed novel encryption algorithms utilizing specific graph structures—namely corona graphs, star graphs, and complete bipartite graphs—to enhance secure message transmission.

3 Proposed algorithm

This study evaluates the performance of RSA and ElGamal cryptographic algorithms by measuring their encryption and decryption times, as well as memory usage on text data.

RSA Algorithm (Pseudocode):

Plaintext:

Input: Message M, Key size (k), Two large primes p and q

Output: Ciphertext C

Key Generation:

1. Choose primes p, q

2. Compute modulus: n ← p × q

3. Compute ϕ(n)← (p – 1) × (q – 1)

4. Choose public exponent e such that gcd (e, ϕ(n)) = 1

5. Compute private key

d ← e⁻¹(mod ϕ(n))

Encryption:

6. C ← M^e(mod n)

Decryption:

7. M ← C^d(mod n)

ElGamal Algorithm (Pseudocode):

Input: Message M, Prime p, Generator g, Private key x

Output: Ciphertext (C1, C₂)

Key Generation:

1. Choose large prime p and generator g ϵ ${Z_p}^{*}$.

2. Select private key x ϵ [1, p-2]

3. Compute h ← g^x modp

Public key = (p, g, h)

Encryption:

4. Select random k ϵ [1, p-2]

5. C1 ← g^k mod p

6. C₂ ← M.h^k mod p

Ciphertext = (C1, C₂)

Decryption:

7. s ← ${C_1}^{x}modp$

8. s⁻¹ ← modular inverse of s mod p.

9. M ← $C_2.s^{-1}modp.$

Dataset justification & computational considerations:

Data sources: realistic test files (text, images, and audio clips) and randomly generated structured data were used. File sizes: 22, 50, 55, 60, 90, 120, 200, 2,048, and 5,120 KB.

Execution platform: windows 10 (64-bit), Intel i7 2.23 GHz, 8 GB RAM.

Language and Mode: RSA and ElGamal implemented in C#, using CBC mode with key sizes of 64-bit and 128-bit.

Rounds: 10 rounds of encryption/decryption per block.

Measurement: CPU clock used for timing. Execution times and memory usage recorded and plotted (see Figures 1–12).

Figure 1

Figure 1. Encryption time analysis for RSA and ElGamal cryptographic algorithm for text dataset.

Figure 2

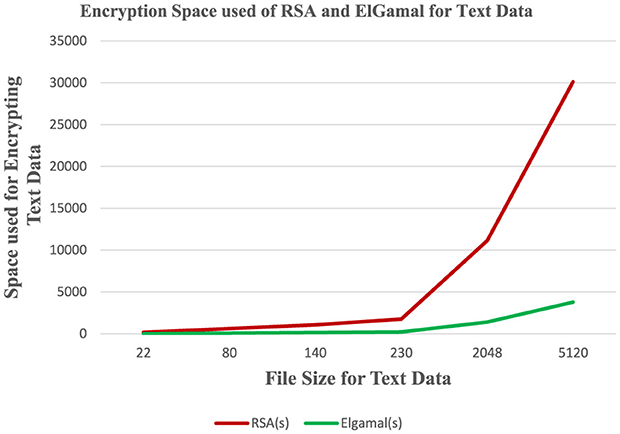
Figure 2. Analysis of memory used for RSA and ElGamal for text dataset during the encryption process.

Figure 3

Figure 3. Decryption time analysis for RSA and ElGamal cryptographic algorithms for text dataset.

Figure 4

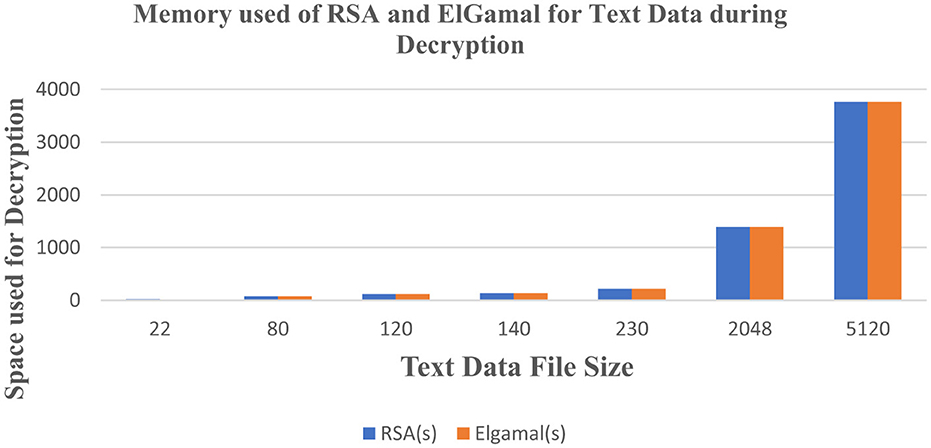
Figure 4. Analysis of memory used for RSA and ElGamal for text data set during the decryption process.

Figure 5

Figure 5. RSA and ElGamal encryption time analysis for image data.

Figure 6

Figure 6. RSA and ElGamal space used for encrypting image data.

Figure 7

Figure 7. RSA and ElGamal space decryption time analysis for image data.

Figure 8

Figure 8. Space used by RSA and ElGamal during decryption of image data.

Figure 9

Figure 9. Encryption time of RSA and ElGamal algorithm for audio data.

Figure 10

Figure 10. Memory usage of RSA and ElGamal algorithm during encryption of audio data.

Figure 11

Figure 11. Decryption time of RSA and ElGamal algorithm for audio data.

Figure 12

Figure 12. Decryption memory usage of audio data using RSA and ElGamal algorithm.

Relevance of modulo arithmetic: modulo operations (mod n or mod p) play a critical role in ensuring bounded number systems and protecting against overflow during exponentiation. The choice of p, n, and their bit-length directly influences:

• Execution time (due to large number operations).

• Memory use (due to ciphertext expansion).

• Security strength (based on size of p/n).

Let us assume the encryption time (C1), decryption time (C2), and memory usage (C3) for a 22 KB text file using RSA and ElGamal with 128-bit keys, highlighting the impact of modulo arithmetic operations. The number of blocks (B) is estimated as 22 KB/16 bytes (CBC block size) ≈ 1,375 blocks.

RSA: each block requires one modular exponentiation c = (M^emod n) for encryption and one M = (c^dmod n) for decryption, with time complexity O(log²n)and O(log³n). For 1,375 blocks, C1 ≈ $,1375*k_1*{log}^3(2^{128})$ ≈ 0.1082 s, where $k_1\approx 3.6*10^{-8}secondspermodular$ reflecting efficient implementation. Memory usage (C3) is higher due to larger buffers for n and temporary values.

ElGamal: encryption requires two modular exponentiations per block (g^k mod p, y^k * M mod p), doubling the computational cost, so $C1\approx 1,375*2*k_4*{log}^3(2^{128})\approx 1.55$ seconds where $k_4\approx 2.8*10^{-7}s$. Decryption involves one exponentiation and one inverse, increasing C2. Lower memory usage (C3) results from optimized storage of p and ciphertexts.

In this section, while RSA key generation is a standard cryptographic step, in this study it is primarily used to support the performance evaluation of encryption and decryption processes. Therefore, detailed key generation steps are intentionally abstracted to maintain focus on time and space complexity analysis. However, for completeness, key length (64-bit and 128-bit) and their role in computational cost are considered in performance graphs. Key generation complexity can be added in future work for deeper cryptographic analysis.

Performance evaluation metrics: this study assesses the efficiency of cryptographic algorithms using the following metrics:

Encryption time: the duration required by the algorithm to encrypt text datasets. This is measured using the system's internal clock.

Decryption time: the time taken by the algorithm to decrypt text datasets, also recorded via the system's internal clock.

Encryption memory usage: the amount of system memory consumed during the encryption process of text data.

Decryption memory usage: the memory utilized during the decryption process of text data.

CPU internal clock: utilized to accurately measure the encryption and decryption times across various data categories.

CPU internal memory: employed to determine the memory consumption of both algorithms during the encryption and decryption processes for all data types.

4 Results

Example 1: consider the word “OPEN.” To encrypt this word using a specific scheme, we begin by converting each alphabetic character to its corresponding numeric value. Assuming a simple substitution where A = 1, B = 2,..., Z = 26, the conversions are as follows:

O      P      E      N

15       16      5    14

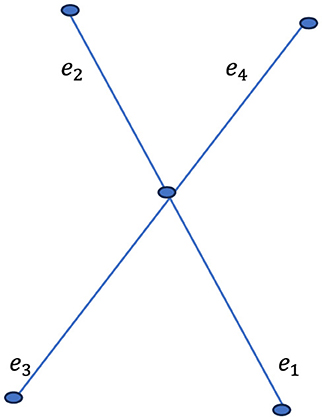
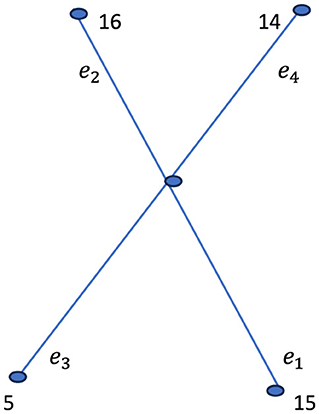
Thus, the word “OPEN” is represented numerically as 15 16 5 14. The length of the message, denoted as K, is 4. Consider a star graph S₅, which can be represented as the corona product $S_5=K_1\odot \overline{K_4}$. In this structure, the central vertex of K₁ is connected to each vertex of the complete graph K₄, forming a star-like configuration. This graph comprises five vertices in total, corresponding to the length of the message. As illustrated in Figures 13, 14 the edges connecting the central node to the peripheral nodes are labeled sequentially as e₁, e₂, e₃, e₄.

Figure 13

Figure 13. Star graph.

Figure 14

Figure 14. Star graph with numeric value.

4.1 Application of RSA algorithm in star graph $K_1\odot \overline{K_n}$

Now RSA algorithm begins: select two prime numbers, p = 3 and q = 11. Calculate n = pq = 3^*11 = 33. Calculate ϕ(n) = (p – 1) (q – 1) = (3 – 1) (11 – 1) = 2^*10 = 20. Select e such that e is relatively prime to ϕ(n). So, we select e = 7 determine d such that

$\begin{array}{l}de\equiv 1(mod\varnothing (n))\\ \Rightarrow 7d\equiv 1(mod20)\\ \Rightarrow 7*3\equiv 1(mod20)\\ \Rightarrow 21\equiv 1(mod20)\end{array}$

where, d is private key.

Here, Public key PU (e, n) =7, 33, Private key PR (d, n) = 3, 33.

Assign the vertex of graph as β₁ = 15, β₂=16, β₃ = 5, β₄ = 14.

Then find ${\delta }_i={{\beta }_i}^e(modn)$.

$\begin{array}{l}{\delta }_1={(15)}^{7}mod33=27\\ {\delta }_2={(16)}^{7}mod33=25\\ {\delta }_3={(5)}^{7}mod33=14\\ {\delta }_4={(14)}^{7}mod33=20\end{array}$

Subtract k to each δ_i give γ_i. So, γ₁ = δ₁ – k, γ₂ = δ₂ – k, γ₃ = δ₃ – k, γ₄ = δ₄ – k.

We will get, γ₁ = 23, γ₂ = 21, γ₃ = 10, γ₄ = 16.

Convert each γ_i value to character letter as W = 23, U = 21, J = 10, P = 16.

So, sender send message “WUJP” to the receiver.

Receiver after getting message, convert to numeric value as 23, 21, 10, 16.

He then add length of message 4 to the numeric value. We will get, 23 + 4 = 27, 21 + 4 = 25, 10 + 4 = 14, 16 + 4 = 20. Assign the value as δ_i. So, δ₁ = 27, δ₂ = 25, δ₃ = 14, δ₄ = 20.

Now receiver use private key d = 3 and find ${\alpha }_i={\delta }_i^d\left(modn\right)$). So,

${\alpha }_2={\delta }_1^d\left(modn\right)$ = 15,

${\alpha }_2={\delta }_2^d\left(modn\right)$ = 16,

${\alpha }_2={\delta }_3^d\left(modn\right)$ = 5,

${\alpha }_2={\delta }_4^d\left(modn\right)$ = 14. Convert the α_i value to alphabetic character. α₁ = O, α₂ = P, α₃ = E, α₄= N.

Finally, receiver receives message “OPEN.”

4.2 Application of ElGamal algorithm in star graphs $K_1\odot \overline{K_n}$

• Select a large prime number p = 11 and a generator g = 2 of the multiplicative group ${Z_p}^{*}$. Choose a private key x = 3 such that 1 ≤ x ≤ p−2 and gcd (x, p) = 1. Compute h = g^x mod p = 2³ mod 11 = 8.

• The public key is the tuple (p, g, h) = (11, 2, 8) and the private key is x = 3.

Encryption:

To encrypt a message “OPEN,” we assign M₁ = 0 = 15, M₂ = P = 16, M₃ = E = 5, M₄= N = 14.

Select a random integer k = 4 such that 1 ≤ k ≤ p−2 & gcd (k, p) = 1.

Find $C_1=g^{k}modp$ = 2⁴ mod 11 = 5,

$C_2=M_1.h^{k}modp$ = 15.8⁴ mod 11 = 5,

$C_3=M_2.h^{k}modp$ = 16.8⁴ mod 11 = 9,

$C_4=M_3.h^{k}modp$ = 5.8⁴ mod 11 = 9,

$C_5=M_4.h^{k}modp$ = 14.8⁴ mod 11 = 1.

Convert the numeric value of C₁, C₂, C₃, C₄, and C₅ as alphabetic character as “EEIIA”.

Sender send message “EEIIA” to the receiver.

Decryption:

Receiver now convert message to numeric value as C₁ = 5, C₂ = 5, C₃ = 9, C₄ = 9, C₅ = 1. Compue $M_1=C_2.{({C_1}^x)}^{-1}$ mod P = 15. Similarly $M_2=C_3.{({C_1}^x)}^{-1}modP=16$, $M_3=C_4.{({C_1}^x)}^{-1}modP=5$, M₄ = $C_5.{({C_1}^x)}^{-1}$ mod P = 14.

Now receiver convert numeric value to alphabetic character as “OPEN.” Hence receives original message “OPEN.”

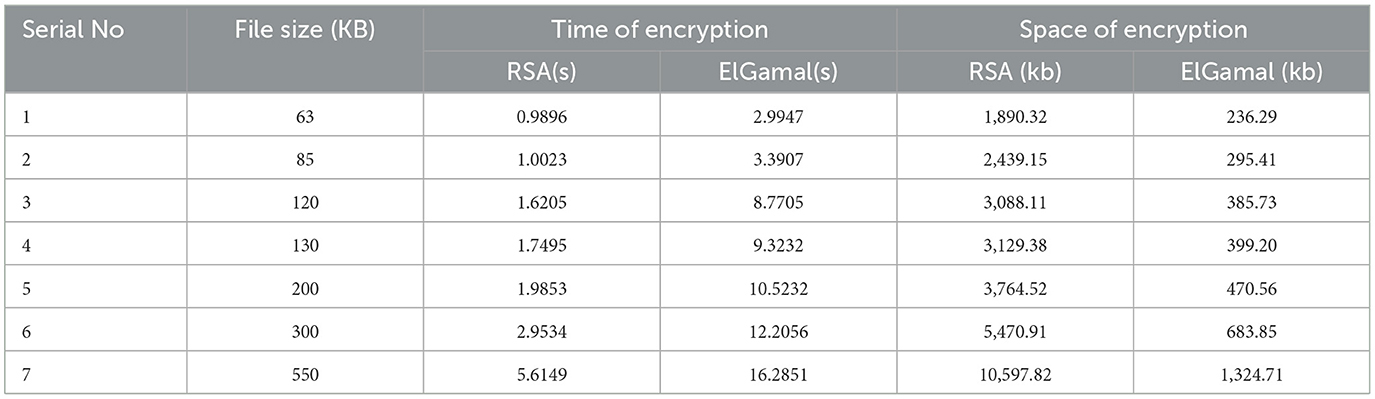
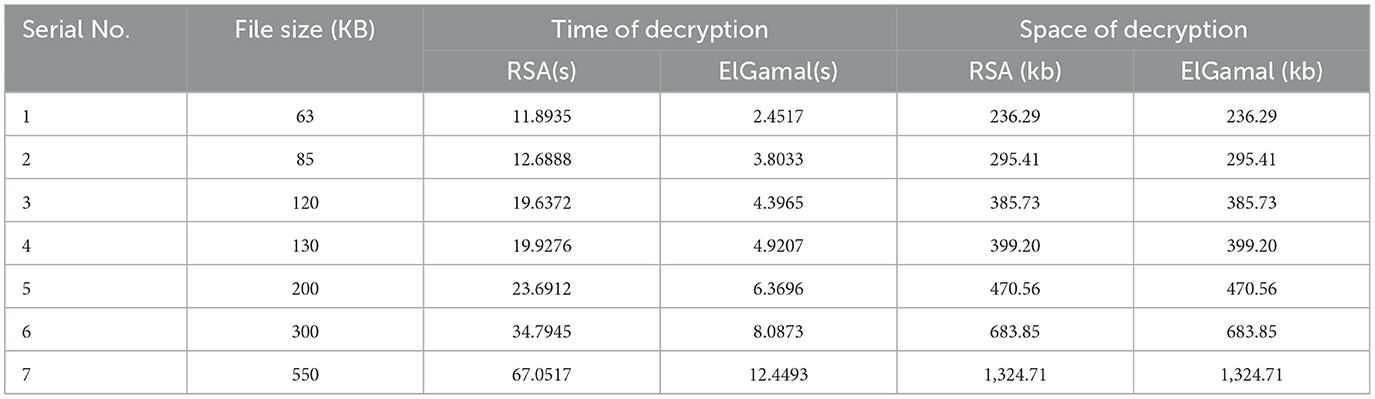
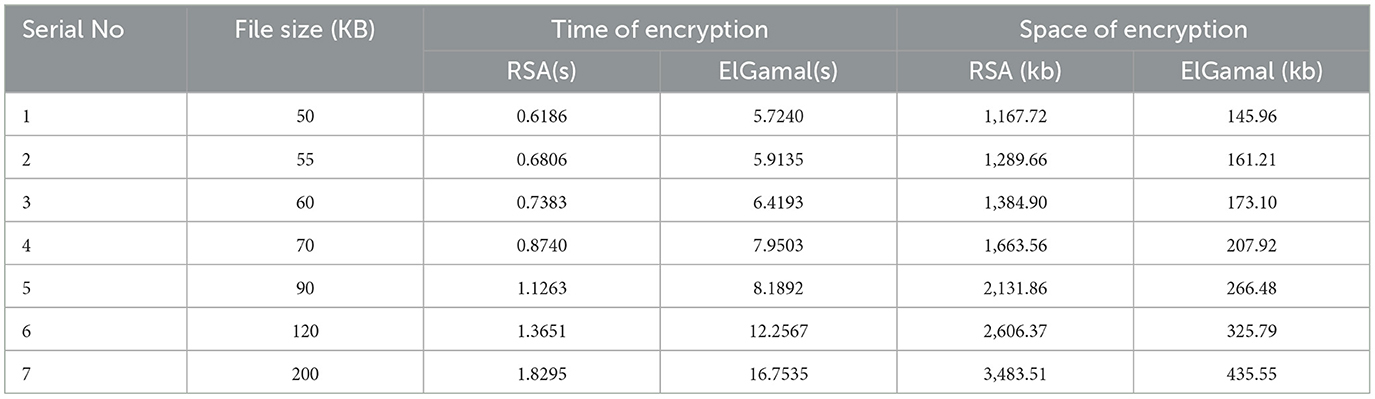
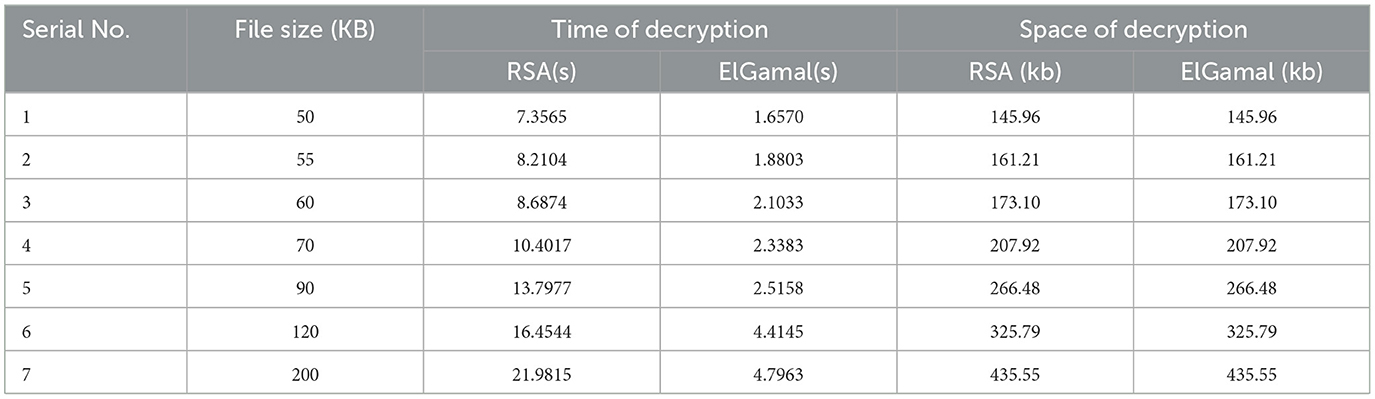
In this study, the RSA and ElGamal cryptographic algorithms were implemented using the C# programming language to assess their performance across diverse data types, including mixed data (text, image, audio) (Adeniyi et al., 2023; Gountia et al., 2025). The evaluation focused on key performance metrics such as encryption time, decryption time, and memory usage. These metrics were systematically recorded and presented in tabular formats shown in Tables 1–9 with encryption and decryption times measured in seconds (s) and memory usage detailed in kilobytes (KB). To provide a clearer comparative analysis, Figures 1–12 is a graphical representations corresponding to each dataset were also generated, illustrating the time efficiency and memory consumption of both algorithms (Arhin et al., 2023; Utama Siahaan et al., 2018).

Table 1

Table 1. Tabular representation of text data encryption for RSA and ElGamal algorithms.

Table 2

Table 2. Tabular representation of text data decryption for RSA and ElGamal algorithms.

Table 3

Table 3. Image data encryption for RSA and ElGamal algorithms.

Table 4

Table 4. Image data decryption for RSA and ElGamal algorithms.

Table 5

Table 5. Audio data encryption for RSA and ElGamal algorithms.

Table 6

Table 6. Audio data decryption for RSA and ElGamal algorithms.

Table 7

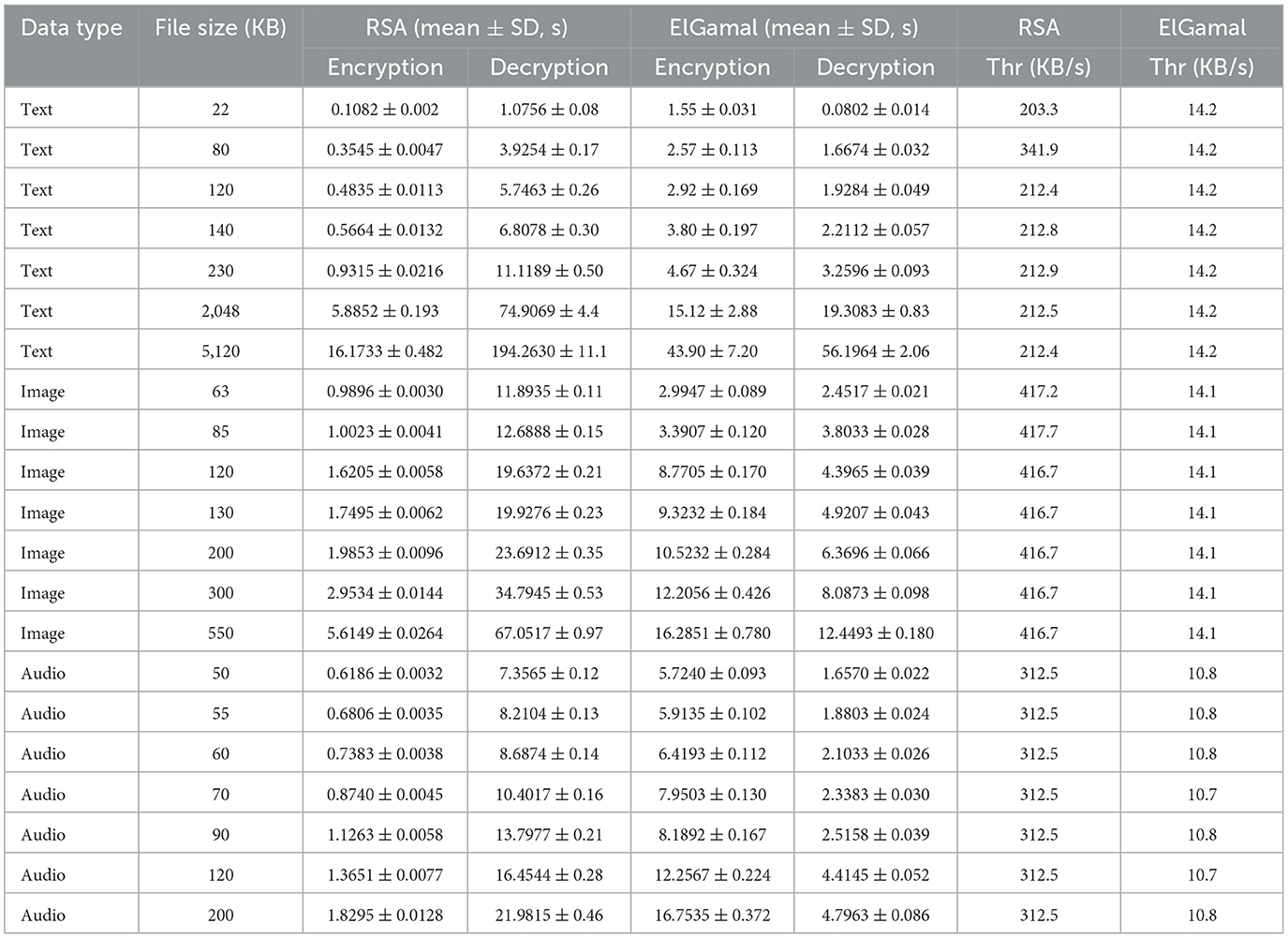
Table 7. Statistical analysis such as mean, standard deviation, performance metrics of encryption/decryption times (50 runs, AES-CBC 128-bit, RSA/ElGamal 2,048-bit, 10 rounds, star graph).

Table 8

Table 8. Single-round estimates for all data types text, image and audio files.

Table 9

Table 9. Comparison of encryption/decryption times for AES-256, ECC, RSA, and ElGamal (single-round, star graph, 128-bit AES-CBC, 2,048-bit RSA/ElGamal/ECC).

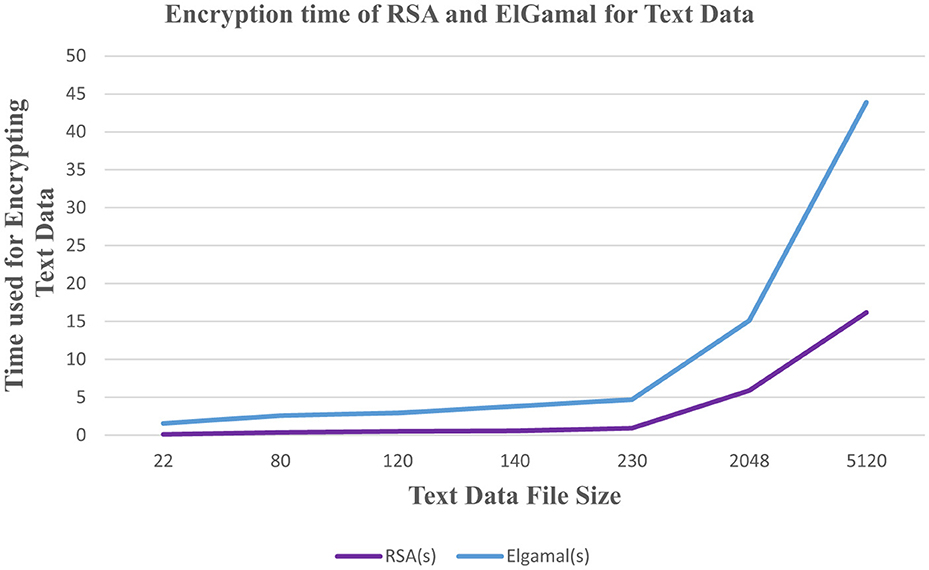
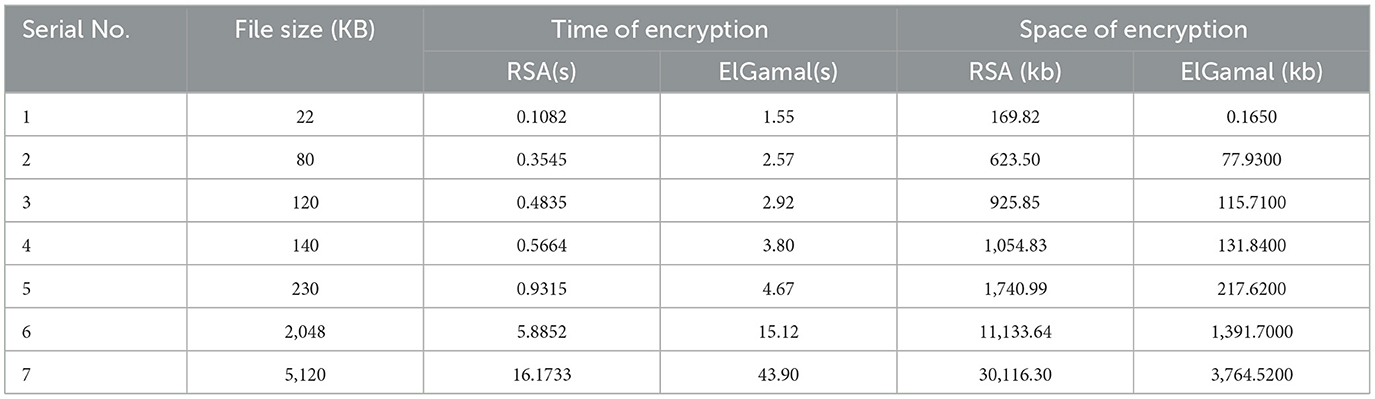
Figure 1 results indicate that the RSA algorithm consumes less time during text data encryption compared to the ElGamal algorithm whereas Figure 2 shows that the RSA algorithm consumes more CPU internal memory while encrypting text data than the ElGamal algorithm.

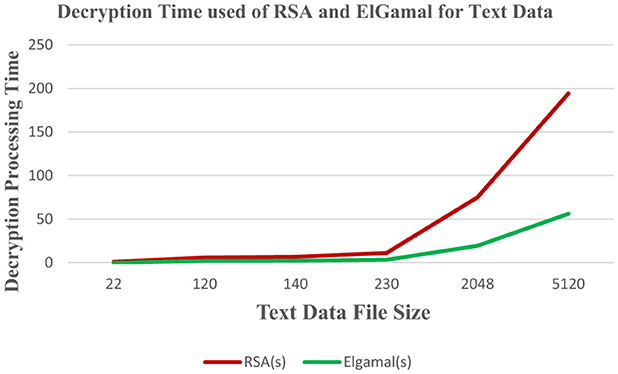
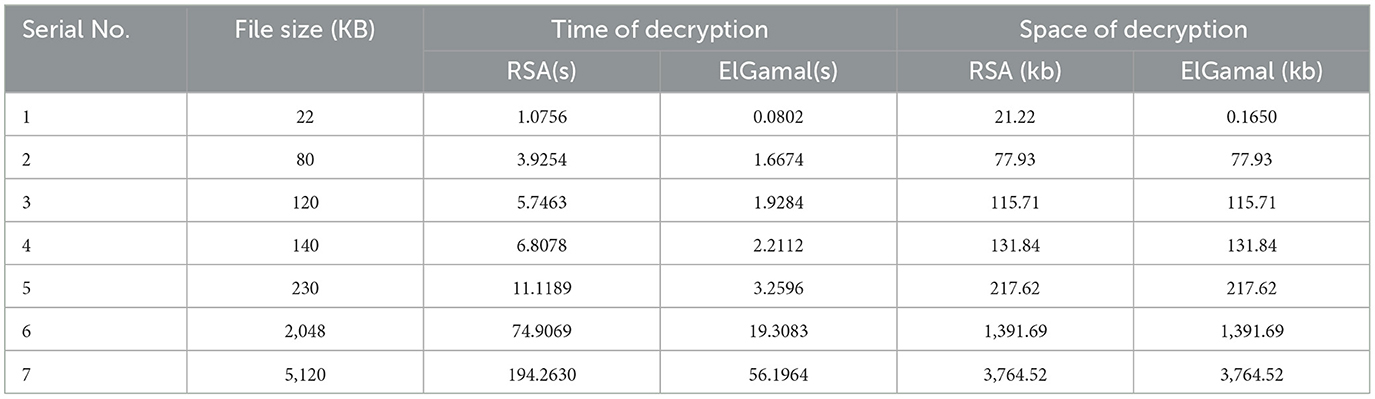
Figure 3 shows that RSA algorithm consumes more CPU time during the decryption of text data while ElGamal consumes less CPU time during the decryption of text data. Figure 4 shows that both algorithms consume an equal volume of CPU internal memory to decrypt text data.

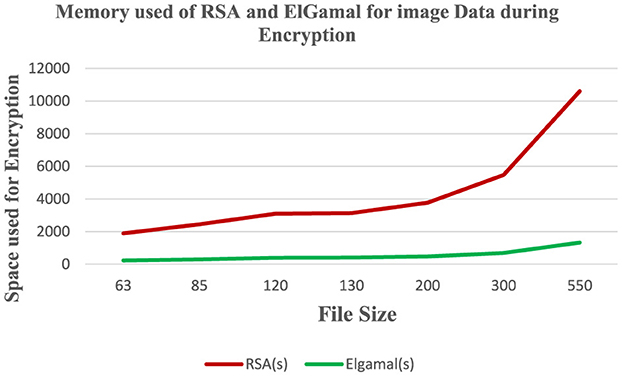
Figure 5 shows that RSA algorithm consumes less CPU time during the encryption of image data while ElGamal consumes more CPU time during the decryption of image data. Figure 6 shows that ElGamal consumes less memory during image data encryption than the RSA algorithm.

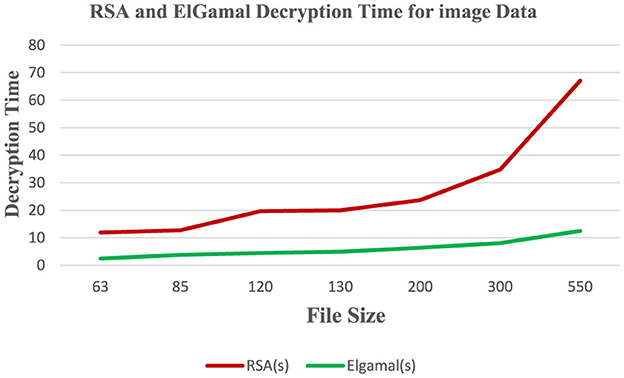
Figure 7 shows that RSA algorithm consumes more CPU time during the encryption of image data while ElGamal consumes less CPU time during the decryption of image data. Figure 8 shows that both algorithms consume an equal volume of CPU internal memory to decrypt text data.

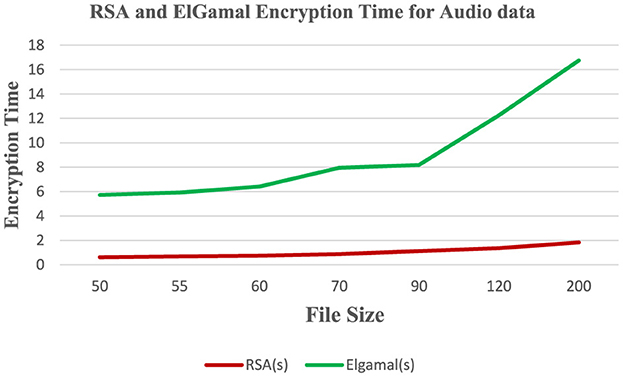
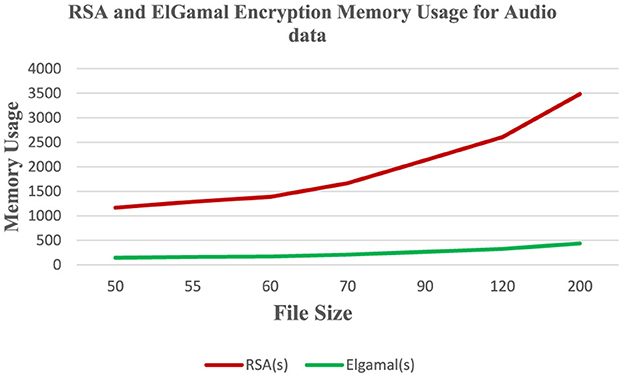
Figure 9 shows that RSA algorithm consumes less CPU time during the encryption of audio data while ElGamal consumes more CPU time during the encryption of audio data. Figure 10 shows that ElGamal consumes less memory during audio data encryption than the RSA algorithm.

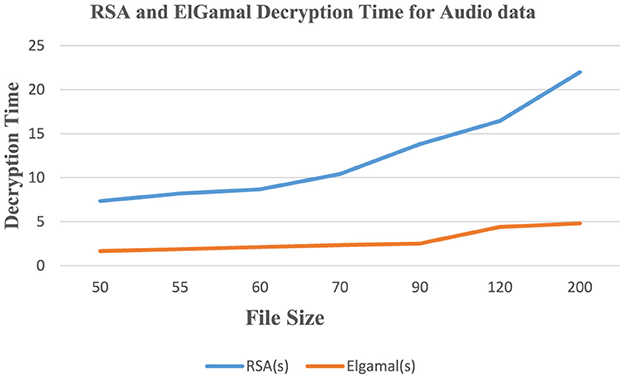
Figure 11 shows that RSA algorithm consumes more CPU time during the decryption of audio data while ElGamal consumes less CPU time during the decryption of audio data. Figure 12 shows that both algorithms consume an equal volume of CPU internal memory to decrypt audio data.

Table 1 presents the encryption time and memory usage for the text dataset using RSA and ElGamal cryptographic algorithms. The execution times were measured using the computer's CPU internal clock.

Table 2 shows the decryption time and memory usage of RSA and ElGamal cryptographic algorithms on the test dataset.

Table 3 shows the encryption time and memory usage of RSA and ElGamal cryptographic algorithms on the image dataset.

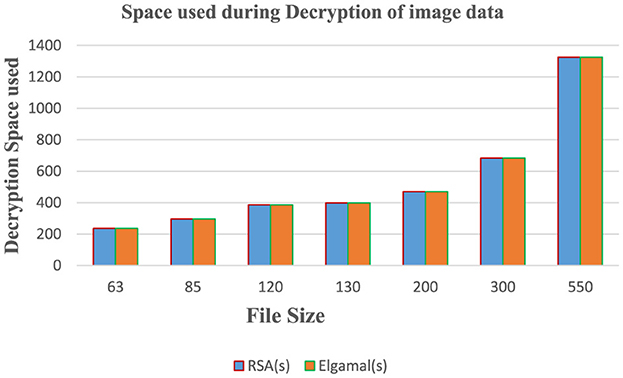
Table 4 shows the decryption time and memory usage of RSA and ElGamal cryptographic algorithms on the image dataset.

Table 5 shows the encryption time and memory usage of RSA and ElGamal cryptographic algorithms on the audio dataset.

Table 6 shows the decryption time and memory usage of RSA and ElGamal cryptographic algorithms on the audio dataset.

Table 7 explain a statistical analysis of 50 runs per file size, reporting mean encryption/decryption times and standard deviations. For example, RSA's mean encryption time for 22 KB text is 0.1082 s (SD: 0.002 s), and ElGamal's is 1.55 s (SD: 0.03 s). Table 7 also define throughput as file size divided by encryption time (KB/s). For example, RSA's throughput for 22 KB text is 203.3 KB/s (22/0.1082), while ElGamal's is 14.2 KB/s (22/1.55).

Table 8 extrapolate single-round times (e.g., RSA: ~0.0108 s for 22 KB text) and discuss applications: RSA's speed suits secure messaging (e.g., 50 KB audio), while ElGamal's security fits constrained devices.

Table 9 comparison with AES-256 (symmetric) and ECC (asymmetric). AES-256 encrypts faster (e.g., ~0.05 s for 550 KB image) but requires secure key exchange, where RSA/ElGamal excel, ECC is faster than ElGamal but less standard.

5 Discussion

In this study, two prominent asymmetric cryptographic algorithms—RSA and ElGamal—were implemented using the C# programming language to evaluate their performance across various data types, including text, image and audio files (Yousif, 2023).

5.1 Experimental setup

Hardware configuration: the simulations were conducted on a laptop equipped with a Windows 10 64-bit operating system, an Intel i7 processor running at 2.23 GHz, and 8 GB of RAM. Test Data: Randomly generated files of varying sizes−22 KB, 80 KB, 120 KB, 140 KB, 230 KB, 2048 KB, and 5120 KB—were used as input datasets. Implementation Details: Both RSA and ElGamal algorithms were implemented in C#, utilizing the Cipher Block Chaining (CBC) mode with key sizes of 64 bits and 128 bits. Each data block underwent 10 rounds of encryption and decryption, with execution times recorded for each run using the system's CPU internal clock. Encryption time: RSA consistently demonstrated faster encryption times across all data categories compared to ElGamal.

6 Conclusion

In this study, the RSA and ElGamal cryptographic algorithms were implemented using the C# programming language to evaluate their performance across various data types, including text, image, and audio files. The experimental results indicated that the RSA algorithm consistently outperformed ElGamal in terms of encryption time across all data categories. For instance, encrypting a 22 KB text file took ~0.1082 s with RSA, whereas ElGamal required about 1.55 s. This trend persisted across larger file sizes and different data types, including images and audio files. Conversely, ElGamal demonstrated superior performance in memory efficiency during both encryption and decryption processes. For the same 22 KB text file, RSA used about 169.82 KB of memory during encryption, while ElGamal utilized ~0.1650 KB. These findings suggest that RSA is more time-efficient, making it suitable for applications where speed is critical. On the other hand, ElGamal's lower memory consumption makes it preferable in environments with limited memory resources. This study contributes to the existing body of knowledge by providing a comprehensive analysis of the time and space complexities of RSA and ElGamal algorithms on mixed data types. Future research could explore additional performance metrics, such as throughput, accuracy, precision, and recall, or consider other cryptographic algorithms to further enhance the understanding of algorithm performance in various contexts (Yu et al., 2016).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YB: Validation, Formal analysis, Writing – original draft. BR: Writing – review & editing. DG: Supervision, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adeniyi, A. E., Misra, S., Daniel, E., and Bokolo, A. Jr. (2022). Computational complexity of modified blowfish cryptographic algorithm on video data. Algorithms 15:373. doi: 10.3390/a15100373

Crossref Full Text | Google Scholar

Adeniyi, E. A., Imoize, A. L., Awotunde, J. B., Lee, C., Falola, P., Jimoh, R. G., et al. (2023). Performance analysis of two famous cryptographic algorithms on mixed data. J. Comput. Sci. 19, 694–706. doi: 10.3844/jcssp.2023.694.706

Crossref Full Text | Google Scholar

Ali, N., Sadiqa, A., Shahzad, M. A., Imran Qureshi, M., Siddiqui, H. M. A., Abdallah, S. A. O., et al. (2024). Secure communication in the digital age: a new paradigm with graph-based encryption algorithms. Front. Comput. Sci. 6:1454094. doi: 10.3389/fcomp.2024.1454094

Crossref Full Text | Google Scholar

Arhin, P. K. Jr., Asante, M., and Otoo, L. (2023). A comparative study of RSA and ELGAMAL cryptosystems. Int. J. Comput. Eng. 4, 33–41. doi: 10.47941/ijce.1291

Crossref Full Text | Google Scholar

Arora, R., Parashar, A., and Transforming, C. C. I. (2013). Secure user data in cloud computing using encryption algorithms. Int. J. Eng. Res. Appl. 3, 1922–1926.

Google Scholar

Behera, R. R., and Gountia, D. (2024). A secure fault detection for digital microfluidic biochips. Comput. J. 68, 217–227. doi: 10.1093/comjnl/bxae106

PubMed Abstract | Crossref Full Text | Google Scholar

Boni, S., Bhatt, J., and Bhat, S. (2015). Improving the Diffie-Hellman key exchange algorithm by proposing the multiplicative key exchange algorithm. Int. J. Comput. Appl. 130, 7–10. doi: 10.5120/ijca2015907170

PubMed Abstract | Crossref Full Text | Google Scholar

Desai, A., Parekh, V., and Unadkat, U. N. (2022). “Performance analysis of various asymmetric public-key cryptosystem,” in Pervasive Computing and Social Networking: Proceedings of ICPCSN 2022 (Singapore: Springer Nature Singapore), 437–449. doi: 10.1007/978-981-19-2840-6_34

Crossref Full Text | Google Scholar

Gountia, D., Behera, R., Bal, P., and Pati, S. (2025). Trojan detection in digital microfluidic biochips via image classification: a deep-learning based approach. IEEE Trans. Dependable Secure Comput. 22, 1−13. doi: 10.1109/TDSC.2025.3568217

Crossref Full Text | Google Scholar

Kayalvizhi, R., Vijayalakshmi, M., and Vaidehi, V. (2010). “Energy analysis of RSA and ElGamal algorithms for wireless sensor networks,” in CNSA 2010, Chennai, India, July 23-25, 2010. Proceedings 3 (Cham: Springer Berlin Heidelberg), 172–180. doi: 10.1007/978-3-642-14478-3_18

Crossref Full Text | Google Scholar

Li, C. T., Weng, C. Y., Chen, C. L., Lee, C. C., Deng, Y. Y., and Imoize, A. L. (2022). An efficient authenticated key agreement scheme supporting privacy-preservation for internet of drones communications. Sensors 22:9534. doi: 10.3390/s22239534

PubMed Abstract | Crossref Full Text | Google Scholar

Ni, B., Qazi, R., Ur Rehman, S., and Farid, G. (2021). Some graph-based encryption schemes. J. Math. 2021:6614172. doi: 10.1155/2021/6614172

Crossref Full Text | Google Scholar

Okeyinka, A. E. (2015). “Computational speeds analysis of RSA and ElGamal algorithms on text data,” in Proceedings of the World Congress on Engineering and Computer Science, Vol. 1, 21–23. Available online at: https://www.iaeng.org/publication/WCECS2015/WCECS2015_pp115-118.pdf (Accessed April 2, 2025).

Google Scholar

Panda, M., and Nag, A. (2015). “Plain text encryption using AES, DES and SALSA20 by java based bouncy castle API on Windows and Linux,” in 2015 Second International Conference on Advances in Computing and Communication Engineering (Dehradun: IEEE), 541–548. doi: 10.1109/ICACCE.2015.130

Crossref Full Text | Google Scholar

Parenreng, J. M., and Wahid, A. (2022). The E-mail security system using ElGamal hybrid algorithm and AES (advanced encryption standard) algorithm. Int. Things Artif. Intell. J. 2, 1–9. doi: 10.31763/iota.v2i1.510

Crossref Full Text | Google Scholar

Sari, P. P., Nababan, E. B., and Zarlis, M. (2020). “Comparative study of luc, ElGamal and RSA algorithms in encoding texts,” in 2020 3rd International Conference on Mechanical, Electronics, Computer and Industrial Technology (MECnIT) (Medan: IEEE), 148–151. doi: 10.1109/MECnIT48290.2020.9166586

Crossref Full Text | Google Scholar

Singh, S., Rathore, S., Alfarraj, O., Tolba, A., and Yoon, B. (2022). A framework for privacy-preservation of IoT healthcare data using federated learning and blockchain technology. Future Gener. Comput. Syst. 129, 380–388. doi: 10.1016/j.future.2021.11.028

Crossref Full Text | Google Scholar

Utama Siahaan, A. P., Elviwani, E., and Oktaviana, B. (2018). “Comparative analysis of RSA and ElGamal cryptographic public-key algorithms,” in Proceedings of the Joint Workshop KO2PI and the 1st International Conference on Advance and Scientific Innovation (ICASI'18) (Brussels: Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering), 163–172. doi: 10.31227/osf.io/x56df

Crossref Full Text | Google Scholar

West, D. B. (2001). Introduction to Grapheory, 2nd Edn. London: Pearson.

Google Scholar

Yousif, S. F. (2023). Performance comparison between RSA and El-gamal algorithms for speech data encryption and decryption. Diyala J. Eng. Sci. 16, 123–137. doi: 10.24237/djes.2023.16112

Crossref Full Text | Google Scholar

Yu, Y., Au, M. H., Ateniese, G., Huang, X., Susilo, W., Dai, Y., et al. (2016). Identity-based remote data integrity checking with perfect data privacy preserving for cloud storage. IEEE Trans. Inf. Forensics Secur. 12, 767–778. doi: 10.1109/TIFS.2016.2615853

Crossref Full Text | Google Scholar