- 1Department of Psychology, Technical University Dortmund, Dortmund, Germany
- 2Department of Education and Psychology, Freie Universität Berlin, Berlin, Germany
The self-concept of ability in math in elementary school is an early predictor for future math-related choices and careers. Unfortunately, already at this early age girls report lower ability self-concepts in math than boys—despite their comparable performances in objective math competence tests. In the present study we focus on teachers' beliefs as factors explaining these gender differences. Women's underrepresentation in math and science in academia has recently been explained by the belief held by the environment that success in these domains requires an innate ability that cannot be taught (“brilliance”). In addition, teachers' beliefs regarding their students' mathematical aptitude have also been found to influence students' self-concepts of ability. Here, we study if teachers' beliefs regarding their students' mathematical aptitude and brilliance beliefs may account for gender differences in elementary school students' self-concept of ability in math and thus potentially contribute to entering the gendered path into math and science professions. In a sample of 830 fourth graders (M = 9.14 years old, 49% female) and 56 elementary school teachers from Germany, we assessed teachers' beliefs regarding their students' mathematical aptitude and their belief that children need brilliance to succeed in math as well as children's mathematical ability self-concept and competencies. In line with prior research, boys reported a statistically significantly more positive math ability self-concept (d = 0.50), although boys and girls reached similar scores in a standardized math competence test (d = 0.07). However, multilevel regression analyses revealed that teachers' math brilliance beliefs were not related to the gender gap in students' ability self-concept in expense of girls whereas the gender gap was mediated by teachers' beliefs about their students' mathematical aptitude. These findings suggest that math brilliance beliefs held by important socializers such as teachers might not play a role in explaining gender differences in math-related motivation in elementary school whereas teachers' beliefs about students' math aptitude do. Results are discussed against the background of teacher expectancy effects, developmental changes in elementary school, and cultural differences.
Introduction
“You need to be a math person to be good at math.” Such beliefs are widespread in Western industrialized societies (Rattan et al., 2012; Chestnut et al., 2018). In the context of higher education, research has already shown their potentially damaging implications for the diversity of the learners. Believing in an innate ability required for success in math—that is, math brilliance, which you either have or have not—seems to be particularly detrimental for women and people of color, two social groups that are stereotyped as lacking an innate ability for math (Storage et al., 2016; Chestnut et al., 2018). Thus, believing in brilliance required for success in a particular domain has been identified as one factor contributing to the underrepresentation of women in domains such as science, technology, engineering, and math (i.e., STEM domains, Wang and Degol, 2016).
Gender differences regarding math, however, do not just emerge when it comes to math course selection in high school or college but much earlier in students' educational careers. Therefore, it is important to understand the school experiences and motivational processes that lay the groundwork for (not) pursuing math-related careers (Wang and Degol, 2013, p. 323, 324). In this study, we focus on students in their last year of elementary school, i.e., fourth grade, and their teachers. We test if teachers' belief that math requires innate ability and the ascription of math aptitude to boys also account for gender differences in these students' motivation in math and thus potentially contribute to entering the gendered path into math and science professions.
In what follows, we shortly summarize empirical evidence on gender differences in students' math achievement and motivation in elementary school, two important predictors of students' math-related choices (e.g., Eccles et al., 1983; Wang and Degol, 2013). Subsequently, we synthesize (a) research on the general role of teachers' beliefs for gender differences in school with (b) research on the belief that math requires brilliance, which seems to be widespread in academia and to be a barrier for women's success and participation in STEM fields (Leslie et al., 2015; Rattan et al., 2018). This results in our research question whether teachers' beliefs about (a) students' math aptitude and (b) brilliance in general explain gender differences in children's math ability self-concept in expense of girls already at the end of elementary school.
Gender Differences in Math Achievement and Motivation in Elementary School
Many people believe that an average male person possesses higher math skills and talent than an average female person (e.g., Nosek et al., 2002; Steffens et al., 2010; Ertl et al., 2017). However, contrary to this stereotype, actual mean gender differences in math competence tests are generally small and often negligible (for meta-analyses see e.g., Else-Quest et al., 2010; Reilly et al., 2015). This has also been found for elementary school students. In the recent Trends in Math and Science Study (TIMSS 2015), for instance, no significant differences between male and female fourth graders were found across all participating countries (Mullis et al., 2016). In countries where boys outperformed girls, differences were mostly small. Other studies with elementary school samples yielded similar results (Herbert and Stipek, 2005; Cvencek et al., 2015). However, while mean differences in boys' and girls' math performance in early years tend to be small or non-existent, larger gender differences are found at the highest ability level (Brunner et al., 2008). Both in earlier and more recent cohorts of early childhood studies, the gender gap developed early at the top of the achievement distribution and spread throughout the distribution during the first few years of elementary school (Cimpian et al., 2016). For example, when considering the combined PIRLS and TIMSS test results the gender ratio in the highest performance level was four girls to five boys (Bergold et al., 2017). Gender differences in math also become larger in older samples concerning both the average performance and the gender gap among top performers (Hyde, 2005; Reilly, 2012). In older students, i.e., PISA 2009 participants, twice as many male (2.5%) than female (1.2%) students reached the highest ability levels in math (Reilly, 2012). However, most researchers agree that gender differences in math ability are not the primary explanation for why female students end up working and majoring less often than male students in math-intensive fields (see also Riegle-Crumb et al., 2012; Wang and Degol, 2013, p. 308).
The seminal Eccles et al. expectancy-value model (e.g., Eccles et al., 1983; Eccles, 2011) provides a popular theoretical model of the processes that lead to gender differences in academic achievement and choices. According to Eccles et al., the two most proximal precursors of academic choices are students' belief about how well they will do on upcoming tasks in the respective domain (i.e., their expectation of success in math) and how much they like, value, and enjoy the respective domain (i.e., their math values), with both constructs being influenced by the child's ability self-concept. The child's ability self-concept is defined as the child's beliefs about its competence in the respective domain (here, math) and is assumed to be directly influenced by socializer's beliefs and stable child characteristics such as child's gender or aptitude (Eccles and Wigfield, 2002, p. 119). As math ability self-concept is an empirically established, powerful predictor of students' math-related career choices (Wang and Degol, 2013; Musu-Gillette et al., 2015) we concentrate on ability self-concepts in the present study. And already in elementary school, boys report a more positive ability self-concept than girls (e.g., Tiedemann, 2000b; Fredricks and Eccles, 2002; Herbert and Stipek, 2005). Importantly, these gender differences in math ability self-concept in expense of female students are larger than those found in test performance, and thus, cannot be traced back on actual competence differences. Moreover, gender gaps in ability self-concepts (or confidence) seem to be larger than in intrinsic motivation (or interest) or the perceived usefulness and importance of math (Wigfield et al., 1997; Ganley and Lubienski, 2016) suggesting that children's competence beliefs are more likely to be affected by prior learning experiences and socializers' beliefs in a gender-specific way than children's valuing of the respective domain. In addition, these findings indicate that a domain that is stereotyped as male will still be highly valued by girls and women irrespective of their perceptions of their own abilities, possibly reflecting the high status of those fields or occupations perceived as male or masculine in our society.
The Role of Socializers' Beliefs
Socializers such as teachers or parents are considered as powerful influences on gender gaps in academic motivation, choices, and achievement during school (see e.g., Gunderson et al., 2012). According to the expectancy-value model (e.g., Eccles et al., 1983) socializers' beliefs directly affect students' beliefs such as their stereotypes and ability self-concepts. As teachers' beliefs are thought to influence parents' beliefs concerning their child competencies more profoundly than vice versa (Simpkins et al., 2015), we concentrate on teachers' beliefs. In general, the important role of teachers' beliefs concerning children's ability self-concept formation has been underlined by many empirical studies (e.g., Keller, 2001; Herbert and Stipek, 2005; Wolter et al., 2015; for related research on the role of parents, see e.g., Tiedemann, 2000b; Tomasetto et al., 2015). For instance, teachers' belief that girls have superior reading skills than boys predicted a decline in boys' reading self-concept whereas girls' reading self-concept was unrelated (Retelsdorf et al., 2015). Regarding math, there is evidence that also elementary school teachers share math-male gender stereotypes (for a review see Li, 1999), that is, they ascribed greater talent and more importance of math to male than female persons (e.g., Fennema et al., 1990; Tiedemann, 2000a,b, 2002; McKown and Weinstein, 2002; Hand et al., 2017). Furthermore, they even revealed a shift in evaluation standards when rating the math performance of a girl compared to a boy's math performance (Holder and Kessels, 2017). Elementary teachers underrated the skills of girls throughout the achievement distribution as early as in Grade 1, when past and current math achievement and behavioral ratings where controlled for (Cimpian et al., 2016). In contrast, only a few studies found no gender differences in teachers' ratings of their students' abilities (e.g., Bennett et al., 1993; Dickhäuser and Stiensmeier-Pelster, 2003) and did not reveal any gender-biased expectations regarding math (Lorenz et al., 2016).
Moreover, teachers (like parents, see e.g., Frome and Eccles, 1998; Herbert and Stipek, 2005; Lazarides and Watt, 2017) seem to transmit stereotyped beliefs (Keller, 2001) to their students supporting or maintaining students' stereotyped belief that math is a “male” domain (e.g., Steffens et al., 2010). The “math-male stereotype” has been consistently found in students in various countries when assessing the stereotyping of domains using implicit measures (like the IAT; Greenwald et al., 1998). Interestingly, the implicit math-male stereotype was evident in children as young as four years old (Cvencek et al., 2011), in elementary school children (Passolunghi et al., 2014), secondary school students (Steffens et al., 2010), and college students (Nosek et al., 2002; Smeding, 2012). However, children at elementary school age did not yet consistently stereotype math as a male domain when expressing their views using explicit measures (e.g., Ambady et al., 2001; Passolunghi et al., 2014). Only later, at adolescence, most students endorsed clear-cut math-male stereotypes and ascribed more talent, ability, and interest in math to boys than to girls (Chatard et al., 2007; Steffens et al., 2010; Steffens and Jelenec, 2011; however compare Passolunghi et al., 2014). The perceived fit between one's own gender and the perceived maleness or femaleness of a domain constitutes a crucial factor for students' willingness to get involved in that domain (Kessels et al., 2014). Accordingly, domain gender stereotypes have been proven important predictors of many domain-related emotions, cognitions, and behaviors. The more female students perceived of math as a male domain, the lower their math achievements, math liking and intentions to follow a respective career were (e.g., Nosek and Smyth, 2011; Steffens and Jelenec, 2011; Lane et al., 2012). According to the expectancy-value model (e.g., Eccles et al., 1983) this view is influenced and shaped by, for example, teachers' beliefs and stereotypes increasing gender gaps in STEM-related ability self-concepts, e.g., mathematical ability self-concepts (e.g., Hand et al., 2017). Indeed, studies with German elementary school samples (Tiedemann, 2000a,b, 2002) showed that the more teachers endorsed gender stereotypes concerning math the greater was their gender-stereotyped view on their students' math abilities. Since teachers' ratings of students' math aptitude predict students' ability self-concepts (e.g., Herbert and Stipek, 2005), this study aims to test whether teachers' gender-stereotyped perception of girls' and boys' math aptitude might explain gender differences in math ability self-concepts.
Brilliance Beliefs and Women's Underrepresentation in STEM
Above and beyond the “traditional” math-male gender stereotype, a different belief has recently gained an increasing amount of interest in research aiming at explaining STEM-related gender differences in the context of academia and higher education in the United States. Originally, it was coined domain-specific ability belief and encompasses the extent to which important agents in the learning environment perceive success in a given domain as requiring an innate ability that cannot be taught (“brilliance”) (Leslie et al., 2015). That is, such beliefs can be interpreted as essentially a domain-specific version of what has been called entity theory of intelligence or fixed mindset before, i.e., the belief that intelligence is fixed (Dweck, 2006, 2007; Gunderson et al., 2017). If the beliefs of important learning agents instead of student's field-specific ability beliefs are in focus, the construct is also closely related to the so-called meta-lay theories of a domain-specific aptitude (Rattan et al., 2018). In what follows, we use the term “brilliance belief” to describe the extent to which success in a given domain is perceived as requiring innate ability.
A larger misfit between female students' self and STEM subjects has been attributed in the past to the clashing perceptions that while learning in STEM depends mainly on high ability and less on effort, female academic success is seen as mainly due to effort and hard work (Kessels, 2015). Research in the context of academia has shown that the stronger success in a given domain was perceived as requiring innate ability, the lower the portion of women in this field (Leslie et al., 2015; Meyer et al., 2015). In higher education, STEM subjects were among those domains strongly requiring innate ability as well as being dominated by male persons. In more detail, different disciplines within the STEM field differ in the degree that innate ability is seen as required, and while on average Social Science/Humanities are regarded as requiring less brilliance than STEM, some of those are seen as requiring more or less of innate ability and thus resulting in smaller or larger proportion of female PhDs (Leslie et al., 2015). Also experimental research suggests that presenting job opportunities as requiring innate ability reduces women's interest and belonging but increases their anxiety (Bian et al., 2018). Similarly, perceiving STEM faculty as believing in a special STEM aptitude (which only some students have and others do not) predicted less sense of belonging among female PhD candidates in STEM. Male PhD candidates' sense of belonging, however, was unrelated to their meta-lay theories (Rattan et al., 2018). These findings with adults raise the question whether similar beliefs and processes are already present in earlier stages of math careers, that is, in elementary school, where gender differences in math ability self-concept seem to emerge (Herbert and Stipek, 2005).
Given the alienating consequences of statements that innate ability is required for a domain or task on female students' engagement, teachers' brilliance beliefs seem crucial for understanding the underrepresentation of female students in STEM. As school students have the full range of domains as school subjects, the relative importance ascribed to innate ability in the different school subjects should signal students which subjects to avoid and to approach instead, according to their gender. First studies showed that U.S. American teachers held more fixed views of intelligence for math and science performance compared to performance in languages (Patterson et al., 2016). The construct of brilliance beliefs has so far been studied only once outside the United States, that is in an elementary school teacher sample from Germany (Heyder et al., 2019). It was found that also this group of socializers held stronger brilliance beliefs for math than language arts although their mean level was lower than in prior US studies with academics or lay persons from the general public (see Meyer et al., 2015). The finding that in both countries, that is, Germany and the US, there are domain differences in brilliance beliefs is in line with the fact that both countries are considered Western industrialized countries that with—at least in parts—shared beliefs and stereotypes (Wilde and Diekman, 2005).
As there is also experimental evidence suggesting that in the United States girls from the age of six on view themselves as less smart than boys and refrain from tasks that require to be smart (Bian et al., 2017), an environment that believes that math requires to be smart might discourage girls from math not just at later stages of their career but already at the very beginning. More precisely, such beliefs if held by the teacher might increase the detrimental effects of the math-male gender stereotype on girls, and thus lead to a larger gender gap in math ability self-concept than if teachers held less pronounced math brilliance beliefs. In a German sample, the present study thus aims to explore whether already in elementary school math brilliance beliefs held by the teacher relate to girls' lower ability self-concept in math, despite boys and girls showing similar math competence.
Study overview
Brilliance beliefs are powerful predictors of women's underrepresentation in certain fields in academia such as STEM domains (e.g., Leslie et al., 2015; Storage et al., 2016). A recent study showed that also German elementary school teachers believed that success in math requires more innate ability than success in language (Heyder et al., 2019). Further, elementary school girls have been found to report a less positive ability self-concept than boys despite their comparable competences (e.g., Herbert and Stipek, 2005; Ganley and Lubienski, 2016) and also teachers perceive boys as more talented in math than girls (e.g., Li, 1999; Tiedemann, 2000a). In this study, we bring these strands of research together. First, we want to explore whether teachers' belief that math requires innate ability predicts a less positive ability self-concept in girls than boys in elementary school. Second, we want to test whether teachers' perceptions of students' math aptitude mediate the gender gap in students' ability self-concept. With teachers' math brilliance beliefs, we thus test a novel facet of students' learning environment in elementary school as an additional factor that might contribute to the beginning of the leaky STEM pipeline for girls and women. More precisely, we test the following hypotheses: (1) Independent from the actual performance girls report lower self-concept of ability in math than boys. (2) Independent from the actual performance teachers perceive girls as less talented in math than boys. (3) Teachers' math brilliance beliefs moderate the effect of gender on teachers' ratings of their students' mathematical aptitude and students' ability self-concept in the expense of girls. That is, we expect larger gender differences in teachers' math aptitude ratings and students' ability self-concept if teachers hold strong brilliance beliefs than if they hold weak brilliance beliefs. (4) Teachers' ratings of their students' mathematical aptitude mediate the effect of gender on students' ability self-concept.
Methods
Sample
For this study, we re-analyzed the elementary school data set from the FA(IR)BULOUS Study, a German research project on social inequality in school transitions (Steinmayr et al., 2017). The FA(IR)BULOUS data set had already been analyzed in a prior study on the role of teachers' math-specific ability beliefs for low-achieving students' intrinsic motivation in math (Heyder et al., 2019). This study exceeds the former study by focusing on gender differences in ability self-concept in math and how they are related to teachers' math-specific ability beliefs.
The FA(IR)BULOUS elementary school sample was collected in 2016 and consisted of 837 fourth graders nested in 56 classes. Seven refugee children were excluded from the full sample because they could not fill out the questionnaire due to a lack of German language skills. The remaining 830 student were on average 9.14 years old (SD = 0.54), 409 of them were female (49.4%, two students did not indicate their gender), and 667 of them reported German to be their first language (80.4%). More than half of the students reported to have 100 books at home or less (59.6%) which serves as an indicator for students' resources for learning at home or their cultural capital. These descriptive characteristics of the sample suggest that the sample can be considered as similar to the representative German PIRLS 2016 elementary school sample with regard to language spoken at home (83.4% always or nearly always German) and number of books (53.5% 100 books or less at home; Hußmann et al., 2017).
In German elementary schools, each class has one (main) teacher. The 56 teachers of the FA(IR)BULOUS elementary school sample were mostly women (94.6%) and 44.56 years old on average (SD = 11.48). The teacher sample corresponds to the total population of primary school teachers in the federal state of Germany in which the study was conducted in terms of gender composition and age (Ministerium für Schule und Weiterbildung des Landes Nordrhein-Westfalen, 2016).
Measures
Students' Math Ability Self-Concept
Students' ability self-concept in math was assessed with a four-item short version of the validated German Scales for the Assessment of School-Related Competence Beliefs (SESSKO; Schöne et al., 2002). Each item was rated on a 5-point scale from 1 = totally disagree to 5 = totally agree. An example item is “In math I know a lot.” The reliability of the scale was high (Cronbach's alpha = 0.90).
Students' Math Competencies
Students' math competencies were assessed using the arithmetic subscale of the DEMAT 3+ (Deutscher Mathematiktest für dritte Klassen; Roick et al., 2004), a standardized German math competence test for third graders. The test consists of 15 arithmetic math tasks and had a good reliability (Cronbach's alpha = 0.82). In the following analyses, we used the raw sum score of the test. In addition, we provide the corresponding T-score, i.e., the score on a standardized scale with a M = 50 and SD = 10.
Teachers' Math Aptitude Ratings
Teachers indicated for each student how talented in math the student is compared with the total student population. Response options were 1 = far below average (ca. 2% of all students), 2 = below average (ca. 14% of all students), 3 = slightly below average (ca. 15.5% of all students), 4 = average (ca. 37% of all students), 5 = slightly above average (ca. 15.5% of all students), 6 = above average (ca. 14% of all students), and 7 = far above average (ca. 2% of all students).
Teachers' Math Brilliance Beliefs
For assessing teachers' math brilliance beliefs, we translated the four items of Leslie et al. (2015) from English to German and adopted them with regard to math and elementary school students. That means, that teachers were asked to indicate to which degree they believe that children need an innate ability to be successful in math. An example item is “If you want to succeed in math, hard work alone just won't cut it; for that, children need to have an innate gift or talent”. Teachers rated each item on a scale from 1 = strongly disagree to 7 = strongly agree. Cronbach's alpha was 0.76.
Procedure
This study was carried out in accordance with the recommendations of the German Research Foundation. In compliance with the guidelines established by the institutional ethic committee, participation was voluntary and parents' written informed consent was given before participation in accordance with the Declaration of Helsinki. Teachers were informed about the study during a staff meeting and declared their informed consent verbally. A formal ethics approval was not required by the TU Dortmund guidelines or German regulations. Data was collected during regular class hours by trained research assistants at the beginning of fourth grade. All self-report items were read aloud to make sure that all students understood the items and worked at the same speed.
Analytic Approach
We applied multilevel regression analyses in Mplus 8 (Muthén and Muthén, 1998-2017) with standard errors corrected for non-normality of variables (MLR). All continuous variables were grand-mean centered. Students' gender was coded 0 = female, 1 = male. Students' first language was coded 0 = German, 1 = other language.
In order to explore, whether teachers' math brilliance beliefs moderate the size of the gender gap in students' and teachers' aptitude ratings, we specified two cross-level interaction models with gender, teachers' math brilliance beliefs and their interaction terms as predictors of students' ability self-concept or teachers' aptitude rating, respectively. In a second step, we added students' math competencies, mother tongue and number of books as control variables to the model which all have been found to be related with students' motivation in prior research (e.g., Evans et al., 2010; Stanat et al., 2010; Ganley and Lubienski, 2016). Hypothesis 4 was tested in a lower level mediation model with teachers' aptitude ratings as a mediator of the effect of gender on students' ability self-concept.
The percentage of missing data was low. Information on gender was missing for 0.2%, number of books for 0.4%, math test scores for 3.4%, and teachers' aptitude ratings for 2.8% of the student sample. The data on class membership, students' ability self-concept, students' mother tongue, and teachers' math brilliance beliefs were complete. Little's MCAR test with all target variables included suggested missing completely at random, X2 = 11.47, df = 9, p = 0.245. Thus, the full information maximum likelihood algorithm (FIML) was applied to handle cases with missing values.
Results
Descriptive Statistics
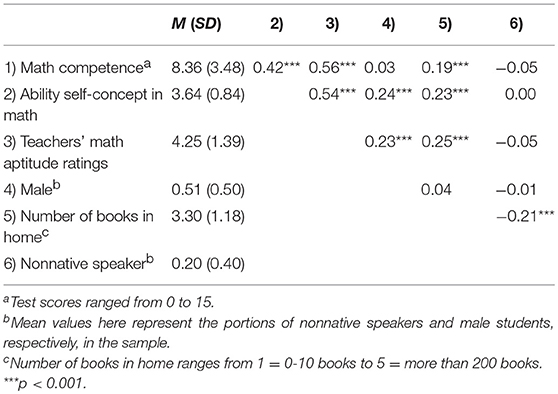
On average, students earned M = 8.36 (SD = 3.48) out of 15 points in the math competence test. This is equivalent to an average T-score of T = 47.81 (SD = 10.48) suggesting that, on average, students performed at the expected level. They further reported a positive ability self-concept, M = 3.64, SD = 0.84. Teachers' aptitude ratings had a mean of M = 4.25 (SD = 1.39). Bivariate correlations between the variables were medium to high. All means, standard deviations, and correlations are presented in Table 1.
Gender Differences in Math
As in prior studies (e.g., Herbert and Stipek, 2005), only negligible and statistically not significant differences between girls' and boys' scores on the math competence test were found; Girls: M = 8.26, SD = 3.42, boys: M = 8.47, SD = 3.53, t(798) = −0.85, p = 0.398, Cohen's d = 0.06. Nonetheless, moderate gender differences in students' ability self-concept and teachers' aptitude ratings were found. Boys reported a more positive ability self-concept than girls, corroborating Hypothesis 1; Girls M = 3.44, SD = 0.83, boys M = 3.84, SD = 0.80, t(826) = −7.15, p < 0.001, d = 0.50. Furthermore, also teachers rated boys as having more math talent than girls, supporting Hypothesis 2; Girls M = 3.03, SD = 1.39, boys M = 4.56, SD = 1.33, t(803) = −6.55, p < 0.001, d = 0.46.
Moderation by Teachers' Math Brilliance Beliefs
As reported in a previous study (Heyder et al., 2019), teachers on average perceived success in math as requiring a moderate amount of innate ability, M = 4.17, SD = 1.12. In order to explore whether this belief relates to the gender gap in students' ability self-concept and teachers' aptitude ratings, we ran two series of cross-level interaction models including different control variables (see Tables 2, 3).
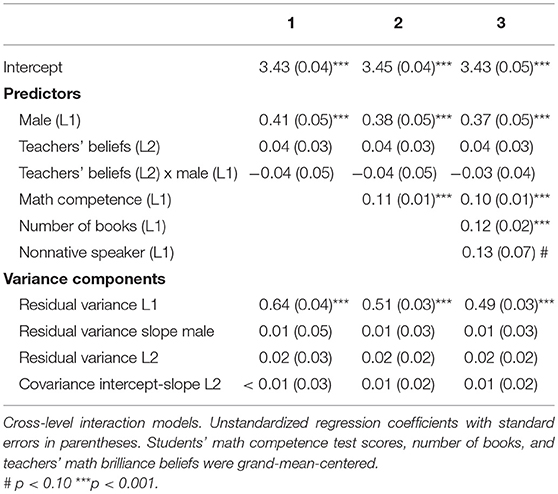
Table 2. Regression of students' ability self-concept in math on students' gender and teachers' math brilliance beliefs.
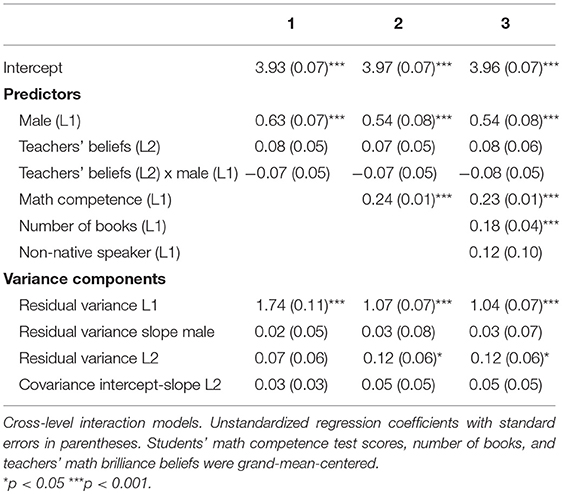
Table 3. Regression of teachers' aptitude ratings on students' gender and teachers' math brilliance beliefs.
As presented in Table 2, girls reported a less positive ability self-concept than boys. Teachers' math brilliance beliefs, however, did not predict students' ability self-concept or the gender gap in students' ability self-concept. Furthermore, there was no significant variation in the relation between gender and students' ability self-concept between classes. Students' math competencies and number of books at home predicted higher scores in students' ability self-concept. Controlling for these variables as well as students' mother tongue only slightly reduced the gender gap in students' ability self-concept. The non-significance of the cross-level interaction remained unaffected.
Table 3 shows the results for the regression analysis of teachers' aptitude ratings. Here again, being male predicted higher scores than being female. However, this gender difference in teachers' aptitude ratings was not related to teachers' belief whether math requires innate ability. That is, the cross-level interaction did not reach statistical significance. Moreover, there was no significant variation in the relation between gender and teachers' math aptitude ratings between classes. With regard to the control variables, students with higher math competences and students who reported a higher number of books at home were rated by the teachers as having higher math aptitude than other students. Controlling for students' math competence, number of books at home and mother tongue did not substantially change the results. Hypothesis 3 was thus not supported by the data.
Mediation by Teachers' Math Aptitude Ratings
The lack of significant variation in the relations between gender and (a) teachers' aptitude ratings, and (b) students' ability self-concept at Level 2 as well as the non-significant cross-level interaction effects suggested that teachers' brilliance beliefs do not moderate the relations in focus. Striving for a parsimonious model in order to ensure model convergence, we thus tested Hypothesis 4 in a lower level mediation model assuming all effects to be fixed. We did not control for actual math performance as we did not find any significant gender differences in the mathematical competency test. As presented in Table 4, all relations specified at Level 1 were statistically significant. Teachers rated boys' math aptitude as higher than girls, and teachers' aptitude ratings in turn predicted students' ability self-concept.
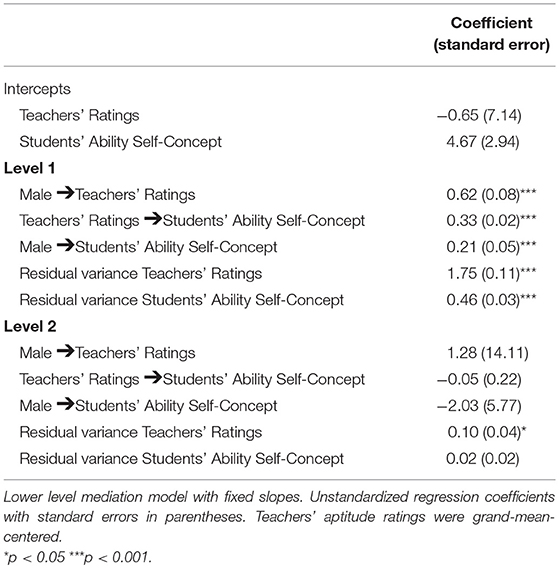
Table 4. Mediation of the effect of gender on students' math ability self-concept via teachers' aptitude ratings.
In support of our hypothesis, teachers' aptitude ratings mediated the effect of gender on students' ability self-concept within classes (indirect effect within = 0.20, SE = 0.03, p < 0.001). The results indicate that approximately half of the gender gap in students' ability self-concepts was statistically explained by teachers' aptitude ratings. No significant indirect effect was found at Level 2 (indirect effect between = −0.07, SE = 0.55, p = 0.905).
Discussion
Why do women end up pursuing less math-intensive careers than men? In this study, we aimed to explain gender differences in a powerful and early predictor of math-related achievement and career choices, that is elementary school students' ability self-concept (e.g., Eccles, 2011; Musu-Gillette et al., 2015). We focused on the role that teachers' beliefs play in gender differences in math ability self-concepts. More precisely, we were interested in exploring whether teachers' ascription of higher math talent to boys compared to girls might contribute to girls' lower ability self-concept in math. In addition, we tested whether teachers' belief that success in math requires an innate ability might be detrimental for girls' but not boys' self-concept of ability. Our analyses were based on an elementary school sample of teachers and fourth graders from Germany. In line with prior meta-analyses (e.g., Else-Quest et al., 2010; Reilly et al., 2015), only negligible gender differences in a standardized math competence test were found. Nonetheless, boys already reported a more positive ability self-concept in math than girls, supporting Hypothesis 1. This finding is in line with findings from earlier studies with elementary students (Tiedemann, 2000b; Fredricks and Eccles, 2002; Herbert and Stipek, 2005; Ganley and Lubienski, 2016; Gentrup and Rjosk, 2018). While male and female students did not differ in their standardized test performance, teachers described their male students as more talented in math than their female students, corroborating Hypothesis 2 and validating earlier studies on teachers' gender-bias in math (e.g., Li, 1999; Cimpian et al., 2016; Hand et al., 2017; Holder and Kessels, 2017; Gentrup and Rjosk, 2018). As expected in Hypotheses 4, these gender-biased aptitude ratings of the teachers proved to account for half of the gender gap in math ability self-concepts. Students at the end of elementary school seem to have internalized their teachers' gender bias in talent ascription in math, with the result that girls perceive their talent for math to be lower than boys. This is an alarming finding, given the importance of math ability self-concepts for future achievement and choices in STEM subjects (e.g., Wang and Degol, 2013; Musu-Gillette et al., 2015).
Based on the literature suggesting detrimental effects of brilliance beliefs for female students' aspirations in STEM (e.g., Leslie et al., 2015; Rattan et al., 2018), we further tested if teachers' brilliance beliefs had a more negative relation with girls' self-concept of ability in math than with boys'. However, our analysis found both boys' and girls' math ability self-concept to be unrelated to their teachers' brilliance beliefs, thus contradicting Hypothesis 3. Whereas such socially shared brilliance beliefs have been found to be related to female students' underrepresentation in STEM careers in higher education (e.g., Leslie et al., 2015; Rattan et al., 2018), our results suggest that teachers' brilliance beliefs may not play a role in explaining the gender gap in math ability self-concept in elementary school.
Several reasons might account for this. First, it is possible that teachers did not transfer their beliefs to the children, so students were not aware of these beliefs, which in turn could not influence their motivation. For instance, teachers might not communicate their beliefs to their students or students might not be able to decipher any messages conveying the respective beliefs (directly or via teaching practices). However, our finding that the students' math ability self-concept was related to the teacher's aptitude rating supports the validity of the expectancy-value model (e.g., Eccles et al., 1983). Moreover, research on teacher expectations has shown many times (e.g., Jussim et al., 2009) that such positive or negative assumptions of a student's (mathematical) abilities can be conveyed in the classroom by the actions of the teacher. In contrast, any deterrent effect of a teacher's brilliance belief on a specific student's ability self-concept seems to be more complicated or subtle and has to be conveyed via several, more abstract intermediate steps than the message “I think you are (not) good at math.”
Another possible explanation for the lacking interaction effect could be found in the understanding of the construct “math.” More precisely, elementary teachers seem to assume that innate ability is needed for children to succeed in “math” (in general), but they might not apply this belief to basic math in elementary school, considering basic math still as relatively easy and accessible not only to exceptional children. An earlier study with teachers from a variety of grade levels did ask separately about domain-specific beliefs toward advanced and basic math, but combined these two in their analyses (Patterson et al., 2016). Our study raises the question to be studied in future research if advanced math might elicit stronger brilliance beliefs than basic math.
Generally, the young age of the students in our study might be another factor explaining the independency of their math ability self-concept from their teachers' brilliance beliefs. Most importantly, younger children do not consistently differentiate the concepts of ability and of effort (Nicholls, 1990), what implies that messages of required innate ability might not result in the conclusion that effort would not help in order to succeed. Accordingly, at earlier ages, teachers' brilliance beliefs might not execute their full range of negative implications for girls compared to later ages. In addition, earlier research showed that even though first and second graders believed that success in an adult job requires more fixed ability in math than reading and writing, the children did not think that their own grades in math were depending more on fixed ability than their reading and writing grades (Gunderson et al., 2017), thus not yet applying the stereotypes on their own achievements.
And while in the U.S., children as young as six were found to endorse the stereotype that brilliant children are male (Bian et al., 2017), evidence from European countries is scarce. Most European studies with school students on the stereotyping of genius and “effortless achievement” as something male and masculine (Jackson, 2003; Jackson and Dempster, 2009; Heyder and Kessels, 2017) have so far concentrated on adolescents. State of research regarding the gender stereotyping of math in younger children is inconclusive, as some studies found implicit gender stereotyping at an early age (Cvencek et al., 2011), but others, using explicit measures, could not find these (Ambady et al., 2001). Research on the perception of adult stereotypes further indicates that Italian elementary school children thought that teachers viewed boys and girls similarly in math (Muzzatti and Agnoli, 2007) and that French fourth graders of each gender reported that people view their own gender as better in math (Martinot and Désert, 2007). A study from the U.S. however found that male, but not female, fourth graders perceived that adults believed that boys are better at math and science than girls (Kurtz-Costes et al., 2008). Taken together, the existing research on elementary school students and teachers seems to find more and stronger math brilliance beliefs and math-male stereotypes in the U.S. than in Europe. Thus, the role not only of students' age but also of the cultural background on math-related beliefs should be studied more explicitly in comparative studies in the future.
In this vein, this study is limited as it focused only on a German sample. Another limitation is its cross-sectional nature. Even if earlier research has shown that socializers' ability beliefs longitudinally predict children's self-concept of ability (Frome and Eccles, 1998; Lazarides and Watt, 2017), we cannot rule out that other mechanisms are behind the relationship between teachers' aptitude perceptions and children's ability self-concept found in our data. For instance, it is possible that a more positive ability self-concept signals to the teacher that this student is talented, while a negative ability self-concept might be interpreted by the teacher as a lack of talent. Thus, any implications for practice should be drawn and interpreted very cautiously. This study's finding that the gender gap in teachers' aptitude ratings was larger than in students' actual math competencies corroborates once more the prevalence of math-male stereotypes in teachers (see also e.g., Li, 1999; Tiedemann, 2002; Hand et al., 2017). Increasing teachers' awareness of their own math-male stereotypes and confronting them with the fact that average gender differences in math competencies are actually very small could be one approach to reduce teachers' math-male stereotypes leading to more accurate perceptions of boys' and girls' math aptitude. This could happen both during teacher education in universities as well as in professional development courses for in-service teachers. Reducing a potential gender bias in elementary school teachers' aptitude perceptions seems also a fruitful means for increasing girls' participation in STEM particularly in Germany because in Germany teachers give tracking recommendations at the end of elementary school, and these have also been found to be predicted by teachers' gender stereotypes (Nürnberger et al., 2016).
Above and beyond testing the research questions derived above from this study's results, future research should study in more detail—and longitudinally—how domain specific brilliance beliefs develop in children. It would be interesting to understand how the emergence of brilliance beliefs in children relates to their ability self-concept as well as to both the emergence of a compensatory concept of effort and ability and to the emergence of a general view on intelligence as fixed. Teachers' entity theories can be both comforting and demotivating for their students (Rattan et al., 2012), and from early adolescence on, girls report lower incremental views on intelligence than boys (Diseth et al., 2014). As the belief that success in a given domain requires innate ability goes along with an underrepresentation of female persons, it is most crucial to understand from what age on children actually infer from their socializers' brilliance beliefs that their own striving for success in math may be useless, and if girls might gain this understanding even earlier than boys might.
Ethics Statement
This study was carried out in accordance with the recommendations of the German Research Foundation. In compliance with the guidelines established by the institutional ethic committee, participation was voluntary and parents' written informed consent was given before participation in accordance with the Declaration of Helsinki. An institutional approval of the protocol by the university ethics board is not typically required for projects of this type.
Author Contributions
AH and RS contributed conception and design of the study. AH provided a first draft of the manuscript and finalized the paper. RS and UK wrote sections of the manuscript and gave valuable feedback on the first draft.
Funding
The research reported in this article is based on the project FA(IR)BULOUS – FAIRe BeUrteilung des LeistungspOtenzials Unterprivilegierter Schülerinnen und Schüler; Fair Evaluation of underprivileged students' potential. The project was funded by the Stiftung Mercator (Foundation Mercator). Furthermore, we acknowledge financial support by Deutsche Forschungsgemeinschaft and Technische Universität Dortmund/TU Dortmund Technical University within the funding programme Open Access Publishing.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Ambady, N., Shih, M., Kim, A., and Pittinsky, T. L. (2001). Stereotype susceptibility in children: effects of identity activation on quantitative performance. Psychol. Sci. 12, 385–390. doi: 10.1111/1467-9280.00371
Bennett, R. E., Gottesman, R. L., Rock, D. A., and Cerullo, F. (1993). Influence of behavior perceptions and gender on teachers' judgments of students' academic skill. J. Educ. Psychol. 85, 347–356.
Bergold, S., Wendt, H., Kasper, D., and Steinmayr, R. (2017). Academic competencies: their interrelatedness and gender differences at their high end. J. Educ. Psychol. 109, 439–449. doi: 10.1037/edu0000140
Bian, L., Leslie, S.-J., and Cimpian, A. (2017). Gender stereotypes about intellectual ability emerge early and influence children's interests. Science 355, 389–391. doi: 10.1126/science.aah6524
Bian, L., Leslie, S.-J., Murphy, M. C., and Cimpian, A. (2018). Messages about brilliance undermine women's interest in educational and professional opportunities. J. Exp. Soc. Psychol. 18, 404–420. doi: 10.1016/j.jesp.2017.11.006
Brunner, M., Krauss, S., and Kunter, M. (2008). Gender differences in mathematics: does the story need to be rewritten? Intelligence 36, 403–421. doi: 10.1016/j.intell.2007.11.002
Chatard, A., Guimond, S., and Selimbegovic, L. (2007). “How good are you in math?” the effect of gender stereotypes on students' recollection of their school marks. J. Exp. Soc. Psychol. 43, 1017–1024. doi: 10.1016/j.jesp.2006.10.024
Chestnut, E., Lei, R., Leslie, S.-J., and Cimpian, A. (2018). The myth that only brilliant people are good at math and its implications for diversity. Educ. Sci. 8:65. doi: 10.3390/educsci8020065
Cimpian, J. R., Lubienski, S. T., Timmer, J. D., Makowski, M. B., and Miller, E. K. (2016). Have gender gaps in math closed? Achievement, teacher perceptions, and learning behaviors across two ECLS-K cohorts. AERA Open 2, 1–19. doi: 10.1177/2332858416673617
Cvencek, D., Kapur, M., and Meltzoff, A. N. (2015). Math achievement, stereotypes, and math self-concepts among elementary-school students in Singapore. Learn. Instruct. 39, 1–10. doi: 10.1016/j.learninstruc.2015.04.002
Cvencek, D., Meltzoff, A. N., and Greenwald, A. G. (2011). Math-gender stereotypes in elementary school children. Child Dev. 82, 766–779. doi: 10.1111/j.1467-8624.2010.01529.x
Dickhäuser, O., and Stiensmeier-Pelster, J. (2003). Wahrgenommene Lehrereinschätzungen und das Fähigkeitsselbstkonzept von Jungen und Mädchen in der Grundschule. [Perceptions of teacher evaluations and the academic self-concept of boys and girls in elementary school]. Psychologie in Erziehung und Unterricht 50, 182–190.
Diseth, Å., Meland, E., and Breidablik, H. J. (2014). Self-beliefs among students: Grade level and gender differences in self-esteem, self-efficacy and implicit theories of intelligence. Learn. Individ. Differ. 35, 1–8. doi: 10.1016/j.lindif.2014.06.003
Dweck, C. S. (2007). “Is math a gift? beliefs that put females at risk,” in Why aren't More Women in Science?: Top Researchers Debate the Evidence, eds S. J. Ceci and W. M. Williams (Washington, DC: American Psychological Association), 47–55.
Eccles, J. S. (2011). Gendered educational and occupational choices: applying the Eccles et al. model of achievement-related choices. Int. J. Behav. Dev. 35, 195–201. doi: 10.1177/0165025411398185
Eccles, J. S., Adler, T. F., Futterman, R., Goff, S. B., Kaczala, C. M., Meece, J. L., et al. (1983). “Expectancies, values, and academic behaviors,”. in A Series of Books in Psychology. Achievement and Achievement Motives. Psychological and Sociological Approaches eds J. T. Spence (San Francisco, CA: W.H. Freeman), 76–146.
Eccles, J. S., and Wigfield, A. (2002). Motivational beliefs, values, and goals. Annu. Rev. Psychol. 53, 109–132. doi: 10.1146/annurev.psych.53.100901.135153
Else-Quest, N. M., Hyde, J. S., and Linn, M. C. (2010). Cross-national patterns of gender differences in mathematics: a meta-analysis. Psychol. Bull. 136, 103–127. doi: 10.1037/a0018053
Ertl, B., Luttenberger, S., and Paechter, M. (2017). The impact of gender stereotypes on the self-concept of female students in STEM subjects with an under-representation of females. Front. Psychol. 8:703. doi: 10.3389/fpsyg.2017.00703
Evans, M. D. R., Kelley, J., Sikora, J., and Treiman, D. J. (2010). Family scholarly culture and educational success: books and schooling in 27 nations. Res. Soc. Stratif. Mobil. 28, 171–197. doi: 10.1016/j.rssm.2010.01.002
Fennema, E., Peterson, P. L., Carpenter, T. P., and Lubinski, C. A. (1990). Teachers' attributions and beliefs about girls, boys, and mathematics. Educ. Stud. Math. 21, 55–69. doi: 10.1007/BF00311015
Fredricks, J. A., and Eccles, J. S. (2002). Children's competence and value beliefs from childhood through adolescence: growth trajectories in two male-sex-typed domains. Dev. Psychol. 38, 519–533. doi: 10.1037/0012-1649.38.4.519
Frome, P. M., and Eccles, J. S. (1998). Parents' influence on children's achievement-related perceptions. J. Pers. Soc. Psychol. 74:435. doi: 10.1037/0022-3514.74.2.435
Ganley, C. M., and Lubienski, S. T. (2016). Mathematics confidence, interest, and performance: examining gender patterns and reciprocal relations. Learn. Individ. Differ. 47, 182–193. doi: 10.1016/j.lindif.2016.01.002
Gentrup, S., and Rjosk, C. (2018). Pygmalion and the gender gap: Do teacher expectations contribute to differences in achievement between boys and girls at the beginning of schooling? Edu. Res. Eval. 18, 1–29. doi: 10.1080/13803611.2018.1550840
Greenwald, A. G., McGhee, D. E., and Schwartz, J. L. K. (1998). Measuring individual differences in implicit cognition: the implicit association test. J. Pers. Soc. Psychol. 74, 1464–1480. doi: 10.1037/0022-3514.74.6.1464
Gunderson, E. A., Hamdan, N., Sorhagen, N. S., and D'Esterre, A. P. (2017). Who needs innate ability to succeed in math and literacy? academic-domain-specific theories of intelligence about peers versus adults. Dev. Psychol. 53, 1188–1205. doi: 10.1037/dev0000282
Gunderson, E. A., Ramirez, G., Levine, S. C., and Beilock, S. L. (2012). The role of parents and teachers in the development of gender-related math attitudes. Sex Roles 66, 153–166. doi: 10.1007/s11199-011-9996-2
Hand, S., Rice, L., and Greenlee, E. (2017). Exploring teachers' and students' gender role bias and students' confidence in STEM fields. Soc. Psychol. Educ. 20, 929–945. doi: 10.1007/s11218-017-9408-8
Herbert, J., and Stipek, D. (2005). The emergence of gender differences in children's perceptions of their academic competence. J. Appl. Dev. Psychol. 26, 276–295. doi: 10.1016/j.appdev.2005.02.007
Heyder, A., and Kessels, U. (2017). Boys don't work? On the psychological benefits of showing low effort in high school. Sex Roles 77, 72–85. doi: 10.1007/s11199-016-0683-1
Heyder, A., Weidinger, A. F., Cimpian, A., and Steinmayr, R. (2019). Teachers' belief that math requires innate ability predicts lower intrinsic motivation among low-achieving students. Manuscript submitted for publication.
Holder, K., and Kessels, U. (2017). Gender and ethnic stereotypes in student teachers' judgments: a new look from a shifting standards perspective. Soc. Psychol. Educ. 20, 471–490. doi: 10.1007/s11218-017-9384-z
Hußmann, A., Wendt, H., Bos, W., Bremerich-Vos, A., Kasper, D., and Lankes, E.-M. (eds.) (2017). IGLU 2016: Lesekompetenzen von Grundschulkindern in Deutschland im Internationalen Vergleich [Elementary School Students' Reading Competencies in Germany in International Comparision]. Münster: Waxmann.
Hyde, J. S. (2005). The gender similarities hypothesis. Am. Psychol. 60, 581–592. doi: 10.1037/0003-066X.60.6.581
Jackson, C. (2003). Motives for ’laddishness’ at school: fear of failure and fear of the ’feminine’. Br. Educ. Res. J. 29, 583–598. doi: 10.1080/01411920301847
Jackson, C., and Dempster, S. (2009). ‘I sat back on my computer … with a bottle of whisky next to me’: constructing ‘cool’ masculinity through ‘effortless’ achievement in secondary and higher education. J. Gender Stud. 18, 341–356. doi: 10.1080/09589230903260019
Jussim, L., Robustelli, S., and Cain, T. (2009). “Teacher expectations and self-fulfilling prophecies,” in Handbook of motivation at school, eds A. Wigfield and K. Wentzel (Mahwah, NJ: Erlbaum), 349–380.
Keller, C. (2001). Effect of teachers' stereotyping on students' stereotyping of mathematics as a male domain. J. Soc. Psychol. 141, 165–173. doi: 10.1080/00224540109600544
Kessels, U. (2015). Bridging the gap by enhancing the fit: How stereotypes about STEM clash with stereotypes about girls. Int. J. Gender Sci. Technol. 7, 280–296.
Kessels, U., Heyder, A., Latsch, M., and Hannover, B. (2014). How gender differences in academic engagement relate to students' gender identity. Educ. Res. 56, 219–228. doi: 10.1080/00131881.2014.898916
Kurtz-Costes, B., Rowley, S. J., Harris-Britt, A., and Woods, T. A. (2008). Gender stereotypes about mathematics and science and self-perceptions of ability in late childhood and early adolescence. Merrill Palmer Q. 54, 386–409. doi: 10.1353/mpq.0.0001
Lane, K. A., Goh, J. X., and Driver-Linn, E. (2012). Implicit science stereotypes mediate the relationship between gender and academic participation. Sex Roles 66, 220–234. doi: 10.1007/s11199-011-0036-z
Lazarides, R., and Watt, H. M. (2017). Student-perceived mothers' and fathers' beliefs, mathematics and english motivations, and career choices. J. Res. Adolesc. 27, 826–841. doi: 10.1111/jora.12317
Leslie, S.-J., Cimpian, A., Meyer, M., and Freeland, E. (2015). Expectations of brilliance underlie gender distributions across academic disciplines. Science 347, 262–265. doi: 10.1126/science.1261375
Li, Q. (1999). Teachers' beliefs and gender differences in mathematics: a review. Educ. Res. 41, 63–76. doi: 10.1080/0013188990410106
Lorenz, G., Gentrup, S., Kristen, C., Stanat, P., and Kogan, I. (2016). Stereotype bei Lehrkräften? eine untersuchung systematisch verzerrter lehrererwartungen. [stereotypes among teachers? a study of systematic bias in teacher expectations]. Kölner Z. Soziol. Sozialpsychol. 68, 89–111. doi: 10.1007/s11577-015-0352-3
Martinot, D., and Désert, M. (2007). Awareness of a gender stereotype, personal beliefs and self-perceptions regarding math ability: when boys do not surpass girls. Soc. Psychol. Educ. 10, 455–471. doi: 10.1007/s11218-007-9028-9
McKown, C., and Weinstein, R. S. (2002). Modeling the role of child ethnicity and gender in children's differential response to teacher expectations. J. Appl. Soc. Psychol. 32, 159–184. doi: 10.1111/j.1559-1816.2002.tb01425.x
Meyer, M., Cimpian, A., and Leslie, S. J. (2015). Women are underrepresented in fields where success is believed to require brilliance. Front. Psychol. 6:235. doi: 10.3389/fpsyg.2015.00235
Ministerium für Schule und Weiterbildung des Landes Nordrhein-Westfalen (2016). Das Schulwesen in Nordrhein-Westfalen aus Quantitativer Sicht 2015/16 [A Quantitative Perspective on Schools in North Rhine-Westphalia 2015/16]. Available online at: https://www.schulministerium.nrw.de/docs/bp/Ministerium/Service/Schulstatistik/Amtliche-Schuldaten/Quantita_2015.pdf (accessed January 7, 2019).
Mullis, I. V. S., Martin, M. O., Foy, P., and Hooper, M. (2016). TIMSS 2015 International Results in Mathematics. Boston, MA: TIMSS & PIRLS International Study Center.
Musu-Gillette, L., Wigfield, A., Harring, J., and Eccles, J. S. (2015). Trajectories of change in students' self-concepts of ability and values in math and college major choice. Educ. Res. Eval. 21, 343–370. doi: 10.1080/13803611.2015.1057161
Muthén, L. K., and Muthén, B. O. (1998-2017). Mplus User's Guide, 8th Edn. Los Angeles, CA: Muthén & Muthén.
Muzzatti, B., and Agnoli, F. (2007). Gender and mathematics: attitudes and stereotype threat susceptibility in Italian children. Dev. Psychol. 43, 747–759. doi: 10.1037/0012-1649.43.3.747
Nicholls, J. G. (1990). “What is ability and why are we mindful of it? A developmental perspective,” in Competence Considered, eds R. J. Sternberg and J. Kolligian (New Haven, CT: Yale University Press), 11–40.
Nosek, B. A., Banaji, M. R., and Greenwald, A. G. (2002). Math = male, me = female, therefore math ≠ me. J. Pers. Soc. Psychol. 83, 44–59. doi: 10.1037/0022-3514.83.1.44
Nosek, B. A., and Smyth, F. L. (2011). Implicit social cognitions predict sex differences in math engagement and achievement. Am. Educ. Res. J. 48, 1125–1156. doi: 10.3102/0002831211410683
Nürnberger, M., Nerb, J., Schmitz, F., Keller, J., and Sütterlin, S. (2016). Implicit gender stereotypes and essentialist beliefs predict preservice teachers' tracking recommendations. J. Exp. Educ. 84, 152–174. doi: 10.1080/00220973.2015.1027807
Passolunghi, M. C., Rueda Ferreira, T. I., and Tomasetto, C. (2014). Math–gender stereotypes and math-related beliefs in childhood and early adolescence. Learn. Individ. Differ. 34, 70–76. doi: 10.1016/j.lindif.2014.05.005
Patterson, M. M., Kravchenko, N., Chen-Bouck, L., and Kelley, J. A. (2016). General and domain-specific beliefs about intelligence, ability, and effort among preservice and practicing teachers. Teach. Teach. Educ. 59, 180–190. doi: 10.1016/j.tate.2016.06.004
Rattan, A., Good, C., and Dweck, C. S. (2012). “It's ok — Not everyone can be good at math”: instructors with an entity theory comfort (and demotivate) students. J. Exp. Soc. Psychol. 48, 731–737. doi: 10.1016/j.jesp.2011.12.012
Rattan, A., Savani, K., Komarraju, M., Morrison, M. M., Boggs, C., and Ambady, N. (2018). Meta-lay theories of scientific potential drive underrepresented students' sense of belonging to science, technology, engineering, and mathematics (STEM). J. Pers. Soc. Psychol. 115, 54–75. doi: 10.1037/pspi0000130
Reilly, D. (2012). Gender, culture, and sex-typed cognitive abilities. PLoS ONE 7:e39904. doi: 10.1371/journal.pone.0039904
Reilly, D., Neumann, D. L., and Andrews, G. (2015). Sex differences in mathematics and science achievement: a meta-analysis of national assessment of educational progress assessments. J. Educ. Psychol. 107, 645–662. doi: 10.1037/edu0000012
Retelsdorf, J., Schwartz, K., and Asbrock, F. (2015). “Michael can't read!” Teachers' gender stereotypes and boys' reading self-concept. J. Educ. Psychol. 107, 186–194. doi: 10.1037/a0037107
Riegle-Crumb, C., King, B., Grodsky, E., and Muller, C. (2012). The more things change, the more they stay the same? prior achievement fails to explain gender inequality in entry into STEM college majors over time. Am. Educ. Res. J. 49, 1048–1073. doi: 10.3102/0002831211435229
Roick, T., Gölitz, D., and Hasselhorn, M. (2004). Deutscher Mathematiktest für dritte Klassen DEMAT 3+ [German math test for third graders]. Göttingen: Hogrefe Publishing.
Schöne, C., Dickhäuser, O., Spinath, B., and Stiensmeier-Pelster, J. (2002). SESSKO Skalen zur Erfassung des schulischen Selbstkonzept [Scales for the Assessment of School-Related Competence Beliefs]. Göttingen: Hogrefe.
Simpkins, S. D., Fredricks, J. A., and Eccles, J. S. (2015). The role of parents in the ontogeny of achievement-related motivation and behavioral choices: IV. child factors and parent belief models. Monogr. Soc. Res. Child Dev. 80, 65–84. doi: 10.1111/mono.12160
Smeding, A. (2012). Women in science, technology, engineering, and mathematics (STEM): an investigation of their implicit gender stereotypes and stereotypes' connectedness to math performance. Sex Roles 67, 617–629. doi: 10.1007/s11199-012-0209-4
Stanat, P., Segeritz, M., and Christensen, G. (2010). “Schulbezogene Motivation und Aspiration von Schülerinnen und Schülern mit Migrationshintergrund [School-related motivation and aspiration of students with migration background],” in Schulische Lerngelegenheiten und Kompetenzentwicklung. Festschrift für Jürgen Baumert, eds W. Bos, E. Klieme, and O. Köller (Münster: Waxmann.), 31–57.
Steffens, M. C., and Jelenec, P. (2011). Separating implicit gender stereotypes regarding math and language: Implicit ability stereotypes are self-serving for boys and men, but not for girls and women. Sex Roles 64, 324–335. doi: 10.1007/s11199-010-9924-x
Steffens, M. C., Jelenec, P., and Noack, P. (2010). On the leaky math pipeline: comparing implicit math-gender stereotypes and math withdrawal in female and male children and adolescents. J. Educ. Psychol. 102, 947–963. doi: 10.1037/a0019920
Steinmayr, R., Michels, J., and Weidinger, A. (2017). Fa(ir)bulous: Faire Beurteilungen des Leistungspotenzials von Schülerinnen und Schülern [Fa(ir)bulous- Fair Judgments of Students' Academic Potential]. Dortmund: Technische Universität Dortmund.
Storage, D., Horne, Z., Cimpian, A., and Leslie, S.-J. (2016). The frequency of “brilliant” and “genius” in teaching evaluations predicts the representation of women and African Americans across fields. PLoS ONE 11:e0150194. doi: 10.1371/journal.pone.0150194
Tiedemann, J. (2000a). Gender-related beliefs of teachers in elementary school mathematics. Educ. Stud. Math. 41, 191–207. doi: 10.1023/A:1003953801526
Tiedemann, J. (2000b). Parents' gender stereotypes and teachers' beliefs as predictors of children's concept of their mathematical ability in elementary school. J. Educ. Psychol. 92, 144–151. doi: 10.1037/0022-0663.92.1.144
Tiedemann, J. (2002). Teachers' gender stereotypes as determinants of teacher perceptions in elementary school mathematics. Educ. Stud. Math. 50, 49–62. doi: 10.1023/A:1020518104346
Tomasetto, C., Mirisola, A., Galdi, S., and Cadinu, M. (2015). Parents' math–gender stereotypes, children's self-perception of ability, and children's appraisal of parents' evaluations in 6-year-olds. Contemp. Educ. Psychol. 42, 186–198. doi: 10.1016/j.cedpsych.2015.06.007
Wang, M.-T., and Degol, J. (2013). Motivational pathways to STEM career choices: using expectancy-value perspective to understand individual and gender differences in STEM Fields. Dev. Rev. 33, 304–340. doi: 10.1016/j.dr.2013.08.001
Wang, M.-T., and Degol, J. L. (2016). Gender gap in science, technology, engineering, and mathematics (STEM): current knowledge, implications for practice, policy, and future directions. Educ. Psychol. Rev. 29, 119–140. doi: 10.1007/s10648-015-9355-x
Wigfield, A., Eccles, J. S., Yoon, K. S., Harold, R. D., Arbreton, A. J. A., Freedman-Doan, C., et al. (1997). Change in children's competence beliefs and subjective task values across the elementary school years: a 3-year study. J. Educ. Psychol. 89, 451–469. doi: 10.1037/0022-0663.89.3.451
Wilde, A., and Diekman, A. B. (2005). Cross-cultural similarities and differences in dynamic stereotypes: a comparison between Germany and the United States. Psychol. Women Q. 29, 188–196. doi: 10.1111/j.1471-6402.2005.00181.x
Keywords: gender differences, ability self-concept, math, teacher beliefs, implicit theories, elementary school
Citation: Heyder A, Steinmayr R and Kessels U (2019) Do Teachers' Beliefs About Math Aptitude and Brilliance Explain Gender Differences in Children's Math Ability Self-Concept? Front. Educ. 4:34. doi: 10.3389/feduc.2019.00034
Received: 08 January 2019; Accepted: 08 April 2019;
Published: 17 May 2019.
Edited by:
Manuela Paechter, University of Graz, AustriaReviewed by:
Gerardo Ramirez, University of California, Los Angeles, United StatesDreisiebner Gernot, University of Graz, Austria
Copyright © 2019 Heyder, Steinmayr and Kessels. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anke Heyder, YW5rZS5oZXlkZXJAdHUtZG9ydG11bmQuZGU=
 Anke Heyder
Anke Heyder Ricarda Steinmayr
Ricarda Steinmayr Ursula Kessels2
Ursula Kessels2