- Department of Curriculum and Instruction, College of Education, University of Houston, Houston, TX, United States
Many preservice teachers (PSTs) enter mathematics methods courses with fixed beliefs about teaching and learning mathematics and their own abilities as doers of mathematics. Using a repeated measures design, I examined changes in PSTs’ beliefs about mathematics teaching and learning at three separate time points-at the beginning of the first semester of a growth mindset-oriented mathematics methods course, midway through the treatment at the end of the first semester, and at the conclusion of the treatment at the end of the second semester of mathematics methods that was forced to pivot to online learning due to the COVID-19 pandemic. Results showed that explicit teaching of growth mindset principles coupled with participation in growth mindset-oriented mathematics methods courses yielded statistically significant improvement for PSTs’ beliefs about Rules and Procedures, Process of Inquiry, Active Learning, and Fixed Ability as measured by the TEDS-M instrument and did not appear to be impacted by the pivot to remote learning. Comparison of a pre-pandemic cohort with the pandemic-disrupted cohort showed no statistically significant difference in Fixed Ability. These findings suggest that resilience, one of the hallmarks of the growth mindset, may serve as a protective asset during periods of profound stress.
Introduction
Fixed mindsets about mathematics teaching and learning held by preservice teachers (PSTs) can impede their developing content and pedagogical knowledge. Dweck (2006) defines mindset as a self-perception people hold about malleability and their brain’s ability to grow and improve. Like all people, a PST’s fixed mindset about mathematical abilities may limit achievement. Many PSTs do not consider themselves to be “good at math.” Research has helped to debunk many myths about who is or is not a math person. For example, neuroscience reveals that the brain’s plasticity allows for growth and change in response to appropriate stimuli and experiences (Maguire et al., 2000). Also, a growing body of research on mindset shows that learning and achievement improve when people transform their perception of themselves as math learners from fixed to growth (Aronson et al., 2002; Blackwell et al., 2007). Students possessing what Boaler (2016b) terms a mathematical mindset achieve at higher levels than those with a fixed mindset (Claro et al., 2016). Differences in achievement may stem from how individuals with differing mindsets respond to mistakes in mathematics. Brain research shows that when confronted with a mistake, synapses in a fixed mindset individual’s brain fire less frequently that those in the brain of a growth mindset individual. The growth mindset individual’s brain engages with the mistake, trying to understand and learn from the error, but the fixed mindset brain remains comparatively static. Simply put—fewer neural connections means less learning (Moser et al., 2011). Thus, adopting a growth mindset increases our brain’s ability to understand mathematics by persisting when it becomes challenging. Another area of research indicates that expanding students’ beliefs about the nature of mathematics itself has positive effects on learning and achievement. Boaler and Zoido (2016) reported that students whose mathematics experiences moved beyond rote procedures and memorization to include grappling with challenging ideas, deep conceptual learning, and creative thinking showed higher achievement than those who characterized mathematics as a series of rules, formulas, and procedures. Most significant to teacher educators, explicit teaching of mathematical mindset principles can alter mindsets (Boaler et al., 2018).
Design
This paper describes the results of a repeated measure design examining the impact of participation in growth mindset-oriented mathematics methods courses coupled with explicit teaching of growth mindset on PSTs’ beliefs and mindsets as measured by the TEDS-M 2008 User Guide for the International Database: Supplement 3 (Brese and Tatto, 2012). The Supplementary Material contains the full survey instrument. PSTs selected responses using a 5-point Likert scale for items from the following categories:
• The Nature of Mathematics – Rules and Procedures (5 items). Example: Mathematics is a collection of rules and procedures that prescribe how to solve a problem. The Nature of Mathematics – Process of Inquiry (6 items). Example: Mathematical problems can be solved correctly in many ways.
• Beliefs about Learning Mathematics – Teacher Direction (8 items). Example: Hands-on mathematics experiences aren’t worth the time and expense. Learning Mathematics – Active Learning (6 items). Example: It is helpful for students to discuss different ways to solve particular problems.
• Mathematics Achievement – Fixed Ability (8 items). Example: Mathematics is a subject in which natural ability matters a lot more than effort.
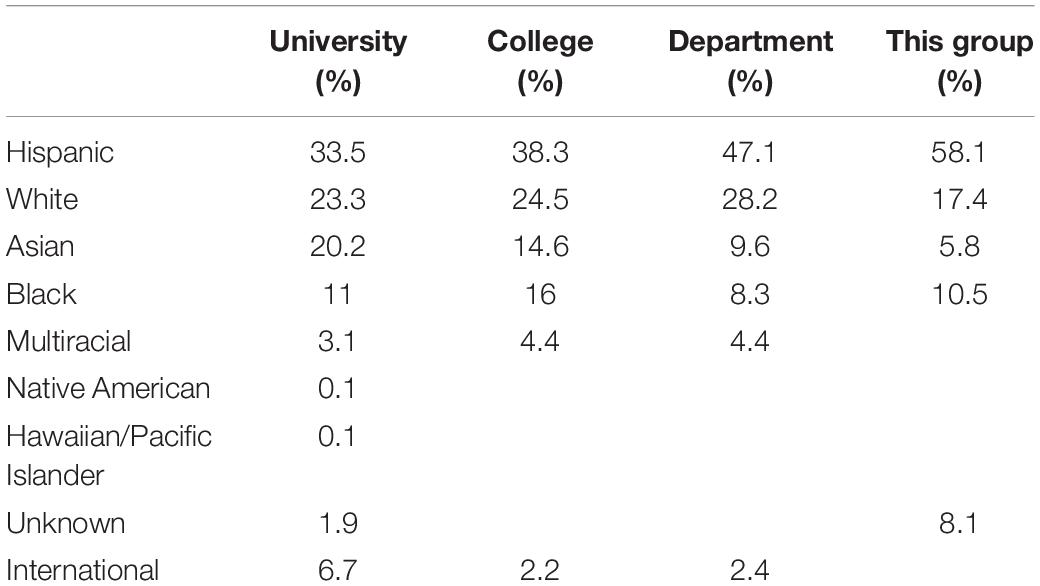
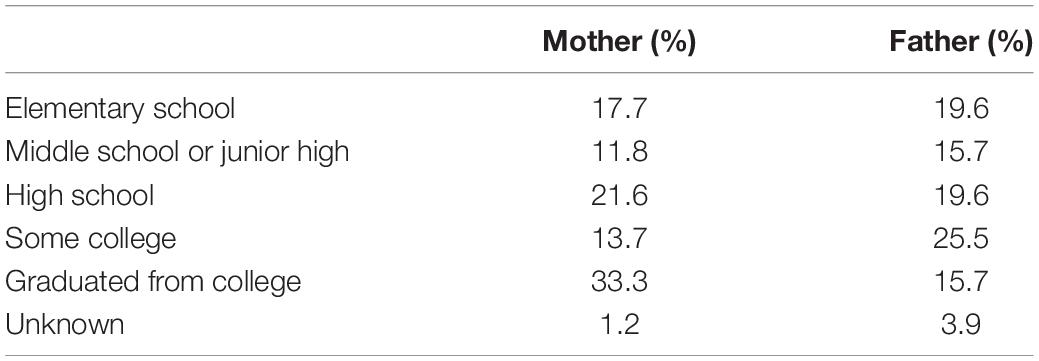
The study, conducted at a large urban university, included PSTs (N = 86) who were enrolled sequentially in two elementary mathematics methods courses required for their undergraduate elementary teacher certification program. I taught the methods courses concurrently with the PSTs’ two-semester student teaching internship in public prekindergarten through sixth grade classrooms. PSTs spent 4 days a week in field work and 1 day in methods classes at the university. I taught the first semester classes face-to-face, providing PSTs with 42 h of instruction. PSTs received 24 h of in-person instruction during the second semester until the COVID-19 pandemic required transition to online instruction for the remaining 6 weeks of the course. The majority (58%) of participants were Hispanic females. Sixty percent of participants were first generation college students. The mean age of participants was 23 years. Tables 1, 2 provide additional demographic information for participants including parental educational levels.
The elementary mathematics methods courses followed recommendations from the Essential Elements of Effective Mathematics Classrooms as outlined in the National Council of Teachers of Mathematics (2014) Principles to Actions. These elements include the following practices:
• Establish mathematics goals to focus learning.
• Implement tasks that promote reasoning and problem solving.
• Use and connect mathematical representations.
• Facilitate meaningful mathematical discourse.
• Pose purposeful questions.
• Build procedural fluency from conceptual understanding.
• Support productive struggle in learning mathematics.
• Elicit and use evidence of student thinking.
As part of their coursework, PSTs completed field-based assignments for inquiry-based instruction implementing the 5E Instructional Model (Bybee and Landes, 1990) and 3 Act Tasks (Meyer, 2015; Fletcher, 2016). They conducted a whole-group discussion with a Number Talk (Parrish, 2014) and a small-group lesson guided by Math Workshop (Lempp, 2020). They also assessed an elementary student’s mathematical thinking using a Cognitively Guided Instruction interview (Carpenter et al., 2015). Though not commonly classified as growth mindset-oriented, these teaching experiences provided PSTs with opportunities to enact feedback, language, and expectations for learners that aligned with growth mindset principles.
Preservice teachers also received explicit instruction in growth mindset through a series of six 45- to 60-min lessons spread over the two semesters. The Supplementary Material addendum includes the complete Growth Mindset Curriculum. These lessons sought to help PSTs become familiar with mindset research, examine the effects of mindset on learning, and explore ways to adopt growth mindset language and behaviors in classroom scenarios. In lesson one, PSTs learned about malleability and contrasted traits such as height (not malleable) and mathematical ability (malleable). PSTs watched and discussed Jo Boaler’s TEDx Stanford Talk “How You Can Be Good at Math and Other Surprising Facts about Learning” (Boaler, 2016a, May). PSTs recorded personal math anxieties on paper and symbolically shredded the papers before tossing them in the trash and pledging to adopt a growth mindset while in math methods classes. In lesson two, PSTs watched Carole Dweck’s TED Talk “The Power of Believing You Can Improve (2014).” They collaborated to contrast characteristics of growth and fixed mindsets. Lesson three placed PSTs in small groups to create posters focused on prompts related to attitudes, goals, and behaviors of fixed and growth mindset individuals. For example, one group discussed the following equity statement from the National Council of Teachers of Mathematics (2014) Principles to Actions: “An excellent mathematics program requires that all students have access to a high-quality mathematics curriculum, effective teaching and learning, high expectations, and the support and resources needed to maximize their learning potential” (p. 59). The group then wrote If/Then statements to explore the relationship between equity and mathematical mindsets. For example, if schools track second language learners into lower math classes, then those students miss out on math curriculum at higher levels. Lesson four focused on teacher language to support mathematical mindsets in the elementary classroom. PSTs revised fixed mindset phrases like “You’re so smart” with alternatives such as “You should feel proud that you stuck with the assignment even though it was tough.” PSTs designed posters with growth mindset phrases and read their posters aloud to create a video shared on social media. The posters were displayed on the classroom walls and the instructor’s university office door. For lesson five, PSTs applied growth mindset actions to challenging classroom scenarios and student teaching obstacles. Working in small groups, they brainstormed growth mindset responses to common challenges such as a university supervisor giving critical feedback or elementary students giving up on extended math problems. Lesson six was completed virtually as the pandemic necessitated moving from face-to-face to remote learning. PSTs watched videos of a math class where Dr. Deborah Ball promoted productive struggle through classroom discussion (Mathematics Teaching and Learning to Teach, 2010) and Angela Duckworth’s TedTalk “Grit: The Power of Passion and Perseverance” (2013). PSTs then reflected on ways in which mathematical mindsets were supported or inhibited by policies, procedures, and expectations in their field placement. Debriefing this lesson was completed via the discussion board feature of Blackboard. PSTs uploaded their observations and reflections after which classmates and the instructor responded to the posts.
Changes in Beliefs About Mathematics Teaching and Learning
Using a repeated measures design, I explored changes in PSTs’ beliefs about mathematics teaching and learning at three separate time points. PSTs completed the survey at the beginning of the first semester of math methods (Time 1), midway through the treatment at the conclusion of the first semester (Time 2), and at the conclusion of the treatment at the end of the second semester (Time 3). PSTs completed the three administrations of the survey as part of the regular course activities using a Google form. I reverse coded survey items as necessary prior to data analysis. For example, the Teacher Direction survey item that states, “Hands-on mathematics experiences aren’t worth the time and expense” was reverse coded to ensure correct scoring of the Likert scale responses. I carried out this study according to the university’s Institutional Review Board guidelines.
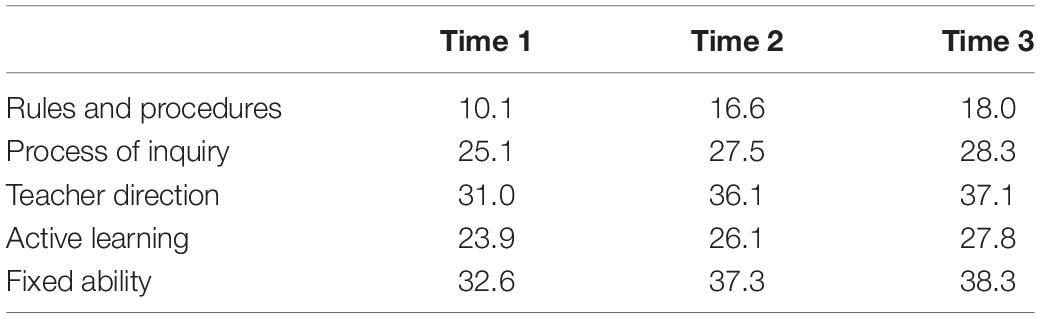
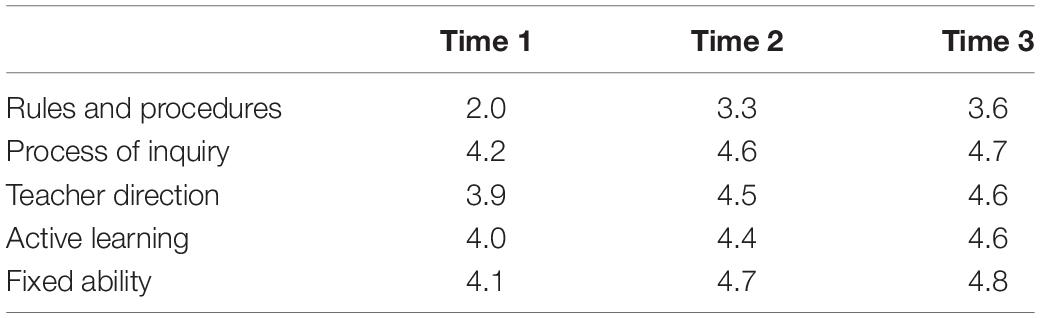
Table 3 contains descriptive statistics for survey results from Time 1 to Time 3. Since the five survey categories (Rules and Procedures, Process of Inquiry, Teacher Direction, Active Learning, and Fixed Ability) included different numbers of questions, I used mean composite scores to explore the topics broadly. These mean scores comparisons showed that from Time 1 to Time 3, PSTs made the largest gains in Rules and Procedures and Teacher Direction. To examine the categories individually, I used grand mean composite scores across time. These results, summarized in Table 4, indicate that PSTs made the most improvement in Rules and Procedures and held steady in their growth in all areas, with Fixed Ability showing the highest outcome when compared to other categories.
As shown in the results of the Time 1 survey, PSTs entered mathematics methods courses with fixed views of mathematics teaching and learning, particularly in the area of Rules and Procedures. They thought mathematics involved remembering and applying definitions, formulas, and mathematical facts and valued the application of procedures to find quick solutions to problems rather focusing on processes. While PSTs scored lowest initially on Rules and Procedures, they made the largest gains in this category over time. Linear Regression from Time 1 to Time 3 showed statistically significant effects for Rules and Procedures (p = 0.023) when controlling for students’ ages, ethnicity, and parental education levels. Tables 5, 6 provide summarized reports of p-values for Linear Regressions performed comparing Time 1 to Time 2 and Time 1 to Time 3.

Table 5. Summary of p values for linear regressions by survey category from Time 1 to Time 2 with Time 2 as the dependent variable.

Table 6. Summary of p values for linear regressions by survey category from Time 1 to Time 3 with Time 3 as the dependent variable.
Process of Inquiry centered on the relevance of mathematics to real-world problem solving as well as the process of discovery as a valid means of building understanding in mathematics. PSTs’ scores increased statistically significantly from Time 1 to Time 2 (p = 0.035) and from Time 1 to Time 3 (p = 0.028) in Process of Inquiry when controlling for age, ethnicity, and parental education level. PSTs showed gains in understanding that mathematics includes elements of creativity and that focused engagement in mathematical tasks leads to personally constructed understanding.
Results for Teacher Direction did not produce statistically significant results; however, single item analysis showed that in Time 1 PSTs responded overwhelmingly that students “need to be taught exact procedures for solving mathematical problems” and would “learn best by attending to the teacher’s explanations.” By Time 3, PSTs showed softening of their Teacher Direction views. All PSTs either Disagreed or Strongly Disagreed with the survey items that stated: “Hands-on mathematics experiences aren’t worth the time and expense.” and “To be good in mathematics you must be able to solve problems quickly.”
Active Learning showed statistically significant differences when controlling for ethnicity (p = 0.053) and mother’s education level (p = 0.022). Active Learning explored PSTs’ beliefs about how teachers should engage students in problem solving and divergent thinking. PSTs made strides in their attitudes about teachers’ support of productive struggle and allocating class time for investigating why solutions work. For example, in Time 3 nearly all PSTs either Agreed or Strongly Agreed with the statement, “Teachers should encourage students to find their own solutions to mathematical problems even if they are inefficient.” The Active Learning category was the only area that yielded statistically significant differences between Hispanic and non-Hispanic participants.
Changes in Beliefs About Mindset
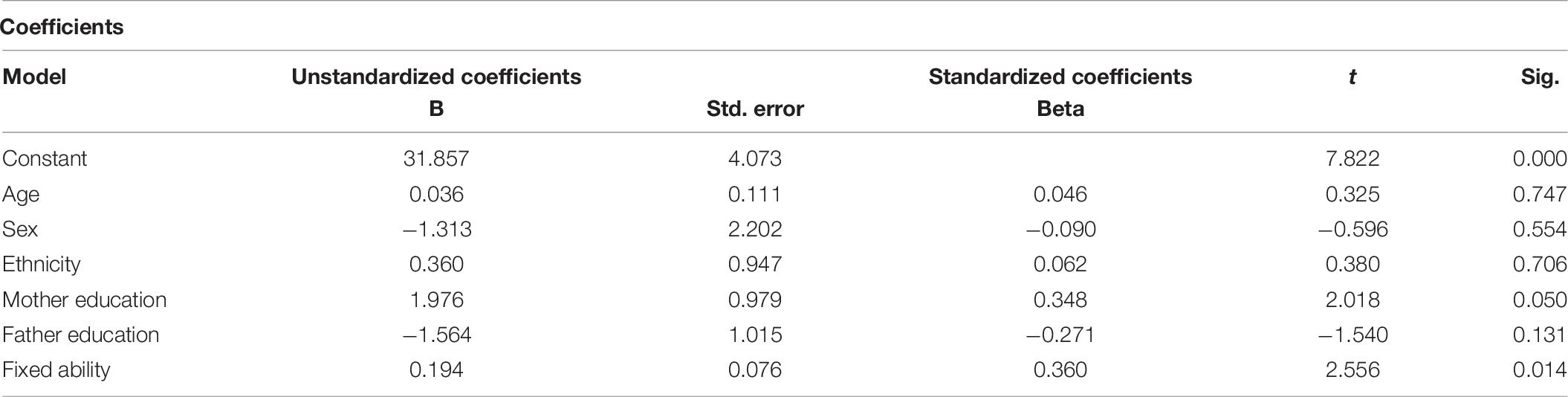
Linear regression showed statistically significant changes in PSTs’ Fixed Ability beliefs from Time 1 to Time 2 (p = 0.016) and from Time 1 to Time 3 (p = 0.014). Particularly interesting was the finding that mother’s education level had a higher impact on Fixed Ability than father’s education level when comparing the standardized coefficients (beta = 0.35 vs. beta = -0.27 from Time 1 to Time 3). See results in Table 7. Mother’s education level was predictive of outcomes on the Fixed Ability measures from Time 1 to Time 2 (p = 0.019) and from Time 2 to Time 3 (p = 0.05). This finding could be interpreted to mean that if a PST’s mother had attended some college or graduated from college, the PST’s responses on survey items related to Fixed Ability were 2.7 points higher than PSTs’ whose mothers had no college experience. Fixed Ability was the only category where mother’s education level impacted beliefs.
The Time 3 survey included an open response item where PSTs responded to the following question: How do you feel being in this class has affected your thinking about math and teaching math? A future study will code these responses; however, a few preliminary observations follow. The term “mindset” appeared in 77% of the responses and “growth mindset” appeared in 43%. Many students mentioned they had once believed they were “not a math person” but had come to understand that was a myth. One PST wrote: “I was guilty of labeling people as a ‘math person’ or not a math person, and this class helped me realize that this was not valid, and that it could actually be detrimental to students’ learning and mindset. Every student is a math student, and effort should be praised! The teacher needs to have a growth mindset about each student and the students will reap those benefits. Loved everything I learned in this class!” Another PST explained how the class affected their views on mathematics teaching: “I feel like I have more of a growth mindset. I believe I can teach math in a more interactive way by having meaningful discussions, hands-on activities, and using manipulatives.”
Attrition among participants may have affected outcomes of this study. Time 1 and Time 2, which occurred prior to COVID-19 forced instruction to move online, included 86 participants. Time 3 was conducted 6 weeks into the pivot to online instruction and included only 51 participants. The attrition in the study was largely due to COVID-19 related challenges. When I followed up with PSTs who did not complete the Time 3 survey, several indicated that the pandemic disrupted regular routines for daily living as well as for completing school work. PSTs reported difficulties managing heavy workloads related to student teaching and college course requirements along with increased family and home responsibilities.
This raises important questions about the mindsets of PSTs who did not complete the Time 3 survey. How would their responses have affected outcomes? Where did these non-responders fall on their growth mindset continuum as shown in Time 2 results? Could the stressors of COVID-19 have presented as fixed mindset triggers (Dweck, 2006) that made PSTs less willing or able to share their views? Was the pandemic challenging the growth mindset PSTs had developed during the previous semester but not serving as a protective force during a time of significant emotional trauma?
Without the insight provided by missing survey data, I could not determine if the mindsets in the pandemic cohort were influenced by the abrupt pivot to remote learning caused by COVID-19. However, by comparing survey results from the pandemic cohort with survey results from my PSTs in the pre-pandemic cohort (Spring 2019/Fall 2019, N = 48), I was able to further explore of the effects of the pandemic on mindset. Since mindset was most closely examined in the Fixed Ability section of the survey, I concentrated on survey responses for only those items. Based on mean comparisons, I found no statistically significant difference between the Fixed Ability responses from the pre-pandemic cohort and the pandemic cohort. See Table 8 for descriptive statistics. Though these findings are preliminary and will require further analysis, they seem to indicate a relationship between mindset and the coping mechanisms employed during a pandemic. Learning about productive struggle and ways to respond to challenges may sustain math-positive mindsets in the face of unprecedented challenges. More fully examining the full survey data from the pre-pandemic cohort and making comparisons with the pandemic cohort in a future study will further inspect the effects of the pivot to remote learning on PSTs’ resiliency in periods of profound stress.

Table 8. Mean composite scores for fixed ability pre-pandemic cohort (Spring 2020/Fall 2019) and Pandemic Cohort (Fall 2019/Spring 2020).
Conclusion
Explicit instruction in growth mindset principles and applications positively affected PSTs’ views of mathematics teaching and learning. These findings were most significant for improvements in PSTs’ beliefs about mathematical Rules and Procedures, Process of Inquiry, Active Learning, and Fixed Beliefs. PSTs appeared to set aside initial views of mathematics as a series of steps to be applied in prescribed ways in favor of what Boaler (2016b) calls an active approach to mathematics knowledge emphasizing understanding and sense making. The positive effects on PSTs’ views on fixed versus growth mindsets confirm studies undertaken with middle school and high school students (Blackwell et al., 2007; Boaler et al., 2018) and clarifies some of the findings among PSTs (Schmude et al., 2017).
This study’s high number of Hispanic PSTs provides particularly important information in light of continued concerns about equity and access in US mathematics classrooms. In their joint position statement, the National Council of Supervisors of Mathematics and Todos: Mathematics for All (2020) encouraged schools to discontinue mathematics course “tracking” that institutionalized fixed mindsets about students’ capacities in mathematics, particularly among students of color. In schools where mathematics is treated as a gateway rather than a gatekeeper to educational advancement, all learners must receive strong support and high expectations for their success. Equipping Latina teachers with mathematical mindsets may assist in disrupting patterns of inequity in mathematics opportunities, expectations, and supports.
The evidence from this repeated measures design shows the impact of changing fixed mindset beliefs and limited views about the nature of teaching and learning mathematics among PSTs. The iterative nature of teacher research allows me to further refine my mathematical mindset curriculum to improve outcomes for the area of Teacher Direction and compels me to connect with former students who are now teachers to explore the longevity of their math-positive mindset views in the face of the complexities of teaching in the midst of a pandemic.
Data Availability Statement
The datasets presented in this article are not readily available because as a condition of the study’s ethical approval data can not be made publicly available to outside researchers. Requests to access the datasets should be directed to corresponding author.
Ethics Statement
The studies involving human participants were reviewed and approved by University of Houston, IRB. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2020.595264/full#supplementary-material
Supplementary Data Sheet 1 | Mathematical Mindset Survey Instrument and Mindset Curriculum.
References
Aronson, J., Fried, C. B., and Good, C. (2002). Reducing the effects of stereotype threat on African American college students by shaping theories of intelligence. J. Appl. Dev. Psychol. 38, 113–125. doi: 10.1006/jesp.2001.1491
Blackwell, L. S., Trzesniewski, K. H., and Dweck, C. S. (2007). Implicit theories of intelligence predict achievement across an adolescent transition: a longitudinal study and an intervention. Child Dev. 78, 246–263. doi: 10.1111/j.1467-8624.2007.00995.x
Boaler, J. (2016a). How You Can be Good at Math and Other Surprising Facts About Learning. [Video file]∗. Available at: https://www.youtube.com/watch?v=3icoSeGqQtY (accessed September 3, 2019).
Boaler, J. (2016b). Mathematical Mindsets: Unleashing Students’ Potential Through Creative Math, Inspiring Messages, and Innovative Teaching. New York, NY: John Wiley & Sons.
Boaler, J., and Zoido, P. (2016). Why math education in the U.S. doesn’t add up. Sci. Am. Mind. 27, 18–19. doi: 10.1038/scientificamericanmind1116-18
Boaler, J., Dieckmann, J. A., Pérez-Núñez, G., Sun, K. L., and Williams, C. (2018). Changing students’ minds and achievement in mathematics: the impact of a free online student course. Front. Educ. 3:26. doi: 10.3389/feduc.2018.00026
Brese, F., and Tatto, M. T. (eds). (2012). TEDS-M 2008 User Guide for the International Database: Supplement 3. Hamburg: International Association for the Evaluation of Educational Achievement (IEA).
Bybee, R., and Landes, N. M. (1990). Science for life and living: an elementary school science program from Biological Sciences Improvement Study (BSCS). Am. Biol. Teach. 52, 92–98. doi: 10.2307/4449042
Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L., and Empson, S. B. (2015). Children’s Mathematics: Cognitively Guided Instruction. Portsmouth, NH: Heinemann.
Claro, S., Paunesku, D., and Dweck, C. S. (2016). Growth mindset tempers the effects of poverty on academic achievement. Proc. Natl. Acad. Sci. U.S.A. 113, 8664–8668. doi: 10.1073/pnas.1608207113
Fletcher, G. (2016). Modeling with Mathematics Through Three-Act Tasks∗. Available at: http://www.nctm.org/Publications/TeachingChildren-Mathematics/Blog/Modeling-withMathematics-through-Three-Act-Tasks/ (accessed February 5, 2020).
Lempp, J. (2020). Math Workshop: Five Steps to Implementing Guided Math, Learning Stations, Reflection, and More. Sausalito, CA: Math Solutions.
Maguire, E. A., Gadian, D. G., Johnsrude, I. S., Good, C. D., Ashburner, J., Frackowiak, R. S., et al. (2000). Navigation-related structural change in the hippocampi of taxi drivers. Proc. Natl. Acad. Sci. U.S.A. 97, 4398–4403. doi: 10.1073/pnas.070039597
Mathematics Teaching and Learning to Teach, (2010). SeanNumbers-Ofala [Video file]. Ann Arbor, MI: University of Michigan.
Meyer, D. (2015). Missing the promise of mathematical modeling. Math. Teach. 108, 578–583. doi: 10.5951/mathteacher.108.8.0578
Moser, J. S., Schroder, H. S., Heeter, C., Moran, T. P., and Lee, Y. H. (2011). Mind your errors evidence for a neural mechanism linking growth mind-set to adaptive posterror adjustments. Psychol. Sci. 22, 1484–1489. doi: 10.1177/0956797611419520
National Council of Supervisors of Mathematics and Todos: Mathematics for All (2020). Mathematics Education Through the Lens of Social Justice: Acknowledgment, Actions, and Accountability. Available at: https://www.todos-math.org/assets/docs2016/2016Enews/3.pospaper16_wtodos_8pp.pdf (acessed on 1 August 2020)
National Council of Teachers of Mathematics (2014). Principles to Actions: Ensuring Mathematical Success for All. Reston, VI: National Council of Teachers of Mathematics.
Keywords: mindset – an established set of attitudes held by someone, teacher – education, math-positive mindsets, teacher beliefs and attitudes, mathematics education, teacher research, online instruction and learning
Citation: Cutler CS (2020) Preservice Teachers’ Mathematical Mindsets During Pandemic-Induced Pivot to Online Learning. Front. Educ. 5:595264. doi: 10.3389/feduc.2020.595264
Received: 15 August 2020; Accepted: 22 October 2020;
Published: 13 November 2020.
Edited by:
Christine Beaudry, Nevada State College, United StatesReviewed by:
Joseph Samuel Backman, Alpine School District, United StatesKimberly Coy, California State University, Fresno, United States
Copyright © 2020 Cutler. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Carrie S. Cutler, Y3NjdXRsZXJAY2VudHJhbC51aC5lZHU=
 Carrie S. Cutler
Carrie S. Cutler