- 1Rossier School of Education, University of Southern California, Los Angeles, CA, United States
- 2School of Education, Indiana University Bloomington, Bloomington, IN, United States
- 3School of Education and Information Studies, University of California, Los Angeles, Los Angeles, CA, United States
Experimental and quasi-experimental designs have been increasingly employed in education. Mediation analysis has long been used to measure the role of mediators. Causal mediation analysis provides a modern approach to evaluate potential causal roles of mediators. Compared with conventional mediation analysis, causal mediation analysis has several advantages, e.g., by enabling us to evaluate necessary assumptions to establish a valid causal role of the mediator of interest. Despite these advantages and the availability of various software programs, causal mediation analysis has not been employed frequently in educational research. In this paper, we provide a step-by-step guide to causal mediation analysis using the free R package mediation in order to promote the more frequent application of causal mediation analysis in education, with an accessible data example from a Comprehensive College Transition Program (CCTP).
Introduction
The randomized control trial (RCT) along with quasi-experimental designs have been increasingly employed in education at the national, state, and district levels to evaluate the effectiveness of intervention programs (e.g., De Witte and Rogge, 2016; Baroni et al., 2019; Kireev et al., 2019; Legaki et al., 2020) and to inform educational policy decision-making (Sadoff, 2014; Raudenbush and Schwartz, 2020). Often in these studies, researchers and practitioners would like to determine if the intervention (e.g., an instructional model, or a new technological tool) impacts the outcome (e.g., student learning outcome, or teacher quality). In addition, underlying causal mechanisms are of interest; in other words, how the intervention influences the outcome through a mediator (e.g., student engagement, or student motivation).
Mediation analysis (Baron and Kenny, 1986; MacKinnon, 2008) is routinely applied to investigate mediation effects. Recently, causal mediation analysis (Robins and Greenland, 1992; Pearl, 2001; Robins, 2003; Imai et al., 2010a,b, 2011; Imai and Yamamoto, 2013; VanderWeele, 2015) has been proposed and provides a new perspective to understanding mediation. Conventional mediation analysis and causal mediation analysis are not completely different in terms of modeling perspectives. However, based on the potential outcomes framework (Holland, 1986), causal mediation analysis provides methods to evaluate the assumptions required in establishing the causal role of a mediator, which may not be the case with conventional analysis. Causal mediation analysis does so by clearly identifying and evaluating required assumptions through sensitivity analysis that supplies measures of how robust results are to violations of the assumptions needed to establish causality.
In addition, causal mediation analysis introduces a more general definition of the causal mediation effect. The approach provides non-parametric definitions of causal mediation effects and allows accommodating various types of models (linear and nonlinear), mediators (continuous and discrete), and outcome variables (continuous and discrete). Based on non-parametric definitions, causal mediation effects can be estimated through various parametric and non-parametric estimation methods.
Despite these advantages and the availability of various software programs (Valente et al., 2020), causal mediation analysis does not appear to be employed as much as conventional mediation analysis in experimental designs found in educational studies (Imai et al., 2010a; Cuartas and McCoy, 2021). The insufficient use of causal mediation methods is notable considering the more recent focus on experimental and quasi-experimental methods to evaluate causal effects (Hufstedler et al., 2021; Yeboah et al., 2021). The current What Works Clearinghouse (WWC) standards for effectiveness studies do not yet include guidance on causal mediation methods (What Works Clearinghouse, 2020). To encourage the use of causal inference in applied studies, in this paper, we provide practical guidance for applied researchers. We provide a step-by-step explanation of causal mediation analysis with an accessible example. Through this guide, we aim to promote and foster more use of causal mediation analysis in applied educational research.
The remainder of this paper is structured as follows: “A Running Example” presents our empirical example of an RCT design in education. “Conventional Mediation Analysis” briefly reviews conventional mediation analysis and how it is typically applied in education research. This section also discusses several assumptions needed to establish a valid causal mediation effect. “Causal Mediation Analysis” introduces causal mediation analysis and compares it with conventional mediation analysis. “A Practical Guide” recommends a four-step procedure that can be applied in practice and illustrates the procedure through an empirical example. “Concluding Remarks” provides a summary and final thoughts.
A Running Example
Comprehensive college transition programs (CCTPs) include several different types of transition programs that range in intensity and comprehensiveness, including summer bridge programs (e.g., Strayhorn, 2011), first-year seminars (e.g., Keup and Barefoot, 2005), paired developmental courses within cohorts (e.g., Weiss et al., 2014), financial awards with intensive advisement (e.g., Page et al., 2019), and learning communities (Taylor, 2003; Price, 2005). The CCTP studied in the present study supports low-income, in-state high school graduates and was offered on three campuses of the University of Nebraska. At each campus, portions of applicants to this program were randomly assigned to three conditions: (a) the CCTP treatment condition, in which the participants received financial assistance and a comprehensive set of supports (e.g., academic classes, and first-year seminars); (b) the college opportunity scholars (COS) condition, where the participants received financial assistance only; and (c) the control condition, where participants received neither financial aid nor the CCTP (Angrist et al., 2016).
Melguizo et al. (2021) compared the participants in the CCTP condition to those in the COS condition and demonstrated that the CCTP participants experienced substantial gains in two psychosocial outcomes: sense of belonging to a campus community and mattering to a campus community. The former is defined as the perception that one is a part of the broader campus community (Hausmann et al., 2007; Hurtado et al., 2008; Chang et al., 2011; Strayhorn, 2012). The latter refers to the sense that one is of consequence to other people in the broader campus community (Rosenberg and McCullough, 1981; Schlossberg, 1989; Gossett et al., 1996; Cooper, 1997; Marshall, 2001; Rayle and Chung, 2007; Dixon and Kurpius, 2008; Klug, 2008; Tovar et al., 2009; France and Finney, 2010; Tovar, 2013). These two psychosocial outcomes were measured through the Longitudinal Survey of Thompson Scholars (STS) at the second follow-up of the program.
To explain the differences between the CCTP and COS conditions in the psychological outcomes, the mediating roles of four types of personal interactions that have been previously associated with them are examined. These interactions between participants and nonprogram faculty and peers are: (a) faculty course-related interaction (e.g., student utilization of faculty office hours); (b) faculty non-course-related interaction (e.g., discussions with faculty about personal problems and ambition); (c) academic peer interaction (e.g., discussing class topics, assignments, and concerns with peers); and (d) social peer interaction (e.g., discussing current events, personal concerns, and social issues with peers). These interactions were measured via the STS at the first follow-up (see Supplementary Material for the survey items).
Aside from the STS data, additional background information was collected from applications to the CCTP and the Free Application for Federal Student Aid, including participants’ unweighted high school grade point average and aggregate gross family income, if their guardian(s) attended college, their gender and race/ethnicity (Black, Latino, White, other), and if they are members of the 2016 cohort.
To illustrate conventional mediation analysis and causal mediation analysis, we use data from this study the sections “Conventional Mediation Analysis” and “Causal Mediation Analysis”, focusing on exploring the causal mechanism of how faculty course-related interaction is impacted by participants’ CCTP status (if they are in the CCTP condition or the COS condition) and in turn influences their sense of belonging to a campus community (i.e., the mediation effect of faculty course-related interaction).
Conventional Mediation Analysis
Conventional mediation analysis (Baron and Kenny, 1986; MacKinnon, 2008) is formulated under a linear structural equation modeling (LSEM) framework.
Common Practices
To address the research question of how faculty course-related interaction is impacted by participants’ CCTP status and in turn influences their sense of belonging to a campus community, with conventional mediation analysis, three linear regression equations are usually specified based on a single mediator model shown in Figure 1:
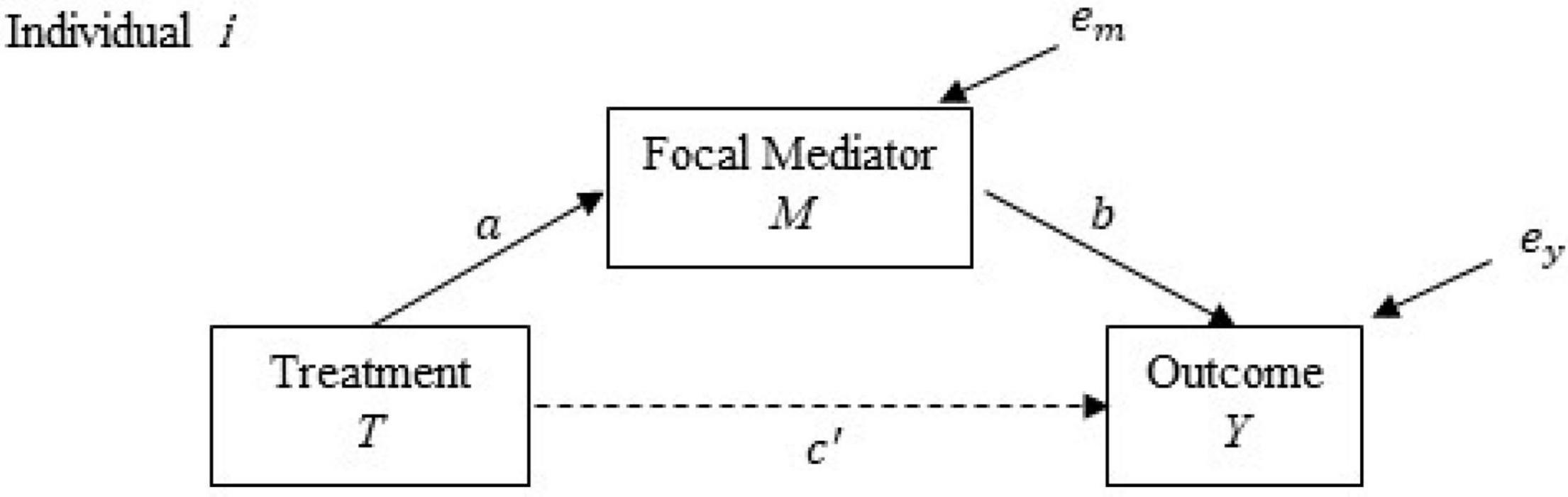
Figure 1. Model with only focal mediator. Path diagram for conventional mediation analysis with only focal mediator.
In the above equations, Y represents the outcome variable, T denotes a binary treatment variable and takes the value of 1 if participant i is in the CCTP condition (Ti = 1) and 0 if the participant is in the COS condition (Ti = 0), and M is the mediator. Equation 1 indicates that participant i’s level of sense of belonging to a campus community is the sum of the intercept, α1, the total effect of the CCTP, cTi, and the unexplained residual, ei. Equation 2 states that Yi is the sum of the intercept, α2, the direct effect of the CCTP, c′Ti, the effect of faculty course-related interaction (i.e., the focal mediator), bMi, and the residual, eyi. Equation 3 shows that the level of the mediator is the sum of the intercept α3, impact of participant i’s CCTP status, aTi, and the residual, emi. Note that measured confounders (e.g., participants unweighted GPA) can be controlled for by incorporating the confounders into the above equations.
The above equations can be estimated, through approaches such as ordinary least squares (OLS) and logistic regression, to obtain parameter estimates and the associated standard errors. The mediation effect is then computed as the product of estimates of a and b parameters, , or the difference between the total and the direct effects, . The presence of a mediation effect can be determined using significance tests or confidence intervals (CIs). It is shown that CIs that account for the non-normal sampling distribution, such as the bias-corrected bootstrap CI and percentile bootstrap CI, generally have higher power to detect a statistically significant mediation effect than normal-theory CIs and significance tests (MacKinnon et al., 2004; Fritz and MacKinnon, 2007; Hayes and Scharkow, 2013).
When other mediators (that are not of major interest) other than the focal mediator are also measured in a study, the effects of these mediators can be incorporated through a multiple mediation model. For example, if both faculty course-related interaction and faculty non-course-related interaction are to be considered and are assumed to be independent (Figure 2A), four linear regression equations can be specified as:
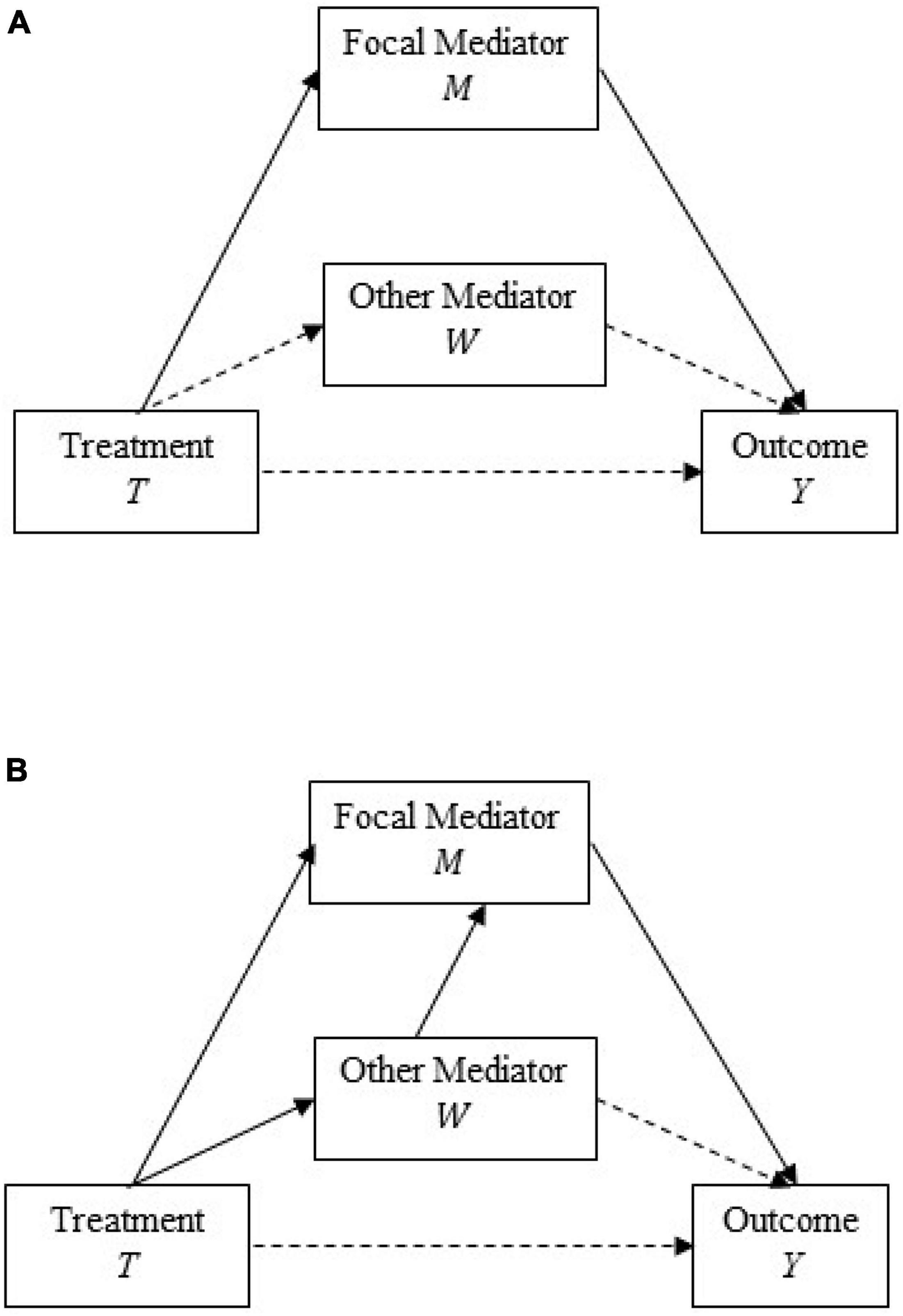
Figure 2. Path diagram for mediation analysis model with multiple mediators. (A) Model with independent mediators. (B) Model with related mediators. In each panel, the solid arrows represent the average causal mediation effect (ACME) through the focal mediator. The solid and dashed arrows, together, represent the total effect of participation in the comprehensive college transition program. In panel (A), the focal mediator is assumed to be independent of the other mediators. With this assumption, ACME estimates for each focal mediator are not allowed to be confounded by post-treatment changes in other mediators. In panel (B), the focal mediator is allowed to depend on other mediators. Figure adapted from Imai and Yamamoto (2013). Copyright 2013 by K. Imai and T. Yamamoto.
Equations 4–7 indicate that the other mediator (faculty non-course-related interaction, denoted by W) is impacted by participants’ CCTP status, and together with the focal mediator influences the levels of the sense of belonging to a campus community. The mediation effect of the focal mediator, M, can then be computed and evaluated. In a subsequent section, we relax this assumption that the causal effect estimate of the focal mediator on the outcome is independent from that of other mediators. Instead, the other mediators are allowed to influence the focal mediator.
Several Key Considerations
Conventional mediation analysis, as just described, establishes the association between the mediator and the outcome, but does not always guarantee a valid conclusion regarding the causal role of the focal mediator. Potential confounders that are either measured or unmeasured may not be adequately considered. Thus, results tend to be over-interpreted (i.e., estimates of the mediation effect have an upward bias) in these studies. In this section, we discuss several key requirements needed for the establishment of the causal role of the focal mediator.
First, it is important to consider if the samples of the comparison groups are balanced in characteristics. Randomization can yield identical comparison groups, on average, but non-random attrition from the samples can confound results. In the running example, if the CCTP group includes a significantly higher number of White participants than the COS group, suggesting non-random attrition, the mediator-outcome effect, the treatment-mediator and treatment-outcome effects could all be biased. The imbalance suggests the possibility that an unmeasured participant characteristic is correlated to both treatment status as well as the levels of the faculty course-related interaction mediator and the sense of belonging to a campus community outcome.
Second, it is prudent to examine how unmeasured pre-treatment or post-treatment confounders would impact the estimates of a mediation effect. Both unmeasured pre-treatment or post-treatment confounders would confound the relationship between the focal mediator and the outcome. An example of pre-treatment confounders in the CCTP example could be participants’ motivation to interact with college peers and faculty before they are assigned to either the CCTP or COS groups. Post-treatment confounders can include unmeasured factors that are induced by the CCTP status, such as the unique CCTP camaraderie. Post-treatment confounders can also include other measured non-focal mediators. The assumption regarding pre-treatment and post-treatment confounders are crucial for a valid inference of the mediation effect of interest; however, they are untestable with observed data.
Third, Equations 2 and 5 indicate that there exists no interaction between the focal mediator and the treatment (i.e., the no-interaction assumption). However, this assumption may not always hold in practice, because the role of mediator can be different in the treatment and control conditions. This assumption can be relaxed by incorporating a treatment-mediator interaction term in Equations 2 and 5. The additional interaction term also reflects the approach taken in conventional mediation analysis (Judd and Kenny, 1981; MacKinnon et al., 2020).
Causal Mediation Analysis
In this section, using the CCTP running example, we first briefly review causal mediation analysis. Next, we present two sensitivity analyses, through which the robustness of the mediation effect estimates can be evaluated. For more technical details, we refer interested readers to Imai et al. (2010a,b, 2011), Imai and Yamamoto (2013), and VanderWeele (2015).
Causal Mediation Effects
In causal mediation analysis, the causal mediation effect is defined in the potential outcome framework. Let Mi(t) represent the potential mediator value for participant i if the participant’s treatment status is Ti = t. Let Yi(t,m) denote the potential outcome value for participant i if Ti = t and participant i has a mediator value Mi = m. The causal mediation effect for participant i captures the difference between the participant’s observed outcome and a counterfactual outcome if the participant’s treatment status remains the same but the mediator value equals the value under the other treatment status (Robins and Greenland, 1992; Pearl, 2001):
where t = 0, 1. If t = 0, the term Yi(0,Mi(1)) is counterfactual and Yi(0,Mi(0)) is observed. δi(0) is also termed pure indirect effect. When t = 1, the term Yi(1,Mi(1)) is observed and Yi(1,Mi(0)) is counterfactual. δi(1) is termed the total indirect effect.
As the causal mediation effect depends on the treatment status, population average causal mediation effects (ACMEs) under the treatment and control conditions are computed separately, denoted by ACME(1) and ACME(0). In addition to the mediation effects, direct effects under the two conditions (also known as the pure direct effect and total direct effect) are also defined,
where t = 0, 1. The total causal effect is defined as τi = δi(t) + ζi(1−t).
In our running example, where the mediation effect of faculty course-related interaction is of major importance, ACME(1) represents the averaged difference between two outcomes associated with the CCTP participants: (a) their observed levels of sense of belonging to a campus community, and (b) the levels of sense of belonging to a campus community when they stay in the CCTP condition, but their faculty course-related interaction levels are what they would be if assigned to the COS group. ACME(0) indicates the difference between two outcomes of the COS participants: (a) their levels of sense of belonging to a campus community when they stay in the COS group, but their faculty course-related interaction levels are what they would be if assigned to the CCTP group, and (b) their observed sense of belonging to a campus community levels. Through fixing participants’ CCTP status (i.e., the treatment), levels of faculty course-related interaction (i.e., the mediator) and sense of belonging to a campus community (i.e., the outcome) are isolated and the causal relationship between the mediator and outcome can be established.
To compute the ACMEs, two regression equations are first specified and fitted, one for the mediator and one for the outcome,
In both Equations, Xi is a vector of control variables, such as the background characteristics of participants. Compared with Equation 5, Equation 11 has an additional treatment-mediator interaction term, MiTi. It is worth noting here that although it is possible in conventional mediation analysis to relax the no-interaction assumption and include this interaction term, this interaction term is rarely estimated and tested in conventional mediation analysis (MacKinnon et al., 2020). Without the interaction term, it is assumed the role of the mediator in influencing the outcome is the same regardless of treatment status.
The mediator and outcome in our example are both continuous; therefore the ACME(1) and ACME(0) can be computed using the product of coefficients approach:
The causal mediation model can be extended easily to various nonlinear models including quantile, probit, and survival models and can accommodate discrete mediators and outcomes (Imai et al., 2010a).
As alluded to earlier, the focal mediator M can either be independent from other mediators W (e.g., faculty non-course-related interaction; Figure 2A) or be impacted by W (Figure 2B). The causal mediation analysis has been extended to the case of multiple causal mechanisms (Imai and Yamamoto, 2013; VanderWeele and Vansteelandt, 2014):
By including the term Wi in Equation 14, the focal mediator can be dependent on the other mediator, which is also impacted by the treatment. Regression coefficients in these two equations vary across participants (via the individual subscript i), allowing for heterogeneous treatment effects. The causal mediation analysis with multiple mediators relaxes the independence assumption but still assumes that the mediator-treatment interaction is homogeneous across participants (which is different from the no-interaction assumption). The inclusion of one or more non-focal mediators allows for a sensitivity analysis to examine if the causal effect of the focal mediator on the outcome depends on treatment status. Such a dependence would mask our primary interest in isolating the effect of the mediator on the outcome.
Sensitivity Analysis
To identify the estimates obtained through causal mediation analysis as a causal mediation effect, it is assumed that there are no unmeasured pre-treatment confounders and no post-treatment confounders. However, these two assumptions are untestable. An important advantage of causal mediation analysis over conventional mediation analysis is that it allows us to examine how sensitive the ACME estimates are to the potential violation of these assumptions.
In causal mediation analysis, the degree of the possible violation of the no unmeasured pre-treatment confounders assumption can be quantified via a measure that is based on the correlation between the residuals of the regression equations,
When the no unmeasured pre-treatment confounders assumption holds, ρ = 0. An extreme value of ρ indicates that there exists strong confounding between the mediator and the outcome variables. We can also set ρ to different values and re-estimate the associated ACME to find the value for ρ at which ACME=0. This value for ρ represents the amount of pre-treatment mediator-outcome confounding necessary to result in no ACME. The larger this value is, the more robust the ACME estimate.
In causal mediation analysis with multiple mediators, we can measure the sensitivity to the homogeneous interaction assumption (i.e., the effect of the treatment-mediator interaction on the outcome is the same across units), which if violated, indicates bias in the effect estimate of the mediator on the outcome from a treatment-mediator interaction. The homogenous interaction assumption can be measured using the standard deviation of the coefficient β3 in Equation 15. The value of σ, at which simulated bounds on the estimated ACME equal zero, divided by its highest possible value represents the degree of the allowable violation of this assumption. Thus, larger values of σ suggest less sensitivity to this type of violation. An approach suggested in Imai and Yamamoto (2013) to help gauge whether the focal mediator is influenced by other mediators is to regress the focal mediator to other mediators. Note that even though this approach accounts for the role of other measured mediators, these methods do not account for unmeasured mediators.
A Practical Guide
In this section, a four-step procedure is recommended to establish a valid causal role of the mediator of major interest in RCT designs. The procedure starts with comparing participants in the control and treatment groups in key background characteristics. In Step 2, mediation, direct, and total effects are computed based on causal mediation models with the focal mediator. In Step 3, the sensitivity of the estimates obtained in Step 2 to unmeasured pre-treatment confounders is examined. In Step 4, the robustness of estimated mediation effects to the assumptions that the focal and other mediators are independent are further examined if multiple mediators are measured in the study.
To illustrate this procedure, we use data collected from the CCTP described in the section “A Running Example” and present sample R code.
Step 1: Comparing Participants in Baseline Characteristics
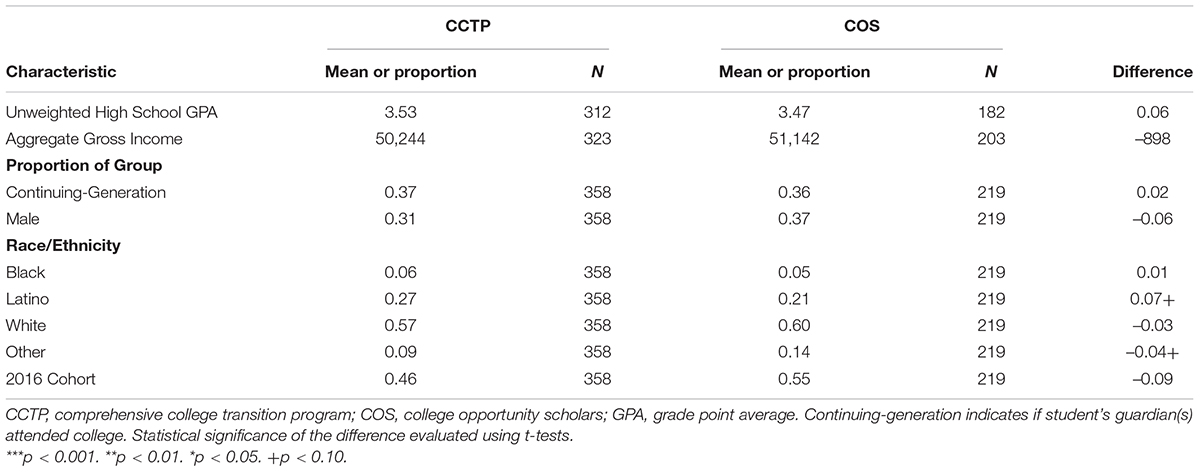
The step of comparing participants in different groups in key background characteristics examines the possibility of non-random attrition from the study after participants are randomized to treatment conditions and before the outcome is observed. The virtue of randomization is that it can provide comparison groups that are, on average, the same. However, if participants with certain characteristics in one treatment condition attrit more frequently, it is possible that the differences in the levels of mediators or outcomes are caused by pre-treatment confounders. The difficulty is that the source of such confounding may not have been measured. To alleviate concerns of non-random attrition, we can compare observed characteristics through statistical techniques such as the t-test.
Table 1 summarizes the means of participants’ unweighted high school grade point average and their aggregate gross family income, and proportions of participants whose guardian(s) attended college, male participants, different race/ethnicities, and of 2016 cohort members in both CCTP and COS groups. Results of t-tests indicate that there are no significant differences between the two groups in these background characteristics at a α = 0.05 level.
If significant differences were detected, suggesting non-random attrition, methods to address the potential for bias from non-random attrition are limited (Duflo et al., 2007). In estimating the total effects of treatments, the traditional parametric method Heckman (1976, 1979) relies on restrictive assumptions, namely joint normality. Non-parametric approaches are also available (Ichimura and Lee, 1991; Ahn and Powell, 1993) but require a valid exclusion restriction: a variable that is not the cause of attrition but correlated to the cause. Such a variable may not be available. More recent methods that do not have these limitations include bound estimators (Lee, 2009). These estimators, however, are limited by the extent of attrition. More importantly, we are unaware of adaptations of these or other methods that address non-random attrition in estimates of causal mediation. To avert these issues, preventing attrition from a study in the first place is paramount.
Step 2: Fitting Causal Mediation Models With the Focal Mediator
The second step involves fitting the mediator and outcome models described in Equations 10 and 11, which assume independence between mediators and include only the focal mediator. In this step, estimates of ACMEs, average direct effects, and the total effect are obtained based on estimates of the regression coefficients. The associated confidence intervals are also computed to evaluate if these effects are statistically significant.
The causal mediation models can be fitted using the mediate() function in the R package mediation. To obtain estimates of interest, two fitted model objects for the mediator (the med object) and the outcome (the out object) need to be specified first. Discrete and other nonlinear mediators and outcomes can be accommodated by using classes other than lm. Next, the mediate() function is applied, using the mediator and outcome model objects as ingredients. R code for fitting causal mediation models with academic peer interaction as the focal mediator and mattering to a campus community as the outcome is shown in Figure 3. This is repeated eight times, each using one of the four mediators and one of the two psychological outcomes. Code for all analyses can be found in the Supplementary Material.

Figure 3. R code for fitting causal mediation models academic peer interaction as the focal mediator and mattering to campus as the outcome. The package mediation is installed first. The mediator object med and the outcome object out are specified first via lm(), since the mediator T1APIR and outcome T2MATC are both continuous. With the mediate() function, the first two arguments indicate the two fitted model objects. Its last three arguments boot = TRUE, boot.ci.type = “bca”, and sims = 5000 indicate that the nonparametric bootstrap estimation approach is used for computing the bias-corrected and accelerated confidence intervals and the number of Monte Carlo draws for nonparametric bootstrap is 5000.
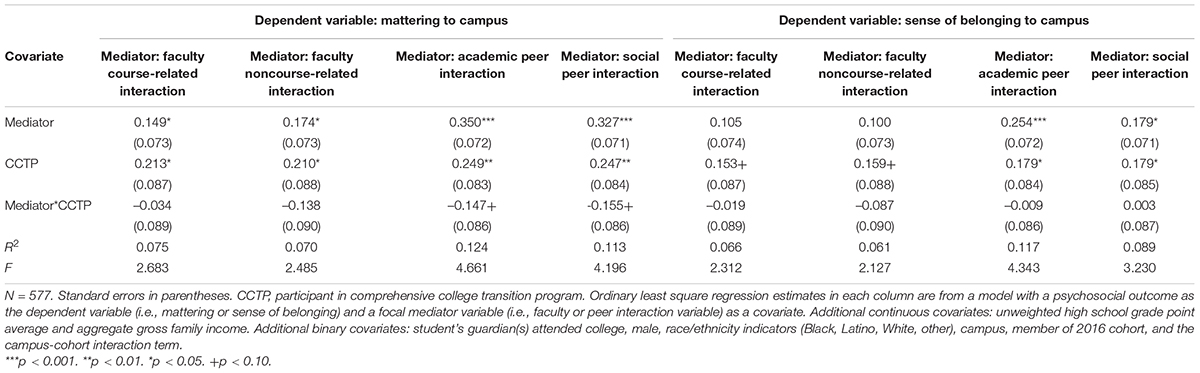
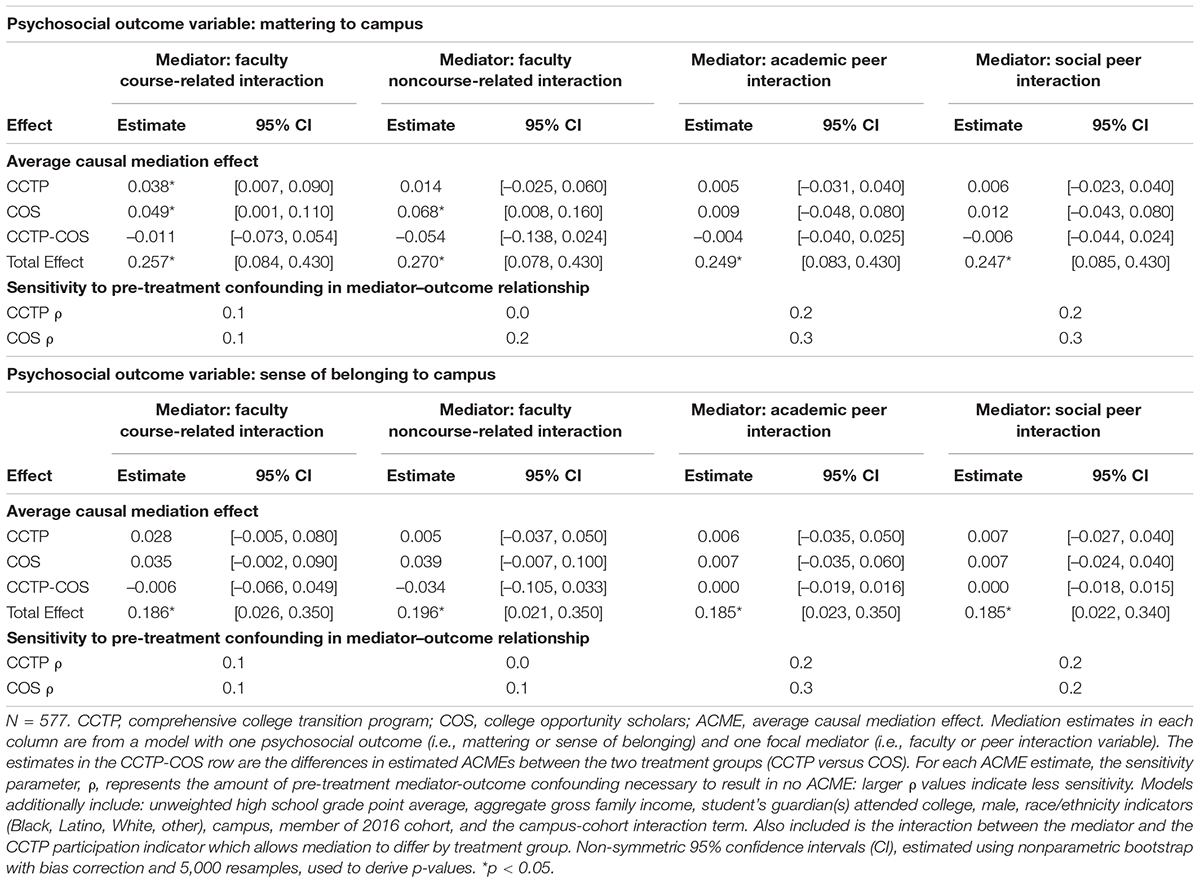
Table 2 shows the estimated effects of CCTP on each of the four interaction-related mediators. Table 3 summarizes the estimates of associations between interaction-related mediators and psychosocial outcomes. Table 4 presents the estimates of ACMEs for the CCTP and COS groups and the total effects, along with their 95% bootstrapped confidence intervals (which account for the non-normality of the mediator and outcome).
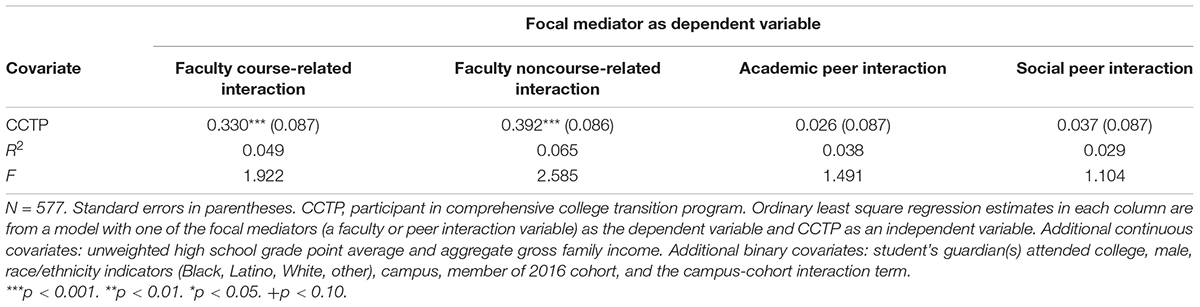
Table 2. Direct effect estimates of comprehensive college transition program on interaction mediators.
According to Table 2, CCTP participation is strongly and positively associated with the two faculty-related interaction measures. In contrast, the positive association between CCTP and the two peer interaction measures is not statistically significant at the 0.10 level. These results suggest that two faculty interaction mediators are dependent on CCTP participation. Therefore, they could be potential post-treatment confounders.
Table 3 indicates that the two peer interaction measures strongly predict greater mattering to a campus community. Faculty interactions also predict greater mattering to a campus community, but with smaller magnitudes. CCTP participation is also significantly positively related to mattering to a campus community. The estimated coefficients of the mediator-CCTP interaction terms all are negative and significant at the 0.10 level for peer interactions but not significant for faculty interactions. Larger and statistically significant coefficient estimates on the interaction term suggest differences between CCTP and COS students in the mediating role of the interaction measure. In the case of sense of belonging to a campus community, results are similar but attenuated.
As shown in Table 4, for mattering to a campus community, ACME estimates for faculty course-related interaction as the mediator are positive and significant at the 0.05 level. For CCTP participants, this mediator explains a 0.038 standard deviation increase in the psychological outcome. For COS students, it explains a 0.049 standard deviation increase. The difference in estimated ACMEs between the two groups suggests the COS students may benefit more from non-CCTP faculty course-related interactions. These estimated ACMEs are relatively small compared to the total effect, which accounts for all observed and unobserved mediational paths between treatment and outcome. This suggests that there could be other mediators that play a larger role in explaining participants’ gain in this psychological outcome.
The ACME estimates with the faculty non-course-related interaction as the mediator are similar but only statistically significant for COS participants. ACME estimates with the peer interaction measures as mediators are all positive but not statistically significant. The differences in ACMEs between CCTP and COS participants for all the interaction measures are negative, which are in line with the negative coefficient estimates on the mediator-CCTP interaction of Equation 11.
For sense of belonging to a campus community, the ACME estimates are all positive but small in magnitude and statistically insignificant. These estimates suggest that faculty and peer interactions may not significantly explain gains in this psychological outcome. The differences in estimated ACMEs between CCTP and COS students are negative except when the social peer interaction is the mediator. The direction of these differences is in line with the coefficient estimates on the mediator-CCTP interaction.
Step 3: Conducting Sensitivity Analysis
If significant mediation effects are found in the previous step, the robustness of these estimates to the potential violation of the assumption of no unmeasured pre-treatment confounders needs to be examined. This is achieved by conducting a sensitivity analysis to find the value for the sensitivity parameter ρ at which ACME=0.
In the package mediation, sensitivity analysis of the estimated ACMEs to such confounding is conducted through the function medsens(). R code is shown in Figure 4. The sensitivity analysis result obtained through the R code includes two tables, one for the COS condition and one for the CCTP condition. In each result table, estimates of the ACME and their 95% confidence intervals that are associated with different values for ρ are presented first. Then, the ρ value at which ACME=0 is shown. If the ρ value is small in magnitude, it means that the ACME estimates obtained in the previous step would be reversed if the errors for the mediation and outcome models are just weakly correlated. In other words, a small value indicates the ACME estimates may not be robust to unobserved confounders. The usefulness of this measure is that it quantifies the sensitivity to such confounding, the presence of which, as mentioned earlier, is untestable with observed data. As such, there is no threshold value that determines whether a result is valid or not (Imai et al., 2011; Keele et al., 2015). Instead, sensitivity values should be compared across studies so that we can judge which analyses are more robust than others (Rosenbaum, 2002). As more causal mediation analysis report values for ρ, more meaningful comparisons can be made.

Figure 4. R code for sensitivity analysis of causal mediation model with one mediator. The medsens() function takes the fitted causal mediation model from the previous step. The argument rho.by indicates the increment for the sensitivity parameter ρ.
Table 4 shows the values for the sensitivity measure ρ at which the estimated ACMEs are zero. These ρ values are relatively small, ranging from 0 to 0.3. Since a higher ρ value indicates less sensitivity to unmeasured pre-treatment confounders, the sensitivity analysis results here suggest that the ACME estimates we obtained in the previous step are sensitive to unobserved confounders. In comparison, the empirical example in Keele et al. (2015) regarded a value of 0.3 to be a “modest” violation (p. 953). For example, the ACME estimate of faculty course-related interaction on mattering to a campus community in the CCTP group is statistically significant; however, its associated ρ value is 0.1, indicating that the true ACME would not be significantly different from zero if there exist an unobserved confounder that causes a small correlation between errors for the mediator and the outcome models. Thus, caution is needed while interpreting the ACMEs and drawing conclusions regarding the mediating roles of the interactions.
Step 4: Examining Multiple Mediation Mechanism
The aim of this step is to examine if the estimates obtained in Step 2 are robust to the assumption that mediation mechanisms are independent when more than one mediator are measured in a study. It involves fitting the multiple mediator models, testing the homogenous interaction assumption, and examining the relationship between the focal mediator and other mediators (if multiple mediators are included). This step can be done through the function multimed (R code shown in Figure 5). The multiple mediator model result obtained through the R code includes two tables. The first result table presents a set of estimates under the homogeneous interaction assumption, including point estimates of ACME in the two groups and the average direct effects, along with their bootstrap confidence intervals. These estimates need to be compared with the corresponding estimates obtained through the single mediator model (Step 2). If large differences are found, there may exist another mediation mechanism that needs to be considered. The second result table shows values of a set of sensitivity parameters, σ, at which ACME and ADE first cross zero in control and treatment groups. Small σ values suggest that the ACME estimates are sensitive to the violation of the homogenous treatment-mediator interaction assumption.

Figure 5. R code for fitting causal mediation model with multiple mediators. In the multimed function, the outcome object, the mediator of interest, the post-treatment confounders, the covariate the treatment variable, are specified. Multiple covariates and confounders can be incorporated.
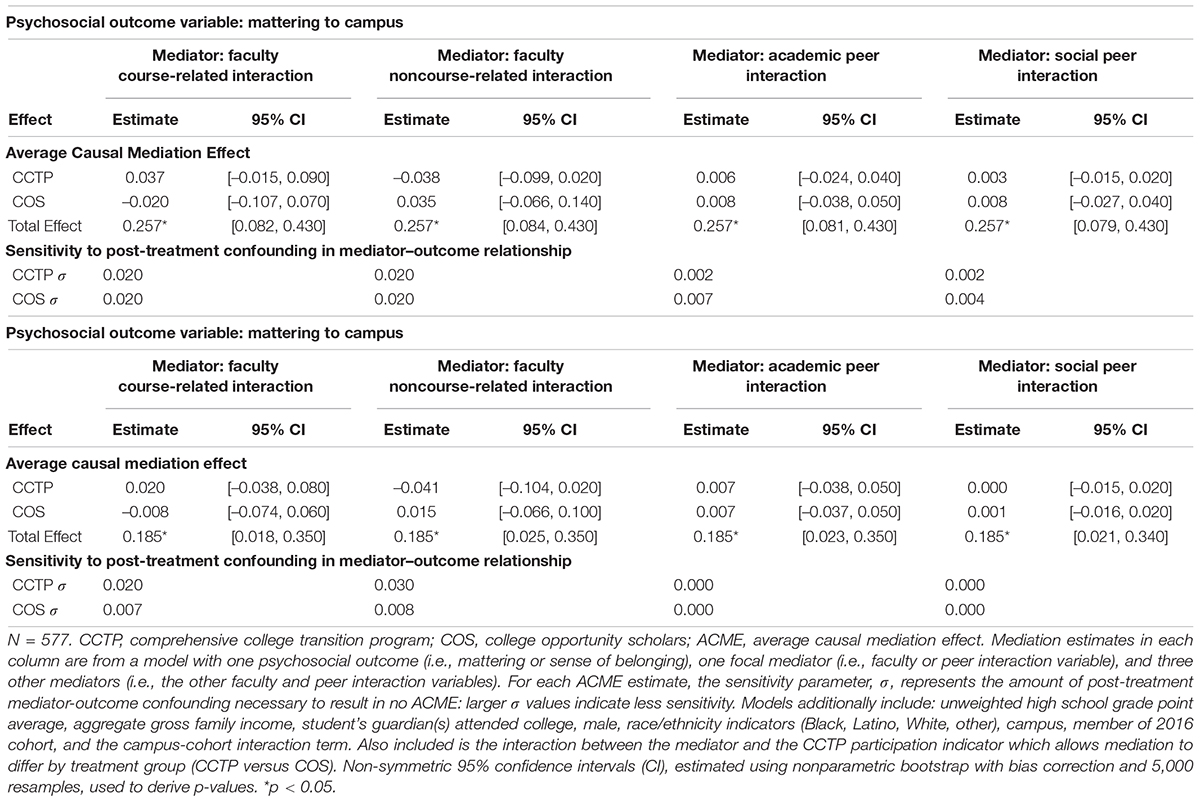
Table 5 presents the results of causal mediation models that allow other measured mediators to be causally related to the focal mediator. Compared with the ACME estimates in the single mediator models, estimates obtained with this weakened assumption are smaller in magnitude, mixed in sign, and all not statistically significant. The differences in ACME estimates from the estimates obtained in Step 2, which assumed independence among mediators, suggest the ACME estimates are sensitive to the focal mediator’s dependence on other mediators.
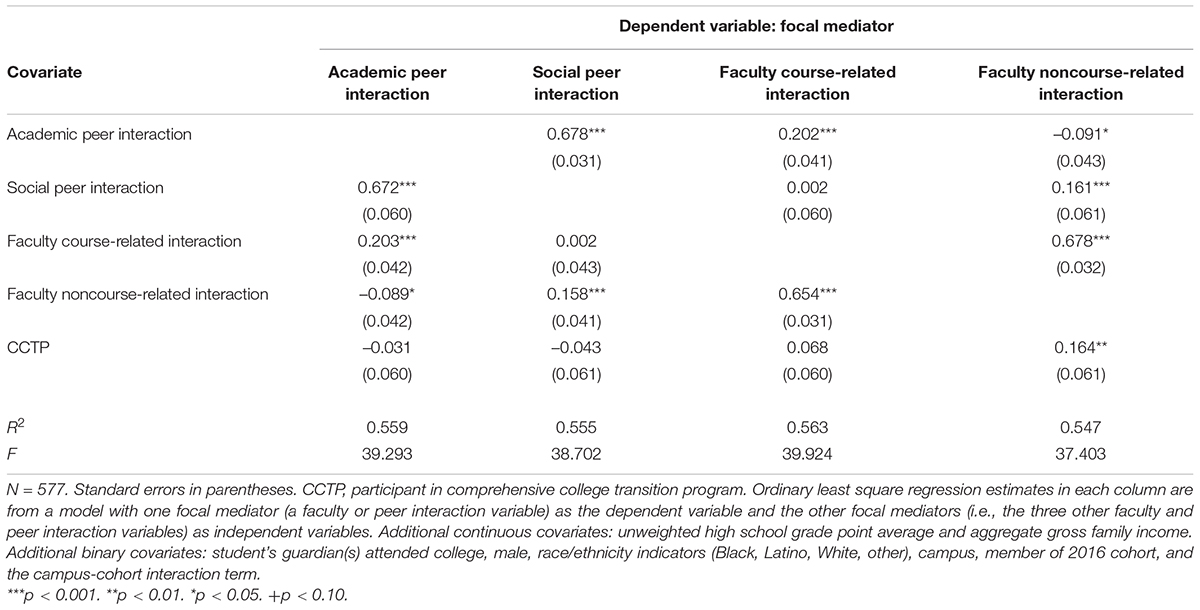
Table 5 also shows values of the parameterσ, with which the homogenous treatment-mediator assumption is assessed. Values of σ at which the ACMEs equal to zero are relatively small, suggesting that the ACME estimates are sensitive to the violation of the homogenous treatment-mediator effect assumption. Table 6 presents the associations of each focal mediator with other mediators. Estimates range from –0.091 to 0.678 standard deviations; most relationships are statistically significant. The significant relationships suggest the violation of the key assumption that there are no post-treatment confounders.
Result Interpretation and Implications
Within the context of this study, student interactions with faculty and peers in the broader campus community likely played a minimal role in explaining Melguizo et al.’s (2021) findings of the large effects on students’ mattering and sense of belonging to the campus. The ACME estimates are minimal because of the small constituent relationships (to and from the mediator) that explain the role of the mediators. Though faculty interactions are affected strongly by CCTP participation, they have a weak association with psychosocial outcomes. Mediational pathways are a product of these relationships; so, even though one part of the pathway may be large, if the other part is small, the overall role of the pathway is diminished. The large effects of CCTP participation on faculty interactions are consistent with qualitative evidence that CCTP supports and trains students to interact with faculty (Kitchen et al., 2021; Perez et al., 2021). If the CCTP seeks to increase students’ mattering and sense of belonging, then increasing the CCTP’s emphasis on interactions with non-CCTP peers may be beneficial.
The CCTP’s much smaller impact on interactions with peers in the broader campus community suggests that the program can increase its emphasis in this area. Qualitative evidence that the program builds a sense of community among program participants soon after students enter their institutions may explain the low level of interaction with non-CCTP peers. Evidence from other institutions suggests that relationships formed early in college are stable and do not expand appreciably to other students later in a student’s college tenure (Nathan, 2005; Chambliss and Takacs, 2014). In the context of CCTPs, the role of interactions with peers in the broader campus community is worthy of additional consideration.
Results of the sensitivity analyses suggest that the ACME estimates are relatively sensitive to the violations of key assumptions required for establishing valid inferences of causal effects. Thus, the results need to be interpreted with caution.
Concluding Remarks
In this article, we review causal mediation analysis, which is a new and insightful method to study mediation effects under the potential outcomes framework. We compare it to conventional mediation analysis. In addition, we provide a step-by-step guide for the application of causal mediation analysis to establish valid causal role of the mediator in RCT designs. Specifically, Step 1 compares participants in baseline characteristics through statistical techniques such as the t-test to alleviate concerns of non-random attrition. Step 2 involves computing estimates of ACMEs, average direct effects, and the total effect, assuming independence between mediators and including only the focal mediator. Step 3 evaluates the robustness of these estimates to the potential violation of the assumption of no unmeasured pre-treatment confounders through sensitivity analysis. Step 4 further examines how robust the estimates obtained in Step 2 are to the assumption that mediation mechanisms are independent when more than one mediator is measured in a study.
We illustrate the proposed procedure with empirical data collected from an educational study to present how causal inference involving a mediator can be performed. The mediation estimates are of small size, suggesting other mediational pathways largely generated the changes in the outcome variables. Additionally, we provide values of the sensitivity parameters which may be benchmarked against sensitivity values from future studies. For the program studied, the suggestion for practitioners is to consider the benefits of nonprogram peer interactions and how they may be further emphasized.
Through the illustration, we aim to offer a practical guide on applying and reporting causal mediation analysis using basic terminology. It is also worth nothing here that although we conduct all analyses with the R package mediation, there are other available programs and approaches for causal mediation analysis (e.g., Hong, 2015; Muthén et al., 2017). Tingley et al. (2014) include a more expanded discussion of the R causal mediation package and references such as Imai et al. (2010a) provide more theoretical and technical details. However, these references are written for a more general readership rather than targeting applied researchers in education; plus, the examples are not from educational studies and the language may not be immediately translative for education research. Additionally, a step-by-step procedure to assist applied education researchers to easily follow and apply to their own data sets is not found in those papers.
Unlike conventional mediation analysis, causal mediation analysis focuses on causal inference in its precise non-parametric definitions of causal mediation effects, clearly demonstrates required assumptions for a valid causal effect and provides measures of sensitivity to these assumptions. By comparing estimates of the mediation effects and the associated sensitivity parameters across analyses and studies, researchers can gain a better understanding of the causal role of mediators. Compared to conventional mediation analyses, causal mediation analysis also accommodates more types of models of the mediator and outcome.
Given the prevalence of RCT and quasi-experiment designs in education and the advantages of causal mediation analysis, we encourage researchers to follow the procedure recommended in this article to fully explore causal mechanisms, including sensitivity analyses, and to carefully interpret estimates of mediation effects. In addition, we argue that causal mediation analysis should be applied more often. We believe causal mediation methods will further our understanding of how different educational contexts result in changes to educational outcomes. Future methodological work is also needed, for instance, simulation studies can help illustrate the potential impacts of violating key assumptions required for to establish a valid causal role of a mediator.
Author’s Note
W. Edward Chi is now at Cerritos College. Elizabeth S. Park is now at Westat.
This article uses data based on a longitudinal study registered with the American Economic Association (Identifier AEARCTR-0000125). The article is related to Melguizo et al. (2021). No conflicts of interest exist. The Susan Thompson Buffett Foundation provided financial support. Opinions are those of the authors alone and do not necessarily reflect those of the Foundation or of the authors’ home institutions. Darnell Cole, Robert Reason, Ronald Hallett, Paco Martorell, Rosemary Perez, Joseph Kitchen, Gwendelyn Rivera, Mark Masterton, Cameron McPhee, Matthew Soldner, Evan Nielsen, Samantha Neiman, and Reed Humphrey gave helpful input. Gregory R. Hancock, Beth Gamse, Rebecca A. Maynard, Vincent Tinto, Harry O’Neil, David Quinn, Chih-Ping Chou, Guanglei Hong, Jennifer Keup, David S. Yeager, Patrick Lapid, Diana Strumbos, Jun Hyung Kim, Xu Qin, and Elise Swanson reviewed prior drafts. Chih-Ping Chou, Gregory R. Hancock, and Teppei Yamamoto provided technical guidance. Gale Sinatra, Mary Helen Immordino-Yang, and Rebecca Gotlieb reviewed related earlier work.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author. The data used in the running example is not publicly available.
Author Contributions
WC conducted the analysis and drafted the manuscript. SH and MJ drafted the article. EP, TM, and AK worked on the analysis. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2022.886722/full#supplementary-material
References
Ahn, H., and Powell, J. L. (1993). Semiparametric estimation of censored selection models with a nonparametric selection mechanism. J. Econ. 58, 3–29.
Angrist, J., Autor, D., Hudson, S., and Pallais, A. (2016). Evaluating Post-Secondary Aid: Enrollment, Persistence, and Projected Completion Effects (Working Paper No. 23015). Cambridge: National Bureau of Economic Research. doi: 10.3386/w23015
Baron, R. M., and Kenny, D. A. (1986). The moderator–mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J. Pers. Soc. Psychol. 51, 1173–1182.
Baroni, A., Dooly, M., García, P. G., Guth, S., Hauck, M., Helm, F., et al. (2019). Evaluating the Impact of Virtual Exchange on Initial Teacher Education: a European Policy Experiment. Dublin: Research-publishing. net.
Chang, M. J., Eagan, M. K., Lin, M. H., and Hurtado, S. (2011). Considering the impact of racial stigmas and science identity: persistence among biomedical and behavioral science aspirants. J. High. Educ. 82, 564–596. doi: 10.1353/jhe.2011.0030
Cooper, J. (1997). Marginality, mattering, and the African American student: creating an inclusive college environment. Coll. Stud Aff. J. 16, 15–20.
Cuartas, J., and McCoy, D. C. (2021). Causal mediation in developmental science: a primer. Int. J. Behav. Dev. 45, 269–274. doi: 10.1177/0165025420981640
De Witte, K., and Rogge, N. (2016). Problem-based learning in secondary education: evaluation by an experiment. Educ. Econ. 24, 58–82. doi: 10.1080/09645292.2014.966061
Dixon, S. K., and Kurpius, S. E. R. (2008). Depression and college stress among university undergraduates: do mattering and self-esteem make a difference? J. Coll. Stud. Dev. 49, 412–424. doi: 10.1353/csd.0.0024
Duflo, E., Glennerster, R., and Kremer, M. (2007). “Using randomization in development economics research: a toolkit,” in Handbook of Development Economics, Vol. 4, eds T. P. Schultz and J. A. Strauss (Amsterdam: Elsevier), 3895–3962. doi: 10.1016/S1573-4471(07)04061-2
France, M. K., and Finney, S. J. (2010). Conceptualization and utility of university mattering: a construct validity study. Meas. Eval. Couns. Dev. 43, 48–65. doi: 10.1177/0748175610362369
Fritz, M. S., and MacKinnon, D. P. (2007). Required sample size to detect the mediated effect. Psychol. Sci. 18, 233–239. doi: 10.1111/j.1467-9280.2007.01882.x
Gossett, B. J., Cuyjex, M. J., and Cockriel, I. (1996). African Americans’ and non-African Americans’ sense of mattering and marginality at public, predominantly White institutions. Equity Excell. Educ. 29, 37–42. doi: 10.1080/1066568960290306
Hausmann, L. R. M., Schofield, J. W., and Woods, R. L. (2007). Sense of belonging as a predictor of intentions to persist among African American and White first-year college students. Res. High. Educ. 48, 803–839. doi: 10.1007/s11162-007-9052-9
Hayes, A. F., and Scharkow, M. (2013). The relative trustworthiness of inferential tests of the indirect effect in statistical mediation analysis: does method really matter? Psychol. Sci. 24, 1918–1927. doi: 10.1177/0956797613480187
Heckman, J. J. (1976). The common structure of statistical models of truncation, sample selection and limited dependent variables and a simple estimator for such models. Ann. Econ. Soc. Meas. 5, 475–492.
Heckman, J. J. (1979). Sample selection bias as a specification error. Econometrica 47, 153–161. doi: 10.2307/1912352
Holland, P. W. (1986). Statistics and causal inference. J. Am. Stat. Assoc. 81, 945–960. doi: 10.2307/2289064
Hufstedler, H., Matthay, E. C., Rahman, S., de Jong, V. M. T., Campbell, H., Gustafson, P., et al. (2021). Current trends in the application of causal inference methods to pooled longitudinal observational infectious disease studies-a protocol for a methodological systematic review. PLoS One 16:e0250778. doi: 10.1371/journal.pone.0250778
Hurtado, S., Eagan, M. K., Cabrera, N. L., Lin, M. H., Park, J., and Lopez, M. (2008). Training future scientists: predicting first-year minority student participation in health science research. Res. High. Educ. 49, 126–152. doi: 10.1007/s11162-007-9068-1
Ichimura, H., and Lee, L.-F. (1991). “Semiparametric least squares estimation of multiple index models: single equation estimation,” in Nonparametric and Semiparametric Methods in Econometrics and Statistics, eds W. A. Barnett, J. Powell, and G. E. Tauchen (Cambridge: Cambridge University Press), 3–49.
Imai, K., Keele, L., and Tingley, D. (2010a). A general approach to causal mediation analysis. Psychol. Methods 15, 309–334. doi: 10.1037/a0020761
Imai, K., Keele, L., and Yamamoto, T. (2010b). Identification, inference and sensitivity analysis for causal mediation effects. Stat. Sci. 25, 51–71. doi: 10.1214/10-STS321
Imai, K., Keele, L., Tingley, D., and Yamamoto, T. (2011). Unpacking the black box of causality: learning about causal mechanisms from experimental and observational studies. Am. Polit. Sci. Rev. 105, 765–789. doi: 10.1017/S0003055411000414
Imai, K., and Yamamoto, T. (2013). Identification and sensitivity analysis for multiple causal mechanisms: revisiting evidence from framing experiments. Polit. Anal. 21, 141–171. doi: 10.1093/pan/mps040
Judd, C. M., and Kenny, D. A. (1981). Process analysis: estimating mediation in treatment evaluations. Eval. Rev. 5, 602–619. doi: 10.1177/0193841X8100500502
Keele, L., Tingley, D., and Yamamoto, T. (2015). Identifying mechanisms behind policy interventions via causal mediation analysis. J. Policy Anal. Manage. 34, 937–963. doi: 10.1002/pam.21853
Keup, J., and Barefoot, B. (2005). Learning how to be a successful student: exploring the impact of first-year seminars on student outcomes. J. First-Year Exp. Stud. Transition 17, 11–47.
Kireev, B., Zhundibayeva, A., and Aktanova, A. (2019). Distance Learning in Higher Education Institutions: results of an Experiment. J. Soc. Stud. Educ. Res. 10, 387–403.
Kitchen, J. A., Cole, D., Rivera, G., and Hallett, R. (2021). The Impact of a College Transition Program Proactive Advising Intervention on Self-Efficacy. J. Stud. Aff. Res. Pract. 58, 29–43. doi: 10.1080/19496591.2020.1717963
Klug, J. M. (2008). A Phenomenological Study on Students’ Perceptions of Mattering at a Selected Midwestern Public Institution (Publication No. 3333970). Ph.D. thesis. Vermillion: University of South Dakota.
Lee, D. S. (2009). Training, wages, and sample selection: estimating sharp bounds on treatment effects. Rev. Econ. Stud. 76, 1071–1102. doi: 10.1111/j.1467-937X.2009.00536.x
Legaki, N.-Z., Xi, N., Hamari, J., Karpouzis, K., and Assimakopoulos, V. (2020). The effect of challenge-based gamification on learning: an experiment in the context of statistics education. Int. J. Hum.-Comput. Stud. 144:102496. doi: 10.1016/j.ijhcs.2020.102496
MacKinnon, D. P. (2008). Introduction to Statistical Mediation Analysis. Milton Park: Taylor & Francis.
MacKinnon, D. P., Lockwood, C. M., and Williams, J. (2004). Confidence limits for the indirect effect: distribution of the product and resampling methods. Multivar. Behav. Res. 39, 99–128. doi: 10.1207/s15327906mbr3901_4
MacKinnon, D. P., Valente, M. J., and Gonzalez, O. (2020). The correspondence between causal and traditional mediation analysis: the link is the mediator by treatment interaction. Prev. Sci. 21, 147–157. doi: 10.1007/s11121-019-01076-4
Marshall, S. K. (2001). Do I matter? Construct validation of adolescents’ perceived mattering to parents and friends. J. Adolesc. 24, 473–490. doi: 10.1006/jado.2001.0384
Melguizo, T., Martorell, P., Swanson, E., Chi, W. E., Park, E., and Kezar, A. (2021). Expanding Student Success: the Impact of a Comprehensive College Transition Program on Psychosocial Outcomes. J. Res. Educ. Effect. 14, 835–860. doi: 10.1080/19345747.2021.1917029
Muthén, B. O., Muthén, L. K., and Asparouhov, T. (2017). Regression and Mediation Analysis Using Mplus. Los Angeles, CA: Muthén & Muthén.
Nathan, R. (2005). My Freshman year: What a Professor Learned by Becoming a Student. Ithaca: Cornell University Press.
Page, L. C., Kehoe, S. S., Castleman, B. L., and Sahadewo, G. A. (2019). More than dollars for scholars: the impact of the Dell Scholars Program on college access, persistence and degree attainment. J. Hum. Resour. 54, 683–725. doi: 10.3368/jhr.54.3.0516.7935R1
Pearl, J. (2001). “Direct and indirect effects,” in Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence, eds B. John and K. Daphne (Burlington: Morgan Kaufmann Publishers), 411–420.
Perez, R. J., Acuña, A., and Reason, R. D. (2021). Pedagogy of validation: autobiographical reading and writing courses for first-year, low-income students. Innov. High. Educ. 46, 623–641. doi: 10.1007/s10755-021-09555-9
Price, D. V. (2005). Learning Communities and Student Success in Postsecondary Education: A Background Paper. New York, NY: MDRC.
Raudenbush, S. W., and Schwartz, D. (2020). Randomized experiments in education, with implications for multilevel causal inference. Annu. Rev. Stat. Appl. 7, 177–208. doi: 10.1146/annurev-statistics-031219-041205
Rayle, A. D., and Chung, K.-Y. (2007). Revisiting first-year college students’ mattering: social support, academic stress, and the mattering experience. J. Coll. Stud. Retent. Res. Theory Pract. 9, 21–37. doi: 10.2190/X126-5606-4G36-8132
Robins, J. M. (2003). “Semantics of causal DAG models and the identification of direct and indirect effects,” in Highly Structured Stochastic Systems, eds P. J. Green, N. L. Hjort, and S. Richardson (Oxford: Oxford University Press), 70–81.
Robins, J. M., and Greenland, S. (1992). Identifiability and exchangeability for direct and indirect effects. Epidemiology 3, 143–155. doi: 10.1097/00001648-199203000-00013
Rosenbaum, P. R. (2002). Covariance adjustment in randomized experiments and observational studies. Stat. Sci. 17, 286–327. doi: 10.1214/ss/1042727942
Rosenberg, M., and McCullough, B. C. (1981). Mattering: inferred significance and mental health among adolescents. Res. Community Ment. Health 2, 163–182.
Sadoff, S. (2014). The role of experimentation in education policy. Oxford Rev. Econ. Policy 30, 597–620. doi: 10.1093/oxrep/grv001
Schlossberg, N. K. (1989). Marginality and mattering: key issues in building community. New Dir. Stud. Serv. 48, 5–15. doi: 10.1002/ss.37119894803
Strayhorn, T. L. (2011). Bridging the pipeline: increasing underrepresented students’ preparation for college through a summer bridge program. Am. Behav. Sci. 55, 142–159. doi: 10.1177/0002764210381871
Strayhorn, T. L. (2012). College Students’ Sense of Belonging: A Key to Educational Success for all Students. Milton Park: Taylor and Francis.
Taylor, K. (2003). Learning Community Research and Assessment: What We Know Now. Ollympia: Washington Center for Improving the Quality of Undergraduate Education.
Tingley, D., Yamamoto, T., Hirose, K., Keele, L., and Imai, K. (2014). Mediation: R package for causal mediation analysis. J. Stat. Softw. 59, 1–38. doi: 10.18637/jss.v059.i05
Tovar, E. (2013). A Conceptual Model on the Impact of Mattering, Sense of Belonging, Engagement/Involvement, and Socio-Academic Integrative Experiences on Community College Students’ Intent to Persist (Publication No. 3557773). Ph.D. thesis. Claremont: Claremont Graduate University.
Tovar, E., Simon, M. A., and Lee, H. B. (2009). Development and validation of the college mattering inventory with diverse urban college students. Meas. Eval. Couns. Dev. 42, 154–178.
Valente, M. J., Rijnhart, J. J., Smyth, H. L., Muniz, F. B., and MacKinnon, D. P. (2020). Causal mediation programs in R, M plus, SAS, SPSS, and Stata. Struct. Equ. Model. Multidiscip. J. 27, 975–984. doi: 10.1080/10705511.2020.1777133
VanderWeele, T. (2015). Explanation in Causal Inference: Methods for Mediation and Interaction. Oxford: Oxford University Press.
VanderWeele, T., and Vansteelandt, S. (2014). Mediation analysis with multiple mediators. Epidemiol. Methods 2, 95–115.
Weiss, M. J., Mayer, A., Cullinan, D., Ratledge, A., Sommo, C., and Diamond, J. (2014). A Random Assignment Evaluation of Learning Communities at Kingsborough Community College: Seven Years Later. New York, NY: MDRC.
What Works Clearinghouse (2020). What Works Clearinghouse standards Handbook (Version 4.1). Washington, DC: Institute of Education Sciences.
Yeboah, E., Mauer, N. S., Hufstedler, H., Carr, S., Matthay, E. C., Maxwell, L., et al. (2021). Current trends in the application of causal inference methods to pooled longitudinal non-randomised data: a protocol for a methodological systematic review. BMJ Open 11:e052969. doi: 10.1136/bmjopen-2021-052969
Keywords: causal mediation analysis, college transition program, psychosocial outcome, educational program evaluation, mediation analysis
Citation: Chi WE, Huang S, Jeon M, Park ES, Melguizo T and Kezar A (2022) A Practical Guide to Causal Mediation Analysis: Illustration With a Comprehensive College Transition Program and Nonprogram Peer and Faculty Interactions. Front. Educ. 7:886722. doi: 10.3389/feduc.2022.886722
Received: 28 February 2022; Accepted: 01 June 2022;
Published: 04 August 2022.
Edited by:
Xinya Liang, University of Arkansas, United StatesReviewed by:
Kyle Cox, University of North Carolina at Charlotte, United StatesYusuf Kara, Southern Methodist University, United States
Copyright © 2022 Chi, Huang, Jeon, Park, Melguizo and Kezar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sijia Huang, c2lqaHVhbmdAaXUuZWR1
 W. Edward Chi
W. Edward Chi Sijia Huang
Sijia Huang Minjeong Jeon3
Minjeong Jeon3 Elizabeth S. Park
Elizabeth S. Park