- Department of Kinesiology and Educational Psychology, Washington State University, Pullman, WA, United States
Item parameter recovery in the compensatory multidimensional graded response model (MGRM) under simple and complex structures with rating-scale item response data was examined. A simulation study investigated factors that influence the precision of item parameter estimation, including sample size, intercorrelation between the dimensions, and test lengths for the MGRM under balanced and unbalanced complex structures, as well as the simple structure. The item responses for the MGRM were generated and analyzed across conditions using the R package mirt. The bias and root mean square error (RMSE) was used to evaluate item parameter recovery. Results suggested that item parameter estimation was more accurate in balanced complex structure conditions than in unbalanced or simple structures, especially when the test length was 40 items, and the sample size was large. Further, the mean bias and RMSE in the recovery of item threshold estimates along the two dimensions for both balanced and unbalanced complex structures were consistent across all conditions.
Introduction
The item response theory (IRT) framework has been used in conjunction with polytomous probabilistic models, such as the graded response model (GRM), to describe the interaction between individuals and items for a wide range of psychological, educational, and medical outcomes measured with rating scales (Samejima, 1969; Bolt and Lall, 2003; Scherbaum et al., 2006). A foundational assumption in the polytomous IRT models is unidimensionality. In practice, many constructs and corresponding measures are multidimensional, such as the Resilience Scale and Cushing Syndrome Scale (Depaoli et al., 2018; Hunsu et al., 2022). As a result, the unidimensionality assumption of IRT models is violated, and consequently, multidimensional IRT models such as the multidimensional GRM (MGRM) are proposed to ensure a deeper grasp of how multiple constructs in the instrument are measured by the item sets. The application of MGRM has occurred in both education (Wang et al., 2004; Friyatmi, 2020) and health-related contexts (e.g., mental health; DeMars, 2013; Nouri et al., 2021). Using GRM (or other multidimensional polytomous IRT models) to describe the interaction of items and examinees necessitates the specification of either a simple or complex structure. Many studies have operationalized the definitions of simple and complex structures (DeMars, 2013; Wetzel and Hell, 2014; Jiang et al., 2016). Wetzel and Hell (2014), for example, used these two structures to investigate which structure best described Holland’s model for vocational interest inventories. In their study, the simple structure was defined as a between-multidimensional model in which several latent traits of the vocational interest scale, as well as the correlation between dimensions, are modeled simultaneously, and each item only measures one latent trait at a time. The complex structure, on the other hand, was referred to as the within-multidimensional model because items were allowed to measure multiple latent traits at the same time. Jiang et al. (2016) and Svetina et al. (2017) operationalized these two structures (i.e., simple and complex) by the number of non-zero discrimination parameters on each dimension.
Despite its capabilities in addressing multidimensionality under both simple and complex structures, the performance of MGRM has not been fully explored and evaluated, especially under complex structure. Only very few studies could be identified that examined the implementation of MGRM across factors, such as sample size (N), test length (L), and intercorrelations between the dimensions (r). All of the studies, however, were conducted assuming a simple structure. Ferrando and Chico’s study (2001), for example, found that using MGRM in the data analysis (N < 500) was insufficient and computationally demanding for test lengths of 20 items. For this reason, the authors used the linear factor analysis (FA) model for their analysis instead of MGRM. As a result of this limitation, Forero and Maydeu-Olivares (2009) and Jiang et al. (2016) conducted simulation studies that investigated the minimum sample size in conjunction with other manipulative factors required in the implementation of MGRM, particularly under a simple structure. In both studies, the authors used various sample sizes (200 ≤ N ≤ 2, 000), test lengths (J = 9,…, 240), and intercorrelations between dimensions (r = 0.2,…,0.8) in their simulations to investigate the performance of MGRM under a simple structure. A more in-depth review of these studies appears below.
While many of the instruments assume a complex structure (e.g., English language proficiency [ELP] assessment; Wolf and Butler, 2017), the performance of MGRM under such a dimensional structure is yet to be explored. Items are frequently associated with more than one latent feature in practice, rather than assuming a simple structure. No simulation studies that we are aware of have employed the MGRM to evaluate the potential variables that may promote better accuracy of item parameter estimation under different data structure complexities. In light of this, our purpose with this article is to extend the current literature by examining the performance of MGRM under both simple and complex structures in the presence of several manipulated factors, including sample size, intercorrelation between dimensions, test lengths, and dimensional structure (level of complexities). This article is structured as follows: first, we provide context and literature on MGRM; second, the design and analysis of simulations are described; third, the results are summarized and discussed; and fourth, the conclusion and recommendation for the implementation of MGRM are presented.
Background and literature
The multidimensional graded response model
The MGRM is an extended version of the conventional GRM extensively as a statistical choice to investigate the correlation among the latent traits in an instrument. Below is the two-parameter logistic form of the MGRM (De Ayala, 1994; Jiang et al., 2016; Wang et al., 2018). See Jiang et al. (2016) and Wang et al. (2018) for more details about Equation 2.
Simplifying, Equation 1 becomes
Where is the probability that observed scores for item j and examinee i given the ability or latent trait θ to obtain a score greater than or equal to category k, D = 1 or 1.7, ajm is the vector of item discrimination parameters for item j on each latent trait m, bjk is the vector of item difficulty parameters for each category k within item j, θm is the vector of the latent traits on mth dimension. However, the number of latent traits and category responses influence the dynamical feature of MGRM to GRM, and other multidimensional IRT models (e.g., multidimensional two-parameter logistic model; De Ayala, 1994; Embretson and Reise, 2000; Penfield, 2014; Dai et al., 2021).
The manner in which the latent traits interact and their respective denominators can be categorized into compensatory and non-compensatory MGRMs. In the non-compensatory model, the probability of an examinee endorsing a certain item response category requires mastery of all required latent traits, and the denominator is the product of the corresponding probability of each dimension. Whereas, in the compensatory model, the probability of endorsing a specific category on an item is non-zero if the examinee is proficient in any of the traits measured by the item (i.e., high ability compensates for lower ability), and the denominator is the exponential sum of the probability of each dimension. In applied settings, the appropriate use of these models varies. Due to its computational flexibility, we focused on the compensatory MGRM in this study.
Application of multidimensional graded response model
We identified 60 articles across various contexts that applied MGRM with empirical data using databases (e.g., Google Scholar and Worldwide Science). Among the identified articles, we noted that MGRM has been gaining attention from researchers in health (e.g., Walton et al., 2008; Depaoli et al., 2018; Haem and Doostfatemeh, 2020) and education (e.g., DeMars, 2013; Wang et al., 2015; Friyatmi, 2020). These studies used MGRM because it improved measurement precision, especially when the correlation between latent traits was taken into account, and the test lengths and sample sizes were modest. For instance, Depaoli et al. (2018) utilized MGRM in health research to analyze the Cushing Quality of Life Questionnaire (CushingQoL) scale that contained 12 five-point rating scale items. The Cushing syndrome instrument consisted of items that were developed to measure two subscales, namely, physical and psychological factors. The authors investigated the accuracy of item parameter estimation and model fit of MGRM with a relatively small sample size (N = 397) as compared to the unidimensional IRT models, such as GRM. Their findings showed that MGRM fit the data better than the unidimensional model based on the nested log-likelihood test. Based on the model fit results, further analysis was conducted to determine the accuracy of item parameter estimates with MGRM. Furthermore, all items in the development of the CushingQoL scale were well discriminative between low and high levels of Cushing syndrome patients, and the item difficulty parameter estimates indicated that the patient with a low QoL level tended to agree more with the items.
Another example is Haem and Doostfatemeh (2020) in which the authors applied MGRM to analyze data from a general health questionnaire (GHQ) that consisted of 12 items with a 4-point rating scale. Their purpose was to investigate which of the 12 items was more informative. They found that one item (i.e., feeling unhappy and depressed) measuring the social dysfunction dimension was more informative than other items. In addition, the authors’ finding on the MGRM model fit was consistent with Depaoli et al. (2018), indicating that MGRM with two dimensions yielded an adequate fit according to all model fit indices. These examples continue in the educational domain, where the MGRM showed better model fit compared to a unidimensional model with data from the Trend in International Mathematics and Science Study (TIMSS) science assessment (DeMars, 2013), and better model fit with data from the 21-item Teacher Observation of Classroom Adaptation (TOCA) scale consisting of three subscales—concentration problems, disruptive behavior, and prosocial behavior (Wang et al., 2015). The evidence supports the MGRM in many applications and across domains.
Literature on the performance of multidimensional graded response model
In the last decade, studies (Reckase, 2009; Finch, 2010; Finch, 2011; Svetina, 2013; Svetina et al., 2017) have investigated the performance of multidimensional polytomous IRT models. In this section, we synthesize the details of these studies and discuss their findings.
According to the concerns raised by Ferrando and Chico (2001), using MGRM under the simple structure to analyze data from a 20-item instrument with a sample size of 500 might influence the accuracy of the item parameter estimations. Based on this, Forero and Maydeu-Olivares (2009) conducted a simulated study that investigated the performance of MGRM across 324 conditions with a variety of manipulated factors (e.g., sample size [200, 500, 2,000], test length [9, 21, and 42 items], and factor loadings [0.4, 0.6, 08]). When using the unweighted least square (ULS) estimation, the authors discovered that a sample size of 500 and an instrument of 40 items would be appropriate to provide relatively accurate item parameter estimates. The use of the weight least square (WLS) estimation under a small sample size of 500 yielded poor standard errors, especially when indicators had extreme item parameters. The authors’ assumption that the three latent traits were uncorrelated, however, posed a limitation to the study. Following this limitation, some studies (Jiang et al., 2016; Wang et al., 2016, 2018; Su et al., 2021) further investigated the impact of different levels of correlation and other manipulative variables (e.g., sample size and test lengths) on the performance of MGRM.
In Jiang et al. (2016), the authors were motivated by the constraints of prior studies to investigate the performance of a three-dimensional simple structure MGRM over five sample sizes (N = 500; 1,000; 1,500; and 2,000), three test lengths (L = 30, 90, and 240), and intercorrelation between the dimensions was specified at r = 0.2, 0.5, and 0.7, respectively. With a test length of 90 or less, the results showed that a sample size of 500 produced reliable parameter estimates. For better parameter estimates, a higher sample size of 1,000 was necessary when the test items were increased to 240. For further work on the performance of MGRM, Wang et al. (2016) conducted a simulation study that estimated the classification accuracy and consistency indices using MGRM across several manipulated variables (i.e., sample size [1,000, 3,000] and levels of correlation [0.00, 0.50, 0.80]). Results of the study revealed that the value of accuracy indices (e.g., bias, absolute bias, and RMSE) increased as the sample size and the correlation between latent traits increased. Another study is a simulation study on the performance of the S- χ2 statistic with MGRM conducted by Su et al. (2021). In this study, the authors utilized the Monte Carlo simulation procedure to evaluate the performance of S- χ2 for detecting item misfits using MGRM across manipulated factors (e.g., sample size [500, 2,000], test length [30, 60, and 90 items], and correlation between dimensions [0.5, 0.7]). In addition, the authors randomly selected 10% of the items as misfitting items in the simulation study. Results of the study regarding false positive rates (FPRs) and true positive rates (TPRs) suggested that increasing the sample size to 2,000 inflated the FPRs from 13 to 14% for the test length of 90 items at α = 0.05, and remained reasonably close to the nominal rates for 30 and 60 items with a sample size of 500, whereas TPR was found higher with 30 and 90 items for a sample size of 2,000.
To further investigate the performance of MGRM, some simulation studies (Kuo and Sheng, 2016; Wang et al., 2018) have incorporated the presence of non-normality of latent traits and several parameter estimation methods via the use of software in their simulation studies. For example, Kuo and Sheng (2016) investigated the performance of MGRM under different estimation methods (e.g., marginal maximum likelihood or MML, Bayesian algorithms) and the use of software (e.g., IRTPRO, BMIRT, and MATLAB). The simulation study was conducted across several manipulated variables (i.e., sample size [500, 1,000], test length [20, 40], inter-trait correlation [0.2, 0.5, 0.8], estimation methods [Bock-Aitkin expectation-maximum algorithm, adaptive quadrature approach], Gibbs, Metropolis-Hastings or MH, Hastings-within-Gibbs, blocked Metropolis, Metropolis-Hastings Robbins-Monro, and software [IRTPRO, BMIRT, and MATLAB]). Results of the study revealed that MH with the three procedures implemented in BMIRT (e.g., TRUE, AIC, or COR) provided better estimates of item discrimination and threshold parameters than other procedures with a sample size of 500, and a test length of 20. However, the procedures implemented in BMIRT resulted in a better estimate, especially with a sample size of 1,000, a test length of 20, and an inter-trait correlation of 0.2. Another study is Wang et al. (2018), where the performance of MGRM in the presence of non-normality of latent traits across several manipulated variables (i.e., sample size [500, 2,000], test length [30, 90], factor loadings [0.5, 0.7], and the number of non-normal dimensions [0, 1, 2, 3]) was investigated. One interesting finding was that skewness on one dimension did not affect the recovery parameter accuracy of the rest of the dimensions, regardless of the level of correlation. The full-information maximum likelihood (FIML) produced more accurate estimates compared to other estimation methods.
In the medical domain, application studies with MGRM have addressed sample size issues (Wang et al., 2018; Haem and Doostfatemeh, 2020). These studies found that the MGRM model provided reliable estimates with sample sizes that are frequently considered small in health research and that the recovery of parameters in one dimension was unaffected by skewness in other dimensions, regardless of the level of correlations among dimensions.
The abovementioned studies investigated the performance of MGRM across different manipulative factors (e.g., sample size, test length, and intercorrelations) but only with a simple structure. To extend the existing literature, the current study investigated the performance of MGRM under both simple and complex structures across sample size, intercorrelation between dimensions, test lengths, and the complexity of dimensional structure (simple, balanced, and unbalanced). The authors of the current study hypothesized that MGRM with a complex structure would yield a better estimate than a simple structure. Furthermore, the authors hypothesized that a higher level of correlation among dimensions under a complex structure would substantially impact the accuracy of the recovery of parameter estimates than when it was modeled using a simple structure, and that the parameter recovery would be better in a balanced structure than unbalanced structure, particularly when a small number of items were unbalanced in terms of the level of complexity. In lieu of this, it would be worthwhile to investigate the accuracy of MGRM parameter estimates under complex structures, which is frequently reflected in assessment settings. To the best of our knowledge, no studies have systematically investigated or evaluated the performance of MGRM, particularly under complex structures. In this study, our goal is to investigate the performance of MGRM under complex structures with several manipulated variables.
Method
Simulation design
We conducted a simulation study using the manipulated factors that have been implemented in previous research (Reise and Yu, 1990; Jiang et al., 2016; Svetina et al., 2017), including sample size (three levels), intercorrelation (three levels), test length (two levels), and structure of data (five levels; see Table 1). A fully crossed design for all these manipulated factors yielded a total of 120 conditions, each of which was replicated 500 times using packages and code written in R (R Core Team, 2021).
Sample size (N) and test length (L)
The influence of sample size and test length for unidimensional and multidimensional models has been investigated (e.g., Reise and Yu, 1990; Jiang et al., 2016; Wang et al., 2018). Wang et al. (2018) examined N = 500 and 2,000 to demonstrate that large sample sizes (>N = 1,000) played a vital role in the accuracy of the MGRM parameter estimates, especially when the non-normality of dimensions under simple structure was taken into account. Thus, we utilized a small sample size (N = 500) to evaluate a lower bound and the 1,500 and 2,000 as an upper bound, assuming a positive relationship with larger sizes and parameter estimation accuracy, and to also reflect the typical applications with large sample size. These levels of sample sizes of N = 500, 1,500, and 2,000, with test lengths of L = 20 and 40 were chosen to be consistent with previous studies and real data. This enhances the contextualization of our results to previous work.
Intercorrelation between dimensions
Several correlations between dimensions have been investigated based on previous simulated and empirical literature (Wetzel and Hell, 2014; Jiang et al., 2016; Svetina et al., 2017; Wang et al., 2018). For this study, the correlation between dimensions was set at r = 0.00, 0.25, 0.50, and 0.75, to increase generalizability with previous work.
Dimensional structure
Only two dimensions were specified for both simple and complex structures. The simple structure (i.e., 0% cross-loadings) was modeled as the baseline conditions. Explicitly, the same number of items in a simple structure measures each dimension. In the 20-item condition, for instance, items 1–10 loaded on the first dimension only and items 11–20 loaded on the second dimension only (see columns 1 and 2 in Table 2). For complex structures, we specified two different types (balanced vs. unbalanced) and degrees of complexity (20 vs. 40% of cross-loaded items). In the balanced complexity condition, the loadings parameters are equal. For instance, a 20% balanced complexity in the 20-item condition means that four items loaded on both dimensions and each item had equal discrimination parameters (i.e., factor loadings) across the dimensions. In the case of unbalanced complexity, the items were assumed to have different discrimination parameters across the dimensions. Specifically, the discrimination parameters of the items in the balanced complex structure were generated from a uniform distribution of U [1.1, 2.8], whereas a value of 0.85 was added to those of the second dimension to obtain the unbalanced structure (Jiang et al., 2016; Svetina et al., 2017). See Table 2 for the item discrimination parameters that we used for different types of dimensional structures under the condition of 20 items with 20% complexity.
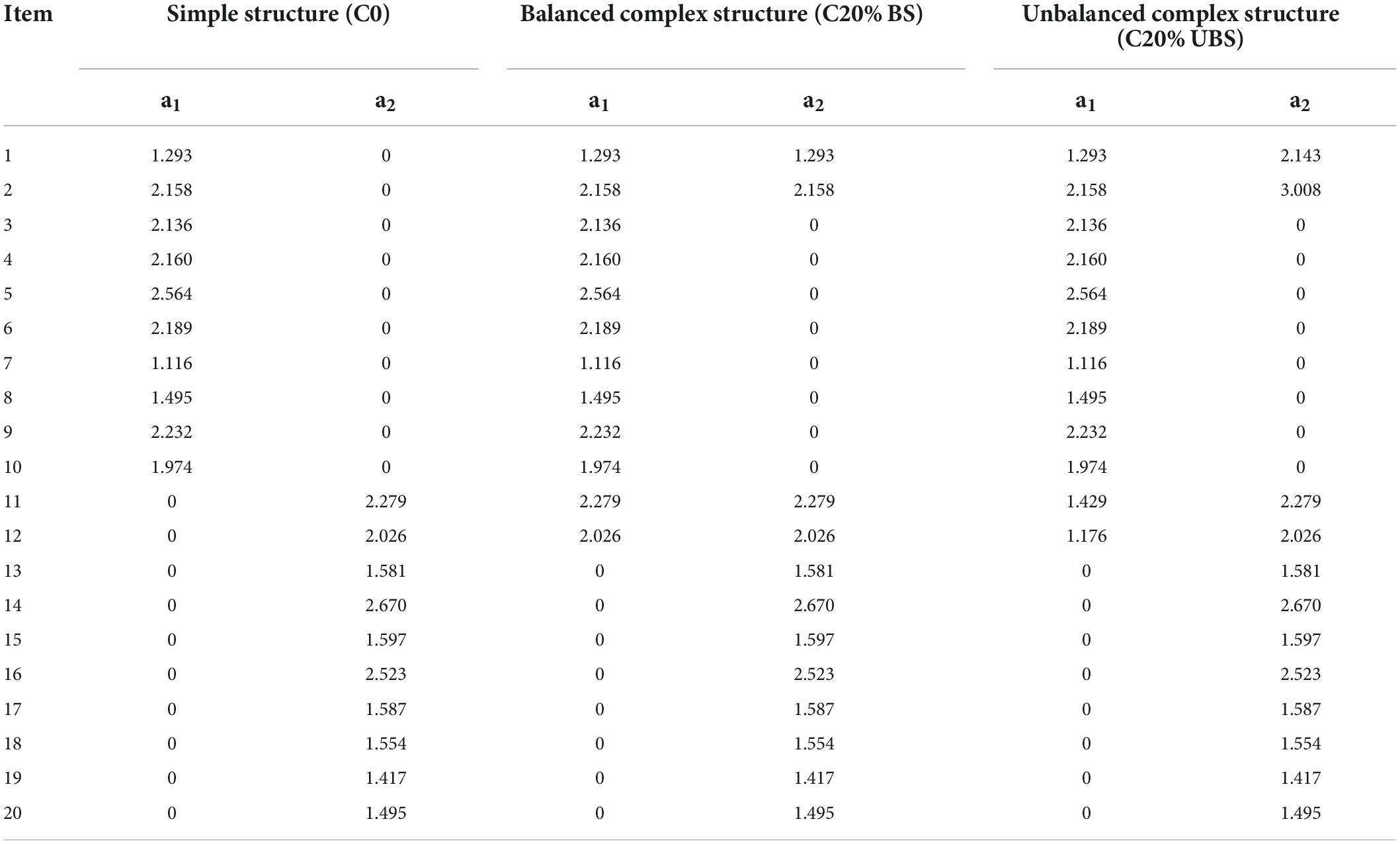
Table 2. Item discrimination parameters for different types of complexity under selected conditions.
Fixed factors
All items followed a 4-point rating scale, and the three threshold parameters were randomly sampled from a uniform (U) distribution, U [−2, −0.67], U [−0.67, 0.67], and U [0.67, 2] (Jiang et al., 2016). The simulees’ latent ability values on the two dimensions were generated using a multivariate normal (MVN) distribution with a specified mean vector of zeros and a variance-covariance matrix with specified covariance (i.e., off-diagonal) elements (e.g., r = 0.25).
Data generation and analysis
We used the simdata function from the mirt R package (Chalmers, 2012, version 1.35.1) to generate the item responses for the MGRM. With fixed quadrature points and a convergence threshold of 0.0001 by default, the item parameters were estimated with maximum likelihood (ML) estimation with the expectation-maximization (EM) algorithm. According to the manual of the package, the EM algorithm was effective for one to three dimensions (Chalmers, 2012). In this simulation study, we monitored and tested the model misfit across all 120 conditions, as well as the 500 replications, by ensuring that the model fit indexes for each condition satisfied the criteria for satisfactory model fit including a non-significant M2 test (i.e., p > 0.05), RMSEA < 0.05, CFI > 0.9, and SRMR < 0.05 (Hu and Bentler, 1999; Weston and Gore, 2006).
Outcome measures for parameter recovery
Both the estimated and true parameters were used to calculate the average bias and root mean square error (RMSE) across the 500 replications. For each replication, bias and RMSE were calculated for the two discrimination and three threshold parameters across items, respectively. Average bias and RMSE were then computed across replications for every condition. For example, the bias and RMSE for the first discrimination parameter were computed as follows:
Where and aj1 are the true and estimated parameters across J items, respectively. L is the test length.
Result
The results for the bias and RMSE of item parameter estimations across the conditions in the study are presented through the profile plots with four main sections: (1) item discrimination estimates for simple structure, (2) discrimination estimates for balanced complex structure, (3) discrimination estimates for unbalanced complex structure, and (4) mean of item threshold estimates for simple, balanced, and unbalanced structures.
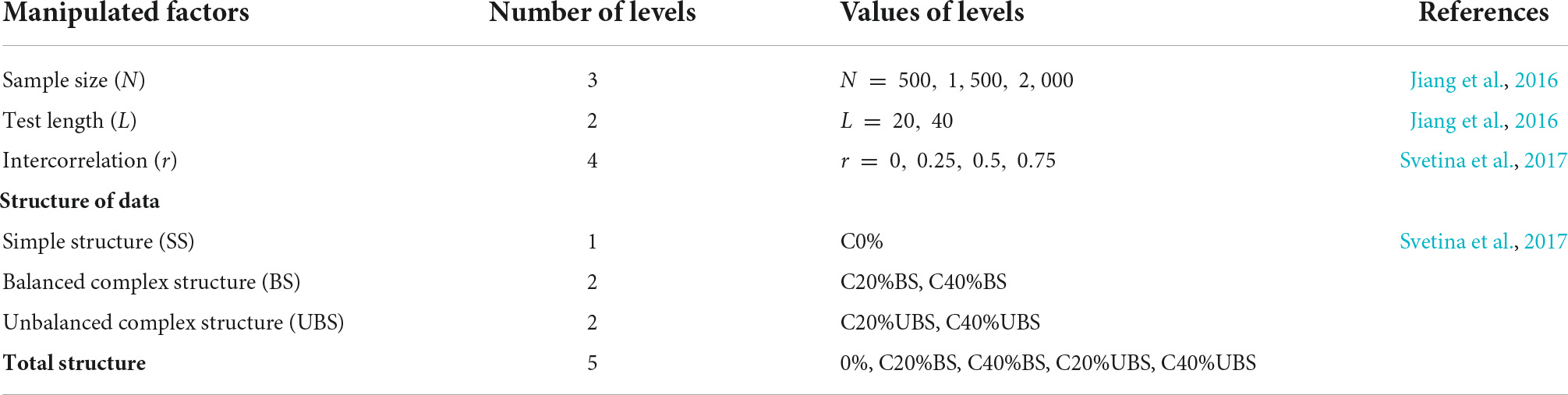
Figure 1 depicts the bias and RMSE of item discrimination parameter estimations for MGRM across conditions under a simple structure. As indicated in the upper panel, a similar pattern was found across test lengths (L = 20, 40), indicating that the bias values for the first and second item discrimination parameters, a1 and a2, were unaffected by the number of items specified. For a1, the upper panel of the figure indicates that the bias values for the zero correlation condition (r = 0, the solid lines with square in the graphs) showed overestimation, while conditions with other correlations (r = 0.25 [dashed lines with circles], 0.5 [dotted lines with triangles], and 0.75 [dot-dash lines with crosses]) showed underestimation, especially when the sample size was 500. The bias, however, only ranged slightly from −0.041 to 0.033 across all conditions except for the condition of r = 0.5 and N = 500 under which the average bias was found to be −0.082. Additionally, the magnitude of the bias values only varied trivially when the sample size was increased from 1,500 to 2,000. For a2, we observed that the bias values ranged only slightly from −0.025 to 0.029 across levels of sample sizes and correlations, despite the different patterns of bias noticed under the r = 0.5 condition. The RMSEs for a1 and a2 are included in the lower panel of Figure 1. Similar patterns were observed across all conditions for both a1 and a2. Across all levels of correlation, the RMSEs for a1 and a2 decreased as the sample size increased. The largest RMSE of a1 was observed to be 0.158 when N = 500 and r = 0.5. There was no discernible difference in RMSE values for a2 across sample sizes and levels of correlations.
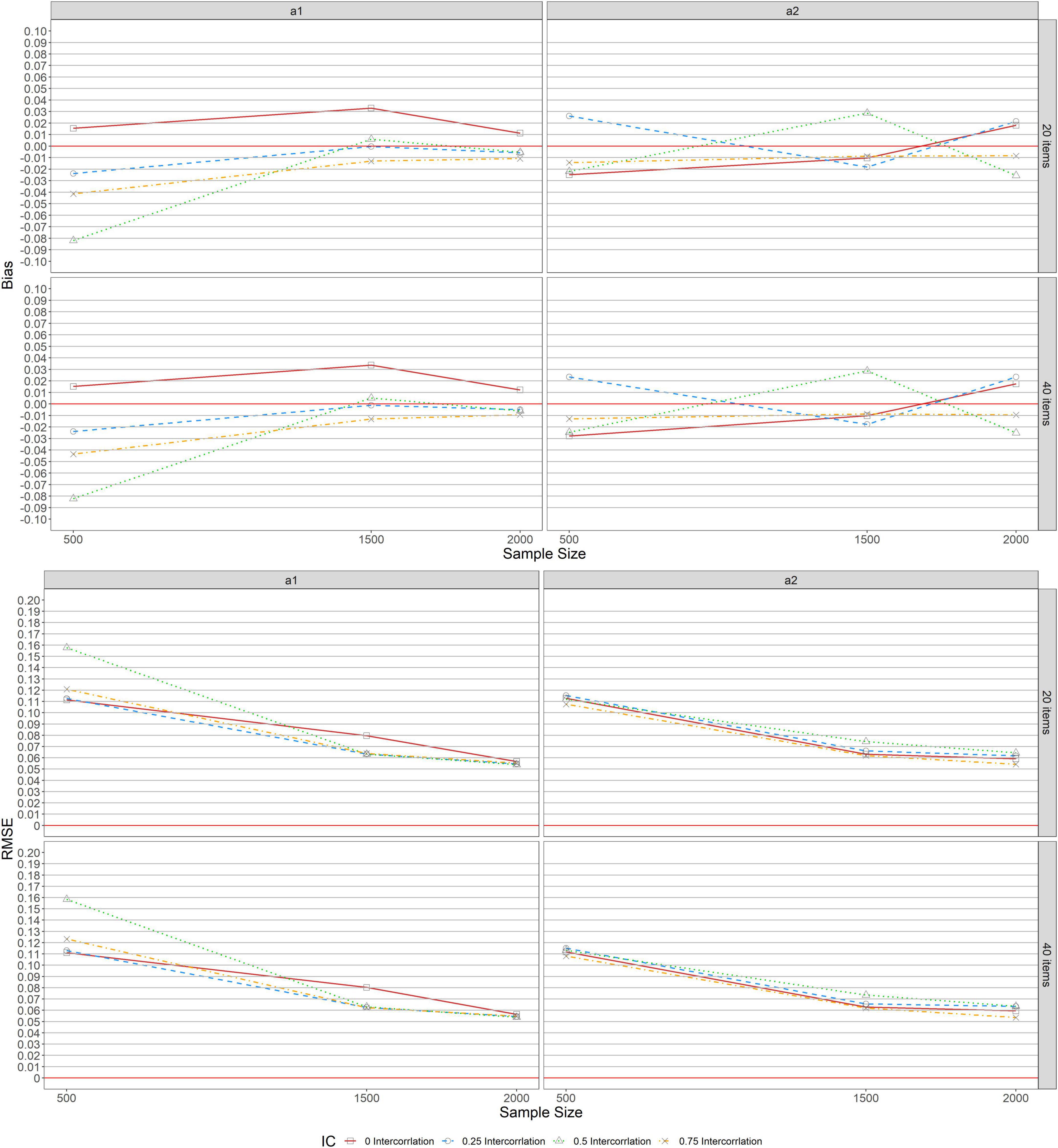
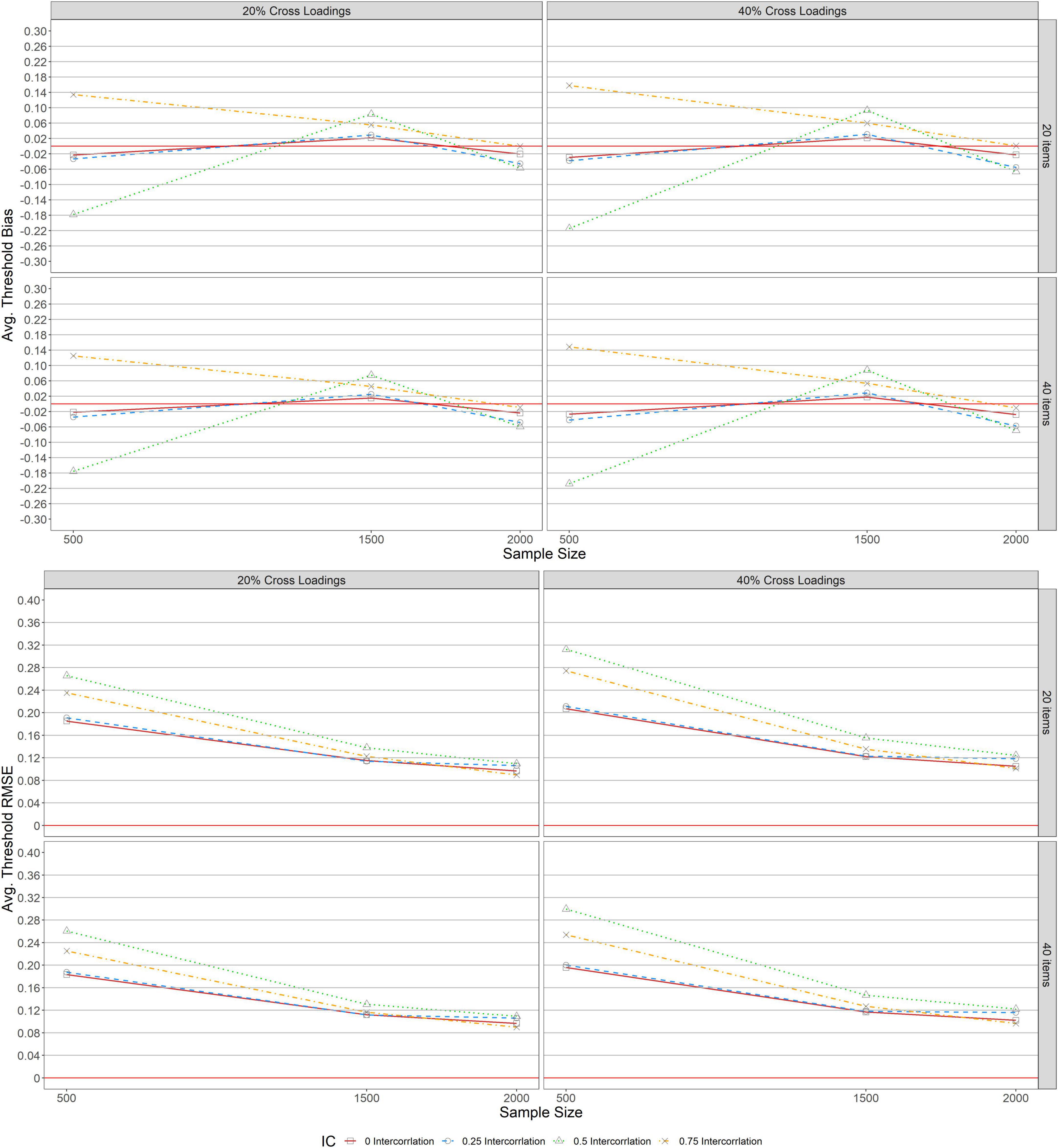
Figure 2 shows the bias and RMSE of item discrimination parameter estimations for MGRM across conditions under a balanced complex structure. Similar patterns of bias were found across test lengths (L = 20, 40) when complexity was 20% balanced for a1 and a2, as seen in the upper panel of the figure. With 20% balanced complexity, bias results revealed overestimation for zero correlation (r = 0, the solid lines with squares in the graphs) and underestimation for other levels of correlation (r = 0.25 [dashed lines with circles], 0.5 [dotted lines with triangles], and 0.75 [dot-dash lines with crosses]) for a1. Further, the bias values ranged slightly from −0.050 to 0.043 across all conditions except for the condition of r = 0.5 and N = 500. Under this condition, the bias was −0.103, which decreased to almost 0 as the sample size increased from 500 to 1,500, and then declined slightly after reaching a steady state (bias of zero) and remained unchanged (1, 500 ≤ N ≤ 2, 000). The bias results for a2 across test lengths (L = 20, 40) with 20% balanced complexity ranged from −0.033 to 0.038 across sample sizes and correlations.
Bias patterns varied across test lengths (L = 20, 40) when complexity was 40% for a1 and a2. When L = 20, the bias values for a1 increased as the level of correlation increased. Further, as the sample size increased for the levels of correlation (r = 0.5 and 0.75), the bias values were high except for the condition of r = 0.5 and N = 500. Under this condition, the bias value was found to be 0.042. However, the bias results decreased as the sample size increased from 500 to 1,500, and then falls below zero and increased to 0.055 for the level of zero correlation (r = 0) as the sample kept increasing from 1,500 to 2,000. Also, when L = 40, the bias values for a1 with 40% balanced complexity exhibited the same pattern of bias for a1 with 20% balanced complexity. For a2, the magnitudes of bias values were similar to the bias results for a1 with 40% balanced complexity when L = 20, whereas, with 40% balanced complexity, bias results for a2 showed the same bias results for a2 with 20% balanced complexity when L = 20.
RMSE for a1 and a2 with 20% balanced complexity at the lower panel of Figure 2 indicated similar patterns across test lengths (L = 20, 40). With 20% balanced complexity across all levels of correlation between a1 and a2, the RMSEs decreased as the sample size increased. Under 40% complexity, the pattern of RMSE differed across test lengths (L = 20, 40) for a1 and a2. RMSE values for correlation (r = 0.75) were high across sample sizes for a1 and a2 when L = 20, and as the sample size increased from 500 to 1,500 across all levels of correlation and test lengths, the RMSE values decreased except for a1 with 40% complexity for correlations (r = 0.5, 0.75). Under this condition, the RMSE increased for correlation (r = 0.75), was stable for correlation (r = 0.5), and decreased across correlation (r = 0, 0.25). With 40% complexity, as the sample size increased from 1,500 to 2,000 when L = 40, RMSE decreased and ranged slightly from 0.064 to 0.095 across all levels of correlation, but when L = 20, RMSE values increased by 0.25 and 0.5 for correlation along a1 and a2, respectively, and remained stable for correlation (r = 0) for both a1 and a2.
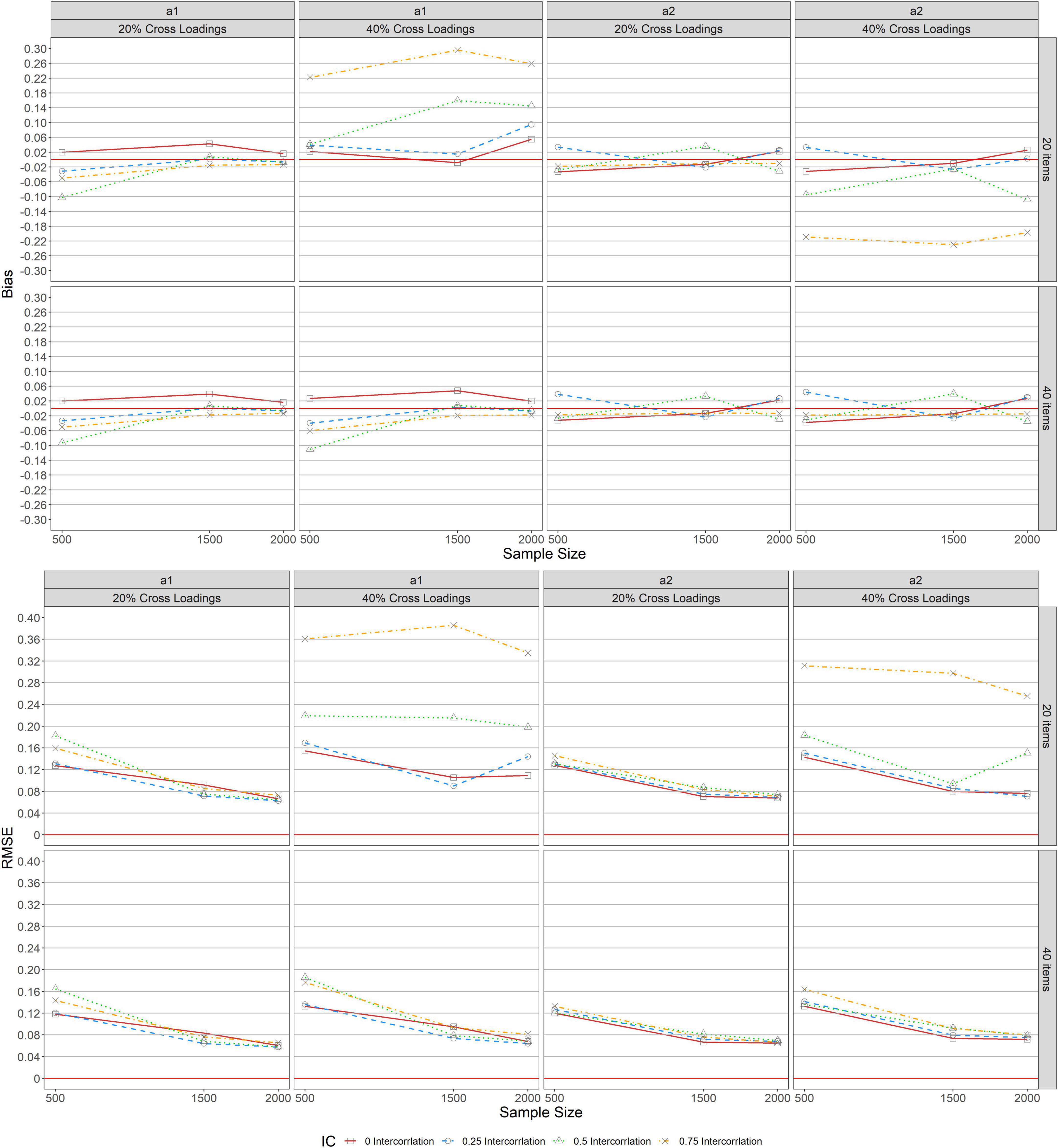
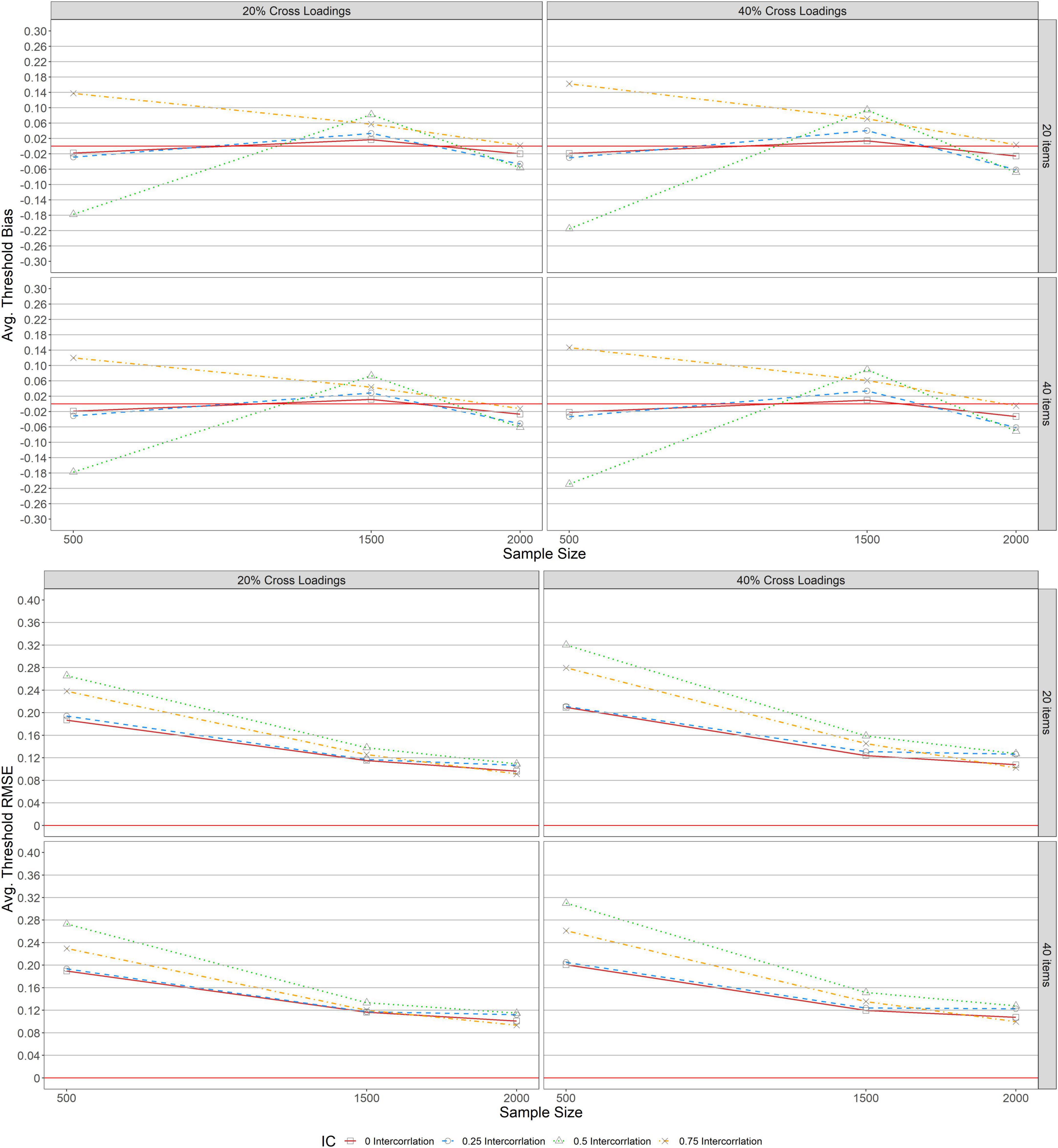
Under the unbalanced complex structure, Figure 3 shows the bias and RMSE item discrimination parameter estimations for MGRM across conditions. As indicated in the upper panel, a similar pattern of bias was identified across test lengths (L = 20, 40) when complexity levels were 20 and 40% unbalanced for a1 and a2, implying that the bias values for both parameters under this condition were unchanged by the number of items specified. However, with 20 and 40% unbalanced complexity for a1, the upper panel of the figure indicates that the bias values for the zero-correlation condition (r = 0, the solid lines with square in the graphs) revealed overestimation, while conditions with other correlations (r = 0.25, 0.5, and 0.75) showed underestimation, particularly when the sample size was 500. The average bias was found to be −0.093 for the condition of r = 0.5 and N = 500 except at L = 20 with 40% unbalanced complexity, where bias values decreased from 0.008 to −0.009 as the sample size increased from 1,500 to 2,000. Furthermore, as the sample size increased, bias values decreased to a steady state (bias of zero), and then declined slightly for the r = 0.25 condition, and when the sample size was increased from 1,500 to 2,000, the magnitude of the bias only changed minimally. Despite the varied pattern of bias detected under the r = 0.5 condition, the bias values for a2 across 20 and 40% unbalanced complexity levels ranged only significantly from −0.039 to 0.048 across levels of sample sizes and correlations.
The RMSE for a1 and a2 across levels of unbalanced complexity (20 and 40%) and test lengths (L = 20, 40) are indicated in the lower panel of the figure. Similar patterns were observed across all conditions for both a1 and a2. Across all levels of correlation between a1 and a2 with 20 and 40% unbalanced, the RMSEs decreased as the sample size increased. However, with 20% unbalanced, the largest RMSE for a1 was observed when N = 500 and r = 0.5, but no noticeable difference was found in RMSE values for a2 across sample sizes and levels of correlations. Additionally, the largest RMSE values observed for a1 and a2 when N = 500 and r = 0.75 with 40% unbalanced complexity across test lengths (L = 20,40).
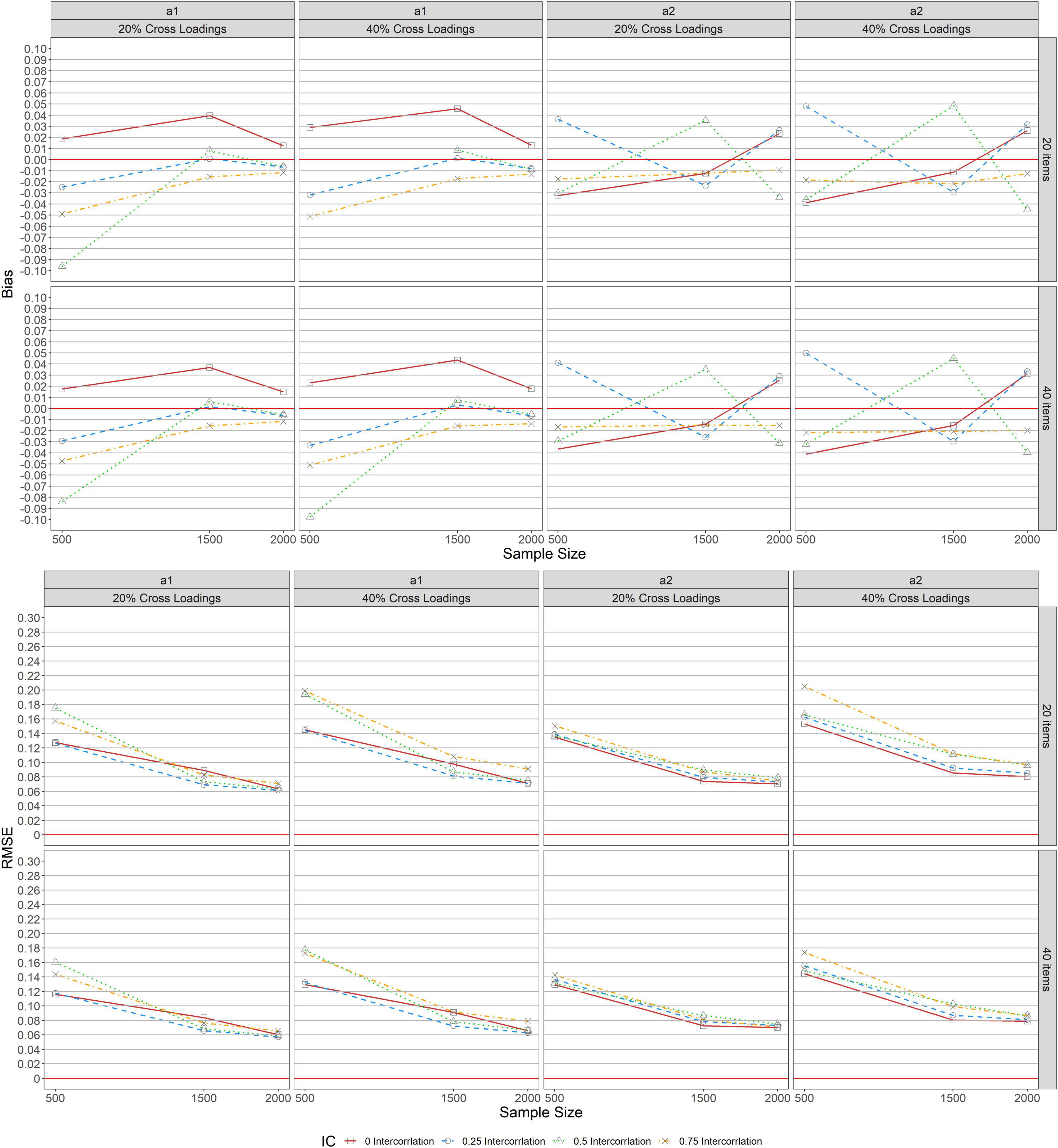
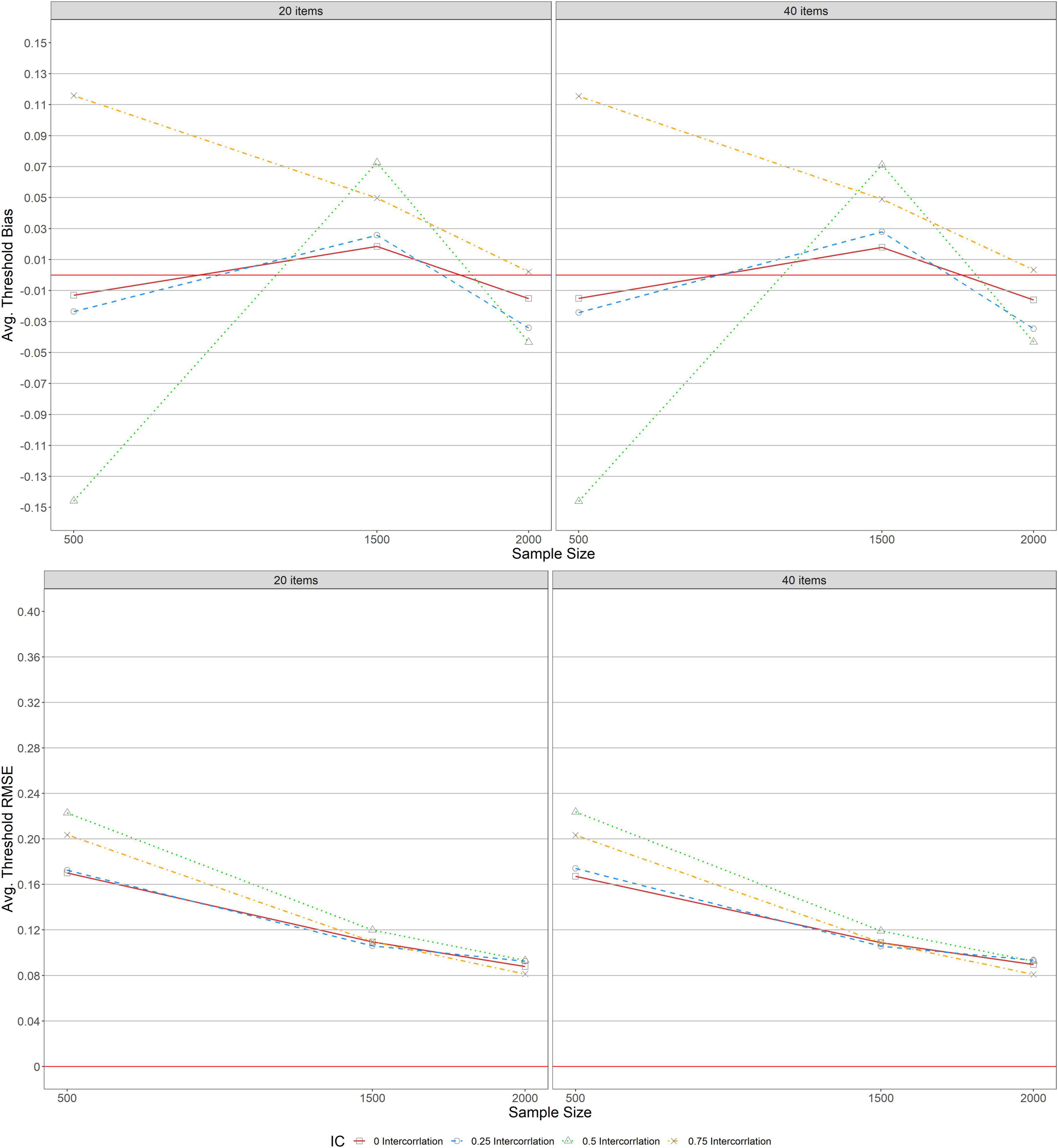
Figure 4 shows the average bias and RMSE of item threshold parameter estimations across conditions under a simple structure. As indicated in the upper panel, a similar pattern of bias was detected across test lengths (L = 20, 40), indicating that average threshold bias was unaffected by items specified. The average bias values ranged from −0.024 to 0.026 for correlations (r = 0, 0.25) and sample sizes (500 ≤ N ≤ 2, 000) except for the conditions of other correlations (r = 0.5, 0.75) and N = 500. Under this condition, the absolute maximum average threshold bias values were found. However, for the condition of r = 0.75, average threshold bias values decreased to almost zero as the sample size increased from 500 to 2,000. Regarding the average threshold RMSE across test lengths (L = 20, 40) in the lower panel, its values decreased and tended to 0.08 as the sample size increased (500 ≤ N ≤ 2, 000) across correlations except for conditions with correlations (r = 0, 0.25, 0.5, and 0.75) and N = 500 under which high average threshold RMSE were identified.
Figures 5, 6 depict the average bias and RMSE of item threshold parameter estimations across conditions under balanced and unbalanced structures. As indicated in all the panels, a similar pattern of bias and RMSE were detected across test lengths (L = 20, 40), indicating that average threshold bias and RMSE values were unaffected by the items specified. Similarly, the average threshold bias and RMSE for both balanced and unbalanced with 20 and 40% exhibited the same patterns as the results for average threshold bias and RMSE under the simple structure.
Conclusion and discussion
Conclusion
A simulation study was conducted to examine the performance of MGRM across several manipulated factors, including sample size, correlation between the dimensions, and test lengths under both simple and different types of complex structures. These factors varied in a completely crossed simulation design to evaluate the recovery of item parameter estimation using bias and RMSE. Results of the simulation study revealed several impacts of the manipulated factors on bias and RMSE of item discrimination and threshold values. Some patterns were identified for the item parameter estimations across all conditions under different complex structures.
Regarding the item parameter estimations for simple structure, the following patterns were observed across the manipulated variables. First, the test length did not influence either the bias or RMSE of item discrimination and threshold values. Second, the level of correlations and sample sizes impacted the accuracy of the item parameter estimations. Third, bias and RMSE of the item parameters of the first dimension were inflated in the presence of small sample size (N = 500) and a correlation of 0.5 (r = 0.5), but a trivial change in the magnitude of bias was observed when the sample size was between 1,500 and 2,000. Fourth, smaller average threshold bias values were yielded under the correlations of r = 0 and 0.25 and sample sizes 500 ≤ N ≤ 2, 000. Fifth, almost zero average RMSE values were obtained for threshold parameters when the correlation was r = 0 and sample sizes were 500 ≤ N ≤ 2, 000.
For complex structures (i.e., balanced and unbalanced), the synthesized results of item parameter estimations are as follows: First, bias and RMSE of item discrimination and threshold values under the balanced structure were more affected by test lengths across all conditions than in the unbalanced structure. Second, bias values under 20% balanced complexity yielded smaller bias values than the 20% unbalanced complexity across sample sizes and level correlations when the test length was 20 and 40 items. Third, the performance of MGRM for 20% complexity under both balanced and unbalanced structures yielded higher bias values across all conditions, especially for a correlation level of 0.5 and a sample size of 500. Fourth, under 40% unbalanced complexity, as the sample size increased (1500 ≤ N ≤ 2, 000) with a low level of correlation (r = 0.25), the bias values declined slightly, especially with a small test length (L = 20). Under 40% balanced complexity, bias values were inflated as the sample size increased (500 ≤ N ≤ 2, 000) with higher levels of correlations (r = 0.5, 0.75) across test lengths. Fifth, under 20% complexity for both balanced and unbalanced structures, RMSE values decreased as the sample size increased across all levels of correlations and test lengths. Sixth, for both balanced and unbalanced structures, a higher correlation (r = 0.75) with 40% complexity yielded higher RMSE values across all conditions, especially with a small sample size (N = 500) under the unbalanced structure. Seventh, bias values under 40% balanced complexity and a moderate test length (L = 40) were stable when there was no correlation (r = 0) between dimensions. The bias values decreased, however, across all levels of correlations in the presence of a moderate to large sample size (1, 500 ≤ N ≤ 2, 000). Eighth, for both complexity levels (20 and 40%) across test lengths (L = 20, 40), bias and RMSE values for threshold parameters under balanced and unbalanced complex structures were the same as those under a simple structure.
Discussion
In practice, the chances of obtaining accurate item parameter estimation based on the assumption that items are tightly restricted to perfect simple structure rather than multiple latent traits are uncertain (Finch, 2011). According to Dai et al. (2021), the choice of polytomous IRT models (e.g., GRM and generalized partial credit model [GPCM]) is beyond the model fit indices, especially when the sample size is less than 300 and the test length is less than 5. Similarly, fitting a complex structure of multidimensionality to a simple structure may be inappropriate in practice. Previous research, however, has provided evidence to support this conclusion (e.g., Finch, 2011; Jiang et al., 2016; Svetina et al., 2017; Wang et al., 2018; Finch and French, 2019). We noted that, however, this evidence was mainly obtained from MGRM models with simple structures and other MIRT models with complex structures (e.g., two- and three-parameter normal ogive and models). Our study differs from the previous studies (e.g., Jiang et al., 2016; Svetina et al., 2017; Wang et al., 2018) in the five following ways: (1) We found that correlation levels influenced the recovery of item parameter estimations under both simple and complex structures, whereas two previous studies (i.e., Jiang et al., 2016; Svetina et al., 2017) revealed that correlation levels had no meaningful impact on parameter recovery under the simple structure. (2) Jiang et al. (2016) revealed that increasing sample size decreased RMSE under simple conditions. Our study went beyond and further revealed that increasing sample size decreased RMSE as correlation and complexity levels increased. (3) Our study found that small sample size (N = 500) and a moderate level of correlation (r = 0.5) affected the bias of the parameter estimates, while previous studies found that sample size had no effect on bias under the simple structure. (4) Bias and RMSE values associated with complex structures yielded larger item discrimination parameters in our study, not only with increased correlations as indicated by Finch (2011) and Svetina et al. (2017) but also with 40% complexity and test lengths of 20 and 40 items. (5) In Svetina et al. (2017), balanced complexity provided better accuracy than when only a few items were unbalanced with respect to complexity, whereas in our study, the accuracy of parameter estimates under complex structures was dependent not only on the number of items being unbalanced with respect to complexity but also on sample size and levels of correlation.
Based on the results of the current study, the choice between balanced and unbalanced complex structures should be made with caution in the presence of levels of complexity, correlation, sample size, and test lengths. In terms of test lengths, the bias results associated with unbalanced complex structures were unaffected when compared to the balanced complex structure. Balanced and unbalanced complex structures might provide better accuracy of item parameter estimations than simple structures depending on the conditions specified, but the accuracy in recovering the item parameters might not be attainable when the correlations between the dimensions are 0.5 and 0.75, particularly with a sample size of 500. Additionally, the average bias and RMSE for item threshold parameters were recovered reasonably well in unbalanced and balanced complex structures than in simple structures across conditions.
Given that the accuracy of item parameter estimations is improved more under complex structures than under simple structures, one of the limitations of this study is that the recovery of the item parameters was the main objective. Also, the study assumed multivariate normality of the latent traits. Based on these limitations, future research would consider non-normality of the dimensions and investigate the impact of missing data on MGRM under complex structures, as well as parameter recovery in MGRM in the presence of more than two dimensions. Although RMSE with a 40-item rating scale decreased under a balanced complex structure, most rating scales on health or education are rarely 40 items in practice. As a result, among the investigated test lengths and sample size, the future study should cover the condition of 30 items and N = 1, 000.
The current simulation study on balanced and unbalanced complexities allows us to make some recommendations to applied researchers in education and health to avoid some challenges in MGRM, and more broadly, MIRT applications that are related to dimensional structures. The complex structure of the MIRT model could be determined and fitted by the Q-matrix developed by subject matter experts (da Silva et al., 2019). For example, if 20 items were developed to measure two latent traits, a Q-matrix representing the mapping of each item to the latent trait, its measures are developed based on the responses of the examinees to the items. Assume that 9 of these 20 items only measure the first latent trait and only 11 items measure the second latent trait. In the case of balanced complexity, the two latent traits will have an equal number of cross-loadings, whereas in the case of unbalanced complexity, the first dimension will have a simple structure, and the second dimension will have four unbalanced items with 45% complexity. To ensure that unbalanced complexity results in better accuracy as the balanced complexity, consider a large sample size and a low level of correlation between dimensions. Adopting MGRM in models with a complex structure could improve validity in both education and health research. Evaluating MGRM under complex structures, the results of our simulation study revealed that a sample size greater than 500 and a correlation between dimensions less than 0.5 should be employed to maximize parameter recovery accuracy because the accuracy of parameter recovery is important in clinical studies of Cushing syndrome, depression, and so on. Furthermore, the accuracy of parameter recovery of a person’s health condition reflects the development of an appropriate treatment plan for the individual. In this context, the presence of biased item estimates does not account for low or high stakes, as opposed to education testing (e.g., TOEFL and GRE), where low and high stakes are based on the biased item or person estimates.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
OK developed the original idea and study design, conducted the data analyses and interpretation, carried out the substantial part of the writing and graphing, and contributed to editing. SD initiated the idea and contributed to conceptualizing the study design, supervised the overall research process, and contributed to editing. BF reviewed the entire study and provided major suggestions that improved the study and contributed immensely to editing throughout the process of the study. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bolt, D. M., and Lall, V. F. (2003). Estimation of Compensatory and Noncompensatory Multidimensional Item Response Models Using Markov Chain Monte Carlo. Appl. Psychol. Measur. 27, 395–414. doi: 10.1177/0146621603258350
Chalmers, R. P. (2012). mirt: A Multidimensional Item Response Theory Package for the R Environment. J. Statist. Softw. 48, 1–29. doi: 10.18637/jss.v048.i06
da Silva, M. A., Liu, R., Huggins-Manley, A. C., and Bazán, J. L. (2019). Incorporating the q-matrix into multidimensional item response theory models. Educat. Psychol. Measur. 79, 665–687. doi: 10.1177/0013164418814898
Dai, S., Vo, T. T., Kehinde, O. J., He, H., Xue, Y., Demir, C., et al. (2021). Performance of Polytomous IRT Models with Rating Scale Data: An Investigation Over Sample Size, Instrument Length, and Missing Data. Front. Educ. 6:372. doi: 10.3389/feduc.2021.721963
De Ayala, R. J. (1994). The influence of multidimensionality on the graded response model. Appl. Psychol. Measur. 18, 155–170. doi: 10.1177/014662169401800205
DeMars, C. E. (2013). A comparison of confirmatory factor analysis and multidimensional Rasch models to investigate the dimensionality of test-taking motivation. J. Appl. Measur. 14, 179–196.
Depaoli, S., Tiemensma, J., and Felt, J. M. (2018). Assessment of health surveys: Fitting a multidimensional graded response model. Psychol. Health Med. 23, 1299–1317. doi: 10.1080/13548506.2018.1447136
Embretson, S. E., and Reise, S. P. (2000). Item Response Theory for Psychologists. Mahwah, NJ: Psychology Press.
Ferrando, P. J., and Chico, E. (2001). The construct of sensation seeking as measured by Zuckerman’s SSS-V and Arnett’s AISS: A structural equation model. Personal. Indiv. Diff. 31, 1121–1133. doi: 10.1016/S0191-8869(00)00208-7
Finch, H. (2010). Item Parameter Estimation for the MIRT Model: Bias and Precision of Confirmatory Factor Analysis—Based Models. Appl. Psychol. Measur. 34, 10–26. doi: 10.1177/0146621609336112
Finch, H. (2011). Multidimensional item response theory parameter estimation with nonsimple structure items. Appl. Psychol. Measur. 35, 67–82. doi: 10.1177/0146621610367787
Finch, H., and French, B. F. (2019). A comparison of estimation techniques for IRT models with small samples. Appl. Psychol. Measur. 32, 77–96.
Forero, C. G., and Maydeu-Olivares, A. (2009). Estimation of IRT graded response models: limited versus full information methods. Psychol. Methods 14:275. doi: 10.1037/a0015825
Friyatmi, M. (2020). Assessing students’ higher order thinking skills using multidimensional item response theory. Probl. Educ. 78:196.
Haem, E., and Doostfatemeh, M. (2020). Multidimensional item response theory to assess psychological properties of GHQ-12 in school children’s parents. Shiraz: Shiraz University of Medical Sciences Medical School.
Hu, L. T., and Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Modeling 6, 1–55.
Hunsu, N. J., Kehinde, O. J., Oje, A. V., and Yli-Piipari, S. (2022). Single Versus Multiple Resilience Factors: An Investigation of the Dimensionality of the Academic Resilience Scale. J. Psychoeducat. Assess. 40, 346–359.
Jiang, S., Wang, C., and Weiss, D. J. (2016). Sample Size Requirements for Estimation of Item Parameters in the Multidimensional Graded Response Model. Front. Psychol. 7:109. doi: 10.3389/fpsyg.2016.00109
Kuo, T. C., and Sheng, Y. (2016). A comparison of estimation methods for a multi-unidimensional graded response IRT model. Front. Psychol. 7:880. doi: 10.3389/fpsyg.2016.00880
Nouri, F., Feizi, A., Roohafza, H., Sadeghi, M., and Sarrafzadegan, N. (2021). How different domains of quality of life are associated with latent dimensions of mental health measured by GHQ-12. Health Qual. Outcomes 19, 1–16. doi: 10.1186/s12955-021-01892-9
Penfield, R. D. (2014). An NCME instructional module on polytomous item response theory models. Educ. Measur. 33, 36–48.
R Core Team (2021). R: A Language and environment for statistical computing. (Version 4.0) [Computer software]. Available online at: https://cran.r-project.org (Accessed on Aprl 01, 2021).
Reckase, M. D. (2009). “Multidimensional Item Response Theory Models,” in Multidimensional Item Response Theory, ed. M. D. Reckase (New York, NY: Springer), 79–112. doi: 10.1007/978-0-387-89976-3_4
Reise, S. P., and Yu, J. (1990). Parameter recovery in the graded response model using MULTILOG. J. Educ. Measur. 27, 133–144.
Samejima, F. (1969). Estimation of latent ability using a response pattern of graded scores. Psychometr. Monogr. Suppl. 34(4, Pt. 2) 100–100.
Scherbaum, C. A., Cohen-Charash, Y., and Kern, M. J. (2006). Measuring General Self-Efficacy: A Comparison of Three Measures Using Item Response Theory. Educ. Psychol. Measur. 66, 1047–1063. doi: 10.1177/0013164406288171
Su, S., Wang, C., and Weiss, D. J. (2021). Performance of the S- χ 2 Statistic for the Multidimensional Graded Response Model. Educ. Psychol. Measur. 81, 491–522. doi: 10.1177/0013164420958060
Svetina, D. (2013). Assessing dimensionality of noncompensatory multidimensional item response theory with complex structures. Educ. Psychol. Measur. 73, 312–338.
Svetina, D., Valdivia, A., Underhill, S., Dai, S., and Wang, X. (2017). Parameter Recovery in Multidimensional Item Response Theory Models Under Complexity and Nonnormality. Appl. Psychol. Measur. 41, 530–544. doi: 10.1177/0146621617707507
Walton, K. E., Roberts, B. W., Krueger, R. F., Blonigen, D. M., and Hicks, B. M. (2008). Capturing abnormal personality with normal personality inventories: An item response theory approach. J. Personal. 76, 1623–1648. doi: 10.1111/j.1467-6494.2008.00533.x
Wang, C., Su, S., and Weiss, D. J. (2018). Robustness of parameter estimation to assumptions of normality in the multidimensional graded response model. Multivar. Behav. Res. 53, 403–418. doi: 10.1080/00273171.2018.1455572
Wang, W. C., Chen, P. H., and Cheng, Y. Y. (2004). Improving measurement precision of test batteries using multidimensional item response models. Psychol. Methods 9:116.
Wang, W., Song, L., Ding, S., and Meng, Y. (2016). “Estimating classification accuracy and consistency indices for multidimensional latent ability,” in Quantitative Psychology Research, eds L. van der Ark, D. Bolt, W. C. Wang, J. Douglas, and M. Wiberg (Cham: Springer), 89–103.
Wang, Z., Rohrer, D., Chuang, C. C., Fujiki, M., Herman, K., and Reinke, W. (2015). Five methods to score the Teacher Observation of Classroom Adaptation Checklist and to examine group differences. J. Exp. Educ. 83, 24–50.
Weston, R., and Gore, P. A. Jr. (2006). A brief guide to structural equation modeling. Couns. Psychol. 34, 719–751.
Wetzel, E., and Hell, B. (2014). Multidimensional item response theory models in vocational interest measurement: An illustration using the AIST-R. J. Psychoeducat. Assess. 32, 342–355.
Keywords: GRM, item parameters, multidimensionality, parameter recovery, complex structure
Citation: Kehinde OJ, Dai S and French B (2022) Item parameter estimations for multidimensional graded response model under complex structures. Front. Educ. 7:947581. doi: 10.3389/feduc.2022.947581
Received: 18 May 2022; Accepted: 02 August 2022;
Published: 20 September 2022.
Edited by:
Yong Luo, Educational Testing Service, United StatesReviewed by:
Xin Qiao, University of Maryland, College Park, United StatesKuan Xing, University of Tennessee Health Science Center (UTHSC), United States
Copyright © 2022 Kehinde, Dai and French. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Olasunkanmi James Kehinde, S2VoaW5kZS5qYW1lc0B3c3UuZWR1
 Olasunkanmi James Kehinde
Olasunkanmi James Kehinde Shenghai Dai
Shenghai Dai Brian French
Brian French