- 1Chair of Mathematics Education, University of Würzburg, Würzburg, Germany
- 2Institute of Mathematics Education and Computer Science Education, University of Münster, Münster, Germany
Providing adaptive, independence-preserving and theory-guided support to students in dealing with real-world problems in mathematics lessons is a major challenge for teachers in their professional practice. This paper examines this challenge in the context of simulations and mathematical modelling with digital tools: in addition to mathematical difficulties when autonomously working out individual solutions, students may also experience challenges when using digital tools. These challenges need to be closely examined and diagnosed, and might – if necessary – have to be overcome by intervention in such a way that the students can subsequently continue working independently. Thus, if a difficulty arises in the working process, two knowledge dimensions are necessary in order to provide adapted support to students. For teaching simulations and mathematical modelling with digital tools, more specifically, these knowledge dimensions are: pedagogical content knowledge about simulation and modelling processes supported by digital tools (this includes knowledge about phases and difficulties in the working process) and pedagogical content knowledge about interventions during the mentioned processes (focussing on characteristics of suitable interventions as well as their implementation and effects on the students’ working process). The two knowledge dimensions represent cognitive dispositions as the basis for the conceptualisation and operationalisation of a so-called adaptive intervention competence for teaching simulations and mathematical modelling with digital tools. In our article, we present a domain-specific process model and distinguish different types of teacher interventions. Then we describe the design and content of a university course at two German universities aiming to promote this domain-specific professional adaptive intervention competence, among others. In a study using a quasi-experimental pre-post design (N = 146), we confirm that the structure of cognitive dispositions of adaptive intervention competence for teaching simulations and mathematical modelling with digital tools can be described empirically by a two-dimensional model. In addition, the effectiveness of the course is examined and confirmed quantitatively. Finally, the results are discussed, especially against the background of the sample and the research design, and conclusions are derived for possibilities of promoting professional adaptive intervention competence in university courses.
1. Introduction
When designing lessons, teachers have a great influence on the performance and learning success of their students (Hattie, 2009). Cognitively activating teaching plays a central role in this context (Baumert and Kunter, 2013). In order to prepare teachers for these teaching situations, explicitly created opportunities for developing professional competences, which is a declared aim of university teacher education (Kunter et al., 2013b), need to be offered in teacher training. In addition to general professional competences, subject- and domain-specific professional competences of teachers are also crucial for teaching content-and process-related competences to their students. One competence of students specific to mathematics education, which is frequently established in national educational standards, is dealing with reality-related problems in modelling and simulation processes (Kaiser, 2020; Geiger et al., 2022). Professional competences for teaching mathematical modelling – i.e., the competences teachers need to teach mathematical modelling in their own lessons – have recently been intensively investigated (e.g., Wess et al., 2021; Greefrath et al., 2022).
In classrooms, digital (mathematics) tools are increasingly used to deal with reality-related problems. Examples for common digital tools are Dynamic Geometry Software, Computer Algebra Systems, spreadsheets, and function plotters. For instance, reality-based problems can be investigated even more realistically with these tools. However, the usage of digital tools puts new demands on education systems and teachers (Drijvers et al., 2016), for example demands on the technical level and demands regarding the interpretation of digitally generated results. These new demands also affect dealing with reality-related problems. In order to initiate simulation and mathematical modelling with digital tools among students in classrooms and to accompany it in a pedagogically meaningful way, a consideration of digital aspects of professional competences for teaching simulations and mathematical modelling is necessary. One of these required competences is the adaptive intervention competence (in this paper, the adaptive intervention competence for teaching simulations and mathematics with digital tools will sometimes be abbreviated to domain-specific adaptive intervention competence). This domain-specific competence describes the professional competence of teachers to provide adaptive content-and process-oriented support to students who have difficulties in dealing with reality-and digital-based tasks, or to decide when this adaptive intervention is necessary. For adaptivity, it is necessary that the intervention is based on a diagnosis of the difficulty and enables the students to continue their working process independently.
The aim of this paper is to theoretically describe and empirically test the structure of adaptive intervention competence for teaching simulations and mathematical modelling with digital tools based on previous research (e.g., Klock and Siller, 2019). In addition, this paper investigates to what extent this competence can be promoted in university teacher training. For this purpose, a course in mathematics education on simulations and mathematical modelling with digital tools was designed and implemented at the universities of Würzburg and Münster. We present the concept of the course and report initial results on the development of cognitive dispositions of the domain-specific professional adaptive intervention competence.
2. Theoretical background
2.1. Using digital tools in simulations and mathematical modelling
The use of digital tools in modelling activities has recently become more important (Geiger, 2011; Siller et al., 2022). On the one hand, this trend might be based on the constant progress of digital tools as well as educational policy requirements. On the other hand, digital tools enable to reproduce and investigate the increasing complexity of reality-related contexts in models in a simplified way (Greefrath and Siller, 2017). New opportunities arise in the selection of reality-related contexts, other focal points in the process emerge, and often a higher degree of realism is achieved when larger amounts of data are processed. Digital tools – when used meaningfully – are characterised by “great assistance for teachers and learners alike, particularly in connection with real-world problems and the discussion of those.” (Greefrath and Siller, 2017, p. 530). Going a little further, digital support is sometimes even seen as a “fundamental component in the reorganisation of the ways of doing modelling” (Molina-Toro et al., 2019, p. 2), i.e., not only as a tool, but even as an essential part of the process.
The support of learning processes through digital tools is well described by a holistic approach (Kaiser and Brand, 2015; Greefrath et al., 2018). This highlights the versatility of digital tools throughout the modelling process as a whole. Nevertheless, in this context it is also worthwhile to look at individual substeps of the use of digital tools for purposefully supporting during the simulation and modelling process (Geiger, 2011). Digital tools can, for example, contribute to the visualisation of contexts, to experimentation, to calculation, to simulation and to the validation and interpretation of results (Siller et al., 2022). Figure 1 provides a compact overview of the possible uses.
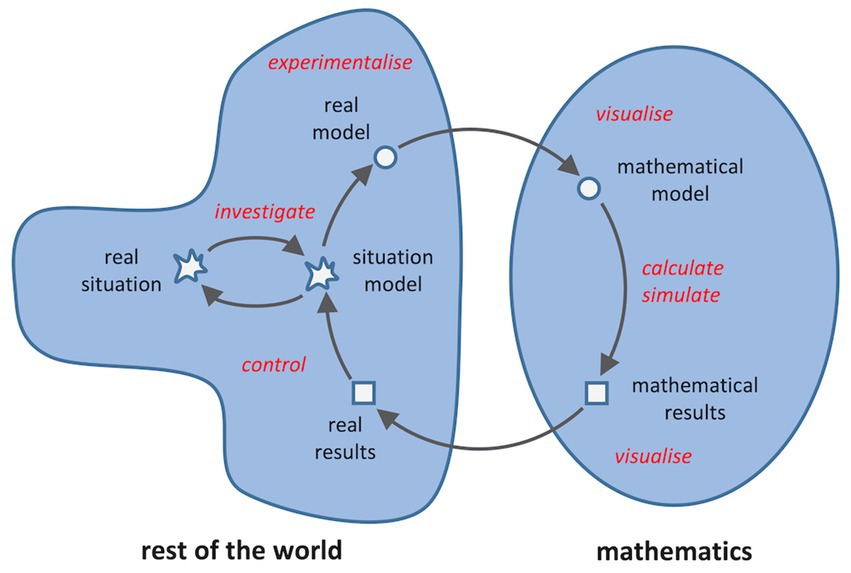
Figure 1. Use of digital tools (terms in italics) when modelling – integrated perspective (see Blum and Leiss, 2007, p. 22; Greefrath, 2011, p. 303).
The use of digital tools also enables a broadening of the thematic range into many other fields, such as natural sciences, under conditions of reduced complexity and resources. One method for the mathematical dealing with reality-based problems are digital simulations. The term simulation combines the properties of experimentation and the model-like imitation of real contexts, e.g., when analysing the number of people in a traffic jam (Gerber et al., 2022). Simulations are based on a mathematical model1 and therefore represent a – possibly complex – extra-mathematical situation in its essential characteristics. By systematically changing variables of the mathematical model, for example parameters (sliders) in an appropriate software, the effects on the real situation are simulated. This results, for example, in numerical solutions or graphical visualisations. Through a structured experiment-like procedure, simulations thus contribute to the comprehension of reality-related situations (Velten, 2009). The repeated running of digital simulations and comparison with real data can also contribute to model validation and optimisation (Shannon, 1975). The experiment-like approach is – compared to modelling processes – specific for simulation processes. At the same time, simulations also require, as mentioned, a model that simplifies reality, as well as a validation of the results.
In terms of dealing with reality-related problems (for further examples see Siller, 2015) in mathematics lessons, the high demands on students and teachers are often emphasised (Blum, 2015). When students have to use digital tools independently, the (additional) tool level is added on top of the already demanding modelling activities. This requires translation processes from mathematics and the mathematical model into the digital tool model and transfer of digitally generated results back into the language of mathematics (see Figure 2; Greefrath et al., 2018; Frenken et al., 2022). Therefore, despite all the advantages and supporting possibilities of digital tools, difficulties can arise for students in every modelling process. Thus, processing can be challenging (Galbraith and Stillman, 2006; Tropper et al., 2015; Klock and Siller, 2020a). To overcome these difficulties teacher interventions are needed. Therefore, teaching simulations and mathematical modelling with digital tools requires domain-specific adaptive intervention competence.
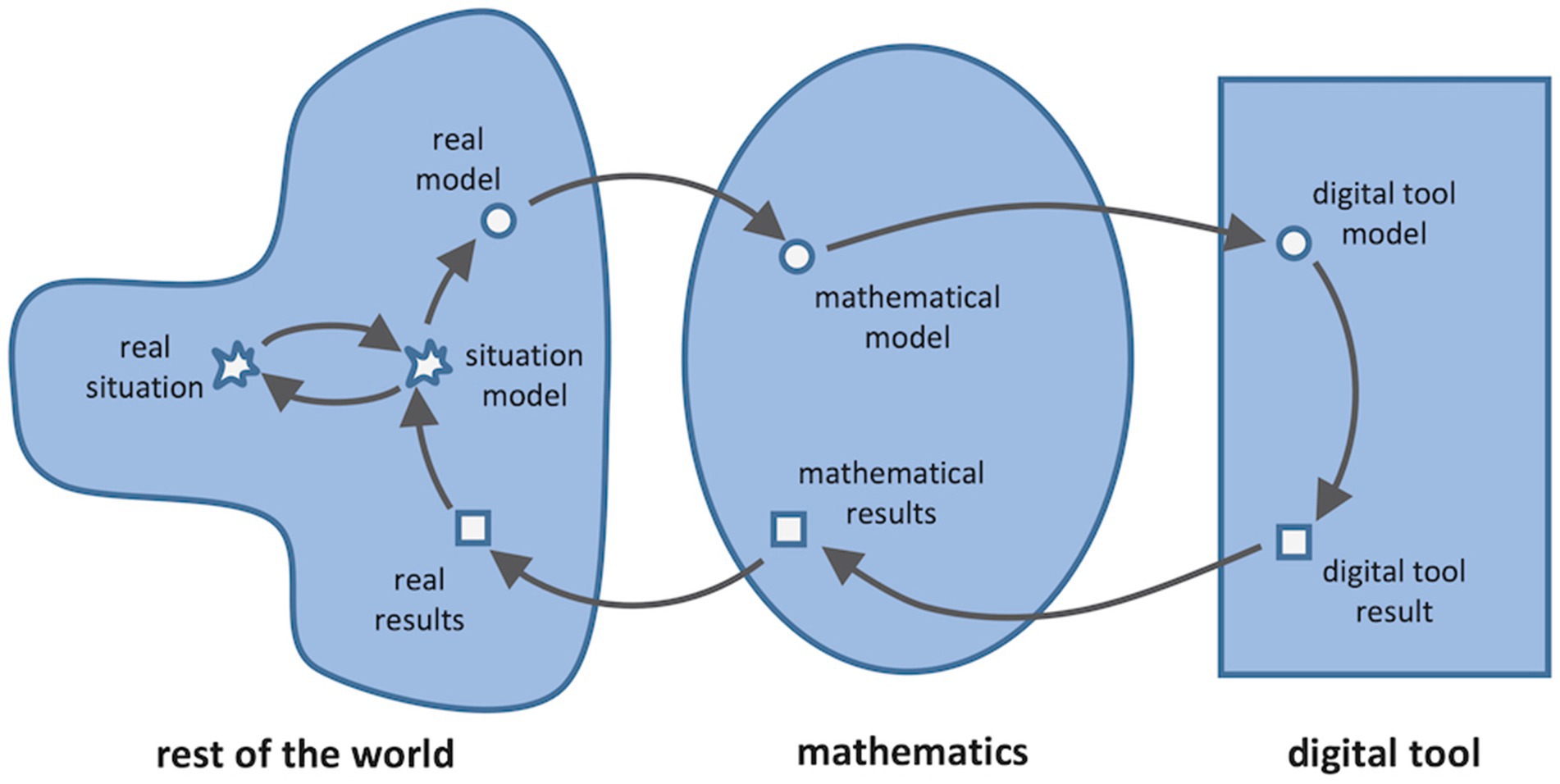
Figure 2. Use of digital tools when modelling – extended perspective (see Siller and Greefrath, 2010, p. 2137).
2.2. Adaptive intervention competence for teaching simulations and mathematical modelling with digital tools
In the following, adaptive intervention is conceptualised as a construct of diagnosis and intervention. This represents the basis for adaptive intervention competence. First, the concept of competence and the concept of pedagogical content knowledge as cognitive dispositions, which are a basis of teacher competences, must be addressed.
2.2.1. Competences and professional competences of teachers
Analysing reality-related situations is an activity in mathematics teaching that is designed to encourage students’ independence (Tropper et al., 2015). Digital-based simulation and modelling tasks are characterised by a high degree of individuality and diversity in terms of content and mathematical approach (see Quarder et al., 2023). As a consequence, the students themselves are highly responsible for their learning process (Tropper et al., 2015) in which the teacher only intervenes when necessary. This intervention is described below as part of a multi-step process.
The knowledge of how to intervene as a teacher during the process of digitally supported, reality-based tasks is part of the adaptive intervention competence of teachers in simulations and mathematical modelling with digital tools and is, as a theory-based competence, a domain-specific interpretation of the general professional competence of teachers. According to Weinert, competences are “intellectual abilities, content-specific knowledge, cognitive skills, domain-specific strategies, routines and subroutines, motivational tendencies, volitional control systems, personal value orientations, and social behaviours” (Weinert, 2001, p. 51). Individual competences are thus influenced by knowledge on the one hand and affective-motivational characteristics on the other hand. Blömeke et al. (2015) describe both aspects in the sense of a disposition as the basis for competence and for concrete observable behaviour (performance). Situation-specific skills such as perception, interpretation, and decision-making are seen as mediators between cognitive and affective-motivational characteristics (dispositions) as influencing prerequisites on one side and performance as a result on the other.
This perspective of competence as a continuum (Blömeke et al., 2015) will subsequently be used as a basis for making statements about the development of adaptive intervention competence of pre-service teachers in the context of our study: Collected data about pedagogical content knowledge are used to be able to evaluate the development of adaptive intervention competence. The importance of knowledge is pointed out by the results and interpretations of the COACTIV study (Kunter et al., 2013a). According to this, knowledge in various forms (pedagogical knowledge, pedagogical content knowledge, content knowledge) is a central element of competence and contributes to the development of competences in interaction with beliefs, motivational orientations and normative aims (Krauss et al., 2013).
The pedagogical content knowledge of teachers is shown to be a stronger predictor of the learning progress of their students than content knowledge (Baumert et al., 2010). At the same time, content knowledge and pedagogical content knowledge correlate at a high level (Krauss et al., 2013). Therefore, we focus on the pedagogical content knowledge of teachers as a central aspect of professional competence [and not, as suggested by Shulman, 1986, on a clearer division of professional knowledge into content knowledge, pedagogical content knowledge and pedagogical knowledge]. In order to be able to make statements about the professional competence of teachers, we also consider additional dispositions of self-efficacy expectations and beliefs, each with special consideration of the use of digital tools in the process of working on a problem as presented in Figure 3 [see also Blömeke et al., 2015 regarding the measurement of competences].
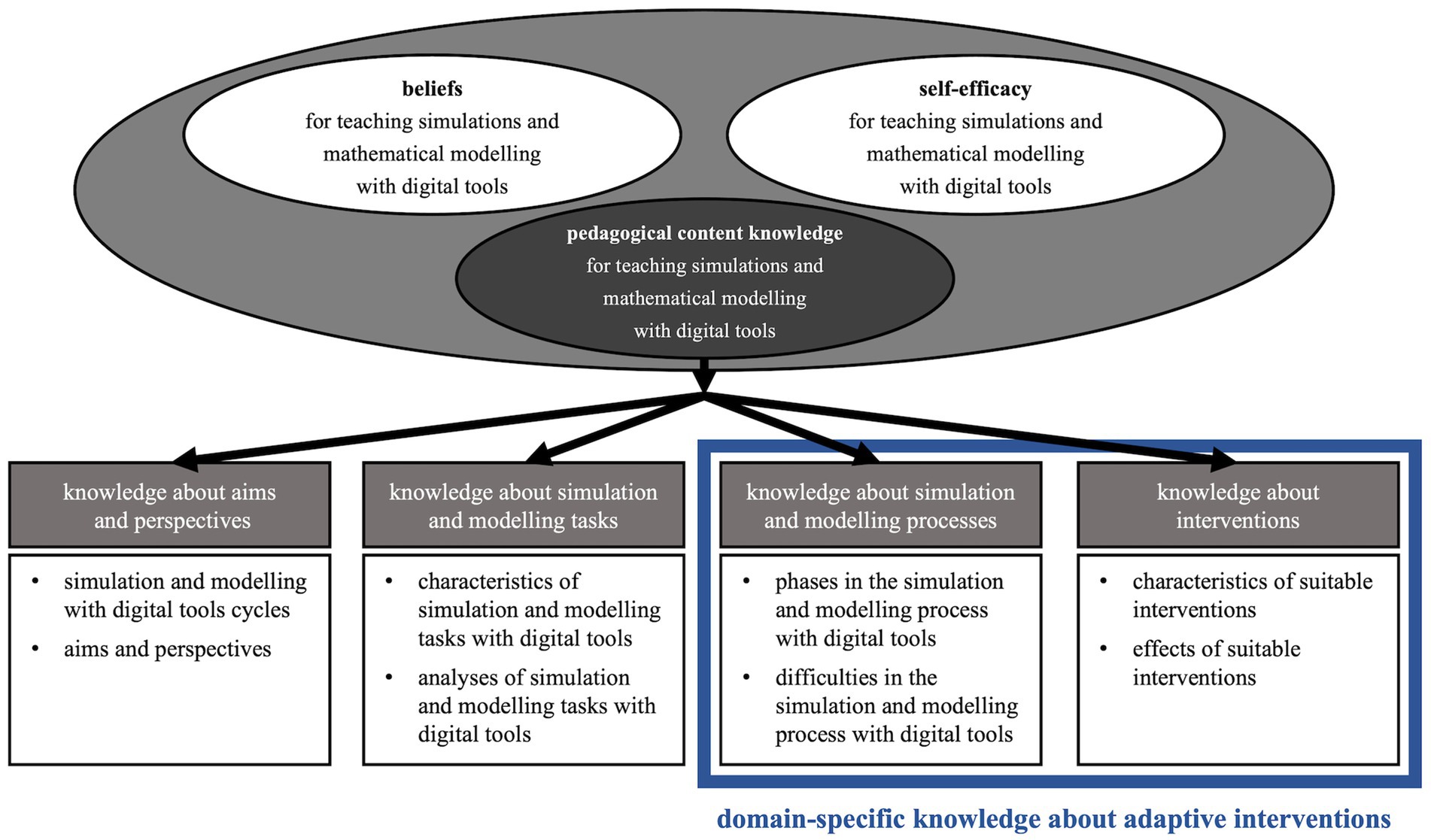
Figure 3. Competence model on domain-specific pedagogical content knowledge; the two knowledge dimensions for adaptive intervention competence for teaching simulations and mathematical modelling with digital tools are highlighted (following Gerber et al., 2022).
The pedagogical content knowledge is divided into four knowledge dimensions that comprise essential knowledge for teaching simulations and mathematical modelling with digital tools. These dimensions are based on the work of Borromeo Ferri and Blum (2010) as well as Greefrath et al. (2022) and were empirically confirmed in our concretisation for the usage of digital tools in simulations and mathematical modelling by means of a test instrument (Gerber et al., 2022; Gerber and Quarder, 2022).
2.2.2. Adaptive intervention competence
Adaptive interventions describe individual support for students in the process of dealing with problems. The competence of teachers to be able to intervene in a theory-based and adapted way is therefore called adaptive intervention competence. In order to adapt this support to the personal difficulty in the best possible way, the intervention must be preceded by a diagnosis of the situation (Leiss and Wiegand, 2005; Vorhölter et al., 2013; Tropper et al., 2015; Klock and Siller, 2019). Therefore, two of the four knowledge dimensions in Figure 3 are focused on: knowledge about simulations and modelling processes (i.e., knowledge necessary for diagnosis) and knowledge about interventions.
Firstly, the process of adaptive intervention is described, focusing on the two activities of diagnosis and intervention in general. Secondly, the knowledge specific for simulations and mathematical modelling with digital tool required for this process, highlighted in Figure 3, is explained in more detail.
2.2.2.1. Diagnosis
In everyday teaching, diagnoses are necessary in order to enable theory-based action decisions. Heitzmann et al. (2019) define diagnostic competences as” individual dispositions enabling people to apply their knowledge in diagnostic activities according to professional standards to collect and interpret data in order to make high-quality decisions” (p. 5). Diagnostic competence is thus an essential component of a teacher’s professional competence.
Diagnoses can also be conscious analyses of situations or difficulties as well as intuitive – i.e., automated – assessments regarding lesson planning, the provision of learning materials or when difficulties arise (Heitzmann et al., 2019; Sommerhoff et al., 2022). Herppich et al. (2018) define diagnostic competence – in accordance with Blömeke et al. (2015) and using the term “teachers’ assessment competence” – as “a measurable cognitive disposition that is acquired by dealing with assessment demands in relevant educational situations and that enables teachers to master these demands quantifiably in a range of similar situations in a relatively stable and relatively consistent way” (p. 10). On the one hand, cognitive knowledge (hence: theory-based) is emphasised as a prerequisite for a meaningful, professionally qualified diagnosis or assessment of students. On the other hand, “competence” describes the classification of diagnosis as an interaction of theoretical knowledge and practical skills of implementation.
Following Sommerhoff et al. (2022), different consecutive diagnostic steps can be identified when a difficulty occurs in the students’ working process:
• Description of the situation in which the difficulty occurred, with particular reference to the processing phase (Figure 3) and the use of the digital tool (Figure 1)
• Evaluation of the information with special attention to the knowledge of typical errors in the working process on a problem
• Description and explanation of the student’s difficulty as a basis for decisions on further action
In our competence model in Figure 3, the knowledge needed for diagnosis is described with the pedagogical content knowledge of simulation and modelling processes with digital tools. This is – more precisely – the knowledge about phases in these simulation and modelling processes and possible or typical difficulties. As an aid to diagnosis, so-called modelling cycles describe dealing with reality-related tasks using digital tools. This includes two modelling cycles to analyse working processes in which digital tools are used: a cycle that shows the possible uses of digital tools (Figure 1) and another cycle that describes translation processes with the digital tool (Figure 2). Here, particular attention is paid to the implementation of the mathematical model in the syntax of the digital tool, as well as the interpretation of the result generated by the digital tool. Both phases are crucial for working with digital tools and can pose great difficulties at the same time.
2.2.2.2. Intervention
In our conceptualisation, diagnosis is followed by assistance to learners, which takes the form of interventions. In the context of reality-related tasks, the term intervention has been implicitly or explicitly mentioned in various fields of research, such as research on scaffolding (Tropper et al., 2015; Klock and Siller, 2019). Leiss (2007) defines interventions as hints” which minimally support the individual learning and solution process of students, so that students can continue to work in a way that allows for maximum independence.” (p. 65; translated from German). Especially in mathematical modelling, independence-preserving work is identified as an essential teaching method (Stender and Kaiser, 2017).
In cooperative learning processes where students work together on tasks, Leiss and Wiegand (2005) consider possibilities for teacher interventions. The basis of the intervention competence is the associated knowledge dimension. In our model (cf. Figure 3), knowledge about interventions includes knowledge about characteristics of interventions and about the effects of these interventions. As part of teacher training, extensive experiential knowledge, where students can draw on group-dependent effects of interventions in classrooms, is not yet available among the students participating in our study presented below. Unfortunately, there are also only few scientific insights into the effect of interventions in the field of reality-based teaching and the use of digital tools. While as an in-service teacher, the assessment of interventions can be trained, among others, through extensive evaluations of the interventions that are made, it must be made by pre-service teachers via an a priori assessment using given characteristics (see below) as a basis for the choice of intervention in later teaching situations.
2.2.2.3. Adaptive intervention as a two-step process of diagnosis and intervention
Therefore, we use the term adaptive intervention as a common construct of diagnosis and intervention, which is characterised as student-oriented, independence-preserving assistance as short-term, selective intervention by the teacher. Four characteristics of adaptive interventions that are important for appropriate intervention and enable an a priori assessment of concrete support, are identified by Klock and Siller (2019). According to them, adaptive interventions (1) are based on a diagnosis, (2) are adapted to the student’s learning process and relate to the analysed difficulty, (3) are kept as minimal as possible, and (4) maintain the independence of the student’s processing.
Overall, Figure 4 illustrates the process of adaptive intervention and pedagogical content knowledge, which is specific to diagnosis and intervention for the (a priori) assessment of an adaptive intervention. This process and competence model is based on the process model for general teacher interventions (Leiss, 2007) and the process model for adaptive interventions in mathematical modelling (Klock and Siller, 2019, 2020b) with special consideration of the use of digital tools in simulations and mathematical modelling.
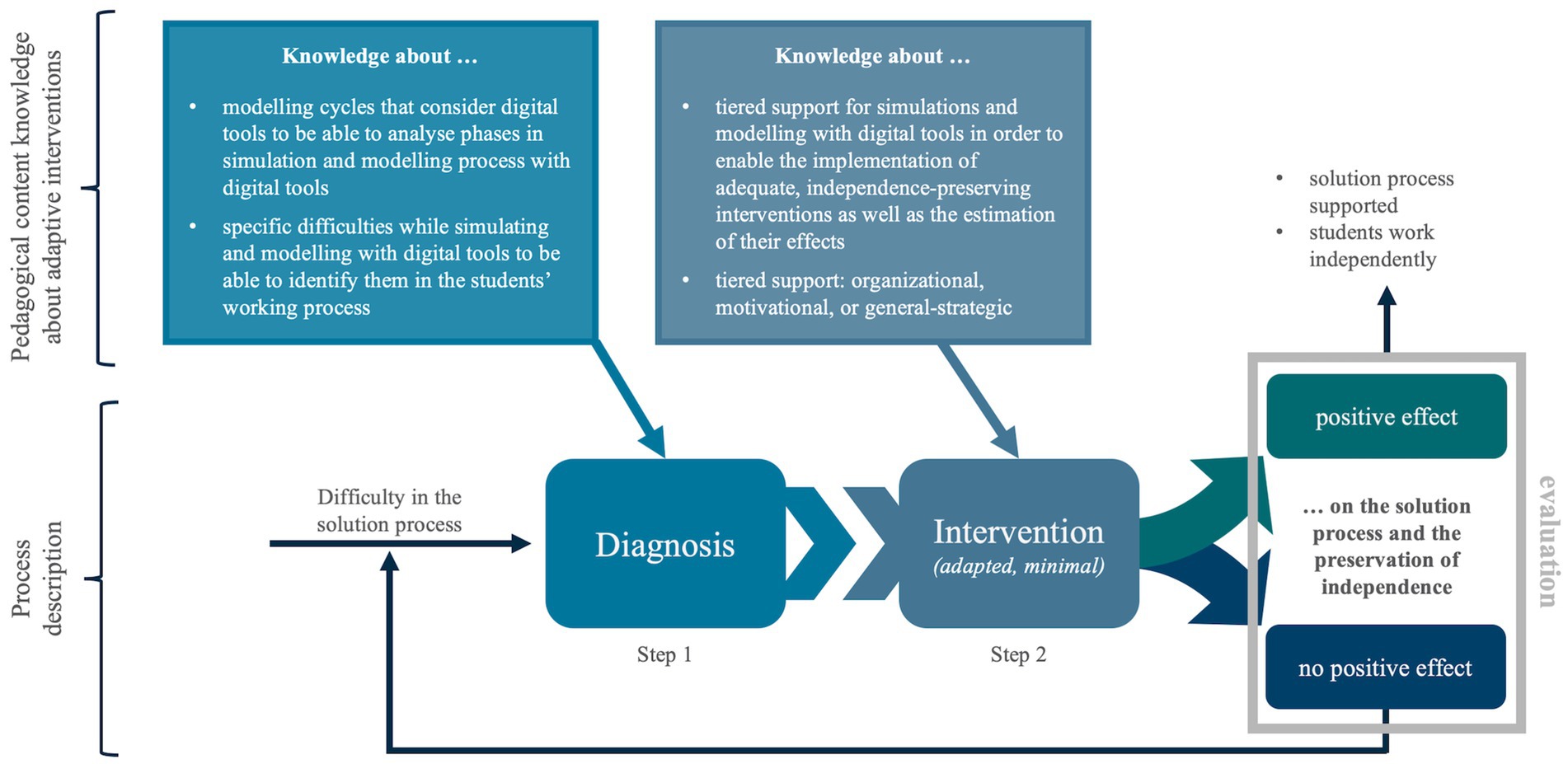
Figure 4. Process and competence model for adaptive intervention in simulation and modelling with digital tools.
2.2.2.4. Knowledge about general-strategic support as adaptive interventions
It is necessary to specify adaptive interventions for the use of digital tools in simulations and mathematical modelling. Following Zech (2002) and Leiss and Wiegand (2005), there are different types of teacher interventions: motivational help, feedback-help, strategic help, content-oriented help and content-related help. These differ in particular in the extent to which they provide content and/or strategic support. To help students to process tasks as independently as possible, we focus on (general-)strategic support: It represents the most abstract level of support which relates to concrete work and is not interchangeable for all activities and difficulties, as is the case with motivational support and feedback support. Strategic support is used when motivational support and feedback support do not sufficiently support students to continue working (Stender and Kaiser, 2017). In addition, we do not consider content-oriented strategic support or content-related support, as these interfere too much with independence-preserving teaching and can limit the individuality of the work. Moreover, content-oriented strategic support and content-related support are often more content-specific than, for example, the general-strategic help. Content-oriented strategic interventions and content-related interventions can often contradict the aim that students work out the solution autonomously (Leiss and Wiegand, 2005) because the help may be no longer minimal. Nevertheless, for some students who have difficulty with the openness of (general-)strategic interventions, they represent an important support in practise.
Considering general-strategic support, these interventions can include operating strategies, problem-solving strategies and reflection strategies (Roth, 2019), also in the area of teaching simulations and mathematical modelling with digital tools:
• Interventions on operating strategies help students to use the digital tool and support them to independently seek help on how it works (Carretero et al., 2017).
• Interventions on problem-solving strategies concern, for example, the (systematic) generation of examples, switching between different representations or creating dynamic visualisations (Henn, 2007; Pierce and Stacey, 2010; Thurm and Barzel, 2022).
• Interventions on reflection strategies encourage students to question the digitally generated result and the significance of the result. These are particularly necessary when the digital result or output is accepted unthinkingly, without validation or verification (Cavanagh and Mitchelmore, 2000).
In the theoretical background we have described – also by using modelling cycles (Figures 1, 2) – theories on the use of digital tools in simulations and mathematical modelling. In addition, we conceptualised knowledge about adaptive interventions as a construct (see also Figure 3), highlighting the importance of both diagnosis and intervention knowledge. This knowledge was an essential basis for adaptive intervention as a competence (Figure 4) to help students to overcome a difficulty in an independence-preserving way.
3. Research questions
The lack of studies on modelling competences of students using digital tools was discussed recently (e.g., Cevikbas et al., 2022). This lack of studies includes studies on the pedagogical content knowledge of (pre-service) teachers on simulations and mathematical modelling with digital tools. Pedagogical content knowledge of teachers in general has a significant influence on teaching and student learning (Baumert et al., 2010). Existing research results on pedagogical content knowledge in mathematical modelling (Greefrath et al., 2022) should therefore be expanded to include the use of digital tools and simulations.
In this paper, we investigate pedagogical content knowledge as cognitive dispositions for teacher competences (according to Blömeke et al., 2015) on how to deal with students’ difficulties constructively and in an independence-preserving manner when teaching simulations and mathematical modelling with digital tools. For this purpose, we focus on adaptive interventions and the corresponding competence which we described on the basis of existing research results on diagnosis and interventions. In addition, we now want to empirically prove the effectiveness of a related course in an early phase of teacher training and thus derive opportunities for the development of this adaptive intervention competence.
The first question therefore is which model describes cognitive dispositions of adaptive intervention competence for teaching simulations and mathematical modelling with digital tools empirically. After clarifying the empirical operationalisation of the construct, the question to what extent pre-service teachers can develop cognitive dispositions of these domain-specific, digitally related professional competences through a university course can then be addressed. Based on pedagogical content knowledge as a cognitive disposition of comprehensive adaptive intervention competences, we concretise the research interest in three research questions:
Research question 1: Can the structure of cognitive dispositions of adaptive intervention competence for teaching simulations and mathematical modelling with digital tools be described empirically rather by a one-dimensional model or rather by a two-dimensional model?
Since theoretical process models for teaching mathematical modelling often distinguish diagnosis from intervention (Leiss and Wiegand, 2005; Leiss, 2007) and the two domains have already been empirically separated as competence dimensions (Klock and Siller, 2019), we formulate hypothesis (H1), stating that the construct of cognitive dispositions of adaptive intervention competence can be described by a two-dimensional Rasch model in our domain-specific interpretation.
Research question 2: To what extent can an improvement in cognitive dispositions of the adaptive intervention competence for teaching simulations and mathematical modelling with digital tools of pre-service teachers who have participated in a specifically designed mathematics education course for the development of this competence be determined?
Research question 3: To what extent can differences in the change in cognitive dispositions of the adaptive intervention competence for teaching simulations and mathematical modelling with digital tools be identified between pre-service teachers who
i. have participated in a specifically designed mathematics education course for the development of this competence, and
ii. have not participated in a specifically designed mathematics education course for the development of this competence?
Previous studies have already shown that aspects of adaptive intervention competence for teaching mathematical modelling can be significantly built up through a semester-long course at university (Greefrath et al., 2022). Based on these findings, we assume that by modifying the course, we also positively develop the digitally related professional adaptive intervention competence for reality-based mathematics teaching. Therefore, we formulate hypothesis (H2), stating that the cognitive dispositions of the adaptive intervention competence improve significantly over the treatment period through participation in the specifically designed mathematics education course. Moreover, we formulate hypothesis (H3), stating that the posttest results of the adaptive intervention competence for teaching simulations and mathematical modelling with digital tools are positively influenced by the group membership in favour of the specifically designed mathematics education course under control of the pretest results.
4. Methods
4.1. Research design
In a quasi-experimental treatment study, data from 146 pre-service mathematics teachers at the University of Würzburg and the University of Münster were collected in the winter semester of 2021/22 and the summer semester of 2022 and cumulatively analysed. The pre-service teachers took an identical test at two measurement points. The pretest (measurement point 1) was conducted at the beginning of the semester and the posttest (measurement point 2) at the end of each semester (duration of the semester: approx. Three months). Between the measurement times, the pre-service teachers in the experimental group took part in a mathematics education course (12 sessions of 90 min each) that focused, among other things, on the development of adaptive intervention skills for teaching simulations and mathematical modelling with digital tools. This course was specifically designed to develop this domain-specific competence and serves as a treatment in the context of this study. The control group consisted of pre-service mathematics teachers who took different courses in mathematics education (lecture, tutorial or seminar) during the same period. Thus, they did not receive any explicit training for the domain-specific adaptive intervention competence.
4.2. Test instrument
In order to measure the pedagogical content knowledge about processes and interventions for simulations and mathematical modelling with digital tools as cognitive dispositions of a corresponding domain-specific adaptive intervention competence, two scales from a self-developed test instrument (Gerber and Quarder, 2022) are used. The processes scale and the interventions scale each consist of 18 single-choice items that are evaluated dichotomously (0 = wrong option selected; 1 = correct option selected). Three items on each of the two scales refer to a teaching situation that is presented in one of a total of six text vignettes in the test instrument. The text vignettes consist of a simulation or modelling task as well as transcripts of associated conversations of students and screenshots depicting their working process on a problem with the digital tool (see Figure 5).
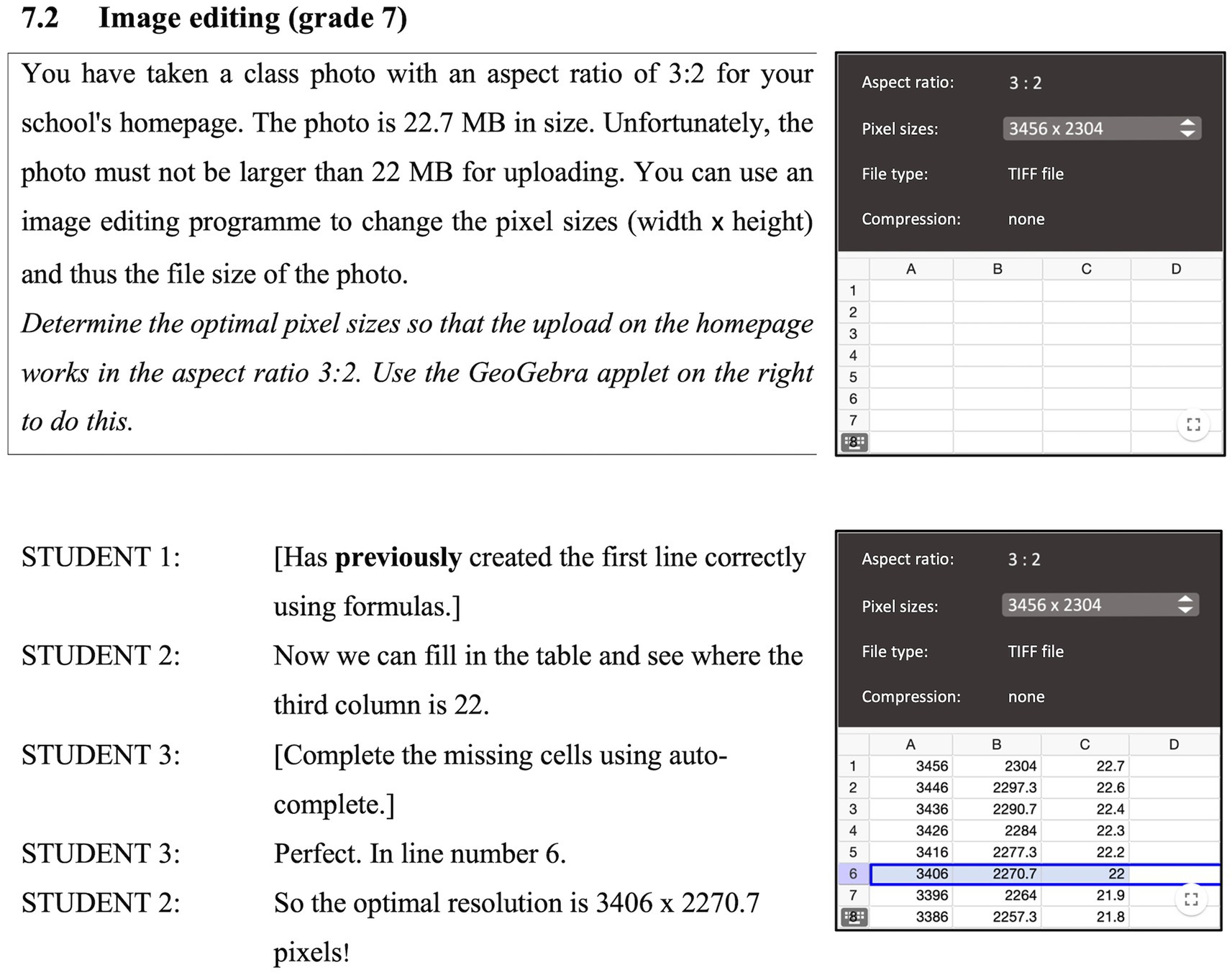
Figure 5. Text vignette for the scale processes and the scale interventions (Gerber and Quarder, 2022, p. 29, translated).
To answer the items, the participants first have to read the corresponding text vignette and analyse it from a mathematics educational point of view. The items of the processes scale contain four answer options each, one of which is correct in relation to the processing situation depicted in the associated text vignette, while the other three are distractors. This is an item that belongs to the processes scale and relates to the text vignette shown in Figure 5 and the modelling cycle shown in Figure 1:
Which function of the digital tools do the students mainly use in this situation? Please place one mark.
• investigate
• calculate
• visualise
• control
The item is intended to measure whether the participants identify which function of digital tools the students mainly use when working on the task in the described situation. Since in the text vignette in Figure 5, the students use the digital tool while working mathematically to calculate the cell values, the second answer option is correct.
The items of the interventions scale each contain a quotation of an oral teaching intervention that refers to a student difficulty in the task processing presented in the text vignette. The participants have to decide whether the statement is a suitable or unsuitable intervention in terms of independence-preserving support by placing a mark at “suitable” or “not suitable.” In order to reduce the guessing probability of the test participants, especially those with little teaching experience, the scale was supplemented by a default category (Wess et al., 2021). Just like selecting the wrong answer option, the “do not know” option is also scored as 0. These are three items of the interventions scale that belong to the text vignette from Figure 5:
Please mark which of the following interventions are suitable for an independence-preserving support of modelling or simulation skills in this situation. Please place one mark for each intervention.
• “Can your result regarding the unit of measurement be correct?”
• “Change the form of representation.”
• “2270.7 pixels do not exist.”
Of the three statements, only the first statement is an appropriate intervention in relation to the situation depicted in the text vignette. The third statement also points out that 2270.7 is an impossible value for pixel as the unit for measurement, but it is strongly content-oriented and not minimal. The first statement, in contrast, is a general-strategic support that is preserving independence. It is more minimal than the third statement, but can still have a positive effect on the working process on the problem. The intervention intends to stimulate a reflection process in which the learners question the output of the digital tool critically.
4.3. Notes on data analysis
The items of the test instrument used in this study are analysed dichotomously and then merged into scale values with the help of a simple Rasch model (Embretson and Reise, 2000). To answer research question 1 and to thus investigate the dimensionality of the construct, the pretest and posttest data are transferred into a long format data matrix. In this concurrent estimation approach, the posttest data are attached to the pretest data as virtual test subjects and the data are considered as if there had only been one measurement point. One advantage of this is that it increases the sample size for dimensionality and model testing in an acceptable way (Hanson and Béguin, 2002).
To answer research questions 2 and 3, a scaling of person parameters is required. For this purpose, the estimated item parameters from the long format data design are saved and the data is transferred back to the wide format. In order to obtain measured values per test person for the pretest and posttest, a multidimensional pre-post model (Adams et al., 1997) is calculated, which takes into account the correlation between the two measurement times, but uses the saved item parameters from the long-format data design. With the person parameters estimated in this way, the final longitudinal investigations are carried out. For this purpose, t-tests and multiple regression analyses are used in classical test theory.
4.4. Treatment: mathematics education course on simulations and mathematical modelling with digital tools
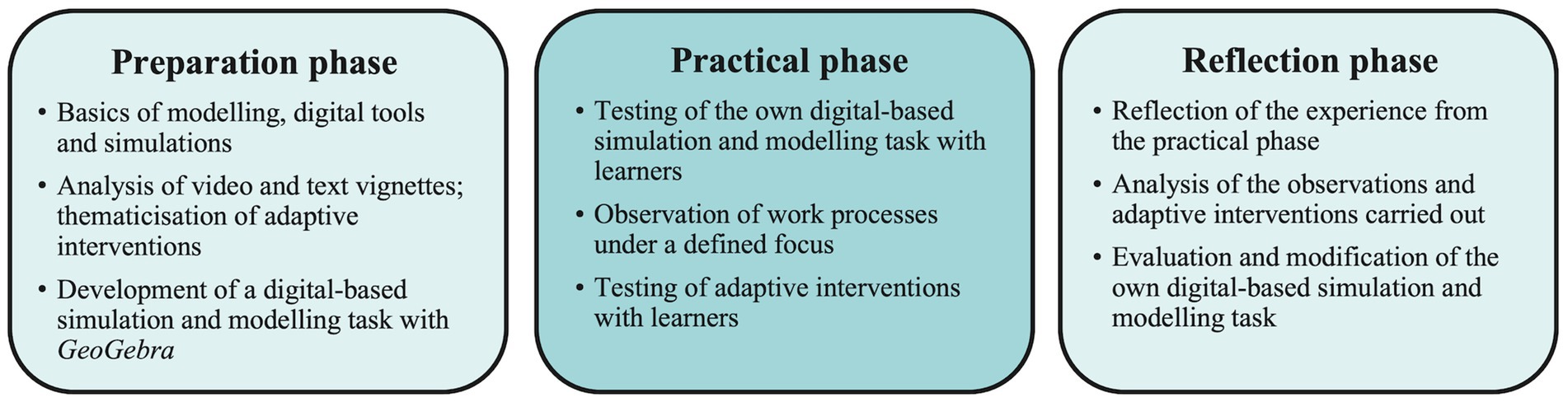
The treatment of this study takes place through a university course that involves practical school elements. The course focuses on simulations and mathematical modelling with digital tools and aims, among other things, to promote pre-service teachers regarding their domain-specific adaptive intervention competence. The course is based on the treatment described by Greefrath et al. (2022) and is divided into a preparation phase, a practical phase, and a reflection phase.
In the preparation phase (six sessions), the basics of simulations and mathematical modelling as well as the use of digital tools are taught. Reference is made to existing theories such as instrumental genesis (Artigue, 2002) or cognitive load theory (Sweller et al., 2011). In addition, various modelling cycles (see theory section Figures 1, 3) are addressed. In the discussion of video and text vignettes, for example, the digital-related modelling cycles shown in Figures 1, 2 are used as diagnostic tools. Pre-service teachers use them to analyse students’ processes when working on a reality-related task with digital tools. In this context, adaptive interventions as diagnosis-based and minimal assistance are also discussed using concrete case examples. In addition, the pre-service teachers develop their own digital-based simulation and modelling task on the basis of an elaborated catalogue of criteria. To illustrate this, the following task serves as an example: In the task, the outside of a half-pipe is to be painted. A student solution could be to model the area in GeoGebra with two rectangles and the integral of a polynomial function. The person depicted in the GeoGebra material can be used as a reference size to obtain a suitable scale for the conversion into square metres (see Figure 6).
In the practical phase (two sessions), the pre-service teachers try out the tasks they have developed themselves tasks with secondary students or with pre-service teachers who take on the role of student learners. While the learners work on the tasks independently in small groups, the pre-service teachers observe the working processes with a defined focus. If necessary, the pre-service teachers support the learners through the adaptive interventions that were theoretically discussed in advance.
In the reflection phase (four sessions), the pre-service teachers reflect on collected experiences from the practical phase. For this purpose, the observations recorded in writing are analysed with recourse to the theory taught and from specific points of view. The effect of the support provided is also critically examined and discussed against the background of adaptive teaching behaviour. With the help of the collected and systematically evaluated experiences, the pre-service teachers evaluate their self-developed task. On this basis, the task is then revised and, if necessary or helpful, made more precise.
Figure 7 shows the tripartite concept of the course including the selected contents.
4.5. Sample
Due to the quasi-experimental design of the study and the lack of randomisation, the sample is an occasional sample. It consists of 146 pre-service teachers who study mathematics as part of their teacher training at the University of Würzburg or the University of Münster in the winter semester of 2021/22 and the summer semester of 2022. Eighty pre-service teachers were assigned to the experimental group due to their participation in the educations course on simulations and mathematical modelling with digital tools described above. The control group consisted of 66 pre-service teachers who did not receive any specific promotion on adaptive intervention competence for teaching simulations and mathematical modelling with digital tools. A detailed sample description can be found in Table 1.
In terms of gender, age, number of semesters studied and Abitur grade (school leaving examination grade), the experimental group and the control group have basically comparable values.
5. Results
5.1. Structure of cognitive dispositions of adaptive intervention competence for teaching simulations and mathematical modelling with digital tools
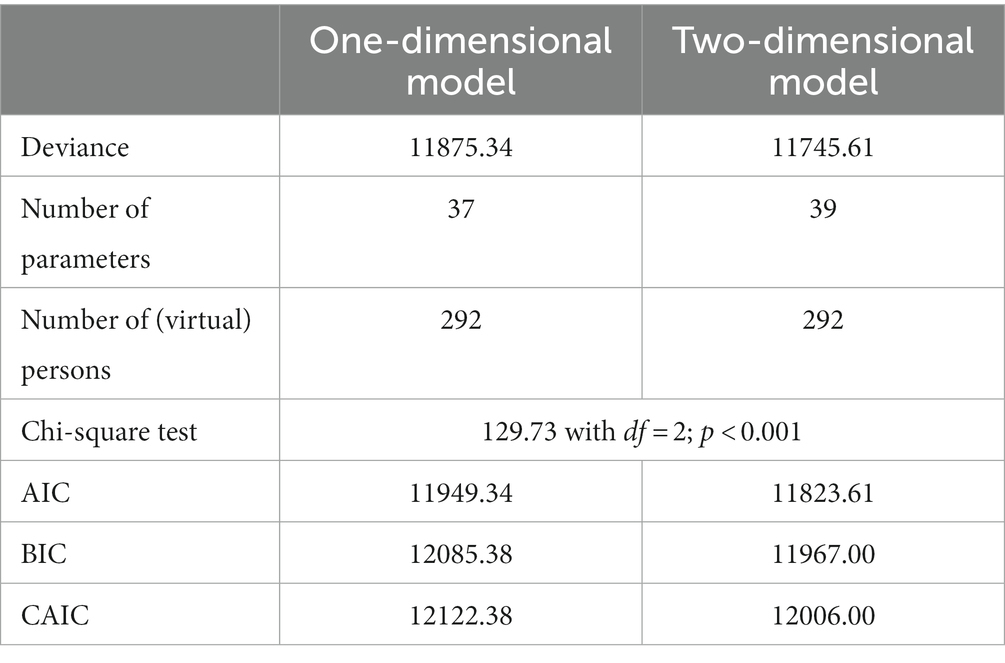
Now it is to be examined whether pedagogical content knowledge as cognitive dispositions of professional adaptive intervention competence in our domain-specific interpretation can be better described empirically by one or by two measured values. Therefore, two within-item Rasch models (Adams et al., 1997; Embretson and Reise, 2000) are compared. While, in the first model, all 36 items load on only one dimension, the second model consists of two dimensions with 18 items each. The second model separates the processes dimension from the interventions dimension instead of combining all items in the adaptive interventions dimension, as it was the case in the first model.
Table 2 summarises the results of the model comparison. All statistical values indicate that the two-dimensional model is better suited to empirically describe the structure of the cognitive dispositions of adaptive intervention competence for teaching simulations and mathematical modelling with digital tools.
The smaller deviance value of the two-dimensional model indicates that the two-dimensional model has a better global fit than the one-dimensional model with respect to the data collected. As the chi-squared difference test becomes significant, this difference in deviance values is statistically significant. The information criteria (AIC, BIC and CAIC), which penalise multidimensional models due to their greater complexity, are also lower for the two-dimensional model. This is another argument in favour of the less restrictive two-dimensional model.
Not only in direct comparison with another model, but also on its own, the two-dimensional model has a sufficient fit: the Weighted Mean Squares (WMNSQ) of the items are in the interval [0.84, 1.13]. According to Bond and Fox (2007), multiple choice items with WMNSQ values in the range of 0.8–1.2 are suitable for so-called High-Stakes Assessments. The EAP reliabilities of the two dimensions processes and interventions with 0.58 and 0.76 are sufficient for group comparisons (Lienert and Raatz, 1998), as intended in our study. Although the two dimensions are empirically separated from each other, they form the common construct of adaptive intervention competence due to the high correlation between them (r = 0.56) according to Cohen (1988). Overall, the hypothesis (H1) formulated for research question 1 could thus be confirmed.
5.2. Development of cognitive dispositions of adaptive intervention competence for teaching simulations and mathematical modelling with digital tools
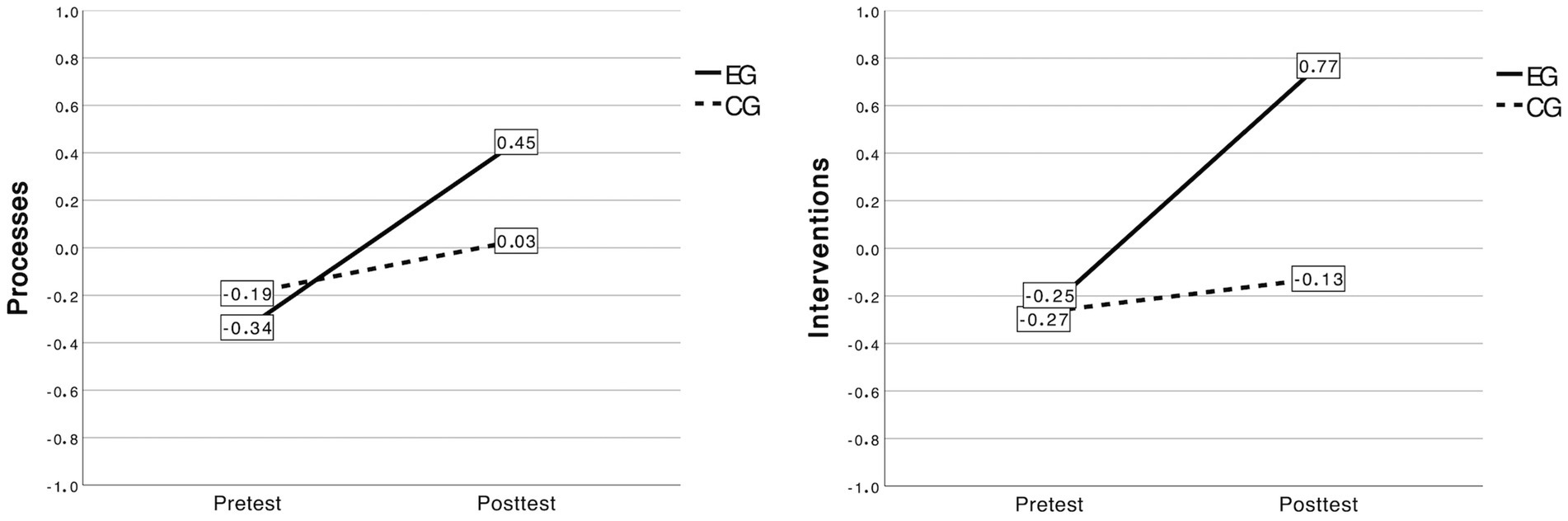
In order to be able to assess the extent of any changes in the cognitive dispositions of domain-specific adaptive intervention competence, we compare the arithmetic mean values of the person parameters of the two knowledge dimensions processes and interventions in relation to the time of measurement and the group membership. First, the dimension processes is considered: In the pretest, the mean value in the experimental group is MPre,EG = −0.34 (SD = 0.68) and in the control group it is MPre,CG = −0.19 (SD = 0.61). In the posttest, the mean value in the experimental group is MPost,EG = 0.45 (SD = 0.78) and in the control group it is MPost,CG = 0.03 (SD = 0.71). A similar finding emerges for the dimension interventions: In the pretest, the mean value in the experimental group is MPre,EG = −0.25 (SD = 0.96) and in the control group a mean value of MPre,CG = −0.27 (SD = 1.21) is calculated. In the posttest, the mean value in the experimental group is MPost,EG = 0.77 (SD = 1.13) and in the control group it is MPost,CG = −0.13 (SD = 1.21). Figure 8 shows the changes in knowledge in the two dimensions in a line chart, separated by measurement time points and the group membership. It can be seen that the pedagogical content knowledge in both dimensions and in both groups increases over time. In both dimensions, however, the increase is more pronounced in the experimental group than in the control group.
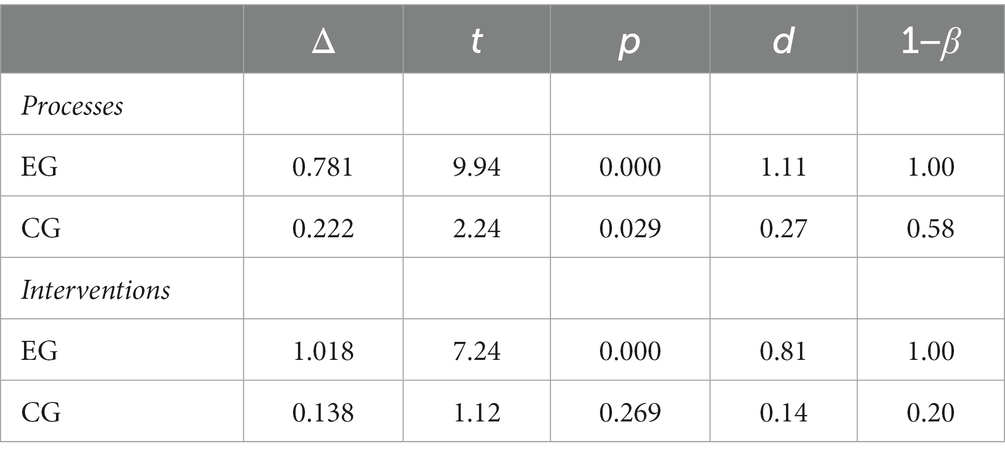
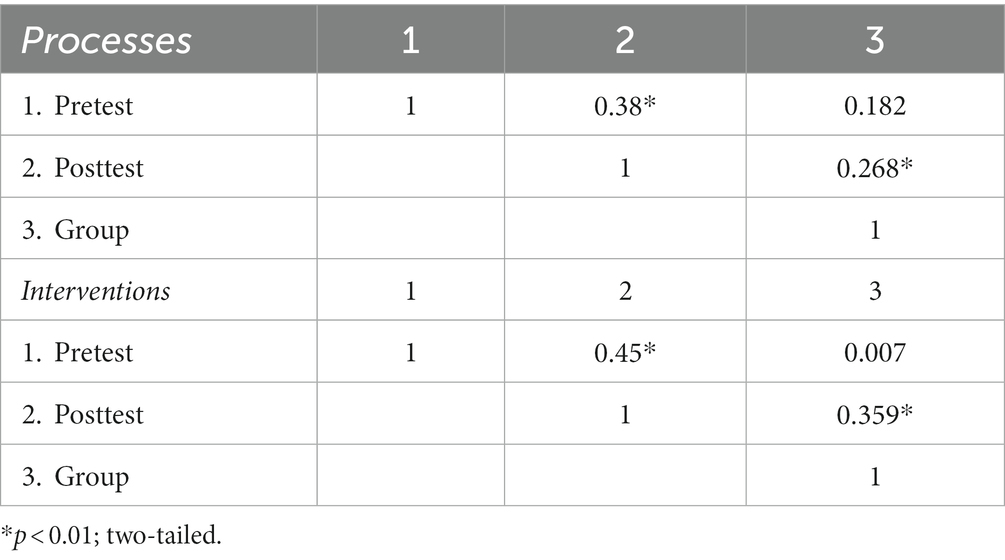
In the following, inferential statistical calculations (t-tests and regression analyses) are carried out to examine to what extent the change in knowledge presented above is significant and to what extent this improvement in knowledge is significantly influenced by group membership. Table 3 shows paired t-tests for the processes dimension and for the interventions dimension, each for the experimental and control group.
Using the t-test, it can be determined that in the experimental group, knowledge improves significantly over time in relation to the dimension processes and the dimension interventions, and with a large effect size according to Cohen (1988). The hypothesis (H2) formulated for research question 2 can thus be confirmed. As already seen, knowledge also develops positively in the control group. However, this change is only significant in the dimension processes and only with a small effect size.
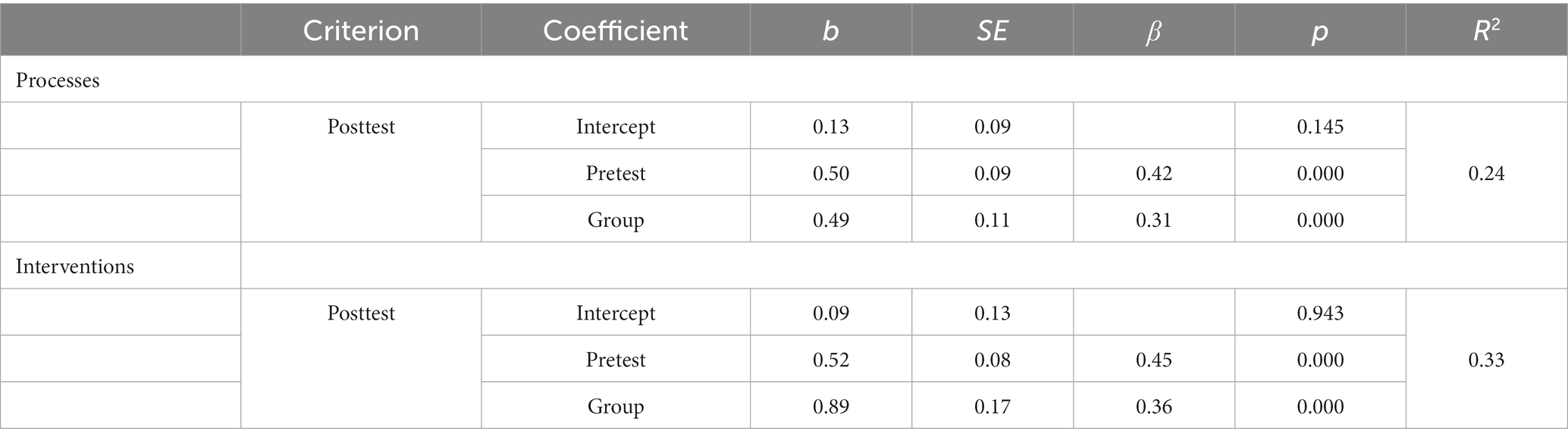
In order to work out the influence of group membership on knowledge development more precisely, regression analyses are carried out for the two dimensions with the linear model equation posttest = b0 + b1 • pretest + b2 • group. The experimental group was coded with one and the control group with zero. To test for multicollinearity, the bivariate correlations between the variables included in the model are considered first. These are summarised for the dimension processes and for the dimension interventions in Table 4.
For both dimensions, only low correlations (according to Cohen, 1988) occur between the independent variables pretest and group and that they are not significant. Multicollinearity, which could have been caused by self-selection effects, for example, can therefore be dismissed.
The resulting coefficients and parameters of the regression analysis are shown in Table 5 for the dimension processes and the dimension interventions. For both dimensions, group membership is a significant, positive predictor with medium effect sizes in each case for the results in the posttest, with the pretest results held constant. Participation in the experimental group thus has a significant influence on knowledge development, both for the dimension processes and for the dimension interventions. This also confirms the hypothesis (H3) formulated for research question 3.
6. Discussion
Independently dealing with reality-related problems with the help of mathematical tools within the framework of modelling and simulation activities is one of the important goals of mathematics education internationally. For this purpose, promoting modelling competences of students is necessary. Studies have shown that the use of digital tools – such as dynamic geometry software – can support the development of mathematical modelling skills (e.g., Greefrath et al., 2018), although there is little substantive research on the properties of technology that support these skills (Cevikbas et al., 2022).
Regardless of the degree to which digital tools support the simulation and modelling process, their use in dealing with reality-based and relevant problems is a great challenge for students and, consequently, for teachers. This paper investigated the adaptive intervention competence of teachers in simulations and mathematical modelling with digital tools. Interventions were presented as support provided by teachers that is taken in the students’ process of working on tasks because of difficulties that arise and that seriously hinder or make it impossible to continue working in a student-oriented, adaptive way. In other words, interventions involve support that enables independent and individual further work. To intervene adaptively, a preceding diagnosis is required. We pointed out that, in our domain-specific interpretation of simulations and mathematical modelling, this diagnosis particularly captures the students’ current processing phase as well as the way in which the digital tool is used. On this basis, the professional decision on how to support is possible.
6.1. Design of the treatment study
To investigate adaptive intervention competence, a treatment study in a pre-post design was conducted with a total of N = 146 pre-service teachers at the University of Würzburg and the University of Münster. The data were collected quantitatively with a self-developed test instrument (Gerber et al., 2022; Gerber and Quarder, 2022) and subsequently evaluated. Following Blömeke et al. (2015), adaptive intervention competence was reduced to two dimensions of knowledge which, as cognitive dispositions, allow statements about the competence itself. Therefore, the scales knowledge about simulation and modelling processes and knowledge about interventions of the test instrument were evaluated and interpreted in terms of the corresponding competence, taking motivational-affective characteristics and the course design into account. Against this background, changes in pedagogical content knowledge allow statements about changes in the corresponding competence (e.g., Baumert et al., 2010). Following Blömeke et al. (2015) again and in accordance with the theoretical conceptualisation of competences (cf. chapter 2.1), a positive development of knowledge can be interpreted as a positive development of competence if one also measures corresponding developments in – for example – self-efficacy. As we measured positive changes in self-efficacy of pre-service mathematics teachers, especially for planning and conducting teaching processes in which simulation and modelling problems can be processed with digital tools [see Gerber et al. (submitted) for the results about self-efficacy], we therefore use our data about development of knowledge of pre-service teachers to draw conclusions about their competences.
6.2. Answers to the research questions
Research question 1 examined the dimensionality of the construct. It was to be examined whether adaptive intervention competence is a one-dimensional or a two-dimensional construct consisting of the knowledge dimension processes and the knowledge dimension interventions. In relation to the above-mentioned test instrument, the dimension processes refers to knowledge about simulations and modelling processes using digital tools. In the test instrument, the dimension interventions refers to the knowledge area of the same name. The results confirm that the construct can be adequately described by a two-dimensional model. This model showed a higher fit than the one-dimensional model through better values in the model comparison (see Chapter 5.1). This replicates results of previous studies, see for example Klock and Siller (2019), who investigated adaptive intervention competence in the area of teaching mathematical modelling (without simulations and digital tools).
The results analysed to answer research questions 2 and 3 confirm the effectiveness of the course at the University of Würzburg and the University of Münster as a treatment. Based on the evaluation with the help of t-tests, a significant positive development with a large effect strength could be determined in the experimental group in the two knowledge dimensions examined during the period of the treatment. The analyses also showed a positive development in the control group. However, this was only significant in relation to the dimension processes with a small effect size. In the dimension intervention the development was not significant. One possible explanation for the significant increases could be the composition of the control group: The pre-service teachers did not receive any domain-specific education course in the area of simulations and mathematical modelling with digital tools. Nevertheless, they generally attended other mathematics education courses between the two measurement points. Among them were also some pre-service teachers who attended seminars on modelling without digital tools, in which modelling cycles were used to describe processing phases. The items of the scale knowledge of simulations and modelling processes addressed in our study, which were used to measure the gains in competence regarding diagnosis, are increasingly oriented towards modelling cycles. If the pre-service teachers in the control group developed more positive beliefs about the use of digital tools in mathematics teaching as a whole and about their use in independence-preserving teaching in particular between the two measurement points, this could have also had an influence on diagnostic competence. It cannot be ruled out that knowledge about these general cycles had a positive effect on a more general diagnostic competence, which was also found using our test instrument.
Using linear regression analyses, however, it could be shown for both dimensions that group membership positively influences the knowledge development of pre-service mathematics teachers in favour of the experimental group, in each case with a medium effect size. Therefore, participating in the specifically designed course has a positive influence on the development of adaptive intervention competence. The treatment can thus be considered effective.
6.3. Limitations and outlook
The composition of the sample already allows for meaningful conclusions in our study. However, this data basis is to be increased in the next semesters in order to confirm the statements or to make them more precise. In addition, the development of knowledge is also to be compared with regard to their correlation with other aspects of competence of our construct. For this purpose, it will be necessary in the future to investigate and include whether other dimensions of pedagogical content knowledge can also be improved through participation in the treatment, as well as beliefs for example.
When assessing the development of competence, it must be taken into account that the study had its focus on the (a priori) analysis of situations on the basis of pedagogical content knowledge, not on the implementation of diagnosis and intervention. The contribution of the practical phase to the positive changes in competence thus remains unclear. Greefrath et al. (2022), contrastingly, state its importance for the teaching of mathematical modelling. Since we could not verify the concrete effect of interventions, we refer to our intervention competence as a priori adaptive intervention competence, following Klock and Siller (2019) and Klock (2020). Furthermore, it would be interesting for future work to consider noticing competences in addition to professional knowledge when researching domain-specific professional competences (Alwast and Vorhölter, 2022).
7. Conclusion
Overall, we presented a process model for adaptive intervention with a focus on the use of digital tools in simulations and mathematical modelling. Following Roth (2019), we have distinguished general-strategic interventions into three categories: interventions on operating strategies, problem-solving strategies and reflection strategies. Regarding the promotion of the domain-specific professional adaptive interventions competence, we consider – based on the results of our study – our mathematics education course to be effective in terms of developing this competence. This confirms the concept of our university course: a theoretical phase (i.e., the teaching of theoretical and empirical findings on teaching simulations and mathematical modelling with digital tools), combined with practical school exercises for theory-based diagnosis and intervention in a practical phase, as well as an extensive reflection phase. According to our analyses, these phases are essential elements of the treatment that can account for the strong increase in professional adaptive intervention competence.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
Author contributions
SG and JQ analysed and carried out the study with content and organisational supervision by GG and H-SS. All authors contributed to the article and approved the submitted version.
Funding
This project is part of the “Qualitätsoffensive Lehrerbildung,” a joint initiative of the German Federal Government and the Länder which aims to improve the quality of teacher training (projects CoTeach, grant number: 01JA2020, and DwD.LeL, grant number: 01JA1921). The programme is funded by the Federal Ministry of Education and Research. This publication was supported by the Open Access Publication Fund of the University of Wuerzburg. The authors are responsible for the content of this publication.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^In this paper we use the term mathematical model as a mathematical representation of a simplified construction of the reality that characteristically describes essential criteria of the real situation, for example, by means of terms, functions and graphs.
References
Adams, R. J., Wilson, M., and Wang, W.-C. (1997). The multidimensional random coefficients multinomial logit model. Appl. Psychol. Meas. 21, 1–23. doi: 10.1177/0146621697211001
Alwast, A., and Vorhölter, K. (2022). Measuring pre-service teachers’ noticing competencies within a mathematical modeling context – an analysis of an instrument. Educ. Stud. Math. 109, 263–285. doi: 10.1007/s10649-021-10102-8
Artigue, M. (2002). Learning mathematics in a cas environment: the genesis of a reflection about instrumentation and the dialectics between technical and conceptual work. Int. J. Comput. Math. Learn. 7, 245–274. doi: 10.1023/A:1022103903080
Baumert, J., and Kunter, M. (2013). “The effect of content knowledge and pedagogical content knowledge on instructional quality and student achievement” in Cognitive activation in the mathematics classroom and professional competence of teachers: Results from the COACTIV project. eds. M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss, and M. Neubrand (Boston, MA: Springer US), 175–205.
Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., Jordan, A., et al. (2010). Teachers’ mathematical knowledge, cognitive activation in the classroom, and student progress. Am. Educ. Res. J. 47, 133–180. doi: 10.3102/0002831209345157
Blömeke, S., Gustafsson, J.-E., and Shavelson, R. J. (2015). Beyond dichotomies: competence viewed as a continuum. Z. Psychol. 223, 3–13. doi: 10.1027/2151-2604/a000194
Blum, W. (2015). “Quality teaching of mathematical modelling: what do we know, what can we do?” in The proceedings of the 12th international congress on mathematical education. ed. S. J. Cho (Cham: Springer International Publishing), 73–96.
Blum, W., and Leiss, D. (2007). “How do students and teachers deal with modelling problems?” in Mathematical modelling: education, engineering and economics. eds. C. Haines, P. Galbraith, W. Blum, and S. Khan (Chichester: Horwood), 222–231.
Bond, T. G., and Fox, C. M. (2007). Applying the rasch model: Fundamental measurement in the human sciences. 2nd. Mahwah: Lawrence Erlbaum Associates.
Borromeo Ferri, R., and Blum, W. (2010). “Mathematical modelling in teacher education – experiences from a modelling seminar” in Proceedings of the sixth congress of the European Society for Research in mathematics education (CERME 6). eds. V. Durand-Guerrier, S. Soury-Lavergne, and F. Arzarello ( Institut National de Recherche Pédagogique and ERME), 2046–2055.
Carretero, S., Vuorikari, R., and Punie, Y. (2017). Digcomp 2.1: the digital competence framework for citizens with eight proficiency levels and examples of use. Luxenburg: Publications Office of the European Union
Cavanagh, M., and Mitchelmore, M. (2000). “Graphics calculators in mathematics learning. Studies of student and teacher understanding” in Proceedings of the 24th International Conference on Technology in Mathematics Education. ed. M. O. J. Thomas (Auckland: Auckland Institute of Technology), 112–119.
Cevikbas, M., Kaiser, G., and Schukajlow, S. (2022). A systematic literature review of the current discussion on mathematical modelling competencies. State-of-the-art developments in conceptualizing, measuring, and fostering. Educ. Stud. Math. 109, 205–236. doi: 10.1007/s10649-021-10104-6
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. 2. New Jersey: Lawrence Erlbaum Associates.
Drijvers, P., Ball, L., Barzel, B., Heid, M. K., Cao, Y., and Maschietto, M. (2016). Uses of technology in lower secondary mathematics education: a concise topical survey. Cham: Springer International Publishing
Embretson, S. E., and Reise, S. P. (2000). Item response theory for psychologists. Mahwah, NJ: L. Erlbaum Associates.
Frenken, L., Greefrath, G., Siller, H.-S., and Wörler, J. F. (2022). Analyseinstrumente zum mathematischen Modellieren mit digitalen Medien und Werkzeugen. mathematica didactica 45, 1–18. doi: 10.18716/ojs/md/2022.1391
Galbraith, P., and Stillman, G. (2006). A framework for identifying student blockages during transitions in the modelling process. Zentralblatt Didaktik Mathematik 38, 143–162. doi: 10.1007/BF02655886
Geiger, V. (2011). “Factors affecting teachers’ adoption of innovative practices with technology and mathematical modelling” in Trends in teaching and learning of mathematical modelling international perspectives on the teaching and learning of mathematical modelling. eds. G. Kaiser, W. Blum, R. B. Ferri, and G. Stillman (Dordrecht: Springer Netherlands), 305–314.
Geiger, V., Galbraith, P., Niss, M., and Delzoppo, C. (2022). Developing a task design and implementation framework for fostering mathematical modelling competencies. Educ. Stud. Math. 109, 313–336. doi: 10.1007/s10649-021-10039-y
Gerber, S., and Quarder, J. (2022). Erfassung von Aspekten professioneller Kompetenz zum Lehren des Simulierens und mathematischen Modellierens mit digitalen Werkzeugen. Ein Testinstrument. Würzburg: Universität Würzburg. doi: 10.25972/OPUS-27359
Gerber, S., Quarder, J., Greefrath, G., and Siller, H.-S. (2022). “Pre-service teachers’ pedagogical content knowledge for teaching simulations and mathematical modelling with digital tools” in Proceedings of the Twelfth Congress of the European Research Society in Mathematics Education (CERME12). eds. J. Hodgen, E. Geraniou, G. Bolondi, and F. Ferretti (Bozen-Bolzano, Italy: ERME/Free University of Bozen-Bolzano), 1051–1058.
Gerber, S., Quarder, J., Greefrath, G., and Siller, H.-S. (submitted). “Pre-service teachers’ self-efficacy for teaching simulations and mathematical modelling with digital tools” in Researching mathematical modelling education in disruptive/challenging times international perspectives on the teaching and learning of mathematical modelling. eds. H.-S. Siller, V. Geiger, and G. Kaiser ( Springer International Publishing)
Greefrath, G. (2011). “Using technologies: new possibilities of teaching and learning modelling – overview” in Trends in teaching and learning of mathematical modelling international perspectives on the teaching and learning of mathematical modelling. eds. G. Kaiser, W. Blum, R. Borromeo Ferri, and G. Stillman (Dordrecht: Springer), 301–304.
Greefrath, G., Hertleif, C., and Siller, H.-S. (2018). Mathematical modelling with digital tools – a quantitative study on mathematising with dynamic geometry software. ZDM 50, 233–244. doi: 10.1007/s11858-018-0924-6
Greefrath, G., and Siller, H.-S. (2017). “Modelling and simulation with the help of digital tools” in Mathematical modelling and applications international perspectives on the teaching and learning of mathematical modelling. eds. G. A. Stillman, W. Blum, and G. Kaiser (Cham: Springer International Publishing), 529–539.
Greefrath, G., Siller, H.-S., Klock, H., and Wess, R. (2022). Pre-service secondary teachers’ pedagogical content knowledge for the teaching of mathematical modelling. Educ. Stud. Math. doi: 10.1007/s10649-021-10038-z
Hanson, B. A., and Béguin, A. A. (2002). Obtaining a common scale for item response theory item parameters using separate versus concurrent estimation in the common-item equating design. Appl. Psychol. Meas. 26, 3–24. doi: 10.1177/0146621602026001001
Hattie, J. (2009). Visible learning: A synthesis of over 800 meta-analyses relating to achievement. Reprinted. London: Routledge.
Heitzmann, N., Seidel, T., Hetmanek, A., Wecker, C., Fischer, M. R., Ufer, S., et al. (2019). Facilitating diagnostic competences in simulations in higher education a framework and a research agenda. FLR, 1–24. doi: 10.14786/flr.v7i4.384
Henn, H.-W. (2007). “Modelling pedagogy – Overview” in Modelling and applications in mathematics education. The 14th ICMI study. eds. W. Blum, P. L. Galbraith, H.-W. Henn, and M. Niss (New York: Springer), 321–324.
Herppich, S., Praetorius, A.-K., Förster, N., Glogger-Frey, I., Karst, K., Leutner, D., et al. (2018). Teachers’ assessment competence: integrating knowledge-, process-, and product-oriented approaches into a competence-oriented conceptual model. Teach. Teach. Educ. 76, 181–193. doi: 10.1016/j.tate.2017.12.001
Kaiser, G. (2020). “Mathematical modelling and applications in education” in Encyclopedia of mathematics education. ed. S. Lerman (Cham: Springer International Publishing), 553–561.
Kaiser, G., and Brand, S. (2015). “Modelling competencies: past development and further perspectives” in Mathematical modelling in education research and practice international perspectives on the teaching and learning of mathematical modelling. eds. G. A. Stillman, W. Blum, and M. Salett Biembengut (Cham: Springer International Publishing), 129–149.
Klock, H. (2020). Adaptive Interventionskompetenz in mathematischen Modellierungsprozessen: Konzeptualisierung, Operationalisierung und Förderung. Wiesbaden: Springer Fachmedien Wiesbaden
Klock, H., and Siller, H.-S. (2019). Measuring an aspect of adaptive intervention competence in mathematical modelling processes. In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education (CERME 11), Eds. U. T. Jankvist, M. Heuvel-Panhuizenvan den, and M. Veldhuis (Utrecht, Netherlands: Freudenthal Group & Freudenthal Institute, Utrecht University and ERME), 1200–1207.
Klock, H., and Siller, H.-S. (2020a). “A time-based measurement of the intensity of difficulties in the modelling process” in Mathematical modelling education and sense-making international perspectives on the teaching and learning of mathematical modelling. eds. G. A. Stillman, G. Kaiser, and C. E. Lampen (Cham: Springer International Publishing), 163–173.
Klock, H., and Siller, H.-S. (2020b). Die Bedeutung der Diagnose für adaptive Interventionen beim mathematischen Modellieren – Intervenieren lernen im Lehr-Lern-Labor. Mathematica Didactica 43, 47–62. doi: 10.18716/ojs/md/2020.1382
Krauss, S., Blum, W., Brunner, M., Neubrand, M., Baumert, J., Kunter, M., et al. (2013). “Mathematics teachers’ domain-specific professional knowledge. Conceptualization and test construction in COACTIV” in Cognitive activation in the mathematics classroom and professional competence of teachers: results from the COACTIV project. eds. M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss, and M. Neubrand (Boston, MA: Springer US), 147–174.
Kunter, M., Baumert, J., Blum, W., Klusmann, U., Krauss, S., and Neubrand, M. eds. (2013a). Cognitive activation in the mathematics classroom and professional competence of teachers: Results from the coactive project. Boston, MA: Springer US
Kunter, M., Kleickmann, T., Klusmann, U., and Richter, D. (2013b). “The development of teachers’ professional competence” in Cognitive activation in the mathematics classroom and professional competence of teachers: Results from the COACTIV project. eds. M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss, and M. Neubrand (Boston, MA: Springer US), 63–77.
Leiss, D. (2007). “Hilf mir, es selbst zu tun”. Lehrerinterventionen beim mathematischen Modellieren. Hildesheim; Berlin: Franzbecker.
Leiss, D., and Wiegand, B. (2005). A classification of teacher interventions in mathematics teaching. Zentralblatt Didaktik Mathematik 37, 240–245. doi: 10.1007/s11858-005-0015-3
Lienert, G. A., and Raatz, U. (1998). Testaufbau und Testanalyse. 6. Weinheim: Beltz Psychologie Verlags Union.
Molina-Toro, J. F., Rendón-Mesa, P. A., and Villa-Ochoa, J. A. (2019). Research trends in digital technologies and modeling in mathematics education. Eurasia J. Math Sci. T 15:em1736. doi: 10.29333/ejmste/108438
Pierce, R., and Stacey, K. (2010). Mapping pedagogical opportunities provided by mathematics analysis software. Int. J. Comput. Math Learn. 15, 1–20. doi: 10.1007/s10758-010-9158-6
Quarder, J., Gerber, S., Siller, H.-S., and Greefrath, G. (2023). “Simulieren und mathematisches Modellieren mit digitalen Werkzeugen im Lehr-Lern-Laborseminar. Förderung und empirische Analyse der bereichsspezifischen Aufgabenkompetenz” in Lehr-Lern-Labore und Digitalisierung Edition Fachdidaktiken. eds. M. Meier, G. Greefrath, M. Hammann, R. Wodzinski, and K. Ziepprecht (Wiesbaden: Springer VS), 33–46.
Roth, J. (2019). “Digitale Werkzeuge im Mathematikunterricht – Konzepte, empirische Ergebnisse und Desiderate” in Vielfältige Zugänge zum Mathematikunterricht: Konzepte und Beispiele aus Forschung und Praxis. eds. A. Büchter, M. Glade, R. Herold-Blasius, M. Klinger, F. Schacht, and P. Scherer (Wiesbaden: Springer Fachmedien), 233–248.
Shannon, R. E. (1975). Simulation. A survey with research suggestions. A I I E Transactions 8, 289–296. doi: 10.1080/05695557508975433
Shulman, L. S. (1986). Those who understand: knowledge growth in teaching. Educ. Res. 15, 4–14. doi: 10.3102/0013189X015002004
Siller, H.-S., Cevikbas, M., Geiger, V., and Greefrath, G. (2022). “The role of digital resources in mathematical modelling research” in Proceedings of the 45th conference of the International Group for the Psychology of mathematics education. eds. C. Fernández, S. Llinares, Á. Gutiérrez, and N. Planas (Alicante, Spain: PME), 152–155.
Siller, H.-S., and Greefrath, G. (2010). “Mathematical modelling in class regarding to technology” in Proceedings of the Sixth Congress of the European Society for Research in Mathematics Education (CERME 6). eds. V. Durand-Guerrier, S. S. Lavergne, and F. Arzarello (Lyon: INRP), 2136–2145.
Sommerhoff, D., Codreanu, E., Nickl, M., Ufer, S., and Seidel, T. (2022). Pre-service teachers’ learning of diagnostic skills in a video-based simulation. Effects of conceptual vs. interconnecting prompts on judgment accuracy and the diagnostic process. Learn. Instr. 101689. doi: 10.1016/j.learninstruc.2022.101689
Stender, P., and Kaiser, G. (2017). “The use of heuristic strategies in modelling activities” in Proceedings of the Tenth Congress of the European Society for Research in Mathematics Education (CERME 10). eds. T. Dooley and G. Gueudet (Dublin, Ireland: DCU Institute of Education & ERME), 1012–1019.
Sweller, J., Ayres, P., and Kalyuga, S. (2011). Cognitive load theory. New York, NY: Springer New York
Thurm, D., and Barzel, B. (2022). Teaching mathematics with technology: a multidimensional analysis of teacher beliefs. Educ. Stud. Math. 109, 41–63. doi: 10.1007/s10649-021-10072-x
Tropper, N., Leiss, D., and Hänze, M. (2015). Teachers’ temporary support and worked-out examples as elements of scaffolding in mathematical modeling. ZDM 47, 1225–1240. doi: 10.1007/s11858-015-0718-z
Velten, K. (2009). Mathematical modeling and simulation. Introduction for scientists and engineers. Weinheim: WILEY-VCH Verlag.
Vorhölter, K., Grünewald, S., Krosanke, N., Beutel, M., and Meyer, N. (2013). “Teacher behaviour in modelling classes” in Proceedings of the Eighth Congress of the European Society for Research in Mathematics Education (CERME 8). eds. B. Ubuz, Ç. Haser, and M. A. Mariotti (Ankara, Turkey: Middle East Technical University and ERME), 1127–1136.
Weinert, F. E. (2001). “Concept of competence: a conceptual clarification” in Defining and selecting key competencies. eds. D. S. Rychen and L. H. Salganik (Kirkland, WA: Hogrefe & Huber), 46–65.
Wess, R., Klock, H., Siller, H.-S., and Greefrath, G. (2021). Measuring professional competence for the teaching of mathematical modelling: A test instrument. Cham: Springer International Publishing
Keywords: adaptive intervention competence, diagnosis, simulation, mathematical modelling, digital tools, teacher education, pedagogical content knowledge, technology
Citation: Gerber S, Quarder J, Greefrath G and Siller H-S (2023) Promoting adaptive intervention competence for teaching simulations and mathematical modelling with digital tools: theoretical background and empirical analysis of a university course in teacher education. Front. Educ. 8:1141063. doi: 10.3389/feduc.2023.1141063
Edited by:
Frederick W. B. Li, Durham University, United KingdomReviewed by:
Eric C. K. Cheng, The Education University of Hong Kong, Hong Kong SAR, ChinaCorey Brady, Vanderbilt University, United States
Copyright © 2023 Gerber, Quarder, Greefrath and Siller. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sebastian Gerber, c2ViYXN0aWFuLmdlcmJlckBtYXRoZW1hdGlrLnVuaS13dWVyemJ1cmcuZGU=
 Sebastian Gerber
Sebastian Gerber Jascha Quarder
Jascha Quarder Gilbert Greefrath
Gilbert Greefrath Hans-Stefan Siller
Hans-Stefan Siller