Dakota/Lakota Math Connections: an epistemological framework for teaching and learning mathematics with Indigenous communities and students

Tribal colleges/universities have and continue to seek out connections between the local heritage and culture and the mainstream education content. In math, calls for culture to be more integrated into the classroom have been met with epistemological challenges as well as a dearth of math and local culture resources. The Dakota/Lakota Math Connections research project addresses both of these challenges. This article will specifically share the collaborative development, pilot, evaluation, and confirmation of an epistemological framework for curriculum development in both the math and language classrooms at Sitting Bull College. Following an Indigenous research paradigm focusing on relationality and relational accountability, the co-authors gathered a group of tribal college math instructors, Lakota language immersion teachers, and fluent elders. Altogether they experienced, evaluated, and confirmed the Dakota/Lakota Math Connections framework as a path for teaching and learning mathematics with Indigenous communities and students. Using an Indigenous research paradigm led to circular, reciprocal research questions for this article: In what ways, if any, did the framework impact the participants? In what ways, if any, did the participants influence the framework? The framework includes four major components (Western Math, Dakota/Lakota Math, the English language, and the Dakota/Lakota language) and the intersections among each component. The framework builds from the assumptions that language is intimately tied with culture and identity and that higher order mathematical thinking is embedded within Dakota/Lakota language and culture. This is based on the assumption that all cultures “do” math. The framework asserts that math fluency and Dakota/Lakota language fluency can grow together. The Dakota/Lakota Math Connections framework lays an epistemological pathway for Dakota/Lakota students to see their culture, identity, and language in the math curriculum as well as for math instructors to honor the call to connect the math classroom with the local heritage and culture.

1. Introduction

Tribally controlled colleges and universities (TCUs) have and continue to seek out connections between the local heritage and culture and the mainstream education content (American Indian Higher Education Consortium, 2023). At Sitting Bull College in Standing Rock Nation, a portion of the mission statement reads “Guided by Lakota/Dakota culture, values, and language, Sitting Bull College is committed to building intellectual capacity through academics.” (Sitting Bull College, 2023). At Sitting Bull College, as well as many other TCUs, every course is required to connect to the culture as demonstrated by the college's syllabus template that specifically has a section on cultural relevance.

“Guided by Dakota/Lakota culture, values, and language” also specifically applies to science, technology, engineering, and math (STEM) courses at Sitting Bull College. Across all TCUs, there are efforts to connect STEM with place-based, community-specific culture, language, and knowledge (Boyer, 2011; American Indian Science Engineering Society, 2020). Calls for culture to be more integrated into the classroom continue at the TCU-level as well as the K-12 level (Lipka et al., 2005; American Indian Science Engineering Society, 2020; Meyer and Aikenhead, 2021a,b; Stevens, 2021). At the K-8 level, the Yup'ik in Alaska have taken major strides in developing their curriculum called “Math in a Cultural Context” (Lipka et al., 2005). The decades of work within this project both answered the call for math and local culture integration and were able to demonstrate its many benefits from increased cultural identity for students to increased math exam scores (Lipka and Adams, 2004; Lipka et al., 2007; Kisker et al., 2012).

At the college level, calls for culture to be more integrated into the math classroom have been met with epistemological challenges as well as a dearth of math and local culture resources (Webb et al., 2017; Ruef et al., 2020; Meyer and Aikenhead, 2021a,b; Stevens, 2021). If Western mathematics is assumed to transcend culture, as it often is in mainstream Western education, then how can the TCU math classrooms connect with Indigenous culture (Bishop, 1990; Aikenhead, 2017; Ernest, 2021; Stevens, 2021)? More specifically, in what ways could Sitting Bull College math classrooms connect with Lakota/Dakota culture, values, and language? The Dakota/Lakota Math Connections research project addresses both challenges of epistemological misalignment and the scarcity of college math and Dakota/Lakota culture resources.

This article will specifically focus on the first challenge of epistemological misalignment between Sitting Bull College's mission of academics guided by D/Lakota culture, value, and language with the Western assumption of mathematics as universal and objective, meaning that math is the same for everyone with no influence from local culture but rather transcends local culture (Bishop, 1990; Aikenhead, 2017; Ernest, 2021; Stevens, 2021). As the Sitting Bull College mission mandates, D/Lakota culture, values, and language are place-based [not universal]; holistically include mind, heart, body, and spirit; and have a strong emphasis on relationship/context. In this tension of epistemological misalignment, the D/Lakota Math Connections project emerged. This article will specifically share the collaborative development, evaluation, and confirmation of an epistemological framework for teaching and learning mathematics in both the math and language classrooms at Sitting Bull College.

Building on the considerable body of STEM education literature for Native students at the K-12 level, the American Indian Science and Engineering Society conducted a literature review with the goal “to provide an understanding of the most effective educational strategies for (primary and secondary). Native learners in the areas of STEM” (American Indian Science Engineering Society, 2020, p. 4). Their concluding statement for K-12 STEM education for Native students follows.

Indigenous people, cultures, and communities have rich histories, traditions, and ways of knowing, being, and connecting with the world around them. For too long mainstream education systems have undervalued and disregarded Indigenous Knowledge and Indigenous Science. Research now suggests these Indigenous assets are not only important for the success of Indigenous people themselves but for the healing and health of our world. Stemming from this foundation of immense wealth, researchers posit improved educational outcomes for Native and non-Native students result when STEM instruction is culturally relevant, rooted in Indigenous ways of knowing, linked to place, and embedded in community (p. 12).

Specific to math education, Garcia-Olp et al. (2019) posit that “Indigenous Knowledge has Always Been Mathematics Education.” They state that Indigenous mathematical knowledge has been passed down from one generation to the next in Indigenous communities through “experiential relationships in the natural world” (p. 11). Furthermore, the D/Lakota Math Connections project builds upon Sanders' (2011) dissertation work that brought together both the idea of a Lakota view of mathematics and the action of a math curriculum designed to follow the community's desire for self-determination in (math) education.

In this context of math education with Indigenous communities, Luecke and initial collaborators (a Sitting Bull College math instructor, a language instructor, and an Indigenous research methodology specialist) applied an Indigenous research paradigm to research in undergraduate math education. Their collaboration laid the groundwork for the Dakota/Lakota Math Connections course and framework (Luecke et al., 2022).

The foundation for the course content was previous research in Lakota math by Sanders (2011). Luecke invited him to co-facilitate the 1-week summer course together. They gathered a group of tribal college math instructors, Lakota language instructors, and fluent elders to further understand D/Lakota math. During the course, participants/contributors collaboratively discussed connections between mathematics and D/Lakota culture, values, and language. Altogether, they experienced and evaluated the “Dakota/Lakota Math Connections Framework.” The course collaboratively confirmed the use and further implementation of the framework while simultaneously further describing D/Lakota math and refining the framework's nuances.

The D/Lakota Math Connections framework (see Figure 1) includes four major components (Western Math, Dakota/Lakota Math, the English language, and the Dakota/Lakota language) and the interactions among each component. The framework builds from the assumptions that language is intimately tied with culture and identity (Wilson, 2008; Ruef et al., 2020; Sitting Bull College, 2023) and that higher order mathematical thinking is embedded within Dakota/Lakota language and culture (Bishop, 1991; Sanders, 2011; Garcia-Olp et al., 2019; Ruef et al., 2020). This assumes that all cultures “do” math (Bishop, 1991; Sanders, 2011). The framework asserts that math fluency and Dakota/Lakota language fluency can grow together. The Dakota/Lakota Math Connections framework, sometimes called the “Four Circles Framework” lays an epistemological pathway for Dakota/Lakota students to see their culture, identity, and language in the math curriculum as well as for math instructors to honor the call to connect the math classroom with the local heritage, culture, values, and language. The college is part of the D/Lakota communities' effort to revitalize the language, and the Four Circles framework shows a path for mathematics teaching and learning to also join that effort.

FIGURE 1

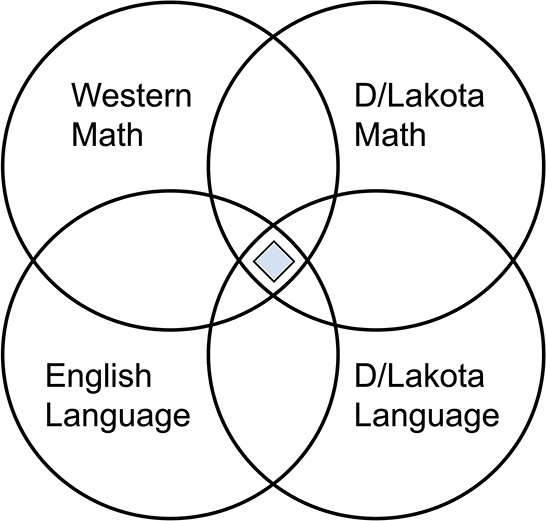
Figure 1. Dakota/Lakota Math Connections framework. The D/Lakota Math Connections framework is a four-circle Venn diagram, and thus sometimes referred to as the “Four Circles framework.” Content in the intersection of all four circles, pictured as a blue diamond, is sometimes called a “D/Lakota math connection.”

The course piloted the D/Lakota Math Connections framework. This article describes the course and framework implementation as well as the research methods, analysis/synthesis, and results from this pilot course. The two research questions guiding this study are as follows:

1. In what ways did the framework impact the participants?

2. In what ways did the participants influence the framework?

Following an Indigenous research paradigm that centers on relationality and relational accountability (Wilson, 2008), these two questions highlight “the process is the product” (Wilson, 2008, p. 103) and the Indigenous value of reciprocity. First, reciprocity is evident in the reciprocal questions reflecting upon each other. In contrast to a more linear process where the framework would be static and pre-determined during data collection, analysis, and synthesis, Question 2 probes how the participants change our understanding of the framework. Fuller comprehension of the framework came through the participants' experience of the course/framework. Additionally, the two guiding questions of this article highlight an Indigenous research paradigm that is circular and iterative. In contrast to a linear research paradigm, these two questions guiding the quantitative analysis were developed after the initial synthesis of relationships throughout the course by the co-authors. “The process is the product” (Wilson, 2008, p. 103). The framework and participants co-inform with one another. Similarly, the data collection and data synthesis/analysis/results co-inform one another (Wilson, 2008). Again, instead of the linear logic for writing/reading an article (introduction to methods to results to discussion), the framework of four interconnected circles also describes the four main sections of this article (introduction, methods, results, and discussion). This research project attempts to follow an Indigenous research paradigm within academia. However, “Indigenous epistemologies challenge the very core of knowledge production and purpose. While this is not a matter of one worldview over another, how we make room to privilege both, while also bridging the epistemic differences, is not going to be easy” (Kovach, 2009, p. 29).

Answering the two reciprocal research questions confirms the D/Lakota Math Connections framework and expands upon the nuances for curriculum development at Sitting Bull College and more generally teaching and learning mathematics with Indigenous communities and students. This article honors the call on TCU math instructors, and more broadly STEM instructors, at all levels, teaching Indigenous students, to bring balance and epistemological alignment between their math curricula and the community/nation's expectation of math education being guided by local culture, values, and language.

2. Methods

2.1. Indigenous research paradigm viewpoint on data collection and synthesis

This subsection is not defending the validity of an Indigenous research paradigm compared with Western research approaches, but rather “a conceptual framework gives researchers a tool to show how their methods are being aligned with a particular way of knowing” (Kovach, 2009, p. 43). As far as the authors are aware, an Indigenous research paradigm collectively described by Archibald (2008), Wilson (2008), and Kovach (2009) has not been applied to research in undergraduate math education to date. Wilson (2008) asserts that an Indigenous research paradigm is built on relationality and relational accountability. Relationality, meaning relationships form reality, is the ontology (what is real?) and epistemology (how do I know what is real?). With relationality as the ontology and epistemology, one does not have relationships but is relationships. Thus, increased understanding does not come from triangulating an object's location/definition, but rather encircling/strengthening the relationships with the central idea/activity. Therefore, knowledge is not contained in this written article, but rather in all the relationships of the participants/co-researchers who have participated in the D/Lakota Math Connections project as well as all who will think about D/Lakota math connections and/or read this article. Relational accountability is the methodology (how do I find out more about this reality?) and axiology (what moral beliefs will guide this search for reality?). Strengthening and being accountable to all relations is the value system and process in which to align all methods and research decisions. Specifically, in this research project and study, the use of story, intuitive synthesis, and non-linear data collection and analysis are all implemented to follow a research paradigm based on relationality and relational accountability.

First, “story as method elevates the research from an extractive exercise serving the fragmentation of knowledge to a holistic endeavor that situates research firmly within the nest of relationships” (Kovach, 2009, p. 99). In this research project and study, story was used for data collection, data synthesis, and in writing/reading this article. Wilson expands to describe non-fragmented, non-linear research as “the methods of data collection and the data analysis blended into one… The analysis was collaborative and ongoing. It shaped the direction of the research” (Wilson, 2008, p. 131). Note how he does not describe research with fixed linear phases of data collection, analysis, results, and discussion.

How one gathers information, interprets information, and verifies knowledge must follow relationality (ontology and epistemology) and relational accountability (methodology and axiology). Wilson further describes analysis in his understanding of an Indigenous research paradigm.

“it [analysis/synthesis] just can't be thought of in a linear one-step-leads-to-another-way. All of the pieces go in, until eventually the new ideas come out… [The Indigenous style is to] look at all those relations as a whole instead of breaking it down, because it just won't work. It has to use a more of an intuitive logic, rather than a linear logic… that is the spiritual [ceremonial] part of it… when those ideas all come together, those connections are made [stronger]. (Wilson, 2008, p. 116, 119, 122)

Finally, a non-linear, spiritual research process reveals itself in writing as well. “It [a tribal epistemology of relationality] demanded that I ‘write knowledge differently' than I had been instructed to do within previous Western research training… Once this tribal epistemology was visible, then all the research choices were considered against it.” All the research decisions in the D/Lakota Math Connections project and this study are made through the lens of an Indigenous research paradigm and sometimes summarized as “the process is the product” (Wilson, 2008, p. 103).

2.2. The Dakota/Lakota Math Connections framework

The D/Lakota Math Connections (Four Circles) framework was developed by the co-authors in preparation for the “D/Lakota Math Connections” course. The course they developed brought together math instructors (middle school through TCU), language instructors (immersion through high school), and fluent elders to discuss math topics.

Course participants were introduced to the framework and worked with it throughout the week. At the end of the week, two exercises were completed so participants could reflect on the framework and give feedback to further define and understand the D/Lakota Math Connections framework. Both of these exercises along with participants' quotes and stories are described in the Results section.

The framework was a way to declare the assumptions and goals of the course (as shared below in the Methods section) and the course was a way to collaboratively envision and define the framework (as shared in the Results and Discussion sections). The course was the avenue to experience the framework and the framework was the avenue to evaluate the course.

The framework set the stage/environment for respectful, asset-based conversation among the three distinct groups of people participating in the course (math instructors, language instructors, and fluent elders). Western math expertise (as held by math instructors) and D/Lakota language expertise (as held by fluent elders) are two distinct areas of expertise, but both are highly valuable. Fluent elders are central to the entire process and essential in every community effort toward language revitalization/reclamation. Their participation, comments, and feedback are pivotal in understanding the framework, the D/Lakota language circle, and the D/Lakota math circle.

Furthermore, language learning and Western math learning can be intimidating. The initial setup of the framework sought to ease these tensions by consistently emphasizing that math fluency and language fluency are both valid and valuable in this course and framework. With English as the medium for communication, the course goals were to further understand and strengthen the D/Lakota Math circle as well as articulate the center intersection, the connections among all four circles, so that TCU math instructors and language instructors can use these connections in their classroom. There are multiple layers of reciprocity and balance between math instructors and language instructors, mathematical knowing and linguistic knowing, and Western ways and D/Lakota ways of knowing.

The process of using the framework determined the product of the framework. Learning how math teachers, language teachers, and fluent elders viewed and responded to the framework brought definition to the framework. Even after this article is published, the D/Lakota Math Connections framework will still be in the process of being defined and understood. Furthermore, each circle, especially D/Lakota math, and the intersections among the circles will continue to be shaped in future by math teachers, language teachers, fluent elders, and whoever else participates in the D/Lakota Math Connections project.

Despite the continual re-understanding and defining of the framework, there were seven initial assumptions/beliefs that were used to describe the framework to participants in the summer 2021 “D/Lakota Math Connections” course. They are as follows.

2.2.1. Each circle is distinct

This assumption describes that Western Math does not contain all mathematical knowledge. Due to the distinct ways of the Western worldview compared to Indigenous ways of knowing, being, and doing, there was no assumption that Western Math contains all mathematical thinking. Similarly, the D/Lakota language is distinct from English not just in vocabulary but also in worldview. Each circle is distinct.

2.2.2. Each circle stands on its own

This assumption describes that D/Lakota math existed before colonization. It passed down from one generation to the next and needed no justification from colonial powers or reinforcement with colonial knowledge. Just like the D/Lakota language does not need the English language to justify its credibility, use, or power, D/Lakota math does not need Western math to justify its credibility, use, or power. Each circle can stand on its own.

2.2.3. Each circle (equally sized) is equally valuable

This assumption describes that despite colonization creating an imbalance of overvaluing Western knowledge and devaluing D/Lakota knowledge, the framework asserts an equal value to both ways of mathematical knowing. This assumption specifically pushes back against the typical training/education that most people receive in the United States, which values the Western way of knowing over an Indigenous way of knowing. Each circle is equally valuable.

2.2.4. Each circle is connected to all the other circles

This assumption describes that every circle is connected to every circle (despite the diagram (Figure 1) missing the visual representation of Western Math connected to the D/Lakota Language and English connected to D/Lakota Math). Furthermore, we assume that the center intersection of all four circles exists. The specific examples within that center spot of connection are called “D/Lakota Math Connections.” Articulating these “D/Lakota Math Connections” for use in math classrooms and language classrooms was and continues to be one of the central goals of this project. Each circle is connected to all the others.

2.2.5. No pre-determined definition is needed

No precise definition was given to what each label meant, nor the intersection between such circles. No precise definition was given for Western or Western Math. It was informally introduced to the course participants as what the U.S. education system typically teaches in math classrooms, math that happens on desks, with paper and pencil, etc. The balance among the four circles demonstrates no negativity or diminishing of the power of Western math, but rather seeks to bring Western math into balance with other ways of knowing. No precise definition was given for D/Lakota Math either. Course participants (more appropriately named co-researchers) collectively defined the circles, in particular the D/Lakota Math circle. A language instructor in preparation for the course explained that in the D/Lakota language, numbers can be the verbs of a sentence instead of just adjectives or nouns depending on the context. This initial understanding of the distinctiveness of how numbers can be viewed was the proof of concept to help confirm that the D/Lakota language instructors and fluent elders were the most appropriate people to define/describe D/Lakota Math, not an outside researcher. Finally, the D/Lakota Math Connections framework was not even named at the start of the week, but rather was simply called the “course and research framework.”

2.2.6. Higher order mathematical concepts are embedded within the language and culture

The decision to have the D/Lakota community define D/Lakota math also comes from the belief that “higher order mathematical concepts are embedded within the language and culture” (Garcia-Olp et al., 2019; Luecke et al., 2022). This builds on the assumption that all cultures “do” math. Bishop (1991) describes six universal math activities [counting, designing, locating, measuring, playing, and explaining] as a framework to articulate the mathematical thinking embedded within every culture. Sanders' dissertation (2011) used Bishop's framework in another Lakota community and became the basis for the summer 2021 pilot course. Again, what defines a “higher order mathematical concept” was left to the research process and co-researchers (participants and D/Lakota community). The higher order mathematical concepts embedded within the language and culture that were part of the summer 2021 pilot course would become the mathematical examples to define/describe the four circles and intersections. These results are shared in the follow-up study addressing the scarcity of resources connecting college math and Dakota/Lakota culture.

2.2.7. Math fluency and language fluency can grow together

Sanders shared a story with Luecke and then again with the summer 2021 pilot course of his math teaching experiences. He shared that the class physically next door to his classroom was the Lakota language classroom, but the physical wall felt like an impermeable wall between the two subjects. He lamented the separation between the subjects (typical in Western ways of education) and that feeling helped inspire the topic of his dissertation.

The Four Circles framework not only asserts balance between Western math and D/Lakota math but also a balance between mathematics and language. Similar to the asset-based approach of developing the framework for math teachers, language teachers, and fluent elders, two distinct expertise genres are assumed by the framework to be in balance by the framework. The co-facilitators for the course (and co-authors) fluent in Western math seek to encourage D/Lakota language fluency through this framework and research. Across the D/Lakota nation, language revitalization efforts are being encouraged and endorsed and the D/Lakota Math Connections framework and the project seek to do the same. The results and discussion of this study will focus on the epistemological stance that math fluency and language fluency grow together.

2.3. The pilot course

The course took place in June 2021 at Sitting Bull College. It was part of a larger language revitalization effort called “D/Lakota Summer Institute” which is co-sponsored by Sitting Bull College and the Standing Rock Iyapi, a branch of the Standing Rock Department of Education. The class was 3 hours long for 5 days. It was framed as a workshop to course participants who signed up through the “D/Lakota Summer Institute” processes. It was viewed as a pilot course and originally named “Lakota Math Connections.” During the course itself, the framework had yet to be named and was simply called “the course and research framework.” The goal at that moment was to be honest about the assumptions the co-facilitators (now co-authors) were bringing to the 1-week summer course and to set a safe place of discussion among the TCU math instructors, Lakota language teachers, and fluent elders.

2.3.1. Participants

A total of 28 people took part in the course. Not every person participated in each of the 5 days and not every person participated in each data collection approach. In non-exclusive groupings, this included seven math teachers, 14 language teachers, nine elders, six elders who speak the D/Lakota language fluently, six miscellaneous people (science teachers, elementary teachers, and non-teachers), two lead facilitators (co-authors Luecke and Sanders), and five small group facilitators. The seven math teachers included four current math instructors (three at TCUs and one at a middle school in Standing Rock) and three past math instructors (one at the middle school and one at the high school level in different reservation communities and one at a mainstream public university). Three of the math instructors were enrolled in D/Lakota Nations and one in another Indigenous Nation. The 14 language teachers included nine second-language learners and five fluent elders. Nine of the language teachers worked in an immersion setting and four worked in a middle school or high school. Twelve of the language teachers were enrolled in D/Lakota Nations and one in another Indigenous Nation. Five of the six fluent elders lived and worked in Standing Rock. The median attendance per day was 21. The median attendance of math teachers, language teachers, elders, and other community members was 7, 10, 5, and 6, respectively.

2.3.2. Course overview

Each day of the course emphasized a specific mathematical activity expressed by Bishop (1991). Sanders used Bishop's framework to establish the Lakota language specific to each activity, thereby showing connections at a basic level between mathematical terms and Lakota words (2011). The course facilitator and lead researcher, Luecke, began each day by introducing an overview of the day's activities. This was followed by a presentation by Sanders who presented a specific universal math activity utilizing content and examples from his dissertation. Luecke then presented the Western mathematical concepts that would be utilized for the subsequent small group discussions leading into a large group discussion. This general rhythm was repeated each day. A summary of the week is given in Figure 2.

FIGURE 2

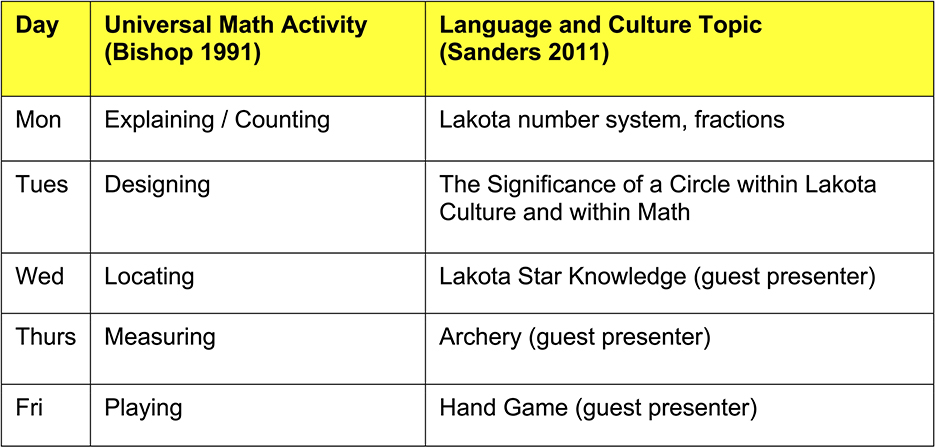
Figure 2. Schedule overview. This table shows the schedule of the week-long pilot course following the Universal Math Activity framework implemented by Sanders in a Lakota community.

2.3.3. Small group discussions

After the presentations by Sanders and Luecke, smaller groups were gathered with the selection of idealized group members based on specific criteria. Each group contained a facilitator and at least one Lakota speaker, one Lakota language teacher, one math teacher, and one elder. The small group discussions consisted of answering the small group discussion questions. Often the discussion included a deeper explanation in English of the mathematical concept introduced by Luecke and Sanders. This was followed by a conversation about the concept/activity itself and an engagement with Lakota language speaker(s) to determine if they could recreate the mathematical concept utilizing the Lakota language with additional questions and support offered by the Lakota language instructors. From the framework perspective, the process looked something like this:

(^*) Western Math → English Language → Lakota word or phrase → Lakota context(s) for word or phrase → Discussion and agreement

At the beginning of the week, all participants were gathered together for the first time, most not knowing the participants from a different group (language teachers and math teachers). Relationships were built during the daily exercises and discussions. Much of the work in Indigenous research methodologies has a heavy dependence on strong trusting relationships. Facilitators ultimately had to gain the trust of all participants in their respective groups while implementing the tasks.

2.4. Methods of data collection and analysis

Following an Indigenous research paradigm as described by Wilson (2008), the data collection and analysis/synthesis for this project are non-linear and instead flow from a reality based on relationship and relational accountability. Specifically, this means that the two reciprocal research questions guiding this article were not clearly articulated until after the data were collected.

During the course, multiple data sources were collected. Non-quantifiable relational outcomes (among the participants and with the content/framework) were experienced, noted by the co-facilitators (now co-authors), and intuitively synthesized to provide initial confirmation of the D/Lakota Math Connections framework (Wilson, 2008). Later, as a process of circling back (Windchief and San Pedro, 2019), the initial confirmation was encircled (that is, brought into greater relationship and a strengthening of the relationships that made up the initial confirmation) by the two reciprocal research (Wilson, 2008).

In the future, circling forward will occur in the continual development of the framework. As math and language teachers implement D/Lakota math connections in their classrooms and fluent elders continue to share their wisdom and expertise, the Four Circles framework will be re-defined. Data collection and data synthesis will continue reciprocally and cyclically. As new relationships are formed through experiencing the framework, the understanding of the framework will grow beyond this written article. The research process used for the D/Lakota Math Connections project emphasizes a relationship-oriented over object-oriented approach, an action-oriented over definition-oriented approach, a cyclical intuitive over a linear disconnected approach (Wilson, 2008; Kovach, 2009; Smith et al., 2018; Windchief and San Pedro, 2019).

The initial confirmation of the Four Circles framework was brought into the greater relationship, that is encircled, by the two research questions. To address how the framework impacted the participants, a quantitative analysis was conducted on participants' self-assessment framework drawings of their change of knowledge from Monday to Friday. To address how the participants influence the framework, two additional methods were employed. First, a quantitative analysis was conducted on the participants' emphasis scale ratings via the framework of the course. Second, and arguably the most important, the knowledge keepers of the community (that is fluent elders) shared their perspectives on the course, framework, and project overall.

3. Results

The results section is divided into three subsections:

- Connections amongst people as an initial confirmation.

- Framework impacts participants.

- Participants influence framework.

3.1. Connections among people as an initial confirmation

Priority is given to relational accountability in an Indigenous research paradigm. It is the crucial concept for both the methodology and axiology (determining what research is valid/credible and what research is valuable, respectively). Generally, non-quantified connections among people may seem insignificant or less credible within some Western research paradigms, but within an Indigenous research paradigm, these relational details are invaluable.

During the summer 2021 “D/Lakota Math Connections” course, multiple relationships began or were strengthened throughout the week. Math teachers, language teachers, and elders all expressed (in off-hand comments and some in their post-surveys and post-interviews) the value of simply being together in the same room with dedicated time to discuss and learn from one another. Even though food was provided each day for the course, during the last 3 days of the week, local language instructors felt invested in the success of the project as evidenced by bringing in additional food to share with the class. The sharing of food created a positive, inclusive environment for all. Furthermore, upon completion of the week, Wahóȟpi Kiŋ (the Lakota Language Immersion Nest) at Sitting Bull College asked Luecke to continue working with the school as a math consultant. They also suggested applying for and co-writing a grant with Luecke to continue the work started during the course. Finally, during the Friday Talking Circle, each person present was able to publicly share their thoughts on the course, the framework, and the future of the project. Elders, along with many participants, shared their public support for the project, framework, and its continuance. Not one person suggested the project be discontinued, but rather every participant encouraged its continuation.

One Wahóȟpi Kiŋ instructor shared publicly during the Friday Talking Circle the following quote:

“I really appreciate everybody that was here because often when something like this happens, and having worked for my tribe, ‘the Lakota thing is always the Lakota teachers.' So you being a Lakota teacher, [you are told] ‘they will do it.' So I'm really grateful to have the math teachers come in and working and asking, how do you get cultural knowledge into content? [In the past] The math people are always like ‘oh you can't do it. Sorry, they are just numbers. It's just not happening.' And then [they] don't come to these things because [they] think it's not possible. So to be open and say yes you can, I think it's important that we have everybody that is working in math move forward with it… We need the cultural knowledge but we also need someone that can clearly articulate and knows the math concept that we are trying to articulate, and like where do we find it. I just think we need all those parts, and it's slower moving to bring everybody. Or you might not think you know a lot about math, but being able to make the connection, ‘oh, I know where I see that in our community, in our lifeways, in things that my grandparents taught me.' Making those connections is important. And just making math relevant for our students, for our Lakota kids, is the most important thing. Because a lot of the time there is not a quick connection [with math] to who we are as Lakota people, but we are learning and it [the framework] makes it [math] more open and that connection is made. This connects to your modern day life and the past as well, about keeping those [traditional and modern] connections strong. I deal with it in our school down the hall, and I'm sorry you guys couldn't come down and see the school, but that's what we do, try to make our education as relevant as possible, maintaining who we are as Lakota people, is the core of what we offer as we teach. I think it [this course] was amazing and I'm really grateful to be here.”

This quote has many key ideas, from connecting with math teachers, the process/framework of making connections across expertise areas, and how Wahóȟpi Kiŋ values D/Lakota identity. The aspect we will draw out from this public statement is the multiple references to the value of making connections among math instructors, language instructors, and fluent elders. The quote began with an appreciation, and even enthusiasm, for math instructors being present for culture and language efforts contrasted with the past math instructors. The language instructor even apologized for not being able to invite the whole class to visit Wahóȟpi Kiŋ. Furthermore, this language instructor emphasized the expertise needed in both mathematics and the culture and the value of people coming together even if it would take more time and effort. Overall, the strengthening relationships among the math instructors, language instructors, and elders and their collective response to the course and framework was an initial confirmation of the research and framework.

3.2. Framework impacts participants

The initial framework confirmation was encircled by the two reciprocal research questions for this article. To answer the question “In what ways, if any, did the framework impact the participants?” a quantitative analysis was conducted on participants' Monday–Friday Drawings (MFDs). MFDs are a self-assessment of personal knowledge via free-hand drawings. On Friday, participants described the amount of their knowledge on both Monday and Friday. Participants were asked to reason with/through the D/Lakota Math Connections framework and self-assess the amount of their knowledge in each of the Four Circles as well as their connection among the Four Circles for both Monday when they entered the course and in that present moment on Friday as they were finishing the course. Since perceptions of D/Lakota Math were anticipated to change, fitting with best practice to manage ‘response-shift bias' (Howard, 1980), both the self-assessment drawing for Monday (reflecting back to the start of the week) and for Friday were completed on Friday.

There are limitations in these pre-post self-assessment MFDs. We realize that this form of self-assessment is subjective and wholly dependent on an individual's perceived understanding of a specific circle at a given moment (Howard, 1980). Despite that, we assumed that growth in a circle meant an increase in knowledge. We also assumed that an intersection meant a connection/relationship between the circles. Some participants provided an additional narrative to the diagrams which helped the researchers with their interpretations. The MFDs were analyzed by the two co-authors separately to compare, contrast, and synthesize their findings and discuss implications for teaching and learning mathematics with Indigenous communities and students.

Using the lens of math fluency and language fluency growing together, the MFDs were analyzed by individual circle growth and by intersection with other circles, all by category of people (math instructor, language instructor, and elder). The first subsection analyzes the data showing how the course/framework impacted the individual math fluency and individual language fluency of the participants. The second subsection focuses on the connections between the Four Circles to describe if/how math and language fluency grow together. For both subsections, a middle school math instructor's MFD will be an exemplar leading to a summary of all MFDs.

3.2.1. Math fluency increases, language fluency increases

This subsection focuses on the size of the circles (through size ordering and circle growth tallies) to describe individual math fluency changes and individual language fluency changes. Figure 3 shows the MFD exemplar.

FIGURE 3

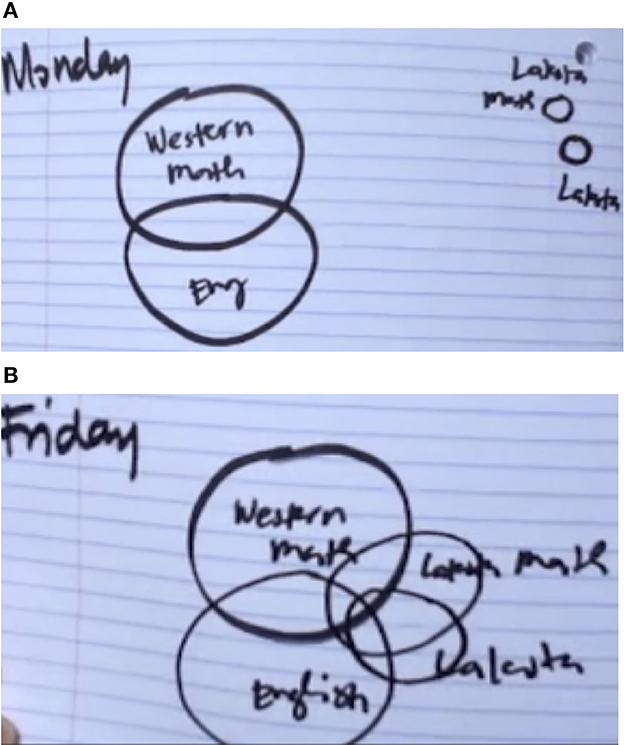
Figure 3. Exemplar of a Monday-Friday drawing by a middle school math teacher in Standing Rock. (A) The Monday drawing of self-assessed knowledge of and connection among the four circles. (B) The Friday drawing of self-assessed knowledge of and connection among the four circles.

To initially describe the MFD, on Monday's pre-self-assessment, this participant only had English and Western Math intersecting, showing a relationship between the two. Lakota Math does not intersect with anything nor does Lakota. They are depicted as far away from Western Math and English as possible in the study. The participant's Friday diagram shows all the areas coming together. All four circles intersect with each other on Friday showing connections and relationships among the four. The circle sizes for Lakota Math and Lakota also substantially increase showing knowledge growth in both areas. Note that not all participants placed their circles similar to the standard depiction of the framework.

First, we will analyze circle size ordering. The exemplar on Monday has order largest to smallest as WM = E and LM = L, meaning the Western Math and English circle tie for largest (most self-assessed knowledge) and the Lakota Math and Lakota circle tie for third largest (least self-assessed knowledge). The exemplar on Friday has order largest to smallest as WM = E, LM, and L. The only change in order is Lakota decreased from third to fourth largest. The circle size ordering for all MFDs is shown in Figure 4.

FIGURE 4

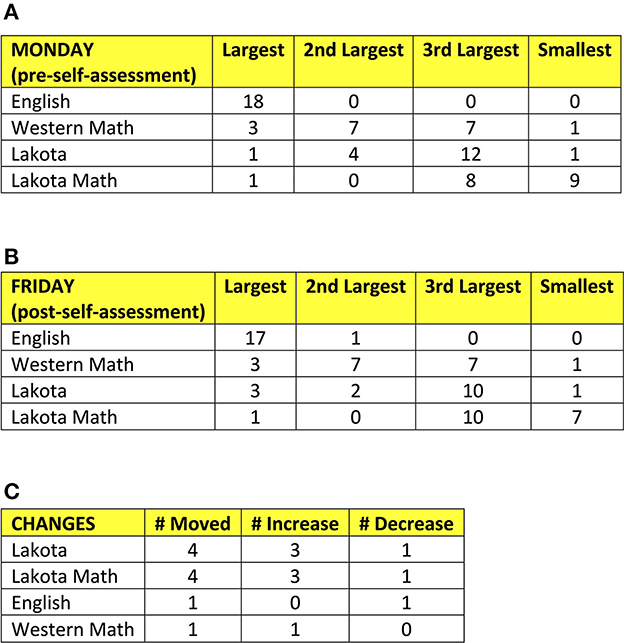
Figure 4. Summary of circle size ordering for all MFDs. (A) Shows circle size ordering on Monday for all MFDs disaggregated by each circle. (B) Shows similarly for Friday. (C) Shows the movement of circle size ordering from Monday to Friday.

Observe that English was identified as the largest circle by all participants signifying their level of comfort regarding their knowledge of English in relation to the other three areas. Lakota Math was an area that was identified by participants as their least knowledgeable area. This demonstrates that most participants do not view themselves as balanced in these four areas of the framework. English and Western Math in general are dramatically over-emphasized in self-assessed knowledge.

Second, we will analyze the growth of each circle compared to itself from Monday to Friday, assumed by the researchers to mean a self-assessed growth in knowledge of that individual circle. Figure 3 exemplar demonstrates growth in Lakota Math and Lakota and no change in Western Math and English. The individual circle growth for all MFDs is shown in Figure 5.

FIGURE 5

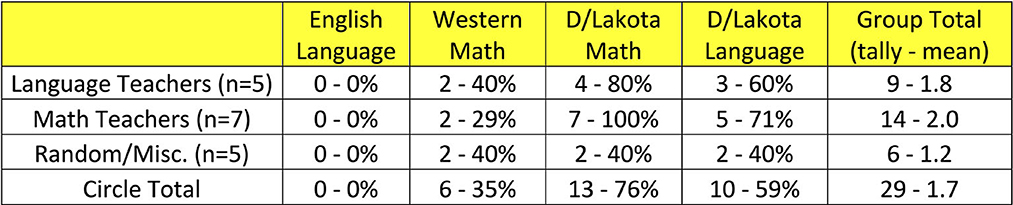
Figure 5. Tallies and percentages of self-assessed knowledge growth. The tallies and percentages are disaggregated by individual circles (columns) and categories of people (rows). The bottom row is the circle total across all MFDs. The far-right column is the total tally and means per category of people across all four circles.

There are multiple trends and notable singularities but only two will be highlighted for brevity. First, observe that the D/Lakota Math Circle had the most people self-assess knowledge growth with 13 out of 17. Second, observe that the Western Math Circle had some people from each category share growth in their knowledge. This is especially interesting for two out of seven math teachers who self-assessed growth in their knowledge of Western Math. Overall, the highest tallies and percentages of the table are for math and language teachers for the D/Lakota Math and D/Lakota Language Circles. This data is the first evidence that math fluency and language fluency can grow together.

To close this subsection, a TCU math instructor's brief explanation of their MFD is unpacked. The TCU math instructor wrote next to their MFD, “English [stayed the] same. Lakota improved. [I] learned more, corrected pronunciations of words I've been saying incorrectly. Western Math [I] learned ways to help students visualize better things I was teaching. Lakota math, I have more ideas on how to integrate culture into the content I teach.” In order of the quote, first note that English as a content area did not see any change. The Lakota did improve, especially in the pronunciation of words. It should not be understated how important this is. Pronunciation of Lakota words is key to the communication between speakers. Lakota language has specific guttural sounds, for instance, that if missed damages the word itself. Pronunciation is the first step to communicating in Lakota. The third comment about Western Math is in relation to teaching. The week-long course allowed this participant a fresh look at how to teach mathematics. It increased Western math understanding, making the participant a better math teacher. The final comment is instructive as well, if this individual teaches Lakota/Dakota students, then the participant is more equipped to make the content more culturally responsive. The participant can now draw on the Dakota/Lakota language to make connections between mathematics and the lives of the students.

3.2.2. Connections between math fluency and language fluency increase

This subsection focuses on the connections between the Four Circles to describe if/how math and language fluency grow together. Once again, the middle school math instructor's MFD is used as an exemplar leading into a summary of all MFDs. Each MFD is redrawn into a standardized diagram as a way to visually see the relationships (and changes in relationships) between the four circles. Only the intersection between two individual circles is depicted. The six intersections among the four circles are ranked in four tiers from no touching to an increase in connection from Monday to Friday. Recall that the amount of intersection of two circles in the MFD is assumed to mean the amount of connection between the two knowledge areas. The Figure 3 exemplar is redrawn as the standardized four-tier intersection diagram in Figure 6.

FIGURE 6

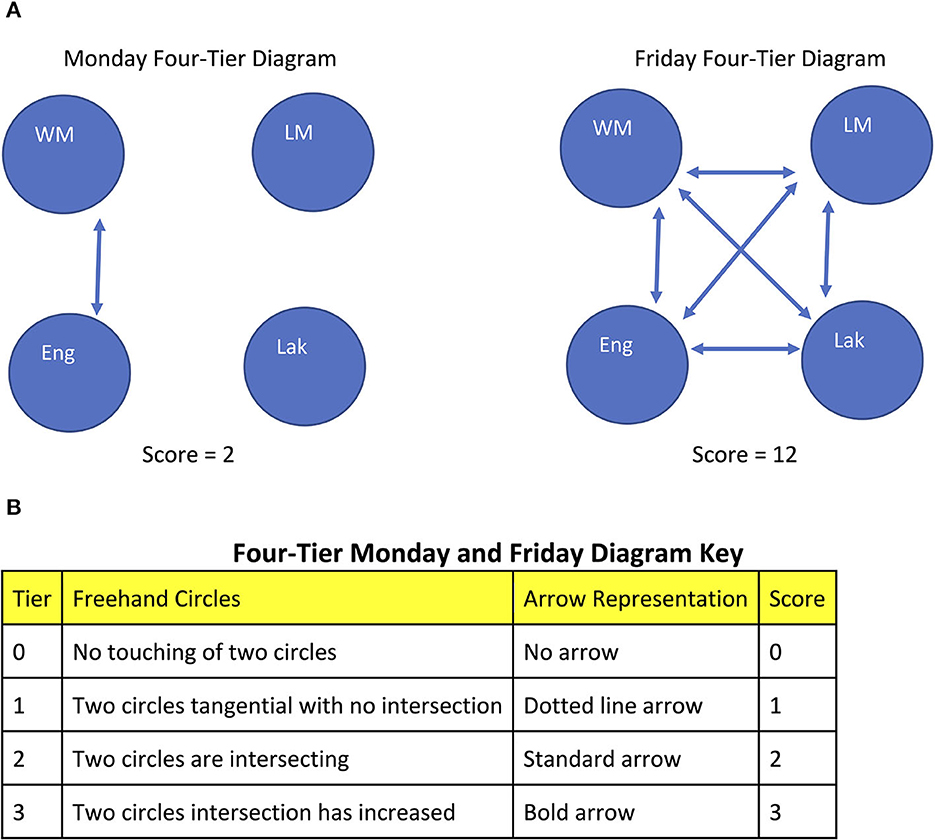
Figure 6. Exemplar of Four-Tier Intersection Diagram from the Monday-Friday drawing by a middle school math teacher in Standing Rock (Figure 3). (A) The Monday Four-Tier Intersection Diagram and Friday Four-Tier Intersection Diagram. (B) Four-Tier Intersection Diagram Key. The single intersection in the exemplar MFD (Figure 3) is represented by a single arrow in the Monday Four-Tier Intersection Diagram.

A deeper analysis of the Monday and Friday Four-Tier Intersection Diagrams leads to the Three-Tier Change Diagram where the arrows and score build off the four-tier rankings. The Figure 3 exemplar is redrawn as the standardized Three-Tier Change diagram in Figure 7.

FIGURE 7

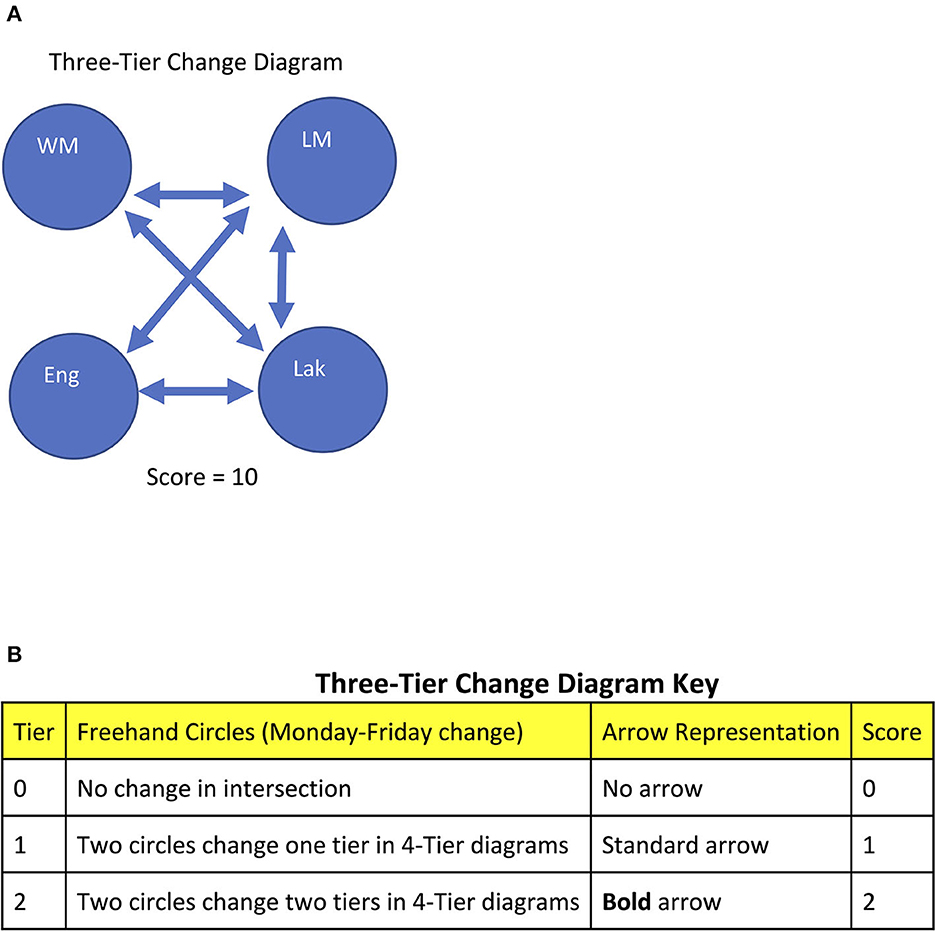
Figure 7. Exemplar of Three-Tier Change Diagram from the Monday-Friday drawing by a middle school math teacher in Standing Rock (Figure 3) and Four-Tier Intersection Diagram (Figure 6). (A) The Three-Tier Change Diagram. (B) Four-Tier Intersection Diagram Key. The single intersection in the exemplar MFD (Figure 3) is represented by a single arrow in the Monday Four-Tier Intersection Diagram.

The standardized Monday and Friday Four-Tier Intersection Diagrams and Three-Tier Change Diagram allow the relationships between any two circles to be visualized as well as compared across all MFDs. The scoring system is an arbitrary quantification (0, 1, 2, 3 chosen for ease), yet it gives some sense of distinction when summing the arrows of each standardized diagram. The standardization and scoring system allow the diagrams to be compared across all MFDs. Specifically, the mean and median intersection scores can be averaged across all MFDs and dis-aggregated across each of the six connections and three groups of people (math teachers n = 7, language teachers n = 5, and all MFD participants n = 17) as shown in Figure 8.

FIGURE 8

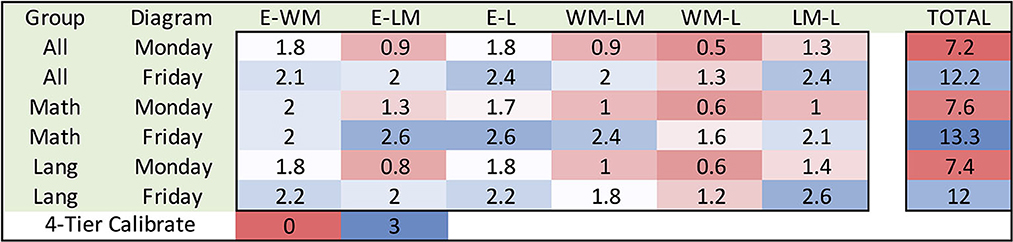
Figure 8. Mean scores heat map of Four-Tier Monday–Friday Intersection Diagrams. The heat map shows the mean scores disaggregated by each two-circle intersection (columns) and category of people (rows). A higher number represents a higher intersection score which means a greater amount of self-assessed intersection/connection among the circles. The far-right column is the sum of the means aggregated across all six intersections emphasizing the overall value for each category of people on Monday and Friday and is calibrated only among the included six numbers (7.2–13.3). The central disaggregated heat map is calibrated 0–3 to match the Four-Tier scoring.

There are multiple trends and notable singularities but only two will be highlighted for brevity. First, observe that the far-right column heat map that shows the average of every group moved toward a larger intersection score from Monday to Friday. Second, observe that the WM-L column has the most red (lowest intersection). Despite being the lowest connection, in the post-surveys, 15 out of 21 people specifically shared the value of vocabulary connecting Western math and Lakota when asked about the implementation of this project in your classroom. This observation could lead to the interpretation of bias from the standard depiction of the Four Circles framework (Figure 1) not visually depicting E-LM and WM-L. However, this was rejected due to the highest score in the table being 2.6 for E-LM.

The Three-Tier Change Diagram can also be analyzed across the six connections and three groups of people (Figure 9).

FIGURE 9

Figure 9. Mean scores heat map of Three-Tier Change Diagrams. The heat map shows the mean scores dis-aggregated by each two-circle intersection (columns) and category of people (rows). A higher number represents a greater change in the Four-Tier intersection score which means a greater amount of self-assessed change in intersection/connection among the circles. The far-right column is the sum of the change of means aggregated across all six intersections emphasizing the overall change for each category of people and is calibrated only among the included three numbers (4.6–5.7). The central disaggregated heat map is calibrated 0–2 to match the Three-Tier change scoring.

Again, there are multiple trends and notable singularities but only two will be highlighted for brevity. First, observe that all numbers are positive, the most significant trend. This means a positive growth of connections among all circles, albeit varying amounts per group of people and connection. Second, observe the most red in the E-WM column. This means that this connection changed the least throughout the week, which was anticipated with the focus of the project on connecting with the Lakota language, culture, and values.

The median heat maps help accentuate additional details. Figure 10 is the median heat map for the same data in Figure 8 mean heat map.

FIGURE 10

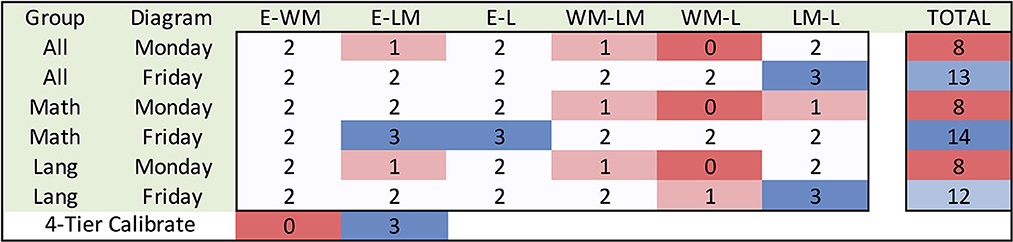
Figure 10. Median scores heat map of Four-Tier Monday–Friday Intersection Diagrams. The heat map shows the median scores dis-aggregated by each two-circle intersection (columns) and category of people (rows). A higher number represents a higher intersection score which means a greater amount of self-assessed intersection/connection among the circles. The far-right column is the sum of the medians aggregated across all six intersections emphasizing the overall value for each category of people on Monday and Friday and is calibrated only among the included six numbers (8–14). The central dis-aggregated heat map is calibrated 0–3 to match the Four-Tier scoring.

Observe similar trends to the mean heat maps. Additionally, observe the same total median score of 8 on Monday for all three groups of people. Furthermore, observe that the total median score on Friday is not identical for math instructors and language instructors. The median heat map for Three-Tier Change Diagrams helps explain this difference (Figure 11).

FIGURE 11

Figure 11. Median scores heat map of Three-Tier Change Diagrams. The heat map shows the median scores disaggregated by each two-circle intersection (columns) and category of people (rows). A higher number represents a greater change in the Four-Tier intersection score which means a greater amount of self-assessed change in intersection/connection among the circles. The far-right column is the sum of the change of medians aggregated across all six intersections emphasizing the overall change for each category of people and is calibrated only among the included three numbers (3–5). The central dis-aggregated heat map is calibrated 0–2 to match the Three-Tier change scoring.

Observe that language instructors have a median change of one for all three connections with D/Lakota math and a median change of zero for the connections with D/Lakota language. In contrast, math instructors also have a median change of one for the connections with the D/Lakota language. This is understandable as language instructors came into the course with a much stronger understanding of the language compared to math instructors and thus experienced less change. However, all groups self-assessed a median change of one for D/Lakota Math.

Furthermore, the median heat maps allow for visual representations similar to the exemplar's Three-Tier Change Diagram (Figure 7) for each of the three groups of people (Figure 12). Note that Figure 12 contains the same information as Figures 10, 11, but the numbers/colors are represented as different types of arrows following the same keys shared in Figures 6, 7. All the same observation trends from the heat maps can be visualized within these nine diagrams.

FIGURE 12

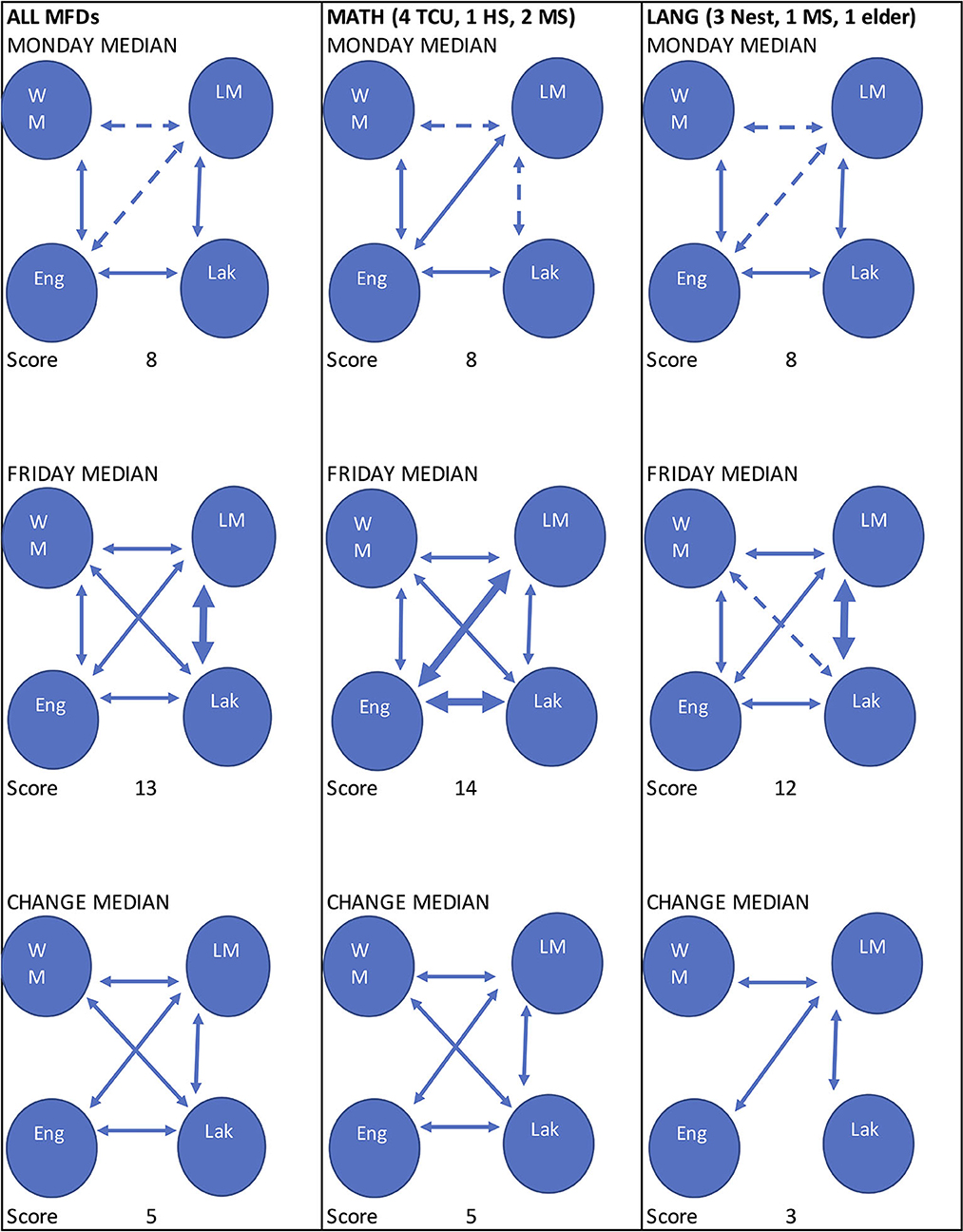
Figure 12. Median Four-Tier Intersection Diagrams and Median Three-Tier Change Diagrams. Each column represents a group of participants (all MFDs, math instructors' MFDs, and language teachers' MFDs). Each row represents the Monday Four-Tier Intersection Diagram, the Friday Four-Tier Intersection Diagram, and the Three-Tier Change Diagram, respectively.

Altogether, it seems that the week-long course provided participants the opportunity to learn more about each topic area individually and also provided participants the opportunity to see that there are indeed connections across the four content areas. Elders, Lakota language instructors, and math instructors all ended up with essentially the same outcomes that there are Dakota/Lakota math connections and that their math and language fluency grew together.

3.3. Participants influence framework

In what ways, if any, did the participants influence the framework?

This subsection is further divided into three subsections.

- Three-color emphasis activity.

- Naming the four circles.

- Significant teachings from elders.

3.3.1. Three-color emphasis activity

Similar to the MFDs, the Three-Color Emphasis Activity asked participants on Friday to rank their perceptions of the course through the lens of the framework. Together, the MFDs and Three-Color Activity are the main methods of data collection using the framework. The MFDs are an interesting tool because no assumption is made that participants enter the course in the balanced state that the framework posits. Similarly, the Three-Color activity makes no assumption that the facilitators taught the course (implicitly and explicitly) from a place of balance. This activity makes clear the perceptions of the participants on what was explicitly and implicitly included/emphasized within the week-long course. The Three-Color Activity allows the participants to evaluate the course and thus influence the framework.

The participants were asked to color three distinct levels (minimal, somewhat, and a lot) showing their perception of the Four Circles and their intersections as experienced through the course. Figure 13 shows an exemplar from a fluent elder.

FIGURE 13

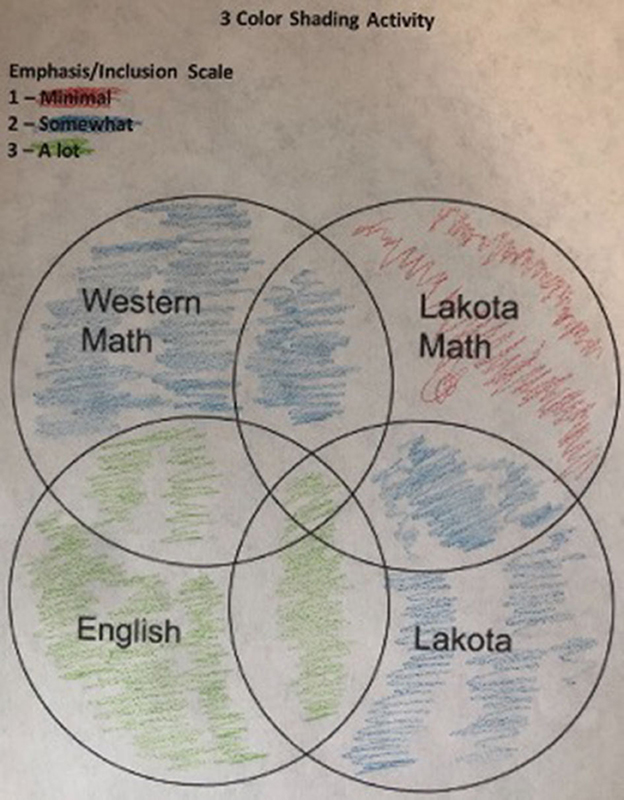
Figure 13. Three-color activity exemplar from a fluent elder. The three colors of shading following the emphasis/inclusion scale in the top left. Here, green means emphasized/included “a lot” and a score of 3. Red means emphasized/included in a “minimal” way and a score of 1.

The Three-Color Emphasis Activity was analyzed into a 3x3 heat map where 1 is “minimal” and 3 is “a lot.” Similar to the MFDs, only the major intersections of two circles are included to make a 3x3 table. The four smaller intersections of three circles and excluding one are not included in the analysis. Furthermore, by the de facto design of a four-circle Venn diagram, two major intersections are missing (Western Math and Lakota, as well as Lakota Math and English). Figure 14 shows the 3x3 heat map representation for a participant in each group of people.

FIGURE 14

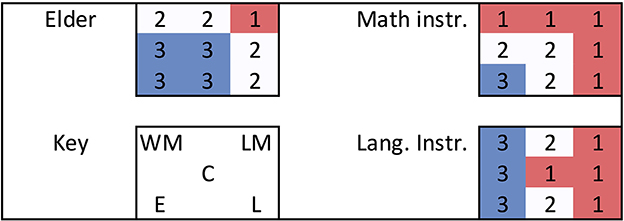
Figure 14. Three-color activity analysis exemplars for an elder, math instructor, and language instructor. Here are three exemplars of analyzed three-color emphasis activities from a fluent elder, a math instructor, and a language instructor. The key follows the standard depiction of the Four Circles framework.

The analysis across all participants reveals the perception of the course through the lens of the framework (Figure 15).

FIGURE 15

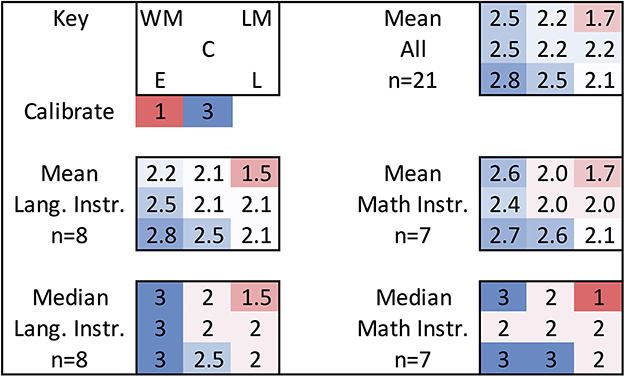
Figure 15. Three-color activity analysis across all participants. Six 3x3 heat maps show the key and five variations of mean and median and groups of people. The heat maps are calibrated between 1 and 3 because the activity allowed those values of coloring.

Observe more blue (higher numbers) on the Western side of the four Circles framework. This means participants perceived that Western Math and English were the most highly emphasized/included. The medium of communication was English almost entirely, except for one small group on 1 day, the medium was Lakota when the math instructor was absent at that moment.

Next observe that Lakota Math is the most red (lowest number) and Lakota language a light pink, light blue, or white. Lakota Math was perceived (and thus evaluated) as the least emphasized or included within the course. This corroborates/triangulates/encircles with what one language instructor shared publicly during the Friday Talking Circle. The language instructor shared about the value of holding space where we can think and discuss traditional Lakota math. There is constant pressure in our colonized society to learn and over-value Western ways of knowing, but if Lakota Math is going to continue we need to learn to hold space and emphasize Lakota math without seeking justification from Western math and English. The language instructor continued by asking how we can make connections to the Lakota math circle without first strengthening it.

Finally, observe that there is basically no substantial difference among the participants when disaggregated into subgroups. The mean values for all participants, the math instructors, and the language instructors had negligible differences.

3.3.2. Naming the four circles

The MFDs and Three-Color Activity were specifically designed from the D/Lakota Math Connections framework. However, during the week, the course was called “Lakota Math Connections” and the framework was called the “course and research framework.” This subsection will share every circle name used across all participants; 11 of the 17 used the names given in the instructions/framework, however, six did not.

One language teacher and elder wrote “DM” and “Dak Math” for their “LM-Lakota Math” circle. This participant's naming along with encouragement from Standing Rock Iyapi brought about the official name change of the circle and framework to “D/Lakota Math” and “D/Lakota Math Connections,” respectively. Furthermore, recall that the summer course happened during a larger language institute called the “D/Lakota Summer Institute.”

One language teacher wrote “Colonial math” in replacement of “WM-Western Math.” The emphasis on colonization through mathematics aligns with the 1990 article by Bishop titled, “Western mathematics: the secret weapon of cultural imperialism.” Some in academia prefer the titles “global math,” “near global math,” or “conventional math.” Most participants seemed fine using Western math for simplicity and to not miss the colonizing nuance of the term Western. D'Ambrosio (2000) makes an analogy of Western Math being like “a great river shored up by its tributaries, water from the tributaries being the contribution of many diverse non-Western peoples, cultures, and societies… However, in the process of building mathematical knowledge, many of the contributions of non-Western cultures have been rendered invisible and have been appropriated, marginalized, lost, silenced, and/or hidden” (p. 79). This language teacher does not miss the nuance in the term “Western math” and chooses to write “Colonial math” in its stead.

Three participants (a community member, math instructor, and language instructor) wrote “M” or “Math” in replacement of “WM-Western Math.” Writing “Math” and “Lakota Math” on the same drawing gives privilege to Western math, whether the naming was intentional or subconscious. It conveys Western math as the “normal” math and D/Lakota math which stood strong for millennia on this continent as the marginalized way of mathematical thinking. The co-authors feel that another reason why the term “Western math” is currently being used in the framework instead of the alternative names such as “near global” or “conventional math” for “Western Math” is that they seem to convey the same sentiment as replacing “Western Math” with just the title “Math,” privileging that over D/Lakota math.

Finally, one elder who completed the MFDs wrote “EM” which is assumed to mean “English Math.” This could potentially be an alternative to “Western Math” because it puts the focus on language for both math circles. It is inferred that this elder saw “D/Lakota math” as referring to the D/Lakota language more than the D/Lakota people.

3.3.3. Significant teachings from elders

The fluent elders are 100% essential to the D/Lakota Math Connections project. Every day began “in a good way” with an elder offering a prayer (in Lakota traditions it is customary for an elder to offer a prayer at a formal gathering that includes the phrase “in a good way”). Their spiritual and intellectual input, wisdom, and guidance cannot be overstated. The co-facilitators, language instructors, math instructors, and everyone in the course deferred to the elders and listened to their stories and contributions. Their contributions and stories hold both the content knowledge of the Lakota language and Lakota math as well as guide the entire course and research process. Their continued participation, sharing of stories and the language, and encouragement to continue the D/Lakota Math Connections project beyond the pilot course described in this study is the single most significant factor in the evaluation of the course, framework, and research process.

Specific stories and input shared by the fluent elders are included here. The co-facilitators asked elders one time to complete any formal surveys, evaluations, or activities, but did not force anything upon them. Each elder chose how to give their own response and input, as described in Indigenous Storywork (Archibald, 2008). That being said, here are some specific stories and input shared by some of the elders. As a note, Lalá means my grandpa, Uŋčí means my grandma, Lekší means my uncle, and all are used as terms of respect.

One fluent elder (who preferred not to be identified) shared a story about hunting a buffalo with a bow and arrow. It was something that he never grew up doing but was given the opportunity later in life. He said he was prepared not because he had done that exact activity before but because he had done many things surrounding that activity. He had made traditional bows and arrows, hunted deer with great accuracy, built the body and arm strength to use a sinew-backed bow, and had relationships with the community that gave him the opportunity. Furthermore, he mentioned some activities that encircled the traditional buffalo hunts including the following:

• Making sinew-backed bows and arrows.

• Learning accurate, instinctive shooting from the hip while riding the horse.

• Building body and arm strength to shoot a bow while riding the horse.

• Riding horse bareback with no hands on the horse so hands could remain on the bow.

• Building the bravery/courage to ride into the buffalo stampede.

• Tracking and training the nose to smell where the game was located (we have lost the skill of smell today but were told that if you can smell a skunk, then you can train your nose to smell every small animal).

• Knowing the land and terrain of where one is riding and recognizing what is up ahead.

He described his story about his buffalo hunt as well as describing past buffalo hunters with the phrases “learn all the peripheral… to really have the center stick,” “you prepare for something by knowing/doing everything around it,” and “you really know something if you understand all the peripheral [relationships/connections].”

This fluent elder's way to describe a buffalo hunt has become the metaphor for defining/encircling both “higher order math concepts” and “D/Lakota Math.” The center (that is, a specific vocabulary word) is not defined as a static object but instead through the relationships and peripheral connections. This is similar to how Wilson (2008) describes an Indigenous research paradigm, “I also need to be clear that I am not promoting this book as a model of Indigenous research or data analysis; it is only one presentation of the view shared by my friends and myself as co-researchers… The very nature of our epistemology is that it will be different in other contexts” (p. 136). He shares the relationships that he has made with the central idea throughout the book but does not claim a single, final definition. There cannot be such a definition because it is dependent on context, that is, all the relationships in that place that give the central idea shape and form. As the fluent elder shared, if you want to really know something, you must encircle it, that is strengthen/learn about all the relationships and connections that make up its web of existence in that place.

Based on an Indigenous research paradigm and because of this fluent elder's story, some of the relationships that the course and co-authors connected to “D/Lakota Math” include:

• D/Lakota language.

• Western math.

• Six universal math activities (counting, designing, locating, measuring, playing, and explaining).

• Embodied and activity-oriented math, instead of a static body of knowledge.

• Math is from nature and a way to describe nature.

• Relationship-oriented (action and verb-oriented), instead of object-oriented (noun and definition-oriented).

• Emphasis on stories.

• Emphasis on spirituality.

Furthermore, some of the peripheral relations that encircle the term “higher order math concepts” include:

• College-level math, not just at the elementary level.

• Building upon the dissertation of Sanders that expressly began looking at base math concepts connected to the language and culture (Sanders, 2011).

• Conceptual strand in the Five Strands of Math Proficiency (National Research Council, 2001).

• Higher levels of student mathematical thinking in APOS (action-process-object-schema) theory (Martin et al., 2010).

Again, none of these individual relationships make the whole concept. Instead, each one of the relationships informs the central activity/idea in some way by someone. Not every person makes all the relational connections and some people emphasize and/or understand one connection far greater than another connection. Overall, encircling the central idea to gain greater understanding fits in with the Indigenous way of thinking that is more relationship-oriented vs. object-oriented.

Uŋčí Ruby Shoestring and Uŋčí Grace Draskovic have consistently been part of translating and editing the videos and data from the summer course to develop the math resource for curriculum development from Dakota/Lakota culture, values, and language (see follow-on study). During these times of collaboratively watching video snippets from the course and translating and describing aspects of the language, multiple discussions around the D/Lakota Math Connections framework emerged. Specifically, three conversations will be shared and taken altogether to have perhaps the largest impact on how the framework is now viewed.

First, co-author Luecke was describing to Uŋčí Grace and Uŋčí Ruby aspects of the D/Lakota Math Connections framework and specifically the Western math circle. Luecke described that some people believe that math has no values attached to it and is distinct/separate from all cultural matters. Uŋčí Grace responded “Héčhetu šni.” Freely translated this means, “That's not right.” Her two-word sentence reinforces the Four Circles framework. Her comment implies that math from a Lakota perspective includes Lakota values and culture, including the Lakota language.

Second, a while later, Uŋčí Ruby shares a comment about her grandparents. She said, “My grandparents never went to [a formal] school but did math all the time.” On the surface, this demonstrates a distinction between Western math and Lakota math, the former being in school, at a desk on paper, and the latter not. At a deeper level, this implies a description of Lakota math as being outside, activity-based, embodied, and experienced. Uŋčí Ruby repeated her statement/sentiment another time later in the discussion.

Third and finally, as Uŋčí Grace and Uŋčí Ruby were working on developing Lakota words for abstract math words, a discussion began about the task. Together they described, “we can translate whatever we want. It's a descriptive language.” This sentiment contains multiple components. First, it says the Lakota language is descriptive in contrast to the English language, which may be considered a definition-based language. Lakota describes what's happening (verb-oriented) and the context instead of a static definition (noun-oriented). Second, their sentiment conveys that the Lakota language is capable of translating whatever is desired by the Lakota people. The language is strong enough and dynamic enough for translation from any other language, including English and Western math. Third and finally, it depends on the desires of the Lakota people and fluent elders specifically. If collectively decided upon, then it can and will happen.

These three quotes from Uŋčí Ruby and Uŋčí Grace describe a powerful description to re-define and re-understand the D/Lakota Math Connections framework. After being introduced to the framework, having some experience using it and thinking through it, their three quotes hugely influence the overall comprehension of the framework and its applications in math classrooms, language classrooms, and the continual development process.

Finally, two stories are shared from Lekší Kevin Locke's experience with the course and framework. When asked to complete the Three-Color Emphasis Activity to evaluate what aspects the course explicitly and implicitly emphasized/included through the Four Circles framework, he shared extremely valuable feedback in his own way. Instead of ranking the circles and intersections via three colors, he used the three colors to make a pretty design with the four-circle Venn diagram and said something like, “I cannot rank these different circles and their intersections separately, they are all interconnected.” By not completing the survey, he powerfully made a statement about the intersections and interconnectedness of all the circles, that black lines on paper can never separate these circles in a Lakota reality. His feedback impacts the framework and specifically helps re-define and re-understand the initial statement “Each circle is connected to all the others.”

Lekší Kevin also shares his thoughts at the Friday Talking Circle that impacts the understanding of the Four Circles framework and its use in future. He shares:

I think it's a brilliant concept, Lakota Math Connections. Cause you know the main thing about the Lakota culture is making, creating relationship, understanding relationship and interrelationship. And then, so we do that through language. And math is a language. The way I understand it's [math] a language that we can really precisely describe the physical creation. But then we look at how that is applied by the dominant culture, I just call it dominant culture, it's pretty much been used to trash out our creation, trash out the world, and everything has gone haywire in the world. So there needs to be this balance, so we can use this powerful language, math to describe the physical world but then we have to infuse it with that understanding of the relationship that we have with the physical creation. So that's why I thought that was such a unique, I've never seen this whole thing, “Lakota Math Connections.” That's a really interesting word. The word Lakota, they say in the books it means allies, but it doesn't mean that. That's false, that's erroneous, that's a different word. You can say allies, kȟolákičhiyapi, there are other words to describe ally. But that's not what Lakota means, so then, I was reading in that book by Albert White Hat, the way he grew up, Lakota means people who pray, people who pray. Then when I asked Mary Louise Defender what does that word “Dakota” mean? It means people who are civilized, people who are civilized. And then, I ask other people and they say Lakota means people who have faith, people who have covenant, people who understand laws. And now, now we can use math, we can express that relationship with the laws and add that insight into the world. It's just kind of like a vision, a dream. It's wonderful because I know that a lot of kids have a hard time with math and we can use it in this way. I think these ways, these perspectives that we have been looking at this week are just fantastic. Epiphanies, that's a good word. Iglúbleza. [Lakota-word-for-epiphanies] (laughing out loud). Insights you could say. Insights that we have, to see new connections, use that to expand our, broaden our thinking. Héčhetu yeló. [Lakota-phrase-to-end-speaking].

Again, Lekší Kevin's comments during the Friday Talking Circle describe how the framework is understood. He describes math as a language to describe nature and infuses the Western understanding of math with an understanding of the relationship to care for nature instead of to destroy nature. He describes how math connects to D/Lakota identity and the power of the phrase “Lakota Math Connections.” He encourages the continuation of the D/Lakota Math Connections process and connects it to the math classroom for D/Lakota students. Lekší Kevin's insight, stories, and wisdom guide the D/Lakota Math Connections project. Before this study was written, Lekší Kevin took his journey to the next world and one of his daughters was consulted for the inclusion of this quote [personal communication, January 2023].

Another second language learning elder, Uŋčí June Szczur, shared during the Friday Talking Circle. She discussed the connection between math and nature, the human relationships strengthened during the week, the hope she has from seeing the younger people being successful in Western math and in the language, and finished with this quote, “I was thoroughly confused by some of the math terms that were thrown out there, but after we started saying the Dakota/Lakota names for some of them, it made a little more sense to me. Those are the things I'll remember.” Again, the values of D/Lakota Math (linked to nature) and the power of connecting D/Lakota language with math is evident in this quote. Furthermore, the connection among the participants is also paramount. Additionally, she shared a metaphor for the strength, value, and applicability of the intersection of D/Lakota Math and Western Math as steel coming from iron, that indeed something stronger comes out when taken in together.

All these stories and insights from fluent and language learning elders re-define the understanding of the Four Circles framework. The elders' validation of the research approach and framework is the strongest and most significant confirmation. No other endorsement or research validation is needed. Altogether, math teachers, language teachers, and elders influenced the framework, sometimes confirming initial assumptions and sometimes expanding and adding new relationships to the framework.

4. Discussion

Circular data collection and synthesis follow an Indigenous research paradigm. The results section is both the process and product. The discussion section will answer the two reciprocal research questions that encircled the initial confirmation of the framework.

4.1. How did the framework impact the participants?

Two major impacts of the framework on participants are synthesized from the results. Math fluency and language fluency did grow together for all individual participants. Second, may relationships were formed among people from different areas of expertise.

Through self-assessment, participants shared their growth in knowledge of math and language. Furthermore, they shared growth in the connection between math and language (and culture). Math fluency and language fluency did grow together for all participants, especially in the areas of D/Lakota math and the D/Lakota language. It happened for math teachers, language teachers, and fluent elders. One TCU math instructor said during the Friday Talking Circle, “I used to focus on content and realized this [connection to language and culture] isn't taking away from the content but enhancing it.” This demonstrates that math and language fluency growth is possible not only for the participants/instructors but also for their students as well. Not only did math fluency and language fluency grow together but the lens of two fluency areas connecting also proved to be a successful avenue to engage fluent speakers with math concepts and to engage math teachers with understanding math in a way new to them. Two different areas of expertise, separated in Western ways of knowing, teaching, and learning, were steered back toward relationship and interconnection, which are essential to a D/Lakota way of knowing, teaching, and learning. This growth and connections of math fluency and language fluency (Western and D/Lakota) by participants influence their teaching and learning of mathematics with Indigenous students.

Second, this all happened within the context of relationships. Focusing on human-to-human relationships, people from every group discussed the value of being with and learning from everyone present. Math teachers, language teachers, and elders built relationships with each other that continue past the course and research. Each group saw that their input and area of expertise were valued. Elders encouraged the process and relationships to continue. Luecke was subsequently hired as a math consultant Wahóȟpi Kiŋ at Sitting Bull College. Language teachers strengthened relationships with math instructors. Math instructors strengthened relationships with language instructors and elders and are now more able to join the language revitalization efforts of the community.

4.2. How did the participants influence the framework?

Three major impacts from participants on the framework are synthesized from the results. First, there is a greater understanding of the nuances and themes of the framework including a stronger understanding of D/Lakota math. Second, the framework is confirmed, both through an initial synthesis of relationships and by encircling the two research questions, for continued use in teaching and learning mathematics at Sitting Bull College and Standing Rock Nation. Third, the participants determined the future direction and implications of using the framework.

Participants experiencing the course and framework were able to better understand, define, and describe the nuances and themes of the framework, including that of D/Lakota Math. Participants gave specific examples, to be elaborated upon in the follow-up study on math resources connected to D/Lakota culture, values, and language. Participants' examples and greater definition of the framework through the MFDs, Three-Color Emphasis Activity, written and oral quotes, and so on helped bridge the epistemological misalignment between Western math (that claims to be culture-free) and the Sitting Bull College mission of D/Lakota culture, values, and language as the guide for every course, including STEM and math. No precise definition for D/Lakota math was shared but a fluent elder discussed a relational metaphor of hunting buffalo to describe/encircle the relationships and themes of D/Lakota math. Another fluent elder emphasized that even though our grandparents did not go to school, they did math all the time. Their math was from nature, relational, through stories, spiritual, action/activity-based, embodied, linked to the language, and now since settler colonialism in this place linked to Western math.

Furthermore, as far as the co-authors are aware, this is the first use of an Indigenous research paradigm in research on undergraduate math education, a collaborative effort among math teachers, language teachers, fluent elders, and facilitators. However, in the context of colonialism's unceasing pressure to overvalue Western Math and English as the main medium of communication, nearly all participants evaluated the course implementation to have an over-emphasis on the practice of English and Western math. Many conversations begin with Western math through English to the D/Lakota language and eventually to D/Lakota Math. What would other directions look like, starting with D/Lakota math or the D/Lakota language? The participants confirmed that despite the framework claiming a balance, the actual experience still can easily favor Western ways of knowing and doing.

Second, the framework was confirmed for continued use at Sitting Bull College and Standing Rock Nation through both the initial synthesis of relationships and encircling the two research questions. The framework meets the challenge of epistemological misalignment for math instructors at TCUs and math instructors at any level teaching D/Lakota students. This prepares the math department to develop a curriculum aligned with the mission of Sitting Bull College. Multiple elders shared the certainty of math and culture and language being interconnected. Not solely for Sitting Bull College, the framework and course are one concrete answer to the call from the American Indian Science and Engineering Society literature positing “improved educational outcomes for Native and non-Native students result when STEM instruction is culturally-relevant, rooted in Indigenous ways of knowing, linked to place, and embedded in community” (American Indian Science Engineering Society, 2020, p. 12). Additionally, the framework meets a need for language teachers and especially those who are teaching math to young children, for example, at Wahóȟpi Kiŋ. Furthermore, the framework was encouraged by elders through their presence, their stories and quotes, and by a continual engagement with the project to this day. They see an area needing more development and are willing to contribute and learn more. Benefits to math instructors and language instructors for the teaching and learning of mathematics and the affirmation from elders confirms the continual use and value of the framework in Standing Rock and other Indigenous communities.

Finally, the participants impacted the framework by giving four future directions for its use. First, participants shared that more work needed to be done specifically in encircling D/Lakota Math. This circle was perceived to be the least emphasized of all circles and intersections (Figures 11–15) and self-assessed as the circle with the most growth in knowledge and new connections (Figures 5, 9, 11, 12). The combination of these two demonstrates a need for more work in this area. Additionally, even though the most growth happened in D/Lakota Math, it is still the lowest in overall ordering (Figure 4), thus needing more attention to pursue balance. Furthermore, participant quotes share the idea that one cannot make “D/Lakota Math Connections” without strengthening “D/Lakota Math,” first by focusing on D/Lakota fluent elders explaining their thinking around mathematical and traditional activities. A math/language course in summer 2022 and 2023 was titled “D/Lakota Math” to follow this path.

Second, participants (math and language teachers) see the value of and have the desire for the framework and process to work toward developing D/Lakota words for Western math terms. Elders shared that their language is capable of translating whatever is desired and that the math concept could be better understood with D/Lakota words. A math/language course in summer 2022 and 2023 was titled “Math Neologisms” (neologisms is the linguists' way to describe developing new words or expressions for modern concepts) to follow this path.

Third, participants emphasized the D/Lakota value of connectedness and relationship. The Four Circles are not meant to be defined, understood, or used in isolation but rather in connection. An elder shared that the Lakota way is that of inter-connectedness and you cannot even discuss/evaluate one circle in isolation because they are all tied together. Furthermore, instead of seeking to define the circles (object/definition-oriented), the intersection areas and relationships among the circles is the future focus area, especially due to its links to teaching and learning mathematics and language in both the math and language classrooms.

Fourth and finally, the participants impacted the framework by guiding its future use to develop a math resource based on D/Lakota culture, values, and language. The framework and course provide the structure and content for the resource. A team of math instructors, language instructors, and fluent elders have been translating/editing specific examples from the course. Examples in the intersections of the four circles, and especially the center spot connecting all four circles, are shared through the lens of the Four Circles framework and called “D/Lakota Math Connections.” The examples and resources are the focus of the follow-up study.

5. Conclusion

When experienced and evaluated by TCU math instructors, D/Lakota language teachers, and elders, the D/Lakota Math Connections framework proved valuable for teaching and learning mathematics in the math department and language department at Sitting Bull College. Specifically, the framework meets the need of TCU math instructors to have the math content and classroom guided by local culture, heritage, and languages. Furthermore, the framework meets the need of language teachers in the area of mathematics, especially those who are teaching math in the language to young children, for example, at immersion schools and in future D/Lakota-medium schools.

The framework was confirmed and re-defined by the stories and input of fluent elders. Following an Indigenous research paradigm, the framework was both a process to follow (used in the course and as a survey structure) and a product of encircling and fuller understanding as a result. Data collection and data synthesis followed a circular and reciprocal pattern. Through the process, the framework was initially confirmed, encircled by the two research questions, and re-understood in a more full and connected way. Similarly, the theme of math fluency and D/Lakota language fluency growing together was confirmed, encircled, and re-understood in a more full and connected way. Overall, through an Indigenous research paradigm for research in undergraduate math education, the power and value of the D/Lakota Math Connections framework for teaching and learning mathematics with Indigenous communities/students was experienced and confirmed in the context of the Sitting Bull College community.

Data availability statement

The datasets presented in this article are not readily available because of data sovereignty. One may view the datasets with written permission from the Standing Rock Iyapi, a branch of the Standing Rock Sioux Tribe Department of Education. Requests to access the datasets should be directed to aW5mbyYjeDAwMDQwO3N0YW5kaW5ncm9jay5vcmc=.

Ethics statement

The studies involving human participants were reviewed and approved by Sitting Bull College IRB and North Dakota State University IRB. The patients/participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

DL and DS contributed to the design and facilitation of the pilot course and framework. DL organized the logistics for the course and invited DS to co-facilitate and co-author. DL analyzed all the data and wrote the first draft. DS analyzed all the Monday–Friday Drawings, some videos, and wrote additional sections. All authors contributed to the manuscript revision and approved the submitted version.

Acknowledgments

There are too many people to name who have had a direct influence in shaping us and our relationships with the ideas we explored in this article. Yet, a few people particularly stand out. We want to thank everyone at Wahóȟpi Kiŋ (the Lakota Language Immersion Nest) at Sitting Bull College. Without them, this project would not have ever happened. In particular, DL thanks the elders who really influenced him while being at Wahóȟpi Kiŋ and contributed greatly to the D/Lakota Math Connections project: Lalá Tom Red Bird, Uŋčí Grace Draskovic, Uŋčí Ruby Shoestring, and the late Lekší Kevin Locke. Furthermore, we want to thank Sunshine Carlow for opening the door for us to co-facilitate the course and for creating the path for the D/Lakota Math Connections project. Also, we are thankful for all the leaders and employees at the D/Lakota Summer Institute. We want to thank all the participants in the D/Lakota Math Connections project in the summer 2021 pilot course and the summer 2022 and 2023 follow-up courses. Truly, we view you all as co-researchers who have influenced and taught us much about the framework, D/Lakota math, the language, and the community. Next, we want to thank the editors of our drafts as we prepared for the final version. Your input in editing this article was invaluable. Thank you Hollie Mackey, Warren Christensen, and Dina Horwedel. Furthermore, DL sincerely and wholeheartedly thanks Hollie and Warren as his Ph.D. mentors in helping him navigate academia, his research, and his identity. And most of all, we each thank our families, children, and spouses. You each are a gift in our life and we are so thankful for you. We would not be the same without you. Thank you for your love and support. With gratefulness, DL and DS.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aikenhead, G. S. (2017). Enhancing school mathematics culturally: a path of reconciliation. Can. J. Sci. Math. Technol. Educ. 17, 73–140. doi: 10.1080/14926156.2017.1308043

CrossRef Full Text | Google Scholar

American Indian Higher Education Consortium (2023). Tribal Colleges and Universities. Available online at: https://www.aihec.org/tribal-colleges-universities/ (accessed June 7, 2023).

Google Scholar

American Indian Science Engineering Society (2020). Literature Review: STEM Education for Native American Students. Available online at: https://www.aises.org/sites/default/files/AISES-Literature-Review.pdf (accessed January 18, 2023).

Google Scholar

Archibald, J. Q. Q. X. (2008). Indigenous Storywork: Educating the Heart, Mind, Body, and Spirit. Vancouver, BC: UBC Press.

Google Scholar

Bishop, A. J. (1990). Western mathematics: the secret weapon of cultural imperialism. Race Class 32, 51–65. doi: 10.1177/030639689003200204

CrossRef Full Text | Google Scholar

Bishop, A. J. (1991). Mathematical Enculturation: A Cultural Perspective on Mathematics Education. Dordrecht; Boston; London: Kluwer Academic Publishers.

Google Scholar

Boyer, P. (2011). Ancient Wisdom, Modern Science: The Integration of Native Knowledge at Tribally Controlled Colleges and Universities. Lincoln, NE: Salish Kootenai College Press and University of Nebraska Press.

Google Scholar

D'Ambrosio, U. (2000). “A Historiographical proposal for non-western mathematics,” in Mathematics Across Cultures: The History of Non-Western Mathematics, eds H. Selin (Dordrecht: Kluwer Academic Publishers), 79–92.

Google Scholar

Ernest, P. (2021). The Ethics of Mathematical Practice: Rejection, Realisation and Responsibility. Philosophy of Mathematics Education Journal. ISSN 1465–2978. University of Exeter, United Kingdom.

Google Scholar

Garcia-Olp, M., Nelson, C., and LeRoy, S. (2019). Conceptualizing a mathematics curriculum: indigenous knowledge has always been mathematics education. Educ. Stud. 55, 689–706. doi: 10.1080/00131946.2019.1680374

CrossRef Full Text | Google Scholar

Howard, G. S. (1980). Response-shift bias: a problem in evaluating interventions with pre/post self-reports. Eval. Rev. 4, 93–106. doi: 10.1177/0193841X8000400105

CrossRef Full Text | Google Scholar

Kisker, E. E., Lipka, J., Adama, B., Rickard, A., Andrew-Ihrke, D., Yanez, E. E., et al. (2012). The potential of a culturally based supplemental mathematics curriculum to improve the mathematics performance of Alaska Native and other students. J. Res. Math. Educ. 2012, 75–113. doi: 10.5951/jresematheduc.43.1.0075

CrossRef Full Text | Google Scholar

Kovach, M. (2009). Indigenous Methodologies: Characteristics, Conversations, and Contexts. Toronto, ON: University of Toronto Press.

Google Scholar

Lipka, J., and Adams, B. (2004). Culturally Based Math Education as a Way to Improve Alaska Native Students' Math Performance. Ohio Univ., Athens. ACCLAIM (Appalachian Collaborative Center for Learning, Assessment, and Instruction in Mathematics) Research Institute.

Google Scholar

Lipka, J., Hogan, M. P., Webster, J. P., Yanez, E., Adams, B., Clark, S., et al. (2005). Math in a cultural context: two case studies of a successful culturally based math project. Anthropol. Educ. Quart. 4, 367–385. doi: 10.1525/aeq.2005.36.4.367

CrossRef Full Text | Google Scholar

Lipka, J., Sharp, N., Adams, B., and Sharp, F. (2007). Creating a third space for authentic biculturalism: examples from math in a cultural context. J. Am. Indian Educ. 46, 94–115. Available online at: http://www.jstor.org/stable/24398545

Google Scholar

Luecke, D., Carlow, S., Mattes, J., Christensen, W., and Mackey, H. (2022). Circulating Conversations Methodology: Co-Connecting Knowledge to Develop Research Questions at Sitting Bull College. Philosophy of Mathematics Education Journal. ISSN 1465–2978. University of Exeter, United Kingdom.

Google Scholar

Martin, W., Loch, S., Cooley, L., Dexter, S., and Vidakovic, D. (2010). Integrating learning theories and application-based modules in teaching linear algebra. Linear Algebra Appl. 432, 2089–2099. doi: 10.1016/j.laa.2009.08.030

CrossRef Full Text | Google Scholar

Meyer, S., and Aikenhead, G. (2021a). Indigenous culture-based school mathematics in action: Part I: Professional development for creating teaching materials. Math. Enthus. 18, 110–118. doi: 10.54870/1551-3440.1516

CrossRef Full Text | Google Scholar

Meyer, S., and Aikenhead, G. (2021b). Indigenous culture-based school mathematics in action: Part II: The study's results: what support do teachers need?. Math. Enthus. 18, 119–138. doi: 10.54870/1551-3440.1517

CrossRef Full Text | Google Scholar

National Research Council. (2001). Adding It Up: Helping Children Learn Mathematics. Washington, DC: The National Academies Press. doi: 10.17226/9822

CrossRef Full Text | Google Scholar

Ruef, J. L., Jacob, M. M., Walker, G. K., and Beavert, V. R. (2020). Why indigenous languages matter for mathematics education: a case study of Ichishkíin. Educ. Stud. Math. 20, 9957. doi: 10.1007/s10649-020-09957-0

CrossRef Full Text | Google Scholar

Sanders, D. (2011). Mathematical Views Within a Lakota Community: Towards a Mathematics for Tribal Self-Determination. (Dissertation). University of Colorado, Boulder, CO, United States.

Google Scholar

Sitting Bull College (2023). Vision and Mission. Available online at: https://sittingbull.edu/about-us/vision-and-mission/ (accessed January 18, 2023).

Google Scholar

Smith, L. T., Tuck, E., and Yang, K. W. (2018). Indigenous and Decolonizing Studies in Education: Mapping the Long View. Routledge.

Google Scholar

Stevens, P. J. (2021). A woodcutter's story: perceptions and uses of mathematics on the San Carlos Apache Reservation. Anthropol. Educ. Quart. 52, 430–450. doi: 10.1111/aeq.12399

CrossRef Full Text | Google Scholar

Webb, D., Groseth, B., and Coggins, P. (2017). “Incorporating culture into the post-secondary mathematics classroom,” in The Mathematics Edcuation for the Future Project - Proceedings of the 14th International Conference: Challenges in Mathematics Education for the Next Decade (Balatonfüred), 347–352.

Google Scholar

Wilson, S. (2008). Research Is Ceremony: Indigenous Research Methods. Halifax & Winnipeg: Fernwood Publishing.

Google Scholar

Windchief, S., and San Pedro, T. (2019). Applying Indigenous Research Methods: Storying with Peoples and Communities (Series: Indigenous and Decolonizing Studies in Education). New York, NY: Routledge.

Google Scholar