Development and initial validation of a mathematics-specific spatial vocabulary scale

This study describes the development and initial validation of a mathematics-specific spatial vocabulary measure for upper elementary school students. Reviews of spatial vocabulary items, mathematics textbooks, and Mathematics Common Core State Standards identified 720 mathematical terms, 148 of which had spatial content (e.g., edge). In total, 29 of these items were appropriate for elementary students, and a pilot study (59 fourth graders) indicated that nine of them were too difficult (< 50% correct) or too easy (> 95% correct). The remaining 20 items were retained as a spatial vocabulary measure and administered to 181 (75 girls, mean age = 119.73 months, SD =4.01) fourth graders, along with measures of geometry, arithmetic, spatial abilities, verbal memory span, and mathematics attitudes and anxiety. A Rasch model indicated that all 20 items assessed an underlying spatial vocabulary latent construct. The convergent and discriminant validity of the vocabulary measure was supported by stronger correlations with theoretically related (i.e., geometry) than with more distantly related (i.e., arithmetic) mathematics content and stronger relations with spatial abilities than with verbal memory span or mathematics attitudes and anxiety. Simultaneous regression analyses and structural equation models, including all measures, confirmed this pattern, whereby spatial vocabulary was predicted by geometry knowledge and spatial abilities but not by verbal memory span, mathematics attitudes and anxiety. Thus, the measure developed in this study helps in assessing upper elementary students' mathematics-specific spatial vocabulary.

Introduction

The development of mathematical competencies is a critical part of children's schooling and sets the foundation for future educational and occupational opportunities and contributes to functioning (e.g., financial decision-making) in other aspects of life in the modern world (National Mathematics Advisory Panel, 2008; Joensen and Nielsen, 2009; Kroedel and Tyhurst, 2012; Ritchie and Bates, 2013). There are many factors that influence children's mathematical development, including spatial abilities. In fact, the relation between some areas of mathematics and conceptions of space can be traced back to the early emergence of mathematics as an academic discipline (Dantiz, 1954). Modern cognitive scientists define spatial abilities as the capacity to perceive, retain, retrieve, and mentally transform the static and dynamic visual information of objects and their relationships (Wai et al., 2009; Uttal et al., 2013a; Verdine et al., 2014). Related studies confirm the relationship between spatial abilities, various aspects of mathematical development (Lachance and Mazzocco, 2006; Li and Geary, 2013, 2017; Gilligan et al., 2017; Verdine et al., 2017; Zhang and Lin, 2017; Geer et al., 2019; Mix, 2019; Hawes and Ansari, 2020; Attit et al., 2021; Geary et al., 2023), innovation in science, technology, engineering, and mathematics (STEM) fields (Wai et al., 2009; Kell et al., 2013; Uttal et al., 2013b) and competence in technical–mechanical blue-collar occupations (Humphreys et al., 1993; Gohm et al., 1998).

Although the relation between general spatial abilities and mathematics is well established, the more specific relations between different aspects of spatial abilities and mathematical learning and knowledge are not well understood. For example, mental rotation abilities predicted standardized mathematics achievement and accuracy of placing whole numbers on a number line for 6- and 7-year-olds but not for older students (Gilligan et al., 2019). For older students, in contrast, visuospatial attention, not mental rotation skills, predicted the accuracy of fractions placements on a number line task (Geary et al., 2021a). Other studies suggest that spatial abilities may be particularly important for learning some types of newly presented mathematical material and may become less important as students become familiar with this material (Casey et al., 1997; Mix et al., 2016).

Most of what we know about these relations is based on measures of spatial abilities, with comparatively less known about the contributions of students' developing spatial vocabulary (below) to their mathematical competencies. Mathematics-specific spatial vocabulary represents explicit statements about the intersection between spatial abilities and mathematical concepts. For instance, spatial ability includes the inherent brain and cognitive systems for processing information about objects which is eventually applied to geometric shapes (Izard and Spelke, 2009); the intersection is represented with, for instance, an understanding of the meaning of edge and face for geometric solids. A full understanding of the spatial-mathematics relation will require tracking developing the spatial vocabulary of students and examining how vocabulary contributes to this relation. To facilitate the study of this relation, we developed and provided the initial validation of a mathematics-focused spatial vocabulary measure for elementary school students.

Mathematics vocabulary and achievement

There is a misconception that early mathematical development largely involves learning symbolic arithmetic and associated concepts and procedural rules (Crosson et al., 2020). It does, of course, involve these but also includes the development of a mathematical language, including a specific mathematics vocabulary (Toll and Van Luit, 2014; Purpura and Logan, 2015; Hornburg et al., 2018). Even though there is no agreed-upon definition, in the most general sense, mathematical language is defined as keywords and concepts representing mathematical activities (for a review, see Turan et al., 2022). Sistla and Feng (2014) highlighted that mathematical language often differs from general language, stating that “In Math, there are many words used for the same operation, for example, ‘add them up, ‘the sum,' ‘the total,' ‘in all,' and ‘altogether' are phrases used to mean to use the addition operation, but these are not terms used in everyday language” (p. 4).

A recent meta-analysis, including 40 studies with 55 independent samples, revealed that mathematics vocabulary is moderately but consistently associated with mathematics achievement (Lin et al., 2021). However, the association is nuanced, depending on students' age and achievement levels, the novelty of topics, and the domain of mathematics (Powell et al., 2017; Peng and Lin, 2019; Lin et al., 2021; Ünal et al., 2021; Espinas and Fuchs, 2022). More specifically, mathematics vocabulary appears to play a more substantial role during the initial learning of mathematics subdomains (e.g., arithmetic) and needs to become increasingly nuanced with the introduction of more complex mathematics across grades (Lin et al., 2021; Ünal et al., 2021). Furthermore, depending on the topic, some aspects of mathematics vocabulary seem more critical than others. For instance, Peng and Lin (2019) found that word problem performance was more strongly associated with measurement and geometry-related vocabulary than with numerical operations-related vocabulary.

The importance of a strong mathematics vocabulary is illustrated by Hughes et al. (2020) finding that seventh-grade mathematics books contained over 450 mathematics vocabulary words. The measurement of mathematics vocabulary is thus an essential component of tracking students' mathematical development, but the content of these measures varies across studies. Some measures combine different areas (e.g., comparative terms, such as combine and take away, and spatial terms, such as near and far; Purpura et al., 2017), whereas others focus on specific areas (e.g., measurement vocabulary, such as decimeter; geometry vocabulary, such as parallelogram; and numerical operations vocabulary, such as fraction) (Peng and Lin, 2019). Although general mathematics vocabulary measures are useful, measures that assess content-specific vocabulary (e.g., geometry related) are important for tracking students' development in specific areas of mathematics (Peng and Lin, 2019).

Mathematics-specific spatial vocabulary is one such area. To be sure, there are mathematics vocabulary assessments that include spatial terms, and these are sometimes found to mediate the relation between spatial abilities and mathematics outcomes for younger students (Purpura and Logan, 2015; Georges et al., 2021; Gilligan-Lee et al., 2021). For instance, Gilligan-Lee et al. (2021) showed that spatial vocabulary was predictive of overall mathematics achievement, controlling spatial abilities, and general vocabulary. However, their measure was composed of items that were focused on spatial direction (e.g., to the right) and location (e.g., above) and not spatial terms that have specific mathematical meanings (e.g., edge of a cube). Moreover, most of these studies have focused on students in early elementary school, kindergarten, or preschool (e.g., Toll and Van Luit, 2014; Purpura and Logan, 2015; Powell and Nelson, 2017; Vanluydt et al., 2020), although there are a few studies focusing on older students (e.g., Peng and Lin, 2019; Ünal et al., 2021).

Hence, there is a need for a mathematics vocabulary assessment explicitly focusing on mathematics-specific spatial terms for upper-elementary school students, hereafter, referred to as spatial vocabulary. This is important because some aspects of spatial-related mathematics vocabulary are not typically included in mathematics vocabulary measures. Some of these measures include terms associated with shape (e.g., cube and parallelogram), operation (e.g., quotient and sum), geometry (e.g., line, angle, and edge), or number (e.g., odd and even) (Powell et al., 2020), but less often include more specific key spatial concepts. For example, “edge” may be a spatial term included in mathematical vocabulary scales; however, those scales may not include terms that represent relationships between objects in space, such as “perpendicular,” “parallel,” “intersecting,” or “adjacent.” The same is true for geometry terms, which may include types of angles and lines and properties of shapes but may be less likely to include words representing relationships between them.

Current study

This study aimed to develop an easy-to-administer measure of elementary students' mathematics-specific spatial vocabulary. We developed the measure by compiling items from multiple existing sources and then assessed its convergent and discriminant validity (Campbell and Fiske, 1959). Convergent validity is established when spatial vocabulary scores are strongly correlated with mathematics and cognitive measures that have a clear spatial component to them, specifically geometry and spatial abilities. Discriminant validity is established when the correlations between spatial vocabulary and geometry and spatial abilities are significantly stronger than the correlations with mathematics and ability domains that do not have a clear spatial component to them, specifically arithmetic and verbal memory span. We also assessed the relation between spatial vocabulary and mathematics attitudes and anxiety as a further control. The latter is often related to concurrent mathematics achievement and longitudinal gains in achievement (Eccles and Wang, 2016; Geary et al., 2021b). Discriminant validity would be further supported when scores on the spatial vocabulary measure are not strongly related to mathematics attitudes and anxiety.

Method

Participants

Participants included 181 fourth graders (mean age = 119.73 months, SD =4.01). In total, 96 students identified as boys, with 75 identified as girls, 1 preferred not to identify their gender, and the remaining did not complete this item. Students were asked whether they preferred to speak a language other than English at home, and 39 students indicated that they did (predominantly Spanish). Students were recruited through advertisements and through schools in several large urban districts in California; specifically, teachers shared information on the project with students in their classrooms, and students within these classrooms volunteered for the study.

Measures

Mathematics measures

The mathematics measures assessed fluency at solving whole number and fractions arithmetic problems, the accuracy of whole and fractions number line placements, accuracy at solving non-standard arithmetic problems, and geometry. The tests were administered in small groups on the students' computers using Qualtrics (Qualtrics, Provo, UT).

Arithmetic fluency

The test included 24 whole-number addition (e.g., 87 + 5), subtraction (e.g., 35–8), and multiplication (e.g., 48 x 2) problems. The problems were presented with an answer, and the student responded Yes (correct) or No (incorrect). Half the problems were incorrect, with the answer +1 or 2 from the correct answer. Students had 2 min to solve as many problems as possible. A composite arithmetic fluency score was based on the correct answer selected across the three operations (M = 9.79, SD = 4.63; α = 0.90).

Fractions arithmetic

The test included 24 fractions addition (e.g., $\frac{1}{4}$ + 1/8 = 3/8) and fractions multiplication problems (e.g., 2$\frac{1}{2}$ x $\frac{1}{4}$ = 5/8). The problems were presented with an answer, and the student responded Yes (correct) or No (incorrect). Half the problems were incorrect, with error foils based on common fractions errors (e.g., $\frac{1}{4}$ + 2/4 = 3/8). A composite fractions arithmetic score was based on the correct number selected (M = 6.55, SD = 4.21; α = 0.80).

Whole number line

The student was asked to place 26 target numbers on a 0-1000 number line. The placements were made by moving a slider to the chosen location on the number line with 0 to 1000 endpoints. Following Siegler and Booth (2004), the accuracy of number line estimation was determined by calculating their mean percent absolute error [PAE = (|Estimate – Target Number|)/1000, M = 7.98%, SD = 4.52%, α = 0.89]. For the analyses, these scores were multiplied by −1 so that positive scores represent better performance.

Fractions number line

The student was asked to place 10 target fractions on a 0–5 number line (10/3, 1/19, 7/5, 9/2, 13/9, 4/7, 8/3, 7/2, 17/4, and 11/4). The placements were made by moving a slider to the chosen location on a number line with 0 to 5 endpoints. Following Siegler et al. (2011), accuracy was determined by calculating their mean percent absolute error [PAE = (|Estimate – Target Number|)/5, M = 27.17%, SD = 10.70%, α = 0.67]. For the analyses, these scores were multiplied by −1 so that positive scores represent better performance.

Equality problems

Students' understanding of mathematical equality (i.e., the meaning of =) can be assessed using problems in non-standard formats, such as 8 = __ + 2 – 3 (Alibali et al., 2007; McNeil et al., 2019). We used the 10-item measure developed by Scofield et al. (2021), where items are presented in a multiple-choice format (4 options). The score was the mean percent correct for the 10 items (M = 70.0, SD = 28.71, α = 0.88).

Geometry

In total, 20 items were from the released item pool from the 4th grade National Assessment of Educational Progress (NAEP; https://nces.ed.gov/nationsreportcard/). The items assess students' knowledge of shapes and solids, including identification (e.g., rectangle and cylinder) and their properties (e.g., number of sides, faces, the diameter of a circle, and angles in a triangle), as well as knowledge of lines (e.g., parallel). The students were given 10 min to complete the test.

The items were submitted to a Rasch model, grounded on an IRT analysis for the core sample of students (n = 170, scores for the remaining students were imputed, below), following Hughes et al. (2020). Three types of fit statistics were used: item difficulty, infit, and outfit statistics. The item difficulty metric provided information about whether the difficulty of each item is suitable to the person's ability levels on the latent trait (Van Zile-Tamsen, 2017). The items within the range of−3.0 to 3.0 were kept in the measure. The infit statistics show unanticipated response patterns based on items targeted to the individuals' imputed latent ability based on prior responses. The outfit statistics are more susceptible to guessing or mistakes, such as when the individual guesses correctly on an item that is well above their imputed ability level or misses an item that should be relatively easy (Runnels, 2012). The acceptable range of mean-square values (MNSQ) is from 0.7 to 1.3 (Linacre, 2007); items with infit–outfit values within that range were retained.

The analyses were conducted using the mirt package in R (Chalmers, 2012; R Core Team, 2022). The results indicated that one item (Item 3) was not contributing to the measurement of geometry knowledge and was dropped, leaving 19 items for the final measure. The IRT-based scores and the total correct from the 19 items were highly correlated (r = 0.99, p < 0.001), and thus total correct was used in the analyses (M = 9.43, SD = 4.09, α = 0.88).

Spatial measures

The spatial measures assessed a range of competencies, including visuospatial attention, mental rotation abilities, and spatial visualization. The measures were administered on the students' computers in small groups. In addition to the measures mentioned below, we also administered the Corsi Block Tapping Task (Corsi, 1972; Kessels et al., 2000), but the scores were not reliable for this sample, and thus the measure was dropped.

Visual spatial attention

Visuospatial attention was assessed using the Judgment of Line Angle and Position test (Collaer and Nelson, 2002; Collaer et al., 2007; JLAP). The task requires students to match the angle of a single line to one of the 15-line options in an array below the target line. There were 20 sequentially presented test items, with students selecting the item that matched the angle of the target. Each trial began immediately after the student's response, or at the 10 s time limit. The score was the number of correct trials (M = 7.72, SD = 3.35, α = 0.88).

Mental rotation

Ganis and Kievit (2015) software was used to generate 24 mental rotation items. The items included a three-dimensional baseline object (constructed from cubes) and a target stimulus that was either the same or different from the baseline object but rotated 0 to 150 degrees (the baseline and target objects were the same for 12 items and different for 12 items). The task was to determine whether the objects were the same or different, and the score was the number of correct trials (M = 15.93, SD = 4.28, α = 0.94).

Spatial visualization

Ekstrom and Harman (1976) Paper Folding Test assessed visualization abilities. Students were asked to imagine a paper being folded and a hole punched through the folds. They were then asked to select the image that represents what that same paper would look like if it were unfolded. Students were shown one example problem with an explanation of the correct answer. Students completed 10 items, and the score was the total correct across items (M = 3.88, SD = 2.28, α = 0.70).

Spatial transformation

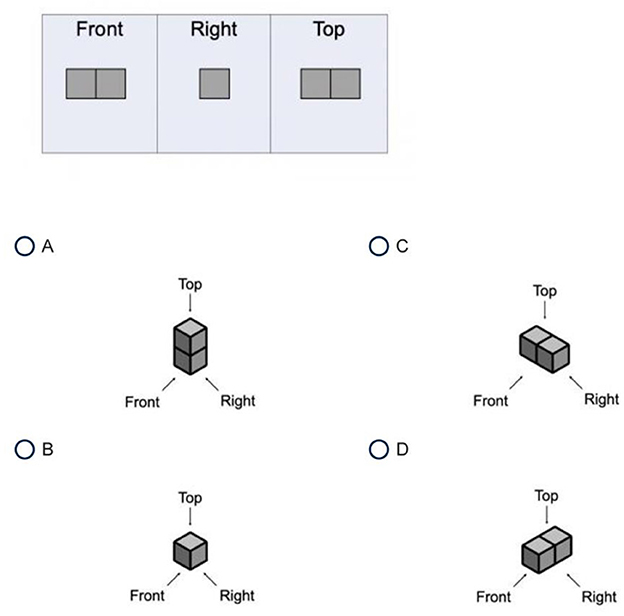
This measure was developed for this project and included items that required students to identify the shape corresponding to two-dimensional representations of the front, right, and top of a figure, as shown in Figure 1. In total, 22 of these items were created and administered to 59 fourth graders in two classrooms. Performance on six items was poorly correlated (rs < 0.20) with performance on the other items and was therefore dropped. The resulting 16-item measure was administered to the current sample, and the score was the number correct (M = 8.58, SD = 3.80, α = 0.72). The measure loaded on the same spatial factor as the other spatial measures (below), confirming it is tapping spatial ability.

FIGURE 1

Figure 1. Practice item from the spatial transformation test.

Beery

Visuomotor skills were assessed with the Beery-Buktenica Developmental Test of Visual-Motor Integration (Beery et al., 2010). The measure includes 30 geometric forms that are arranged from simple to more complex. The task is to draw the figures, which are then scored as correct (1) or not (0) based on standard procedures (M = 23.65, SD = 4.09).

Memory span measures

Digit span

Both forward and backward verbal digit spans were assessed. The former started with three digits and the latter with two. For each trial, students heard a sequence of digits at 1 s intervals. The task was to recall the digit list by tapping on a circle of digits displayed on the student's computer screen. The student advanced to the next level if the response was correct (in digits and presentation order). If the response was incorrect, the same level was presented a second time. If a consecutive error occurred, the student regressed one level. Each direction (forward and then backward) ended after 14 trials. The student's score was the highest digit span correctly recalled before making two consecutive errors at the same span length.

Mathematics attitudes

Interest

The 10 items were from the student attitudes assessment of the Trends in International Mathematics and Science Study (TIMSS; Martin et al., 2015). The items assessed interest in mathematics (e.g., “I learn many interesting things in mathematics,” “I like mathematics”). The items were on a 1 (Disagree a lot) to 4 (Agree a lot) scale, with negatively worded items (e.g., “Mathematics is boring”) reverse coded. The score was the mean across items (M = 3.12, SD = 0.85, α = 0.90).

Self-efficacy

The 9 items were from the student attitudes assessment of the TIMSS (Martin et al., 2015). The items assessed mathematics self-efficacy (e.g., “I usually do well in mathematics,” “I learn things quickly in mathematics”). The items were on a 1 (Disagree a lot) to 4 (Agree a lot) scale, with negatively worded items (e.g., “I am just not good at mathematics”) reverse coded. The score was the mean across items (M = 3.04, SD = 0.81, α = 0.72).

Anxiety

Ramirez et al. (2013) 8-item measure was used to assess students' mathematics anxiety (e.g., “How do you feel when taking a big test in math class?”, “How do you feel when you have to solve 27 + 15?”). Students responded by clicking on one of the three options in Figure 2, and thus higher scores (1 to 3) reflected lower anxiety (M = 2.90, SD = 0.32, α = 0.83).

FIGURE 2

Figure 2. Response options for the anxiety measure.

Spatial vocabulary

Scale development

We began with four main mathematics education resources: (1) Cannon et al. (2007) Spatial Language Coding Manual; (2) the Quantile Framework for Mathematics (a standardized measure of mathematical skills and concepts based on the Lexile Framework for Reading; Cuberis, 2021); (3) the Mathematics Common Core State Standards (focusing on grades third through fifth; http://www.corestandards.org/Math/); and (4) a mathematics vocabulary measure developed by Powell et al. (2017) based on three common third and fifth-grade mathematics textbooks.

A total of 720 mathematical terms were extracted from these resources, and three independent researchers determined that 148 of them were spatially relevant. Two independent researchers then assessed whether the items were appropriate for elementary school children, which yielded 29 words for the initial version of the measure. This version contained seven parts that focused on position, direction, pattern, dimension, orientation, action, and geometry-relevant vocabulary. An electronic version of the assessment was created using Qualtrics.

The assessment was piloted on 36 incoming 5th-grade students through a virtual STEAM course that provided hands-on learning experiences related to spatial reasoning and problem-solving through origami. Students were asked to complete the Qualtrics version of the assessment before and after completion of the virtual course. An item-level analysis was conducted to determine internal consistency and level of difficulty. Items were determined to be too easy if >95% of students answered correctly before the lessons. Words were considered too difficult if < 50% of students answered correctly before the lessons. Based on these criteria, nine words were excluded.

The remaining 20 items were submitted to an IRT analysis, following the same procedures described for the geometry test for the core sample of students (n = 170, scores for the remaining students were imputed, see below). The results indicated that all items contributed to the measurement of spatial vocabulary and were retained for the final measure. The items, along with an Item Person Map (Supplementary Figure A1), are shown in the Supplementary material. The IRT-based scores and the total correct from the 20 items were highly correlated (r = 0.99, p < 0.001), and thus total correct was used in the analyses (M = 12.72, SD = 4.16, α = 0.81).

Procedures

After receiving parent consent and student assent, students completed a battery of assessments online on the students' computer, including the spatial vocabulary, mathematics, and spatial ability measures. Students completed measures in virtual groups of 6–8 students that were proctored by trained researchers. Assessments were given once a week over the course of 3 weeks. Sessions were approximately 1 h long. Students were scheduled to meet at the same time and day of the week over the 3 weeks with the same proctor. Most of the measures were assessed through a Qualtrics survey, but the spatial and verbal memory span measures were administered using customized programs developed through Inquisit by Millisecond (https://www.millisecond.com).

During the first session, students were provided a Qualtrics link and were asked about their sex, preferred language, and attitudes toward math. After completing these assessments, they completed the digit span and the JLAP, mental rotation, and Corsi measures on the Inquisit platform. During the second session, students completed the Beery assessment and a second battery of assessments on Qualtrics. Each student was sent a Beery assessment to their homes. The assessment was sealed in a manila envelope with instructions not to open it until instructed to do so, along with a pre-addressed mailer to return the test. Once students were ready to begin, the researcher gave explicit instructions on how to proceed. Once a student had completed the Beery form, the researcher would watch as they placed the form into the pre-addressed mailer and sealed the envelope. Students were then sent a battery of assessments on Qualtrics. The assessments included arithmetic fluency, fractions arithmetic, spatial transformation, and the two number line estimation tasks. At the end of the second session, the researchers then gave students instructions to leave the mailer with the Beery assessment outside their homes for UPS pickup or to drop it off at their nearest post office. During the third session, students were provided a final Qualtrics link that included the spatial vocabulary assessment, Paper Folding, geometry assessment, and equality problems.

Analyses

The 11% of missing values were estimated using the multiple imputations procedure in SAS (2014). The imputations were based on all key variables and were the average across five imputations. Scores were then standardized (M = 0, SD = 1). The first goal was to reduce the number of variables by creating composite measures. The five arithmetic measures were submitted to principal components factor analyses with Promax rotation (allowing correlated factors) using proc factor (SAS, 2014), as were the seven cognitive (i.e., spatial, verbal memory span) measures and three attitude measures. Factors with Eigenvalues > 1 were retained; the next lowest Eigenvalue was 0.77 for the arithmetic measures and cognitive measures and 0.38 for the attitudes measures. The composite measures were then used to assess the convergent and discriminant validity of the spatial measure.

We then ran follow-up structural equation models (SEM) in Proc Calis (SAS, 2014). The goal was to isolate variance common to all measures (composites for arithmetic, spatial, verbal memory span, and mathematics attitudes), which included general cognitive ability (e.g., top-down attentional control; Ünal et al., 2023) and any method variance (Campbell and Fiske, 1959). All variables defined a general factor for the baseline model. For Model 2, paths from geometry and spatial abilities were added to the baseline model. For Model 3, paths from the alternative measures (i.e., arithmetic, verbal memory span, and mathematics attitudes) were added to the baseline model. Convergent validity would be supported by the finding of significant geometry to spatial vocabulary and spatial abilities to spatial vocabulary paths in Model 2, and discriminant validity by non-significant paths from alternative measures to spatial vocabulary in Model 3.

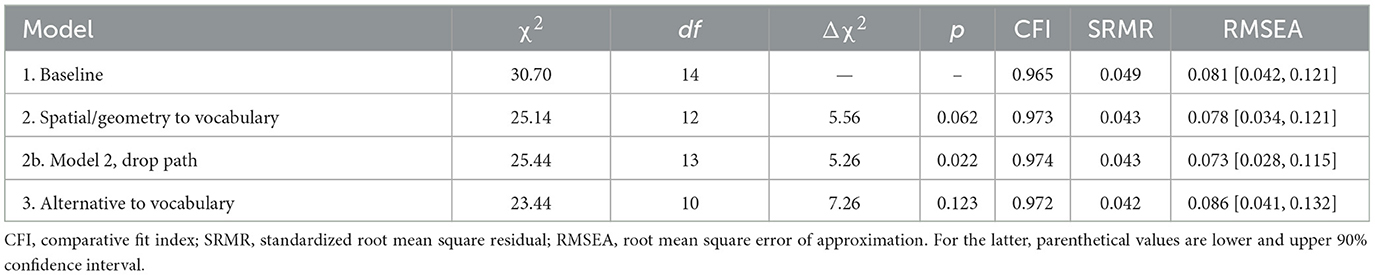
We estimated the fit of the various models using standard measures, that is, χ² (non-significant effects indicate better model fit), root mean square error approximation (RMSEA), standardized root mean square residual (SRMR values < 0.06 indicate good model fit), and the comparative fit index (CFI). The χ² value varies directly with the sample size and thus is not always a good measure of model fit. The combination of absolute (RMSEA, SRMR) and comparative (CFI) measures reduces the overall proportion of Type I and Type II errors (Hu and Bentler, 1999). Hu and Bentler suggested that good fit is obtained when CFI > 0.95 and RMSEA < 0.06. However, others have recommended a more graded set of guidelines for RMSEA, such that an RMSEA < 0.05 is considered good, values between 0.05 and 0.08 are considered acceptable, and values between 0.08 and 0.10 are considered marginal (Fabrigar et al., 1999).

Results

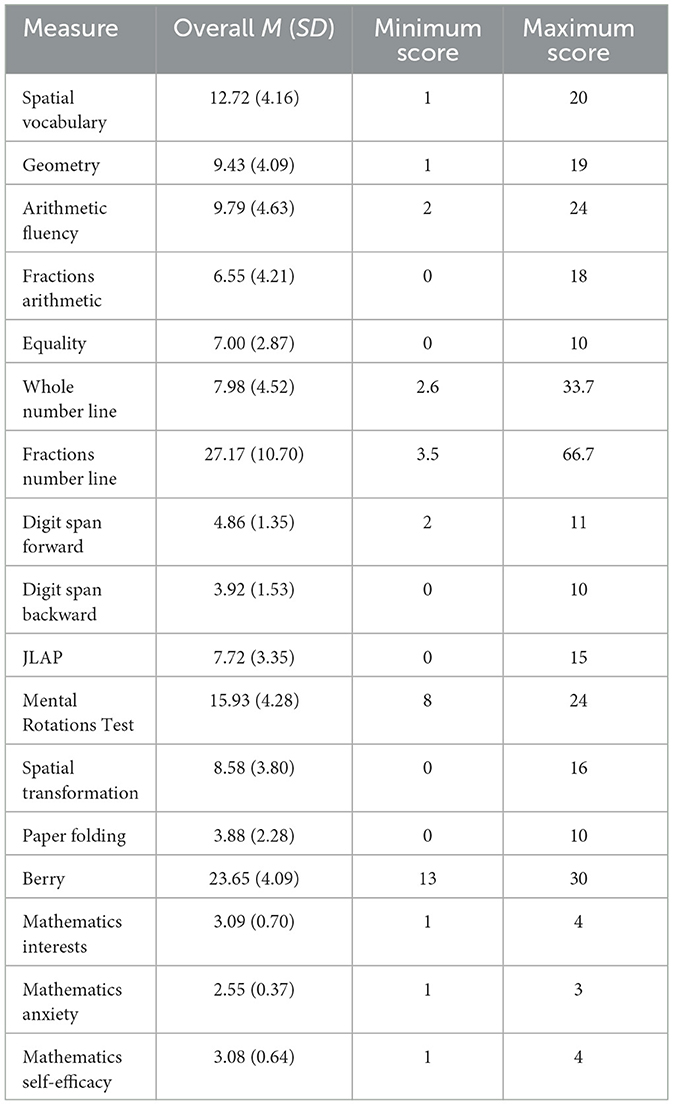
Mean unstandardized scores for all the measures are shown in Table 1.

TABLE 1

Table 1. Mean scores.

Factor structure

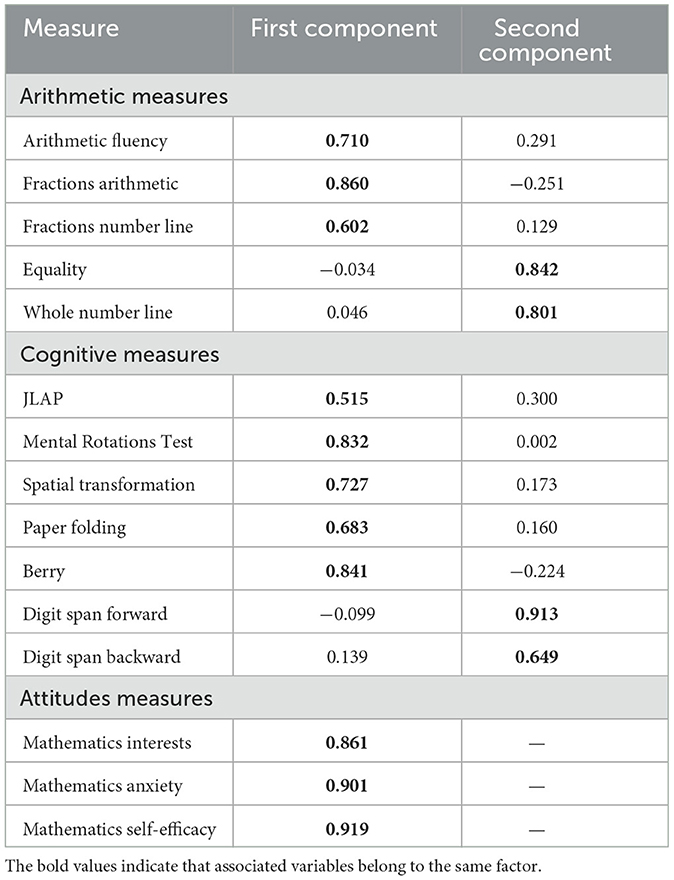
Two components emerged from the correlation matrix among the arithmetic measures (standardized loadings > 0.50). The first had an Eigenvalue of 2.01 and explained 40% of the covariance between measures and the second had an Eigenvalue of 1.15 and explained 23% of the covariance. The standardized regressions from the rotated factor pattern are shown in the top section of Table 2. The first factor, hereafter simple arithmetic, was defined by the mean of the arithmetic fluency, fractions arithmetic, and fractions number line measures. The second factor, hereafter complex arithmetic, was defined by the mean of the equality and whole number line measures.

TABLE 2

Table 2. Factor pattern for arithmetic, cognitive, and attitudes measures.

As shown in the second section in Table 2, two components emerged for the cognitive measures. The first had an Eigenvalue of 3.26 and explained 47% of the covariance among measures, whereas the second had an Eigenvalue of 1.02 and explained 15% of the covariance. The first factor, hereafter spatial abilities, was defined by means of paper folding, spatial transformation, JLAP, MRT, and Berry measures. The second factor, hereafter memory span, was defined by the mean of the digit span forward and digit span backward measures.

As shown in the third section of Table 2, the mathematics attitudes measures defined a single factor that explained 80% of the covariance among them (Eigenvalue = 2.41). The score was defined by means of the three attitude and anxiety measures. The spatial vocabulary and geometry measures were not included in the factors analyses because the former is the core dependent measure in the analyses, and the latter is a core measure for the assessment of the convergent validity of the spatial vocabulary measure.

Convergent and discriminant validity

Correlational and regression analyses

As noted, the convergent and discriminant validity of the spatial vocabulary measure can be assessed by the pattern of correlations with mathematics measures that have a clear spatial component to them (i.e., the geometry test) and those that do not (i.e., the arithmetic tests; Campbell and Fiske, 1959). Similarly, if the development of spatial vocabulary is influenced by spatial abilities, then the measure should be more strongly correlated with spatial ability than memory span.

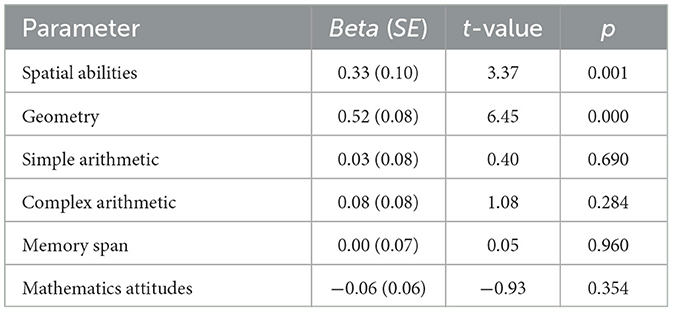
As shown in Table 3, both patterns emerged. The table presents correlations among the measures and reliabilities (alphas) on the diagonal. The key correlations are in bold, and all are higher than other correlations in the matrix. Spatial vocabulary is more strongly related to geometry (r = 0.73, p < 0.001) than simple (r = 0.32, p < 0.001) or complex (r = 0.52, p < 0.001) arithmetic, and more strongly related to spatial abilities (r =0.65, p < 0.001) than Memory Span (r =0.35, p < 0.001). Table 4 shows the results of a simultaneous regression analysis, whereby spatial vocabulary was regressed on the geometry, simple arithmetic, complex arithmetic, spatial abilities, memory span, and mathematics attitudes measures. The results revealed that only geometry (p < 0.001) and spatial abilities (p < 0.001) were significant predictors of spatial vocabulary (all other ps > 0.283); R² = 0.57, F_{(6, 174)} = 39.04, p < 0.001.

TABLE 3

Table 3. Correlation matrix.

TABLE 4

Table 4. Regression model predicting spatial vocabulary.

Structural equation models

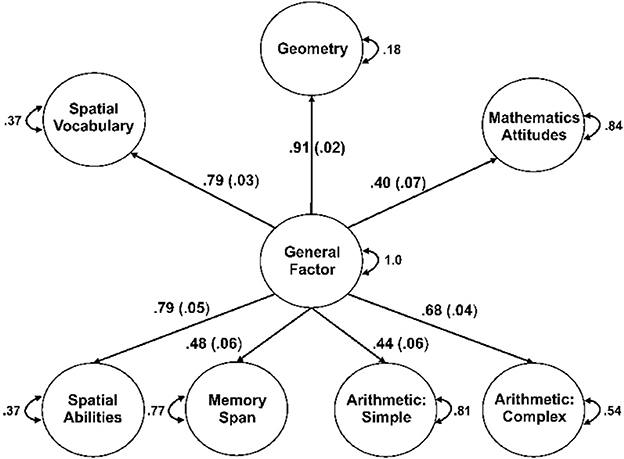
As noted, the baseline model involved estimating paths from a general factor to spatial vocabulary, spatial abilities, geometry, simple arithmetic, complex arithmetic, memory span, and mathematics attitudes. As can be seen in Table 5, the fit statistics for the baseline model were acceptable for CFI, SRMR, and marginal for RMSEA. The standardized path estimates for this model are shown in Figure 3, all of which were significant (ps < 0.001).

TABLE 5

Table 5. Fit indices for structural equation models.

FIGURE 3

Figure 3. Standardized estimates for baseline model.

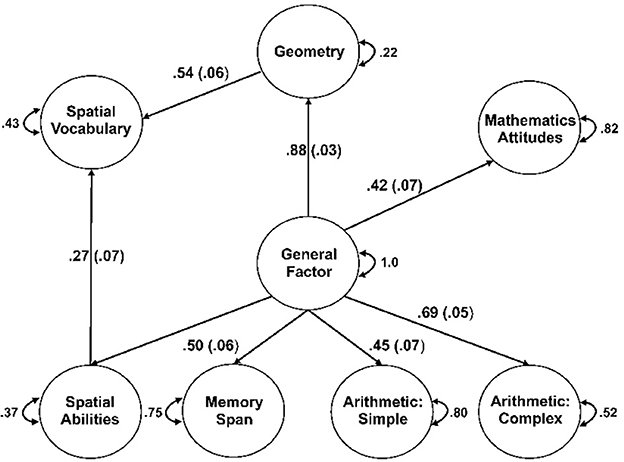
Estimating paths from spatial abilities and geometry to spatial vocabulary (Model 2) resulted in an improvement in overall model fit, Δχ²(2) = 5.56, p = 0.062, relative to the baseline model, and improvements in all fit statistics. Examination of the paths from this model indicated that the path from the general factor to spatial vocabulary was no longer significant (p = 0.597) and thus was dropped, creating Model 2b. The overall fit of Model 2b, Δχ²(1) = 5.26, p = 0.022, was improved relative to the baseline model, and all fit indices were acceptable.

Estimating paths from simple and complex arithmetic, memory span, and mathematics attitudes to spatial vocabulary (Model 3) did not improve overall model fit, Δχ²(4) = 7.26, p = 0.123, relative to the baseline model. Moreover, only the path from mathematics attitudes to spatial vocabulary was significant, but the coefficient was negative, β = −0.11, se = 0.058, t = −1.98, p = 0.047.

The results indicate that Model 2b is the best representation of the covariance among the variables. The associated standardized path coefficients are shown in Figure 4.

FIGURE 4

Figure 4. Standardized estimates for model 2b.

Discussion

The goal of this study was to develop and provide the initial validation for a mathematics-specific spatial vocabulary measure for late elementary school students. The goal stemmed from the contribution of mathematics vocabulary to students' mathematical development (Toll and Van Luit, 2014; Purpura and Logan, 2015; Hornburg et al., 2018), and its correlation with mathematics achievement (Lin et al., 2021). The goal was also based on the relationship between spatial abilities and mathematical development and innovation in STEM fields (Kell et al., 2013; Geary et al., 2023), as well as its importance for performance in technical-mechanical blue-collar fields (Humphreys et al., 1993; Gohm et al., 1998). The latter is a critical but underappreciated occupation that are particularly attractive to adolescent boys and men from blue-collar backgrounds (Stoet and Geary, 2022), and the cognitive abilities associated with success in them include spatial and mechanical abilities (Gohm et al., 1998). In any case, the study builds on prior studies that have largely focused on younger students and typically include vocabulary items that cover different mathematics topics (Toll and Van Luit, 2014; Purpura and Logan, 2015; Powell and Nelson, 2017; Vanluydt et al., 2020; e.g., measurement, number) or include spatial items that are not mathematics specific (Gilligan-Lee et al., 2021).

As an example of the latter, Gilligan-Lee et al. (2021) developed a spatial vocabulary measure for elementary school students that focused on spatial-specific terms (e.g., under, over, to the right of). Performance on this measure was correlated with spatial abilities and was predictive of overall mathematics achievement, controlling spatial abilities. Our focus, in contrast, was on spatial terms that have a specific mathematics meaning and are frequently used in mathematics textbooks (Powell et al., 2017) and included in the Mathematics Common Core State Standards for upper elementary school students (http://www.corestandards.org/Math/). The utility of our spatial vocabulary measure was evaluated following a combination of Hughes et al.'s (2020). Rasch model procedure for developing a mathematic vocabulary measure and Campbell and Fiske's (1959) convergent and discriminant validity approach.

Convergent validity requires the measure to be more strongly related to conceptually similar than dissimilar measures. Thus, our inclusion of a geometry measure composed of items from the high-stakes NAEP and standard spatial ability measures. Much of geometry has a spatial component to it (Clements and Battista, 1992), and prior research shows that the development of spatial abilities and spatial vocabulary co-occurs (e.g., Gilligan-Lee et al., 2021). Although spatial abilities and spatial vocabulary are correlated with aspects of arithmetic performance and may contribute to development in these areas (Geary and Burlingham-Dubree, 1989; Gilligan et al., 2019; Geary et al., 2021a; Gilligan-Lee et al., 2021), these correlations should, in theory, be weaker than those between spatial vocabulary and geometry. This is what we found: a result that supports the convergent and discriminant validity of the measure within mathematics. If the spatial vocabulary measure is simply a reflection of general cognitive ability, which is correlated with vocabulary and academic achievement broadly (Roth et al., 2015), then it should show similar relations to spatial abilities and verbal memory span, but it did not. In keeping with the convergent and discriminant validity within the cognitive domain, spatial vocabulary was more strongly related to spatial abilities than to verbal memory span.

Moreover, mathematics outcomes are often related to mathematics attitudes and anxiety (Eccles and Wang, 2016; Geary et al., 2021a), and they were significantly correlated with geometry and arithmetic scores, as well as with spatial vocabulary, in this study (Table 3). The key finding here is that spatial vocabulary was unrelated to mathematics attitudes (combined attitudes and anxiety) once spatial abilities and geometry performance were controlled. In total, the results suggest that our spatial vocabulary measure is capturing aspects of mathematical competencies that have a strong spatial component to them (geometry in this case; Clements and Battista, 1992), and are related to spatial abilities, as expected (Gilligan-Lee et al., 2021) and, critically, is only weakly related to performance in mathematical and cognitive domains that are not strongly spatial and is not influenced by students' mathematics attitudes and anxiety.

Limitations

The primary limitation is the correlational nature of the data. In the regression analyses, we used mathematics, cognitive, and attitudes measures to predict spatial vocabulary scores but we could have just as easily used spatial vocabulary to predict performance on these measures. The regressions, however, were not used to imply some type of causal relation between geometry and spatial abilities and students' emerging spatial vocabulary but to show that the latter was not tapping individual differences in non-spatial arithmetic abilities, verbal memory span, or attitudes. In other words, the regression results and the correlations show that spatial vocabulary is more strongly related to spatial-related mathematics and abilities than to alternative constructs that are related to children's mathematical development.

Another potential limitation is that we did not have a more general mathematics vocabulary measure. The assessment of our spatial vocabulary measure would have been strengthened with a demonstration that it is related to geometry and spatial abilities above and beyond the relation between general mathematics vocabulary and these constructs. Despite these limitations, this study provides a first step in the development of a mathematics-specific spatial vocabulary measure for older elementary school students, adding to prior studies that have largely focused on younger students, general mathematics, and spatial-specific vocabulary measures.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material. Data and R codes are available on Open Science Framework (https://osf.io/f6phe/?view_only=8a91da5d41304cc8b1f41e68c72596a8). Further inquiries can be directed to the corresponding authors.

Ethics statement

The studies involving human participants were reviewed and approved by the University of San Diego (IRB-2019-479). Written informed consent to participate in this study was provided by the participants' legal guardian/next of kin.

Author contributions

LR, YL, CG, TR, and PM collected the data. ZÜ and DG analyzed the data and wrote the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This study was supported by the grants DRL-1920546 and DRL-1659133 from the National Science Foundation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1189674/full#supplementary-material

References

Alibali, M. W., Knuth, E. J., Hattikudur, S., McNeil, N. M., and Stephens, A. C. (2007). A longitudinal examination of middle school students' understanding of the equal sign and equivalent equations. Mathematic Thinking Learn. 9, 221–247. doi: 10.1080/10986060701360902

CrossRef Full Text | Google Scholar

Attit, K., Power, J. R., Pigott, T., Lee, J., Geer, E. A., Uttal, D. H., et al. (2021). Examining the relationships between spatial skills and mathematical performance: a meta-analysis. Psychonomic Bullet. Rev. 1, 1–22. doi: 10.3758/s13423-021-02012-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Beery, K. E., Beery, N. A., and Beery, V. M. I. (2010). The Beery-Buktenica Developmental Test of Visual-motor Integration with Supplemental Developmental Tests of Visual Perception and Motor Coordination: And, Stepping Stones Age Norms from Birth to Age Six. Framingham, CT: Therapro.

Google Scholar

Campbell, D. T., and Fiske, D. W. (1959). Convergent and discriminant validation by the multitrait-multimethod matrix. Psychol. Bulletin 56, 81–105. doi: 10.1037/h0046016

PubMed Abstract | CrossRef Full Text | Google Scholar

Cannon, J., Levine, S., and Huttenlocher, J. (2007). A system for analyzing children and caregivers' language about space in structured and unstructured contexts. Ashburn, VC: Spatial Intelligence and Learning Center (SILC) Technical Report.

Google Scholar

Casey, M. B., Nuttall, R. L., and Pezaris, E. (1997). Mediators of gender differences in mathematics college entrance test scores: A comparison of spatial skills with internalized beliefs and anxieties. Dev. Psychol. 33, 669–680. doi: 10.1037/0012-1649.33.4.669

PubMed Abstract | CrossRef Full Text | Google Scholar

Chalmers, R. P. (2012). Mirt: A multidimensional item response theory package for the R environment. J. Stat. Software 48, 1–29. doi: 10.18637/jss.v048.i06

CrossRef Full Text | Google Scholar

Clements, D. H., and Battista, M. T. (1992). “Geometry and spatial reasoning,” in Handbook of Research on Mathematics Teaching and Learning, ed D. A. Grouws (New York, NY: Macmillan), 420–464.

Google Scholar

Collaer, M. L., and Nelson, J. D. (2002). Large visuospatial sex difference in line judgment: Possible role of attentional factors. Brain Cognit. 49, 1–12. doi: 10.1006/brcg.2001.1321

PubMed Abstract | CrossRef Full Text | Google Scholar

Collaer, M. L., Reimers, S., and Manning, J. T. (2007). Visuospatial performance on an internet line judgment task and potential hormonal markers: Sex, sexual orientation, and 2D: 4D. Archives Sexual Behav. 36, 177–192. doi: 10.1007/s10508-006-9152-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Corsi, P. M. (1972). Human memory and the medial temporal region of the brain. Unpublished doctoral dissertation. McGill University, Montreal, Canada.

Google Scholar

Crosson, A. C., Hughes, E. M., Blanchette, F., and Thomas, C. (2020). What's the point? Emergent bilinguals' understanding of multiple-meaning words that carry everyday and discipline-specific mathematical meanings. Reading Writing Q. 36, 84–103. doi: 10.1080/10573569.2020.1715312

CrossRef Full Text | Google Scholar

Cuberis. (2021). The Quantile Framework for Mathematics. Quantile. Available online at: https://www.quantiles.com/ (accessed July 1, 2021).

Google Scholar

Dantiz, T. (1954). Number: The Language of Science, 4th Edn. NY, New York: Scribner.

Google Scholar

Eccles, J. S., and Wang, M. T. (2016). What motivates females and males to pursue careers in mathematics and science? International J. Behav. Dev. 40, 100–106. doi: 10.1177/0165025415616201

CrossRef Full Text | Google Scholar

Ekstrom, R. B., and Harman, H. H. (1976). Manual for Kit of Factor-Referenced Cognitive Tests. Princeton, NJ: Educational Testing Service.

Google Scholar

Espinas, D. R., and Fuchs, L. S. (2022). The effects of language instruction on math development. Child Dev. Perspectives 16, 69–75. doi: 10.1111/cdep.12444

PubMed Abstract | CrossRef Full Text | Google Scholar

Fabrigar, L. R., Wegener, D. T., MacCallum, R. C., and Strahan, E. J. (1999). Evaluating the use of exploratory factor analysis in psychological research. Psychol. Methods 4, 272–299. doi: 10.1037/1082-989X.4.3.272

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganis, G., and Kievit, R. A. (2015). A new Set of three-dimensional shapes for investigating mental rotation processes: Validation data and stimulus set. J. Open Psychol. Data 3, e3. doi: 10.5334/jopd.ai

CrossRef Full Text | Google Scholar

Geary, D. C., and Burlingham-Dubree, M. (1989). External validation of the strategy choice model for addition. J. Exp. Child Psychol. 47, 175–192. doi: 10.1016/0022-0965(89)90028-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Geary, D. C., Hoard, M. K., Nugent, L., and Scofield, J. E. (2021a). In-class attentive behavior, spatial ability, and mathematics anxiety predict across-grade gains in adolescents' mathematics achievement. J. Educ. Psychol. 113, 754–769. doi: 10.1037/edu0000487

PubMed Abstract | CrossRef Full Text | Google Scholar

Geary, D. C., Hoard, M. K., and Nugent, L. Ünal, Z. E. (2023). Sex differences in developmental pathways to mathematical competence. J. Educ. Psychol. 115, 212–228. doi: 10.1037/edu0000763

PubMed Abstract | CrossRef Full Text | Google Scholar

Geary, D. C., Scofield, J. E., Hoard, M. K., and Nugent, L. (2021b). Boys' advantage on the fractions number line is mediated by visuospatial attention: evidence for a parietal-spatial contribution to number line learning. Dev. Sci. 24, e13063. doi: 10.1111/desc.13063

PubMed Abstract | CrossRef Full Text | Google Scholar

Geer, E. A., Quinn, J. M., and Ganley, C. M. (2019). Relations between spatial skills and math performance in elementary school children: a longitudinal investigation. Dev. Psychol. 55, 637–652. doi: 10.1037/dev0000649

PubMed Abstract | CrossRef Full Text | Google Scholar

Georges, C., Cornu, V., and Schiltz, C. (2021). The importance of visuospatial abilities for verbal number skills in preschool: Adding spatial language to the equation. J. Exp. Child Psychol. 201, 104971. doi: 10.1016/j.jecp.2020.104971

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilligan, K. A., Flouri, E., and Farran, E. K. (2017). The contribution of spatial ability to mathematics achievement in middle childhood. J. Exp. Child Psychol. 163, 107–125. doi: 10.1016/j.jecp.2017.04.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilligan, K. A., Hodgkiss, A., Thomas, M. S. C., and Farran, E. K. (2019). The developmental relations between spatial cognition and mathematics in primary school children. Dev. Sci. 22, 786. doi: 10.1111/desc.12786

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilligan-Lee, K. A., Hodgkiss, A., Thomas, M. S., Patel, P. K., and Farran, E. K. (2021). Aged-based differences in spatial language skills from 6 to 10 years: Relations with spatial and mathematics skills. Learning Instr. 73, 101417. doi: 10.1016/j.learninstruc.2020.101417

CrossRef Full Text | Google Scholar

Gohm, C. L., Humphreys, L. G., and Yao, G. (1998). Underachievement among spatially gifted students. Am. Educ. Res. J. 35, 515–531. doi: 10.3102/00028312035003515

PubMed Abstract | CrossRef Full Text | Google Scholar

Hawes, Z., and Ansari, D. (2020). What explains the relationship between spatial and mathematical skills? A review of evidence from brain and behavior. Psycho. Bullet. Rev. 27, 465–482. doi: 10.3758/s13423-019-01694-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hornburg, C. B., Schmitt, S. A., and Purpura, D. J. (2018). Relations between preschoolers' mathematical language understanding and specific numeracy skills. J. Exp. Child Psychol. 176, 84–100. doi: 10.1016/j.jecp.2018.07.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, L. T., and Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives. Struc. Eq. Model. 6, 1–55. doi: 10.1080/10705519909540118

PubMed Abstract | CrossRef Full Text | Google Scholar

Hughes, E. M., Powell, S. R., and Lee, J. Y. (2020). Development and psychometric report of a middle-school mathematics vocabulary measure. Assessment Eff. Interv. 45, 226–234. doi: 10.1177/1534508418820116

CrossRef Full Text | Google Scholar

Humphreys, L. G., Lubinski, D., and Yao, G. (1993). Utility of predicting group membership and the role of spatial visualization in becoming an engineer, physical scientist, or artist. J. Appl. Psychol. 78, 250–261. doi: 10.1037/0021-9010.78.2.250

PubMed Abstract | CrossRef Full Text | Google Scholar

Izard, V., and Spelke, E. S. (2009). Development of sensitivity to geometry in visual forms. Human Evol. 23, 213–248.

PubMed Abstract | Google Scholar

Joensen, J. S., and Nielsen, H. S. (2009). Is there a causal effect of high school math on labor market outcomes? J Hum. Res. 44, 171–198. doi: 10.1353/jhr.2009.0004

CrossRef Full Text | Google Scholar

Kell, H. J., Lubinski, D., Benbow, C. P., and Steiger, J. H. (2013). Creativity and technical innovation: spatial ability's unique role. Psychol. Sci. 24, 1831–1836. doi: 10.1177/0956797613478615

PubMed Abstract | CrossRef Full Text | Google Scholar

Kessels, R. P. C., van Zandvoort, M. J. E., Postma, A., Kappelle, L. J., and Haan, E. H. F. (2000). The corsi block-tapping task: standardization and normative data. Appl. Neuropsychol. 7, 252–258. doi: 10.1207/S15324826AN0704_8

PubMed Abstract | CrossRef Full Text | Google Scholar

Kroedel, C., and Tyhurst, E. (2012). Math skills and labor-market outcomes: evidence from a resume-based field experiment. Econ. Educ. Rev. 31, 131–140. doi: 10.1016/j.econedurev.2011.09.006

CrossRef Full Text | Google Scholar

Lachance, J. A., and Mazzocco, M. M. (2006). A longitudinal analysis of sex differences in math and spatial skills in primary school age children. Learn. Ind. Diff. 16, 195–216. doi: 10.1016/j.lindif.2005.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., and Geary, D. C. (2013). Developmental gains in visuospatial memory predict gains in mathematics achievement. PloS ONE 8, e70160. doi: 10.1371/journal.pone.0070160

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., and Geary, D. C. (2017). Children's visuospatial memory predicts mathematics achievement through early adolescence. PloS ONE 12, e0172046. doi: 10.1371/journal.pone.0172046

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, X., Peng, P., and Zeng, J. (2021). Understanding the relation between mathematics vocabulary and mathematics performance: A meta-analysis. Elementary School J. 121, 504–540. doi: 10.1086/712504

CrossRef Full Text | Google Scholar

Linacre, J. M. (2007). A User's Guide to WINSTEPS-MINISTEP: Rasch-Model > Computer Programs. Chicago, IL: winsteps.com.

Google Scholar

Martin, M. O., Mullis, I. V. S., Hooper, M., Yin, L., Foy, P., and Palazzo, L. (2015). “Creating and interpreting the TIMSS 2015 context questionnaire scales,” in Methods and Procedures in TIMSS 2015,eds M. O. Martin, I. V. S. Mullis, and M. Hooper (Chestnut Hill, MA: Boston College), 558–869.

Google Scholar

McNeil, N. M., Hornburg, C. B., Devlin, B. L., Carrazza, C., and McKeever, M. O. (2019). Consequences of individual differences in children's formal understanding of mathematical equivalence. Child Dev. 90, 940–956. doi: 10.1111/cdev.12948

PubMed Abstract | CrossRef Full Text | Google Scholar

Mix, K. S. (2019). Why are spatial skill and mathematics related? Child Dev. Persp. 13, 121–126. doi: 10.1111/cdep.12323

CrossRef Full Text | Google Scholar

Mix, K. S., Levine, S. C., Cheng, Y.-L., Young, C., Hambrick, D. Z., Ping, R., et al. (2016). Separate but correlated: The latent structure of space and mathematics across development. J. Exp. Psychol. Gen. 145, 1206–1227. doi: 10.1037/xge0000182

PubMed Abstract | CrossRef Full Text | Google Scholar

National Mathematics Advisory Panel. (2008). Foundations for Success: Final Report of the National Mathematics Advisory Panel. Washington, DC: United States Department of Education.

Google Scholar

Peng, P., and Lin, X. (2019). The relation between mathematics vocabulary and mathematics performance among fourth graders. Learning and Individual Differences 69, 11–21. doi: 10.1016/j.lindif.2018.11.006

CrossRef Full Text | Google Scholar

Powell, S. R., Berry, K. A., and Tran, L. M. (2020). Performance differences on a measure of mathematics vocabulary for English Learners and non-English Learners with and without mathematics difficulty. Reading Writing Q. Overcoming Learning Difficulties 36, 124–141. doi: 10.1080/10573569.2019.1677538

CrossRef Full Text | Google Scholar

Powell, S. R., Driver, M. K., Roberts, G., and Fall, A. M. (2017). An analysis of the mathematics vocabulary knowledge of third-and fifth-grade students: Connections to general vocabulary and mathematics computation. Learn. Ind. Diff. 57, 22–32. doi: 10.1016/j.lindif.2017.05.011

CrossRef Full Text | Google Scholar

Powell, S. R., and Nelson, G. (2017). An investigation of the mathematics-vocabulary knowledge of first-grade students. Elementary School J. 117, 664–686. doi: 10.1086/691604

CrossRef Full Text | Google Scholar

Purpura, D. J., and Logan, J. A. (2015). The nonlinear relations of the approximate number system and mathematical language to early mathematics development. Dev. Psychol. 51, 1717. doi: 10.1037/dev0000055

PubMed Abstract | CrossRef Full Text | Google Scholar

Purpura, D. J., Logan, J. A., Hassinger-Das, B., and Napoli, A. R. (2017). Why do early mathematics skills predict later reading? The role of mathematical language. Dev. Psychol. 53, 1633. doi: 10.1037/dev0000375

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team. (2022). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Vienna, Austria.

Google Scholar

Ramirez, G., Gunderson, E. A., Levine, S. C., and Beilock, S. L. (2013). Math anxiety, working memory, and math achievement in early elementary school. J. Cognit. Dev. 14, 187–202. doi: 10.1080/15248372.2012.664593

PubMed Abstract | CrossRef Full Text | Google Scholar

Ritchie, S. J., and Bates, T. C. (2013). Enduring links from childhood mathematics and reading achievement to adult socioeconomic status. Psychol. Sci. 24, 1301–1308. doi: 10.1177/0956797612466268

PubMed Abstract | CrossRef Full Text | Google Scholar

Roth, B., Becker, N., Romeyke, S., Schäfer, S., Domnick, F., Spinath, F. M., et al. (2015). Intelligence and school grades: a meta-analysis. Intelligence 53, 118–137. doi: 10.1016/j.intell.2015.09.002

CrossRef Full Text | Google Scholar

Runnels, J. (2012). Using the Rasch model to validate a multiple choice English achievement test. Int. J. Lang. Studies 6, 141–155.

Google Scholar

SAS. (2014). Statistical Analysis System 9, 2. Cary, NC: SAS.

Google Scholar

Scofield, J. E., Hoard, M. K., Nugent, L., LaMendola, J. V., and Geary, D. C. (2021). Mathematics clusters reveal strengths and weaknesses in adolescents' mathematical competencies, spatial abilities, and mathematics attitudes. J. Cognit. Dev. 22, 695–720. doi: 10.1080/15248372.2021.1939351

PubMed Abstract | CrossRef Full Text | Google Scholar

Siegler, R. S., and Booth, J. L. (2004). Development of numerical estimation in young children. Child Develop. 75, 428–444. doi: 10.1111/j.1467-8624.2004.00684.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Siegler, R. S., Thompson, C. A., and Schneider, M. (2011). An integrated theory of whole number and fractions development. Cognitive Psychol. 62, 273–296. doi: 10.1016/j.cogpsych.2011.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Sistla, M., and Feng, J. (2014). “More than numbers: Teaching ELLs mathematics language in primary grades,” in Proceedings of the Chinese American Educational Research & Development Association Annual Conference (Philadelphia, PA).

Google Scholar

Stoet, G., and Geary, D. C. (2022). Sex differences in adolescents' occupational aspirations: variations across time and place. Plos ONE 17, e0261438. doi: 10.1371/journal.pone.0261438

PubMed Abstract | CrossRef Full Text | Google Scholar

Toll, S. W., and Van Luit, J. E. (2014). The developmental relationship between language and low early numeracy skills throughout kindergarten. Excep. Children 81, 64–78. doi: 10.1177/0014402914532233

CrossRef Full Text | Google Scholar

Turan, E., and Smedt, D. e. B. (2022). Mathematical language and mathematical abilities in preschool: A systematic literature review. Educ. Res. Rev. 4, 100457. doi: 10.1016/j.edurev.2022.100457

CrossRef Full Text | Google Scholar

Ünal, Z. E., Greene, N. D., Lin, X., and Geary, D. C. (2023). What is the source of the correlation between reading and mathematics achievement? Two meta-analytic studies. Educ. Psychol. Rev. 35, 4. doi: 10.1007/s10648-023-09717-5

CrossRef Full Text | Google Scholar

Ünal, Z. E., Powell, S. R., Özel, S., Scofield, J. E., and Geary, D. C. (2021). Mathematics vocabulary differentially predicts mathematics achievement in eighth grade higher-versus lower-achieving students: Comparisons across two countries. Learning Ind. Diff. 92, 102061. doi: 10.1016/j.lindif.2021.102061

CrossRef Full Text | Google Scholar

Uttal, D. H., Meadow, N. G., Tipton, E., Hand, L. L., Alden, A. R., Warren, C., et al. (2013a). The malleability of spatial skills: A meta-analysis of training studies. Psychol. Bulletin 139, 352–402. doi: 10.1037/a0028446

PubMed Abstract | CrossRef Full Text | Google Scholar

Uttal, D. H., Miller, D. I., and Newcombe, N. S. (2013b). Exploring and enhancing spatial thinking. Curr. Direc. Psychol. Sci. 22, 367–373. doi: 10.1177/0963721413484756

CrossRef Full Text | Google Scholar

Van Zile-Tamsen, C. (2017). Using Rasch analysis to inform rating scale development. Res. Higher Educ. 58, 922–933. doi: 10.1007/s11162-017-9448-0

CrossRef Full Text | Google Scholar

Vanluydt, E., Supply, A. S., Verschaffel, L., and Van Dooren, W. (2020). (2021). The importance of specific mathematical language for early proportional reasoning. Early Childhood Res. Q. 55, 193–200. doi: 10.1016/j.ecresq.2020.12.003

CrossRef Full Text | Google Scholar

Verdine, B. N., Golinkoff, R. M., Hirsh-Pasek, K., and Newcombe, N. S. (2017). I. Spatial skills, their development, and their links to mathematics. Monographs Soc. Res. Child Dev. 82, 7–30. doi: 10.1111/mono.12280

PubMed Abstract | CrossRef Full Text | Google Scholar

Verdine, B. N., Golinkoff, R. M., Hirsh-Pasek, K., Newcombe, N. S., Filipowicz, A. T., and Chang, A. (2014). Deconstructing building blocks: preschoolers' spatial assembly performance relates to early mathematical skills. Child Dev. 85, 1062–1076. doi: 10.1111/cdev.12165

PubMed Abstract | CrossRef Full Text | Google Scholar

Wai, J., Lubinski, D., and Benbow, C. P. (2009). Spatial ability for STEM domains: aligning over 50 years of cumulative psychological knowledge solidifies its importance. J. Educ. Psychol. 101, 817–835. doi: 10.1037/a0016127

CrossRef Full Text | Google Scholar

Zhang, X., and Lin, D. (2017). Does growth rate in spatial ability matter in predicting early arithmetic competence? Learning Instr. 49, 232–241. doi: 10.1016/j.learninstruc.2017.02.003

CrossRef Full Text | Google Scholar