Mathematics education research on algebra over the last two decades: quo vadis?

Veith, Joaquin Marc; Beste, Meeri-Liisa; Kindervater, Marco; Krause, Michel; Straulino, Michael; Greinert, Franziska; Bitzenbauer, Philipp

doi:10.3389/feduc.2023.1211920

REVIEW article

Front. Educ., 09 August 2023

Sec. STEM Education

Volume 8 - 2023 | https://doi.org/10.3389/feduc.2023.1211920

Mathematics education research on algebra over the last two decades: quo vadis?

$\r\nJoaquin Marc Veith$ Joaquin Marc Veith¹^*

Meeri-Liisa Beste¹

Marco Kindervater¹

Michel Krause¹

Michael Straulino²

Franziska Greinert³

Philipp Bitzenbauer²

¹Institut für Mathematik und Angewandte Informatik, Stiftung Universität Hildesheim, Hildesheim, Germany
²Professur für Didaktik der Physik, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany
³Institut für Fachdidaktik der Naturwissenschaften, Technische Universität Braunschweig, Braunschweig, Germany

Algebra is a crucial component of mathematics education as it introduces learners to the mathematical world of modeling relationships and handling abstract quantities. The increasing volume of scholarly work in the field has been analyzed qualitatively in numerous systematic reviews—a quantitative breakdown of the field, however, remains a desideratum to date. With this study we contribute to closing this gap by reporting on the results of a bibliometric analysis. We retrieved data from Scopus and Web of Science databases and analyzed 1,825 articles published between 2003 and 2022. On the one hand, we provide insight into the current state of algebra education from primary up to tertiary education by describing the scientific production and its bibliographic topography. On the other hand, we analyzed the data to identify trends and future directions. The results of our study indicate, among other aspects, that APOS Theory and Realistic Mathematics Education are emerging themes in the field that have great potential to shape future research.

1. Introduction

Algebra education is a critical subject in mathematics education that provides the foundation for higher-level mathematics concepts and is essential in many STEM fields (science, technology, engineering, and mathematics). It is often seen as “the gateway to higher mathematics” (Stein et al., 2011, p. 454) and as researchers and educators alike seek to better understand how to improve students' understanding and achievement in algebra it “is subject to worldwide scrutiny” (Drijvers et al., 2011b, p. 5). Thus, over the years, numerous studies have investigated various aspects of algebra education, such as the effect of different instructional approaches (Haas, 2005; Rakes et al., 2010; Durkin et al., 2021), the impact of technology (Drijvers et al., 2011a; Hegedus et al., 2015), the role of teacher training (McCrory et al., 2012; Pincheira and Alsina, 2021), and the influence of student characteristics (Britt and Irwin, 2008; Blanton et al., 2015b). The relevance of algebra education in this collective effort is summarized memorably by Tall and Thomas who argued that “there is a stage in the curriculum when the introduction of algebra may make simple things hard, but not teaching algebra will soon render it impossible to make hard things simple” (Tall and Thomas, 1991, p. 128). Consequently, the body of research has been vastly expanding over the past two decades and this rapid growth in the number of scientific publications has led to the need to compile results and summarize findings, resulting in several systematic literature reviews, e.g., concerned with classroom instructions (Rakes et al., 2010), professional development (Pincheira and Alsina, 2021), early algebra (Eriksson, 2022), algebraic thinking (Sibgatullin et al., 2022), and student misconceptions (Bush and Karp, 2013).

However, in recent years, advances in research methodologies and the availability of large-scale bibliometric data sets have opened new avenues for investigating algebra education research. Applying sophisticated and fine-grained search queries to extensive online databases now entails a coherent network of bibliographical data that can be analyzed quantitatively – a perspective which “amazing new means of literature study are emerging from” (Drijvers et al., 2020, p. 1455). This article aims to contribute to the existing body of research on algebra education by leveraging the method of bibliometric analysis and analysing the progression of this scientific field over the last two decades from a bibliometric viewpoint. In doing so, we will focus on both cognitive and affective aspects of learning throughout all educational levels to obtain a holistic perspective of the entire body of research. Specifically, we will (a) identify the most influential works, authors and journals, (b) examine emerging or declining trends, and (c) discuss possible future directions for algebra education as a whole.

To provide unfamiliar readers with a short perspective on algebra education research, we will first outline the structure of the field. It is noteworthy, however, that no summary can do this vast and complex research field justice. As such, we will only present educational key components that have been developed over the past years and shaped the field as we know it now. This qualitative depiction will then be complemented by a quantitative one by means of our assessed data.

2. Research background

2.1. Algebra education in school mathematics

Algebra education research in school settings reaches from elementary school contexts (Carpenter et al., 2005; Carraher et al., 2008; Powell et al., 2020; Kieran and Martínez-Hernández, 2022) to middle or high school contexts (Molina et al., 2017; Jiang et al., 2022; Papadopoulos and Thoma, 2022) and are linked by the broad notion of early algebra which “focuses on principles and representations of algebra that can be and presumably need to be mastered by young students as the foundations for later learning” (Carraher and Schliemann, 2020, p. 249). Several key notions have been developed to better describe students' understanding of algebraic concepts, such as algebraic reasoning (Kaput, 1998), algebraic thinking (Kieran, 2004), relational thinking (Carpenter et al., 2005), and functional thinking (Blanton and Kaput, 2011). These notions are linked through a variety of recurring mathematical foci such as patterns, structure, operations, and relations. The notion of algebraic reasoning, for example, goes back to Kaput (1998) who enunciated its core characteristics, among others, as

• generalizing and formalizing patterns and regularities,

• studying structures and systems abstracted from computations and relations.

• and studying functions and relations.

This characterization formed the basis for a later definition of relational thinking by Jacobs et al. who conceived it as “looking at expressions and equations in their entirety, noticing number relations among and within these expressions and equations” (Jacobs et al., 2007, p. 260). Similarly, algebraic thinking is often described as a combination of operating on unknown, thinking in terms of variables and their relations as well as acknowledging algebraic structures (Carraher and Schliemann, 2020). According to Kieran (2004), algebraic thinking includes a focus on (a) relations, (b) operations as well as their inverses, (c) representing and solving a problem instead of just solving it, and (d) working with letters that represent unknown quantities. For a detailed analysis of algebraic thinking and the respective body of research we refer the reader to a recent literature review by Sibgatullin et al. (2022).

Consequently, a predominant focus in early algebra education research lies on how students reason and think algebraically (Amit and Neria, 2008; Ayala-Altamirano and Molina, 2020; Pitta-Pantazi et al., 2020; Levin and Walkoe, 2022), often building upon Kaput's framework for algebraic reasoning (Kaput, 2008). A prime example is the widely cited early algebra learning progression (EALP) by Blanton et al. (2015b) which is dedicated to fostering the development of children's algebraic thinking.

Other influential didactical products are presented by Brosseau's Theory of didactical situations (Brosseau, 1997) as a theory to describe student engagement (cf. Nyman and Kilhamn, 2014) and Realistic Mathematics Education (RME) which will constitute a recurring theme throughout this article. Realistic Mathematics Education dates back to Freudenthal (Treffers, 1993) and can be described as a domain-specific instruction theory that focuses on exploring mathematical concepts by providing real life contexts. The underlying goal is to provide learners with a sense of meaningfulness to “make them more independent and able to think more critically” (Phan et al., 2022, p. 1,134). Its growing relevance is reflected in a vastly increasing number of articles, as shown in a recent bibliometric analysis by Phan et al. (2022). Many of these publications incorporated this theory for algebraic contexts, e.g., by using it to connect algebra to geometry (Jupri, 2016) or by employing it into a design-based research intervention dedicated to fostering algebraic thinking (Apsari et al., 2019). The importance of RME radiates even into higher educational contexts such as university mathematics where interventions have been built on this theory (Veith and Bitzenbauer, 2022).

2.2. Algebra education in university mathematics

In university mathematics, algebra courses are often separated by algebraic structures. On the one hand, groups, rings, and fields are studied in abstract algebra courses. On the other hand, vector spaces are studied in linear algebra courses. Educational research follows this distinction and splits into linear algebra education research (Payton, 2019; Stewart and Thomas, 2019; Wawro et al., 2019) and abstract algebra education research (Soto-Johnson et al., 2008; Melhuish et al., 2023). Regarding the field of linear algebra education research, a comprehensive overview of the years 2008 to 2017 is provided by Stewart et al. (2019a)—themes, results and perspectives from contemporary research are discussed detailing how “students reason about a variety of topic areas in linear algebra, as well as studies that provide evidence of promising directions for supporting students success through various teaching interventions and experiments in the classroom” (Stewart et al., 2019a, p. 1,017) in order to derive possible directions for future research. Moreover, several frameworks for student understanding of linear algebra concepts have been developed in recent years, for example by

• Zandieh et al. (2019) in the context of bases of vector spaces, or

• Larson and Zandieh (2013) regarding a conceptual framework concerned with the interpretation of matrix equations which was later expanded to include more general systems of linear equations (Zandieh and Andrews-Larson, 2019).

A central theory about learning abstract algebraic concepts which the above-mentioned frameworks—and many other works in the field—are based on is the APOS Theory developed by Dubinsky and McDonald (2001)—a constructivist learning theory according to which students mentally construct their own representations of mathematical models in a progressive sequence of stages. Each letter in the acronym APOS represents one of four cognitive stages:

• Actions are transformations of a mathematical object that are perceived as essentially external, meaning that algorithms or step-by-step instructions are required to conduct them.

• On the next stage, actions turn into processes when they are repeated through exercise until an internal representation has been built.

• Objects are then constructed from processes when the learner becomes aware of this process and is able to derive a generalization of the mathematical object through it.

• Lastly, all actions, processes and objects that belong to a specific mathematical object are collected in a schema. Learners then make sense of abstract algebraic notions by coordinating different schemas for different objects.

More details regarding this theory are provided by Arnon et al. (2001) and its use in the context of mental constructions involved in the learning of linear algebra topics is substantiated by Altieri and Schirmer (2019), Okta (2019), and Trigueros (2019).

Another widely used framework is presented by Tall's Three Worlds of Mathematics (Tall, 2004) which aims at describing general development of mathematical thinking by categorizing three different mental worlds of mathematics: conceptual embodiment, operational symbolism and axiomatic formalism (Tall, 2013). This was used, for example, by Stewart et al. (2019b) who tracked an instructor's movement between these three worlds in order to examine his reflection on teaching linear algebra. In addition, Stewart and Thomas used this framework to analyse students' “views on understanding of proof, the purpose of a proof, and when and how proofs communicate to them” (Stewart and Thomas, 2019, p. 1,069) in a linear algebra course. Additional works can be located in the area of tension between linear algebra and abstract algebra as they are concerned with investigating how students make sense of algebraic structures like vector spaces (Caglayan, 2019; Wawro et al., 2019).

In the case of abstract algebra, APOS Theory has been a recurring theme as well: Especially in the development of concept inventories, namely the Group Theory Concept Assessment (GTCA; Melhuish, 2019) and the Concept Inventory for Introductory Group Theory (CI²GT; Veith et al., 2022a). Both instruments aim at empirically assessing students' conceptual understanding of group theory notions and leveraged APOS Theory to (a) gain insights into learners' cognitive progression and to (b) uncover learning difficulties that were encountered along the way (Veith et al., 2022b). An overarching review on research in abstract algebra education, however, constitutes a desideratum to date.

2.3. Affective aspects of teaching and learning algebra

According to Philipp (2007) affect can be perceived as “a disposition or tendency or an emotion or feeling attached to an idea or object”. This concept sets itself apart from cognition and encompasses many more specific terms like attitudes, emotions and beliefs (McLeod, 1992). Beliefs can be described as “psychologically held understandings, premises, or propositions about the world that are thought to be true” (Philipp, 2007, p. 259). A lot of research has shown that teachers' beliefs have a huge influence on their decision making and classroom practices regarding algebra education (Raymond, 1997; Beswick et al., 2012). In particular, the teachers' beliefs about mathematics content has been established as a key factor in prior research (Beswick, 2012). On the other hand, students' beliefs in algebra classrooms can be influenced by the teachers' beliefs (Patterson and Norwood, 2004) and different instructional approaches (Cifarelli et al., 2010), while changing the teachers' beliefs themselves has been proven to be a difficult endeavor (Lau, 2021).

Affective learner characteristics, e.g., students' sense of belonging (Barbieri et al., 2021), their attitudes (Murphy et al., 2016) or their ideas regarding prospective careers (Champion et al., 2011), have been found to be significant predictors of algebra achievement. Another fundamental pillar of affective learner characteristics is motivation which “refers to those energizing/arousing mechanisms with relatively direct access to the final common motor pathways, which have the potential to facilitate and direct some motor circuits while inhibiting others” (Kleinginna and Kleinginna, 1981, p. 272). Potential connections of students' achievement in school algebra (O'Shea et al., 2016; Simzar et al., 2016) and college algebra (Nguyen, 2015) to their motivation have been investigated, indicating that critical differences in motivation were most evident between high-achieving and low-achieving students. Thus, improving learners' motivation constitutes a central goal in algebra classroom and different instructional approaches have already shown positive impact, e.g., by using computer-based feedback (Corbalan et al., 2010) or putting an emphasis on cooperative learning strategies (Habtamu et al., 2022).

The last notion that needs to be introduced in this section and that has fundamentally shaped the research into affective learner characteristics is the concept of self-efficacy. Self-efficacy can be traced back to Bandura who described it as “a judgement of one's ability to organize and execute given types of performances” (Bandura, 1997, p. 21). In simpler terms, self-efficacy can be seen as the belief in one's own ability to succeed. The role of self-efficacy in algebra classrooms has been thoroughly investigated in numerous studies (Hodges and Murphy, 2009; Cifarelli et al., 2010; Topcu, 2011; Peters, 2012). Recently, the Algebra Teacher Self-Efficacy Instrument (ATSEI) has been developed by Wilkerson et al. (2018) – an instrument which allows for measuring self-efficacy in the context of algebra teaching in high school.

3. Research rationale

As outlined above, numerous frameworks, teaching concepts, theories about teaching and learning as well as test instruments have been developed and empirically evaluated over the past two decades in algebra education research. Several reviews and meta-analyses have been conducted which summarized these notions' impact in terms of future perspectives of this research field (Buteau et al., 2010; Rakes et al., 2010; Watt et al., 2016). With the latest review dating back to 2016, however, recent developments aren't captured. In addition, it is not clear from such reviews how to determine the importance of contributions and authors. Lastly, it is impossible for such qualitative reviews to set a scope beyond a specific sub-field of algebra education – however, with patterns, structures, equations and relations being at the very core of algebra education throughout all levels (cf. Section 2) it is necessary to assess whether developed ideas and notions may perhaps be unified across boundaries presented by the separation into primary, secondary and tertiary education. In other words: What emerging notions have been proven fruitful in some aspects of algebra education and can they be utilized in others? Thus, with this accumulated knowledge it is now time to take a step back and take a snapshot of the progression in algebra education over the last 20 years from a quantitative perspective—which works and authors have influenced and shaped this research field as a whole, which journals have significantly contributed to this progression and which emerging themes can be identified for future investigations?

4. Research questions

With our study we aim to address the following research questions:

RQ1: How has the scientific output in terms of research publications and citations of articles on algebra education developed over time from 2002 to 2022 in mathematics education research?

RQ2: Who are the most active authors and countries publishing articles on algebra education from 2002 to 2022?

RQ3: What are the most relevant publishing venues in mathematics education research through which studies on algebra education are disseminated from 2002 to 2022 and which are the most cited articles?

RQ4: How can the collaboration among countries be described in the context of algebra education?

RQ5: What are the most relevant key words and which co-occurrence patterns can be observed in articles on algebra education?

RQ6: What emerging topics can be identified and which topics are relevant but underdeveloped so far?

5. Methods

5.1. Study design

The research questions were investigated by means of a bibliometric analysis. Bibliometric studies are established in the educational context and especially suited for “deciphering and mapping the cumulative scientific knowledge and evolutionary nuances of well-established fields by making sense of large volumes of unstructured data in rigorous ways” (Donthu et al., 2021, p. 1). To ensure a valid procedure that is in line with up-to-date standards regarding bibliometric analyses, we closely followed the workflow recommended by Aria and Cuccurullo (2017) which comprises the following aspects:

• Study design: Defining research questions and selecting databases.

• Data collection: Selecting databases and filtering the core document set.

• Data analysis: Employing statistical software tools to analyze the document set.

• Data visualization: Deciding which visualization methods are suited for the research questions and employing appropriate mapping software.

• Interpretation: Interpreting and describing the findings.

We outline our decisions regarding all these aspects in the following subsections.

5.2. Data collection

For gathering the final set of documents for bibliometric analysis, we employed the online databases Scopus by Elsevier and Web of Science by Clarivate Analytics because of the index of impact they provide: The Scimago Journal and Country Rank (SJR) in the case of Elsevier and the Journal Citation Reports (JCR) by Clarivate, respectively. Both databases are well-established within the corpus of educational research and are usually consulted when conducting a bibliometric analysis (Hartley and Ho, 2017; Drijvers et al., 2020; Hou et al., 2022; Hou and Yu, 2023).

Both sets of document data were extracted on 20.10.2022 from the respective database. Our search strategy was to apply a broad and non-restrictive search-string in a first step to obtain a comprehensive sample of research in algebra education. To this end, we only used the search field TITLE-ABS-KEY¹ in our Scopus query and the search field TS¹ in our Web of Science query, respectively. In a subsequent co-word analysis (cf. Section 5.3) we identified commonly used keywords in the obtained articles that do not contain the word algebra but are located in algebra education, i.e., functional thinking or relational thinking. Both search queries were then extended by those missing key notions to ensure that no relevant work was omitted. The resulting search-strings are provided in Table 1 alongside the refinements and the number of documents they yielded.

TABLE 1

Table 1. Search-strings applied to the respective databases alongside the number of resulting documents.

The data sets were exported in BibTex format from the data bases and the preliminary sample was obtained by (a) merging both BibTex files (n = 3, 549), and by (b) removing all duplicates using the R-package bibliometrix (Aria and Cuccurullo, 2017) (n = 726 duplicates). The non-restrictive and broad nature of both search-strings, however, led to the inclusion of many off-topic works that needed to be filtered out. Thus, in a next step, the preliminary data set was subjected to a title-abstract screening. For this step of data collection, we adapted the PRISMA 2020 instructions (Page, 2021) as well as their extension statement PRISMA-S (Rethlefsen et al., 2021) which are commonly used in systematic literature reviews by formulating rigorous inclusion and exclusion criteria. An article was included in our bibliometric analysis if and only if all inclusion criteria.

• Investigation scope relates to algebra education in mathematics research.

• Abstract and Title in English to ensure that the manuscript is not off-topic during screening.

• Publication year is between 2003 and 2022.

• Article published in peer-reviewed Journal.

were met and if and only if none of the exclusion criteria.

• Investigation is aimed at contexts other than mathematics education (e.g., physics or computer sciences).

• Articles published in proceedings, books, etc. since there is no guarantee that a rigorous peer review process was conducted to ensure quality control.

was met. By using these inclusion and exclusion criteria the sample was refined to fit the research questions more precisely. For example, Scopus returned a research article by Maat and Zakaria (2011) because the keyword computer algebraic system was listed. However, this article reports on an investigation of students' understanding of ordinary differential equations using Maple software and is therefore off-topic. The title-abstract screening was conducted by two independent raters and dissenting judgements were resolved through discussion among the authors until full agreement was reached. This analysis step led to the exclusion of 869 entries in the Scopus file and 129 entries in the Web of Science file. Thus, the final sample to be explored in our bibliometric analysis consisted of 1,825 articles. An overview of the data selection process is provided in Figure 1 and an overview of the final sample is provided in Table 2.

FIGURE 1

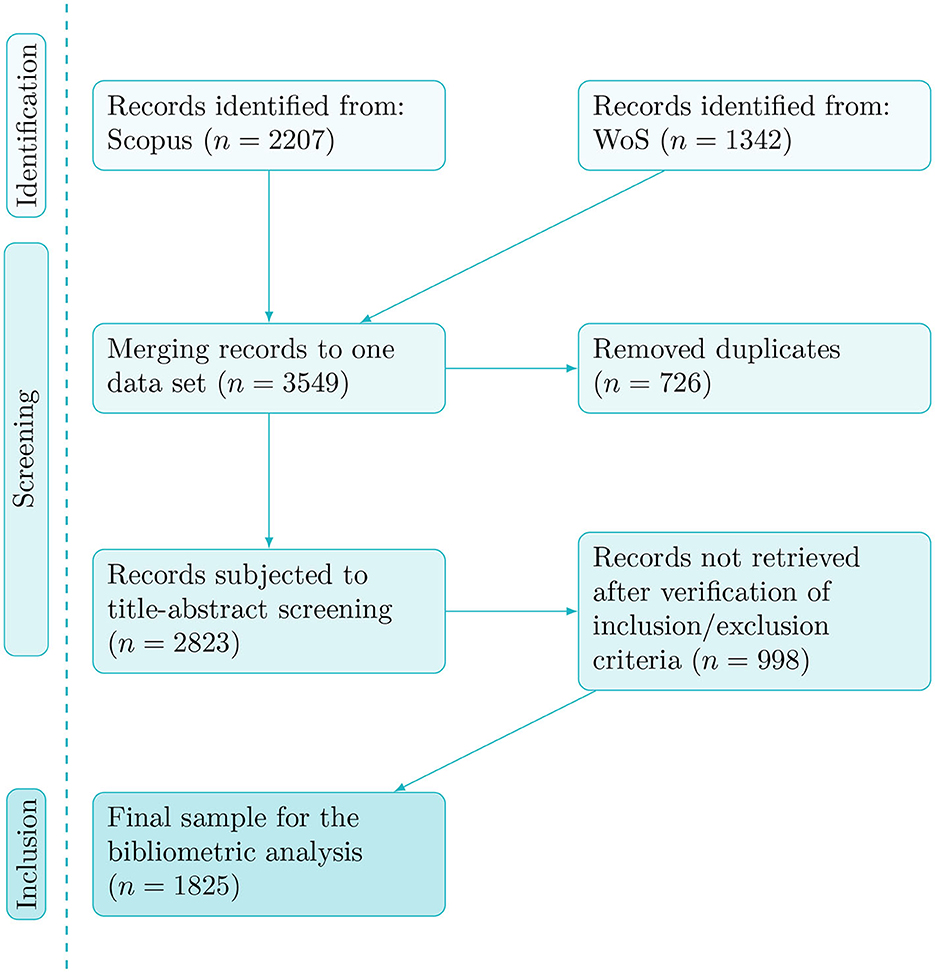
Figure 1. Flowchart of the literature review process to obtain our final sample in accordance with the PRISMA guidelines.

TABLE 2

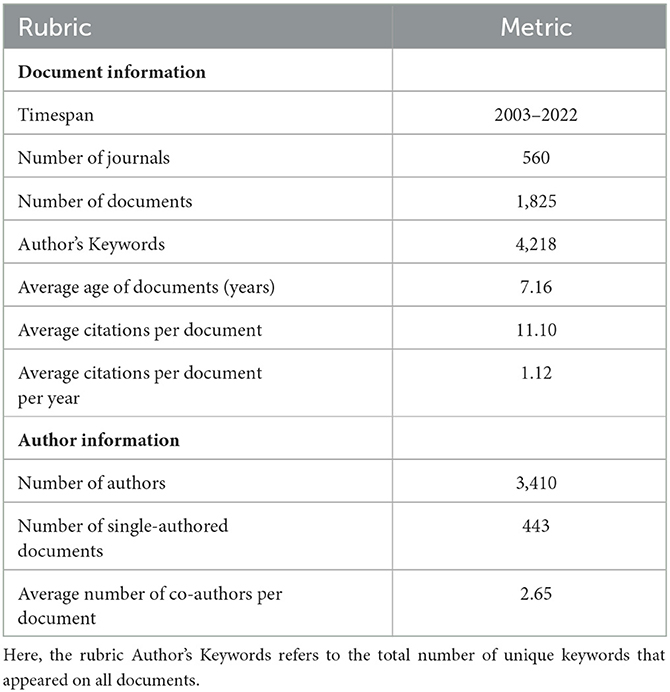
Table 2. Overview of the final data set (without duplicates) we analyzed in terms of document and author metrics.

5.3. Data analysis and visualization

The techniques for bibliometric analyses are commonly separated into the two categories performance analysis and science mapping (Bitzenbauer, 2021; Donthu et al., 2021). Performance analysis encompasses quantitative measures that aim to capture the scientific performance of different research constituents, e.g., authors, institutions, or journals. This scientific outcome is expressed in two different aspects, namely measure of productivity (e.g., number of publications per year) as well as measure of impact (e.g., number of citations per publication). Science mapping, on the other hand, analyzes the “relationships between research constituents and a field's intellectual structure” (Baker et al., 2021, p. 2) and comprises citation analysis (Appio et al., 2014), co-citation analysis (White and McCain, 1998), bibliographic coupling (Boyack and Klavans, 2010), co-word analysis (Burton et al., 2020) as well as co-authorship analysis (Kumar, 2015). In this article we follow Bitzenbauer (2021) and synthesize both performance analysis and science mapping to obtain a comprehensive overview of the field. Additionally, we have adopted an approach by Callon et al. (1991) to quantify and visualize the evolution of a research field by means of a thematic map. A thematic map is a “strategic diagram [that] is a two-dimensional space built by plotting themes according to their centrality and density rank values [...]” (Cobo et al., 2011, p. 150) where,

• “Centrality measures for a given cluster the intensity of its links with other clusters” (Callon et al., 1991, p. 164). It is therefore used as a measure of the importance of a theme in the development of a research field.

• “Density characterizes the strength of the links that tie the words making up the cluster together” (Callon et al., 1991, p. 165). It is therefore used as a measure of a theme's development.

Each theme then is located within one of four quadrants of a two-dimensional map, depending on its centrality and density value. According to Callon et al. (1991), the quadrants can be described as,

• Motor Themes (upper right): These themes are both central to the research field and well-developed. If a theme is located here, this suggests that it has been researched systematically over a long period of time.

• Niche Themes (upper left): Here reside well-developed themes that are very specialized and thus not of high relevance to the research field as a whole.

• Basic Themes (lower right): Basic Themes are relevant and as such exhibit strong connections to other clusters, but are still underdeveloped, suggesting that only a small amount of researchers work on the corresponding theme.

• Emerging or Declining Themes (lower left): Themes that have both a low relevance and development degree are located within this quadrant. They might either increase or decrease in those metrics and only a comparative analysis (comparison with other networks) allows to determine their contribution to the field (Callon et al., 1991).

Identifying key themes and their location within such a map will allow for a more detailed description of research foci of algebra education research.

An assignment of each research question to the respective bibliometric method is provided in Table 3. Our study was conducted using the statistical software R alongside the package bibliometrix (Aria and Cuccurullo, 2017) in version 4.1.3, the R-code is provided in the Appendix. For scalability and visual coherence we recreated the graphical output from bibliometrix regarding the performance analysis with PGF-TikZ in version 3.1.10, while for the science mapping we used software VOSviewer in version 1.6.19. Mathematical details regarding the co-occurrence patterns generated by this software are discussed by van Eck and Waltman (2010).

TABLE 3

Table 3. Overview of the bibliometric methods that we used to clarify each research question.

6. Results

6.1. Scientific output in algebra education research

With regards to the first research question we analyzed the number of articles published per year and their average number of citations between 2003 and 2022. Figure 2 shows the annual production with an annual growth rate of 14.26%. This significant growth is reflected by the observation that the first 5 years only account for about 7% of all publications in our sample while over 53% were published between 2017 and 2022, as indicated by the blue dashed line. Figure 2 also contains the average number of citations per article per year. It ranges from 0.5 (2022) to 3.2 (2004) and averages 1.51. In contrast to the annual scientific production, however, the number of citations is under constant change. In terms of citations, newer articles are at a natural disadvantage to the earlier articles in our time frame. As such, the observed decline from 2015 onward is plausible.

FIGURE 2

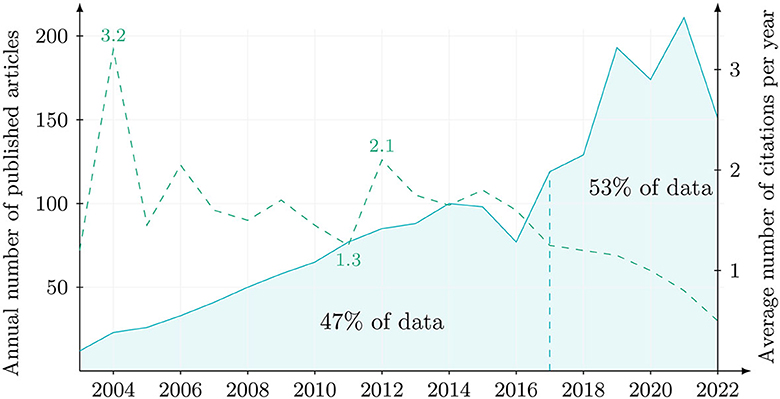
Figure 2. Annual scientific production in algebra education research from 2003 to 2022. The green dashed line indicates the average number of citations per year while the blue dashed line roughly splits the sample into two halves.

6.2. Most active authors and countries in algebra education research

In a next step, we identified the most active authors and countries publishing articles on algebra education over the past two decades. Table 4 lists the ten most productive authors in this regard alongside (a) their scientific output expressed by the number of published articles and (b) an example reference. Since the number of articles of the most productive authors ranges between 11 and 16, the data show that the field of algebra education research is not dominated by a few, outstanding authors but is rather constituted by a range of many equivalently active researchers. In addition, the articles that lead to this enumeration are not disjoint in terms of authorship (Rittle-Johnson and Star, 2007; Durkin et al., 2021; Powell et al., 2021).

TABLE 4

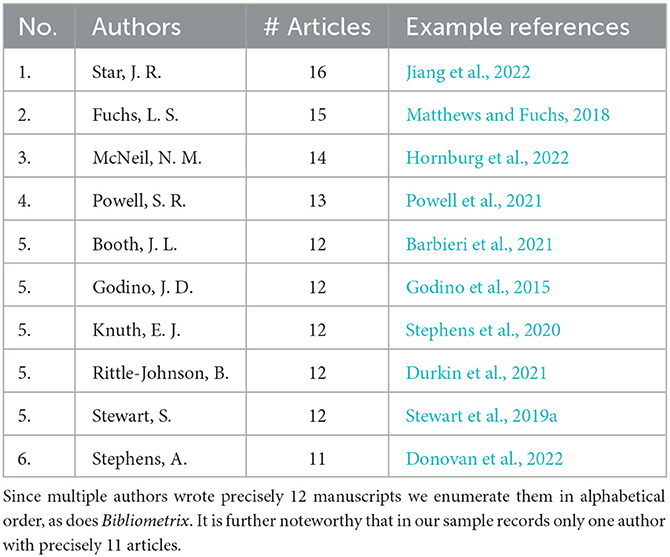
Table 4. Most productive authors in the field of algebra education over the past 2 decades according to the databases Scopus and Web of Science.

While the total number of published articles in Table 4 adequately measures scientific activity, it does not provide a deeper perspective into each researchers' body of work. A better clarification as to how recent their activity is and how impactful it is on algebra education in general is enabled by Figure 3.

FIGURE 3

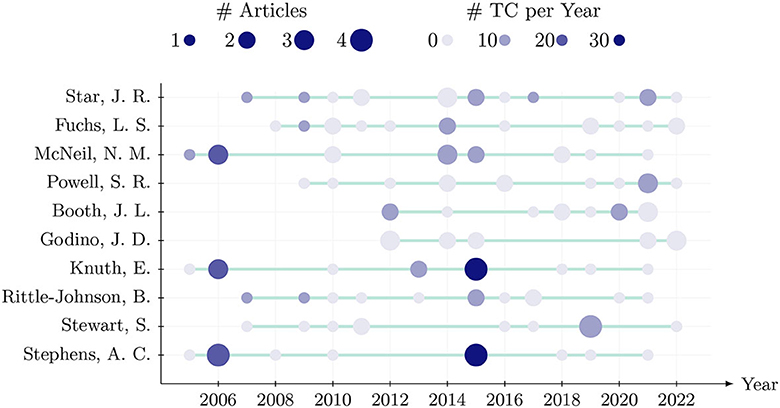
Figure 3. The top authors' scientific output over the past two decades, including the total number of published articles (Articles) as well as the total number of citations per year (TC).

While other bibliometric analyses detected that the set of the most active authors splits into (a) one part comprised of new and emerging authors that actively contributed within a short time span and (b) a longevity part consisting of authors that have consistently contributed over a long period of time (Bitzenbauer, 2021), we observe that the top authors in algebra education have been active almost the entirety of our time frame and published even in the last recorded year (2022). Figure 3 further indicates that the impact of their work (measured by the number of citations) is in most cases not concentrated within a single publication but rather spreads evenly across the whole body of work. In summary, a coherent picture emerges for algebra education research where influential works have been consistently contributed over a large period of time up to the most recent year 2022.

The list of most active authors with only one non-american author (Juan D. Godino) further suggests that algebra education research is mainly driven in the USA. This is substantiated by Figure 4 providing an overview of the total number of published articles per country, split into (a) the number of single country publications and (b) the number of multiple country publications.

FIGURE 4

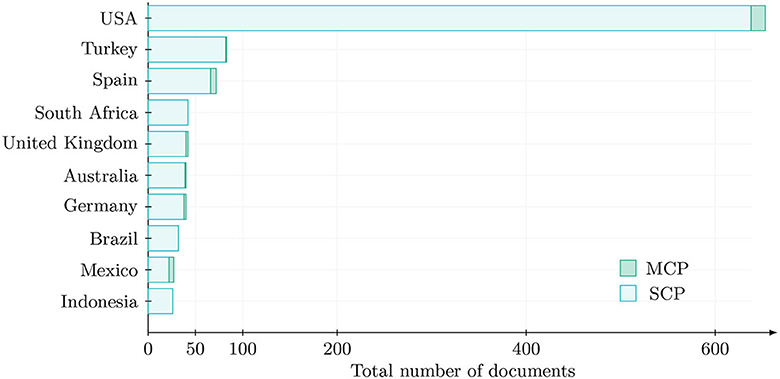
Figure 4. Total number of articles per country, including single country publications (SCP) as well as multiple country publications (MCP).

With 653 articles in total, USA-based publications account for 35.7% of articles in the sample with the runner-up being Turkey contributing a significantly lower amount of 83 publications (4.5%). This imbalance is in accordance with findings from Julius et al. (2021) who conducted a bibliometric analysis on mathematics education in general, finding that 34.64% of the 46,798 articles could be ascribed to the USA. This is underpinned by the fraction of multiple country publications being low and never exceeding 20%, with Mexico having the highest and only two-digit MCP ratio of 18.5%.

6.3. Most relevant publishing venues in algebra education research

The most relevant sources in the field of algebra education research are listed in Table 5. In the following, we will refer to these journals using the abbreviations provided in parentheses.

TABLE 5

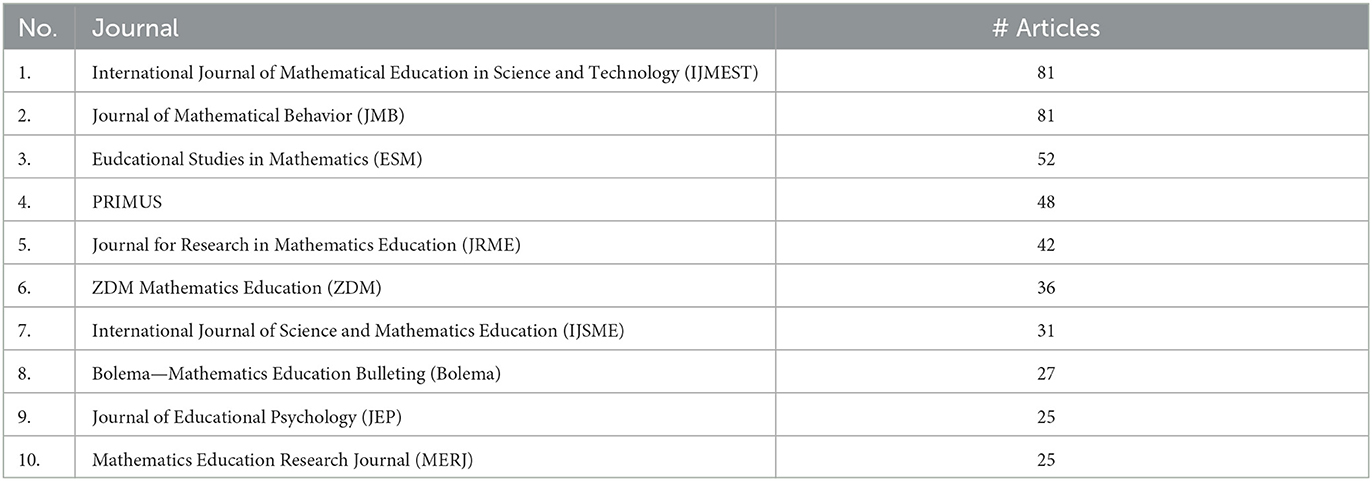
Table 5. Most relevant sources in the field of algebra education over the past two decades according to the databases Scopus and Web of Science.

The IJMEST and the JMB are tied for the first position and we observe a subsequent steep decline in the number of articles. Out of the ten entries listed in Table 5, eight match precisely with the most prolific journals listed by Julius et al. (2021), with even their order being almost identical. This suggests that algebra education research reflects well the entirety of mathematics education research in this regard. It is further noteworthy that the top two journals for algebra education research published merely 8.9% of all documents published within the time frame under investigation. This number is significantly lower when compared to bibliometric analyses of other research topics in science, such as Realistic Mathematics Education with 40.4% (Phan et al., 2022) or Quantum Physics Education with 62.0% (Bitzenbauer, 2021). This discrepancy suggests a greater diversification in terms of journals publishing articles on algebra education—the articles spread more evenly and there are numerous attractive publishing venues for researchers in the field. The source dynamics for the leading six journals in this regard are visualized in Figure 5.

FIGURE 5

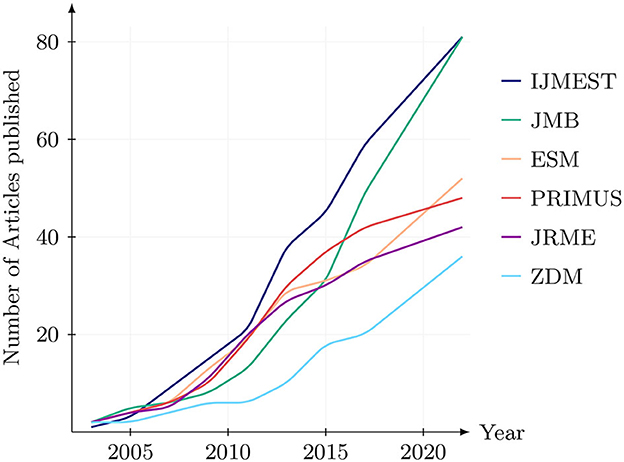
Figure 5. Cumulative number of annually published articles on algebra education research for the six most relevant sources.

The development over time shows a sharp increase in publications after 2011 for the leading journals IJMEST and JMB. The Journals ESM and ZDM also show a growing potential and a significantly increased inclination from 2017 onward. Interestingly, however, out of the top ten journals only the JRME published more than one of the most cited manuscripts in the sample (cf. Table 6) and only one further journals make an appearance in this regard, namely the JEP.

TABLE 6

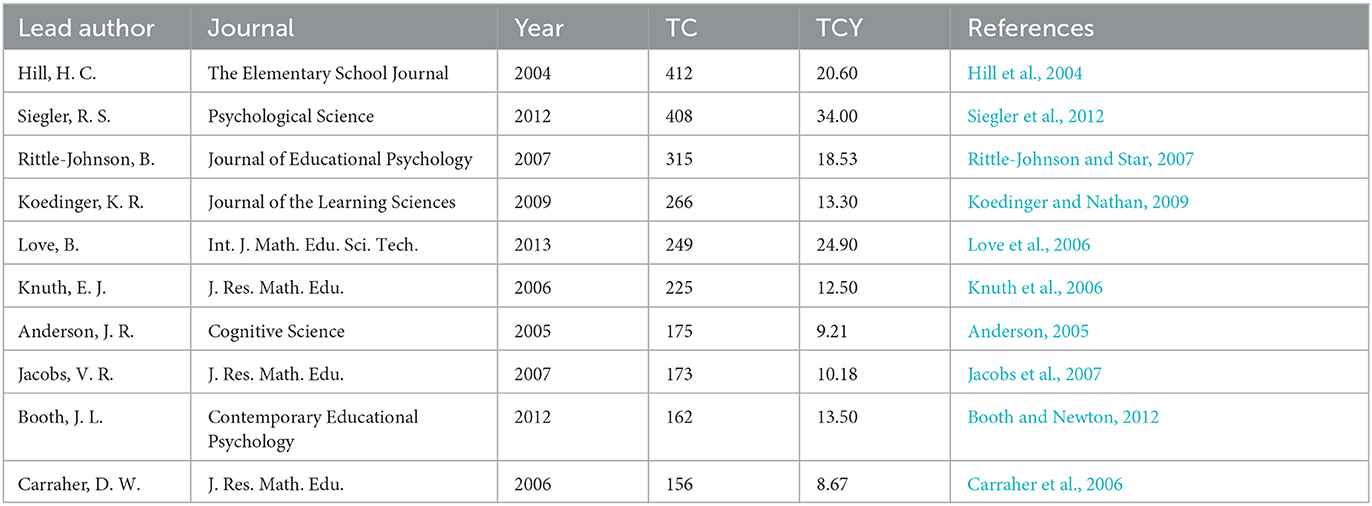
Table 6. Most globally cited manuscripts in the field of algebra education research over the past two decades, including the total number of citations (TC) as well as the total number of citations per year (TCY).

A complete list of the ten most cited manuscripts is presented in Table 6 alongside their total and yearly citation counts as well as the corresponding journal. Since journals published earlier have a head start in terms of gathering citations, the number of citations per year is sometimes used as a metric to more accurately reflect the impact of a given manuscript—we therefore provide both, the total number of citations (TC) as well as the number of citations per year (TCY).

Since the citation count in Table 6 also takes citations from outside algebra education research into account the relevance for algebra itself may be skewed. To more specifically identify the most impactful manuscripts for algebra education, we thus further investigated how many times a given article has been cited within our sample. The resulting metric of local citations (LC) leads to a list of the ten most locally cited manuscripts provided in Table 7. Precisely four entries appear in both lists (Carraher et al., 2006; Rittle-Johnson and Star, 2007; Booth and Newton, 2012; Siegler et al., 2012) and it is noteworthy, that all of them deal with concepts of school algebra education rather that university algebra education.

TABLE 7

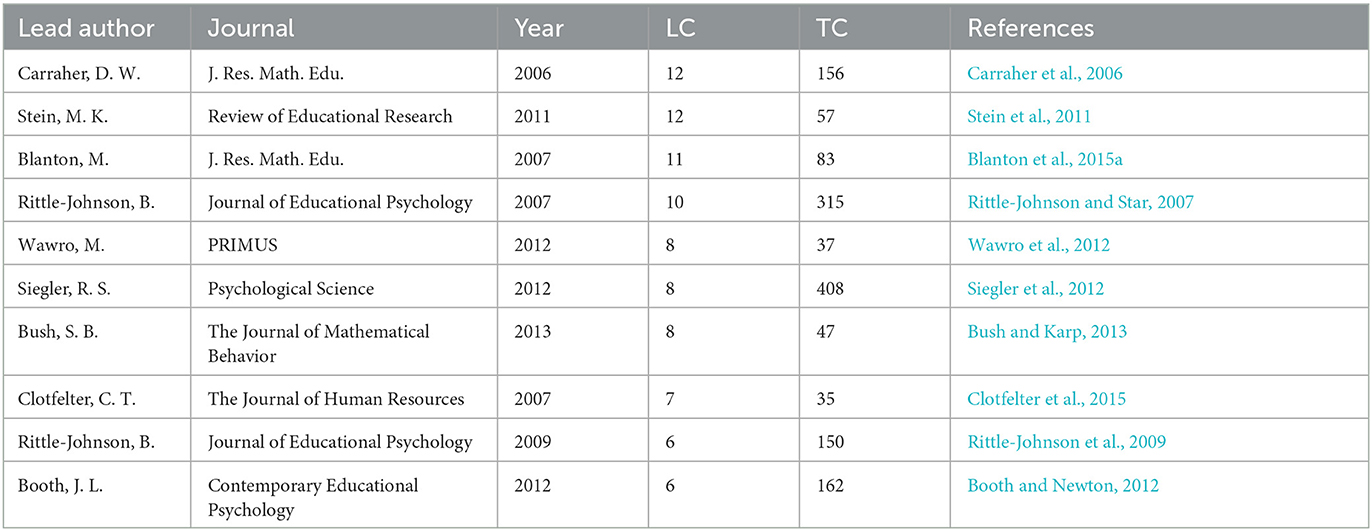
Table 7. Most locally cited manuscripts in the field of algebra education research over the past two decades, including the number of local citations (LC) as well as the global number of citations (TC).

6.4. Country co-authorships in algebra education research

To explore the co-authorship between countries, we computed a co-authorship network where each country is represented by a circle node and each collaboration between two countries is represented by a corresponding edge. The resulting Figure 6 complements Figure 4 by exploring how the multiple country publications are synthesized.

FIGURE 6

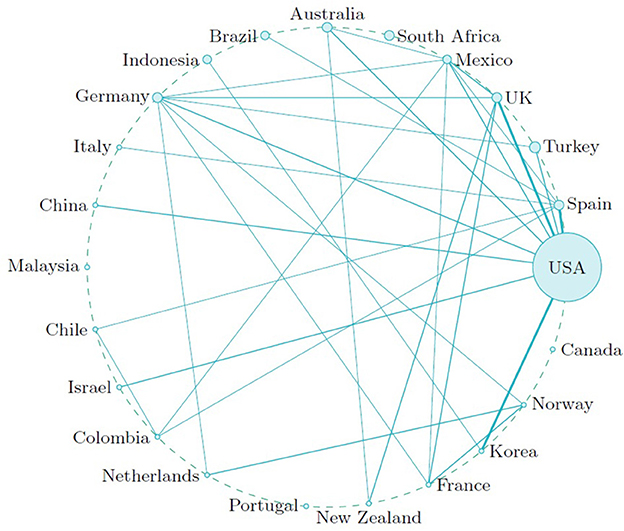
Figure 6. Co-authorship network regarding the authors' countries. Node size indicates total number of publications per country and line width indicates the number of collaborative publications.

Consequently to our earlier observations the USA constitutes the largest node. With 9 edges it also exhibits the largest amount of different country collaborations. In descending order follow Mexico and Germany (seven edges each), Spain (6), UK (5), and France (4).

6.5. Key word co-occurrences

The fifth research question addresses the most relevant key words in algebra education research articles and the emerging co-occurrence pattern connecting them. In our frequency analysis we manually excluded trivial terms like algebra or student as their general nature does not contribute much to an exploration of research foci. Additionally, a minimum of 10 documents had to contain the respective key word in order for it to appear in our analysis (Bitzenbauer, 2021; Julius et al., 2021). This resulted in a total of 435 key words, the pattern of which is visualized in Figure 7.

FIGURE 7

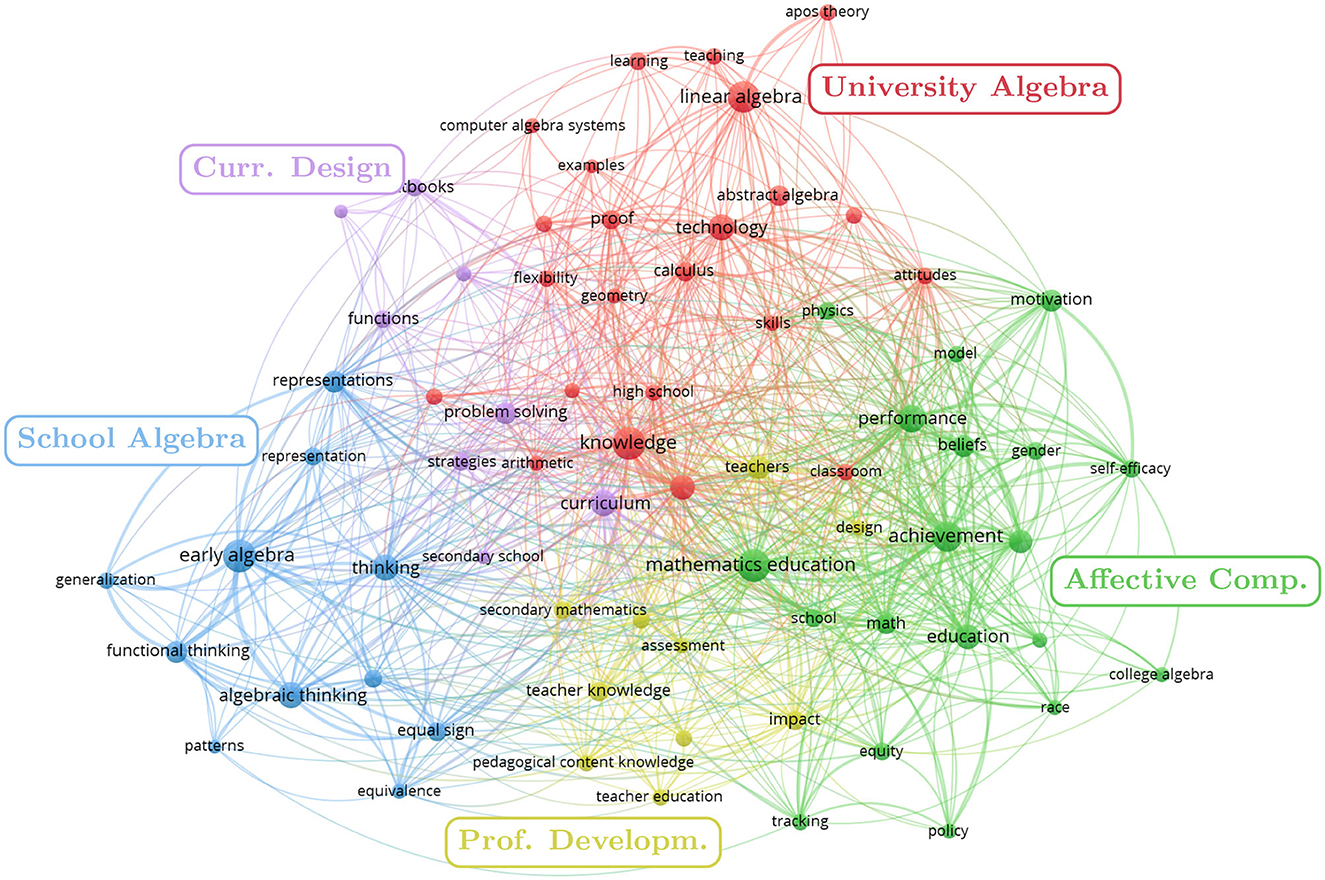
Figure 7. Co-occurrence pattern of key words in algebra education research articles, generated by VOSviewer. The size of each node is proportional to the frequency with which the key word has been mentioned in articles and each co-occurrence is indicated by a line connecting two nodes. The line width scales with the number of co-occurences.

As indicated by the different colors, three primary clusters (blue, red, and green) and two secondary clusters (violet and yellow) emerge. Of these five clusters none takes a central position but they instead share a common center consisting of the broad notions knowledge, teachers, curriculum, and mathematics education. The clusters become progressively specific and diverse with increasing distance from the center. Among the non-central notions the most frequently used key words in each cluster are early algebra (87 mentions, blue), linear algebra (82 mentions, red), achievement (67 mentions, green), problem solving (32 mentions, violet), and teacher knowledge (21 mentions, yellow). Comparing this finding with the remaining key words of each cluster draws a coherent picture:

• The blue cluster indicates a research focus on the teaching of school algebra. Students either visit secondary schools or learn early algebra. Key notions are functional thinking, algebraic thinking, patterns, representations and equivalences.

• The red cluster, on the contrary, hints to a research focus on university-level algebra, e.g., in the context of linear algebra or abstract algebra. Algebra education in this cluster also manifests in terms of geometry and calculus, demonstrating its characteristic trait of connecting different mathematics disciplines. Examples for key notions are proofs and APOS Theory.

• The green cluster highlights research that focusses on affective learner characteristics. Respective articles deal with beliefs, self-efficacy, and motivation in the context of algebra education research. It is noteworthy that the green cluster is located diametrically opposed to the blue cluster, indicating that those affective notions exhibit stronger links with key words of the red cluster of university-level algebra education and the yellow cluster. The yellow cluster is represented via the notions teacher knowledge, teacher education, and pedagogical content knowledge and thus summarizes the aspects of professional development. Consequently, its primary connections are to the blue and green cluster.

• Lastly, the violet cluster links the blue and red cluster by focusing on curriculum design. Its position between those clusters suggests that the design of a school curriculum and corresponding textbooks are informed by university-level mathematics which are represented by the red cluster.

In summary, a holistic perspective on algebra education emerges that factorizes into self-contained subdomains which cover various educational aspects. A deeper look into the movement of algebra education as a research field is enabled by applying a temporal topography to the co-occurrence pattern. The resulting Figure 8 uses a color gradient to indicate the recency of each key word—the brighter the node color the more recent the research activity on the respective notion.

FIGURE 8

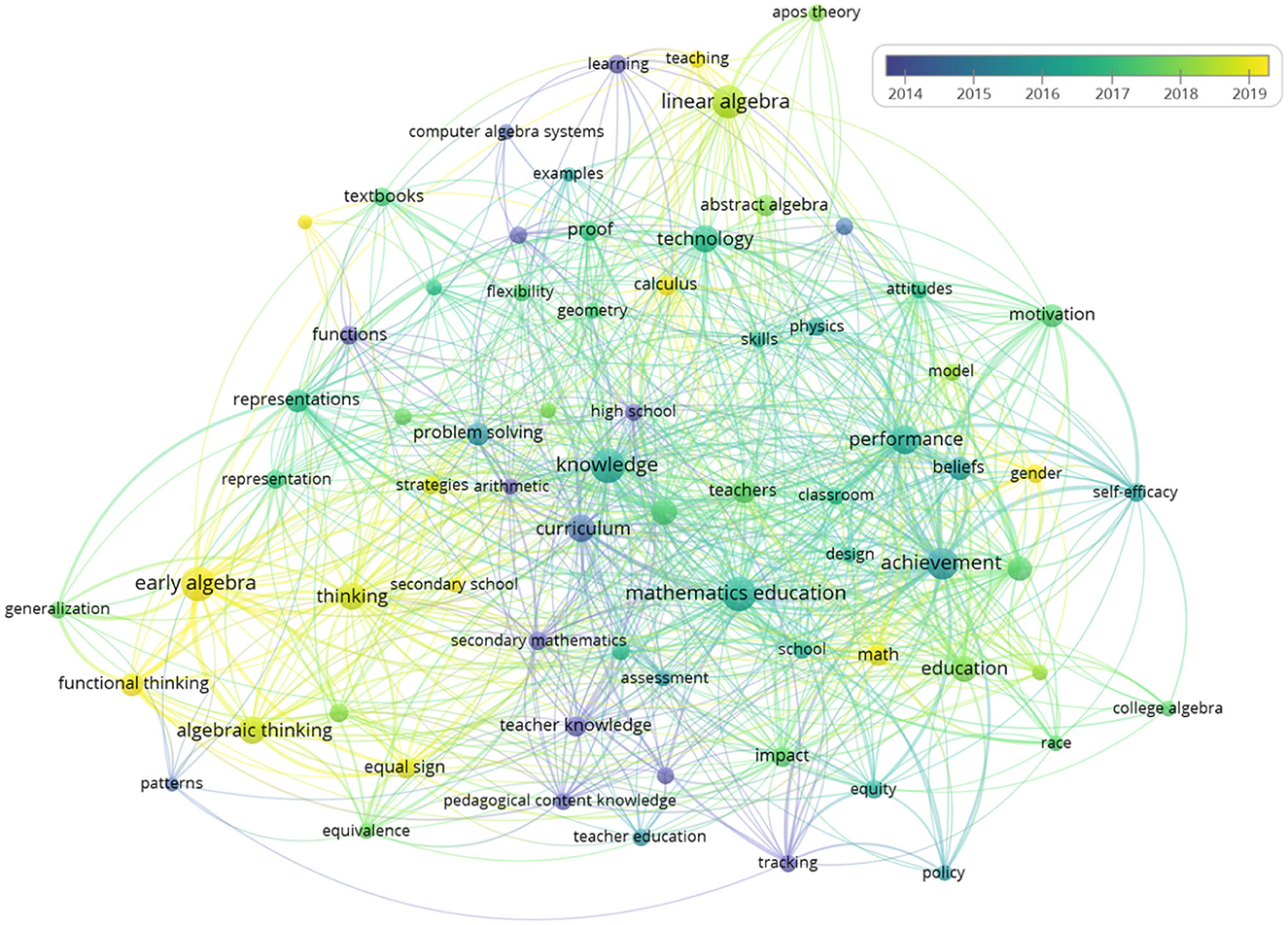
Figure 8. Co-occurrence pattern of key words in algebra education research articles, generated by VOSviewer. The size of each node is proportional to the frequency the key word has been mentioned in articles and each co-occurrence is indicated by a line connecting two nodes. Here, the recency scales with the brightness.

In accordance with our findings in Section 6.6, early algebra and its core notions of functional and algebraic thinking remain pertinent up to date. Another striking observation can be made regarding the cluster of affective learning variables: While beliefs and self-efficacy can be mainly located in the years 2016 and older, the research on the role that gender partakes in algebra education seems highly topical (Hardebolle et al., 2022; Sproesser et al., 2022; Geary et al., 2023).

6.6. Emerging and underdeveloped topics in algebra education research

In a final step, we leverage the science mapping method (cf Section 5) to assess different key word clusters of algebra education research in terms of their relevance and derive future directions for the research field as a whole (cf. Section 5). The thematic map for our sample is provided in Figure 9.

FIGURE 9

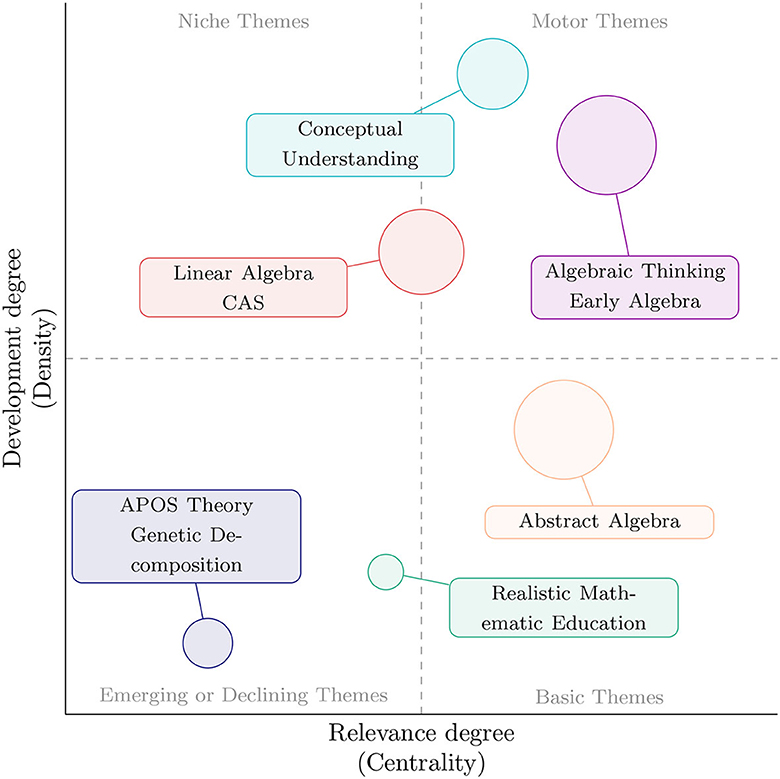
Figure 9. Thematic map of the entire research field of algebra education. The node size is directly proportional to the number of occurrences of the respective key words that constitute the theme.

Under the plotting conditions (cf. Appendix) six themes occurred in our thematic map of which only Linear Algebra and CAS are partially located in the Niche Themes quadrant. The most developed theme is tied to conceptual understanding which comes to no surprise, as some of the most influential works presented earlier, especially by Rittle-Johnson, are directly concerned with this notion, both inside (Rittle-Johnson, 2014; Rittle-Johnson and Schneider, 2014; Rittle-Johnson et al., 2015, 2016) and outside of our time frame (Rittle-Johnson et al., 2001).

In terms of development, there is a strict descending hierarchy in Early Algebra, Linear Algebra, and Abstract Algebra. While the different algebra themes differ only slightly in terms of relevance, the non-university context is by far the most developed. This might be connected to Early Algebra being a necessary stage in every educational pathway regarding algebra, while Linear Algebra and Abstract Algebra are far more specialized and complex fields. Consequently, more work has been put into paving the way for school students by laying the foundations of algebra understanding [e.g., by developing dedicated notions such as algebraic thinking (Kieran, 2004) or algebraic reasoning (Kaput, 2008)]. Coherently, APOS Theory as a constructivist framework for conceptual understanding developed specifically for university-level algebra (Arnon et al., 2001; Dubinsky and McDonald, 2001) shows a comparatively low development degree. As mentioned above, to further explore whether this marks an emerging or declining theme we will connect these findings with the ones from Section 6.5 in the discussion section of this article. Lastly, Realistic Mathematics Education (van den Heuvel-Panhuizen and Drijvers, 2020) emerges at the borderline between Basic Themes and Emerging or Declining Themes, indicating that this didactical approach is central but underdeveloped so far. This will be further discussed in the next section as well.

7. Discussion

In this article we report on the results of a bibliometric analysis of the algebra education research field with 1,825 articles which, in the following, serve as a foundation to (a) derive a concise overview of said field by exploring the results of the performance analysis and (b) discuss implications for future research suggested by the science mapping analysis.

7.1. Discussion of performance analysis results

The performance analysis clearly displays the vastly growing output of research in algebra education. More than half of all published articles in the years 2003 to 2022 can be located in the most recent quarter of this time frame. Additionally, the data show that the most prolific authors excel in a steady and impactful contribution over both decades and influential works spread evenly. The research field as a whole is especially driven by authors from the USA and in this regard accurately reflects mathematics education in general (Julius et al., 2021). As such, more than every third (35.7%) manuscript is written by an author from the USA. The publishing venues through which such articles are disseminated are dominated by the International Journal of Mathematical Education in Science and Technology and the Journal of Mathematical Behavior with the ZDM Mathematics Education and Educational Studies in Mathematics on the rise since around 2017. Even though the impact of the top two journals exceeds the rest of the field there exist a plethora of attractive journals and in comparison to other research areas algebra education can be described as highly diversified in this regard. Consequently the research foci of the top articles exhibit a large diversification as well, ranging from secondary school algebra (Anderson, 2005; Knuth et al., 2006; Booth and Newton, 2012), professional development contexts (Hill et al., 2004; Jacobs et al., 2007), or theoretical notions such as conceptual and procedural knowledge (Rittle-Johnson and Star, 2007; Siegler et al., 2012) to quantitative reasoning (Koedinger and Nathan, 2009). In summary, the results of the performance analysis provide a comprehensive overview of what research has been conducted so far in the field of algebra education. This overview is now to be complemented by a look into the future asking how the results from the science mapping may inform subsequent research and in which aspects the field may still improve upon.

7.2. Discussion of science mapping results

Regarding research question 4, we record no strong collaboration among countries—the amount of multiple country publications is negligible (cf. Figure 4) and only USA, Germany, Spain and UK have connections to 5 or more other countries (cf. Figure 6). In other words, the algebra education research community can still improve in terms of collaborative networks. More than 25% of all documents in our collection were authored by a single researcher whereas other fields record fractions <20% as shown in a recent study on co-authorship networks (Anderson et al., 2017). This is especially important to pollinate ideas across different islands of research groups. A prime example in this regard is illustrated by the didactical approach of Realistic Mathematics Education (RME) which originated in the Netherlands – a country with only two recorded collaborations in Figure 6. The thematic map presented in Figure 9 showed that RME is either an emerging or declining theme. The recent publication of a dedicated chapter in the Encyclopedia of Mathematics Education (van den Heuvel-Panhuizen and Drijvers, 2020) and up-to-date articles leveraging it (Veith and Bitzenbauer, 2022) suggest that it is more emerging than declining, underpinned by a bibliometric analysis of RME showing that the number of articles drastically increased in recent years (Phan et al., 2022). However, the development degree of RME is still very low, indicating that future research needs to further build connections to other algebra education topics.

A similar observation can be made regarding APOS Theory. According to the thematic map (cf. Figure 9) its relevance and development degree are both rather low which locates it in the same quadrant as RME. Again, however, it can be assumed that it constitutes an emerging theme rather than a declining theme as expressed by the temporal topography in Figure 8 and a plethora of recent articles concerned with this theory (Zhong et al., 2022; Kemp and Vidakovic, 2023). Since APOS Theory helps to understand learning of university-level students, the question arises as to whether it may also serve as a sensible endeavor for research of learning algebra in the context of higher secondary education. After all, prospective high-school graduates and 1st-year university students are almost identical target groups on a cognitive level which is in conflict with the fact that APOS Theory is at the very end of its cluster (cf. Figure 7) with not a single link to school algebra. We argue that a lot of potential here is still unutilized and future research should focus more on excavating educational connections between high school and university algebra. First steps in this regard have already been made by Lee and Heid (2018) who developed the so-called EDUS framework that bridges the gap between said disciplines by connecting notions of APOS Theory with those of algebraic thinking. In order to develop a structural perspective on mathematics, according to the EDUS framework, university students should follow a progression through four different stages of learning:

1. The E in EDUS stands for “extending a context in which a set of existing understandings are situated” (Lee and Heid, 2018, p. 309). For example, in the case of developing a structural perspective through dihedral groups, it implies that learners may look at regular polygons which have already been established in geometry lessons in school. The set of existing understandings may then be extended by exploring symmetrical behavior of these mathematical objects.

2. The D in EDUS stands for “deepening the level of existing understandings of a certain, single mathematical object” (Lee and Heid, 2018, p. 309). Again, in the case of dihedral groups, this may be achieved by establishing symbols for rotations and reflections and learning to reason about those abstract quantities.

3. The U in EDUS stands for “unifying existing understandings (that were previously unrelated by the student) under a specific overarching mathematical object” (Lee and Heid, 2018, p. 309). In the case of dihedral groups, exploring the isometries of regular polygons allows for the conclusion that they can be concatenated, yielding yet another isometry of the exact same polygon. In other words, there is a binary operation on the set of all isometries of a given polygon which on fundamental level works precisely like previously known operations such as an addition + on ℤ.

4. Lastly, the S in EDUS stands for “strengthening the links between existing understandings of more than one mathematical object” (Lee and Heid, 2018, p. 309). In our example, this may be realized by observing that in both cases additional insights about mathematical objects could be gained by equipping a set with a binary operation and derive the notion of magmas which is the abstract link between (D_n, °) and (ℤ, +).

The above example shows how this framework may guide a transition from school algebra to university algebra step by step and we further argue that these notions are strongly related to the notions usually linked with algebraic thinking. For example, Blanton et al. (2015b) list different components of algebraic thinking among which there are

• Noticing regularities in arithmetic situations. When replacing the word arithmetic with geometric, this is precisely what was aimed at in the frist step of the above context. A geometric regularity that is shared among all (D_n, °) is that each n-gon has precisly n rotations and n reflections.

• Reasoning about abstract quantities. Again, this is precisely what happened in the second progression step outlined above. When exploring the symmetric behavior of an n-gon in a deeper manner it is necessary to express all occurring isometries in abstract ways so that one can formulate algebraic expressions at a later stage.

• Developing a relational understanding. This accurately reflects the third step of EDUS where a unification was achieved by relating different mathematical objects to one another before they are generalized in the last step.

• Generalizing mathematical structures. This is arguably the ultimate goal of abstract algebra and as such constitutes the last step in the EDUS progression. Here, general algebraic structures are derived from previous examinations and a generalization of their abstract nature is resolved.

When comparing both the EDUS framework and algebraic thinking we observe isomorphic ideas emerging both in secondary and tertiary algebra education that are (as of now) disjoint. As such, future research may investigate further connections and flesh out the pedagogical coherence underlying those different notions (cf. Table 8).

TABLE 8

Table 8. Summary of the similarities between the different algebra education concepts EDUS and algebraic thinking.

Another finding related to this is revealed by the thematic map (cf. Figure 9): Abstract Algebra is highly relevant for algebra education in general but underdeveloped so far. Since the development degree is expressed by the average strength of all links that connect the different notions within this theme it is apparent that more work needs to be done to better unify and combine the notions of university mathematics education. Because an essential ingredient of university mathematics is proof activity, a corresponding node can be found in the very center of the university algebra cluster that emerged from our co-occurence analysis (see Figure 7). It seems apparent that further strengthening of this themes' internal bonds may be achieved by developing respective frameworks that can be utilized in different abstract algebra contexts. One example of such a framework has recently been published by Melhuish et al. (2022)—the Authentic Mathematical Proof Activity (AMPA) framework has been developed to help analyzing and documenting mathematical activity in proof-based settings and to expand “what competency can look like in the undergraduate mathematics classroom” (Melhuish et al., 2022, p. 28).

Another approach to unify research in abstract algebra education could be further development of more general notions such as conceptual and procedural understanding as suggested by Rittle-Johnson et al. (2015). The idea of separating different dimensions of knowledge and understanding and researching links between those concepts has already proven very fruitful in early algebra education research (cf. Table 6). In this regard, a recent study by Gerasimova et al. (2023) showed that achievement in high school algebra is mediated statistically significant via conceptual teaching approaches but not via procedural teaching approaches. While for abstract algebra great effort has been put into the operationalization of conceptual understanding (cf. Section 2.2) other dimensions are yet to be explored.

On another note, it seems counter-intuitive that the cluster concerned with affective learning variables such as beliefs and motivation is located diametrically opposed to the school algebra cluster in the co-occurrence pattern and its connections to university algebra outweigh its links to school algebra by a large margin (cf. Figure 7). Since “motivation in teaching and learning activities is the overall driving force within students that raises, ensures continuity, and provides direction for learning activities” (Wardani et al., 2020, p. 275) it seems apparent that school algebra should be equally concerned with notions of motivation and self-efficacy and more corresponding connections should be established in future research.

7.3. Limitations

Even though the workflow (Aria and Cuccurullo, 2017) and guidelines (Page, 2021; Rethlefsen et al., 2021) we used are helpful in circumventing methodological flaws, there are some limitations inherent to bibliometric analyses that need to be addressed to contextualize our results: Most importantly, as for any review of literature, there is a huge variety of databases to choose from and the list of indexed journals is constantly growing. As it is necessary to select specific databases, conducting a bibliometric analysis inherently entails the risk of excluding relevant research. Additionally, some country-specific journals publish papers in the English language but do not contain english words like education, learning, or teaching in their name and thus are not detected by any respective search-string. Moreover, there are no widely-used structures for the creation of titles, abstracts and keywords which severely limits the data selection process. To some extent we accommodated for this limitation by iterative growing of the search-string by means of preceding co-word analyses. However, published research articles on algebra education that never mention key notions (e.g., algebraic thinking or functional thinking) in the corresponding search fields are not returned by any sensible search query. Another limitation relates to the fact that the extracted BibTex-files do not contain any information about Altmetrics and thus the scientific impact can not be expressed in terms of social media activity.

8. Conclusion

The results of our bibliometric analysis demonstrated that the field of algebra education research is proficiently developed on the surface level—all target groups of education (primary, secondary, and tertiary students as well as teachers) constituted their own cluster in the co-occurence map developed based on algebra education articles published between 2003 and 2022 (cf. Figure 7) and cognitive variables were matched with a cluster concerned with affective variables. Possible future directions that emerged from the data can be summarized as (a) a need for stronger collaboration in the academic discourse between the different countries, (b) putting into effect unutilized potentials by connecting different key notions and frameworks of the respective clusters such as APOS Theory and Realisitic Mathematics Education, (c) excavating structural similarities of school, and university algebra education and (d) develop linking elements in abstract algebra education, e.g., by operationalizing proof activity or dimensions of understanding beyond conceptual understanding. With this, some currently disjoint areas of algebra education could converge and different ideas and insights could be cross-pollinated to improve educational outcomes. In contrast to these shortages, the foundation of algebra education, namely Early Algebra, is both well-developed and relevant and it constitutes a very active and ever-growing part of algebra education.

In summary, with the results presented in this article, we spotlight the current status-quo of algebra education research. At the same time, we identified perspectives for future research in this field and pave the way for a further intensification of activities on teaching and learning algebra along the entire educational chain. In this respect, it is up to the mathematics education research community and all of us to shape the answer to the question raised in the title of this article: Algebra education research, quo vadis?

Author contributions

JV: conceptualization, methodology, investigation, data curation, writing—original draft, writing—review and editing, and visualization. M-LB and MKi: conceptualization and writing—original draft. MKr and MS: data curation. FG: conceptualization. PB: conceptualization, methodology, investigation, and writing—review and editing. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1211920/full#supplementary-material

Footnotes

1. ^These field tags search for topics in titles, abstracts, and keywords.

References

Altieri, M., and Schirmer, E. (2019). Learning the concept of eigenvalues and eigenvectors: a comparative analysis of achieved concept construction in linear algebra using apos theory among students from different educational backgrounds. ZDM Math. Educ. 51, 1125–1140. doi: 10.1007/s11858-019-01074-4