- 1Faculty of Education, University of Melbourne, Melbourne, VIC, Australia
- 2School of Education and Tertiary Access, University of Sunshine Coast, Sunshine Coast, QLD, Australia
This conceptual analysis paper argues for an expansion to the definition of tools in Goos et al. model of numeracy. As the digitalization of society progresses at an ever-quickening pace, mathematical processes that were once considered only necessary for higher level occupations and tasks are now everyday requirements for successful participation in modern life and workplaces. Mathematical acts are routinely undertaken on a normal day because of the technology we use in daily life. For example, the act of driving a car has a mathematical basis; the driver has awareness of the location of the destination, reads multiple instruments and indicators including speed and fuel consumption, and interprets digital maps or navigation aids. Authentic digital tools and devices that are used in the real world that undertake mathematical processes can change the mathematics that is to be done. Rapid developments in mathematical technology, alongside the ubiquity of digital devices, the broad scope of functions and ease of use, has advanced the mathematical processes that digital tools can perform. The specificity and functionality of current digital tools can influence both the approach to and the application of the mathematics. To keep pace with society trends and demands, the tools used in the teaching and learning of numeracy should reflect the level of mathematical knowledge and skills required for successful participation in 21st Century life. Given that the digitalization of tools means they are no longer bound by time and space, they can be shared instantaneously. This agile ease of use suggests these tools may be suitable for use in the classroom. It is important therefore that educators find pedagogical ways to use real-world digital tools in authentic ways. This paper explores the current definition of numeracy tools found in literature and curricula and considers an expansion to the definition to fit with current technological directions. A model for implementation will be considered, and a suggested evaluation of the expanded model as a vehicle for learning numeracy is proposed.
1 Introduction
Technology has become an integral part of life. It is found in our workplaces, our day-to-day activities, at home, and in the community. Today, it is commonplace to carry a personal device such as a smartphone or smartwatch with us, and this digital tool overlaps the different domains of personal and work life. In Australia, for example, from a total population of 25,978,935 (Australian Bureau of Statistics, 2022) there were 28 million active smartphone users in June, 2022 according to the ACCC (2022), far outpacing predictions of 23.6 million users by 2026 (Hughes, 2021). In 2022, there were 255 billion app downloads worldwide (Ceci, 2021), many of which could be considered tools with a numerical basis such as banking and mapping apps. One consequence of the wide use of these current technologies is the speed of the processes that occur, making mathematical calculations efficient and in many instances hidden. Given the rapid and seemingly infinite expansion of digital capabilities today, we contend with digital representations of mathematics in more and more aspects of our modern lives. Steen (1990) made the bold prediction that by the year 2000, algebra calculations would be routinely completed using digital tools rather than with paper and pencil. Today, technology can undertake complex algorithms and produce visual representations of data that was unimaginable even to the foresightedness of Steen.
Mobile apps can be seen as the basis for accessing life in a modern society (Zhao et al., 2019). Zhao et al. (2019) contend that key adaptations of smartphones include the functionality of personalization and ease of installation at the point of need. The implications for education are that mathematical processes which used to be done algorithmically or by modeling, can now be carried out by a purpose designed application. The modern evolution of banking provides a clear example. In Australia society has moved from the first automatic teller machine in the Australian state of Queensland in 1967, followed by EFTPOS in 1984 (Worthington, 2017), which was superseded by online banking in the mid-1990s. Today, many people use banking and payment software applications such as tap and pay systems with a smartphone. Accounts information can be linked to the application and financial data may be displayed instantaneously on a smart device.
Rapid advances in mathematical technology, alongside the ubiquity of digital devices, the broad scope of functions, and ease of use, has changed the mathematical processes that digital tools can perform. Given that tools are no longer bound by time and space, they can be digitally shared instantaneously. To keep pace with society trends and demands, the tools used in the teaching and learning of numeracy should reflect the realities of life and work.
Thus, the aim of this paper is to argue that technology is an important component of numeracy in our everyday lives at home, in school and at work. As such we need to consider the need to revisit the examples given in the definition of tools in the model of numeracy put forward by Goos et al. (2012a) and shown in Figure 1.
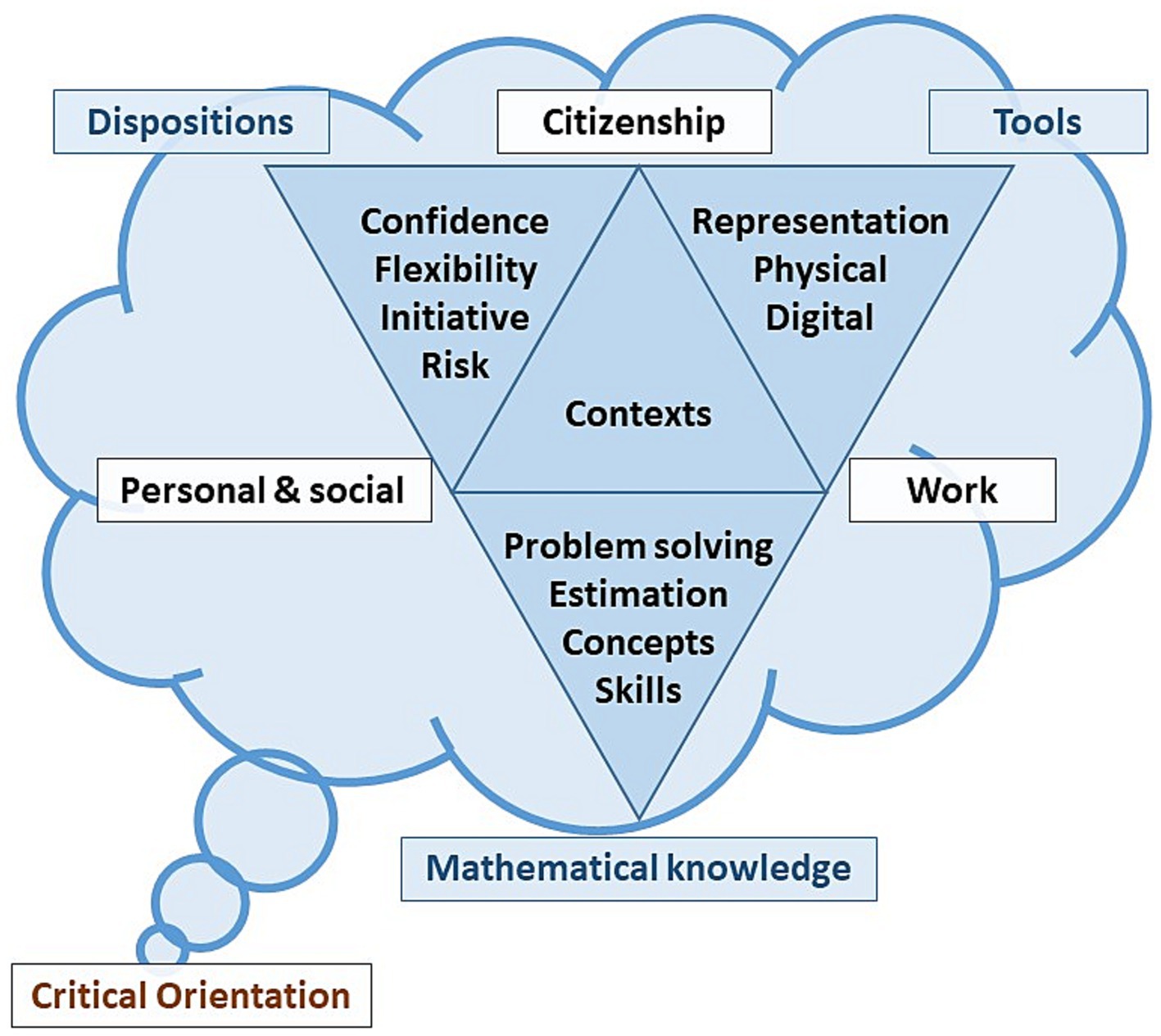
Figure 1. Goos et al. (2012a) Reprinted: A model for Numeracy in the 21st century (two dimensional).
2 Conceptual analysis of numeracy: current state of the field
In this section we will examine the origins of numeracy education and definitions used in the educational landscape. We will then consider the definition of tools used in the Goos et al. (2012a) model for embedding numeracy across the curriculum. This will be supported by a brief analysis of numeracy demands found in society.
2.1 Numeracy
Numeracy, a term first attributed to Lord Crowther in 1957 in the United Kingdom parliament, referred to the enhanced mathematical requirements of post-Second World War workplaces. As an economist, Lord Crowther connected labor market outcomes to the levels of numeracy in the workforce. He inferred that increased numeracy would lead to greater productivity (Cockcroft, 1982), an observation still made today (Shergold et al., 2020). Until the mid-19th century, calculations were manually completed by workers known as calculators, with ciphering books recording mathematical processes (Hertel, 2016). At this time numerical demands were largely arithmetic, and tools were largely limited to pen and paper, and books and tables such as logarithmic and trigonometric tables.
The advent of affordable desktop calculators in 1964 saw a revolution in how mathematics was undertaken. Calculators made previously slow laborious processes, fast and accurate, and accessible to a wider range of workers (Chiba et al., 2012). Around this same time, Douglas Engelbart’s theories of computing asserted that computers were not intended to be a data storage and manipulation tool, but a vehicle to enable human beings to explore and critically think about data and to solve problems in a novel way (Bardini, 2000). By the 1970s, Ehrenberg (1977) further defined numeracy to the two categories of: reading and writing mathematics, and extracting and presenting mathematics. This definition was further expanded in the 1980s to reflect the demands of society at that time, where statistics were deemed to be a useful and common form of communication (Ehrenberg, 1981). Ehrenberg saw that communication of mathematical ideas through workplace tables and graphs was an essential but poorly executed skill. At this time numerical tools were commonly adding machines and desktop calculators.
In 1990, Steen stated that “numeracy is to mathematics as literacy is to language” (p. 2011). Steen noted that the emergence of the digital age had led to a proliferation of data in society and at work which required higher levels of mathematical literacy in the population. Since this identification of the importance of numeracy, the research literature has expanded to include idea of incorporating the contexts and tools of the real world (Goos et al., 2012a; AAMT and AIG, 2014; Geiger et al., 2015a,b). Numeracy has importance in the educational policies and school curricula of some countries, which is evidenced in Australia New Zealand, South Africa, and Ireland (Goos and O’Sullivan, 2022). However, given the role of tools in numeracy according to the Goos et al. (2012a) model, not all of these jurisdictions place importance on the use of tools including technology. To address the growing mathematical requirements for successful participation in society, the AAMT (1998) published a policy for numeracy education in schools. They noted that the coming digital age required a workforce that was technologically literate, and that a higher level of numeracy would be required with the anticipated changes. The policy defined numeracy as the ability to use the contexts of home, vocational, community and civic, as the basis for effectively applying mathematics knowledge and skills (1998). Their assertion was that numeracy is the responsibility of all teachers across the curriculum and not just mathematics teachers in mathematics classrooms. The definition of numeracy on the AAMT website, which is still relevant today, acknowledges the need to prepare students who are mathematically and technologically literate: however, it does not specifically include technology in the definition.
In this paper we use the numeracy definition from Goos et al. (2012a) as illustrated in Figure 1 and incorporate ideas from current research about numeracy. In the Goos et al. (2012a) model, numeracy starts with the real-life context from which the mathematical knowledge and skills should be taught. This is in conjunction with the students’ dispositions, values and identity (Hill et al., 2021) where values and identity are essential components of a students’ dispositions, and importantly tools, both analog and digital in nature. Contexts are drawn from the domains of personal, vocational, recreational, financial, health and civic (Gal et al., 2020; VCAA, 2022). In the model the students’ critical orientation toward mathematics is defined as their ability to solve problems in the real world, to relate their mathematics back to the real-world questions and evaluate its effectiveness.
Goos and O’Sullivan (2022) describe three key approaches to didactical numeracy in school curricula. Firstly, numeracy may be a function of the mathematics classroom such as seen in Japan. Secondly, numeracy can be taught as a distinct subject separate to mainstream mathematics courses. The Australian states of New South Wales and Victoria use this approach in upper secondary schools, as does South Africa and the Canadian state of Ontario which offers Mathematics for work and everyday life (Ontario Curriculum, 2023). Lastly, numeracy can be embedded across all subject disciplines in the school, such as in New Zealand and in primary and lower secondary in Australia. In the Australian Curriculum, numeracy is regarded as one of seven general capabilities to be developed in all subjects, not just in mathematics. The Australian Curriculum Assessment and Reporting Authority (ACARA), in the latest definition of numeracy included in the new Australian Curriculum: Mathematics V9.0 (ACARA, 2023) include the underpinning elements found in the Goos et al. model of context, dispositions and tools.
Considering as an example of numeracy embedded across the curriculum, in the new model for numeracy in Australia (ACARA, 2023), there are six strands of mathematics encompassing mathematical knowledge and skills. Namely: number, algebra, measurement, space, statistics and probability. There are also sub strands in place for each of these three strands. For example, in the number and algebra strand there are nine sub strands which include: number and place value, counting processes, additive strategies, multiplicative strategies, interpreting fractions, proportional thinking, number patterns and algebraic thinking and understanding money. Drawing on previous versions of numeracy, ACARA have retained the notion that numeracy is mathematics that is undertaken purposively and include students’ behaviors and dispositions toward the act of doing mathematics. However, in the latest definition of numeracy in the Australian Curriculum: Mathematics V9.0 there is no specific mention of analog tools or digital devices. Rather, tools appear only incidentally in discussions of how the general capability of numeracy may be addressed within specific learning area subjects, such as Technologies. This approach contrasts with the Goos et al. model (Figure 1) where tools are an underpinning numeracy concept. In the Technology learning area, the mathematical concepts of number, geometry, scale, proportion, measurement and volume are listed as appropriate for learning with digital software. Mathematical concepts such as statistics, probability or algebra are not mentioned, even though researchers have highlighted the importance of technology as a critical component for mathematical pedagogies for all mathematics topics (Zevenbergen, 2004; Wing, 2006, 2019; Goos et al., 2012a; Geiger et al., 2015a, 2020).
The numeracy literature supports the significance of an array of tools for numeracy (Hutton et al., 2010; Goos et al., 2012a; Monaghan and Trouche, 2016; Goos and O’Sullivan, 2022) Yet, even in countries that aim to address numeracy across the school curriculum, there are inconsistencies in how the role of digital technologies are interpreted. For example, in the Australian states and territories there are contradictions about the importance, status and provision for technology in numeracy. In Victoria, the Department of Education states that numeracy encompasses the ideas of dispositions, behaviors, and mathematical knowledge and skills which are mapped across the curriculum and are underpinned by the elements including real life contexts, applications of mathematics, and the use of tools (Department of Education Victoria, 2022; Victorian Curriculum and Assessment Authority, 2023). Tools for numeracy are mentioned in their definition of numeracy, however, they are not expounded further in the advice. The New South Wales curriculum (New South Wales Government-Education, 2023) similarly to ACARA, does not mention tools as an important aspect of numeracy. It suggests that numeracy is required for daily life and that mathematics is used to make sense of life through critical evaluation, interpretation, application, and communication. These skills are considered to be a general capability, similarly to Victoria, but with no reference to the role of technologies in numeracy. Similarly, the Western Australian curriculum refers to developing dispositions and capacities to purposively use mathematics (West Australian School Curriculum and Standards Authority, 2023), with no direct mention of the role of technology in numeracy. Both the South Australian curriculum (South Australia Department of Education, 2022) and Queensland curriculum (Queensland Curriculum and Assessment Authority, 2021) use the ACARA definition, while the Tasmanian curriculum is yet to define Numeracy (The Department for Education, Children and Young People Tasmania, 2023). Thus, there seems to be lingering confusion and even doubt as to how digital technologies can play a part in supporting young people’s numeracy development and practice in the real world.
2.2 Definition of tools in Goos et al. numeracy model
In the model for numeracy shown in Figure 1 (Goos et al., 2012a), tools are defined as representational, physical or digital. Representational tools are graphical and visual and include maps, charts, drawings, tables and images. Physical tools include the use of manipulatives (concrete or physical materials) for deepening student understanding, but also analog tools used in industry such as measuring devices (e.g., measuring tapes, syringes, and trundle wheels). Digital tools include computers, software, calculators and internet (Goos et al., 2012a; Geiger et al., 2020). The digital tool given as an example in the seminal paper by Goos et al. (2012a) is the teacher using spreadsheets as a pedagogical tool to aid in the learning of mathematical concepts. While the tenets of this definition hold true in the practice of many classrooms today (Attard and Holmes, 2020), all three categories of numeracy tools (physical, representational, digital) have undergone transformations and can be seen to be converging as a result of the increased use of technologies in the digital age. Hence the examples of tools that were originally used to illustrate the model have changed over time. For example, physical measuring tapes have been superseded with digital alternatives, such as lasers, drones and satellite measures. Many functions of representational tools such as maps are now carried out by mobile apps such as navigation systems in cars which provide step-by-step verbal instructions. The evolution in digital tools can be typified by the advent of artificial intelligence and purpose specific tools such as online mortgage calculators.
In support of the approach to the inclusion of digital tools in the numeracy model, Geiger et al. (2015a,b) investigated the connections of modern technologies that may be found in life and in industry, to pedagogical opportunities in the classroom. Their study involved ten pairs of teachers of students in years six to twelve, from public schools in Australia in a design-based research approach. Data sources included classroom observations, pre-and post-intervention semi-structured interviews of teachers and students, audio, artifacts, field notes, computer files and student work samples. The teachers engaged in collaboration with their counterpart as they embedded technology into numeracy practices in a diverse range of subjects including Sciences, Mathematics, English, Health, and Social and Design studies. In one example given, a physical education teacher used Excel for students to record their number of steps across a whole week and investigated trends in overall distances walked among different student groups. Their study demonstrated that inclusion of technologies in the numeracy lesson is not only possible but also supported the assertion that when teaching numeracy all aspects of the model should be pedagogically considered in concert.
Currently, much of the numeracy literature focusses on statistical literacy (Geiger et al., 2020), and on analog or digital workplace tools such as measurement tools (e.g., Gravemeijer et al., 2017). Gravemeijer et al. (2017) cast doubt on the pedagogical use of these tools in the classroom setting, noting that they are often used by teachers to motivate students, and not in context to the real-world problem to be solved. The authentic use of these tools in learning numeracy is highlighted by Gravemeijer et al. (2017) as they assert the need for this approach to effectively prepare students for the numeracy demands that they will meet in the workforce and in life.
3 Discussion
The importance of tools in the Goos et al. numeracy model is evident in the level of mathematical skills required to carry out commonplace everyday tasks whether overt (such as measurement in industry) or hidden (such as in a bill-splitting application). For example, driving a car requires mathematical understandings of location, distance, time and speed, undertaken through the interpretation of automated instruments. Taylor et al. (2019) predicted that by 2030, increased numeracy skills will be needed across industries due to automation and digitization. They suggest that healthcare will see increased numeracy requirements up to 29%, and retail may have increases between 29 and 75%. The projected increases in mathematical skills and knowledge in these industries can be observed with the digitization of previously manual or technical tasks such as in healthcare with advances in the technology for intravenous drips, imaging, and dosages of medicines. Likewise in retail, financial understanding of the market and economics at local, state, national and international levels, alongside navigation of taxation, employee transactions and money management, require increasingly sophisticated levels of mathematics.
Further evidence of increased numeracy requirements in the workforce of the future due to technological advances is found in the OECD automation and skills report (Nedelkoska and Quintini, 2018). It is predicted that 32% of jobs are likely to be automated, and that between 50 and 70% of jobs will undergo transformations due to digital automation by the year 2030. Digital tools and automated systems change the mathematics, and consequently they will change the way that we think about problems. Goos et al. (2003) identified ways in which technology mediated the mathematics in a three-year study of five classrooms of senior school mathematics students. They found examples of the technology being used in four key ways: (i) technology as a servant to the student (e.g., computing), (ii) master of the student (student struggled to use the technology), (iii) partner to the student (learning facilitated by the technology) and (iv) as an extension of the student (exploration of the mathematics through technology). Today, technology as a partner or servant can be seen ubiquitously in workplaces. For example, a drone can measure the dimensions of a house roof, digitally apply the data to software, resulting in a quotation. The mathematics for the user now lies in the checking the reasonableness of the data generated and the interpretation of the result provided.
3.1 Expanding the definition of digital tools in the Goos et al. numeracy model
The definition of tools in the Goos et al. (2012a) model of numeracy encompasses three categories of physical, representational, and digital. This paper aims to demonstrate that digital transformations in society and at work have digitalized all three categories of tools in the model.
The nature, ubiquity and computational power of digital tools has fundamentally changed the way that we see and do mathematics outside of the school setting. The resultant changes in the thinking required to undertake numerical tasks using digital tools might look like increased creative thinking, interpretation of information, decision making and problem-solving skills (Shergold et al., 2020). It is well established in the computational thinking literature that digital tools are faster, more accurate, less error prone when performing mathematical operations and representations, and that these digital tools allow the user to spend their efforts on more complex ideas and problem solving than previously (Wing, 2006, 2019; Lodi and Martini, 2021). Attard and Holmes (2019) noted that “technology can and should be regarded as a disruptive pedagogy” (p.2). It is important therefore, that educators find pedagogical ways to use the digital tools of the real world to be used in an authentic way in the classroom (Mak-van der Vossen et al., 2018). This would allow students to have the opportunity to not only learn with the digital tools necessary for life and work skills, but also to learn how to use these tools efficiently to solve problems. Additionally, students should be able to critically interpret any outputs from digital tools. The mathematical skills and knowledge required in the workplace in modern industries tend to utilize the competencies of reading and interpreting the mathematics, as opposed to traditional calculations (FitzSimons and Björklund Boistrup, 2017; Hoogland, 2023).
Given the effect of digitization and automation on everyday life including both at home and at work we argue that the definition of digital tools in the numeracy model (Goos et al., 2012a) needs to be expanded to include digitalization in all categories: physical devices and implements (both analog and digital), physical and digital representational tools (virtual manipulatives, graphs, maps, diagrams, charts, tables), and automated and digital tools (which includes general and purpose specific applications and software, artificial intelligence and emerging technologies).
3.2 Transformations in physical tools
It can be observed that as technology becomes more pervasive, there is a convergence of physical and digital tools. The literature from computing and communication research highlights this entwining of digital smart systems (Romero et al., 2021). The current technological age has seen an ever-increasing immersion of life with technology, with digital capabilities including sensing, networking, communicating, conversion of intention, and powerful computing (Das, 2016). In this section we will consider firstly the importation of real world computing as possible numerical tools. Secondly we will examine the changes to manipulatives, a well-researched mathematical didactic tool.
The implications of the wide-ranging functions of technology described by Das (2016), can be seen in smart devices such as smartphones. These devices have overtaken many previously analog functions in life. Analog calendars and clocks have been superseded by digital versions, as have analog measuring devices such as measuring tapes, rulers and thermometers, which can now be found as digital tools or analog tools with digital capabilities. Successive iterations of new and emerging digital products (such as fitness or mapping applications) leverage data that are collected during usage of apps to further drive innovation. Additionally, digitally focused tools are leveraged off the data to individualize tools. In the past these tools were produced for the mass market, with one size fits all. The implications for personalization of digital tools can be seen in industries such as health, where focused data allows for targeted approaches to improving health and well-being.
Das (2016) notes that there is a convergence between the physical, internet, and social domains, and the interactions between these are complex, adaptable and constantly changing. This interweaving of domains can also be commercially harnessed, as is evidenced in the evolution of apps that use data-driven metrics to drive the technology (Romero et al., 2021). In the past digital technology such as software applications were mass produced and distributed as developers had no easy way to gather and interrogate consumer data. Today, big data can be analyzed to optimize technology specific to users’ needs. An example of this can be seen with current health applications on smart devices, which allow users to track their sleep and exercise, with the aim to increase productivity. The implications of these applications for numeracy are therefore inferred to be an increased use of technology with the mathematical demands of understanding the inputs and outputs of this technology with the resultant skills of interpreting and analyzing the mathematical information.
The internet of things (IoT) is defined by Atzori et al. (2010) as a three-way convergence of physical and virtual “things,” with the internet, and semantic technologies. In this early definition, the user accesses the web using smart technology which employs applications and software to support the decoding of the information such as text or video capability. With recent rapid advances in technology driven by Covid disruptions, the IoT has had a further evolution with increased interactivity between “things,” and the supporting applications. For example, self-check-out stations at retail stores shift the burden of the mathematics to the customer, who must check and interpret the mathematical information presented by the machine such as weight of goods, number, and cost.
Additionally in the advancement of IoT, there is the practice of twinning. Twinning is the pairing of immersive data driven virtual models with physical models to allow for multiple virtual iterations before making decisions in the real world (Li et al., 2023). Li et al. (2023) describe the example of a car brake where successive digital iterations are tested virtually before a physical model is produced for testing, saving time and money. Another advantage of providing a virtual model can be effective cost saving, for example, in retail where modeling can predict trends in human behavior to drive sales to draw in and keep customers. Additionally, the IoT can also be found in smart-homes, smart-cities, smart-cars, where the commonality of systems includes sensors, storage, the ability to code, processing, connectivity to the internet, and control. In a modern society it is difficult to find an area of life that is not impacted by the IoT (Atzori et al., 2010; Li et al., 2023).
The implications of these innovations in IoT for numerical thinking are yet to be fully seen, but numerical requirements are constantly evolving alongside the technology (Taylor et al., 2019). Mathematical requirements of software engineers and coders are in increasing demand to satisfy the increase in technologies and applications (Al-Emran et al., 2020). Moreover, Taylor et al. predict that by 2030, workers will spend up to 60% more of their time using digital technologies. Given this prediction, the mathematical demands of users of technology are poorly studied in the research literature. Extrapolating the mathematical requirements of each system would require accounting for the ubiquity and uniqueness of the myriad of systems available. Yet, it can reasonably be assumed that mathematical demands are present and, in some cases, may be increasing in the IoT.
Additionally, the IoT is well identified in the literature as being systems driven (Vermesan et al., 2015). The multiple systems include a global network, intelligent interfaces, information networks, programming networks, communication interfaces, and physical and virtual things (Vermesan et al., 2015). There is a trend with the IoT toward evermore interconnected systems such as made possible by artificial intelligence and Web 3.0, which is the shift to decentralization from individual devices to the internet (Chen et al., 2022). Therefore, the numeracy demands reflect systems thinking as foreseen in the future of education and skills: Education 2030 report (Organisation for Economic Co-operation and Development (OECD), 2018). The OECD identified that, given the fragile nature of climate issues, the pervasiveness of automation, and the resultant changes to society, education should embrace design and systems thinking to prepare students for the demands of an increasingly complex world. Likewise, the OECD (2022b) identify systems thinking as a 21st Century skill in the PISA mathematics framework. Therefore, numeracy learning with technology should embrace systems thinking as a logical vehicle for which students can consider messy real world problems. Systems thinking is traditionally in the domain of high-level mathematics education with strong sociotechnical or engineering applications (Scribante and Pretorius, 2022). However, given the interconnectedness of technology where complex systems thinking underpins the coding, simple systems thinking can be found within commonplace applications and software that is used in everyday life. For example, users of the health and fitness application, Strava (2023), use the numeracy-based application to track their running activity. Through GPS technology, routes are shown on satellite maps, analysis of performance and comparisons for different routes are shown. On Strava, changes to one variable can affect the whole system, and the user should understand how the variables influence the whole. Hence, we argue that there may be a place for mathematically driven systems thinking through technology in numeracy education. This may be as a sub-strand in the definition of tools.
Manipulatives, previously largely considered as physical pedagogical tools, have strong digital counterparts (Sarama and Clements, 2016). It is noted that virtual manipulatives are well represented in the research literature (Moyer-Packenham and Westenskow, 2013). Virtual manipulatives as defined by Moyer et al. (2002) are visual representations of dynamic objects which may be found online and can be useful for developing student mathematical understanding. In acknowledgment of the developments in technology over the ensuing decade, this definition has been expanded by Moyer-Packenham and Bolyard (2016) to include student interactivity with the manipulative, and the ability to program different features.
In a review of the literature on mathematical manipulatives, Sarama and Clements (2016) hark back to Dewey (1933) noting that concrete understanding precedes abstract thinking. Additionally, virtual manipulatives have been shown to be as meaningful to students as physical manipulatives when engaging cognitively with mathematical ideas (Sarama and Clements, 2016). They observe that the research largely finds that student use of manipulative tools can lead to deeper learning. It is noted that virtual manipulatives have the ability to mimic the real world through the advances in software and applications. Although manipulatives have long been seen in the research to cross the physical-digital divide, they are as with many software applications, evolving with time.
Virtual manipulatives are additionally demonstrated in the literature to have the affordances of developing abstract reasoning and providing opportunity for learners to extract greater meaning and understanding from the mathematics (Carbonneau et al., 2013). Stronger meaning and understanding of a mathematical concept can lead to greater memory retention, and a more useful conceptualism that has transferability (Buckner et al., 1999; Sousa, 2015). Additionally, virtual manipulatives can simulate mathematical objects or scenarios that may be found in the real world (Carbonneau et al., 2013; Keldgord and Ching, 2022). The use of real-life contextualization of the mathematics has been shown to help with students’ development mathematical concepts (Goos et al., 2012b; Gravemeijer et al., 2017; Nieminen et al., 2022).
Most importantly, virtual manipulatives provide opportunities for student led exploration of the mathematics, driving curiosity, and meaning making (Reiten, 2020). In a study of 14 middle school mathematics teachers, Reiten (2020) observed that when professionally supported in quality pedagogical use of virtual manipulatives, their students were able to have time for exploration of the mathematics and to connect multiple mathematical ideas. The use of manipulatives affords students the capacity to meaningfully explore mathematical concepts, that would not be possible with traditional pen and paper. Additionally, virtual manipulatives are time efficient, showing changes instantaneously (Reiten, 2020). Taken together these affordances mean that virtual manipulatives are an important consideration in the examples of representational tools in the numeracy toolkit as defined by Goos et al. (2012a).
3.3 Transformations in representational tools
Representational tools are defined in the Goos et al. (2012a) model of numeracy as including “symbol systems, graphs, maps, diagrams, drawings, tables, ready reckoners” (p. 5). These tools, like others, have in recent decades undergone transformations through advances in technology. Software platforms such as online websites, mobile and desktop applications may have didactical affordances as representational tools for teaching mathematics. For example, software applications may have calculating functions, and the act of typing a mathematical equation into an internet search function will in many cases produce an answer.
Statistical technology is well documented in the literature for the pedagogical benefits it provides students. In a fresh approach, Cai et al. (2020) argue that augmented reality can be a useful tool for bringing statistical and probability concepts to life in the classroom. Augmented reality is an extension of virtual reality where virtual information or data is superimposed on the real time image from the real world (Berryman, 2012). Berryman contends that augmented reality enhances the user’s understanding of the physical world that they are observing. In a study of 68 grade seven students in the United States looking at student attainment of probability and statistical concepts through didactical use of augmented reality technology, Cai et al. (2020) found the experimental group has statistically significant improvements compared to the control group. In one example, the students in this study used augmented reality when tossing coins. The screen displayed animated information with each coin toss, linking the act of coin tossing to ideas of probability. Additionally, the same technology was then used to construct graphs, thereby affording the opportunity for students to observe when their experimental results matched the expected theoretical outcomes.
Additionally, technology has the capacity to represent static two-dimensional models, graphs and diagrams as interactive three-dimensional objects (Cavus and Deni̇z, 2022). A meta-analysis study of dynamic geometry in the education research literature by Cavus and Deni̇z (2022) examined 98 studies considering the effect of technology on learning geometry and mathematics as compared to learning by traditional pedagogies. They concluded that using technology has greater effect sizes for both geometry and mathematics, indicating that technology assists in students’ attainment of mathematical concepts. Given there is a plethora of representational software freely available on the internet, representational software could be utilized in classrooms for the purposes of developing numeracy. Kidman and Chang (2022) argue that in a globally connected world that is undergoing societal changes, students require numerical skills to decode the information they might encounter in the media or on social media. Real life contexts can be linked with graphing or spreadsheet technology in a classroom setting to teach numeracy, and this approach is supported by the Goos et al. (2012a) model.
Finally, the use of common digital navigation software applications such Google Maps can usefully bridge the mathematical skills required in learning location concepts with the reality of how maps are utilized in everyday life (Gravemeijer et al., 2017). Mapping software applications are found on everyday digital handheld devices, and the large scale data collected from usage of these apps has commercial applications. For example, Ghazali et al. (2019) designed an application that used data from Google Maps to streamline rubbish collection in a local community. Additionally real-time feedback of map users provides travel time estimations which instantaneously update as the traffic conditions vary. Given that in many countries digital navigation software has superseded paper-based maps, the resultant required mathematical skills too have changed.
3.4 Transformations in digital tools
The evolution of digital technology in society has had impacts on all three categories of tools (physical, representational and digital) in the Goos et al. (2012a) model of numeracy. As we argue that physical and representational tools are converging with digital tools, in this section, we will examine the transformations to digital tools generally. In schools, learning is increasingly mediated through technology (Epaminonda et al., 2022). The prevalence of handheld devices, laptops, and tablets and the ease of use of devices creates an environment that is conducive to learning with and through technology.
The use of an expanded repertoire of digital tools can change the nature of the numeracy problems that can be investigated and expand the types of problems that can be investigated. Online mortgage calculators, health and fitness applications, digital planning tools in the construction industry, blockchain, and ChatGPT are but a few examples. In this sense they can be considered revolutionary tools. Digital tools and automation can also change how the problem is conceptualized, its specifications, possible solutions, processes, criteria for success, none of which are observable in a physical sense, which makes digital tools different from previously used conventional tools such as calculators and spreadsheets.
Calculators, a key tool used in mathematics classrooms, are superseded in the real world by mathematical computing software, software applications on mobile handheld devices, and purpose specific software or computing tools. There are computational literacy considerations for using customized tools and a variety of software applications when learning numeracy, such as students learning to engage with the mathematical inputs, analyzing and interpreting these results and developing a sense of when to use technology and which tool to select for each purpose (Wolfram, 2020).
According to the OECD digital economy paper (2022), artificial intelligence may provide an immersive window into numeracy education, changing the way we interact and engage with the mathematics. Artificial intelligence is pervasive and rapidly encroaching on multiple realms of life and work. Hence, the advances in artificial intelligence are also rapidly changing the mathematical education landscape. The roles that artificial intelligence can play in the classroom are limited only by the scope of the chosen technology. Artificial intelligence draws pedagogical affordances from its multifunctionalities of machine learning, speech, vision, language processing, expert systems, planning and optimization and robotics (Qiu et al., 2022). The pedagogical implications are that the technology can be a teacher or trainer, as it can compare, analyze and justify, but only within the parameters of its capability. Artificial intelligence can mimic the tools of the workplace, allowing for safe and affordable training, and allowing students to develop numeracy skills while using tools found in the workplace.
The area of artificial intelligence pedagogical uses in education is an intriguing one which could be usefully explored in further research. Given this field is constantly evolving, work needs to be done to first establish the pedagogical affordances of artificial intelligence, and secondly the impacts of the pedagogies. Further, digital tools are becoming smarter and more automated (OECD, 2022a). Likewise, research on how these digital tools contribute to students’ engagement with, and attainment of numeracy skills and concepts warrants further research. It has long been identified that continued research into the pedagogical role of tools in numeracy must keep apace of the emerging technologies (Jorgensen Zevenbergen, 2011; Geiger et al., 2015b).
The literature provides evidence of the changes that digital tools bring to workplace numeracy. Jorgensen Zevenbergen (2011) observed many changes to digital numerical tasks being used in the retail industry. She noted that the mathematics had shifted from mostly in-head counting and calculations, to mechanical with manual cash registers, and then to digital scanners. The observable mathematics skills in the retail context transformed from accurate counting, to estimating to check the reasonableness of the resultant totals from a digital tool.
Likewise, a relationship exists between the use of industry specific tools and numeracy efficacy as demonstrated by Hutton et al. (2010). They created a specific-purpose assessment simulation tool using artificial intelligence for nurses in training. The simulation tool assessed nurses on their ability to correctly administer medication dosages. The significance of their multi-stage quantitative study of 50 nurses has two facets. Firstly, the tool allowed for safe training and assessment, as the consequences of incorrect dosages in real life can be fatal. Secondly, the tool allowed for simulated real life training with minimal resourcing.
When considered from the perspective of the Master-Servant-Partner-Extension of Self framework for technology (Goos et al., 2003), artificial intelligence may support students’ mathematical learning. There is potential for artificial intelligence to fulfill all four roles as described in the framework. Given the immense power of artificial intelligence, we argue that these tools might be considered when learning numeracy for the following reasons. Firstly, there is inherent danger in the student being subservient to the technology (technology as master) if the student does not have the requisite numeracy skills to determine if the results are reasonable. Gravemeijer et al. (2017) postulate that a key skill required to effectively undertake numeracy with technology is being able to critically evaluate the results of digital calculations, as opposed to performing calculations.
Secondly, artificial intelligence is commonly considered as a servant to the user (Dwivedi et al., 2021). This functionality has freed time for users to engage in other less routine tasks such as creative and critical thinking. Thirdly, in considering artificial intelligence as a partner technology, artificial intelligence has the capacity to produce step-by-step calculations thereby providing solution pathways. The students can consider artificial technology as an additional smart resource in the classroom, and this is seen in online tutoring systems, chatbots, and adaptive learning systems (Chen et al., 2020). Lastly, artificial intelligence has the power to extend a students’ mathematical thinking and skills by removing calculations and producing instantaneous visualizations of the mathematics. The interactive capabilities of artificial intelligence mean that changes have immediacy, and the changes are applied across all interconnected systems. Additionally, artificial intelligence is continuously improving as artificial intelligence is by design self-learning (OECD, 2022b). As such, the effects of artificial intelligence on extending student thinking are yet to be fully observed. It is recommended that further research may be conducted into the relationship of artificial intelligence in respect to mathematical learning with the Master-Servant-Partner-Extension of Self framework for technology (Goos et al., 2003).
3.5 Changes to numeracy pedagogical opportunities
An important aspect of the Goos et al. (2012a) model lies in the strength it brings to the pedagogy of numeracy. Monaghan and Trouche (2016) asserts that schools continue to focus on computers as a tool for semiotic mediation, ignoring the workplace requirements of multiple technologies and the way in which these tools are used. This follows the long-held idea of technology as a “black-box” (p. 139), where the user inputs information and interprets the results, and the importance lies in the act of understanding as opposed to computing (Hansson, 2020). Monaghan and Trouche (2016), in a survey of local schools identifying which technologies and how technology is used in the classroom, argues that there is a difference between using technology for artifacts to teach mathematical concepts and using technology as an authentic tool to mimic real-life contexts.
Siller and Greefrath (2010) proposed a model to demonstrate the link between the real-world, mathematics, and technology. Their model has a focus on the technology as a tool for aiding mathematical modeling of problems, and they postulate the technological affordances of: increased relevance for students, alongside the ability to work with large data sets, and the ability to quickly see visualizations of the mathematics. In contrast, Monaghan and Trouche (2016) questions why the focus should remain solely on the tool as means of didactical understanding and ignoring the possibilities of the technology as a functional tool. The real world comprises of massive and ever-evolving range of technologies, many requiring intuition with the technology (Hansson, 2020). Supporting Monaghan’s approach is a six-year study of 11–14 year-old students in 3 schools by Downes and Bishop (2012). Their well-accepted study included equipping schools with new laptops, professionally educating the teachers, and partnering with the students to understand their perspectives with learning with technology. They describe students that identify as digital natives, who embrace the technology as a tool for bringing the real-world into the classroom. Students in this study report that technology and applications that are relevant in the real-world, are worthwhile and have purpose to support their learning.
The existing extensive body of literature on modeling and problem solving in mathematics has strong transferability for numeracy learning (Wake, 2015; Geiger et al., 2015b; Tout, 2021). PISA has a problem solving cycle as the basis for mathematical literacy testing (OECD, 2022b). The PISA cycle has three key stages: formulate the mathematics from a real world context, undertake and use mathematics to solve the problem, and interpret the results in relation to the context and reflect on their reasonableness. The use of software and tools from life can authenticate this problem solving cycle through strengthening the applicability of the problem’s context to the underlying mathematics found in real life (Mak-van der Vossen et al., 2018). Wake (2015) demonstrated two lessons drawn from a lesson study that used authentic workplace contexts as the basis for learning numeracy through a problem solving cycle. Wake draws the conclusion that mathematical models should reflect the reality of the real world problem. One pedagogical implication of this finding could be the validity of using the tools that would be used to solve this problem in the real life, in the numeracy classroom.
These studies demonstrate the importance of embedding current digital software and tools in numeracy learning. The literature examining the use of authentic tools of the real world in the numeracy classroom, such as software applications used in everyday life or at work, highlight the need to further examine these from a didactic perspective.
4 Conclusion
This paper has argued for an augmentation to the definition of tools in the model for embedding numeracy across the curriculum as described by Goos et al. (2012a). Given the Goos et al. model is a leader in the literature for numeracy practices in educational contexts, it is important to consider how tools are evolving in the current digital age. Digital tools greatly expand the kinds of numeracy that can be tackled and how these numeracy problems are conceptualized and expressed. They allow for the numeracy skills and knowledge required in the workplace and in life to be authentically replicated in the classroom (AAMT and AIG, 2014; Gravemeijer et al., 2017; FYA, 2018).
Numeracy tools, whether they be physical, digital, or representational, are undergoing large scale change at an accelerating pace due to the widespread transformations in digital technologies. Tools which were previously only physical or 2-dimensionally represented, may now be digital (virtual, interactive, automated). This change is happening in the world of life and work and hence there is a compelling argument for educators to consider the role of digital tools in the classroom. Preparing students to have the skills and transferability of skills to cope with the requirements of numeracy in the workforce can happen if the digital tools that are found in the real world and industry are utilized for educational purposes. Through artificial intelligence, tools may be developed that approximate the workplace experience and simulate the mathematical skills. Additionally, the scope of artificial intelligence on work on everyday life is as yet unknown, however, it will change the type of mathematics that is undertaken, and this process is already underway at a rapid pace.
The curriculum requirements of numeracy at present largely do not consider the important role that digital tools play in the act of doing numeracy. Curriculum drives the content that is taught, and as such, the curriculum must consider the importance of digital tools to prepare students who are ready for the numeracy demands due to the functionality of the technologies. Curriculum may draw on real life contexts such as personal, societal, occupational, and civic advocated by PISA, yet the tools used to examine the mathematics in these categories are given by traditional software such as spreadsheets and lists on graphing calculators (OECD, 2022b). These tools are evidenced in the literature as supporting students developing cognitive understanding of the underlying mathematics, however, the literature is yet to fully examine if the tools of the real world can provide cognitive didactic affordances. These tools may include: mapping applications to consider ideas of location and direction, a farming software tool to consider the amount of chemicals and water in a boom sprayer may consider ideas of proportion and algebra, or financial planning applications such as those calculating and displaying the interest on loans. Students learning numeracy with these tools may consider the underpinning mathematics from the real life contexts expected in curricula and international testing such as PISA.
Pedagogically, digital tools found in the real world may have strong affordances for the classroom given their relevance, ubiquity, connectivity and speed. The benefits of the internet of things, can bring the same strengths to numeracy education. Transformations in the way we teach numeracy may occur with the embrace of the digitalized automated world, including a strong preparation of students for a future which is firmly embedded in technology.
To further understand the increasing role that technology plays in the act of doing numeracy, it is intended that a model for implementation of tools when embedding numeracy across the curriculum be considered. Building on from a model, an evaluation of this within a research setting will be designed and evaluated to understand how these tools are used mathematically in the act of learning numeracy. Given numeracy has roots in the demands of the real world, further research should be carried out to understand the mathematical skills and knowledge required when using digital tools in life and at work.
Author contributions
JS: Writing – original draft, Writing – review & editing. MG: Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
AAMT. (1998). Numeracy education in schools. Australian Association of Mathematics Teachers. Available at: https://primarystandards.aamt.edu.au/About-AAMT/Position-statements/Numeracy-education (Accessed October 11, 2022).
AAMT and AIG. (2014). Identifying and supporting quantitative skills of 21st century workers. Adelaide: Australian Association of Mathematics Teachers, and Australian Industry Group. Available at: http://www.aamt.edu.au/Activities-and-projects/Workplace-maths-skills %02.
ACARA. (2023). ACARA Numeracy Australian. Curriculum Assessment and Reporting Authority. Numeracy. Available at: https://v9.australiancurriculum.edu.au/teacher-resources/understand-this-general-capability/numeracy#accordion-ec50a82d77-item-a3563679db.
ACCC. (2022). June 2022 report. Australian Competition Consumer Commission. Available at: https://www.accc.gov.au/regulated-infrastructure/telecommunications-and-internet/telecommunications-industry-record-keeping-and-reporting-rules/internet-activity-record-keeping-rule/june-2022-report (Accessed February 7, 2023).
Al-Emran, M., Malik, S. I., and Al-Kabi, M. N. (2020). “A survey of internet of things (IoT) in education: opportunities and challenges” in Toward social internet of things (SIoT): Enabling technologies, architectures and applications: Emerging technologies for connected and smart social objects studies in computational intelligence. eds. A. E. Hassanien, R. Bhatnagar, N. E. M. Khalifa, and M. H. N. Taha (Cham: Springer International Publishing), 197–209.
Attard, C., and Holmes, K. (2019). Technology-enabled Mathematics Education: Optimising Student Engagement. Abingdon: Routledge.
Attard, C., and Holmes, K. (2020). “It gives you that sense of hope”: an exploration of technology use to mediate student engagement with mathematics. Heliyon 6:e02945. doi: 10.1016/j.heliyon.2019.e02945
Atzori, L., Iera, A., and Morabito, G. (2010). The internet of things: a survey. Comput. Netw. 54, 2787–2805. doi: 10.1016/j.comnet.2010.05.010
Australian Bureau of Statistics. National, State and Territory Population. (2022). Available at: https://www.abs.gov.au/statistics/people/population/national-state-and-territory-population/jun-2022 (Accessed August 24, 2023).
Bardini, T. (2000). Bootstrapping: Douglas Engelbart, coevolution, and the origins of personal computing. California: Stanford University Press.
Berryman, D. R. (2012). Augmented reality: a review. Med. Ref. Serv. Q. 31, 212–218. doi: 10.1080/02763869.2012.670604
Buckner, R. L., Kelley, W. M., and Petersen, S. E. (1999). Frontal cortex contributes to human memory formation. Nat. Neurosci. 2, 311–314. doi: 10.1038/7221
Cai, S., Liu, E., Shen, Y., Liu, C., Li, S., and Shen, Y. (2020). Probability learning in mathematics using augmented reality: impact on student’s learning gains and attitudes. Interact. Learn. Environ. 28, 560–573. doi: 10.1080/10494820.2019.1696839
Carbonneau, K. J., Marley, S. C., and Selig, J. P. (2013). A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives. J. Educ. Psychol. 105, 380–400. doi: 10.1037/a0031084
Cavus, H., and Deni̇z, S. (2022). The effect of technology assisted teaching on success in mathematics and geometry: a meta-analysis study. Particip. Educ. Res. 9, 358–397. doi: 10.17275/per.22.45.9.2
Ceci, L. (2021). Annual number of mobile app downloads worldwide 2022. Statista. Available at: https://www.statista.com/statistics/271644/worldwide-free-and-paid-mobile-app-store-downloads/ (Accessed February 7, 2023).
Chen, L., Chen, P., and Lin, Z. (2020). Artificial intelligence in education: a review. IEEE Access 8, 75264–75278. doi: 10.1109/ACCESS.2020.2988510
Chen, C., Zhang, L., Li, Y., Liao, T., Zhao, S., Zheng, Z., et al. (2022). When digital economy meets Web3.0: applications and challenges. IEEE Open J. Comput. Soc. 3, 233–245. doi: 10.1109/OJCS.2022.3217565
Chiba, T., Iwase, T., Yoshida, Y., and Shirakawa, I. (2012). History of developing and commercializing families of solid-state calculators. In: 2012 third IEEE history of electro-technology conference, pp. 1–5.
Das, S. (2016). Cyber-physical-social convergence in smart living: challenges and opportunities. In: 2016 IEEE international conference on pervasive computing and communication workshops (PerCom workshops), pp., 1–1.
Department of Education Victoria. (2022). Numeracy for all learners. Numeracy math. Available at: https://www.education.vic.gov.au:443/school/teachers/teachingresources/discipline/maths/Pages/numeracy-for-all-learners.aspx (Accessed March 14, 2023).
Dewey, J. (1933). Why have progressive schools? Curr. Hist. N. Y. 38, 441–448. doi: 10.1525/curh.1933.38.4.441
Downes, J. M., and Bishop, P. (2012). Educators engage digital natives and learn from their experiences with technology: integrating technology engages students in their learning. Middle Sch. J. 43, 6–15. doi: 10.1080/00940771.2012.11461824
Dwivedi, Y. K., Hughes, L., Ismagilova, E., Aarts, G., Coombs, C., Crick, T., et al. (2021). Artificial intelligence (AI): multidisciplinary perspectives on emerging challenges, opportunities, and agenda for research, practice and policy. Int. J. Inf. Manag. 57, 101994–101947. doi: 10.1016/j.ijinfomgt.2019.08.002
Ehrenberg, A. S. C. (1977). Rudiments of numeracy. J. R. Stat. Soc. Ser. Gen. 140, 277–297. doi: 10.2307/2344922
Epaminonda, E., Efthymiou, L., and Doukanari, E. (2022). Linking digital transformation to learning strategies and pedagogy. In: 2022 IEEE global engineering education conference (EDUCON), pp. 2088–2092.
FitzSimons, G. E., and Björklund Boistrup, L. (2017). In the workplace mathematics does not announce itself: towards overcoming the hiatus between mathematics education and work. Educ. Stud. Math. 95, 329–349. doi: 10.1007/s10649-017-9752-9
FYA. (2018). The new work order: report series. Foundation for Young Australians. Available at: https://www.fya.org.au/report/new-work-order-summary/ %08.
Gal, I., Grotlüschen, A., Tout, D., and Kaiser, G. (2020). Numeracy, adult education, and vulnerable adults: a critical view of a neglected field. ZDM 52, 377–394. doi: 10.1007/s11858-020-01155-9
Geiger, V., Goos, M., and Dole, S. (2015a). The role of digital technologies in numeracy teaching and learning. Int. J. Sci. Math. Educ. 13, 1115–1137. doi: 10.1007/s10763-014-9530-4
Geiger, V., Goos, M., and Forgasz, H. (2015b). A rich interpretation of numeracy for the 21st century: a survey of the state of the field. ZDM 47, 531–548. doi: 10.1007/s11858-015-0708-1
Geiger, V., Yasukawa, K., Bennison, A., Wells, J. F., and Sawatzki, C. (2020). “Facets of numeracy: teaching, learning and practices” in Research in mathematics education in Australasia 2016–2019. eds. J. Way, C. Attard, J. Anderson, J. Bobis, H. McMaster, and K. Cartwright (Singapore: Springer), 59–89.
Ghazali, M. A. A., Kassim, M., Ya’acob, N., Idris, A., and Saaidin, S. (2019). Mobile application on garbage collector tracker using Google maps. In: 2019 IEEE 9th international conference on system engineering and technology (ICSET), pp. 287–291.
Goos, M., Dole, S., and Geiger, V. (2012a). Numeracy across the curriculum. Aust. Math. Teach. 68, 3–7.
Goos, M., Galbraith, P., Renshaw, P., and Geiger, V. (2003). Perspectives on technology mediated learning in secondary school mathematics classrooms. J. Math. Behav. 22, 73–89. doi: 10.1016/S0732-3123(03)00005-1
Goos, M., Geiger, V., and Dole, S. (2012b). Auditing the numeracy demands of the middle years curriculum. PNA Rev. Investig. En Didáctica Matemática 6, 147–158. doi: 10.30827/pna.v6i4.6138
Goos, M., and O’Sullivan, K. (2022). Numeracy across the curriculum. In: Oxford Research Encyclopedia of Education. Oxford: Oxford University Press.
Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15, 105–123. doi: 10.1007/s10763-017-9814-6
Hansson, S. O. (2020). Technology and mathematics. Philos. Technol. 33, 117–139. doi: 10.1007/s13347-019-00348-9
Hertel, J. T. (2016). Investigating the implemented mathematics curriculum of new England navigation cyphering books. Learn. Math. 36, 4–10.
Hill, J. L., Kern, M. L., Seah, W. T., and van Driel, J. (2021). Feeling good and functioning well in mathematics education: exploring students’ conceptions of mathematical well-being and values. ECNU Rev. Educ. 4, 349–375. doi: 10.1177/2096531120928084
Hoogland, K. (2023). The changing nature of basic skills in numeracy. Front. Educ. 8:754. doi: 10.3389/feduc.2023.1293754
Hughes, C. (2021). Australia: Smartphone Users 2026. Statista. Available at: https://www-statista-com.eu1.proxy.openathens.net/statistics/467753/forecast-of-smartphone-users-in-australia/ (Accessed February 7, 2023).
Hutton, M., Coben, D., Hall, C., Rowe, D., Sabin, M., Weeks, K., et al. (2010). Numeracy for nursing, report of a pilot study to compare outcomes of two practical simulation tools – an online medication dosage assessment and practical assessment in the style of objective structured clinical examination. Nurse Educ. Today 30, 608–614. doi: 10.1016/j.nedt.2009.12.009
Jorgensen Zevenbergen, R. (2011). Young workers and their dispositions towards mathematics: tensions of a mathematical habitus in the retail industry. Educ. Stud. Math. 76, 87–100. doi: 10.1007/s10649-010-9267-0
Keldgord, F., and Ching, Y.-H. (2022). Teachers’ experiences with and perceptions of virtual manipulatives following the COVID-19 pandemic. TechTrends 66, 957–967. doi: 10.1007/s11528-022-00796-9
Kidman, G., and Chang, C.-H. (2022). Numbers and graphs - what sort of mathematical literacy do we need for geographical education in uncertain times. Int. Res. Geogr. Environ. Educ. 31, 1–4. doi: 10.1080/10382046.2022.2018756
Li, K., Cui, Y., Li, W., Lv, T., Yuan, X., Li, S., et al. (2023). When internet of things meets metaverse: convergence of physical and cyber worlds. IEEE Internet Things J. 10, 4148–4173. doi: 10.1109/JIOT.2022.3232845
Lodi, M., and Martini, S. (2021). Computational thinking, between Papert and Wing. Sci. Educ. 30, 883–908. doi: 10.1007/s11191-021-00202-5
Mak-van der Vossen, M., Teherani, A., van Mook, W. N. K. A., Croiset, G., and Kusurkar, R. A. (2018). Investigating US medical students’ motivation to respond to lapses in professionalism. Med. Educ. 52, 838–850. doi: 10.1111/medu.13617
Monaghan, J., and Trouche, L. (2016). Mathematics teachers and digital tools. Tools Math. 110, 357–384. doi: 10.1007/978-3-319-02396-0_15
Moyer, P. S., Bolyard, J. J., and Spikell, M. A. (2002). What are virtual manipulatives? Teach. Child. Math. 8, 372–377. doi: 10.5951/TCM.8.6.0372
Moyer-Packenham, P. S., and Bolyard, J. J. (2016). “Revisiting the definition of a virtual manipulative” in International perspectives on teaching and learning mathematics with virtual manipulatives mathematics education in the digital era. ed. P. S. Moyer-Packenham (Cham: Springer International Publishing), 3–23.
Moyer-Packenham, P. S., and Westenskow, A. (2013). Effects of virtual manipulatives on student achievement and mathematics learning. Int. J. Virtual Pers. Learn. Environ. IJVPLE 4, 35–50. doi: 10.4018/jvple.2013070103
New South Wales Government-Education (2023). Literacy and numeracy. Numeracy. Available at: https://education.nsw.gov.au/teaching-and-learning/curriculum/literacy-and-numeracy/teaching-and-learning-resources/numeracy.html (Accessed March 14, 2023).
Nieminen, J. H., Chan, M. C. E., and Clarke, D. (2022). What affordances do open-ended real-life tasks offer for sharing student agency in collaborative problem-solving? Educ. Stud. Math. 109, 115–136. doi: 10.1007/s10649-021-10074-9
OECD. (2022a). Harnessing the power of AI and emerging technologies: Background paper for the CDEP ministerial meeting. Paris: OECD Publishing.
OECD. (2022b). PISA 2022: Mathematics framework. Available at: https://pisa2022-maths.oecd.org/ca/index.html (Accessed August 19, 2023).
Ontario Curriculum. (2023). Mathematics. Available at: https://www.dcp.edu.gov.on.ca/en/curriculum/secondary-mathematics (Accessed August 24, 2023).
Organisation for Economic Co-operation and Development (OECD) (2018). The future of education and skills: Education 2030. Paris: OECD. Available at: http://www.oecd.org/education/2030/oecd-education-2030-position-paper.pdf
Qiu, Y., Pan, J., and Ishak, N. A. (2022). Effectiveness of artificial intelligence (AI) in improving pupils’ deep learning in primary school mathematics teaching in Fujian Province. Comput. Intell. Neurosci. 2022, 1–10. doi: 10.1155/2022/1362996
Queensland Curriculum and Assessment Authority (2021). General capabilities: Numeracy. Available at: https://www.qcaa.qld.edu.au/p-10/aciq/version-8/general-capabilities/numeracy (Accessed March 14, 2023).
Reiten, L. (2020). Why and how secondary mathematics teachers implement virtual manipulatives. Contemp. Issues Technol. Teach. Educ. 20, 55–84.
Romero, A. M., Quesada, A. A., and Estepa, C. A. (2021). Promoting critical thinking through mathematics and science teacher education: the case of argumentation and graphs interpretation about climate change. Eur. J. Teach. Educ. 2021, 1–19. doi: 10.1080/02619768.2021.1961736
Sarama, J., and Clements, D. H. (2016). “Physical and virtual manipulatives: what is ‘concrete’?” in International perspectives on teaching and learning mathematics with virtual manipulatives mathematics education in the digital era. ed. P. S. Moyer-Packenham (Cham: Springer International Publishing), 71–93.
Scribante, N., and Pretorius, L. (2022). Can systems thinking as a process be used to solve real-world problems? In [Pretoria: international council on systems engineering (INCOSE)]. Available at: https://www.researchgate.net/publication/366953328_CAN_SYSTEMS_THINKING_AS_A_PROCESS_BE_USED_TO_SOLVE_REAL-WORLD_PROBLEMS.
Shergold, P., Calma, T., and Russo, S. (2020). Looking to the future. Education Council of Australia. Available at: https://apo.org.au/node/307138.
Siller, H.-S., and Greefrath, G. (2010). Mathematical modelling in class regarding to technology. In: Proceedings of the sixth congress of the European Society for Research in Mathematics Education, pp. 2136–2145.
South Australia Department of Education. (2022). Curriculum in South Australia–From early years to year 12. Available at: https://www.education.sa.gov.au/students/curriculum-and-learning/curriculum-birth-year-10 (Accessed March 14, 2023).
Strava. (2023). Strava features. Available at: https://www.strava.com/features (Accessed September 4, 2023).
Taylor, C., Carrigan, J., Noura, H., Ungur, S., Van Halder, J., and Singh Dandona, G. (2019). Australia’s automation opportunity: reigniting productivity and inclusive income growth. McKinsey. Available at: http://hdl.voced.edu.au/10707/498608 %2020.
The Department for Education, Children and Young People Tasmania. (2023). Literacy and numeracy. The Department for Education, Children and Young People Tasmania. Available at: https://www.decyp.tas.gov.au/parents-carers/literacy-and-numeracy/ (Accessed March 14, 2023).
Tout, D. (2021). Critical connections between numeracy and mathematics. Available at: https://www.education.vic.gov.au/school/teachers/teachingresources/discipline/maths/Pages/research_connectionsbetweennumeracyandmaths.aspx.
VCAA. (2022). VCE vocational major numeracy. Victorian Curriculum and Assessment Authority. Major Numeracy. Available at: https://www.vcaa.vic.edu.au/curriculum/vce/vce-study-designs/VCEVMNumeracy/Pages/Index.aspx.
Vermesan, O., Friess, P., Guillemin, P., Giaffreda, R., Grindvoll, H., Eisenhauer, M., et al. (2015). “Building the hyperconnected society-internet of things research and innovation value chains, ecosystems and markets” in Building the hyperconnected society-internet of things research and innovation value chains, ecosystems and markets communications. eds. O. Vermesan and P. Friess (Aalborg, Denmark: River Publishers), 119–143.
Victorian Curriculum and Assessment Authority (2023). Numeracy. Available at: https://www.vcaa.vic.edu.au/curriculum/foundation-10/crosscurriculumresources/Pages/Numeracy.aspx (Accessed March 14, 2023).
Wake, G. (2015). Preparing for workplace numeracy: a modelling perspective. ZDM 47, 675–689. doi: 10.1007/s11858-015-0704-5
West Australian School Curriculum and Standards Authority (2023). West Australia general capabilities. Available at: https://k10outline.scsa.wa.edu.au/home/teaching/curriculum-browser/mathematics-v8/overview/general-capabilities (Accessed March 14, 2023).
Wing, J. M. (2019). A conversation about computational thinking. NSW Department of Education. NSW Department. Available at: https://policies.education.nsw.gov.au/content/dam/main-education/teaching-and-learning/education-for-a-changing-world/media/documents/Computational-Conversation_1_A.pdf.
Wolfram, C. (2020). Covid-19 and excel-07: When will we fix the failed education that lead to yet another data science disaster? Available at: http://www.conradwolfram.com/home/covid19-excel07.
Worthington, S. (2017). The ATM celebrates 50 years but we’re using it less. The Conversation. Available at: http://theconversation.com/the-atm-celebrates-50-years-but-were-using-it-less-79847 (Accessed February 7, 2023).
Zevenbergen, R. (2004). Technologizing numeracy: intergenerational differences in working mathematically in new times. Educ. Stud. Math. 56, 97–117. doi: 10.1023/B:EDUC.0000028399.76056.91
Keywords: numeracy, digital, technology, tools, education, mathematical literacy
Citation: Sakurai J and Goos M (2023) Revisiting tools in numeracy learning: the role of authentic digital tools. Front. Educ. 8:1291407. doi: 10.3389/feduc.2023.1291407
Edited by:
Dominik E. Froehlich, University of Vienna, AustriaReviewed by:
Brandon McMillan, Brigham Young University, United StatesValerie Harlow Shinas, Lesley University, United States
Copyright © 2023 Sakurai and Goos. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Justine Sakurai, ai5zYWt1cmFpQHVuaW1lbGIuZWR1LmF1
 Justine Sakurai
Justine Sakurai Merrilyn Goos
Merrilyn Goos