- 1Institute of Educational Sciences, Leuphana University, Lüneburg, Germany
- 2Institute of Mathematics and its Didactics, Leuphana University, Lüneburg, Germany
- 3German Studies Institute, Ruhr University Bochum, Bochum, Germany
Introduction: Many teachers consider real-life tasks problematic for students because of their linguistic demands. However, it is unclear how the linguistic demands of real-life tasks actually affect students' solution rates for these tasks.
Method: Against this background, this experimental study systematically varied the linguistic demands of real-life mathematical tasks. It examined (1) the extent to which teachers (N = 72) estimate the influence of linguistic modifications on students' solution rates, (2) the extent to which linguistic modification influences actual student test results (N = 1, 346), and (3) whether students' language skills mitigate this effect.
Results: The results showed that the teachers expected linguistic modification to strongly influence the students' problem-solving processes (effect sizes: 0.73 < d < 1.67). However, the effect size for the actual student performance (d = 0.12) was considerably lower than the teachers' expectations.
Discussion: The findings indicate that in mathematics teachers' education, additional attention should be paid to the role of language in solving reality-based tasks.
Introduction
Mathematical problem-solving tasks embedded in real-world contexts, commonly known as reality-based tasks, are challenging for both educators and students. Unlike traditional mathematical exercises, these require students to not only apply mathematical concepts but also comprehend and interpret textual information within a contextual scenario (Khoshaim, 2020). Consequently, they are often perceived as particularly demanding and can pose significant hurdles for students, especially those with varying language proficiency levels.
Within the educational landscape, recognition of the intricate interplay between students' language proficiency and their performance on mathematical text tasks is growing (Prediger et al., 2018). However, the exact mechanisms underlying this interplay, particularly in the context of reality-based tasks, remain elusive. Moreover, research investigating teachers' perceptions of students' difficulties with reality-based tasks and the accuracy of these perceptions is lacking.
Understanding how teachers perceive students' difficulties is crucial for several reasons. Misalignments between teachers' perceptions and students' actual performance may impede effective instructional planning and hinder students' academic progress. By identifying and addressing these discrepancies, educators can optimize their support strategies and create more inclusive learning environments that cater to all students' diverse needs.
However, existing studies' methodological limitations pose a notable challenge in addressing this research gap. Non-experimental approaches often struggle to disentangle the dual demands of mathematical content and linguistic comprehension inherent in reality-based tasks (e.g., Walkington et al., 2018). Non-experimental studies investigating how language demands affect solution rates in mathematical text tasks frequently rely on data from large-scale assessments with large data sets. However, in these studies, mathematically demanding tasks are often those with higher linguistic demands, making it difficult to distinguish between the two aspects of tasks. These effects can only be investigated separately through systematic experimental variation of linguistic and mathematical demands. Thus, rigorous experimental designs that systematically manipulate the language demands of reality-based tasks while controlling for mathematical complexity are necessary.
This study aims to address this research deficit by employing a rigorous experimental design. By systematically varying the language demands of reality-based tasks while keeping the mathematical content constant, we investigate the impact on teachers' expectations and students' actual performance, while accounting for students' varying levels of language proficiency. Through this approach, we aim to provide valuable insights into the nuanced relationship between linguistic demands, mathematical content, and student outcomes in the context of reality-based tasks.
Theoretical background
This section describes the process of solving reality-based mathematical tasks. Subsequently, we illustrate the language process's role in solving such tasks and elaborate on student characteristics that affect their ability to respond to them. Furthermore, we elaborate on teachers' attitudes concerning students' language difficulties with mathematical tasks. Finally, we review empirical studies that have rigorous experimental designs with varying linguistic task attributes.
Solving reality-based mathematical tasks
Reality-based tasks (Blum and Leiss, 2007) involve authentic problem situations in a realistic setting. They are usually presented in a descriptive text (Verschaffel et al., 2020) and play a strongly growing role in mathematics education [e.g., Boaler, 2001; National Council of Teachers of Mathematics (NCTM), 2003]. How a student approaches such a task—and, subsequently, its degree of difficulty—is principally determined by the mathematic demands it contains, such as the mathematical attributes and competencies focused or the number and kind of mathematical operations required (Blomhøj and Jensen, 2003; Maaß, 2010; OECD., 2003; Schleicher et al., 2009).
All phases in a reality-based mathematical task's solution process contain potential difficulties for students (Galbraith and Stillman, 2006; Newman, 1977; Stillman et al., 2010). However, the first step is reading and comprehending the text prompt (Blum and Leiss, 2007; Leiss et al., 2019), where the reader seeks to establish the task situation's mental model that sets the foundation for a precise understanding (Heine et al., 2018). Following the established models of reading, this comprehension process can be understood as the construction of a situation model, an individual cognitive representation, with a combination of the bottom-up and top-down processes. The textual elements are decoded and provide situational data; however, they are simultaneously interpreted based on prior knowledge and integrated into the existing knowledge structures (Kintsch and van Dijk, 1978; McNamara et al., 2010; Caccamise et al., 2008). Comprehension can be considered successful when the readers' resulting situation model converges with the author's intended meaning (Reusser, 1989). In reality-based tasks, the text comprehension processes form the basis for any appropriate application of mathematical knowledge and skills, thus putting particular weight on this element (Cummins et al., 1988), especially since the presentation of an authentic problem situation from daily life often requires an extensive text, compared to word problems describing only a simple situation (“In a bowl, there are two apples and three pears...”). Therefore, reality-based tasks often require high language proficiency (Leiss et al., 2019). Several studies have shown that comprehension problems in this phase cause errors in the following solution steps (Leiss et al., 2010; Mayer and Hegarty, 1996; Wijaya et al., 2014). Thus, language proficiency is an essential student variable, comprising the ability to decode words and sentences, as well as strategies such as analyzing text structure, summarizing, or annotating texts (Artelt et al., 2009).
Role of the language process in solving reality-based mathematical tasks
A general and extremely basic assumption in general linguistics is that language provides various alternatives for expressing ideas. Hence, the same content can be linguistically represented in diverse ways (Cummins, 2000, 2008; Schleppegrell, 2007, 2010, 2012). One can decide on the vocabulary level regarding how to present ideas verbally. One can use highly frequent verbs and nouns with a clear, straightforward meaning, with which even beginners will be familiar. Alternatively, one can utilize infrequent vocabulary poorly represented in everyday linguistic input. One can use short sentences with an evident, canonical structure or compress large amounts of information into one single, complex sentence. Most conceptual contents and ideas always have several possibilities of linguistic expression that can theoretically serve the same purpose. However, they could differ in readability and be more difficult to understand for students with low language competencies.
Accordingly, the same reality-based tasks can be presented in linguistically different versions. Imagine two different variants, A and B, of realistic tasks. Variant A presents a reality-based situation regarding a mathematical task with highly familiar vocabulary and simple sentence structures. Variant B denotes the same situation through infrequent vocabulary and long, complex syntactic structures. The mathematical demands for solving both tasks are the same; however, Variant B obviously requires higher text comprehension demands than Variant A. Since the former will put greater constraints on linguistic knowledge and processing, students with identical mathematical skills will presumably score lower on Variant B than A.
A comprehensive study on the influence of language factors on solving mathematical tasks was conducted by Walkington et al. (2018). Using data from 20 years of the National Assessment of Educational Progress (NAEP) and Trends in International Mathematics and Science Study (TIMSS), they examined the effect of readability factors such as word length, polysemous and technical vocabulary, vocabulary size, and syntactic complexity in mathematics word problems on students' solution rates. The results of the analyses showed that these factors influenced the difficulty of the mathematics word problems and that they also interacted to some extent with students' background characteristics, such as race/ethnicity, math achievement, and socioeconomic status.
Student characteristics that affect solving reality-based mathematical tasks
Students' mathematical and language proficiency can be considered one of the most important characteristics influencing the likelihood of successfully solving a mathematical word problem (Prediger, 2019).
The level of students' mathematical knowledge and skills affects the identification of mathematical relationships and concepts when solving mathematical word problems, for instance, by identifying mathematical operation patterns. In several studies, pre-knowledge was the most significant predictor of achievement (Nguyen et al., 2016; Hailikari et al., 2008). Furthermore, mathematical problem-solving strategies (Schoenfeld, 2014; Polya, 1945) are also relevant. Regarding reality-based math tasks, researchers have emphasized the importance of problem-solving strategies as mental tools for solving mathematical tasks (Capraro et al., 2012; Galbraith and Stillman, 2006; Schukajlow and Leiss, 2011). Leiss et al. (2019) and Wienecke et al. (2023) showed that strategies such as note-taking are conducive to finding solutions to reality-based math problems.
A sufficient language proficiency level is essential to develop a proper situation model for reality-based tasks. Specifically, presenting an authentic situation from daily life is often provided by a considerably longer text than “traditional” word problems. Thus, such tasks often require high-level language proficiency (Leiss et al., 2019). Studies on linguistic tasks' attributes showed that students belonging to sub-groups, such as low-achieving (Wheeler and McNutt, 1983), bilingual (Moschkovich, 2002), and English as an additional language (Barwell, 2005), encounter specific challenges when solving mathematical word problems. Moschkovich and Scott (2021) summarized language issues in mathematics word problems, especially for English language learners. They summarized that the most relevant language features are on three levels: (a) the cultural background, (b) syntactic (sentences and paragraphs), and (c) lexical levels (words and phrases).
Teachers' perceptions of students' difficulties with solving reality-based mathematical tasks
This section addresses mathematics teachers' perceptions of students' language difficulties when solving reality-based mathematical tasks. Given the limited research evidence in this area, we draw upon findings examining the broader role of language in educational processes. For example, Skinnari and Nikula (2017) showed that (Finnish) teachers possess some awareness of the subject-specific language within their discipline and the value of multiliteracy practices. However, the role of multilingualism, encompassing the diversity of students' languages and its impact on pedagogical practice, was only minor. Seah (2016) showed that teachers perceive a wide range of student difficulties related to language use, especially concerning the use of technical terms. Contrastingly, few studies to date have addressed the perception of difficulties in solving reality-based mathematical tasks.
Khoshaim's (2020) study shed light on teachers' reluctance to incorporate word problems into their instruction, citing perceived challenges faced by students. These include insufficient mathematical skills and a negative disposition toward mathematics when engaging with such tasks. Consequently, these difficulties in task engagement can exacerbate classroom stress and anxiety, potentially leading to math-related anxiety disorders among students.
Pearce et al. (2013) contributed insights into teachers' perceptions of their students' primary hurdle in solving word problems—namely, the ability to comprehend the text. Teachers in the study predominantly recommended keyword searching as a strategy for overcoming this perceived difficulty. Interestingly, the study highlighted a gap in teachers' pedagogical approaches, as none reported explicitly teaching problem-solving strategies to their students.
Basaraba et al.'s (2019) study analyzed teachers' perceptions and elucidated factors contributing to difficulty in math word problems. Particularly, teachers identified language presentation as a more formidable challenge for English language learners (ELLs) than for native English speakers. These findings underscore teachers' awareness of the linguistic demands inherent in mathematical tasks, especially for diverse learner populations.
Despite these valuable insights, the extent to which mathematics teachers' perceptions align with actual language-related difficulties in reality-based tasks remains ambiguous. Teachers should be aware that both linguistic and mathematical demands influence the solving of reality-based mathematical tasks. If linguistic demands are significantly overestimated or underestimated, teachers may not select the appropriate difficulty level for their students and thus overwhelm or underwhelm them. Particularly for students with low language skills, this can contribute to increasing the disadvantage of these students and widening social disparities in the education system. Addressing this discrepancy is therefore crucial for teacher training. By understanding and anticipating potential linguistic challenges in learning materials and assessments, teachers can better support student learning and adapt teaching strategies to effectively meet the needs of different learners.
In summary, an in-depth exploration of teachers' perceptions of students' difficulties with reality-based mathematical tasks offers valuable insights into the intersection of language and mathematics learning. By bridging the gap between perceived and actual challenges, educators can enhance pedagogical practices and promote equitable access to high-quality mathematics education for all learners.
Literature review of empirical studies employing rigorous experimental designs to vary linguistic task attributes
A challenge in researching student characteristics' impact on reality-based tasks (or on mathematics word problems, too) is that mathematical and language task attributes are often confounded and, due to the methodological design, cannot be analyzed independently. For example, mathematically complex problems that require multiple solving steps often have longer problem descriptions with more and possibly longer sentences.
As mentioned, Walkington et al. (2018) showed that the influence of linguistic factors such as length, word difficulty, and pronouns makes processing mathematical word problems more difficult. However, this study was based on a cross-sectional design (observed data from large-scale assessments) and failed to separate the confounding factors between a task's linguistic and mathematical demands. Additionally, students' language proficiency could not be controlled, so no differentiated analyses for weak and strong students were possible. Therefore, although this research provided strong evidence that language factors are relevant, no causal relationships could be demonstrated.
Moreover, how the factors at the student and task levels work together or interact remains unclear. Many researchers assume that student characteristics moderate the influence of mathematical and linguistic task attributes on the successful solving of mathematical word problems (Abedi et al., 1997; Abedi and Lord, 2001; Haag et al., 2013; Daroczy et al., 2015; Martiniello, 2008; Prins and Ulijn, 1998).
An experimental research design is required to analyse the effects of the interaction of student characteristics and mathematical and language task characteristics. This is the only way to control or systematically vary linguistic and mathematical factors in a targeted manner. However, experimental studies that vary readability factors or the linguistic dimensions of test items in experimental designs under tight control of other factors are rare. Given these methodological challenges, we have summarized the state of research in the following section, considering only studies with a strict experimental design.
Abedi and Lord (2001) investigated the importance of language on student test performance in mathematical word problems. Overall, 1,174 students were given items released from the National Assessment of Educational Progress mathematics assessment and parallel ones modified to reduce their linguistic demands. The linguistic modification (seven factors on syntactic and lexical levels) of 20 test items caused significant differences in the mathematics performance; the linguistically modified version's scores were slightly higher (effect size: d = 0.09). Some student groups benefited more from the items' linguistic modification, particularly those in low-level and average mathematics classes, ELLs, and those with a low socio-economic status.
Johnson and Monroe (2004) examined the impact of simplified language on one state's mathematics performance assessment through 20 items. The simplified language was received by applying seven recommendations designed to improve the accessibility of text material from Kopriva (2000). Overall, 1,232 seventh-grade students had participated. The variance analysis indicated no benefit for those in general education (effect size: d = 0.05) and ELLs. Only those receiving special education services (N = 138) benefitted from the simplified language (effect size: d = 0.17); nonetheless, their scores remained significantly below those of their general education counterparts.
From a test accommodation perspective, Sato et al. (2010) evaluated whether ELLs significantly benefitted from a linguistic simplification (different modification strategies on syntactic and lexical levels) of 25 multiple-choice mathematics items. Four different item response theory-based (IRT) scoring approaches, commonly used by the states in analyzing the performance data from the United States state-wide testing, assessed their mathematics performance. Differences across sub-groups (ELLs, English language proficiency, and Non-English language proficiency) in the effects of linguistic modification on the students' mathematics performance depended on the scoring approach. Only when the scores were constructed based on the 1-PL item response model (Rasch model) a significant difference in the theta scores on the two item sets (original and linguistically modified) was detected across the student subgroups (effect size: d = 0.16). An analysis based on the raw scores or other IRT models revealed no significant effects of linguistic simplification.
Moreover, Haag et al. (2015) tested the impact of simplifying mathematics word problems' language (19 factors on syntactic and lexical levels). Using a randomized experimental design, they conducted a large-scale linguistic simplification study to test whether the performance gap between those who use a heritage language at home and monolinguals was smaller when assessed with linguistically simplified items in the schooling language. They utilized data from 17,738 fourth graders. Although the differences between the multilingual and monolingual students in mathematics achievement were related to those in their language proficiency and socioeconomic status, they found no significant primary effects of linguistic simplification. However, the multilingual students' differential effects emerged, indicating that some might profit from linguistic simplification during elementary school.
Pöhler et al. (2017) investigated whether students with low and high language proficiency score differently on mathematical word problems and whether this was due to the items' text format or conceptual mathematical challenges. A test with percentage problems of different types, in a purely mathematical, text, or visual format, was given to 308 seventh graders, with the scores analyzed statistically using a cognitive diagnosis model. The probability for those with a low language proficiency to solve the text format items was not lower than that for the pure format, indicating that conceptual challenges might have a stronger impact than language ones.
Walkington et al. (2019) systematically manipulated six different language features (number of sentences, pronouns, word concreteness, word hypernyms, consistency of sentences, and problem topic) of algebra story problems and analyzed the effects on student performance. They found limited evidence suggesting individual language features considerably affect the mathematics word problem-solving performance of the general student population. Among other differential results, language modifications were suggested to benefit or harm students depending on their familiarity with the computer-based assessment instrument employed.
Experimental studies so far have provided crucial empirical evidence regarding linguistic task characteristics' influence on task difficulty. Despite this research progress, a significant gap persists concerning the generalizability of the studies' findings across diverse student populations. While some studies have identified substantial effects of linguistic task characteristics, particularly for multilingual students or those with special educational needs (Haag et al., 2015), none have consistently demonstrated a larger effect across the entire student sample. This discrepancy highlights a critical gap in the literature, suggesting that the impact of language demands on task difficulty may vary significantly depending on individual student characteristics, particularly their language proficiency levels. Furthermore, existing research has often failed to adequately consider students' language proficiency levels in a nuanced manner, leading to potential confounding effects in the analyses. Consequently, the true relationship between linguistic task characteristics, student language proficiency, and task difficulty remains inadequately understood. This study aims to address these research gaps by adopting a comprehensive approach that considers students' language proficiency levels as a crucial factor influencing task difficulty. By measuring and controlling for students' language proficiency levels, we aim to provide a more nuanced understanding of the interplay between linguistic task characteristics and task difficulty across diverse student populations. We believe that elucidating the differential effects of language demands on task difficulty and considering the moderating role of students' language proficiency levels will help bridge the existing research gap and advance knowledge in this area. Through rigorous empirical investigation, we aim to elucidate the nuanced dynamics of task difficulty in reality-based mathematical tasks and inform more effective instructional practices considering students' diverse linguistic needs.
Research questions and hypotheses
This study aims to address three research questions. Each question investigates the linguistic demands of the impact of reality-based tasks on teachers' perceptions. Two questions also analyse student performance (one without controlling for and the other controlling for background characteristics). The three questions are designed to address existing research gaps and provide insights into the discrepancies between teachers' estimations and students' actual performance, as well as the interplay between language demands and task difficulty.
1. Teacher perceptions and task difficulty
Research Question 1: How do mathematics teachers assess the likelihood of students solving reality-based tasks with systematically varied linguistic difficulties?
Hypothesis 1: We hypothesize that the linguistic demands of reality-based tasks will influence teachers' perceptions of task difficulty. Specifically, tasks with higher linguistic demands will be perceived as having lower solution probabilities than content-equivalent tasks with lower linguistic demands.
2. Student performance and task difficulty
Research Question 2: How do the linguistic demands of reality-based tasks influence the solution rate of these tasks when solved by students?
Hypothesis 2: Drawing from the literature (e.g., Walkington et al., 2019), we hypothesize that reality-based tasks with higher linguistic demands will pose greater complexity for students than tasks with lower linguistic demands. Additionally, we aim to compare teachers' estimations of solution probabilities with students' actual solution rates to explore any discrepancies between them. Such discrepancies can provide valuable insights into the effectiveness of instructional practices. If teachers consistently overestimate or underestimate certain tasks' difficulty, it may indicate the need to adjust teaching methods or task designs to better align with students' abilities and learning needs.
3. Moderating effect of language proficiency
Research Question 3: To what extent is the influence of linguistic demands on the solution rate of a task moderated by students' language proficiency in the schooling language?
Hypothesis 3: Building on previous findings (e.g., Haag et al., 2015), we hypothesize that the effect of linguistic demands on task difficulty will vary depending on students' language proficiency. Specifically, students with lower general language proficiency will experience a stronger impact of linguistic demands on task difficulty than those with higher language proficiency.
Materials and methods
Modifying the reality-based tasks' linguistic demands
We constructed three linguistically different versions each (low, medium, and high linguistic demands) of five reality-based tasks. All items' mathematical content addressed reality-based problems in the linear functions' content area. In constructing these tasks, we accounted for various design criteria, which were intended to ensure that they were reality-based tasks in the sense of Depaepe et al. (2015). This means that the processing phases of Understanding, Structuring, Mathematizing, Working mathematically, Interpreting, and Validating had to be completed. Besides that, the students should not be deterred from seriously starting the solution process by elements that are too unfamiliar, such as an unusually long description of a real-life situation or the still unfamiliar making of assumptions of required quantities. In this respect, the tasks used in our study can be characterized by the following content-related features:
- A written task stimulus that describes a daily-life context relatively briefly (M = 121 words and SD = 14 words) should be familiar to most students from their own experience.
- There are no illustrating or motivating figures, so the text is the central basis for forming the situation model.
- An item prompt (question) aims to recognize a connection between the described parameters of everyday life.
- Three to four numbers are required to solve a problem. In addition, the task contains two superfluous numbers.
- All the data necessary to solve the task are given in the text.
- Accordingly, one solution can be marked as unambiguously correct for each task.
- Our test comprises three tasks designed in a single-choice format and two in an open-task format.
- The titles of the items are as follows: “Oven,” “Car wash,” “Bicycle courier,” “Thermal insulation,” and “Filling up” (example in Table 1).
Considering the numerous aspects different researchers apply to “real” mathematical modeling tasks (Wess et al., 2021), our tasks are deliberately placed in a middle range on this continuum of normative specifications. They are neither clothed tasks whose context does not play a role nor authentic modeling tasks that leave a lot of freedom for the individual processing and answering of the central question. Rather, our reality-based tasks have the particular element that linear functions imply a fixed mathematical model for dealing with the real-life context. However, the students must translate worldly objects into mathematics, including the linguistic identification of constant starting elements (ordinate intercept) and changing quantities (variables and slope). Our preliminary studies have shown that many students have problems comprehending and translating functional relations even in these well-structured tasks (Leiss et al., 2019). Accordingly, the goal was for the students to process many tasks, the analysis of which yields findings whose transfer to more complex modeling tasks seems obvious but requires further studies.
Our study was conducted in Germany; therefore, the reality-based tasks were offered in German. Our approach to modifying these tasks' linguistic demands was described comprehensively by Heine et al. (2018).1 Their model integrated several difficulties, inducing linguistic surface features.
Regarding the linguistic elements' frequency, the less frequent it is, presumably the less it is part of the language users' knowledge base and the less automated it is, thus creating gaps or vagueness in comprehension. These gaps must be filled from the linguistic co-text or world knowledge (Heine et al., 2018). However, on the syntax level, the frequency dimensions play an important role (Chen and Meurers, 2018). Thus far, the most frequent sentence structures were short main clauses with canonical word order in an active voice (Heine et al., 2018), while more complex sentences were generally rare and more typical for specific contexts (e.g., academic language use) and, thus, less familiar to the language users in general.
In our study, linguistic demand refers to the varying linguistic features present in reality-based mathematical tasks, which may influence task difficulty and student performance. We employed a systematic approach to vary the tasks' linguistic demands, as elaborately outlined in Heine et al. (2018). The specific linguistic features encompassed syntactic structures, verb forms, semantic transparency, stylistic elements, deixis, and impersonal expressions. These variations were meticulously designed and implemented by a team of linguists, ensuring consistency in mathematical demands in each version while systematically manipulating linguistic complexity. The aim was to ensure consistency in the mathematical requirements in each version while systematically varying the linguistic complexity. Starting from a task at the intermediate language level, simpler and more complex variants were then designed. Particular care was taken to ensure that the mathematical content and requirements remained consistent.
Heine et al.'s (2018) model serves as a basis for systematically manipulating texts into linguistically different versions on the word and sentence levels while keeping the mathematical task constant. A research team of linguists and mathematicians applied this approach to the five mathematical word problems and modified each text prompt systematically into linguistically simple, medium, and advanced language levels (LL1–LL3). The linguistic modifications only affected the task stimuli. The item questions and single-choice response options remained constant for all three versions of the five tasks. They were carefully formulated on a linguistically low demand level. The mathematics experts reviewed the linguistic modification process to ensure that all versions of the mathematically relevant information needed to solve the reality-based tasks remained constant. Table 1 illustrates an example task stimulus with low (LL1) and high (LL3) levels of linguistic demands.
In addition to the theoretically based model's systematic application, we conducted a simple modification examination and quantified the difference between LL1 and LL3 of the two German versions in Table 1 using the Flesch Reading Ease Readability Formula (Flesch, 1948; Schöll, 2021). After applying the index, the results revealed 86 (“easy”) and 57 (“fairly difficult”) score points for the low and high complex variants, respectively, validating that the texts should be relatively easily understood by students aged 13–15 years.
Study design and sample
This study employed an experimental design with the within-factor items' linguistic demand level (low vs. high), controlling for language proficiency as a metric moderator variable. The sample comprised 1,346 students from 17 schools in northern Germany (female: 49.4%, male: 50.6%). The average age was 14.0 years. Approximately 34% of the students had an immigrant background (=parents were not born in Germany).
This research is part of a larger study that, besides mathematics, comprises other subject domains (physics, music, physical education, and German).2 The elicitation duration was 90 min, with 60 and 30 min for the test and background variables, respectively (c-test and questionnaire).
It was decided post-hoc to exclude items with a medium language level and use only those with low and high linguistic demands for further analysis. Due to time constraints, only the two extreme variants could be employed within the teacher survey; nevertheless, no significant differences between the medium and low or high variants were found regarding the empirical item difficulty. Thus, we focused on the contrast between the low and high demand levels that could be more sensitive in detecting the effects of linguistic demands on the students' performance. The sample size remained unchanged by this decision because each student solved only one or two items with a medium linguistic demand.
Teachers ratings
The first research question's sample comprised 72 mathematics teachers from secondary schools in northern Germany (82.1% male, 17.9% female). It included a convenience sample drawn from the teacher professional development courses and was independent of the student sample. On average, the teachers had 13 years of teaching experience (SD = 10.1 years).
We requested the sample to review the reality-based tasks and estimate if they expected difficulties for the students. To establish a common reference base, we advised them to imagine a fictitious class characterized by information about the number of female and male students (14 and 10, respectively), the percentage of migration background students (33%), and the distribution of school grades within the class in mathematics and German (given by two tables). We instructed them regarding three different ratings: (1) “Guess what percentage of the students can solve the reality-based tasks correctly.” The response format was a percentage value between 0 and 100%. (2) “Evaluate the following statement regarding the class described at the beginning: the students will have linguistic difficulties solving the problem.” (3) “Judge the following statement regarding the class described at the beginning: the students will have mathematical difficulties solving the problem.” The response format of ratings (2) and (3) was as follows: 1 = “disagree,” 2 = “somewhat disagree,” 3 = “partly disagree/partly agree,” 4 = “somewhat agree,” and 5 = “fully agree.”
Language proficiency
A condensed version of a c-test, which is a specific format of the cloze test, was administered to assess the students' language proficiency over a 10-min duration. This test is widely recognized for its reliability and validity in measuring language proficiency, offering insights into both receptive and productive language skills (Grotjahn, 2010; Grotjahn et al., 2002; Grotjahn and Drackert, 2020). Previous research has demonstrated the discriminative validity (DCLL+3) of texts utilized in this assessment. Each c-test comprised two texts, with 30 gaps in each test for students to complete. The total of 60 gaps were treated as individual items (Harsch and Hartig, 2010), resulting in a high internal consistency, as indicated by a Cronbach's alpha coefficient of 0.96. Item responses were calibrated using the Rasch model, and the resulting scale scores were standardized to a mean of 0 and a standard deviation of 1.
Statistical modeling procedure
We calculated the descriptive statistics for research questions 1 and 2 and assessed significant group differences between the LL1 and LL3 task versions by conducting t-tests. For all analyses, we chose a significance level of α = 0.05.
Sato et al.'s (2010) study suggested that applying the IRT models for estimating students' achievement scores, compared to using the sum scores or the percentage correct, is more suitable for detecting the effects of the linguistic task attributes. Moreover, for analyzing the moderator effects between the personal characteristics (e.g., reading proficiency) and item attributes (e.g., language demands), explanatory item response models (EIRMs) seemed (Meulders and Xie, 2004) adequate and sensitive (De Boeck and Wilson, 2004). The EIRM is an approach to cognitive assessment that employs explanatory measurements utilizing item and person covariates to explain what is being measured, thus adding an explanatory value to the measurements (De Boeck et al., 2016).
Thus, for the third research question, we employed the EIRMs that provide a framework for modeling the item responses directly as a function of the item, as personal predictors, or as a combination of both (De Boeck and Wilson, 2004). This makes them especially suitable for the present analysis, as we expected the item responses to depend on an interaction between the item's linguistic level and the students' language proficiency. In our case, the item responses were binary, and we modeled the students' propensity to answer the items correctly, which were the logarithmised odds of a correct answer (e.g., Wilson and De Boeck, 2004). The models were specified as hierarchical generalized linear mixed models, with item responses nested within students and items (e.g., De Boeck et al., 2011).
The modification status of the reality-based tasks and the student characteristics (general language proficiency) and their interactions were defined as fixed effects. A possible primary effect of general language proficiency indicated an overall effect when solving reality-based tasks. The interaction effects of the general language proficiency (student characteristic) with the linguistic task level (item characteristic) demonstrated differences in the effect of linguistic demands related to the students' general language proficiency (Beretvas et al., 2012; Meulders and Xie, 2004). The models were estimated using the lmer function of the lme4 package in R (Bates et al., 2012).
Results
Results concerning RQ1: how do mathematics teachers assess the likelihood of students solving reality-based tasks with systematically varied linguistic difficulties?
Table 2 provides the results of how our sample's mathematics teachers rated the expected difficulties regarding the language and mathematical demands on a Likert scale. On average, the teachers expected exceedingly large differences (all five items' effect size: d = 1.68, p < 0.001) between the reality-based tasks with low and high linguistic demand levels (Table 2). This indicated that they anticipated a considerable effect of linguistic modification on the students, suggesting that they expected high linguistic demands to result in serious language difficulties. Table 2 demonstrates an example task of this language modification.
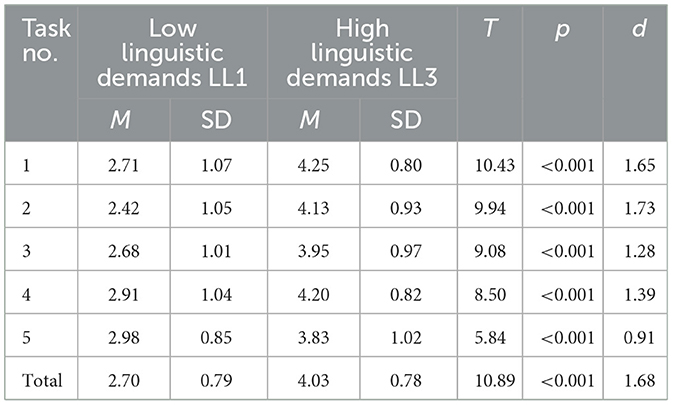
Table 2. Teacher ratings concerning the students' expected language difficulties in solving reality-based tasks with low and high linguistic demands.
Furthermore, the teachers expected mathematical difficulties between the tasks with low linguistic demands (LL1) and high linguistic demands (LL3; Table 3). The mean values between them were statistically significantly different; the total scale's effect size was d = 0.51. Sullivan and Feinn (2012) rated an effect size of 0.2, 0.5, 0.8, and 1.3 as small, medium, large, and very large, respectively.
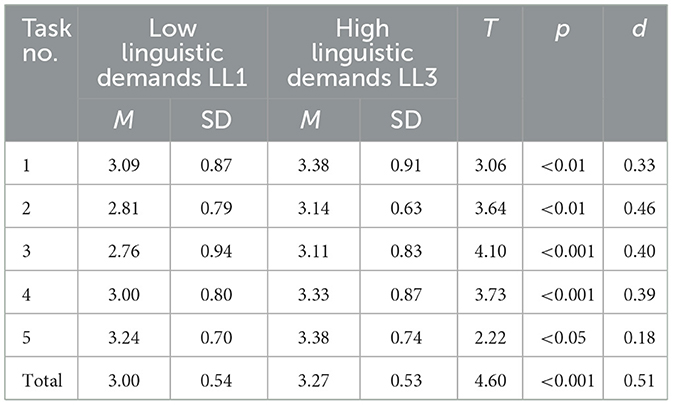
Table 3. Teacher ratings concerning the students' expected mathematical difficulties in solving the reality-based tasks with low and high linguistic demands.
Finally, we requested the mathematics teachers to estimate how many students in a fictitious class would find each task version's correct solution (Table 4). On average, they expected that the LL1 and LL3 task versions would be solved by ~53% and only 36% of the students, respectively. The mean difference was statistically significant (p < 0.001). The effect size of the mean difference was approximately d = 0.73, which was a practically relevant effect. The results showed that the teachers anticipated a task's linguistic shape to strongly affect the students' success. As a manipulation check's form, the linguistic demand model's application (Heine et al., 2018) could be considered successful regarding face validity.
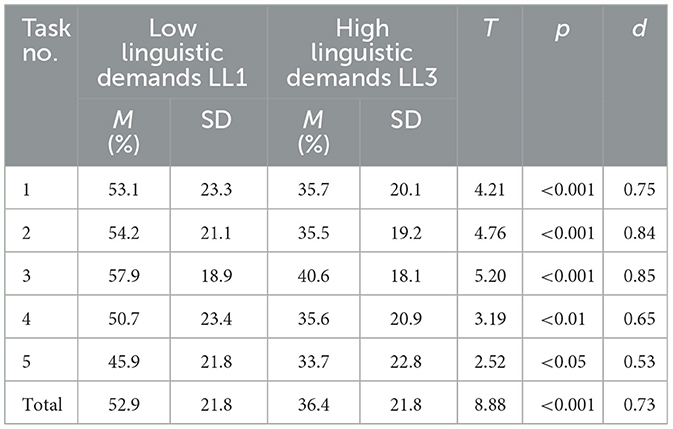
Table 4. Teacher estimates of the percentage of students who could correctly solve the reality-based tasks with low and high linguistic demands.
Results concerning RQ2: how do the linguistic demands of reality-based tasks influence the solution rate of these tasks when solved by students?
Regarding the second research question, 29 and 24% of the students successfully solved the mathematics tasks for the LL1 and LL3 versions, respectively (Table 5). The effect size of this mean difference was 0.12.
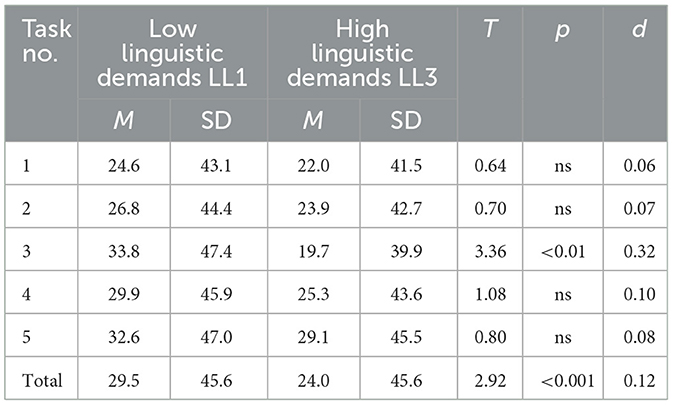
Table 5. Percentage of the students that could correctly solve the reality-based tasks with low and high linguistic demands.
Noticeably, four out of five mean differences were not statistically significant. However, the LL1 versions were easier than the LL3 ones in all five tasks. Comparing the results (effect sizes) between the teachers' assessments (d = 0.73) and the students' performance (d = 0.12), the results show that teachers significantly overestimated the influence of linguistic requirements in real-life math problems. Their expected language difficulties were much higher than the students' empirical difficulties. This effect's overestimation was also accompanied by underestimating the tasks' absolute difficulty.
Results concerning RQ3: to what extent is the influence of linguistic demands on the solution rate of a task moderated by students' language proficiency in the schooling language?
Regarding the third research question, we divided the student sample into four quartiles based on their language proficiency test results. Comparing the difficulties between the LL1 and LL3 task versions, we found the following effect sizes for the four quartiles: first (=25% of the students with the lowest language proficiency): d = 0.20 (p < 0.05); second quartile: d = 0.17 (p < 0.05); third quartile: d = 0.15 (ns); and fourth quartile (highest language proficiency): d = 0.03 (ns). These descriptive results indicated that the students' language proficiency influences the effect of a task's linguistic demands on its overall difficulty. Therefore, the language requirements of reality-based tasks are essential for students with low language proficiency.
To establish the moderation effect in a more advanced model, we applied an EIRM that allowed direct modeling of the interaction effect between personal abilities (language proficiency) and item characteristics (low vs. high linguistic demands) (De Boeck and Wilson, 2004). We investigated whether the effect of a task's linguistic demands was higher for the students with a low language proficiency than those with a high language proficiency.
Table 6 provides the three analyses' results. In Model 1, we found a statistically significant primary effect for a task's linguistic demands (β = −0.338, p < 0.01). This replicated the descriptive finding in Table 5: the students' performance is lower if the tasks' linguistic demands are high.
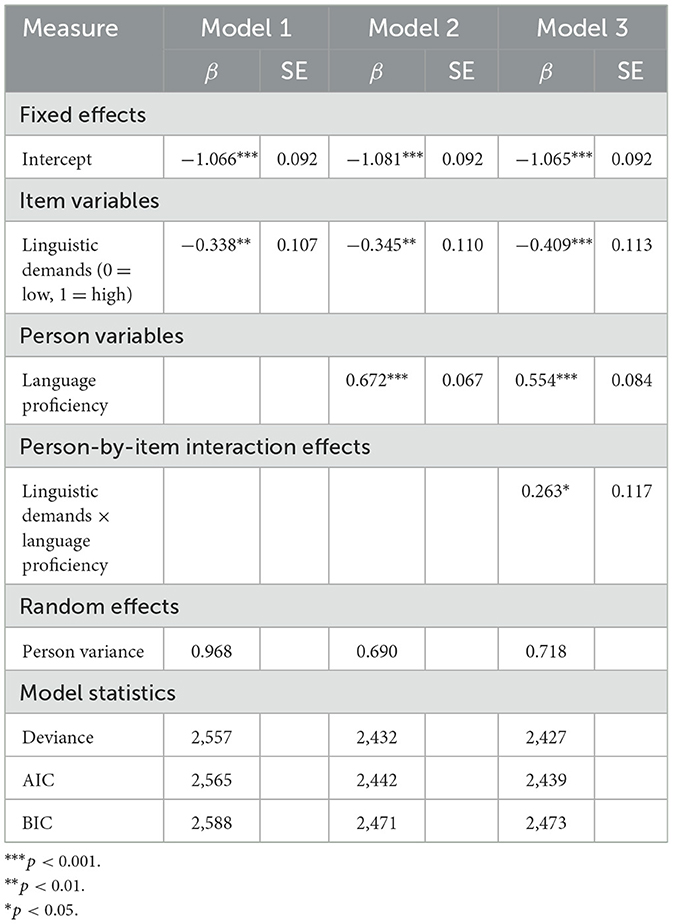
Table 6. Effects of the task's linguistic demands and the students' language proficiency on the students' performance in the reality-based mathematical tasks.
Model 2 additionally accounted for the students' language proficiency. The results showed that both student-level predictors, namely the students' language proficiency (β = 0.672, p < 0.001) and item-level predictors such as the task's linguistic demands (β = −0.345, p < 0.001), are predictive of students' performance on the reality-based tasks. This indicated that those with a high language proficiency have a higher propensity for solving a task than those with a low proficiency. Furthermore, the probability of correctly solving a task decreases as the task's linguistic demands increase.
Finally, in Model 3 (Model 2 plus the interaction effect), the students' language proficiency, along with the task's linguistic demands, was included in the analyses. The results demonstrated a significant interaction effect (β = 0.263, p < 0.05), indicating that the students' language proficiency moderates the effect of a task's linguistic demands regarding successfully solving an item.
Discussion
Our study investigated the role of language difficulty in solving reality-based mathematical tasks, aiming to contribute to the current understanding of this complex relationship. By employing a rigorous experimental design, we systematically manipulated language demands while controlling for mathematical content, providing unbiased evidence of the impact of language demands on task difficulty.
Firstly, our findings highlighted the importance of disentangling mathematical and linguistic demands in reality-based tasks. Previous correlational studies often failed to address this confounding factor, making it challenging to attribute task difficulty solely to language demands. By isolating the effect of language demands through experimental manipulation, we extended the empirical state of research and provided clear evidence of their influence on task difficulty.
Additionally, our study shed light on mathematics teachers' perceptions toward language demands in reality-based tasks, an area that has been relatively underexplored in previous research. While teachers anticipated significant linguistic demands, the observed discrepancy between their expectations and students' actual performance underscored the need for further investigation into the factors shaping teachers' perceptions.
Moreover, our findings regarding the effects of language modification on student solution rates revealed a small but statistically significant impact, contrasting with previous studies that failed to demonstrate a verifiable effect. The comparison between teachers' expectations and students' actual performance showed that teachers may overestimate the influence of linguistic requirements. The result points to the relevance of teaching. If teachers overestimate the requirements of tasks, they may only select tasks for their lessons that have low linguistic requirements.
Furthermore, our study elucidated the moderating role of students' language proficiency, with students with lower language proficiency being more negatively influenced by language-demanding tasks. This novel pattern of results extends the current state of research by demonstrating the nuanced interplay between students' language proficiency and task demands in reality-based tasks. The promotion of language skills is therefore also central to mathematics education.
In summary, our study offers valuable insights into the multifaceted relationship between language demands, mathematical task difficulty, and students' performance. However, this study's limitation was that our scale for the reality-based mathematical tasks only comprised five items. We focused on the linear functions' content area for those five items to keep it as a constant influence factor. However, whether similar effects would be obtained in other content areas remains unclear. The same holds for the mathematical competencies [National Council of Teachers of Mathematics (NCTM), 2003]. All five items required mathematical modeling competence. It can be assumed that the linguistic effects were relatively lower for mathematical items requiring primarily technical skills. We focused the items' mathematical demands on specific aspects to keep them constant. However, further research should address different mathematical item attributes and assess if this study's effects can be replicated. In our tasks, a high linguistic requirement occasionally includes less frequent words that are less common in everyday language. In retrospect, our study cannot distinguish which linguistic factors are particularly relevant and which are less relevant. Further in-depth studies would be necessary to do so.
Recommendations for further research
We see implications for further research in the following areas in particular:
(1) Concerning the characteristics of reality-based tasks, the role played by the mathematical demands of the tasks to be solved should be further investigated. Linguistic demands may be negligible when it comes to simple mathematical reproduction tasks. However, as the mathematical demands of tasks increase, high linguistic demands could pose an additional hurdle and result in students exceeding their cognitive capacity and being unable to construct an adequate mental model of the task.
(2) Our study has shown that modeling the interaction of person and task traits using linear mixed models such as the EIRM approach is reasonable. Therefore, we recommend using this method for future research in this area.
(3) To allow a more differentiated analysis, recording the students' situational motivation when solving such tasks seems promising. For example, whether tasks with high linguistic demands negatively affect the willingness to make an effort or the students' situational motivation could be analyzed. The subjective interest of the task context could also play a moderating role.
(4) Finally, what effective interventions are available to teachers to support students with language difficulties in solving reality-related tasks could be examined. There are many suggestions for language support (Sharma and Sharma, 2022), but to what extent these are also effective for solving reality-based tasks is still unclear.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
Ethical approval was not required for the studies involving humans because the authors stated that all relevant ethical guidelines and principles were carefully considered in the preparation of this scientific article. The conduct of the research, as well as data collection, analysis, and interpretation, was performed in strict adherence to ethical standards to ensure that potential impacts on humans and the environment were minimized. Owing to the fact that in Germany no formal approval by an Ethics Committee is required prior to conducting a scientific study, no such statement exists. However, prior to data collection, an audit is conducted by the state education authority of Lower Saxony, which reviews the study design, instruments, and process in advance. The authors further stated that this review includes compliance with ethical standards in the research process (including anonymity of subjects, voluntariness of participation, and confidentiality in data management) and only after successful assessment can the study be implemented. A comprehensive ethical evaluation was conducted prior to the study; this weighed all potential risks and benefits of the research. Any interaction with human participants was voluntary and informed consent was obtained. Participant privacy and confidentiality were always respected, and appropriate measures were taken to maintain anonymity. All study participants provided informed consent. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
TE: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Writing – original draft, Writing – review & editing. DL: Conceptualization, Data curation, Investigation, Methodology, Project administration, Writing – original draft, Writing – review & editing. LH: Conceptualization, Formal analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This publication was funded by the German Research Foundation (DFG).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^Since the task texts described real-life situations, mathematical terminology did not play a role. Accordingly, the modifications addressed only the students' language proficiency.
2. ^The domain-specific results for physics are published by Höttecke et al. (2017), Leiss et al. (2019) and those for music and sports by Leiss et al. (2019).
References
Abedi, J., and Lord, C. (2001). The language factor in mathematics tests. Appl. Meas. Educ. 14, 219–234. doi: 10.1207/S15324818AME1403_2
Abedi, J., Lord, C., and Plummer, J. R. (1997). Final Report of Language Background as a Variable in NAEP Mathematics Performance. Los Angeles, CA: National Center for Research on Evaluation, Standards, and Student Testing.
Artelt, C., Beinicke, A., Schlagmüller, M., and Schneider, W. (2009). Diagnose von strategiewissen beim textverstehen. Z. Entwicklungspsychol. Padagog. Psychol. 41, 96–103. doi: 10.1026/0049-8637.41.2.96
Barwell, R. (2005). Integrating language and content: Issues from the mathematics classroom. Linguist. Educ. 16, 205–218. doi: 10.1016/j.linged.2006.01.002
Basaraba, D., Walkington, C., Baker, D. L., Ketterlin-Geller, L., and Yovanoff, P. (2019). “Teacher perceptions of factors that make mathematics word problems more difficult for English learners,” in Presentation at the American Educational Research Association (AERA) annual meeting, April 5th – 9th, Toronto, Ontario, Canada. doi: 10.3102/1442418
Bates, D., Maechler, M, and Bolker, B. (2012). lme4: Linear Mixed-Effects Models Using S4 Classes. R package version 0.999999-0.
Beretvas, S. N., Cawthon, S. W., Lockhart, L. L., and Kaye, A. D. (2012). Assessing impact, DIF, and DFF in accommodated item scores: a comparison of multilevel measurement model parameterisations. Educ. Psychol. Meas. 72, 754–773. doi: 10.1177/0013164412440998
Blomhøj, M., and Jensen, T. H. (2003). Developing mathematical modelling competence: conceptual clarification and educational planning. Teach. Math. Appl. 22, 123–139. doi: 10.1093/teamat/22.3.123
Blum, W., and Leiss, D. (2007). “How do students and teachers deal with modelling problems?” in Mathematical modelling (ICTMA 12). Education, Engineering and Economics: Proceedings from the Twelfth International Conference on the Teaching of Mathematical Modelling and Applications, ed. C. Haines (Chichester: Horwood), 222–231.
Boaler, J. (2001). Mathematical modelling and new theories of learning. Teach. Math. Appl. 220, 121–127. doi: 10.1093/teamat/20.3.121
Caccamise, D., Synder, L., and Kintsch, E. (2008). “Constructivist theory and the situation model. Relevance to future assessment of reading comprehension,” in Comprehension Instruction. Research-Based Best Practices, eds. C. C. Block, and M. Pressley (New York, NY: The Guildford Press).
Capraro, R. M., Capraro, M. M., and Rupley, W. H. (2012). Reading-enhanced word problem solving: a theoretical model. Eur. J. Psychol. Educ. 27, 91–114. doi: 10.1007/s10212-011-0068-3
Chen, X., and Meurers, D. (2018). Word frequency and readability: predicting the text-level readability with a lexical-level attribute. J. Res. Read. 41, 486–510. doi: 10.1111/1467-9817.12121
Cummins, D. D., Kintsch, W., Reusser, K., and Weimer, R. (1988). The role of understanding in solving word problems. Cogn. Psychol. 20, 405–438. doi: 10.1016/0010-0285(88)90011-4
Cummins, J. (2000). Language, Power and Pedagogy: Bilingual Children in the Crossfire. Clevedon: Multilingual Matters. doi: 10.21832/9781853596773
Cummins, J. (2008). “BICS and CALP: empirical and theoretical status of the distinction,” in Encyclopedia of Language and Education, Vol. 2, eds. B. Street and N. H. Hornberger (New York, NY: Springer), 71–83. doi: 10.1007/978-0-387-30424-3_36
Daroczy, G., Wolska, M., Meurers, W. D., and Nuerk, H. C. (2015). Word problems: a review of linguistic and numerical factors contributing to their difficulty. Front. Psychol. 6:348. doi: 10.3389/fpsyg.2015.00348
De Boeck, P., Bakker, M., Zwitser, R., Nivard, M., Hofman, A., Tuerlinckx, F., et al. (2011). The estimation of item response models with the lmer function from the lme4 package in R. J. Stat. Softw. 39, 1–28. doi: 10.18637/jss.v039.i12
De Boeck, P., Cho, S. J., and Wilson, M. (2016). “Explanatory item response models,” in The Handbook of Cognition and Assessment, eds. A. A. Rupp, and J. P. Leighton (Hoboken, NJ: John Wiley and Sons, Inc), 247–266. doi: 10.1002/9781118956588.ch11
De Boeck, P., and Wilson, M. (Eds.). (2004). Explanatory Item Response Models. A generalized liNear and Nonlinear Approach. New York, NY: Springer. doi: 10.1007/978-1-4757-3990-9
Depaepe, F., De Corte, E., and Verschaffel, L. (2015). “Students' non-realistic mathematical modeling as a drawback of teachers' beliefs about and approaches to word problem solving,” in From Beliefs to Dynamic Affect Systems in Mathematics Education (New York, NY: Springer), 137–156. doi: 10.1007/978-3-319-06808-4_7
Galbraith, P., and Stillman, G. (2006). A framework for identifying student blockages during transitions in the modelling process. ZDM Math. Educ. 38, 143–162. doi: 10.1007/BF02655886
Grotjahn, R. (2010). The C-Test: Contributions from Current Research. Frankfurt am Main: Peter Lang GmbH Internationaler Verlag der Wissenschaften.
Grotjahn, R., and Drackert, A. (2020). The Electronic C-test Bibliography: Version October 2020. Available online at: http://www.c-test.de
Grotjahn, R., Klein-Braley, C., and Raatz, U. (2002). “C-tests: an overview,” in University Language Testing and the C-Test, eds. J. A. Coleman, R. Grotjahn, and U. Raatz (Bochum: AKS-Verlag), 93–114.
Haag, N., Heppt, B., Roppelt, A., and Stanat, P. (2015). Linguistic simplification of mathematics items: effects for language minority students in Germany. Eur. J. Psychol. Educ. 30, 145–167. doi: 10.1007/s10212-014-0233-6
Haag, N., Heppt, B., Stanat, P., Kuhl, P., and Pant, H. A. (2013). Second language learners' performance in mathematics: disentangling the effects of academic language features. Learn. Instr. 28, 24–34. doi: 10.1016/j.learninstruc.2013.04.001
Hailikari, T., Nevgi, A., and Komulainen, E. (2008). Academic self-beliefs and prior knowledge as predictors of student achievement in mathematics: a structural model. Educ. Psychol. 28, 59–71. doi: 10.1080/01443410701413753
Harsch, C., and Hartig, J. (2010). “Empirische und inhaltliche analyse lokaler abhängigkeiten im C-test,” in Der C-Test: Beiträge aus der Aktuellen Forschung, ed. R. Grotjahn (Frankfurt am Main: Peter Lang GmbH Internationaler Verlag der Wissenschaften), 193–204.
Heine, L., Domenech, M., Otto, L., Neumann, A., Krelle, M., Leiss, D., et al. (2018). Modellierung sprachlicher Anforderungen in Testaufgaben verschiedener Unterrichtsfächer: Theoretische und empirische Grundlagen. Z. fur Angew. Linguist. 69, 69–96.
Höttecke, D., Ehmke, T., Krieger, C., and Kulik, M. A. (2017). Vergleichende Messung fachsprachlicher Fähigkeiten in den Domänen Physik und Sport. ZfDN 23, 53–69. doi: 10.1007/s40573-017-0055-6
Johnson, E., and Monroe, B. (2004). Simplified language as an accommodation on math tests. Assess. Eff. Interv. 29, 35–45. doi: 10.1177/073724770402900303
Khoshaim, H. B. (2020). Mathematics teaching using word-problems: is it a phobia! Int. J. Instr. 13, 855–868. doi: 10.29333/iji.2020.13155a
Kintsch, W., and van Dijk, T. (1978). Toward a model of text comprehension and production. Psychol. Rev. 85, 363–394. doi: 10.1037/0033-295X.85.5.363
Kopriva, R. (2000). Ensuring Accuracy in Testing for English Language Learners. Washington, DC: Council of Chief State School Officers.
Leiss, D., Plath, J., and Schwippert, K. (2019). Language and mathematics - Key factors influencing the comprehension process in reality-based tasks. Math. Think. Learn. 21, 131–153. doi: 10.1080/10986065.2019.1570835
Leiss, D., Schukajlow, S., Blum, W., Messner, R., and Pekrun, R. (2010). Zur Rolle des Situationsmodells beim mathematischen Modellieren - Aufgabenanalysen, Schülerkompetenzen und Lehrerinterventionen. J. Math.-Didakt. 31, 119–141.
Maaß, K. (2010). Classification scheme for modelling tasks. J. Math.-Didakt. 31, 285–311. doi: 10.1007/s13138-010-0010-2
Martiniello, M. (2008). Language and the performance of English-language learners in math word problems. Harv. Educ. Rev. 78, 333–368. doi: 10.17763/haer.78.2.70783570r1111t32
Mayer, R. E., and Hegarty, M. (1996). “The process of understanding mathematical problems,” in Studies in Mathematical Thinking and Learning Series. The Nature of Mathematical Thinking, eds. R. J. Sternberg and T. Ben-Zeev (Mahwah, NJ: Lawrence Erlbaum Associates, Inc.), 29–53.
McNamara, D. S., Louwerse, M. M., McCarthy, P. M., and Graesser, A. C. (2010) Coh-metrix: capturing linguistic features of cohesion. Discourse Process. 47, 292–330. doi: 10.1080/01638530902959943
Meulders, M., and Xie, Y. (2004). “Person-by-item predictors,” in Explanatory Item Response Models: A Generalized Linear and Nonlinear Approach, eds. P. De Boeck and M. Wilson (New York, NY: Springer), 213–240. doi: 10.1007/978-1-4757-3990-9_7
Moschkovich, J. (2002). A situated and sociocultural perspective on bilingual mathematics learners. Math. Think. Learn. 4, 189–212. doi: 10.1207/S15327833MTL04023_5
Moschkovich, J., and Scott, J. (2021). “Language issues in mathematics word problems for English learners,” in Diversity Dimensions in Mathematics and Language Learning: Perspectives on Culture, Education and Multilingualism, eds. A. Fritz, E. Gürsoy, and M. Herzog (Berlin: De Gruyter), 331–349. doi: 10.1515/9783110661941-017
National Council of Teachers of Mathematics (NCTM) (2003). Principles and Standards for School Mathematics. Reston: National Council of Teachers of Mathematics.
Newman, K. (1977). “An analysis of sixth-grade pupils' errors on written mathematical tasks,” in Research in Mathematics Education in Australia (Hawthorn, VIC: Swinburne Press), 239–258.
Nguyen, T., Watts, T. W., Duncan, G. J., Clements, D. H., Sarama, J. S., Wolfe, C., et al. (2016). Which preschool mathematics competencies are most predictive of fifth grade achievement? Early Child. Res. Q. 36, 550–560. doi: 10.1016/j.ecresq.2016.02.003
OECD. (2003). The PISA 2003 Assessment Framework: Mathematics, Reading, Science and Problem Solving Knowledge and Skills. Paris: OECD Publishing.
Pearce, D. L., Bruun, F., Skinner, K., and Lopez-Mohler, C. (2013). What teachers say about student difficulties solving mathematical word problems in grades 2-5. Int. Electron. J. Math. Educ. 8, 3–19. doi: 10.29333/iejme/271
Pöhler, B., George, A. C., Prediger, S., and Weinert, H. (2017). Are word problems really more difficult for students with low language proficiency? Investigating percent items in different formats and types. Int. Electron. J. Math. Educ. 12, 667–687. doi: 10.29333/iejme/641
Polya, G. (1945). How to Solve It. Princeton, NJ: Princeton University Press. doi: 10.1515/9781400828678
Prediger, S. (2019). Investigating and promoting teachers' expertise for language-responsive mathematics teaching. Math. Educ. Res. J. 31, 367–392. doi: 10.1007/s13394-019-00258-1
Prediger, S., Wilhelm, N., Büchter, A., Gürsoy, E., and Benholz, C. (2018). Language proficiency and mathematics achievement: empirical study of language-induced obstacles in a high stakes test, the central exam ZP10. J. Math.-Didak. 39(Suppl 1), 1–26. doi: 10.1007/s13138-018-0126-3
Prins, E., and Ulijn, J. (1998). Linguistic and cultural factors in the readability of mathematics texts: the Whorfian hypothesis revisited with evidence from the South African context. J. Res. Read. 21, 139–159. doi: 10.1111/1467-9817.00050
Reusser, K. (1989). Vom Text zur Situation zur Gleichung. Kognitive Simulation von Sprachverständnis und Mathematisierung beim Lösen von Textaufgaben. Bern: Habilitationsschrift Universität Bern.
Sato, E., Rabinowitz, S., Gallagher, C., and Huang, C. W. (2010). Accommodations for English Language Learner Students: The Effect of Linguistic Modification of Math Test Item Sets. Final Report. NCEE 2009-4079. Washington, DC: National Center for Education Evaluation and Regional Assistance.
Schleicher, A., Zimmer, K., Evans, J., and Clements, N. (2009). PISA 2009 Assessment Framework: Key Competencies in Reading, Mathematics and Science. OECD Publishing.
Schleppegrell, M. J. (2007). The linguistic challenges of mathematics teaching and learning: a research review. Read. Writ. Q. 23, 139–159. doi: 10.1080/10573560601158461
Schleppegrell, M. J. (2010). The Language of Schooling. A Functional Linguistics Perspective. London: Routledge.
Schleppegrell, M. J. (2012). Academic language in teaching and learning. Elem. Sch. J. 112, 409–418. doi: 10.1086/663297
Schöll, P. (2021). Flesch-Index Berechnen. Available online at: https://fleschindex.de
Schukajlow, S., and Leiss, D. (2011). Selbstberichtete Strategienutzung und mathematische Modellierungskompetenz. J. Math.-Didakt. 32, 53–77.
Seah, L. H. (2016). Elementary teachers' perception of language issues in science classrooms. Int. J. Sci. Math. Educ. 14, 1059–1078. doi: 10.1007/s10763-015-9648-z
Sharma, S., and Sharma, S. (2022). Successful teaching practices for English Language Learners in multilingual mathematics classrooms: a meta-analysis. Math. Educ. Res. J. 1–28. doi: 10.1007/s13394-022-00414-0
Skinnari, K., and Nikula, T. (2017). Teachers' perceptions on the changing role of language in the curriculum. Eur. J. Appl. Linguist. 5, 223–244. doi: 10.1515/eujal-2017-0005
Stillman, G., Brown, J., and Galbraith, P. (2010). “Identifying challenges within transition phases of mathematical modelling activities at year 9,” in Modeling Students' Mathematical Modeling Competencies. ICTMA 13, eds. R. Lesh, P. Galbraith, C. Haines, and A. Hurford (Berlin: Springer), 385–398. doi: 10.1007/978-1-4419-0561-1_33
Sullivan, G. M., and Feinn, R. (2012). Using effect size - or why the P value is not enough. J. Grad. Med. Educ. 4, 279–282. doi: 10.4300/JGME-D-12-00156.1
Verschaffel, L., Schukajlow, S., Star, J., and Van Dooren, W. (2020). Word problems in mathematics education: a survey. ZDM: Int. J. Math. Educ. 52, 1–16. doi: 10.1007/s11858-020-01130-4
Walkington, C., Clinton, V., and Shivraj, P. (2018). How readability factors are differentially associated with performance for students of different backgrounds when solving mathematics word problems. Am. Educ. Res. J. 55, 362–414. doi: 10.3102/0002831217737028
Walkington, C., Clinton, V., and Sparks, A. (2019). The effect of language modification of mathematics story problems on problem-solving in online homework. Instr. Sci. 47, 499–529. doi: 10.1007/s11251-019-09481-6
Wess, R., Klock, H., Siller, H. S., and Greefrath, G. (2021). “Mathematical modelling,” in Measuring Professional Competence for the Teaching of Mathematical Modelling: A Test Instrument, eds. R. Wess, H. Klock, H. S. Siller, and G. Greefrath (Berlin: Springer International Publishing), 3–20. doi: 10.1007/978-3-030-78071-5_1
Wheeler, L. J., and McNutt, G. (1983). The effect of syntax on low-achieving students' abilities to solve mathematical word problems. J. Spec. Educ. 17, 309–315. doi: 10.1177/002246698301700307
Wienecke, L. M., Leiss, D., and Ehmke, T. (2023). Taking notes as a strategy for solving reality-based tasks in mathematics. Int. Elect. J. Math. Ed. 18:em0744.
Wijaya, A., van den Heuvel-Panhuizen, M., Doorman, M., and Robitzsch, A. (2014). Difficulties in solving context-based PISA mathematics tasks: an analysis of students' errors. Math. Enthusiast 11, 555–584. doi: 10.54870/1551-3440.1317
Keywords: linguistic modification, mathematical word problems, reality-based tasks, teachers' expectations, teachers' beliefs
Citation: Ehmke T, Leiss D and Heine L (2025) Effects of linguistic demands of reality-based mathematical tasks: discrepancy between teachers' expectations and students' performance. Front. Educ. 10:1528806. doi: 10.3389/feduc.2025.1528806
Received: 15 November 2024; Accepted: 12 May 2025;
Published: 10 June 2025.
Edited by:
Eduardo Encabo-Fernández, University of Murcia, SpainReviewed by:
Stefan Daniel Keller, University of Teacher Education Zuerich, SwitzerlandJosé Ginés Espín Buendía, University of Murcia, Spain
Copyright © 2025 Ehmke, Leiss and Heine. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Timo Ehmke, dGltby5laG1rZUBsZXVwaGFuYS5kZQ==
 Timo Ehmke
Timo Ehmke Dominik Leiss2
Dominik Leiss2