- 1Education Academy and Faculty of Informatics, Vytautas Magnus University, Kaunas, Lithuania
- 2Education Academy, Vytautas Magnus University, Kaunas, Lithuania
- 3Department of Teacher Education, University of Turku, Turku, Finland
The influence of teachers’ self-efficacy on the effectiveness of teaching is well-documented in educational research. The aim of this study was to investigate the construct of self-efficacy in mathematics teachers. The sample consisted of 222 Lithuanian pre-service teachers who were divided into four groups according to their length of teaching experience. Using a confirmatory factor analysis, the study identified different but highly correlated dimensions of teacher self-efficacy, in particular knowledge, recognition and (use of) methods. The results showed significant differences in general teacher self-efficacy and in the specific subscales according to career stage. Teachers at the beginning of their career or still in training (with less than 1 year of experience) generally reported lower levels of self-efficacy than more experienced groups; however, this difference was not statistically significant within the knowledge self-efficacy category. In addition, teachers with more than 30 years of experience reported lower levels of self-efficacy than teachers with 1–29 years of teaching experience.
Introduction
In today’s ever-changing world, individuals must be able to adapt quickly and meet the demands of modern society. Desired skills include critical and analytical thinking, creative problem solving, effective information processing, logical reasoning and other skills (Trei, 2015) that are associated with mathematical literacy (Gravemeijer et al., 2017). Mathematics teachers are trusted to prepare new generaration for future, to provide all of these skills. Thus it comes to no surprise that the quality of mathematics education is largely dependent on the teachers’ capability to teach - their teaching quality (e.g., Hattie, 2003; Shulman, 1986). There is strong research evidence showing the teachers’ ability to teach efficiently is one of the most important factors for the quality of students’ learning (e.g., Darling-Hammond and Young, 2002, Hattie, 2003).
Research on teacher effectiveness has identified numerous factors that contribute to the teaching quality (e.g., Norton, 2019; Darling-Hammond, 2009). Among these, a growing body of evidence highlights the significant role of teachers’ beliefs and the ways in which these beliefs influence their instructional practices (Muhtarom et al., 2024; Peterson et al., 1989; Stipek et al., 2001).
One belief to be identified as essential in successful teaching is the belief in one’s own capabilities (Hoy et al., 2009, Gregoire, 2003). In educational contexts, this self-belief is referred to by two key terms: self-confidence and self-efficacy. While “confidence” is the term more commonly used to describe this belief in everyday language, research literature often favors “self-efficacy” due to its focus on specific facets of belief in self (Bandura, 1977). Self-confidence is generally understood as a broad sense of trust in oneself and one’s abilities (Callingham and Watson, 2014), whereas self-efficacy pertains more precisely to belief in one’s capacity to execute particular tasks or reach certain performance levels, a concept rooted in social cognitive theory as defined by Bandura (1977).
Teaching self-efficacy and teaching experience
Over the past two decades, extensive research has explored the concept of teaching self-efficacy (TSE), emphasizing its critical role in promoting teaching effectiveness. In a comprehensive review of 218 studies, Klassen et al. (2011) underscored the growing scholarly interest in this construct and its wide-ranging implications. Since then, numerous review and meta-analytic studies have examined specific dimensions of TSE, including its relationship with personality traits and teaching performance (Klassen and Tze, 2014), its role in educational leadership (Alanoğlu, 2022), its relevance in online teaching contexts (Corry and Stella, 2018), the effectiveness of TSE-focused interventions (Täschner et al., 2024), its function in the context of educational reforms (Gordon et al., 2023), and its predictive value for teacher commitment (Chesnut and Burley, 2015). Despite this growing body of literature, no systematic review to date has specifically addressed the relationship between TSE and teachers’ length of professional experience.
While much of the existing literature has concentrated on the effects and outcomes of TSE, relatively few studies have examined its developmental origins, particularly how TSE evolves throughout a teacher’s career (e.g., Mishal et al., 2024; Gale et al., 2021). Most research in this area has focused on the development of TSE during teacher education (e.g., Siegle and McCoach, 2007; Yurekli et al., 2020), the transition from pre-service training to the early years of teaching (e.g., Ma et al., 2022), or comparisons between novice teachers and those with limited teaching experience (Gale et al., 2021). There is evidence that early-career mathematics teachers often lack self-efficacy in their teaching skills, leading to self-doubt (Wolters and Daugherty, 2007). Additionally, some studies have reported correlations between TSE and years of teaching experience, though often without offering a detailed analysis of how TSE develops across different career stages. Overall, findings suggest that teaching self-efficacy tends to increase during both teacher preparation and early teaching experiences, with a general positive association between greater experience and higher levels of TSE.
Although numerous studies have demonstrated a general positive relationship between teaching experience and self-efficacy, only a limited number have examined in depth how teaching self-efficacy develops across the different stages of a teacher’s career. It is essential to also consider the later phases of the teaching profession, as research on teacher effectiveness and expertise indicates that the development of instructional competence and components such as pedagogical content knowledge does not follow a linear trajectory (authors, in review; Grigaliuniene et al., 2025a). This focus becomes particularly relevant in educational systems with an aging teaching workforce, such as in Lithuania (Pec̆iuliauskienė et al., 2023).
However, there is very little research evidence about the changes of TSE during later phases of teaching profession. One of the few exceptions is the large-scale study of 1,430 teachers by Klassen and Chiu (2010) which focused on the development of TSE during later years of teaching career. They found that there was a positive relationship between increasing teaching experience and teacher self-efficacy in the first 20–25 years, whereas thereafter experience was associated with decreasing teacher self-efficacy. This non-monotonic relationship was similar for all measured aspects of self-efficacy, teaching strategies, classroom management, and student engagement (Klassen and Chiu, 2010).
Mathematics teachers’ self-efficacy
In mathematics education, self-efficacy has been conceptualized as teachers’ confidence in their ability to promote students’ learning in mathematics, a construct distinct from the simple possession of mathematical knowledge (Hackett and Betz, 1989, Hoy, 2000). An important distinction exists between “mathematics self-efficacy” and “self-efficacy for teaching mathematics.” Just as performing mathematics and teaching mathematics are separate domains, believing in one’s ability to perform mathematics is different from believing in one’s ability to effectively teach mathematics to others (Hoy, 2000; Kahle, 2008).
Self-efficacy of teaching mathematics has been researched from many perspectives, including its effects on teacher wellbeing (e.g., Perera and John, 2020), instructional practices (Siegle and McCoach, 2007; Tschannen-Moran and Hoy, 2001; Ünsal et al., 2016), and student outcomes (Perera and John, 2020; Siegle and McCoach, 2007).
Many studies have used Bandura’s description of the sources of self-efficacy as a general framework for studies of teacher self-efficacy development (see the review Morris et al., 2017). Own success (mastery experience), observation of others (vicarious experience), and positive feedback (social persuasion), as well as various physiological and affective states, are the sources of self-efficacy proposed by Bandura (1977). These have been used in many studies on the development of teacher self-efficacy (Morris et al., 2017). All of these factors relate to experience as an influencing factor for development, but also show that it is not only the increase in experience that matters, but also the quality of the experience.
Numerous studies show that self-efficacy in mathematics teaching can develop during teacher training (e.g., Emmer and Stough, 2001; Siegle and McCoach, 2007) or in the early stages of a teacher’s career (Işıksal-Bostan, 2016; Thomson et al., 2021; Tschannen-Moran and Hoy, 2001). These findings underline the importance of targeted training and early teaching experience in promoting self-efficacy.
However, contrasting evidence exists as well. For example, Ünsal et al. (2016) found that mathematics teachers’ confidence in their teaching abilities remained relatively stable over time, suggesting that initial self-efficacy levels may be maintained rather than significantly changed over the course of teachers’ careers.
Measuring teaching self-efficacy
One of the important aspects of all self-efficacy studies is the instrument used to measure it. Numerous measurement instruments have been used in studies on teacher self-efficacy; however, the validity and reliability of these tools have been a topic of critical discussion (e.g., Henson, 2010; Klassen and Chiu, 2010; Morris et al., 2017; Wyatt, 2012). Among these instruments, the Teacher Efficacy Scale developed by Gibson and Dembo (1984) has been the most widely utilized since the 1980s. Drawing from Bandura’s (1977) theory of self-efficacy, this scale assesses two dimensions: (1) the general belief in a teacher’s ability to influence the educational environment and student outcomes despite external constraints such as family background, student capabilities, or school conditions, and (2) the teacher’s belief in their personal capacity to support and enhance student learning. Notably, the items on this scale are general and do not address content-specific teaching scenarios.
In contrast, the Teacher’ Sense of Efficacy Scale (TSES), developed by Tschannen-Moran and Hoy (2001), incorporates some domain-specific elements, although these remain relatively broad. The TSES offers a nuanced approach by addressing general teaching contexts while still capturing elements tied to specific teaching domains, making it a versatile tool for self-efficacy research in education.
Bandura (1977) emphasized the importance of the specificity of self-efficacy measures, as measures that focus on specific content areas are more predictive of outcomes. In developing mathematics-specific self-efficacy measures, researchers have distinguished between teacher mathematics self-efficacy and mathematics teaching self-efficacy (McGee and Wang, 2014). For example, McGee and Wang developed a mathematics teaching test that focused on teachers’ beliefs about how well they could teach specific mathematics topics.
Present study
Present study follows Bandura’s (1977) recommendation to measure self-efficacy in relation to specific content areas, this study aims to measure mathematics teachers’ self-efficacy in a way that parallels measures of mathematics teachers’ pedagogical content knowledge (Depaepe et al., 2013) and focuses on known difficult topics and misconceptions as well as appropriate teaching strategies. The second aim was to investigate how teachers’ self-efficacy and its subdomains change at different stages of the teaching career.
The aim of the present study is 2-fold. First, it seeks to develop a measure of mathematics teaching self-efficacy that centers on the practical teaching activities commonly examined in research on mathematics teachers’ pedagogical content knowledge [see review by Grigaliuniene et al. (2025b)]. Second, the study aims to investigate how various dimensions of mathematics teaching self-efficacy evolve across different stages of teachers’ professional careers.
This study aims to answer the following research questions:
1. Is mathematics teachers’ self-efficacy a unidimensional construct or is it possible to identify various factors?
Expectation is for mathematics teachers’ self-efficacy to have several factors related to different aspects of teaching.
2. Are there differences in overall teaching self-efficacy between math teachers at different stages of their careers?
Findings on the confidence of preservice and in-service teachers are somewhat mixed. While expectation could be for self-efficacy to develop as experience grows, studies show preservice teachers to be overconfident in some cases.
3. Are there differences in the subscales of teaching self-efficacy between mathematics teachers at different stages of their careers?
The results of previous research are not conclusive, and many conclusions have been drawn about this phenomenon. Further findings are required.
Materials and methods
Participants
The participants were selected using convenience sampling, majority of the respondents were invited to participate in the study while they attended free teachers’ in-service training seminar held by Vytautas Magnus university (Lithuania). The aim was to get a sample which includes teachers from all phases of teacher profession from teacher training to teachers close to retiring. The sample group was very diverse - both from perspective of region (of Lithuania) and length of their career. Participant inclusion criteria was limited to them either working as mathematics teachers or learning to become mathematics teachers (in Lithuania). The total number of participants was 222 (58 preservice teachers and 164 in-service teachers). Data collection took place within school-year of 2023/2024.
For the purpose of this analysis, all participants were grouped according to the length of their professional careers. This grouping was used because many of the student teachers have had teaching experience before they started their formal teacher education. Cut-off points for groups were determined partly based on the grouping used in previous studies (e.g., Klassen and Chiu, 2010) and partly on distribution of the career length to form four similar size groups (quartiles).
The first group comprised pre-service teachers and teachers who had just started teaching - up to 1 year of teaching (n = 50); the second group comprised teachers at the beginning of their career - 1–6 years of teaching (n = 61); the third group comprised teachers working in schools between 7 and 29 years (n = 51) and the fourth group - teachers who had been teaching for more than 30 years (max. 47 years, n = 60).
Measures
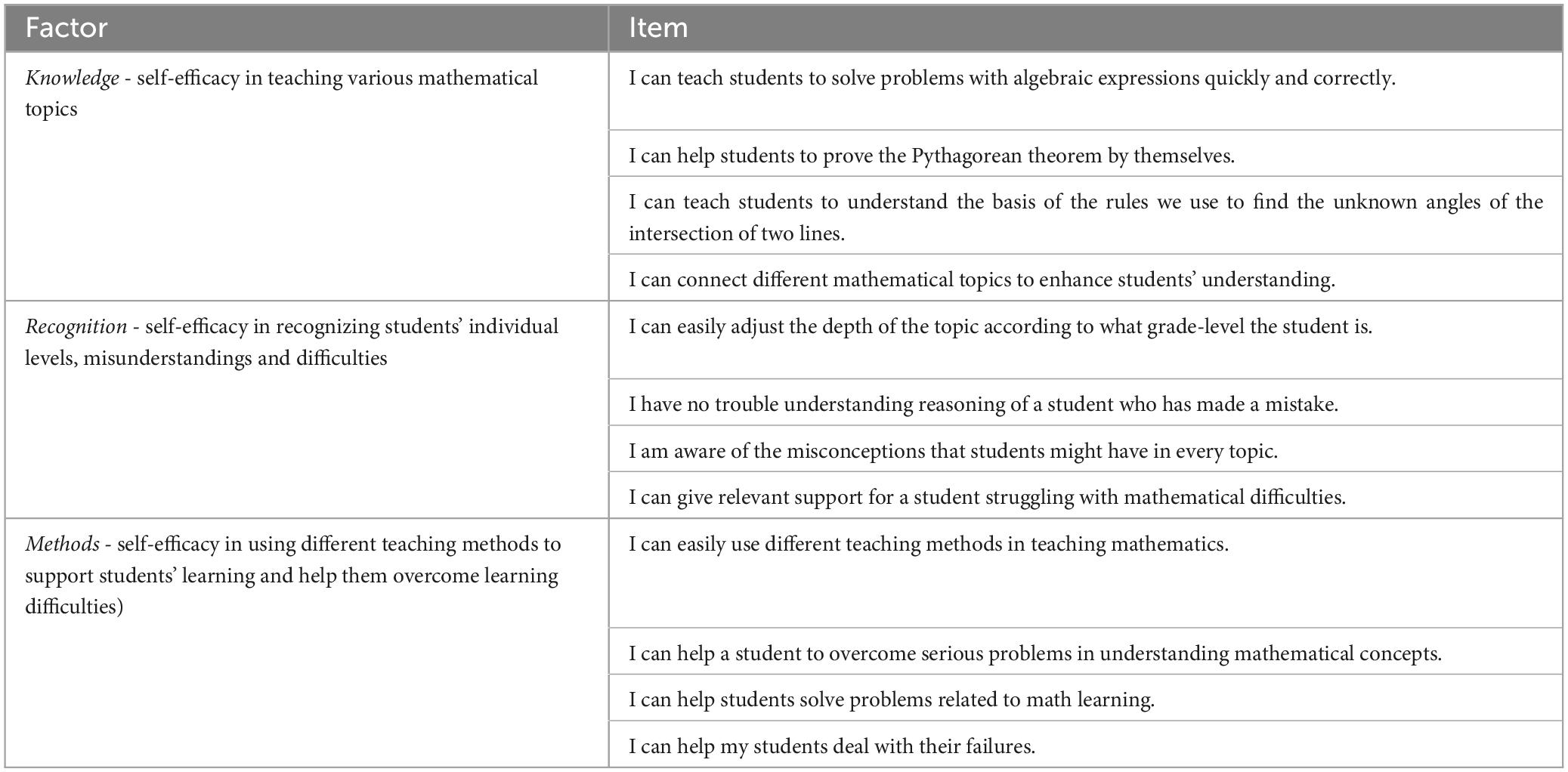
A self-efficacy questionnaire was developed for this study. The aim was to develop a short test with subscales covering the most important aspects of mathematics teachers’ pedagogical tasks, activities, and instructional challenges described in the current review of measures of mathematics pedagogical content knowledge (Grigaliuniene et al., 2025b; Depaepe et al., 2013). The questionnaire differed from some previously developed measurement instruments in that it focused entirely on mathematics teaching and did not include general classroom management questions. The first version of the questionnaire consisted of 47 statements. All statements were related to self-efficacy in teaching mathematics, but from different perspectives - procedural skills, conceptual skills, curriculum knowledge, teaching methods, recognizing learning difficulties and misconceptions, learning support, and emotional/social support.
Statements in the questionnaire appeared in random order with no similar statements appearing near each other. Respondents were asked to “Rate the following statements on a scale from “1-I have no confidence in my abilities” to “7-I have full confidence in my abilities”.” using a seven-point Likert scale.
Pilot study and sample group
Pilot study for overall validity of the questionnaire was held with more than 20 participants. After pilot study, minor adjustments were made that led to more clearly formulated statements. After the final data collection 12 items with serious ceiling effect (more than 50 percent selected six or seven) were removed from the data.
Data analysis
The items included in the teaching self-efficacy instrument were designed to align with the dimensions commonly employed in assessments of mathematics teachers’ pedagogical content knowledge (Grigaliuniene et al., 2025b). To identify the underlying latent variables that explain the correlations among observed items, as well as to reduce the total number of items and retain those that best represent these latent constructs, an exploratory factor analysis was conducted (Watkins, 2018).
The confirmatory factor analysis was used to assess the fit of the subscales derived from the exploratory factor analysis. An initial pilot study was conducted using a small sample, and minor revisions were made to the items based on preliminary findings. Thus, the exploratory factor analysis was made with the final dataset. Because repeating explorative and confirmatory factor analyses with the same data may lead to overfitting results, we followed the recommendation of Fokkema and Greiff (2017) to split the data into separate subsets for exploratory and confirmatory analyses. A subgroup of 50 students was used to run an exploratory factor analysis. Based on the results of the exploratory factor analysis, subscales were created and tested by confirmatory factor analysis by using another sub-group of the sample (N = 172). A one-way analysis of variance (ANOVA) was conducted to compare teaching self-efficacy across groups with different levels of teaching experience. Descriptive statistics, exploratory factor analysis, and ANOVA were performed using SPSS version 28, while confirmatory factor analysis was conducted with AMOS version 28.
Results
The skewness and kurtosis values of the 35 variables were between –1 and +1 and showed that the data was approximately, normally distributed with the exception that three variables’ skewness values were between 1 and 1.08, and four variables had the kurtosis values between 1 and 1.3. Factor analysis of the 35 items was conducted. Kaiser-Meyer-Olkin value 0.879 (p < 0.001) showed that the data was suitable for factor analysis (Lloret et al., 2017). The factor analysis resulted in three factors which explained 78 percent of the total variance. The factors and items with high loadings are presented in Table 1. The communalities of the 12 variables varied between 0.697 and 0.827.
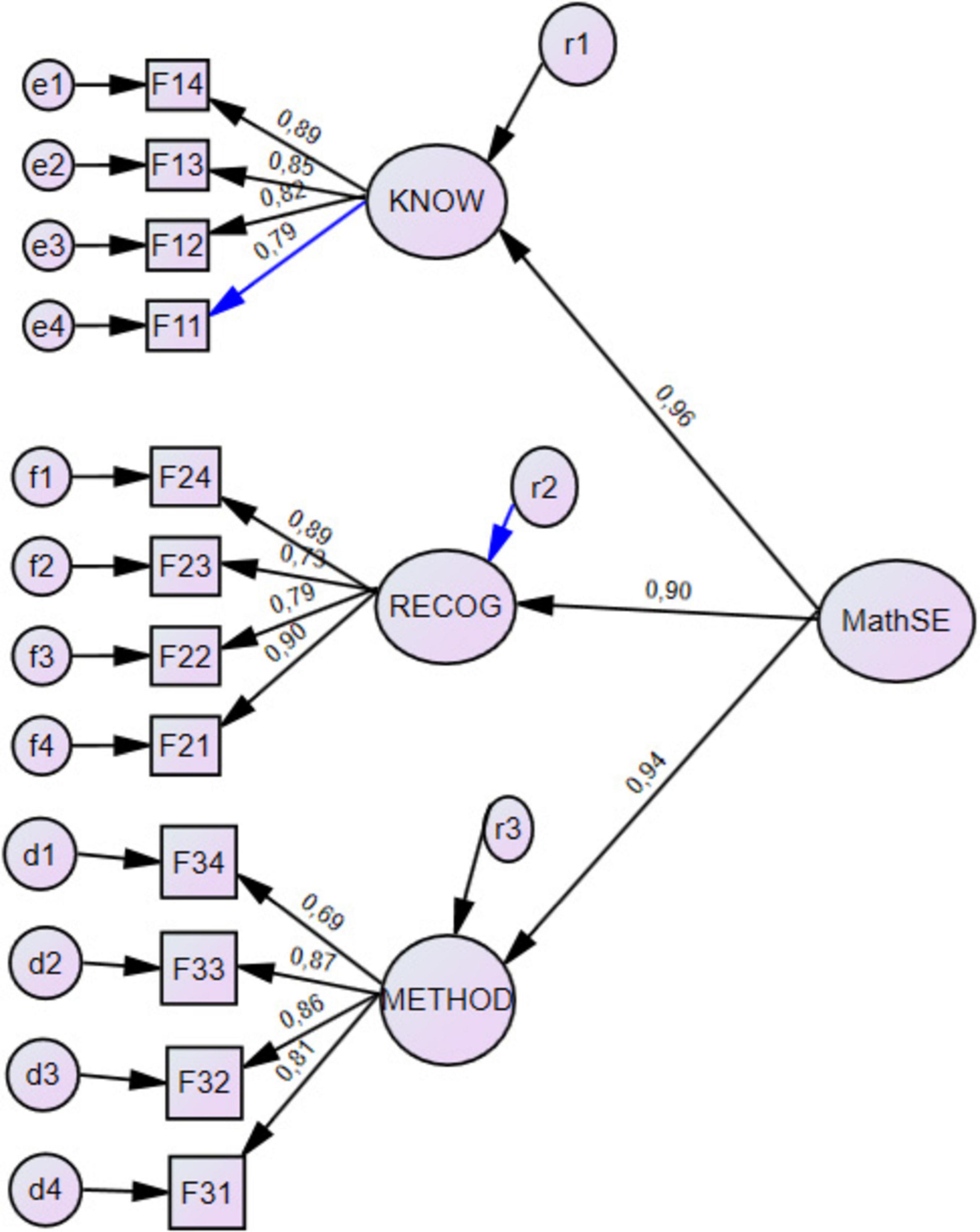
To answer the first research question, the three subscales model was compared with the one-factor model. The three-factor model showed a good data fit, Chi-square (df = 48) = 87.60 (p < 0.001), PCMIN/DF = 1.825, RMSEA = 0.069 (p = 0.084), while the model fit of the one-factor model was unacceptable, Chi-square (df = 47) 137.72 (p < 0.001), PCMIN/DF = 2.93, RMSEA = 0.093 (p < 0.001). The correlations between the latent variables were between 0.84 and 0.90.
The model in which general self-efficacy in mathematics education was the second-order latent variable (Figure 1) showed a good model fit, Chi-square (46) = 77.03, p = 0.003, PCMIN/DF = 1.675, RMSEA = 0.055 (p = 0.323).
The Cronbach’s alpha for the overall mathematics self-efficacy (MathSE) test was 0.95, Knowledge subscale 0.91, Recognition subscale 0.89, and the Methods subscale 0.88. The sum variables of the overall test and its three subscales are used in the following analyses.
The descriptive statistics of the overall test and the three subscales are shown in Table 2.
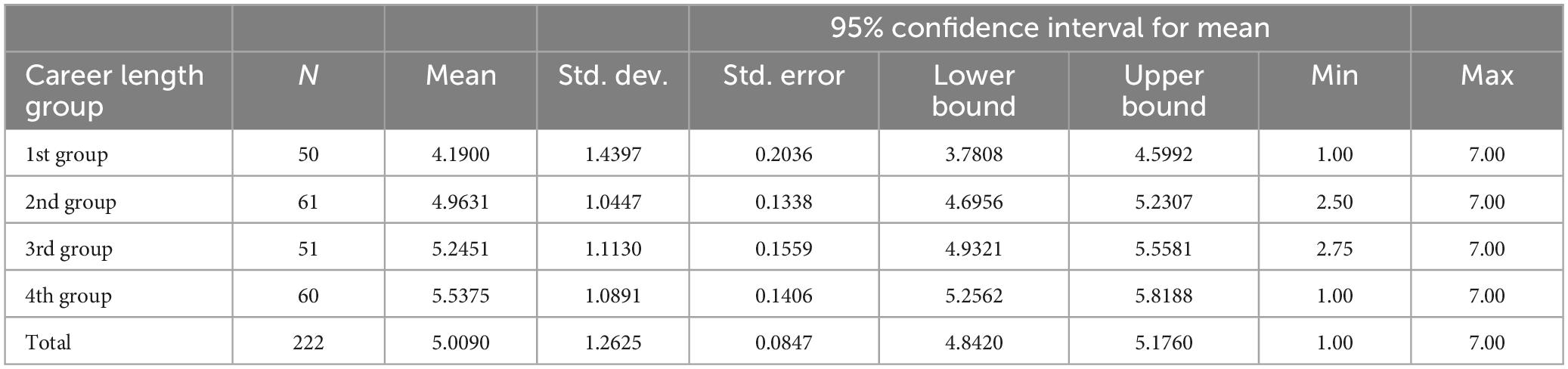
Based on the Skewness and Kurtosis values, all the subscale variables were approximately normally distributed. The differences between teaching career length groups were analyzed by One-Way ANOVA. The mean values and standard deviations of overall teaching self-efficacy are presented in Table 3.
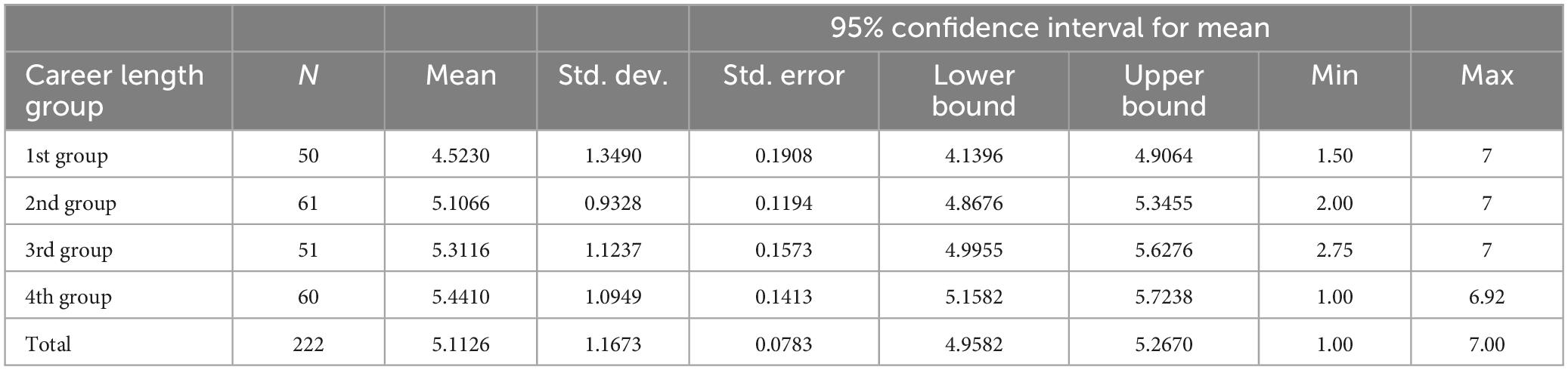
Table 3. Means and standards deviations of the overall mathematics teaching self-efficacy of different teaching career length groups.
There was medium size significant difference in overall teaching self-efficacy between career length groups, F(3) = 6.83, p < 0.001, η2 = 0.086. Because the Levene test (2.712, p = 0.046) showed that the homogeneity assumption of the variances is not met, the results were confirmed with the robust Welch tests, 6.65 (3), p < 0.001. The Post hoc analysis showed that there was significant difference between the group 1 (shortest career) and all other groups but no significant differences between other groups.
The mean values and standard deviations for self-efficacy Knowledge subscale are presented in Table 4.
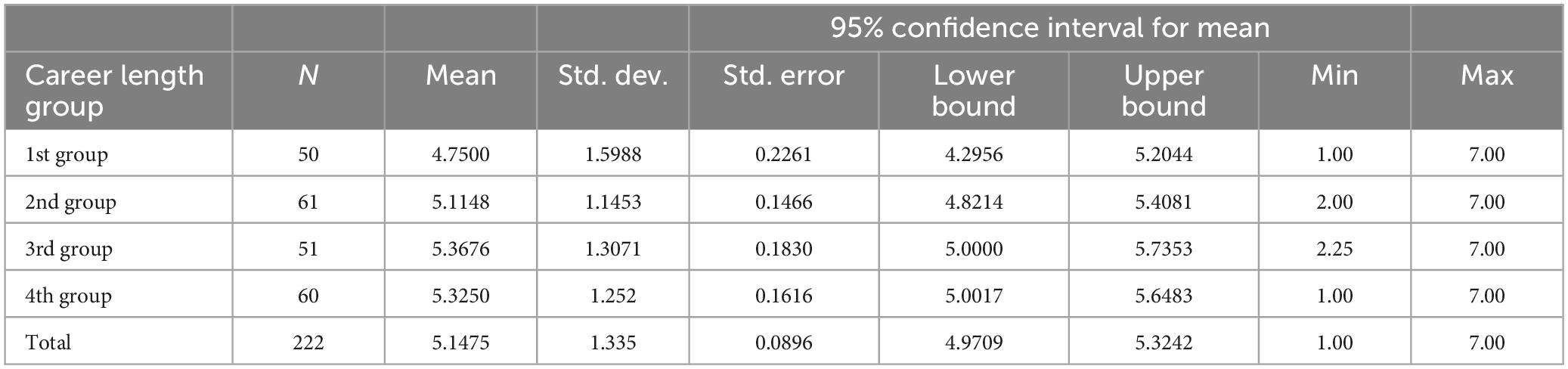
Table 4. Means and standards deviations of self-efficacy Knowledge subscale of the different teaching career length groups.
There were no statistically significant differences between the career length groups. F(3) = 2.35, p = 0.74. Because Levene’s test (3.030, p = 0.030) shown that the homogeneity assumption of the variances is not met, the results were confirmed with the robust Welch test [1.869 (3), p = 0.139].
The mean values and standard deviations for self-efficacy of students’ difficulty Recognition are presented in Table 5.
The ANOVA revealed that the differences between the groups were statistically significant [F(3) = 12.947, p < 0.001], with a large effect size (η2 = 0.151). The Levene test showed that the homogeneity assumption was met (2.063, p = 0.106).
The Bonferroni post hoc analysis shows that the 1st career group (up to 1 year of teaching) has lower self-efficacy for recognition than all other teacher groups.
A further statistically significant difference exists between the second group of teachers (1–6 years of teaching) and the teachers with the longest career (fourth group), with the fourth group showing a significantly higher value for self-efficacy in Recognition compared to the second group.
The mean values and standard deviations for self-efficacy in supporting students learning with Methods are presented in Table 6.
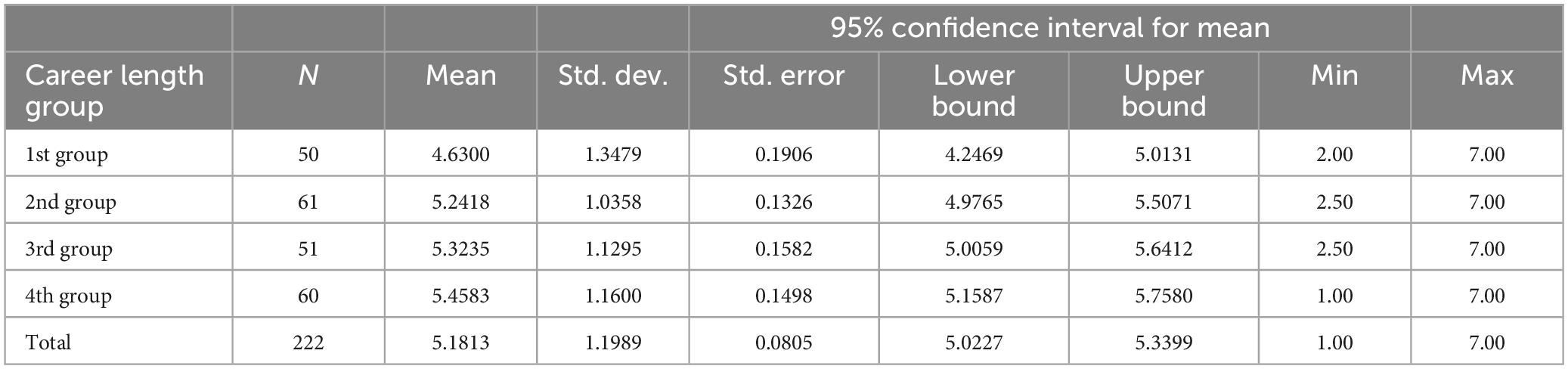
Table 6. Means and standard deviations of self-efficacy Methods subscale between teaching career length groups.
The results show that the differences between the groups are statistically significant [F(3) = 7.019, p = 0.002] with a mean effect size (η2 = 0.066). The Levene test showed that the homogeneity assumption was met (1.526, p = 0.209).
The Bonferroni post hoc analysis shows that the first group of teachers (up to 1 year of teaching experience) has lower methodological self-efficacy than all other teacher groups. No further statistically significant differences were found between the groups for the factor method self-efficacy.
Discussion and conclusion
The aim of this study was to investigate the dimensionality of a novel measure of teacher self-efficacy and the level of teacher self-efficacy of Lithuanian mathematics teachers at different stages of their teaching careers. The analysis identified three different latent self-efficacy variables and 1 s order latent variable. The results indicate that teachers who are at the beginning of their careers generally have lower levels of self-efficacy, while teachers with the longest careers tend to have higher levels of self-efficacy compared to other groups.
To answer the first research question “Is mathematics teachers’ self-efficacy a unidimensional construct or is it possible to identify various factors?” - three different dimensions of teachers’ self-efficacy were identified and confirmed in the study: Knowledge, Recognition, and Methods. The Knowledge factor reflects teachers’ confidence in their ability to teach a wide range of mathematical topics in a way that improves students’ understanding. The Recognition factor reflects teachers’ belief that they are able to recognize students’ mathematical misconceptions or more general learning difficulties and adapt their teaching accordingly, it represents instruction that is oriented toward recognizing the difficulties of individual students (Dindyal et al., 2021). Finally, the Methods factor captures teachers’ confidence in using a variety of instructional techniques tailored to address both specific and general challenges and learning difficulties that students encounter during the learning process. The Method factor focuses on teaching methods that take into account the diversity of students (Rowan et al., 2021). In addition, the model in which general self-efficacy in math instruction was a latent second-order factor fit the data well.
The second and third research questions focus on examining self-efficacy in relation to career length. This perspective is particularly important, as it is widely assumed that teaching competencies evolve over the course of a teacher’s career (Berliner, 2005). However, existing literature suggests that this progression is not uniform, and that the development of teaching skills over time is marked by considerable variability (Kini and Podolsky, 2016; Kraft and Papay, 2014). For instance, research by Hanushek (2011), Hanushek and Rivkin (2010) indicates that teacher effectiveness tends to improve during the initial years of teaching, but subsequently plateaus, with little further change. A similar pattern is observed in the work of Kraft and Papay (2004), who found that while instructional quality generally improves in the early stages of a teaching career, divergent developmental trajectories emerge thereafter - suggesting that not all educators continue to grow professionally over time. Thus, raising question about teachers’ self-efficacy at different stages of their career in Lithuania where the amount of teachers with very long teaching experience is exceptionally high in international comparison (Pec̆iuliauskienė et al., 2023).
In response to the second research question, “Are there differences in overall teaching self-efficacy between math teachers at different stages of their careers?”, the analysis revealed a medium-sized, statistically significant difference in overall teaching self-efficacy across career stages. Results indicated that overall self-efficacy scores tend to increase as teachers advance in their careers; however, only the early-career teacher group demonstrated a statistically significant difference in overall self-efficacy compared to other groups.
Despite forementioned difference, all participants reported relatively high levels of self-efficacy across statements related to their perceived teaching capabilities. It is important to consider that previous research has highlighted the potential for early career teachers to overestimate their instructional competence (Weinstein, 1988). The present findings align with prior studies (George et al., 2018; Klassen and Chiu, 2010).
The analyses to answer the third research question “Are there differences in the subscales of teaching self-efficacy between mathematics teachers at different stages of their careers?” showed that there was no difference in the Knowledge factor. Relatively high score of Knowledge for early career teachers could be explained by variety of sources of self-efficacy. Recent study shows that not only experience, but social and affective sources construct early career mathematics teachers’ self-efficacy (Marschall, 2023). It can also mean that teacher education succeeds in imparting knowledge and skills for teaching in different mathematical subjects, so that prospective teachers already have a relatively high self-efficacy in terms of their ability to impart content knowledge.
The ability to recognize pupils’ learning difficulties is closely associated with pedagogical content knowledge (PCK), which has been identified as a critical component of effective teaching (Depaepe et al., 2013; Kunter et al., 2013; Blömeke and Kaiser, 2017). Recent research on Lithuanian mathematics teachers indicates that early career teachers might have high levels of PCK (authors, in review; Grigaliuniene et al., 2025a). However, the findings also suggest that early career teachers may not be fully aware of their capacity to identify students’ difficulties. Specifically, on the Recognition subscale, the two groups with the shortest teaching experience reported significantly lower levels of self-efficacy compared to their more experienced colleagues. These results indicate that practical teaching experience may play a crucial role in fostering the self-efficacy necessary to effectively address student diversity through varied instructional approaches. However, even relatively short experience leads to the same level of self-efficacy as is evident for Methods factor.
The findings on differences in self-efficacy at different stages of the teaching career are consistent with previous research showing that teachers who are at the beginning of their career or still in training have lower self-efficacy than established teachers, but the differences might be minor (e.g., Gale et al., 2021; Klassen and Chiu, 2010; Ünsal et al., 2016; Wolters and Daugherty, 2007).
The findings of this study indicate that early-career teachers may benefit from targeted support aimed at enhancing their confidence in classroom practice. While the benefits of high self-efficacy are well documented (e.g., Perera and John, 2020, Siegle and McCoach, 2007; Tschannen-Moran and Hoy, 2001), this should not imply that increasing self-efficacy is an end in itself. Considering that some teachers may overestimate their instructional abilities (Weinstein, 1988), it may be more effective for preservice teacher education to prioritize the development of competencies in areas that are both challenging for teachers and essential for improving student outcomes.
While early-career teachers demonstrated high levels of self-efficacy concerning their subject-specific knowledge for teaching mathematics, they reported comparatively lower self-efficacy in their ability to recognize pupils’ learning difficulties. The distinction between these two subscales suggests that teachers perceive the skill of recognizing student difficulties as a discrete component of teaching, despite its integral role in effective instruction (Hill et al., 2008) and its status as a foundational element of pedagogical content knowledge (Cochran, 1997). Improving self-efficacy in this area—which reflects the broader concept of pedagogical content knowledge—may be supported by placing more emphasis on PCK in preservice teacher education, especially since PCK has been shown to be at least partly teachable through direct instruction (Depaepe et al., 2018).
Future studies should look more closely at the construct of self-efficacy and attempt to capture its differentiated dimensions in different teaching contexts. Further exploration of potential self-efficacy or lack of self-efficacy in teachers, particularly in relation to their actual teaching skills, could provide valuable insights. This line of research would contribute to a more comprehensive understanding of how self-efficacy beliefs match - or diverge from - demonstrated teaching abilities and would have implications for both teacher education and professional development.
A limitation of the study was the relatively small convenient sample which limits the generalizability of the results. The data was also small for splitting the data for explorative and confirmatory factor analyses. A separate pilot study with bigger number of participants would have been beneficial for conducting the explorative and confirmatory factor analyses with different data sets. While a more representative sample might have enhanced the generalizability of the findings, the selected sample was deemed sufficient to provide valuable insights within the scope of the study. Despite these limitations, this study offers valuable insights into mathematics teachers’ self-efficacy and, in particular, brings attention to an underrepresented group—Lithuanian mathematics teachers.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by Ethics Committee of Vytautas Magnus University. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
MG: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review and editing. EL: Conceptualization, Methodology, Supervision, Validation, Writing – original draft, Writing – review and editing, Formal Analysis, Visualization.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The authors declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alanoğlu, M. (2022). The role of instructional leadership in increasing teacher self-efficact: A meta-analytic review. Asia Pac. Educ. Rev. 23, 233–244. doi: 10.1007/s12564-021-09726-5
Bandura, A. (1977). Self-efficacy. Toward a unifying theory of behavioral change. Psychol. Rev. 84, 191–215. doi: 10.1037/0033-295X.84.2.191
Berliner, D. C. (2005). The near impossibility of testing for teacher quality. J. Teach. Educ. 56, 205–213. doi: 10.1177/0022487105275904
Blömeke, S., and Kaiser, G. (2017). “Understanding the development of teachers’ professional competencies as personally, situationally and socially determined,” in The Sage Handbook of Research on Teacher Education, eds D. J. Clandinin and J. Husu (Thousand Oaks, CA: Sage).
Callingham, R., and Watson, J. (2014). “Teachers’ confidence in teaching statistical ideas,” in Sustainability in Statistics Education: Proceedings of the Ninth International Conference on Teaching Statistics, eds K. Makar, B. Sousa, and R. Gould (Flagstaff, AZ: International Statistical Institute).
Chesnut, S., and Burley, H. (2015). Self-efficacy as a predictor of commitment to the teaching profession: A meta-analysis. Educ. Res. Rev. 15, 1–16. doi: 10.1016/j.edurev.2015.02.001
Cochran, K. F. (1997). “Pedagogical Content Knowledge: Teachers’ Integration of Subject Matter, Pedagogy, Students, and Learning Environments,” in Research Matters – to the Science Teacher. Available online at: https://home.miracosta.edu/rfrench/documents/NARST_%20Publications%20-%20Research%20Matters%20-%20to%20the%20Science%20Teacher.pdf
Corry, M., and Stella, J. (2018). Teacher self-efficacy in online education: A review of the literature. Res. Learn. Technol. 26:2047. doi: 10.25304/rlt.v26.2047
Darling-Hammond, L. (2009). Recognizing and enhancing teacher effectiveness. Int. J. Educ. Psychol. Assess. 3, 1–24.
Darling-Hammond, L., and Young, P. (2002). Defining ‘highly qualified teachers’: What does ‘scientifically-based research’ actually tell us? Educ. Res. 31, 13–25. doi: 10.3102/0013189X031009013
Depaepe, F., Van Roy, P., Torbeyns, J., Kleickmann, T., Dooren, W., and Verschaffel, L. (2018). Stimulating pre-service teachers’ content and pedagogical content knowledge on rational numbers. Educ. Stud. Mathem. 99, 197–216. doi: 10.1007/s10649-018-9822-7
Depaepe, F., Verschaffel, L., and Kelchtermans, G. (2013). Pedagogical content knowledge: A systematic review of the way in which the concept has pervaded mathematics educational research. Teach. Teach. Educ. 34, 12–25. doi: 10.1016/j.tate.2013.03.001
Dindyal, J., Schack, E., Choy, B., and Sherin, M. (2021). Exploring the terrains of mathematics teacher noticing. ZDM Math. Educ. 53, 1–16. doi: 10.1007/s11858-021-01249-y
Emmer, E., and Stough, L. (2001). Classroom management: A critical part of educational psychology, with implications for teacher education. Educ. Psychol. 36, 103–112. doi: 10.1207/S15326985EP3602_5
Fokkema, M., and Greiff, S. (2017). How performing PCA and CFA on the same data equals trouble: Overfitting in the assessment of internal structure and some editorial thoughts on it. Eur. J. Psychol. Assess. 33, 399–402. doi: 10.1027/1015-5759/a000460
Gale, J., Alemdar, M., Cappelli, C., and Morris, D. (2021). A Mixed methods study of self-efficacy, the sources of self-efficacy, and teaching experience. Front. Educ. 6:750599. doi: 10.3389/feduc.2021.750599
George, S., Richardson, P., and Watt, H. (2018). Early career teachers’ self-efficacy: A longitudinal study from Australia. Aust. J. Educ. 62, 217–233. doi: 10.1177/0004944118779601
Gibson, S., and Dembo, M. (1984). Teacher efficacy: A construct validation. J. Educ. Psychol. 76, 569–582. doi: 10.1037/0022-0663.76.4.569
Gordon, D., Blundell, C., Mills, R., and Bourke, T. (2023). Teacher self-efficacy and reform: A systematic literature review. Austr. Educ. Res. 50, 801–821. doi: 10.1007/s13384-022-00526-3
Gravemeijer, K., Stephan, M., Julie, C., Lin, F., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 151, 115–123. doi: 10.1007/s10763-017-9814-6
Gregoire, M. (2003). Is it a challenge or a threat? A dual process model of teachers’ cognition and appraisal processes during conceptual change. Educ. Psychol. Rev. 15, 147–179. doi: 10.1023/A:1023477131081
Grigaliuniene, M., Lehtinen, E., Verschaffel, L., and Depaepe, F. (2025b). Systematic review of research on pedagogical content knowledge in mathematics: Insights from a topic-specific approach. ZDM Math. Educ.
Grigaliuniene, M., Rutkienë, A., and Lehtinen, E. (2025a). How Lithuanian mathematics teachers interpret student thinking at the different career stages. Int. Electronic J. Math. Educ. 20: em0835. doi: 10.29333/iejme/16235
Hackett, G., and Betz, N. (1989). An exploration of the mathematics self-efficacy/mathematics performance. J. Res. Math. Educ. 20, 261–273. doi: 10.2307/749515
Hanushek, E. (2011). A. The economic value of higher teacher quality. Econ. Educ. Rev. 30, 466–479. doi: 10.1016/j.econedurev.2010.12.006
Hanushek, E., and Rivkin, S. (2010). Generalizations about using value-added measures of teacher quality. Am. Econ. Rev. 100, 267–271. doi: 10.1257/aer.100.2.267
Hattie, J. (2003). Teachers make a difference: What is the research evidence? Interpretations 36, 27–28.
Henson, R. K. (2010). From adolescent angst to adulthood: Substantive implications and measurement dilemmas in the development of teacher efficacy research. Educ. Psychol. 37, 137–150. doi: 10.1207/S15326985EP3703_1
Hill, H., Deborah, C., Ball, L., and Schilling, S. G. (2008). Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers’ topic-specific knowledge of students. J. Res. Math. Educ. 39 4, 372–400.
Hoy, A. W. (2000). Changes in Teacher Efficacy during the Early Years of Teaching. Paper presented at the Annual Meeting of the American Educational Research Association. New Orleans, LA.
Hoy, A. W., Hoy, W., and Davis, H. (2009). “Teachers’ self-efficacy beliefs,” in Handbook of Motivation at School, eds R. Kathryn, Wenzel, and David Miele (Milton Park: Routledge), 627–653.
Işıksal-Bostan, M. A. (2016). Longitudinal study on mathematics teaching efficacy: Which factors (Un)support the development? Eurasia J. Math. Sci. Technol. Educ. 12, 2085–2102. doi: 10.12973/eurasia.2016.1277a
Kahle, D. K. (2008). How Elementary School Teachers’ Mathematical Self-Efficacy and Mathematics Teaching Self-Efficacy Relate to Conceptually and Procedurally Oriented Teaching Practices. PhD diss. Ohio: Ohio State University.
Kini, T., and Podolsky, A. (2016). Does Teaching Experience Increase Teacher Effectiveness? A Review of the Research. Palo Alto: Learning Policy Institute.
Klassen, R., and Chiu, M. (2010). Effects on teachers’ self-efficacy and job satisfaction: Teacher gender, years of experience, and job stress. J. Educ. Psychol. 102, 741–756. doi: 10.1037/a0019237
Klassen, R., and Tze, V. (2014). Teachers’ self-efficacy, personality, and teaching effectiveness: A meta-analysis. Educ. Res. Rev. 12, 59–76. doi: 10.1016/j.edurev.2014.06.001
Klassen, R., Tze, V., Betts, S., and Gordon, K. (2011). Teacher efficacy research 1998–2009: Signs of progress or unfulfilled promise? Educ. Psychol. Rev. 23, 21–43. doi: 10.1007/s10648-010-9141-8
Kraft, M., and Papay, J. (2014). Can professional environments in schools promote teacher development? Explaining heterogeneity in returns to teaching experience. Educ. Eval. Policy Anal. 36, 476–500. doi: 10.3102/0162373713519496
Kunter, M., Baumert, J., Blum, W., Klusmann, U., Krauss, S., and Neubrand, M. (2013). Cognitive Activation in the Mathematics Classroom and Professional Competence of Teachers. Results from the COACTIV Project. Berlin: Springer.
Lloret, S., Ferreres, A., Hernandez, A., and Tomas, I. (2017). The exploratory factor analysis of items: Guided analysis based on empirical data and software. Anal. Psicol. 33, 417–432. doi: 10.6018/analesps.33.2.270211
Ma, K., Chutlyami, M., and Nicoll, S. (2022). Transitioning into the first year of teaching: Changes and sources of teacher self-efficacy. Aust. Educ. Res. 49, 943–960. doi: 10.1007/s13384-021-00481-5
Marschall, G. (2023). Teacher self-efficacy sources during secondary mathematics initial teacher education. Teach. Teach. Educ. 132:104203. doi: 10.1016/j.tate.2023.104203
McGee, J., and Wang, C. (2014). Validity-supporting evidence of the self-efficacy for teaching mathematics instrument. J. Psychoeduc. Assess. 32, 390–403. doi: 10.1177/0734282913516280
Mishal, A., Naseem, A., Zahid, H., and Naseer, I. (2024). Relationship between teacher’s sense of self-efficacy and teaching experience. J. Asian Dev. Stud. 13, 1530–1537. doi: 10.62345/jads.2024.13.3.124
Morris, D., Usher, E., and Chen, J. (2017). Reconceptualizing the sources of teaching self-efficacy: A critical review of emerging literature. Educ. Psychol. Rev. 27, 795–833. doi: 10.1007/s10648-016-9378-y
Muhtarom, M., Sutrisno, S., Nizaruddin, N., and Murtianto, Y. (2024). Research on mathematical beliefs: Systematic literature review. Int. J. Eval. Res. Educ. 13, 693–704. doi: 10.11591/ijere.v13i2.25968
Norton, S. (2019). Middle school mathematics pre-service teachers’ content knowledge, confidence, and self-efficacy. Teach. Dev. 23, 529–548. doi: 10.1080/13664530.2019.1668840
Pec̆iuliauskienė, P., Kaminskienė, L., and Lehtinen, E. (2023). Science teachers’ collaborative innovative activities: The role of professional development and professional experience. Human. Soc. Sci. Commun. 10:324. doi: 10.1057/s41599-023-01833-5
Perera, H., and John, J. (2020). Teachers’ self-efficacy beliefs for teaching math: Relations with teacher and student outcomes. Contemp. Educ. Psychol. 61:101842. doi: 10.1016/j.cedpsych.2020.101842
Peterson, P., Fennema, E., Carpenter, T., and Loef, M. (1989). Teachers’ pedagogical content beliefs in mathematics. Cogn Instruct. 6, 1–40.
Rowan, L., Bourke, T., L’Estrange, L., Lunn Brownlee, J., Ryan, M., Walker, S., et al. (2021). How does initial teacher education research frame the challenge of preparing future teachers for student diversity in schools? A systematic review of literature. Rev. Educ. Res. 91, 112–158. doi: 10.3102/0034654320979171
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educ. Res. 15, 4–14. doi: 10.3102/0013189X015002004
Siegle, D., and McCoach, D. (2007). Increasing student mathematics self-efficacy through teacher training. J. Adv. Acad. 18, 278–312. doi: 10.4219/jaa-2007-353
Stipek, D., Givvin, K., Salmon, J., and MacGyvers, V. (2001). Teachers’ beliefs and practices related to mathematics instruction. Teach. Teach. Educ. 17, 213–226. doi: 10.1016/S0742-051X(00)00052-4
Täschner, J., Dicke, T., Reinhold, S., and Holzberger, S. (2024). ‘Yes, I can!’ A systematic review and meta-analysis of intervention studies promoting teacher self-efficacy. Rev. Educ. Res. 95, 3–52. doi: 10.3102/00346543231221499
Thomson, M. M., Gray, D., Walkowiak, T., and Alnizami, R. (2021). Developmental trajectories for novice elementary teachers: Teaching efficacy and mathematics knowledge. J. Teach. Educ. 73, 338–351. doi: 10.1177/00224871211014128
Trei, K. (2015). Science, technology, engineering and math (STEM) academic librarian positions during 2013: What carnegie classifications reveal about desired STEM skills. Issues Sci. Technol. Librarianship 80, doi: 10.5062/F4XG9P57
Tschannen-Moran, M., and Hoy, A. (2001). Teacher efficacy: Capturing an elusive concept. Teach. Teach. Educ. 17, 783–805. doi: 10.1016/S0742-051X(01)00036-1
Ünsal, S., Korkmaz, F., and Percin, S. (2016). Analysis of mathematics teachers’ self-efficacy levels concerning the teaching process. J. Educ. Pract. 7 24, 99–107.
Watkins, M. W. (2018). Exploratory factor analysis: A guide to best practice. J. Black Psychol. 44, 219–246. doi: 10.1177/0095798418771807
Weinstein, C. S. (1988). Preservice teachers’ expectations about the first year of teaching. Teach. Teach. Educ. 4, 31–40. doi: 10.1016/0742-051X(88)90022-4
Wolters, C. A., and Daugherty, S. G. (2007). Goal structures and teachers’ sense of efficacy: Their relation and association to teaching experience and academic level. J. Educ. Psychol. 99, 181–193. doi: 10.1037/0022-0663.99.1.181
Wyatt, M. (2012). Towards a re-conceptualization of teachers’ self-efficacy beliefs: Tackling enduring problems with the quantitative research and moving on. Int. J. Res. Method Educ. 37, 166–189. doi: 10.1080/1743727X.2012.742050
Keywords: mathematics, teaching self-efficacy, preservice teachers, in-service teachers, Lithuania
Citation: Grigaliuniene M and Lehtinen E (2025) Mathematics teachers’ career length and teaching self-efficacy. Front. Educ. 10:1536429. doi: 10.3389/feduc.2025.1536429
Received: 28 November 2024; Accepted: 02 May 2025;
Published: 18 June 2025.
Edited by:
Lynn McGarvey, University of Alberta, CanadaReviewed by:
Jupeth Toriano Pentang, Central Luzon State University, PhilippinesVeronika Fitri Rianasari, Sanata Dharma University, Indonesia
Copyright © 2025 Grigaliuniene and Lehtinen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Monika Grigaliuniene, bW9uaWthLmdyaWdhbGl1bmllbmVAdmR1Lmx0
 Monika Grigaliuniene
Monika Grigaliuniene Erno Lehtinen
Erno Lehtinen